

Preview text:
thuvienhoclieu.com
MỘT SỐ BÀI TOÁN TỌA ĐỘ HÓA MỘT SỐ HÌNH HỌC KHÔNG GIAN
VÀ ỨNG DỤNG THỰC TẾ
Phương pháp: Để tọa độ hóa một số hình học không gian thì ta thực hiện như sau:
■ Bước 1: Chọn hệ trục tọa độ. Trong bước này ta sẽ xác định 3 đường vuông góc có trong bài
toán và gọi đó là 3 đường cơ sở. Thông thường thì ta sẽ quy ước trục Ox hướng vào mình, trục
Oy nằm ngang, còn lại là trục Oz .
■ Bước 2: Xác định tọa độ các điểm liên trên hình liên quan tới bài toán. Với những bạn chưa
quen thì chúng ta xác định tọa độ hình chiếu của điểm cần tìm lên các trục, từ đó sẽ suy ra được
tọa độ điểm cần tính.
■ Bước 3: Áp dụng công thức. Sau đây chúng ta sẽ nhắc lại một số công thức cần nhớ trong phần này:
Diện tích và thể tích: Diện tích tam giác, thể tích tứ diện, thể tích hình hộp, thể tích hình lăng trụ.
Góc: Góc giữa 2 mặt phẳng, góc giữa 2 đường thẳng, góc giữa đường thẳng và mặt phẳng.
Khoảng cách: Khoảng cách từ điểm đến mặt phẳng, Khoảng cách từ một điểm đến 1 đường
thẳng, Khoảng cách giữa hai đường thẳng chéo nhau.
Chú ý: Thông thường các bài mà không có 3 đường vuông góc thì ta sẽ phải tự dựng thêm để gắn tọa độ
và những bài liên quan tới hình lập phương, hình hộp chữ nhật, chối chóp có 3 đường vuông góc, lăng trụ
đứng thì khi áp dụng phương pháp này sẽ giải rất nhanh.
A. BÀI TẬP TRẮC NGHIỆM
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
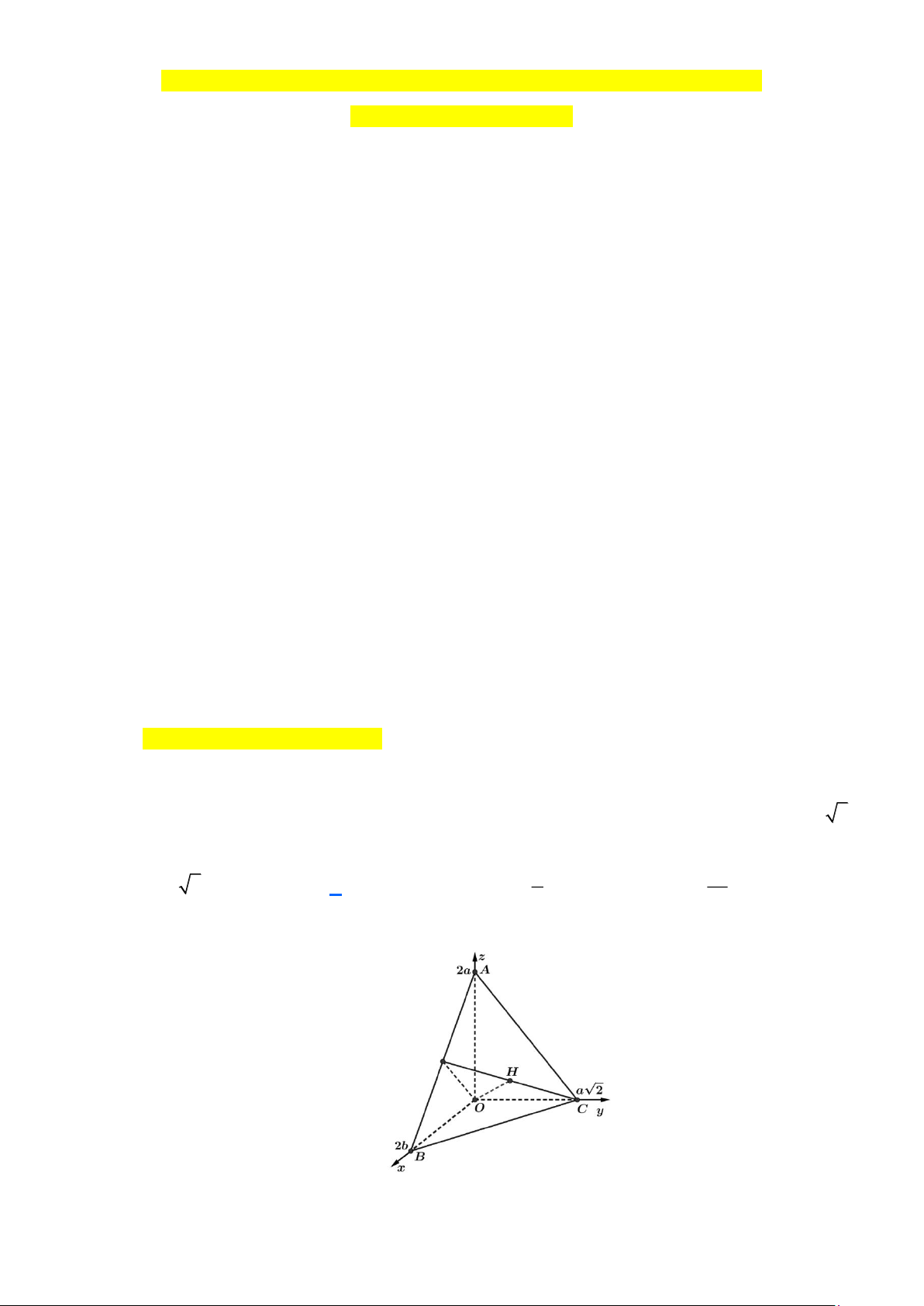
Câu 1: Cho tứ diện OABC có OA, OB , OC đôi một vuông góc và OA = OB = 2a , OC = a 2 .
Khoảng cách từ điểm O đến mặt phẳng ( ABC) bằng a 3a A. a 2 . B. a . C. . D. . 2 4 Lời giải
Xét hệ trục tọa độ Oxyz như sau điểm O là gốc tọa độ OA Oz ; OB Ox và OC Oy .
thuvienhoclieu.com Trang 1 thuvienhoclieu.com
Khi đó ta có O(0;0;0); A(0;0;2a) ; B(2 ;
a 0;0) và C(0;a 2;0) . x y z
Phương trình mặt phẳng ( ABC) là + +
= 1 x + 2y + z − 2a = 0 . 2a a 2 2a + + − a
Khoảng cách từ điểm O đến mặt phẳng ( ABC) là d (O ( ABC)) 0 2.0 0 2 , = = a . 1+ 2 +1
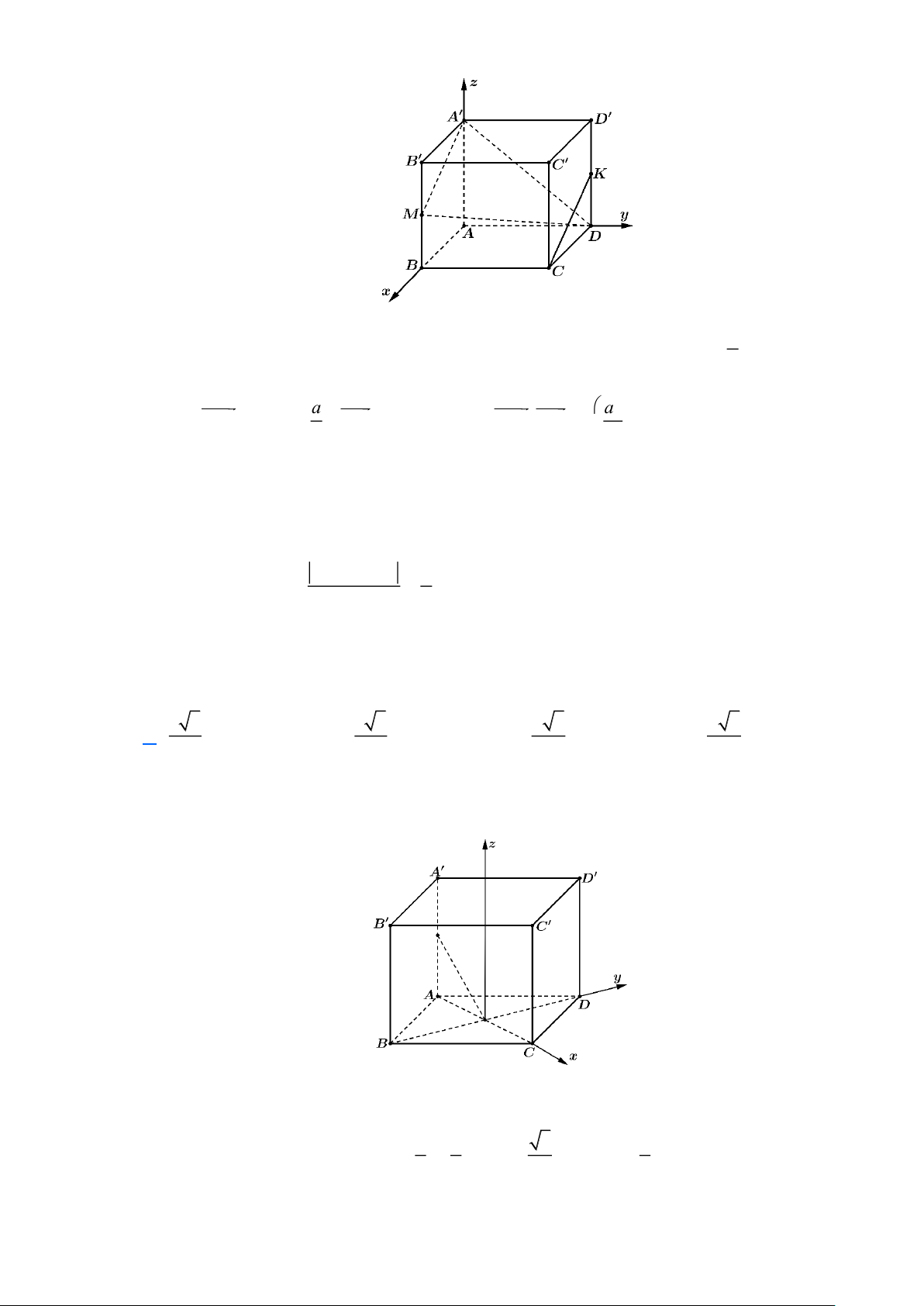
Câu 2: Cho hình lập phương ABCDA B C D cạnh bằng a . Khoảng cách giữa A B và B C bằng 1 1 1 1 1 1 a a A. . B. . C. a 3 . D. a 6 . 3 6 Lời giải
Đặt a =1. Chọn B A là trục Ox , B C là trục Oy , B B là trục Oz 1 1 1 1 1
Suy ra B 0;0;0 , A 1;0;0 ,C 0;1;0 , B 0;0;1 ,C 0;1;1 1 ( ) 1( ) 1( ) ( ) ( )
Ta có A B = 1
− ;0;1 , B B = 0;0;1 , B C = 0;1;1 1 ( ) 1 ( ) 1 ( )
A B,B C.B B 1
Vậy d ( A B,B C) 1 1 1 = = 1 1 A B,B C 3 1 1
Câu 3: Trong không gian với hệ tọa độ Oxyz , cho hai mặt phẳng 4x − 4y + 2z −1 = 0 và
2x − 2y + z +1 = 0 chứa hai mặt của hình lập phương. Thể tích khối lập phương đó bằng 1 1 1 1 A. V = .
B. V = . C. V = . D. V = . 27 8 3 3 2 2 Lời giải
Giả sử (P) :4x − 4y + 2z −1= 0 , (Q) : 2x − 2y + z +1= 0. Ta thấy (P)∥ (Q) . Mặt khác lấy điểm M (0;0;− )
1 (Q). Gọi a là độ dài cạnh hình lập phương 3 − 1 3 1 1
Khi đó ta có: a = d ((P),(Q)) = d (M;(P)) = = nên 3 V = a = = . 2 2 2 4 + 4 + 2 2 2 8
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là tam giác vuông với AB = AC = 2 . Cạnh bên SA
vuông góc với đáy và SA = 3 . Gọi M là trung điểm của SC . Tính khoảng cách giữa AM và BC . 3 2 3 3 22 22 A. . B. . C. . D. . 2 3 11 6 Lời giải
Gắn hệ trụ tọa độ ta có A(0;0;0) là gốc tọa độ, S (0;0; )
3 , B(2;0;0),C(0;2;0) . 3
3 Điểm M 0;1; . Ta có AM = 0;1; , BC = ( 2
− ;2;0). Gọi n = AM,BC = ( 3 − ; 3 − ;2) 2 2
thuvienhoclieu.com Trang 2 thuvienhoclieu.com
Gọi (P) là mặt phẳng qua B(2;0;0) nhận n = ( 3 − ; 3
− ;2) làm vectơ pháp tuyến. ( 3.0 − − 3.0 + 2.0 + 6 3 22 P) : 3
− x − 3y + 2z + 6 = 0. Ta có d ( AM , BC) = d ( , A (P)) = = . (− )2 + (− )2 2 11 3 3 + 2
Câu 5: Cho hình chóp S.ABC có AB = a, AC = a 3 , SB 2a và 0
ABC = BAS = BCS = 90 . Biết sin 11
của góc giữa đường thẳng SB và mặt phẳng (SAC) bằng
. Tính thể tích khối chóp 11 S.ABC 3 a 6 3 a 3 3 2a 3 3 a 6 A. . B. . C. . D. . 6 9 9 3 Lời giải
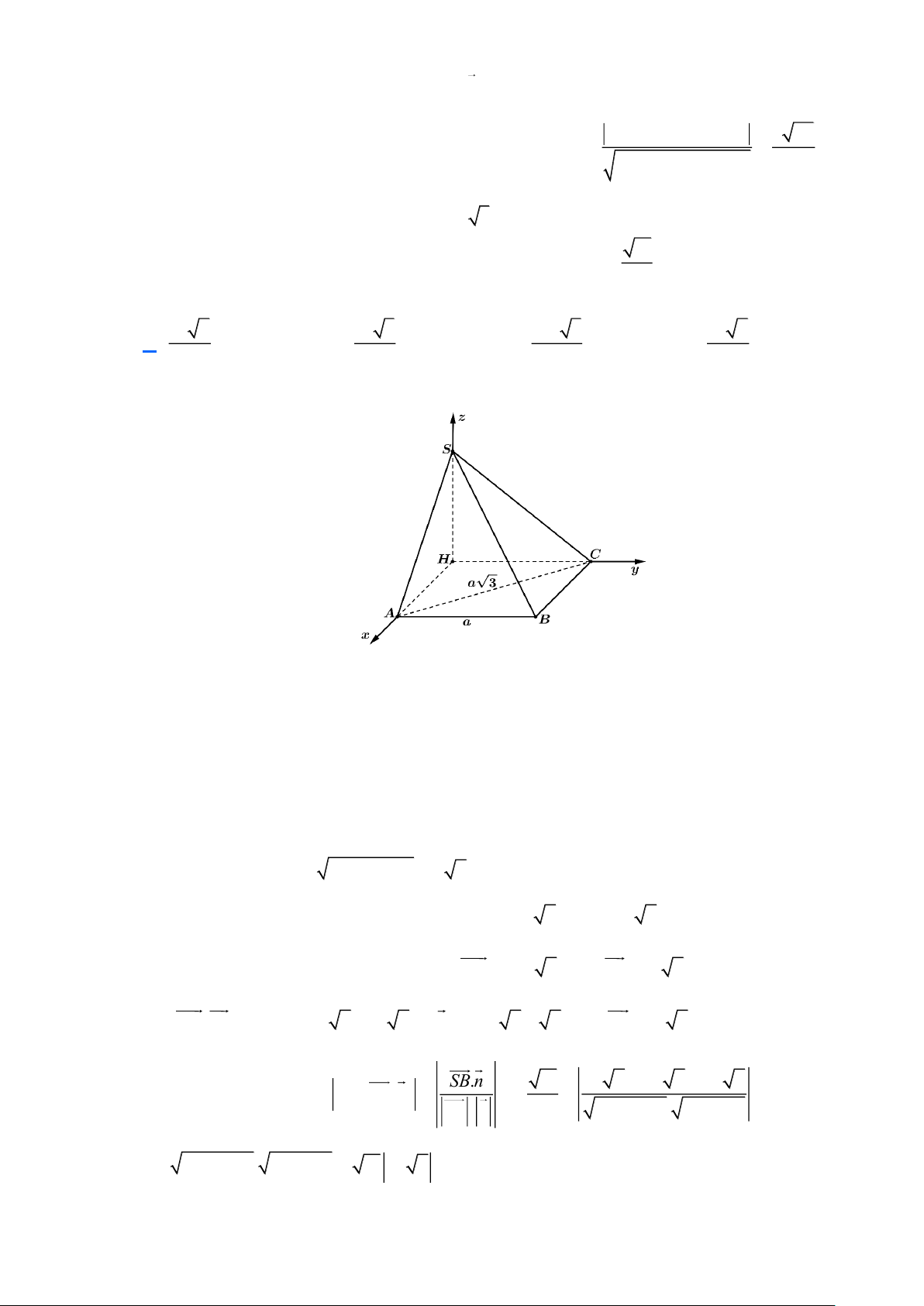
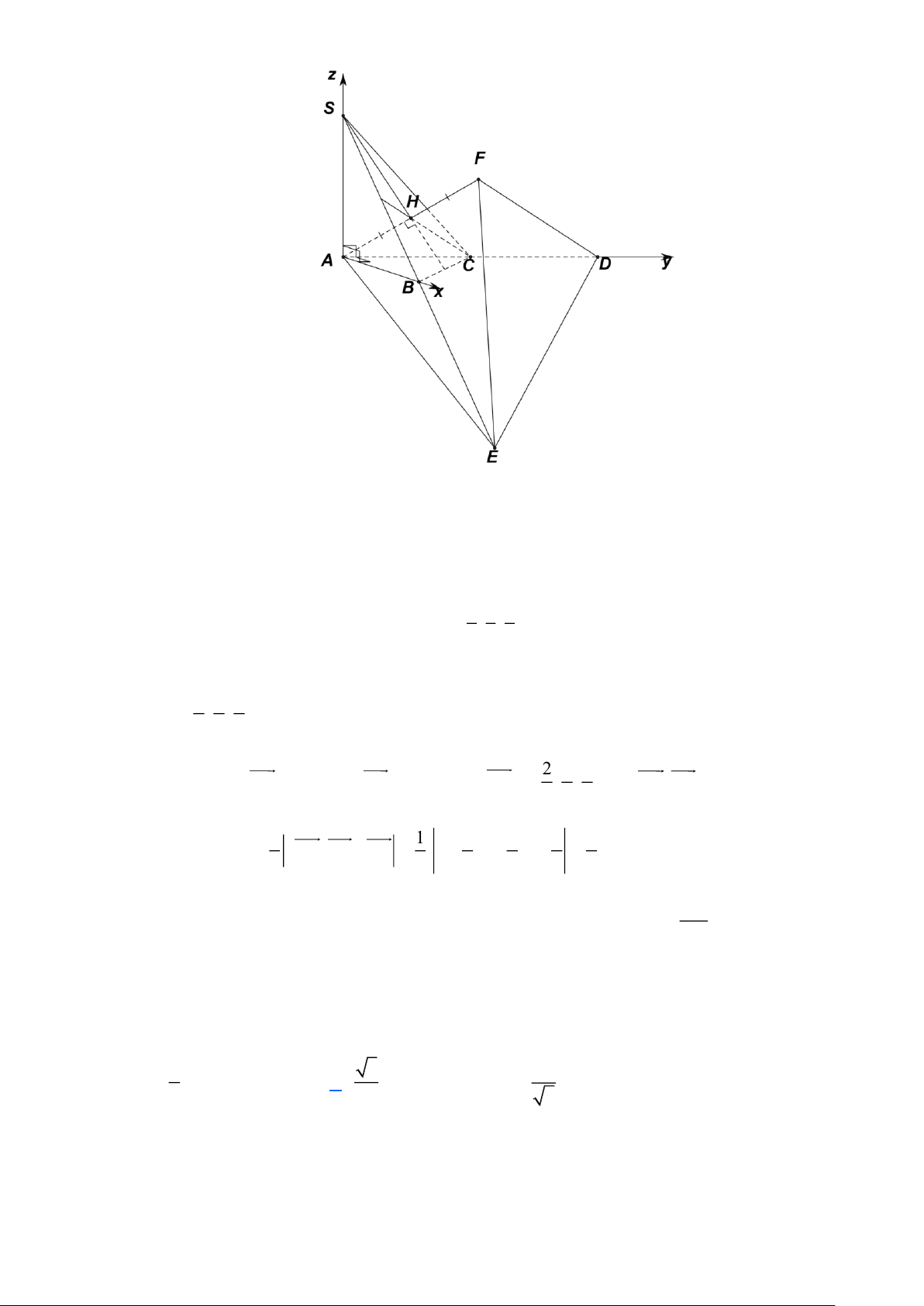
Gọi H là hình chiếu vuông góc của S trên mặt phẳng ( ABC) . AB ⊥ BC
Ta có SH ⊥ ( ABC) SH ⊥ AB và SH ⊥ BC mà
ABC = BAS = BCS = 90 AB ⊥ SA . BC ⊥ SC
Suy ra AB ⊥ (SH )
A AB ⊥ AH và BC ⊥ (SHC) BC ⊥ HC nên tứ giác ABCH là hình chữ nhật. Suy ra 2 2
BC = AC − AB = a 2 .
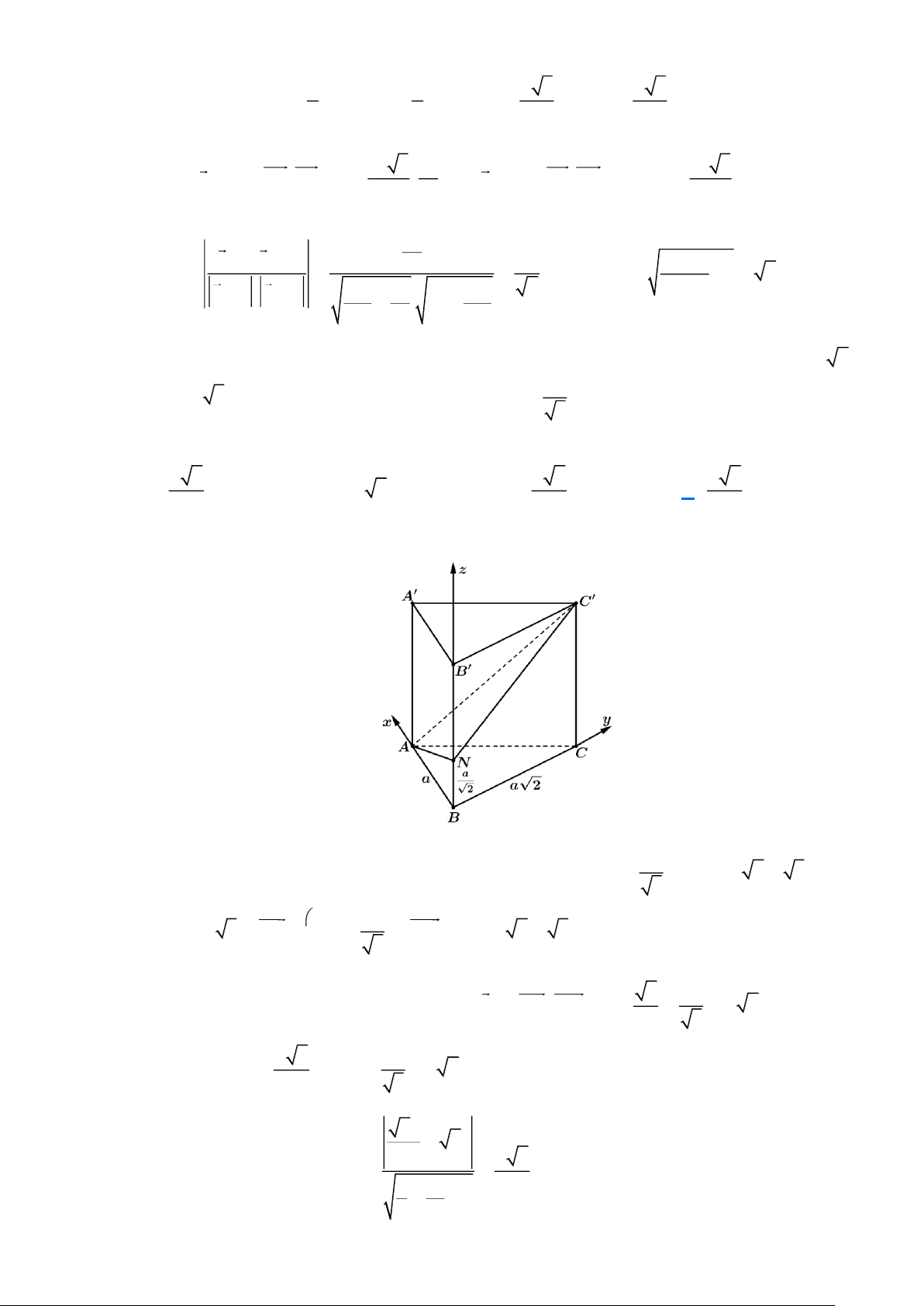
Gắn hệ trục toạ độ như hình vẽ ta có H (0;0;0), A(a 2;0;0),B(a 2; ; a 0),C(0; ; a 0) .
Giả sử SH = x(x 0) S (0;0;x). Ta có AC = (−a 2; ;
a 0),SA = (a 2;0;−x) AC SA = ( 2 , −a ;
x −ax 2;−a 2 ) / /n =
( ;xx 2;a 2) mà SB =(a 2; ;a−x). SB n 11
xa 2 + xa 2 − xa 2 Suy ra (SB (SAC)) = (SB n) . sin , cos , = = SB . n 2 2 2 2 11
3x + 2a . 3a + x 2 2 2 2
3x + 2a . 3a + x = 11 xa 2 ( 2 2 x + a )( 2 2 a + x ) = ( 2 2 3 2 3 11 2a x ) 2 2 4 4 2 2 2 2
9a x + 3x + 6a + 2a x = 22x a 4 2 2 4
3x −11x a + 6a = 0 ( 2 2 x − a )( 2 2 3 2 x − 3a ) = 0
thuvienhoclieu.com Trang 3 thuvienhoclieu.com 2 2 2 x = a 3
. HB = AC = a 3 nên với 2 2 2 2
SH = x = 3a SB = SH + HB = a 6 2a 2 2 x = 3a 2 1 a 2
(thoả mãn). Do đó SH = a 3 . Diện tích của tam giác ABC là S = . AB BC = . ABC 2 2 2 3 1 1 a 2 a 6 Vậy V = .SH.S = .a 3. = . S.ABC 3 A BC 3 2 6
Câu 6: Cho hình lập phương ABC . D A B C D
có cạnh bằng 2a . Tính góc giữa CC và mặt phẳng (AB C ) A. 60. B. 30. C. 45. D. 90 .
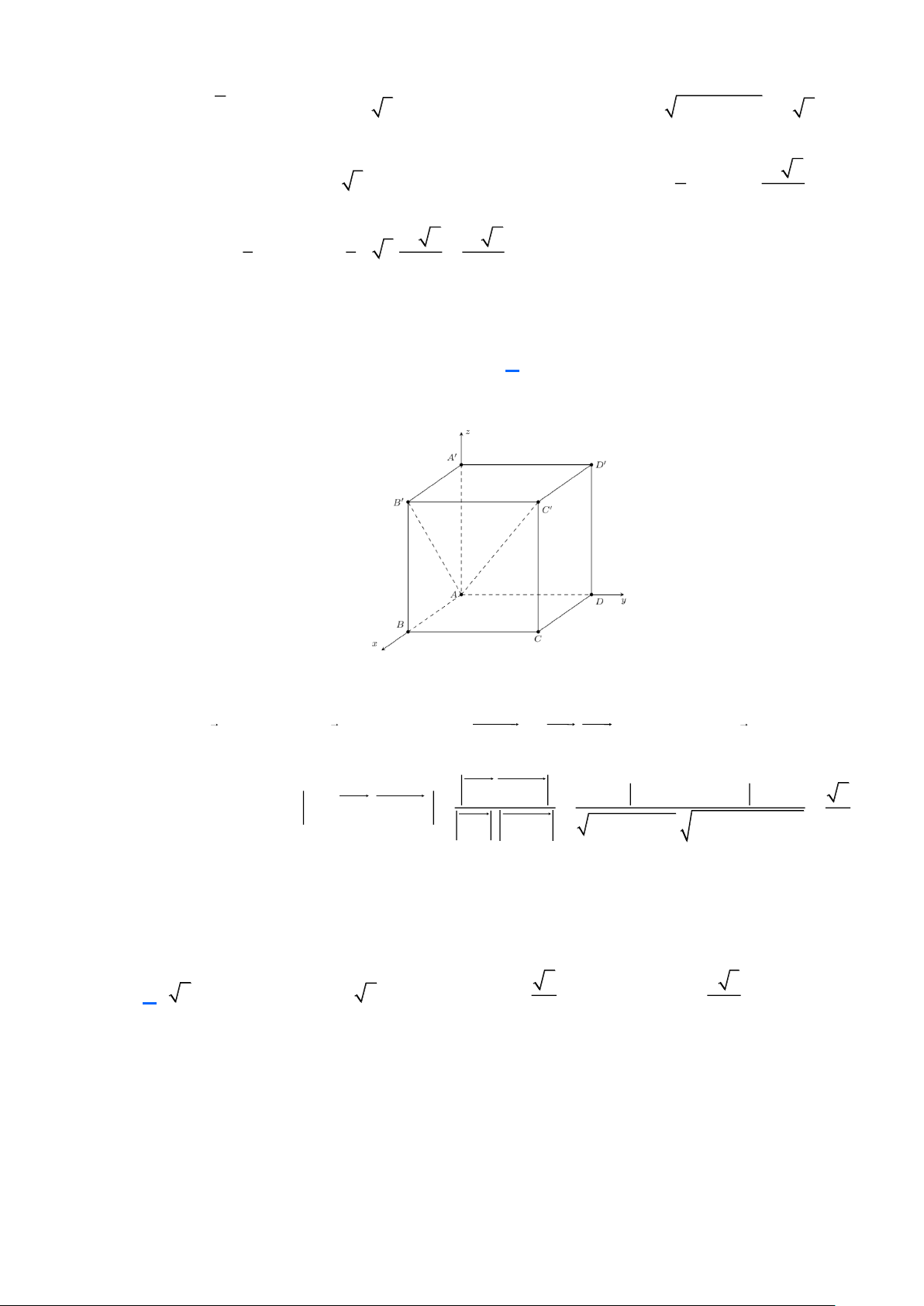
Chọn hệ trục Oxyz như hình vẽ
Gắn tọa độ A(0;0;0) , C(2;2;0) , B'(2;0;2) , C'(2;2;2) .
Ta có AB = (2;0;2) , AC = (2;2;2) suy ra n
= AB ; AC = − , CC = (0;0;2) . ( 4;0;4 AB C ) ( )
(
CC '.n − + + CC ( AB C )) = ( AB C 4.0 0.0 4.2 2 sin '; ' ' cos CC ';n = =
= AB 'C ' ) ( ' ') ( ) 2 2 2 2 2 2 CC ' . n 2 (AB 'C ') 0 + 0 + 2 . ( 4 − ) + 0 + 4
Vậy (CC ;( AB C )) = 45
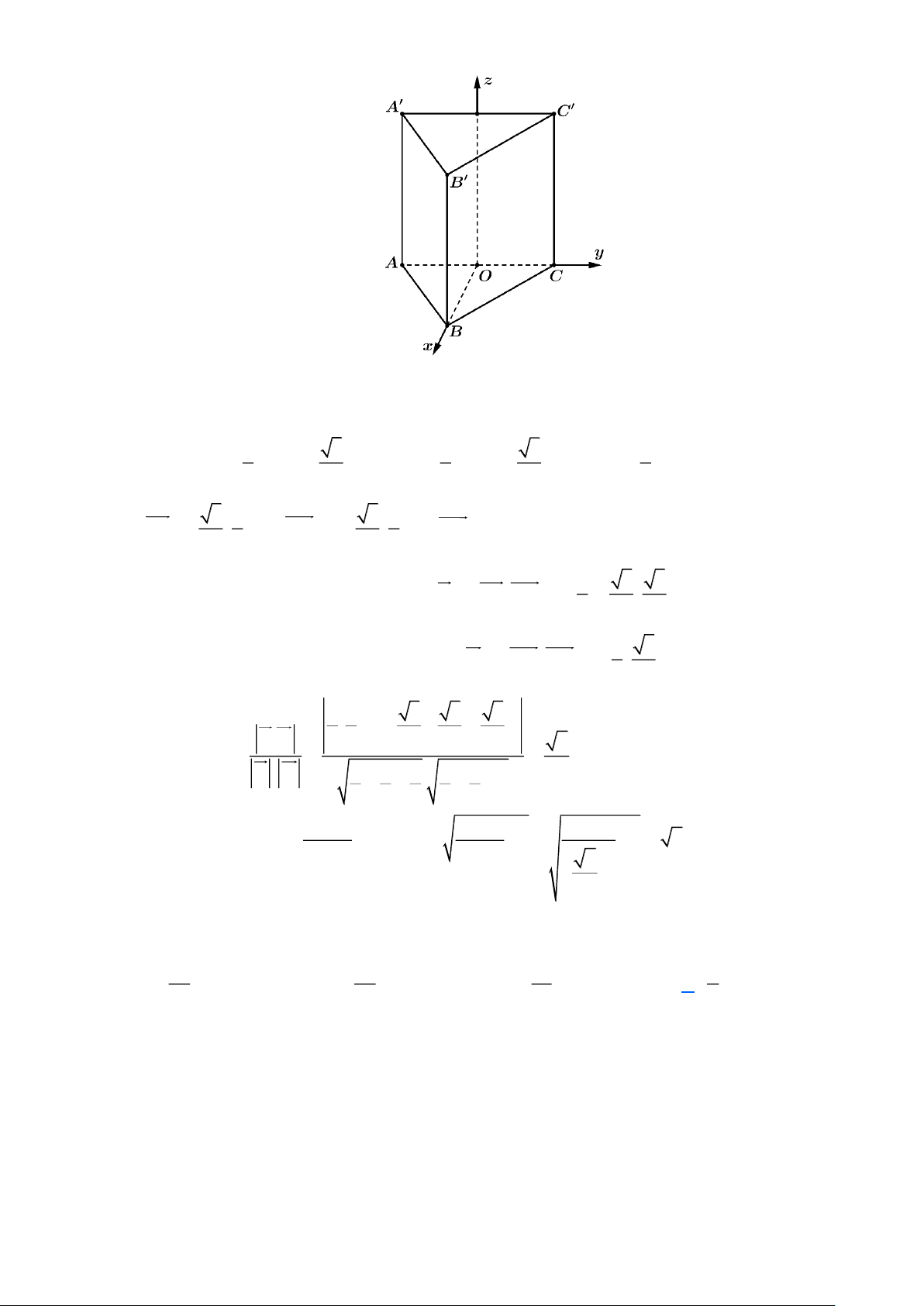
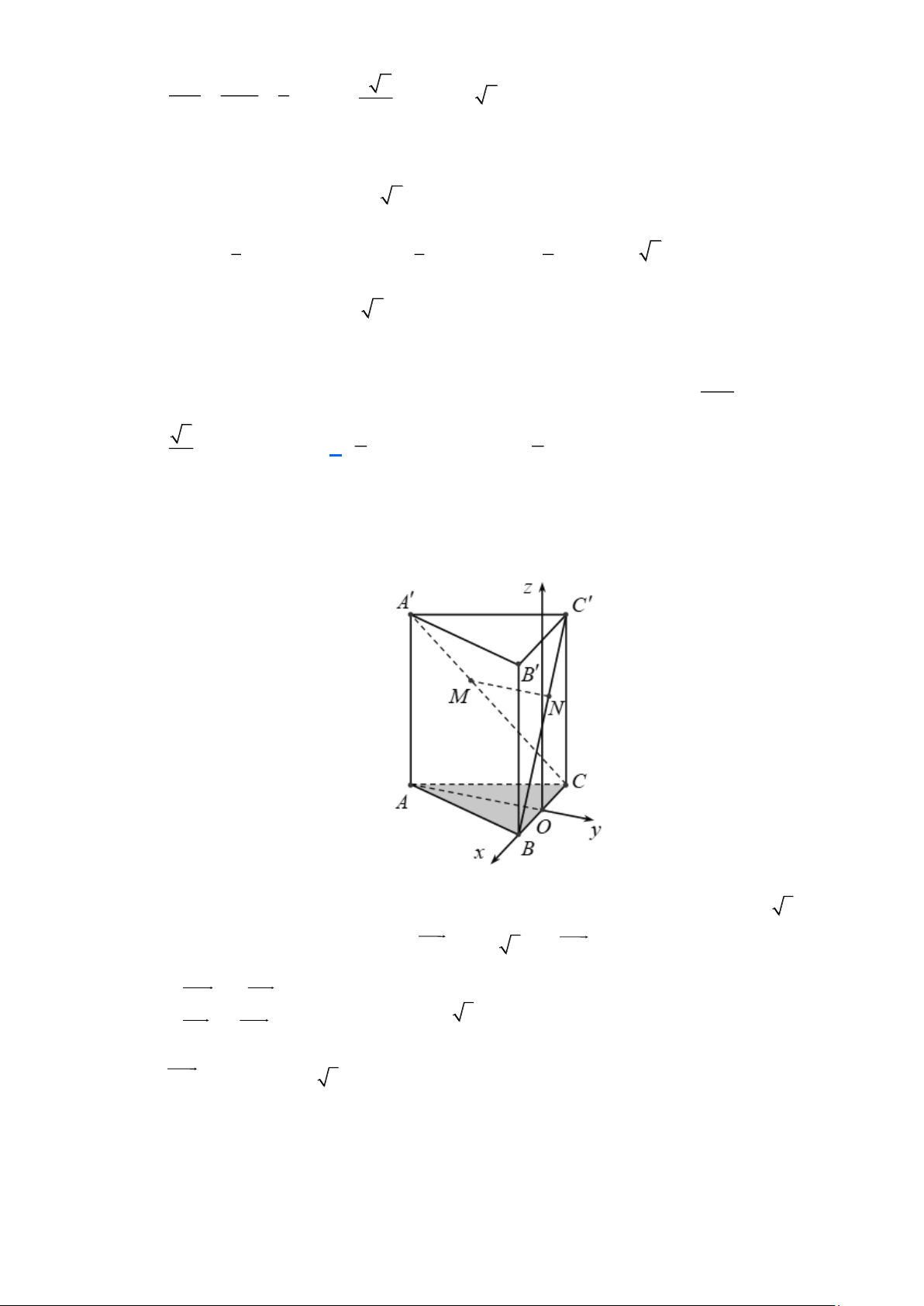
Câu 7: Cho hình lăng trụ tam giác đều AB . C A B C
có tất cả các cạnh bẳng nhau. Gọi là góc tạo
bởi hai mặt phẳng (C A
B) và (BCC B
) . Giá trị tan bằng 6 2 3 A. 6 . B. 2 . C. . D. . 2 3 Lời giải
thuvienhoclieu.com Trang 4 thuvienhoclieu.com
Giả sử lăng trụ tam giác đều AB . C A B C
có tất cả các cạnh bằng 1.
Chọn hệ trục Oxyz , với O là trung điểm AC , BOx , C Oy . 1 3 1 3 1 Ta có A 0;− ;0 , B ;0;0 , C 0; ;0 , B ;0;1 , C ' 0; ;1 . 2 2 2 2 2
3 1 3 1 AB = ; ;0 , BC = −
; ;1 , CC = (0;0; ) 1 2 2 2 2
1 3 3 Mặt phẳng (C B
) có vectơ pháp tuyến n = AB,BC = ;− ; . 1 2 2 2
1 3 Mặt phẳng (BCC B
) có vectơ pháp tuyến n = BC ,CC = ; ;0. 2 2 2 1 1 3 3 3 . + − . + .0 n .n 2 2 2 2 2 7 Ta có 1 2 cos = = = . n . n 1 3 3 1 3 7 1 2 + + . + + 0 4 4 4 4 4 1 1 1 Ta lại có 2 1+ tan = tan = −1 = −1 = 6 . 2 cos 2 2 cos 7 7
Câu 8: Cho hình lập phương ABC . D A B C D
cạnh bằng a . Gọi K là trung điểm DD . Tính khoảng
cách giữa hai đường thẳng CK và AD . 2a 4a 3a a A. . B. . C. . D. . 3 3 4 3 Lời giải
Gọi M là trung điểm BB thì ta có CK∥ A M
CK∥ ( A M D)
Suy ra d (CK, A D
) = d (CK,(A M
D)) = d (C,(A M D))
Chọn trục toạ độ như hình vẽ:
thuvienhoclieu.com Trang 5 thuvienhoclieu.com a
Ta có A(0;0;0), B( ; a 0;0), D(0; ;
a 0), A(0;0;a),C ( ; a ; a 0), B( ; a 0;a), M ; a 0; 2 2 a
a Khi đó A M = a − A D = ( a − a) 2 2 ;0; , 0; ; A M , A D = ;a ;a . 2 2
Suy ra mặt phẳng ( A M
D) có một vectơ pháp tuyến là (1;2;2)
Phương trình mặt phẳng ( A M
D) có dạng: x + 2y + 2z − 2a = 0 .
a + a − a a
Vậy d (C ( A M D)) 2 2 , = = . 3 3
Câu 9: Cho lăng trụ đứng ABC . D A B C D
có đáy ABCD là hình thoi tâm O cạnh a , AA = a và góc
ABC = 60 . Gọi M là trung điểm của cạnh AA . Khoảng cách giữa hai đường thẳng MO và C D bằng 3 5 3 5 2 5 2 5 A. a . B. a . C. a . D. a . 10 5 12 5 Lời giải
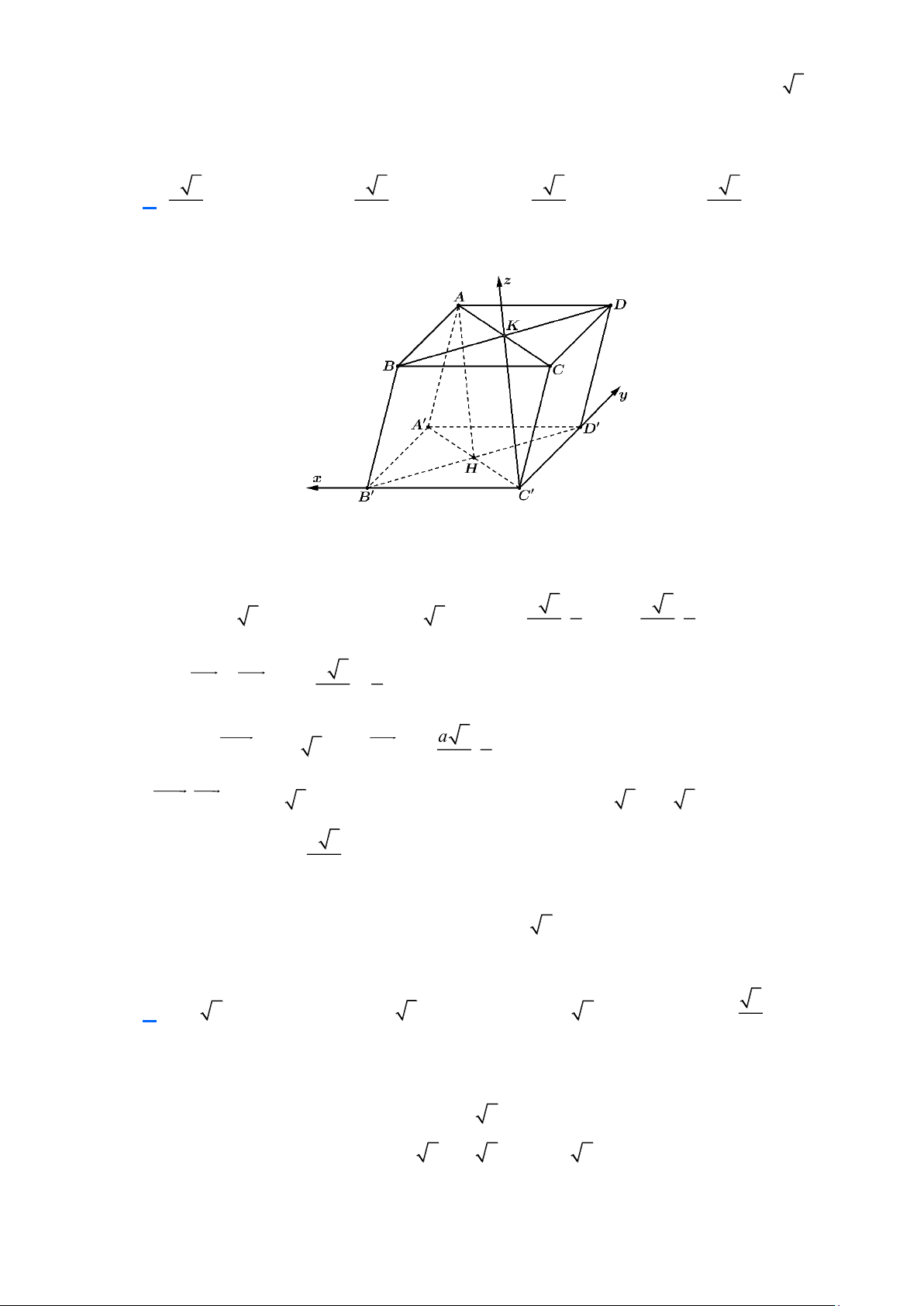
Dựng hệ trục tọa độ như hình vẽ.
Gọi O là giao điểm của AC và BD . Chọn a =1. 1 1 3 1
Dễ dàng tính được O(0;0;0), M − ;0; , D0; ;0 và C ;0;1 . 2 2 2 2
thuvienhoclieu.com Trang 6 thuvienhoclieu.com
1 1 1 3 1 Suy ra OM = − ;0; , C D = − ; ;−1 và OC = ;0;1 . 2 2 2 2 2 3 3 − − 3
Khi đó OM ,C D = − ; ; . 4 4 4 − 3 − 3 + OM ,C D .OC 8 4 3 5 3a 5
Khi đó khoảng cách : d (OM ;C D ) = = = = . OM ,C D 3 9 3 10 10 + + 16 16 16
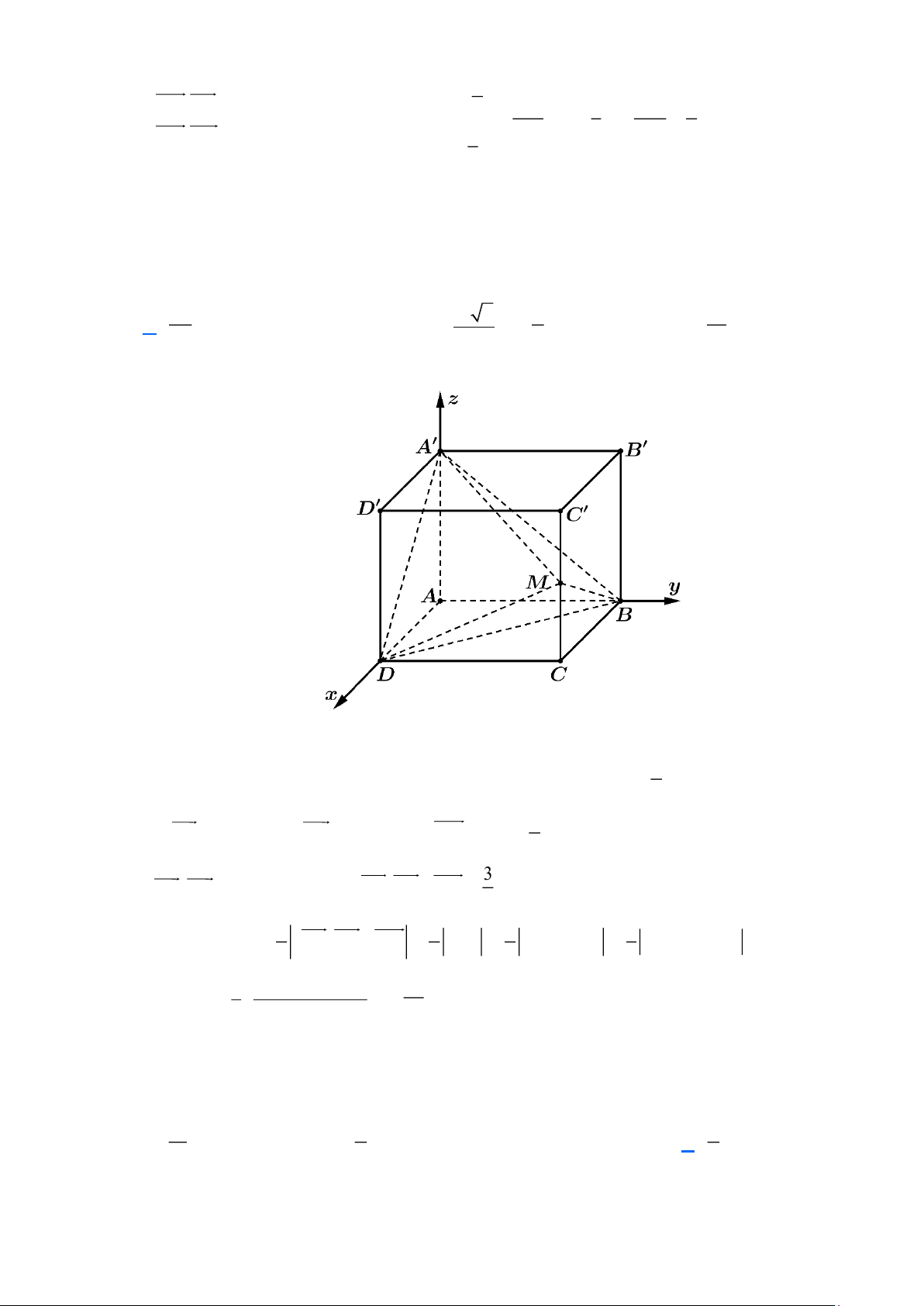
Câu 10: Cho hình lập phương ABC . D A B C D
có độ dài cạnh bằng 1. Gọi M , N, P,Q , lần lượt là
trung điểm của các cạnh AB , BC , C D
và DD . Thể tích khối tứ diện MNPQ là 1 1 3 1 A. . B. . C. . D. . 12 8 8 24 Lời giải
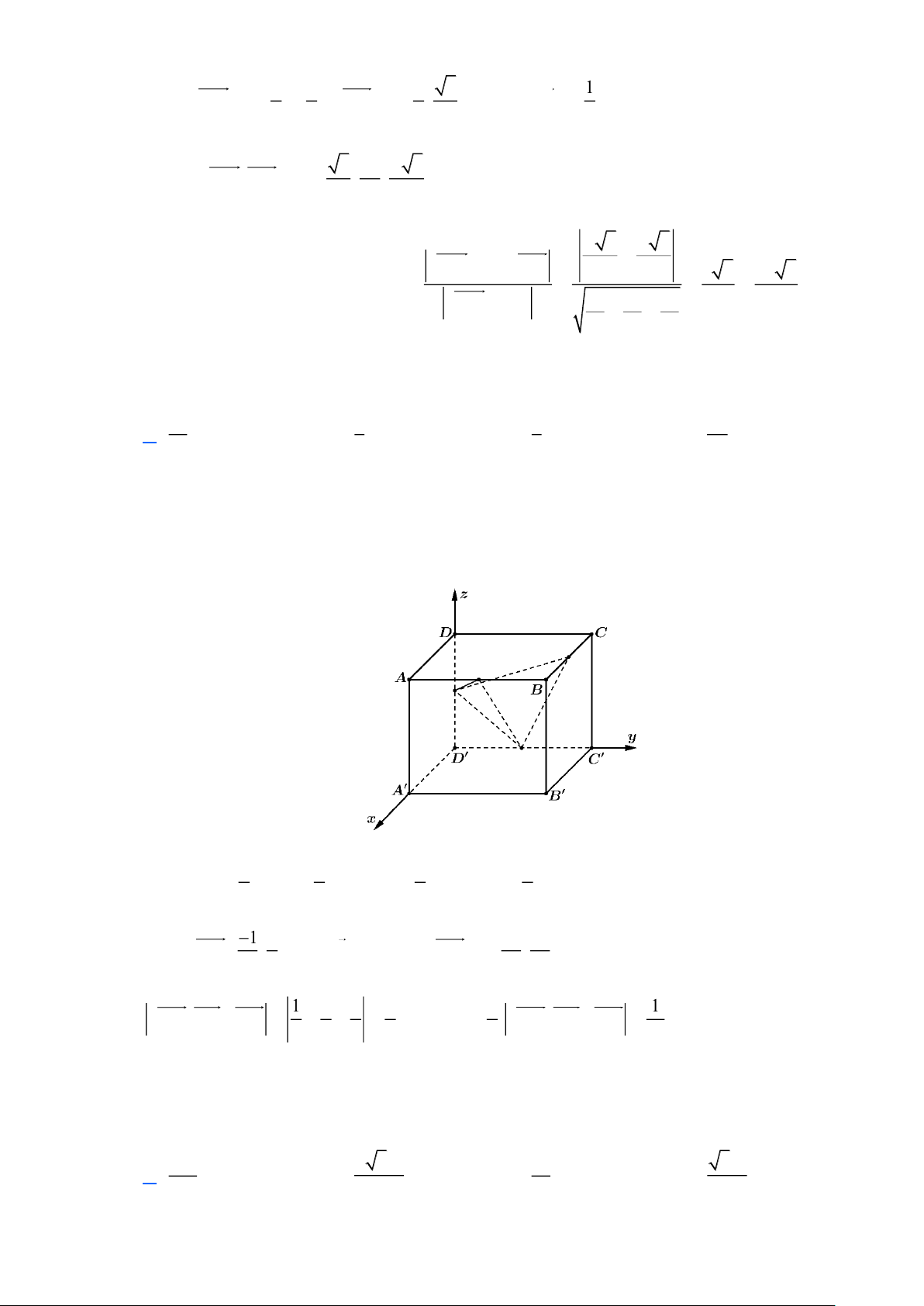
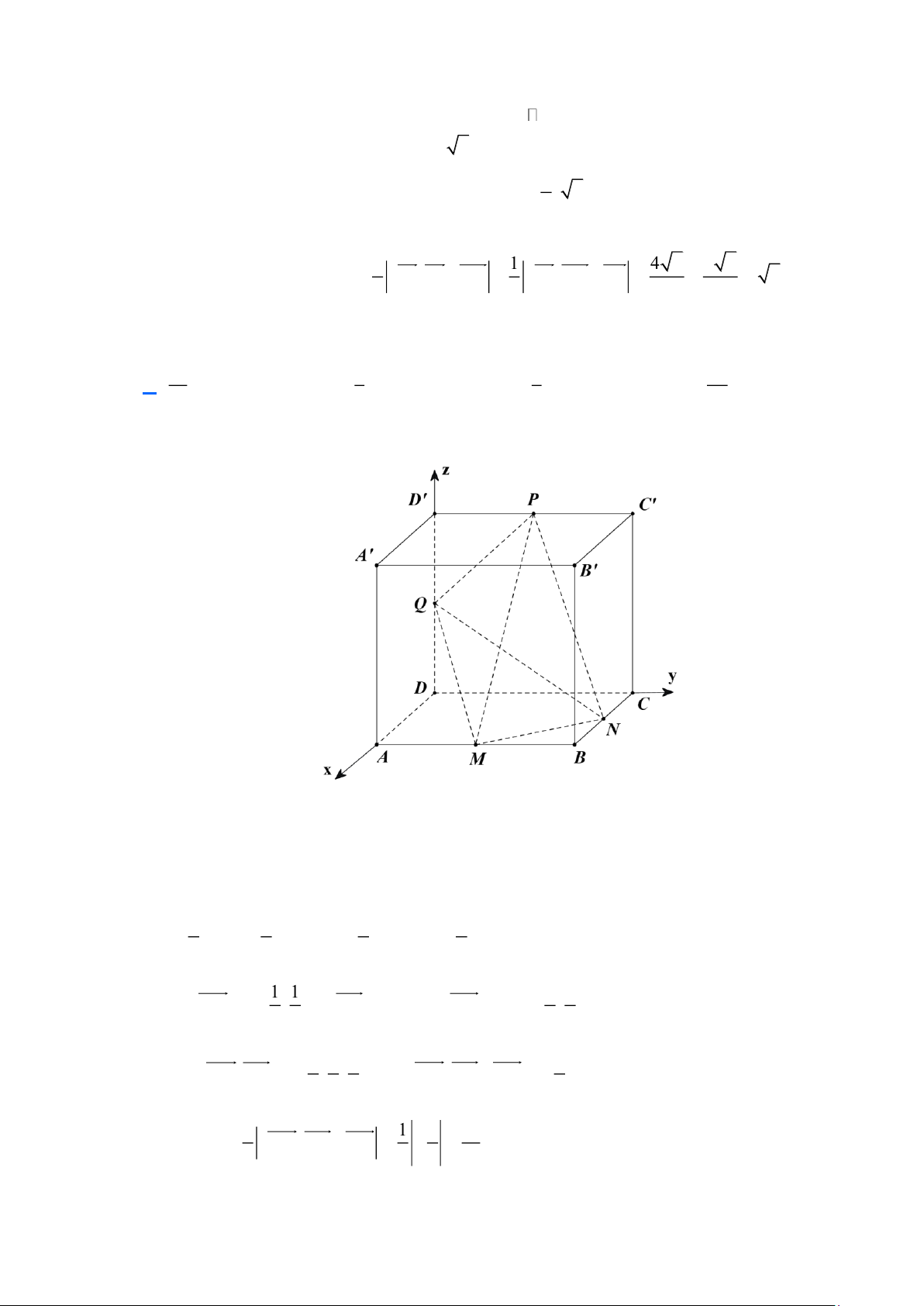
Chọn hệ trục tọa độ Oxyz sao cho: D ; O Ox D A
; Oy D C
; Oz D D . Khi đó: A(1;0; ) 1 , B(1;1; ) 1 , C (0;1; ) 1 , D(0;0; )
1 , A(1;0;0) , B(1;1;0) , C(0;1;0) 1 1 1 1 Ta có: M 1; ;1 , N ;1;1 , P 0; ;0 , Q 0;0; . 2 2 2 2 −
1 1 −1 −1 Ta có: MN ; ;0 , MP( 1 − ;0;− ) 1 , MQ 1 − ; ; 2 2 2 2
1 1 1 1
1 1
MN, MP.MQ = + − = V
= . MN,MP.MQ = . 2 4 4 2 MNPQ 6 12
Câu 11: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A và AB = a , cạnh bên SA
vuông góc với mặt phẳng đáy và SA = a . Gọi D , E , F lần lượt là điểm đối xứng của A qua
C , của S qua B và của A qua mặt phẳng (SBC). Thể tích của khối tứ diện ADEF bằng 3 2a 3 2 3a 3 a 3 3a A. . B. . C. . D. . 3 3 3 3 Lời giải
thuvienhoclieu.com Trang 7 thuvienhoclieu.com
Chọn hệ trục tọa độ Axyz như hình vẽ với độ dài vectơ đơn vị bằng a , ta được tọa độ các điểm như sau:
A(0;0;0) , B(1;0;0) , C(0;1;0) , S (0;0; )
1 D(0;2;0) , E(2;0;− ) 1 . 1 1 1
Gọi H là trọng tâm tam giác SBC H ; ;
. Vì tam giác SBC là tam giác đều nên H 3 3 3
cũng là trực tâm của tam giác SBC AH ⊥ (SBC) F là điểm đối xứng với A qua H 2 2 2 F ; ; . 3 3 3 2 2 2
Ta tính được: AD = (0;2;0), AE = (2;0;− ) 1 , AF = ; ; A , D AE = ( 2 − ;0; 4 − ) 3 3 3
1 1 2 2 2 2 Khi đó: V
= AD, AE.AF = . 2 − . + 0. − 4. = . . A DEF 6 6 3 3 3 3 3 2a
Vì độ dài vectơ đơn vị trên trục bằng a nên ta được thể tích cần tính là . 3
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a . Cạnh bên SA = a vuông
góc với đáy ( ABCD) . Gọi M là điểm nằm trên cạnh SD sao cho SM = 2MD. Hãy tính cosin
của góc tạo bởi hai mặt phẳng ( AMC) và (SBC)? 1 3 2 A. . B. . C. . D. 1. 2 2 5 Lời giải
thuvienhoclieu.com Trang 8 thuvienhoclieu.com
Chọn hệ trục tọa độ Oxyz sao cho điểm A O , các điểm B, D, S lần lượt thuộc chiều dương
các trục tọa độ Ox,Oy,Oz . Suy ra tọa độ các điểm như trên hình vẽ.
Do M là điểm nằm trên cạnh SD sao cho SM = 2MD suy ra
2a a 2 2 2
AM = 0; ; 2 2a a a a 2a
SM = SD M 0; ;
3 3 AM , AC = − ; ;− 3 3 3 AC = (a a ) 3 3 3 ; ;0 2 a SB = (a;0;− a) = − (1; 1
− ;2) . Ta có
SB,SC = ( 2 2 a ;0;a ) 2 = a (1;0; ) 1 . 3 SC =
(a;a;− a)
Chọn vectơ pháp tuyến của mặt phẳng ( AMC) là n = 1;−1;2 . 1 ( )
Chọn vec tơ pháp tuyến của mặt phẳng (SBC) là n = 1;0;1 . 2 ( ) n .n 3 3
Khi đó: cos(( AMC),(SBC)) 1 2 = = = . n . n 6 2 2 1 2
Câu 13: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và độ dài cạnh SA = a và vuông
góc với ( ABC) . Góc giữa mặt phẳng (SAB) và mặt phẳng (SBC) là . Khi đó tan bằng: 1 A. 1. B. 3 . C. 6 . D. . 2 2 Lời giải
Gắn hệ tọa độ Oxyz như hình vẽ:
thuvienhoclieu.com Trang 9 thuvienhoclieu.com a a a 3 a 3
Ta có: H (0;0;0), C ;0;0 , B − ;0;0 , A 0; ;0, S 0; ;a 2 2 2 2 2 2 a 3 a 2 a 3 Suy ra = 2 = ( n AB AS = − , n
BS, BC = 0;a ;− SAB) , ; ;0 2 2 (SBC) 2 4 a ( n n SAB). (SBC) 1 2 1 cos = = = . Vậy tan = −1 = 6 4 4 4 n . n 3a a 3a 7 2 cos (SAB) (SBC) 4 + . a + 4 4 4
Câu 14: Cho lăng trụ đứng AB . C A B C
có đáy ABC là tam giác vuông tại B , AB = a, BC = a 2 , a
AA = a 3 . Trên BB lấy điểm N sao cho BN =
. Khoảng cách từ B đến mặt phẳng 3 (AC N ) bằng a 6 a 6 a 6 A. . B. a 6 . C. . D. . 2 6 3 Lời giải a
Chọn hệ trục tọa độ như hình vẽ, khi đó ta có: A(a;0;0), N 0;0;
, C(0;a 2;a 3) , 3 a
B(0;0;a 3). AN = −a;0;
, AC = (−a;a 2;a 3) . 3 6 4a Mặt phẳng ( AC N
)đi qua A(a;0;0) có vtpt n = AN , AC = − a; ;− a 2 có phương 3 3 − 6 4 trình là: ( AC N ): (x − a) + y − 2z = 0. 3 3 6a − 6a 3 a 6
Khoảng cách: d (B,( AC N )) = = . 6 16 3 + + 2 9 3
thuvienhoclieu.com Trang 10 thuvienhoclieu.com
Câu 15: Cho lăng trụ ABC . D A B C D
có đáy ABCD là hình chữ nhật và AB = a, AD = a 3 . Hình
chiếu vuông góc của điểm A lên mặt phẳng ( A B C D
) trùng với giao điểm của A C và B D
. Khoảng cách từ điểm B đến ( AB D ) bằng a 3 a 3 a 3 a 3 A. . B. . C. . D. . 2 4 3 6 Lời giải Gọi H = A C B D
và K = AC BD .
Chọn hệ toạ độ Oxyz như hình vẽ với C O, BOx, DOy, K Oz .
Đặt AH = m 0.
a 3 a a 3 a
Khi đó B(a 3;0;0),D(0; ;
a 0), A(a 3; ; a 0), H ; ;0, A ; ;m . 2 2 2 2 a 3 a Ta có B B = A A B ;− ;m . 2 2 a a Mặt khác B D = (−a a ) 3 3; ;0 , B A = − ; ;m nên ( AB D
) có véctơ pháp tuyến là 2 2 B D , B A = (a ; m 3a ; m 0) nên ( AB D
) có phương trình x + 3y − a 3 = 0. a
Vậy d (B ( AB D )) 3 ; = . 2
Câu 16: Trong không gian Oxyz , cho hình chóp S.ABCD có đáy ABCD là hình thoi, AC cắt BD tại
gốc tọa độ O . Biết A(2;0;0) , B(0;1;0) , S (0;0;2 2). Gọi M là trung điểm của cạnh SC .
Mặt phẳng ( ABM ) cắt đường thẳng SD tại điểm N . Tính thể tích khối chóp S.ABMN . 3
A. V = 2 .
B. V = 2 3 .
C. V = 3 2 . D. V = . 4 Lời giải
Điểm O là trung điểm của AC, BD C( 2 − ;0;0),D(0; 1 − ;0) .
Điểm M là trung điểm của SC M ( 1 − ;0; 2 ).
Phương trình mặt phẳng ( ABM ) là 2x + 2 2y + 3z − 2 2 = 0 .
thuvienhoclieu.com Trang 11 thuvienhoclieu.com x = 0
Phương trình đường thẳng SD là y = 1
− + t (t ) . z = 2 2t 1
Điểm N là giao điểm của ( ABM ) và SD N 0;− ; 2 . 2
Vậy thể tích khối chóp S.ABMN là: 1 1
4 2 2 2 V = V +V = S , A SB.SM + S , A SM .SN = + = 2 . S.ABM S.AMN 6 6 6 6
Câu 17: Cho hình lập phương ABC . D A B C D
có độ dài cạnh bằng 1. Gọi M , N , P , Q lần lượt là
trung điểm của các cạnh AB , BC , C D
và DD . Tính thể tích khối tứ diện MNPQ . 1 1 3 1 A. . B. . C. . D. . 12 8 8 24 Lời giải
Gắn hệ trục toạ độ như hình vẽ ta có D(0;0;0), A(1;0;0), B(1;1;0),C(0;1;0), A(1;0; ) 1 , B(1;1; ) 1 , C(0;1; ) 1 , D(0;0; ) 1 .
Vì M , N , P , Q lần lượt là trung điểm của các cạnh AB , BC , C D và DD nên: 1 1 1 1 M 1; ;0 , N
;1;0 , P 0; ;1 ,Q 0;0; . 2 2 2 2 1 1
1 1
Suy ra MN = − ; ;0 , MP = ( 1 − ;0; ) 1 , MQ = 1 − ;− ; 2 2 2 2
1 1 1
1
Suy ra MN;MP = ; ;
, MN;MP.MQ = − . 2 2 2 2 1 1
1 1 Vậy V
= MN;MP.MQ = − = . MNPQ 6 6 2 12
thuvienhoclieu.com Trang 12 thuvienhoclieu.com
Câu 18: Cho tứ diện .
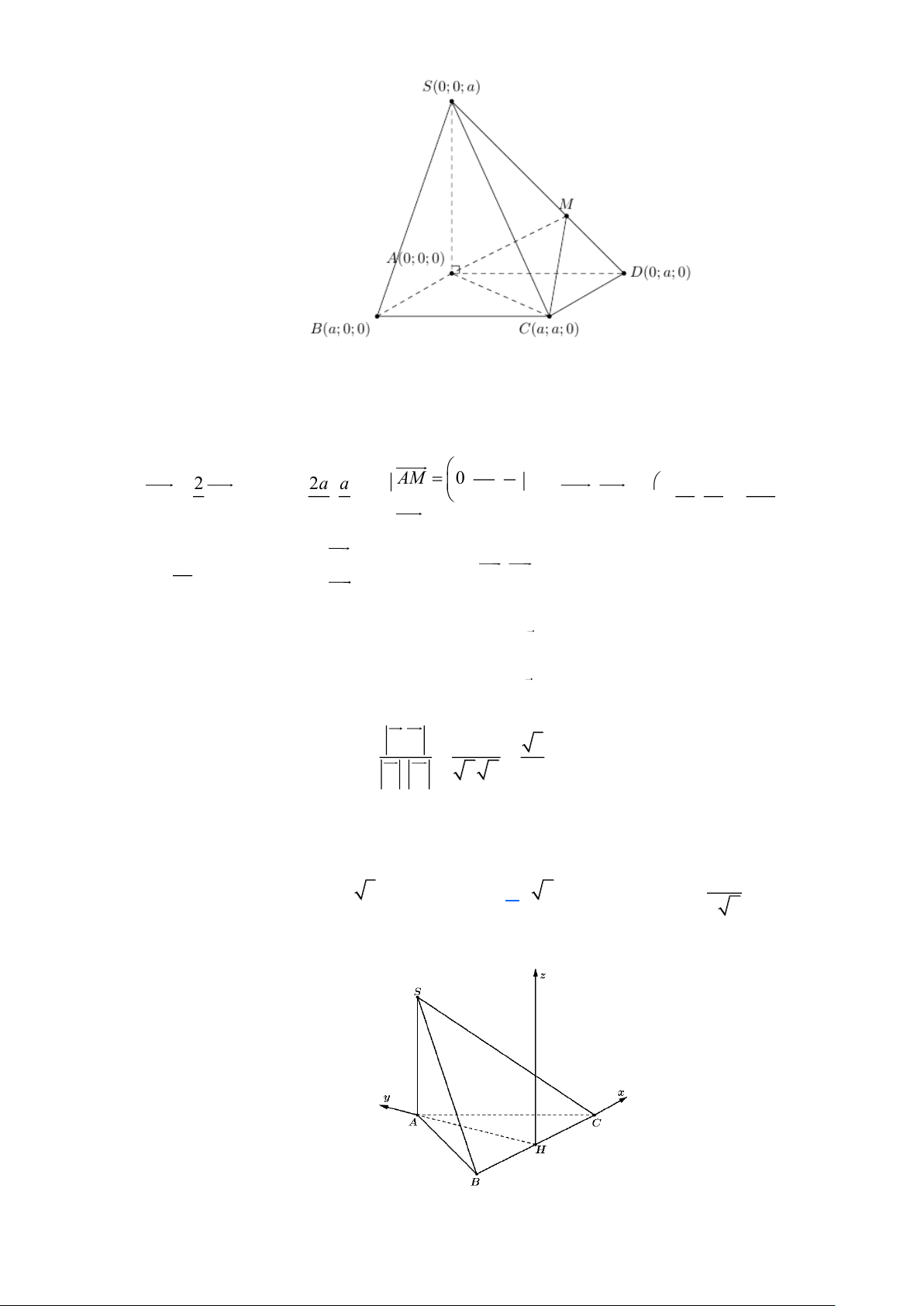
O ABC có OA, OB , OC đôi một vuông góc với nhau OA = a và OB = OC = 2a
. Gọi P là trung điểm của BC (minh họa như hình vẽ). Khoảng cách giữa hai đường thẳng
OP và AB bằng: 2a 6a 2 5a A. . B. . C. a . D. . 2 3 5 Lời giải Đặt khối tứ diện .
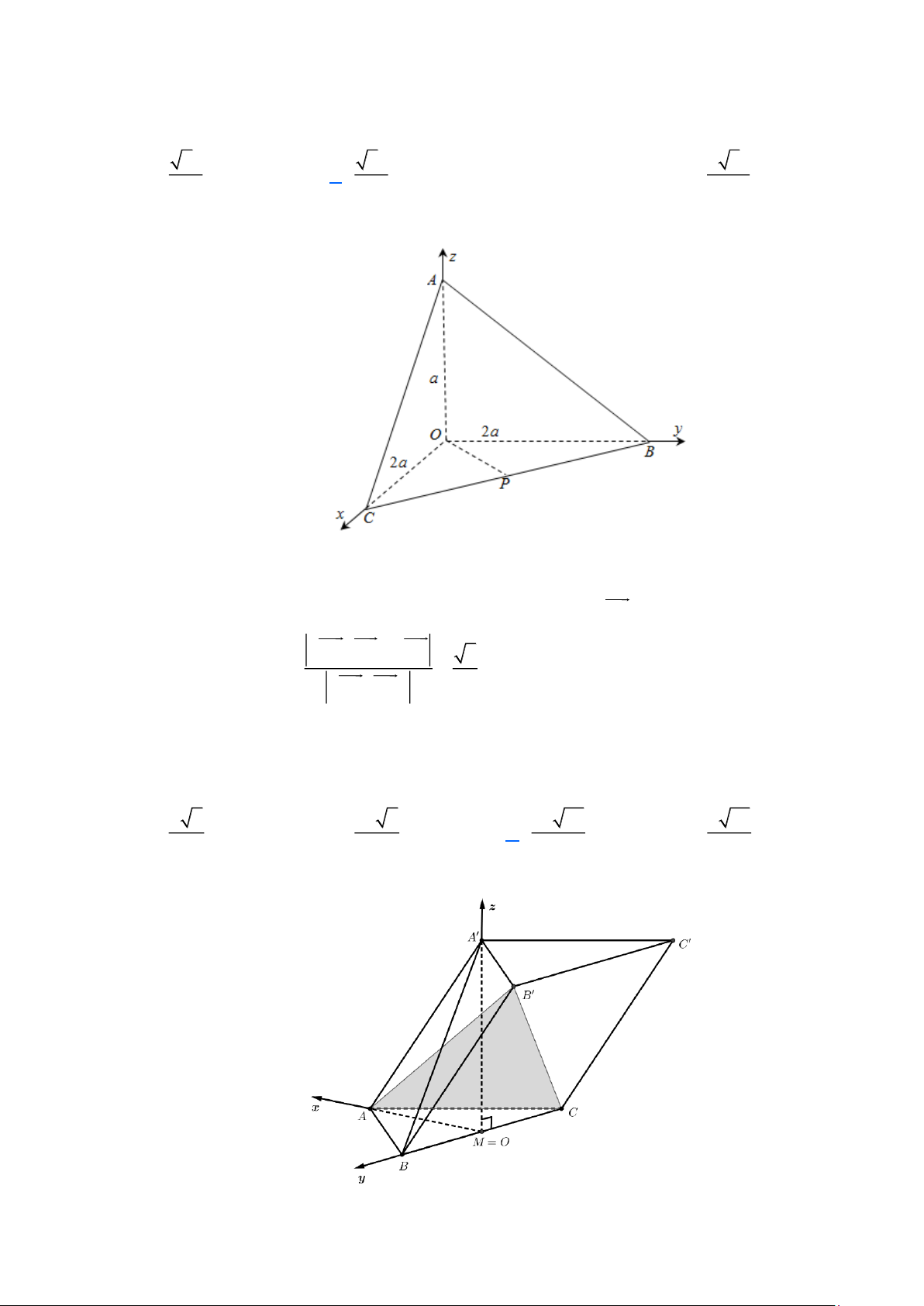
O ABC vào hệ trục tọa độ gốc Oxyz : các điểm ,
A B,C lần lượt thuộc các trục
tọa độ Oz,Oy,Ox .
Ta có: O(0;0;0), A(0;0; )
1 , B(0;2;0) , C(2;0;0), P(1;1;0) , AB = (0;2;− ) 1 .
OP ; AB OB 6 Khi đó: d (O ; P AB) = = (a) . OP ; AB 3
Câu 19: Cho lăng trụ AB . C A B C
có tam giác ABC đều cạnh bằng 2a . Hình chiếu vuông góc của A
lên mặt phẳng ( ABC) trùng với trung điểm M của BC . Biết góc tạo bởi AB và mặt đáy
bằng 60. Khoảng cách từ B đến mặt phẳng ( AB C ) là a 7 2a 7 2a 39 a 39 A. . B. . C. . D. . 7 7 13 13 Lời giải
Góc giữa AB và mặt phẳng ( ABC) là góc A B M = 60 .
thuvienhoclieu.com Trang 13 thuvienhoclieu.com 3 Ta có A M
= BM.tan60 = a 3 ; AM = . AB sin 60 = 2 . a = a 3 . 2
Đặt hệ trục toạ Oxyz như hình vẽ. Coi a =1 khi đó A( 3;0;0), B(0;1;0) , C(0; 1 − ;0) ,
A(0;0; 3) . Gọi B(x ; y ;z , A B
= (x ; y ;z − 3 , AB = (− 3;1;0). 0 0 0 ) 0 0 0 ) = − x 3 0
Vì AB = AB nên y =1 B(− 3;1; 3). 0 z = 3 0 AC = (− 3; 1 − ;0) Ta có
n = (1;− 3;3) là vectơ pháp = (
AC AB = − − AB 2 − 3;1; 3) , ( 3;3; 3 3)
tuyến của mp ( ACB). Phương trình mặt phẳng ( ACB) là: x − 3y + 3z − 3 = 0 . − − 2a 39
d (B ( ACB)) 3 3 2 39 , = =
. Vậy khoảng cách từ B đến ( AB C ) là . 1+ 3 + 9 13 13 x = 0 x = 2
Câu 20: Trong không gian Oxyz , cho hai đường thẳng : y = 2 + t và d : y = 1+ t . Biết rằng có z = t − z = 1 − + t một hình hộp ABC . D A B C D
thỏa mãn A , C cùng thuộc Ox , B , C cùng thuộc và D ,
B cùng thuộc d . Thể tích của khối hộp ABC . D A B C D là A. 9 2 . B. 18 2 . C. 9 . D. 18. Lời giải AC ⊥ BC
Nhận xét rằng các đường thẳng , d , Ox đôi một vuông góc với nhau nên BC ⊥ B D . B D ⊥ AC
Gọi I là tâm của hình bình hành ABCD và M là giao của D I và B D . IM ID 1 1 B D ⊥ AC Ta có =
= IM = ID . Mặt khác B D ⊥ ( AD C ) . MD B D 2 3 B D
⊥ BC B D ⊥ AD
Kẻ MH // AD ( H AC ) MH ⊥ AC suy ra MH là đoạn vuông góc chung của AC, B D
MH = d ( AC,B D ) = d (O ; x d ) = 2 . MH IM 1 Vì = = AD = . AD ID 3 2 3
Kẻ MK // AC ( K AD ) MK ⊥ AD suy ra MK là đoạn vuông góc chung của AD , B D .
MK = d ( AD ,B D ) = d ( ; d ) = 2
thuvienhoclieu.com Trang 14 thuvienhoclieu.com MK D M 2 3 2 Vì = = AI = AC = 3 2 . AI ID 3 2
Ta lại có BC//( AD C
) d (BC ; AC) = d (BC ;(AD C )) = d ( ; B ( AD C )) = d ( ; D ( AD C )) d ( ; D ( AD C )) = d (O ; x ) = 2 1 1 1 V = = .d ( ; D ( AD C )) = .d D AD C S . AD AC 3 2 DAD C ( ;( )). 3 AD C 3 2 V = = . 6V 18 2 ABC . D A B C D DAD 'C
Câu 21: Cho lăng trụ tam giác đều AB . C A B C
có cạnh bên bằng cạnh đáy. Đường thẳng MN ( NB M A C
; N BC) là đường vuông góc chung của A C
và BC . Tỷ số NC bằng 5 3 2 A. . B. . C. . D. 1. 2 2 3 Lời giải
Kết quả bài toán sẽ không thay đổi nếu ta xét lăng trụ đều AB . C A B C
có cạnh bên bằng cạnh đáy bằng 2 .
Chọn hệ trục tọa độ Oxyz như hình vẽ ( O là trung điểm của BC ) thì ta có: A(0;− 3;2), B(1;0;0), C( 1 − ;0;0), C( 1
− ;0;2), CA = (1;− 3;2) , BC = ( 2 − ;0;2) . C
M = mCA
Do nên ta có M ( 1 − + ; m − 3 ;
m 2m) , N (1− 2 ; n 0;2n)
BN = nBC
MN = (−m − 2n + 2; 3 ;
m 2n − 2m).
Đường thẳng MN là đường vuông góc chung của A C và BC nên:
thuvienhoclieu.com Trang 15 thuvienhoclieu.com 2 = MN.CA = 0 4 − m + 2n = 1 − m BN 3 NB 3
5 = n = = MN.BC = 0 −m + 4n = 2 3 BC 5 NC . 2 n = 5
Câu 22: Trong không gian với hệ tọa độ Oxyz , cho hình hộp chữ nhật AB . CD A B C D
có A trùng với
gốc tọa độ O . Biết rằng B( ; m 0;0) , D(0; ;
m 0) , A(0;0;n) với m , n là các số dương và
m + n = 4. Gọi M là trung điểm của cạnh CC . Thể tích lớn nhất của khối tứ diện BDAM bằng 64 9 75 A. .
B. d (M (P)) 11 2 ; = . C. . D. . 27 6 4 32 Lời giải
Ta có A(0;0;0) , B( ; m 0;0) , D(0; ;
m 0) , A(0;0;n) . n Suy ra C ( ; m ; m 0) , B( ;
m 0;n) , C( ; m ; m n) , D(0; ; m n) , M ; m ; m . 2 n Và BD = (− ; m ;
m 0), BA = (− ;
m 0;n) , BM = 0; ; m . 2
3 BD BA = = ( 2 , m ; n m ; n m ) ; 2
BD, BA .BM m n . 2
1 1 1 1 Ta được V = 2 = 2 = m .(4 − m) = . m . m (8 − 2m)
BD, BA .BM m .n BDA M . 6 4 4 8 3 64 V
1 m + m + 8 − 2m = BDA M . 8 3 27
Câu 23: Trong không gian với hệ tọa độ Oxyz cho hình chóp tứ giác đều S.ABCD có các điểm
A(1;2;0) B(4;6;0) , D( 3
− ;5;0) . Gọi I là tâm hình vuông ABCD. Tính khoảng cách từ
đường vuông góc chung của đường thẳng SI và BC đến đường thẳng AB . 15 3 5 A. . B. . C. 5 . D. . 2 2 2 Lời giải
Vì I là tâm hình vuông ABCD nên I là trung điểm của BD .
thuvienhoclieu.com Trang 16 thuvienhoclieu.com 1 11 Tọa độ I ; ;0
. Suy ra tọa độ điểm C(0;9;0) . 2 2 15
Gọi H là trung điểm
BC khi đó tọa độ H 2; ;0
và IH ⊥ BC (1). 2
Vì hình chóp S.ABCD là hình chóp đều nên SI ⊥ ( ABCD) SI ⊥ IH (2).
Từ (1) và (2) suy ra đường vuông góc chung của SI và BC là đường thẳng IH . AB 5
Vì IH ∥ AB nên khoảng cách từ IH đến AB bằng = . 2 2
Câu 24: Cho hình lăng trụ tam giác đều AB . C A B C
có cạnh đáy bằng 1, cạnh bên bằng 3 . Gọi I là 1
điểm trên cạnh BB sao cho BI = BB , điểm M di động trên cạnh AA . Biết diện tích của 3 AM a
tam giác MIC nhỏ nhất khi tỷ số = (a ;
b *,(a,b) = )
1 . P = a + b là AA b A. 4 . B. 3 . C. 7 . D. 5 . Lời giải 3 1
Chọn hệ toạ độ Axyz sao cho: A(0;0;0), B(0;1;0),C ; ;0, A(0;0;3). 2 2 3 1
Khi đó B(0;1;3);C ; ;3; I (0;1; ) 1 . 2 2
3 1
Gọi toạ độ điểm M (0;0;x) AA(0 x ) 3 ; IC = ;− ;2; IM = (0; 1 − ; x − ) 1 2 2 1 1 1
Diện tích của tam giác MIC là: S = IC ',IM = 4x −16x + 31 = 4(x − 2)2 2 +15 2 4 4 AM a 2
Do đó S nhỏ nhất khi x = 2 . Khi đó tỉ số
= = a + b = 5 AA . b 3
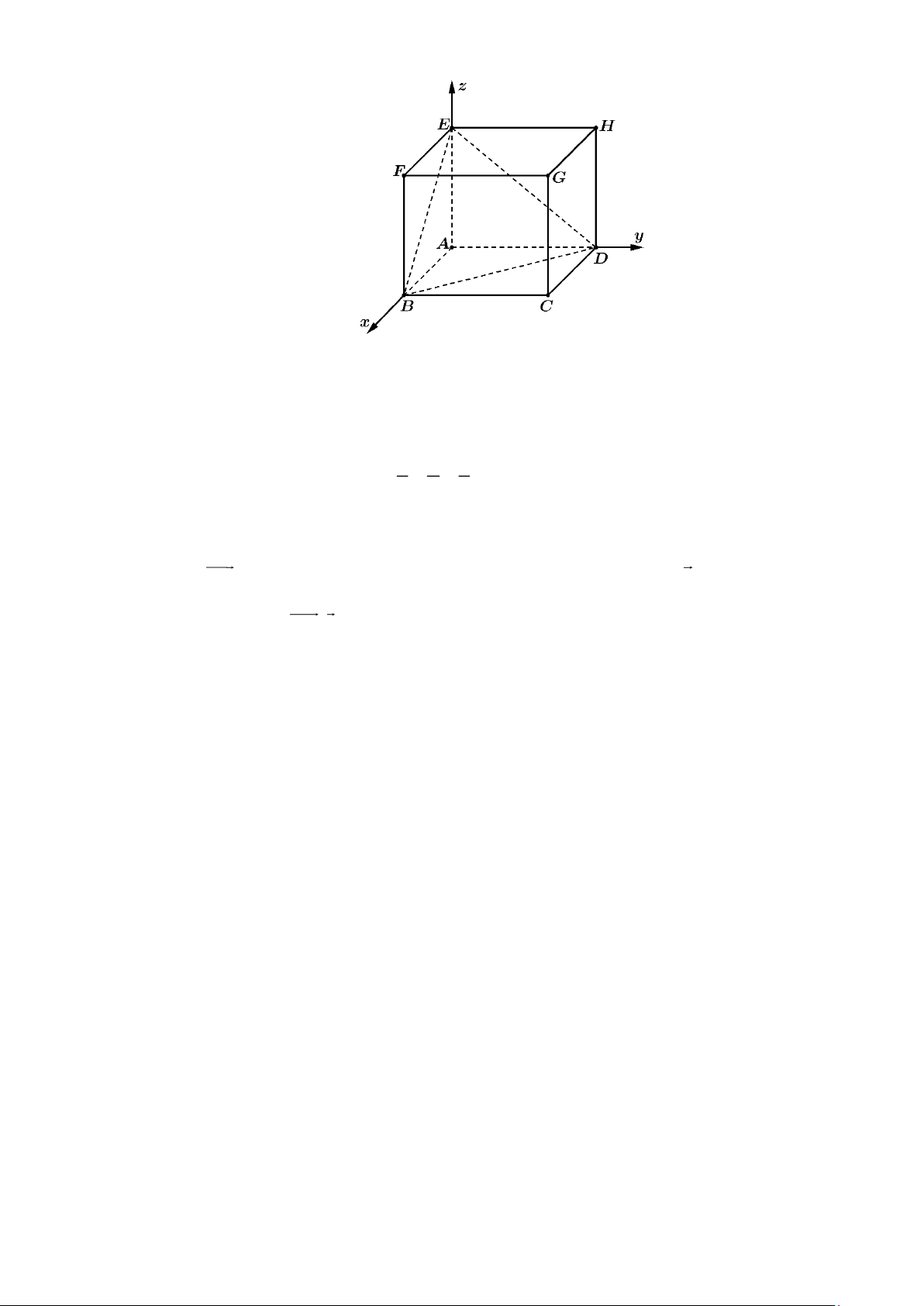
Câu 25: Cho hình lập phương ABC .
D EFGH có cạnh bằng 4. Gọi d là đường thẳng đi qua trọng tâm
của tứ diện EABD , cắt đường thẳng AE tại M và song song với mặt phẳng (EBD) . Tính AM .
A. AM = 1.
B. AM = 2 .
C. AM = 3. D. AM = 4 . Lời giải
Chọn hệ trục tọa độ như hình vẽ.
thuvienhoclieu.com Trang 17 thuvienhoclieu.com
Ta có: A(0;0;0);B(4;0;0);D(0;4;0); E(0;0;4) .
Gọi T là trọng tâm của tứ diện EABD suy ra T (1;1; ) 1 . x y z
Phương trình mặt phẳng (EBD) : + + = 1 x + y + z − 4 = 0 . 4 4 4
Đường thẳng d cắt đường thẳng AE tại M suy ra M (0;0;m) .
Khi đó, MT = (1;1;1− m) và vectơ pháp tuyến của mặt phẳng (EBD) là n = (1;1; ) 1 .
Do d∥(EBD) nên MT .n = 0 1+1+1− m = 0 m = 3 .
Suy ra M (0;0;3) nên AM = 3.
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho hình chóp S.ABC có đường cao SA = h và có đáy là tam giác ABC vuông tại C . Biết rằng
thuvienhoclieu.com Trang 18 thuvienhoclieu.com
AC = b, BC = a . Gọi M là trung điểm của AC và N là điểm sao cho 1
SN = SB và được gắn 3
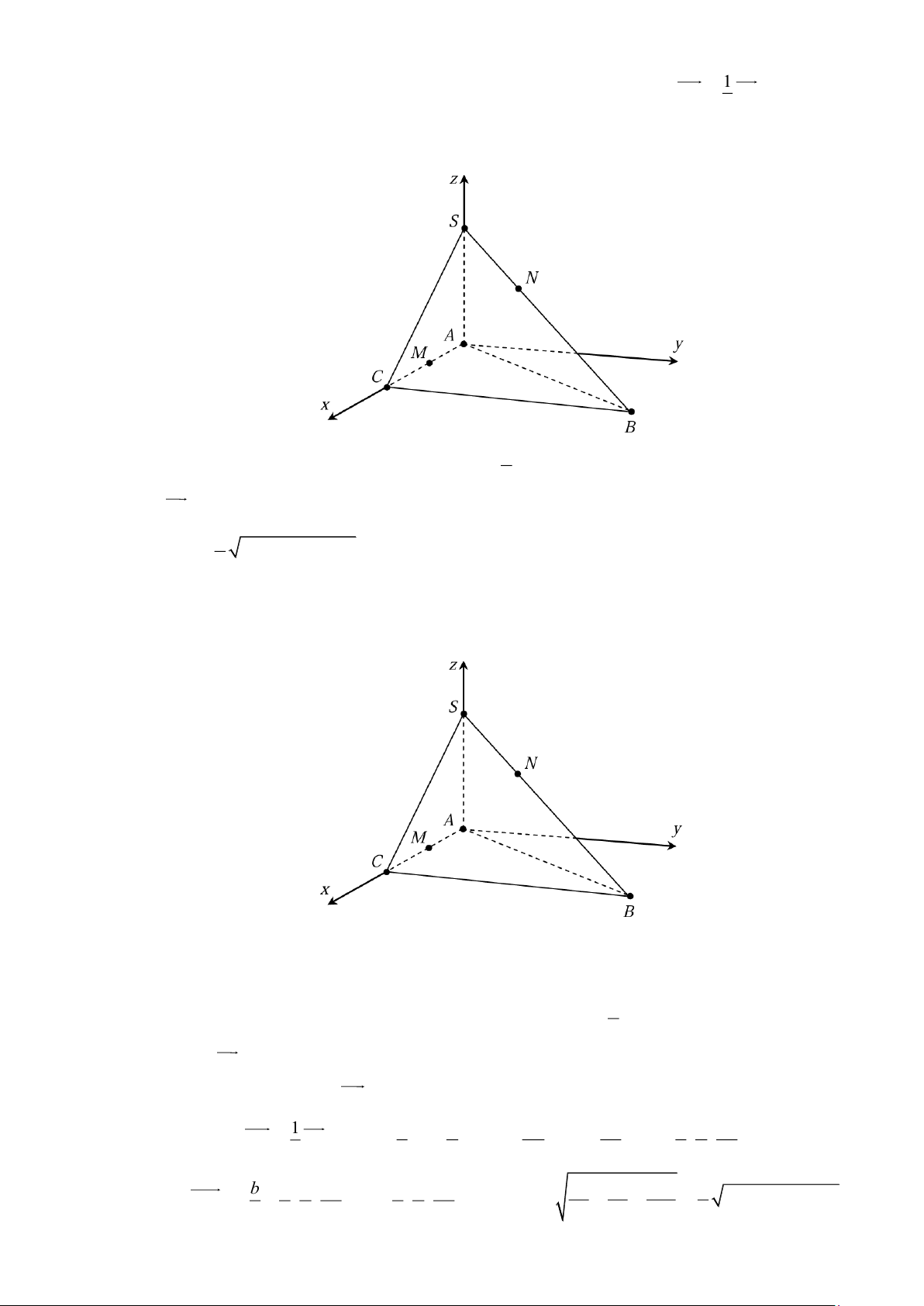
vào hệ trục tọa độ Oxyz (với A O ) như hình vẽ dưới đây. Xét tính đúng sai của các khẳng định sau: a) ( b A 0;0;0),C ( ; b 0;0), B( ; b ;
a 0), S (0;0;h), M ;0;0 2 b) SB = ( ; a ; b −h) c) 1 2 2 2 MN =
b + 4a + 16h 2 b) Khi 2 2 2
4h = 2a − b thì hai đường thẳng MN và SB vuông góc với nhau. Lời giải
Ta chọn hệ trục tọa độ Oxyz có gốc O trùng với A , tia Ox trùng với tia AC , tia Oz trùng
với tia AS sao cho điểm B nằm trong góc xOy . a) Đúng: Khi đó ( b A 0;0;0),C ( ; b 0;0), B( ; b ;
a 0), S (0;0;h), M ;0;0 2 b) Đúng: SB = ( ; b ;
a −h) c) Sai: Gọi N ( ; x ;
y z) thì SN = ( ; x ; y z − h) b a −h 2h b a 2h Từ điều kiện 1
SN = SB nên x = ; y = , z − h = z = N ; ; 3 3 3 3 3 3 3 3
b b a 2h b a 2h 2 2 2 b a 4h 1 Ta có MN = − ; ; = − ; ; nên 2 2 2 MN = + + =
b + 4a +16h 3 2 3 3 6 3 3 36 9 9 6
thuvienhoclieu.com Trang 19 thuvienhoclieu.com
d) Sai: Hai đường thẳng MN và SB vuông góc với nhau khi và chỉ khi: 2 2 2 b − a 2 − h 2 2 2 MN.SB = 0 + +
= 0 4h = 2a − b 6 3 3
Câu 2: Cho tứ diện S.ABC có SC = CA = AB = a 2 và SC ⊥ ( ABC) . Biết rằng tam giác ABC là
tam giác vuông tại A . Các điểm M ,
SA N BC sao cho AM = CN = t (0 t 2a) . Gắn tứ
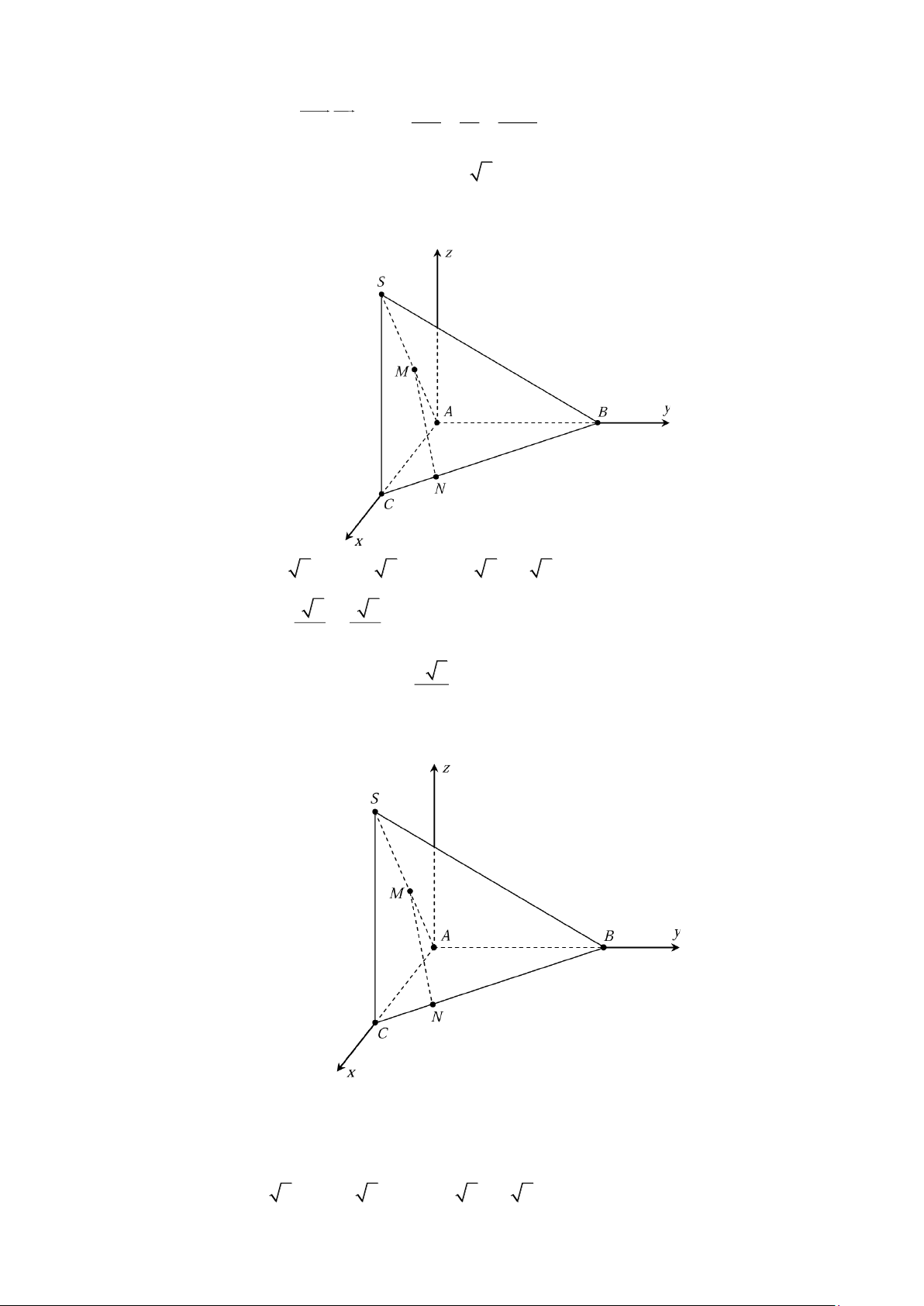
diện vào hệ trục tọa độ Oxyz với A O . Xét tính đúng sai của các khẳng định sau:
a) A(0;0;0), B(0;a 2;0),C(a 2;0;0),S (a 2;0;a 2) t 2 t 2
b) Tọa độ điểm M ;0; 2 2 a 6
c) Đoạn thẳng MN ngắn nhất bằng 2
d) Khi MN ngắn nhất thì MN là đường vuông góc chung của BC và SA Lời giải
a) Đúng: Ta chọn hê trục Oxyz sao cho gốc tọa độ O A . Trục Ox chứa AC , trục Oy chứa
AB và trục Oz ⊥ ( ABC) . Khi đó cạnh SC song song với trục Oz và ta có:
A(0;0;0), B(0;a 2;0),C(a 2;0;0),S (a 2;0;a 2 )
thuvienhoclieu.com Trang 20




