

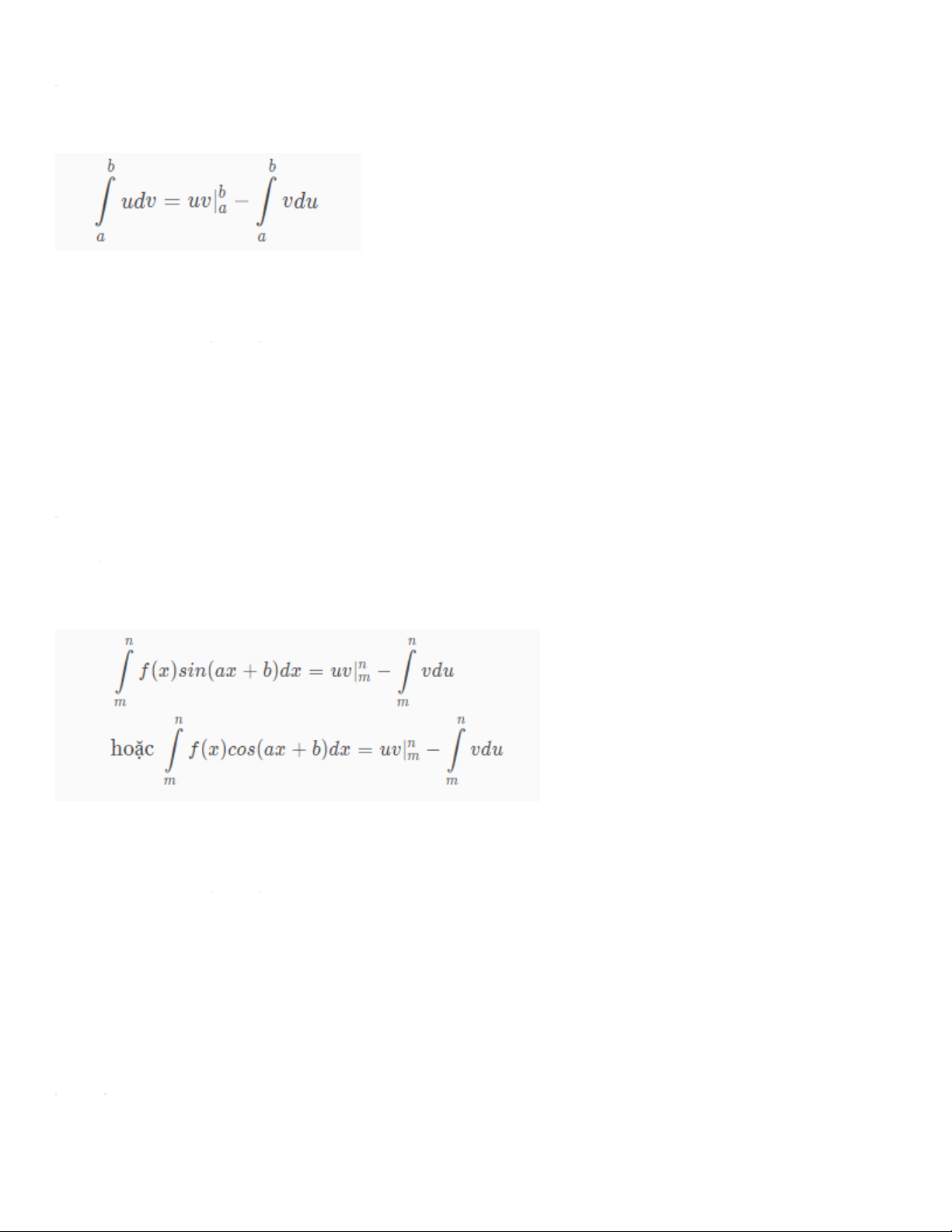

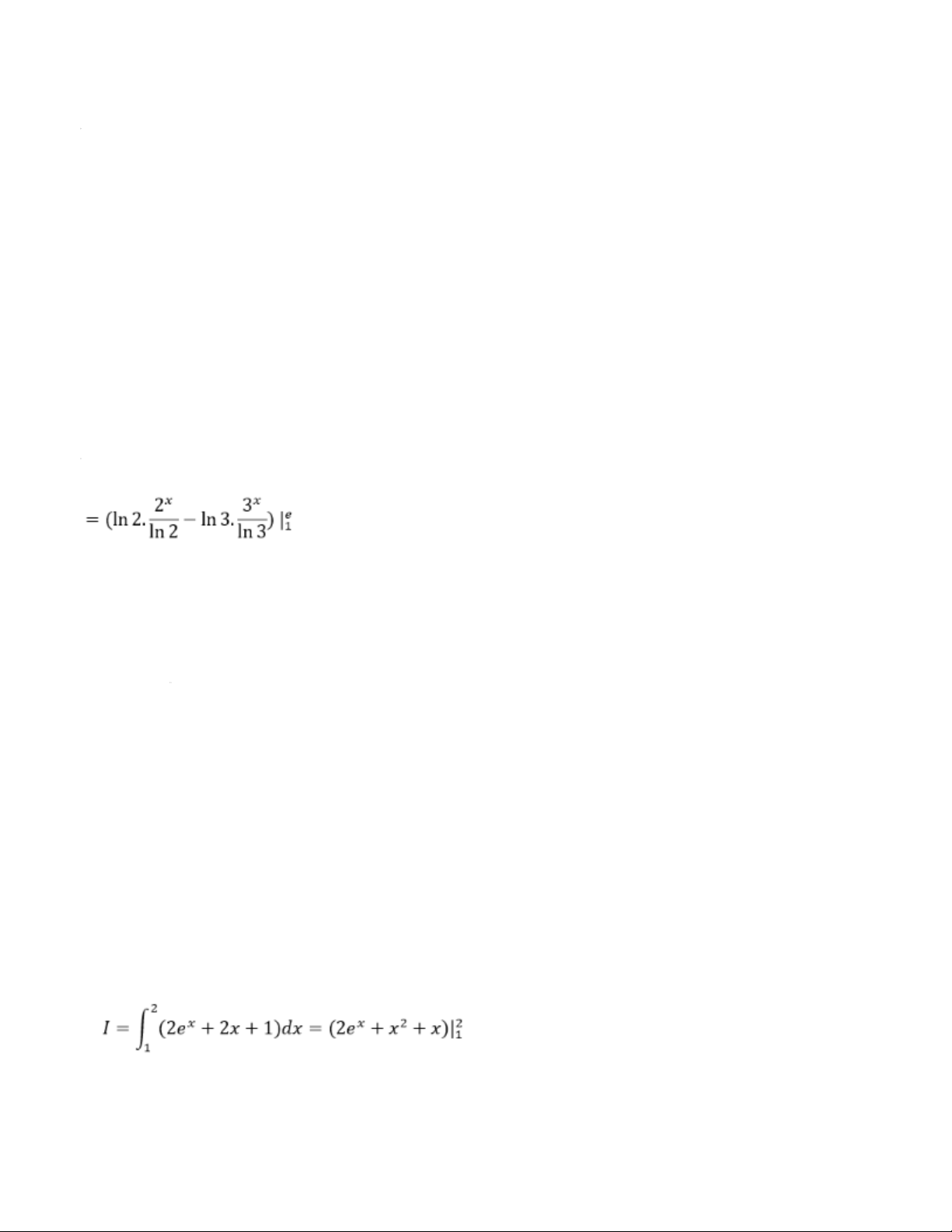








Preview text:
Phương pháp tính tích phân từng phần cực hay
1. Tích phân từng phần là gì ?
- Tích phân từng phần là phương pháp tính tìm tích phân của các hàm số có dạng dựa trên việc phân tích
các nguyên hàm và đạo hàm của hàm số đó. Phương pháp này thường được sử dụng để biến đổi nguyên
hàm của tích các hàm số thành một nguyên hàm đơn giản hơn. Quy tắc có thể suy ra bằng cách tích hợp
quy tắc nhân của đạo hàm.
- Tích phân từng phần được sử dụng để tính tích phân nếu biểu thức dưới dấu tích phân có chưa 2 hàm số
khác nhau trong 4 hàm số, bao gồm: Hàm logarit, hàm đa thức, hàm lượng giá và hàm số mũ.
- Cho f là hàm số liên tục trên đoạn [a;b]. Giả sử F là một nguyên hàm của f trên [a;b]. Hiệu số F(b) - F(a)
được gọi là tích phân từ a đến b (hay tích phân xác định trên đoạn [a;b] của hàm số f(x), kí hiệu là - Ta dùng kí hiệu
để chỉ kí hiệu số F(b) - F(a). Vậy Covers content Not interested Inappropriate Seen too often =
- Nhận xét: Tích phân của hàm số f từ a đến b có thể kí hiệu bởi
. Tích phân đó chỉ phụ thuộc
vào f và cận a, b mà không phụ thuộc vào cách ghi biển số.
- Ý nghĩa hình học của tích phân: Nếu hàm số f liên tục và không âm trên đoạn [a;b] thì tích phân là
diện tích S của hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục Ox và hai đường thẳng x = a, x = b. Vậy S = .
2. Công thức tính tích phân từng phần và dấu hiệu nhận biết
Cho 2 hàm số u = u (x) và v = v(x) có đạo hàm liên tục trên đoạn [a;b] thì ta có công thức:
Có thể viết gọn thành công thức tổng quát:
- Dấu hiệu nhân biết: Dấu hiệu Có thể đặt Ví dụ 1 Có t = I = . Đặt t = 2 Có (ax+b)n t = ax +b I = . Đặt t = x - 1 3 Có af(x) t = f(x)
4 Có dx / x và lnx t = lnx hoặc biểu thức chứa lnx I = . Đặt t = lnx 5 Có ex dx
t = ex hoặc biểu thức chứa ex I = . Đặt t = 6 Có sinx dx t = cos 7 Có cosx dx t = -sinxdx 8 Có dx / cos2x t = tanx 9 Có dx / sin2x t = cot
3. Một số dạng bài tích phân thường gặp và cách giải cụ thể
3.1. Dạng 1: Hàm đa thức và hàm logarit - Công thức chung:
Trong đó f(x) là một hàm đa thức - Phương pháp giải:
KHi gặp dạng toán này, hãy thức hiện các bước sau:
Bước 1: Ta tiến hành đặt
Bước 2: Tính tích phân theo công thức:
3.2. Dạng 2: Hàm đa thức và hàm lượng giác - Công thức chung: hoặc
Trong đó, f(x) là một hàm đa thức - Phương pháp giải:
Bước 1: Ta tiến hành đặt hoặc
Bước 2: Tính tích phân theo công thức:
3.3. Dạng 3: Hàm mũ và hàm lượng giác - Công thức chung: hoặc - Phương pháp giải:
Với dạng toán tìm tích phân của một biểu thức cho chứa hàm mũ và hàm lượng giác, hãy thực hiện giải toán bằng 2 bước:
Bước 1: Ta tiến hành đặt hoặc
Bước 2: Suy ra được công thức theo u và v như sau:
3.4. Dạng 4: Hàm mũ và hàm đa thức - Công thức chung:
Trong đó, P(x) là một hàm đa thức
- Phương pháp giải: để tính tích phân của biểu thức chưa hàm đa thức và hãm mũ, các em tiến hành: Đặt
4. Một số bài tập áp dụng Bài 1. Tính I = Cho kết quả đúng: A. 6 B. -3 C. 3 D. -6 Lời giải: Ta có: = 9 - 12 = -3 Chọn đáp án B Bài 2. Tính I = A. ln2.2e - ln3.3e B. ln2.2e - ln3.3e +1 C. 2e - 3e D. 2e - 3e +1 Lời giải: Ta có: I = A. 2e2 - 2e + 4 B. 2e3 + 2e + 2 C. 2e2 - 2e + 8 D.2e2 + 2e + 8 Lời giải: Ta có: I = <=> I = 2e - 3e + 1 Chọn đáp án D Bài 3: Tính I = A. 2e2 - 2e + 4 B. 2e3 + 2e + 2 C. 2e2 - 2e + 8 D. 2e2 + 2e +8 Lời giải: Ta có: I =
<=> I = 2.e2 + 4 + 2 - ( 2.e + 1 + 1 ) = 2e2 - 2e + 4 Chọn đáp án A Bài 4. Cho:
với a; b; c là các số nguyên. Mệnh đề nào dưới đây đúng ? A. a + b + c = 0 B. a - 2b + c = 0 C. a - b + c = -1 D. a + 2b = 0 Lời giải: Ta có: = 2ln5 + 4ln7 - 2ln3 - 4ln5 = -2ln5 + 4ln7 - 2ln3 => a = -2; b = 4; c = - 2 => a + b + c = 0 Chọn đáp án A Bài 5. Cho
Khi đó giá trị của m là: A. m = 1 B. m = 3 C, m = 4 D. m = 0 Lời giải: Điều kiện m > 0 Ta có: Theo giả thiết ta có: 2ln(m+1) - 2ln2 = 2ln2 <=> 2ln(m+1) = 4ln2 <=> ln(m+1) = ln4 <=> m + 1 = 4 <=> m = 3 Chọn đáp án B Bài 6. Tính I = A. 0 B. 1 + C. 2 - D. 2 + 1 / Lời giải: Ta có: Chọn đáp án C Bài 7. Tính I = A. 251 / 18432 B. 25 / 1432 C. 215 / 432 D. Đáp án khác Lời giải: Ta có: I = = = 251 / 18432 Chọn đáp án A Bài 8. Tính I = A. 128 B. 128ln2 C. 124 / ln2 D. 248 Lời giải: Ta có: I = ( vì ln25 - 2.ln5) Chọn đáp án D Bài 9. Cho I = Tìm m ? A. m = 20 B. m = 16 C. m = 4 D. m = 8 Lời giải: Ta có: Theo giả thiết ta có: Chọn đáp án B Bài 10: Tính I biết A. 0 B. -2 C.4 D. -3 Lời giải: Ta có:
<=> I = (1 - 4) - (-1 - 4.0) = - 2 Chọn đáp án B Bài 11. Tính I = A. 929 / 4561 B. 271 / 1982 C. 45 / 2654 D. 2348 / 6561 Lời giải: Ta có: I = = = = 2348 / 6561 Chọn đáp án D
Bài 12: Cho m là số thực dương thỏa mãn:
Mệnh đề nào sau đây là đúng ? A. B. C. D. Đáp án khác Lời giải: Ta có: = Theo giả thiết ta có:
1 / 4 - 1 / 4(1 + m2)2 = 3 / 16
<=> 1 / 4(1+m2)2 = 1 / 16 <=> ( 1 + m2)2 = 4 <=> 1 + m2 = 2 <=> m =
Kết hợp với điều kiện m > 0 nên m = 1 Chọn đáp án B Bài 13. Tính I = A. 3 / 7 B. 3 / 8 C. 7 / 8 D. 3 / 4 Lời giải: Ta có: I = Hay I = 3 / 8 Chọn đáp án B Bài 14. Tính I = A. I = 2 - ln2 B. I = 2 - 5ln2 C. I = 2 + 5lin2 D. I = 4 - 5ln2 Lời giải Ta có: = Do đó: I = 2 - 5ln2 Chọn đáp án B Bài 15: Tính A. -1 / 16 B. -1 / 8 C. - 1 / 6 D. 1 / 16 Lời giải:
Đặt t = x4=> dt = 4x3dx <=> x3dx = dt / 4 Đổi cận: Suy ra: Chọn đáp án A Bài 16. Cho I =
Hỏi I gần với giá trị nào nhất ? A. 186 B. 168 C. 197 D. 174 Lời giải Ta có: => I = = Đặt t = Đổi cận => I = Chọn đáp án C
Bài 17. Tính các tích phân sau a) I = b) I = c) I = Lời giải: a) I = = = 3 / 8 b) I = = = 1 - ln2 c) I = = 3 + 6ln2 - 3ln3
Bài 18: Tính tích phân sau: a) I = b) I = Lời giải chi tiết: a) Đặt u = 1 - x; dv = exdx Ta có: du = - dx; v = e x Vậy I = e - 2
b) Đặt u = x2, dv = e-x dx, ta có: du = 2xdx, chọn v = -e-x Với K =
Tính K: Đặt u = x2, dv = e - x dx
Ta có: du = dx, chọn v = e-x
= - 1 / e - (1 / e - 1 ) = - 2 / e + 1 Vậy I = - 5 / e + 2




