Bảng tóm tắt kiến thức toán 12 học kỳ 1

Bảng tóm tắt kiến thức toán 12 học kỳ 1 giúp các em học sinh nắm chắc các dạng Toán hình thường gặp trong đề thi, luyện giải đề thật nhuần nhuyễn để ôn thi lớp 12 HK 1 năm 2023 - 2024 đạt kết quả cao. Đề thi được thiết kế dưới dạng PDF bao gồm 50 trang. Mời các em tham khảo.

27 14 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Trang 1

PHẦN I. HÀM SỐ

1. SỰ ĐỒNG BIẾN NGHỊCH BIẾN CỦA HÀM SỐ

1.1. Định nghĩa

Kí hiệu

là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số

 

y f x

x{c định trên

ta có:

 Hàm số

 

y f x

được gọi là đồng biến(tăng) trên

nếu:

   

    x x K x x f x f x

1 2 1 2 1 2

 Hàm số

 

y f x

được gọi là nghịch biến(giảm) trên

nếu:

Hàm số đồng biến hoặc nghịch biến trên

được gọi chung là đơn điệu trên

* Nhận xét:

 Hàm số

 

đồng biến trên K

   



    



f x f x

x x K x x

1 2 1 2

 0 , , .

Khi đó đồ thị

của hàm số đi lên từ trái sang phải.

 Hàm số

 

nghịch biến trên K

   



    



f x f x

x x K x x

1 2 1 2

 0 , , .

Khi đó đồ thị

của hàm số đi xuốngtừ trái sang phải.

 Nêu

   



   f x x a b0, ;

h|m sô

 

đông biến trên khoảng

 

ab;.

 Nêu

   

0, ;f x x a b



   

h|m sô

 

nghịch biên trên khoảng

 

ab;.



Nêu

   



  f x x a b0, ;



h|m sô

 

không đôi trên khoảng

 

ab;.

 Nêu

 

đông biến trên khoảng

     



   a b f x x a b; 0, ; .

 Nếu

 

nghịch biên trên khoảng

     

a b f x x a b; 0, ; .



   

 Nêu thay đôi khoảng

 

ab;

bằng môt đoan hoặc nửa khoảng thì phải bô sung thêm

giả thiêt “h|m sô

 

liên tuc trên đoan hoặc nửa khoảng đó”.

1.2. Quy tắc và công thức tính đạo hàm

Quy tắc tính đạo hàm:Cho

   

u u x v v x C; ; :

là hằng số .

 Tổng, hiệu:

 





  u v u v .

 Tích:

   



  

   u v u v v u C u C u. . . . . .

   

    x x K x x f x f x

1 2 1 2 1 2

Trang 2

 Thƣơng:

 



   

  



    

   

   

u u v v u C C u

. . .

 Đạo hàm hàm hợp: Nếu

   

  

   

x u x

y f u u u x y y u,.

1.3. Bảng công thức tính đạo hàm

Đạo hàm của hàm sơ cấp

Đạo hàm của hàm hợp

 



C 0

(C là hằng số).

 









xx

 









xx





  





( 0)





 



xx

 

..u u u











 







  









 





 



xxsin cos

 



u u usin .cos

 



xxcos sin

 



u u ucos .sin

 



x

tan

cos

 





tan

cos

 



x

cot

sin

 





cot

sin

 





 





e u e.

 





a a a.ln

 





a u a a. .ln

 



x

 





 

log





 





log

.ln

1.4 . Công thức tính nhanh đạo hàm hàm phân thức



 

















ax b ad bc

cx d



 

c b c

f e f

a b a

d e d

ax bx c

dx ex f

  

  





















1.5. Đạo hàm cấp 2

1.5.1. Định nghĩa

Trang 3

   

f x f x





 





1.5.2. Ý nghĩa cơ học

Gia tốc tức thời của chuyển động

 

s f t

tại thời điểm

là:

   



a t f t

1.5.3. Đạo hàm cấp cao

 







  







f x f x n n

, , 2

* Một số chú ý:

 Nếu hàm số

 

và

 

cùng đồng biến (nghịch biến) trên

thì hàm số

   

f x g x

cũng đồng biến (nghịch biến) trên

Tính chất này có thể không đúng

đối với hiệu

   

f x g x

 Nếu hàm số

 

và

 

là các hàm số dương v| cùng đồng biến (nghịch biến) trên

thì hàm số

   

f x g x.

cũng đồng biến (nghịch biến) trên

Tính chất này có thể

không đúng khi c{c h|m số

   

f x g x,

không là các hàm số dương trên

 Cho hàm số

 

u u x

, x{c định với

 

x a b;

và

   

u x c d;

. Hàm số

 

f u x





cũng

x{c định với

 

x a b;

Ta có nhận xét sau:

 Giả sử hàm số

 

u u x

đồng biến với

 

x a b;

. Khi đó, h|m số

 

f u x





đồng biến

với

   

x a b f u;

đồng biến với

 

;u c d

 Giả sử hàm số

 

u u x

nghịch biến với

 

;x a b

. Khi đó, h|m số

 





f u x

nghịch

biến với

   

;x a b f u

nghịch biến với

 

u c d;

Quy tắc xét tính đơn điệu của hàm số.

Giả sử hàm số

có đạo hàm trên

 Nếu

 

fx'0

với mọi

xK

và

 

fx'0

chỉ tại một số hữu hạn điểm

xK

thì hàm số

đồng biến trên

 Nếu

 

fx'0

với mọi

xK

và

 

fx'0

chỉ tại một số hữu hạn điểm

xK

thì hàm số

nghịch biến trên

Chú ý:

* Đối với hàm phân thức hữu tỉ

ax b d

y x

cx d c





  







thì dấu

""

khi xét dấu

đạo hàm



không xảy ra.

Giả sử

   

y f x ax bx cx d f x ax bx c

3 2 2

3 2 .



        

Hàm số đồng biến trên



Hàm số nghịch biến trên



Trang 4

 

f x x

0; .



























    



























 

f x x

0; .



























    



























Trường hợp 2 thì hệ số

khác

vì khi

a b c 0  

thì

 

f x d

(Đường thẳng song song hoặc trùng với trục Ox thì không đơn điệu)

* Với dạng toán tìm tham số m để hàm số bâc ba đơn điệu một chiều trên khoảng có độ

dài bằng

ta giải như sau:

Bước 1: Tính

 

y f x m ax bx c



   

Bước 2: Hàm số đơn điệu trên

 

x x y





có

nghiệm phân biệt

















 

Bước 3: Hàm số đơn điệu trên khoảng có độ dài bằng

x x l

  

 

x x x x l

1 2 1 2

4   

4  S P l

 

Bước 4: Giải

 

và giao với

 

để suy ra giá trị m cần tìm.

2. CỰC TRỊ HÀM SỐ

2.1. Định nghĩa

Giả sử hàm số

x{c định trên tập K và

xK

. Ta nói:



là điểm cực tiểu của hàm số

nếu tồn tại một khoảng

 

;ab

chứa

sao cho

 

;a b K

và

       

  f x f x x a b x

, ; \

.Khi đó

 

được gọi là giá trị cực tiểu

của hàm số



là điểm cực đại của hàm số

nếu tồn tại một khoảng

 

ab;

chứa

sao cho

 

;a b K

và

       

  f x f x x a b x

, ; \

.Khi đó

 

được gọi là giá trị cực đại

của hàm số

 Điểm cực đại v| điểm cực tiểu gọi chung là điểm cực trị.

 Giá trị cực đại và giá trị cực tiểu gọi chung là cực trị.

 Điểm cực đại v| điểm cực tiểu được gọi chung là điểm cực trị củahàm số v| điểm cực

trị phải là một điểm trong tập hợp K.

 Giá trị cực đại và giá trị cực tiểu được gọi chung là giá trịcực trị (hay cực trị)

củahàmsố.

Trang 5

 Nếu

l| điểm cực trị của hàm số thì điểm

 

x f x

;

được gọi là điểm cực trị của

đồ thị hàm số

* Nhận xét:

 Giá trị cực đại (cực tiểu)

 

nói chung không phải là giá trị lớn nhất (nhỏ nhất) của

hàm số

trên tập D;

 

chỉ là giá trị lớn nhất (nhỏ nhất) của hàm số

trên một

khoảng

 

ab;

n|o đó chứa

hay nói cách khác khi

điểm cực đại ( cực tiểu) sẽ tồn

tại khoảng (a;b) chứa

sao cho

 

là giá trị lớn nhất (nhỏ nhất) của hàm số

trên

khoảng

 

ab; .

 Hàm số

có thể đạt cực đại hoặc cực tiểu tại nhiều điểm trên tập

. Hàm số có thể

không có cực trị trên một tập cho trước.

2.2. Điều kiện cần để hàm số đạt cực trị

Định lí 1:

Giả sử hàm số

 

y f x

đạt cực trị tại điểm

. Khi đó, nếu

 

y f x

có đạo hàm tại điểm

thì

 



fx

Chú ý:

 Đạo hàm

 



có thể bằng

tại điểm

nhưng h|m số

không đạt cực trị tại điểm

 Hàm số có thể đạt cực trị tại một điểm mà tại đó h|m số không có đạo hàm.

 Hàm số chỉ có thể đạt cực trị tại một điểm mà tại đó đạo hàm của hàm số bằng

hoặc

tại đó h|m số không có đạo hàm.

2.3. Điều kiện đủ để hàm số đạt cực trị

Định lí 2:

Giả sử hàm số

đạt cực trị tại điểm

. Khi đó, nếu hàm số

có đạo hàm tại điểm

thì

 

'0fx

 Nêu

 



fx 0

trên khoảng

 

x h x

;

và

 



fx 0

trên khoảng

 

x x h

;

thì

là

môt điểm cực đại của h|m số

 

fx.

 Nêu

 

fx 0





trên khoang

 

x h x

;

và

 

fx 0





trên khoảng

 

;x x h

thì

là

môt điểm cực tiểu của h|m sô

 

fx.

2.4. Quy tắc tìm cực trị

Quy tắc 1:

 Bước 1: Tìm tập x{c định. Tìm

 



fx.

Trang 6

 Bước 2: Tìm c{c điểm

 

i 1;2;...

mà tại đó đạo hàm của hàm số bằng 0 hoặc hàm số

liên tục nhưng không có đạo hàm.

 Bước 3: Lập bảng biến thiên hoặc bảng xét dấu

 



. Nếu

 



đổi dấu khi đi qua

thì hàm số đạt cực trị tại

Định lí 3:

Giả sử

 

y f x

có đạo h|m c}p 2 trong khoảng

 

x h x h

;

vơi

h 0.

Khi đó:

 Nếu

 



fx

 



fx

thì hàm số

đạt cực đại tại

 Nếu

 

0,fx





 



fx

thì hàm số

đạt cực tiểu tại

Từ định lí trên, ta có một quy tắc khác để tìm cực trị của hàm số

Quy tắc 2:

 Bước 1: Tìm tập x{c định. Tìm

 



fx.

 Bước 2: Tìm các nghiệm

 

i 1;2;...

của phương trình

 



fx 0.

 Bước 3:Tính

 



và tính

 

fx.



 Nếu

 





fx 0

thì hàm số

đạt cực đại tại điểm

x .

 Nếu

 





fx 0

thì hàm số

đạt cực tiểu tại điểm

3. MỘT SỐ DẠNG TOÁN LIÊN QUAN ĐẾN CỰC TRỊ HÀM SỐ

3.1. Cực trị của hàm đa thức bậc ba

y ax bx cx d

.   

3.1.1. Tìm điều kiện để hàm số có cực đại, cực tiểu thỏa mãn hoành độ cho trƣớc

Bài toán tông quat:

Cho hàm số

 

y f x m ax bx cx d

;.    

Tìm tham số m để hàm số có cực

đại, cực tiểu tại

thỏa mãn điều kiện

cho trước?

Phương pháp:

 Bước 1:

 Tập x{c định:

D . 

 Đạo hàm:

y ax bx c Ax Bx C



     

 Bước 2:

Hàm số có cực trị (hay có hai cực trị, hai cực trị phân biệt hay có cực đại và

cực tiểu)

y 0





có hai nghiệm phân biệt và



đổi dấu qua 2 nghiệm đó



phương trình

y 0





có hai nghiệm phân biệt

A a a

B AC b ac b ac

2 2 2

3 0 0

4 4 12 0 3 0





  



   



       





 Bước 3:

Trang 7

Gọi

là hai nghiệm của phương trình

y 0.





Khi đó:



    













 Bước 4:

Biên đôi điều kiện

vê dang t ổng

v| tich

. Từ đó giải ra tìm đươc

.

 Bước 5:

Kêt luận các giá trị m thỏa mãn:

m D D

.

* Chú ý: Hàm số bậc ba:

 

y ax bx cx d a

0.    

Ta có:

y ax bx c

' 3 2 .  

Điều kiện

Kết luận

b ac

30

Hàm số không có cực trị.

b ac

30

Hàm số có hai điểm cực trị.

 Điều kiện để hàm số có cực trị cùng dấu, trái dấu.

 Hàm số có 2 cực trị trái dấu



phương trình

y 0





có hai nghiệm phân biệt trái dấu

AC ac ac. 3 0 0.    

 Hàm số có hai cực trị cùng dấu



phương trình

y 0





có hai nghiệm phân biệt cùng dấu

P x x













  





 Hàm số có hai cực trị cùng dấu dương



phương trình

y 0





có hai nghiệm dương ph}n biệt

S x x

P x x









     





  





 Hàm số có hai cực trị cùng dấu âm



phương trình

y 0





có hai nghiệm âm phân biệt

S x x

P x x







     





  





 Tìm điều kiện để hàm số có hai cực trị

thỏa mãn:

Trang 8





 Hai cực trị

thỏa mãn





    

x x x x x x

1 2 1 2 1 2

0 . 0

   

        

 Hai cực trị

thỏa mãn





    

x x x x x x

x x x x

1 2 1 2 1 2

1 2 1 2

0 . 0

   





      







   





 Hai cực trị

thỏa mãn





    

x x x x x x

x x x x

1 2 1 2 1 2

1 2 1 2

0 . 0

   





      







   





 Phương trình bậc 3 có 3 nghiệm lập thành cấp số cộng

khi có 1 nghiệm là





, có 3 nghiệm lập thành cấp số nhân khi có 1 nghiệm là



3.1.2. Tìm điều kiện để đồ thị hàm số có các điểm cực đại, cực tiểu nằm cùng phía, khác

phía so với một đƣờng thẳng

Vị trí tương đối gia 2 điểm vi đương thng:

Cho 2 điêm

   

A A B B

A x y B x y; , ;

v| đường thẳng

ax by c: 0.   

Nêu

  

A A B B

ax by c ax by c 0    

thì hai điểm

A B,

năm về

hai phía so với đương thẳng

.

Nêu

  

A A B B

ax by c ax by c 0    

thì hai điểm

A B,

năm cung

phía so với đương thẳng

.

Một số trương hp đăc biệt:

 C{c điểm cực trị của đồ thị nằm cùng về 1 phía đối với trục Oy



hàm số có 2 cực trị cùng dấu



phương trình

y 0





có hai nghiệm phân biệt cùng dấu

 C{c điểm cực trị của đồ thị nằm cùng về 2 phía đối với trục Oy



hàm số có 2 cực trị trái dấu



phương trình

y 0





có hai nghiệm trái dấu

 C{c điểm cực trị của đồ thị nằm cùng về 1 phía đối với trục Ox



phương trình

y 0





có hai nghiệm phân biệt và

CC T

yy.0

Đặc biệt:

 C{c điểm cực trị của đồ thị nằm cùng về phía trên đối với trục Ox

Trang 9



phương trình

y 0





có hai nghiệm phân biệt và

CTC















 C{c điểm cực trị của đồ thị nằm cùng về phía dưới đối với trục Ox



phương trình

y 0





có hai nghiệm phân biệt và

CTC















 C{c điểm cực trị của đồ thị nằm về 2 phía đối với trục Ox



phương trình

y 0





có hai nghiệm phân biệt và

CC T

yy.0

(áp dụng khi không nhm đươc nghiệm và viết được phương trình đường thẳng đi qua

hai điểm cực trị của đồ thị hàm số)

Hoặc: C{c điểm cực trị của đồ thị nằm về 2 phía đối với trục Ox



đồ thị cắt trục Ox tại 3 điểm phân biệt



phương trinh ho|nh đô giao điểm

 

fx 0

có 3 nghiêm phân biệt (áp

dụng khi nhm được nghiệm)

3.1.3. Phƣơng trình đƣờng thẳng qua các điểm cực trị

 

c b bc

g x x d

3 9 9



   





hoặc

 

 



g x y

hoặc

 

g x y

 





3.1.4. Khoảng cách giữa hai điểm cực trị của đồ thị hàm số bậc 3 là

4 16



với

b ac





3.2. Cực trị của hàm bậc 4 trùng phƣơng

 

y ax bx c a

,0   

3.2.1. Một số kết quả cần nhớ

 Hàm số có một cực trị

ab 0.

 Hàm số có ba cực trị

ab 0.

 Hàm số có đúng một cực trị và cực trị là cực tiểu

















 Hàm số có đúng một cực trị và cực trị là cực đại

















 Hàm số có hai cực tiểu và một cực đại

















 Hàm số có một cực tiểu và hai cực đại

















3.2.2. Một số công thức tính nhanh

Giả sử hàm số

y ax bx c

  

có

cực trị:

A c B C

a a a a

(0; ), ; , ;

2 4 2 4

   



   

    

   

   

tạo thành tam giác

ABC

thỏa mãn dữ kiện:

ab 0

Đặt:

BAC a=



Trang 10

Tổng quát:

cot







Dữ kiện

Công thức

thỏa mãn

ab c0; 0

Tam giác

ABC

vuông cân tại

8

Tam giác

ABC

đều

24

Tam giác

ABC

có diện tích

ABC

0



a S b

3 2 5

32 ( ) 0

Tam giác

ABC

có diện tích

max S

()



Tam giác

ABC

có b{n kính đường tròn nội

tiếp

ABC

0



4 1 1













Tam giác

ABC

có b{n kính đường tròn ngoại

tiếp

ABC









Tam giác

ABC

có độ dài cạnh

BC m



am b

20

Tam giác

ABC

có độ dài

AB AC n



a n b ab

2 2 4

16 8 0  

Tam giác

ABC

có cực trị

B C Ox, 

b ac

4

Tam giác

ABC

có

góc nhọn

b a b

(8 ) 0

Tam giác

ABC

có trọng tâm

b ac

6

Tam giác

ABC

có trực tâm

b a ac

8 4 0  

Tam giác

ABC

cùng điểm

tạo thành hình

thoi

b ac

2

Tam giác

ABC

có

l| t}m đường tròn nội

tiếp

b a abc

8 4 0  

Tam giác

ABC

có

l| t}m đường tròn ngoại

tiếp

b a abc

8 8 0  

Tam giác

ABC

có cạnh

BC kAB kAC

b k a k

3 2 2

. 8 ( 4) 0  

Trục hoành chia tam giác

ABC

thành

hai phần có diện tích bằng nhau

b ac

42

Tam giác

ABC

có điểm cực trị c{ch đều trục

hoành

b ac

8

Đồ thị hàm số

 

C y ax bx c

:   

cắt trục

b ac

100



Trang 11

tại 4 điểm phân biệt lập thành cấp số

cộng

Định tham số để hình phẳng giới hạn bởi đồ

thị

 

C y ax bx c

:   

và trục hoành có

diện tích phần trên và phần dưới bằng nhau.

b ac



Phương trình đường tròn ngoại tiếp

ABC

là:

x y c y c

b a b a

   



      

   

   

4. GIÁ TRỊ LỚN NHẤT - GIÁ TRỊ NHỎ NHẤT

4.1. Định nghĩa.

Cho hàm số

 

y f x

x{c định trên tập

 Số M gọi là giá trị ln nhất của hàm số

 

y f x

trên

nếu:

f x M x D

x D f x M

( ) ,

, ( )



  





  





. Kí

hiệu:

max ( )

M f x





 Số

gọi là giá trị nhỏ nhất của hàm số

 

y f x

trên

nếu:

f x m x D

x D f x m

( ) ,

, ( )



  





  





. Kí

hiệu:

m f xmin ( )





4.2. Phƣơng pháp tìm GTLN,GTNN

4.2.1. Tìm GTLN, GTNN của hàm số bằng cách khảo sát trực tiếp

 Bước 1: Tính

 



v| tìm c{c điểm



x x x D

, ,...,

mà tại đó

 



fx 0

hoặc hàm số

không có đạo hàm.

 Bước 2:Lập bảng biến thiên và từ đó suy ra gi{ trị lớn nhất, giá trị nhỏ nhất của hàm

số.

4.2.2. Tìm GTLN, GTNN của hàm số trên một đoạn

 Bước 1:

 Hàm số đã cho

 

y f x

x{c định và liên tục trên đoạn





ab;.

 Tìm c{c điểm

x x x

, ,...,

trên khoảng

 

ab;

, tại đó

 



fx 0

hoặc

 



không xác

định.

 Bước 2: Tính

         

f a f x f x f x f b

, , ,..., , .

 Bước 3: Khi đó:



           

 

max f x max f x f x f x f a f b

, ,..., , , .









           

 







min f x min f x f x f x f a f b

, ,. .., , , .

4.2.3. Tìm GTLN, GTNN của hàm số trên một khoảng

 Bước 1:Tính đạo hàm

fx()



Trang 12

 Bước 2:Tìm tất cả các nghiệm

x a b( ; )

của phương trình

fx( ) 0





và tất cả c{c điểm

ab( ; )





làm cho

fx()



không x{c định.

 Bước 3. Tính

A f xlim ( )







B f xlim ( )







fx()

f ()



 Bước 4.So sánh các giá trị tính được và kết luận

M f x

( ; )

max ( )

m f x

( ; )

min ( )

Nếu giá trị lớn nhất (nhỏ nhất) là A hoặc B thì ta kết luận không có giá trị lớn nhất (nhỏ nhất).

Chú ý:

 Nêu

 

y f x

đông biến trên

ab;





thì

   

f x f a

f x f b

;

min

max























 Nêu

 

y f x

nghịch biến trên

ab;





thì

 























f x f b

f x f a

;

min ( )

max ( )

 Hàm số liên tục trên một khoảng có thể không có giá trị lớn nhất, giá trị nhỏ nhất

trên khoảng đó.

5. ĐƢỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ

5.1. Đƣờng tiệm cận ngang

Cho hàm số

y f x()

x{c định trên một khoảng vô hạn (là khoảng dạng

   

 ab; , ;

hoặc

 

; 

). Đường thẳng



l| đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị

hàm số

y f x()

nếu ít nhất một trong c{c điều kiện sau được thỏa mãn:

f x y f x y

lim ( ) , lim ( )

 



5.2. Đƣờng tiệm cận đứng

Đường thẳng

xx

được gọi l| đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị

hàm số

()y f x

nếu ít nhất một trong c{c điều kiện sau được thỏa mãn:





   

x x x x

f x f x

lim ( ) , lim ( ) ,

lim ( ) , lim ( )

x x x x

f x f x





   

Lưu ý: Với đồ thị hàm phân thức dạng

 



   



ax b

y c ad bc

cx d

0; 0

luôn có tiệm cận

ngang là



và tiệm cận đứng



6. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ HÀM SỐ

6.1.Khảo sát một số hàm đa thức và hàm phân thức

6.1.1. Hàm số bậc ba

 

    y ax bx cx d a

TRƢỜNG HỢP

a 0

0a 

Trang 13

Phương trình

y

có

2 nghiệm phân biệt

Phương trình

y

có

nghiệm kép

Phương trình

0y 

vô

nghiệm

6.1.2. Hàm số trùng phƣơng

 

   y ax bx c a

TRƢỜNG HỢP

a 0

0a 

Phương trình

y

có

3 nghiệm phân biệt

(ab<0)

Phương trình

y

có

1 nghiệm.

6.1.3. Hàm số nhất biến

 

0, 0

ax b

y c ad bc

cx d



   



Trang 14

  D ad bc 0

  D ad bc 0

6.2. Một số phép biến đổi đồ thị

6.2.1. Dạng 1

Từ đồ thị

   

C y f x:

suy ra đồ thị

 



C y f x:

Ta có:

 

f x khi x

y f x

f x khi x

















và

 

y f x

là hàm chẵn nên đồ thị

 



nhận Oy làm trục đối xứng.

* Cách vẽ

 



từ

 

 Giữ nguyên phần đồ thị bên phải Oy của đồ thị

   

C y f x:

 Bỏ phần đồ thị bên trái Oy của

 

, lấy đối xứng phần đồ thị được giữ qua Oy.

Ví dụ: Từ đồ thị

   

  C y f x x x

suy ra đồ thị

 



C y x x

Biến đổi

 

 Bỏ phần đồ thị của

 

bên trái

Oy,

giữ nguyên

 

bên phải

.Oy

 Lấy đối xứng phần đồ thị được

giữ qua

6.2.2. Dạng 2

Từ đồ thị

   

C y f x:

suy ra đồ thị

   



C y f x:

Ta có:

 

   

















f x khi f x

y f x

f x khi f x

* Cách vẽ

 



từ

 

 Giữ nguyên phần đồ thị phía trên Oxcủa đồ thị (C):

 

y f x

-2

-1

-2

-1

 



C y x x

 

C y x x

Trang 15

 Bỏ phần đồ thị phía dưới Oxcủa (C), lấy đối xứng phần đồ thị bị bỏ qua Ox.

Ví dụ: Từ đồ thị

   

:3C y f x x x  

suy ra đồ thị

y x x

Biến đổi

 

 Bỏ phần đồ thị của

 

dưới

,Ox

giữ nguyên

 

phía trên

.Ox

 Lấy đối xứng phần đồ thị bị bỏ

qua

Chú ý với dạng:

 

y f x

ta lần lượt biến đổi 2 đồ thị

 

y f x

và

 

y f x

Ví dụ: Từ đồ thị

   

  C y f x x x

suy ra đồ thị

y x x

. Biến đổi

 

để được đồ thị

 



C y x x

Biến đổi

 



C y x x

ta được đồ

thị

 



C y x x

6.2.3. Dạng 3

Từ đồ thị

     

C y u x v x:.

suy ra đồ thị

     



C y u x v x:.

Ta có:

   

       

u x v x f x khi u x

y u x v x

u x v x f x khi u x











  





* Cách vẽ

 



từ

 

 Giữ nguyên phần đồ thị trên miền

 

ux 0

của đồ thị

   

C y f x:

 Bỏ phần đồ thị trên miền

 

ux 0

của

 

, lấy đối xứng phần đồ thị bị bỏ qua Ox.

Ví dụ

a) Từ đồ thị

   

   C y f x x x

: 2 3 1

suy ra đồ thị

 



   C y x x x

: 1 2 1

b) Từ đồ thị

   





C y f x

suy

ra đồ thị

 







 







    









f x khi x

y x x x

f x khi x

1 2 1

 



 













  





khi x

-2

-1

 

:3C y x x

 



C y x x

 



C y x x

Trang 16

Đồ thị (C’):

 Giữ nguyên (C) với

1x 

 Bỏ (C) với

x 1

. Lấy đối xứng

phần đồ thị bị bỏ qua Ox.

Nhận xét: Trong quá trình thực hiện

phép suy đồ thị nên lấy đối xứng các điểm

đặc biệt của (C): giao điểm với Ox, Oy,

CĐ, CT…

Đồ thị (C’):

 Bỏ phần đồ thị của

 

với

x ,1

giữ nguyên

 

với

1.x 

 Lấy đối xứng phần đồ thị bị bỏ

qua

Ox.

Nhận xét: Đối với hàm phân thức thì

nên lấy đối xứng các đường tiệm cận để

thực hiện phép suy đồ thị một cách

tương đối chính xác.

7. TIẾP TUYẾN

7.1. Tiếp tuyến

Cho hàm số

 

y f x

, có đồ thị (C). Tiếp tuyến của đồ thị (C) tại điểm

 

M x y C

0 0 0

; ( )

có

dạng:

  



  y f x x x y

0 0 0

Trong đó:

Điểm

 

M x y C

0 0 0

; ( )

được gọi là tiếp điểm. ( với

 

y f x

) và

 

k f x

là hệ số góccủa

tiếp tuyến.

7.2. Điều kiện tiếp xúc

Cho hai hàm số

   

C y f x:

và

   

C y g x': 

. Đồ thị

 

và

 



tiếp xúc nhau khi chỉ

khi hệ phương trình:

   















f x g x

có nghiệm.

8. TƢƠNG GIAO ĐỒ THỊ

Cho hàm số

y f x()

có đồ thị

()

và

y g x()

có đồ thị

()C

Phương trình ho|nh độ giao điểm của

()

và

()C

là

 

f x g x ( ) ( ) 1

. Khi đó:

 Số giao điểm của

()C

và

()

bằng với số nghiệm của phương trình

 

 Nghiệm

của phương trình

 

chính l| ho|nh độ

của giao điểm.

(C)

(C')

Trang 17

 Để tính tung độ

của giao điểm, ta thay ho|nh độ

vào

 

y f x

hoặc

 

y g x

 Điểm

 

;M x y

l| giao điểm của

()

và

()

9. ĐIỂM ĐẶC BIỆT CỦA HỌ ĐƢỜNG CONG

9.1. Bài toán tìm điểm cố định của họ đƣờng cong

Xét họ đường cong

C()

có phương trình

y f x m( , )

, trong đó

là h|m đa thức theo biến

với

là tham số sao cho bậc của m không quá 2. Tìm những điểm cố định thuộc họ đường

cong khi

thay đổi?

Phƣơng pháp giải:

 Bước 1: Đưa phương trình

( , )y f x m

về dạng phương trình theo ẩn

có dạng sau:

Am B 0

hoặc

  Am Bm C

 Bước 2:Cho các hệ số bằng

, ta thu được hệ phương trình v| giải hệ phương trình:















hoặc

















 Bước 3:Kết luận:

- Nếu hệ vô nghiệm thì họ đường cong

C()

không có điểm cố định.

- Nếu hệ có nghiệm thì nghiệm đó l| điểm cố định của

C()

9.2. Bài toán tìm điểm có tọa độ nguyên

Cho đường cong

C()

có phương trình

y f x()

(hàm phân thức). Hãy tìm những điểm có

tọa độ nguyên của đường cong?

Những điểm có tọa độ nguyên là những điểm sao cho cả hoành độ và tung độ của điểm đó đều là số

nguyên.

Phƣơng pháp giải:

 Bước 1:Thực hiện phép chia đa thức chia tử số cho mẫu số.

 Bước 2:Lập luận để giải bài toán.

9.3. Bài toán tìm điểm có tính chất đối xứng

Cho đường cong

()C

có phương trình

y f x()

. Tìm những điểm đối xứng nhau qua một

điểm, qua đường thẳng.

Bài toán 1: Cho đồ thị

 

   C y Ax Bx Cx D

trên đồ thị

 

tìm những cặp điểm đối xứng

nhau qua điểm

I x y( , )

Phƣơng pháp giải:

 Gọi

   

     M a Aa Ba Ca D N b Ab Bb Cb D

3 2 3 2

; , ;

l| hai điểm trên

 

đối

xứng nhau qua điểm

Trang 18

 Ta có

 









      





a b x

A a b B a b C a b D y

3 3 2 2

( ) 2 2

Giải hệ phương trình tìm được

ab,

từ đó tìm được toạ độ M, N.

Bài toán 2: Cho đồ thị

 

   C y Ax Bx Cx D

. Trên đồ thị

 

tìm những cặp điểm đối

xứng nhau qua gốc tọa độ.

Phƣơng pháp giải:

 Gọi

   

     M a Aa Ba Ca D N b Ab Bb Cb D

3 2 3 2

, , ,

l| hai điểm trên

 

đối

xứng nhau qua gốc tọa độ.

 Ta có

 









      





A a b B a b C a b D

3 3 2 2

( ) 2 0

 Giải hệ phương trình tìm được

ab,

từ đó tìm được toạ độ

MN,

Bài toán 3: Cho đồ thị

 

   C y Ax Bx Cx D

trên đồ thị

 

tìm những cặp điểm đối xứng

nhau qua đường thẳng

d y A x B

Phƣơng pháp giải:

 Gọi

   

3 2 3 2

; , ;M a Aa Ba Ca D N b Ab Bb Cb D     

l| hai điểm trên

 

đối xứng

nhau qua đường thẳng

 Ta có:















 

MN u

(1)

. 0 (2)

(với

l| trung điểm của

và



l| vectơ chỉ phương của

đường thẳng

 Giải hệ phương trình tìm được M, N.

9.4. Bài toán tìm điểm đặc biệt, khoảng cách

9.4.1. Lý thuyết:

 Cho hai điểm

   

A x y B x y

1 1 2 2

; ; ;

   

    AB x x y y

2 1 2 1

 Cho điểm

 

M x y

;

v| đường thẳng

:0d Ax By C  

, thì khoảng cách từ

đến

là

 







Ax By C

h M d

;

 Cho hàm phân thức:

ax b

cx d







tiếp tuyến tại M cắt TCĐ,TCN ở A và B thì M là

trung điểm của AB. Thì diện tích tam giác

MA B

không đổi:



MAB

S ad bc

9.4.2. Các bài toán thƣờng gặp

Bài toán 1: Cho hàm số

 



   



ax b

c ad bc

cx d

y 0, 0

có đồ thị

 

. Hãy tìm trên

C()

hai điểm

và

thuộc hai nhánh đồ thị hàm số sao cho khoảng cách

ngắn nhất.

Phƣơng pháp giải:

Trang 19



 

có tiệm cận đứng



do tính chất của hàm phân thức, đồ thị nằm về hai

phía của tiệm cận đứng. Nên gọi hai số



là hai số dương.

 Nếu

thuộc nhánh trái:



       

d d d

c c c

;



y f x()

 Nếu

thuộc nhánh phải:



       

d d d

c c c

;



y f x()

 Sau đó tính:

         





         



B A B A B A

AB x x y y a a y y

2 2 2

 Áp dụng bất đẳng thức Cauchy sẽ tìm ra kết quả.

Bài toán 2: Cho đồ thị hàm số

 

có phương trình

y f x()

. Tìm tọa độ điểm

thuộc

()C

để tổng

khoảng cách từ

đến hai trục tọa độ nhỏ nhất.

Phƣơng pháp giải:

 Gọi

 

M x y;

và tổng khoảng cách từ

đến hai trục tọa độ là

thì

d x y .

 Xét các khoảng cách từ

đến hai trục tọa độ khi

nằm ở các vị trí đặc biệt: Trên

trục hoành, trên trục tung.

 Sau đó xét tổng quát, những điểm

có ho|nh độ, hoặc tung độ lớn hơn ho|nh độ

hoặc tung độ của

khi nằm trên hai trục thì loại đi không xét đến.

 Những điểm còn lại ta đưa về tìm giá trị nhỏ nhất của đồ thi hàm số dựa v|o đạo

hàm rồi tìm được giá trị nhỏ nhất của

Bài toán 3: Cho đồ thị

C()

có phương trình

()y f x

. Tìm điểm

trên

C()

sao cho khoảng cách từ

đến Ox bằng

lần khoảng cách từ

đến trục

Phƣơng pháp giải:

Theo đầu bài ta có

 







  









y kx f x kx

y k x

y kx

f x kx

Bài toán 4: Cho đồ thị hàm số

C()

có phương trình

 

( ) 0, 0

ax b

y f x c ad bc

cx d



    



. Tìm tọa độ

điểm

trên

()C

sao cho độ dài

ngắn nhất (với I là giao điểm hai tiệm cận).

Phƣơng pháp giải:

 Tiệm cận đứng





; tiệm cận ngang



 Ta tìm được tọa độ giao điểm









;

của hai tiệm cận.

 Gọi

 

Mx y;

l| điểm cần tìm, thì:

 

   

    

   

   

M M M

IM x y g x

 Sử dụng phương ph{p tìm GTLN - GTNN cho hàm số

để thu được kết quả.

Bài toán 5: Cho đồ thị hàm số

C()

có phương trình

y f x()

và đường thẳng

  d Ax By C:0

Tìm điểm

trên

C()

sao cho khoảng cách từ

đến

là ngắn nhất.

Phƣơng pháp giải:

Trang 20

 Gọi

thuộc

C()

 

I x y y f x

0 0 0 0

; ; ( )

 Khoảng cách từ

đến

là

 







Ax By C

g x h I d

( ) ;

 Khảo sát hàm số

y g x()

để tìm ra điểm

thỏa mãn yêu cầu.

Trang 21

PHẦN II. MŨ VÀ LOGARIT

1. LŨY THỪA VÀ HÀM SỐ LŨY THỪA

1.1. Khái niệm lũy thừa

1.1.1. Lũy thừa với số mũ nguyên

Cho

là một số nguyên dương.

Với

là số thực tùy ý, lũy thừa bậc

của a là tích của

thừa số





a a a a. ......

(

thừa số).

Với

a 0.

thì





Ta gọi

l| cơ số,

l| mũ số. Và chú ý

và

n

không có nghĩa.

1.1.2. Một số tính chất của lũy thừa

 Giả thuyết rằng mỗi biểu thức được xét đều có nghĩa:

   



a a a ;











;

   

aa

( ) ;

  

ab a b( ) ;











;





   



   

   

 Nếu

a 1

thì



  aa

;

 Nếu

a01

thì



  aa

 Với mọi

ab0

, ta có:

  

a b m 0

  

a b m 0

Chú ý:

 Các tính chất trên đúng trong trường hợp số mũ nguyên hoặc không nguyên.

 Khi xét lũy thừa với số mũ

và số mũ nguyên }m thì cơ số

phải khác

 Khi xét lũy thừa với số mũ không nguyên thì cơ số

phải dương.

1.2. Phƣơng trình



xb.

Ta có kết quả biện luận số nghiệm của phương trình

xb

như sau:

 Trường hợp n lẻ:

Với mọi số thực

, phương trình có nghiệm duy nhất.

 Trường hợp n chẵn:

 Với

0b 

, phương trình vô nghiệm.

 Với

b 0

, phương trình có một nghiệm

x 0.

 Với

b 0

, phương trình có hai nghiệm trái dấu, kí hiệu giá trị dương l|

, còn

giá trị âm là



1.3. Một số tính chất của căn bậc

Với

ab

, ;n

, ta có:

Trang 22





a a a





 

a a a



   

ab a b ab



  

  

n n n

ab a b a b

2 1 2 1 2 1





   



ab b

, 0, 0





   



 

  

a a a,0

nguyên dương,

nguyên



  

m nm

a a a,0

nguyên dương

 Nếu



thì

  

a a a m n, 0, ,

nguyên dương

pq,

nguyên

Đặc biệt:





1.4. Hàm số lũy thừa

1.4.1. Khái niệm

Xét hàm số



yx

, với



là số thực cho trước.

Hàm số



yx

, với





, được gọi là hàm số lũy thừa.

Chú ý.

Tập x{c định của hàm số lũy thừa



yx

tùy thuộc vào giá trị của



. Cụ thể.

 Với



nguyên dương, tập x{c định là

.

 Với



nguyên âm hoặc bằng

, tập x{c định là

 

\ 0 .

 Với



không nguyên, tập x{c định

 

0; .

1.4.2. Khảo sát hàm số lũy thừa



yx

Tập x{c định của hàm số lũy thừa



yx

luôn chứa khoảng

 

0;

với mọi



 

Trong

trường hợp tổng quát, ta khảo sát hàm số



yx

trên khoảng này.



yx, 0.



yx, 0.

Trang 23

1. Tập x{c định:

 

0; .

2. Sự biến thiên





   y x x

' . 0 0.

Giới hạn đặc biệt:









  

lim 0, lim .

Tiệm cận: không có.

3. Bảng biến thiên.



y’





1. Tập x{c định:

 

0; .

2. Sự biến thiên





   y x x

' . 0 0.

Giới hạn đặc biệt:

lim , lim 0.









  

Tiệm cận:

Ox là tiệm cận ngang.

Oy là tiệm cận đứng.

3. Bảng biến thiên.



y’





Đồ thị của hàm số.

Đồ thị của hàm số lũy thừa





luôn đi qua điểm

 

I 1; 1 .

1.5. Khảo sát hàm số mũ

 

, 0, 1

y a a a  

 



y a a,1

 

y a a

1. Tập x{c định:

 .

2. Sự biến thiên.

' ln 0, .

y a a x  

Giới hạn đặc biệt:

 

  

aalim 0, lim .

Tiệm cận:

Ox là tiệm cận ngang.

3. Bảng biến thiên.



0 1



1. Tập x{c định:

.

2. Sự biến thiên.

  

y a a x' ln 0,

Giới hạn đặc biệt:

 

  

aalim , lim 0.

Tiệm cận:

Ox là tiệm cận ngang.

3. Bảng biến thiên.



0 1

Trang 24

y '





Đồ thị như hình sau.



y '





Đồ thị như hình sau.

2. LOGARIT

2.1.Khái niệm Logarit

Cho hai số dương

ab,

với

1a 

. Số



thỏa mãn đẳng thức



ab

được gọi l| logarit cơ số

của

v| được kí hiệu là

blog

log .

b a b



  

Không có logarit của số âm và số 0.

2.2. Bảng tóm tắt công thức Mũ-loarrit thƣờng gặp



 

aa

1, 0 .



 

aa



 





a



 













     

.a b a

   







     

  

a b a b..



 













   

 





aa



 







aa



 

  

alog 1 0, 0 1



 

  

aalog 1, 0 1



 



  

aalog , 0 1



 

log , 0 1



  



 

log .log , , 0, 1

b b a b a



  







log .log



log .log











 



a a a

b c bclog log log











a a a

log l og log

Trang 25



 



  

a b blog





log

3. BẤT PHƢƠNG TRÌNH MŨ VÀ LOGARIT.

3.1. Bất phƣơng trình mũ cơ bản

Bất phương trình mũ cơ bản có dạng



(hoặc

xxx

a b a b a b

) với

aa0, 1.

Ta xét bất phương trình có dạng



ab.

 Nếu

b 0

, tập nghiệm của bất phương trình l|



, vì

   

a b x,.

 Nếu

b 0

thì bất phương trình tương đương với



log

 Với

a 1

, nghiệm của bất phương trình l|

xblog .

 Với

a01

, nghiệm của bất phương trình l|

xblog .

Ta minh họa bằng đồ thị sau:

 Với

a 1

, ta có đồ thị sau.

 Với

a01

, ta có đồ thị sau.

3.2. Bất phƣơng trình logarit cơ bản

Bất phương trình logarit cơ bản có dạng

log

xb

(hoặc

log ,log ,log

aaa

x b x b x b

) với

aa0, 1.

Xét bất phương trình



xblog .

 Trường hợp

a 1

, ta có:

  

x b x alog .

 Trường hợp

a01

, ta có:

log 0 .

x b x a   

Ta minh họa bằng đồ thị như sau.

Trang 26

 Với

a 1

, ta có đồ thị sau.

 Với

a01

, ta có đồ thị sau.

Quan s{t đồ thị, ta thấy rằng:

 Trường hợp

a 1

log

xb

khi và chỉ khi



xa.

 Trường hợp

01a



xblog

khi và chỉ khi



xa0

4. BÀI TOÁN LÃI SUẤT NGÂN HÀNG

4.1. Lãi đơn

4.1.1. Định nghĩa

Lãi đơn là số tiền lãi chỉ tính trên số tiền gốc mà không tính trên số tiền lãi do số tiền gốc

sinh ra, tức là tiền lãi của kì hạn trước không được tính vào vốn để tính lãi cho kì hạn kế tiếp,

cho dù đến kì hạn người gửi không đến rút tiền ra.

4.1.2. Công thức tính

Khách hàng gửi vào ngân hàng

đồng với lãi đơn

/kì hạn thì số tiền khách hàng

nhận được cả vốn lẫn lãi sau

kì hạn (

n * 

) là:

 

S A nAr A nr1   

Chú ý:trong tính toán các bài toán lãi suất và các bài toán liên quan, ta nhớ

là

100

4.2. Lãi kép

4.2.1. Định nghĩa

Lãi kép làtiền lãi của kì hạn trước nếu người gửi không rút ra thì được tính vào vốn để

tính lãi cho kì hạn sau.

4.2.2. Công thức tính

Khách hàng gửi vào ngân hàng

đồng với lãi kép

/kì hạn thì số tiền khách hàng

nhận được cả vốn lẫn lãi sau

kì hạn (

n * 

) là:

 

log













Trang 27

 

S A r1

%1

 





4.3. Tiền gửi hàng tháng

4.3.1. Định nghĩa

Tiền gửi hàng tháng là mỗi tháng gửi đúng cùng một số tiền vào 1 thời gian cố định.

4.3.2. Công thức tính

Đầu mỗi tháng khách hàng gửi vào ngân hàng số tiền

đồng với lãi kép

/tháng thì số

tiền khách hàng nhận được cả vốn lẫn lãi sau

tháng (

n * 

) ( nhận tiền cuối tháng, khi

ng}n h|ng đã tính lãi) l|

 

log 1















   

1 1 1





  





4.4. Gửi ngân hàng và rút tiền gửi hàng tháng

Công thức tính

Gửi ngân hàng số tiền là

đồng với lãi suất

/tháng. Mỗi tháng vào ngày ngân hàng

tính lãi, rút ra số tiền là

đồng. Tính số tiền còn lại sau

tháng là bao nhiêu?

4.5. Vay vốn trả góp

4.5.1. Định nghĩa

Vay vốn trả góp là vay ngân hàng số tiền là

đồng với lãi suất

/th{ng. Sau đúng một

tháng kể từ ngày vay, bắt đầu hoàn nợ; hai lần hoàn nợ c{ch nhau đúng một tháng, mỗi hoàn

nợ số tiền là

đồng và trả hết tiền nợ sau đúng

tháng.

4.5.2. Công thức tính

Cách tính số tiền còn lại sau

tháng giống hoàn toàn công thức tính gửi ngân hàng và rút

tiền hàng tháng nên ta có

 

S A r X



  

Để sau đúng

tháng trả hết nợ thì

S 0

nên

   

S r r

1 1 1



   







 

S A r X



  

 

X A r S



  







Trang 28

 

A r X



  

 

A r r







4.6. Bài toán tăng lƣơng

4.6.1. Định nghĩa

B|i to{n tăng lương được mô tả như sau: Một người được lãnh lương khởi điểm là

đồng/tháng. Cứ sau

th{ng thì lương người đó được tăng thêm

/tháng. Hỏi sau

th{ng người đó lĩnh được tất cả số tiền là bao nhiêu?

4.6.2. Công thức tính

Tổng số tiền nhận được sau

tháng là

 

S Ak

11



4.7. Bài toán tăng trƣởng dân số

Công thức tính tăng trưởng dân số

 

X X r m n m n1 , , ,





   

Trong đó:

% là tỉ lệ tăng d}n số từ năm

đến năm

dân số năm

Từ đó ta có công thức tính tỉ lệ tăng d}n số là





4.8. Lãi kép liên tục

Gửi vào ngân hàng

đồng với lãi kép

/năm thì số tiền nhận được cả vốn lẫn lãi sau

năm

 

 

là:

 

S A r1

. Giả sử ta chia mỗi năm th|nh

kì hạn để tính lãi và lãi

suất mỗi kì hạn là

thì số tiền thu được sau

năm l|:









Khi tăng số kì hạn của mỗi năm lên vô cực, tức là

m  

, gọi là hình thức lãi kép tiên

tục thì người ta chứng minh được số tiền nhận được cả gốc lẫn lãi là:

S Ae



( công thức tăng trưởng mũ)

Trang 29

PHẦN III.NGUYÊN HÀM - TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN

1. NGUYÊN HÀM

1.1. Định nghĩa

Cho hàm số

 

x{c định trên

(

là khoảng, đoạn hay nửa khoảng). Hàm số

 

được gọi là nguyên hàm của hàm số

 

trên

nếu

   

F x f x'

với mọi

xK

Kí hiệu:

   





f x dx F x C

Định lí:

1) Nếu

 

là một nguyên hàm của

 

trên

thì với mỗi hằng số

, hàm số

   

G x F x C

cũng l| một nguyên hàm của

 

trên

2) Nếu

 

là một nguyên hàm của hàm số

 

trên

thì mọi nguyên hàm của

 

trên

đều có dạng

 

F x C

, với

là một hằng số.

Do đó

 

F x C C,

là họ tất cả các nguyên hàm của

 

trên

1.2. Tính chất của nguyên hàm



 







f x dx f x

và

   





f x dx f x C'

;

 





d f x f xdx dx

 Nếu F(x) có đạo hàm thì:

 





d F x F x C( ) ( )



   





kf x dx k f x dx

với

là hằng số khác



       



  



  

f x g x dx f x dx g x dx

 Công thức đổi biến số: Cho

 

y f u

và

 

u g x .

Nếu





f x dx F x C( ) ( )

thì

 





f g x g x dx f u du( ) '( ) ( )

F u C()

1.3. Sự tồn tại của nguyên hàm

Định lí:

Mọi hàm số

 

liên tục trên

đều có nguyên hàm trên

1.4. Bảng nguyên hàm các hàm số thƣờng gặp





dx C0





dx x C

 







   





x dx x C

16.

 



    





ax b

ax b c

dx , 1



  



dx C

17.





xdx C





dx x C

18.

  





ax b c

ax b a

dx 1

Trang 30





e dx e C

19.







ax b ax b

e dx e C





a dx C

aln

20.







kx b

a dx C





xdx x Ccos sin

21.

   

   



ax b dx ax b C

cos sin

xdx x Csin cos  



22.

   

    



ax b dx ax b C

sin cos

10.

  



x dx x Ctan . ln | cos |

23.

   

    



ax b ax b C

tan dx ln cos

11.





x dx x Ccot . ln | sin |

24.

   

   



ax b ax b C

cot dx ln sin

12.





dx x C

tan

cos

25.

 

  





dx ax b C

ax b

tan

cos

13.

  



dx x C

cot

sin

26.

 

   





dx ax b C

ax b

cot

sin

14.

 

  



x dx x C

1 tan tan

27.

 

    



ax b dx ax b C

1 tan tan

15.

 

   



x dx co x C

1 cot t

28.

 

     



ax b dx co ax b C

1 cot t

1.5. Bảng nguyên hàm mở rộng







dx 1

arctg

   



x a x C

arcsin dx arcsin









a a x

dx 1

   



x a x C

arccos dx arccos

 

   





x x a C

 

   



x x a

x a x C

arctan dx arctan ln







arcsin

 

   



x x a

x a x C

arccot dx arccot ln







x x a

dx 1

arccos



  





a x a

x x a

dx 1

 









ax b

dx 1

ln tan

sin

   



     







ax b x ax b x C

ln dx ln

 









e a bx b bx

e bx C

cos sin

cos dx



   



x a x a x

a x C

2 2 2

dx arcsin

 









e a bx b bx

e bx C

sin cos

sin dx

Trang 31

2. CÁC PHƢƠNG PHÁP TÍNH NGUYÊN HÀM

2.1. Phƣơng pháp đổi biến

2.1.1. Đổi biến dạng 1

Nếu :





f x dx F x C( ) ( )

và với

 

u t





là hàm số có đạo hàm thì :





f u du F t C( ) ( ( ))



2.1.1.1. Phƣơng pháp chung

 Bước 1: Chọn

 





, trong đó

 



là hàm số mà ta chọn thích hợp .

 Bước 2: Lấy vi phân hai vế :

 



dx t dt'

 Bước 3: Biến đổi :

     









f x dx f t t dt g t dt( ) '

 Bước 4: Khi đó tính :

  



f x dx g t dt G t C( ) ( ) ( )

2.1.1.2. Các dấu hiệu đổi biến thƣờng gặp

Dấu hiệu

Cách chọn

ax

Đặt

x a sint

; với











t ;.

hoặc

x a cost

;

với









t 0; .

xa

Đặt



sint

; với

 











t ; \ 0

hoặc



cost

với















t 0; \ .

ax

Đặt

x a tant

; với











t ;.

hoặc

x a tcot

với

 



t 0; .





hoặc





Đặt

x acos t2

  

x a b x

Đặt

x a b a sin t

–()

ax

Đặt

x atant

; với











t ;.

2.1.2. Đổi biến dạng 2

Nếu hàm số f(x) liên tục thì đặt

 



xt

. Trong đó

 



cùng với đạo hàm của nó (

 



là những hàm số liên tục) thì ta được :

   





   



  

f x dx f t t dt g t dt G t C( ) ' ( ) ( )

2.1.2.1. Phƣơng pháp chung

Trang 32

 Bước 1: Chọn t=

 



. Trong đó

 



là hàm số mà ta chọn thích hợp .

 Bước 2: Tính vi phân hai vế :

 



dt t dt'

 Bước 3: Biểu thị :

   









f x dx f t t dt g t dt( ) ' ( )

 Bước 4: Khi đó :

   



I f x dx g t dt G t C( ) ( ) ( )

2.1.2.2. Các dấu hiệu đổi biến thƣờng gặp :

Dấu hiệu

Cách chọn

Hàm số mẫu số có

là mẫu số

Hàm số :

 



f x x;

 



tx

Hàm

 



a inx+b.cosx

c inx+d.cosx+e









t cos

tan ; 0

Hàm

 

  





x a x b

Với :

xa0

và

xb0

 Đặt :

   t x a x b

Với

xa0

và

xb0

Đặt :

     t x a x b

2.2. Phƣơng pháp nguyên hàm từng phần

Nếu u(x) , v(x) là hai hàm số có đạo hàm liên tục trên K:





u x v x dx u x v x v x u x dx( ). '( ) ( ). ( ) ( ). '( )

Hay





udv uv vdu

( với

   

du u x dx dv v x dx’ , ’

)

2.2.1. Phƣơng pháp chung

 Bước 1: Ta biến đổi tích ph}n ban đầu về dạng :





I f x dx f x f x dx

( ) ( ). ( )

 Bước 2: Đặt :



















du f x dx

u f x

dv f x

v f x dx

' ( )

()

 Bước 3: Khi đó :





u dv u v v du. . .

2.2.2. Các dạng thƣờng gặp

2.2.2.1.Dạng 1





















I P x x dx

sin

( ) cos .

. Đặt





























u P x

dv x dx

()

sin

cos .

































u du P x dx

'. '( )

cos

sin

Vậy:

I P x x

cos

( ) sin





























x P x dx

cos

sin . '( )

2.2.2.2.Dạng 2

Trang 33

I P x xdx( ).ln



. Đặt















dv P x dx

()



















du dx

v P x dx Q x

( ) ( )

Vậy

 

QI lnx Q xx dx

( ).. 



2.2.2.3.Dạng 3



















I e dx

sin

cos

.Đặt



























dv dx

sin

cos































du e dx

cos

sin

Vậy I =

cos

sin





































e dx

cos

sin

Bằng phương ph{p tương tự ta tính được



















e dx

cos

sin

sau đó thay v|o

3. TÍCH PHÂN

3.1. Công thức tính tích phân

  



f x dx F x F b F a( ) ( ) ( ) ( )

* Nhận xét:Tích phân của hàm số

từ a đến b có thể kí hiệu bởi



f x dx()

hay



f t dt( ) .

Tích

ph}n đó chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào cách ghi biến số.

3.2. Tính chất của tích phân

Giả sử cho hai hàm số

( )

và

( )

liên tục trên

, , ,K a b c

là ba số bất kỳ thuộc

. Khi đó ta

có :





f x dx( ) 0





f x dx f x dx( ) ( )



  

b c b

a a c

f x dx f x dx f x dx( ) ( ) ( )



  



  

b b b

a a a

f x g x dx f x dx g x dx( ) ( ) ( ) ( )





kf x dx k f x dx( ) . ( )

6. Nếu f(x)

x a b0, ;



  



thì :



  





f x dx x a b( ) 0 ;

Trang 34

7. Nếu

x a b f x g x f x dx g x dx; : ( ) ( ) ( ) ( )



    





8. Nếu







x a b;

Nếu

M f x N()

thì

   

   



M b a f x dx N b a()

4. PHƢƠNG PHÁP TÍNH TÍCH PHÂN

4.1. Phƣơng pháp đổi biến

4.1.1. Phƣơng pháp đổi biến số dạng 1

4.1.1.1. Định lí

Nếu 1) Hàm

x u t()

có đạo hàm liên tục trên







;

2) Hàm hợp

f u t( ( ))

được x{c định trên







;



u a u b( ) , ( )

Khi đó:









I f x dx f u t u t dt

( ) ( ( )) ( )

4.1.1.2. Phƣơng pháp chung

 Bước 1: Đặt

 

x u t

 Bước 2: Tính vi phân hai vế :

  x u t dx u t dt( ) '( )

Đổi cận:











x b t

x a t

 Bước 3: Chuyển tích ph}n đã cho sang tích ph}n theo biến t

Vậy:







  



  

I f x dx f u t u t dt g t dt( ) ( ) '( ) ( )







  G t G G( ) ( ) ( )

4.1.2. Phƣơng pháp đổi biến dạng 2

4.1.2.1. Định lí

Nếu hàm số

u u x()

đơn điệu v| có đạo hàm liên tục trên đoạn





ab;

sao cho

 

f x dx g u x u x dx g u du( ) ( ) '( ) ( )

thì:





a u a

I f x dx g u du

()

( ) ( )

4.1.2.2. Phƣơng pháp chung

 Bước 1: Đặt

  u u x du u x dx

( ) ( )

 Bước 2: Đổi cận :







x b u u b

x a u u a

()

 Bước 3:Chuyển tích ph}n đã cho sang tích ph}n theo

Vậy:



  



  

a a u a

I f x dx g u x u x dx g u du

()

( ) ( ) . '( ) ( )

4.2. Phƣơng pháp tích phân từng phần

4.2.1. Định lí

Trang 35

Nếu

( )

và

( )

là các hàm số có đạo hàm liên tục trên





ab;

thì:

 





u x v x dx u x v x v x u x dx

( ) ( ) ( ) ( ) ( ) ( )

Hay



udv







vdu

4.2.2. Phƣơng pháp chung

 Bước 1: Viết

( )

f x dx

dưới dạng

udv uv dx

bằng cách chọn một phần thích hợp

của

( )

làm

( )

và phần còn lại

dv v x dx'( )

 Bước 2: Tính

du u dx'

và





v dv





v x dx'( )

 Bước 3: Tính



vu x dx'( )

và

*Cách đặt u và dv trong phƣơng pháp tích phân từng phần.

Đặt u theo thứ tự ưu

tiên:

Lốc-đa-mũ-lưng



P x e dx()



P x xdx( )ln



P x xdx( )cos



e xdxcos

P(x)

lnx

P(x)

e dx

P(x)dx

cosxdx

Chú ý: Nên chọn

là phần của

( )

mà khi lấy đạo h|m thì đơn giản, chọn

dv v dx

là phần

của

( )

f x dx

là vi phân một hàm số đã biết hoặc có nguyên hàm dễ tìm.

5. TÍCH PHÂN CÁC HÀM SỐ SƠ CẤP CƠ BẢN

5.1. Tích phân hàm hữu tỉ

5.1.1. Dạng 1

I =









  





dx adx

ax b

ax b a ax b a

. (với a≠0)

Chú ý: Nếu I =









  

   







ax b adx ax b

a a k

ax b

( ) . .( )

(1 )

()

5.1.2. Dạng 2

 











ax bx c

(

  ax bx c

với mọi









x ;

)

Xét

  b ac

 Nếu

0 

thì

     



;



  



    





a x x x x a x x x x x x

ax bx c

1 2 1 2 1 2

1 1 1 1 1

( )( ) ( )

thì :

I dx x x x x

a x x x x x x a x x

a x x x x

1 2 1 2 1 2

1 2 2

1 1 1 1

ln ln

( ) ( )

()













     







   











Trang 36

 Nếu

0 

thì









  



ax bx c a x x

()

thì I =









  



  



dx dx

a a x x

ax bx c x x

()

 Nếu

0

thì































dx dx

ax bx c

Đặt

 

 

    

x t dx t dt

tan 1 tan

5.1.3. Dạng 3

 













mx n

I dx a

ax bx c

(trong đó







mx n

ax bx c

()

liên tục trên đoạn







;

)

 Bằng phương ph{p đồng nhất hệ số, ta tìm

và

sao cho:

  



     

mx n A ax bx c B

ax bx c ax bx c ax bx c

2 2 2

( )'





   

A ax b B

ax bx c ax bx c

(2 )

 Ta có I=















     



mx n A ax b B

dx dx dx

ax bx c ax bx c ax bx c

2 2 2

(2 )

Tích phân











A ax b

ax bx c

(2 )





A ax bx c

Tích phân









ax bx c

thuộc dạng 2.

5.1.4. Dạng 4





I dx

()

với

( )

và

( )

là đa thức của

 Nếu bậc của

( )

lớn hơn hoặc bằng bậc của

( )

thì dùng phép chia đa thức.

 Nếu bậc của

( )

nhỏ hơn bậc của

( )

thì có thể xét c{c trường hợp:

 Khi

( )

chỉ có nghiệm đơn

  

n12

, ,...,

thì đặt

  

   

  

A A A

Q x x x x

()

...

()

 Khi

( )

có nghiệm đơn v| vô nghiệm

 



       Q x x x px q p q

( ) , 4 0

thì đặt











P x A Bx C

Q x x

x px q

()

 Khi

( )

có nghiệm bội



  Q x x x

( ) ( )( )

với  thì đặt

Trang 37

 





  





P x B C

Q x x x

()



  Q x x x

( ) ( ) ( )

với  thì đặt



    

    



    

P x A B C D E

x x x x x

2 3 2 3 2

()

( ) ( ) ( ) ( ) ( )

5.2. Tích phân hàm vô tỉ



R x f x dx( , ( ))

Trong đó

( )

, R x f x

có dạng:













Đặt

x acos t t2, 0;























R x a x

, 

Đặt

x atsin

hoặc

x atcos



ax b

cx d











Đặt

ax b







 

R x f x

ax b x x

()

  



  

Với

 

x k x bx a

  

 

Đặt

t x x

  

  

, hoặc Đặt

ax b











R x a x

, 

Đặt

x attan

t ;

















R x x a

, 

Đặt

xcos



t [0; ]\



















n n n

R x x x

; ;...;

Gọi

( )

; ;...;

k BSCNN n n n=

. Đặt

xt=

5.2.1. Dạng 1

 







I dx a

ax bx c





Từ :

















       





















f(x)=ax bx c a x du dx

Khi đó ta có :

 Nếu

 

        a f x a u k f x a u k

2 2 2 2

0, 0 ( ) ( ) .

(1)

 Nếu :









     





  







f x a x

f x a x a u

0 ( )

( ) .

(2)

 Nếu :

0

Trang 38

 Với

0a >

     

      f x a x x x x f x a x x x x

1 2 1 2

( ) ( ) .

(3)

 Với

0a <

     

        f x a x x x x f x a x x x x

1 2 1 2

( ) ( ) .

(4)

Căn cứ vào phân tích trên , ta có một số cách giải sau :

 Phƣơng pháp :

* Trường hợp :

 

        a f x a u k f x a u k

2 2 2 2

0, 0 ( ) ( ) .

Khi đó đặt :

   

ax bx c t a x.



















  









     







  







x dx tdt

bx c t ax

x t t x t t

t a x t a

;

* Trường hợp :









     





  







f x a x

f x a x a u

0 ( )

( ) .

Khi đó :

















  









  









   











I dx dx

a x x

ln : 0

1 1 1

ln : 0

* Trường hợp :

  a0, 0

. Đặt :

  

 







     







x x t

ax bx c a x x x x

x x t

* Trường hợp :

  a0, 0

. Đặt :

  

 







     







x x t

ax bx c a x x x x

x x t

5.2.2. Dạng 2

 









mx n

I dx a

ax bx c





 Phƣơng pháp :

 Bước 1:

Phân tích





 





  

     

2 2 2

A d ax bx c

mx n B

ax bx c ax bx c ax bx c

( ) 1

 Bước 2:

Quy đồng mẫu số , sau đó đồng nhất hệ số hai tử số để suy ra hệ hai ẩn số

,AB

 Bước 3:

Giải hệ tìm

,AB

thay vào (1)

 Bước 4 :

Tính





I A ax bx c B dx

ax bx c









   





(2)

Trang 39

Trong đó

 











dx a

ax bx c

đã biết cách tính ở trên

5.2.3. Dạng 3

 







  



I dx a

mx n ax bx c

 Phƣơng pháp :

 Bước 1:

Phân tích :

 





  





mx n ax bx c

m x ax bx c

. (1)

 Bước 2:

Đặt :





    











  



   



         

   



   



y t dy dx

x t m x t

x t ax bx c a t b t c

y y y

1 1 1

 Bước 3:

Thay tất cả vào (1) thì I có dạng :











Ly My N

. Tích ph}n n|y chúng ta đã

biết cách tính .

5.2.4. Dạng 4

 

























I R x y dx R x dx

;;

( Trong đó :

( )

;R x y

là hàm số hữu tỷ đối với hai biến số x,y và

   

, , ,

là các hằng số đã biết

)

 Phương pháp :

 Bước 1:

Đặt :









(1)

 Bước 2:

Tính x theo t : Bằng c{ch n}ng lũy thừa bậc m hai vế của (1) ta có dạng

 



xt

 Bước 3:

Tính vi phân hai vế :

 



dx t dt'

v| đổi cận

 Bước 4:

Tính :

 



























R x dx R t t t dt

; ; '

5.3. Tích phân hàm lƣợng giác

5.3.1. Một số công thức lƣợng giác

Trang 40

5.3.1.1. Công thức cộng

 a b a b a bcos cos .c() os  sin . sin

a b a b b asin sin .cos sin .) os( c  

atan tan

()

1 tan .tan

tan 





5.3.1.2. Công thức nhân đôi

a a a a

2 2 2

cos2 cos – sin 2 cos – 1

1 tan

1 – 2 sin

1 tan

  







a a a

sin2 2sin .cos

2tan

1 tan



;





2tan

tan 2

1 tan

cos3 4cos 3cos

  



;

sin 3 3sin 4sin

  



5.3.1.3. Công thức hạ bậc

1 cos2

sin





;

1 cos2

cos





;







1 cos2

tan

1 cos2









3sin sin 3

sin

;

cos3 3cos

cos









5.3.1.4. Công thức tính theo

Với

t tan



Thì

sin





;

cos







;

tan





5.3.1.5. Công thức biến đổi tích thành tổng

     



   





   





   



cos .cos cos( ) cos( )

sin .sin cos( ) cos( )

sin .cos sin( ) sin( )

5.3.1.6. Công thức biến đổi tổng thành tích

Công thức thƣờng dùng:

Hệ quả:

   



   



   



   









  

















cos cos 2cos .cos

cos cos 2si n .sin

sin sin 2sin .cos

sin sin 2cos .sin

sin( )

tan tan

cos cos

sin( )

tan tan

cos cos

















3 cos4

cos sin

5 3cos4

cos sin

Trang 41

5.3.2. Một số dạng tích phân lƣợng giác

 Nếu gặp

 





sin .cos

I f x xdx

ta đặt

 sintx

 Nếu gặp dạng

 





cos .sin

I f x xdx

ta đặt

 costx

 Nếu gặp dạng

 





tan

cos

I f x

ta đặt

 tantx

 Nếu gặp dạng

 





cot

sin

I f x

ta đặt

 cottx

5.3.2.1. Dạng 1

   

= sinx dx ; cosx dx



* Phƣơng pháp

 Nếu

chẵn thì sử dụng công thức hạ bậc

 Nếu

3n =

thì sử dụng công thức hạ bậc hoặc biến đổi

 Nếu

lẻ

()21np=+

thì thực hiện biến đổi:

   

 

n 2p+1

= sinx dx = sinx dx    

   

I x xdx x d x

sin sin 1 cos cos

 





        











       









p p p p

C C x C x C x d x

C x C x C x C x c

0 1 2 2 2

2 1 2 1

0 1 3

cos ... 1 cos .. . 1 cos cos

1 1 1

cos cos ... cos ... cos

3 2 1 2 1

   

 

n 2p+1

= cosx dx = cosx dx   

   

I x xdx x d x

cos cos 1 sin sin

 





       











      









p p p p

C C x C x C x d x

C x C x C x C x c

0 1 2 2 2

2 1 2 1

0 1 3

sin ... 1 sin ... 1 sin sin

1 1 1

sin sin ... sin ... sin

3 2 1 2 1

5.3.2.2. Dạng 2

( )

sin cos ,

I x xdx m n N=Î

* Phƣơng pháp

 Trường hp 1:

,mn

là các số nguyên

a. Nếu

chẵn,

chẵn thì sử dụng công thức hạ bậc, biến đổi tích thành tổng.

b. Nếu

chẵn,

lẻ

()21np=+

thì biến đổi:



   



   

   

    

   

   

   

     

   

   

cos sin 2 cos 2 sin

Trang 42

   

     

 

m 2p+1

I = sinx cosx dx   

  

m p m

x x xdx x x d x

sin cos cos sin 1 sin sin

   

 

   

 

     



        









       

     







m k p

p p p p

m m k m p m

p p p p

x C C x C x C x d x

x x x x

C C C C c

m m k m p m

0 1 2 2 2

1 3 2 1 2 1

sin sin ... 1 sin ... 1 sin sin

sin sin sin sin

... 1 ... 1

1 3 2 1 2 1

c. Nếu

lẻ

( )

21mp=+

chẳn thì biến đổi:

   

     

 

2p+1 n

I = sinx cosx dx    

  

n p n

x x xdx x x d x

cos sin sin cos 1 cos cos

   

 

   

 

     



         









        

     







n k p

p p p p

n n k n p n

p p p p

x C C x C x C x d x

x x x x

C C C C c

n n k n p n

0 1 2 2 2

1 3 2 1 2 1

cos cos ... 1 cos ... 1 cos cos

cos cos cos cos

... 1 ... 1

1 3 2 1 2 1

d. Nếu

lẻ,

lẻ thì sử dụng biến đổi 1.2. hoặc 1.3. cho số mũ lẻ bé hơn.

 Nếu

,mn

là các số hu tỉ thì biến đổi và đặt

u sinx=

 

   



   

  

m n m

B x xdx x x xdx u u du

sin cos sin cos cos 1

(*)

Tích ph}n (*) tính được  1 trong 3 số

  m n m k11

;;

2 2 2

là số nguyên

5.3.2.3. Dạng 3

().nNÎ



 

    

  

x dx d x x c

1 tan tan tan

cos



 

      

  

x dx d x x C

1 cot cot cot

sin



6. ỨNG DỤNG TÍCH PHÂN

6.1. Diện tích hình phẳng

6.1.1. Diện tích hình phẳng giới hạn bởi 1 đƣờng cong và trục hoành

Diện tích hình phẳng giới hạn bởi đồ thị hàm số

y f x()

liên tục trên đoạn





ab;

, trục

ho|nh v| hai đường thẳng

xa

xb

được x{c định:





S f x dx()

   

= tan x dx ; = cot x dx



 

     

  

x d x

xdx dx x C

sin cos

tan ln cos

cos cos

 

   

  

x d x

xdx dx x C

cos sin

cot ln sin

sin sin





















()

y f x

 ()y f x





S f x dx()

Trang 43

6.1.2. Diện tích hình phẳng giới hạn bởi 2 đƣờng cong

Diện tích hình phẳng giới hạn bởi đồ thị hàm số

y f x()

y g x()

liên tục trên đoạn





ab;

v| hai đường thẳng

xa

xb

được x{c định:





S f x g x dx( ) ( )

- Nếu trên đoạn

[a b];

, hàm số

fx()

không đổi dấu thì:





f x dx f x dx( ) ( )

- Nắm vững cách tính tích phân của hàm số có chứa giá trị tuyệt đối

- Diện tích của hình phẳng giới hạn bởi c{c đường

x g y()

x h y()

v| hai đường thẳng

yc

yd

được x{c định:





S g y h y dy( ) ( )

6.2. Thể tích vật thể và thể tích khối tròn xoay

6.2.1. Thể tích vật thể

Gọi

là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại c{c điểm a và

Sx()

là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm

a x b()

. Giả sử

Sx()

là hàm số liên tục trên đoạn

[a b];

6.2.2. Thể tích khối tròn xoay

- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi c{c đường

y f x()

, trục ho|nh v| hai đường thẳng

xa

xb

quanh trục Ox:

- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi c{c đường

x g y()

, trục ho|nh v| hai đường thẳng

yc

yd

quanh trục Oy:

( ): ( )

( ):





















C y f x

Ox y 0

 

()

V f x dx



 ()y f x





S x dxV ()

()V

S(x)





















( ): ( )

()

C y f x

()C





S f x f x dx

( ) ( )

( ): ( )

( ):





















C x g y

Oy x 0

 

()

V g y dy



Trang 44

- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới

hạn bởi c{c đường

y f x()

y g x()

v| hai đường thẳng

xa

xb

quanh trục Ox:

V f x g x dx

( ) ( )







Trang 45

PHẦN IV. SỐ PHỨC

1. SỐ PHỨC

1.1. Khái niệm số phức

 Số phức (dạng đại số) :

 

z a bi a b;,   

. Trong đó :

là phần thực,

là phần

ảo,

l| đơn vị ảo,

1.

 Tập hợp số phức kí hiệu:





là số thực



phần ảo của

bằng

 

b 0



là số ảo (hay còn gọi là thuần ảo)



phần thực bằng

 

a 0

 Số

vừa là số thực vừa là số ảo.

1.2. Hai số phức bằng nhau

 Hai số phức

 

z a bi a b

,   

và

 

z c di c d

,   

bằng nhau khi phần thực

và phần ảo của chúng tương đương bằng nhau.

 Khi đó ta viết

z z a bi c di







     









1.3. Biểu diễn hình học số phức

Số phức

 

z a bi a b,   

được biểu diễn bởi điểm

 

M a b;

hay bởi

 

u a b;



trong mặt phẳng phức với hệ tọa độ

Oxy

1.4. Số phức liên hợp

Số phức liên hợp của

 

z a bi a b,   

là

z a bi



là số thực

zz

;

là số ảo

zz

1.5. Môđun của số phức

Độ dài của vectơ



được gọi là môđun của số phức

và kí hiệu là

. Vậy

z OM



hay

z a bi OM a b

    



Một số tính chất:



z a b zz OM

   



;

zz



zz0, ;   

zz00  



z z z z

1 2 1 2

..

;



;

z z z

1 1 2

.

z z z z z z z z z z z z a b

; ' ' ; . ' . '; ; . .



       





M (a;b)

Trang 46



z z z z z z

1 2 1 2 1 2

    

2. PHÉP CỘNG TRỪ NHÂN CHIA SỐ PHỨC

2.1. Phép cộng và phép trừ số phức

Cho hai số phức

 

z a bi a b

,   

và

 

z c di c d

,   

. Khi đó:

   

z z a c b d i

    

 Số đối của số phức

z a bi

là

z a bi   

 Tổng của một số phức với số phức liên hợp của nó bằng hai lần phần thực của số

thực đó:

z a bi z z a,2   

2.2. Phép nhân số phức

 Cho hai số phức

 

z a bi a b

,   

và

 

z c di c d

,   

Khi đó:

      

z z a bi c di ac bd ad bc i

–     

 Với mọi số thực

và mọi số phức

 

z a bi a b,   

, ta có

 

k z k a bi ka kbi. . .   

Đặc biệt:

z0. 0

với mọi số phức

 Lũy thừa của

i i i i i i i i

0 1 2 3 2

1, , 1, .      

n n n n

i i i i i i n

4 4 1 4 2 4 3

1, , 1, ,

   

        

2.3. Chia hai số phức

Số phức nghịch đảo của

khác

là số





Phép chia hai số phức

z '

và

z 0

là

z z z z z

z z z

' '. '.



  

3. TẬP HỢP ĐIỂM BIỂU DIỄN SỐ PHỨC

Một số tập hợp điểm biểu diễn số phức z thường gặp:



ax by c 0   

tập hợp điểm l| đường thẳng



x 0

tập hợp điểm là trục tung Oy



y 0

tập hợp điểm là trục hoành Ox



   

x a y b R

    

tập hợp điểm là hình tròn tâm

 

I a b;,

bán kính



   

x a y b R

x y ax by c

2 2 0



   







    



tập hợp điểm là đường tròn có tâm

 

I a b;,

bán kính

R a b c

  



0x 

tập hơp điểm là miền bên phải trục tung



y 0

tập hợp điểm là miền phía dưới trục hoành



x 0

tập hợp điểm là miền bên trái trục tung



y 0

tập hợp điểm là phía trên trục hoành

Trang 47



y ax bx c

   

tập hợp điểm l| đường Parabol



1  

tập hợp điểm l| đường Elip



1  

tập hợp điểm l| đường Hyperbol

4. PHƢƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC

4.1. Căn bậc hai của số thực âm

 Cho số

, nếu có số phức

sao cho



thì ta nói

là một căn bậc hai của

 Mọi số phức

z 0

đều có hai căn bậc hai.

 Căn bậc hai của số thực

âm là

iz

Tổng qu{t, c{c căn bậc hai của số thực

âm là

ia

4.2. Phƣơng trình bậc hai với hệ số thực

Cho phương trình bậc hai

ax bx c a b c a

0, , , , 0     

. Xét biệt số

b ac

4  

của

phương trình. Ta thấy:

 Khi

0

, phương trình có một nghiệm thực



 Khi

0

, phương trình có hai nghiệm thực phân biệt

1,2

  



 Khi

0

, phương trình có hai nghiệm phức

  



1,2

5. BÀI TOÁN LIÊN QUAN ĐẾN MAX – MIN MÔ ĐUN SỐ PHỨC

 Cho số phức

thỏa mãn

 

. , 0z z z r r  

max

min

















 Cho số phức

thỏa mãn

 

1 2 1 1

. , 0z z z r r  

max   

và

min   

 Cho số phức

thỏa mãn

 

z z z z z z k k

1 2 1 2

. . , 0    

max



và

min





MỤC LỤC

PHẦN I. HÀM SỐ ................................................................................................................................. 1

1. SỰ ĐỒNG BIẾN NGHỊCH BIẾN CỦA HÀM SỐ ........................................................................ 1

Trang 48

1.1. Định nghĩa ................................................................................................................................ 1

1.2. Quy tắc và công thức tính đạo hàm ......................................................................................... 1

1.3. Bảng công thức tính đạo hàm ................................................................................................... 2

1.4 . Công thức tính nhanh đạo hàm hàm phân thức ..................................................................... 2

1.5. Đạo hàm cấp 2 .......................................................................................................................... 2

2. CỰC TRỊ HÀM SỐ ........................................................................................................................ 4

2.1. Định nghĩa ................................................................................................................................ 4

2.2. Điều kiện cần để hàm số đạt cực trị ......................................................................................... 5

2.3. Điều kiện đủ để hàm số đạt cực trị .......................................................................................... 5

2.4. Quy tắc tìm cực trị .................................................................................................................... 5

3. MỘT SỐ DẠNG TOÁN LIÊN QUAN ĐẾN CỰC TRỊ HÀM SỐ ................................................ 6

3.1. Cực trị của h|m đa thức bậc ba

y ax bx cx d

.   

..................................................... 6

3.2. Cực trị của hàm bậc 4 trùng phƣơng

 

y ax bx c a

,0   

.................................... 9

4. GIÁ TRỊ LỚN NHẤT - GIÁ TRỊ NHỎ NHẤT ........................................................................... 11

4.1. Định nghĩa. ............................................................................................................................. 11

4.2. Phƣơng pháp tìm GTLN,GTNN .......................................................................................... 11

5. ĐƢỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ ........................................................................... 12

5.1. Đƣờng tiệm cận ngang .......................................................................................................... 12

5.2. Đƣờng tiệm cận đứng............................................................................................................ 12

6. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ HÀM SỐ .......................................................... 12

6.1. Khảo sát một số hàm đa thức và hàm phân thức .................................................................. 12

6.2. Một số phép biến đổi đồ thị ................................................................................................... 14

7. TIẾP TUYẾN ................................................................................................................................ 16

7.1. Tiếp tuyến .............................................................................................................................. 16

7.2. Điều kiện tiếp xúc ................................................................................................................... 16

8. TƢƠNG GIAO ĐỒ THỊ .............................................................................................................. 16

9. ĐIỂM ĐẶC BIỆT CỦA HỌ ĐƢỜNG CONG ............................................................................. 17

9.1. B|i to{n tìm điểm cố định của họ đường cong ....................................................................... 17

9.2. B|i to{n tìm điểm có tọa độ nguyên ....................................................................................... 17

9.3. B|i to{n tìm điểm có tính chất đối xứng ................................................................................ 17

9.4. B|i to{n tìm điểm đặc biệt, khoảng cách ................................................................................ 18

PHẦN II. MŨ VÀ LOGARIT .............................................................................................................. 21

1. LŨY THỪA VÀ HÀM SỐ LŨY THỪA ....................................................................................... 21

1.1. Khái niệm lũy thừa ................................................................................................................. 21

1.2. Phương trình



xb.

............................................................................................................ 21

1.3. Một số tính chất của căn bậc

.............................................................................................. 21

1.4. Hàm số lũy thừa ..................................................................................................................... 22

1.5. Khảo sát hàm số mũ

 

, 0, 1

y a a a  

. ................................................................... 23

Trang 49

2. LOGARIT ..................................................................................................................................... 24

2.1. Khái niệm Logarit................................................................................................................... 24

2.2. Bảng tóm tắt công thức Mũ-logarit thường gặp ..................................................................... 24

3. BẤT PHƢƠNG TRÌNH MŨ VÀ LOGARIT. .............................................................................. 25

3.1. Bất phương trình mũ cơ bản .................................................................................................. 25

3.2. Bất phương trình logarit cơ bản ............................................................................................. 25

4. BÀI TOÁN LÃI SUẤT NGÂN HÀNG........................................................................................ 26

4.1. Lãi đơn ................................................................................................................................... 26

4.2. Lãi kép .................................................................................................................................... 26

4.3. Tiền gửi hàng tháng ............................................................................................................... 27

4.4. Gửi ngân hàng và rút tiền gửi hàng tháng ............................................................................. 27

4.5. Vay vốn trả góp ...................................................................................................................... 27

4.6. B|i to{n tăng lương ................................................................................................................ 28

4.7. B|i to{n tăng trưởng dân số ................................................................................................... 28

4.8. Lãi kép liên tục ....................................................................................................................... 28

PHẦN III. NGUYÊN HÀM - TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN ......................................... 29

1. NGUYÊN HÀM............................................................................................................................ 29

1.1. Định nghĩa .............................................................................................................................. 29

1.2. Tính chất của nguyên hàm ..................................................................................................... 29

1.3. Sự tồn tại của nguyên hàm ..................................................................................................... 29

1.4. Bảng nguyên hàm các hàm số thường gặp ............................................................................ 29

1.5. Bảng nguyên hàm mở rộng .................................................................................................... 30

2. CÁC PHƢƠNG PHÁP TÍNH NGUYÊN HÀM .......................................................................... 31

2.1. Phương ph{p đổi biến ............................................................................................................ 31

2.2. Phương ph{p nguyên h|m từng phần ................................................................................... 32

3. TÍCH PHÂN ................................................................................................................................. 33

3.1. Công thức tính tích phân ........................................................................................................ 33

3.2. Tính chất của tích phân .......................................................................................................... 33

4. PHƢƠNG PHÁP TÍNH TÍCH PHÂN ......................................................................................... 34

4.1. Phương ph{p đổi biến ............................................................................................................ 34

4.2. Phương ph{p tích ph}n từng phần ........................................................................................ 34

5. TÍCH PHÂN CÁC HÀM SỐ SƠ CẤP CƠ BẢN ......................................................................... 35

5.1. Tích phân hàm hữu tỉ ............................................................................................................. 35

5.2. Tích phân hàm vô tỉ ............................................................................................................... 37

5.3. Tích ph}n h|m lượng giác ...................................................................................................... 39

6. ỨNG DỤNG TÍCH PHÂN .......................................................................................................... 42

6.1. Diện tích hình phẳng .............................................................................................................. 42

6.2. Thể tích vật thể và thể tích khối tròn xoay ............................................................................. 43

PHẦN IV. SỐ PHỨC ........................................................................................................................... 45

Trang 50

1. SỐ PHỨC ..................................................................................................................................... 45

1.1. Khái niệm số phức .................................................................................................................. 45

1.2. Hai số phức bằng nhau .......................................................................................................... 45

1.3. Biểu diễn hình học số phức .................................................................................................... 45

1.4. Số phức liên hợp ..................................................................................................................... 45

1.5. Môđun của số phức ................................................................................................................ 45

2. PHÉP CỘNG TRỪ NHÂN CHIA SỐ PHỨC .............................................................................. 46

2.1. Phép cộng và phép trừ số phức .............................................................................................. 46

2.2. Phép nhân số phức ................................................................................................................. 46

2.3. Chia hai số phức ..................................................................................................................... 46

3. TẬP HỢP ĐIỂM BIỂU DIỄN SỐ PHỨC ..................................................................................... 46

4. PHƢƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC....................................................................... 47

4.1. Căn bậc hai của số thực âm .................................................................................................... 47

4.2. Phương trình bậc hai với hệ số thực ....................................................................................... 47

5. BÀI TOÁN LIÊN QUAN ĐẾN MAX – MIN MÔ ĐUN SỐ PHỨC ............................................ 47

Bấm Tải xuống để xem toàn bộ.

| 1/50

| | Tải xuống

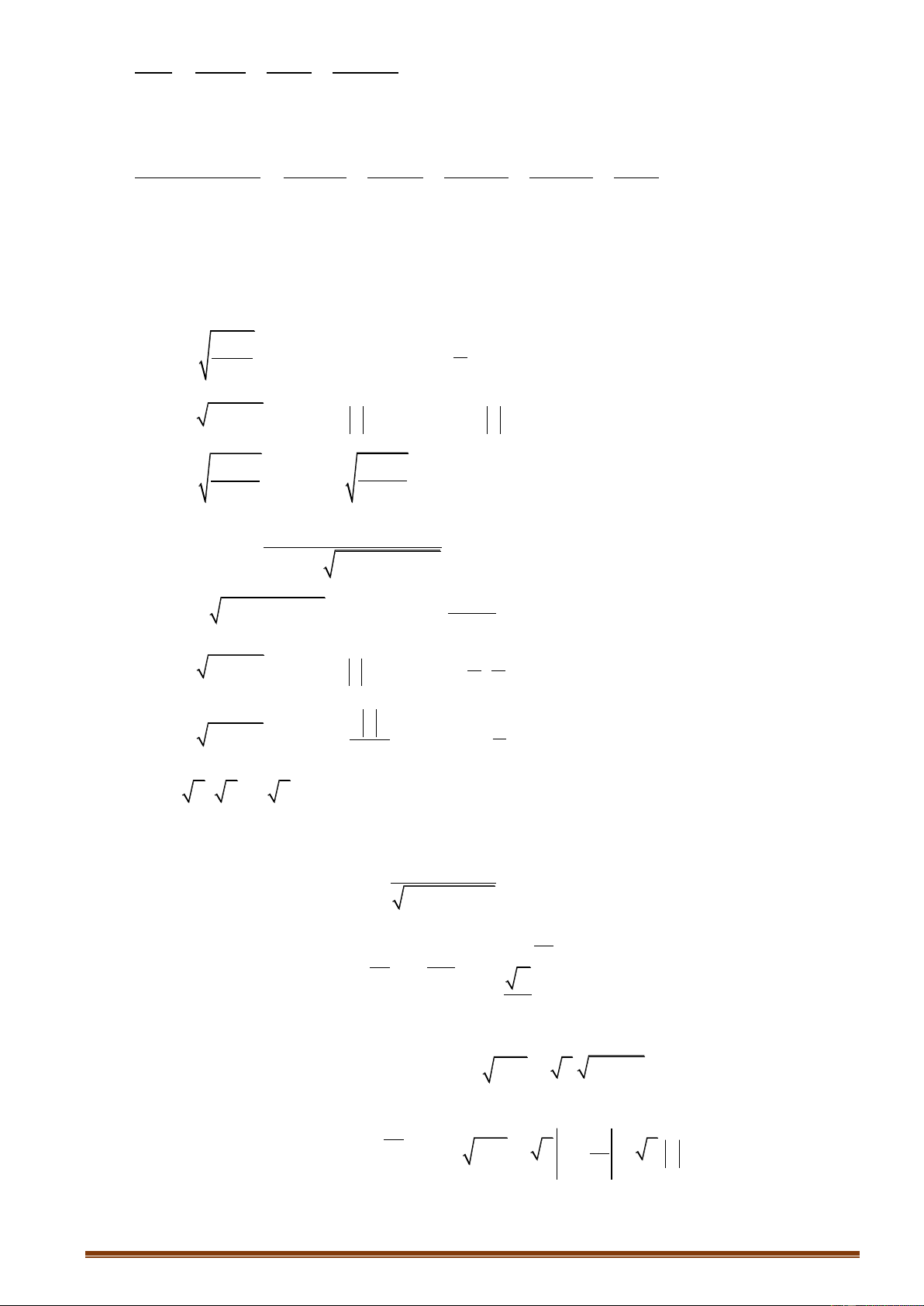
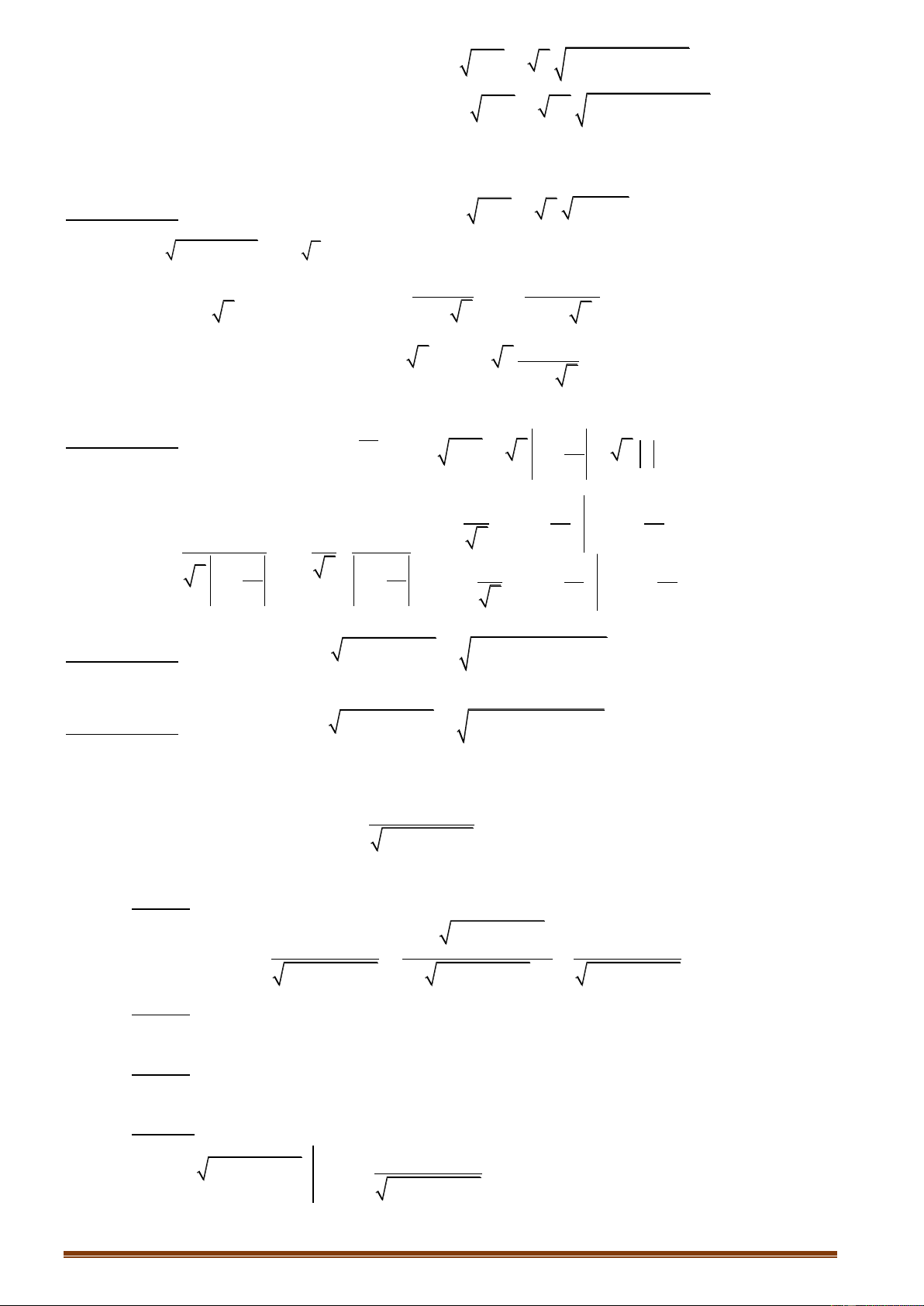
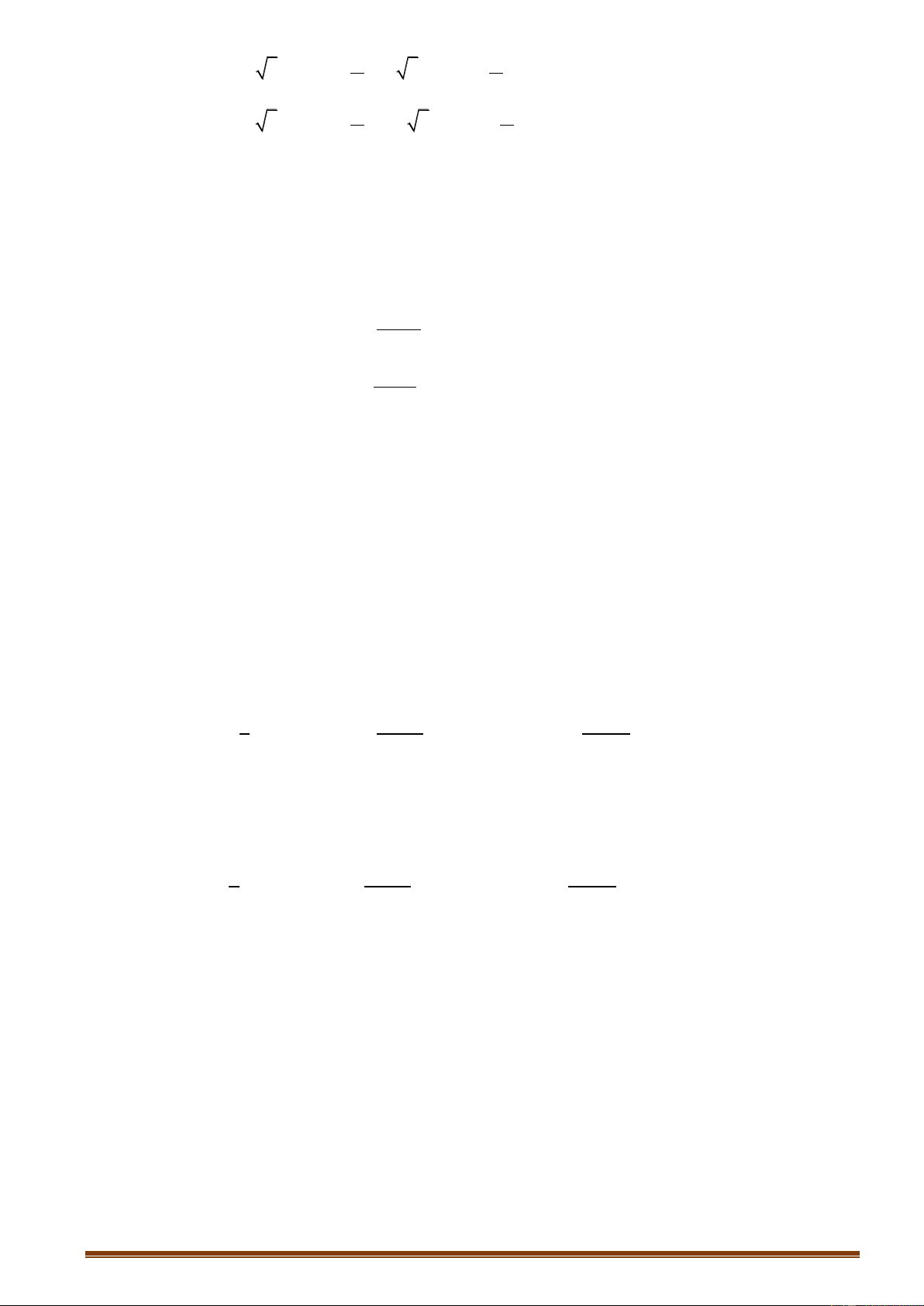
Preview text:

PHẦN I. HÀM SỐ
1. SỰ ĐỒNG BIẾN NGHỊCH BIẾN CỦA HÀM SỐ 1.1. Định nghĩa
Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y  f x  x{c định trên K ta có:
 Hàm số y  f x  được gọi là đồng biến(tăng) trên K nếu:
x ,x  K ,x  x  f x   f x 1 2 1 2 1 2 
 Hàm số y  f x  được gọi là nghịch biến(giảm) trên K nếu:
x ,x  K ,x  x  f x   f x 1 2 1 2 1 2 
Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K * Nhận xét:
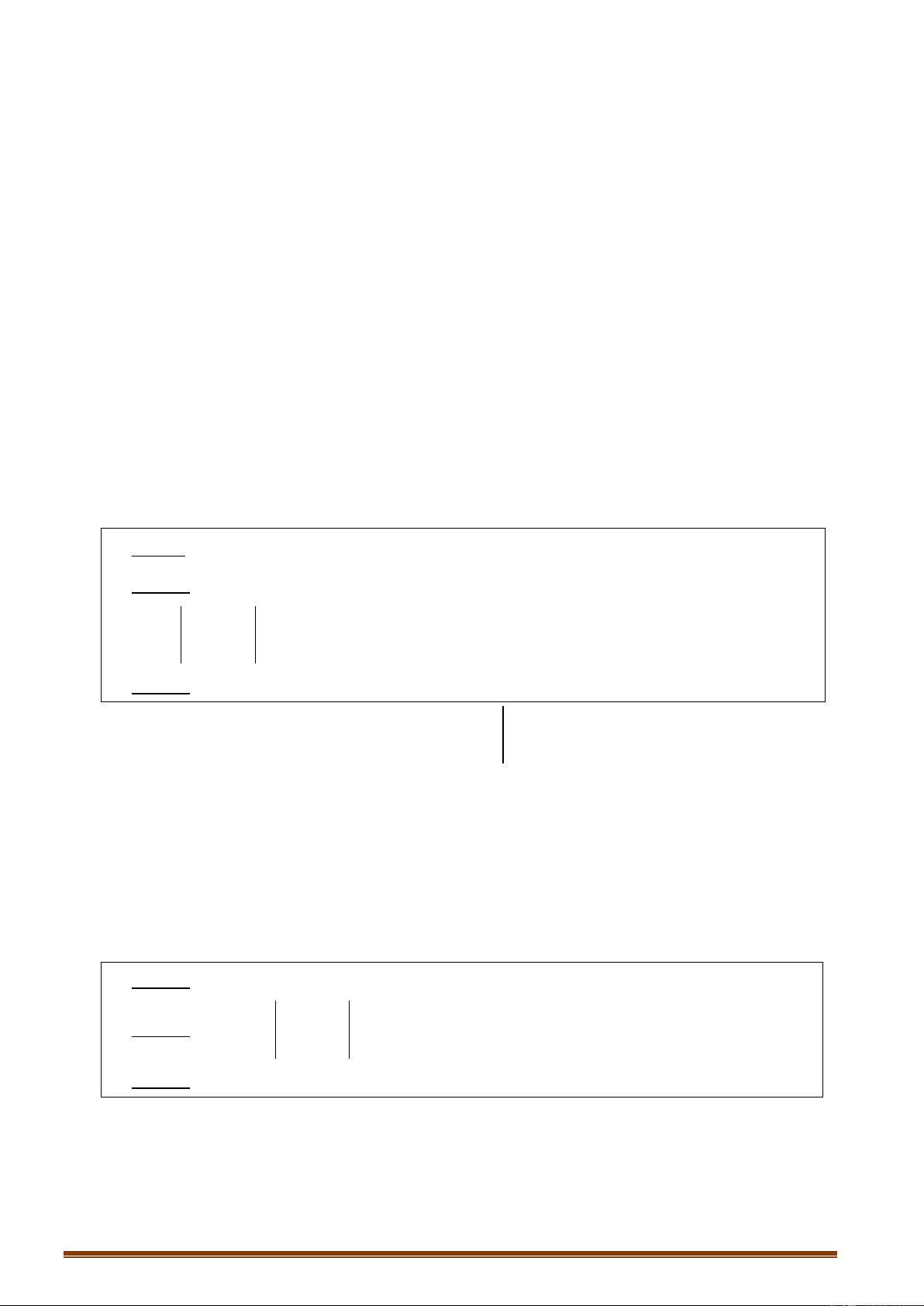
f x2   f x1 
 Hàm số f x đồng biến trên K   0 
x , x  K , x  x . Khi đó đồ thị x  x 1 2 1 2 2 1
của hàm số đi lên từ trái sang phải.
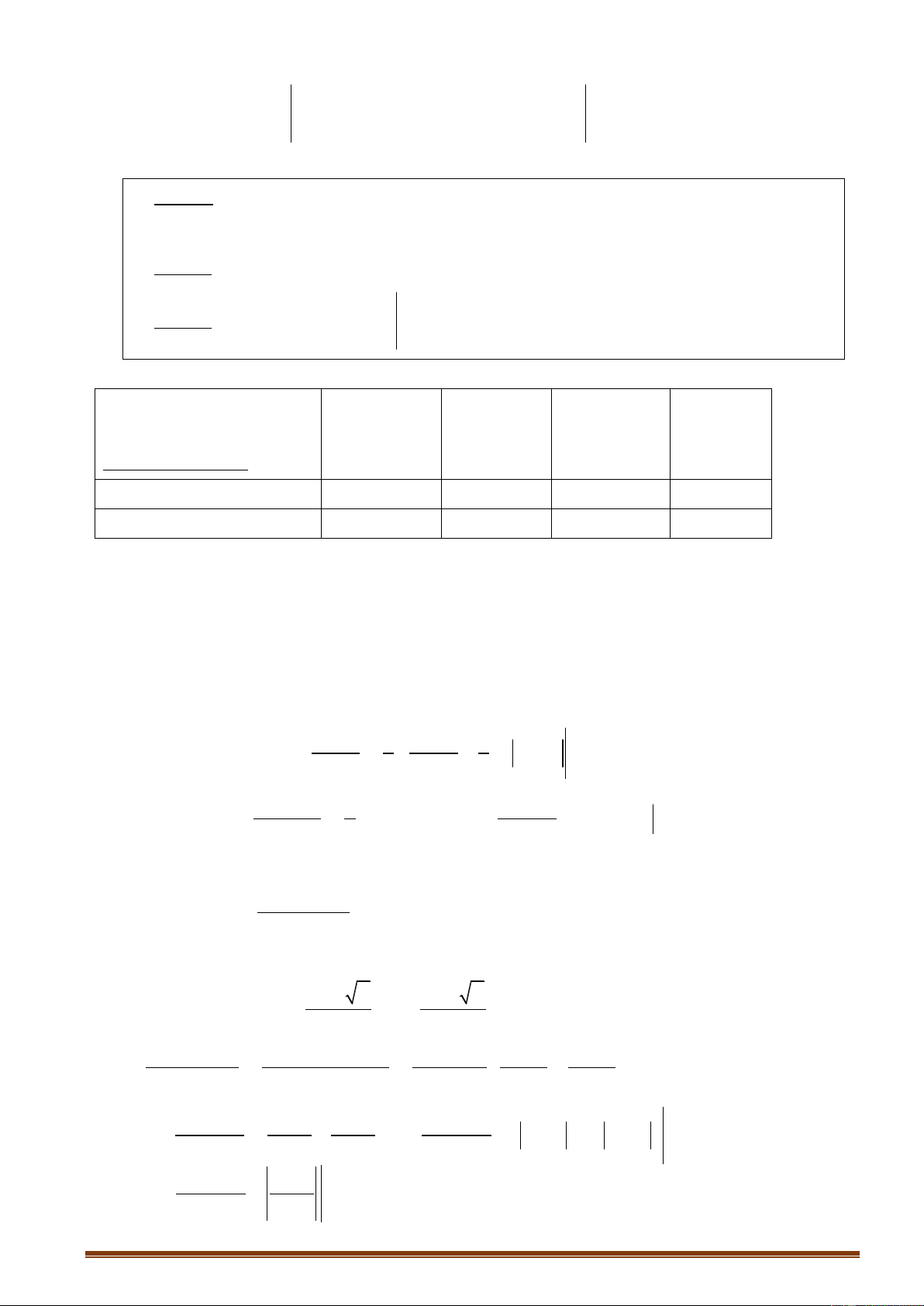
f x2   f x1 
 Hàm số f x nghịch biến trên K   0 
x , x  K , x  x . Khi đó đồ thị x  x 1 2 1 2 2 1
của hàm số đi xuốngtừ trái sang phải.
 Nếu f x   0, x  a;b  h|m số f x đồng biến trên khoảng a;b.
 Nếu f x  0, x   ;
a b  h|m số f x nghịch biến trên khoảng a;b.
f  x  0, x    Nếu  
a;b h|m số f xkhông đổi trên khoảng a;b.
 Nếu f x đồng biến trên khoảng a;b  f x   0, x  a b ; .
 Nếu f x nghịch biến trên khoảng a;b  f x   0, x
  a;b.
 Nếu thay đổi khoảng a;b bằng một đoạn hoặc nửa khoảng thì phải bổ sung thêm
giả thiết “h|m số f x liên tục trên đoạn hoặc nửa khoảng đó”.
1.2. Quy tắc và công thức tính đạo hàm
Quy tắc tính đạo hàm:Cho u  u x ; v  v x ; C : là hằng số .
 Tổng, hiệu: u  v  u  v.    Tích: u v .   uv .  v u .  C u .   C u . . Trang 1 
 u  uv.  vu . C  C u . 
 Thƣơng:   , 0 2
v         v  v  u  u 2
 Đạo hàm hàm hợp: Nếu y  f u, u  u x   y  y u. . x u x
1.3. Bảng công thức tính đạo hàm
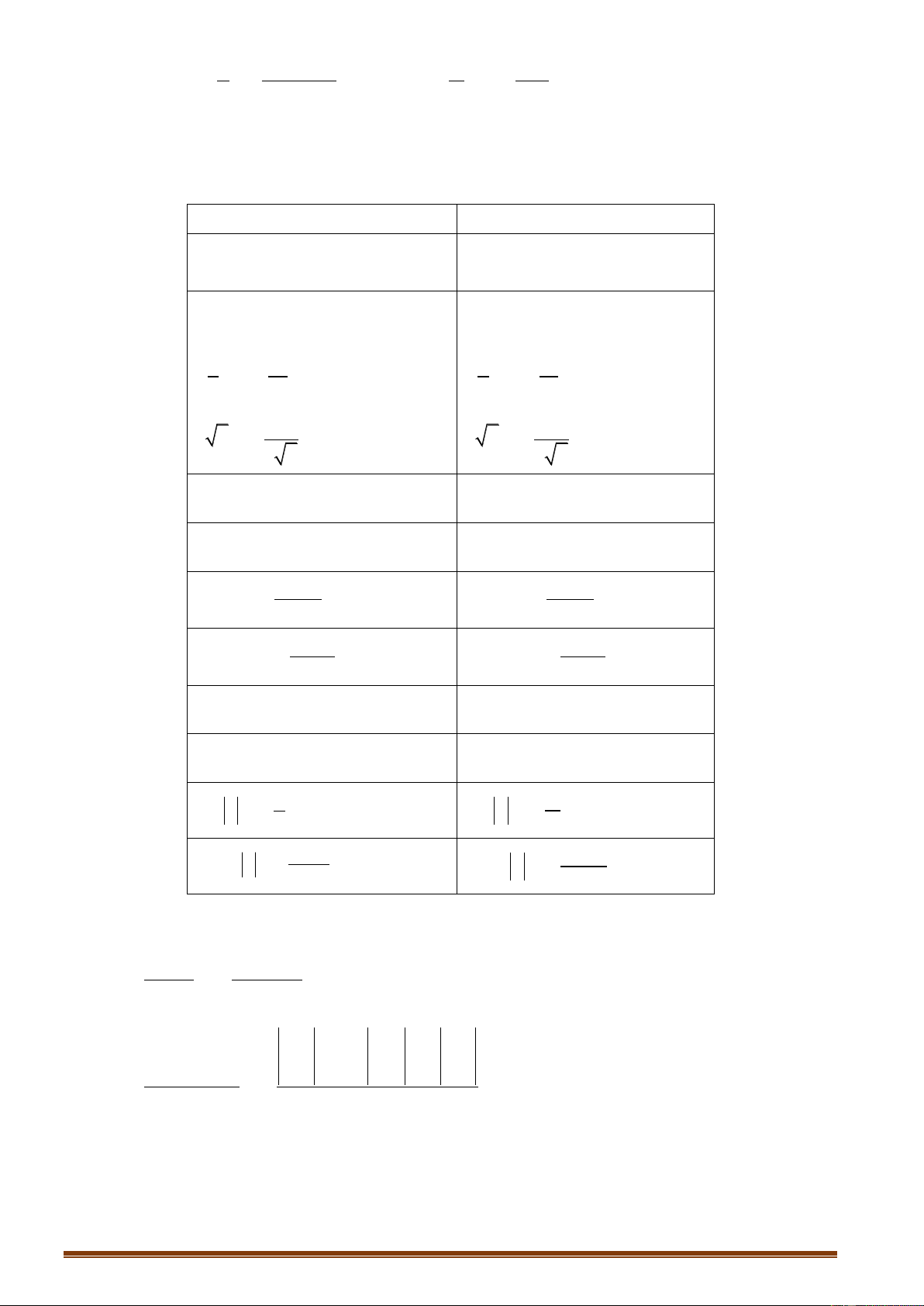
Đạo hàm của hàm sơ cấp
Đạo hàm của hàm hợp    
C   0 (C là hằng số). x     x 1 .      x      x 1 . u  1
.u  .u    1  1  1  u     (x  0)     u  0  x  x 2  u  u 2  1  u  x   x  0
 u  u  0 2 x 2 u
sinx cosx
sinu u.cosu
cosx  sinx
cosu  u.sinu  1  t an x   tan    u u 2 cos x 2 cos u  1  cot x    cot     u u 2 sin x 2 sin u
 x   x e e
 u    u e u e .
 x   x a a . ln a
 u    u a u a . . ln a  1  ln x   ln    u u x u    u x  log u a    a  1 log x ln a u. ln a
1.4 . Công thức tính nhanh đạo hàm hàm phân thức   ax  b  ad   bc    . cx   d   2 cx  d  a b a c b c x 2  2 x   2     d e d f e f  ax bx c    .
dx 2  ex  f    2
dx 2  ex  f 
1.5. Đạo hàm cấp 2 1.5.1. Định nghĩa Trang 2 
f  x   f 
 x
1.5.2. Ý nghĩa cơ học
Gia tốc tức thời của chuyển động s  f t  tại thời điểm t là: a t   f  t . 0 0  0
1.5.3. Đạo hàm cấp cao n 1 f x n  f x    
, n  , n    2   . * Một số chú ý:
 Nếu hàm số f x  và g x  cùng đồng biến (nghịch biến) trên K thì hàm số
f x   g x  cũng đồng biến (nghịch biến) trên K.Tính chất này có thể không đúng
đối với hiệu f x   g x  .
 Nếu hàm số f x  và g x  là các hàm số dương v| cùng đồng biến (nghịch biến) trên
K thì hàm số f x  g
. x  cũng đồng biến (nghịch biến) trên K.Tính chất này có thể
không đúng khi c{c h|m số f x ,g x  không là các hàm số dương trên K.
 Cho hàm số u  u x , x{c định với x  a b
;  và u x   c;d  . Hàm số f ux   cũng
x{c định với x  a b ;  .
Ta có nhận xét sau:
 Giả sử hàm số u  u x  đồng biến với x  a b
;  . Khi đó, h|m số f ux   đồng biến
với x  a;b  f u  đồng biến với uc;d .
 Giả sử hàm số u  u x  nghịch biến với xa;b . Khi đó, h|m số f u x    nghịch
biến với x a;b  f u nghịch biến với u  c d ;  .
Quy tắc xét tính đơn điệu của hàm số.
Giả sử hàm số f có đạo hàm trên K
 Nếu f 'x   0 với mọi x  K và f 'x   0 chỉ tại một số hữu hạn điểm
xK thì hàm số f đồng biến trên K .
 Nếu f 'x   0 với mọi x  K và f 'x   0 chỉ tại một số hữu hạn điểm
x  K thì hàm số f nghịch biến trên K . Chú ý: ax  b  d 
* Đối với hàm phân thức hữu tỉ y 
x    thì dấu "  " khi xét dấu cx  d c  
đạo hàm y  không xảy ra.
Giả sử y  f x   ax 3  bx2  cx  d  f x   ax2 3  b 2 x  c.
Hàm số đồng biến trên 
Hàm số nghịch biến trên  Trang 3  a   0 a  0      0    0    
f  x   0; x     a   0 . 
 f x   0; x     a   0 .     b   0  b   0   c  0  c  0 
Trường hợp 2 thì hệ số c khác 0 vì khi a  b  c  0 thì f x   d
(Đường thẳng song song hoặc trùng với trục Ox thì không đơn điệu)
* Với dạng toán tìm tham số m để hàm số bậc ba đơn điệu một chiều trên khoảng có độ
dài bằng l ta giải như sau:
Bước 1: Tính y  f x m   ax2 ;  bx  c.
Bước 2: Hàm số đơn điệu trên x ;x   y  0 có 2 nghiệm phân biệt 1 2   0   * a  0 
Bước 3: Hàm số đơn điệu trên khoảng có độ dài bằng l  2 x  x
 l  x  x  4  2 2
 S  4P  l * * 1 2  x x l2 1 2 1 2
Bước 4: Giải * và giao với * * để suy ra giá trị m cần tìm.
2. CỰC TRỊ HÀM SỐ 2.1. Định nghĩa
Giả sử hàm số f x{c định trên tập K và x  K . Ta nói: 0
 x là điểm cực tiểu của hàm số f nếu tồn tại một khoảng  ;ab chứa x sao cho 0 0
 ;ab  K và f x  f x ,x a b;\ x .Khi đó f x được gọi là giá trị cực tiểu 0  0 0 của hàm số f .
 x là điểm cực đại của hàm số f nếu tồn tại một khoảng a;b chứa x sao cho 0 0
 ;ab  K và f x  f x ,x a b;\ x .Khi đó f x được gọi là giá trị cực đại 0  0 0 của hàm số f .
 Điểm cực đại v| điểm cực tiểu gọi chung là điểm cực trị.
 Giá trị cực đại và giá trị cực tiểu gọi chung là cực trị.
 Điểm cực đại v| điểm cực tiểu được gọi chung là điểm cực trị củahàm số v| điểm cực
trị phải là một điểm trong tập hợp K.
 Giá trị cực đại và giá trị cực tiểu được gọi chung là giá trịcực trị (hay cực trị) củahàmsố. Trang 4
 Nếu x l| điểm cực trị của hàm số thì điểm x ;f x được gọi là điểm cực trị của 0 0  0
đồ thị hàm số f . * Nhận xét:
 Giá trị cực đại (cực tiểu) f x nói chung không phải là giá trị lớn nhất (nhỏ nhất) của 0 
hàm số f trên tập D; f x chỉ là giá trị lớn nhất (nhỏ nhất) của hàm số f trên một 0 
khoảng a;b n|o đó chứa x hay nói cách khác khi x điểm cực đại ( cực tiểu) sẽ tồn 0 0
tại khoảng (a;b) chứa x sao cho f x là giá trị lớn nhất (nhỏ nhất) của hàm số f trên 0  0
khoảng a;b.
 Hàm số f có thể đạt cực đại hoặc cực tiểu tại nhiều điểm trên tập K . Hàm số có thể
không có cực trị trên một tập cho trước.
2.2. Điều kiện cần để hàm số đạt cực trị
Định lí 1:
Giả sử hàm số y  f x  đạt cực trị tại điểm x . Khi đó, nếu y  f x  có đạo hàm tại điểm 0
x thì f  x 0. 0   0 Chú ý:
 Đạo hàm f x có thể bằng 0 tại điểm x nhưng h|m số f không đạt cực trị tại điểm 0 x . 0
 Hàm số có thể đạt cực trị tại một điểm mà tại đó h|m số không có đạo hàm.
 Hàm số chỉ có thể đạt cực trị tại một điểm mà tại đó đạo hàm của hàm số bằng 0 hoặc
tại đó h|m số không có đạo hàm.
2.3. Điều kiện đủ để hàm số đạt cực trị
Định lí 2:
Giả sử hàm số f đạt cực trị tại điểm x . Khi đó, nếu hàm số f có đạo hàm tại điểm x thì 0 0 f 'x  0. 0 
 Nếu f x   0 trên khoảng x  h;x và f x   0 trên khoảng x ;x  h thì x là 0 0  0 0  0
một điểm cực đại của h|m số f x .
 Nếu f x   0 trên khoảng x  h;x và f x   0 trên khoảng x ;x  h thì x là 0 0  0 0  0
một điểm cực tiểu của h|m số f x .
2.4. Quy tắc tìm cực trị Quy tắc 1:
 Bước 1: Tìm tập x{c định. Tìm f x . Trang 5
 Bước 2: Tìm c{c điểm x i  1;2;... mà tại đó đạo hàm của hàm số bằng 0 hoặc hàm số i
liên tục nhưng không có đạo hàm.
 Bước 3: Lập bảng biến thiên hoặc bảng xét dấu f x . Nếu f x đổi dấu khi đi qua x i
thì hàm số đạt cực trị tại x . i
Định lí 3:
Giả sử y  f x  có đạo h|m c}́p 2 trong khoảng x  h;x  h với h  0. Khi đó: 0 0 
 Nếu f x 0, f  x
0 thì hàm số f đạt cực đại tại x . 0   0   0
 Nếu f x  0, f  x
0 thì hàm số f đạt cực tiểu tại x . 0   0  0
Từ định lí trên, ta có một quy tắc khác để tìm cực trị của hàm số Quy tắc 2:
 Bước 1: Tìm tập x{c định. Tìm f x .
 Bước 2: Tìm các nghiệm x i  1;2;... của phương trình f x   0. i
 Bước 3:Tính f  x  và tính f  x . i 
 Nếu f  x   0 thì hàm số f đạt cực đại tại điểm x . i i
 Nếu f  x   0 thì hàm số f đạt cực tiểu tại điểm x . i i
3. MỘT SỐ DẠNG TOÁN LIÊN QUAN ĐẾN CỰC TRỊ HÀM SỐ
3.1. Cực trị của hàm đa thức bậc ba y  ax 3  bx 2  cx  d.
3.1.1. Tìm điều kiện để hàm số có cực đại, cực tiểu thỏa mãn hoành độ cho trƣớc
Bài toán tổng quát:
Cho hàm số y  f x m   ax 3  bx2 ;
 cx  d. Tìm tham số m để hàm số có cực
đại, cực tiểu tại x , x thỏa mãn điều kiện K cho trước? 1 2 Phương pháp:  Bước 1:
 Tập x{c định: D   .
 Đạo hàm: y  ax2  bx  c  Ax2 3 2  Bx C  Bước 2:
Hàm số có cực trị (hay có hai cực trị, hai cực trị phân biệt hay có cực đại và cực tiểu)
 y  0 có hai nghiệm phân biệt vày đổi dấu qua 2 nghiệm đó
 phương trình y  0 có hai nghiệm phân biệt A   a 3  0 a   0        m  D .   B 2  A 4 C  b2 4  1 a 2 c  0 b2  a 3 c 1  0  y    Bước 3: Trang 6
Gọi x , x là hai nghiệm của phương trình y   0. 1 2  B b 2 x  x      1 2 Khi đó: A a 3  . C c x  x.   1 2  A a 3  Bước 4:
Biến đổi điều kiện K về dạng t ổng S v| tích P . Từ đó giải ra tìm được m  D . 2  Bước 5:
Kết luận các giá trị m thỏa mãn: m  D  D . 1 2
* Chú ý: Hàm số bậc ba: y  ax 3  bx 2  cx  d a  0.
Ta có: y  ax 2 ' 3  b 2 x  c. Điều kiện Kết luận b2  a 3 c  0
Hàm số không có cực trị. b2  a 3 c  0
Hàm số có hai điểm cực trị.
 Điều kiện để hàm số có cực trị cùng dấu, trái dấu.
 Hàm số có 2 cực trị trái dấu
 phương trình y  0 có hai nghiệm phân biệt trái dấu  AC .  a
3 c  0  ac  0.
 Hàm số có hai cực trị cùng dấu
 phương trình y  0 có hai nghiệm phân biệt cùng dấu   0 y     C P  x x .   0  1 2  A
 Hàm số có hai cực trị cùng dấu dương
 phương trình y  0 có hai nghiệm dương ph}n biệt    0 y   B  S
  x  x    0 1 2 A  C
P  x x.   0 1 2  A
 Hàm số có hai cực trị cùng dấu âm
 phương trình y  0 có hai nghiệm âm phân biệt    0 y '  B  S
  x  x    0 1 2 A  C
P  x x.   0 1 2  A
 Tìm điều kiện để hàm số có hai cực trị x , x thỏa mãn: 1 2 Trang 7 x    x 1 2
x  x   1 2   x  x 1 2
 Hai cực trị x , x thỏa mãn x    x 1 2 1 2
 x  x    0  x x.   x  x  2    0 1 2 1 2 1 2
 Hai cực trị x , x thỏa mãn x  x   1 2 1 2
x x   0 x
 x.   x  x  2    0 1 2 1 2 1 2     x  x  2 x  x  2  1 2   1 2 
 Hai cực trị x , x thỏa mãn   x  x 1 2 1 2
x x   0 x
 x.   x  x  2    0 1 2 1 2 1 2     x  x  2 x  x  2  1 2   1 2 
 Phương trình bậc 3 có 3 nghiệm lập thành cấp số cộng b 
khi có 1 nghiệm là x 
, có 3 nghiệm lập thành cấp số nhân khi có 1 nghiệm là a 3 d x 3   . a
3.1.2. Tìm điều kiện để đồ thị hàm số có các điểm cực đại, cực tiểu nằm cùng phía, khác
phía so với một đƣờng thẳng
Vị trí tương đối giữa 2 điểm với đường thẳng:
Cho 2 điểm A x ;y , B x ;y v| đường thẳng  : ax  by  c  0. A A   B B 
Nếu ax  by  c ax  by  c  0 thì hai điểm A, B nằm về A A  B B 
hai phía so với đường thẳng . 
Nếu ax  by  c ax  by  c  0 thì hai điểm A, B nằm cùng A A  B B 
phía so với đường thẳng . 
Một số trường hợp đặc biệt:
 C{c điểm cực trị của đồ thị nằm cùng về 1 phía đối với trục Oy
 hàm số có 2 cực trị cùng dấu
 phương trình y  0 có hai nghiệm phân biệt cùng dấu
 C{c điểm cực trị của đồ thị nằm cùng về 2 phía đối với trục Oy
 hàm số có 2 cực trị trái dấu
 phương trình y  0 có hai nghiệm trái dấu
 C{c điểm cực trị của đồ thị nằm cùng về 1 phía đối với trục Ox
 phương trình y  0 có hai nghiệm phân biệt và y y.  0 C Đ CT
Đặc biệt:
 C{c điểm cực trị của đồ thị nằm cùng về phía trên đối với trục Ox Trang 8 y  y .  0
 phương trình y  0 có hai nghiệm phân biệt và CĐ CT  y  y  0  CĐ CT 
 C{c điểm cực trị của đồ thị nằm cùng về phía dưới đối với trục Ox y  y .  0
 phương trình y  0 có hai nghiệm phân biệt và CĐ CT  y  y  0  CĐ CT 
 C{c điểm cực trị của đồ thị nằm về 2 phía đối với trục Ox
 phương trình y  0 có hai nghiệm phân biệt và y y.  0 C Đ CT
(áp dụng khi không nhẩm được nghiệm và viết được phương trình đường thẳng đi qua
hai điểm cực trị của đồ thị hàm số)
Hoặc: C{c điểm cực trị của đồ thị nằm về 2 phía đối với trục Ox
 đồ thị cắt trục Ox tại 3 điểm phân biệt
 phương trình ho|nh độ giao điểm f x   0 có 3 nghiệm phân biệt (áp
dụng khi nhẩm được nghiệm)
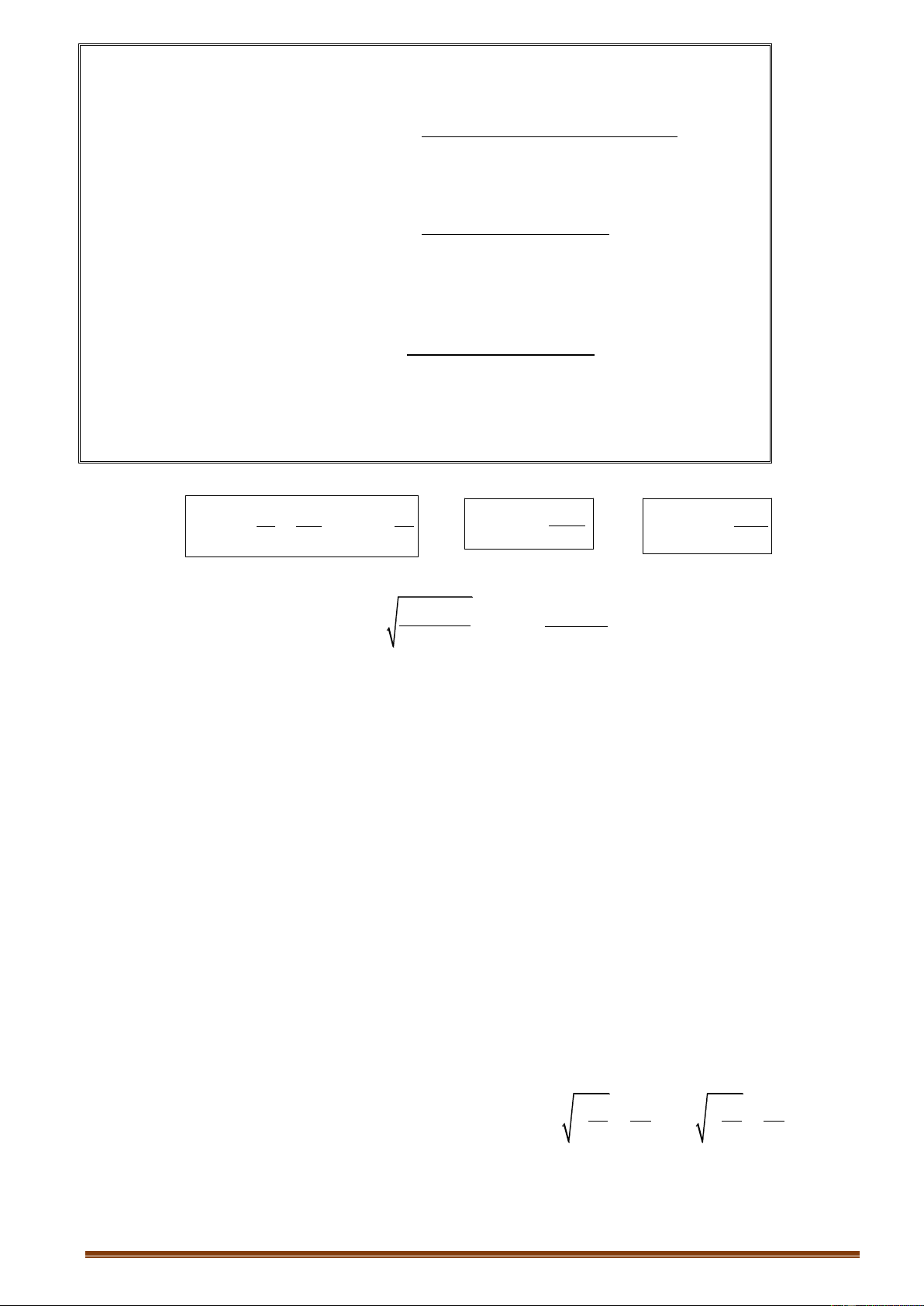
3.1.3. Phƣơng trình đƣờng thẳng qua các điểm cực trị    c b2 2 2  bc y y .  g x    x  d  hoặc g x  
 y  . . hoặc   y y g x  y  3 a 9 a 9   18a y 3 
3.1.4. Khoảng cách giữa hai điểm cực trị của đồ thị hàm số bậc 3 là e  e3 4 16 b2  a 3 c A B  với e  a a 9
3.2. Cực trị của hàm bậc 4 trùng phƣơng y  ax 4  bx 2  c, a  0
3.2.1. Một số kết quả cần nhớ
 Hàm số có một cực trị  ab  0.
 Hàm số có ba cực trị  ab  0. a   0
 Hàm số có đúng một cực trị và cực trị là cực tiểu   . b  0  a   0
 Hàm số có đúng một cực trị và cực trị là cực đại   . b  0  a   0
 Hàm số có hai cực tiểu và một cực đại   . b  0  a   0
 Hàm số có một cực tiểu và hai cực đại   . b  0 
3.2.2. Một số công thức tính nhanh     b  b  Giả sử hàm số y ax 4 bx 2  
 c có 3cực trị:A(0;c),B    ;  ,C   ;    a 2 a 4   a 2 a 4     
tạo thành tam giác A BC thỏa mãn dữ kiện: ab  0 Đặt: · BAC = a  Trang 9 y  b3  2  Tổng quát: cot 2 a 8 A O x B C Dữ kiện Công thức
thỏa mãn ab  0;c  0
Tam giác A BC vuông cân tại A b3   a 8 Tam giác A BC đều b3   a 24
Tam giác A BC có diện tích S  S a 3 32 S 2 ( )  b5  0 A  BC 0 0
Tam giác A BC có diện tích max S ( ) 5 0 b S   0 a 3 32
Tam giác A BC có b{n kính đường tròn nội b2 r  tiếp r  r  3  A  BC 0 b 4 a 1  1    a 8   
Tam giác A BC có b{n kính đường tròn ngoại b3  a 8 tiếp R  R R  A  BC 8 a b
Tam giác A BC có độ dài cạnh BC  m 2   am b 2 0 0 0
Tam giác A BC có độ dài A B  A C  n a 16 n 2 2  b4  a 8 b  0 0 0
Tam giác A BC có cực trị B ,C Ox b2  a 4 c
Tam giác A BC có 3 góc nhọn b a  b3 (8 )  0
Tam giác A BC có trọng tâm O b2  a 6 c
Tam giác A BC có trực tâm O b3  a 8  a 4 c  0
Tam giác A BC cùng điểm O tạo thành hình b2  a 2 c thoi
Tam giác A BC có O l| t}m đường tròn nội b3  a 8  a 4 bc  0 tiếp
Tam giác A BC có O l| t}m đường tròn ngoại b3  a 8  a 8 bc  0 tiếp
Tam giác A BC có cạnh BC  kA B  kA C
b3 k 2  a k 2 . 8 (  4)  0
Trục hoành chia tam giác A BC thành b2  4 2 ac
hai phần có diện tích bằng nhau
Tam giác A BC có điểm cực trị c{ch đều trục b2  a 8 c hoành
Đồ thị hàm số C  y ax 4 bx2 :    c cắt trục 100 b2  ac 9 Trang 10
Ox tại 4 điểm phân biệt lập thành cấp số cộng
Định tham số để hình phẳng giới hạn bởi đồ 36
thị C  y ax 4 bx2 :  
 c và trục hoành có b2  ac 5
diện tích phần trên và phần dưới bằng nhau.
Phương trình đường tròn ngoại tiếp ABC  là:  2    2  
x 2  y 2   
 c y  c     0 b a 4 b a 4    
4. GIÁ TRỊ LỚN NHẤT - GIÁ TRỊ NHỎ NHẤT 4.1. Định nghĩa.
Cho hàm số y  f x  x{c định trên tập . D
f (x)  M, x   D
 Số M gọi là giá trị lớn nhất của hàm số y  f x  trên D nếu:  . Kí x
  D, f (x )  M  0 0 
hiệu: M  max f (x) . x D 
f (x)  m, x   D
 Số m gọi là giá trị nhỏ nhất của hàm số y  f x  trên D nếu:  . Kí x
  D, f (x )  m  0 0 
hiệu: m  min f (x ) . x D 
4.2. Phƣơng pháp tìm GTLN,GTNN
4.2.1. Tìm GTLN, GTNN của hàm số bằng cách khảo sát trực tiếp
 Bước 1: Tính f x v| tìm c{c điểm x ,x ,...,x D mà tại đó f x   0 hoặc hàm số 1 2 n không có đạo hàm.
 Bước 2:Lập bảng biến thiên và từ đó suy ra gi{ trị lớn nhất, giá trị nhỏ nhất của hàm số.
4.2.2. Tìm GTLN, GTNN của hàm số trên một đoạn  Bước 1:
 Hàm số đã cho y  f x  x{c định và liên tục trên đoạn a;b  .
 Tìm c{c điểm x ,x ,...,x trên khoảng a;b , tại đó f x   0 hoặc f x  không xác 1 2 n định.
 Bước 2: Tính f a, f x , f x ,..., f x , f b . 1 2 n   
 Bước 3: Khi đó:
 max f x   max  
f x ,f x ,...,f x ,f a ,f b . 1 2 n      a b ,  
 min f x   min f x , f x ,..., f x , f a , f b .  1 2 a b ,      
 n       
4.2.3. Tìm GTLN, GTNN của hàm số trên một khoảng
 Bước 1:Tính đạo hàm f (x) . Trang 11
 Bước 2:Tìm tất cả các nghiệm x  a
( ;b) của phương trình f (
 x)  0 và tất cả c{c điểm i   a
( ;b) làm cho f (
 x) không x{c định. i
 Bước 3. Tính A  lim f x
( ) , B  lim f x
( ) , f (x ) , f ( ) .   i i x a  x b 
 Bước 4.So sánh các giá trị tính được và kết luận M  maxf x
( ) , m  min f x ( ) . (a b ; ) (a b ; )
Nếu giá trị lớn nhất (nhỏ nhất) là A hoặc B thì ta kết luận không có giá trị lớn nhất (nhỏ nhất). Chú ý:
min f x   f a     Nếu a b ;
y  f x  đồng biến trên a  ;b   thì    . max f 
x  f b a  b ;    
min f (x)  f b   a b;
Nếu y  f x  nghịch biến trên a  ;b   thì    . max f (x)   f a  a b ;    
 Hàm số liên tục trên một khoảng có thể không có giá trị lớn nhất, giá trị nhỏ nhất trên khoảng đó.
5. ĐƢỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
5.1. Đƣờng tiệm cận ngang
Cho hàm số y  f (x ) x{c định trên một khoảng vô hạn (là khoảng dạng a;, ;b hoặc  ;
 ). Đường thẳng y  y l| đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị 0
hàm số y  f (x ) nếu ít nhất một trong c{c điều kiện sau được thỏa mãn:
lim f (x )  y , lim f (x )  y x 0  x 0 
5.2. Đƣờng tiệm cận đứng
Đường thẳng x  x được gọi l| đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị 0
hàm số y  f (x) nếu ít nhất một trong c{c điều kiện sau được thỏa mãn:
lim f (x )  , lim f (x )  , lim f (x)  , lim f (x)       x x x x xx xx 0 0 0 0 ax  b
Lưu ý: Với đồ thị hàm phân thức dạng y 
c  0; ad  bc  0 luôn có tiệm cận cx  d ngang là  a y
và tiệm cận đứng   d x . c c
6. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ HÀM SỐ
6.1.Khảo sát một số hàm đa thức và hàm phân thức
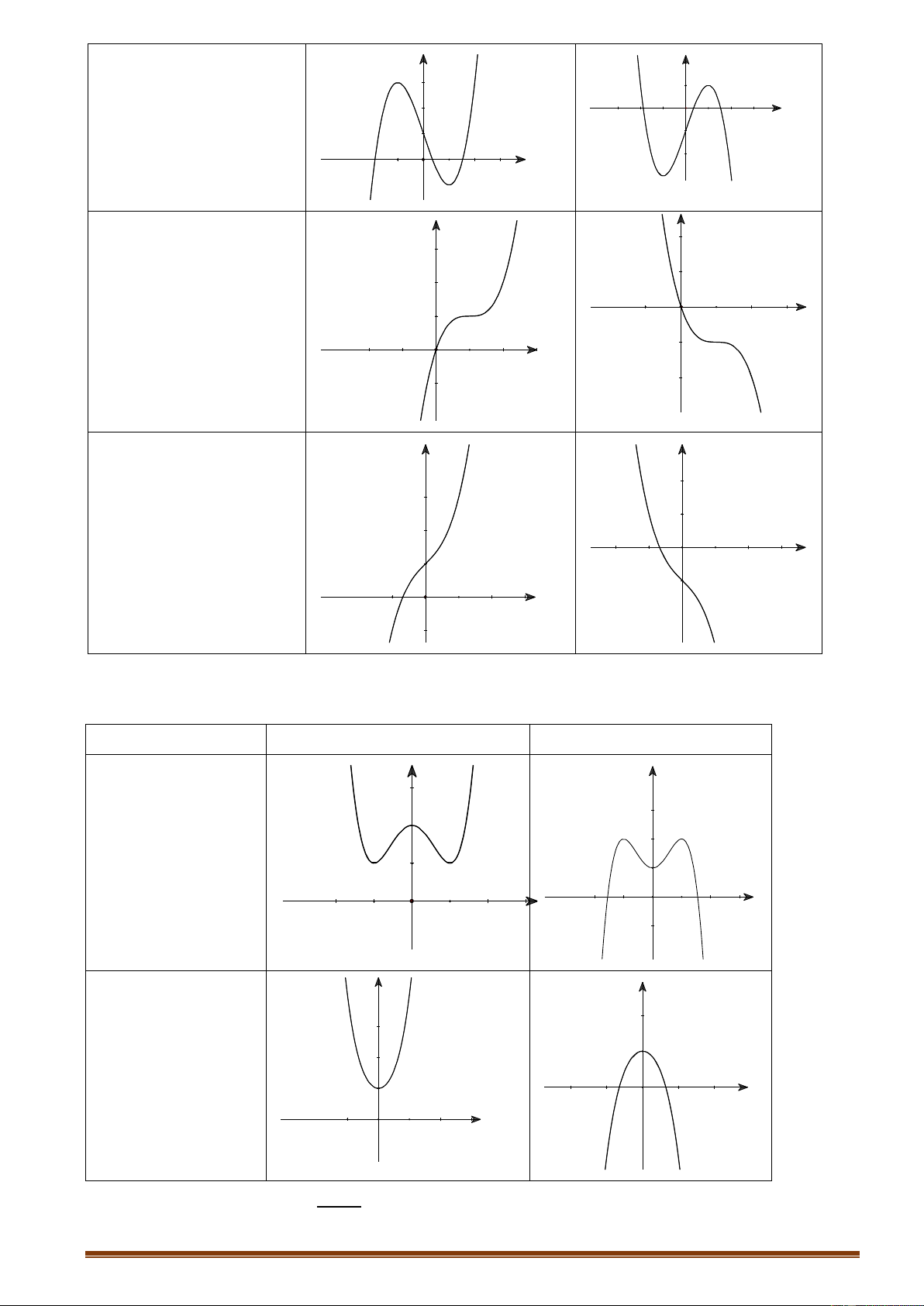
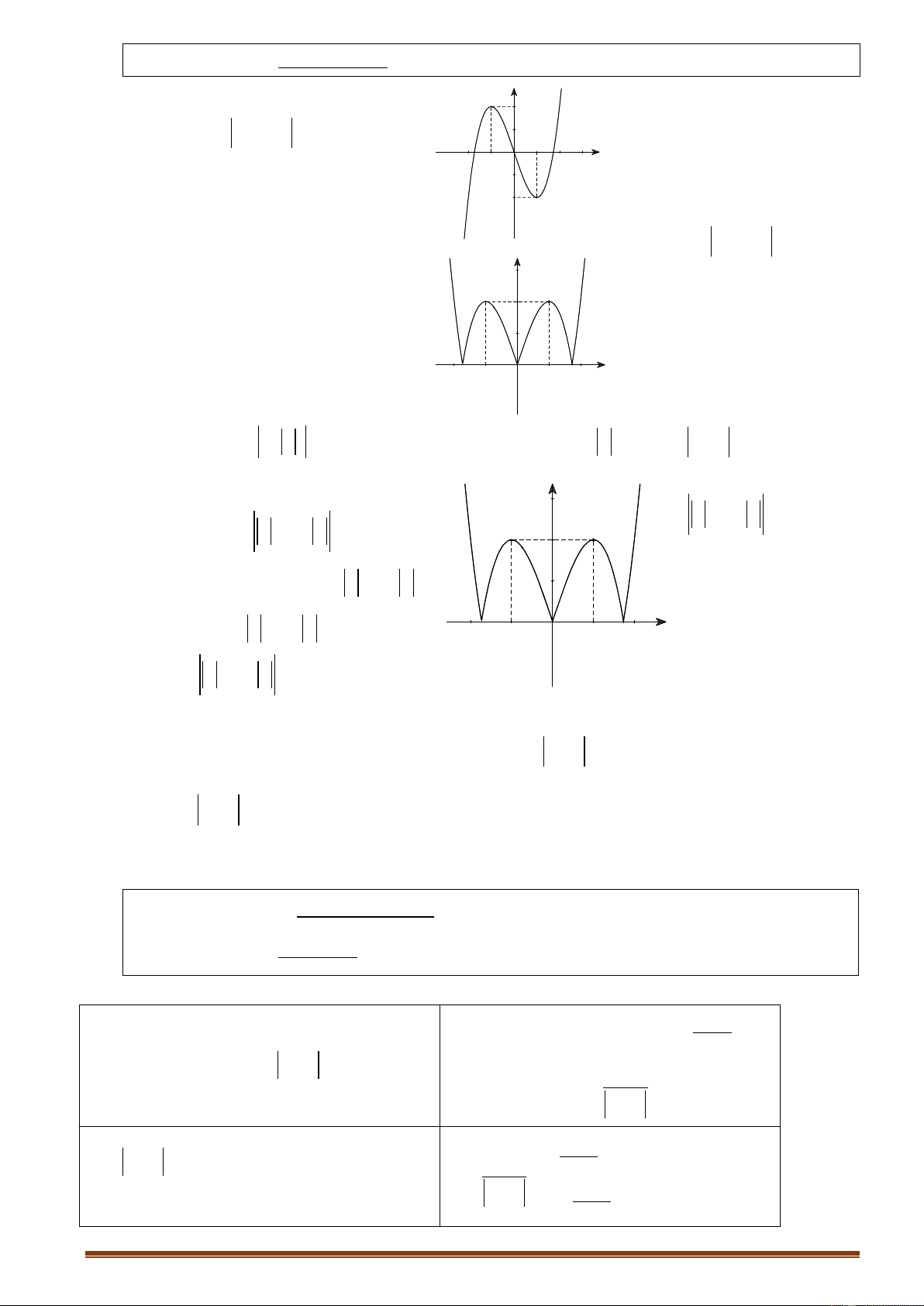
6.1.1. Hàm số bậc ba y  ax 3  bx 2  cx  d a  0 TRƢỜNG HỢP a  0 a  0 Trang 12
Phương trình y/  0 có y y 1
2 nghiệm phân biệt 1 O x 1 1 O x Phương trình y y /  0 có y nghiệm kép 1 1 1 O x 1 O x Phương trình / y  0 vô y y nghiệm 1 O 1 1 x 1 O x
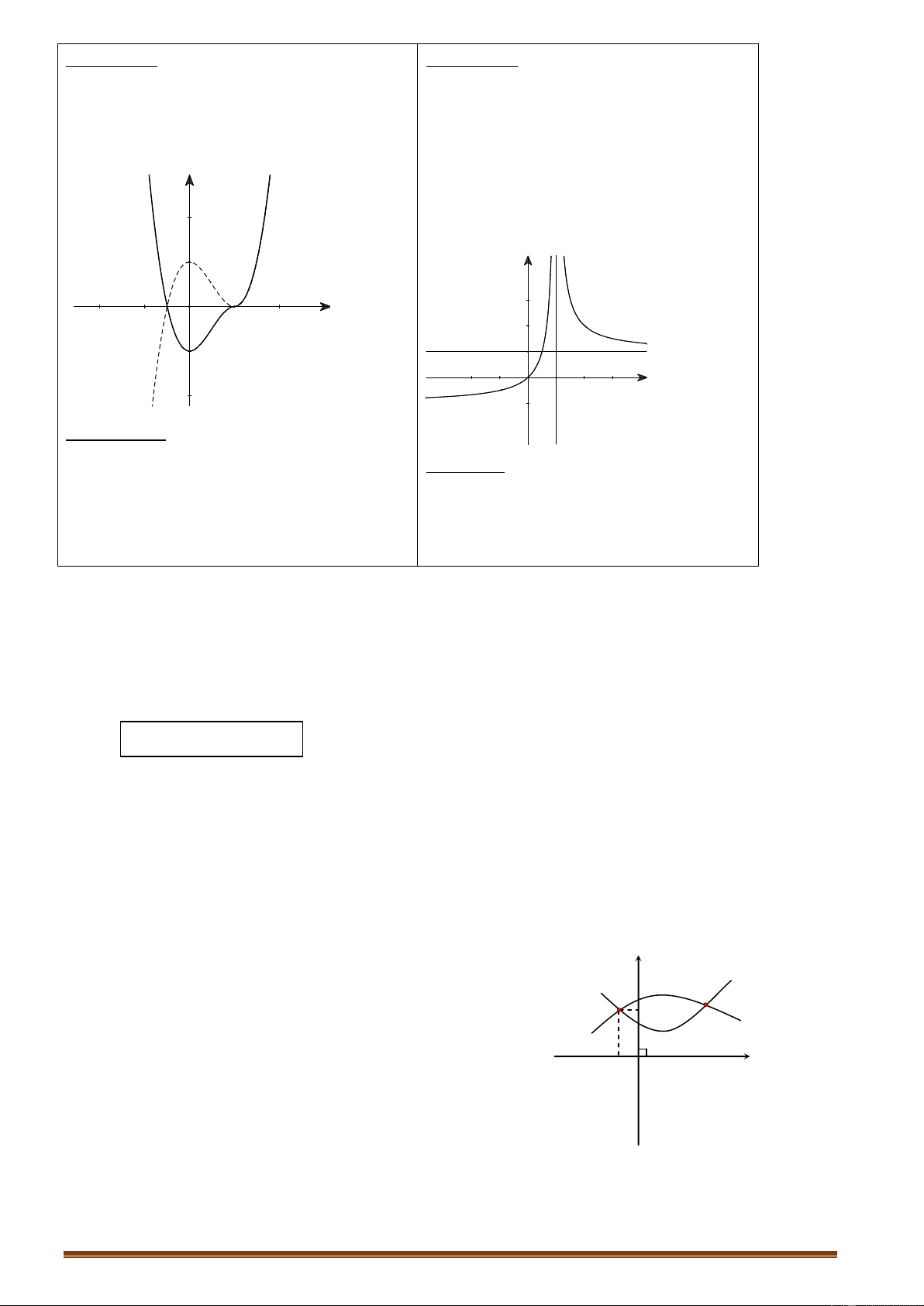
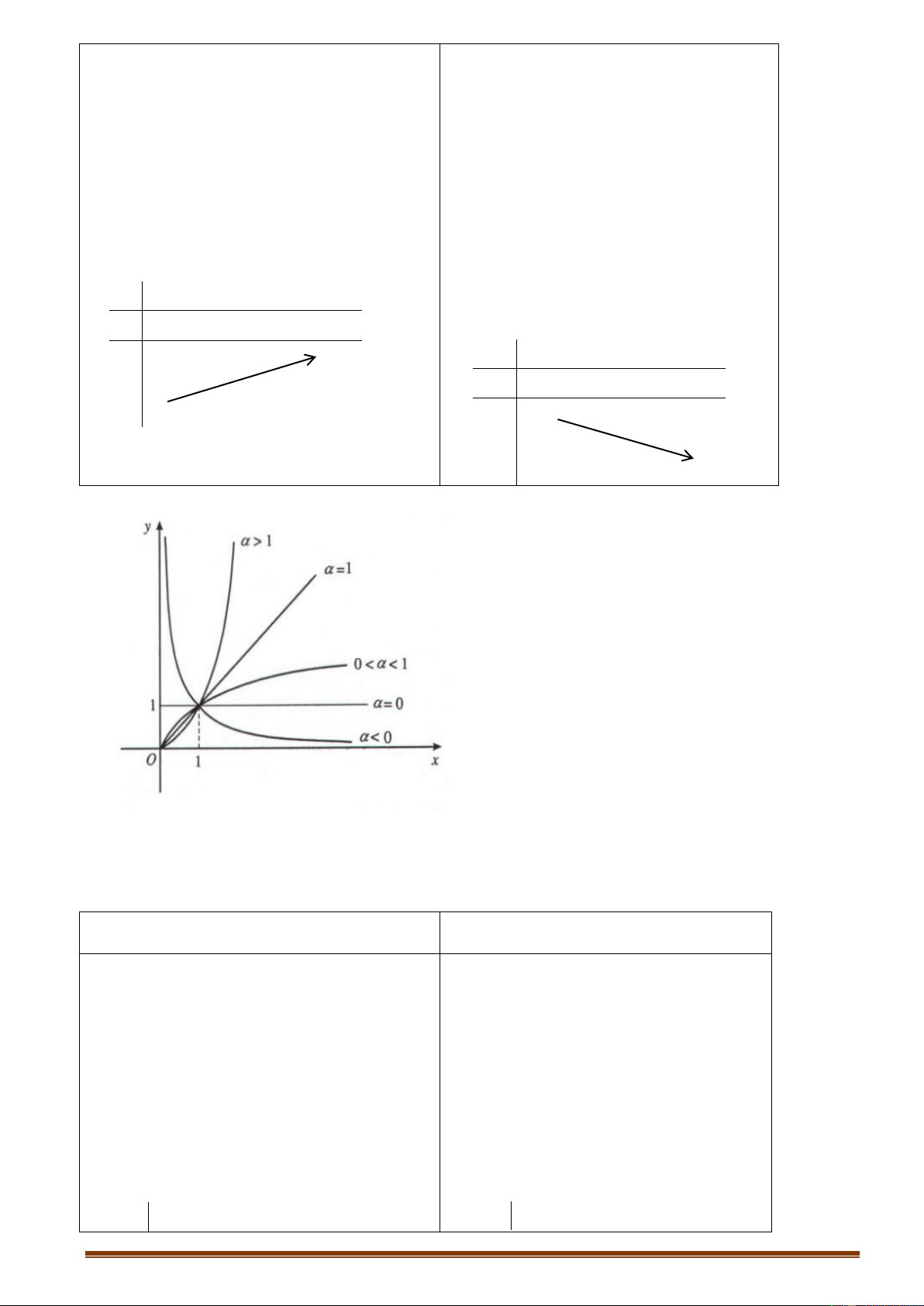
6.1.2. Hàm số trùng phƣơngy  ax 4  bx 2  c a  0 TRƢỜNG HỢP a  0 a  0
Phương trình y/  0 y y có
3 nghiệm phân biệt (ab<0) 1 1 1 1 O O x x
Phương trình y/  0 y y có 1 nghiệm. 1 1 1 O x 1 O x ax  b
6.1.3. Hàm số nhất biến y 
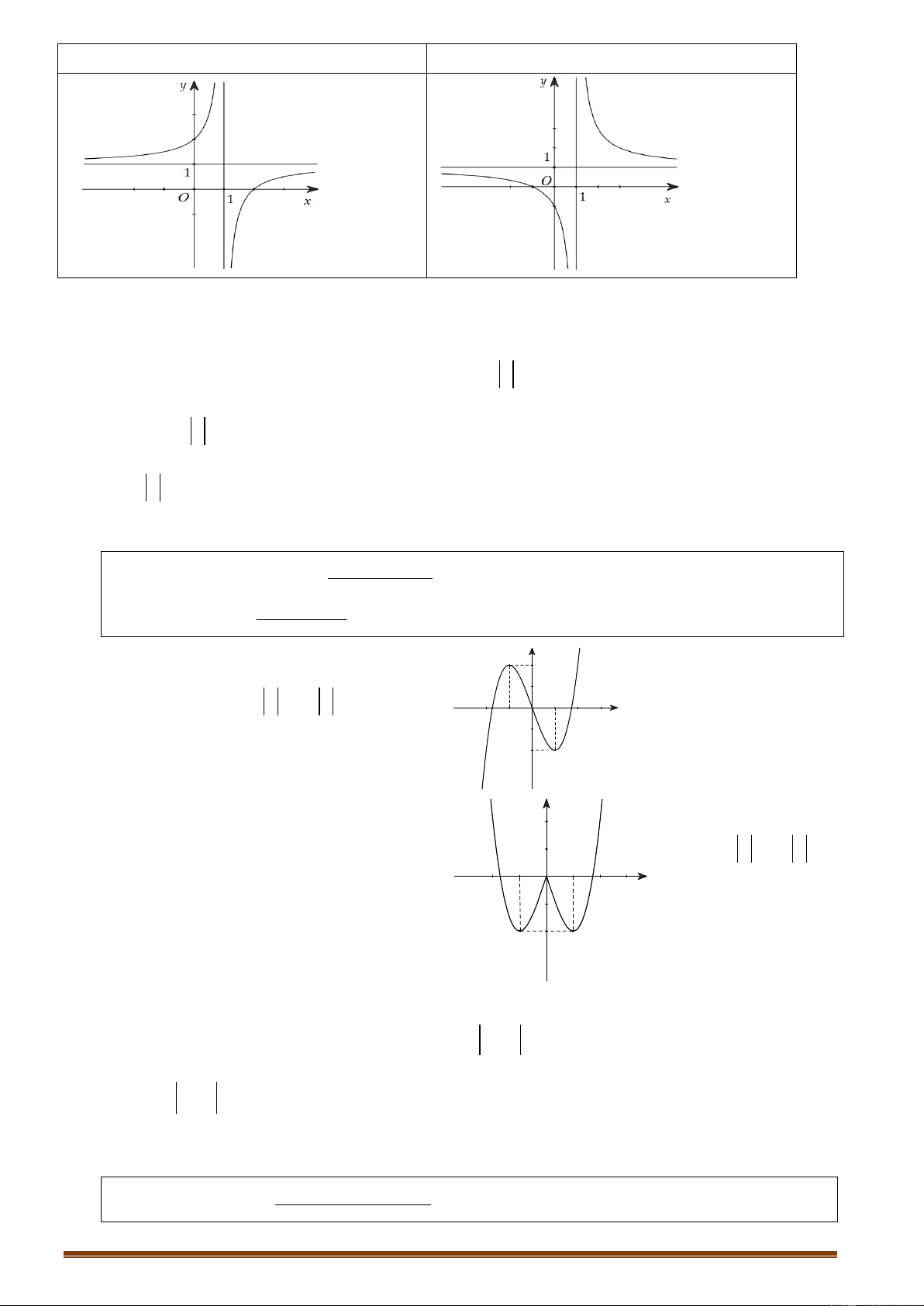
c  0, ad  bc  0 cx  d Trang 13
D  ad  bc  0
D  ad  bc  0
6.2. Một số phép biến đổi đồ thị 6.2.1. Dạng 1
Từ đồ thị C  : y  f x  suy ra đồ thị C  : y  f  x  . f x khi x  0
Ta có:y  f  x      f   x   khi x  0
và y  f  x  là hàm chẵn nên đồ thị C nhận Oy làm trục đối xứng.
* Cách vẽ C  từ C  :
 Giữ nguyên phần đồ thị bên phải Oy của đồ thị C  : y  f x .
 Bỏ phần đồ thị bên trái Oy của C  , lấy đối xứng phần đồ thị được giữ qua Oy.
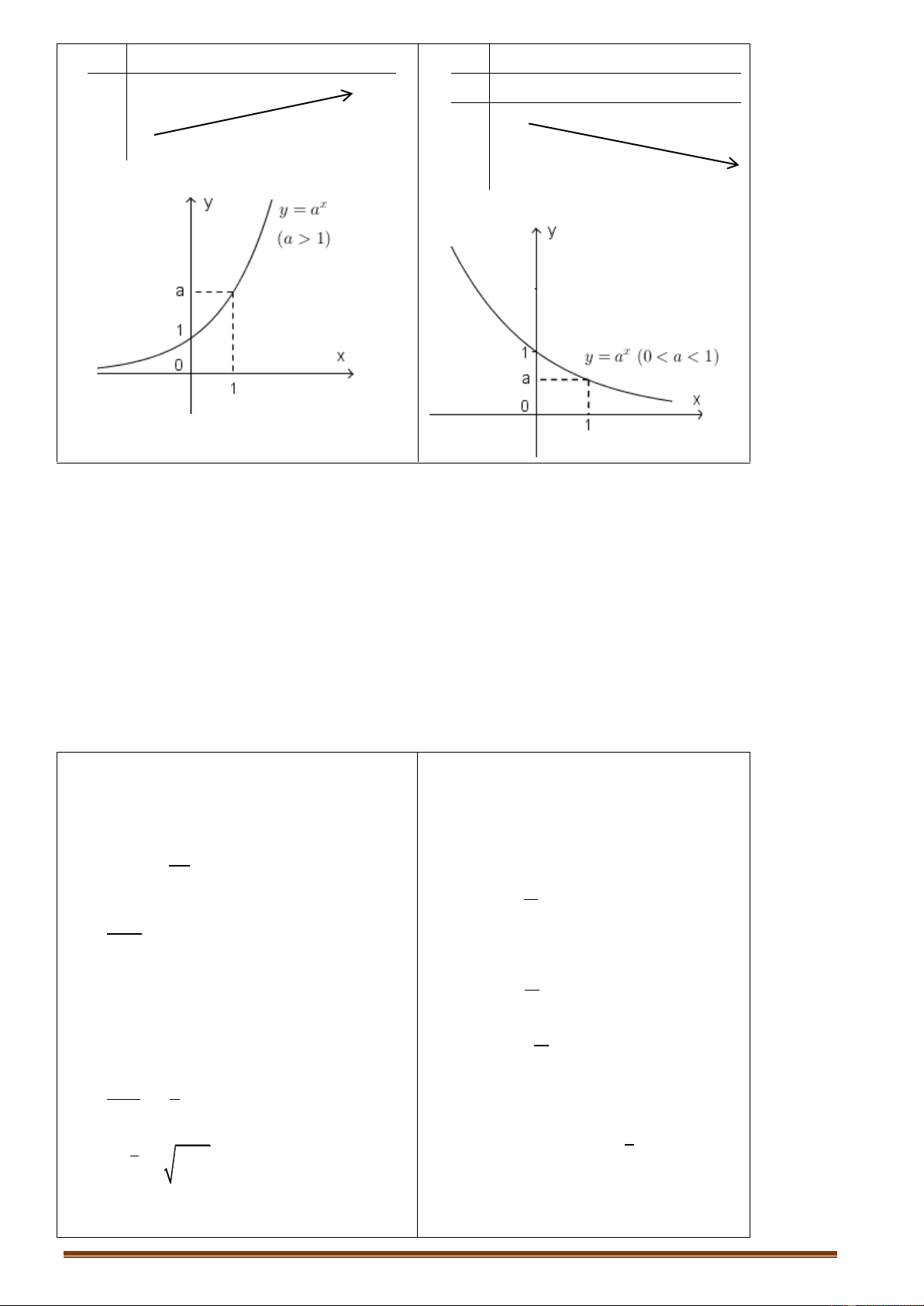
Ví dụ: Từ đồ thị C  y  f x   x 3 :  x 3 y 2
C  y  x3 :  x 3 3
suy ra đồ thị C  : y  x  3 x . 1 O -1 x
Biến đổi C  : -2
 Bỏ phần đồ thị của C  bên trái y
Oy, giữ nguyên C  bên phải . Oy  3
C  : y  x   3 x
Lấy đối xứng phần đồ thị được -1 O 1 giữ qua Oy . x -2 6.2.2. Dạng 2
Từ đồ thị C  : y  f x  suy ra đồ thị C  : y  f x  . f x khi f x  0
Ta có: y  f x       
f x  khi f x    0
* Cách vẽ C  từ C :
 Giữ nguyên phần đồ thị phía trên Oxcủa đồ thị (C):y  f x  . Trang 14
 Bỏ phần đồ thị phía dưới Oxcủa (C), lấy đối xứng phần đồ thị bị bỏ qua Ox.
Ví dụ: Từ đồ thị C y  f x 3 :  x  3x y 2 C 3
: y  x  3x
suy ra đồ thị y  x 3  x 3 . 1 O -1 x
Biến đổi C :  -2
Bỏ phần đồ thị của C  dưới
C y  x3 :  x 3
Ox, giữ nguyên C  phía trên y . Ox 2
 Lấy đối xứng phần đồ thị bị bỏ qua Ox . -1 O 1 x
Chú ý với dạng: y  f  x  ta lần lượt biến đổi 2 đồ thị y  f  x  và y  f x 
Ví dụ: Từ đồ thị C  y  f x   x 3 :  x 3 y  3
C  : y  x  3 x 3
suy ra đồ thị y  x  3 x . Biến đổi 2  3
C  để được đồ thị C  : y  x  3 x . 3
Biến đổi C  : y  x  3 x ta được đồ -1 O 1 x 3
thị C  : y  x  3 x . 6.2.3. Dạng 3
Từ đồ thị C  : y  u x  v
. x  suy ra đồ thị C  : y  u x  v . x  . u
 x v. x  f x khi u x  0
Ta có: y  u x  v . x            u 
 x  v. x   f x  khi u x   0
* Cách vẽ C  từ C :
 Giữ nguyên phần đồ thị trên miền u x   0 của đồ thị C  : y  f x .
 Bỏ phần đồ thị trên miềnu x   0 của C  , lấy đối xứng phần đồ thị bị bỏ qua Ox. Ví dụ
a) Từ đồ thị C  y  f x   x 3  x2 : 2 3  1 x
b) Từ đồ thị C  : y  f x   suy x  1
suy ra đồ thị C  y  x   x2 : 1 2  x   1 x
ra đồ thị C  : y  x  1 f x khi x 1  x khi x  x 1;  
y  x  1  x2 2
 x      
1  f x khi x   x  1  1 y    . x  1
 x khi x    ;1  x  1 Trang 15 Đồ thị (C’): Đồ thị (C’):
 Giữ nguyên (C) với x  1.
 Bỏ phần đồ thị của C  với
 Bỏ (C) với x  1. Lấy đối xứng x  ,
1 giữ nguyên C  với
phần đồ thị bị bỏ qua Ox. x  1. y (C')
 Lấy đối xứng phần đồ thị bị bỏ qua Ox. 1 y O 1 x 1 O (C) 1 x
Nhận xét: Trong quá trình thực hiện
phép suy đồ thị nên lấy đối xứng các điểm Nhận xét: Đối với hàm phân thức thì
đặc biệt của (C): giao điểm với Ox, Oy, nên lấy đối xứng các đường tiệm cận để CĐ, CT…
thực hiện phép suy đồ thị một cách tương đối chính xác. 7. TIẾP TUYẾN 7.1. Tiếp tuyến
Cho hàm số y  f  x , có đồ thị (C). Tiếp tuyến của đồ thị (C) tại điểm M x ;y   C ( ) có 0 0 0
dạng: y  f  x x  x   y . 0 0 0 Trong đó:
Điểm M x ;y   C
( ) được gọi là tiếp điểm. ( với y  f x ) và k  f ' x là hệ số góccủa 0  0 0  0 0 0 tiếp tuyến.
7.2. Điều kiện tiếp xúc
Cho hai hàm số C  : y  f x  và C ' : y  g x . Đồ thị C  và C  tiếp xúc nhau khi chỉ y
f x   gx 
khi hệ phương trình:  có nghiệm. f / x    /  g x  y0 x
8. TƢƠNG GIAO ĐỒ THỊ x0 O
Cho hàm số y  f (x ) có đồ thị C (
) và y  g(x ) có đồ thị (C ) . 1 2
Phương trình ho|nh độ giao điểm của C (
) và (C ) là f x ( )  g x ( )   1 . Khi đó: 1 2
 Số giao điểm của (C ) và C (
) bằng với số nghiệm của phương trình   1 . 1 2
 Nghiệm x của phương trình 1 chính l| ho|nh độ x của giao điểm. 0 0 Trang 16
 Để tính tung độ y của giao điểm, ta thay ho|nh độ x vào y  f x  hoặc y  g x . 0 0
 Điểm M x ; y l| giao điểm của C ( ) và C ( ) . 0 0  1 2
9. ĐIỂM ĐẶC BIỆT CỦA HỌ ĐƢỜNG CONG
9.1. Bài toán tìm điểm cố định của họ đƣờng cong
Xét họ đường cong C (
) có phương trình y  f (x, m ) , trong đó f là h|m đa thức theo biến m
x với m là tham số sao cho bậc của m không quá 2. Tìm những điểm cố định thuộc họ đường
cong khi m thay đổi? Phƣơng pháp giải:
 Bước 1: Đưa phương trình y  f (x, )
m về dạng phương trình theo ẩn m có dạng sau:
A m  B  0 hoặc A m 2  Bm  C  0 .
 Bước 2:Cho các hệ số bằng 0 , ta thu được hệ phương trình v| giải hệ phương trình: A   0 A  0   hoặc B  0 . B   0 C   0
 Bước 3:Kết luận:
- Nếu hệ vô nghiệm thì họ đường cong C (
) không có điểm cố định. m
- Nếu hệ có nghiệm thì nghiệm đó l| điểm cố định của C ( ) . m
9.2. Bài toán tìm điểm có tọa độ nguyên Cho đường cong C
( ) có phương trình y  f (x ) (hàm phân thức). Hãy tìm những điểm có
tọa độ nguyên của đường cong?
Những điểm có tọa độ nguyên là những điểm sao cho cả hoành độ và tung độ của điểm đó đều là số nguyên. Phƣơng pháp giải:
 Bước 1:Thực hiện phép chia đa thức chia tử số cho mẫu số.
 Bước 2:Lập luận để giải bài toán.
9.3. Bài toán tìm điểm có tính chất đối xứng
Cho đường cong (C) có phương trình y  f (x ) . Tìm những điểm đối xứng nhau qua một
điểm, qua đường thẳng.
Bài toán 1: Cho đồ thị C  y  Ax 3  Bx2 :
Cx  D trên đồ thị C  tìm những cặp điểm đối xứng
nhau qua điểmI (x , y ) . I I Phƣơng pháp giải:
 Gọi M a Aa3 Ba2 Ca D  N b Ab3 Bb2 ; , ;
Cb D  l| hai điểm trên C  đối
xứng nhau qua điểm I . Trang 17
a  b  x 2   Ta có  I . A a 3 (
 b3)  B a2 b2  C a b  D 2   y 2 I
Giải hệ phương trình tìm được a,b từ đó tìm được toạ độ M, N.
Bài toán 2: Cho đồ thị C  y  Ax 3  Bx2 :
Cx  D . Trên đồ thị C  tìm những cặp điểm đối
xứng nhau qua gốc tọa độ. Phƣơng pháp giải:
 Gọi M a Aa3 Ba2 Ca D  N b Ab3 Bb2 , , ,
Cb D  l| hai điểm trên C đối
xứng nhau qua gốc tọa độ. a  b  0   Ta có  . A a 3 (
 b3)  B a2 b2 C a b  D 2   0
 Giải hệ phương trình tìm đượca,b từ đó tìm được toạ độ M , N .
Bài toán 3: Cho đồ thị C  y  Ax 3  Bx2 :
Cx  D trên đồ thị C  tìm những cặp điểm đối xứng
nhau qua đường thẳng d : y  A x  B . 1 1 Phƣơng pháp giải:  Gọi M 3 2
a Aa  Ba Ca D  N  3 2 ; ,
b;Ab Bb C
 b D  l| hai điểm trên C đối xứng
nhau qua đường thẳng d . I d (1)   
Ta có:  
(với I l| trung điểm của MN và ud l| vectơ chỉ phương của MN u . d   0 (2) đường thẳng d ).
 Giải hệ phương trình tìm được M, N.
9.4. Bài toán tìm điểm đặc biệt, khoảng cách 9.4.1. Lý thuyết:  2 2
Cho hai điểm A x ;y ;B x ;y  A B  x  x 2 1   y  y 2 1  1 1 2 2 
 Cho điểm M x ;y v| đường thẳng d : Ax  By C  0 , thì khoảng cách từ M đến d 0 0  A x By C
là h M ;d     0 0 . A2  B 2   ax b
Cho hàm phân thức: y  cx  tiếp tuyến tại M cắt TCĐ,TCN ở A và B thì M là d 2
trung điểm của AB. Thì diện tích tam giác MA B không đổi: S  ad  bc . MA B c2
9.4.2. Các bài toán thƣờng gặp ax  b
Bài toán 1: Cho hàm số y 
c  0, ad bc  0 có đồ thị C . Hãy tìm trên C() hai điểm cx  d
A và B thuộc hai nhánh đồ thị hàm số sao cho khoảng cách A B ngắn nhất. Phƣơng pháp giải: Trang 18
 C  có tiệm cận đứng  d x
do tính chất của hàm phân thức, đồ thị nằm về hai c
phía của tiệm cận đứng. Nên gọi hai số  ,  là hai số dương.  d d d
Nếu A thuộc nhánh trái: x  
 x       ; y  f x ( ) . A A c c c A A  d d d
Nếu B thuộc nhánh phải: x  
 x       ; y  f (x ) . B B c c c B B  Sau đó tính: 2 2 2 2
A B 2  x  x y y a a y y . B A     B A 
              B A 
 Áp dụng bất đẳng thức Cauchy sẽ tìm ra kết quả.
Bài toán 2: Cho đồ thị hàm số C  có phương trình y  f (x). Tìm tọa độ điểm M thuộc (C) để tổng
khoảng cách từ M đến hai trục tọa độ nhỏ nhất.
Phƣơng pháp giải:
 Gọi M x;y và tổng khoảng cách từ Mđến hai trục tọa độ là d thì d  x  y .
 Xét các khoảng cách từ M đến hai trục tọa độ khi M nằm ở các vị trí đặc biệt: Trên
trục hoành, trên trục tung.
 Sau đó xét tổng quát, những điểm M có ho|nh độ, hoặc tung độ lớn hơn ho|nh độ
hoặc tung độ của M khi nằm trên hai trục thì loại đi không xét đến.
 Những điểm còn lại ta đưa về tìm giá trị nhỏ nhất của đồ thi hàm số dựa v|o đạo
hàm rồi tìm được giá trị nhỏ nhất của d .
Bài toán 3: Cho đồ thị C
( ) có phương trình y  f (x). Tìm điểm M trên C
( ) sao cho khoảng cách từ
M đến Ox bằng k lần khoảng cách từ M đến trụcOy . Phƣơng pháp giải: y  kx
f x   kx
Theo đầu bài ta có y  k x     . y    kx  
f x   kx ax  b
Bài toán 4: Cho đồ thị hàm số C
( ) có phương trình y  f (x) 
c  0, adbc  0 . Tìm tọa độ cx  d
điểm M trên (C) sao cho độ dài MI ngắn nhất (với I là giao điểm hai tiệm cận). Phƣơng pháp giải: 
 Tiệm cận đứng  d x
; tiệm cận ngang  a y . c c  d a 
 Ta tìm được tọa độ giao điểm I  ;  của hai tiệm cận.  c c   2 2 2 d   a 
 Gọi M x ;y l| điểm cần tìm, thì:IM  x  y g x M     M    M  M M   c   c 
 Sử dụng phương ph{p tìm GTLN - GTNN cho hàm số g để thu được kết quả.
Bài toán 5: Cho đồ thị hàm số C
( ) có phương trình y  f (x ) và đường thẳng d : A x  By  C  0 . Tìm điểm I trên C
( ) sao cho khoảng cách từ I đến d là ngắn nhất. Phƣơng pháp giải: Trang 19
 Gọi I thuộc C
( )  I x ;y ; y  f x ( ) . 0 0 0 0 A x By C
 Khoảng cách từ I đến d là g x ( )
h I ;d      0 0 0 A2  B 2
 Khảo sát hàm số y  g(x) để tìm ra điểm I thỏa mãn yêu cầu. Trang 20
PHẦN II. MŨ VÀ LOGARIT
1. LŨY THỪA VÀ HÀM SỐ LŨY THỪA
1.1. Khái niệm lũy thừa
1.1.1. Lũy thừa với số mũ nguyên
Cho n là một số nguyên dương.
Với a là số thực tùy ý, lũy thừa bậc n của a là tích của n thừa số a . n a    a a .  ...  . . a . ( n thừa số). n 1 Với a  0. thì 0  a  n 1 a  n a
Ta gọi a l| cơ số, n l| mũ số. Và chú ý 0
0 và 0n không có nghĩa.
1.1.2. Một số tính chất của lũy thừa
 Giả thuyết rằng mỗi biểu thức được xét đều có nghĩa:     a      a  a  a ;  a ;     a  a . ( ) ; a
( b)  a  b ;  a       a  a a   b     ;         b  b  b  a 
 Nếu a  1 thì   a
 a     ;
 Nếu 0  a  1 thì   a
 a     .
 Với mọi 0  a  b , ta có: m  m a b  m  0 m  m a b  m  0 Chú ý:
 Các tính chất trên đúng trong trường hợp số mũ nguyên hoặc không nguyên.
 Khi xét lũy thừa với số mũ 0 và số mũ nguyên }m thì cơ số a phải khác 0 .
 Khi xét lũy thừa với số mũ không nguyên thì cơ số a phải dương. n
1.2. Phƣơng trình x  b.
Ta có kết quả biện luận số nghiệm của phương trình n
x  b như sau:  Trường hợp n lẻ:
Với mọi số thực b , phương trình có nghiệm duy nhất.  Trường hợp n chẵn:
 Với b  0 , phương trình vô nghiệm.
 Với b  0 , phương trình có một nghiệm x  0.
 Với b  0 , phương trình có hai nghiệm trái dấu, kí hiệu giá trị dương l| n b , còn
giá trị âm là n b .
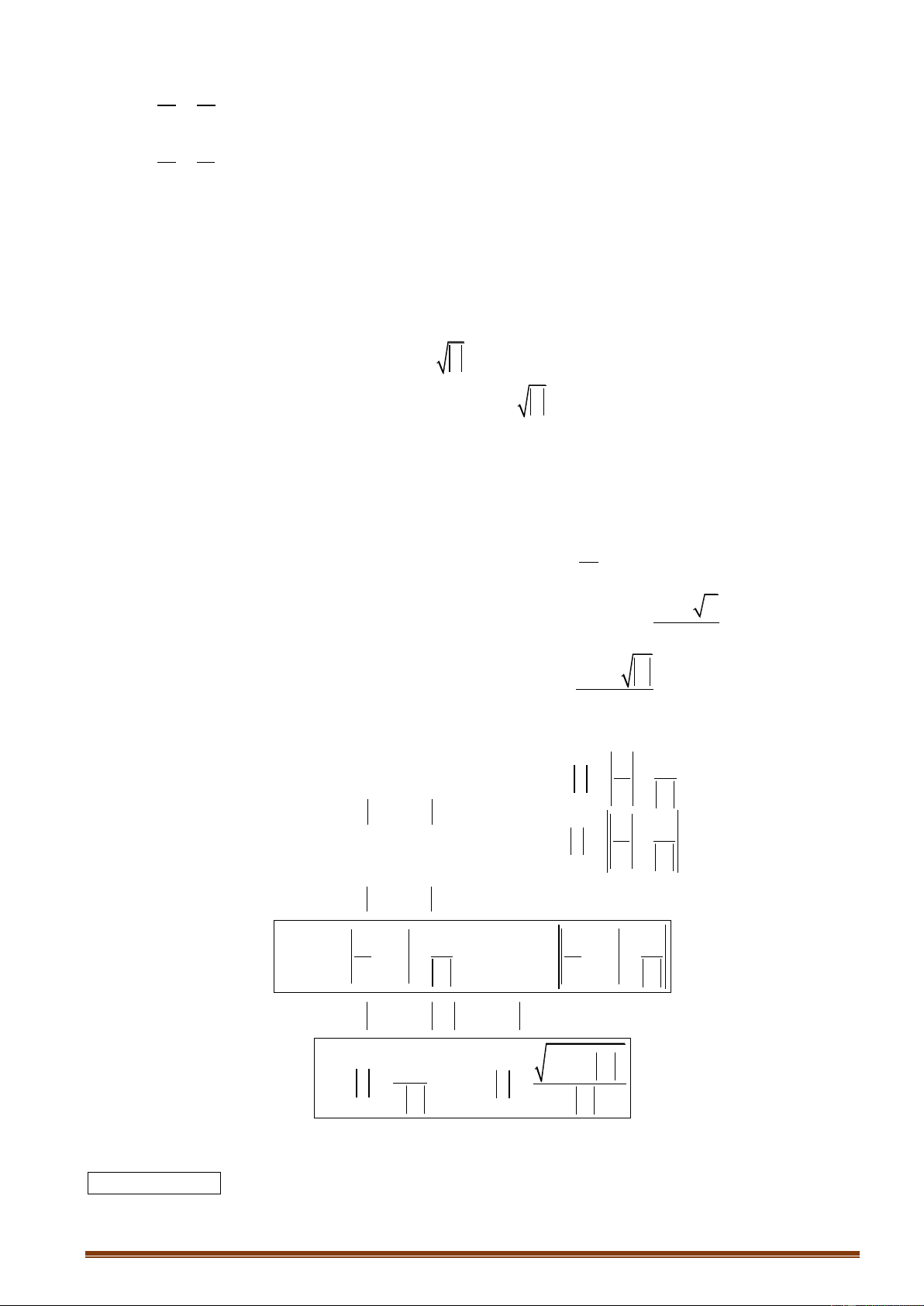
1.3. Một số tính chất của căn bậc n Với a b     * , ; n , ta có: Trang 21 2n 2n  a  a  a  n21 n2 a
1  a a  n2
 n2 n ab a 2  b , ab  0  2n1 2n 1 2n  ab  a 
1 b a,b 2n a   a 2n 
, ab  0,b  0 2n b  b n 2 1  a a n 2 1 
a, b  0 n 2  b 1 b m  n m a  n a 
, a  0 , n nguyên dương, m nguyên  n m  nm a
a, a  0 , n ,m nguyên dương  p q Nếu 
thì n p  m q a
a , a  0, m , n nguyên dương p,q nguyên n m Đặc biệt: n   m n m a a
1.4. Hàm số lũy thừa 1.4.1. Khái niệm Xét hàm số 
y  x , với  là số thực cho trước. Hàm số 
y  x , với   , được gọi là hàm số lũy thừa. Chú ý.
Tập x{c định của hàm số lũy thừa 
y  x tùy thuộc vào giá trị của  . Cụ thể.
 Với  nguyên dương, tập x{c định là  .
 Với  nguyên âm hoặc bằng 0 , tập x{c định là   \  0 .
 Với  không nguyên, tập x{c định 0;.
1.4.2. Khảo sát hàm số lũy thừa  y  x
Tập x{c định của hàm số lũy thừa 
y  x luôn chứa khoảng 0;  với mọi    . Trong
trường hợp tổng quát, ta khảo sát hàm số 
y  x trên khoảng này. 
y  x ,  0. 
y  x ,  0. Trang 22
1. Tập x{c định: 0;.
1. Tập x{c định: 0;. 2. Sự biến thiên 2. Sự biến thiên   y    x 1 ' .  0 x  0. y    x 1 ' .  0 x  0. Giới hạn đặc biệt: Giới hạn đặc biệt:     lim x
 0, lim x  .
lim x   , lim x  0.   x  x  0 x0 x Tiệm cận: không có. Tiệm cận: 3. Bảng biến thiên. Ox là tiệm cận ngang. x 0  Oy là tiệm cận đứng. y’  3. Bảng biến thiên. y  x 0  y’  0 y  0 Đồ thị của hàm số.
Đồ thị của hàm số lũy thừa y x 
luôn đi qua điểm I 1;  1 .
1.5. Khảo sát hàm số mũ x y  a ,
a  0,a  1.  x y a , a   1 x
y  a ,a   1
1. Tập x{c định:  .
1. Tập x{c định:  . 2. Sự biến thiên. 2. Sự biến thiên. ' x
y  a ln a  0, . x '  x y
a ln a  0, x Giới hạn đặc biệt: Giới hạn đặc biệt: x lim a  0, lim a  . x lim a   x , lim a  0. x  x  x  x  Tiệm cận: Tiệm cận:
Ox là tiệm cận ngang.
Ox là tiệm cận ngang.
3. Bảng biến thiên. 3. Bảng biến thiên. x  0 1  x  0 1 Trang 23
y '     a  y '    y 1  0 y 1 Đồ thị như hình sau. a 0 Đồ thị như hình sau. 2. LOGARIT
2.1.Khái niệm Logarit
Cho hai số dương a,b với a  1. Số  thỏa mãn đẳng thức  a
 b được gọi l| logarit cơ số
a của b v| được kí hiệu là log b . a log b a     . b a
Không có logarit của số âm và số 0.
2.2. Bảng tóm tắt công thức Mũ-loarrit thƣờng gặp
 a0  1, a  0.
 log 1  0, 0  a  1 a   1
a   a
 log a  1, 0  a  1 a    log a  , 0  a    1 1 a   a     a 1   log     a ,0 a 1 a  a      a     
 log b  .log b, a b  a  a a  , 0, 1 a  1       log b 
a .b  a   .log b a a   
 a .b  a b.  log     b .log b a a     a    a
 log b  log c     ,  log bc a a a    b 0    b b  b  
 log b  log c  log a a a     a  
 a    * ,  c      
a   a  Trang 24
 a  b    log b  1 a log b  . a log a b
3. BẤT PHƢƠNG TRÌNH MŨ VÀ LOGARIT.
3.1. Bất phƣơng trình mũ cơ bản
Bất phương trình mũ cơ bản có dạng x
a  b (hoặc x  , x  , x a b a
b a  b ) với a  0,a  1.
Ta xét bất phương trình có dạng x a  b.
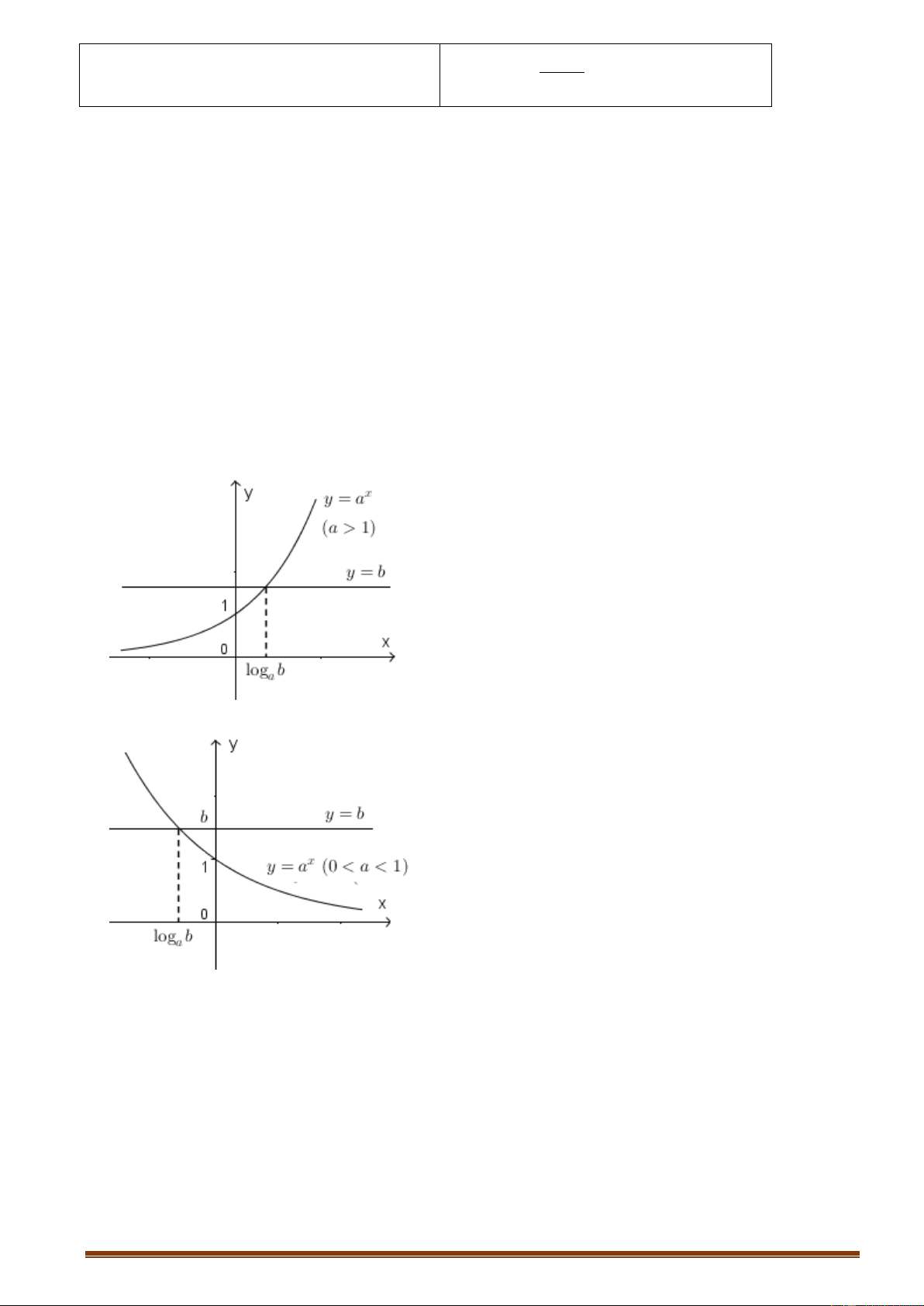
 Nếu b  0, tập nghiệm của bất phương trình l|  , vì x
a  b, x   . .
 Nếu b  0 thì bất phương trình tương đương với x a  b a a log .
 Với a  1, nghiệm của bất phương trình l| x  log b. a
 Với 0  a  1, nghiệm của bất phương trình l| x  log b. a
Ta minh họa bằng đồ thị sau:
 Với a  1, ta có đồ thị sau.
 Với 0  a  1, ta có đồ thị sau.
3.2. Bất phƣơng trình logarit cơ bản
Bất phương trình logarit cơ bản có dạng log x  b (hoặc log x  , b log x  ,
b log x  b ) với a a a a
a  0,a  1.
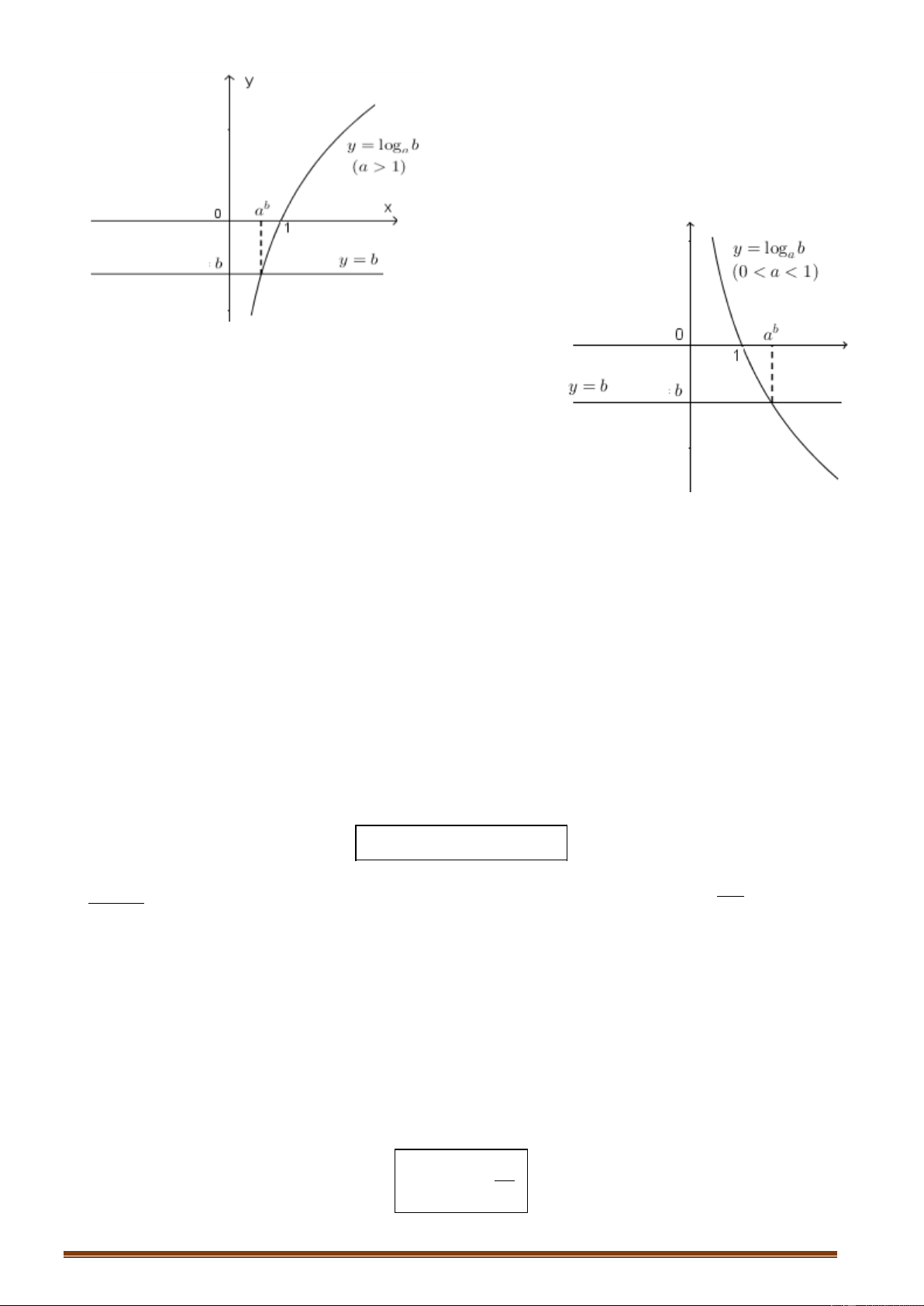
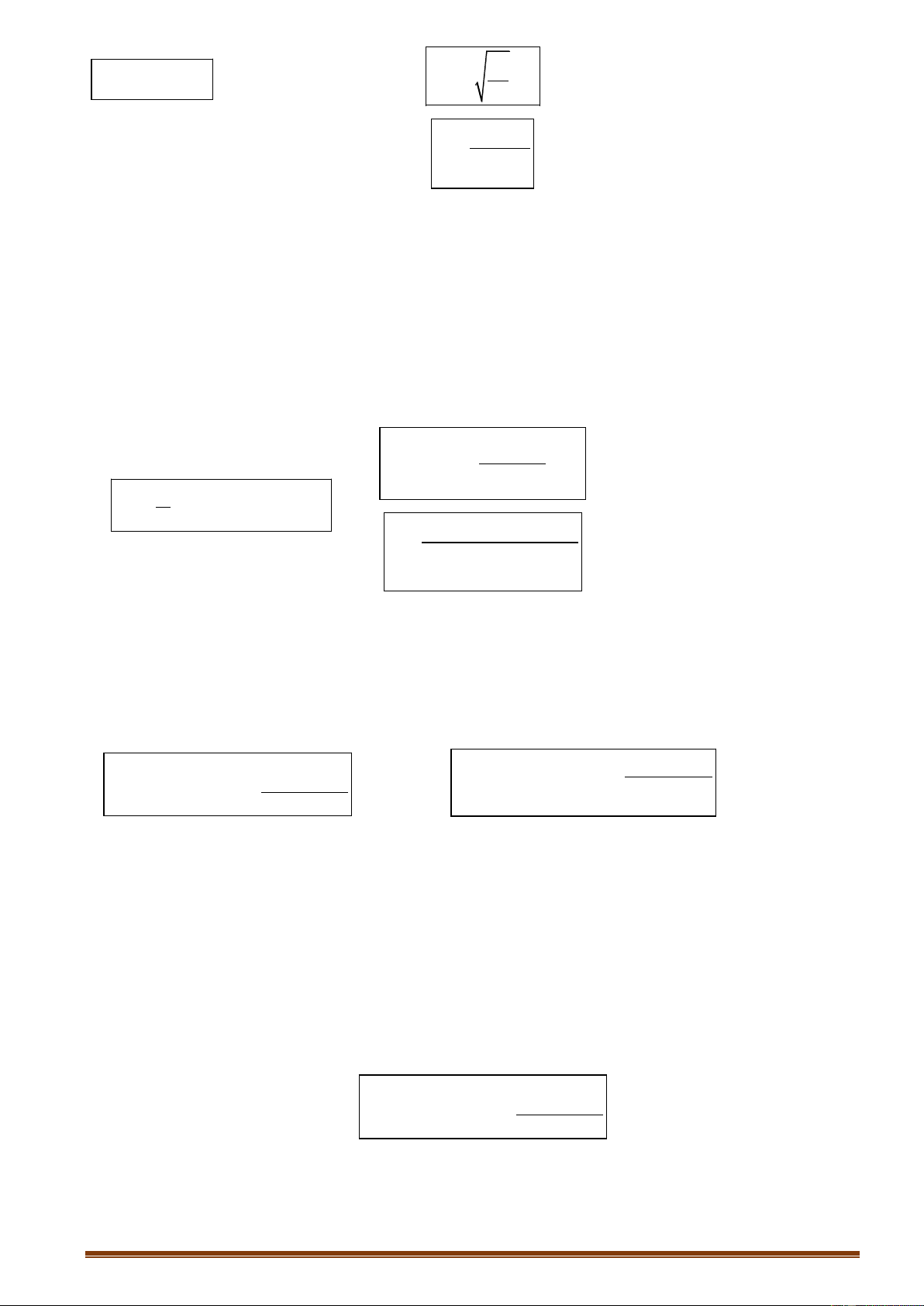
Xét bất phương trình log x  b. a
 Trường hợp a  1, ta có: log x  b  x  b a . a
 Trường hợp 0  a  1, ta có: log x  b  0 b  x  a . a
Ta minh họa bằng đồ thị như sau. Trang 25
 Với a  1, ta có đồ thị sau.
 Với 0  a  1, ta có đồ thị sau.
Quan s{t đồ thị, ta thấy rằng:
 Trường hợp a  1: log x  b khi và chỉ khi a  b x a .
 Trường hợp 0  a  1: log x  b khi và chỉ khi a 0   b x a .
4. BÀI TOÁN LÃI SUẤT NGÂN HÀNG 4.1. Lãi đơn 4.1.1. Định nghĩa
Lãi đơn là số tiền lãi chỉ tính trên số tiền gốc mà không tính trên số tiền lãi do số tiền gốc
sinh ra, tức là tiền lãi của kì hạn trước không được tính vào vốn để tính lãi cho kì hạn kế tiếp,
cho dù đến kì hạn người gửi không đến rút tiền ra.
4.1.2. Công thức tính
Khách hàng gửi vào ngân hàng A đồng với lãi đơn r % /kì hạn thì số tiền khách hàng
nhận được cả vốn lẫn lãi sau n kì hạn ( n   * ) là:
S  A  nA r  A 1  nr n   r
Chú ý:trong tính toán các bài toán lãi suất và các bài toán liên quan, ta nhớ r % là . 100 4.2. Lãi kép 4.2.1. Định nghĩa
Lãi kép làtiền lãi của kì hạn trước nếu người gửi không rút ra thì được tính vào vốn để tính lãi cho kì hạn sau.
4.2.2. Công thức tính
Khách hàng gửi vào ngân hàng A đồng với lãi kép r % /kì hạn thì số tiền khách hàng
nhận được cả vốn lẫn lãi sau n kì hạn ( n   * ) là:  S  n n  log   1 r    A     Trang 26 S
S  A 1  r n n n r %   1 n A S n A   1  r n
4.3. Tiền gửi hàng tháng 4.3.1. Định nghĩa
Tiền gửi hàng tháng là mỗi tháng gửi đúng cùng một số tiền vào 1 thời gian cố định.
4.3.2. Công thức tính
Đầu mỗi tháng khách hàng gửi vào ngân hàng số tiền A đồng với lãi kép r % /tháng thì số
tiền khách hàng nhận được cả vốn lẫn lãi sau n tháng ( n   * ) ( nhận tiền cuối tháng, khi
ng}n h|ng đã tính lãi) l| S . n   S r . n n  log     1 1 r    A  n  1  r    A   S  1  r  1 1  r n     r   S r . n A    
1  r  1  r n  1  
4.4. Gửi ngân hàng và rút tiền gửi hàng tháng Công thức tính
Gửi ngân hàng số tiền là A đồng với lãi suất r % /tháng. Mỗi tháng vào ngày ngân hàng
tính lãi, rút ra số tiền là X đồng. Tính số tiền còn lại sau n tháng là bao nhiêu? n   r 1   1 X  A
 1  r   S 
S  A 1  r   rn n  X n 
 1  r n  n 1 r 
4.5. Vay vốn trả góp 4.5.1. Định nghĩa
Vay vốn trả góp là vay ngân hàng số tiền là A đồng với lãi suất r % /th{ng. Sau đúng một
tháng kể từ ngày vay, bắt đầu hoàn nợ; hai lần hoàn nợ c{ch nhau đúng một tháng, mỗi hoàn
nợ số tiền là X đồng và trả hết tiền nợ sau đúng n tháng.
4.5.2. Công thức tính
Cách tính số tiền còn lại sau n tháng giống hoàn toàn công thức tính gửi ngân hàng và rút
tiền hàng tháng nên ta có 1  r  1
S  A 1  r   n n  X n r
Để sau đúng n tháng trả hết nợ thì S  0 nên n Trang 27 1   1 1   n n r A r  X  0 r
A 1  r n r. X  
1  r n  1
4.6. Bài toán tăng lƣơng 4.6.1. Định nghĩa
B|i to{n tăng lương được mô tả như sau: Một người được lãnh lương khởi điểm là A
đồng/tháng. Cứ sau n th{ng thì lương người đó được tăng thêm r % /tháng. Hỏi sau kn
th{ng người đó lĩnh được tất cả số tiền là bao nhiêu?
4.6.2. Công thức tính
1rk 1
Tổng số tiền nhận được sau kn tháng là S  Ak kn r
4.7. Bài toán tăng trƣởng dân số
Công thức tính tăng trưởng dân số  X
X 1 r m n , m,n   
  ,m  n m n   Trong đó:
r % là tỉ lệ tăng d}n số từ năm n đến năm m
X dân số năm m m
X dân số năm n n X
Từ đó ta có công thức tính tỉ lệ tăng d}n số là m r %  m n   1 X n
4.8. Lãi kép liên tục
Gửi vào ngân hàng A đồng với lãi kép r % /năm thì số tiền nhận được cả vốn lẫn lãi sau n năm n *
   là: S  A 1  r n . Giả sử ta chia mỗi năm th|nh m kì hạn để tính lãi và lãi n m n . r  r  suất mỗi kì hạn là
% thì số tiền thu được sau n năm l|: S  A 1   m n m  
Khi tăng số kì hạn của mỗi năm lên vô cực, tức là m   , gọi là hình thức lãi kép tiên
tục thì người ta chứng minh được số tiền nhận được cả gốc lẫn lãi là: n r S A e . 
( công thức tăng trưởng mũ) Trang 28
PHẦN III.NGUYÊN HÀM - TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN 1. NGUYÊN HÀM 1.1. Định nghĩa
Cho hàm số f x  x{c định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F x 
được gọi là nguyên hàm của hàm số f x  trên K nếu F 'x   f x  với mọi x  K . Kí hiệu:        f x dx F x C . Định lí:
1) Nếu F x  là một nguyên hàm của f x  trên K thì với mỗi hằng số C , hàm số
G x   F x  C cũng l| một nguyên hàm của f x  trên K .
2) Nếu F x  là một nguyên hàm của hàm số f x  trên K thì mọi nguyên hàm của
f x  trên K đều có dạng F x   C , với C là một hằng số.
Do đó F x  C,C   là họ tất cả các nguyên hàm của f x  trên K .
1.2. Tính chất của nguyên hàm         f x dx f x  và '      
 f x dx f x C ; d  f x dx   f x  dx
 Nếu F(x) có đạo hàm thì:  ( )  ( )  d F x F x C
 kf x dx  
k  f x dx với k là hằng số khác 0 .  
 f x   gx dx   f x dx   
gx dx
 Công thức đổi biến số: Cho y  f u và u  g x . Nếu ( )  ( ) 
 f x dx F x C thì f g x()g x '( d ) x  
 f u( d)u  F(u) C
1.3. Sự tồn tại của nguyên hàm Định lí:
Mọi hàm số f x  liên tục trên K đều có nguyên hàm trên K .
1.4. Bảng nguyên hàm các hàm số thƣờng gặp 1. 0   dx C 2.   dx x C 1   1    1 3.     1  x dx x C   1   1 16.    dx   ,    ax b ax b c 1 a   1 1 1 2 4.     dx C 17.    x xdx C x 2 x 2 1 dx 1 5.  ln   dx x C 18.  ln    ax b c x ax  b a Trang 29 6.    x x e dx e C 1 19.      ax b ax b e dx e C a x a kx b 1 a 7. x a dx    C 20. kx b a dx    C ln a k ln a 8. cos  sin   xdx x C 1 21. cos 
   sin      ax b dx ax b C a
9. sin xdx   co s x  C  1 22. sin 
    cos     ax b dx ax b C a 10. t an .   ln | cos |   x dx x C 1 23. t an    dx   ln cos      ax b ax b C a 11. cot .  ln | sin |   x dx x C 1 24. cot    dx  ln sin      ax b ax b C a 1 1 1 12.  tan   dx x C 25.  tan    dx ax b C 2 cos x 2
cos ax  b   a 1 1 1 13.   cot   dx x C 26.   cot    dx ax b C 2 sin x 2
sin ax  b   a 14.   2 1 t an   tan   x dx x C 1 27. 1  2 t an     tan      ax b dx ax b C a 15.   2 1 cot    t   x dx co x C 1 28. 1  2 cot      t      ax b dx co ax b C a
1.5. Bảng nguyên hàm mở rộng dx  1 arctg   x C   2  2 arcsin dx arcsin   x x x a x C a2  x 2 a a a a dx 1   ln   a x C   2  2 arccos dx arccos   x x x a x C a2  x 2 a 2 a  x a a dx  ln   2  2    x x a C    2  2 arct an dx arct an ln    x x a x a x C x 2  a2 a a 2 dx  arcsin   x C    2  2 arc cot dx arc cot ln    x x a x a x C 2  2 a a x a a 2 dx  1 arccos   x C 2  2 a a x x a dx 1  2  2   ln   a x a C dx 1  2  2 a x  ln tan  x x a  ax b sin  C ax  b a 2 ln      dx   b ax b x  ln  
ax  b  x  C ax
e a cosbx b sin bx ax    a  e cosbx dx    C a2  b2 ax
e a sin bx b cosbx ax   2 2  2 2 2  dx   arcsin   x a x a x a x  C e sin bx dx  C 2 2 2 2 a a  b Trang 30
2. CÁC PHƢƠNG PHÁP TÍNH NGUYÊN HÀM
2.1. Phƣơng pháp đổi biến
2.1.1. Đổi biến dạng 1 Nếu : ( )  ( ) 
 f x dx F x C và với u   t  là hàm số có đạo hàm thì : ( )  ( (  ))   f u du F t C
2.1.1.1. Phƣơng pháp chung
 Bước 1: Chọn x   t  , trong đó  t  là hàm số mà ta chọn thích hợp .
 Bước 2: Lấy vi phân hai vế : dx   't dt
 Bước 3: Biến đổi : f (x d ) x  f 
 t  't dt   
g t dt
 Bước 4: Khi đó tính : f x ( d ) x  g t ( d ) t  G t ( )    C .
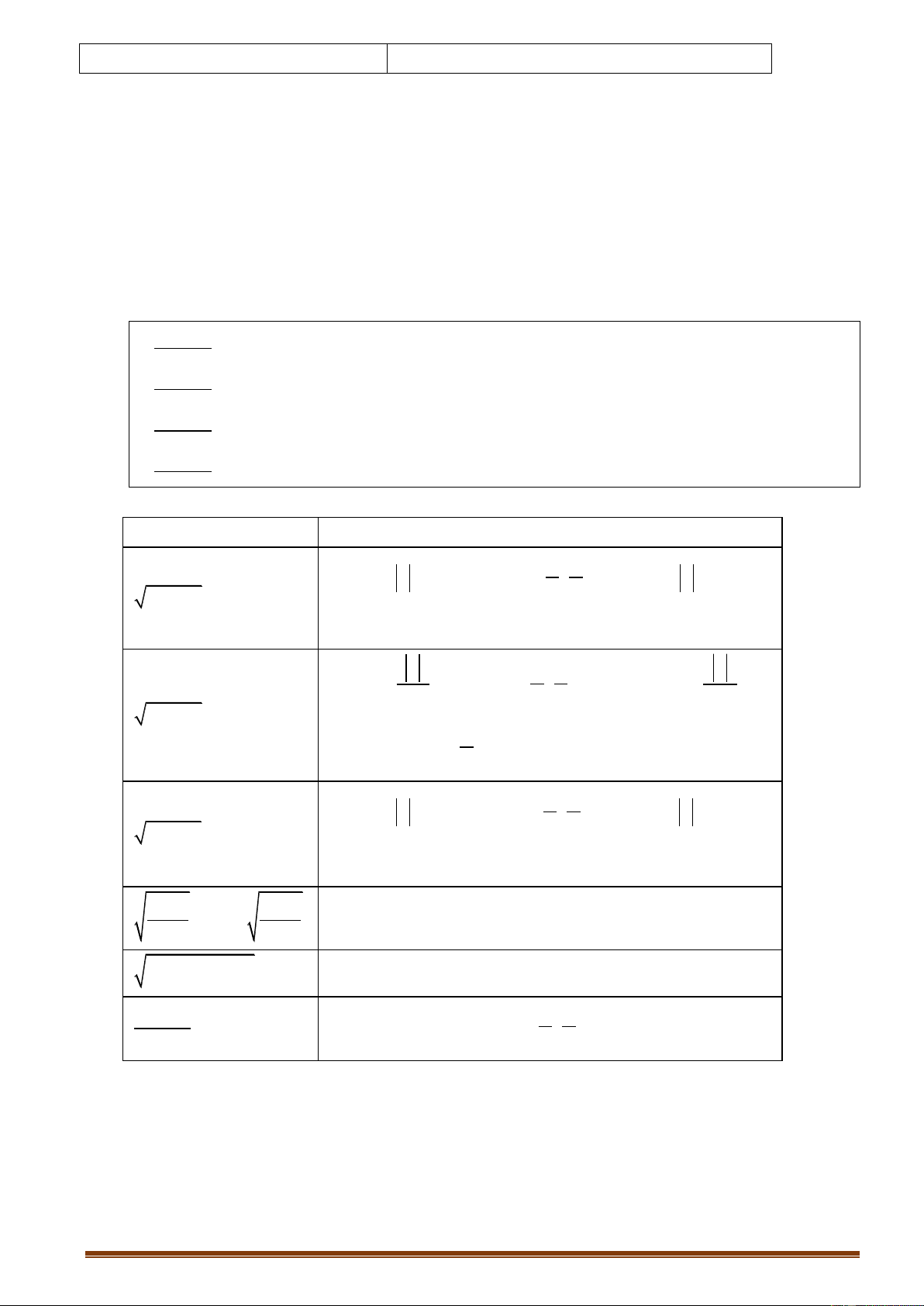
2.1.1.2. Các dấu hiệu đổi biến thƣờng gặp Dấu hiệu Cách chọn    
Đặt x  a sint ; với t    ;
. hoặc x  a cost ;  2 2  a2  x 2
với t  0;   . a     a Đặt x  .; với t    ;  \   0 hoặc x  sint  2 2  cost x 2  a2  
với t  0;    \  .  2     
Đặt x  a tant ; với t    ; . hoặc x  a cot t  2 2  a2  x 2
với t  0; . a  x a  x . hoặc
. Đặt x  acos t 2 a  x a  x
x ab x
Đặt x  a  b ( a s ) in t 2 – 1    
Đặt x  atant ; với t    ; . a2  x 2  2 2 
2.1.2. Đổi biến dạng 2
Nếu hàm số f(x) liên tục thì đặt x   t  . Trong đó  t  cùng với đạo hàm của nó ( ' t 
là những hàm số liên tục) thì ta được : f (x d ) x  f    
t  't dt  g t( d)t G t()     C .
2.1.2.1. Phƣơng pháp chung Trang 31
 Bước 1: Chọn t= x . Trong đó  x  là hàm số mà ta chọn thích hợp .
 Bước 2: Tính vi phân hai vế : dt   't dt .
 Bước 3: Biểu thị : f (x d ) x  f 
 t  't dt    g t ( d ) t .
 Bước 4: Khi đó : I  f x ( d ) x  g t ( d ) t  G t ( )    C
2.1.2.2. Các dấu hiệu đổi biến thƣờng gặp : Dấu hiệu Cách chọn Hàm số mẫu số có t là mẫu số
Hàm số : f x;  x  t   x  . s x  x 
Hàm    a inx+b.cosx f x t  t an ; cos  0
c. s inx+d.cosx+e 2  2  1
Với : x  a  0 và x  b  0 .
Hàm f x   
x  a x  b
 Đặt : t  x  a  x  b
Với x  a  0 và x  b  0 .
Đặt : t  x  a  x  b
2.2. Phƣơng pháp nguyên hàm từng phần
Nếu u(x) , v(x) là hai hàm số có đạo hàm liên tục trên K: u x ( ) v . '(x dx )
 u(x) v . (x)  
v(x) u. '(x dx )
Hay udv  uv  
vdu ( với du  u’xdx, d v  v’xdx )
2.2.1. Phƣơng pháp chung
 Bước 1: Ta biến đổi tích ph}n ban đầu về dạng : I  f x ( dx )  
 f x().f (x dx ) 1 2
u  f (x)
du  f ' x ( dx )  1 
Bước 2: Đặt :    1 dv  f x ( ) v   ( ) 2   f x dx 2
 Bước 3: Khi đó : u dv .  u v .   vdu .
2.2.2. Các dạng thƣờng gặp 2.2.2.1.Dạng 1
u  P(x) u ' d
. u  P '(x d ) x     sin x       sin x    cos x
I   P(x) cosx  d.x . Đặt           dv   cosx  d . x v   sin x  x  e    x    x   e   e   cosx       cos x 
Vậy: I  P (x ) sin x  -  sin x  P . '(x d ) x  x   x  e   e  2.2.2.2.Dạng 2 Trang 32 u  ln x    1 du  dx I  P x ( ). ln xdx  . Đặt    x   dv 
v  P (x d
) x  Q(x )  P (x d ) x   1
Vậy I  lnx Q
. x   Q(x). dx  x 2.2.2.3.Dạng 3 u  x du  x  e e dx sin x      I   x e  dx .Đặt sin x         cosx  cosx  dv     d . x v      cosx   sin x 
cosx cosx  Vậy I = x I  e   -    x e dx sin x   sin x  cosx 
Bằng phương ph{p tương tự ta tính được    x
e dx sau đó thay v|o I sin x  3. TÍCH PHÂN
3.1. Công thức tính tích phân b f (x d ) x  b
F (x )  F b ( )   F a ( ) . a a b b
* Nhận xét:Tích phân của hàm số f từ a đến b có thể kí hiệu bởi  f (x d
) x hay  f t( d ) t. Tích a a
ph}n đó chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào cách ghi biến số.
3.2. Tính chất của tích phân
Giả sử cho hai hàm số f (x)và g (x)liên tục trên K , a,b, c là ba số bất kỳ thuộc K . Khi đó ta có : a 1. f (x d ) x   0 a b a 2. f (x d ) x   
 f x( d)x . a b b c b 3. f (x dx )  f x ( dx )     f x( dx ) a a c b b b
4. f (x)  g x ( )dx  f x ( d ) x     
g x( d)x . a a a b b 5. kf x ( dx )   k. f x ( dx ) . a a b 6. Nếu f(x)  0, x   a  ;b 
 thì : f (x dx )  
0 x  a;b    a Trang 33 b b 7. Nếu x   a
 ;b : f (x)  g(x)  f (x dx )  g x ( dx )     . a a b
8. Nếu x  a;b 
 Nếu M  f (x)  N thì M b  a   f x ( dx )  N b   a  . a
4. PHƢƠNG PHÁP TÍNH TÍCH PHÂN
4.1. Phƣơng pháp đổi biến
4.1.1. Phƣơng pháp đổi biến số dạng 1 4.1.1.1. Định lí
Nếu 1) Hàm x  u t
( ) có đạo hàm liên tục trên   ;    
2) Hàm hợp f (u t
( )) được x{c định trên   ;     , 3) u 
( )  a, u( )  b b 
Khi đó: I  f x dx    f u t u' ( ) ( ( )) t ( dt ) . a 
4.1.1.2. Phƣơng pháp chung
 Bước 1: Đặt x  u t 
 Bước 2: Tính vi phân hai vế : x  u t()  dx  u ' t( d ) t x  b t   Đổi cận:  x  a t  
 Bước 3: Chuyển tích ph}n đã cho sang tích ph}n theo biến t b   
Vậy: I  f x ( dx )
 f u t()u ' t( dt )      g t( dt )  G t()
 G() G   ( ) a  
4.1.2. Phƣơng pháp đổi biến dạng 2 4.1.2.1. Định lí
Nếu hàm số u  u(x ) đơn điệu v| có đạo hàm liên tục trên đoạn a;b   sao cho b u (b) f x ( d
) x  g u x ( )u x '( d ) x  g u ( d ) u thì: I  f (x d ) x  
 g u( d)u . a u (a )
4.1.2.2. Phƣơng pháp chung
 Bước 1: Đặt u  u x  du  u' ( ) (x d ) x x  b u  u b ( )
 Bước 2: Đổi cận :  x  a u  u a ( )
 Bước 3:Chuyển tích ph}n đã cho sang tích ph}n theou b b u b ( )
Vậy: I  f (x d
) x  g u(x ) u . '(x d ) x     
 g u( d)u a a u (a )
4.2. Phƣơng pháp tích phân từng phần 4.2.1. Định lí Trang 34
Nếu u(x)và v(x)là các hàm số có đạo hàm liên tục trên a;b   thì: b b b b b b
u x v' x dx  u x v x    v x u' ( ) ( ) ( ) ( ) ( ) x ( d
) x Hay udv  uv vdu a a a a a a
4.2.2. Phƣơng pháp chung
 Bước 1: Viết f (x)dx dưới dạng udv  uv d'x bằng cách chọn một phần thích hợp
của f (x)làm u(x)và phần còn lại dv  v ' x ( d ) x
 Bước 2: Tính du  u 'dx và v  dv  v x '( dx ) b b
 Bước 3: Tính vu '(x d)x và uv a a
*Cách đặt u và dv trong phƣơng pháp tích phân từng phần.
Đặt u theo thứ tự ưu b b b b  x P x ( e ) dx
P(x)lnxdx P(x)cosxdx  xe cosxdx tiên: a a a a
Lốc-đa-mũ-lượng u P(x) lnx P(x) x e dv x e dx P(x)dx cosxdx cosxdx
Chú ý: Nên chọn u là phần của f (x)mà khi lấy đạo h|m thì đơn giản, chọn dv  v d ' x là phần
của f (x)dx là vi phân một hàm số đã biết hoặc có nguyên hàm dễ tìm.
5. TÍCH PHÂN CÁC HÀM SỐ SƠ CẤP CƠ BẢN
5.1. Tích phân hàm hữu tỉ 5.1.1. Dạng 1    dx 1 adx 1 I =   ln ax    b . (với a≠0) ax  b a ax    b a    dx 1 1 Chú ý: Nếu I =   1   ax (  b) adx .  . ax (    k k b) k  ax (  b) a a(1    k) 5.1.2. Dạng 2    dx I
0 (ax 2  bx  c  0 với mọi x    ;   ) 2 a     ax  bx   c
Xét   b2  a 4 c . b   b  
 Nếu   0thìx  ;x  1 a 2 2 a 2 1 1 1  1 1       thì : 2  
ax  bx  c
a(x  x )(x  x )
a(x  x ) x  x x  1 2 1 2  x 1 2   1  1 1  1  I    d  x 
ln x  x  ln x  x     
a(x  x ) x  x x  x a(x  x 1 2 )    1 2  1 2 1 2 1 x  x1   ln
a(x  x ) x  x  1 2 2 Trang 35 1 1  b   Nếu   0 thì  2 2 x  0 
ax  bx  c a x (  x ) 2 0  a    dx 1 dx 1 thì I =      2  2 
ax  bx  c a (x  x ) a(x    x ) 0 0    dx dx
Nếu   0 thì I    2 
ax  bx  c  2 2     b       a x       a  2 2       a 4    b  1  Đặt x  
t an t  dx  1 t an 2 2   2tdt a 2 a 4 2 a 5.1.3. Dạng 3     mx n I dx, 0 . 2 a   ax  bx   c mx  n
(trong đó f (x)  liên tục trên đoạn   ;     )
ax 2  bx  c
 Bằng phương ph{p đồng nhất hệ số, ta tìm A và B sao cho: mx  n A a ( x 2  bx   c) ' A ax (2   B  b)  B
ax 2  bx  c
ax 2  bx  c
ax 2  bx  c
ax 2  bx  c
ax 2  bx  c    mx  n A ax (2   b) B Ta có I=  dx  dx  2  2  dx
ax  bx  c
ax  bx  c ax 2  bx     c  (2  ) 
Tích phân  A ax b dx = A ax2 ln  bx  c ax 2  bx    c  Tích phân  dx thuộc dạng 2. ax 2  bx   c 5.1.4. Dạng 4 b   P(x) I
dx với P(x)và Q(x)là đa thức của x . Q(x ) a
 Nếu bậc của P(x)lớn hơn hoặc bằng bậc của Q(x)thì dùng phép chia đa thức.
 Nếu bậc của P(x)nhỏ hơn bậc của Q(x)thì có thể xét c{c trường hợp:
 Khi Q(x)chỉ có nghiệm đơn  , ,..., thì đặt 1 2 n
P (x )  A1  A2  ...  An . Q(x ) x   x   x   1 2 n
 Khi Q(x)có nghiệm đơn v| vô nghiệm
Q x  x   x2  px  q   p2 ( ) ,  q 4  0 thì đặt P(x) A Bx    C . Q x ( ) x  
x 2  px  q
 Khi Q(x)có nghiệm bội
Q x  x   x   2 ( ) ( )( ) với  thì đặt Trang 36
P (x )  A  B  C . Q(x ) x   x    2 x   
Q x  x   2 x   3 ( ) ( ) ( ) với  thì đặt P (x )  A  B  C  D  E (x   2 ) (x   3 ) (x   2 ) (x  ) (x   3 ) (x   2 ) x  
5.2. Tích phân hàm vô tỉ b
R(x, f(x) d)x Trong đó R( ,
x f (x))có dạng: a        a x R x,     Đặt x acos t 2 , t 0;   a  x    2  
 R x a2 x2 , 
 Đặt x  a sint hoặc x  a cost      ax b ax b n R x,    Đặt n t cx  d    cx  d  1
R x, f x  
Với x2  x   '  k  x a  b a
( x  b) x 2  x   1 Đặt t  x 2 
 x   , hoặc Đặt t  ax  b    
 R x a2 x2 , 
 Đặt x  a tant , t   ;   2 2   a  
 R x x2 a2 , 
 Đặt x  ,t [0;]\   cos x 2    n n n R  1 2 i
x ; x ;...; x  Gọi k = BSCNN(n ;n ;...;n . Đặt k x = t 1 2 i ) 5.2.1. Dạng 1  1 I   dx a  0 
ax 2  bx  c   2   b x     u b 2   Từ :           a f(x)=ax bx c a x 2  du  dx  a 2  a2 4        K  a 2 Khi đó ta có :
 Nếu   a   f x  a u2  k2   f x  a u2  k2 0, 0 ( ) ( ) . (1) 2 a   0 b  
 Nếu :   0  f (x)  a x     (2) a 2 ( )   b f x a x     a . u  a 2  Nếu :   0. Trang 37
 Với a > 0: f x
( )  a x  x x  x   f x
( )  a . x  x x  x (3) 1 2 1 2 
 Với a < 0: f x
( )  a x  x x  x   f x ( ) 
a. x  x x  x (4) 1 2 1 2 
Căn cứ vào phân tích trên , ta có một số cách giải sau :  Phƣơng pháp :
* Trường hợp :   a 
 f x  a u2  k2   f x  a u2  k2 0, 0 ( ) ( ) . Khi đó đặt : 2
ax  bx  c  t  a x .  t 2  c 2 x  ;dx   tdt
bx  c  t 2  2 ax  b   2 a b 2 a      x  t t , x        t   t  t 2 0 1  t  a x .  t  c  a  b  2 a 2 a   0 b  
* Trường hợp :   0  f (x )  a x     a 2 ( )   b f x a x     a . u  a 2  1  b    b ln x   : x   0   1 1 1 a 2     a a 2 Khi đó : I  dx  dx     b a b 1  b     a x  x   b ln x   : x   0 a 2 a 2  a 2     a a 2  x  x t
* Trường hợp :   0,a  0 . Đặt : 2
ax  bx  c  a x  x
1  x  x 2   1 
 x x2t  x  x t
* Trường hợp :   0,a  0 . Đặt : 2
ax  bx  c  a x  x 1 x  x 2   1 
 x x 2 t 5.2.2. Dạng 2     mx n I dx a  0 
ax 2  bx  c  Phƣơng pháp :  Bước 1: A d .  2 ax  bx   c mx n  B
Phân tích f (x)     1 2 ax  bx  2 c ax  bx  2 c
ax  bx  c  Bước 2:
Quy đồng mẫu số , sau đó đồng nhất hệ số hai tử số để suy ra hệ hai ẩn số , A B  Bước 3: Giải hệ tìm , A B thay vào (1)  Bước 4 :   1 Tính I  A 2  2
ax  bx  c   B dx   (2) 2 
ax  bx  c Trang 38  1 Trong đó  dx
a  0đã biết cách tính ở trên 
ax 2  bx  c 5.2.3. Dạng 3  1 I   dx a  0
 mx  n  ax 2  bx  c  Phƣơng pháp :  Bước 1: 1 1 Phân tích :  . (1) mx n   2  n  
ax  bx  c m x   2
ax  bx  c  m   Bước 2:  1  n  1 y  t    dy   dx 1 n  x  t m x    t Đặt :  x    2 y m 1  1   1 
x   t  2
ax  bx  c  a   t   b   t    c  y  y   y   Bước 3:  '
Thay tất cả vào (1) thì I có dạng :    dy I
. Tích ph}n n|y chúng ta đã  Ly 2 '  My  N biết cách tính . 5.2.4. Dạng 4 
I  R x;y    x    dx  R  m x;     dx x        ( Trong đó : R( ;
x y)là hàm số hữu tỷ đối với hai biến số x,y và , ,  ,  là các hằng số đã biết )
 Phương pháp :  Bước 1: x   Đặt :  m t  (1) x    Bước 2:
Tính x theo t : Bằng c{ch n}ng lũy thừa bậc m hai vế của (1) ta có dạng x   t   Bước 3:
Tính vi phân hai vế : dx   ' t dt v| đổi cận  Bước 4:     ' x    Tính : R  m x; dx  
 R  t ;t  't    dt x        '
5.3. Tích phân hàm lƣợng giác
5.3.1. Một số công thức lƣợng giác Trang 39
5.3.1.1. Công thức cộng cos a
(  b)  cosa. cosb  sin a. sin b sin a
(  b)  sin a. cosb  sin b. os c a
t an a  t an b t an a
(  b)  1  tana.tanb
5.3.1.2. Công thức nhân đôi 2  2 2 2 2 a cos a
2  cos a – sin a  2 cos a – 1 1 t an  1 – 2 sin a  2 1  t an a 2 t an a 2 t an a sin a
2  2 sin a. cosa  ; t an a 2  3
cos 3  4 cos   3 cos ; 2 1  t an a 1  2 t an a 3
sin 3  3 sin   4 sin 
5.3.1.3. Công thức hạ bậc 1  cos 2 1  cos 2 1 cos 2 2  a 2 a 2 a sin a  ; cos a  ; t an a  2 2 1  cos a 2 3 sin sin 3 cos 3 3 cos  3   sin    ; 3 cos    4 4
5.3.1.4. Công thức tính theo t a t 2 1  t 2 t 2 Với t  t an Thì sin a  ; cosa  ; t an a  2 1  t 2 1  t 2 1  t 2
5.3.1.5. Công thức biến đổi tích thành tổng    1 cos . cos co  s(  )  co  s(  )   2    1 sin . sin co  s(  )  co  s(  )   2    1 sin . cos sin  (  )  sin  (  )   2
5.3.1.6. Công thức biến đổi tổng thành tích       cos   cos   2 cos . cos 2 2      
cos   cos   2 sin . sin 2 2       sin   sin   2 sin . cos 2 2       sin   sin   2 cos . sin 2 2 sin  (       ) t an t an cos  cos  sin  (       ) t an t an cos  cos 
Công thức thƣờng dùng: 3 cos 4 4 4   cos   sin   4 5 3 cos 4 6 6   cos   sin   8 Hệ quả: Trang 40       cos   sin   2 cos     2 sin     4   4        cos   sin   2 cos  
   2 sin     4   4 
5.3.2. Một số dạng tích phân lƣợng giác b
 Nếu gặp I   f sinx.cosxdx ta đặt t  sinx . a b
 Nếu gặp dạng I   f cosx.sinxdx ta đặt t  cosx . a b  dx
Nếu gặp dạng I   f tanx
ta đặt t  tan x . 2 cos x a b  dx
Nếu gặp dạng I   f cotx
ta đặt t  cot x . 2 sin x a 5.3.2.1. Dạng 1 I =
sinxn dx ; I cosxn dx   1 2 * Phƣơng pháp
 Nếu n chẵn thì sử dụng công thức hạ bậc
 Nếu n = 3thì sử dụng công thức hạ bậc hoặc biến đổi
 Nếu 3nlẻ (n = 2 p + )
1 thì thực hiện biến đổi: 2p I =
sinxn dx = sinx2p+1 dx   x  xdx     2 sin sin 1
cos x  d cos x      p 1 C 0 C 1 2 cos x ...  1k C  2 cos x  ...  1p k p C  2 cos x            d cos x   k p  p p p p   1  1k p  1 0 1 3     2 1 2 1 C cos x 
C cos x  ...  k
C cos x  k     ...  p
C cos x  p   c  p p 3 k 2  p 1 2p  p 1  2p I =
cosxn dx = cosx2p+1 dx   x  xdx    2 cos cos 1
sin x  d sin x      p 2 C 0 C 1 2 sin x ...  1k C  2 sin x  ...  1p k p C  2 sin x           d sin x   k p  p p p p   1  k p  1 1 0 1 3    2 1 2 1 C sin x 
C sin x  ...  k
C sin x  k     ...  p
C sin x  p   c  p p 3 k 2  p 1 2p  p 1  5.3.2.2. Dạng 2 = sinm cosn I x xdx ( , m n Î N) ò * Phƣơng pháp
 Trường hợp 1: ,
m n là các số nguyên
a. Nếu m chẵn, n chẵn thì sử dụng công thức hạ bậc, biến đổi tích thành tổng.
b. Nếu m chẵn, n lẻ (n = 2 p + ) 1 thì biến đổi: Trang 41  m  2p+1 m 2p m I = sinx cosx dx   x   x  xdx   x    2 sin cos cos sin 1
sin x  d sin x     p
sin x m C 0 C 1 2 sin x ...  k 1 C  2 sin x  ...  p k p 1 C  2 sin x          
d sin x    k p  p p p p    1 3 2 1 2 1 c. Nếu sin sin sin sin 0 x m   1 x m  k  m p  m  C C  ...   k  x  x k 1 C  ...  1p   p C   c  p m  p 1 m  p 3 k 2  1  p m
2p  1  m 
m lẻ(m = 2 p + )
1 , n chẳn thì biến đổi:  2p+1  n n 2p n I = sinx cosx dx   x   x  xdx    x    2 cos sin sin cos 1
cos x  d cos x     p
cosx n C 0 C 1 2 cos x ...  1k C  2 cos x  ...  1p k p C  2 cos x           
d cos x    k p  p p p p    1 3 2 1 2 1 cos cos cos cos 0 x n   1 x n  k  n p  n   C C  ...   k  x  x k 1 C  ...  1p   p C   c  p n  p 1 n  p 3 k 2  1  p n
2p  1  n 
d. Nếu m lẻ, n lẻ thì sử dụng biến đổi 1.2. hoặc 1.3. cho số mũ lẻ bé hơn.  Nếu ,
m n là các số hữu tỉ thì biến đổi và đặt u = sinx n 1 n 1    m m n  2  2  m B x xdx x x xdx
u   u 2     2 sin cos sin cos cos 1 du (*)
m  1 n  1 m  k
Tích ph}n (*) tính được  1 trong 3 số ; ; là số nguyên 2 2 2 5.3.2.3. Dạng 3 I =
tan xn dx ; I = cot xn dx (n Î N).   1 2  2 dx
1  tan x dx 
 d tan x   tan x    2  c cos x  2 dx
1  cot x dx 
  d cot x    cot x    2  C sin x sin x d cos x   tan xdx  dx  
  ln cosx C    cos x cos x cos x d sin x   cot xdx  dx 
 ln sin x C    sin x sin x
6. ỨNG DỤNG TÍCH PHÂN
6.1. Diện tích hình phẳng
6.1.1. Diện tích hình phẳng giới hạn bởi 1 đƣờng cong và trục hoành
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y  f (x ) liên tục trên đoạn a;b   , trục b
ho|nh v| hai đường thẳng x  a , x  b được x{c định: S   f x ( ) dx a y
y  f (x)
y  f (x)  b y  0
S   f (x) dx (H ) x   a a O a c c c x 1 2 3 b  x  b Trang 42
6.1.2. Diện tích hình phẳng giới hạn bởi 2 đƣờng cong
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y  f (x ) , y  g(x ) liên tục trên đoạn a;b   b
v| hai đường thẳng x  a , x  b được x{c định: S  f (x )  
g(x ) dx a y
(C ) : y  f ( ) x (C ) 1  1 1
(C ) : y  f ( ) x (H )  2 2 x  a (C ) 2 x  b b S  f (x )  a c O c 1 2 b x  f (x ) dx 1 2 a b b
- Nếu trên đoạn [a;b] , hàm số f (x ) không đổi dấu thì: f (x) dx  
 f(x d)x a a
- Nắm vững cách tính tích phân của hàm số có chứa giá trị tuyệt đối
- Diện tích của hình phẳng giới hạn bởi c{c đường x  g(y) , d
x  h(y ) v| hai đường thẳng y  c , y  d được x{c định: S  g y ( )   h y ( ) dy c
6.2. Thể tích vật thể và thể tích khối tròn xoay
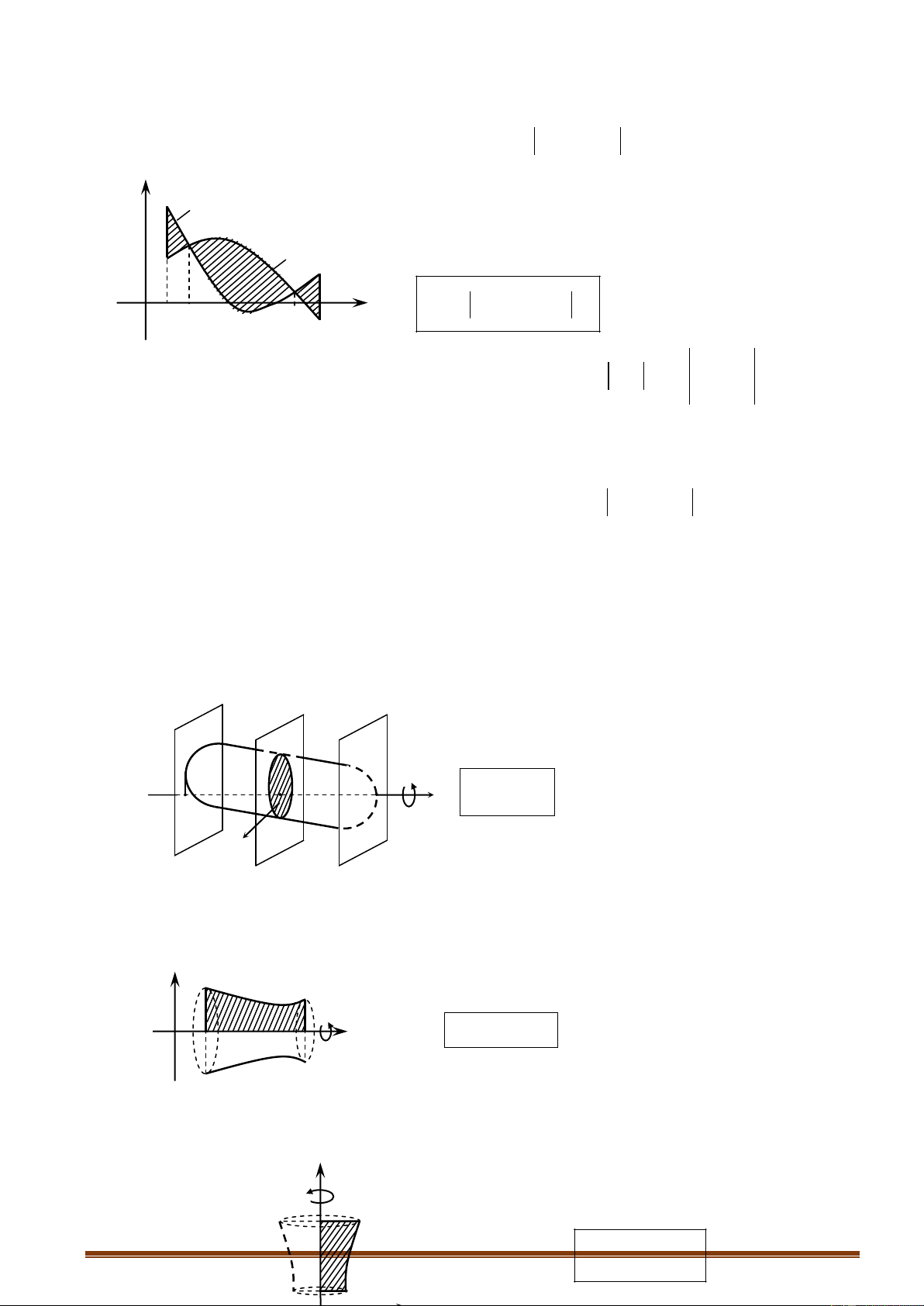
6.2.1. Thể tích vật thể
Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại c{c điểm a và
b; S (x ) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm x , a
(  x  b) . Giả sử S (x ) là hàm số liên tục trên đoạn [a;b] . (V) b x V  a
S(x d)x O b x a S(x)
6.2.2. Thể tích khối tròn xoay
- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi c{c đường
y  f (x ) , trục ho|nh v| hai đường thẳng x  a , x  b quanh trục Ox: y
y  f (x) (
 C) : y  f ( ) x  (  O )
x : y  0 b  V   f x dx a  x  2 ( ) O b x x   a a  x  b
- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi c{c đường
x  g(y ) , trục ho|nh v| hai đường thẳng y  c , y  d quanh trục Oy: y d (  C) : x  ( g ) y
(O )y: x  0 d  V   g y dy  y  2 ( ) y   c c Trang 43  c y  d O x
- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới
hạn bởi c{c đường y  f (x ) , y  g(x ) v| hai đường thẳng x  a , x  b quanh trục Ox: b V  
f 2 x  g2 ( ) (x) dx  a Trang 44 PHẦN IV. SỐ PHỨC 1. SỐ PHỨC
1.1. Khái niệm số phức
 Số phức (dạng đại số) : z  a  bi; a,b    . Trong đó : a là phần thực, b là phần
ảo, i l| đơn vị ảo, i2  1.
 Tập hợp số phức kí hiệu:  .
 z là số thực  phần ảo của z bằng 0 b  0 .
 z là số ảo (hay còn gọi là thuần ảo)  phần thực bằng 0 a  0.
 Số 0 vừa là số thực vừa là số ảo.
1.2. Hai số phức bằng nhau
 Hai số phức z  a  bi a, b   và z  c  di c, d   bằng nhau khi phần thực 2  1 
và phần ảo của chúng tương đương bằng nhau. a   c
 Khi đó ta viết z  z  a  bi  c  di   1 2 b  d  y
1.3. Biểu diễn hình học số phức M (a;b)
Số phức z  a  bi a, b    được biểu diễn bởi điểm M a;b  hay bởi O u  a b
;  trong mặt phẳng phức với hệ tọa độ Oxy . x
1.4. Số phức liên hợp
Số phức liên hợp của z  a  bi a, b    là z  a  bi .    z z z  z ;
z  z '  z  z ' ; z z . '  z z 1 1 . ';    ; z z
.  a 2  b2.  z  z  2  2
 z là số thực  z  z ; z là số ảo z  z  .
1.5. Môđun của số phức  
Độ dài của vectơ OM được gọi là môđun của số phức z và kí hiệu là z . Vậy z  OM  hay z a bi OM a 2 b2      . Một số tính chất:   z a2 b2  
 zz  OM ; z  z  z  0, z
   ; z  0  z  0. z z  z z z z z .  z . z ; 1 1  ; 1 1 2  . 1 2 1 2 z z z 2 2 2 2 z2 Trang 45
 z  z  z  z  z  z . 1 2 1 2 1 2
2. PHÉP CỘNG TRỪ NHÂN CHIA SỐ PHỨC
2.1. Phép cộng và phép trừ số phức
Cho hai số phức z  a  bi a, b   và z  c  di c, d   . Khi đó: 2  1 
z  z  a  c  b  d i 1 2
 Số đối của số phức z  a  bi là z   a   bi .
 Tổng của một số phức với số phức liên hợp của nó bằng hai lần phần thực của số
thực đó: z  a  bi, z  z  a 2 .
2.2. Phép nhân số phức
 Cho hai số phức z  a  bi a, b   và z  c  di c, d   . 2  1 
Khi đó: z z  a  bi c  di   ac – bd   ad  bci . 1 2
 Với mọi số thực k và mọi số phức z  a  bi a, b   , ta có k z
.  k. a  bi   ka  kbi.Đặc biệt: 0 z
.  0 với mọi số phức z .
 Lũy thừa củai :i0  i1  i i2   i3  i2 1, , 1, i .  i  n 4 n 4 1  n 4 2  n i i i i i 4 3 1, , 1, i, n           .
2.3. Chia hai số phức  1
Số phức nghịch đảo của z khác 0 là số z 1  z . 2 z z '  '. '. 1 z z z z
Phép chia hai số phức z ' và z  0 là  z 'z   . z 2 z z z .
3. TẬP HỢP ĐIỂM BIỂU DIỄN SỐ PHỨC
Một số tập hợp điểm biểu diễn số phức z thường gặp:
 ax  by  c  0  tập hợp điểm l| đường thẳng
 x  0  tập hợp điểm là trục tung Oy
 y  0  tập hợp điểm là trục hoành Ox  2 2 x a  y b R2    
 tập hợp điểm là hình tròn tâm I a;b, bán kính R   2 2
x  a   y  b 2   R
 tập hợp điểm là đường tròn có tâm I a;b, bán kính x 2   y2  a 2 x  b 2 y  c  0  R a2 b2    c
 x  0  tập hơp điểm là miền bên phải trục tung
 y  0  tập hợp điểm là miền phía dưới trục hoành
 x  0  tập hợp điểm là miền bên trái trục tung
 y  0  tập hợp điểm là phía trên trục hoành Trang 46  y ax2 
 bx  c  tập hợp điểm l| đường Parabol 2 2  x y 
 1  tập hợp điểm l| đường Elip a2 b2 2 2  x y 
 1  tập hợp điểm l| đường Hyperbol a2 b2
4. PHƢƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC
4.1. Căn bậc hai của số thực âm
 Cho số z , nếu có số phức z sao cho z 2  z thì ta nói z là một căn bậc hai của z . 1 1 1
 Mọi số phức z  0 đều có hai căn bậc hai.
 Căn bậc hai của số thực z âm là i  z .
Tổng qu{t, c{c căn bậc hai của số thực a âm là i a .
4.2. Phƣơng trình bậc hai với hệ số thực
Cho phương trình bậc hai ax 2  bx  c  0, a
 ,b,c   ,a  0 . Xét biệt số   b2  a 4 c của phương trình. Ta thấy:  b
Khi   0 , phương trình có một nghiệm thực x   . a 2     b
Khi   0 , phương trình có hai nghiệm thực phân biệt x  . 1,2 a 2 b  i 
 Khi   0 , phương trình có hai nghiệm phức x  . 1,2 a 2
5. BÀI TOÁN LIÊN QUAN ĐẾN MAX – MIN MÔ ĐUN SỐ PHỨC  z r max z 2   z  z  1
Cho số phức z thỏa mãn z .z  z  r, r  0 1  . 1 2   z  r min z 2    z z 1 1 
 Cho số phức z thỏa mãn z .z  z  r , r  0 . 1 2 1  1  z r z r max P 2   z 1  và min P 2   z 1  z 3 z z 3 z 1 1 1 1
 Cho số phức z thỏa mãn z z.  z  z z.  z  k, k  0 . 1 2 1 2  2 2 k k  4 z2 max z  và min z  2 z 2 z 1 1 MỤC LỤC
PHẦN I. HÀM SỐ ................................................................................................................................. 1
1. SỰ ĐỒNG BIẾN NGHỊCH BIẾN CỦA HÀM SỐ ........................................................................ 1 Trang 47
1.1. Định nghĩa ................................................................................................................................ 1
1.2. Quy tắc và công thức tính đạo hàm ......................................................................................... 1
1.3. Bảng công thức tính đạo hàm ................................................................................................... 2
1.4 . Công thức tính nhanh đạo hàm hàm phân thức ..................................................................... 2
1.5. Đạo hàm cấp 2 .......................................................................................................................... 2
2. CỰC TRỊ HÀM SỐ ........................................................................................................................ 4
2.1. Định nghĩa ................................................................................................................................ 4
2.2. Điều kiện cần để hàm số đạt cực trị ......................................................................................... 5
2.3. Điều kiện đủ để hàm số đạt cực trị .......................................................................................... 5
2.4. Quy tắc tìm cực trị .................................................................................................................... 5
3. MỘT SỐ DẠNG TOÁN LIÊN QUAN ĐẾN CỰC TRỊ HÀM SỐ ................................................ 6
3.1. Cực trị của h|m đa thức bậc ba y  ax 3  bx 2  cx  d. ..................................................... 6
3.2. Cực trị của hàm bậc 4 trùng phƣơng y  ax 4  bx 2  c, a  0 .................................... 9
4. GIÁ TRỊ LỚN NHẤT - GIÁ TRỊ NHỎ NHẤT ........................................................................... 11
4.1. Định nghĩa. ............................................................................................................................. 11
4.2. Phƣơng pháp tìm GTLN,GTNN .......................................................................................... 11
5. ĐƢỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ ........................................................................... 12
5.1. Đƣờng tiệm cận ngang .......................................................................................................... 12
5.2. Đƣờng tiệm cận đứng............................................................................................................ 12
6. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ HÀM SỐ .......................................................... 12
6.1. Khảo sát một số hàm đa thức và hàm phân thức .................................................................. 12
6.2. Một số phép biến đổi đồ thị ................................................................................................... 14
7. TIẾP TUYẾN ................................................................................................................................ 16
7.1. Tiếp tuyến .............................................................................................................................. 16
7.2. Điều kiện tiếp xúc ................................................................................................................... 16
8. TƢƠNG GIAO ĐỒ THỊ .............................................................................................................. 16
9. ĐIỂM ĐẶC BIỆT CỦA HỌ ĐƢỜNG CONG ............................................................................. 17
9.1. B|i to{n tìm điểm cố định của họ đường cong ....................................................................... 17
9.2. B|i to{n tìm điểm có tọa độ nguyên ....................................................................................... 17
9.3. B|i to{n tìm điểm có tính chất đối xứng ................................................................................ 17
9.4. B|i to{n tìm điểm đặc biệt, khoảng cách ................................................................................ 18
PHẦN II. MŨ VÀ LOGARIT .............................................................................................................. 21
1. LŨY THỪA VÀ HÀM SỐ LŨY THỪA ....................................................................................... 21
1.1. Khái niệm lũy thừa ................................................................................................................. 21 n 1.2. Phương trình x
 b. ............................................................................................................ 21
1.3. Một số tính chất của căn bậc n .............................................................................................. 21
1.4. Hàm số lũy thừa ..................................................................................................................... 22
1.5. Khảo sát hàm số mũ x y  a ,
a  0,a  1. ................................................................... 23 Trang 48
2. LOGARIT ..................................................................................................................................... 24
2.1. Khái niệm Logarit................................................................................................................... 24
2.2. Bảng tóm tắt công thức Mũ-logarit thường gặp ..................................................................... 24
3. BẤT PHƢƠNG TRÌNH MŨ VÀ LOGARIT. .............................................................................. 25
3.1. Bất phương trình mũ cơ bản .................................................................................................. 25
3.2. Bất phương trình logarit cơ bản ............................................................................................. 25
4. BÀI TOÁN LÃI SUẤT NGÂN HÀNG........................................................................................ 26
4.1. Lãi đơn ................................................................................................................................... 26
4.2. Lãi kép .................................................................................................................................... 26
4.3. Tiền gửi hàng tháng ............................................................................................................... 27
4.4. Gửi ngân hàng và rút tiền gửi hàng tháng ............................................................................. 27
4.5. Vay vốn trả góp ...................................................................................................................... 27
4.6. B|i to{n tăng lương ................................................................................................................ 28
4.7. B|i to{n tăng trưởng dân số ................................................................................................... 28
4.8. Lãi kép liên tục ....................................................................................................................... 28
PHẦN III. NGUYÊN HÀM - TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN ......................................... 29
1. NGUYÊN HÀM............................................................................................................................ 29
1.1. Định nghĩa .............................................................................................................................. 29
1.2. Tính chất của nguyên hàm ..................................................................................................... 29
1.3. Sự tồn tại của nguyên hàm ..................................................................................................... 29
1.4. Bảng nguyên hàm các hàm số thường gặp ............................................................................ 29
1.5. Bảng nguyên hàm mở rộng .................................................................................................... 30
2. CÁC PHƢƠNG PHÁP TÍNH NGUYÊN HÀM .......................................................................... 31
2.1. Phương ph{p đổi biến ............................................................................................................ 31
2.2. Phương ph{p nguyên h|m từng phần ................................................................................... 32
3. TÍCH PHÂN ................................................................................................................................. 33
3.1. Công thức tính tích phân ........................................................................................................ 33
3.2. Tính chất của tích phân .......................................................................................................... 33
4. PHƢƠNG PHÁP TÍNH TÍCH PHÂN ......................................................................................... 34
4.1. Phương ph{p đổi biến ............................................................................................................ 34
4.2. Phương ph{p tích ph}n từng phần ........................................................................................ 34
5. TÍCH PHÂN CÁC HÀM SỐ SƠ CẤP CƠ BẢN ......................................................................... 35
5.1. Tích phân hàm hữu tỉ ............................................................................................................. 35
5.2. Tích phân hàm vô tỉ ............................................................................................................... 37
5.3. Tích ph}n h|m lượng giác ...................................................................................................... 39
6. ỨNG DỤNG TÍCH PHÂN .......................................................................................................... 42
6.1. Diện tích hình phẳng .............................................................................................................. 42
6.2. Thể tích vật thể và thể tích khối tròn xoay ............................................................................. 43
PHẦN IV. SỐ PHỨC ........................................................................................................................... 45 Trang 49
1. SỐ PHỨC ..................................................................................................................................... 45
1.1. Khái niệm số phức .................................................................................................................. 45
1.2. Hai số phức bằng nhau .......................................................................................................... 45
1.3. Biểu diễn hình học số phức .................................................................................................... 45
1.4. Số phức liên hợp ..................................................................................................................... 45
1.5. Môđun của số phức ................................................................................................................ 45
2. PHÉP CỘNG TRỪ NHÂN CHIA SỐ PHỨC .............................................................................. 46
2.1. Phép cộng và phép trừ số phức .............................................................................................. 46
2.2. Phép nhân số phức ................................................................................................................. 46
2.3. Chia hai số phức ..................................................................................................................... 46
3. TẬP HỢP ĐIỂM BIỂU DIỄN SỐ PHỨC ..................................................................................... 46
4. PHƢƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC....................................................................... 47
4.1. Căn bậc hai của số thực âm .................................................................................................... 47
4.2. Phương trình bậc hai với hệ số thực ....................................................................................... 47
5. BÀI TOÁN LIÊN QUAN ĐẾN MAX – MIN MÔ ĐUN SỐ PHỨC ............................................ 47 Trang 50

Bảng tóm tắt kiến thức toán 12 học kỳ 1

Thông tin :

Tài liệu liên quan:

Hình nón là gì? Công thức tính diện tích xung quanh hình nón | Toán 12

Đề tham khảo kỳ thi tốt nghiệp THPT từ năm 2025 môn Toán

Đề thi thử TN THPT 2025 lần 1 môn Toán trường THPT Lương Tài 2 – Bắc Ninh

Lời giải chi tiết đề tham khảo kỳ thi tốt nghiệp THPT môn Toán từ năm 2025

Đề chọn đội tuyển thi HSG QG môn Toán THPT năm 2024 – 2025 sở GD&ĐT Bắc Giang