Bảng Tóm Tắt Lý Thuyết Toán 12 Cả Năm

TÓM TẮT KIẾN THỨC TOÁN 12 I.BẢNG ĐẠO HÀM  
1)u  v'  u ' v' 15) .
u v' u '.v . u v ' '  u  u '.v  . u v' 2)    2  v  v
16)k.u'  k.u '
3)(c)' = 0
17)(x)' = 1 n n n n- 4)(x ) 1 ' . n x - = 18)(u ) 1 ' = . n u .u ' ' ' 1 æ ö 1 1 æ ö u ' 5)ç ÷ ç ÷ = - ç ÷ ç ÷ 19)ç ÷ = - 2 èxø ç ÷ x 2 èuø u ' 1 ' u ' 6)( x) = 20)( u ) = 2. x 2. u
7)sin x'  cos x
21)sinu'  u '.cosu
8)cos x'  sin x
22)cosu'  u  '.sinu 1 u ' 9) tan x 2 '  1 tan x
23) tan u'  2 cos x 2 cos u 1  u  '
10)cot x'    2 1 cot x
24)cot u '  2  sin x 2 sin u 11) x ' x e  e
25) u '  '. u e u e 12) x ' x a
 a .ln a
26) u '  '. u a
u a .ln a u 13) x 1 ln '  27) u ' ln '  x u u 14) x  28) u  a  ' log ' a  1 log ' . x ln a . u ln a ' ' '  . a x  b  . a d  . b c 29) 2
sin x  sin 2x. 30) 2
cos x  sin 2x . 31)    .  . c x  d 
 .cx  d 2 Trang1 ' 2 2
 ax  bx  c 
(ab ' a 'b)x  2(ac ' a 'c)x  (bc ' b 'c) 32)   2 2 2
a ' x  b ' x  c '
(a ' x  b ' x  c ')  
Cách nhớ công thức 32 là : “anh ba, ăn cơm hai lần, ba chén”
II.DẠNG TOÁN TÍNH GTLN, GTNN CỦA HS: y  f (x) TRÊN ĐOẠN  ; a b  
-Hàm số xác định và liên tục trên  ; a b  
-Tính y’, gpt y’= 0. Tìm các nghiệm x , x ,... ; a b . 1 2 -Tính f ( ) a ,f ( )
b ,f (x ),f (x ) … -Số nào lớn là GTLN, số nào nhỏ là GTNN. 1 2
Chú ý: 1) Nếu đề bài yêu cầu tính GTLN, GTNN trên khoảng a;b thì ta lập BBT của hàm
số trên khoảng đó rồi kết luận.
2) Nếu đề bài không cho đoạn, khoảng thì ta tìm trên TXĐ
III. Các hàm cơ bản và tính chất:
HSDB tren   a  0
1) Hàm bậc nhất y  .
a x  b a) y  . a x  b
HSNB tren   a  0
b) Không cực trị, không tiệm cận. 2) Hàm 3 2 y  . a x  . b x  .
c x  d a  0 a  0 a  0 a) HSĐB trên R khi  b) HSNB trên R khi  2 b   3ac  0 2 b   3ac  0 a  0
c) HS có 2 cực trị khi  2 b   3ac  0
d) ĐTHS có 2 hoặc 0 cực trị, không có tiệm cận. 3 cuc tri khi . a b  0 3) Hàm bậc bốn 4 2
y  ax  bx  c a  0 1 cuc tri khi .ab  0
a) HS không bao giờ ĐB, NB trên R d) ĐTHS có 3 hoặc 1 cực trị, không có tiệm cận. . a x  b d  . a d  . b c 4) Hàm y 
ad bc  0;c  0a)TXĐ: D   \  , tính y'  . c x  d  c  cx  d2
b) Hàm số ĐB trên từng khoảng XĐ  y '  0 x  D  . a d  . b c  0
c) Hàm số NB trên từng khoảng XĐ  y '  0 x  D  . a d  . b c  0 Trang2 d) ĐTHS có 2 đườ a
ng tiệm cận. TCN: y  ; TCĐ: d x   c c
5) DẠNG TOÁN Tìm m để hs đạt cực trị tại x . 0 y'  x  0 0 
- Tính y' , Tính y ' . Hs đạt cực trị tại x   . Giải tìm m. 0 y'  x  0 0 
6) DẠNG TOÁN Tìm m để hs đạt cực tiểu tại x . 0 y'  x  0 0 
- Tính y' , Tính y ' . Hs đạt cực tiểu tại x   . Giải tìm m. 0 y'  x  0 0 
7) DẠNG TOÁN Tìm m để hs đạt cực đại tại x . 0 y'  x  0 0 
- Tính y' , Tính y ' . Hs đạt cực đại tại x   . Giải tìm m. 0 y'  x  0 0 
8) Cách tìm tiệm cận hàm số TS y  MS x  x x 1  1
a) MS  0  x  x
b)Nhập TS cal x kq  0 hoặc MR thì loại, còn lại là TCĐ 2  2 x  ....  ... 10 TS 10 c)Nhập cal
kết quả bằng số thì y bằng số đó là TCN. 10 MS 10 
IV. LŨY THỪA-MŨ-LOGA m  a mn m n m n 1) a  a .a 2) a  3) n m m.n a  a n a n m n a  a  4)   n n n a .b a.b 5) n n m a  a 6)    n b  b  n n  1  a   b  n 7) a  8)      n a  b   a  f ( x ) f ( x ) g( x ) 9) a
b  f ( x )lo    a g b 10) a a f ( x ) g( x ) 11) f ( x ) a b f ( x ) a b
  f ( x )  log   a b 12)  f ( x ) loga b a 1  0  a 1  Trang3 f ( x ) g( x ) a a  f ( x ) g( x ) a a  13)
  f ( x )  g( x ) 14)
  f ( x ) g( x ) a 1  0  a 1  b 15)log b .b
 log b  log b 16) 1 log
 log b  log b a  1 2  a 1 a 2 a a 1 a 2 b2 m 1 17)log b  m.log b 18)log b  .log b 19) a a a m a m m m log b  .log b
20)log b.log c  log c a n a b a a n log b 1 21) c log b  22)log b  a log a a log a c b 23) b log    a f ( x ) b f ( x ) a 24)
 f ( x )  g( x )  log   a f ( x ) loga g( x )  g( x )  0   hoac f(x) 0
25) Nếu đề bài chưa cho đúng dạng CT nghiệm thì ta đặt điều kiện sau đó áp dụng các CT biến
đổi pt về đúng dạng CT nghiệm.
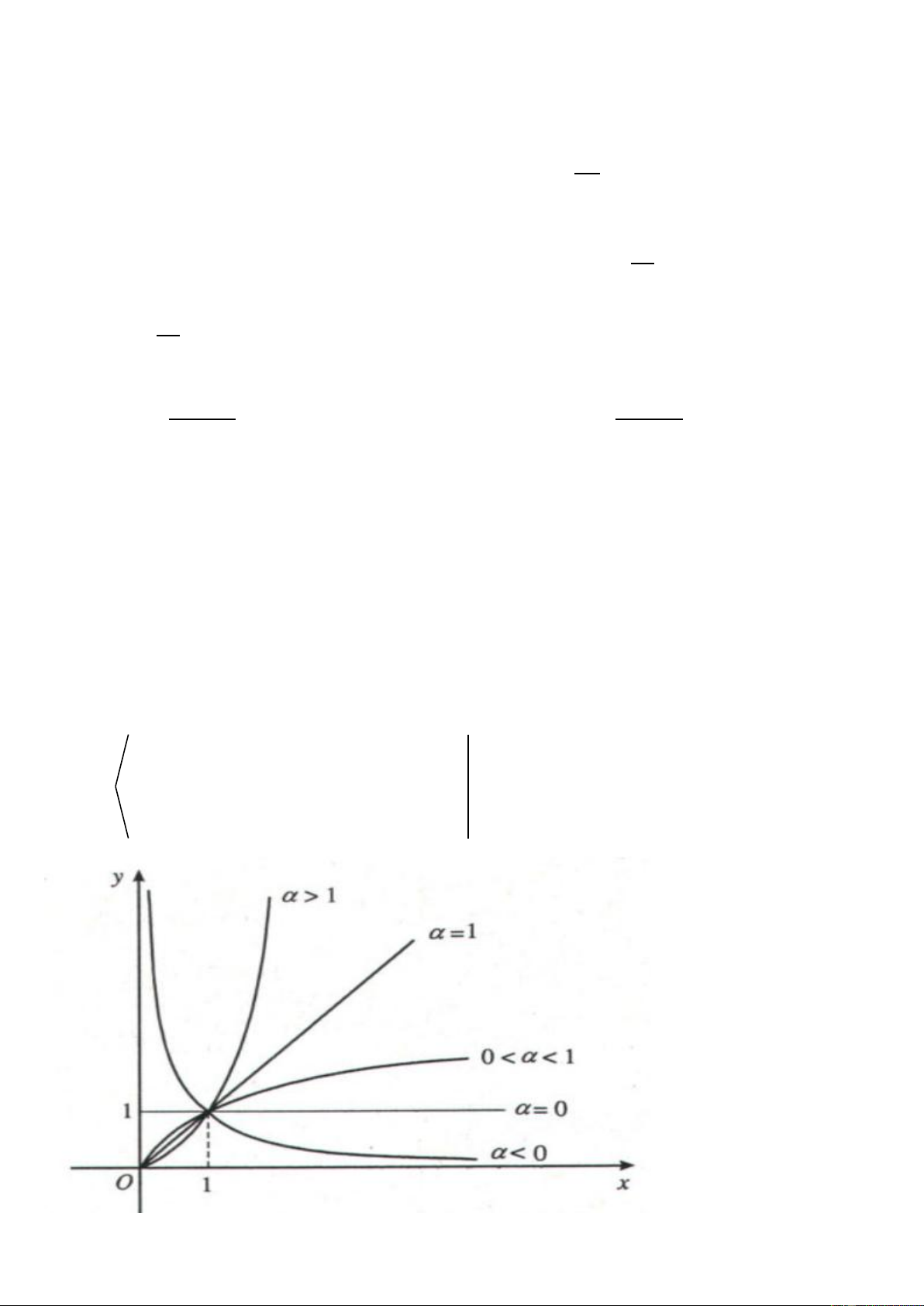
V. BẢNG TÓM TẮT HÀM SỐ LŨY THỪA y ua =
 nguyên duong . TXD: u   . R
y  u  nguyên â . m TXD: u  0.
 không nguyên. TXD: u  0. Trang4 BẢNG NGUYÊN HÀM
NGUYÊN HÀM CĂN BẢN
NGUYÊN HÀM MỞ RỘNG 1) dx  x  C  adx  ax  C  1 x 1    1 (ax  b) 2) x dx   C (  -1)  (ax  b) dx  .  C (  -1)    1 a  1 1 dx 1 3) dx  ln | x | C   ln | ax  b | C  x ax  b a 4) x x e dx  e  C  ;  x  x e dx  e   C  x  1 a ax b axb e dx  e  C  x ; a dx = + C ò a ln a 5) sin xdx  cos x  C  1
sin(ax  b)dx   cos(ax  b)  C  a 6) cos xdx  sin x  C  1
cos(ax  b)dx  sin(ax  b)  C  a dx dx 1 7)  cot x  C    cot(ax  b)  C  2 sin x 2 sin (ax  b) a dx dx 1 8)  tan x  C   tan(ax  b)  C  2 cos x 2 cos (ax  b) a dx dx 1 9)  2 x  C   2 a.x  b  C  x a.x  b a 1 1 1 1 1 10) dx    C  dx   .  C  2 x x a.x  b2 a a.x  b 11) tan xdx = - ln cos x + C ò 1 tan(a.x + b)dx = - ln cos(a.x + b) + C ò a 12) cot xdx ò = ln sin x + C 1 co t(a.x + b)dx = ln sin(a.x + b) + C ò a 13) ln . = .ln - + ò xdx x x x c . x = . x x - + = ( - ) 1 . x x e dx x e e c x e + c ò
VI. Định nghĩa và tính chất:
1) Định nghĩa nguyên hàm: Trang5 Nếu ( )'
F(x) = f (x) thì F(x) được gọi là một nguyên hàm của f (x) .
2) ĐỊNH NGHĨA TÍCH PHÂN:
-Giả sử F(x) là một nguyên hàm của f (x) trên đoạn[a;b]. b
Khi đó hiệu số F(b) - F(a) được gọi là tích phân từ a đến b của hàm số f (x) , kí hiệu f (x)dx ò . a b b f (x)dx = F(x) = F(b) - F(a) ò a a 3)Các tính chất: ,
3.1) ( f (x).dx ò
) = f (x) 3.2) f ('x).dx = f (x)+ c ò 3.3)
k. f (x).dx = k. f (x).dx ò ò
(k là hằng số khác 0) 3.4) f
é (x)± g(x).d ù x =
f (x).dx ± g(x).dx ò ë û ò ò 1 3.5) f ( .
a x + b)dx = .F ( .
a x + b)+ c (a ¹ ) 0 ò a b b 3.6)
k. f (x).dx = k. f (x).dx ò ò (k là hằng số) a a
Chỉ tính chất 3 và 6 giữa nguyên hàm và tích phân khác nhau, cá tính chất còn lại giống nhau.
3) Dạng 3: Vận dụng phương pháp tính NGUYÊN HÀM TỪNG PHẦN:
-Nếu hai hàm u = u(x); v = v(x) có đạo hàm liên tục, ' '
v (x)dx = dv;u (x)dx = du . Ta có công b b b
thức tính tích phân từng phần: udv = uv - vdu ò ò a a a
-Các bước tính nguyên hàm từng phần: Đặt u = u(x) DH ¾ ¾® du = ' u (x)dx dv = phần còn lại NH ¾ ¾® v = v(x) . Thế vào công thức.
*Một số kỹ thuật khi tính NGUYÊN HÀM TỪNG PHẦN : p(x).sin xdx ò p(x).ln xdx ò 1 ln xdx ò xa
( p(x) là đa thức) (a ¹ - ) 1 Trang6 p(x).cos xdx ò x p(x).e dx ò u = p(x) ln x dv = Phần còn lại
Tóm lại: Đặt u theo thứ tự ln, đa, lượng = mũ b
-Hình phẳng giới hạn bởi y = f (x), trục hoành Ox, x = a, x = b được tính S = f (x)dx ò a b
-Hình phẳng giới hạn bởi y = f (x), y = f (x) , x = a, x = b được tính S = f (x) - f (x)dx ò 1 2 1 2 a
*Để tính diện tích hình phẳng ta cần tìm đủ 4 đường; hai đường y , hai đường x . Nếu thiếu
đương x ta tìm bằng cách giải phương trình hoành độ giao điểm.
2) Tính thể tích vật thể tròn xoay:
-Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi y = f (x) , hai đường thẳng b
x = a;x = b quanh trục hoành: 2 V = p. y dx ò a
Chú ý: Đối với bài toán tính thể tích vật thể tròn xoay không giải phương trình hoành độ
giao điểm nếu tích phân đã có đủ hai cận.
* công thức tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox
tại các điểm x = a , x = b (a < b)có diện tích thiết diện bị cắt bởi mặt phẳng vuông góc với trục a V = S x x
Ox tại điểm có hoành độ x (a £ x £ b) là S (x ). Thể tích là : ò ( )d . b Phần 4: SỐ PHỨC
I.Định nghĩa và các tính chất căn bản -Số i: 2 i = - 1 -Với n = 4q + r , ta có: n r i = i
-Số phức z = a + bi với a,bR , a gọi là phần thực, b gọi là phần ảo -Môđun của số phức 2 2 z  a  bi  a  b Trang7
-Điểm biểu diễn của z = a + bi là M(a; b)
-Số phức z = a + bi có số phức liên hợp là: z  a  bi
-Hai số phức bằng nhau khi phần thực bằng phần thực, phần ảo bằng phần ảo. a  c a  .
b i  c  d.i  b   d íï z + z = 2a ï -Lưu ý ì 2 2 ïï z.z = a + b î
-Số phức z = bi với b  R b  0 được gọi là số thuần ảo.
-Cộng trừ hai số phức a  bi  c  di   a  c   b  d i
-Phép nhân hai số phức thực hiện như nhân hai số thực với lưu ý 2 i = - 1.
-Phép chia số phức thực hiện bằng cách nhân tử và mẫu cho số phức liên hợp với mẫu.
-Căn bậc hai của số thực a âm là i | a | -Phương trình bậc hai 2
ax  bx  c  0 với trường hợp b  i |  | 2
  b  4ac  0 thì pt có hai nghiệm phức xác định bởi công thức x  1,2 2a
*Chú ý: Phương trình bậc hai 2
ax  bx  c  0 với trường hợp 2
  b  4ac  0 có hai nghiệm
phức là hai số phức là hai số phức liên hợp.
Phần 5:HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
I. Lý thuyết căn bản      1) OM  . x i  .
y j  z.k  M  ;
x y; z  AB   x  x ; y  y ; z  z B A B A B A   
Cho a  a ;a ;a , b  b ;b ;b , A x ; y ; z , B x ; y ; z , C  x ; y ; z . C C C  A A A B B B  1 2 3  1 2 3   2) Độ dài vecto 2 2 2
a  a  a  a 1 2 3 
3) Độ dài đoạn AB: AB= AB   x  x 2   y  y 2   z  z 2 B A B A B A   . a b
4) Góc giữa hai vecto: cos    (tích vô hướng chia tich độ dài) a . b x  x y  y z  z
5) Gọi I là trung điểm AB: A B x  , A B y  , A B z  I 2 I 2 I 2
x  x  x
y  y  y
z  z  z
6) Gọi G là trọng tâm  ABC : A B C x  , A B C y  , A B C z  G 3 G 3 G 3 Trang8    
7) Tích vô hướng hai vecto: .
a b  a .b  a .b  a .b . Suy ra: a  b  a .b  a .b  a .b  0 1 1 2 2 3 3 1 1 2 2 3 3    a a a a a a 
8) Tích có hướng hai vecto: 2 3 3 1 1 2
a,b   ; ;    b b b b b b  2 3 3 1 1 2  ér r ùr ér r ùr
-Chú ý: +Tích có hướng của 2 vecto vuông góc cả hai vecto đó.( a;b .a = 0; a;b .b = ê ú ê ú ë û ë û ) 0 . r r ér r ù r
+Hai vecto a;b cùng phương Û a;b = 0 ê ú ë û r r ur ér r ùur
+Ba vecto u; v; w đồng phẳng Û u; v .w = 0 ê ú ë û    1
9) A, B, C là 3 đỉnh tam giác (không thẳng hàng)     A , B AC  0 
    S  A , B AC ABC  2  
  
1   
10) A, B, C, D là 4 đỉnh tứ diện     A , B AC.AD  0   V  A , B AC . AD ABCD 6  
  
11) Thể tích hình hộp ' ' ' ' ABC . D A B C D bằng: ' V
 AB, AD. AA ' ' ' ' ABCD. A B C D  
12) Khoảng cách từ M  x , y , z đến mp P : Ax  By  Cz  D  0 là: o o o o  
Ax  By  Cz  D d M , P 0 0 0  0 2 2 2
A  B  C 
13) Cho đường thẳng (  ) qua M và có VTCP u .   M M ,u  
Khoảng cách từ M  x , y , z đến (  ) là: d M ,    0  0 o o o o  u  
14) Cho đường thẳng  qua M , VTCP u ,  qua M , VTCP u 2  1  1 1 2 2
  
  
u ,u .M M   
,  chéo nhau  u
 ,u .M M  0  d  ,    1 2  1 2 1 2 1 2 1 2 1 2   u ,u  1 2   tâm I ; a ; b c 2 2 2 2
15) PTMC  S  
 S:xa yb zc  R bán kính R tâm I  ; a ; b c PT: 2 2 2
x  y  z  2ax  2by  2cz  d  0 là PTMC S  2 2 2
R  a  b  c  d  2 2 2
DK dê (S) là ptmc là : a  b  c  d  0
 Muốn viết PTMC cần biết tâm và bán kính Trang9 tâm I
a) Mặt cầu tâm I và đi qua A   S 
R  IA   x  x  y  y  z  z A I 2
 A I 2  A I 2 uur
(R bằng độ dài đoạn IA hay AI hay độ dài vecto IA đều đúng)
b) Mặt cầu tâm I  x ; y z tiếp xúc mp(P): P : Ax  By  Cz  D  0 0 0; 0  tâm I  S     R  d  Ax By Cz D I;(P) 0 0 0  2 2 2
A  B  C
c) Mặt cầu (S) đường kính AB:
 x  x y  y z  z  tâm A B I ; A B ; A B là trung diem AB   uur    AB  S  2 2 2
R = IA = IB = đều 2 AB
x  x  y  y  z  z B A 2
 B A2  B A2 R   2 2 đúng.
d) Mặt cầu qua bốn điểm A, B, C, D -Nêu dạng   2 2 2
S : x  y  z  2ax  2by  2cz  d  0 . Thế tọa độ 4 điểm vào (S) được hệ 4 pt 4
ẩn. Giải hệ tìm 4 ẩn a, b, c, d.
16) Phương trình mặt phẳng 
*VTPT là vecto khác 0 có giá vuông góc với mp. Muốn viết ptmp: 
-Cần M  x ; y ; z n  o o
o o (P) và một VTPT  ; A ;
B C  . (P) có dạng:
A x  x   B y  y  C  z  z o o
o   0 , biến đổi về dạng: Ax + By + Cz + D = 0 
Hoặc cần một VTPT n   ; A ;
B C  và một điều kiện khác, suy ra (P): Ax  By  Cz  D  0 . Từ
điều kiện khác giải tìm D
 Đặc biệt: Mp (Oxy): z = 0 (Oyz): x = 0 (Oxz): y = 0
 A Î (Oxy)Þ A(a ;a ;0) ;B Î (Oxz)Þ B(b ;0;b ) ;CÎ (Oyz) Þ C(0;c ;c ) 1 2 1 3 2 3  x y z
Ptmp qua A(a;0;0),B(0;b;0),C(0;0;c)có dạng: + + = 1 (a ¹ 0;b ¹ 0;c ¹ 0) a b c
 (P) //(Q) : Ax  By  Cz  D  0  (P) có dạng: Ax + By + Cz + m = 0(m ¹ D)
17) Phương trình đường thẳng(D ): Trang10 
*VTCP là vecto khác 0 có giá song hoặc trùng (D ). Muốn viết pt đường thẳng cần x  x  .  a t  0 
M  x ; y ;z u  y  y 
o o o o (D )và một VTCP
 ,a ,bc. Pt tham số (D):  . b t 0  z  z  .  c t 0 x - x y - y z - z
-Nếu a ¹ 0;b ¹ 0;c ¹ 0 thì pt chính tắc đt (D ) có dạng: 0 0 0 = = a b c
Đặc biệt: A Î Ox Þ A(a;0;0) ;B Î Oy Þ B(0;b;0) ;C Î Oz Þ C(0;0;c)
18) Một số tình huống tìm VTPT của mp, VTCP của đường thẳng:   
a) mp(P) vuông góc với AB VTPT là n  AB hoac BA P
 x  x y  y z  z  qua A B I ; A B ; A B la td AB  
b) (P) là mp trung trực đoạn AB:   P  2 2 2     
VTPT : n  AB hoac IA hoac IB P  qua A
c) mp(P)tiếp xúc mc (S) tâm I bán kính R tại A  S :   P  
VTPT : n  AI P 
d)  qua A, B. Suy ra VTCP là AB
19) Sáu VTTĐ cần nhớ giúp ta tìm VTPT của mp, VTCP của đường thẳng    
1)  P  Q  n  n 2) P Q  n  n P Q
  / /  chon P Q    
3) d    u  u 4) d / /  chon u  u d  d        P d / /(P) 5)
 d  chon n = u 6)   u  n P d d  (P) d P    n  a     Nêu 
  thì chon n   ; a b   n  b  
Phần 7: HÌNH HỌC KHÔNG GIAN
I. Công thức tính thể tích và cách tìm góc: S
1)Thể tích khối chóp bằng một phần ba diện tích đáy A' B' nhân với chiều cao.
2)Thể tích khối lăng trụ bằng diện tích đáy nhân với A C' B chiều cao. C Trang11 V
SA' SB ' SC '
3)Tỉ số thể tích: S.A'B'C' = . . V SA SB SC S.ABC
4)Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó lên mặt
phẳng. Để xác định hình chiếu của đường thẳng lên mặt phẳng ta cần một giao điểm và một điểm vuông góc.
5)Góc giữa hai mặt phẳng: Cần một giao tuyến, một đường thẳng nằm trong mặt phẳng này
vuông góc giao tuyến, một đường thẳng nằm trong mặt phẳng kia và vuông góc giao tuyến, góc
giữa hai mặt phẳng là góc giữa hai đường thẳng mới tìm. II. Tam giác
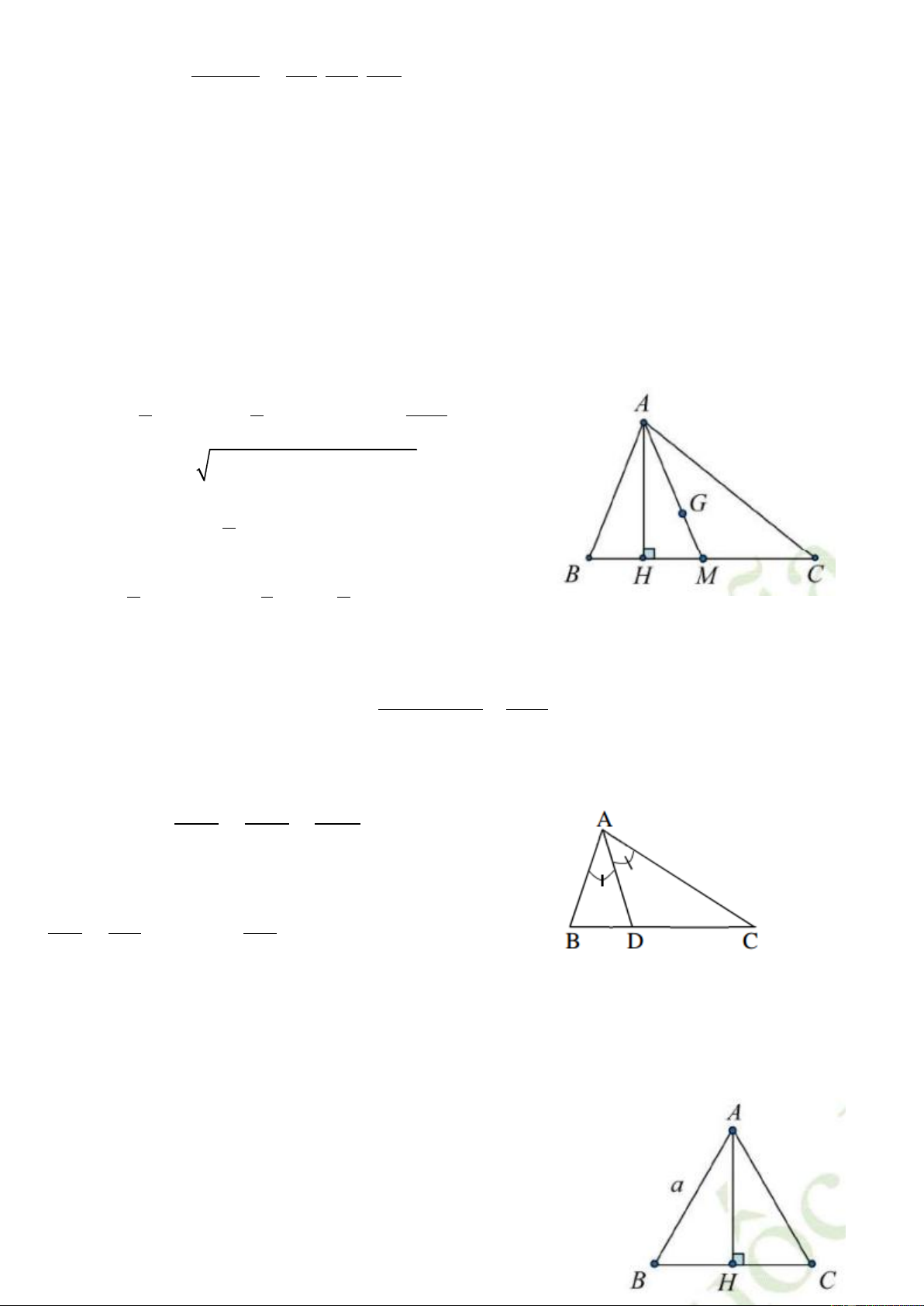
a) Tam giác thường: 1 1 . a . b c 1)S = .BC.AH = . . AB AC.sin A = D ABC 2 2 4R = . p r =
p(p - a)(p - b)(p - c) 1 2) S = S = S D ABM ACM 2 DABC 2 1 1 3) AG = AM ; GM = AM = AG 3 3 2
(G là trọng tâm D ABC ) 2 2 2 4) Độ AB + AC BC
dài đường trung tuyến: 2 AM = - 2 4 5) Định lí cosin: 2 2 2
BC = AB + AC - 2.A . B AC.cos A 6) Đị a b c nh lí sin: = = = 2.R sin A sin B sin C
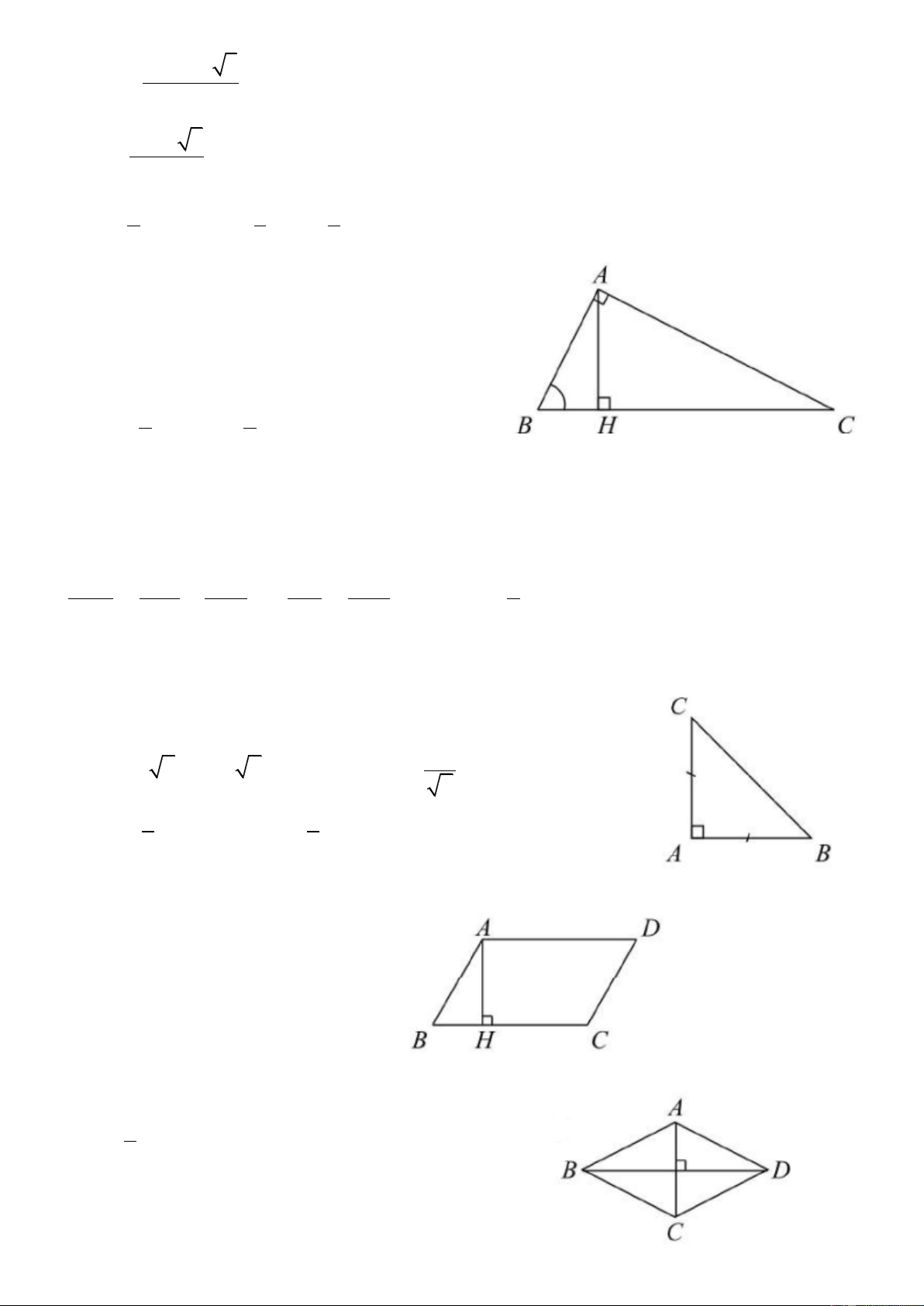
7) Gọi D là chân đường phân giác trong góc A. Ta có: DB AB uuur AB uuur = Þ DB = - .DC DC AC AC
8) Trực tâm tam giác là giao điểm ba đường cao.
Trọng tâm tam giác là giao điểm ba đường trung tuyến.
Tâm đường tròn ngoại tiếp là giao điểm ba đường trung trực.
Tâm đường tròn nội tiếp là giao điểm ba đường phân giác.
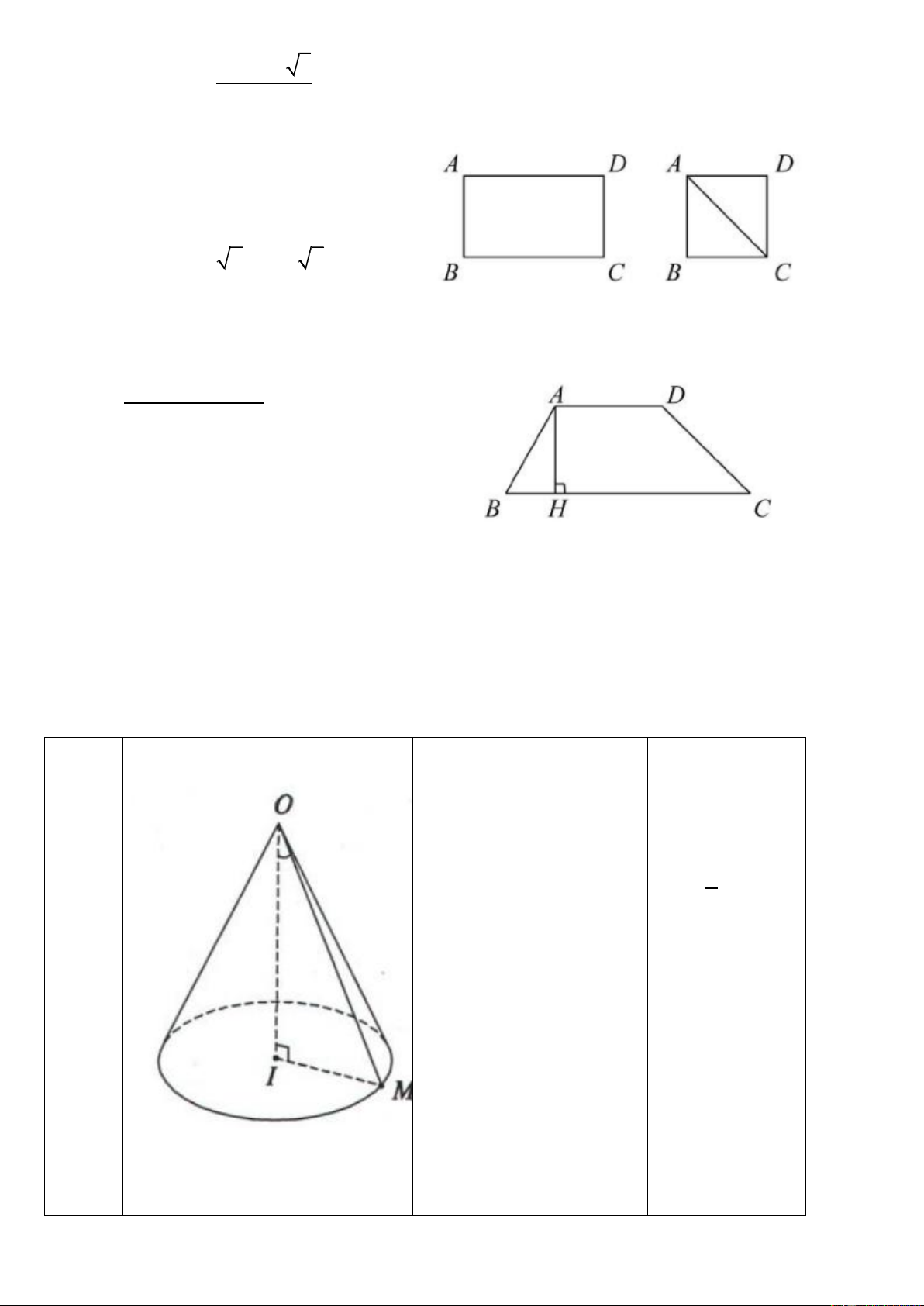
b) Tam giác đều cạnh a . Trang12 (canh)2 3 1) S = D ABC 4 can . h 3 2) AH = 2 2 1 1 3) AG = AH; GH = AH = AG (G là trọng 3 3 2 tâm D ABC )
4) Tâm đường tròn ngoại tiếp là trọng tâm tam giác.
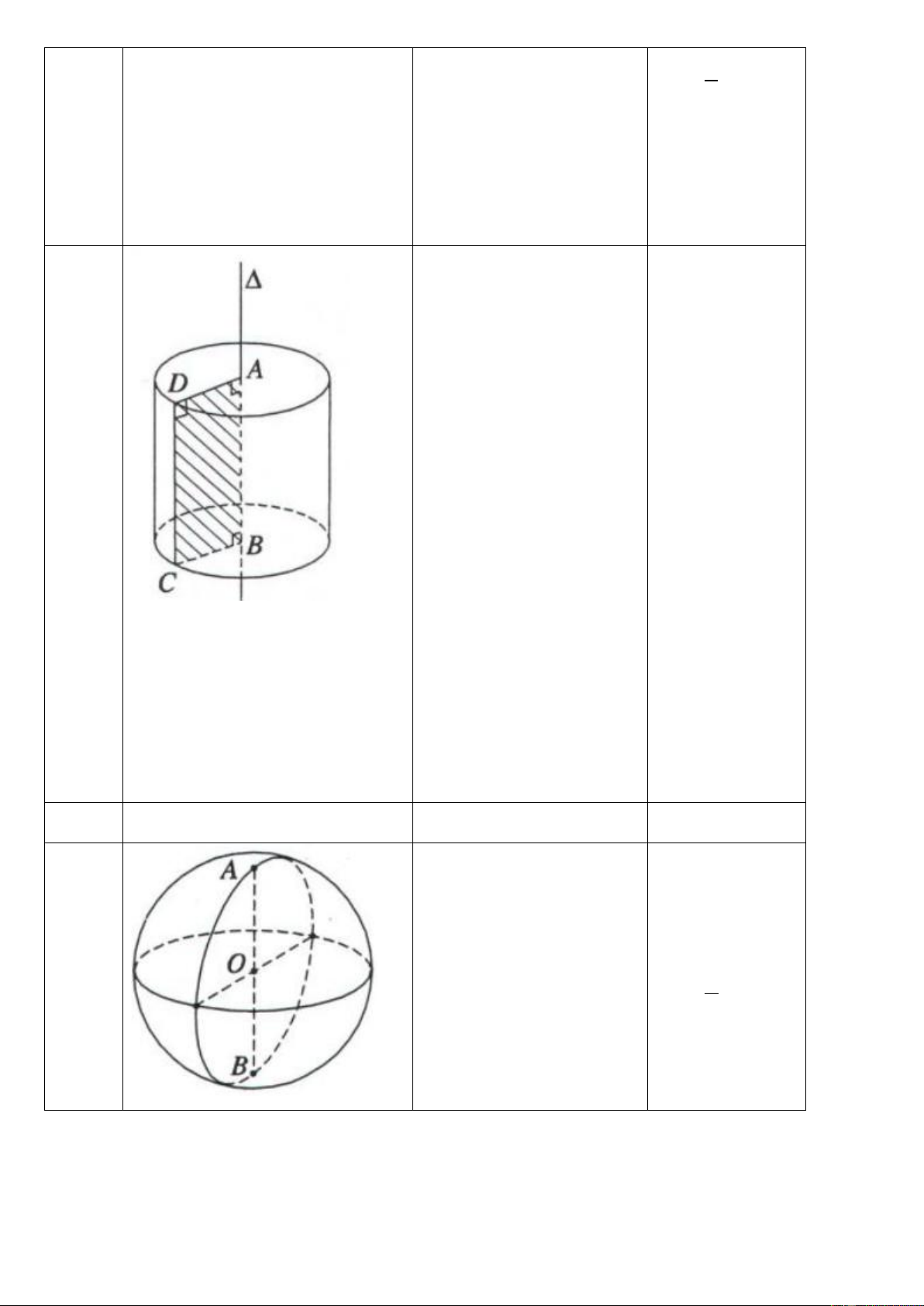
c) Tam giác vuông tại A. 1 1 1)S = A . B AC = AH.BC D ABC 2 2 2 2 2
2)BC = AB + AC 2 2
3) AB = BC.BH 4) AC = BC.CH 2 5) AH = H .
B HC 6) AH.BC = A . B AC 2 1 1 1 HB AB 1 7) = + 8) = 9) AM = BC 2 2 2 2 AH AB AC HC AC 2
10) Tâm đường tròn ngoại tiếp là trung điểm cạnh huyền.
d) Tam giác vuông cân tại A BC 1)BC = A .
B 2 = AC. 2 2) AB = AC = 2 1 1 3)S = canh n = BC D ABC ( huyê )2 2 4 4 III. Tứ giác: a) Hình bình hành: S = B . C AH = A . B A . D sin A ABCD b) Hình thoi: 1 S =
AC.BD = A . B A . D sin A ABCD 2 Đặ · c biệt: Nếu 0
ABC = 60 thì DABC, DADC đều. Trang13 (canh)2 3 S = 2.S = ABCD D ABC 2
c) Hình chữ nhật: S = A . B AD ABCD d) Hình vuông: 2 S = AB ABCD Đường chéo:
AC = BD = (canh) 2 = AB 2 d) Hình thang:
(AD + BC).AH S = ABCD 2
Đặc biệt: Nếu ABCD là hình thang cân thì:
AD = BC - 2.BH
e) Tứ giác có hai đường chéo vuông góc: Diện tích bằng một phần 2 tích độ dài hai đường chéo.
f) Tứ giác có hai đường chéo tạo nhau góc a : Diện tích bằng một phần 2 tích độ dài hai
đường chéo nhân sina .
Phần 8: KIẾN THỨC TRỌNG TÂM PHẦN MẶT TRÒN XOAY Tên Các yếu tố Diện tích Thể tích Hình
Diện tích xung quanh: nón 1 tròn S = . . p q xq . Trong xoay 2 1
đó: p là chu vi đáy của V = . . B h . 3
hình chóp đều nội tiếp Trong đó: B là
hình nón; q là khoảng diện tích đáy;
cách từ O tới một cạnh h là chiều cao.
đáy của hình chóp đều. S = p.r.l xq Diện tích đáy: 2
S = p.r d Các yếu tố gồm:
Diện tích toàn phần: Trang14
Đường sinh: l = OM . S = S + S 1 tp xq d 2 V = .p.r .h
Chiều cao: h = OI . 2
S = p.r.l + p.r 3 tp
Bán kính đường tròn đáy:
S = p.r r + l tp ( . ) r = IM . ·
Góc ở đỉnh mặt nón: 2.IOM Hình
Diện tích xung quanh: trụ S = . p h . Trong đó: V = . B h. xq tròn Trong đó: B p là là chu vi đáy của xoay diện tích đáy;
hình lăng trụ đều nội h là chiều cao.
tiếp hình trụ; h là chiều cao. S = 2p.r.l xq . Diện tích 2 đáy: 2
S = 2.p.r 2 d 2
V = p.r .h
Diện tích toàn phần: Các yếu tố gồm: S = S + S Đườ tp xq 2 d
ng sinh: l = CD. 2
S = 2p.r.l + 2p.r tp
Chiều cao: h = l = AB .
S = 2p.r r + l tp ( . )
Bán kính đường tròn đáy:
r = AD = BC . Tên Các yếu tố Diện tích Thể tích Mặt cầu 2
S = 4p.R 4 3 V = p.R 3
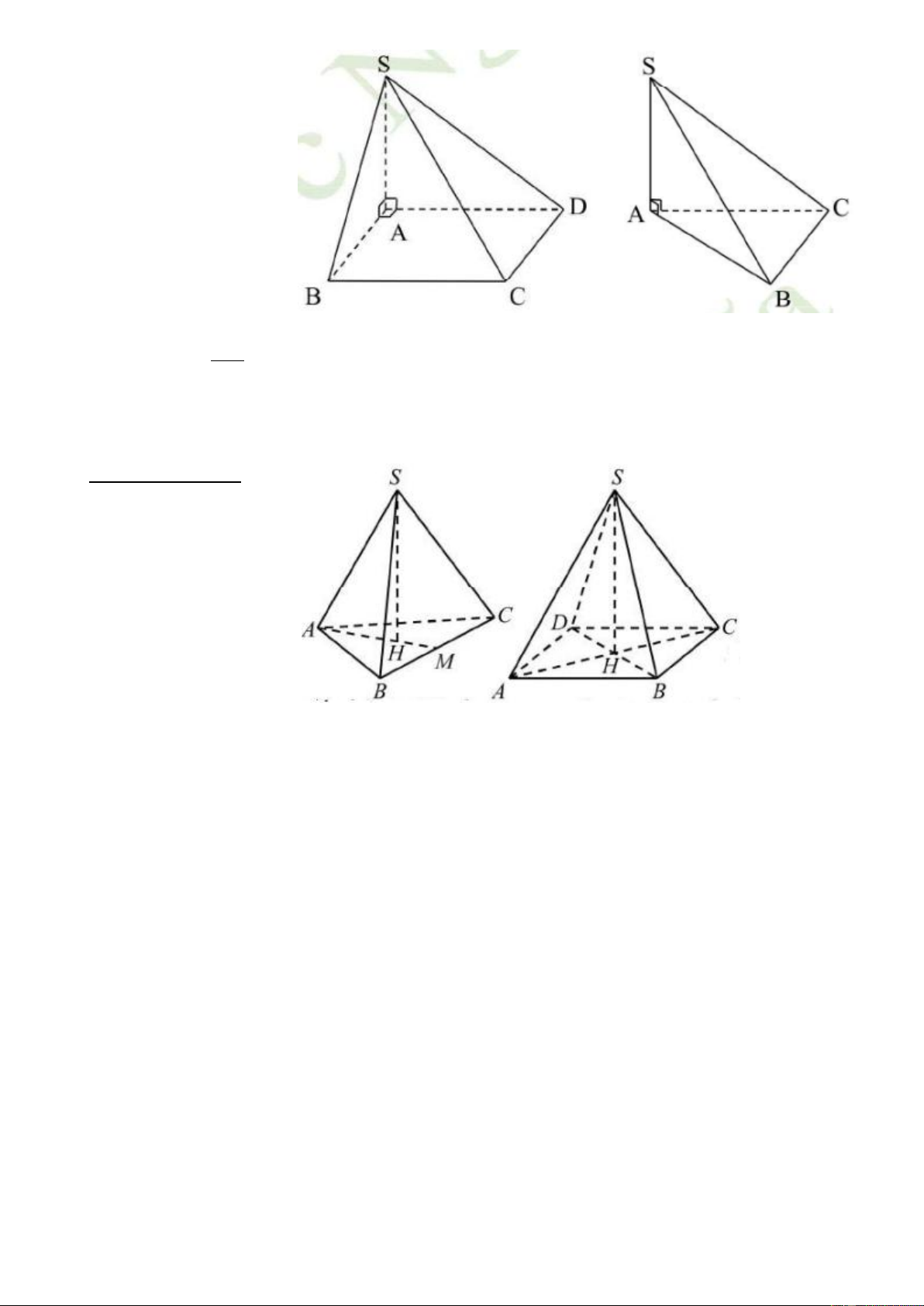
Đặc biệt: Một số cách xác định tâm bán kính mặt cầu (S) ngoại tiếp hình chóp: Trang15
1) Đối với hình chóp S.ABCD có
SA ^ (ABCD), ABCD
là hình vuông hoặc hình chữ nhật; hình chóp
S.ABC có SA ^ (ABC),
DABC vuông tại B. Khi
đó mặt cầu (S) có đường
kính SC, tâm là trung điểm SC SC, bán kính R = . 2
2) Đối với hình chóp có chân đường cao trùng tâm mặt đáy thì bán kính (S ) canh n2 bê R  2  ch ê i u cao Trang16