Báo Cáo Bài Tập Lớn | Môn Hóa lý 1,2 - Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

BÁO CÁO BÀI TẬP LỚN lOMoAR cPSD| 58728417 Câu hỏi 1 Chu trình Rankine
Hơi nước đi vào turbine của một nhà máy điện ở 500 C và 10 MPa rồi được ngưng tụ ở 125 kPa.
Giả sử nhà máy vận hành theo chu trình Rankine lý tưởng. Bài làm
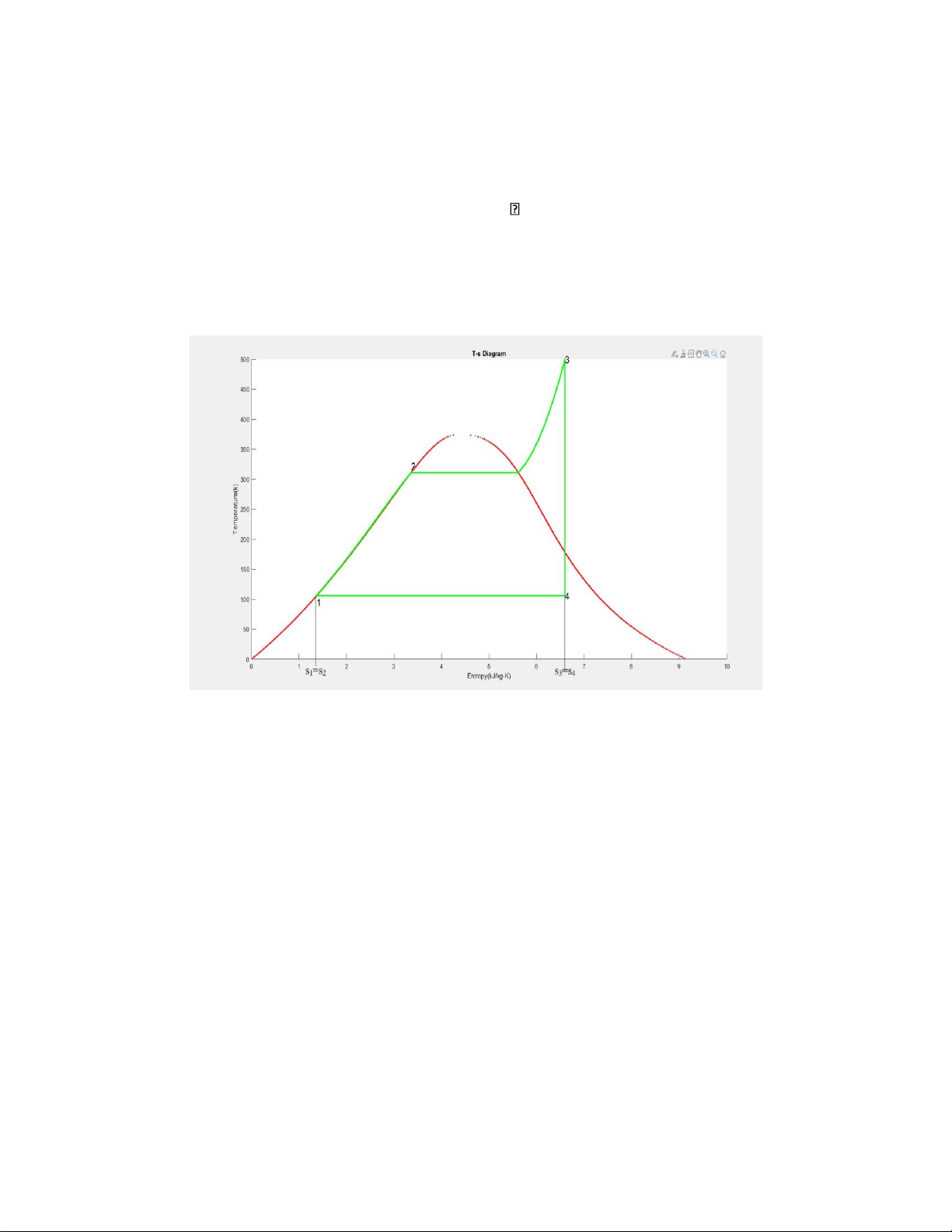
a) Vẽ giản đồ T-s của chu trình
Hình 1.Giản đồ T-s của chu trình Rankine
b) Công sinh ra trên mỗi kg nước: X=600; Y=5; Z=75; H=84
Công sinh ra trên mỗi kg nước là tổng công sinh ra của toàn chu trình Rankine (wnet ¿ Được tính bằng:
Wnet = Wt - Wp = ( h3 – h4 ) – Wp với Wp = v1 ( P2 – P1 ) h1, h2, h3, h4
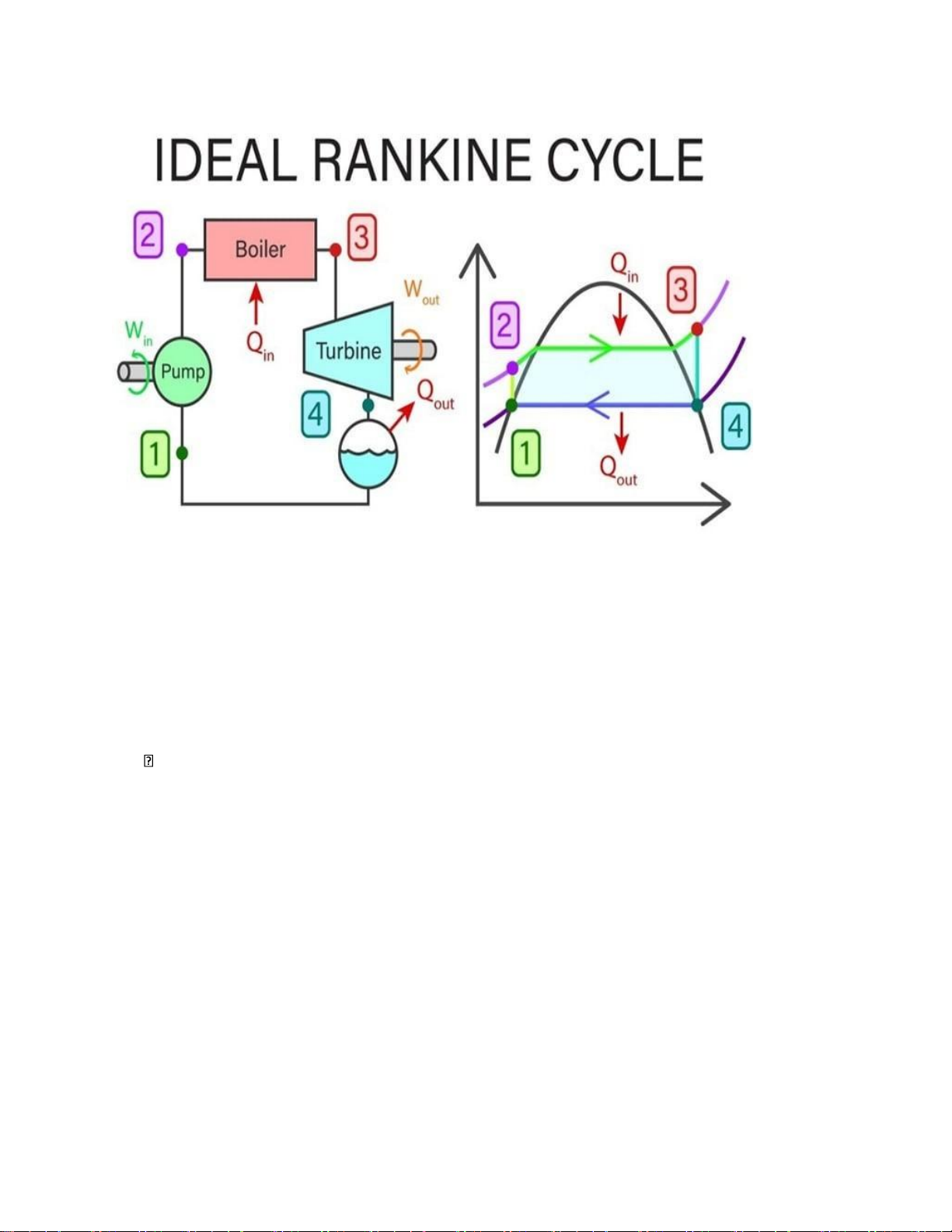
của nước tương ứng với các giai đoạn trong giản đồ sau: lOMoAR cPSD| 58728417
Hình 2. Giản đồ chu trình Rankine cơ bản
P1=P4=125kPa
Ta có: P2=P3=10 MPa { T3=500℃ Ở 10 MPavà 500℃:
h3=¿3375.1 kJ/kg ( bảng A-6 )
h1=444.36kJ /kg
Ở 125 kPa: v1=0.001048m3 (bảng A-5)
{ h4=2684.9kJ /kg
wp = h2 – h1 = v (P2 – P1) = 0.001048 (10x103 – 125) = 10.349 kJ/kg
=> h2 = wp + h1 = 875 + 444.36 = 1319.36 kJ/kg
wt = h3 – h4 = 3375.1 – 2684.9 = 690.2 kJ/kg
wnet = wt – wp = 690.2 – 10.349 = 679.851 kJ/kg
c) Tỷ lệ công cần trích từ turbine để nén lưu chất được tính như sau: lOMoAR cPSD| 58728417 Wt 690.2 = =65.69 W p 10.349
P2=P3=5 MPa
d) Tính hiệu suất nhiệt
{c ủa chu trình: X=600;
Y=5; Z=75; H=84 P1=P4=75kPa T 3=600∘C
Trạng thái 1 (Bảng A-5): kJ h1 = hf = 384,44 kg v1 = vf = 0,001037 m3 kg kJ
Wp = v1 ( P2 – P1 ) = 0,001037 ( 5000 – 75 ) = 5,1072 = h2 – h1 kg kJ
=> h2 = h1 + Wp = 384,44 + 5,1072 = 389,5472 kg
Trạng thái 3 (Bảng A-6) : kJ h3 = 3666,9 kg kJ S3 = 7,2605 kg. K
Trạng thái 4 (Bảng A-6):
S4 = S3 => Sf < S4 < Sg S4 = Sf + x4 .sfg
(=) 7,2605 = 1,2132 + x4 . 6,2426 =) x4 = 0,9687 kJ
h4 = hf + x4.hfg = 384,44 + 0,9687. 2278 = 2591,1386 kg
* Hiệu suất của chu trình W net 1070,6542
ƞ = = = 32,67% q∈¿¿ 3277,3528 lOMoAR cPSD| 58728417
Wnet = Wt - Wp = ( h3 – h4 ) – Wp = 1075,7614 – 5,1072 = 1070,6542 qin
= h3 – h2 = 3666,9 – 389,5472 = 3277,2582
e) So sánh hiệu suất nhiệt vừa tính được với hiệu suất nhiệt của chu trình Carnot. Giải thích: X=600; Y=5; Z=75; H=84 Th = 600oC = 873oK Tc = 91,76oC = 364,76oK Tc 364,76 ƞ = 1 - = 1- = 58,21% Th 873
Hiệu suất nhiệt của chu trình Carnot được tính dựa trên lý thuyết hoàn hảo và không có mất mát
nhiệt. Nó đạt được khi quá trình nhiệt xảy ra một cách lý tưởng, không có mất mát nhiệt và không
có mất mát ma sát. Do đó, hiệu suất Carnot là một giới hạn lý thuyết và thường cao hơn so với các chu trình thực tế.
Trong khi đó, chu trình Rankine là một chu trình công nghiệp thực tế được sử dụng trong nhà
máy điện nhiệt. Nó sử dụng nguyên lý hoạt động của máy quay turbine. Chu trình Rankine bao
gồm các quá trình như nhiệt mở rộng trong turbine, ngưng tụ trong bình ngưng tụ và nén trong
bơm. Chu trình này thường bị mất mát nhiệt và có mất mát ma sát, do đó hiệu suất nhiệt của chu
trình Rankine thường thấp hơn so với hiệu suất Carnot.
Vì vậy, sự khác nhau giữa hiệu suất nhiệt của chu trình Carnot và chu trình Rankine nằm ở mức
độ mất mát nhiệt và mất mát ma sát trong quá trình hoạt động thực tế. Chu trình Carnot không có
mất mát nhiệt và mất mát ma sát, trong khi chu trình Rankine thường có mất mát nhiệt và mất mát
ma sát, dẫn đến hiệu suất nhiệt thấp hơn.
f ) Tính lại công tổng và hiệu suất nhiệt của chu trình Rankine nếu hiệu suất đẳng entropy
của turbine và bơm cùng là 83%: X=600; Y=5; Z=75; H=84 ƞp = ƞT = 84% kJ h1=384,44 kg Trạng thái 1 : 3 m v 1=0,001037 kg lOMoAR cPSD| 58728417 kJ { Trạng thái 3 : h3=3666,9 kg kJ S3=7,2605 kg.K
Trong thực tế sẽ có tổn thất do ma sát, tổn thất truyền nhiệt trong turbine hoặc máy bơm . Xác định
những tổn thất đó thông qua hiệu suất đẳng entropy. Ký hiệu h2 , h4 ( lý tưởng ) ; h2’ và h4’ ( thực tế ) Máy bơm :
v 1(P2−P1) 5,1072 kJ
Ƞp = h2'−h1 (=) 0,84 =
h2'−384,44 => h2’ = 390,52 kg Turbine :
ƞT = h3−h 4' (=) 0,84 = 3666,9−h4'
h4’ = 2763,26 kJ h3−h 4 kg
Hiệu suất nhiệt của chu trình : Wnet 897.56
ƞ = = = 27,39 % q∈¿¿ 3276,38 kJ
Wnet = WT – Wp = ( h3 – h4’ ) – ( h2’ – h1 ) = 897,56 kg kJ
qin = h3 – h2’ = 3666,9 – 390,52 = 3276,38 kg Câu hỏi 2
Hydrogen là nguồn nhiên liệu sạch để sản xuất điện, có thể được tổng hợp từ phản ứng phân huỷ ethanol: lOMoAR cPSD| 58728417
CH3CH2OHg ↔ CH3CHOg + H2 g
a) Tính hằng số cân bằng áp suất của phản ứng ở nhiệt độ thường:
Ở nhiệt độ thường, T = 298K, P = 1 bar
Hằng số cân bằng áp suất KP của phản ứng ở nhiệt độ thường: ΔG0T = - RTlnKP (μ0CH −μ0
3CHO +μ0H2
C2H5OH) = - RTlnKP
(-128,86 + 168,49). 103 = - 8,314. 298. lnKP KP = 1,13.10-7
b) Tính hằng số cân bằng áp suất của phản ứng ở 390oC và 1 bar, nếu Δ H 0
rxn được xem là không đổi: X=390
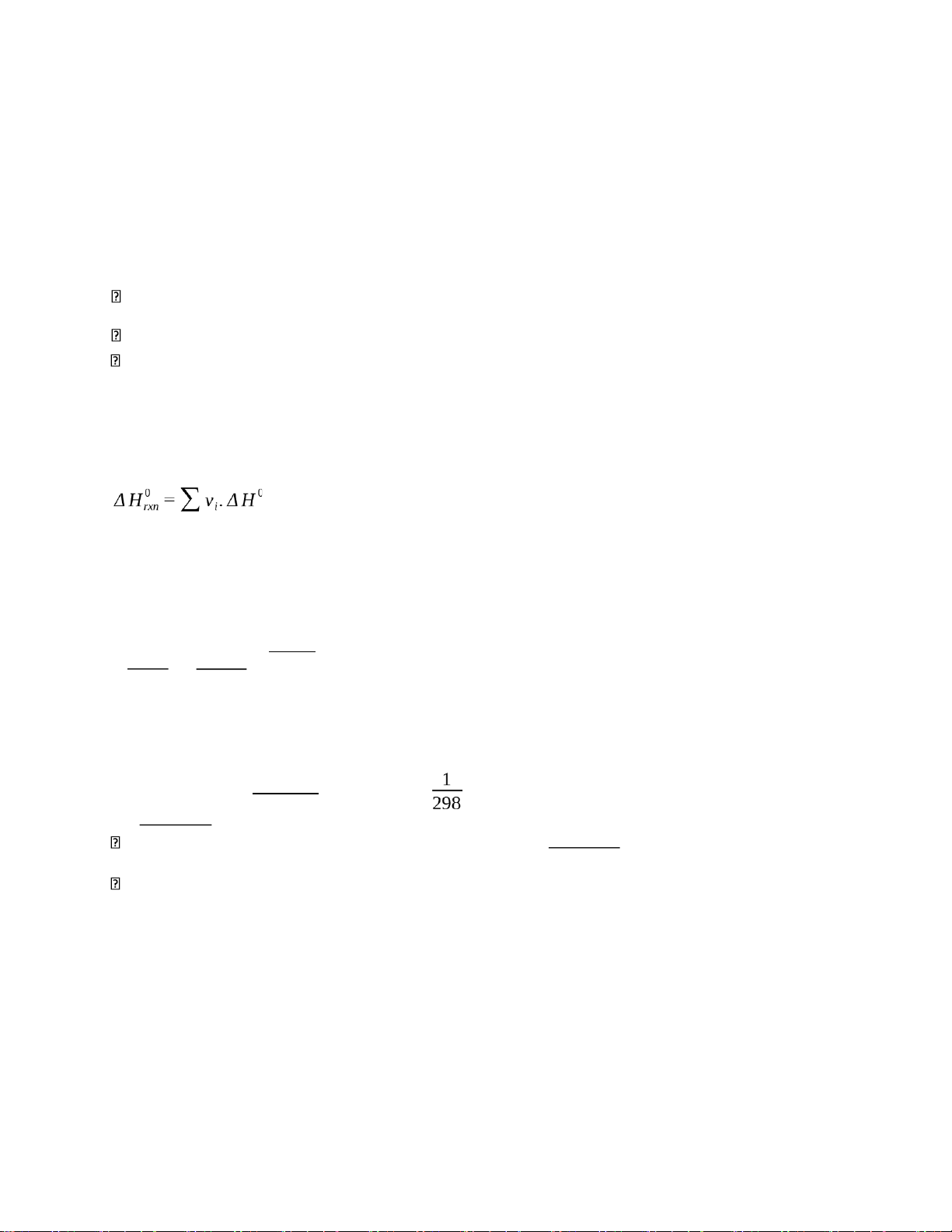
- Theo định luật Hess, ta có: 0
sảnphẩm−∑ vi .ΔH phảnứng
= (- 166,19 + 235,10).103 = 68,91.103 (J/mol)
- Hằng số cân bằng áp suất của phản ứng ở 390oC và 1 bar: KP, T2 ΔH0rxn 1 1 ln = - .( − ) KP, T1 R T2 T1 K P,T 68,91.103 1 2 ln 1,13.10−7 = - 8,314 .(390 +273− )
K P,T = 0,505 c) Tính độ chuyển hoá của ethanol và thành phần của hệ khi đạt trạng thái cân 2
bằng ở 390°
C và 1 bar: X=390
Hằng số cân bằng áp suất của phản ứng ở 390°C, 1 bar: KP = 0,505
Giả sử có 1 mol CH3CH2OH ban đầu x mol CH3CH2OH phản ứng lOMoAR cPSD| 58728417
CH3CH2OHg ↔ CH3CHOg + H2 g 1 0 0 (mol) x x x 1-x x x P ∆n Ta có: Kp = Kn cb ∆ n = 2-1 = 1
∑ ni = 1 – x + x + x = 1 + x 1 1 => 0,505 ( ) = Kn 1+x
=> Kn = 0,505×(1+x) = x2 1−x => x = 0,579 => Độ chuyển hóa = ×100%=59,7 %
d) Tính độ chuyển hoá của ethanol và thành phần của hệ khi đạt trạng thái cân bằng ở 390
°C và 0,50 bar: X=390; Y=0,50
Do hằng số cân bằng áp suất chỉ phụ thuộc vào nhiệt độ nên K Pở 390℃, 0,5 bar cũng bằng 0,505 P ∆n Ta có: Kp = Kn cb 0,5 1
Thay P = 0,5 ta được: 0,505 = Kn ( ) 1+x lOMoAR cPSD| 58728417 2
=> Kn = 1,01×(1+x) = x 1−x => x = 0,709 => Độ chuyển hóa = ×100%=70,9%
e) Tính hằng số cân bằng áp suất của phản ứng ở 390°C và 1 bar, nếu Δ H 0
rxn thay đổi theo nhiệt độ: X=390 T ❑ ∫(∑ v ) i(cp)i dT i 663 dT (1) 298 i
Theo bảng tra A.2.1, ta có A, B, C, D, E Ta có: - CH3CH2OH
c p = 3, 518 + 20,001.10-3.663+(-6,002).106.6632 = 14,1404 => cp=117,57 R - CH3CHO
c p =1, 693 + 17,978.10-3.663 - 6,158.10-6.6632 = 10,91 => cp= 90,67 R - H c p 2
= -3.663 +_0,083.10-5.663-2 = 3,54 =>cp= 29,45 3,249 + 0,442.10 R lOMoAR cPSD| 58728417 (1) dT
= 68,91 + 86758,11914 = 86827,03 (kJ/mol)
Hằng số cân bằng áp suất của phản ứng ở 390°C và 1 bar, nếu ΔH 0
rxn thay đổi theo nhiệt độ: KP, T2 Δ H0rxn,663 1 1 ln = - 1 .( − ) KP, T R T2 T1 K P,T 2 ln −7 = - .( − ) 1,13.10
K P,T = 4,726.10 2 -16 Câu hỏi 3
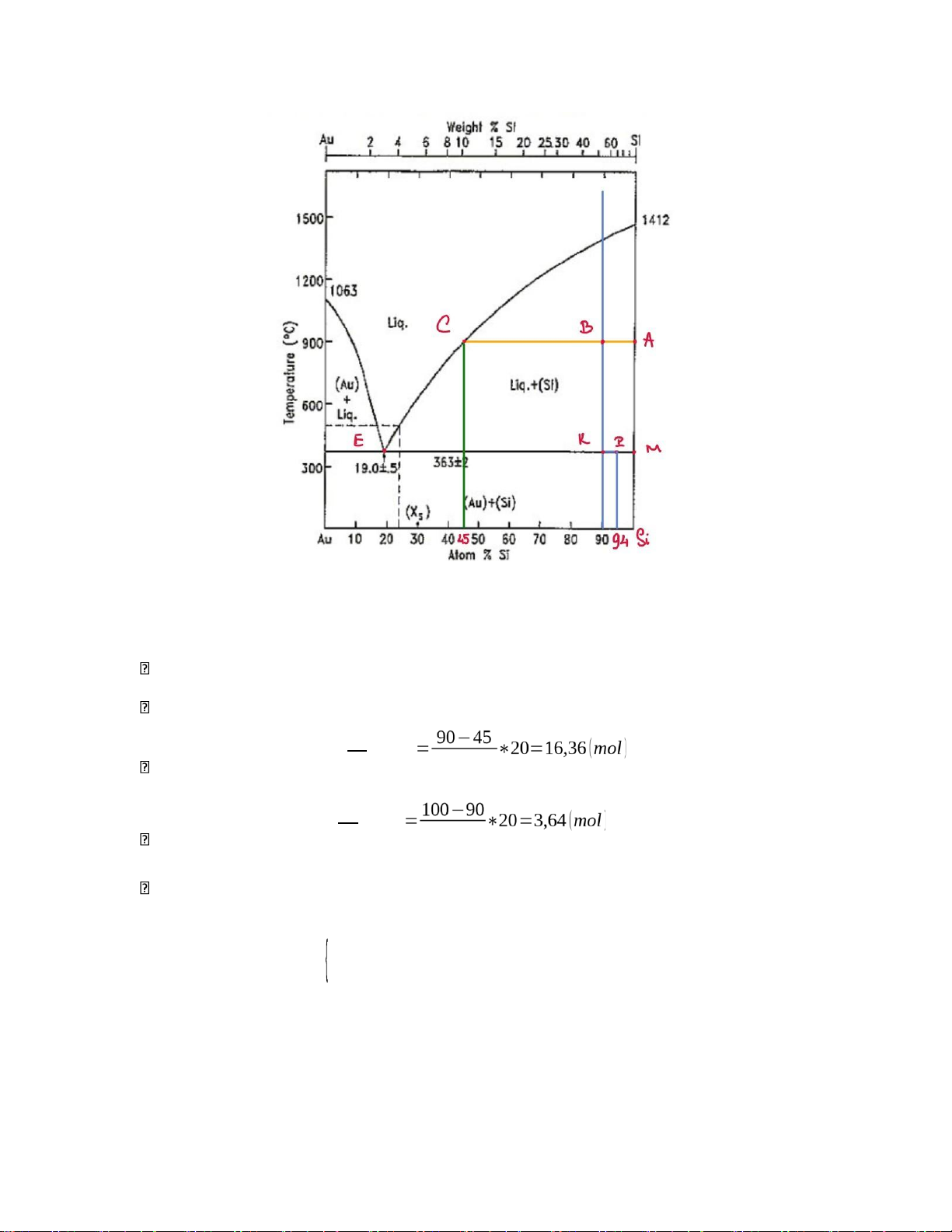
Xét giản đồ nhiệt độ – thành phần ở 1 atm của hệ cân bằng lỏng – rắn gồm 2 cấu tử Au và Si: lOMoAR cPSD| 58728417
a) Xác định những pha cân bằng khi trộn 2 mol Au và 18 mol Si ở 1200o C: X=2; Y=18; Z=900
Tính số mol của từng cấu tử trong mỗi pha.
Tại 2 mol Au và 18 mol Si ở nhiệt độ 1200o C gồm 2 pha: lỏng và Si rắn.
Số mol tổng: ntổng=2+18=20 (mol) BC
Lượng mol rắn Si: nA= AC ∗ntổng 100−45 AB
Lượng mol lỏng: nC = AC∗ntổng 100−45
Tại C, Si chiếm 45% và Au chiếm 55%
¿>nSi (C )=nC∗0,45=3,64∗0,68=1,638(mol)
nAu (C )=nC∗0,55=3,64∗0,32=2,002(mol) E(19,363) K (90,363 ) lOMoAR cPSD| 58728417 { Tọa độ các điểm: P (94,363 ) M (100,363)
b) Tính khối lượng lớn nhất có thể có của pha lỏng eutectic?
Khối lượng eutectic tối đa khi P trùng với M tại E Lượng mol lỏng e: − 90
nE= KMEM ×ntổng=100100 −19 ×20=2,47mol
Tại E: Si chiếm 19% và Au chiếm 81%
Lượng mol pha lỏng eutectic :
{nnAuSi((EE))==nnEE××00,,1981==22,,4747××00,,1981==0,46932,0007molmol { Khốilượng:⇒
mSi( ()E)=nSi( (E) )×28,09=0,4693×28,09=13,18g
mAu E =nAu E ×196,97=2,0007×196,97=393,48g
Vậy khối lượng lớn nhất mà pha lỏng eutectic có thể nhận là
393,48 + 13,18 ¿ 406,66g
c) Tính khối lượng của pha lỏng eutectic và các pha rắn khi MP/MK = 60% (H=60)
Điểm hệ tại K: Hệ K= lỏng e + rắn chung P MP
=0,6⇒ MP=0,6. MK=0,6.(100−90)=6 MK Tọa độ P: (94,363) 19
Lượng mol Rắn chung: nP= PEKE ×ntổng=9490−− 19 ×20=18,93mol lOMoAR cPSD| 58728417
Tại P: Si chiếm 94% và Au chiếm 6% Lượng mol pha rắn
P:{nnSiAu(P(P)=)=nnPP××00,94,06==1818,93,93××00,94,06≈≈171,,1479molmol Khối lượng pha rắn
P:{mmAuSi(P(P)=)=nnAuSi((PP))××196,9728,09==171,,7914××28196,97,09≈≈499,72224,55gg KP
Lượng mol lỏng e: ne= PE ×ntổng 94−19 mol
Tại E: Si chiếm 19% và Au chiếm 81%
Lượng mol pha lỏng eutecric : {nn Si Au ( E ) = n × 1
( E ) = nEE ×00,,1981== 1,,0707××00,,1981≈≈00,,2186molmol
Khối lượng:⇒{m Aum(ESi)=( E)n=Aun(
ESi)(×E)196,97×28,09==00,86,21××196,9728,09≈≈5169,39,90 g g
Khối lượng lỏng eutectic⇒me=5,90+169,39=175,29g