Bending Deformation in Construction Materials | Môn Vật liệu xây dựng - Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

lOMoAR cPSD| 58931565 Bending lOMoAR cPSD| 58931565
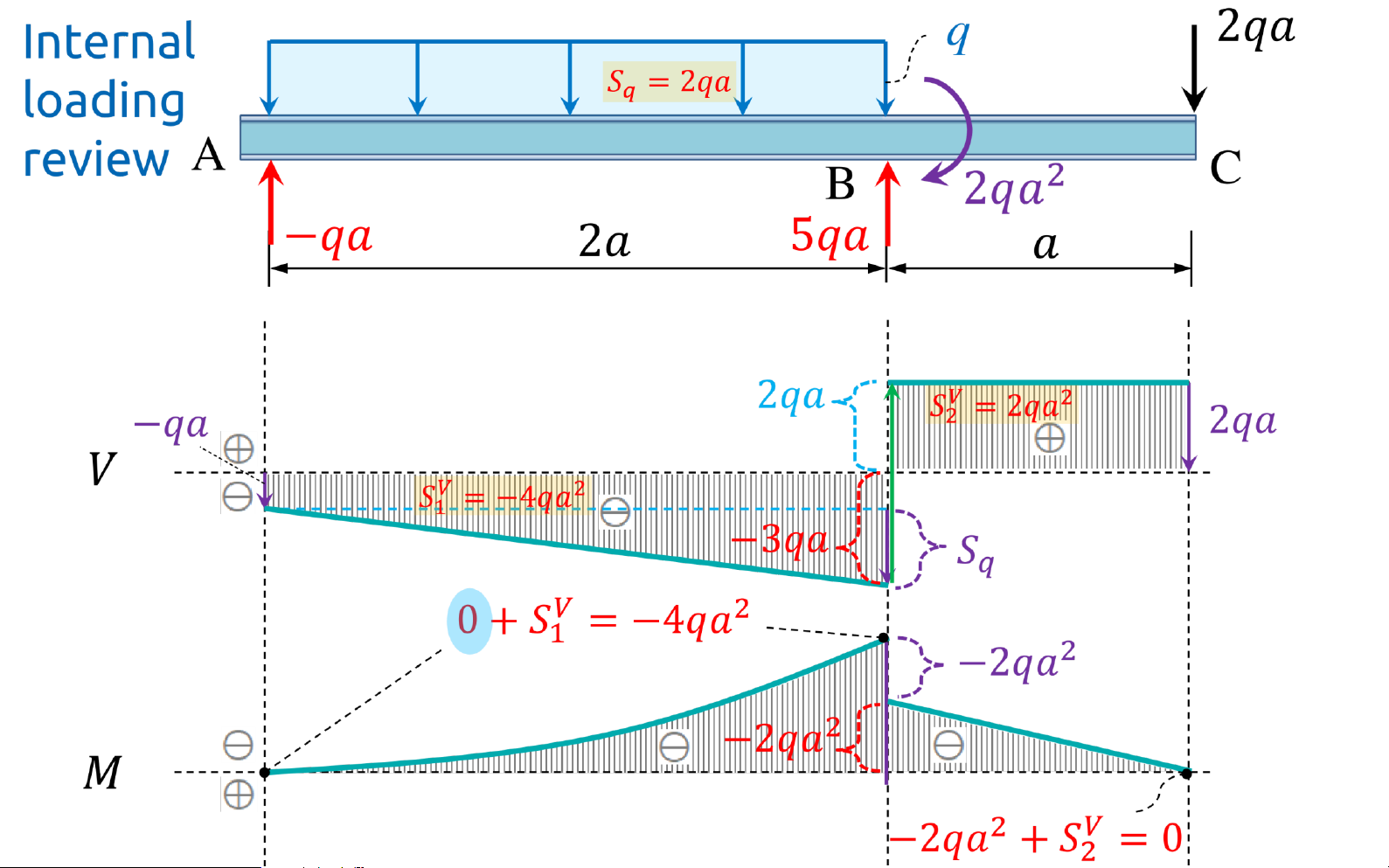
↑∑=0 ⇒𝑌𝐴+𝑌𝐵−4𝑞𝑎=0
⇒ቐ𝑌𝐴 =−𝑞𝑎 𝑌𝐵 lOMoAR cPSD| 58931565
↺∑𝐴 =0⇒2𝑎𝑌𝐵−10𝑞𝑎2 =0 =5𝑞𝑎 lOMoAR cPSD| 58931565 q 2 𝑞𝑎 A 2 C B 2 𝑞𝑎 2 𝑎 𝑎 𝑞𝑎 2 2 𝑞𝑎 𝑋 𝐴 A C B 2 𝑌 2 𝑞𝑎 𝐴 𝑌 𝑎 𝑎 𝐵 𝑎 𝑋 𝐴 =0 →∑=0 ⇒𝑋𝐴 =0 lOMoAR cPSD| 58931565 lOMoAR cPSD| 58931565
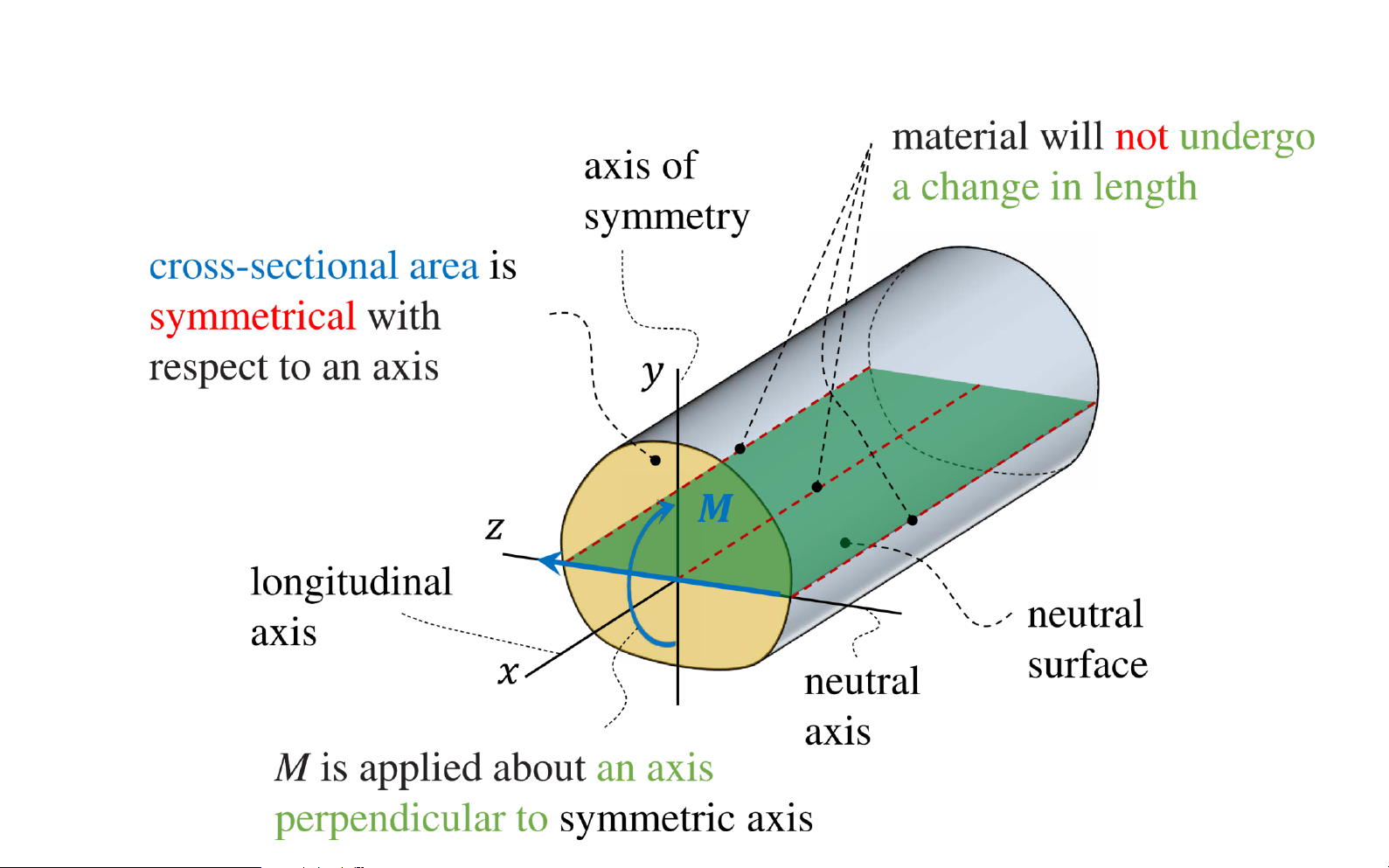
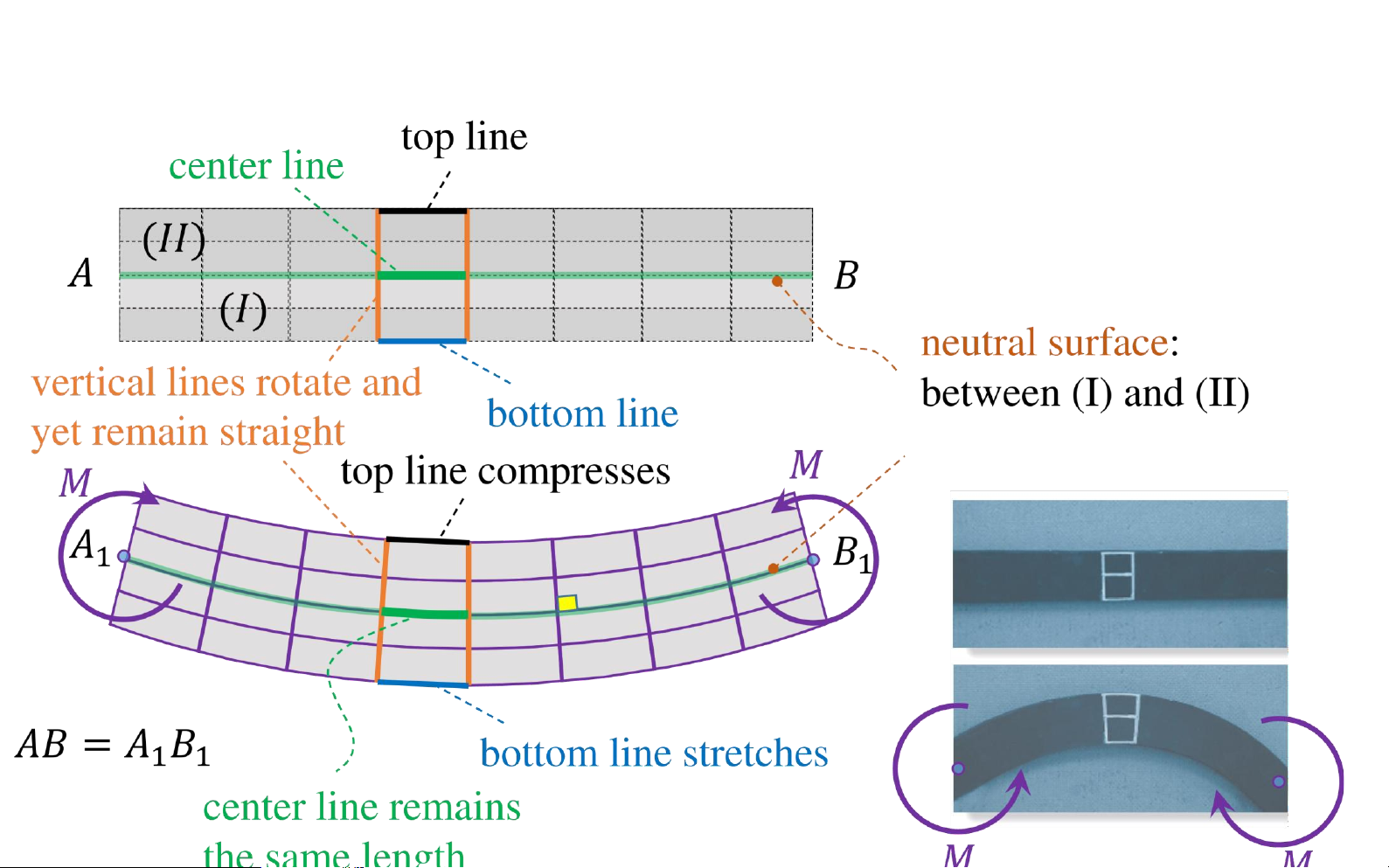
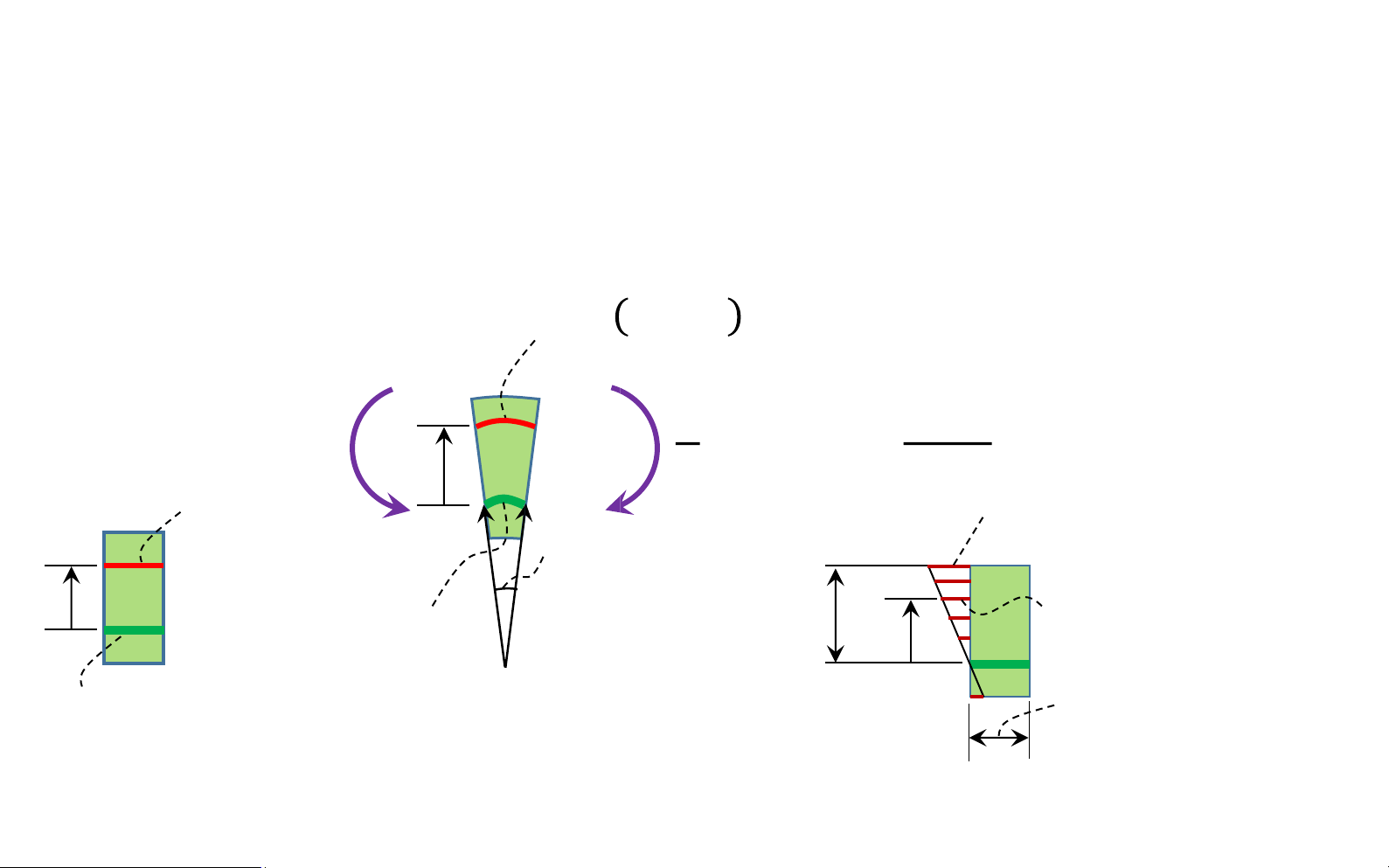
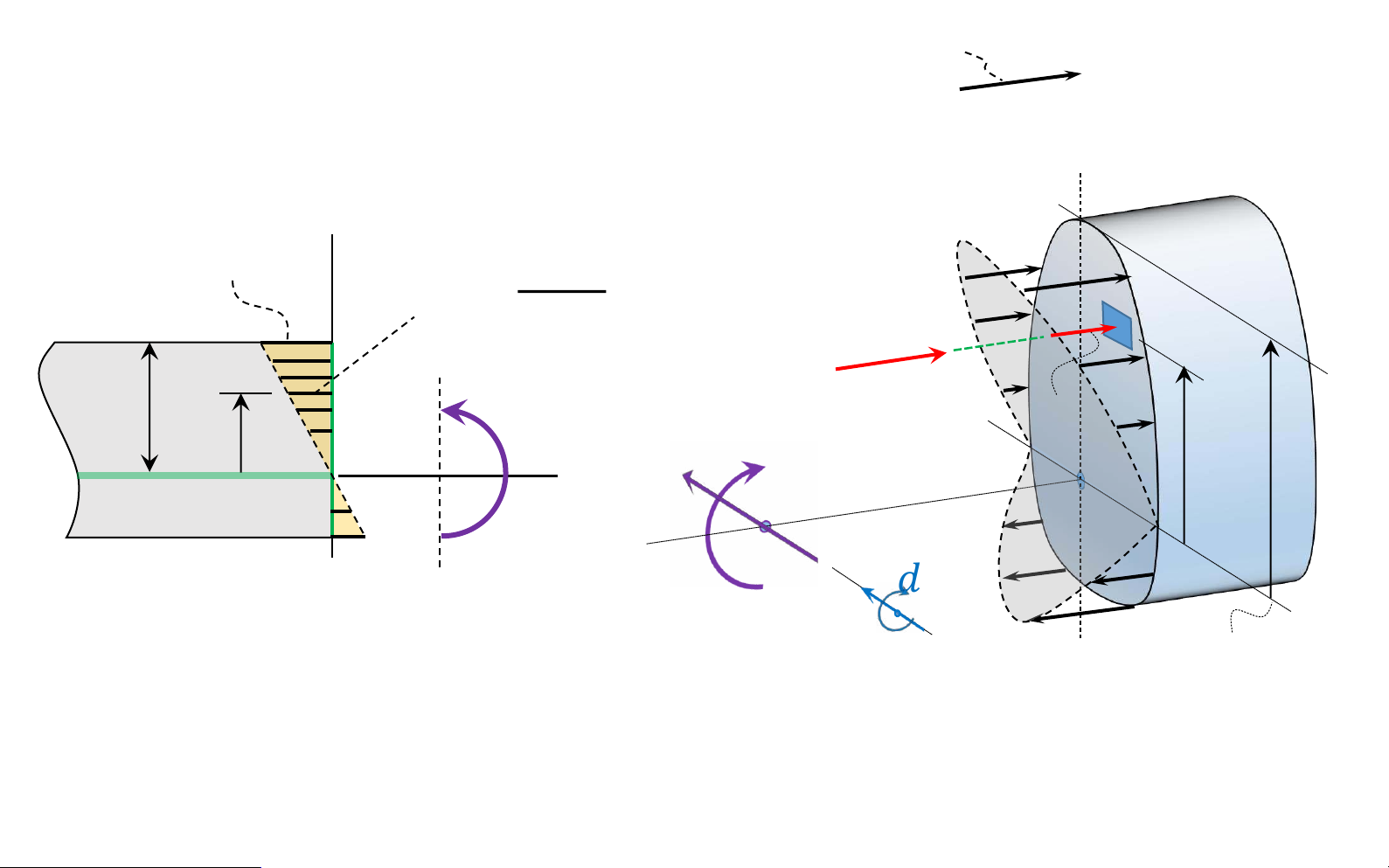
Bending deformation of a straight member horizontal fibers of the lOMoAR cPSD| 58931565
Bending deformation of a straight member lOMoAR cPSD| 58931565
Bending deformation of a straight member 𝑀
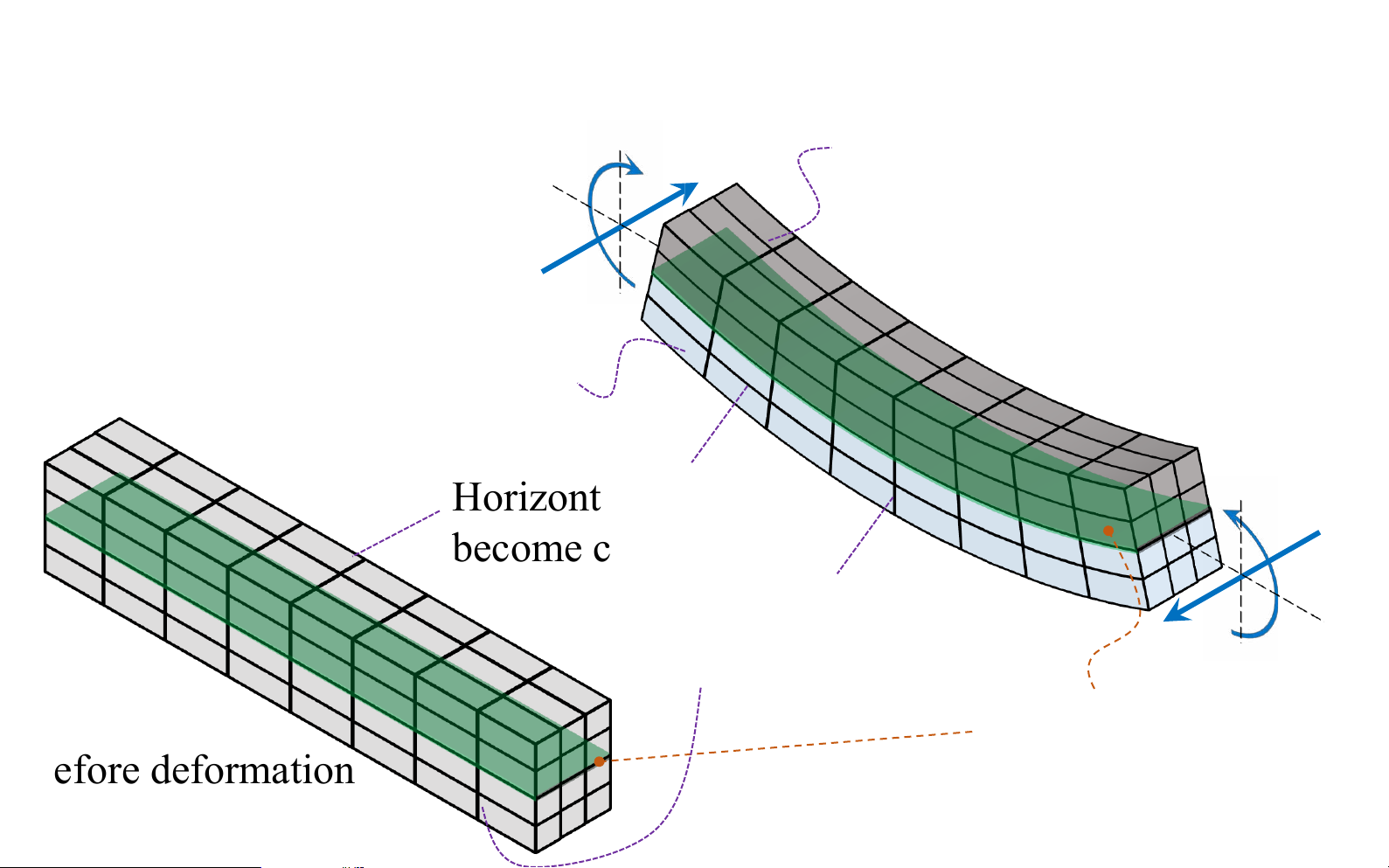
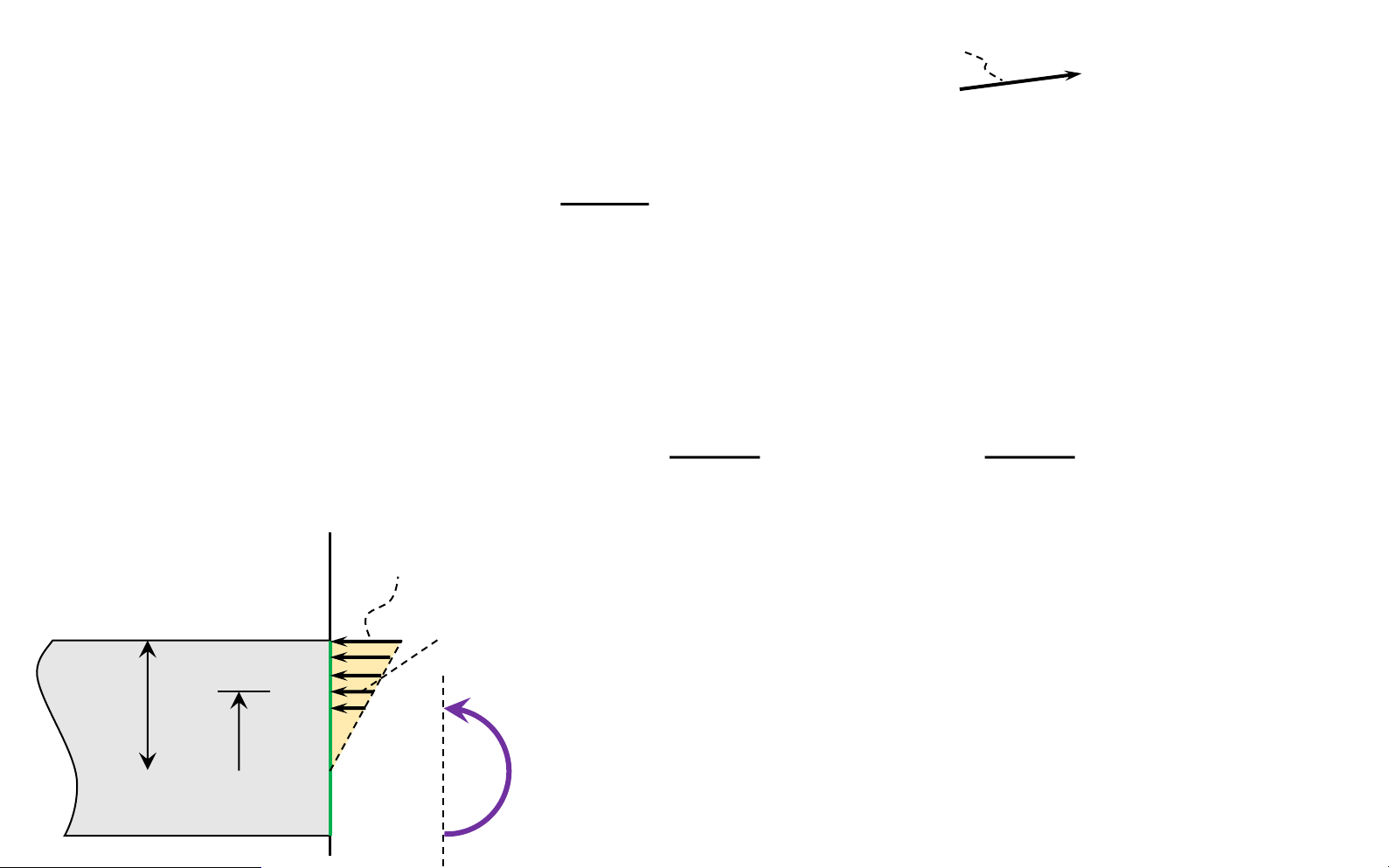
top portion (II) of the After deformation bar to compress bottom portion (I) of the bar to stretch Horizontal lines 𝑀 become curved vertical lines remain straight, yet rotate neutral surface : Before deformation between (I) and (II) lOMoAR cPSD| 58931565
Bending deformation of a straight member
top portion (II) of the 𝑀 bar to compress After deformation horizontal fibers of the material will not undergo a change in length bottom portion (I) of 𝑀 the bar to stretch neutral surface : between (I) and ( II) lOMoAR cPSD| 58931565
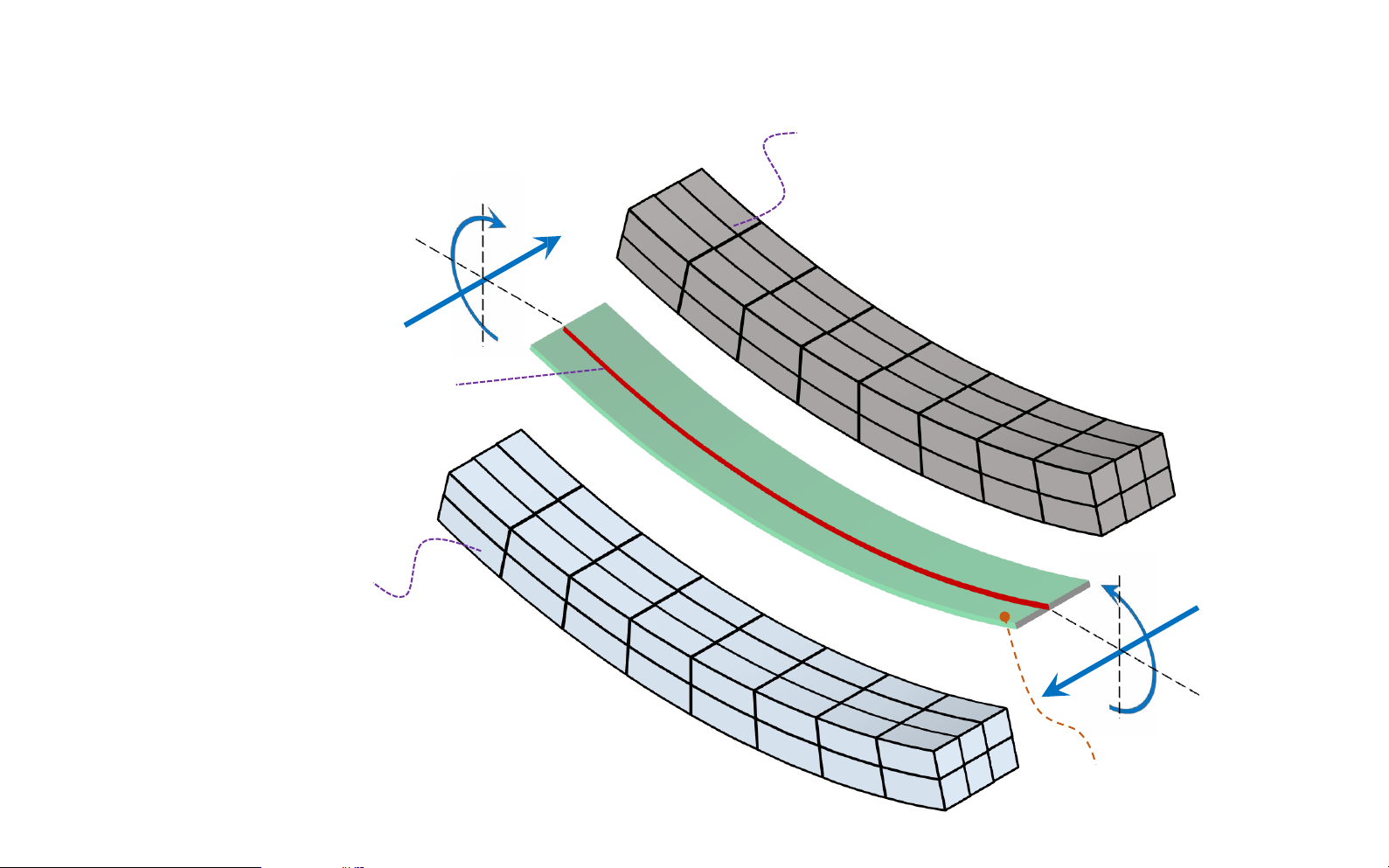
Bending deformation of a straight member lOMoAR cPSD| 58931565
Bending deformation of a straight member ( 𝐼𝐼 ) 𝐴 𝐵 ( 𝐼 ) 𝐶 lOMoAR cPSD| 58931565
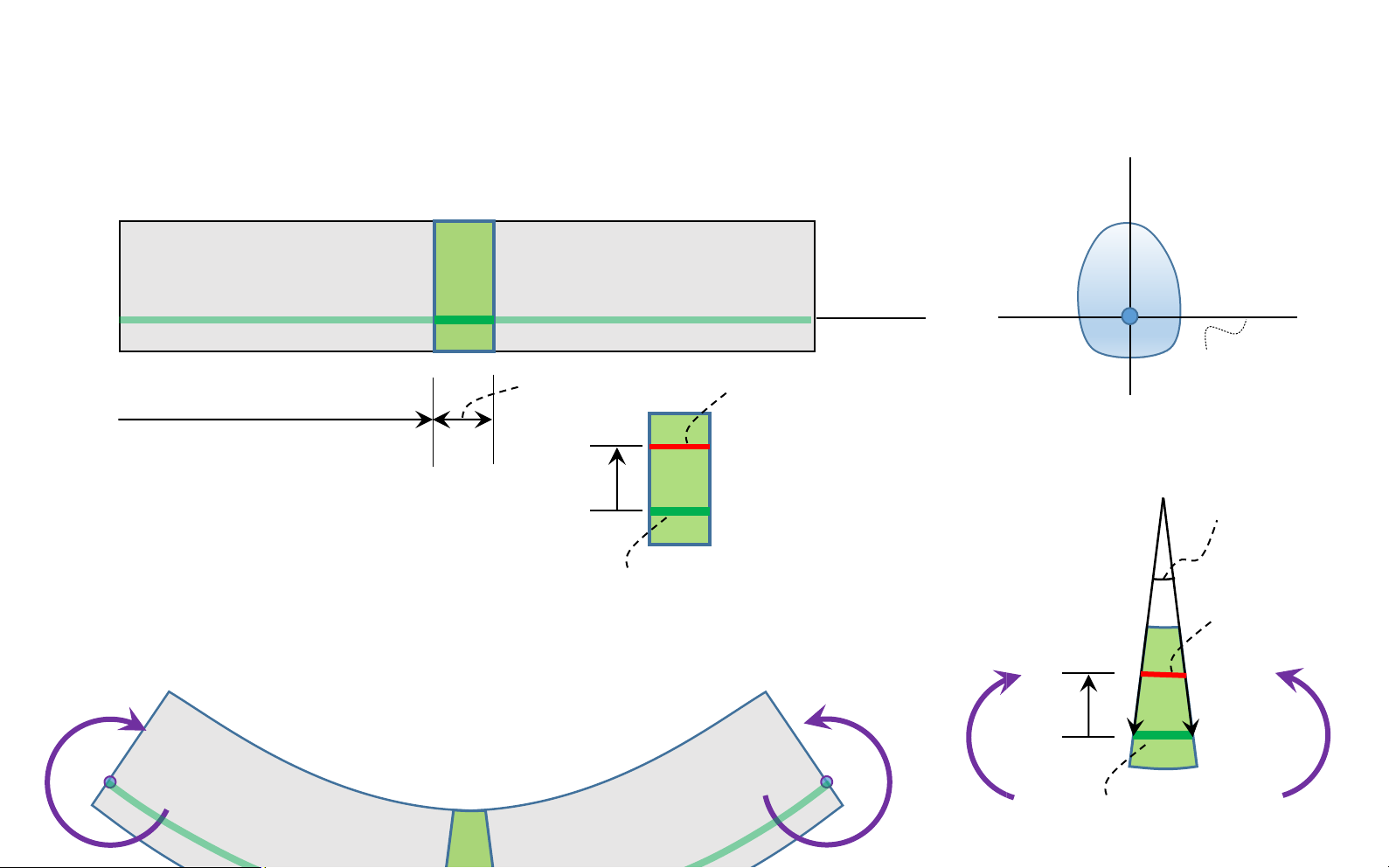
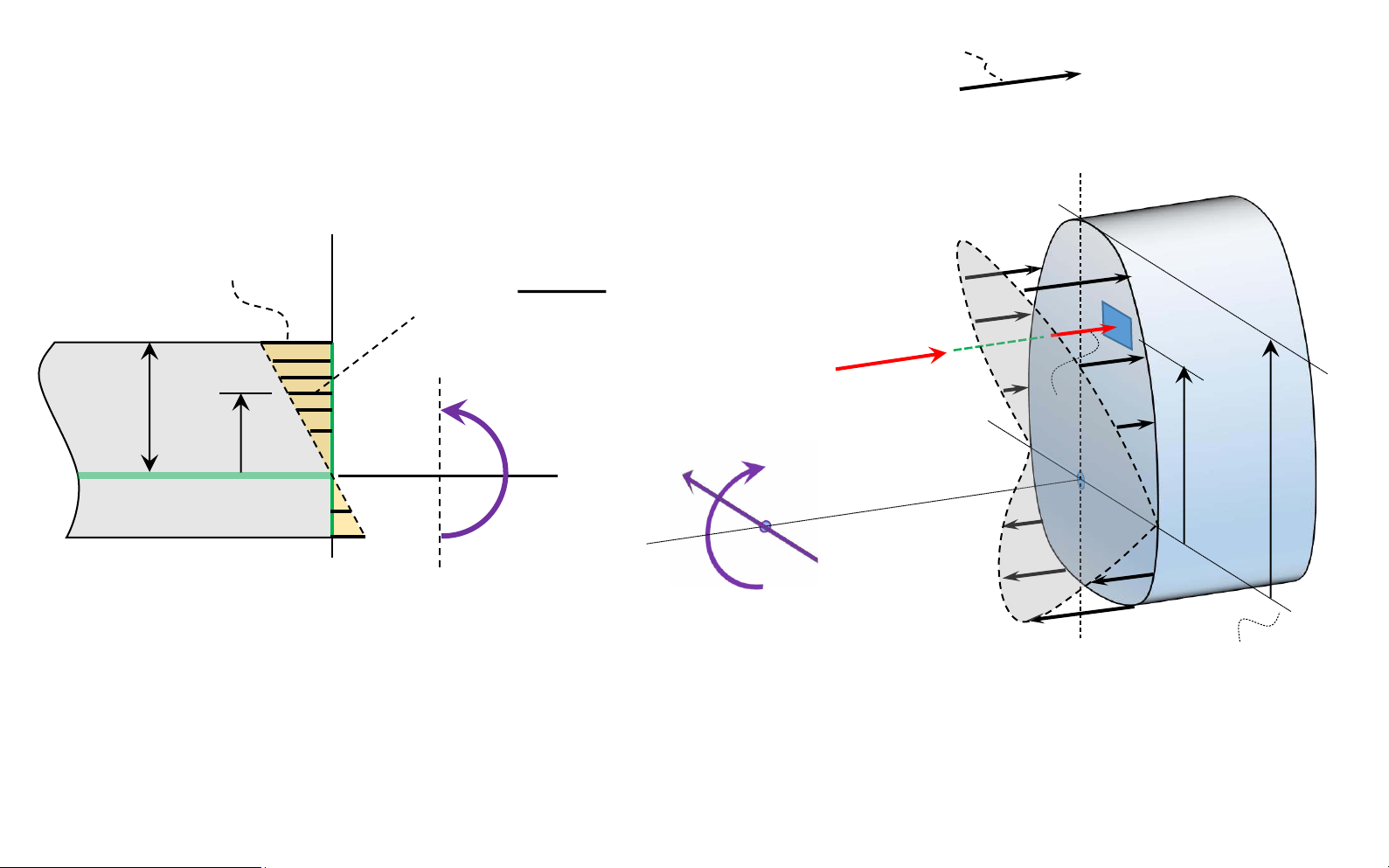
Bending deformation of a straight member ∆𝑥 Before ∆𝑠 deformation 𝑀 𝑦 Normal 𝐴 𝐵 𝑥 𝑧 neutral 𝑥 ∆𝑥 ∆𝑠 = 0 ∆𝑥 axis ( N - A ) 𝑦 𝑂 ∆𝜃 𝜌 𝑀 𝑦 𝐴 1 𝐵 1 ∆𝑥 After lOMoAR cPSD| 58931565
Bending deformation of a straight member
strain along ∆s0 is determined by ∆𝑠 − ∆𝑠0 𝜀 = lim = lim ∆𝑠0→0 ∆𝑠0 ∆𝜃→0 𝑦 𝑀
𝜌 is radius of curvature of the ∆𝑥 longitudinal axis of Before ∆𝑥 = 𝜌∆𝜃 𝑂 the element
𝜌 − 𝑦 ∆𝜃 − 𝜌∆𝜃 −𝑦∆𝜃 𝑦 ∆𝜃 = lim = − ∆𝑠 ∆𝑠 0 = ∆𝑥 𝜌∆𝜃 ∆𝜃→0 𝜌∆𝜃 𝜌 𝜌 𝑦 𝑦 𝑦𝑚𝑎𝑥 lOMoAR cPSD| 58931565
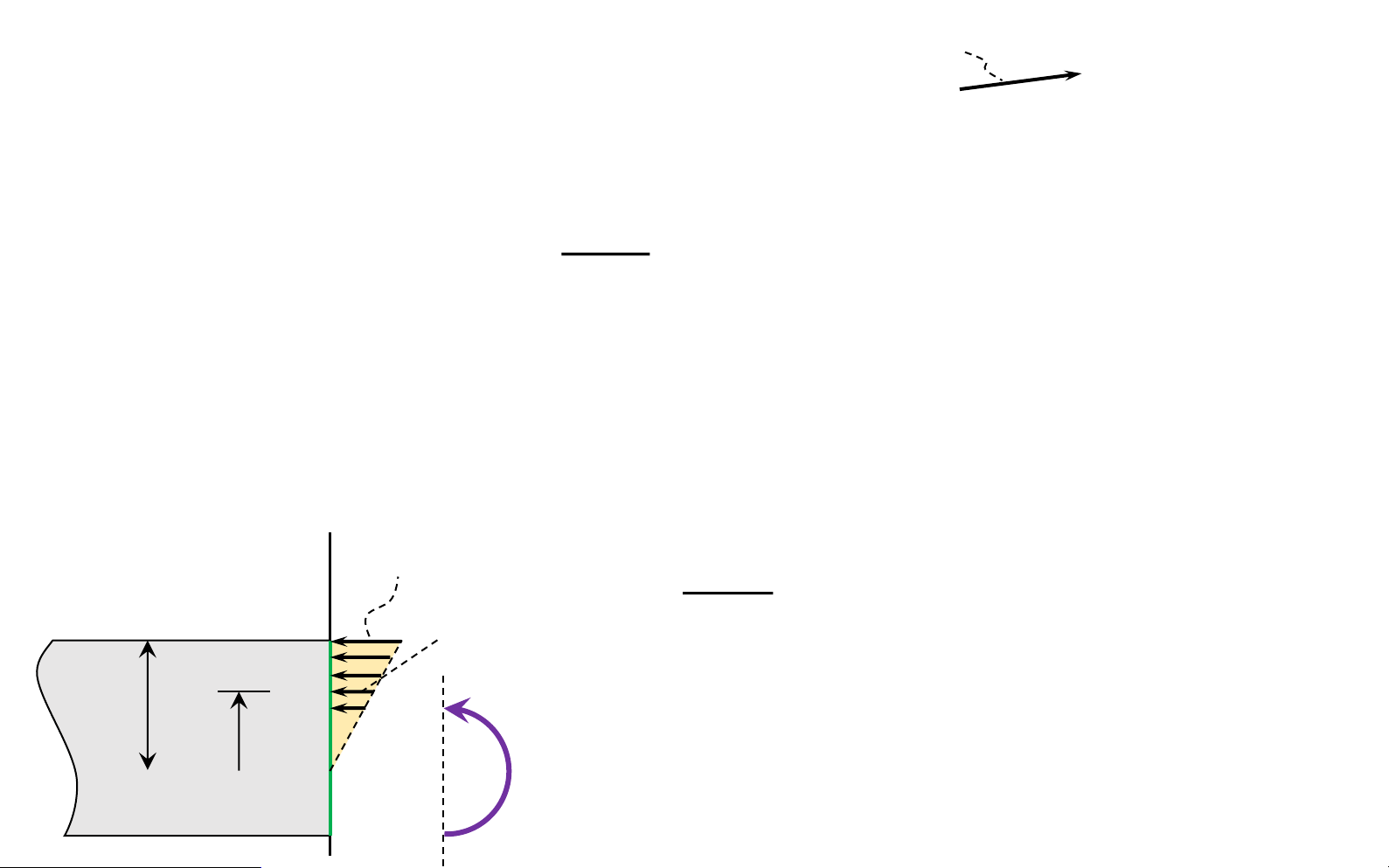
Bending deformation of a straight member 𝜀 = − 𝜀𝑚𝑎𝑥 = 𝑀 𝑦 𝜌 𝜌 𝑦𝑚𝑎𝑥 𝜀 = − 𝑦 𝑦 𝑚𝑎𝑥 𝜀𝑚𝑎𝑥 ∆𝑥 = 𝜌 − 𝑦 ∆𝜃 𝜀 𝑚𝑎𝑥 deformation After deformation Normal strain distribution
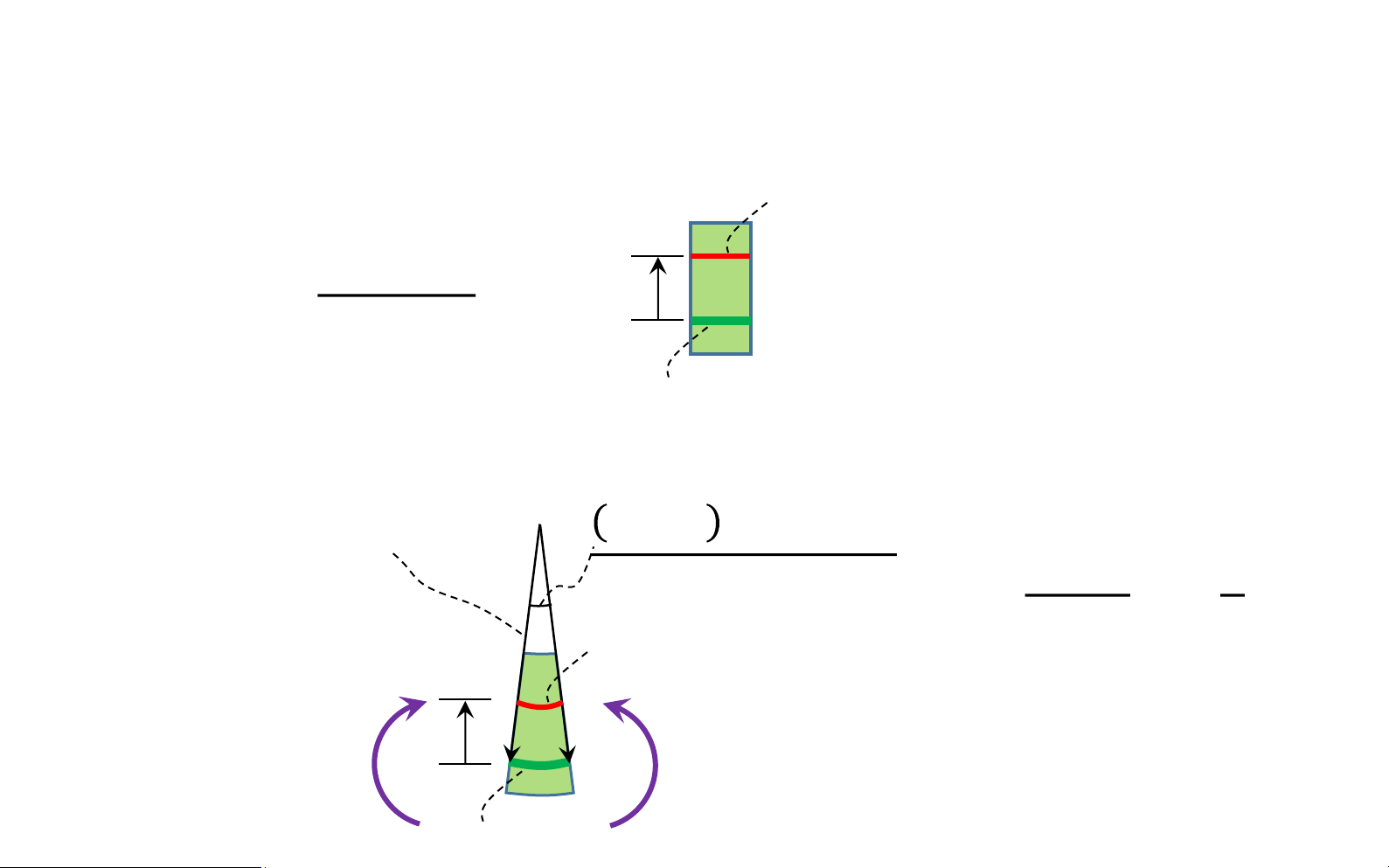
Normal strain along ∆s0 is determined by ∆𝑠 − ∆𝑠0
𝜌 + 𝑦 ∆𝜃 − 𝜌∆𝜃 𝑦∆𝜃 𝑦 𝜀 = lim = lim = lim = lOMoAR cPSD| 58931565
Bending deformation of a straight member ∆𝑠0→0 ∆𝑠0 ∆𝜃→0 𝜌∆𝜃 ∆𝜃→0 𝜌∆𝜃 𝜌 ∆𝑠 = 𝜌 + 𝑦 ∆𝜃 𝑦
𝑦𝑚𝑎𝑥 𝑀 𝑀 𝜀 = 𝜌 𝜀𝑚𝑎𝑥 = 𝜌 𝑦 𝜌 ∆𝑠0 = ∆𝑥𝜀𝑚𝑎𝑥 ∆𝜃 𝑦 lOMoAR cPSD| 58931565
Bending deformation of a straight member 𝑦 𝜌∆𝜃 = ∆𝑥 𝑦𝑚𝑎𝑥 𝜀 = 𝑦𝑚𝑎𝑥𝑦 𝜀𝑚𝑎𝑥 ∆𝑥 𝑂∆𝑥 Before deformation After deformation Normal strain distribution The Flexure Formula 𝜎𝑚𝑎𝑥 𝑦 lOMoAR cPSD| 58931565 𝜀𝑚𝑎𝑥 𝑦 𝑦 𝜀=− 𝜀 𝑦 𝑚𝑎𝑥 𝑚𝑎𝑥 𝑑𝐴 𝑦 𝑚𝑎𝑥 𝑀 𝑑𝐹=𝜎𝑑𝐴 𝜎 𝑦 𝑧 𝑥 𝑦 𝑦 𝑚𝑎𝑥 𝑥 Hooke′ slaw: 𝜎= 𝑀 𝐸𝜀 neutral Location of Neutral Axis axis (N-A) The Flexure Formula 𝜎𝑚𝑎𝑥 𝑦 lOMoAR cPSD| 58931565 𝜀𝑚𝑎𝑥 𝑦 𝑦 𝑦 𝐹𝑅 = Σ𝐹𝑥 = 0 𝜎 = − 𝜎𝑚𝑎𝑥 𝑦𝑚𝑎𝑥 න
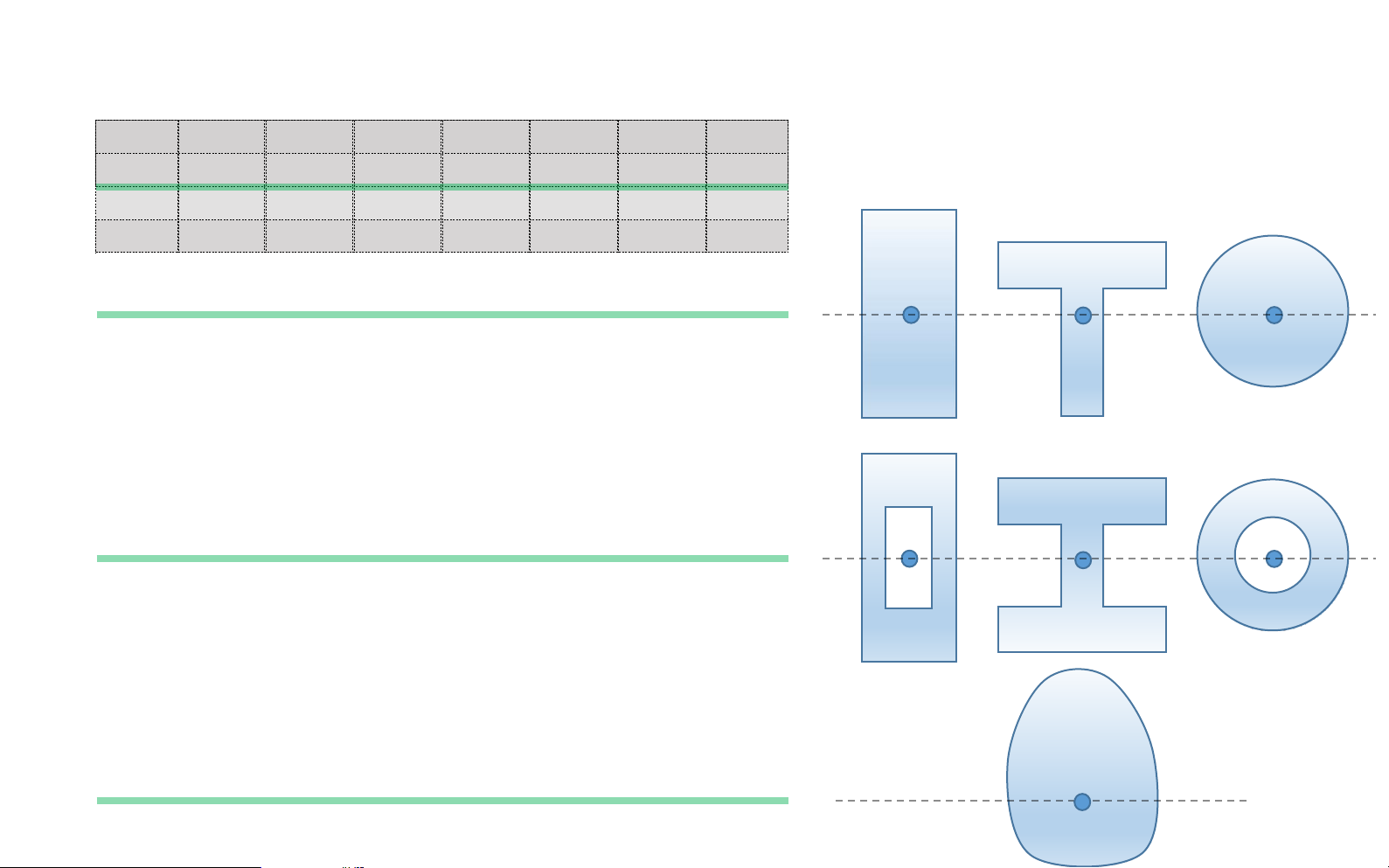
𝑑𝐹 = න 𝜎𝑑𝐴 = 0 𝑀 𝐴 𝐴 𝜎𝑚𝑎𝑥 𝑦 𝜎 𝑚𝑎𝑥 −
න 𝑦𝑑𝐴 = 0 ⇒ 𝑆𝑧 = න 𝑦𝑑𝐴 = 0 𝑦𝑚𝑎𝑥 𝐴 𝐴 𝑦 𝑚𝑎𝑥 𝑦 The Flexure Formula 𝜎𝑚𝑎𝑥 𝑦 lOMoAR cPSD| 58931565 𝜀𝑚𝑎𝑥 𝑦 𝑦 𝑑𝑀 = 𝑦𝑑𝐹 𝜀=− 𝜀 =− 𝑦𝜎𝑑𝐴 𝑦 𝑚𝑎𝑥 𝑚𝑎𝑥 𝑑𝐴 𝑦 𝑚𝑎𝑥 𝑀 𝑑𝐹=𝜎𝑑𝐴 𝜎 𝑦 𝑥 𝑧 𝑦 𝑦 𝑚𝑎𝑥 𝑥 𝑑𝑀 Hooke′ slaw: 𝜎= 𝑀 𝐸𝜀 neutral Bending moment axis (N-A) 𝑦 The Flexure Formula 𝜎𝑚𝑎𝑥 𝑦 lOMoAR cPSD| 58931565 𝜀𝑚𝑎𝑥 𝑦 𝑦 𝜎 = −
𝑦𝑚𝑎𝑥 𝜎𝑚𝑎𝑥 𝑀 = න𝐴 𝑑𝑀 = − න𝐴 𝑦𝜎𝑑𝐴 𝑀 = 𝜎𝑚𝑎𝑥
2𝑑𝐴 = 𝜎𝑚𝑎𝑥 𝐼𝑧 moment of inertia න 𝑦 𝑦𝑚𝑎𝑥 𝐴 𝑦𝑚𝑎𝑥 𝐼𝑧 = න 𝑦2𝑑𝐴 𝑦 𝜎 𝐴 𝑚𝑎𝑥 𝑦 𝑚𝑎𝑥 𝑦