Bộ đề cuối học kì 2 Toán 9 Kết Nối Tri Thức Với Cuộc Sống cấu trúc mới.

ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 – MÔN TOÁN – LỚP 9 – BỘ SÁCH KẾT NỐI TRI THỨC ĐỀ SỐ 01
A. MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 – TOÁN 9 – KẾT NỐI TRI THỨC
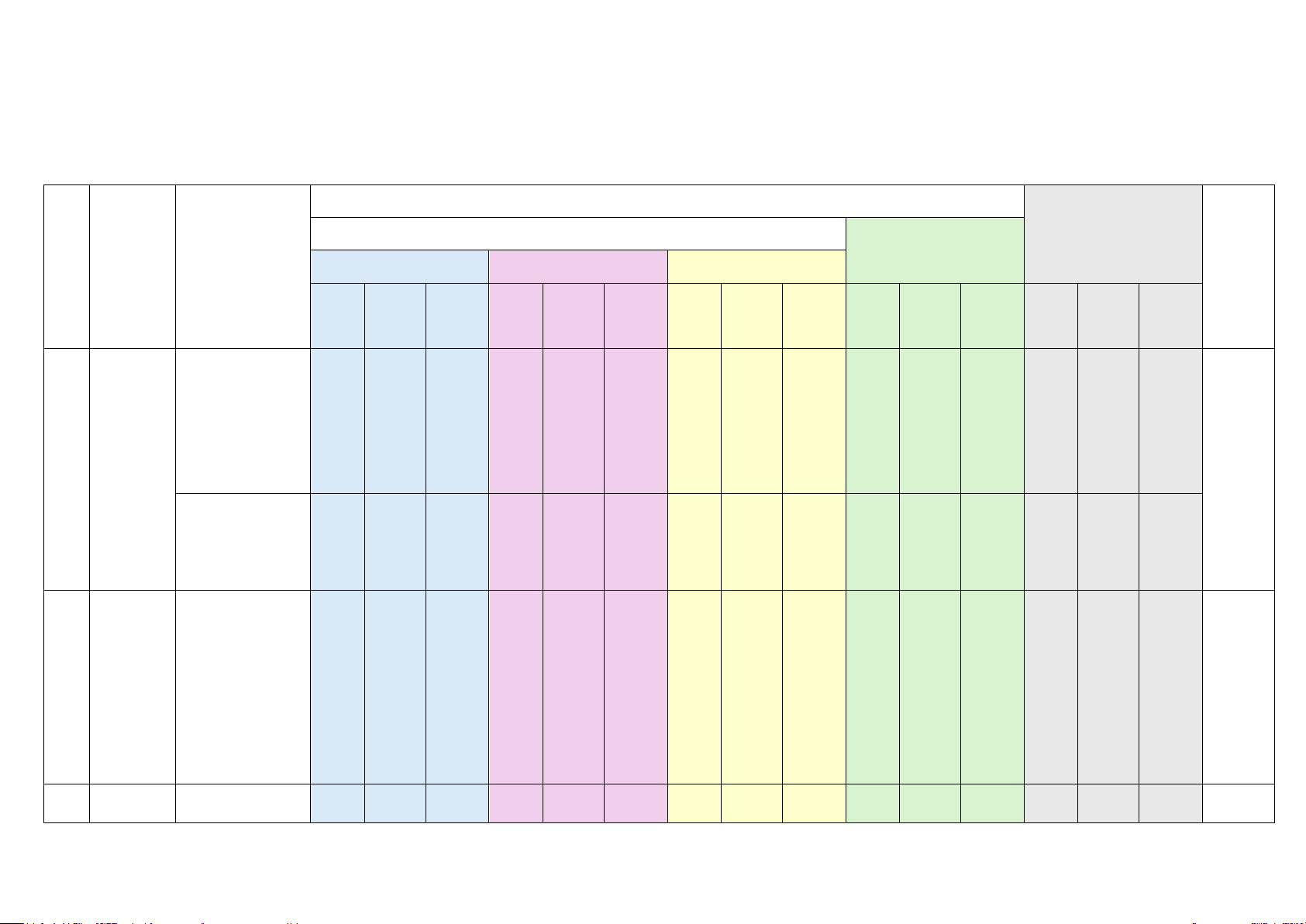
Mức độ đánh giá TNKQ Tổng Tỉ lệ
Chủ đề/ Nội dung/ đơn Tự luận TT Nhiều lựa chọn “Đúng – Sai” Trả lời ngắn % Chương vị kiến thức Vận Vận Vận Vận Vận điểm Biết Hiểu Biết Hiểu Biết Hiểu Biết Hiểu Biết Hiểu dụng dụng dụng dụng dụng Hàm số Hàm số 2 y = ax 2 y = ax 1 1 1 1
(a ≠ 0). (a ≠ 0) và đồ 1 Phương thị 25% trình Phương trình
bậc hai bậc hai một ẩn. 2 4 1 6 1 một ẩn Định lí Viète
Tần số Bảng tần số,
và tần số biểu đồ tần số, tương Bảng tần số 2 3 1 1 4 1 17,5% đối tương đối, biểu đồ tần số tương đối
3 Xác suất Phép thử ngẫu 1 1 1 1 2 12,5%
của biến nhiên và không
cố trong gian mẫu. Xác
một số suất của biến cố
mô hình trong một số
xác suất mô hình xác
đơn giản suất đơn giản Đường Đường tròn tròn ngoại tiếp tam ngoại giác. Đường 1 1 1 1 1
tiếp và tròn nội tiếp 4 30% đường tam giác
tròn nội Tứ giác nội tiếp 1 1 1 1 1 1 tiếp Đa giác đều và 1 1 1 1 phép quay
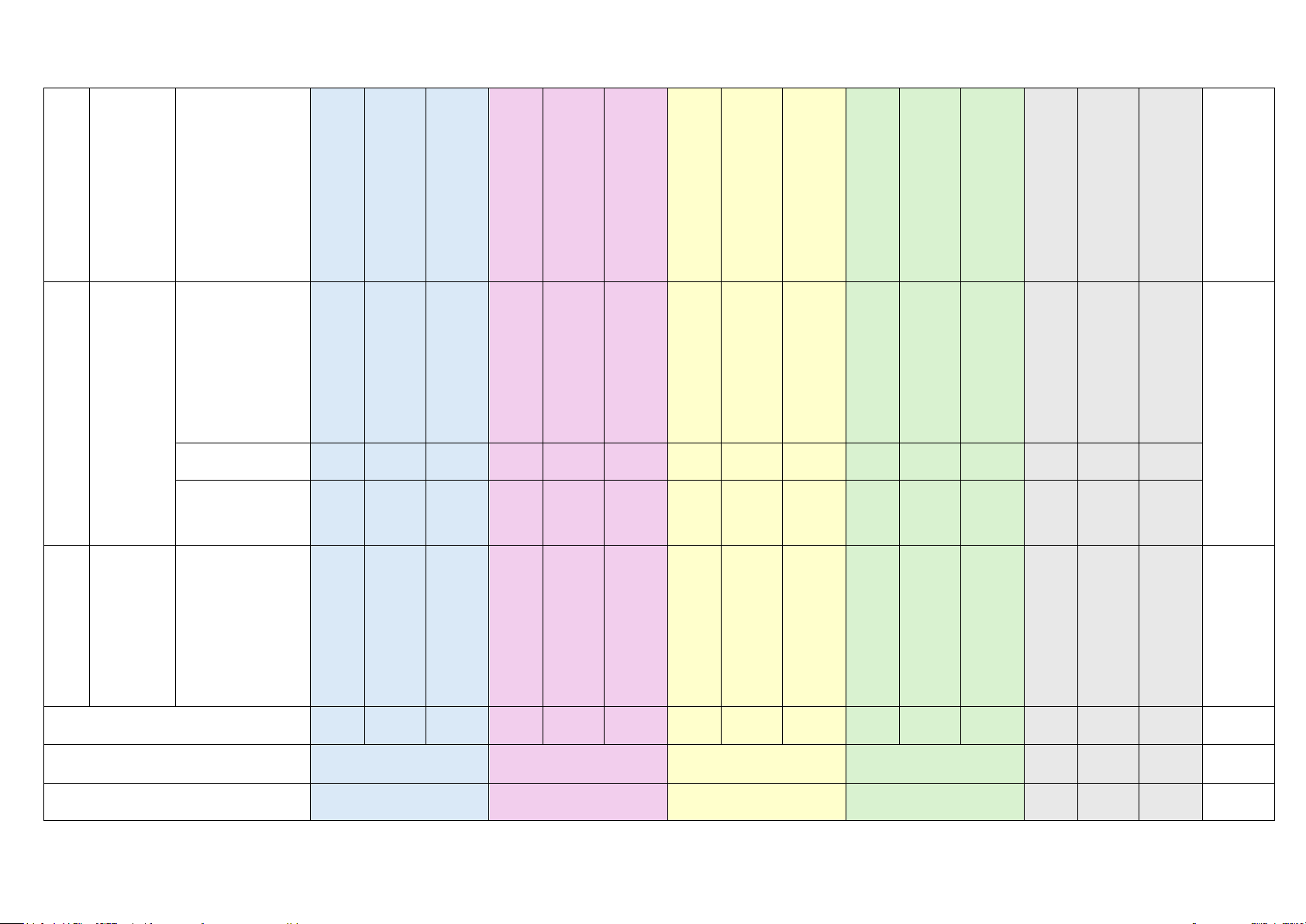
Một số Hình trụ. Hình hình nón. Hình cầu 5 khối 2 2 1 2 2 1 15% trong thực tiễn Tổng số câu 10 2 6 2 3 2 1 1 4 17 7 7 31 Tổng số điểm 3,0 2,0 2,0 3,0 4,0 3,0 3,0 10,0 Tỉ lệ % 30 20 20 30 40 30 30 100 Lưu ý:
– Các dạng thức trắc nghiệm gồm:
+ Nhiều lựa chọn: mỗi câu cho 04 phương án, chọn 01 phương án đúng. Mỗi câu chọn đáp án đúng được 0,25 điểm.
+ “Đúng – Sai: mỗi câu hỏi có 04 ý, tại mỗi mỗi ý thí sinh lựa chọn đúng hoặc sai.
⦁ Trả lời đúng 1 ý được 0,1 điểm;
⦁ Trả lời đúng 2 ý được 0,25 điểm;
⦁ Trả lời đúng 3 ý được 0,5 điểm;
⦁ Trả lời đúng 4 ý được 1,0 điểm.
+ Trả lời ngắn: với mỗi câu hỏi, viết câu trả lời/ đáp án vào bài thi. Mỗi câu trả lời đúng được 0,5 điểm.
– Số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ điểm được quy định trong ma trận.
B. BẢN ĐẶC TẢ ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 – TOÁN 9 – KẾT NỐI TRI THỨC Nội
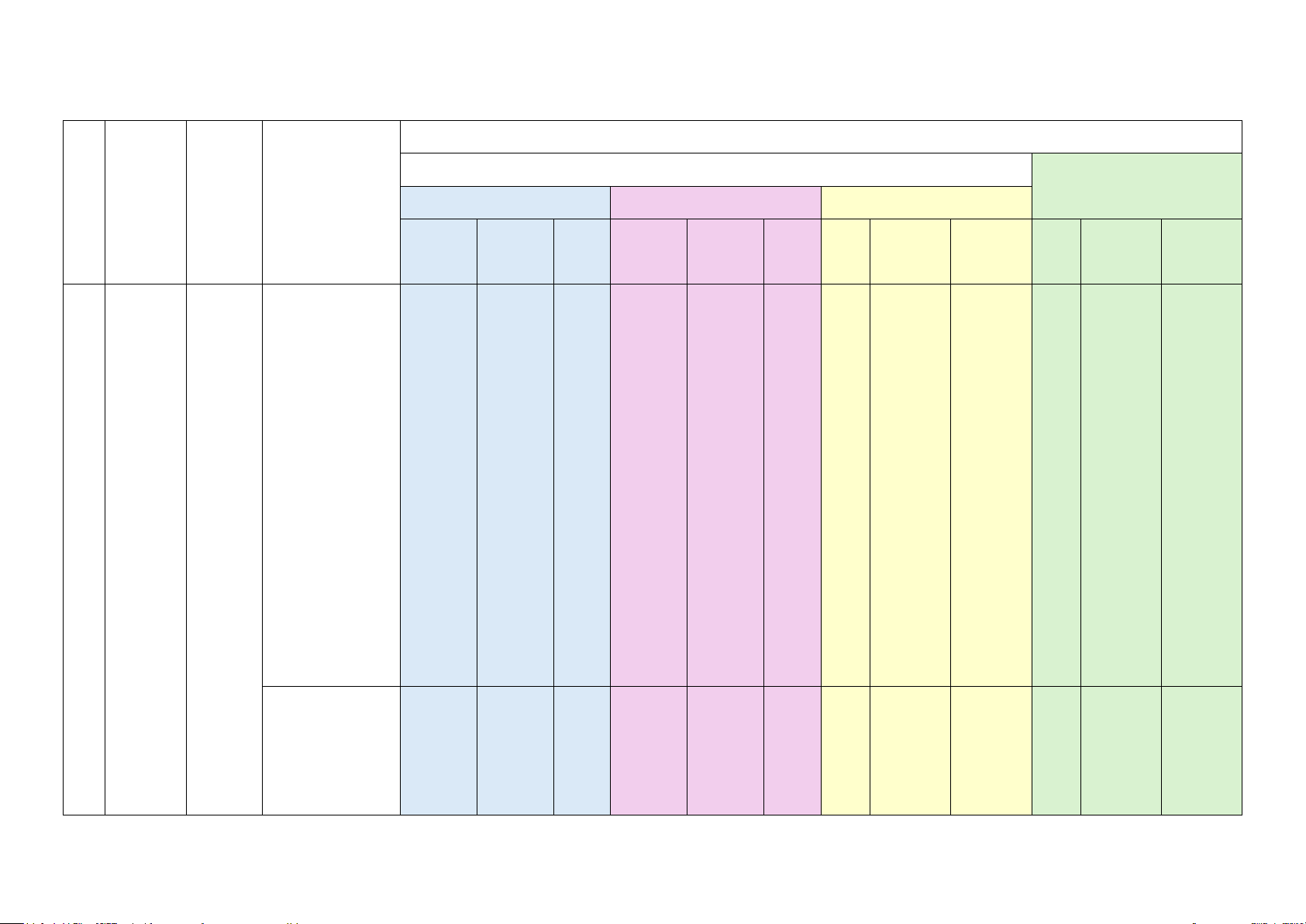
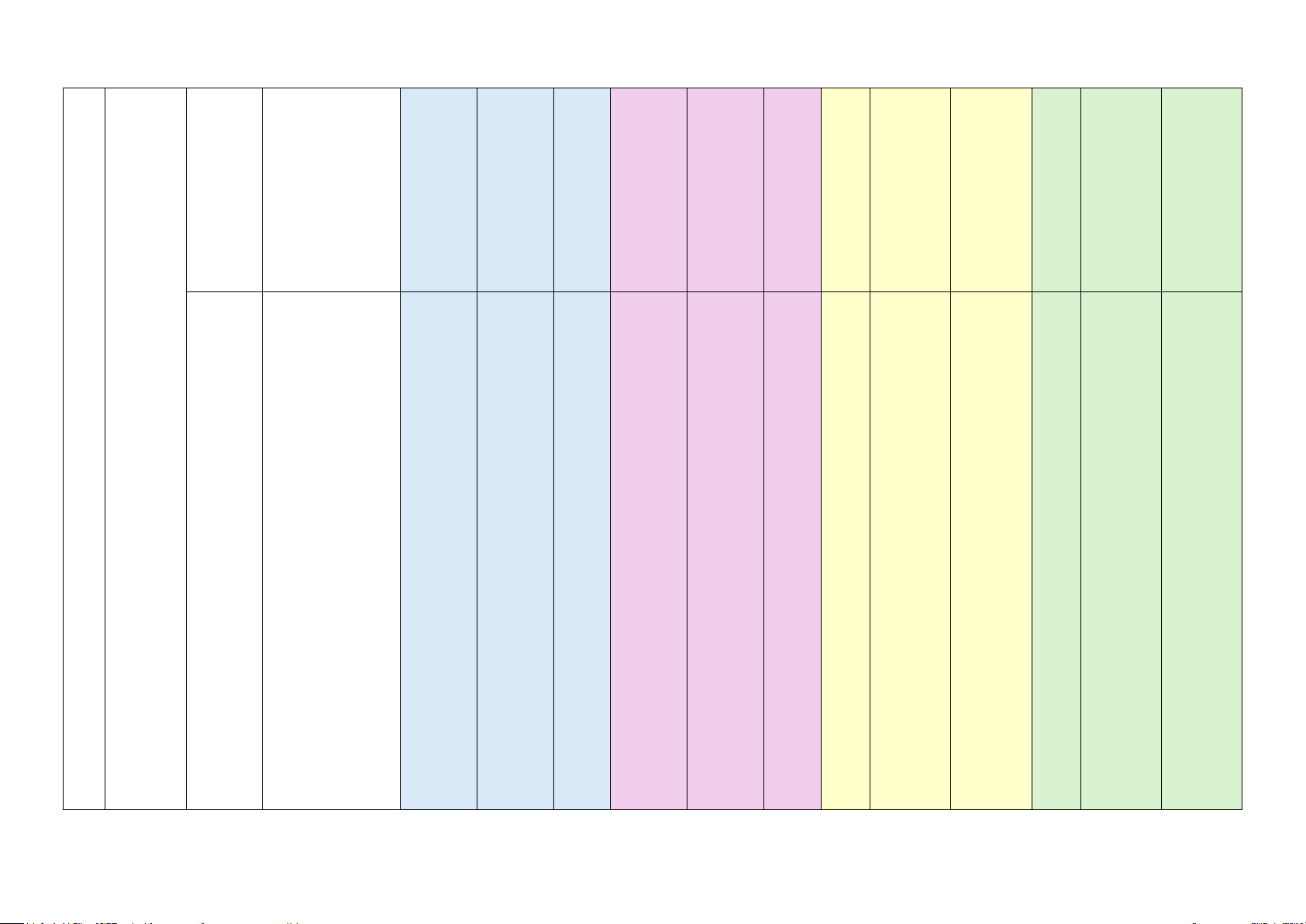
Số câu hỏi ở các mức độ đánh giá dung/ TNKQ Chủ đề/ Yêu cầu cần Tự luận TT đơn vị Nhiều lựa chọn “Đúng – Sai” Trả lời ngắn Chương đạt kiến Vận Vận Vận Vận Biết Hiểu Biết Hiểu Biết Hiểu Biết Hiểu thức dụng dụng dụng dụng
1 Hàm số Hàm số Biết: Câu 1 2 y = ax 2
y = ax – Nhận biết (GTTH)
(a ≠ 0). (a ≠ 0) được tính đối xứng (trục) và
Phương và đồ trục đối xứng trình thị của đồ thị hàm bậc hai số 2 y = ax một ẩn (a ≠ 0). – Xác định được giá trị của hàm số khi biết giá trị của biến. Hiểu: Câu 2 – Thiết lập được (SD bảng giá trị của CCPT) hàm số 2
y = ax (a ≠ 0). – Xác định được
hệ số a khi biết đồ thị hàm số đi qua một điểm cho trước.
Phương Biết: Câu 3, Câu trình – Nhận biết Câu 4 13a,
bậc hai được khái niệm (GTTH) Câu một ẩn. phương trình 13b,
Định lí bậc hai một ẩn. Câu Viète – Xác định các 13c, hệ số a, , b c Câu của phương 13d, trình bậc hai (GTTH/ một ẩn. TD) – Xác định được số nghiệm của phương trình khi biết dấu của biệt thức/ biệt thức thu gọn. Hiểu: – Tính được nghiệm phương trình bậc hai một ẩn bằng máy tính cầm tay. – Giải được phương trình bậc hai một ẩn. – Giải thích được định lí Viète. Vận dụng: Câu 15 – Ứng dụng (TD/ được định lí GQVĐ) Viète vào tính nhẩm nghiệm của phương trình bậc hai, tìm hai số biết tổng và tích của chúng, ... – Vận dụng được phương trình bậc hai vào giải quyết bài toán thực tiễn (đơn giản, quen thuộc). – Vận dụng được phương trình bậc hai vào giải quyết bài toán thực tiễn (phức hợp, không quen
thuộc). 2 Tần số Bảng Biết: Câu 5,
và tần tần số, – Xác định được Câu 6, số biểu đồ tần số Câu 7 tương
tần số. (frequency) của (GTTH) đối Bảng một giá trị.
tần số – Xác định được tương tần số tương đối đối, (relative
biểu đồ frequency) của tần số một giá trị. tương – Nhận biết đối được mối liên hệ thống kê với những kiến thức của các môn học khác trong Chương trình lớp 9 và trong thực tiễn. Hiểu: Bài 1.1a – Giải thích (GQVĐ) được ý nghĩa và vai trò của tần số, tần số tương đối trong thực tiễn. – Xác định tần số (frequency), tần số tương đối (relative frequency) của một giá trị. Vận dụng: Bài 1.1b – Thiết lập được (GQVĐ/ bảng tần số MHH) ghép nhóm, bảng tần số tương đối ghép nhóm. – Thiết lập được biểu đồ tần số tương đối ghép nhóm (histogram) (ở dạng biểu đồ cột hoặc biểu đồ
đoạn thẳng). 3 Xác Phép Biết: Câu 8 suất của thử
– Nhận biết (GTTH) biến cố ngẫu được phép thử trong nhiên ngẫu nhiên và một số và không gian
mô hình không mẫu. xác suất gian Hiểu: Câu 16 Bài 1.2 đơn mẫu. – Tính được xác (TD/ (GQVĐ/ giản Xác suất của biến cố GQVĐ) MHH) suất bằng cách kiểm của đếm số trường
biến cố hợp có thể và số trong trường thuận lợi
một số trong một số mô mô
hình đơn giản. hình xác suất đơn giản
4 Đường Đường Biết: Câu 9 tròn tròn
– Nhận biết (GTTH) ngoại ngoại được định nghĩa tiếp và tiếp đường tròn đường tam ngoại tiếp tam tròn nội giác. giác, đường tròn tiếp Đường nội tiếp tam tròn nội giác. tiếp – Xác định được tam tâm đường tròn giác ngoại tiếp tam giác, trong đó có tâm và bán kính đường tròn nội tiếp, ngoại tiếp tam giác vuông, tam giác đều. Hiểu: – Tính độ dài của bán kính đường tròn nội tiếp, ngoại tiếp. – Tính diện tích hình vuông, hình tam giác thông qua việc áp dụng tính bán kính đường tròn nội tiếp, ngoại tiếp. Vận dụng: Bài 2b – Chứng minh (GQVĐ) các tính chất liên quan đến đường tròn ngoại tiếp, đường tròn nội tiếp tam giác (ba đường thẳng đồng quy, thẳng hàng, hai góc bằng nhau, …)
Tứ giác Biết: Câu 10
nội tiếp – Nhận biết (GTTH) được tứ giác nội tiếp đường tròn. Hiểu: Câu 17 – Giải thích (GQVĐ) được định lí về tổng hai góc đối của tứ giác nội tiếp bằng 180 .° – Xác định được tâm và bán kính đường tròn ngoại tiếp hình chữ nhật, hình vuông. Vận dụng: Bài 2a, – Chứng minh Bài 2c được tứ giác nội (GQVĐ/ tiếp. MHH) – Giải quyết được một số vấn đề thực tiễn (đơn giản, quen thuộc) gắn với đường tròn. – Giải quyết được một số vấn đề thực tiễn (phức hợp, không quen
thuộc) gắn với đường tròn.
Đa giác Biết: Câu 11
đều và – Nhận biết (GTTH) phép được đa giác quay đều. – Nhận biết được phép quay. – Nhận biết được những hình phẳng đều trong tự nhiên, nghệ thuật, kiến trúc, công nghệ, chế tạo,… Hiểu: Câu 12 – Mô tả được (GTTH) các phép quay giữ nguyên hình đa giác đều, biến điểm này thành điểm khác. – Tính số cạnh, góc của đa giác đều. 5 Một số Hình Biết: Câu hình trụ. – Mô tả (đường 14a, khối Hình sinh, chiều cao, Câu trong nón. bán kính đáy), 14b thực Hình tạo lập được (GTTH) tiễn cầu hình trụ, hình nón, hình cầu. Nhận biết được phần xung quanh của mặt phẳng và mặt cầu. diện tích quanh của hình trụ, hình nón, hình cầu. Hiểu: Câu – Tính được 14c, diện tích xung Câu quanh, thể tích 14d của hình trụ, (GTTH) hình nón, hình cầu. Vận dụng: Câu 18 – Giải quyết (GQVĐ) được một số vấn đề thực tiễn gắn với việc tính diện tích xuang quanh của hình trụ, hình nón, hình cầu (ví dụ: tính thể tích và diện tích xung quanh của một số đồ vật quen thuộc có dạng hình trụ, hình nón, hình cầu,...). Tổng số câu 10 2 6 2 3 2 1 1 4 Tổng số điểm 3,0 2,0 2,0 3,0 Tỉ lệ % 30 20 20 30
C. ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 – TOÁN 9 – KẾT NỐI TRI THỨC
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 TRƯỜNG …
MÔN: TOÁN – LỚP 9 MÃ ĐỀ MT 101
NĂM HỌC: … – … Thời gian: 90 phút
(không kể thời gian giao đề)
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Câu 1. Trong các hàm số sau, hàm số nào đồng biến trên ? A y = 3 − x + 2 . B. 1 x y − = . C. x y = −1. D. y =1− 2x . 2 3
Câu 2. Cho hàm số y = ( m + ) 2 3 2 x với 2
m = − . Giá trị của tham số m để đồ thì hàm số đã cho đi 3 qua điểm ( 1; − 2) là A. 2 m = − . B. m = 0. C. m = 1. − D. m =1. 3
Câu 3. Cho phương trình 2
ax + bx + c = 0 (a ≠ 0) có biệt thức 2
∆ = b − 4ac . Phương trình đã cho vô nghiệm khi A. ∆ < 0 . B. ∆ > 0 . C. ∆ ≥ 0 . D. ∆ ≤ 0 .
Câu 4. Phương trình nào sau đây có hai nghiệm trái dấu? A. 2
x − 6x + 5 = 0 . B. 2
x − 5x + 6 = 0 . C. 2
−x − 5x − 6 = 0. D. 2
x − 5x − 6 = 0.
Câu 5. Biểu đồ tần số dạng cột là
A. biểu đồ đoạn thẳng với trục ngang biểu diễn tần số.
B. biểu đồ cột với trục ngang biểu diễn tần số.
C. biểu đồ đoạn thẳng với trục đứng biểu diễn tần số.
D. biểu đồ cột với trục đứng biểu diễn tần số.
Câu 6. Cho bảng khảo sát về chiều cao học sinh trong lớp như sau: Chiều cao (cm)
[150; 160) [160; 167) [167; 170) [170; 175) [175; 180) Số học sinh 12 18 8 3 1
Bảng số liệu ghép nhóm trên có số nhóm số liệu là A. 40 . B. 4 . C. 5. D. 6 .
Câu 7. Số lượng đôi giày thể thao bán được của một cửa hàng trong bốn năm gần đây được biểu diễn ở biểu đồ sau đây:
Số lượng đôi giày thể thao bán được của một cửa hàng Tần số 800 700 700 600 600 500 400 400 300 300 200 100 0 2020 2021 2022 2023 Năm
Số đôi giày cửa hàng đã bán được vào năm 2023 là A. 400. B. 600. C. 700. D. 300.
Câu 8. Khi gieo hai con xúc xắc cân đối và đồng chất, gọi T là tổng số chấm trên hai con xúc xắc
thì kết quả nào sau đây không thể xảy ra? A. T =1. B. T = 2. C. T = 3. D. T = 4.
Câu 9. Tâm đường tròn nội tiếp của một tam giác là giao của các đường A. trung trực. B. phân giác trong. C. phân giác ngoài. D. đường cao.
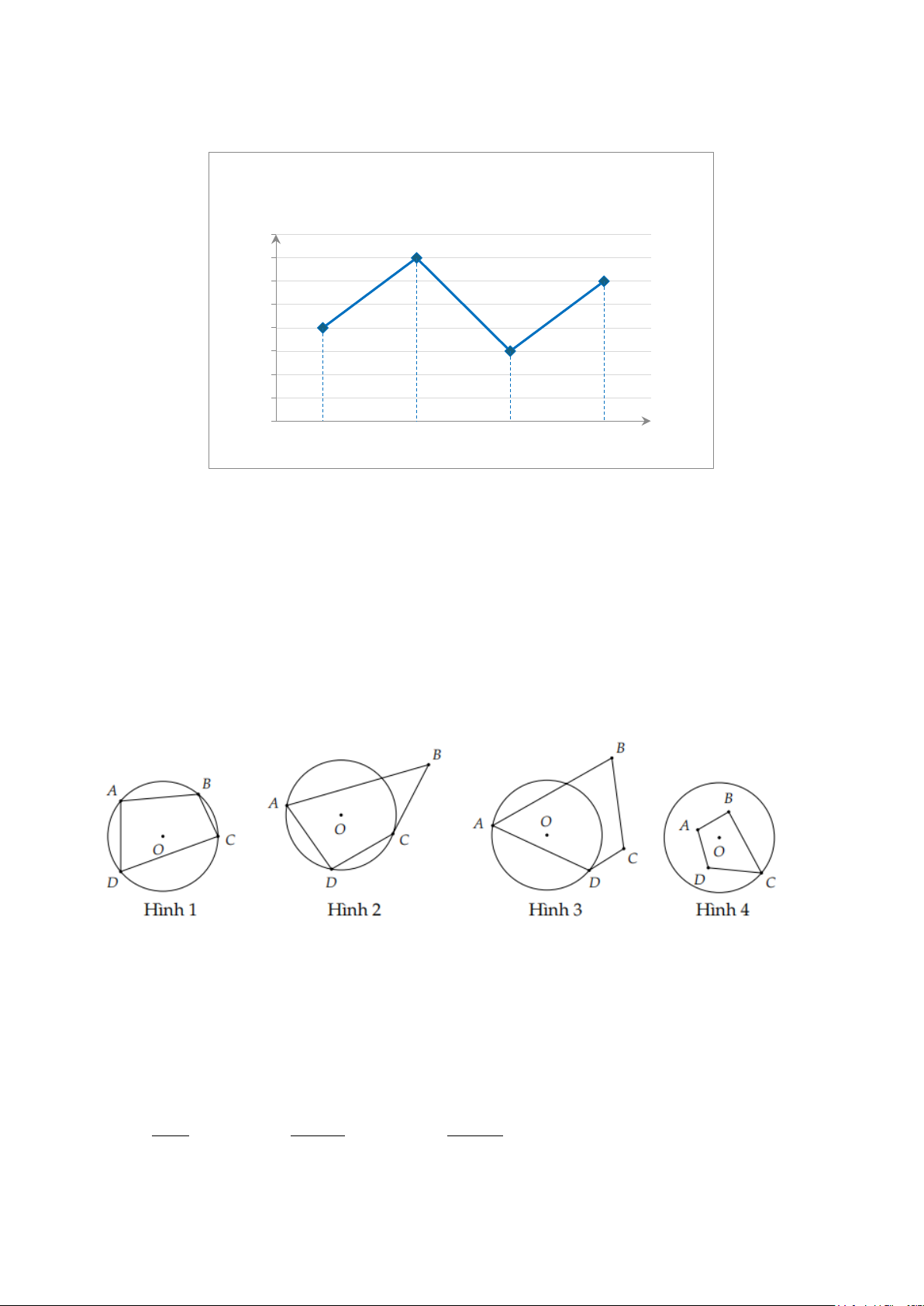
Câu 10. Cho các hình vẽ sau:
Trong các hình trên, hình nào đang nội tiếp đường tròn? A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Câu 11. Phép quay giữ nguyên mọi điểm là phép quay A. 0°. B. 360° .
C. Cả A và B đều đúng. D. Cả A và B đều sai.
Câu 12. Cho tam giác ABC đều nội tiếp đường tròn (O). Các phép quay giữ nguyên tam giác ABC là A. o 360° o 3⋅360° o 2⋅360 α 120 ; α 360 ; α ° = = ° = = ° = = 240 .° 1 2 3 3 3 3 B. o 2⋅360° o 360° o 3⋅360 α 240 ; α 120 ; α ° = = ° = = ° = = 360 .° 1 2 3 3 3 3 C. o 360° o 2⋅360° o 3⋅360 α 120 ; α 240 ; α ° = = ° = = ° = = 360 .° 1 2 3 3 3 3 D. o 3⋅360° o 2⋅360° o 360 α 360 ; α 240 ; α ° = = ° = = ° = = 120 .° 1 2 3 3 3 3
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Trong câu 13 và câu 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Câu 13. Cho phương trình 2
x + (m + 2) x + m −1 = 0 .
a) Phương trình đã cho là phương trình bậc hai một ẩn.
b) Phương trình luôn có hai nghiệm x , x với mọi . m 1 2
c) Tổng và tích hai nghiệm của phương trình lần lượt là x + x = m + 2; x x = m −1. 1 2 1 2
d) Không có giá trị của m để phương trình có hai nghiệm x , x thoả mãn 2 2
x − x + x − x = 6. 1 2 1 1 2 2 Hướng dẫn giải Đáp án: a) Đúng. b) Đúng. c) Sai. d) Sai. Xét phương trình 2
x + (m + 2) x + m −1 = 0 với m là tham số.
⦁ Phương trình đã cho là phương trình bậc hai ẩn x có a =1 ≠ 0; b = m + 2; c = m −1. Do đó ý a) là đúng.
⦁ Phương trình có biệt thức ∆ = (m + )2 − ⋅ ⋅(m − ) 2 2 4 1
1 = m + 8 > 0 nên phương trình luôn có nghiệm
x , x với mọi m∈ . 1 2  Do đó ý b) là đúng.
⦁ Theo định lí Viète, ta có: x + x = − m + 2 ; x x = m −1. Do đó ý c) là sai. 1 2 ( ) 1 2 ⦁ Ta có 2 2
x + 2x x + x − 2x x − x + x = 6 1 1 2 2 1 2 ( 1 2)
(x + x )2 − 2x x − x + x = 6 1 2 1 2 ( 1 2) (m + )2 2 − 2(m − ) 1 + (m + 2) = 6 2
m + 4m + 4 − 2m + 2 + m + 2 = 6 2
m + 3m + 2 = 0 .
Phương trình này có tổng các hệ số a − b + c =1− 3+ 2 = 0 nên phương trình này có các nghiệm m = 1, − m = 2 − . 1 2
Vậy có hai giá trị cần tìm của m là m = 1, − m = 2 − . Do đó ý d) là sai. 1 2
Câu 14. Một chiếc kem ốc quế có dạng hình nón với phần vỏ quế có đường kính
đáy là 4,4 cm, chiều cao vỏ quế 12 cm. Người ta lấy phần kem từ một hộp hình
trụ có chiều cao là 15 cm với diện tích đáy π ( 2 100
cm ) để cho vào vỏ ốc quế (coi
phần vỏ kem có độ dày không đáng kể).
a) Thể tích hình trụ có bán kính đáy R và chiều cao h , được tính bằng công thức: 1 2 V = π R . h 3
b) Bán kính đáy của chiếc kem ốc quế là R = 2,2 cm.
c) Thể tích của chiếc kem là 1452 π ( 3 cm ). 5 2
d) Ta có thể lấy kem từ hộp làm được tối đa 75 chiếc kem ốc quế.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Trong mỗi câu hỏi từ câu 15 đến câu 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Câu 15. Theo kế hoạch 2 tổ phải sản xuất 700 sản phẩm. Nhưng do tổ 1 làm vượt mức 15% và tổ 2
vượt mức 20% so với kế hoạch nên cả 2 tổ làm được 820 sản phẩm. Tính số sản phẩm mỗi tổ phải làm theo kế hoạch?
Câu 16. Tập hợp A gồm các số có ba chữ số, trong đó có 15 số nguyên tố. Bạn An chọn ngẫu nhiên một số từ tập hợp .
A Biết rằng xác suất của biến cố “Chọn được số là hợp số” là 0,7. Hỏi tập hợp A có bao nhiêu phần tử?
Câu 17. Cho tứ giác nội tiếp ABCD đường tròn (O) . Hai đường thẳng AB và DC cắt nhau tại X. Biết  = ° 
BAD 70 ; ABC =130 .° Tính số đo góc BXC (đơn vị độ).
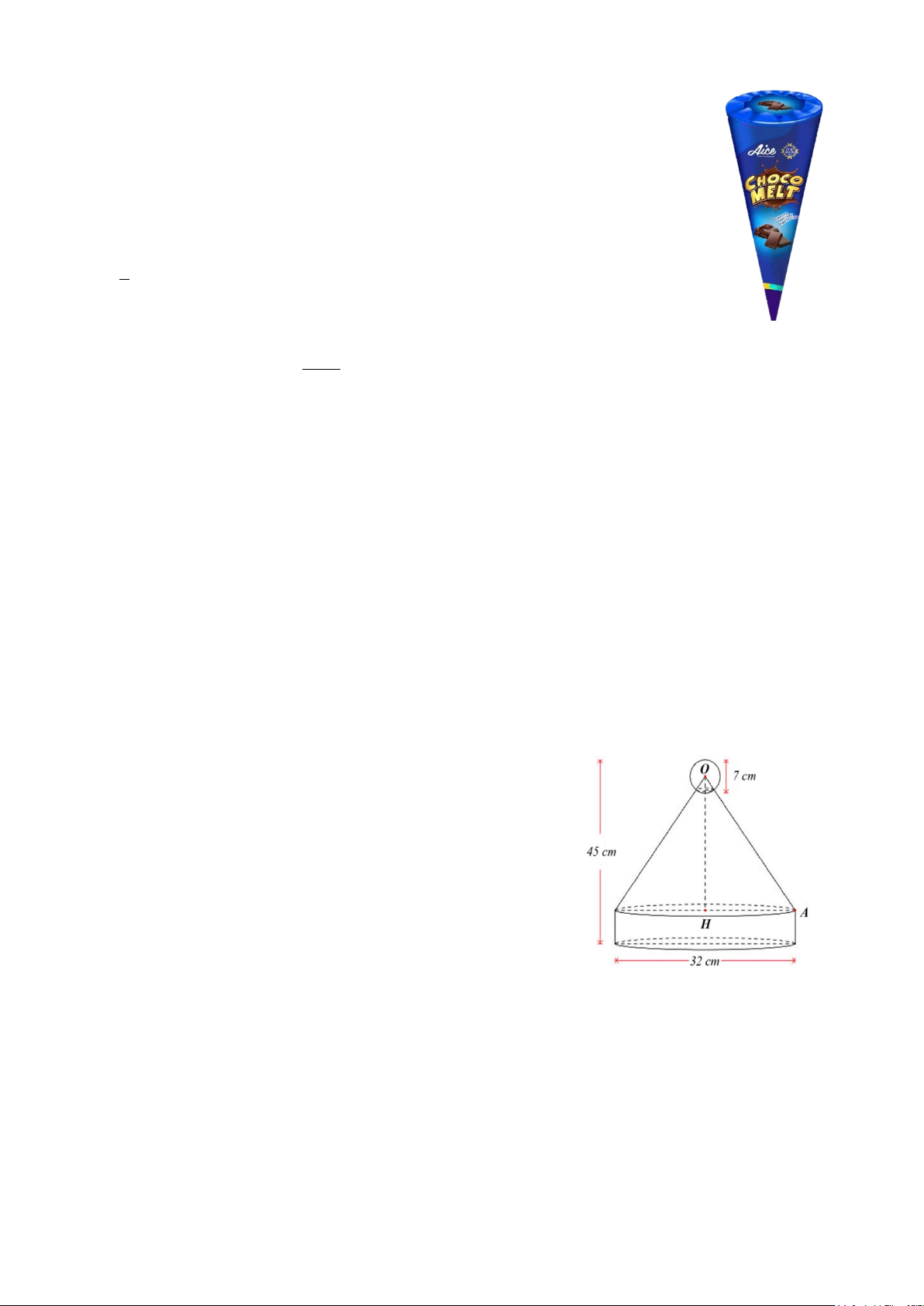
Câu 18. Một chiếc nón ông già Noel thường gồm có ba phần:
Hình trụ để làm đế nón, phần mũ chính là hình nón, trên đỉnh nón
là quả bóng trắng có hình cầu và có các kích thước tương ứng
như hình vẽ. Tính tổng diện tích phần vải để may nón, biết rằng
chiều cao của đế nón bằng đường kính của quả bóng (kết quả làm
tròn đến hàng đơn vị với đơn vị 2 cm ).
B. TỰ LUẬN (3,0 điểm)
Bài 1. (1,5 điểm)
1. Biểu đồ dưới đây biểu diễn tỉ lệ về cân nặng của các bạn học sinh lớp 9A (đơn vị: kg).