Bộ đề giữa học kì 2 Toán 8 Kết Nối Tri Thức Với Cuộc Sống cấu trúc mới có đáp án

ĐỀ KIỂM TRA, ĐÁNH GIÁ GIỮA HỌC KÌ II – BỘ SÁCH: KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
MÔN: TOÁN − LỚP 8 ĐỀ SỐ 01
A. MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ II
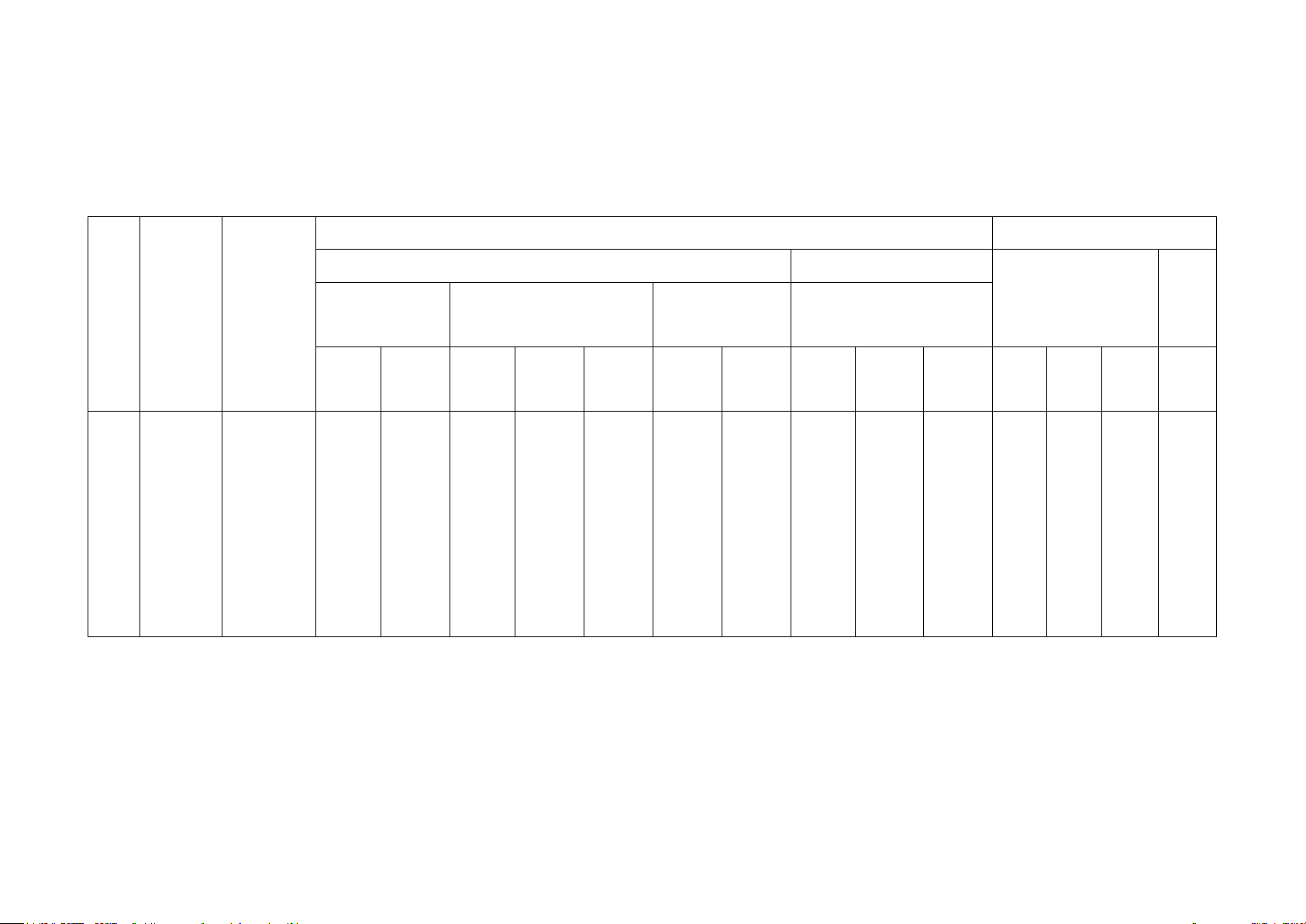
Số câu hỏi ở các mức độ đánh giá Tổng Nội TNKQ Tự luận Tỉ lệ Chủ đề/ dung/ % STT Nhiều lựa chọn Đúng - Sai Trả lời ngắn Chương Đơn vị điểm kiến thức Vận Vận Vận Vận Biết Hiểu Biết Hiểu Hiểu Biết Hiểu Biết Hiểu Tổng dụng dụng dụng dụng Phân thức Chương đại số. 2 VI. Tính chất TD, 1 Phân cơ bản 4 3 2 30% GTTH thức của phân 0,5đ đại số thức đại số. Phép cộng và phép trừ phân thức 1 1 1 2 2 đại số. TD, TD, TD, TD, TD, Phép GQVĐ GQVĐ GQVĐ GTTH GQVĐ nhân và 0,5đ 0,5đ 0,5đ 0,5đ 0,5đ phép chia phân thức đại số Phương Chương 2 1 trình bậc VII. TD, TD, nhất một Phương GTTH GQVĐ ẩn trình 0,5đ 0,5đ 2. bậc 4 2 2 30% Giải bài 1 nhất và 2 1 1 toán bằng TD, hàm số TD, TD, TD, cách lập GQVĐ bậc GTTH GQVĐ GQVĐ phương MHH nhất. 0,5đ 0,25đ 0,25đ trình 1,0đ
Chương Hai tam 1 2 1 1 3 IX. giác đồng TD, TD, TD, TD, 7 2 3 40% Tam dạng. Ba GTTH GTTH GQVĐ GQVĐ giác trường 0,25đ 0,5đ 0,25đ 0,25đ đồng hợp bằng dạng nhau của hai tam giác Định lí 1 1 1 Pythagore TD, TD, TD, và ứng GTTH GQVĐ GTTH dụng 0,25đ 0,5đ 0,5đ Các trường hợp bằng 2 1 1 nhau của TD, TD, TD, tam giác GTTH GQVĐ GQVĐ vuông. 0,5đ 0,5đ 0,5đ Hình đồng dạng Tổng số câu 10 2 4 2 2 2 2 1 1 3 15 7 7 29 Tổng số điểm 3,0 2,0 2,0 3,0 4,0 3,0 3,0 10 Tỉ lệ % 30% 20% 20% 30% 40% 30% 30% 100
B. BẢN ĐẶC TẢ ĐỀ KIỂM TRA GIỮA HỌC KÌ II – TOÁN 8
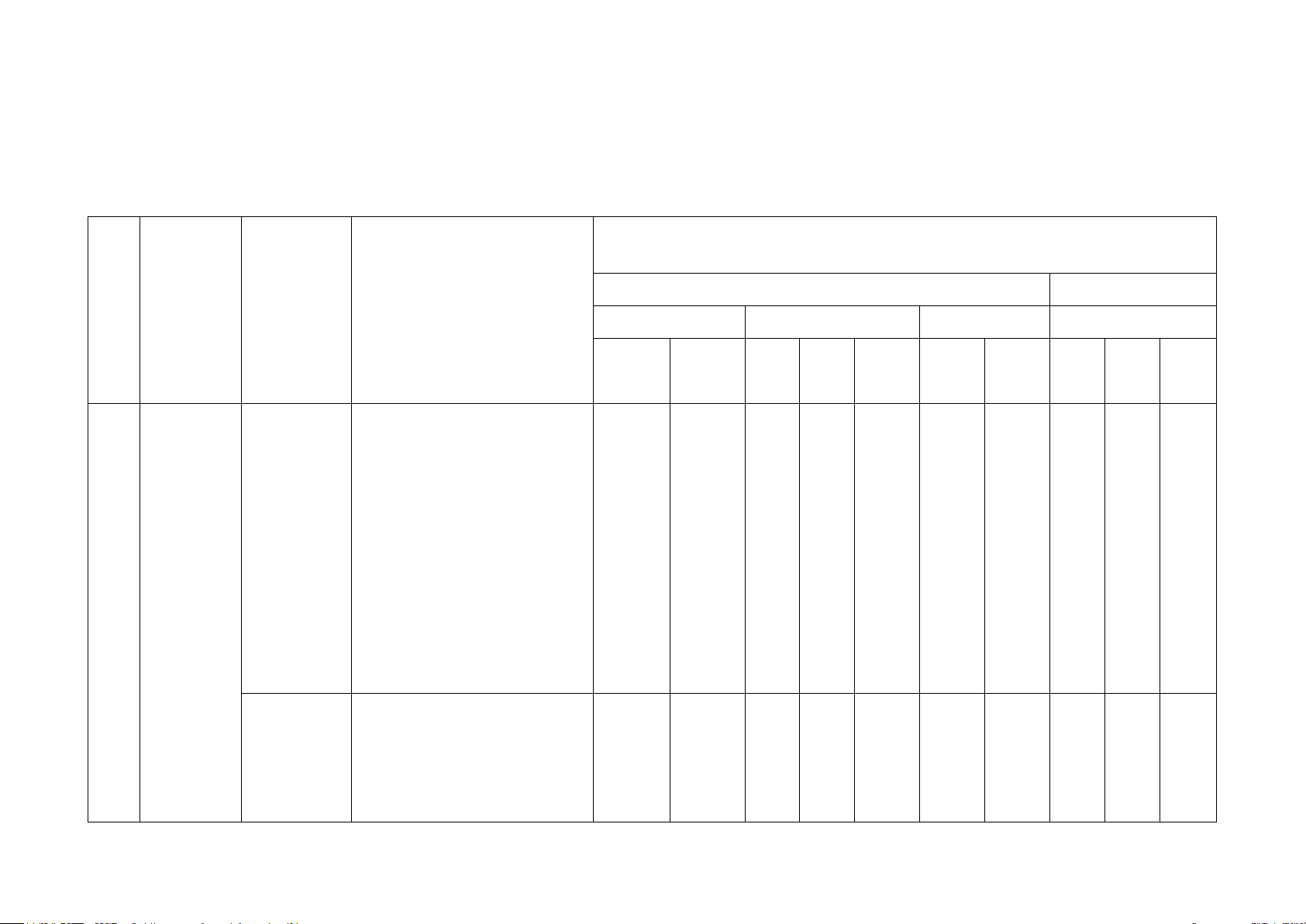
Số câu hỏi ở mức độ đánh giá Nội dung/ Chủ đề/ TNKQ Tự luận STT Đơn vị kiến
Yêu cầu cần đạt chương Nhiều lựa chọn Đúng – Sai Trả lời ngắn thức Vận Vận Vận Biết Hiểu Biết Hiểu Hiểu Biết Hiểu dụng dụng dụng Nhận biết:
- Nhận biết được các khái
Phân thức niệm cơ bản về phân thức đại
đại số. Tính số: định nghĩa, điều kiện xác Câu 1,
chất cơ bản định, giá trị của phân thức đại Chương Câu 2
của phân số, hai phân thức bằng nhau. VI. Phân 1
thức đại số. Thông hiểu: thức đại
- Mô tả được những tính chất số
cơ bản của phân thức đại số.
Phép cộng Nhận biết:
và phép trừ - Phân biệt được phép cộng, Câu Câu 3 Câu 4 Bài 3
phân thức trừ hai phân thức cùng mẫu và 15 đại số. khác mẫu.
- Thực hiện cộng, trừ hai phân
thức cùng mẫu đơn giản. Thông hiểu:
- Thực hiện được các phép
tính: phép cộng, phép trừ đối
với hai phân thức đại số. Vận dụng:
- Vận dụng được các phép tính
giao hoán, kết hợp, phân phối
của phép nhân với phép cộng,
quy tắc dấu ngoặc với phân
thức đại số trong tính toán. Nhận biết:
- Nhận biết được phân thức
đối, phân thức nghịch đảo của một phân thức.
Phép nhân Thông hiểu: và phép Câu
- Thực hiện được các phép Câu 5 Câu 6 chia phân 16
tính: phép nhân, phép chia đối
thức đại số với hai phân thức đại số. Vận dụng:
- Vận dụng được các phép tính
giao hoán, kết hợp, phân phối
của phép nhân với phép cộng,
quy tắc dấu ngoặc với phân
thức đại số trong tính toán. Nhận biết:
- Trình bày được khái niệm
phương trình bậc nhất một ẩn. Chương
- Nhận biết được một số là VII.
nghiệm của phương trình bậc Phương Phương nhất một ẩn. trình bậc Câu 7, Câu 2 trình bậc Thông hiểu: nhất một ẩn Câu 8 17 nhất và
- Giải được phương trình bậc hàm số nhất một ẩn. bậc nhất. Vận dụng:
- Giải quyết được một số vấn
đề thực tiễn gắn liền với
phương trình bậc nhất một ẩn. Thông hiểu: Giải bài
- Lập được phương trình bậc Câu
toán bằng nhất một ẩn từ dữ kiện của bài 13a, Câu Câu cách lập toán thực tế. Bài 1 Câu 13c 13d phương Vận dụng: 13b trình
- Giải quyết được một số vấn
đề thực tiễn gắn với phương
trình bậc nhất (ví dụ: các bài
toán liên quan đến chuyển
động trong vật lí, các bài toán
liên quan đến hóa học,….) Nhận biết:
- Mô tả được định nghĩa của hai tam giác đồng dạng.
- Nhận biết được cách viết kí
hiệu hai tam giác đồng dạng. Hai tam
- Từ kí hiệu hai tam giác đồng
giác đồng dạng chỉ ra được hai góc Chương dạng. Ba
tương ứng bằng nhau và tỉ số Câu
IX. Tam trường hợp hai cạnh tương ứng. 14a, Câu Câu 3 Câu 9
giác đồng bằng nhau Thông hiểu: Câu 14c 14d dạng
của hai tam - Giải thích được các trường 14b giác
hợp đồng dạng của hai tam giác. Vận dụng:
- Giải quyết được một số vấn
đề thực tiễn gắn với việc vận
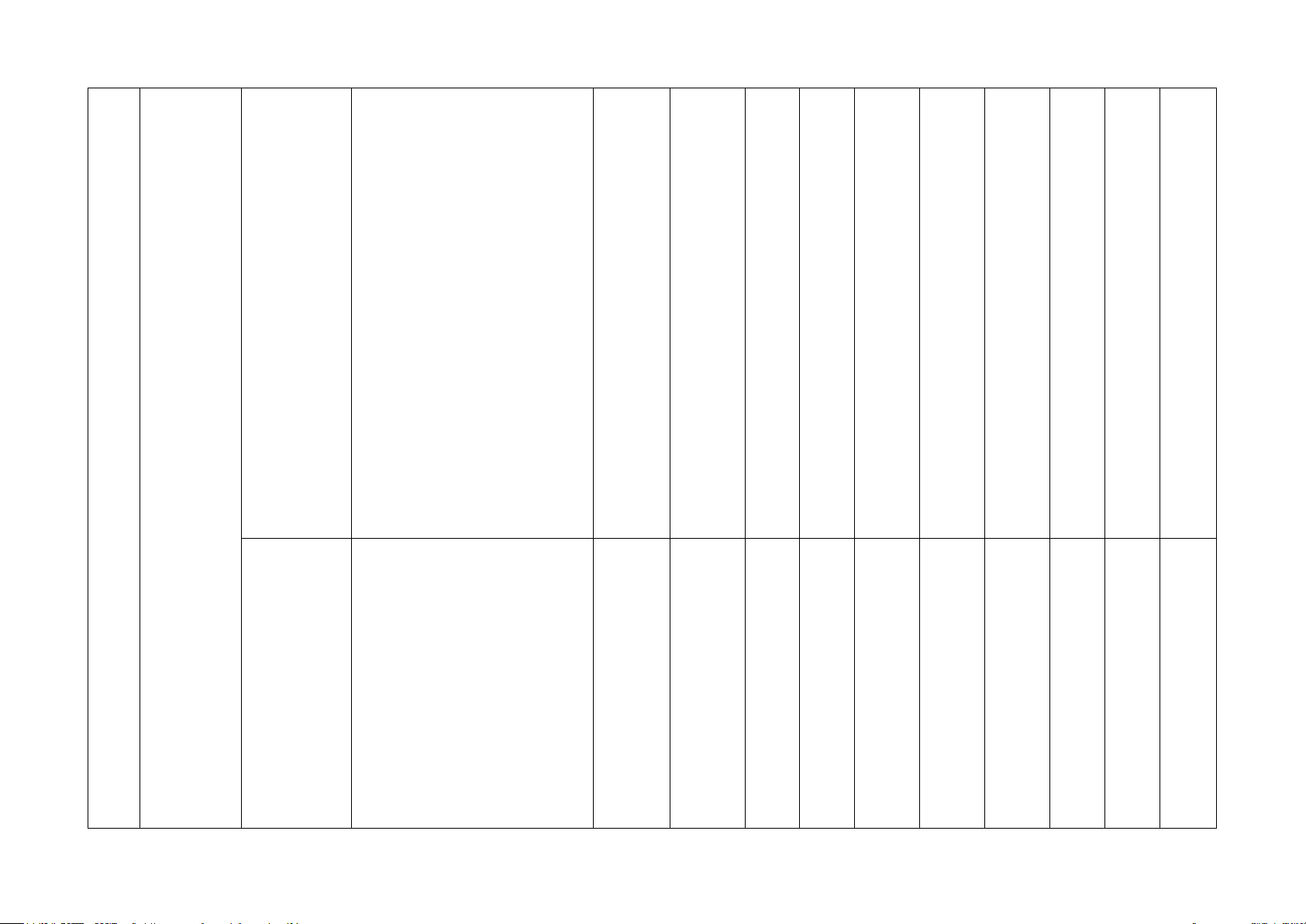
dụng kiến thức về hai tam giác đồng dạng. Nhận biết:
- Trình bày được định lí Pythagore. Thông hiểu:
- Tính được độ dài các cạnh Định lí trong tam giác vuông bằng
Pythagore cách sử dụng định lí Câu Bài Câu 10
và ứng dụng Pythagore. 18 2a Vận dụng:
- Giải quyết được một số vấn
đề thực tiễn gắn với việc vận
dụng định lí Pythagore (ví dụ:
tính khoảng cách giữa hai vị trí). Nhận biết:
- Nhận biết được hình đồng
Các trường dạng phối cảnh, hình đồng
hợp bằng dạng qua các hình ảnh cụ thể. nhau của Câu 11, Bài Bài Thông hiểu: tam giác Câu 12 2b 2c
- Giải thích được các trường
vuông. Hình hợp đồng dạng của hai tam
đồng dạng giác vuông. Vận dụng:
- Giải quyết được một số vấn
đề thực tiễn gắn với việc vận
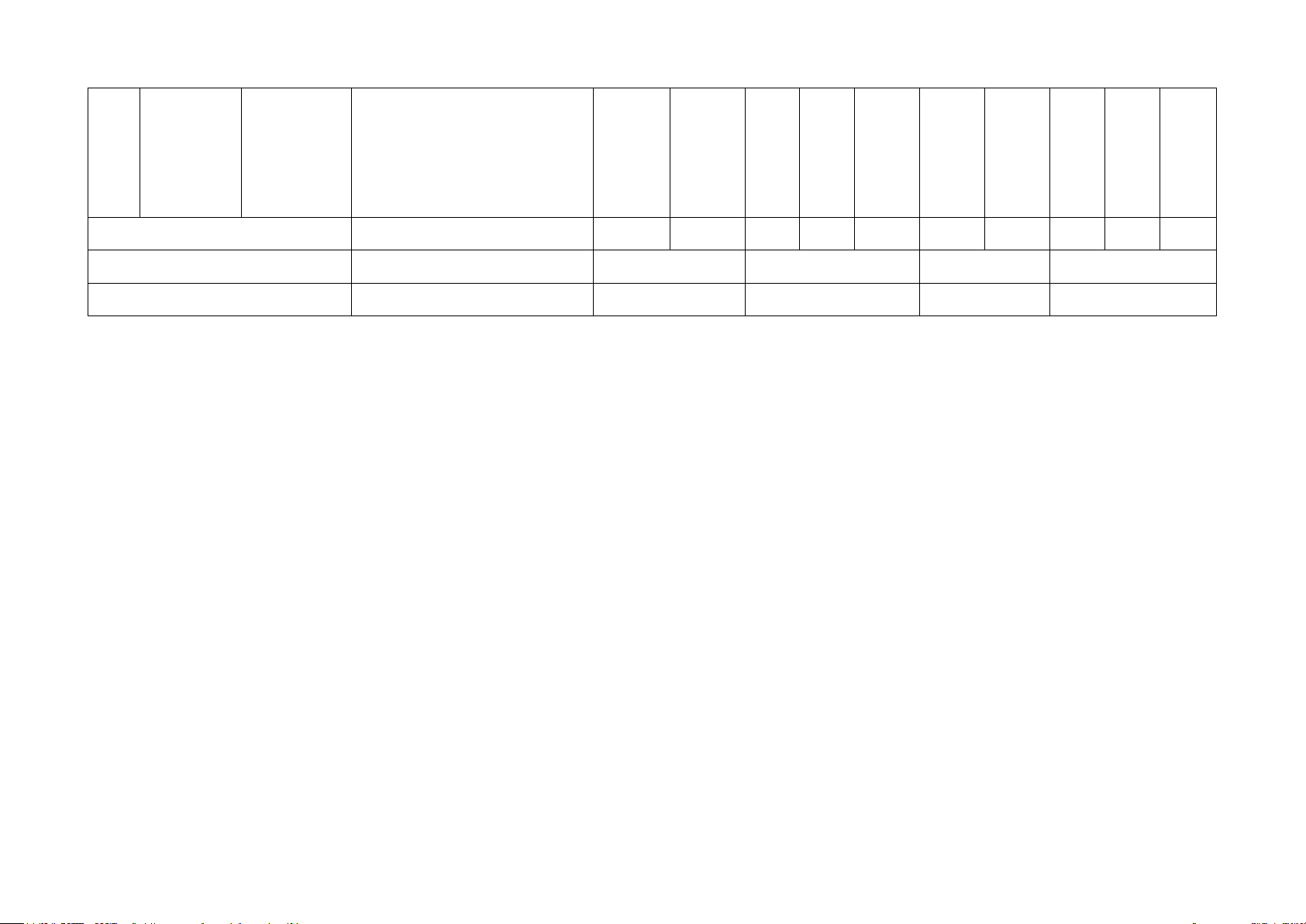
dụng kiến thức về hai tam giác vuông đồng dạng. Tổng số câu 29 10 2 4 2 2 2 2 1 1 3 Tổng số điểm 10 3,0 2,0 2,0 3,0 Tỉ lệ phần trăm 100% 30 20 20 30 Lưu ý:
– Các dạng thức trắc nghiệm gồm:
+ Dạng thức 1: Dạng câu hỏi trắc nghiệm nhiều lựa chọn, mỗi câu cho 04 phương án, chọn 01 phương án đúng. Mỗi câu chọn đáp án đúng được 0,25 điểm.
+ Dạng thức 2: Dạng câu hỏi trắc nghiệm Đúng/Sai, mỗi câu hỏi có 04 ý với tối đa là 1 điểm/câu, tại mỗi ý thí sinh lựa chọn đúng hoặc sai. Nếu thí
sinh chỉ lựa chọn chính xác 01 ý trong 1 câu được 0,1 điểm; 02 ý trong 1 câu được 0,25 điểm; 03 ý trong một câu được 0,5 điểm và chọn chính xác
cả 04 ý trong câu được 1 điểm.
+ Dạng thức 3: Dạng câu hỏi trắc nghiệm trả lời ngắn, với mỗi câu hỏi, viết câu trả lời/ đáp án vào bài thi. Mỗi câu trả lời đúng được 0,5 điểm.
– Số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ điểm được quy định trong ma trận.
C. ĐỀ THI KIỂM TRA GIỮA HỌC KÌ II – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐỀ KIỂM TRA GIỮA HỌC KÌ II TRƯỜNG …
MÔN: TOÁN – LỚP 8 MÃ ĐỀ MT101
NĂM HỌC: … – … Thời gian: 90 phút
(không kể thời gian giao đề)
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Câu 1. Trong các biểu thức sau biểu thức nào là phân thức đại số? A. x . B. 2x +1. C. 2x −1. D. 2x +1 . x − 3 x − 3 x − 3 3x − 2
Câu 2. Phân thức 2x +1 xác định khi x − 3 A. x = 3. B. x ≠ 3. C. x ≥ 3. D. x ≤ 3.
Câu 3. Phân thức x +1 có phân thức đối là 2x − y A. x −1 . B. x +1 x + x − − . C. 1 . D. 2 y . 2x + y 2x − y 2x + y x +1
Câu 4. Giả sử các biểu thức đều có nghĩa, kết quả của phép tính a 3 − là a − 3 a + 3 2 2 2 2 A. a + 9 . B. a − 9 . C. a + 6 . D. a − 6 . 2 a − 9 2 a + 9 2 a − 6 2 a + 6 2
Câu 5. Phân thức x y +1 là phân thức nghịch đảo của 2 3x y + 2x 2 2 2 2 A. x y +1 x y + x y + x y − − . B. 3 2x . C. 3 2 − x . D. 1 . 2 3x y + 2x 2 x y +1 2 x y +1 2 3x y − 2x 2 2
Câu 6. Giả sử các biểu thức đều có nghĩa, kết quả của phép tính x − 25 x + 5 : x là 2 2 x − 3x x − 9 (x −3)(x −5) (x +3)(x −5) (x −3)(x +5) A. x − 5 . B. . C. . D. . 2 x 2 x 2 x 2 x
Câu 7. Trong các phương trình sau, phương trình nào không phải là phương trình bậc nhất một ẩn? A. 0x x + 2 = 0.
B. 2x +1 = 0. C. 2 − x = 0. D. + 3 = 0 . 2
Câu 8. Phương trình 2x 1
+ = 0 có hạng tử tự do là 3 2 A. 2 . B. 1. C. 2 . D. 1 . 3 3 2
Câu 9. Cho tam giác ABC đồng dạng với tam giác ′
A B′C′ . Chọn khẳng định đúng trong các khẳng định dưới đây: A. B =  B′. B. A =  B′. C. A =  C′ .
D. B = C .
Câu 10. Cho tam giác MNP vuông tại P khi đó A. 2 2 2
MN = MP − NP . B. 2 2 2
MN = NP + MP . C. 2 2 2
NP = MN + MP . D. 2 2 2
MP = MN + NP .
Câu 11. Cho các mệnh đề sau:
(I). Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam
giác vuông ấy đồng dạng.
(II). Nếu một cạnh góc vuông của tam giác vuông này bằng một cạnh góc vuông của tam giác vuông
kia thì hai tam giác vuông ấy đồng dạng.
Khẳng định nào dưới đây là đúng?
A. Chỉ có (I) đúng.
B. Chỉ có (II) đúng.
C. Cả (I) và (II) đúng.
D. Cả (I) và (II) sai.
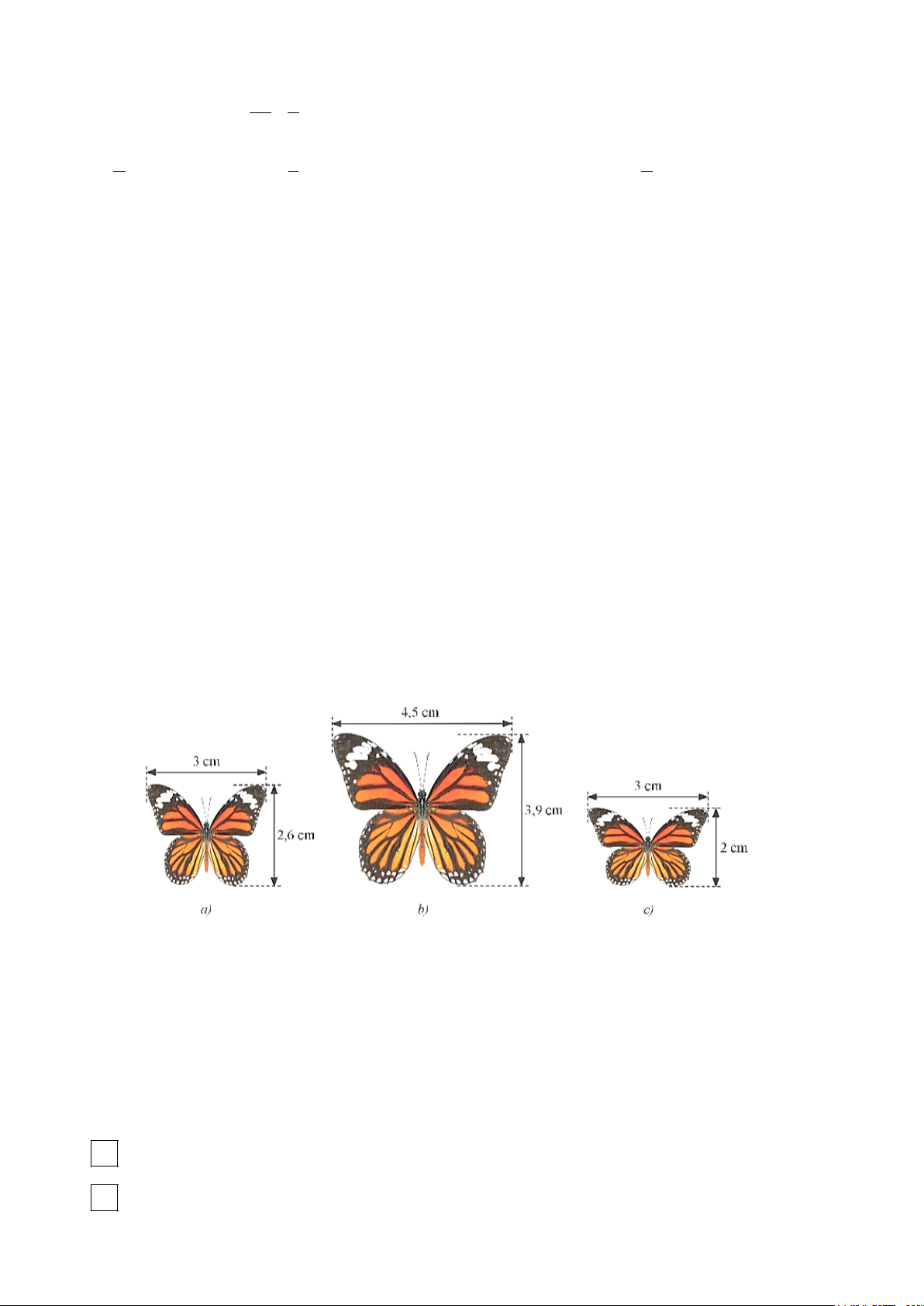
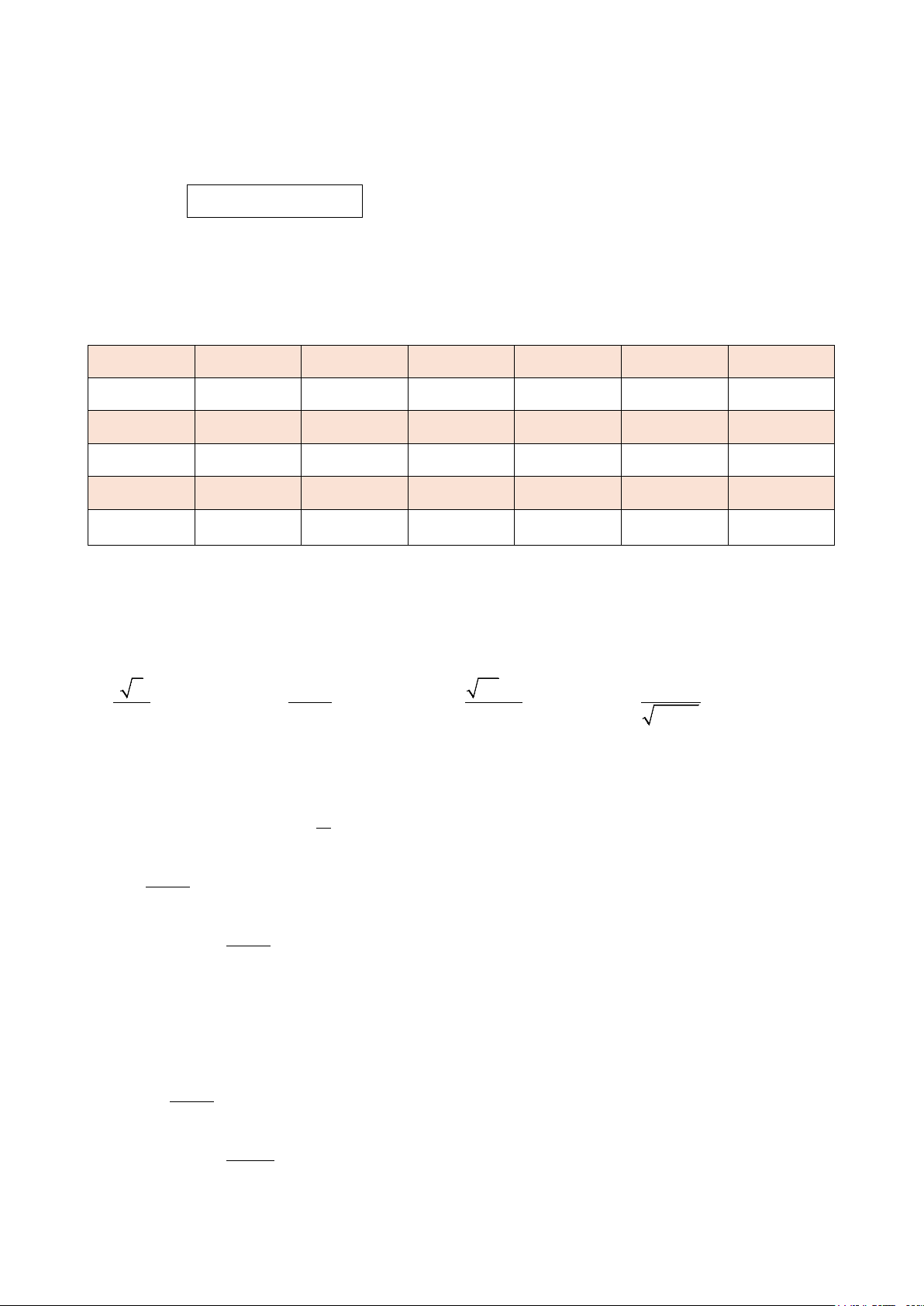
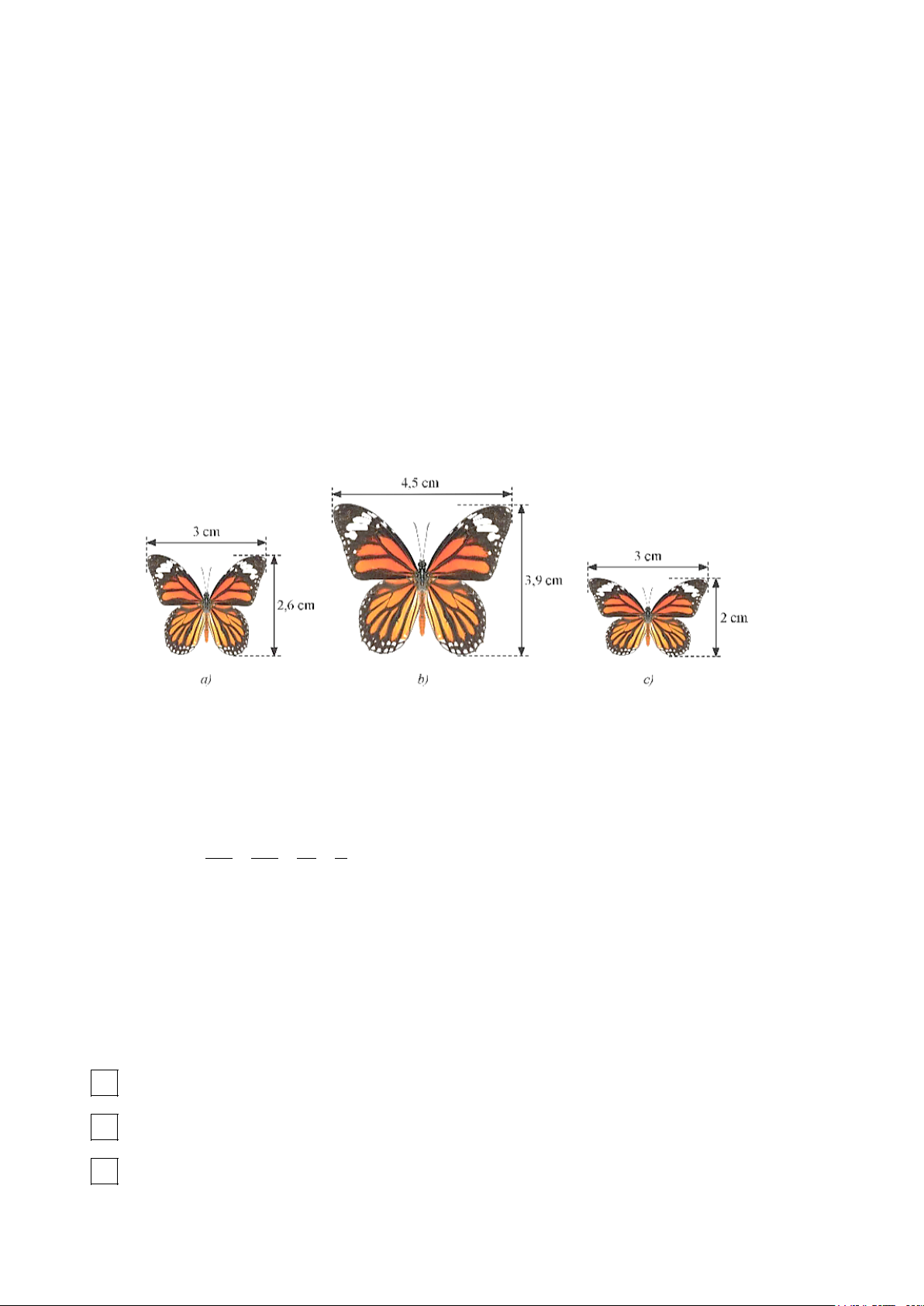
Câu 12. Trong các hình dưới đây, hình nào đồng dạng với nhau?
A. Hình a) và hình b).
B. Hình a) và hình c).
C. Hình b) và hình c). D. Cả ba hình.
Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai
Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Câu 13. Năm nay tuổi bố gấp 10 lần tuổi Minh. Bố Minh tính rằng sau 24 năm nữa thì tuổi bố chỉ
gấp 2 lần tuổi Minh. Gọi tuổi của Minh hiện nay là x (x∈) .
a) Sau 24 năm nữa tuổi của Minh là x + 24 (tuổi).
b) Sau 24 năm nữa tuổi của bố Minh là 10x + 24 (tuổi).
c) Sau 24 năm nữa thì tuổi bố chỉ gấp 2 lần tuổi Minh nên phương trình mô tả bài toán là:
10x + 24 = 2x + 24 .
d) Tuổi của bố Minh hiện tại là 30 tuổi.
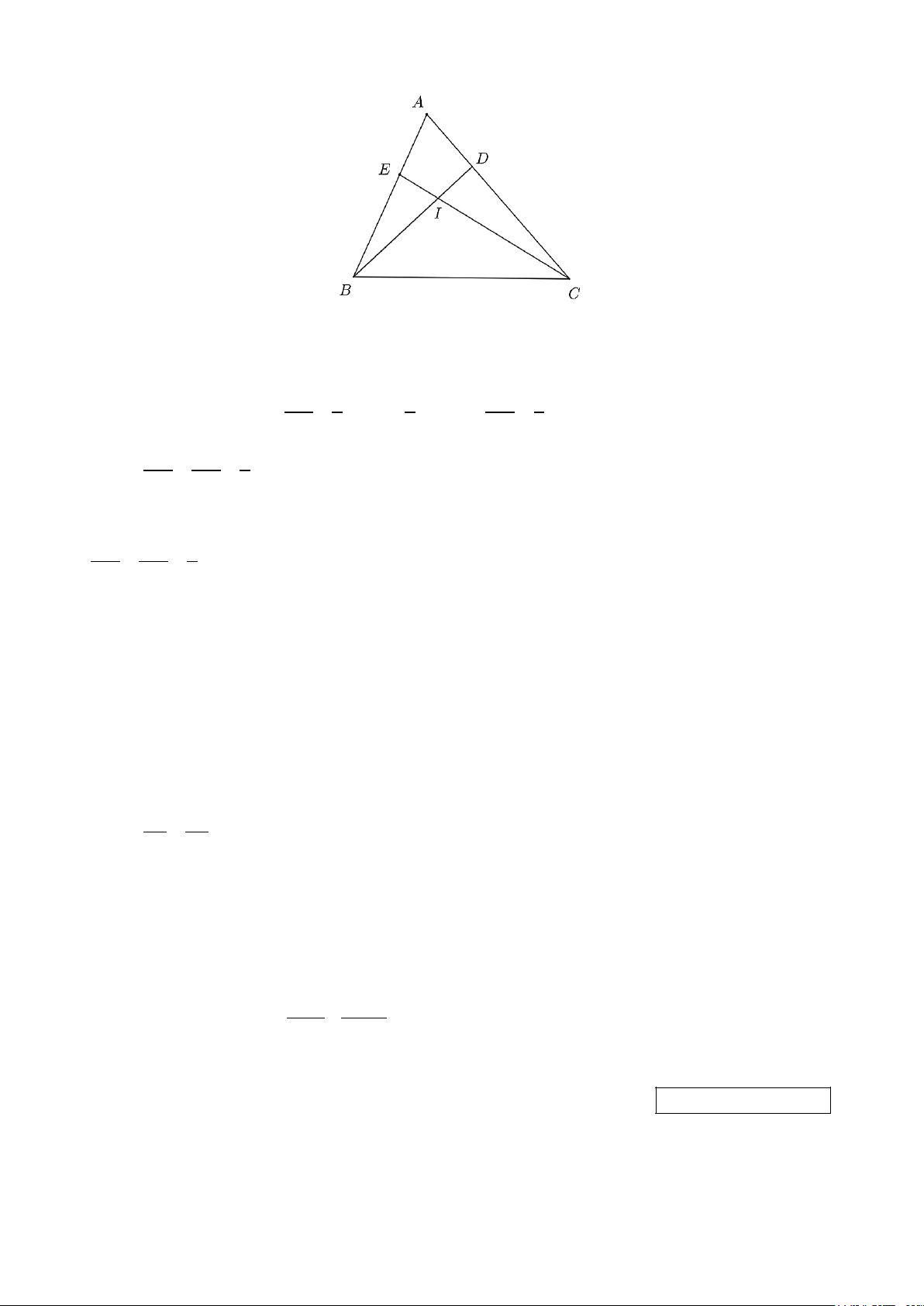
Câu 14. Cho tam giác ABC . Trên cạnh AB, AC lần lượt lấy các điểm E, D sao cho AC = 3AE và 1
AD = AB . Gọi I là giao điểm của BD và EC . Biết rằng ∆ABD ∽ ∆ACE . 3 a)  ADB =  AEC . b) AE AD 1 = = . AC AB 3
c) ∆ADE ∽ ∆ACB . d) .
ID IB = IE.IC .
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Câu 15. Cho biểu thức 3 12 A = −
( x ≠ 2 ; x ≠ 2
− ). Tính giá trị của biểu thức A tại x = 4. 2 x − 2 x − 4
(Kết quả ghi dưới dạng số thập phân) Trả lời: 2  − 
Câu 16. Cho biểu thức x 2 1 x +1 M =  +  : với x ≠ 2, − x ≠ 1
− và x ≠ 0 . Hỏi có bao nhiêu 2
 x + 2x x + 2  x
giá trị nguyên của x thỏa mãn để M nhận giá trị nguyên? Trả lời:
Câu 17. Cho phương trình ( 2
m − 3m + 2) x = m − 2 với m là tham số. Hỏi giá trị của m bằng bao nhiêu
để phương trình có vô số nghiệm? Trả lời:
Câu 18. Cho tam giác nhọn ABC có AB =13 cm , AC =15 cm. Kẻ AD ⊥ BC (D∈ BC). Biết
BD = 5 cm , hỏi cạnh BC có độ dài bao nhiêu centimet? Trả lời:
B. TỰ LUẬN (3,0 điểm)
Bài 1. (1,0 điểm) Một xe tải và một xe con cùng khởi hành từ tỉnh A đến tỉnh B. Xe tải đi với vận tốc
30 km/h , xe con đi với vận tốc 45 km/h . Sau khi đi được 3 quãng đường AB, xe con tăng vận tốc 4
5 km/h trên quãng đường còn lại thì đến B sớm hơn xe tải là 2 giờ 27 phút. Tính quãng đường AB.
Bài 2. (1,5 điểm) Cho ∆ABC vuông tại A có AB = 6 cm , AC = 8 cm .
a) Tính độ dài cạnh BC .
b) Vẽ đường cao AH . Chứng minh rằng ∆ABC ∽ ∆HAC .
c) Trên cạnh AH lấy điểm M sao cho AM = 3,2 cm , từ điểm M kẻ đường thẳng d song song với
BC lần lượt cắt AB, AC tại E, F . Tính SAEF . SABC
Bài 3. (0,5 điểm) Với * n∈ 1 1 1 1
 , tính tổng sau: A = + + + ...+ . 1.3 3.5 5.7 (2n − ) 1 (2n + ) 1
D. ĐÁP ÁN & HƯỚNG DẪN ĐỀ KIỂM TRA HỌC KÌ II – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐỀ KIỂM TRA GIỮA HỌC KÌ II TRƯỜNG …
MÔN: TOÁN – LỚP 8 MÃ ĐỀ MT101
NĂM HỌC: … – … Thời gian: 90 phút
(không kể thời gian giao đề)
A. TRẮC NGHIỆM (7,0 điểm) BẢNG ĐÁP ÁN Câu 1 2 3 4 5 6 Đáp án B B B A B C Câu 7 8 9 10 11 12 Đáp án A C A B A A Câu 13 14 15 16 17 18 Đáp án Đ Đ S Đ Đ Đ S Đ , 0 5 2 2 14
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Câu 1. Trong các biểu thức sau biểu thức nào là phân thức đại số? A. x . B. 2x +1. C. 2x −1. D. 2x +1 . x − 3 x − 3 x − 3 3x − 2 Hướng dẫn giải Đáp án đúng là: B
Một phân thức đại số có dạng A với ,
A B là các đa thức và B ≠ 0 . B
Do đó, 2x +1 là một phân thức đại số. x − 3
Câu 2. Phân thức 2x +1 xác định khi: x − 3 A. x = 3. B. x ≠ 3. C. x ≥ 3. D. x ≤ 3. Hướng dẫn giải Đáp án đúng là: B
Phân thức 2x +1 xác định khi x − 3 ≠ 0 hay x ≠ 3. x − 3
Câu 3. Phân thức x +1 có phân thức đối là 2x − y A. x −1 . B. x +1 x + x − − . C. 1 . D. 2 y . 2x + y 2x − y 2x + y x +1 Hướng dẫn giải Đáp án đúng là: B
Phân thức đối của x +1 là x +1 − . 2x − y 2x − y
Câu 4. Giả sử các biểu thức đều có nghĩa, kết quả của phép tính a 3 − là a − 3 a + 3 2 2 2 2 A. a + 9 . B. a − 9 . C. a + 6 . D. a − 6 . 2 a − 9 2 a + 9 2 a − 6 2 a + 6 Hướng dẫn giải Đáp án đúng là: A a 3 a(a + 3) 3(a −3) 2 2 Ta có:
a + 3a − 3a + 9 a + 9 − = − = = .
a − 3 a + 3 (a + 3)(a −3) (a −3)(a + 3) 2 2 a − 9 a − 9 2
Câu 5. Phân thức x y +1 là phân thức nghịch đảo của 2 3x y + 2x 2 2 2 2 A. x y +1 x y + x y + x y − − . B. 3 2x . C. 3 2 − x . D. 1 . 2 3x y + 2x 2 x y +1 2 x y +1 2 3x y − 2x Hướng dẫn giải Đáp án đúng là: B 2 2
Phân thức nghịch đảo của x y +1 là 3x y + 2x . 2 3x y + 2x 2 x y +1 2 2
Câu 6. Giả sử các biểu thức đều có nghĩa, kết quả của phép tính x − 25 x + 5 : x là 2 2 x − 3x x − 9 (x −3)(x −5) (x +3)(x −5) (x −3)(x +5) A. x − 5 . B. . C. . D. . 2 x 2 x 2 x 2 x Hướng dẫn giải Đáp án đúng là: C 2 2
Ta có: x − 25 x + 5 : x 2 2 x − 3x x − 9 2 2 x − 25 x − 9 = . 2 2
x − 3x x + 5x
(x −5)(x +5) (x +3)(x −3) = x(x − ) . 3 x(x + 5)
(x −5)(x +5)(x −3)(x +3) (x −5)(x +3) = . x( =
x − 3) x(x + 5) 2 x Vậy chọn C.
Câu 7. Trong các phương trình sau, phương trình nào không phải là phương trình bậc nhất một ẩn? A. 0x x + 2 = 0. B. 2x +1 = 0. C. 2 − x = 0. D. + 3 = 0 . 2 Hướng dẫn giải Đáp án đúng là: A
Ta có phương trình bậc nhất một ẩn có dạng ax + b = 0 với a ≠ 0 nên phương trình 0x + 2 = 0 không
là phương trình bậc nhất một ẩn.
Câu 8. Phương trình 2x 1
+ = 0 có hạng tử tự do là: 3 2 A. 2 . B. 1. C. 2 . D. 1 . 3 3 2 Hướng dẫn giải. Đáp án đúng là: C
Hạng tử tự do của phương trình bậc nhất một ẩn 2x 1 + = 0 là 1 . 3 2 2
Câu 9. Cho tam giác ABC đồng dạng với tam giác ′
A B′C′ . Chọn khẳng định đúng trong các khẳng định dưới đây: A. B =  B′. B. A =  B′. C. A =  C′ .
D. B = C . Hướng dẫn giải Đáp án đúng là: A
Có ∆ABC ∽ ∆ ′
A B′C′ thì ta có A = ′  A B =  B′ C =  ; ; C′.
Câu 10. Cho tam giác MNP vuông tại P khi đó A. 2 2 2
MN = MP − NP . B. 2 2 2
MN = NP + MP . C. 2 2 2
NP = MN + MP . D. 2 2 2
MP = MN + NP . Hướng dẫn giải Đáp án đúng là: B
Ta có tam giác MNP vuông tại P nên theo định lí Pythagore, ta có: 2 2 2
MN = NP + MP .
Câu 11. Cho các mệnh đề sau:
(I). Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam
giác vuông ấy đồng dạng.
(II). Nếu một cạnh góc vuông của tam giác vuông này bằng một cạnh góc vuông của tam giác vuông
kia thì hai tam giác vuông ấy đồng dạng.
Khẳng định nào dưới đây là đúng?
A. Chỉ có (I) đúng.
B. Chỉ có (II) đúng.
C. Cả (I) và (II) đúng.
D. Cả (I) và (II) sai. Hướng dẫn giải Đáp án đúng là: A
Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam
giác vuông ấy đồng dạng.
Do đo mệnh đề (I) là đúng.
Mệnh đề (II) là sai vì khi sử dụng điều kiện về cạnh thì ta cần ít nhất hai cặp tỉ số cạnh bằng nhau. Vậy chỉ có (I) đúng.
Câu 12. Trong các hình dưới đây, hình nào đồng dạng với nhau?
A. Hình a) và hình b).
B. Hình a) và hình c).
C. Hình b) và hình c). D. Cả ba hình. Hướng dẫn giải Đáp án đúng là: A Nhận thấy tỉ lệ 3 4,5 15 3 = = ≠ . 2,6 3,9 13 2
Do đó ta có hình a) và hình b) đồng dạng.
Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai
Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Câu 13. Năm nay tuổi bố gấp 10 lần tuổi Minh. Bố Minh tính rằng sau 24 năm nữa thì tuổi bố chỉ
gấp 2 lần tuổi Minh. Gọi tuổi của Minh hiện nay là x (x∈) .
a) Sau 24 năm nữa tuổi của Minh là x + 24 (tuổi).
b) Sau 24 năm nữa tuổi của bố Minh là 10x + 24 (tuổi).
c) Sau 24 năm nữa thì tuổi bố chỉ gấp 2 lần tuổi Minh nên phương trình mô tả bài toán là:
10x + 24 = 2x + 24 .
d) Tuổi của bố Minh hiện tại là 30 tuổi. Hướng dẫn giải Đáp án đúng là: a) Đ b) Đ c) S d) Đ
Gọi tuổi của Minh hiện nay là x (x∈) .
Theo đề, sau 24 năm nữa tuổi của Minh là x + 24 (tuổi).
Sau 24 năm nữa tuổi của bố Minh là 10x + 24 (tuổi).
Sau 24 năm nữa thì tuổi bố chỉ gấp 2 lần tuổi Minh nên ta có phương trình:
10x + 24 = 2(x + 24)
Giải phương trình, ta được:
10x + 24 = 2(x + 24)
10x + 24 = 2x + 2.24
10x + 24 = 2x + 48
10x − 2x = 48 − 24 8x = 24 x = 3 (thỏa mãn).
Do đó, tuổi của Minh hiện tại là 3 tuổi.
Suy ra tuổi của bố Minh hiện tại là 3.10 = 30 (tuổi).
Vậy hiện tại bố Minh 30 tuổi.
Câu 14. Cho tam giác ABC . Trên cạnh AB, AC lần lượt lấy các điểm E, D sao cho AC = 3AE và 1
AD = AB . Gọi I là giao điểm của BD và EC . Biết rằng ∆ABD ∽ ∆ACE . 3 a)  ADB =  AEC . b) AE AD 1 = = . AC AB 3
c) ∆ADE ∽ ∆ACB . d) .
ID IB = IE.IC . Hướng dẫn giải
Đáp án đúng là: a) Đ b) Đ c) S d) Đ
a) Theo đề, ta có ∆ABD ∽ ∆ACE nên  ADB = 
AEC (hai góc tương ứng). Do đó ý a) đúng.
b) Ta có: AC = 3AE hay AE 1 = ; 1
AD = AB hay AD 1 = . AC 3 3 AB 3 Suy ra AE AD 1 = = . Do đó, ý b) đúng. AC AB 3
c) Xét ∆ADE và ∆ABC , có: AE AD 1 = = (cmt) AC AB 3 A chung (gt)
Do đó, ∆ADE ∽ ∆ABC (c.g.c) Do đó, ý c) sai.
d) Vì ∆ABD ∽ ∆ACE nên  ABD = 
ACE (2 góc tương ứng) (1) Lại có,  EIB = 
DIC (hai góc đối đỉnh) (2)
Từ (1) và (2) suy ra ∆EIB ∽ ∆DIC (g.g)
Suy ra IE = IB suy ra IE.IC = . IB ID . ID IC Do đó, ý d) đúng.
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Câu 15. Cho biểu thức 3 12 A = −
( x ≠ 2 ; x ≠ 2
− ). Tính giá trị của biểu thức A tại x = 4. 2 x − 2 x − 4
(Kết quả ghi dưới dạng số thập phân) Trả lời: Hướng dẫn giải Đáp án: , 0 5
Thay x = 4 (thỏa mãn) vào biểu thức A , ta được: 3 12 3 1 A = − = −1 = = 0,5 . 2 4 − 2 4 − 4 2 2
Vậy A = 0,5 tại x = 4. 2 Câu 16.  −  Cho biểu thức x 2 1 x +1 M =  +  : với x ≠ 2, − x ≠ 1
− và x ≠ 0 . Hỏi có bao nhiêu 2
 x + 2x x + 2  x
giá trị nguyên của x thỏa mãn để M nhận giá trị nguyên? Trả lời: Hướng dẫn giải Đáp án: 2 Với x ≠ 2, − x ≠ 1
− và x ≠ 0 , ta có: 2  x − 2 1  x +1 M =  +  : 2
 x + 2x x + 2  x 2  x − 2 x  x M =  ( +
x + ) x (x + ) . 2 2 x x +1  2
x + x − 2 x M = ( x + ) . 2 x x +1 (x − ) 1 (x + 2) x M = ( x + ) . 2 x x +1 x −1 M = . x +1 Nhận thấy x −1 x +1− 2 2 M = = = 1− . x +1 x +1 x +1
Để M nhận giá trị nguyên thì 2 1− nhận giá trị nguyên. x +1
Suy ra 2 nhận giá trị nguyên. x +1
Do đó x +1 là ước của 2 . Mà Ư(2) = { 2 − ; 1; − 1; } 2 . Ta có bảng sau: x +1 2 − 1 − 1 2 x 3 − (t/m) 2 − (l) 0 (l) 1 (t/m)
Vậy có 2 giá trị nguyên của x thỏa mãn để M nhận giá trị nguyên.