Bộ Đề Kiểm Tra Giữa Học Kỳ 2 Môn Toán 12 Năm 2022 Có Đáp Án

Bộ đề kiểm tra giữa HK2 môn Toán 12 năm 2022 được biên soạn dưới dạng file PDF gồm 24 trang. Tài liệu là kiến thức từ cơ bản đến nâng cao khác nhau và kèm sẵn đáp án để các em học sinh dễ dàng so sánh kết quả sao cho chuẩn xác nhất. Mời các em tham khảo thêm nhé!

15 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 12

Môn: Toán 12

Thông tin:

24 trang 6 tháng trước

Tác giả:

Profile ha phan
Trang1
ĐỀ 1
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 - NĂM HỌC 2021 –2022
MÔN TOÁN 12
Câu 1.Cho
()u u x=
,
()v v x=
là hai hàm s o hàm liên tc, kh
A.
.udv uv vdu=+
òò
B.
.udv uv vdu=-
òò
C.
.
u
udv vdu
v
=+
òò
D.
.vdu uv vdu=+
òò
Câu 2. Hàm s
( ) 2
xx
f x e=-
có nguyên hàm là
A.
. B.
.
C.
2
F( )
ln 2
x
x
x e C= + +
. D.
.
Câu 3. Trong không gian Oxyz
23a i j k

. To  c
a
là
A.
( )
2; 1; 3--
. B.
( )
2; 1;3--
. C.
( )
2;1;3-
. D.
( )
2;1; 3--
.
Câu 4. Trong không gian Oxyzt cu tâm O, bán kính R = 2 có dng là
A.
2 2 2
2 2 2 1 0.x y z x y z
B.
2 2 2
2.x y z
C.
2 2 2
2 2 2 1 0.x y z x y z
D.
2 2 2
4.x y z
Câu 5. Trong không gian Oxyzm
1;2;0A
,
1;0; 1B
 n thng AB bng?
A. 2. B.
2
. C. 1. D.
5.
Câu 6. Trong không gian Oxyzm
( 1;2; 3), (3;2; 1)AB
. T m I cn
thng AB là
A.
1;2; 2I
. B.
2;4; 4I
. C.
4;0;2I
. D.
1;2;2 .I
Câu7. Cho
fx
,
gx
là các hàm s nh và liên tc trên
. Trong các m sau, m
nào sai?
A.
d d . df x g x x f x x g x x
. B.
2 d 2 df x x f x x

.
C.
d d df x g x x f x x g x x


. D.
dddf x g x x f x x g x x


.
Câu8. M đúng?
A.
2
2
3
3d
ln3
x
x
xC
. B.
2
9
3d
ln3
x
x
xC
.
Trang2
C.
2
2
3
3d
ln9
x
x
xC
. D.
21
2
3
3d
21
x
x
xC
x

.
Câu9. Tìm m sai trong các m sau.
A.
4
3
d.
4
xC
xx
B.
1
d ln .x x C
x

C.
sin d cos .x x C x
D.
2e d 2 e .
xx
xC
Câu10. Hàm s nào sau không phải là mt nguyên hàm ca hàm s
5
( ) 3 1f x x
?
A.
6
31
8
18
x
Fx

. B.
6
31
2
18
x
Fx

.
C.
6
31
18
x
Fx
. D.
6
31
6
x
Fx
.
Câu 11. Cho
( )
Fx
là nguyên hàm ca hàm s
( )
fx
trên
;ab
éù
êú
ëû
. Phát bisai ?
A.
( ) ( ) ( )
.
b
a
f x dx F b F a=-
ò
B.
( ) ( )
.
bb
aa
f x dx f t dt¹
òò
C.
( )
0.
a
a
f x dx =
ò
D.
( ) ( )
.
ba
ab
f x dx f x dx=-
òò
Câu 12. Cho
01a<¹
. Chn khnh đúng trong các kh
A. B.
d.
ln
x
x
a
a x C
a
=+
ò
C.
d.
xx
a x a C=+
ò
D.
d ln .
xx
a x a a C=+
ò
Câu 13. Cho hàm s
( )
4
2
23
,0
x
f x x
x
+
=¹
. Ch
A.
( )
3
23
.
3
x
f x dx C
x
= - +
ò
B.
( )
3
23
.
3
x
f x dx C
x
= + +
ò
C.
( )
3
3
2.f x dx x C
x
= - +
ò
D.
( )
3
23
.
32
x
f x dx C
x
= + +
ò
Câu 14. Cho
2
. 1.I x x dx=+
ò
. Vi bin
2
1tx=+
c kt qu là
A.
2
..I t dt=
ò
B.
2
2 . .I t dt=
ò
C.
2
1
..
2
I t dt=
ò
D.
..I t dt=
ò
Câu 15. m
(3; 1;2)M
. Hình chiu cm M lên các trc t Ox, Oy, Oz lt có t
là
A.
(3;0;0), (0; 1;0), (0;0;2).
B.
( 3;0;0), (0;1;0), 0;0; 2 .
C.
( 1;0;0), (0;3;0), (0;0;2).
D.
(2;0;0), (0; 1;0), (0;0;3).
1
d
x
x
a
a x C
x
+
=+
ò
Trang3
Câu 16. m
(3;2; 5)P
. Gi Q là hình chiu vuông góc ca P trên mt phng Oxy. T m
Q là
A.
( 3;2;0)
. B.
( 3; 2;0).
C.
(3; 2;0).
D.
(3;2;0).
Câu 17. Trong không gian Oxyzm
(2;1; 3)M
. Gi N i xng ca M qua trc Ox.
T m N
A.
( 2;1; 3)
. B.
(2; 1;3)
. C.
(2;1;3)
. D.
(2; 1; 3).
Câu 18. Vit công thc tính th tích V ca khc to ra khi quay hình thang cong, gii
hn b th hàm s y f(x), trc Ox ng thng x a, x b (a b) quay xung quanh trc Ox.
A.
2
( ) .
b
a
V f x dx
B.
2
( ) .
b
a
V f x dx
C.
( ) .
b
a
V f x dx
D.
( ) .
b
a
V f x dx
Câu 19.Cho hàm s
fx
liên tc trên. Gi
S
là din tích hình phng gii hn bng
y f x
,
0y
,
1x 
và
5x
 bên). M đúng?
A.
15
11
S f x dx f x dx

. B.
15
11
S f x dx f x dx


.
C.
15
11
S f x dx f x dx


. D.
15
11
S f x dx f x dx

.
Câu 20. Gi
S
là din tích hình phng gii hn bng
e
x
y
,
0y
,
0x
,
2x
. M

A.
2
2
0
ed
x
Sx
.B.
2
0
ed
x
Sx
.C.
2
0
ed
x
Sx
. D.
2
2
0
ed
x
Sx
.
Câu 21. Cho hình phng gii hn bi ng cong , tr    ng thng
. Khi tròn xoay to thành khi quay quanh trc hoành có th tích bng bao nhiêu?
A. . B. . C. . D. .
Câu 22.Ông Bo xây mt cng có dng hình Parabol
󰇛
󰇜
( b lõm quay xung), có chiu ngang
ca chân cn chân bên kia là 4 mét và chiu cao t n mt là 3 mét. Ông Bo
làm ca cc gii hn bi
󰇛
󰇜
n thng ni hai chân cng mt) bng g. Din tích
ca ca cng là
D
2
1yx
0, 1xx
D
V
4
3
V
2V
4
3
V
2V
Trang4
A.7
2
. B. 8
2
. C. 9
2
. D. 10
2
.
Câu 23. Nu
( )
5
d
a
f x dx =
ò
và
( )
2
d
b
f x dx =
ò
vi
adb<<
thì
( )
b
a
f x dx
ò
bng
A.
2.-
B.
7.
C.
3.-
D.
3.
Câu 24.Trong không gian
Oxyz
, gi
()P
là mt phm
(1;3;5)M
và ct các tia
, , Ox Oy Oz
lt ti
, , A B C
sao cho th tích ca t din
OABC
nh nht phng
()P
là
A.
15 3 29 0x y z
. B.
15 5 3 45 0x y z
.
C.
15 7 5 61 0x y z
. D.
5 3 19 0x y z
.
Câu 25.Cho
d
( 2) 2 ( 1) 1
21
x
a x x b x x C
xx
= + + + + + +
+ + +
ò
. Tính
3S a b=+
.
A.
2
.
3
S
-
=
B.
1
.
3
S =
C.
4
.
3
S =
D.
2
.
3
S =
Câu 26. Din tích phn hình phng gch chéo trong hình v  c tính
theo công th
A.
2
2
1
2 2 4 d

x x x
. B.
2
1
2 2 d

xx
. C.
2
1
2 2 d
xx
. D.
2
2
1
2 2 4 d
x x x
.
Câu 27.Tính tích phân
( )
1
0
xx
I e e dx
-
=+
ò
.
A.
1
Ie
e
=-
. B.
1
2Ie
e
= + -
. C.
1
Ie
e
=+
. D.
1
2Ie
e
= + +
.
Câu 28.Trong không gian , cho hình hp ch nht .  có trùng vi gc t .
Bit rng
󰇛
; 0; 0
󰇜
,
󰇛
0; ; 0
󰇜
, 
󰇛
0; 0;
󰇜
vi , là các s  + = 6. Gi là trung
m ca cnh . Th tích ln nht ca khi t din  bng
A.6 B.10. C.8. D.12.
Câu 29. Mc ít nht 5 giây) vi vn tc 60 / i lái xe nhìn thy
mng ngi vp phanh. T thng chm du vi vn tc
󰇛
󰇜
= 60 6 là thi gian ( tính bng giây ) k t 
c trong 12 giây cui cùng bng
A.80. B.288. C.60. D.420.
x
y
O
2
21y x x
2
3yx
2
1
Trang5
Câu 30. Cho tích phân
2
0
8 sinx
sinx cos
a dx
x
p
p
=
+
ò
, hàm s
󰇛
󰇜
liên tc trên o hàm tha mãn
󰇛
󰇜
+ 
󰇛
󰇜
= 2
3
,  và
󰇛
0
󰇜
= 1. Tích phân
( )
3
0
f x dx
ò
bng
A.3. B. 6. C. 9. D. 12.
ĐÁP ÁN
1
B
6
A
11
B
16
D
21
A
26
D
2
A
7
A
12
B
17
B
22
B
27
A
3
C
8
C
13
A
18
A
23
D
28
C
4
D
9
B
14
A
19
B
24
B
29
D
5
D
10
D
15
A
20
B
25
C
30
B
ĐỀ 2
Thuvienhoclieu.com
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 - NĂM HỌC 2021 –2022
MÔN TOÁN 12
Câu 1: 

Oxyz
, 


:
10 0.x y z




.
A.
10;2022;2022 .A
B.
10;11;1 .B
C.
10;1;1 .C
D.
2;3;;1 .D
Câu 2: 

Oxyz
, 
1; 2;9M
lên
mp(Oxy).
A.
0; 2;9P
B.
1;0;9Q
C.
1; 2;0N
D.
1; 2;0N 
Câu 3: 
A.
.
xx
e dx e C

B.
2
.
2
x
xdx C
C.
1
ln .dx x C
x

D.
sin cos .x dx x C
Câu 4: Cho
fx



;ab

Fx
. 




A.
.
b
a
f x dx F b F a
B.
.
b
a
f x dx F a F b
C.
.
b
a
F x dx f b f a
D.
.
a
b
a
b
f x dx
Fx
Câu 5:

Oxyz
, cho hai vecto
1;3;4 , 3;2; 5 .ab


2 3 .c a b
Trang6
A.
11;12;7 .c
B.
11;12; 7 .c
C.
11;12; 7 .c 
D.
11; 12; 7 .c
Câu 6:
34
.
27
zi
A.
.i
B.
4
.
7
i
C.
4
.
7
D.
3
.
2
Câu 7:

Oxyz


;;i j k
,
2 3 4 .a i j k
A.
2;3; 4 .a 
B.
4;3;2 .a 
C.
2; 4;3 .a 
D.
2;3;4 .a
Câu 8:











y f x
(
y f x
liên

;ab
), 
Ox
, 


xa

xb
?
A.
.
a
b
S f x dx
B.
.S f b f a
C.
.
b
a
S f x dx
D.
.
b
a
S f x dx
Câu 9: 
A.
.f x g x dx f x dx g x dx


B.
,.f x kg x dx k f x dx g x dx k


C.
..f x g x dx f x dx g x dx


D.
.f x g x dx f x dx g x dx


Câu 10:
33 41
.
27
zi
A.
.i
B.
33
.
2
C.
41
.
7
i
D.
41
.
7
Câu 11:

Oxyz
, 

1;1;1 , B 2;4;3 ,C 3;7; .Am
m 
A,B,C 

.
A.
4.m
B.
2.m
C.
5.m
D.
3.m
Câu 12:Cho
Fx

fx
. 


A.
.f x dx F x
B.
.F x dx f x C
C.
.f x dx F x C
D.
.f x dx F x C
Câu 13:


, .
A.
2022 .zi
B.
3 4 .zi
C.
2022 2023 .zi
D.
1 2 .zi
Câu 14:
3
.
2
x
dx
x
A.
ln 2 .xx
B.
ln 2 .x x C
C.
ln 2 .x x C
D.
ln 2 .x x C
Câu 15: 

Oxyz
, 




1;1; 2M



2;3;2 .n
Trang7
A.
2 1 0.x y z
B.
2 3 2 2 0.x y z
C.
2 3 2 1 0.x y z
D.
2 2 0.x y z
Câu 16: 

Oxyz
, 


:
4 6 2 7 0.x y z





.
A.
6;4; 2 .b 
B.
2; 3;1 .n
C.
4;6; 2 .m

D.
4;6; 1 .a 
Câu 17::
2
2y x x
,
2
4y x x
,
0x
,
3x
.
A.
7.
B.
9.
C.
6.
D.
8.
Câu 18:
quanh Ox:
32
1
3
y x x
,
0y
,
0, 3.xx
A.
8
.
35
B.
16
.
35
C.
27
.
35
D.
81
.
35
Câu 19::
2
2y x x
, ,
1x 
,
2x
.
A.
4
.
3
B.
5
.
3
C.
8
.
3
D.
7
.
3
Câu 20: 
sin 3cos .x x dx
A.
cos 3sinx x C
B.
cos 3sinx x C
C.
cos 3sinx x C
D.
cos 3sinx x C
Câu 21:

Oxyz
, 

4;3;2 , N 1;2;3 .M

.MN
A.
3;1; 1 .MN 
B.
3;1;1 .MN 
C.
3; 1;1 .MN
D.
3; 1;1 .MN 
Câu 22:
A.
b b b
a a a
f x dx g x dx f x g x dx


B.
b d b
a c a
f x dx g x dx f x g x dx


C.
,.
bb
aa
kf x dx k f x dx k

D.
.
ba
ab
f x dx f x dx

Câu 23: 
A.
.
b d d
a c b
f x dx f x dx f x dx
B.
.
b d d
a c a
f x dx f x dx f x dx
C.
.
b d c
a c a
f x dx f x dx f x dx
D.
.
b d d
a b a
f x dx f x dx f x dx
Câu 24:










?
Trang8
A.
2 3 .zi
B.
3 2 .zi
C.
2.zi
D.
3 2 .zi
Câu 25:
1
2
0
1.x dx
A.
11
3
B.
7
3
C.
2
3
D.
1
Câu 26:
4 5 .zi
A.
4 5 .zi
B.
4 5 .zi
C.
4 5 .zi
D.
5.zi
Câu 27: 
A.
2
.
3
x
xdx C
B.
3
22
2.
3
x
x x dx x C
C.
1 2 2 .x dx x C
D.
2022
2021
.
2022
x
x dx
Câu 28:
1;3; 26a
A.
26.a
B.
10.a
C.
6.a
D.
36.a
Câu 29: 
Fx

23x
f x e
, 
3
1
0 1.
2
Fe
A.
23
1
1.
2
x
e

B.
23
1
2.
2
x
e
C.
23
.
x
e
D.
23
1
1.
2
x
e
Câu 30:







 D 

, D 
y f x
(
y f x


;ab
), 
Ox
, 


xa

xb
?
A.
.
b
a
V f x dx
B.
2
.
b
a
V f x dx
C.
.
b
a
V f x dx
D.
.
b
a
V f x dx
Câu 31:

Oxyz
, 




1;0;0 , B 0;2;0 , C 0;0;3 ,A
?
A.
1 0.
1 2 3
x y z
B.
1.
1 2 3
x y z
C.
1.
2 1 3
x y z
D.
1.
3 2 1
x y z
Câu 32:
2
4
0
sin cos .x x dx
A.
1
.
4
B.
2
.
2
C.
2.
D.
1
.
42
Câu 33:
1
0
3 2 .xdx
A.
1 3 3
.
3

B.
1 2 3
.
6

C.
1 3 3
.
3
D.
1 3 3
.
3

Câu 34:D 
y f x
(
y f x


;ab
),

Ox
, 


xa

xb
(


). D?
Trang9
A.
.
b
D
a
S f x dx
B.
.
cb
D
ac
S f x dx f x dx

C.
.
cb
D
ac
S f x dx f x dx

D.
.
cb
D
ac
S f x dx f x dx

Câu 35:

Oxyz
, 




2; 1;3 , B 4;2;1 , C 1;2;3 ,A 
?
A.
2 2 5 17 0.x y z
B.
2 2 5 17 0.x y z
C.
2 2 5 17 0.x y z
D.
2 2 5 17 0.x y z
Câu 36:Cho s phc
5 4 .zi
S phi cm bi
c là
A.(5;4) B.(-5;-4) C.(5;-4) D.(-5;4)
Câu 37:Tp hp tt c m biu din s phc z tha mãn
24zi
ng tròn có tâm I và
bán kính R lt là :
A.I(-2;-1); R = 4 B.I(-2;-1); R = 2 C.I(2;-1); R = 4 D.I(2;-1); R = 2
Câu 38:Cho
1
x
F x x e
là mt nguyên hàm ca hàm s
3
.
x
f x e
Tìm nguyên hàm ca hàm s
3
.
x
f x e
A.
3
21
xx
f x e dx x e C
B.
3
63
xx
f x e dx x e C
C.
3
63
xx
f x e dx x e C
D.
3
63
xx
f x e dx x e C
Câu 39:Trong không gian vi h t m A(1;1;1) và hai mt phng
: 2 3 1 0,( ) : 0.P x y z Q y
Vit phng (R) cha A, vuông góc vi c hai mt
phng (P) và (Q)?
A.
3 2 2 0x y z
B.
3 2 2 4 0x y z
C.
3 2 1 0xz
D.
3 2 0xz
Câu 40:

Oxyz
, 





A,B, 
0;1; 3 , B 4;3;1 .A
A.
2 2 2
2 2 1 9.x y z
B.
2 2 2
2 2 1 3.x y z
C.
2 2 2
2 2 1 9.x y z
D.
2 2 2
2 2 1 9.x y z
Câu 41:Cho hàm s
4 3 2
4 3 1, .f x x x x x x
Tính
1
2
0
.'I f x f x dx
Trang10
A.
7
3
B.
7
3
C. 2 D. -2
Câu 42:Cho tích phân
1
7
5
2
0
,
1
x
I dx
x
gi s t
2
1.tx
Tìm m 
A.
3
2
5
1
1t
I dt
t
B.
3
2
4
1
1
1
2
t
I dt
t
C.
3
2
5
1
1
1
2
t dt
I
t
D.
3
2
4
1
1
3
2
t
I dt
t
Câu 43:Din tích hình phng gii hn b th hàm s
2
21y x x
và
2
2 4 1y x x
là
A. 6 B. 7 C. 5 D. 4
Câu 44:Tìm h nguyên hàm ca hàm s
5
tanf x x
A.
42
11
tan tan ln cos
42
f x dx x x x C
B.
42
11
tan tan ln cos
42
f x dx x x x C
C.
42
11
tan tan ln cos
42
f x dx x x x C
D.
42
11
tan tan ln cos
42
f x dx x x x C
Câu 45:Trong không gian vi h t m
2;1;0 , 1;1;3 , 2; 1;3 ,A B C
1; 1;0 .D
Bán kính mt cu ngoi tip t din ABCD là
A.
5
B.
15
2
C. 2 D.
14
2
Câu 46:. ng thng song song vng thng
12
:
1 1 1
x y z
d


và cng
thng
12
1 1 2 1 2 3
: ; :
1 1 1 1 1 3
x y z x y z
dd
là
A.
1 2 3
1 1 1
x y z

B.
112
1 1 1
x y z


C.
11
1 1 1
x y z

D.
11
1 1 1
x y z

Câu 47:Cho hàm s
fx
có
fx
liên tc trên na khong
0;
tha mãn
2
3 1 3
x
f x f x e
bit
11
0.
3
f
Giá tr
1
ln6
2
f



bng
A.
56
9
B.
56
18
C. 1. D.
1
2
Câu 48:
t bn hoa hình tròn có tâm O. Mt nhóm hc sinh lp
c giao thit k bn hoa, nhóm này chia bn hoa thành bn phn, bng Parabol có cùng
i xng Parabol này cng tròn ti bm A, B, C, D to
thành mt hình vuông có cnh b). Phn di trng hoa, phn
di trng c (Din hàng pht kinh phí trng
ng/ 1
2
,m
kinh phí trng c ng/1
2
m
. Hi c ng cn bao nhiêu tin
 trng b tin hàng chc nghìn).
Trang11
A. B.
C. D.5.790.000 
Câu 49:Cho hàm s
y f x
 nh trên
1
\
2
R



th  u kin
2
,
21
fx
x
0 1, 1 2.ff
Giá tr ca biu thc
13ff
bng
A.
3 ln15
B.
4 ln15
C.
2 ln15
D.
ln15
Câu 50:Cho s phc
z
tha mãn
1 1,zi
s phc
w
tha mãn
2 3 2.wi
Tính giá tr nh nht
ca
zw
A.
13 3
B.
17 3
C.
13 3
D.
17 3
------ HẾT ------
ĐÁP ÁN
1
A
6
C
11
C
16
B
21
C
26
A
31
B
36
D
41
B
46
D
2
C
7
A
12
C
17
B
22
B
27
B
32
D
37
A
42
C
47
B
3
A
8
D
13
A
18
D
23
D
28
C
33
A
38
A
43
D
48
D
4
C
9
D
14
D
19
C
24
B
29
D
34
D
39
C
44
A
49
A
5
C
10
B
15
C
20
B
25
B
30
B
35
A
40
A
45
D
50
D
ĐỀ 3
Thuvienhoclieu.com
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 - NĂM HỌC 2021 –2022
MÔN TOÁN 12
Câu 1. 
()Fx

()fx

K

A.
'( ) ( ), .F x f x x K
B.
'( ) ( ), .f x F x x K
C.
'( ) ( ), .F x f x x K
D.
'( ) ( ), .f x F x x K
Câu 2.
4
dx x
: A.
5
1
5
xC
B.
3
4xC
C.
5
xC
D.
5
5xC
Câu 3. 
3
(x)
x
fe

A.
3
x
eC
. B.
3
1
3
x
eC
. C.
1
3
x
eC
. D.
3
3
x
eC
.
Câu 4. 
2
1
3
x
yx
x
.
Trang12
A.
3
2
31
,
3 ln3
x
x
CC
x
. B.
3
2
1
3 ,
3
x
x
CC
x
C.
3
3
ln ,
3 ln3
x
x
x C C
. D.
3
3
ln ,
3 ln3
x
x
x C C
.
Câu 5. 
2
3 sinf x x x
là
A.
3
cosx x C
. B.
6 cosx x C
. C.
3
cosx x C
. D.
6 cosx x C
.
Câu 6. Hàm s
y f x
liên tc trên
2;9
.
Fx
là mt nguyên hàm ca hàm s
fx
trên
2;9
và
2 5; 9 4FF
. M đúng
A.
9
2
d1f x x 
. B.
9
2
d1f x x
. C.
9
2
d 20f x x
. D.
9
2
d7
f x x
.
Câu 7. 
2
1
d2f x x 
và
3
2
d1f x x
thì
3
1
df x x

A.
3
. B.
1
. C.
1
. D.
3
.
Câu 8. 
1
0
d4f x x
thì
1
0
2df x x

A.
16
. B.
4
. C.
2
. D.
8
.
Câu 9. Tính tích phân
1
4
0
( 1) I x x dx
A.
7
10
I
B.
7
3
I
C.
10
7
I
D.
7
10
I 
Câu 10 .
y f x

;ab


y f x

,x a x b


A.
d
b
a
S f x x
. B.
d
b
a
S f x x
. C.
d
b
a
S f x x
. D.
d
a
b
S f x x
.
Câu 11. 
S

2
x
y
,
0y
,
0x
,
2x
.

A.
2
0
2d
x
Sx
B.
2
0
2d
x
Sx
C.
2
2
0
2d
x
Sx
D.
2
2
0
2d
x
Sx
Câu12. 
fx


, 0, 1, 2y f x y x x

Trang13
A.
12
11
dx + dxS f x f x

. B.
12
11
dx dxS f x f x

.
C.
12
11
dx+ dxS f x f x


. D.
12
11
dx dxS f x f x


.
Câu13.
V


y f x

Ox

,x a x b a b
, xung quanh

Ox
.
A.
b
a
V f x dx
B.
2
b
a
V f x dx
C.
2
b
a
V f x dx
D.
b
a
V f x dx
Câu 14.
D

x
ye

0x
,
1x

D

V

A.

2
1
2
e
V
B.
2
1
2
e
V
C.
2
3
e
V
D.

2
1
2
e
V
Câu 15.
1

3
là
A.
13i
B.
13i
C.
13i
D.
13i
Câu 16:
34zi
là:
A.
34zi
B.
34zi
C.
34zi
D.
34zi
Câu 17.
2zi
. Tính
z
.
A.
5z
B.
5z
C.
2z
D.
3z
Câu 18.
12zi
?
A.
1;2Q
. B.
2;1M
. C.
2;1P
. D.
1; 2N
.
Câu 19.
12zi
?
A.
P
B.
M
C.
Q
D.
N
Trang14
Câu 20.Trong không gian
Oxyz
,   m
2;4;1 1;1;3A ,B
và mt phng
: 3 2 5 0P x y z
. Lt phng
Q
m
A
,
B
và vuông góc vi
mt phng
P
.
A.
2 3 11 0xy
. B.
2 3 11 0yz
. C.
3 2 5 0x y z
. D.
3 2 11 0yz
.
Câu 21.Cho 
x
và
y

2 3 3 5 4x yi i x i

i

x+y=?
A.3. B.-2. C.0. D.2.
Câu 22.
1
12zi
và
2
2zi

12
zz

A.
3 i
B.
3 i
C.
3 i
D.
3 i
Câu 23.
1
32zi
và
2
2zi

12
zz

A.
13i
. B.
13i
. C.
13i
. D.
13i
.
Câu 24.
1
3zi=-
và
2
1zi= - +

12
zz

A.
4
. B.
4i
. C.
1
. D.
2
.
Câu 25.
13zi
và
1wi

.zw

A.
25
. B.
22
. C.
20
. D.
8
.
Câu 26.  
A. . B. . C. . D. .
Câu 27.Cho    
A. B. C. D.
Câu 28.Trong không gian  và  
A. B. C. D.
Câu 29.Trong không gian    

A. . B. . C. . D. .
Câu 30. , cho  là
A. . B. . C. . D. .
Câu 31.OxyzA , B . 
.
A. 26. B. 22. C. . D.
Câu 32.  , , . Tìm
 sao cho là hình bình hành.
A. . B. . C. . D. .
Câu 33.Trong không gian
Oxyz
t cu có tâm I(a;b;c) bán kính R là:
z
1 3 5z i i
z
17z
16z
17z
4z
,ab
2 1 3a bi i a i
i
ab
4
10
4
10
Oxyz
1;1; 2A
2;2;1B
AB
1; 1; 3
3;1;1
1;1;3
3;3; 1
Oxyz
2; 2;1M
Oxy
2;0;1
2; 2;0
0; 2;1
0;0;1
Oxyz
23a i j k
a
1;2; 3
2; 3; 1
2; 1; 3
3;2; 1
1; 3;1
3;0; 2
AB
26
22.
Oxyz
1;0;3A
2;3; 4B
3;1;2C
D
ABCD
4; 2;9D 
4;2;9D
4; 2;9D
4;2; 9D
Trang15
A.
2 2 2
2
: . . S x a y b z c R
. B.
2 2 2
2
: S x a y b z c R
.
C.
2 2 2
2
: S x a y b z c R
. D.
2 2 2
: S x a y b z c R
.
Câu 34.Trong không gian
Oxyz
, cho mt cu
2 2 2
: 8 10 6 49 0S x y z x y z
. Tính bán kính
R
ca mt cu
S
.
A.
1R
. B.
7R
. C.
151R
. D.
99R
.
Câu 35.Trong h trc t
Oxyz
t cu tâm
2;1; 2I
bán kính
2R
là:
A.
2 2 2
2 1 2 2 x y z
. B.
2 2 2
2 1 2 4 x y z
.
C.
2 2 2
2 1 2 4 x y z
. D.
2 2 2
2 1 2 2x y z
.
Câu 36.Trong không gian vi h trc
Oxyz
   
2 2 2 2
2 2 4 2 5 9 0x y z m x my mz m
. Tìm các giá tr ca
m
   
a mt mt cu.
A.
5m

1m
. B.
51m
.
C.
5m 

1m
. D.
51 m
.
Câu 37.Trong không gian
Oxyz
, cho mt phng
:2 3 1 0P x y z
  
mn ca
P
?
A.
3
2;3;1n
. B.
1
2; 1; 3n

. C.
4
2;1;3n
. D.
2
2; 1;3n 
.
Câu 38.Trong không gian
Oxyz
m
1;0;0A
,
0;2;0B
và
0;0;3C
. Mt phng
ABC

A.
1
1 2 3
x y z
. B.
1
1 2 3
x y z
. C.
1
1 2 3
x y z
. D
1
1 2 3
x y z
.
Câu 39.Trong không gian vi h t
Oxyz
t
phm
1;2; 3M
và có mn
1; 2;3n 
.
A.
2 3 12 0x y z
B.
2 3 6 0x y z
C.
2 3 12 0x y z
D.
2 3 6 0x y z
Câu40.Trong không gian vi h t
Oxyz
m
0;1;1A
) và
1;2;3B
. Vi
trình ca mt phng
P

A
và vuông góc vng thng
AB
.
A.
2 3 0x y z
B.
2 6 0x y z
C.
3 4 7 0x y z
D.
3 4 26 0x y z
Câu 41. Cho hàm s
fx
tha mãn
1
2
25
f
và
2
3
4


f x x f x
vi mi
x
. Giá tr
ca
1f
bng
A.
391
400
B.
1
40
C.
41
400
D.
1
10
Lờigiải
ChọnD
Trang16
Ta có
2
3
4


f x x f x
3
2
4


fx
x
fx
3
1
4



x
fx
4
1
xC
fx
Do
1
2
25
f
, nên ta có
9C

4
1
9

fx
x
1
1
10
f
.
Câu 42. Cho
4
3
2
.ln 2 ln 3
1
x
dx a b c
x
, vi
,,a b c
là các s hu t. Giá tr ca
6P a b c
bng:
A.
1
. B.
1
. C.
2
. D.3.
Câu 43. Cho hàm s
()fx
nh trên
1
\
2



tha mãn
2
, 0 1, 1 2
21
f x f f
x
. Giá tr
ca biu thc
13ff
bng
A.
2 ln15
B.
3 ln15
C.
4 ln15
D.
ln15
Lờigiải
ChọnC
2
ln 2 1
21
dx x C f x
x

1
2
x
,
01f
1C
nên
1 1 ln3f

1
, 1 2 2
2
x f C
nên
3 2 ln5f 
Nên
1 3 3 ln15ff
Câu 44. Cho hàm s
fx
tha mãn
2
0
1 d 9A x f x x
và
3 2 0 12ff
. Tính
2
0
dI f x x
A.
3I
. B.
3I
. C.
6I 
. D.
6I
.
Li gii:
2
0
1 d 9A x f x x
t u=x+1 suy ra du=dx

Vy
2
2
0
0
( 1) ( ) | d 9 3 (2) (0) 9
3

A x f x f x x f f I
I
Câu 45. Cho hàm s
y f x
o hàm trên
 th hàm s
y f x
. Bit
din tích hình phng phn sc k bng
3
. Tính giá tr ca biu thc:
2 3 4
1 2 3
1 dx 1 dx 2 8 dxT f x f x f x

Trang17
A.
9
2
T
. B.
6T
. C.
0T
. D.
3
2
T
.
Lờigiải
n tích phn k sc là:
0
2
dxS f x
3
.
Vì
0fx
2;0x
00
22
3 dx dxf x f x




0
2
dx 3fx
.

4
3
2 8 dxI f x
.
t
28tx
dt 2dx
;
32xt
;
40xt
.
Suy ra:
0
2
1
. dt
2
I f t
0
2
1
dx
2
fx
3
2

.
y
2 3 4
1 2 3
1 dx 1 dx 2 8 dxT f x f x f x

23
12
11f x f x I
3
3 2 2 1
2
f f f f
33
21
22
.
Câu 46. Din tích
S
ca hình phng gii hng
2
1y x x
;
0y
;2x
là
1a
S
c
Giá tr ca biu thc
P a c
bng
A.
3P
. B.
122P
. C.
112P
.D.
22P
.
Câu 47. Mt xe la chuyng chm du và dng li hn sau
20
s k t lúc bu hãm
phanh. Trong th c
120
m. Cho bit công thc tính vn tc ca chuyn
ng biu là
0
v v at

a
(
2
m/s
) là gia tc,
v
(m/s) là vn tc ti thm
t
(s). Hãy tính gia tc
a
ca xe la khi hãm phanh.
A.
2
0,6 /ms
. B.
2
0,6 / ms
. C.
2
12 /ms
. D.
2
1,2 /ms
.
Câu 48. Cho
z
là s phc tha mãn
2z z i
. Giá tr nh nht ca
1 2 1 3z i z i
là
A.
52
. B.
13
. C.
29
. D.
5
.

,z a bi a b
.
Trang18
Ta có:
2
2 2 2
22z z i a b a b
4 4 0 1bb
z a i
.
Xét:
1 2 1 3 1 1 4 z i z i a i a i
22
22
1 1 1 4 aa
.

2 2 2 2
22
1 1 1 4 1 1 1 4 a a a a
4 25 29
.
Suy ra:
1 2 1 3z i z i

29
khi
3
4 1 1
5
a a a
.
Câu 49. Cho s phc
z a bi
, ab
tha mãn
1 3 0z i z i
. Tính
23S a b
.
A.
6S 
. B.
3S
. C.
2S
. D.
5S
.
Câu 50.       
Oxyz
   
3; 2;6 , 0;1;0AB
  
2 2 2
: 1 2 3 25S x y z
 
: 2 0P ax by cz
 
,AB
 
S
theo
Hãy tìm chu vi cng tròn có bán kính nh
nht.
A.
2
. B.
45
. C.
25
. D.
10 5
.
Lờigiải

S
có tâm
1; 2; 3I
và bán kính
5R
Ta có


3 2 6 2 0
20
AP
a b c
b
BP
22
2
ac
b

22
2
; 25 ;r R d I P d I P

;d I P

Ta có

2 2 2
2 3 2
,
a b c
d I P
a b c
2
22
2 2 4 3 2
2 2 2
cc
cc

2
2
4
5 8 8
c
cc
Xét

2
2
4
5 8 8
c
fc
cc



2
2
2
2
2
48 144 192
4
5 8 8
5 8 8
cc
fc
c
cc
cc



1
0
4
c
fc
c

Trang19
Vy
;d I P
ln nht bng
5
.




2
2
25 ; 25 5 2 5r d I P
2 2 .2 5 4 5Cr
ĐỀ 4
Thuvienhoclieu.com
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 - NĂM HỌC 2021 –2022
MÔN TOÁN 12
Câu 1:Trong không gian
Oxyz
, cho mt cu
2 2 2
:( 3) ( 1) ( 1) 2S x y z
. Tâm ca
()S
có t là
A.
(3; 1;1)
. B.
( 3; 1;1)
. C.
(3;1; 1)
. D.
( 3;1; 1)
.
Câu 2: Tính tích phân
1
32
0
1I x x dx
A.
5
12
I 
B.
1
2
I
. C.
7
3
I
. D.
1
3
I
.
Câu 3:Cho hai s phc
12
1 2 ; 3z i z i
.Tìm
12
zz
A.13. B.
13
. C.5. D.
5
.
Câu 4:S phc liên hp ca s phc
z
bit
1
(1 )(3 2 )
3
z i i
i
là:
A.
13 9
10 10
i
. B.
53 9
10 10
i
. C.
53 9
10 10
i
. D.
13 9
10 10
i
.
Câu 5:Phn thc ca s phc
54zi
là
A.
5
.B.
4
.C.
5
.D.
4
.
Câu 6: Tìm s phc z tha mãn
2 3 3 2z i i
A.
15zi
. B.
1zi
. C.
55zi
. D.
1zi
.
Câu 7:Cho s phc
32zi
, s phc
1 iz
bng
A.
5 i
. B.
5 i
. C.
15i
. D.
15i
Câu 8:Trên mt phng t Oxym biu din s phc
12zi
?
A.
2;1Q
. B.
1;2N
. C.
1; 2M
. D.
2; 1P
.
Câu 9:Trong không gian vi h t Oxyzt phm
0
y
x
'y
-¥
+¥
4-
0
1
5
5
1
5
-
-
1
0
+
Trang20
(1;2; 3)M
và có mn
(1; 2;3)n 
?
A.
2 3 12 0x y z
. B.
2 3 6 0x y z
. C.
2 3 12 0x y z
. D.
2 3 6 0x y z
.
Câu 10:Cho s phc
43zi
a s phc
w 2 1z
là:
A.
117
. B.
2 13
. C.5. D.
3 10
.
Câu 11:Trong không gian
Oxyz
, cho mt cu
2 2 2
( ): 1 2 3 4S x y z
. bán kính ca mt c
cho bng
A.
16
. B.
2
. C.
4
. D.
10
.
Câu 12:Cho
2;2;1 , 1;0;2 , 1;2;3 , 1;1; 2 , 0;2; 1A B C D E
,
:4 3 1 0x y z
. Có bao nhiêu
m trên mt phng
?
A. 2. B.4. C. 1. D.
3
.
Câu 13: Cho hai hàm s
32
( ) 1f x ax bx cx
và
2
1
( ) ( , , , , )
2
g x dx ex a b c d e
. Bit r th ca
hàm s
()y f x
và
()y g x
ct nhau t lt là
3
;
1
;
2
(tham kho hình v bên) .
Hình phng gii hn b th n tích bng
A.
125
12
. B.
253
12
. C.
253
48
. D.
125
48
.
Câu 14: Tìm các s thc x, y tha mãn:
(x 2y) (2x 2y)i x y 1 y 3 i.
A.
x 1,y 1.
B.
11 1
x ,y .
33
C.
x 1,y 1.
D.
31
x ,y .
42
Câu 15:Trong không gian
Oxyz
, cho mt phng
: 2 4 1 0x y z

tuyn ca mt phng
?
A.
4
1;2;4n

.B.
2
1;2;4n
. C.
1
1;2; 4n

. D.
3
1; 2;4n

.
Câu 16:
2
31
1
ed
x
x
bng
A.
52
1
ee
3
. B.
52
1
ee
3
. C.
52
1
ee
3
. D.
52
ee
.
Câu 17: Din tích S ca hình phng gii hn b th ca hàm s
y f x
liên tc trên
;ab
, trc hoành và
ng thng
x a,x b
c tính theo công thc:
Trang21
A.
b
a
S f x dx.
B.
b
a
S f x dx.
C.
0b
a0
S f x dx f x dx.

D.
0b
a0
S f x dx f x dx.

Câu 18:Trong không gian vi h t
Oxyz
ng thng
1
13
:2
2
xt
d y t
z

,
2
12
:
2 1 2
x y z
d


và
mt phng
( ): 2 2 3 0P x y z
t phm ca
1
d
và (Png thi vuông góc vi
2
d
.
A.
2 2 13 0x y z
. B.
2 2 22 0x y z
.
C.
2 2 13 0x y z
. D.
2 2 22 0x y z
.
Câu 19:Tích phân
2
1
d
32
x
x
bng
A.
2ln2
. B.
2
ln 2
3
. C.
1
ln 2
3
. D.
ln2
.
Câu 20:Trong không gian
Oxyz
ng thng
3 1 5
:
2 2 1
x y z
d

c
d
?
A.
2;2; 1P
. B.
2;2;1Q
. C.
3;1;5M
. D.
3;1; 5N
.
Câu 21: Cho
1
0
11
ln2 ln3
12
dx a b
xx




vi a, b là các s nguyên. M đúng ?
A.
2ab
. B.
2ab
. C.
20ab
. D.
20ab
.
Câu 22:Cho s phc
z
tha mãn
3 2 3 10z i i z i
a
z
bng
A.
3
. B.
5
. C. . D.
5
.
Câu 23:Trong không gian
Oxyz
, mt phng
Oxz

A.
0x y z
. B.
0x
. C.
0z
. D.
0y
.
Câu 24:S phc liên hp ca s phc
34i
là
A.
34i
. B.
34i
. C.
43i
. D.
34i
.
Câu 25:Kí hiu
12
,zz
là hai nghim phc c
2
60zz
. Tính
12
11
P
zz

A.
1
6
P 
. B.
1
6
P
. C.
6P
. D.
1
12
P
Câu 26: 
e
1
ln dI x x x
A.
2
e1
4
I
. B.
1
2
I
. C.
2
e2
2
I
. D.
2
e1
4
I
.
3
Trang22
Câu 27: Cho
2
1
(1 ln )d
e
x x x ae be c
vi
,,abc
là các s hu t. M đúng ?
A.
a b c
. B.
a b c
. C.
a b c
. D.
a b c
.
Câu 28:m nào trong hình v m biu din ca s phc
2?zi
A.
Q
. B.
N
. C.
M
. D.
P
.
Câu 29:Cho hai s phc . Trên mt phng t Oxym biu din s phc có
t là:
A. .B. . C. . D. .
Câu 30: Bit
1
0
2f x dx 
và
1
0
3,g x dx

1
0
f x g x dx


bng
A.
5.
B.
1.
C.
5.
D.
1.
Câu 31:Trong không gian
Oxyz
, 

1;1; 1A
,
2;3;2B

AB
uuur

A.
1; 2;3
. B.
3;5;1
. C.
1;2;3
. D.
3;4;1
.
Câu 32: Tìm th tích
V
ca khc to ra khi quay hình thang cong, gii hn b th hàm s
y f x
liên tc trên
;ab
, trc Ox ng thng
x a, x b a b ,
xung quanh trc Ox.
A.
d
b
a
V f x x.
B.
d
b
2
a
V f x x.
C.
d
b
a
V f x x.
D.
d
b
2
a
V f x x.
Câu 33:Gi
12
,zz
là hai nghim phc c
2
30zz

12
zz
bng
A.
3
. B.
23
C.
6
. D.
3
.
Câu 34:Cho s phc
2zi
. Tính
z
.
A.
3z
. B.
2z
. C.
5z
. D.
5z
.
Câu 35:Cho hai s phc
1
32zi
và
2
2zi
. S phc
12
zz
bng
A.
13i
. B.
13i
. C.
13i
. D.
13i
.
Câu 36: Nguyên hàm ca hàm s
3
f x x x
là
A.
2
31xC
. B.
42
11
42
x x C
. C.
3
x x C
. D.
42
x x C
.
Câu 37:
2
4 3 1y x x ,y x

?
12
2 , 1z i z i
12
2zz
5;0
1;5
5; 1
0;5
Trang23
A.
4
2
1
3 2 xx x d
. B.
4
2
1
5 4 xx x d
.
C.
4
2
1
3 2 xx x d
. D.
4
2
1
5 4 xx x d
.
Câu 38:Trong không gian
Oxyz
, 

2;2; 5A
,
4;6;1B
.
m M cn thng AB 
A.
2;4;6
. B.
3;4; 2
.C.
2; 4; 6
. D.
3;4; 3
.
Câu 39:Trong không gian vi h t Oxyz, cho mt phng
( ): 2 5 0P x y z
c
()P
?
A.
(2; 1;5)Q
. B.
(0;0; 5)P
. C.
( 5;0;0)N
. D.
(1;1;6)M
.
Câu 40:Trong không gian
Oxyz
    u vuông góc c m
3;4;1A
trên mt
phng
Oxy
?
A.
0;0;1M
. B.
3;4;0N
.C.
3;0;1P
.D.
0;4;1Q
.
Câu 41: Cho hình phng D gii hn bng cong
x
ye
, trng thng
0, 1xx
. Khi
tròn xoay to thành khi quay D quanh trc hoành có th tích V bng bao nhiêu ?
A.
2
1
2
e
V
B.
2
2
e
V
C.
2
( 1)
2
e
V
D.
2
( 1)
2
e
V
Câu 42:Trong không gian Oxyz  ng thng
12
:
2 1 2
x y z
và mt phng
( ): 1 0P x y z
.
ng thng nm trong
()P
ng thi ct và vuông góc vi

A.
3
24
2
xt
yt
zt


. B.
32
26
2
xt
yt
zt


.C.
3
24
23
xt
yt
zt


. D.
1
4
3
xt
yt
zt


.
Câu 43:Trong không gian
Oxyz
 ng th  
2; 1;3M
và vuông góc vi mt phng
:4 3 2 0x y z

A.
42
3
13
xt
yt
zt



.B.
24
13
3
xt
yt
zt


. C.
24
23
2
xt
yt
zt

. D.
24
43
2
xt
yt
zt

.
Câu 44: Cho hàm s
fx
liên tc trên
R
. Gi
S
là din tích hình phng gii hn b  ng
, 0, 1y f x y x
và
4x
 bên). M đúng?
Trang24
A.
14
11
S f x dx f x dx


. B.
14
11
S f x dx f x dx

.
C.
14
11
S f x dx f x dx

. D.
14
11
S f x dx f x dx


.
Câu 45:Gi
2
4 11 0zz
, kt qu nghim là:
A.
2 7.
2 7.
zi
zi


. B.
3 2.
3 2.
zi
zi


. C.
1 5.
1 5.
zi
zi


. D.
17
zi
22
17
zi
22


.
Câu 46:Trong không gian
Oxyz
 cng thng d 
2;3;1M
và có vecto ch

(1; 2;2)u 
r
là
A.
12
23
2
xt
yt
zt


. B.
2
32
12
xt
yt
zt


.C.
2
32
12
xt
yt
zt

. D.
12
23
2
xt
yt
zt


.
Câu 47:Trong không gian
Oxyz
, khong cách gia hai mt phng
: 2 2 10 0P x y z
và
: 2 2 3 0Q x y z
bng
A.
8
3
. B.
7
3
. C.
4
3
. D.
3
.
Câu 48:Xét các s phc
z
tha mãn
2z
. Trên mt phng t
Oxy
, tp hm biu din ca các s
phc
4
w
1
iz
z
là mng tròn có bán kính bng
A.
26.
B.
26.
C.
34.
D.
34.
Câu 49:S phc
37i
có phn o bng
A.
7
.B.
7
. C.
3
. D.
7i
.
Câu 50:Tìm s phc liên hp ca s phc
2
1 2 3 4 5z i i i
.
A.
3 22i
. B.
3 22i
. C.
3 22i
. D.
3 22i
.
ĐÁP ÁN
1
B
6
B
11
B
16
C
21
C
26
D
31
C
36
B
41
D
46
B
2
A
7
B
12
A
17
A
22
D
27
A
32
D
37
D
42
C
47
B
3
B
8
B
13
C
18
C
23
D
28
D
33
B
38
B
43
D
48
C
4
B
9
A
14
C
19
B
24
D
29
C
34
C
39
D
44
A
49
A
5
A
10
A
15
D
20
D
25
B
30
A
35
C
40
B
45
A
50
A
| 1/24
| | Tải xuống

Có thể bạn quan tâm:

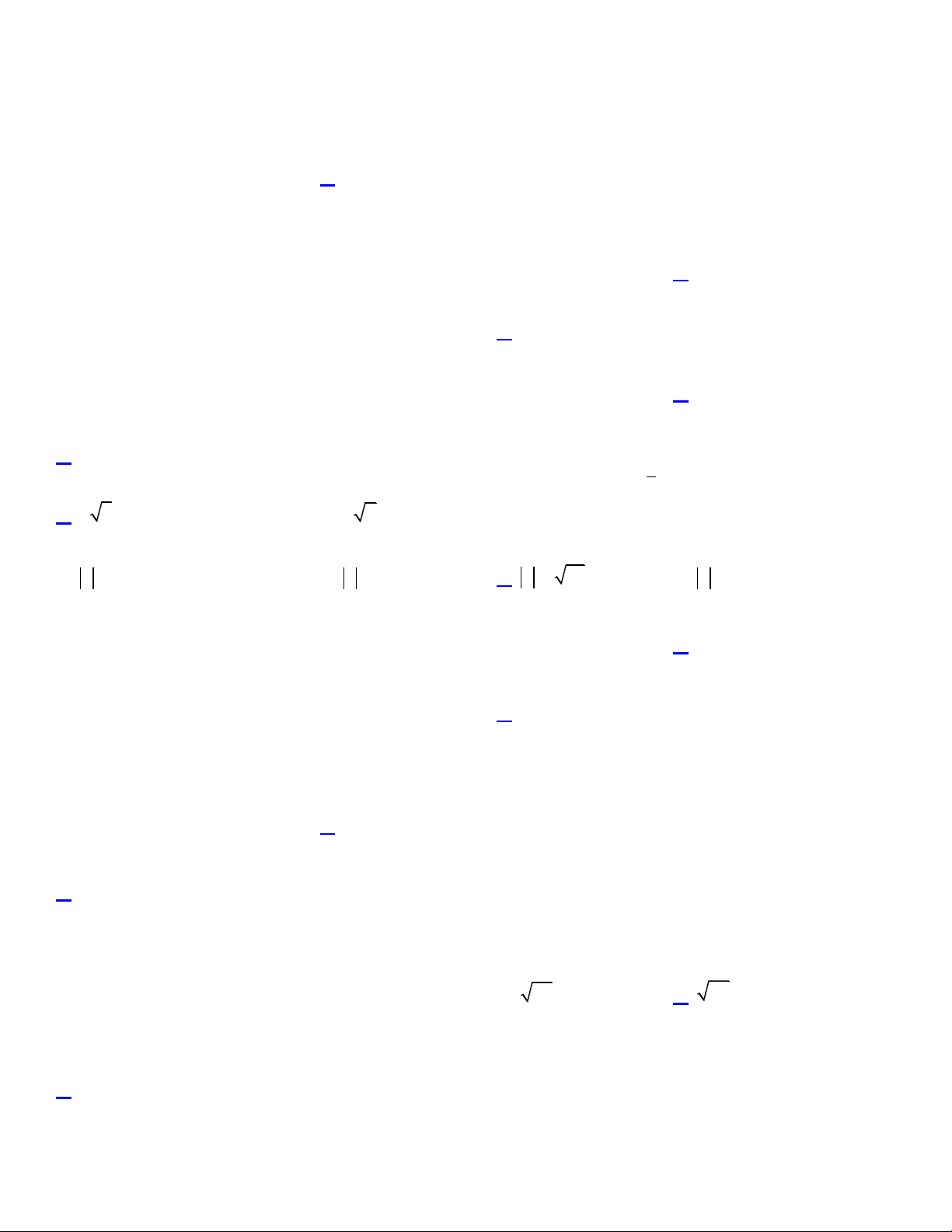
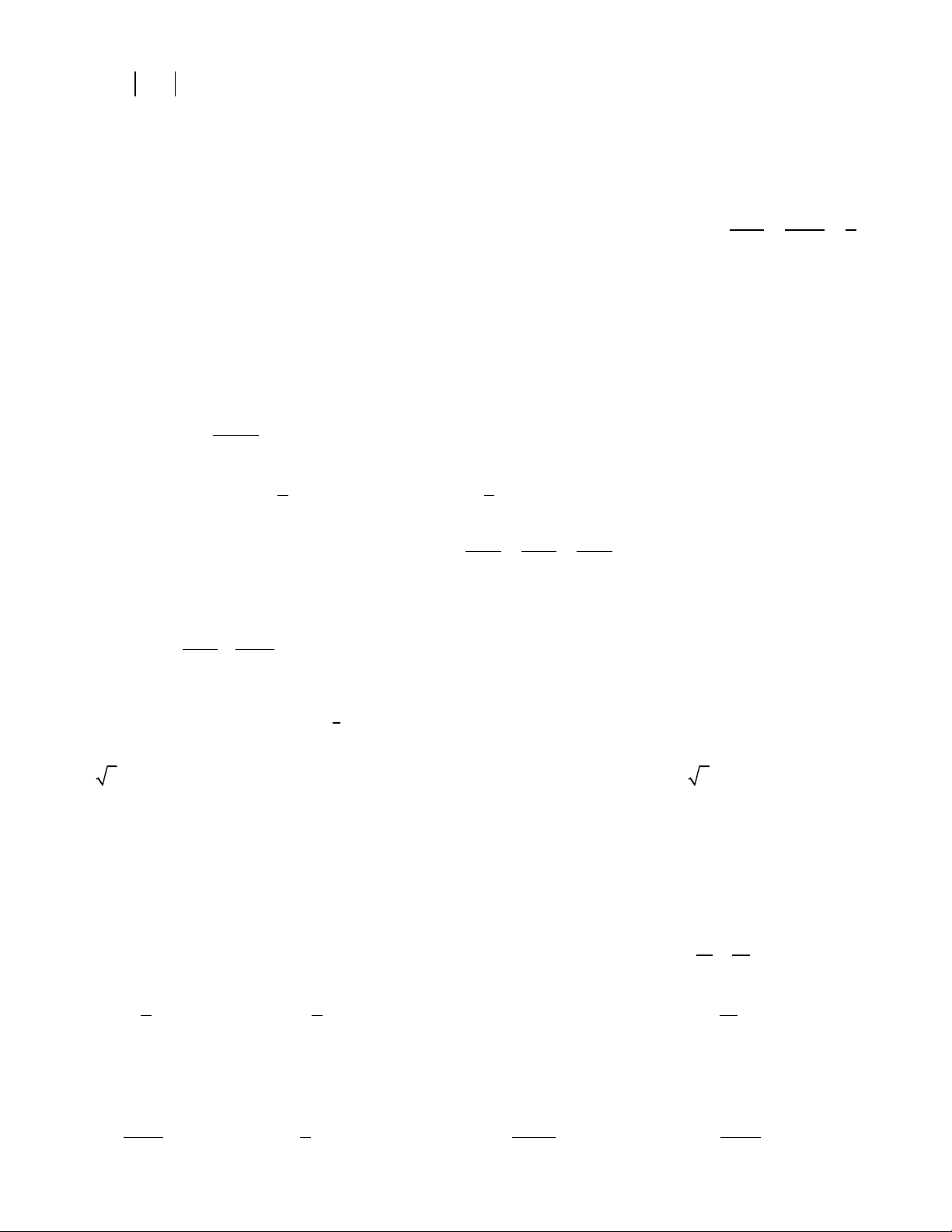
Preview text:

ĐỀ 1
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 - NĂM HỌC 2021 –2022 MÔN TOÁN 12
Câu 1.Cho u = u(x ) ,v = v(x ) là hai hàm số có đạo hàm liên tục, khẳng định nào sau đây là đúng ? A. udv = uv + vdu. ò ò B. udv = uv - vdu. ò ò u C. udv = + vdu. ò ò D. vdu = uv + vdu. ò ò v Câu 2. Hàm số ( ) x = - 2x f x e có nguyên hàm là x 2x
A. F(x) = e - + C . B. F( ) x x x = e - + C . ln 2 ln 2 x 2x x ln 2
C. F(x) = e + + C .
D. F(x) = e - + C . ln 2 2x     
Câu 3. Trong không gian Oxyz, cho vectơ a  2
i j  3k . Toạ độ của vectơ a là A.(2;- 1;- ) 3 . B.(- 2;- 1; ) 3 . C.(- 2;1; ) 3 . D.(- 2;1;- ) 3 .
Câu 4. Trong không gian Oxyz, phương trình mặt cầu tâm O, bán kính R = 2 có dạng là A. 2 2 2
x y z  2x  2 y  2z 1  0. B. 2 2 2
x y z  2. C. 2 2 2
x y z  2x  2 y  2z 1  0. D. 2 2 2
x y z  4.
Câu 5. Trong không gian Oxyz, cho hai điểm A1;2;0 , B 1;0;  
1 . Độ dài đoạn thẳng AB bằng? A. 2. B. 2 . C. 1. D. 5.
Câu 6. Trong không gian Oxyz, cho hai điểm ( A 1  ;2; 3  ), B(3;2; 1
 ) . Tọa độ trung điểm I của đoạn thẳng AB là A. I 1;2; 2
 . B. I 2;4; 4
  . C. I 4;0;2 . D. I 1;2;2.
Câu7. Cho f x , g x là các hàm số xác định và liên tục trên  . Trong các mệnh đề sau, mệnh đề nào sai? A. f
 xgxdx f
 xd .x g  xdx. B. 2 f
 xdx  2 f  xdx . C. f
 x gxdx f
 xdxg  xdx . D. f
 x gxdx f
 xdxg  xdx.
Câu8. Mệnh đề nào dưới đây đúng? 2 x 9x x 3 x A. 2 3 dx   C  . B. 2 3 dx   C  . ln 3 ln 3 Trang1 2 2 x 1  x 3 x 3 x C. 2 3 dx   C  . D. 2 3 dx   C  . ln 9 2x 1
Câu9. Tìm mệnh đề sai trong các mệnh đề sau. 4 x C 1 A. 3 x dx  .  B.
dx  ln x C.  4 x C. sin d
x x C  cos . xD. 2exd  2  ex xC.
Câu10. Hàm số nào sau đây không phải là một nguyên hàm của hàm số f x   x  5 ( ) 3 1 ? x x
A. F x  6 3 1  8 .
B. F x  6 3 1   2 . 18 18 x x
C. F x  6 3 1  .
D. F x  6 3 1  . 18 6
Câu 11. Cho F (x ) là nguyên hàm của hàm số f (x ) trên a é ;bù
êë úû. Phát biểu nào sau đây sai ? b b b A. f
ò (x)dx = F (b)- F (a). B. f ò (x)dx ¹ f ò (t)dt. a a a a b a C. f ò (x)dx = 0. D. f
ò (x)dx = - f ò (x)dx. a a b
Câu 12. Cho 0 < a ¹ 1. Chọn khẳng định đúng trong các khẳng định sau đây? x + 1 x a x a A. a dx = + C B. x a dx = + C . ò ò C. x d x a
x =a + C . ò D. x d x a
x =a ln a + C . ò x ln a 4 2x + 3
Câu 13. Cho hàm số f (x ) =
, x ¹ 0 . Chọn phương án đúng. 2 x 3 2x 3 3 2x 3 A. f ò (x)dx = - + C . B. f ò (x)dx = + + C . 3 x 3 x 3 3 2x 3 C. f ò (x) 3 dx = 2x - + C . D. f ò (x)dx = + + C . x 3 2x Câu 14. Cho 2 I =
x. x + 1.dx ò . Với phép đổi biến 2 t =
x + 1 ta được kết quả là 1 A. 2 I = t .dt. ò B. 2 I = 2t .dt. ò C. 2 I = t .dt. ò D. I = t .dt. ò 2
Câu 15. Cho điểm M (3; 1
 ;2) . Hình chiếu của điểm M lên các trục tọa độ Ox, Oy, Oz lần lượt có tọa độ là A. (3;0;0), (0; 1  ;0), (0;0;2). B. ( 3  ;0;0), (0;1;0), 0;0; 2  . C. ( 1  ;0;0), (0;3;0), (0;0;2). D. (2;0;0), (0; 1  ;0), (0;0;3). Trang2
Câu 16. Cho điểm P(3; 2; 5) . Gọi Q là hình chiếu vuông góc của P trên mặt phẳng Oxy. Tọa độ điểm Q là A. (3; 2; 0) . B. ( 3  ; 2  ;0). C. (3; 2  ;0). D. (3; 2; 0).
Câu 17. Trong không gian Oxyz, cho điểm M (2;1; 3
 ) . Gọi N là điểm đối xứng của M qua trục Ox. Tọa độ điểm N A. (2;1; 3) . B. (2; 1  ;3) . C. (2;1;3) . D. (2; 1; 3).
Câu 18. Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới
hạn bởi đồ thị hàm số y f(x), trục Ox và hai đường thẳng x a, x b (a b) quay xung quanh trục Ox. b b b b A. 2 V   f (x)d . x  B. 2 V f (x)d . x
C.V   f (x)d . x
D.V f (x)d . xa a a a
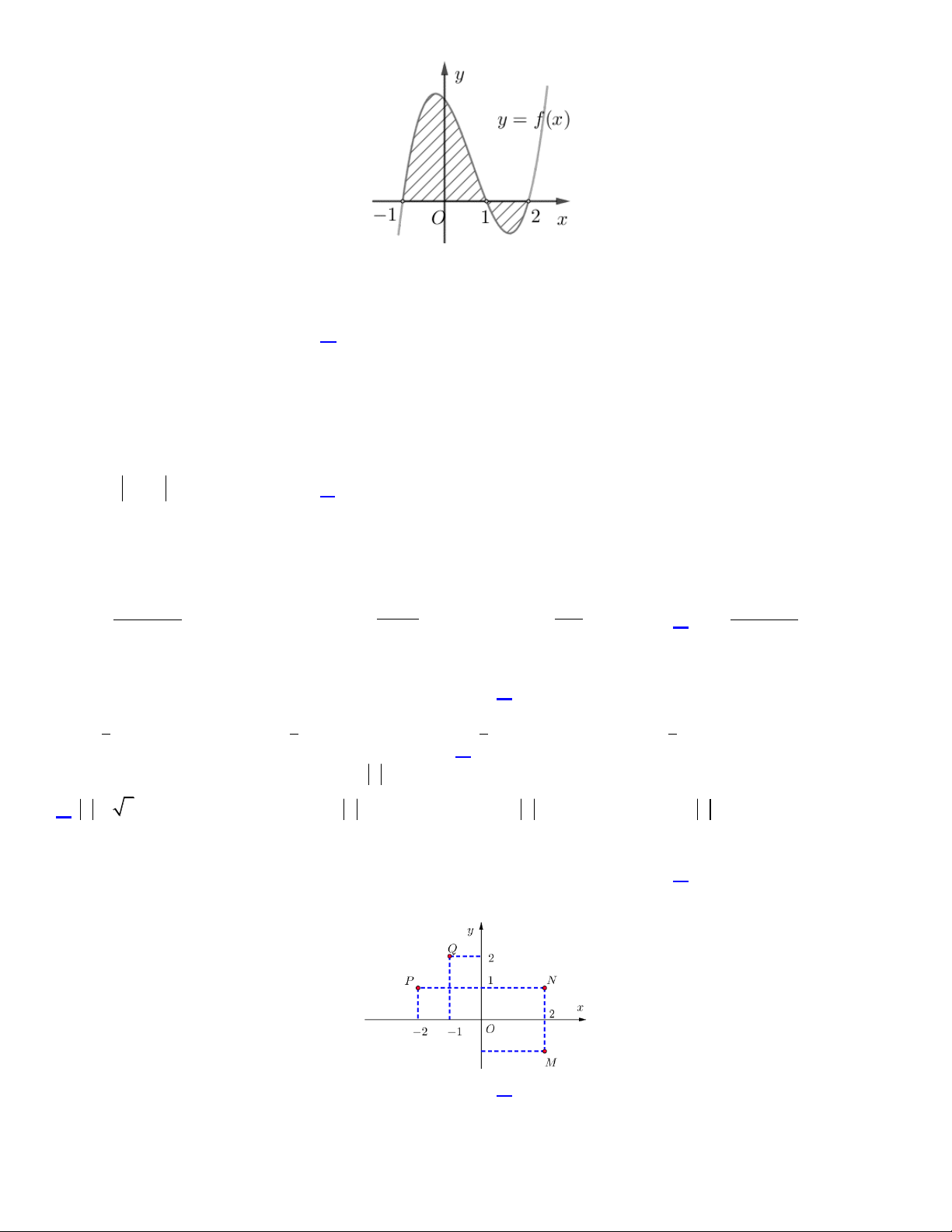
Câu 19.Cho hàm số f x liên tục trên𝑅. Gọi S là diện tích hình phẳng giới hạn bởi các đường
y f x , y  0, x  1
 và x  5 (như hình vẽ bên). Mệnh đề nào dưới đây là đúng? 1 5 1 5 A. S   f
 xdxf
 xdx . B.S f
 xdxf  xdx. 1  1 1  1 1 5 1 5 C. S f
 xdxf
 xdx . D.S   f
 xdxf  xdx. 1  1 1  1
Câu 20. Gọi S là diện tích hình phẳng giới hạn bởi các đường ex y
, y  0 , x  0 , x  2 . Mệnh đề nào dưới đây đúng? 2 2 2 2 A. 2   e x S dx  .B.  ex S dx  .C.   ex S dx  . D. 2  e x S dx  . 0 0 0 0
Câu 21. Cho hình phẳng D giới hạn bởi đường cong 2 y
x 1 , trục hoành và các đường thẳng
x  0, x  1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? 4 A.V  . B.V  4 2 . C.V  . D.V  2 . 3 3
Câu 22.Ông Bảo xây một cổng trường có dạng hình Parabol 𝑃 ( bề lõm quay xuống), có chiều ngang
của chân cổng bên đây đến chân bên kia là 4 mét và chiều cao từ đỉnh đến mặt đất là 3 mét. Ông Bảo
làm cửa cổng ( được giới hạn bởi 𝑃 và đoạn thẳng nối hai chân cổng ở mặt đất) bằng gỗ. Diện tích của cửa cổng là Trang3 A.7𝑚2. B. 8𝑚2. C. 9𝑚2. D. 10𝑚2. d d b Câu 23. Nếu f
ò (x)dx = 5 và f
ò (x)dx = 2 với a < d < b thì f (x)dx ò bằng a b a A.- 2. B. 7. C.- 3. D. 3.
Câu 24.Trong không gian Oxyz , gọi (P) là mặt phẳng đi qua điểm M (1;3;5) và cắt các tia Ox, Oy, Oz lần lượt tại ,
A B, C sao cho thể tích của tứ diện OABC nhỏ nhất. Phương trình mặt phẳng (P) là
A.15x  3y z  29  0 .
B.15x  5y  3z  45  0 .
C.15x  7 y  5z  61  0 .
D. 5x  3y z 19  0 . dx Câu 25.Cho
= a(x + 2) x + 2 + (
b x + 1) x + 1 + C ò
. Tính S = 3a + b . x + 2 + x + 1 - 2 1 4 2 A.S = . B.S = . C.S = . D.S = . 3 3 3 3 y 2
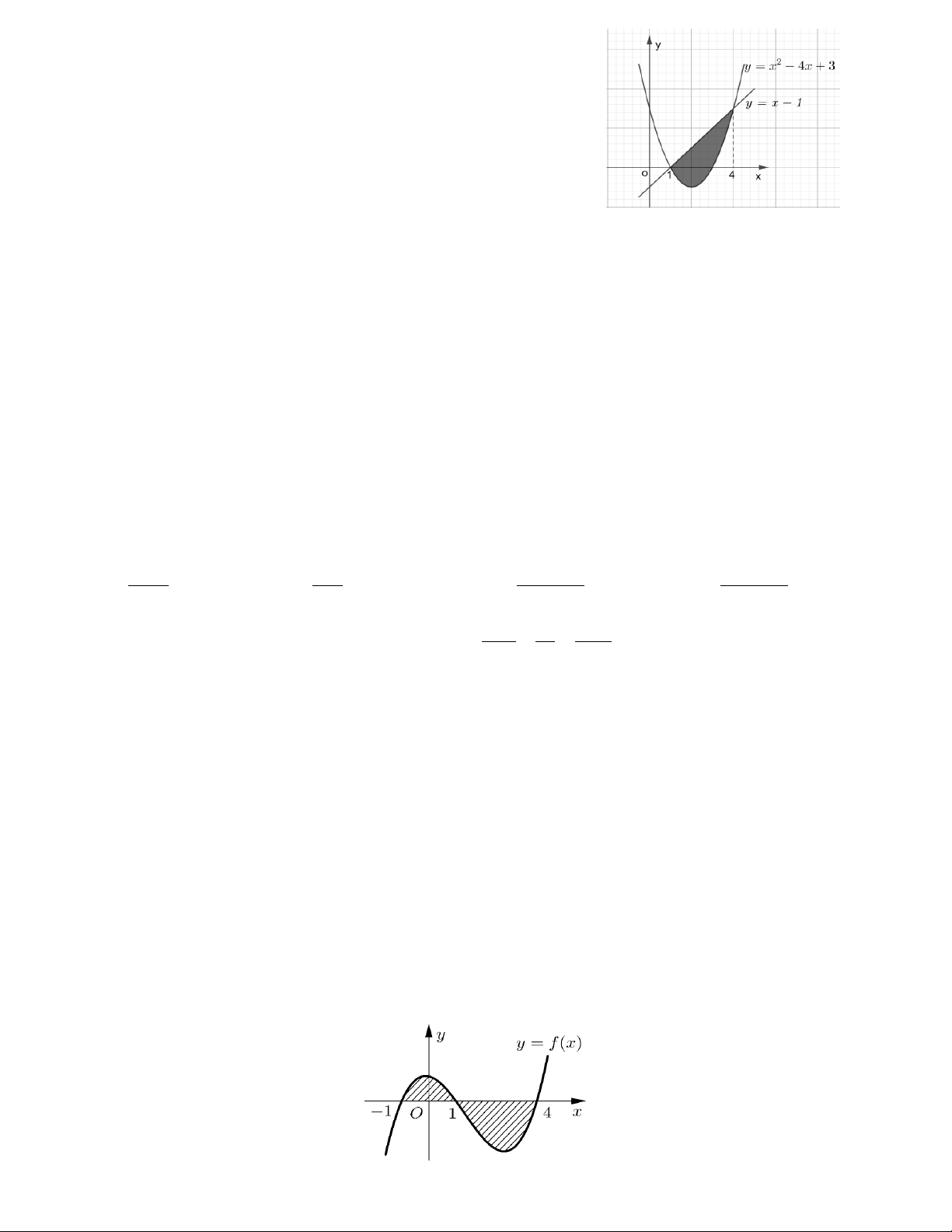
y x  2x 1
Câu 26. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính 2
theo công thức nào dưới đây?  x 1 O 2
y   x  3 2 2 2 2 A.  2
2x  2x  4dx . B.   2
x  2dx . C.  2x2dx. D.   2 2
x  2x  4dx . 1  1  1  1  1
Câu 27.Tính tích phân = ò ( x - x I e + e )dx . 0 1 1 1 1
A. I = e - .
B. I = e + - 2 .
C. I = e + .
D. I = e + + 2 . e e e e
Câu 28.Trong không gian 𝑂𝑥𝑦𝑧, cho hình hộp chữ nhật 𝐴𝐵𝐶𝐷. 𝐴′𝐵′𝐶′𝐷′ có 𝐴 trùng với gốc tọa độ 𝑂.
Biết rằng 𝐵 𝑚; 0; 0 , 𝐷 0; 𝑚; 0 , 𝐴′ 0; 0; 𝑛 với 𝑚, 𝑛 là các số dương và 𝑚 + 𝑛 = 6. Gọi 𝑀 là trung
điểm của cạnh 𝐶𝐶′. Thể tích lớn nhất của khối tứ diện 𝐵𝐷𝐴′𝑀 bằng A.6 B.10. C.8. D.12.
Câu 29. Một xe ô tô đang chạy đều ( được ít nhất 5 giây) với vận tốc 60 𝑚/𝑠 thì người lái xe nhìn thấy
một chướng ngại vật nên đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc
𝑣 𝑡 = 60 − 6𝑡, trong đó 𝑡 là thời gian ( tính bằng giây ) kể từ lúc đạp phanh. Quãng đường mà ô tô đi
được trong 12 giây cuối cùng bằng A.80𝑚. B.288𝑚. C.60𝑚. D.420𝑚. Trang4 p 2 8 s inx
Câu 30. Cho tích phân a = dx ò
, hàm số 𝑓 𝑥 liên tục trên 𝑅 có đạo hàm thỏa mãn p s inx + cos x 0 3
𝑓′ 𝑥 + 𝑎𝑥𝑓 𝑥 = 2𝑥3, ∀𝑥 ∈ 𝑅 và 𝑓 0 = −1. Tích phân f (x )dx ò bằng 0 A.3. B. 6. C. 9. D. 12. ĐÁP ÁN 1 B 6 A 11 B 16 D 21 A 26 D 2 A 7 A 12 B 17 B 22 B 27 A 3 C 8 C 13 A 18 A 23 D 28 C 4 D 9 B 14 A 19 B 24 B 29 D 5 D 10 D 15 A 20 B 25 C 30 B ĐỀ 2
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 - NĂM HỌC 2021 –2022 Thuvienhoclieu.com MÔN TOÁN 12
Câu 1: Trong không gian to ̣a đô ̣ Oxyz , cho mă ̣t phẳng   có phương trình: x y z 10  0.Tìm một
điểm thuô ̣c mp  . A. A 1
 0;2022;2022. B. B 1  0;11  ;1 .
C. C 10;1;  1 . D. D 2;3;  ;1 .
Câu 2: Trong không gian to ̣a đô ̣ Oxyz , tìm tọa độ hình chiếu vuông góc của điểm M 1; 2  ;9 lên mp(Oxy). A. P 0; 2  ;9
B. Q 1;0;9 C. N 1; 2  ;0 D. N  1  ; 2  ;0
Câu 3: Chọn khẳng định sai trong các khẳng định dưới đây 2 x A. xx e dx e  . CB. xdx   C.  2 1 C.
dx  ln x C.  D. sin
 xdx  cosx . C x
Câu 4: Cho f x liên tu ̣c trên đoa ̣n a;b và có đạo hàm là F x . Chọn khẳng định đúng trong các
khẳng đi ̣nh dưới đây b b A. f
 xdx FbFa. B. f
 xdx FaF b. a a b a b C. F
 xdx f b f a. D.
f xdx   F x . a a b     
Câu 5:Trong không gian to ̣a đô ̣ Oxyz , cho hai vecto a  1;3; 4, b  3; 2; 5
 .Tính c  2a 3 . b Trang5    
A. c  11;12;7.
B. c  11;12; 7.
C. c  11;12; 7  .
D. c  11; 12; 7.
Câu 6:Tìm phần ảo của số phức 3 4 z   .i 2 7 4 4  3 A. i. B. . i C. . D. . 7 7 2       
Câu 7:Trong không gian to ̣a đô ̣ Oxyz vớiba vecto đơn vi ̣  ;i j;k ,tính tọa độ vecto a  2i  3 j  4k.    
A. a  2;3; 4  . B. a   4  ;3;2. C. a  2; 4  ;3.
D. a  2;3; 4.
Câu 8:Nêu công thức tính diê ̣n tích hình phẳng giới ha ̣n bởi đồ thi ̣ hàm số y f x (hàm y f x liên
tục trên a;b), trục Ox , đường thẳng x a và đường thẳng x b ? a b b A. S f
 xd .x
B. S f b  f a. C. S f
 xd .x D. S f
 xd .x b a a
Câu 9: Chọn khẳng định đúng trong các khẳng định dưới đây A. f
 x gxdx f
 xdxg
 xd .x B. f
 xkgxdx k f
 xdxg
 xd ,xk   . C. f
 xgxdx  
f xdx. gxdx. D. f
 x gxdx f
 xdxg
 xd .x
Câu 10:Tìm phần thực của số phức 33 41 z   . i 2 7 33 41 41 A. i. B. . C. i. D. . 2 7 7
Câu 11:Trong không gian to ̣a đô ̣ Oxyz , cho ba điểm A1;1 
;1 , B2; 4;3, C3;7; m. Tìm m để ba điểm A,B,C thẳng hàng. A. m  4. B. m  2. C. m  5. D. m  3.
Câu 12:Cho F x là một nguyên hàm của hàm f x . Chọn khẳng định đúng trong các khẳng định dưới đây A. f
 xdx Fx. B. F
 xdx f x . C C. f
 xdx Fx . C D. f
 xdx  FxC.
Câu 13:Trong các số phức bên dưới, tìm số thuần ảo. A. z  2022 . i
B. z  3 4 . i
C. z  2022  2023 . i D. z 1 2 . i x Câu 14:Tính 3 . dxx  2
A. x  ln x  2 .
B. x  ln x  2  C.
C. x  ln x  2  C.
D. x  ln x  2  C.
Câu 15: Trong không gian to ̣a đô ̣ Oxyz , viết phương trình mă ̣t phẳng đi qua điểm M 1;1; 2  và có 
vecto pháp tuyến n  2;3;2. Trang6
A. x y  2z 1  0.
B. 2x  3y  2z  2  0.
C. 2x  3y  2z 1  0.
D. x y  2z  2  0.
Câu 16: Trong không gian to ̣a đô ̣ Oxyz , cho mă ̣t phẳng   có phương trình: 4x  6y  2z  7  0.Tìm
mô ̣t vecto pháp tuyến của mp  .    
A. b  6; 4; 2  .
B. n  2; 3;  1 . C. m   4  ;6; 2  .
D. a  4;6;   1 .
Câu 17:Tính diện tích hình phẳng giới hạn bởi các đường sau: 2
y x  2x , 2
y  x  4x , x  0 , x  3. A. 7. B. 9. C. 6. D. 8.
Câu 18:Tính thể tích vật thể tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường sau khi quay 1 quanh Ox: 3 2 y
x x , y  0 , x  0, x  3. 3 8 16 27 81 A. . B. . C. . D. . 35 35 35 35
Câu 19:Tính diện tích hình phẳng giới hạn bởi các đường sau: 2
y x  2x , trục hoành, x  1  , x  2 . 4 5 8 7 A. . B. . C. . D. . 3 3 3 3
Câu 20: Tính sin x 3cos xd .x
A. cos x  3sin x C
B. cos x  3sin x C
C. cos x  3sin x C
D. cos x  3sin x C 
Câu 21:Trong không gian to ̣a đô ̣ Oxyz , cho hai điểm M 4;3;2, N 1;2;3. Tính tọa độ MN.    
A. MN  3;1;   1 . B. MN   3  ;1;  1 .
C. MN  3; 1;  1 .
D. MN  3; 1  ;  1 .
Câu 22:Chọn khẳng định sai trong các khẳng định dưới đây b b b b d b A. f
 xdxg
 xdx   f
  xgxdxB. f
 xdxg
 xdx   f
  x gxdxa a a a c a b b b a C.
kf xdx k
f xd , x k      . D. f
 xdx   f
 xd .x a a a b
Câu 23: Chọn khẳng định đúng trong các khẳng định dưới đây b d d b d d A. f
 xdxf
 xdx f
 xd .x B. f
 xdxf
 xdx f
 xd .x a c b a c a b d c b d d C. f
 xdxf
 xdx f
 xd .x D. f
 xdxf
 xdx f
 xd .x a c a a b a
Câu 24:Điểm M trong hình ảnh bên dưới là điểm biểu diễn của số phức nào? Trang7
A. z  2  3 . i
B. z  3 2 . i C. z  2 . i D. z  3   2 .i 1 2 Câu 25:Tính x    1 d . x 0 11 7 2 A. B. C. D.1 3 3 3
Câu 26:Tìm số phức liên hơp của số phức z  4  5 . i
A. z  4  5 . i B. z  4   5 .i C. z  4   5 .i D. z  5  .i
Câu 27: Chọn khẳng định đúng trong các khẳng định dưới đây 2 x x A. xdx   C. 
B. x x 3 2 2 2 dx   x C. 3 3 2022 x
C. x  
1 dx  2x  2  . C D. 2021 x dx  .  2022 
Câu 28:Tính độ dài của vecto a   1  ;3; 26     A. a  26. B. a  10. C. a  6. D. a  36. 1
Câu 29: Tìm F x là một nguyên hàm của hàm f x 2 x 3 e   , biết F 0 3  e 1. 2 1 1 1 A. 2 x 3 e   1. B. 2 x 3 e   2. C. 2x 3 e  . D. 2 x 3 e  1. 2 2 2
Câu 30:Nêu công thức tính thể tích khối tròn xoay đươ ̣c ta ̣o thành khi quay miền D quay quanh tru ̣c
hoành, biết D là hình phẳng giới hạn bởi đồ thị hàm số y f x (hàm y f x liên tu ̣c trên a;b ), trục
Ox , đường thẳng x a và đường thẳng x b ? b b b b
A.V     f xd .x B.V     f x2 d .x C.V f
 xd .x D.V   f
 xd .x a a a a
Câu 31:Trong không gian to ̣a đô ̣ Oxyz , phương trình mă ̣t phẳng đi qua ba điểm
A1;0;0, B0; 2;0, C0;0;3, là phương trình nào trong các phương trình dưới đây? x y z x y z x y z x y z A.   1  0. B.    1. C.    1. D.    1. 1 2 3 1 2 3 2 1 3 3 2 1 
Câu 32:Tính  sin x  cos x2 4 d . x 0  1  2  1 A. . B. . C. 2. D.  . 4 2 4 2
Câu 33:Tính 1 3  2xd . x  0 1   3 3 1   2 3 1 3 3 1   3 3 A. . B. . C. . D. . 3 6 3 3
Câu 34:Biết D là hình phẳng giới hạn bởi đồ thị hàm số y f x (hàm y f x liên tu ̣c trên a;b ),
trục Ox , đường thẳng x a và đường thẳng x b (xem hình vẽ bên dưới). Tính diện tích của miền D? Trang8 b c b A. S f x dxB. S   f x dx f x dx   D     . D   . a a c c b c b C. S f x dx f x dx   D. S f x dx f x dx   D     . D     . a c a c
Câu 35:Trong không gian to ̣a đô ̣ Oxyz , phương trình mă ̣t phẳng đi qua ba điểm A2; 1  ;3, B4;2  ;1 , C  1
 ;2;3, là phương trình nào trong các phương trình dưới đây?
A. 2x  2 y  5z 17  0. B. 2
x  2y  5z 17  0. C. 2x  2y  5z 17  0. D. 2x  2y  5z 17  0.
Câu 36:Cho số phức z  5  4 .
i Số phức đối của z có điểm biểu diễn hình học là A.(5;4) B.(-5;-4) C.(5;-4) D.(-5;4)
Câu 37:Tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn z  2  i  4 là đường tròn có tâm I và
bán kính R lần lượt là : A.I(-2;-1); R = 4 B.I(-2;-1); R = 2 C.I(2;-1); R = 4 D.I(2;-1); R = 2 Câu 38:Cho       1 x F x x
e là một nguyên hàm của hàm số   3x
f x e . Tìm nguyên hàm của hàm số   3x f x e . A.     3x  2    1 x f x e dx x e C B.     3x  6    3 x f x e dx x e C C.
   3x 63  x f x e dx x e C D.
   3x 63  x f x e dx x e C
Câu 39:Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;1;1) và hai mặt phẳng
P:2x y 3z 1 0,(Q): y  0. Viết phương trình mặt phẳng (R) chứa A, vuông góc với cả hai mặt phẳng (P) và (Q)?
A. 3x y  2z  2  0
B. 3x  2y  2z  4  0
C. 3x  2z 1  0
D. 3x  2z  0
Câu 40:Trong không gian to ̣a đô ̣ Oxyz , viết phương trình mă ̣t cầu có đường kính là A,B, biết A0;1; 3  , B4;3  ;1 . A.  2 2 2
x  2   y  2   z  2 2 2 1  9.
B. x  2   y  2  z   1  3. C.  2 2 2
x  2   y  2   z  2 2 2 1  9.
D. x  2   y  2  z   1  9. 1 Câu 41:Cho hàm số 2 f x 4 3 2  x 4
x 3x x 1, x
  . Tính I f
 x.f 'xdx 0 Trang9 7 7 A. B. C. 2 D. -2 3 3 1 7 x
Câu 42:Cho tích phân I    dx giả sử đặt 2
t  1 x . Tìm mệnh đề đúng? 1 x  , 5 2 0 2  2 3 t  3 1 2 2 1 t  3 1 1 t   1 dt 3 t  3 1 A. I dtB. I dtC. I   D. I dt  5 t 4 2 t 5 2 t 4 2 t 1 1 1 1
Câu 43:Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 2
y  x 2x  1 và 2
y  2x  4x 1 là A. 6 B. 7 C. 5 D. 4
Câu 44:Tìm họ nguyên hàm của hàm số f x 5  tan x 1 1 1 1 A. f  x 4 2 dx  tan x
tan x  ln cos x C B. f  x 4 2 dx  tan x
tan x  ln cos x C 4 2 4 2 1 1 1 1 C. f  x 4 2 dx  tan x
tan x  ln cos x C D. f  x 4 2 dx  tan x
tan x  ln cos x C 4 2 4 2
Câu 45:Trong không gian với hệ tọa độ Oxyz, cho các điểm A2;1;0, B 1;1;3 , C 2; 1  ;3 , D1; 1  ;0.
Bán kính mặt cầu ngoại tiếp tứ diện ABCD là 15 14 A. 5 B. C. 2 D. 2 2 x 1 y  2 z
Câu 46:. Phương trình đường thẳng song song với đường thẳng d :   1 1 1  và cắt hai đường x 1 y 1 z  2 x 1 y  2 z  3 thẳng d :   ; d :   1 2 1  1 1  1  là 1 3 x 1 y  2 z  3 x 1 y 1 z  2 x 1 y z 1 x 1 y z 1 A.         1 1 1  B. 1  C. 1 1 1 1  D. 1 1 1 1  Câu 47:Cho hàm số f x có
f  x liên tục trên nửa khoảng 0;  thỏa mãn       2 1 3  13 x f x f x e  biết f   11 0  . Giá trị f ln 6   bằng 3  2  5 6 5 6 1 A. B. C. 1. D. 9 18 2
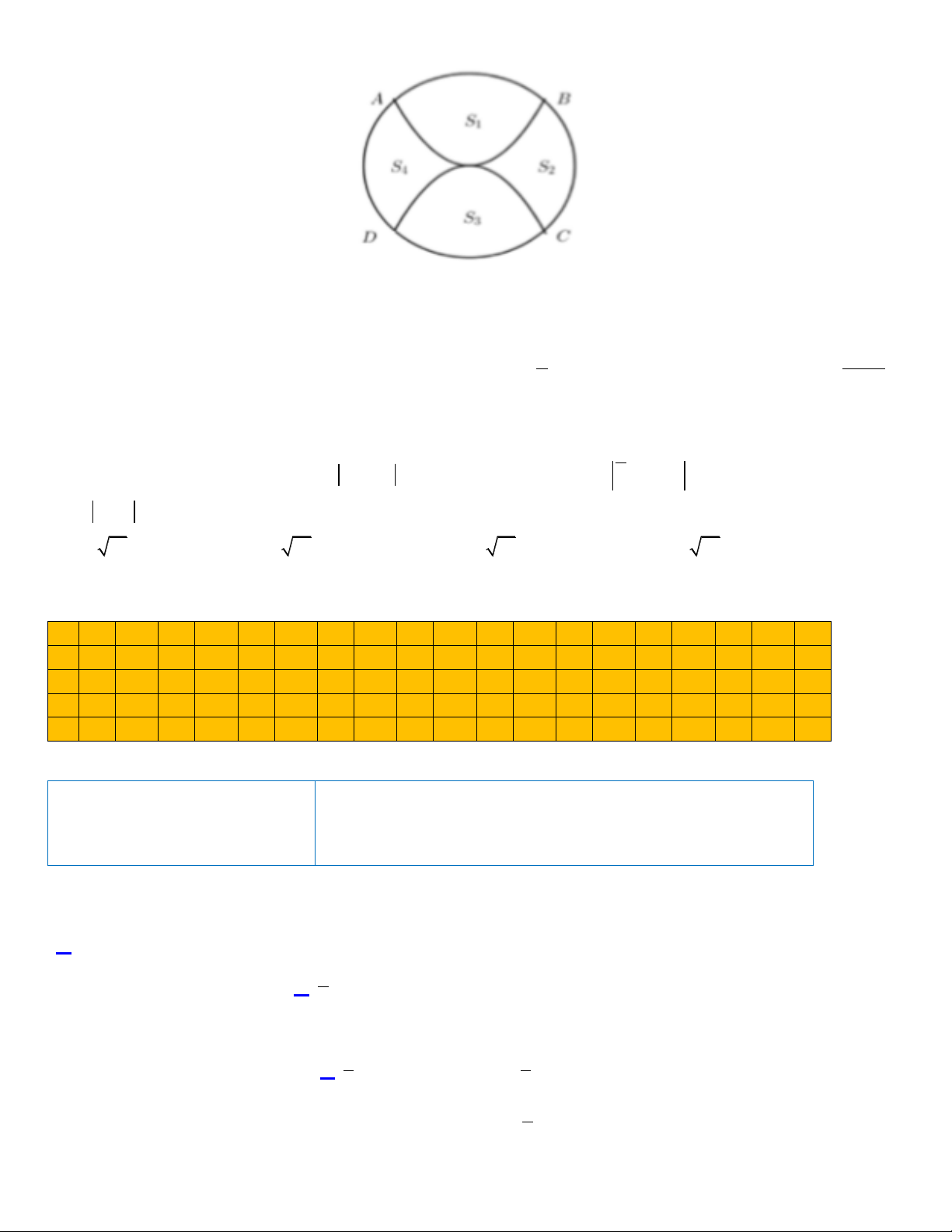
Câu 48:Khuân viên trường THPT Cam Lô ̣ có một bồn hoa hình tròn có tâm O. Một nhóm học sinh lớp
12 được giao thiết kế bồn hoa, nhóm này chia bồn hoa thành bốn phần, bởi hai đường Parabol có cùng
đỉnh O và đối xứng nhau qua O. Hai đường Parabol này cắt đường tròn tại bốn điểm A, B, C, D tạo
thành một hình vuông có cạnh bằng 4m (như hình vẽ). Phần diện tích S1, S2 dùng để trồng hoa, phần
diện tích S3, S4 dùng để trồng cỏ (Diện tích được làm tròn đến hàng phần trăm). Biết kinh phí trồng hoa là 150.000 đồng/ 1 2
m , kinh phí trồng cỏ là 100.000 đồng/1 2
m . Hỏi cả trường cần bao nhiêu tiền
để trồng bồn hoa đó? (Số tiền làm tròn đến hàng chục nghìn). Trang10 A.6.060.000 đồng B.3.270.000 đồng C.3.000.000 đồng D.5.790.000 đồng 1 
Câu 49:Cho hàm số y f x xác định trên R \   thỏa mãn điều kiện f  x 2  , 2  2x 1
f 0  1, f  
1  2. Giá trị của biểu thức f   1  f 3 bằng A. 3  ln15 B. 4  ln15 C. 2  ln15 D. ln15
Câu 50:Cho số phức z thỏa mãn z 1 i  1, số phức w thỏa mãn w  2  3i  2. Tính giá trị nhỏ nhất của z w A. 13  3 B. 17  3 C. 13  3 D. 17  3
------ HẾT ------ ĐÁP ÁN 1 A 6 C 11 C 16
B 21 C 26 A 31 B 36 D 41 B 46 D 2 C 7 A 12 C 17
B 22 B 27 B 32 D 37 A 42 C 47 B 3 A 8
D 13 A 18 D 23 D 28 C 33 A 38 A 43 D 48 D 4 C 9
D 14 D 19 C 24 B 29 D 34 D 39 C 44 A 49 A 5 C 10 B 15 C 20
B 25 B 30 B 35 A 40 A 45 D 50 D ĐỀ 3
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 - NĂM HỌC 2021 –2022 Thuvienhoclieu.com MÔN TOÁN 12
Câu 1. Hàm số F (x) là một nguyên hàm của hàm số f (x) trên khoảng K nếu
A. F '(x)   f (x), x
  K.B. f '(x)  F(x), x   K.
C. F '(x)  f (x), x   K.
D. f '(x)  F(x), x   K. 1 Câu 2. 4 x dx  bằng: A. 5
x C B. 3
4x C C. 5 x C D. 5 5x C 5
Câu 3. Họ nguyên hàm của hàm số 3 (x)  x f
e là hàm số nào sau đây? 1 1 A. 3 x e C . B. 3x eC . C. x e C . D. 3 3 x eC . 3 3 1
Câu 4. Tìm họ nguyên hàm của hàm số 2   3x y x  . x Trang11 3 3x x 1 3 x x 1 A.  
C, C   . B.  3   C, C   2 3 ln 3 x 2 3 x 3 3x x 3 3x x C.
 ln x C, C   . D.
 ln x C, C   . 3 ln 3 3 ln 3
Câu 5. Họ nguyên hàm của hàm số f x 2
 3x  sin x là A. 3
x  cos x C .
B. 6x  cos x C . C. 3
x  cos x C .
D. 6x  cos x C .
Câu 6. Hàm số y f x liên tục trên2;9. F x là một nguyên hàm của hàm số f x trên
2;9 và F 2  5; F 9  4. Mệnh đề nào sau đây đúng 9 9 9 9
A. f xdx  1   . B. f
 xdx 1. C. f
 xdx  20. D.f xdx  7. 2 2 2 2 2 3 3
Câu 7. Nếu f xdx  2   và f
 xdx 1 thì f xdx  bằng 1 2 1 A. 3  . B. 1. C.1. D. 3 . 1 1 Câu 8. Nếu f
 xdx  4 thì 2 f xdx  bằng 0 0 A.16. B. 4 . C. 2 . D. 8 . 1 Câu 9. Tính tích phân 4
I  (x x 1)dx  0 7 7 10 7 A. I B. I C. I D. I   10 3 7 10
Câu 10 .Cho hàm số y f x xác định và liên tục trên đoạn  ;
a b . Diện tích hình phẳng giới
hạn bởi đồ thị hàm số y f x , trục hoành và hai đường thẳng x a, x b được tính theo công thức b b b a A. S f  x dx.
B. S f  xdx .
C. S   f
 xdx. D.S f  x dx. a a a b
Câu 11. Gọi S là diện tích của hình phẳng giới hạn bởi các đường 2x y
, y  0 , x  0 , x  2 .
Mệnh đề nào dưới đây đúng? 2 2 2 2 A.   2x S dx B.  2x S dx C. 2   2 x S dx D. 2  2 x S dx  0 0 0 0
Câu12. Cho hàm số f x liên tục trên  . Gọi S là diện tích hình phẳng giới hạn bởi các đường
y f x, y  0, x  1
 , x  2 (như hình vẽ bên). Mệnh đề nào dưới đây đúng? Trang12 1 2 1 2 A. S f
 x dx + f
 x dx . B.S   f
 x dx f
 x dx . 1  1 1  1 1 2 1 2
C. S   f
 x dx+ f
 x dx . D.S f
 x dx  f
 x dx . 1  1 1  1
Câu13.Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong,
giới hạn bởi đồ thị hàm số y f x , trục Ox và hai đường thẳng x  ,
a x b a b , xung quanh trục Ox . b b b b A.V f
 xdx B. 2 V   f
 xdx C. 2 V f
 xdx
D.V   f  xdx a a a a
Câu 14.Cho hình phẳng D giới hạn bởi đường cong  x y
e , trục hoành và các đường thẳng x  0
, x  1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu?  2e   1 2  2e   e  1  2 e 1 A. V B. V C. V D. V  2 2 3 2
Câu 15.Số phức có phần thực bằng 1 và phần ảo bằng 3 là A.1 3i B. 1  3i
C.1 3i D. 1  3i
Câu 16:Số phức liên hợp của số phức z  3  4i là: A. z  3   4i B. z  3   4i
C. z  3  4i
D. z  3  4i
Câu 17.Cho số phức z  2  i . Tính z .
A. z  5
B. z  5
C. z  2 D. z  3
Câu 18.Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn số phức z  1 2i ? A. Q1;2 . B. M 2  ;1 . C. P  2   ;1 .
D. N 1; 2 .
Câu 19.Điểm nào trong hình vẽ bên là điểm biểu diễn của số phức z  1   2i ? A. P B. M C. Q D. N Trang13
Câu 20.Trong không gian
Oxyz , cho hai điểm A2;4;  1 ,B  1  ;1;3và mặt phẳng
P:x 3y  2z 5  0. Lập phương trình mặt phẳng Q đi qua hai điểm A , B và vuông góc với
mặt phẳng P .
A. 2x  3y 11  0 .
B. 2 y  3z 11  0 .
C. x  3y  2z  5  0 . D. 3y  2z 11  0 .
Câu 21.Cho hai số thực x và y thỏa mãn 2x  3yi  3 i  5x  4i với i là đơn vị ảo.Khi đó x+y=? A.3. B.-2. C.0. D.2.
Câu 22.Cho hai số phức z  1 2i và z  2  i . Số phức z z bằng 1 2 1 2
A. 3 i B. 3  i
C. 3i D. 3  i
Câu 23.Cho hai số phức z  3  2i và z  2  i . Số phức z z bằng 1 2 1 2 A. 1   3i . B. 1   3i . C.1 3i . D.1 3i .
Câu 24.Cho hai số phức z = 3- i và z = - 1+ i . Phần ảo của số phức z z bằng 1 2 1 2 A. 4 . B. 4i . C. 1. D. 2  .
Câu 25.Cho hai số phức z 1 3i và w 1 i . Môđun của số phức z.w bằng A. 2 5 . B. 2 2 . C. 20 . D.8 .
Câu 26.Cho số phức z thỏa mãn z 1 i  3 5i . Tính môđun của z A. z  17 . B. z  16 . C. z  17 . D. z  4 .
Câu 27.Cho a,b   và thỏa mãn a bii  2a 1 3i , với i là đơn vị ảo. Giá trị a b bằng A. 4 B. 10  C. 4  D.10 
Câu 28.Trong không gian Oxyz , cho hai điểm A1;1; 2 và B 2; 2 
;1 . Vectơ AB có tọa độ là A.  1  ;1; 3 B. 3;1;  1 C. 1;1;3 D. 3;3;   1
Câu 29.Trong không gian Oxyz , hình chiếu vuông góc của điểm M 2; 2;  1 trên mặt phẳng
Oxy có tọa độ là A. 2;0;  1 . B. 2; 2;0 . C. 0; 2;  1 . D. 0;0;  1 .     
Câu 30.Trong không gian với hệ trục tọa độ Oxyz , cho a i
  2 j 3k . Tọa độ của vectơ a là A.  1  ;2; 3   . B. 2; 3  ;  1 . C. 2; 1  ; 3   . D.  3  ;2;  1 .
Câu 31.Trong không gian với hệ tọa độ Oxyz, cho hai điểm A1; 3  ;  1 , B3;0; 2   . Tính độ dài AB . A. 26. B. 22. C. 26 . D. 22.
Câu 32.Trong không gian với hệ tọa độ Oxyz , cho các điểm A1;0;3 , B2;3; 4 , C  3  ;1;2. Tìm
tọa độ điểm D sao cho ABCD là hình bình hành. A. D 4  ; 2;9. B. D  4  ;2;9 .
C. D 4; 2;9 .
D. D 4;2; 9 .
Câu 33.Trong không gian Oxyz , phương trình mặt cầu có tâm I(a;b;c) bán kính R là: Trang14 A.  2 2 2
S   x a2  y b2 z c2 2 : . .  R .
B. S   x a
y b z c 2 :       R . C.  2 2 2
S   x a2  y b2  z c2 2 :       R .
D. S  :x a   y b  z c  R .
Câu 34.Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x y z  8x 10 y  6z  49  0. Tính bán kính
R của mặt cầu  S  . A. R  1 . B. R  7 . C. R  151 . D. R  99 .
Câu 35.Trong hệ trục tọa độ Oxyz , phương trình mặt cầu tâm I 2;1; 2 bán kính R  2 là: A.  2 2 2
x  2   y  2   z  2 2 1 2  2 .
B. x  2   y  
1   z  2  4 . C.  2 2 2
x  2   y  2   z  2 2 1 2  4 .
D. x  2   y  
1   z  2  2 . Câu 36.Trong không gian với hệ trục Oxyz , cho phương trình 2 2 2
x y z  m   2 2
2 x  4my  2mz  5m  9  0 . Tìm các giá trị của m để phương trình trên là
phương trình của một mặt cầu. A. m  5  hoặc m 1 . B. 5   m  1. C. m  5  hoặc m  1. D. 5   m 1.
Câu 37.Trong không gian Oxyz , cho mặt phẳng P : 2x y  3z 1  0 . Vectơ nào dưới đây là
một vectơ pháp tuyến của P ?    
A. n  2;3;1 . B. n  2; 1  ; 3  .
C. n  2;1;3 .
D. n  2; 1;3 . 2   4   1   3  
Câu 38.Trong không gian Oxyz , cho 3 điểm A 1
 ;0;0 , B0;2;0 và C 0;0;3 . Mặt phẳng  ABC có phương trình là x y z x y z x y z x y z A.    1. B.    1. C.
   1. D   1. 1 2 3  1 2  3 1  2 3 1 2 3
Câu 39.Trong không gian với hệ tọa độ Oxyz , phương trình nào dưới đây là phương trình mặt 
phẳng đi qua điểm M 1;2; 3
  và có một vectơ pháp tuyến n  1;2;3 .
A. x  2 y  3z 12  0
B. x  2 y  3z  6  0 C. x  2 y  3z 12  0 D. x  2y  3z  6  0
Câu40.Trong không gian với hệ tọa độ Oxyz , cho hai điểm A0;1;1 ) và B1;2;3 . Viết phương
trình của mặt phẳng P đi qua A và vuông góc với đường thẳng AB .
A. x y  2z  3  0
B. x y  2z  6  0
C. x  3y  4z  7  0 D. x  3y  4z  26  0 Câu 41.
Cho hàm số f x thỏa mãn f   1 2  
và f x  x f x 2 3 4  
 với mọi x . Giá trị 25 của f   1 bằng 391 1 41 1 A. B. C. D.  400 40 400 10 Lờigiải ChọnD Trang15f  x  1  1
Ta có f x  x f x 2 3 4    3     x 3     4  x 4   x C f x 4 2   f xf x    1 Do f   1 2   , nên ta có C  9
 . Do đó f x    f   1 1   . 25 4 x  9 10 4 x Câu 42. Cho dx a  . b ln 2  
c ln 3 , với a,b,c là các số hữu tỷ. Giá trị của P  6a b c 2 3  x   1 bằng: A. 1 . B. 1 . C. 2 . D.3. 1 2
Câu 43. Cho hàm số f (x) xác định trên  \   thỏa mãn f  x 
, f 0  1, f   1  2 . Giá trị 2 2x 1
của biểu thức f  
1  f 3 bằng A. 2  ln15 B. 3 ln15 C. 4  ln15 D. ln15 Lờigiải ChọnC 2
dx  ln 2x 1  C f  x 2x 1 Với 1 x
, f 0  1  C 1 nên f   1  1 ln 3 2 Với 1 x  , f  
1  2  C  2 nên f 3  2  ln 5 2 Nên f  
1  f 3  3  ln15 2
Câu 44. Cho hàm số f x thỏa mãn A  x  
1 f  x dx  9 và 3 f 2  f 0  12 . Tính 0 2 I f
 xdx 0 A. I  3  . B. I  3. C. I  6  . D. I  6. 2
Lời giải: A  x  
1 f  xdx  9 0 Đặt u=x+1 suy ra du=dx dv=f’(x)dx suy ra v=f(x) 2 2
A  (x 1) f (x) |  f x dx  9  3 f (2)  f (0)  I  9  0   Vậy 0  I  3
Câu 45. Cho hàm số y f x có đạo hàm trên  , đồ thị hàm số y f x như hình vẽ. Biết
diện tích hình phẳng phần sọc kẻ bằng 3 . Tính giá trị của biểu thức: 2 3 4 T f
 x 1dx  f
 x 1dx  f  2x8dx 1 2 3 Trang16 9 3 A.T  . B.T  6 . C.T  0 . D.T  . 2 2 Lờigiải 0
 Diện tích phần kẻ sọc là: S f  x dx 3. 2  0 0 0
Vì f x  0 x   2  ;0  3  f
 x dx   f   xdx 
f xdx  3   . 2  2  2  4
 Tính I f  2x8dx . 3
Đặt t  2x 8  dt  2dx ; x  3t  2
 ; x  4 t  0. 0 1 0 1 3 Suy ra: I f  t. dt  f
 xdx   . 2 2 2 2  2  2 3 4
 Vậy T f
 x  1dx  f
 x 1dx  f  2x 8dx 1 2 3
f x   2 1
f x   3 1
I f    f    f    f   3 3 2 2 1      3 3 2 1   . 1 2 2 2 2 a 1
Câu 46. Diện tích S của hình phẳng giới hạn các đường 2
y x x  1 ; y  0 ; x  2 là S c
Giá trị của biểu thức P a c bằng
A. P  3.
B. P  122 .
C. P  112 .D. P  22 .
Câu 47. Một xe lửa chuyển động chậm dần đều và dừng lại hẳn sau 20 s kể từ lúc bắt đầu hãm
phanh. Trong thời gian đó xe chạy được 120m. Cho biết công thức tính vận tốc của chuyển
động biến đổi đều là v v at ; trong đó a ( 2
m/s ) là gia tốc, v (m/s) là vận tốc tại thời điểm t 0
(s). Hãy tính gia tốc a của xe lửa khi hãm phanh. A. 2
0, 6 m / s . B. 2 0  ,6 m / s . C. 2
12 m / s . D. 2 1  ,2 m / s .
Câu 48. Cho z là số phức thỏa mãn z z  2i . Giá trị nhỏ nhất của z 1 2i z 1 3i là A. 5 2 . B. 13 . C. 29 . D. 5 .
Đặt z a bi a, b  . Trang17
Ta có: z z i a b a  b  2 2 2 2 2 2
 4b  4  0  b  1 
z a i . Xét: 2 2
z 1 2i z 1 3i a 1 i a 1 4i    a 2     a 2 1 1 1  4 . Áp dụng BĐT Mincôpxki:
  a2     a2     a   a2    2 2 2 1 1 1 4 1 1 1 4  4  25  29 .
Suy ra: z 1 2i z 1 3i đạt GTNN là 29 khi   a 3 4 1
 1 a a  . 5
Câu 49. Cho số phức z a bi a, b  thỏa mãn z 1 3i z i  0 . Tính S  2a 3b. A. S  6  .
B. S  3.
C. S  2 . D. S  5.
Câu 50. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A3; 2
 ;6, B0;1;0 và mặt cầu
S x 2 y  2 z  2 : 1 2 3
 25. Mặt phẳng P: ax by cz  2  0 đi qua ,
A B và cắt S  theo
giao tuyến là đường tròn có bán kính nhỏ nhất. Hãy tìm chu vi của đường tròn có bán kính nhỏ nhất. A. 2 . B. 4 5 . C. 2 5 . D.10 5 . Lờigiải
Mặt cầu S có tâm I 1;2;3 và bán kính R  5 A 
P 3a2b6c2  0 a  22c Ta có    B 
P  b2   0 b   2
Bán kính của đường tròn giao tuyến là r R   2 2 2
dI;P  25   
d I;P
Bán kính của đường tròn giao tuyến nhỏ nhất khi và chỉ khi dI;P lớn nhất 2 a 2b 3c 2
2  2c  4  3c  2 c 4
Ta có dI,P       2 2 a  2 b  2 c  5c  8c  2  2c2  2 2  2 c 8 c  2 4  2
48c  144c  192 Xét f c   
f c  2 5c  8c  8 2  c
5c  8c  82 4 2    2 5c  8c  8 f c c     1 0  c    4 Bảng biến thiên Trang18 x - ¥ - 4 1 + ¥ y ' - 0 + 0 - 1 y 5 5 0 1 5
Vậy dI;P lớn nhất bằng 5 . 2 2
r  25  d I;P  25    5      2 5 C   2 r   2 .2 5   4 5 ĐỀ 4
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 - NĂM HỌC 2021 –2022 Thuvienhoclieu.com MÔN TOÁN 12
Câu 1:Trong không gian Oxyz , cho mặt cầu S  2 2 2
: (x  3)  ( y 1)  (z 1)  2 . Tâm của (S) có tọa độ là A. (3; 1  ;1) . B. ( 3  ; 1  ;1) . C. (3;1; 1  ) . D. ( 3  ;1; 1  ) . 1
Câu 2: Tính tích phân I   3 2 x x   1dx 0 5 1 7 1 A. I   B. I  . C. I  . D. I  . 12 2 3 3
Câu 3:Cho hai số phức z  1 2i; z  3  i .Tìm z z 1 2 1 2 A.13. B. 13 . C.5. D. 5 . 1
Câu 4:Số phức liên hợp của số phức z biết z  (1 i)(3  2i)  là: 3  i 13 9 53 9 53 9 13 9 A.i . B.i . C.i . D.i . 10 10 10 10 10 10 10 10
Câu 5:Phần thực của số phức z  5  4i là
A. 5 .B. 4 .C. 5  .D. 4  .
Câu 6: Tìm số phức z thỏa mãn z  2  3i  3  2i
A. z  1 5i .
B. z  1 i .
C. z  5  5i .
D. z  1 i .
Câu 7:Cho số phức z  3
  2i , số phức 1 iz bằng
A. 5  i . B. 5   i . C.1 5i . D. 1  5i
Câu 8:Trên mặt phẳng tọa độ Oxy, điểm nào dưới đây là điểm biểu diễn số phức z  1   2i ? A. Q  2  ;  1 . B. N  1  ;2 . C. M 1; 2   .
D. P 2;   1 .
Câu 9:Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm Trang19M (1; 2; 3
 ) và có một vectơ pháp tuyến n  (1; 2  ;3) ?
A. x  2 y  3z  12  0 . B. x  2 y  3z  6  0 .
C. x  2 y  3z 12  0 .
D. x  2 y  3z  6  0 .
Câu 10:Cho số phức z  4  3i . Môđun của số phức w  2z 1 là: A. 117 . B. 2 13 . C.5. D. 3 10 . 2 2 2
Câu 11:Trong không gian Oxyz , cho mặt cầu (S) :  x  
1   y  2   z  3  4 . bán kính của mặt cầu đã cho bằng
A.16 . B. 2 . C. 4 . D. 10 .
Câu 12:Cho A2;2;  1 ,B1;0;  2 ,C1;2;  3 ,D 1;1;  2 ,E0;2; 
1 ,   : 4x y  3z 1  0 . Có bao nhiêu
điểm đã cho nằm trên mặt phẳng   ? A. 2. B.4. C. 1. D. 3 . 1
Câu 13: Cho hai hàm số 3 2
f (x)  ax bx cx 1 và 2
g(x)  dx ex  (a, ,
b c, d , e   ) . Biết rằng đồ thị của 2
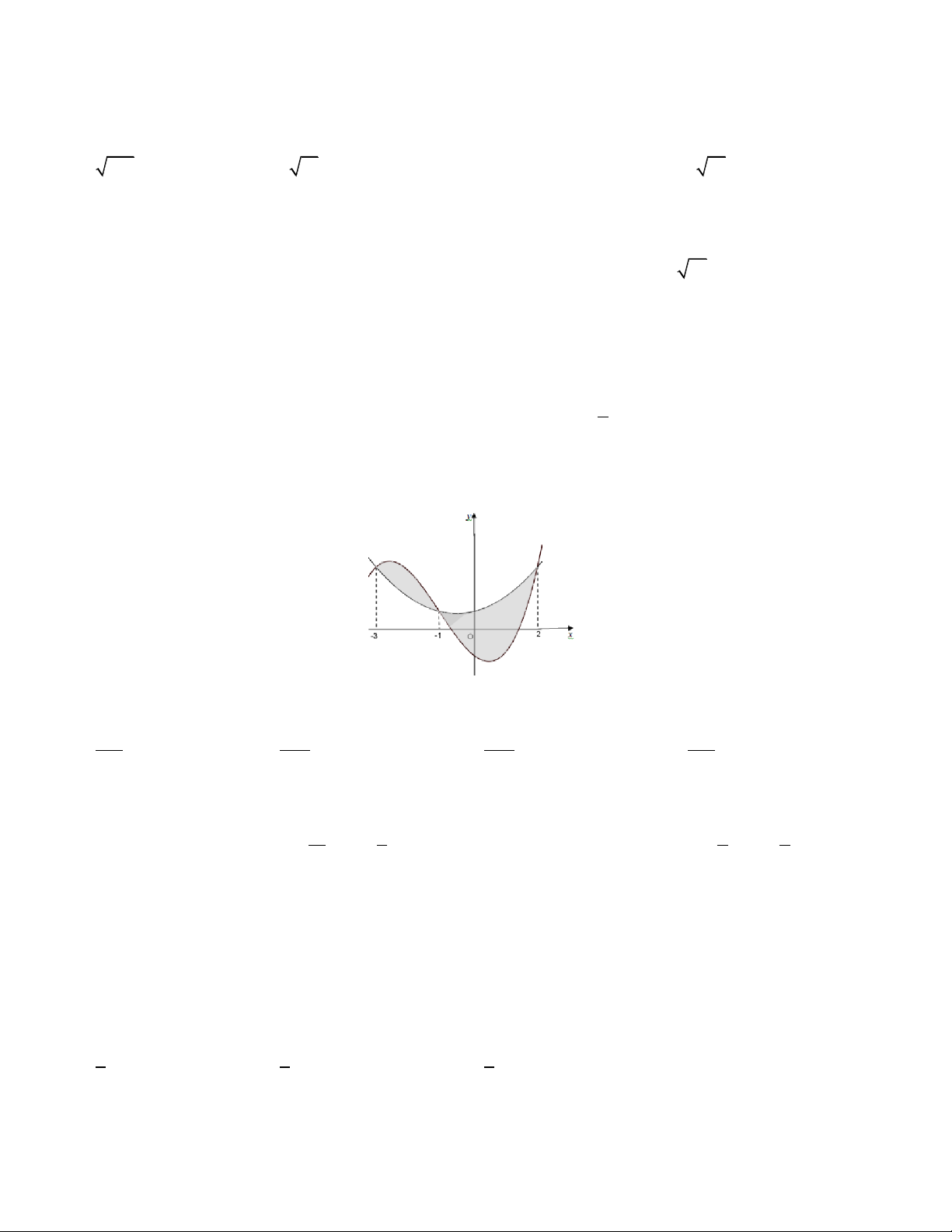
hàm số y f (x) và y g(x) cắt nhau tại ba điểm có hoành độ lần lượt là 3  ; 1
 ; 2 (tham khảo hình vẽ bên) .
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng 125 253 253 125 A. . B. . C. . D. . 12 12 48 48
Câu 14: Tìm các số thực x, y thỏa mãn: (x  2y)  (2x  2y)i  x  y   1  y  3i. 11 1 3 1 A. x  1  , y 1. B. x  , y   . C. x  1, y  1  . D. x  , y   . 3 3 4 2
Câu 15:Trong không gian Oxyz , cho mặt phẳng   : x  2 y  4z 1  0 .Vectơ nào dưới đây là một vectơ pháp
tuyến của mặt phẳng   ?     A. n  1
 ;2;4 .B. n  1;2;4 . C. n  1;2; 4
 . D. n  1; 2  ;4 . 3   1   2   4   2 Câu 16: 3x 1 e   dx bằng 1 1 1 1 A. 5 2 e  e . B.  5 2 e  e  . C.  5 2 e  e  . D. 5 2 e  e . 3 3 3
Câu 17: Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y  f x liên tục trên a;b , trục hoành và
hai đường thẳng x  a , x  b được tính theo công thức: Trang20 b b A. S  f  x dx. B. S  f  xdx. a a 0 b 0 b C. S  f
 xdx  f xdx. D. S  f
 xdx  f xdx. a 0 a 0 x  1 3tx 1 y  2 z
Câu 18:Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng d :  y  2   t , d :   và 1  2 2 1  2 z  2 
mặt phẳng (P) : 2x  2 y  3z  0 . Phương trình nào dưới đây là phương trình mặt phẳng đi qua giao điểm của
d và (P), đồng thời vuông góc với d . 1 2
A. 2x y  2z  13  0 .
B. 2x y  2z  22  0 .
C. 2x y  2z 13  0 .
D. 2x y  2z  22  0 . 2 dx Câu 19:Tích phân  bằng 3x  2 1 2 1 A. 2 ln 2 . B. ln 2 . C. ln 2 . D. ln 2 . 3 3 x  3 y 1 z  5
Câu 20:Trong không gian Oxyz , cho đường thẳng d :  
. Điểm nào dưới đây thuộc d ? 2 2 1 
A. P 2; 2;  
1 . B. Q 2; 2  ;1 .
C. M 3;1;5 . D. N 3;1; 5  . 1  1 1  Câu 21: Cho 
dx a ln 2  b ln 3  
với a, b là các số nguyên. Mệnh đề nào dưới đây đúng ?
x 1 x  2  0
A. a b  2  .
B. a b  2 .
C. a  2b  0 .
D. a  2b  0 .
Câu 22:Cho số phức z thỏa mãn 3z i 2 iz  310i . Mô đun của z bằng A. 3 . B. 5 . C. 3 . D. 5 .
Câu 23:Trong không gian Oxyz , mặt phẳng Oxz  có phương trình là
A. x y z  0 . B. x  0 . C. z  0 . D. y  0 .
Câu 24:Số phức liên hợp của số phức 3  4i là A. 3   4i . B. 3   4i . C. 4  3i .
D. 3  4i . 1 1
Câu 25:Kí hiệu z , z là hai nghiệm phức của phương trình 2
z z  6  0 . Tính P   1 2 z z 1 2 1 1 1 A. P   . B. P  . C. P  6 . D. P  6 6 12 e
Câu 26: Tính tích phân I x ln d x x  1 2 e 1 1 2 e  2 2 e 1 A. I  . B. I  . C. I . D. I . 4 2 2 4 Trang21 e Câu 27: Cho 2
(1 x ln x)dx ae be c
với a, b, c là các số hữu tỉ. Mệnh đề nào dưới đây đúng ? 1
A. a b c .
B. a b c  .
C. a b c .
D. a b c  .
Câu 28:Điểm nào trong hình vẽ bên là điểm biểu diễn của số phức z  2   i? A. Q . B. N . C. M . D. P .
Câu 29:Cho hai số phức z  2  i, z  1 i . Trên mặt phẳng tọa độ Oxy, điểm biểu diễn số phức 2z z có 1 2 1 2 tọa độ là:
A. 5;0 .B.  1  ;5 . C. 5; 1
. D.0;5 . 1 1 1 Câu 30: Biết
f xdx  2   và g
 xdx  3, khi đó  f
 x gxdx  bằng 0 0 0 A. 5.  B.1. C. 5. D. 1.  uuur
Câu 31:Trong không gian Oxyz , cho hai điểm A1;1; 1  , B 2;3; 2 . Vectơ AB có tọa độ là
A. 1;  2;3 . B. 3;5  ;1 . C. 1;2;3 . D. 3;4;  1 .
Câu 32: Tìm thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số
y  f x liên tục trên a;b , trục Ox và hai đường thẳng x  a, x  b a  b, xung quanh trục Ox. b b b b
A. V   f xdx. B. V   2
f x dx. C. V   f x dx.D. V   2 f x dx. a a a a
Câu 33:Gọi z , z là hai nghiệm phức của phương trình 2
z z  3  0 . Khi đó z z bằng 1 2 1 2 A. 3 . B. 2 3 C. 6 . D. 3 .
Câu 34:Cho số phức z  2  i . Tính z . A. z  3. B. z  2 . C. z  5 . D. z  5 .
Câu 35:Cho hai số phức z  3  2i và z  2  i . Số phức z z bằng 1 2 1 2 A. 1
  3i . B. 1
  3i . C.1 3i . D.1 3i .
Câu 36: Nguyên hàm của hàm số   3
f x x x là 1 1 A. 2 3x 1 C . B. 4 2 x x C . C. 3
x x C . D. 4 2
x x C . 4 2
Câu 37:Diện tích phần hình phẳng tô đậm trong hình vẽ giới hạn bởi các đường 2
y x  4x  3, y x 1được
tính theo công thức nào dưới đây? Trang22 4 4 A.  2
x  3x  2 x d . B.  2
x  5x  4 x d . 1 1 4 4 C.  2
x  3x  2 x d . D.  2
x  5x  4 x d . 1 1
Câu 38:Trong không gian Oxyz , cho hai điểm A2; 2;  5  , B 4;6  ;1 .
Trung điểm M của đoạn thẳng AB có tọa độ là
A. 2; 4;6 . B. 3; 4;  2 .C.  2
 ; 4; 6 . D.3;4;3 .
Câu 39:Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) : x  2 y z  5  0 . Điểm nào dưới đây thuộc (P) ? A. Q(2; 1  ;5) .
B. P(0; 0; 5) . C. N ( 5
 ;0;0) . D. M (1;1;6) .
Câu 40:Trong không gian Oxyz , điểm nào dưới đây là hình chiếu vuông góc của điểm A3; 4  ;1 trên mặt phẳng Oxy ? A. M 0;0 
;1 . B. N 3; 4;0 .C. P 3;0 
;1 .D. Q 0; 4  ;1 .
Câu 41: Cho hình phẳng D giới hạn bởi đường cong x
y e , trục hoành và các đường thẳng x  0, x  1. Khối
tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu ? 2 e 1 2  e 2  (e 1) 2  (e 1) A.V B.V C.V D.V  2 2 2 2 x 1 y z  2
Câu 42:Trong không gian Oxyz, cho đường thẳng  :  
và mặt phẳng (P) : x y z 1  0 . 2 1  2
Đường thẳng nằm trong (P) đồng thời cắt và vuông góc với  có phương trình là x  3  t            x 3 2tx 3 tx 1 t
A. y  2  4t . B. y  2  6t .C. y  2  4t . D. y  4t . z  2  t  z  2  t
z  2  3t  z  3t
Câu 43:Trong không gian Oxyz , đường thẳng đi qua M 2; 1
 ;3 và vuông góc với mặt phẳng
 :4x 3y z  2  0 có phương trình là
x  4  2t
x  2  4tx  2   4tx  2   4t    
A. y  3  t .B. y  1
  3t . C. y  2
  3t . D. y  4   3t .     z  1 3tz  3  tz  2  tz  2  t
Câu 44: Cho hàm số f x liên tục trên R . Gọi S là diện tích hình phẳng giới hạn bởi các đường
y f x, y  0, x  1
 và x  4 (như hình vẽ bên). Mệnh đề nào dưới đây là đúng? Trang23 1 4 1 4 A. S f
 xdxf
 xdx.
B. S   f
 xdxf
 xdx. 1  1 1  1 1 4 1 4
C. S   f
 xdxf
 xdx. D. S f
 xdxf
 xdx. 1  1 1  1
Câu 45:Giải phương trình : 2
z  4z 11  0 , kết quả nghiệm là:  1 7  z   i z  2  7.i
z  3 2.iz 1 5.i A.  . B.  . C.  . D. 2 2  .
z  2  7.i
z  3 2.i
z 1 5.i  1 7 z   i  2 2
Câu 46:Trong không gian Oxyz , phương trình tham số của đường thẳng d đi qua M  2  ;3  ;1 và có vecto chỉ r phương u  (1; 2  ;2) là x 1 2tx  2   tx  2  tx 1 2t     A. y  2
  3t . B. y  3 2t .C. y  3
  2t . D. y  2   3t .     z  2  tz  1 2tz  1   2tz  2  t
Câu 47:Trong không gian Oxyz , khoảng cách giữa hai mặt phẳng  P : x  2y  2z 10  0 và
Q: x  2y  2z 3  0 bằng 8 7 4 A. . B. . C. . D. 3 . 3 3 3
Câu 48:Xét các số phức z thỏa mãn z  2 . Trên mặt phẳng tọa độ Oxy , tập hợp điểm biểu diễn của các số 4  iz phức w 
là một đường tròn có bán kính bằng 1 z A. 26. B. 26. C. 34. D. 34. Câu 49:Số phức 3
  7i có phần ảo bằng A. 7 .B. 7  . C. 3  . D. 7i .
Câu 50:Tìm số phức liên hợp của số phức z    i  i2 1 2 3  4  5i . A. 3  22i . B. 3  22i . C. 3   22i . D. 3   22i . ĐÁP ÁN 1 B 6 B 11 B 16 C 21 C 26 D 31 C 36 B 41 D 46 B 2 A 7 B 12 A 17 A 22 D 27 A 32 D 37 D 42 C 47 B 3 B 8 B 13 C 18 C 23 D 28 D 33 B 38 B 43 D 48 C 4 B 9 A 14 C 19 B 24 D 29 C 34 C 39 D 44 A 49 A 5 A 10 A 15 D 20 D 25 B 30 A 35 C 40 B 45 A 50 A Trang24