

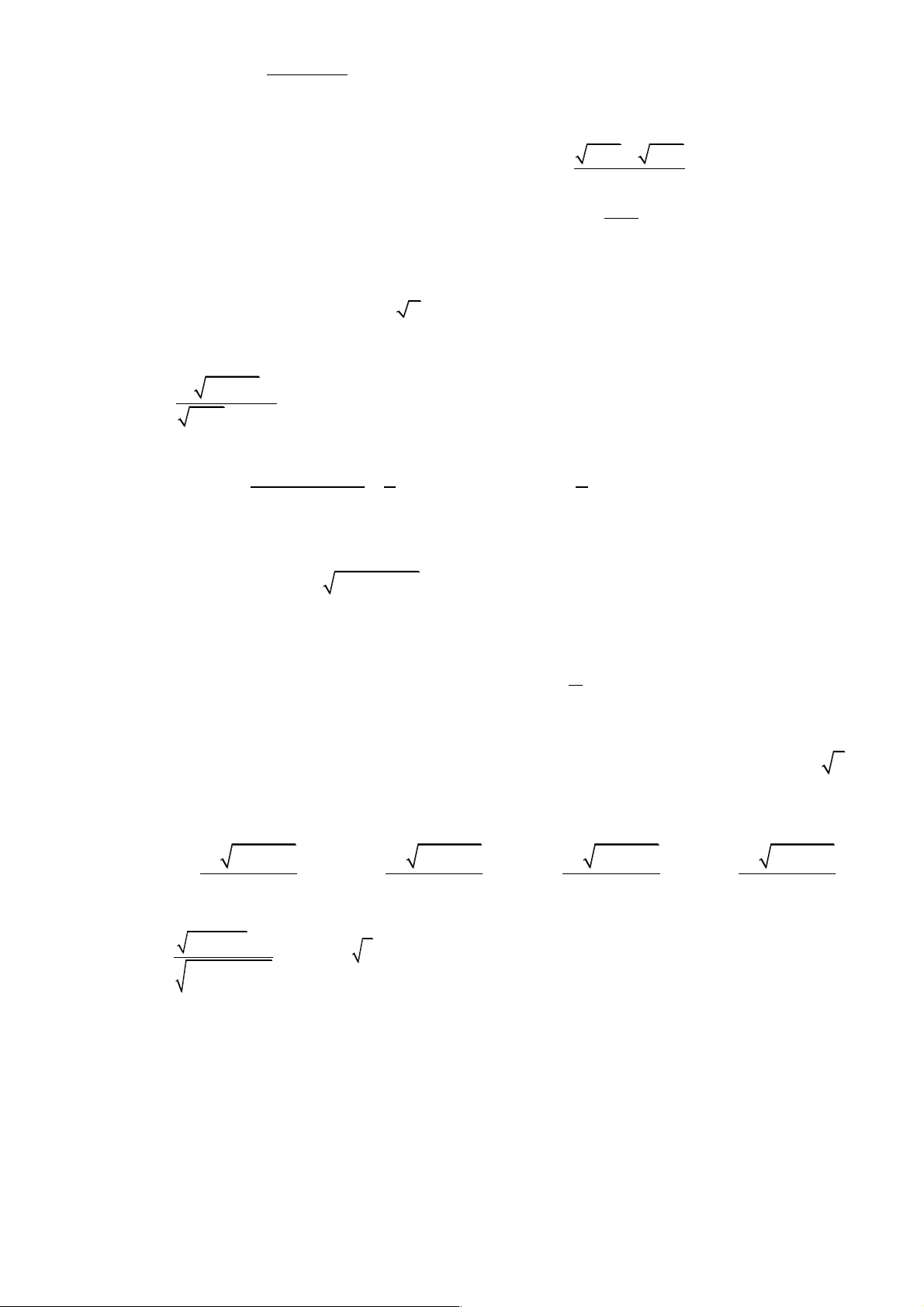





































Preview text:
ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KỲ II
Môn: TOÁN 11 – ĐỀ 1
Thời gian làm bài: 90 phút, không tính thời gian phát đề 4n + 2023 Câu 1: lim bằng 2n +1 1 A. 4 . B. 2 . C. 2023. D. . 2 Câu 2: ( 3
lim x - 2023x - 2024) bằng x®+¥ A. 0 . B. 1. C. -¥ . D. +¥ .
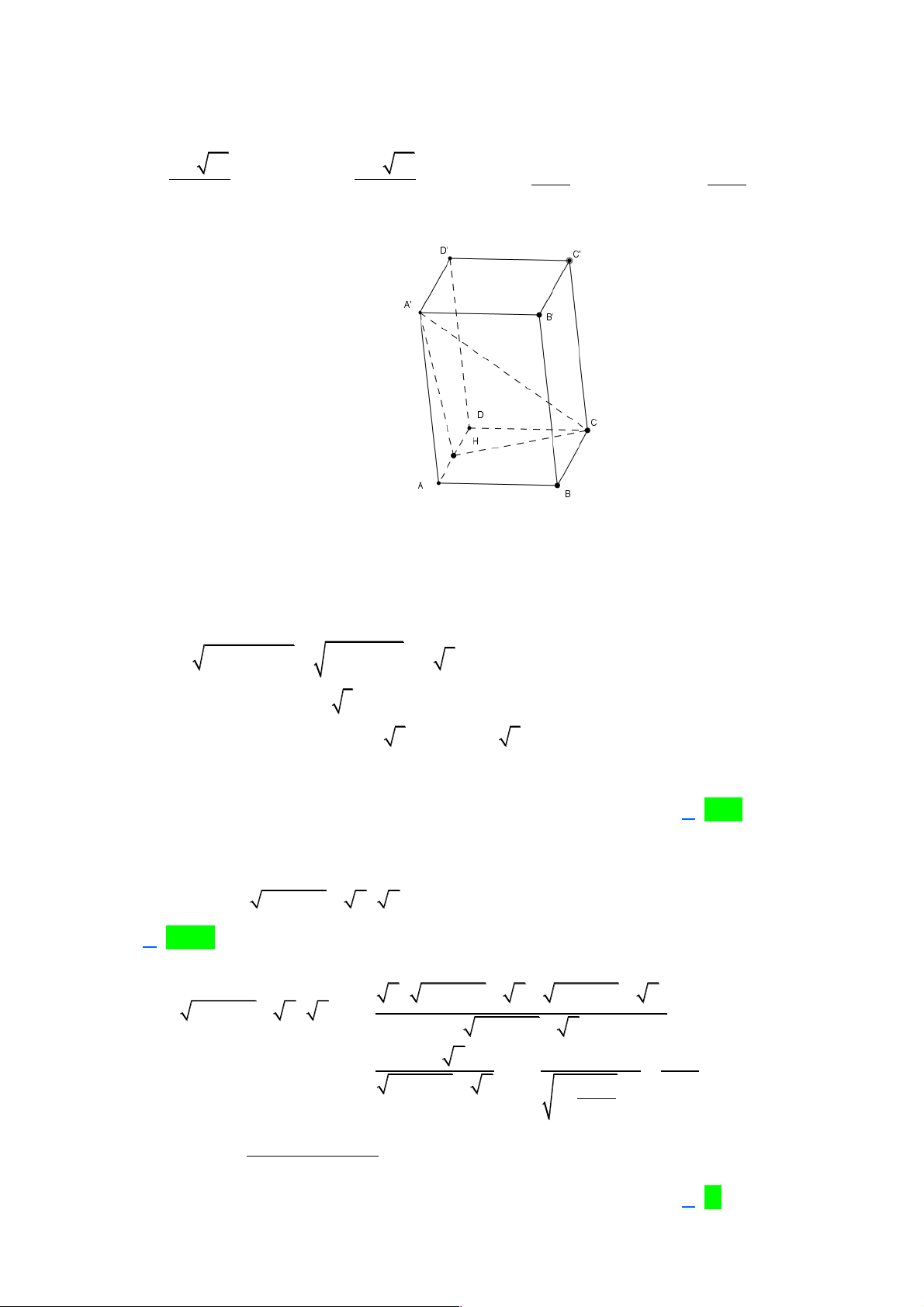
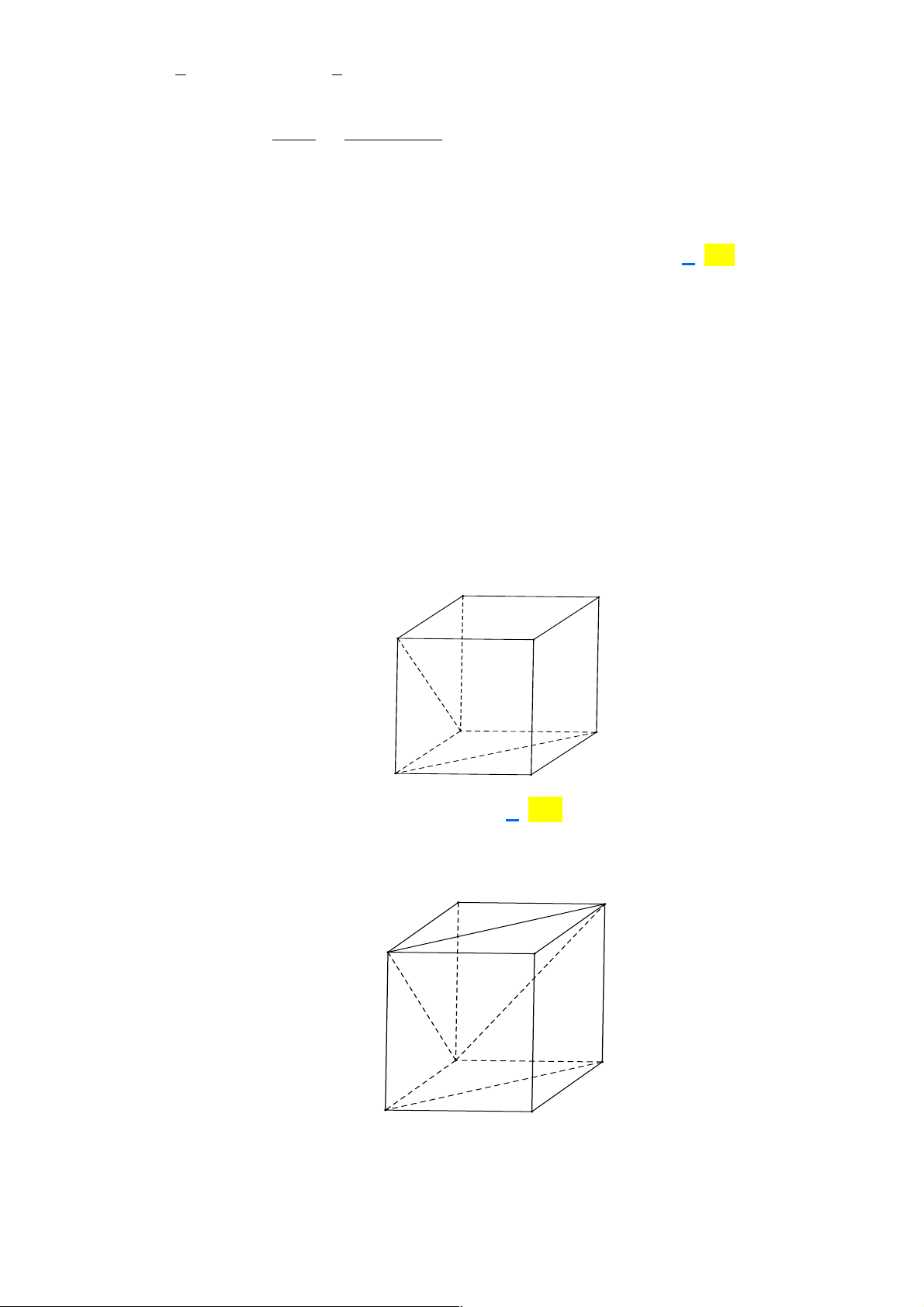
Câu 3: Cho hình lập phương ABC .
D A' B 'C ' D ' . Tìm mệnh đề sai trong các mệnh đề sau. A. ( AC B D ) o
, ' ' = 90 . B. (BD BD ) o ,
' = 60 . C. (BD BA ) o ,
' = 60 . D. ( AB DD ) o , ' = 90 . 5x -1 Câu 4: lim có giá trị bằng x®-¥ 2 - x 1 A. - . B. 5 - 3 . C. . D. 5 . 2 2
Câu 5: Cho hình hộp ABCD.A' B 'C ' D ' . Các véc tơ có điểm đầu và điểm cuối là các đỉnh của hình !!!"
hộp và bằng véc tơ AB là uuur uuuur uuuur uuur uuuur uuuur A. ;
CD D'C '; A'B '.
B. DC; A' B '; C ' D'. uuur uuuur uuuur uuur uuuur uuuur
C. DC; C ' D '; B ' A'.
D. DC; A' B '; D'C '.
Câu 6: Cho a,b là các số thực khác 0 . Tìm hệ thức liên hệ giữa a,b để hàm số ì ax +1 -1 ï ¹ f (x) khi x 0 = í x
liên tục tại x = 0 . ï 2
î4x + 5b khi x = 0
A. a = 5b .
B. a = 10b .
C. a = b .
D. a = 2b . u ì = 5 -
Câu 7: Biết (u lim(u + 2.5n) n ) 1 : í . Khi đó là: u = 5u - 20,n * Î î • n n 1 + n A. 100 . B. -¥ . C. 100 - . D. 5 .
Câu 8: Cho tứ diện ABCD , các điểm M , N, P lần lượt thuộc các cạnh AB, BC,CD nhưng không
trùng với các đỉnh của tứ diện. Thiết diện của tứ diện khi cắt bởi mp(MNP)là: A. Một ngũ giác. B. Một lục giác. C. Một tứ giác. D. Một tam giác.
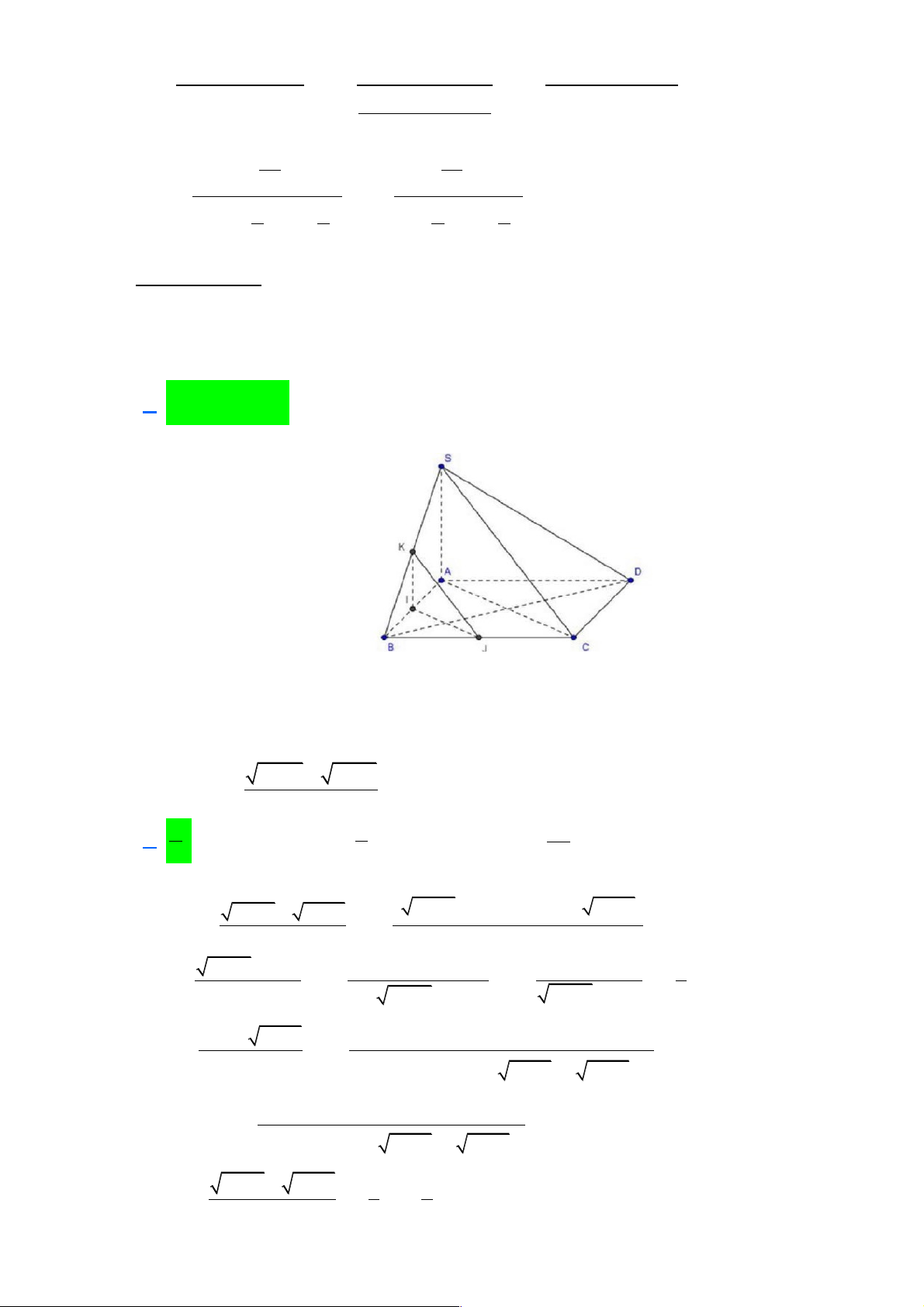
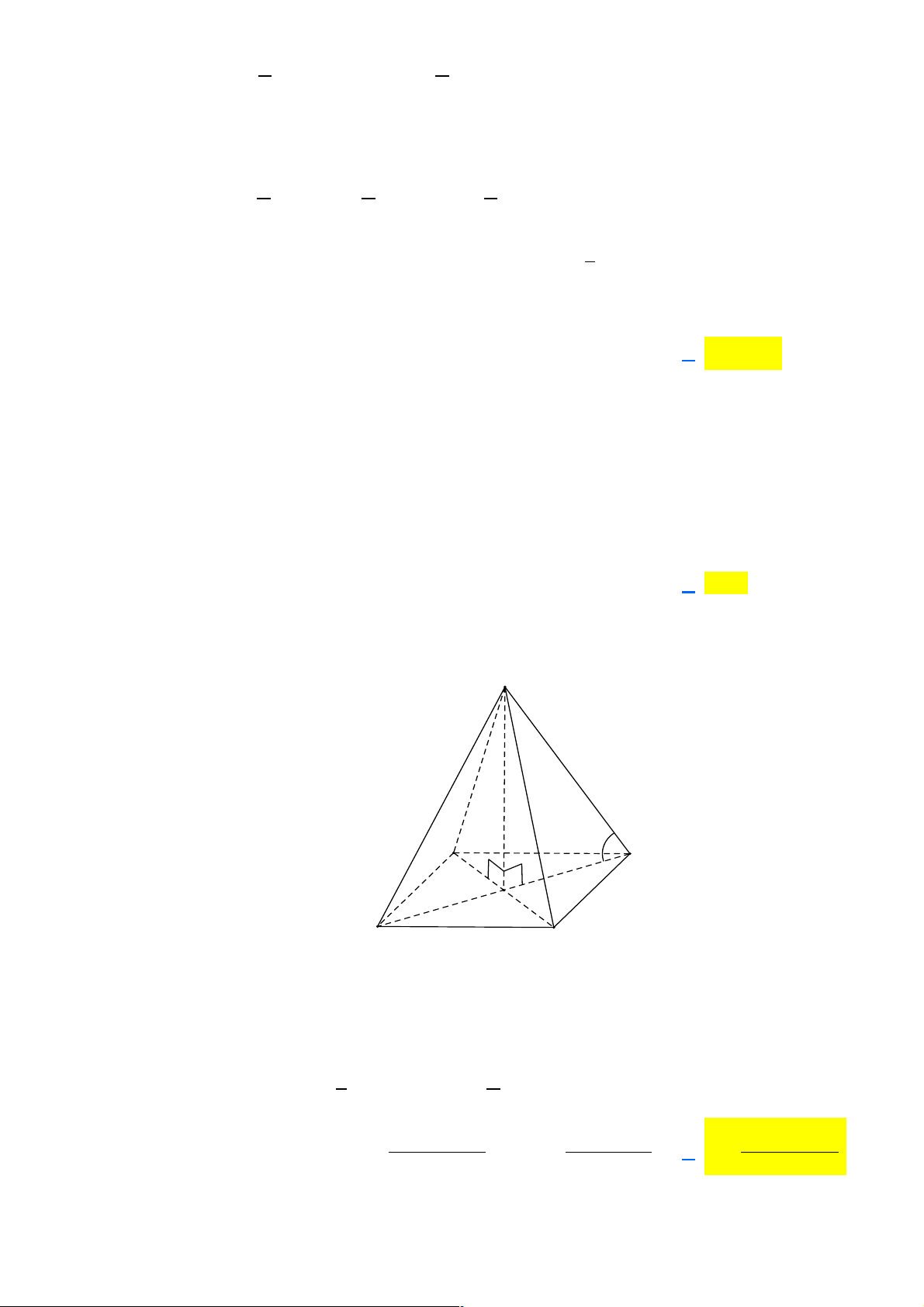
Câu 9: Cho hình chóp SABCD có đáy là hình vuông cạnh a , có cạnh SA = a 2 và SA vuông góc với
đáy. Tính góc giữa đường thẳng SC và mp(ABCD) A. 30!. B. 45! . C. 60! . D. 90!.
Câu 10: lim (2x + )
1 có giá trị bằng x 2 ®- A. . -¥ B. 5. C. 3. - D. + . ¥ 2 3n - 2n -1 Câu 11: lim có giá trị bằng 2 - n + 3 3 A. - . B. + . ¥ C. . -¥ 3 D. . 2 2 3n + 4n Câu 12: lim có giá trị bằng n 1 2 - 4 + Trang 1 1 1 A. +¥ 1 . B. . C. . D. - . 4 2 4
Câu 13: Giá trị của m để 2
lim mx + x + 2 = -¥ là x®-¥ ( ) A. m < 0 . B. m > 1 - . C. m > 0 . D. m > 1 .
Câu 14: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Ba đường thẳng cắt nhau đôi một thì đồng quy.
B. Ba đường thẳng cắt nhau đôi một và không đồng phẳng thì đồng quy.
C. Ba đường thẳng đồng quy thì đồng phẳng.
D. Ba đường thẳng cắt nhau đôi một thì đồng phẳng. 2 5n + 3n - 7
Câu 15: limu , với u = bằng n n 2 n A. 0. B. 5. C. 3. D. 7. - !!!" " !!!" " !!!" "
Câu 16: Cho tứ diện ABCD . Gọi M là trung điểm của BC , biết AB = a, AC = b và AD = c . Đẳng thức nào sau đây đúng? !!!!" 1 " " " !!!!" 1 " " "
A. DM = (a + c - 2b).
B. DM = (b + c - 2a). 2 2 !!!!" 1 " " " !!!!" 1 " " "
C. DM = (a + b - 2c).
D. DM = (a + b - c). 2 2 n n 1 3 4.2 - - - 3 Câu 17: lim bằng 3.2n + 4n A. +¥ . B. -¥ . C. 0 . D. 1.
Câu 18: Cho hàm số f (x) 3 2
= x - 3x +1. Giá trị lim f (x) bằng x®-¥ A. -3 . B. +¥ . C. 3. D. -¥ . 2 3 x - 2 Câu 19: lim bằng x®-¥ x A. -¥ . B. +¥ . C. 3. D. -3 .
Câu 20: Hàm số nào sau đây gián đoạn tại x = 1? 2x +1 x A. y = . B. 3
y = x + x +1. C. y = .
D. y = sin x . 2 x +1 2 x -1
Câu 21: Cho hình hộp ABC .
D A B C D . Đẳng thức nào sau đây sai? 1 1 1 1 !!!!" !!!" !!!" !!!!" !!!" !!!!" "
A. AC + AC = 2AC .
B. AC + CA + 2C C = 0. 1 1 1 1 1 !!!" !!!" !!!!" !!!!" !!!" !!!!"
C. CA + AC = CC .
D. AC + CD = A D . 1 1 1 1 1 ∑ ∑
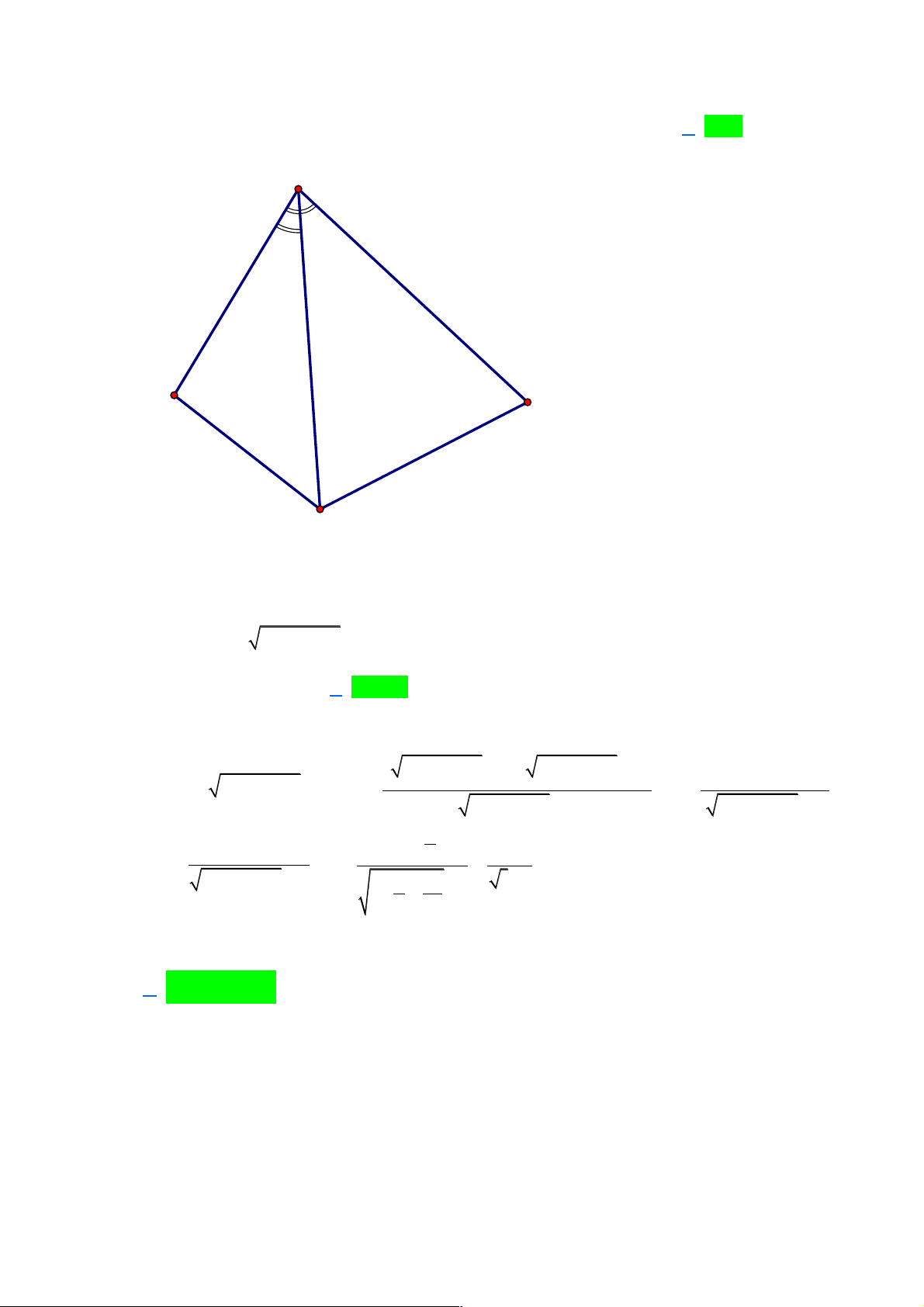
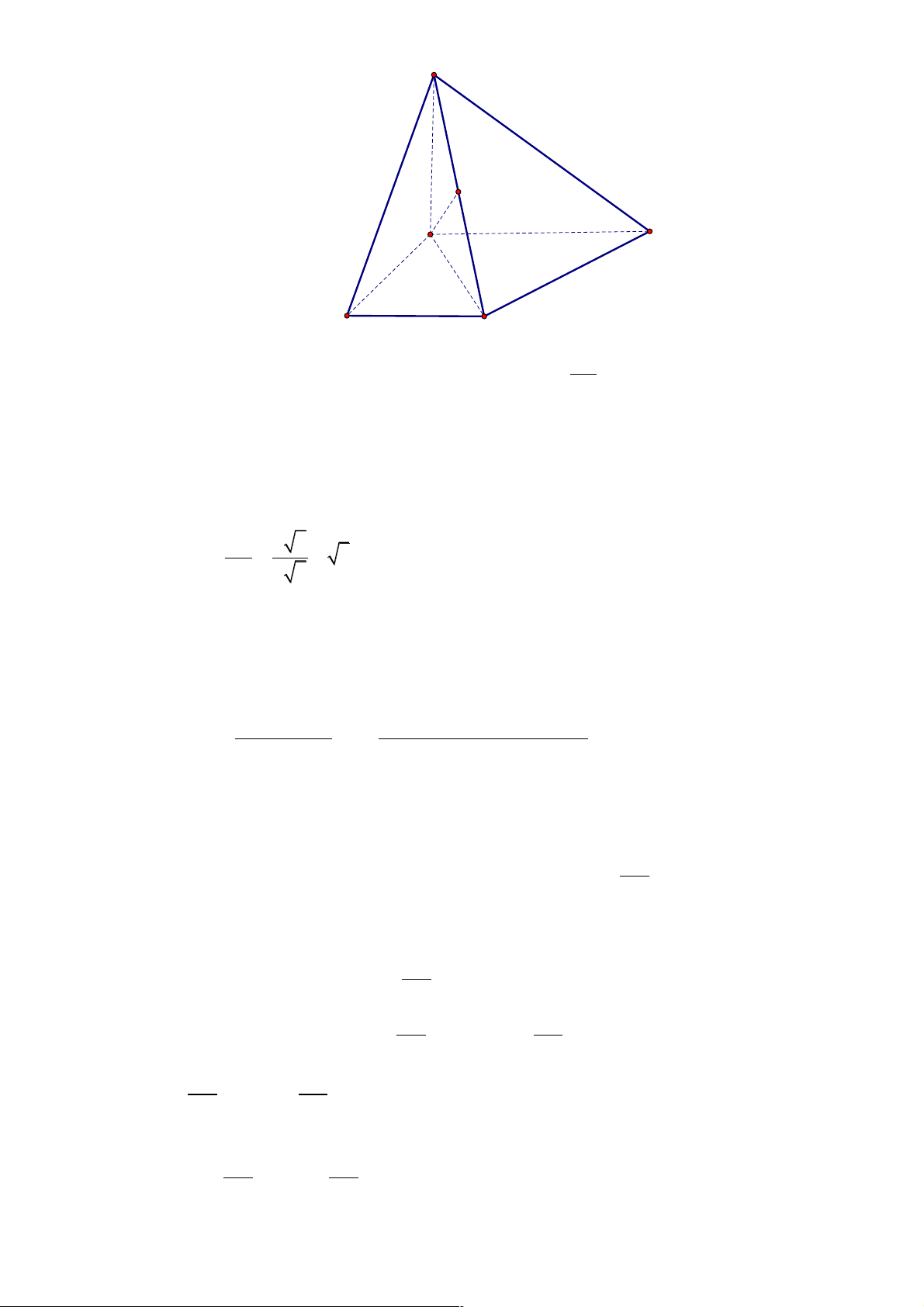
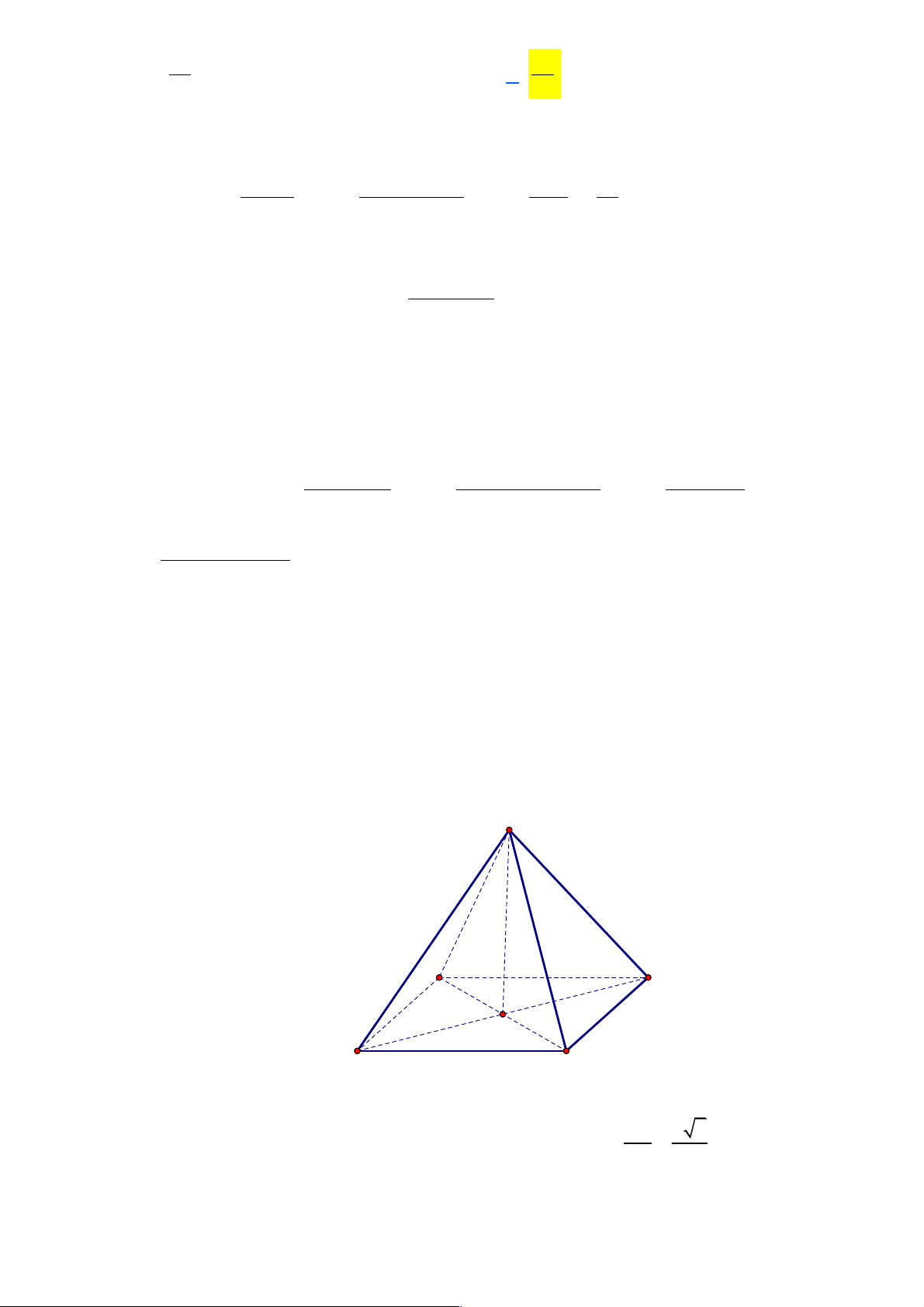
Câu 22: Cho tứ diện ABCD có AB = AC = AD và BAC = BAD = 60°. Tính góc giữa hai đường thẳng AB và CD . A. 30° . B. 45° . C. 60° . D. 90° . Câu 23: Tính 2 I = lim
n - 2n + 3 - n . ( ) A. I = 1. B. I = 1. - C. I = 0. D. I = + . ¥
Câu 24: Cho hình chóp S.ABC có đáy là tam giác cân tại A, SA vuông góc với đáy, M là trung điểm của
BC, J là trung điểm của BM . Khẳng định nào sau đây đúng?
A. BC ^ (SAM ).
B. BC ^ (SAC).
C. BC ^ (SAB).
D. BC ^ (SAJ ). Trang 2 x +1
Câu 25: Hàm số f ( x) =
liên tục trên khoảng nào sau đây? 2 x - 5x + 4 A. ( ; -¥ 4). B. ( 1 - ;2) . C. [1;+¥). D. (2;3) . ì 1- x - 1+ x ï khi x < 0 ï
Câu 26: Tìm tất cả các giá trị của tham số m để hàm số ( ) x f x = í liên tục tại 1- x ïm + khi x ³ 0 ïî 1+ x x = 0. A. m = 1. B. m = 2 - . C. m = 1 - . D. m = 0
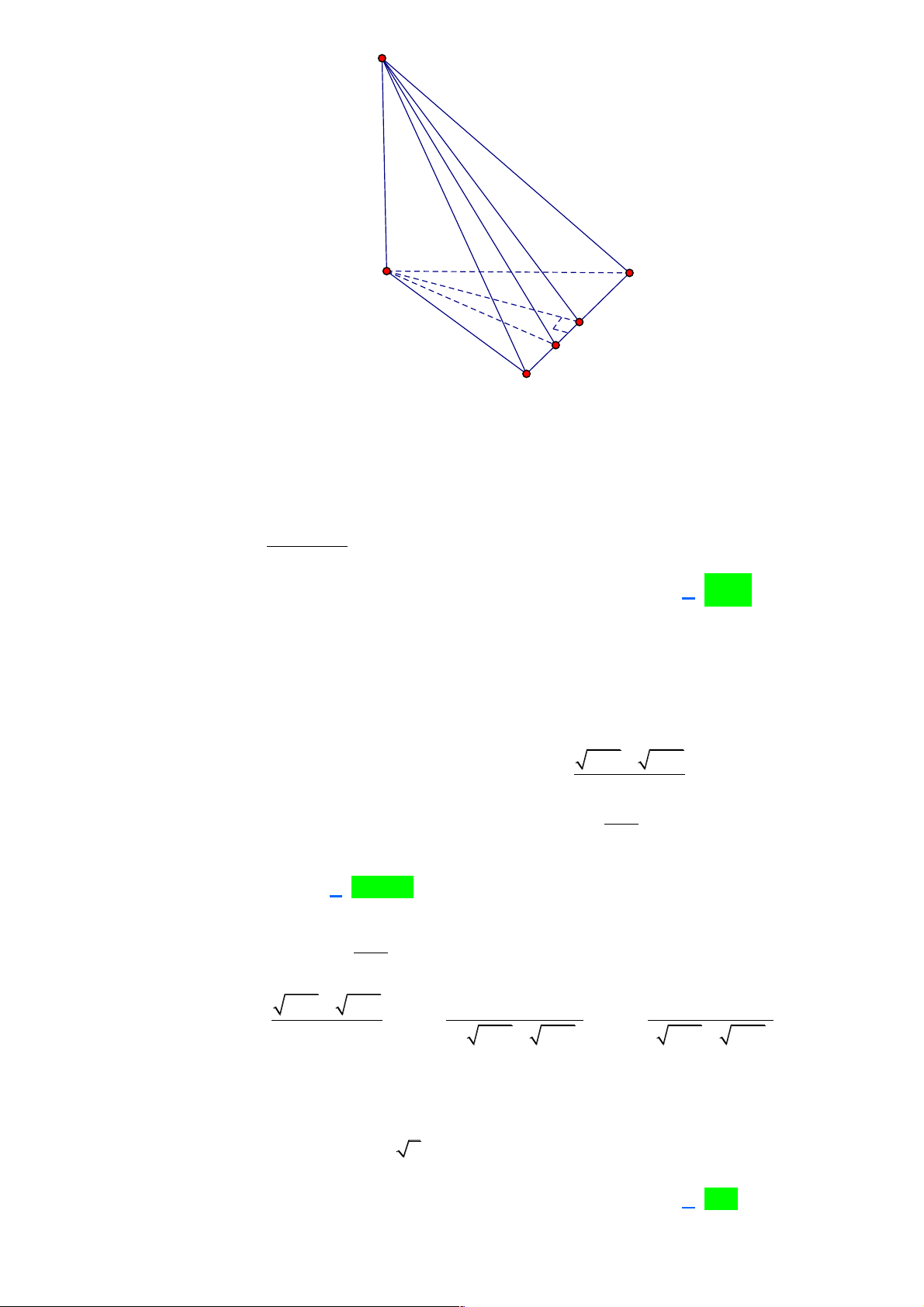
Câu 27: Cho hình chóp S.ABC có BC = 2 , các cạnh còn lại bằng 1. Tính góc giữa hai đường thẳng SB và AC . A. 0 120 . B. 0 90 . C. 0 30 . D. 0 60 . 3 2 x - x Câu 28: lim có giá trị bằng x 1+ ® x -1 +1- x A. 0 . B. 1 - . C. +¥ . D. 1. 3 3 3 1 + 2 +!+ n b Câu 29: Cho biết lim = , a bΕ b 4 (
), đồng thời là phân số tối giản. Giá trị của n +1 a a 2 2 2a + b là A. 99. . B. 33. . C. 73. . D. 51. Câu 30: Tìm m sao cho 2
lim x + x + mx + 2 = 2 x®-¥( ) A. m = 0 . B. m = 2 . C. m = 4 - . D. m = 5 - .
Câu 31: Trong hộp đựng 9 tấm thẻ được đánh số từ 1 đến 9. Gọi x là số lần rút thẻ ít nhất từ hộp để xác
suất có ít nhất một thẻ ghi số chia hết cho 4 phải lớn hơn 5 . Hãy cho biết x thuộc tập nào? 6 A. (2;6). B. (4;8). C. (0;4). D. (6;9) .
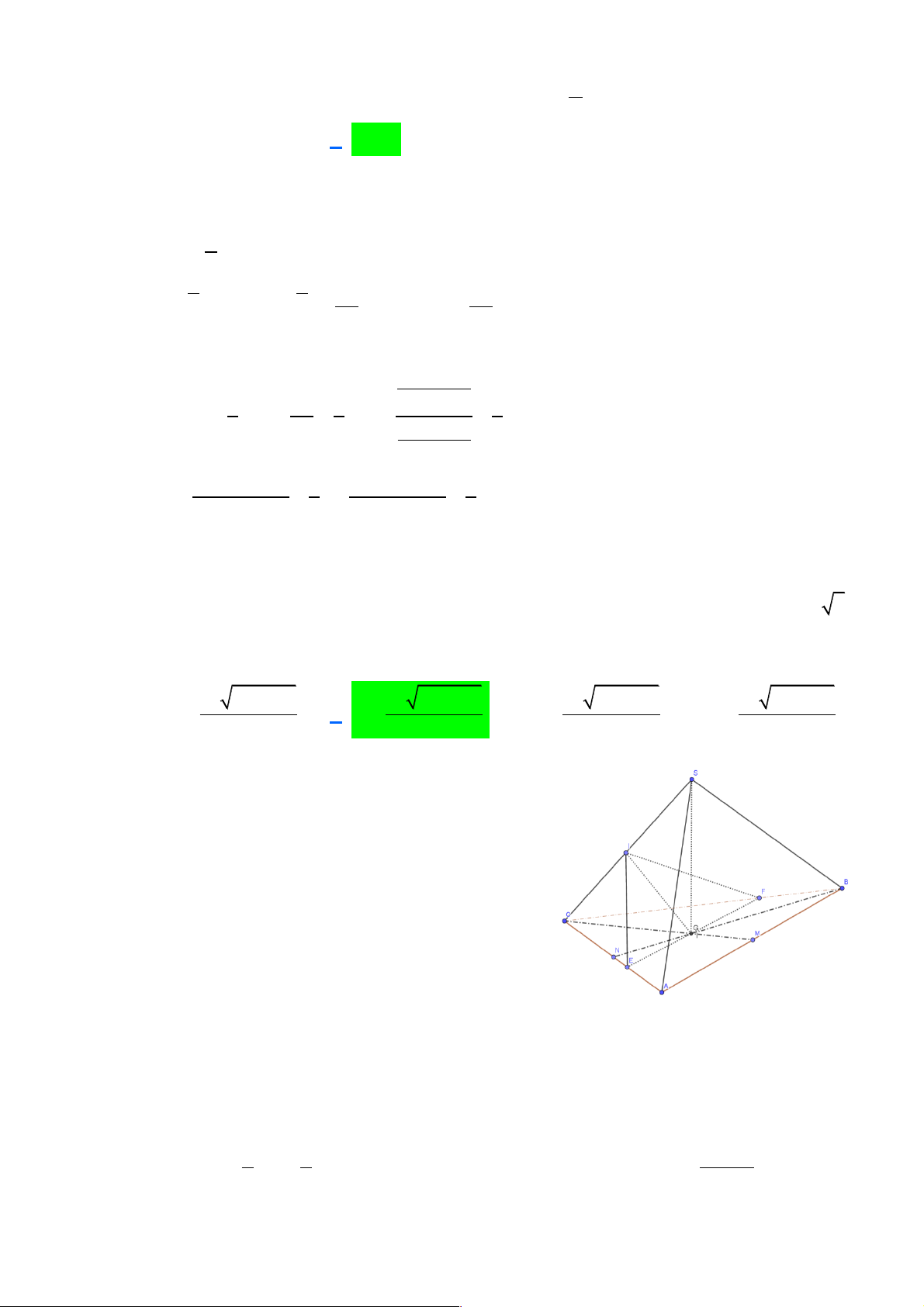
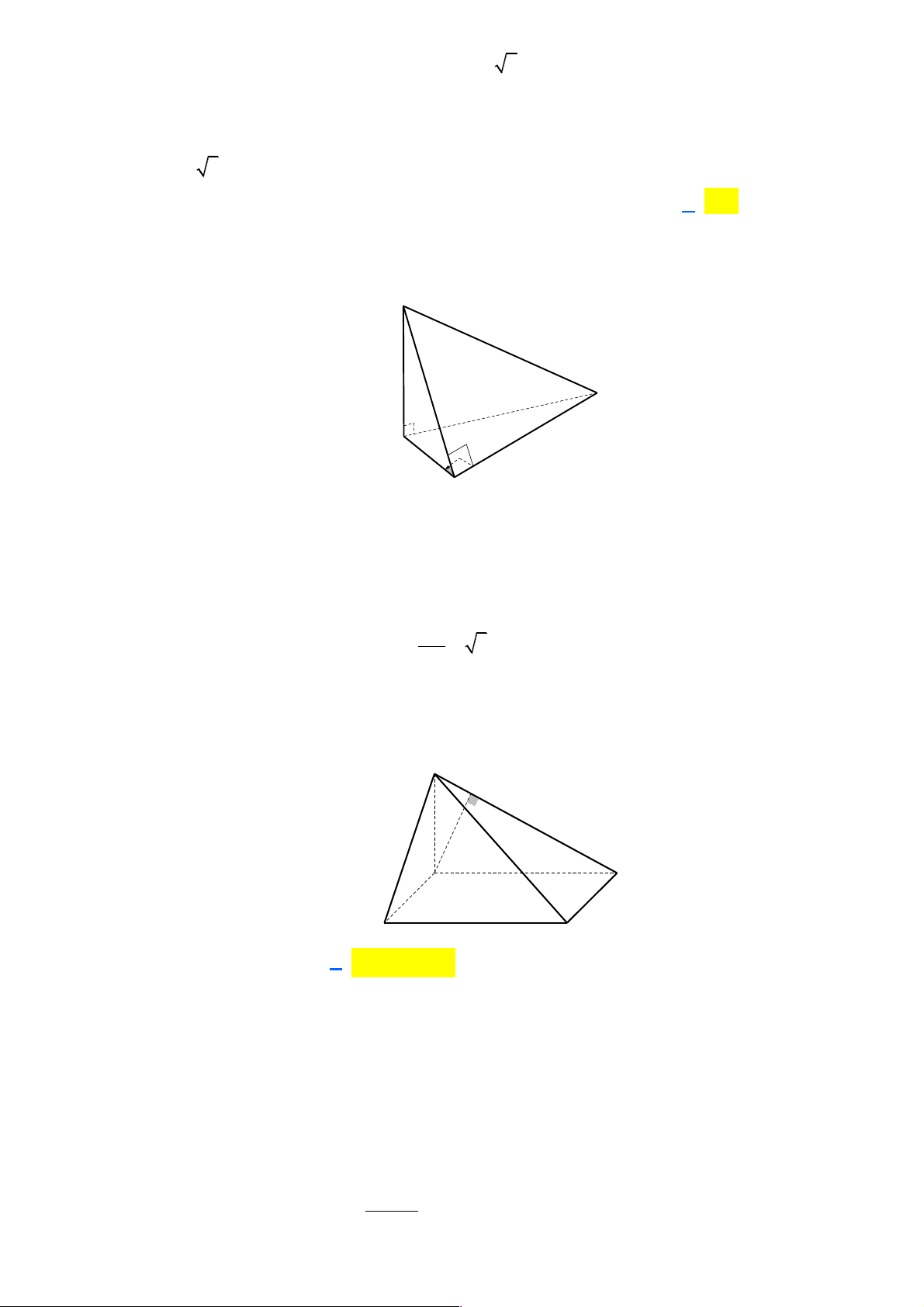
Câu 32: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA = SB = SC = b (a > b 2).
Gọi G là trọng tâm ABC D
. Xét mặt phẳng (P) đi qua G vuông góc với SC tại điểm I nằm
giữa S và C . Diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng (P) là? 2 2 2 a 3b + a 2 2 2 a 3b - a 2 2 2 a 3b + a 2 2 2 a 3b - a A. S = . B. S = . C. S = . D. S = . 2b 9b 9b 2b
Câu 33: Cho ba số dương a,b,c theo thứ lập thành cấp số cộng. Giá trị lớn nhất của biểu thức a2 + b
8 c + 3 có dạng x y (x,yΕ ).Hỏi x + y bằng bao nhiêu: P = ( 2 a + 2c) +1 A. 11.. B. 13.. C. 9.. D. 7.
Câu 34: Cho hàm số f x = ( 2 + m ) 8 5 3 ( ) 1
x - m x + mx - . Ch 1
ọn mệnh đề đúng trong các mệnh đề sau:
A. Phương trình f (x) = 0 vô nghiệm với mọi m .
B. f (x) gián đoạn tại x =1 .
C. Phương trình f (x) = 0 có ít nhất hai nghiệm phân biệt với mọi m .
D. f (x) luôn nhận giá trị âm với mọi m . Trang 3 ì 2x - 4 +3, khi x ³ 2 ï
Câu 35: Cho hàm số f (x) = í x +1
. Tìm tất cả các giá trị của tham số thực m để , khi x < 2 ï 2
î x - 2mx + 3m + 2
hàm số liên tục trên ! . A. m = 3. B. m = 4 . C. m = 5. D. m = 6 .
Câu 36: Mệnh đề nào sau đây là mệnh đề đúng
A. Mọi dãy số có giới hạn thì luôn luôn tăng hoặc luôn luôn giảm. B. Nếu (u limu = +¥
n ) là dãy số tăng thì . n
C. Nếu limu = +¥ và limv = +¥ thì lim(u - v = n n ) 0 . n n D. Nếu n u = a và 1
- < a < 0 thì limu = 0. n n 3 n + n
Câu 37: Giới hạn lim bằng: 2 2 2 1 + 2 + ... + n A. 2018. B. 6 . C. +¥ . D. 3.
Câu 38: Trong các mệnh đề sau, mệnh đề nào sai? 1 1 A. lim = +¥. B. 1 1 lim = +¥. C. lim = -¥. D. lim = -¥. x 0- ® x - 4 - 3 x®0 x x 0- ® x x®0 x 3 x + 2 2
Câu 39: Tính giới hạn I = lim 2 x®- 2 x - 2 2 -3 2 A. -1. B. 1 . C. . D. . 2 2 2 2 1 1 1
Câu 40: Tìm limu biết u = + +...+ . n n 2 2 2 2 -1 3 -1 n -1 A. 3 . B. 3 . C. 2 D. 4 . 4 5 3 3
Câu 41: Cho lăng trụ tứ giác ABC .
D A' B 'C ' D ' . Có đáy là hình vuông và cạnh bên bằng 2a . Hình
chiếu của A' trên mặt phẳng ( ABCD) là trung điểm của cạnh AD , đường thẳng A'C hợp với
mặt phẳng ( ABCD)một góc 45o . Thể tích khối lăng trụ đã cho bằng 3 8a 30 3 8a 30 3 16a 3 16a A. . B. . C. . D. . 9 27 3 9 lim f ( x) = 5 lim é3 - 4 ë f ( x)ù Câu 42: Nếu û x®2 thì x®2 bằng A. 18 - . B. 1 - . C. 1. D. 17 - .
Câu 43: Giới hạn lim ( n + 2018 - n ) n bằng A. 1009 . B. 2018 . C. +¥ . D. 0 . 3 n + n
Câu 44: Giới hạn lim bằng: 2 2 2 1 + 2 + ... + n A. 2018. B. 6 . C. +¥ . D. 3.
Câu 45: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA ^ (ABCD). Gọi I , J , K lần lượt là
trung điểm của AB, BC và SB . Tong các khẳng định sau, khẳng định nào sai? Trang 4 A. ! (SD BC) 0 , = 60 .
B. BD ^ (SAC).
C. BD ^ (IJK).
D. (IJK) / /(SAC). 3 1+ 2x - 1+ 3x
Câu 46: Giới hạn lim có giá trị là: 2 x®0 x A. 1 . B. 2 . C. 9 - . D. 0 . 2 5 20 2 3
x + x + 2 - 7x +1 a 2 Câu 47: Biết lim = + c với a
a , b , c Î ! và
là phân số tối giản. Giá trị của x 1 ® 2 (x - ) 1 b b
a + b + c bằng: A. 5 . B. 37 . C. 13. D. 51. 2 4x - x + 3
Câu 48: Giới hạn: lim
bằng kết quả nào trong các kết quả sau? x®-¥ x A. 2. B. 2 - . C. - 2 . D. 0 . 4
Câu 49: Giới hạn: 2x - 3 lim
bằng kết quả nào trong các kết quả sau? x®+¥ 2 x +1 + x A. 0 . B. -¥ . C. +¥ . D. 1. 3 3x + 5 - x + 3 Câu 50: lim có giá trị bằng: x 1 ® x -1 1 1 1 A. - . B. 0 . C. . D. - . 6 4 5
---------- HẾT ----------
HƯỚNG DẪN GIẢI CHI TIẾT 4n + 2023 Câu 1: lim bằng 2n +1 1 A. 4 . B. 2 . C. 2023. D. . 2 Lời giải 2023 4 + 4n + 2023 Ta có lim = lim n = 2 . 2n +1 1 2 + n Câu 2: ( 3
lim x - 2023x - 2024) bằng x®+¥ A. 0 . B. 1. C. -¥ . D. +¥ . Lời giải æ 2 20 3 2024 ö Ta có: lim ( 3 x - 2023x - 0 2 24) 3 = lim x 1- - . ç 2 3 ÷ x®+¥ x®+¥ è x x ø æ 2023 2024 ö Vì 3 lim x = +¥ và lim 1- - =1 > 0 ç ÷ x®+¥ 2 3 x®+¥ è x x ø nên theo quy tắc 2, ( 3 lim x - 2x + ) 1 = +¥. x®+¥
Câu 3: Cho hình lập phương ABC .
D A' B 'C ' D ' . Tìm mệnh đề sai trong các mệnh đề sau. A. ( AC B D ) o
, ' ' = 90 . B. (BD BD ) o ,
' = 60 . C. (BD BA ) o ,
' = 60 . D. ( AB DD ) o , ' = 90 . Lời giải Chọn B Trang 5 A' D' B' C' A D B C
Đáp án A ta có ( AC B D ) = ( AC BD) o , ' ' , = 90 Đáp án B ta có ( DD ' 1 BD BD ) ∑ ,
' = DBD'. Xét BD D D ' có ∑ ∑ o o tan DBD ' = =
Þ DBD' » 35,26 ¹ 60 . BD 2
Đáp án C ta có (BD BA ) ∑ o ,
' = DBA' = 60 vì D
D BA' là tam giác đều
Đáp án D ta có ( AB DD ) = (CD DD ) ∑ o , ' , ' = CDD' = 90 5x -1 Câu 4: lim có giá trị bằng x®-¥ 2 - x 1 A - . B. 5 - 3 . C. . D. 5 . 2 2 Lời giải 1 5 - 5x -1 5 - 0 1 2 Ta có: lim = lim x = = -5. (Vì lim = 0; lim = 0). x®-¥ 2 x - x ®-¥ 2 0 -1 -1 x®-¥ x x ®-¥ x x
Câu 5: Cho hình hộp ABCD.A' B 'C ' D ' . Các véc tơ có điểm đầu và điểm cuối là các đỉnh của hình !!!"
hộp và bằng véc tơ AB là uuur uuuur uuuur uuur uuuur uuuur A. ;
CD D'C '; A'B '. B. DC; A'B'; C 'D'. uuur uuuur uuuur uuur uuuur uuuur
C. DC; C ' D '; B ' A'. D. DC; A' B '; D 'C '. Lời giải Trang 6
Dựa vào hình ta có: Các véc tơ có điểm đầu và điểm cuối là các đỉnh của hình hộp và bằng véc !!!" uuur uuuur uuuur
tơ AB là DC; A' B '; D 'C '.
Câu 6: Cho a,b là các số thực khác 0 . Tìm hệ thức liên hệ giữa a,b để hàm số ì ax +1 -1 ï ¹ f (x) khi x 0 = í x
liên tục tại x = 0 . ï 2
î4x + 5b khi x = 0
A. a = 5b .
B. a = 10b .
C. a = b .
D. a = 2b . Lời giải TXĐ: D = ! .
Hàm số đã cho liên tục tại x = 0 khi và chỉ khi lim f (x) = f (0). x®0 ax +1 -1 a a
Mà lim f (x) = lim = lim = ; x 0 ® x 0 ® x 0 x ® ax +1 +1 2 f (0) = 5b. Suy ra a
lim f ( x) = f (0) Û = 5b Û a =10b. x®0 2 u ì = 5 -
Câu 7: Biết (U lim(u + 2.5n) n ) 1 : í . Khi đó là: u = 5u - 20,n * Î î • n n 1 + n A. 100 . B. -¥ . C. 100 - . D. 5 . Lời giải
Đặt u = v + 5, n *
" Î • Þ u = v + 5 n n n 1 + n 1 +
Û v = u -5 Û v = 5u - 20-5 Û v = 5 v + 5 - 25, n * " Ε n 1 + n 1 + n 1 + n n 1 + ( n )
Û v = 5v , n * " Î • n 1 + n Vậy (v
q = 5 v = u - 5 = 1 - 0 n 1 v 10.5 - , n * = - " Î •
n ) là cấp số nhân với công bội , và SHTQ: 1 1 n Suy ra n 1 u - u - - = - + Þ + = - + + = n ( n n ) ( n 1 n 1 10.5 5 lim 2.5 lim 10.5 10.5 5) 5.
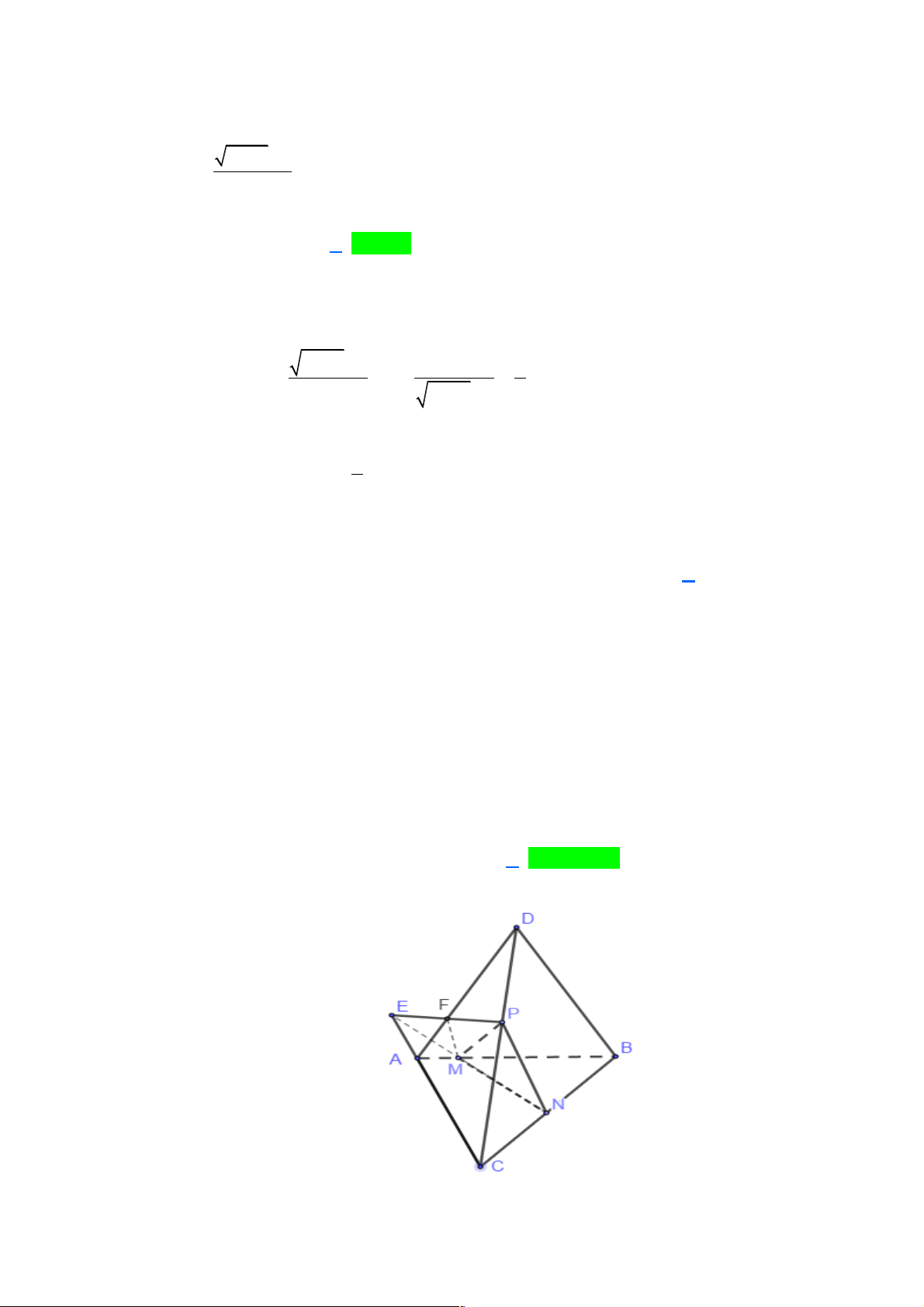
Câu 8: Cho tứ diện ABCD , các điểm M , N, P lần lượt thuộc các cạnh AB, BC,CD nhưng không
trùng với các đỉnh của tứ diện. Thiết diện của tứ diện khi cắt bởi mp(MNP)là: A. Một ngũ giác. B. Một lục giác. C. Một tứ giác. D. Một tam giác. Lời giải
Gọi E = MN Ç AC, F = EP Ç DA ta có thiết diện cần tìm là tứ giác MNPF . Trang 7
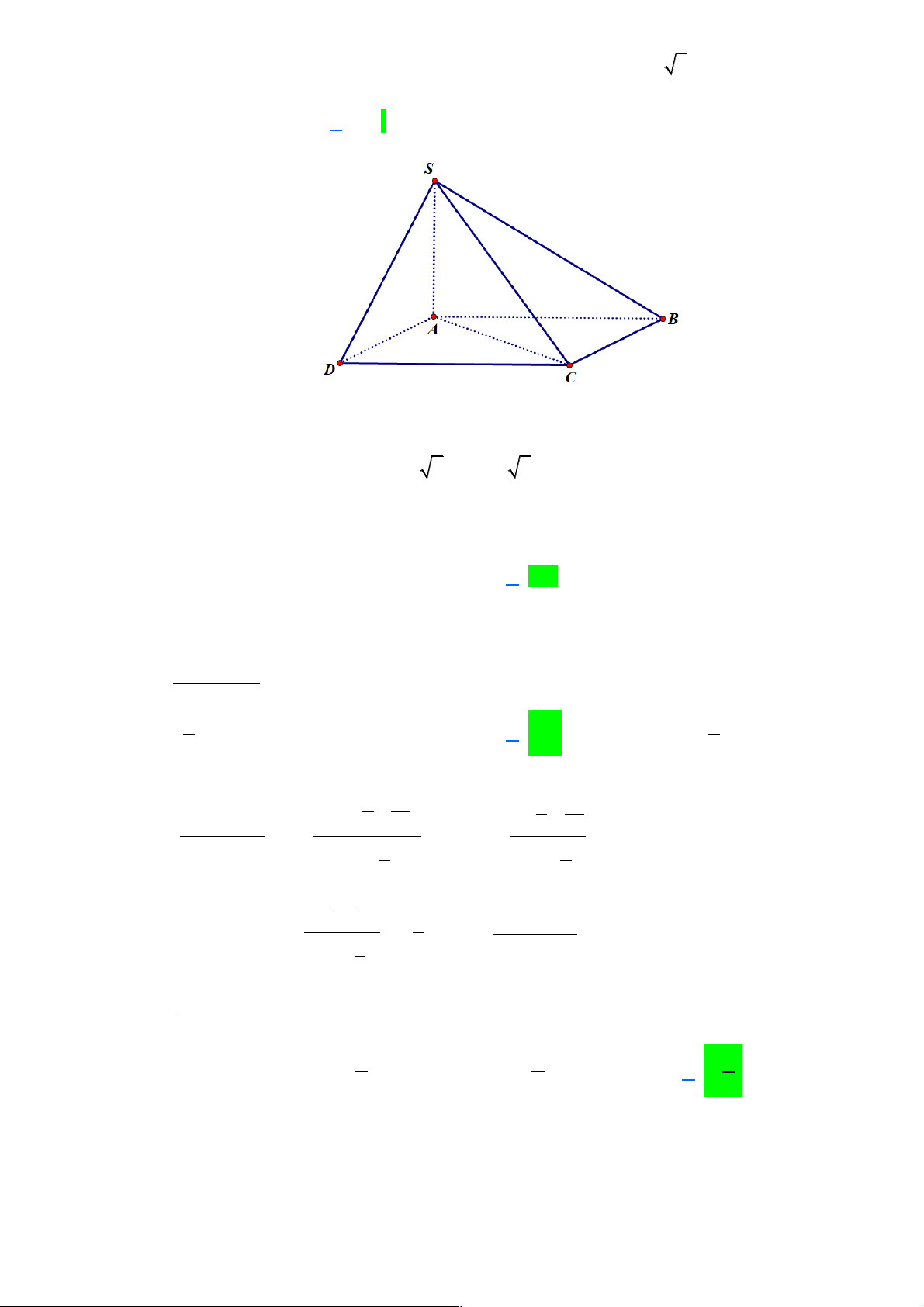
Câu 9: Cho hình chóp SABCD có đáy là hình vuông cạnh a , có cạnh SA = a 2 và SA vuông góc với
đáy. Tính góc giữa đường thẳng SC và mp(ABCD) A. 30!. B. 45! . C. 60! . D. 90!. Lời giải
Ta có AC là hình chiếu vuông góc của SC lên mp(ABCD) nên góc giữa SC và mp(ABCD) là góc ∑ SCA
Xét tam giác vuông SAC có SA = a 2, AC = a 2 ( đường chéo của hình vuông) Hay SA D
C là tam giác vuông cân tại A . Vậy ∑ 0 SCA = 45 .
Câu 10: lim (2x + )
1 có giá trị bằng x 2 ®- A. . -¥ B. 5. C. 3. - D. + . ¥ Lời giải Ta có: lim (2x + ) 1 = 2.( 2 - )+1= 3 - . x 2 ®- 2 3n - 2n -1 Câu 11: lim có giá trị bằng 2 - n + 3 3 A. - . B. + . ¥ C. . -¥ 3 D. . 2 2 Lời giải æ 2 1 ö 2 1 . n 3 - - 2 ç ÷ - - 2 3 2 3n - 2n -1 è n n lim lim ø = = lim .lim n n n 2 - n + 3 3 3 2 - + 2 - + n n 2 1 3 - - 2 3 2 3n - 2n -1 Mà lim = + ; ¥ lim n n n = - nên lim = - . ¥ 3 2 2 - + 2 - n + 3 n 3n + 4n Câu 12: lim có giá trị bằng n 1 2 - 4 + 1 1 A. +¥ 1 . B. . C. . D. - . 4 2 4 Lời giải Trang 8 æ 3 n ö +1 3n 4n 3n 4n ç ÷ + + è 4 ø 1 lim = lim = lim = - . n 1 2 - 4 + 2 - 4.4n æ 1 n ö 4 2 - 4 ç ÷ è 4 ø
Câu 13: Giá trị của m để 2
lim mx + x + 2 = -¥ là x®-¥ ( ) A. m < 0 . B. m > 1 - . C. m > 0 . D. m > 1 . Lời giải æ ö Ta có: 2 2
lim mx + x + 2 = lim xçm - 1+ ÷ x®-¥ ( ) 2 x®-¥ ç x ÷ è ø ì lim x = -¥ x®-¥ ïï æ 2 ö Mà í æ ö
Þ Để lim xçm - 1+
÷ = -¥ Û m -1 > 0 Û m >1. 2 ç ÷ ï lim ç m - 1+ ÷ = m -1 2 x®-¥ x è ø 2 x®-¥ ç x ÷ ïî è ø
Câu 14: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Ba đường thẳng cắt nhau đôi một thì đồng quy.
B. Ba đường thẳng cắt nhau đôi một và không đồng phẳng thì đồng quy.
C. Ba đường thẳng đồng quy thì đồng phẳng.
D. Ba đường thẳng cắt nhau đôi một thì đồng phẳng. Lời giải 2 5n + 3n - 7
Câu 15: limu , với u = bằng n n 2 n A. 0. B. 5. C. 3. D. 7. - Lời giải 2 æ 5n 3n 7 ö æ 3 7 ö Ta có limu = limç + - ÷ = lim 5+ - = 5. n 2 2 2 ç 2 ÷ è n n n ø è n n ø !!!" " !!!" " !!!" "
Câu 16: Cho tứ diện ABCD . Gọi M là trung điểm của BC , biết AB = a, AC = b và AD = c . Đẳng thức nào sau đây đúng? !!!!" 1 " " " !!!!" 1 " " "
A. DM = (a + c - 2b). B. DM = (b + c - 2a). 2 2 !!!!" 1 " " " !!!!" 1 " " "
C. DM = (a + b - 2c). D. DM = (a + b - c). 2 2 Lời giải Ta có !!!!" 1 !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" " " "
DM = (DB + DC) 1
= (DA+ AB + DA+ AC) 1
= (AB + AC - AD) 1 2
= (a +b- 2c). 2 2 2 2 n n 1 3 4.2 - - - 3 lim Câu 17: 3.2n + 4n bằng A. +¥ . B. -¥ . C. 0 . D. 1. Lời giải Ta có Trang 9 æ 3 ön æ 2 ön æ 1 ön - 2. - 3. n n 1 3 4.2 - 3 3n 2.2n 3 ç ÷ ç ÷ ç ÷ - - - - è 4 ø è 4 ø è 4 lim lim lim ø = = = 0. 3.2n + 4n 3.2n + 4n æ 2 ön 3. +1 ç ÷ è 4 ø
Câu 18: Cho hàm số f (x) 3 2
= x - 3x +1. Giá trị lim f (x) bằng x®-¥ A. -3 . B. +¥ . C. 3. D. -¥ . Lời giải æ 3 1 ö
Ta có: lim f (x) = lim ( 3 2 x - 3x + ) 3 1 = lim x 1- + . ç 3 ÷ x®-¥ x®-¥ x®-¥ è x x ø æ 3 1 ö Do 3
lim x = -¥ và lim 1- +
= 1 nên lim f (x) = -¥. ç ÷ x®-¥ 3 x®-¥ è x x ø x®-¥ 2 3 x - 2 lim Câu 19: x®-¥ x bằng A. -¥ . B. +¥ . C. 3. D. -3 . Lời giải 2 2 - - - 2 3 x 1 3x 1 2 2 3 x - 2 x x æ 2 ö Ta có: lim = lim = lim = lim ç 3 - 1- ÷ = 3 - . 2 x®-¥ x®-¥ x®-¥ x x x x ®-¥ x è ø
Câu 20: Hàm số nào sau đây gián đoạn tại x = 1? 2x +1 x A. y = . B. 3
y = x + x +1. C. y = .
D. y = sin x . 2 x +1 2 x -1 Lời giải x Xét hàm số y =
, hàm số này không xác định tại x = 1 . Do đó hàm số gián đoạn tại x = 1 . 2 x -1
Câu 21: Cho hình hộp ABC .
D A B C D . Đẳng thức nào sau đây sai? 1 1 1 1 !!!!" !!!" !!!" !!!!" !!!" !!!!" "
A. AC + AC = 2AC . B. AC + CA + 2C C = 0. 1 1 1 1 1 !!!" !!!" !!!!" !!!!" !!!" !!!!"
C. CA + AC = CC .
D. AC + CD = A D . 1 1 1 1 1 Lời giải
!!!!" !!!" !!!" !!!!" !!!" !!!" !!!"
+ AC + AC = AC + CC + A A+ AC = 2AC . 1 1 1 1 !!!!" !!!"
!!!!" !!!!" !!!!" !!!" !!!!" !!!" !!!!" "
+ AC + CA + 2C C = AC + C C + CA + C C = AC +C A = 0. 1 1 1 1 1 1 1 1 1 !!!" !!!" !!!" !!!!"
+ CA + AC = AA = CC . 1 1 1 !!!!" !!!" !!!!" !!!!" !!!!"
+ AC + CD = AC + C D = AD . 1 1 1 1 1 Trang 10 ∑ ∑
Câu 22: Cho tứ diện ABCD có AB = AC = AD và BAC = BAD = 60°. Tính góc giữa hai đường thẳng AB và CD . A. 30° . B. 45° . C. 60° . D. 90° . Lời giải A B D C !!!" !!!" !!!" !!!" !!!"
Ta có AB CD = AB ( AD - AC) ∑ ∑ . . = A . B A .
D cos BAD - A .
B AC.cos BAC = 0 . !!!" !!!"
Do đó AB ^ CD, tức AB ^ CD . Vậy ( AB CD) 0 , = 90 . I = ( 2 lim
n - 2n + 3 - n) Câu 23: Tính . A. I = 1. B. I = 1. - C. I = 0. D. I = + . ¥ Lời giải Ta có
( 2n -2n+3-n)( 2n -2n+3+n) ( 2n -2n+3) 2 - n I = ( 2
lim n - 2n + 3 - n) = lim = lim 2
n - 2n + 3 + n 2
n - 2n + 3 + n 3 - + 2 - n + 3 2 = 2 - lim = lim n = = 1 - . 2
n - 2n + 3 + n 2 3 1 +1 1- + +1 2 n n
Câu 24: Cho hình chóp S.ABC có đáy là tam giác cân tại A, SA vuông góc với đáy, M là trung điểm của
BC, J là trung điểm của BM . Khẳng định nào sau đây đúng?
A. BC ^ (SAM ).
B. BC ^ (SAC).
C. BC ^ (SAB).
D. BC ^ (SAJ ). Lời giải Trang 11 S C A M J B
Ta có SA ^ ( ABC) Þ SA ^ BC ( ) 1 . ABC D
cân tại A Þ AM ^ BC (2). Từ ( )
1 và (2) suy ra BC ^ (SAM ). x +1
Câu 25: Hàm số f ( x) =
liên tục trên khoảng nào sau đây? 2 x - 5x + 4 A. ( ; -¥ 4). B. ( 1 - ;2) . C. [1;+¥). D. (2;3) . Lời giải
Ta có f (x) là hàm số phân thức hữu tỉ có tập xác định là D = ! \{1; }
4 nên f (x) liên tục trên các khoảng (-¥ ) ;1 , (1;4), (4;+¥).
Do đó f (x) liên tục trên (2;3). ì 1- x - 1+ x ï khi x < 0 ï
Câu 26: Tìm tất cả các giá trị của tham số m để hàm số ( ) x f x = í liên tục tại 1- x ïm + khi x ³ 0 ïî 1+ x x = 0. A. m = 1. B. m = 2 - . C. m = 1 - . D. m = 0 Lời giải æ 1- x ö
Ta có: lim f (x) = lim m + = m +1 ç ÷ x 0+ x 0+ ® ® è 1+ x ø æ ö - æ ö 2x -2 f (x)
æ 1- x - 1+ x ö lim = limç ÷= lim ç ÷= limç ÷= 1 - x x ç ÷ 0- 0- ® ® è x ø x 0- ® ç x ( 1 x 1 x ) ÷ - + + x 0- ® ç ( 1- x + 1+ è x ) ÷ è ø ø f (0) = m + 1
f (x) liên tục tại x = 0 khi và chỉ khi lim f (x) = lim f (x) = f (0) Û m +1= 1 - Þ m = 2 - . x 0+ x 0- ® ®
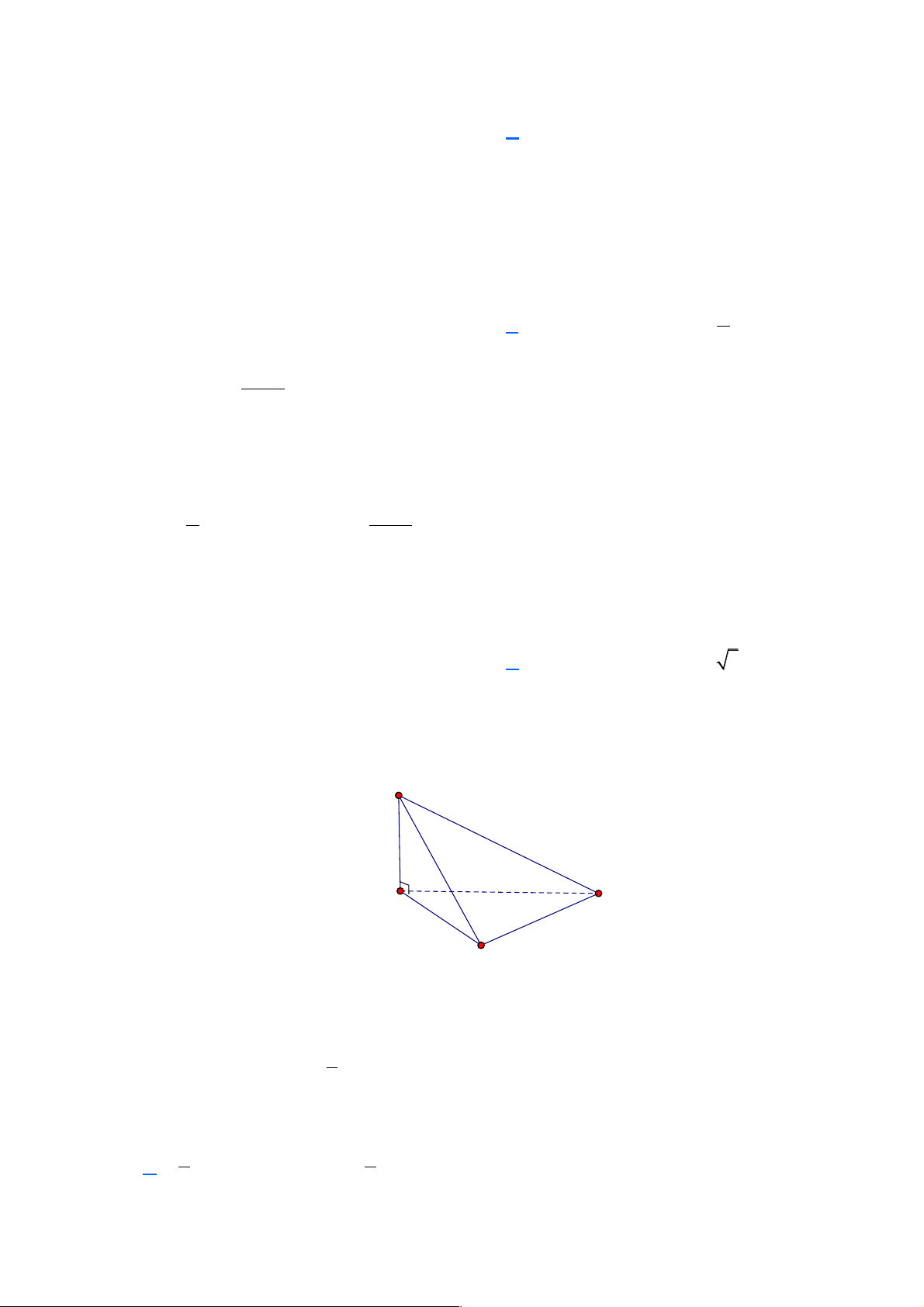
Câu 27: Cho hình chóp S.ABC có BC = 2 , các cạnh còn lại bằng 1. Tính góc giữa hai đường thẳng SB và AC . A. 0 120 . B. 0 90 . C. 0 30 . D. 0 60 . Lời giải Trang 12 S A B I C
Ta có SB = SC = 1, BC = 2 nên tam giác SBC vuông cân tại S .
Vì SA = SB = AB = 1 nên tam giác SAB là tam giác đều. !!" !!!" !!" !!!" . SB AC Ta có cos( ,
SB AC) = cos(SB, AC) = . . SB AC !!" !!!" !!" !!!" !!" !!" !!!" !!" !!" .
SB AC = SB SC - SA = . SB SC - . SB SA = . SB SC.cos90° - . SB . SA cos 60° 1 = - . ( ) 2 1 - cos( AB, SC) 2 1 = = Þ (∑, AB SC) = 60° . 1 2 3 2 x - x Câu 28: lim có giá trị bằng x 1+ ® x -1 +1- x A. 0 . B. 1 - . C. +¥ . D. 1. Lời giải 3 2 x - x x x -1 x 1 Ta có: lim = lim = lim = =1. x 1+ x 1 x -1 +1- x +
x -1 - (x - ) x 1 1 + ® ® ® 1- x -1 1- 1-1 3 3 3 1 + 2 +!+ n b Câu 29: Cho biết lim = , a bΕ b 4 (
), đồng thời là phân số tối giản. Giá trị của n +1 a a 2 2 2a + b là A. 99. . B. 33. . C. 73. . D. 51. Lời giải n + n 3 3 3 ( )2 2 Ta có 1 + 2 +!+ n =
(có thể chứng minh đẳng thức này bằng quy nạp). Do đó 4 3 3 3 4 3 2 b 1 + 2 +!+ n
n + 2n + n 1 = lim = lim = 4 a n +1 4( 4 n + ) 1 4 b
Mà theo đề, đồng thời là phân số tối giản nên ta suy ra b = 1, a = 4. Vậy 2 2 2a + b = 33. a
x + x + mx + = x®-¥ ( 2 lim 2) 2 Câu 30: Tìm m sao cho A. m = 0 . B. m = 2 . C. m = 4 - . D. m = 5 - . Lời giải
x - x + mx + - mx +
lim x + x + mx + = = x®-¥ ( 2 ) 2 ( 2 2 2 2 ) ( ) lim lim x®-¥ 2 x®-¥ 2
x + x + mx + 2
x + x + mx + 2 2 . -m - -m = lim x = = 2 Þ m = -4 x®-¥ m 2 2 1+ 1+ + 2 x x Trang 13
Câu 31: Trong hộp đựng 9 tấm thẻ được đánh số từ 1 đến 9. Gọi x là số lần rút thẻ ít nhất từ hộp để xác
suất có ít nhất một thẻ ghi số chia hết cho 4 phải lớn hơn 5 . Hãy cho biết x thuộc tập nào? 6 A. (2;6). B. (4;8). C. (0;4). D. (6;9) . Lời giải
Số cách chọn x thẻ (1£ x £ 9, xΕ )từ 9 thẻ là: x Þ (W) x C n = C 9 9
Gọi A : “trong x thẻ rút ra có ít nhất một thẻ ghi số chia hết cho 4”
Suy ra: A “Trong x thẻ rút ra không có thẻ nào mang số chia hết cho 4” Þ n(A) x x C C x = C Þ P A = Þ P A =1- . 7 ( ) 7x ( ) 7 x C C 9 9 Ta có: 7! x - P ( A) 5 C 5 x! 7 x ! 5 7 ( ) > Û 1- > Û 1- > 6 x C 6 9! 6 9 x ( ! 9 - x)! (9 - x)(8 - x) 5 (9 - x)(8 - x) 1 2 Û 1- > Û
< Û x -17x + 60 < 0 Û 5 < x < 12. 72 6 72 6
Kết hợp điều kiện, ta có 6 £ x £ 9, x Î • .
Vậy phải rút ít nhất 6 thẻ nên xÎ(4;8).
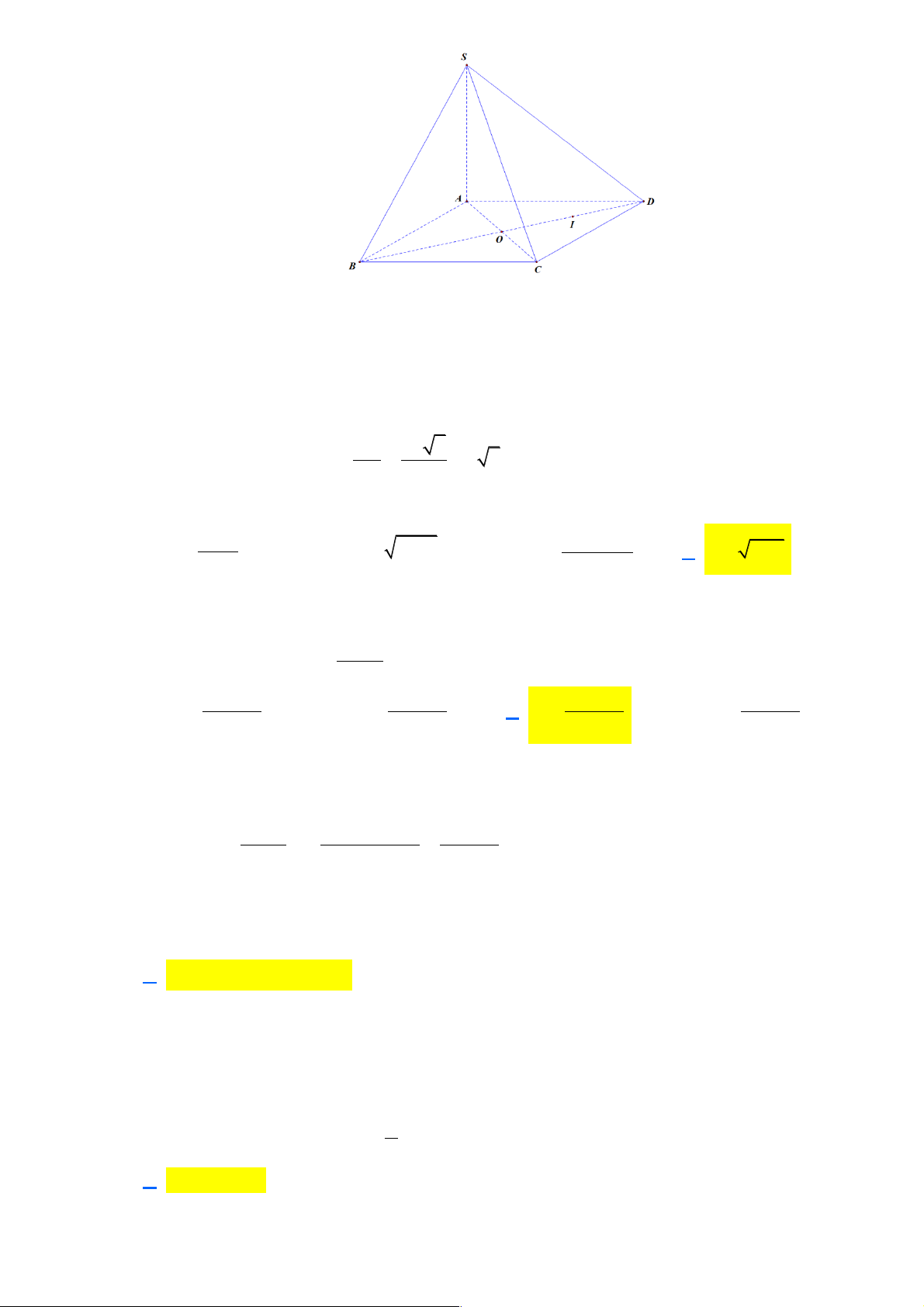
Câu 32: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA = SB = SC = b (a > b 2).
Gọi G là trọng tâm ABC D
. Xét mặt phẳng (P) đi qua G vuông góc với SC tại điểm I nằm
giữa S và C . Diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng (P) là? 2 2 2 a 3b + a 2 2 2 a 3b - a 2 2 2 a 3b + a 2 2 2 a 3b - a A. S = . B. S = . C. S = . D. S = . 2b 9b 9b 2b Lời giải
Trong ( ABC) kẻ đường thẳng đi qua G song song với AB cắt AC, BC lần lượt tại E, F .
Khi đó, EF ^ CG (1)
Theo giả thiết ta suy ra hình chóp S.ABC là hình chóp đều suy ra: SG ^ ( ABC) (2).
Từ (1) và (2) ta suy ra SC ^ EF Þ (P) º (IEF). Þ thiết diện có được là tam giác IEF . Ta có: 2 2 GC.GS EF =
AB = a . Tam giác SGC vuông tại G , GI ^ SC Þ GI = . 3 3 SC Trang 14 a 2 2 3 3 3 2 2 2 2 2 - 2 GC = 3 a S . G GC a b a
, GS = SC - GC = b - =
3b - a Þ GI = = . 3 9 3 SC 3b a2 b2 - a2 1 3
Diện tích tam giác IEF là . FE GI = . 2 9b .
Câu 33: Cho ba số dương a,b,c theo thứ lập thành cấp số cộng. Giá trị lớn nhất của biểu thức a2 + b
8 c + 3 có dạng x y (x,yΕ ).Hỏi x + y bằng bao nhiêu: P = ( 2 a + 2c) +1 A. 11.. B. 13.. C. 9.. D. 7. Lời giải
Vì a,b,c theo thứ lập thành cấp số cộng 2
Þ a + c = 2b Þ a +8bc = a + 2c (a + 2c)+3 Þ P =
. Dễ thấy P > 0. (a + 2c)2 +1
Đặt a + 2c = t (t > 0) 2 t + 3 t + 6t + 9 Ta có 2 2 2 2 2 P = Û P =
Û P t + P = t + 6t + 9 Û ( 2 P - ) 2 2
1 t - 6t + P - 9 = 0 * 2 ( ) 2 t +1 t +1
Để tồn tại P thì phương trình ( )
* phải có nghiệm t > 0 2
P -1 = 0 Û P = 1 ± , ( ) 4
* Û t = - < 0 (không thỏa mãn, do đó loại P = 1 ± ). 3 ( ) * có hai nghiệm dương
ì9ï-( 2p - )1( 2p -9)³0 2 ìP ìD¢ ³ ( 2 10 - P ) ³ 0 0 ï 2 ï ï 6 ïï ìïP £10 2 Û t í + t > 0 Û í > 0 Û íP -1> 0 Û í Þ P £ 10 1 2 2 2 P -1 ï ï ï ïîP > 9 2 t .t > 0 î - > 1 2 2 P 9 0 ï P -9 ï 0 î > ï 2 î P -1
Vậy P = 10 Þ x =1; y =10 Þ x + y = . 11 max
Câu 34: Cho hàm số f x = ( 2 + m ) 8 5 3 ( ) 1
x - m x + mx - . Ch 1
ọn mệnh đề đúng trong các mệnh đề sau:
A. Phương trình f (x) = 0 vô nghiệm với mọi m .
B. f (x) gián đoạn tại x = 1.
C. Phương trình f (x) = 0 có ít nhất hai nghiệm phân biệt với mọi m .
D. f (x) luôn nhận giá trị âm với mọi m . Lời giải
FB Tác giả: Anh Bùi
f (x) là hàm đa thức nên liên tục trên ! Þ Loại. B.
lim f ( x) = +¥ Þ Loại. D. x®+¥ f (0) = 1
- , lim f (x) = +¥ Þ f (x) có nghiệm thuộc (0;+¥) Þ Loại. A. x®+¥ Vậy đáp án đúng là. C. Trang 15 ì 2x - 4 +3, khi x ³ 2 ï
Câu 35: Cho hàm số f (x) = í x +1
. Tìm tất cả các giá trị của tham số thực m để , khi x < 2 ï 2
î x - 2mx + 3m + 2
hàm số liên tục trên ! . A. m = 3. B. m = 4 . C. m = 5. D. m = 6 . Lời giải Ta có f (2) = 3. lim f (x) = lim x - + = + + ( 2 4 3) 3. x®2 x®2 x +1 3 lim f (x) = lim = . - - 2 x®2
x®2 x - 2mx + 3m + 2 6 - m
Hàm số liên tục tại x = 2 khi và chỉ khi f x = f x = f ( ) 3 lim ( ) lim ( ) 2 Û = 3 Û m = 5. 0 x 2+ x 2- ® ® 6 - m
Suy ra khi m = 5 thì hàm số đã cho liên tục tại x = 2. 0
Mặt khác, với x ³ 2 thì f (x) = 2x - 4 + 3liên tục. x +1
Với x < 2 thì hàm f (x) = liên tục. 2 x -10x +17
Vậy với m = 5 thì hàm f liên tục trên ! .
Câu 36: Mệnh đề nào sau đây là mệnh đề đúng
A. Mọi dãy số có giới hạn thì luôn luôn tăng hoặc luôn luôn giảm. B. Nếu (u limu = +¥
n ) là dãy số tăng thì . n
C. Nếu limu = +¥ và limv = +¥ thì lim(u - v = n n ) 0 . n n D. Nếu n u = a và 1
- < a < 0 thì limu = 0. n n Lời giải
A sai. Vì có dãy số không tăng cũng không giảm, ví dụ dãy hằng. B sai. Phản ví dụ: n u =
là dãy tăng nhưng limu =1. n n +1 n ìlimu = +¥ u ì = 2n n ï C sai. Phản ví dụ: n Þ ílimv = +¥ . ív = n n î n ïlim(u -v = +¥ î n n ) D đúng vì lim n
a = 0 với a < . 1 3 n + n
Câu 37: Giới hạn lim bằng: 2 2 2 1 + 2 + ... + n A. 2018. B. 6 . C. +¥ . D. 3. Lời giải Trang 16 n + n n + n 6( 3 3 3 n + n ) lim = lim = lim 2 2 2 1 + 2 + ... + n n(n + ) 1 (2n + ) 1 n(n + ) 1 (2n + ) 1 6 3 æ 1 ö æ 1 ö 6n +1 6 +1 ç ÷ ç ÷ 2 2 è n ø è n lim lim ø = = = 3 3 æ 1 öæ 1 ö æ 1 öæ 1 ö n 1+ 2 + 1+ 2 + ç ÷ç ÷ ç ÷ç ÷ è n øè n ø è n øè n ø 3 n + n Vậy lim = 3. 2 2 2 1 + 2 +...+ n
Câu 38: Trong các mệnh đề sau, mệnh đề nào sai? 1 1 A. lim = +¥. B. 1 1 lim = +¥. C. lim = -¥. D. lim = -¥. x 0- ® x - 4 - 3 x®0 x x 0- ® x x®0 x Lời giải 1 1
xác định với x > 0 nên không tồn tại lim
. Dó đó phương án A sai. x x 0- ® x
Các phương án còn lại đều đúng. 3 x + 2 2 I = lim 2
Câu 39: Tính giới hạn x®- 2 x - 2 2 -3 2 A. -1. B. 1 . C. . D. . 2 2 2 2 Lời giải Ta có: x + (x+ 2)( 2 3 x - 2x + 2 2 2 ) I = lim = lim 2 x®- 2 x®- 2 x - 2 (x+ 2)(x- 2)
( 2x - 2x+2) 2+2+2 3- 2 = lim = = . x®- 2 (x- 2) 2 - 2 2
Câu 40: Tìm limu biết 1 1 1 u = + +...+ . n n 2 2 2 2 -1 3 -1 n -1 A. 3 . B. 3 . C. 2 D. 4 . 4 5 3 3 Lời giải Chọn A 1 1 1 1 1 1 1 Ta có: u = + +...+ = + + +...+ n 2 2 2 2 -1 3 -1 n -1 1.3 2.4 3.5 (n- )1(n+ )1 1 æ1 1 1 1 1 1 1 1 ö = - + - + - +...+ - 1 æ1 1 1 ö 3 1 ç ÷ = + - = - . 2 è1 3 2 4 3 5 n -1 n +1ø ç ÷
2 è1 2 n +1ø 4 2(n + ) 1 é3 1 ù 3 Suy ra: limu = lim ê - ú = . n 4 2(n + ë )1 4 û Trang 17
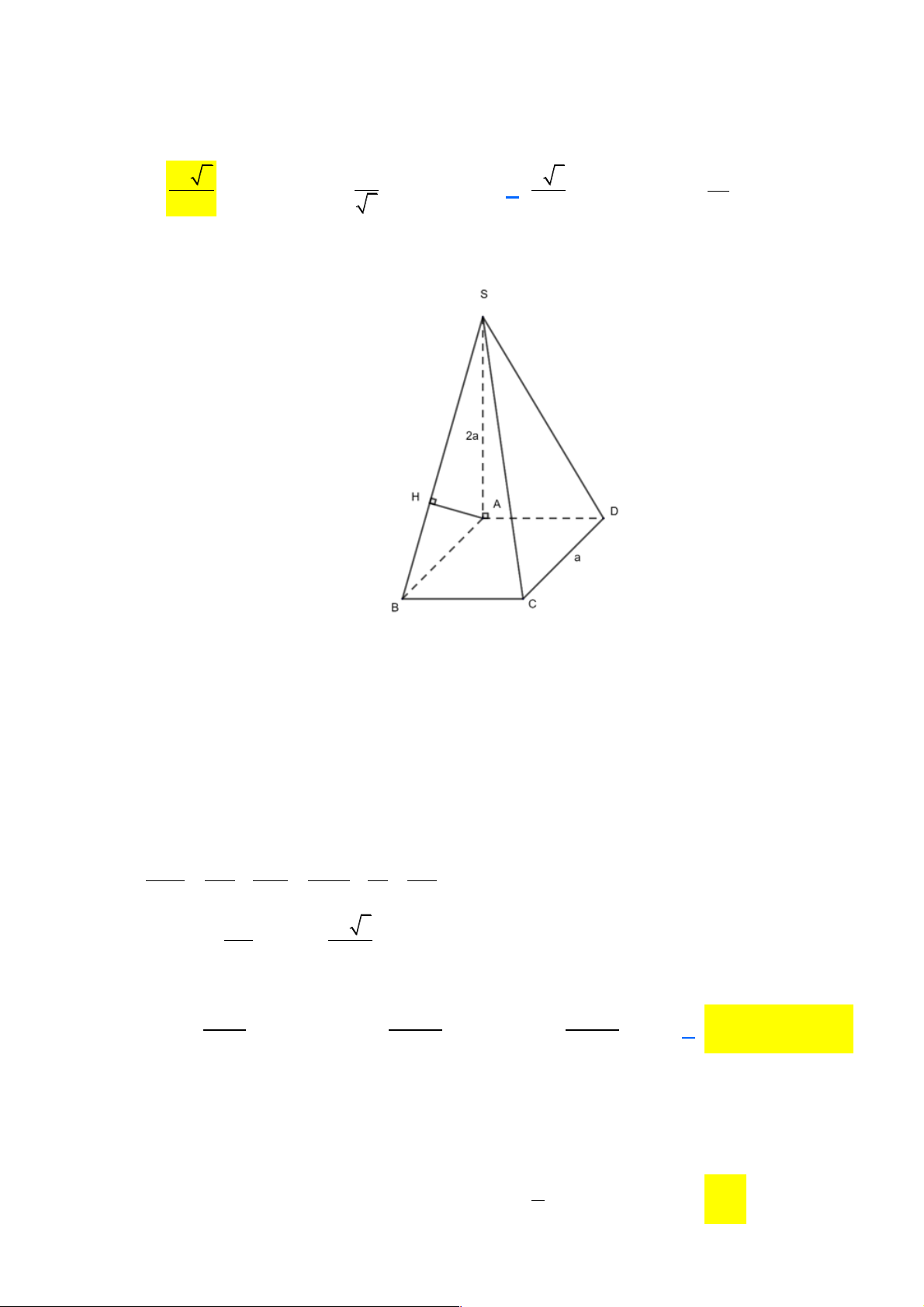
Câu 41: Cho lăng trụ tứ giác ABC .
D A' B 'C ' D ' . Có đáy là hình vuông và cạnh bên bằng 2a . Hình
chiếu của A' trên mặt phẳng ( ABCD) là trung điểm của cạnh AD , đường thẳng A'C hợp với
mặt phẳng ( ABCD)một góc 45o . Thể tích khối lăng trụ đã cho bằng 3 8a 30 3 8a 30 3 16a 3 16a A. 9 . B. 27 . C. 3 . D. 9 . Lời giải:
Gọi H là trung điểm AD, ta có: A' H ^ (ABCD)
Þ HC là hình chiếu của A'C trên ( ABCD) ∑ ∑ ∑ Þ ( ' ,( )) = ( ' , ) = ' = 45o A C ABCD A C HC HCA
Áp dụng định lý Pitago cho tam giác HDC vuông tại D ta có:
HC = HD + DC = a + ( a)2 2 2 2 2 = a 5 Þ ' = .tan 45o A H HC = a 5 ÞV = A'H.S
= a 5. 2a = 4a 5 ABC .
D A'B'C'D' ABCD ( )2 3 . lim f ( x) = 5 lim é3 - 4 ë f ( x)ù Câu 42: Nếu û x®2 thì x®2 bằng A. 18 - . B. 1 - . C. 1. D. 17 - . Lời giải Ta có lim é3 - 4 ë
f ( x)ù = lim3 - 4lim û
f ( x) = 3 - 4.5 = 1 - 7 . x®2 x®2 x®2
lim ( n + 2018 - n ) n Câu 43: Giới hạn bằng A. 1009 . B. 2018 . C. +¥ . D. 0 . Lời giải n n + - n n + + n
lim( n + 2018 - n) ( 2018 )( 2018 ) n = lim n + 2018 + n . 2018 n 2018 2018 = lim = lim = =1009 n + 2018 + n 2018 1+1 1+ +1 n 3 n + n
Câu 44: Giới hạn lim bằng: 2 2 2 1 + 2 + ... + n A. 2018. B. 6 . C. +¥ . D. 3. Lời giải Trang 18 n + n n + n 6( 3 3 3 n + n ) lim = lim = lim 2 2 2 1 + 2 + ... + n n(n + ) 1 (2n + ) 1 n(n + ) 1 (2n + ) 1 6 3 æ 1 ö æ 1 ö 6n +1 6 +1 ç ÷ ç ÷ 2 2 è n ø è n lim lim ø = = = 3 3 æ 1 öæ 1 ö æ 1 öæ 1 ö n 1+ 2 + 1+ 2 + ç ÷ç ÷ ç ÷ç ÷ è n øè n ø è n øè n ø 3 n + n Vậy lim = 3. 2 2 2 1 + 2 +...+ n
Câu 45: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA ^ (ABCD). Gọi I, J , K lần lượt là
trung điểm của AB, BC và SB . Tong các khẳng định sau, khẳng định nào sai? A. ! (SD BC) 0 , = 60 .
B. BD ^ (SAC)..
C. BD ^ (IJK)..
D. (IJK) / /(SAC). Lời giải Ta có: ! (SD BC) ! = (SD AD) ∑ , , = SDA
Mà theo giả thiết không có số liệu AD, SA nên đáp án A là sai. 3 1+ 2x - 1+ 3x
Câu 46: Giới hạn lim có giá trị là: 2 x®0 x A. 1 . B. 2 . C. 9 - . D. 0 . 2 5 20 Lời giải + - + ( 1+2x -1- x)+( 3 3 1+ x - 1+ 3 1 2 1 3 x x x ) Ta có lim = lim . 2 2 x®0 x®0 x x 1+ 2x -1- x 1+ 2x - (1+ x)2 +) 1 - 1 lim = lim = lim = - . 2 x 0 ® x 0 ® 2 x
x ( 1+ 2x +1+ x) x 0 ® 1+ 2x +1+ x 2 1+ x - 1+ 3x (1+ x)3 3 - (1+ 3x) +) lim = lim 2 x® x® x é x (1 x)
(1 x) 1 3x ( 1 3x)2 0 0 2 2 3 3 ù + + + + + + êë úû 3 + x = lim =1
x®0 (1+ x) + (1+ x) 3 1+ 3x + (3 1+3x)2 2 3 1+ 2x - 1+ 3x 1 1 Vậy lim = - +1= . 2 x®0 x 2 2 Trang 19 2 3
x + x + 2 - 7x +1 a 2 Câu 47: Biết lim = + c với a
a , b , c Î ! và
là phân số tối giản. Giá trị của x 1 ® 2 (x - ) 1 b b
a + b + c bằng: A. 5 . B. 37 . C. 13. D. 51. Lời giải Chọn C 2 3 2 3
x + x + 2 - 7x +1
x + x + 2 - 2 + 2 - 7x +1 Ta có lim = lim x 1 ® 2 (x - ) x 1 1 ® 2 (x - ) 1 2 3 x + x + 2 - 2 2 - 7x +1 = lim + lim = I + J . x 1 ® 2 (x - ) x 1 1 ® 2 (x - ) 1 2 2 Tính x + x + 2 - 2 x + x + 2 - 4 I = lim = lim x 1 ® 2 ( x - ) x 1 1 ® 2 ( x - ) 1 ( 2 x + x + 2 + 2) (x - ) 1 ( x + 2) x + 2 3 = lim = lim = . x 1 ® 2 ( x - )
1 ( 2x + x + 2 + 2) x 1 ®
2 ( 2x + x + 2 + 2) 4 2 3 2 - 7x +1 8 - 7x -1 và J = lim = lim x® 2 (x - ) 1 x® 2 (x - ) 1 é4 + 2 7x +1 + ê ( 7x+1)2 1 1 3 3 ù ë úû 7 - 7 - = lim = . x® é + x + + ( x + ê )2 1 3 3 ù 12 2 2 4 2 7 1 7 1 ë úû 2 3
x + x + 2 - 7x +1 2 Do đó lim = I + J = x 1 ® 2 (x - ) 1 12
Suy ra a = 1, b = 12 , c = 0 . Vậy a + b + c = 13. 2 4x - x + 3
Câu 48: Giới hạn: lim
bằng kết quả nào trong các kết quả sau? x®-¥ x A. 2. B. 2 - . C. - 2 . D. 0 . Lời giải Chọn B 2 æ 1 3 ö 1 3 x 4 - + ç ÷ - + 2 2 x 4 2 4x - x + 3 è x x ø lim = lim = lim x x x®-¥ x®-¥ x x x ®-¥ x 1 3 1 3 - . x 4 - + . - 4 - + 2 2 = lim x x = lim x x = 2 - x®-¥ x x ®-¥ 1 . . 4
Câu 49: Giới hạn: 2x - 3 lim
bằng kết quả nào trong các kết quả sau? x®+¥ 2 x +1 + x A. 0 . B. -¥ . C. +¥ . D. 1. Lời giải Trang 20 Chọn C 4 æ 3 ö 2 3 x 2 - ç ÷ - 4 4 x 2 4 2x - 3 è x ø lim = lim = lim x x®+ ¥ 2 x +1 x + x ®+¥ æ 1 x®+ ¥ ö 1 2 x 1+ + x x 1+ + x ç 2 ÷ 2 è x ø x 2 3 3 x 2 - x 2 - 4 4 = lim x = lim x = +¥ x®+ ¥ æ 1 x®+ ¥ ö 1 x ç 1+ +1÷ 1+ +1 2 2 x x è ø 3 3x + 5 - x + 3 Câu 50: lim có giá trị bằng: x 1 ® x -1 1 1 1 A. - . B. 0 . C. . D. - . 6 4 5 Lời giải 3 3x + 5 - x + 3
3 3x + 5 - 2 + 2 - x + 3 Ta có lim = lim x 1 ® x -1 x 1 ® x -1 æ ö 1 3x + 5 - 8 4 - x - 3 lim ç ÷ = + x 1 ® x -1ç + + ÷ 3 ( x + )2 3 2 x 3 3 5 + 2 3x + 5 + 4 è ø æ ö 1 3( x - ) 1 x -1 lim ç ÷ = - x 1 ® x -1ç + + ÷ 3 ( x + )2 3 2 x 3 3 5 + 2 3x + 5 + 4 è ø æ ö 3 1 3 1 1 1 lim ç ÷ = - = - = - = 0. x 1 ® ç + + ÷ 3 ( x + )2 3 2 x 3 3 5 + 2 3x + 5 + 4 4 + 4 + 4 2 + 2 4 4 è ø
ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KỲ II
Môn: TOÁN 11 – ĐỀ 2
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Trong không gian, cho tam giác ABC có M là trung điểm BC . Tìm khẳng định đúng trong các khẳng định sau. !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!!" !!!" !!!" !!!!"
A. AB - AC = . BC
B. AB + AC = . BC
C. AB + AC = AM. D. AB + AC = 2AM.
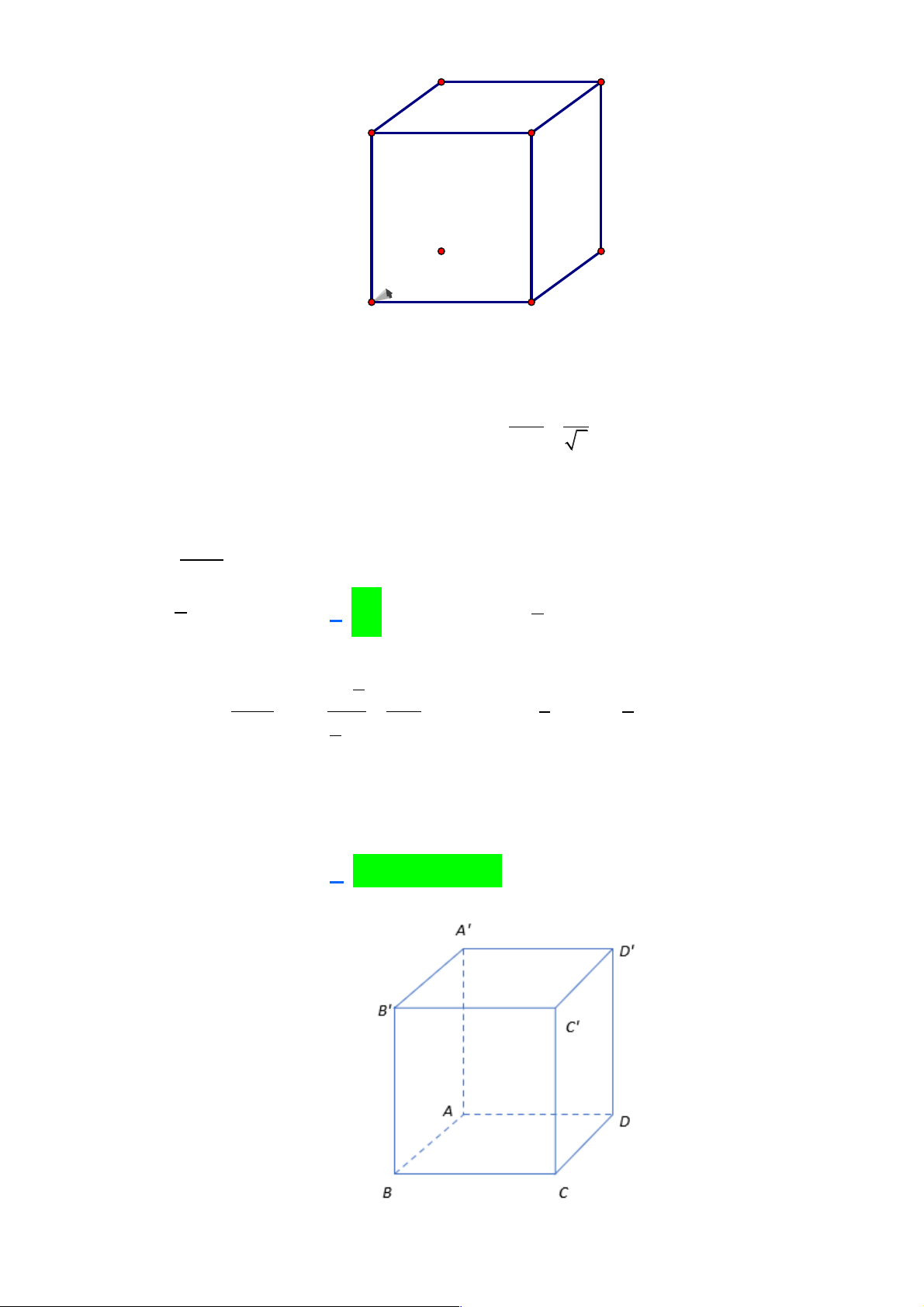
Câu 2: Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh a . Khoảng cách giữa đường thẳng AC và mặt
phẳng ( A'B'C'D'). a A. . B. a 2. C. 2 . a D. . a 2
Câu 3: Đạo hàm của hàm số y = xsin x là.
A. y ' = cos x.
B. y ' = sin x + xcos .
x C. y' = sin x + cos .x D. y' = sin x - xcos .x Trang 21
Câu 4: Cho hai hàm số f (x) và g ( x) có f '(0) =1 và g '(0) = 2. Đạo hàm của hàm số
y = 2 f (x) -3g (x) tại điểm x = 0 bằng A. 4 . B. 3 - . C. 4 - . D. 3.
Câu 5: Tìm khẳng định đúng trong các khẳng định sau p
A. (sin 2x)' = cos2 , x x " Î! . B. ( x) 2
tan ' =1+ tan x, x
" ¹ + kp,k Î! 2 1 C. (cot x)' = , x
" ¹ kp,k Î!. D. ( 2
sin x)' = 2sin ,x x " Î! . 2 sin x
Câu 6: Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng ( ABC), góc giữa mặt bên
(SBC) và mặt đáy (ABC) bằng 0
60 . Tính diện tích tam giác ABC biết diện tích tam giác SBC bằng 10. A. 20 . B. 8 . C. 5 . D. 5 3 .
Câu 7: Cho hàm số y = f (x) 2 = x + x + . T
1 ập nghiệm của phương trình 2 f '(x) -3 = 0 là ì1 ü ì3ü A. í ý. B. í ý. C. { } 1 . D. { } 0 . î4þ î2þ Câu 8: lim (x - ) 1 (x + 2)bằng x®+¥ A. 1. B. 0 . C. +¥ . D. -¥ . Câu 9: lim( 3 2
-x + 2x - x + ) 1 bằng x 1 ® A. -¥ . B. 1. C. +¥ . D. 0 .
Câu 10: Đạo hàm của hàm số y = x tại điểm x = 4 là 1 A. . B. 2. C. 0. D. 1. 4
Câu 11: Đạo hàm của hàm số y = sin x + cos x là A. y¢ = 2sin . x
B. y¢ = cos x + sin . x
C. y¢ = cos x - sin .
x D. y¢ = -cos x - sin . x
Câu 12: Cho tứ diện đều ABC .
D Góc giữa hai đường thẳng AB và AC bằng A. 60 . ° B. 30 . ° C. 90 . ° D. 45 . °
Câu 13: Cho u = u(x) và v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Khẳng
định nào dưới đây là sai?
A. (u + v)' = u'+ v'.
B. (ku)' = k 'u', với k là một hằng số.
C. (uv)' = u'v + v'u .
D. (u - v)' = u'- v'. 1
Câu 14: Đạo hàm của hàm số y = là x 1 1 1 1 A. y ' = . B. y ' = . C. y ' = - . D. y ' = - . 2 x (x - )2 1 (x + )2 1 2 x Trang 22
Câu 15: Cho hàm số y = f (x) có đồ thị (C) và có đạo hàm tại điểm x . Phương trình tiếp tuyến của 0
đồ thị (C) tại điểm M (x ; f x 0 ( 0)) là
A. y = f '(x x + x + f x
y = f '(x x + x - f x 0 )( 0 ) ( 0) 0 )( 0 ) ( 0). B. .
C. y = f '(x x - x + f x
y = f '(x x - x - f x 0 )( 0 ) ( 0) 0 )( 0 ) ( 0). D. .
Câu 16: Cho hai dãy số (u (v lim(u +5 = limv = 2 n ) 0 n ) n )và thỏa mãn và . n
Giá trị của lim(u + v n n ) bằng A. 7 - . B. 3 - . C. 7 . D. 0 .
Câu 17: Trong không gian, cho mặt phẳng (P) và đường thẳng (d ) vuông góc với mặt phẳng (P) có
bao nhiêu mặt phẳng chứa d và vuông góc với mặt phẳng (P)? A. 0 . B. Vô số. C. 2 . D. 1. 2n -1 Câu 18: lim bằng 3 - n 2 A. 1. B. . C. 0 . D. 2 - . 3
Câu 19: Đạo hàm của hàm số 3
y = x - 2x là A. 2
y ' = x + 2. B. 3
y ' = 2x - 2. C. 2
y ' = 3x - 2. D. 2
y ' = 3x . 2 n æ ö Câu 20: lim bằng ç ÷ è 3 ø A. 1. B. + . ¥ C. . -¥ D. 0. x - 2
Câu 21: Đạo hàm của hàm số y = là x +1 1 3 3 1 A. y ' = . B. y ' = - . C. y ' = . D. y ' = - . 2 (x +1) 2 (x +1) 2 (x +1) 2 (x +1)
Câu 22: Đạo hàm của hàm số 2 5
y = (x + 3) là A. 2 4
y ' = 2x(x + 3) . B. 2 4
y ' = 5(x + 3) . C. 2 4
y ' =10x(x + 3) . D. 2 5
y ' = 2x(x + 3) .
Câu 23: Tiếp của đồ thị hàm số 2
y = x - 2x tại điểm M có hoành độ bằng 2 có hệ số góc là: A. 2. B. 1. C. 1. - D. 2. -
Câu 24: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a . Tính khoảng cách từ đỉnh S đến
mặt phẳng (ABCD). a 3 a
A. d(S,(ABCD)) = 3 .
B. d(S,(ABCD)) = . 2 4 a 2 a
C. d(S,(ABCD)) = .
D. d(S,(ABCD)) = . 2 2
Câu 25: Cho hình lập phương ABC .
D A' B 'C ' D '.Mặt phẳng ( ABCD) vuông góc với mp nào sau đây?
A. ( ABC 'D') B. (BDC ')
C. ( AB'D')
D. ( ACC ' A') Trang 23
Câu 26: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a .Cạnh bên SA vuông góc với mặt phẳng
(ABCD) và SA= a 2 .Góc giữa đường thẳng SC và mặt phẳng (ABCD)bằng: A. 0 45 B. 0 30 C. 0 60 D. 0 90
Câu 27: Tìm khẳng định đúng trong các khẳng định sau:
A. Nếu hàm số y = f (x) gián đoạn tại điểm x và hàm số y = g (x) liên tục tại điểm x thì 0 0
hàm số y = f (x) + g (x) liên tục tại điểm x . 0
B. Nếu hàm số y = f (x) và y = g (x) cùng gián đoạn tại điểm x thì hàm số y = f (x) + g (x) 0
gián đoạn tại điểm x . 0
C. Nếu hàm số y = f (x) và y = g (x) cùng gián đoạn tại điểm x thì hàm số 0
y = f (x) + g (x) liên tục tại điểm x . 0
D. Nếu hàm số y = f (x) và y = g (x) cùng liên tục tại điểm x thì hàm số y = f (x) + g (x) 0
liên tục tại điểm x . 0
Câu 28: Cho hàm số y = tan x . Tìm khẳng định đúng trong các khẳng định sau. A. 2
y - y '+1 = 0. B. 2
y - y '-1 = 0. C. 2
y + 2y '+1 = 0. D. 2
y - 2y '+1 = 0 .
Câu 29: Đạo hàm của hàm số y = sin(cosx)là
A. y' = -sinx.cos(sinx). B. y' = -sinx.cos(cosx).
C. y' = sinx.cos(cosx). D. y' = cos(cosx). !" !!" !" !!" !" !!"
Câu 30: Trong không gian, cho hai vectơ u và u có u = 2 , u = 3 và u .u = 3 - . Góc giữa 2 vectơ 1 2 1 2 1 2 !" !!"
u và u bằng 1 2 A. 0 60 . B. 0 120 . C. 0 30 . D. 0 90 .
Câu 31: Đạo hàm cấp hai của hàm số 10
y = x là A. 8
y '' = 19x . B. 8
y '' = 90x . C. 8
y '' = 9x . D. 9 y '' = 10x .
Câu 32: Đạo hàm của hàm số y = cos3x là A. 3 - cos3x . B. 3 - sin 3x .
C. 3cos3x . D. 3sin 3x .
Câu 33: Trong không gian cho hai đường thẳng a,b phân biệt và mặt phẳng (P). Khẳng định nào sau đây là sai?
A. Nếu a ! (P) và b ^ (P) thì b ^ a .
B. Nếu a Ì (P) và b ^ (P) thì b ^ a .
C. Nếu a ^ (P) và b ^ (P) thì a ! b.
D. Nếu a ^ (P) và b ^ a thì b ! (P).
Câu 34: Cho hàm số y = sin x. Tìm khẳng định đúng trong các khẳng định sau:
A. y¢ + y¢ = 0.
B. y¢ + y = 0.
C. y¢ + y = 0.
D. y¢ + y¢ + y = 0.
Câu 35: Cho cấp số nhân lùi vô hạn (u u = 2 u = 1 (un) n ) có và
. Tổng của cấp số nhân lùi vô hạn 1 2 bằng Trang 24 1 A. 4. B. 2. C. D. 1. 2 II. PHẦN TỰ LUẬN Câu 36: Cho hàm số ( ) 4 2
f x = ax + bx + c với a, ,
b c Î! . Biết rằng đồ thị hàm số đi qua hai điểm A(1; 3
- ) và B(2;3), đồng thời tiếp tuyến của đồ thị tại điểm có hoành độ bằng 1 - có hệ số
góc bằng 2. Xác định giá trị của a,b, c.
Câu 37: Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a , góc giữa mặt bên
và mặt đáy bằng 30° . Tính độ dài đường cao của hình chóp S.ABCD . Câu 38:
a. Giả sử hàm số y = f (x) liên tục trên ° và thỏa mãn f (5) = 4 f ( ) 1 . Chứng minh rằng
phương trình 2 f (x) - f (x + 2) = 0 luôn có nghiệm trên đoạn [1; ] 3 . x - 2 b. Cho hàm số y =
có đồ thị (C). Tìm điểm M trên đồ thị (C) sao cho tiếp tuyến của x + 3 ( 18
C) tại M tạo với hai trục tọa độ một tam giác có diện tích bằng . 5 ----- HẾT -----
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM
Câu 1: Trong không gian, cho tam giác ABC có M là trung điểm BC . Tìm khẳng định đúng trong các khẳng định sau. !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!!" !!!" !!!" !!!!"
A. AB - AC = . BC
B. AB + AC = . BC
C. AB + AC = AM. D. AB + AC = 2AM. Lời giải Chọn D
Câu 2: Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh a . Khoảng cách giữa đường thẳng AC và mặt
phẳng ( A'B'C'D'). a A. . B. a 2. C. 2 . a D. . a 2 Lời giải Chọn D
Ta có: AC || ( A'B'C'D') Þ d ( AC,( A'B'C'D')) = d ( ,
A ( A'B'C'D')) = AA' = . a
Câu 3: Đạo hàm của hàm số y = xsin x là.
A. y ' = cos x.
B. y ' = sin x + xcos .
x C. y' = sin x + cos .
x D. y ' = sin x - xcos . x Lời giải Chọn B
Ta có: y' = (x)'sin x + .
x (sin x)' = sin x + xcos . x Trang 25
Câu 4: Cho hai hàm số f (x) và g (x) có f '(0) =1 và g '(0) = 2. Đạo hàm của hàm số
y = 2 f (x) -3g (x) tại điểm x = 0 bằng A. 4 . B. 3 - . C. 4 - . D. 3. Lời giải Chọn C
y' = 2 f '(x) -3g '(x) Þ y'(0) = 2 f '(0) -3g '(0) = 2.1-3.2 = 4 - .
Câu 5: Tìm khẳng định đúng trong các khẳng định sau p
A. (sin 2x)' = cos2 , x x " Î! . B. ( x) 2 tan ' = 1+ tan x, x
" ¹ + kp ,k Î! 2 1 C. (cot x)' = , x
" ¹ kp ,k Î!. D. ( 2 sin x)' = 2sin , x x " Î! . 2 sin x Lời giải Chọn B p x
" ¹ + kp ,k Î! :(tan x) 1 2 ' = =1+ tan . x 2 2 cos x
Câu 6: Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng ( ABC), góc giữa mặt bên
(SBC) và mặt đáy (ABC) bằng 0
60 . Tính diện tích tam giác ABC biết diện tích tam giác SBC bằng 10. A. 20 . B. 8 . C. 5 . D. 5 3 . Lời giải Chọn C S A C B
Hình chiếu vuông góc của tam giác SBC lên mặt phẳng ( ABC) là tam giác ABC . Do đó, 1 0 S
= S .cos60 =10. = 5 (đơn vị diện tích). ABC SBC 2
Câu 7: Cho hàm số y = f (x) 2 = x + x + . T
1 ập nghiệm của phương trình 2 f '(x) -3 = 0 là ì1 ü ì3ü A. í ý. B. í ý. C. { } 1 . D. { } 0 . î4þ î2þ Lời giải Trang 26 Chọn A
Ta có: y' = f '(x) = 2x +1 nên f (x) - = Û ( x + ) 1 2 ' 3 0 2 2
1 - 3 = 0 Û 4x -1 = 0 Û x = . 4 Câu 8: lim (x - ) 1 (x + 2)bằng x®+¥ A. 1. B. 0 . C. +¥ . D. -¥ . Lời giải Chọn C æ 1 2 ö Ta có: lim ( x - ) 1 ( x + 2) = lim ( 2 x + x - 2) 2 = lim x 1+ - = +¥ . ç 2 ÷ x®+¥ x®+¥ x®+¥ è x x ø Câu 9: lim( 3 2
-x + 2x - x + ) 1 bằng x 1 ® A. -¥ . B. 1. C. +¥ . D. 0 . Lời giải Chọn B Ta có: lim( 3 2
-x + 2x - x + ) 3 2 1 = 1 - + 2.1 -1+1 =1. x 1 ®
Câu 10: Đạo hàm của hàm số y = x tại điểm x = 4 là 1 A. . B. 2. C. 0. D. 1. 4 Lời giải Chọn A 1 1 Ta có y¢ = Þ y¢(4) = . 2 x 4
Câu 11: Đạo hàm của hàm số y = sin x + cos x là A. y¢ = 2sin . x
B. y¢ = cos x + sin . x
C. y¢ = cos x - sin .
x D. y¢ = -cos x - sin . x Lời giải Chọn C
Ta có y¢ = cos x - sin . x
Câu 12: Cho tứ diện đều ABC .
D Góc giữa hai đường thẳng AB và AC bằng A. 60 . ° B. 30 . ° C. 90 . ° D. 45 . ° Lời giải Chọn A
Tứ diện đều là tứ diện có 4 mặt là tam giác đều. Nên (∑ AB AC) ∑ , = BAC = 60 . °
Câu 13: Cho u = u(x) và v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Khẳng
định nào dưới đây là sai? Trang 27
A. (u + v)' = u'+ v'.
B. (ku)' = k 'u', với k là một hằng số.
C. (uv)' = u'v + v'u .
D. (u - v)' = u'- v'. Lời giải Chọn B 1
Câu 14: Đạo hàm của hàm số y = là x 1 1 1 1 A. y ' = . B. y ' = . C. y ' = - . D. y ' = - . 2 x (x - )2 1 (x + )2 1 2 x Lời giải Chọn D
Câu 15: Cho hàm số y = f (x) có đồ thị (C) và có đạo hàm tại điểm x . Phương trình tiếp tuyến của 0
đồ thị (C) tại điểm M (x ; f x 0 ( 0)) là
A. y = f '(x x + x + f x
y = f '(x x + x - f x 0 )( 0 ) ( 0) 0 )( 0 ) ( 0). B. .
C. y = f '(x x - x + f x
y = f '(x x - x - f x 0 )( 0 ) ( 0) 0 )( 0 ) ( 0). D. . Lời giải Chọn C
Câu 16: Cho hai dãy số (u (v lim(u +5 = limv = 2 n ) 0 n ) n )và thỏa mãn và . n
Giá trị của lim(u + v n n ) bằng A. 7 - . B. 3 - . C. 7 . D. 0 . Lời giải Chọn B
Ta có lim(u +5 = Û u = - n ) 0 lim 5 n
Khi đó lim(u + v = - + = - n n ) 5 2 3.
Câu 17: Trong không gian, cho mặt phẳng (P) và đường thẳng (d ) vuông góc với mặt phẳng (P) có
bao nhiêu mặt phẳng chứa d và vuông góc với mặt phẳng (P)? A. 0 . B. Vô số. C. 2 . D. 1. Lời giải Chọn B 2n -1 Câu 18: lim bằng 3 - n 2 A. 1. B. . C. 0 . D. 2 - . 3 Lời giải Chọn D Trang 28 1 2 - 2n -1 Ta có lim = lim n = 2. - 3 - n 3 -1 n
Câu 19: Đạo hàm của hàm số 3
y = x - 2x là A. 2
y ' = x + 2. B. 3
y ' = 2x - 2. C. 2
y ' = 3x - 2. D. 2
y ' = 3x . Lời giải Chọn C 2 n æ ö Câu 20: lim bằng ç ÷ è 3 ø A. 1. B. + . ¥ C. . -¥ D. 0. Lời giải Chọn D 2 2 n æ ö Vì 0 < <1 nên lim = 0. ç ÷ 3 è 3 ø x - 2
Câu 21: Đạo hàm của hàm số y = là x +1 1 3 3 1 A. y ' = . B. y ' = - . C. y ' = . D. y ' = - . 2 (x +1) 2 (x +1) 2 (x +1) 2 (x +1) Lời giải Chọn C x - 2 3 3 Ta có: y = =1- Þ y' = . 2 x +1 x +1 (x +1)
Câu 22: Đạo hàm của hàm số 2 5
y = (x + 3) là A. 2 4
y ' = 2x(x + 3) . B. 2 4
y ' = 5(x + 3) . C. 2 4
y ' =10x(x + 3) . D. 2 5
y ' = 2x(x + 3) . Lời giải Chọn C 2 4 2 ' 2 4 2 4
y ' = 5.(x + 3) .(x + 3) = 5.(x + 3) .2x =10 ( x x + 3) .
Câu 23: Tiếp của đồ thị hàm số 2
y = x - 2x tại điểm M có hoành độ bằng 2 có hệ số góc là: A. 2. B. 1. C. 1. - D. 2. - Lời giải Chọn A Ta có: ' y = 2x - 2
Suy ra hệ số góc của phương trình tiếp tuyến tại điểm M có hoành độ bằng 2 là: '
k = y (2) = 2.2 - 2 = 2. Trang 29
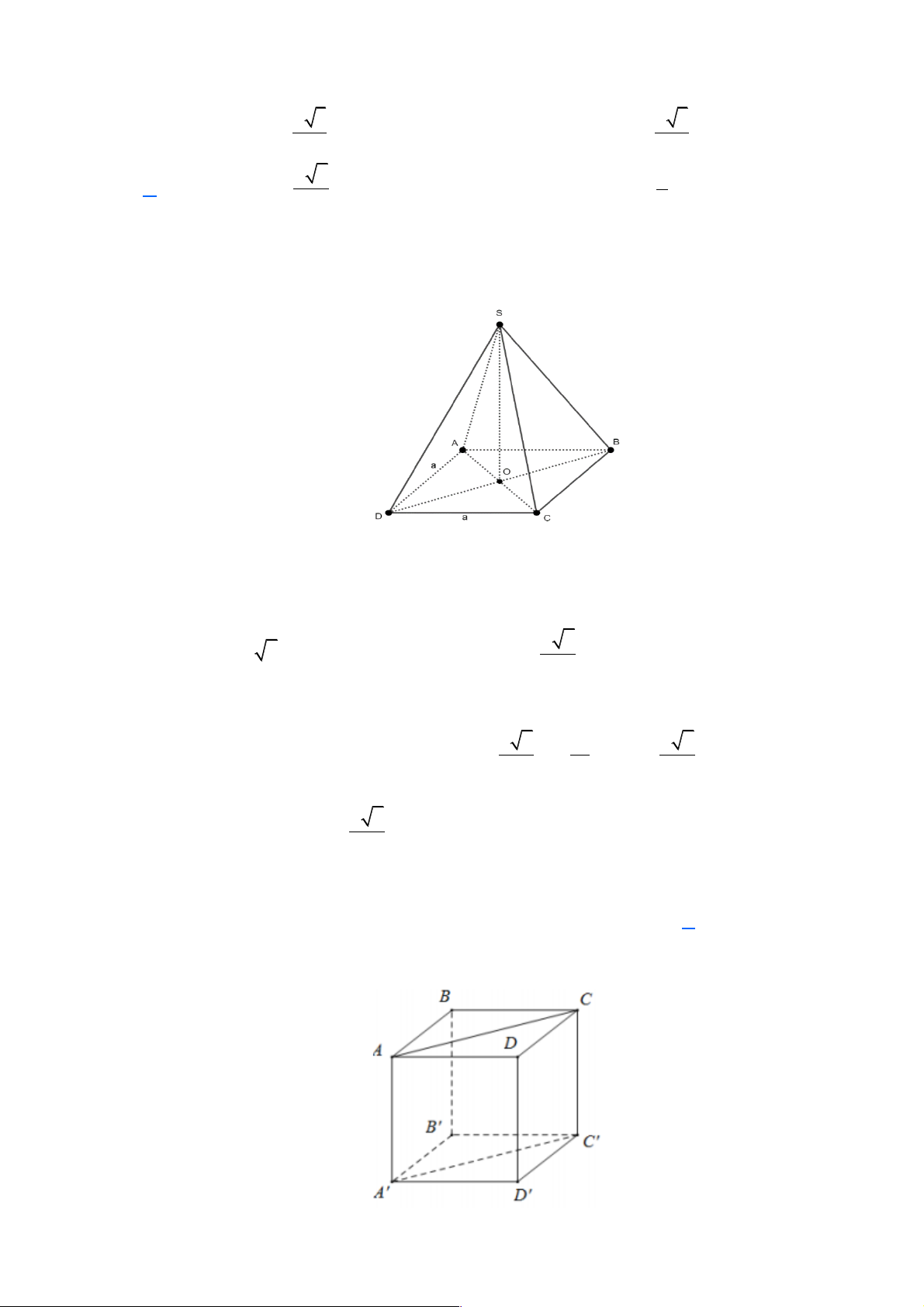
Câu 24: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a . Tính khoảng cách từ đỉnh S đến
mặt phẳng (ABCD). a 3 a
A. d(S,(ABCD)) = 3 .
B. d(S,(ABCD)) = . 2 4 a 2 a
C. d(S,(ABCD)) = .
D. d(S,(ABCD)) = . 2 2 Lời giải Chọn C
Gọi O là tâm của hình vuông ABC .
D Suy ra SO ^ (ABCD) hay SO ^ BD
Xét hình vuông ABCD cạnh a, ta có AD = AB = . a a Suy ra BD = 2
a 2 (đường chéo hình vuông) Þ OD = 2
Xét tam giác vuông SDO vuông tại O, áp dụng định lý Pitago ta có: 2 2 æ a 2 ö a a 2 2 2 2 2 2 2 2
SD = SO + OD Þ SO = SD - OD = a - ç ÷ = Þ SO = ç 2 ÷ 2 2 è ø a 2
Vậy d(S,(ABCD)) = SO = . 2
Câu 25: Cho hình lập phương ABC .
D A' B 'C ' D '.Mặt phẳng ( ABCD) vuông góc với mp nào sau đây?
A. ( ABC 'D') B. (BDC ')
C. ( AB'D')
D. ( ACC ' A') Lời giải Trang 30 Chọn D
Câu 26: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a .Cạnh bên SA vuông góc với mặt phẳng
(ABCD) và SA= a 2 .Góc giữa đường thẳng SC và mặt phẳng (ABCD)bằng: A. 0 45 B. 0 30 C. 0 60 D. 0 90 Lời giải Chọn A SC ( ∑
( ABCD) = SC AC =SCA ) ∑ ( ) ∑ , ,
Tam giác SAC có SA ^ AC, SA = AC = a 2 Suy ra ∑ 0 SCA = 45 .
Câu 27: Tìm khẳng định đúng trong các khẳng định sau:
A. Nếu hàm số y = f (x) gián đoạn tại điểm x và hàm số y = g (x) liên tục tại điểm x thì 0 0
hàm số y = f (x) + g (x) liên tục tại điểm x . 0
B. Nếu hàm số y = f (x) và y = g (x) cùng gián đoạn tại điểm x thì hàm số y = f (x) + g (x) 0
gián đoạn tại điểm x . 0
C. Nếu hàm số y = f (x) và y = g (x) cùng gián đoạn tại điểm x thì hàm số 0
y = f (x) + g (x) liên tục tại điểm x . 0
D. Nếu hàm số y = f (x) và y = g (x) cùng liên tục tại điểm x thì hàm số y = f (x) + g (x) 0
liên tục tại điểm x . 0 Lời giải Chọn D
Câu 28: Cho hàm số y = tan x . Tìm khẳng định đúng trong các khẳng định sau. A. 2
y - y '+1 = 0. B. 2
y - y '-1 = 0. C. 2
y + 2y '+1 = 0. D. 2
y - 2y '+1 = 0 . Lời giải Chọn A Ta có: 2
(tan x)' = tan x +1. Vậy 2 2
(tan x) - (tan x +1) +1 = 0 hay 2 y - y '+1 = 0.
Câu 29: Đạo hàm của hàm số y = sin(cosx)là Trang 31
A. y' = -sinx.cos(sinx). B. y' = -sinx.cos(cosx).
C. y' = sinx.cos(cosx). D. y' = cos(cosx). Lời giải Chọn B
Ta có: (sin u)' = u '.cosu .
Vậy (sin(cosx))' = (cosx)'.cos(cosx) = -sinx.cos(cosx). !" !!" !" !!" !" !!"
Câu 30: Trong không gian, cho hai vectơ u và u có u = 2 , u = 3 và u .u = 3 - . Góc giữa 2 vectơ 1 2 1 2 1 2 !" !!"
u và u bằng 1 2 A. 0 60 . B. 0 120 . C. 0 30 . D. 0 90 . Lời giải Chọn B !" !!" !" !!" !" !!" !" !!" !" !!" u .u Ta có: 1 2
u .u = u . u .cos(u ,u ) Þ cos(u ,u ) = !" !!" !" !!" 1 2 1 2 1 2 1 2
u .u = u . u 1 2 1 2 !" !!" 3 - 1 - Þ cos(u ,u ) = = . 1 2 2.3 2 !" !!" Vậy 0 (u ,u ) =120 . 1 2
Câu 31: Đạo hàm cấp hai của hàm số 10
y = x là A. 8
y '' = 19x . B. 8
y '' = 90x . C. 8
y '' = 9x . D. 9 y '' = 10x . Lời giải Chọn B Ta có: 9 8
y ' =10x ; y ' = 90x .
Câu 32: Đạo hàm của hàm số y = cos3x là A. 3 - cos3x . B. 3 - sin 3x .
C. 3cos3x . D. 3sin 3x . Lời giải Chọn B
Ta có: y' = (cos3x)' = 3 - sin3x.
Câu 33: Trong không gian cho hai đường thẳng a,b phân biệt và mặt phẳng (P). Khẳng định nào sau đây là sai?
A. Nếu a ! (P) và b ^ (P) thì b ^ a .
B. Nếu a Ì (P) và b ^ (P) thì b ^ a .
C. Nếu a ^ (P) và b ^ (P) thì a ! b.
D. Nếu a ^ (P) và b ^ a thì b ! (P). Lời giải Trang 32 Chọn D
Xét đáp án D, Sai vì nếu a ^ (P) và b ^ a thì b ! (P) hoặc b Ì (P) .
Câu 34: Cho hàm số y = sin x. Tìm khẳng định đúng trong các khẳng định sau:
A. y¢ + y¢ = 0.
B. y¢ + y = 0.
C. y¢ + y = 0.
D. y¢ + y¢ + y = 0. Lời giải Chọn C
y = sin x Þ y¢ = cos ; x y¢ = -sin x
Do đó: y¢ + y = -sin x + sin x = 0.
Câu 35: Cho cấp số nhân lùi vô hạn (u u = 2 u = 1 (un) n ) có và
. Tổng của cấp số nhân lùi vô hạn 1 2 bằng 1 A. 4. B. 2. C. D. 1. 2 Lời giải Chọn A 1
Ta có u = 2 và u = 1 mà u = u .q Þ q = . 1 2 2 1 2 u 2
Tổng của cấp số nhân lùi vô hạn (u 1 S = = = 4. n )bằng: 1- q 1 1- 2 II. PHẦN TỰ LUẬN Câu 36: Cho hàm số ( ) 4 2
f x = ax + bx + c với a, ,
b c Î! . Biết rằng đồ thị hàm số đi qua hai điểm A(1; 3
- ) và B(2;3), đồng thời tiếp tuyến của đồ thị tại điểm có hoành độ bằng 1 - có hệ số
góc bằng 2. Xác định giá trị của a,b, c. Lời giải
Đồ thị hàm số đi qua điểm A(1; 3 - ) nên 3
- = a + b + c ( ) 1
Đồ thị hàm số đi qua điểm B(2;3) nên 16a + 4b + c = 3 (2)
Tiếp tuyến của đồ thị tại điểm có hoành độ bằng 1
- có hệ số góc bằng 2 nên f ¢(- ) 1 = 2 Û 4 - a - 2b = 2 - Û 2a + b = 1 (3) Từ ( )
1 , (2), (3) ta có hệ phương trình:
ìa + b + c = 3 - ìa =1 ï ï 16
í a + 4b + c = 3 Û b í = 3 - ï2a b 1 ï + = - c = 1 - î î Vậy a =1;b = 3 - ;c = 1 - . Trang 33
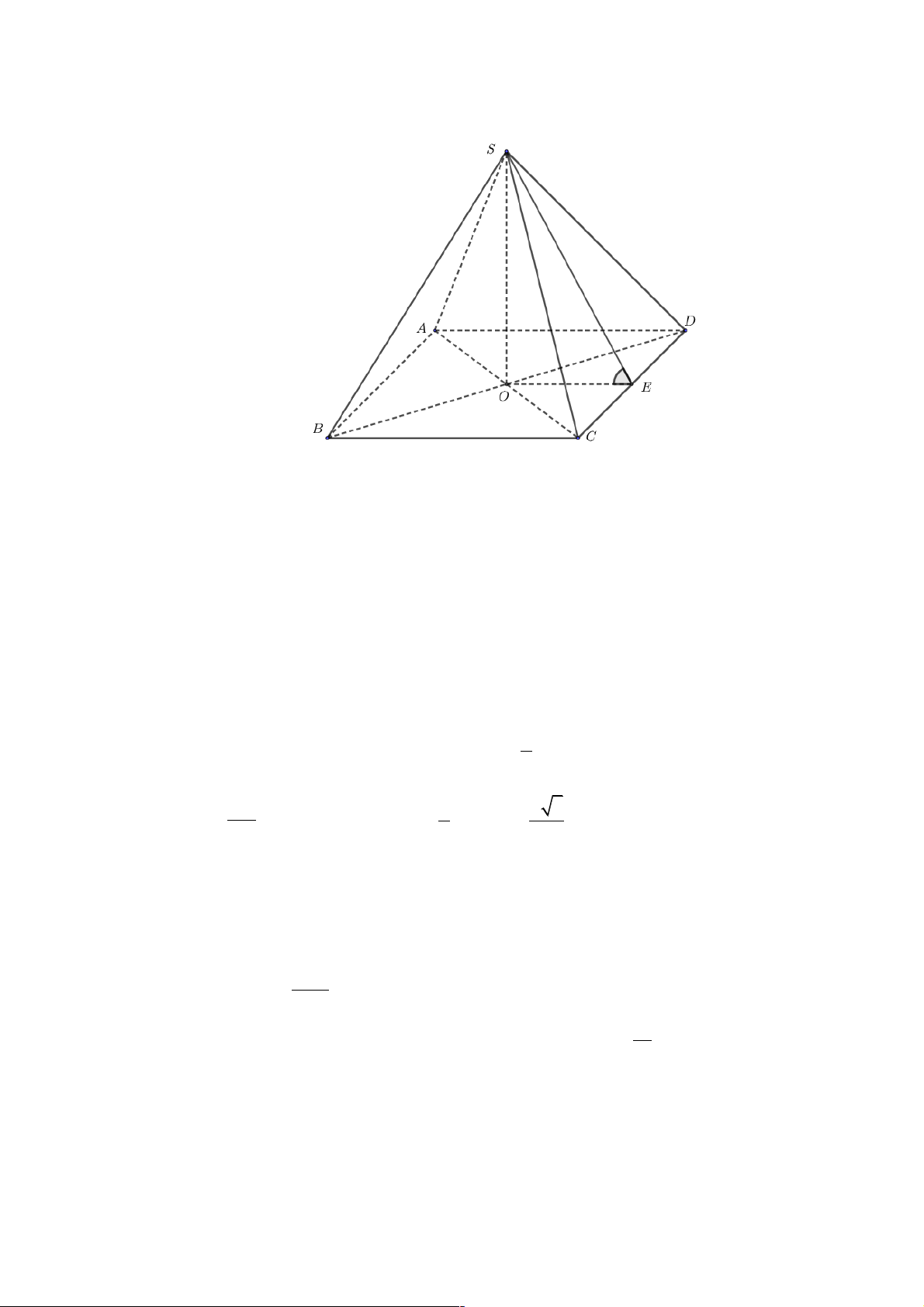
Câu 37: Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a , góc giữa mặt bên
và mặt đáy bằng 30° . Tính độ dài đường cao của hình chóp S.ABCD . Lời giải
Gọi O = AC Ç BD ; E là trung điểm của CD . SA
D C cân nên SO ^ AC ; SB
D D cân nên SO ^ BD
Mà AC, BD Ì ( ABCD) nên SO ^ ( ABCD)
Khi đó độ dài đường cao của hình chóp S.ABCD là SO .
Gọi E là trung điểm của CD Þ SE ^ CD và EO ^ CD Þ ( SCD) ∑(ABCD)) =(∑ SE EO) ∑ , , = SEO = 30° a
Áp dụng hệ thức lượng vào D vuông ∑
SEO,OM = , SEO = 30°, ta có: 2 ∑ SO a a tan SEO = ∑ 3 Þ SO = E .
O tan SEO = .tan 30° = . EO 2 6 Câu 38:
a. Giả sử hàm số y = f (x) liên tục trên ° và thỏa mãn f (5) = 4 f ( ) 1 . Chứng minh rằng
phương trình 2 f (x) - f (x + 2) = 0 luôn có nghiệm trên đoạn [1; ] 3 . x - 2 b. Cho hàm số y =
có đồ thị (C). Tìm điểm M trên đồ thị (C) sao cho tiếp tuyến của x + 3 ( 18
C) tại M tạo với hai trục tọa độ một tam giác có diện tích bằng . 5 Lời giải
a.Xét hàm số g (x) = 2 f (x) - f (x + 2) liên tục trên [1; ] 3 . Ta có: Trang 34 ìg ï ( ) 1 = 2 f ( ) 1 - f (3) í ïg
î (3) = 2 f (3) - f (5) g ( )
1 .g (3) = é2 f ( )
1 - f (3)ù é2 f (3) - f (5)ù = é2 f ( )
1 - f (3)ù é2 f (3) - 4 f ( ) 1 ù ë û ë û ë û ë û = 2 é2 f ë
( )1- f (3)ù é f û ë (3) - 2 f ( ) 1 ù £ 0 û
Vậy phương trình 2 f (x) - f (x + 2) = 0 luôn có nghiệm trên đoạn [1; ] 3 .
b.Tập xác định D = ° \{- } 3 æ a - 2 ö Gọi M ; a Î ç ÷ (C). è a + 3 ø 5 y ' = (x +3)2 5 a - 2
Phương trình tiếp tuyến của (C) tại M : y = x - a + D 2 ( ) ( ) (a +3) a + 3 2
æ -a + 4a + 6 ö
A = Ox Ç D Þ A ;0 ç ÷ è 5 ø 2 æ a 4a 6 ö - -
B = Oy Ç D Þ B ç 0; ÷ ç (a 3)2 ÷ + è ø 2 2 1
1 -a + 4a + 6 a - 4a - 6 18 S = . OA OB Û . = OAB 2 2 5 (a +3)2 5
Û (a - 4a - 6)2 = 36(a + 3)2 2 2
éa -10a - 24 = 0 éa = 12 Û ê Û ê 2
ëa + 2a +12 = 0 : vn ëa = 2 - æ 2 ö Vậy M 12; hoặc M ( 2; - 4 - ) ç ÷ . è 3 ø
ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KỲ II
Môn: TOÁN 11 – ĐỀ 3
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Cho hàm số f (x) liên tục tại điểm x , khi đó lim f ( x)bằng 0 x® 0 x A. f (x f (x) x x 0 ). B. . C. . D. . 0 Dy
Câu 2: Cho hàm số y = 2x - . G 1
iả sử Dx là một số gia của đối số x . Tính . Dx
A. 2.Dx . B. 2 .
C. 2xDx . D. 2x .
Câu 3: Tính đạo hàm cấp hai của hàm số y = sin 2x .
A. y¢¢ = 4sin 2x. B. y¢¢ = 4c - os 2x. C. y¢¢ = 4 - sin 2x.
D. y¢¢ = 4cos 2x. Trang 35 2 n - 20n + 21 lim Câu 4: 2
20 - 21n + 2n bằng 21 20 1 1 A. . B. . C. . D. . 20 2 20 2
Câu 5: Tính ddaoj hàm của hàm số 2 y = cos 2x . A. y¢ = 2c - os 4x. B. y¢ = 2 - sin 4x.
C. y¢ = -sin 4x .
D. y¢ = 2sin 4x.
Câu 6: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , SA ^ ( ABC). Tìm mệnh đề
đúng trong các mệnh đề sau.
A. SA ^ BC .
B. SA ^ SB .
C. SA ^ SC .
D. SB ^ SC .
Câu 7: Tính đạo hàm của hàm số 2
y = x - 3x + 2 . 2x - 3 1 2x - 3 2x - 3 A. y¢ = . B. y¢ = . C. y¢ = .D. y¢ = - . 2 x - 3x + 2 2 2 2 2 x - 3x + 2 2 x - 3x + 2 2 x -3x + 2 1 * lim , k Î • Câu 8: k n bằng A. 1. B. 0. C. . -¥ D. + . ¥ x + 3
Câu 9: Tìm đạo hàm của hàm số y = . 2x -1 7 - 7 5 5 - A. y¢ = . B. y¢ = . C. y¢ = . D. y¢ = . 2 (2x -1) 2 (2x -1) 2 (2x -1) 2 (2x -1)
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA ^ (ABCD). Trong các khẳng
định sau, khẳng định nào sai?
A. BD ^ (SAC).
B. SA ^ ( ABCD).
C. BC ^ (SAB).
D. CD ^ (SAD).
Câu 11: Trong không gian, xét các mệnh đề:
(I): Hai đường thẳng a và b phân biệt cùng vuông góc với đường thẳng D thì a và b song song với nhau.
(II): Hai đường thẳng a và b phân biệt cùng vuông góc với đường thẳng D thì a và b vuông góc với nhau.
Chọn khẳng định đúng trong những khẳng định sau: A. Chỉ có (I) đúng.
B. Cả (I) và (II) đều đúng.
C. Cả (I) và (II) đều sai. D. Chỉ có (II) đúng.
Câu 12: Giả sử ta có lim f (x) = a và lim ( g x) = .
b Trong các mệnh đề sau, mệnh đề nào sai? x®+¥ x®+¥
A. lim é f (x) + ( g x)ù = a + . b B.
é f x - g x ù = a - b ë û lim ( ) ( ) . ë û x®+¥ x®+¥ f x a
C. lim f (x). ( g x) = ( ) . a . b D. lim = . x®+¥ x®+¥ ( g x) b
Câu 13: Tập hợp tất cả các điểm trong không gian cách đều hai điểm ,
A B phân biệt cho trước là tập
hợp nào sau đây? Mặt phẳng trung trực của đoạn thẳng . AB
A. Mặt phẳng trung trực của đoạn thẳng . AB
B. Đường trung trực của đoạn thẳng . AB
C. Một đường thẳng song song với . AB
D. Một mặt phẳng song song với . AB Trang 36
Một chất điểm chuyển động có phương trình s(t) 3 2
= t -3t -9t (t tính bằng giây, s tính bằng Câu 14: =
mét). Tính gia tốc tức thời tại thời điểm t 3s ? A. 2 0m / s . B. 2 15m / s . C. 2 18m / s . D. 2 12m / s .
Câu 15: Cho hàm số f (x) 2
= 3x và x Î!. Chọn khẳng định đúng. 0
A. f ¢(x = 3x .
f ¢(x = 6x . 0 ) 0 ) B. 0 0 C. f ¢(x
f ¢(x = 3x . 0 ) 2 0 ) không tồn tại. D. 0
Câu 16: Chọn khẳng định SAI trong các khẳng định sau: ¢ æ x ö 1 A. = .
B. (3x)¢ = 3. ç ÷ è 3 ø 3 1 ¢ æ ö 1 ¢ C. = . D. ( x) 1 = ; x > 0. ç ÷ 2 è x ø x 2 x 2 x - x + 3 2
ax + bx + c
Câu 17: Cho hàm số y = , biết y¢ =
. Tính a + b + . c x +1 (x + )2 1 A. 1. B. 3. C. 4. D. 1. - !!!" !!!"
Câu 18: Cho hình lập phương ABC .
D EFGH có cạnh bằng .
a Kết quả của phép toán . AB EG bằng 2 a 2 A. 2 a 2. B. 2 a . C. 2 2a 2. D. . 2
Câu 19: Tính lim 2 .n A. . -¥ B. 0. C. 2. D. + . ¥
Câu 20: Chọn phát biểu đúng trong các khẳng định sau:
A. Đường vuông góc chung của hai đường thẳng chéo nhau là khoảng cách giữa hai đường thẳng đó.
B. Khoảng cách giữa hai đường thẳng song song là khoảng cách giữa hai đường thẳng bất kì
lần lượt nằm trên hai đường thẳng đó.
C. Khoảng cách giữa hai mặt phẳng song song bằng khoảng cách từ một điểm bất kì trên mặt
phẳng này đến mặt phẳng kia.
D. Khoảng cách giữa đường thẳng và mặt phẳng song song bằng khoảng cách từ một điểm bất
kì trên mặt phẳng đến đường thẳng kia.
Câu 21: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh ,
a SA ^ ( ABCD) và SA = a 6 .
Tính góc giữa SC và mặt phẳng ( ABCD). A. 120o. B. 60o. C. 30o. D. 45o.
Câu 22: Cho các mệnh đề sau ( 1
I ) : (sin x)' = cosx (II ) : (cosu)' = u
- 'sinu (III ) : (tan x)' = 2 sin x
A. Chỉ có mệnh đề (I ) đúng.
B. Mệnh đề (I ),(III ) đúng.
C. Các mệnh đề (I ),(II ),(III ) đúng.
D. Mệnh đề (I ),(II ) đúng.
Câu 23: Chọn khẳng định đúng trong các khẳng định sau
A. (C)' = 1,C là hằng số. B. ( n x ) n 1 ' . n x - =
(nÎ N,n > ) 1 . Trang 37
C. (x)' = x. D. ( n x )' = n . x
Câu 24: Giả sử u(x),v(x)là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định và k là hằng số. xét các đẳng thức: ' æ u ö
u 'v - uv ' ' æ 1 ö v ' (I) : ( .
u v)' = u 'v + uv' (II) : =
(v = v(x) ¹ 0) (III) : = -
(v = v(x) ¹ 0) ç ÷ 2 ç ÷ è v ø v 2 è v ø v
Số đẳng thức đúng trong các đẳng thức trên là A. 0 B. 2 C. 3 D. 1
Câu 25: Chọn mệnh đề sai trong các mệnh đề sau: ! ! !
A. Ba vectơ a,b, c được gọi là đồng phẳng nếu giá của chúng cùng song song với một mặt phẳng. !!!" !!!" !!!!" "
B. Nếu G là trọng tâm của tam giác ABC thì với mọi điểm M , ta có MA+ MB + MC = 0 !!" !!" "
C. Nếu I là trung điểm của đoạn thẳng AB thì IA+ IB = 0. !!!" !!!" !!!"
D. Nếu ABCD là hình bình hành thì AB + AD = . AC
Câu 26: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh bên SA = 2a và vuông
góc với mặt đáy. Tính khoảng cách từ A đến mặt phẳng (SBC)? 2a 5 a a 5 2a A. B. C. D. 5 5 2 5
Câu 27: Tìm đạo hàm của hàm số y = cot 3x 1 - 1 - 3 A. y¢ = B. y¢ = C. y¢ = D. y¢ = - ( 2 3 1+ cot 3x) 2 sin x 2 sin 3x 2 sin 3x (u (v lim(u = c lim(v = d lim(u - v n n ) n ) n ) n ) n )
Câu 28: Cho hai dãy số và thỏa mãn và . Giá trị của bằng c
A. c + d . B. cd . C. .
D. c - d . d 1 3
Câu 29: Tìm đạo hàm của hàm số 3 2
y = x - x - 2x +1 3 2 1 3 A. 2
y ' = x - x - 2 . B. 2
y ' = 3x - 2x - 2. C. 2
y ' = x - 3x - 2. D. 3 2
y ' = x -3x - 2. 9 4
Câu 30: Tính đạo hàm của hàm số y = cos 2x A. y¢ = 2 - sin 2x. B. y¢ = 2 - sin x.
C. y¢ = 2sin 2x .
D. y¢ = 2sin x . lim ( 2 2021x - 2x) Câu 31: x 1 ®- bằng A. 2023. B. 2023 - . C. 2019 . D. 2019 - . sin 2x
Câu 32: Tìm giới hạn lim . x®0 x 1 A. . B. 0 . C. 2 . D. 1. 2 æ p ö æ p ö y = cos - 3x ç ÷ f ¢ ? ç ÷ Câu 33: Cho hàm số è 2 ø . Tính è 3 ø Trang 38 A. 1. B. 3. C. 3 - . D. 1 - .
Câu 34: Chọn phát biểu đúng trong các khẳng định dưới đây.
A. Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì chúng song song với nhau.
B. Nếu hai mặt phẳng vuông góc với nhau và cắt nhau theo một giao tuyến thì mọi đường thẳng
nằm trong mặt này vuông góc với giao tuyến sẽ vuông góc với mặt phẳng kia.
C. Nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằmg trong mặt này vuông góc với mặt phẳng kia.
D. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thứ ba thì chúng vuông góc với nhau.
Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AD = 2a, AB = 3a . Cạnh bên SA
vuông góc với đáy, SA = 2a . Khoảng cách giữa hai đường thẳng AB và SD bằng 2a A. a 2. B. . C. 2 . a D. . a 5
II. PHẦN TỰ LUẬN (4 câu – 3,0 điểm) 3 + -
Câu 36: Tính giới hạn x 1 1 lim . x®0 x
Câu 37: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại , A D với AB AD = DC = = ;
a SA = a 6,SA ^ (ABCD). Xác định góc giữa đường thẳng AC với mặt 2 phẳng (SBC)
f (x) = x(x - )
1 (x - 2)....(x -1000) f ¢(0)
Câu 38: (0,5 điểm) Cho hàm số . Tính . 2 2a
Câu 39: (0,5 điểm) Chứng minh rằng tiếp tuyến của đồ thị hàm số y =
( a là hằng số khác 0 ) tạo x
với các trục tọa độ thành một tam giác có diện tích không đổi.
---------- HẾT ----------
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm)
Câu 1: Cho hàm số f (x) liên tục tại điểm x , khi đó lim f ( x)bằng 0 x® 0 x A. f (x f (x) x x 0 ). B. . C. . D. . 0 Lời giải Chọn A
Ta có: hàm số f (x) liên tục tại điểm x khi và chỉ khi lim f ( x) = f (x0 ). 0 x® 0 x Dy
Câu 2: Cho hàm số y = 2x - . G 1
iả sử Dx là một số gia của đối số x . Tính . Dx
A. 2.Dx . B. 2 .
C. 2xDx . D. 2x . Lời giải Chọn B Dy
f (x + Dx) - f (x) 2(x + Dx) -1- (2x - ) 1 Ta có: = = = 2. Dx Dx Dx
Câu 3: Tính đạo hàm cấp hai của hàm số y = sin 2x . Trang 39
A. y¢¢ = 4sin 2x. B. y¢¢ = 4c - os 2x. C. y¢¢ = 4 - sin 2x.
D. y¢¢ = 4cos 2x. Lời giải Chọn C
Ta có: y¢ = 2cos 2x y¢¢ = 4 - sin 2x. 2 n - 20n + 21 lim Câu 4: 2
20 - 21n + 2n bằng 21 20 1 1 A. . B. . C. . D. . 20 2 20 2 Lời giải Chọn D 20 21 2 1- + 2 n - 20n + 21 1 lim = lim n n = . 2 20 - 21n + 2n 20 21 2 - + 2 2 n n
Câu 5: Tính ddaoj hàm của hàm số 2 y = cos 2x . A. y¢ = 2c - os 4x. B. y¢ = 2 - sin 4x.
C. y¢ = -sin 4x .
D. y¢ = 2sin 4x. Lời giải Chọn A y ( 2
cos 2x)¢ 2cos2x(cos2x)¢ ¢ = = = 4 - cos2 . x sin 2x = 2 - sin 4x.
Câu 6: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , SA ^ ( ABC). Tìm mệnh đề
đúng trong các mệnh đề sau.
A. SA ^ BC .
B. SA ^ SB .
C. SA ^ SC .
D. SB ^ SC . Lời giải Chọn A SA ^ ( ABC) üï Ta có: ý Þ SA ^ BC . BC Ì ( ABC)ïþ
Câu 7: Tính đạo hàm của hàm số 2
y = x - 3x + 2 . 2x - 3 1 A. y¢ = . B. y¢ = . 2
x - 3x + 2 2
2 x - 3x + 2 2x - 3 2x - 3 C. y¢ = . D. y¢ = - . 2 2 x - 3x + 2 2 2 x - 3x + 2 Lời giải Chọn C ( 2x 3x 2 ¢ - + 2x - 3 2 )
Ta có: y = x - 3x + 2 Þ y¢ = = . 2 2 2 x - 3x + 2 2 x - 3x + 2 1 * lim , k Î • Câu 8: k n bằng A. 1. B. 0. C. . -¥ D. + . ¥ Lời giải Trang 40 Chọn B 1 Ta có: * lim
= 0, k Ε . k n x + 3
Câu 9: Tìm đạo hàm của hàm số y = . 2x -1 7 - 7 5 5 - A. y¢ = . B. y¢ = . C. y¢ = . D. y¢ = . 2 (2x -1) 2 (2x -1) 2 (2x -1) 2 (2x -1) Lời giải Chọn A x + 3
(x 3)¢ (2x )1 (2x )1¢ + - -
- (x + 3) 2x -1- 2(x + 3) 7 - Ta có: y = Þ y¢ = = = . 2x -1 (2x - )2 1 (2x - )2 1 (2x - )2 1
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA ^ (ABCD). Trong các khẳng
định sau, khẳng định nào sai?
A. BD ^ (SAC).
B. SA ^ ( ABCD).
C. BC ^ (SAB).
D. CD ^ (SAD). Lời giải Chọn A
Giả sử BD ^ (SAC) Þ BD ^ AC mâu thuẫn do ABCD là hình chữ nhật.
Vậy khẳng định sai là BD ^ (SAC).
Câu 11: Trong không gian, xét các mệnh đề:
(I): Hai đường thẳng a và b phân biệt cùng vuông góc với đường thẳng D thì a và b song song với nhau.
(II): Hai đường thẳng a và b phân biệt cùng vuông góc với đường thẳng D thì a và b vuông góc với nhau.
Chọn khẳng định đúng trong những khẳng định sau: A. Chỉ có (I) đúng.
B. Cả (I) và (II) đều đúng.
C. Cả (I) và (II) đều sai. D. Chỉ có (II) đúng. Lời giải Chọn C
Câu 12: Giả sử ta có lim f (x) = a và lim ( g x) = .
b Trong các mệnh đề sau, mệnh đề nào sai? x®+¥ x®+¥
A. lim é f (x) + ( g x)ù = a + . b B.
é f x - g x ù = a - b ë û lim ( ) ( ) . ë û x®+¥ x®+¥ f x a
C. lim f (x). ( g x) = ( ) . a . b D. lim = . x®+¥ x®+¥ ( g x) b Trang 41 Lời giải Chọn D f x a Vì lim f (x) = ( ) a và lim (
g x) = b ¹ 0 Þ lim = . x®+¥ x®+¥ x®+¥ ( g x) b
Câu 13: Tập hợp tất cả các điểm trong không gian cách đều hai điểm ,
A B phân biệt cho trước là tập
hợp nào sau đây? Mặt phẳng trung trực của đoạn thẳng . AB
A. Mặt phẳng trung trực của đoạn thẳng . AB
B. Đường trung trực của đoạn thẳng . AB
C. Một đường thẳng song song với . AB
D. Một mặt phẳng song song với . AB Lời giải Chọn A
Một chất điểm chuyển động có phương trình s(t) 3 2
= t -3t -9t (t tính bằng giây, s tính bằng Câu 14:
mét). Tính gia tốc tức thời tại thời điểm t = 3s ? A. 2 0m / s . B. 2 15m / s . C. 2 18m / s . D. 2 12m / s . Lời giải Chọn D
Ta có: a(t) = v¢(t) = s¢ (t) s(t) 3 2
= t - t - t Þ s¢(t) 2 3 9
= 3t -6t -9 Þ s¢ (t) = 6t -6
Vậy gia tốc tức thời tại thời điểm t = 3s là a( ) 2
3 = 6.3- 6 =12m / s .
Câu 15: Cho hàm số f (x) 2
= 3x và x Î!. Chọn câu đúng. 0
A. f ¢(x = 3x .
f ¢(x = 6x . 0 ) 0 ) B. 0 0 C. f ¢(x
f ¢(x = 3x . 0 ) 2 0 ) không tồn tại. D. 0 Lời giải Chọn B Ta có: f (x) 2
= 3x Þ f ¢(x) = 6 .x
Vậy f ¢(x = 6x . 0 ) 0
Câu 16: Chọn khẳng định SAI trong các khẳng định sau: ¢ æ x ö 1 A. = . B. (3x)¢ = 3. ç ÷ è 3 ø 3 1 ¢ æ ö 1 ¢ C. = . D. ( x) 1 = ; x > 0. ç ÷ 2 è x ø x 2 x Lời giải Chọn C 2 x - x + 3 2
ax + bx + c
Câu 17: Cho hàm số y = , biết y¢ =
. Tính a + b + . c x +1 (x + )2 1 A. 1. B. 3. C. 4. D. 1. - Lời giải Chọn D Trang 42 2 2 x - x + 3 x + 2x - 4 y = Þ y¢ = x +1 (x + )2 1
Do đó: a + b + c = 1+ 2 - 4 = 1. - !!!" !!!"
Câu 18: Cho hình lập phương ABC .
D EFGH có cạnh bằng .
a Kết quả của phép toán . AB EG bằng 2 a 2 A. 2 a 2. B. 2 a . C. 2 2a 2. D. . 2 Lời giải Chọn B E H G F A D B C Ta có ABC .
D EFGH là hình lập phương cạnh a nên AB = a, EG = a 2. Khi đó, !!!" !!!" !!!" !!!" !!!" !!!" . AB EG = . AB .
EG cos( AB, EG) = .aa 2.cos( AB, AC) o 2 2 ∑ 2 2 2
= a 2.cosBAC = a 2.cos45 = a 2.
= a . Vậy chọn đáp án B. 2
Câu 19: Tính lim 2 .n A. . -¥ B. 0. C. 2. D. + . ¥ Lời giải Chọn D
Theo các kết quả giới hạn đặc biệt, vì 2 > 1 nên lim 2n = + . ¥ Do đó chọn đáp án D
Câu 20: Chọn phát biểu đúng trong các khẳng định sau:
A. Đường vuông góc chung của hai đường thẳng chéo nhau là khoảng cách giữa hai đường thẳng đó.
B. Khoảng cách giữa hai đường thẳng song song là khoảng cách giữa hai đường thẳng bất kì
lần lượt nằm trên hai đường thẳng đó.
C. Khoảng cách giữa hai mặt phẳng song song bằng khoảng cách từ một điểm bất kì trên mặt
phẳng này đến mặt phẳng kia.
D. Khoảng cách giữa đường thẳng và mặt phẳng song song bằng khoảng cách từ một điểm bất
kì trên mặt phẳng đến đường thẳng kia. Lời giải Chọn C
Theo định nghĩa khoảng cách giữa hai mặt phẳng song song ta có khẳng định ở câu C là đúng.
Do đó chọn đáp án C.
Câu 21: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh ,
a SA ^ ( ABCD) và SA = a 6 .
Tính góc giữa SC và mặt phẳng ( ABCD). A. 120o. B. 60o. C. 30o. D. 45o. Trang 43 Lời giải Chọn B
Ta có: A là hình chiếu của S lên ( ABCD)
C là hình chiếu của C lên ( ABCD)
Suy ra: AC là hình chiếu của SC lên ( ABCD) Þ (SC,( ABCD)) = (SC, AC) SA a
Xét tam giác SAC vuông tại C : (SCA) 6 tan = = = 3 SC a 2 SA a tan (SCA) 6 0 = =
= 3 Þ SAC = 60 Þ (SC,( ABCD)) = 60o. SC a 2
Câu 22: Cho các mệnh đề sau ( 1
I ) : (sin x)' = cosx (II ) : (cosu)' = u
- 'sinu (III ) : (tan x)' = 2 sin x
A. Chỉ có mệnh đề (I ) đúng.
B. Mệnh đề (I ),(III ) đúng.
C. Các mệnh đề (I ),(II ),(III ) đúng.
D. Mệnh đề (I ),(II ) đúng. Lời giải Chọn D (sin x)' = cosx (cosu)' = u - 'sinu ( x) 1 tan ' = 2 cos x
Câu 23: Chọn khẳng định đúng trong các khẳng định sau
A. (C)' = 1,C là hằng số. B. ( n x ) n 1 ' . n x - =
(nÎ N,n > ) 1 .
C. (x)' = x. D. ( n x )' = n . x Lời giải Chọn B
Câu 24: Giả sử u(x),v(x)là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định và k là hằng số. xét các đẳng thức: ' æ u ö
u 'v - uv ' ' æ 1 ö v ' (I) : ( .
u v)' = u 'v + uv' (II) : =
(v = v(x) ¹ 0) (III) : = -
(v = v(x) ¹ 0) ç ÷ 2 ç ÷ è v ø v 2 è v ø v
Số đẳng thức đúng trong các đẳng thức trên là A. 0 B. 2 C. 3 D. 1 Lời giải Chọn C
Câu 25: Chọn mệnh đề sai trong các mệnh đề sau: ! ! !
A. Ba vectơ a,b, c được gọi là đồng phẳng nếu giá của chúng cùng song song với một mặt phẳng. !!!" !!!" !!!!" "
B. Nếu G là trọng tâm của tam giác ABC thì với mọi điểm M , ta có MA+ MB + MC = 0 !!" !!" "
C. Nếu I là trung điểm của đoạn thẳng AB thì IA+ IB = 0. !!!" !!!" !!!"
D. Nếu ABCD là hình bình hành thì AB + AD = . AC Lời giải Trang 44 Chọn B !!!" !!!" !!!!" !!!!"
Nếu G là trọng tâm của tam giác ABC thì với mọi điểm M , ta có MA+ MB + MC = 3MG
Câu 26: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh bên SA = 2a và vuông
góc với mặt đáy. Tính khoảng cách từ A đến mặt phẳng (SBC)? 2a 5 a a 5 2a A. B. C. D. 5 5 2 5 Lời giải Chọn A
Vì SA ^ ( ABCD) Þ SA ^ BC
Mặt khác ABCD là hình vuông AB ^ BC Þ BC ^ (SAB) ìAH ^ SB
Từ A Kẻ AH ^ SB Þ í Þ AH ^ (SBC) îAH ^ BC Þ d( ; A (SBC)) = AH
Vì SA ^ ( ABCD) Þ SA ^ AB
Áp dụng hệ thức lượng trong SA
D B vuông tại A đường cao AH 1 1 1 1 1 5 = + = + = 2 2 2 2 2 2 AH SA AB (2a) a 4a 2 4a 2a 5 2 Þ AH = Þ AH = . 5 5
Câu 27: Tìm đạo hàm của hàm số y = cot 3x 1 - 1 - 3 A. y¢ = B. y¢ = C. y¢ = D. y¢ = - ( 2 3 1+ cot 3x) 2 sin x 2 sin 3x 2 sin 3x Lời giải Chọn D
Câu 28: Cho hai dãy số (u (v lim(u = c lim(v = d lim(u - v n n ) n ) n ) n ) n ) và thỏa mãn và . Giá trị của bằng c
A. c + d . B. cd . C. .
D. c - d . d Trang 45 Chọn D Lời giải
Ta có: lim(u -v ) = lim(u ) -lim v = c - d n n n ( n ) . 1 3
Câu 29: Tìm đạo hàm của hàm số 3 2
y = x - x - 2x +1 3 2 1 3 A. 2
y ' = x - x - 2 . B. 2
y ' = 3x - 2x - 2. C. 2
y ' = x - 3x - 2. D. 3 2
y ' = x -3x - 2. 9 4 Chọn C Lời giải ' æ 1 3 ö Ta có: 3 2 2 y ' =
x - x - 2x +1 = x - 3x - 2. ç ÷ è 3 2 ø
Câu 30: Tính đạo hàm của hàm số y = cos 2x A. y¢ = 2 - sin 2x. B. y¢ = 2 - sin x.
C. y¢ = 2sin 2x .
D. y¢ = 2sin x . Lời giải Chọn A
Ta có: y = cos 2x Þ y = -(2x)¢ ¢ sin 2x = 2 - sin 2x . lim ( 2 2021x - 2x) Câu 31: x 1 ®- bằng A. 2023. B. 2023 - . C. 2019 . D. 2019 - . Lời giải Chọn A Ta có: lim ( 2 2021x - 2x) = (- )2 2021 1 - 2.(- ) 1 = 2023. x 1 ®- sin 2x lim
Câu 32: Tìm giới hạn x®0 x . 1 A. . B. 0 . C. 2 . D. 1. 2 Lời giải Chọn C sin 2x æ sin 2x ö sin 2x Ta có: lim = lim 2. = lim 2.lim = 2.1 = 2. ç ÷ x®0 x®0 x è
2x ø x®0 x®0 2x æ p ö æ p ö y = cos - 3x ç ÷ f ¢ ? ç ÷ Câu 33: Cho hàm số è 2 ø . Tính è 3 ø A. 1. B. 3. C. 3 - . D. 1 - . Lời giải Chọn C æ p ö æ p ö Ta có: y = cos - 3x Þ f ¢ ç ÷ (x) = 3sin -3x ç ÷ è 2 ø è 2 ø æ p ö Do đó: f ¢ = 3 - ç ÷ è 3 ø
Câu 34: Chọn phát biểu đúng trong các khẳng định dưới đây.
A. Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì chúng song song với nhau. Trang 46
B. Nếu hai mặt phẳng vuông góc với nhau và cắt nhau theo một giao tuyến thì mọi đường thẳng
nằm trong mặt này vuông góc với giao tuyến sẽ vuông góc với mặt phẳng kia.
C. Nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằmg trong mặt này vuông góc với mặt phẳng kia.
D. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thứ ba thì chúng vuông góc với nhau. Lời giải Chọn B
Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AD = 2a, AB = 3a . Cạnh bên SA
vuông góc với đáy, SA = 2a . Khoảng cách giữa hai đường thẳng AB và SD bằng 2a A. a 2. B. . C. 2 . a D. . a 5 Lời giải Chọn A
Vẽ: Từ A kẻ AH ^ SD Þ AH là đường vuông góc chung
Chứng minh: Ta có AB ^ AH (Do AB ^ (SAD))và AH ^ SD Þ AH là đường vuông góc chung Þ d ( A , B SD) = AH. AS.AD 2 . a 2a Tính AH : AH = = = a 2. 2 2 AS + AD (2a)2 +(2a)2 II. TỰ LUẬN 3 + -
Câu 36: Tính giới hạn x 1 1 lim . x®0 x Lời giải 3 x +1 -1 x 1 1 Ta có lim = lim = lim = . x®0 x®0 x ® é ù é ù x ê( x + )2 x 0 3 3 + x + + ú ê( 3 x + )2 3 3 1 1 1 1 + x +1 +1ú ë û ë û
Câu 37: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại , A D với AB AD = DC = = ;
a SA = a 6,SA ^ (ABCD). Xác định góc giữa đường thẳng AC với mặt 2 phẳng (SBC) Lời giải Trang 47 S H B A D C AB
Do ABCD là hình thang vuông tại ,
A D với AD = DC =
= a nên tam giác ABC vuông tại 2
C , tức là AC ^ BC . Suy ra BC ^ (SAC).
Trong tam giác SAC , hạ AH ^ SC , suy ra AH ^ (SBC).
Tức là HC là hình chiếu của AC trên mặt phẳng (SBC). (AC SBC ) ∑ ,(
) = (AC, HC) = SCA. ∑ SA a 6 ∑ 0 tan SCA = = = 3 Þ SAC = 60 . AC a 2
f (x) = x(x - )
1 (x - 2)....(x -1000) f ¢(0)
Câu 38: (0,5 điểm) Cho hàm số . Tính . Lời giải
Theo định nghĩa đạo hàm của hàm số tại một điểm: ¢( f x - f x x - x - x - f 0) ( ) (0) ( )1( 2)....( 1000) = lim = lim x®0 x®0 x x = lim éë(x - )
1 ( x - 2)....( x -1000)ù = û (- ) 1 .( 2 - ).( 3 - )....( 1 - 000) =1000! x®0 Vậy f ¢(0) =1000 ! 2 2a
Câu 39: (0,5 điểm) Chứng minh rằng tiếp tuyến của đồ thị hàm số y =
( a là hằng số khác 0 ) tạo x
với các trục tọa độ thành một tam giác có diện tích không đổi. Lời giải 2 2a
Tập xác định: D = ! \{ } 0 , y¢ = - . 2 x 2 2a 2 æ 2a ö
Tiếp tuyến của đồ thị hàm số y = tại điểm ç x ;
là đường thẳng (d ) có dạng: ÷ x 0 x è 0 ø 2 2 2a 2a y = - . x - x +
, x ¹ 0, a ¹ 0 . 2 ( 0 ) ( 0 ) x x 0 0
+ Gọi A = d Ç Ox :Cho 2 2 2a 2a y = 0 Þ - x - x +
= 0 Û x - x - x = 0 Û x = 2x Þ A 2x ;0 . 2 ( 0 ) 0 0 0 ( 0 ) x x 0 0 Trang 48 2 2 2 2 2 2 2a 2a 2a 2a 4a æ 4a ö
+ Gọi B = d ÇOy : Cho x = 0 Þ y = - . -x + = + = Þ Bç0; ÷. 2 ( 0) x x x x x x 0 0 0 0 0 è 0 ø 2 1 1 4a
+ Diện tích tam giác OAB : 2 S = O . AOB = . 2x .
= 4a ( không đổi). 0 2 2 x0 2 2a
Vậy tuyến của đồ thị hàm số y =
( a ¹ 0 ) tạo với các trục tọa độ thành một tam giác có x diện tích không đổi.
ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KỲ II
Môn: TOÁN 11 – ĐỀ 4
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) !!!" !!!" !!!" !!!!"
Câu 1: Cho hình hộp ABC .
D A B C D . Giá trị k thích hợp thỏa mãn BA+ BC + BB = kBD là: 1 1 1 1 1 1
A. k = 1×
B. k = 0×
C. k = 2×
D. k = 4×
Câu 2: Trong các mệnh đề sau đây, mệnh đề nào sai?
A. Hình chóp tứ giác đều có đáy là hình vuông.
B. Hình chóp tứ giác đều có hình chiếu của đỉnh lên mặt đáy trùng với tâm của đáy.
C. Hình chóp tứ giác đều có tất cả các cạnh bằng nhau.
D. Hình chóp tứ giác đều có tất cả các cạnh bên bằng nhau.
f ( x) - f (6)
Câu 3: Cho hàm số y = f (x) có đạo hàm thỏa mãn f ¢(6) = 2. Giá trị của biểu thức lim x®6 x - 6 bằng 1 A. × B. 12× 1 C. × D. 2× 2 3 ! !
Câu 4: Trong không gian, cho hai đường thẳng a và b lần lượt có các vectơ chỉ phương là u , v . Biết
hai đường thẳng a và b vuông góc với nhau. Mệnh đề nào dưới đây đúng? ! ! ! ! ! ! ! ! ! A. . u v = 1 - . B. . u v = 0. C. . u v = 0. D. . u v =1. 2022 Câu 5: lim bằng 2n + 3 A. 1001. B. 2022 . C. +¥ . D. 0 .
Câu 6: Cho các hàm số u = u (x); v = v(x) có đạo hàm trên tập xác định của nó. Tìm mệnh đề sai? A. ( n u )¢ n 1
= nu - .u¢(nΕ ,n > ) 1 .
B. (u + v)¢ = u¢+ v¢. æ 1 ¢ö u¢ ¢ u¢ C. = u ¹ 0 ç ÷ ( u) = (u >0) 2 ( ). D. . è u ø u 2 u
Câu 7: Trong các mệnh đề sau đây, mệnh đề nào sai? x 1 1 A. lim = -¥ . B. lim = 0. C. 2 lim x = +¥. D. lim = 0. x®-¥ x +1 x®+¥ x x®-¥ 3 x®+¥ x Trang 49
Câu 8: Cho hàm số y = f (x) xác định trên khoảng ( ; a b) và x Î ; a b y = f (x) 0 ( ). Hàm số được gọi
là liên tục tại x0 nếu
A. lim f ( x) = a .
B. lim f ( x) = b.
C. lim f ( x) = f (x
lim f ( x) = x 0 ) . D. . 0 x® ® ® ® 0 x x 0 x x 0 x x 0 x
Câu 9: Cho các hàm số u = u(x); v = v(x) có đạo hàm trên tập xác định của nó. Có bao nhiêu công
thức sai trong các công thức dưới đây
(1): (u -v)¢ = u¢ -v¢.
(2): (u ×v)¢ = u¢×v¢.
æ u ¢ö u¢×v + u ×v¢
(3): (ku)¢ = k ×u¢, k là hằng số (4): =
(v = v(x) ¹ 0) ç ÷ 2 è v ø v A. 1. B. 0 . C. 2 . D. 3.
Câu 10: Cho đường thẳng a không vuông góc với mặt phẳng (a ). Có bao nhiêu mặt phẳng chứa a và vuông góc với (a )? A. 0 . B. 2 . C. 1. D. Vô số.
Câu 11: Đạo hàm của hàm số y = sin3x là:
A. y¢ = -cos3x .
B. y¢ = 3cos3x.
C. y¢ = cos3x.
D. y¢ = 3cos x .
Câu 12: Cho hàm số f (x) thoả mãn lim f (x) = 2 - . Tính lim é f ë ( x) + xù? û x 3 ® x®3 A. 5 . B. 11. C. 1. D. 6 .
Câu 13: Đạo hàm của hàm số 2022 y = x là: A. ( 2022 x )¢ 2021
= 2022x . B. ( 2022 x )¢ 2022 = 2022x . C. ( 2022 x
)¢ = 2022x. D. ( 2022 x )¢ 2023 = 2022x .
Câu 14: Trong các mệnh đề sau, mệnh đề nào sai? 3 æ 1 ö A. 2 lim n = +¥ . B. lim = 0. ç ÷ è n ø
C. lim c = c ( c là hằng số). D. lim n q = 0, q Î! .
Câu 15: Chọn khẳng định đúng trong các khẳng định sau: ¢ 2 ¢ 1 A. ( x) = ( x " > 0). B. ( x) = ( x " > 0). x 2 x ¢ 1 ¢ 1 C. ( x) = ( x " > 0). D. ( x) = ( x " Î! ). x 2 x
Câu 16: Cho hình lăng trụ đứng ABC.A' B 'C ' . Khoảng cách giữa hai mặt phẳng ( ABC) và ( A'B'C ') bằng A. AB ' . B. AA' . C. BC '. D. AC ' .
Câu 17: Khẳng định nào sau đây đúng? sin x sin 3x sin 3x sin x A. lim =1. B. lim = 0. C. lim =1. D. lim = 0 . x®0 x x®0 x x®0 x x®0 x x
Câu 18: Đạo hàm của hàm số y = là 3 Trang 50 x ¢ æ ö x ¢ æ ö 1 x ¢ æ ö x ¢ æ ö 1 A. = 3x . B. = - . C. = 3. D. = . ç ÷ ç ÷ ç ÷ ç ÷ è 3 ø è 3 ø 9 è 3 ø è 3 ø 3
Câu 19: Cho x ¹ 0 , tìm mệnh đề đúng? 1 ¢ æ ö 1 1 ¢ æ ö 1 1 ¢ æ ö 1 1 ¢ æ ö 1 A. - = - . B. - = . C. = . D. = - . ç ÷ 2 ç ÷ ç ÷ ç ÷ è x ø x 2 è x ø x 2 è x ø x è x ø x
Câu 20: Hàm số g (x) = -sin x là đạo hàm của hàm số nào sau đây? 1 A. y = .
B. y = -sin x.
C. y = - cos x .
D. y = cos x . sin x
Câu 21: Hệ số góc của tiếp tuyến của đồ thị hàm số y = f (x) 3 2
= 2x + x -1 tại điểm x = 2 - bằng 0 A. 13 - . B. 20 . C. 19. D. 28 .
Câu 22: Cho hàm số f ( x) = (x - )2 2 1 + 2.Tính f ¢¢( ) 1 ? A. f ¢¢( ) 1 =12 . B. f ¢¢( ) 1 = 0 . C. f ¢¢( ) 1 =16 . D. f ¢¢( ) 1 = 8.
Câu 23: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 4a , SA ^ ( ABCD).Gọi I
là trung điểm của DO . Khi đó khoảng cách từ điểm I đến mặt phẳng (SAC) bằng A. 2a . B. 4a . C. a 2. D. 2a 2 .
Câu 24: Hàm số nào trong các hàm số dưới đây liên tục trên ! ? 3 x -1 x A. y = . B. 3 y = x + sin 3 1. C. y = . D. 3 y = x -1. x -1 cos3x +1 4 - 3x
Câu 25: Đạo hàm của hàm số y =
là kết quả nào sau đây: x - 2 -5 -11 2 10 A. y¢ = . B. y¢ = . C. y¢ = . D. y¢ = . (x - 2)2 (x - 2)2 (x - 2)2 (x - 2)2
Câu 26: Đạo hàm của hàm số 3
y = x .sin x là kết quả nào sau đây: A. 2
y¢ = x (3sin x - xcos x). B. 2
y¢ = x (3cos x + xsin x). C. 2
y¢ = x (3sin x + xcos x). D. 2
y¢ = x (3cos x - xsin x). æ p ö
Câu 27: Đạo hàm của hàm số y = 2cos - 3x +
1 là kết quả nào sau đây: ç ÷ è 2 ø
A. y¢ = 6cos3x .
B. y¢ = 6cos3x + . 1 æ p ö æ p ö C. y¢ = -2sin - 3x . D. y¢ = 2sin - 3x . ç ÷ ç ÷ è 2 ø è 2 ø 1
Câu 28: Một chất điểm chuyển động có phương trình S = f (t) 3 2
= t - t + 4t + 5 ( S là quãng đường 3
chuyển động tính bằng mét và t là thời gian tính bằng giây). Gia tốc của chuyển động tại thời
điểm t = 2 giây là: A. ( 2 3 m / s ). B. ( 2 4 m / s ). C. ( 2 1 m / s ). D. ( 2 2 m / s ). Trang 51
Câu 29: Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O . Góc giữa cạnh bên
SB và mặt phẳng (ABCD) là A. BSD . B. SBA. C. SBC . D. SBO . 1 æ p ö
Câu 30: Đạo hàm của hàm số y = (5 - tan x)5 , x ¹ + kp ,k Î! là kết quả nào sau đây: ç ÷ 5 è 2 ø -(5- tan x)4 (5- tan x)4 -(5- tan x)4 A. y¢ = ( - x)4 5 tan . B. y¢ = . C. y¢ = . D. y¢ = . 2 sin x 2 cos x 2 cos x
Câu 31: Tính đạo hàm của hàm số y = (x - x )2 5 2 2 ta thu được kết quả 9 6 3
y¢ = ax + bx + cx . Khi đó tổng
a + b + c bằng A. 3 - . B. 3. C. 2 . D. 2 - .
Câu 32: Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ (hình vẽ bên dưới). Góc giữa hai đường thẳng DA¢ và B D ¢ ¢ bằng A B D C A' B' D' C' A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 .
Câu 33: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , BC = a . SA ^ mp( ABC)và
SA = a 3 . Góc giữa hai mặt phẳng (SBC)và ( ABC) bằng A. 0 30 . B. 0 90 . C. 0 45 . D. 0 60 .
Câu 34: Cho hình chóp S.ABCD có SA ^ ( ABCD)và đáy ABCD là hình vuông. Từ A kẻ AH ^ SD
(hình vẽ bên dưới). Khẳng định nào sau đây đúng? S H A D B C
A. AH ^ (SAB).
B. AH ^ (SCD).
C. AH ^ (SBD).
D. SD ^ (HAC). æ x - a ö
Câu 35: Cho a ¹ 0. Kết quả của lim bằng ç 2 2 ÷
x®a è x - a ø -1 1 A. . B. 2a . C. . D. 2 - a . 2a 2a
II. PHẦN TỰ LUẬN. (4 CÂU – 3 ĐIỂM) Trang 52 3 ì x + 27 ï khi x < 3 -
Câu 36: Tìm số thực m để hàm số f ( x) 2 = í x -3x -18 liên tục trên ! ?
ïî2x+ m khi x ³ 3 -
Câu 37: Cho hình chóp đều tứ giác đều S .A BCD có tất cả các cạnh bằng a . Gọi O là giao điểm AC
và BD . Tính khoảng cách từ O đến mặt phẳng (SCD)? 3 + - +
Câu 38: Tính giới hạn của hàm số sau: 1 2x 1 3x lim ? 2 x x - 5
Câu 39: Cho hàm số y =
có đồ thị là đường cong (C). Lập phương trình tiếp tuyến của đồ thị x -1
(C) sao cho tiếp tuyến này cắt các trục Ox, Oy lần lượt tại các điểm ,
A B phân biệt sao cho OB = 4OA .
---------- HẾT ---------- BẢNG ĐÁP ÁN 1.A 2.C 3.D 4.C 5.D 6.C 7.A 8.C 9.C 10.D 11.B 12.C 13.A 14.D 15.B 16.B 17.A 18.D 19.B 20.D 21.B 22.D 23.C 24.D 25.C 26.C 27.A 28.D 29.D 30.D 31.D 32.C 33.D 34.B 35.C
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm) !!!" !!!" !!!" !!!!"
Câu 1: Cho hình hộp ABC .
D A B C D . Giá trị k thích hợp thỏa mãn BA+ BC + BB = kBD là: 1 1 1 1 1 1
A. k = 1×
B. k = 0×
C. k = 2×
D. k = 4× Lời giải Chọn A !!!" !!!" !!!" !!!!"
BA+ BC + BB = BD (theo quy tắc hình hộp). 1 1
Câu 2: Trong các mệnh đề sau đây, mệnh đề nào sai?
A. Hình chóp tứ giác đều có đáy là hình vuông.
B. Hình chóp tứ giác đều có hình chiếu của đỉnh lên mặt đáy trùng với tâm của đáy.
C. Hình chóp tứ giác đều có tất cả các cạnh bằng nhau.
D. Hình chóp tứ giác đều có tất cả các cạnh bên bằng nhau. Lời giải Chọn C
f ( x) - f (6)
Câu 3: Cho hàm số y = f (x) có đạo hàm thỏa mãn f ¢(6) = 2. Giá trị của biểu thức lim x®6 x - 6 bằng 1 A. × B. 12× 1 C. × D. 2× 2 3 Lời giải Chọn D ¢( f x - f f x - f f 6) ( ) (6) ( ) (6) = lim Þ lim = 2. x®6 x®6 x - 6 x - 6 ! !
Câu 4: Trong không gian, cho hai đường thẳng a và b lần lượt có các vectơ chỉ phương là u , v . Biết Trang 53
hai đường thẳng a và b vuông góc với nhau. Mệnh đề nào dưới đây đúng? ! ! ! ! ! ! ! ! ! A. . u v = 1 - . B. . u v = 0. C. . u v = 0. D. . u v =1. Lời giải Chọn C ! ! ! !
a ^ b Û u ^ v Û . u v = 0. 2022 lim Câu 5: 2n + 3 bằng A. 1001. B. 2022 . C. +¥ . D. 0 . Lời giải Chọn D 2022 Ta có lim = 0. 2n + 3
Câu 6: Cho các hàm số u = u (x); v = v(x) có đạo hàm trên tập xác định của nó. Tìm mệnh đề sai? ¢ A. ( n u ) n 1
= nu - .u¢(nΕ ,n > ) 1 .
B. (u + v)¢ = u¢ + v¢. æ 1 ¢ö u¢ ¢ u¢ C. = u ¹ 0 ç ÷ ( u) = (u >0) 2 ( ). D. . è u ø u 2 u Lời giải Chọn C æ 1 ¢ö u¢ Công thức = - u ¹ 0 ç ÷ 2 ( ). è u ø u
Câu 7: Trong các mệnh đề sau đây, mệnh đề nào sai? x 1 1 A. lim = -¥ . B. lim = 0. C. 2 lim x = +¥. D. lim = 0. x®-¥ x +1 x®+¥ x x®-¥ 3 x®+¥ x Lời giải Chọn A x Ta có lim =1. x®-¥ x +1
Câu 8: Cho hàm số y = f (x) xác định trên khoảng ( ; a b) và x Î ; a b y = f (x) 0 ( ). Hàm số được gọi
là liên tục tại x nếu 0
A. lim f ( x) = a .
B. lim f ( x) = b.
C. lim f ( x) = f (x
lim f ( x) = x 0 ) . D. . 0 x® ® ® ® 0 x x 0 x x 0 x x 0 x Lời giải Chọn C
Hàm số y = f (x) được gọi là liên tục tại x nếu lim f (x) = f (x0 ) . 0 x® 0 x
Câu 9: Cho các hàm số u = u(x); v = v(x) có đạo hàm trên tập xác định của nó. Có bao nhiêu công
thức sai trong các công thức dưới đây
(1): (u -v)¢ = u¢ -v¢. (2): (u ×v)¢ = u¢×v¢. Trang 54
æ u ¢ö u¢×v + u ×v¢
(3): (ku)¢ = k ×u¢, k là hằng số (4): =
(v = v(x) ¹ 0) ç ÷ 2 è v ø v A. 1. B. 0 . C. 2 . D. 3. Lời giải Chọn C Ta có:
(1): (u -v)¢ = u¢ -v¢ Þcông thức (1) trong giả thiết đúng.
(2): (u ×v)¢ = u¢×v + v¢×u Þ công thức (2) trong giả thiết sai.
(3): (ku)¢ = k ×u¢, k là hằng số Þcông thức (3) trong giả thiết đúng.
æ u ¢ö u¢×v - u ×v¢ (4): =
(v = v(x) ¹ 0) Þcông thức (4) trong giả thiết sai. ç ÷ 2 è v ø v
Câu 10: Cho đường thẳng a không vuông góc với mặt phẳng (a ). Có bao nhiêu mặt phẳng chứa a và vuông góc với (a )? A. 0 . B. 2 . C. 1. D. Vô số. Lời giải Chọn D
Nếu a Ì (a ) suy ra có duy nhất một mặt phẳng chứa a và vuông góc với (a )
Nếu a Ì (a ) suy ra có vô số mặt phẳng chứa a và vuông góc với (a ).
Câu 11: Đạo hàm của hàm số y = sin3x là:
A. y¢ = -cos3x .
B. y¢ = 3cos3x.
C. y¢ = cos3x.
D. y¢ = 3cos x . Lời giải Chọn B Ta có: y (sin3x)¢ ¢ = = 3cos3x.
Câu 12: Cho hàm số f (x) thoả mãn lim f (x) = 2 - . Tính lim é f ë ( x) + xù? û x 3 ® x®3 A. 5 . B. 11. C. 1. D. 6 . Lời giải Chọn C
Ta có: lim x = 3 và lim f ( x) = 2
- là các giới hạn hữu hạn. x 3 ® x 3 ® Do đó: lim é f
ë ( x) + xù = lim f û (x)+ lim x = 2 - + 3 =1. x®3 x®3 x®3
Câu 13: Đạo hàm của hàm số 2022 y = x là: A. ( 2022 x )¢ 2021
= 2022x . B. ( 2022 x )¢ 2022 = 2022x . C. ( 2022 x
)¢ = 2022x. D. ( 2022 x )¢ 2023 = 2022x . Trang 55 Lời giải Chọn A Ta có ( 2022 x )¢ 2021 = 2022x .
Câu 14: Trong các mệnh đề sau, mệnh đề nào sai? 3 æ 1 ö A. 2 lim n = +¥ . B. lim = 0. ç ÷ è n ø
C. lim c = c ( c là hằng số). D. lim n q = 0, q Î! . Lời giải Chọn D lim n q = 0, q <1.
Câu 15: Chọn khẳng định đúng trong các khẳng định sau: ¢ 2 ¢ 1 A. ( x) = ( x
" > 0). B. ( x) = ( x " > 0). x 2 x ¢ 1 ¢ 1 C. ( x) = ( x
" > 0). D. ( x) = ( x " Î! ). x 2 x Lời giải Chọn B ¢ 1 Ta có ( x) = ( x " > 0). 2 x
Câu 16: Cho hình lăng trụ đứng ABC.A' B 'C ' . Khoảng cách giữa hai mặt phẳng ( ABC) và ( A'B'C ') bằng A. AB ' . B. AA' . C. BC '. D. AC ' . Lời giải Chọn B
Do ( ABC)//( A'B'C ') Þ d (( ABC),( A'B'C ')) = d (A',(ABC)) = AA'.
Câu 17: Khẳng định nào sau đây đúng? sin x sin 3x sin 3x sin x A. lim =1. B. lim = 0. C. lim =1. D. lim = 0 . x®0 x x®0 x x®0 x x®0 x Lời giải Chọn A x
Câu 18: Đạo hàm của hàm số y = là 3 x ¢ æ ö x ¢ æ ö 1 x ¢ æ ö x ¢ æ ö 1 A. = 3x . B. = - . C. = 3. D. = . ç ÷ ç ÷ ç ÷ ç ÷ è 3 ø è 3 ø 9 è 3 ø è 3 ø 3 Lời giải Chọn C x ¢ æ ö 1 1 Ta có . ç ÷ (x)¢ = = . è 3 ø 3 3
Câu 19: Cho x ¹ 0 , tìm mệnh đề đúng? Trang 56 1 ¢ æ ö 1 1 ¢ æ ö 1 1 ¢ æ ö 1 1 ¢ æ ö 1 A. - = - . B. - = . C. = . D. = - . ç ÷ 2 ç ÷ ç ÷ ç ÷ è x ø x 2 è x ø x 2 è x ø x è x ø x Lời giải Chọn B 1 ¢ æ ö æ 1 ö 1 Ta có - = - - = . ç ÷ ç 2 ÷ 2 è x ø è x ø x
Câu 20: Hàm số g (x) = -sin x là đạo hàm của hàm số nào sau đây? 1 A. y = .
B. y = -sin x.
C. y = - cos x .
D. y = cos x . sin x Lời giải Chọn D
Ta có (cos x)¢ = -sin x.
Câu 21: Hệ số góc của tiếp tuyến của đồ thị hàm số y = f (x) 3 2
= 2x + x -1 tại điểm x = 2 - bằng 0 A. 13 - . B. 20 . C. 19. D. 28 . Lời giải Chọn B
Ta có: f ¢(x) 2 = 6x + 2x
Suy ra, hệ số góc k = f ¢( 2 - ) = 20.
Câu 22: Cho hàm số f ( x) = (x - )2 2 1 + 2.Tính f ¢¢( ) 1 ? A. f ¢¢( ) 1 =12 . B. f ¢¢( ) 1 = 0 . C. f ¢¢( ) 1 =16 . D. f ¢¢( ) 1 = 8. Lời giải Chọn D
Ta có: f ¢(x) = x( 2 x - ) 3 4 1 = 4x - 4x Þ f ¢¢(x) 2 =12x - 4 Vậy f ¢¢( ) 1 = 8.
Câu 23: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 4a , SA ^ ( ABCD).Gọi I
là trung điểm của DO . Khi đó khoảng cách từ điểm I đến mặt phẳng (SAC) bằng A. 2a . B. 4a . C. a 2. D. 2a 2 . Lời giải Chọn C Trang 57 ìIO ^ AC ïIO ^ SA ï Ta có í Þ IO ^ (SAC)
AC Ì (SAC), SA Ì ï (SAC)
ïîAC ÇSA = A BD a
Do đó, d (I,(SAC)) = 4 2 IO = = = a 2 . 4 4
Câu 24: Hàm số nào trong các hàm số dưới đây liên tục trên ! ? 3 x -1 x A. y = . B. 3 y = x + sin 3 1. C. y = . D. 3 y = x -1. x -1 cos3x +1 Lời giải Chọn D 4 - 3x
Câu 25: Đạo hàm của hàm số y =
là kết quả nào sau đây: x - 2 -5 -11 2 10 A. y¢ = . B. y¢ = . C. y¢ = . D. y¢ = . (x - 2)2 (x - 2)2 (x - 2)2 (x - 2)2 Lời giải Chọn C æ 4 - 3x ¢ö 3. - ( 2 - ) -1.4 2 Ta có: y¢ = = = ç ÷ è x - 2 ø (x -2)2 (x -2)2
Câu 26: Đạo hàm của hàm số 3
y = x .sin x là kết quả nào sau đây: 2
y¢ = x (3sin x - xcos x) 2
y¢ = x (3cos x + xsin x) A. . B. . C. 2
y¢ = x (3sin x + xcos x). D. 2
y¢ = x (3cos x - xsin x). Lời giải Chọn C Ta có y¢ = ( 3 x x)¢ = ( 3 x )¢ 3 x + x ( x)¢ 2 3 2 .sin .sin . sin
= 3x sin x + x cos x = x (3sin x + xcos x). æ p ö
Câu 27: Đạo hàm của hàm số y = 2cos - 3x +
1 là kết quả nào sau đây: ç ÷ è 2 ø
A. y¢ = 6cos3x .
B. y¢ = 6cos3x + . 1 Trang 58 æ p ö æ p ö C. y¢ = -2sin
- 3x . D. y¢ = 2sin - 3x . ç ÷ ç ÷ è 2 ø è 2 ø Lời giải Chọn A p ¢ æ ö æ p ö æ p ö Ta có y¢ = 2 - - 3x .sin - 3x = 6sin - 3x = 6cos3x . ç ÷ ç ÷ ç ÷ è 2 ø è 2 ø è 2 ø 1
Câu 28: Một chất điểm chuyển động có phương trình S = f (t) 3 2
= t - t + 4t + 5 ( S là quãng đường 3
chuyển động tính bằng mét và t là thời gian tính bằng giây). Gia tốc của chuyển động tại thời
điểm t = 2 giây là: A. ( 2 3 m / s ). B. ( 2 4 m / s ). C. ( 2 1 m / s ). D. ( 2 2 m / s ). Lời giải Chọn D Ta có 2
v = s¢ = t - 2t + 4
Vậy phương trình gia tốc là: a = v¢ = t - Þ a( ) = ( 2 2 2 2 2 m / s ).
Câu 29: Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O . Góc giữa cạnh bên
SB và mặt phẳng ( ABCD) là A. BSD . B. SBA. C. SBC . D. SBO . Lời giải Chọn D S A B O D C
Vì S.ABCD là hình chóp tứ giác đều nên SO ^ ( ABCD) Þ SB có hình chiếu vuông góc lên
mặt phẳng ( ABCD) là OB . Do đó, góc giữa SB và mặt phẳng ( ABCD) là góc giữa SB và
OB , chính là góc SBO . 1 æ p ö
Câu 30: Đạo hàm của hàm số y = (5 - tan x)5 , x ¹ + kp ,k Î! là kết quả nào sau đây: ç ÷ 5 è 2 ø -(5- tan x)4 (5- tan x)4 -(5- tan x)4 A. y¢ = ( - x)4 5 tan . B. y¢ = . C. y¢ = . D. y¢ = . 2 sin x 2 cos x 2 cos x Lời giải Chọn D Trang 59 1 y = ( - x)5 1 5 tan
Þ y = .5.(5- tan x)4 .(5- tan x)¢ ¢ 5 5 = ( æ ö - - x 5 - tan x) 1 (5 tan )4 4 . - = . ç 2 ÷ 2 è cos x ø cos x
Câu 31: Tính đạo hàm của hàm số y = (x - x )2 5 2 2 ta thu được kết quả 9 6 3
y¢ = ax + bx + cx . Khi đó tổng
a + b + c bằng A. 3 - . B. 3. C. 2 . D. 2 - . Lời giải Chọn D
y = (x - x )2 5 2 Þ y = ( 5 2 x - x )( 5 2 2 2 2 x - 2x )¢ ¢ = ( 5 2 x - x )( 4 x - x) 9 6 3 2 2 5
4 =10x - 28x +16x ìa =10 ï Þ b í = 28
- Þ a + b + c = 2 - . ïc =16 î
Câu 32: Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ (hình vẽ bên dưới). Góc giữa hai đường thẳng DA¢ và B D ¢ ¢ bằng A B D C A' B' D' C' A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 . Lời giải Chọn C A B D C A' B' D' C' Do BD / /B D
¢ ¢ nên góc giữa hai đường thẳng DA¢ và B D
¢ ¢ bằng góc giữa hai đường thẳng DA¢ và BD . Trang 60
Xét tam giác BDA¢ có BD = DA¢ = A B
¢ = AB 2 nên tam giác BDA¢ đều. Vậy góc giữa hai
đường thẳng DA¢ và B D ¢ ¢ 0 bằng 60 .
Câu 33: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , BC = a . SA ^ mp( ABC)và
SA = a 3 . Góc giữa hai mặt phẳng (SBC)và ( ABC) bằng A. 0 30 . B. 0 90 . C. 0 45 . D. 0 60 . Lời giải Chọn D S C A α B ìBC ^ AB
Ta có BC = ( ABC)!(SBC) và í Þ BC ^ SB îBC ^ SA
Khi đó góc ((SBC) ( ABC)) = goc(SB AB) ∑ ; ; = SBA SA
Trong tam giác SAB có ∑ tan (SBA) = = 3 suy ra ∑ 0
SBA = 60 . Chọn D AB
Câu 34: Cho hình chóp S.ABCD có SA ^ ( ABCD)và đáy ABCD là hình vuông. Từ A kẻ AH ^ SD
(hình vẽ bên dưới). Khẳng định nào sau đây đúng? S H A D B C
A. AH ^ (SAB).
B. AH ^ (SCD).
C. AH ^ (SBD).
D. SD ^ (HAC). Lời giải Chọn B
Ta có AH ^ SD (1) CD ì ^ AD Và í Þ CD ^ AH (2) CD î ^ SA
Từ (1), (2) suy ra AH ^ (SCD). æ x - a ö
Câu 35: Cho a ¹ 0. Kết quả của lim bằng ç 2 2 ÷
x®a è x - a ø Trang 61 -1 1 A. . B. 2a . C. . D. 2 - a . 2a 2a Lời giải Chọn C æ x - a ö æ x - a ö æ 1 ö 1 Ta tính lim = lim ç ÷ ç ÷ = lim = . 2 2 ç ÷ ç ÷ x®a x®a è x - a ø
è (x - a)(x + a) x®a ø
è x + a ø 2a
II. Phần tự luận. (4 câu – 3 điểm) 3 ì x + 27 ï khi x < 3 -
Câu 36: Tìm số thực m để hàm số f ( x) 2 = í x -3x -18 liên tục trên ! ?
ïî2x+ m khi x ³ 3 - Lời giải
Hàm số liên tục trên khoảng ( ; -¥ - ) 3 và [ 3; - +¥) Ta tính được x + (x +3)( 2 3 x - 3x + 9 27 ) 2 x - 3x + 9
. lim f (x) = lim = lim = lim x ( )- x ( )- 2 3 3
x - 3x -18 x ( 3)- (x +3)(x -6) x ( 3)- ® - ® - ® - ® - x - 6 (- )2 3 - 3( 3 - ) + 9 = = 3 - 3 - - 6
. lim f (x) = lim (2x + m) = 6 - + m x ( 3)+ x ( 3)+ ® - ® -
Để hàm số liên tục trên ! thì hàm số phải liên tục tại x = 3 -
suy ra lim f (x) = lim f (x) = f ( 3 - ) hay là 3 - = 6 - + m Û m = 3 x ( 3)- x ( 3)+ ® - ® -
Câu 37: Cho hình chóp đều tứ giác đều S .A BCD có tất cả các cạnh bằng a . Gọi O là giao điểm AC
và BD . Tính khoảng cách từ O đến mặt phẳng (SCD)? Lời giải S A D O B C
Theo giả thiết S .A BCD là hình chóp đều tứ giác đều có tất cả các cạnh đáy bằng a nên ba AC a 2
cạnh SO,OC,OD đôi một vuông góc nhau và OS = OC = OD = = . 2 2 Trang 62 1 1 1 1 3 6 a 6 Gọi h = d ( ,
O (SCD)) khi đó ta có = + + = = suy ra h = . 2 2 2 2 2 2 h OS OC OD æ 2 ö a a 6 ç ÷ 2 è ø a
Vậy d (O (SCD)) 6 , = . 6 3 1+ 2x - 1+ 3x
Câu 38: Tính giới hạn của hàm số sau: lim ? 2 x Lời giải é 1+ 2x - + - +
(1+ x)ù + é(1+ x) 3 3 - 1+ 3 1 2 1 3 x x x ù Ta có lim lim ë û ë û = 2 2 x 0 ® x x 0 ® x æ ö 1 1+ 2x - ç (1+ x)2 (1+ x)3 -1-3x lim ÷ = + 2 x 0
® x çç 1 2x (1 x) ( ÷ + + +
1+ x)2 + (1+ x) 3 3
1+ 3x + (1+ 3x)2 ÷ è ø æ 2 3 2 ö 1 -x x + 3x lim ç ÷ = + 2 x 0
® x çç 1 2x (1 x) ( ÷ + + +
1+ x)2 + (1+ x) 3 3
1+ 3x + (1+ 3x)2 ÷ è ø æ ö x + 3 1 lim ç ÷ = - x 0 ® çç ( + )2 +( + ) 3 ÷ 3 + + ( + )2 1+ 2x + (1 1 1 1 3 1 3 + x x x x x ) ÷ è ø 1 = . 2 x - 5
Câu 39: Cho hàm số y =
có đồ thị là đường cong (C). Lập phương trình tiếp tuyến của đồ thị x -1
(C) sao cho tiếp tuyến này cắt các trục Ox, Oy lần lượt tại các điểm ,
A B phân biệt sao cho OB = 4OA . Lời giải
Giả sử d là tiếp tuyến của đồ thị (C) tại điểm M (x ; y 0 0 ) .
Do d cắt các trục Ox, Oy lần lượt tại các điểm ,
A B sao cho OB = 4OA nên ∑ OB tan OAB =
= 4. Suy ra hệ số góc k của d bằng 4 hoặc 4 - . OA 4
Ta có k = y¢( x = > 0 k = 4 0 ) nên (x - )2 1 0 4 éx -1=1 éx = 2 Û = 4 Û x -1 =1Û Û 2 ( 0 )2 0 0 . ( ê ê x - ) 1 x -1 = 1 - x = 0 ë 0 ë 0 0
+) Với x = 2: phương trình của d là y = 4(x - 2) + y(2) = 4x -1 . 1 0
+) Với x = 0: phương trình của d là y = 4(x -0) + y(0) = 4x + . 5 0
Vậy có 2 tiếp tuyến của đồ thị (C) thỏa mãn là y = 4x -11 và y = 4x + 5. Trang 63




