Bộ đề thi giữa HK2 toán 12 năm 2022-2023 (Có đáp án)

Bộ đề thi giữa HK2 Toán 12 năm 2022-2023 có đáp án được soạn dưới dạng file PDF gồm 34 trang. Các bạn xem và tải về ở dưới.

 

85 43 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 12

Môn: Toán 12

Thông tin:

34 trang 8 tháng trước

Tác giả:

Profile Hoàng Yến
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 1
MÔN TOÁN 12
Câu 1: Trong không gian
Oxyz
cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 2 3 25S x y z− + − + − =
.Tìm tọa độ tâm I và bán
kính R của mặt cầu.
A.
( )
1; 2; 3I − − −
,
5R =
. B.
( )
1;2;3I
,
5R =−
.
C.
,
5R =
. D.
( )
1; 2; 3I − − −
,
5R =−
.
Câu 2: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
1;2
và thỏa mãn
( )
1 1,f =
( )
2 2.f =
Tính
( )
2
1
d.I f x x
¢
=
ò
A.
= 1.I
B.
=-1.I
C.
7
2
I =×
D.
3.I =
Câu 3: Trong không gian
Oxyz
, một véc tơ pháp tuyến của mặt phẳng
( )
:3 2 5 0P x y z− + + =
là:
A.
( )
3;1;2n
→
=
. B.
( )
2; 1;3n
→
=−
. C.
( )
3;1;2n
→
=−
. D.
( )
3; 1;2n
→
=−
.
Câu 4: Cho hai hàm số
()fx
và
()gx
liên tục trên
;ab
. Diện tích hình phẳng giới hạn bởi đồ thị của các
hàm số
()y f x=
,
()y g x=
và các đường thẳng
xa=
,
xb=
bằng:
A.
( ) ( ) d
b
a
f x g x x−
. B.
( ) ( ) d
b
a
f x g x x+
. C.
( ) ( ) d
b
a
f x g x x−
. D.
( ) ( ) d
b
a
f x g x x−
.
Câu 5: Cho hàm số liên tục trên . Chọn khẳng định sai:
A. . B. .
C. . D. .
Câu 6: Cho hàm số
( )
fx
thỏa mãn
3
1
( ) 2022f x dx =
và
4
3
( ) 2023f x dx =
Tính tích phân
( )
4
1
d.I f x x=
ò
A.
1.I =-
B.
4045I =−
C.
4045I =
D.
1.I =
Câu 7: Trong không gian với hệ tọa độ
Oxyz
cho
(1;2;3), ( 4;4;6).AB−
Tọa độ trọng tâm G của tam giác
OAB là
A.
( 3;6;9)G −
. B.
( 1;2;3)G −
. C.
(1; 2; 3)G −−
. D.
39
;3;
22
G

−


.
Câu 8: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( )
1;3; 2A −
và
( )
4; 5;2 .B −
Tính tọa độ của vectơ
AB
→
.
A.
( )
5; 2;0 .AB =−
→
B.
( )
3; 8;4 .AB =−
→
C.
( )
3;8; 4 .AB = − −
→
D.
5
; 1;0 .
2
AB

=−


→
Câu 9: Hàm số
( )
fx
có nguyên hàm trên
K
nếu:
A.
( )
fx
liên tục trên
K
. B.
( )
fx
xác định trên
K
.
C.
( )
fx
có giá trị nhỏ nhất trên
K
. D.
( )
fx
có giá trị lớn nhất trên
K
.
Câu 10: Cho
( )
fx
,
( )
gx
là các hàm số xác định và liên tục trên R. Trong các mệnh đề sau, mệnh đề nào
đúng?
A.
( ) ( ) ( ) ( )
dddf x g x x f x x g x x+ = −


. B.
( ) ( )
2 d 2 df x x f x x=

.
()y f x=
;ab
( )
( ) ( ) ( ) , ;
b c c
a a b
f x dx f x dx f x dx c a b+ =
(x)dx ( )
ba
ab
f f x dx=−

( )
( ) ( ) ( ) , ;
b c b
a a c
f x dx f x dx f x dx c a b= +
( ) 0
a
a
f x dx =
C.
( )
( )
( )
( )
d
d
d
f x x
fx
x
gx
g x x
=
. D.
( ) ( ) ( ) ( )
. d d . df x g x x f x x g x x=


.
Câu 11: Để tính
. osxdx c x
ò
theo phương pháp tính nguyên hàm từng phần, ta đặt:
A.
osx
.
dd
uc
v x x
ì
=
ï
ï
í
ï
=
ï
î
B.
osx
.
d
uc
vx
ì
=
ï
ï
í
ï
=
ï
î
C.
.
d osx
ux
vc
ì
=
ï
ï
í
ï
=
ï
î
D.
.
d osxd
ux
v c x
ì
=
ï
ï
í
ï
=
ï
î
Câu 12: Trong không gian với hệ tọa độ
Oxyz
cho
(2;0;3), ( 3;1;0).uv
→→
= = −
Tích vô hướng của
u
→
và
v
→
là:
A.
.0uv
→→
=
. B.
.6uv
→→
=−
. C.
. ( 3; 11,2)uv
→→
= − −
. D.
. 10uv
→→
=
.
Câu 13: Viết công thức tính thể tích
V
của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi
đồ thị hàm số
( )
,y f x=
trục
Ox
và hai đường thẳng
( )
, ,x a x b a b= = <
xung quanh trục
.Ox
A.
( )
d.
b
a
V f x xp=
ò
B.
( )
2
d.
b
a
V f x x=
ò
C.
( )
2
d.
b
a
V f x xp=
ò
D.
( )
d.
b
a
V f x x=
ò
Câu 14: Cho
( ) ( )
2
1
3 d 10f x g x x
éù
-=
ëû
ò
và
( )
2
1
d 3.f x x =
ò
Khi đó
( )
2
1
dg x x
ò
bằng:
A. 17. B. 1. C. -1. D. -4.
Câu 15: Một nguyên hàm của hàm số
( )
cos3f x x=
thoả
1
18 6
f

=


.
A.
sin3 1
36
x
+
. B.
1
3sin 3
2
x −
. C.
3sin3 1x+
. D.
sin 3
3
x
.
Câu 16: Trong không gian Oxyz mặt phẳng (P) đi qua điểm M( - 1;2;0) và có véc tơ pháp tuyến
n (4;0; 5)=−
có phương trình là:
A. 4x - 5z - 4 = 0. B. 4x - 5z + 4 = 0. C. 4x - 5y + 4 = 0. D. 4x - 5y - 4 = 0.
Câu 17: Tìm nguyên hàm của hàm số
2
)(
x
xexf
−
=
.
A.
Cedxxf
x
+−=
−
2
2
1
)(
. B.
Cedxxf
x
+=
−
2
2
1
)(
.
C.
Cxedxxf
x
+−=
−
2
2
1
)(
. D.
Cxedxxf
x
+=
−
2
2
1
)(
.
Câu 18: Cho
6
0
( ) 12f x dx =
. Tính
2
0
(3 )I f x dx=
.
A.
4I =
. B.
2I =
. C.
6I =
. D.
36I =
.
Câu 19: Cho điểm A(1;-2;1) và (P): x + 2y – z – 1 = 0. Viết phương trình mặt phẳng (Q) đi qua A và song
song với (P).
A.
(Q):x 2y z 4 0− − + =
. B.
(Q):x 2y z 4 0+ − − =
. C.
(Q):x 2y z 4 0+ − + =
. D.
(Q):x 2y z 2 0+ − + =
.
Câu 20: Trong không gian Oxyz ,cho mặt phẳng (P): và điểm A(3;3;3). Tìm khoảng
cách từ điểm A đến mp(P).
A. -14. B.
14
. C.
14
. D.
14
14
.
Câu 21: Tính
2
0
sinx.dx
bằng:
A.
cos cos0
2
−
. B.
sin sin0
2
−
. C.
cos0 cos
2
−
. D.
sin0 sin
2
−
.
Câu 22: Một nguyên hàm của hàm số thỏa mãn F(1) = 0 là:
A. . B. . C. . D. .
( )
2
31f x x=+
3
2xx+−
3
1x −
3
xx+
3
2xx++
Câu 23: Gọi
D
là hình phẳng giới hạn bởi các đường
4
, 0, 0
x
y e y x= = =
và
1x =
. Thể tích của khối tròn
xoay tạo thành khi quay
D
quanh trục
Ox
bằng
A.
1
8
0
d
x
ex
. B.
1
4
0
d
x
ex
. C.
1
4
0
d
x
ex
. D.
1
8
0
d
x
ex
.
Câu 24: Định
m
để hai mặt phẳng sau vuông góc với nhau:
( ):3 5 3 0,P x y mz− + − =
( ): 3 2 5 0Q mx y z+ + + =
A.
4m =
. B.
1m =
. C.
3m =
. D.
2m =
.
Câu 25: Trong không gian với hệ tọa độ
Oxyz
, mặt phẳng
( )
P
đi qua điểm
( )
1;2;3M
và cắt các tia
Ox
,
Oy
,
Oz
lần lượt tại
N
,
H
,
K
sao cho thể tích của tứ diện
ONHK
đạt giá trị nhỏ nhất. Phương trình của mặt
phẳng
( )
P
là
A.
6 3 2 6 0x y z+ − − =
. B.
6 3 2 6 0x y z− + − =
. C.
6 3 2 6 0x y z− + + − =
. D.
6 3 2 18 0x y z+ + − =
.
Câu 26: Cho hàm số
( ) ( )
32
, , , , 0y f x ax bx cx d a b c R a= = + + +
có đồ thị
( )
C
. Biết rằng đồ thị
( )
C
tiếp
xúc với đường thẳng
4y =
tại điểm có hoành độ âm và đồ thị hàm số
( )
y f x
=
cho bởi hình vẽ dưới đây:
Tính diện tích
S
của hình phẳng giới hạn bởi đồ thị
( )
C
và trục hoành.
A.
5
4
. B.
27
4
S =
. C.
21
4
. D.
9S =
.
Câu 27: Trong không gian
Oxyz
, cho điểm
( )
1; 2;3M −
. Gọi
I
là hình chiếu vuông góc của
M
trên trục
Ox
. Phương trình nào dưới đây là phương trình mặt cầu tâm
I
bán kính
IM
?
A.
( )
2
22
1 13.x y z+ + + =
B.
( )
2
22
1 13.x y z− + + =
C.
( ) ( ) ( )
2 2 2
1 2 3 13.x y z− + + + − =
D.
( )
2
22
1 13.x y z− + + =
Câu 28: Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?
A.
( )
2
2
1
2 2 4 .x x dx
−
−−
B.
( )
2
1
2 2 .x dx
−
−
C.
( )
2
1
2 2 .x dx
−
−+
D.
( )
2
2
1
2 2 4 .x x dx
−
− + +
Câu 29: Tính tích phân
2
2
1
2 1dI x x x=−
bằng cách đặt
2
1,ux=−
mệnh đề nào dưới đây đúng ?
A.
2
1
1
d.
2
I u u=
B.
3
0
d.I u u=
C.
2
1
d.I u u=
D.
3
0
2 d .I u u=
Câu 30: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
1;1 ,-
thỏa mãn
( )
0,fx>
x"Ρ
và
( ) ( )
2 0.f x f x
¢
+=
Biết rằng
( )
1 1,f =
tính
( )
1.f -
A.
( )
1 3.f -=
B.
( )
2
1.fe
-
-=
C.
( )
3
1.fe-=
D.
( )
4
1.fe-=
Câu 31: Giá trị của a, b thoả
.sin xd osx + bsinx + Cx x axc=
là:
A. a = - 1; b = - 1. B. a = 1; b = - 1. C. a = 1; b = 1. D. a = -1; b = 1.
Câu 32: Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( ) ( )
2;3; 1 , 1;1;1MN−−
,
( )
0; ;0Pm
. Tìm giá trị
của m để tam giác MNP vuông tại M.
A.
7.m =−
B.
13
.
2
m =
C.
7.m =
D.
15
.
2
m =
------ HẾT ------
ĐÁP ÁN
1
C
6
A
11
D
16
B
21
C
26
B
31
D
2
A
7
B
12
B
17
A
22
A
27
B
32
C
3
D
8
B
13
C
18
A
23
A
28
D
4
D
9
A
14
C
19
C
24
C
29
B
5
A
10
B
15
D
20
B
25
D
30
D
Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 2
MÔN TOÁN 12
Câu 1: Trong không gian
Oxyz
, cho biểu diễn của vectơ
a
qua các vectơ đơn vị là
23a i j k= − +
. Tọa độ
của vectơ
a
là
A.
( )
2; 3;1−
. B.
( )
1;2; 3−
. C.
( )
2;1; 3−
. D.
( )
1; 3;2−
.
Câu 2: Cho
( )
Fx
là một nguyên hàm của hàm
( )
1
21
fx
x
=
+
; biết
( )
02F =
. Tính
( )
1F
.
A.
( )
1
1 3 2
2
F ln=-
. B.
( )
1 2 3 2F ln=-
. C.
( )
1 3 2F ln=+
. D.
( )
1
1 3 2
2
F ln=+
.
Câu 3: Trong không gian
,Oxyz
cho điểm
( )
1; 2;3A −
. Hình chiếu vuông góc của điểm
A
trên mặt phẳng
( )
Oxz
là điểm
.M
Tọa độ của điểm
M
là
A.
( )
0;1;0M
. B.
( )
0; 2;3M −
. C.
( )
1; 2;0M −
. D.
( )
1;0;3M
.
Câu 4: Cho hàm số
( )
fx
xác định và liên tục trên
\0
thỏa mãn
( ) ( ) ( ) ( )
2 2 '
2 1 1x f x x f x xf x+ − = −
với
mọi
\0x
, đồng thời thỏa
( )
12f =−
. Tính
( )
3
1
d.f x x
A.
3
ln3
2
−−
. B.
ln3
1
3
−−
. C.
2
ln3
3
−−
. D.
ln3 2
33
−−
.
Câu 5: Cho
( )
Fx
là một nguyên hàm của hàm số
( )
sinf x x x=+
và thỏa mãn
( )
01F =
. Tìm
( )
Fx
.
A.
( )
2
cos
2
x
F x x=+
. B.
( )
2
cos 2
2
x
F x x= − −
. C.
( )
2
1
cos
22
x
F x x= + +
. D.
( )
2
cos 2
2
x
F x x= − +
.
Câu 6: Cho hàm số
( )
y f x=
xác định và liên tục trên đoạn
;ab
. Diện tích hình phẳng giới hạn bởi đồ thị
hàm số
( )
y f x=
, trục hoành và hai đường thẳng
,x a x b==
được tính theo công thức
A.
( )
d
b
a
S f x x=
. B.
( )
d
b
a
S f x x=−
. C.
( )
d
b
a
S f x x=
. D.
( )
d
a
b
S f x x=
.
Câu 7: Trong không gian với hệ tọa độ
Oxyz
cho hai điểm
( ) ( )
1;2; 1 ; 2;1;0AB−
mặt phẳng
( )
:2 3 1 0P x y z+ − + =
. Gọi
( )
Q
là mặt phẳng chứa
;AB
và vuông góc với
( )
P
. Phương trình mặt phẳng
( )
Q
là
A.
2 5 0x y z+ − − =
. B.
2 6 0x y z− − − =
. C.
2 3 7 0x y z+ − − =
. D.
2 5 3 9 0x y z+ + − =
.
Câu 8: Trong không gian với hệ tọa độ Oxyz, cho
( ) ( ) ( )
1;2;3 , 1;2;4 ; 4; 1;2A B C −
. Tìm tọa độ điểm M trên
mặt phẳng (Oyz) sao cho:
MA MB MC++
ngắn nhất?
A.
( )
0;1;3M
B.
( )
2;1;3M
C.
( )
2;0;3M
D.
( )
0;2;3M
Câu 9: Trong không gian
Oxyz
, mặt phẳng
( )
: 2 3 3 0P x y z+ − + =
có một vectơ pháp tuyến là
A.
( )
1;2;3
. B.
( )
1;2; 3−−
. C.
( )
1;2; 3−
. D.
( )
1; 2;3−
.
Câu 10: Trong không gian với hệ trục tọa độ
Oxyz
cho hai vectơ
( )
4;5; 3a = − −
,
( )
2; 2;1b =−
. Tìm tọa độ của
vectơ
2x a b=+
.
A.
( )
0; 1;1x =−
. B.
( )
0;1; 1x =−
. C.
( )
2;3; 2x =−
. D.
( )
8;9;1x =−
.
Câu 11: Biết
( )
=
3
2
f x dx 3
và
( )
=−
3
2
g x dx 2
. Khi đó:
( ) ( )
3
2
f x g x dx

−

bằng
A.
5
. B.
1
. C.
5−
. D.
6−
.
Câu 12: Trong không gian với hệ trục tọa độ
,Oxyz
mặt phẳng
( )
: 2 2 3 0P x y z+ − + =
cắt mặt cầu
( )
S
tâm I
(2; 1; -1) theo giao tuyến là một đường tròn có bán kính bằng 4. Tính bán kính mặt cầu (S).
A. 5. B. 4. C. 3. D. 6.
Câu 13: Tính
sin xdx
A.
2 cos 2sinx x x C− − +
. B.
2 sin 2sinx x x C−+
.
C.
2 sin 2cosx x x C− + +
. D.
2 s 2sinxco x x C− + +
.
Câu 14: Hàm số nào sau đây không phải là một nguyên hàm của hàm số
( )
3
( ) 2 3f x x=−
?
A.
( )
( )
4
23
3
8
x
Fx
−
=−
.B.
( )
( )
4
23
8
x
F x x
−
=+
. C.
( )
( )
4
23
8
x
Fx
−
=
. D.
( )
( )
4
23
8
8
x
Fx
−
=+
.
Câu 15: Công thức nào sau đây là đúng?
A.
cos d sinx x x C= − +
. B.
sin d cosx x x C=+
.
C.
sin d cosx x x C= − +
. D.
cos d sinx x x C− = +
.
Câu 16: Tìm nguyên hàm của hàm số
( ) 7
x
fx=
.
A.
1
77
xx
dx C
+
=+
. B.
1
7
7
1
x
x
dx C
x
+
=+
+
. C.
7 7 ln7
xx
dx C=+
. D.
7
7
ln7
x
x
dx C=+
.
Câu 17: Biết tích phân
ln6
0
e
d ln 2 ln3
1 e 3
x
x
x a b c= + +
++
, với
a
,
b
,
c
là các số nguyên. Tính tổng
T a b c= + +
.
A.
1T =−
. B.
1T =
. C.
0T =
. D.
2T =
.
Câu 18: Gọi
D
là hình phẳng giới hạn bởi các đường
, 0, 0
x
y e y x= = =
và
1x =
. Thể tích của khối tròn xoay
tạo thành khi quay
D
quanh trục
Ox
bằng
A.
1
0
x
e dx
. B.
1
2
0
x
e dx
. C.
1
0
x
e dx
D.
1
2
0
x
e dx
.
Câu 19: Gọi S là diện tích hình phẳng giới hạn bởi các đường
( )
=y f x
, trục hoành (phần gạch sọc trong
hình vẽ). Đặt
( ) ( )
12
21
,a f x dx b f x dx
−
==

. Mệnh đề nào đúng?
A.
.ba−
B.
.ba−−
C.
.ab−
D.
.ab+
Câu 20: Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( 2; 3;1)a = − −
,
(1;0;1)b =
. Tính
cos( , )ab
.
A.
1
cos( , )
27
ab =
. B.
1
cos( , )
27
ab
−
=
. C.
3
cos( , )
27
ab =
. D.
3
cos( , )
27
ab
−
=
.
Câu 21: Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
( )
S
:
2 2 2
6 4 8 4 0x y z x y z+ + − + − + =
. Tìm tọa
độ tâm
I
của mặt cầu
( )
S
.
A.
( )
3; 2;4I −
. B.
( )
3;2; 4I −−
. C.
( )
6; 4;8I −
. D.
( )
6;4; 8I −−
.
Câu 22: Thể tích của khối tròn xoay sinh bởi hình phẳng giới hạn bởi đồ thị hai hàm số
2
3y x x=−
,
2
9yx=−
khi nó quay quanh trục hoành là
A.
648
5
. B.
34101
160
. C.
1296
5
. D.
2673
32
.
Câu 23: Nếu
( )
1
1
d4f x x
−
=−
thì
( )
1
1
3 1 df x x
−

−+

bằng
A.
10−
. B.
11−
. C.
11
. D.
14
.
Câu 24: Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
: 2 0P x y z+ − + =
và hai điểm
( ) ( )
3;4;1 ; 7; 4; 3AB−−
. Tìm điểm
( )( )
; ; 2M a b c a
thuộc
( )
P
sao cho tam giác
ABM
vuông tại
M
và có
diện tích nhỏ nhất.
A.
4 7 5
;;
3 3 3
M

−


. B.
5 4 7
;;
3 3 3
M

−


. C.
5 7 4
;;
3 3 3
M

−


. D.
457
;;
333
M



.
Câu 25: Tích phân
3
0
d
2
x
I
x
=
+
có giá trị bằng
A.
5
ln
2
I =
. B.
4581
5000
I =
. C.
5
log
2
I =
. D.
21
100
I =−
.
Câu 26: Trong không gian
Oxyz
, cho ba điểm
( )
1; 0; 0A
,
( )
0; 2; 0B
,
( )
0; 0; 4C
. Tính khoảng cách từ gốc
tọa độ
O
đến mặt phẳng
( )
ABC
.
A.
3 21
21
. B.
2 21
21
. C.
21
21
. D.
4 21
21
.
Câu 27: Giả sử các biểu thức sau đều có nghĩa, công thức nào sau đây sai?
A.
=+
ò
d .ln .
xx
a x a a C
B.
=+
ò
2
1
d tan .
cos
x x C
x
C.
1
ln .dx x C
x
=+
D.
=+
ò
cos d sin .x x x C
Câu 28: Trong các khẳng định sau, khẳng định nào đúng khi nói về tích phân
2
0
sin 2I x xdx
=
?
A.
22
00
1
2 sin 2 .
24
x
I cos x x

=−
B.
22
00
1
2 sin 2 .
24
x
I cos x x

= − +
C.
22
00
1
2 sin 2 .
22
x
I cos x x

= − +
D.
22
00
1
2 sin 2 .
24
x
I cos x x

= − −
Câu 29: Tìm nguyên hàm của hàm số
( )
cos3f x x=
.
A.
sin3
cos3 .
3
x
xdx C=+
B.
cos3 sin3 .xdx x C=+
C.
sin3
cos3 .
3
x
xdx C= − +
D.
cos3 3sin3 .xdx x C=+
.
Câu 30: Cho hàm số
( )
gx
liên tục trên . Mệnh đề nào sau đây đúng?
A.
( )
2021
2021
d 2021g x x =
. B.
( )
2021
2021
d0g x x =
. C.
( )
2021
2021
d1g x x =
. D.
( )
2021
2021
d 2021g x x =−
.
Câu 31: Cho
( )
Fx
là một nguyên hàm của hàm số
( )
fx
trên
0;5
. Mệnh đề nào sau đây đúng?
A.
( )
5
0
d (0) (5).f x x F F=−
B.
( )
5
0
d (5) (0).f x x F F=+
C.
( )
5
0
d (5) (0).f x x f f=−
D.
( )
5
0
d (5) (0).f x x F F=−
Câu 32: Tính diện tích
S
của hình phẳng
()H
giới hạn bởi các đường cong
3
12y x x= − +
và
2
yx=−
.
A.
937
12
S =
. B.
343
12
S =
. C.
793
4
S =
. D.
397
4
S =
.
------ HẾT ------
Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 3
MÔN TOÁN 12
Câu 1: Tính
2
1
2dI x x
−
=
.
A.
3I =−
. B.
3I =
. C.
5I =
. D.
6I =−
.
Câu 2: Mệnh đề nào sau đây sai?
A.
xx
e dx e C=+
. B.
sinx osdx c x C=+
.
C.
dx x C=+
. D.
5
4
5
x
x dx C=+
.
Câu 3: Cho
( )
Fx
là một nguyên hàm của hàm số
( )
e2
x
f x x=+
thỏa mãn
( )
3
0
2
F =
. Tìm
( )
.Fx
A.
( )
2
5
e
2
x
F x x= + +
. B.
( )
2
3
e
2
x
F x x= + +
.
C.
( )
2
1
2e
2
x
F x x= + −
. D.
( )
2
1
e
2
x
F x x= + +
.
Câu 4: Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
P
đi qua điểm
( )
0; 1;4A −
và có một véctơ
pháp tuyến
( )
2;2; 1n =−
. Phương trình của
( )
P
là
A.
2 2 6 0x y z+ + − =
. B.
2 2 6 0x y z+ − − =
. C.
2 2 6 0x y z+ − + =
. D.
2 2 6 0x y z− − − =
.
Câu 5: Tính diện tích
S
của hình phẳng giới hạn bởi đường cong
2
3= − +y x x
và đường thẳng
21=+yx
.
A.
4
5
=S
. B.
9
2
=S
. C.
2
3
=S
. D.
1
6
=S
.
Câu 6: Trong không gian với hệ toạ độ
Oxyz
, cho mặt cầu
( )
S
có phương trình:
( ) ( ) ( )
2 2 2
1 2 3 4x y z− + + + − =
. Tìm toạ độ tâm
I
và bán kính
R
của
( )
S
.
A.
(1; 2;3)I −
và
4R =
. B.
( 1;2; 3)I −−
và
4R =
.
C.
(1; 2;3)I −
và
2R =
. D.
( 1;2; 3)I −−
và
2R =
.
Câu 7: Cho tích phân
2
0
sinI x x dx
=
. Bằng cách đặt
, sinu x dv x dx==
ta được:
A.
2
2
0
0
( cos ) cosI x x xdx
=−
. B.
2
2
0
0
( cos ) cosI x x xdx
= − −
.
C.
2
2
0
0
( cos ) cosI x x xdx
=+
. D.
2
2
0
0
( cos ) cosI x x xdx
= − +
.
Câu 8: Trong không gian
Oxyz
, phương trình của mặt phẳng
( )
P
đi qua điểm
( )
2;1; 3B −
, đồng thời vuông
góc với hai mặt phẳng
( )
: 3 0Q x y z+ + =
,
( )
:2 0R x y z− + =
là
A.
4 5 3 22 0x y z+ − + =
. B.
2 3 14 0x y z+ − − =
.
C.
4 5 3 22 0x y z+ − − =
. D.
4 5 3 12 0x y z− − − =
.
Câu 9: Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường:
2
=−y x x
,
0=y
quanh
trục
Ox
là:
A.
( )
30
= tV đvt
. B.
( )
15
= tV đvt
. C.
( )
5
=V đvtt
. D.
( )
10
= tV đvt
.
Câu 10: Trong không gian
Oxyz
, cho hai điểm
( )
1;2; 3A −
và
( )
3; 2; 1B −−
. Tọa độ trung điểm
I
của đoạn
thẳng
AB
là
A.
( )
1; 2;1I −
. B.
( )
1;0; 2I −
. C.
( )
2;0; 2I −
. D.
( )
4;0; 4I −
.
Câu 11: Biết
( )
3 3 3
d , .
x x x
xe x axe be C a b= + +
Tính tích
ab
.
A.
1
27
ab =
. B.
1
9
ab =
. C.
1
27
ab =−
. D.
1
9
ab =−
.
Câu 12: Góc tạo bởi hai véc tơ
( ) ( )
2;2;4 , 3; 3;0ab= = −
bằng
A.
45
. B.
90
. C.
135
. D.
30
.
Câu 13: Cho hàm số
( )
fx
liên tục trên và có
( )
1
0
d2f x x =
;
( )
1
3
d6f x x =
. Tính
( )
3
0
dI f x x=
.
A.
4I =−
. B.
36I =
. C.
4I =
. D.
8I =
.
Câu 14: Cho biết
( )
Fx
là một nguyên hàm của hàm số
( )
fx
trên
¡
. Tìm
( )
2 1 dI f x x=+


A.
( )
2I xF x x C= + +
. B.
( )
2I F x x C= + +
. C.
( )
21I F x C= + +
. D.
( )
21I xF x C= + +
.
Câu 15: Trong không gian Oxyz, cho mặt phẳng (P): 3x – 2y - 2z - 5 = 0 và điểm A(2;3;-1). Khoảng cách từ
điểm A đến mặt phẳng
()P
bằng:
A.
3
.
17
B.
3
.
7
C.
3
.
17
D.
3
.
7
Câu 16: Tìm nguyên hàm của hàm số
( )
2018
(1 )
xx
f x e e=−
A.
( )
2018
d ( ) .
2018
x
x
e
f x x e x C= − +
B.
( )
2019
d.
2019
x
x
e
f x x e C= + +
C.
( )
2019
d.
2019
x
x
e
f x x e C= − +
D.
( )
2019
d 2019 .
xx
f x x e e C= − +
Câu 17: Hàm số
( )
2
2F x x x=+
là một nguyên hàm của hàm số:
A.
( )
41f x x=+
. B.
( )
1f x x=+
. C.
( )
21f x x=+
. D.
( )
2
3
2
32
x
f x x=+
.
Câu 18: Trong không gian
Oxyz
, một véctơ pháp tuyến của mặt phẳng
( )
: 2 3 1 0x y z
− + + =
là
A.
( )
1; 2; 3n =−
. B.
( )
1; 2; 3n = − −
. C.
( )
3; 2; 1n =−
. D.
( )
1; 2; 3n =−
.
Câu 19: Diện tích hình phẳng giới hạn bởi đồ thị hàm số
( )
y f x=
liên tục trên
;ab
và các đường
0, ,y x a x b= = =
với
( )
ab
là
A.
2
()
b
a
S f x dx=
. B.
()
b
a
S f x dx
=
. C.
()
b
a
S f x dx=
. D.
2
()
b
a
S f x dx
=
.
Câu 20: Cho
4
2
( ) 5f x dx =
. Tính
2
1
(2 )I f x dx=
A.
5I =
. B .
5
2
I =
. C.
10I =
D.
3
2
I =
.
Câu 21: Thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong giới hạn bởi đồ thị hàm số y =
f(x), trục Ox và hai đường thẳng x = a, x = b (a b) xung quanh trục Ox là
A.
( ) .
b
a
V f x dx=
B.
2
( ) .
b
a
V f x dx
=
C.
( ) .
b
a
V f x dx
=
D.
2
( ) .
b
a
V f x dx=
Câu 22: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
3; 1; 2M −−
và mặt phẳng
( )
:3 2 4 0P x y z− + + =
.
Phương trình mặt phẳng đi qua
M
và song song với
( )
P
là
A.
3 2 14 0x y z− − − =
. B.
3 2 14 0x y z+ − − =
. C.
3 2 6 0x y z− + + =
. D.
3 2 6 0x y z− + − =
.
Câu 23: Cho tích phân
e
1
3ln 1
d
x
Ix
x
+
=
. Nếu đặt
lntx=
thì
A.
( )
e
1
3 1 dI t t=+
. B.
( )
1
0
3 1 dI t t=+
. C.
1
0
31
d
e
t
t
It
+
=
. D.
e
1
31
d
t
It
t
+
=
.
Câu 24: Trong không gian với hệ tọa độ
Oxyz
, cho các điểm
( )
1;0;3A
,
( )
2;3; 4B −
,
( )
3;1;2C −
. Tìm tọa độ
điểm
D
sao cho tứ giác
ABCD
là hình bình hành.
A.
( )
4;2;9D
. B.
( )
6;2; 3D −
. C.
( )
4; 2;9D −−
. D.
( )
2;4; 5D −−
.
Câu 25: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( )
2;2; 2A −−
;
( )
3; 3;3B −
. Điểm
M
trong
không gian thỏa mãn
2
3
MA
MB
=
. Khi đó độ dài
OM
lớn nhất bằng
A.
12 3
. B.
53
2
. C.
63
. D.
53
.
Câu 26: Cho hàm số
()fx
có đạo hàm liên tục trên , biết
(6) 1f =
và
1
0
(6 ) 1xf x dx =
. Đặt
6
2
0
'( )m x f x dx=
. Mệnh đề nào sau đây đúng ?
A.
0 34m
. B.
5 37m
. C.
50m−
. D.
34m −
.
Câu 27: Cho hàm số
( )
y f x=
liên tục trên đoạn
3;3−
. Biết rằng diện tích hình phẳng
1
S
,
2
S
giới hạn bởi
đồ thị hàm số
( )
y f x=
và đường thẳng
d
lần lượt là
M
,
m
. Tính tích phân
( )
3
3
df x x
−
A.
6 mM−−
. B.
6Mm−+
. C.
6 mM+−
. D.
6mM−−
.
Câu 28: Cho
( )
1
2
0
l
2
n2 ln3a
xdx
x
bc=
+
++
với
,,abc
là các số hữu tỷ. Giá trị của
3abc++
bằng
A.
1−
. B.
1
. C.
2
. D.
2−
.
Câu 29: Biết
( )
2
sin2 cos2 d cos4
a
x x x x x C
b
− = + +
, với
a
,
b
là các số nguyên dương,
a
b
là phân số tối
giản và
C
. Giá trị của
ab+
bằng
A.
4
. B.
5
. C.
2
. D.
3
.
Câu 30: Cho hàm số
()y f x=
có đạo hàm trên
1;2
thỏa mãn
'
( 1) ( ) ( ) 2
x
x f x xf x e+ + =
với mọi
1;2x
,biết
(1)fe=
. Mệnh đề nào sau đây đúng?
A.
(2) 3e f e
. B.
(2) 0ef−
. C.
4 (2) 6e f e
. D.
24
(2)e f e
.
Câu 31: Cho nguyên hàm
1
d
4
x
Ix
e
=
+
. Nếu đặt
4
x
te=+
thì
A.
( )
2
d
4
t
It
tt
=
−
. B.
( )
2
2
d
4
It
tt
=
−
. C.
2
2
d
4
t
It
t
=
−
. D.
( )
2
2
d
4
It
t
=
−
.
Câu 32: Trong không gian với hệ tọa độ
Oxyz
, mặt phẳng
( )
P
qua hai điểm
( )
1;8;0M
,
( )
0;0;3C
cắt các
tia
Ox
,
Oy
lần lượt tại
A
,
B
sao cho
OG
nhỏ nhất, với
( )
;;G a b c
là trọng tâm tam giác
ABC
.
Tính
T a b c= + +
.
A.
6T =
. B.
7T =
. C.
3T =
. D.
12T =
.
---------------------------------
HẾT
-------------------------------
(Cán bộ coi thi không giải thích gì thêm).
ĐÁP ÁN
1
B
6
C
11
C
16
C
21
B
26
D
31
D
2
B
7
D
12
B
17
A
22
D
27
D
32
A
3
D
8
C
13
A
18
D
23
B
28
A
4
C
9
A
14
B
19
C
24
C
29
B
5
D
10
C
15
A
20
B
25
A
30
A
Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 4
MÔN TOÁN 12
Câu 1: Trong không gian
Oxyz
với hệ tọa độ
( )
; , ,O i j k
cho
25OA i k j= − − +
. Tìm tọa độ điểm
A
.
A.
( )
2; 5;1−−
. B.
( )
2;1; 5−−
. C.
( )
2; 5;1−−
. D.
( )
5; 2;1−
.
Câu 2: Trong không gian với hệ trục tọa độ
Oxyz
, mặt phẳng đi qua ba điểm
( )
0;0;5A
,
( )
1;0;0B −
và
( )
0;3;0C
có phương trình là:
A.
1
2 1 3
x y z
+ + =
. B.
1
1 3 5
x y z
+ + = −
. C.
1
1 3 5
x y z
+ + =
−
. D.
1
1 3 5
x y z
+ − =
.
Câu 3: Trong không gian
Oxyz
, cho hai điểm
( )
7;2; 3A −−
và
( )
3; 2; 1B −−
. Tọa độ trung điểm
I
đoạn thẳng
AB
là:
A.
( )
2;0; 4I −−
. B.
( )
2;0; 2I −−
. C.
( )
5;0;1I
. D.
( )
2;0; 2I −
.
Câu 4: Cho hình phẳng
( )
D
được giới hạn bởi các đường
( )
71f x x=+
,
, 0, 1Ox x x==
. Thể tích
V
của
khối tròn xoay tạo thành khi quay
( )
D
xung quanh trục
Ox
được tính theo công thức?
A.
1
0
7 1dV x x
=+
. B.
( )
1
0
7 1 dV x x
=+
. C.
1
0
7 1dV x x=+
. D.
( )
1
0
7 1 dV x x=+
.
Câu 5: Một vật thể được giới hạn bởi hai mặt phẳng vuông góc với trục
Ox
tại các điểm
xa=
,
xb=
( )
ab<
, biết diện tích thiết diện bị cắt bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
x
( )
a x b££
là
( )
Sx
. Tính thể tích
V
của vật thể đó.
A.
( )
2
d.
b
a
V S x xp=
ò
B.
( )
d.
a
b
V S x xp=
ò
C.
( )
d.
a
b
V S x x=
ò
D.
( )
d.
b
a
V S x x=
ò
Câu 6: Cho hàm số
( )
3
25f x x=+
. Khẳng định nào dưới đây đúng?
A.
( )
4
1
d5
2
f x x x x C= + +
. B.
( )
4
d 4 5f x x x x C= − +
.
C.
( )
4
1
d5
2
f x x x C= + +
. D.
( )
4
1
d5
4
f x x x x C= + +
.
Câu 7: Tích phân
3
2
0
1x x dx+
có giá trị là:
A.
7
. B.
3−
. C.
4
3
. D.
7
3
.
Câu 8: Cho hai hàm số
( )
y f x=
và
( )
y g x=
liên tục trên . Trong các mệnh đề sau, mệnh đề nào sai?
A.
( ) ( ) ( ) ( )
f x g x dx f x dx g x dx− = −


.
B.
( ) ( ) ( ) ( )
..f x g x dx f x dx g x dx=
.
C.
( ) ( ) ( ) ( )
f x g x dx f x dx g x dx+ = +


.
D.
( ) ( )
kf x dx k f x dx=

với mọi hằng số
\0k
.
Câu 9: Trong không gian
Oxyz
, cho hai điểm
( )
1; 1; 2A −−
và
( )
2; 1; -5B
. Tọa độ của
AB
bằng:
A.
( )
3;2; 7AB = − −
. B.
( )
3;2; 7AB =−
. C.
( )
3;0;3AB =
. D.
( )
3;2;1AB =
.
Câu 10: Hình phẳng giới hạn bởi đồ thị hàm số
( )
y f x=
, trục hoành và hai đường thẳng
xa=
,
xb=
trong
hình dưới đây (phần gạch sọc) có diện tích
S
bằng:
A.
( )
| d |
b
a
f x x
. B.
( ) ( )
dd
cb
ac
f x x f x x+

.
C.
( ) ( )
dd
cb
ac
f x x f x x−

. D.
( ) ( )
dd
cb
ac
f x x f x x−+

.
Câu 11: Cho hai hàm số
( )
u u x=
và
( )
v v x=
có đạo hàm liên tục trên . Khẳng định nào sau đây đúng?
A.
( ) ( ) ( ) ( ) ( ) ( )
' ' ' 'u x v x dx u x v x u x v x dx=−

. B.
( ) ( ) ( ) ( ) ( ) ( )
' ' 'u x v x dx u x v x u x v x dx=−

.
C.
( ) ( ) ( ) ( ) ( ) ( )
''u x v x dx u x v x u x v x dx=−

. D.
( ) ( ) ( ) ( ) ( ) ( )
''u x v x dx u x v x u x v x dx=−

.
Câu 12: Hàm số
( )
sin3F x x=
là nguyên hàm của hàm số:
A.
( )
3cos3f x x=−
. B.
( )
cos3
3
x
fx=
. C.
( )
os3f x c x=
. D.
( )
3cos3f x x=
.
Câu 13: Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
( )
:2 3 10 0P x z− − =
. Mặt phẳng
( )
P
có
một vectơ pháp tuyến là:
A.
( )
2; 3;1n =−
. B.
( )
2; 3n =−
. C.
( )
2; 3;0n =−
. D.
( )
2;0; 3n =−
.
Câu 14: Cho hàm số
( )
fx
liên tục trên đoạn
2;3−
. Gọi
( )
Fx
là một nguyên hàm của hàm số
( )
fx
trên
2;3−
và
( ) ( )
3 8; 2 4FF= − − = −
. Tính
( )
3
2
I f x dx
−
=
.
A.
4
. B.
4−
. C.
2−
D.
2
.
Câu 15: Trong không gian
Oxyz
, mặt cầu
( ) ( ) ( )
2 2 2
4 2 3 25x y z− + − + + =
có tâm và bán kính lần lượt là:
A.
( )
4;2; 3I −
;
5R =
. B.
( )
1; 2;3I −−
;
5R =
. C.
( )
4;2; 3I −
;
25R =
. D.
( )
4; 2;3I −
;
2R =
.
Câu 16: Trong không gian
,Oxyz
cho mặt phẳng
( )
: 2 20 0x y z
− + − =
. Mặt phẳng nào dưới đây song song
với
( )
?
A.
( )
: 2 1 0.S x y z+ − + =
B.
( )
: 2 2 0.P x y z− + + =
C.
( )
: 2 1 0.Q x y z+ − − =
D.
( )
: 2 20 0.R x y z− + − =
Câu 17: Tìm họ nguyên hàm của hàm số
( )
7
x
fx=
.
A.
( )
d 7 ln7
x
f x x C=+
. B.
( )
1
7
d
1
x
f x x C
x
+
=+
+
.
C.
( )
7
d
ln7
x
f x x C=+
. D.
( )
d7
x
f x x C=+
.
Câu 18: Cho hàm số
( )
y f x=
liên tục trên khoảng
K
và
,,a b c K
. Mệnh đề nào sau đây sai?
A.
( ) ( )
dd
ba
ab
f x x f x x=−

. B.
( ) ( ) ( )
d d d
b b c
a c a
f x x f x x f x x+=
.
C.
( ) ( )
d dt
bb
aa
f x x f t=

. D.
( )
d0
a
a
f x x =
.
Câu 19: Trong không gian
Oxyz
, cho mặt phẳng
( )
:3 2 3 8 0P x y z+ + + =
điểm nào sau đây thuộc mặt phẳng
( )
P
?
A.
( )
1;2;3M
B.
( )
3; 2;0P −
C.
( )
1; 1; 3N −−
D.
( )
1; 1;1Q −−
Câu 20: Cho hàm số
( )
fx
liên tục trên
R
và có
( )
1
0
d 2,f x x =−
và
( )
3
1
d8f x x =
. Tính
( )
3
0
d.I f x x=
A.
4I =
. B.
6I =
. C.
6I =
. D.
12I =
.
Câu 21: Cho
( )
3
2
d7f x x =
và
( )
3
2
d3g t t =−
. Giá trị của
( ) ( )
3
2
3 5 dA f x g x x=+


là:
A.
6A =
. B.
1A =−
. C.
5A =
. D.
9A =
.
Câu 22: Biết
( )
4 4 4
d , .
x x x
xe x axe be C a b= + +
Tính tích
ab+
.
A.
. B.
2
9
ab+ = −
. C.
3
16
ab+=
. D.
2
9
ab+=
.
Câu 23: Cho hình phẳng
( )
H
giới hạn bởi đồ thị
2
3y x x=−
và trục hoành. Tính thể tích
V
vật thể tròn xoay
sinh ra khi cho
( )
H
quay quang
Ox
.
A.
9
2
V
=
. B.
81
10
V =
. C.
81
7
V
=
. D.
81
10
V
=
.
Câu 24: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
2 os 2,y c x=+
trục hoành và hai đường thẳng
0x =
và
5
6
x
=
.
A.
5
1
3
−
B.
37
1
23
++
C.
5
1
3
+
D.
6
Câu 25: Trong không gian
Oxyz
, cho hai điểm
( )
5;2;3M −
và
( )
1;4; 7N −−
. Mặt cầu đường kính
MN
có
phương trình là:
A.
( ) ( )
22
2
( 3) 3 2 30x y z+ + − + + =
. B.
( ) ( )
22
2
( 3) 3 2 30x y z+ + − + + =
.
C.
( ) ( )
22
2
( 3) 3 2 81x y z+ + + + + =
. D.
( ) ( )
22
2
( 3) 3 1 9x y z+ + − + − =
.
Câu 26: Trong không gian
,Oxyz
khoảng cách từ điểm
( )
2;4; 3A −−
đến mặt phẳng
2 2 13 0x y z− − − =
bằng:
A.
1
.
3
B.
7
.
3
−
C.
5.
D.
7
.
3
Câu 27: Giả sử hàm số
( )
y f x=
liên tục trên và
( )
5
2
d3f x x a=
,
( )
a
. Tích phân
( )
2
1
3 1 dI f x x=−
có
giá trị là:
A.
2Ia=
. B.
Ia=
. C.
21Ia=+
. D.
1
1
2
Ia=+
.
Câu 28: Tích phân
2022
0
8d
x
Ix=
bằng
A.
2022
2021.8
. B.
2022
81−
. C.
2022
8
ln8
. D.
2022
81
3ln2
−
.
Câu 29: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( )
1;6;9A −
và
( )
3;2;3B
. Phương trình mặt
phẳng trung trực đoạn
AB
là:
A.
2 2 3 13 0x y z− − + =
. B.
2 2 3 24 0x y z− − + =
.
C.
2 2 3 23 0x y z− − + =
. D.
2 3 17 0x y z− + + =
.
Câu 30: Cho
4
1
(4 1)ln d ln4x x x a b+ = +
,
( )
,ab
. Tính
ab+
.
A.
18ab+=
. B.
43
3
ab
−
+=
. C.
43
3
ab+=
. D.
4ab+=
.
Câu 31: Cho hàm số
( )
3
3 khi 0 1
8 5 khi 1 2
xx
fx
xx

=
−
. Tính
( )
2
0
dI f x x=
.
A.
1
2
I =−
. B.
4I =
. C.
3
2
I =
. D.
5
4
I =
.
Câu 32: Cho hàm số
( ) ( )
3
13f x x=−
. Khẳng định nào dưới đây đúng?
A.
( ) ( )
4
1
d 1 3
12
f x x x C= − − +
. B.
( ) ( )
4
d 4 1 3f x x x C= − +
.
C.
( ) ( )
4
1
d 1 3
12
f x x x C= − +
. D.
( ) ( )
4
1
d 1 3
4
f x x x C= − +
.
Câu 33: Trong không gian với hệ trục
Oxyz
, mặt phẳng chứa 2 điểm
(1;0;1)A
và
( )
1;2;2B −
và song song
với trục
Oz
có phương trình là
A.
10xy+ − =
. B.
2 1 0xy+ − =
. C.
10xy+ + =
. D.
20xz− − =
.
Câu 34: Trong không gian
Oxyz
, gọi
là góc giữa hai vectơ
( )
1; 2; 2a = − −
và
( )
2; 2; 1b = − −
. Tính
cos
.
A.
2
9
−
. B. 0. C.
8
9
. D.
8
9
.
Câu 35: Khi đặt
1tx=−
thì
1dx x x−
được viết lại bởi kết quả nào:
A.
42
(2 )t t dt−
. B.
42
2 ( )t t dt+
. C.
42
2 ( )t t dt−
. D.
42
()t t dt−
.
ĐÁP ÁN
1
B
6
A
11
D
16
B
21
A
26
C
31
D
2
C
7
D
12
D
17
C
22
C
27
B
32
A
3
B
8
B
13
D
18
B
23
D
28
D
33
A
4
B
9
B
14
B
19
C
24
C
29
B
34
D
5
D
10
D
15
A
20
B
25
A
30
A
35
B
------ HẾT ------
Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 5
MÔN TOÁN 12
Câu 1: Cho hình phẳng
()H
giới hạn bởi các đường
2
3yx=−
,
0y =
,
1x =
,
2x =
. Gọi
V
là thể tích của
khối tròn xoay được tạo thành khi quay
()H
xung quanh trục
Ox
. Mệnh đề nào dưới đây đúng?
A.
2
2
1
( 3)V x dx=−
. B.
2
2
1
( 3)V x dx= −
. C.
2
22
1
( 3)V x dx=−
. D.
2
22
1
( 3)V x dx= −
.
Câu 2: Trong không gian
Oxyz
cho ba điểm
(2; 3;4), (1; ; 1), ( ;4;3)A B y C x−−
. Để ba điểm
,,A B C
thẳng hàng
thì giá trị của
5xy+
bằng:
A.
23−
. B.
42
. C.
41
. D.
40
.
Câu 3: Nếu
4
1
( ) 2f x dx =−
và
9
4
( ) 1f x dx =
thì
9
1
()f x dx
bằng
A.
1−
. B.
3−
. C.
1
. D.
3
.
Câu 4: Trong không gian với hệ tọa độ
Oxyz
, cho tứ diện
ABCD
có đỉnh
(8;14;10)A
,
,,AD AB AC
đôi một
vuông góc. Viết phương trình mặt phẳng
( )
BCD
biết trực tâm tam giác
BCD
là
(7;16;15)H
.
A.
2 5 50 0x y z+ − − =
B.
3
7 16 15
x y z
+ + =
−−
C.
2 5 100 0x y z− − + =
D.
1
7 16 15
x y z
+ + =
−−
Câu 5: Trong không gian
,Oxyz
cho hai mặt phẳng
( )
:2 2 5 0x y z− + − =
và
( )
:2 2 9 0x y z− + + =
.
Khoảng cách giữa
( )
và
( )
bằng
A.
14
.
3
B.
14
.
9
C.
4
.
9
D.
4
.
3
Câu 6: Cho
()Fx
là một nguyên hàm của
3
( ) 4 3f x x=−
, biết
(1) 2F =
. Tính
(2)F
.
A.
(2) 8F =
. B.
(2) 10F =
. C.
(2) 14F =
. D.
(2) 76F =
.
Câu 7: Trong không gian
Oxyz
, cho mặt cầu
()S
có tâm
(2;1;1)I
và mặt phẳng
( ):2 2 8 0P x y z− − + =
. Mặt
phẳng
()P
cắt mặt cầu
()S
theo giao tuyến là một đường tròn có bán kính bằng
1
. Tìm phương trình mặt cầu
()S
.
A.
2 2 2
( 2) ( 1) ( 1) 10x y z+ + + + + =
. B.
2 2 2
( 2) ( 1) ( 1) 8x y z+ + + + + =
.
C.
2 2 2
( 2) ( 1) ( 1) 10x y z− + − + − =
. D.
2 2 2
( 2) ( 1) ( 1) 8x y z− + − + − =
.
Câu 8: Cho
( 1)
xx
xe dx x e C= − +
và
ln2
22
0
2ln ln2
x
x e dx a b c= + +
.Tính
.= + +P a b c
A.
16.P =−
B.
12.P =−
C.
6.P =−
D.
0.P =
Câu 9: Trong không gian
Oxyz
, cho điểm
( 1; 2;3)M −−
. Tìm tọa độ điểm
N
đối xứng với
M
qua mặt phẳng
()Oxy
A.
( 1; 2;3)N −−
. B.
(1;2;0)N
. C.
( 1; 2; 3)N − − −
. D.
(1;2; 3)N −
.
Câu 10: Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
3
1yx=+
,
2
21y x x= − +
và trục
Ox
là.
A.
5
12
. B.
13
12
. C.
2
3
. D.
7
12
.
Câu 11: Tìm họ nguyên hàm của hàm số
4
32
( ) 4
x
f x x e
+
=
.
A.
4
2x
eC
+
+
. B.
4
2
1
4
x
eC
+
+
. C.
4
2x
eC
+
−+
. D.
4
2
4
x
eC
+
+
.
Câu 12: Cho hai hàm số
( ), ( )f x g x
liên tục trên
;ab
và
k
là số thực khác không thì mệnh đề nào sau đây
sai.
A.
( ) ( ) ( ) ( )
b b b
a a a
f x g x dx f x dx g x dx=
. B.
( ) ( )
b
b
a
a
f x dx f x
=
.
C.
( ) ( )
bb
aa
kf x dx k f x=

. D.
( ) ( ) ( ) ( )
b b b
a a a
f x g x dx f x dx g x dx+ = +
.
Câu 13: Cho hàm số
()y f x=
liên tục trên đoạn
;ab
. Gọi
D
là miền hình phẳng giới hạn bởi đồ thị hàm số
()y f x=
, trục hoành và các đường thẳng
, ( )x a x b a b= =
. Diện tích
S
của
D
cho bởi công thức nào sau
đây?
A.
2
()
b
a
S f x dx=
. B.
2
()
b
a
S f x dx=
. C.
()
b
a
S f x dx=
. D.
()
b
a
S f x dx=
.
Câu 14: Tìm họ nguyên hàm
1
31
dx
x −
A.
11
ln 3 1
3 1 3
dx x C
x
= − +
−
. B.
11
ln(3 1)
3 1 3
dx x C
x
= − +
−
.
C.
1
3ln 3 1
31
dx x C
x
= − +
−
. D.
1
3ln(3 1)
31
dx x C
x
= − +
−
.
Câu 15: Trong không gian
Oxyz
cho vectơ
(0;2; 1)a =−
,
(2; 3;3)b =−
,
(0;2;1)c =
. Tìm tọa độ vectơ
32u a b c= + +
.
A.
(2;1;3)u =
. B.
(4;2;4)u =
. C.
(4; 2;2)u =−
. D.
(2;1;2)u =
.
Câu 16: Tính
4
2
3
4
x
K dx
x
=
−
.
A.
1 12
ln
25
K =
. B.
1 12
ln
35
K =
. C.
12
ln
5
K =
. D.
4ln2K =
.
Câu 17: Tìm họ nguyên hàm
sin(4 2 )x dx−
A.
1
sin(4 2 ) cos(4 2 )
2
x dx x C− = − − +
. B.
sin(4 2 ) 2cos(4 2 )x dx x C− = − +
.
C.
1
sin(4 2 ) cos(4 2 )
2
x dx x C− = − +
. D.
sin(4 2 ) 2cos(4 2 )x dx x C− = − − +
.
Câu 18: Tìm nguyên hàm của hàm số
2022 3
()
x
f x e
+
=
A.
2022 3
()
x
f x dx e C
+
=+
. B.
2022 3
1
()
3
x
f x dx e C
+
=+
.
C.
2022 3
1
()
2022
x
f x dx e C
+
=+
. D.
2022 3
( ) 2022
x
f x dx e C
+
=+
.
Câu 19: Trong không gian
Oxyz
, cho hai điểm
(2;4; 1), ( 2;2;3)AB−−
. Phương trình mặt cầu đường kính
AB
là.
A.
2 2 2
( 3) (z+1) 3xy+ − + =
. B.
2 2 2
( 3) (z 1) 9xy+ + + − =
.
C.
2 2 2
( 3) (z+1) 9xy+ − + =
. D.
2 2 2
( 3) (z 1) 9xy+ − + − =
.
Câu 20: Biết
2
2
( ) 3f x dx
−
=−
. Giá trị của
2
2
2
2 ( ) 3f x dx x dx
−

−

bằng.
A.
40−
. B.
8−
. C.
19−
. D.
22−
.
Câu 21: Biết
()Fx
là một nguyên hàm của hàm số
()fx
trên và
(1) 6F =
,
( ) 2Fe=
. Tính giá trị của
1
()
e
f x dx
bằng.
A.
1e −
. B.
8
. C.
4
. D.
4−
.
Câu 22: Tính
2019
1
2022
x
dx
A.
2019
2022 2022
ln2022
−
. B.
2019
2022
ln2022
. C.
2019
2022 2022
ln2022
−
. D.
2019
2022 2022−
.
Câu 23: Cho hàm số
()fx
có đạo hàm
()fx
liên tục trên và thỏa mãn
( ) 2 ( )f x xf x
=
,
x
; Biết
(0) 4f =
và
( ) 0fx
,
x
. Tính
1
0
()xf x dx
.
A.
22e−
. B.
7
2
. C.
21e −
. D. 2
e
.
Câu 24: Trong không gian
Oxyz
, cho mặt phẳng
()P
:
2 2 5 0x y z+ + − =
và điểm
( 4; 3;1)M −−
. Tính khoảng
cách từ
M
đến
()P
.
A.
9
. B.
18
. C.
7
. D.
6
.
Câu 25: Cho tích phân
1
2
3
0
3
2
x
I dx
x
=
+
, giả sử đặt
3
2tx=+
. Tìm mệnh đề đúng.
A.
3
2
3
dt
I
t
=
. B.
1
0
1
3
dt
I
t
=
. C.
3
2
1
3
dt
I
t
=
. D.
3
2
dt
I
t
=
.
Câu 26: Trong không gian
Oxyz
, cho hai điểm
(4;2; 3), (0;0;3)AB−
. Khi đó tọa độ trung điểm
I
của đoạn
thẳng
AB
.
A.
(2;1;0)I
. B.
(2;1;2)I
. C.
(2; 1; 1)I −−
. D.
(2; 1;2)I −
.
Câu 27: Họ nguyên hàm của hàm số
( ) 3sin 2023f x x=+
là
A.
3cos 2023x x C++
. B.
3 os 2023c x x C− + +
. C.
3cos 2023xx−+
. D.
3cos 2023xC− + +
.
Câu 28: Hình
()H
giới bởi các đường
2
,3y x y x==
. Thể tích vật thể tròn xoay khi
()H
xoay quanh trục
Ox
bằng
a
b
giá trị của
2ab+
là.
A.
141
. B.
157
. C.
172
. D.
131
.
Câu 29: Tính tích phân
1
2
0
(2 2)
x
x e dx−
bằng
A.
2
53
4
e−−
. B.
2
3
2
e−
. C.
2
53
4
e+
. D.
2
2 e−
.
Câu 30: Khẳng định nào sau đây đúng?
A.
1
11
dx
C
xx
= − +
++
. B.
ln( 1)
1
dx
xC
x
= + +
+
. C.
ln 1
1
dx
xC
x
= + +
+
. D.
2
1
1 ( 1)
dx
C
xx
= − +
++
.
Câu 31: Biết
cos2 sin2 cos2x xdx ax x b x C= + +
với
,ab
là các số hữu tỉ. Tính
ab+
?
A.
1
4
. B.
3
4
. C.
1
4
−
. D.
1
8
−
.
Câu 32: Mặt phẳng nào sau đây có vectơ pháp tuyến
(3; 1; 7)n −−
?
A.
6 2 14 1 0x y z− + − =
. B.
3 7 1 0x y z− − + =
. C.
3 7 0xy+ − =
. D.
3 7 0xz+ − =
.
------ HẾT ------
ĐÁP ÁN
ĐÁP ÁN
1
D
6
C
11
A
16
A
21
D
26
A
31
B
2
C
7
C
12
A
17
C
22
C
27
B
32
B
3
A
8
D
13
C
18
C
23
A
28
C
4
C
9
C
14
A
19
D
24
D
29
B
5
A
10
B
15
B
20
D
25
D
30
C
Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 6
MÔN TOÁN 12
Câu 1.
Trong các mệnh đề sau, mệnh đề nào
sai ?
A.
sinxd cosx x C=+
B.
1
x
1
x
x d C
+
=+
+
(
1
−
)
C.
d
xx
e x e C=+
. D.
1
d lnx x C
x
=+
.
Câu 2. Trong không gian
Oxyz
, hình chiếu vuông góc của điểm
( )
2;1; 1M −
trên mặt phẳng
( )
Oxz
có tọa độ
là:
A.
( )
0;1;0
. B.
( )
2;1;0
. C.
( )
0;1; 1−
. D.
( )
2;0; 1−
.
Câu 3. Cho
( ) ( )
,f x g x
là các hàm số liên tục trên
R
. Tìm khẳng định đúng trong các khẳng định sau?
A.
( ) ( )
.k f x dx k f x dx=+

với k là hằng số B.
( ) x
()
()
( ) x
f x d
fx
dx
gx
g x d
=
C.
( ) ( ) ( ) ( )
..f x g x dx f x dx g x dx=


D.
( ) ( ) ( ) ( )
f x g x dx f x dx g x dx+ = +


Câu 4. Cho hàm số
( )
y f x=
liên tục trên
;ab
. Diện tích hình phẳng
S
giới hạn bởi đường cong
( )
y f x=
,
trục hoành và các đường thẳng
xa=
,
xb=
được xác định bởi công thức nào sau đây?
A.
( )
d
b
a
S f x x=
. B.
( )
d
b
a
S f x x=
. C.
( )
d
b
a
S f x x=
. D.
( )
d
a
b
S f x x=
.
Câu 5. Trong không gian
Oxyz
với hệ tọa độ
( )
; ; ;O i j k
cho
2 3 5OA i j k= − +
. Tìm tọa độ điểm
A
?
A.
( )
2;3;0−
. B.
( )
2;3; 5−−
. C.
( )
2;3;5−
. D.
( )
2; 3;5−
.
Câu 6. Nếu u = (x) và v = v(x) là 2 hàm số có đạo hàm liên tục trên đoạn K thì:
A.
∫
𝑢. 𝑑𝑣 = 𝑢. 𝑣 −
∫
𝑣. 𝑑𝑢 B.
∫
𝑢. 𝑑𝑣 = 𝑢. 𝑣 +
∫
𝑣. 𝑑𝑢
C.
∫
𝑢. 𝑑𝑣 = 𝑢. 𝑣 −
∫
𝑢. 𝑑𝑣 D.
∫
𝑣. 𝑑𝑢 = 𝑢. 𝑣 −
∫
𝑣. 𝑑𝑢
Câu 7. Trong không gian
Oxyz
, cho
( ) ( )
1;3;5 , 2;3;1uv==
. Tọa độ của
uv+
là:
A.
( )
3;6;6
B.
( )
1;2;2
C.
( )
1;0;4−
D.
( )
3;6;5
Câu 8. Xét hàm số
( )
fx
,
( )
Fx
là một nguyên hàm của
( )
fx
trên đoạn
;ab
. Mệnh đề nào dưới đây đúng
?
A.
( ) ( ) ( )
d
b
a
f x x F b F a=−
. B.
( ) ( ) ( )
d
b
a
f x x F a F b=−
.
C.
( ) ( ) ( )
d
b
a
f x x F a F b=+
. D.
( ) ( ) ( )
d
b
a
f x x F a F b= − −
.
Câu 9. Trong không gian
,Oxyz
cho mặt phẳng
( ): 3 5 2 9 0.P x y z− + − =
Một vectơ pháp tuyến của mặt
phẳng
()P
là:
A.
(4; 6;5).n =−
B.
( 3;5;2).n =−
C.
(3; 5;2).n =−
D.
(2; 3; 7).n = − −
Câu 10. Hình cong giới hạn bởi đồ thị hàm số
( )
y f x=
, trục
Ox
, hai đường thẳng
xa=
và
xb=
( )
ab
quay quanh trục
Ox
tạo thành một khối tròn xoay có thể tích là:
A.
( )
2
d
b
a
V f x x=
. B.
( )
2
d
b
a
V f x x
=
. C.
( )
d
b
a
V f x x
=
. D.
( )
d
b
a
V f x x=
.
Câu 11. Trong không gian
Oxyz
, cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 2 4 1 9S x y z− + + + − =
. Xác định tọa độ tâm
I
và
bán kính
R
của mặt cầu
( ).S
A.
( )
2;4; 1 ; 9IR− − =
. B.
( )
2; 4;1 ; 3IR−=
. C.
( )
2;4;1 ; 9IR=
. D.
( )
2; 4;1 ; 3IR−=
Câu 12. Tính tích phân
2
0
(2x-1)dx
bằng:
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 13. Cho
( ) ( )
,f x g x
là các hàm số liên tục trên
1;4
. Nếu
4
1
( ) 6f x dx =−
và
4
1
( ) 5g x dx =−
thì
4
1
]()[ ()f x g x dx−
bằng:
A.
1−
. B.
11−
. C. 1 . D.
11
.
Câu 14. Trong không gian
Oxyz
, cho mặt phẳng
( )
: 2 6 1 0P x y z+ − − =
. Trong các điểm sau đây, điểm nào
thuộc mặt phẳng (P)?
A.
( )
3;2;0P −
. B.
( )
1;2; 6N −
. C.
( )
1; 4;1M −−
. D.
( )
1; 2;1Q −−
.
Câu 15. Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
1;4
và
( )
12f =
,
( )
4
1
' 10f x dx =
.Tính
( )
4.f
A. 12. B. 8. C. - 8. D. 5.
Câu 16. Cho
()Fx
là một nguyên hàm của hàm số
( ) 2
x
f x e x=+
thỏa mãn
(0) 0F =
. Tìm
()Fx
.
A.
2
( ) 1.
x
F x e x= + +
B.
2
( ) 2 1.
x
F x e x= + -
C.
2
( ) 1.
x
F x e x= + -
D.
2
( ) .
x
F x e x=+
Câu 17. Trong không gian với hệ toạ độ
Oxyz
, cho mặt phẳng
( )
P
:
2 2 4 0x y z− − − =
và điểm
( 1; 2;2)A −−
.
Tính khoảng cách
d
từ
A
đến mặt phẳng
( )
P
?
A.
4
3
d =
B.
8
3
d =
C.
2
3
d =
D.
5
9
d =
Câu 18. Cho hàm số
2
( ) 3f x x=+
. Khẳng định nào sau đây đúng?
A.
2
( ) 3f x dx x x C= + +
B.
3
( ) 3
3
x
f x dx x C= + +
.
C.
3
( ) 3f x dx x x C= + +
. D.
( ) 2f x dx x C=+
.
Câu 19. Cho hàm số
( )
fx
liên tục trên đoạn
1;5
. Nếu
( )
5
1
7f x dx =
và
( )
3
1
2f x dx =
thì có giá trị
bằng:
A.
5−
.
B.
9
.
C.
9−
.
D.
5
.
5
3
()f x dx
Câu 20. Trong không gian
,Oxyz
cho mặt phẳng (Q) :
2 – 3 - 1 0x y z+=
. Viết phương trình tổng quát
của mặt phẳng song song với (Q) và qua điểm
( )
2,3,4A
?
A.
2 – 3 0.x y z+=
B.
2 – 3 + 5 0.x y z+=
C.
2 – 3 +1 0.x y z+=
D.
2 – 3 - 5 0.x y z+=
Câu 21. Tích phân bằng:
A. B. C. D. 0
Câu 22. Diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục Ox và hai đường thẳng
1; 2xx==
là:
A. B. C. D.
Câu 23. Trong không gian với hệ tọa độ
,Oxyz
cho ba điểm
( )
2; 1;3 ,A −
( )
4;0;1B
và
( )
10;5;3 .C −
Véctơ nào
dưới đây là véctơ pháp tuyến của mặt phẳng
( )
ABC
?
A.
( )
1
1;2;0 .n =
B.
( )
2
1;2;2 .n =
C.
( )
3
1;8;2 .n =
D.
( )
4
1; 2;2 .n =−
Câu 24. Khi tính nguyên hàm
lnx
dx
x ln x + 1
, bằng cách đặt
t ln x + 1=
ta được nguyên hàm nào sau đây?
A.
2
2(t 1)dt−
B.
3
2
( t 2t)dt
3
−
C.
3
2
( t 2t)dt
3
+
D.
2
2(t 1)dt+
Câu 25. Trong không gian Oxyz, cho hai điểm . Phương trình mặt cầu đường kính
là:
A. . B.
C. . D.
Câu 26. Cho phần hình phẳng (H) giới hạn bởi các đường , quanh trục Ox ta thu được khối
tròn xoay có thể tích V bằng:
A. B. C. D. .
Câu 27. Trong không gian với hệ tọa độ , cho điểm
(1;1;0)A
, mặt phẳng (P) và mặt cầu (S) lần lượt có
phương trình
3 6 2 23 0x y z+ − − =
,
2 2 2 2
2 2 0x y z x y m+ + − − − =
. (P) cắt (S) theo giao tuyến là một đường
tròn có bán kính bằng
2
OA
, khi đó số dương thuộc khoảng nào sau đây ?
A.
5
(2; )
2
m
B.
9
(4; )
2
m
C.
5
( ;3)
2
m
D.
9
(4; )
4
m
Câu 28. Biết
( )
2
2
1
aln2 b
I x 1 lnxdx
c
+
= − =
; a, b, c là các số nguyên có ước chung lớn nhất bằng 1.
Tính 𝑎 − 𝑏 + 𝑐 ?
A. 5 B. 13 C. 1 D. 17
Câu 29. Trong không gian
,Oxyz
cho
( )
6;3;2M
.Gọi (P) là mặt phẳng qua M cắt các tia
;;Ox Oy Oz
lần lượt tại
các điểm
;;A B C
sao cho
23OA OB OC==
. Khi đó (P) qua điểm nào trong các điểm sau?
A.
(0;6;0).
B.
(0;9;0).
C.
(0;8;0).
D.
(6;0;0).
Câu 30. Cho hàm số
( )
32
f x ax bx cx d= + + +
( )
0a
và đường thẳng
( )
y g x mx n= = +
là tiếp tuyến của đồ
thị hàm số
( )
fx
tại điểm có hoành độ
3
2
x =−
(tham khảo hình vẽ). Khi đó diện tích phần được tô đậm trong
hình vẽ bằng:
2
0
cos x.sin xdx
2
3
−
2
3
3
2
2
y x 4x 3= − + −
1
3
2
3
10
3
8
3
( )
2;1;1 ,A −
( )
0; 1;1B −
AB
( ) ( )
22
2
1 1 8x y z+ + + − =
( ) ( )
22
2
1 1 2.x y z+ + + − =
( ) ( )
22
2
1 1 8x y z+ + + + =
( ) ( )
22
2
1 1 2.x y z− + + − =
2
2y x x=−
0y =
16
3
V
=
16
5
V
=
16
15
V
=
15
16
V
=
Oxyz
m
A.
2041
567
. B.
2104
576
. C.
2410
567
. D.
2401
576
.
Câu 31. Trong không gian với hệ tọa độ
Oxyz
, cho
( )
;0;0Aa
,
( )
0; ;0Bb
,
( )
0;0;Cc
với
a
,
b
,
c
dương thỏa
mãn
4abc+ + =
. Biết rằng khi
a
,
b
,
c
thay đổi thì tâm
I
mặt cầu ngoại tiếp tứ diện
OABC
thuộc mặt phẳng
( )
P
cố định. Tính khoảng cách
d
từ
( )
1; 1; 1M −−
tới mặt phẳng
( )
P
?
A.
3d =
. B.
3
2
d =
. C.
3
3
d =
. D.
0d =
.
Câu 32. Cho hàm số
( )
y f x=
liên tục trên đoạn
[0; ]a
, biết rằng với mọi
x [0; ]a
ta có
( ) 0fx
và
2
( ). ( )f x f a x k−=
(với
k
là hằng số,
k
>0). Giá trị của tích phân
0
x
()
a
d
k f x+
bằng:
A.
a
k
. B.
2
a
k
. C.
T ak=
. D.
2
ak
T =
.
- Hết –
(Giám thị coi thi không giải thích gì thêm)
ĐÁP ÁN
1
A
6
A
11
B
16
C
21
B
26
C
31
A
2
D
7
A
12
B
17
B
22
B
27
A
32
B
3
D
8
A
13
A
18
B
23
B
28
B
4
C
9
C
14
A
19
D
24
A
29
B
5
D
10
B
15
A
20
B
25
B
30
D
Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 7
MÔN TOÁN 12
Câu 1.
Họ nguyên hàm của hàm số
( )
32
3 2 3xx
fx
x
+−
=
là:
A.
2
3
6 2 .xC
x
+ + +
B.
32
3ln .x x x C+ − +
C.
32
3ln .x x x C+ + +
D.
32
3ln .x x x C+ − +
Câu 2.
Cho hai vectơ
( ) ( )
1;2;5 , 2; 5;4ab= − = −
.Tích vô hướng của hai véc tơ
.ab
bằng:
A. -28. B. 12. C. -32.
D. 8.
Câu 3.
Cho hàm số
( )
fx
có đạo hàm liên tục trên
1;2
thỏa mãn
( )
2
1
'5f x dx =
và
( )
( )
2
1
'
ln2
fx
dx
fx
=
. Biết rằng
( )
0, 1;2f x x
, tính
( )
2f
bằng:
A.
2.
B.
5.
C.
3.
D.
10.
Câu 4.
Gọi
( )
Fx
là một nguyên hàm của hàm số f(x) liên tục trên
;.ab
Trong các đẳng thức sau, đẳng thức
nào là
sai
?
A.
( ) ( ) ( )
'.
b
a
f x dx f b f a=−
B.
( ) ( ) ( )
.
b
a
f x dx F a F b=−
C.
( )
0.
a
a
f x dx =
D.
( ) ( ) ( ) ( )
.
bb
aa
f x dx f t dt F b F a= = −

Câu 5.
Mệnh đề nào dưới đây
đúng
?
A.
cos d cos .x x x C= − +
B.
cos d sin .x x x C=+
C.
2
1
cos d cos .
2
x x x C=+
D.
cos d sin .x x x C= − +
Câu 6.
Trong không gian Oxyz Cho 2 điểm A(2; 1; 4), B(-2; 2; -6). Tọa độ véc tơ
AB
là:
A.
( 4;1;10)AB =−
.
B.
( 4;1; 10)AB = − −
C.
(4; 1;10)AB =−
.
D.
(0;3; 2).AB =−
Câu 7.
Diện tích hình phẳng được giới hạn bởi các đường
2
2y x x=-
và
yx=
là S =
.
a
b
Trong đó
.
a
b
là phân số tối giản kết quả nào sau đây đúng?
A.
a = 3b.
B.
a + b = -11.
C.
a.b =18.
D.
2a = b.
Câu 8.
Kết quả tích phân
1
0
( 2) d
x
I x e x=+
ò
được viết dưới dạng I = ae + b với
, abÎ ¤
. Khẳng định nào sau
đây là đúng?
A.
a + b = 3.
B.
a - b = 2.
C.
a + 2b = 0.
D.
a.b = 3.
Câu 9.
Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P) đi qua điểm H(2; 1;1) và cắt các trục Ox, Oy,
Oz lần lượt tại A; B; C (khác gốc toạ độ O) sao cho H là trực tâm tam giác ABC, phương trình mặt phẳng (P)
là:
A.
2x+ y - z + 6 = 0.
B.
2x+ y + z - 6= 0.
C.
2x + y + z+ 6 = 0.
D.
2x - y + z +6 = 0.
Câu 10.
Trong không gian với hệ tọa độ Oxyz, cho điểm I(1;2;-2) và mặt phẳng
(P): 2x + 2y + z + 5 = 0. Viết phương trình mặt cầu (S) có tâm I sao cho mặt phẳng (P) cắt mặt cầu (S) theo
giao tuyến là một đường tròn có chi vi bằng
8.
A.
( ) ( ) ( )
2 2 2
1 2 2 25.x y z− + − + + =
B.
( ) ( ) ( )
2 2 2
1 2 2 5.x y z− + − + + =
C.
( ) ( ) ( )
2 2 2
1 2 2 5.x y z+ + + + − =
D.
( ) ( ) ( )
2 2 2
1 2 2 25.x y z+ + + + − =
Câu 11.
Khẳng định nào sau đây là
sai
?
A.
( ) ( )
'.f x dx f x C=+
B.
( ) ( ) ( ) ( )
.f x g x dx f x dx g x dx+ = +


C.
( ) ( )
,kf x dx k f x dx=

k
là hằng số khác 0.
D.
( ) ( ) ( ) ( )
..f x g x dx f x dx g x dx=


Câu 12.
Viết phương trình mặt phẳng(P)đi qua điểm A(2;-1;2)và có VTPT
( )
1; 3;4n =−
.
A.
(P): x - 3y + 4z -13 = 0.
B.
(P):2x - y + 2z + 3 = 0.
C.
(P):
-x - 3y + 4z + 13 = 0.
D.
(P):2x - y + 2z - 13 = 0.
Câu 13.
Tính nguyên hàm
( )
ln ln
d
x
Ix
x
=
ò
được kết quả nào sau đây?
A.
( )
ln .ln ln ln .I x x x C= - +
B.
( )
ln .ln ln ln .I x x x C= + +
C.
( )
ln ln ln .I x x C= + +
D.
( )
ln .ln ln .I x x C=+
Câu 14.
Tìm nguyên hàm của hàm số
( )
cos
1 sinx
x
fx=
+
?
A.
( ) ln 1 osx .F x c C= + +
B.
( ) ln 1 sinx .F x C= − +
C.
( ) ln 1 sinx .F x C= + +
D.
( ) ln 1 osx .F x c C= − +
Câu 15.
Biết hàm số
( )
Fx
là một nguyên hàm của hàm số
( )
1
x
f x e
x
=+
và
( )
1.Fe=
Tìm
( )
?Fx
A.
( )
2
e.
2
x
x
Fx=+
B.
( )
e ln .
x
F x x=+
C.
( )
1
e.
x
Fx
x
=−
D.
( )
e ln .
x
F x x=−
Câu 16.
Biết
( ) ( )
14
00
3, 7f x dx f x dx==

.khi đó
( )
4
1
f x dx
có kết quả là:
A.
-4
.
B.
4
.
C.
5.
D.
10
.
Câu 17.
Biết rằng
1
2
0
2
ln
1
x
I dx a
x
==
+
ò
với
aRÎ
. Khi đó giá trị của a bằng:
A.
a =
2.
B.
a =
1
2
.
C.
a =4.
D.
a=2.
Câu 18.
Diện tích của hình phẳng giới hạn bởi:
( )
12
: ln ; : 1; : 1C y x d y d y x= = = − +
là:
A.
3
.
2
−e
B.
1
.
2
+e
C.
1
.
2
−e
D.
3
.
2
+e
Câu 19.
Phương trình mặt cầu tâm
( )
I 1; 2; 3-
,bán kính R = 5 là:
A.
2 2 2
(x 1) (y 2) (z 3) 25+ + + + - =
B.
2 2 2
(x 1) (y 2) (z 3) 5.- + - + + =
C.
2 2 2
(x 1) (y 2) (z 3) 25.- + - + + =
D.
2 2 2
(x 1) (y 2) (z 3) 5.+ + + + - =
Câu 20.
Cho I =
1
ln 1
e
x
dx
x
+
và đặt u = lnx+1. Chọn khẳng đúng trong các khẳng định sau:
A.
I=
1
.
e
du
u
B.
I=
1
e
udu
.
C.
I=
2
1
.
du
u
D.
I=
2
1
udu
.
Câu 21.
Mặt phẳng (P): 3x -5y + 8z -12 = 0 có một véctơ pháp tuyến là:
A.
( )
3; 3;8n =−
.
B.
( )
3;5;8n =
.
C.
( )
5; 8;12 .n =−
D.
( )
3; 5;8n =−
Câu 22.
Cho hai mặt phẳng (P): 2x + y -3z + 1 = 0 và (Q): 4x + 2y - 6z - 3 = 0. Khẳng định nào sau đây đúng?
A.
(P) vuông góc với (Q).
B.
(P) song song (Q
). C.
(P) trùng (Q).
D.
(P) cắt (Q).
Câu 23.
Khoảng cách từ điểm M(-2; -4; 3) đến mặt phẳng (P): 2x - y + 2z - 3 = 0 bằng:
A.
1.
B.
3.
C.
4.
D.
2.
Câu 24.
Tìm nguyên hàm của hàm số
( )
x
f x xe=
A.
( )
2 x
f x dx x e C=+
.
B.
( )
x
f x dx xe C=+
.
C.
( ) ( )
1
x
f x dx x e C= + +
D.
( ) ( )
1
x
f x dx x e C= − +
Câu 25.
Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
;ab
. Hãy chọn mệnh đề
sai
dưới đây:
A.
k.f(x)d f(x)d ( )
bb
aa
x k x k R= " Î
òò
.
B.
( ) ( ) ( )
[ ( )]d d d
b b b
a a a
f x g x x f x x g x x± = ±
ò ò ò
.
C.
( ) ( ) ( )
d d d
b c b
a a c
f x x f x x f x x=+
ò ò ò
với
[ ]
;c a bÎ
.
D.
( ) ( )
d
ba
ab
f x dx f x x=
òò
Câu 26.
Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số
( )
y f x=
liên tục trên [a;b], trục hoành và
hai đường thẳng x = a, x = b được tính theo công thức:
A.
( ) ( )
=−

.
b
a
S f x d x f x dx
0
0
B.
( ) ( )
=+

.
b
a
S f x dx f x dx
0
0
C.
( )
=
.
b
a
S f x dx
D.
( )
=
.
b
a
S f x dx
Câu 27.
Thể tích khối tròn xoay sinh ra do quay hình phẳng giới hạn bởi các đường
3
yx=
, trục Ox,
1x =-
,
1x =
một vòng quanh trục Ox là:
A.
6
.
7
p
B.
2
.
7
p
C.
2.p
D.
.p
Câu 28.
Đặt
( )
2
1
2 1 dI mx x=+
ò
(
m
là tham số thực). Tìm
m
để
4I =
.
A.
1m =
.
B.
1m =-
.
C.
2m =
.
D.
2m =-
.
Câu 29.
Thể tích khối tròn xoay được tạo thành khi quay quanh trục Ox hình phẳng (H) được giới hạn bởi các
đường sau:
( )
y f x=
, trục Ox và hai đường thẳng x = a, x = b
( )
ab
là:
A.
( )
=
.
b
a
V f x dx
2
2
B.
( )
=
.
b
a
V f x dx
2
C.
( )
=
.
b
a
V f x dx
D.
( )
=
.
b
a
V f x dx
2
Câu 30.
Cho
a
= (2; -3; 3),
b
= (0; 2; -1). Khi đó tọa độ của vecto
u 2a 3b=+
bằng:
A.
(2; -1; 2).
B.
(4; 0; 3).
C.
(4; -12; 3).
D.
(-2; 5; -4).
Câu 31.
Cho hai mặt phẳng (P): 3x + 3y -z + 1 =0 và (Q): (m-1)x + y - (m+2)z - 3 = 0. Xác định m để hai mặt
phẳng (P), (Q) vuông góc với nhau.
A.
1
.
2
m =
B.
3
.
2
m =−
C.
m =2.
D.
1
.
2
m =−
Câu 32.
Cho hai hàm số
( ) ( )
,u u x v v x==
có đạo hàm liên tục trên tập
K
. Công thức tính nguyên hàm từng
phần là:
A.
.udu uv vdu=+

B.
.udv uv vdu=−

C.
.udu uv vdu=−

D.
.udv uv vdu=+

=====HẾT=====
ĐÁP ÁN
1
D
6
B
11
D
16
B
21
D
26
C
31
D
2
D
7
C
12
A
17
D
22
B
27
B
32
B
3
D
8
C
13
A
18
A
23
A
28
A
4
B
9
B
14
C
19
C
24
D
29
B
5
B
10
A
15
B
20
D
25
D
30
B
Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 8
MÔN TOÁN 12
Câu 1. Trong không gian
Oxyz
, mặt phẳng
( )
Oxy
có phương trình là
A.
0y =
. B.
0x =
. C.
0xy+=
. D.
0z =
.
Câu 2. Trong không gian
Oxyz
, cho các điểm
( )
2; 2;1A −
,
( )
1; 1;3B −
. Tìm tọa độ của vectơ
AB
.
A.
( )
3; 3;4−
. B.
( )
1;1;2−
. C.
( )
1; 1; 2−−
. D.
( )
3;3; 4−−
.
Câu 3. Cho hàm số
2
3
( ) 2
cos
f x x
x
=+
. Trong các khẳng định sau, khẳng định nào đúng?
A.
( )d 3tan 2f x x x C= + +
. B.
2
( )d 3tanf x x x x C= − + +
.
C.
2
( )d 3tanf x x x x C= + +
. D.
( )d 3tan 2f x x x C= − + +
.
Câu 4. Nếu
( )
2
1
d3f x x =
,
( )
5
2
d1f x x =−
thì
( )
5
1
df x x
bằng
A.
3
. B.
4
. C.
2
. D.
2−
.
Câu 5. Trong không gian
Oxyz
, điểm nào sau đây là hình chiếu vuông góc của điểm
(1;4;2)A
trên mặt phẳng
Oxy
?
A.
(1;0;2)
. B.
(1;4;0)
. C.
(0;0;2)
. D.
(0;4;2)
.
Câu 6. Trong không gian
Oxyz
, cho mặt phẳng
( )
: 2 3 1 0P x y z− + − =
. Mặt phẳng
( )
P
có một vectơ pháp
tuyến là
A.
( )
2;1;3n =−
. B.
( )
1; 2;3n =−
. C.
( )
1;3; 2n =−
. D.
( )
1; 2;1n =−
.
Câu 7. Tính tích phân
0
sin3 dxx
A.
2
3
. B.
1
3
. C.
2
3
−
. D.
1
3
−
.
Câu 8. Tìm họ nguyên hàm của hàm số
( )
sin 2f x x=
.
A.
cos2
3
x
C−+
. B.
2cos2xC+
. C.
cos2
2
x
C−+
. D.
cos2
2
x
C+
.
Câu 9. Cho
( )
6
0
d 12f x x =
. Tính
( )
2
0
3dI f x x=
.
A.
6I =
. B.
36I =
. C.
2I =
. D.
4I =
.
Câu 10. Cho hàm số
( )
2
31f x x=−
. Trong các khẳng định sau, khẳng định nào đúng?
A.
( )
3
1
d
3
f x x x x C= − +
. B.
( )
3
df x x x C=−
.
C.
( )
3
df x x x x C= − +
. D.
( )
3
d3f x x x x C= − +
.
Câu 11. Trong không gian
Oxyz
, cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 2 3 4S x y z− + + + + =
. Tìm tọa độ tâm của mặt cầu
( )
S
.
A.
( )
1; 2; 3−−
. B.
( )
2; 4; 6−−
. C.
( )
2;4;6−
. D.
( )
1;2;3−
.
Câu 12. Nguyên hàm của hàm số
31
e
x
y
−+
=
là
A.
31
1
e
3
x
C
−+
+
. B.
31
3e
x
C
−+
+
. C.
31
3e
x
C
−+
−+
. D.
31
1
e
3
x
C
−+
−+
.
Câu 13. Tìm nguyên hàm của hàm số
( )
2
43
fx
x
=
−
.
A.
2d 1
ln 4 3
4 3 2
x
xC
x
= − +
−
. B.
2d 1 3
ln 2
4 3 2 2
x
xC
x

= − +

−

.
C.
2d 3
2ln 2 C
4 3 2
x
x
x

= − +

−

. D.
2d 1
ln 4 3
4 3 4
x
xC
x
= − +
−
.
Câu 14. Nguyên hàm
( )
1 ln
d0
x
xx
x
+
bằng
A.
2
lnx x C++
. B.
2
1
ln
2
x x C++
. C.
2
ln lnx x C++
. D.
2
1
ln ln
2
x x C++
.
Câu 15. Cho tích phân
( )
4
0
1 sin 2 d .I x x x
=−
Tìm đẳng thức đúng.
A.
( )
4
0
1 cos2 cos2 dI x x x x
= − − −
. B.
( )
4
4
0
0
1 cos2 cos2 dI x x x x
= − − +
.
C.
( )
4
4
0
0
11
1 cos2 cos2 d
22
I x x x x
= − − +
. D.
( )
4
4
0
0
1
1 cos2 cos2 d
2
I x x x x
= − − −
.
Câu 16. Trong không gian
Oxyz
, cho ba điểm
( )
3; 2; 2A −−
,
( )
3;2;0B
,
( )
0;2;1C
. Viết phương trình mặt phẳng
( )
ABC
.
A.
2 3 6 12 0x y z+ + + =
. B.
2 3 6 12 0x y z− + + =
.
C.
2 3 6 0x y z− + =
. D.
2 3 6 12 0xyz+ − − =
.
Câu 17. Trong không gian
Oxyz
, phương trình mặt phẳng đi qua hai điểm
( ) ( )
0;1;0 , 2;0;1AB
và vuông góc
với mặt phẳng
( )
: 1 0P x y− − =
là:
A.
2 6 2 0x y z− − + =
. B.
2 2 5 2 0x y z+ − − =
. C.
10x y z+ − − =
. D.
3 1 0x y z+ − − =
.
Câu 18. Họ nguyên hàm của hàm số
( )
cos2f x x x=
là
A.
sin2 cos2
24
x x x
C++
. B.
cos2
sin2
2
x
x x C−+
.
C.
cos2
sin2
2
x
x x C++
. D.
sin2 cos2
24
x x x
C−+
.
Câu 19. Biết
( )
22xx
x e dx x mx n e C= + + +
. Tính
.mn
.
A.
6
. B.
4−
. C.
0
. D.
4
.
Câu 20. Khi tính nguyên hàm
3
d
1
x
x
x
−
+
, bằng cách đặt
1ux=+
ta được nguyên hàm nào?
A.
( )
2
4duu−
. B.
( )
2
2 4 du u u−
. C.
( )
2
3duu−
. D.
( )
2
2 4 duu−
.
Câu 21. Cho tích phân
( )
1
7
5
2
0
d
1
x
Ix
x
=
+
, giả sử đặt
2
1tx=+
. Tìm mệnh đề đúng.
A.
( )
3
2
4
1
1
1
d
2
t
It
t
−
=
. B.
( )
3
4
4
1
1
3
d
2
t
It
t
−
=
. C.
( )
3
3
5
1
1
d
t
It
t
−
=
. D.
( )
3
2
5
1
1
1
d
2
t
It
t
−
=
.
Câu 22. Biết
3
2
0
3
d ln
cos
x
I x b
xa
= = −
. Khi đó, giá trị của
2
ab+
bằng
A.
11
. B.
7
. C.
9
. D.
13
.
Câu 23. Trong không gian
Oxyz
cho hai điểm
( )
1;1;1I
và
( )
1;2;3A
. Viết phương trình mặt cầu có tâm I và đi
qua A.
A.
( ) ( ) ( )
2 2 2
1 1 1 5x y z− + − + − =
. B.
( ) ( ) ( )
2 2 2
1 1 1 29x y z+ + + + + =
.
C.
( ) ( ) ( )
2 2 2
1 1 1 25x y z− + − + − =
. D.
( ) ( ) ( )
2 2 2
1 1 1 5x y z+ + + + + =
.
Câu 24. Biết
( )
2
2 d sin lnf x x x x C= + +
. Tìm nguyên hàm
( )
df x x
.
A.
( )
2
d 2sin 2ln
2
x
f x x x C= + +
. B.
( )
2
d 2sin 2 2lnf x x x x C= + +
.
C.
( )
2
d sin ln
2
x
f x x x C= + +
. D.
( )
2
d 2sin 2lnf x x x x C= + +
.
Câu 25. Biết
2
e
1
ln 2
d ln
11
(1 )
xa
x b c
ee
x
= + +
++
+
, với
, , .abc
. Tính
abc++
.
A.
3
. B.
2
. C.
1
. D.
1−
.
Câu 26. Cho hàm số
( )
fx
có đạo hàm trên
4;2−
, thỏa mãn
( )
3
0
' 2 4 8xf x dx−=
và
( )
22f =
.
Tính
( )
1
2
2I f x dx
−
=
.
A.
10I =−
. B.
10I =
. C.
5I =−
. D.
5I =
.
Câu 27. Cho
2
2
0
cos 4
d ln
sin 5sin 6
x
xa
x x b
=
−+
. Giá trị của
ab+
bằng
A.
3
. B.
0
. C.
1
. D.
4
.
Câu 28. Trong không gian
Oxyz
, cho bốn điểm
( )
0;1; 1A −
,
( )
1;1;2B
,
( )
1; 1;0C −
và
( )
0;0;1D
. Mặt phẳng
( )
song song với mặt phẳng
( )
BCD
và chia khối tứ diện
ABCD
thành hai khối đa diện sao cho tỉ số thể tích
của khối đa diện có chứa điểm
A
và khối tứ diện
ABCD
bằng
1
27
. Viết phương trình mặt phẳng
( )
.
A.
40yz− + − =
. B.
40yz+ − =
. C.
10yz− − =
. D.
3 3 4 0xz− − =
.
Câu 29. Trong không gian
Oxyz
, cho điểm
( )
3;1; 1−I
và mặt phẳng
( )
: 2 2 3 0− − + =P x y z
. Phương trình
mặt cầu
( )
S
có tâm
I
và tiếp xúc với mặt phẳng
( )
P
là
A.
( ) ( ) ( )
2 2 2
3 1 1 16+ + + + − =x y z
. B.
( ) ( ) ( )
2 2 2
3 1 1 16− + − + + =x y z
.
C.
( ) ( ) ( )
2 2 2
3 1 1 4− + − + + =x y z
. D.
( ) ( ) ( )
2 2 2
3 1 1 4+ + + + − =x y z
.
Câu 30. Biết
2
52
2
xb
I e dx ae ce
−
−
= = +
, với
,,abc
là các số nguyên. Tính
P ab c=+
.
A.
0P =
. B.
12P =
. C.
4P =
. D.
6P =
.
Câu 31. Trong không gian
Oxyz
, cho mặt cầu
( )
2 2 2
: 2 6 4 2 0S x y z x y z+ + − + − − =
và mặt phẳng
( )
: 4 -11 0x y z
+ + =
. Viết phương trình mặt phẳng
( )
P
song song với giá của vectơ
( )
1;6;2v =
, vuông góc
với
( )
và tiếp xúc với
( )
S
.
A.
4 3 5 0
4 3 27 0
x y z
x y z
− − + =
− − − =
. B.
2 3 0
2 21 0
x y z
x y z
− + + =
− + − =
.
C.
2 2 3 0
2 2 21 0
x y z
x y z
− + + =
− + − =
. D.
3 4 1 0
3 4 2 0
x y z
x y z
+ + + =
+ + − =
.
Câu 32. Trong không gian
Oxyz
, cho điểm
( )
1;1;1A
và mặt phẳng
( )
:P x+ y 2z 6 = 0−−
. Gọi
( )
; ; M a b c
là điểm thuộc
( )
P
sao cho
MA
ngắn nhất. Tính
S a b c= + +
.
A.
= 4S
. B.
= 0S
. C.
= 3S
. D.
= -3S
.
------ HẾT ------
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
D
B
C
C
B
B
A
C
D
C
A
D
A
D
C
C
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
C
A
B
D
D
A
A
A
C
A
D
C
C
D
C
C
Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 9
MÔN TOÁN 12
Câu 1. Cho hình phẳng giới hạn bởi đường cong , trục hoành và các đường thẳng .
Khối tròn xoay tạo thành khi quay quanh trục hoành có thể tích bằng bao nhiêu?
A. . B. . C. . D. .
Câu 2. Cho
( )
Fx
là nguyên hàm của hàm số
( )
fx
trên
;ab
éù
êú
ëû
. Phát biểu nào sau đây đúng ?
A.
( ) ( ) ( )
.
b
a
f x dx F a F b=-
ò
B.
( ) ( ) ( )
.
b
a
f x dx F b F a=-
ò
C.
( ) ( ) ( )
.
b
a
f x dx F a F b=+
ò
D.
( ) ( ) ( )
.
b
a
f x dx F b F a=+
ò
Câu 3. Viết phương trình mặt cầu (S) có tâm I(-1;2;1) và tiếp xúc với mặt phẳng (P):
2 2 1 0x y z− − + =
A.
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 4S x y z+ + − + + =
. B.
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 4S x y z+ + − + − =
.
C.
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 2S x y z+ + − + − =
. D.
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 2S x y z+ + − + + =
.
Câu 4. Cho hàm số
( )
fx
liên tục trên . Gọi S là diện tích hình phẳng giới hạn bởi các đường
( )
, 0, 1, 2y f x y x x= = = − =
(như hình vẽ bên). Mệnh đề nào dưới đây đúng?
A.
( ) ( )
12
11
dx dxS f x f x
−
= − −

. B.
( ) ( )
12
11
dx+ dxS f x f x
−
=−

.
C.
( ) ( )
12
11
dx + dxS f x f x
−
=

. D.
( ) ( )
12
11
dx dxS f x f x
−
=−

.
Câu 5. Trong không gian với hệ tọa độ
Oxyz
, phương trình nào dưới đây là phương trình mặt phẳng đi qua
điểm
( )
1;2; 3M −
và có một vectơ pháp tuyến
( )
1; 2; 3n = − −
.
A.
2 3 12 0x y z− + − =
B.
2 3 6 0x y z− − + =
C.
2 3 6 0x y z− − − =
D.
2 3 12 0x y z− + + =
Câu 6. Cho
()u u x=
,
()v v x=
là hai hàm số có đạo hàm liên tục, khẳng định nào sau đây là đúng ?
A.
.
u
udv vdu
v
=+
òò
B.
.udv uv vdu=-
òò
C.
.vdu uv vdu=+
òò
D.
.udv uv vdu=+
òò
D
2
1yx=+
0, 1xx==
D
V
2V =
4
3
V
=
4
3
V =
2V
=
Câu 7. Trong không gian tọa độ
( )
Oxyz
, cho hai vecto
( ) ( )
1;3;4 , 3; 2;5ab=−
Tính T =
.ab
A.
11T =−
. B.
29T =
. C.
11T =
. D.
17T =
.
Câu 8. Tính
3
sin
(1 3cos )
xdx
I
x
=
+
A.
( )
2
1
+C
6 1 3cos
I
x
=
+
. B.
( )
2
1
+C
12 1 3cos
I
x
=
+
.
C.
( )
2
1
+C
12 1 3cos
I
x
=−
+
. D.
( )
2
1
+C
6 1 3cos
I
x
=−
+
.
Câu 9. Cho
1
0
()fx
dx
1=
;
3
0
()fx
dx
5=
. Tính
3
1
()fx
dx
A. 6. B. 5. C. 4. D. 1.
Câu 10. Trong không gian tọa độ
( )
Oxyz
, cho hai vecto
( ) ( )
1;3; 4 , 3;2;5ab= − =
Tính
2 3 .c a b=+
A.
( )
11;12;7 .c =
B.
( )
11; 12; 7 .c = − −
C.
( )
11;12; 7 .c =−
D.
( )
11;12; 7 .c = − −
Câu 11. Cho
( )
fx
,
( )
gx
là các hàm số xác định và liên tục trên . Trong các mệnh đề sau, mệnh đề nào
sai?
A.
( ) ( ) ( ) ( )
dddf x g x x f x x g x x− = −


. B.
( ) ( ) ( ) ( )
d d . df x g x x f x x g x x=
.
C.
( ) ( ) ( ) ( )
d d df x g x x f x x g x x+ = +


. D.
( ) ( )
2 d 2 df x x f x x=

.
Câu 12. Cho hàm số
()y f x=
có đạo hàm liên tục trên đoạn [1 ; 2] thỏa mãn
(1) 2f =
và
2
( ) ( 1) ( ) 2 ( ), [1;2]f x x f x xf x x
− + =
. Giá trị của
2
1
()f x dx
bằng
A.
1
ln2
2
−
. B.
1
ln2
2
+
. C.
1 ln 2+
. D.
1 ln 2.−
Câu 13. Tính
( 1).sinI x xdx=+
A.
( 1)cosx +sinx+CIx= − +
. B.
( 1) cosx sinx+CIx= − + −
.
C.
( 1)cosx sinx+CIx= + −
. D.
( 1)cosx +sinx+CIx=+
.
Câu 14. Trong không gian , cho hai điểm và . Vectơ
BA
có tọa độ là
A. . B. . C. . D. .
Câu 15. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới
đây?
A.
( )
2
1
2 2 d
−
−+
xx
. B.
( )
2
2
1
2 2 4 d
−
−−
x x x
. C.
( )
2
1
2 2 d
−
−
xx
. D.
( )
2
2
1
2 2 4 d
−
− + +
x x x
.
Câu 16. Một cái cổng hình Parabol như hình vẽ sau. Chiều cao
4GH m=
, chiều rộng
4AB m=
,
0,9AC BD m==
. Chủ nhà làm hai cánh cồng khi đóng lại là hình chữ nhật CDEF tô đậm có giá là
1200000 đồng
2
/m
, còn các phần để trắng làm xiên hoa có giá là 900000 đồng
2
/m
. Hỏi tồng số
tiền để làm hai phần nói trên gần nhất với số tiền nào dưới đây?
Oxyz
( )
1;1; 2A −
( )
2;2;1B
( )
1;1;3
( )
3;1;1
( )
3;3; 1−
( )
1; 1; 3− − −
A. 11445000 đồng. B. 7368000 đồng. C. 4077000 đồng. D. 11370000 đồng.
Câu 17. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm
(2;1;3), (6;5;5)AB
. Gọi
()S
là mặt cầu
đường kính AB. Mặt phẳng
()P
vuông góc với AB tại
H
sao cho khối nón đinh
A
và đáy là hình
tròn tâm
H
(giao của mặt cầu
()S
và mặt phẳng
()P
) có thể tích lớn nhất, biết rằng
( ):2 0P x by cz d+ + + =
với
,,b c d
. Tính
S b c d= + +
.
A.
12S =−
. B.
18S =−
. C.
24S =
. D.
18S =
.
Câu 18. . Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng
( )
:2 2 3 0x y z
+ + − =
và điểm
, khi đó khoảng cách từ điểm đến mặt phẳng bằng:
A. 3. B. 7. C. 5. D. 1.
Câu 19. Cho hình phẳng (H) giới hạn bởi các đường
bxaxyxfy ==== ,,0),(
(
ba
) quay xung quanh trục
hoành tạo vật thể tròn xoay. Công thức tính thể tích là
A.
( ) .
b
a
V f x dx=
B.
2
( ) .
b
a
V f x dx
=
C.
( ) .
b
a
V f x dx
=
D.
2
( ) .
b
a
V f x dx=
Câu 20. Biết
1
ln
2
1 ln
e
x
dx a b
xx
=+
+
với
,ab
là các số hữu tỷ. Tính
S a b=+
.
A.
3
4
S =
. B.
2
3
S =
. C.
1S =
. D.
1
2
S =
.
Câu 21. Cho số
1a ¹-
. Hàm số
()f x x
a
=
có nguyên hàm là
A.
d.
x
x x C
a
a
a
=+
ò
B.
1
d.
1
x
x x C
a
a
a
+
=+
+
ò
C.
d.
1
x
x x C
a
a
a
=+
+
ò
D.
1
d.
1
x
x x C
a
a
a
-
=+
-
ò
Câu 22. Nguyên hàm của hàm số
( )
3
2f x x x= + +
là hàm số nào trong các hàm số sau?
A. . B. .
C. . D. .
Câu 23. Cho hình phẳng (H) giới hạn bởi các đường
bxaxyxfy ==== ,,0),(
(
ba
).Diện tích hình phẳng
(H) tính bằng công thức nào sau đây?
A.
( )
.
a
b
S f x dx=
B.
( ) ( )
.S f b f a=−
C.
( )
.
b
a
S f x dx=
D.
( )
.
b
a
S f x dx=
Câu 24. Cho
1
0
( ) 2f x dx =
. Goi F(x) là 1 nguyên hàm của f(x). Biết F(0)= 3. Tính F(1)
A.
( )
11F =−
. B.
( )
15F =
. C.
( )
15F =−
. D.
( )
11F =
.
Câu 25. Trong không gian
Oxyz
, cho mặt phẳng
( )
:2 3 1 0P x y z− − + =
. Vectơ nào dưới đây là một vectơ
pháp tuyến của
( )
P
?
A.
( )
4
2;1;3n =
. B.
( )
2
2; 1;3n =−
. C.
( )
3
2;3;1n =
. D.
( )
1
2; 1; 3n = − −
.
(1;2;1)M
M
()
( )
42
2
42
xx
F x x C= + + +
( )
2
33F x x x C= + +
( )
4
2
32
3
x
F x x x C= + + +
( )
42
3
2
42
xx
F x x C= + + +
Câu 26. Trong hệ trục tọa độ
Oxyz
, phương trình mặt cầu tâm
( )
2; 1;2I −−
bán kính
2R =
là:
A.
( ) ( ) ( )
2 2 2
2 1 2 4− + − + + =x y z
. B.
( ) ( ) ( )
2 2 2
2 1 2 4+ + + + − =x y z
.
C.
( ) ( ) ( )
2 2 2
2 1 2 2x y z− + − + + =
. D.
( ) ( ) ( )
2 2 2
2 1 2 2+ + + + − =x y z
.
Câu 27. Trong không gian Oxyz cho mp(Q): 5x - 12z + 3 = 0 và mặt cầu (S): mp(P)
song song với (Q) và tiếp xúc với (S) có phương trình là:
A. 5x - 12z - 18 = 0. B. 5x - 12z + 8 = 0.
C. 5x - 12z - 8 = 0 hoặc 5x - 12z + 18 = 0. D. 5x - 12z + 8 = 0 hoặc 5x - 12z - 18 = 0.
Câu 28. Chọn khẳng định sai trong các khẳng định dưới đây
A.
( ) ( ) ( ) ( )
b d b
a c a
f x dx g x dx f x g x dx+ = +


B.
( ) ( ) ( ) ( )
b b b
a a a
f x dx g x dx f x g x dx− = −


C.
( ) ( )
.
ba
ab
f x dx f x dx=−

D.
( ) ( ) ( )
,.
bb
aa
kf x dx k f x dx k=

Câu 29. Trong không gian Oxyz, cho vectơ
23a i j k= − + −
. Toạ độ của vectơ
a
là
A.
( )
2;1;3-
. B.
( )
2;1; 3--
. C.
( )
2; 1; 3--
. D.
( )
2; 1;3--
.
Câu 30. Tìm một nguyên hàm
( )
Fx
của hàm số
( )
2
2f x x=−
biết
( )
5
2
3
F =
A.
( )
3
21
3
x
F x x= − +
. B.
( )
3
1
2
33
x
F x x= − +
.
C.
( )
3
19
2
3
F x x x= − +
. D.
( )
3
23
3
x
F x x= − +
.
Câu 31. Cho hai mặt phẳng
( ) ( ) ( ) ( )
:3 3 1 0; : 1 2 3 0P x y z Q m x y m z+ − + = + − − − − =
. Xác định m để hai mặt
phẳng (P), (Q) vuông góc với nhau.
A. . B. . C. . D. .
Câu 32. Cho tích phân
0
2
2
cos sin .I x x dx
−
=
,giả sử đặt
costx=
. Tìm mệnh đề đúng?
A.
1
2
0
I t dt=−
B.
0
2
2
I t dt
−
=
C.
1
2
0
I t dt=
D.
0
2
2
I t dt
−
=−
------ HẾT ------
ĐÁP ÁN
1
B
6
B
11
B
16
A
21
B
26
B
31
D
2
B
7
D
12
B
17
B
22
A
27
D
32
A
3
B
8
A
13
A
18
D
23
C
28
A
4
D
9
C
14
D
19
B
24
B
29
B
5
C
10
A
15
D
20
B
25
D
30
B
Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 10
MÔN TOÁN 12
Câu 1. Nếu
1
0
( ) 4f x dx =
và
3
1
( ) 6f x dx =
thì
3
0
()f x dx
bằng
A.
10−
. B.
2−
. C.
2
. D.
10
.
2 2 2
x y z 2x 0+ + − =
3
2
m
−
=
2m =
1
2
m
−
=
1
2
m =
Câu 2. Họ tất cả các nguyên hàm của hàm số
2
1
()
cos
fx
x
=
là
A.
tan xC+
. B.
cot xC−+
. C.
tan xC−+
. D.
cot xC+
.
Câu 3. Trong không gian cho hai điểm
( )
1; 2;0A −
và
( )
2;1; 4B −
Tọa độ của vectơ là.
A.
( )
1; 3;4−−
. B.
( )
1;3;4
. C.
( )
2; 2;0−
. D.
( )
1;3; 4−
.
Câu 4. Trong không gian
Oxyz
, Cho mặt phẳng
( )
:
2 4 1 0x y z− + + =
. Vectơ nào dưới đây là một vectơ
pháp tuyến của mặt phẳng
( )
?
A.
( )
4
4; 2;1n −
r
. B.
( )
3
0; 2;4n −
r
. C.
( )
2
1;2;4n
r
. D.
( )
1
1; 2;4n −
r
.
Câu 5. Cho hàm số
( )
fx
có đạo hàm
( )
'fx
trên đoạn
1;3
. Biết
( )
12f =
,
( )
37f =
. Tích phân
3
1
'( )f x dx
bằng
A.
5−
. B.
14
. C.
9
. D.
5
.
Câu 6. Họ tất cả các nguyên hàm của hàm số
52
()f x x x=+
là
A.
6
2
6
x
xC++
. B.
4
52x x C++
. C.
63
63
xx
C++
. D.
52
52
xx
C++
.
Câu 7. Cho hình phẳng
( )
H
được giới hạn bởi các đường
2
5yx=+
,
0y =
,
0x =
,
2x =
. Gọi
V
là thể tích
khối tròn xoay được tạo thành khi quay
( )
H
xung quanh trục
Ox
. Mệnh đề nào dưới đây đúng?
A.
( )
2
2
2
0
5V x dx=+
. B.
( )
2
2
0
5V x dx=+
. C.
( )
2
2
0
5V x dx
=+
. D.
( )
2
2
0
5V x dx
=+
.
Câu 8. Trong không gian
Oxyz
. Cho hai vectơ
( )
1; 2;1a =−
và
( )
3;0;4b =
. Tọa độ tích có hướng
;ab


là
A.
( )
6; 1; 8−−
. B.
( )
8; 1;6−−
. C.
( )
2;2;3
. D.
( )
8;1;6
.
Câu 9. Trong không gian
Oxyz
, cho
34a i j k= + −
r r r r
. Tọa độ
a
r
là
A.
( )
3;4; 1−
. B.
( )
1;4;3−
. C.
( )
3;4;1
. D.
( )
3;4;0
.
Câu 10. Nếu
3
1
( ) 3f x dx =
và
3
1
( ) 1g x dx =−
thì
( ) ( )
3
1
23f x g x dx

+

bằng
A.
2
. B.
5−
. C.
3
. D.
5
.
Câu 11.
( )
23
xx
e dx−
bằng
A.
23
xx
eC++
. B.
3
2
ln3
x
x
eC−+
. C.
2 3 ln3
xx
eC−+
. D.
23
xx
eC−+
.
Câu 12. Tích phân
3
2
2xdx
bằng
A.
5
. B.
5−
. C.
2−
. D.
2
.
Câu 13. Cho hàm số
( )
fx
liên tục trên
R
. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
( )
, 0, 1y f x y x= = = −
và
4x =
(như hình vẽ bên). Mệnh đề nào dưới đây là đúng?
,Oxyz
AB
A.
( ) ( )
14
11
S f x dx f x dx
−
=+

. B.
( ) ( )
14
11
S f x dx f x dx
−
= − +

.
C.
( ) ( )
14
11
S f x dx f x dx
−
= − −

. D.
( ) ( )
14
11
S f x dx f x dx
−
=−

.
Câu 14. Trong không gian
Oxyz
, phương trình tổng quát của mặt phẳng đi qua điểm
( )
2;1;0M
và có vectơ
pháp tuyến
( )
1; 1;3n =−
r
là.
A.
3 1 0x y z− + + =
. B.
3 1 0x y z− + − =
. C.
3 1 0x y z+ + − =
. D.
3 1 0x y z− + + =
.
Câu 15. Tính tích phân
5
2
lnI xdx=
bằng phương pháp tích phân từng phần, đặt
lnux
dv dx
=
=
. Khẳng định nào
dưới đây đúng?
A.
( )
5
5
2
2
1
ln | .I x x x dx
x
=−
. B.
( )
5
5
2
2
1
ln | .I x x x dx
x
=+
.
C.
( )
5
52
2
2
ln |I x x x dx=−
. D.
( )
5
5
2
2
1
ln | .I x x x dx
x
= − +
.
Câu 16. Cho
2
1
1
ln
2 1 2
dx a
xb
=
+
, với
,ab
là các số nguyên dương và
a
b
là phân số tối giản. Giá trị
ab+
bằng
A.
2−
. B.
8
. C.
2
. D.
15
.
Câu 17. Trong không gian
Oxyz
, khoảng cách từ
( )
2;4; 3A −
đến mặt phẳng
( )
:
2 2 9 0x y z− + − =
bằng
A.
1
3
. B.
1
. C.
4
3
. D.
5
.
Câu 18. Trong không gian
Oxyz
, cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 2 3 9S x y z− + + + − =
. Tọa độ tâm
I
của mặt
cầu
( )
S
là
A.
( )
1; 2;3I −
. B.
( )
1;2;3I
. C.
( )
1;2; 3I −−
. D.
( )
3; 2;1I −
.
Câu 19.
( )
2
x
x e dx+
bằng
A.
( )
2
x
x e C++
. B.
( 3)
x
x e C++
. C.
( )
1
x
x e C++
. D.
( )
1
x
x e C−+
.
Câu 20. Nếu
4
2
( ) 4f x dx
−
=−
thì
2
1
(2 )f x dx
−
bằng
A.
2
. B.
2−
. C.
8−
. D.
8
.
Câu 21. Diện tích hình phẳng được giới hạn bởi parabol
2
2yx=-
và đường thẳng
yx=-
bằng
A.
3
. B.
7
2
. C.
9
4
. D.
9
2
.
Câu 22. Cho hình phẳng
( )
H
giới hạn bởi các đường
2
2y x x= − +
, trục hoành. Quay hình
( )
H
quanh trục
Ox
ta được khối tròn xoay có thể tích là
A.
32
15
. B.
16
15
. C.
16
15
. D.
4
3
.
Câu 23. Trong không gian
Oxyz
, cho
( )
2; 1;3a −
r
,
( )
1;3; 2b −
r
. Tọa độ
2c a b=−
r r r
là
A.
( )
0; 7;7−
. B.
( )
4; 7;7−
. C.
( )
0; 7; 7−−
. D.
( )
0;7;7
.
Câu 24. Khi tìm nguyên hàm
( )
2
2
2
3
x
dx
x +
, bằng cách đặt
2
3tx=+
ta được nguyên hàm nào dưới đây?
A.
2
2
dt
t
. B.
2
1
dt
t
−
. C.
2
1
dt
t
. D.
2
1
2
dt
t
.
Câu 25. Họ tất cả nguyên hàm của hàm số
( ) sin 4f x x=
là
A.
1
cos4
4
xC−+
. B.
1
cos4
4
xC+
. C.
cos4xC−+
. D.
cos4xC+
.
Câu 26. Trong không gian
Oxyz
, gọi
S
là tập hợp tất cả giá trị thực của
m
để hai mặt phẳng
( )
: 2 3 3 0mx y z
+ − + =
và
( ) ( )
: 1 2 5 0m x my z
− + + − =
vuông góc. Tổng các phần tử của
S
bằng
A.
1−
. B.
6
. C.
6−
. D.
1
.
Câu 27. Cho hàm số
( )
y f x=
liên tục trên
( )
0;+
thỏa mãn
2
2 '( ) ( ) 3xf x f x x x+=
. Biết
( )
1
1
2
f =
, giá trị
( )
4f
bằng
A.
4
. B.
24
. C.
14
. D.
16
.
Câu 28. Cho
1
0
2
ln2
1
x
dx a b
x
−
=−
+
, với
,ab
là các số nguyên dương. Giá trị
2ab+
bằng
A.
7
. B.
4
. C.
5−
. D.
2−
.
Câu 29. Cho hàm số
()fx
xác định trên
1
\
2



thỏa mãn
2
'( )
21
fx
x
=
−
, biết
(0) 1f =
và
(1) 2f =
. Giá trị
của biểu thức
( 1) (3)P f f= − +
bằng
A.
3 ln5+
. B.
3 ln15+
. C.
3 ln15−
. D.
3 ln3+
.
Câu 30. Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
).3;2;1(M
Mặt phẳng
)(P
qua
M
cắt các tia
OzOyOx ,,
lần lượt tại
,,A B C
sao cho thể tích khối tứ diện
OABC
nhỏ nhất có phương trình là:
A.
018236 =−++ zyx
. B.
01432 =−++ zyx
.
C.
0236 =++ zyx
. D.
06 =−++ zyx
.
Câu 31. Cho hàm số
()fx
có đạo hàm liên tục trên , biết
( )
23f =
và
( )
1
0
25xf x dx =
. Khi đó
2
2
0
'( )x f x dx
bằng
A.
13−
. B.
52
. C.
36−
. D.
28−
.
Câu 32. Trong không gian
Oxyz
, cho mặt cầu
( )
S
có tâm
( )
1;0; 1I −
và cắt mặt phẳng
( )
:2 2 16 0P x y z+ − − =
theo giao tuyến là một đường tròn có bán kính bằng 3. Phương trình của mặt cầu
( )
S
là
A.
( ) ( )
22
2
1 1 9x y z+ + + − =
.
B.
( ) ( )
22
2
1 1 25x y z+ + + − =
.
C.
( ) ( )
22
2
1 1 9x y z− + + + =
.
D.
( ) ( )
22
2
1 1 25x y z− + + + =
.
-----------------------------------Hết -----------------------------
ĐÁP ÁN
1. D
6. C
11. B
16. B
21. D
26. A
31. D
2. A
7. D
12. A
17. D
22. C
27. D
32. D
3. D
8. B
13. D
18. A
23. A
28. A
4. D
9. A
14. B
19. C
24. C
29. B
5. D
10. C
15. A
20. B
25. A
30. A
| 1/34
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 1 MÔN TOÁN 12 2 2 2
Câu 1: Trong không gian Oxyz cho mặt cầu (S ) : ( x − )
1 + ( y − 2) + ( z − 3) = 25 .Tìm tọa độ tâm I và bán kính R của mặt cầu. A. I ( 1 − ; 2 − ; 3 − ) , R = 5.
B. I (1;2;3) , R = 5 − .
C. I (1;2;3) , R = 5. D. I ( 1 − ; 2 − ; 3 − ) , R = 5 − .
Câu 2: Cho hàm số f (x) có đạo hàm liên tục trên đoạn [1;2] và thỏa mãn f ( ) 1 = 1, f (2)= 2. Tính 2 I = f ( ¢ x)dx. ò 1 7 A. I = 1. B. I = - 1. C. I = × D. I = 3. 2
Câu 3: Trong không gian Oxyz , một véc tơ pháp tuyến của mặt phẳng (P) : 3x − y + 2z + 5 = 0 là: → → → →
A. n = (3;1;2) .
B. n = (2;−1; ) 3 . C. n = ( 3 − ;1;2) .
D. n = (3;−1;2) .
Câu 4: Cho hai hàm số f (x) và g(x) liên tục trên a ;b. Diện tích hình phẳng giới hạn bởi đồ thị của các
hàm số y = f (x) , y = g(x) và các đường thẳng x = a , x = b bằng: b b b b
A.  f (x) − g(x)dx . B. f (x) + g(x) dx  .
C.  f (x) − g(x)dx . D. f (x) − g(x) dx  . a a a a
Câu 5: Cho hàm số y = f (x) liên tục trên  ;
a b . Chọn khẳng định sai: b c c b a A.
f (x)dx + f (x)dx =
f (x)dx, (c    
a;b) . B.
f (x) dx = − f (x)dx .   a a b a b b c b a C.
f (x)dx = f (x)dx +
f (x)dx, (c      ;ab) . D.
f (x)dx = 0 .a a c a 3 4 4
Câu 6: Cho hàm số f (x) thỏa mãn f (x)dx = 2022  và
f (x)dx = 2023  Tính tích phân I = f (x )dx. ò 1 3 1 A. I = - 1. B. I = 4045 − C. I = 4045 D. I = 1.
Câu 7: Trong không gian với hệ tọa độ Oxyz cho ( A 1; 2;3), B( 4
− ;4;6). Tọa độ trọng tâm G của tam giác OAB là  3 9  A. G( 3 − ;6;9) . B. G( 1 − ;2;3) . C. G(1; 2 − ; 3 − ) . D. G − ;3;   .  2 2 
Câu 8: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A(1;3; 2 − ) và B(4; 5
− ;2). Tính tọa độ của vectơ → AB . → → → →  5 
A. AB = (5; −2;0).
B. AB = (3; −8; 4).
C. AB = (−3;8; −4). D. AB = ; 1 − ;0 .    2 
Câu 9: Hàm số f (x) có nguyên hàm trên K nếu:
A. f (x) liên tục trên K .
B. f (x) xác định trên K .
C. f (x) có giá trị nhỏ nhất trên K .
D. f (x) có giá trị lớn nhất trên K .
Câu 10: Cho f ( x) , g ( x) là các hàm số xác định và liên tục trên R. Trong các mệnh đề sau, mệnh đề nào đúng? A. f
 (x)+ g(x)dx = f
 (x)dx− g  (x)dx . B. 2 f
 (x)dx = 2 f  (x)dx . f ( x) f  (x)dx C.  ( ) dx = . D. f
 (x).g(x)dx = f   (x)d .x g  (x)dx . g x g  (x)dx Câu 11: Để tính . x osx c dx ò
theo phương pháp tính nguyên hàm từng phần, ta đặt: ìï u = cosx ìï u = cosx ìï u = x ìï u = x A. ïí ï ï ï . B. í . C. í . D. í .
ï dv = xdx ïî ï dv = x ïî ï dv = o c sx ïî ï dv = o c sxdx ïî → → → →
Câu 12: Trong không gian với hệ tọa độ Oxyz cho u = (2; 0;3), v = ( 3
− ;1;0). Tích vô hướng của u và v là: → → → → → → → → A. . u v = 0 . B. . u v = 6 − . C. . u v = ( 3 − ; 1 − 1, 2) . D. . u v = 10 .
Câu 13: Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi
đồ thị hàm số y = f (x), trục Ox và hai đường thẳng x = ,
a x = b (a < )
b , xung quanh trục Ox. b b b b A. V = p f (x )dx. ò B. 2 V = f (x )dx. ò C. 2 V = p f (x )dx. ò D. V =
f (x ) dx. ò a a a a 2 2 2 Câu 14: Cho 3
é f (x)- g(x) d ù x = 10 ò ë û và
f (x )dx = 3. ò Khi đó g(x )dx ò bằng: 1 1 1 A. 17. B. 1. C. -1. D. -4.    1
Câu 15: Một nguyên hàm của hàm số f ( x) = cos3x thoả f =   . 18  6 sin 3x 1 1 sin 3x A. + . B. 3sin 3x − . C. 3sin 3x +1. D. . 3 6 2 3
Câu 16: Trong không gian Oxyz mặt phẳng (P) đi qua điểm M( - 1;2;0) và có véc tơ pháp tuyến n = (4; 0; 5 − ) có phương trình là:
A. 4x - 5z - 4 = 0. B. 4x - 5z + 4 = 0. C. 4x - 5y + 4 = 0. D. 4x - 5y - 4 = 0. 2 −
Câu 17: Tìm nguyên hàm của hàm số f (x) x = xe . 1 1 A.
f (x)dx = − e−x + C  2 . B. f (x)dx = e−x + C  2 . 2 2 1 1 C.
f (x)dx = −
xe−x + C  2 .
D. f (x)dx =
xe−x + C  2 . 2 2 6 2 Câu 18: Cho
f (x)dx = 12  . Tính I = f (3x)dx  . 0 0 A. I = 4 . B. I = 2 . C. I = 6 . D. I = 36 .
Câu 19: Cho điểm A(1;-2;1) và (P): x + 2y – z – 1 = 0. Viết phương trình mặt phẳng (Q) đi qua A và song song với (P).
A. (Q) : x− 2 y− z+ 4 = 0 . B. (Q) : x+ 2 y− z− 4 = 0 . C. (Q) : x+ 2 y− z+ 4 = 0 . D. (Q) : x+ 2 y− z+ 2 = 0 .
Câu 20: Trong không gian Oxyz ,cho mặt phẳng (P):
và điểm A(3;3;3). Tìm khoảng
cách từ điểm A đến mp(P). 14 A. -14. B. 14 . C. 14 . D. . 14  2
Câu 21: Tính sinx.dx  bằng: 0     A. cos − cos0 . B. sin − sin 0 . C. cos0 − cos . D. sin 0 − sin . 2 2 2 2
Câu 22: Một nguyên hàm của hàm số f ( x) 2
= 3x +1 thỏa mãn F(1) = 0 là: A. 3 x + x − 2 . B. 3 x −1 . C. 3 x + x . D. 3 x + x + 2 .
Câu 23: Gọi D là hình phẳng giới hạn bởi các đường 4 x
y = e , y = 0, x = 0 và x = 1 . Thể tích của khối tròn
xoay tạo thành khi quay D quanh trục Ox bằng 1 1 1 1 A. 8 xe dx  . B. 4 x e dx  . C. 4 xe dx  . D. 8 x e dx  . 0 0 0 0
Câu 24: Định m để hai mặt phẳng sau vuông góc với nhau: (P) : 3x − 5y + mz − 3 = 0,
(Q) : mx + 3y + 2z + 5 = 0 A. m = 4 . B. m = 1. C. m = 3 . D. m = 2 .
Câu 25: Trong không gian với hệ tọa độ Oxyz , mặt phẳng (P) đi qua điểm M (1;2;3) và cắt các tia Ox , Oy
, Oz lần lượt tại N , H , K sao cho thể tích của tứ diện ONHK đạt giá trị nhỏ nhất. Phương trình của mặt phẳng (P) là
A. 6x + 3y − 2z − 6 = 0 . B. 6x − 3y + 2z − 6 = 0 . C. 6
− x + 3y + 2z − 6 = 0 . D. 6x + 3y + 2z −18 = 0 .
Câu 26: Cho hàm số y = f ( x) 3 2
= ax + bx + cx + d,( , a , b c  ,
R a  0) có đồ thị (C) . Biết rằng đồ thị (C) tiếp
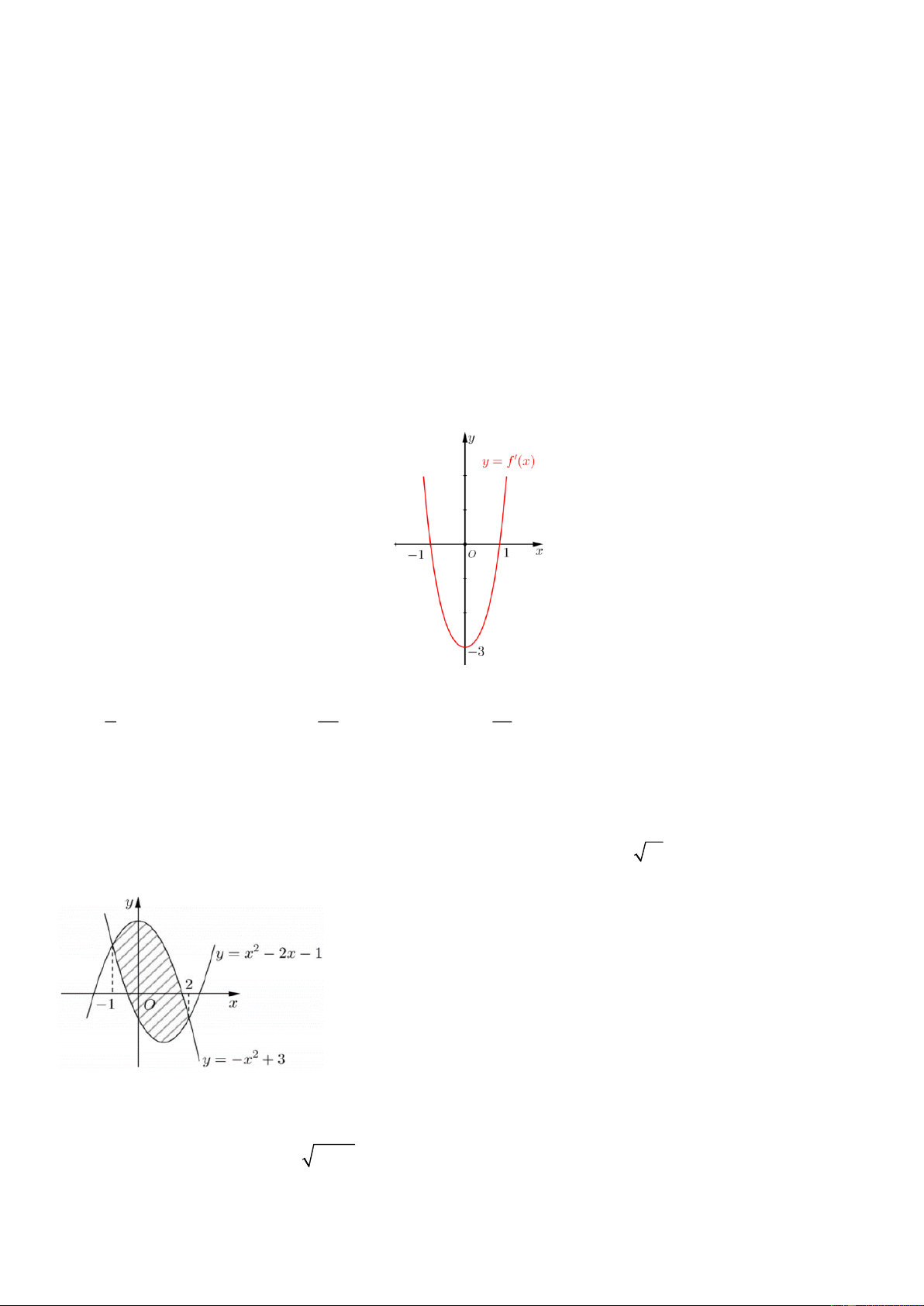
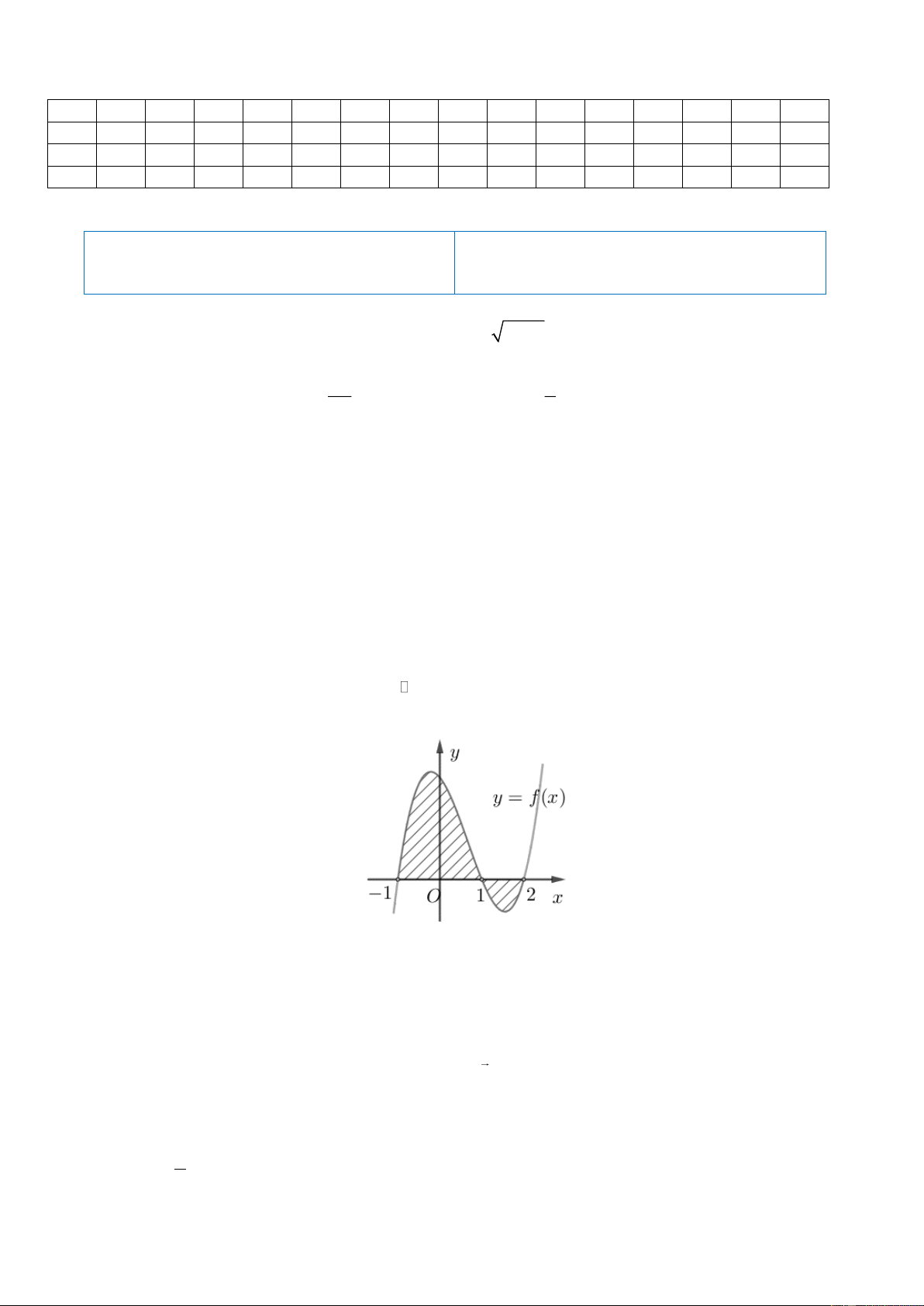
xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị hàm số y = f ( x) cho bởi hình vẽ dưới đây:
Tính diện tích S của hình phẳng giới hạn bởi đồ thị (C) và trục hoành. 5 27 21 A. . B. S = . C. . D. S = 9 . 4 4 4
Câu 27: Trong không gian Oxyz , cho điểm M (1; 2
− ;3) . Gọi I là hình chiếu vuông góc của M trên trục Ox
. Phương trình nào dưới đây là phương trình mặt cầu tâm I bán kính IM ? A. ( x + )2 2 2 1 + y + z = 13. B. ( x − )2 2 2 1 + y + z = 13. 2 2 2 C. ( x − )
1 + ( y + 2) + ( z − 3) = 13. D. ( x − )2 2 2 1 + y + z = 13.
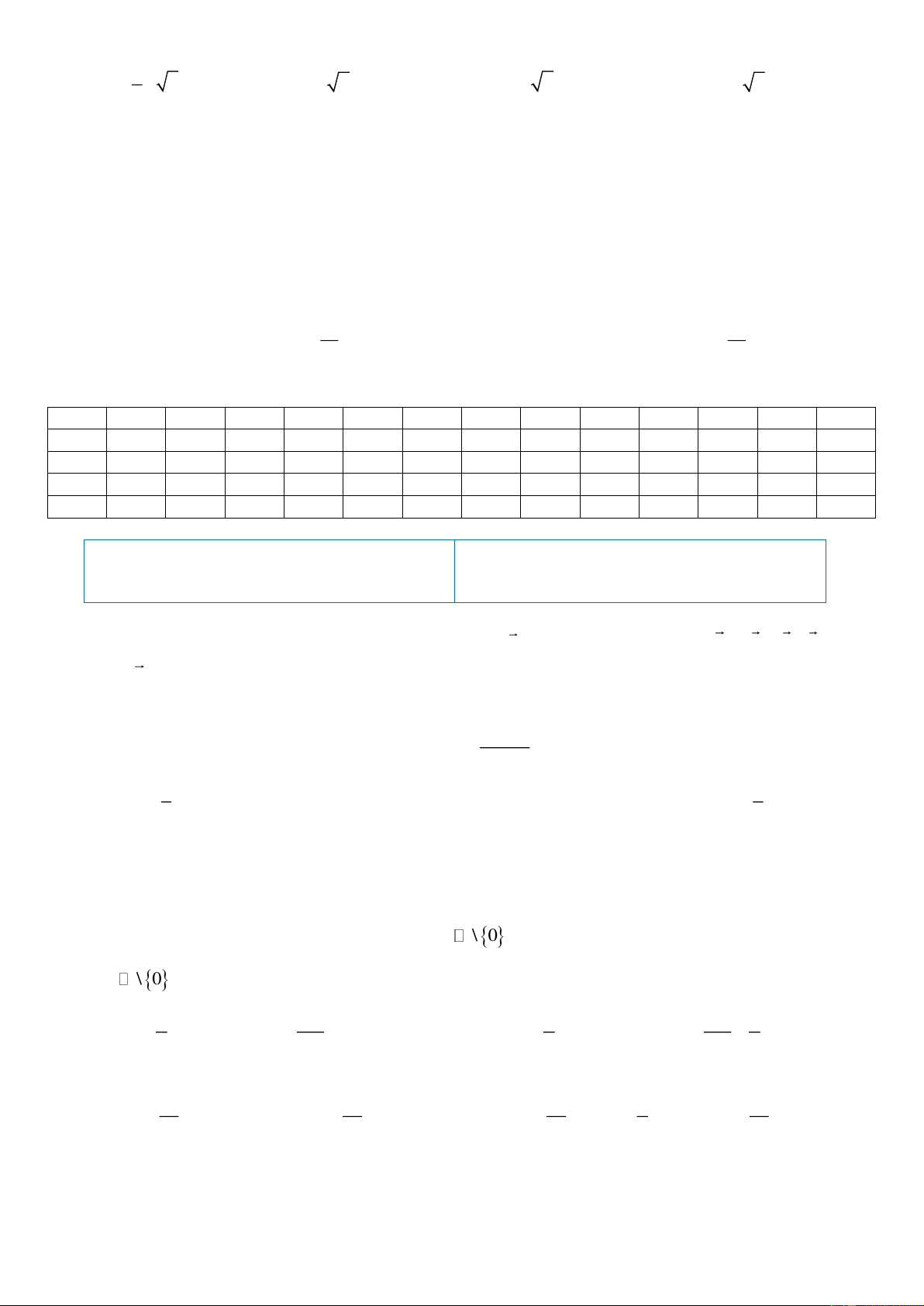
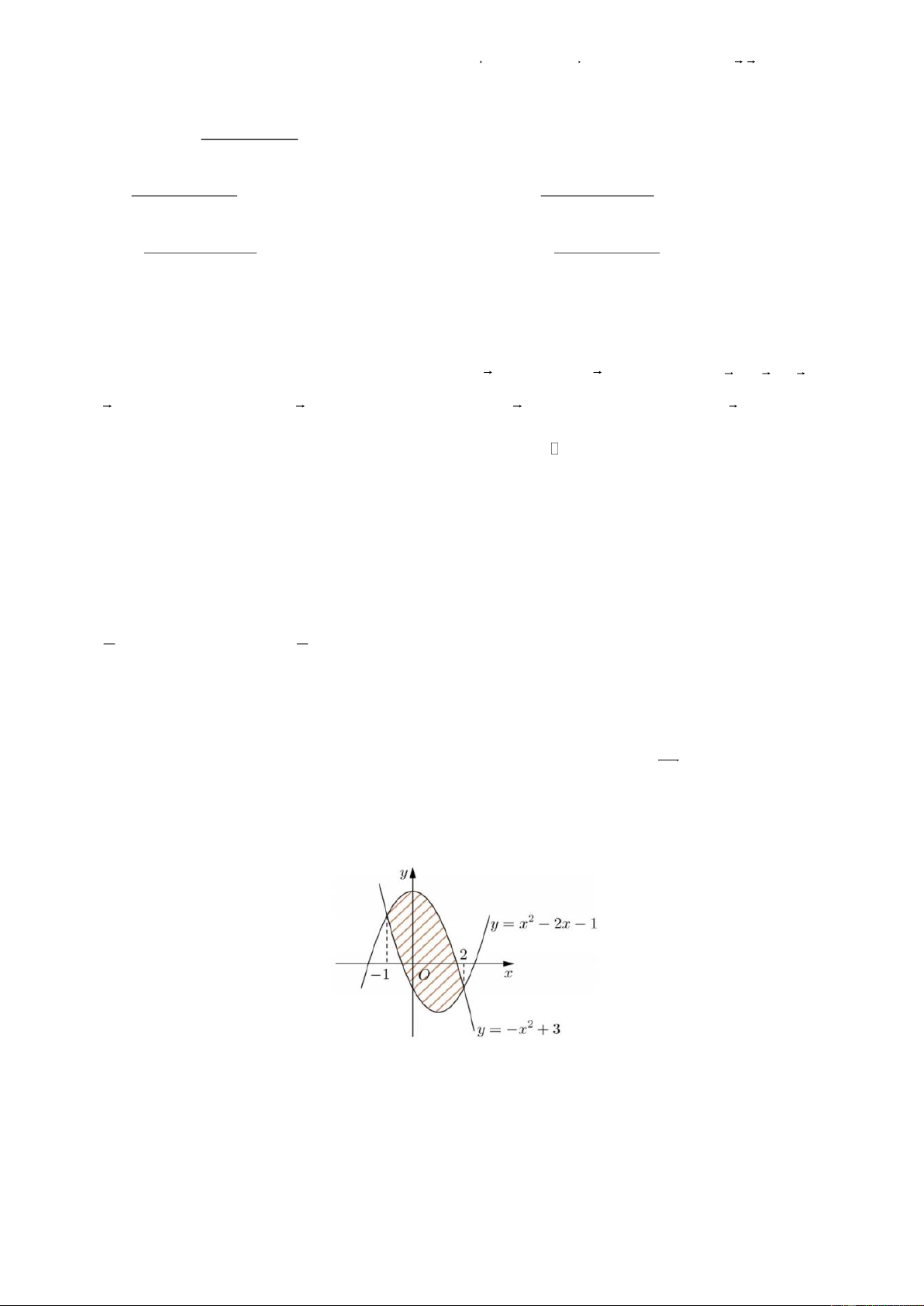
Câu 28: Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 2 2 2 2 A.  ( 2
2x − 2x − 4)d .
x B.  (2x − 2)d .x C.  ( 2
− x + 2)d .x D.  ( 2 2
− x + 2x + 4)d .x 1 − 1 − 1 − 1 − 2
Câu 29: Tính tích phân 2
I = 2x x −1dx  bằng cách đặt 2
u = x −1, mệnh đề nào dưới đây đúng ? 1 2 1 3 2 3 A. I = ud . uB. I = udu.  C. I = ud . uD. I = 2 ud . u  2 1 0 1 0
Câu 30: Cho hàm số f (x) có đạo hàm liên tục trên đoạn [- 1; ]
1 , thỏa mãn f (x)> 0, " x Î ¡ và f (
¢ x)+ 2 f (x)= 0. Biết rằng f ( ) 1 = 1, tính f (- ) 1 . A. f (- ) 1 = 3. B. f ( ) 2 1 e- - = . C. f (- ) 3 1 = e . D. f (- ) 4 1 = e .
Câu 31: Giá trị của a, b thoả .
x sin xdx = ax o c sx + bsinx + C  là:
A. a = - 1; b = - 1. B. a = 1; b = - 1. C. a = 1; b = 1. D. a = -1; b = 1.
Câu 32: Trong không gian với hệ tọa độ Oxyz , cho ba điểm M (2;3;− ) 1 , N ( 1 − ;1; ) 1 , P (0; ; m 0) . Tìm giá trị
của m để tam giác MNP vuông tại M. 13 15 A. m = 7. − B. m = . C. m = 7. D. m = . 2 2
------ HẾT ------ ĐÁP ÁN 1 C 6 A 11 D 16 B 21 C 26 B 31 D 2 A 7 B 12 B 17 A 22 A 27 B 32 C 3 D 8 B 13 C 18 A 23 A 28 D 4 D 9 A 14 C 19 C 24 C 29 B 5 A 10 B 15 D 20 B 25 D 30 D Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 2 MÔN TOÁN 12
Câu 1: Trong không gian Oxyz , cho biểu diễn của vectơ a qua các vectơ đơn vị là a = 2i − 3 j + k . Tọa độ
của vectơ a là A. (2; − 3; ) 1 . B. (1; 2; − 3) . C. (2;1; − 3) . D. (1; − 3; 2) .
Câu 2: Cho F (x ) là một nguyên hàm của hàm f (x ) 1 =
; biết F (0) = 2 . Tính F ( ) 1 . 2x + 1 A. F ( ) 1 1 = ln 3 - 2 . B. F ( ) 1 = 2ln 3 - 2 . C. F ( ) 1 = ln 3 + 2 . D. F ( ) 1 1 = ln 3 + 2 . 2 2
Câu 3: Trong không gian Oxyz, cho điểm A(1; 2
− ;3) . Hình chiếu vuông góc của điểm A trên mặt phẳng
(Oxz) là điểm M. Tọa độ của điểm M là A. M (0;1;0) . B. M (0; 2 − ;3) . C. M (1; 2 − ;0). D. M (1;0;3) .
Câu 4: Cho hàm số f ( x) xác định và liên tục trên \   0 thỏa mãn 2 2
x f ( x) + ( x − ) f ( x) ' 2 1
= xf (x) −1 với 3 mọi x  \  
0 , đồng thời thỏa f ( ) 1 = 2
− . Tính f (x)d . x 1 3 ln 3 2 ln 3 2 A. − ln 3 − . B. − −1. C. − ln 3 − . D. − − . 2 3 3 3 3
Câu 5: Cho F ( x) là một nguyên hàm của hàm số f ( x) = x + sin x và thỏa mãn F (0) = 1. Tìm F ( x) . x x x x
A. F ( x) 2 =
+ cos x . B. F (x) 2 =
− cos x − 2. C. F (x) 2 1 =
+ cos x + . D. F (x) 2 = − cos x + 2 . 2 2 2 2 2
Câu 6: Cho hàm số y = f ( x) xác định và liên tục trên đoạn  ;
a b . Diện tích hình phẳng giới hạn bởi đồ thị
hàm số y = f ( x) , trục hoành và hai đường thẳng x = a, x = b được tính theo công thức b b b a A. S = f  (x) dx.
B. S = − f  (x)dx. C. S = f  (x)dx . D. S = f  (x) dx. a a a b
Câu 7: Trong không gian với hệ tọa độ Oxyz cho hai điểm A(1;2;− )
1 ; B (2;1;0) mặt phẳng
(P):2x+ y −3z +1= 0 . Gọi (Q) là mặt phẳng chứa ;
A B và vuông góc với (P) . Phương trình mặt phẳng (Q) là
A. 2x + y − z − 5 = 0 .
B. x − 2 y − z − 6 = 0 .
C. 2x + y − 3z − 7 = 0 .
D. 2x + 5 y + 3z − 9 = 0 .
Câu 8: Trong không gian với hệ tọa độ Oxyz, cho A(1;2;3), B(1;2;4);C (4; 1
− ;2) . Tìm tọa độ điểm M trên
mặt phẳng (Oyz) sao cho: MA + MB + MC ngắn nhất? A. M (0;1;3) B. M (2;1;3) C. M (2;0;3) D. M (0;2;3)
Câu 9: Trong không gian Oxyz , mặt phẳng (P) : x + 2y − 3z + 3 = 0 có một vectơ pháp tuyến là A. (1;2; ) 3 . B. ( 1 − ;2; 3 − ). C. (1;2; 3 − ). D. (1; 2 − ;3) .
Câu 10: Trong không gian với hệ trục tọa độ Oxyz cho hai vectơ a = ( 4 − ;5; 3 − ) , b = (2;−2; ) 1 . Tìm tọa độ của
vectơ x = a + 2b . A. x = (0; 1 − ) ;1 .
B. x = (0;1;− ) 1 . C. x = (2;3; 2 − ) . D. x = ( 8 − ;9 ) ;1 . 3 3 3
Câu 11: Biết f (x)dx =  3 và g(x)dx = −  2 . Khi đó: f  (x)−g(x) dx  bằng 2 2 2 A. 5 . B. 1. C. 5 − . D. 6 − .
Câu 12: Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng (P) : x + 2y − 2z + 3 = 0 cắt mặt cầu (S ) tâm I
(2; 1; -1) theo giao tuyến là một đường tròn có bán kính bằng 4. Tính bán kính mặt cầu (S). A. 5. B. 4. C. 3. D. 6.
Câu 13: Tính sin xdx − − + − +
A. 2 xcos x 2sin x C .
B. 2 x sin x 2 sin x C . − + + − + +
C. 2 x sin x 2 cos x C .
D. 2 xco s x 2sin x C .
Câu 14: Hàm số nào sau đây không phải là một nguyên hàm của hàm số f x = ( x − )3 ( ) 2 3 ? x − x − x − x −
A. F ( x) ( )4 2 3 =
− 3 .B. F (x) ( )4 2 3 =
+ x . C. F (x) ( )4 2 3 = .
D. F ( x) ( )4 2 3 = + 8 . 8 8 8 8
Câu 15: Công thức nào sau đây là đúng? A. cos d
x x = − sin x + C. B. sin d
x x = cos x + C. C. sin d
x x = − cos x + C. D. − cos d
x x = sin x + C  .
Câu 16: Tìm nguyên hàm của hàm số ( ) 7x f x = . x 1 + x 7x x 7 A. x x 1 7 dx 7 + = + C  . B. 7 dx = + C  . C. 7x = 7x dx ln 7 + C  . D. 7 dx = + C  . x + 1 ln 7 ln 6 ex
Câu 17: Biết tích phân
dx = a + b ln 2 + c ln 3 
, với a , b , c là các số nguyên. Tính tổng x + + 0 1 e 3
T = a + b + c . A. T = 1 − . B. T = 1. C. T = 0 . D. T = 2 .
Câu 18: Gọi D là hình phẳng giới hạn bởi các đường x
y = e , y = 0, x = 0 và x = 1 . Thể tích của khối tròn xoay
tạo thành khi quay D quanh trục Ox bằng 1 1 1 1 A. x e dx  . B. 2 x e dx  . C. xe dxD. 2 xe dx  . 0 0 0 0
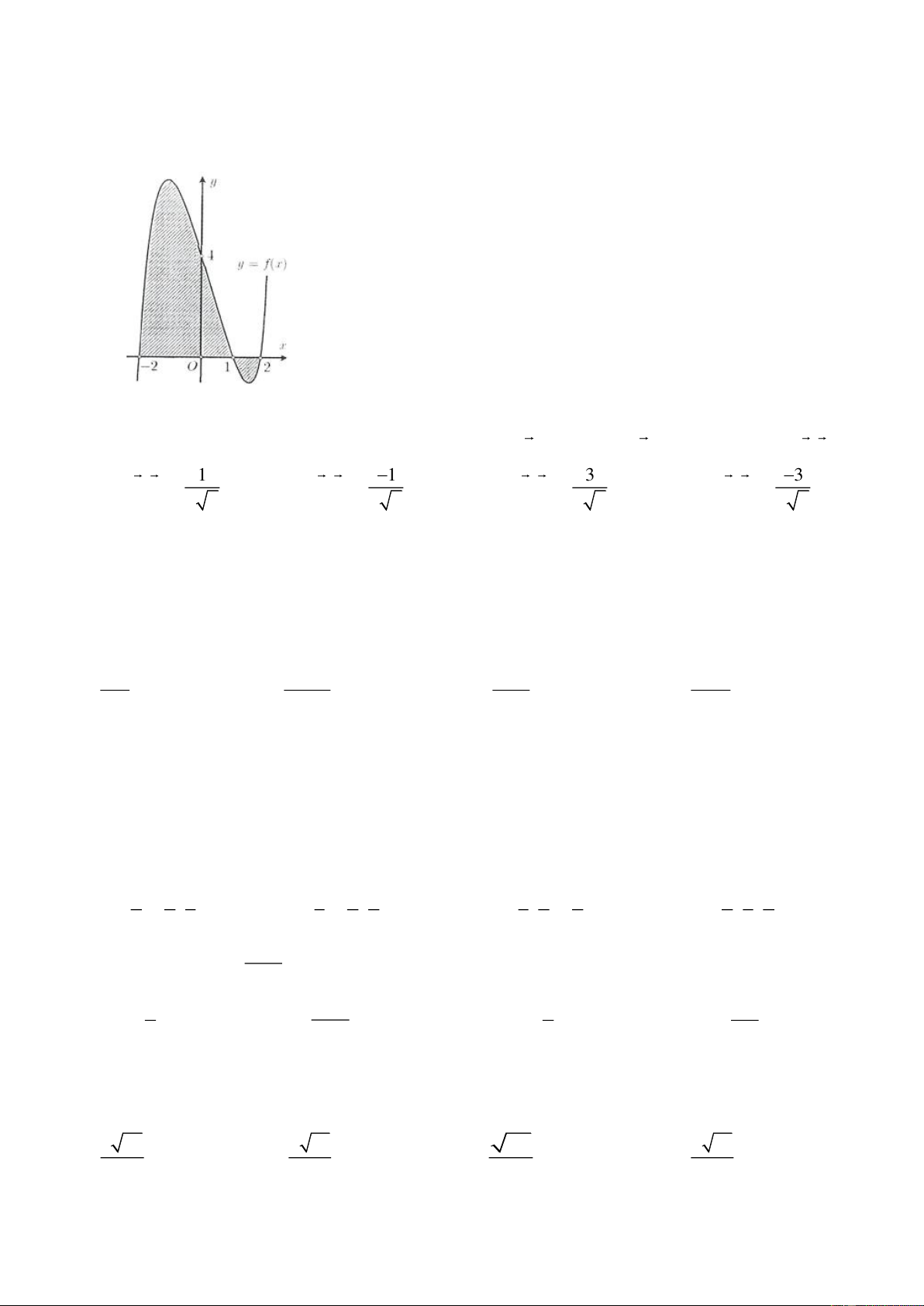
Câu 19: Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f ( x) , trục hoành (phần gạch sọc trong 1 2 hình vẽ). Đặt a = f
 (x)dx,b = f
 (x)dx. Mệnh đề nào đúng? 2 − 1 A. b − . a B. b − − . a C. a − . b D. a + . b
Câu 20: Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a = ( 2 − ; 3
− ;1) , b = (1;0;1) . Tính cos(a,b) . 1 1 − 3 3 −
A. cos (a, b) = .
B. cos (a, b) = .
C. cos (a, b) = .
D. cos (a, b) = . 2 7 2 7 2 7 2 7
Câu 21: Trong không gian với hệ tọa độ Oxyz , cho mặt cầu (S ) : 2 2 2
x + y + z − 6x + 4 y − 8z + 4 = 0 . Tìm tọa
độ tâm I của mặt cầu (S ) . A. I (3; 2 − ;4) . B. I ( 3 − ;2; 4 − ) . C. I (6; 4 − ;8). D. I ( 6 − ;4; 8 − ) .
Câu 22: Thể tích của khối tròn xoay sinh bởi hình phẳng giới hạn bởi đồ thị hai hàm số 2
y = x − 3x , 2 y = 9 − x
khi nó quay quanh trục hoành là 648 34101 1296 2673 A.  . B.  . C.  . D.  . 5 160 5 32 −1 1 Câu 23: Nếu f
 (x)dx = −4 thì  3 − f
  (x)+1dx  bằng 1 1 − A. 10 − . B. 11 − . C. 11. D. 14 .
Câu 24: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( P) :x + y − z + 2 = 0 và hai điểm A(3;4; ) 1 ; B (7; 4 − ; 3
− ) . Tìm điểm M ( ; a ;
b c)(a  2) thuộc (P) sao cho tam giác ABM vuông tại M và có
diện tích nhỏ nhất.  4 7 5   5 4 7   5 7 4   4 5 7  A. M ; − ;   . B. M ; − ;   . C. M ; ; −   . D. M ; ;   .  3 3 3   3 3 3   3 3 3   3 3 3  3 dx
Câu 25: Tích phân I =  có giá trị bằng x + 2 0 5 4581 5 21 A. I = ln . B. I = . C. I = log . D. I = − . 2 5000 2 100
Câu 26: Trong không gian Oxyz , cho ba điểm A(1; 0 ; 0) , B (0 ; 2 ; 0) , C (0 ; 0 ; 4) . Tính khoảng cách từ gốc
tọa độ O đến mặt phẳng ( ABC) . 3 21 2 21 21 4 21 A. . B. . C. . D. . 21 21 21 21
Câu 27: Giả sử các biểu thức sau đều có nghĩa, công thức nào sau đây sai? 1 1 A. x = x a x a a + ò d . ln C. B. dx = tan x + ò C. C.
dx = ln x + C.  D. x x = x + ò cos d sin C. 2 cos x x  2
Câu 28: Trong các khẳng định sau, khẳng định nào đúng khi nói về tích phân I = x sin 2xdx  ? 0     2 2 x 1 2 2 x 1 A. I = cos2x − sin 2x . B. I = − cos2x + sin 2x . 2 4 2 4 0 0 0 0     2 2 x 1 2 2 x 1 C. I = − cos2x + sin 2x . D. I = − cos2x − sin 2x . 2 2 2 4 0 0 0 0
Câu 29: Tìm nguyên hàm của hàm số f ( x) = cos3x . sin 3x A. cos 3xdx = + C. 
B. cos 3xdx = sin 3x + C.  3 sin 3x
C. cos 3xdx = − + C. 
D. cos 3xdx = 3sin 3x + C.  . 3
Câu 30: Cho hàm số g ( x) liên tục trên . Mệnh đề nào sau đây đúng? 2021 2021 2021 2021 A. g
 (x)dx = 2021. B. g  (x)dx = 0. C. g  (x)dx =1. D. g  (x)dx = 20 − 21 . 2021 2021 2021 2021
Câu 31: Cho F ( x) là một nguyên hàm của hàm số f ( x) trên 0; 
5 . Mệnh đề nào sau đây đúng? 5 5 A. f
 (x)dx = F(0)− F(5). B. f
 (x)dx = F(5)+ F(0). 0 0 5 5 C. f
 (x)dx = f (5)− f (0). D. f
 (x)dx = F(5)− F(0). 0 0
Câu 32: Tính diện tích S của hình phẳng (H ) giới hạn bởi các đường cong 3
y = −x +12x và 2
y = −x . 937 343 793 397 A. S = . B. S = . C. S = . D. S = . 12 12 4 4
------ HẾT ------ Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 3 MÔN TOÁN 12 2 I = 2 d x xCâu 1: Tính 1 − . A. I = −3 . B. I = 3 . C. I = 5 . D. I = −6 . Câu 2:
Mệnh đề nào sau đây sai? A. x x
e dx = e + C  . B. sinxdx = o c sx + C  . 5 x 4
C. dx = x + C  . D. x dx = + C  . 5 F ( x) ( ) = ex f x + 2x F ( x). Câu 3: Cho
là một nguyên hàm của hàm số thỏa mãn F ( ) 3 0 = . Tìm 2 x 3 x 5 A. F ( x) 2 = e + x + . B. F ( x) 2 = e + x + . 2 2 x 1 x 1 C. F ( x) 2 = 2e + x − . D. F ( x) 2 = e + x + . 2 2 Câu 4:
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) đi qua điểm A(0; 1 − ;4) và có một véctơ
pháp tuyến n = (2;2;− )
1 . Phương trình của ( P) là
A. 2x + 2 y + z − 6 = 0 . B. 2x + 2 y − z − 6 = 0 . C. 2x + 2 y − z + 6 = 0 . D. 2x − 2 y − z − 6 = 0 . Câu 5:
Tính diện tích S của hình phẳng giới hạn bởi đường cong 2
y = x − x + 3 và đường thẳng y = 2x +1. 4 9 2 1 A. S = . B. S = . C. S = . D. S = . 5 2 3 6 Câu 6:
Trong không gian với hệ toạ độ Oxyz , cho mặt cầu (S ) có phương trình:
(x − )2 +( y + )2 +(z − )2 1 2 3
= 4 . Tìm toạ độ tâm I và bán kính R của (S ) . A. I (1; 2 − ;3) và R = 4 . B. I ( 1
− ; 2; −3) và R = 4 . C. I (1; 2 − ;3) và R = 2 . D. I ( 1
− ; 2; −3) và R = 2 .  2 Câu 7: Cho tích phân I = x sin x dx
. Bằng cách đặt u = x, dv = sin x dx ta được: 0    2  2 A. = 2 I (x cos x) − cos xdx  . B. = − 2 I ( x cos x) − cos xdx  . 0 0 0 0    2  2 C. = 2 I (x cos x) + cos xdx  . D. = − 2 I ( x cos x) + cos xdx  . 0 0 0 0 Câu 8:
Trong không gian Oxyz , phương trình của mặt phẳng ( P) đi qua điểm B (2;1; − 3) , đồng thời vuông
góc với hai mặt phẳng (Q) : x + y + 3z = 0 , (R) : 2x − y + z = 0 là
A. 4x + 5 y − 3z + 22 = 0 .
B. 2x + y − 3z −14 = 0 .
C. 4x + 5 y − 3z − 22 = 0 .
D. 4x − 5 y − 3z −12 = 0 . Câu 9:
Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường: 2
y = x − x , y = 0 quanh trục Ox là:     A. V = (đvtt) . B. V = (đvtt) . C. V = (đvtt) . D. V = (đvtt) . 30 15 5 10
Câu 10: Trong không gian Oxyz , cho hai điểm A(1; 2; 3 − ) và B(3; 2 − ;− )
1 . Tọa độ trung điểm I của đoạn
thẳng AB là A. I (1; 2 − ) ;1 . B. I (1;0; 2 − ) . C. I (2;0; 2 − ) . D. I (4;0; 4 − ) . 3x 3x 3 d x xe
x = axe + be + C (a, b   ). Câu 11: Biết Tính tích ab . 1 1 1 1 A. ab = . B. ab = . C. ab = − . D. ab = − . 27 9 27 9
Câu 12: Góc tạo bởi hai véc tơ a = (2; 2; 4), b = (3; 3 − ;0) bằng A. 45 . B. 90 . C. 135 . D. 30 . 1 1 3 f
 (x)dx = 2 f  (x)dx = 6 I = f  (x)dx
Câu 13: Cho hàm số f ( x) liên tục trên và có 0 ; 3 . Tính 0 . A. I = −4 . B. I = 36 . C. I = 4 . D. I = 8 .
Câu 14: Cho biết F ( x) là một nguyên hàm của hàm số f ( x) trên ¡ . Tìm I = 2 f
 (x)+1dx
A. I = 2xF ( x) + x + C . B. I = 2F ( x) + x + C . C. I = 2F ( x) +1+ C . D. I = 2xF ( x) +1+ C .
Câu 15: Trong không gian Oxyz, cho mặt phẳng (P): 3x – 2y - 2z - 5 = 0 và điểm A(2;3;-1). Khoảng cách từ
điểm A đến mặt phẳng (P) bằng: 3 3 3 3 A. . B. . C. . D. . 17 7 17 7
Câu 16: Tìm nguyên hàm của hàm số ( ) x 2018 = (1 x f x e − e ) x e x e A. f  (x) 2018 d x
x = e (x − ) + C. B. f  (x) 2019 d x x = e + + C. 2018 2019 x e C. f  (x) 2019 d x x = e − + C. D.  ( ) x 2019 d = − 2019 x f x x e e + C. 2019
Câu 17: Hàm số F ( x) 2
= 2x + x là một nguyên hàm của hàm số: 2 x
A. f ( x) = 4x +1.
B. f ( x) = x +1 .
C. f ( x) = 2x +1. D. f ( x) 2 3 = x + . 3 2
Câu 18: Trong không gian Oxyz , một véctơ pháp tuyến của mặt phẳng ( ) : x − 2 y + 3z +1 = 0 là
A. n = (1; 2; − 3) .
B. n = (1; − 2; − 3) .
C. n = (3; − 2; ) 1 .
D. n = (1; − 2; 3) .
Câu 19: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f ( x) liên tục trên a;b và các đường
y = 0, x = a, x = b với (a b) là b b b b
A. S =  f x 2 ( ) dx . B. S =  f (x) dx  . C. S = f (x) dx  .
D. S =   f x 2 ( ) dx . a a a a 4 2
f (x)dx = 5  I = f (2x)dxCâu 20: Cho 2 . Tính 1 5 3
A. I = 5 . B . I = . C. I = 10 D. I = . 2 2
Câu 21: Thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong giới hạn bởi đồ thị hàm số y =
f(x), trục Ox và hai đường thẳng x = a, x = b (a b) xung quanh trục Ox là b b b b A. V = f (x) d . xB. 2 V =  f (x)d . xC. V =  f (x)d . xD. 2 V = f (x)d . xa a a a
Câu 22: Trong không gian với hệ tọa độ Oxyz , cho điểm M (3; 1 − ; 2
− ) và mặt phẳng(P) :3x − y + 2z + 4 = 0 .
Phương trình mặt phẳng đi qua M và song song với (P) là
A. 3x − y − 2z −14 = 0 . B. 3x + y − 2z −14 = 0 . C. 3x − y + 2z + 6 = 0 . D. 3x − y + 2z − 6 = 0 . e 3ln x +1
Câu 23: Cho tích phân I = dx
. Nếu đặt t = ln x thì x 1 e 1 1 e 3t +1 3t +1
A. I = (3t +  )1dt .
B. I = (3t +  ) 1 dt . C. I = dt  . D. I = dt  . et t 1 0 0 1
Câu 24: Trong không gian với hệ tọa độ Oxyz , cho các điểm A(1;0;3) , B (2;3; 4 − ) , C ( 3 − ;1;2) . Tìm tọa độ
điểm D sao cho tứ giác ABCD là hình bình hành. A. D (4; 2;9) . B. D (6; 2; 3 − ). C. D ( 4 − ; 2 − ;9) . D. D ( 2 − ;4; 5 − ).
Câu 25: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A( 2 − ;2; 2 − ) ; B(3; 3
− ;3) . Điểm M trong
không gian thỏa mãn MA 2
= . Khi đó độ dài OM lớn nhất bằng MB 3 5 3 A. 12 3 . B. . C. 6 3 . D. 5 3 . 2 1
Câu 26: Cho hàm số f (x) có đạo hàm liên tục trên , biết f (6) = 1 và
xf (6x)dx = 1  . Đặt 0 6 2
m = x f '(x)dx
. Mệnh đề nào sau đây đúng ? 0
A. 0  m  34 .
B. 5  m  37 . C. −5  m  0 .
D. m  −34 . Câu 27:
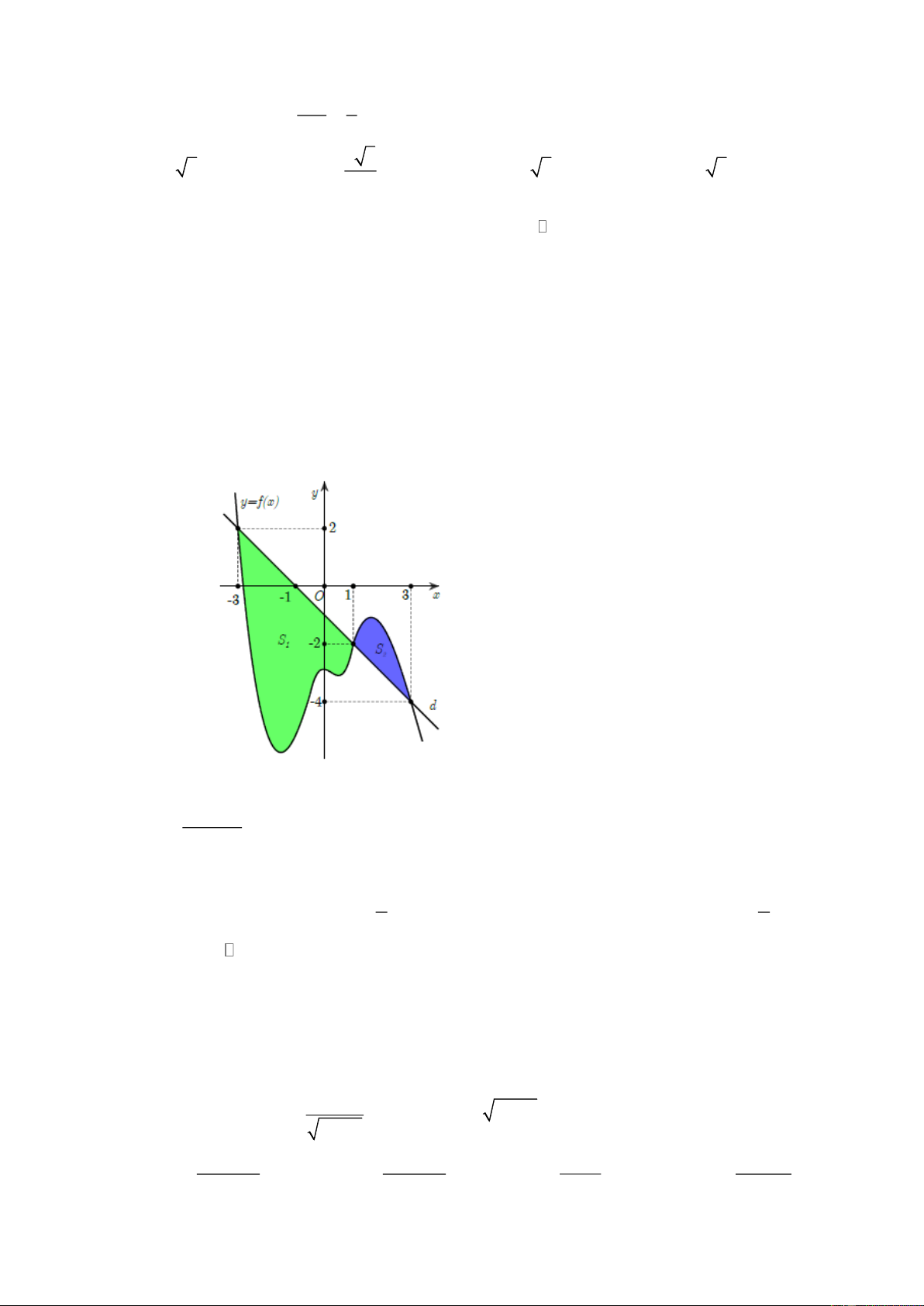
Cho hàm số y = f ( x) liên tục trên đoạn −3; 
3 . Biết rằng diện tích hình phẳng S , S giới hạn bởi 1 2 3
đồ thị hàm số y = f ( x) và đường thẳng d lần lượt là M , m . Tính tích phân f  (x)dx 3 −
A. 6 − m − M .
B. M − m + 6 .
C. 6 + m − M .
D. m − M − 6 . 1 xdx Câu 28: Cho = + +  + + (
a b n 2 c ln 3 với a, b, c là các số hữu tỷ. Giá trị của 3a b c bằng x + 2) l 2 0 A. 1 − . B. 1. C. 2 . D. 2 − . a Câu 29: Biết ( x − x)2 sin 2 cos 2 dx = x +
cos 4x + C , với a , b là các số nguyên dương, a là phân số tối b b
giản và C  . Giá trị của a + b bằng A. 4 . B. 5 . C. 2 . D. 3 .
Câu 30: Cho hàm số y = f (x) có đạo hàm trên 1; 2thỏa mãn ' ( +1) ( ) + ( ) = 2 x x f x xf x
e với mọi x 1; 2 ,biết
f (1) = e . Mệnh đề nào sau đây đúng?
A. e f (2)  3e .
B. −e f (2)  0 .
C. 4e f (2)  6e . D. 2 4
e f (2)  e . 1
Câu 31: Cho nguyên hàm I = dx  . Nếu đặt x t = e + 4 thì x e + 4 t 2 2t 2 A. I =  . B. I = dt  . C. I = dt  . D. I = dt  . t ( dt 2 t − 4) t ( 2 t − 4) 2 t − 4 ( 2t −4)
Câu 32: Trong không gian với hệ tọa độ Oxyz , mặt phẳng ( P) qua hai điểm M (1;8;0) , C (0;0;3) cắt các
tia Ox , Oy lần lượt tại A , B sao cho OG nhỏ nhất, với G ( ; a ;
b c) là trọng tâm tam giác ABC .
Tính T = a + b + c . A. T = 6 . B. T = 7 . C. T = 3 . D. T = 12 .
--------------------------------- HẾT -------------------------------
(Cán bộ coi thi không giải thích gì thêm). ĐÁP ÁN 1 B 6 C 11 C 16 C 21 B 26 D 31 D 2 B 7 D 12 B 17 A 22 D 27 D 32 A 3 D 8 C 13 A 18 D 23 B 28 A 4 C 9 A 14 B 19 C 24 C 29 B 5 D 10 C 15 A 20 B 25 A 30 A Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 4 MÔN TOÁN 12
Câu 1: Trong không gian Oxyz với hệ tọa độ ( ;
O i , j, k ) cho OA = 2
− i − 5k + j . Tìm tọa độ điểm A . A. ( 2 − ; 5 − ; ) 1 . B. ( 2 − ;1; 5 − ). C. ( 2 − ; 5 − ; ) 1 . D. (5; 2 − ; ) 1 .
Câu 2: Trong không gian với hệ trục tọa độ Oxyz , mặt phẳng đi qua ba điểm A(0;0;5) , B( 1 − ;0;0) và
C (0;3;0) có phương trình là: x y z x y z x y z x y z A. + + = 1. B. + + = −1. C. + + = 1 + − = . 2 1 3 1 3 5 − . D. 1 1 3 5 1 3 5
Câu 3: Trong không gian Oxyz , cho hai điểm A( 7 − ;2; 3 − ) và B(3; 2 − ;− )
1 . Tọa độ trung điểm I đoạn thẳng AB là: A. I ( 2 − ;0; 4 − ) . B. I ( 2 − ;0; 2 − ) . C. I (5;0; ) 1 . D. I (2;0; 2 − ).
Câu 4: Cho hình phẳng ( D) được giới hạn bởi các đường f ( x) = 7x +1 , Ox, x = 0, x = 1. Thể tích V của
khối tròn xoay tạo thành khi quay ( D) xung quanh trục Ox được tính theo công thức? 1 1 1 1 A. V =  7x +1dx
. B. V =  (7x +  )1dx . C. V = 7x +1dx  .
D. V = (7x +  )1dx . 0 0 0 0
Câu 5: Một vật thể được giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm x = a , x = b
(a < b), biết diện tích thiết diện bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x
(a £ x £ b) là S (x). Tính thể tích V của vật thể đó. b a a b A. 2 V = p S
ò (x)dx. B. V = p S ò (x)dx. C. V = S ò (x)dx. D. V = S ò (x)dx. a b b a
Câu 6: Cho hàm số f ( x) 3
= 2x + 5. Khẳng định nào dưới đây đúng? 1 A. f  (x) 4 dx =
x + 5x + C . B. f  (x) 4
dx = 4x − 5x + C . 2 1 1 C. f  (x) 4 dx = x + 5 + C . D. f  (x) 4 dx =
x + 5x + C . 2 4 3 Câu 7: Tích phân 2 x x +1dx  có giá trị là: 0 4 7 A. 7 . B. 3 − . C. . D. . 3 3
Câu 8: Cho hai hàm số y = f ( x) và y = g ( x) liên tục trên
. Trong các mệnh đề sau, mệnh đề nào sai? A. f
 (x)− g(x)dx = f
 (x)dx− g  (x)dx. B. f
 (x).g(x)dx = f
 (x)d .x g  (x)dx. C. f
 (x)+ g(x)dx = f
 (x)dx+ g  (x)dx . D. kf
 (x)dx = k f
 (x)dx với mọi hằng số k \  0 .
Câu 9: Trong không gian Oxyz , cho hai điểm A( 1 − ; 1
− ; 2) và B(2; 1; -5) . Tọa độ của AB bằng: A. AB = ( 3 − ;2; 7 − ).
B. AB = (3; 2; 7 − ).
C. AB = (3;0;3) . D. AB = (3; 2 ) ;1 .
Câu 10: Hình phẳng giới hạn bởi đồ thị hàm số y = f ( x) , trục hoành và hai đường thẳng x = a , x = b trong
hình dưới đây (phần gạch sọc) có diện tích S bằng: b c b A. | f  (x)dx|. B. f
 (x)dx+ f
 (x)dx . a a c c b c b C. f
 (x)dx− f  (x)dx. D. − f
 (x)dx+ f  (x)dx . a c a c
Câu 11: Cho hai hàm số u = u ( x) và v = v( x) có đạo hàm liên tục trên
. Khẳng định nào sau đây đúng? A. u
 (x)v'(x)dx = u'(x)v'(x)− u'
 (x)v(x)dx. B. u
 (x)v'(x)dx = u(x)v(x)− u'
 (x)v'(x)dx. C. u
 (x)v'(x)dx = u'(x)v(x)− u
 (x)v(x)dx . D. u
 (x)v'(x)dx = u(x)v(x)− u'
 (x)v(x)dx .
Câu 12: Hàm số F ( x) = sin 3x là nguyên hàm của hàm số: x
A. f ( x) = 3
− cos3x . B. f (x) cos3 = .
C. f ( x) = o c s3x .
D. f ( x) = 3cos3x . 3
Câu 13: Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng (P) : 2x − 3z −10 = 0 . Mặt phẳng ( P) có
một vectơ pháp tuyến là:
A. n = (2;− 3; ) n = (2; − 3) n = (2;− 3;0) n = (2;0;− ) 1 . B. . C. . D. 3 . f ( x)  2 − ;  3 F ( x) f ( x)
Câu 14: Cho hàm số liên tục trên đoạn . Gọi
là một nguyên hàm của hàm số trên  2 − ;  3 3 và F ( ) 3 = 8 − ; F ( 2 − ) = 4
− . Tính I = f  (x)dx. 2 − A. 4 . B. 4 − . C. 2 − D. 2 . 2 2 2
Câu 15: Trong không gian Oxyz , mặt cầu ( x − 4) + ( y − 2) + ( z + 3) = 25 có tâm và bán kính lần lượt là: A. I (4;2; 3
− ) ; R = 5. B. I ( 1 − ; 2
− ;3); R = 5. C. I (4;2; 3
− ) ; R = 25 . D. I (4; 2 − ;3) ; R = 2 .
Câu 16: Trong không gian Oxyz, cho mặt phẳng ( ) : x − y + 2z − 20 = 0 . Mặt phẳng nào dưới đây song song với ( )?
A. (S ) : x + y − 2z +1 = 0.
B. ( P) : x − y + 2z + 2 = 0.
C. (Q) : x + y − 2z −1 = 0.
D. (R) : x − y + 2z − 20 = 0.
Câu 17: Tìm họ nguyên hàm của hàm số ( ) 7x f x = . x+
A.  ( )d = 7x f x x ln 7 + C . B. f  (x) 1 7 dx = + C . x +1 x C. f  (x) 7 dx = + C .
D.  ( )d = 7x f x x + C . ln 7
Câu 18: Cho hàm số y = f ( x) liên tục trên khoảng K và a, ,
b c K . Mệnh đề nào sau đây sai? b a b b c A. f
 (x)dx = − f  (x)dx. B. f
 (x)dx+ f
 (x)dx = f  (x)dx. a b a c a b b a C. f
 (x)dx = f  (t)dt . D. f  (x)dx = 0 . a a a
Câu 19: Trong không gian Oxyz , cho mặt phẳng ( P) : 3x + 2y + 3z + 8 = 0 điểm nào sau đây thuộc mặt phẳng (P)? A. M (1;2;3) B. P (3; 2 − ;0) C. N (1; 1 − ; 3 − ) D. Q ( 1 − ; 1 − ; ) 1 1 3 f  (x)dx = 2 − , I = f  (x)d .x 3
Câu 20: Cho hàm số f ( x) liên tục trên R và có 0 và f
 (x)dx =8. Tính 0 1 A. I = 4 . B. I = 6 . C. I = 6 . D. I = 12 . 3 g  (t) − 3 dt = 3 3 Câu 21: Cho f
 (x)dx = 7 và 2
. Giá trị của A = 3 f
 (x)+5g(x)dx  là: 2 2 A. A = 6 . B. A = 1 − . C. A = 5 . D. A = 9 . Câu 22: Biết 4 x 4 x 4 d x xe x = axe
+ be + C (a, b 
). Tính tích a +b . 2 3 2
A. a + b = 0 .
B. a + b = − .
C. a + b = .
D. a + b = . 9 16 9
Câu 23: Cho hình phẳng ( H ) giới hạn bởi đồ thị 2
y = 3x − x và trục hoành. Tính thể tích V vật thể tròn xoay
sinh ra khi cho ( H ) quay quang Ox . 9 81 81 81 A. V =  . B. V = . C. V =  . D. V =  . 2 10 7 10
Câu 24: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = 2 o
c sx + 2, trục hoành và hai đường thẳng 5 x = 0 và x = . 6 5 3 7 5 A. −1 B. + +1 C. 1 + D. 6 3 2 3 3
Câu 25: Trong không gian Oxyz , cho hai điểm M ( 5 − ;2;3) và N ( 1
− ;4;− 7) . Mặt cầu đường kính MN có phương trình là: 2 2 2 2 A. 2
(x + 3) + ( y − 3) + ( z + 2) = 30 . B. 2
(x + 3) + ( y − 3) + ( z + 2) = 30 . 2 2 2 2 C. 2
(x + 3) + ( y + 3) + ( z + 2) = 81. D. 2
(x + 3) + ( y − 3) + ( z − ) 1 = 9 .
Câu 26: Trong không gian Oxyz, khoảng cách từ điểm A( 2 − ;4; 3
− ) đến mặt phẳng 2x − y − 2z −13 = 0 bằng: 1 −7 7 A. . B. . C. 5. D. . 3 3 3 5 2
Câu 27: Giả sử hàm số y = f ( x) liên tục trên và f
 (x)dx = 3a , (a ). Tích phân I = f (3x−  ) 1 dx có 2 1 giá trị là: 1
A. I = 2a .
B. I = a .
C. I = 2a +1 . D. I = a +1 . 2 2022 Câu 28: Tích phân = 8x I dx  bằng 0 2022 8 2022 8 −1 A. 2022 2021.8 . B. 2022 8 −1. C. . D. . ln 8 3ln 2
Câu 29: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A( 1
− ;6;9) và B(3;2;3) . Phương trình mặt
phẳng trung trực đoạn AB là:
A. 2x − 2 y − 3z +13 = 0 . B. 2x − 2 y − 3z + 24 = 0 . C. − − + = − + + = 2x 2 y 3z 23 0 .
D. x 2y 3z 17 0 . 4
Câu 30: Cho (4x +1) ln d
x x = a ln 4 + b
, (a,b  ) . Tính a + b . 1 −43 43
A. a + b = 18 .
B. a + b = .
C. a + b = .
D. a + b = 4 . 3 3 2 I = f  (x)dx 3 3  x khi 0  x  1
Câu 31: Cho hàm số f ( x) =  . Tính 0 . 8
 − 5x khi 1 x  2 1 3 5 A. I = − . B. I = 4 . C. I = . D. I = . 2 2 4
Câu 32: Cho hàm số f ( x) = ( − x)3 1 3
. Khẳng định nào dưới đây đúng? 1 A. f
 (x)dx = − (1−3x)4 +C . B. f
 (x) x = ( − x)4 d 4 1 3 + C . 12 1 1 C. f
 (x)dx = (1−3x)4 +C . D. f
 (x)dx = (1−3x)4 +C . 12 4
Câu 33: Trong không gian với hệ trục Oxyz , mặt phẳng chứa 2 điểm (
A 1; 0;1) và B ( 1 − ;2;2) và song song
với trục Oz có phương trình là
A. x + y −1 = 0 .
B. 2x + y −1 = 0 .
C. x + y +1 = 0 .
D. x − z − 2 = 0 . 
Câu 34: Trong không gian Oxyz , gọi
là góc giữa hai vectơ a = (1; 2 − ; 2 − ) và b = (2; 2 − ;− ) 1 . Tính cos . 2 8 8 A. − . B. 0. C. . D. . 9 9 9
Câu 35: Khi đặt t =
x −1 thì x x −1dx
được viết lại bởi kết quả nào: A. 4 2
(2t − t )dt  . B. 4 2
2 (t + t )dt  . C. 4 2
2 (t − t )dt  . D. 4 2
(t − t )dt  . ĐÁP ÁN 1 B 6 A 11 D 16 B 21 A 26 C 31 D 2 C 7 D 12 D 17 C 22 C 27 B 32 A 3 B 8 B 13 D 18 B 23 D 28 D 33 A 4 B 9 B 14 B 19 C 24 C 29 B 34 D 5 D 10 D 15 A 20 B 25 A 30 A 35 B
------ HẾT ------ Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 5 MÔN TOÁN 12
Câu 1: Cho hình phẳng (H ) giới hạn bởi các đường 2
y = x − 3 , y = 0 , x = 1 , x = 2 . Gọi V là thể tích của
khối tròn xoay được tạo thành khi quay (H ) xung quanh trục Ox . Mệnh đề nào dưới đây đúng? 2 2 2 2 A. 2
V = (x − 3)dx  . B. 2
V =  (x − 3)dx  . C. 2 2
V = (x − 3) dx  . D. 2 2
V =  (x − 3) dx  . 1 1 1 1
Câu 2: Trong không gian Oxyz cho ba điểm ( A 2; 3
− ;4), B(1; y; 1 − ),C( ;
x 4;3) . Để ba điểm ,
A B,C thẳng hàng
thì giá trị của 5x + y bằng: A. 23 − . B. 42 . C. 41 . D. 40 . 4 9 9 Câu 3: Nếu
f (x)dx = 2 −  và
f (x)dx = 1  thì f (x)dx  bằng 1 4 1 A. −1. B. 3 − . C. 1. D. 3 .
Câu 4: Trong không gian với hệ tọa độ Oxyz , cho tứ diện ABCD có đỉnh (
A 8;14;10) , AD, AB, AC đôi một
vuông góc. Viết phương trình mặt phẳng ( BCD) biết trực tâm tam giác BCD là H (7;16;15) . x y z x y z
A. x + 2 y − 5z − 50 = 0 B. + + = 3
x − y − z + = D. + + = 1 7 −16 − C. 2 5 100 0 15 7 −16 1 − 5
Câu 5: Trong không gian Oxyz, cho hai mặt phẳng ( ) : 2x − y + 2z − 5 = 0 và ( ) : 2x − y + 2z + 9 = 0 .
Khoảng cách giữa ( ) và ( ) bằng 14 14 4 4 A. . B. . C. . D. . 3 9 9 3
Câu 6: Cho F (x) là một nguyên hàm của 3
f (x) = 4x − 3 , biết F (1) = 2 . Tính F (2) . A. F (2) = 8 . B. F (2) = 10 . C. F (2) = 14 . D. F (2) = 76 .
Câu 7: Trong không gian Oxyz , cho mặt cầu (S ) có tâm I (2;1;1) và mặt phẳng (P) :2x − y − 2z + 8 = 0 . Mặt
phẳng (P) cắt mặt cầu (S ) theo giao tuyến là một đường tròn có bán kính bằng 1. Tìm phương trình mặt cầu (S ) . A. 2 2 2
(x + 2) + ( y +1) + (z +1) = 10 . B. 2 2 2
(x + 2) + ( y +1) + (z +1) = 8 . C. 2 2 2
(x − 2) + ( y −1) + (z −1) = 10 . D. 2 2 2
(x − 2) + ( y −1) + (z −1) = 8 . ln 2 Câu 8: Cho x ( = −1) x xe dx x e + C  và 2 x 2
x e dx = a ln 2 + b ln 2 + c
.Tính P = a + b + . c 0 A. P = 16. − B. P = 12. − C. P = 6. − D. P = 0.
Câu 9: Trong không gian Oxyz , cho điểm M ( 1 − ; 2
− ;3) . Tìm tọa độ điểm N đối xứng với M qua mặt phẳng (Oxy) A. N ( 1 − ; 2 − ;3) .
B. N (1; 2; 0) . C. N ( 1 − ; 2 − ; 3 − ) . D. N (1; 2; 3 − ) .
Câu 10: Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 3 y = x +1 , 2
y = x − 2x +1và trục Ox là. 5 13 2 7 A. . B. . C. . D. . 12 12 3 12 4
Câu 11: Tìm họ nguyên hàm của hàm số 3 2 ( ) 4 x f x x e + = . 4 4 1 4 4 A. x +2 e + C . B. x +2 + + e + C . C. x 2 −e + C . D. 2 4 x e + C . 4
Câu 12: Cho hai hàm số f (x), g(x) liên tục trên  ;
a b và k là số thực khác không thì mệnh đề nào sau đây sai. b b b b A.
f (x)g(x)dx =
f (x)dx g(x)dx    . B. f (
x)dx = f (x) b  . a a a a a b b b b b
C. kf (x)dx = k f (x)   .
D.  f (x) + g(x)dx = f (x)dx + g(x)dx   . a a a a a
Câu 13: Cho hàm số y = f (x) liên tục trên đoạn  ;
a b . Gọi D là miền hình phẳng giới hạn bởi đồ thị hàm số
y = f (x) , trục hoành và các đường thẳng x = a, x = b(a b) . Diện tích S của D cho bởi công thức nào sau đây? b b b b A. 2 S = f (x)dx  . B. 2
S =  f (x)dx  . C. S = f (x) dx  . D. S = f (x)dx  . a a a a 1
Câu 14: Tìm họ nguyên hàm dx  3x −1 1 1 1 1 A. dx = ln 3x −1 + C  . B. dx = ln(3x −1) + C  . 3x −1 3 3x −1 3 1 1 C.
dx = 3ln 3x −1 + C  . D.
dx = 3ln(3x −1) + C  . 3x −1 3x −1
Câu 15: Trong không gian Oxyz cho vectơ a = (0; 2; −1) , b = (2; − 3;3) , c = (0; 2;1) . Tìm tọa độ vectơ
u = 3a + 2b + c .
A. u = (2;1;3) .
B. u = (4; 2; 4) .
C. u = (4; − 2; 2) .
D. u = (2;1; 2) . 4 x
Câu 16: Tính K = dx  . 2 x − 4 3 1 12 1 12 12 A. K = ln . B. K = ln . C. K = ln . D. K = 4 ln 2 . 2 5 3 5 5
Câu 17: Tìm họ nguyên hàm sin(4 − 2x)dx  1
A. sin(4 − 2x)dx = −
cos(4 − 2x) + C  .
B. sin(4 − 2x)dx = 2 cos(4 − 2x) + C  . 2 1
C. sin(4 − 2x)dx =
cos(4 − 2x) + C  .
D. sin(4 − 2x)dx = 2
− cos(4 − 2x) + C  . 2
Câu 18: Tìm nguyên hàm của hàm số 2022 3 ( ) x f x e + = 1 A. 2022 +3 + ( ) x f x dx = e + C  . B. 2022 x 3 f (x)dx = e + C  . 3 1 C. 2022 x+3 f (x)dx = e + C  . D. 2022 +3 ( ) = 2022 x f x dx e + C  . 2022
Câu 19: Trong không gian Oxyz , cho hai điểm ( A 2; 4; 1 − ), B( 2
− ;2;3) . Phương trình mặt cầu đường kính AB là. A. 2 2 2
x + ( y − 3) + (z+1) = 3 . B. 2 2 2
x + ( y + 3) + (z −1) = 9 . C. 2 2 2
x + ( y − 3) + (z+1) = 9 . D. 2 2 2
x + ( y − 3) + (z −1) = 9 . 2 2 Câu 20: Biết
f (x)dx = 3 −  . Giá trị của 2
2 f (x)dx −3x dx    bằng. 2 − 2 − A. 40 − . B. 8 − . C. 19 − . D. −22 .
Câu 21: Biết F (x) là một nguyên hàm của hàm số f (x) trên
và F (1) = 6 , F (e) = 2 . Tính giá trị của e f (x)dx  bằng. 1 A. e −1. B. 8 . C. 4 . D. 4 − . 2019 Câu 22: Tính 2022x dx  1 2019 2022 − 2022 2019 2022 2019 2022 − 2022 A. . B. . C. . D. 2019 2022 − 2022 . ln 2022 ln 2022 ln 2022
Câu 23: Cho hàm số f (x) có đạo hàm f (
x) liên tục trên và thỏa mãn f (x) = 2xf (x) , x   ; Biết 1
f (0) = 4 và f (x)  0 , x
  . Tính xf (x)dx  . 0 7 A. 2e − 2 . B. . C. 2e −1. D. 2 e . 2
Câu 24: Trong không gian Oxyz , cho mặt phẳng (P) : 2x + 2 y + z − 5 = 0 và điểm M ( 4 − ; 3 − ;1). Tính khoảng
cách từ M đến (P) . A. 9 . B. 18 . C. 7 . D. 6 . 1 2 3x
Câu 25: Cho tích phân I = dx  , giả sử đặt 3
t = x + 2 . Tìm mệnh đề đúng. 3 + 0 x 2 3 dt 1 1 dt 3 1 dt 3 dt A. I = 3 . B. I =  . C. I =  . D. I =  . t 3 t 3 t t 2 0 2 2
Câu 26: Trong không gian Oxyz , cho hai điểm ( A 4; 2; 3
− ), B(0;0;3) . Khi đó tọa độ trung điểm I của đoạn thẳng AB .
A. I (2;1; 0) . B. I (2;1; 2) . C. I (2; 1 − ; 1 − ) . D. I (2; 1 − ;2) .
Câu 27: Họ nguyên hàm của hàm số f (x) = 3sin x + 2023 là
A. 3cos x + 2023x + C . B. −3 o
c sx + 2023x + C . C. 3
− cos x + 2023x .
D. −3cos x + 2023 + C .
Câu 28: Hình (H ) giới bởi các đường 2
y = x , y = 3x . Thể tích vật thể tròn xoay khi (H ) xoay quanh trục Ox a bằng 
giá trị của a + 2b là. b A. 141. B. 157 . C. 172 . D. 131. 1
Câu 29: Tính tích phân 2 (2 − 2) x x e dx  bằng 0 2 5 − − 3e 2 3 − e 2 5 + 3e A. . B. . C. . D. 2 2 − e . 4 2 4
Câu 30: Khẳng định nào sau đây đúng? dx 1 dx dx dx 1 A. = − + C  . B. = ln(x +1) + C  . C. = ln x +1 + C  . D. = − + C  . x +1 x +1 x +1 x +1 2 x +1 (x +1)
Câu 31: Biết x cos 2xdx = ax sin 2x + b cos 2x + C
với a, b là các số hữu tỉ. Tính a + b ? 1 3 1 1 A. . B. . C. − . D. − . 4 4 4 8
Câu 32: Mặt phẳng nào sau đây có vectơ pháp tuyến n(3; 1 − ; 7 − ) ?
A. 6x − 2 y +14z −1 = 0 . B. 3x − y − 7z +1 = 0 .
C. 3x + y − 7 = 0 .
D. 3x + z − 7 = 0 .
------ HẾT ------ ĐÁP ÁN ĐÁP ÁN 1 D 6 C 11 A 16 A 21 D 26 A 31 B 2 C 7 C 12 A 17 C 22 C 27 B 32 B 3 A 8 D 13 C 18 C 23 A 28 C 4 C 9 C 14 A 19 D 24 D 29 B 5 A 10 B 15 B 20 D 25 D 30 C Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 6 MÔN TOÁN 12
Câu 1. Trong các mệnh đề sau, mệnh đề nào sai ?  1 +  x
A. sinxdx = cos x + CB. x x d = + C    −  ( 1 ) +1 1 C. xd x
e x = e + C  . D.
dx = ln x + C  . x
Câu 2. Trong không gian Oxyz , hình chiếu vuông góc của điểm M (2;1; − )
1 trên mặt phẳng (Oxz) có tọa độ là: A. (0;1;0) . B. (2;1;0) . C. (0;1; − ) 1 . D. (2;0; − ) 1 .
Câu 3. Cho f ( x), g ( x) là các hàm số liên tục trên R . Tìm khẳng định đúng trong các khẳng định sau? f (x)dx f (x)  A. k. f
 (x)dx = k + f
 (x)dx với k là hằng số B. dx =  g(x) g(x)dx  C.f
 (x).g(x)dx = f
 (x)d .x g  (x)dx D.f
 (x)+ g(x)dx = f
 (x)dx + g  (x)dx
Câu 4. Cho hàm số y = f ( x) liên tục trên  ;
a b . Diện tích hình phẳng S giới hạn bởi đường cong y = f ( x) ,
trục hoành và các đường thẳng x = a , x = b được xác định bởi công thức nào sau đây? b b b a A. S = f
 (x)dx . B. S = f
 (x)dx . C. S = f
 (x) dx . D. S = f  (x) dx . a a a b
Câu 5. Trong không gian Oxyz với hệ tọa độ ( ;
O i ; j; k ) cho OA = 2i − 3 j + 5k . Tìm tọa độ điểm A ? A. (−2;3;0) . B. ( 2 − ;3; 5 − ) . C. (−2;3;5) . D. (2; −3;5) .
Câu 6. Nếu u = (x) và v = v(x) là 2 hàm số có đạo hàm liên tục trên đoạn K thì:
A. ∫ 𝑢. 𝑑𝑣 = 𝑢. 𝑣 − ∫ 𝑣. 𝑑𝑢
B. ∫ 𝑢. 𝑑𝑣 = 𝑢. 𝑣 + ∫ 𝑣. 𝑑𝑢
C. ∫ 𝑢. 𝑑𝑣 = 𝑢. 𝑣 − ∫ 𝑢. 𝑑𝑣
D. ∫ 𝑣. 𝑑𝑢 = 𝑢. 𝑣 − ∫ 𝑣. 𝑑𝑢
Câu 7. Trong không gian Oxyz , cho u = (1;3;5), v = (2;3 )
;1 . Tọa độ của u + v là: A. (3;6;6) B. (1; 2; 2) C. (−1;0; 4) D. (3;6;5)
Câu 8. Xét hàm số f ( x) , F ( x) là một nguyên hàm của f ( x) trên đoạna;b . Mệnh đề nào dưới đây đúng ? b b A. f
 (x)dx = F (b)− F (a). B. f
 (x)dx = F (a)− F (b). a a b b C. f
 (x)dx = F (a)+ F (b). D. f
 (x)dx = −F (a)− F (b). a a
Câu 9. Trong không gian Oxyz, cho mặt phẳng (P) : 3x − 5 y + 2z − 9 = 0. Một vectơ pháp tuyến của mặt
phẳng (P) là: A. n = (4; 6 − ;5). B. n = ( 3 − ;5;2). C. n = (3; 5 − ;2). D. n = (2; 3 − ; 7 − ).
Câu 10. Hình cong giới hạn bởi đồ thị hàm số y = f ( x) , trục Ox , hai đường thẳng x = a và x = b (a b)
quay quanh trục Ox tạo thành một khối tròn xoay có thể tích là: b b b b A. 2 V = f  (x)dx . B. 2 V =  f
 (x)dx . C. V = f
 (x)dx . D. V = f  (x)dx . a a a a 2 2 2
Câu 11. Trong không gian Oxyz , cho mặt cầu (S ) : ( x − 2) + ( y + 4) + ( z − ) 1
= 9 . Xác định tọa độ tâm I và
bán kính R của mặt cầu (S ). A. I ( 2 − ;4;− ) 1 ; R = 9 . B. I (2; 4 − )
;1 ; R = 3 . C. I (2; 4; )
1 ; R = 9 . D. I (2; 4 − ) ;1 ; R = 3 2
Câu 12. Tính tích phân (2x-1)dx  bằng: 0 A. 1. B. 2 . C. 3 . D. 0 . 4 4
Câu 13. Cho f ( x), g ( x) là các hàm số liên tục trên 1; 4. Nếu
f (x)dx = 6 −  và
g(x)dx = 5 −  thì 1 1
4 [f (x) − g(x)]dx  bằng: 1 A. 1 − . B. −11. C. 1 . D. 11.
Câu 14. Trong không gian Oxyz , cho mặt phẳng ( P) : x + 2 y − 6z −1 = 0 . Trong các điểm sau đây, điểm nào thuộc mặt phẳng (P)? A. P ( 3 − ;2;0) .
B. N (1; 2; − 6) . C. M ( 1; − − 4; ) 1 . D. Q ( 1; − − 2; ) 1 . 4
Câu 15. Cho hàm số f ( x) có đạo hàm liên tục trên đoạn1; 4 và f ( ) 1 = 2 , f '
 (x)dx =10.Tính f (4). 1 A. 12. B. 8. C. - 8. D. 5.
Câu 16. Cho F (x ) là một nguyên hàm của hàm số ( ) x
f x = e + 2x thỏa mãn F (0) = 0 . Tìm F (x ) . A. x 2
F (x ) = e + x + 1. B. x 2
F (x ) = 2e + x - 1. C. x 2
F (x ) = e + x - 1. D. x 2
F (x ) = e + x .
Câu 17. Trong không gian với hệ toạ độ Oxyz , cho mặt phẳng ( P ) : 2x − y − 2z − 4 = 0 và điểm ( A −1; −2; 2) .
Tính khoảng cách d từ A đến mặt phẳng ( P) ? 4 8 2 5 A. d = B. d = C. d = D. d = 3 3 3 9 Câu 18. Cho hàm số 2
f (x) = x + 3 . Khẳng định nào sau đây đúng? 3 x A. 2
f (x)dx = x + 3x + CB. f (x)dx = + 3x + C  . 3 C. 3
f (x)dx = x + 3x + C  . D.
f (x)dx = 2x + C  . 5 3 5
Câu 19. Cho hàm số f ( x) liên tục trên đoạn 1;5 . Nếu f
 (x)dx = 7 và f
 (x)dx = 2 thì f (x)dx có giá trị  1 1 3 bằng: A. 5 − . B. 9 . C. 9 − . D. 5 .
Câu 20. Trong không gian Oxyz, cho mặt phẳng (Q) : 2x + y – 3z - 1 = 0 . Viết phương trình tổng quát
của mặt phẳng song song với (Q) và qua điểm A(2,3,4) ?
A. 2x + y – 3z = 0.
B. 2x + y – 3z + 5 = 0.
C. 2x + y – 3z +1 = 0.
D. 2x + y – 3z - 5 = 0.  Câu 21. Tích phân 2 cos x.sin xdx bằng:  0 2 3 A. − 2 B. C. D. 0 3 3 2
Câu 22. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = −x + 4x − 3, trục Ox và hai đường thẳng
x = 1; x = 2 là: 1 2 10 8 A. B. C. D. 3 3 3 3
Câu 23. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2; 1 − ;3), B(4;0 ) ;1 và C ( 10 − ;5;3). Véctơ nào
dưới đây là véctơ pháp tuyến của mặt phẳng ( ABC ) ?
A. n = 1; 2; 0 .
B. n = 1; 2; 2 . C. n = 1;8; 2 . D. n = 1; 2 − ;2 . 4 ( ) 3 ( ) 2 ( ) 1 ( ) ln x
Câu 24. Khi tính nguyên hàm dx 
, bằng cách đặt t = ln x + 1 ta được nguyên hàm nào sau đây? x ln x + 1 2 A. 2 2(t −1)dt  B. 3 ( t − 2t)dt  3 2 C. 3 ( t + 2t)dt  D. 2 2(t +1)dt  3
Câu 25. Trong không gian Oxyz, cho hai điểm A( 2 − ;1 ) ;1 , B (0; 1 − )
;1 . Phương trình mặt cầu đường kính AB là: 2 2 2 2 A. ( x + ) 2
1 + y + ( z − ) 1 = 8 . B. ( x + ) 2
1 + y + ( z − ) 1 = 2. 2 2 2 2 C. ( x + ) 2 1 + y + ( z + ) 1 = 8 . D. ( x − ) 2
1 + y + ( z − ) 1 = 2.
Câu 26. Cho phần hình phẳng (H) giới hạn bởi các đường 2
y = x − 2x , y = 0 quanh trục Ox ta thu được khối
tròn xoay có thể tích V bằng: 16    A. V = 16 B. V = 16 C. V = 15 D. V = . 3 5 15 16
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho điểm (
A 1;1; 0) , mặt phẳng (P) và mặt cầu (S) lần lượt có
phương trình 3x + 6y − 2z − 23 = 0 , 2 2 2 2
x + y + z − 2x − 2 y − m = 0 . (P) cắt (S) theo giao tuyến là một đường tròn có bán kính bằng 2
OA , khi đó số dương m thuộc khoảng nào sau đây ? 5 9 5 9 A. m  (2; ) B. m  (4; ) C. m  ( ;3) D. m  (4; ) 2 2 2 4 2 a ln 2 + b Câu 28. Biết I = ( 2 x − ) 1 ln xdx = 
; a, b, c là các số nguyên có ước chung lớn nhất bằng 1. c 1 Tính 𝑎 − 𝑏 + 𝑐 ? A. 5 B. 13 C. 1 D. 17
Câu 29. Trong không gian Oxyz, cho M (6;3; 2) .Gọi (P) là mặt phẳng qua M cắt các tia ;
Ox Oy;Oz lần lượt tại các điểm ; A ;
B C sao cho OA = 2OB = 3OC . Khi đó (P) qua điểm nào trong các điểm sau? A. (0; 6; 0). B. (0;9; 0). C. (0;8; 0). D. (6; 0; 0). Câu 30. Cho hàm số ( ) 3 2
f x = ax + bx + cx + d (a  0) và đường thẳng y = g ( x) = mx + n là tiếp tuyến của đồ 3
thị hàm số f ( x) tại điểm có hoành độ x = − (tham khảo hình vẽ). Khi đó diện tích phần được tô đậm trong 2 hình vẽ bằng: 2041 2104 2410 2401 A. . B. . C. . D. . 567 576 567 576
Câu 31. Trong không gian với hệ tọa độ Oxyz , cho A( ; a 0;0) , B (0; ;
b 0) , C (0;0;c) với a , b , c dương thỏa
mãn a + b + c = 4 . Biết rằng khi a , b , c thay đổi thì tâm I mặt cầu ngoại tiếp tứ diện OABC thuộc mặt phẳng
(P) cố định. Tính khoảng cách d từ M (1; 1 − ;− )
1 tới mặt phẳng ( P) ? 3 3 A. d = 3 . B. d = . C. d = . D. d = 0 . 2 3
Câu 32. Cho hàm số y = f ( x) liên tục trên đoạn [0; a] , biết rằng với mọi x [0; a] ta có f (x)  0 và 2 a x d
f (x). f (a − x) = k (với k là hằng số, k >0). Giá trị của tích phân  bằng:
0 k + f (x) a a ak A. . B. .
C. T = ak . D. T = . k 2k 2 - Hết –
(Giám thị coi thi không giải thích gì thêm) ĐÁP ÁN 1 A 6 A 11 B 16 C 21 B 26 C 31 A 2 D 7 A 12 B 17 B 22 B 27 A 32 B 3 D 8 A 13 A 18 B 23 B 28 B 4 C 9 C 14 A 19 D 24 A 29 B 5 D 10 B 15 A 20 B 25 B 30 D Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 7 MÔN TOÁN 12 x + x −
Câu 1. Họ nguyên hàm của hàm số f ( x) 3 2 3 2 3 = là: x 3 3 2 3 2 A. 6x + 2 + + C. B. 3 2
x + x − 3ln x + C. C. x + x + 3ln x + C. D. x + x − 3ln x + C. 2 x
Câu 2. Cho hai vectơ a = ( 1 − ;2;5), b = (2; 5
− ;4).Tích vô hướng của hai véc tơ a .b bằng: A. -28. B. 12. C. -32. D. 8. 2 2 f '( x)
Câu 3. Cho hàm số f ( x) có đạo hàm liên tục trên 1; 2 thỏa mãn f '
 (x)dx = 5 và dx = ln 2  . Biết rằng f x 1 ( ) 1
f ( x)  0, x
 1;2 , tính f (2) bằng: A. 2. B. 5. C. 3. D. 10.
Câu 4. Gọi F ( x) là một nguyên hàm của hàm số f(x) liên tục trên a;b. Trong các đẳng thức sau, đẳng thức nào là sai? b b A. f '
 (x)dx = f (b)− f (a). B. f
 (x)dx = F (a) − F (b). a a a b b C. f  (x)dx = 0. D.
f ( x) dx =
f (t ) dt = F (b) F −   (a). a a a
Câu 5. Mệnh đề nào dưới đây đúng? A. cos d
x x = − cos x + C.  B. cos d
x x = sin x + C.  1 C. 2 cos d x x = cos x + C.  D. cos d
x x = − sin x + C.  2
Câu 6. Trong không gian Oxyz Cho 2 điểm A(2; 1; 4), B(-2; 2; -6). Tọa độ véc tơ AB là: A. AB = ( 4
− ;1;10) . B. AB = ( 4 − ;1; 10 − ) C. AB = (4; 1 − ;10) .
D. AB = (0;3; 2) − . a
Câu 7. Diện tích hình phẳng được giới hạn bởi các đường 2
y = x - 2x và y = x là S = . b a
Trong đó . là phân số tối giản kết quả nào sau đây đúng? b
A. a = 3b. B. a + b = -11. C. a.b =18. D. 2a = b. 1
Câu 8. Kết quả tích phân = ( + 2) x I x e dx ò
được viết dưới dạng I = ae + b với ,
a b Î ¤ . Khẳng định nào sau 0 đây là đúng?
A. a + b = 3. B. a - b = 2. C. a + 2b = 0. D. a.b = 3.
Câu 9. Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P) đi qua điểm H(2; 1;1) và cắt các trục Ox, Oy,
Oz lần lượt tại A; B; C (khác gốc toạ độ O) sao cho H là trực tâm tam giác ABC, phương trình mặt phẳng (P) là:
A. 2x+ y - z + 6 = 0. B. 2x+ y + z - 6= 0.
C.2x + y + z+ 6 = 0. D. 2x - y + z +6 = 0.
Câu 10. Trong không gian với hệ tọa độ Oxyz, cho điểm I(1;2;-2) và mặt phẳng
(P): 2x + 2y + z + 5 = 0. Viết phương trình mặt cầu (S) có tâm I sao cho mặt phẳng (P) cắt mặt cầu (S) theo
giao tuyến là một đường tròn có chi vi bằng 8 .  2 2 2 2 2 2 A. ( x − )
1 + ( y − 2) + ( z + 2) = 25. B. ( x − )
1 + ( y − 2) + ( z + 2) = 5. 2 2 2 2 2 2 C. ( x + )
1 + ( y + 2) + ( z − 2) = 5. D. ( x + )
1 + ( y + 2) + ( z − 2) = 25.
Câu 11. Khẳng định nào sau đây là sai? A. f '
 (x)dx = f (x) + C. B.f
 (x)+ g(x) dx = f
 (x)dx + g
 (x)d .x C. kf
 (x)dx = k f
 (x)dx, k là hằng số khác 0. D.f
 (x)g(x) dx = f
 (x)d .x g
 (x)d .x
Câu 12. Viết phương trình mặt phẳng(P)đi qua điểm A(2;-1;2)và có VTPT n = (1; 3 − ;4) .
A. (P): x - 3y + 4z -13 = 0.
B. (P):2x - y + 2z + 3 = 0.
C. (P): -x - 3y + 4z + 13 = 0. D. (P):2x - y + 2z - 13 = 0. ln (ln x )
Câu 13. Tính nguyên hàm I = dx ò
được kết quả nào sau đây? x
A. I = ln x. ln (ln x )- ln x + C. B. I = ln x. ln (ln x )+ ln x + C.
C. I = ln (ln x )+ ln x + C. D. I = ln x. ln (ln x )+ C. x
Câu 14. Tìm nguyên hàm của hàm số f ( x) cos = 1+ ? s inx
A. F (x) = ln 1+ osx c + C.
B. F (x) = ln 1− sinx + C.
C. F (x) = ln 1+ s inx + C.
D. F (x) = ln 1− osx c + C.
Câu 15. Biết hàm số F ( x) là một nguyên hàm của hàm số f ( x) x 1 = e + và F ( ) 1 = .
e Tìm F ( x) ? x x A. F ( x) 2 = ex + . B. ( ) = ex F x + ln x .
C. F ( x) x 1
= e − . D. ( ) = ex F x − ln x . 2 x 1 4 4
Câu 16. Biết f
 (x)dx = 3, f
 (x)dx = 7 .khi đó f (x)dx  có kết quả là: 0 0 1 A. -4. B. 4. C. 5. D. 10. 1 2x
Câu 17. Biết rằng I = dx = ln a ò
với a Î R . Khi đó giá trị của a bằng: 2 x + 1 0 1 A. a = 2. B. a = . C. a =4. D. a=2. 2
Câu 18. Diện tích của hình phẳng giới hạn bởi: (C ) : y = ln ;
x d : y = 1; d : y = −x +1 là: 1 2 3 1 1 3 A. e − . B. e + . C. e − . D. e + . 2 2 2 2
Câu 19. Phương trình mặt cầu tâm I(1; 2; - ) 3 ,bán kính R = 5 là: A. 2 2 2
(x + 1) + (y + 2) + (z - 3) = 25 B. 2 2 2
(x - 1) + (y - 2) + (z + 3) = 5. C. 2 2 2
(x - 1) + (y - 2) + (z + 3) = 25. D. 2 2 2
(x + 1) + (y + 2) + (z - 3) = 5. e ln x +1 Câu 20. Cho I = dx
và đặt u = lnx+1. Chọn khẳng đúng trong các khẳng định sau: x 1 e du e 2 du 2 A. I= .  B. I= udu  . C. I= .  D. I= udu  . u u 1 1 1 1
Câu 21. Mặt phẳng (P): 3x -5y + 8z -12 = 0 có một véctơ pháp tuyến là: A. n = (3; 3 − ;8).
B. n = (3;5;8) . C. n = (5; 8 − ;12). D. n = (3; 5 − ;8)
Câu 22. Cho hai mặt phẳng (P): 2x + y -3z + 1 = 0 và (Q): 4x + 2y - 6z - 3 = 0. Khẳng định nào sau đây đúng?
A. (P) vuông góc với (Q). B. (P) song song (Q). C. (P) trùng (Q). D. (P) cắt (Q).
Câu 23. Khoảng cách từ điểm M(-2; -4; 3) đến mặt phẳng (P): 2x - y + 2z - 3 = 0 bằng: A. 1. B. 3. C. 4. D. 2.
Câu 24. Tìm nguyên hàm của hàm số ( ) x f x = xe A.  ( ) 2 x
f x dx = x e + C . B.  ( ) x
f x dx = xe + C . C.  ( ) = ( + ) 1 x f x dx x e + C D.  ( ) = ( − ) 1 x f x dx x e + C
Câu 25. Cho hàm số f (x ) liên tục trên đoạn [ ;
a b]. Hãy chọn mệnh đề sai dưới đây: b b b b b A. k . f(x)dx = k
f(x)dx (" k Î R ) ò ò . B. [f (x)± ( g x )]dx =
f (x )dx ± g(x )dx ò ò ò . a a a a a b c b b a C.
f (x )dx =
f (x )dx + f (x )dx ò ò ò với c Î [ ; a b]. D.
f (x )dx = f (x )dx ò ò a a c a b
Câu 26. Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f (x ) liên tục trên [a;b], trục hoành và
hai đường thẳng x = a, x = b được tính theo công thức: 0 b 0 b A.S =
f (x )dx − 
f (x )dx. B.S =
f (x )dx + 
f (x )dx. a 0 a 0 b b
C. S =  f (x ) dx.
D. S =  f (x )dx. a a
Câu 27. Thể tích khối tròn xoay sinh ra do quay hình phẳng giới hạn bởi các đường 3
y = x , trục Ox,
x = - 1, x = 1 một vòng quanh trục Ox là: 6p 2p A. . B. . C. 2p. D. p. 7 7 2
Câu 28. Đặt I = (2mx + ò )
1 dx (m là tham số thực). Tìm m để I = 4 . 1 A. m = 1. B. m = - 1 . C. m = 2 . D. m = - 2 .
Câu 29. Thể tích khối tròn xoay được tạo thành khi quay quanh trục Ox hình phẳng (H) được giới hạn bởi các
đường sau:y = f (x ), trục Ox và hai đường thẳng x = a, x = b (a  b) là: b b 2 2 A. V = 
2  f (x )dx.
B. V =  f (x )dx. a a b b 2
C. V =  f (x )dx.
D. V =  f (x )dx. a a
Câu 30. Cho a = (2; -3; 3), b = (0; 2; -1). Khi đó tọa độ của vecto u = 2a + 3b bằng: A. (2; -1; 2). B. (4; 0; 3). C. (4; -12; 3). D. (-2; 5; -4).
Câu 31. Cho hai mặt phẳng (P): 3x + 3y -z + 1 =0 và (Q): (m-1)x + y - (m+2)z - 3 = 0. Xác định m để hai mặt
phẳng (P), (Q) vuông góc với nhau. 1 3 1 A. m = . B. m = − . C. m =2. D. m = − . 2 2 2
Câu 32. Cho hai hàm số u = u ( x) , v = v ( x) có đạo hàm liên tục trên tập K . Công thức tính nguyên hàm từng phần là:
udu = uv + vd . u  
udv = uv − vd . u  
udu = uv − vd . u  
udv = uv + vd . u   A. B. C. D. =====HẾT===== ĐÁP ÁN 1 D 6 B 11 D 16 B 21 D 26 C 31 D 2 D 7 C 12 A 17 D 22 B 27 B 32 B 3 D 8 C 13 A 18 A 23 A 28 A 4 B 9 B 14 C 19 C 24 D 29 B 5 B 10 A 15 B 20 D 25 D 30 B Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 8 MÔN TOÁN 12
Câu 1. Trong không gian Oxyz , mặt phẳng (Oxy) có phương trình là
A. y = 0 .
B. x = 0 .
C. x + y = 0 . D. z = 0 .
Câu 2. Trong không gian Oxyz , cho các điểm A(2; 2 − ) ;1 , B (1; 1
− ;3) . Tìm tọa độ của vectơ AB .
A. (3; −3; 4) .
B. (−1;1; 2) . C. (1; 1 − ; 2 − ) . D. ( 3 − ;3; 4 − ) . 3
Câu 3. Cho hàm số f (x) =
+ 2x . Trong các khẳng định sau, khẳng định nào đúng? 2 cos x A.
f (x)dx = 3 tan x + 2 + C  . B. 2
f (x)dx = 3
− tan x + x + C. C. 2
f (x)dx = 3 tan x + x + C  . D.
f (x)dx = 3
− tan x + 2 + C. 2 5 5 Câu 4. Nếu f
 (x)dx = 3, f (x)dx = 1 −  thì f ( x) dx  bằng 1 2 1 A. 3 . B. 4 . C. 2 . D. 2 − .
Câu 5. Trong không gian Oxyz , điểm nào sau đây là hình chiếu vuông góc của điểm (
A 1; 4; 2) trên mặt phẳng Oxy ? A. (1; 0; 2) . B. (1; 4; 0) . C. (0; 0; 2) . D. (0; 4; 2) .
Câu 6. Trong không gian Oxyz , cho mặt phẳng ( P) : x − 2 y + 3z −1 = 0 . Mặt phẳng ( P) có một vectơ pháp tuyến là A. n = ( 2 − ;1;3). B. n = (1; 2 − ;3). C. n = (1;3; 2 − ) . D. n = (1; 2 − ) ;1 . 
Câu 7. Tính tích phân sin 3 d x x  0 2 1 2 1 A. . B. . C. − . D. − . 3 3 3 3
Câu 8. Tìm họ nguyên hàm của hàm số f ( x) = sin 2x . cos 2x cos 2x cos 2x A. − + C .
B. 2 cos 2x + C . C. − + C . D. + C . 3 2 2 6 2 Câu 9. Cho f
 (x)dx =12. Tính I = f  (3x)dx. 0 0
A. I = 6 .
B. I = 36 .
C. I = 2 . D. I = 4 .
Câu 10. Cho hàm số f ( x) 2
= 3x −1. Trong các khẳng định sau, khẳng định nào đúng? 1 A. f  (x) 3 dx =
x − x + C . B. f  (x) 3
dx = x − C . 3 C. f  (x) 3
dx = x − x + C . D. f  (x) 3
dx = 3x − x + C . 2 2 2
Câu 11. Trong không gian Oxyz , cho mặt cầu (S ) : ( x − )
1 + ( y + 2) + ( z + 3) = 4 . Tìm tọa độ tâm của mặt cầu (S). A. (1; 2 − ; 3 − ) . B. (2; 4 − ; 6 − ) .
C. (−2; 4; 6) . D. (−1; 2;3) .
Câu 12. Nguyên hàm của hàm số 3 1 e x y − + = là 1 − + − + − + 1 − + A. 3x 1 e + C . B. 3 1
3e x + C . C. 3 1
−3e x + C . D. 3x 1 − e + C . 3 3
Câu 13. Tìm nguyên hàm của hàm số f ( x) 2 = 4x− . 3 2dx 1 2dx 1  3  A.
= ln 4x − 3 + C  . B. = ln 2x − + C    . 4x − 3 2 4x − 3 2  2  2dx  3  2dx 1 C. = 2ln 2x − + C    . D.
= ln 4x − 3 + C  . 4x − 3  2  4x − 3 4 1+ ln x Câu 14. Nguyên hàm dx  (x  0) bằng x 1 1 A. 2
x + ln x + C . B. 2 x +
ln x + C . C. 2
ln x + ln x + C . D. 2
ln x + ln x + C . 2 2  4
Câu 15. Cho tích phân I = ( x −  ) 1 sin 2 d x .
x Tìm đẳng thức đúng. 0   
A. I = − ( x − ) 4 1 cos2x − cos2 d x x  .
B. I = − ( x − ) 4 4 1 cos2x + cos2 d x x  . 0 0 0     1 1 1
C. I = − ( x − ) 4 4 1 cos2x + cos2 d x x  .
D. I = − ( x − ) 4 4 1 cos2x − cos2 d x x  . 2 2 2 0 0 0 0
Câu 16. Trong không gian Oxyz , cho ba điểm A(3; 2 − ; 2
− ), B(3;2;0) ,C (0;2 )
;1 . Viết phương trình mặt phẳng ( ABC).
A. 2x + 3y + 6z +12 = 0 .
B. 2x − 3y + 6z +12 = 0 .
C. 2x − 3y + 6z = 0 .
D. 2x + 3y − 6z −12 = 0 .
Câu 17. Trong không gian Oxyz , phương trình mặt phẳng đi qua hai điểm A(0;1;0), B (2;0 ) ;1 và vuông góc
với mặt phẳng (P) : x − y −1 = 0 là:
A. x − 2 y − 6z + 2 = 0 . B. 2x + 2 y − 5z − 2 = 0 .
C. x + y − z −1 = 0 .
D. x + y − 3z −1 = 0 .
Câu 18. Họ nguyên hàm của hàm số f ( x) = x cos 2x là x sin 2x cos 2x cos 2x A. + + C .
B. x sin 2x − + C . 2 4 2 cos 2x x sin 2x cos 2x
C. x sin 2x + + C . D. − + C . 2 2 4 Câu 19. Biết 2 x =  ( 2 + + ) x x e dx x mx
n e + C . Tính . m n . A. 6 . B. −4 . C. 0 . D. 4 . x − 3
Câu 20. Khi tính nguyên hàm dx
, bằng cách đặt u = x +1 ta được nguyên hàm nào? x + 1 A.  ( 2
u − 4)du . B. u  ( 2 2
u − 4)du . C.  ( 2
u − 3)du . D.  ( 2 2 u − 4)du . 1 7 x
Câu 21. Cho tích phân I =  ( x , giả sử đặt 2
t = 1+ x . Tìm mệnh đề đúng. 1+ x ) d 5 2 0 1 (t − )3 2 1 3 (t − )3 4 1 (t − )3 3 1 1 (t − )3 2 1 A. I = dt  . B. I = dt  . C. I = dt  . D. I = dt  . 4 2 t 4 2 t 5 t 5 2 t 1 1 1 1  3 x 3
Câu 22. Biết I = dx =  − lnb  . Khi đó, giá trị của 2 a + b bằng 2 cos x a 0 A. 11. B. 7 . C. 9 . D. 13 .
Câu 23. Trong không gian Oxyz cho hai điểm I (1;1; )
1 và A(1; 2;3) . Viết phương trình mặt cầu có tâm I và đi qua A. 2 2 2 2 2 2 A. ( x − ) 1 + ( y − ) 1 + ( z − ) 1 = 5 . B. ( x + ) 1 + ( y + ) 1 + ( z + ) 1 = 29 . 2 2 2 2 2 2 C. ( x − ) 1 + ( y − ) 1 + ( z − ) 1 = 25. D. ( x + ) 1 + ( y + ) 1 + ( z + ) 1 = 5 . Câu 24. Biết f  ( x) 2 2
dx = sin x + ln x + C . Tìm nguyên hàm f ( x) dx  . x A. f  (x) 2 dx = 2sin
+ 2ln x + C . B. f  (x) 2
dx = 2sin 2x + 2 ln x + C . 2 x C. f  (x) 2 dx = sin
+ ln x + C . D. f  (x) 2
dx = 2sin x + 2 ln x + C . 2 e ln x a 2 Câu 25. Biết d x = + bln + c
, với a,b,c  .. Tính a + b + c . 2 (1 + x) e + 1 e + 1 1 A. 3 . B. 2 . C. 1. D. 1 − . 3
Câu 26. Cho hàm số f ( x) có đạo hàm trên −4; 2 , thỏa mãn xf '
 (2x−4)dx =8 và f (2) = 2 . 0 1 Tính I = f
 (2x)dx. 2 −
A. I = −10 .
B. I = 10 .
C. I = −5 . D. I = 5 .  2 cos x 4 Câu 27. Cho dx = a ln 
. Giá trị của a + b bằng 2
sin x − 5sin x + 6 b 0 A. 3 . B. 0 . C. 1. D. 4 .
Câu 28. Trong không gian Oxyz , cho bốn điểm A(0;1; − )
1 , B (1;1; 2) , C (1; 1 − ;0) và D(0;0 ) ;1 . Mặt phẳng
( ) song song với mặt phẳng (BCD) và chia khối tứ diện ABCD thành hai khối đa diện sao cho tỉ số thể tích
của khối đa diện có chứa điểm A và khối tứ diện ABCD bằng 1 . Viết phương trình mặt phẳng ( ) . 27
A. − y + z − 4 = 0 .
B. y + z − 4 = 0 .
C. y − z −1 = 0 .
D. 3x − 3z − 4 = 0 .
Câu 29. Trong không gian O xyz , cho điểm I (3;1; 1
− ) và mặt phẳng (P ): x − 2y − 2z + 3 = 0 . Phương trình
mặt cầu (S ) có tâm I và tiếp xúc với mặt phẳng (P ) là 2 2 2 2 2 2
A. ( x + 3) + ( y + ) 1 + ( z − ) 1 =16 .
B. ( x − 3) + ( y − ) 1 + ( z + ) 1 =16 . 2 2 2 2 2 2
C. ( x − 3) + ( y − ) 1 + ( z + ) 1 = 4 .
D. ( x + 3) + ( y + ) 1 + ( z − ) 1 = 4 . Câu 30. Biết 2 5−2 x b I = e
dx = ae + ce
, với a,b, c là các số nguyên. Tính P = ab + c . 2 −
A. P = 0 .
B. P = 12 .
C. P = 4 . D. P = 6 .
Câu 31. Trong không gian Oxyz , cho mặt cầu (S ) 2 2 2
: x + y + z − 2x + 6 y − 4z − 2 = 0 và mặt phẳng
( ): x + 4y + z -11= 0. Viết phương trình mặt phẳng (P) song song với giá của vectơ v = (1;6;2) , vuông góc
với ( ) và tiếp xúc với (S ) .
4x − 3y − z + 5 = 0
x − 2y + z + 3 = 0 A.  . B.  .
4x − 3y − z − 27 = 0
x − 2y + z − 21 = 0
2x − y + 2z + 3 = 0
3x + y + 4z +1 = 0 C.  . D.  .
2x − y + 2z − 21 = 0
3x + y + 4z − 2 = 0
Câu 32. Trong không gian Oxyz , cho điểm A(1;1; )
1 và mặt phẳng ( P) : x+ y − 2z − 6 = 0 . Gọi M (a ; b ; c)
là điểm thuộc (P) sao cho MA ngắn nhất. Tính S = a + b + c .
A. S = 4 .
B. S = 0 .
C. S = 3 . D. S = -3 .
------ HẾT ------ ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 D B C C B B A C D C A D A D C C 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 C A B D D A A A C A D C C D C C Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 9 MÔN TOÁN 12
Câu 1. Cho hình phẳng D giới hạn bởi đường cong 2 y =
x +1 , trục hoành và các đường thẳng x = 0, x = 1 .
Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu?  A. V = 4 2 . B. V = 4 . C. V = .
D. V = 2 . 3 3
Câu 2. Cho F (x ) là nguyên hàm của hàm số f (x ) trên a é ;bù
êë úû. Phát biểu nào sau đây đúng ? b b A. f
ò (x)dx = F (a)- F (b). B. f
ò (x)dx = F (b)- F (a). a a b b C. f
ò (x)dx = F (a)+ F (b). D. f
ò (x)dx = F (b)+ F (a). a a
Câu 3. Viết phương trình mặt cầu (S) có tâm I(-1;2;1) và tiếp xúc với mặt phẳng (P): x − 2 y − 2z +1 = 0 2 2 2 2 2 2
A. (S ) : ( x + ) 1
+ ( y − 2) + (z + ) 1 = 4 .
B. (S ) : ( x + ) 1
+ ( y − 2) + (z − ) 1 = 4 . 2 2 2 2 2 2
C. (S ) : ( x + ) 1
+ ( y − 2) + (z − ) 1 = 2 .
D. (S ) : ( x + ) 1
+ ( y − 2) + (z + ) 1 = 2 .
Câu 4. Cho hàm số f ( x) liên tục trên
. Gọi S là diện tích hình phẳng giới hạn bởi các đường
y = f ( x), y = 0, x = 1
− , x = 2 (như hình vẽ bên). Mệnh đề nào dưới đây đúng? 1 2 1 2 A. S = − f  (x) dx − f  (x) dx . B. S = − f  (x) dx+ f  (x) dx . 1 − 1 1 − 1 1 2 1 2 C. S = f  (x) dx + f  (x) dx . D. S = f  (x) dx − f  (x) dx . 1 − 1 1 − 1
Câu 5. Trong không gian với hệ tọa độ Oxyz , phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm M (1;2; 3
− ) và có một vectơ pháp tuyến n = (1; 2 − ; 3 − ) .
A. x − 2 y + 3z −12 = 0
B. x − 2 y − 3z + 6 = 0
C. x − 2 y − 3z − 6 = 0
D. x − 2 y + 3z +12 = 0
Câu 6. Cho u = u(x ) , v = v(x ) là hai hàm số có đạo hàm liên tục, khẳng định nào sau đây là đúng ? u A. udv = + vdu. ò ò B. udv = uv - vdu. ò ò v C. vdu = uv + vdu. ò ò D. udv = uv + vdu. ò ò
Câu 7. Trong không gian tọa độ (Oxyz) , cho hai vecto a = (1;3;4) , b(3; 2 − ;5) Tính T = . a b
A. T = −11.
B. T = 29 .
C. T = 11 . D. T = 17 . sin xdx I =  3 + Câu 8. Tính (1 3cos x) 1 1 A. I = . B. I = +C . 6(1+ 3cos x) +C 2 12(1+ 3cos x)2 1 1 C. I = − . D. I = − +C . 12(1+ 3cos x) +C 2 6(1+ 3cos x)2 1 3 3 Câu 9. Cho f (x) 
dx = 1 ; f (x)  dx = 5 . Tính f (x)  dx 0 0 1 A. 6. B. 5. C. 4. D. 1.
Câu 10. Trong không gian tọa độ (Oxyz) , cho hai vecto a = (1;3; 4
− ) , b = (3;2;5)Tính c = 2a +3 . b
A. c = (11;12;7). B. c = (11; 12 − ; 7 − ). C. c = (11;12; 7 − ). D. c = ( 11 − ;12; 7 − ).
Câu 11. Cho f ( x) , g ( x) là các hàm số xác định và liên tục trên . Trong các mệnh đề sau, mệnh đề nào sai? A. f
 (x)− g(x)dx = f
 (x)dx − g
 (x)dx. B. f
 (x)g(x)dx = f  (x)d .x g  (x)dx . C. f
 (x)+ g(x)dx = f
 (x)dx + g
 (x)dx . D. 2 f
 (x)dx = 2 f  (x)dx .
Câu 12. Cho hàm số y = f (x) có đạo hàm liên tục trên đoạn [1 ; 2] thỏa mãn f (1) = 2 và  2 2
f (x) − (x +1) f (x) = 2xf (x), x
 [1;2] . Giá trị của f (x)dx  bằng 1 1 1 A. − ln 2 . B. + ln 2. C. 1+ ln 2 . D. 1− ln 2. 2 2
I = (x +1).sin xdxCâu 13. Tính
A. I = −(x +1)cosx + s inx+C .
B. I = −(x +1) cosx − s inx+C .
C. I = (x +1)cosx − s inx+C .
D. I = (x +1)cosx + s inx+C .
Câu 14. Trong không gian Oxyz , cho hai điểm A(1;1; − 2) và B (2; 2; )
1 . Vectơ BA có tọa độ là A. (1;1;3) . B. (3;1; ) 1 . C. (3;3; − ) 1 . D. ( 1 − ;−1;− 3).
Câu 15. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 2 2 2 2 A.  ( 2
− x + 2)dx . B.  ( 2
2x − 2x − 4)dx .
C.  (2x −2)dx. D.  ( 2 2
− x + 2x + 4)dx . 1 − 1 − 1 − 1 −
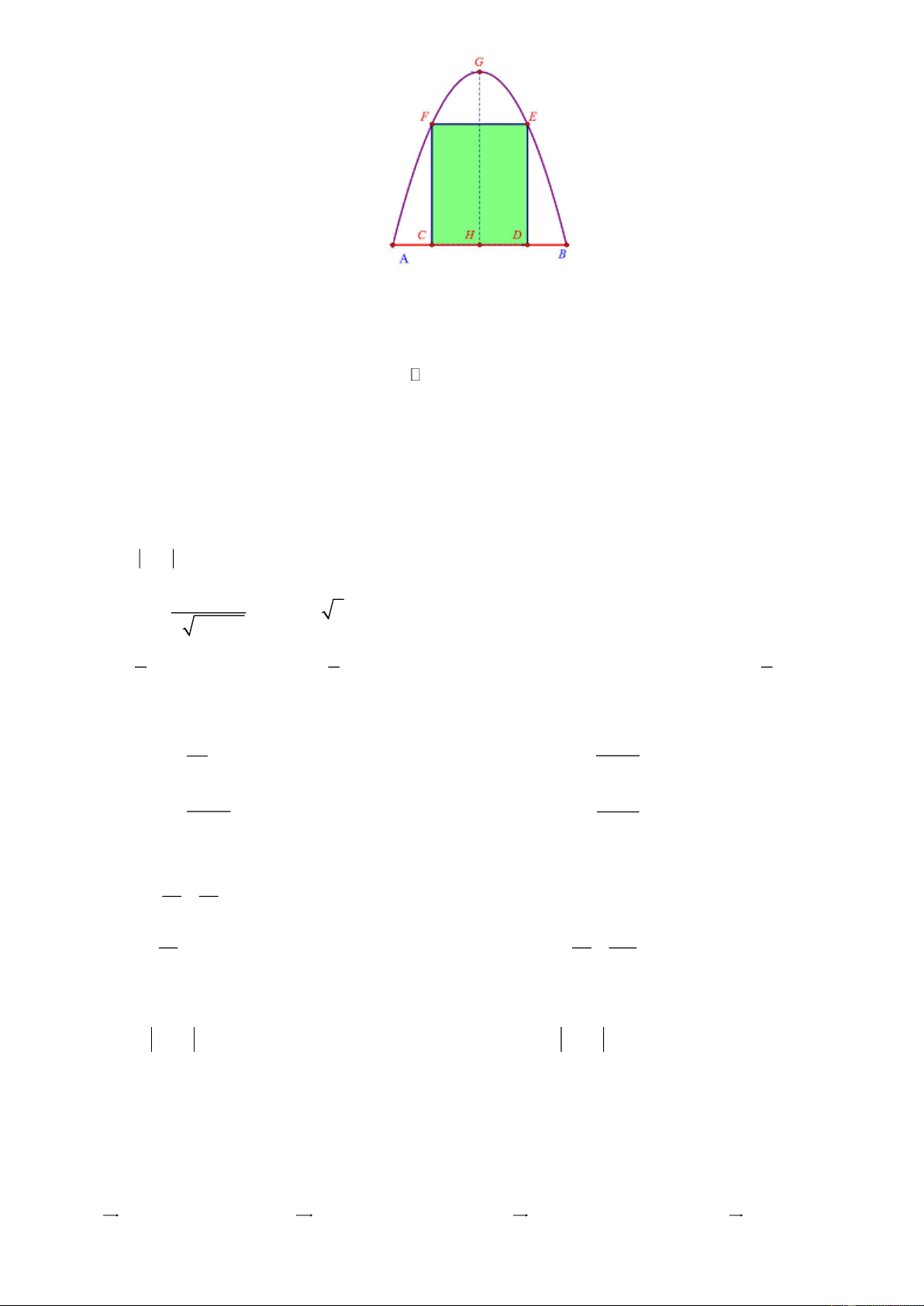
Câu 16. Một cái cổng hình Parabol như hình vẽ sau. Chiều cao GH = 4m , chiều rộng AB = 4m ,
AC = BD = 0, 9m . Chủ nhà làm hai cánh cồng khi đóng lại là hình chữ nhật CDEF tô đậm có giá là 1200000 đồng 2
/m , còn các phần để trắng làm xiên hoa có giá là 900000 đồng 2 /m . Hỏi tồng số
tiền để làm hai phần nói trên gần nhất với số tiền nào dưới đây?
A. 11445000 đồng.
B. 7368000 đồng.
C. 4077000 đồng. D. 11370000 đồng.
Câu 17. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm (
A 2;1;3), B(6;5;5) . Gọi (S ) là mặt cầu
đường kính AB. Mặt phẳng (P) vuông góc với AB tại H sao cho khối nón đinh A và đáy là hình
tròn tâm H (giao của mặt cầu (S ) và mặt phẳng (P) ) có thể tích lớn nhất, biết rằng
(P) : 2x + by + cz + d = 0 với , b c, d
. Tính S = b + c + d .
A. S = −12 .
B. S = −18 .
C. S = 24 .
D. S = 18 .
Câu 18. . Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng ( ) : 2x + y + 2z − 3 = 0 và điểm M (1; 2;1)
, khi đó khoảng cách từ điểm M đến mặt phẳng ( ) bằng: A. 3. B. 7. C. 5. D. 1.
Câu 19. Cho hình phẳng (H) giới hạn bởi các đường y = f (x), y = ,
0 x = a, x = b ( a b ) quay xung quanh trục
hoành tạo vật thể tròn xoay. Công thức tính thể tích là b b b b
A. V = f (x)d . x B. 2 V =  f (x)d . x
C. V =  f (x)d . x D. 2 V = f (x)d . xa a a a e ln x Câu 20. Biết
dx = a + b 2 
với a, b là các số hữu tỷ. Tính S = a + b . x 1+ ln x 1 3 2 1 A. S = . B. S = . C. S =1. D. S = . 4 3 2
Câu 21. Cho số a ¹ - 1 . Hàm số f (x ) x a = có nguyên hàm là a + 1 a x a x a A. x dx = + C . ò B. x dx = + C . ò a a + 1 a - 1 a x a a x C. x dx = + C . ò D. x dx = + C . ò a + 1 a - 1
Câu 22. Nguyên hàm của hàm số f ( x) 3
= x + x + 2 là hàm số nào trong các hàm số sau? x x A. F ( x) 4 2 = +
+ 2x + C . B. F ( x) 2
= 3x + 3x + C . 4 2 x x x
C. F ( x) 4 2 =
+ 3x + 2x + C . D. F ( x) 4 2 3 = + + 2x + C . 3 4 2
Câu 23. Cho hình phẳng (H) giới hạn bởi các đường y = f (x), y = ,
0 x = a, x = b ( a b ).Diện tích hình phẳng
(H) tính bằng công thức nào sau đây? a b b A. S = f
 (x) d .x
B. S = f (b) − f (a). C. S = f
 (x) d .x D. S = f
 (x)d .x b a a 1 Câu 24. Cho
f (x)dx = 2 
. Goi F(x) là 1 nguyên hàm của f(x). Biết F(0)= 3. Tính F(1) 0 A. F ( ) 1 = 1 − . B. F ( ) 1 = 5 . C. F ( ) 1 = 5 − . D. F ( ) 1 = 1.
Câu 25. Trong không gian Oxyz , cho mặt phẳng ( P) : 2x − y − 3z +1 = 0 . Vectơ nào dưới đây là một vectơ
pháp tuyến của (P) ?
A. n = 2;1;3 . B. n = 2; 1 − ;3 .
C. n = 2;3;1 . D. n = 2; 1 − ; 3 − . 1 ( ) 3 ( ) 2 ( ) 4 ( )
Câu 26. Trong hệ trục tọa độ Oxyz , phương trình mặt cầu tâm I ( 2
− ;−1;2) bán kính R = 2 là: 2 2 2 2 2 2
A. ( x − 2) + ( y − )
1 + ( z + 2) = 4 .
B. ( x + 2) + ( y + ) 1 + ( z − 2) = 4 . 2 2 2 2 2 2
C. ( x − 2) + ( y − )
1 + ( z + 2) = 2 .
D. ( x + 2) + ( y + ) 1 + ( z − 2) = 2 .
Câu 27. Trong không gian Oxyz cho mp(Q): 5x - 12z + 3 = 0 và mặt cầu (S): 2 2 2 x + y + z − 2x = 0 mp(P)
song song với (Q) và tiếp xúc với (S) có phương trình là:
A. 5x - 12z - 18 = 0. B. 5x - 12z + 8 = 0.
C. 5x - 12z - 8 = 0 hoặc 5x - 12z + 18 = 0.
D. 5x - 12z + 8 = 0 hoặc 5x - 12z - 18 = 0.
Câu 28. Chọn khẳng định sai trong các khẳng định dưới đây b d b b b b A. f
 (x)dx+ g
 (x)dx =  f
  (x)+ g(x)dx B. f
 (x)dx− g
 (x)dx =  f
  (x)− g(x)dxa c a a a a b a b b C. f
 (x)dx = − f
 (x)d .x D.
kf ( x) dx = k
f ( x) d , x ( k     ). a b a a
Câu 29. Trong không gian Oxyz, cho vectơ a = 2
− i + j − 3k . Toạ độ của vectơ a là A. (- 2;1; ) 3 . B. (- 2;1;- ) 3 . C. (2;- 1;- ) 3 . D. (- 2;- 1; ) 3 .
Câu 30. Tìm một nguyên hàm F ( x) của hàm số f ( x) 2
= 2 − x biết F ( ) 5 2 = 3 x x A. F ( x) 3 = 2x − +1. B. F ( x) 3 1 = 2x − + . 3 3 3 19 x C. F ( x) 3 = 2x − x + . D. F ( x) 3 = 2x − + 3. 3 3
Câu 31. Cho hai mặt phẳng ( P) : 3x + 3y − z +1 = 0; (Q) : (m + )
1 x − y − (m − 2) z − 3 = 0 . Xác định m để hai mặt
phẳng (P), (Q) vuông góc với nhau. 3 − − A. m = . B. m = 1 2 . C. m = 1 . D. m = . 2 2 2 0
Câu 32. Cho tích phân 2 I = cos x sin . x dx
,giả sử đặt t = cos x . Tìm mệnh đề đúng?  − 2 1 0 1 0 2 2 2 2
A. I = − t dt B. I = t dt
C. I = t dt D. I = − t dt  0   − 0 − 2 2
------ HẾT ------ ĐÁP ÁN 1 B 6 B 11 B 16 A 21 B 26 B 31 D 2 B 7 D 12 B 17 B 22 A 27 D 32 A 3 B 8 A 13 A 18 D 23 C 28 A 4 D 9 C 14 D 19 B 24 B 29 B 5 C 10 A 15 D 20 B 25 D 30 B Thuvienhoclieu.Com
ĐỀ THI GIỮA HỌC KỲ II-ĐỀ 10 MÔN TOÁN 12 1 3 3
Câu 1. Nếu
f (x)dx = 4  và
f (x)dx = 6  thì f (x)dx  bằng 0 1 0 A. −10 . B. −2 . C. 2 . D. 10 . 1
Câu 2. Họ tất cả các nguyên hàm của hàm số f (x) = là 2 cos x
A. tan x + C .
B. − cot x + C .
C. − tan x + C .
D. cot x + C .
Câu 3. Trong không gian Oxyz, cho hai điểm A(1; 2 − ;0) và B(2;1; 4
− ) Tọa độ của vectơ AB là. A. ( 1 − ; 3 − ;4) . B. (1;3; 4) .
C. (2; −2;0) .
D. (1;3; −4) .
Câu 4. Trong không gian Oxyz , Cho mặt phẳng ( ) : x − 2 y + 4z +1 = 0 . Vectơ nào dưới đây là một vectơ
pháp tuyến của mặt phẳng ( ) ? r r r r A. n − − 4 ( 4; 2 ) ;1 . B. n − 3 (0; 2; 4) .
C. n2 (1; 2; 4) . D. 1 n (1; 2; 4) . 3
Câu 5. Cho hàm số f ( x) có đạo hàm f '( x) trên đoạn 1;  3 . Biết f ( )
1 = 2 , f (3) = 7 . Tích phân f '(x)dx  1 bằng A. 5 − . B. 14 . C. 9 . D. 5 .
Câu 6. Họ tất cả các nguyên hàm của hàm số 5 2
f (x) = x + x là 6 x 6 3 x x 5 2 x x A. + 2x + C . B. 4
5x + 2x + C . C. + + C . D. + + C . 6 6 3 5 2
Câu 7. Cho hình phẳng ( H ) được giới hạn bởi các đường 2
y = x + 5 , y = 0 , x = 0 , x = 2 . Gọi V là thể tích
khối tròn xoay được tạo thành khi quay ( H ) xung quanh trục Ox . Mệnh đề nào dưới đây đúng? 2 2 2 2 2 2 A. V = ( 2 x + 5) dx . B. V = ( 2 x + 5)dx .
C. V =  ( 2 x + 5)dx .
D. V =  (x + 5) dx . 0 0 0 0
Câu 8. Trong không gian Oxyz . Cho hai vectơ a = (1; 2 − )
;1 và b = (3;0; 4) . Tọa độ tích có hướng a;b   là A. (6; 1 − ; 8 − ) . B. ( 8 − ; 1 − ;6) . C. (2; 2;3) . D. (8;1;6) . r r r r r
Câu 9. Trong không gian Oxyz , cho a = 3i + 4 j − k . Tọa độ a là A. (3; 4; − ) 1 .
B. (−1; 4;3) . C. (3; 4; ) 1 . D. (3; 4;0) . 3 3 3 Câu 10. Nếu
f (x)dx = 3 
và g(x)dx = 1 −  thì 2 f
 (x)+3g(x) dx  bằng 1 1 1 A. 2 . B. 5 − . C. 3 . D. 5 .
Câu 11. (2 x −3x e )dx bằng x 3x
A. 2 x + 3x e + C . B. 2e − + C .
C. 2 x − 3x e ln 3 + C .
D. 2 x − 3x e + C . ln 3 3
Câu 12. Tích phân 2xdx  bằng 2 A. 5 . B. 5 − . C. −2 . D. 2 .
Câu 13. Cho hàm số f ( x) liên tục trên R . Gọi S là diện tích hình phẳng giới hạn bởi các đường
y = f ( x), y = 0, x = 1
− và x = 4 (như hình vẽ bên). Mệnh đề nào dưới đây là đúng? 1 4 1 4 A. S = f
 (x)dx+ f
 (x)dx. B. S = − f
 (x)dx+ f
 (x)dx . 1 − 1 1 − 1 1 4 1 4 C. S = − f
 (x)dx− f
 (x)dx . D. S = f
 (x)dx− f  (x)dx . 1 − 1 1 − 1
Câu 14. Trong không gian Oxyz , phương trình tổng quát của mặt phẳng đi qua điểm M (2;1;0) và có vectơ r pháp tuyến n = (1; 1 − ;3) là.
A. x − 3y + z +1 = 0 .
B. x − y + 3z −1 = 0 .
C. x + 3y + z −1 = 0 .
D. x − y + 3z +1 = 0 . 5 u = ln x
Câu 15. Tính tích phân I = ln xdx
bằng phương pháp tích phân từng phần, đặt  . Khẳng định nào  = 2 dv dx  dưới đây đúng? 5 5 1 1
A. I = ( x ln x) 5| − . x dx.
B. I = ( x ln x) 5| + . x dx. 2 x 2 x 2 2 5 5 1
C. I = ( x ln x) 5 2 | − x dx.
D. I = − ( x ln x) 5| + . x dx. 2 2 x 2 2 2 dx 1 a Câu 16. Cho = ln 
, với a, b là các số nguyên dương và a là phân số tối giản. Giá trị a + b bằng 2x +1 2 b b 1 A. −2 . B. 8 . C. 2 . D. 15 .
Câu 17. Trong không gian Oxyz , khoảng cách từ A(2; 4; 3
− ) đến mặt phẳng ( ) : 2x − y + 2z − 9 = 0 bằng 1 4 A. . B. 1. C. . D. 5 . 3 3 2 2 2
Câu 18. Trong không gian Oxyz , cho mặt cầu (S ) : ( x − ) 1
+ ( y + 2) + (z − 3) = 9 . Tọa độ tâm I của mặt cầu (S ) là A. I (1; 2 − ;3) . B. I (1; 2;3) . C. I ( 1 − ;2; 3 − ) . D. I (3; 2 − ) ;1 .
Câu 19. ( + 2) x x e dx bằng A. ( + 2) x x e + C . B. ( + 3) x x e + C . C. ( + ) 1 x x e + C . D. ( − ) 1 x x e + C . 4 2 Câu 20. Nếu
f (x)dx = 4 −  thì f (2x)dx  bằng 2 − 1 − A. 2 . B. −2 . C. 8 − . D. 8 .
Câu 21. Diện tích hình phẳng được giới hạn bởi parabol 2
y = 2 - x và đường thẳng y = - x bằng 7 9 9 A. 3 . B. . C. . D. . 2 4 2
Câu 22. Cho hình phẳng ( H ) giới hạn bởi các đường 2
y = −x + 2x , trục hoành. Quay hình ( H ) quanh trục
Ox ta được khối tròn xoay có thể tích là 32 16 16 4 A. . B. . C. . D. . 15 15 15 3 r r r r r
Câu 23. Trong không gian Oxyz , cho a (2; 1 − ;3) , b(1;3; 2
− ) . Tọa độ c = a − 2b là A. (0; −7;7) . B. (4; −7;7) . C. (0; 7 − ; 7 − ) . D. (0;7;7) . 2x
Câu 24. Khi tìm nguyên hàm  (
dx , bằng cách đặt 2
t = x + 3 ta được nguyên hàm nào dưới đây? x + 3)2 2 2 1 1 1 A. dt  . B. − dt  . C. dt  . D. dt  . 2 t 2 t 2 t 2 2t
Câu 25. Họ tất cả nguyên hàm của hàm số f (x) = sin 4x là 1 1 A. − cos4x + C . B. cos4x + C .
C. − cos 4x + C .
D. cos 4x + C . 4 4
Câu 26. Trong không gian Oxyz , gọi S là tập hợp tất cả giá trị thực của m để hai mặt phẳng
( ):mx + 2y −3z +3 = 0 và ( ):(m − )
1 x + my + 2z − 5 = 0 vuông góc. Tổng các phần tử của S bằng A. 1 − . B. 6 . C. 6 − . D. 1.
Câu 27. Cho hàm số y = f ( x) liên tục trên (0; +) thỏa mãn 2
2xf '(x) + f (x) = 3x x . Biết f ( ) 1 1 = , giá trị 2 f (4) bằng A. 4 . B. 24 . C. 14 . D. 16 . 1 x − 2 Câu 28. Cho
dx = a − b ln 2 
, với a, b là các số nguyên dương. Giá trị a + 2b bằng x +1 0 A. 7 . B. 4 . C. 5 − . D. −2 . 1  2
Câu 29. Cho hàm số f (x) xác định trên
\   thỏa mãn f '(x) =
, biết f (0) = 1 và f (1) = 2 . Giá trị 2 2x −1
của biểu thức P = f ( 1 − ) + f (3) bằng A. 3 + ln 5 . B. 3 + ln15 . C. 3 − ln15 . D. 3 + ln 3 .
Câu 30. Trong không gian với hệ trục tọa độ Oxyz , cho điểm M ; 1 ( ). 3 ; 2
Mặt phẳng (P) qua M cắt các tia
Ox,Oy,Oz lần lượt tại ,
A B, C sao cho thể tích khối tứ diện OABC nhỏ nhất có phương trình là:
A. 6x + 3y + 2z − 18 = 0 .
B. x + 2 y + 3z − 14 = 0 .
C. 6x + 3y + 2z = 0 .
D. x + y + z − 6 = 0 . 1 2
Câu 31. Cho hàm số f (x) có đạo hàm liên tục trên
, biết f (2) = 3 và xf
 (2x)dx = 5. Khi đó 2x f '(x)dx  0 0 bằng A. −13 . B. 52 . C. −36 . D. −28 .
Câu 32. Trong không gian Oxyz , cho mặt cầu (S ) có tâm I (1;0; − ) 1 và cắt mặt phẳng
(P):2x + y − 2z −16 = 0 theo giao tuyến là một đường tròn có bán kính bằng 3. Phương trình của mặt cầu (S) là ( 2 2
x + )2 + y + ( z − )2 2 1 1 = 9 . (x + ) 2 1 + y + (z − ) 1 = 25. A. B. ( 2 2
x − )2 + y + ( z + )2 2 1 1 = 9 . (x − ) 2 1 + y + (z + ) 1 = 25. C. D.
-----------------------------------Hết ----------------------------- ĐÁP ÁN 1. D 6. C 11. B 16. B 21. D 26. A 31. D 2. A 7. D 12. A 17. D 22. C 27. D 32. D 3. D 8. B 13. D 18. A 23. A 28. A 4. D 9. A 14. B 19. C 24. C 29. B 5. D 10. C 15. A 20. B 25. A 30. A