Bộ đề thi giữa kỳ Giải tích 2 dành cho thi online | Đại học Bách Khoa Hà Nội

Bộ đề thi giữa kỳ Giải tích 2 dành cho thi online | Đại học Bách Khoa Hà Nội. Tài liệu được biên soạn giúp các bạn tham khảo, củng cố kiến thức, ôn tập và đạt kết quả cao kết thúc học phần. Mời các bạn đọc đón xem!

41 21 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Giải tích 2

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

70 trang 1 tháng trước

Tác giả:

Profile Thùy Dương
BK – ĐẠI CƯƠNG MÔN PHÁI
ĐỀ Ệ TRẮC NGHI M GIẢI TÍCH 2
NHÓM NGÀNH 1 + 2
TẬP 1: GIỮA K Ỳ
THỰ ỆC HI N: TEAM GIẢI TÍCH 2
MỤC LỤC
LỜI NÓI ĐẦU ................................................................................................................................. 1
PHẦ ẮN I: CÂU HỎI TR C NGHIỆM 2 ............................................................................................
I. HÀM NHI U BIỀ ẾN ................................................................................................................. 2
1.1. GI I H N C A HÀM NHI U BIỚ Ạ Ủ Ề ẾN.............................................................................. 2
1.2. KH O SÁT TÍNH LIÊN T C C A HÀM NHIẢ Ụ Ủ ỀU BIẾN .............................................. 3
1.3. ĐẠO HÀM RIÊNG VÀ VI PHÂN TOÀN PHẦN............................................................ 4
1.4. ĐẠO HÀM CỦA HÀM HỢP ............................................................................................ 6
1.5. ĐẠO HÀM CỦA HÀM ẨN .............................................................................................. 7
1.6. TÍNH GẦN ĐÚNG NHỜ VI PHÂN ................................................................................. 8
1.7. C C TRỰ Ị C A HÀM NHI U BIỦ Ề ẾN ................................................................................ 8
1.8. KHAI TRI N TAYLORỂ ................................................................................................. 10
1.9. TÌM GTLN, GTNN C A HÀM SỦ Ố ............................................................................... 10
II. ỨNG D NG C A PHÉP TÍNH VI PHÂNỤ Ủ .......................................................................... 11
III. TÍCH PHÂN B I & NG DỘ Ứ ỤNG ...................................................................................... 11
3.1. TÍCH PHÂN KÉP ........................................................................................................... 12
3.2. TÍCH PHÂN B I BAỘ ..................................................................................................... 14
3.3. NG D NG C A TÍCH PHÂN BỨ Ụ Ủ ỘI............................................................................. 15
IV. TÍCH PHÂN PH THU C THAM SỤ Ộ Ố: ............................................................................ 16
4.1. TÍCH PHÂN XÁC ĐỊNH PHỤ THUỘC THAM SỐ ..................................................... 16
4.2. TÍCH PHÂN SUY R NG PH THU C THAM SỘ Ụ Ộ Ố .................................................... 17
PHẦN II: LỜI GIẢI VÀ ĐÁP ÁN ................................................................................................ 19
I. HÀM NHI U BIỀ ẾN ............................................................................................................... 19
1.1. GI I H N C A HÀM NHI U BIỚ Ạ Ủ Ề ẾN............................................................................ 19
1.2. KHẢO SÁT TÍNH LIÊN TỤC: ...................................................................................... 23
1.3. ĐẠO HÀM RIÊNG VÀ VI PHÂN TOÀN PHẦN .......................................................... 25
1.4. ĐẠO HÀM CỦA HÀM ẨN ............................................................................................ 27
1.5. TÍNH GẦN ĐÚNG NHỜ VI PHÂN ............................................................................... 29
1.6. C C TRỰ Ị C A HÀM NHI U BIỦ Ề ẾN .............................................................................. 30
1.7. KHAI TRI N TAYLORỂ ................................................................................................. 35
1.8. TÌM GTLN, GTNN C A HÀM SỦ Ố ............................................................................... 35
II. NG D NG C A PHÉP TÍNH VI PHÂN:Ứ Ụ Ủ ......................................................................... 40
III. TÍCH PHÂN B I & NG DỘ Ứ ỤNG ...................................................................................... 44
3.1. TÍCH PHÂN KÉP ........................................................................................................... 44
3.2. TÍCH PHÂN B I BAỘ ..................................................................................................... 49
3.3. NG D NG C A TÍCH PHÂN BỨ Ụ Ủ ỘI............................................................................. 55
IV. TÍCH PHÂN PH THU C THAM SỤ Ộ Ố ............................................................................. 59
4.1. TÍCH PHÂN XÁC ĐỊNH PHỤ THUỘC THAM SỐ ..................................................... 59
4.2. TÍCH PHÂN SUY R NG PH THU C THAM SỘ Ụ Ộ Ố .................................................... 64
TEAM GI I TÍCH 2 Ả
1
LỜI NÓI ĐẦU
n nay, v i hình th i m i t thi t n sang hình th c thi Hiệ ớ ức thi đổ ớ ừ ự luậ ứ
trắc nghi m, chính vì v y nhi u b n sinh viên s g p khó khệ ậ ề ạ ẽ ặ ăn trong việc
ôn tập. Trong tình hình đó, nhóm “BK – ĐẠI CƯƠNG MÔN PHÁI” đã
biên so C NGHI M GI giúp các b n thuạn “BỘ ĐỀ TRẮ Ệ ẢI TÍCH 2” để ạ ận
tiện hơn trong việc ôn tập.
Do th i gian c p bách nên vi c biên so n tài li u không thờ ấ ệ ạ ệ ể tránh được
những sai sót. Mọi ý kiến đóng góp củ ạn đọ fanpage “BÁCH a b c xin gửi về
KHOA LEARNING”.
Nhóm tác gi : Team GI I TÍCH 2 nhóm BK ả Ả – ĐẠI CƯƠNG MÔN PHÁI
(Admin: Đỗ Tuấn Cường, Đinh Tiến Long, Phạm Thanh Tùng, Tr n Trung ầ
Dũng, Đỗ Ngọc Hiế ễ ều, Nguy n Thu Hi n, Nguyễn Minh Hiếu)
TEAM GI I TÍCH 2 Ả
2
PHẦN I: CÂU H I TR C NGHI M Ỏ Ắ Ệ
I. HÀM NHI U BI N Ề Ế
1.1. I H N CGIỚ Ạ ỦA HÀM NHI U BI N Ề Ế
Câu 1. Tính 𝐥𝐢𝐦
(𝒙,𝒚)→(𝟎,𝟎)
𝒙
𝟐
𝒚
𝒙
𝟐
+𝒚
𝟐
A.0 B.1 C.2 D. Không t n t i gi i h n ồ ạ ớ ạ
Câu 2. Tính 𝐥𝐢𝐦
(𝒙,𝒚)→(𝟎,𝟎)
𝒙𝒚
𝒙
𝟐
+𝒚
𝟐
A.0 B.1 C.2 D. Không t n t i gi i h n ồ ạ ớ ạ
Câu 3. Tính 𝐥𝐢𝐦
(𝒙,𝒚)→(𝟎,𝟎)
𝒙𝒚
√
𝒙
𝟐
+𝒚
𝟐
A.0 B.+∞ C. −∞ D.
−1
2
Câu 4. Tính 𝐥𝐢𝐦
(𝒙,𝒚)→(𝟎,𝟎)
𝒙
𝟐
−𝒚
𝟐
𝒙
𝟐
+𝒚
𝟐
A.
1
2
B.
−1
2
C.0 D. Không t n t i giồ ạ ới h n ạ
Câu 5. Tính 𝐥𝐢𝐦
(𝒙,𝒚)→(𝟎,𝟎)
𝒙
𝟑
−𝒚
𝟑
𝒙
𝟐
+𝒚
𝟐
A.
𝜋
4
B.
𝜋
2
C.0 D. Không t n t i giồ ạ ới h n ạ
Câu 6. Tính 𝐥𝐢𝐦
(𝒙,𝒚)→(𝟎,𝟎)
𝒙
𝟐
𝒚−𝒙𝒚
𝟐
𝒙
𝟑
+𝒚
𝟑
A.
1
2
B.
−1
2
C.0 D. Không t n t i giồ ạ ới h n ạ
Câu 7. Tính 𝐥𝐢𝐦
(𝒙,𝒚)→(𝟎,𝟎)
𝒚.(𝒆
𝟑𝒙
−𝟏)− .(𝒆 −𝟏)𝟑𝒙
𝒚
𝒙
𝟐
+𝒚
𝟐
A.
√
2
2
B.
−
√
2
2
C.0 D. Không t n t i gi i h n ồ ạ ớ ạ
TEAM GI I TÍCH 2 Ả
3
Câu 8. Tính 𝐥𝐢𝐦
(𝒙,𝒚)→(𝟎,𝟎)
(𝒙
𝟐
+𝒚
𝟐
)
𝒙
𝟐
𝒚
𝟐
A.1 B.
1
𝑒
C.0 D. Không t n t i giồ ạ ới hạn
Câu 9. Tính 𝐥𝐢𝐦
(𝐱,𝐲)→(𝟎,𝟎)
(
(
(
((
𝟏+𝐱
𝟐
𝐲
𝟐
)
)
)
))
𝟏
𝐱
𝟐
+𝐲
𝟐
A.1 B.
1
𝑒
C.0 D. Không t n t i giồ ạ ới hạn
Câu 10.Tính 𝐥𝐢𝐦
(𝒙,𝒚)→(𝟎,𝟎)
𝒙
𝟐
+𝒚
𝟐
𝒆
𝒙+𝒚
A.1 B. C.0 D. Không t n t i gi i h n −1 ồ ạ ớ ạ
Câu 11.Tính 𝐥𝐢𝐦
(𝐱,𝐲)→(𝟎,𝟎)
𝟏+𝟑𝐱
(
𝟐
)
𝟏
𝐱
𝟐
+𝐲
𝟐
A.1 B.
1
𝑒
C.0 D. Không t n t i giồ ạ ới hạn
Câu 12.Tính 𝐥𝐢𝐦
(𝐱,𝐲)→(𝟎,𝟎)
𝐜𝐨𝐬 (
𝐱
𝟐
+𝐲
𝟐
)
−𝟏
𝐱
𝟐
+𝐲
𝟐
A.1 B.
1
𝑒
C.0 D. Không t n t i giồ ạ ới hạn
1.2. KH O SÁT TÍNH LIÊN T C C A HÀM NHI U BI N Ả Ụ Ủ Ề Ế
Câu 1:
Cho hàm số 𝒇
(
(
(
((
𝒙,𝒚
)
)
)
))
=
{
{
{
{{
𝒙⋅𝐚𝐫𝐜𝐭𝐚𝐧
(
(
(
((
𝒚
𝒙
)
)
)
))
𝟐
, nếu 𝒙 ≠ 𝟎
𝟎, nếu 𝒙 = 𝟎
Xét tính liên tục của
𝒇
(
(
(
((
𝒙,𝒚
)
)
)
))
tại 𝑩 𝟎,𝟏 .
(
(
(
((
)
)
)
))
A.
𝑓
( )
𝑥,𝑦 liên tục
tại 𝐵(0,1) B. 𝑓
( )
𝑥,𝑦 không liên tục
tại 𝐵(0,1)
Câu 2. Cho hàm s
ố 𝒇(𝒙,𝒚) = {
𝟐𝒙
𝟐
𝒚−𝒚
𝟐
𝒙
𝒙
𝟐
+𝒚
𝟐
, 𝒙 nếu
𝟐
+𝒚
𝟐
≠ 𝟎
𝒂 ,nếu 𝒙 +𝒚 = 𝟎
𝟐 𝟐
. Tìm a để hàm s liên ố
tục t i (0; 0). ạ
A.0 B.1 C.2 D. ∀𝑎 ∈ 𝑅
TEAM GI I TÍCH 2 Ả
4
Câu 3.
Cho hàm số 𝒇(𝒙,𝒚) = {
𝐬𝐢𝐧 (
𝒙𝒚+𝒚
𝟐
𝒙 +𝒚
𝟐 𝟐
), nếu (𝒙,𝒚) ≠ (𝟎,𝟎)
𝟎 , nếu (𝒙,𝒚) = 𝟎
.
Xét tính liên tục của
𝒇
(
(
(
((
𝒙,𝒚
)
)
)
))
tại 𝑩 𝟎,𝟎 .
(
(
(
((
)
)
)
))
A.
𝑓
( )
𝑥,𝑦 liên tục
tại 𝐵(0,1) B. 𝑓
( )
𝑥,𝑦 không liên tục
tại 𝐵(0,1)
Câu 4. Cho hàm s
ố 𝒇(𝒙,𝒚) = {
𝒙𝒚−𝒙
𝟐
𝒙 +𝒚
𝟐 𝟐
, nếu (𝒙,𝒚) ≠ (𝟎,𝟎)
𝟎, nếu (𝒙,𝒚) = 𝟎
Kh
ảo sát s liên t c c a hàm sự ụ ủ ố 𝒇(𝒙,𝒚) tại 𝑩
(
(
(
((
𝟎,𝟎 .
)
)
)
))
A.
𝑓
( )
𝑥,𝑦 liên tục
tại 𝐵(0,1) B. 𝑓
( )
𝑥,𝑦 không liên tục
tại 𝐵(0,1)
1.3. ĐẠO HÀM RIÊNG VÀ VI PHÂN TOÀN PH N Ầ
Câu 1. Đạo hàm riêng theo biến x c a hàm z = ln( x + ) ủ √𝒙 +𝒚
𝟐 𝟐
A.
z’
x
=
1
√𝑥 +𝑦
2 2
B. z’
x
=
𝑥
√𝑥 +𝑦
2 2
C.
z’
x
=
2
√𝑥 +𝑦
2 2
D. z’
x
=
2𝑥
√𝑥 +𝑦
2 2
Câu 2. Đạo hàm riêng theo biến y của hàm z = ln( x + √𝒙 +𝒚
𝟐 𝟐
)
A.
z’
y
=
𝑦
(𝑥+√𝑥 +𝑦
2 2
)√𝑥 +𝑦
2 2
B. z’
y
=
√𝑥
2
+𝑦
2
(𝑥+√𝑥 +𝑦 )√𝑥 +𝑦
2 2 2 2
C.
z’
y
=
𝑦
2
(𝑥+√𝑥 +𝑦
2 2
)√𝑥 +𝑦
2 2
D. z’
y
=
2√𝑥
2
+𝑦
2
(𝑥+√𝑥 +𝑦 )√𝑥 +𝑦
2 2 2 2
Câu 3. Vi phân toàn ph n c a hàm z = ln( x + ầ ủ √𝒙 +𝒚
𝟐 𝟐
)
A. 𝑑𝑧 =
1
√𝑥 +𝑦
2 2
.𝑑𝑥+
𝑦
(𝑥+√𝑥 +𝑦
2 2
)√𝑥 +𝑦
2 2
.𝑑𝑦
B. 𝑑𝑧 =
𝑥
√𝑥 +𝑦
2 2
.𝑑𝑥+
√𝑥
2
+𝑦
2
(𝑥+√𝑥 +𝑦 )√𝑥 +𝑦
2 2 2 2
.𝑑𝑦
C. 𝑑𝑧 =
2
√𝑥 +𝑦
2 2
.𝑑𝑥+
𝑦
2
(𝑥+√𝑥 +𝑦
2 2
)√𝑥 +𝑦
2 2
.𝑑𝑦
D. 𝑑𝑧 =
2𝑥
√𝑥 +𝑦
2 2
.𝑑𝑥+
2√𝑥
2
+𝑦
2
(𝑥+√𝑥 +𝑦 )√𝑥 +𝑦
2 2 2 2
.𝑑𝑦
Câu 4. Đạo hàm riêng theo biến y của hàm u = 𝒙
𝒚
𝟐
𝒛
A. u’
y
= 𝑥
𝑦
2
𝑧
.𝑙𝑛𝑥𝑦𝑧
B. u’
y
= 𝑥
𝑦
2
𝑧
.𝑙𝑛𝑥𝑦
2
𝑧
TEAM GI I TÍCH 2 Ả
5
C. u’
y
= 𝑥
𝑦
2
𝑧
.𝑙𝑛𝑥2𝑦𝑧
D. u’
y
= 𝑥
𝑦𝑧
.𝑙𝑛𝑥𝑦𝑧
Câu 5. Vi phân toàn ph n c a hàm u = ầ ủ 𝒆
(𝒙
𝟐
+𝟐𝒚
𝟐
+𝒛 )
𝟐 −𝟏
t -1; 1) ại (𝟏;
A. -1; 1) = 𝑑𝑢(1;
2
𝑒
−4
.16
.dx +
−4
𝑒
−4
.16
.dy -
2
𝑒
−4
.16
.dz
B. -1; 1) = 𝑑𝑢(1;
−2
𝑒
−4
.16
.dx +
4
𝑒
−4
.16
.dy -
2
𝑒
−4
.16
.dz
C. -1; 1) = 𝑑𝑢(1;
2
𝑒
−4
.16
.dx +
4
𝑒
−4
.16
.dy +
2
𝑒
−4
.16
.dz
D. -1; 1) = 𝑑𝑢(1;
2
𝑒
−4
.16
.dx +
−4
𝑒
−4
.16
.dy +
2
𝑒
−4
.16
.dz
Câu 6. Tính 𝒛
𝒙
′
,𝒛
𝒚
′
của hàm số 𝒛 =
∫
∫
∫
∫∫
𝒙
𝒚
𝒙𝒚
𝒕
𝟐
𝐬𝐢𝐧 𝟐𝒕𝒅𝒕
A.
{
𝑧
𝑥
′
=
−1
𝑦
⋅(
𝑥
𝑦
)sin
2𝑥
𝑦
−𝑦⋅( )𝑥𝑦
2
⋅sin 2𝑥𝑦
𝑧
𝑦
′
=
−𝑥
𝑦
2
⋅(
𝑥
𝑦
)
2
sin
2𝑥
𝑦
−𝑥⋅ (𝑥𝑦)
2
⋅sin 2𝑥𝑦
B.
{
𝑧
𝑥
′
=
1
𝑦
⋅(
𝑥
𝑦
)sin
2𝑥
𝑦
+𝑦⋅( )𝑥𝑦
2
⋅sin 2𝑥𝑦
𝑧
𝑦
′
=
−𝑥
𝑦
2
⋅(
𝑥
𝑦
)
2
sin
2𝑥
𝑦
+𝑥⋅ (𝑥𝑦)
2
⋅sin 2𝑥𝑦
C.
{
𝑧
𝑥
′
=
1
𝑦
⋅(
𝑥
𝑦
)sin
2𝑥
𝑦
+𝑦⋅( )𝑥𝑦
2
⋅sin 2𝑥𝑦
𝑧
𝑦
′
=
𝑥
𝑦
2
⋅(
𝑥
𝑦
)
2
sin
2𝑥
𝑦
−𝑥⋅( )𝑥𝑦
2
⋅sin 2𝑥𝑦
D.
{
𝑧
𝑥
′
=
1
𝑦
⋅(
𝑥
𝑦
)sin
2𝑥
𝑦
−𝑦⋅(𝑥𝑦)
2
⋅sin 2𝑥𝑦
𝑧
𝑦
′
=
−𝑥
𝑦
2
⋅(
𝑥
𝑦
)
2
sin
2𝑥
𝑦
−𝑥⋅( )𝑥𝑦
2
⋅sin 2𝑥𝑦
Câu 7. Vi phân toàn ph n c a hàm
ầ ủ u =
𝒛
√
𝒙
𝟐
+𝒚
𝟐
A. 𝑑𝑢 = −𝑧𝑥 (𝑥 +𝑦
2 2 2
)
−3
2
𝑑𝑥+ (𝑥 +𝑦 )z y
2 2
−3
2
𝑑𝑦 + (𝑥 + 𝑦 )
2 2
−1
2
𝑑𝑧
B. 𝑑𝑢 = − (𝑥 +𝑦 )𝑧𝑥
2 2
−3
2
𝑑𝑥+ z y (𝑥 +𝑦
2 2
)
−3
2
𝑑𝑦 + 𝑥𝑦(𝑥 +𝑦
2 2
)
−1
2
𝑑𝑧
C. 𝑑𝑢 = − (𝑥 +𝑦 )𝑧𝑥
2 2
−3
2
𝑑𝑥− z y (𝑥 +𝑦
2 2
)
−3
2
𝑑𝑦 + (𝑥 +𝑦 )
2 2
−1
2
𝑑𝑧
D. 𝑑𝑢 = − (𝑥 +𝑦 )𝑧𝑥
2 2
−3
2
𝑑𝑥+ z y (𝑥 +𝑦
2 2
)
−3
2
𝑑𝑦 −(𝑥 +𝑦
2 2
)
−1
2
𝑑𝑧
Câu 8. Cho hàm s f(x,y) =
ố {
𝒚.𝒂𝒓𝒕𝒂𝒏(
𝒙
𝒚
)
𝟐
, 𝒏ế𝒖 𝒚 ≠ 𝟎
𝟎, 𝒏ế𝒖 𝒚 = 𝟎
TEAM GI I TÍCH 2 Ả
6
Tính 𝒇 (𝟏,𝟎)
′
𝒚
A.
π
2
B.
π
3
C.
π
4
D.
π
6
Câu 9. Tính đạo hàm riêng z’(x, y) của hàm số:
𝒛 = {
𝒂𝒓𝒄𝒕𝒂𝒏
𝒚
𝒙
𝒌𝒉𝒊 (𝒙,𝒚) ≠ (𝟎,𝟎)
𝟎 𝒌𝒉𝒊 (𝒙,𝒚) = (𝟎,𝟎)
A.
{
𝑧′
𝑥
= 0
𝑧′ = 0
𝑦
C. {
𝑧′
𝑥
= +∞
𝑧′ = +∞
𝑦
B.
{
𝑧′
𝑥
= 0
𝑧′ = +∞
𝑦
D. {
𝑧′
𝑥
= +∞
𝑧′ = 0
𝑦
1.4. ĐẠO HÀM C A HÀM H P Ủ Ợ
Câu 1. Xác định đạo hàm c a hàm h z = v i u = cosx ; v = sinx ủ ợp 𝒖
𝒗
ớ
A. .sinx + z’ = 𝑣.𝑢
𝑣−1
𝑢
𝑣
.𝑙𝑛𝑢.𝑐𝑜𝑠𝑥
B. - z’ = 𝑣.𝑢
𝑣−1
.(-sinx) 𝑢
𝑣
.𝑙𝑛𝑢.𝑐𝑜𝑠𝑥
C. -sinx) + z’ = 𝑣.𝑢
𝑣−1
.( 𝑢
𝑣
.𝑙𝑛𝑢.𝑐𝑜𝑠𝑥
D. .sinx - z’ = 𝑣.𝑢
𝑣−1
𝑢
𝑣
.𝑙𝑛𝑢.𝑐𝑜𝑠𝑥
Câu 2. Xác định đạo hàm c a hàm h z = 2 v i u = cosx ; v = sinx ủ ợp 𝒖
𝟐
– 𝒗
𝟐
ớ
A. -3.sin2x z’ =
B. z’ = -3.cos2x
C. z’ = 3.sin2x
D. 2x z’ = 3.cos
Câu 3. Xác định đạo hàm c a hàm h z = ln( v i u = x.y và v = ủ ợp 𝒖
𝟐
+𝒗 )
𝟐
ớ
𝒙
𝒚
A.
{
𝑧′
𝑥
=
2𝑢
𝑢
2
+𝑣
2
.𝑥 +
2𝑣
𝑢
2
+𝑣
2
.
1
𝑦
𝑧′
𝑦
=
2𝑢
𝑢
2
+𝑣
2
.𝑦 +
2𝑣
𝑢
2
+𝑣
2
.(
−𝑥
𝑦
2
)
B.
{
𝑧′
𝑥
=
2𝑢
𝑢
2
+𝑣
2
.𝑦 +
2𝑣
𝑢
2
+𝑣
2
.
1
𝑦
𝑧′
𝑦
=
2𝑢
𝑢
2
+𝑣
2
.𝑥 +
2𝑣
𝑢
2
+𝑣
2
.(
−𝑥
𝑦
2
)
TEAM GI I TÍCH 2 Ả
7
C.
{
𝑧′
𝑥
=
2𝑢
𝑢
2
+𝑣
2
.𝑦 +
2𝑣
𝑢
2
+𝑣
2
.
𝑥
𝑦
𝑧′
𝑦
=
2𝑢
𝑢
2
+𝑣
2
.𝑥 +
2𝑣
𝑢
2
+𝑣
2
.(
𝑥
𝑦
2
)
D.
{
𝑧′
𝑥
=
2𝑢
𝑢
2
+𝑣
2
.𝑦−
2𝑣
𝑢
2
+𝑣
2
.
1
𝑦
𝑧′
𝑦
=
2𝑢
𝑢
2
+𝑣
2
.𝑥−
2𝑣
𝑢
2
+𝑣
2
.(
−𝑥
𝑦
2
)
1.5. ĐẠO HÀM C A HÀM N Ủ Ẩ
Câu 1. Xác định đạo hàm c a hàm n sau ủ ẩ 𝒙 +𝟐𝒚 +𝟑𝒙 𝒚 =𝟐
𝟑 𝟑 𝟐
A. y’
x
= −
x
2
−2𝑥𝑦
2y −𝑥
2 2
B.
y’
x
=
x
2
+2𝑥𝑦
2y −𝑥
2 2
C.
y’
x
=
x
2
−2𝑥𝑦
2y −𝑥
2 2
D. y’
x
= −
x
2
+2𝑥𝑦
2y −𝑥
2 2
Câu 2. Cho 𝒙 .𝒂𝒓𝒄𝒕𝒂𝒏𝒙 + +𝒚 +𝟐𝒛 = 𝟏
𝟐
𝟐𝒙𝒚
𝟐 𝟒 𝟑
. Tính z’
x
và z’
y
A.
{
𝑧′
𝑥
=
2𝑥.𝑎𝑟𝑐𝑡𝑎𝑛𝑥+
𝑥
2
1+𝑥
2
+2𝑦
2
6𝑧
2
𝑧′
𝑦
=
2xy+2𝑦
3
3𝑧
2
B.
{
𝑧′
𝑥
=
2𝑥.𝑎𝑟𝑐𝑡𝑎𝑛𝑥−
𝑥
2
1+𝑥
2
−2𝑦
2
6𝑧
2
𝑧′ = −
𝑦
2xy+2𝑦
3
3𝑧
2
C.
{
𝑧′
𝑥
= −
2𝑥.𝑎𝑟𝑐𝑡𝑎𝑛𝑥+
𝑥
2
1+𝑥
2
+2𝑦
2
6𝑧
2
𝑧′ = −
𝑦
2xy+2𝑦
3
3𝑧
2
D.
{
𝑧′
𝑥
=−
2𝑥.𝑎𝑟𝑐𝑡𝑎𝑛𝑥−
𝑥
2
1+𝑥
2
−2𝑦
2
6𝑧
2
𝑧′
𝑦
=
2xy+2𝑦
3
3𝑧
2
Câu 3. Cho hàm số 𝒙
𝟑
−𝒚
𝟑
+𝟑𝒙𝒚− = 𝟎𝟏𝟑 . Xác định hàm n y = y(x). ẩ
Viết phương trình tiếp tuyến của đồ thị hàm ẩn này t m A(-1; -2) ại điể
TEAM GI I TÍCH 2 Ả
8
A. y = −
1
5
.
(
𝑥+1
)
−2
B. y =
1
5
.
(
𝑥+1
)
−2
C. y =
1
5
.
(
𝑥+1
)
+2
D. y = −
1
5
.
(
𝑥+1
)
+2
Câu 4. Cho hàm ẩn z=z(x,y) được xác định t ừ phương trình sau
𝒛
𝟐
+
𝟐
𝒙
=
√
𝒚
𝟐
−𝒛
𝟐
Tính 𝒙 𝒛′
𝟐
𝒙
+
𝟏
𝒚
𝒛′
𝒚
=?
A.
1
𝑧
B.
−1
𝑧
C.
−1
𝑧
2
D.
1
𝑧
2
1.6. TÍNH GẦN ĐÚNG NHỜ VI PHÂN
Câu 1. Tính g
ần đúng giá trị sau nhờ vi phân A = (1,02) . (0.97)
3 2
A. 0 B. 1 C. 2 D. 3
Câu 2. Tính gần đúng giá trị sau nhờ vi phân A = √(𝟏, ) +(𝟎,𝟎𝟐
𝟐
𝟎𝟓)
𝟐
𝟑
A.
1
5
B.
1
15
C.
1
3
D.
76
75
Câu 3. Tính g
ần đúng giá trị sau nhờ vi phân A = √𝟐.(𝟐, −𝟑. 𝟒,𝟗𝟖)
𝟑
(
𝟎𝟏
)
𝟐
+𝟐
𝟑
A. B. 1,76 1,89 C. 1, 1,93 D. 67
Câu 4. Tính gần đúng giá trị sau nhờ vi phân S = √(𝟑, ) +(𝟑,𝟎𝟏
𝟐
𝟗𝟗)
𝟐
A. B. 2,76 3,29 C. 4, 1,988 D. 58
1.7. C C TR CỰ Ị ỦA HÀM NHI U BI N Ề Ế
Câu 1. Cho hàm s z = ố 𝒙 +𝒚 −𝒚
𝟐
+𝒙𝒚
𝟐
−𝟐𝒙 . Xác định điểm c i và c c tiực đạ ự ểu
của hàm số n u có. ế
A. Hàm s có m m c i M(1; 0) ố ột điể ực đạ
B. Hàm s có m m c c ti u M(1; 0) ố ột điể ự ể
C. Hàm s có m m c i M(-1; 0) ố ột điể ực đạ
TEAM GI I TÍCH 2 Ả
9
A. Hàm s có m m c c ti u M(0; -1) ố ột điể ự ể
Câu 2. Cho hàm s z = ố 𝟐𝒙 𝟒𝒙 𝟐𝒚
𝟒
+𝒚
𝟒
−
𝟐
+
𝟐
. Điểm N(1; 0) là điể ực đạm c i hay
cực ti u c a hàm sể ủ ố và xác định n𝒛
𝒎𝒂𝒙
; 𝒛
𝒎𝒊𝒏
ếu có.
A. m c c ti u v i f -2 N(1; 0) là điể ự ể ớ
min
=
B. m c i v i f = 2 N(1; 0) là điể ực đạ ớ
min
C. m c i v i f 4 N(1; 0) là điể ực đạ ớ
min
=
D. m c u v i f = 2 N(1; 0) là điể ực tiể ớ
min
Câu 3. Cho hàm s z = 2 m c i và c c tiố 𝒙 +𝟑𝒚 −𝒆
𝟐 𝟑 −(𝒙
𝟐
+𝒚
𝟐
)
. Xác định điể ực đạ ự ểu
của hàm số n u có. ế
A. M(0; 0) là điểm cực tiểu
B. M(0; 0) là điể ực đạm c i
C. N(1; 0) là điểm cực tiểu
D. N(1; 0) là điể ực đạm c i
Câu 4. Cho hàm số với điều kiệ𝒛 = 𝟐𝒙 +𝒚
𝟐 𝟐
n 𝒙 +𝒚 = 𝟏.
𝟐 𝟐
Hàm s trên có bao ố
nhiêu điể ực đại và điểm c m c ực tiểu.
A. 1 c i và 3 c c ti u ực đạ ự ể
B. 2 c i và c c ti u ực đạ ự ể
C. 3 c i và 1 c c ti u ực đạ ự ể
D. 3 c i ực đạ
Câu 5. Tìm c c tr c a hàm sự ị ủ ố 𝒛 =
𝒙
𝟒
+
𝒚
𝟑
với điều kiệ . Điển 𝒙 +𝒚 = 𝟏
𝟐 𝟐
m
𝑴(
𝟑
𝟓
;
𝟒
𝟓
) là điể ực đạm c i hay cực tiểu của hàm s nh giá tr z t m M. ố và xác đị ị ại điể
A. 𝑀(
3
5
;
4
5
) là điể ực đạm c i và 𝑧
(
𝑀
)
=
1
2
B. 𝑀(
3
5
;
4
5
) là điểm cực tiểu và 𝑧
(
𝑀
)
=
5
6
C. 𝑀(
3
5
;
4
5
) là điể ực đạm c i và 𝑧
(
𝑀
)
=
5
12
D. 𝑀(
3
5
;
4
5
) là điểm cực tiểu và 𝑧
(
𝑀
)
=
5
12
Câu 6. Cho hàm s sau: z= . Hàm số 𝒙 +𝒚 +(𝒙+𝒚)
𝟑 𝟑 𝟐
ố trên có bao nhiêu điểm
cực tr . ị
A. 1 B. 2
TEAM GI I TÍCH 2 Ả
10
C. 3 D. 4
Câu 7. Cho hàm s sau . Hàm số 𝒛 = 𝟐𝒙 +𝒙𝒚 + 𝒚 +𝟐
𝟐 𝟐 𝟑
ố trên có bao nhiêu điểm
cực tr . ị
A. 0 B. 1
C. 2 D. 3
1.8. KHAI TRI N TAYLOR Ể
Câu 1. Vi t khai tri n Taylor c a hàm s sau t m M(1; 2) ế ể ủ ố ại điể
𝒇(𝒙,𝒚) = 𝒙 +𝒚 +𝟏
𝟐 𝟐
+ + +𝒙𝒚 𝟐𝒙 𝟐𝒚
A. 𝑓(𝑥,𝑦) = +3(𝑥 −1)+7(𝑦 −2)+2(𝑥 −1) + 2(𝑥−1)(𝑦 −2)+(𝑦 −2)14
2 2
B. 𝑓(𝑥,𝑦) = +6(𝑥 −1)+7(𝑦 −2)+(𝑥 −1) +(𝑥 −1)(𝑦− 2)+(𝑦−2)14
2 2
C. 𝑓(𝑥,𝑦) = 7+6(𝑥−1)+ (𝑦−2)+(𝑥−1) +(𝑥 −1)(𝑦− 2)+(𝑦−2)14
2 2
D. 𝑓(𝑥,𝑦) = 7+6(𝑥−1)+ (𝑦−2)+(𝑥−1) +(𝑥−1)(𝑦− 2)+(𝑦−2)14
2 2
Câu 2. Vi t khai tri n Taylor c a hàm s sau t m M(0; 1) ế ể ủ ố ại điể
𝒇
(
𝒙,𝒚
)
= 𝒙
𝟑
+𝒙 𝒚+𝒚
𝟐 𝟑
A.
𝑓
( (
𝑥,𝑦
)
= 1+3 𝑦− 1
)
+
1
2
𝑥
2
+3(𝑦−1)
2
+𝑥
3
+𝑥
2
(
𝑦−1
)
+(𝑦−1)
3
B.
𝑓
( (
𝑥,𝑦
)
= 1−3 𝑦− 1
)
+
1
2
𝑥
2
−3 𝑦−1
( )
2
+𝑥
3
−𝑥
2
(
𝑦−1
)
+(𝑦− 1)
3
C.
𝑓
( (
𝑥,𝑦
)
= 1+3 𝑦− 1
)
+
1
2
𝑥
2
+3(𝑦−1)
2
+𝑥
3
+𝑥
2
(
𝑦−1
)
+
1
6
(𝑦−1)
3
D.
𝑓
( (
𝑥,𝑦
)
= 1−3 𝑦− 1
)
+
1
2
𝑥
2
−3 𝑦−1
( )
2
+𝑥
3
−𝑥
2
(
𝑦−1
)
+
1
6
(𝑦−1)
3
1.9. TÌM GTLN, GTNN C A HÀM S Ủ Ố
Câu 1. Tìm của 𝒎𝒊𝒏,𝒎𝒂𝒙 𝒛 = 𝐬𝐢𝐧 𝒙 +𝐬𝐢𝐧 𝒚 +𝐬𝐢𝐧 (𝒙+𝒚) 𝟎 ≤ 𝒙,𝒚 ≤ với
𝝅
𝟐
A. 𝑧
𝑚𝑎𝑥
=
3 3
√
2
,𝑧
𝑚𝑖𝑛
= 0
B. 𝑧
𝑚𝑎𝑥
=
√
3
2
,𝑧
𝑚𝑖𝑛
= 0
C. 𝑧
𝑚𝑎𝑥
=
1
2
,𝑧
𝑚𝑖𝑛
= −1
D. 𝑧
𝑚𝑎𝑥
=
3 3
√
2
,𝑧
𝑚𝑖𝑛
=
−1
2
TEAM GI I TÍCH 2 Ả
11
Câu 2. Tìm GTLN, GTNN của trong miền hình elip 𝒛 = 𝒙 −𝟗𝒚 ,
𝟐 𝟐
𝒙
𝟐
𝟗
+𝒚
𝟐
≤ 𝟏
A. 𝑧 = 9,𝑍
𝑚𝑎𝑥 𝑚𝑖𝑛
= −9
B. 𝑧 = 3,𝑍
𝑚𝑎𝑥 𝑚𝑖𝑛
= −3
C. 𝑧 = 3,𝑍
𝑚𝑎𝑥 𝑚𝑖𝑛
= −9
D. 𝑧 = 9,𝑍
𝑚𝑎𝑥 𝑚𝑖𝑛
= −3
Câu 3.
Tìm giá trị lớn nhất, giá trị ỏ ất trong miề ΔOAB với O(0,0);A(7,0);B(0,7) của nh nh n
𝒛 = 𝒙 +𝟐𝒚 +𝟑𝒙𝒚−
𝟑 𝟐
𝟏𝟑𝒙 𝟏𝟖𝒚−
A. 𝑧 ; 𝑧
𝑚𝑎𝑥
= 252
𝑚𝑖𝑛
= −
81
2
B. 𝑧 ; 𝑧 = −
𝑚𝑎𝑥
= 64
𝑚𝑖𝑛
1
2
C. 𝑧 ; 𝑧
𝑚𝑎𝑥
= 212
𝑚𝑖𝑛
=
1
2
D. 𝑧 ; 𝑧
𝑚𝑎𝑥
= 252
𝑚𝑖𝑛
= −
1
2
II. NG D NG C A PHÉP TÍNH VI PHÂN Ứ Ụ Ủ
Câu 1.
Tìm hình bao c a h ng cong , c là tham s . ủ ọ đườ 𝑐 𝑦 −𝑐 = 𝑥
( )
2
ố
A. 𝑦 = 𝑥
B. 𝑦 = −2𝑥
C. 𝑦 = 2𝑥
D. 𝑦 = ±2𝑥
Câu 2. Phương trình pháp diện tại 𝐴(
𝜋
4
;1;1) của đường {
𝑥 = 𝑡
𝑦 = 2.cos𝑡
√
𝑧 = 2.sin𝑡
√
là :
A. 𝑥+𝑦 +𝑧 = 0
B. 𝑥 −𝑦+𝑧 =
𝜋
4
C. 𝑦−𝑧 =
𝜋
4
D. 𝑥 +𝑦−𝑧 =
𝜋
4
Câu 3. Phương trình tiếp diện tại 𝐴(1;1;−1) của mặt 𝑧 = 𝑥 −3 +𝑦
2
𝑥𝑦
2
là :
A. 𝑥+𝑦 +𝑧 = 1
B. 𝑥 +𝑦−𝑧 = 1
C. 𝑥 +𝑦−𝑧+1 = 0
D. 𝑥 +𝑦+𝑧 = 3
Câu 4.
Tính độ cong c ng ủa đườ {
𝑥 =2𝑡−𝑡
2
𝑦 = 3𝑡− 𝑡
3
tại điểm 𝑡 =−1.
A.
1
2
B.
3
8
C. 1
D.
5
8
Câu 5. Viết phương trình tiếp diện của mặt 𝑧 = 4𝑥 −𝑦 +2𝑦
2 2
tại (−1;2;4) :
TEAM GI I TÍCH 2 Ả
12
A. 8𝑥+2𝑦 +𝑧 = 0
B. 8𝑥+2𝑦−𝑧=0
C. 𝑥 +2𝑦+𝑧=7
D. 4𝑥+2𝑦−𝑧+4 = 0
Câu 6.
Viết phương trình tiếp diện của mặt cong t𝑧 =𝑒
𝑥
2
−𝑦
2
ại
(
1;−1;1
)
∶
A. 2𝑥+2𝑦 −𝑧+1 = 0
B. 𝑥 +2𝑦−𝑧+2 = 0
C. 2𝑥−2𝑦+𝑧−5 = 0
D. Các câu tr lả ời đều sai
Câu 7. Viết phương trình tiế ủa đườ ại giao điểp tuyến c ng cong t𝑦 = 𝑒
1−𝑥
2
m của
đường cong v ng thới đườ ẳng : 𝑦 = 1
A. 𝑥−2𝑦 +1 = 0
B. 2𝑥+𝑦−3=0
C. 2𝑥−𝑦+3=0
D. 𝑥 −𝑦+1 =0
Câu 8. Viết phương tình pháp tuyế ủa đườn c ng cong 𝑥
2
3
+𝑦
2
3
= 5 𝑀(8;1) tại điểm
A. 𝑥+2𝑦 − = 010
B. 2𝑥+𝑦+5=0
C. 2𝑥−𝑦− = 015
D. 𝑥 −2𝑦+ =010
Câu 9. Tính độ cong t c ng là giao c a m t trại điểm 𝑀(1;0;−1) ủa đườ ủ ặ ụ 4𝑥 +𝑦 =
2 2
4
và m t ph ng ặ ẳ 𝑥 −3𝑧 = 4
A. 0
B. 1
C. 2
D. 9
Câu 10.
Viết phương trình tiế ủa đườp tuyến c ng {
𝑥
2
+𝑦
2
= 10
𝑦
2
+𝑧
2
= 25
t m A(1,3,4) : ại điể
A.
𝑥−1
12
=
𝑦−3
−4
=
𝑧−4
3
B. 12x 4y 3z 12− + − =0
C.
𝑥+1
6
=
𝑦−4
3
=
𝑧−3
4
D. Các đáp án đều sai
III. TÍCH PHÂN B I NG D Ộ & Ứ ỤNG
3.1. TÍCH PHÂN KÉP
Câu 1: 𝑇í𝑛ℎ 𝑥𝑦𝑑𝑥𝑑𝑦
∬
𝐷
v c gi i h n bới D đượ ớ ạ ởi 𝑥+𝑦 =4 𝑣à 𝑥 = 2𝑦
2
A.90 -90 -72 D.72 B. C.
Câu 2:𝑇í𝑛ℎ 2𝑦𝑑𝑥𝑑𝑦
∬
𝐷
𝑣ớ𝑖 𝐷 𝑥á𝑐 đị𝑛ℎ 𝑏ở𝑖 𝑥
2
+𝑦
2
≤1,𝑥+𝑦 ≥1
A.
1
3
B.
1
6
C.
2
3
D.
4
3
Câu 3:
𝑇í𝑛ℎ
∫
𝑑𝑥
1
0
∫
(𝑥
2
3
2
𝑦−2𝑦
2
)𝑑𝑦
A.−
62
6
B.
72
7
C.−
71
6
D.
62
6
Câu 4:
∫
𝑑𝑥
1
0
∫
sin
(
𝑦
2
)
𝑑𝑦
1
𝑥
=
𝑎−𝑐𝑜𝑠𝑏
𝑐
.𝑇í𝑛ℎ 𝑎−𝑏 +𝑐
TEAM GI I TÍCH 2 Ả
13
A.0 B.1 C.2 D.3
Câu 5:𝑇í𝑛ℎ +𝑦
∬
𝑥
√
𝑥
2 2
𝐷
𝑑𝑥𝑑𝑦 𝑣ớ𝑖 𝐷 𝑥á𝑐 đị𝑛ℎ 𝑏ở𝑖 𝑥
2
+𝑦
2
≤ 𝑥;𝑦 ≥ 0
A.
1
15
B.
2
15
C.
4
15
D.
8
15
Câu 6:𝑇í𝑛ℎ (2𝑥+𝑠𝑖𝑛𝑦)𝑑𝑥𝑑𝑦
∬
𝐷
𝑣ớ𝑖 𝐷: 𝑥 −2
( )
2
+𝑦
2
≤ 1
A.2𝜋 4𝜋 6𝜋 8𝜋 B. C. D.
𝐂â𝐮 𝟕:
∬
𝑑𝑥𝑑𝑦
(
𝑥
2
+𝑦
2
)
3
=
𝑎
𝑏
+𝑙𝑛𝑐,𝐷:𝑥 ≤ 𝑥 +𝑦 ≤ 2𝑥
2 2
𝐷
,−𝑥 ≤ 𝑦 ≤0.
𝑎
𝑏
𝑡ố𝑖 ả𝑛.𝑔𝑖
Tổng a+b+c=?
A.20 B.21 C.22 D.23
𝐂â𝐮 𝟖: 𝑇í𝑛ℎ 2𝑥− 𝑥 −𝑦∬√
2 2
𝑑𝑥𝑑𝑦
𝐷
𝑣ớ𝑖 ề𝑛 𝐷 𝑙à ề𝑛 𝑥𝑚𝑖 𝑚𝑖
2
+𝑦
2
≤ 2𝑥,𝑦 ≥ 0
A.
𝜋
4
B.
𝜋
3
C.
𝜋
2
D.𝜋
𝑪â𝒖 𝟗:𝑇í𝑛ℎ
∬𝑦
2
( )
6𝑥 −𝑦 𝑑𝑥𝑑𝑦,𝑣ớ𝑖 𝐷 ớ𝑖 ℎạ𝑛 𝑏ở𝑖:𝑥 =0,𝑥 + = 1.𝑔𝑖
|
𝑦
|
𝐷
A.
1
5
B.
1
3
D.1 C.3
𝐂â𝐮 :𝑇í𝑛ℎ 𝑥+𝑦
𝟏𝟎 ∬
( )
2
𝑑𝑥𝑑𝑦
𝐷
𝑣ớ𝑖 ề𝑛 𝐷:5𝑥𝑚𝑖
2
+6 +5𝑦𝑥𝑦
2
≤ 4
𝐴.
𝜋
8
B.𝜋 C.
𝜋
2
D.
π
4
𝐂â𝐮 ề𝑛 𝐷 ớ𝑖 ℎạ𝑛 𝑏ở𝑖 𝑥 = 1,𝑦 = 0 𝑥 = 𝑦.𝟏𝟏:𝑀𝑖 𝑔𝑖 ,
∬
𝑑𝑥𝑑𝑦
𝑥+𝑦+1
=
𝑎
2
𝑙𝑛𝑏−𝑐𝑙𝑛2
𝐷
𝑇ổ 𝑎+𝑏+𝑐 =?𝑛𝑔
A.5 B.6 C.7 D.8
𝐂â𝐮 : ề𝑛 𝐷: 𝑥 + 𝑦 ≤ 6.
𝟏𝟐 𝑀𝑖
2 2
∬
3𝑥
2
−𝑦
2
+1
𝑥
2
+𝑦 +1
2
𝑑𝑥𝑑𝑦
𝐷
= 𝑎𝜋+𝑙𝑛𝑏.
Tổng a+b=?
A.6 B.7 C.8 D.9
TEAM GI I TÍCH 2 Ả
14
3.2. TÍCH PHÂN BỘI BA
𝐂â𝐮 𝟏:𝑇í𝑛ℎ 𝑡í𝑐ℎ 𝑝ℎâ𝑛 ∫ 𝑑𝑥
1
0
∫
𝑑𝑧
1−𝑥
0
∫
(𝑦+𝑧)
2
0
𝑑𝑦
A.
1
3
B.
2
3
C.1 D.
4
3
𝐂â𝐮 𝟐:𝑇í𝑛ℎ 3𝑥 −2𝑦
∭
(
2
)
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧 𝑣ớ𝑖 𝑉:0 ≤ 𝑥 ≤ 1,0 ≤ 𝑦 ≤ 𝑥,0 ≤ 𝑧 ≤𝑥
2
A.
3
10
B.
1
10
C.
7
10
D.
9
10
𝐂â𝐮 𝟑:𝑇í𝑛ℎ +𝑦
∭
(
𝑥
2 2
)
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧,𝑉 ớ𝑖 ℎạ𝑛 𝑏ở𝑖 𝑥𝑔𝑖
2
+𝑦
2
−2𝑧 = 0,𝑧 = 2
A.
64
15
B.
64𝜋
15
C.
16𝜋
3
D.
24𝜋
5
𝐂â𝐮 𝟒: ∫ 𝑑𝑥
1
0
∫
𝑑𝑧
1
0
∫
𝑥𝑧𝑒
𝑥𝑦
2
𝑑𝑦
1
𝑧
2
=
𝑒
𝑎
−
𝑏
𝑐
.𝑎 +𝑏 +𝑐 =?
A.6 B.7 C.8 D.9
𝐶â𝐮 𝟓:
∭
𝑑𝑥𝑑𝑦𝑑𝑧
( )
𝑥+𝑦 +𝑧+2
2
=
𝑎
𝑏
+𝑐. 2−𝑑. 3 ,𝑉: {𝑙𝑛 𝑙𝑛
𝑥+ 𝑦+𝑧 ≤1
𝑥,𝑦,𝑧 ≥ 0
𝑉
𝑎+𝑏 +𝑐 −𝑑 =?
A.10 B.11 C.12 D.13
𝐂â𝐮 𝟔: 4𝑥 +𝑦 +𝑧 +2
∭
(
2 2 2
𝑥𝑦
)
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧 =
𝑎𝜋
𝑏
,𝑉:4𝑥
2
+𝑦
2
+𝑧
2
≤ 4,𝑧 ≥ 0.
𝑎−𝑏 =?
A.2 B.3 C.11 D.7
𝐂â𝐮 𝟕: +𝑦 +𝑧∭√𝑥
2 2 2
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧 =
𝜋
𝑎
,𝑉:𝑥
2
+𝑦
2
+𝑧
2
≤ 𝑦.𝑇ì𝑚 𝑎?
A.9 B.12 C.8 D.10
𝐂â𝐮 𝟖:, ề𝑛 𝑉: +𝑦 ≤ 𝑧 ≤ 4−𝑥 −𝑦 𝑧𝑐𝑜𝑠 + 𝑦
𝑀𝑖 √𝑥
2 2
√
2 2
.∭
(
𝑥
2 2
)
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧
= 𝜋 𝑎−𝑐𝑜𝑠𝑏 .𝑇ổ 𝑎 +𝑏 =?
( )
𝑛𝑔
A.3 B.4 C.5 D.6
𝐂â𝐮 𝟗: ề𝑛 𝑉:{
𝑀𝑖
𝑥
2
+𝑦
2
+𝑧
2
≤ 8
𝑥
2
+𝑦
2
≤ 2
.
∭(
𝑥
2
+𝑦
2
)
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧 =
𝑎
√
8−𝑏 6
√
15
𝜋.
TEAM GI I TÍCH 2 Ả
15
𝑏−𝑎 =?
A.16 B.42 24 D.8 C.
𝐂â𝐮 :𝑇í𝑛ℎ 𝑥+𝑦−2𝑧
𝟏𝟎 ∭
( )
2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
=
𝑎𝜋
𝑏
,𝑣ớ𝑖 𝑉:𝑥
2
+𝑦
2
+𝑧
2
≤ 1.
𝑎−𝑏 =?
A.-3 B.4 C.1 -2 D.
3.3. NG DỨ Ụ ỦNG C A TÍCH PHÂN B I Ộ
𝑪
𝑪
𝑪
𝑪𝑪â
𝒖
𝒖
𝒖
𝒖𝒖
𝟏
𝟏
𝟏
𝟏𝟏:𝐷𝑖ệ𝑛 𝑡í𝑐ℎ 𝑝ℎầ𝑛 𝑚ặ𝑡 𝑧 =𝑥 +𝑦 +2 𝑛ằ𝑚 𝑡𝑟𝑜𝑛𝑔 𝑚ặ𝑡 ụ 𝑥 +𝑦 = 9 𝑙à
2 2
𝑡𝑟
2 2
𝑎
√
𝑎−𝑏
𝑐
𝜋.𝑇ổ𝑛𝑔 𝑎 +𝑏+ 𝑐 =?
A.32 B.36 C.44 D.48
𝐂
𝐂
𝐂
𝐂𝐂â
𝒖
𝒖
𝒖
𝒖𝒖
𝟐
𝟐
𝟐
𝟐𝟐:𝐷𝑖ệ𝑛 𝑡í𝑐ℎ ℎì𝑛ℎ 𝑝ℎẳ ớ𝑖 ℎạ𝑛 𝑏ở𝑖 𝑦 = 3𝑥,𝑦 = 0,𝑥 +𝑦 = 2𝑥 𝑙à𝑛𝑔 𝑔𝑖
√
2 2
𝜋
𝑎
+
√𝑏
𝑐
.𝑇ổ𝑛𝑔 𝑎 +𝑏+𝑐 =?
A.7 B.8 C.9 D.10
𝐂
â
𝒖
𝒖
𝒖
𝒖𝒖
𝟑
𝟑
𝟑
𝟑𝟑:𝑇ℎể 𝑡í𝑐ℎ ề𝑛 ớ𝑖 ℎạ𝑛 𝑏ở𝑖 𝑥 = 1+𝑦 +𝑧 𝑣à 𝑥 = 2 +𝑧𝑚𝑖 𝑔𝑖
2 2
(
𝑦
2 2
)
𝑙à
𝜋
𝑎
.𝑉ậ𝑦 𝑎 =
A.
1
2
B.
5
4
C.3 D.2
𝐶
𝐶
𝐶
𝐶𝐶
â
𝑢
𝑢
𝑢
𝑢𝑢 4:𝑀𝑖ề𝑛 𝐷 ớ𝑖 ℎạ𝑛 𝑏ở𝑖 +𝑦 = 2𝑥 .𝑆𝑔𝑖
(
𝑥
2 2
)
2 3
𝐷
=
𝑎𝜋
𝑏
.𝑇í𝑛ℎ 𝑏 −𝑎?
A.3 B.4 C.5 D.7
𝐂â𝐮 𝟓:𝑇í𝑛ℎ 𝑣ậ𝑡 𝑡ℎể 𝑉 𝑥á𝑐 đị𝑛ℎ 𝑏ở𝑖 +𝑦√𝑥
2 2
≤ 𝑧 ≤ 6−𝑥 −𝑦
2 2
A.
16𝜋
3
B.
32𝜋
3
𝐶.
64𝜋
3
D.
35𝜋
3
Câu 6: 𝑇í𝑛ℎ 𝑡ℎể 𝑡í𝑐ℎ 𝑣ậ𝑡 𝑡ℎể ớ𝑖 ℎạ𝑛 𝑏ở𝑖 𝑐á𝑐 𝑚ặ𝑡 𝑧 = 𝑥 + 3𝑦𝑔𝑖
2 2
và
𝑧 = 4−3𝑥 −𝑦
2 2
A.
16𝜋
3
B.
8𝜋
3
C.2 𝜋 D.4𝜋
TEAM GI I TÍCH 2 Ả
16
IV. TÍCH PHÂN PH THU C THAM S : Ụ Ộ Ố
4.1. TÍCH PHÂN XÁC ĐỊNH PHỤ THU C THAM SỘ Ố
Câu 1: Tính
∫
ln (1
𝜋/2
0
+y𝑠𝑖𝑛
2
𝑥) 𝑣ớ𝑖 𝑦𝑑𝑥 >1
A.𝜋ln(1+ 𝑦+ 1
√
)−𝜋𝑙𝑛2
B. 𝜋ln(1+ 𝑦+1
√
)+𝜋𝑙𝑛2
C. 𝜋−𝜋𝑙𝑛2
D.1
Câu 2: Tính gi i h n sau: ớ ạ
lim
𝑦⟶0
∫ √
𝑥
3
+𝑦
3
𝑑𝑥
1
0
A.
3
5
B.0,4 C.
1
5
D. 0,8
Câu3: Tính gi i h n: ớ ạ
lim
𝑦⟶0
∫
𝑥
2015
cos (𝑥𝑦)
1+𝑥 +𝑦
2 2
𝑑𝑥
1
−1
A. .
3
7
B. .
3
5
C. .
1
3
D. .
2
3
Câu 4: Tính :
lim
𝑦⟶0
∫
𝑎𝑟𝑐cot (𝑥+𝑦)
1+𝑥 +𝑦
2 2
𝑑𝑥
𝑠𝑖𝑛𝑦
𝑐𝑜𝑠𝑦
A. .
−3𝜋
2
32
B. .
3𝜋
16
C. .
−𝜋
32
D. .
3𝜋
2
32
Câu 5: Cho I(y)=
∫
sin ( 𝑥
2
+𝑥𝑦
1
𝑦
+𝑦
2
) .𝑇í𝑛ℎ 𝐼𝑑𝑥
′
(0)
A. .
𝑠𝑖𝑛1
2
B.
𝜋
2
C.
1
2
D. 1
Câu 6: Cho I(y)=
∫
ln ( 𝑦 𝑠𝑖𝑛 𝑥+𝑐𝑜𝑠 𝑥)
2 2 2
𝜋
2
0
𝑑𝑥. Tính 𝐼
′
(1)
A.0 B. .
𝜋
2
C.
1
2
D.2
Câu 7: Tìm
TEAM GI I TÍCH 2 Ả
17
lim
𝑦⟶1
∫
𝑎𝑟𝑐tanx
𝑥
2
+𝑦
2
𝑑𝑥
𝑦
0
A.
𝜋
2
B.
𝜋
2
32
C.
−𝜋
2
32
D.
−3𝜋
2
32
Câu 8: Tính
lim
𝑦⟶0
∫
𝑎𝑟𝑐tan (𝑥+𝑦)
1+𝑥 +𝑦
2 2
𝑑𝑥
𝑐𝑜𝑠𝑦
𝑠𝑖𝑛𝑦
A.
𝜋
2
B.
−𝜋
2
32
C.
𝜋
2
32
D.
−3𝜋
2
32
Câu 9: Tính lim
𝑦⟶1
∫
𝑥
2
sin (𝜋𝑦𝑥)
2𝑦
𝑦
𝑑𝑥.
A.
2−5𝜋
𝜋
2
B.
2+5𝜋
𝜋
2
C.2 D. .
𝜋
4
Câu 10 (Đề cuối kì- 20152): Tính gi i h n ớ ạ
lim
𝑦⟶0
∫
𝑥
2020
+𝑦
2021
1+𝑥
2
+2021𝑦
2
𝑑𝑥
1
−1
4.2. TÍCH PHÂN SUY R NG PH THU C THAM SỘ Ụ Ộ Ố
Câu 1:
Tính I(y)=
∫
arctan (x+y)
𝑥
2
+1
𝑑𝑥
+∞
0
A.
2𝜋
𝑦
2
+𝑦
B.
2𝜋
𝑦
2
+𝑦
C.
2
𝑦
2
+𝑦
D.
2𝜋
𝑦
2
Câu
2: Tính
∫
𝑒
− −𝑎𝑥
−𝑒
𝑏𝑥
𝑥
𝑑𝑥
+∞
0
A. -lna+lnb B. ln(ab) C. lna lnb D. 1 –
Câu 3: Tính
lim
𝑦⟶0
∫
𝑐𝑜𝑠xy
𝑥
2
+1
𝑑𝑥
𝑦
0
A. 𝜋/2 𝜋/2 B. 0 C. -
D.2
Câu 4: Tính
∫
𝑒
−𝑎𝑥
sin − sin ( )
(
𝑏𝑥
)
𝑐𝑥
𝑥
𝑑𝑥
+∞
0
A.
arctan(
𝑏
𝑎
) - arcrtan(
𝑐
𝑎
) C. arctan(
𝑏
𝑐
) - arcrtan(
𝑐
𝑎
)
B. 0 D. arctan(
𝑐
𝑎
) -arcrtaln(
𝑐
𝑏
)
TEAM GI I TÍCH 2 Ả
18
Câu 5:
Tính
∫
2 −3
−𝑥 −𝑥
𝑥
𝑑𝑥
+∞
0
A.
ln(
𝑙𝑛3
𝑙𝑛
2
) B. ln(
𝑙𝑛2
𝑙𝑛
3
) C.0 D. ln6
TEAM GI I TÍCH 2 Ả
19
PHẦN II: L I GI Ờ ẢI VÀ ĐÁP ÁN
I. HÀM NHI U BI N Ề Ế
1.1. GI I H N C A HÀM NHI U BI N Ớ Ạ Ủ Ề Ế
Câu 1:
I = lim
(𝑥,𝑦)→(0,0)
𝑥
2
𝑦
𝑥
2
+𝑦
2
Nguyên lý k p: 0 |ẹ ≤
𝑥
2
𝑦
𝑥
2
+𝑦
2
| ≤ |
𝑥
2
𝑦
𝑥
2
| = |y|
Mà lim
(𝑥,𝑦)→(0,0)
|𝑦| = 0
I = lim
(𝑥,𝑦)→(0,0)
𝑥
2
𝑦
𝑥
2
+𝑦
2
= 0
Đáp án A
Câu 2:
I= lim
(𝑥,𝑦)→(0,0)
𝑥𝑦
𝑥
2
+𝑦
2
Đặt y = kx
I= lim
(𝑥,𝑦)→(0,0)
𝑥.𝑘𝑥
𝑥
2
+(𝑘𝑥)
2
= lim
(𝑥,𝑦)→(0,0)
𝑘
1+(𝑘)
2
= f(k)
Không t n t i gi i h n ồ ạ ớ ạ
Đáp án D
Câu 3:
I= lim
(𝑥,𝑦)→(0,0)
𝑥𝑦
√𝑥 +𝑦
2 2
Theo b ng th c Cô 2xy ất đẳ ứ – si: 𝑥
2
+𝑦
2
≥
Ta có: 0 | ≤
𝑥𝑦
√𝑥 +𝑦
2 2
| ≤ |
𝑥𝑦
√
2𝑥𝑦
| = |
√
𝑥𝑦
√
2
|
Mà lim
(𝑥,𝑦)→(0,0)
|
√
𝑥𝑦
√
2
| = 0
I= lim
(𝑥,𝑦)→(0,0)
𝑥𝑦
√𝑥 +𝑦
2 2
= 0
Đáp án A
Câu 4:
TEAM GI I TÍCH 2 Ả
20
I= lim
(𝑥,𝑦)→(0,0)
𝑥
2
−𝑦
2
𝑥
2
+𝑦
2
t y = kx Đặ
=> I= lim
(𝑥,𝑦)→(0,0)
𝑥
2
−(𝑘𝑥)
2
𝑥
2
+(𝑘𝑥)
2
= lim
(𝑥,𝑦)→(0,0)
1−(𝑘)
2
1+(𝑘)
2
=f(k)
=> Không t n t i gi i h n ồ ạ ớ ạ
Đáp án D
Câu 5:
I= lim
(𝑥,𝑦)→(0,0)
𝑥
3
−𝑦
3
𝑥
2
+𝑦
2
= lim
(𝑥,𝑦)→(0,0)
(𝑥−𝑦 .(𝑥 +𝑦 ))
2
+𝑥𝑦
2
𝑥
2
+𝑦
2
Ta có: 0 |≤
(
𝑥−𝑦 .(𝑥 +𝑦 ))
2
+𝑥𝑦
2
𝑥
2
+𝑦
2
| ≤ |
(
𝑥−𝑦).(𝑥
2
+
𝑥
2
2
+
𝑦
2
2
+𝑦
2
)
𝑥
2
+𝑦
2
| = |
3
2
.(x-y)|
Mà: lim
(𝑥,𝑦)→(0,0)
|
3
2
.(x-y)| = 0
I= lim
(𝑥,𝑦)→(0,0)
𝑥
3
−𝑦
3
𝑥
2
+𝑦
2
= 0
Đáp án C
Câu 6:
I = lim
(𝑥,𝑦)→(0,0)
𝑥
2
𝑦−𝑥𝑦
2
𝑥
3
+𝑦
3
t y = kx Đặ
=> I = lim
(𝑥,𝑦)→(0,0)
𝑥
2
.𝑘𝑥−𝑥.(𝑘𝑥)
2
𝑥
3
+(𝑘𝑥)
3
= lim
(𝑥,𝑦)→(0,0)
𝑘−(𝑘)
2
1+(𝑘)
3
= f(k)
=> Không t n t i gi i h n ồ ạ ớ ạ
Đáp án D
Câu 7:
I = lim
(𝑥,𝑦)→(0,0)
𝑦.(𝑒
3𝑥
−1)−3𝑥.(𝑒 −1)
𝑦
𝑥
2
+𝑦
2
Sử d ng khai tri n Maclaurin: ụ ể
I = lim
(𝑥,𝑦)→(0,0)
𝑦.(3𝑥+
9𝑥
2
2
+0(𝑥
2
))−3𝑥.(𝑦+
𝑦
2
2
+0(𝑦
2
))
𝑥
2
+𝑦
2
= lim
(𝑥,𝑦)→(0,0)
𝑦.(
9𝑥
2
2
)−3𝑥.(
𝑦
2
2
)
𝑥
2
+𝑦
2
= lim
(𝑥,𝑦)→(0,0)
𝑥𝑦.(
9
2
.𝑥−
3
2
.𝑦)
𝑥
2
+𝑦
2
Theo b ng th c Cô 2xy ất đẳ ứ – si: 𝑥
2
+𝑦
2
≥
TEAM GI I TÍCH 2 Ả
21
Ta có: 0
≤ |
𝑥𝑦.(
9
2
.𝑥−
3
2
.𝑦)
𝑥
2
+𝑦
2
| ≤
1
2
. |
(𝑥
2
+𝑦
2
).(
9
2
.𝑥−
3
2
.𝑦)
𝑥
2
+𝑦
2
| =
1
2
. |
9
2
.𝑥 −
3
2
.𝑦|
Mà lim
(𝑥,𝑦)→(0,0)
1
2
. |
9
2
.𝑥 −
3
2
.𝑦| = 0
I = lim
(𝑥,𝑦)→(0,0)
𝑦.(𝑒
3𝑥
−1)−3𝑥.(𝑒 −1)
𝑦
𝑥
2
+𝑦
2
= 0
Đáp án C
Câu 8: (Mẹo: i bỞ đây dạng hàm mũ nên có thể loạ ỏ ngay được các giá trị ≤ 0 =>
loại C)
I = lim
(𝑥,𝑦)→(0,0)
(𝑥 +𝑦
2 2
)
𝑥
2
𝑦
2
= 𝑒
lim
(𝑥,𝑦)→(0,0)
𝑥
2
𝑦
2
.𝑙𝑛(𝑥
2
+𝑦
2
)
= 𝑒
lim
(𝑥,𝑦)→(0,0)
𝑥
2
𝑦
2
𝑥
2
+𝑦
2
.(𝑥
2
+𝑦
2
). (𝑥𝑙𝑛
2
+𝑦
2
)
= 𝑒
lim
(𝑥,𝑦)→(0,0)
𝐼
1
.𝐼
2
+ Xét: lim
(𝑥,𝑦)→(0,0)
𝐼
1
= lim
(𝑥,𝑦)→(0,0)
𝑥
2
𝑦
2
𝑥
2
+𝑦
2
Ta có: 0 |≤
𝑥
2
𝑦
2
𝑥
2
+𝑦
2
| ≤ |
𝑥
2
𝑦
2
2
𝑥𝑦
| = |
𝑥𝑦
2
|
Mà lim
(𝑥,𝑦)→(0,0)
|
𝑥𝑦
2
| = 0
+ Xét: lim
(𝑥,𝑦)→(0,0)
𝐼
2
= lim
(𝑥,𝑦)→(0,0)
(
𝑥
2
+𝑦
2
)
.𝑙𝑛
(𝑥 +𝑦 )
2 2
Đặt: 𝑥
2
+𝑦
2
= t
Khi:
{
𝑥 → 0
𝑦 → 0
=> t → 0
lim
(𝑥,𝑦)→(0,0)
𝐼
2
= lim
𝑡→0
𝑡.𝑙𝑛𝑡 lim =
𝑡→0
𝑙𝑛𝑡
1
𝑡
= lim
𝑡→0
1
𝑡
−1
𝑡
2
= lim (−
𝑡→0
𝑡) = 0
I = lim
(𝑥,𝑦)→(0,0)
(𝑥 +𝑦
2 2
)
𝑥
2
𝑦
2
= 𝑒
lim
(𝑥,𝑦)→(0,0)
𝐼
1
.𝐼
2
= 𝑒
0.0
= 1
Đáp án A
Câu 9:
Do 𝑥 → 0,𝑦 → 0 nên 𝑥
2
𝑦
2
→0,𝑥 +𝑦
2 2
→ 0,
1
𝑥
2
+𝑦
2
→ ∞
⇒ lim
(𝑥,𝑦 0,0)
→
( )
1+𝑥
(
2
𝑦
2
)
1
𝑥
2
+𝑦
2
là dạng vô định 1
∞
TEAM GI I TÍCH 2 Ả
22
⇒ s d ng ử ụ (1+
1
𝑢
)
𝑢
∼ 𝑒 𝑢 → +∞ với
lim 1+𝑥
(𝑥,𝑦)→(0,0)
(
2
𝑦
2
)
1
𝑥
2
+𝑦
2
= lim
(𝑥,𝑦)→(0,0)
(1+
1
1
𝑥
2
𝑦
2
)
1
𝑥
2
𝑦
2
𝑥
2
𝑦
2
1
𝑥
2
+𝑦
2
= 𝑒
lim
(𝑥,𝑦)→(0,0)
𝑥
2
𝑦
2
𝑥
2
+𝑦
2
Ta có:
|
𝑥
2
+𝑦
2
|
≥ |2 |𝑥𝑦 (Cauchy) ⇒
1
|
𝑥
2
+𝑦
2
|
≤
1
|2
𝑥𝑦|
⇒ |
𝑥
2
𝑦
2
𝑥
2
+𝑦
2
| ≤ |
𝑥
2
𝑦
2
2
𝑥𝑦
| = |
𝑥𝑦
2
|
⇒ 0 ≤ |
𝑥
2
𝑦
2
𝑥
2
+𝑦
2
| ≤ |
𝑥𝑦
2
| ⇒ lim
(𝑥,𝑦)→(0,0)
|
𝑥𝑦
2
| = |
0
2
| = 0 ⇒ lim
(𝑥,𝑦)→(0,0)
𝑥
2
𝑦
2
𝑥
2
+𝑦
2
= 0 (định
lý k p) ẹ
⇒ lim 1+𝑥
(𝑥,𝑦)→(0,0)
(
2
𝑦
2
)
1
𝑥
2
+𝑦
2
= 𝑒
0
= 1
Đáp án A
Câu 10:
I = lim
(𝑥,𝑦)→(0,0)
𝑥
2
+𝑦
2
𝑒
𝑥+𝑦
= lim
(𝑥,𝑦)→(0,0)
(𝑥+𝑦 .(𝑥 +𝑦 ))
2 2
𝑒
𝑥+𝑦
.(𝑥+𝑦)
= lim
(𝑥,𝑦)→(0,0)
(
𝑥+𝑦
𝑒
𝑥+𝑦
.
𝑥
2
+𝑦
2
𝑥+𝑦
) = lim
(𝑥,𝑦)→(0,0)
𝐼
1
.𝐼
2
Xét: lim
(𝑥,𝑦)→(0,0)
𝐼
1
= lim
(𝑥,𝑦)→(0,0)
𝑥+𝑦
𝑒
𝑥+𝑦
Đặt x + y = t
Khi:
{
𝑥 → 0
𝑦 → 0
=> t → 0
lim
(𝑥,𝑦)→(0,0)
𝐼
1
= lim
𝑡→0
𝑡
𝑒
𝑡
= 0
Xét: lim
(𝑥,𝑦)→(0,0)
𝐼
2
= lim
(𝑥,𝑦)→(0,0)
𝑥
2
+𝑦
2
𝑥+𝑦
Ta có: 0 ≤ |
𝑥
2
+𝑦
2
𝑥+𝑦
| ≤ |
𝑥
2
+𝑦
2
+2𝑥𝑦
𝑥+𝑦
| = |x + y|
Mà lim
(𝑥,𝑦)→(0,0)
|x + y| = 0
I = 0
Đáp án C
Câu 11:
TEAM GI I TÍCH 2 Ả
23
Do
(𝑥,𝑦) → (0,0) ⇒ 3𝑥 → 0,𝑥 +𝑦
2 2 2
→ 0,
1
𝑥
2
+𝑦
2
→ ∞ ⇒ Dạng vô định 1
∞
lim
(𝑥,𝑦)→(0,0)
1+3𝑥
(
2
)
1
𝑥
2
+𝑦
2
= lim
(𝑥,𝑦)→(0,0)
(1+
1
1
3𝑥
2
)
1
3𝑥
2
⋅3𝑥
2
1
𝑥
2
+𝑦
2
= 𝑒
(𝑥,𝑦)→(0,0)
3𝑥
2
𝑥
2
+𝑦
2
Xét (𝑥,𝑦) → (0,0) theo phương 𝑦 = 𝑘𝑥
⇒ lim
(𝑥,𝑦)→(0,0)
3𝑥
2
𝑥
2
+𝑦
2
= lim
(𝑥, )→(0,0)
𝑘𝑥
3𝑥
2
𝑥
2
+(𝑘𝑥)
2
= lim
(𝑥, )→(0,0)
𝑘𝑥
3
1+𝑘
2
=
3
1+𝑘
2
Vậy v i m khác nhau ớ ỗi 𝑘 lim
(𝑥,𝑦)→(0,0)
3𝑥
2
𝑥
2
+𝑦
2
tiến đến những giá trị giới hạn khác
nhau.
⇒∄ lim
(𝑥,𝑦)→(0,0)
3𝑥
2
𝑥
2
+𝑦
2
⇒ ∄ lim
(𝑥,𝑦)→(0,0)
1+ 3𝑥
(
2
)
1
𝑥
2
+𝑦
2
Đáp án D
Câu 12:
Do (𝑥,𝑦) → (0,0) ⇒ 𝑥 +𝑦 → 0
2 2
⇒ cos
(
𝑥
2
+𝑦
2
)
−1 = − 1−cos
[ (
𝑥
2
+𝑦
2
)]
∼
− +𝑦
(
𝑥
2 2
)
2
2
⇒ lim
(𝑥,𝑦)→(0,0)
cos
(
𝑥
2
+𝑦
2
)
−1
𝑥
2
+𝑦
2
= lim
(𝑥,𝑦)→(0,0)
−
(
𝑥
2
+𝑦
2
)
2
2
1
𝑥
2
+𝑦
2
= lim
(𝑥,𝑦)→(0,0)
−
(
𝑥
2
+𝑦
2
)
2
= 0
Đáp án C
1.2. KH O SÁT TÍNH LIÊN T Ả ỤC:
Câu 1:
{
Do
−𝜋
2
< arctan(
𝑦
𝑥
)
2
<
𝜋
2
⇒ 0 ≤ |𝑥⋅ arctan(
𝑦
𝑥
)
2
| ≤ |
𝜋
2
𝑥|
Mà lim
(
𝑥,𝑦
)
→
(
0,1)
|
𝜋
2
𝑥| = 0
⇒ lim
(𝑥,𝑦)→(0,1)
𝑥⋅arctan (
𝑦
𝑥
)
2
= 0
TEAM GI I TÍCH 2 Ả
24
⇒ 𝑓(𝑥,𝑦) 𝐵(0,1) liên tục tại .
Đáp án A
Câu 2:
𝑥
2
+𝑦 = 0
2
chỉ x y ra khi ả 𝑥 = 𝑦 = 0.
Để 𝑓(𝑥,𝑦) liên tục tại (0,0) ⇔ lim
(𝑥,𝑦)→(0,0)
𝑓(𝑥,𝑦) = 𝑓(0,0) = 𝑎
Theo Cauchy: 𝑥
2
+𝑦 ≥ 2|
2
𝑥𝑦| ⇒
1
𝑥
2
+𝑦
2
≤
1
2| |𝑥𝑦
⇒ 0 ≤ |
2𝑥
2
𝑦−𝑦
2
𝑥
𝑥
2
+𝑦
2
|≤ |
2𝑥
2
𝑦−𝑦
2
𝑥
2
𝑥𝑦
| = |
2𝑥− 𝑦
2
|
Mà lim |
(𝑥,𝑦)→(0,0)
2𝑥−𝑦
2
| =0
⇒ lim
(𝑥,𝑦)→(0,0)
2𝑥
2
𝑦−𝑦
2
𝑥
𝑥
2
+𝑦
2
= 0 (Kẹp)
Vậy hàm s liên t c t khi và ch khi ố 𝑓(𝑥,𝑦) ụ ại (0,0) ỉ 𝑎 = 0
Đáp án A
Câu 3:
Xét theo phương 𝑦 =𝑘𝑥
⇒ lim
(𝑥,𝑦)→(0,0)
sin (
𝑥𝑦+𝑦
2
𝑥
2
+𝑦
2
) = lim
(𝑥, )→(0,0)
𝑘𝑥
sin (
𝑘𝑥 +𝑘
2 2
𝑥
2
𝑥 𝑥
2
+𝑘
2 2
)
= lim
𝑥→0
𝑘𝑥
→0
sin (
𝑘 +𝑘
2
1+𝑘
2
) = sin (
𝑘 +𝑘
2
1+𝑘
2
)
Vậy v i m khác nhau ớ ỗi 𝑘 lim sin (
(𝑥,𝑦)→(0,0)
𝑥𝑦+𝑦
2
𝑥
2
+𝑦
2
) tiến đến những giá tr i h n ị giớ ạ
khác nhau.
⇒ Không t n tồ ại lim sin(
(𝑥,𝑦 → 0,0) ( )
𝑥𝑦+𝑦
2
𝑥
2
+𝑦
2
)
⇒ Hàm s n tố gián đoạ ại (0,0)
Đáp án B
Câu 4:
Với (𝑥,𝑦) ∈ 𝑅 ∖{(0,0)}
2
thì hàm s liên t c. Xét tính liên t c c a hàm s ố 𝑓(𝑥,𝑦) ụ ụ ủ ố
TEAM GI I TÍCH 2 Ả
25
𝑓(𝑥,𝑦) (0,0) tại .
Khi (𝑥,𝑦) → (0,0), xét theo phương 𝑦 = 𝑘𝑥
⇒ lim
(𝑥,𝑦)→(0,0)
𝑥𝑦−𝑥
2
𝑥
2
+𝑦
2
= lim
(𝑥, )→(0,0)
𝑘𝑥
𝑘𝑥
2
−𝑥
2
𝑥
2
+(𝑘𝑥)
2
=
𝑘−1
1+𝑘
2
Vậy v i m khác nhau ớ ỗi 𝑘 lim
(𝑥,𝑦)→(0,0)
𝑥𝑦−𝑥
2
𝑥
2
+𝑦
2
tiến đến những giá trị giới h n khác ạ
nhau.
⇒ Không t n tồ ại lim
(𝑥,𝑦 → 0,0) ( )
𝑥𝑦−𝑥
2
𝑥
2
+𝑦
2
⇒ Hàm s n tố gián đoạ ại (0,0)
Vậy hàm s liên t c v n t ố 𝑓(𝑥,𝑦) ụ ới (𝑥,𝑦) ∈𝑅 ∖{(0,0)}
2
, gián đoạ ại (0,0)
Đáp án B
1.3. ĐẠO HÀM RIÊNG VÀ VI PHÂN TOÀN PH N Ầ
Câu 1:
z’
x
=
1
√𝑥 +𝑦
2 2
Đáp án A
Câu 2:
z’
y
=
𝑦
(𝑥+√𝑥 +𝑦
2 2
)√𝑥 +𝑦
2 2
Đáp án A
Câu 3:
dz = z’ + z’
x
.dx
y
.dy =
1
√𝑥 +𝑦
2 2
.𝑑𝑥 +
𝑦
(𝑥+√𝑥 +𝑦
2 2
)√𝑥 +𝑦
2 2
.𝑑𝑦
Đáp án A
Câu 4:
u’
y
= 𝑥
𝑦
2
𝑧
.𝑙𝑛𝑥.2.𝑦.𝑧
Đáp án C
Câu 5:
TEAM GI I TÍCH 2 Ả
26
u’
x
= 𝑒
(𝑥
2
+2𝑦
2
+𝑧
2
)
−1
. (
−2𝑥
(
𝑥
2
+2𝑦
2
+𝑧
2
)
2
)
u’
y
= 𝑒
(𝑥
2
+2𝑦
2
+𝑧
2
)
−1
. (
−4𝑦
(
𝑥
2
+2𝑦
2
+𝑧
2
)
2
)
u’
z
= 𝑒
(𝑥
2
+2𝑦
2
+𝑧
2
)
−1
. (
−2𝑧
(
𝑥
2
+2𝑦
2
+𝑧
2
)
2
)
du = 𝑒
(𝑥
2
+2𝑦
2
+𝑧
2
)
−1
. (
−2𝑥
(
𝑥
2
+2𝑦
2
+𝑧
2
)
2
).dx +
𝑒
(𝑥
2
+2𝑦
2
+𝑧
2
)
−1
. (
−4𝑦
(
𝑥
2
+2𝑦
2
+𝑧
2
)
2
).dy +
𝑒
(𝑥
2
+2𝑦
2
+𝑧
2
)
−1
. (
−2𝑧
(
𝑥
2
+2𝑦
2
+𝑧
2
)
2
)
𝑑𝑢(1; -1; 1) =
−2
𝑒
−4
.16
.dx +
4
𝑒
−4
.16
.dy -
2
𝑒
−4
.16
.dz
Đáp án B
Câu 6:
Đặt 𝑢 =
𝑥
𝑦
,𝑣 = ⇒ 𝑢𝑥𝑦
𝑥
′
=
1
𝑦
,𝑢
𝑦
′
=
−𝑥
𝑦
2
,𝑣
𝑥
′
= 𝑦,𝑣
𝑦
′
= 𝑥
+ 𝑧
𝑥
′
= 𝑧
𝑢
′
⋅𝑢
𝑥
′
+𝑧
𝑣
′
⋅𝑣
𝑥
′
=𝑢
𝑥
′
⋅𝑓(𝑢)−𝑣
𝑥
′
⋅𝑓(𝑣)
=
1
𝑦
⋅(
𝑥
𝑦
)
2
sin
2𝑥
𝑦
−𝑦⋅(𝑥𝑦)
2
⋅sin 2𝑥𝑦
+ 𝑧
𝑦
′
=𝑧
𝑢
′
⋅𝑢
𝑦
′
+𝑧
𝑣
′
⋅𝑣
𝑦
′
= 𝑢
𝑦
′
⋅𝑓(𝑢)−𝑣
𝑦
′
⋅𝑓(𝑣)
=
−𝑥
𝑦
2
⋅(
𝑥
𝑦
)
2
sin
2𝑥
𝑦
−𝑥⋅(𝑥𝑦)
2
⋅sin 2𝑥𝑦
Đáp án D
Câu 7:
u’
x
= z. 2x.
−1
2
. (𝑥 +𝑦 )
2 2
−3
2
= - z. x. (𝑥 +𝑦
2 2
)
−3
2
u’
y
= - z. y. (𝑥 +𝑦 )
2 2
−3
2
u’
z
= (𝑥 +𝑦
2 2
)
−1
2
du = - z. x. (𝑥 +𝑦
2 2
)
−3
2
.𝑑𝑥 - z. y. (𝑥 +𝑦
2 2
)
−3
2
.𝑑𝑦 + (𝑥 +𝑦 )
2 2
−1
2
.𝑑𝑧
Đáp án C
Câu 8:
𝑓
𝑦
′
(1,0) = lim
Δ𝑦→0
𝑓(1,0+ Δ𝑦)−𝑓(1,0)
Δ𝑦
= lim
Δ𝑦→0
Δ𝑦⋅arctan
1
Δ𝑦
−0
Δ𝑦
TEAM GI I TÍCH 2 Ả
27
=lim arctan
Δ𝑦→0
1
Δ𝑦
Với Δ𝑦 →0⇒
1
Δ𝑦
→ +∞
⇒ arctan
1
Δ𝑦
→
𝜋
2
⇒ lim
Δ𝑦→0
arctan
1
Δ𝑦
=
𝜋
2
⇒ 𝑓
𝑦
′
(1,0) = lim
Δ𝑦→0
arctan
1
Δ𝑦
=
𝜋
2
Đáp án A
Câu 9:
Sử dụng định nghĩa:
𝑧
′
𝑥
(
0,0
)
=lim
𝑥→0
𝑧
(
𝑥,0
)
−𝑧(0,0)
𝑥−0
= lim
𝑥→0
arctan (0)−0
𝑥−0
= 0
𝑧
′
𝑦
(
0,0
)
= lim
𝑦→0
𝑧
(
0,𝑦
)
−𝑧(0,0)
𝑦−0
= lim
𝑦→0
arctan (∞)−0
𝑦− 0
= lim
𝑦→0
𝜋
2
𝑦
= ∞
Đáp án B
1.4. ĐẠO HÀM CỦA HÀM N Ẩ
Câu 1:
𝑥
3
+2𝑦 +3𝑥 𝑦 = 2
3 2
F(x, y) = 𝑥
3
+2𝑦 + 3𝑥 𝑦 −2 = 0
3 2
{
F’x = 3x
2
+6𝑥𝑦
F’y = 6y −3𝑥
2 2
TEAM GI I TÍCH 2 Ả
28
y’
x
= −
F’x
F’y
= −
x
2
+2𝑥𝑦
2y −𝑥
2 2
Đáp án D
Câu 2:
Ta có: F(x, y, z) = 𝑥
2
.𝑎𝑟𝑐𝑡𝑎𝑛𝑥 +2𝑥𝑦 + 𝑦 +2𝑧 −1=0
2 4 3
{
f′
x
= 2𝑥.𝑎𝑟𝑐𝑡𝑎𝑛𝑥+
𝑥
2
1+𝑥
2
+2𝑦
2
f′ =4xy+ 4𝑦
y
3
f′ = 6𝑧
z
2
z’
x
= −
f′
x
f′
z
= −
2𝑥.𝑎𝑟𝑐𝑡𝑎𝑛𝑥+
𝑥
2
1+𝑥
2
+2𝑦
2
6𝑧
2
z’
y
= −
f′
y
f′
z
= −
2xy+2𝑦
3
3𝑧
2
Đáp án C
Câu 3:
PTTT: y = y’(x
0
).(x - x ) + y
0 0
Có:
{
𝑥
0
𝑦
0
) → Xác định y’(x
0
Ta có: F(x, y, z) = 𝑥
3
−𝑦 +3 = 0
3
𝑥𝑦−13
{
f′
x
= 3x
2
+3𝑦
f′ = −3y +3𝑥
y
2
y’
x
= −
F’x
F’y
=
x
2
+𝑥
y
2
−𝑥
y’(-1) = −
1
5
Pttt: y = −
1
5
.
(
𝑥+1
)
−2
Đáp án A
Câu 4:
Đặt F(x,y,z) = 𝑧
2
+
2
𝑥
−
√
𝑦
2
−𝑧
2
=>
{
F′ = −
x
2
x
2
F′
y
=
−y
√y −z
2 2
F′
z
= 2z+
z
√y −z
2 2
𝑧′ = −
𝑥
F
′
x
F
′
z
=
2
x
2
2z
+
z
√
y
2
−z
2
; 𝑧′ =−
𝑦
F
′
y
F
′
z
=
y
√
y
2
−z
2
2z
+
z
√
y
2
−z
2
TEAM GI I TÍCH 2 Ả
29
𝑥
2
𝑧′
𝑥
=
2
z.(2+
1
√
y
2
−z
2
)
;
1
𝑦
𝑧′
𝑦
=
1
√
y
2
−z
2
z.(2+
1
√
y
2
−z
2
)
𝑥
2
𝑧′
𝑥
+
1
𝑦
𝑧′
𝑦
=
2+
1
√
y
2
−z
2
z.(2+
1
√
y
2
−z
2
)
=
1
𝑧
(đpcm)
Đáp án A
1.5. TÍNH GẦN ĐÚNG NHỜ VI PHÂN
Câu 1:
D
ạng: f(x, y) = x
3
.y
2
Ta có:
{
𝑥
0
=1
𝑦
0
= 1
và {
∆𝑥 = 0,02
∆𝑦 = −0,03
ADCT: A ≈ f(1; 1) + f’
x
(1; 1).0,02 + f’
y
(1; 1).(−0, )03
= 1 + 3. 0,02 + 2. (−0, )03
= 1
Đáp án A
Câu 2:
Dạng: f(x, y) =
√
𝑥
2
+𝑦
2
3
Ta có:
{
𝑥
0
=1
𝑦
0
= 0
và {
∆𝑥 = 0,02
∆𝑦 = 0,05
ADCT: A ≈ f(1; 1) + f’
x
(1; 0).0,02 + f’
y
(1; 0).0,05
= 1 +
2
3
.0,02 + 0
=
76
75
Đáp án D
Câu 3:
D
ạng: f(x, y) =
√2𝑥 −3𝑦 +2
3 2
3
Ta có:
{
𝑥
0
=3
𝑦
0
= 4
và {
∆𝑥 = −0,02
∆𝑦 = 0,01
ADCT: A ≈ f(3; 4) + f’
x
(3; 4).(−0,02) + f’
y
(3; 4).0,01
= 2 + 4,5. - 2.0,01 (−0,02)
= 1,89
TEAM GI I TÍCH 2 Ả
30
Đáp án B
Câu 4:
Đặt f(x,y)=
√
𝑥
2
+𝑦
2
=> 𝑓′
𝑥
=
𝑥
√𝑥 +𝑦
2 2
; 𝑓′
𝑦
=
𝑦
√𝑥 +𝑦
2 2
Áp d ng công th c : ụ ứ
f(x +∆x;y +∆y) ≈ f ;y
0 0
(
x
0 0
)
+∆xf (x ;y )+∆yf (x ;y
′
x 0 0
′
y 0 0
)
Chọn x
0
=3;y = 4; ∆x=0, ;∆y=−0,
0
01 01
S ≈ 4,988
Đáp án C
1.6. CỰC TR C A HÀM NHI U BI N Ị Ủ Ề Ế
Câu 1:
z = 𝑥
2
+𝑥𝑦 +𝑦 −2𝑥 −𝑦
2
Ta có: z = f(x, y) = 𝑥
2
+𝑥𝑦+𝑦 −2𝑥 −𝑦
2
T
ập xác định: D = R
2
_ i h
Giả ệ phương trình: {
𝑓′
𝑥
= 2𝑥+𝑦 −2 = 0
𝑓′ = 𝑥+2𝑦−1 = 0
𝑦
{
𝑥 = 1
𝑦 = 0
=> Điểm d ng M(1; 0) ừ
_ Ta có:
𝑓 𝑓′′
𝑥𝑥
= 2 ; ′′
𝑥𝑦
= 0 ; 𝑓′′
𝑦𝑦
=2
Tại M(1; 0): {
𝐴 = 𝑓
′′
𝑥𝑥
(
1;0
)
= 2
𝐵 = 𝑓
′′
𝑥𝑦
(
1;0
)
= 0
𝐶 = 𝑓
′′
𝑦𝑦
(
1;0
)
= 2
∆= 𝐵 = 0 −2.2 = −4 < 0
2
−𝐴𝐶
2
Và A = 2 > 0 => M(1; 0) là điểm c c ti u ự ể
Đáp án B
Câu 2:
Ta có: z = f(x, y) = 2𝑥 +𝑦 −4𝑥 +2𝑦
4 4 2 2
T
ập xác định: D = R
2
TEAM GI I TÍCH 2 Ả
31
_ i h
Giả ệ phương trình: {
𝑓′
𝑥
= 8𝑥
3
−8𝑥 = 0
𝑓′ = 4𝑦 + 4𝑦 = 0
𝑦
3
2 điểm dừng: M(0; 0), N(1; 0)
_ Ta có:
{
𝑓′′
𝑥𝑥
= 24𝑥
2
−8
𝑓′′
𝑥𝑦
= 0
𝑓′′
𝑦𝑦
= 12𝑦
2
+4
+ T i M(0; 0):
ạ {
𝐴 = −8
𝐵 = 0
𝐶 =4
=> ∆ = > 032 => Không ph i c c tr ả ự ị
+ T i N(1; 0):
ạ {
𝐴 = 16
𝐵 = 0
𝐶 =4
=> ∆ = − < 064 và A = 16 > 0
N(1; 0) là điểm cực tiểu với f -2
min
=
Đáp án A
Câu 3:
Ta có: z = f(x, y) = 2 𝑥
2
+3𝑦 −𝑒
3 −(𝑥
2
+𝑦
2
)
1, Gi i h
ả ệ phương trình: {
𝑓′
𝑥
= 4𝑥+2𝑥.𝑒
−(𝑥
2
+𝑦
2
)
= 0
𝑓′ = 9𝑦 +2𝑦.𝑒 =0
𝑦
2 −(𝑥
2
+𝑦
2
)
Điểm d ng M(0; 0) ừ
2, Ta có:
{
𝑓′′
𝑥𝑥
= 4+ 2.𝑒 −4𝑥 .𝑒
−(𝑥
2
+𝑦
2
) 2 −(𝑥
2
+𝑦
2
)
𝑓′′
𝑥𝑦
= −4𝑥𝑦.𝑒
−(𝑥
2
+𝑦
2
)
𝑓
′′
𝑦𝑦
= 18𝑦+2.𝑒 −4𝑦 .𝑒
−(𝑥
2
+𝑦
2
) 2 −(𝑥
2
+𝑦
2
)
Tại M( 0; 0): {
𝐴 = 6
𝐵 = 0
𝐶 = 2
=> ∆=− < 012 và A = 6 > 0
M( 0; 0) là điểm cực tiểu với f -1
min
=
Đáp án A
Câu 4:
Điề ệu ki n 𝑥
2
+𝑦 = 1 ⇔ 𝑥 + 𝑦 −1 = 0
2 2 2
Đặ
t hàm phụ: 𝐿(𝑥,𝑦,𝑘) = 2𝑥 +𝑦 +𝑘 +𝑦 −1
2 2
(
𝑥
2 2
)
Xét
{
𝐿
𝑥
′
= 0
𝐿
𝑦
′
= 0
𝐿
𝑘
′
= 0
⇔ {
4𝑥+ 2 = 0(1)𝑘𝑥
2𝑦+2 =0(2)(∗)𝑘𝑦
𝑥
2
+𝑦
2
= 1(3)
TEAM GI I TÍCH 2 Ả
32
TH1: (1) ⇔ 2𝑥(𝑘+2) = 0 ⇒ 𝑘 = −2
V
ới 𝑘 =−2, hệ (∗) trở thành {
−2𝑦 = 0
𝑥
2
+𝑦 = 1
2
⇒ {
𝑥 = ±1
𝑦 = 0
TH2:(2) ⇔ 2𝑦(𝑘+1) ⇒ 𝑘 = −1
V
ới 𝑘 =−1, hệ (∗) trở thành {
2𝑥 = 0
𝑥
2
+𝑦 = 1
2
⇒ {
𝑥 = 0
𝑦 = ±1
⇒ (∗) có các b nghi ộ ệm (𝑥,𝑦,𝑘) = {(1,0,−2);(−1,0,−2);(0,1,−1);(0,−1,−1)}
Xét vi phân c p hai: ấ 𝑑
2
𝐿(𝑥,𝑦,𝑘) = 𝐿
𝑥𝑥
′′
𝑑𝑥
2
+2𝐿
𝑥𝑦
′′
𝑑𝑥𝑑𝑦+𝐿
𝑦𝑦
′′
𝑑𝑦
2
⇒ 𝑑 𝐿(𝑥,𝑦,𝑘) = (2+ 𝑘)𝑑𝑥 +0.𝑑𝑥𝑑𝑦+(1+𝑘)𝑑𝑦
2 2 2
⇒ 𝑑 𝐿(𝑥,𝑦,𝑘) = (1+ 𝑘)𝑑𝑥 +(1+𝑘)𝑑𝑦
2 2 2
Với (𝑘,𝑥,𝑦) = (1,0,−2) ⇒𝑑 𝐿(1,0,−2) = −𝑑𝑦 < 0
2 2
⇒ 𝑀
1
(1,0) 𝑧 là điể ực đại có điềm c u kiên của hàm số,
CD
= 𝑧 𝑀
(
1
)
= 2
Vói (𝑥,𝑦,𝑘)=(−1,0,−2) ⇒ 𝑑 𝐿(−1,0,−2) = −𝑑𝑦 < 0
2 2
⇒ 𝑀
2
(−1,0) là điểm c u kiên c a hàm sực đại có điề ủ ố, 𝑧 = 𝑧 𝑀
C𝐷
(
2
)
= 2
Với (𝑥,𝑦,𝑘) = (0,1,−1) ⇒ 𝑑 𝐿(0,1,−1) = 𝑑𝑥 > 0
2 2
⇒ 𝑀
3
(0,1) là điể ểu có điềm cực ti u kiên c a hàm sủ ố, 𝑧
CT
= 𝑧 𝑀
(
3
)
= 1
Với (𝑥,𝑦,𝑘) = (0,−1,−1) ⇒𝑑 𝐿(0,−1,−1) = 𝑑𝑥 > 0
2 2
⇒ 𝑀
4
(0,−1) 𝑧 là điể ểu có điềm cực ti u kiên của hàm số,
CT
= 𝑧 𝑀
(
4
)
= 1
Đáp án B
Câu 5:
Điề ệu ki n 𝑥
2
+𝑦 = 1 ⇔ 𝑥 + 𝑦 −1 = 0
2 2 2
Đặt 𝐿(𝑥,𝑦,𝑘) =
𝑥
4
+
𝑦
3
+𝑘
(
𝑥
2
+𝑦
2
−1
)
Xét
{
𝐿
𝑥
′
= 0
𝐿
𝑦
′
= 0
𝐿
𝑘
′
= 0
⇔
{
1
4
+2𝑘𝑥 = 0
1
3
+2𝑘𝑦 =0
𝑥
2
+𝑦 = 1
2
⇔
{
𝑥 =
−1
8𝑘
𝑦 =
−1
6𝑘
𝑥
2
+𝑦 = 1
2
(𝑘 ≠ 0)
⇒ (
−1
8𝑘
)
2
+(
−1
6𝑘
)
2
= 1 ⇒ 𝑘 = ±
5
24
Với 𝑘 =
5
24
⇒ 𝑥 =
−3
5
,𝑦 =
−4
5
Với
𝑘 =−
5
24
⇒ 𝑥 =
3
5
,𝑦 =
4
5
TEAM GI I TÍCH 2 Ả
33
Xét vi phân c p 2 c ấ ủa 𝐿(𝑥,𝑦,𝑘)
Xét vi phân c p 2 c ấ ủa 𝐿(𝑥,𝑦,𝑘)
𝑑
2
𝐿(𝑥,𝑦,𝑘) = 𝐿
𝑥𝑥
′′
(𝑥,𝑦,𝑘)𝑑𝑥
2
+2𝐿
𝑥𝑦
′′
(𝑥,𝑦,𝑘)+𝐿
𝑦𝑦
′′
(𝑥,𝑦,𝑘)𝑑𝑦
2
= 2𝑘d𝑥
2
+2𝑘d𝑦
2
Với (𝑥,𝑦,𝑘)=(
−3
5
,
−4
5
,
5
24
) ⇒ 𝑑
2
𝐿(
−3
5
,
−4
5
,
5
24
)=
5
12
(
d𝑥
2
+d𝑦
2
)
> 0
⇒ 𝑀
1
(
−3
5
,
−4
5
) là điểm cực tiểu có điều kiện của hàm số, 𝑧
CT
= 𝑧 𝑀
(
1
)
=
−5
12
Với (𝑥,𝑦,𝑘) = (
3
5
,
4
5
,
5
24
) ⇒ 𝑑
2
𝐿(
3
5
,
4
5
,
−5
24
)=
−5
12
(
d𝑥
2
+d𝑦
2
)
< 0
⇒ 𝑀
2
(
3
5
,
4
5
) là điể ực đại có điềm c u kiện của hàm số, 𝑧
𝐶Ð
= 𝑧 𝑀
(
2
)
=
5
12
Đáp án C
Câu 6:
z= 𝑥 + 𝑦 +(𝑥+𝑦)
3 3 2
Xét {
𝑧′
𝑥
= 3𝑥
2
+2 𝑥+𝑦 = 0∗
( )
𝑧′ = 3𝑦 +2 𝑥+𝑦 = 0∗∗
𝑦
2
( )
=> 𝑥
2
= 𝑦
2
<=> ⌈
𝑥 = 𝑦
𝑥 = −𝑦
Với x=y thay vào * ta có
3𝑥 +4𝑥 = 0
2
[
𝑥 = 0 => 𝑦 = 0
𝑥 =
−4
3
=> 𝑦 =
−4
3
Với x=-y thay vào * ta có
3𝑥 = 0
2
x=y=0
V m t i h n M(
ậy có 2 điể ớ ạ
−4
3
;
−4
3
) và N(0,0)
Đặt A= ; B= ; C= 𝑧 =6𝑥+2′′
𝑥𝑥
𝑧 = 2′′
𝑥𝑦
𝑧 =6𝑦+2′′
𝑦𝑦
Tại M(
−4
3
;
−4
3
) thì {
𝐴= −6 < 0
∆= 𝐵 = − < 0
2
−𝐴𝐶 32
=> M là điể ực đạ
m c i ; 𝑧 = 𝑧
𝐶Đ
(
𝑀
)
=
64
27
Tại N(0,0) : ∆= 𝐵 = 0
2
−𝐴𝐶
Giả s m H( lân c m N (-1< ử các điể ∆𝑥;∆𝑦) ận điể ∆𝑥;∆𝑦 < 1)
Xét ∆𝑧 = 𝑧 −𝑧 0,0 = ∆𝑥 +∆𝑦 +(∆𝑥+∆𝑦)
(
𝐻
) ( )
3 3 2
+ V m H( ới các điể ∆𝑥;0) ∈ 𝑂𝑥
∆𝑧 = ∆𝑥 +∆𝑥 = ∆𝑥 (1+∆𝑥)
3 2 2
B ng xét d u: ả ấ
∆𝑥
TEAM GI I TÍCH 2 Ả
34
∆z < 0 khi ∆x qua 0đi
+ V m H có t ( (ới các điể ọa độ ∆𝑥;−2∆𝑥) ∆𝑦 =−2∆𝑥)
∆𝑧 = −7∆𝑥 +∆𝑥 = ∆𝑥 (1−7∆𝑥)
3 2 2
B ng xét d u: ả ấ
∆𝑥
-1/7 0 1/7
∆𝑧
0 + 0 + 0 --- ---
∆z > 0 khi ∆x qua 0đi
Từ ị đổ 2 trường hợp trên => ∆𝑧 = 𝑧 −𝑧 0,0
(
𝐻
) ( )
b i dâu v m H lân ới các điể
cận N(0,0)
N(0,0) không là điểm c c tr c a hàm s ự ị ủ ố
Đáp án A
Câu 7:
Xét {
𝑧
𝑥
′
= 0
𝑧
𝑦
′
= 0
⇔ {
4𝑥 +𝑦
2
= 0
2
𝑥𝑦+3𝑦 = 0
2
⇔ {
2𝑥 =
−𝑦
2
2
(1)
2𝑥𝑦+3𝑦 = 0(2)
2
Thế (1) vào (2) ⇒
−𝑦
2
2
y+3𝑦
2
= 0 ⇒ [
𝑦 = 6 ⇒ 𝑥 = −9
𝑦 = 0 ⇒ 𝑥 =0
⇒ Hàm s m t i h n ố có hai điể ớ ạ 𝑀
1
(−9,6) 𝑀 và
2
(0,0)
Đặt 𝐴 = 𝑧
𝑥𝑥
′′
= 4,𝐵 = 𝑧
𝑥𝑦
′′
= 2𝑦,𝐶 = 𝑧
𝑦𝑦
′′
= 2𝑥 +6𝑦
T
ại 𝑀
1
(−9,6):{
𝐴 = 4 > 0
Δ = 𝐵 > 0
2
−𝐴𝐶 = 72
⇒ 𝑀
1
không là điểm cực trị của hàm số.
Tại 𝑀
2
(0,0):Δ = 0
Xét các điểm lân c n ậ 𝑀
2
(0,0) 𝑁(0;Δ𝑦) Δ𝑦 n m trên trằ ục 𝑂𝑦 : với r t nh . ấ ỏ
⇒ Δ𝑧 = 𝑓(𝑁)−𝑓 𝑀
(
2
)
= 2.0+0.(Δ𝑦)
2 3
+(Δ𝑦) +2−(0+0+0+ 2) = (Δ𝑦)
3
Bảng xét d u: ấ
Δ𝑦
0
−
0
0
+
Δ𝑧 = (Δ𝑦)
3
−
0
+
⇒ Δ𝑧 Δ𝑦 0⇒𝑀 đổi dấu khi đi qua
2
(0,0) không là điểm c c tr . ự ị
∆𝑧
TEAM GI I TÍCH 2 Ả
35
Vậy hàm s không có c c tr . ố ự ị
Đáp án A
1.7. KHAI TRIỂN TAYLOR
Câu 1:
Đặt 𝑧(𝑥,𝑦) = 𝑓(𝑥,𝑦) = 𝑥 +𝑦 +2𝑥+2𝑦 +1
2 2
+𝑥𝑦
Ta có: 𝑧
𝑥
′
= 2𝑥+𝑦 +2,𝑧
𝑦
′
= 2𝑦+𝑥 +2,𝑧
𝑥𝑥
′′
= 2,𝑧
𝑦𝑦
′′
= 2,𝑧
𝑥𝑦
′′
= 1
Các đạo hàm riêng c p 2 c a hàm s là nh ng h ng s ấ ủ ố ữ ằ ố
⇒ vi ph n toàn ph n c p 3 tr lên b ng 0 . ầ ầ ấ ở ằ
Sử d ng công th c khai tri n Taylor t ụ ứ ể ại điểm 𝑀(1,2)
𝑧(𝑥,𝑦) = z 𝑥 ;𝑦
(
0 0
)
+∑
+∞
𝑘=1
1
𝑘!
𝑑
𝑘
𝑧
(
𝑥
0
;𝑦
0
)
=z
(
𝑥
0
;𝑦
0
)
+
1
1!
𝑑𝑧
(
𝑥
0
;𝑦
0
)
+
1
2!
𝑑
2
𝑧
(
𝑥
0
;𝑦
0
)
Ta có: {
𝑧(1,2) = 14
𝑑𝑧(1,2)𝑧 (1,2)⋅(𝑥 −1) +𝑧 (1,2)⋅(𝑦−2) = 6(𝑥 −1)+7(𝑦 −2)
′
𝑥
′
𝑑
2
𝑧(1,2) = 2(𝑥 −1) +2(𝑥 −1)(𝑦 −2)+2(𝑦 −2)
2 2
Vậy khai tri n Taylor c a hàm s tể ủ ố ại 𝑀(1,2) là:
𝑧 = +6(𝑥− 1)+7(𝑦−2) +(𝑥−1) +(𝑥 −1)(𝑦 −2)+(𝑦−2)14
2 2
Đáp án B
Câu 2:
Làm tương tự câu 1
Đáp án C
1.8. TÌM GTLN, GTNN C A HÀM S Ủ Ố
Câu 1:
Miền giá tr c là hình vuông ị ủa (𝑥,𝑦) 𝐴𝐵𝐶𝐷
Xét các điểm phía trong mi n ề 0 < 𝑥,𝑦 <
𝜋
2
Tìm các điểm t i h n: ớ ạ
TEAM GI I TÍCH 2 Ả
36
Xét {
𝑧
𝑥
′
= 0
𝑧
𝑦
′
= 0
⇔ {
cos 𝑥+cos (𝑥+𝑦) = 0
cos 𝑦 +cos (𝑥+𝑦) = 0
⇔ {
cos 𝑥 = cos 𝑦
cos 𝑦 +cos (𝑥+ 𝑦) = 0
⇔ {
𝑥 = 𝑦
cos 𝑥 +cos 2𝑥 =0
⇔ {
𝑥 = 𝑦
2cos
3𝑥
2
cos
𝑥
2
= 0
⇒ Trong miền có một điểm tới hạn 𝐷,𝑧 𝑀
1
(𝜋/3,𝜋/3)
Xét trên biên 𝐷𝐶:𝑦 = 0,0<𝑥 <
𝜋
2
𝑧 = 2sin 𝑥 ⇒𝑧 = 2cos 𝑥
′
𝑧
′
= 0 ⇔ 2cos 𝑥 =0⇔𝑥 =
𝜋
2
(loại) ⇒ Trên 𝐷𝐶 (trừ hai đầu mút) không có điểm tới
hạn
Xét trên biên 𝐴𝐷:𝑥 =0;0 < 𝑦 <
𝜋
2
⇒ 𝑧 = 2sin 𝑦 ⇒𝑧 = 2cos 𝑦
′
𝑧
′
= 0 ⇔ 2cos 𝑦 = 0⇔𝑦=
𝜋
2
(loại)
Trên 𝐴𝐷 (trừ hai đầu mút) không có điểm dừng
Tương tự tại các biên và m t i h n 𝐴𝐵 𝐵𝐶 ta tìm được điể ớ ạ
TEAM GI I TÍCH 2 Ả
37
Ta có:
{
𝑀
2
(
𝜋
4
,
𝜋
2
) và 𝑀
3
(
𝜋
2
𝜋
4
)
𝑧
(
𝑀
1
)
=
3
√
3
2
𝑧
(
𝑀
2
)
= 𝑧 𝑀
(
2
)
= √2+1 ⇒ 𝑧
max
=
3
√
3
2
,𝑧
min
= 0
𝑧(𝐷) = 0
𝑧(𝐵) = 𝑧(𝐴) = 2
Đáp án A
Câu 2:
Xét trong mi n elip
ề
𝑥
2
9
+𝑦
2
<1
Xét {
𝑧
𝑥
′
= 0
𝑧
′
𝑦
= 0
⇔ {
2𝑥 = 0
− 𝑦 = 0
18
⇔ 𝑥 = 𝑦 = 0
⇒ Trong mi n elip có m m t i h n ề ột điể ớ ạ 𝑂(0,0)
Xét
ở biên c a elip ủ
𝑥
2
9
+𝑦
2
= 1
Tìm điểm tới hạn của 𝑧 với điều kiện
𝑥
2
9
+𝑦
2
= 1
Đặt hàm phụ
𝐿(𝑥,𝑦,𝑘) = 𝑥 −9𝑦 +𝑘(
2 2
𝑥
2
9
+𝑦
2
−1)
Xét
{
𝐿
𝑥
′
= 0
𝐿
𝑦
′
= 0
𝐿
𝑘
′
= 0
⇔
{
2𝑥+
2𝑘
9
𝑥 = 0
− 𝑦 +2 = 018 𝑘𝑦
𝑥
2
9
+𝑦
2
= 1
⇔
{
𝑥(1+
𝑘
9
)= 0
𝑦(𝑘 −9) = 0
𝑥
2
9
+𝑦
2
= 1
TH1:x = y = 0 ⇒ không ph i nghi m c a h ả ệ ủ ệ
TH2:k = −9 => y = 0 ⇒ x = ±3
TH3:k = 9 => x = 0 ⇒ y = ±1
TEAM GI I TÍCH 2 Ả
38
Với 𝑘 =−9,𝑧 có hai điểm tới hạn 𝐴(3,0),𝐵(−3,0)
Với 𝑘 =9,𝑧 có 2 điểm tới hạn 𝐶(0,1),𝐷(0,−1)
Ta có:
{
𝑧(𝑂) = 0
𝑧(𝐴) = 9
𝑧(𝐵) = −9
𝑧(𝐷) = −9
⇒ 𝑧
min max
= −9,𝑧 = 9
Đáp án A
Câu 3:
Phương trình AB:y = 7−x
Xét trong mi n ề Δ𝑂𝐴𝐵
Xét hệ {
𝑧
𝑥
′
= 0
𝑧
𝑦
′
= 0
⇔ {
3𝑥
2
+3𝑦− = 013
4𝑦+3𝑥 − = 018
{
3𝑥
2
+3𝑦− =013
3𝑦+
9
4
𝑥−
27
2
= 0
⇒ 3𝑥
2
−
9
4
𝑥+
1
2
= 0
⇒ Trong mi n ề Δ𝑂𝐴𝐵 không có điểm tới hạn
Xét trên biên u mút): 𝑂𝐵 (không tính hai đầ 𝑥 = 0,0 <𝑦 <7
⇒ 𝑧 = 2𝑦 𝑦⇒𝑧 = 4𝑦− ⇒ 𝑧 = 0 𝑦 = 4,5
2
−18
′
18
′
khi
⇒ trên biên 𝑂𝐵 có m m t i h n ột điể ớ ạ 𝑀(0;4,5)
Xét trên biên u mút): 𝑂𝐴 (không tính hai đầ 𝑦 = 0,0 < 𝑥 < 7
TEAM GI I TÍCH 2 Ả
39
⇒ 𝑥 𝑥 ⇒ 𝑧 = 𝑥 ⇒ 𝑥 =
3
−13
′ 2
−13
√
13
3
(Không lấy trường họp nghiệm âm)
⇒
Trên biên 𝑂𝐴 có một điểm tới hạn 𝑁(
√
13
3
,0)
Ta có: {
𝑧(𝑂) = 0
𝑧(𝐴) = 252
𝑧(𝐵) = −17
𝑧(𝑀) = − ,5
40
⇒ 𝑧
min
= − ,5;𝑧40
max
= 252
𝑧(𝑁) =
−26
√
39
9
Đáp án A
TEAM GI I TÍCH 2 Ả
40
II. NG D NG C A PHÉP TÍNH VI PHÂN: Ứ Ụ Ủ
Câu 1:
Lời gi i : ả
Bước 1 : Kiểm tra điểm kì dị(thi trắc nghiệm thườ qua bước này đểng bỏ
tiết kiệm th i gian) ờ
{
2𝑥 = 0
𝑐 = 0
𝑐𝑦
−𝑐 −𝑥 = 0
2 2
⇒ 𝑥 = 𝑐 = 0, nhưng điểm kì d c h ị đó không thuộ ọ
đường cong đã cho nên hệ đường cong không điể m kì d . ị
Bước 2 : Tìm hình bao
{
𝑦−2𝑐 = 0
𝑐𝑦
−𝑐 −𝑥 = 0
2 2
⟹ 𝑦 = ±2𝑥
Đáp án : D
Câu 2:
Lời gi i : ả
Bư
ớc 1 : {
𝑥
′
(
𝑡
)
= 1
𝑦
′
(
𝑡
)
=−
√
2.sin𝑡
𝑧
′
(
𝑡
)
=
√
2.cos𝑡
𝑣ớ𝑖 𝑡 =
𝜋
4
; Suy ra :
{
𝑥
′
(
𝜋
4
) =1
𝑦
′
(
𝜋
4
) = −1
𝑧
′
(
𝜋
4
) = 1
Bước 2 : Phương trình pháp diện :
(𝑥−
𝜋
4
)− 𝑦 −1 𝑧−1 = 0 ℎ 𝑥−𝑦+𝑧 =
( )
+
( )
𝑎𝑦
𝜋
4
Đáp án : B
Câu 3:
L i gi i : ờ ả
Bư
ớc 1 : Đặ 𝑥,𝑦,𝑧 = 𝑥 −3 +𝑦 −𝑧 ⟹ {t 𝐹
( )
2
𝑥𝑦
2
𝐹
𝑥
′
= 2𝑥 −3𝑦
𝐹
𝑦
′
= −3𝑥+2𝑦
𝐹
𝑧
′
= −1
⟹ {
𝐹
𝑥
′
(
𝐴
)
= −1
𝐹
𝑦
′
(
𝐴
)
= −1
𝐹
𝑧
′
(
𝐴
)
= −1
Bước 2 : Phương trình tiế ệp di n
−
(
𝑥−1
)
−
( (
𝑦− 1
)
−𝑧 𝑧+1
)
= 0 ℎ
𝑎𝑦 𝑥 +𝑦+𝑧 = 1
Đáp án : A
Câu 4:
L i gi i : ờ ả
TEAM GI I TÍCH 2 Ả
41
Áp d ng công th c : ụ ứ
𝐾 =
|
𝑥
′
𝑦
′
𝑥
′′
𝑦
′′
|
(
𝑥
′2
+𝑦
′2
)
3
2
Đáp án : A
Câu 5:
L i gi i : ờ ả
Bư
ớc 1 : Đặ 𝑥,𝑦,𝑧 = 4𝑥 −𝑦t 𝐹
( )
2 2
+2𝑦−𝑧 {
𝐹
𝑥
′
= 8𝑥
𝐹
𝑦
′
= −2𝑦+2
𝐹
𝑧
′
= −1
𝑣ớ𝑖 𝐴 −1;2;4
( )
⟹ {
𝐹
𝑥
′
(
𝐴
)
= −8
𝐹
𝑦
′
(
𝐴
)
= −2
𝐹
𝑧
′
(
𝐴
)
= −1
Bước 2 : Phương trình tiế ệp di n :
−8 𝑥 +1 −2 𝑦 −2 𝑧−4 = 0 ℎ 8𝑥 +2𝑦 +𝑧 =0
( ) ( )
−
( )
𝑎𝑦
Đáp án : A
Câu 6:
L i gi i : ờ ả
Bư
ớc 1 : Đặ 𝑥,𝑦,𝑧 = 𝑧−𝑒 ⟹ {t 𝐹
( )
𝑥
2
−𝑦
2
𝐹
𝑥
′
= −2𝑥.𝑒
𝑥
2
−𝑦
2
𝐹
𝑦
′
= 2𝑦.𝑒
𝑥
2
+𝑦
2
𝐹
𝑧
′
= 1
𝑣ớ𝑖 𝐴 1;−1;1
( )
⟹ {
𝐹
𝑥
′
(
𝐴
)
= −2
𝐹
𝑦
′
(
𝐴
)
= −2
𝐹
𝑧
′
(
𝐴
)
= 1
Bước 2: Phương trình tiế ệp di n
−2 𝑥−1 −2 𝑦 +1 𝑧−1 = 0 ℎ 2𝑥+2𝑦 −𝑧 +1 = 0
( ) ( )
+
( )
𝑎𝑦
Đáp án : A
Câu 7:
L i gi i : ờ ả
Bư
ớc 1 : Tìm giao điể = 1 ⟹ 𝑥 = ±1 ⟹ 𝐴 1;1 ;𝐴m : 𝑒
1−𝑥
2
( )
′
( )
−1;1 là giao
điể ầm c n tìm
Bướ = −2𝑥.𝑒c 2 : Ta có : 𝑦
′ 1−𝑥
2
฀ =1 ⟹ ฀
′
(
1 2
)
= −
฀ =−1 ⟹ ฀
′
(
−1
)
= 2
TEAM GI I TÍCH 2 Ả
42
Bước 3 :
฀ −1 = −2
(
฀ −1
)
⟹ 2฀ + −฀ 3 = 0
฀ −1 = 2
(
฀ +1
)
⟹ 2฀ −฀ +3 = 0
Đáp án : B,C
Câu 8:
L i gi i : ờ ả
Bư
ớc 1 : Đặ 𝑥;𝑦 = 𝑥t 𝐹
( )
2
3
+𝑦
2
3
−5 ⟹ {
𝐹
𝑥
′
=
2
3
√
𝑥
3
𝐹
𝑦
′
=
2
3
√
𝑦
3
⟹ {
𝐹
𝑥
′
(
𝑀
)
=
1
3
𝐹
𝑦
′
(
𝑀
)
=
2
3
Bước 2 : Phương trình pháp tuyến
𝑥−8
1
3
=
𝑦−1
2
3
⟹ 2𝑥− 𝑦−15 = 0
Đáp án : C
Câu 9:
L i : ời giả
Bư
ớc 1 : Đặt {
𝑥 =cos𝑡
𝑦 = 2sin𝑡
𝑧 =
cos𝑡−4
3
Bước 2 : Áp dụng công thức tính :
𝐾 =
√
|
𝑥
′
𝑦
′
𝑥
′′
𝑦
′′
|
2
+|
𝑦
′
𝑧
′
𝑦
′′
𝑧
′′
|
2
+|
𝑧
′
𝑥
′
𝑧
′′
𝑥
′′
|
2
(
𝑥
′2
+𝑦
′2
+𝑧
′2
)
3
2
Đáp án : A
Câu 10:
L i gi i : ờ ả
Đặ
t {
𝐹 = 𝑥
2
+𝑦
2
−10
𝐺 = 𝑦 +𝑧
2 2
−25
𝑛
𝐹
= (𝐹
𝑥
′
(
𝐴
)
;𝐹
𝑦
′
( )
𝐴 ;𝐹
𝑧
′
( ) ( )
𝐴 ) = 2;6;0 ; 𝑛
𝐺
= (𝐺
𝑥
′
(
𝐴
)
;𝐺
𝑦
′
(
𝐴
)
;𝐺
𝑧
′
(
𝐴
)
) = (0;6;8)
Ta có
𝒏
𝒕𝒕
= 𝑛 ×𝑛 = ( ;−4;3)
𝐹 𝐺
12
TEAM GI I TÍCH 2 Ả
43
Phương trình tiếp tuyến:
𝑥 −1
12
=
𝑦−3
−4
=
𝑧−4
3
Đáp án : A
TEAM GI I TÍCH 2 Ả
44
III. TÍCH PHÂN B I & NG D Ộ Ứ ỤNG
3.1. TÍCH PHÂN KÉP
Câu 1: 𝑇í𝑛ℎ 𝑥𝑦𝑑𝑥𝑑𝑦
∬
𝐷
v c gi i h n bới D đượ ớ ạ ởi 𝑥+𝑦 =4 𝑣à 𝑥 = 2𝑦
2
𝑀𝑖
ề𝑛 𝐷:{
−4 ≤ 𝑥 ≤ 2
𝑥
2
2
≤ 𝑦 ≤ 4−𝑥
∬
𝑥𝑦𝑑𝑥𝑑𝑦
𝐷
= ∫
𝑑𝑥
2
−4
∫ 𝑥𝑦𝑑𝑦
4−𝑥
𝑥
2
2
=
∫
𝑥𝑦
2
2
|
𝑦=
𝑥
2
2
𝑦=4−𝑥
𝑑𝑥
2
−4
=
∫
𝑥
( )
4−𝑥
2
2
−
𝑥(
𝑥
2
2
)
2
2
𝑑𝑥
2
−4
= −90. Ch n B ọ
Câu 2: 𝑇í𝑛ℎ 2𝑦𝑑𝑥𝑑𝑦
∬
𝐷
𝑣ớ𝑖 𝐷 𝑥á𝑐 đị𝑛ℎ 𝑏ở𝑖 𝑥
2
+𝑦
2
≤ 1,𝑥+ 𝑦 ≥ 1
𝑀𝑖
ề𝑛 𝐷:{
0 ≤ 𝑥 ≤ 1
1−𝑥 ≤ 𝑦 ≤ 1−𝑥
√
2
∬
2𝑦𝑑𝑥𝑑𝑦
𝐷
= ∫
𝑑𝑥
1
0
∫
2𝑦𝑑𝑦
√
1−𝑥
2
1−𝑥
=
∫ [
(
1−𝑥
2
)
−
( )
1−𝑥
2
]𝑑𝑥
1
0
=
1
3
.𝐶ℎọ𝑛 𝐴
Câu 3: 𝑇í𝑛ℎ
∫
𝑑𝑥
1
0
∫
(𝑥
2
3
2
𝑦−2𝑦
2
)𝑑𝑦
=
∫ (
𝑥
2
𝑦
2
2
−
2𝑦
3
3
)
|
𝑦=2
𝑦=3
𝑑𝑥
1
0
=
∫ [
𝑥
2
.(3
2
−2
2
)
2
−
2(3
3
−2
3
)
3
1
0
]𝑑𝑥
= −
71
6
.𝐶ℎọ𝑛 𝐶
Câu 4:
TEAM GI I TÍCH 2 Ả
45
∫
𝑑𝑥
1
0
∫
sin
(
𝑦
2
)
𝑑𝑦
1
𝑥
𝐷:{
0 ≤ 𝑥 ≤ 1
𝑥 ≤ 𝑦 ≤ 1
→{
0 ≤ 𝑦 ≤ 1
0 ≤ 𝑥 ≤ 𝑦
→ ∫ 𝑑𝑥
1
0
∫
sin
(
𝑦
2
)
𝑑𝑦
1
𝑥
= ∫
𝑑𝑦
1
0
∫
sin
(
𝑦
2
)
𝑑𝑥
𝑦
0
=
∫ 𝑥𝑠𝑖𝑛
(
𝑦
2
)|
𝑥=0
𝑥=𝑦
1
0
𝑑𝑦
=
∫ 𝑦𝑠𝑖𝑛
(
𝑦
2
)
1
0
𝑑𝑦
=
∫
1
2
𝑠𝑖𝑛
(
𝑦
2
)
1
0
𝑑
(
𝑦
2
)
=
∫
1
2
𝑠𝑖𝑛𝑡
1
0
𝑑𝑡 =
1−𝑐𝑜𝑠1
2
.𝐶ℎọ𝑛 𝐶
Câu 5: 𝑇í𝑛ℎ +𝑦
∬
𝑥
√
𝑥
2 2
𝐷
𝑑𝑥𝑑𝑦 𝑣ớ𝑖 𝐷 𝑥á𝑐 đị𝑛ℎ 𝑏ở𝑖 𝑥
2
+𝑦
2
≤ 𝑥;𝑦 ≥ 0
Đặ𝑡 {
𝑥 = 𝑟𝑐𝑜𝑠𝜑
𝑦 = 𝑟𝑠𝑖𝑛𝜑
|
𝐽
|
= 𝑟.
𝑀𝑖
ề𝑛 𝐷 ở 𝑡ℎà𝑛ℎ {𝑡𝑟
0 ≤ 𝑟 ≤ 𝑐𝑜𝑠𝜑
0 ≤ 𝜑 ≤
𝜋
2
∬
𝑥
√
𝑥
2
+𝑦
2
𝐷
𝑑𝑥𝑑𝑦 = ∬
𝑟
3
𝑐𝑜𝑠𝜑
𝐷
𝑑𝑟𝑑𝜑
= ∫ 𝑑𝜑
𝜋
2
0
∫
𝑟
3
𝑐𝑜𝑠𝜑
𝑐𝑜𝑠𝜑
0
𝑑𝑟𝑑𝜑
=
∫
( )
𝑐𝑜𝑠𝜑
4
4
.𝑐𝑜𝑠𝜑𝑑𝜑
𝜋
2
0
=
∫
( ( )
1− 𝑠𝑖𝑛𝜑
)
2 2
4
.𝑑(𝑠𝑖𝑛𝜑)
𝜋
2
0
=
2
15
.𝐶ℎọ𝑛 𝐵
Câu 6:𝑇í𝑛ℎ (2𝑥+ )𝑑𝑥𝑑𝑦
∬
𝑠𝑖𝑛𝑦
𝐷
𝑣ớ𝑖 𝐷: 𝑥 −2
( )
2
+𝑦
2
≤ 1
TEAM GI I TÍCH 2 Ả
46
Ta th y f(x,y)=siny là hàm l i v i y và mi i x ng qua Ox ấ ẻ đố ớ ền D đố ứ
→ ∬𝑠𝑖𝑛𝑦𝑑𝑥𝑑𝑦 = 0
𝐷
Đặ𝑡 {
𝑥 = 2+ 𝑟𝑐𝑜𝑠𝜑
𝑦 = 𝑟𝑠𝑖𝑛𝜑
|
𝐽
|
=𝑟.
𝑀𝑖
ề𝑛 𝐷 ở 𝑡ℎà𝑛ℎ {𝑡𝑟
0 ≤ 𝑟 ≤1
0 ≤ 𝜑 ≤ 2𝜋
∬
2𝑥
𝐷
𝑑𝑥𝑑𝑦 = 2+𝑟𝑐𝑜𝑠𝜑 𝑟𝑑𝑟𝑑𝜑∬
2
( )
𝐷
= ∫ 𝑑𝜑
2𝜋
0
∫
4𝑟𝑑𝑟
1
0
+∫
𝑐𝑜𝑠𝜑
2𝜋
0
𝑑𝜑∫
2𝑟
2
1
0
𝑑𝑟 =4𝜋.𝐶ℎọ𝑛 𝐵
𝐂â𝐮 𝟕:
∬
𝑑𝑥𝑑𝑦
(
𝑥
2
+𝑦
2
)
3
=
𝑎
𝑏
+𝑙𝑛𝑐,𝐷:𝑥 ≤ 𝑥 +𝑦 ≤ 2𝑥
2 2
𝐷
,−𝑥 ≤ 𝑦 ≤0.
𝑎
𝑏
𝑡ố𝑖 ả𝑛.𝑔𝑖
Tổng a+b+c=?
Đặ𝑡 {
𝑥 = 𝑟𝑐𝑜𝑠𝜑
𝑦 = 𝑟𝑠𝑖𝑛𝜑
|
𝐽
|
= 𝑟.
𝑀𝑖
ề𝑛 𝐷 ở 𝑡ℎà𝑛ℎ {𝑡𝑟
𝑐𝑜𝑠𝜑 ≤ 𝑟 ≤ 2𝑐𝑜𝑠𝜑
−
𝜋
4
≤ 𝜑 ≤ 0
∬
𝑑𝑥𝑑𝑦
(
𝑥
2
+𝑦
2
)
3
= ∬
𝑑𝑟𝑑𝜑
𝑟
5
𝐷𝐷
= ∫ 𝑑𝜑
0
−
𝜋
4
∫
𝑑𝑟
𝑟
5
2𝑐𝑜𝑠𝜑
𝑐𝑜𝑠𝜑
=
15
64
∫
1
(
𝑐𝑜𝑠𝜑
)
4
𝑑𝜑
0
−
𝜋
4
=
15
64
∫
(
𝑡𝑎𝑛𝜑
)
2
+1
(
𝑐𝑜𝑠𝜑
)
2
𝑑𝜑
0
−
𝜋
4
=
15
64
∫
[
(
𝑡𝑎𝑛𝜑
)
2
+1]𝑑(𝑡𝑎𝑛𝜑)
0
−
𝜋
4
=
5
16
→ 𝑎 = 5,𝑏 =16,𝑐 = 1.𝐶ℎọ𝑛 𝐶
𝐂â𝐮 𝟖: 2𝑥−𝑥 − 𝑦 𝑑𝑥𝑑𝑦∬√
2 2
𝐷
𝑣ớ𝑖 ề𝑛 𝐷:𝑥𝑚𝑖
2
+𝑦
2
≤ 2𝑥,𝑦 ≥ 0
TEAM GI I TÍCH 2 Ả
47
Đặ𝑡 {
𝑥 = 1+ 𝑟𝑐𝑜𝑠𝜑
𝑦 = 𝑟𝑠𝑖𝑛𝜑
|
𝐽
|
=𝑟.
𝑀𝑖
ề𝑛 𝐷 ở 𝑡ℎà𝑛ℎ {𝑡𝑟
0 ≤ 𝑟 ≤ 1
0 ≤ 𝜑 ≤ 𝜋
→ ∬√
2𝑥− 𝑥
2
−𝑦
2
𝑑𝑥𝑑𝑦
𝐷
= ∬
√
1−𝑟
2
.𝑟𝑑𝑟𝑑𝜑
𝐷
= ∫ 𝑑𝜑
𝜋
0
∫
−
1
2
√
1−𝑟
2
1
0
𝑑(1 −𝑟
2
)
= 𝜋.
∫
√
𝑢
2
𝑑𝑢 =
𝜋
3
1
0
.𝐶ℎọ𝑛 𝐵
𝐂â𝐮 𝟗:𝑇í𝑛ℎ
∬𝑦
2
( )
6𝑥 −𝑦 𝑑𝑥𝑑𝑦,𝑣ớ𝑖 𝐷 ớ𝑖 ℎạ𝑛 𝑏ở𝑖:𝑥 = 0,𝑥+ = 1.𝑔𝑖
|
𝑦
|
𝐷
𝐷:{
0 ≤ 𝑥 ≤ 1
𝑥−1 ≤ 𝑦 ≤ 1−𝑥
∬
𝑦
2
(6𝑥−𝑦)
𝐷
𝑑𝑥𝑑𝑦 = ∫
𝑑𝑥
1
0
∫
𝑦
2
(
6𝑥−𝑦
)
𝑑𝑦
1−𝑥
𝑥−1
=
∫ (2𝑥𝑦
3
−
𝑦
4
4
)
|
𝑦=𝑥−1
𝑦=1−𝑥
1
0
𝑑𝑥
=
∫ (2𝑥 1− 𝑥
( )
3
−
(1−𝑥)
4
4
−2𝑥 𝑥 −1
( )
3
+
(𝑥−1)
4
4
)
1
0
𝑑𝑥
=
1
5
.𝐶ℎọ𝑛 𝐴
𝐂â𝐮 𝑥+𝑦
𝟏𝟎:∬
( )
2
𝑑𝑥𝑑𝑦
𝐷
𝑣ớ𝑖 ề𝑛 𝐷:5𝑥𝑚𝑖
2
+6 +5𝑦𝑥𝑦
2
≤ 4
𝐷:4 𝑥 +𝑦
( )
2
+
( )
𝑥− 𝑦
2
≤ 4
Đặ𝑡 {
𝑢 = 𝑥 +𝑦
𝑣 = 𝑥 −𝑦
→
|
𝐽
|
=
1
2
𝑀𝑖ề𝑛 𝐷 ở 𝑡ℎà𝑛ℎ 4𝑢 +𝑣 ≤ 4𝑡𝑟
2 2
→
∬
(
𝑥+ 𝑦
)
2
𝑑𝑥𝑑𝑦
𝐷
= ∬
𝑢
2
2
𝑑𝑢𝑑𝑣
𝐷
Đặ𝑡 {
𝑢 = 𝑟𝑐𝑜𝑠𝜑
𝑣 = 2𝑟𝑠𝑖𝑛𝜑
→ = 2𝑟
|
𝐽
|
TEAM GI I TÍCH 2 Ả
48
𝑀𝑖
ề𝑛 𝐷 ở 𝑡ℎà𝑛ℎ {𝑡𝑟
0 ≤ 𝑟 ≤1
0 ≤ 𝜑 ≤ 2𝜋
→ ∬2𝑢 𝑑𝑢𝑑𝑣
2
𝐷
= ∬
𝑟
3
(𝑐𝑜𝑠𝜑)
2
𝑑𝑟𝑑𝜑
𝐷
= ∫ (𝑐𝑜𝑠𝜑)
2
𝑑𝜑
2𝜋
0
∫
𝑟
3
𝑑𝑟
1
0
=
𝜋
4
.𝐶ℎọ𝑛 𝐷
𝐂â𝐮 ề𝑛 𝐷 ớ𝑖 ℎạ𝑛 𝑏ở𝑖 𝑥 = 1,𝑦 = 0,𝑥 = 𝑦.
𝟏𝟏:𝑀𝑖 𝑔𝑖 ∬
𝑑𝑥𝑑𝑦
𝑥+𝑦 +1
=
𝑎
2
𝑙𝑛𝑏−𝑐𝑙𝑛2
𝐷
.
𝑇ổ 𝑎+𝑏+𝑐 =?𝑛𝑔
𝑀𝑖
ề𝑛 𝐷:{
0 ≤ 𝑥 ≤ 1
0 ≤ 𝑦 ≤ 𝑥
∬
1
𝑥+𝑦 +1
𝑑𝑥𝑑𝑦
𝐷
= ∫
𝑑𝑥
1
0
∫
1
𝑥+𝑦 +1
𝑑𝑦
𝑥
0
=
∫ ln
| |
𝑦+𝑥 +1
𝑦=0
𝑦=𝑥
𝑑𝑥
1
0
= ∫ ln|2x+1|𝑑𝑥
1
0
−∫
ln|x+1|𝑑𝑥
1
0
=
∫ ln
(
2x+1
)
𝑑𝑥
1
0
−∫
ln
(
x+1
)
𝑑𝑥
1
0
(
𝑑𝑜 0 ≤ 𝑥 ≤ 1
)
=
∫
1
2
ln
(
2x+1
)
𝑑(2𝑥 +1)
1
0
−∫
ln
(
x+1
)
𝑑(𝑥 +1)
1
0
= [
( (
2𝑥+ 1
)
ln 2𝑥 +1 2𝑥 +1
)
−
( )
2
−
(
𝑥+ 1
)
ln
(
𝑥 +1 +(𝑥+1)]
) |
𝑥=0
𝑥=1
=
3
2
𝑙𝑛 𝑙𝑛3−2 2. Ch n D. ọ
𝐂â𝐮 : ề𝑛 𝐷: 𝑥 + 𝑦 ≤ 6.𝟏𝟐 𝑀𝑖
2 2
∬
3𝑥
2
−𝑦
2
+1
𝑥
2
+𝑦 +1
2
𝑑𝑥𝑑𝑦
𝐷
= 𝑎𝜋+𝑙𝑛𝑏, Tổng a+b=?
Ta th y trong bi u th nh mi i x ng nhau nên có th i vai trò ấ ể ức xác đị ền D, x và y đố ứ ể đổ
của x và y trong bi u th c l y tích phân. ể ứ ấ
→
∬
3𝑥
2
−𝑦
2
+1
𝑥
2
+𝑦 +1
2
𝑑𝑥𝑑𝑦 =
∬
3𝑦
2
−𝑥
2
+1
𝑦
2
+𝑥 +1
2
𝑑𝑥𝑑𝑦
𝐷𝐷
→
∬
3𝑥
2
−𝑦
2
+1
𝑥
2
+𝑦 +1
2
𝑑𝑥𝑑𝑦 =
1
2
∬
3𝑥
2
−𝑦
2
+1+3𝑦
2
−𝑥
2
+1
𝑥
2
+𝑦
2
+1
𝑑𝑥𝑑𝑦
𝐷𝐷
TEAM GI I TÍCH 2 Ả
49
=
1
2
∬
2(𝑥
2
+𝑦
2
+1)
𝑥
2
+𝑦 +1
2
𝐷
𝑑𝑥𝑑𝑦
= ∬𝑑𝑥𝑑𝑦
𝐷
= 𝑆
𝐷
= 6𝜋.→ 𝑎 = 6,𝑏 = 1 → 𝐶ℎọ𝑛 𝐴
3.2. TÍCH PHÂN BỘI BA
𝐂â𝐮 𝟏:𝑇í𝑛ℎ 𝑡í𝑐ℎ 𝑝ℎâ𝑛 ∫ 𝑑𝑥
1
0
∫
𝑑𝑧
1−𝑥
0
∫
(𝑦+𝑧)
2
0
𝑑𝑦
= ∫ 𝑑𝑥
1
0
∫
( )
2+2𝑧
1−𝑥
0
𝑑𝑧
=
∫
(
2𝑧+𝑧
2
)
|
𝑧=0
𝑧=1−𝑥
1
0
𝑑𝑥
=
∫ 2
(
1−𝑥
)
+
( )
1−𝑥
2
1
0
𝑑𝑥
=
4
3
.𝐶ℎọ𝑛 𝐷
𝐂â𝐮 𝟐:𝑇í𝑛ℎ 3𝑥 −2𝑦
∭
(
2
)
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧 𝑣ớ𝑖 𝑉:0 ≤ 𝑥 ≤ 1,0 ≤ 𝑦 ≤ 𝑥,0 ≤ 𝑧 ≤𝑥
2
∭
(
3𝑥
2
−2𝑦
)
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧
= ∫ 𝑑𝑥
1
0
∫
𝑑𝑦
𝑥
0
∫
(3𝑥
2
−2𝑦)
𝑥
2
0
𝑑𝑧
= ∫ 𝑑𝑥
1
0
∫
𝑥
2
(3𝑥
2
−2𝑦)
𝑥
0
𝑑𝑦
= ∫ (3𝑥 −𝑥 )
5 4
1
0
𝑑𝑥 =
3
10
.𝐶ℎọ𝑛 𝐴
𝐂â𝐮 𝟑:𝑇í𝑛ℎ
∭
(
𝑥
2
+𝑦
2
)
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧,𝑉 𝑔𝑖ớ𝑖 ℎạ𝑛 𝑏ở𝑖 𝑥
2
+𝑦
2
−2𝑧 = 0,𝑧 = 2
Đặ𝑡 {
𝑥 = 𝑟𝑐𝑜𝑠𝜑
𝑦 = 𝑟𝑠𝑖𝑛𝜑
𝑧 = 𝑧
→ = 𝑟
|
𝐽
|
TEAM GI I TÍCH 2 Ả
50
𝑀𝑖
ề𝑛 𝑉 ở 𝑡ℎà𝑛ℎ𝑡𝑟 {
𝑟
2
2
≤ 𝑧 ≤ 2
0 ≤ 𝑟 ≤ 2
0 ≤ 𝜑 ≤ 2𝜋
∭
(
𝑥
2
+𝑦
2
)
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧 = ∭
𝑟
3
𝑉
𝑑𝑟𝑑𝜑𝑑𝑧
= ∫ 𝑑𝜑
2𝜋
0
∫
𝑑𝑟
2
0
∫
𝑟
3
𝑑𝑧
2
𝑟
2
2
= 2𝜋 (2−
∫ 𝑟
3
𝑟
2
2
)
2
0
𝑑𝑟
=
16𝜋
3
.𝐶ℎọ𝑛 𝐶
𝐂â𝐮 𝟒: ∫ 𝑑𝑥
1
0
∫
𝑑𝑧
1
0
∫
𝑥𝑧𝑒
𝑥𝑦
2
𝑑𝑦
1
𝑧
2
=
𝑒
𝑎
−
𝑏
𝑐
.𝑎 +𝑏 +𝑐 =?
𝑀𝑖
ề𝑛 {
0 ≤ 𝑥 ≤ 1
0 ≤ 𝑧 ≤ 1
𝑧
2
≤ 𝑦 ≤ 1
⇔ {
0 ≤ 𝑥 ≤ 1
0 ≤ 𝑦 ≤ 1
0 ≤ 𝑧 ≤
√
𝑦
∫
𝑑𝑥
1
0
∫
𝑑𝑧
1
0
∫
𝑥𝑧𝑒
𝑥𝑦
2
𝑑𝑦
1
𝑧
2
= ∫ 𝑑𝑥
1
0
∫
𝑑𝑦
1
0
∫
𝑥𝑧𝑒
𝑥𝑦
2
𝑑𝑧
√
𝑦
0
= ∫ 𝑑𝑥
1
0
∫
𝑧
2
2
𝑥𝑒
𝑥𝑦
2
1
0
|
𝑧=0
𝑧=
√
𝑦
𝑑𝑦
=
1
2
∫
𝑑𝑥
1
0
∫
𝑥𝑦𝑒
𝑥𝑦
2
1
0
𝑑𝑦
=
1
4
∫
𝑑𝑥
1
0
∫
𝑒
𝑥𝑦
2
1
0
𝑑
(
𝑥𝑦
2
)
=
1
4
∫
(𝑒
𝑥
−1)
1
0
𝑑𝑥 =
𝑒
4
−
1
2
.𝐶ℎọ𝑛 𝐵
𝐂â𝐮 𝟓:𝑇í𝑛ℎ
∭
𝑑𝑥𝑑𝑦𝑑𝑧
( )
𝑥+𝑦 +𝑧+2
2
,𝑉: {
𝑥 +𝑦+𝑧 ≤ 1
𝑥,𝑦,𝑧 ≥ 0
𝑉
TEAM GI I TÍCH 2 Ả
51
𝑀𝑖
ề𝑛 𝑉:{
0 ≤ 𝑧 ≤ 1−𝑥 −𝑦
0 ≤ 𝑦 ≤ 1−𝑥
0 ≤ 𝑥 ≤ 1
∭
𝑑𝑥𝑑𝑦𝑑𝑧
(
𝑥+ 𝑦+𝑧+2
)
2
𝑉
= ∫
𝑑𝑥
1
0
∫
𝑑𝑦
1−𝑥
0
∫
𝑑𝑧
( )
𝑥+𝑦 +𝑧+2
2
1−𝑥−𝑦
0
= ∫ 𝑑𝑥
1
0
∫
−1
𝑥+𝑦 +𝑧+2
|
𝑧=0
𝑧=1−𝑥−𝑦
𝑑𝑦
1−𝑥
0
= ∫ 𝑑𝑥
1
0
∫
(
−1
3
+
1
𝑥+𝑦 +2
)𝑑𝑦
1−𝑥
0
=
∫ (
−𝑦
3
+ln
( )
𝑥+𝑦+ 2 )
|
𝑦=0
𝑦=1−𝑥
1
0
𝑑𝑥
=
∫ (
𝑥−1
3
+ln
(
3
)
−ln
(
𝑥+2
)
)
1
0
𝑑𝑥
=
5
6
+2𝑙𝑛2−2𝑙𝑛3.𝐶ℎọ𝑛 𝐵
𝐂â𝐮 𝟔:𝑇í𝑛ℎ 4𝑥 +𝑦 + 𝑧 +2
∭
(
2 2 2
𝑥𝑦
)
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧,𝑉:4𝑥
2
+𝑦
2
+𝑧
2
≤ 4,𝑧 ≥ 0
𝐼 = 4𝑥 + 𝑦 +𝑧 +2
∭
(
2 2 2
𝑥𝑦
)
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧
𝐶ó 𝑓 𝑥,𝑦 = 2 𝑙à ℎà𝑚 𝑙ẻ đố𝑖 𝑣ớ𝑖 𝑥 𝑣à ề𝑛 𝑉 đố𝑖 𝑥ứ 𝑞𝑢𝑎 𝑚ặ𝑡 𝑥 = 0
( )
𝑥𝑦 𝑚𝑖 𝑛𝑔
→ ∭2𝑥𝑦𝑑𝑥𝑑𝑦𝑑𝑧 = 0
𝑉
Đặ𝑡 {
𝑥 = 𝑟𝑐𝑜𝑠𝜑𝑠𝑖𝑛𝜃
𝑦 = 2𝑟𝑠𝑖𝑛𝜑𝑠𝑖𝑛𝜃
𝑧 = 2𝑟𝑐𝑜𝑠𝜃
→
|
𝐽
|
= 4𝑟
2
𝑠𝑖𝑛𝜃
𝑀𝑖
ề𝑛 𝑉 ở 𝑡ℎà𝑛ℎ 𝑡𝑟 {
0 ≤ 𝑟 ≤ 1
0 ≤ 𝜃 ≤
𝜋
2
0 ≤ 𝜑 ≤ 2𝜋
→ 𝐼 = 4𝑟 𝑠𝑖𝑛𝜃𝑑𝑟𝑑𝜃𝑑𝜑∭
4
𝑉
= ∫ 𝑑𝜑
2𝜋
0
∫
𝑠𝑖𝑛𝜃𝑑𝜃
𝜋
2
0
∫
4𝑟
4
𝑑𝑟
1
0
=
8𝜋
5
.𝐶ℎọ𝑛 𝐵
TEAM GI I TÍCH 2 Ả
52
𝐂â𝐮 𝟕: +𝑦 +𝑧∭√𝑥
2 2 2
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧 =
𝜋
𝑎
,𝑉:𝑥
2
+𝑦
2
+𝑧
2
≤ 𝑦.𝑇ì𝑚 𝑎?
Đặ𝑡 {
𝑥 = 𝑟𝑐𝑜𝑠𝜑𝑠𝑖𝑛𝜃
𝑦 = 𝑟𝑐𝑜𝑠𝜃
𝑧 = 𝑟𝑠𝑖𝑛𝜑𝑠𝑖𝑛𝜃
→
|
𝐽
|
= 𝑟
2
𝑠𝑖𝑛𝜃
𝑀𝑖
ề𝑛 𝑉 ở 𝑡ℎà𝑛ℎ𝑡𝑟 {
0 ≤ 𝑟 ≤ 𝑐𝑜𝑠𝜃
0 ≤ 𝜃 ≤
𝜋
2
0 ≤ 𝜑 ≤ 2𝜋
∭√
𝑥
2
+𝑦
2
+𝑧
2
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧 = ∭
𝑟
3
𝑠𝑖𝑛𝜃
𝑉
𝑑𝑟𝑑𝜑𝑑𝜃
= ∫ 𝑑𝜑
2𝜋
0
∫
𝑑𝜃
𝜋
2
0
∫
𝑟
3
𝑠𝑖𝑛𝜃
𝑐𝑜𝑠𝜃
0
𝑑𝑟
= 2𝜋.
∫
(
𝑐𝑜𝑠𝜃
)
4
4
.𝑠𝑖𝑛𝜃
𝜋
2
0
𝑑𝜃
=
𝜋
2
.
∫
−
(
𝑐𝑜𝑠𝜃
)
4
𝜋
2
0
𝑑(𝑐𝑜𝑠𝜃)
=
𝜋
2
∫
𝑢
4
𝑑𝑢
1
0
=
𝜋
10
.𝐶ℎọ𝑛 𝐷
𝐂â𝐮 𝟖: 𝑧𝑐𝑜𝑠 +𝑦
∭
(
𝑥
2 2
)
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧,𝑉:√
𝑥
2
+𝑦
2
≤ 𝑧 ≤ 4−𝑥√
2
−𝑦
2
Đặ𝑡{
𝑥 = 𝑟𝑐𝑜𝑠𝜑
𝑦 = 𝑟𝑠𝑖𝑛𝜑
𝑧 = 𝑧
→ = 𝑟
|
𝐽
|
𝑀𝑖
ề𝑛 𝑉 ở 𝑡ℎà𝑛ℎ{𝑡𝑟
𝑟 ≤ 𝑧 ≤ 4− 𝑟
√
2
0 ≤ 𝑟 ≤ √2
0 ≤ 𝜑 ≤ 2𝜋
∭
𝑧𝑐𝑜𝑠
(
𝑥
2
+𝑦
2
)
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧 = 𝑧𝑐𝑜𝑠∭
(
𝑟
2
)
.𝑟
𝑉
𝑑𝑟𝑑𝜑𝑑𝑧
= ∫ 𝑑𝜑
2𝜋
0
∫
𝑑𝑟
√
2
0
∫
𝑧𝑟𝑐𝑜𝑠
(
𝑟
2
)
𝑑𝑧
√
4−𝑟
2
𝑟
= 2𝜋
∫
𝑧
2
2
𝑟𝑐𝑜𝑠
(
𝑟
2
)|
𝑧=𝑟
𝑧= 4−𝑟√
2
√
2
0
𝑑𝑟
TEAM GI I TÍCH 2 Ả
53
= 2𝜋
∫
4−𝑟
2
−𝑟
2
2
𝑟𝑐𝑜𝑠
(
𝑟
2
)|
𝑧=𝑟
𝑧= 4−𝑟√
2
√
2
0
𝑑𝑟
= 𝜋 2−𝑟
∫
(
2
)
cos
(
𝑟
2
)
𝑑
(
𝑟
2
)
√
2
0
= 𝜋
∫
(
2−𝑢
)
𝑐𝑜𝑠𝑢
2
0
𝑑𝑢
= 𝜋 2−𝑢
∫
( )
2
0
𝑑
(
𝑠𝑖𝑛𝑢
)
= 𝜋[ 2−𝑢 𝑠𝑖𝑛𝑢
( ) |
𝑢=0
𝑢=2
+∫
𝑠𝑖𝑛𝑢
2
0
𝑑𝑢]
= 𝜋 0−𝑐𝑜𝑠𝑢
( |
𝑢=0
𝑢=2
)
= 𝜋 1−𝑐𝑜𝑠2 .𝐶ℎọ𝑛 𝐴
( )
𝐂â𝐮 𝟗: ề𝑛 𝑉:{
𝑀𝑖
𝑥
2
+𝑦
2
+𝑧
2
≤ 8
𝑥
2
+𝑦
2
≤ 2
.∭
(
𝑥
2
+𝑦
2
)
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧 =
𝑎
√
8−𝑏 6
√
15
𝜋.
𝑏−𝑎 =?
Đặ𝑡 {
𝑥 = 𝑟𝑐𝑜𝑠𝜑
𝑦 = 𝑟𝑠𝑖𝑛𝜑
𝑧 = 𝑧
→
|
𝐽
|
= 𝑟
𝑀𝑖
ề𝑛 𝑉 ở 𝑡ℎà𝑛ℎ {𝑡𝑟
− 8−𝑟
√
2
≤ 𝑧 ≤ 8−𝑟
√
2
0 ≤ 𝑟 ≤ √2
0 ≤ 𝜑 ≤ 2𝜋
∭
(
𝑥
2
+𝑦
2
)
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧 = ∭
𝑟
3
𝑉
𝑑𝑟𝑑𝜑𝑑𝑧
= ∫ 𝑑𝜑
2𝜋
0
∫
𝑑𝑟
√
2
0
∫
𝑟
3
𝑑𝑧
√
8−𝑟
2
−
√8−𝑟
2
= 2𝜋 2𝑟 8−𝑟
∫
3
√
2
√
2
0
𝑑𝑟
= 2𝜋 − 8−8+𝑟
∫
(
2
)
√
8−𝑟
2
√
2
0
𝑑
(
8−𝑟
2
)
= 2𝜋 8−𝑢
∫
( )
√
𝑢
8
6
𝑑𝑢
TEAM GI I TÍCH 2 Ả
54
= 2𝜋(
16
3
𝑢
3
2
−
2
5
𝑢
5
2
)
|
𝑢=6
𝑢=8
=
512
√
8−528
√
6
15
𝜋.𝐶ℎọ𝑛 𝐴.
𝐂â𝐮 :𝑇í𝑛ℎ 𝑥+𝑦−2𝑧
𝟏𝟎 ∭
( )
2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
=
𝑎𝜋
𝑏
,𝑣ớ𝑖 𝑉:𝑥
2
+𝑦
2
+𝑧
2
≤ 1.
𝑎−𝑏 =?
𝐼 = 𝑥 +𝑦−2𝑧
∭
( )
2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∭(𝑥 +𝑦 +4𝑧 +2
2 2 2
𝑥𝑦−4𝑥𝑧−4𝑦𝑧)
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧
𝑋é𝑡 𝑓 𝑥,𝑦,𝑧 = 2 𝑙à ℎà𝑚 𝑙ẻ đố𝑖 𝑣ớ𝑖 𝑥, ề𝑛 𝑉 đố𝑖 𝑥ứ 𝑞𝑢𝑎 𝑥 =0
( )
𝑥𝑦 𝑚𝑖 𝑛𝑔
→ ∭2𝑥𝑦
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧 = 0
𝑇 𝑡ự 𝑐ó −4ươ𝑛𝑔 ∭ 𝑥𝑧
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧 = −4∭ 𝑦𝑧
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧 = 0
→ 𝐼 = (𝑥 +𝑦 +4𝑧 )∭
2 2 2
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧
Đặ𝑡 {
𝑥 = 𝑟𝑐𝑜𝑠𝜑𝑠𝑖𝑛𝜃
𝑦 = 𝑟𝑠𝑖𝑛𝜑𝑠𝑖𝑛𝜃
𝑧 = 𝑟𝑐𝑜𝑠𝜃
→
|
𝐽
|
= 𝑟
2
𝑠𝑖𝑛𝜃
𝑀𝑖
ề𝑛 𝑉 ở 𝑡ℎà𝑛ℎ {𝑡𝑟
0 ≤ 𝑟 ≤1
0 ≤ 𝜃 ≤ 𝜋
0 ≤ 𝜑 ≤ 2𝜋
→ 𝐼 =
∭
(
𝑟
2
+𝑟
2
(
𝑐𝑜𝑠𝜃
) )
2
.𝑟
2
𝑠𝑖𝑛𝜃
𝑉
𝑑𝑟𝑑𝜑𝑑𝜃
=
∭(𝑟 𝑠𝑖𝑛𝜃+𝑟 𝑠𝑖𝑛𝜃)
4 4
(
𝑐𝑜𝑠𝜃
)
2
𝑉
𝑑𝑟𝑑𝜑𝑑𝜃
= ∫ 𝑑𝜑
2𝜋
0
∫
𝑠𝑖𝑛𝜃
𝜋
0
𝑑𝜃∫
𝑟
4
1
0
𝑑𝑟+∫ 𝑑𝜑
2𝜋
0
∫
(
𝑐𝑜𝑠𝜃
)
2
𝑠𝑖𝑛𝜃
𝜋
0
𝑑𝜃∫
𝑟
4
1
0
𝑑𝑟
= 2𝜋.2.
1
5
+2𝜋.
2
3
.
1
5
=
16𝜋
15
.𝐶ℎọ𝑛 𝐶
TEAM GI I TÍCH 2 Ả
55
3.3. NG DỨ Ụ ỦNG C A TÍCH PHÂN B I Ộ
𝐂â𝐮 𝟏: ệ𝑛 𝑡í𝑐ℎ 𝑝ℎầ𝑛 𝑚ặ𝑡 𝑧 = 𝑥 +𝑦 +2 𝑛ằ𝑚 𝑡𝑟𝑜𝑛𝑔 𝑚ặ𝑡 ụ 𝑥 +𝑦 = 9 𝑙à𝐷𝑖
2 2
𝑡𝑟
2 2
𝑎
√
𝑎−𝑏
𝑐
𝜋.𝑇ổ𝑛𝑔 𝑎 +𝑏+ 𝑐 =?
𝐻ì𝑛ℎ 𝑐ℎ𝑖ế𝑢 𝑐ủ𝑎 𝑚ặ𝑡 𝑡𝑟𝑜𝑛𝑔 𝑚ặ𝑡
𝑡𝑟ụ 𝑙ê𝑛 𝑂𝑥𝑦 𝑙à 𝐷:{
𝑧 = 0
𝑥
2
+𝑦 ≤ 9
2
𝑆 = 1+𝑧∬ √
𝑥
′
2
+𝑧
𝑦
′2
𝐷
𝑑𝑥𝑑𝑦 = 1+4𝑥∬√
2
+4𝑦
2
𝐷
𝑑𝑥𝑑𝑦
Đặ𝑡 {
𝑥 = 𝑟𝑐𝑜𝑠𝜑
𝑦 = 𝑟𝑠𝑖𝑛𝜑
= 𝑟
|
𝐽
|
𝑀𝑖
ề𝑛 𝐷 ở 𝑡ℎà𝑛ℎ ∶{𝑡𝑟
0 ≤ 𝑟 ≤ 3
0 ≤ 𝜑 ≤ 2𝜋
→ 𝑆 = 1+4𝑟
∬
√
2
𝐷
.𝑟𝑑𝑟𝑑𝜑
= ∫ 𝑑𝜑
2𝜋
0
∫
√1+4𝑟
2
8
3
0
𝑑
(
1+4𝑟
2
)
=
2𝜋
8
∫
√
𝑢𝑑𝑢
37
1
=
37
√
37−1
6
𝜋.𝐶ℎọ𝑛 𝐶
𝐂â𝐮 𝟐:𝑇í𝑛ℎ ệ𝑛 𝑡í𝑐ℎ ℎì𝑛ℎ 𝑝ℎẳ ớ𝑖 ℎạ𝑛 𝑏ở𝑖 𝑦 = √3𝑑𝑖 𝑛𝑔 𝑔𝑖 𝑥,𝑦 = 0,𝑥 +𝑦 = 2𝑥
2 2
𝑆
𝐷
= ∬
𝑑𝑥𝑑𝑦
𝐷
Đặ𝑡 {
𝑥 = 𝑟𝑐𝑜𝑠𝜑
𝑦 = 𝑟𝑠𝑖𝑛𝜑
= 𝑟
|
𝐽
|
𝑀𝑖
ề𝑛 𝐷 ở 𝑡ℎà𝑛ℎ ∶{𝑡𝑟
0 ≤ 𝑟 ≤ 2𝑐𝑜𝑠𝜑
0 ≤ 𝜑 ≤
𝜋
3
𝑆
𝐷
= ∬
𝑟𝑑𝑟𝑑𝜑
𝐷
= ∫ 𝑑𝜑
𝜋
3
0
∫
𝑟𝑑𝑟
2𝑐𝑜𝑠𝜑
0
=
∫ 2
( )
𝑐𝑜𝑠𝜑
2
𝑑𝜑
𝜋
3
0
TEAM GI I TÍCH 2 Ả
56
=
∫
( )
1+𝑐𝑜𝑠2𝜑
𝑑𝜑
𝜋
3
0
=
𝜋
3
+
√
3
4
.𝐶ℎọ𝑛 𝐷
𝐂â𝐮 𝟑:𝑇í𝑛ℎ 𝑡ℎể 𝑡í𝑐ℎ ề𝑛 ớ𝑖 ℎạ𝑛 𝑏ở𝑖 𝑥 = 1+𝑦 +𝑧 𝑣à 𝑥 = 2(𝑦 +𝑧 )𝑚𝑖 𝑔𝑖
2 2 2 2
𝑉
𝑉
= ∭
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
Đặ𝑡 {
𝑥 = 𝑥
𝑦 = 𝑟𝑐𝑜𝑠𝜑
𝑧 = 𝑟𝑠𝑖𝑛𝜑
→
|
𝐽
|
= 𝑟
𝑀𝑖
ề𝑛 𝑉 ở 𝑡ℎà𝑛ℎ{𝑡𝑟
2𝑟
2
≤ 𝑥 ≤ 1+𝑟
2
0 ≤ 𝑟 ≤ 1
0 ≤ 𝜑 ≤ 2𝜋
→ ∭𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∭
𝑟𝑑𝑟𝑑𝜑𝑑𝑥
𝑉
= ∫ 𝑑𝜑
2𝜑
0
∫
𝑑𝑟
1
0
∫
𝑟𝑑𝑥
1+𝑟
2
2𝑟
2
= 2𝜋 𝑟(1+𝑟 −2𝑟∫
2 2
)𝑑𝑟
1
0
=
𝜋
2
.𝐶ℎọ𝑛 𝐷
𝐂â𝐮 𝟒: ề𝑛 𝐷 ớ𝑖 ℎạ𝑛 𝑏ở𝑖 +𝑦 = 2𝑥 .𝑆
𝑀𝑖 𝑔𝑖
(
𝑥
2 2
)
2 3
𝐷
=
𝑎𝜋
𝑏
.𝑇í𝑛ℎ 𝑎+𝑏?
Đặ𝑡 {
𝑥 = 𝑟𝑐𝑜𝑠𝜑
𝑦 = 𝑟𝑠𝑖𝑛𝜑
=𝑟
|
𝐽
|
𝑀𝑖
ề𝑛 𝐷 ở 𝑡ℎà𝑛ℎ {𝑡𝑟
0 ≤ 𝑟 ≤ 2 𝑐𝑜𝑠𝜑
( )
3
−
𝜋
2
≤ 𝜑 ≤
𝜋
2
𝑆
𝐷
= ∬
𝑑𝑥𝑑𝑦
𝐷
= ∫
𝑑𝜑
𝜋
2
−𝜋
2
∫
𝑟𝑑𝑟
2(𝑐𝑜𝑠𝜑)
3
0
= 2 𝑐𝑜𝑠𝜑
∫
( )
6
𝑑𝜑
𝜋
2
−
𝜋
2
= 4 𝑐𝑜𝑠𝜑
∫
( )
6
𝑑𝜑
𝜋
2
0
= 4.
𝜋
2
.
5‼
6‼
(𝑇í𝑐ℎ 𝑝ℎâ𝑛 𝑊𝑎𝑙𝑙𝑖𝑠)
TEAM GI I TÍCH 2 Ả
57
=
5𝜋
8
.𝐶ℎọ𝑛 𝐴
∗𝑇í𝑐ℎ 𝑝ℎâ𝑛 𝑊𝑎𝑙𝑙𝑖𝑠
∫
(
𝑠𝑖𝑛
)
𝑛
𝑑𝜑
𝜋
2
0
= ∫
( )
𝑐𝑜𝑠𝜑
𝑛
𝑑𝜑
𝜋
2
0
= {
𝜋
2
.
( )
𝑛−1 ‼
𝑛‼
𝑛ế𝑢 𝑛 𝑐ℎẵ𝑛
( )
𝑛−1 ‼
𝑛‼
𝑛ế𝑢 𝑛 𝑙ẻ
𝐂â𝐮 𝟓:𝑇í𝑛ℎ 𝑣ậ𝑡 𝑡ℎể 𝑉 𝑥á𝑐 đị𝑛ℎ 𝑏ở𝑖 +𝑦√𝑥
2 2
≤ 𝑧 ≤ 6−𝑥 −𝑦
2 2
𝑉
𝑉
= ∭
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
Đặ𝑡 {
𝑥 = 𝑟𝑐𝑜𝑠𝜑
𝑦 = 𝑟𝑠𝑖𝑛𝜑
𝑧 = 𝑧
→ = 𝑟
|
𝐽
|
𝑀𝑖
ề𝑛 𝑉 ở 𝑡ℎà𝑛ℎ {𝑡𝑟
𝑟 ≤ 𝑧 ≤ 6− 𝑟
2
0 ≤ 𝑟 ≤ 2
0 ≤ 𝜑 ≤ 2𝜋
→ ∭𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∭
𝑟𝑑𝑟𝑑𝜑𝑑𝑧
𝑉
= ∫ 𝑑𝜑
2𝜋
0
∫
𝑑𝑟
2
0
∫
𝑟𝑑𝑧
6−𝑟
2
𝑟
= 2𝜋 𝑟(6−𝑟 − 𝑟)∫
2
𝑑𝑟
2
0
=
32𝜋
3
.𝐶ℎọ𝑛 𝐵
𝐂â𝐮 𝟔:𝑇í𝑛ℎ 𝑡ℎể 𝑡í𝑐ℎ 𝑣ậ𝑡 𝑡ℎể ớ𝑖 ℎạ𝑛 𝑏ở𝑖 𝑐á𝑐 𝑚ặ𝑡 𝑧 = 𝑥 +3𝑦𝑔𝑖
2 2
và
𝑧 = 4−3𝑥 −𝑦
2 2
𝑉
𝑉
= ∭
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
→
𝑀𝑖ề𝑛 𝑉:{
𝑥
2
+3𝑦
2
≤ 𝑧 ≤ 4−3𝑥
2
−𝑦
2
𝑥
2
+𝑦 ≤ 1.
2
(
𝐷
)
∭
𝑑𝑥𝑑𝑦𝑑𝑧 =
∬
(
4−3𝑥
2
−𝑦
2
−𝑥
2
−3𝑦
2
)
𝑑𝑥𝑑𝑦
𝐷𝑉
= 4 1−𝑥 −𝑦
∬
(
2 2
)
𝑑𝑥𝑑𝑦
𝐷
Đặ𝑡 {
𝑥 = 𝑟𝑐𝑜𝑠𝜑
𝑦 = 𝑟𝑠𝑖𝑛𝜑
= 𝑟
|
𝐽
|
TEAM GI I TÍCH 2 Ả
58
𝑀𝑖
ề𝑛 𝐷 ở 𝑡ℎà𝑛ℎ ∶{𝑡𝑟
0 ≤ 𝑟 ≤ 1
0 ≤ 𝜑 ≤ 2𝜋
→ 𝑉
𝑉
= 4 1−𝑟∬
(
2
)
𝑟𝑑𝑟𝑑𝜑
𝐷
= 4∫ 𝑑𝜑
2𝜋
0
∫
(
1−𝑟
2
)
𝑟𝑑𝑟
1
0
= 2𝜋.𝐶ℎọ𝑛 𝐶.
TEAM GI I TÍCH 2 Ả
59
IV. PHÂN PH THU C THAM STÍCH Ụ Ộ Ố
( Vì là thi TN nên chúng ta s t ng gi i nhanh nh t có ẽ ập làm theo cách và hướ ả ấ
thể, không lan man suy nghĩ đến điề câu tích phân xác địu kiện ở 1 số nh hay
suy r ng ph thu c tham s n chúng ta s thay tr c ti p s vào ộ ụ ộ ố ữa, mà đa số ẽ ự ế ố
để ả ấ ờ ở ố ở dướ có thể gi i 1 cách nhanh nh t. Vì vậy, l i giải 1 s câu i sẽ trực tiếp
thay s và b u ki n c n ). ố ỏ qua xét các điề ệ ầ
4.1. TÍCH PHÂN XÁC ĐỊNH PHỤ THU C THAM SỘ Ố
Câu 1: Tính
∫
ln (1
𝜋/2
0
+y𝑠𝑖𝑛
2
𝑥) 𝑣ớ𝑖 𝑦𝑑𝑥 >1
Đáp án: A. 𝜋ln(1+ 𝑦+1
√
)−𝜋𝑙𝑛2
Giải:
Nhận th y: I(y)=ấ
∫
ln (1
𝜋
2
0
+y𝑠𝑖𝑛
2
𝑥) 𝑙à ℎà𝑚 𝑠ố 𝑘ℎả ê𝑛 (1,+∞)𝑑𝑥 𝑣𝑖 𝑡𝑟
⇒ 𝐼
′
(
𝑦
)
= ∫
1
𝑦+
1
𝑠𝑖𝑛 𝑥
2
𝜋/2
0
𝑑𝑥
Đặt t= tanx ⇒ 𝑑𝑡 =
1
𝑐𝑜𝑠
2
𝑥
𝑑𝑥 =
(
1+𝑡𝑎𝑛
2
𝑥
)
𝑑𝑥 =
𝑑𝑡
𝑡
2
+1
Với x=0 ; x=⇒ 𝑡 =0
𝜋
2
⇒ 𝑡 →+∞
⇒ 𝐼
′
= ∫
1
𝑦+
1
𝑠𝑖𝑛 𝑥
2
𝜋
2
0
𝑑𝑥 = ∫
1
𝑦+ 1+ 𝑐𝑜𝑡
(
2
𝑥
)
.
1
𝑡
2
+1
𝑑𝑡
+∞
0
=
∫
1
𝑦+(1+
1
𝑡𝑎𝑛
2
𝑥
)
.
1
𝑡
2
+1
𝜋
2
0
𝑑𝑥 =∫
1
𝑦+(1+
1
𝑡
2
)
.
1
𝑡
2
+1
𝜋
2
0
=
∫
𝑡
2
𝑡
2
𝑦+𝑡 +1
2
.
𝑑𝑡
𝑡
2
+1
=
1
𝑦
∫
1
𝑡
2
+1
−
1
𝑡
2
(1+𝑦) +1
𝑑𝑡
+∞
0
𝜋
2
0
=
1
𝑦
[𝑎𝑟𝑐𝑡𝑎𝑛𝑡−
1
√
1+𝑦
arctan𝑡 1+𝑦 |
√
𝑡 = +∞
𝑡 = 0
]
=
1
𝑦
(
𝜋
2
−
𝜋
2
√
1+𝑦
) =
𝜋
2
√
1+𝑦.(1+ 1+𝑦)
√
⇒ 𝐼 =
(
𝑦
)
∫𝐼
′
(
𝑦
)
𝑑𝑦=𝜋∫
1
2
√
1+𝑦.(1+ 1+𝑦)
√
𝑑𝑦
TEAM GI I TÍCH 2 Ả
60
= 𝜋
∫
1
(1+ 1+𝑦
√
)
𝑑(1+ 1+𝑦) = 𝜋 (1+ 𝑦+1)+𝐶
√
ln
√
Do I(0)= 0 ⇒ 𝐶 = −𝜋𝑙𝑛2
Vậy I(y)= 𝜋ln(1+ 𝑦+1
√
)−𝜋𝑙𝑛2
Câu 2: Tính gi i h n sau:ớ ạ
lim
𝑦⟶0
∫ √
𝑥
3
+𝑦
3
𝑑𝑥
1
0
Đáp án: B.0,4
Giải:
Thay s c ti p: ố trự ế
lim
𝑦⟶0
∫ √
𝑥
3
+𝑦
3
𝑑𝑥 = 𝐼 =
(
0
)
∫
√
𝑥
3
𝑑𝑥 =
2
5
1
0
1
0
Vậy ch n B. ọ
Câu 3:Tính gi i h n: ớ ạ
lim
𝑦⟶0
∫
𝑥
2015
cos (𝑥𝑦)
1+𝑥 +𝑦
2 2
𝑑𝑥
1
−1
Đáp án: D.
2
3
Giải:
Thay s vào tr c ti p: ố ự ế
lim
𝑦⟶0
∫
𝑥
2015
cos (𝑥𝑦)
1+𝑥 +𝑦
2 2
𝑑𝑥 = 𝐼 =
(
0
)
1
−1
∫
𝑥
2015
1+𝑥
2
𝑑𝑥 =
2
3
1
−1
Câu 4: Tính :
lim
𝑦⟶0
∫
𝑎𝑟𝑐cot (𝑥+𝑦)
1+𝑥 +𝑦
2 2
𝑑𝑥
𝑠𝑖𝑛𝑦
𝑐𝑜𝑠𝑦
Đáp án: A.
−3𝜋
2
32
Giải:
Thay s c ti p: ố trự ế
TEAM GI I TÍCH 2 Ả
61
lim
𝑦⟶0
∫
𝑎𝑟𝑐cot (𝑥 +𝑦)
1+𝑥 +𝑦
2 2
𝑑𝑥
𝑠𝑖𝑛𝑦
𝑐𝑜𝑠𝑦
=𝐼 =
(
0
)
∫
𝑎𝑟𝑐cot (𝑥)
1+𝑥
2
𝑑𝑥
0
1
= ∫ 𝑎𝑟𝑐cot (𝑥)𝑑(𝑎𝑟𝑐cot 𝑥)
1
0
=
𝑎𝑟𝑐cot (𝑥)
2
2
|
1
0
=
−3𝜋
2
32
Câu 5: Cho I(y)=
∫
sin ( 𝑥
2
+𝑥𝑦
1
𝑦
+𝑦
2
) .𝑇í𝑛ℎ 𝐼𝑑𝑥
′
(0)
Đáp án:
A.
𝑠𝑖𝑛1
2
Giải:
*Phân tích:
Hàm f(x,y)= sin ( 𝑥 ) 𝑥á𝑐 đị𝑛ℎ 𝑣ớ𝑖 𝑚ọ𝑖 𝑥,𝑦 ∈
2
+𝑥𝑦 +𝑦
2
R
Chọn ng u nhiên [-1,1]x[-1,1] ( ch m y=0) ẫ ứa điể
*Nhận th y: ấ
{
𝑓
(
𝑥,𝑦
)
𝑘ℎả 𝑣à ê𝑛 𝑡ụ𝑐 ê𝑛 [−1,1]x[−1,1] 𝑣𝑖 𝑙𝑖 𝑡𝑟
𝑎
(
𝑦 𝑦
)
= 𝑦,𝑏
( )
=1 𝑣à 𝑘ℎả 𝑣𝑖 𝑡𝑟ê𝑛 −1,1
[ ]
𝑓
𝑦
′
(
𝑥,𝑦
)
𝑙𝑖ê𝑛 𝑡ụ𝑐 𝑡𝑟ê𝑛 [−1,1]x[−1,1]
Áp d ng công ụ thức:
𝐼
′
(
𝑦
)
=𝑓 ,𝑦 .𝑏
(
𝑏
(
𝑦
) )
𝑦
′
( ( (
𝑦
)
.𝑓 𝑎 𝑦
)
,𝑦
)
.𝑎
𝑦
′
(
𝑦
)
+
∫
𝑓
𝑦
′
(
𝑥,𝑦
)
𝑑𝑥
𝑏(𝑦)
𝑎(𝑦)
= 𝑓 1,𝑦 𝛽.0−𝑓 𝑦,𝑦 .1+ (𝑥+2𝑦)cos (𝑥 +𝑦
( ) ( )
∫
2
+𝑥𝑦
2
)𝑑𝑥
1
𝑦
⇒ 𝐼
′
(
0
)
=𝑓 1,0 .0−𝑓 0,0 .1
( ) ( )
+
∫ 𝑥𝑐𝑜𝑠
(
𝑥
2
)
𝑑𝑥 =
1
2
∫
cos
(
𝑥
2
)
𝑑
(
𝑥
2
)
=
1
2
sin
(
𝑥
2
)
|
1
0
=
𝑠𝑖𝑛1
2
1
0
1
0
Câu 6: Cho I(y)=
∫
ln ( 𝑦 𝑠𝑖𝑛 𝑥+𝑐𝑜𝑠 𝑥)
2 2 2
𝜋
2
0
𝑑𝑥. Tính 𝐼
′
(1)
Đáp án:
B.
𝜋
2
Giải:
*Phân tích :
Cho [
𝛼,𝛽] 𝑠𝑎𝑜 𝑐ℎ𝑜 𝑦 = 1 ∈ 𝛼,𝛽 𝑣à á𝑛ℎ 𝑘ℎô ợ𝑐 để 𝑦 ∈
[ ]
𝑡𝑟 𝑛𝑔 đư
[
𝛼,𝛽
]
𝑙à𝑚 𝑐ℎ𝑜 ℎà𝑚 𝑓 𝑥,𝑦 á𝑛 đ𝑜ạ𝑛
( )
𝑔𝑖
Hàm
𝑓 𝑥,𝑦 𝑦 𝑠𝑖𝑛 𝑥+𝑐𝑜𝑠 𝑏ị á𝑛 đ𝑜ạ𝑛 𝑡ạ𝑖 𝑦 = 0,𝑥 =
( )
= ln
(
2 2 2
𝑥
)
𝑔𝑖
𝜋
2
TEAM GI I TÍCH 2 Ả
62
⇒ á𝑛ℎ để đ𝑖ể𝑚 𝑦 = 0 𝑛ằ𝑚 𝑡𝑟𝑜𝑛𝑔 𝛼,𝛽 ,𝑐ℎọ𝑛 𝑘ℎ𝑜ả 𝑏ấ𝑡 𝑘ì [1,2]
𝑡𝑟
[ ]
𝑛𝑔
*Tính toán:
𝑇𝑎 𝑐ó: 𝑓
𝑦
′
=
2𝑦𝑠𝑖𝑛
2
𝑥
𝑦
2
𝑠𝑖𝑛 𝑥+𝑐𝑜𝑠
2 2
𝑥
Áp d ng công thụ ức:
𝐼
′
(
𝑦
)
=
∫
𝑓
𝑦
′
(𝑥,𝑦)𝑑𝑥
𝑏
𝑎
Thay s : ố
𝐼
′
(
1
)
= ∫ 𝑓
𝑦
′
(𝑥,𝑦)𝑑𝑥
𝜋
2
0
= ∫
2𝑠𝑖𝑛
2
𝑥
𝑠𝑖𝑛 𝑥 +𝑐𝑜𝑠 𝑥
2 2
𝜋
2
0
=
𝜋
2
Câu 7: Tìm
lim
𝑦⟶1
∫
𝑎𝑟𝑐tanx
𝑥
2
+𝑦
2
𝑑𝑥
𝑦
0
Đáp án: B.
π
2
32
Giải:
Thay tr c ti p: ự ế
lim
𝑦⟶1
∫
𝑎𝑟𝑐tanx
𝑥
2
+𝑦
2
𝑑𝑥 =𝐼
(
1
)
𝑦
0
= ∫
𝑎𝑟𝑐tanx
𝑥
2
+1
𝑑𝑥
1
0
=
∫ 𝑎𝑟𝑐𝑡𝑎𝑛𝑥 𝑑 𝑎𝑟𝑐𝑡𝑎𝑛𝑥 = (
( )
(arctan𝑥)
2
2
)|
1
0
=
1
0
𝜋
2
32
Câu 8: Tính
lim
𝑦⟶0
∫
𝑎𝑟𝑐tan (𝑥𝑦)
1+𝑥 + 𝑦
2 2
𝑑𝑥
𝑐𝑜𝑠𝑦
𝑠𝑖𝑛𝑦
Đáp án :
C.
𝜋
2
32
Giải:
Thay s c ti p: ố trự ế
TEAM GI I TÍCH 2 Ả
63
lim
𝑦⟶0
∫
𝑎𝑟𝑐tan (𝑥+𝑦)
1+𝑥 +𝑦
2 2
𝑑𝑥
𝑐𝑜𝑠𝑦
𝑠𝑖𝑛𝑦
=𝐼
(
0
)
= ∫
arctan 𝑥
1+𝑥
2
𝑑𝑥
1
0
=
∫ 𝑎𝑟𝑐𝑡𝑎𝑛𝑥 𝑑 𝑎𝑟𝑐𝑡𝑎𝑛𝑥 = (
( )
(arctan𝑥)
2
2
)|
1
0
=
1
0
𝜋
2
32
Câu 9: Tính lim
𝑦⟶1
∫
𝑥
2
sin (𝜋𝑦𝑥)
2𝑦
𝑦
𝑑𝑥.
Đáp án: A.
2−5𝜋
𝜋
2
Giải:
Thay tr c ti p: ự ế
lim
𝑦⟶1
∫
𝑥
2
sin (𝜋𝑦𝑥)
2𝑦
𝑦
𝑑𝑥 =𝐼
(
1
)
= ∫ 𝑥
2
sin ( )𝜋𝑥 𝑑𝑥
2
1
Đặ
t {
𝑥
2
= 𝑢
sin =
(
𝜋𝑥
)
𝑑𝑥 𝑑𝑣
⟹ {
2𝑥𝑑𝑥 = 𝑑𝑢
−𝑐𝑜𝑠(𝜋𝑥)
𝜋
= 𝑣
Ta có:
𝐼
(
1
)
=
∫
𝑥
2
sin ( )𝜋𝑥 𝑑𝑥
2
1
=
−𝑥
2
𝑐𝑜𝑠
(
𝜋𝑥
)
𝜋
|
2
1
+
2
𝜋
∫
xcos ( )𝜋𝑥 𝑑𝑥
2
1
Đặ
t: {
𝑥 = 𝑢
cos
(
𝜋𝑥
)
𝑑𝑥 𝑑𝑣=
⟹ {
𝑑𝑥 = 𝑑𝑢
sin ( )𝜋𝑥
𝜋
= 𝑣
Ta có:
𝐼
(
1
)
=
−5
𝜋
+
2
𝜋
(
sin
(
𝜋𝑥
)
𝜋
𝑥|
2
1
−
1
𝜋
∫
sin ( ) ) =𝜋𝑥 𝑑𝑥
2
1
−5
𝜋
+
cos
(
𝜋𝑥
)
𝜋
2
|
2
1
=
2−5𝜋
𝜋
2
Câu 10:Tính gi i h n ớ ạ
lim
𝑦⟶0
∫
𝑥
2020
+𝑦
2021
1+𝑥
2
+2021𝑦
2
𝑑𝑥
1
−1
Đáp án:
Giải:
Thay s c ti p: ố trự ế
lim
𝑦⟶0
∫
𝑥
2020
+𝑦
2021
1+𝑥
2
+2021𝑦
2
𝑑𝑥 = 𝐼
(
0
)
= ∫
𝑥
2020
1+𝑥
2
𝑑𝑥
1
−1
1
−1
Đặ
t {
𝑥
2020
= 𝑢
1
1+𝑥
2
𝑑𝑥 𝑑𝑣=
⇒ {
2020𝑥
2019
𝑑𝑥 = 𝑑𝑢
𝑎𝑟𝑐𝑡𝑎𝑛𝑥 = 𝑣
TEAM GI I TÍCH 2 Ả
64
𝐼
(
0
)
=𝑎𝑟𝑐𝑡𝑎𝑛𝑥
2020
|
1
−1
−2020∫ 𝑎𝑟𝑐𝑡𝑎𝑛𝑥.
1
−1
𝑥
2019
𝑑𝑥
4.2. TÍCH PHÂN SUY R NG PH THU C THAM SỘ Ụ Ộ Ố
Câu 1:
Tính I(y)=
∫
arctan (x+y)
𝑥
2
+1
𝑑𝑥
+∞
0
Đáp
án: A.
2𝜋
𝑦
2
+𝑦
Lời gi ải:
Ta có:
𝑓
(
𝑥,𝑦
)
=
arctan x+y( )
𝑥
2
+1
𝑙𝑖ê𝑛 𝑡ụ𝑐 ê𝑛 [0,+∞𝑡𝑟 ) x R
⇒ 𝑓
𝑦
′
=
1
(
1+𝑥
2
)
[1+(
𝑥+𝑦
)
2
]
𝑙𝑖ê𝑛 𝑡ụ𝑐 ê𝑛 [0,+∞𝑡𝑟 ) x R
I
′
(
𝑦
)
= 𝑓∫
𝑦
′
𝑑𝑥 = ∫
1
(
1+𝑥
2
)
[1+ 𝑥+𝑦
( )
2
]
𝑑𝑥
+∞
0
+∞
0
Đặ𝑡
1
(
1+𝑥
2
)
[1+ 𝑥+𝑦
( )
2
]
=
𝐴𝑥+ 𝐵
1+𝑥
2
+
𝐶𝑥 +𝐷
1+ 𝑥+𝑦
( )
2
Đồ ứng nhất th c hệ số, ta được:
𝐴 =
−2
𝑦(𝑦 +4)
2
,𝐵 =
2
𝑦(𝑦 +4)
2
,𝐶 =
1
(𝑦 +4)
2
,𝐷 =
3
(𝑦 +4)
2
I
′
(
𝑦
)
=
1
(𝑦 +4)
2
∫
[
−2𝑥+ 𝑦
1+𝑥
2
+
2𝑥+3𝑦
1+ 𝑥+𝑦
( )
2
]𝑑𝑥
+∞
0
=
1
(𝑦 +4)
2
[
−ln
(
1+𝑥
2
)
+𝑦.𝑎𝑟𝑐𝑡𝑎𝑛𝑥
+
ln
[
1+ 𝑥+𝑦 + 𝑦.arctan 𝑥 +𝑦 |
( )
2
] ( )]
1
0
=
2𝜋
𝑦
2
+𝑦
Câu 2:
Tính
∫
𝑒
− −𝑎𝑥
−𝑒
𝑏𝑥
𝑥
𝑑𝑥
+∞
0
Đáp án: A. -lna+lnb
Lời giải:
Đặ𝑡 𝐼 𝑥,𝑎
( )
= ∫
𝑒
−𝑎𝑥
−𝑒
−𝑏𝑥
𝑥
𝑑𝑥
(
𝑐𝑜𝑖 𝑏 𝑙à 𝑡ℎ
𝑎𝑚 𝑠ố
)
+∞
0
𝑓
(
𝑥,𝑎
)
=
𝑒
−𝑎𝑥
−𝑒
−𝑏𝑥
𝑥
⇒ 𝑓
𝑎
′
(
𝑥,𝑎
)
= −𝑒
−𝑎𝑥
TEAM GI I TÍCH 2 Ả
65
𝐼
′
(
𝑎
)
= ∫ 𝑓
𝑎
′
(
𝑥,𝑎
)
𝑑𝑥 =∫ −𝑒
−𝑎𝑥
𝑑𝑥 =
−1
𝑎
+∞
0
+∞
0
⇒ 𝐼 =
(
𝑎
)
∫𝐼
′
(
𝑎
)
𝑑𝑎 =∫
−1
𝑎
𝑑𝑎 = −𝑙𝑛𝑎+𝐶
𝑑𝑜
𝐼
(
𝑏
)
= ∫
𝑒
−𝑎𝑥
−𝑒
−𝑏𝑥
𝑥
𝑑𝑥 = 0 ⇒ −𝑙𝑛𝑏 +𝐶 = 0 ⇒ 𝐶 = 𝑙𝑛𝑏
+∞
0
𝑉ậ𝑦
∫
𝑒
−𝑎𝑥
−𝑒
−𝑏𝑥
𝑥
𝑑𝑥 = −𝑙𝑛𝑎+𝑙𝑛𝑏 = ln(
𝑏
𝑎
)
+∞
0
Câu 3: Tính
lim
𝑦⟶0
∫
𝑐𝑜𝑠xy
𝑥
2
+1
𝑑𝑥
𝑦
0
Đáp án: A. 𝜋/2
Lời gi ải:
Thay s c ti p: ố trự ế
lim
𝑦→0
∫
𝑐𝑜𝑠𝑦𝑥
1+𝑥
2
𝑑𝑥 = 𝐼
(
0
)
= ∫
1
1+𝑥
2
𝑑𝑥 =
+∞
0
+∞
0
𝜋
2
Câu 4: Tính
∫
𝑒
−𝑎𝑥
sin − sin ( )
(
𝑏𝑥
)
𝑐𝑥
𝑥
𝑑𝑥
+∞
0
Đáp án:
A. arctan(
𝑏
𝑎
) - arcrtan(
𝑐
𝑎
)
Lời gi ải:
𝑇𝑎
𝑐ó: 𝑒
−𝑎𝑥
sin − sin ( )
(
𝑏𝑥
)
𝑐𝑥
𝑥
= 𝐹 𝑥,𝑏 −𝐹 𝑥,𝑐
( ) ( )
=
∫ 𝐹
𝑦
′
( )
𝑥,𝑦 𝑑𝑦 =∫ 𝑒
−𝑎𝑥
.cos ( )𝑦𝑥 𝑑𝑦
𝑏
𝑐
𝑏
𝑐
𝐼 = .cos )
∫ (∫ 𝑒
−𝑎𝑥
(
𝑦𝑥
)
𝑑𝑦 𝑑𝑥
𝑏
𝑐
)
+∞
0
= (−
𝑎
𝑎
2
+𝑦
2
.𝑒
−𝑎𝑥
.cos
(
𝑦𝑥
)
+
𝑏
𝑎
2
+𝑏
2
.𝑒
−𝑎𝑥
.sin
(
𝑦𝑥
)
))|
+∞
0
=
𝑎
𝑎
2
+𝑦
2
TEAM GI I TÍCH 2 Ả
66
𝐼 = .cos )
∫ (∫ 𝑒
−𝑎𝑥
(
𝑦𝑥
)
𝑑𝑦 𝑑𝑥
𝑏
𝑐
)
+∞
0
= ∫
(
∫
𝑒
−𝑎𝑥
.cos )
(
𝑦𝑥
)
𝑑𝑥 𝑑𝑦
+∞
0
)
𝑏
𝑐
=
∫
𝑎
𝑎
2
+𝑦
2
𝑑𝑦 = 𝑎𝑟𝑐𝑡𝑎𝑛
𝑦
𝑎
|
𝑏
𝑐
= arctan(
𝑏
𝑎
) − arcrtan(
𝑐
𝑎
)
𝑏
𝑐
Câu 5: Tính
∫
2
−𝑥
−3
−𝑥
𝑥
𝑑𝑥
+∞
0
Đáp án: B. ln(
𝑙𝑛2
𝑙𝑛
3
)
Lời giải:
𝑇𝑎 𝑐ó: ∫ 𝑡
−𝑥−1
𝑑𝑡 =
𝑡
−𝑥
−𝑥
|
3
2
=
2
−𝑥
−3
−𝑥
𝑥
3
2
𝐼
2
= ∫
(
∫
𝑡
−𝑥−1
𝑑𝑡
3
2
)𝑑𝑥
+∞
0
= ∫
(
∫
𝑡
−𝑥−1
𝑑𝑥
+∞
0
)𝑑𝑡 =
3
2
∫
(
𝑡
−𝑥−1
−𝑙𝑛𝑡
|
+∞
0
)𝑑𝑡
3
2
=
∫
1
𝑡.𝑙𝑛𝑡
𝑑𝑡 = ln
(
𝑙𝑛𝑡
)
|
3
4
= ln(
𝑙𝑛2
𝑙𝑛
3
)
3
2
---HẾT---
TEAM GI I TÍCH 2 Ả
67
| 1/70
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


BK – ĐẠI CƯƠNG MÔN PHÁI
ĐỀ TRẮC NGHIỆM GIẢI TÍCH 2 NHÓM NGÀNH 1 + 2
TẬP 1: GIỮA KỲ
THỰC HIỆN: TEAM GIẢI TÍCH 2
MỤC LỤC
LỜI NÓI ĐẦU ................................................................................................................................. 1
PHẦN I: CÂU HỎI TRẮC NGHIỆM ............................................................................................ 2
I. HÀM NHIỀU BIẾN ................................................................................................................. 2
1.1. GIỚI HẠN CỦA HÀM NHIỀU BIẾN.............................................................................. 2
1.2. KHẢO SÁT TÍNH LIÊN TỤC CỦA HÀM NHIỀU BIẾN .............................................. 3
1.3. ĐẠO HÀM RIÊNG VÀ VI PHÂN TOÀN PHẦN............................................................ 4
1.4. ĐẠO HÀM CỦA HÀM HỢP ............................................................................................ 6
1.5. ĐẠO HÀM CỦA HÀM ẨN .............................................................................................. 7
1.6. TÍNH GẦN ĐÚNG NHỜ VI PHÂN ................................................................................. 8
1.7. CỰC TRỊ CỦA HÀM NHIỀU BIẾN ................................................................................ 8
1.8. KHAI TRIỂN TAYLOR ................................................................................................. 10
1.9. TÌM GTLN, GTNN CỦA HÀM SỐ ............................................................................... 10
II. ỨNG DỤNG CỦA PHÉP TÍNH VI PHÂN .......................................................................... 11
III. TÍCH PHÂN BỘI & ỨNG DỤNG ...................................................................................... 11
3.1. TÍCH PHÂN KÉP ........................................................................................................... 12
3.2. TÍCH PHÂN BỘI BA ..................................................................................................... 14
3.3. ỨNG DỤNG CỦA TÍCH PHÂN BỘI............................................................................. 15
IV. TÍCH PHÂN PHỤ THUỘC THAM SỐ: ............................................................................ 16
4.1. TÍCH PHÂN XÁC ĐỊNH PHỤ THUỘC THAM SỐ ..................................................... 16
4.2. TÍCH PHÂN SUY RỘNG PHỤ THUỘC THAM SỐ .................................................... 17
PHẦN II: LỜI GIẢI VÀ ĐÁP ÁN ................................................................................................ 19
I. HÀM NHIỀU BIẾN ............................................................................................................... 19
1.1. GIỚI HẠN CỦA HÀM NHIỀU BIẾN............................................................................ 19
1.2. KHẢO SÁT TÍNH LIÊN TỤC: ...................................................................................... 23
1.3. ĐẠO HÀM RIÊNG VÀ VI PHÂN TOÀN PHẦN .......................................................... 25
1.4. ĐẠO HÀM CỦA HÀM ẨN ............................................................................................ 27
1.5. TÍNH GẦN ĐÚNG NHỜ VI PHÂN ............................................................................... 29
1.6. CỰC TRỊ CỦA HÀM NHIỀU BIẾN .............................................................................. 30
1.7. KHAI TRIỂN TAYLOR ................................................................................................. 35
1.8. TÌM GTLN, GTNN CỦA HÀM SỐ ............................................................................... 35
II. ỨNG DỤNG CỦA PHÉP TÍNH VI PHÂN:......................................................................... 40
III. TÍCH PHÂN BỘI & ỨNG DỤNG ...................................................................................... 44
3.1. TÍCH PHÂN KÉP ........................................................................................................... 44
3.2. TÍCH PHÂN BỘI BA ..................................................................................................... 49
3.3. ỨNG DỤNG CỦA TÍCH PHÂN BỘI............................................................................. 55
IV. TÍCH PHÂN PHỤ THUỘC THAM SỐ ............................................................................. 59
4.1. TÍCH PHÂN XÁC ĐỊNH PHỤ THUỘC THAM SỐ ..................................................... 59
4.2. TÍCH PHÂN SUY RỘNG PHỤ THUỘC THAM SỐ .................................................... 64
LỜI NÓI ĐẦU
Hiện nay, với hình thức thi đổi mới từ thi tự luận sang hình thức thi
trắc nghiệm, chính vì vậy nhiều bạn sinh viên sẽ gặp khó khăn trong việc
ôn tập. Trong tình hình đó, nhóm “BK – ĐẠI CƯƠNG MÔN PHÁI” đã
biên soạn “BỘ ĐỀ TRẮC NGHIỆM GIẢI TÍCH 2” để giúp các bạn thuận
tiện hơn trong việc ôn tập.
Do thời gian cấp bách nên việc biên soạn tài liệu không thể tránh được
những sai sót. Mọi ý kiến đóng góp của bạn đọc xin gửi về fanpage “BÁCH KHOA LEARNING”.
Nhóm tác giả: Team GIẢI TÍCH 2 nhóm BK – ĐẠI CƯƠNG MÔN PHÁI
(Admin: Đỗ Tuấn Cường, Đinh Tiến Long, Phạm Thanh Tùng, Trần Trung
Dũng, Đỗ Ngọc Hiếu, Nguyễn Thu Hiền, Nguyễn Minh Hiếu) TEAM GIẢI TÍCH 2 1
PHẦN I: CÂU HỎI TRẮC NGHIỆM
I. HÀM NHIỀU BIẾN
1.1. GIỚI HẠN CỦA HÀM NHIỀU BIẾN Câu 1. Tính 𝐥𝐢𝐦 𝒙𝟐𝒚
(𝒙,𝒚)→(𝟎,𝟎)𝒙𝟐+𝒚𝟐
A.0 B.1 C.2 D. Không tồn tại giới hạn 𝒙𝒚 Câu 2. Tính 𝐥𝐢𝐦
(𝒙,𝒚)→(𝟎,𝟎)𝒙𝟐+𝒚𝟐
A.0 B.1 C.2 D. Không tồn tại giới hạn 𝒙𝒚 Câu 3. Tính 𝐥𝐢𝐦
(𝒙,𝒚)→(𝟎,𝟎)√𝒙𝟐+𝒚𝟐
A.0 B.+∞ C. −∞ D. −1 2 𝒙𝟐−𝒚𝟐 Câu 4. Tính 𝐥𝐢𝐦
(𝒙,𝒚)→(𝟎,𝟎)𝒙𝟐+𝒚𝟐
A.1 B. −1 C.0 D. Không tồn tại giới hạn 2 2 𝒙𝟑−𝒚𝟑 Câu 5. Tính 𝐥𝐢𝐦
(𝒙,𝒚)→(𝟎,𝟎)𝒙𝟐+𝒚𝟐
A.𝜋 B. 𝜋 C.0 D. Không tồn tại giới hạn 4 2 𝒙𝟐𝒚−𝒙𝒚𝟐 Câu 6. Tính 𝐥𝐢𝐦
(𝒙,𝒚)→(𝟎,𝟎) 𝒙𝟑+𝒚𝟑
A.1 B. −1 C.0 D. Không tồn tại giới hạn 2 2
𝒚.(𝒆𝟑𝒙−𝟏)−𝟑 . 𝒙 (𝒆𝒚−𝟏) Câu 7. Tính 𝐥𝐢𝐦 (𝒙,𝒚)→(𝟎,𝟎) 𝒙𝟐+𝒚𝟐
A.√2 B. −√2 C.0 D. Không tồn tại giới hạn 2 2 TEAM GIẢI TÍCH 2 2 Câu 8. Tính
𝐥𝐢𝐦 (𝒙𝟐 + 𝒚𝟐)𝒙𝟐𝒚𝟐 (𝒙,𝒚)→(𝟎,𝟎)
A.1 B. 1 C.0 D. Không tồn tại giới hạn 𝑒 𝟏
Câu 9. Tính 𝐥𝐢𝐦 (𝟏 + 𝐱𝟐𝐲𝟐)𝐱𝟐+𝐲𝟐 (𝐱,𝐲)→(𝟎,𝟎)
A.1 B. 1 C.0 D. Không tồn tại giới hạn 𝑒 𝒙𝟐+𝒚𝟐 Câu 10.Tính 𝐥𝐢𝐦
(𝒙,𝒚)→(𝟎,𝟎) 𝒆𝒙+𝒚
A.1 B. −1 C.0 D. Không tồn tại giới hạn 𝟏
Câu 11.Tính 𝐥𝐢𝐦 (𝟏 + 𝟑𝐱𝟐)𝐱𝟐+𝐲𝟐 (𝐱,𝐲)→(𝟎,𝟎)
A.1 B. 1 C.0 D. Không tồn tại giới hạn 𝑒
Câu 12.Tính 𝐥𝐢𝐦 𝐜𝐨𝐬 (𝐱𝟐+𝐲𝟐)−𝟏 (𝐱,𝐲)→(𝟎,𝟎) 𝐱𝟐+𝐲𝟐
A.1 B. 1 C.0 D. Không tồn tại giới hạn 𝑒
1.2. KHẢO SÁT TÍNH LIÊN TỤC CỦA HÀM NHIỀU BIẾN 𝟐
Câu 1: Cho hàm số 𝒇(𝒙, 𝒚) = {𝒙 ⋅ 𝐚𝐫𝐜𝐭𝐚𝐧 (𝒚) , nếu 𝒙 ≠ 𝟎 𝒙 𝟎, nếu 𝒙 = 𝟎
Xét tính liên tục của 𝒇(𝒙, 𝒚) tại 𝑩(𝟎, ( 𝟏).) A. 𝑓(𝑥, 𝑦)
liên tục tại 𝐵(0,1) B. 𝑓(𝑥, 𝑦) không liên tục tại 𝐵(0,1)
𝟐𝒙𝟐𝒚−𝒚𝟐𝒙, nếu 𝒙 𝟐 + 𝒚𝟐 ≠ 𝟎
Câu 2. Cho hàm số 𝒇(𝒙, 𝒚) = { 𝒙𝟐+𝒚𝟐
. Tìm a để hàm số liên
𝒂 ,nếu 𝒙𝟐 + 𝒚𝟐 = 𝟎
tục tại (0; 0).
A.0 B.1 C.2 D. ∀𝑎 ∈ 𝑅 TEAM GIẢI TÍCH 2 3
Câu 3. Cho hàm số 𝒇(𝒙, 𝒚) = {𝐬𝐢𝐧 (𝒙𝒚+𝒚𝟐
𝒙𝟐+𝒚𝟐) , nếu (𝒙, 𝒚) ≠ (𝟎, 𝟎) .
𝟎 ,nếu (𝒙, 𝒚) = 𝟎
Xét tính liên tục của 𝒇(𝒙, 𝒚) tại 𝑩(𝟎, ( 𝟎).) A. 𝑓(𝑥, 𝑦)
liên tục tại 𝐵(0,1) B. 𝑓(𝑥, 𝑦) không liên tục tại 𝐵(0,1) 𝒙𝒚−𝒙𝟐
Câu 4. Cho hàm số 𝒇(𝒙, 𝒚) = {
𝒙𝟐+𝒚𝟐 , nếu (𝒙, 𝒚) ≠ (𝟎, 𝟎)
𝟎, nếu (𝒙,𝒚) = 𝟎
Khảo sát sự liên tục của hàm số 𝒇(𝒙, 𝒚) tại 𝑩(𝟎, 𝟎). ) A. 𝑓(𝑥, 𝑦)
liên tục tại 𝐵(0,1) B. 𝑓(𝑥, 𝑦) không liên tục tại 𝐵(0,1)
1.3. ĐẠO HÀM RIÊNG VÀ VI PHÂN TOÀN PHẦN
Câu 1. Đạo hàm riêng theo biến x của hàm z = ln( x + √𝒙𝟐 + 𝒚𝟐) A. z’x = 1 B. z’ √𝑥2+𝑦2 x = 𝑥 √𝑥2+𝑦2 C. z’x = 2 D. z’ √𝑥2+𝑦2 x = 2𝑥 √𝑥2+𝑦2
Câu 2. Đạo hàm riêng theo biến y của hàm z = ln( x + √𝒙𝟐 + 𝒚𝟐) A. z’y = 𝑦 B. z’
(𝑥+√𝑥2+𝑦2)√𝑥2+𝑦2 y = √𝑥2+𝑦2
(𝑥+√𝑥2+𝑦2)√𝑥2+𝑦2 C. z’y = 𝑦2 D. z’
(𝑥+√𝑥2+𝑦2)√𝑥2+𝑦2 y = 2√𝑥2+𝑦2
(𝑥+√𝑥2+𝑦2)√𝑥2+𝑦2
Câu 3. Vi phân toàn phần của hàm z = ln( x + √𝒙𝟐 + 𝒚𝟐) A. 𝑑𝑧 = 1 . 𝑑𝑥 + 𝑦 . 𝑑𝑦 √𝑥2+𝑦2
(𝑥+√𝑥2+𝑦2)√𝑥2+𝑦2 B. 𝑑𝑧 = 𝑥 . 𝑑𝑥 + √𝑥2+𝑦2 . 𝑑𝑦 √𝑥2+𝑦2
(𝑥+√𝑥2+𝑦2)√𝑥2+𝑦2 C. 𝑑𝑧 = 2 . 𝑑𝑥 + 𝑦2 . 𝑑𝑦 √𝑥2+𝑦2
(𝑥+√𝑥2+𝑦2)√𝑥2+𝑦2
D. 𝑑𝑧 = 2𝑥 . 𝑑𝑥 + 2√𝑥2+𝑦2 . 𝑑𝑦 √𝑥2+𝑦2
(𝑥+√𝑥2+𝑦2)√𝑥2+𝑦2
Câu 4. Đạo hàm riêng theo biến y của hàm u = 𝒙𝒚𝟐𝒛
A. u’y = 𝑥𝑦2𝑧. 𝑙𝑛𝑥𝑦𝑧
B. u’y = 𝑥𝑦2𝑧. 𝑙𝑛𝑥𝑦2𝑧 TEAM GIẢI TÍCH 2 4
C. u’y = 𝑥𝑦2𝑧. 𝑙𝑛𝑥2𝑦𝑧
D. u’y = 𝑥𝑦𝑧. 𝑙𝑛𝑥𝑦𝑧
Câu 5. Vi phân toàn phần của hàm u = 𝒆(𝒙𝟐+𝟐𝒚𝟐+𝒛𝟐)−𝟏 tại (𝟏; -1; 1)
A. 𝑑𝑢(1; -1; 1) = 2 .dx + −4 .dy - 2 .dz 𝑒−4.16 𝑒−4.16 𝑒−4.16
B. 𝑑𝑢(1; -1; 1) = −2 .dx + 4 .dy - 2 .dz 𝑒−4.16 𝑒−4.16 𝑒−4.16
C. 𝑑𝑢(1; -1; 1) = 2 .dx + 4 .dy + 2 .dz 𝑒−4.16 𝑒−4.16 𝑒−4.16
D. 𝑑𝑢(1; -1; 1) = 2 .dx + −4 .dy + 2 .dz 𝑒−4.16 𝑒−4.16 𝑒−4.16 𝒙
Câu 6. Tính 𝒛′ ′
𝒙, 𝒛𝒚 của hàm số 𝒛 = ∫ 𝒚 𝒙𝒚 𝒕𝟐𝐬𝐢𝐧 𝟐𝒕𝒅𝒕 𝑧′ 2
𝑥 = −1 ⋅ (𝑥 ) sin 2𝑥 − 𝑦 ⋅ (𝑥𝑦) ⋅ sin 2𝑥𝑦 𝑦 𝑦 𝑦 A. { 2
𝑧′𝑦 = −𝑥 ⋅ (𝑥) sin2𝑥 − 𝑥 ⋅ (𝑥𝑦)2 ⋅ sin 2𝑥𝑦 𝑦2 𝑦 𝑦 𝑧′ 2
𝑥 = 1 ⋅ (𝑥 ) sin 2𝑥 + 𝑦 ⋅ (𝑥𝑦) ⋅ sin 2𝑥𝑦 𝑦 𝑦 𝑦 B. { 2
𝑧′𝑦 = −𝑥 ⋅ (𝑥) sin2𝑥 + 𝑥 ⋅ (𝑥𝑦)2 ⋅ sin 2𝑥𝑦 𝑦2 𝑦 𝑦 𝑧′ 2
𝑥 = 1 ⋅ (𝑥) sin 2𝑥 + 𝑦 ⋅ (𝑥𝑦) ⋅ sin 2𝑥𝑦 𝑦 𝑦 𝑦 C. { 2 𝑧′ 2
𝑦 = 𝑥 ⋅ (𝑥) sin 2𝑥 − 𝑥 ⋅ (𝑥𝑦) ⋅ sin 2𝑥𝑦 𝑦2 𝑦 𝑦
𝑧′𝑥 = 1 ⋅ (𝑥)sin 2𝑥 − 𝑦 ⋅ (𝑥𝑦)2 ⋅ sin 2𝑥𝑦 𝑦 𝑦 𝑦 D. { 2 𝑧′ 2
𝑦 = −𝑥 ⋅ (𝑥 ) sin
2𝑥 − 𝑥 ⋅ (𝑥𝑦) ⋅ sin 2𝑥𝑦 𝑦2 𝑦 𝑦
Câu 7. Vi phân toàn phần của hàm u = 𝒛 √𝒙𝟐+𝒚𝟐
A. 𝑑𝑢 = −𝑧𝑥2(𝑥2 + 𝑦2)−32 𝑑𝑥 +z y (𝑥2 + 𝑦2 −3
) 2 𝑑𝑦 + (𝑥2 + 𝑦2 −1 ) 2 𝑑𝑧 −3 −1
B. 𝑑𝑢 = −𝑧𝑥(𝑥2 + 𝑦2 −3
) 2 𝑑𝑥 + z y (𝑥2 + 𝑦2) 2 𝑑𝑦 + 𝑥𝑦(𝑥2 + 𝑦2) 2 𝑑𝑧 −3
C. 𝑑𝑢 = −𝑧𝑥(𝑥2 + 𝑦2) 2 𝑑𝑥 − z y (𝑥2 + 𝑦2)−32𝑑𝑦 + (𝑥2 + 𝑦2 −1 ) 2 𝑑𝑧 −3 −1
D. 𝑑𝑢 = −𝑧𝑥(𝑥2 + 𝑦2) 2 𝑑𝑥 + z y (𝑥2 + 𝑦2)−32𝑑𝑦 −(𝑥2 + 𝑦2) 2 𝑑𝑧
𝒚. 𝒂𝒓𝒕𝒂𝒏(𝒙)𝟐, 𝒏ế𝒖 𝒚 ≠ 𝟎
Câu 8. Cho hàm số f(x,y) = { 𝒚 𝟎, 𝒏ế𝒖 𝒚 = 𝟎 TEAM GIẢI TÍCH 2 5
Tính 𝒇′ (𝟏, 𝟎) 𝒚 A. π B. π C. π D. π 2 3 4 6
Câu 9. Tính đạo hàm riêng z’(x, y) của hàm số: 𝒚
𝒛 = {𝒂𝒓𝒄𝒕𝒂𝒏𝒙 𝒌𝒉𝒊 (𝒙, 𝒚) ≠ (𝟎, 𝟎)
𝟎 𝒌𝒉𝒊 (𝒙, 𝒚) = (𝟎, 𝟎) 𝑧′ A. {𝑧′𝑥 = 0 𝑥 = +∞ 𝑧′ C. { 𝑦 = 0 𝑧′𝑦 = +∞ 𝑧′ B. { 𝑧′𝑥 = 0 𝑥 = +∞ 𝑧′ D. { 𝑦 = +∞ 𝑧′𝑦 = 0
1.4. ĐẠO HÀM CỦA HÀM HỢP
Câu 1. Xác định đạo hàm của hàm hợp z = 𝒖𝒗 với u = cosx ; v = sinx
A. z’ = 𝑣. 𝑢𝑣−1.sinx + 𝑢𝑣. 𝑙𝑛𝑢. 𝑐𝑜𝑠𝑥
B. z’ = 𝑣. 𝑢𝑣−1.(-sinx) - 𝑢𝑣. 𝑙𝑛𝑢. 𝑐𝑜𝑠𝑥
C. z’ = 𝑣. 𝑢𝑣−1.(-sinx) + 𝑢𝑣. 𝑙𝑛𝑢. 𝑐𝑜𝑠𝑥
D. z’ = 𝑣. 𝑢𝑣−1.sinx - 𝑢𝑣. 𝑙𝑛𝑢. 𝑐𝑜𝑠𝑥
Câu 2. Xác định đạo hàm của hàm hợp z = 𝒖𝟐 – 2𝒗𝟐 với u = cosx ; v = sinx A. z’ = -3.sin2x B. z’ = -3.cos2x C. z’ = 3.sin2x D. z’ = 3.cos2x
Câu 3. Xác định đạo hàm của hàm hợp z = ln(𝒖𝟐 + 𝒗𝟐) với u = x.y và v = 𝒙 𝒚
𝑧′𝑥 = 2𝑢 . 𝑥 + 2𝑣 .1 A. { 𝑢2+𝑣2 𝑢2+𝑣2 𝑦
𝑧′𝑦 = 2𝑢 . 𝑦 + 2𝑣 .(−𝑥 ) 𝑢2+𝑣2 𝑢2+𝑣2 𝑦2
𝑧′𝑥 = 2𝑢 . 𝑦 + 2𝑣 .1 B. { 𝑢2+𝑣2 𝑢2+𝑣2 𝑦
𝑧′𝑦 = 2𝑢 . 𝑥 + 2𝑣 .(−𝑥 ) 𝑢2+𝑣2 𝑢2+𝑣2 𝑦2 TEAM GIẢI TÍCH 2 6
𝑧′𝑥 = 2𝑢 . 𝑦 + 2𝑣 .𝑥 C. { 𝑢2+𝑣2 𝑢2+𝑣2 𝑦
𝑧′𝑦 = 2𝑢 . 𝑥 + 2𝑣 .( 𝑥 ) 𝑢2+𝑣2 𝑢2+𝑣2 𝑦2
𝑧′𝑥 = 2𝑢 . 𝑦 − 2𝑣 .1 D. { 𝑢2+𝑣2 𝑢2+𝑣2 𝑦
𝑧′𝑦 = 2𝑢 . 𝑥 − 2𝑣 .(−𝑥 ) 𝑢2+𝑣2 𝑢2+𝑣2 𝑦2
1.5. ĐẠO HÀM CỦA HÀM ẨN
Câu 1. Xác định đạo hàm của hàm ẩn sau 𝒙𝟑 + 𝟐𝒚𝟑 + 𝟑𝒙𝟐𝒚 = 𝟐 A. y’x = − x2−2𝑥𝑦 2y2−𝑥2 B. y’x = x2+2𝑥𝑦 2y2−𝑥2 C. y’x = x2−2𝑥𝑦 2y2−𝑥2 D. y’x = − x2+2𝑥𝑦 2y2−𝑥2
Câu 2. Cho 𝒙𝟐. 𝒂𝒓𝒄𝒕𝒂𝒏𝒙 + 𝟐𝒙𝒚𝟐 + 𝒚𝟒 + 𝟐𝒛𝟑 = 𝟏. Tính z’x và z’y
A. {𝑧′𝑥 = 2𝑥.𝑎𝑟𝑐𝑡𝑎𝑛𝑥+ 𝑥2 1+𝑥2+2𝑦2 6𝑧2 𝑧′𝑦 = 2xy+2𝑦3 3𝑧2
B. {𝑧′𝑥 = 2𝑥.𝑎𝑟𝑐𝑡𝑎𝑛𝑥− 𝑥21+𝑥2−2𝑦2 6𝑧2 𝑧′ 2xy+2𝑦3 𝑦 = − 3𝑧2
C. {𝑧′𝑥 = − 2𝑥.𝑎𝑟𝑐𝑡𝑎𝑛𝑥+ 𝑥2 1+𝑥2+2𝑦2 6𝑧2 𝑧′ 2xy+2𝑦3 𝑦 = − 3𝑧2
D. {𝑧′𝑥 = − 2𝑥.𝑎𝑟𝑐𝑡𝑎𝑛𝑥− 𝑥21+𝑥2−2𝑦2 6𝑧2 𝑧′𝑦 = 2xy+2𝑦3 3𝑧2
Câu 3. Cho hàm số 𝒙𝟑 − 𝒚𝟑 + 𝟑𝒙𝒚 − 𝟏𝟑 = 𝟎. Xác định hàm ẩn y = y(x).
Viết phương trình tiếp tuyến của đồ thị hàm ẩn này tại điểm A(-1; -2) TEAM GIẢI TÍCH 2 7
A. y = − 1 . (𝑥 + 1) − 2 5 B. y = 1 . (𝑥 + 1) − 2 5 C. y = 1 . (𝑥 + 1) + 2 5 D. y = − 1 . (𝑥 + 1) + 2 5
Câu 4. Cho hàm ẩn z=z(x,y) được xác định từ phương trình sau 𝟐
𝒛𝟐 + 𝒙 = √𝒚𝟐 − 𝒛𝟐
Tính 𝒙𝟐𝒛′𝒙 + 𝟏𝒛′ 𝒚 𝒚 =? A. 1 B. −1 C. −1 𝑧 𝑧 𝑧2 D. 1 𝑧2
1.6. TÍNH GẦN ĐÚNG NHỜ VI PHÂN
Câu 1. Tính gần đúng giá trị sau nhờ vi phân A = (1,02)3. (0.97)2 A. 0 B. 1 C. 2 D. 3
Câu 2. Tính gần đúng giá trị sau nhờ vi phân A = √
𝟑 (𝟏,𝟎𝟐)𝟐 + (𝟎, 𝟎𝟓)𝟐 A. 1 B. 1 C. 1 D. 76 5 15 3 75
Câu 3. Tính gần đúng giá trị sau nhờ vi phân A = √
𝟑 𝟐.(𝟐,𝟗𝟖)𝟑 − 𝟑. (𝟒, 𝟎𝟏)𝟐 + 𝟐
A. 1,76 B. 1,89 C. 1,93 D. 1,67
Câu 4. Tính gần đúng giá trị sau nhờ vi phân S = √(𝟑, 𝟎𝟏)𝟐 + (𝟑, 𝟗𝟗)𝟐
A. 2,76 B. 3,29 C. 4,988 D. 1,58
1.7. CỰC TRỊ CỦA HÀM NHIỀU BIẾN
Câu 1. Cho hàm số z = 𝒙𝟐 + 𝒙𝒚 + 𝒚𝟐 − 𝟐𝒙 − 𝒚. Xác định điểm cực đại và cực tiểu
của hàm số nếu có.
A. Hàm số có một điểm cực đại M(1; 0)
B. Hàm số có một điểm cực tiểu M(1; 0)
C. Hàm số có một điểm cực đại M(-1; 0) TEAM GIẢI TÍCH 2 8
A. Hàm số có một điểm cực tiểu M(0; -1)
Câu 2. Cho hàm số z = 𝟐𝒙𝟒 + 𝒚𝟒 − 𝟒𝒙𝟐 + 𝟐𝒚𝟐. Điểm N(1; 0) là điểm cực đại hay
cực tiểu của hàm số và xác định 𝒛 n
𝒎𝒂𝒙; 𝒛𝒎𝒊𝒏 ếu có.
A. N(1; 0) là điểm cực tiểu với fmin = -2
B. N(1; 0) là điểm cực đại với fmin = 2
C. N(1; 0) là điểm cực đại với fmin = 4
D. N(1; 0) là điểm cực tiểu với fmin = 2
Câu 3. Cho hàm số z = 2𝒙𝟐 + 𝟑𝒚𝟑 − 𝒆−(𝒙𝟐+𝒚𝟐). Xác định điểm cực đại và cực tiểu
của hàm số nếu có.
A. M(0; 0) là điểm cực tiểu
B. M(0; 0) là điểm cực đại
C. N(1; 0) là điểm cực tiểu
D. N(1; 0) là điểm cực đại
Câu 4. Cho hàm số 𝒛 = 𝟐𝒙𝟐 + 𝒚𝟐 với điều kiện 𝒙𝟐 + 𝒚𝟐 = 𝟏. Hàm số trên có bao
nhiêu điểm cực đại và điểm cực tiểu.
A. 1 cực đại và 3 cực tiểu
B. 2 cực đại và cực tiểu
C. 3 cực đại và 1 cực tiểu D. 3 cực đại
Câu 5. Tìm cực trị của hàm số 𝒛 = 𝒙 + 𝒚 với điều kiện 𝒙𝟐 + 𝒚𝟐 = 𝟏. Điểm 𝟒 𝟑
𝑴 (𝟑 ; 𝟒) là điểm cực đại hay cực tiểu của hàm số và xác định giá trị z tại điểm M. 𝟓 𝟓
A. 𝑀 (3 ; 4) là điểm cực đại và 𝑧(𝑀) = 1 5 5 2
B. 𝑀 (3 ; 4) là điểm cực tiểu và 𝑧(𝑀) = 5 5 5 6
C. 𝑀 (3 ; 4) là điểm cực đại và 𝑧(𝑀) = 5 5 5 12
D. 𝑀 (3 ; 4) là điểm cực tiểu và 𝑧(𝑀) = 5 5 5 12
Câu 6. Cho hàm số sau: z=
𝒙𝟑 + 𝒚𝟑 + (𝒙 + 𝒚)𝟐. Hàm số trên có bao nhiêu điểm
cực trị. A. 1 B. 2 TEAM GIẢI TÍCH 2 9 C. 3 D. 4
Câu 7. Cho hàm số sau 𝒛 = 𝟐𝒙𝟐 + 𝒙𝒚𝟐 + 𝒚𝟑 + 𝟐. Hàm số trên có bao nhiêu điểm
cực trị. A. 0 B. 1 C. 2 D. 3
1.8. KHAI TRIỂN TAYLOR
Câu 1. Viết khai triển Taylor của hàm số sau tại điểm M(1; 2)
𝒇(𝒙, 𝒚) = 𝒙𝟐 + 𝒚𝟐 + 𝒙𝒚 + 𝟐𝒙 + 𝟐𝒚 + 𝟏
A. 𝑓(𝑥, 𝑦) = 14 + 3(𝑥 − 1) + 7(𝑦 − 2) + 2(𝑥 − 1)2 + 2(𝑥 − 1)(𝑦 − 2) + (𝑦 − 2)2
B. 𝑓(𝑥, 𝑦) = 14 + 6(𝑥 − 1) + 7(𝑦 − 2) + (𝑥 − 1)2 + (𝑥 − 1)(𝑦 − 2) + (𝑦 − 2)2
C. 𝑓(𝑥, 𝑦) = 7 + 6(𝑥 − 1) + 14(𝑦 − 2) + (𝑥 − 1)2 + (𝑥 − 1)(𝑦 − 2) + (𝑦 − 2)2
D. 𝑓(𝑥, 𝑦) = 7 + 6(𝑥 − 1) + 14(𝑦 − 2) + (𝑥 − 1)2 + (𝑥 − 1)(𝑦 − 2) + (𝑦 − 2)2
Câu 2. Viết khai triển Taylor của hàm số sau tại điểm M(0; 1)
𝒇(𝒙, 𝒚) = 𝒙𝟑 + 𝒙𝟐𝒚 + 𝒚𝟑
A. 𝑓(𝑥, 𝑦) = 1 + 3(𝑦 − 1) + 1𝑥2 + 3(𝑦 − 1)2 + 𝑥3 + 𝑥2(𝑦 − 1) + (𝑦 − 1)3 2
B. 𝑓(𝑥, 𝑦) = 1 − 3(𝑦 − 1) + 1𝑥2 − 3(𝑦 − 1)2 + 𝑥3 − 𝑥2(𝑦 − 1) + (𝑦 − 1)3 2
C. 𝑓(𝑥, 𝑦) = 1 + 3(𝑦 − 1) + 1𝑥2 + 3(𝑦 − 1)2 + 𝑥3 + 𝑥2(𝑦 − 1) + 1 (𝑦 − 1)3 2 6
D. 𝑓(𝑥, 𝑦) = 1 − 3(𝑦 − 1) + 1𝑥2 − 3(𝑦 − 1)2 + 𝑥3 − 𝑥2(𝑦 − 1) + 1 (𝑦 − 1)3 2 6
1.9. TÌM GTLN, GTNN CỦA HÀM SỐ
Câu 1. Tìm 𝒎𝒊𝒏, 𝒎𝒂𝒙 của 𝒛 = 𝐬𝐢𝐧 𝒙 + 𝐬𝐢𝐧 𝒚 + 𝐬𝐢𝐧 (𝒙 + 𝒚) với 𝟎
≤ 𝒙, 𝒚 ≤ 𝝅 𝟐 A. 𝑧 √ 𝑚𝑎𝑥 = 3 3 , 𝑧 2 𝑚𝑖𝑛 = 0
B. 𝑧𝑚𝑎𝑥 = √3 , 𝑧 2 𝑚𝑖𝑛 = 0 C. 𝑧𝑚𝑎𝑥 = 1 , 𝑧 2 𝑚𝑖𝑛 = −1 D. 𝑧 √ 𝑚𝑎𝑥 = 3 3 , 𝑧 2 𝑚𝑖𝑛 = −1 2 TEAM GIẢI TÍCH 2 10
Câu 2. Tìm GTLN, GTNN của 𝒛 = 𝒙𝟐 − 𝟗𝒚𝟐, trong miền hình elip 𝒙𝟐 + 𝒚𝟐 ≤ 𝟏 𝟗
A. 𝑧𝑚𝑎𝑥 = 9, 𝑍𝑚𝑖𝑛 = −9
B. 𝑧𝑚𝑎𝑥 = 3, 𝑍𝑚𝑖𝑛 = −3
C. 𝑧𝑚𝑎𝑥 = 3, 𝑍𝑚𝑖𝑛 = −9
D. 𝑧𝑚𝑎𝑥 = 9, 𝑍𝑚𝑖𝑛 = −3 Câu 3.
Tìm giá trị lớn nhất, giá trị nhỏ n ấ
h t trong miền ΔOAB với O(0,0);A(7,0);B(0,7) của
𝒛 = 𝒙𝟑 + 𝟐𝒚𝟐 + 𝟑𝒙𝒚 − 𝟏𝟑𝒙 − 𝟏𝟖𝒚
A. 𝑧𝑚𝑎𝑥 = 252; 𝑧𝑚𝑖𝑛 = − 81 2 B. 𝑧 1 𝑚𝑎𝑥 = 64; 𝑧𝑚𝑖𝑛 = − 2
C. 𝑧𝑚𝑎𝑥 = 212; 𝑧𝑚𝑖𝑛 = 1 2
D. 𝑧𝑚𝑎𝑥 = 252; 𝑧𝑚𝑖𝑛 = − 1 2
II. ỨNG DỤNG CỦA PHÉP TÍNH VI PHÂN
Câu 1. Tìm hình bao của họ đường cong
𝑐(𝑦 − 𝑐) = 𝑥2 , c là tham số. A. 𝑦 = 𝑥 B. 𝑦 = −2𝑥 C. 𝑦 = 2𝑥 D. 𝑦 = ±2𝑥 𝑥 = 𝑡
Câu 2. Phương trình pháp diện tại 𝐴 (𝜋 ; 1; 1)
của đường { 𝑦 = √2. cos 𝑡 là : 4 𝑧 = √2. sin 𝑡 A. 𝑥 + 𝑦 + 𝑧 = 0
B. 𝑥 − 𝑦 + 𝑧 = 𝜋 4 C. 𝑦 − 𝑧 = 𝜋 D. 4 𝑥 + 𝑦 − 𝑧 = 𝜋4
Câu 3. Phương trình tiếp diện tại 𝐴(1; 1; −1) của mặt 𝑧 = 𝑥2 − 3𝑥𝑦 + 𝑦2 là : A. 𝑥 + 𝑦 + 𝑧 = 1 B. 𝑥 + 𝑦 − 𝑧 = 1
C. 𝑥 + 𝑦 − 𝑧 + 1 = 0 D. 𝑥 + 𝑦 + 𝑧 = 3
Câu 4. Tính độ cong của đường {𝑥 = 2𝑡 − 𝑡2
𝑦 = 3𝑡 − 𝑡3 tại điểm 𝑡 = −1. A. 1 3 B. 2 8 C. 1 D. 5 8
Câu 5. Viết phương trình tiếp diện của mặt 𝑧 = 4𝑥2 − 𝑦2 + 2𝑦 tại (−1; 2; 4) : TEAM GIẢI TÍCH 2 11 A. 8𝑥 + 2𝑦 + 𝑧 = 0 B. 8𝑥 + 2𝑦 − 𝑧 = 0 C. 𝑥 + 2𝑦 + 𝑧 = 7
D. 4𝑥 + 2𝑦 − 𝑧 + 4 = 0
Câu 6. Viết phương trình tiếp diện của mặt cong 𝑧 = 𝑒𝑥2−𝑦2 tại (1; −1; 1) ∶
A. 2𝑥 + 2𝑦 − 𝑧 + 1 = 0
B. 𝑥 + 2𝑦 − 𝑧 + 2 = 0
C. 2𝑥 − 2𝑦 + 𝑧 − 5 = 0
D. Các câu trả lời đều sai
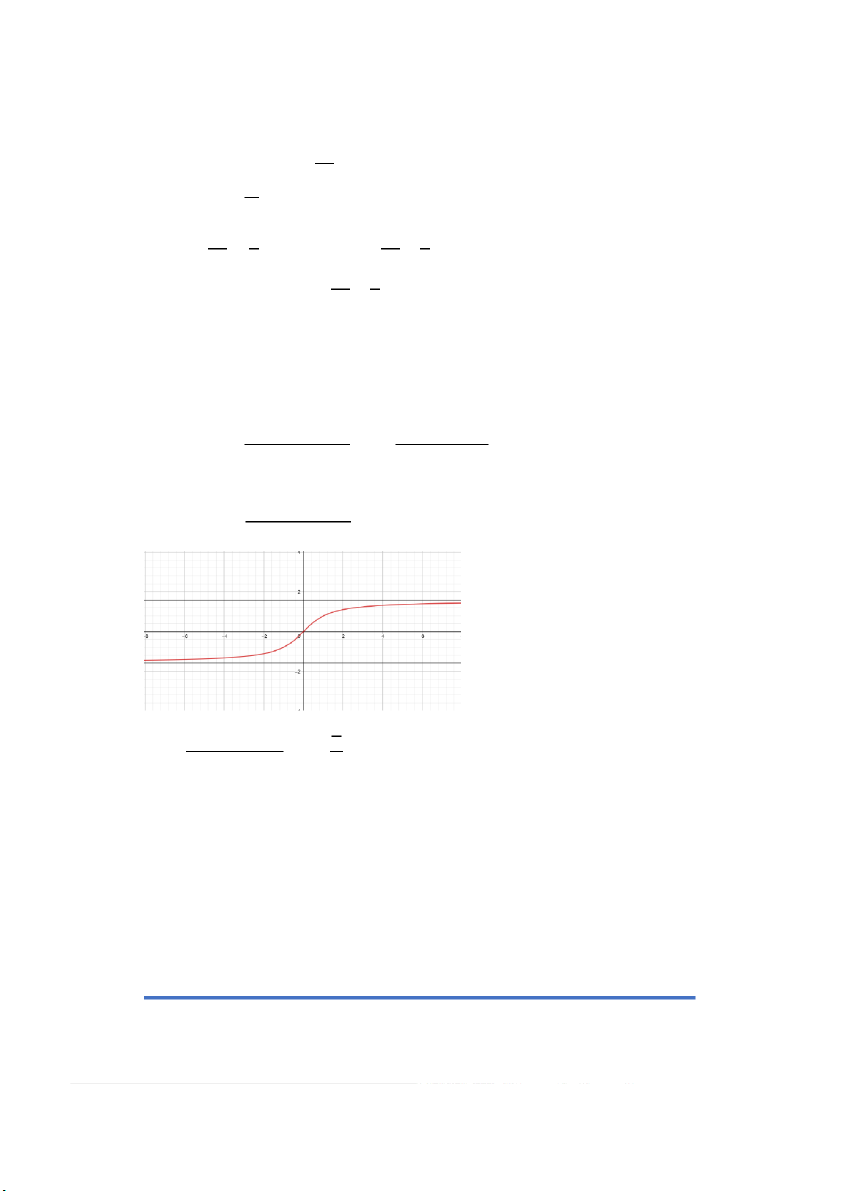
Câu 7. Viết phương trình tiếp tuyến của đường cong 𝑦 = 𝑒1−𝑥2 tại giao điểm của
đường cong với đường thẳng 𝑦 = 1: A. 𝑥 − 2𝑦 + 1 = 0 B. 2𝑥 + 𝑦 − 3 = 0 C. 2𝑥 − 𝑦 + 3 = 0 D. 𝑥 − 𝑦 + 1 = 0 2
Câu 8. Viết phương tình pháp tuyến của đường cong 𝑥23 + 𝑦3 = 5 tại điểm 𝑀(8; 1) A. 𝑥 + 2𝑦 − 10 = 0 B. 2𝑥 + 𝑦 + 5 = 0 C. 2𝑥 − 𝑦 − 15 = 0 D. 𝑥 − 2𝑦 + 10 = 0
Câu 9. Tính độ cong tại điểm 𝑀(1; 0; −1) của đường là giao của mặt trụ 4𝑥2 + 𝑦2 = 4
và mặt phẳng 𝑥 − 3𝑧 = 4 A. 0 B. 1 C. 2 D. 9
Câu 10. Viết phương trình tiếp tuyến của đường {𝑥2 + 𝑦2 = 10
𝑦2 + 𝑧2 = 25 tại điểm A(1,3,4) : A. 𝑥−1 = 𝑦−3 = 𝑧−4 B. 12x − 4y + 3z − 12 = 0 12 −4 3 C. 𝑥+1 = 𝑦−4 = 𝑧−3 D. Các đáp án đều sai 6 3 4
III. TÍCH PHÂN BỘI & ỨNG DỤNG 3.1. TÍCH PHÂN KÉP
Câu 1: 𝑇í𝑛ℎ ∬ 𝑥𝑦𝑑𝑥𝑑𝑦 ới D đượ ớ ạ ở 2 𝐷 v
c gi i h n b i 𝑥 + 𝑦 = 4 𝑣à 𝑥 = 2𝑦 A.90 B - . 90 C - . 72 D.72
Câu 2:𝑇í𝑛ℎ ∬ 2𝑦𝑑𝑥𝑑𝑦 𝐷
𝑣ớ𝑖 𝐷 𝑥á𝑐 đị𝑛ℎ 𝑏ở𝑖 𝑥2 + 𝑦2 ≤ 1, 𝑥 + 𝑦 ≥ 1 A.1 B.1 C.2 D.4 3 6 3 3
Câu 3: 𝑇í𝑛ℎ ∫1 𝑑𝑥 3 0 ∫ (𝑥2 2 𝑦 − 2𝑦2)𝑑𝑦 A.− 62 B.72 C.− 71 D.62 6 7 6 6 Câu 4:∫1 𝑑𝑥 1
= 𝑎−𝑐𝑜𝑠𝑏 . 𝑇í𝑛ℎ 𝑎− 𝑏 + 𝑐 0 ∫ sin(𝑦2) 𝑥 𝑑𝑦 𝑐 TEAM GIẢI TÍCH 2 12 A.0 B.1 C.2 D.3
Câu 5:𝑇í𝑛ℎ ∬ 𝑥√𝑥2 + 𝑦2 𝐷
𝑑𝑥𝑑𝑦 𝑣ớ𝑖 𝐷 𝑥á𝑐 đị𝑛ℎ 𝑏ở𝑖 𝑥2 + 𝑦2 ≤ 𝑥; 𝑦 ≥ 0 A. 1 B. 2 C. 4 D. 8 15 15 15 15
Câu 6:𝑇í𝑛ℎ ∬ (2𝑥 + 𝑠𝑖𝑛𝑦)𝑑𝑥𝑑𝑦 ( )2 𝐷
𝑣ớ𝑖 𝐷: 𝑥 − 2 + 𝑦2 ≤ 1 A.2𝜋 B 4 . 𝜋 C 6 . 𝜋 D.8𝜋 𝑑𝑥𝑑𝑦 𝑎 𝐂â𝐮 𝟕: ∬ 𝑎 2 2 , −𝑥 ≤ 𝑦 ≤ 0. 𝑔𝑖
𝐷 (𝑥2 + 𝑦2)3 = 𝑏 + 𝑙𝑛𝑐, 𝐷: 𝑥 ≤ 𝑥 + 𝑦 ≤ 2𝑥 𝑏 𝑡ố𝑖 ả𝑛. Tổng a+b+c=? A.20 B.21 C.22 D.23
𝐂â𝐮 𝟖: 𝑇í𝑛ℎ ∬ √2𝑥 − 𝑥2 − 𝑦2𝑑𝑥𝑑𝑦 𝑣ớ𝑖 𝑚 ề 𝑖 𝑛 𝐷 𝑙à 𝑚 ề
𝑖 𝑛 𝑥2 + 𝑦2 ≤ 2𝑥, 𝑦 ≥ 0 𝐷 A.𝜋 B.𝜋 C.𝜋 D.𝜋 4 3 2
𝑪â𝒖 𝟗: 𝑇í𝑛ℎ ∬ 𝑦2(6𝑥 − 𝑦)𝑑𝑥𝑑𝑦, 𝑣ớ𝑖 𝐷 𝑔 ớ
𝑖 𝑖 ℎạ𝑛 𝑏ở𝑖: 𝑥 = 0, 𝑥 + |𝑦| = 1. 𝐷 A.1 B.1 C.3 D.1 5 3
𝐂â𝐮 𝟏𝟎: 𝑇í𝑛ℎ ∬ (𝑥 + 𝑦)2𝑑𝑥𝑑𝑦 𝑣ớ𝑖 𝑚 ề
𝑖 𝑛 𝐷: 5𝑥2 + 6𝑥𝑦 + 5𝑦2 ≤ 4 𝐷 𝐴. 𝜋 B.𝜋 C.𝜋 D.π 8 2 4
𝐂â𝐮 𝟏𝟏: 𝑀𝑖ề𝑛 𝐷 𝑔 ớ
𝑖 𝑖 ℎạ𝑛 𝑏ở𝑖 𝑥 = 1, 𝑦 = 0, 𝑥 = 𝑦. ∬ 𝑑𝑥𝑑𝑦
= 𝑎 𝑙𝑛𝑏 − 𝑐𝑙𝑛2 𝐷 𝑥+𝑦+1 2
𝑇ổ𝑛𝑔 𝑎+ 𝑏 + 𝑐 =? A.5 B.6 C.7 D.8 3𝑥2 − 𝑦2 + 1
𝐂â𝐮 𝟏𝟐: 𝑀𝑖ề𝑛 𝐷: 𝑥2 + 𝑦2 ≤ 6. ∬
𝑥2 + 𝑦2 + 1 𝑑𝑥𝑑𝑦 = 𝑎𝜋 + 𝑙𝑛𝑏. 𝐷 Tổng a+b=? A.6 B.7 C.8 D.9 TEAM GIẢI TÍCH 2 13
3.2. TÍCH PHÂN BỘI BA 1 1−𝑥 2
𝐂â𝐮 𝟏: 𝑇í𝑛ℎ 𝑡í𝑐ℎ 𝑝ℎâ𝑛 ∫ 𝑑𝑥 ∫ 𝑑𝑧 ∫ (𝑦 + 𝑧) 𝑑𝑦 0 0 0 A.1 B.2 C.1 D.4 3 3 3
𝐂â𝐮 𝟐: 𝑇í𝑛ℎ ∭(3𝑥2 − 2𝑦) 𝑑𝑥𝑑𝑦𝑑𝑧 𝑣ớ𝑖 𝑉: 0 ≤ 𝑥 ≤ 1, 0 ≤ 𝑦 ≤ 𝑥, 0 ≤ 𝑧 ≤ 𝑥2 𝑉 A. 3 B. 1 C. 7 D. 9 10 10 10 10
𝐂â𝐮 𝟑: 𝑇í𝑛ℎ ∭(𝑥2 + 𝑦2) 𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉 𝑔 ớ
𝑖 𝑖 ℎạ𝑛 𝑏ở𝑖 𝑥2 + 𝑦2 − 2𝑧 = 0, 𝑧 = 2 𝑉 A.64 B.64𝜋 C.16𝜋 D.24𝜋 15 15 3 5 1 1 1 𝑒 𝑏
𝐂â𝐮 𝟒: ∫ 𝑑𝑥 ∫ 𝑑𝑧 ∫ 𝑥𝑧𝑒𝑥𝑦2𝑑𝑦 = 0 0 𝑧2
𝑎 − 𝑐 . 𝑎 + 𝑏 + 𝑐 =? A.6 B.7 C.8 D.9 𝑑𝑥𝑑𝑦𝑑𝑧 𝑎 𝐶â𝐮 𝟓: ∭ 𝑥 + 𝑦 + 𝑧 ≤ 1
(𝑥 + 𝑦 + 𝑧 + 2)2 = 𝑏 + 𝑐. 𝑙 2 𝑛 − 𝑑. 𝑙 3
𝑛 ,𝑉: { 𝑥,𝑦,𝑧 ≥ 0 𝑉
𝑎 + 𝑏 + 𝑐 − 𝑑 =? A.10 B.11 C.12 D.13 𝑎𝜋
𝐂â𝐮 𝟔: ∭(4𝑥2 + 𝑦2 + 𝑧2 + 2𝑥𝑦) 𝑑𝑥𝑑𝑦𝑑𝑧 = 𝑉
𝑏 , 𝑉: 4𝑥2 + 𝑦2 + 𝑧2 ≤ 4, 𝑧 ≥ 0. 𝑎 − 𝑏 =? A.2 B.3 C.11 D.7 𝜋
𝐂â𝐮 𝟕: ∭√𝑥2 + 𝑦2 + 𝑧2 𝑑𝑥𝑑𝑦𝑑𝑧 = 𝑉
𝑎 ,𝑉: 𝑥2 + 𝑦2 + 𝑧2 ≤ 𝑦. 𝑇ì𝑚 𝑎? A.9 B.12 C.8 D.10
𝐂â𝐮 𝟖: , 𝑀𝑖ề𝑛 𝑉: √𝑥2 + 𝑦2 ≤ 𝑧 ≤ √4 − 𝑥2 − 𝑦2. ∭𝑧𝑐𝑜𝑠(𝑥2 + 𝑦2) 𝑑𝑥𝑑𝑦𝑑𝑧 𝑉
= 𝜋(𝑎 − 𝑐𝑜𝑠𝑏). 𝑇ổ𝑛𝑔 𝑎 + 𝑏 =? A.3 B.4 C.5 D.6 𝑎√8 − 𝑏√6
𝐂â𝐮 𝟗: 𝑀𝑖ề𝑛 𝑉: {𝑥2 + 𝑦2 + 𝑧2 ≤ 8
𝑥2 + 𝑦2 ≤ 2 . ∭(𝑥2 + 𝑦2)𝑑𝑥𝑑𝑦𝑑𝑧 = 𝑉 15 𝜋. TEAM GIẢI TÍCH 2 14 𝑏 − 𝑎 =? A.16 B.42 C 2 . 4 D.8 𝑎𝜋
𝐂â𝐮 𝟏𝟎: 𝑇í𝑛ℎ ∭(𝑥 + 𝑦 − 2𝑧)2𝑑𝑥𝑑𝑦𝑑𝑧 = 𝑉
𝑏 ,𝑣ớ𝑖 𝑉: 𝑥2 + 𝑦2 + 𝑧2 ≤ 1. 𝑎 − 𝑏 =? A.-3 B.4 C.1 D.-2
3.3. ỨNG DỤNG CỦA TÍCH PHÂN BỘI
𝑪â𝒖 𝟏:𝐷𝑖ệ𝑛 𝑡í𝑐ℎ 𝑝ℎầ𝑛 𝑚ặ𝑡 𝑧= 𝑥2 + 𝑦2 + 2 𝑛ằ𝑚 𝑡𝑟𝑜𝑛𝑔 𝑚ặ𝑡 𝑡 ụ 𝑟 𝑥2 + 𝑦2 = 9 𝑙à 𝑎√𝑎 − 𝑏 𝑐
𝜋. 𝑇ổ𝑛𝑔 𝑎+ 𝑏 + 𝑐 =? A.32 B.36 C.44 D.48
𝐂â𝒖 𝟐:𝐷𝑖ệ𝑛 𝑡í𝑐ℎ ℎì𝑛ℎ 𝑝ℎẳ𝑛𝑔 𝑔 ớ
𝑖 𝑖 ℎạ𝑛 𝑏ở𝑖 𝑦 = √3𝑥, 𝑦 = 0, 𝑥2 + 𝑦2 = 2𝑥 𝑙à 𝜋 √𝑏
𝑎 + 𝑐 . 𝑇ổ𝑛𝑔 𝑎 + 𝑏 + 𝑐 =? A.7 B.8 C.9 D.10
𝐂â𝒖 𝟑:𝑇ℎể 𝑡í𝑐ℎ 𝑚 ề 𝑖 𝑛 𝑔 ớ
𝑖 𝑖 ℎạ𝑛 𝑏ở𝑖 𝑥 = 1 + 𝑦2 + 𝑧2 𝑣à 𝑥 = 2(𝑦2 + 𝑧2) 𝑙à 𝜋 𝑎 . 𝑉ậ𝑦 𝑎 = A.1 B.5 C.3 D.2 2 4
𝐶â𝑢 4:𝑀𝑖ề𝑛 𝐷 𝑔 ớ
𝑖 𝑖 ℎạ𝑛 𝑏ở𝑖 (𝑥2 + 𝑦2)2 = 2𝑥3. 𝑆𝐷 = 𝑎𝜋 . 𝑇í𝑛ℎ 𝑏− 𝑎? 𝑏 A.3 B.4 C.5 D.7
𝐂â𝐮 𝟓: 𝑇í𝑛ℎ 𝑣ậ𝑡 𝑡ℎể 𝑉 𝑥á𝑐 đị𝑛ℎ 𝑏ở𝑖 √𝑥2 + 𝑦2 ≤ 𝑧 ≤ 6 − 𝑥2 − 𝑦2 A.16𝜋 B.32𝜋 𝐶. 64𝜋 D.35𝜋 3 3 3 3
Câu 6: 𝑇í𝑛ℎ
𝑡ℎể 𝑡í𝑐ℎ 𝑣ậ𝑡 𝑡ℎể 𝑔 ớ
𝑖 𝑖 ℎạ𝑛 𝑏ở𝑖 𝑐á𝑐 𝑚ặ𝑡 𝑧= 𝑥2 + 3𝑦2 và 𝑧 = 4 − 3𝑥2 − 𝑦2 A.16𝜋 B.8𝜋 C.2𝜋 D.4𝜋 3 3 TEAM GIẢI TÍCH 2 15
IV. TÍCH PHÂN PHỤ THUỘC THAM SỐ:
4.1. TÍCH PHÂN XÁC ĐỊNH PHỤ THUỘC THAM SỐ
Câu 1: Tính ∫𝜋/2 ln (1 0 +y𝑠𝑖𝑛2𝑥)𝑑𝑥 𝑣ớ𝑖 𝑦>1
A.𝜋 ln(1 + √𝑦 + 1) − 𝜋𝑙𝑛2
B. 𝜋 ln(1 + √𝑦 + 1) + 𝜋𝑙𝑛2
C. 𝜋 − 𝜋𝑙𝑛2 D.1
Câu 2: Tính giới hạn sau: 1
lim ∫ √𝑥3 + 𝑦3𝑑𝑥 𝑦⟶0 0 A.3 B.0,4 C. 1 D. 0,8 5 5
Câu3: Tính giới hạn: 𝑥 1 2015cos (𝑥𝑦) lim ∫
𝑦⟶0 −1 1 + 𝑥2 + 𝑦2 𝑑𝑥 A. .3 B. .3 C. .1 D. .2 7 5 3 3 Câu 4: Tính : 𝑠𝑖𝑛 𝑎 𝑦 𝑟𝑐cot (𝑥 + 𝑦) lim ∫
𝑦⟶0 𝑐𝑜𝑠𝑦 1 + 𝑥2 + 𝑦2 𝑑𝑥
A. .−3𝜋2 B. .3𝜋 C. .−𝜋 D. .3𝜋2 32 16 32 32
Câu 5: Cho I(y)= ∫1sin (𝑥2 + 𝑥𝑦 ′ 𝑦 +𝑦2)𝑑𝑥 . 𝑇í𝑛ℎ 𝐼(0) A. .𝑠𝑖𝑛1 B. 𝜋 C. 1 D. 1 2 2 2 Câu 6: Cho I(y)= 𝜋 ∫ 2 ln
(𝑦2𝑠𝑖𝑛2𝑥 + 𝑐𝑜𝑠2𝑥) 0 𝑑𝑥. Tính 𝐼′(1) A.0 B. . 𝜋 C. 1 D.2 2 2 Câu 7: Tìm TEAM GIẢI TÍCH 2 16 𝑎 𝑦 𝑟𝑐tanx lim ∫ 𝑦⟶1 𝑥2 0 + 𝑦2 𝑑𝑥 A. 𝜋 −𝜋2 −3𝜋2 B. 𝜋2 C. D. 2 32 32 32 Câu 8: Tính
𝑐𝑜𝑠𝑦 𝑎𝑟𝑐tan (𝑥 + 𝑦) lim ∫
𝑦⟶0 𝑠𝑖𝑛𝑦 1 + 𝑥2 + 𝑦2 𝑑𝑥 A. 𝜋 𝜋2 −3𝜋2
B. −𝜋2 C. D. 2 32 32 32
Câu 9: Tính lim ∫ 2𝑦𝑥2sin (𝜋𝑦𝑥) 𝑦⟶1 𝑦 𝑑𝑥. A. 2−5𝜋 𝜋 C.2 D. . 𝜋2 B. 2+5𝜋 𝜋2 4
Câu 10 (Đề cuối kì- 20152): Tính giới hạn 1 𝑥2020 + 𝑦2021 lim ∫
𝑦⟶0 −1 1 + 𝑥2 + 2021𝑦2 𝑑𝑥
4.2. TÍCH PHÂN SUY RỘNG PHỤ THUỘC THAM SỐ
Câu 1: Tính I(y)= ∫+∞ arctan (x+y) 𝑑𝑥 0 𝑥2+1 A. 2𝜋 2 B. 2𝜋 C. D. 2𝜋 𝑦2+𝑦 𝑦2+𝑦 𝑦2+𝑦 𝑦2 𝑎𝑥 Câu2: +∞ Tính ∫ 𝑒− − −𝑒 𝑏𝑥 𝑑𝑥 0 𝑥
A. -lna+lnb B. ln(ab) C. lna – lnb D. 1 Câu 3: Tính 𝑦 𝑐𝑜𝑠xy lim ∫ 𝑦⟶0 𝑥2 0 + 1 𝑑𝑥
A. 𝜋/2 B. 0 C. - 𝜋/2 D.2 Câu 4: Tính +∞ sin(𝑏𝑥) − sin (𝑐𝑥) ∫ 𝑒−𝑎𝑥 0 𝑥 𝑑𝑥
A. arctan(𝑏) - arcrtan(𝑐 ) C. arctan(𝑏) - arcrtan(𝑐) 𝑎 𝑎 𝑐 𝑎
B. 0 D. arctan(𝑐) -arcrtaln(𝑐) 𝑎 𝑏 TEAM GIẢI TÍCH 2 17 −𝑥 −𝑥
Câu 5: Tính ∫+∞ 2 −3 𝑑𝑥 0 𝑥
A. ln(𝑙𝑛3) B. ln(𝑙𝑛2) C.0 D. ln6 𝑙𝑛2 𝑙𝑛3 TEAM GIẢI TÍCH 2 18
PHẦN II: LỜI GIẢI VÀ ĐÁP ÁN
I. HÀM NHIỀU BIẾN
1.1. GIỚI HẠN CỦA HÀM NHIỀU BIẾN Câu 1: I = lim 𝑥2𝑦
(𝑥,𝑦)→(0,0) 𝑥2+𝑦2
Nguyên lý kẹp: 0 ≤ | 𝑥2𝑦 | ≤ |𝑥2𝑦 | = |y| 𝑥2+𝑦2 𝑥2 Mà lim |𝑦| = 0 (𝑥,𝑦)→(0,0) 𝑥2𝑦  I = lim = 0
(𝑥,𝑦)→(0,0) 𝑥2+𝑦2 Đáp án A Câu 2: I= lim 𝑥𝑦
(𝑥,𝑦)→(0,0) 𝑥2+𝑦2 Đặt y = kx 𝑥.𝑘𝑥 𝑘  I= lim = lim = f(k)
(𝑥,𝑦)→(0,0) 𝑥2+(𝑘𝑥)2 (𝑥,𝑦)→(0,0) 1+(𝑘)2
 Không tồn tại giới hạn Đáp án D Câu 3: I= lim 𝑥𝑦
(𝑥,𝑦)→(0,0) √𝑥2+𝑦2
Theo bất đẳng thức Cô – si: 𝑥2 + 𝑦2 ≥ 2xy Ta có: 0
≤ | 𝑥𝑦 | ≤ | 𝑥𝑦 | = |√𝑥𝑦 | √𝑥2+𝑦2 √2𝑥𝑦 √2 Mà lim |√𝑥𝑦| = 0 (𝑥,𝑦)→(0,0) √2 𝑥𝑦  I= lim = 0
(𝑥,𝑦)→(0,0) √𝑥2+𝑦2 Đáp án A Câu 4: TEAM GIẢI TÍCH 2 19 I=
lim 𝑥2−𝑦2 Đặt y = kx
(𝑥,𝑦)→(0,0) 𝑥2+𝑦2 => I= lim 𝑥2−(𝑘𝑥)2 = lim 1−(𝑘)2 =f(k)
(𝑥,𝑦)→(0,0) 𝑥2+(𝑘𝑥)2 (𝑥,𝑦)→(0,0) 1+(𝑘)2
=> Không tồn tại giới hạn Đáp án D Câu 5: 2 2 I= lim 𝑥3−𝑦3 = lim (𝑥−𝑦).(𝑥 +𝑥 + 𝑦 𝑦 )
(𝑥,𝑦)→(0,0) 𝑥2+𝑦2 (𝑥,𝑦)→(0,0) 𝑥2+𝑦2 2 2 (𝑥−𝑦).(𝑥2+𝑥2
Ta có: 0 ≤ |(𝑥−𝑦).(𝑥 +𝑥𝑦+𝑦 )| ≤ |
2 +𝑦22 +𝑦2)| = |3 .(x-y)| 𝑥2+𝑦2 𝑥2+𝑦2 2 Mà: lim |3 .(x-y)| = 0 (𝑥,𝑦)→(0,0) 2 𝑥3−𝑦3  I= lim = 0
(𝑥,𝑦)→(0,0) 𝑥2+𝑦2 Đáp án C Câu 6: I =
lim 𝑥2𝑦−𝑥𝑦2 Đặt y = kx
(𝑥,𝑦)→(0,0) 𝑥3+𝑦3 => I =
lim 𝑥2.𝑘𝑥−𝑥.(𝑘𝑥)2 = lim 𝑘−(𝑘)2 = f(k) (𝑥,𝑦)→(0,0) 𝑥3+(𝑘𝑥)3 (𝑥,𝑦)→(0,0) 1+(𝑘)3
=> Không tồn tại giới hạn Đáp án D Câu 7: 𝑦 I =
lim 𝑦.(𝑒3𝑥−1)−3𝑥.(𝑒 −1) (𝑥,𝑦)→(0,0) 𝑥2+𝑦2
Sử dụng khai triển Maclaurin: 𝑦.(3𝑥+9𝑥2 I = lim
2 +0(𝑥2))−3𝑥.(𝑦+𝑦2 2 +0(𝑦2)) (𝑥,𝑦)→(0,0) 𝑥2+𝑦2 𝑦.(9𝑥2 𝑥𝑦.(9 = lim 2 )−3𝑥.(𝑦22 ) = lim 2.𝑥−32.𝑦) (𝑥,𝑦)→(0,0) 𝑥2+𝑦2
(𝑥,𝑦)→(0,0) 𝑥2+𝑦2
Theo bất đẳng thức Cô – si: 𝑥2 + 𝑦2 ≥ 2xy TEAM GIẢI TÍCH 2 20
Ta có: 0 ≤ | 𝑥𝑦.(92.𝑥−32.𝑦)| ≤ 1. | (𝑥2+𝑦2).(92.𝑥−32.𝑦)| = 1 . | 9 . 𝑥 − 3 . 𝑦| 𝑥2+𝑦2 2 𝑥2+𝑦2 2 2 2 Mà
lim 1. |9 . 𝑥 − 3. 𝑦| = 0 (𝑥,𝑦)→(0,0) 2 2 2
𝑦.(𝑒3𝑥−1)−3𝑥.(𝑒𝑦−1)  I = lim = 0 (𝑥,𝑦)→(0,0) 𝑥2+𝑦2 Đáp án C
Câu 8: (Mẹo: Ở đây dạng hàm mũ nên có thể loại bỏ ngay được các giá trị ≤ 0 => loại C) I = lim (𝑥2 + 𝑦2)𝑥2𝑦2 (𝑥,𝑦)→(0,0) 𝑥2𝑦2
= 𝑒 lim 𝑥2𝑦2.𝑙𝑛(𝑥2+𝑦2) 𝑙𝑛 2+𝑦2) (𝑥,𝑦)→(0,0) = 𝑒 lim
(𝑥,𝑦)→(0,0)𝑥2+𝑦2.(𝑥2+𝑦2). (𝑥 𝐼 = 𝑒 lim (𝑥,𝑦)→(0,0) 1.𝐼2 + Xét: lim 𝐼 𝑥2𝑦2 (𝑥,𝑦)→(0,0) 1 = lim (𝑥,𝑦)→(0,0)𝑥2+𝑦2
Ta có: 0 ≤ | 𝑥2𝑦2 | ≤ |𝑥2𝑦2 | = |𝑥𝑦 | 𝑥2+𝑦2 2𝑥𝑦 2 Mà lim |𝑥𝑦 | = 0 (𝑥,𝑦)→(0,0) 2 + Xét: lim 𝐼
(𝑥2 + 𝑦2). 𝑙𝑛(𝑥2 + 𝑦2) (𝑥,𝑦)→(0,0) 2 = lim (𝑥,𝑦)→(0,0) Đặt: 𝑥2 + 𝑦2 = t Khi: {𝑥 → 0 𝑦 → 0 => t → 0 𝑙𝑛𝑡  lim 𝐼 𝑡. 𝑙𝑛𝑡 = l im (𝑥,𝑦)→(0,0) 2 = lim 𝑡→0 𝑡→0 1𝑡 1 = lim 𝑡 = lim (− 𝑡) = 0 𝑡→0 −1 𝑡2 𝑡→0 𝐼1.𝐼2  I =
lim (𝑥2 + 𝑦2)𝑥2𝑦2 = 𝑒 lim (𝑥,𝑦)→(0,0) = 𝑒0.0 = 1 (𝑥,𝑦)→(0,0) Đáp án A Câu 9:
Do 𝑥 → 0, 𝑦 → 0 nên 𝑥2𝑦2 → 0, 𝑥2 + 𝑦2 → 0, 1 → ∞ 𝑥2+𝑦2 1 ⇒ lim 2
(𝑥,𝑦)→(0,0) (1 + 𝑥 𝑦2)𝑥2+𝑦2 là dạng vô định 1∞ TEAM GIẢI TÍCH 2 21 𝑢
⇒ sử dụng (1 + 1) ∼ 𝑒 với 𝑢 → +∞ 𝑢 1 𝑥2𝑦2𝑥2𝑦2 1 𝑥2+𝑦2 1 1 lim 2
(𝑥,𝑦)→(0,0) (1 + 𝑥 𝑦2)𝑥2+𝑦2 = lim(𝑥,𝑦)→(0,0) (1 + 1 ) 𝑥2𝑦2
= 𝑒lim(𝑥,𝑦)→(0,0) 𝑥2𝑦2 𝑥2+𝑦2
Ta có: |𝑥2 + 𝑦2| ≥ |2𝑥𝑦| (Cauchy) ⇒ 1
≤ 1 ⇒ | 𝑥2𝑦2 | ≤ |𝑥2𝑦2 | = |𝑥𝑦 | |𝑥2+𝑦2| |2𝑥𝑦| 𝑥2+𝑦2 2𝑥𝑦 2
⇒ 0 ≤ | 𝑥2𝑦2 | ≤ |𝑥𝑦| ⇒ lim | = |0| = 0 ⇒ lim = 0 (định 𝑥2+𝑦2 2 (𝑥,𝑦)→(0,0) |𝑥𝑦 2 2 (𝑥,𝑦)→(0,0) 𝑥2𝑦2 𝑥2+𝑦2 lý kẹp) 1 ⇒ lim 2
(𝑥,𝑦)→(0,0) (1 + 𝑥 𝑦2)𝑥2+𝑦2 = 𝑒0 = 1 Đáp án A Câu 10: 2 2 I =
lim 𝑥2+𝑦2 = lim (𝑥+𝑦).(𝑥 +𝑦 )
(𝑥,𝑦)→(0,0) 𝑒𝑥+𝑦
(𝑥,𝑦)→(0,0) 𝑒𝑥+𝑦.(𝑥+𝑦)
= lim ( 𝑥+𝑦 . 𝑥2+𝑦2 ) = lim 𝐼
(𝑥,𝑦)→(0,0) 𝑒𝑥+𝑦 𝑥+𝑦 (𝑥,𝑦)→(0,0) 1. 𝐼2 Xét: lim 𝐼 𝑥+𝑦 Đặt x + y = t (𝑥,𝑦)→(0,0) 1 = lim
(𝑥,𝑦)→(0,0) 𝑒𝑥+𝑦 Khi: {𝑥 → 0 𝑦 → 0 => t → 0 𝑡  lim 𝐼 = 0 (𝑥,𝑦)→(0,0) 1 = lim 𝑡→0 𝑒𝑡 Xét: lim 𝐼 𝑥2+𝑦2 (𝑥,𝑦)→(0,0) 2 = lim (𝑥,𝑦)→(0,0) 𝑥+𝑦
Ta có: 0 ≤ | 𝑥2+𝑦2 | ≤ | 𝑥2+𝑦2+2𝑥𝑦 | = |x + y| 𝑥+𝑦 𝑥+𝑦 Mà lim |x + y| = 0 (𝑥,𝑦)→(0,0)  I = 0 Đáp án C Câu 11: TEAM GIẢI TÍCH 2 22 1
Do (𝑥, 𝑦) → (0,0) ⇒ 3𝑥2 → 0, 𝑥2 + 𝑦2 → 0,𝑥2 + 𝑦2 → ∞ ⇒ Dạng vô định 1∞ 1 1 1 3𝑥2⋅3𝑥2 1 𝑥2+𝑦2
lim (1 + 3𝑥2)𝑥2+𝑦2 = lim (1 + )
= 𝑒(𝑥,𝑦)→(0,0) 3𝑥2 (𝑥,𝑦)→(0,0) (𝑥,𝑦)→(0,0) 1 𝑥2 + 𝑦2 3𝑥2
Xét (𝑥, 𝑦) → (0,0) theo phương 𝑦 = 𝑘𝑥 3𝑥2 3𝑥2 3 3 ⇒ lim
(𝑥,𝑦)→(0,0) 𝑥2 + 𝑦2 = lim
(𝑥,𝑘𝑥)→(0,0) 𝑥2 + (𝑘𝑥)2 = lim
(𝑥,𝑘𝑥)→(0,0) 1 + 𝑘2 = 1 + 𝑘2
Vậy với mỗi 𝑘 khác nhau lim(𝑥,𝑦)→(0,0) 3𝑥2 tiến đến những giá trị giới hạn khác 𝑥2+𝑦2 nhau. 3𝑥2 1 ⇒ ∄ lim (1 + 3𝑥2)𝑥2+𝑦2
(𝑥,𝑦)→(0,0) 𝑥2 + 𝑦2 ⇒ ∄ lim (𝑥,𝑦)→(0,0) Đáp án D Câu 12:
Do (𝑥, 𝑦) → (0,0) ⇒ 𝑥2 + 𝑦2 → 0 −(𝑥2 + 𝑦2)2 ⇒ cos
(𝑥2 + 𝑦2) − 1 = −[1 − cos (𝑥2 + 𝑦2)] ∼ 2 cos (𝑥2 + 𝑦2) − 1 ⇒ lim −(𝑥2 + 𝑦2)2 1 (𝑥,𝑦)→(0,0) 𝑥2 + 𝑦2 = lim(𝑥,𝑦)→(0,0) 2 𝑥2 + 𝑦2 −(𝑥2 + 𝑦2) = lim(𝑥,𝑦)→(0,0) 2 = 0 Đáp án C
1.2. KHẢO SÁT TÍNH LIÊN TỤC : Câu 1: −𝜋 𝑦 2 𝜋 𝑦 2 𝜋 Do < | ≤ | { 2 < arctan (𝑥)
2 ⇒ 0 ≤ |𝑥 ⋅ arctan ( 𝑥) 2 𝑥| 𝜋 Mà lim |
(𝑥,𝑦)→(0,1) 2 𝑥| = 0 𝑦 2 ⇒ lim 𝑥 ⋅ arctan ( = 0 (𝑥,𝑦)→(0,1) 𝑥) TEAM GIẢI TÍCH 2 23
⇒ 𝑓(𝑥, 𝑦) liên tục tại 𝐵(0,1). Đáp án A Câu 2:
𝑥2 + 𝑦2 = 0 chỉ xảy ra khi 𝑥 = 𝑦 = 0.
Để 𝑓(𝑥, 𝑦) liên tục tại (0,0) ⇔ lim(𝑥,𝑦)→(0,0) 𝑓(𝑥, 𝑦) = 𝑓(0,0) = 𝑎
Theo Cauchy: 𝑥2 + 𝑦2 ≥ 2|𝑥𝑦| ⇒ 1 ≤ 1 𝑥2+𝑦2 2|𝑥𝑦| 2𝑥2𝑦 − 𝑦2𝑥 2𝑥2𝑦 − 𝑦2𝑥 2𝑥 − 𝑦
⇒ 0 ≤ | 𝑥2 + 𝑦2 | ≤ | 2𝑥𝑦 | = | 2 | Mà lim 2𝑥−𝑦 (𝑥,𝑦)→(0,0) | | = 0 2 2𝑥2𝑦 − 𝑦2𝑥 ⇒ lim (𝑥,𝑦)→(0,0) 𝑥2 + 𝑦2 = 0 (Kẹp)
Vậy hàm số 𝑓(𝑥, 𝑦) liên tục tại (0,0) khi và chỉ khi 𝑎 = 0 Đáp án A Câu 3:
Xét theo phương 𝑦 = 𝑘𝑥 𝑥𝑦 + 𝑦2 𝑘𝑥2 + 𝑘2𝑥2 ⇒ lim sin ( sin ( (𝑥,𝑦)→(0,0) 𝑥2 + 𝑦2) = lim (𝑥,𝑘𝑥)→(0,0) 𝑥2 + 𝑘2𝑥2 ) 𝑘 + 𝑘2 𝑘 + 𝑘2 = lim sin ( 𝑥→0 1 + 𝑘2) = sin ( 1 +𝑘2) 𝑘𝑥→0
Vậy với mỗi 𝑘 khác nhau lim 𝑥𝑦+𝑦2 (𝑥,𝑦)→(0,0) sin (
) tiến đến những giá trị giới hạn 𝑥2+𝑦2 khác nhau. ⇒ Không tồn tại lim 𝑥𝑦+𝑦2 (𝑥,𝑦)→(0,0) sin ( ) 𝑥2+𝑦2
⇒ Hàm số gián đoạn tại (0,0) Đáp án B Câu 4:
Với (𝑥, 𝑦) ∈ 𝑅2 ∖ {(0,0)} thì hàm số 𝑓(𝑥, 𝑦) liên tục. Xét tính liên tục của hàm số TEAM GIẢI TÍCH 2 24
𝑓(𝑥, 𝑦) tại ( 0,0).
Khi (𝑥, 𝑦) → (0,0), xét theo phương 𝑦 = 𝑘𝑥 𝑥𝑦 − 𝑥2 𝑘𝑥2 − 𝑥2 𝑘 − 1 ⇒ lim
(𝑥,𝑦)→(0,0) 𝑥2 + 𝑦2 = lim
(𝑥,𝑘𝑥)→(0,0) 𝑥2 + (𝑘𝑥)2 = 1 + 𝑘2
Vậy với mỗi 𝑘 khác nhau lim(𝑥,𝑦)→(0,0) 𝑥𝑦−𝑥2 tiến đến những giá trị giới hạn khác 𝑥2+𝑦2 nhau.
⇒ Không tồn tại lim(𝑥,𝑦)→(0,0) 𝑥𝑦−𝑥2 𝑥2+𝑦2
⇒ Hàm số gián đoạn tại (0,0)
Vậy hàm số 𝑓(𝑥, 𝑦) liên tục với (𝑥, 𝑦) ∈ 𝑅2 ∖ {(0,0)}, gián đoạn tại (0,0) Đáp án B
1.3. ĐẠO HÀM RIÊNG VÀ VI PHÂN TOÀN PHẦN Câu 1: z’x = 1 √𝑥2+𝑦2 Đáp án A Câu 2: z’y = 𝑦
(𝑥+√𝑥2+𝑦2)√𝑥2+𝑦2 Đáp án A Câu 3:
dz = z’x.dx + z’y.dy = 1 . 𝑑𝑥 + 𝑦 . 𝑑𝑦 √𝑥2+𝑦2
(𝑥+√𝑥2+𝑦2)√𝑥2+𝑦2 Đáp án A Câu 4:
u’y = 𝑥𝑦2𝑧. 𝑙𝑛𝑥. 2. 𝑦. 𝑧 Đáp án C Câu 5: TEAM GIẢI TÍCH 2 25
u’x = 𝑒(𝑥2+2𝑦2+𝑧2)−1. ( −2𝑥 ) (𝑥2+2𝑦2+𝑧2)2
u’y = 𝑒(𝑥2+2𝑦2+𝑧2)−1. ( −4𝑦 ) (𝑥2+2𝑦2+𝑧2)2
u’z = 𝑒(𝑥2+2𝑦2+𝑧2)−1. ( −2𝑧 ) (𝑥2+2𝑦2+𝑧2)2
 du = 𝑒(𝑥2+2𝑦2+𝑧2)−1. ( −2𝑥 ).dx + (𝑥2+2𝑦2+𝑧2)2
𝑒(𝑥2+2𝑦2+𝑧2)−1. ( −4𝑦 ).dy + (𝑥2+2𝑦2+𝑧2)2
𝑒(𝑥2+2𝑦2+𝑧2)−1. ( −2𝑧 ) (𝑥2+2𝑦2+𝑧2)2
 𝑑𝑢(1; -1; 1) = −2 .dx + 4 .dy - 2 .dz 𝑒−4.16 𝑒−4.16 𝑒−4.16 Đáp án B Câu 6:
Đặt 𝑢 = 𝑥 , 𝑣 = 𝑥𝑦 ⇒ 𝑢′ = 1 , 𝑢′ = −𝑥 , 𝑣′ = 𝑦, 𝑣′ = 𝑥 𝑦 𝑥 𝑦 𝑦 𝑦2 𝑥 𝑦 + 𝑧′ ′ ′ ′ ′ ′ ′
𝑥 = 𝑧𝑢 ⋅ 𝑢𝑥 + 𝑧𝑣 ⋅ 𝑣𝑥 = 𝑢𝑥 ⋅ 𝑓(𝑢) − 𝑣𝑥 ⋅ 𝑓(𝑣) 1 2 = 𝑥 2𝑥
𝑦 ⋅ (𝑦) sin 𝑦 − 𝑦 ⋅ (𝑥𝑦)2 ⋅ sin 2𝑥𝑦 + 𝑧′ ′ ′ ′ ′ ′ 𝑦 = 𝑧𝑢 ⋅ 𝑢 ′
𝑦 + 𝑧𝑣 ⋅ 𝑣𝑦 = 𝑢𝑦 ⋅ 𝑓(𝑢) − 𝑣𝑦 ⋅ 𝑓(𝑣) −𝑥 2 = 𝑥 2𝑥
𝑦2 ⋅ (𝑦) sin 𝑦 − 𝑥 ⋅ (𝑥𝑦)2 ⋅ sin 2𝑥𝑦 Đáp án D Câu 7: −3 u’ 2 2 −3 2 2
x = z. 2x. −1. (𝑥 + 𝑦 ) 2 = - z. x. (𝑥 + 𝑦 ) 2 2 u’ 2 2 −3 y = - z. y. (𝑥 + 𝑦 ) 2 u’ 2 2 z = (𝑥 + 𝑦 )−1 2 −3
 du = - z. x. (𝑥2 + 𝑦2)−32. 𝑑𝑥 - z. y. (𝑥2 + 𝑦2) 2 . 𝑑𝑦 + (𝑥2 + 𝑦2 −1 ) 2 . 𝑑𝑧 Đáp án C Câu 8:
𝑓(1,0 + Δ𝑦) − 𝑓(1,0) Δ𝑦 ⋅ arctan 1 𝑓′ Δ𝑦 − 0 𝑦(1,0) = limΔ𝑦→0 Δ𝑦 = limΔ𝑦→0 Δ𝑦 TEAM GIẢI TÍCH 2 26 1 = limΔ𝑦→0 arctan Δ𝑦
Với Δ𝑦 → 0 ⇒ 1 → +∞ Δ𝑦 1 𝜋 1 𝜋
⇒ arctan Δ𝑦 → 2 ⇒ limΔ𝑦→0 arctan Δ𝑦 = 2 1 𝜋
⇒ 𝑓′𝑦(1,0) = limΔ𝑦→0 arctan Δ𝑦 = 2 Đáp án A Câu 9: Sử dụng định nghĩa: 𝑧(𝑥, 0) − 𝑧(0,0) arctan (0) − 0 𝑧′𝑥(0,0) = lim 𝑥→0 𝑥 − 0 = lim 𝑥→0 𝑥 − 0 = 0 𝑧(0, 𝑦) − 𝑧(0,0) 𝑧′𝑦(0,0) = lim 𝑦→0 𝑦 − 0 𝜋 arctan (∞) − 0 = lim 2 𝑦→0 𝑦 − 0 = lim 𝑦→0 𝑦 = ∞ Đáp án B
1.4. ĐẠO HÀM CỦA HÀM ẨN Câu 1:
𝑥3 + 2𝑦3 + 3𝑥2𝑦 = 2
F(x, y) = 𝑥3 + 2𝑦3 + 3𝑥2𝑦 − 2 = 0  {F’x = 3x2 + 6𝑥𝑦 F’y = 6y2 − 3𝑥2 TEAM GIẢI TÍCH 2 27
 y’x = − F’x = − x2+2𝑥𝑦 F’y 2y2−𝑥2 Đáp án D Câu 2:
Ta có: F(x, y, z) = 𝑥2. 𝑎𝑟𝑐𝑡𝑎𝑛𝑥 + 2𝑥𝑦2 + 𝑦4 + 2𝑧3 − 1 = 0
f′x = 2𝑥. 𝑎𝑟𝑐𝑡𝑎𝑛𝑥 + 𝑥2 + 2𝑦2 1+𝑥2  { f′ 3 y = 4xy + 4𝑦 f′ 2 z = 6𝑧
 z’x = − f′x = − 2𝑥.𝑎𝑟𝑐𝑡𝑎𝑛𝑥+ 𝑥21+𝑥2+2𝑦2 f′z 6𝑧2
 z’y = − f′y = − 2xy+2𝑦3 f′z 3𝑧2 Đáp án C Câu 3:
PTTT: y = y’(x0).(x - x0) + y0 Có: {𝑥0
𝑦 → Xác định y’(x0) 0
Ta có: F(x, y, z) = 𝑥3 − 𝑦3 + 3𝑥𝑦 − 13 = 0  { f′x = 3x2 + 3𝑦 f′ 2 y = −3y + 3𝑥
 y’x = − F’x = x2+𝑥 F’y y2−𝑥  y’(-1) = − 1 5
 Pttt: y = − 1 . (𝑥 + 1) − 2 5 Đáp án A Câu 4: 2 F′x = − x2  Đặt F(x,y,z) =
𝑧2 + 2 − √𝑦2 − 𝑧2 => F′y = −y 𝑥 √y2−z2 {F′z = 2z + z √y2−z2 y 2 F′ F′y √y2−z2  𝑧′ x x2 𝑥 = − = ; 𝑧′𝑦 = − = F′z 2z+ z F′z 2z+ z √y2−z2 √y2−z2 TEAM GIẢI TÍCH 2 28 1 √y2−z2  𝑥2𝑧′𝑥 = 2 ; 1 𝑧′ z.(2+ 1 ) 𝑦 𝑦 = z.(2+ 1 ) √y2−z2 √y2−z2 2+ 1 √y2−z2
 𝑥2𝑧′𝑥 + 1 𝑧′ = 1 (đpcm) 𝑦 𝑦 = z.(2+ 1 ) 𝑧 √y2−z2 Đáp án A
1.5. TÍNH GẦN ĐÚNG NHỜ VI PHÂN Câu 1: Dạng: f(x, y) = x3.y2 Ta có: {𝑥0 = 1 𝑦0 = 1 và { ∆𝑥 = 0,02 ∆𝑦 = −0,03
 ADCT: A ≈ f(1; 1) + f’x(1;
1).0,02 + f’y(1; 1).(−0,03) = 1 + 3. 0,02 + 2. (−0,03) = 1 Đáp án A Câu 2:
Dạng: f(x, y) = √3𝑥2 + 𝑦2 Ta có: {𝑥0 = 1 𝑦0 = 0 và {∆𝑥 = 0,02 ∆𝑦 = 0,05
 ADCT: A ≈ f(1; 1) + f’x(1; 0).0,02 + f’y(1; 0).0,05 = 1 + 2.0,02 + 0 3 = 76 75 Đáp án D Câu 3:
Dạng: f(x, y) = √32𝑥3 − 3𝑦2 + 2 Ta có: {𝑥0 = 3
𝑦0 = 4 và {∆𝑥 = −0,02 ∆𝑦 = 0,01
 ADCT: A ≈ f(3; 4) + f’x(3;
4).(−0,02) + f’y(3; 4).0,01 = 2 + 4,5.(−0,02) - 2.0,01 = 1,89 TEAM GIẢI TÍCH 2 29 Đáp án B Câu 4:
 Đặt f(x,y)=√𝑥2 + 𝑦2 => 𝑓′𝑥 = 𝑥 ; 𝑓′ √𝑥2+𝑦2 𝑦 = 𝑦 √𝑥2+𝑦2  Áp dụng công thức : f(x ′ ′
0 + ∆x; y0 + ∆y) ≈ f(x0; y0) + ∆xf x(x0; y0) + ∆yf y(x0; y0) Chọn x 01 01 0 = 3; y0 = 4; ∆x = 0, ;∆y = −0,  S ≈ 4,988 Đáp án C
1.6. CỰC TRỊ CỦA HÀM NHIỀU BIẾN Câu 1:
z = 𝑥2 + 𝑥𝑦 + 𝑦2 − 2𝑥 − 𝑦
Ta có: z = f(x, y) = 𝑥2 + 𝑥𝑦 + 𝑦2 − 2𝑥 − 𝑦 Tập xác định: D = R2
_ Giải hệ phương trình: {𝑓′𝑥 = 2𝑥 + 𝑦 − 2 = 0 𝑓′ 𝑦 = 𝑥 + 2𝑦 − 1 = 0 {𝑥 = 1
𝑦 = 0 => Điểm dừng M(1; 0) _ Ta có:
𝑓′ 𝑥𝑥= 2 ; 𝑓′ 𝑥𝑦 = 0 ; 𝑓′ 𝑦𝑦 = 2 𝐴 = 𝑓′ ( 𝑥𝑥 1; 0) = 2
 Tại M(1; 0): {𝐵 = 𝑓′ ( 𝑥𝑦 1; 0) = 0 𝐶 = 𝑓′ ( 𝑦𝑦 1; 0) = 2
 ∆= 𝐵2 − 𝐴𝐶 = 02 − 2.2 = −4 < 0
Và A = 2 > 0 => M(1; 0) là điểm cực tiểu Đáp án B Câu 2:
Ta có: z = f(x, y) = 2𝑥4 + 𝑦4 − 4𝑥2 + 2𝑦2 Tập xác định: D = R2 TEAM GIẢI TÍCH 2 30
_ Giải hệ phương trình: {𝑓′𝑥 = 8𝑥3 − 8𝑥 = 0 𝑓′ 3 𝑦 = 4𝑦 + 4𝑦 = 0
 2 điểm dừng: M(0; 0), N(1; 0)
𝑓′ 𝑥𝑥 = 24𝑥2 − 8 _ Ta có: { 𝑓′ 𝑥𝑦 = 0 𝑓′ 𝑦𝑦 = 12𝑦2 + 4 𝐴 = −8
+ Tại M(0; 0): {𝐵 = 0 => ∆
= 32 > 0 => Không phải cực trị 𝐶 = 4 𝐴 = 16
+ Tại N(1; 0): {𝐵 = 0 => ∆
= −64 < 0 và A = 16 > 0 𝐶 = 4
 N(1; 0) là điểm cực tiểu với fmin = - 2 Đáp án A Câu 3:
Ta có: z = f(x, y) = 2𝑥2 + 3𝑦3 − 𝑒−(𝑥2+𝑦2)
1, Giải hệ phương trình: { 𝑓′𝑥 = 4𝑥 + 2𝑥. 𝑒−(𝑥2+𝑦2) = 0 𝑓′ 2 −(𝑥2+𝑦2) 𝑦 = 9𝑦 + 2𝑦. 𝑒 = 0  Điểm dừng M(0; 0) 𝑓′ −(𝑥2+𝑦2) 2 −(𝑥2+𝑦2) 𝑥𝑥 = 4 + 2. 𝑒 − 4𝑥 . 𝑒 2, Ta có: {
𝑓′ 𝑥𝑦 = −4𝑥𝑦.𝑒−(𝑥2+𝑦2) 𝑓′ −(𝑥2+𝑦2) 2 −(𝑥2+𝑦2) 𝑦𝑦 = 18𝑦 + 2. 𝑒 − 4𝑦 . 𝑒 𝐴 = 6
 Tại M( 0; 0): {𝐵 = 0 => ∆= −12 < 0 và A = 6 > 0 𝐶 = 2
 M( 0; 0) là điểm cực tiểu với fmin = -1 Đáp án A Câu 4:
Điều kiện 𝑥2 + 𝑦2 = 1 ⇔ 𝑥2 + 𝑦2 − 1 = 0
Đặt hàm phụ: 𝐿(𝑥, 𝑦, 𝑘) = 2𝑥2 + 𝑦2 + 𝑘(𝑥2 + 𝑦2 − 1) 𝐿′𝑥 = 0 4𝑥 + 2𝑘𝑥 = 0(1)
Xét {𝐿′𝑦 = 0 ⇔ {2𝑦 + 2𝑘𝑦 = 0(2)(∗) 𝐿′𝑘 = 0 𝑥2 + 𝑦2 = 1(3) TEAM GIẢI TÍCH 2 31
TH1: (1) ⇔ 2𝑥(𝑘 + 2) = 0 ⇒ 𝑘 = −2
Với 𝑘 = −2, hệ (∗) trở thành { −2𝑦 = 0
𝑥2 + 𝑦2 = 1 ⇒ {𝑥 = ±1 𝑦 = 0
TH2: (2) ⇔ 2𝑦(𝑘 + 1) ⇒ 𝑘 = −1
Với 𝑘 = −1, hệ (∗) trở thành { 2𝑥 = 0
𝑥2 + 𝑦2 = 1 ⇒ { 𝑥 = 0 𝑦 = ±1
⇒ (∗) có các bộ nghiệm (𝑥, 𝑦, 𝑘) = {(1,0, −2); (−1,0, −2); (0,1, −1); (0, −1, −1)}
Xét vi phân cấp hai: 𝑑2𝐿(𝑥, 𝑦, 𝑘) = 𝐿′ ′ ′
𝑥𝑥𝑑𝑥2 + 2𝐿𝑥𝑦 𝑑𝑥𝑑𝑦 + 𝐿𝑦𝑦 𝑑𝑦2
⇒ 𝑑2𝐿(𝑥, 𝑦, 𝑘) = (2 + 𝑘)𝑑𝑥2 + 0. 𝑑𝑥𝑑𝑦 + (1 + 𝑘)𝑑𝑦2
⇒ 𝑑2𝐿(𝑥, 𝑦, 𝑘) = (1 + 𝑘)𝑑𝑥2 + (1 + 𝑘)𝑑𝑦2
Với (𝑘, 𝑥, 𝑦) = (1,0, −2) ⇒ 𝑑2𝐿(1,0, −2) = −𝑑𝑦2 < 0
⇒ 𝑀1(1,0) là điểm cực đại có điều kiên của hàm số, 𝑧CD = 𝑧(𝑀1) = 2
Vói (𝑥, 𝑦, 𝑘) = (−1,0, −2) ⇒ 𝑑2𝐿(−1,0, −2) = −𝑑𝑦2 < 0
⇒ 𝑀2(−1,0) là điểm cực đại có điều kiên của hàm số, 𝑧C𝐷 = 𝑧(𝑀2) = 2
Với (𝑥, 𝑦, 𝑘) = (0,1, −1) ⇒ 𝑑2𝐿(0,1, −1) = 𝑑𝑥2 > 0
⇒ 𝑀3(0,1) là điểm cực tiểu có điều kiên của hàm số, 𝑧CT = 𝑧(𝑀3) = 1
Với (𝑥, 𝑦, 𝑘) = (0, −1, −1) ⇒ 𝑑2𝐿(0, −1, −1) = 𝑑𝑥2 > 0
⇒ 𝑀4(0,−1) là điểm cực tiểu có điều kiên của hàm số, 𝑧CT = 𝑧(𝑀4) = 1 Đáp án B Câu 5:
Điều kiện 𝑥2 + 𝑦2 = 1 ⇔ 𝑥2 + 𝑦2 − 1 = 0
Đặt 𝐿(𝑥, 𝑦, 𝑘) = 𝑥 + 𝑦 + 𝑘(𝑥2 + 𝑦2 − 1) 4 3 1 −1 𝑥 = 𝐿′𝑥 = 0 4 + 2𝑘𝑥 = 0 8𝑘 Xét 𝐿′ = 0 ⇔ 1 ⇔ −1 (𝑘 ≠ 0) 𝑦 𝑦 = 𝐿′𝑘 = 0 3 + 2𝑘𝑦 = 0 6𝑘 { {𝑥2 + 𝑦2 = 1 {𝑥2 + 𝑦2 = 1 −1 2 2 ⇒ ( −1 5
8𝑘) + ( 6𝑘) = 1 ⇒ 𝑘 = ± 24 5 −3 −4
Với 𝑘 = 24 ⇒ 𝑥 = 5 ,𝑦 = 5 5 3 4
Với 𝑘 = − 24 ⇒ 𝑥 = 5,𝑦 = 5 TEAM GIẢI TÍCH 2 32
Xét vi phân cấp 2 của 𝐿(𝑥, 𝑦, 𝑘)
Xét vi phân cấp 2 của 𝐿(𝑥, 𝑦, 𝑘)
𝑑2𝐿(𝑥, 𝑦, 𝑘) = 𝐿′ ′ ′ 2 2
𝑥𝑥(𝑥, 𝑦, 𝑘)𝑑𝑥2 + 2𝐿𝑥𝑦 (𝑥, 𝑦, 𝑘) + 𝐿𝑦𝑦(𝑥, 𝑦, 𝑘)𝑑𝑦2 = 2𝑘 d𝑥 + 2𝑘 d𝑦 −3 −4 5 −3 −4 5 5
Với (𝑥, 𝑦, 𝑘) = ( 5 , 5 , 24) ⇒ 𝑑2𝐿( 5 , 5 , 24) = 12( d𝑥2 + d𝑦2) > 0 −3 ⇒ 𝑀 −4 −5 1 ( (
5 , 5 ) là điểm cực tiểu có điều kiện của hàm số, 𝑧CT = 𝑧 𝑀1) = 12
Với (𝑥, 𝑦, 𝑘) = (3 , 4, 5 ) ⇒ 𝑑2𝐿 (3 , 4 , −5) = −5 ( d𝑥2 + d𝑦2) < 0 5 5 24 5 5 24 12
⇒ 𝑀2 (3 , 4) là điểm cực đại có điều kiện của hàm số, 𝑧 ( 5 5 𝐶Ð = 𝑧 𝑀2) = 512 Đáp án C Câu 6: z=
𝑥3 + 𝑦3 + (𝑥 + 𝑦)2 ( ) 𝑥 = 𝑦
 Xét { 𝑧′𝑥 = 3𝑥2 + 2 𝑥 + 𝑦 = 0 ∗ 𝑧′ 2
=> 𝑥2 = 𝑦2 <=> ⌈ 𝑥 = −𝑦
𝑦 = 3𝑦 + 2(𝑥 + 𝑦) = 0 ∗∗
 Với x=y thay vào * ta có 𝑥 = 0 => 𝑦 = 0
3𝑥2 + 4𝑥 = 0  [𝑥 = −4 => 𝑦 = −4 3 3
 Với x=-y thay vào * ta có 3𝑥2 = 0  x=y=0
Vậy có 2 điểm tới hạn M(−4; −4) và N(0,0) 3 3
 Đặt A=𝑧′ 𝑥𝑥 = 6𝑥 + 2 ; B=𝑧′ 𝑥𝑦 = 2 ; C=𝑧′ 𝑦𝑦 = 6𝑦 + 2  Tại M(−4; −4) thì { 𝐴 = −6 < 0 3 3
∆= 𝐵2 − 𝐴𝐶 = −32 < 0
=> M là điểm cực đại ; 𝑧𝐶Đ = 𝑧(𝑀) = 64 27
 Tại N(0,0) : ∆= 𝐵2 − 𝐴𝐶 = 0
Giả sử các điểm H(∆𝑥; ∆𝑦) lân cận điểm N (-1< ∆𝑥; ∆𝑦 < 1)
 Xét ∆𝑧 = 𝑧(𝐻) − 𝑧(0,0) =
∆𝑥3 + ∆𝑦3 + (∆𝑥 + ∆𝑦)2
+ Với các điểm H(∆𝑥; 0) ∈ 𝑂𝑥 ∆𝑧 =
∆𝑥3+∆𝑥2 = ∆𝑥2(1 + ∆𝑥) Bảng xét dấu: ∆𝑥 -1 0 1 TEAM GIẢI TÍCH 2 33 ∆𝑧 + 0 --- 0 --- 0 +  ∆z < 0 khi ∆x đi qua 0
+ Với các điểm H có tọa độ (∆𝑥; −2∆𝑥) (∆𝑦 = −2∆𝑥)
∆𝑧 = −7∆𝑥3+∆𝑥2 = ∆𝑥2(1 − 7∆𝑥) Bảng xét dấu: ∆𝑥 -1/7 0 1/7 ∆𝑧 --- 0 + 0 + 0 ---  ∆z > 0 khi ∆x đi qua 0
 Từ 2 trường hợp trên => ∆𝑧 = 𝑧(𝐻) − 𝑧(0,0) ị
b đổi dâu với các điểm H lân cận N(0,0)
 N(0,0) không là điểm cực trị của hàm số Đáp án A Câu 7: ′ = 0 −𝑦2 Xét {𝑧𝑥 𝑧′ ⇔ { 2𝑥 = 2 (1)
𝑦 = 0 ⇔ { 4𝑥 + 𝑦2 = 0 2𝑥𝑦 + 3𝑦2 = 0 2𝑥𝑦 + 3𝑦2 = 0(2)
Thế (1) vào (2) ⇒ −𝑦2 y + 3𝑦2 = 0 ⇒ [𝑦 = 6 ⇒ 𝑥 = −9 2 𝑦 = 0 ⇒ 𝑥 = 0
⇒ Hàm số có hai điểm tới hạn 𝑀1(−9,6) và 𝑀2(0,0) Đặt 𝐴 = 𝑧′ ′ ′
𝑥𝑥 = 4, 𝐵 = 𝑧𝑥𝑦 = 2𝑦, 𝐶 = 𝑧𝑦𝑦 = 2𝑥 + 6𝑦 Tại 𝑀1(−9,6): { 𝐴 = 4 > 0
Δ = 𝐵2 − 𝐴𝐶 = 72 > 0 ⇒ 𝑀1 không là điểm cực trị của hàm số. Tại 𝑀2(0,0): Δ = 0
Xét các điểm lân cận 𝑀2(0,0) nằm trên trục 𝑂𝑦 : 𝑁 (0; Δ𝑦) với Δ 𝑦 rất nhỏ.
⇒ Δ𝑧 = 𝑓(𝑁) − 𝑓(𝑀2) = 2.0 + 0. (Δ𝑦)2 3
+ (Δ𝑦) + 2 − (0 + 0 + 0 + 2) = (Δ𝑦)3 Bảng xét dấu: Δ𝑦 0− 0 0+ Δ𝑧 = (Δ𝑦)3 − 0 +
⇒ Δ𝑧 đổi dấu khi Δ𝑦 đi qua 0 ⇒ 𝑀2(0,0) không là điểm cực trị. TEAM GIẢI TÍCH 2 34
Vậy hàm số không có cực trị. Đáp án A
1.7. KHAI TRIỂN TAYLOR Câu 1:
Đặt 𝑧(𝑥, 𝑦) = 𝑓(𝑥, 𝑦) = 𝑥2 + 𝑦2 + 𝑥𝑦 + 2𝑥 + 2𝑦 + 1 Ta có: 𝑧′ ′ ′ ′ ′
𝑥 = 2𝑥 + 𝑦 + 2, 𝑧𝑦 = 2𝑦 + 𝑥 + 2, 𝑧𝑥𝑥 = 2, 𝑧𝑦𝑦 = 2, 𝑧𝑥𝑦 = 1
Các đạo hàm riêng cấp 2 của hàm số là những hằng số
⇒ vi phần toàn phần cấp 3 trở lên bằng 0 .
Sử dụng công thức khai triển Taylor tại điểm 𝑀(1,2) +∞ 1 1 1
𝑧(𝑥, 𝑦) = z(𝑥0;𝑦0) + ∑ 𝑘!𝑑𝑘𝑧(𝑥0;𝑦0) = z(𝑥0;𝑦0) + 1!𝑑𝑧(𝑥0;𝑦0) + 2!𝑑2𝑧(𝑥0;𝑦0) 𝑘=1 𝑧(1,2) = 14
Ta có: {𝑑𝑧(1,2)𝑧′ ( ′
𝑥 1,2) ⋅ (𝑥 − 1) + 𝑧 (1,2) ⋅ (𝑦 − 2) = 6(𝑥 − 1) + 7(𝑦 − 2)
𝑑2𝑧(1,2) = 2(𝑥 − 1)2 + 2(𝑥 − 1)(𝑦 − 2) + 2(𝑦 − 2)2
Vậy khai triển Taylor của hàm số tại 𝑀(1,2) là:
𝑧 = 14 + 6(𝑥 − 1) + 7(𝑦 − 2) + (𝑥 − 1)2 + (𝑥 − 1)(𝑦 − 2) + (𝑦 − 2)2 Đáp án B Câu 2: Làm tương tự câu 1 Đáp án C
1.8. TÌM GTLN, GTNN CỦA HÀM SỐ Câu 1:
Miền giá trị của (𝑥, 𝑦) là hình vuông 𝐴𝐵𝐶𝐷
Xét các điểm phía trong miền 0 < 𝑥, 𝑦 < 𝜋 2
Tìm các điểm tới hạn: TEAM GIẢI TÍCH 2 35 ′ = 0 Xét {𝑧𝑥
𝑧′𝑦 = 0 ⇔ {cos 𝑥+ cos (𝑥 + 𝑦) = 0 cos 𝑦 + cos (𝑥 + 𝑦) = 0 cos 𝑥 = cos 𝑦
⇔ {cos 𝑦+ cos (𝑥 + 𝑦) = 0 ⇔ { 𝑥 = 𝑦 cos 𝑥 + cos 2𝑥 = 0 𝑥 = 𝑦 ⇔ { 3𝑥 𝑥 2cos 2 cos 2= 0
⇒ Trong miền 𝐷, 𝑧 có một điểm tới hạn 𝑀1(𝜋/3, 𝜋/3)
Xét trên biên 𝐷𝐶: 𝑦 = 0,0 < 𝑥 < 𝜋 2 𝑧 = 2sin 𝑥 ⇒ 𝑧′ = 2cos 𝑥 𝑧′ = 0 ⇔ 2cos
𝑥 = 0 ⇔ 𝑥 = 𝜋 (loại) ⇒ Trên 𝐷𝐶 (trừ hai đầu mút) không có điểm tới 2 hạn
Xét trên biên 𝐴𝐷: 𝑥 = 0; 0 < 𝑦 < 𝜋 2 ⇒ 𝑧 = 2sin 𝑦 ⇒ 𝑧′ = 2cos 𝑦 𝜋 𝑧′ = 0 ⇔ 2cos 𝑦 = 0 ⇔ 𝑦 = 2 (loại)
Trên 𝐴𝐷 (trừ hai đầu mút) không có điểm dừng
Tương tự tại các biên 𝐴𝐵 và 𝐵𝐶 ta tìm được điểm tới hạn TEAM GIẢI TÍCH 2 36 𝜋 𝜋 𝜋 𝜋 𝑀2 (4 ,2) và 𝑀3(2 4) 3 𝑧(𝑀 √3 1) = Ta có: 2 𝑧( 3 𝑀 √3
2) = 𝑧(𝑀2) = √2 + 1 ⇒ 𝑧max = 2 ,𝑧min = 0 𝑧(𝐷) = 0 { 𝑧(𝐵) = 𝑧(𝐴) = 2 Đáp án A Câu 2:
Xét trong miền elip 𝑥2 + 𝑦2 < 1 9 ′ = 0 Xét {𝑧𝑥 𝑧′ ⇔ 𝑥 = 𝑦 = 0 𝑦 = 0 ⇔ { 2𝑥 = 0 −18𝑦 = 0
⇒ Trong miền elip có một điểm tới hạn 𝑂(0,0)
Xét ở biên của elip 𝑥2 + 𝑦2 = 1 9
Tìm điểm tới hạn của 𝑧 với điều kiện 𝑥2 + 𝑦2 = 1 9 Đặt hàm phụ
𝐿(𝑥, 𝑦, 𝑘) = 𝑥2 − 9𝑦2 𝑥2 + 𝑘 ( 9 + 𝑦2 − 1) 2𝑘 𝑘 2𝑥 + 𝑥 (1 + 𝐿′𝑥 = 0 9 𝑥 = 0 9) = 0
Xét 𝐿′ = 0 ⇔ −18𝑦 + 2𝑘𝑦 = 0 ⇔ 𝑦(𝑘 − 9) = 0 𝑦 𝐿′𝑘 = 0 𝑥2 𝑥2 { { 9 + 𝑦2 = 1 { 9 + 𝑦2 = 1
TH1: x = y = 0 ⇒ không phải nghiệm của hệ
TH2: k = −9 => y = 0 ⇒ x = ±3
TH3: k = 9 => x = 0 ⇒ y = ±1 TEAM GIẢI TÍCH 2 37
Với 𝑘 = −9, 𝑧 có hai điểm tới hạn 𝐴(3,0), 𝐵(−3,0)
Với 𝑘 = 9, 𝑧 có 2 điểm tới hạn 𝐶(0,1), 𝐷(0, −1) 𝑧(𝑂) = 0 𝑧(𝐴) = 9
Ta có: {𝑧(𝐵) = −9 ⇒ 𝑧min = −9,𝑧max = 9 𝑧(𝐷) = −9 Đáp án A Câu 3:
Phương trình AB: y = 7 − x
Xét trong miền Δ𝑂𝐴𝐵 ′ = 0 13 Xét hệ {𝑧𝑥
𝑧′𝑦 = 0 ⇔ {3𝑥2 + 3𝑦 − = 0 4𝑦 + 3𝑥 − 18 = 0 3𝑥2 + 3𝑦 − 13 = 0 9 1 { 9 27 ⇒ 3𝑥2 − 3𝑦 + 4 𝑥 + 2 = 0 4 𝑥 − 2 = 0
⇒ Trong miền Δ𝑂𝐴𝐵 không có điểm tới hạn
Xét trên biên 𝑂𝐵 (không tính hai đầu mút): 𝑥 = 0,0 < 𝑦 < 7
⇒ 𝑧 = 2𝑦2 − 18𝑦 ⇒ 𝑧′ = 4𝑦 − 18 ⇒ 𝑧′ = 0 khi 𝑦 = 4,5
⇒ trên biên 𝑂𝐵 có một điểm tới hạn 𝑀(0; 4,5)
Xét trên biên 𝑂𝐴 (không tính hai đầu mút): 𝑦 = 0,0 < 𝑥 < 7 TEAM GIẢI TÍCH 2 38
⇒ 𝑥3 − 13𝑥 ⇒ 𝑧′ = 𝑥2 − 13 ⇒ 𝑥 = √133 (Không lấy trường họp nghiệm âm)
⇒ Trên biên 𝑂𝐴 có một điểm tới hạn 𝑁 (√133 ,0) 𝑧(𝑂) = 0 𝑧(𝐴) = 252
Ta có: { 𝑧(𝐵) = −17 ⇒ 𝑧min = −40,5;𝑧max = 252 𝑧(𝑀) = −40,5 −26 𝑧(𝑁) = √39 9 Đáp án A TEAM GIẢI TÍCH 2 39
II. ỨNG DỤNG CỦA PHÉP TÍNH VI PHÂN: Câu 1: Lời giải :
Bước 1 : Kiểm tra điểm kì dị(thi trắc nghiệm thường bỏ qua bước này để tiết kiệm thời gian) 2𝑥 = 0 { 𝑐 = 0
⇒ 𝑥 = 𝑐 = 0, nhưng điểm kì dị đó không thuộc họ
𝑐𝑦 − 𝑐2 − 𝑥2 = 0
đường cong đã cho nên hệ đường cong không điểm kì dị.
Bước 2 : Tìm hình bao 𝑦 − 2𝑐 = 0
{𝑐𝑦 − 𝑐2 − 𝑥2 = 0 ⟹ 𝑦 = ±2𝑥 Đáp án : D Câu 2: Lời giải : 𝑥′(𝑡) = 1 ) = 1 𝑥′ (𝜋4
Bước 1 : {𝑦′(𝑡) = −√2. sin 𝑡 𝑣ớ𝑖 𝑡= 𝜋
; Suy ra : 𝑦′ (𝜋 ) = −1 4 4
𝑧′(𝑡) = √2. cos 𝑡 { 𝑧′ (𝜋 ) = 1 4
Bước 2 :Phương trình pháp diện : 𝜋 (𝑥 − 𝜋
4) − (𝑦 − 1) + (𝑧 − 1) = 0 ℎ𝑎𝑦 𝑥− 𝑦 + 𝑧 = 4 Đáp án :B Câu 3: Lời giải : 𝐹′ ′ 𝑥 = 2𝑥 − 3𝑦 𝐹𝑥(𝐴) = −1
Bước 1 :Đặt 𝐹(𝑥, 𝑦, 𝑧) = 𝑥2 − 3𝑥𝑦 + 𝑦2 − 𝑧 ⟹ { 𝐹′ ′
𝑦 = −3𝑥 + 2𝑦 ⟹ { 𝐹𝑦(𝐴) = −1 𝐹′𝑧 = −1 𝐹′𝑧(𝐴) = −1
Bước 2 :Phương trình tiếp diện
−(𝑥 − 1) − (𝑦 − 1) − 𝑧(𝑧 + 1) = 0 ℎ𝑎𝑦 𝑥+ 𝑦 + 𝑧 = 1 Đáp án :A Câu 4: Lời giải : TEAM GIẢI TÍCH 2 40 Áp dụng công thức : |𝑥′ 𝑦′ 𝐾 = 𝑥′ 𝑦′ | (𝑥′2 + 𝑦′2)32 Đáp án :A Câu 5: Lời giải : 𝐹′𝑥 = 8𝑥
Bước 1 :Đặt 𝐹(𝑥, 𝑦, 𝑧) = 4𝑥2 − 𝑦2 + 2𝑦 − 𝑧 { 𝐹′𝑦 = −2𝑦 + 2 𝑣ớ𝑖 𝐴 (−1; 2; 4) 𝐹′𝑧 = −1 𝐹′𝑥(𝐴) = −8
⟹ {𝐹′𝑦(𝐴) = −2 𝐹′𝑧(𝐴) = −1
Bước 2 :Phương trình tiếp diện :
−8(𝑥 + 1) − 2(𝑦 − 2) − (𝑧 − 4) = 0 ℎ𝑎 8 𝑦 𝑥 + 2𝑦 + 𝑧 = 0 Đáp án :A Câu 6: Lời giải :
𝐹′𝑥 = −2𝑥. 𝑒𝑥2−𝑦2
Bước 1 :Đặt 𝐹(𝑥, 𝑦, 𝑧) = 𝑧 − 𝑒𝑥2−𝑦2 ⟹ { 𝐹′𝑦 = 2𝑦. 𝑒𝑥2+𝑦2 𝑣ớ𝑖 𝐴 (1;−1; 1) 𝐹′𝑧 = 1 𝐹′𝑥(𝐴) = −2 ⟹ {𝐹′𝑦(𝐴) = −2 𝐹′𝑧(𝐴) = 1
Bước 2: Phương trình tiếp diện
−2(𝑥 − 1) − 2(𝑦 + 1) + (𝑧 − 1) = 0 ℎ𝑎𝑦 2𝑥 + 2𝑦 − 𝑧 + 1 = 0 Đáp án :A Câu 7: Lời giải :
Bước 1 :Tìm giao điểm : 𝑒1−𝑥2 = 1 ⟹ 𝑥 = ±1 ⟹ 𝐴(1; 1); 𝐴′(−1; 1) là giao điểm cần tìm
Bước 2 : Ta có : 𝑦′ = −2𝑥. 𝑒1−𝑥2  ฀ = 1 ⟹ ฀′(1 2 ) = −
 ฀ = −1 ⟹ ฀′(−1) = 2 TEAM GIẢI TÍCH 2 41 Bước 3 :
 ฀ − 1 = −2(฀ − 1) ⟹ 2฀ + ฀ − 3 = 0
 ฀ − 1 = 2(฀ + 1) ⟹ 2฀ − ฀ + 3 = 0 Đáp án :B,C Câu 8: Lời giải : ′ ′ 2 𝐹𝑥 = 23 𝐹 (𝑀) = 1 Bước 1 :Đặ 2 𝑥 t 𝐹(𝑥; 𝑦) = 𝑥 3 3 + 𝑦 √𝑥 3 − 5 ⟹ { ⟹ { 3 𝐹′𝑦 = 2 𝐹′(𝑀) = 2 3 √3𝑦 𝑦 3
Bước 2 :Phương trình pháp tuyến 𝑥 − 8 𝑦 − 1
1 = 2 ⟹ 2𝑥 − 𝑦 − 15 = 0 3 3 Đáp án :C Câu 9: Lời giải : 𝑥 = cos 𝑡
Bước 1 :Đặt { 𝑦 = 2 sin 𝑡 𝑧 = cos𝑡−4 3
Bước 2 : Áp dụng công thức tính : 2 2 √ 2 |𝑥′ 𝑦′
𝑥′ 𝑦′ | + |𝑦′ 𝑧′
𝑦′ 𝑧′ | + |𝑧′ 𝑥′ 𝑧′ 𝑥′ | 𝐾 =
(𝑥′2 + 𝑦′2 + 𝑧′2)32 Đáp án :A Câu 10: Lời giải :
Đặt {𝐹 = 𝑥2 + 𝑦2 − 10 𝐺 = 𝑦2 + 𝑧2 − 25 𝑛 ′
𝐹 = (𝐹𝑥(𝐴); 𝐹′ ′ 𝑦(𝐴); 𝐹 ′ 𝑧(𝐴)) = (2; 6; 0); 𝑛 ′ 𝐺 = (𝐺𝑥(𝐴); 𝐺 ′
𝑦(𝐴); 𝐺𝑧(𝐴)) = (0; 6; 8) Ta có
𝒏𝒕𝒕 = 𝑛𝐹 × 𝑛𝐺 = (12;−4;3) TEAM GIẢI TÍCH 2 42
Phương trình tiếp tuyến: 𝑥 − 1 𝑦 − 3 𝑧 − 4 12 = −4 = 3 Đáp án :A TEAM GIẢI TÍCH 2 43
III. TÍCH PHÂN BỘI & ỨNG DỤN G 3.1. TÍCH PHÂN KÉP
Câu 1: 𝑇í𝑛ℎ ∬ 𝑥𝑦𝑑𝑥𝑑𝑦 ới D đượ ớ ạ ở 2 𝐷 v
c gi i h n b i 𝑥 + 𝑦 = 4 𝑣à 𝑥 = 2𝑦 −4 ≤ 𝑥 ≤ 2
𝑀𝑖ề𝑛 𝐷: {𝑥22 ≤𝑦 ≤4−𝑥 2 4−𝑥
∬ 𝑥𝑦𝑑𝑥𝑑𝑦 = ∫ 𝑑𝑥 ∫ 𝑥𝑦𝑑𝑦 𝐷 −4 𝑥2 2 2 𝑥𝑦2 = ∫ 𝑦=4−𝑥 −4 2 | 𝑑𝑥 𝑦=𝑥22 2
2 𝑥(4 − 𝑥)2 𝑥 (𝑥2 = ∫ 2 ) −4 2 − 2 𝑑𝑥 = −90. Chọn B
Câu 2: 𝑇í𝑛ℎ ∬ 2𝑦𝑑𝑥𝑑𝑦 𝐷
𝑣ớ𝑖 𝐷 𝑥á𝑐 đị𝑛ℎ 𝑏ở𝑖 𝑥2 + 𝑦2 ≤ 1, 𝑥 + 𝑦 ≥ 1 0 ≤ 𝑥 ≤ 1
𝑀𝑖ề𝑛 𝐷: {1− 𝑥 ≤ 𝑦 ≤ √1−𝑥2 1 √1−𝑥2
∬ 2𝑦𝑑𝑥𝑑𝑦 = ∫ 𝑑𝑥 ∫ 2𝑦𝑑𝑦 𝐷 0 1−𝑥 1
= ∫ [(1 − 𝑥2) − (1 − 𝑥)2]𝑑𝑥 0 1 = 3.𝐶ℎọ𝑛 𝐴 Câu 3: 1 3
𝑇í𝑛ℎ ∫ 𝑑𝑥 0 ∫ (𝑥2 2
𝑦 − 2𝑦2)𝑑𝑦 1 𝑥2𝑦2 2𝑦3 = ∫ ( 𝑦=3 0 2 − 3 ) |𝑦=2 𝑑𝑥
1 𝑥2. (32 − 22) 2(33 − 23) = ∫ [ ]𝑑𝑥 0 2 − 3 71 = − 6 .𝐶ℎọ𝑛 𝐶 Câu 4: TEAM GIẢI TÍCH 2 44 1 1
∫ 𝑑𝑥 ∫ sin(𝑦2) 𝑑𝑦 0 𝑥 𝐷: {0 ≤ 𝑥 ≤ 1
𝑥 ≤ 𝑦 ≤ 1 → {0 ≤ 𝑦 ≤ 1 0 ≤ 𝑥 ≤ 𝑦 1 1 1 𝑦
→ ∫ 𝑑𝑥 ∫ sin(𝑦2) 𝑑𝑦 = ∫ 𝑑𝑦 ∫ sin(𝑦2) 𝑑𝑥 0 𝑥 0 0 1
= ∫ 𝑥𝑠𝑖𝑛(𝑦2)| 𝑥=𝑦 𝑥=0 𝑑𝑦 0 1
= ∫ 𝑦𝑠𝑖𝑛(𝑦2) 𝑑𝑦 0 11 = ∫ 𝑑(𝑦2) 0 2 𝑠𝑖𝑛(𝑦2) 11 1 − 𝑐𝑜𝑠1 = ∫ 𝑑𝑡 = 0 2 𝑠𝑖𝑛𝑡 2 . 𝐶ℎọ𝑛 𝐶
Câu 5: 𝑇í𝑛ℎ ∬ 𝑥√𝑥2 + 𝑦2 𝐷
𝑑𝑥𝑑𝑦 𝑣ớ𝑖 𝐷 𝑥á𝑐 đị𝑛ℎ 𝑏ở𝑖 𝑥2 + 𝑦2 ≤ 𝑥; 𝑦 ≥ 0 𝑥 = 𝑟𝑐𝑜𝑠𝜑
Đặ𝑡 {𝑦 = 𝑟𝑠𝑖𝑛𝜑 |𝐽| = 𝑟.
0 ≤ 𝑟 ≤ 𝑐𝑜𝑠𝜑
𝑀𝑖ề𝑛 𝐷 𝑡𝑟ở 𝑡ℎà𝑛ℎ { 𝜋 0 ≤ 𝜑 ≤ 2
∬ 𝑥√𝑥2 + 𝑦2 𝑑𝑥𝑑𝑦 = ∬𝑟3𝑐𝑜𝑠𝜑 𝑑𝑟𝑑𝜑 𝐷 𝐷 𝜋 𝑐𝑜𝑠𝜑 = ∫ 𝑑
2 𝜑 ∫ 𝑟3𝑐𝑜𝑠𝜑 𝑑𝑟𝑑𝜑 0 0 𝜋(2𝑐𝑜𝑠𝜑)4 = ∫ 0 4 . 𝑐𝑜𝑠𝜑𝑑𝜑
𝜋(21 − (𝑠𝑖𝑛𝜑)2)2 = ∫ 0 4 . 𝑑(𝑠𝑖𝑛𝜑) 2 = 15.𝐶ℎọ𝑛 𝐵
Câu 6:𝑇í𝑛ℎ ∬ (2𝑥 + 𝑠𝑖𝑛𝑦)𝑑𝑥𝑑𝑦 ( )2 𝐷
𝑣ớ𝑖 𝐷: 𝑥 − 2 + 𝑦2 ≤ 1 TEAM GIẢI TÍCH 2 45
Ta thấy f(x,y)=siny là hàm lẻ đối với y và miền D đối xứng qua Ox
→ ∬ 𝑠𝑖𝑛𝑦𝑑𝑥𝑑𝑦 = 0 𝐷
Đặ𝑡 {𝑥 = 2 + 𝑟𝑐𝑜𝑠𝜑
𝑦 = 𝑟𝑠𝑖𝑛𝜑 |𝐽| = 𝑟.
𝑀𝑖ề𝑛 𝐷 𝑡𝑟ở 𝑡ℎà𝑛ℎ { 0 ≤ 𝑟 ≤ 1 0 ≤ 𝜑 ≤ 2𝜋
∬ 2𝑥 𝑑𝑥𝑑𝑦 = ∬2(2 + 𝑟𝑐𝑜𝑠𝜑)𝑟𝑑𝑟𝑑𝜑 𝐷 𝐷 2𝜋 1 2𝜋 1
= ∫ 𝑑𝜑 ∫ 4𝑟𝑑𝑟 + ∫ 𝑐𝑜𝑠𝜑 𝑑𝜑 ∫ 2𝑟2 𝑑𝑟 = 4𝜋. 𝐶ℎọ𝑛 𝐵 0 0 0 0 𝑑𝑥𝑑𝑦 𝑎 𝑎 𝐂â𝐮 𝟕: ∬ 2 2 , −𝑥 ≤ 𝑦 ≤ 0. 𝑔𝑖
𝐷 (𝑥2 + 𝑦2)3 = 𝑏 + 𝑙𝑛𝑐, 𝐷: 𝑥 ≤ 𝑥 + 𝑦 ≤ 2𝑥 𝑏 𝑡ố𝑖 ả𝑛. Tổng a+b+c=? 𝑥 = 𝑟𝑐𝑜𝑠𝜑
Đặ𝑡 {𝑦 = 𝑟𝑠𝑖𝑛𝜑 |𝐽| = 𝑟.
𝑐𝑜𝑠𝜑 ≤ 𝑟 ≤ 2𝑐𝑜𝑠𝜑
𝑀𝑖ề𝑛 𝐷 𝑡𝑟ở 𝑡ℎà𝑛ℎ { 𝜋 − 4 ≤ 𝜑 ≤ 0 𝑑𝑥𝑑𝑦 𝑑𝑟𝑑𝜑 ∬ (𝑥2 + 𝑦2)3 = ∬ 𝐷 𝑟5 𝐷 0 2𝑐𝑜𝑠𝜑 𝑑𝑟 = ∫ 𝑑𝜑 ∫ −𝜋 𝑐𝑜𝑠𝜑 𝑟5 4 15 0 = 1 64 ∫ (
−𝜋 𝑐𝑜𝑠𝜑)4 𝑑𝜑 4 15 0(𝑡𝑎𝑛𝜑)2 + 1 = 64∫ ( −𝜋 𝑐𝑜𝑠𝜑)2 𝑑𝜑 4 15 0
= 64∫ [(𝑡𝑎𝑛𝜑)2 + 1]𝑑(𝑡𝑎𝑛𝜑) −𝜋4 5
= 16 → 𝑎 = 5,𝑏 = 16,𝑐 = 1.𝐶ℎọ𝑛 𝐶
𝐂â𝐮 𝟖: ∬ √2𝑥 − 𝑥2 − 𝑦2𝑑𝑥𝑑𝑦 𝑣ớ𝑖 𝑚𝑖ề𝑛 𝐷: 𝑥2 + 𝑦2 ≤ 2𝑥, 𝑦 ≥ 0 𝐷 TEAM GIẢI TÍCH 2 46
Đặ𝑡 {𝑥 = 1 + 𝑟𝑐𝑜𝑠𝜑
𝑦 = 𝑟𝑠𝑖𝑛𝜑 |𝐽| = 𝑟.
𝑀𝑖ề𝑛 𝐷 𝑡𝑟ở 𝑡ℎà𝑛ℎ { 0 ≤ 𝑟 ≤ 1 0 ≤ 𝜑 ≤ 𝜋
→ ∬ √2𝑥 − 𝑥2 − 𝑦2𝑑𝑥𝑑𝑦 = ∬√1 − 𝑟2. 𝑟𝑑𝑟𝑑𝜑 𝐷 𝐷 𝜋 1 1
= ∫ 𝑑𝜑 ∫ − √1 − 𝑟2 𝑑(1 − 𝑟2) 0 0 2 1 𝜋
= 𝜋. ∫ √𝑢2 𝑑𝑢 = .𝐶ℎọ𝑛 𝐵 0 3
𝐂â𝐮 𝟗: 𝑇í𝑛ℎ ∬ 𝑦2(6𝑥 − 𝑦)𝑑𝑥𝑑𝑦, 𝑣ớ𝑖 𝐷 𝑔 ớ
𝑖 𝑖 ℎạ𝑛 𝑏ở𝑖: 𝑥 = 0, 𝑥 + |𝑦| = 1. 𝐷 𝐷: { 0 ≤ 𝑥 ≤ 1
𝑥 − 1 ≤ 𝑦 ≤ 1 − 𝑥 1 1−𝑥
∬ 𝑦2(6𝑥 − 𝑦) 𝑑𝑥𝑑𝑦 = ∫ 𝑑𝑥 ∫ 𝑦2(6𝑥 − 𝑦)𝑑𝑦 𝐷 0 𝑥−1 1 𝑦4 = ∫ (2𝑥𝑦3 − 𝑦=1−𝑥 𝑑𝑥 0 4 ) |𝑦=𝑥−1 1 (1 − 𝑥)4 = ∫ (2𝑥(1 − 𝑥)3 − (𝑥 − 1)4 𝑑𝑥 0 4 − 2𝑥(𝑥 − 1)3 + 4 ) 1 = 5.𝐶ℎọ𝑛 𝐴
𝐂â𝐮 𝟏𝟎: ∬ (𝑥 + 𝑦)2𝑑𝑥𝑑𝑦 𝑣ớ𝑖 𝑚 ề
𝑖 𝑛 𝐷: 5𝑥2 + 6𝑥𝑦 + 5𝑦2 ≤ 4 𝐷
𝐷: 4(𝑥 + 𝑦)2 + (𝑥 − 𝑦)2 ≤ 4 1 Đặ𝑡 {𝑢 = 𝑥 + 𝑦
𝑣 = 𝑥 − 𝑦 → |𝐽| = 2
𝑀𝑖ề𝑛 𝐷 𝑡𝑟ở 𝑡ℎà𝑛ℎ 4𝑢2 + 𝑣2 ≤ 4 𝑢2
→ ∬ (𝑥 + 𝑦)2𝑑𝑥𝑑𝑦 = ∬ 𝐷 2 𝑑𝑢𝑑𝑣 𝐷 𝑢 = 𝑟𝑐𝑜𝑠𝜑
Đặ𝑡 {𝑣 = 2𝑟𝑠𝑖𝑛𝜑 → |𝐽| = 2𝑟 TEAM GIẢI TÍCH 2 47
𝑀𝑖ề𝑛 𝐷 𝑡𝑟ở 𝑡ℎà𝑛ℎ { 0 ≤ 𝑟 ≤ 1 0 ≤ 𝜑 ≤ 2𝜋
→ ∬ 2𝑢2𝑑𝑢𝑑𝑣 = ∬𝑟3(𝑐𝑜𝑠𝜑)2𝑑𝑟𝑑𝜑 𝐷 𝐷 2𝜋 1 𝜋
= ∫ (𝑐𝑜𝑠𝜑)2𝑑𝜑 ∫ 𝑟3𝑑𝑟 = 0 0 4 . 𝐶ℎọ𝑛 𝐷 𝑑𝑥𝑑𝑦 𝑎
𝐂â𝐮 𝟏𝟏: 𝑀𝑖ề𝑛 𝐷 𝑔 ớ
𝑖 𝑖 ℎạ𝑛 𝑏ở𝑖 𝑥 = 1, 𝑦 = 0, 𝑥 = 𝑦. ∬
𝑥 + 𝑦 + 1 = 2 𝑙𝑛𝑏 − 𝑐𝑙𝑛2. 𝐷
𝑇ổ𝑛𝑔 𝑎+ 𝑏 + 𝑐 =?
𝑀𝑖ề𝑛 𝐷: {0 ≤ 𝑥 ≤ 1 0 ≤ 𝑦 ≤ 𝑥 1 1 𝑥 1
∬ 𝑥 + 𝑦 + 1𝑑𝑥𝑑𝑦 = ∫ 𝑑𝑥 ∫ 𝐷 0 0 𝑥 + 𝑦 + 1 𝑑𝑦 1
= ∫ ln|𝑦 + 𝑥 + 1| 𝑦=𝑥 𝑦=0 𝑑𝑥 0 1 1
= ∫ ln|2x + 1|𝑑𝑥 − ∫ ln|x + 1|𝑑𝑥 0 0 1 1
= ∫ ln(2x + 1) 𝑑𝑥 − ∫ ln(x + 1) 𝑑𝑥 (𝑑𝑜 0 ≤ 𝑥 ≤ 1) 0 0 11 1 = ∫
− ∫ ln(x + 1) 𝑑(𝑥 + 1) 0 2 ln(2x + 1) 𝑑(2𝑥 + 1) 0
(2𝑥 + 1) ln(2𝑥 + 1) − (2𝑥 + 1) = [ ) |𝑥=1 2
− (𝑥 + 1) ln(𝑥 + 1 + (𝑥 + 1)] 𝑥=0
= 3 𝑙𝑛3 − 2𝑙𝑛2. Chọn D. 2
𝐂â𝐮 𝟏𝟐: 𝑀𝑖ề𝑛 𝐷: 𝑥2 + 𝑦2 ≤ 6. ∬ 3𝑥2−𝑦2+1 𝑑𝑥𝑑𝑦 𝐷
= 𝑎𝜋 + 𝑙𝑛𝑏, Tổng a+b=? 𝑥2+𝑦2+1
Ta thấy trong biểu thức xác định miền D, x và y đối xứng nhau nên có thể đổi vai trò
của x và y trong biểu thức lấy tích phân. 3𝑥2 − 𝑦2 + 1 3𝑦2 − 𝑥2 + 1 → ∬
𝐷 𝑥2 + 𝑦2 + 1 𝑑𝑥𝑑𝑦 = ∬ 𝑦2 + 𝑥2 + 1 𝑑𝑥𝑑𝑦 𝐷 3𝑥2 − 𝑦2 + 1 → ∬
1 3𝑥2 − 𝑦2 + 1 + 3𝑦2 − 𝑥2 + 1
𝐷 𝑥2 + 𝑦2 + 1 𝑑𝑥𝑑𝑦 = 2 ∬ 𝑥2 + 𝑦2 + 1 𝑑𝑥𝑑𝑦 𝐷 TEAM GIẢI TÍCH 2 48 1 2(𝑥2 + 𝑦2 + 1) = 2∬ 𝑥 𝑑𝑥𝑑𝑦 2 + 𝑦2 𝐷 + 1 = ∬ 𝑑𝑥𝑑𝑦 𝐷 = 𝑆𝐷
= 6𝜋. → 𝑎 = 6, 𝑏 = 1 → 𝐶ℎọ𝑛 𝐴
3.2. TÍCH PHÂN BỘI BA 1 1−𝑥 2
𝐂â𝐮 𝟏: 𝑇í𝑛ℎ 𝑡í𝑐ℎ 𝑝ℎâ𝑛 ∫ 𝑑𝑥 ∫ 𝑑𝑧 ∫ (𝑦 + 𝑧) 𝑑𝑦 0 0 0 1 1−𝑥
= ∫ 𝑑𝑥 ∫ (2 + 2𝑧) 𝑑𝑧 0 0 1
= ∫ (2𝑧 + 𝑧2)| 𝑧=1−𝑥 𝑧=0 𝑑𝑥 0 1
= ∫ 2(1 − 𝑥) + (1 − 𝑥)2 𝑑𝑥 0 4 = 3.𝐶ℎọ𝑛 𝐷
𝐂â𝐮 𝟐: 𝑇í𝑛ℎ ∭(3𝑥2 − 2𝑦) 𝑑𝑥𝑑𝑦𝑑𝑧 𝑣ớ𝑖 𝑉: 0 ≤ 𝑥 ≤ 1, 0 ≤ 𝑦 ≤ 𝑥, 0 ≤ 𝑧 ≤ 𝑥2 𝑉
∭(3𝑥2 − 2𝑦)𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 1 𝑥 𝑥2
= ∫ 𝑑𝑥 ∫ 𝑑𝑦 ∫ (3𝑥2 − 2𝑦) 𝑑𝑧 0 0 0 1 𝑥
= ∫ 𝑑𝑥 ∫ 𝑥2(3𝑥2 − 2𝑦) 𝑑𝑦 0 0 1 3
= ∫ (3𝑥5 − 𝑥4) 𝑑𝑥 = 0 10 . 𝐶ℎọ𝑛 𝐴
𝐂â𝐮 𝟑: 𝑇í𝑛ℎ ∭(𝑥2 + 𝑦2) 𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉 𝑔𝑖ớ𝑖 ℎạ𝑛 𝑏ở𝑖 𝑥2 + 𝑦2 − 2𝑧 = 0, 𝑧 = 2 𝑉 𝑥 = 𝑟𝑐𝑜𝑠𝜑
Đặ𝑡 {𝑦 = 𝑟𝑠𝑖𝑛𝜑 → |𝐽| = 𝑟 𝑧 = 𝑧 TEAM GIẢI TÍCH 2 49 𝑟2 𝑀𝑖ề𝑛 𝑉 𝑡 ở
𝑟 𝑡ℎà𝑛ℎ { 2 ≤ 𝑧 ≤ 2 0 ≤ 𝑟 ≤ 2 0 ≤ 𝜑 ≤ 2𝜋
∭(𝑥2 + 𝑦2)𝑑𝑥𝑑𝑦𝑑𝑧 = ∭𝑟3 𝑑𝑟𝑑𝜑𝑑𝑧 𝑉 𝑉 2𝜋 2 2
= ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ 𝑟3𝑑𝑧 0 0 𝑟2 2 2 = 2𝜋 ∫ 𝑟3 𝑟2 (2 − 𝑑𝑟 0 2 ) 16𝜋 = 3 .𝐶ℎọ𝑛 𝐶 1 1 1 𝑒
𝐂â𝐮 𝟒: ∫ 𝑑𝑥 ∫ 𝑏
𝑑𝑧 ∫ 𝑥𝑧𝑒𝑥𝑦2𝑑𝑦 = 0 0 𝑧2
𝑎 − 𝑐 . 𝑎 + 𝑏 + 𝑐 =? 0 ≤ 𝑥 ≤ 1 0 ≤ 𝑥 ≤ 1
𝑀𝑖ề𝑛 { 0 ≤ 𝑧 ≤ 1 ⇔ { 0 ≤ 𝑦 ≤ 1 𝑧2 ≤ 𝑦 ≤ 1 0 ≤ 𝑧 ≤ √𝑦 1 1 1
∫ 𝑑𝑥 ∫ 𝑑𝑧 ∫ 𝑥𝑧𝑒𝑥𝑦2𝑑𝑦 0 0 𝑧2 1 1 √𝑦
= ∫ 𝑑𝑥 ∫ 𝑑𝑦 ∫ 𝑥𝑧𝑒𝑥𝑦2𝑑𝑧 0 0 0 1 𝑧 1 2 = ∫ 𝑑𝑥 ∫ | 𝑧=√𝑦 𝑧=0 𝑑𝑦 0 0 2 𝑥𝑒𝑥𝑦2 1 1 1
= 2∫ 𝑑𝑥 ∫ 𝑥𝑦𝑒𝑥𝑦2 𝑑𝑦 0 0 1 1 1 = ∫
4 ∫ 𝑑𝑥 𝑒𝑥𝑦2 𝑑(𝑥𝑦2) 0 0 1 1 𝑒 1 = 𝑑𝑥 = 4 ∫ (𝑒𝑥 − 1) 0 4 − 2 . 𝐶ℎọ𝑛 𝐵 𝑑𝑥𝑑𝑦𝑑𝑧
𝐂â𝐮 𝟓: 𝑇í𝑛ℎ ∭ (𝑥 +𝑦 +𝑧 +2)2,𝑉: {𝑥 +𝑦 + 𝑧 ≤ 1 𝑥, 𝑦, 𝑧 ≥ 0 𝑉 TEAM GIẢI TÍCH 2 50
0 ≤ 𝑧 ≤ 1 − 𝑥 − 𝑦
𝑀𝑖ề𝑛 𝑉: { 0 ≤ 𝑦 ≤ 1 − 𝑥 0 ≤ 𝑥 ≤ 1 𝑑𝑥𝑑𝑦𝑑𝑧 1 1−𝑥 1−𝑥−𝑦 𝑑𝑧 ∭ ( = ∫ ∫ 𝑥 + 𝑦 + 𝑧 + 2)2 𝑑𝑥 𝑑𝑦 ∫ 2 𝑉 0 0 0 (𝑥 + 𝑦 + 𝑧 + 2) 1 1−𝑥 −1 = ∫ 𝑑𝑥 ∫ 𝑧=1−𝑥−𝑦𝑑𝑦 0 0 𝑥 + 𝑦 + 𝑧 + 2 |𝑧=0 1 1−𝑥 −1 1 = ∫ 𝑑𝑥 ∫ ( 0 0 3 + 𝑥 + 𝑦 + 2) 𝑑𝑦 1 −𝑦 = ∫ ( 𝑦=1−𝑥 𝑑𝑥 0
3 + ln(𝑥 + 𝑦 + 2)) |𝑦=0 1 𝑥 − 1 = ∫ ( 𝑑𝑥 0 3 + ln(3) − ln(𝑥 + 2)) 5
= 6 + 2𝑙𝑛2 − 2𝑙𝑛3.𝐶ℎọ𝑛 𝐵
𝐂â𝐮 𝟔: 𝑇í𝑛ℎ ∭(4𝑥2 + 𝑦2 + 𝑧2 + 2𝑥𝑦) 𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉: 4𝑥2 + 𝑦2 + 𝑧2 ≤ 4, 𝑧 ≥ 0 𝑉
𝐼 = ∭(4𝑥2 + 𝑦2 + 𝑧2 + 2𝑥𝑦) 𝑑𝑥𝑑𝑦𝑑𝑧 𝑉
𝐶ó 𝑓(𝑥, 𝑦) = 2𝑥𝑦 𝑙à ℎà𝑚 𝑙ẻ đố𝑖 𝑣ớ𝑖 𝑥 𝑣à 𝑚 ề
𝑖 𝑛 𝑉 đố𝑖 𝑥ứ𝑛𝑔 𝑞𝑢𝑎 𝑚ặ𝑡 𝑥 = 0
→ ∭2𝑥𝑦𝑑𝑥𝑑𝑦𝑑𝑧 = 0 𝑉
𝑥 = 𝑟𝑐𝑜𝑠𝜑𝑠𝑖𝑛𝜃
Đặ𝑡 {𝑦 = 2𝑟𝑠𝑖𝑛𝜑𝑠𝑖𝑛𝜃 → |𝐽| = 4𝑟2𝑠𝑖𝑛𝜃 𝑧 = 2𝑟𝑐𝑜𝑠𝜃 0 ≤ 𝑟 ≤ 1 𝜋 𝑀𝑖ề𝑛 𝑉 𝑡 ở
𝑟 𝑡ℎà𝑛ℎ { 0 ≤ 𝜃 ≤ 2 0 ≤ 𝜑 ≤ 2𝜋
→ 𝐼 = ∭4𝑟4𝑠𝑖𝑛𝜃𝑑𝑟𝑑𝜃𝑑𝜑 𝑉 2𝜋 𝜋 1 8𝜋
= ∫ 𝑑𝜑 ∫ 𝑠2𝑖𝑛𝜃𝑑𝜃 ∫ 4𝑟4𝑑𝑟 = 0 0 0 5 . 𝐶ℎọ𝑛 𝐵 TEAM GIẢI TÍCH 2 51 𝜋
𝐂â𝐮 𝟕: ∭√𝑥2 + 𝑦2 + 𝑧2 𝑑𝑥𝑑𝑦𝑑𝑧 = 𝑉
𝑎 ,𝑉: 𝑥2 + 𝑦2 + 𝑧2 ≤ 𝑦. 𝑇ì𝑚 𝑎?
𝑥 = 𝑟𝑐𝑜𝑠𝜑𝑠𝑖𝑛𝜃
Đặ𝑡 { 𝑦 = 𝑟𝑐𝑜𝑠𝜃 → |𝐽| = 𝑟2𝑠𝑖𝑛𝜃
𝑧 = 𝑟𝑠𝑖𝑛𝜑𝑠𝑖𝑛𝜃
0 ≤ 𝑟 ≤ 𝑐𝑜𝑠𝜃𝜋 𝑀𝑖ề𝑛 𝑉 𝑡 ở
𝑟 𝑡ℎà𝑛ℎ { 0 ≤ 𝜃 ≤ 2 0 ≤ 𝜑 ≤ 2𝜋
∭√𝑥2 + 𝑦2 + 𝑧2 𝑑𝑥𝑑𝑦𝑑𝑧 = ∭𝑟3𝑠𝑖𝑛𝜃 𝑑𝑟𝑑𝜑𝑑𝜃 𝑉 𝑉 2𝜋 𝜋 𝑐𝑜𝑠𝜃
= ∫ 𝑑𝜑 ∫ 𝑑2𝜃 ∫
𝑟3𝑠𝑖𝑛𝜃 𝑑𝑟 0 0 0 ( 𝜋 2 𝑐𝑜𝑠𝜃)4 = 2𝜋. ∫ 𝑑𝜃 0 4 . 𝑠𝑖𝑛𝜃 𝜋 𝜋 = 2
2 . ∫ −(𝑐𝑜𝑠𝜃)4 𝑑(𝑐𝑜𝑠𝜃) 0 𝜋 1 = 𝜋 2 ∫ 𝑢4 𝑑𝑢 = 0 10 . 𝐶ℎọ𝑛 𝐷
𝐂â𝐮 𝟖: ∭𝑧𝑐𝑜𝑠(𝑥2 + 𝑦2) 𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉: √𝑥2 + 𝑦2 ≤ 𝑧 ≤ √4 − 𝑥2 − 𝑦2 𝑉 𝑥 = 𝑟𝑐𝑜𝑠𝜑
Đặ𝑡 {𝑦 = 𝑟𝑠𝑖𝑛𝜑 → |𝐽| = 𝑟 𝑧 = 𝑧
𝑟 ≤ 𝑧 ≤ √4 − 𝑟2 𝑀𝑖ề𝑛 𝑉 𝑡 ở 𝑟 𝑡ℎà𝑛ℎ { 0 ≤ 𝑟 ≤ √2 0 ≤ 𝜑 ≤ 2𝜋
∭𝑧𝑐𝑜𝑠(𝑥2 + 𝑦2)𝑑𝑥𝑑𝑦𝑑𝑧 = ∭𝑧𝑐𝑜𝑠(𝑟2). 𝑟 𝑑𝑟𝑑𝜑𝑑𝑧 𝑉 𝑉 2𝜋 √2 √4−𝑟2
= ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫
𝑧𝑟𝑐𝑜𝑠(𝑟2)𝑑𝑧 0 0 𝑟 √ 𝑧 2 2 = 2𝜋 ∫ 𝑧=√4−𝑟2 𝑑𝑟 0
2 𝑟𝑐𝑜𝑠(𝑟2)|𝑧=𝑟 TEAM GIẢI TÍCH 2 52 √ 4 2 − 𝑟2 − 𝑟2 = 2𝜋 ∫ 𝑧=√4−𝑟2 𝑑𝑟 0 2
𝑟𝑐𝑜𝑠(𝑟2)|𝑧=𝑟 √2
= 𝜋 ∫ (2 − 𝑟2) cos(𝑟2) 𝑑(𝑟2) 0 2
= 𝜋 ∫ (2 − 𝑢)𝑐𝑜𝑠𝑢 𝑑𝑢 0 2
= 𝜋 ∫ (2 − 𝑢) 𝑑(𝑠𝑖𝑛𝑢) 0 2
= 𝜋[(2 − 𝑢)𝑠𝑖𝑛𝑢|𝑢=2
𝑢=0 + ∫ 𝑠𝑖𝑛𝑢 𝑑𝑢] 0
= 𝜋(0 − 𝑐𝑜𝑠𝑢|𝑢=2 𝑢=0)
= 𝜋(1 − 𝑐𝑜𝑠2). 𝐶ℎọ𝑛 𝐴 𝑎√8 − 𝑏√6
𝐂â𝐮 𝟗: 𝑀𝑖ề𝑛 𝑉: {𝑥2 + 𝑦2 + 𝑧2 ≤ 8 𝑑𝑥𝑑𝑦𝑑𝑧 =
𝑥2 + 𝑦2 ≤ 2 . ∭(𝑥2 + 𝑦2) 𝑉 15 𝜋. 𝑏 − 𝑎 =? 𝑥 = 𝑟𝑐𝑜𝑠𝜑
Đặ𝑡 {𝑦 = 𝑟𝑠𝑖𝑛𝜑 → |𝐽| = 𝑟 𝑧 = 𝑧
−√8 − 𝑟2 ≤ 𝑧 ≤ √8 − 𝑟2 𝑀𝑖ề𝑛 𝑉 𝑡 ở 𝑟 𝑡ℎà𝑛ℎ { 0 ≤ 𝑟 ≤ √2 0 ≤ 𝜑 ≤ 2𝜋
∭(𝑥2 + 𝑦2)𝑑𝑥𝑑𝑦𝑑𝑧 = ∭𝑟3 𝑑𝑟𝑑𝜑𝑑𝑧 𝑉 𝑉 2𝜋 √2 √8−𝑟2
= ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ 𝑟3𝑑𝑧 0 0 −√8−𝑟2 √2
= 2𝜋 ∫ 2𝑟3√8 − 𝑟2 𝑑𝑟 0 √2
= 2𝜋 ∫ −(8 − 8 + 𝑟2)√8 − 𝑟2 𝑑(8 − 𝑟2) 0 8
= 2𝜋 ∫ (8 − 𝑢)√𝑢 𝑑𝑢 6 TEAM GIẢI TÍCH 2 53 16 3 2 5 = 2𝜋 ( 2 − 𝑢=8 3 𝑢 5 𝑢2) |𝑢=6 512 = √8 − 528√6 15 𝜋. 𝐶ℎọ𝑛 𝐴. 𝑎𝜋
𝐂â𝐮 𝟏𝟎: 𝑇í𝑛ℎ ∭(𝑥 + 𝑦 − 2𝑧)2𝑑𝑥𝑑𝑦𝑑𝑧 = 𝑉
𝑏 ,𝑣ớ𝑖 𝑉: 𝑥2 + 𝑦2 + 𝑧2 ≤ 1. 𝑎 − 𝑏 =?
𝐼 = ∭(𝑥 + 𝑦 − 2𝑧)2𝑑𝑥𝑑𝑦𝑑𝑧 𝑉
= ∭(𝑥2 + 𝑦2 + 4𝑧2 + 2𝑥𝑦 − 4𝑥𝑧 − 4𝑦𝑧) 𝑑𝑥𝑑𝑦𝑑𝑧 𝑉
𝑋é𝑡 𝑓(𝑥, 𝑦, 𝑧) = 2𝑥𝑦 𝑙à ℎà𝑚 𝑙ẻ đố𝑖 𝑣ớ𝑖 𝑥, 𝑚 ề
𝑖 𝑛 𝑉 đố𝑖 𝑥ứ𝑛𝑔 𝑞𝑢𝑎 𝑥 = 0
→ ∭2𝑥𝑦𝑑𝑥𝑑𝑦𝑑𝑧 = 0 𝑉
𝑇ươ𝑛𝑔 𝑡ự 𝑐ó ∭−4𝑥𝑧 𝑑𝑥𝑑𝑦𝑑𝑧 = ∭−4𝑦𝑧 𝑑𝑥𝑑𝑦𝑑𝑧 = 0 𝑉 𝑉
→ 𝐼 = ∭(𝑥2 + 𝑦2 + 4𝑧2) 𝑑𝑥𝑑𝑦𝑑𝑧 𝑉
𝑥 = 𝑟𝑐𝑜𝑠𝜑𝑠𝑖𝑛𝜃
Đặ𝑡 {𝑦 = 𝑟𝑠𝑖𝑛𝜑𝑠𝑖𝑛𝜃 → |𝐽| = 𝑟2𝑠𝑖𝑛𝜃 𝑧 = 𝑟𝑐𝑜𝑠𝜃 0 ≤ 𝑟 ≤ 1 𝑀𝑖ề𝑛 𝑉 𝑡 ở
𝑟 𝑡ℎà𝑛ℎ { 0 ≤ 𝜃 ≤ 𝜋 0 ≤ 𝜑 ≤ 2𝜋
→ 𝐼 = ∭(𝑟2 + 𝑟2(𝑐𝑜𝑠𝜃)2). 𝑟2𝑠𝑖𝑛𝜃 𝑑𝑟𝑑𝜑𝑑𝜃 𝑉
= ∭(𝑟4𝑠𝑖𝑛𝜃 + 𝑟4(𝑐𝑜𝑠𝜃)2𝑠𝑖𝑛𝜃) 𝑑𝑟𝑑𝜑𝑑𝜃 𝑉 2𝜋 𝜋 1 2𝜋 𝜋 1
= ∫ 𝑑𝜑 ∫ 𝑠𝑖𝑛𝜃 𝑑𝜃 ∫ 𝑟4 𝑑𝑟 + ∫ 𝑑𝜑 ∫ (𝑐𝑜𝑠𝜃)2𝑠𝑖𝑛𝜃 𝑑𝜃 ∫ 𝑟4 𝑑𝑟 0 0 0 0 0 0 1 = 2𝜋. 2. 2 1 16𝜋
5 + 2𝜋.3 . 5 = 15 . 𝐶ℎọ𝑛 𝐶 TEAM GIẢI TÍCH 2 54
3.3. ỨNG DỤNG CỦA TÍCH PHÂN BỘI 𝐂â𝐮 𝟏: 𝐷 ệ
𝑖 𝑛 𝑡í𝑐ℎ 𝑝ℎầ𝑛 𝑚ặ𝑡 𝑧= 𝑥2 + 𝑦2 + 2 𝑛ằ𝑚 𝑡𝑟𝑜𝑛𝑔 𝑚ặ𝑡 𝑡𝑟ụ 𝑥2 + 𝑦2 = 9 𝑙à 𝑎√𝑎 − 𝑏 𝑐
𝜋. 𝑇ổ𝑛𝑔 𝑎+ 𝑏 + 𝑐 =?
𝐻ì𝑛ℎ 𝑐ℎ𝑖ế𝑢 𝑐ủ𝑎 𝑚ặ𝑡 𝑡𝑟𝑜𝑛𝑔 𝑚ặ𝑡 𝑡𝑟ụ 𝑙ê𝑛 𝑂𝑥𝑦 𝑙à 𝐷: { 𝑧 = 0 𝑥2 + 𝑦2 ≤ 9 𝑆 = ∬ √1 + 𝑧′2 2 𝑥 + 𝑧′2 𝑦
𝑑𝑥𝑑𝑦 = ∬ √1 + 4𝑥 + 4𝑦2 𝑑𝑥𝑑𝑦 𝐷 𝐷 𝑥 = 𝑟𝑐𝑜𝑠𝜑
Đặ𝑡 {𝑦 = 𝑟𝑠𝑖𝑛𝜑 |𝐽| = 𝑟
𝑀𝑖ề𝑛 𝐷 𝑡𝑟ở 𝑡ℎà𝑛ℎ ∶ { 0 ≤ 𝑟 ≤ 3 0 ≤ 𝜑 ≤ 2𝜋
→ 𝑆 = ∬ √1 + 4𝑟2 . 𝑟𝑑𝑟𝑑𝜑 𝐷 2𝜋 √ 3 1 + 4𝑟2 = ∫ 𝑑𝜑 ∫ 𝑑(1 + 4𝑟2) 0 0 8 2𝜋 37 37√37 − 1 = = 8 ∫ √𝑢𝑑𝑢 1 6 𝜋. 𝐶ℎọ𝑛 𝐶
𝐂â𝐮 𝟐: 𝑇í𝑛ℎ 𝑑 ệ
𝑖 𝑛 𝑡í𝑐ℎ ℎì𝑛ℎ 𝑝ℎẳ𝑛𝑔 𝑔 ớ
𝑖 𝑖 ℎạ𝑛 𝑏ở𝑖 𝑦 = √3𝑥, 𝑦 = 0, 𝑥2 + 𝑦2 = 2𝑥
𝑆𝐷 = ∬𝑑𝑥𝑑𝑦 𝐷 𝑥 = 𝑟𝑐𝑜𝑠𝜑
Đặ𝑡 {𝑦 = 𝑟𝑠𝑖𝑛𝜑 |𝐽| = 𝑟
0 ≤ 𝑟 ≤ 2𝑐𝑜𝑠𝜑
𝑀𝑖ề𝑛 𝐷 𝑡𝑟ở 𝑡ℎà𝑛ℎ ∶ { 𝜋 0 ≤ 𝜑 ≤ 3
𝑆𝐷 = ∬𝑟𝑑𝑟𝑑𝜑 𝐷 𝜋 2𝑐𝑜𝑠𝜑 = ∫ 𝑑 3 𝜑 ∫ 𝑟𝑑𝑟 0 0 𝜋 = ∫ 2 3 (𝑐𝑜𝑠𝜑)2𝑑𝜑 0 TEAM GIẢI TÍCH 2 55 𝜋 𝜋 = ∫ (3 √3
1 + 𝑐𝑜𝑠2𝜑)𝑑𝜑 = 0 3 + 4 . 𝐶ℎọ𝑛 𝐷
𝐂â𝐮 𝟑: 𝑇í𝑛ℎ 𝑡ℎể 𝑡í𝑐ℎ 𝑚 ề 𝑖 𝑛 𝑔 ớ
𝑖 𝑖 ℎạ𝑛 𝑏ở𝑖 𝑥 = 1 + 𝑦2 + 𝑧2 𝑣à 𝑥 = 2(𝑦2 + 𝑧2)
𝑉𝑉 = ∭𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 𝑥 = 𝑥
Đặ𝑡 {𝑦 = 𝑟𝑐𝑜𝑠𝜑 → |𝐽| = 𝑟 𝑧 = 𝑟𝑠𝑖𝑛𝜑 2𝑟2 ≤ 𝑥 ≤ 1 + 𝑟2 𝑀𝑖ề𝑛 𝑉 𝑡 ở 𝑟 𝑡ℎà𝑛ℎ { 0 ≤ 𝑟 ≤ 1 0 ≤ 𝜑 ≤ 2𝜋
→ ∭𝑑𝑥𝑑𝑦𝑑𝑧 = ∭𝑟𝑑𝑟𝑑𝜑𝑑𝑥 𝑉 𝑉 2𝜑 1 1+𝑟2
= ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ 𝑟𝑑𝑥 0 0 2𝑟2 1 𝜋
= 2𝜋 ∫ 𝑟(1 + 𝑟2 − 2𝑟2)𝑑𝑟 = 0 2 . 𝐶ℎọ𝑛 𝐷 𝑎𝜋
𝐂â𝐮 𝟒: 𝑀𝑖ề𝑛 𝐷 𝑔 ớ
𝑖 𝑖 ℎạ𝑛 𝑏ở𝑖 (𝑥2 + 𝑦2)2 = 2𝑥3. 𝑆𝐷 =
𝑏 . 𝑇í𝑛ℎ 𝑎+ 𝑏? 𝑥 = 𝑟𝑐𝑜𝑠𝜑
Đặ𝑡 {𝑦 = 𝑟𝑠𝑖𝑛𝜑 |𝐽| = 𝑟
0 ≤ 𝑟 ≤ 2(𝑐𝑜𝑠𝜑)3
𝑀𝑖ề𝑛 𝐷 𝑡𝑟ở 𝑡ℎà𝑛ℎ { 𝜋 𝜋 − 2 ≤ 𝜑 ≤ 2 𝜋 2(𝑐𝑜𝑠𝜑)3 𝑆 2
𝐷 = ∬ 𝑑𝑥𝑑𝑦 = ∫ 𝑑𝜑 ∫ 𝑟𝑑𝑟 𝐷 −𝜋 2 0 𝜋 = 2 ∫ ( 2 𝑐𝑜𝑠𝜑)6𝑑𝜑 −𝜋2 𝜋
= 4 ∫ (2𝑐𝑜𝑠𝜑)6𝑑𝜑 0 𝜋 5‼
= 4. 2.6‼(𝑇í𝑐ℎ 𝑝ℎâ𝑛 𝑊𝑎𝑙𝑙𝑖𝑠) TEAM GIẢI TÍCH 2 56 5𝜋 = 8 .𝐶ℎọ𝑛 𝐴 𝜋 𝜋 𝜋 (𝑛 − 1)‼
∗ 𝑇í𝑐ℎ 𝑝ℎâ𝑛 𝑊𝑎𝑙𝑙𝑖𝑠 ∫ (2 2
𝑠𝑖𝑛)𝑛𝑑𝜑 = ∫ (𝑐𝑜𝑠𝜑)𝑛𝑑𝜑 = {2 .
𝑛‼ 𝑛ế𝑢 𝑛 𝑐ℎẵ𝑛 0 0 (𝑛 − 1)‼ 𝑛‼ 𝑛ế𝑢 𝑛 𝑙ẻ
𝐂â𝐮 𝟓: 𝑇í𝑛ℎ 𝑣ậ𝑡 𝑡ℎể 𝑉 𝑥á𝑐 đị𝑛ℎ 𝑏ở𝑖 √𝑥2 + 𝑦2 ≤ 𝑧 ≤ 6 − 𝑥2 − 𝑦2
𝑉𝑉 = ∭𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 𝑥 = 𝑟𝑐𝑜𝑠𝜑
Đặ𝑡 {𝑦 = 𝑟𝑠𝑖𝑛𝜑 → |𝐽| = 𝑟 𝑧 = 𝑧 𝑟 ≤ 𝑧 ≤ 6 − 𝑟2 𝑀𝑖ề𝑛 𝑉 𝑡 ở 𝑟 𝑡ℎà𝑛ℎ { 0 ≤ 𝑟 ≤ 2 0 ≤ 𝜑 ≤ 2𝜋
→ ∭𝑑𝑥𝑑𝑦𝑑𝑧 = ∭𝑟𝑑𝑟𝑑𝜑𝑑𝑧 𝑉 𝑉 2𝜋 2 6−𝑟2
= ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ 𝑟𝑑𝑧 0 0 𝑟 2 32𝜋
= 2𝜋 ∫ 𝑟(6−𝑟2 − 𝑟)𝑑𝑟 = 0 3 . 𝐶ℎọ𝑛 𝐵
𝐂â𝐮 𝟔: 𝑇í𝑛ℎ 𝑡ℎể 𝑡í𝑐ℎ 𝑣ậ𝑡 𝑡ℎể 𝑔 ớ
𝑖 𝑖 ℎạ𝑛 𝑏ở𝑖 𝑐á𝑐 𝑚ặ𝑡 𝑧= 𝑥2 + 3𝑦2 và 𝑧 = 4 − 3𝑥2 − 𝑦2
𝑉𝑉 = ∭𝑑𝑥𝑑𝑦𝑑𝑧 𝑉
→ 𝑀𝑖ề𝑛 𝑉: {𝑥2 + 3𝑦2 ≤ 𝑧 ≤ 4 − 3𝑥2 − 𝑦2 𝑥2 + 𝑦2 ≤ 1. (𝐷)
∭ 𝑑𝑥𝑑𝑦𝑑𝑧 = ∬(4 − 3𝑥2 − 𝑦2 − 𝑥2 − 3𝑦2)𝑑𝑥𝑑𝑦 𝑉 𝐷
= 4 ∬ (1 − 𝑥2 − 𝑦2)𝑑𝑥𝑑𝑦 𝐷 𝑥 = 𝑟𝑐𝑜𝑠𝜑
Đặ𝑡 {𝑦 = 𝑟𝑠𝑖𝑛𝜑 |𝐽| = 𝑟 TEAM GIẢI TÍCH 2 57
𝑀𝑖ề𝑛 𝐷 𝑡𝑟ở 𝑡ℎà𝑛ℎ ∶ { 0 ≤ 𝑟 ≤ 1 0 ≤ 𝜑 ≤ 2𝜋 → 𝑉 2
𝑉 = 4 ∬ (1 − 𝑟 )𝑟𝑑𝑟𝑑𝜑 𝐷 2𝜋 1
= 4 ∫ 𝑑𝜑 ∫ (1 − 𝑟2)𝑟𝑑𝑟 0 0 = 2𝜋. 𝐶ℎọ𝑛 𝐶. TEAM GIẢI TÍCH 2 58
IV. TÍCH PHÂN PHỤ THUỘC THAM SỐ
( Vì là thi TN nên chúng ta sẽ tập làm theo cách và hướng giải nhanh nhất có
thể, không lan man suy nghĩ đến điều kiện ở 1 số câu tích phân xác định hay
suy rộng phụ thuộc tham số nữa, mà đa số chúng ta sẽ thay trực tiếp số vào
để có thể giải 1 cách nhanh nhất. Vì vậy, lời giải ở 1 số câu ở dưới sẽ trực tiếp
thay số và bỏ qua xét các điều kiện cần ).
4.1. TÍCH PHÂN XÁC ĐỊNH PHỤ THUỘC THAM SỐ
Câu 1: Tính ∫𝜋/2 ln (1 0 +y𝑠𝑖𝑛2𝑥)𝑑𝑥 𝑣ớ𝑖 𝑦>1
Đáp án: A. 𝜋 ln(1 + √𝑦 + 1) − 𝜋𝑙𝑛2 Giải: 𝜋
Nhận thấy: I(y)= ∫2 ln (1 0 +y𝑠𝑖𝑛2𝑥)𝑑𝑥
𝑙à ℎà𝑚 𝑠ố 𝑘ℎả 𝑣𝑖 𝑡 ê 𝑟 𝑛 (1, +∞) 𝜋/2 1 ⇒ 𝐼′(𝑦) = ∫ 𝑑𝑥 0 𝑦 + 1 𝑠𝑖𝑛2𝑥 Đặt t= tanx ⇒
𝑑𝑡 = 1 𝑑𝑥 = ( 1+ 𝑡𝑎𝑛2𝑥)𝑑𝑥 = 𝑑𝑡 𝑐𝑜𝑠2𝑥 𝑡2+1 Với x=0 ⇒
𝑡 = 0 ; x=𝜋 ⇒ 𝑡→ +∞ 2 𝜋 2 1 +∞ 1 1 ⇒ 𝐼′ = ∫ 𝑑𝑥 = ∫ 2 0 𝑦 + 1 0
𝑦 + (1 + 𝑐𝑜𝑡 𝑥) . 𝑡2 + 1 𝑑𝑡 𝑠𝑖𝑛2𝑥 𝜋 𝜋 2 1 = ∫ 1 2 1 1 . 𝑑𝑥 = ∫ . 0 𝑦 + (1 + 1 𝑡2 + 1 0 𝑡2 + 1 𝑡𝑎𝑛2𝑥) 𝑦 + (1 + 1𝑡2) 𝜋 2 𝑡2 𝑑𝑡 1 +∞ 1 1 = ∫
0 𝑡2𝑦 + 𝑡2 + 1 . 𝑡2 + 1 = 𝑦 ∫0
𝑡2 + 1 − 𝑡2(1 + 𝑦) + 1 𝑑𝑡 1 =
1 arctan𝑡√1+𝑦 |𝑡 = +∞
𝑦 [𝑎𝑟𝑐𝑡𝑎𝑛𝑡 − √1 + 𝑦 𝑡 = 0 ] 1 𝜋 = 𝜋 𝜋 ) = 𝑦 (2 − 2√1 + 𝑦
2√1 + 𝑦. (1 + √1 + 𝑦) 1
⇒ 𝐼(𝑦) = ∫ 𝐼′(𝑦)𝑑𝑦 = 𝜋 ∫ 𝑑𝑦
2√1 + 𝑦. (1 + √1 + 𝑦) TEAM GIẢI TÍCH 2 59 1 = 𝜋 ∫
𝑑( 1 + √1 + 𝑦) = 𝜋 ln(1 + √𝑦 + 1) + 𝐶 (1 + √1 + 𝑦)
Do I(0)= 0 ⇒ 𝐶 = −𝜋𝑙𝑛2
Vậy I(y)= 𝜋 ln(1 + √𝑦 + 1) − 𝜋𝑙𝑛2
Câu 2: Tính giới hạn sau: 1
lim ∫ √𝑥3 + 𝑦3𝑑𝑥 𝑦⟶0 0 Đáp án: B.0,4 Giải: Thay số trực tiếp: 1 1 2
lim ∫ √𝑥3 + 𝑦3𝑑𝑥 = 𝐼(0) = ∫ √𝑥3𝑑𝑥 = 𝑦⟶0 0 0 5 Vậy chọn B.
Câu 3:Tính giới hạn: 𝑥 1 2015cos (𝑥𝑦) lim ∫
𝑦⟶0 −1 1 + 𝑥2 + 𝑦2 𝑑𝑥 Đáp án: D. 2 3 Giải: Thay số vào trực tiếp: 𝑥 1 2015cos (𝑥𝑦) 1 𝑥2015 2 lim ∫ (0) ∫
𝑦⟶0 −1 1 + 𝑥2 + 𝑦2 𝑑𝑥 = 𝐼 = −11+ 𝑥2𝑑𝑥 = 3 Câu 4: Tính : 𝑠𝑖𝑛 𝑎 𝑦 𝑟𝑐cot (𝑥 + 𝑦) lim ∫
𝑦⟶0 𝑐𝑜𝑠𝑦 1 + 𝑥2 + 𝑦2 𝑑𝑥 Đáp án: A.−3𝜋2 32 Giải: Thay số trực tiếp: TEAM GIẢI TÍCH 2 60
𝑠𝑖𝑛𝑦𝑎𝑟𝑐cot (𝑥 + 𝑦) 𝑎0𝑟𝑐cot (𝑥) lim ∫ = 𝐼(0) = ∫
𝑦⟶0 𝑐𝑜𝑠𝑦 1 + 𝑥2 + 𝑦2 𝑑𝑥 1 + 𝑥2 𝑑𝑥 1 1 𝑎𝑟𝑐cot (𝑥)2 −3𝜋2 = ∫ 𝑎𝑟𝑐cot
(𝑥)𝑑(𝑎𝑟𝑐cot 𝑥) = 0 2 |10 = 32
Câu 5: Cho I(y)= ∫1 sin (𝑥2 + 𝑥𝑦 ′ 𝑦 +𝑦2)𝑑𝑥 . 𝑇í𝑛ℎ 𝐼(0) Đáp án: A. 𝑠𝑖𝑛1 2 Giải: *Phân tích: Hàm f(x,y)= sin
(𝑥2 + 𝑥𝑦 +𝑦2) 𝑥á𝑐 đị𝑛ℎ 𝑣ớ𝑖 𝑚ọ𝑖 𝑥, 𝑦 ∈ R
Chọn ngẫu nhiên [-1,1]x[-1,1] ( chứa điểm y=0) *Nhận thấy:
𝑓(𝑥, 𝑦)𝑘ℎả 𝑣𝑖 𝑣à 𝑙ê
𝑖 𝑛 𝑡ụ𝑐 𝑡𝑟ê𝑛 [−1,1]x[−1,1]
{ 𝑎(𝑦) = 𝑦, 𝑏(𝑦) = 1 𝑣à 𝑘ℎả 𝑣𝑖 𝑡𝑟ê𝑛 [−1,1]
𝑓′𝑦(𝑥,𝑦)𝑙𝑖ê𝑛 𝑡ụ𝑐 𝑡𝑟ê𝑛 [−1,1]x[−1,1] Áp dụng công thức: 𝑏(𝑦)
𝐼′(𝑦) = 𝑓(𝑏(𝑦), 𝑦). 𝑏′ ′ ′
𝑦(𝑦). 𝑓(𝑎(𝑦), 𝑦). 𝑎𝑦(𝑦) + ∫ 𝑓𝑦(𝑥, 𝑦)𝑑𝑥 𝑎(𝑦) 1
= 𝑓(1, 𝑦)𝛽. 0 − 𝑓(𝑦, 𝑦). 1 + ∫ (𝑥 + 2𝑦)cos
(𝑥2 + 𝑥𝑦 + 𝑦2)𝑑𝑥 𝑦
⇒ 𝐼′(0) = 𝑓(1,0). 0 − 𝑓(0,0). 1 1 1 1 1 𝑠𝑖𝑛1
+ ∫ 𝑥𝑐𝑜𝑠(𝑥2)𝑑𝑥 = 2∫ cos(𝑥2)𝑑(𝑥2) = 0 0 2 sin(𝑥2) |10 = 2 Câu 6: Cho I(y)= 𝜋 ∫ 2 ln
(𝑦2𝑠𝑖𝑛2𝑥 + 𝑐𝑜𝑠2𝑥) 0 𝑑𝑥. Tính 𝐼′(1) Đáp án: B. 𝜋 2 Giải: *Phân tích : Cho [𝛼, 𝛽]
𝑠𝑎𝑜 𝑐ℎ𝑜 𝑦 = 1 ∈ [𝛼, 𝛽] 𝑣à 𝑡 á
𝑟 𝑛ℎ 𝑘ℎô𝑛𝑔 đượ𝑐 để 𝑦 ∈
[𝛼,𝛽] 𝑙à𝑚 𝑐ℎ𝑜 ℎà𝑚 𝑓(𝑥, 𝑦) 𝑔 á 𝑖 𝑛 đ𝑜ạ𝑛 Hàm
𝑓(𝑥, 𝑦) = ln( 𝑦2𝑠𝑖𝑛2𝑥 + 𝑐𝑜𝑠2𝑥) 𝑏ị 𝑔 á
𝑖 𝑛 đ𝑜ạ𝑛 𝑡ạ𝑖 𝑦 = 0, 𝑥 = 𝜋 2 TEAM GIẢI TÍCH 2 61 ⇒ 𝑡 á
𝑟 𝑛ℎ để đ𝑖ể𝑚 𝑦 = 0 𝑛ằ𝑚 𝑡𝑟𝑜𝑛𝑔 [𝛼, 𝛽], 𝑐ℎọ𝑛 𝑘ℎ𝑜ả𝑛𝑔 𝑏ấ𝑡 𝑘ì [1,2] *Tính toán: 2𝑦𝑠𝑖𝑛2𝑥
𝑇𝑎 𝑐ó: 𝑓′𝑦 = 𝑦2𝑠𝑖𝑛2𝑥 + 𝑐𝑜𝑠2𝑥 Áp dụng công thức: 𝑏
𝐼′(𝑦) = ∫ 𝑓′𝑦(𝑥,𝑦)𝑑𝑥 𝑎 Thay số: 𝜋 𝜋 𝜋 𝐼′(1) = ∫ 𝑓 2 ′ 2 2𝑠𝑖𝑛2𝑥 𝑦(𝑥, 𝑦)𝑑𝑥 = ∫ = 2 2 0
0 𝑠𝑖𝑛 𝑥 + 𝑐𝑜𝑠 𝑥 2 Câu 7: Tìm 𝑎 𝑦 𝑟𝑐tanx lim ∫
𝑦⟶1 0 𝑥2 + 𝑦2 𝑑𝑥 Đáp án: B. π2 32 Giải: Thay trực tiếp: 𝑎 𝑦 𝑟𝑐tanx lim ∫
𝑦⟶1 0 𝑥2 + 𝑦2 𝑑𝑥 = 𝐼(1) 𝑎 1 𝑟𝑐tanx = ∫0 𝑥2 +1 𝑑𝑥 1 𝜋2
= ∫ 𝑎𝑟𝑐𝑡𝑎𝑛𝑥 𝑑(𝑎𝑟𝑐𝑡𝑎𝑛𝑥) (arctan 𝑥)2 = ( 0 2 ) |10 = 32 Câu 8: Tính
𝑐𝑜𝑠𝑦 𝑎𝑟𝑐tan (𝑥𝑦) lim ∫ 𝑦⟶0 1 + 𝑥2 + 𝑦2 𝑑𝑥 𝑠𝑖𝑛𝑦 Đáp án : C. 𝜋2 32 Giải: Thay số trực tiếp: TEAM GIẢI TÍCH 2 62 𝑐𝑜𝑠 𝑎 𝑦 𝑟𝑐tan (𝑥 + 𝑦) a1rctan 𝑥 lim ∫ = 𝐼(0) = ∫
𝑦⟶0 𝑠𝑖𝑛𝑦 1 + 𝑥2 + 𝑦2 𝑑𝑥 0 1 + 𝑥2 𝑑𝑥 1
= ∫ 𝑎𝑟𝑐𝑡𝑎𝑛𝑥 𝑑(𝑎𝑟𝑐𝑡𝑎𝑛𝑥) (arctan 𝑥)2 = ( 𝜋2 2 ) |10 = 0 32
Câu 9: Tính lim ∫2𝑦 𝑥2 𝑦 sin (𝜋𝑦𝑥) 𝑑𝑥. 𝑦⟶1 Đáp án: A. 2−5𝜋 𝜋2 Giải: Thay trực tiếp: 2𝑦 2 lim ∫ 𝑥2sin
(𝜋𝑦𝑥) 𝑑𝑥 = 𝐼(1) = ∫ 𝑥2sin (𝜋𝑥)𝑑𝑥 𝑦⟶1 𝑦 1 2𝑥𝑑𝑥 = 𝑑𝑢 Đặt { 𝑥2 = 𝑢
sin(𝜋𝑥) 𝑑𝑥 = 𝑑𝑣 ⟹ { −𝑐𝑜𝑠(𝜋𝑥) = 𝑣 𝜋 Ta có: 2
−𝑥2𝑐𝑜𝑠(𝜋𝑥) 2 2 2 𝐼(1) = ∫ 𝑥2sin (𝜋𝑥)𝑑𝑥 = 𝜋𝑥 𝑑𝑥 1 𝜋 | 1 + 𝜋∫ xcos ( ) 1 𝑑𝑥 = 𝑑𝑢 Đặt: { 𝑥 = 𝑢
cos(𝜋𝑥) 𝑑𝑥 = 𝑑𝑣 ⟹ {sin (𝜋𝑥) = 𝑣 𝜋 Ta có: −5 2 sin(𝜋𝑥) 2 1 2
−5 cos(𝜋𝑥) 2 2 − 5𝜋
𝐼(1) = 𝜋 + 𝜋( 𝜋 𝑥|1 −𝜋∫ sin (𝜋𝑥)𝑑𝑥) = 1 𝜋 + 𝜋2 | 1 = 𝜋2
Câu 10:Tính giới hạn 1 lim 𝑥2020 + 𝑦2021 ∫
𝑦⟶0 −1 1 + 𝑥2 + 2021𝑦2 𝑑𝑥 Đáp án: Giải: Thay số trực tiếp: 1 𝑥2020 + 𝑦2021 1 𝑥2020 lim ∫
𝑦⟶0 −1 1 + 𝑥2 + 2021𝑦2 𝑑𝑥 = 𝐼(0) = ∫ 1 + 𝑥2 𝑑𝑥 −1 𝑥2020 = 𝑢
Đặt { 1 𝑑𝑥 = 𝑑𝑣 ⇒ {2020𝑥2019𝑑𝑥 = 𝑑𝑢 1+𝑥2
𝑎𝑟𝑐𝑡𝑎𝑛𝑥 = 𝑣 TEAM GIẢI TÍCH 2 63 1
𝐼(0) = 𝑎𝑟𝑐𝑡𝑎𝑛𝑥2020 | 1
−1 − 2020 ∫ 𝑎𝑟𝑐𝑡𝑎𝑛𝑥. 𝑥2019𝑑𝑥 −1
4.2. TÍCH PHÂN SUY RỘNG PHỤ THUỘC THAM SỐ
Câu 1: Tính I(y)= ∫+∞ arctan (x+y) 𝑑𝑥 0 𝑥2+1 Đáp án: A. 2𝜋 𝑦2+𝑦
Lời giải : Ta có:
𝑓(𝑥, 𝑦) = arctan(x+y) 𝑙𝑖ê𝑛 𝑡ụ𝑐 𝑡 ê 𝑟 𝑛 [0, +∞) x R 𝑥2+1 ⇒ 𝑓′𝑦 = 1 𝑙𝑖ê𝑛
𝑡ụ𝑐 𝑡𝑟ê𝑛 [0, +∞) x R (1+𝑥2)[1+(𝑥+𝑦)2] +∞ +∞ 1
I′ (𝑦) = ∫ 𝑓′𝑦𝑑𝑥 = ∫ ( 0 0
1 + 𝑥2)[1 + (𝑥 + 𝑦)2] 𝑑𝑥 1 𝐴𝑥 + 𝐵 𝐶𝑥 + 𝐷
Đặ𝑡 (1 + 𝑥2)[1 + (𝑥 + 𝑦)2] = 1 + 𝑥2 + 1 + (𝑥 + 𝑦)2
Đồng nhất thức hệ số, ta được: −2 𝐴 = 2 1 3
𝑦(𝑦2 + 4) , 𝐵 = 𝑦(𝑦2 + 4) ,𝐶 = (𝑦2 + 4) , 𝐷 = (𝑦2 + 4) 1 +∞ I′ (𝑦) = −2𝑥 + 𝑦 2𝑥 + 3𝑦 (𝑦2 + 4) ∫ [ 0
1 + 𝑥2 + 1 + (𝑥 + 𝑦)2] 𝑑𝑥 1 = [
(𝑦2 + 4) − ln(1 + 𝑥2) + 𝑦. 𝑎𝑟𝑐𝑡𝑎𝑛𝑥 2𝜋
+ ln[1 + (𝑥 + 𝑦)2] + 𝑦. arctan(𝑥 + 𝑦) ]|10 = 𝑦2 +𝑦 𝑎𝑥 Câu 2: +∞ Tính ∫ 𝑒− − −𝑒 𝑏𝑥 𝑑𝑥 0 𝑥 Đáp án: A. -lna+lnb Lời giải: + 𝑒
∞ −𝑎𝑥 − 𝑒−𝑏𝑥
Đặ𝑡 𝐼(𝑥, 𝑎) = ∫ 0 𝑥
𝑑𝑥 (𝑐𝑜𝑖 𝑏 𝑙à 𝑡ℎ𝑎𝑚 𝑠ố)
𝑒−𝑎𝑥 − 𝑒−𝑏𝑥 𝑓(𝑥, 𝑎) = ′ 𝑥
⇒ 𝑓𝑎(𝑥,𝑎) = −𝑒−𝑎𝑥 TEAM GIẢI TÍCH 2 64 +∞ +∞ −1
𝐼′(𝑎) = ∫ 𝑓′𝑎(𝑥, 𝑎)𝑑𝑥 = ∫ −𝑒−𝑎𝑥𝑑𝑥 = 0 0 𝑎 −1
⇒ 𝐼(𝑎) = ∫ 𝐼′(𝑎)𝑑𝑎 = ∫
𝑎 𝑑𝑎 = −𝑙𝑛𝑎 + 𝐶 + 𝑒
∞ −𝑎𝑥 − 𝑒−𝑏𝑥 𝑑𝑜 𝐼(𝑏) = ∫ 𝑥
𝑑𝑥 = 0 ⇒ −𝑙𝑛𝑏 + 𝐶 = 0 ⇒ 𝐶 = 𝑙𝑛𝑏 0 + 𝑒
∞ −𝑎𝑥 − 𝑒−𝑏𝑥 𝑉ậ𝑦 ∫ 𝑏 0 𝑥
𝑑𝑥 = −𝑙𝑛𝑎 + 𝑙𝑛𝑏 = ln ( 𝑎) Câu 3: Tính 𝑦 𝑐𝑜𝑠xy lim ∫ 𝑦⟶0 0 𝑥2 + 1 𝑑𝑥 Đáp án: A. 𝜋/2
Lời giải : Thay số trực tiếp: + 𝑐𝑜𝑠 ∞ 𝑦𝑥 +∞ 1 𝜋 lim ∫
𝑦→0 0 1 + 𝑥2 𝑑𝑥 = 𝐼(0) = ∫ 1 + 𝑥2 𝑑𝑥 = 0 2 Câu 4: Tính +∞ sin(𝑏𝑥) − sin (𝑐𝑥) ∫ 𝑒−𝑎𝑥 0 𝑥 𝑑𝑥
Đáp án: A. arctan(𝑏) - arcrtan(𝑐 ) 𝑎 𝑎
Lời giải : (𝑏𝑥) 𝑐𝑥
𝑇𝑎 𝑐ó: 𝑒−𝑎𝑥 sin − sin ( ) 𝑥
= 𝐹(𝑥, 𝑏) − 𝐹(𝑥, 𝑐) 𝑏 𝑏
= ∫ 𝐹′𝑦(𝑥, 𝑦)𝑑𝑦 = ∫ 𝑒−𝑎𝑥.cos (𝑦𝑥)𝑑𝑦 𝑐 𝑐 +∞ 𝑏
𝐼 = ∫ (∫ 𝑒−𝑎𝑥. cos(𝑦𝑥) 𝑑𝑦) 𝑑𝑥 ) 0 𝑐 𝑎 𝑏 𝑎
= (− 𝑎2 + 𝑦2.𝑒−𝑎𝑥.cos(𝑦𝑥) + 𝑎2 + 𝑏2.𝑒−𝑎𝑥.sin(𝑦𝑥)))|+∞0 = 𝑎2 + 𝑦2 TEAM GIẢI TÍCH 2 65 +∞ 𝑏 𝑏 +∞
𝐼 = ∫ (∫ 𝑒−𝑎𝑥. cos(𝑦𝑥) 𝑑𝑦) 𝑑𝑥 ) = ∫ (∫ 𝑒−𝑎𝑥. cos(𝑦𝑥) 𝑑𝑥) 𝑑𝑦 ) 0 𝑐 𝑐 0 𝑏 𝑎 𝑦 𝑏 𝑏 𝑐 = ∫
𝑐 𝑎2 + 𝑦2 𝑑𝑦 = 𝑎𝑟𝑐𝑡𝑎𝑛𝑎 | 𝑐 = arctan ( 𝑎) − arcrtan (𝑎) Câu 5: Tính +∞2−𝑥 − 3−𝑥 ∫ 0 𝑥 𝑑𝑥 Đáp án: B. ln(𝑙𝑛2) 𝑙𝑛3
Lời giải: 3 𝑡−𝑥 2−𝑥 − 3−𝑥
𝑇𝑎 𝑐ó: ∫ 𝑡−𝑥−1𝑑𝑡 = 2 −𝑥 |32 = 𝑥 +∞ 3
𝐼2 = ∫ (∫ 𝑡−𝑥−1𝑑𝑡 ) 𝑑𝑥 0 2 3 +∞ 3 𝑡−𝑥−1
= ∫ (∫ 𝑡−𝑥−1𝑑𝑥 )𝑑𝑡 = ∫ ( 2 0 2 −𝑙𝑛𝑡 |+∞ 0 ) 𝑑𝑡 3 1 𝑙𝑛2 = ∫
2 𝑡. 𝑙𝑛𝑡 𝑑𝑡 = ln(𝑙𝑛𝑡) |3 4 = ln ( 𝑙𝑛3) ---HẾT--- TEAM GIẢI TÍCH 2 66 TEAM GIẢI TÍCH 2 67