Bộ đề thi giữa kỳ học phần Giải tích 2 | Đại học Bách Khoa Hà Nội

Bộ đề thi giữa kỳ học phần Giải tích 2 | Đại học Bách Khoa Hà Nội. Tài liệu được biên soạn giúp các bạn tham khảo, củng cố kiến thức, ôn tập và đạt kết quả cao kết thúc học phần. Mời các bạn đọc đón xem!

30 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Giải tích 2

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

82 trang 1 tháng trước

Tác giả:

Profile Thùy Dương
BÁCH KHOA- I C ÔN PHĐẠ ƯƠNG M ÁI
BÀI GI I THAM KH Ả ẢO
GIẢI TÍCH II
______________________________________________
Đề ữ thi gi a kì 20163-20193
Người biên soạn: Phạm Thanh Tùng
(Tự Động H óa – ĐHBKHN)
H Nà ội, áng 5 n 1 Th ăm 202
TÀI LI U THAM KH Ệ ẢO:
− Bài gi ng môn Gi i tích II, th y Bùi Xuân Diả ả ầ ệu.
− Bài t p gi i s n Gi i tích 2 (Tóm t t lý thuy t và chậ ả ẵ ả ắ ế ọn l c), th y Tr n Bình.ọ ầ ầ
− Bài t p Toán h c cao c p, t p hai: Gi i tích, GS.TS Nguyậ ọ ấ ậ ả ễn Đình Trí (chủ
biên), PGS.TS. Tr n Viầ ệt Dũng, PGS.TS. Trần Xuân Hi n, PGS.TS Nguyề ễn
Xuân Thảo.
− Bộ đề cương Giải tích II, Viện Toán ng d ng và Tin hứ ụ ọc.
− Bộ đề thi Gi a kì và Cu i kì môn Giữ ố ải tích II Trường ĐH Bách Khoa Hà Nội.
Tài li c biên so n d a trên kinh nghiệu đượ ạ ự ệm cá nhân, dù đã rất cố gắng
nhưng với những hạ ấ địn chế nh t nh về kiến th c, kứ ĩ n c chăng chắ ắn vẫn sẽ
tồn t i các l i sai tính toán, l ạ ỗ ỗi đánh máy, … chưa được kiểm tra hết, m i ý ọ
kiến góp ý b c vui lòng g i ạn đọ ử qua link fb “fb.com/tungg810” để mình có thể
kiểm tra, hoàn thi n b tài li u. Xin chân thành cệ ộ ệ ảm ơn!
PHẦN I:
ĐỀ THI
VIỆN TOÁN NG D NG VÀ TIN H C Ứ Ụ Ọ
ĐỀ ĐỀ Ữ 1 THI GI A KỲ MÔN GI I TÍCH 2 H c kì 20163 Ả – ọ
i gian: 60 phút Thờ
Chú ý: Thí sinh không được sử dụng tài liệu và Giám thị phải kí xác nhận số đề vào bài thi
của sinh viên.
Câu 1: (1đ). Viết phương trình tiếp diện và pháp tuyến của mặt cong t𝑥
2
+ 3𝑦+ 2𝑧
3
= 3 ại
𝑀
(
2; −1; 1
)
Câu 2: (1đ). Tìm hình bao c a h ng th ng v là tham s . ủ ọ đườ ẳ 𝑦= 2𝑐𝑥− 𝑐
2
ới 𝑐 ố
Câu 3: (1đ). Tìm điểm có độ ủa đườ cong lớn nhất c ng cong 𝑦= ln 𝑥
Câu 4: (1đ). Đổi th t l y tích phân: ứ ự ấ
∫ 𝑑𝑥
1
0
∫ 𝑓(𝑥, 𝑦)𝑑𝑦
1
√
2𝑥−𝑥
2
Câu 5: (2đ). Tính các tích phân kép sau:
𝑎) ∬
(
3𝑥+ 2𝑦𝑑𝑥𝑑𝑦
)
𝐷
, 𝐷 ền ới hạn bởi các 𝑦= 𝑥là mi gi đường
2
và 𝑦= 1
𝑏) ∬
𝑥𝑦
𝑥
2
+ 𝑦
2
𝑑𝑥𝑑𝑦
𝐷
với 𝐷=
{(
𝑥, 𝑦
)
∈𝑅
2
: 1 ≤ 𝑥
2
+ 𝑦
2
≤ 2𝑥, 𝑦≥ 0
}
Câu 6: (1đ). Tính th tích c a v t th gi i h n b i các m t ể ủ ậ ể 𝑉 ớ ạ ở ặ
𝑧= 𝑥
2
+ 𝑦
2
và 𝑧= 2𝑥+ 4𝑦
Câu 7: (2đ). Tính tích phân b i ba ộ
∭
𝑦𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
trong đó:
a) 𝑉 gi i h n b i các m ớ ạ ở ặt
𝑧= 0, 𝑧= 𝑥 𝑦= 4 + 𝑥
2
, 𝑦= 2𝑥
2
và
2
b) 𝑉 là hình cầu 𝑥
2
+ 𝑦 + 𝑧
2 2
≤ 2𝑦
Câu 8: (1đ). Tính tích phân
∫
𝑒
−𝛼𝑥
2
− 1
𝑥
2
𝑒
𝑥
2
𝑑𝑥
+∞
0
với 𝛼≥ 0
VIỆN TOÁN NG D NG VÀ TIN H C Ứ Ụ Ọ
ĐỀ ĐỀ Ữ 2 THI GI A KỲ MÔN GI I TÍCH 2 H c kì 20172 Ả – ọ
i gian: 60 phút Thờ
Chú ý: Thí sinh không được sử dụng tài liệu và Giám thị phải kí xác nhận số đề vào bài thi
của sinh viên.
Câu 1: (1đ).
Viết phương trình tiếp diện và pháp tuyến của mặt cong tln
(
𝑥
2
+ 3𝑦 − 3𝑧
)
3
= 2 ại
điể
m 𝑀
(
1,0, −1
)
.
Câu 2: (1đ). Tìm hình bao c a h ng cong v là tham s . ủ ọ đườ 𝑐𝑥 − 2𝑦− 𝑐
2 3
+ 1 = 0 ới 𝑐 ố
Câu 3: (1đ).
Tính độ ủa đườ ại điể cong c ng t𝑦= ln
(
sin 𝑥
)
m ứng với 𝑥= 𝜋/4.
Câu 4: (2đ). Tính các tích phân sau:
𝑎) ∬
(
𝑥
2
− 4𝑦
2
)
𝑑𝑥𝑑𝑦
𝐷
, 𝐷 ền ới hạn bởi 𝑦= 𝑥, 𝑥= 1 𝑦= 0là mi gi và
𝑏) ∬
(
𝑥
2
− 𝑥𝑦+ 𝑦
2
)
𝑑𝑥𝑑𝑦
𝐷
, 𝐷 ền ới hạn bởi 𝑦= −3𝑥+ 1, 𝑦= −3𝑥+ 2, 𝑦= 𝑥là mi gi
và 𝑦= 𝑥+ 2
Câu 5: (1đ). Tính tích phân sau:
∫ 𝑑𝑥
1
0
∫
1
𝑦
5
+ 1
𝑑𝑦
1
√
𝑥
4
Câu 6: (1đ). Tính th tích c a v t th gi i h n b i các m t ể ủ ậ ể 𝑉 ớ ạ ở ặ
𝑧= 𝑥
2
+ 2𝑦 − 𝑦
2
và 𝑧= 3 − 2𝑥
2 2
Câu 7: (1đ).
Tính tích phân b i ba ộ
∭
(
3𝑥𝑦 − 4𝑥𝑦𝑧𝑑𝑥𝑑𝑦𝑑𝑧
2
)
𝑉
trong đó ền xác đị𝑉 là mi nh bởi
1 ≤ 𝑦≤ 2, 0 ≤ 𝑥𝑦≤ 2,0 ≤ 𝑧≤ 2
Câu 8: (1đ).
Tính tích phân b i ba ộ
∭
(
𝑥
2
+ 𝑦 + 𝑧
2 2
)
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
trong đó 𝑉 là miền giới hạn bởi
các mặt 𝑦=
√
𝑥
2
+ 4𝑧
2
, 𝑦= 2.
Câu 9: (1đ). Tính tích phân
∫
𝑒
−𝑎𝑥
2
− 𝑒
−𝑏𝑥
2
𝑥
𝑑𝑥
+∞
0
với 𝑎, 𝑏> 0
VIỆN TOÁN NG D NG VÀ TIN H C Ứ Ụ Ọ
ĐỀ ĐỀ Ữ 4 THI GI A KỲ MÔN GI I TÍCH 2 H c kì 20172 Ả – ọ
i gian: 60 phút Thờ
Chú ý: Thí sinh không được sử dụng tài liệu và Giám thị phải kí xác nhận số đề vào bài thi
của sinh viên.
Câu 1: (1đ). Viết phương trình tiế ủa đườp tuyến và pháp diện c ng cong 𝑥= 4 sin
2
𝑡,𝑦=
4 cos 𝑡, 𝑧= 2 sin 𝑡+ 1 tại điểm 𝑀(1; −2 3
√
; 2)
Câu 2: (1đ). Tìm hình bao c a h ng th ng v là tham s . ủ ọ đườ ẳ 3𝑐𝑥− 𝑦− 𝑐
3
= 0, ới 𝑐 ố
Câu 3: (1đ). Tính độ ủa đườ ại điể cong c ng cong t𝑥= sin 𝑡+ 𝑡cos 𝑡, 𝑦= cos 𝑡+ 𝑡sin 𝑡 m ứng
với 𝑡= 𝜋
Câu 4: (2đ). Tính các tích phân kép sau:
a) ∬2𝑥𝑑𝑥𝑑𝑦
𝐷
, 𝐷 ền ới hạn bởi 𝑦= 𝑥là mi gi
2
𝑦= 2 − 𝑥 và
b) ∬𝑦
√
𝑥
2
+ 𝑦
2
𝑑𝑥𝑑𝑦
𝐷
, vớ𝑖 𝐷=
{(
𝑥, 𝑦
)
∈𝑅
2
: 𝑥
2
+ 𝑦
2
≤ 𝑦
}
Câu 5: (1đ). Tính th tích v t th gi i h n b i các m ể ậ ể 𝑉 ớ ạ ở ặt
𝑥= 9𝑦
2
+ 𝑧
2
𝑥= 9và
Câu 6: (1đ). Tính tích phân sau:
∫ 𝑑𝑦
1
0
∫ 𝑑𝑥
1
0
∫ 𝑥𝑦𝑒
𝑦𝑧
2
𝑑𝑧
1
𝑥
2
Câu 7: (1đ).
Tính
∬
(
4 + 3𝑦𝑑𝑥𝑑𝑦𝑥𝑦
)
𝐷
v ới 𝐷: 1 ≤ 𝑥𝑦≤ 4, 𝑥≤ 𝑦≤ 9𝑥.
Câu 8: (1đ). : Tính tích phân b i ba ộ
∭
𝑧𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
trong đó ền xác đị𝑉 là mi nh bởi
𝑥 𝑥
2
+ 𝑦 + 𝑧
2 2
≤ 𝑧, 𝑧≤
√
2
+ 𝑦
2
Câu 9: (1đ). Tính tích phân
∫
𝑒
−𝑎𝑥
3
− 𝑒
−𝑏𝑥
3
𝑥
𝑑𝑥
+∞
0
với 𝑎, 𝑏> 0
VIỆN TOÁN NG D NG VÀ TIN H C Ứ Ụ Ọ
ĐỀ ĐỀ Ữ 1 THI GI A KỲ MÔN GI I TÍCH 2 H c kì 20173 Ả – ọ
i gian: 60 phút Thờ
Chú ý: Thí sinh không được sử dụng tài liệu và Giám thị phải kí xác nhận số đề vào bài thi
của sinh viên.
Câu 1: (1đ).
Tính độ ủa đườ cong tại 𝑡= 0 c ng {
𝑥= 𝑒
−𝑡
− sin𝑡
𝑦= 𝑒
−𝑡
− cos 𝑡
Câu 2: (1đ).
Lập phương trình pháp tuyến và tiếp diện tại 𝐴
(
1,1,0
)
của mặt 𝑧= ln
(
3𝑥− 2𝑦
)
Câu 3: (1đ).
Cho hàm vecto 𝑝 sin 2𝑡, 2𝑡, 𝑒
(
𝑡
)
=
(
cos
−𝑡
)
và 𝑟 + 1 𝑝
(
𝑡
)
=
(
𝑡
2
) (
𝑡
)
. Tính 𝑟
′
(
0
)
Câu 4: (1đ). Đổi th t l y tích phân ứ ự ấ 𝐼= 𝑑𝑥
∫
2
−1
∫
𝑓
(
𝑥, 𝑦𝑑𝑥𝑑𝑦
)
2−𝑥
2
−𝑥
Câu 5: (1đ).
Tính
∬
(
3𝑥+ 2𝑦𝑑𝑥𝑑𝑦
)
𝐷
, 𝐷 gi i h n b ớ ạ ởi:
𝑥= 0, 𝑦= 0, 𝑥+ 𝑦= 1
Câu 6: (1đ).
Tính
∬
(
𝑥+ 𝑦 𝑥− 2𝑦− 1
)( )
2
𝑑𝑥𝑑𝑦
𝐷
, 𝐷 gi i h n bớ ạ ởi 𝑥+ 𝑦= 0, 𝑥+ 𝑦= 3, 𝑥−
2𝑦= 1, 𝑥− 2𝑦= 2
Câu 7: (1đ). Tính
∭
𝑧√𝑥 + 𝑦
2 2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
, 𝑉 gi i h n bớ ạ ởi 𝑥
2
+ 𝑦
2
= 1, 𝑧= 0, 𝑧= 2
Câu 8: (1đ). Tính th tích v t th gi i h n b ể ậ ể 𝑉 ớ ạ ởi
𝑥=
√
𝑦
2
+ 𝑧
2
, 𝑥=
√
1 − 𝑥
2
− 𝑦
2
Câu 9: (1đ). Tính
∭
3𝑥
2
− 𝑦
2
+ 𝑧
2
+ 1
𝑥
2
+ 𝑦 + 𝑧
2 2
+ 1
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
Với 𝑉 là nửa khối cầu 𝑥
2
+ 𝑦 + 𝑧
2 2
≤ 1, 𝑧≥ 0
Câu 10: (1đ) Tìm gi i h n ớ ạ
lim
𝑦→0
∫
arctan 𝑥+ 𝑦
( )
1 + 𝑥 + 𝑦
2 2
𝑑𝑥
cos𝑦
sin 𝑦
VIỆN TOÁN NG D NG VÀ TIN H C Ứ Ụ Ọ
ĐỀ ĐỀ Ữ 2 THI GI A KỲ MÔN GI I TÍCH 2 H c kì 20182 Ả – ọ
i gian: 60 phút Thờ
Chú ý: Thí sinh không được sử dụng tài liệu và Giám thị phải kí xác nhận số đề vào bài thi
của sinh viên.
Câu 1: (1đ). Viết phương trình tiếp diện và pháp tuyến của mặt cong 𝑥
2
+ 𝑦 − 𝑒
2 𝑧
− 2𝑦𝑥𝑧= 0
t
ại điểm 𝑀
(
1,0,0 .
)
Câu 2: (1đ).
Tìm hình bao c a h ng cong sau: ủ ọ đườ
(
𝑥+ 𝐶
)
2
+
(
𝑦− 2𝐶
)
2
= 5.
Câu 3: (1đ).
Tính tích phân kép
∬
(
𝑥− 4𝑦𝑑𝑥𝑑𝑦
)
𝐷
với 𝐷 ới hạn bởi parabol 𝑦= 𝑥gi
2
− 1 và
trục 𝑂𝑥.
Câu 4: (1đ). Tính tích phân l p: ặ
∫ 𝑑𝑥
2
1
∫
1 − cos 𝜋𝑦
𝑦
2
1
√
𝑥−1
𝑑𝑦
Câu 5: (1đ). Tính di n tích ph n hình tròn n ng tròn ệ ầ 𝑥
2
+ 𝑦
2
= 2𝑦 ằm ngoài đườ 𝑥
2
+ 𝑦
2
= 1
Câu 6: (3đ). Tính các tích phân b i ba sau: ộ
𝑎) ∭
(
3𝑥 + 2𝑦𝑑𝑥𝑑𝑦𝑑𝑧
2
)
𝑉
, trong ền 𝑉 xác đị bởi 0 ≤ 𝑥≤ 1, 0 ≤ 𝑦≤ 𝑥, 0 ≤ 𝑧≤ 𝑥đó mi nh
2
𝑏) ∭
(
𝑥− 𝑦+ 2𝑧𝑑𝑥𝑑𝑦𝑑𝑧
)
𝑉
, trong 𝑉 ợc ới hạn bởi các mặt đó đư gi
𝑥− 𝑦= 0, 𝑥− 𝑦= 2, 𝑥+ 𝑦= 0, 𝑥+ 𝑦= 1, 𝑧= 0, 𝑧= 1
𝑐) ∭
𝑦
2
√4𝑧− 𝑥 − 𝑧
2 2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
, trong V ền xác đị bởi 𝑥đó là mi nh
2
+ 𝑦
2
+ 𝑧
2
≤ 4𝑧, 𝑦≥ 0
Câu 7: (1đ).
Tính độ ại điể ủa đườ cong t m 𝑀
(
−1,0, −1
)
c ng cong là giao của mặt trụ 4𝑥 +
2
𝑦
2
= 4 và m t ph ng ặ ẳ 𝑥− 3𝑧= 2.
Câu 8: (1đ).
Chứng minh r ng hàm sằ ố 𝐼
(
𝑦
)
=
∫
𝑒
−𝑥
1−cos
(
𝑥𝑦
)
𝑥
𝑑𝑥
+∞
0
khả vi trên 𝑅.
VIỆN TOÁN NG D NG VÀ TIN H C Ứ Ụ Ọ
ĐỀ ĐỀ Ữ 3 THI GI A KỲ MÔN GI I TÍCH 2 H c kì 201 Ả – ọ 82
i gian: 60 phút Thờ
Chú ý: Thí sinh không được sử dụng tài liệu và Giám thị phải kí xác nhận số đề vào bài thi
của sinh viên.
Câu 1: (1đ). Viết phương trình tiếp tuyến và pháp diện của đường cong 𝑥= sin 𝑡, 𝑦=
cos
𝑡, 𝑧= 𝑒
2𝑡
tại điểm 𝑀
(
0,1,1 .
)
Câu 2: (1đ). Tính độ ủa đườ ại điể cong c ng t𝑥= 𝑡
2
, 𝑦= 𝑡ln𝑡, 𝑡> 0 m ứng với 𝑡= 𝑒
Câu 3: (1đ). Đổi th t l y tích phân ứ ự ấ
∫ 𝑑𝑥
1
0
∫ 𝑓𝑥, 𝑦𝑑𝑦
( )
1
𝑥
3
Câu 4: (2đ). Tính các tích phân sau:
𝑎) ∬
√
𝑥
2
+ 𝑦
2
𝑑𝑥𝑑𝑦
𝐷
, trong 𝐷: 1 ≤ 𝑥đó
2
+ 𝑦
2
≤ 4, 𝑥+ 𝑦≥ 0
𝑏) ∬
|
cos
(
𝑥+ 𝑦 𝑑𝑥𝑑𝑦
)|
𝐷
, trong 𝐷= [0;đó
𝜋
2
] × [0;
𝜋
2
]
Câu 5: (1đ). Tính tích phân:
∫ 𝑑𝑥
1
0
∫ 𝑑𝑧
1−𝑥
0
∫ 𝑦+ 𝑧𝑑𝑦
( )
2
0
Câu 6: (1đ).
Tính th tích c a mi n gi i h n b i hai parabol và ể ủ ề ớ ạ ở 𝑥= 1 + 𝑦
2
+ 𝑧
2
𝑥= 2
(
𝑦
2
+ 𝑧
2
)
Câu
7: (1đ). Cho hàm vecto kh vi ả 𝑟
(
𝑡
)
: 𝑅→ 𝑅
3
\{0
}.
Ký hi u ệ
|
𝑟 𝑟 .
(
𝑡
)|
dài clà độ ủa
(
𝑡
)
ng Chứ
minh:
𝑑
(|
𝑟
(
𝑡
)|)
𝑑𝑡
=
1
|
𝑟
(
𝑡
)|
𝑟 . 𝑟
(
𝑡
)
′
(
𝑡
)
.
Câu 8: (1đ).
Tính tích phân
∭
(
2𝑦− 𝑧
)
2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
là hình c u trong đó 𝑉 ầ 𝑥
2
+ 𝑦
2
+ 𝑧
2
≤ 1
Câu 9: (1đ).
Chứng minh r ng hàm sằ ố 𝐼
(
𝑦
)
=
∫
𝑒
−𝑥
sin
(
𝑥𝑦
)
𝑥
𝑑𝑥
+∞
0
khả vi trên 𝑅.
VIỆN TOÁN NG D NG VÀ TIN H C Ứ Ụ Ọ
ĐỀ ĐỀ Ữ 1 THI GI A KỲ MÔN GI I TÍCH 2 H c kì 20183 Ả – ọ
i gian: 60 phút Thờ
Chú ý: Thí sinh không được sử dụng tài liệu và Giám thị phải kí xác nhận số đề vào bài thi
của sinh viên.
Câu 1: (1đ). Tìm hình bao c a h ng th ng ủ ọ đườ ẳ 𝑥− 𝑐𝑦+ 𝑐
3
= 0
Câu 2: (1đ).
Viết phương trình tiế ại điểp diện và pháp tuyến của t m 𝐴
(
1; 0; 1
)
của mặt 𝑧= 𝑥𝑒
sin2𝑦
Câu 3: (1đ). Đổi th t l y tích phân: ứ ự ấ
∫ 𝑑𝑥
1
0
∫ 𝑓
(
𝑥, 𝑦𝑑𝑦
)
𝑥
2
−𝑥
Câu 4: (1đ).
Tính
∬
sin + 2𝑦
(
𝑥
2 2
)
𝑑𝑥𝑑𝑦
𝐷
, v là mi n: ới 𝐷 ề
𝑥
2
+ 2𝑦
2
≤
𝜋
2
, 𝑦≥ 0
Câu 5: (1đ). Tính
∭
𝑥+ 𝑦+ 2
(
𝑥+ 1 𝑦+ 1
)( )
𝑧
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
Với i 𝑉 nh bxác đị ở 0 ≤ 𝑥≤ 1, 1 ≤ 𝑦≤ 2, 1 ≤ 𝑧≤ 𝑒
Câu 6: (1đ).
Tính th tích mi n gi i h n b i các mể ề 𝑉 ớ ạ ở ặt 𝑥= −
(
𝑦
2
+ 𝑧
2
)
và 𝑥= −1
Câu 7: (1đ). Tìm gi i h n ớ ạ lim
𝑦→0
∫
arctan 𝑥− 𝑦𝑑𝑥
( )
cos𝑦
sin 𝑦
Câu 8: (1đ). Tìm điểm có độ ủa đườ cong nhỏ nhất c ng 𝑥
2
+ 4𝑦
2
= 4𝑥
Câu 9: (1đ). Tính
∭
(
𝑦+ 1
)
2
𝑥
2
+ 𝑦 + 𝑧 + 3
2 2
𝑑𝑥𝑑𝑦𝑑𝑧
Với i 𝑉 nh bxác đị ở 𝑥
2
+ 𝑦 + 𝑧
2 2
≤ 1
Câu 10: (1đ).
Cho hàm s ố 𝐼
(
𝑦
)
=
∫
ln
(
1+𝑥𝑦
)
1+𝑥
2
𝑦
0
𝑑𝑥. Tính 𝐼
′
( )
1
VIỆN TOÁN NG D NG VÀ TIN H C Ứ Ụ Ọ
ĐỀ ĐỀ Ữ 2 THI GI A KỲ MÔN GI I TÍCH 2 H c kì 20192 Ả – ọ
i gian: 60 phút Thờ
Chú ý: Thí sinh không được sử dụng tài liệu và Giám thị phải kí xác nhận số đề vào bài thi
của sinh viên.
Câu 1: (1đ). Viết phương trình tiế ủa đườp tuyến và pháp tuyến c ng cong t𝑥
3
+ 𝑦
3
= 9𝑥𝑦 ại
điể
m
(
4,2
)
Câu 2: (1đ).
Tính độ ủa đườ cong c ng {
𝑥= 2
(
𝑡− sin𝑡
)
𝑦= 2
(
1 − cos 𝑡
)
t ng v ại điểm ứ ới 𝑡= 𝜋/2
Câu 3: (1đ). Tìm hình bao c a h ng cong ủ ọ đườ
2𝑥 − 4 + 2𝑦 + 𝑐
2
𝑥𝑐
2 2
= 0, 𝑐 là tham số, 𝑐≠ 0
Câu 4: (1đ). Tìm gi i h n ớ ạ
lim
𝑦→0
∫ cos
(
𝑥
2
𝑦+ 3𝑥+ 𝑦
2
)
𝑑𝑥
𝜋
2
0
Câu 5: (1đ). Đổi th t l y tích phân: ứ ự ấ
∫ 𝑑𝑥
1
0
∫ 𝑓
(
𝑥, 𝑦𝑑𝑦
)
√
2−𝑥
2
𝑥
2
Với i 𝑉 nh bxác đị ở 0 ≤ 𝑥≤ 1, 1 ≤ 𝑦≤ 2, 1 ≤ 𝑧≤ 𝑒
Câu 6: (1đ). Tính di n tích ph n m n m trong m ệ ầ ặt 𝑧= 𝑥
2
+ 𝑦 + 2
2
ằ ặt 𝑥
2
+ 𝑦
2
= 9
Câu 7: (1đ). Tính th tích c a mi n gi i h n b i các m t cong và mể ủ ề ớ ạ ở ặ 𝑦= 𝑥
2
, 𝑥= 𝑦
2
, 𝑧= 𝑥
2
ặt
𝑂𝑥𝑦.
Câu 8: (1đ).
Tính
∬
(
2𝑦 + 3 𝑑𝑥𝑑𝑦
2
)
𝐷
, v là mi nh b ới 𝐷 ền xác đị ởi
𝑥
2
+
(
𝑦− 1
)
2
≤ 1
Câu 9: (1đ). Tính
∭
𝑧𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
với i 𝑉 nh bxác đị ở
𝑥
2
+ 𝑦 + 𝑧
2
≤ 1, 𝑦
2 2
≤ 4, 𝑧≥ 0
Câu 10: (1đ). Tính tích phân b i ba ộ
∭
𝑦
2
𝑒
𝑧
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
, trong đó
𝑉: 0 ≤ 𝑥≤ 1, 𝑥≤ 𝑦≤ 1, ≤ 𝑧≤ 𝑥𝑦+ 2
VIỆN TOÁN NG D NG VÀ TIN H C Ứ Ụ Ọ
ĐỀ ĐỀ Ữ 3 THI GI A KỲ MÔN GI I TÍCH 2 H c kì 20192 Ả – ọ
i gian: 60 phút Thờ
Chú ý: Thí sinh không được sử dụng tài liệu và Giám thị phải kí xác nhận số đề vào bài thi
của sinh viên.
Câu 1: (1đ).
Viết phương ủa đườtrình tiếp diện và pháp tuyến c ng cong {
𝑥= 2
(
𝑡− sin 𝑡
)
𝑦= 2
(
1 − cos 𝑡
)
tại
𝑡= 𝜋/2
Câu 2: (1đ).
Tính độ ủa đườ cong c ng cong t𝑦= 𝑒
2𝑥
ại 𝐴
(
0,1
)
Câu 3: (1đ). Tìm hình bao c a h ng cong ủ ọ đườ
𝑦= 4𝑐𝑥
3
+ 𝑐
4
, với 𝑐 tham sốlà
Câu 4: (1đ). Đổi th t l y tích phân ứ ự ấ
∫ 𝑑𝑦
1
0
∫ 𝑓
(
𝑥, 𝑦𝑑𝑥
)
√
2−𝑦
2
√
𝑦
Câu 5: (1đ). Tính
∬
4𝑦𝑑𝑥𝑑𝑦
𝐷
, v là mi nh b ới 𝐷 ền xác đị ởi:
𝑥
2
+ 𝑦
2
≤ 1, 𝑥+ 𝑦≥ 1
Câu 6: (1đ). Tính th tích mi n gi i h n b i m và m ể ề 𝑉 ớ ạ ở ặt 𝑂𝑥𝑦 ặt 𝑧= 𝑥
2
+ 𝑦 − 4
2
Câu 7: (1đ). Tính
∭
√
𝑥
2
+ 𝑦 + 𝑧
2 2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
V
ới i 𝑉 nh bxác đị ở 𝑥 𝑥
2
+ 𝑦 + 𝑧
2 2
≤ 1, √3
(
2
+ 𝑦
2
)
≤ 𝑧
Câu 8: (1đ). Tính
∭
𝑧𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
, v nh bới 𝑉xác đị ởi 𝑥
2
+ 𝑦
2
+ 𝑧
2
≤ 6, 𝑧≥ 𝑥
2
+ 𝑦
2
Câu 9: (1đ). Tính di n tích c a mi n gi i h n b ệ ủ ề ớ ạ ởi
(
𝑥
2
+ 𝑦
2
)
2
= 4𝑥𝑦
Câu 10: (1đ).
Cho hàm s ố 𝐼
(
𝑦
)
=
∫
sin + 𝑦
(
𝑥
2
+ 𝑥𝑦
2
)
𝑑𝑥
1
𝑦
. Tính 𝐼
′
( )
0
VIỆN TOÁN NG D NG VÀ TIN H C Ứ Ụ Ọ
ĐỀ ĐỀ Ữ 1 THI GI A KỲ MÔN GI I TÍCH 2 H c kì 20193 Ả – ọ
i gian: 60 phút Thờ
Chú ý: Thí sinh không được sử dụng tài liệu và Giám thị phải kí xác nhận số đề vào bài thi
của sinh viên.
Câu 1: (1đ).
Xác định độ ại đườ ại điể cong t ng cong t𝑥=
√
4𝑦+ 1
m
(
3,1
)
Câu
2: (1đ). Viết phương trình pháp tuyến và tiếp diện của mặt cong 𝑦
2
= 3
(
𝑥
2
+ 𝑧
2
)
tại điểm
(
√
2, 3,1)
Câu 3: (1đ).
Tìm hình bao c a h ng cong: ủ ọ đườ 𝑦=
(
2𝑥+ 3𝑐
)
4
Câu 4: (1đ). Tính
∬
√𝑥 + 𝑦
2 2
𝑑𝑥𝑑𝑦
𝐷
, với D ền phía trên parabol 𝑦= 𝑥là mi
2
nằm phía và
trong tròn 𝑥đường
2
+ 𝑦
2
= 2
Câu 5: (1đ). Tính
∭
√6𝑦− 𝑥 − 𝑦 − 𝑧
2 2 2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
với 𝑉: 𝑥
2
+ 𝑦
2
+ 𝑧
2
≤ 6𝑦
Câu 6: (1đ). Tính di n tích mi n gi i h n b ng cong và ệ ề ớ ạ ởi hai đườ 𝑦= 𝑥
2
𝑥= 𝑦
2
Câu 7: (1đ). Tính th tích mi n gi i h n b i các m t cong và ể ề ớ ạ ở ặ 𝑥= 𝑦
2
+ 𝑧
2
𝑥
2
+ 𝑦 + 𝑧
2 2
= 2
nằm trong phần không gian có không âm. 𝑥
Câu 8: (1đ). Tính di n tích m t cong n m trong hình tr ệ ặ 𝑧= 2𝑥
2
− 2𝑦
2
ằ ụ 𝑥
2
+ 𝑦
2
= 1
Câu 9: (1đ). Tính lim
𝑦→0
∫
(
𝑥+ 3𝑦√𝑥
)
2
+ 𝑦
3
+ 1𝑑𝑥
1
0
Câu 10: (1đ). Khảo sát tính liên t c và kh vi c a hàm s : ụ ả ủ ố
𝑔
(
𝑦
)
= ∫
𝑑𝑥
𝑥
2
+ 𝑦
2
1
0
PHẦN II:
LỜI GIẢI
THAM
KHẢO
PHAM THANH TUNG
LỜI GI I THAM KH THI GI Ả ẢO ĐỀ ỮA KÌ 20163 (ĐỀ 1)
Câu 1: Viết phương trình tiếp diện và pháp tuyến của mặt cong t𝑥
2
+ 3𝑦+ 2𝑧 = 3
3
ại
𝑀
(
2; −1; 1
)
Gi i:ả
Đặ
t 𝐹
(
𝑥, 𝑦, 𝑧 = 𝑥 + 3𝑦+ 2𝑧 − 3 ⇒𝐹
)
2 3
𝑥
′
= 2𝑥, 𝐹
𝑦
′
= 3, 𝐹
𝑧
′
= 6𝑧
2
T
ại 𝑀
(
2, −1,1 ,
)
ta có 𝐹
𝑥
′
(
𝑀
)
= 4, 𝐹
𝑦
′
(
𝑀
)
= 3, 𝐹
𝑧
′
(
𝑀
)
= 6
Phương trình pháp tuyế ủa đườ
n c ng cong tại 𝑀
(
2, −1,1
)
là:
𝑥− 2
4
=
𝑦+ 1
3
=
𝑧− 1
6
Phương trình tiế ủa đườ
p diện c ng cong tại 𝑀
(
2, −1,1
)
là:
4
(
𝑥− 2 + 3 𝑦+ 1 + 6 𝑧− 1 = 0 ⇔4𝑥+ 3𝑦+ 6𝑧−
) ( ) ( )
11 = 0
Câu 2: Tìm hình bao c a h ng th ng v là tham s . ủ ọ đườ ẳ 𝑦= 2𝑐𝑥− 𝑐
2
ới 𝑐 ố
Gi i:ả
Đặ
t 𝐹
(
𝑥, 𝑦, 𝑐 = 𝑦− 2𝑐𝑥+ 𝑐
)
2
Xét:
{
𝐹
𝑥
′
= 0
𝐹
𝑦
′
= 0
⇔{
−2𝑐= 0
1 = 0
⇒ Vô nghi H ng th m kì d . ệm ⇒ ọ đườ ẳng không có điể ị
Xét
{
𝐹= 0
𝐹
𝑐
′
= 0
⇔{
𝑦− 2𝑐𝑥+ 𝑐
2
= 0
−2𝑥+ 2𝑐= 0
⇔{
𝑦− 2𝑐𝑥+ 𝑐
2
= 0 (1)
𝑥= 𝑐 (2)
Thế (2) vào (1) ta có: 𝑦− 2𝑥 + 𝑥 = 0 ⇔𝑦= 𝑥
2 2 2
Vậy hình bao c a hủ ọ đường thẳng là: 𝑦= 𝑥
2
Câu 3: Tìm điểm có độ ủa đườ cong lớn nhất c ng cong 𝑦= ln 𝑥
Gi i:ả
𝑦= 𝑥(𝑥> 0) ⇒𝑦
ln
′
=
1
𝑥
, 𝑦
′′
=
−1
𝑥
2
Độ ấ cong c ng t bủa đườ 𝑦= ln 𝑥 ại điểm 𝑀(𝑥, 𝑦) t kì : là
PHAM THANH TUNG
𝐶
(
𝑀
)
=
|
𝑦
′′
|
(1 + 𝑦
′
2
)
3
2
=
|
−1
𝑥
2
|
(1 +
1
𝑥
2
)
3
2
=
1
𝑥
2
(
1 + 𝑥
2
𝑥
2
)
3
2
=
1
𝑥
2
(
1 + 𝑥
2
)
3
2
. (
1
𝑥
2
)
3
2
=
1
(
1 + 𝑥
2
)
3
2
. (
1
𝑥
2
)
1
2
=
1
(
1 + 𝑥
2
)
3
2
.
1
𝑥
=
𝑥
(
1 + 𝑥
2
)
3
2
= 𝑓
(
𝑥
)
⇒𝑓
′
(
𝑥
)
=
(
1 + 𝑥
2
)
3
2
−
3
2
. 2𝑥.
(
1 + 𝑥
2
)
1
2
. 𝑥
(
1 + 𝑥
2
)
3
=
(
1 + 𝑥
2
)
3
2
− 3𝑥
2
.
(
1 + 𝑥
2
)
1
2
(
1 + 𝑥
2
)
3
=
(
1 + 𝑥
2
)
1
2
. (1 + 𝑥
2
− 3𝑥
2
)
(
1 + 𝑥
2
)
3
=
(
1 + 𝑥
2
)
1
2
. (1 − 2𝑥
2
)
(
1 + 𝑥
2
)
3
Ta
: 𝑓có
′
(
𝑥
)
= 0 ⇔𝑥=
1
√
2
Bảng bi n thiên: ế
𝑥
0
1
√
2
+ ∞
𝑓
′
(𝑥)
+ 0 −
𝑓(𝑥)
𝑓(
1
√
2
)
Vậy độ ủa đườ ại điể cong c ng l𝑦= ln 𝑥 ớn nhất t m 𝑀(
1
√
2
, ln
1
√
2
)
Câu 4: Đổi th t l y tích phân: ứ ự ấ
∫ 𝑑𝑥
1
0
∫ 𝑓(𝑥,𝑦)𝑑𝑦
1
√
2𝑥−𝑥
2
Gi i:ả
Mi
ền 𝐷: {
0 ≤ 𝑥≤ 1
√2𝑥− 𝑥
2
≤ 𝑦≤ 1
(
√
2𝑥− 𝑥
2
≤ 𝑦⇔2𝑥− 𝑥
2
≤ 𝑦
2
⇔{
(
𝑥− 1
)
2
+ 𝑦
2
≥ 1
𝑦≥ 0
)
PHAM THANH TUNG
Đổ ứ ự ấ
i th t l y tích phân 𝐷: {
0 ≤ 𝑥≤ 1 − √1 − 𝑦
2
0 ≤ 𝑦≤ 1
⇒∫ 𝑑𝑥
1
0
∫ 𝑓(𝑥, 𝑦)𝑑𝑦
1
√
2𝑥−𝑥
2
= ∫ 𝑑𝑦
1
0
∫ 𝑓(𝑥, 𝑦)𝑑𝑥
1− 1−𝑦√
2
0
Câu 5: Tính các tích phân kép sau:
𝑎) ∬
(
3𝑥+ 2𝑦𝑑𝑥𝑑𝑦
)
𝐷
, 𝐷 ền ới hạn bởi các 𝑦= 𝑥là mi gi đường
2
𝑦= 1và
𝑏) ∬
𝑥𝑦
𝑥
2
+ 𝑦
2
𝑑𝑥𝑑𝑦
𝐷
với 𝐷=
{(
𝑥, 𝑦
)
∈𝑅
2
: 1 ≤ 𝑥
2
+ 𝑦
2
≤ 2𝑥, 𝑦≥ 0
}
Gi i:ả
𝑎) ∬
(
3𝑥+ 2𝑦𝑑𝑥𝑑𝑦
)
𝐷
, 𝐷 ền ới hạn bởi các 𝑦= 𝑥là mi gi đường
2
và 𝑦= 1
Mi
ền
(
𝐷
)
: {
−1 ≤ 𝑥≤ 1
𝑥
2
≤ 𝑦≤ 1
PHAM THANH TUNG
∬
𝑥𝑦
𝑥
2
+ 𝑦
2
𝑑𝑥𝑑𝑦
𝐷
= ∫ 𝑑𝑥
1
−1
∫(3𝑥+ 2𝑦)𝑑𝑦
1
𝑥
2
= ∫(3𝑥+ 1 − 3𝑥
3
− 𝑥
4
)𝑑𝑥
1
−1
=
8
5
Hình minh h a câu ọ 𝑎
𝑏) ∬
𝑥𝑦
𝑥
2
+ 𝑦
2
𝑑𝑥𝑑𝑦
𝐷
với 𝐷=
{(
𝑥, 𝑦
)
∈𝑅
2
: 1 ≤ 𝑥
2
+ 𝑦
2
≤ 2𝑥, 𝑦≥ 0
}
Đặ
t {
𝑥= 𝑟cos 𝜑
𝑦= 𝑟sin 𝜑
|
𝐽
|
= 𝑟
Mi
ền
(
𝐷
)
: {
1 ≤ 𝑟≤ 2 cos 𝜑
0 ≤ 𝜑≤ 𝜋/3
PHAM THANH TUNG
∬
𝑥𝑦
𝑥
2
+ 𝑦
2
𝑑𝑥𝑑𝑦
𝐷
= ∫ 𝑑𝜑
𝜋
3
0
∫
𝑟cos 𝜑. 𝑟sin 𝜑
𝑟
2
𝑟𝑑𝑟
2 cos 𝜑
1
= ∫ 𝑑𝜑
𝜋
3
0
∫ 𝑟cos 𝜑sin 𝜑𝑑𝑟
2 cos 𝜑
1
=
1
2
∫
[
4
(
cos 𝜑
)
2
− 1
]
cos 𝜑sin𝜑𝑑𝜑
𝜋
3
0
=
−1
2
∫
[
4
(
cos 𝜑
)
2
− 1
]
cos 𝜑𝑑(cos 𝜑)
𝜋
3
0
=
−1
2
∫
(
4𝑡
2
− 1
)
𝑡𝑑𝑡
1
2
1
=
9
32
Câu 6: Tính th tích c a v t th gi i h n b i các m t ể ủ ậ ể 𝑉 ớ ạ ở ặ
𝑧= 𝑥 + 𝑦
2 2
và 𝑧= 2𝑥+ 4𝑦
Gi i:ả
Xét giao tuy n c
ế ủa {
𝑧= 𝑥
2
+ 𝑦
2
𝑧= 2𝑥+ 4𝑦
⇒𝑥
2
+ 𝑦
2
= 2𝑥+ 4𝑦⇔(𝑥− 1)
2
+ (𝑦− 2)
2
= 5
Hình chi u c lên là:
ế ủa (𝑉) 𝑂𝑥𝑦
(
𝐷
)
: (𝑥− 1)
2
+ (𝑦− 2) ≤ 5
2
Thể ề tích mi n là: (𝑉)
𝑉
(
𝑉
)
= ∭𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∬𝑑𝑥𝑑𝑦 ∫ 𝑑𝑧
2𝑥+4𝑦
𝑥
2
+𝑦
2
=
𝐷
∬(2𝑥+ 4𝑦− 𝑥
2
−
𝐷
𝑦
2
)𝑑𝑥𝑑𝑦
= ∬
{
5 − (𝑥− 1) + (𝑦− 2)
[
2 2
]}
𝐷
𝑑𝑥𝑑𝑦
Đặ
t {
𝑥= 1 + 𝑟cos𝜑
𝑦= 2 + 𝑟sin𝜑
|
𝐽
|
= 𝑟. Mi n ề
(
𝐷
)
: {
0 ≤ 𝑟≤ √5
0 ≤ 𝜑≤ 2𝜋
⇒𝑉
(
𝑉
)
= ∬5 − 𝑟
(
2
)
𝑟
𝐷
𝑑𝑟𝑑𝜑= ∫ 𝑑𝜑
2𝜋
0
∫
(
5 − 𝑟
2
)
𝑟𝑑𝑟
√
5
0
= 2𝜋.
25
4
=
25𝜋
2
(
đvtt
)
PHAM THANH TUNG
Câu 7: Tính tích phân b i ba ộ
∭
𝑦𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
trong đó:
a) 𝑉 gi i h n b i các m ớ ạ ở ặt
𝑧= 0, 𝑧= 𝑥 𝑦= 4 + 𝑥
2
, 𝑦= 2𝑥
2
và
2
b) 𝑉 là hình cầu 𝑥
2
+ 𝑦 + 𝑧 ≤ 2𝑦
2 2
Gi i:ả
a) 𝑉 gi i h n b i các m ớ ạ ở ặt
𝑧= 0, 𝑧= 𝑥 𝑦= 4 + 𝑥
2
, 𝑦= 2𝑥
2
và
2
Hình chi u c lên gi i h n b
ế 𝐷 ủa 𝑉 𝑂𝑥𝑦 ớ ạ ởi {
𝑦= 2𝑥
2
𝑦= 4 + 𝑥
2
⇒
(
𝐷
)
{
−2 ≤ 𝑥≤ 2
2𝑥 ≤ 𝑦≤ 4 + 𝑥
2 2
∭𝑦𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∫ 𝑑𝑥
2
−2
∫ 𝑑𝑦
4+𝑥
2
2𝑥
2
∫ 𝑦𝑑𝑧
𝑥
2
0
= ∫ 𝑑𝑥
2
−2
∫ 𝑦𝑥
2
𝑑𝑦
4+𝑥
2
2𝑥
2
=
1
2
∫ 𝑥
2
[(
4 + 𝑥
2
)
2
− 4𝑥
4
]
𝑑𝑥
2
−2
=
4096
105
b) 𝑉 là hình cầu 𝑥
2
+ 𝑦 + 𝑧 ≤ 2𝑦
2 2
Miền 𝑉: 𝑥
2
+ 𝑦 + 𝑧 ≤ 2𝑦⇔𝑥 + (𝑦− 1) + 𝑧 ≤ 1
2 2 2 2 2
Đặ
t {
𝑥= 𝑟sin 𝜃cos 𝜑
𝑦= 1 + 𝑟sin𝜃sin 𝜑
𝑧= 𝑟
cos 𝜃
|
𝐽
|
= 𝑟
2
sin 𝜃 . Mi n ề
(
𝑉
)
: {
0 ≤ 𝑟≤ 1
0 ≤ 𝜃≤ 𝜋
0 ≤ 𝜑≤ 2𝜋
∭𝑦𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∫ 𝑑𝜑
2𝜋
0
∫ 𝑑𝜃
𝜋
0
∫
(
1 + 𝑟sin 𝜃sin 𝜑
)
𝑟
2
sin 𝜃𝑑𝑟
1
0
= ∫ 𝑑𝜑
2𝜋
0
∫ (
1
3
sin 𝜃+
1
4
(
sin 𝜃
)
2
sin 𝜑) 𝑑𝜃
𝜋
0
= ∫ (
2
3
+
𝜋
8
sin 𝜑) 𝑑𝜑
2𝜋
0
=
4𝜋
3
Câu 8: Tính tích phân
∫
𝑒
−𝛼𝑥
2
− 1
𝑥
2
𝑒
𝑥
2
𝑑𝑥
+∞
0
với 𝛼≥ 0
Gi i:ả
∫
𝑒
−𝛼𝑥
2
− 1
𝑥
2
𝑒
𝑥
2
𝑑𝑥
+∞
0
= ∫
𝑒
−𝛼𝑥
2
− 𝑒
−0.𝑥
2
𝑥
2
𝑒
𝑥
2
𝑑𝑥
+∞
0
PHAM THANH TUNG
Đặt 𝐹
(
𝑥, 𝑦
)
=
𝑒
−𝑦𝑥
2
𝑥
2
𝑒
𝑥
2
𝑒
−𝑎𝑥
2
− 𝑒
−0.𝑥
2
𝑥
2
𝑒
𝑥
2
= 𝐹
(
𝑥, 𝑎
)
− 𝐹
(
𝑥, 0
)
= ∫ 𝐹
𝑦
′
(
𝑥, 𝑦
)
𝑑𝑦
𝑎
0
= ∫ −𝑒
−
(
𝑦+1
)
𝑥
2
𝑑𝑦
𝑎
0
= ∫ 𝑒
−
(
𝑦+1
)
𝑥
2
𝑑𝑦
0
𝑎
∫
𝑒
−𝛼𝑥
2
− 𝑒
−0.𝑥
2
𝑥
2
𝑒
𝑥
2
𝑑𝑥
+∞
0
= ∫ ∫ 𝑒(
−
(
𝑦+1
)
𝑥
2
𝑑𝑦
0
𝑎
)
𝑑𝑥
+∞
0
= ∫ ∫ 𝑒(
−
(
𝑦+1
)
𝑥
2
𝑑𝑥
+∞
0
)
𝑑𝑦
0
𝑎
Xét ∫ 𝑒 𝑑𝑥
−
(
𝑦+1
)
𝑥
2
+∞
0
Đặt
(
𝑦+ 1
)
𝑥
2
= 𝑡⇒𝑥=
√
𝑡
√
1 + 𝑦
⇒𝑑𝑥=
1
2 1 + 𝑦
√
. 𝑡
−1
2
𝑑𝑡
⇒∫ 𝑒
−
(
𝑦+1
)
𝑥
2
𝑑𝑥
+∞
0
= ∫ 𝑒
−𝑡
.
1
2 1 + 𝑦
√
. 𝑡
−1
2
𝑑𝑡
+∞
0
=
1
2
√
1 + 𝑦
∫ 𝑒
−𝑡
. 𝑡
1
2
−1
𝑑𝑡
+∞
0
=
1
2 1 + 𝑦
√
. Γ (
1
2
)
=
√
𝜋
2
√
1 + 𝑦
⇒∫ ∫ 𝑒(
−
(
𝑦+1
)
𝑥
2
𝑑𝑥
+∞
0
)
𝑑𝑦
0
𝑎
= ∫
√
𝜋
2 1 + 𝑦
√
𝑑𝑦
0
𝑎
=
√
𝜋
2
. 2(
√
𝑎+ 1 − 1) =
√
𝜋(
√
𝑎+ 1 − 1)
*Kiểm tra điều kiện khả tích:
Đặt 𝑓
(
𝑥, 𝑦 = 𝑒
)
−
(
𝑦+1
)
𝑥
2
−
Hàm liên t c trên n 𝑓
(
𝑥, 𝑦
)
ụ miề
[ [
0; +∞
)
× 0; 𝑎
]
−
Tích phân 𝐼
(
𝑦
)
=
∫
𝑒
−
(
𝑦+1
)
𝑥
2
𝑑𝑥
+∞
0
h i t u trên ộ ụ đề
[
0, 𝑎
]
Do
{
𝑒
−
(
𝑦+1
)
𝑥
2
≤ 𝑒
−
(
𝑦 +1
0
)
𝑥
2
với 𝑦
0
≥ 0
∫ 𝑒
−
(
𝑦
0
+1
)
𝑥
2
+∞
0
𝑑𝑥=
√
𝜋
2 1 + 𝑦
√
0
hội tụ
⇒∫ 𝑒
−
(
𝑦+1
)
𝑥
2
𝑑𝑥
+∞
0
hội tụ đều trên
[
0; 𝑎
]
Vậy điề ện đổu ki i thứ tự lấy tích phân thỏa mãn.
PHAM THANH TUNG
❖ Mẹo:
Trong các bài t p s d i th t l o ậ ử ụng phương pháp đổ ứ ự ấy tích phân và phương pháp đạo hàm đạ
hàm qua d u tích phân, chúng ta s , t c là c áp dấ ẽ “tiền tr m h u tả ậ ấu” ứ ứ ụng hai phương pháp trên
để ế ả ồ ệ ả ả ả tính tích phân, khi ra k t qu r i mới ki u kiểm tra điề n kh vi, kh tích, giống lời gi i tham
khảo trên. Khi làm như vậ ếu không đủ ứng minh điềy, n thời gian ch u kiện khả vi, khả tích,
chúng ta v ẫn được 0.5đ nếu tính toán đúng tích phân.
PHAM THANH TUNG
LỜI GI I THAM KH THI GI Ả ẢO ĐỀ ỮA KÌ 20172 (ĐỀ 2)
Câu 1:
Viết phương trình tiếp di n và pháp tuy n c a m t cong ệ ế ủ ặ ln
(
𝑥
2
+ 3𝑦 − 3𝑧 = 2
)
3
tại điểm
𝑀
(
1,0, −1
)
.
Gi i:ả
Đặt 𝐹
(
𝑥, 𝑦, 𝑧 + 3𝑦 − 3𝑧 − 2 ⇒
)
= ln
(
𝑥
2
)
3
{
𝐹
𝑥
′
=
2𝑥
𝑥
2
+ 3𝑦
𝐹
𝑦
′
=
3
𝑥
2
+ 3𝑦
𝐹
𝑧
′
= −9𝑧
2
T
ại 𝑀
(
1,0, −1 ,
)
ta có: {
𝐹
𝑥
′
(
𝑀
)
= 2
𝐹
𝑦
′
(
𝑀
)
= 3
𝐹
𝑧
′
(
𝑀
)
= −9
Phương trình tiế
p diện của mặt cong tại 𝑀
(
1,0, −1
)
là:
2
(
𝑥− 1 + 3 𝑦− 0 − 9 𝑧+ 1 = 0 ⇔2𝑥+ 3𝑦− 9𝑧−
) ( ) ( )
11 = 0
Phương trình pháp tuyế
n của mặt cong tại 𝑀
(
1,0, −1
)
là:
𝑥− 1
2
=
𝑦
3
=
𝑧+ 1
−9
Câu 2: Tìm hình bao c a h ng cong v là tham s . ủ ọ đườ 𝑐𝑥 − 2𝑦− 𝑐 + 1 = 0
2 3
ới 𝑐 ố
Gi i:ả
Đặ
t 𝐹
(
𝑥, 𝑦, 𝑐 = 𝑐𝑥 − 2𝑦− 𝑐 + 1
)
2 3
Xét
{
𝐹
𝑥
′
(
𝑥, 𝑦, 𝑐
)
= 0
𝐹
𝑦
′
(
𝑥, 𝑦, 𝑐
)
= 0
⇔{
2𝑐𝑥= 0
−2 = 0
⇒ Vô nghi H m kì d . ệm ⇒ ọ đường cong không có điể ị
Xét {
𝐹
(
𝑥, 𝑦, 𝑐
)
= 0
𝐹
𝑐
′
(
𝑥, 𝑦, 𝑐
)
= 0
⇔{
𝑐𝑥
2
− 2𝑦− 𝑐
3
+ 1 = 0
𝑥
2
− 3𝑐
2
= 0
⇔{
𝑐. 3𝑐
2
− 2𝑦− 𝑐
3
+ 1 = 0
𝑥
2
= 3𝑐
2
⇔{
2𝑐
3
= 2𝑦− 1
𝑐
2
=
𝑥
2
3
⇔{
𝑐
3
=
2𝑦− 1
2
𝑐
2
=
𝑥
2
3
⇒(
𝑥
2
3
)
3
− (
2𝑦− 1
2
)
2
= 0
Vậy hình bao của họ cong
đường là đường
𝑥
6
27
=
(
2𝑦− 1
)
2
4
PHAM THANH TUNG
Câu 3:
Tính độ ủa đườ ại điể cong c ng t𝑦= sin𝑥ln
( )
m ứng với 𝑥= 𝜋/4.
Gi i:ả
𝑦= sin𝑥 ⇒𝑦
ln
( )
′
(
𝑥
)
=
cos 𝑥
sin 𝑥
= cot 𝑥, 𝑦
′′
(
𝑥
)
=
−1
sin
2
𝑥
Tại 𝑥=
𝜋
4
, ta : 𝑦có
′
(
𝜋
4
) = 1, 𝑦
′′
(
𝜋
4
) = −2
Độ ạ
cong c tủa đường 𝑦= ln
(
sin 𝑥
)
i 𝑥= 𝜋/4
𝐶(𝑥=
𝜋
4
) =
|
−2
|
(
1 + 1
)
3
2
=
2
2
√
2
=
1
√
2
Câu 4: Tính các tích phân sau:
𝑎) ∬
(
𝑥
2
− 4𝑦
2
)
𝑑𝑥𝑑𝑦
𝐷
, 𝐷 ền ới hạn bởi 𝑦= 𝑥,𝑥= 1 𝑦= 0là mi gi và
𝑏) ∬
(
𝑥
2
− 𝑥𝑦+ 𝑦
2
)
𝑑𝑥𝑑𝑦
𝐷
, 𝐷 ền ới hạn bởi 𝑦= −3𝑥+ 1,𝑦= −3𝑥+ 2, 𝑦= 𝑥là mi gi
và 𝑦= 𝑥+ 2
Gi i:ả
𝑎) ∬
(
𝑥
2
− 4𝑦
2
)
𝑑𝑥𝑑𝑦
𝐷
, 𝐷 ền ới hạn bởi 𝑦= 𝑥, 𝑥= 1 𝑦= 0là mi gi và
Mi
ền 𝐷: {
0 ≤ 𝑥≤ 1
0 ≤ 𝑦≤ 𝑥
∬ − 4𝑦
(
𝑥
2 2
)
𝑑𝑥𝑑𝑦
𝐷
= ∫ 𝑑𝑥
1
0
∫
(
𝑥
2
− 4𝑦
2
)
𝑑𝑦
𝑥
0
= ∫ . 𝑥−
(𝑥
2
4
3
𝑥
3
) 𝑑𝑥
1
0
=
−1
12
PHAM THANH TUNG
𝑏) ∬
(
𝑥
2
− 𝑥𝑦+ 𝑦
2
)
𝑑𝑥𝑑𝑦
𝐷
, 𝐷 ền ới hạn bởi 𝑦= −3𝑥+ 1,𝑦= −3𝑥+ 2, 𝑦= 𝑥là mi gi
và 𝑦= 𝑥+ 2
Mi
ề ạn gi𝐷 ới h n bởi {
𝑦= −3𝑥+ 1
𝑦= −3𝑥+ 2
𝑦= 𝑥
𝑦= 𝑥+ 2
⇔
{
𝑦+ 3𝑥= 1
𝑦+ 3𝑥= 2
𝑦− 𝑥= 0
𝑦− 𝑥= 2
Đặ
t {
𝑢= 𝑦+ 3𝑥
𝑣= 𝑦− 𝑥
⇒𝐽
−1
= |
3 1
−1 1
| = 4 ⇒𝐽= 1/4
Mi
ền 𝐷
𝑢𝑣
trong t m gi i h n bọa độ ới 𝑂𝑢𝑣 ớ ạ ởi {
𝑢= 1
𝑢= 2
𝑣= 0
𝑣= 2
⇒𝐷
𝑢𝑣
: {
1 ≤ 𝑢≤ 2
0 ≤ 𝑣≤ 2
{
𝑢= 𝑦+ 3𝑥
𝑣= 𝑦− 𝑥
⇒
{
𝑥=
𝑢− 𝑣
4
𝑦=
𝑢+ 3𝑣
4
⇒∬ + 𝑦
(
𝑥
2
− 𝑥𝑦
2
)
𝑑𝑥𝑑𝑦
𝐷
=
1
4
∬[(
𝑢− 𝑣
4
)
2
−
𝑢− 𝑣
4
.
𝑢+ 3𝑣
4
+ (
𝑢+ 3𝑣
4
)
2
] 𝑑𝑢𝑑𝑣
𝐷
𝑢𝑣
=
1
64
∬
(
𝑢
2
+ 2𝑢𝑣 13+ 𝑣
2
)
𝑑𝑢𝑑𝑣
𝐷
𝑢𝑣
=
1
64
∫ 𝑑𝑢
2
1
∫
(
𝑢
2
+ 2𝑢𝑣 13+ 𝑣
2
)
𝑑𝑣
2
0
=
1
64
∫ (
2𝑢
2
+ 4𝑢+
104
3
) 𝑑𝑢
2
1
=
17
24
Câu 5: Tính tích phân sau:
∫ 𝑑𝑥
1
0
∫
1
𝑦
5
+ 1
𝑑𝑦
1
√
𝑥
4
Gi i:ả
Mi
ền 𝐷: {
0 ≤ 𝑥≤ 1
√
𝑥
4
≤ 𝑦≤ 1
PHAM THANH TUNG
Đổ ứ ự ấ ề
i th t l y tích phân, mi n 𝐷: {
0 ≤ 𝑥≤ 𝑦
4
0 ≤ 𝑦≤ 1
∫ 𝑑𝑥
1
0
∫
1
𝑦
5
+ 1
𝑑𝑦
1
√
𝑥
4
= ∫ 𝑑𝑦
1
0
∫
1
𝑦
5
+ 1
𝑑𝑥
𝑦
4
0
= ∫
𝑦
4
𝑦
5
+ 1
𝑑𝑦
1
0
=
1
5
∫
𝑑
(
𝑦
5
)
𝑦
5
+ 1
1
0
=
ln
(
𝑦
5
+ 1
)
5
|
1
0
=
ln 2
5
Câu 6: Tính th tích c a v t th gi i h n b i các m t ể ủ ậ ể 𝑉 ớ ạ ở ặ
𝑧= 𝑥 + 2𝑦 𝑧= 3 − 2𝑥 − 𝑦
2 2
và
2 2
Gi i:ả
Miền 𝑉: 𝑥 + 2𝑦 ≤ 𝑧≤ 3 − 2𝑥 − 𝑦
2 2 2 2
Giao tuy n c a m và ế ủ ặt 𝑧= 𝑥 + 2𝑦
2 2
𝑧= 3 − 2𝑥 − 𝑦
2 2
⇒𝑥 + 2𝑦 = 3 − 2𝑥 − 𝑦 ⇔𝑥 + 𝑦 = 1
2 2 2 2 2 2
Hình chi u c lên là ế ủa 𝑉 𝑂𝑥𝑦 𝐷: 𝑥
2
+ 𝑦 ≤ 1
2
Đặ
t {
𝑥= 𝑟cos 𝜑
𝑦= 𝑟sin 𝜑
, 𝐽= 𝑟⇒𝐷: {
0 ≤ 𝑟≤ 1
0 ≤ 𝜑≤ 2𝜋
Thể ậ ể tích v t th 𝑉 là:
PHAM THANH TUNG
𝑉= ∭𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∬ 3 − 2𝑥
[(
2
− 𝑦
2
)
−
(
𝑥
2
+ 2𝑦
2
)]
𝑑𝑥𝑑𝑦
𝐷
= ∬
[
3 − 3
(
𝑥
2
+ 𝑦
2
)]
𝑑𝑥𝑑𝑦
𝐷
= ∫ 𝑑𝜑
2𝜋
0
∫
(
3 − 3𝑟
2
)
𝑟𝑑𝑟
1
0
=
3
2
𝜋
(
đvtt
)
Câu 7:
Tính tích phân b i ba ộ
∭
(
3𝑥𝑦 − 4𝑥𝑦𝑧𝑑𝑥𝑑𝑦𝑑𝑧
2
)
𝑉
trong đó ền xác đị𝑉 là mi nh bởi
1 ≤ 𝑦≤ 2, 0 ≤ ≤ 2, 0 ≤ 𝑧≤ 2𝑥𝑦
Gi i:ả
Cách 1: Đổi biến số:
Đặ
t {
𝑢= 𝑦
𝑣= 𝑥𝑦
𝑤= 𝑧
⇒𝐽
−1
= |
0 1 0
𝑦 𝑥 0
0 0 1
| = −𝑦⇒𝐽= −1/𝑦= −1/𝑢
Mi
ền mới 𝑉
𝑢𝑣𝑤
trong h t m i là ệ ọa độ ớ 𝑉
𝑢𝑣𝑤
: {
1 ≤ 𝑢≤ 2
0 ≤ 𝑣≤ 2
0 ≤ 𝑤≤ 2
∭3𝑥𝑦 − 4𝑥𝑦𝑧𝑑𝑥𝑑𝑦𝑑𝑧
(
2
)
𝑉
= ∭3 − 4
(
𝑢𝑣 𝑣𝑤
)
.
1
𝑢
𝑑𝑢𝑑𝑣𝑑𝑤
𝑉
𝑢𝑣𝑤
= ∫ 𝑑𝑤
2
0
∫ 𝑑𝑣
2
0
∫ (
3𝑣−
4𝑣𝑤
𝑢
) 𝑑𝑢
2
1
= ∫ 𝑑𝑤
2
0
∫
(
3𝑣− 4 2 . 𝑑𝑣ln 𝑣𝑤
)
2
0
= ∫ 6 − 8 2 . 𝑤𝑑𝑤
(
ln
)
2
0
= 12 16− ln 2
Cách 2: Tính thông thường:
Hình chi u c a mi n gi i h n b
ế 𝐷 ủ ề 𝑉 ớ ạ ởi {
𝑦= 1, 𝑦= 2
𝑦= 2/𝑥
⇒Hình chiếu 𝐷: {
0 ≤ 𝑥≤
2
𝑦
1 ≤ 𝑦≤ 2
⇒Miền 𝑉: {
0 ≤ 𝑧≤ 2
0 ≤ 𝑥≤
2
𝑦
1 ≤ 𝑦≤ 2
∭3𝑥𝑦 − 4𝑥𝑦𝑧𝑑𝑥𝑑𝑦𝑑𝑧
(
2
)
𝑉
= ∫ 𝑑𝑦
2
1
∫ 𝑑𝑧
2
0
∫
(
3𝑥𝑦
2
− 4𝑥𝑦𝑧𝑑𝑥
)
2
𝑦
0
= 12 16− ln 2
PHAM THANH TUNG
Câu 8:
Tính tích phân b i ba ộ
∭
(
𝑥
2
+ 𝑦 + 𝑧
2 2
)
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
trong đó 𝑉 là miền giới hạn bởi các
mặt 𝑦= + 4𝑧
√
𝑥
2 2
, 𝑦= 2.
Gi i:ả
Hình chi u c a mi n lên là ế ủ ề 𝑉 𝑂𝑥𝑧 𝐷: 𝑥 + 4𝑧
2 2
≤ 4
Đặt {
2𝑧= 𝑟cos 𝜑
𝑥= 𝑟sin 𝜑
𝑦= 𝑦
⇔ {
𝑧=
𝑟cos𝜑
2
𝑥= 𝑟sin 𝜑
𝑦= 𝑦
, 𝐽=
𝑟
2
𝑉: {
√𝑥
2
+ 4𝑧
2
≤ 𝑦≤ 2
𝐷: 𝑥
2
+ 4𝑧
2
≤ 4
⇔{
𝑟≤ 𝑦≤ 2
0 ≤ 𝜑≤ 2𝜋
0 ≤ 𝑟≤ 2
∭ + 𝑦 + 𝑧
(
𝑥
2 2 2
)
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∫ 𝑑𝜑
2𝜋
0
∫ 𝑑𝑟
2
0
∫ (𝑟
2
sin
2
𝜑+ 𝑦
2
+
𝑟
2
4
cos
2
𝜑) .
𝑟
2
𝑑𝑦
2
𝑟
= ∫ 𝑑𝜑
2𝜋
0
∫ [(
𝑟
3
sin
2
𝜑
2
+
𝑟
3
cos
2
𝜑
8
)
(
2 − 𝑟
)
+
8
3
−
𝑟
3
3
] 𝑑𝑟
2
0
= ∫ (
4
5
sin
2
𝜑+
1
5
cos
2
𝜑+ 4) 𝑑𝜑
2𝜋
0
=
4
5
𝜋+
1
5
𝜋+ 8𝜋= 9𝜋
Câu 9: Tính tích phân
∫
𝑒
−𝑎𝑥
2
− 𝑒
−𝑏𝑥
2
𝑥
𝑑𝑥
+∞
0
với 𝑎, 𝑏> 0
Gi i:ả
Đặt 𝐹
(
𝑥, 𝑦
)
=
𝑒
−𝑦𝑥
2
𝑥
𝑒
−𝑎𝑥
2
− 𝑒
−𝑏𝑥
2
𝑥
= 𝐹
(
𝑥, 𝑎
)
− 𝐹
(
𝑥, 𝑏
)
= ∫ 𝐹
𝑦
′
(
𝑥, 𝑦
)
𝑑𝑦
𝑎
𝑏
= ∫ −𝑥𝑒
−𝑦𝑥
2
𝑑𝑦
𝑎
𝑏
= ∫ 𝑥𝑒
−𝑦𝑥
2
𝑑𝑦
𝑏
𝑎
∫
𝑒
−𝑎𝑥
2
− 𝑒
−𝑏𝑥
2
𝑥
𝑑𝑥
+∞
0
= ∫ (
∫ 𝑥𝑒
−𝑦𝑥
2
𝑑𝑦
𝑏
𝑎
)
𝑑𝑥
+∞
0
= ∫ ∫ 𝑥𝑒(
−𝑦𝑥
2
𝑑𝑥
+∞
0
)
𝑑𝑦
𝑏
𝑎
PHAM THANH TUNG
= ∫
(
1
2
∫ 𝑒
−𝑦𝑥
2
𝑑
(
𝑥
2
)
+∞
0
)
𝑑𝑦
𝑏
𝑎
= ∫ (
1
2
.
−1
𝑦
𝑒
−𝑦𝑥
2
|
+∞
0
) 𝑑𝑦
𝑏
𝑎
= ∫
1
2𝑦
𝑑𝑦
𝑏
𝑎
=
1
2
ln
𝑏
𝑎
*Kiểm tra điều kiện khả tích:
Đặt 𝑓
(
𝑥, 𝑦 = 𝑥𝑒
)
−𝑦𝑥
2
−
Hàm liên t c trên mi n 𝑓
(
𝑥, 𝑦
)
ụ ề
[ [
0; +∞
)
× 𝑏; 𝑎
]
−
Tích phân 𝐼
(
𝑦
)
=
∫
𝑥𝑒
−𝑦𝑥
2
𝑑𝑥
+∞
0
h i t u trên ộ ụ đề
[ ]
𝑏, 𝑎
(
𝑎, 𝑏> 0
)
Do
{
𝑥𝑒
−𝑦𝑥
2
≤ 𝑥𝑒
−𝑦
0
𝑥
2
với 𝑦
0
≥ 𝑏> 0
∫ 𝑥𝑒
−𝑦
0
𝑥
2
+∞
0
𝑑𝑥=
1
2𝑦
0
hội tụ
⇒∫ 𝑥𝑒
−𝑦𝑥
2
𝑑𝑥
+∞
0
hội tụ đều trên
[ ]
𝑏; 𝑎
Vậy điề ện đổu ki i thứ tự lấy tích phân thỏa mãn.
❖ Mẹo:
Trong các bài t p s dậ ử ụng phương pháp đổi thứ t lự ấy tích phân và phương pháp đạo hàm đạo hàm
qua d u tích phân, chúng ta s , t là c áp d ấ ẽ “tiền tr m h u tả ậ ấu” ức ứ ụng hai phương pháp trên để
tính tích phân, khi ra k t qu r i m i ki u ki n kh vi, kh tích, gi ng l i gi i tham khế ả ồ ớ ểm tra điề ệ ả ả ố ờ ả ảo
trên. Khi làm như vậy, nếu không đủ thời gian chứng minh điều ki n kh vi, kh tích, chúng ta v n ệ ả ả ẫ
đượ ếc 0.5đ n u tính toán đúng tích phân.
PHAM THANH TUNG
LỜI GI I THAM KH THI Ả ẢO ĐỀ GIỮA KÌ 20172 (ĐỀ 4)
Câu 1: Viết phương trình tiế ủa đườp tuyến và pháp diện c ng cong 𝑥= 4 sin 𝑡,𝑦= 4
2
cos 𝑡,
𝑧= 2 sin 𝑡+ 1 𝑀(1; −2 3 tại điểm
√
; 2)
Gi i:ả
T
ại 𝑀(1; −2 3; 2),
√
ta có: {
1 = 4 sin
2
𝑡
−2
√
3 = 4 𝑡cos
2 = 2 sin𝑡+ 1
⇔𝑡= 5𝜋/6
{
𝑥= 4 sin
2
𝑡
𝑦= 4 𝑡cos
𝑧= 2 sin 𝑡+ 1
⇒{
𝑥
′
(
𝑡
)
= 8 sin 𝑡cos 𝑡
𝑦
′
(
𝑡
)
= −4 sin𝑡
𝑧
′
(
𝑡
)
= 2 cos𝑡
. Tại 𝑡=
5𝜋
6
, ta : có
{
𝑥
′
(
5𝜋
6
) = −2√3
𝑦
′
(
5𝜋
6
) = −2
𝑧
′
(
5𝜋
6
) = −
√
3
Phương trình tiế ủa đườp tuyến c ng cong tại 𝑀(1; −2 3
√
; 2) là:
𝑥− 1
−2
√
3
=
𝑦+ 2
√
3
−2
=
𝑧− 2
−
√
3
Phương trình pháp diện của đường cong tại 𝑀(1; −2 3; 2)
√
là:
−2 3
√
(
𝑥− 1 − 2(𝑦+ 2 3 𝑧− 2 = 0 ⇔−2 3
)
√
) − 3
√
( )
√
𝑥− 2𝑦− 3𝑧= 0
√
Câu 2: Tìm hình bao c a h ng th ng v là tham s . ủ ọ đườ ẳ 3𝑐𝑥− 𝑦− 𝑐 = 0,
3
ới 𝑐 ố
Gi i:ả
Đặ ố
t 𝐹
(
𝑥, 𝑦, 𝑐 = 3𝑐𝑥− 𝑦− 𝑐
)
3
với 𝑐 là tham s .
Xét
{
𝐹
𝑥
′
(
𝑥, 𝑦, 𝑐
)
= 0
𝐹
𝑦
′
(
𝑥, 𝑦, 𝑐
)
= 0
⇔{
3𝑐= 0
−1 = 0
⇒ Vô nghi H m kì d . ệm ⇒ ọ đường cong không có điể ị
Xét {
𝐹
(
𝑥, 𝑦, 𝑐
)
= 0
𝐹
𝑐
′
(
𝑥, 𝑦, 𝑐
)
= 0
⇔{
3𝑐𝑥− 𝑦− 𝑐
3
= 0
3𝑥− 3𝑐
2
= 0
⇔{
3𝑐. 𝑐
2
− 𝑦− 𝑐
3
= 0
𝑥= 𝑐
2
⇔{
𝑦= 2𝑐
3
𝑥= 𝑐
2
⇔{
𝑦
2
= 𝑐
3
𝑥= 𝑐
2
⇒𝑥 − (
3
𝑦
2
)
2
= 0 ⇔𝑦
2
= 4𝑥
3
Vậy hình bao của họ cong 𝑦 đường là đường
2
= 4𝑥
3
PHAM THANH TUNG
Câu 3: Tính độ ại điể cong của đường cong t𝑥= sin 𝑡+ 𝑡 𝑡, 𝑦= 𝑡+ 𝑡sin𝑡cos cos m ứng với
𝑡= 𝜋
Gi i:ả
{
𝑥= sin 𝑡+ 𝑡cos 𝑡
𝑦= 𝑡+ 𝑡sin 𝑡
cos
⇒{
𝑥
′
(
𝑡
)
= 2 𝑡− 𝑡sin𝑡cos
𝑦
′
(
𝑡
)
= 𝑡cos 𝑡
⇒{
𝑥
′′
(
𝑡
)
= −3 sin 𝑡− 𝑡cos𝑡
𝑦
′′
(
𝑡
)
= cos 𝑡− 𝑡sin 𝑡
T
ại 𝑡= 𝜋, ta có: {
𝑥
′
(
𝜋
)
= −2, 𝑥
′′
(
𝜋
)
= 𝜋
𝑦
′
(
𝜋
)
= −𝜋, 𝑦
′′
(
𝜋
)
= −1
Độ ứ cong c ng cong tủa đườ ại điểm ng với 𝑡= 𝜋 là:
𝐶
(
𝑡= 𝜋
)
=
|
𝑥
′
. 𝑦
′′
− 𝑥
′′
. 𝑦′
|
(𝑥 + 𝑦
′
2
′
2
)
3
2
=
|( )|
−2
)
.
(
−1
)
− 𝜋.
(
−𝜋
(
4 + 𝜋
2
)
3
2
=
2 + 𝜋
2
(
4 + 𝜋
2
)
3
2
Câu 4: Tính các tích phân kép sau:
a) ∬2𝑥𝑑𝑥𝑑𝑦
𝐷
, 𝐷 ền ới hạn bởi 𝑦= 𝑥là mi gi
2
và 𝑦= 2 − 𝑥
b) ∬𝑦
√
𝑥
2
+ 𝑦
2
𝑑𝑥𝑑𝑦
𝐷
, vớ𝑖 𝐷=
{(
𝑥, 𝑦
)
∈𝑅
2
: 𝑥
2
+ 𝑦
2
≤ 𝑦
}
Gi i:ả
a) ∬2𝑥𝑑𝑥𝑑𝑦
𝐷
, 𝐷 ền ới hạn bởi 𝑦= 𝑥là mi gi
2
𝑦= 2 − 𝑥 và
Mi
ền 𝐷: {
−2 ≤ 𝑥≤ 1
𝑥
2
≤ 𝑦≤ 2 − 𝑥
∬2𝑥𝑑𝑥𝑑𝑦
𝐷
= ∫ 𝑑𝑥
1
−2
∫ 2𝑥𝑑𝑦
2−𝑥
𝑥
2
= ∫ 2𝑥
(
2 − 𝑥− 𝑥
2
)
𝑑𝑥
1
−2
=
−9
2
PHAM THANH TUNG
b) ∬𝑦
√
𝑥
2
+ 𝑦
2
𝑑𝑥𝑑𝑦
𝐷
, vớ𝑖 𝐷=
{(
𝑥, 𝑦
)
∈𝑅
2
: 𝑥
2
+ 𝑦
2
≤ 𝑦
}
Đăt
{
𝑥= 𝑟cos 𝜑
𝑦= 𝑟sin 𝜑
, 𝐽= 𝑟
Mi
ền {
0 ≤ 𝑟≤ sin 𝜑
0 ≤ 𝜑≤ 𝜋
∬𝑦 + 𝑦
√
𝑥
2 2
𝑑𝑥𝑑𝑦
𝐷
= ∫ 𝑑𝜑
𝜋
0
∫ 𝑟sin 𝜑
√
𝑟
2
𝑟𝑑𝑟
sin 𝜑
0
=
1
4
∫ sin 𝜑. sin
4
𝜑𝑑𝜑
𝜋
0
=
−1
4
∫
(
1 − cos
2
𝜑
)
2
𝑑
(
cos 𝜑
)
𝜋
0
=
−1
4
∫
(
1 − 𝑢
2
)
2
𝑑𝑢
−1
1
=
−1
4
.
−16
15
=
4
15
Câu 5: Tính th tích v t th gi i h n b i các m ể ậ ể 𝑉 ớ ạ ở ặt
𝑥= 9𝑦 + 𝑧
2 2
𝑥= 9và
Gi i:ả
Xét giao tuy n c và ế ủa 𝑥= 9𝑦 + 𝑧
2 2
𝑥= 9
9𝑦 + 𝑧 = 9 ⇔ 3𝑦
2 2
( )
2
+ 𝑧 = 3
2 2
Hình chi u c lên là
ế ủa 𝑉 𝑂𝑦𝑧 𝐷:
(
3𝑦
)
2
+ 𝑧 ≤ 3
2 2
PHAM THANH TUNG
Thể ậ ể tích v t th 𝑉 là:
𝑉= ∭𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∬9 − 9𝑦
[ (
2
+ 𝑧
2
)]
𝑑𝑦𝑑𝑧
𝐷
Đặt {
3𝑦= 𝑟cos 𝜑
𝑧= 𝑟sin 𝜑
⇔{
𝑦=
𝑟
3
cos 𝜑
𝑧= 𝑟sin 𝜑
, 𝐽=
𝑟
3
⇒𝐷: {
0 ≤ 𝑟≤ 3
0 ≤ 𝜑≤ 2𝜋
⇒𝑉= ∬9 − 9𝑦 + 𝑧
[ (
2 2
)]
𝑑𝑦𝑑𝑧
𝐷
= ∫ 𝑑𝜑
2𝜋
0
∫
(
9 − 𝑟
2
)
.
𝑟
3
𝑑𝑟
3
0
= 2𝜋.
27
4
=
27𝜋
2
(
đvtt
)
Câu 6: Tính tích phân sau:
∫ 𝑑𝑦
1
0
∫ 𝑑𝑥
1
0
∫ 𝑥𝑦𝑒
𝑦𝑧
2
𝑑𝑧
1
𝑥
2
Gi i:ả
Mi
ền 𝑉: {
0 ≤ 𝑥≤ 1
0 ≤ 𝑦≤ 1
𝑥
2
≤ 𝑧≤ 1
.Đổ ứ ự ấ ềi th t l y tích phân: mi n 𝑉trở thanh 𝑉: {
0 ≤ 𝑥≤
√
𝑧
0 ≤ 𝑦≤ 1
0 ≤ 𝑧≤ 1
Hình v minh h a trên m t ph ng i th t c n và ẽ ọ ặ ẳ 𝑂𝑥𝑧khi đổ ứ ự ậ 𝑥 𝑧
PHAM THANH TUNG
⇒∫ 𝑑𝑦
1
0
∫ 𝑑𝑧
1
0
∫ 𝑥𝑦𝑒
𝑦𝑧
2
𝑑𝑥
√
𝑧
0
=
1
2
∫ 𝑑𝑦
1
0
∫ 𝑦𝑧𝑒
𝑦𝑧
2
𝑑𝑧
1
0
=
1
2
∫ 𝑑𝑦
1
0
∫ 𝑒
𝑦𝑧
2
𝑑(
𝑦𝑧
2
2
)
1
0
=
1
4
∫ 𝑑𝑦
1
0
∫ 𝑒
𝑦𝑧
2
𝑑
(
𝑦𝑧
2
)
1
0
=
1
4
∫
(
𝑒
𝑦
− 1
)
𝑑𝑦
1
0
=
1
4
(
𝑒− 2
)
Câu 7:
Tính
∬
(
4 + 3𝑦𝑑𝑥𝑑𝑦𝑥𝑦
)
𝐷
v ới 𝐷: 1 ≤ ≤ 4, 𝑥≤ 𝑦≤ 9𝑥.𝑥𝑦
Gi i:ả
Mi
ền 𝐷: 1 ≤ 𝑥𝑦≤ 4, 𝑥≤ 𝑦≤ 9𝑥⇔1 ≤ ≤ 4, 1 ≤𝑥𝑦
𝑦
𝑥
≤ 9
Đặ𝑡 {
𝑢= 𝑥𝑦
𝑣=
𝑦
𝑥
⇒𝐽
−1
= |
𝑢
𝑥
′
𝑢
𝑦
′
𝑣
𝑥
′
𝑣
𝑦
′
| = |
𝑦 𝑥
−𝑦
𝑥
2
1
𝑥
| =
2𝑦
𝑥
⇒𝐽=
1
2
.
𝑥
𝑦
=
1
2𝑣
Mi
ề ện trong h𝐷 t mọa độ ới 𝑂
𝑢𝑣
là 𝐷
𝑢𝑣
: {
1 ≤ 𝑢≤ 4
1 ≤ 𝑣≤ 9
∬4 + 3𝑦𝑑𝑥𝑑𝑦
(
𝑥𝑦
)
𝐷
= ∬(4𝑢+ 3
√
𝑢𝑣)
1
2𝑣
𝑑𝑢𝑑𝑣
𝐷
𝑢𝑣
= ∫ 𝑑𝑣
9
1
∫ (
2𝑢
𝑣
+
3
2
√
𝑢
𝑣
) 𝑑𝑢
4
1
= 30 28ln 3 +
Câu 8: Tính tích phân b i ba ộ
∭
𝑧𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
là mi nh btrong đó 𝑉 ền xác đị ởi 𝑥
2
+ 𝑦
2
+ 𝑧
2
≤ 𝑧
𝑧≤ + 𝑦
√
𝑥
2 2
Gi i:ả
PHAM THANH TUNG
Cách 1: T : ọa độ trụ
Mi
ền 𝑉: {
𝑥
2
+ 𝑦
2
+ 𝑧
2
≤ 𝑧
𝑧≤ + 𝑦
√
𝑥
2 2
⇔{
𝑥
2
+ 𝑦
2
+ (
𝑧−
1
2
)
2
≤
1
4
𝑧≤ + 𝑦
√
𝑥
2 2
𝑥
2
+ 𝑦 𝑧−
2
+ (
1
2
)
2
≤
1
4
: Dấu ≤ thể hiện miền 𝑉 nằm trong mặt cầu.
𝑧≤ + 𝑦
√
𝑥
2 2
: Dấu ể ện ền 𝑉 nằm ới mặt nón.≤ th hi mi dư
⇒𝑉:
1
2
−
√
1
4
−
(
𝑥
2
+ 𝑦
2
)
≤ 𝑧≤ + 𝑦
√
𝑥
2 2
Xét giao tuy n c a hai m
ế ủ ặt {
𝑥
2
+ 𝑦
2
+ 𝑧
2
= 𝑧
𝑧= √𝑥 + 𝑦
2 2
⇒
(
𝑥
2
+ 𝑦
2
)
+
(
𝑥
2
+ 𝑦
2
)
=
√
𝑥
2
+ 𝑦
2
⇔2 + 𝑦
(
𝑥
2 2
)
−
√
𝑥
2
+ 𝑦
2
= 0
⇒
√
𝑥
2
+ 𝑦
2
=
1
2
⇔𝑥
2
+ 𝑦
2
=
1
4
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 𝐷: 𝑥
là
2
+ 𝑦
2
≤
1
4
Miền V:
{
1
2
−
√
1
4
−
(
𝑥
2
+ 𝑦
2
)
≤ 𝑧≤
√
𝑥
2
+ 𝑦
2
𝐷: 𝑥
2
+ 𝑦
2
≤
1
4
Đặt {
𝑥= 𝑟cos 𝜑
𝑦= 𝑟sin 𝜑
𝑧= 𝑧
, 𝐽= 𝑟⇒𝑉:
{
1
2
−
√
1
4
− 𝑟
2
≤ 𝑧≤ 𝑟
0 ≤ 𝑟≤
1
2
0 ≤ 𝜑≤ 2𝜋
∭𝑧𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∫ 𝑑𝜑
2𝜋
0
∫ 𝑑𝑟
1
2
0
∫ 𝑧. 𝑟𝑑𝑧
𝑟
1
2
−
√
1
4
−𝑟
2
=
1
2
∫ 𝑑𝜑
2𝜋
0
∫ [𝑟
2
− (
1
2
−
√
1
4
− 𝑟
2
)
2
] 𝑟𝑑𝑟
1
2
0
=
1
2
∫ 𝑑𝜑
2𝜋
0
∫ [𝑟
3
−
𝑟
4
+ 𝑟
√
1
4
− 𝑟
2
− 𝑟(
1
4
− 𝑟
2
)
] 𝑑𝑟
1
2
0
PHAM THANH TUNG
∫ 𝑟
√
1
4
− 𝑟
2
𝑑𝑟
1
2
0
=
1
2
∫
√
1
4
− 𝑟
2
𝑑
(
𝑟
2
)
1
2
0
=
1
2
∫
√
1
4
− 𝑢𝑑𝑢
1
4
0
=
1
24
⇒
1
2
∫ 𝑑𝜑
2𝜋
0
∫ [𝑟
3
−
𝑟
4
+ 𝑟
√
1
4
− 𝑟
2
− 𝑟(
1
4
− 𝑟
2
)
] 𝑑𝑟
1
2
0
=
1
2
∫ (
−1
32
+
1
24
) 𝑑𝜑
2𝜋
0
=
𝜋
96
Cách 2: T c ọa độ ầu:
Đặ
t {
𝑥= 𝑟 𝜑sin 𝜃cos
𝑦= 𝑟sin 𝜑sin 𝜃
𝑧= 𝑟
cos 𝜃
,
|
𝐽
|
= 𝑟
2
sin 𝜃⇒Miền 𝑉: {
0 ≤ 𝑟≤ cos 𝜃
𝜋/4 ≤ 𝜃≤ 𝜋 /2
0 ≤ 𝜑≤ 2𝜋
∭𝑧𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∫ 𝑑𝜑
2𝜋
0
∫ 𝑑𝜃
𝜋
2
𝜋
4
∫ 𝑟cos 𝜃. 𝑟
2
sin 𝜃𝑑𝑟
cos𝜃
0
=
1
4
∫ 𝑑𝜑
2𝜋
0
∫ cos
4
𝜃cos 𝜃sin 𝜃𝑑𝜃
𝜋
2
𝜋
4
=
−1
4
∫ 𝑑𝜑
2𝜋
0
∫ cos
5
𝜃𝑑
(
cos 𝜃
)
𝜋
2
𝜋
4
=
−1
4
∫ 𝑑𝜑
2𝜋
0
∫ 𝑢
5
𝑑𝑢
0
√
2
2
=
𝜋
96
Câu 9: Tính tích phân
∫
𝑒
−𝑎𝑥
3
− 𝑒
−𝑏𝑥
3
𝑥
𝑑𝑥
+∞
0
với 𝑎, 𝑏> 0
Gi i:ả
Đặt 𝐹
(
𝑥, 𝑦
)
=
𝑒
−𝑦𝑥
3
𝑥
𝑒
−𝑎𝑥
3
− 𝑒
−𝑏𝑥
3
𝑥
= 𝐹
(
𝑥, 𝑎
)
− 𝐹
(
𝑥, 𝑏
)
= ∫ 𝐹
𝑦
′
(
𝑥, 𝑦
)
𝑑𝑦
𝑎
𝑏
= ∫ −𝑥
2
𝑒
−𝑦𝑥
3
𝑑𝑦
𝑎
𝑏
= ∫ 𝑥
2
𝑒
−𝑦𝑥
3
𝑑𝑦
𝑏
𝑎
∫
𝑒
−𝑎𝑥
3
− 𝑒
−𝑏𝑥
3
𝑥
𝑑𝑥
+∞
0
= ∫ ∫ 𝑥(
2
𝑒
−𝑦𝑥
3
𝑑𝑦
𝑏
𝑎
)
𝑑𝑥
+∞
0
= ∫ ∫ 𝑥(
2
𝑒
−𝑦𝑥
3
𝑑𝑥
+∞
0
)
𝑑𝑦
𝑏
𝑎
PHAM THANH TUNG
= ∫
(
1
3
∫ 𝑒
−𝑦𝑥
3
𝑑
(
𝑥
3
)
+∞
0
)
𝑑𝑦
𝑏
𝑎
= ∫ (
1
3
.
−1
𝑦
𝑒
−𝑦𝑥
3
|
+∞
0
) 𝑑𝑦
𝑏
𝑎
= ∫
1
3𝑦
𝑑𝑦
𝑏
𝑎
=
1
3
ln
𝑏
𝑎
*Kiểm tra điều kiện khả tích:
Đặt 𝑓
(
𝑥, 𝑦 = 𝑥
)
2
𝑒
−𝑦𝑥
3
−
Hàm liên t c trên mi n 𝑓
(
𝑥, 𝑦
)
ụ ề
[ [
0; +∞
)
× 𝑏; 𝑎
]
−
Tích phân 𝐼
(
𝑦
)
=
∫
𝑥
2
𝑒
−𝑦𝑥
3
𝑑𝑥
+∞
0
h i t u trên ộ ụ đề
[ ]
𝑏, 𝑎
(
𝑎, 𝑏> 0
)
Do
{
𝑥
2
𝑒
−𝑦𝑥
3
≤ 𝑥
2
𝑒
−𝑦
0
𝑥
3
với 𝑦
0
≥ 𝑏> 0
∫ 𝑥
2
𝑒
−𝑦
0
𝑥
3
+∞
0
𝑑𝑥=
1
3𝑦
0
hội tụ
⇒∫ 𝑥
2
𝑒
−𝑦𝑥
3
𝑑𝑥
+∞
0
hội tụ đều trên
[
𝑏; 𝑎
]
Vậy điề ện đổu ki i thứ tự lấy tích phân thỏa mãn.
❖ Mẹo:
Trong các bài t p s dậ ử ụng phương pháp đổi thứ t lự ấy tích phân và phương pháp đạo hàm đạo hàm
qua d u tích phân, chúng ta s , t c là c áp d ấ ẽ “tiền tr m h u tả ậ ấu” ứ ứ ụng hai phương pháp trên để
tính tích phân, khi ra k t qu r i m i ki u ki n kh vi, kh tích, gi ng l i gi i tham khế ả ồ ớ ểm tra điề ệ ả ả ố ờ ả ảo
trên. Khi làm như vậy, nếu không đủ thời gian chứng minh điều ki n kh vi, kh tích, chúng ta v n ệ ả ả ẫ
được 0.5đ nếu tính toán đúng tích phân.
PHAM THANH TUNG
LỜI GI I THAM KH THI GI Ả ẢO ĐỀ ỮA KÌ 20173 (ĐỀ 1)
Câu 1:
Tính độ ủa đườ cong tại 𝑡= 0 c ng {
𝑥= 𝑒 − sin 𝑡
−𝑡
𝑦= 𝑒
−𝑡
− cos 𝑡
Gi i:ả
{
𝑥= 𝑒 − sin 𝑡
−𝑡
𝑦= 𝑒
−𝑡
− cos 𝑡
⇒{
𝑥
′
(
𝑡
)
= −𝑒
−𝑡
− cos𝑡, 𝑥
′′
(
𝑡
)
= 𝑒
−𝑡
+ sin 𝑡
𝑦
′
(
𝑡
)
= −𝑒 + sin 𝑡, 𝑦
−𝑡 ′′
(
𝑡
)
= 𝑒
−𝑡
+ cos𝑡
V
ới 𝑡= 0 ⇒{
𝑥
′
(
0
)
= −2, 𝑥
′′
(
0
)
= 1
𝑦
′
(
0 = −1, 𝑦
)
′′
(
0 = 2
)
Độ ạ cong c ng cong tủa đườ i 𝑡= 0 là:
𝐶
(
𝑡= 0
)
=
|
𝑥
′
. 𝑦
′′
− 𝑥
′′
. 𝑦
′
|
(𝑥 + 𝑦
′
2
′
2
)
3
2
=
|( )|
−2
)
. 2 − 1.
(
−1
(
2
2
+ 1
2
)
3
2
=
3
5
√
5
Câu 2:
Lập phương trình pháp tuyến và tiếp diện tại 𝐴
(
1,1,0
)
của mặt 𝑧= 3𝑥− 2𝑦ln
( )
Gi i:ả
Đặt 𝐹
(
𝑥, 𝑦, 𝑧 = 𝑧− 3𝑥− 2𝑦 ⇒𝐹
)
ln
( )
𝑥
′
=
−3
3𝑥− 2𝑦
, 𝐹
𝑦
′
=
2
3𝑥− 2𝑦
, 𝐹
𝑧
′
= 1
T
ại 𝐴
(
1,1,0 ⇒𝐹
)
𝑥
′
(
𝐴
)
= −3, 𝐹
𝑦
′
(
𝐴
)
= 2, 𝐹
𝑧
′
(
𝐴
)
= 1
Phương trình pháp tuyế
n của mặt cong tại 𝐴
(
1,1,0
)
là:
𝑥− 1
−3
=
𝑦− 1
2
=
𝑧
1
Phương trình tiế
p diện của mặt cong tại 𝐴
(
1,1,0
)
là:
−3 𝑥− 1 + 2 𝑦− 1 + 𝑧= 0 ⇔−3𝑥+ 2𝑦+ 𝑧+ 1 = 0
( ) ( )
Câu 3:
Cho hàm vecto 𝑝 sin 2𝑡, 2𝑡,𝑒
(
𝑡
)
=
(
cos
−𝑡
)
và 𝑟 + 1 𝑝
(
𝑡
)
=
(
𝑡
2
) (
𝑡
)
. Tính 𝑟
′
(
0
)
Gi i:ả
𝑟 + 1 𝑝 ⇒𝑟
(
𝑡
)
=
(
𝑡
2
) (
𝑡
)
′
( )
𝑡
)
=
[(
𝑡
2
+ 1 𝑝
(
𝑡
)]
′
=
(
𝑡
2
+ 1
)
′
𝑝 + 1
(
𝑡
)
+
(
𝑡
2
)
𝑝
′
(
𝑡
)
= 2𝑡.
(
sin 2𝑡, 2𝑡,𝑒cos
−𝑡
)
+
(
𝑡
2
+ 1 2𝑡, −2 sin 2𝑡,−𝑒
)(
2 cos
𝑡
)
⇒𝑟
′
(
0
)
= 2.0.
(
sin 0 , cos 0 , 𝑒
−0
)
+ 1.
(
2 cos 0 , −2 sin 0, −𝑒
0
)
=
( )
2,0, −1
PHAM THANH TUNG
Câu 4: Đổi th t l y tích phân ứ ự ấ 𝐼= 𝑑𝑥
∫
2
−1
∫
𝑓
(
𝑥, 𝑦𝑑𝑥𝑑𝑦
)
2−𝑥
2
−𝑥
Gi i:ả
Miền
(
𝐷
)
: {
−1 ≤ 𝑥≤ 2
−𝑥≤ 𝑦≤ 2 − 𝑥
2
Đổ ứ ự ấ ề ầ
i th t l y tích phân. Chia mi n thành 2 ph
(
𝐷
)
n
(
𝐷
1
)
: {
−
√
2 − 𝑦≤ 𝑥≤ 2 − 𝑦
√
1 ≤ 𝑦≤ 2
và
(
𝐷
2
)
: {
−𝑦≤ 𝑥≤ 2 − 𝑦
√
−2 ≤ 𝑦≤ 1
⇒𝐼= ∫ 𝑑𝑦
1
−2
∫ 𝑓(𝑥,𝑦)𝑑𝑥
√
2−𝑦
−𝑦
+ ∫𝑑𝑦
2
1
∫ 𝑓(𝑥, 𝑦)𝑑𝑥
√
2−𝑦
−
√
2−𝑦
Câu 5:
Tính
∬
(
3𝑥+ 2𝑦𝑑𝑥𝑑𝑦
)
𝐷
, 𝐷 gi i h n b ớ ạ ởi:
𝑥= 0, 𝑦= 0, 𝑥+ 𝑦= 1
Gi i:ả
Mi
ền
(
𝐷
)
: {
0 ≤ 𝑥≤ 1
0 ≤ 𝑦≤ 1 − 𝑥
∬3𝑥+ 2𝑦𝑑𝑥𝑑𝑦
( )
𝐷
= ∫ 𝑑𝑥
1
0
∫
(
3𝑥+ 2𝑦𝑑𝑦
)
1−𝑥
0
= ∫ 3𝑥1 − 𝑥 1 − 𝑥 𝑑𝑥
[ ( )
+
( )
2
]
1
0
=
5
6
PHAM THANH TUNG
Câu 6:
Tính
∬
(
𝑥+ 𝑦 𝑥− 2𝑦− 1
)( )
2
𝑑𝑥𝑑𝑦
𝐷
, 𝐷 𝑥+ 𝑦= 0, 𝑥+ 𝑦= 3, 𝑥− 2𝑦= 1, gi i h n bớ ạ ởi
𝑥− 2𝑦= 2
Gi i:ả
Đặ
t {
𝑥+ 𝑦= 𝑢
𝑥− 2𝑦= 𝑣
⇒𝐽
−1
= |
1 1
1 −2
| = −3 ⇒
|
𝐽
|
= 1/3
Mi
ền
(
𝐷
′
)
m i trong hớ ệ t mọa độ ới 𝑂𝑢𝑣 là
(
𝐷
′
)
: {
0 ≤ 𝑢≤ 3
1 ≤ 𝑣≤ 2
⇒∬𝑥+ 𝑦 𝑥− 2𝑦− 1
( )( )
2
𝑑𝑥𝑑𝑦
𝐷
=
1
3
∬𝑢
(
𝑣− 1
)
2
𝑑𝑢𝑑𝑣
𝐷
′
=
1
3
∫ 𝑑𝑢
3
0
∫ 𝑢𝑣− 1
( )
2
𝑑𝑣
2
1
=
1
2
Câu 7: Tính
∭
𝑧√𝑥 + 𝑦 𝑑𝑥𝑑𝑦𝑑𝑧
2 2
𝑉
, 𝑉 gi i h n bớ ạ ởi 𝑥
2
+ 𝑦
2
= 1, 𝑧= 0,𝑧= 2
Gi i:ả
Hình chi u c lên là ế ủa 𝑉 𝑂𝑥𝑦 𝐷: 𝑥
2
+ 𝑦 ≤ 1
2
Đặ
t {
𝑥= 𝑟cos 𝜑
𝑦= 𝑟sin 𝜑
𝑧= 𝑧
𝐽= 𝑟. Mi n ề
(
𝐷
)
: {
0 ≤ 𝑟< 1
0 ≤ 𝜑≤ 2𝜋
⇒
n Miề
(
𝑉
)
trong t ọa độ trụ: {
0 ≤ 𝑟≤ 1
0 ≤ 𝜑≤ 2𝜋
0 ≤ 𝑧≤ 2
⇒∭𝑧 + 𝑦
√
𝑥
2 2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∫ 𝑑𝜑
2𝜋
0
∫ 𝑑𝑟
1
0
∫ 𝑧. 𝑟. 𝑟𝑑𝑧
2
0
= 2 ∫ 𝑑𝜑
2𝜋
0
∫ 𝑟
2
𝑑𝑟
1
0
=
4𝜋
3
Câu 8: Tính th tích v t th gi i h n b ể ậ ể 𝑉 ớ ạ ởi
𝑥= + 𝑧
√
𝑦
2 2
, 𝑥=
√
1 − 𝑥
2
− 𝑦
2
PHAM THANH TUNG
Gi i:ả
Hình minh h a mi n c v l i theo quy t c tam di n thu n ọ ề 𝑉 đượ ẽ ạ ắ ệ ậ
Đặ
t {
𝑦= 𝑟sin 𝜃cos 𝜑
𝑧= 𝑟sin 𝜃sin 𝜑
𝑥= 𝑟
cos 𝜃
|
𝐽
|
= 𝑟
2
sin 𝜃. Miền
(
𝑉
)
: {
0 ≤ 𝑟≤ 1
0 ≤ 𝜃≤ 𝜋/4
0 ≤ 𝜑≤ 2𝜋
Thể ề tích mi n là: 𝑉
𝑉
(
𝑉
)
= ∭𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∫ 𝑑𝜑
2𝜋
0
∫ 𝑑𝜃
𝜋
4
0
∫ 𝑟
2
sin 𝜃𝑑𝑟
1
0
=
1
3
∫ 𝑑𝜑
2𝜋
0
∫ sin 𝜃𝑑𝜃
𝜋
4
0
=
2𝜋
3
(1 −
√
2
2
)
(
đvtt
)
Câu 9: Tính
∭
3𝑥 − 𝑦 + 𝑧 + 1
2 2 2
𝑥
2
+ 𝑦 + 𝑧 + 1
2 2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
V khới 𝑉 là nửa ối cầu 𝑥
2
+ 𝑦 + 𝑧 ≤ 1, 𝑧≥ 0
2 2
Gi i:ả
PHAM THANH TUNG
Khi đổ không thay đổi vai trò của 𝑥 và cho nhau thì mi𝑦 ền 𝑉 i
⇒𝐼= ∭
3𝑥
2
− 𝑦
2
+ 𝑧
2
+ 1
𝑥
2
+ 𝑦 + 𝑧 + 1
2 2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∭
3𝑦
2
− 𝑥
2
+ 𝑧
2
+ 1
𝑥
2
+ 𝑦 + 𝑧 + 1
2 2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
⇒2𝐼= ∭
3𝑥
2
− 𝑦
2
+ 𝑧
2
+ 1
𝑥
2
+ 𝑦 + 𝑧 + 1
2 2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
+ ∭
3𝑦
2
− 𝑥
2
+ 𝑧
2
+ 1
𝑥
2
+ 𝑦 + 𝑧 + 1
2 2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= 2 ∭𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
⇒𝐼= ∭𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
=
1
2
.
4
3
𝜋=
2𝜋
3
Câu 10: Tìm gi i h n ớ ạ
lim
𝑦→0
∫
arctan 𝑥+ 𝑦
( )
1 + 𝑥 + 𝑦
2 2
𝑑𝑥
cos 𝑦
sin 𝑦
Gi i:ả
{
cos x , siny liên tục ∀y ∈𝑅
arctan x + y
( )
1 + x + y
2 2
liên tục trên 𝑅
2
⇒𝐼
(
𝑦
)
= ∫
arctan
(
x + y
)
1 + x + y
2 2
𝑑𝑥
cos𝑦
sin 𝑦
liên tục trên 𝑅
⇒lim
𝑦→0
∫
arctan x + y
( )
1 + x + y
2 2
𝑑𝑥
cos 𝑦
sin 𝑦
= ∫
arctan 𝑥+ 0
( )
1 + 𝑥 + 0
2 2
𝑑𝑥
cos0
sin 0
= ∫
arctan
(
𝑥
)
1 + 𝑥
2
𝑑𝑥
1
0
= ∫ arctan
(
𝑥
)
𝑑
(
arctan
(
𝑥
))
1
0
= ∫ 𝑡𝑑𝑡
𝜋
4
0
=
𝜋
2
32
PHAM THANH TUNG
LỜI GI I THAM KH Ả ẢO ĐỀ GIỮA KỲ 20182 (ĐỀ 2)
Câu 1: Viết phương trình tiếp diện và pháp tuyến của mặt cong t𝑥
2
+ 𝑦 − 𝑒 − 2𝑦𝑥𝑧= 0
2 𝑧
ại
điể
m 𝑀
(
1,0,0 .
)
Gi i:ả
Đặ
t 𝐹
(
𝑥, 𝑦, 𝑧 = 𝑥 + 𝑦 − 𝑒 − 2𝑦𝑥𝑧⇒{
)
2 2 𝑧
𝐹
𝑥
′
= 2𝑥− 2𝑦𝑧
𝐹
𝑦
′
= 2𝑦− 2𝑥𝑧
𝐹
𝑧
′
= −𝑒
𝑧
− 2𝑦𝑥
T
ại 𝑀
(
1,0,0 ,
)
ta có: 𝐹
𝑥
′
(
𝑀
)
= 2, 𝐹
𝑦
′
(
𝑀
)
= 0, 𝐹
𝑧
′
(
𝑀
)
= −1
Phương trình tiế
p diện của mặt cong tại 𝑀
(
1,0,0
)
là:
2
(
𝑥− 1 + 0 𝑦− 0 𝑧− 0 = 0 ⇔2𝑥− 𝑧− 2 = 0
) ( )
−
( )
Phương trình pháp tuyế
n của mặt cong tại 𝑀
(
1,0,0
)
là: {
𝑥= 1 + 2𝑡
𝑦= 0
𝑧= −𝑡
Câu 2:
Tìm hình bao c a h ng cong sau: ủ ọ đườ
(
𝑥+ 𝐶
)
2
+
(
𝑦− 2𝐶
)
2
= 5.
Gi i:ả
Đặ
t 𝐹
(
𝑥, 𝑦, 𝑐 𝑥+ 𝑐
)
=
( )
2
+
(
𝑦− 2𝑐
)
2
− 5
Xét
{
𝐹
𝑥
′
= 0
𝐹
𝑦
′
= 0
⇔{
2
(
𝑥+ 𝑐 = 0
)
2 𝑦− 2𝑐 = 0
( )
⇔
{
𝑥= −𝑐
𝑦= 2𝑐
Đi
ể ộ ọ đườm
(
−𝑐, 2𝑐
)
không thu c h ng tròn
(
𝑥+ 𝑐
)
2
+
(
𝑦− 2𝑐
)
2
= 5
H m kì d . ⇒ ọ đường tròn không có điể ị
Xét
{
𝐹= 0
𝐹
𝑐
′
= 0
⇔{
(
𝑥+ 𝑐
)
2
+
(
𝑦− 2𝑐
)
2
− 5 = 0
2 𝑥+ 𝑐 − 4 𝑦− 2𝑐
( ) ( )
= 0
⇔{
(
𝑥+ 𝑐
)
2
+
(
𝑦− 2𝑐
)
2
− 5 = 0
𝑥+ 𝑐= 2 𝑦− 2𝑐
( )
⇔{
(
2𝑦− 4𝑐
)
2
+
(
𝑦− 2𝑐
)
2
= 5
𝑥+ 𝑐= 2 𝑦− 2𝑐
( )
⇔{
(
𝑦− 2𝑐
)
2
= 1
𝑥= 2 𝑦− 2𝑐 − 𝑐
( )
⇔{
[
𝑦= 1 + 2𝑐
𝑦= −1 + 2𝑐
𝑥= 2 𝑦− 2𝑐 − 𝑐
( )
⇔[
{
𝑥= 2 − 𝑐
𝑦= 1 + 2𝑐
{
𝑥= −2 − 𝑐
𝑦= −1 + 2𝑐
⇔
[
{
−𝑥+ 2 = 𝑐
𝑦− 1
2
= 𝑐
{
−𝑥− 2 = 𝑐
𝑦+ 1
2
= 𝑐
⇒[
𝑦− 1
2
+ 𝑥− 2 = 0
𝑦+ 1
2
+ 𝑥+ 2 = 0
⇔[
𝑦+ 2𝑥− 5 = 0
𝑦+ 2𝑥+ 5 = 0
Vậy hình bao c a hủ ọ đường tròn là: và 𝑦= −2𝑥+ 5 𝑦= −2𝑥− 5
PHAM THANH TUNG
Câu 3: Tính tích phân kép ∬
(
𝑥− 4𝑦𝑑𝑥𝑑𝑦
)
𝐷
trong 𝐷 ới hạn bởi parabol 𝑦= 𝑥đó gi
2
− 1
và tr ục 𝑂𝑥.
Gi i:ả
Mi
ền 𝐷: {
−1 ≤ 𝑥≤ 1
𝑥
2
− 1 ≤ 𝑦≤ 0
∬𝑥− 4𝑦𝑑𝑥𝑑𝑦
( )
𝐷
= ∫ 𝑑𝑥
1
−1
∫
(
𝑥− 4𝑦𝑑𝑦
)
0
𝑥
2
−1
= ∫ [𝑥1 − 𝑥
(
2
)
+ 4.
1
2
(
𝑥
2
− 1
)
2
] 𝑑𝑥
1
−1
=
32
15
Câu 4: Tính tích phân l p: ặ
∫ 𝑑𝑥
2
1
∫
1 − cos 𝜋𝑦
𝑦
2
1
√
𝑥−1
𝑑𝑦
Gi i:ả
PHAM THANH TUNG
Đổ ứ ự ấ ề
i th t l y tích phân, mi n 𝐷: {
1 ≤ 𝑥≤ 𝑦
2
+ 1
0 ≤ 𝑦≤ 1
⇒∫ 𝑑𝑥
2
1
∫
1 − cos 𝜋𝑦
𝑦
2
1
√
𝑥−1
𝑑𝑦= ∫ 𝑑𝑦
1
0
∫
1 − cos 𝜋𝑦
𝑦
2
𝑦
2
+1
1
𝑑𝑥= ∫ (
𝑦
2
.
1 − cos 𝜋𝑦
𝑦
2
) 𝑑𝑦
1
0
= ∫ 1 − 𝑑𝑦
(
cos 𝜋𝑦
)
1
0
= 1
Câu 5: Tính di n tích ph n hình tròn n ng tròn ệ ầ 𝑥
2
+ 𝑦 = 2𝑦
2
ằm ngoài đườ 𝑥
2
+ 𝑦 = 1
2
Gi i:ả
Gọi miền cần tính diện tích là 𝐷.
Đặ
t {
𝑥= 𝑟cos 𝜑
𝑦= 𝑟sin 𝜑
,
|
𝐽
|
= 𝑟. Mi n ề 𝐷: {
1 ≤ 𝑟≤ 2 sin 𝜑
𝜋/6 ≤ 𝜑≤ 5𝜋 /6
Diệ ền tích mi n là: 𝐷
PHAM THANH TUNG
𝑆= ∬𝑑𝑥𝑑𝑦
𝐷
= ∫ 𝑑𝜑
5𝜋
6
𝜋
6
∫ 𝑟𝑑𝑟
2 sin 𝜑
1
=
1
2
∫
(
4sin
2
𝜑− 1
)
𝑑𝜑
5𝜋
6
𝜋
6
= ∫ (
2
(
1 − 2𝑥cos
)
2
−
1
2
) 𝑑𝜑
5𝜋
6
𝜋
6
⇒𝑆=
𝜋
3
+
√
3
2
(
đvdt
)
Câu 6: Tính các tích phân b i ba sau: ộ
𝑎) ∭
(
3𝑥 + 2𝑦𝑑𝑥𝑑𝑦𝑑𝑧
2
)
𝑉
, trong ền 𝑉 xác đị bởi 0 ≤ 𝑥≤ 1, 0 ≤ 𝑦≤ 𝑥, 0 ≤ 𝑧≤ 𝑥đó mi nh
2
Gi i:ả
∭3𝑥 + 2𝑦𝑑𝑥𝑑𝑦𝑑𝑧
(
2
)
𝑉
= ∫ 𝑑𝑥
1
0
∫ 𝑑𝑦
𝑥
0
∫
(
3𝑥
2
+ 2𝑦𝑑𝑧
)
𝑥
2
0
= ∫ 𝑑𝑥
1
0
∫ 𝑥
2
(
3𝑥
2
+ 2𝑦𝑑𝑦
)
𝑥
0
= ∫ 3𝑥 + 𝑥 . 𝑥
(
5 2 2
)
𝑑𝑥
1
0
=
7
10
𝑏) ∭
(
𝑥− 𝑦+ 2𝑧𝑑𝑥𝑑𝑦𝑑𝑧
)
𝑉
, trong 𝑉 ợc ới hạn bởi các mặt đó đư gi
𝑥− 𝑦= 0, 𝑥− 𝑦= 2, 𝑥+ 𝑦= 0, 𝑥+ 𝑦= 1, 𝑧= 0, 𝑧= 1
Gi i:ả
Đặ
t {
𝑢= 𝑥− 𝑦
𝑣= 𝑥+ 𝑦
𝑤= 𝑧
⇒𝐽
−1
= |
𝑢
𝑥
′
𝑢
𝑦
′
𝑢
𝑧
′
𝑣
𝑥
′
𝑣
𝑦
′
𝑣
𝑧
′
𝑤
𝑥
′
𝑤
𝑦
′
𝑤
𝑧
′
| = |
1 −1 0
1 1 0
0 0 1
| = 2 ⇒𝐽= 1/2
Mi
ền trong t m𝑉 ọa độ ới 𝑂𝑢𝑣𝑤 là 𝑉
𝑢𝑣𝑤
: {
0 ≤ 𝑢≤ 2
0 ≤ 𝑣≤ 1
0 ≤ 𝑤≤ 1
⇒∭𝑥− 𝑦+ 2𝑧𝑑𝑥𝑑𝑦𝑑𝑧
( )
𝑉
= ∭
1
2
(
𝑢+ 2𝑤
)
𝑑𝑢𝑑𝑣𝑑𝑤
𝑉𝑢𝑣𝑤
=
1
2
∫ 𝑑𝑢
2
0
∫ 𝑑𝑣
1
0
∫ 𝑢+ 2𝑤
( )
1
0
𝑑𝑤
=
1
2
∫ 𝑑𝑢
2
0
∫ 𝑢+ 1 𝑑𝑣
( )
1
0
=
1
2
∫
(
𝑢+ 1
)
𝑑𝑢= 2
2
0
PHAM THANH TUNG
𝑐) ∭
𝑦
2
√4𝑧− 𝑥 − 𝑧
2 2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
, trong V ền xác đị bởi 𝑥đó là mi nh
2
+ 𝑦
2
+ 𝑧
2
≤ 4𝑧, 𝑦≥ 0
Mi
ền 𝑉: {
𝑥
2
+ 𝑦
2
+ 𝑧
2
≤ 4𝑧
𝑦≥ 0
⇔{
𝑦
2
≤ −𝑥
2
− 𝑧
2
+ 4𝑧
𝑦≥ 0
⇔0 ≤ 𝑦≤ 4 − 𝑧− 2√
[
𝑥
2
+
( )
2
]
Hình chi u c lên là
ế ủa 𝑉 𝑂𝑥𝑧 𝐷: 𝑥
2
+
(
𝑧− 2
)
2
≤ 4
Đặ
t {
𝑧= 𝑟cos 𝜑
𝑦= 2 + 𝑟sin𝜑
𝑧= 𝑧
, 𝐽= 𝑟
𝑉: {
0 ≤ 𝑦≤ 4 − 𝑧− 2
√ [
𝑥
2
+
( )
2
]
𝐷: 𝑥
2
+
(
𝑧− 2
)
2
≤ 4
⇔{
0 ≤ 𝑦≤ 4 − 𝑟
√
2
0 ≤ 𝑟≤ 2
0 ≤ 𝜑≤ 2𝜋
∭
𝑦
2
√
4 − 𝑧− 2
[
𝑥
2
+
( )
2
]
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∫ 𝑑𝜑
2𝜋
0
∫ 𝑑𝑟
2
0
∫
𝑦
2
. 𝑟
√4 − 𝑟
2
𝑑𝑦
√
4−𝑟
2
0
= ∫ 𝑑𝜑
2𝜋
0
∫
(
4 − 𝑟
2
)
𝑟
3
𝑑𝑟
2
0
=
8𝜋
3
PHAM THANH TUNG
Câu 7:
Tính độ ại điể ủa đườ cong t m 𝑀
(
−1,0, −1
)
c ng cong là giao của mặt trụ 4𝑥 + 𝑦 = 4
2 2
và m t ph ng ặ ẳ 𝑥− 3𝑧= 2.
Gi i:ả
Tham s hóa
ố {
𝑥= cos 𝑡
𝑦= 2 sin 𝑡
(do ng có d ng 𝑥
2
+ 𝑦 /4 = 1) ⇒
2
Đườ 𝐿 ạ {
𝑥= cos 𝑡
𝑦= sin 𝑡
𝑧=
cos 𝑡−2
3
⇒
{
𝑥
′
= − sin𝑡, 𝑥
′′
= − cos𝑡
𝑦
′
= 2 cos 𝑡, 𝑦
′′
= −2 sin 𝑡
𝑧
′
=
− sin 𝑡
3
, 𝑧
′′
=
− cos 𝑡
3
. Tại 𝑀
(
−1,0, −1
)
⇔ 𝑡= 𝜋⇒{
𝑥
′
(
𝑀
)
= 0, 𝑥
′′
(
𝑀
)
= 1
𝑦
′
(
𝑀
)
= 2, 𝑦
′′
(
𝑀
)
= 0
𝑧
′
(
𝑀
)
= 0, 𝑧
′′
(
𝑀
)
=
1
3
Áp d ng công th cong: ụ ức tính độ
𝐶
(
𝑀
)
=
√
|
𝑦
′
(𝑡
0
) 𝑧
′
(𝑡
0
)
𝑦
′′
(𝑡
0
) 𝑧
′′
(𝑡
0
)
|
2
+ |
𝑧
′
(𝑡
0
) 𝑥
′
(𝑡
0
)
𝑧
′′
(𝑡
0
) 𝑥
′′
(𝑡
0
)
|
2
+ |
𝑥
′
(𝑡
0
) 𝑦
′
(𝑡
0
)
𝑥
′′
(𝑡
0
) 𝑦
′′
(𝑡
0
)
|
2
(𝑥 + 𝑦 + 𝑧
′
2
′
2
′
2
)
3
2
=
√
10
12
Câu 8:
Chứng minh r ng hàm s ằ ố 𝐼
(
𝑦
)
=
∫
𝑒
−𝑥
1−cos
(
𝑥𝑦
)
𝑥
𝑑𝑥
+∞
0
khả vi trên 𝑅.
Gi i:ả
Đặt 𝑓
(
𝑥, 𝑦 = 𝑒
)
−𝑥
1 − cos
(
𝑥𝑦
)
𝑥
Hàm nh t
𝑓
(
𝑥, 𝑦
)
không xác đị ại 𝑥= 0 nhưng
lim
𝑥→0
+
𝑓
(
𝑥, 𝑦
)
=lim
𝑥→0
−
𝑓
(
𝑥, 𝑦 = lim
)
𝑥→0
𝑒
−𝑥
1 − cos
(
𝑥𝑦
)
𝑥
= lim
𝑥→0
𝑒
−𝑥
𝑥
2
𝑦
2
𝑥
= lim
𝑥→0
𝑒
−𝑥
𝑥𝑦
2
= 0
Ta
có: 𝑓𝑥, 𝑦 = {
( )
𝑒
−𝑥
1 − cos
(
𝑥𝑦
)
𝑥
, 𝑥≠ 0
0 , 𝑥= 0
, 𝑓
𝑦
′
= 𝑒
−𝑥
sin
(
𝑥𝑦
)
liên tục trên 𝑅
2
{
|
𝑒
−𝑥
sin
(
𝑥𝑦
)|
≤ 𝑒
−𝑥
, ∀𝑦∈𝑅
Mà ∫ 𝑒 𝑑𝑥
−𝑥
+∞
0
= −𝑒
−𝑥
|
+∞
0
= 0 −
(
−1
)
= 1 hội tụ
⇒∫ 𝑒
−𝑥
sin
(
𝑥𝑦
)
𝑑𝑥
+∞
0
hội tụ đều trên 𝑅
(
theo tiêu chuẩn Weierstrass
)
PHAM THANH TUNG
𝐼
(
𝑦
)
= ∫ 𝑒
−𝑥
1 − cos
(
𝑥𝑦
)
𝑥
𝑑𝑥
+∞
0
= ∫ 𝑒
−𝑥
1 − cos
(
𝑥𝑦
)
𝑥
𝑑𝑥
1
0
+ ∫ 𝑒
−𝑥
1 − cos
(
𝑥𝑦
)
𝑥
𝑑𝑥
+∞
1
{
|
𝑒
−𝑥
cos
(
𝑥𝑦
)
𝑥
| ≤ 𝑒
−𝑥
, ∀𝑦∈𝑅
∫ 𝑒 𝑑𝑥
−𝑥
+∞
1
= −𝑒
−𝑥
|
+∞
1
=
1
𝑒
hội tụ
∫ 𝑒 𝑑𝑥
−𝑥
1
0
= 1 −
1
𝑒
hội tụ
⇒
{
∫ 𝑒
−𝑥
1 − cos
(
𝑥𝑦
)
𝑥
𝑑𝑥
1
0
hội tụ
∫ 𝑒
−𝑥
1 − cos
(
𝑥𝑦
)
𝑥
𝑑𝑥
+∞
1
hội tụ
⇒𝐼
(
𝑦
)
hội tụ
V
ậy kh𝐼
(
𝑦
)
ả vi trên 𝑅
PHAM THANH TUNG
LỜI GI I THAM KH THI GI Ả ẢO ĐỀ ỮA KÌ 20182 (ĐỀ 3)
Câu 1: Viết phương trình tiế ủa đườp tuyến và pháp diện c ng cong 𝑥= sin 𝑡, 𝑦= 𝑡,𝑧= 𝑒cos
2𝑡
t
ại điểm 𝑀
(
0,1,1 .
)
Gi i:ả
T
ại 𝑀
(
0,1,1 ⇒{
)
0 = sin 𝑡
1 = 𝑡cos
1 = 𝑒
2𝑡
⇔𝑡= 0
Ta có:
{
𝑥
′
(
𝑡
)
= cos 𝑡
𝑦
′
(
𝑡
)
= − sin𝑡
𝑧
′
(
𝑡
)
= 2𝑒
2𝑡
. Tại 𝑡= 0 ⇒{
𝑥
′
(
0
)
= 1
𝑦
′
(
0 = 0
)
𝑧
′
(
0 = 2
)
T
ại 𝑀
(
0,1,1 ,
)
p tuy n c ng cong là: phương trình tiế ế ủa đườ
{
𝑥= 𝑡
𝑦= 1
𝑧= 1 + 2𝑡
T
ại 𝑀
(
0,1,1 ,
)
n c ng cong là: phương trình pháp diệ ủa đườ 𝐿
𝑥+ 0. 𝑦− 1 + 2 𝑧− 1 = 0 ⇔𝑥+ 2𝑧− 2 = 0
( ) ( )
Câu 2: Tính độ ủa đườ ại điể cong c ng t𝑥= 𝑡 , 𝑦= 𝑡 𝑡, 𝑡> 0
2
ln m ứng với 𝑡= 𝑒
Gi i:ả
Ta có
{
𝑥= 𝑡
2
𝑦= 𝑡
ln 𝑡
⇒{
𝑥
′
= 2𝑡 , 𝑥
′′
= 2
𝑦
′
= ln 𝑡+ 1,𝑦
′′
= 1/𝑡
T
ại 𝑡= 𝑒⇒{
𝑥
′
(
𝑒
)
= 2𝑒 , 𝑥
′′
(
𝑒
)
= 2
𝑦
′
(
𝑒
)
= 2 , 𝑦
′′
(
𝑒
)
= 1/𝑒
Độ ạ cong c ng cong tủa đườ i 𝑡= 𝑒 là:
𝐶
(
𝑡= 𝑒
)
=
|2𝑒.
1
𝑒
− 2.2|
(4𝑒 + 2
2 2
)
3
2
=
2
(4𝑒 + 2
2 2
)
3
2
Câu 3: Đổi th t l y tích phân ứ ự ấ
∫ 𝑑𝑥
1
0
∫ 𝑓𝑥, 𝑦𝑑𝑦
( )
1
𝑥
3
PHAM THANH TUNG
Gi i:ả
Mi
ền 𝐷: {
0 ≤ 𝑥≤ 1
𝑥
3
≤ 𝑦≤ 1
Thay đổi thứ tự lấy tích phân
Mi
ền 𝐷: {
0 ≤ 𝑥≤ 𝑦
√
3
0 ≤ 𝑦≤ 1
⇒∫ 𝑑𝑥
1
0
∫ 𝑓𝑥, 𝑦𝑑𝑦
( )
1
𝑥
3
= ∫ 𝑑𝑦
1
0
∫ 𝑓𝑥, 𝑦𝑑𝑥
( )
√
𝑦
3
0
Câu 4: Tính các tích phân sau:
𝑎) ∬
√
𝑥
2
+ 𝑦
2
𝑑𝑥𝑑𝑦
𝐷
, trong 𝐷: 1 ≤ 𝑥đó
2
+ 𝑦
2
≤ 4, 𝑥+ 𝑦≥ 0
𝑏) ∬
|
cos
(
𝑥+ 𝑦 𝑑𝑥𝑑𝑦
)|
𝐷
, trong 𝐷= [0;đó
𝜋
2
] × [0;
𝜋
2
]
Gi i:ả
𝑎) ∬
√
𝑥
2
+ 𝑦 𝑑𝑥𝑑𝑦
2
𝐷
, trong 𝐷: 1 ≤ 𝑥đó
2
+ 𝑦
2
≤ 4, 𝑥+ 𝑦≥ 0
Đặ
t {
𝑥= 𝑟cos 𝜑
𝑦= 𝑟sin 𝜑
, 𝐽= 𝑟
Mi
ền 𝐷: {
1 ≤ 𝑟≤ 2
−𝜋
4
≤ 𝜑≤
3𝜋
4
∬
√
𝑥
2
+ 𝑦
2
𝑑𝑥𝑑𝑦
𝐷
= ∫ 𝑑𝜑
2𝜋
0
∫
√
𝑟
2
. 𝑟𝑑𝑟
2
1
=
14𝜋
3
PHAM THANH TUNG
𝑏) ∬
|
cos
(
𝑥+ 𝑦 𝑑𝑥𝑑𝑦
)|
𝐷
, trong 𝐷= [0;đó
𝜋
2
] × [0;
𝜋
2
]
Ta
: có {
|
cos
(
𝑥+ 𝑦 𝑥+ 𝑦
)|
= cos
( )
khi
−𝜋
2
≤ 𝑥+ 𝑦≤
𝜋
2
⇔
−𝜋
2
− 𝑥≤ 𝑦≤
𝜋
2
− 𝑥
|
cos
(
𝑥+ 𝑦 = −
)|
cos
(
𝑥+ 𝑦
)
khi
𝜋
2
≤ 𝑥+ 𝑦≤
3𝜋
2
⇔
𝜋
2
− 𝑥≤ 𝑦≤
3𝜋
2
− 𝑥
𝐾ế𝑡 ℎợ𝑝 𝑐ù ề𝑛 𝐷= [0;
𝑛𝑔𝑚𝑖
𝜋
2
] × [0;
𝜋
2
] , 𝑡𝑎 𝑐ó:
|
cos
(
𝑥+ 𝑦
)|
= cos
(
𝑥+ 𝑦
)
khi {
0 ≤ 𝑦≤
𝜋
2
− 𝑥
0 ≤ 𝑥≤
𝜋
2
|
cos
(
𝑥+ 𝑦 = −
)|
cos
(
𝑥+ 𝑦
)
khi {
𝜋
2
− 𝑥≤ 𝑦≤
𝜋
2
0 ≤ 𝑥≤
𝜋
2
Chia mi n thành: ề 𝐷
𝐷
+
: {
0 ≤ 𝑦≤
𝜋
2
− 𝑥
0 ≤ 𝑥≤
𝜋
2
và 𝐷
−
: {
𝜋
2
− 𝑥≤ 𝑦≤
𝜋
2
0 ≤ 𝑥≤
𝜋
2
∬ 𝑥+ 𝑦 𝑑𝑥𝑑𝑦
|
cos
( )|
𝐷
= ∬ 𝑥+ 𝑦 𝑑𝑥𝑑𝑦cos
( )
𝐷
+
+ ∬− 𝑥+ 𝑦 𝑑𝑥𝑑𝑦cos
( )
𝐷
−
PHAM THANH TUNG
= ∫ 𝑑𝑥
𝜋
2
0
∫ cos
(
𝑥+ 𝑦𝑑𝑦
)
𝜋
2
−𝑥
0
− ∫ 𝑑𝑥
𝜋
2
0
∫ cos
(
𝑥+ 𝑦𝑑𝑦
)
𝜋
2
𝜋
2
−𝑥
= ∫ (sin
𝜋
2
− sin 𝑥) 𝑑𝑥
𝜋
2
0
− ∫ [sin (𝑥+
𝜋
2
) − sin
𝜋
2
] 𝑑𝑥
𝜋
2
0
=
𝜋
2
− 1 +
𝜋
2
− 1 = 𝜋− 2
Câu 5: Tính tích phân:
∫ 𝑑𝑥
1
0
∫ 𝑑𝑧
1−𝑥
0
∫ 𝑦+ 𝑧𝑑𝑦
( )
2
0
Gi i:ả
∫ 𝑑𝑥
1
0
∫ 𝑑𝑧
1−𝑥
0
∫
(
𝑦+ 𝑧𝑑𝑦
)
2
0
= ∫ 𝑑𝑥
1
0
∫ 𝑑𝑦
2
0
∫
(
𝑦+ 𝑧𝑑𝑧
)
1−𝑥
0
= ∫ 𝑑𝑥
1
0
∫ [(
𝑦𝑧+
1
2
𝑧
2
) |
1 − 𝑥
0
] 𝑑𝑦
2
0
= ∫ 𝑑𝑥
1
0
∫ [𝑦1 − 𝑥
( )
+
1
2
(
1 − 𝑥
)
2
] 𝑑𝑦
2
0
= ∫ 2 1 − 𝑥 1 − 𝑥 𝑑𝑥
[ ( )
+
( )
2
]
1
0
=
4
3
Câu 6:
Tính th tích c a mi n gi i h n b i hai parabol và ể ủ ề ớ ạ ở 𝑥= 1 + 𝑦 + 𝑧
2 2
𝑥= 2 + 𝑧
(
𝑦
2 2
)
Gi i:ả
Xét giao tuy n c và
ế ủa 𝑥= 1 + 𝑦 + 𝑧
2 2
𝑥= 2 + 𝑧
(
𝑦
2 2
)
1 + 𝑦 + 𝑧 = 2 + 𝑧
2 2
(
𝑦
2 2
)
⇔𝑦 + 𝑧 = 1
2 2
Hình chi u c lên là ế ủa 𝑉 𝑂𝑦𝑧 𝐷: 𝑦
2
+ 𝑧 ≤ 1
2
Đặ
t {
𝑦= 𝑟cos 𝜑
𝑧= 𝑟sin 𝜑
, 𝐽= 𝑟⇒𝐷: {
0 ≤ 𝑟≤ 1
0 ≤ 𝜑≤ 2𝜋
Thể ậ ể tích v t th 𝑉 là:
PHAM THANH TUNG
𝑉= ∭𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∬ 1 + 𝑦
[(
2
+ 𝑧
2
)
− 2
(
𝑦
2
+ 𝑧
2
)]
𝑑𝑦𝑑𝑧
𝐷
= ∬
(
1 − 𝑦 − 𝑧
2 2
)
𝑑𝑦𝑑𝑧
𝐷
= ∫ 𝑑𝜑
2𝜋
0
∫ 1 − 𝑟
(
2
)
𝑟𝑑𝑟
1
0
=
𝜋
2
(
đvtt
)
Câu 7:
Cho hàm vecto kh vi ả 𝑟
(
𝑡
)
: 𝑅→ 𝑅 \{0
3
}.
Ký hi u ệ
|
𝑟
(
𝑡
)|
là độ dài của 𝑟 .
(
𝑡
)
Chứng minh:
𝑑
(|
𝑟
(
𝑡
)|)
𝑑𝑡
=
1
|
𝑟
(
𝑡
)|
𝑟 . 𝑟
(
𝑡
)
′
(
𝑡
)
.
Gi i:ả
Đặ
t 𝑟 = (𝑥 ,𝑦 , 𝑧 ) ⇒{
(
𝑡
) (
𝑡
) (
𝑡
) (
𝑡
)
|
𝑟 = √𝑥
(
𝑡
)|
2
(
𝑡
)
+ 𝑦
2
(
𝑡
)
+ 𝑧
2
(
𝑡
)
𝑟′
(
𝑡
)
= (𝑥
′
(
𝑡
)
, 𝑦
′
(
𝑡
)
, 𝑧
′
(
𝑡
)
)
Biến đổi tương đương
𝑑
(|
𝑟
(
𝑡
)|)
𝑑𝑡
=
1
|
𝑟
(
𝑡
)|
𝑟 . 𝑟
(
𝑡
)
′
(
𝑡
)
⇔
𝑑
𝑑𝑡
(
√
𝑥
2
(
𝑡
)
+ 𝑦
2
(
𝑡
)
+ 𝑧
2
(
𝑡
)
) =
𝑥
′
(
𝑡
)
. 𝑥
(
𝑡
)
+ 𝑦
′
(
𝑡
)
. 𝑦
(
𝑡
)
+ 𝑧
′
(
𝑡
)
. 𝑧
(
𝑡
)
√𝑥
2
(
𝑡
)
+ 𝑦
2
(
𝑡
)
+ 𝑧
2
(
𝑡
)
⇔
2𝑥
′
(
𝑡
)
. 𝑥
(
𝑡
)
+ 2𝑦
′
(
𝑡
)
. 𝑦
(
𝑡
)
+ 2𝑧
′
(
𝑡
)
. 𝑧
(
𝑡
)
2√𝑥
2
(
𝑡
)
+ 𝑦
2
(
𝑡
)
+ 𝑧
2
(
𝑡
)
=
𝑥
′
(
𝑡
)
. 𝑥
(
𝑡
)
+ 𝑦
′
(
𝑡
)
. 𝑦
(
𝑡
)
+ 𝑧
′
(
𝑡
)
. 𝑧
(
𝑡
)
√𝑥
2
(
𝑡
)
+ 𝑦
2
(
𝑡
)
+ 𝑧
2
(
𝑡
)
⇔
𝑥
′
(
𝑡
)
. 𝑥
(
𝑡
)
+ 𝑦
′
(
𝑡
)
. 𝑦
(
𝑡
)
+ 𝑧
′
(
𝑡
)
. 𝑧
(
𝑡
)
√𝑥
2
(
𝑡
)
+ 𝑦
2
(
𝑡
)
+ 𝑧
2
(
𝑡
)
=
𝑥
′
(
𝑡
)
. 𝑥
(
𝑡
)
+ 𝑦
′
(
𝑡
)
. 𝑦
(
𝑡
)
+ 𝑧
′
(
𝑡
)
. 𝑧
(
𝑡
)
√𝑥
2
(
𝑡
)
+ 𝑦
2
(
𝑡
)
+ 𝑧
2
(
𝑡
)
⇒ Điề ả ứu ph i ch ng minh.
Câu 8:
Tính tích phân
∭
(
2𝑦− 𝑧
)
2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
là hình c u trong đó 𝑉 ầ 𝑥
2
+ 𝑦
2
+ 𝑧
2
≤ 1
Gi i:ả
∭4𝑦 − 4 + 𝑧
(
2
𝑦𝑧
2
)
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∭4𝑦
(
2
+ 𝑧
2
)
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
+ ∭−4 𝑑𝑥𝑑𝑦𝑑𝑧
(
𝑦𝑧
)
𝑉
PHAM THANH TUNG
{
𝑓
(
𝑥, 𝑦, 𝑧
)
= −4𝑦𝑧 là hàm lẻ với biến 𝑦
Mi
ền 𝑉 đối xứ qua 𝑂𝑥𝑧ng
⇒∭
(
−4𝑦𝑧
)
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= 0
Đặ
t {
𝑥= 𝑟sin 𝜃cos 𝜑
𝑦= 𝑟s 𝜃sin𝜑in
𝑧= 𝑟
cos 𝜃
, 𝐽= −𝑟
2
sin 𝜃
Mi
ề ần trong t c𝑉 ọa độ u là 𝑉: {
0 ≤ 𝑟≤ 1
0 ≤ 𝜃≤ 𝜋
0 ≤ 𝜑≤ 2𝜋
∭4𝑦 + 𝑧
(
2 2
)
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∫ 𝑑𝜑
2𝜋
0
∫ 𝑑𝜃
𝜋
0
∫
[
4
(
𝑟sin 𝜃sin 𝜑
)
2
+
(
𝑟cos 𝜃
)
2
]
1
0
𝑟
2
sin 𝜃𝑑𝑟
= ∫ 𝑑𝜑
2𝜋
0
∫ [
4
5
(
sin 𝜃sin𝜑
)
2
+
1
5
(
cos 𝜃
)
2
] sin 𝜃𝑑𝜃
𝜋
0
= ∫ [
16
15
(
sin 𝜑
)
2
+
2
15
] 𝑑𝜑
2𝜋
0
=
4
3
𝜋
Câu 9:
Chứng minh r ng hàm s ằ ố 𝐼
(
𝑦
)
=
∫
𝑒
−𝑥
sin
(
𝑥𝑦
)
𝑥
𝑑𝑥
+∞
0
khả vi trên 𝑅.
Gi i:ả
Đặt 𝑓
(
𝑥, 𝑦 = 𝑒
)
−𝑥
sin
(
𝑥𝑦
)
𝑥
Hàm nh t
𝑓
(
𝑥, 𝑦
)
không xác đị ại 𝑥= 0 nhưng
lim
𝑥→0
+
𝑓
(
𝑥, 𝑦
)
=lim
𝑥→0
−
𝑓
(
𝑥, 𝑦 = lim
)
𝑥→0
𝑒
−𝑥
sin
(
𝑥𝑦
)
𝑥
= lim
𝑥→0
𝑒
−𝑥
𝑥𝑦
𝑥
= lim
𝑥→0
𝑒
−𝑥
𝑦= 𝑦
Ta
có: 𝑓𝑥, 𝑦 = {
( )
𝑒
−𝑥
sin
(
𝑥𝑦
)
𝑥
, 𝑥≠ 0
𝑦 , 𝑥= 0
, 𝑓
𝑦
′
= 𝑒
−𝑥
cos
(
𝑥𝑦
)
liên tục trên 𝑅
2
{
|
𝑒
−𝑥
cos
(
𝑥𝑦
)|
≤ 𝑒
−𝑥
, ∀𝑦∈𝑅
Mà ∫ 𝑒 𝑑𝑥
−𝑥
+∞
0
= −𝑒
−𝑥
|
+∞
0
= 0 −
(
−1
)
= 1 hội tụ
⇒∫ 𝑒
−𝑥
cos
(
𝑥𝑦
)
𝑑𝑥
+∞
0
hội tụ đều trên 𝑅
(
theo tiêu chuẩn Weierstrass
)
𝐼
(
𝑦
)
= ∫ 𝑒
−𝑥
sin
(
𝑥𝑦
)
𝑥
𝑑𝑥
+∞
0
= ∫ 𝑒
−𝑥
sin
(
𝑥𝑦
)
𝑥
𝑑𝑥
1
0
+ ∫ 𝑒
−𝑥
sin
(
𝑥𝑦
)
𝑥
𝑑𝑥
+∞
1
PHAM THANH TUNG
{
|
𝑒
−𝑥
sin
(
𝑥𝑦
)
𝑥
| ≤ 𝑒
−𝑥
, ∀𝑦∈𝑅
∫ 𝑒 𝑑𝑥
−𝑥
+∞
1
= −𝑒
−𝑥
|
+∞
1
=
1
𝑒
hội tụ
∫ 𝑒 𝑑𝑥
−𝑥
1
0
= 1 −
1
𝑒
hội tụ
⇒𝐼
(
𝑦
)
= ∫ 𝑒
−𝑥
sin
(
𝑥𝑦
)
𝑥
𝑑𝑥
1
0
+ ∫ 𝑒
−𝑥
sin
(
𝑥𝑦
)
𝑥
𝑑𝑥
+∞
1
hội tụ
V
ậy kh𝐼
(
𝑦
)
ả vi trên 𝑅
PHAM THANH TUNG
LỜI GI I THAM KH THI GIẢ ẢO ĐỀ ỮA KỲ 20183 (ĐỀ 1)
Câu 1: Tìm hình bao c a h ng th ng ủ ọ đườ ẳ 𝑥− 𝑐𝑦+ 𝑐 = 0
3
Gi i:ả
Đặt 𝐹
(
𝑥, 𝑦, 𝑐 = 𝑥− 𝑐𝑦+ 𝑐
)
3
Xét
{
𝐹
𝑥
′
(
𝑥, 𝑦, 𝑐
)
= 0
𝐹
𝑦
′
(
𝑥, 𝑦, 𝑐
)
= 0
⇔{
1 = 0
−𝑐= 0
⇒ Vô nghi H m kì d . ệm ⇒ ọ đường cong không có điể ị
Xét {
𝐹
(
𝑥, 𝑦, 𝑐
)
= 0
𝐹
𝑐
′
(
𝑥, 𝑦, 𝑐
)
= 0
⇔{
𝑥− 𝑐𝑦+ 𝑐
3
= 0
−𝑦+ 3𝑐
2
= 0
⇔{
𝑥− 𝑐.3𝑐
2
+ 𝑐
3
= 0
𝑦= 3𝑐
2
⇔{
𝑥= 2𝑐
3
𝑦= 3𝑐
2
⇔{
𝑥
2
= 𝑐
3
𝑦
3
= 𝑐
2
⇒(
𝑥
2
) − (
2
𝑦
3
)
3
= 0 ⇔𝑦
3
=
27
4
𝑥
2
Vậy hình bao của họ cong 𝑦
đường là đường
3
=
27
4
𝑥
2
Câu 2:
Viết phương trình tiế ại điểp diện và pháp tuyến của t m 𝐴
(
1; 0; 1
)
của mặt 𝑧= 𝑥𝑒
sin 2𝑦
Gi i:ả
Đặ
t 𝐹
(
𝑥, 𝑦, 𝑧 = 𝑧− 𝑥𝑒
)
sin 2𝑦
⇒{
𝐹
𝑥
′
= −𝑒
sin2𝑦
𝐹
𝑦
′
= −2𝑥 𝑦𝑒cos
sin2𝑦
𝐹
𝑧
′
= 1
T
ại 𝐴
(
1; 0; 1 {
)
, ta có:
𝐹
𝑥
′
(
𝐴
)
= −1
𝐹
𝑦
′
(
𝐴
)
= −2
𝐹
𝑧
′
(
𝐴
)
= 1
Phương trình tiế
p diện của mặt cong tại 𝐴
(
1; 0; 1
)
là:
−1. 𝑥− 1 − 2. 𝑦− 0 + 1. 𝑧− 1 = 0 ⇔−𝑥− 2𝑦+ 𝑧= 0
( ) ( ) ( )
Phương trình pháp tuyế
n của mặt cong tại 𝐴
(
1; 0; 1
)
là:
𝑥− 1
−1
=
𝑦
−2
=
𝑧− 1
1
PHAM THANH TUNG
Câu 3: Đổi th t l y tích phân: ứ ự ấ
∫ 𝑑𝑥
1
0
∫ 𝑓𝑥, 𝑦𝑑𝑦
( )
𝑥
2
−𝑥
Gi i:ả
Mi
ền 𝐷: {
0 ≤ 𝑥≤ 1
−𝑥≤ 𝑦≤ 𝑥
2
Đổ ứ ự ấ ề
i th t l y tích phân, chia thanh hai mi𝐷 n 𝐷
1
: {
−𝑦≤ 𝑥≤ 1
−1 ≤ 𝑦≤ 0
và 𝐷
2
: {
√
𝑦≤ 𝑥≤ 1
0 ≤ 𝑦≤ 1
⇒∫ 𝑑𝑥
1
0
∫ 𝑓𝑥, 𝑦𝑑𝑦
( )
𝑥
2
−𝑥
= ∫ 𝑑𝑦
0
−1
∫ 𝑓𝑥, 𝑦𝑑𝑥
( )
1
−𝑦
+ ∫𝑑𝑦
1
0
∫ 𝑓𝑥, 𝑦𝑑𝑥
( )
1
√
𝑦
Câu 4:
Tính
∬
sin + 2𝑦
(
𝑥
2 2
)
𝑑𝑥𝑑𝑦
𝐷
, v là mi n: ới 𝐷 ề
𝑥
2
+ 2𝑦
2
≤
𝜋
2
, 𝑦≥ 0
Gi i:ả
Đặt {
𝑥= 𝑟cos 𝜑
√
2𝑦= 𝑟sin 𝜑
⇔{
𝑥= 𝑟
cos 𝜑
𝑦=
𝑟
√
2
sin 𝜑
, 𝐽=
1
√
2
𝑟
PHAM THANH TUNG
Mi
ền 𝐷 trong tọa độ cực suy rộ 𝐷: {ng
0 ≤ 𝑟≤
√
𝜋
2
0 ≤ 𝜑≤ 𝜋
∬sin + 2𝑦
(
𝑥
2 2
)
𝑑𝑥𝑑𝑦
𝐷
= ∫ 𝑑𝜑
𝜋
0
∫ sin
(
𝑟
2
)
.
𝑟
√
2
𝑑𝑟
√
𝜋
2
0
=
1
2
√
2
∫ 𝑑𝜑
2𝜋
0
∫ sin
(
𝑟
2
)
𝑑
(
𝑟
2
)
√
𝜋
2
0
=
1
2
√
2
∫ 𝑑𝜑
𝜋
0
∫ sin 𝑢𝑑𝑢
𝜋
2
0
=
1
2
√
2
∫ 𝑑𝜑
𝜋
0
=
𝜋
2 2
√
Câu 5: Tính
∭
𝑥+ 𝑦+ 2
(
𝑥+ 1 𝑦+ 1
)( )
𝑧
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
Với i 𝑉 nh bxác đị ở 0 ≤ 𝑥≤ 1, 1 ≤ 𝑦≤ 2, 1 ≤ 𝑧≤ 𝑒
Gi i:ả
∭
𝑥+ 𝑦+ 2
( )
𝑥+ 1 𝑦+ 1
)(
𝑧
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∫ 𝑑𝑥
1
0
∫ 𝑑𝑦
2
1
∫
𝑥+ 𝑦+ 2
(
𝑥+ 1 𝑦+ 1
)( )
𝑧
𝑑𝑧
𝑒
1
= ∫ 𝑑𝑥
1
0
∫ [
𝑥+ 𝑦+ 2
(
𝑥+ 1 𝑦+ 1
)(
)
ln 𝑧] |
𝑒
1
𝑑𝑦
2
1
= ∫ 𝑑𝑥
1
0
∫
𝑥+ 𝑦+ 2
(
𝑥+ 1 𝑦+ 1
)( )
𝑑𝑦
2
1
= ∫ 𝑑𝑥
1
0
∫
(
𝑥+ 1
)
+
(
𝑦+ 1
)
(
𝑥+ 1 𝑦+ 1
)( )
𝑑𝑦
2
1
= ∫ 𝑑𝑥
1
0
∫
1
𝑦+ 1
𝑑𝑦
2
1
+ ∫ 𝑑𝑥
1
0
∫
1
𝑥+ 1
𝑑𝑦
2
1
PHAM THANH TUNG
= ∫ 3 − 𝑑𝑥
(
ln ln 2
)
1
0
+ ∫
1
𝑥+ 1
𝑑𝑥
1
0
=
(
ln ln ln ln3 − 2
)
+ 2 = 3
Câu 6:
Tính th tích mi n gi i h n b i các mể ề 𝑉 ớ ạ ở ặt 𝑥= − + 𝑧
(
𝑦
2 2
)
và 𝑥= −1
Gi i:ả
Xét giao tuy n c a hai m
ế ủ ặt 𝑥= − + 𝑥
(
𝑦
2 2
)
và 𝑥= −1
⇒− + 𝑧
(
𝑦
2 2
)
= −1 ⇔𝑦 + 𝑧 = 1
2 2
Hình chi u c a mi n lên là ế ủ ề 𝑉 𝑂𝑦𝑧 𝐷: 𝑦 ≤ 1
2
+ 𝑧
2
Thể ề tích mi n là: 𝑉
𝑉= ∭𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∬1 −
[ (
𝑦
2
+ 𝑧
2
)]
𝐷
𝑑𝑦𝑑𝑧
Đặ
t {
𝑦= 𝑟cos 𝜑
𝑧= 𝑟sin 𝜑
, 𝐽= 𝑟⇒𝐷: {
0 ≤ 𝑟≤ 1
0 ≤ 𝜑≤ 2𝜋
⇒𝑉= ∭𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∬1 −
[ (
𝑦
2
+ 𝑧
2
)]
𝐷
𝑑𝑦𝑑𝑧= ∫ 𝑑𝜑
2𝜋
0
∫
(
1 − 𝑟
2
)
. 𝑟𝑑𝑟
1
0
=
𝜋
2
(
đvtt
)
Câu 7: Tìm gi i h n ớ ạ lim
𝑦→0
∫
arctan 𝑥− 𝑦𝑑𝑥
( )
cos𝑦
sin𝑦
Gi i:ả
Đặt 𝐼
(
𝑦
)
= ∫ arctan
(
𝑥− 𝑦𝑑𝑥
)
cos𝑦
sin 𝑦
Ta có:
{
𝑓
(
𝑥, 𝑦
)
= arctan
(
𝑥− 𝑦
)
liên tục với
(
𝑥, 𝑦
)
∈𝑅
2
cos 𝑦 liên tục với y ∈R
sin 𝑦 liên tục với y ∈R
⇒𝐼
(
𝑦
)
liên t c trên ụ 𝑅
⇒lim
𝑦→0
∫ arctan
(
𝑥− 𝑦𝑑𝑥
)
cos 𝑦
sin 𝑦
= 𝐼 0 = ∫ arctan 𝑥𝑑𝑥
( )
1
0
Đặt
{
𝑢= arctan 𝑥
𝑑𝑣= 𝑑𝑥
⇒{
𝑑𝑢=
1
1 + 𝑥
2
𝑑𝑥
𝑣= 𝑥
PHAM THANH TUNG
∫ arctan 𝑥𝑑𝑥
1
0
= 𝑥. arctan 𝑥|
1
0
− ∫
𝑥
1 + 𝑥
2
𝑑𝑥
1
0
=
𝜋
4
−
1
2
∫
1
1 + 𝑥
2
𝑑
(
𝑥
2
)
1
0
=
𝜋
4
−
ln 2
2
Vậy lim
𝑦→0
∫ arctan
(
𝑥− 𝑦𝑑𝑥
)
cos 𝑦
sin 𝑦
=
𝜋
4
−
ln 2
2
Câu 8: Tìm điểm có độ ủa đườ cong nhỏ nhất c ng 𝑥
2
+ 4𝑦 = 4𝑥
2
Gi i:ả
Ta
: 𝑥có
2
+ 4𝑦 = 4𝑥⇔ 𝑥− 2
2
( )
2
+ 4𝑦 = 4 ⇔
2
(
𝑥− 2
)
2
4
+ 𝑦
2
= 1
Đặ𝑡 {
𝑥= 2 + 2 cos 𝑡
𝑦= sin 𝑡
⇒{
𝑥
′
= −2 sin 𝑡, 𝑥
′′
= −2 cos𝑡
𝑦
′
= cos 𝑡, 𝑦
′′
= − sin 𝑡
Độ ủ cong c a đường cong t i m ng v b t k là: ạ ột điểm ứ ới 𝑡 ấ ỳ
𝐶=
|
𝑥
′
𝑦
′′
− 𝑥
′′
. 𝑦
′
|
(𝑥 + 𝑦
′
2
′
2
)
3/2
=
2
(
5
2
−
3
2
cos 2𝑡)
3/2
= 2. (
5
2
−
3
2
cos 2𝑡)
−3/2
Xét 𝐶
′
(
𝑡
)
= 2.
−3
2
.
3
2
. 2. sin 2𝑡. (
5
2
−
3
2
cos 2𝑡)
−5/2
=
−9 sin 2𝑡
(
5
2
−
3
2
cos 2𝑡)
5/2
=
−18 sin 𝑡. 𝑡cos
(
5
2
−
3
2
cos 2𝑡)
5/2
𝐶
′
(
𝑡
)
= 0 ⇔[
sin 𝑡= 0
cos
𝑡= 0
⇔[
𝑡= 0
𝑡= 𝜋
𝑡= ±
𝜋
2
(Để ạ ủ bài toan bớt phức t p, chỉ xét giá trị c a 𝑡 trong m ng giác) ột vòng lượ
𝑡
−2𝜋 −
𝜋
2
0
𝜋
2
𝜋
𝐶
′
(
𝑡
)
+ + − + − 0 − 0 0 0 0
𝐶
(
𝑡
)
T
ừ bảng biến thiên ⇒𝐶
(
𝑡
)
đạt giá tr nhị ỏ nhất tại các điểm làm cho cos 𝑡= 1
(𝑡=
−𝜋
2
,
𝜋
2
, … )
PHAM THANH TUNG
V
ới cos 𝑡= 0 ⇔sin 𝑡= ±1 ⇒[
𝑥= 2, 𝑦= −1
𝑥= 2, 𝑦= 1
V
ậy đường cong có độ ại điể cong nhỏ nhất t m
(
2, −1
)
hoặc
(
2,1
)
Câu 9: Tính
∭
(
𝑦+ 1
)
2
𝑥
2
+ 𝑦 + 𝑧 + 3
2 2
𝑑𝑥𝑑𝑦𝑑𝑧
Với i 𝑉 nh bxác đị ở 𝑥
2
+ 𝑦 + 𝑧 ≤ 1
2 2
Gi i:ả
Đặ𝑡 𝐼= ∭
(𝑦− 1)
2
𝑥
2
+ 𝑦 + 𝑧 + 3
2 2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
𝐼= ∭
𝑦
2
+ 2𝑦+ 1
𝑥
2
+ 𝑦 + 𝑧 + 3
2 2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∭
𝑦
2
+ 1
𝑥
2
+ 𝑦 + 𝑧 + 3
2 2
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧+ ∭
2𝑦𝑑𝑥𝑑𝑦𝑑𝑧
𝑥
2
+ 𝑦 + 𝑧 + 3
2 2
𝑉
{
2𝑦
𝑥
2
+ 𝑦 + 𝑧 + 3
2 2
lẻ với biến 𝑦
Mi
ền 𝑉 đối xứ q 𝑂𝑥𝑧ng ua
⇒∭
2𝑦
𝑥
2
+ 𝑦 + 𝑧 + 3
2 2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= 0
⇒𝐼= ∭
𝑦
2
+ 1
𝑥
2
+ 𝑦 + 𝑧 + 3
2 2
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧
(
1
)
PHAM THANH TUNG
Đổ ủ ềi vai trò c a 𝑥, 𝑦 mi n 𝑉không thay đổi
⇒𝐼= ∭
𝑥
2
+ 1
𝑥
2
+ 𝑦 + 𝑧 + 3
2 2
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧
(
2
)
Đổ ủ ềi vai trò c a 𝑦, 𝑧 mi n 𝑉không thay đổi
⇒𝐼= ∭
𝑧
2
+ 1
𝑥
2
+ 𝑦 + 𝑧 + 3
2 2
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧
(
3
)
( (
1
)
+
(
2
)
+ 3
)
⇒3𝐼= ∭
𝑥
2
+ 𝑦
2
+ 𝑧
2
+ 3
𝑥
2
+ 𝑦 + 𝑧 + 3
2 2
𝑉
𝑑𝑥𝑑𝑦𝑑𝑧= ∭𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
=
4
3
𝜋⇒𝐼=
4
9
𝜋
Câu 10:
Cho hàm s ố 𝐼
(
𝑦
)
=
∫
ln
(
1+𝑥𝑦
)
1+𝑥
2
𝑦
0
𝑑𝑥. Tính 𝐼
′
( )
1
Gi i:ả
Đặt 𝑓
(
𝑥, 𝑦
)
=
ln
(
1 + 𝑥𝑦
)
1 + 𝑥
2
⇒𝑓
𝑦
′
(
𝑥, 𝑦
)
=
𝑥
(
1 + 𝑥
2
)(
1 + 𝑥𝑦
)
Ta có:
{
𝑓
(
𝑥, 𝑦
)
liên tục, ả trên kh vi
[ [ ]
0; 2
]
× 0; 2
𝑓
𝑦
′
(
𝑥, 𝑦
)
liên tục trên
[ [ ]
0; 2
]
× 0; 2
𝑦
2
= 𝑦 liên tục, ả trên kh vi
[
0; 2
]
⇒𝐼
(
𝑦
)
kh vi v ả ới 𝑦∈ 0; 2
[ ]
𝐼
′
(
𝑦
)
= 𝑓𝑦
(
2
(
𝑦
)
,𝑦. 𝑦
)
2
′
(
𝑦
)
− 𝑓
(
𝑦
1
( ) )
𝑦, 𝑦. 𝑦
1
′
(
𝑦
)
+ ∫ 𝑓
𝑦
′
(
𝑥, 𝑦
)
𝑦
2
(
𝑦
)
𝑦
1
(
1
)
𝑑𝑥
⇒𝐼
′
(
𝑦
)
=
ln
(
1 + 𝑦
2
)
1 + 𝑦
2
−
ln 1
1
. 0 + ∫
𝑥
(
1 + 𝑥
2
)(
1 + 𝑥𝑦
)
𝑦
0
𝑑𝑥
⇒𝐼
′
(
1
)
=
ln 2
2
+ ∫
𝑥
(
1 + 𝑥
2
)( )
1 + 𝑥
1
0
𝑑𝑥
∫
𝑥
(
1 + 𝑥
2
)( )
1 + 𝑥
1
0
𝑑𝑥= ∫
−1
2 1 + 𝑥
( )
1
0
𝑑𝑥+ ∫
𝑥+ 1
2
(
1 + 𝑥
2
)
1
0
𝑑𝑥= −
ln 2
2
+
ln 2
4
+
1
2
. arctan 1
⇒𝐼
′
(
1
)
=
ln 2
4
+
𝜋
8
PHAM THANH TUNG
LỜI GI I THAM KH THI GI Ả ẢO ĐỀ ỮA KÌ 20192 (ĐỀ 2)
Câu 1: Viết phương trình tiế ủa đườ ại điểp tuyến và pháp tuyến c ng cong t𝑥
3
+ 𝑦 = 9
3
𝑥𝑦 m
(
4,2
)
Gi i:ả
Đặ
t 𝐹
(
𝑥, 𝑦 = 𝑥 + 𝑦 − 9 ⇒𝐹
)
3 3
𝑥𝑦
𝑥
′
= 3𝑥
2
− 9𝑦, 𝐹
𝑦
′
= 3𝑦
2
− 9𝑥
T
ại
(
4,2 ,
)
tai có 𝐹
𝑥
′
(
4,2
)
= 30,𝐹
𝑦
′
= −24
Phương trình tiế ủa đườ
p tuyến c ng cong tại
(
4,2
)
là:
30 24 30 24 72
(
𝑥− 4
)
−
(
𝑦− 2 = 0 ⇔
)
𝑥− 𝑦− = 0
Phương trình ủa đườ
pháp tuyến c ng cong tại
(
4,2
)
là:
𝑥− 4
30
=
𝑦− 2
−24
Câu 2:
Tính độ ủa đườ cong c ng {
𝑥= 2
(
𝑡− sin 𝑡
)
𝑦= 2 1 −
(
cos 𝑡
)
t ng vại điểm ứ ới 𝑡= 𝜋/2
Gi i:ả
Ta có
{
𝑥= 2
(
𝑡− sin 𝑡
)
𝑦= 2 1 −
(
cos 𝑡
)
⇒{
𝑥
′
(
𝑡
)
= 2 − 2cos 𝑡
𝑦
′
(
𝑡
)
= 2 sin 𝑡
⇒{
𝑥
′′
(
𝑡
)
= 2 sin𝑡
𝑦
′′
(
𝑡
)
= 2 cos 𝑡
Tại 𝑡= 𝜋/2 ⇒
{
𝑥
′
(
𝜋
2
) = 2 , 𝑥
′′
(
𝜋
2
) = 2
𝑦
′
(
𝜋
2
) = 2 , 𝑦
′′
(
𝜋
2
) = 0
Độ ủ ạ cong c a 𝐿 t i 𝑡= 𝜋/2 là:
𝐶
(
𝑡= 0
)
=
|
2.0 − 2.2
|
(2 + 2
2 2
)
3
2
=
2
2
2
9
2
=
√
2
8
Câu 3: Tìm hình bao c a h ng cong ủ ọ đườ
2𝑥 − 4 + 2𝑦 + 𝑐 = 0, 𝑐 , 𝑐≠ 0
2
𝑥𝑐
2 2
là tham số
Gi i:ả
Đặt 𝐹 với 𝑐≠ 0
(
𝑥, 𝑦, 𝑐 = 2𝑥 − 4 + 2𝑦 + 𝑐
)
2
𝑥𝑐
2 2
PHAM THANH TUNG
Xét
{
𝐹
𝑥
′
(
𝑥, 𝑦, 𝑐
)
= 0
𝐹
𝑦
′
(
𝑥, 𝑦, 𝑐
)
= 0
⇔{
4𝑥− 4𝑐= 0
4𝑦= 0
⇔
{
𝑥= 𝑐
𝑦= 0
Đi
ể ộ ọ đườm
(
𝑐, 0
)
không thu c h ng cong 2𝑥 − 4 + 2𝑦 + 𝑐 = 0
2
𝑥𝑐
2 2
H m kì d . ⇒ ọ đường cong không có điể ị
Xét {
𝐹
(
𝑥, 𝑦, 𝑐
)
= 0
𝐹
𝑐
′
(
𝑥, 𝑦, 𝑐
)
= 0
⇔{
2𝑥
2
− 4 + 2𝑦 + 𝑐 = 0𝑥𝑐
2 2
−4𝑥+ 2𝑐= 0
⇔{
2𝑥
2
− 4 + 2𝑦 + 𝑐 = 0𝑥𝑐
2 2
𝑐= 2𝑥
⇒2𝑥 − 4𝑥. 2𝑥+ 2𝑦 2𝑥
2 2
+
( )
2
= 0 ⇔−𝑥 + 𝑦
2 2
= 0 ⇔𝑦= ±𝑥
Do nên và 𝑐≠ 0 𝑥≠ 0 𝑦≠ 0
Vậy hình bao của họ cong 𝑦= ±𝑥 ừ 𝑂
đường là đường tr
(
0,0
)
Câu 4: Tìm gi i h n ớ ạ
lim
𝑦→0
∫ cos
(
𝑥
2
𝑦+ 3𝑥+ 𝑦
2
)
𝑑𝑥
𝜋
2
0
Gi i:ả
Ta có:
𝑓
(
𝑥, 𝑦 𝑦+ 3𝑥+ 𝑦
)
= cos
(
𝑥
2 2
)
là hàm s liên t c trên ố ụ
[
0; 𝜋/2
]
× 𝑅
⇒𝐼 = ∫ 𝑦+ 3𝑥+ 𝑦
(
𝑦
)
cos
(
𝑥
2 2
)
𝑑𝑥
𝜋
2
0
là hàm số liên tục trên 𝑅.
⇒lim
𝑦→0
∫ cos
(
𝑥
2
𝑦+ 3𝑥+ 𝑦
2
)
𝑑𝑥
𝜋
2
0
= 𝐼0 = ∫ 3𝑥𝑑𝑥
( )
cos
( )
𝜋
2
0
=
−1
3
Câu 5: Đổi th t l y tích phân: ứ ự ấ
∫ 𝑑𝑥
1
0
∫ 𝑓
(
𝑥, 𝑦𝑑𝑦
)
√
2−𝑥
2
𝑥
2
Gi i:ả
Mi
ền 𝐷: {
0 ≤ 𝑥≤ 1
𝑥
2
≤ 𝑦≤ √2 − 𝑥
2
Đổ ứ ự ấi th t l y tích phân
PHAM THANH TUNG
Chia n thành hai mi n miề 𝐷 ề
𝐷
1
: {
0 ≤ 𝑥≤ 𝑦
√
0 ≤ 𝑦≤ 1
, 𝐷
2
: {
0 ≤ 𝑥≤ 2 − 𝑦
√
2
1 ≤ 𝑦≤
√
2
⇒∫ 𝑑𝑥
1
0
∫ 𝑓
(
𝑥, 𝑦𝑑𝑦
)
√
2−𝑥
2
𝑥
2
= ∫ 𝑑𝑦
1
0
∫ 𝑓𝑥 , 𝑦𝑑𝑥
( )
√
𝑦
0
+ ∫ 𝑑𝑦
√
2
1
∫ 𝑓
(
𝑥, 𝑦𝑑𝑥
)
√
2−𝑦
2
0
Câu 6: Tính di n tích ph n m n m trong m ệ ầ ặt 𝑧= 𝑥 + 𝑦 + 2
2 2
ằ ặt 𝑥
2
+ 𝑦 = 9
2
Gi i:ả
Hình chi u c n m n m trong m t tr ế ủa phầ ặt 𝑧= 𝑥 + 𝑦 + 2
2 2
ằ ặ ụ
𝑥
2
+ 𝑦 = 9 𝑂𝑥𝑦
2
lên là:
𝐷: 𝑥 + 𝑦
2 2
≤ 9
Ta có:
𝑧
𝑥
′
= 2𝑥, 𝑧
𝑦
′
= 2𝑦
Diệ ần tích c n tính là:
𝑆= ∬ 1 + 𝑧
√
(
𝑥
′
)
2
+ (𝑧
𝑦
′
)
2
𝑑𝑥𝑑𝑦
𝐷
= ∬ 1 + 4𝑥
√
2
+ 4𝑦
2
𝑑𝑥𝑑𝑦
𝐷
Đặ
t {
𝑥= 𝑟cos 𝜑
𝑦= 𝑟sin 𝜑
, 𝐽= 𝑟⇒𝐷: {
0 ≤ 𝑟≤ 3
0 ≤ 𝜑≤ 2𝜋
PHAM THANH TUNG
⇒𝑆= ∫ 𝑑𝜑
2𝜋
0
∫
√
1 + 4𝑟
2
. 𝑟𝑑𝑟
3
0
=
1
2
∫ 𝑑𝜑
2𝜋
0
∫
√
1 + 4𝑟
2
𝑑
(
𝑟
2
)
3
0
=
1
2
∫ 𝑑𝜑
2𝜋
0
∫
√
1 + 4𝑢𝑑𝑢
9
0
=
1
2
. 2𝜋.
1
6
(37 37
√
− 1 ) =
(37 37
√
− 1)𝜋
6
(
đvdt
)
Câu 7: Tính th tích c a mi n gi i h n b i các m t cong và m ể ủ ề ớ ạ ở ặ 𝑦= 𝑥 , 𝑥= 𝑦 , 𝑧= 𝑥
2 2 2
ặt 𝑂𝑥𝑦
Gi i:ả
Gọi miền cần tính thể tích là 𝑉.
Hình chi u c lên là mi n gi i h n b
ế ủa 𝑉 𝑂𝑥𝑦 ề 𝐷 ớ ạ ởi {
𝑦= 𝑥
2
𝑥= 𝑦
2
⇒𝐷: {
𝑥
2
≤ 𝑦≤
√
𝑥
0 ≤ 𝑥≤ 1
Mi
ền 𝑉: {
0 ≤ 𝑧≤ 𝑥
2
0 ≤ 𝑥≤ 1
𝑥
2
≤ 𝑦≤
√
𝑥
Thể ề tích mi n là: 𝑉
𝑉= ∭𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∬𝑥
2
𝑑𝑥𝑑𝑦
𝐷
= ∫ 𝑑𝑥
1
0
∫ 𝑥
2
𝑑𝑦
√
𝑥
𝑥
2
= ∫ 𝑥
2
(
√
𝑥− 𝑥
2
)𝑑𝑥
1
0
=
3
35
(
đvtt
)
Câu 8:
Tính
∬
(
2𝑦 + 3 𝑑𝑥𝑑𝑦
2
)
𝐷
, v là mi nh b ới 𝐷 ền xác đị ởi
𝑥
2
+
(
𝑦− 1
)
2
≤ 1
Gi i:ả
Đặ
t {
𝑥= 𝑟cos 𝜑
𝑦= 1 + 𝑟sin𝜑
, 𝐽= 𝑟
Mi
ền 𝐷: {
0 ≤ 𝑟≤ 1
0 ≤ 𝜑≤ 2𝜋
∬2𝑦 + 3 𝑑𝑥𝑑𝑦
(
2
)
𝐷
= 2 ∬𝑦
2
𝑑𝑥𝑑𝑦
𝐷
+ 3. 𝑆
𝐷
PHAM THANH TUNG
= 2 ∫ 𝑑𝜑
2𝜋
0
∫
(
1 + 𝑟sin 𝜑
)
2
. 𝑟𝑑𝑟
1
0
+ 3. 𝜋. 1
2
= 2 ∫ (
1
2
+
2
3
sin 𝜑+
1
4
sin
2
𝜑) 𝑑𝜑
2𝜋
0
+ 3𝜋
= 2
(
2𝜋
2
+
𝜋
4
) + 3𝜋=
11
2
𝜋
Câu 9: Tính
∭
𝑧𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
với i 𝑉 nh bxác đị ở
𝑥
2
+ 𝑦 + 𝑧
2
≤ 1, 𝑦
2 2
≤ 4, 𝑧≥ 0
Gi i:ả
Hình chi u c lên là ế ủa 𝑉 𝑂𝑥𝑦 𝐷: 𝑥
2
+ 𝑦 ≤ 1
2
Mi
ền 𝑉: {
0 ≤ 𝑧≤ √4 − 𝑦
2
𝐷: 𝑥
2
+ 𝑦 ≤ 1
2
⇒𝐼= ∭𝑧𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∬𝑑𝑥𝑑𝑦
𝐷
∫ 𝑧𝑑𝑧
√
4−𝑦
2
0
=
1
2
∬
(
4 − 𝑦
2
)
𝑑𝑥𝑑𝑦
𝐷
Đặ
t {
𝑥= 𝑟cos 𝜑
𝑦= 𝑟sin 𝜑
, 𝐽= 𝑟⇒𝐷: {
0 ≤ 𝑟≤ 1
0 ≤ 𝜑≤ 2𝜋
⇒𝐼=
1
2
∫ 𝑑𝜑
2𝜋
0
∫
[
4 −
(
𝑟sin 𝜑
)
2
]
. 𝑟𝑑𝑟
1
0
=
1
2
∫ [2 −
1
4
(
sin 𝜑
)
2
] 𝑑𝜑
2𝜋
0
=
1
2
.
15𝜋
4
=
15𝜋
8
Hình v minh h a ẽ ọ
PHAM THANH TUNG
Câu 10: Tính tích phân b i ba ộ
∭
𝑦
2
𝑒
𝑧
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
, trong đó
𝑉: 0 ≤ 𝑥≤ 1, 𝑥≤ 𝑦≤ 1, ≤ 𝑧≤ + 2𝑥𝑦
Gi i:ả
Mi
ền 𝑉: {
0 ≤ 𝑥≤ 1
𝑥≤ 𝑦≤ 1
1 ≤ 𝑧≤ + 2
𝑥𝑦
⇔{
0 ≤ 𝑥≤ 𝑦
0 ≤ 𝑦≤ 1
1 ≤ 𝑧≤ + 2
𝑥𝑦
(
Đổi ứ tự lấy tích phân 𝑥 𝑦th và
)
⇒𝐼= ∫ 𝑑𝑦
1
0
∫ 𝑑𝑥
𝑦
0
∫ 𝑦
2
𝑒
𝑧
𝑑𝑧
𝑥𝑦+2
1
= ∫ 𝑑𝑦
1
0
∫ 𝑦
2
(
𝑒
𝑥𝑦+2
− 𝑒𝑑𝑥
)
𝑦
0
∫ 𝑦
2
(
𝑒
𝑥𝑦+2
− 1 𝑑𝑥
)
𝑦
0
= ∫ 𝑦
2
𝑒
𝑥𝑦+2
𝑑𝑥
𝑦
0
− ∫ 𝑦
2
𝑑𝑥
𝑦
0
= ∫ 𝑦𝑒
𝑥𝑦+2
𝑑
(
𝑥𝑦+ 2
)
𝑦
0
− 𝑒.𝑦
3
= 𝑦𝑒
𝑥𝑦+2
|
𝑦
0
− 𝑒.𝑦
3
= 𝑦𝑒
𝑦
2
+2
− 𝑒
2
𝑦− 𝑒. 𝑦
3
⇒∫ 𝑑𝑦
1
0
∫ 𝑦
2
(
𝑒
𝑥𝑦+2
− 1 𝑑𝑥
)
𝑦
0
= ∫(𝑦𝑒
𝑦
2
+2
− 𝑒
2
𝑦− 𝑦
3
)𝑑𝑦
1
0
=
1
2
∫ 𝑒
𝑦
2
+2
𝑑
(
𝑦
2
)
1
0
−
𝑒
2
2
−
𝑒
4
=
1
2
𝑒
3
− 𝑒
2
−
𝑒
4
PHAM THANH TUNG
LỜI GI I THAM KH THI GI Ả ẢO ĐỀ ỮA KÌ 20192 (ĐỀ 3)
Câu 1: Viết phương trình tiế ủa đườp diện và pháp tuyến c ng cong
{
𝑥= 2
(
𝑡− sin 𝑡
)
𝑦= 2 1 −
(
cos 𝑡
)
tại 𝑡=
𝜋
2
Gi i:ả
{
𝑥= 2
(
𝑡− sin 𝑡
)
𝑦= 2 1 −
(
cos 𝑡
)
⇒{
𝑥
′
(
𝑡
)
= 2 − 2 cos 𝑡
𝑦
′
(
𝑡
)
= 2 sin𝑡
.
Tại 𝑡=
𝜋
2
⇒{
𝑥
′
(
𝜋
2
) = 2, 𝑥(
𝜋
2
) = 𝜋− 2
𝑦
′
(
𝜋
2
) = 2, 𝑦(
𝜋
2
) = 2
Tại 𝑡=
𝜋
2
⇒{
phương trình tiếp tuyến:
𝑥− 𝜋+ 2
2
=
𝑦− 2
2
⇔𝑦= 𝑥− 𝜋+ 4
phương trình pháp tuyến:
𝑥− 𝜋+ 2
2
= −
𝑦− 2
2
⇔𝑦= 𝜋− 𝑥
Câu 2:
Tính độ ủa đườ cong c ng cong t𝑦= 𝑒
2𝑥
ại 𝐴
(
0,1
)
Gi i:ả
𝑦= 𝑒 ⇒𝑦
2𝑥 ′
(
𝑥
)
= 2𝑒 , 𝑦
2𝑥 ′′
(
𝑥
)
= 4𝑒
2𝑥
. Tại 𝐴
(
0,1 ⇒𝑦
)
′
(
0 = 2, 𝑦
)
′′
(
0 = 4
)
Độ
cong c ng cong t là: ủa đườ ại điểm 𝐴
(
0,1
)
𝐶
(
𝐴
)
=
|
𝑦
′′
(
0
)|
(1 + 𝑦
′
(
0
)
2
)
3
2
=
4
5
√
5
Câu 3: Tìm hình bao c a h ng cong ủ ọ đườ
𝑦= 4𝑐𝑥 + 𝑐
3 4
, với c tham sốlà
Gi i:ả
Đặ
t 𝐹
(
𝑥, 𝑦, 𝑐 = 𝑦− 4𝑐𝑥 − 𝑐
)
3 4
Xét
{
𝐹
𝑥
′
= 0
𝐹
𝑦
′
= 0
⇔{
−12
𝑐𝑥
2
= 0
1 = 0
⇒ Vô nghi H m kì d . ệm ⇒ ọ đường cong không có điể ị
Xét
{
𝐹= 0
𝐹
𝑐
′
= 0
⇔{
𝑦− 4𝑐𝑥
3
− 𝑐
4
= 0
−4𝑥 − 4𝑐
3 3
= 0
⇔{
𝑦− 4𝑐𝑥
3
− 𝑐
4
= 0
−𝑥= 𝑐
PHAM THANH TUNG
⇒𝑦− 4 −𝑥 — 𝑥4 = 0 ⇔𝑦+ 4𝑥 − 𝑥
( )
𝑥
3 4 4
= 0
Vậy hình bao c a hủ ọ đường cong là 𝑦= −3𝑥
4
Câu 4: Đổi th t l y tích phân ứ ự ấ
∫ 𝑑𝑦
1
0
∫ 𝑓
(
𝑥, 𝑦𝑑𝑥
)
√
2−𝑦
2
√
𝑦
Gi i:ả
Mi
ề ấn l y tích phân
(
𝐷
)
: {
√
𝑦≤ 𝑥≤ √2 − 𝑦
2
0 ≤ 𝑦≤ 1
Đổ ứ ự ấ ề ầ
i th t l y tích phân, chia mi n thành 2 ph
(
𝐷
)
n:
(
𝐷
1
)
: {
0 ≤ 𝑥≤ 1
0 ≤ 𝑦≤ 𝑥
2
và
(
𝐷
2
)
: {
1 ≤ 𝑥≤ 2
√
0 ≤ 𝑦≤ √2 − 𝑥
2
⇒𝐼= ∫ 𝑑𝑥
1
0
∫ 𝑓𝑥, 𝑦𝑑𝑦
( )
𝑥
2
0
+ ∫ 𝑑𝑥
√
2
1
∫ 𝑓
(
𝑥, 𝑦𝑑𝑦
)
√
2−𝑥
2
0
PHAM THANH TUNG
Câu 5: Tính
∬
4𝑦𝑑𝑥𝑑𝑦
𝐷
, v là mi nh b ới 𝐷 ền xác đị ởi:
𝑥
2
+ 𝑦
2
≤ 1, 𝑥+ 𝑦≥ 1
Gi i:ả
Mi
ền 𝐷: {
1 − 𝑥≤ 𝑦≤ √1 − 𝑥
2
0 ≤ 𝑥≤ 1
∬4𝑦
𝐷
𝑑𝑥𝑑𝑦= ∫ 𝑑𝑥
1
0
∫ 4𝑦𝑑𝑦
√
1−𝑥
2
1−𝑥
= ∫ (
2𝑥
2
|
√
1 − 𝑥
2
1 − 𝑥
) 𝑑𝑥
1
0
= 2 ∫
[(
1 − 𝑥
2
)
−
(
1 − 𝑥 𝑑𝑥
)
2
]
1
0
=
2
3
Câu 6: Tính th tích mi n gi i h n b i m và m ể ề 𝑉 ớ ạ ở ặt 𝑂𝑥𝑦 ặt 𝑧= 𝑥 + 𝑦 − 4
2 2
Gi i:ả
Mi
ền
(
𝑉
)
: 𝑥
2
+ 𝑦 − 4 ≤ 𝑧≤ 0
2
Hình chi u c lên là:
ế ủa
(
𝑉
)
𝑂𝑥𝑦
(
𝐷
)
: 𝑥 + 𝑦
2 2
≤ 4
Đặ
t {
𝑥= 𝑟cos 𝜑
𝑦= 𝑟sin 𝜑
𝐽= 𝑟. Mi n ề
(
𝐷
)
: {
0 ≤ 𝑟≤ 2
0 ≤ 𝜑≤ 2𝜋
Mi
ền trong t
(
𝑉
)
ọa độ trụ là:
(
𝑉
)
: {
0 ≤ 𝑟≤ 2
0 ≤ 𝜑≤ 2𝜋
𝑟
2
− 4 ≤ 𝑧≤ 0
Thể ề tích mi n là: 𝑉
𝑉
(
𝑉
)
= ∭𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∫ 𝑑𝜑
2𝜋
0
∫ 𝑑𝑟
2
0
∫ 𝑟𝑑𝑧
0
𝑟
2
−4
= ∫ 𝑑𝜑
2𝜋
0
∫ 𝑟(−𝑟
2
+ 4)𝑑𝑟
1
0
= 8𝜋
(
đvtt
)
PHAM THANH TUNG
Câu 7: Tính
∭
√
𝑥
2
+ 𝑦 + 𝑧
2 2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
V
ới i 𝑉 nh bxác đị ở 𝑥 𝑥
2
+ 𝑦 + 𝑧 ≤ 1, √3
2 2
(
2
+ 𝑦
2
)
≤ 𝑧
Gi i:ả
Mi
ền 𝑉: √3
(
𝑥
2
+ 𝑦 ≤ 𝑧≤ √1 − + 𝑦
2
) (
𝑥
2 2
)
Đặ
t {
𝑥= 𝑟sin 𝜃cos 𝜑
𝑦= 𝑟sin 𝜃sin 𝜑
𝑧= 𝑟
cos 𝜃
|
𝐽
|
= 𝑟
2
sin 𝜃
Mi
ền
(
𝑉
)
: {
0 ≤ 𝑟≤ 1
0 ≤ 𝜃≤ 𝜋/6
0 ≤ 𝜑≤ 2𝜋
∭
√
𝑥
2
+ 𝑦 + 𝑧
2 2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∫ 𝑑𝜑
2𝜋
0
∫ 𝑑𝜃
𝜋
6
0
∫ 𝑟.
1
0
𝑟
3
sin 𝜃𝑑𝑟=
2 − 3
√
4
𝜋
Câu 8: Tính
∭
𝑧𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
, v nh bới 𝑉xác đị ởi 𝑥
2
+ 𝑦
2
+ 𝑧
2
≤ 6, 𝑧≥ 𝑥
2
+ 𝑦
2
Gi i:ả
Mi
ền nh b
(
𝑉
)
xác đị ởi {
𝑥
2
+ 𝑦
2
+ 𝑧
2
≤ 6
𝑧≥ 𝑥 + 𝑦
2 2
Hình chi u c lên là:
ế ủa
(
𝑉
)
𝑂𝑥𝑦
(
𝐷
)
: 𝑥
2
+ 𝑦 ≤ 2
2
Đặ
t {
𝑥= 𝑟cos 𝜑
𝑦= 𝑟sin 𝜑
𝑧= 𝑧
𝐽= 𝑟⇒ n Miề
(
𝑉
)
: {
0 ≤ 𝑟≤
√
2
0 ≤ 𝜑≤ 2𝜋
𝑟
2
≤ 𝑧≤ √6 − 𝑟
2
∭𝑧𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∫ 𝑑𝜑
2𝜋
0
∫ 𝑑𝑟
√
2
0
∫ 𝑧. 𝑟𝑑𝑧
√
6−𝑟
2
𝑟
2
=
1
2
∫ 𝑑𝜑
2𝜋
0
∫
(
6 − 𝑟
2
− 𝑟
4
)
. 𝑟𝑑𝑟
√
2
0
=
11
3
𝜋
PHAM THANH TUNG
Câu 9: Tính di n tích c a mi n gi i h n b ệ ủ ề ớ ạ ởi
(
𝑥
2
+ 𝑦
2
)
2
= 4𝑥𝑦
Gi i:ả
Mi
ề ạn gi
(
𝐷
)
ới h n bởi (𝑥 + 𝑦 = 4
2 2
)
2
𝑥𝑦
Đặ
t {
𝑥= 𝑟cos 𝜑
𝑦= 𝑟sin 𝜑
𝐽= 𝑟⇒ n Miề
(
𝐷
)
c gi i h n b ng đượ ớ ạ ởi đườ 𝑟= 2 sin 2𝜑
√
Ta có:
sin 2𝜑≥ 0 ⇔sin 𝜑 𝜑≥ 0 ⇔[cos
{
sin 𝜑≥ 0
cos 𝜑≥ 0
{
sin 𝜑≤ 0
cos
𝜑≤ 0
⇔[
0 ≤ 𝜑≤ 𝜋 /2
𝜋≤ 𝜑≤ 3𝜋 /2
n c chia thành 2 ph n
⇒Miề
(
𝐷
)
đượ ầ
(
𝐷
1
)
: {
0 ≤ 𝑟≤ 2 sin 2𝜑
√
0 ≤ 𝜑≤ 𝜋/2
và
(
𝐷
2
)
: {
0 ≤ 𝑟≤ 2 sin 2𝜑
√
𝜋≤ 𝜑≤ 3𝜋 /2
𝑆
(
𝐷
1
)
= ∬𝑑𝑥𝑑𝑦
𝐷
1
= ∫ 𝑑𝜑
𝜋
2
0
∫ 𝑟𝑑𝑟
√2 sin 2𝜑
0
=
1
2
∫ 2 sin2𝜑𝑑𝜑
𝜋
2
0
= 1
𝑆
(
𝐷
2
)
= ∬𝑑𝑥𝑑𝑦
𝐷
2
= ∫ 𝑑𝜑
3𝜋
2
𝜋
∫ 𝑟𝑑𝑟
√2 sin 2𝜑
0
=
1
2
∫ 2 sin 2𝜑𝑑𝜑
3𝜋
2
𝜋
= 1
⇒𝑆
(
𝐷
)
= 𝑆
(
𝐷
1
)
+ 𝑆
(
𝐷
2
)
= 2
PHAM THANH TUNG
Câu 10:
Cho hàm s ố 𝐼
(
𝑦
)
=
∫
sin + 𝑦
(
𝑥
2
+ 𝑥𝑦
2
)
𝑑𝑥
1
𝑦
. Tính 𝐼
′
(
0
)
Gi i:ả
Đặ
t 𝑓
(
𝑥, 𝑦 = sin + 𝑦
) (
𝑥
2
+ 𝑥𝑦
2
)
⇒𝑓
𝑦
′
=
(
𝑥+ 2𝑦
)
cos
(
𝑥
2
+ 𝑥𝑦+ 𝑦
2
)
Ta có:
{
𝑓
(
𝑥, 𝑦
)
liên tục, ả trên kh vi
[
−1,1
]
×
[ ]
−1,1
𝑎
(
𝑦 𝑦
)
= 𝑦, 𝑏
( )
= 1 liên tục, khả vi trên
[
−1,1
]
𝑓
𝑦
′
(
𝑥, 𝑦
)
liên tục trên
[
−1,1
]
×
[
−1,1
]
⇒ Hàm kh vi trên 𝐼
(
𝑦
)
ả
[ ]
−1,1
𝐼
′
(
𝑦 𝑦
)
= 𝑓
(
𝑏
( )
, 𝑦
)
. 𝑏
𝑦
′
( ( (
𝑦
)
− 𝑓𝑎𝑦
)
, 𝑦
)
. 𝑎
𝑦
′
(
𝑦
)
+ ∫ 𝑓
𝑦
′
(
𝑥, 𝑦
)
𝑑𝑥
𝑏
(
𝑦
)
𝑎
(
𝑦
)
⇒𝐼
′
(
𝑦
)
= 𝑓1,𝑦.0 − 𝑓𝑦, 𝑦. 1 + ∫ 𝑥+ 2𝑦 + 𝑦
( ) ( ) ( )
cos
(
𝑥
2
+ 𝑥𝑦
2
)
𝑑𝑥
1
𝑦
⇒𝐼
′
(
0 = 𝑓1,0 . 0 − 𝑓0,0 . 1 + ∫ 𝑥
) ( ) ( )
cos
(
𝑥
2
)
𝑑𝑥
1
0
=
1
2
∫ cos
(
𝑥
2
)
𝑑
(
𝑥
2
)
1
0
=
sin 1
2
PHAM THANH TUNG
LỜI GI I THAM KH Ả ẢO ĐỀ GIỮA KÌ 20193 (ĐỀ 1)
Câu 1:
Xác định độ ại đườ ại điể cong t ng cong t𝑥= 4𝑦+ 1
√
m
(
3,1
)
Gi i:ả
𝑥= 4𝑦+ 1 ⇔ 4𝑦= 𝑥− 1 ⇔𝑦=
√ √
(
𝑥− 1
)
2
4
(
𝑥≥ 1
)
⇒𝑦
′
(
𝑥
)
=
𝑥− 1
2
, 𝑦
′′
(
𝑥
)
=
1
2
Tại
(
3,1 ⇒𝑦 = 1, 𝑦
)
′ ′′
=
1
2
Độ ạ
cong c ng cong tủa đườ i
(
3,1
)
là:
𝐶
(
3,1
)
=
|
𝑦′′
|
(1 + 𝑦′
2
)
3
2
=
√
2
8
Câu 2:
Viết phương trình pháp tuyến và tiếp diện của mặt cong 𝑦
2
= 3 + 𝑧
(
𝑥
2 2
)
tại điểm
(
√
2, 3,1)
Gi i:ả
Đặ
t 𝐹
(
𝑥, 𝑦, 𝑧 = 𝑦 − 3 + 𝑧
)
2
(
𝑥
2 2
)
⇒{
𝐹
𝑥
′
= −6𝑥
𝐹
𝑦
′
= 2𝑦
𝐹
𝑧
′
= −6𝑧
T
ại (
√
2, 3,1), 𝐹 ta có:
𝑥
′
= −6 2, 𝐹
√
𝑦
′
= 6, 𝐹
𝑧
′
= −6
Phương trình pháp tuyến của mặt cong tại (
√
2, 3,1) là:
𝑥− 2
√
−6
√
2
=
𝑦− 3
6
=
𝑧− 1
−6
⇔
𝑥−
√
2
−
√
2
=
𝑦− 3
1
=
𝑧− 1
−1
Phương trình tiếp diện của mặt cong tại (
√
2, 3,1) là:
−6 2(𝑥− 2) + 6 𝑦− 3 − 6 𝑧− 1 = 0 ⇔− 2𝑥+ 𝑦− 𝑧= 0
√ √
( ) ( )
√
Câu 3:
Tìm hình bao c a h ng cong: ủ ọ đườ 𝑦= 2𝑥+ 3𝑐
( )
4
Gi i:ả
Đặt 𝐹
(
𝑥, 𝑦, 𝑐 = 𝑦− 2𝑥+ 3𝑐
) ( )
4
PHAM THANH TUNG
Xét
{
𝐹
𝑥
′
(
𝑥, 𝑦, 𝑐
)
= 0
𝐹
𝑦
′
(
𝑥, 𝑦, 𝑐
)
= 0
⇔{
−8
(
2𝑥+ 3𝑐
)
3
= 0
1 = 0
⇒ Vô nghi ệm
⇒ H m kì d . ọ đường cong không có điể ị
Xét {
𝐹
(
𝑥, 𝑦, 𝑐
)
= 0
𝐹
𝑐
′
(
𝑥, 𝑦, 𝑐
)
= 0
⇔{
𝑦=
(
2𝑥+ 3𝑐
)
4
−
12
(
2𝑥+ 3𝑐
)
3
= 0
⇔{
𝑦=
(
2𝑥+ 3𝑐
)
4
−2
3
𝑥= 𝑐
⇒𝑦= 2𝑥−(
3.2
3
𝑥)
4
= 0
Vậy hình bao của họ cong 𝑦= 0 đường là đường
𝐂â𝐮 𝟒: Tính ∬
√
𝑥
2
+ 𝑦 𝑑𝑥𝑑𝑦
2
𝐷
, với D ền phía trên parabol 𝑦= 𝑥là mi
2
và nằm phía
trong tròn 𝑥 = 2 đường
2
+ 𝑦
2
Gi i:ả
Đặ
t {
𝑥= 𝑟cos 𝜑
𝑦= 𝑟sin 𝜑
|
𝐽
|
= 𝑟
Chia thành hai mi n: 𝐷 ề
𝐷
1
:
{
0 ≤ 𝑟≤
sin 𝜑
(
cos 𝜑
)
2
𝜑∈[0;
𝜋
4
] ∪[
3𝜋
4
; 𝜋]
và 𝐷
2
: {
0 ≤ 𝑟≤ 2
√
𝜋
4
≤ 𝜑≤
3𝜋
4
PHAM THANH TUNG
⇒∬ + 𝑦
√
𝑥
2 2
𝑑𝑥𝑑𝑦
𝐷
= ∫ 𝑑𝜑
𝜋
4
0
∫ 𝑟. 𝑟𝑑𝑟
sin 𝜑
( )
cos𝜑
2
0
+ ∫ 𝑑𝜑
𝜋
3𝜋
4
∫ 𝑟. 𝑟𝑑𝑟
sin 𝜑
(
cos 𝜑
)
2
0
+ ∫ 𝑑𝜑
3𝜋
4
𝜋
4
∫ 𝑟. 𝑟𝑑𝑟
√
2
0
=
1
3
∫
(
sin 𝜑
)
3
( )
cos 𝜑
6
𝑑𝜑
𝜋
4
0
+
1
3
∫
(
sin 𝜑
)
3
(
cos 𝜑
)
6
𝑑𝜑
𝜋
3𝜋
4
+
√
2𝜋
3
=
−1
3
∫
(
sin 𝜑
)
2
(
cos 𝜑
)
6
𝑑
(
cos 𝜑
)
𝜋
4
0
−
1
3
∫
(
sin 𝜑
)
2
(
cos 𝜑
)
6
𝑑
(
cos 𝜑
)
𝜋
3𝜋
4
+
√
2𝜋
3
=
−1
3
∫
1 − 𝑢
2
𝑢
6
𝑑𝑢
√
2
2
1
−
1
3
∫
1 − 𝑢
2
𝑢
6
𝑑𝑢
−1
−
√
2
2
+
√
2𝜋
3
=
4 + 4
√
2
45
+
√
2𝜋
3
𝐂â𝐮 𝟓: Tính ∭
√
6𝑦− 𝑥
2
− 𝑦 − 𝑧 𝑑𝑥𝑑𝑦𝑑𝑧
2 2
𝑉
với 𝑉: 𝑥
2
+ 𝑦
2
+ 𝑧
2
≤ 6𝑦
Gi i:ả
Mi
ền 𝑉: 𝑥
2
+ 𝑦 + 𝑧 ≤ 6𝑦⇔𝑥 𝑦− 3
2 2 2
+
( )
2
+ 𝑧 ≤ 9
2
Đặ
t {
𝑥= 𝑟sin 𝜃cos 𝜑
𝑦= 3 + 𝑟sin𝜃sin 𝜑
𝑧= 𝑟
cos 𝜃
, 𝐽= −𝑟
2
sin 𝜃
Mi
ề ầ ộn trong t c𝑉 ọa độ u suy r ng là 𝑉: {
0 ≤ 𝑟≤ 3
0 ≤ 𝜃≤ 𝜋
0 ≤ 𝜑≤ 2𝜋
⇒𝐼= ∭ 9 − 𝑥 − 6𝑦+ 9 − 𝑧
√
2
−
(
𝑦
2
)
2
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∭ 9 − 𝑦− 3
√ [
𝑥
2
+
( )
2
+ 𝑧
2
]
𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
PHAM THANH TUNG
= ∫ 𝑑𝜑
2𝜋
0
∫ 𝑑𝜃
𝜋
0
∫
√
9 − 𝑟
2
. 𝑟
2
sin 𝜃𝑑𝑟
3
0
Đặt 𝑟= 3 sin 𝑡⇒𝑑𝑟= 3 𝑡𝑑𝑡cos
⇒∫ 9 − 𝑟
√
2
. 𝑟 𝑑𝑟
2
3
0
= ∫ 9 − 9 sin 𝑡
√ ( )
2
. 9 sin 𝑡
( )
2
. 3 cos 𝑡
𝜋
2
0
𝑑𝑡= ∫ 3 𝑡.9 sin 𝑡cos
( )
2
. 3 cos 𝑡
𝜋
2
0
𝑑𝑡
=
81 ∫
(
sin 𝑡cos 𝑡
)
2
𝑑𝑡
𝜋
2
0
= 81 ∫ (
sin 2𝑡
2
)
2
𝑑𝑡
𝜋
2
0
=
81
4
∫
(
sin 2𝑡
)
2
𝑑𝑡
𝜋
2
0
=
81
4
∫
1 − cos 4𝑡
2
𝑑𝑡
𝜋
2
0
=
81𝜋
16
⇒𝐼=
81𝜋
16
∫ 𝑑𝜑
2𝜋
0
∫ sin 𝜃𝑑𝜃
𝜋
0
=
81
4
𝜋
2
Câu 6: Tính di n tích mi n gi i h n b i hai ng cong và ệ ề ớ ạ ở đườ 𝑦= 𝑥
2
𝑥= 𝑦
2
Gi i:ả
Mi
ền 𝐷: {
0 ≤ 𝑥≤ 1
𝑥
2
≤ 𝑦≤
√
𝑥
Diệ ền tích mi n là: 𝐷
𝑆= ∬𝑑𝑥𝑑𝑦
𝐷
= ∫ 𝑑𝑥
1
0
∫ 𝑑𝑦
√
𝑥
𝑥
2
= ∫(
√
𝑥− 𝑥
2
)𝑑𝑥
1
0
=
1
3
(
đvdt
)
𝑟
3
0
𝑡
𝜋
2
0
PHAM THANH TUNG
Câu 7: Tính th tích mi n gi i h n b i các m t cong và nể ề ớ ạ ở ặ 𝑥= 𝑦 + 𝑧
2 2
𝑥
2
+ 𝑦 + 𝑧 = 2
2 2
ằm
trong ph n không gian có không âm. ầ 𝑥
Gi i:ả
Xét giao tuy n c a hai m ế ủ ặt 𝑥
2
+ 𝑦 + 𝑧 = 2, 𝑥= 𝑦 + 𝑧
2 2 2 2
⇒
(
𝑦
2
+ 𝑧
2
)
+
(
𝑦
2
+ 𝑧 = 2 ⇒𝑦 + 𝑧 = 1
2
)
2 2 2
Hình chi u c lên là ế ủa 𝑉 𝑂𝑦𝑧 𝐷: 𝑦 + 𝑧
2 2
≤ 1
Đặ
t {
𝑦= 𝑟cos 𝜑
𝑧= 𝑟sin 𝜑
𝑥= 𝑥
, 𝐽= 𝑟
Mi
ền 𝑉: {
𝑦
2
+ 𝑧
2
≤ 𝑥≤ √2 −
(
𝑦
2
+ 𝑧
2
)
𝐷: 𝑦
2
+ 𝑧
2
≤ 1
⇒
Miền 𝑉 trong tọa độ trụ là 𝑉: {
𝑟
2
≤ 𝑥≤ √2 − 𝑟
2
𝐷: {
0 ≤ 𝑟≤ 1
0 ≤ 𝜑≤ 2𝜋
Thể ề tích mi n là: 𝑉
𝑉= ∭𝑑𝑥𝑑𝑦𝑑𝑧
𝑉
= ∫ 𝑑𝜑
2𝜋
0
∫ 𝑑𝑟
1
0
∫ 𝑟𝑑𝑥
√
2−𝑟
2
𝑟
2
= ∫ 𝑑𝜑
2𝜋
0
∫ 𝑟( 2 − 𝑟
√
2
− 𝑟
2
) 𝑑𝑟
1
0
∫ 𝑟( 2 − 𝑟
√
2
− 𝑟 ) 𝑑𝑟
2
1
0
= ∫ 𝑟 2 − 𝑟
√
2
𝑑𝑟
1
0
− ∫ 𝑟
3
𝑑𝑟
1
0
=
1
2
∫
√
2 − 𝑟
2
𝑑
(
𝑟
2
)
1
0
−
1
4
=
−7 + 8
√
2
12
⇒𝑉= ∫ 𝑑𝜑
2𝜋
0
∫ 𝑟( 2 − 𝑟
√
2
− 𝑟
2
) 𝑑𝑟
1
0
=
−7 + 8 2
√
6
𝜋
(
đvtt
)
Câu 8: Tính di n tích m t cong n m trong hình tr ệ ặ 𝑧= 2𝑥 − 2𝑦
2 2
ằ ụ 𝑥
2
+ 𝑦 = 1
2
Gi i:ả
Hình chi u c n m n m trong m t tr lên là: ế ủa phầ ặt 2𝑥 − 2𝑦
2 2
ằ ặ ụ 𝑥
2
+ 𝑦 = 1
2
𝑂𝑥𝑦 𝐷: 𝑥 + 𝑦 ≤ 1
2 2
Ta có:
𝑧
𝑥
′
= 4𝑥, 𝑧
𝑦
′
= 4𝑦
Diệ ần tích c n tính là:
PHAM THANH TUNG
𝑆= ∬ 1 + 𝑧
√
(
𝑥
′
)
2
+ (𝑧
𝑦
′
)
2
𝑑𝑥𝑑𝑦
𝐷
= ∬ 1 +
√
16𝑥
2
+ 16𝑦
2
𝑑𝑥𝑑𝑦
𝐷
Đặ
t {
𝑥= 𝑟cos 𝜑
𝑦= 𝑟sin 𝜑
, 𝐽= 𝑟⇒𝐷: {
0 ≤ 𝑟≤ 1
0 ≤ 𝜑≤ 2𝜋
⇒𝑆= ∫ 𝑑𝜑
2𝜋
0
∫
√
1 + 16𝑟
2
. 𝑟𝑑𝑟
1
0
=
1
2
∫ 𝑑𝜑
2𝜋
0
∫
√
1 + 16𝑟
2
𝑑
(
𝑟
2
)
1
0
=
1
2
∫ 𝑑𝜑
2𝜋
0
∫
√
1 + 𝑢𝑑𝑢16
1
0
=
1
2
. 2𝜋.
1
24
(17
√
17 − 1 ) =
(17
√
17 − 1)𝜋
24
(
đvdt
)
𝐂â𝐮 𝟗: Tính lim
𝑦→0
∫
(
𝑥+ 3𝑦
)√
𝑥
2
+ 𝑦
3
+ 1𝑑𝑥
1
0
Gi i:ả
Ta có: liên t c trên mi n
(
𝑥+ 3𝑦√𝑥 + 𝑦 + 1
)
2 3
ụ ề
[ [ ]
0,1
]
× −1,1
⇒𝐼 = ∫ 𝑥+ 3𝑦 + 𝑦 + 1𝑑𝑥
(
𝑦
) ( )√
𝑥
2 3
1
0
liên tục trên ứa 𝑦= 0
[ ]
−1,1
ch
⇒𝐼 = ∫ 𝑥+ 3𝑦 + 𝑦 + 1
(
𝑦
) ( )√
𝑥
2 3
𝑑𝑥
1
0
liên tục tại 𝑦= 0
lim
𝑦→0
∫ 𝑥+ 3𝑦
( )√
𝑥
2
+ 𝑦
3
+ 1𝑑𝑥
1
0
= 𝐼 0 = ∫ 𝑥
( )
√
𝑥
2
+ 1𝑑𝑥
1
0
=
1
2
∫
√
𝑥
2
+ 1𝑑
(
𝑥
2
)
1
0
=
−1 + 2 2
√
3
Câu 10: Khảo sát tính liên t c và kh vi c a hàm s : ụ ả ủ ố
𝑔
(
𝑦
)
= ∫
𝑑𝑥
𝑥
2
+ 𝑦
2
1
0
Gi i:ả
Đặt 𝑓
(
𝑥, 𝑦
)
=
1
𝑥
2
+ 𝑦
2
*Khảo sát tính liên tục:
PHAM THANH TUNG
Xét hàm s t
ố 𝑔
(
𝑦
)
ại 𝑦≠ 0
𝑔
(
𝑦
)
= ∫
𝑑𝑥
𝑥
2
+ 𝑦
2
1
0
=
1
𝑦
arctan
𝑥
𝑦
|
1
0
=
1
𝑦
arctan
1
𝑦
Xét hàm s t
ố 𝑔
(
𝑦
)
ại 𝑦= 0
𝑔
(
0 = ∫
)
𝑑𝑥
𝑥
2
1
0
=
−1
𝑥
|
1
0
= −∞
⇒𝑔 𝑦= 0
(
𝑦
)
nh tkhông xác đị ại
V
ậy hàm số 𝑔
(
𝑦
)
liên tục v ới 𝑦≠ 0
*Khảo sát tính khả vi:
Xét hàm s t
ố 𝑔
(
𝑦
)
ại 𝑦≠ 0
{
Vớ𝑖 𝑦∈𝑅\{0}, 𝑓
(
𝑥, 𝑦
)
là hàm số liên tục trên
[ ]
0; 1
𝑓
𝑦
′
=
−2𝑦
(
𝑥
2
+ 𝑦
2
)
2
là hàm số liên tục trên
[
0; 1
]
×
(
−∞; 0
)
và
[ )
0; 1
]
×
(
0; +∞
⇒𝑔 𝑦≠ 0
(
𝑦
)
là hàm s kh vi vố ả ới
Xét hàm s t
ố 𝑔
(
𝑦
)
ại 𝑦≠ 0
Với 𝑦= 0 ⇒𝑓
(
𝑥, 𝑦
)
=
1
𝑥
2
+ 𝑦
2
=
1
𝑥
2
bị gián đoạn tại 𝑥= 0
⇒Với 𝑦= 0 thì 𝑓 không liên tục trên
(
𝑥, 𝑦
) [
0; 1
]
⇒
𝑔
(
𝑦
)
không kh vi tả ại 𝑦= 0
V
ậy hàm số 𝑔
(
𝑦
)
khả vi v ới 𝑦≠ 0
| 1/82
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

BÁCH KHOA-ĐẠI CƯƠNG MÔN PHÁI
BÀI GIẢI THAM KHẢO GIẢI TÍCH II
______________________________________________
Đề thi giữa kì 20163-20193
Người biên soạn: Phạm Thanh Tùng
(Tự Động Hóa – ĐHBKHN) Hà Nội, T á
h ng 5 năm 2021
TÀI LIỆU THAM KHẢO :
− Bài giảng môn Giải tích II, thầy Bùi Xuân Diệu.
− Bài tập giải sẵn Giải tích 2 (Tóm tắt lý thuyết và chọn lọc), thầy Trần Bình.
− Bài tập Toán học cao cấp, tập hai: Giải tích, GS.TS Nguyễn Đình Trí (chủ
biên), PGS.TS. Trần Việt Dũng, PGS.TS. Trần Xuân Hiền, PGS.TS Nguyễn Xuân Thảo.
− Bộ đề cương Giải tích II, Viện Toán ứng dụng và Tin học.
− Bộ đề thi Giữa kì và Cuối kì môn Giải tích II Trường ĐH Bách Khoa Hà Nội.
Tài liệu được biên soạn dựa trên kinh nghiệm cá nhân, dù đã rất cố gắng
nhưng với những hạn chế n ấ
h t định về kiến thức, kĩ năng chắc chắn vẫn sẽ
tồn tại các lỗi sai tính toán, lỗi đánh máy, … chưa được kiểm tra hết, mọi ý
kiến góp ý bạn đọc vui lòng gửi qua link fb “fb.com/tungg810” để mình có thể
kiểm tra, hoàn thiện bộ tài liệu. Xin chân thành cảm ơn! PHẦN I: ĐỀ THI
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 1
ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 2 – Học kì 20163
Thời gian: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và Giám thị phải kí xác nhận số đề vào bài thi
của sinh viên.
Câu 1: (1đ). Viết phương trình tiếp diện và pháp tuyến của mặt cong 𝑥2 + 3𝑦 + 2𝑧3 = 3 tại 𝑀(2; −1; 1)
Câu 2: (1đ). Tìm hình bao c a h ủ
ọ đường thẳng 𝑦 = 2𝑐𝑥 − 𝑐2 với 𝑐 là tham s . ố
Câu 3: (1đ). Tìm điểm có độ cong lớn nhấ ủa đườ t c ng cong 𝑦 = ln 𝑥
Câu 4: (1đ). Đổi thứ t l ự ấy tích phân: 1 1 ∫ 𝑑𝑥 ∫ 𝑓(𝑥, 𝑦)𝑑𝑦 0 √2𝑥−𝑥2
Câu 5: (2đ). Tính các tích phân kép sau:
𝑎) ∬(3𝑥 + 2𝑦)𝑑𝑥𝑑𝑦 , 𝐷 là m ền i g ới hạn bởi i
các đường 𝑦 = 𝑥2 và 𝑦 = 1 𝐷 𝑥𝑦 𝑏) ∬
𝑑𝑥𝑑𝑦 với 𝐷 = {(𝑥, 𝑦) ∈ 𝑅2: 1 ≤ 𝑥2 + 𝑦2 ≤ 2𝑥, 𝑦 ≥ 0} 𝑥2 + 𝑦2 𝐷
Câu 6: (1đ). Tính thể tích c a v ủ
ật thể 𝑉 giới hạn bởi các mặt
𝑧 = 𝑥2 + 𝑦2 và 𝑧 = 2𝑥 + 4𝑦
Câu 7: (2đ). Tính tích phân b i ba ộ
∭ 𝑦𝑑𝑥𝑑𝑦𝑑𝑧 trong đó: 𝑉
a) 𝑉 giới hạn bởi các mặt
𝑧 = 0, 𝑧 = 𝑥2, 𝑦 = 2𝑥2 v à 𝑦 = 4 + 𝑥2
b) 𝑉 là hình cầu 𝑥2 + 𝑦2 + 𝑧2 ≤ 2𝑦
Câu 8: (1đ). Tính tích phân +∞𝑒−𝛼𝑥2 − 1 ∫ 𝑑𝑥 với 𝛼 ≥ 0 𝑥2𝑒𝑥2 0
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 2
ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 2 – Học kì 20172
Thời gian: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và Giám thị phải kí xác nhận số đề vào bài thi
của sinh viên.
Câu 1: (1đ). Viết phương trình tiếp diện và pháp tuyến của mặt cong ln(𝑥2 + 3𝑦) − 3𝑧3 = t 2 ại điểm 𝑀(1,0, −1).
Câu 2: (1đ). Tìm hình bao c a h ủ
ọ đường cong 𝑐𝑥2 − 2𝑦 − 𝑐3 + 1 = v 0 ới 𝑐 là tham s . ố
Câu 3: (1đ). Tính độ cong của đường 𝑦 = ln(sin 𝑥) tại điểm ứng với 𝑥 = 𝜋/4.
Câu 4: (2đ). Tính các tích phân sau:
𝑎) ∬(𝑥2 − 4𝑦2)𝑑𝑥𝑑𝑦 , 𝐷 là m ền i g ới hạn bởi i 𝑦 = 𝑥, 𝑥 = 1 v à 𝑦 = 0 𝐷
𝑏) ∬(𝑥2 − 𝑥𝑦 + 𝑦2)𝑑𝑥𝑑𝑦 , 𝐷 l à m ền i g ới
i hạn bởi 𝑦 = −3𝑥 + 1, 𝑦 = −3𝑥 + 2, 𝑦 = 𝑥 𝐷 và 𝑦 = 𝑥 + 2
Câu 5: (1đ). Tính tích phân sau: 1 1 1 ∫ 𝑑𝑥 ∫ 𝑑𝑦 𝑦5 + 1 0 √ 4 𝑥
Câu 6: (1đ). Tính thể tích c a v ủ
ật thể 𝑉 giới hạn bởi các mặt
𝑧 = 𝑥2 + 2𝑦2 và 𝑧 = 3 − 2𝑥2 − 𝑦2
Câu 7: (1đ). Tính tích phân b i ba ộ
∭ (3𝑥𝑦2 − 4𝑥𝑦𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 trong đó 𝑉 ền xác đị là mi nh bởi 𝑉
1 ≤ 𝑦 ≤ 2, 0 ≤ 𝑥𝑦 ≤ 2,0 ≤ 𝑧 ≤ 2
Câu 8: (1đ). Tính tích phân b i ba ộ
∭ (𝑥2 + 𝑦2 + 𝑧2)𝑑𝑥𝑑𝑦𝑑𝑧 trong đó 𝑉 là miền giới hạn bởi 𝑉
các mặt 𝑦 = √𝑥2 + 4𝑧2, 𝑦 = 2.
Câu 9: (1đ). Tính tích phân
+∞𝑒−𝑎𝑥2 − 𝑒−𝑏𝑥2 ∫
𝑑𝑥 với 𝑎, 𝑏 > 0 𝑥 0
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 4
ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 2 – Học kì 20172
Thời gian: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và Giám thị phải kí xác nhận số đề vào bài thi
của sinh viên.
Câu 1: (1đ). Viết phương trình tiếp tuyến và pháp diện của đường cong 𝑥 = 4 sin2 𝑡 , 𝑦 =
4 cos 𝑡 , 𝑧 = 2 sin 𝑡 + 1 tại điểm 𝑀(1; −2√3; 2)
Câu 2: (1đ). Tìm hình bao c a h ủ
ọ đường thẳng 3𝑐𝑥 − 𝑦 − 𝑐3 = v 0, ới 𝑐 là tham s . ố
Câu 3: (1đ). Tính độ cong của đường cong 𝑥 = sin 𝑡 + 𝑡 cos 𝑡 , 𝑦 = cos 𝑡 + 𝑡 sin 𝑡 tại điểm ứng với 𝑡 = 𝜋
Câu 4: (2đ). Tính các tích phân kép sau:
a) ∬ 2𝑥𝑑𝑥𝑑𝑦 , 𝐷 là m ền i g ớ
i i hạn bởi 𝑦 = 𝑥2 và 𝑦 = 2 − 𝑥 𝐷
b) ∬ 𝑦√𝑥2 + 𝑦2𝑑𝑥𝑑𝑦 , vớ𝑖 𝐷 = {(𝑥, 𝑦) ∈ 𝑅2: 𝑥2 + 𝑦2 ≤ 𝑦} 𝐷
Câu 5: (1đ). Tính thể tích vật thể 𝑉 giới hạn bởi các mặt 𝑥 = 9𝑦2 + 𝑧2 v à 𝑥 = 9
Câu 6: (1đ). Tính tích phân sau: 1 1 1
∫ 𝑑𝑦 ∫ 𝑑𝑥 ∫ 𝑥𝑦𝑒𝑦𝑧2𝑑𝑧 0 0 𝑥2
Câu 7: (1đ). Tính ∬ (4𝑥𝑦 + 3𝑦)𝑑𝑥𝑑𝑦 với 𝐷: 1 ≤ 𝑥𝑦 ≤ 4, 𝑥 ≤ 𝑦 ≤ 9𝑥 . 𝐷
Câu 8: (1đ). : Tính tích phân b i ba ộ
∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧 trong đó 𝑉 ền xác đị là mi nh bởi 𝑉
𝑥2 + 𝑦2 + 𝑧2 ≤ 𝑧, 𝑧 ≤ 𝑥 √ 2 + 𝑦2
Câu 9: (1đ). Tính tích phân
+∞𝑒−𝑎𝑥3 − 𝑒−𝑏𝑥3 ∫
𝑑𝑥 với 𝑎, 𝑏 > 0 𝑥 0
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 1
ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 2 – Học kì 20173
Thời gian: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và Giám thị phải kí xác nhận số đề vào bài thi
của sinh viên.
Câu 1: (1đ). Tính độ cong tại 𝑡 = 0 của đường {𝑥 = 𝑒−𝑡 − sin 𝑡
𝑦 = 𝑒−𝑡 − cos 𝑡
Câu 2: (1đ). Lập phương trình pháp tuyến và tiếp diện tại 𝐴(1,1,0) của mặt 𝑧 = ln(3𝑥 − 2𝑦)
Câu 3: (1đ). Cho hàm vecto 𝑝 (𝑡) = (sin 2𝑡 , cos 2𝑡 , 𝑒−𝑡) và 𝑟 (𝑡) = (𝑡2 + 1)𝑝 (𝑡). Tính 𝑟′ (0)
Câu 4: (1đ). Đổi thứ t l ự ấy tích phân 2−𝑥2 𝐼 = ∫ 2𝑑𝑥 ∫
𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 −1 −𝑥
Câu 5: (1đ). Tính ∬ (3𝑥 + 2𝑦)𝑑𝑥𝑑𝑦 , 𝐷 giới hạn bởi: 𝐷
𝑥 = 0, 𝑦 = 0, 𝑥 + 𝑦 = 1
Câu 6: (1đ). Tính ∬ (𝑥 + 𝑦)(𝑥 − 2𝑦 − 1)2𝑑𝑥𝑑𝑦
, 𝐷 giới hạn bởi 𝑥 + 𝑦 = 0, 𝑥 + 𝑦 = 3, 𝑥 − 𝐷 2𝑦 = 1, 𝑥 − 2𝑦 = 2
Câu 7: (1đ). Tính ∭ 𝑧√𝑥2 + 𝑦2𝑑𝑥𝑑𝑦𝑑𝑧 , 𝑉 giới hạn bởi 𝑥2 + 𝑦2 = 1, 𝑧 = 0, 𝑧 = 2 𝑉
Câu 8: (1đ). Tính thể tích vật thể 𝑉 giới hạn bởi 𝑥 = √𝑦2 + 𝑧2,
𝑥 = √1 − 𝑥2 − 𝑦2 Câu 9: (1đ). Tính 3𝑥2 − 𝑦2 + 𝑧2 + 1 ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 𝑥2 + 𝑦2 + 𝑧2 + 1 𝑉
Với 𝑉 là nửa khối cầu 𝑥2 + 𝑦2 + 𝑧2 ≤ 1, 𝑧 ≥ 0
Câu 10: (1đ) Tìm giới hạn cos 𝑦arctan(𝑥 + 𝑦) lim ∫ 𝑑𝑥 𝑦→0 1 + 𝑥2 + 𝑦2 sin 𝑦
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 2
ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 2 – Học kì 20182
Thời gian: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và Giám thị phải kí xác nhận số đề vào bài thi
của sinh viên.
Câu 1: (1đ). Viết phương trình tiếp diện và pháp tuyến của mặt cong 𝑥2 + 𝑦2 − 𝑒𝑧 − 2𝑦𝑥𝑧 = 0 tại điểm 𝑀(1,0,0).
Câu 2: (1đ). Tìm hình bao c a h ủ
ọ đường cong sau: (𝑥 + 𝐶)2 + (𝑦 − 2𝐶)2 = 5.
Câu 3: (1đ). Tính tích phân kép ∬ (𝑥 − 4𝑦)𝑑𝑥𝑑𝑦 với 𝐷 g ới hạn bởi i
parabol 𝑦 = 𝑥2 − 1 và 𝐷 trục 𝑂𝑥.
Câu 4: (1đ). Tính tích phân lặp: 2 11 − cos 𝜋𝑦 ∫ 𝑑𝑥 ∫ 𝑑𝑦 𝑦2 1 √𝑥−1
Câu 5: (1đ). Tính diện tích phần hình tròn 𝑥2 + 𝑦2 = 2𝑦 nằm ngoài đường tròn 𝑥2 + 𝑦2 = 1
Câu 6: (3đ). Tính các tích phân b i ba sau: ộ
𝑎) ∭(3𝑥2 + 2𝑦)𝑑𝑥𝑑𝑦𝑑𝑧 , trong đó m ền i
𝑉 xác định bởi 0 ≤ 𝑥 ≤ 1, 0 ≤ 𝑦 ≤ 𝑥, 0 ≤ 𝑧 ≤ 𝑥2 𝑉
𝑏) ∭(𝑥 − 𝑦 + 2𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 , trong đ ó 𝑉 đ ợc ư g ới hạn bởi i các mặt 𝑉
𝑥 − 𝑦 = 0, 𝑥 − 𝑦 = 2, 𝑥 + 𝑦 = 0, 𝑥 + 𝑦 = 1, 𝑧 = 0, 𝑧 = 1 𝑦2 𝑐) ∭
𝑑𝑥𝑑𝑦𝑑𝑧 , trong đó V l à m ền xác đị i
nh bởi 𝑥2 + 𝑦2 + 𝑧2 ≤ 4𝑧, 𝑦 ≥ 0 √4𝑧 − 𝑥2 − 𝑧2 𝑉
Câu 7: (1đ). Tính độ cong tại điểm 𝑀(−1,0, −1) của đường cong là giao của mặt trụ 4𝑥2 +
𝑦2 = 4 và mặt phẳng 𝑥 − 3𝑧 = 2.
Câu 8: (1đ). Chứng minh rằng hàm số +∞ 𝐼(𝑦) = ∫ 𝑒−𝑥 1−cos(𝑥𝑦)
𝑑𝑥 khả vi trên 𝑅. 0 𝑥
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 3
ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 2 – Học kì 2018 2
Thời gian: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và Giám thị phải kí xác nhận số đề vào bài thi
của sinh viên.
Câu 1: (1đ). Viết phương trình tiếp tuyến và pháp diện của đường cong 𝑥 = sin 𝑡 , 𝑦 =
cos 𝑡 , 𝑧 = 𝑒2𝑡 tại điểm 𝑀(0,1,1).
Câu 2: (1đ). Tính độ cong của đường 𝑥 = 𝑡2, 𝑦 = 𝑡 ln 𝑡 , 𝑡 > t
0 ại điểm ứng với 𝑡 = 𝑒
Câu 3: (1đ). Đổi thứ t l ự ấy tích phân 1 1
∫ 𝑑𝑥 ∫ 𝑓(𝑥, 𝑦)𝑑𝑦 0 𝑥3
Câu 4: (2đ). Tính các tích phân sau:
𝑎) ∬ √𝑥2 + 𝑦2𝑑𝑥𝑑𝑦 , trong đó 𝐷: 1 ≤ 𝑥2 + 𝑦2 ≤ 4, 𝑥 + 𝑦 ≥ 0 𝐷 𝜋 𝜋
𝑏) ∬|cos(𝑥 + 𝑦)|𝑑𝑥𝑑𝑦 , trong đó 𝐷 = [0; ] × [0; ] 2 2 𝐷
Câu 5: (1đ). Tính tích phân: 1 1−𝑥 2
∫ 𝑑𝑥 ∫ 𝑑𝑧 ∫(𝑦 + 𝑧)𝑑𝑦 0 0 0
Câu 6: (1đ). Tính thể tích c a mi ủ
ền giới hạn bởi hai parabol 𝑥 = 1 + 𝑦2 + 𝑧2 và 𝑥 = 2(𝑦2 + 𝑧2)
Câu 7: (1đ). Cho hàm vecto khả vi 𝑟(𝑡) : 𝑅 → 𝑅3\{0}. Ký hiệu |𝑟 (𝑡)| là độ dài của 𝑟 (𝑡). Ch ng ứ minh: 𝑑(|𝑟 (𝑡)|) 1 = (𝑡) ′(𝑡). 𝑑𝑡 |𝑟 (𝑡)| 𝑟 . 𝑟
Câu 8: (1đ). Tính tích phân ∭ (2𝑦 − 𝑧)2𝑑𝑥𝑑𝑦𝑑𝑧 trong đó 𝑉 là hình cầu 𝑥2 + 𝑦2 + 𝑧2 ≤ 1 𝑉
Câu 9: (1đ). Chứng minh rằng hàm số +∞ 𝐼(𝑦) = ∫ 𝑒−𝑥 sin(𝑥𝑦)
𝑑𝑥 khả vi trên 𝑅. 0 𝑥
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 1
ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 2 – Học kì 20183
Thời gian: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và Giám thị phải kí xác nhận số đề vào bài thi
của sinh viên.
Câu 1: (1đ). Tìm hình bao c a h ủ
ọ đường thẳng 𝑥 − 𝑐𝑦 + 𝑐3 = 0
Câu 2: (1đ). Viết phương trình tiếp diện và pháp tuyến của tại điểm 𝐴(1; 0; 1) của mặt 𝑧 = 𝑥𝑒sin2𝑦
Câu 3: (1đ). Đổi thứ t l ự ấy tích phân: 1 𝑥2
∫ 𝑑𝑥 ∫ 𝑓(𝑥, 𝑦)𝑑𝑦 0 −𝑥
Câu 4: (1đ). Tính ∬ sin(𝑥2 + 2𝑦2) 𝑑𝑥𝑑𝑦 , với 𝐷 là miền: 𝐷 𝜋 𝑥2 + 2𝑦2 ≤ , 𝑦 ≥ 0 2 Câu 5: (1đ). Tính 𝑥 + 𝑦 + 2 ∭ ( 𝑑𝑥𝑑𝑦𝑑𝑧 𝑥 + 1)(𝑦 + 1)𝑧 𝑉
Với 𝑉 xác định bởi 0 ≤ 𝑥 ≤ 1, 1 ≤ 𝑦 ≤ 2, 1 ≤ 𝑧 ≤ 𝑒
Câu 6: (1đ). Tính thể tích miền 𝑉 giới hạn bởi các mặt 𝑥 = −(𝑦2 + 𝑧2) và 𝑥 = − 1
Câu 7: (1đ). Tìm giới hạn lim ∫ cos𝑦arctan(𝑥 − 𝑦)𝑑𝑥 𝑦→0 sin 𝑦
Câu 8: (1đ). Tìm điểm có độ cong nhỏ nhất của đường 𝑥2 + 4𝑦2 = 4𝑥 Câu 9: (1đ). Tính (𝑦 + 1)2 ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 𝑥2 + 𝑦2 + 𝑧2 + 3
Với 𝑉 xác định bởi 𝑥2 + 𝑦2 + 𝑧2 ≤ 1 Câu 10: (1đ). Cho hàm s ố 𝑦
𝐼(𝑦) = ∫ ln(1+𝑥𝑦) 𝑑𝑥. Tính 𝐼′(1) 0 1+𝑥2
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 2
ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 2 – Học kì 20192
Thời gian: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và Giám thị phải kí xác nhận số đề vào bài thi
của sinh viên.
Câu 1: (1đ). Viết phương trình tiếp tuyến và pháp tuyến của đường cong 𝑥3 + 𝑦3 = 9 t 𝑥𝑦 ại điểm (4,2) 𝑥 = 2(𝑡 − sin 𝑡)
Câu 2: (1đ). Tính độ cong của đường { ại điểm ứ ới 𝑡 = 𝜋/2 𝑦 = 2(1 − cos 𝑡) t ng v
Câu 3: (1đ). Tìm hình bao c a h ủ ọ đường cong
2𝑥2 − 4𝑥𝑐 + 2𝑦2 + 𝑐2 = 0, 𝑐 là tham số, 𝑐 ≠ 0
Câu 4: (1đ). Tìm giới hạn 𝜋 2
lim ∫ cos(𝑥2𝑦 + 3𝑥 + 𝑦2)𝑑𝑥 𝑦→0 0
Câu 5: (1đ). Đổi th t ứ ự lấy tích phân: 1 √2−𝑥2 ∫ 𝑑𝑥 ∫ 𝑓(𝑥, 𝑦)𝑑𝑦 0 𝑥2
Với 𝑉 xác định bởi 0 ≤ 𝑥 ≤ 1, 1 ≤ 𝑦 ≤ 2, 1 ≤ 𝑧 ≤ 𝑒
Câu 6: (1đ). Tính diện tích phần mặt 𝑧 = 𝑥2 + 𝑦2 + 2 nằm trong mặt 𝑥2 + 𝑦2 = 9
Câu 7: (1đ). Tính thể tích c a mi ủ
ền giới hạn bởi các mặt cong 𝑦 = 𝑥2, 𝑥 = 𝑦2, 𝑧 = 𝑥2 và mặt 𝑂𝑥𝑦.
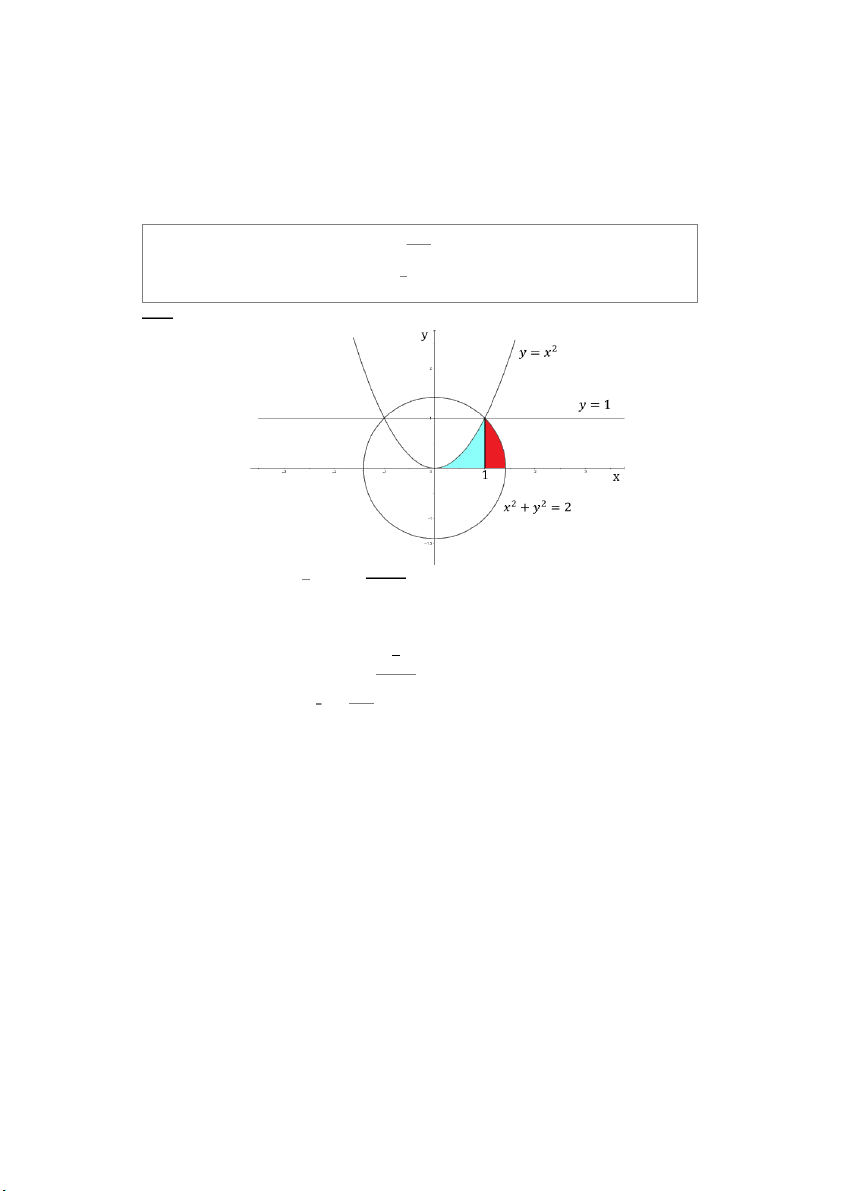
Câu 8: (1đ). Tính ∬ (2𝑦2 + 3)𝑑𝑥𝑑𝑦 , với 𝐷 là mi nh b ền xác đị ởi 𝐷 𝑥2 + (𝑦 − 1)2 ≤ 1
Câu 9: (1đ). Tính ∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧 với 𝑉 xác định bởi 𝑉 𝑥2 + 𝑦2 ≤ 1, 𝑦2 + 𝑧2 ≤ 4, 𝑧 ≥ 0
Câu 10: (1đ). Tính tích phân b i ba ộ
∭ 𝑦2𝑒𝑧𝑑𝑥𝑑𝑦𝑑𝑧 , trong đó 𝑉
𝑉: 0 ≤ 𝑥 ≤ 1, 𝑥 ≤ 𝑦 ≤ 1, ≤ 𝑧 ≤ 𝑥𝑦 + 2
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 3
ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 2 – Học kì 20192
Thời gian: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và Giám thị phải kí xác nhận số đề vào bài thi
của sinh viên. 𝑥 = 2(𝑡 − sin 𝑡)
Câu 1: (1đ). Viết phương trình tiếp diện và pháp tuyến của đường cong { 𝑦 = 2(1 − cos 𝑡) tại 𝑡 = 𝜋/2
Câu 2: (1đ). Tính độ cong của đường cong 𝑦 = 𝑒2𝑥 tại 𝐴(0,1)
Câu 3: (1đ). Tìm hình bao c a h ủ ọ đường cong
𝑦 = 4𝑐𝑥3 + 𝑐4, với 𝑐 l tham số à
Câu 4: (1đ). Đổi thứ t l ự ấy tích phân 1 √2−𝑦2 ∫ 𝑑𝑦 ∫ 𝑓(𝑥, 𝑦)𝑑𝑥 0 √𝑦
Câu 5: (1đ). Tính ∬ 4𝑦𝑑𝑥𝑑𝑦 , với 𝐷 là mi nh b ền xác đị ởi: 𝐷 𝑥2 + 𝑦2 ≤ 1, 𝑥 + 𝑦 ≥ 1
Câu 6: (1đ). Tính thể tích miền 𝑉 giới hạn bởi mặt 𝑂𝑥𝑦 và mặt 𝑧 = 𝑥2 + 𝑦2 − 4 Câu 7: (1đ). Tính
∭ √𝑥2 + 𝑦2 + 𝑧2𝑑𝑥𝑑𝑦𝑑𝑧 𝑉
Với 𝑉 xác định bởi 𝑥2 + 𝑦2 + 𝑧2 ≤ 1, √3(𝑥2 + 𝑦2) ≤ 𝑧
Câu 8: (1đ). Tính ∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧 , với 𝑉 xác định bởi 𝑥2 + 𝑦2 + 𝑧2 ≤ 6, 𝑧 ≥ 𝑥2 + 𝑦2 𝑉
Câu 9: (1đ). Tính diện tích c a mi ủ ền giới hạn bởi (𝑥2 + 𝑦2)2 = 4𝑥𝑦 1 Câu 10: (1đ). Cho hàm s
ố 𝐼(𝑦) = ∫ sin(𝑥2 + 𝑥𝑦 + 𝑦2)𝑑𝑥 . Tính 𝐼′(0) 𝑦
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 1
ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 2 – Học kì 20193
Thời gian: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và Giám thị phải kí xác nhận số đề vào bài thi
của sinh viên.
Câu 1: (1đ). Xác định độ ại đườ cong t ng cong 𝑥 = √4𝑦 + t 1 ại điểm (3,1)
Câu 2: (1đ). Viết phương trình pháp tuyến và tiếp diện của mặt cong 𝑦2 = 3(𝑥2 + 𝑧2) tại điểm (√2, 3,1)
Câu 3: (1đ). Tìm hình bao c a h ủ
ọ đường cong: 𝑦 = (2𝑥 + 3𝑐)4
Câu 4: (1đ). Tính ∬ √𝑥2 + 𝑦2𝑑𝑥𝑑𝑦 , với D là m ền
i phía trên parabol 𝑦 = 𝑥2 v nằm phía à 𝐷
trong đường tròn 𝑥2 + 𝑦2 = 2
Câu 5: (1đ). Tính ∭ √6𝑦 − 𝑥2 − 𝑦2 − 𝑧2𝑑𝑥𝑑𝑦𝑑𝑧
với 𝑉: 𝑥2 + 𝑦2 + 𝑧2 ≤ 6𝑦 𝑉
Câu 6: (1đ). Tính diện tích miền giới hạn bởi hai đường cong 𝑦 = 𝑥2 và 𝑥 = 𝑦2
Câu 7: (1đ). Tính thể tích miền giới hạn bởi các mặt cong 𝑥 = 𝑦2 + 𝑧2 và 𝑥2 + 𝑦2 + 𝑧2 = 2
nằm trong phần không gian có 𝑥 không âm.
Câu 8: (1đ). Tính diện tích mặt cong 𝑧 = 2𝑥2 − 2𝑦2 nằm trong hình tr ụ 𝑥2 + 𝑦2 = 1 1
Câu 9: (1đ). Tính lim ∫ (𝑥 + 3𝑦)√𝑥2 + 𝑦3 + 1𝑑𝑥 𝑦→0 0
Câu 10: (1đ). Khảo sát tính liên t c và kh ụ ả vi của hàm s : ố 1 𝑑𝑥 𝑔(𝑦) = ∫ 𝑥2 + 𝑦2 0 PHẦN II: LỜI GIẢI THAM KHẢO
LỜI GIẢI THAM KHẢO ĐỀ THI GIỮA KÌ 20163 (ĐỀ 1)
Câu 1: Viết phương trình tiếp diện và pháp tuyến của mặt cong 𝑥2 + 3𝑦 + 2𝑧3 = t 3 ại 𝑀(2; −1; 1) Giải:
Đặt 𝐹(𝑥, 𝑦, 𝑧) = 𝑥2 + 3𝑦 + 2𝑧3 − 3 ⇒ 𝐹′ = 2 ′ = 3, ′ = 6 𝑥 𝑥, 𝐹𝑦 𝐹𝑧 𝑧2
Tại 𝑀(2, −1,1), ta có 𝐹′( ′( ′(
𝑥 𝑀) = 4, 𝐹𝑦 𝑀) = 3, 𝐹𝑧 𝑀) = 6
Phương trình pháp tuyến của đường cong tại 𝑀(2, −1,1) là: 𝑥 − 2 𝑦 + 1 𝑧 − 1 = = 4 3 6
Phương trình tiếp diện của đường cong tại 𝑀(2, −1,1) là:
4(𝑥 − 2) + 3(𝑦 + 1) + 6(𝑧 − 1) = 0 ⇔ 4𝑥 + 3𝑦 + 6𝑧 − 11 = 0
Câu 2: Tìm hình bao của h
ọ đường thẳng 𝑦 = 2𝑐𝑥 − 𝑐2 với 𝑐 là tham s . ố Giải:
Đặt 𝐹(𝑥, 𝑦, 𝑐) = 𝑦 − 2𝑐𝑥 + 𝑐2 𝐹′ = 0 Xét: { 𝑥 ệm 𝐹′ ⇒ ọ đườ ẳng không có điể ị 𝑦 = 0 ⇔ {−2𝑐 = 0 1 = 0 ⇒ Vô nghi H ng th m kì d . 𝐹 = 0 Xét {
⇔ {𝑦 − 2𝑐𝑥 + 𝑐2 = 0 (1)
𝐹′ = 0 ⇔ {𝑦 − 2𝑐𝑥 + 𝑐2 = 0 𝑐 −2𝑥 + 2𝑐 = 0 𝑥 = 𝑐 (2)
Thế (2) vào (1) ta có: 𝑦 − 2𝑥2 + 𝑥2 = 0 ⇔ 𝑦 = 𝑥2
Vậy hình bao của họ đường thẳng là: 𝑦 = 𝑥2
Câu 3: Tìm điểm có độ cong lớn nhấ ủa đườ t c ng cong 𝑦 = ln 𝑥 Giải: 1 −1
𝑦 = ln 𝑥 (𝑥 > 0) ⇒ 𝑦′ = , 𝑦′ = 𝑥 𝑥2
Độ cong của đường 𝑦 = ln 𝑥 tại điểm 𝑀(𝑥, 𝑦) ấ b t kì là: PHAM THANH TUNG −1 1 1 |𝑦′ | | 1 𝐶(𝑀) = 𝑥2 | = 𝑥2 𝑥2 3 = = 3 3 = 3 1 (1 + 𝑦′2) 2 1 2 3 2 3 2 (1 + 1 + 2 1 1 ( 𝑥2 (1 + 𝑥2) 2. ( (1 + 𝑥2) 2. ( 𝑥2) 𝑥2 ) 𝑥2) 𝑥2) 1 𝑥 = = 3 = 3 𝑓(𝑥) (1 + 1 𝑥2) 2. (1 + 𝑥2) 2 𝑥 3 3 1 3 1
(1 + 𝑥2) 2 − 2 .2𝑥.(1 + 𝑥2) 2.𝑥 (1 + 𝑥2) 2 − 3𝑥2. (1 + 𝑥2) 2 ⇒ 𝑓′(𝑥) = = (1 + 𝑥2)3 (1 + 𝑥2)3 1 1
(1 + 𝑥2) 2. (1 + 𝑥2 − 3𝑥2) (1 + 𝑥2) 2. (1 − 2𝑥2) = = ( 1 + 𝑥2)3 (1 + 𝑥2)3 1 Ta c :
ó 𝑓′(𝑥) = 0 ⇔ 𝑥 = √2 Bảng biến thiên: 𝑥 0 1 + ∞ √2 𝑓′(𝑥) + 0 − 𝑓(𝑥) 𝑓 ( 1 ) √2 Vậy độ ủa đườ cong c
ng 𝑦 = ln 𝑥 lớn nhấ ại điể t t m 𝑀 ( 1 , ln 1 ) √2 √2
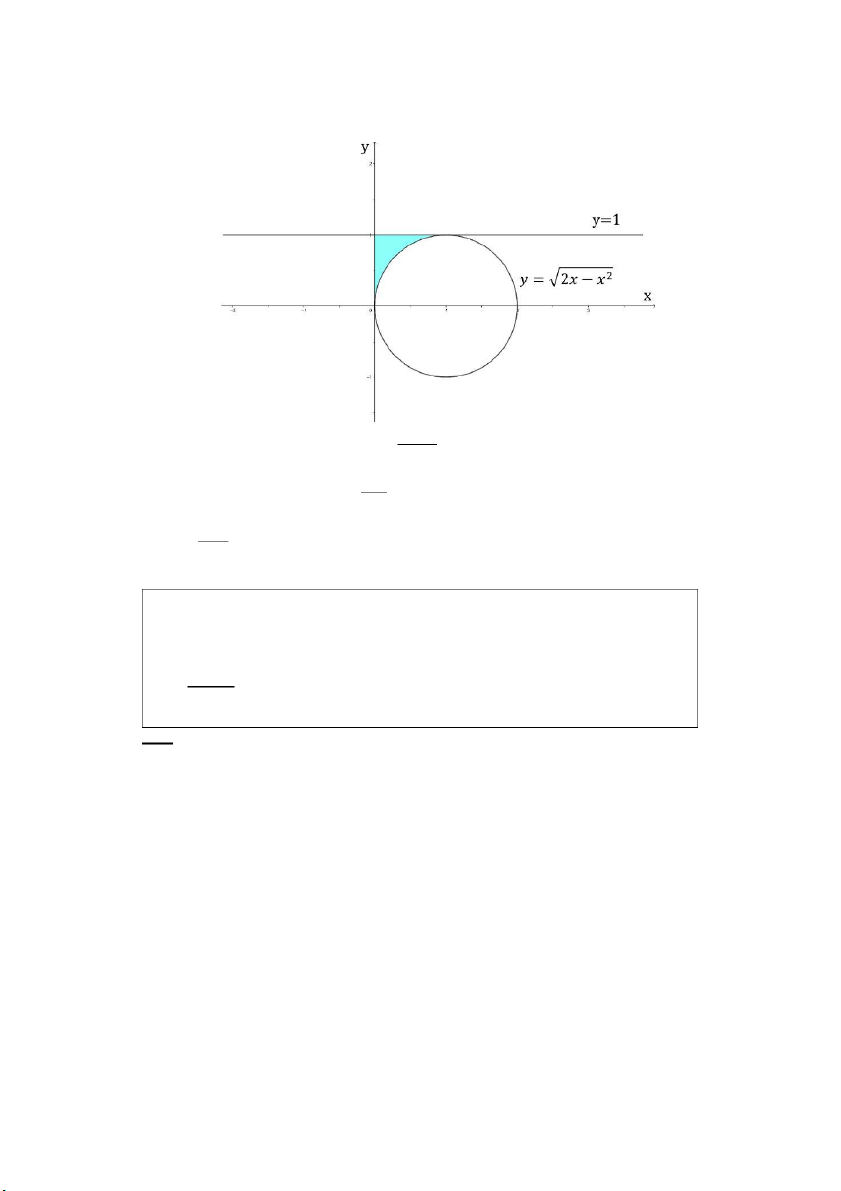
Câu 4: Đổi thứ t l ự ấy tích phân: 1 1 ∫ 𝑑𝑥 ∫ 𝑓(𝑥, 𝑦)𝑑𝑦 0 √2𝑥−𝑥2 Giải: 0 ≤ 𝑥 ≤ 1 Miền 𝐷: {
√2𝑥 − 𝑥2 ≤ 𝑦 ≤ 1 ( (√ 𝑥 − 1)2 + 𝑦2 ≥ 1
2𝑥 − 𝑥2 ≤ 𝑦 ⇔ 2𝑥 − 𝑥2 ≤ 𝑦2 ⇔ { ) 𝑦 ≥ 0 PHAM THANH TUNG
Đổi thứ tự lấy tích phân 𝐷: {0 ≤ 𝑥 ≤ 1 − √1 − 𝑦2 0 ≤ 𝑦 ≤ 1 1 1 1 1−√1−𝑦2 ⇒ ∫ 𝑑𝑥 ∫ 𝑓(𝑥, 𝑦)𝑑𝑦 = ∫ 𝑑𝑦 ∫ 𝑓(𝑥, 𝑦)𝑑𝑥 0 √2𝑥−𝑥2 0 0
Câu 5: Tính các tích phân kép sau:
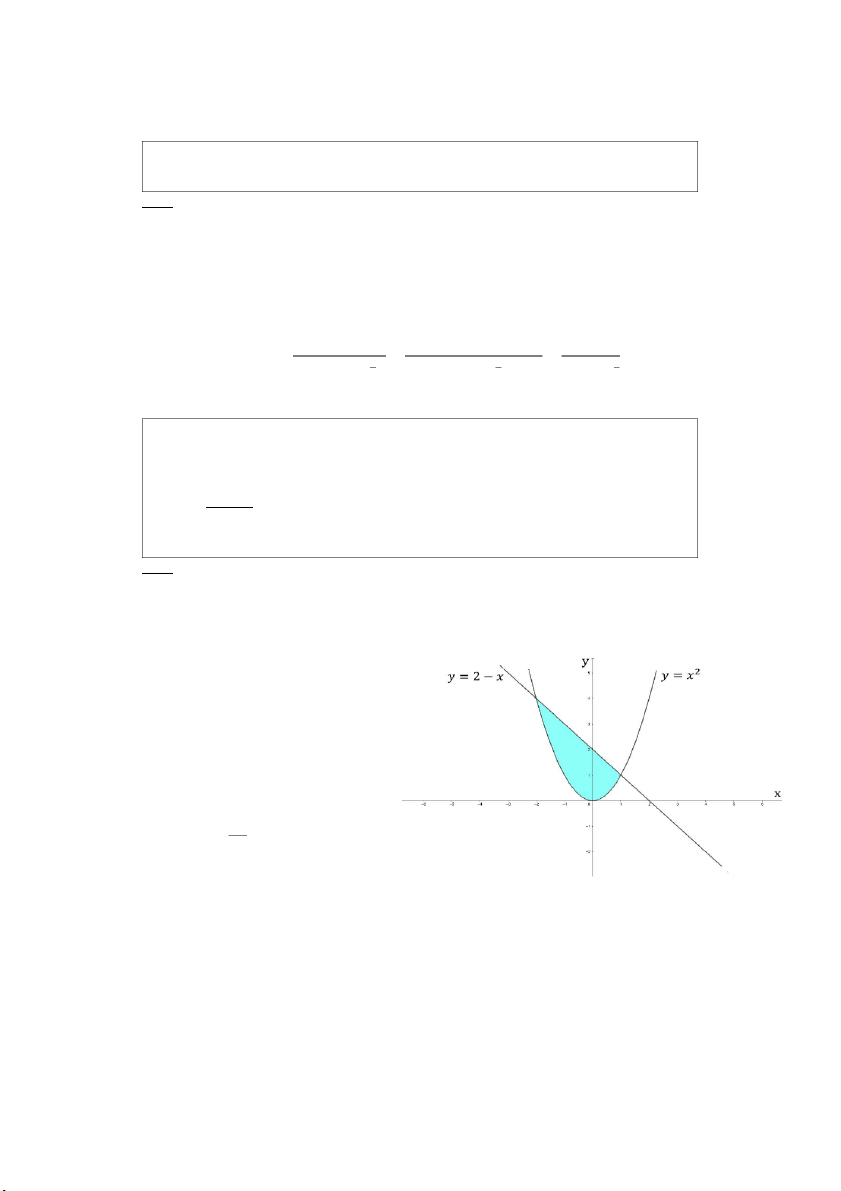
𝑎) ∬(3𝑥 + 2𝑦)𝑑𝑥𝑑𝑦 , 𝐷 l à m ền i g ới hạn bởi i
các đường 𝑦 = 𝑥2 v à 𝑦 = 1 𝐷 𝑥𝑦 𝑏) ∬
𝑑𝑥𝑑𝑦 với 𝐷 = {(𝑥, 𝑦) ∈ 𝑅2: 1 ≤ 𝑥2 + 𝑦2 ≤ 2𝑥, 𝑦 ≥ 0} 𝑥2 + 𝑦2 𝐷 Giải:
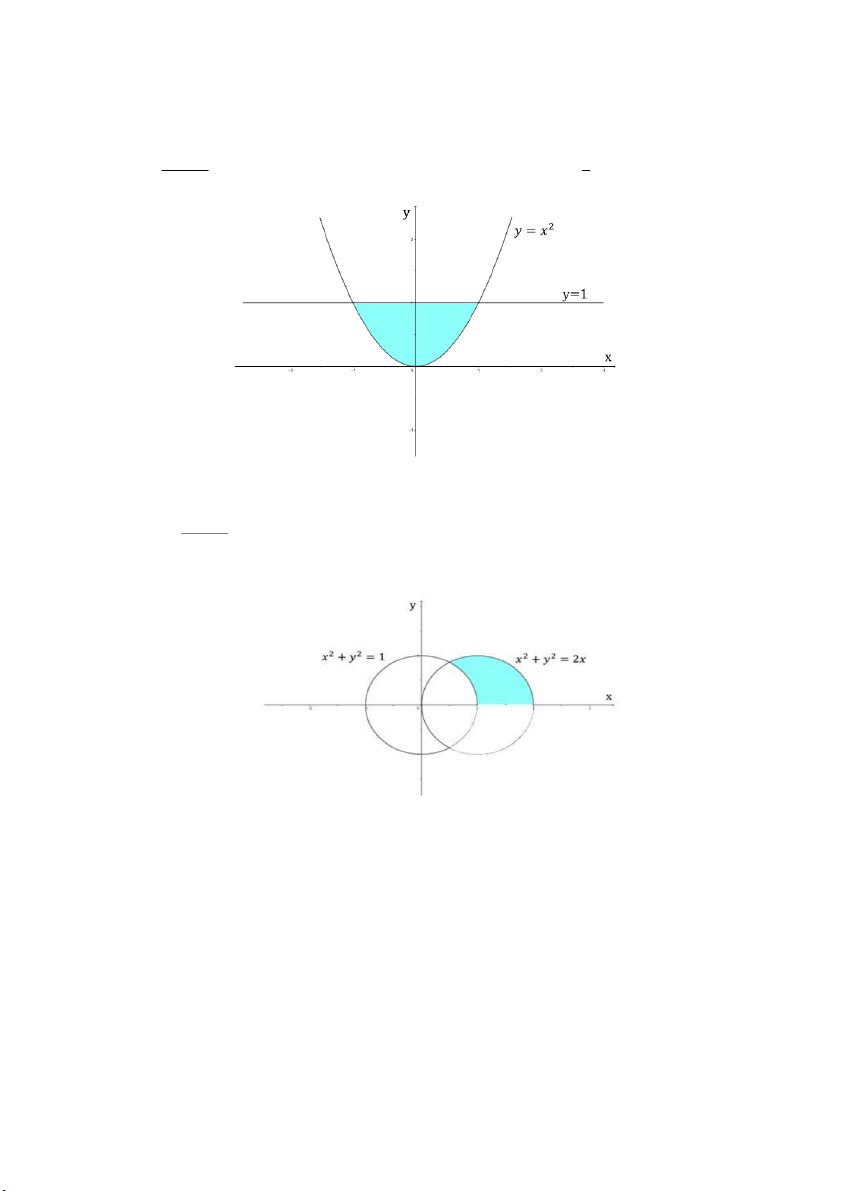
𝑎) ∬(3𝑥 + 2𝑦)𝑑𝑥𝑑𝑦 , 𝐷 là m ền i g ới hạn bởi i
các đường 𝑦 = 𝑥2 và 𝑦 = 1 𝐷 −1 ≤ 𝑥 ≤ 1
Miền (𝐷): { 𝑥2 ≤ 𝑦 ≤ 1 PHAM THANH TUNG 1 1 1 𝑥𝑦 8 ∬
𝑑𝑥𝑑𝑦 = ∫ 𝑑𝑥 ∫(3𝑥 + 2𝑦)𝑑𝑦
= ∫(3𝑥 + 1 − 3𝑥3 − 𝑥4)𝑑𝑥 = 𝑥2 + 𝑦2 5 𝐷 −1 𝑥2 −1 Hình minh họa câu 𝑎 𝑥𝑦 𝑏) ∬
𝑑𝑥𝑑𝑦 với 𝐷 = {(𝑥, 𝑦) ∈ 𝑅2: 1 ≤ 𝑥2 + 𝑦2 ≤ 2𝑥, 𝑦 ≥ 0} 𝑥2 + 𝑦2 𝐷 𝑥 = 𝑟 cos 𝜑 Đặt { |
𝑦 = 𝑟 sin 𝜑 𝐽| = 𝑟 1 ≤ 𝑟 ≤ 2 cos 𝜑
Miền (𝐷): { 0 ≤ 𝜑 ≤ 𝜋/3 PHAM THANH TUNG 𝜋 𝜋 3 2 cos 𝜑 3 2 cos 𝜑 𝑥𝑦 𝑟 cos 𝜑. 𝑟 sin 𝜑 ∬
𝑑𝑥𝑑𝑦 = ∫ 𝑑𝜑 ∫ 𝑟𝑑𝑟 = ∫ 𝑑𝜑
∫ 𝑟 cos 𝜑 sin 𝜑 𝑑𝑟 𝑥2 + 𝑦2 𝑟2 𝐷 0 1 0 1 𝜋 𝜋 3 3 1 −1 =
∫[4(cos 𝜑)2 − 1] cos 𝜑 sin 𝜑 𝑑𝜑 =
∫[4(cos 𝜑)2 − 1] cos 𝜑 𝑑(cos 𝜑) 2 2 0 0 1 2 −1 9 = ∫(4𝑡2 − 1)𝑡𝑑𝑡 = 2 32 1
Câu 6: Tính thể tích của vật thể 𝑉 giới hạn bởi các mặt
𝑧 = 𝑥2 + 𝑦2 và 𝑧 = 2𝑥 + 4𝑦 Giải:
Xét giao tuyến của {𝑧 = 𝑥2 + 𝑦2 ⇒ 𝑥2 + 𝑦2 = 2𝑥 + 4𝑦 ⇔ (𝑥 − 1)2 + (𝑦 − 2)2 = 5 𝑧 = 2𝑥 + 4𝑦
Hình chiếu của (𝑉) lên 𝑂𝑥𝑦 là: (𝐷): (𝑥 − 1)2 + (𝑦 − 2)2 ≤ 5 Thể tích miền (𝑉 là: ) 2𝑥+4𝑦 𝑉( =
𝑉) = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧
∬ 𝑑𝑥𝑑𝑦 ∫ 𝑑𝑧
= ∬(2𝑥 + 4𝑦 − 𝑥2 − 𝑦2)𝑑𝑥𝑑𝑦 𝑉 𝐷 𝑥2+𝑦2 𝐷
= ∬{5 − [(𝑥 − 1)2 + (𝑦 − 2)2]} 𝑑𝑥𝑑𝑦 𝐷 𝑥 = 1 + 𝑟 cos 𝜑 Đặt {
|𝐽| = 𝑟. Miền (𝐷): {0 ≤ 𝑟 ≤ √5 𝑦 = 2 + 𝑟 sin 𝜑 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 √5 25 25𝜋 ⇒ 𝑉( ( 2) ∫ (5 − = 𝑉) = ∬ 5 − 𝑟 𝑟
𝑑𝑟𝑑𝜑 = ∫ 𝑑𝜑 𝑟2)𝑟𝑑𝑟 = 2𝜋. (đvtt) 4 2 𝐷 0 0 PHAM THANH TUNG
Câu 7: Tính tích phân b i ba ộ
∭ 𝑦𝑑𝑥𝑑𝑦𝑑𝑧 trong đó: 𝑉
a) 𝑉 giới hạn bởi các mặt
𝑧 = 0, 𝑧 = 𝑥2, 𝑦 = 2𝑥2 và 𝑦 = 4 + 𝑥2
b) 𝑉 là hình cầu 𝑥2 + 𝑦2 + 𝑧2 ≤ 2𝑦 Giải:
a) 𝑉 giới hạn bởi các mặt
𝑧 = 0, 𝑧 = 𝑥2, 𝑦 = 2𝑥2 v à 𝑦 = 4 + 𝑥2 𝑦 = 2𝑥2 −2 ≤ Hình chiếu 𝑥 ≤ 2
𝐷 của 𝑉 lên 𝑂𝑥𝑦 giới hạn bởi { 2 2
𝑦 = 4 + 𝑥2 ⇒ (𝐷) { 2𝑥 ≤ 𝑦 ≤ 4 + 𝑥 2 4+𝑥2 𝑥2 2 4+𝑥2 2 1 4096
∭ 𝑦𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝑥 ∫ 𝑑𝑦
∫ 𝑦𝑑𝑧 = ∫ 𝑑𝑥 ∫ 𝑦𝑥2𝑑𝑦 =
∫ 𝑥2[(4 + 𝑥2)2 − 4𝑥4]𝑑𝑥 = 2 105 𝑉 −2 2𝑥2 0 −2 2𝑥2 −2
b) 𝑉 là hình cầu 𝑥2 + 𝑦2 + 𝑧2 ≤ 2𝑦
Miền 𝑉: 𝑥2 + 𝑦2 + 𝑧2 ≤ 2𝑦 ⇔ 𝑥2 + (𝑦 − 1)2 + 𝑧2 ≤ 1 𝑥 = 𝑟 sin 𝜃 cos 𝜑 0 ≤ 𝑟 ≤ 1
Đặt {𝑦 = 1 + 𝑟 sin 𝜃 sin 𝜑 |𝐽| = 𝑟2 sin 𝜃 . Miền (𝑉): { 0 ≤ 𝜃 ≤ 𝜋 𝑧 = 𝑟 cos 𝜃 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 𝜋 1
∭ 𝑦𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝜃 ∫(1 + 𝑟 sin 𝜃 sin 𝜑)𝑟2 sin 𝜃 𝑑𝑟 𝑉 0 0 0 2𝜋 𝜋 2𝜋 1 1 2 𝜋 4𝜋 = ∫ 𝑑𝜑∫ ( sin 𝜃 +
(sin 𝜃)2 sin 𝜑) 𝑑𝜃 = ∫ ( + sin 𝜑) 𝑑𝜑 = 3 4 3 8 3 0 0 0
Câu 8: Tính tích phân +∞𝑒−𝛼𝑥2 − 1 ∫ 𝑑𝑥 với 𝛼 ≥ 0 𝑥2𝑒𝑥2 0 Giải: +∞ +∞ 𝑒−𝛼𝑥2 − 1
𝑒−𝛼𝑥2 − 𝑒−0.𝑥2 ∫ 𝑑𝑥 = ∫ 𝑑𝑥 𝑥2𝑒𝑥2 𝑥2𝑒𝑥2 0 0 PHAM THANH TUNG 𝑒−𝑦𝑥2 Đặt 𝐹(𝑥, 𝑦) = 𝑥2𝑒𝑥2 𝑎 𝑎 0
𝑒−𝑎𝑥2 − 𝑒−0.𝑥2 = 𝐹(𝑥,𝑎) − 𝐹(𝑥,0) = ∫𝐹′(𝑥,𝑦)𝑑𝑦
= ∫ −𝑒−(𝑦+1)𝑥2𝑑𝑦
= ∫ 𝑒−(𝑦+1)𝑥2𝑑𝑦 𝑥2𝑒𝑥2 𝑦 0 0 𝑎 +∞ +∞ 0 0 +∞
𝑒−𝛼𝑥2 − 𝑒−0.𝑥2 ∫
𝑑𝑥 = ∫ (∫ 𝑒−(𝑦+1)𝑥2𝑑𝑦 ) 𝑑𝑥 = ∫ ∫ ( 𝑒−(𝑦+1)𝑥2𝑑𝑥 ) 𝑑𝑦 𝑥2𝑒𝑥2 0 0 𝑎 𝑎 0 +∞
Xét ∫ 𝑒−(𝑦+1)𝑥2𝑑𝑥 0 √𝑡 1 −1
Đặt (𝑦 + 1)𝑥2 = 𝑡 ⇒ 𝑥 = ⇒ 𝑑𝑥 = . 𝑡 2 𝑑𝑡 √1 + 𝑦 2 1 √ + 𝑦 +∞ +∞ +∞ 1 −1 1 1 1 1
⇒ ∫ 𝑒−(𝑦+1)𝑥2𝑑𝑥 = ∫ 𝑒−𝑡. . 𝑡 2 𝑑𝑡 =
∫ 𝑒−𝑡. 𝑡 2−1𝑑𝑡 = . Γ ( ) 2 1 √ + 𝑦 2√1 + 𝑦 2 1 √ + 𝑦 2 0 0 0 √𝜋 = 2√1 + 𝑦 0 +∞ 0 √𝜋 √𝜋
⇒ ∫ (∫ 𝑒−(𝑦+1)𝑥2𝑑𝑥 ) 𝑑𝑦 = ∫ 𝑑𝑦 =
. 2(√𝑎 + 1 − 1) = √𝜋(√𝑎 + 1 − 1) 2 1 √ + 𝑦 2 𝑎 0 𝑎
*Kiểm tra điều kiện khả tích:
Đặt 𝑓(𝑥, 𝑦) = 𝑒−(𝑦+1)𝑥2
− Hàm 𝑓(𝑥, 𝑦 liên t ) c trên ụ miền [0; +∞) × [0; 𝑎] − +∞ Tích phân 𝐼(𝑦) = ∫ 𝑒−(𝑦+1)𝑥2𝑑𝑥 h i t ộ ụ đều trên [0, 𝑎] 0
𝑒−(𝑦+1)𝑥2 ≤ 𝑒−(𝑦 +1 0 )𝑥2 với 𝑦0 ≥ 0 +∞ +∞ Do √𝜋
⇒ ∫ 𝑒−(𝑦+1)𝑥2𝑑𝑥
hội tụ đều trên [0; 𝑎] ∫ 𝑒−(𝑦0+1)𝑥2 𝑑𝑥 = hội tụ { 2 1 √ + 𝑦 0 0 0
Vậy điều kiện đổi thứ tự lấy tích phân thỏa mãn. PHAM THANH TUNG
❖ Mẹo: Trong các bài tập s d
ử ụng phương pháp đổi thứ t l
ự ấy tích phân và phương pháp đạo hàm đạo
hàm qua dấu tích phân, chúng ta sẽ “tiền trảm hậu tấu”, tức là c áp d ứ
ụng hai phương pháp trên
để tính tích phân, khi ra kết quả ồ r i mới ki u ki ểm tra điề ệ ả
n kh vi, khả tích, giống lời giải tham
khảo trên. Khi làm như vậy, nếu không đủ thờ ứng minh điề i gian ch
u kiện khả vi, khả tích,
chúng ta vẫn được 0.5đ nếu tính toán đúng tích phân. PHAM THANH TUNG
LỜI GIẢI THAM KHẢO ĐỀ THI GIỮA KÌ 20172 (ĐỀ 2)
Câu 1: Viết phương trình tiếp diện và pháp tuyến của mặt cong ln(𝑥2 + 3𝑦) − 3𝑧3 = 2 tại điểm 𝑀(1,0, −1). Giải: 2𝑥 𝐹′ = 𝑥 𝑥2 + 3𝑦
Đặt 𝐹(𝑥, 𝑦, 𝑧) = ln(𝑥2 + 3𝑦) − 3𝑧3 − 2 ⇒ 3 𝐹′ = 𝑦 𝑥2 + 3𝑦 { 𝐹′𝑧 = −9𝑧2 𝐹′( 𝑥 𝑀) = 2
Tại 𝑀(1,0, −1), ta có: { 𝐹′( 𝑦 𝑀) = 3 𝐹′( 𝑧 𝑀) = −9
Phương trình tiếp diện của mặt cong tại 𝑀(1,0, −1) là:
2(𝑥 − 1) + 3(𝑦 − 0) − 9(𝑧 + 1) = 0 ⇔ 2𝑥 + 3𝑦 − 9𝑧 − 11 = 0
Phương trình pháp tuyến của mặt cong tại 𝑀(1,0, −1) là: 𝑥 − 1 𝑦 𝑧 + 1 = = 2 3 −9
Câu 2: Tìm hình bao của h
ọ đường cong 𝑐𝑥2 − 2𝑦 − 𝑐3 + 1 = v 0 ới 𝑐 là tham s . ố Giải:
Đặt 𝐹(𝑥, 𝑦, 𝑐) = 𝑐𝑥2 − 2𝑦 − 𝑐3 + 1 𝐹′(𝑥, 𝑦, 𝑐) = 0 Xét { 𝑥
ệm ⇒ ọ đường cong không có điể ị 𝐹′(
𝑦 𝑥, 𝑦, 𝑐) = 0 ⇔ {2𝑐𝑥 = 0 −2 = 0 ⇒ Vô nghi H m kì d . 𝐹(𝑥, 𝑦, 𝑐) = 0 Xét {
⇔ {𝑐𝑥2 − 2𝑦 − 𝑐3 + 1 = 0 ⇔ {𝑐. 3𝑐2 − 2𝑦 − 𝑐3 + 1 = 0 𝐹′( 𝑐 𝑥, 𝑦, 𝑐) = 0 𝑥2 − 3𝑐2 = 0 𝑥2 = 3𝑐2 2𝑦 − 1 2𝑐3 = 2𝑦 − 1 𝑐3 = 3 2 2 𝑥2 2𝑦 − 1 ⇔ { 𝑥2 ⇔ { ⇒ ( ) − ( ) = 0 𝑐2 = 𝑥2 3 2 3 𝑐2 = 3 𝑥6 (2𝑦 − 1)2
Vậy hình bao của họ đường cong là đường = 27 4 PHAM THANH TUNG
Câu 3: Tính độ cong của đường 𝑦 = ln(sin 𝑥) tại điểm ứng với 𝑥 = 𝜋/4. Giải: cos 𝑥 −1
𝑦 = ln(sin 𝑥) ⇒ 𝑦′(𝑥) = = cot 𝑥 , 𝑦′ (𝑥) = sin 𝑥 sin2 𝑥 𝜋 𝜋 𝜋 Tại 𝑥 = , ta c : ó 𝑦′ ( ) = 1, 𝑦′ ( ) = −2 4 4 4
Độ cong của đường 𝑦 = ln(sin 𝑥) tại 𝑥 = 𝜋/4 𝜋 |−2| 2 1 𝐶 (𝑥 = ) = = = 4 3 (1 + 1) 2 2√2 √2
Câu 4: Tính các tích phân sau:
𝑎) ∬(𝑥2 − 4𝑦2)𝑑𝑥𝑑𝑦 , 𝐷 là m ền i g ới hạn b i ởi 𝑦 = 𝑥, 𝑥 = 1 v à 𝑦 = 0 𝐷
𝑏) ∬(𝑥2 − 𝑥𝑦 + 𝑦2)𝑑𝑥𝑑𝑦 , 𝐷 là m ền i g ới
i hạn bởi 𝑦 = −3𝑥 + 1, 𝑦 = −3𝑥 + 2, 𝑦 = 𝑥 𝐷 và 𝑦 = 𝑥 + 2 Giải:
𝑎) ∬(𝑥2 − 4𝑦2)𝑑𝑥𝑑𝑦 , 𝐷 là m ền i g ới hạn bởi i 𝑦 = 𝑥, 𝑥 = 1 v à 𝑦 = 0 𝐷 0 ≤ 𝑥 ≤ 1 Miền 𝐷: {0 ≤ 𝑦 ≤ 𝑥 1 𝑥
∬(𝑥2 − 4𝑦2)𝑑𝑥𝑑𝑦
= ∫ 𝑑𝑥 ∫(𝑥2 − 4𝑦2)𝑑𝑦 𝐷 0 0 1 4 −1 = ∫ (𝑥2. 𝑥 − 𝑥3) 𝑑𝑥 = 3 12 0 PHAM THANH TUNG
𝑏) ∬(𝑥2 − 𝑥𝑦 + 𝑦2)𝑑𝑥𝑑𝑦 , 𝐷 l à m ền i g ới
i hạn bởi 𝑦 = −3𝑥 + 1, 𝑦 = −3𝑥 + 2, 𝑦 = 𝑥 𝐷 và 𝑦 = 𝑥 + 2 𝑦 = −3𝑥 + 1 𝑦 + 3𝑥 = 1 𝑦 = −3𝑥 + 2 𝑦 + 3𝑥 = 2
Miền 𝐷 giới hạn bởi { 𝑦 = 𝑥 ⇔ { 𝑦 − 𝑥 = 0 𝑦 = 𝑥 + 2 𝑦 − 𝑥 = 2 𝑢 = 𝑦 + 3𝑥 Đặt { ⇒ 𝐽−1 = | 3 1 | = 4 ⇒ 𝐽 = 1/4 𝑣 = 𝑦 − 𝑥 −1 1 𝑢 = 1 Miền 𝐷 𝑢 = 2
𝑢𝑣 trong tọa độ mới 𝑂𝑢𝑣 giới hạn bởi { ⇒ 𝐷 𝑣 = 0 𝑢𝑣 : {1 ≤ 𝑢 ≤ 2 0 ≤ 𝑣 ≤ 2 𝑣 = 2 𝑢 − 𝑣 𝑥 = 𝑢 = 𝑦 + 3𝑥 4 { ⇒ { 𝑣 = 𝑦 − 𝑥 𝑢 + 3𝑣 𝑦 = 4 1 𝑢 − 𝑣 2 𝑢 − 𝑣 𝑢 + 3𝑣 𝑢 + 3𝑣 2
⇒ ∬(𝑥2 − 𝑥𝑦 + 𝑦2)𝑑𝑥𝑑𝑦 = ∬ [( ) − . + ( ) ] 𝑑𝑢𝑑𝑣 4 4 4 4 4 𝐷 𝐷𝑢𝑣 2 2 1 1 =
∬(𝑢2 + 2𝑢𝑣 + 13𝑣2)𝑑𝑢𝑑𝑣 =
∫ 𝑑𝑢 ∫(𝑢2 + 2𝑢𝑣 + 13𝑣2)𝑑𝑣 64 64 𝐷𝑢𝑣 1 0 2 1 104 17 = ∫ (2𝑢2 + 4𝑢 + ) 𝑑𝑢 = 64 3 24 1
Câu 5: Tính tích phân sau: 1 1 1 ∫ 𝑑𝑥 ∫ 𝑑𝑦 𝑦5 + 1 0 √4𝑥 Giải: 0 ≤ 𝑥 ≤ 1 Miền 𝐷: { √4𝑥 ≤ 𝑦 ≤ 1 PHAM THANH TUNG 0 ≤
Đổi thứ tự lấy tích phân, miền 𝑥 ≤ 𝑦4 𝐷: { 0 ≤ 𝑦 ≤ 1 1 1 1 𝑦4 1 1 1 1 𝑦4 1 𝑑(𝑦5) ln(𝑦5 + 1) 1 ln 2 ∫ 𝑑𝑥 ∫ 𝑑𝑦 = ∫ 𝑑𝑦 ∫ 𝑑𝑥 = ∫ 𝑑𝑦 = ∫ = | = 𝑦5 + 1 𝑦5 + 1 𝑦5 + 1 5 𝑦5 + 1 5 5 0 0 √ 4 𝑥 0 0 0 0
Câu 6: Tính thể tích của vật thể 𝑉 giới hạn bởi các mặt
𝑧 = 𝑥2 + 2𝑦2 và 𝑧 = 3 − 2𝑥2 − 𝑦2 Giải:
Miền 𝑉: 𝑥2 + 2𝑦2 ≤ 𝑧 ≤ 3 − 2𝑥2 − 𝑦2 Giao tuyến c a m ủ
ặt 𝑧 = 𝑥2 + 2𝑦2 và 𝑧 = 3 − 2𝑥2 − 𝑦2
⇒ 𝑥2 + 2𝑦2 = 3 − 2𝑥2 − 𝑦2 ⇔ 𝑥2 + 𝑦2 = 1
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 1 𝑥 = 𝑟 cos 𝜑 0 ≤ 𝑟 ≤ 1 Đặt { ,
𝑦 = 𝑟 sin 𝜑 𝐽 = 𝑟 ⇒ 𝐷: { 0 ≤ 𝜑 ≤ 2𝜋
Thể tích vật thể 𝑉 là: PHAM THANH TUNG
𝑉 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 = ∬[(3 − 2𝑥2 − 𝑦2) − (𝑥2 + 2𝑦2)]𝑑𝑥𝑑𝑦 𝑉 𝐷 2𝜋 1 3
= ∬[3 − 3(𝑥2 + 𝑦2)]𝑑𝑥𝑑𝑦
= ∫ 𝑑𝜑 ∫(3 − 3𝑟2)𝑟𝑑𝑟 = 𝜋 (đvtt) 2 𝐷 0 0
Câu 7: Tính tích phân b i ba ộ
∭ (3𝑥𝑦2 − 4𝑥𝑦𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 trong đó 𝑉 ền xác đị là mi nh bởi 𝑉
1 ≤ 𝑦 ≤ 2, 0 ≤ 𝑥𝑦 ≤ 2, 0 ≤ 𝑧 ≤ 2 Giải:
Cách 1: Đổi biến số: 𝑢 = 𝑦 0 1 0
Đặt {𝑣 = 𝑥𝑦 ⇒ 𝐽−1 = | 𝑦 𝑥 0| = −𝑦 ⇒ 𝐽 = −1/𝑦 = −1/𝑢 𝑤 = 𝑧 0 0 1 1 ≤ 𝑢 ≤ 2
Miền mới 𝑉𝑢𝑣𝑤 trong hệ tọa độ mới là 𝑉𝑢𝑣𝑤: {0 ≤ 𝑣 ≤ 2 0 ≤ 𝑤 ≤ 2 2 2 2 1 4𝑣𝑤
∭(3𝑥𝑦2 − 4𝑥𝑦𝑧)𝑑𝑥𝑑𝑦𝑑𝑧
= ∭(3𝑢𝑣 − 4𝑣𝑤).
𝑑𝑢𝑑𝑣𝑑𝑤= ∫ 𝑑𝑤 ∫ 𝑑𝑣 ∫ (3𝑣 − ) 𝑑𝑢 𝑢 𝑢 𝑉 𝑉𝑢𝑣𝑤 0 0 1 2 2 2
= ∫ 𝑑𝑤 ∫(3𝑣 − 4 ln 2 . 𝑣𝑤)𝑑𝑣
= ∫(6 − 8 ln 2 . 𝑤)𝑑𝑤 = 12 − 16 ln 2 0 0 0
Cách 2: Tính thông thường: 𝑦 = 1, 𝑦 = 2 Hình chiếu 𝐷 c a mi ủ ền 𝑉 giới hạn bởi { 𝑦 = 2/𝑥 2 0 ≤ 𝑧 ≤ 2 0 ≤ 𝑥 ≤ 2 ⇒ Hình chiếu 𝐷: {
𝑦⇒ Miền 𝑉: { 0 ≤ 𝑥 ≤ 𝑦 1 ≤ 𝑦 ≤ 2 1 ≤ 𝑦 ≤ 2 2 2 2 𝑦
∭(3𝑥𝑦2 − 4𝑥𝑦𝑧)𝑑𝑥𝑑𝑦𝑑𝑧
= ∫ 𝑑𝑦 ∫ 𝑑𝑧 ∫(3𝑥𝑦2 − 4𝑥𝑦𝑧)𝑑𝑥
= 12 − 16 ln 2 𝑉 1 0 0 PHAM THANH TUNG
Câu 8: Tính tích phân b i
ộ ba ∭ (𝑥2 + 𝑦2 + 𝑧2)𝑑𝑥𝑑𝑦𝑑𝑧 trong đó 𝑉 là miền giới hạn bởi các 𝑉
mặt 𝑦 = √𝑥2 + 4𝑧2, 𝑦 = 2. Giải: Hình chiếu c a mi ủ
ền 𝑉 lên 𝑂𝑥𝑧 là 𝐷: 𝑥2 + 4𝑧2 ≤ 4 𝑟 cos 𝜑 2𝑧 = 𝑟 cos 𝜑 𝑧 = 𝑟 Đặt { 𝑥 = 𝑟 sin 𝜑 2
⇔ { 𝑥 = 𝑟 sin 𝜑, 𝐽 = 𝑦 = 𝑦 2 𝑦 = 𝑦 𝑟 ≤ 𝑦 ≤ 2
𝑉: {√𝑥2 + 4𝑧2 ≤ 𝑦 ≤ 2⇔ { 0 ≤ 𝜑 ≤ 2𝜋 𝐷: 𝑥2 + 4𝑧2 ≤ 4 0 ≤ 𝑟 ≤ 2 2𝜋 2 2 𝑟2 𝑟
∭(𝑥2 + 𝑦2 + 𝑧2)𝑑𝑥𝑑𝑦𝑑𝑧
= ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ (𝑟2 sin2 𝜑 + 𝑦2 + cos2 𝜑) . 𝑑𝑦 4 2 𝑉 0 0 𝑟 2𝜋 2 2𝜋 𝑟3 sin2 𝜑 𝑟3 cos2 𝜑 8 𝑟3 4 1 = ∫ 𝑑𝜑 ∫ [( + ) (2 − 𝑟) + − ] 𝑑𝑟 = ∫ ( sin2 𝜑 + cos2 𝜑 + 4) 𝑑𝜑 2 8 3 3 5 5 0 0 0 4 1 = 𝜋 + 𝜋 + 8𝜋 = 9𝜋 5 5
Câu 9: Tính tích phân
+∞𝑒−𝑎𝑥2 − 𝑒−𝑏𝑥2 ∫
𝑑𝑥 với 𝑎, 𝑏 > 0 𝑥 0 Giải: 𝑒−𝑦𝑥2 Đặt 𝐹(𝑥, 𝑦) = 𝑥 𝑎 𝑎 𝑏
𝑒−𝑎𝑥2 − 𝑒−𝑏𝑥2
= 𝐹(𝑥, 𝑎) − 𝐹(𝑥, 𝑏) = ∫ 𝐹′(𝑥, 𝑦)𝑑𝑦
= ∫ −𝑥𝑒−𝑦𝑥2𝑑𝑦
= ∫ 𝑥𝑒−𝑦𝑥2𝑑𝑦 𝑥 𝑦 𝑏 𝑏 𝑎 +∞ +∞ 𝑏 𝑏 +∞
𝑒−𝑎𝑥2 − 𝑒−𝑏𝑥2 ∫
𝑑𝑥 = ∫ (∫ 𝑥𝑒−𝑦𝑥2𝑑𝑦 ) 𝑑𝑥 = ∫ ∫ ( 𝑥𝑒−𝑦𝑥2𝑑𝑥 ) 𝑑𝑦 𝑥 0 0 𝑎 𝑎 0 PHAM THANH TUNG 𝑏 +∞ 𝑏 1 1 −1 +∞
= ∫ ( ∫ 𝑒−𝑦𝑥2𝑑(𝑥2) ) 𝑑𝑦 = ∫ ( . 𝑒−𝑦𝑥2 | ) 𝑑𝑦 2 2 𝑦 0 𝑎 0 𝑎 𝑏 1 1 𝑏 = ∫ 𝑑𝑦 = ln 2𝑦 2 𝑎 𝑎
*Kiểm tra điều kiện khả tích:
Đặt 𝑓(𝑥, 𝑦) = 𝑥𝑒−𝑦𝑥2
− Hàm 𝑓(𝑥, 𝑦 liên t ) c trên mi ụ
ền [0; +∞) × [𝑏; 𝑎] − +∞ Tích phân 𝐼(𝑦) = ∫
𝑥𝑒−𝑦𝑥2𝑑𝑥 h i t ộ ụ đều trên [𝑏, 𝑎 ] (𝑎, 𝑏 > 0) 0
𝑥𝑒−𝑦𝑥2 ≤ 𝑥𝑒−𝑦0𝑥2 với 𝑦0 ≥ 𝑏 > 0 +∞ +∞ Do 1
⇒ ∫ 𝑥𝑒−𝑦𝑥2𝑑𝑥
hội tụ đều trên [𝑏; 𝑎]
∫ 𝑥𝑒−𝑦0𝑥2 𝑑𝑥 = hội tụ 2 { 𝑦0 0 0
Vậy điều kiện đổi thứ tự lấy tích phân thỏa mãn.
❖ Mẹo:
Trong các bài tập sử dụng phương pháp đổi thứ tự lấy tích phân và phương pháp đạo hàm đạo hàm
qua dấu tích phân, chúng ta sẽ “tiền trảm hậu tấu”, tức là cứ áp dụng hai phương pháp trên để
tính tích phân, khi ra kết quả r i ồ mới kiểm tra u ki điề
ện khả vi, khả tích, gi ng l ố ời giải tham khảo
trên. Khi làm như vậy, nếu không đủ thời gian chứng minh điều kiện khả vi, khả tích, chúng ta vẫn được 0.5đ ế
n u tính toán đúng tích phân. PHAM THANH TUNG
LỜI GIẢI THAM KHẢO ĐỀ THI GIỮA KÌ 20172 (ĐỀ 4)
Câu 1: Viết phương trình tiếp tuyến và pháp diện của đường cong 𝑥 = 4 sin2 𝑡 , 𝑦 = 4 cos 𝑡,
𝑧 = 2 sin 𝑡 + 1 tại điểm 𝑀(1; −2√3; 2) Giải: 1 = 4 sin2 𝑡
Tại 𝑀(1; −2√3; 2), ta có: { −2√3 = 4 cos 𝑡 ⇔ 𝑡 = 5𝜋/6 2 = 2 sin 𝑡 + 1 5𝜋 𝑥′ ( ) = −2√3 6 𝑥 = 4 sin2 𝑡
𝑥′(𝑡) = 8 sin 𝑡 cos 𝑡 5𝜋 5 { 𝜋 𝑦 = 4 cos 𝑡 ⇒ { 𝑦′(𝑡) = −4 sin 𝑡 . Tại 𝑡 = , ta c : ó ) = −2 6 𝑦′ ( 6 𝑧 = 2 sin 𝑡 + 1 𝑧′(𝑡) = 2 cos 𝑡 5𝜋 { 𝑧′ ( ) = −√3 6
Phương trình tiếp tuyến của đường cong tại 𝑀(1; −2√3; 2) là: 𝑥 − 1 𝑦 + 2√3 𝑧 − 2 = = −2√3 −2 −√3
Phương trình pháp diện của đường cong tại 𝑀(1; −2√3; 2) là:
−2√3(𝑥 − 1) − 2(𝑦 + 2√3) − √3(𝑧 − 2) = 0 ⇔ −2√3𝑥 − 2𝑦 − √3𝑧 = 0
Câu 2: Tìm hình bao của h
ọ đường thẳng 3𝑐𝑥 − 𝑦 − 𝑐3 = v 0, ới 𝑐 là tham số. Giải:
Đặt 𝐹(𝑥, 𝑦, 𝑐) = 3𝑐𝑥 − 𝑦 − 𝑐3 với 𝑐 ố là tham s . 𝐹′(𝑥, 𝑦, 𝑐) = 0 Xét { 𝑥
ệm ⇒ ọ đường cong không có điể ị 𝐹′(
𝑦 𝑥, 𝑦, 𝑐) = 0 ⇔ { 3𝑐 = 0 −1 = 0 ⇒ Vô nghi H m kì d . 𝑦 𝐹(𝑥, 𝑦, 𝑐) = 0 Xét { =
⇔ {3𝑐𝑥 − 𝑦 − 𝑐3 = 0 𝑐3
⇔ {3𝑐. 𝑐2 − 𝑦 − 𝑐3 = 0 ⇔ {𝑦 = 2𝑐3 ⇔ { 2 𝐹′( 𝑐 𝑥, 𝑦, 𝑐) = 0 3𝑥 − 3𝑐2 = 0 𝑥 = 𝑐2 𝑥 = 𝑐2 𝑥 = 𝑐2 𝑦 2
⇒ 𝑥3 − ( ) = 0 ⇔ 𝑦2 = 4𝑥3 2
Vậy hình bao của họ đường cong là đường 𝑦2 = 4𝑥3 PHAM THANH TUNG
Câu 3: Tính độ cong của đường cong 𝑥 = sin 𝑡 + 𝑡 cos 𝑡 , 𝑦 = cos 𝑡 + 𝑡 sin 𝑡 tại điểm ứng với 𝑡 = 𝜋 Giải:
𝑥 = sin 𝑡 + 𝑡 cos 𝑡
𝑥′(𝑡) = 2 cos 𝑡 − 𝑡 sin 𝑡
𝑥′ (𝑡) = −3 sin 𝑡 − 𝑡 cos 𝑡 { ⇒ { 𝑦 = cos ⇒ { 𝑡 + 𝑡 sin 𝑡 𝑦′(𝑡) = 𝑡 cos 𝑡
𝑦′ (𝑡) = cos 𝑡 − 𝑡 sin 𝑡
𝑥′(𝜋) = −2, 𝑥′ (𝜋) = 𝜋 Tại 𝑡 = 𝜋, ta có: {
𝑦′(𝜋) = −𝜋, 𝑦′ (𝜋) = −1
Độ cong của đường cong tại điểm ứng với 𝑡 = 𝜋 là:
|𝑥′. 𝑦′ − 𝑥′ . 𝑦′|
|(−2). (−1) − 𝜋. (−𝜋)| 2 + 𝜋2 𝐶(𝑡 = 𝜋) = = 3 = 3 3 (𝑥′2 + 𝑦′2) 2 (4 + 𝜋2) 2 (4 + 𝜋2) 2
Câu 4: Tính các tích phân kép sau:
a) ∬ 2𝑥𝑑𝑥𝑑𝑦 , 𝐷 l à m ền i g ớ
i i hạn bởi 𝑦 = 𝑥2 và 𝑦 = 2 − 𝑥 𝐷
b) ∬ 𝑦√𝑥2 + 𝑦2𝑑𝑥𝑑𝑦 , vớ𝑖 𝐷 = {(𝑥, 𝑦) ∈ 𝑅2: 𝑥2 + 𝑦2 ≤ 𝑦} 𝐷 Giải:
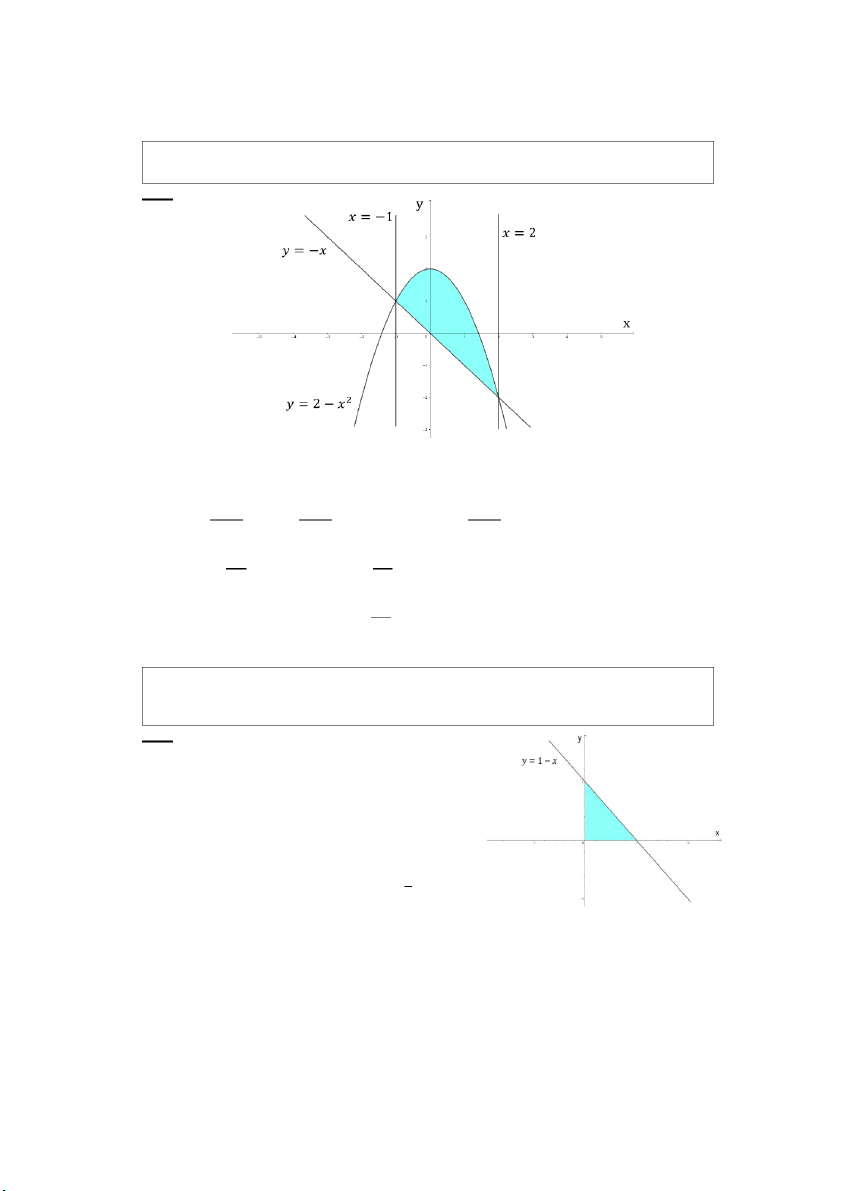
a) ∬ 2𝑥𝑑𝑥𝑑𝑦 , 𝐷 là m ền i g ớ
i i hạn bởi 𝑦 = 𝑥2 và 𝑦 = 2 − 𝑥 𝐷 −2 ≤ 𝑥 ≤ 1 Miền 𝐷: { 𝑥2 ≤ 𝑦 ≤ 2 − 𝑥 1 2−𝑥
∬ 2𝑥𝑑𝑥𝑑𝑦 = ∫ 𝑑𝑥 ∫ 2𝑥𝑑𝑦 𝐷 −2 𝑥2 1
= ∫ 2𝑥(2 − 𝑥 − 𝑥2)𝑑𝑥 −2 −9 = 2 PHAM THANH TUNG
b) ∬ 𝑦√𝑥2 + 𝑦2𝑑𝑥𝑑𝑦 , vớ𝑖 𝐷 = {(𝑥, 𝑦) ∈ 𝑅2: 𝑥2 + 𝑦2 ≤ 𝑦} 𝐷 𝑥 = 𝑟 cos 𝜑 Đăt { ,
𝑦 = 𝑟 sin 𝜑 𝐽 = 𝑟 0 ≤ 𝑟 ≤ sin 𝜑 Miền { 0 ≤ 𝜑 ≤ 𝜋 𝜋 sin 𝜑
∬ 𝑦√𝑥2 + 𝑦2𝑑𝑥𝑑𝑦 = ∫ 𝑑𝜑
∫ 𝑟 sin 𝜑 √𝑟2𝑟𝑑𝑟 𝐷 0 0 𝜋 𝜋 1 −1 =
∫ sin 𝜑 . sin4 𝜑 𝑑𝜑 =
∫(1 − cos2 𝜑)2𝑑(cos 𝜑) 4 4 0 0 −1 −1 −1 −16 4 = ∫ (1 − 𝑢2)2𝑑𝑢 = . = 4 4 15 15 1
Câu 5: Tính thể tích vật thể 𝑉 giới hạn bởi các mặt 𝑥 = 9𝑦2 + 𝑧2 v à 𝑥 = 9 Giải:
Xét giao tuyến của 𝑥 = 9𝑦2 + 𝑧2 và 𝑥 = 9
9𝑦2 + 𝑧2 = 9 ⇔ (3𝑦)2 + 𝑧2 = 32
Hình chiếu của 𝑉 lên 𝑂𝑦𝑧 là 𝐷: (3𝑦)2 + 𝑧2 ≤ 32 PHAM THANH TUNG
Thể tích vật thể 𝑉 là:
𝑉 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 = ∬ 9
[ − (9𝑦2 + 𝑧2)]𝑑𝑦𝑑𝑧 𝑉 𝐷 𝑟 3𝑦 = 𝑟 cos 𝜑 cos 𝜑 𝑟 0 ≤ 𝑟 ≤ 3 Đặt { ⇔ {𝑦 = 3 , 𝐽 = ⇒ 𝐷: { 𝑧 = 𝑟 sin 𝜑 0 ≤ 𝑧 = 𝑟 sin 𝜑 3 𝜑 ≤ 2𝜋 2𝜋 3 𝑟 27 27𝜋
⇒ 𝑉 = ∬[9 − (9𝑦2 + 𝑧2)]𝑑𝑦𝑑𝑧
= ∫ 𝑑𝜑 ∫(9 − 𝑟2). 𝑑𝑟 = 2𝜋. = (đvtt) 3 4 2 𝐷 0 0
Câu 6: Tính tích phân sau: 1 1 1
∫ 𝑑𝑦 ∫ 𝑑𝑥 ∫ 𝑥𝑦𝑒𝑦𝑧2𝑑𝑧 0 0 𝑥2 Giải: 0 ≤ 𝑥 ≤ 1 0 ≤ 𝑥 ≤ √𝑧
Miền 𝑉: {0 ≤ 𝑦 ≤ 1 .Đổ ứ
i th tự lấy tích phân: miền 𝑉 trở thanh 𝑉: { 0 ≤ 𝑦 ≤ 1 𝑥2 ≤ 𝑧 ≤ 1 0 ≤ 𝑧 ≤ 1 Hình vẽ minh h a trên m ọ
ặt phẳng 𝑂𝑥𝑧 khi đổi thứ t c ự ận 𝑥 và 𝑧 PHAM THANH TUNG 1 1 √𝑧 1 1 1 1 1 1 𝑦𝑧2
⇒ ∫ 𝑑𝑦 ∫ 𝑑𝑧 ∫ 𝑥𝑦𝑒𝑦𝑧2𝑑𝑥 =
∫ 𝑑𝑦 ∫ 𝑦𝑧𝑒𝑦𝑧2𝑑𝑧 =
∫ 𝑑𝑦 ∫ 𝑒𝑦𝑧2𝑑 ( ) 2 2 2 0 0 0 0 0 0 0 1 1 1 1 1 1 =
∫ 𝑑𝑦 ∫ 𝑒𝑦𝑧2𝑑(𝑦𝑧2) = ∫(𝑒𝑦 − 1)𝑑𝑦 = (𝑒 − 2) 4 4 4 0 0 0
Câu 7: Tính ∬ (4𝑥𝑦 + 3𝑦)𝑑𝑥𝑑𝑦 với 𝐷: 1 ≤ 𝑥𝑦 ≤ 4, 𝑥 ≤ 𝑦 ≤ 9𝑥. 𝐷 Giải: 𝑦
Miền 𝐷: 1 ≤ 𝑥𝑦 ≤ 4, 𝑥 ≤ 𝑦 ≤ 9𝑥 ⇔ 1 ≤ 𝑥𝑦 ≤ 4, 1 ≤ ≤ 9 𝑥 𝑢 = 𝑥𝑦 𝑦 𝑥 𝑢 ′ 𝑢′ 2𝑦 1 𝑥 1 Đặ𝑡 { 𝑦 𝑥 𝑦 −𝑦 1| = ⇒ 𝐽 = . = 𝑣 = ⇒ 𝐽−1 = | 𝑣′ 𝑣′ | = | 𝑥 2 𝑦 2 𝑥 𝑥 𝑦 𝑣 𝑥2 𝑥
Miền 𝐷 trong hệ tọa độ mới 𝑂𝑢𝑣 là 𝐷𝑢𝑣 : {1 ≤ 𝑢 ≤ 4 1 ≤ 𝑣 ≤ 9 9 4 1 2𝑢 3 𝑢
∬(4𝑥𝑦 + 3𝑦)𝑑𝑥𝑑𝑦 = ∬(4𝑢 + 3√𝑢𝑣) 𝑑𝑢𝑑𝑣= ∫ 𝑑𝑣 ∫ (
+ √ ) 𝑑𝑢 = 30 ln 3 + 28 2𝑣 𝑣 2 𝑣 𝐷 𝐷𝑢𝑣 1 1
Câu 8: Tính tích phân b i ba ộ
∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧 trong đó 𝑉 là mi nh b ền xác đị
ởi 𝑥2 + 𝑦2 + 𝑧2 ≤ 𝑧 𝑉 𝑧 ≤ √𝑥2 + 𝑦2 Giải: PHAM THANH TUNG
Cách 1: Tọa độ trụ: 1 2 1 𝑥2 + 𝑦2 + 𝑧2 ≤ 𝑧 𝑥2 + 𝑦2 + ( ) ≤ Miền 𝑧 − 𝑉: { ⇔ { 2 4 𝑧 ≤ √𝑥2 + 𝑦2 𝑧 ≤ √𝑥2 + 𝑦2 1 2 1 𝑥2 + 𝑦2 + (𝑧 − ) ≤
: Dấu ≤ thể hiện miền 𝑉 nằm trong mặt cầu. 2 4
𝑧 ≤ √𝑥2 + 𝑦2: Dấu ≤ thể h ện i m ền i 𝑉 nằm d ới mặt nón ư . 1 1 ⇒ 𝑉: − √
− (𝑥2 + 𝑦2) ≤ 𝑧 ≤ √𝑥2 + 𝑦2 2 4 𝑥2 + 𝑦2 + 𝑧2 = 𝑧
Xét giao tuyến của hai mặt { 𝑧 = √𝑥2 + 𝑦2
⇒ (𝑥2 + 𝑦2) + (𝑥2 + 𝑦2) = √𝑥2 + 𝑦2 ⇔ 2(𝑥2 + 𝑦2) − √𝑥2 + 𝑦2 = 0 1 1 ⇒ √𝑥2 + 𝑦2 = ⇔ 𝑥2 + 𝑦2 = 2 4 1
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 l à 𝐷: 𝑥2 + 𝑦2 ≤ 4 1 1
− √ − (𝑥2 + 𝑦2) ≤ 𝑧 ≤ √𝑥2 + 𝑦2 Miền V: 2 4 1 { 𝐷: 𝑥2 + 𝑦2 ≤ 4 1 1 𝑥 = 𝑟 cos 𝜑 − √ − 𝑟2 ≤ 𝑧 ≤ 𝑟 2 4
Đặt {𝑦 = 𝑟 sin 𝜑, 𝐽 = 𝑟 ⇒ 𝑉: 1 𝑧 = 𝑧 0 ≤ 𝑟 ≤ 2 { 0 ≤ 𝜑 ≤ 2𝜋 1 1 2 2 𝜋 2 𝑟 2𝜋 2 1 1 1
∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ 𝑧. 𝑟𝑑𝑧 = ∫ 𝑑𝜑 ∫ [𝑟2 − ( − √ − 𝑟2) ] 𝑟𝑑𝑟 2 2 4 𝑉 0 0 1 0 0 2−√14−𝑟2 1 2𝜋 2 1 𝑟 1 1
= ∫ 𝑑𝜑 ∫ [𝑟3 − + 𝑟√ − 𝑟2 − 𝑟 ( − 𝑟2)] 𝑑𝑟 2 4 4 4 0 0 PHAM THANH TUNG 1 1 1 2 2 4 1 1 1 1 1 1 ∫ 𝑟√ − 𝑟2𝑑𝑟 = ∫ √ − 𝑟2𝑑(𝑟2) = ∫ √ − 𝑢𝑑𝑢 = 4 2 4 2 4 24 0 0 0 1 2𝜋 2 2𝜋 1 𝑟 1 1 1 −1 1 𝜋
⇒ ∫ 𝑑𝜑 ∫ [𝑟3 − + 𝑟√ − 𝑟2 − 𝑟 ( − 𝑟2)] 𝑑𝑟 = ∫ ( + ) 𝑑𝜑 = 2 4 4 4 2 32 24 96 0 0 0
Cách 2: Tọa độ cầu: 𝑥 = 𝑟 cos 𝜑 sin 𝜃 0 ≤ 𝑟 ≤ cos 𝜃
Đặt {𝑦 = 𝑟 sin 𝜑 sin 𝜃 , |𝐽| = 𝑟2 sin 𝜃 ⇒ Miền 𝑉: { 𝜋/4 ≤ 𝜃 ≤ 𝜋/2 𝑧 = 𝑟 cos 𝜃 0 ≤ 𝜑 ≤ 2𝜋 𝜋 𝜋 2𝜋 2 cos 𝜃 2𝜋 2 1
∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝜃 ∫ 𝑟 cos 𝜃 . 𝑟2 sin 𝜃 𝑑𝑟 =
∫ 𝑑𝜑 ∫ cos4 𝜃 cos 𝜃 sin 𝜃 𝑑𝜃 4 𝑉 0 𝜋 0 0 𝜋 4 4 𝜋 2𝜋 2 2𝜋 0 −1 −1 𝜋 =
∫ 𝑑𝜑 ∫ cos5 𝜃 𝑑(cos 𝜃) =
∫ 𝑑𝜑 ∫ 𝑢5𝑑𝑢 = 4 4 96 0 𝜋 0 √2 4 2
Câu 9: Tính tích phân
+∞𝑒−𝑎𝑥3 − 𝑒−𝑏𝑥3 ∫
𝑑𝑥 với 𝑎, 𝑏 > 0 𝑥 0 Giải: 𝑒−𝑦𝑥3 Đặt 𝐹(𝑥, 𝑦) = 𝑥 𝑎 𝑎 𝑏
𝑒−𝑎𝑥3 − 𝑒−𝑏𝑥3
= 𝐹(𝑥, 𝑎) − 𝐹(𝑥, 𝑏) = ∫ 𝐹′(𝑥, 𝑦)𝑑𝑦
= ∫ −𝑥2𝑒−𝑦𝑥3𝑑𝑦
= ∫ 𝑥2𝑒−𝑦𝑥3𝑑𝑦 𝑥 𝑦 𝑏 𝑏 𝑎 +∞ +∞ 𝑏 𝑏 +∞
𝑒−𝑎𝑥3 − 𝑒−𝑏𝑥3 ∫
𝑑𝑥 = ∫ (∫ 𝑥2𝑒−𝑦𝑥3𝑑𝑦 ) 𝑑𝑥 = ∫ ∫
( 𝑥2𝑒−𝑦𝑥3𝑑𝑥 ) 𝑑𝑦 𝑥 0 0 𝑎 𝑎 0 PHAM THANH TUNG 𝑏 +∞ 𝑏 1 1 −1 +∞
= ∫ ( ∫ 𝑒−𝑦𝑥3𝑑(𝑥3) ) 𝑑𝑦 = ∫ ( . 𝑒−𝑦𝑥3 | ) 𝑑𝑦 3 3 𝑦 0 𝑎 0 𝑎 𝑏 1 1 𝑏 = ∫ 𝑑𝑦 = ln 3𝑦 3 𝑎 𝑎
*Kiểm tra điều kiện khả tích:
Đặt 𝑓(𝑥, 𝑦) = 𝑥2𝑒−𝑦𝑥3
− Hàm 𝑓(𝑥, 𝑦 liên t ) c trên mi ụ
ền [0; +∞) × [𝑏; 𝑎] − +∞ Tích phân 𝐼(𝑦) = ∫
𝑥2𝑒−𝑦𝑥3𝑑𝑥 h i t ộ ụ đều trên [𝑏, 𝑎 ] (𝑎, 𝑏 > 0) 0
𝑥2𝑒−𝑦𝑥3 ≤ 𝑥2𝑒−𝑦0𝑥3 với 𝑦0 ≥ 𝑏 > 0 +∞ +∞ Do 1
⇒ ∫ 𝑥2𝑒−𝑦𝑥3𝑑𝑥
hội tụ đều trên [𝑏; 𝑎]
∫ 𝑥2𝑒−𝑦0𝑥3 𝑑𝑥 = hội tụ { 3𝑦0 0 0
Vậy điều kiện đổi thứ tự lấy tích phân thỏa mãn.
❖ Mẹo:
Trong các bài tập sử dụng phương pháp đổi thứ tự lấy tích phân và phương pháp đạo hàm đạo hàm
qua dấu tích phân, chúng ta sẽ “tiền trảm hậu tấu”, tức là cứ áp dụng hai phương pháp trên để
tính tích phân, khi ra kết quả r i ồ mới kiểm tra u ki điề
ện khả vi, khả tích, gi ng l ố ời giải tham khảo
trên. Khi làm như vậy, nếu không đủ thời gian chứng minh điều kiện khả vi, khả tích, chúng ta vẫn
được 0.5đ nếu tính toán đúng tích phân. PHAM THANH TUNG
LỜI GIẢI THAM KHẢO ĐỀ THI GIỮA KÌ 20173 (ĐỀ 1) −𝑡
Câu 1: Tính độ cong tại 𝑡 = 0 của đường {𝑥 = 𝑒 − sin 𝑡
𝑦 = 𝑒−𝑡 − cos 𝑡 Giải: −𝑡
𝑥′(𝑡) = −𝑒−𝑡 − cos 𝑡 , 𝑥′ (𝑡) = 𝑒−𝑡 + sin 𝑡
{𝑥 = 𝑒 − sin 𝑡 ⇒ {
𝑦 = 𝑒−𝑡 − cos 𝑡
𝑦′(𝑡) = −𝑒−𝑡 + sin 𝑡 , 𝑦′ (𝑡) = 𝑒−𝑡 + cos 𝑡
𝑥′(0) = −2, 𝑥′ (0) = 1
Với 𝑡 = 0 ⇒ { 𝑦′(0) = −1,𝑦′ (0) = 2 Độ cong của đườ ạ ng cong t i 𝑡 = 0 là:
|𝑥′. 𝑦′ − 𝑥′ . 𝑦′| |(−2). 2 − 1. (−1)| 3 𝐶(𝑡 = 0) = = 3 3 = ( 5√5 𝑥′2 + 𝑦′2) 2 (22 + 12) 2
Câu 2: Lập phương trình pháp tuyến và tiếp diện tại 𝐴(1,1,0) của mặt 𝑧 = ln(3𝑥 − 2𝑦) Giải: −3 2
Đặt 𝐹(𝑥, 𝑦, 𝑧) = 𝑧 − ln(3𝑥 − 2𝑦) ⇒ 𝐹′ = , 𝐹′ = , ′ = 1 𝑥 𝐹 3𝑥 − 2𝑦 𝑦 3𝑥 − 2𝑦 𝑧 Tại 𝐴(1,1,0) ⇒ 𝐹′( ′( ′(
𝑥 𝐴) = −3, 𝐹𝑦 𝐴) = 2, 𝐹𝑧 𝐴) = 1
Phương trình pháp tuyến của mặt cong tại 𝐴(1,1,0) là: 𝑥 − 1 𝑦 − 1 𝑧 = = −3 2 1
Phương trình tiếp diện của mặt cong tại 𝐴(1,1,0) là:
−3(𝑥 − 1) + 2(𝑦 − 1) + 𝑧 = 0 ⇔ −3𝑥 + 2𝑦 + 𝑧 + 1 = 0
Câu 3: Cho hàm vecto 𝑝 (𝑡) = (sin 2𝑡 , cos 2𝑡 , 𝑒−𝑡) và 𝑟 (𝑡) = (𝑡2 + 1)𝑝 (𝑡). Tính 𝑟′ (0) Giải:
𝑟 (𝑡) = (𝑡2 + 1)𝑝 (𝑡) ⇒ 𝑟′ (𝑡) = [(𝑡2 + )
1 𝑝 (𝑡)]′ = (𝑡2 + 1)′𝑝 (𝑡) + (𝑡2 + 1)𝑝′ (𝑡)
= 2𝑡. (sin 2𝑡 , cos 2𝑡 , 𝑒−𝑡) + (𝑡2 + 1)(2 cos 2𝑡 , −2 sin 2𝑡 , −𝑒𝑡)
⇒ 𝑟′(0) = 2.0. (sin 0 , cos 0 , 𝑒−0) + 1. (2 cos 0 , −2 sin 0 , −𝑒0) = (2,0, −1) PHAM THANH TUNG
Câu 4: Đổi thứ t l ự ấy tích phân 2−𝑥2 𝐼 = ∫ 2𝑑𝑥 ∫
𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 −1 −𝑥 Giải: Miền −1 ≤ ( 𝑥 ≤ 2
𝐷): {−𝑥 ≤ 𝑦 ≤ 2 − 𝑥2
Đổi thứ tự lấy tích phân. Chia miền (𝐷) ầ thành 2 ph n √ √
(𝐷1): {−√2 − 𝑦 ≤ 𝑥 ≤ 2 − 𝑦 và (𝐷 1 ≤ 2): {−𝑦 ≤ 𝑥 ≤ 2 − 𝑦 𝑦 ≤ 2 −2 ≤ 𝑦 ≤ 1 1 √2−𝑦 2 √2−𝑦
⇒ 𝐼 = ∫ 𝑑𝑦 ∫ 𝑓(𝑥, 𝑦)𝑑𝑥 + ∫ 𝑑𝑦 ∫ 𝑓(𝑥, 𝑦)𝑑𝑥 −2 −𝑦 1 −√2−𝑦
Câu 5: Tính ∬ (3𝑥 + 2𝑦)𝑑𝑥𝑑𝑦 , 𝐷 giới hạn bởi: 𝐷
𝑥 = 0, 𝑦 = 0, 𝑥 + 𝑦 = 1 Giải: 0 ≤ 𝑥 ≤ 1 Miền (𝐷): {0 ≤ 𝑦 ≤ 1 − 𝑥 1 1−𝑥
∬(3𝑥 + 2𝑦)𝑑𝑥𝑑𝑦 = ∫ 𝑑𝑥 ∫ (3𝑥 + 2𝑦)𝑑𝑦 𝐷 0 0 1 5
= ∫[3𝑥(1 − 𝑥) + (1 − 𝑥)2]𝑑𝑥 = 6 0 PHAM THANH TUNG
Câu 6: Tính ∬ (𝑥 + 𝑦)(𝑥 − 2𝑦 − 1)2𝑑𝑥𝑑𝑦
, 𝐷 giới hạn bởi 𝑥 + 𝑦 = 0, 𝑥 + 𝑦 = 3, 𝑥 − 2𝑦 = 1, 𝐷 𝑥 − 2𝑦 = 2 Giải: 𝑥 + 𝑦 = 𝑢 Đặt { ⇒ 𝐽−1 = |1 1 | = −3 ⇒ |𝐽| = 1/3 𝑥 − 2𝑦 = 𝑣 1 −2
Miền (𝐷′) mới trong hệ tọa độ mới 𝑂𝑢𝑣 là (𝐷′): {0 ≤ 𝑢 ≤ 3 1 ≤ 𝑣 ≤ 2 3 2 1 1 1
⇒ ∬(𝑥 + 𝑦)(𝑥 − 2𝑦 − 1)2𝑑𝑥𝑑𝑦
= ∬ 𝑢(𝑣 − 1)2𝑑𝑢𝑑𝑣 =
∫ 𝑑𝑢 ∫ 𝑢(𝑣 − 1)2𝑑𝑣 = 3 3 2 𝐷 𝐷′ 0 1
Câu 7: Tính ∭ 𝑧√𝑥2 + 𝑦2𝑑𝑥𝑑𝑦𝑑𝑧 , 𝑉 giới hạn bởi 𝑥2 + 𝑦2 = 1, 𝑧 = 0, 𝑧 = 2 𝑉 Giải:
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 1 𝑥 = 𝑟 cos 𝜑 0 ≤ Đặ 𝑟 < 1
t {𝑦 = 𝑟 sin 𝜑𝐽 = 𝑟. Miền (𝐷): { 0 ≤ 𝜑 ≤ 2𝜋 𝑧 = 𝑧 0 ≤ 𝑟 ≤ 1
⇒ Miền (𝑉) trong tọa độ trụ: {0 ≤ 𝜑 ≤ 2𝜋 0 ≤ 𝑧 ≤ 2 2𝜋 1 2
⇒ ∭ 𝑧√𝑥2 + 𝑦2𝑑𝑥𝑑𝑦𝑑𝑧
= ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ 𝑧. 𝑟. 𝑟𝑑𝑧 𝑉 0 0 0 2𝜋 1 4𝜋 = 2 ∫ 𝑑𝜑 ∫ 𝑟2𝑑𝑟 = 3 0 0
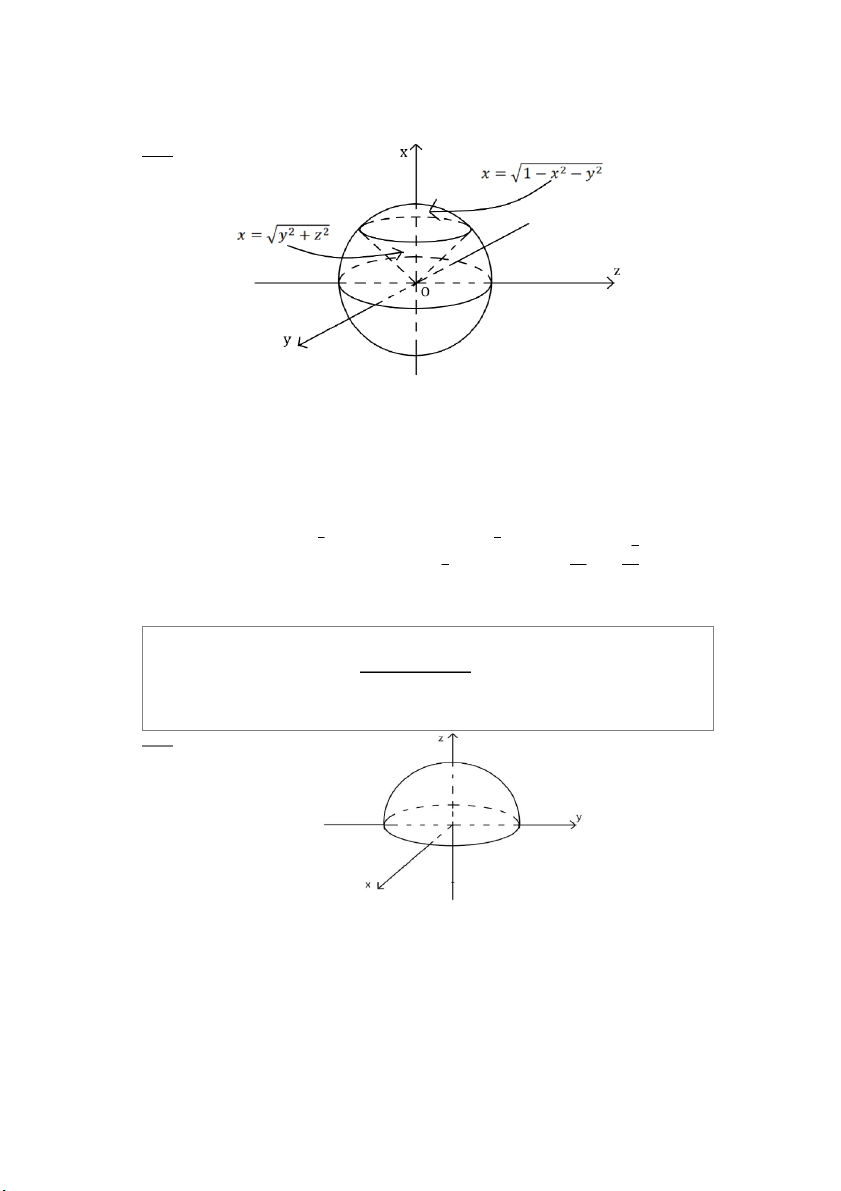
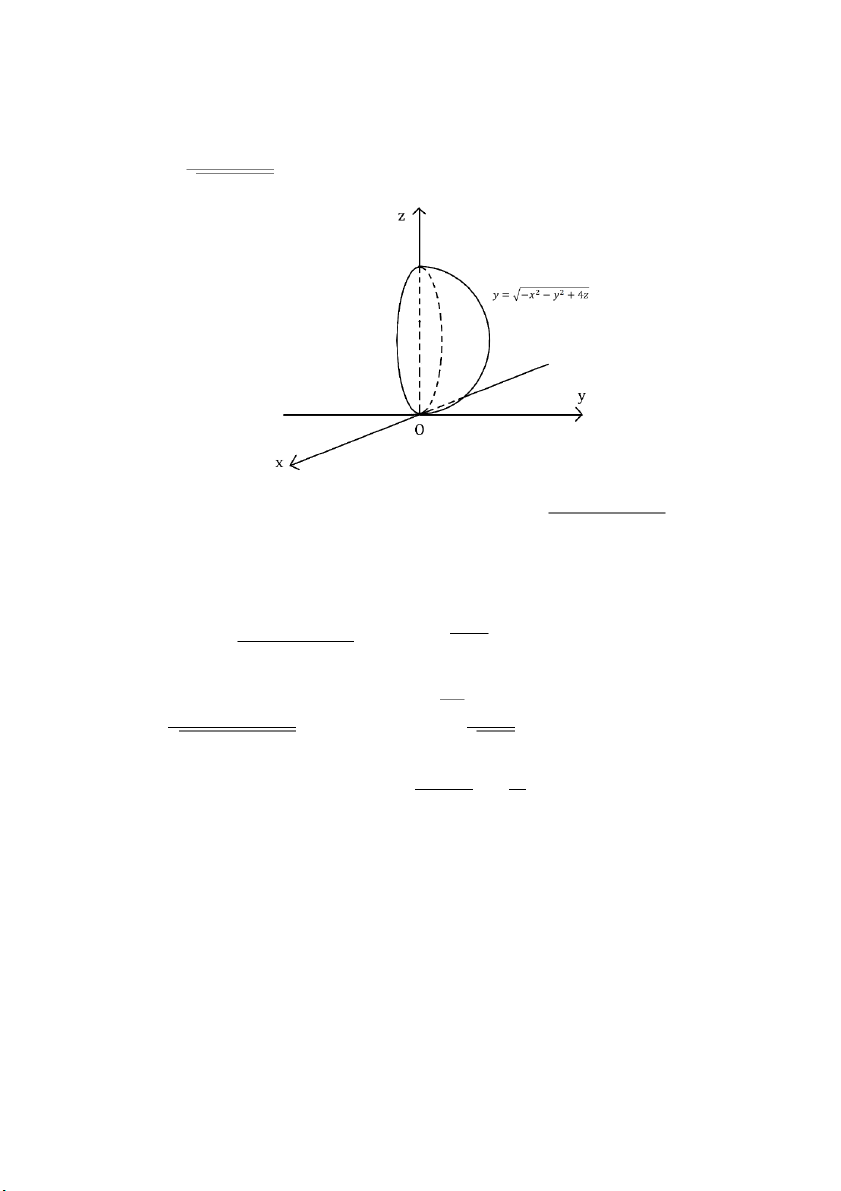
Câu 8: Tính thể tích vật thể 𝑉 giới hạn bởi 𝑥 = √𝑦2 + 𝑧2,
𝑥 = √1 − 𝑥2 − 𝑦2 PHAM THANH TUNG Giải:
Hình minh họa miền 𝑉 được vẽ lại theo quy tắc tam diện thuận 𝑦 = 𝑟 sin 𝜃 cos 𝜑 0 ≤ 𝑟 ≤ 1
Đặt {𝑧 = 𝑟 sin 𝜃 sin 𝜑 |𝐽| = 𝑟2 sin 𝜃. Miền (𝑉): { 0 ≤ 𝜃 ≤ 𝜋/4 𝑥 = 𝑟 cos 𝜃 0 ≤ 𝜑 ≤ 2𝜋 Thể tích miền 𝑉 là: 𝜋 𝜋 2𝜋 4 1 2𝜋 4 1 2𝜋 √2 𝑉( (1 −
𝑉) = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧
= ∫ 𝑑𝜑 ∫ 𝑑𝜃 ∫ 𝑟2 sin 𝜃 𝑑𝑟 =
∫ 𝑑𝜑 ∫ sin 𝜃 𝑑𝜃 = ) (đvtt) 3 3 2 𝑉 0 0 0 0 0 Câu 9: Tính 3𝑥2 − 𝑦2 + 𝑧2 + 1 ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 𝑥2 + 𝑦2 + 𝑧2 + 1 𝑉 Với 𝑉 là nửa kh
ối cầu 𝑥2 + 𝑦2 + 𝑧2 ≤ 1, 𝑧 ≥ 0 Giải: PHAM THANH TUNG
Khi đổi vai trò của 𝑥 và 𝑦 cho nhau thì miền 𝑉 không thay đổi 3𝑥2 − 𝑦2 + 𝑧2 + 1 3𝑦2 − 𝑥2 + 𝑧2 + 1 ⇒ 𝐼 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 𝑥2 + 𝑦2 + 𝑧2 + 1 𝑥2 + 𝑦2 + 𝑧2 + 1 𝑉 𝑉 3𝑥2 − 𝑦2 + 𝑧2 + 1 3𝑦2 − 𝑥2 + 𝑧2 + 1 ⇒ 2𝐼 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 + ∭ 𝑑𝑥𝑑𝑦𝑑𝑧
= 2 ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 𝑥2 + 𝑦2 + 𝑧2 + 1 𝑥2 + 𝑦2 + 𝑧2 + 1 𝑉 𝑉 𝑉 1 4 2𝜋
⇒ 𝐼 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 = . 𝜋 = 2 3 3 𝑉
Câu 10: Tìm giới hạn cos 𝑦 arctan(𝑥 + 𝑦) lim ∫ 𝑑𝑥 𝑦→0 1 + 𝑥2 + 𝑦2 sin 𝑦 Giải:
cos x , sin y liên tục ∀y ∈ 𝑅 cos 𝑦 arctan(x + y) { arctan(x + y)
𝑑𝑥 liên tục trên 𝑅
liên tục trên 𝑅2 ⇒ 𝐼(𝑦) = ∫ 1 + x2 + y2 1 + x2 + y2 sin 𝑦 cos 𝑦 cos 0 1 arctan(x + y) arctan(𝑥 + 0) arctan(𝑥) ⇒ lim ∫ 𝑑𝑥 = ∫ 𝑑𝑥 = ∫ 𝑑𝑥 𝑦→0 1 + x2 + y2 1 + 𝑥2 + 02 1 + 𝑥2 sin 𝑦 sin 0 0 𝜋 1 4 𝜋2
= ∫ arctan(𝑥) 𝑑(arctan(𝑥)) = ∫ 𝑡𝑑𝑡 = 32 0 0 PHAM THANH TUNG
LỜI GIẢI THAM KHẢO ĐỀ GIỮA KỲ 20182 (ĐỀ 2)
Câu 1: Viết phương trình tiếp diện và pháp tuyến của mặt cong 𝑥2 + 𝑦2 − 𝑒𝑧 − 2𝑦𝑥𝑧 = 0 tại điểm 𝑀(1,0,0). Giải:
𝐹′𝑥 = 2𝑥 − 2𝑦𝑧
Đặt 𝐹(𝑥, 𝑦, 𝑧) = 𝑥2 + 𝑦2 − 𝑒𝑧 − 2𝑦𝑥𝑧 ⇒ {
𝐹′𝑦 = 2𝑦 − 2𝑥𝑧
𝐹′𝑧 = −𝑒𝑧 − 2𝑦𝑥
Tại 𝑀(1,0,0), ta có: 𝐹′( ′( ′(
𝑥 𝑀) = 2, 𝐹𝑦 𝑀) = 0, 𝐹𝑧 𝑀) = −1
Phương trình tiếp diện của mặt cong tại 𝑀(1,0,0) là:
2(𝑥 − 1) + 0(𝑦 − 0) − (𝑧 − 0) = 0 ⇔ 2𝑥 − 𝑧 − 2 = 0 𝑥 = 1 + 2𝑡
Phương trình pháp tuyến của mặt cong tại 𝑀(1,0,0) là: { 𝑦 = 0 𝑧 = −𝑡
Câu 2: Tìm hình bao của h
ọ đường cong sau: (𝑥 + 𝐶)2 + (𝑦 − 2𝐶)2 = 5. Giải:
Đặt 𝐹(𝑥, 𝑦, 𝑐) = (𝑥 + 𝑐)2 + (𝑦 − 2𝑐)2 − 5 𝐹′ = 0 2(𝑥 + 𝑐) = 0 𝑥 = −𝑐 Xét { 𝑥 𝐹′ 2( ) ⇔ { 𝑦 = 2𝑐 𝑦 = 0 ⇔ { 𝑦 − 2𝑐 = 0
Điểm (−𝑐, 2𝑐) không thuộc họ đườ
ng tròn (𝑥 + 𝑐)2 + (𝑦 − 2𝑐)2 = 5 ⇒ H
ọ đường tròn không có điểm kì dị. 𝐹 = 0 (
(𝑥 + 𝑐)2 + (𝑦 − 2𝑐)2 − 5 = 0 Xét {
𝑥 + 𝑐)2 + (𝑦 − 2𝑐)2 − 5 = 0 ⇔ {
𝐹′𝑐 = 0 ⇔ { 2(𝑥 + 𝑐) − 4(𝑦 − 2𝑐) = 0
𝑥 + 𝑐 = 2(𝑦 − 2𝑐) 𝑦 = 1 + 2𝑐
(2𝑦 − 4𝑐)2 + (𝑦 − 2𝑐)2 = 5 (𝑦 − 2𝑐)2 = 1 [ ⇔ { 𝑦 = −1 + 2𝑐
𝑥 + 𝑐 = 2(𝑦 − 2𝑐) ⇔ { 𝑥 = 2(𝑦 − 2𝑐) ⇔ { − 𝑐
𝑥 = 2(𝑦 − 2𝑐) − 𝑐 −𝑥 + 2 = 𝑐 { 𝑥 = 2 − 𝑐 { 𝑦 − 1 𝑦 − 1 𝑦 = 1 + 2𝑐 = 𝑐 + 𝑥 − 2 = 0 𝑦 + 2𝑥 − 5 = 0 ⇔ [ ⇔ 2 ⇒ [ 2 ⇔ [ 𝑥 = −2 − 𝑐 −𝑥 − 2 = 𝑐 𝑦 + 1 { 𝑦 + 2𝑥 + 5 = 0 𝑦 = −1 + 2𝑐 { 𝑦 + 1 + 𝑥 + 2 = 0 2 [ = 𝑐 2
Vậy hình bao của họ đường tròn là: 𝑦 = −2𝑥 + và 5 𝑦 = −2𝑥 − 5 PHAM THANH TUNG
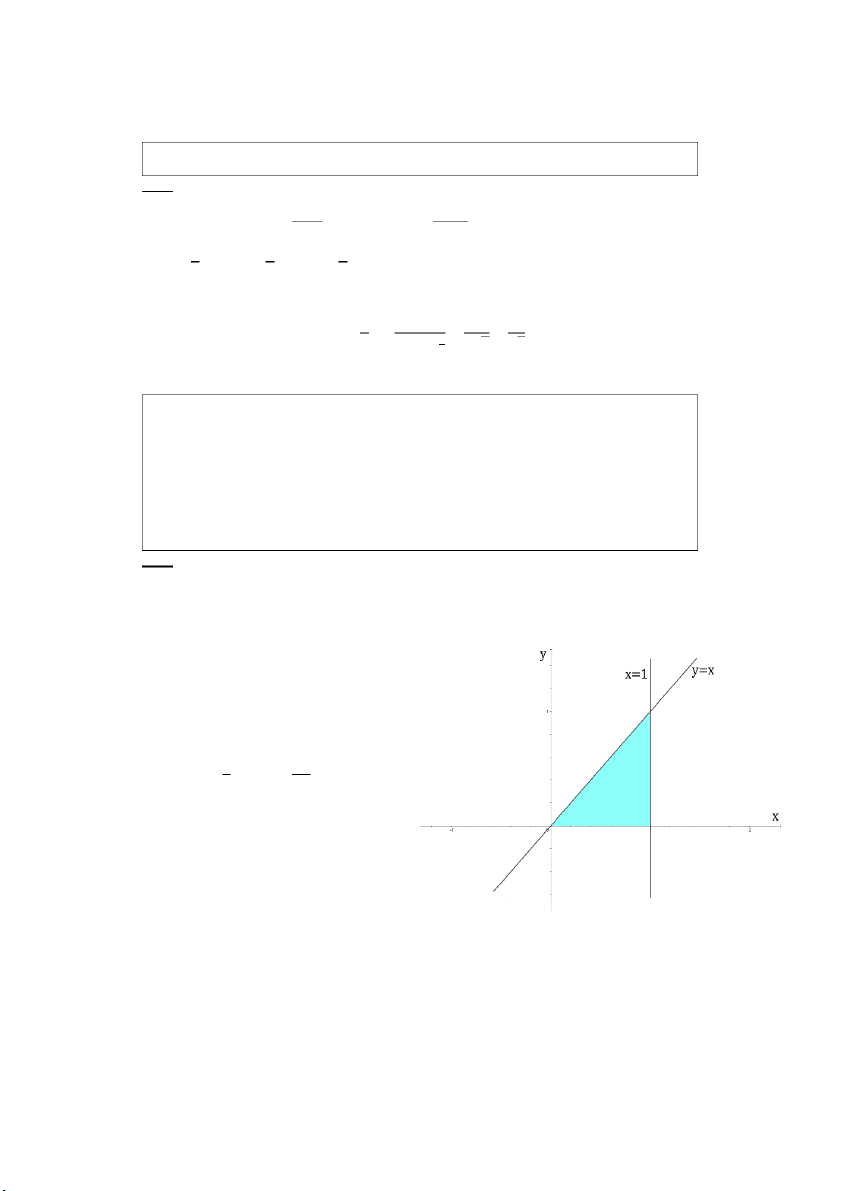
Câu 3: Tính tích phân kép ∬(𝑥 − 4𝑦)𝑑𝑥𝑑𝑦 trong đ
ó 𝐷 giới hạn bởi parabol 𝑦 = 𝑥2 − 1 𝐷 và trục 𝑂𝑥 . Giải: −1 ≤ 𝑥 ≤ 1
Miền 𝐷: {𝑥2 − 1 ≤ 𝑦 ≤ 0 1 0
∬(𝑥 − 4𝑦)𝑑𝑥𝑑𝑦
= ∫ 𝑑𝑥 ∫ (𝑥 − 4𝑦)𝑑𝑦 𝐷 −1 𝑥2−1 1 1 32 = ∫ [𝑥(1 − 𝑥2) + 4. (𝑥2 − 1)2] 𝑑𝑥 = 2 15 −1
Câu 4: Tính tích phân lặp: 2 11 − cos 𝜋𝑦 ∫ 𝑑𝑥 ∫ 𝑑𝑦 𝑦2 1 √𝑥−1 Giải: PHAM THANH TUNG 1 ≤
Đổi thứ tự lấy tích phân, miền 𝑥 ≤ 𝑦2 + 1 𝐷: { 0 ≤ 𝑦 ≤ 1 2 1 1 𝑦2+1 1 1 − cos 𝜋𝑦 1 − cos 𝜋𝑦 1 − cos 𝜋𝑦 ⇒ ∫ 𝑑𝑥 ∫ 𝑑𝑦 = ∫ 𝑑𝑦 ∫ 𝑑𝑥 = ∫ (𝑦2. ) 𝑑𝑦 𝑦2 𝑦2 𝑦2 1 √𝑥−1 0 1 0 1
= ∫(1 − cos 𝜋𝑦)𝑑𝑦 = 1 0
Câu 5: Tính diện tích phần hình tròn 𝑥2 + 𝑦2 = 2𝑦 nằm ngoài đường tròn 𝑥2 + 𝑦2 = 1 Giải:
Gọi miền cần tính diện tích là 𝐷. 𝑥 = 𝑟 cos 𝜑 1 ≤ 𝑟 ≤ 2 sin 𝜑 Đặt { , | ề
𝑦 = 𝑟 sin 𝜑 𝐽| = 𝑟. Mi n 𝐷: { 𝜋/6 ≤ 𝜑 ≤ 5𝜋/6 Diện tích miền 𝐷 là: PHAM THANH TUNG 5𝜋 5𝜋 5𝜋 6 2 sin 𝜑 6 6 1 2(1 − cos 2𝑥) 1
𝑆 = ∬ 𝑑𝑥𝑑𝑦 = ∫ 𝑑𝜑 ∫ 𝑟𝑑𝑟 = ∫ (4sin2 𝜑 − 1)𝑑𝜑 = ∫ ( − ) 𝑑𝜑 2 2 2 𝐷 𝜋 1 𝜋 𝜋 6 6 6 𝜋 √3 ⇒ 𝑆 = + (đvdt) 3 2
Câu 6: Tính các tích phân b i ba sau: ộ
𝑎) ∭(3𝑥2 + 2𝑦)𝑑𝑥𝑑𝑦𝑑𝑧 , trong đó m ền i
𝑉 xác định bởi 0 ≤ 𝑥 ≤ 1, 0 ≤ 𝑦 ≤ 𝑥, 0 ≤ 𝑧 ≤ 𝑥2 𝑉 Giải: 1 𝑥 𝑥2 1 𝑥
∭(3𝑥2 + 2𝑦)𝑑𝑥𝑑𝑦𝑑𝑧
= ∫ 𝑑𝑥 ∫ 𝑑𝑦 ∫ (3𝑥2 + 2𝑦)𝑑𝑧
= ∫ 𝑑𝑥 ∫ 𝑥2(3𝑥2 + 2𝑦)𝑑𝑦 𝑉 0 0 0 0 0 1 7
= ∫(3𝑥5 + 𝑥2. 𝑥2)𝑑𝑥 = 10 0
𝑏) ∭(𝑥 − 𝑦 + 2𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 , trong đ ó 𝑉 đ ợc ư g ới hạn bởi i các mặt 𝑉
𝑥 − 𝑦 = 0, 𝑥 − 𝑦 = 2, 𝑥 + 𝑦 = 0, 𝑥 + 𝑦 = 1, 𝑧 = 0, 𝑧 = 1 Giải: ′ ′ ′ 𝑢 = 𝑥 − 𝑦 𝑢𝑥 𝑢𝑦 𝑢𝑧 1 −1 0
Đặt {𝑣 = 𝑥 + 𝑦⇒ 𝐽−1 = | 𝑣′ ′ ′ 𝑥
𝑣𝑦 𝑣𝑧| = | 1 1 0| = 2 ⇒ 𝐽 = 1/2 𝑤 = 𝑧 𝑤′ ′ ′ 0 0 1 𝑥 𝑤𝑦 𝑤𝑧 0 ≤ 𝑢 ≤ 2
Miền 𝑉 trong tọa độ mới 𝑂𝑢𝑣𝑤 là 𝑉𝑢𝑣𝑤: {0 ≤ 𝑣 ≤ 1 0 ≤ 𝑤 ≤ 1 2 1 1 1 1
⇒ ∭(𝑥 − 𝑦 + 2𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 = ∭
(𝑢 + 2𝑤)𝑑𝑢𝑑𝑣𝑑𝑤 =
∫ 𝑑𝑢 ∫ 𝑑𝑣 ∫(𝑢 + 2𝑤) 𝑑𝑤 2 2 𝑉 𝑉𝑢𝑣𝑤 0 0 0 2 1 2 1 1
= ∫ 𝑑𝑢 ∫(𝑢 + 1)𝑑𝑣 = ∫(𝑢 + 1)𝑑𝑢 = 2 2 2 0 0 0 PHAM THANH TUNG 𝑦2 𝑐) ∭
𝑑𝑥𝑑𝑦𝑑𝑧 , trong đó V l à m ền xác đị i
nh bởi 𝑥2 + 𝑦2 + 𝑧2 ≤ 4𝑧, 𝑦 ≥ 0 √4𝑧 − 𝑥2 − 𝑧2 𝑉
Miền 𝑉: {𝑥2 + 𝑦2 + 𝑧2 ≤ 4𝑧 ⇔ {𝑦2 ≤ −𝑥2 − 𝑧2 + 4𝑧 √ [𝑥2 + ( )2] 𝑦 ≥ 0 𝑦 ≥ 0 ⇔ 0 ≤ 𝑦 ≤ 4 − 𝑧 − 2
Hình chiếu của 𝑉 lên 𝑂𝑥𝑧 là 𝐷: 𝑥2 + (𝑧 − 2)2 ≤ 4 𝑧 = 𝑟 cos 𝜑
Đặt {𝑦 = 2 + 𝑟 sin 𝜑, 𝐽 = 𝑟 𝑧 = 𝑧 √ [ 0 ≤ √ 2 𝑥2 + ( )2] 𝑦 ≤ 4 − 𝑟 𝑉: {0 ≤ 𝑦 ≤ 4 − 𝑧 − 2 ⇔ { 0 ≤ 𝑟 ≤ 2
𝐷: 𝑥2 + (𝑧 − 2)2 ≤ 4 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 2 √4−𝑟2 𝑦2 𝑦2. 𝑟 ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ 𝑑𝑦
√4 − [𝑥2 + (𝑧 − 2)2] √4 − 𝑟2 𝑉 0 0 0 2𝜋 2 (4 − 𝑟2)𝑟 8𝜋 = ∫ 𝑑𝜑 ∫ 𝑑𝑟 = 3 3 0 0 PHAM THANH TUNG
Câu 7: Tính độ cong tại điểm 𝑀(−1,0, −1) của đường cong là giao của mặt trụ 4𝑥2 + 𝑦2 = 4
và mặt phẳng 𝑥 − 3𝑧 = 2. Giải: 𝑥 = cos 𝑡 𝑥 = cos 𝑡 Tham s hóa ố { (do 𝑥2 + 𝑦2/4 = 1) ⇒ ng Đườ 𝐿 có dạng { 𝑦 = sin 𝑡 𝑦 = 2 sin 𝑡 𝑧 = cos 𝑡−2 3
𝑥′ = − sin 𝑡 , 𝑥′ = − cos 𝑡
𝑥′(𝑀) = 0, 𝑥′ (𝑀) = 1
𝑦′ = 2 cos 𝑡, 𝑦′ = −2 sin 𝑡
𝑦′(𝑀) = 2, 𝑦′ (𝑀) = 0 ⇒ { − sin
. Tại 𝑀(−1,0, −1) ⇔ 𝑡 = 𝜋 ⇒ { 𝑡 − cos 𝑡 1 𝑧′ = , 𝑧′ = 3
𝑧′(𝑀) = 0, 𝑧′ (𝑀) = 3 3 Áp d ng công th ụ ức tính độ cong: 2 2 2 √ 𝑦′(𝑡 𝑧′(𝑡 𝑥′(𝑡 | 0)
𝑧′(𝑡0) | + | 0) 𝑥′(𝑡0) | + | 0) 𝑦′(𝑡0) |
𝑦′ (𝑡0) 𝑧′ (𝑡0)
𝑧′ (𝑡0) 𝑥′ (𝑡0)
𝑥′ (𝑡0) 𝑦′ (𝑡0) √10 𝐶(𝑀) = = 3 12
(𝑥′2 + 𝑦′2 + 𝑧′2) 2
Câu 8: Chứng minh rằng hàm s ố +∞ 𝐼(𝑦) = ∫ 𝑒−𝑥 1−cos(𝑥𝑦)
𝑑𝑥 khả vi trên 𝑅. 0 𝑥 Giải: 1 − cos(𝑥𝑦)
Đặt 𝑓(𝑥, 𝑦) = 𝑒−𝑥 𝑥 Hàm 𝑓(𝑥, 𝑦
) không xác định tại 𝑥 = 0 nhưng 1 − cos(𝑥𝑦) 𝑥2𝑦2 lim 𝑓(𝑥, 𝑦) =lim
𝑓(𝑥, 𝑦) = lim 𝑒−𝑥 = lim 𝑒−𝑥
= lim 𝑒−𝑥𝑥𝑦2 = 0 𝑥→0+ 𝑥→0− 𝑥→0 𝑥 𝑥→0 𝑥 𝑥→0 1 − cos(𝑥𝑦) Ta có: ,
𝑓(𝑥, 𝑦) = {𝑒−𝑥 𝑥 ≠ 0 ′ 𝑥
, 𝑓𝑦 = 𝑒−𝑥 sin(𝑥𝑦) liên tục trên 𝑅2 0 , 𝑥 = 0
|𝑒−𝑥 sin(𝑥𝑦)| ≤ 𝑒−𝑥, ∀𝑦 ∈ 𝑅 +∞ +∞ { +∞
⇒ ∫ 𝑒−𝑥 sin(𝑥𝑦) 𝑑𝑥 hội tụ đều trên 𝑅
Mà ∫ 𝑒−𝑥𝑑𝑥 = −𝑒−𝑥 | = 0 − (−1) = 1 hội tụ 0 0 0
(theo tiêu chuẩn Weierstrass) PHAM THANH TUNG +∞ 1 +∞ 1 − cos(𝑥𝑦) 1 − cos(𝑥𝑦) 1 − cos(𝑥𝑦) 𝐼(𝑦) = ∫ 𝑒−𝑥 𝑑𝑥 = ∫ 𝑒−𝑥 𝑑𝑥 + ∫ 𝑒−𝑥 𝑑𝑥 𝑥 𝑥 𝑥 0 0 1 𝑒−𝑥 cos(𝑥𝑦) |
| ≤ 𝑒−𝑥, ∀𝑦 ∈ 𝑅 𝑥 1 1 − cos(𝑥𝑦) +∞ +∞ ∫ hội tụ 1 𝑒−𝑥 𝑑𝑥 𝑥
∫ 𝑒−𝑥𝑑𝑥 = −𝑒−𝑥 | = hội tụ 0 𝑒 ⇒ +∞ ⇒ 𝐼(𝑦) hội tụ 1 1 1 − cos(𝑥𝑦) 1 ∫ 𝑒−𝑥 𝑑𝑥 hội tụ 1 𝑥
∫ 𝑒−𝑥𝑑𝑥 = 1 − hội tụ { 1 { 𝑒 0
Vậy 𝐼(𝑦) khả vi trên 𝑅 PHAM THANH TUNG
LỜI GIẢI THAM KHẢO ĐỀ THI GIỮA KÌ 20182 (ĐỀ 3)
Câu 1: Viết phương trình tiếp tuyến và pháp diện của đường cong 𝑥 = sin 𝑡 , 𝑦 = cos 𝑡 , 𝑧 = 𝑒2𝑡 tại điểm 𝑀(0,1,1). Giải: 0 = sin 𝑡
Tại 𝑀(0,1,1) ⇒ { 1 = cos 𝑡⇔ 𝑡 = 0 1 = 𝑒2𝑡 𝑥′(𝑡) = cos 𝑡 𝑥′(0) = 1
Ta có: { 𝑦′(𝑡) = − sin 𝑡. Tại 𝑡 = 0 ⇒ { 𝑦′(0) = 0 𝑧′(𝑡) = 2𝑒2𝑡 𝑧′(0) = 2
Tại 𝑀(0,1,1), phương trình tiếp tuyến c ng cong là: ủa đườ 𝑥 = 𝑡 { 𝑦 = 1 𝑧 = 1 + 2𝑡
Tại 𝑀(0,1,1), phương trình pháp diện c ng cong ủa đườ 𝐿 là:
𝑥 + 0. (𝑦 − 1) + 2(𝑧 − 1) = 0 ⇔ 𝑥 + 2𝑧 − 2 = 0
Câu 2: Tính độ cong của đường 𝑥 = 𝑡2, 𝑦 = 𝑡 ln 𝑡 , 𝑡 > t
0 ại điểm ứng với 𝑡 = 𝑒 Giải: 𝑥′ = 2𝑡 , 𝑥′ = 2 Ta có { 𝑥 = 𝑡2 ⇒ { 𝑦 = 𝑡 ln 𝑡
𝑦′ = ln 𝑡 + 1, 𝑦′ = 1/𝑡
𝑥′(𝑒) = 2𝑒 , 𝑥′ (𝑒) = 2 Tại 𝑡 = 𝑒 ⇒ {
𝑦′(𝑒) = 2 , 𝑦′ (𝑒) = 1/𝑒 Độ cong của đườ ạ ng cong t i 𝑡 = 𝑒 là: 1 |2𝑒. − 2.2| 𝑒 2 𝐶(𝑡 = 𝑒) = 3 = 3 (4𝑒2 + 22) 2 (4𝑒2 + 22) 2
Câu 3: Đổi thứ t l ự ấy tích phân 1 1
∫ 𝑑𝑥 ∫ 𝑓(𝑥, 𝑦)𝑑𝑦 0 𝑥3 PHAM THANH TUNG Giải: 0 ≤ 𝑥 ≤ 1
Miền 𝐷: {𝑥3 ≤ 𝑦 ≤ 1
Thay đổi thứ tự lấy tích phân 0 ≤ Miền 𝑥 ≤ 𝑦 √3 𝐷: { 0 ≤ 𝑦 ≤ 1 1 1 1 √ 3 𝑦
⇒ ∫ 𝑑𝑥 ∫ 𝑓(𝑥, 𝑦)𝑑𝑦 = ∫ 𝑑𝑦 ∫ 𝑓(𝑥, 𝑦)𝑑𝑥 0 𝑥3 0 0
Câu 4: Tính các tích phân sau:
𝑎) ∬ √𝑥2 + 𝑦2𝑑𝑥𝑑𝑦
, trong đó 𝐷: 1 ≤ 𝑥2 + 𝑦2 ≤ 4, 𝑥 + 𝑦 ≥ 0 𝐷 𝜋 𝜋
𝑏) ∬|cos(𝑥 + 𝑦)|𝑑𝑥𝑑𝑦 , trong đó 𝐷 = [0; ] × [0; ] 2 2 𝐷 Giải:
𝑎) ∬ √𝑥2 + 𝑦2𝑑𝑥𝑑𝑦 , trong đó 𝐷: 1 ≤ 𝑥2 + 𝑦2 ≤ 4, 𝑥 + 𝑦 ≥ 0 𝐷 𝑥 = 𝑟 cos 𝜑 Đặt { , 𝑦 = 𝑟 sin 𝜑 𝐽 = 𝑟 1 ≤ 𝑟 ≤ 2 Miền 𝐷: {−𝜋 3𝜋 ≤ 𝜑 ≤ 4 4 2𝜋 2 14𝜋
∬ √𝑥2 + 𝑦2𝑑𝑥𝑑𝑦
= ∫ 𝑑𝜑 ∫ √𝑟2. 𝑟𝑑𝑟 = 3 𝐷 0 1 PHAM THANH TUNG 𝜋 𝜋
𝑏) ∬|cos(𝑥 + 𝑦)|𝑑𝑥𝑑𝑦 , trong đó 𝐷 = [0; ] × [0; ] 2 2 𝐷 −𝜋 𝜋 −𝜋 𝜋
|cos(𝑥 + 𝑦)| = cos(𝑥 + 𝑦) khi ≤ 𝑥 + 𝑦 ≤ ⇔ − 𝑥 ≤ 𝑦 ≤ − 𝑥 Ta c : ó { 2 2 2 2 𝜋 3𝜋 𝜋 3𝜋
|cos(𝑥 + 𝑦)| = −cos(𝑥 + 𝑦) khi ≤ 𝑥 + 𝑦 ≤ ⇔ − 𝑥 ≤ 𝑦 ≤ − 𝑥 2 2 2 2 𝜋 𝜋
𝐾ế𝑡 ℎợ𝑝 𝑐ù𝑛𝑔 𝑚𝑖ề𝑛 𝐷 = [0; ] × [0; ] , 𝑡𝑎 𝑐ó: 2 2 𝜋 0 ≤ 𝑦 ≤ − 𝑥
|cos(𝑥 + 𝑦)| = cos(𝑥 + 𝑦) khi { 2𝜋 0 ≤ 𝑥 ≤ 2 𝜋 𝜋 − 𝑥 ≤ 𝑦 ≤
|cos(𝑥 + 𝑦)| = − cos(𝑥 + 𝑦) khi { 2 2 𝜋 0 ≤ 𝑥 ≤ 2 Chia miền 𝐷 thành: 𝜋 𝜋 𝜋 0 ≤ 𝑦 ≤ − 𝑥 − 𝑥 ≤ 𝑦 ≤ 2 𝐷+ : { 2 2 𝜋 và 𝐷− : { 𝜋 0 ≤ 𝑥 ≤ 0 ≤ 2 𝑥 ≤ 2
∬|cos(𝑥 + 𝑦)|𝑑𝑥𝑑𝑦
= ∬ cos(𝑥 + 𝑦) 𝑑𝑥𝑑𝑦 + ∬ −cos(𝑥 + 𝑦) 𝑑𝑥𝑑𝑦 𝐷 𝐷+ 𝐷− PHAM THANH TUNG 𝜋 𝜋 𝜋 𝜋 2 2−𝑥 2 2
= ∫ 𝑑𝑥 ∫ cos(𝑥 + 𝑦)𝑑𝑦 − ∫ 𝑑𝑥 ∫ cos(𝑥 + 𝑦)𝑑𝑦 0 0 0 𝜋 2−𝑥 𝜋 𝜋 2 2 𝜋 𝜋 𝜋 𝜋 𝜋 = ∫ (sin
− sin 𝑥) 𝑑𝑥 − ∫ [sin (𝑥 + ) − sin ] 𝑑𝑥 = − 1 + − 1 = 𝜋 − 2 2 2 2 2 2 0 0
Câu 5: Tính tích phân: 1 1−𝑥 2 ∫ 𝑑𝑥 ∫ 𝑑𝑧 ∫(𝑦 + 𝑧)𝑑𝑦 0 0 0 Giải: 1 1−𝑥 2 1 2 1−𝑥 1 2 1 1 − 𝑥 ∫ 𝑑𝑥 ∫ 𝑑𝑧 ∫(𝑦 + 𝑧)𝑑𝑦
= ∫ 𝑑𝑥 ∫ 𝑑𝑦 ∫ (𝑦 + 𝑧)𝑑𝑧
= ∫ 𝑑𝑥 ∫ [(𝑦𝑧 + 𝑧2) | ] 𝑑𝑦 2 0 0 0 0 0 0 0 0 0 1 2 1
= ∫ 𝑑𝑥 ∫ [𝑦(1 − 𝑥) + (1 − 𝑥)2] 𝑑𝑦 2 0 0 1 4
= ∫[2(1 − 𝑥) + (1 − 𝑥)2]𝑑𝑥 = 3 0
Câu 6: Tính thể tích của miền giới hạn bởi hai parabol 𝑥 = 1 + 𝑦2 + 𝑧2 và 𝑥 = 2(𝑦2 + 𝑧2) Giải:
Xét giao tuyến của 𝑥 = 1 + 𝑦2 + 𝑧2 và 𝑥 = 2(𝑦2 + 𝑧2)
1 + 𝑦2 + 𝑧2 = 2(𝑦2 + 𝑧2) ⇔ 𝑦2 + 𝑧2 = 1
Hình chiếu của 𝑉 lên 𝑂𝑦𝑧 là 𝐷: 𝑦2 + 𝑧2 ≤ 1 𝑦 = 𝑟 cos 𝜑 0 ≤ 𝑟 ≤ 1 Đặt { ,
𝑧 = 𝑟 sin 𝜑 𝐽 = 𝑟 ⇒ 𝐷: { 0 ≤ 𝜑 ≤ 2𝜋
Thể tích vật thể 𝑉 là: PHAM THANH TUNG
𝑉 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 = ∬[(1 + 𝑦2 + 𝑧2) − 2(𝑦2 + 𝑧2)]𝑑𝑦𝑑𝑧 𝑉 𝐷 2𝜋 1 𝜋
= ∬(1 − 𝑦2 − 𝑧2)𝑑𝑦𝑑𝑧
= ∫ 𝑑𝜑 ∫(1 − 𝑟2)𝑟𝑑𝑟 = (đvtt) 2 𝐷 0 0
Câu 7: Cho hàm vecto khả vi 𝑟(𝑡) : 𝑅 → 𝑅3\{0 }. Ký hiệu |𝑟 (𝑡)| là độ dài của 𝑟 (𝑡). Chứng minh: 𝑑(|𝑟 (𝑡)|) 1 = 𝑟 (𝑡). 𝑟′(𝑡). 𝑑𝑡 |𝑟 (𝑡)| Giải:
|𝑟 (𝑡)| = √𝑥2(𝑡) + 𝑦2(𝑡) + 𝑧2(𝑡)
Đặt 𝑟 (𝑡) = (𝑥(𝑡), 𝑦(𝑡), 𝑧(𝑡)) ⇒ {
𝑟′ (𝑡) = (𝑥′(𝑡), 𝑦′(𝑡), 𝑧′(𝑡))
Biến đổi tương đương 𝑑(|𝑟 (𝑡)|) 1 = (𝑡) ′(𝑡) 𝑑𝑡 |𝑟 (𝑡)| 𝑟 . 𝑟 𝑑
𝑥′(𝑡). 𝑥(𝑡) + 𝑦′(𝑡). 𝑦(𝑡) + 𝑧′(𝑡). 𝑧(𝑡) ⇔
(√𝑥2(𝑡) + 𝑦2(𝑡) + 𝑧2(𝑡)) = 𝑑𝑡
√𝑥2(𝑡) + 𝑦2(𝑡) + 𝑧2(𝑡)
2𝑥′(𝑡). 𝑥(𝑡) + 2𝑦′(𝑡). 𝑦(𝑡) + 2𝑧′(𝑡). 𝑧(𝑡)
𝑥′(𝑡). 𝑥(𝑡) + 𝑦′(𝑡). 𝑦(𝑡) + 𝑧′(𝑡). 𝑧(𝑡) ⇔ =
2√𝑥2(𝑡) + 𝑦2(𝑡) + 𝑧2(𝑡)
√𝑥2(𝑡) + 𝑦2(𝑡) + 𝑧2(𝑡)
𝑥′(𝑡). 𝑥(𝑡) + 𝑦′(𝑡). 𝑦(𝑡) + 𝑧′(𝑡). 𝑧(𝑡)
𝑥′(𝑡). 𝑥(𝑡) + 𝑦′(𝑡). 𝑦(𝑡) + 𝑧′(𝑡). 𝑧(𝑡) ⇔ =
√𝑥2(𝑡) + 𝑦2(𝑡) + 𝑧2(𝑡)
√𝑥2(𝑡) + 𝑦2(𝑡) + 𝑧2(𝑡) ⇒ Điề ả u ph i chứng minh.
Câu 8: Tính tích phân ∭ (2𝑦 − 𝑧)2𝑑𝑥𝑑𝑦𝑑𝑧 trong đó 𝑉 là hình cầu 𝑥2 + 𝑦2 + 𝑧2 ≤ 1 𝑉 Giải:
∭(4𝑦2 − 4𝑦𝑧 + 𝑧2)𝑑𝑥𝑑𝑦𝑑𝑧
= ∭(4𝑦2 + 𝑧2)𝑑𝑥𝑑𝑦𝑑𝑧
+ ∭(−4𝑦𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 𝑉 𝑉 PHAM THANH TUNG
𝑓(𝑥, 𝑦, 𝑧) = −4𝑦𝑧 là hàm lẻ với biến 𝑦 {
⇒ ∭(−4𝑦𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 = 0
Miền 𝑉 đối xứng qua 𝑂𝑥𝑧 𝑉 𝑥 = 𝑟 sin 𝜃 cos 𝜑
Đặt {𝑦 = 𝑟 sin 𝜃 sin 𝜑 , 𝐽 = −𝑟2 sin 𝜃 𝑧 = 𝑟 cos 𝜃 0 ≤ 𝑟 ≤ 1
Miền 𝑉 trong tọa độ cầu là 𝑉: { 0 ≤ 𝜃 ≤ 𝜋 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 𝜋 1
∭(4𝑦2 + 𝑧2)𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝜃 ∫[4(𝑟 sin 𝜃 sin 𝜑)2 + (𝑟 cos 𝜃)2] 𝑟2 sin 𝜃 𝑑𝑟 𝑉 0 0 0 2𝜋 𝜋 2𝜋 4 1 16 2 4 = ∫ 𝑑𝜑 ∫ [ (sin 𝜃 sin 𝜑)2 +
(cos 𝜃)2 ] sin 𝜃 𝑑𝜃 = ∫ [ (sin 𝜑)2 + ] 𝑑𝜑 = 𝜋 5 5 15 15 3 0 0 0
Câu 9: Chứng minh rằng hàm s ố +∞ 𝐼(𝑦) = ∫ 𝑒−𝑥 sin(𝑥𝑦)
𝑑𝑥 khả vi trên 𝑅. 0 𝑥 Giải: sin(𝑥𝑦)
Đặt 𝑓(𝑥, 𝑦) = 𝑒−𝑥 𝑥 Hàm 𝑓(𝑥, 𝑦
) không xác định tại 𝑥 = 0 nhưng sin(𝑥𝑦) 𝑥𝑦 lim 𝑓(𝑥, 𝑦) =lim
𝑓(𝑥, 𝑦) = lim 𝑒−𝑥 = lim 𝑒−𝑥 = lim 𝑒−𝑥𝑦 = 𝑦 𝑥→0+ 𝑥→0− 𝑥→0 𝑥 𝑥→0 𝑥 𝑥→0 sin(𝑥𝑦) Ta có: ,
𝑓(𝑥, 𝑦) = {𝑒−𝑥 𝑥 ≠ 0 ′ 𝑥
, 𝑓𝑦 = 𝑒−𝑥 cos(𝑥𝑦) liên tục trên 𝑅2 𝑦 , 𝑥 = 0
|𝑒−𝑥 cos(𝑥𝑦)| ≤ 𝑒−𝑥, ∀𝑦 ∈ 𝑅 +∞ +∞ { +∞
⇒ ∫ 𝑒−𝑥 cos(𝑥𝑦) 𝑑𝑥 hội tụ đều trên 𝑅
Mà ∫ 𝑒−𝑥𝑑𝑥 = −𝑒−𝑥 | = 0 − (−1) = 1 hội tụ 0 0 0
(theo tiêu chuẩn Weierstrass) +∞ 1 +∞ sin(𝑥𝑦) sin(𝑥𝑦) sin(𝑥𝑦) 𝐼(𝑦) = ∫ 𝑒−𝑥 𝑑𝑥 = ∫ 𝑒−𝑥 𝑑𝑥 + ∫ 𝑒−𝑥 𝑑𝑥 𝑥 𝑥 𝑥 0 0 1 PHAM THANH TUNG 𝑒−𝑥 sin(𝑥𝑦) |
| ≤ 𝑒−𝑥, ∀𝑦 ∈ 𝑅 𝑥 +∞ +∞ 1 1 +∞
∫ 𝑒−𝑥𝑑𝑥 = −𝑒−𝑥 | = hội tụ sin(𝑥𝑦) sin(𝑥𝑦) 𝑒
⇒ 𝐼(𝑦) = ∫ 𝑒−𝑥 𝑑𝑥 + ∫ 𝑒−𝑥 𝑑𝑥 hội tụ 1 1 𝑥 𝑥 1 0 1 1
∫ 𝑒−𝑥𝑑𝑥 = 1 − hội tụ { 𝑒 0
Vậy 𝐼(𝑦) khả vi trên 𝑅 PHAM THANH TUNG
LỜI GIẢI THAM KHẢO ĐỀ THI GIỮA KỲ 20183 (ĐỀ 1)
Câu 1: Tìm hình bao của h
ọ đường thẳng 𝑥 − 𝑐𝑦 + 𝑐3 = 0 Giải:
Đặt 𝐹(𝑥, 𝑦, 𝑐) = 𝑥 − 𝑐𝑦 + 𝑐3 𝐹′(𝑥, 𝑦, 𝑐) = 0 Xét { 𝑥
ệm ⇒ ọ đường cong không có điể ị 𝐹′(
𝑦 𝑥, 𝑦, 𝑐) = 0 ⇔ { 1 = 0 −𝑐 = 0 ⇒ Vô nghi H m kì d . 𝑥 = 𝐹(𝑥, 𝑦, 𝑐) = 0 𝑥 − 𝑐𝑦 + 𝑐3 = 0 𝑐3 Xét {
⇔ {𝑥 − 𝑐. 3𝑐2 + 𝑐3 = 0 2 𝐹′( 𝑦
𝑐 𝑥, 𝑦, 𝑐) = 0 ⇔ { −𝑦 + 3𝑐2 = 0 𝑦 = 3𝑐2 ⇔ {𝑥 = 2𝑐3 𝑦 = 3𝑐2 ⇔ { = 𝑐2 3 𝑥 2 𝑦 3 27 ⇒ ( ) − ( ) = 0 ⇔ 𝑦3 = 𝑥2 2 3 4 27
Vậy hình bao của họ đường cong là đường 𝑦3 = 𝑥2 4
Câu 2: Viết phương trình tiếp diện và pháp tuyến của tại điểm 𝐴(1; 0; 1) của mặt 𝑧 = 𝑥𝑒sin 2𝑦 Giải: 𝐹′𝑥 = −𝑒sin2𝑦
Đặt 𝐹(𝑥, 𝑦, 𝑧) = 𝑧 − 𝑥𝑒sin 2𝑦 ⇒ { 𝐹′ sin 2𝑦 𝑦 = −2𝑥 cos 𝑦 𝑒 𝐹′𝑧 = 1 𝐹′( 𝑥 𝐴) = −1 Tại 𝐴(1; 0; 1), { ta có: 𝐹′( 𝑦 𝐴) = −2 𝐹′( 𝑧 𝐴) = 1
Phương trình tiếp diện của mặt cong tại 𝐴(1; 0; 1) là:
−1. (𝑥 − 1) − 2. (𝑦 − 0) + 1. (𝑧 − 1) = 0 ⇔ −𝑥 − 2𝑦 + 𝑧 = 0
Phương trình pháp tuyến của mặt cong tại 𝐴(1; 0; 1) là: 𝑥 − 1 𝑦 𝑧 − 1 = = −1 −2 1 PHAM THANH TUNG
Câu 3: Đổi thứ t l ự ấy tích phân: 1 𝑥2
∫ 𝑑𝑥 ∫ 𝑓(𝑥, 𝑦)𝑑𝑦 0 −𝑥 Giải: 0 ≤ 𝑥 ≤ 1
Miền 𝐷: {−𝑥 ≤ 𝑦 ≤ 𝑥2 −𝑦 ≤ 𝑥 ≤ 1
Đổi thứ tự lấy tích phân, chia 𝐷 thanh hai miền 𝐷1 : {−1 ≤
𝑦 ≤ 0 và 𝐷2 : {√𝑦 ≤ 𝑥 ≤ 1 0 ≤ 𝑦 ≤ 1 1 𝑥2 0 1 1 1
⇒ ∫ 𝑑𝑥 ∫ 𝑓(𝑥, 𝑦)𝑑𝑦 = ∫ 𝑑𝑦
∫ 𝑓(𝑥, 𝑦)𝑑𝑥 + ∫ 𝑑𝑦 ∫ 𝑓(𝑥, 𝑦)𝑑𝑥 0 −𝑥 −1 −𝑦 0 √𝑦
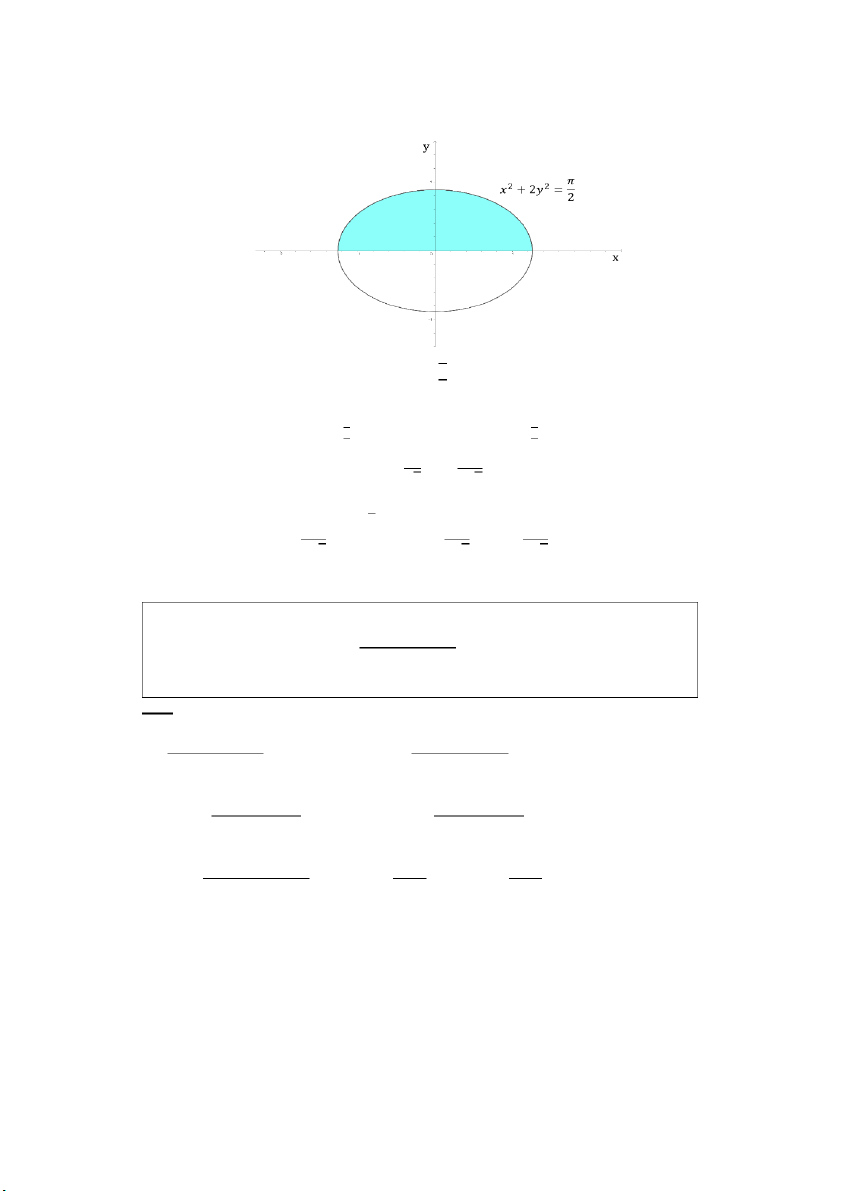
Câu 4: Tính ∬ sin(𝑥2 + 2𝑦2) 𝑑𝑥𝑑𝑦 , với 𝐷 là miền: 𝐷 𝜋 𝑥2 + 2𝑦2 ≤ , 𝑦 ≥ 0 2 Giải: 𝑥 = 𝑟 cos 𝜑 𝑥 = 𝑟 cos 𝜑 1 Đặt { 𝑟 √2 ⇔ { 𝑟 𝑦 = 𝑟 sin 𝜑 𝑦 = sin 𝜑 , 𝐽 = √2 √2 PHAM THANH TUNG 𝜋 Miền 0 ≤
𝐷 trong tọa độ cực suy rộng 𝐷: { 𝑟 ≤ √ 2 0 ≤ 𝜑 ≤ 𝜋 √𝜋 √𝜋 𝜋 2 2𝜋 2 𝑟 1
∬ sin(𝑥2 + 2𝑦2) 𝑑𝑥𝑑𝑦
= ∫ 𝑑𝜑 ∫ sin(𝑟2) . 𝑑𝑟 =
∫ 𝑑𝜑 ∫ sin(𝑟2) 𝑑(𝑟2) √2 2√2 𝐷 0 0 0 0 𝜋 𝜋 2 𝜋 1 1 𝜋
= ∫ 𝑑𝜑 ∫ sin 𝑢 𝑑𝑢 = ∫ 𝑑𝜑 = 2√2 2√2 2√2 0 0 0 Câu 5: Tính 𝑥 + 𝑦 + 2 ∭ ( 𝑑𝑥𝑑𝑦𝑑𝑧 𝑥 + 1)(𝑦 + 1)𝑧 𝑉
Với 𝑉 xác định bởi 0 ≤ 𝑥 ≤ 1, 1 ≤ 𝑦 ≤ 2, 1 ≤ 𝑧 ≤ 𝑒 Giải: 1 2 𝑒 𝑥 + 𝑦 + 2 𝑥 + 𝑦 + 2 ∭
= ∫ 𝑑𝑥 ∫ 𝑑𝑦 ∫ ( 𝑑𝑥𝑑𝑦𝑑𝑧 𝑑𝑧 𝑥 + 1)(𝑦 + ) 1 𝑧 (𝑥 + 1)(𝑦 + 1)𝑧 𝑉 0 1 1 1 2 𝑒 1 2 𝑥 + 𝑦 + 2 𝑥 + 𝑦 + 2 = ∫ 𝑑𝑥 ∫ [ ln = ∫ ( 𝑧] | 𝑑𝑦 𝑑𝑥 ∫ 𝑥 + 1)(𝑦 + 1) 1 (𝑥 + 1)(𝑦 + 1) 𝑑𝑦 0 1 0 1 1 2 1 2 1 2 (𝑥 + 1) + (𝑦 + 1) 1 1 = ∫ 𝑑𝑥 ∫ ∫ ∫ ( = ∫ 𝑑𝑥 𝑑𝑦 + ∫ 𝑑𝑥 𝑑𝑦 𝑥 + 1)(𝑦 + 1) 𝑑𝑦 𝑦 + 1 𝑥 + 1 0 1 0 1 0 1 PHAM THANH TUNG 1 11 = ∫(ln 3 − ln 2)𝑑𝑥 + ∫
𝑑𝑥 = (ln 3 − ln 2) + ln 2 = ln 3 𝑥 + 1 0 0
Câu 6: Tính thể tích miền 𝑉 giới hạn bởi các mặt 𝑥 = −(𝑦2 + 𝑧2) và 𝑥 = −1 Giải:
Xét giao tuyến của hai mặt 𝑥 = −(𝑦2 + 𝑥2) và 𝑥 = −1
⇒ −(𝑦2 + 𝑧2) = −1 ⇔ 𝑦2 + 𝑧2 = 1 Hình chiếu c a mi ủ
ền 𝑉 lên 𝑂𝑦𝑧 là 𝐷: 𝑦2 + 𝑧2 ≤ 1 Thể tích miền 𝑉 là:
𝑉 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 = ∬ 1 [ − (𝑦2 + 𝑧2)] 𝑑𝑦𝑑𝑧 𝑉 𝐷 𝑦 = 𝑟 cos 𝜑 0 ≤ Đặt { , 𝑟 ≤ 1
𝑧 = 𝑟 sin 𝜑 𝐽 = 𝑟 ⇒ 𝐷: { 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 1 𝜋
⇒ 𝑉 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 = ∬ 1 [ − (𝑦2 + 𝑧2)]
𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫(1 − 𝑟2). 𝑟𝑑𝑟 = (đvtt) 2 𝑉 𝐷 0 0 cos
Câu 7: Tìm giới hạn lim 𝑦 ∫ arctan(𝑥 − 𝑦)𝑑𝑥 𝑦→0 sin 𝑦 Giải: cos 𝑦
Đặt 𝐼(𝑦) = ∫ arctan(𝑥 − 𝑦)𝑑𝑥 sin 𝑦
𝑓(𝑥, 𝑦) = arctan(𝑥 − 𝑦) liên tục với (𝑥, 𝑦) ∈ 𝑅2 Ta có: {
cos 𝑦 liên tục với y ∈ R
⇒ 𝐼(𝑦) liên t c trên ụ 𝑅
sin 𝑦 liên tục với y ∈ R cos 𝑦 1
⇒ lim ∫ arctan(𝑥 − 𝑦)𝑑𝑥
= 𝐼(0) = ∫ arctan 𝑥 𝑑𝑥 𝑦→0 sin 𝑦 0 1
Đặt {𝑢 = arctan 𝑥⇒ {𝑑𝑢 = 𝑑𝑥 𝑑𝑣 = 𝑑𝑥 1 + 𝑥2 𝑣 = 𝑥 PHAM THANH TUNG 1 1 1 1 𝑥 𝜋 1 1 𝜋 ln 2
∫ arctan 𝑥 𝑑𝑥 = 𝑥. arctan 𝑥 | − ∫ 𝑑𝑥 = − ∫ = − 1 + 𝑑(𝑥2) 𝑥2 4 2 1 + 𝑥2 4 2 0 0 0 0 cos 𝑦 𝜋 ln 2
Vậy lim ∫ arctan(𝑥 − 𝑦)𝑑𝑥 = − 𝑦→0 4 2 sin 𝑦
Câu 8: Tìm điểm có độ cong nhỏ nhất của đường 𝑥2 + 4𝑦2 = 4𝑥 Giải: (𝑥 − 2)2 Ta c :
ó 𝑥2 + 4𝑦2 = 4𝑥 ⇔ (𝑥 − 2)2 + 4𝑦2 = 4 ⇔ + 𝑦2 = 1 4 𝑥 = 2 + 2 cos 𝑡 Đặ
𝑥′ = −2 sin 𝑡 , 𝑥′ = −2 cos 𝑡 𝑡 { ⇒ { 𝑦 = sin 𝑡
𝑦′ = cos 𝑡 , 𝑦′ = − sin 𝑡 Độ ủ
cong c a đường cong tại một điểm ng v ứ ới 𝑡 bất k là: ỳ
|𝑥′𝑦′ − 𝑥′ . 𝑦′| 2 5 3 −3/2 𝐶 = = = 2. ( − cos 2𝑡) 3/2 3/2 (𝑥′2 + 𝑦′2) 5 3 2 2 ( 2 − 2cos2𝑡) −3 3 5 3 −5/2 −9 sin 2𝑡 −18 sin 𝑡 . cos 𝑡 Xét 𝐶′(𝑡) = 2. . . 2. sin 2𝑡 . ( − cos 2𝑡) = = 2 2 2 2 5 3 5/2 5 3 5/2 ( 2 − 2 cos2𝑡) ( 2 − 2 cos2𝑡) 𝑡 = 0
𝐶′(𝑡) = 0 ⇔ [sin 𝑡 = 0 ⇔ [ 𝑡 = 𝜋 cos 𝑡 = 0 𝜋 𝑡 = ± 2
(Để bài toan bớt phức tạp, chỉ xét giá trị của 𝑡 trong một vòng lượng giác) 𝑡 𝜋 𝜋 −2𝜋 − 0 𝜋 2 2 𝐶′(𝑡) + 0 − + 0 − 0 + 0 0 − 𝐶(𝑡)
Từ bảng biến thiên ⇒ 𝐶(𝑡) đạt giá trị nhỏ nhất tại các điểm làm cho cos 𝑡 = 1 −𝜋 𝜋 (𝑡 = , , … ) 2 2 PHAM THANH TUNG 𝑥 = 2, 𝑦 = −1
Với cos 𝑡 = 0 ⇔ sin 𝑡 = ±1 ⇒ [ 𝑥 = 2, 𝑦 = 1
Vậy đường cong có độ cong nhỏ nhấ ại điể t t m (2, −1) hoặc (2,1) Câu 9: Tính (𝑦 + 1)2 ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 𝑥2 + 𝑦2 + 𝑧2 + 3
Với 𝑉 xác định bởi 𝑥2 + 𝑦2 + 𝑧2 ≤ 1 Giải: (𝑦 − 1)2 Đặ𝑡 𝐼 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 𝑥2 + 𝑦2 + 𝑧2 + 3 𝑉 𝑦2 + 2𝑦 + 1 𝑦2 + 1 2𝑦𝑑𝑥𝑑𝑦𝑑𝑧 𝐼 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 + ∭ 𝑥2 + 𝑦2 + 𝑧2 + 3 𝑥2 + 𝑦2 + 𝑧2 + 3 𝑥2 + 𝑦2 + 𝑧2 + 3 𝑉 𝑉 𝑉 2𝑦 lẻ với biến 𝑦 2𝑦 { 𝑥2 + 𝑦2 + 𝑧2 + 3 ⇒ ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 = 0 𝑥2 + 𝑦2 + 𝑧2 + 3 Miền 𝑉 đối xứng qu a 𝑂𝑥𝑧 𝑉 𝑦2 + 1 ⇒ 𝐼 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 (1) 𝑥2 + 𝑦2 + 𝑧2 + 3 𝑉 PHAM THANH TUNG
Đổi vai trò của 𝑥, 𝑦 miền 𝑉 không thay đổi 𝑥2 + 1 ⇒ 𝐼 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 (2) 𝑥2 + 𝑦2 + 𝑧2 + 3 𝑉
Đổi vai trò của 𝑦, 𝑧 miền 𝑉 không thay đổi 𝑧2 + 1 ⇒ 𝐼 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 (3) 𝑥2 + 𝑦2 + 𝑧2 + 3 𝑉 𝑥2 + 𝑦2 + 𝑧2 + 3 4 4
(1) + (2) + (3) ⇒ 3𝐼 = ∭
𝑑𝑥𝑑𝑦𝑑𝑧 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 = 𝜋 ⇒ 𝐼 = 𝜋 𝑥2 + 𝑦2 + 𝑧2 + 3 3 9 𝑉 𝑉 Câu 10: Cho hàm s ố 𝑦
𝐼(𝑦) = ∫ ln(1+𝑥𝑦) 𝑑𝑥. Tính 𝐼′( ) 1 0 1+𝑥2 Giải: ln(1 + 𝑥𝑦) 𝑥 Đặt 𝑓(𝑥, 𝑦) = ⇒ 𝑓′(𝑥, 𝑦) = 1 + 𝑥2 𝑦 (1 + 𝑥2)(1 + 𝑥𝑦)
𝑓(𝑥, 𝑦) liên tục, k ả h vi trên [0; 2] × [0; ] 2 Ta có: { 𝑓′( 0; 2] × 0; 2
𝑦 𝑥, 𝑦) liên tục trên [ [ ]
⇒ 𝐼(𝑦) khả vi với 𝑦 ∈ 0; [ 2 ]
𝑦2 = 𝑦 liên tục, k ả h vi trên [0; 2] 𝑦2(𝑦) 𝐼′(𝑦) = 𝑓(𝑦 ′ ′ ( ′(
2(𝑦), 𝑦). 𝑦2(𝑦) − 𝑓(𝑦1(𝑦), 𝑦). 𝑦1 𝑦) + ∫ 𝑓𝑦 𝑥, 𝑦) 𝑑𝑥 𝑦1(1) 𝑦 ln(1 + 𝑦2) ln 1 𝑥 ⇒ 𝐼′(𝑦) = − . 0 + ∫ 𝑑𝑥 1 + 𝑦2 1 (1 + 𝑥2)(1 + 𝑥𝑦) 0 1 ln 2 𝑥 ⇒ 𝐼′(1) = + ∫ 𝑑𝑥 2 (1 + 𝑥2)(1 + 𝑥) 0 1 1 1 𝑥 −1 𝑥 + 1 ln 2 ln 2 1 ∫ 𝑑𝑥 = ∫ 𝑑𝑥 + ∫ 𝑑𝑥 = − + + . arctan 1 (1 + 𝑥2)(1 + 𝑥) 2(1 + 𝑥) 2(1 + 𝑥2) 2 4 2 0 0 0 ln 2 𝜋 ⇒ 𝐼′(1) = + 4 8 PHAM THANH TUNG
LỜI GIẢI THAM KHẢO ĐỀ THI GIỮA KÌ 20192 (ĐỀ 2)
Câu 1: Viết phương trình tiếp tuyến và pháp tuyến của đường cong 𝑥3 + 𝑦3 = 9𝑥 𝑦 tại điểm (4,2) Giải:
Đặt 𝐹(𝑥, 𝑦) = 𝑥3 + 𝑦3 − 9𝑥𝑦 ⇒ 𝐹′ = 3 ′ = 3 𝑥 𝑥2 − 9𝑦, 𝐹𝑦 𝑦2 − 9𝑥
Tại (4,2), tai có 𝐹′(4,2) = 30, ′ = −24 𝑥 𝐹𝑦
Phương trình tiếp tuyến của đường cong tại (4,2) là:
30(𝑥 − 4) − 24(𝑦 − 2) = 0 ⇔ 30𝑥 − 24𝑦 − 72 = 0
Phương trình pháp tuyến của đường cong tại (4,2) là: 𝑥 − 4 𝑦 − 2 = 30 −24 𝑥 = 2(𝑡 − sin 𝑡)
Câu 2: Tính độ cong của đường { ại điểm ứ ới 𝑡 = 𝜋/2 𝑦 = 2(1 − cos 𝑡) t ng v Giải: 𝑥 = 2(𝑡 − sin 𝑡)
𝑥′(𝑡) = 2 − 2 cos 𝑡 𝑥′ (𝑡) = 2 sin 𝑡 Ta có { ⇒ { 𝑦 = 2(1 − cos 𝑡) ⇒ { 𝑦′(𝑡) = 2 sin 𝑡 𝑦′ (𝑡) = 2 cos 𝑡 𝜋 𝜋 𝑥′ ( ) = 2 , 𝑥′ ( ) = 2 Tại 𝑡 = 𝜋/2 ⇒ { 2 2 𝜋 𝜋 𝑦′ ( ) = 2 , 𝑦′ ( ) = 0 2 2 Độ ủ
cong c a 𝐿 tại 𝑡 = 𝜋/2 là: |2.0 − 2.2| 22 √2 𝐶(𝑡 = 0) = 3 = 9 = (22 + 22) 8 2 22
Câu 3: Tìm hình bao của h ọ đường cong
2𝑥2 − 4𝑥𝑐 + 2𝑦2 + 𝑐2 = 0, 𝑐 là tham s , ố 𝑐 ≠ 0 Giải:
Đặt 𝐹(𝑥, 𝑦, 𝑐) = 2𝑥2 − 4𝑥𝑐 + 2𝑦2 + 𝑐2 với 𝑐 ≠ 0 PHAM THANH TUNG 𝐹′(𝑥, 𝑦, 𝑐) = 0 4𝑥 − 4𝑐 = 0 𝑥 = 𝑐 Xét { 𝑥 𝐹′( 4 𝑦 = 0
𝑦 𝑥, 𝑦, 𝑐) = 0 ⇔ { 𝑦 = 0 ⇔ {
Điểm (𝑐, 0) không thuộc họ đườ
ng cong 2𝑥2 − 4𝑥𝑐 + 2𝑦2 + 𝑐2 = 0 ⇒ H
ọ đường cong không có điểm kì dị. 𝐹(𝑥, 𝑦, 𝑐) = 0 Xét { 𝑥𝑐 2 2 𝑥𝑐 2 2 ⇔ {2𝑥2 − 4 + 2𝑦 + 𝑐 = 0 𝐹′(
𝑐 𝑥, 𝑦, 𝑐) = 0 ⇔ {2𝑥2 − 4 + 2𝑦 + 𝑐 = 0 −4𝑥 + 2𝑐 = 0 𝑐 = 2𝑥
⇒ 2𝑥2 − 4𝑥. 2𝑥 + 2𝑦2 + (2𝑥)2 = 0 ⇔ −𝑥2 + 𝑦2 = 0 ⇔ 𝑦 = ±𝑥
Do 𝑐 ≠ 0 nên 𝑥 ≠ và 0 𝑦 ≠ 0
Vậy hình bao của họ đường cong là đường 𝑦 = ±𝑥 trừ 𝑂(0,0)
Câu 4: Tìm giới hạn 𝜋 2
lim ∫ cos(𝑥2𝑦 + 3𝑥 + 𝑦2)𝑑𝑥 𝑦→0 0 Giải:
Ta có: 𝑓(𝑥, 𝑦) = cos(𝑥2𝑦 + 3𝑥 + 𝑦2) là hàm s liên t ố c trên ụ [0; 𝜋/2] × 𝑅 𝜋 2
⇒ 𝐼(𝑦) = ∫ cos(𝑥2𝑦 + 3𝑥 + 𝑦2)𝑑𝑥
là hàm số liên tục trên 𝑅. 0 𝜋 𝜋 2 2 −1
⇒ lim ∫ cos(𝑥2𝑦 + 3𝑥 + 𝑦2)𝑑𝑥
= 𝐼(0) = ∫ cos(3𝑥)𝑑𝑥 = 𝑦→0 3 0 0
Câu 5: Đổi thứ t l ự ấy tích phân: 1 √2−𝑥2 ∫ 𝑑𝑥 ∫ 𝑓(𝑥, 𝑦)𝑑𝑦 0 𝑥2 Giải: 0 ≤ 𝑥 ≤ 1 Miền 𝐷: {
𝑥2 ≤ 𝑦 ≤ √2 − 𝑥2
Đổi thứ tự lấy tích phân PHAM THANH TUNG
Chia miền 𝐷 thành hai miền 0 ≤ 𝑥 ≤ 𝑦 √ 0 ≤ 𝑥 ≤ 2 √ − 𝑦2 𝐷1 : { , 𝐷 0 ≤ 2 : { 𝑦 ≤ 1 1 ≤ 𝑦 ≤ √2 1 √2−𝑥2 1 √𝑦 √2 √2−𝑦2 ⇒ ∫ 𝑑𝑥 ∫ 𝑓(𝑥, 𝑦)𝑑𝑦
= ∫ 𝑑𝑦 ∫ 𝑓(𝑥, 𝑦)𝑑𝑥 + ∫ 𝑑𝑦 ∫ 𝑓(𝑥, 𝑦)𝑑𝑥 0 𝑥2 0 0 1 0
Câu 6: Tính diện tích phần mặt 𝑧 = 𝑥2 + 𝑦2 + n
2 ằm trong mặt 𝑥2 + 𝑦2 = 9 Giải:
Hình chiếu của phần mặt 𝑧 = 𝑥2 + 𝑦2 + n 2 ằm trong mặt tr ụ 𝑥2 + 𝑦2 = 9 𝑂𝑥𝑦 lên là: 𝐷: 𝑥2 + 𝑦2 ≤ 9 Ta có: 𝑧′ = 2 ′ = 2 𝑥 𝑥, 𝑧𝑦 𝑦 Diệ ầ n tích c n tính là: 2 𝑆 = ∬ 1 √ + (𝑧′ ′ = √ 2 + 4 𝑥)2 + (𝑧 ∬ 1 + 4𝑥 𝑦2𝑑𝑥𝑑𝑦 𝑦) 𝑑𝑥𝑑𝑦 𝐷 𝐷 𝑥 = 𝑟 cos 𝜑 0 ≤ 𝑟 ≤ 3 Đặt { ,
𝑦 = 𝑟 sin 𝜑 𝐽 = 𝑟 ⇒ 𝐷: { 0 ≤ 𝜑 ≤ 2𝜋 PHAM THANH TUNG 2𝜋 3 2𝜋 3 1
⇒ 𝑆 = ∫ 𝑑𝜑 ∫ √1 + 4𝑟2. 𝑟𝑑𝑟 =
∫ 𝑑𝜑 ∫ √1 + 4𝑟2𝑑(𝑟2) 2 0 0 0 0 2𝜋 9 1 1 1 (37√37 − 1)𝜋
= ∫ 𝑑𝜑 ∫ √1 + 4𝑢𝑑𝑢 = . 2𝜋. (37√37 − 1 ) = (đvdt) 2 2 6 6 0 0
Câu 7: Tính thể tích của miền giới hạn bởi các mặt cong 𝑦 = 𝑥2, 𝑥 = 𝑦2, 𝑧 = 𝑥2 và mặt 𝑂𝑥𝑦 Giải:
Gọi miền cần tính thể tích là 𝑉. 𝑦 = 𝑥2
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là miền 𝐷 giới hạn bởi {𝑥 = 𝑦2
⇒ 𝐷: {𝑥2 ≤ 𝑦 ≤ √𝑥 0 ≤ 𝑥 ≤ 1 0 ≤ 𝑧 ≤ 𝑥2
Miền 𝑉: { 0 ≤ 𝑥 ≤ 1 𝑥2 ≤ 𝑦 ≤ √𝑥 Thể tích miền 𝑉 là: 1 √𝑥 1 3
𝑉 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 = ∬ 𝑥2𝑑𝑥𝑑𝑦 = ∫ 𝑑𝑥
∫ 𝑥2𝑑𝑦 = ∫ 𝑥2(√𝑥 − 𝑥2)𝑑𝑥 = (đvtt) 35 𝑉 𝐷 0 𝑥2 0
Câu 8: Tính ∬ (2𝑦2 + 3)𝑑𝑥𝑑𝑦 , với 𝐷 là mi nh b ền xác đị ởi 𝐷 𝑥2 + (𝑦 − 1)2 ≤ 1 Giải: 𝑥 = 𝑟 cos 𝜑 Đặt { ,
𝑦 = 1 + 𝑟 sin 𝜑 𝐽 = 𝑟 0 ≤ 𝑟 ≤ 1 Miền 𝐷: {0 ≤ 𝜑 ≤ 2𝜋
∬(2𝑦2 + 3)𝑑𝑥𝑑𝑦
= 2 ∬ 𝑦2𝑑𝑥𝑑𝑦 + 3. 𝑆𝐷 𝐷 𝐷 PHAM THANH TUNG 2𝜋 1 2𝜋 1 2 1
= 2 ∫ 𝑑𝜑 ∫(1 + 𝑟 sin 𝜑)2. 𝑟𝑑𝑟 + 3. 𝜋. 12 = 2 ∫ ( + sin 𝜑 + sin2 𝜑) 𝑑𝜑 + 3𝜋 2 3 4 0 0 0 2𝜋 𝜋 11 = 2 ( + ) + 3𝜋 = 𝜋 2 4 2
Câu 9: Tính ∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧 với 𝑉 xác định bởi 𝑉 𝑥2 + 𝑦2 ≤ 1, 𝑦2 + 𝑧2 ≤ 4, 𝑧 ≥ 0 Giải:
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 1 0 ≤ Miền 𝑧 ≤ √4 − 𝑦2 𝑉: { 𝐷: 𝑥2 + 𝑦2 ≤ 1 √4−𝑦2 1
⇒ 𝐼 = ∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧 = ∬ 𝑑𝑥𝑑𝑦 ∫ 𝑧𝑑𝑧 =
∬(4 − 𝑦2)𝑑𝑥𝑑𝑦 2 𝑉 𝐷 0 𝐷 𝑥 = 𝑟 cos 𝜑 0 ≤ Đặt { , 𝑟 ≤ 1
𝑦 = 𝑟 sin 𝜑 𝐽 = 𝑟 ⇒ 𝐷: { 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 1 2𝜋 1 1 1 1 15𝜋 15𝜋 ⇒ 𝐼 =
∫ 𝑑𝜑 ∫[4 − (𝑟 sin 𝜑)2]. 𝑟𝑑𝑟 = ∫ [2 − (sin 𝜑)2] 𝑑𝜑 = . = 2 2 4 2 4 8 0 0 0 Hình vẽ minh họa PHAM THANH TUNG
Câu 10: Tính tích phân bội ba ∭ 𝑦2𝑒𝑧𝑑𝑥𝑑𝑦𝑑𝑧, trong đó 𝑉
𝑉: 0 ≤ 𝑥 ≤ 1, 𝑥 ≤ 𝑦 ≤ 1, ≤ 𝑧 ≤ 𝑥𝑦 + 2 Giải: 0 ≤ 𝑥 ≤ 1 0 ≤ 𝑥 ≤ 𝑦
Miền 𝑉: { 𝑥 ≤ 𝑦 ≤ 1 ⇔ { 0 ≤ 𝑦 ≤ 1
(Đổi thứ tự lấy tích phân 𝑥 v à 𝑦) 1 ≤ 𝑧 ≤ 𝑥𝑦 + 2 1 ≤ 𝑧 ≤ 𝑥𝑦 + 2 1 𝑦 𝑥𝑦+2 1 𝑦
⇒ 𝐼 = ∫ 𝑑𝑦 ∫ 𝑑𝑥 ∫ 𝑦2𝑒𝑧𝑑𝑧
= ∫ 𝑑𝑦 ∫ 𝑦2(𝑒𝑥𝑦+2 − 𝑒)𝑑𝑥 0 0 1 0 0 𝑦 𝑦 𝑦 𝑦
∫ 𝑦2(𝑒𝑥𝑦+2 − 1)𝑑𝑥
= ∫ 𝑦2𝑒𝑥𝑦+2𝑑𝑥 − ∫ 𝑦2𝑑𝑥
= ∫ 𝑦𝑒𝑥𝑦+2𝑑(𝑥𝑦 + 2) − 𝑒. 𝑦3 0 0 0 0 𝑦 = 𝑦𝑒𝑥𝑦+2 |
− 𝑒. 𝑦3 = 𝑦𝑒𝑦2+2 − 𝑒2𝑦 − 𝑒. 𝑦3 0 1 𝑦 1 1 1 𝑒2 𝑒
⇒ ∫ 𝑑𝑦 ∫ 𝑦2(𝑒𝑥𝑦+2 − 1)𝑑𝑥
= ∫(𝑦𝑒𝑦2+2 − 𝑒2𝑦 − 𝑦3)𝑑𝑦 = ∫ 𝑒𝑦2+2𝑑(𝑦2) − − 2 2 4 0 0 0 0 1 𝑒 = 𝑒3 − 𝑒2 − 2 4 PHAM THANH TUNG
LỜI GIẢI THAM KHẢO ĐỀ THI GIỮA KÌ 20192 (ĐỀ 3)
Câu 1: Viết phương trình tiếp diện và pháp tuyến của đường cong 𝑥 = 2(𝑡 − sin 𝑡) {
𝑦 = 2(1 − cos 𝑡) tại 𝑡 = 𝜋 2 Giải: 𝑥 = 2(𝑡 − sin 𝑡)
𝑥′(𝑡) = 2 − 2 cos 𝑡 { . 𝑦 = 2(1 − cos 𝑡) ⇒ { 𝑦′(𝑡) = 2 sin 𝑡 𝜋 𝜋 𝜋 𝑥′ ( ) = 2, 𝑥 ( ) = 𝜋 − 2 Tại 2 2 𝑡 = ⇒ { 2 𝜋 𝜋 𝑦′ ( ) = 2, 𝑦 ( ) = 2 2 2 𝑥 − 𝜋 + 2 𝑦 − 2 𝜋
phương trình tiếp tuyến: = ⇔ 𝑦 = 𝑥 − 𝜋 + 4 Tại 2 2 𝑡 = ⇒ { 2 𝑥 − 𝜋 + 2 𝑦 − 2
phương trình pháp tuyến: = − ⇔ 𝑦 = 𝜋 − 𝑥 2 2
Câu 2: Tính độ cong của đường cong 𝑦 = 𝑒2𝑥 tại 𝐴(0,1) Giải:
𝑦 = 𝑒2𝑥 ⇒ 𝑦′(𝑥) = 2𝑒2𝑥, 𝑦′ (𝑥) = 4𝑒2𝑥. Tại 𝐴(0,1) ⇒ 𝑦′(0) = 2, 𝑦′ (0) = 4
Độ cong của đường cong tại điểm 𝐴(0,1) là: |𝑦′ (0)| 4 𝐶(𝐴) = 3 = (1 + 𝑦′(0)2) 2 5√5
Câu 3: Tìm hình bao của h ọ đường cong
𝑦 = 4𝑐𝑥3 + 𝑐4, với c là tham số Giải:
Đặt 𝐹(𝑥, 𝑦, 𝑐) = 𝑦 − 4𝑐𝑥3 − 𝑐4 𝐹′ = 0 Xét { 𝑥
⇒ Vô nghiệm ⇒ Họ đường cong không có điểm kì dị.
𝐹′𝑦 = 0 ⇔ {−12𝑐𝑥2 = 0 1 = 0 𝐹 = 0 Xét {
⇔ {𝑦 − 4𝑐𝑥3 − 𝑐4 = 0 𝐹′ 3 3
𝑐 = 0 ⇔ {𝑦 − 4𝑐𝑥3 − 𝑐4 = 0 −4𝑥 − 4𝑐 = 0 −𝑥 = 𝑐 PHAM THANH TUNG
⇒ 𝑦 − 4(−𝑥)𝑥3— 𝑥4 = 0 ⇔ 𝑦 + 4𝑥4 − 𝑥4 = 0
Vậy hình bao của họ đường cong là 𝑦 = −3𝑥4
Câu 4: Đổi thứ t l ự ấy tích phân 1 √2−𝑦2 ∫ 𝑑𝑦 ∫ 𝑓(𝑥, 𝑦)𝑑𝑥 0 √𝑦 Giải:
Miền lấy tích phân (𝐷): {√𝑦 ≤ 𝑥 ≤ √2 − 𝑦2 0 ≤ 𝑦 ≤ 1
Đổi thứ tự lấy tích phân, chia miền (𝐷) ầ thành 2 ph n: 0 ≤ 𝑥 ≤ 1 1 ≤ √ ( 𝑥 ≤ 2 𝐷1): {
0 ≤ 𝑦 ≤ 𝑥2 và (𝐷2): { 0 ≤ 𝑦 ≤ √2 − 𝑥2 1 𝑥2 √2 √2−𝑥2
⇒ 𝐼 = ∫ 𝑑𝑥 ∫ 𝑓(𝑥, 𝑦)𝑑𝑦 + ∫ 𝑑𝑥
∫ 𝑓(𝑥, 𝑦)𝑑𝑦 0 0 1 0 PHAM THANH TUNG
Câu 5: Tính ∬ 4𝑦𝑑𝑥𝑑𝑦, với 𝐷 là mi nh b ền xác đị ởi: 𝐷 𝑥2 + 𝑦2 ≤ 1, 𝑥 + 𝑦 ≥ 1 Giải:
Miền 𝐷: {1 − 𝑥 ≤ 𝑦 ≤ √1 − 𝑥2 0 ≤ 𝑥 ≤ 1 1 √1−𝑥2 1 √1 − 𝑥2
∬ 4𝑦 𝑑𝑥𝑑𝑦 = ∫ 𝑑𝑥
∫ 4𝑦𝑑𝑦 = ∫ (2𝑥2 | ) 𝑑𝑥 𝐷 0 1−𝑥 0 1 − 𝑥 1 2
= 2 ∫[(1 − 𝑥2) − (1 − 𝑥)2]𝑑𝑥 = 3 0
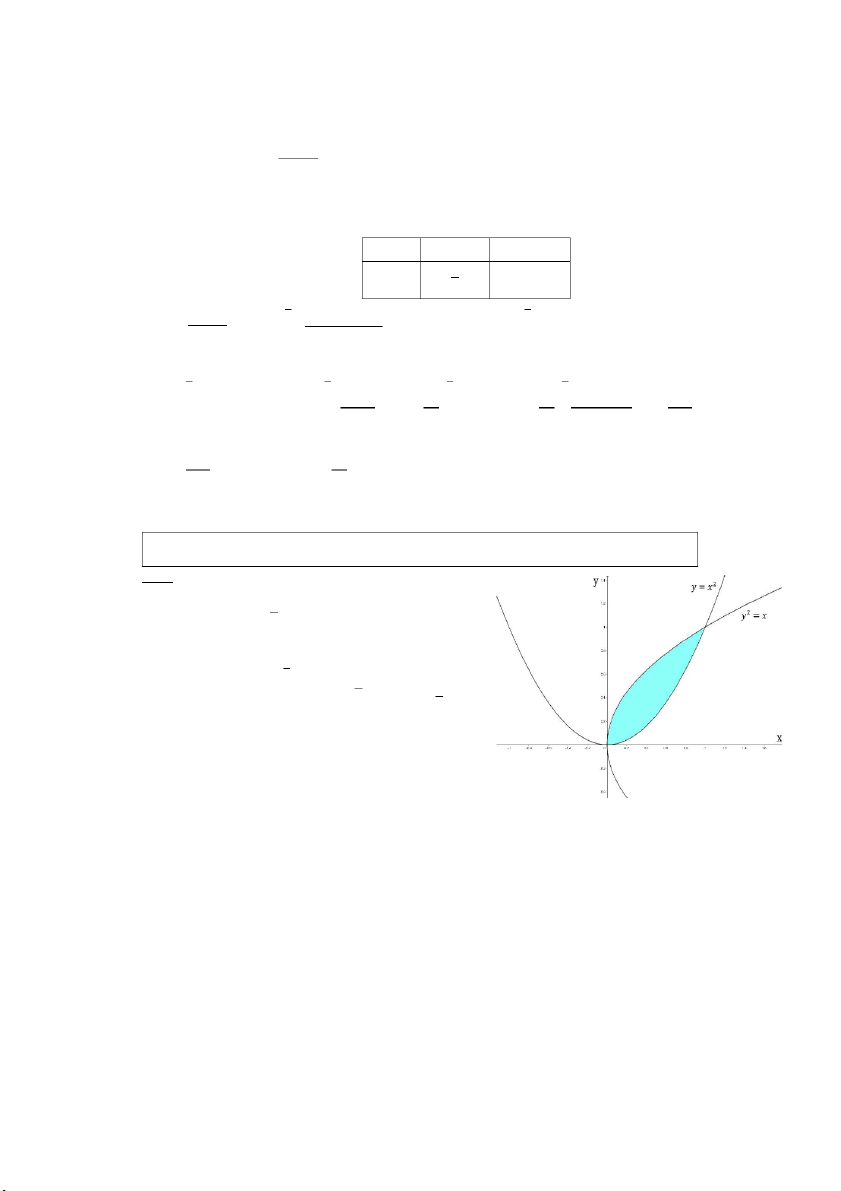
Câu 6: Tính thể tích miền 𝑉 giới hạn bởi mặt 𝑂𝑥𝑦 và mặt 𝑧 = 𝑥2 + 𝑦2 − 4 Giải:
Miền (𝑉): 𝑥2 + 𝑦2 − 4 ≤ 𝑧 ≤ 0
Hình chiếu của (𝑉) lên 𝑂𝑥𝑦 là: (𝐷): 𝑥2 + 𝑦2 ≤ 4 𝑥 = 𝑟 cos 𝜑 0 ≤ Đặt { 𝑟 ≤ 2 ề (
𝑦 = 𝑟 sin 𝜑 𝐽 = 𝑟. Mi n 𝐷): { 0 ≤ 𝜑 ≤ 2𝜋 0 ≤ 𝑟 ≤ 2
Miền (𝑉) trong tọa độ trụ là: (𝑉): { 0 ≤ 𝜑 ≤ 2𝜋 𝑟2 − 4 ≤ 𝑧 ≤ 0 Thể tích miền 𝑉 là: 2𝜋 2 0 2𝜋 1 𝑉( = ∫ ∫ ∫ ∫
𝑉) = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 𝑑𝜑 𝑑𝑟 𝑟𝑑𝑧 = ∫ 𝑑𝜑 𝑟(−𝑟2 + 4)𝑑𝑟 = 8𝜋 (đvtt) 𝑉 0 0 𝑟2−4 0 0 PHAM THANH TUNG Câu 7: Tính
∭ √𝑥2 + 𝑦2 + 𝑧2𝑑𝑥𝑑𝑦𝑑𝑧 𝑉
Với 𝑉 xác định bởi 𝑥2 + 𝑦2 + 𝑧2 ≤ 1, √3(𝑥2 + 𝑦2) ≤ 𝑧 Giải:
Miền 𝑉: √3(𝑥2 + 𝑦2) ≤ 𝑧 ≤ √1 − (𝑥2 + 𝑦2) 𝑥 = 𝑟 sin 𝜃 cos 𝜑
Đặt {𝑦 = 𝑟 sin 𝜃 sin 𝜑 |𝐽| = 𝑟2 sin 𝜃 𝑧 = 𝑟 cos 𝜃 0 ≤ 𝑟 ≤ 1
Miền (𝑉): {0 ≤ 𝜃 ≤ 𝜋/6 0 ≤ 𝜑 ≤ 2𝜋 𝜋 2𝜋 6 1 2 − √3
∭ √𝑥2 + 𝑦2 + 𝑧2𝑑𝑥𝑑𝑦𝑑𝑧
= ∫ 𝑑𝜑 ∫ 𝑑𝜃 ∫ 𝑟. 𝑟3 sin 𝜃 𝑑𝑟 = 𝜋 4 𝑉 0 0 0
Câu 8: Tính ∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧, với 𝑉 xác định bởi 𝑥2 + 𝑦2 + 𝑧2 ≤ 6, 𝑧 ≥ 𝑥2 + 𝑦2 𝑉 Giải: 𝑥2 + 𝑦2 + 𝑧2 ≤ 6
Miền (𝑉) xác định bởi { 𝑧 ≥ 𝑥2 + 𝑦2
Hình chiếu của (𝑉) lên 𝑂𝑥𝑦 là: (𝐷): 𝑥2 + 𝑦2 ≤ 2 𝑥 = 𝑟 cos 𝜑
Đặt {𝑦 = 𝑟 sin 𝜑 𝐽 = 𝑟 ⇒ Miền 𝑧 = 𝑧 0 ≤ 𝑟 ≤ √2 (𝑉): { 0 ≤ 𝜑 ≤ 2𝜋
𝑟2 ≤ 𝑧 ≤ √6 − 𝑟2 2𝜋 √2 √6−𝑟2 2𝜋 √2 1 11
∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ 𝑧. 𝑟𝑑𝑧 =
∫ 𝑑𝜑 ∫ (6 − 𝑟2 − 𝑟4). 𝑟𝑑𝑟 = 𝜋 2 3 𝑉 0 0 𝑟2 0 0 PHAM THANH TUNG
Câu 9: Tính diện tích của miền giới hạn bởi (𝑥2 + 𝑦2)2 = 4𝑥𝑦 Giải:
Miền (𝐷) giới hạn bởi (𝑥2 + 𝑦2)2 = 4𝑥𝑦 𝑥 = 𝑟 cos 𝜑 Đặt { Miề ( đượ ớ ạ ởi đườ
𝑦 = 𝑟 sin 𝜑 𝐽 = 𝑟 ⇒ n 𝐷) c gi i h n b ng 𝑟 = 2 √ sin 2𝜑 sin 𝜑 ≥ 0 { cos𝜑 ≥ 0 0 ≤ 𝜑 ≤ 𝜋/2
Ta có: sin 2𝜑 ≥ 0 ⇔ sin 𝜑 cos 𝜑 ≥ 0 ⇔ [ sin ⇔ [ 𝜑 ≤ 0 𝜋 ≤ 𝜑 ≤ 3𝜋/2 {cos𝜑 ≤ 0 0 ≤ 𝑟 ≤ 2 √ sin 2𝜑 0 ≤ 𝑟 ≤ 2 √ sin 2𝜑 ⇒ Miền (𝐷
) được chia thành 2 phần (𝐷1): { và (𝐷 0 ≤ 2): { 𝜑 ≤ 𝜋/2 𝜋 ≤ 𝜑 ≤ 3𝜋/2 𝜋 𝜋 2 √2 sin 2𝜑 2 1 𝑆(𝐷 = ∫ 𝑑𝜑 ∫ 𝑟𝑑𝑟
= ∫ 2 sin 2𝜑 𝑑𝜑 = 1 1) = ∬ 𝑑𝑥𝑑𝑦 2 𝐷1 0 0 0 3𝜋 3𝜋 2 √2 sin 2𝜑 2 1 𝑆(𝐷 = ∫ 𝑑𝜑 ∫ 𝑟𝑑𝑟 = ∫ 2 sin 2𝜑 𝑑𝜑 = 1 2) = ∬ 𝑑𝑥𝑑𝑦 2 𝐷2 𝜋 0 𝜋
⇒ 𝑆(𝐷) = 𝑆(𝐷1) + 𝑆(𝐷2) = 2 PHAM THANH TUNG Câu 10: Cho hàm s ố 1
𝐼(𝑦) = ∫ sin(𝑥2 + 𝑥𝑦 + 𝑦2)𝑑𝑥 . Tính 𝐼′(0) 𝑦 Giải:
Đặt 𝑓(𝑥, 𝑦) = sin(𝑥2 + 𝑥𝑦 + 𝑦2) ⇒ 𝑓′𝑦 = (𝑥 + 2𝑦) cos(𝑥2 + 𝑥𝑦 + 𝑦2)
𝑓(𝑥, 𝑦) liên tục, k ả
h vi trên [−1,1] × [−1,1]
Ta có: { 𝑎(𝑦) = 𝑦, 𝑏(𝑦) = 1 liên tục, khả vi trên [−1,1] ⇒ Hàm 𝐼(𝑦 kh ) ả vi trên [−1,1] 𝑓′( trên [−1,1] × [−1,1] 𝑦 𝑥, 𝑦) liên tục 𝑏(𝑦)
𝐼′(𝑦) = 𝑓(𝑏(𝑦), 𝑦). 𝑏 ′ (𝑦) − 𝑓(𝑎( ′ ( ′( 𝑦
𝑦), 𝑦). 𝑎𝑦 𝑦) + ∫ 𝑓𝑦 𝑥, 𝑦)𝑑𝑥 𝑎(𝑦) 1
⇒ 𝐼′(𝑦) = 𝑓(1, 𝑦). 0 − 𝑓(𝑦, 𝑦). 1 + ∫(𝑥 + 2𝑦) cos(𝑥2 + 𝑥𝑦 + 𝑦2) 𝑑𝑥 𝑦 1 1 1 sin 1
⇒ 𝐼′(0) = 𝑓(1,0). 0 − 𝑓(0,0). 1 + ∫ 𝑥 cos(𝑥2) 𝑑𝑥 = ∫ cos(𝑥2) 𝑑(𝑥2) = 2 2 0 0 PHAM THANH TUNG
LỜI GIẢI THAM KHẢO ĐỀ GIỮA KÌ 20193 (ĐỀ 1)
Câu 1: Xác định độ ại đườ cong t ng cong 𝑥 = 4 √ 𝑦 + t 1 ại điểm (3,1) Giải: (𝑥 − 1)2 𝑥 = 4 √ 𝑦 + 1 ⇔ 4
√ 𝑦 = 𝑥 − 1 ⇔ 𝑦 = (𝑥 ≥ 1) 4 𝑥 − 1 1 ⇒ 𝑦′(𝑥) = , 𝑦′ (𝑥) = 2 2 1
Tại (3,1) ⇒ 𝑦′ = 1, 𝑦′ = 2 Độ cong của đườ ạ ng cong t i (3,1) là: |𝑦′ | √2 𝐶(3,1) = = 3 (1 + 8 𝑦′2) 2
Câu 2: Viết phương trình pháp tuyến và tiếp diện của mặt cong 𝑦2 = 3(𝑥2 + 𝑧2) tại điểm (√2, 3,1) Giải: 𝐹′𝑥 = −6𝑥
Đặt 𝐹(𝑥, 𝑦, 𝑧) = 𝑦2 − 3(𝑥2 + 𝑧2) ⇒ { 𝐹′𝑦 = 2𝑦 𝐹′𝑧 = −6𝑧 Tại (√2, 3,1), 𝐹 ta có: ′ ′ = 6, ′ = −6 𝑥 = −6√2, 𝐹𝑦 𝐹𝑧
Phương trình pháp tuyến của mặt cong tại (√2, 3,1) là: 𝑥 − √2 𝑦 − 3 𝑧 − 1 𝑥 − √2 𝑦 − 3 𝑧 − 1 = = ⇔ = = −6√2 6 −6 −√2 1 −1
Phương trình tiếp diện của mặt cong tại (√2, 3,1) là:
−6√2(𝑥 − √2) + 6(𝑦 − 3) − 6(𝑧 − 1) = 0 ⇔ −√2𝑥 + 𝑦 − 𝑧 = 0
Câu 3: Tìm hình bao của h
ọ đường cong: 𝑦 = (2𝑥 + 3𝑐)4 Giải:
Đặt 𝐹(𝑥, 𝑦, 𝑐) = 𝑦 − (2𝑥 + 3𝑐)4 PHAM THANH TUNG 𝐹′(𝑥, 𝑦, 𝑐) = 0 Xét { 𝑥 ⇒ Vô nghiệm 𝐹′(
𝑦 𝑥, 𝑦, 𝑐) = 0 ⇔ {−8(2𝑥 + 3𝑐)3 = 0 1 = 0 ⇒ H
ọ đường cong không có điểm kì dị. 𝑦 = (2𝑥 + 3𝑐)4 𝐹(𝑥, 𝑦, 𝑐) = 0 4 𝑦 = (2𝑥 + 3𝑐)4 3.2 Xét { ⇔ { −2 ⇒ 𝑦 = 2 ( 𝑥 − 𝑥) = 0 𝐹′(
𝑐 𝑥, 𝑦, 𝑐) = 0 ⇔ { −12(2𝑥 + 3𝑐)3 = 0 𝑥 = 𝑐 3 3
Vậy hình bao của họ đường cong là đường 𝑦 = 0
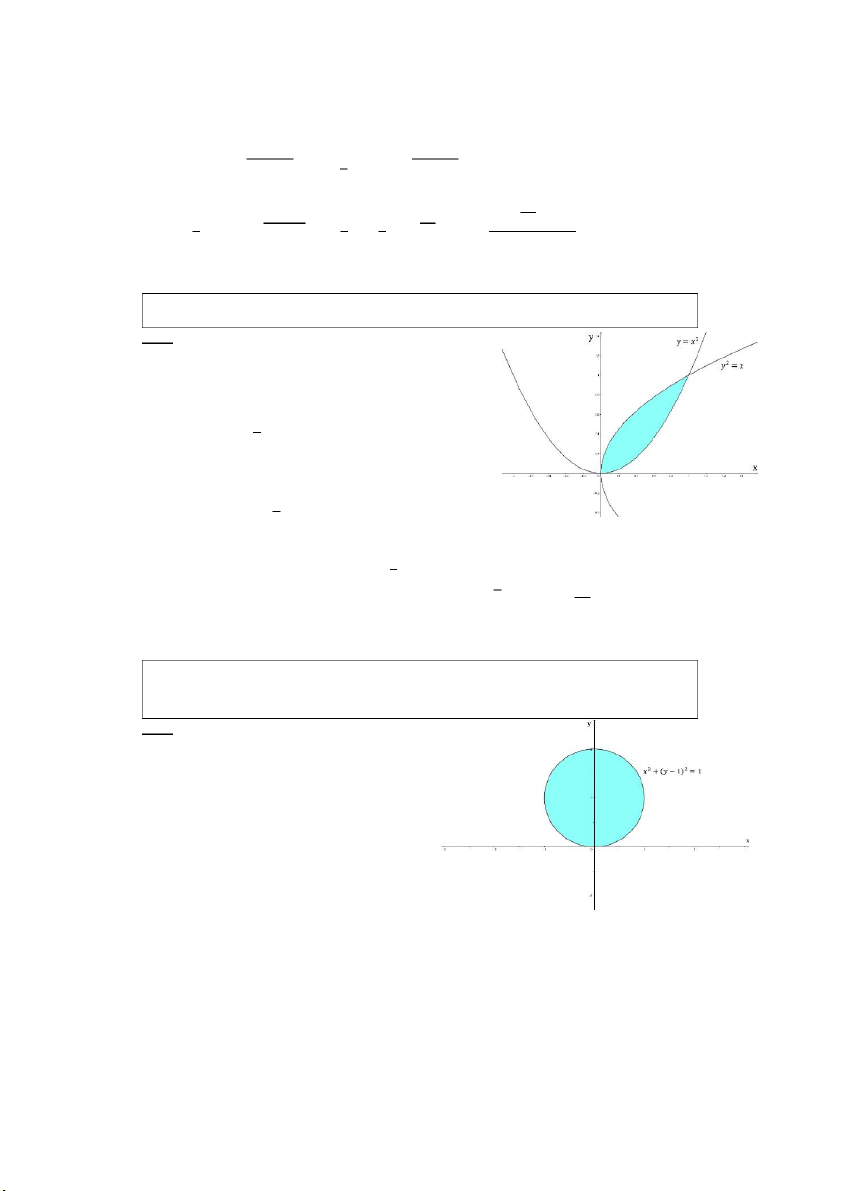
𝐂â𝐮 𝟒: Tính ∬ √𝑥2 + 𝑦2𝑑𝑥𝑑𝑦 , với D l à m ền
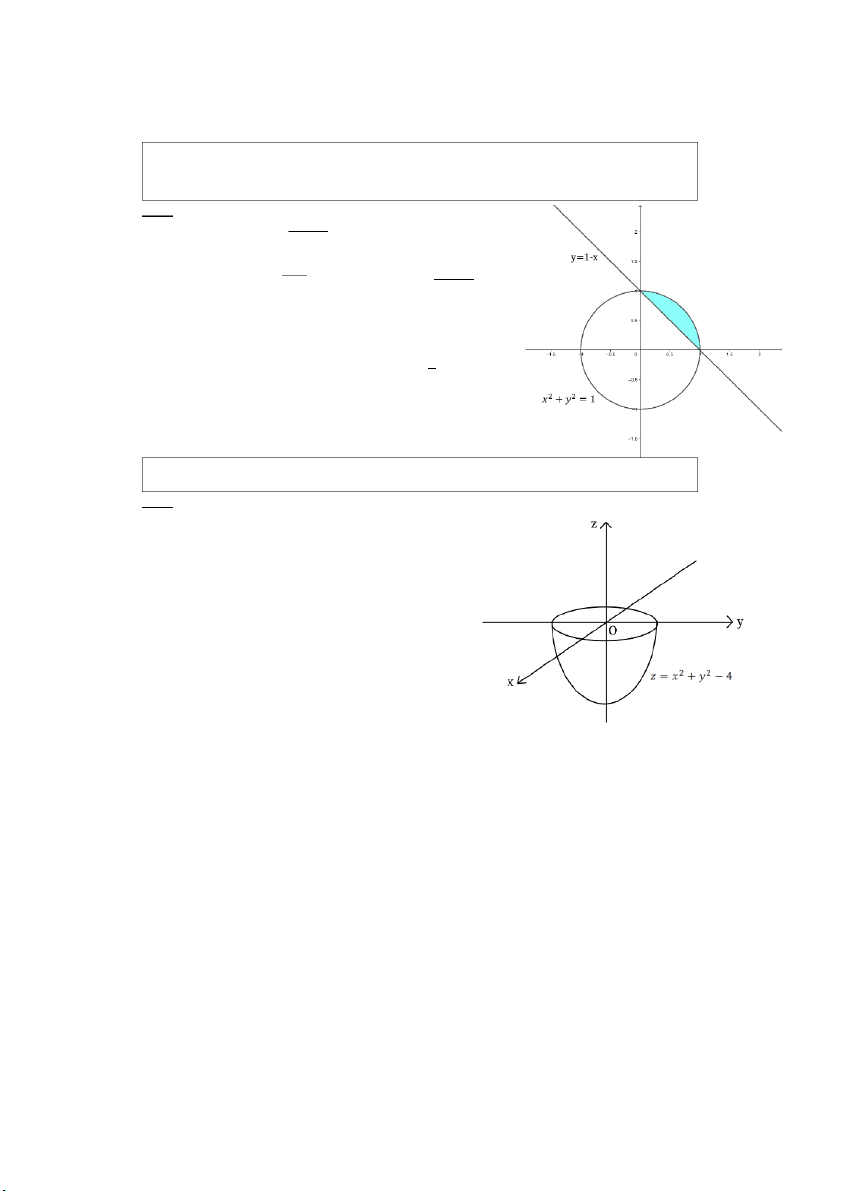
i phía trên parabol 𝑦 = 𝑥2 và nằm phía 𝐷
trong đường tròn 𝑥2 + 𝑦2 = 2 Giải: 𝑥 = 𝑟 cos 𝜑 Đặt { |
𝑦 = 𝑟 sin 𝜑 𝐽| = 𝑟 Chia 𝐷 thành hai miền: sin 𝜑 0 ≤ 𝑟 ≤ (cos𝜑)2 0 ≤ 𝑟 ≤ √2 𝐷1: và 𝐷 𝜋 3𝜋 𝜋 3𝜋 2: { ≤ 𝜑 ≤ { 𝜑 ∈ [0; ] ∪ [ ; 𝜋] 4 4 4 4 PHAM THANH TUNG 𝜋 sin 𝜑 sin 𝜑 3𝜋 4 (cos 𝜑)2 𝜋 (cos 𝜑)2 4 √2
⇒ ∬ √𝑥2 + 𝑦2𝑑𝑥𝑑𝑦 = ∫ 𝑑𝜑 ∫ 𝑟. 𝑟𝑑𝑟 + ∫ 𝑑𝜑
∫ 𝑟. 𝑟𝑑𝑟 + ∫ 𝑑𝜑 ∫ 𝑟. 𝑟𝑑𝑟 𝐷 0 0 3𝜋 0 𝜋 0 4 4 𝜋4 𝜋 1 (sin 𝜑)3 1 (sin 𝜑)3 √2𝜋 = ∫ + ∫ + 3 (cos 𝜑)6 𝑑𝜑 3 (cos 𝜑)6 𝑑𝜑 3 0 3𝜋 4 𝜋 4 𝜋 −1 (sin 𝜑)2 1 (sin 𝜑)2 √2𝜋 = ∫ − ∫ + 3 (cos 𝜑)6 𝑑(cos 𝜑) 3 (cos 𝜑)6 𝑑(cos 𝜑) 3 0 3𝜋 4 √2 2 −1 −1 1 − 𝑢2 1 1 − 𝑢2 √2𝜋 4 + 4√2 √2𝜋 = ∫ 𝑑𝑢 − ∫ 𝑑𝑢 + = + 3 𝑢6 3 𝑢6 3 45 3 1 −√2 2
𝐂â𝐮 𝟓: Tính ∭ √6𝑦 − 𝑥2 − 𝑦2 − 𝑧2𝑑𝑥𝑑𝑦𝑑𝑧
với 𝑉: 𝑥2 + 𝑦2 + 𝑧2 ≤ 6𝑦 𝑉 Giải:
Miền 𝑉: 𝑥2 + 𝑦2 + 𝑧2 ≤ 6𝑦 ⇔ 𝑥2 + (𝑦 − 3)2 + 𝑧2 ≤ 9 𝑥 = 𝑟 sin 𝜃 cos 𝜑
Đặt {𝑦 = 3 + 𝑟 sin 𝜃 sin 𝜑 , 𝐽 = −𝑟2 sin 𝜃 𝑧 = 𝑟 cos 𝜃 0 ≤ 𝑟 ≤ 3
Miền 𝑉 trong tọa độ cầu suy rộng là 𝑉: { 0 ≤ 𝜃 ≤ 𝜋 0 ≤ 𝜑 ≤ 2𝜋 ⇒ 𝐼 = ∭ 9
√ − 𝑥2 − (𝑦2 − 6𝑦 + 9) − 𝑧2𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 = ∭ 9
√ − [𝑥2 + (𝑦 − 3)2 + 𝑧2]𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 PHAM THANH TUNG 2𝜋 𝜋 3
= ∫ 𝑑𝜑 ∫ 𝑑𝜃 ∫ √9 − 𝑟2. 𝑟2 sin 𝜃 𝑑𝑟 0 0 0
Đặt 𝑟 = 3 sin 𝑡 ⇒ 𝑑𝑟 = 3 cos 𝑡 𝑑𝑡 𝑟 3 0 𝑡 𝜋 0 2 𝜋 𝜋 3 2 2 ⇒ ∫ 9 √ − 𝑟2. 𝑟2𝑑𝑟 = ∫ 9
√ − 9(sin 𝑡)2. 9(sin 𝑡)2. 3 cos 𝑡
𝑑𝑡 = ∫ 3 cos 𝑡 . 9(sin 𝑡)2. 3 cos 𝑡 𝑑𝑡 0 0 0 𝜋 𝜋 𝜋 𝜋 2 2 2 2 sin 2𝑡 2 81 81 1 − cos 4𝑡 81𝜋
= 81 ∫(sin 𝑡 cos 𝑡)2𝑑𝑡 = 81 ∫ ( ) 𝑑𝑡 = ∫(sin 2 = ∫ = 2 𝑡)2𝑑𝑡 𝑑𝑡 4 4 2 16 0 0 0 0 2𝜋 𝜋 81𝜋 81 ⇒ 𝐼 =
∫ 𝑑𝜑 ∫ sin 𝜃 𝑑𝜃 = 𝜋2 16 4 0 0
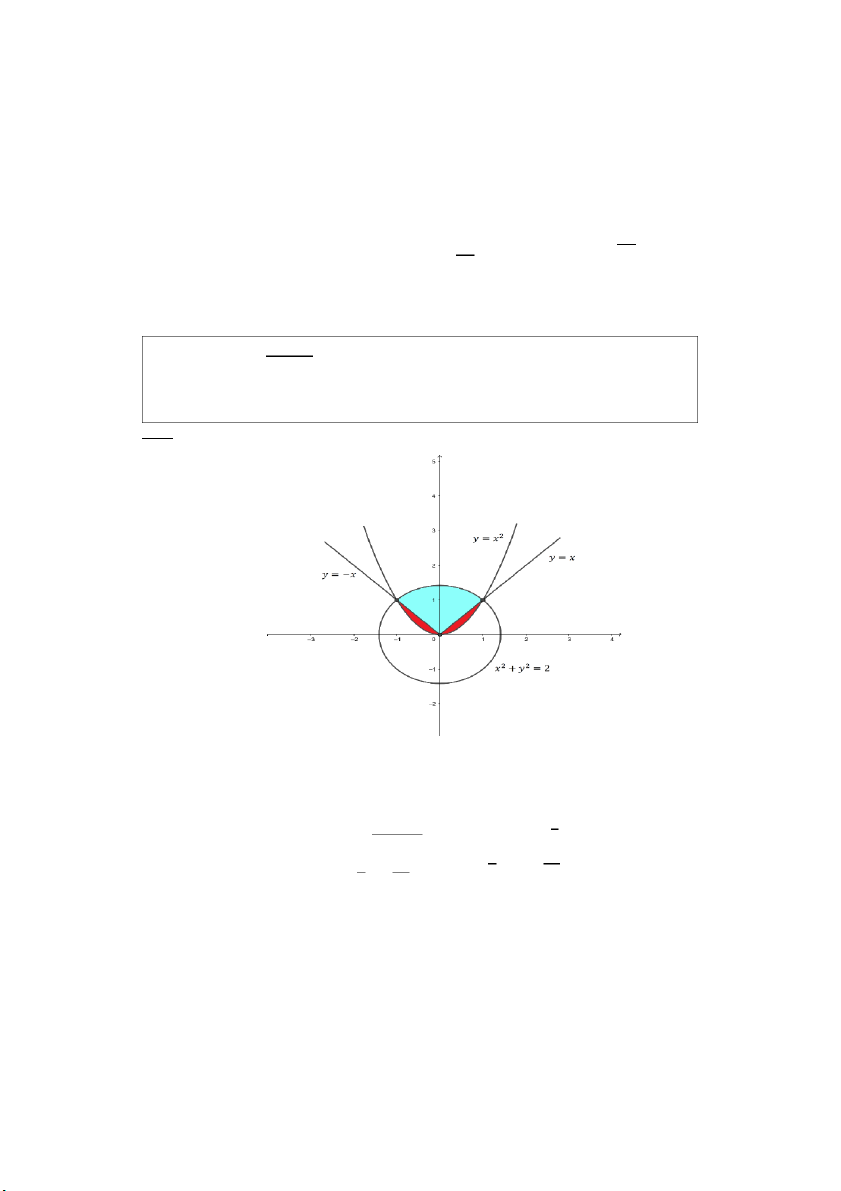
Câu 6: Tính diện tích miền giới hạn bởi hai đường cong 𝑦 = 𝑥2 và 𝑥 = 𝑦2 Giải: 0 ≤ 𝑥 ≤ 1 Miền 𝐷: { 𝑥2 ≤ 𝑦 ≤ √𝑥 Diện tích miền 𝐷 là: 1 √𝑥 1 1
𝑆 = ∬ 𝑑𝑥𝑑𝑦 = ∫ 𝑑𝑥
∫ 𝑑𝑦 = ∫(√𝑥 − 𝑥2)𝑑𝑥 = (đvdt) 3 𝐷 0 𝑥2 0 PHAM THANH TUNG
Câu 7: Tính thể tích miền giới hạn bởi các mặt cong 𝑥 = 𝑦2 + 𝑧2 và 𝑥2 + 𝑦2 + 𝑧2 = 2 nằm
trong phần không gian có 𝑥 không âm. Giải:
Xét giao tuyến của hai mặt 𝑥2 + 𝑦2 + 𝑧2 = 2, 𝑥 = 𝑦2 + 𝑧2
⇒ (𝑦2 + 𝑧2) + (𝑦2 + 𝑧2)2 = 2 ⇒ 𝑦2 + 𝑧2 = 1
Hình chiếu của 𝑉 lên 𝑂𝑦𝑧 là 𝐷: 𝑦2 + 𝑧2 ≤ 1 𝑦 = 𝑟 cos 𝜑
Đặt {𝑧 = 𝑟 sin 𝜑, 𝐽 = 𝑟 𝑥 = 𝑥
Miền 𝑉: {𝑦2 + 𝑧2 ≤ 𝑥 ≤ √2 − (𝑦2 + 𝑧2) 𝐷: 𝑦2 + 𝑧2 ≤ 1
𝑟2 ≤ 𝑥 ≤ √2 − 𝑟2
⇒ Miền 𝑉 trong tọa độ trụ là 𝑉: { 0 ≤ 𝑟 ≤ 1 𝐷: {0 ≤ 𝜑 ≤ 2𝜋 Thể tích miền 𝑉 là: 2𝜋 1 √2−𝑟2 2𝜋 1
𝑉 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ 𝑟𝑑𝑥 = ∫ 𝑑𝜑 ∫ 𝑟 ( 2
√ − 𝑟2 − 𝑟2) 𝑑𝑟 𝑉 0 0 𝑟2 0 0 1 1 1 1 1 1 −7 + 8√2 ∫ 𝑟 ( 2
√ − 𝑟2 − 𝑟2) 𝑑𝑟 = ∫ 𝑟 2 √ − 𝑟2𝑑𝑟 − ∫ 𝑟3𝑑𝑟 = ∫ √2 − 𝑟2𝑑(𝑟2) − = 2 4 12 0 0 0 0 2𝜋 1 −7 + 8√2
⇒ 𝑉 = ∫ 𝑑𝜑 ∫ 𝑟 ( 2
√ − 𝑟2 − 𝑟2) 𝑑𝑟 = 𝜋 (đvtt) 6 0 0
Câu 8: Tính diện tích mặt cong 𝑧 = 2𝑥2 − 2𝑦2 nằm trong hình tr ụ 𝑥2 + 𝑦2 = 1 Giải:
Hình chiếu của phần mặt 2𝑥2 − 2𝑦2 nằm trong mặt tr ụ 𝑥2 + 𝑦2 = lên 1
𝑂𝑥𝑦 là: 𝐷: 𝑥2 + 𝑦2 ≤ 1 Ta có: 𝑧′ = 4 ′ = 4 𝑥 𝑥, 𝑧𝑦 𝑦 Diệ ầ n tích c n tính là: PHAM THANH TUNG 2 𝑆 = ∬ √1 + (𝑧′ ′
𝑥)2 + (𝑧𝑦) 𝑑𝑥𝑑𝑦 = ∬ 1
√ + 16𝑥2 + 16𝑦2𝑑𝑥𝑑𝑦 𝐷 𝐷 𝑥 = 𝑟 cos 𝜑 0 ≤ Đặt { , 𝑟 ≤ 1
𝑦 = 𝑟 sin 𝜑 𝐽 = 𝑟 ⇒ 𝐷: { 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 1 2𝜋 1 2𝜋 1 1 1
⇒ 𝑆 = ∫ 𝑑𝜑 ∫ √1 + 16𝑟2. 𝑟𝑑𝑟 =
∫ 𝑑𝜑 ∫ √1 + 16𝑟2𝑑(𝑟2) = ∫ 𝑑𝜑 ∫ √1 + 1 𝑢 6 𝑑𝑢 2 2 0 0 0 0 0 0 1 1 (17√17 − 1)𝜋 = . 2𝜋. (17√17 − 1 ) = (đvdt) 2 24 24 1
𝐂â𝐮 𝟗: Tính lim ∫(𝑥 + 3𝑦)√𝑥2 + 𝑦3 + 1𝑑𝑥 𝑦→0 0 Giải:
Ta có: (𝑥 + 3𝑦)√𝑥2 + 𝑦3 + liên t 1 c trên mi ụ ền [0,1] × [−1,1 ] 1
⇒ 𝐼(𝑦) = ∫(𝑥 + 3𝑦)√𝑥2 + 𝑦3 + 1𝑑𝑥 liên tục trên [−1,1 ] c ứa h 𝑦 = 0 0 1
⇒ 𝐼(𝑦) = ∫(𝑥 + 3𝑦)√𝑥2 + 𝑦3 + 1𝑑𝑥 liên tục tại 𝑦 = 0 0 1 1 1 1 −1 + 2√2
lim ∫(𝑥 + 3𝑦)√𝑥2 + 𝑦3 + 1𝑑𝑥
= 𝐼(0) = ∫ 𝑥√𝑥2 + 1𝑑𝑥 = ∫ √𝑥2 + 1𝑑(𝑥2) = 𝑦→0 2 3 0 0 0
Câu 10: Khảo sát tính liên t c và kh ụ ả vi của hàm s : ố 1𝑑𝑥 𝑔(𝑦) = ∫ 𝑥2 + 𝑦2 0 Giải: 1 Đặt 𝑓(𝑥, 𝑦) = 𝑥2 + 𝑦2
*Khảo sát tính liên tục: PHAM THANH TUNG
Xét hàm số 𝑔(𝑦) tại 𝑦 ≠ 0 1𝑑𝑥 1 𝑥 1 1 1 𝑔(𝑦) = ∫ = arctan | = arctan 𝑥2 + 𝑦2 𝑦 𝑦 𝑦 𝑦 0 0
Xét hàm số 𝑔(𝑦) tại 𝑦 = 0 1 𝑑𝑥 −1 1 𝑔(0) = ∫ = | = −∞ 𝑥2 𝑥 0 0
⇒ 𝑔(𝑦) không xác định tại 𝑦 = 0
Vậy hàm số 𝑔(𝑦) liên tục với 𝑦 ≠ 0 *Khảo sát tính khả vi:
Xét hàm số 𝑔(𝑦) tại 𝑦 ≠ 0
Vớ𝑖 𝑦 ∈ 𝑅\{0}, 𝑓(𝑥, 𝑦) là hàm số liên tục trên [0; ] 1 { −2𝑦 𝑓′ = 0; 1] × (0; +∞ 𝑦
là hàm số liên tục trên [0; 1] × (−∞; 0) và [ ) (𝑥2 + 𝑦2)2 ⇒ 𝑔(𝑦) là hàm s kh ố ả vi với 𝑦 ≠ 0
Xét hàm số 𝑔(𝑦) tại 𝑦 ≠ 0 1 1
Với 𝑦 = 0 ⇒ 𝑓(𝑥, 𝑦) = =
bị gián đoạn tại 𝑥 = 0 𝑥2 + 𝑦2 𝑥2
⇒ Với 𝑦 = 0 thì 𝑓(𝑥, 𝑦) không liên tục trên [0; 1]
⇒ 𝑔(𝑦) không khả vi tại 𝑦 = 0
Vậy hàm số 𝑔(𝑦) khả vi với 𝑦 ≠ 0 PHAM THANH TUNG