Tứ Giác Điều Hòa Và Một Số Bài Toán Bùi Đắc Hiên Soạn ngày 24/05/2018
Các bài toán về tứ giác điều hòa đã chẳng còn xa lạ gì với một số bạn, ngay cả khi bạn đã là một
học sinh lớp 9 thì ít nhiều đã được tiếp xúc với mô hình này mà chính bạn đã không nhận ra. Đây là
một chủ đề có lẽ đã quen thuộc với nhiều bạn yêu toán trong cả nước. Nhưng đối với một số bạn
mới tìm hiểu về chủ đề này thì thực sự ít nhiều đều gặp khó khăn. Bài viết này ra đời với mục đích
đó, ngoài ra tác giả của bài viết còn muốn được nâng cao trình độ bản thân, muốn chăm chút cho
một số bài viết sắp tới của mình. Do tuổi đời còn hạn chế nên khó tránh khỏi những sai sót, mong bạn đọc thông cảm. I.
Khái niệm về tứ giác điều hòa và một số tính chất liên quan. 1) Khái niệm
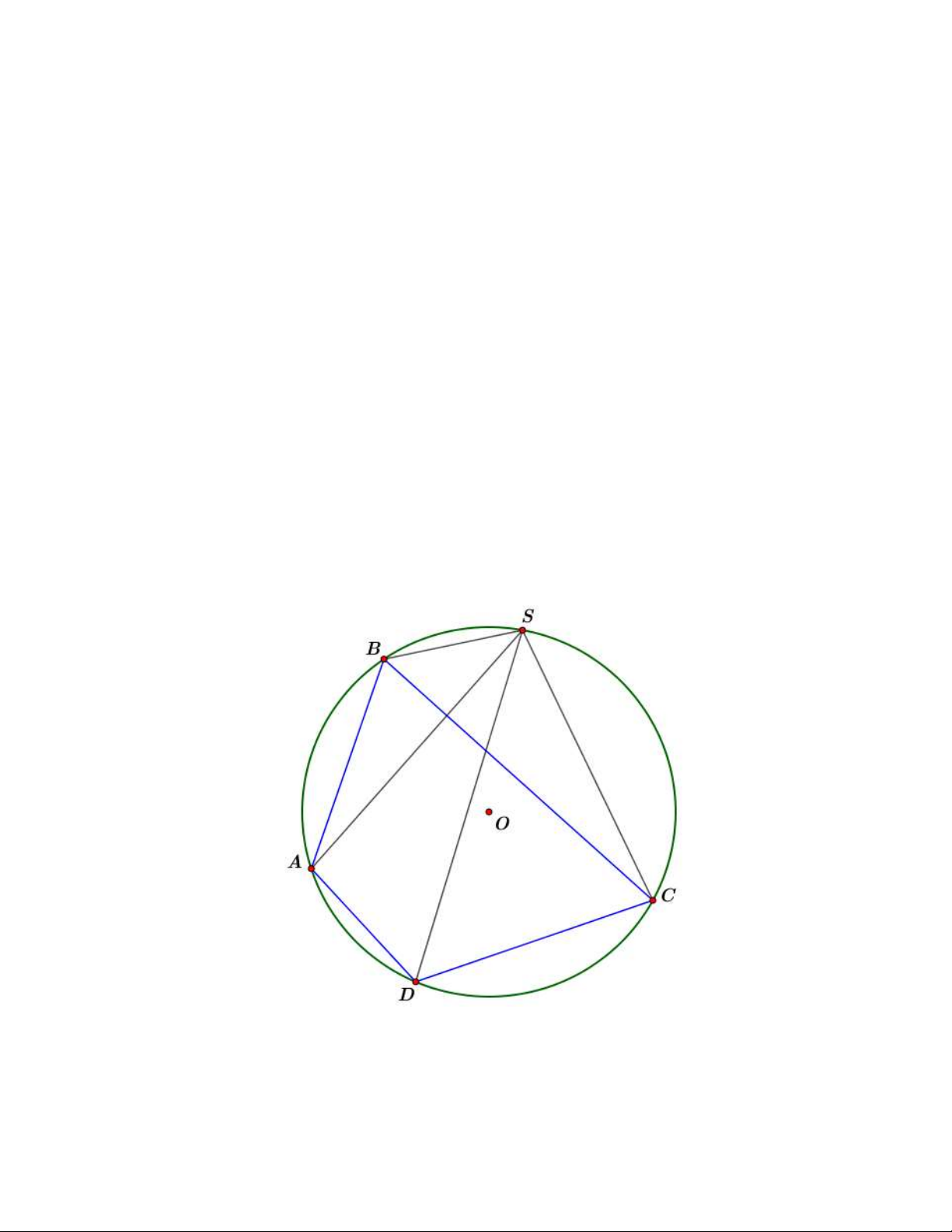
Tứ giác ABCD nội tiếp đường tròn O , điểm S là một điểm cố định bất kỳ trên O . Khi đó
S  ACBD  const (là tỷ số kép của bốn điểm đồng viên ,
A B,C, D , ký hiệu là  ACBD ), với
trường S  ACBD  1 thì ta nói tứ giác ABCD là tứ giác điều hòa. 2) Tính chất
Sau đây tác giả sẽ giới thiệu với bạn đọc một số tính chất về mô hình tứ giác điều hòa để các bạn có
thể vận dụng khi làm bài tập.
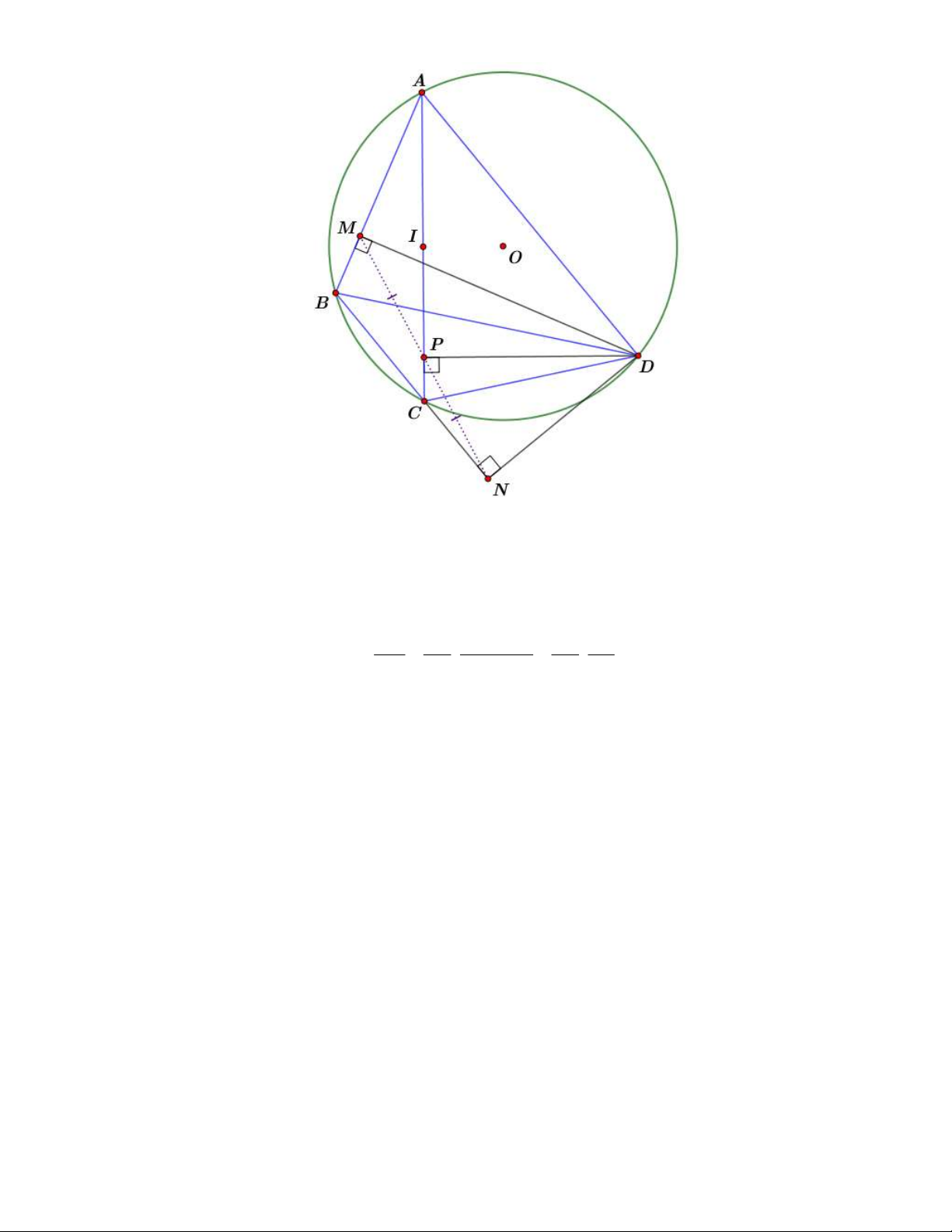
Tính chất 1. Cho tứ giác ABCD nội tiếp trong đường tròn. Gọi M , N, P lần lượt là hình chiếu của
D lên AB, BC,CA ; I, J lần lượt là trung điểm của AC, BD . Khi đó tứ giác ABCD là tứ giác điều
hòa khi và chỉ khi một trong các điều kiện sau xảy ra: a) A . B CD  A . D BC
b) AC là đường đối trung của tam giác ABD (tương tự cho BD)
c) Các tiếp tuyến tại hai đỉnh đối diện B, D cắt nhau tại một điểm nằm trên đường chéo
AC . Tương tự thì các tiếp điểm tại hai đỉnh đối diện ,
A C cắt nhau tại một điểm nằm trên đường chéo BD.
d) Phân giác của các góc B
 AD và DCB cắt nhau tại một điểm nằm trên đường chéo
BD . Tương tự thì phân giác các góc ABC và CDA cắt nhau tại một điểm nằm trên đường chéo AC .
e) AC là tia phân giác BID , BD là tia phân giác AJC
f) P là trung điểm của MN . Chứng minh
Ta ký hiệu  ACBD là tỷ số kép của bốn điểm đồng viên ,
A B,C, D . Theo tính chất của tỉ số kép ta có:     SB SA SD SA ACBD S , A SC, SB, SD sin  ,  sin ,   SB SC : sin , sin SD, SC 
Sử dụng định lý sin vào các tam giác: SC , A SCB, SD , A S  DB ta thu được:   BA DA ACBD  : BC DC
Từ đó  ACBD  1  A . B CD  AD.CB .
Ta chứng minh điều kiện (a) và (b) là tương đương nhau.
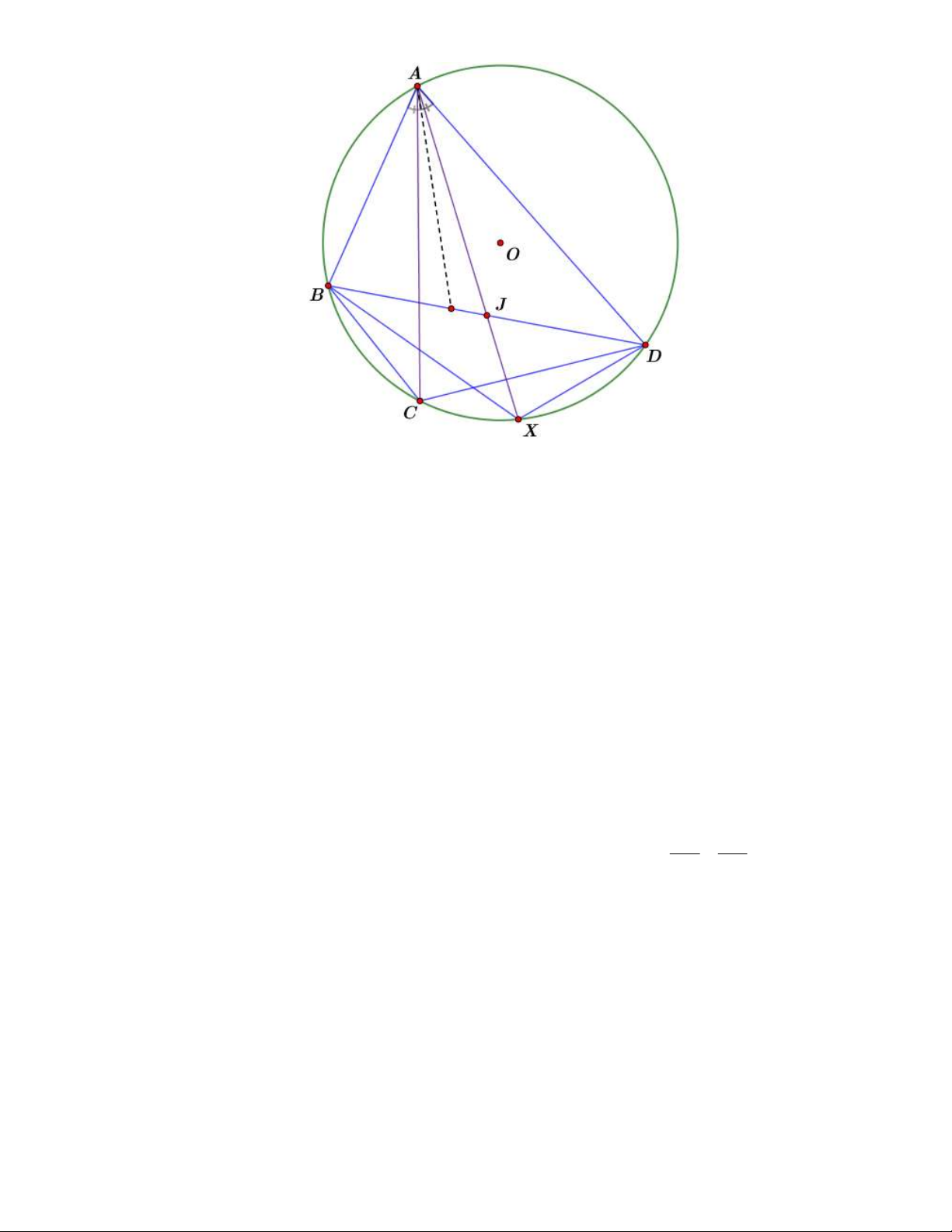
Gọi X là giao điểm của AJ và O . Khi đó ta dễ thấy rằng ABX và ADX có cùng diện tích.
Theo công thức tính diện tích liên quan đến sin suy ra B . A BX  D . A DX .
Nếu AJ và AC đối xứng nhau qua phân giác BAD suy ra:
BAC  XAD   BC   XD  BC  XD   A . B CD  A . D BC BAX  C  AD  BX  DC
Điều ngược lại khá đơn giản xin dành cho bạn đọc.
Vậy (a) và (b) tương đương nhau.
Ta chứng minh (a) và (c) tương đương.
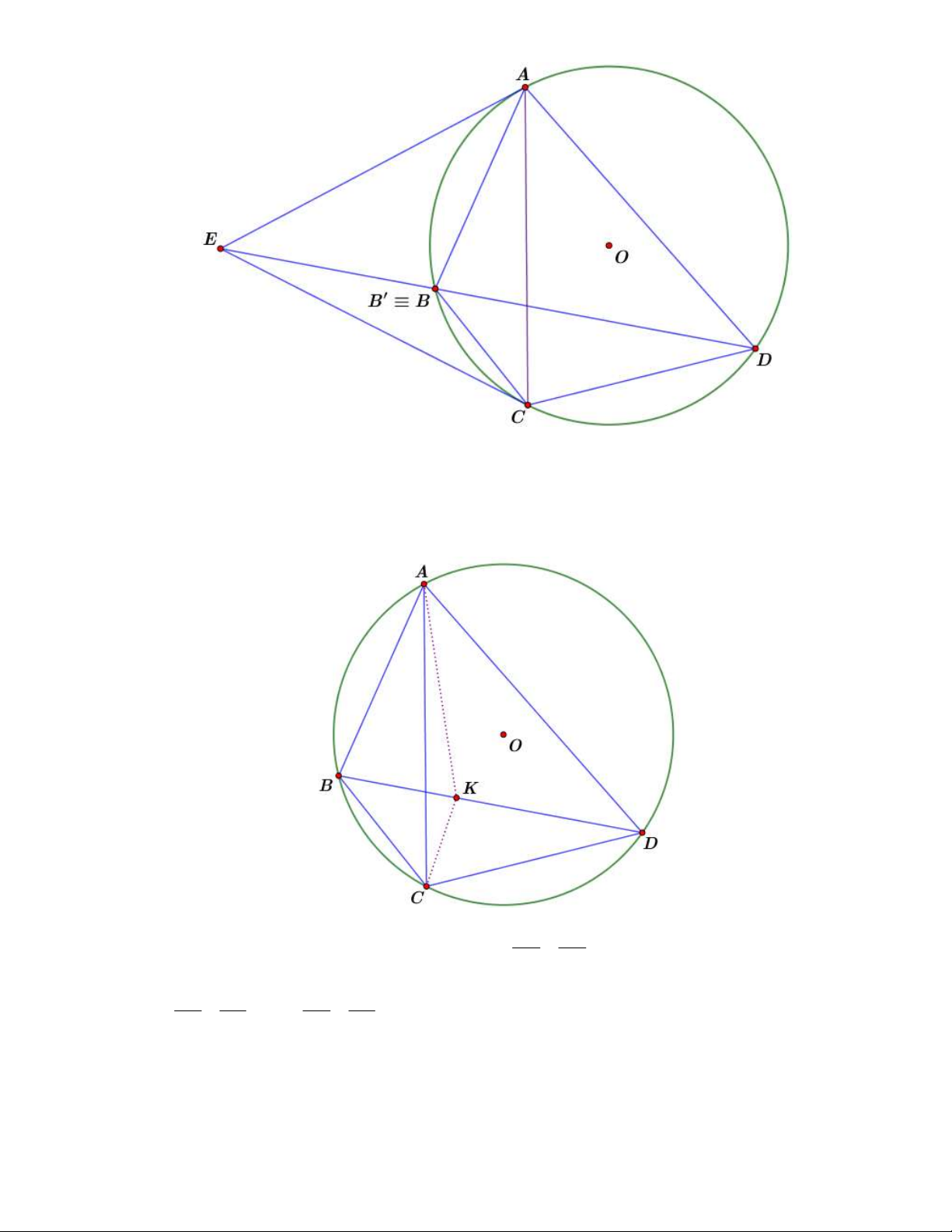
Giả sử tiếp tuyến tại ,
A C cắt nhau tại E thuộc đường thẳng BD . Khi đó : EAB ~ E  D , A E  DC ~ E  CB Hơn nữa EA  EC  A . B CD  A . D BC
Ngược lại giả sử rằng A . B CD  A .
D BC . Gọi E là giao điểm hai tiếp tuyến tại , A C ; B ' là giao AB ' CB '
điểm của ED và O . Theo phần thuận ta có: AB '.CD  A . D B 'C , suy ra   k . AB CB Mà AB 'C  ABC  A
 BC ~ AB 'C  k  1  ABC  AB 'C  B '  B  E  BD
Vậy (a) và (c) tương đương hay (a), (b) và (c) tương đương nhau.
Ta chứng minh (a) và (d) tương đương nhau. KB AB
Gọi K là chân đường phân giác của BAD suy ra  . KD AD AB CB KB CB Mà  suy ra 
 CK là tia phân giác BCD AD CD KD CD
Vậy (a) và (d) tương đương nhau hay (a), (b), (c) và (d) tương đương.
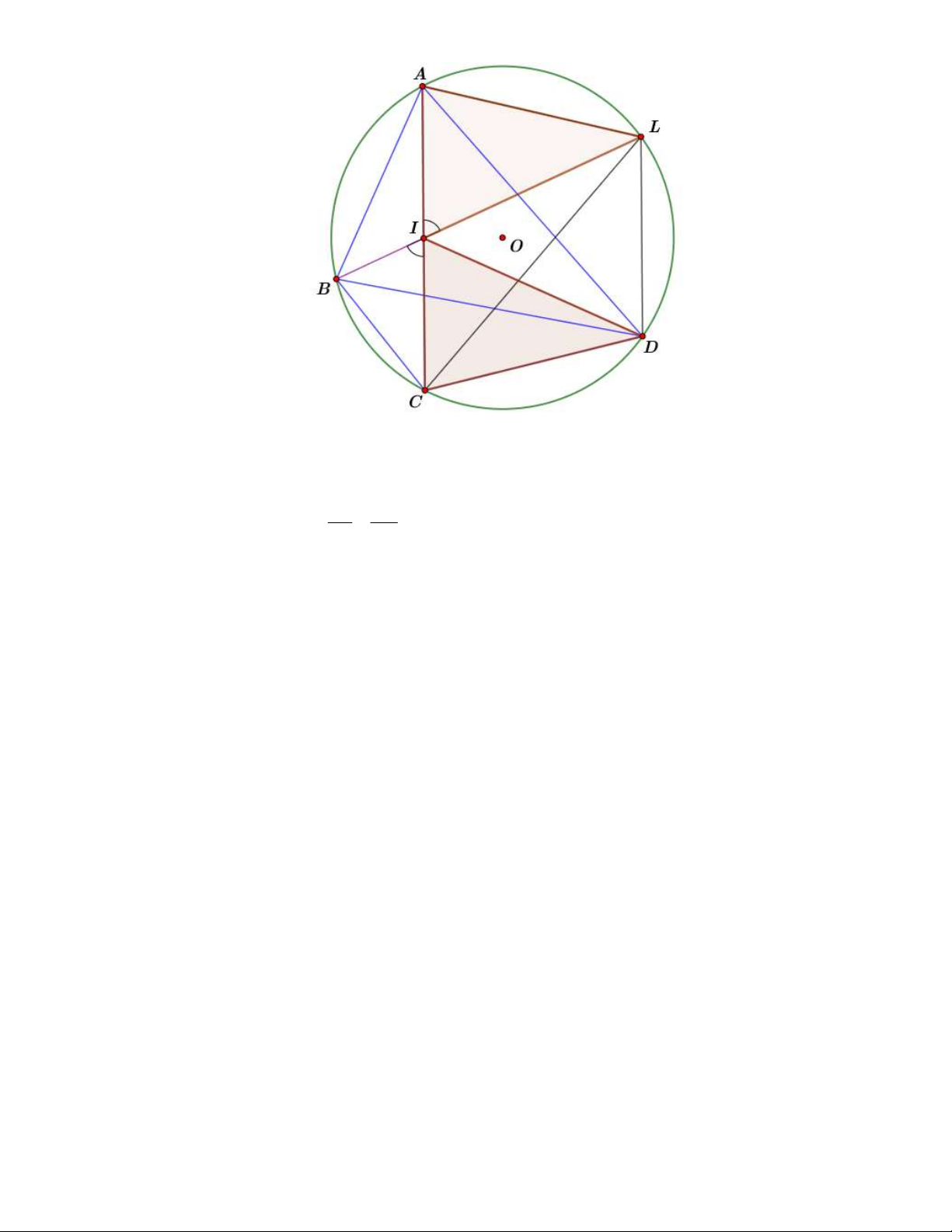
Ta chứng minh (a) và (e) tương đương.
Gọi L là giao điểm của BI và O . Do I là trung điểm của AC nên suy ra BAL và BCL có cùng diện tích. Suy ra A . B AL  CB.CL . AL CD Nếu A . B CD  A . D BC  
 ADL ~ CLD , mà hai tam giác này cùng nội tiếp trong 1 CL AD
đường tròn nên chúng bằng nhau. Suy ra AD  CL, AL  CD  I  AD  I  CL . Suy ra
BIA  CIL  DIA  AC là tia phân giác B  ID .
Ngược lại nếu AC là tia phân giác B
 ID thì dễ thấy rằng L đối xứng với D qua trung trực OI .
Suy ra CL  AD, AL  CD  A . B CD  A . D BC
Vậy (a) và (e) tương đương nhau.
Ta chứng minh (a) và (f) tương đương.
Thực chất đây là một bài toán có trong đề thi IMO 2003, nhưng nhiều bài toán mở rộng hơn đã sử
dụng IMO 2003 làm tính chất, chìa khóa quan trọng để giải bài toán khó hơn.
Sử dụng định lý về hàm số sin đối với các tam giác DPM , DPN ta có: PM  A . D sin M  DP  A . D sin BAC PN  C .
D sin NDP  CD.sin BCA PM AD sin BAC AD BC       1 PN CD sin BCA CD AB
Điều ngược lại khá dễ xin dành cho bạn đọc !
Vậy (a), (b), (c), (d), (e) và (f) tương đương nhau.
Với các tính chất trên thì việc nắm rõ là rất quan trọng khi giải các bài toán. Để xem tính chất nào
quan trọng hơn cả thì tùy mức độ của bài toán và tùy từng bài mà ta sẽ sử dụng những tính chất khác nhau.
Các bạn lưu ý rằng để vẽ được một tứ giác điều hòa thì đơn giản nhất chính là vẽ theo ý điều kiện
(c). Tức là ta chỉ vẽ 2 tiếp tuyến của một điểm nằm ngoài đường tròn, và một đường cát tuyến cắt
đường tròn tại hai điểm là có thể vẽ được tứ giác điều hòa.
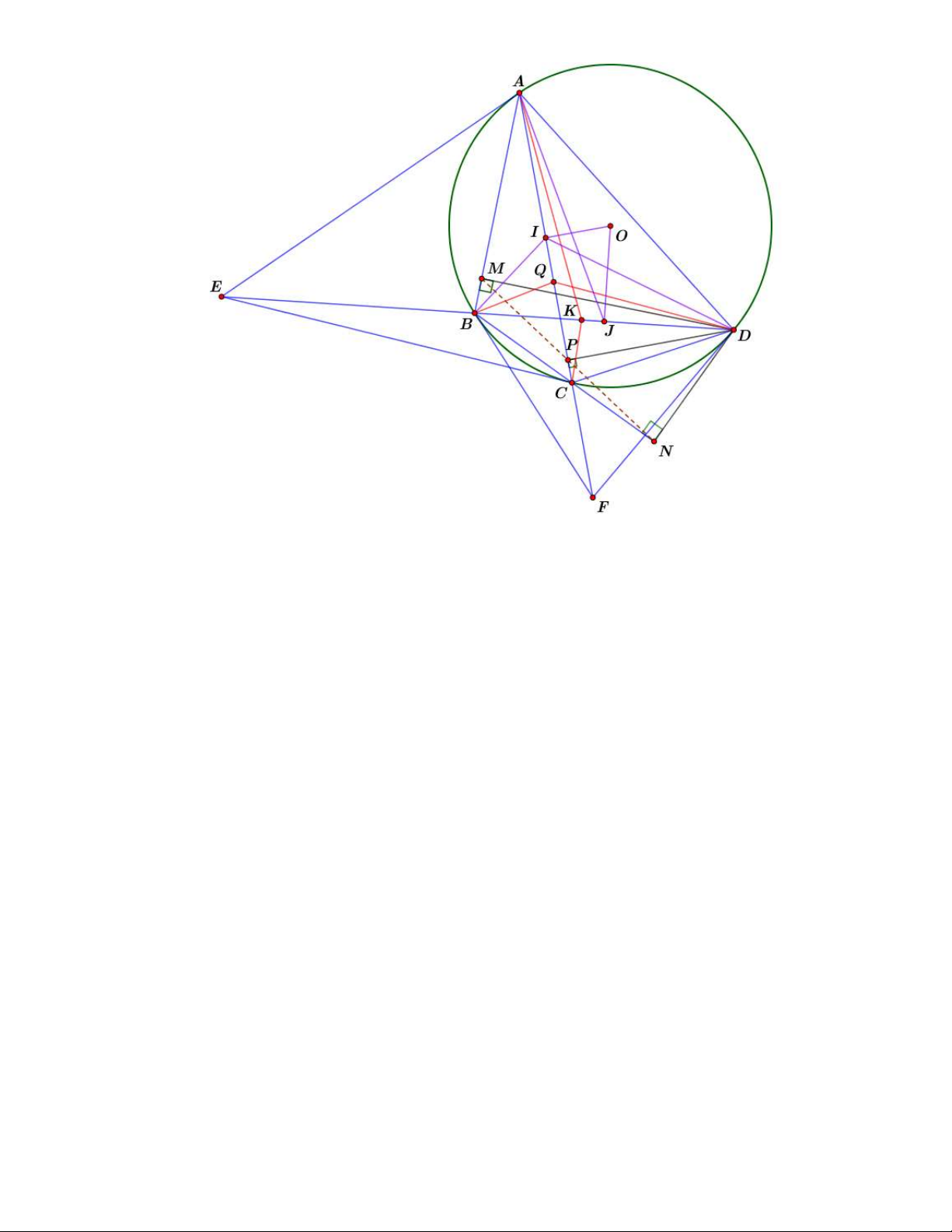
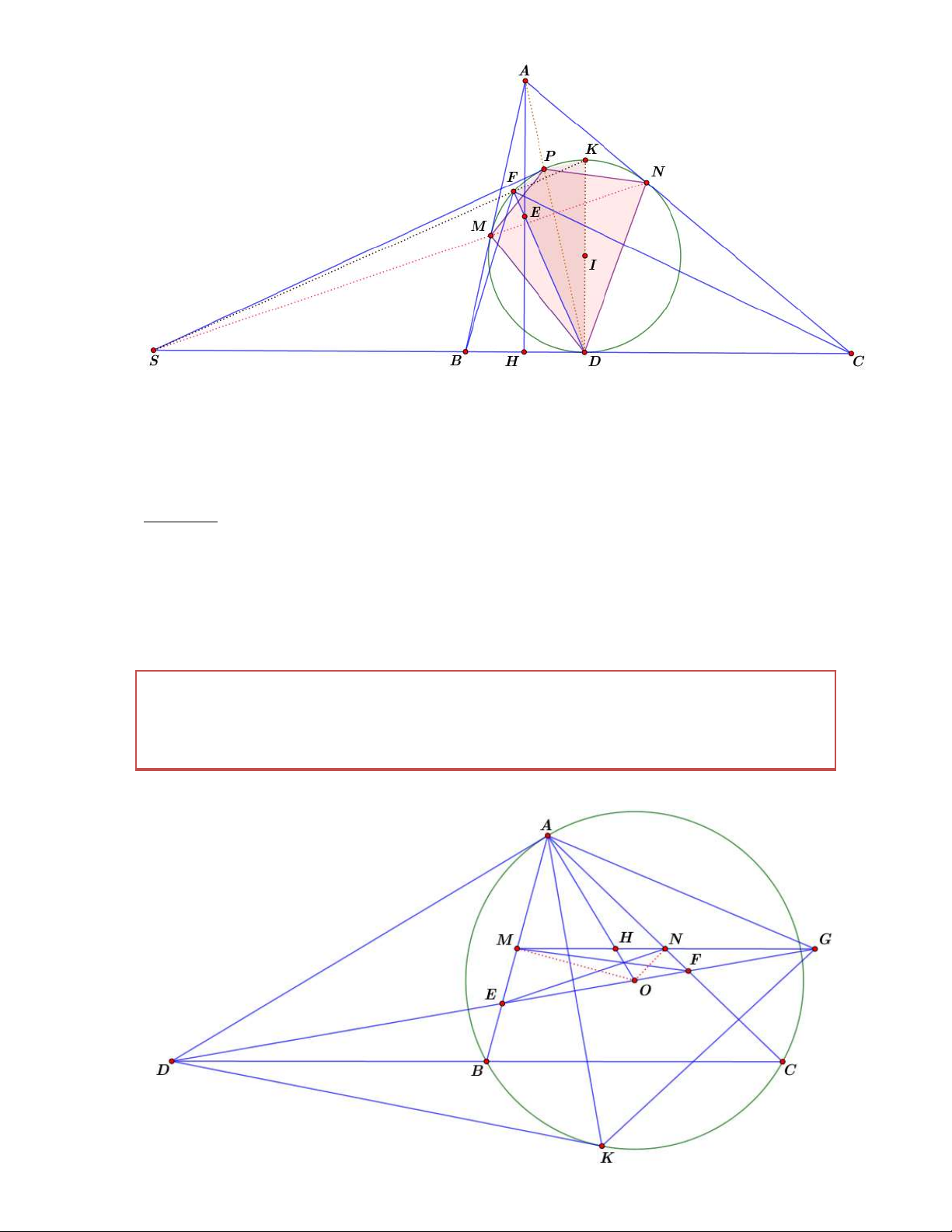
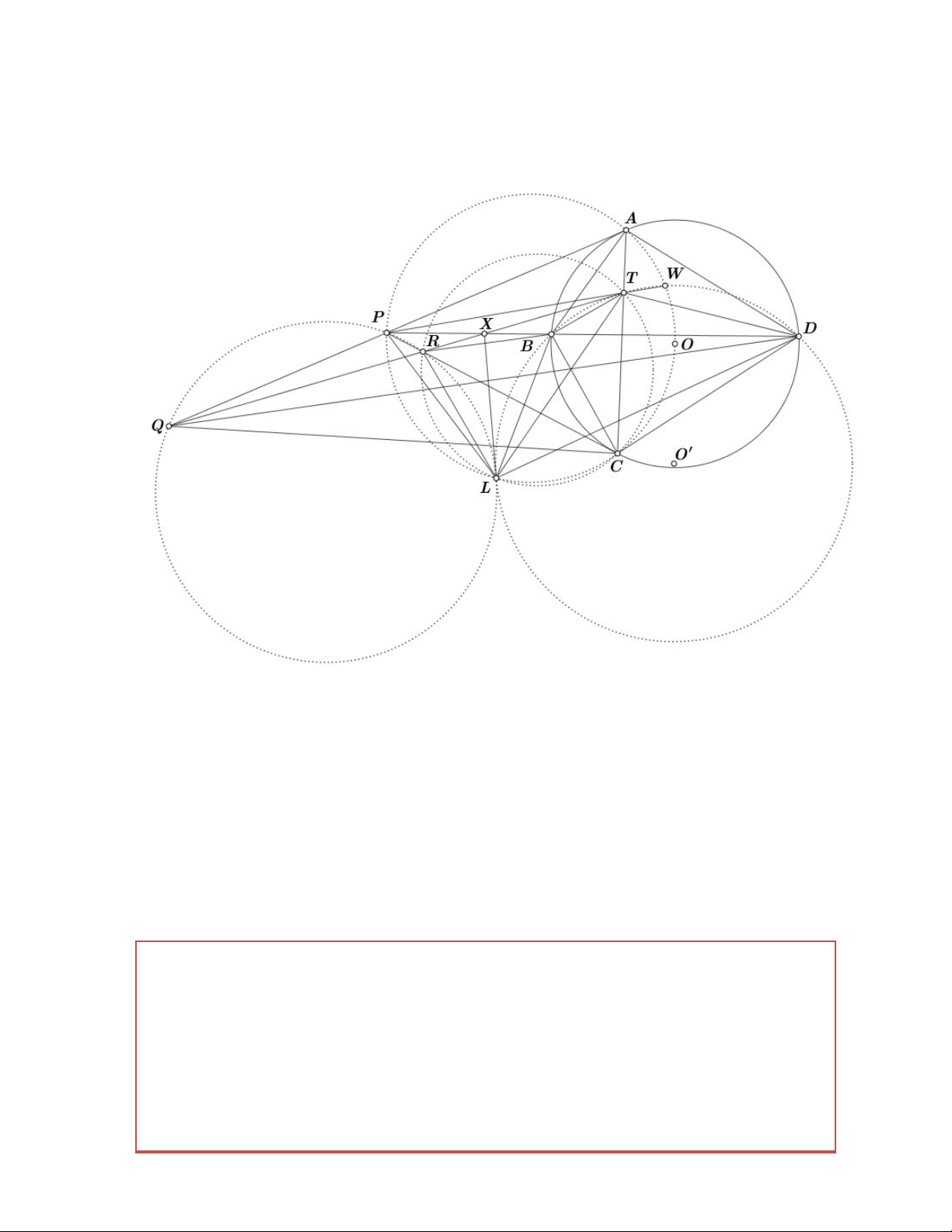
Để tổng quát các tính chất trên mời các bạn xem hình vẽ sau:
Tính chất 2. Tứ giác ABCD là tứ giác điều hòa. Khi đó ta có hệ thức: AC.BD  2A . B CD  2BC.AD Chứng minh
Tính chất này có thể chứng minh đơn giản bằng định lý ptolemy như sau:
Áp dụng định lý ptolemy cho tứ giác nội tiếp ABCD ta có: AC.BD  A . B CD  A . D BC  2A . B CD  2A . D BC
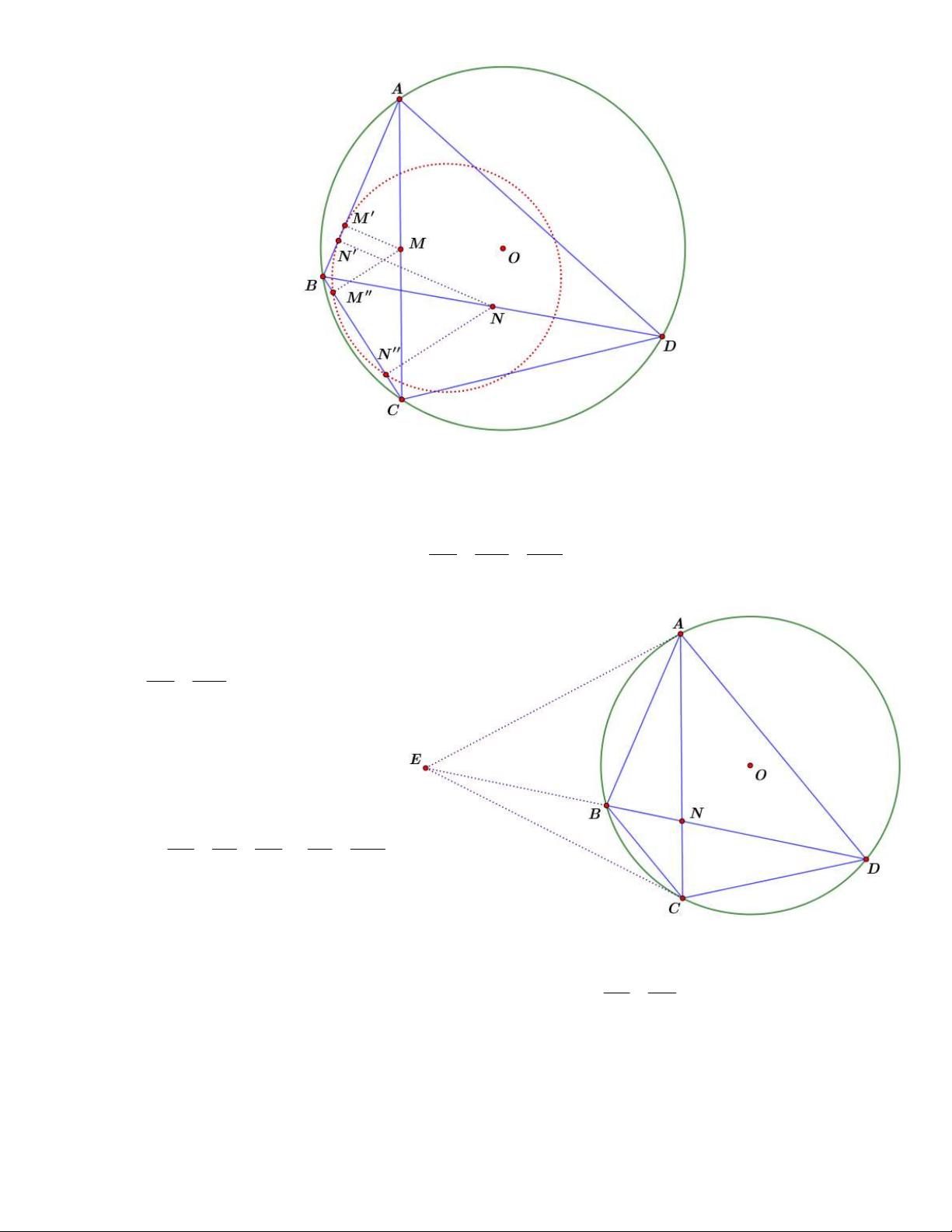
Tính chất 3. Cho tứ giác ABCD nội tiếp đường tròn O . Khi đó hình chiếu của trung điểm của
hai đường chéo trên các cạnh B ,
A BC cùng nằm trên một đường tròn khi và chỉ khi: A . B CD  A . D BC Chứng minh
Nếu tứ giác M ' N ' M ' N ' nội tiếp suy ra BN '.BM '  BN ' .BM '  BM ' M ' ~ BN ' N ' .
Đồng thời ta dễ thấy rằng các tứ giác BM ' MM ', BN ' NN ' nội tiếp. Bằng xoay góc ta dễ dàng suy
ra được ABM  CBD .
Từ đó theo tính chất 1 suy ra tứ giác ABCD là tứ giác điều hòa suy ra A . B CD  A . D BC .
Tính chất 4. Tứ giác ABCD điều hòa. Gọi N là giao điểm của AC và BD . Khi đó ta có: 2 2 NA BA DA   2 2 NC BC DC Chứng minh Ta chỉ cần chứng minh 2 NA BA  . 2 NC BC
Theo tính chất 1 suy ra tiếp tuyến tại ,
A C nằm trên BD gọi là E. Dễ thấy E  AB ~ E  DA 2 EA EB AB EB AB      2 ED EA AD EA AD
Vậy ta có điều phải chứng minh. AB DA
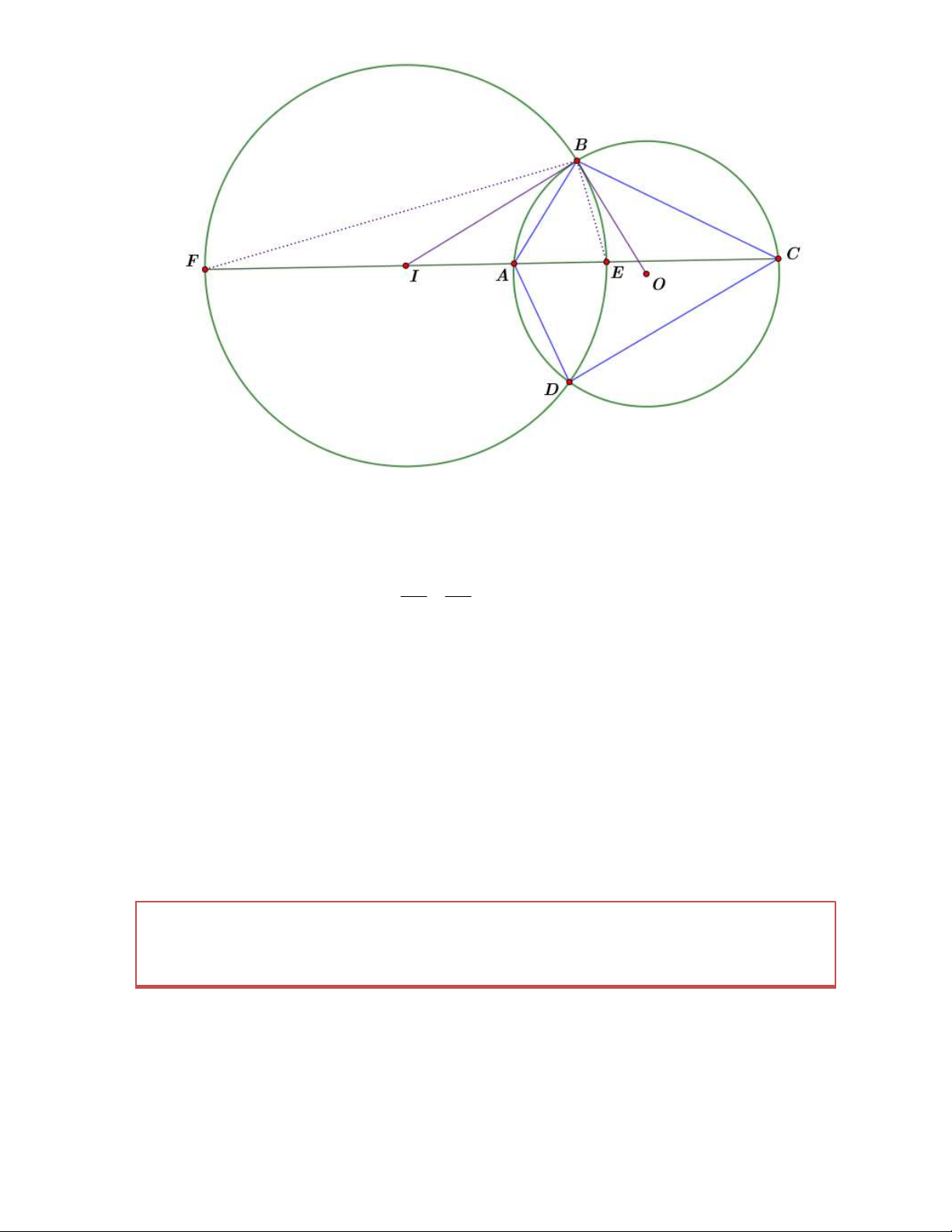
Tính chất 5. Cho tứ giác ABCD nội tiếp đường tròn O có 
 k , khi đó đường tròn BC DC
O trực giao với đường tròn Apollonius với tỉ số k trên đoạn AC . Chứng minh
Vẽ đường phân giác trong và ngoài của ABC lần lượt là BE, BF . Gọi I là trung điểm của EF ,
suy ra I là tâm của đường tròn Apollonius có bán kính là IE . Dễ thấy D cũng thuộc đường tròn
Apollonius. Theo tính chất đường phân giác ta có: EA FA    ACEF   1 EC FC Mà I là trung điểm 2 2 EF  IE  I . A IC  IB  I .
A AC  IB là tiếp tuyến của O .
Vậy ta có điều phải chứng minh.
Trên đây là toàn bộ tính chất mà tác giả muốn truyền đạt đến các bạn trong chủ đề này, hi vọng nó
sẽ giúp ích ! Còn bây giờ hãy bước vào phần bài tập để phụ đạo !
II. Một số bài tập bổ trợ.
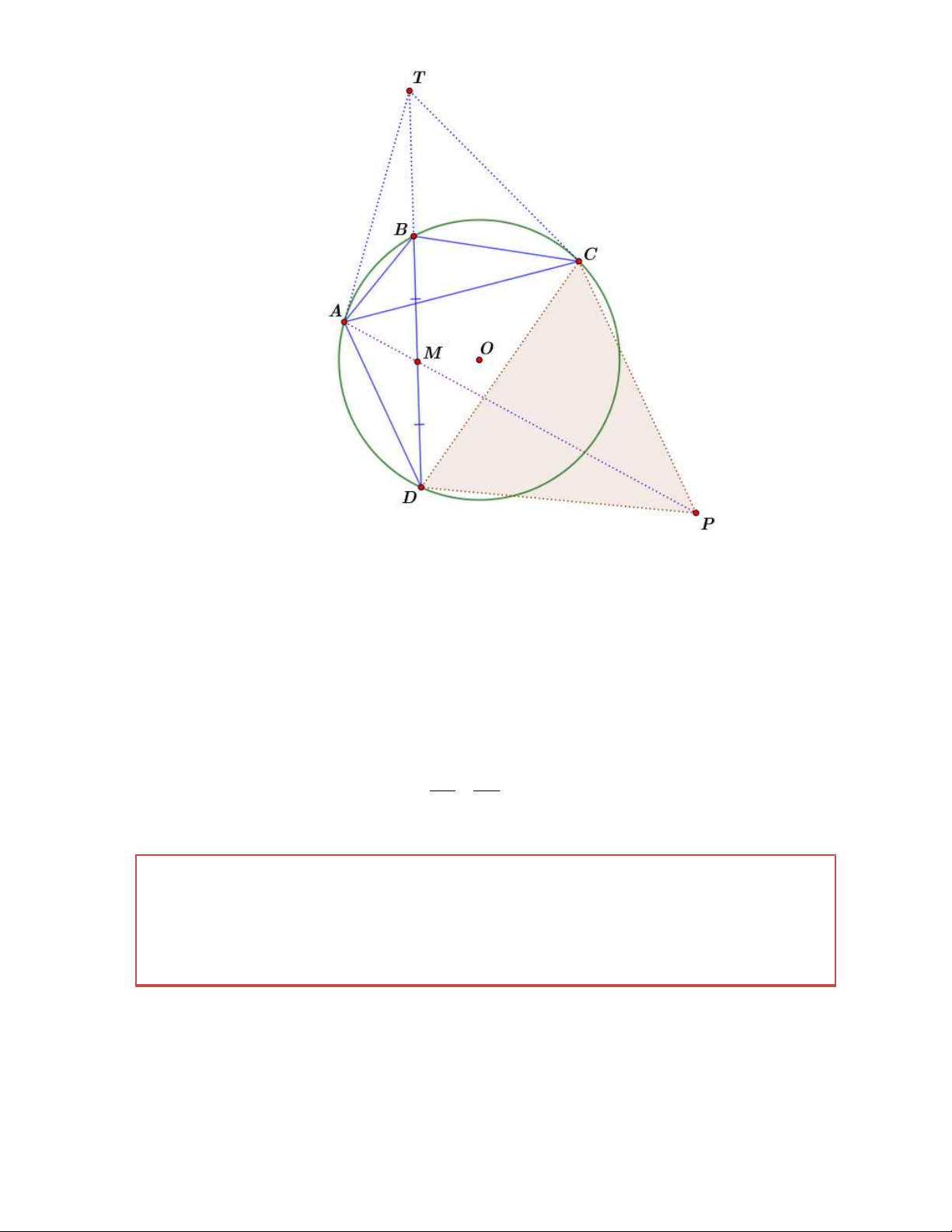
Bài 1. Cho tứ giác ABCD nội tiếp đường tròn, đường phân giác góc BAD , BCD cắt nhau
trên đường chéo BD . Đường thẳng qua C song song với AD cắt đường thẳng đi qua A và
trung điểm BD tại P . Chứng minh rằng tam giác PCD là tam giác cân. (Moldova 2014) Chứng minh
Gọi M là trung điểm của AP . Theo bài ra suy ra tứ giác ABCD là tứ giác điều hòa. Gọi T là giao
điểm hai tiếp tuyến tại , A C  T  BD .
Theo tính chất 1b suy ra AC là đường đối trung của ABD suy ra:
DAM  CAB  CDB  CDT
Mà AD / /CP  DAM  CPA  CPA  CDT (1). Cũng vì AD / /CP suy ra ADC  DCP  T
 CA  DCP  TCD  PCA (2) CT CD
Từ (1) và (2) suy ra DCT ~ PCA  
(3). Cũng do TCA  DCP (4) nên từ (3) và CA CP
(4) suy ra TAC ~ DCP . Mà do tam giác TAC cân nên suy ra DPC cân tại D .
Bài 2. Cho tam giác ABC nội tiếp đường tròn O , có A cố định và B,C thay đổi sao cho BC
luôn song song với đường thẳng cố định cho trước. Tiếp tuyến tại B và C với đường tròn O
cắt nhau tại K . Gọi M là trung điểm của BC , đường thẳng AM cắt O tại N . Chứng minh
rằng đường thẳng KN luôn đi qua một điểm cố định.
(Đề thi chọn đội tuyển PTNK, ĐHKHTN TPHCM) Chứng minh
Gọi I là giao điểm thứ hai của KN và O . Suy ra tứ giác IBNC là tứ giác điều hòa.
Suy ra  AB, AC, AN, AI   1 mà M là trung điểm của BC suy ra AI / /BC nên I cố định.
Vậy ta có điều phải chứng minh.
Nhận xét: Bài toán khá là đơn giản khi chỉ kết hợp tính chất quen thuộc của hàng điểm điều hòa
và mô hình tứ giác điều hòa. Ở đây việc phát hiện điểm I là hoàn toàn tự nhiên và khá đơn giản
nhờ mô hình tứ giác điều hòa.
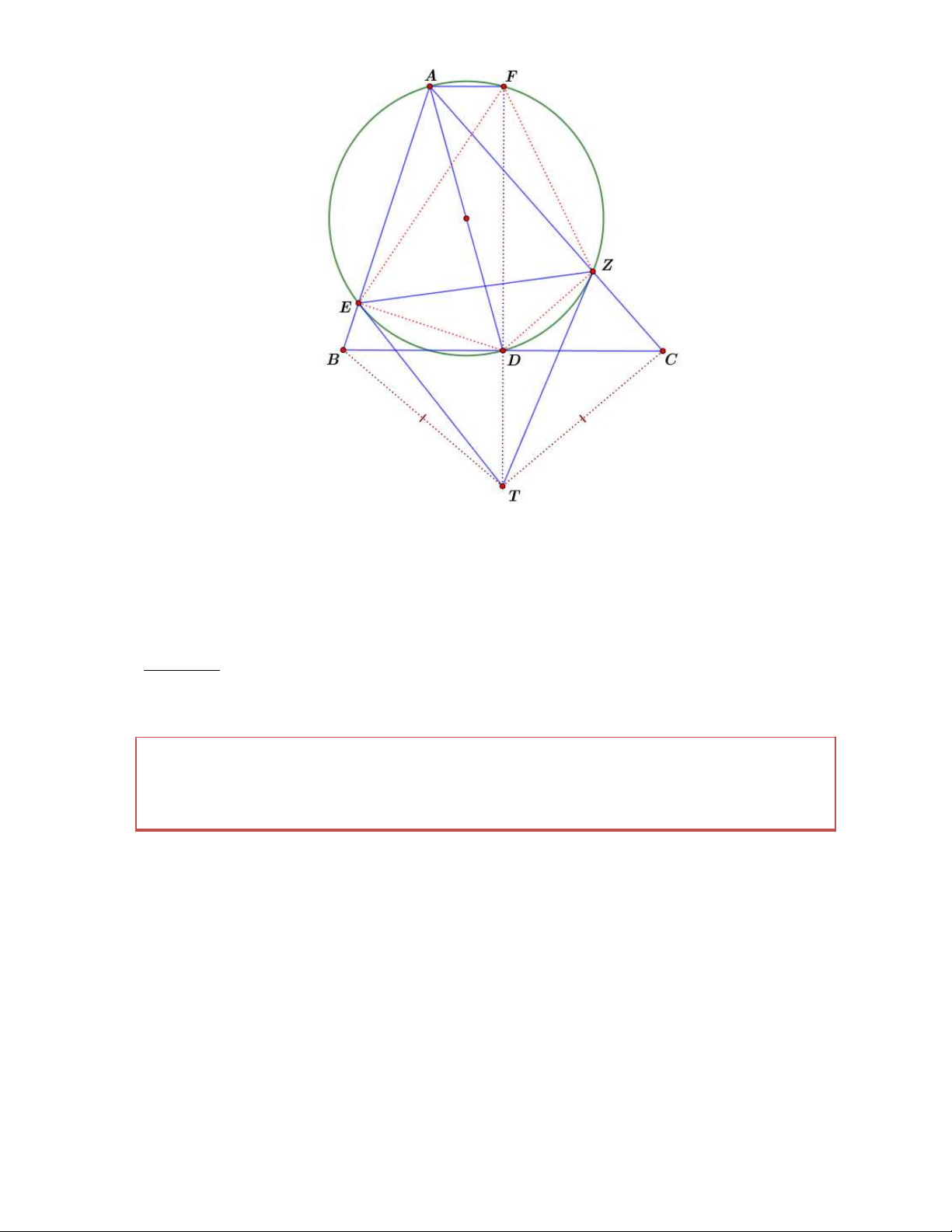
Bài 3. Cho tam giác ABC , D là trung điểm của cạnh BC , và E, Z lần lượt là hình chiếu của
D lên AB, AC . Gọi T là giao điểm của các tiếp tuyến tại E, Z của đường tròn đường kính AD
. Chứng minh rằng TB  TC . Chứng minh
Gọi F là giao điểm của TD với đường tròn đường kính AD . Suy ra tứ giác FEDZ là tứ giác điều
hòa. Từ đó suy ra AFDEZ   1 mà D là trung điểm của BC nên theo định lý quen thuộc về
hàng điểm điều hòa suy ra AF / /BC  TD  BC  TB  TC .
Vậy ta có điều phải chứng minh.
Nhận xét: Bài toán có phần khá giống với bài toán trước, đều cùng một ý tưởng là tạo dựng mô
hình tứ giác điều hòa và hàng điểm điều hòa. Từ đó bạn đọc thấy rằng việc kết hợp các định lý của
hàng điểm điều hòa trong các bài toán về tứ giác điều hòa là rất phổ biến.
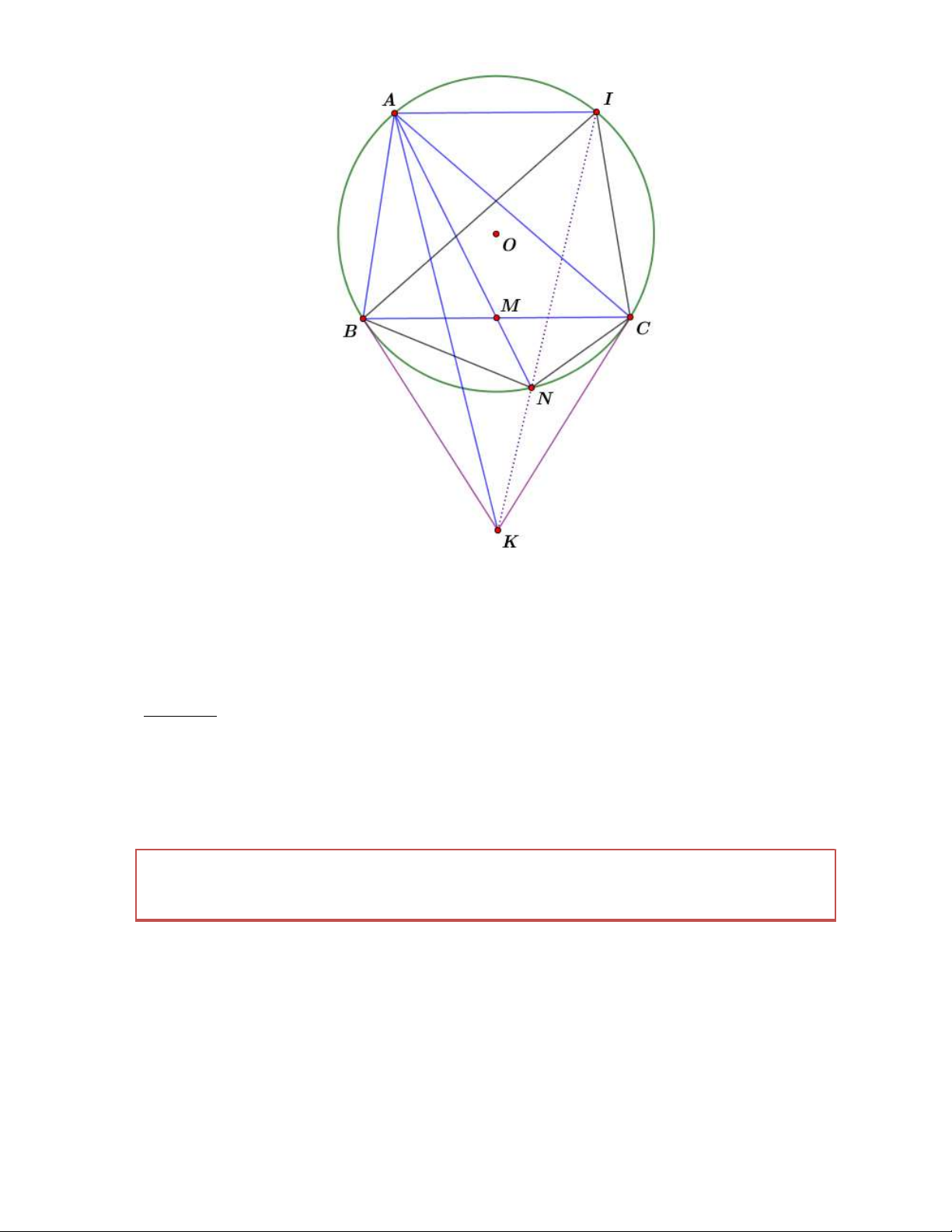
Bài 4. Cho tam giác ABC cân tại A nội tiếp O . Trên cung BC chứa điểm A của đường tròn
lấy điểm D bất kì. Gọi E là giao điểm của AD và BC . Phân giác BDC cắt đường tròn
đường kính AE tại M , N . Chứng minh rằng tứ giác BMCN là tứ giác điều hòa. (Sưu tầm) Chứng minh
Theo bài ra dễ thấy rằng DA  DM  D là trung điểm của MN . Suy ra EQCB  1
 trong đó P là trung điểm của BC và Q là giao điểm của BC và MN .
Theo hệ thức Newton ta có: Q . P QE  QC.QB . Mà Q .
P QE  QM .QN suy ra QM .QN  Q . B QC
hay tứ giác BMCN nội tiếp. Lại có NM là phân giác BDC (giả thiết), D là trung điểm của MN
nên theo tính chất 1(e) ta có điều phải chứng minh.
Nhận xét: Bài toán thực sự không quá khó nhưng đòi hỏi bạn đọc phải nắm vững các tính chất một
cách linh hoạt mới giải quyết được bài toán.
Bài 5. Cho tam giác ABC đường cao AH , E là trung điểm của AH . Đường tròn nội tiếp  I 
tiếp xúc với cạnh BC ở D . DE cắt lại I  ở F . Chứng minh rằng FD là tia phân giác của góc BFC . (Mathscope) Chứng minh
Gọi M , N theo thứ tự là tiếp điểm của  I  với AB, AC . AD cắt I  tại điểm thứ hai là P .
Kẻ đường kính DK của đường tròn  I  .
Do DK / / AH , EA  EH  D HAEK   1 DDPFK   1
 . Từ đó suy ra tứ giác DPFK là tứ giác điều hòa.
Suy ra FK và tiếp tuyến tại P, D đồng quy. Dễ thấy tứ giác DMPN cũng là tứ giác điều hòa nên
tiếp tuyến tại P, D và MN đồng quy. Từ đó suy ra FK, MN, BC đồng quy tại S .
Từ đó suy ra SDBC   1 F SDBC   1
 . Mà DF  SK  DF là tia phân giác BFC .
Nhận xét : Bài toán này tương đối khó hơn các bài toán trước nhưng nếu để ý thì nó cũng chỉ là mô
hình quen thuộc vì thế các điểm P, K, S xuất hiện rất tự nhiên theo mô hình của tứ giác điều hòa.
Bài toán này còn một kết quả tương đối kinh điển là đường tròn I  tiếp xúc với BFC . Để chứng
minh điều này cũng không khó khăn. Một gợi ý nho nhỏ cho các bạn là tiếp tuyến tại F của đường
tròn  I  đi qua trung điểm của SD .
Bài 6. Cho đường tròn O ngoại tiếp ABC . Tiếp tuyến tại A của đường tròn cắt BC tại D .
Đường thẳng DO cắt AB, AC tại E, F . Gọi M , N lần lượt là trung điểm của AB, AC . Chứng
minh rằng EN, FM , AO đồng quy. (Sưu tầm) Chứng minh
Gọi H và G lần lượt là giao điểm của MN với AO và EF . K là tiếp điểm của tiếp tuyến thứ hai
từ điểm D với O .
Ta có: tứ giác ABKC là tứ giác điều hòa, do đó: ADKBC  1. Mà do OM  AB , ON  AC ,
OH  AD, OG  AK nên theo định lý quen thuộc suy ra O MNHG  1 MNHG  1
Suy ra AMNHG  1 AEFOG  1. Từ đây suy ra AO, EN, MF đồng quy.
Vậy ta có điều phải chứng minh. 
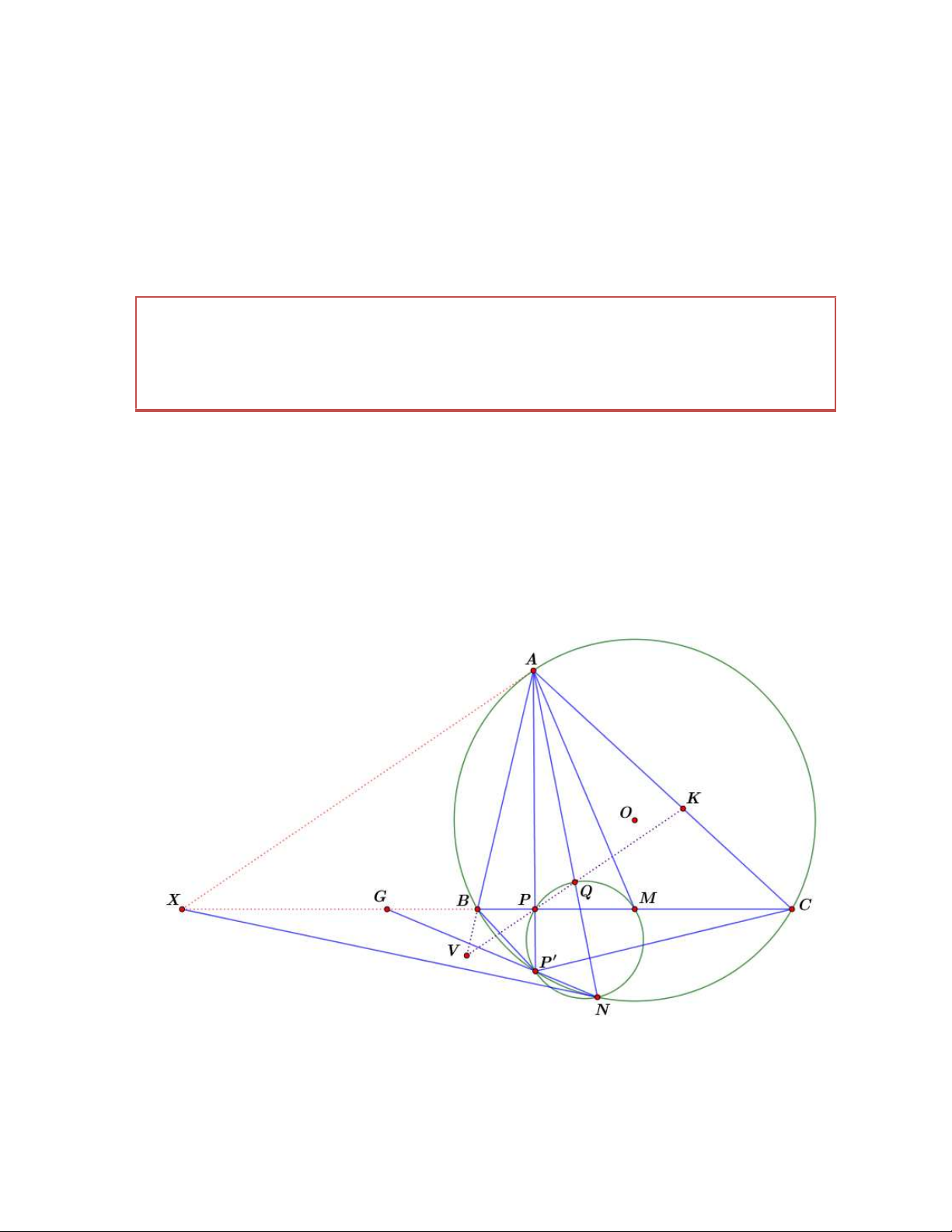
Bài 7. Cho tam giác ABC nội tiếp O . P là một điểm nằm trên cạnh BC , M là trung điểm
của BC . AP cắt O tại điểm thứ hai là P ' . Đường tròn ngoại tiếp tam giác PP 'M cắt O
tại điểm thứ hai là N . Q là giao điểm của AN và PP 'M  . Đường thẳng PQ cắt đường thẳng
AB, AC lần lượt tại V , K . Chứng minh rằng Q là trung điểm của KV . Chứng minh
Gọi G là giao điểm của P ' N và BC . Ta có: G . B GC  GP '.GN  G . P GM
Suy ra GPBC  1 P 'GPBC  1 suy ra P ' ,
A P ' N, P ' B, P 'C   1. Từ đó suy ra tứ giác
ABNC là tứ giác điều hòa. Suy ra tiếp tuyến tại ,
A N và BC đồng quy tại X . Ta có: X  AN  A  CN 180  A  P ' N  P
 QN suy ra PQ / / AX . Nên theo định lý quen thuộc
của hàng điểm điều hòa suy ra Q là trung điểm của VK .
Nhận xét : Việc chứng minh trung điểm đã làm ta liên tưởng tới định lý quen thuộc của hàng điểm
điều hòa từ đó nên ta dẫn đến việc đi chứng minh tứ giác điều hòa và tạo ta điểm G trong bài toán.
Bài toán có thể mở rộng hơn nữa, công việc dành cho bạn đọc !
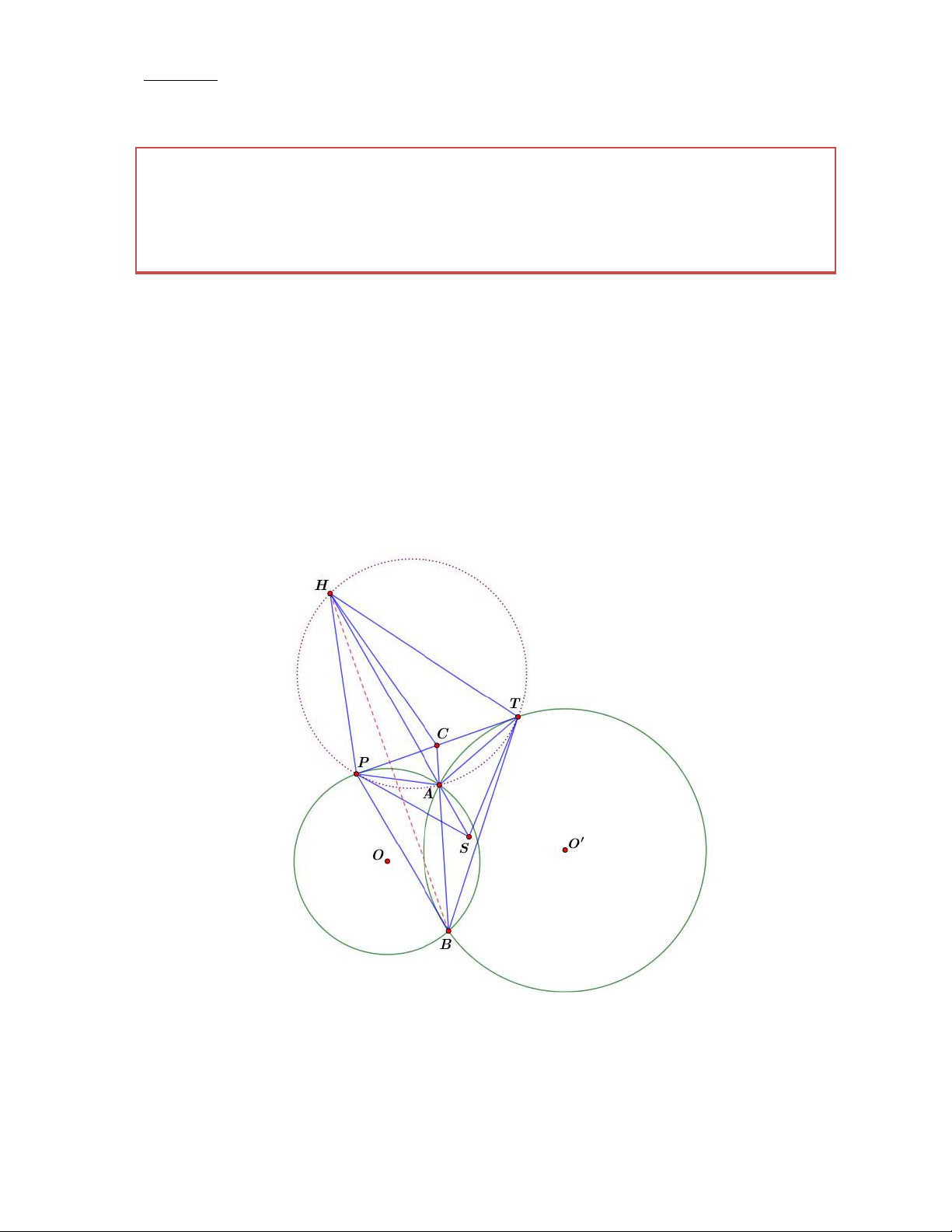
Bài 8. Trong mặt phẳng chứa hai đường tròn O, O ' cắt nhau ở hai điểm , A B . Một tiếp
tuyến chung của hai đường tròn tiếp xúc với O tại P , với O ' tại T . Các tiếp tuyến tại P,T
của đường tròn ngoại tiếp tam giác APT cắt nhau tại S . Gọi H đối xứng với B qua PT . Chứng minh ba điểm , A S, H thẳng hàng. (Việt Nam TST 2001) Chứng minh
Gọi C là giao điểm của AB và PT . Ta có: 2 2 CP  C . A CB, CT  C .
A CB  CP  CT hay C là trung điểm của PT .
Đầu tiên ta sẽ chứng minh tứ giác APHT nội tiếp, thật vậy ta có: P  AT  P  AB  B  AT  B  PT  B  TP  180  P  BT 180  P  HT
Vậy tứ giác APHT nội tiếp. Dễ chứng minh được: C  AP ~ C  PB,  CAT ~ C  TB suy ra: A . P BT  AT.BP  A . P HT  AT.HP
Từ đó suy ra tứ giác APHT điều hòa suy ra , A S, H thẳng hàng.
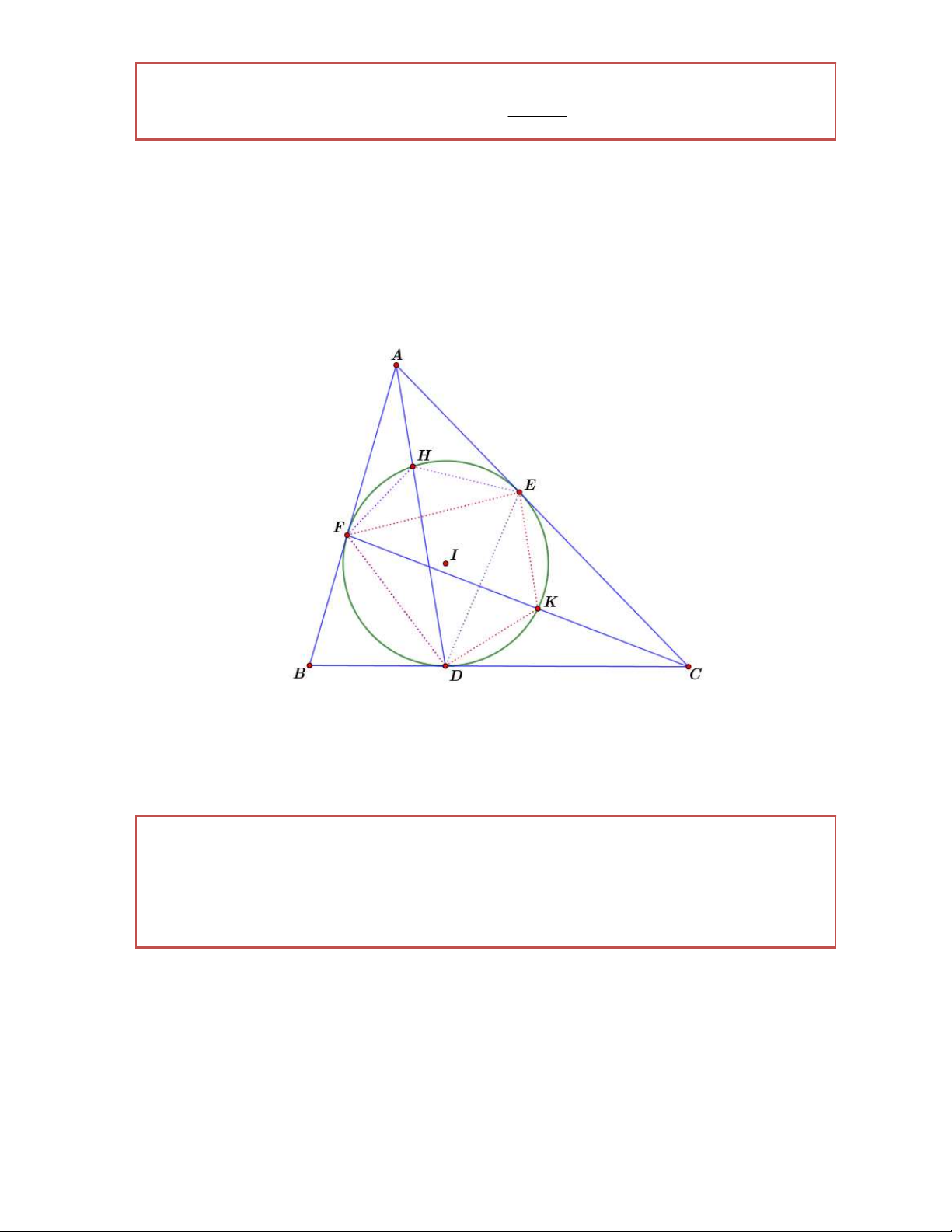
Bài 9. Đường tròn  I  nội tiếp tam giác ABC tiếp xúc với BC tại D và AB tại F , cắt đường FD.HK
thẳng AD tại H và CF tại K . Chứng minh rằng:  3 FH.DK Chứng minh
Dễ thấy rằng các tứ giác FHED và FEKD điều hòa. Sử dụng tính chất của tứ giác điều hòa và
định lý ptolemy ta được: 2EK.FD  2FE.DK  E . D FK 2HF.DE  2HE.DF  H . D FE  4HF.DE.FK.DK  H . D FE.DE.FK  H . D FK  4FH.DK
Sử dụng định lý ptolemy cho tứ giác FHDK suy ra F . D HK  3FH.DK
Vậy ta có điều phải chứng minh.
Bài 10. Tứ giác ABCD điều hòa, tiếp tuyến tại ,
A C và BD cắt nhau tại P . Điểm T thuộc AC
. Gọi O ' là đường tròn ngoại tiếp tam giác TBD . Tiếp tuyến với O ' tại T cắt AP,CP tại Q, R . Chứng minh rằng:
a) Đường tròn ngoại tiếp tam giác PQR tiếp xúc với O ' .
b) B, D,Q, R cùng thuộc một đường tròn. Chứng minh
a) Gọi W là giao điểm của PT và PAC . Dễ thấy 2 P  AT ~ P  WA  PA  PT.PW  PT.PW  P . B PD  W O ' .
Gọi L là giao điểm khác W của PAC và O ' . Bằng cộng góc ta chứng minh được tứ giác
RTCL nội tiếp suy ra L là điểm Miquel của tứ giác toàn phần APRTQC . Hay tứ giác PQRL cũng nội tiếp.
Gọi Lx là tiếp tuyến kẻ từ L của PQR . Ta có:
xLT  RLT  xLR  PCA  CAL  RCL  RTL  TDL
Suy ra xL là tiếp tuyến chung. Suy ra điều phải chứng minh.
b) Gọi X là giao điểm của tiếp tuyến từ L,T của O ' . Dễ thấy AC, BD, LW đồng quy vì lần lượt
là trục đẳng phương của O,O ',PCA .
Nếu gọi AC  BD  Z suy ra PZBD  1 W PZBD  1 W TBLD  1 tứ giác
TBLD là tứ giác điều hòa suy ra 2 2 X  BD  XL  X . R XQ  XT  X . B XD  Q, R, B, D cùng
thuộc một đường tròn.
 Bài toán tương đối khó vì phải vẽ thêm và làm xuất hiện thêm một số điểm phụ, ngoài ra
Còn phải phát hiện ra điểm tiếp xúc là điểm Miquel.
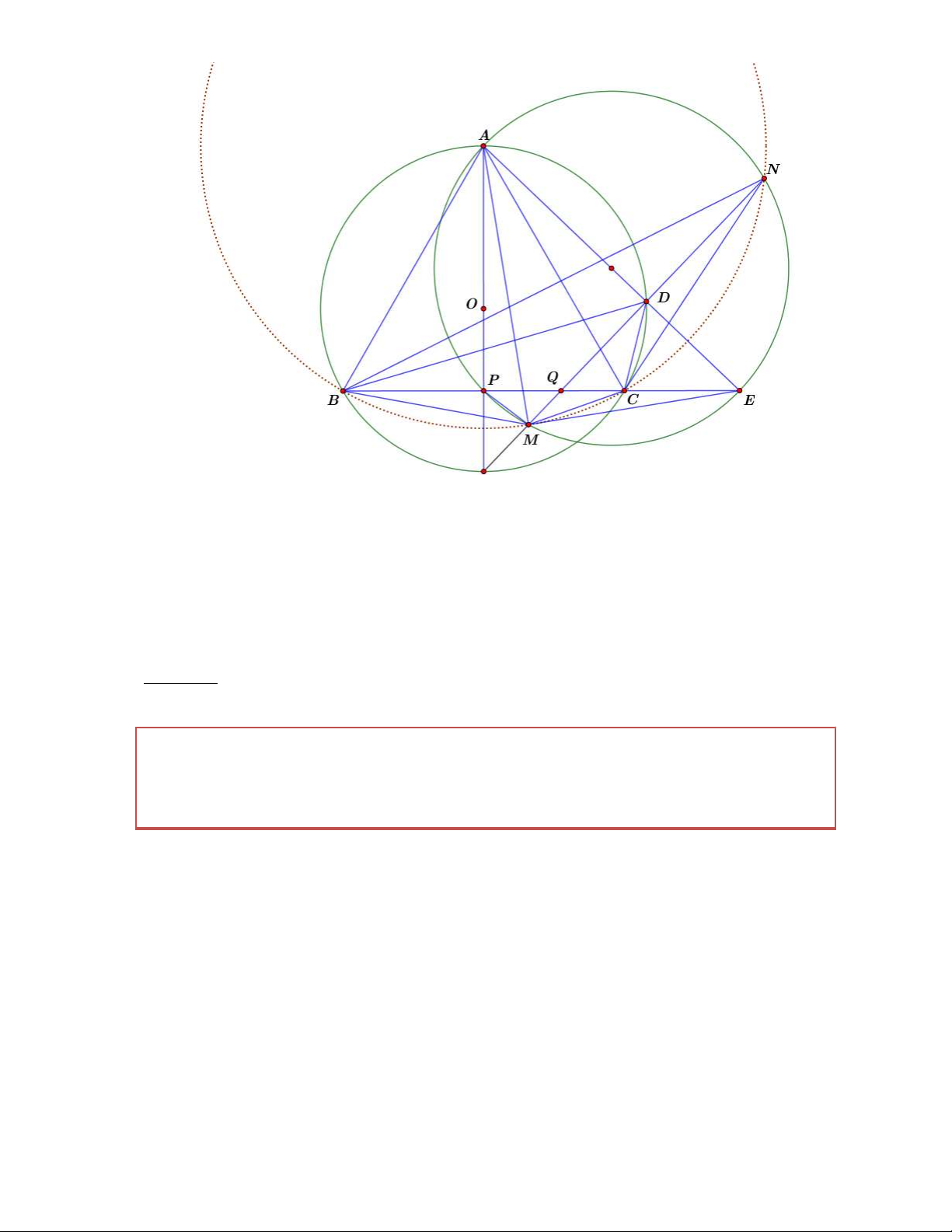
Bài 11. Cho tam giác nhọn ABC nội tiếp đường tròn O , trong đó B,C cố định và A thay đổi
trên đường tròn O . Trên các tia AB, AC lấy lần lượt các điểm M , N sao cho MA  MC và
NA  NB . Các đường tròn ngoại tiếp  AMN  và  ABC cắt nhau tại P khác A . Đường thẳng MN cắt BC tại Q . a) Chứng minh rằng , A P,Q thẳng hàng.
b) Gọi D là trung điểm của BC , các đường tròn có tâm M , N cùng đi qua A cắt nhau
tại K khác A . Đường thẳng đi qua A và vuông góc với AK cắt BC tại E . Đường tròn ngoại
tiếp ADE cắt O tại F khác A . Chứng minh rằng AF luôn đi qua một điểm cố định. (VMO 2014) Chứng minh
a) Do MA  MC, NA  NB nên các tam giác MAC, NAB là các tam giác cân.
Suy ra ABN  BAC  ACM  Tứ giác MBNC là các tứ giác nội tiếp nên Q . B QC  QM .QN
Từ đây suy ra Q thuộc trục đẳng phương của  AMN  và  ABC hay , A P,Q thẳng hàng.
b) Vì O thuộc đường trung trực của AB, AC nên O là trực tâm của AMN . Suy ra AO  MN .
Mà AK là trục đẳng phương của M ;MA và  N; NA nên suy ra AK  MN hay , A O, K thẳng
hàng. Hay EA là tiếp tuyến của O . Dễ thấy 5 điểm ,
A O, E, F, D cùng nằm trên một đường tròn.
Hay OF  EF  EF cũng là tiếp tuyến của O . Hay tứ giác BFCA là tứ giác điều hòa. Từ đó
AF luôn đi qua một điểm cố định là giao điểm hai tiếp tuyến tại B,C .
 Bài toán khá hay nhưng không khó, đặc trưng tiêu biểu cho mô hình về tứ giác điều hòa,
ngoài ra sự xuất hiện của mô típ về trục đẳng phương cũng là gợi ý không nhỏ để giúp cho lời
giải của bài toán. Việc nắm vững các tính chất về tứ giác điều hòa đã giúp chúng ta giải quyết bài
toán không mấy khó khăn.
Bài 12. Cho tam giác ABC , trung tuyến AM cắt đường tròn nội tiếp  I  của tam giác tại X ,
Y . Các điểm Z,T thuộc  I  sao cho XZ / /YT / /BC . Đường thẳng AZ giao với  I  tại điểm
thứ hai là J . Chứng minh rằng tứ giác JYTX là tứ giác điều hòa. Chứng minh
Trước hết ta chứng minh bổ đề sau:
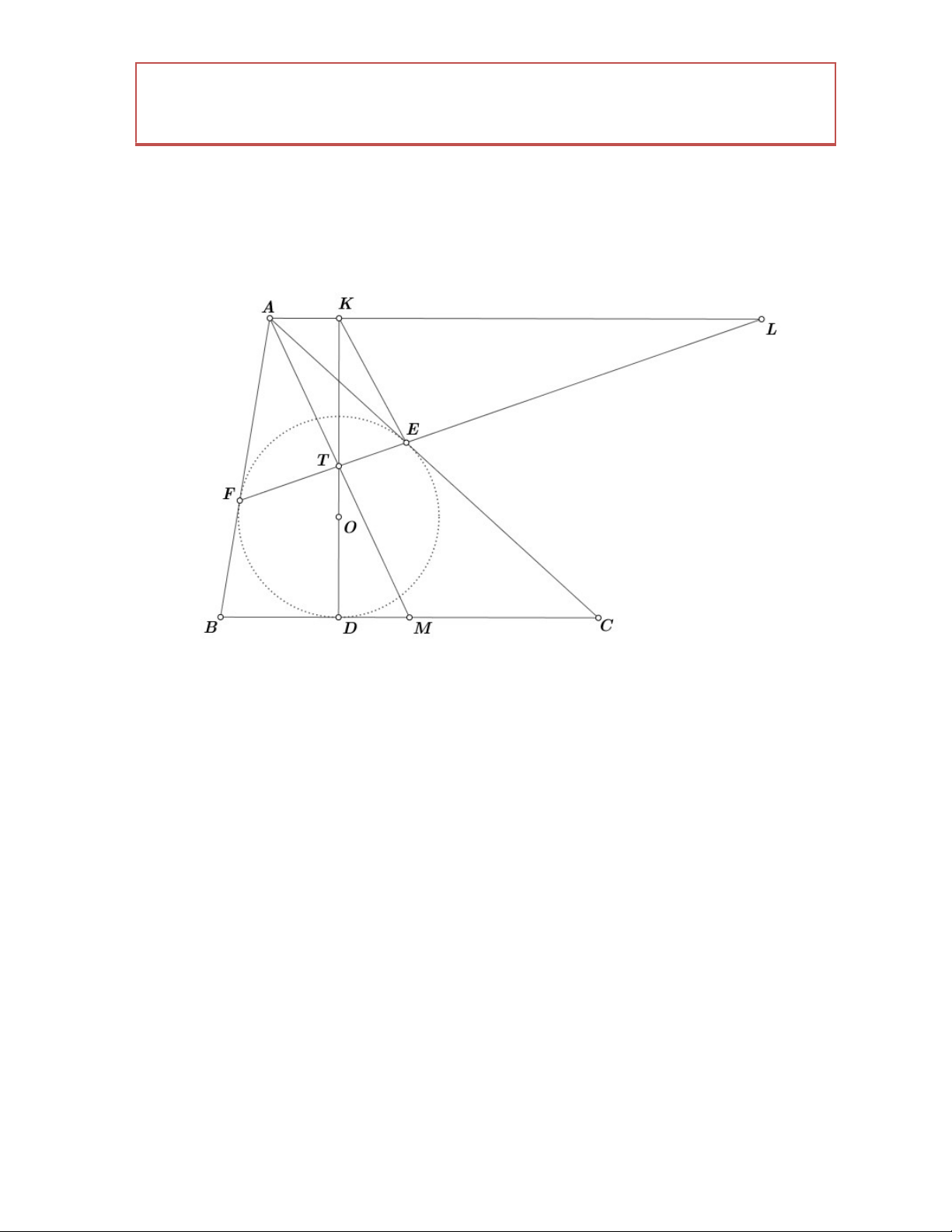
Bổ đề. Cho tam giác ABC ngoại tiếp O . BC,C ,
A AB tiếp xúc với O lần lượt tại D, E, F . Gọi
T là giao điểm của OD và EF . AT cắt BC tại M , thì ta có M là trung điểm của BC .
Qua A kẻ đường thẳng song song với BC cắt FE và DT tại L, K. Dễ thấy 5 điểm ,
A K, E, O, F cùng nằm trên một đường tròn suy ra O  KF  OKE
 KT là tia phân giác của FKE , mà KT  KL . Suy ra K FE,TL  1   FE,TL  1  .
 AFE,TL  1 M là trung điểm của BC . Quay trở lại bài toán.