Các công thức lượng giác cần nhớ - Toán 9

Các công thức lượng giác cần nhớ
I. Các hệ thức cơ bản. 1. sin2x + cos2x = 1 sin x  cos x   2. tan x ; cot x ; tanx.cotx = 1
sin2x = 1 – cos2x = (1 – cosx)(1 + cosx) cos x sin x
 cos2x = 1 – sin2x = (1 – sinx)(1 + sinx) 1 1 3. 2 1  tan x  ; 2 1  cot x  2 cos x 2 sin x
II. Công thức nhân đôi – nhân ba. 1
7. sin3x = 3sinx – 4sin3x = sinx( 3 – 4sin2x)
4. sin2x = 2sinxcosx  sinxcosx = sin2x 2
8. cos3x = 4cos3x – 3cosx = cosx(4cos2x -3)
5. cos2x = cos2x – sin2x = 1 – 2sin2x 3 tan x 3  tan x 9. tan 3x 
= 2cos2x – 1 = (cosx – sinx) (cosx + sinx) 2 1  3 tan x 2 tan x cot 2 x 1 3 x  6. tan 2x  ; cot 2x  cot 3 cot x  x 2 10. cot 3 1  tan x 2 cot x 3 cot 2 x  1
III. Công thức hạ bậc. 1 1 1  cos 2x 11. sin 2 x  1 (  cos 2x) 12. cos 2 x  1 (  cos 2x) 13. tan 2 x  2 2 1  cos 2x 1 1
3sin x  sin 3x 14. sin3x = (3sinx – sin3x) 15. cos3x = (3cosx + cos3x) 16. tan 3 x  4 4
3 cos x  cos 3x 1 1 3 1 1 3 17. sin4x = cos4x - cos2x + 18. cos4x = cos4x + cos2x + 8 2 8 8 2 8 x
IV. Công thức biểu diễn theo t = tan . 2 2t 2  2t 2  19. sinx = 1 t 1 t 20. cosx = 21. tanx = 22. cotx = 2 1  t 2 2 1 t 1  t t 2
V. Công thức qui gọn góc( góc có liên quan đặc biệt).
23. Hai cung đối nhau( cos – đối): sin(- x) = - sin x; cos( - x) = cosx; tan(-x) = - tanx
24. Hai cung bù nhau( sin – bù) : sin(  - x) = sinx ; cos(  - x) = - cosx ; tan( - x) = - tanx         
25. Hai cung phụ nhau( phụ-chéo): sin 
 x = cosx; cos   x = sinx ; tan  x = cotx  2   2   2 
26. Hai cung hơn kém  (tan, cot): sin(  + x) = - sinx ; cos(  + x) = - cosx; tan(  + x) = tanx           27. Hai cung hơn kém (chéo-sin): sin 
 x = cosx; cos  x = - sinx; tan  x = - cotx 2  2   2   2  28. sin(x + k2  ) = sinx 29. cos(x + k2  ) = cosx 30. tan(x + k  ) = tanx 31. cot(x + k  ) = cotx
VI. Công thức cộng cung.
32. sin(a + b) = sinacosb + sinbcosa
33. sin(a – b) = sinacosb – sinbcosa
24. cos(a + b) = cosacosb - sinasinb
35. cos(a – b) = cosacosb + sinasinb tan a  tan b tan a  tan b 36. tan(a + b) = 37. tan(a - b) =
1  tan a tan b
1  tan a tan b
VII. Công thức biến đổi tổng thành tích.  a  b   a  b   a  b   a  b  38. sina + sinb = 2sin   cos  39. sina - sinb = 2cos   sin   2   2   2   2   a  b   a  b   a  b   a  b  40. cosa + cosb = 2cos  cos  
41. cosa – cosb = - 2 sin   sin    2   2   2   2  sin( a  b) sin( a  b) 42. tana + tanb = 43. tana – tanb = cos a cos b cos a cos b sin( a  b) sin( b  a) 44. cota + cotb = 45. cota – cotb = sin a sin b sin a sin b       2
46. sinx + cosx = 2 sin  x 
 = 2 cos x   47. cotx + tanx =  4   4  sin 2x      
48. sinx - cosx = 2 sin  x 
 = - 2 cos  x   49. cotx – tanx = 2cot2x  4   4 
VIII. Công thức biến đổi tích thành tổng. 1 1
50. sinacosb = sin( a  b)  sin( a  b)
51. cosacosb = cos(a  b)  cos(a  b) 2 2 1 1
52. cosasinb = sin( a  b)  sin( a  b)
53. sinasinb = cos(a  b)  cos(a  b) 2 2
IX. Một số công thức cần nhớ khác.
54. cos4x = 8cos4x – 8cos2x + 1
55. cos5x = 16cos5x – 20cos3x + 5cosx 1 1 3
56. cos6x = 32cos6x – 48cos4x + 18cos2x – 1 57. sin4x + cos4x = 1 - sin22x = cos 4x  2 4 4 3 3 5
58. sin6x + cos6x = 1 – 3sin2xcos2x = 1 - sin22x = cos 4x  4 8 8
59. Họ nghiệm x =   k 
2 có 1 điểm biểu diễn trên đường tròn lượng giác. k 2
60. Họ nghiệm x    (n  ,
2 n  N ) có n điểm biểu diễn cách đều nhau trên ĐTLG. n
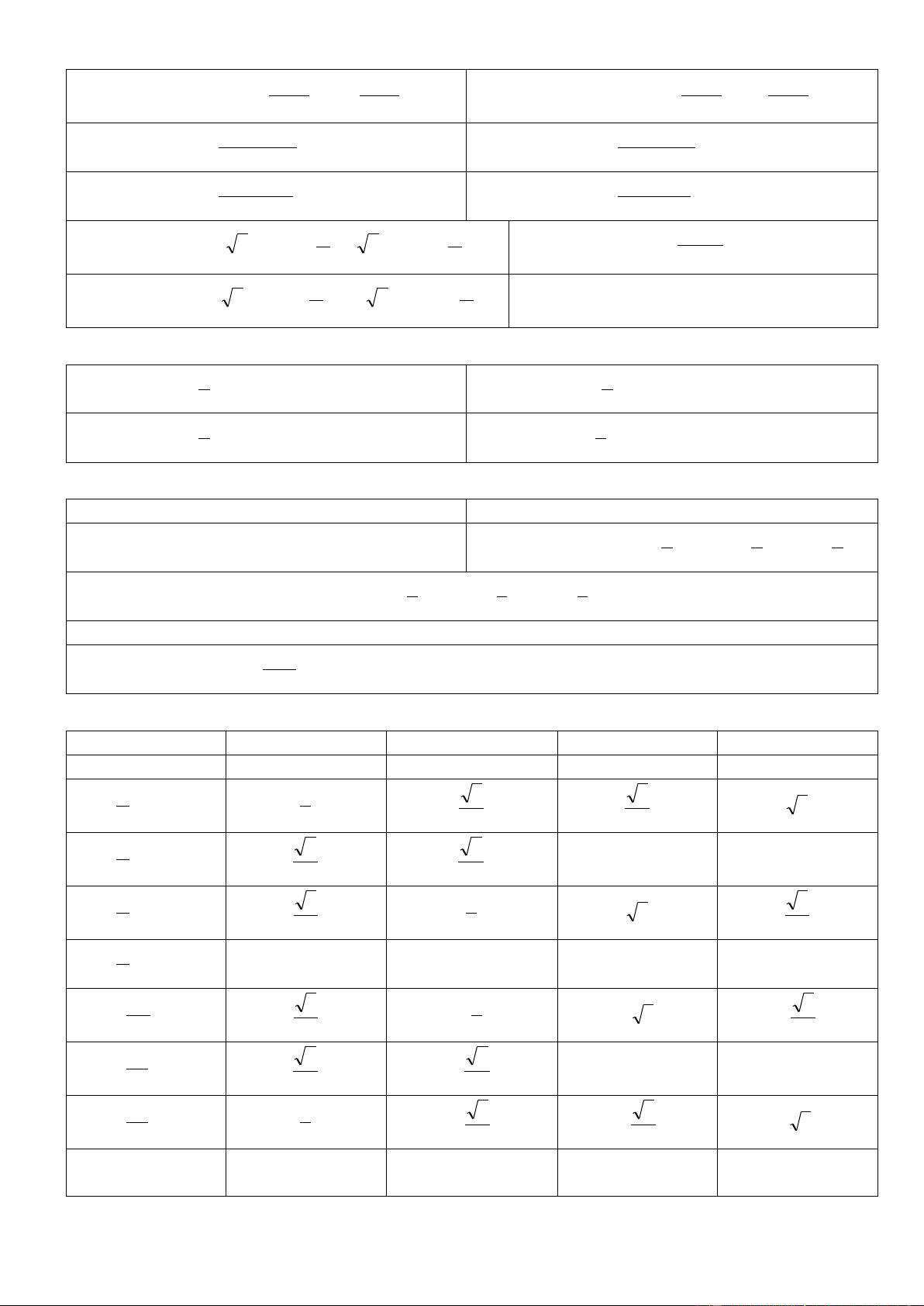
X. Bảng giá trị lượng giác của một số góc đặc biệt. Góc x/ GTLG sinx cosx tanx cotx 00 ( 0 Rad) 0 1 0 ||  1 3 3 300 ( Rad) 3 6 2 2 3  2 2 450 ( Rad) 1 1 4 2 2  3 1 3 600 ( Rad) 3 3 2 2 3  900 ( Rad) 1 0 || 0 2 2 3 1 3 1200 ( Rad) - - 3 - 3 2 2 3 3 2 2 1350 ( Rad) - - 1 - 1 4 2 2 5 1 3 3 1500 ( Rad) - - - 3 6 2 2 3 1800 (  Rad) 0 - 1 0 ||