Các dạng bài tập bồi dưỡng học sinh giỏi môn Toán 9
Tài liệu gồm 319 trang, tuyển tập các dạng bài tập bồi dưỡng học sinh giỏi môn Toán 9, có đáp án và lời giải chi tiết.
+ Chuyên đề 1. Hàm số.
+ Chuyên đề 2. Phương trình.
+ Chuyên đề 3. Hệ phương trình.
+ Chuyên đề 4. Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
+ Chuyên đề 5. Chứng minh đẳng thức và biểu thức.
+ Chuyên đề 6. Hình học (phần 1).
+ Chuyên đề 7. Hình học (phần 2).
+ Chuyên đề 8. Số học.
+ Chuyên đề 9. Chứng minh bất đẳng thức.
+ Chuyên đề 10. Giá trị lớn nhất và giá trị nhỏ nhất (GTLN – GTNN).
Chủ đề: Tài liệu chung Toán 9 129 tài liệu
Môn: Toán 9 3.4 K tài liệu
Tác giả:
Preview text:
CHUYÊN ĐỀ HÀM SỐ Câu 1.
(HSG 9 Tỉnh Bắc Kạn 2023-2024) 2
m + ( 5 − 3) m − 15
Trong mặt phẳng với hệ trục tọa độ Oxy, cho hàm số y = x + 2024. 2 m − 8m + 3
Tìm tất cả các giá trị của tham số m để hàm số nghịch biến. Lời giải 2
m + ( 5 − 3) m − 15
+ Để hàm số nghịch biến thì a = 0 2 m − 8m + 3 + Ta có m − m + = (m − )2 2 8 3 2 +1 0 m + Nên 2
m − ( 3 + 5)m + 15 0
m − 3 0 m 3 (tm) m + 5 0 m − 5 + Ta có 2
m + ( 5 − 3)m − 15 = (m − 3)(m + 5) 0 m− 3 0 m 3 (ktm) m + 5 0 m − 5
Vậy − 5 m 3 thỏa mãn yêu cầu bài toán. Câu 2.
(HSG 9 Tỉnh Bình Phước 2023-2024) Cho Parabol 2
(P) : y = x và đường thẳng (d ) : y = mx + 4 (với m là tham số).
a) Chứng minh đường thẳng (d ) luôn cắt đồ thị (P) tại hai điểm phân biệt .
b) Gọi x , x là hoành độ giao điểm của (P)
d . Tìm m để 1 2 và ( )
2mx − x x + 2mx + 3 1 1 2 2 T = 2 2 x + nhận giá trị nguyên. x 1 2 Lời giải
a) Phương trình hoành độ giao điểm của (d ) và (P) là: 2 2
x = mx + 4 x − mx − 4 = 0 . Ta có 2
= m +16 0 , với mọi m nên phương trình luôn có 2 nghiệm phân biệt, suy ra đường thẳng
(d) luôn cắt (P) tại hai điểm phân biệt.
x + x = m
b) Theo định lý Viet ta có: 1 2 x .x = 4 − 1 2
2m ( x + x − x x + 3 2 2m + 7 1 2 ) Khi đó 1 2 T = = 2 2 x + x 2 m + 8 1 2 9 T = 2 − 2
T m + 8U (9) 2 m + 8 Mà 2 2 m + 8 8, m
m + 8 = 9 m = 1. Câu 3.
(HSG 9 Tỉnh Hà Nam 2023-2024)
Trong mặt phẳng với hệ trục tọa độ Oxy, cho Parabol ( P) 2
: y = 12x và đường thẳng (d) 12 2
: y = 6mx − m + 4 −
, với m 0 là tham số. Tìm các giá trị của m để (d ) và ( P) có các 2 m
điểm chung lần lượt có hoành độ x , x sao cho 3 3
x + x đạt giá trị lớn nhất, giá trị nhỏ nhất. 1 2 1 2 Lời giải
Phương trình hoành độ giao điểm là 12 2 2
12x − 6mx + m − 4 + = 0 1 2 ( ) m 12 144 3 2 2 2
' = 9m −12 m − 4 + = 3 − m + 48 − = − ( 4 2 m −16m + 48 2 2 2 ) m m m Phương trình ( )
1 có nghiệm khi và chỉ khi: 3 ' 0 − ( 4 2 m −16m + 48) 4 2
0 m −16m + 48 0 2 m ( 2 m − )( 2
4 m −12) 0 2 m 2 3 (*)
Với điều kiện (*), pt đã cho có hai nghiệm x , x 1 2 6m m x + x = = 1 2 12 2
Theo hệ thức vi - ét ta có: 12 2 m − 4 + 2 2 m − 4 1 m x x = = + 1 2 2 12 12 m
Do ñoù A = x + x = ( x + x )3 3 3
− 3x .x x + x 1 2 1 2 1 2 ( 1 2 ) 3 2 3 3 2 m m − 4 1 m m m m 3 m − 3 = − 3 + = − + − = 2 2 12 m 2 8 8 2 2m 2m 3 3 3 3 Ta chứng minh A
bằng cách chứng minh A −
0, với điều kiện (*). 4 4 Với điều kiện (*): 2 2 3 3 m − 3 3 3
2m − 3 3 m − 6 A − 0 0 − 0 0 4 2 m 4 4. m 3 2
2m − 3 3 m − 6 0 − m 2 3 (*1) 2
Do có điều kiện (*) nên (*1) luôn đúng. Tức là 3 3 3 3 3 3 A − 0 − A 4 4 4 3 − 3 3 3 Vậy min A = m = 2 − 3 , max A = m = 2 3 . 4 4 Câu 4.
(HSG 9 Đồng Tháp 2023-2024 )
Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d ) 1 : y =
x − 3 cắt hai trục tọa độ Ox , Oy lần lượt 2 tại , A B . a) Tìm tọa độ của , A B .
b) Viết phương trình đường thẳng () đi qua M (2; −2) và cắt đoạn thẳng OA tại C sao cho diện tích
tam giác AMC bằng 5 . Lời giải a) Tìm tọa độ của , A B .
Xét x = 0 y = 3 − B (0; 3 − )
Xét y = 0 x = 6 A(6;0)
b) Viết phương trình đường thẳng () đi qua M (2; 2
− ) và cắt đoạn thẳng OA tại C sao cho diện tích
tam giác AMC bằng 5 .
Gọi H là chân đường cao của M trong AMC , suy ra MH = 2 . 1 Ta có S
= MH.AC = 5, suy ra AC = 5. A MC 2
Vì C thuộc đoạn OA nên C (1;0) . a + b = 0 a = 2 −
Giả sử () : y = ax + b , khi đó 2a + b = 2 − b = 2 Suy ra () : y = 2 − x + 2 . Câu 5.
(HSG 9 Hà Tĩnh 2023-2024 )
Cho đường thẳng (d ) : y = (m − )
1 x + 3 . Tìm tất cả các giá trị của m để đường thẳng (d ) cắt trục
Ox , Oy lần lượt tại hai điểm A và B sao cho tam giác AOB vuông cân. Lời giải
Nếu m = 1 thì (d ) song song với . 3 −
Xét m 1. Ta có tọa độ A ; 0 , B (0;3). m −1
Để tam giác AOB vuông cân thì OA = OB 3 − m −1 =1 m = 2 = 3 m −1 =1 . m −1 m −1 = 1 − m = 0 Câu 6.
(HSG 9 Buôn Ma Thuật 2023-2024 ) Cho Parabol ( P) 2
: y = x và đường thẳng (d ) : y = 2(m − )
1 x − m + 3 . Tìm m để (d ) cắt ( P) tại hai điểm phân biệt ,
A B sao cho A và B cách đều trục Oy . Khi đó tính độ dài đường trung tuyến OM của tam giác OAB . Lời giải
Xét phương trình hoành độ giao điểm của (P) và (d ) là : 2 x = (m − ) 2 2
1 x − m + 3 x − 2 (m − )
1 x + m − 3 = 0 ( ) 1
Điều kiện để (d ) và (P) cắt nhau tại hai điểm phân biệt là phương trình (1) có hai nghiệm phân biệt 2 3 7
hay ' 0 m − + 0 (luôn đúng) 2 4
Kẻ AH , BK ⊥ Oy ( H , K Oy) .
Không mất tính tổng quát, do ,
A B cách đều trục Oy, ,
A B phân biệt, giả sử x 0, x 0 . A B
Khi đó AH = x , BK = −x . Vì AH = BK nên x = −x hay x + x = 0 A B A B A B
Theo định lý Vi-ét, ta có x + x = 2(m − ) 1 . A B
Vậy khi đó 2 (m − ) 1 = 0 nên m = 1
Lúc này (d ) : y = 2.A( 2,2), B(− 2,2) . Vậy nên ,
A B đối xứng qua Oy .
Do đó Oy đi qua trung điểm M của AB
Giao điểm của Oy với d là M (0;2) . Vậy OM = 2
Tóm lại m = 1;OM = 2 . Câu 7.
(HSG 9 Hòa Bình 2023-2024 )
Cho hàm số bậc nhất y = x + 3 và 2 y = 2
− x + m + m −18 ( m là tham số). Tìm tất cả các giá trị của m
để đồ thị hai hàm số trên cắt nhau tại một điểm trên trục hoành. Lời giải
Đồ thị hàm số y = x + 3 cắt trục hoành thì y = 0 nên x = −3
Để đồ thị hai hàm số y = x + 3 và 2 y = 2
− x + m + m −18 (cắt nhau tại một điểm trên trục hoành trên
trục hoành thì đồ thị hàm số 2 y = 2
− x + m + m −18 đi qua điểm có tọa độ (−3;0) . m = 3 Do đó 2 0 = 2 − .( 3
− ) + m + m −18 m = 4 Câu 8.
(HSG 9 Kon Tum 2023-2024)
Đồ thị d của hàm số y = x − 2 cắt trục Oy tại điểm A = −
và cắt đường thẳng d : y
2x 5 tại điểm B. 1
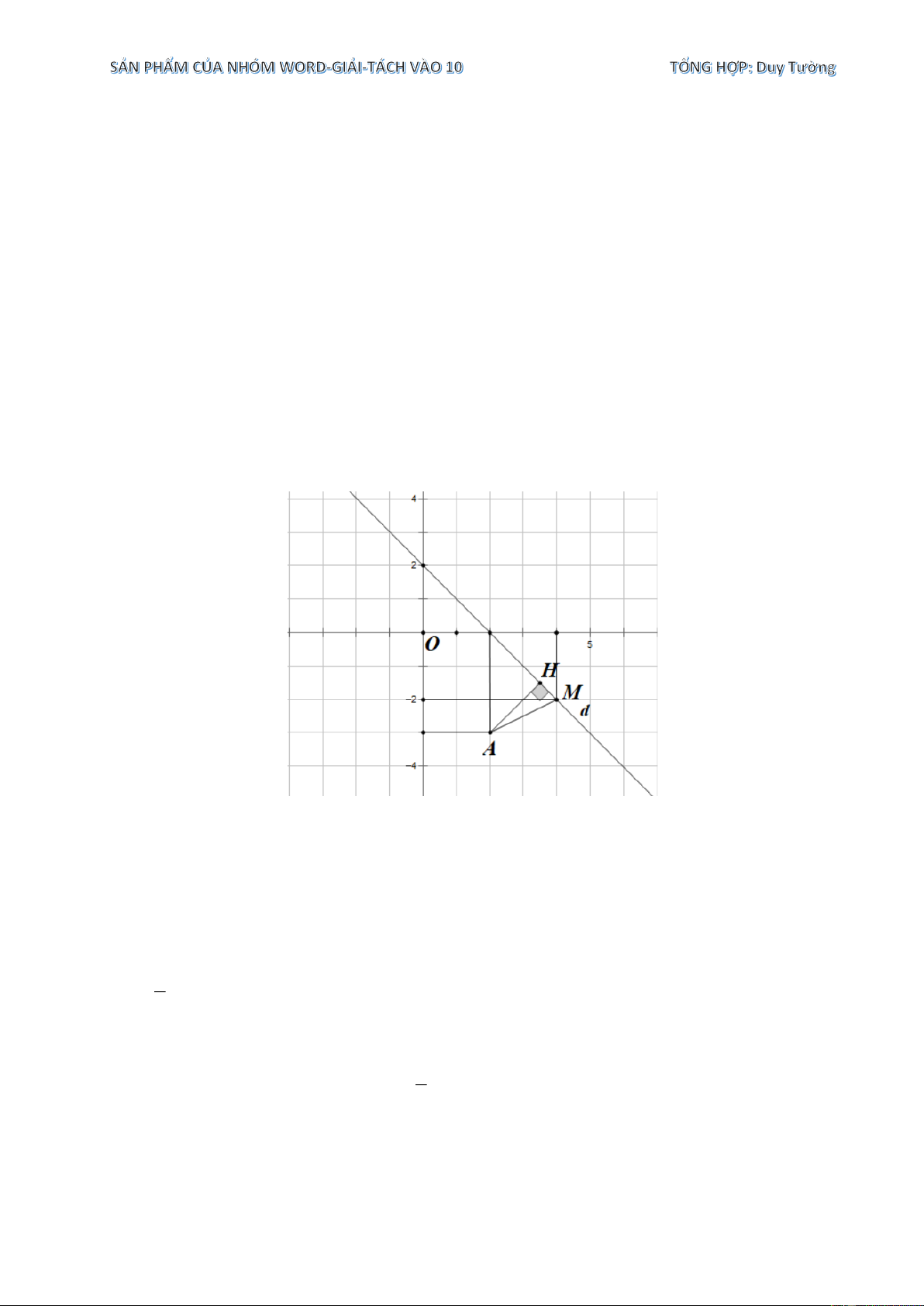
Tính diện tích tam giác OAB và khoảng cách từ điểm O đến đường thẳng AB (với O (0;0) là gốc tọa độ). Lời giải
Giao điểm của d : y = x − 2 với Oy là A(0; 2 − ).
Giao của d : y = x − 2 và d : y = 2x − 5 là B (3; ) 1 . 1
Quan sát hình vẽ bên, với H là hình chiếu vuông góc của B lên trục Oy .
Ta có OA = 2, BH = 3.
Diện tích tam giác OAB BH.OA S = = 3. O AB 2
Gọi I là hình chiếu vuông góc của O lên . AB
Khoảng cách từ điểm O đến đường thẳng AB là độ dài đoạn OI.
Tam giác ABH vuông cân tại H có AH = 3 AB = 3 2. A . B OI 2S 2.3 O AB S = OI = = = 2. O AB 2 AB 3 2 Câu 9.
(HSG 9 Hưng Yên 2023-2024)
Trong mặt phẳng toạ độ Oxy , cho điểm M (3;5) . Lập phương trình đường thẳng d đi qua M và
cắt các tia Ox,Oy tại ,
A B sao cho diện tích tam giác OAB bằng 30 . Lời giải
Phương trình đường thẳng (d ) : y = m( x − 3) + 5 y = mx − 3m + 5 ( − d ) 3m 5
Ox = A A ; 0 m
(d)Oy = B B(0;5−3m)
Điều kiện để d cắt các tia Ox,Oy tại hai điểm ,
A B phân biệt là: m 0 . 1 (3m−5)2 S = O . A OB = 30 = 60 m −
= − m (do m 0 ) OAB (3 5)2 60 2 m 5
m = − (thỏa mãn) 3
Vậy phương trình đường thẳng 5 d là y = − x +10 . 3
Câu 10. (HSG 9 Bến Tre 2023-2024 )
Trong hệ trục tọa độ Oxy cho hai đường thẳng (d : y = x + 3 = − + + − 1 ) , (d ) 2 : y 2x m
m 18 với m là 2
tham số. Tìm tất cả các giá trị của m để hai đường thẳng (d , d cắt nhau tại điểm có hoành độ 1 ) ( 2 ) bằng 0 . Lời giải
Hoành độ giao điểm của (d , d là nghiệm của phương trình: 1 ) ( 2 ) 2 m + m − 21 2 x + 3 = 2
− x + m + m −18 x = 3
(d , d cắt nhau tại điểm tại điểm có hoành độ bằng 0 khi 1 ) ( 2 ) 2 m + m − 21 1 − 85 2 x =
= 0 m + m − 21 = 0 m = 3 2 1 − 85 Vậy m = 2
Câu 11. (HSG 9 Hậu Giang 2023-2024 )
Cho đa thức f ( x) 5 3
= ax + bx + cx + 2 thỏa mãn f (−1) = 2024. Tính f ( ) 1 . Lời giải f ( 1
− ) = −a − b − c + 2 = 2024 a + b + c = 20
− 22 f (1) = a + b + c + 2 = 20 − 22 + 2 = 20 − 20.
Câu 12. (HSG 9 Sơn La 2023-2024 )
Trong mặt phẳng với hệ trục tọa độ Oxy . Cho điểm A(1;3) parabol ( P) và đường thẳng (d ) có
phương trình lần lượt là: 2
y = x và y = ax + 3 − a .
a) Chứng minh rằng với mọi giá trị của a đường thẳng (d ) luôn cắt parabol ( P) tại hai điểm phân
biệt. Giả sử B và C là hai giao điểm của (d ) và ( P) . Tìm a để AB = 2AC .
b) Gọi x , x là hoành độ giao điểm của B , C . Tìm giá trị lớn nhất, nhỏ nhất của biểu thức 1 2 (x +1 x +1 1 )( 2 ) P = 2 2 x + x + . 6 x + x 1 2 ( 1 2) Lời giải
a) Chứng minh rằng đường thẳng (d ) luôn cắt parabol ( P) tại hai điểm phân biệt. Giả sử B và C là
hai giao điểm của (d ) và (P). Tìm a biết rằng AB = 2AC.
Xét phương trình hoành độ giao điểm: 2
x = ax + 3 − a 2
x − ax + a − 3 = 0 ( ) 1
Ta có = a − (a − ) = a − a + = (a − )2 2 2 4 3 4 12 2
+ 8 0 với mọi a Do đó phương trình ( )
1 luôn có hai nghiệm phân biệt.
Như vậy, phương trình hoành độ giao điểm của (d ) và (P) luôn có hai nghiệm phân biệt, tức là (d )
luôn cắt ( P) tại hai điểm phân biệt.
Giả sử x , x là nghiệm của phương trình ( )
1 và B ( x ; y , C ( x ; y thì 2 2 ) 1 1 ) 1 2
(x −1 x −1 = x x − x + x +1= a −3 − a +1= −2 0 1 )( 2 ) 1 2 ( 1 2) ( )
Vậy điểm A nằm giữa B và C . Do đó AB = 2 AC
(1− x = 2 x −1 x = 3− 2x 2 1 ) ( 2 ) 1 2 ( )
Mặt khác x + x = a kết hợp với (2) ta được x = 3 − a 1 2 2 Thay vào phương trình ( ) 2
1 ta được: (3 − a) − a (3 − a) + a − 3 = 0 2
a − 4a + 3 = 0
Phương trình trên có nghiệm a = 1, a = 3.
Vậy a = 1 hoặc a = 3 .
b) Gọi x , x là hoành độ giao điểm của B , C . Tìm giá trị lớn nhất, nhỏ nhất của biểu thức 1 2 (x +1 x +1 1 )( 2 ) P = . 2 2
x + x + 6 x + x 1 2 ( 1 2) (x +1 x +1
x x + x + x +1 1 )( 2 ) 1 2 1 2 P = = 2 2
x + x + 6 x + x + + + − 1 2 ( 2 1 2 ) (x x 6 x x 2x x 1 2 ) ( 1 2) 1 2
x + x = a Vì 0, a
nên theo định lý Vi-ét: 1 2 x x = a − 3 1 2 a − 3 + a +1 2a − 2 P = = 2 a + 6a − 2(a − 3) 2 a + 4a + 6 P( 2
a + 4a + 6) = 2a − 2 2
Pa + 2(2P − )
1 a + 6P + 2 = 0 (*) +) 2
P = 0 a = 2 x − 2x −1 = 0 x = 1 2
Coi (*) là phương trình bậc hai ẩn a , P là tham số. 2
Khi đó: = ( P − ) − P ( P + ) 2 2 1 6 2 = 2 − P − 6P +1
Để phương trình (*) có nghiệm thì 3 − − 11 3 − + 11 3 − − 11 −(2P − ) 1 2 0 2
− P − 6P +1 0 P P = a = =1− 11 2 2 min 2 P (thoả mãn) 3 − + 11 −(2P − ) 1 P = a = =1+ 11 (thoả mãn) max 2 P 3 − − 11 3 − + 11 Vậy P =
a =1− 11 ; P = a =1+ 11 . min 2 max 2
Câu 13. (HSG 9 An Giang 2023 - 2024 ) Cho bai hàm số : 2 y = x và 2
y = 3ax - a ( a là tham số khác 0 ) . Chứng minh rằng đồ thị của hai hàm
số luôn cắt nhau tại bai điểm gọi bai điểm đã cho là ( x ; y , x ; y . Tìm các giá trị của a để 1 1 ) ( 2 2 ) y + y = 28 1 2 Lời giải
* Xét tương giao của hai đồ thị hàm số : 2 y = x và 2
y = 3ax − a ta có 2 2 2 2
x = 3ax − a
hay x − 3ax + a = 0 ( ) 1 2 2 2
= (−3a) − 4a = 5a ; 0 với a 0
Vậy : hai hàm số luôn cắt nhau tại hai điểm phân biệt ( Với a 0 )
* Tìm các giá trị của a để y + y = 28 1 2
hai hàm số luôn cắt nhau tại hai điểm là ( x ; y , x ; y . Thì x ; x là nghiệm của phương trình 1 1 ) ( 2 2 ) 1 2 ( ) 1 Ta có :
y + y = 28 ( 2 2 x + x = 28 1 2 1 2 )
(x + x )2 − 2x .x = 28 (2) 1 2 1 2 ( )
x + x = 3a 1 Theo VI-ET ta có : 1 2 thay vào (2) ta được : 2 x x = a 1 2 ( a)2 2 3 − 2a = 28 2 2
9a − 2a = 28 2 7a = 28 2 a = 4 a = 2 a = 2 −
Vậy : a = 2 thì y + y = 28 1 2
Câu 14. (HSG 9 Tiền Giang 2022-2023 )
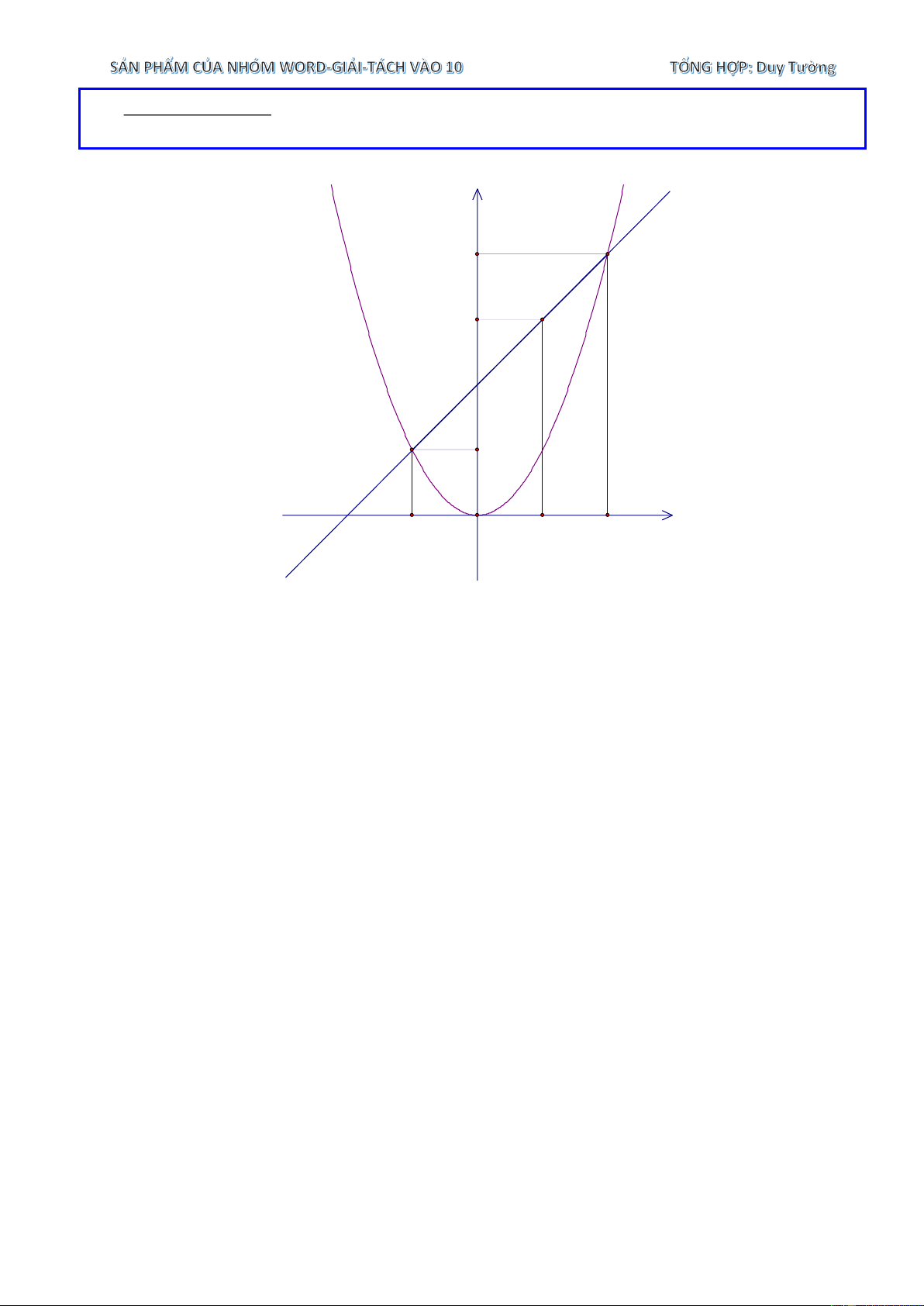
Trong mặt phẳng tọa độ Oxy , cho parabol ( P) 2
: y = x và đường thẳng (d ) : y = 2x+ 3
1. Vẽ đồ thị ( P) và (d ) trên cùng một hệ tọa độ Oxy . 2. Gọi ,
A B là giao điểm của ( P) và (d ) . Điểm M là một điểm thay đổi trên ( P) và có hoành độ là m ( 1
− m m) . Tìm m để tam giác MAB có diện tích lớn nhất. Lời giải 1. Bảng giá trị của 2 y = x x −2 1 − 0 1 2 2 y = x 4 1 0 1 4
Bảng giá trị của y = 2x + 3 x 1 − 0 y = 2x + 3 1 3
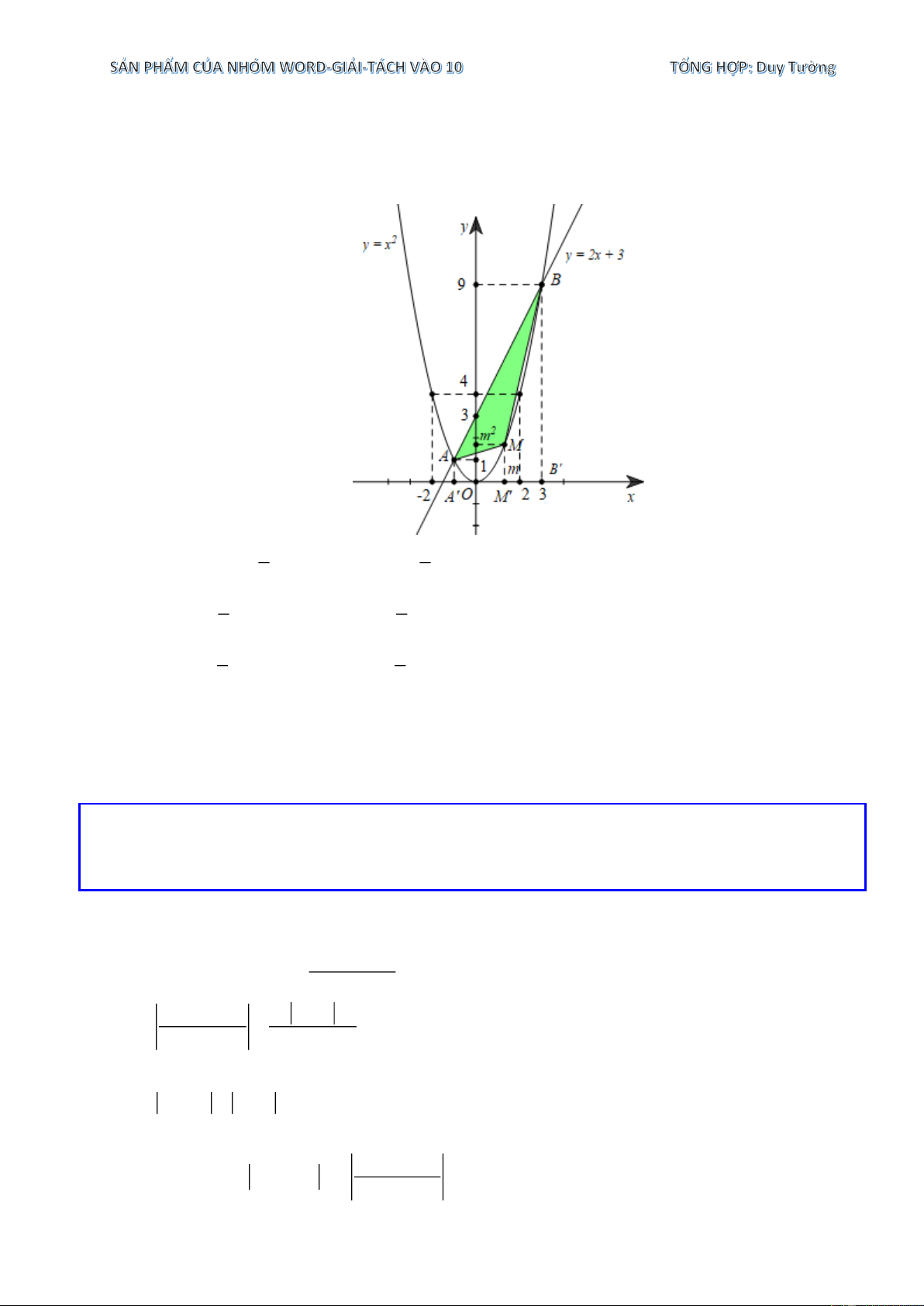
Vẽ ( P) và (d ) 2. Gọi M ( 2 ;
m m )(P) với −1 m 3.
Các điểm A', B ', M ' lần lượt là hình chiếu vuông góc của ,
A B, M trên trục hoành 1 1 Ta có S =
AA'+ BB ' .A' B ' = 1+ 9 .4 = 20 . ABB ' A' ( ) ( ) 2 2 1 S = AA + MM A M = + m + m AMM A ( ) 1 ' ' . ' ' ( 2 1 . 1 . ' ' ) ( ) 2 2 1 S = MM + BB B M = m + − m MBB M ( ) 1 ' ' . ' ' ( 2 9 . 3 . ' ' ) ( ) 2 2 S = S − S − S = 8 − 2 m −
, với mọi −1 m 3. A AMM A MBB M ( )2 1 8 MAB ABB ' ' ' ' ' '
Suy ra tam giác MAB có diện tích lớn nhất bằng 8 m = 1.
Vậy m = 1 là giá trị cần tìm
Câu 15. (HSG 9 Yên Bái 2023-2024 ) Cho đường thẳng 2
(d ) : y = (m − 5m + 8)x − m + 2 với m là tham số thực. Tìm tất cả các giá trị của m để
đường thẳng (d) cắt trục Ox,Oy lần lượt tại hai điểm A và B sao cho OB = 4OA Lời giải 2. Cho (
A x ; y ) y = 0 A A A m − 2
Thay y = 0 vào (d) x = ( 2
m − 5m + 8 0) A A 2 m − 5m + 8 m − 2 m − 2 OA = = 2 2 m − 5m + 8 m − 5m + 8
Cho B(x ; y ) x = 0 .Thay y = −m + 2 vào (d) y = −m + 2 B B B B B
OB = −m + 2 = 2 − m
Để để đường thẳng (d) cắt trục Ox,Oy lần lượt tại hai điểm A và B m 2 m − 2
Ta có OB = 4OA − (m − 2) = 4 2 m − 5m + 8 4 m − 2 m − 2 = m − 2 ( 2
m − 5m + 8 = 4 m − 2 2 ) m − 5m + 8 m − = m − 2 ( 2 0 2
m − 5m + 4) = 0 2
m −5m + 4 = 0 m = 2(L) m = 4(T/m) m =1 (T/m)
Vậy m = 1; m = 4 .
Câu 16. (HSG 9 Bắc Giang 2023-2024 )
Trong mặt phẳng toạ độ Oxy , cho đường thẳng d : y = (m − )
1 x + m − 2 (m )
1 . Tìm tất cả các giá trị
của tham số m để đường thẳng d tạo với hai trục toạ độ một tam giác có diện tích bằng 2 . Lời giải 2 − m
d cắt trục Ox tại A ; 0
, d cắt trục Oy tại B(0;m − 2) m −1 2 − m
Tam giác AOB vuông tại O , có OA = ,OB = m − 2 m − 1 1 1 2 − m S = 2 O . A OB = 2 . . m − 2 = 2 AOB 2 2 m − 1
(m − 2)2 = 4 m −1 1 2 ( ) ( )
(m − 2) = 4 m −1 (m − 2)2 = 4 − (m − )1 (2) + ( ) 2
1 m − 8m + 8 = 0 m = 4 2 2 (thoả mãn) + ( ) 2
2 m = 0 m = 0 (thoả mãn).
Vậy các giá trị cần tìm của m là m = 0, m = 4 2 2.
Câu 17. (HSG 9 Cà Mau 2023-2024 ) 1 1 Cho Parabol ( P) : 2 y =
x và đường thẳng (d ) : y = mx + 2 2
a) Chứng minh rằng (d ) luôn đi qua một điểm cố định với mọi m .
b) Chứng minh rằng (d ) luôn cắt ( P) tại hai điểm phân biệt với mọi m .
c) Gọi A và B là giao điểm của đường thẳng (d ) và Parabol ( P) , tìm tập hợp các trung điểm
C của đoạn thẳng AB khi m thay đổi. Lời giải
a) Chứng minh rằng (d ) luôn đi qua một điểm cố định với mọi m .
Gọi ( x ; y là điểm cố định mà đường thẳng (d ) đi qua với mọi giá trị của m . Khi đó ta có 0 0 ) 1 1 y = mx +
x .m = y − 0 0 0 0 2 2 x = 0 x = 0 0 0 Suy ra: 1 1 y − = 0 y = 0 2 0 2 1
Vậy điểm cố định mà đường thẳng (d ) đi qua với mọi giá trị của m là 0; 2
b) Chứng minh rằng (d ) luôn cắt ( P) tại hai điểm phân biệt với mọi m .
Phương trình hoành độ giao điểm 2
x − 2mx −1 = 0 Có ' 2 = m +1 Vì ' 2
= m +11 0 với m
. Nên Phương trình hoành độ giao điểm luôn có hai nghiệm phân biệt.
Vậy (d ) luôn cắt ( P) tại hai điểm phân biệt với mọi m .
c) Gọi A và B là giao điểm của đường thẳng (d ) và Parabol ( P) , tìm tập hợp các trung
điểm C của đoạn thẳng AB khi m thay đổi.
Gọi A và B là giao điểm của đường thẳng (d ) và Parabol ( P) , tìm tập hợp các trung điểm C của
đoạn thẳng AB khi m thay đổi. 1 x = x + x C ( A B ) 2
Gọi C ( x ; y là trung điểm của đoạn thẳng AB thì . C C ) 1 2 y = x + C C 2 1 1 Theo Viet thì x = x + x = m = m . C ( A B ) .2 2 2 1 1 Khi đó 2 2 y = x + = m + . C C 2 2 1
Vậy tập hợp trung điểm C của đoạn thẳng AB là các điểm thỏa mãn biểu thức 2 y = x + 2
Câu 18. (HSG 9 Đà Nẵng 2023-2024 )
Trên mặt phẳng tọa độ, cho đường thẳng y = mx − 2m + 4 (d ) , với m là tham số và O là gốc tọa độ.
a) Tìm tọa độ điểm A cố định mà đường thẳng (d ) luôn đi qua với mọi m .
b) Với mỗi giá trị của m , gọi R là bán kính của đường tròn tâm O tiếp xúc (d ) . Tìm m để
bán kính R lớn nhất. Lời giải
a) A(a ; b) là điểm cố định của (d ) nên:
b = ma − 2m + 4 với mọi m
(a − 2).m = b − 4 với mọi m a − 2 = 0 b − 4 = 0 a = 2 b = 4 Vậy A = (2 ; 4)
b) Gọi H là tiếp điểm của (d ) với đường tròn (O ; R) thì OH ⊥ (d ) Ta có: y = ax A A 4 = 2a a = 2
Lại có: OA ⊥ d . a a ' = −1 2m = −1 1 − m = 2 1 − Vậy m = 2
Câu 19. (HSG 9 Điện Biên 2023-2024 )
Tìm m sao cho khoảng cách từ gốc tọa độ O đến đường thẳng (d ) : y = mx + 2m + 2 ( m 0 ) đạt giá trị lớn nhất. Lời giải
Gọi M ( x ; y là điểm cố định của của đường thẳng (d ) : y = mx + 2m + 2 o o )
Khi đó: y = mx + 2m + 2 y − mx − 2m – 2 = 0 o o o o + = = − −( x 2 0 x 2
x + 2) m + y – 2 = 0 với mọi m khi o o o o y − 2 = 0 y = 2 o o Vậy điểm M ( 2
− ;2)là điểm cố định của d .
Kẻ OH vuông góc với (d ) tại H , ta có khoảng cách từ O đến (d ) bằng OH .
Khi (d ) thay đổi theo m và luôn đi qua M ( 2
− ;2) cố định ta luôn có OH OM . Suy ra OH
= OM = x + y = − + =
H trùng với M OM ⊥ (d) tại M . a m m ( 2)2 2 2 2 2 2 2 m x
Đường thẳng OM có dạng y = ax đi qua M ( 2 − ; 2) 2 = . a ( 2 − ) a = 1 − .
Điều kiện để đường thẳng OM vuông góc với (d ) là: . m (− ) 1 = 1 − m = 1
Vậy với m = 1 thì khoảng cách từ O tới (d ) là lớn nhất bằng 2 2
Câu 20. (HSG 9 Hòa Bình 2023-2024)
Cho đường thẳng (d ) : mx + (2m − 3) y = 6 ( m là tham số).
a) Tìm điểm cố định mà đường thẳng (d ) luôn đi qua với mọi m .
b) Tìm giá trị của m để khoảng cách từ điểm A(2;−3) đến đường thẳng (d ) lớn nhất. Lời giải
a) Cho đường thẳng (d): mx + (2m − 3) y = 6 ( m là tham số)
Gọi M ( x ; y ) là điểm cố định mà đường thẳng (d ) luôn đi qua với mọi m . Ta có: M M
mx + (2m − 3) y = 6 m M M
mx + 2my − 3y = 6 m M M M
m( x + 2y ) = 3y + 6 m M M M 3y + 6 = 0 M x − 2 y = 0 M M y = 2 − M x = 4 M Vậy M (4 : 2
− )là tọa độ điểm cố định cần tìm
b) Ta có hình vẽ minh họa Do A( 2; 3 − ),M ( 4; 2
− ) cố định nên AM không đổi
Gọi y = ax + b( a,b R,a 0 ) là phương trình đường thẳng AM 2a + b = 3 − 4a + b = 2 − 1 a = ( tmdk ) 2 b = 4 − 1
Vậy phương trình đường thẳng AM là y = x − 4 2
Kẻ AM vuông góc với (d ) tại H nêm AH là độ dài từ A đến (d )
AH AM ( Quan hệ đường vuông góc và đường xiên)
Mà AM không đổi nên dấu “ ”
= xảy ra khi H trùng M
AM ⊥ ( d ) tại M
Ta có (d ) mx + (2m − 3) y = 6
mx − 6 = (3− 2m) y 3 3 Với m =
x − 6 = 0 x = 4 ( Không t/m) 2 2 3 m 6 Với m ( d ) : x − = y 2 3 − 2m 3 − 2m 1 m
Vì AM ⊥ ( d ) tại m . = 1 − 2 3 − 2m
m = (2m −3) 2 . m = 4m − 6 m = 2( t / m )
Vậy m=2 là giá trị thỏa mãn.
Câu 21. (HSG 9 Đắk Lắk 2023-2024 )
Trong mặt phẳng Oxy , cho đường thẳng (d ) : y = (m − 2) x + m +1, ( m là tham số) và Parabol (P) 1 2 : y =
x . Chứng minh rằng với mọi số thực m đường thẳng (d ) luôn cắt Parabol ( P) tại hai 2 điểm phân biệt. Lời giải
Xét phương trình hoành độ 1
giao điểm của ( P) và (d) (d ) 2 :
x = (m − 2) x + m +1 2 2
x − 2(m − 2) x − 2(m + ) 1 = 0 ( I ) Ta có: 2
Δ = (m − 2) + 2(m + ) 1
Do ∆’ = (m - 1)2 + 5 ' 0, m
nên phương trình (I) luôn có 2 nghiệm phân biệt với mọi m
Do đó (P) luôn cắt (d ) tại hai điểm phân biệt với mọi m .
Câu 22. (HSG 9 Sơn La 2023-2024 )
Trong mặt phẳng với hệ trục tọa độ Oxy . Cho điểm A (1; 3), parabol ( P) và đường thẳng (d ) có
phương trình lần lượt là: 2
y = x và y = ax + 3 − a .
a) Chứng minh rằng với mọi giá trị của a đường thẳng (d ) luôn cắt parabol ( P) tại hai điểm phân
biệt. Giả sử B và C là hai giao điểm của (d ) và ( P). Tìm a để AB = 2AC.
b) Gọi x , x là hoành độ giao điểm của B, C . Tìm giá trị lớn nhất, nhỏ nhất của biểu thức 1 2 (x +1)(x +1) 1 2 P = . 2 2
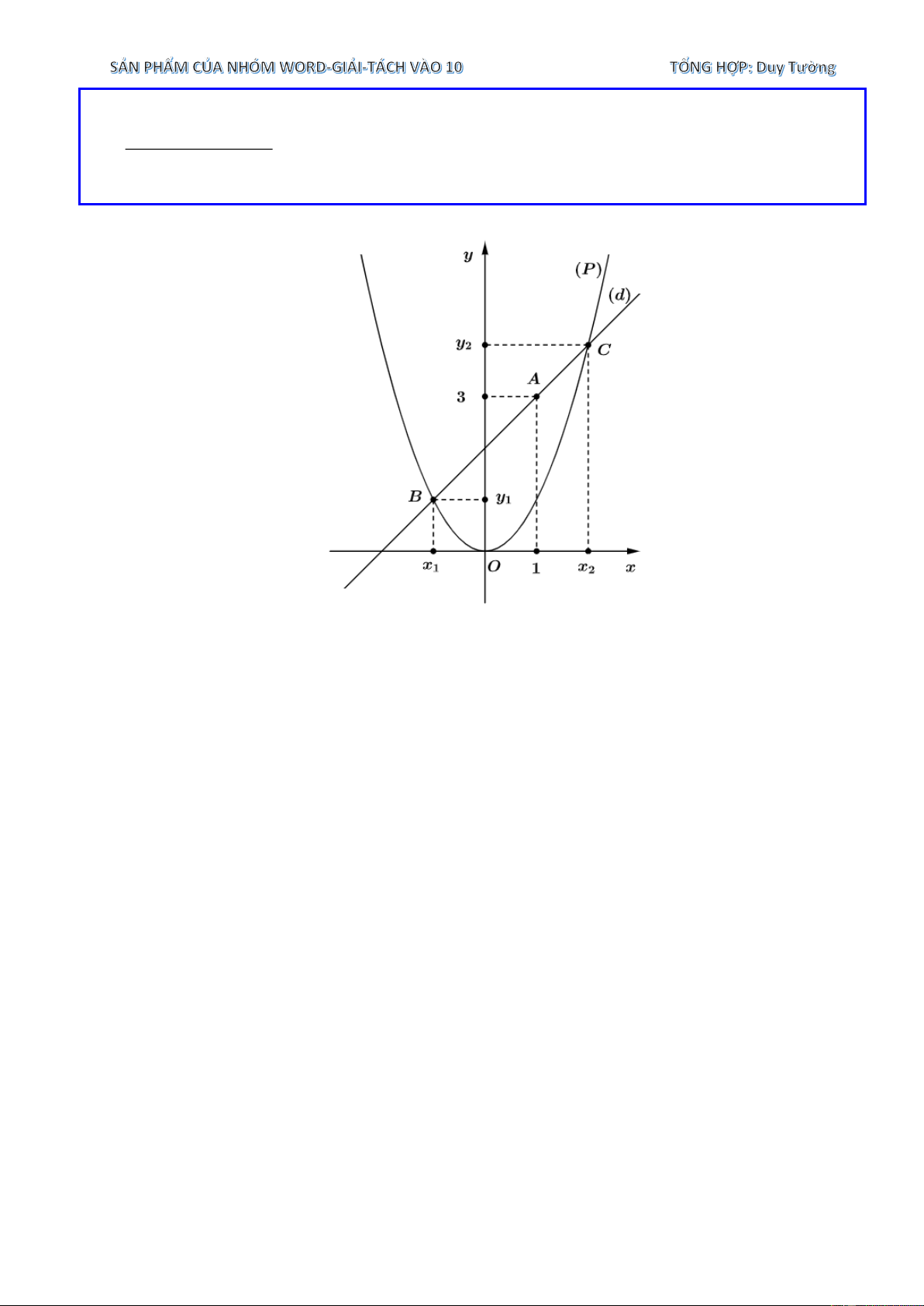
x + x + 6(x + x ) 1 2 1 2 Lời giải y y2 C 3 A y1 B x1 x2 O 1 x
a) Chứng minh rằng với mọi giá trị của a đường thẳng (d ) luôn cắt parabol ( P) tại hai điểm phân
biệt. Giả sử B và C là hai giao điểm của (d ) và ( P). Tìm a để AB = 2AC.
Xét phương trình hoành độ giao điểm: 2 2
x = ax + 3 − a x
− ax + a − 3 = 0 ( )1
Ta có = a − (a − ) = a − a + = (a − )2 2 2 4 3 4 12 2 + 8 0 với a
Do đó phương trình (1) luôn có hai nghiệm phân biệt.
Như vậy, phương trình hoành độ giao điểm của (d ) và (P) luôn có hai nghiệm phân biệt, tức là (d )
luôn cắt ( P) tại hai điểm phân biệt. Giả sử x , x
là nghiệm của phương trình (1) và B ( x ; y , C x ; y thì 1 1 ) ( 2 2) 1 2
( x −1 x −1 = x x − x + x +1 = a − 3 − a +1 = −2 0 1 )( 2 ) 1 2 ( 1 2) ( )
Vậy điểm A nằm giữa B và C . Do đó
AB = 2 AC (1− x = 2 x −1 x = 3 − 2x 2 1 ) ( 2 ) 1 2 ( )
Mặt khác x + x = a kết hợp với (2) ta được x = 3 − a 1 2 2
Thay vào phương trình (1) ta đượ 2
c: (3 − a) − a (3 − a) + a − 3 = 0 2 a − 4a + 3 = 0
Phương trình trên có nghiệm a = 1, a = 3.
Vậy a = 1 hoặc a = 3 .
b) Gọi x , x là hoành độ giao điểm của B, C . Tìm giá trị lớn nhất, nhỏ nhất của biểu thức 1 2 (x +1)(x +1) 1 2 P = . 2 2
x + x + 6(x + x ) 1 2 1 2 (x +1)(x +1)
x x + x + x +1 1 2 1 2 1 2 P = = 2 2 2
x + x + 6(x + x )
(x + x ) + 6(x + x ) − 2x x 1 2 1 2 1 2 1 2 1 2
x + x = a Vì 0, a
nên theo định lý Vi-ét: 1 2 x x = a − 3 1 2 a − 3 + a +1 2a − 2 P = = 2 2
a + 6a − 2(a − 3) a + 4a + 6 2 2
P(a + 4a + 6) = 2a − 2 Pa + 2(2P −1)a + 6P + 2 = 0 (*) 2
+)P = 0 a = 2 x − 2x −1 = 0 x = 1 2
Coi (*) là phương trình bậc hai ẩn a, P là tham số. Khi đó: 2 2
' = (2P −1) − P(6P + 2) = 2 − P − 6P +1
Để phương trình (*) có nghiệm thì 3 − − 11 3 − + 11 2 0 2
− P − 6P +1 0 P 2 2 3 − − 11 −(2P −1) P = a = =1− 11( ) tm min 2 P 3 − + 11 −(2P −1) P = a = =1+ 11( ) tm max 2 P 3 − − 11 Vậy P = a =1− 11 min 2 3 − + 11 P = a =1+ 11 max 2
Câu 23. (HSG 9 Tây Ninh 2023-2024 ) Cho parabol ( P) 2
: y = x và đường thẳng (d ) : y = 2(m − 3) x − m + 5. Tìm các giá trị nguyên của tham
số m để ( P) cắt (d ) tại hai điểm phân biệt ,
A B sao cho tọa độ của ,
A B là các số nguyên. Lời giải
Hoành độ giao điểm của (P) và (d ) là nghiệm của phương trình 2 x = (m − ) 2 2
3 x − m + 5 x − 2 (m − 3) x + m − 5 = 0 (1)
(P) cắt (d) tại hai điểm phân biệt 2
Δ = m − 7m +14 0 ( * ) Do tọa độ của ,
A B là các số nguyên nên (1) có hai nghiệm phân biệt đều nguyên. Suy ra 2 = k (k ) 2 2 Δ
m − 7m +14 = k ( 2 m − m + ) 2 4 7
14 = 4k (2m − 7 − 2k )(2m − 7 + 2k ) = 7 −
Từ (1) ta có 4 trường hợp
2m − 7 − 2k = 1 − m = 5 + Trường hợp 1:
(thỏa ( * ) và m )
2m − 7 + 2k = 7 k = 2
2m − 7 − 2k =1 m = 2 + Trường hợp 2:
(thỏa (*) và m )
2m − 7 + 2k = 7 − k = 2 −
2m − 7 − 2k = 7 m = 5 + Trường hợp 3:
( thỏa ( * ) và m )
2m − 7 + 2k = 1 − k = 2 −
2m − 7 − 2k = 7 − m = 2 + Trường hợp 4:
(thỏa ( * ) và m )
2m − 7 + 2k = 1 k = 2
Vậy m = 5, m = 2 là các giá trị cần tìm.
Câu 24. (HSG 9 Thái Bình 2023-2024 )
Trên trục tọa độ Oxy cho điểm hai điểm A(−1; ) 1 , B ( 5 − ; 3
− ) và đường thẳng (d): y = ax + b
a) Tính diện tích tam giác OAB .
b) Tìm a và b biết đường thẳng d vuông góc với đường thẳng AB và tiếp xúc đường tròn tâm
O (0;0) bán kính R = 4 2 . Lời giải
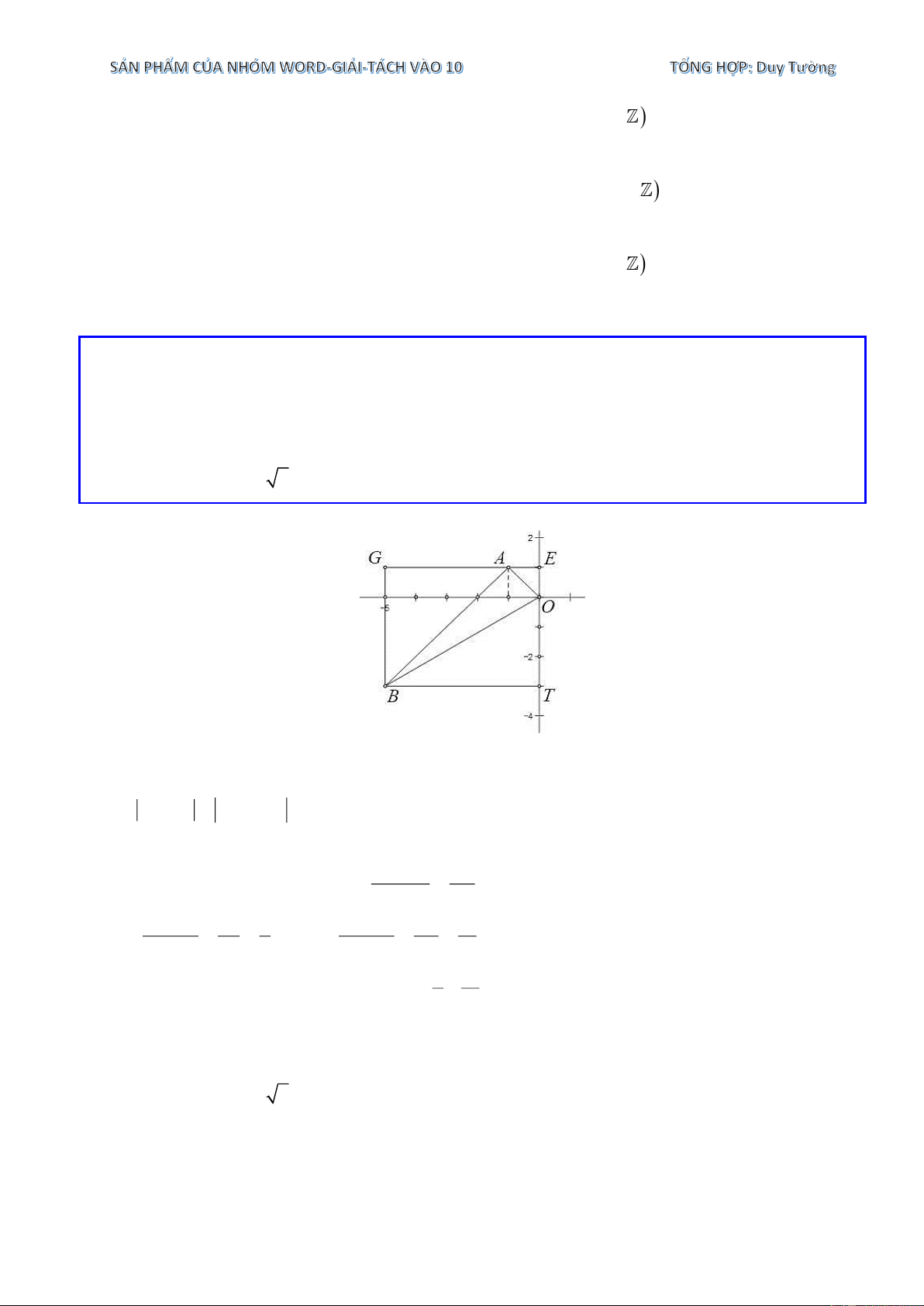
a) Tính diện tích tam giác OAB .
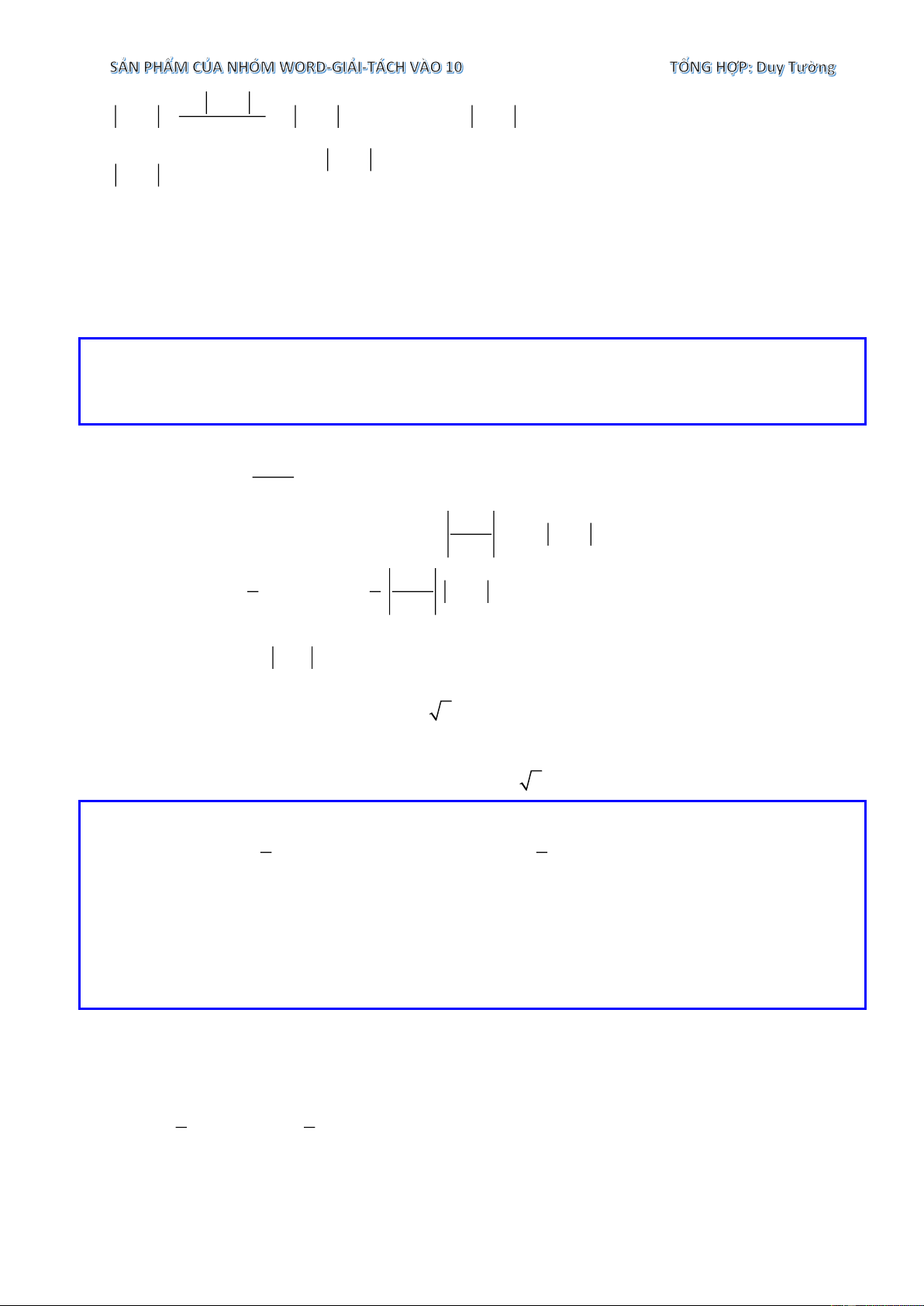
Dựng hình chữ nhật GETB như hình vẽ dưới đây. Theo bài ra ta có:
AG = x − x = 5 − − (− ) 1 = 4 . G A
Tương tự ta có: AE = OE = 1; BG = 4 ; OT = 3; BT = 5 . B . G AG 4.4 S = .
BG BT = 4.5 = 20 ; S = = = 8 ; GEBT GAB 2 2 OE.AE 1.1 1 OT.BT 3.5 15 S = = = ; S = = = . OAE 2 2 2 OTB 2 2 2 1 15 S = S − S − S − S = 20 −8 − − = 4 (đvdt). OAB GEBT GAB OAE OTB 2 2 Vậy S = 4 (đvdt). OAB
b) Tìm a và b biết đường thẳng d vuông góc với đường thẳng AB và tiếp xúc đường tròn tâm
O (0;0) bán kính R = 4 2 .
Gọi đường thẳng ( AB) : y = mx + k đi qua A(−1; ) 1 , B ( 5 − ; 3 − ) nên −m + k =1 m =1
( AB): y = x + 2 . Vì (d ) ⊥ ( AB) nên a = −1, khi đó (d ) : y = −x + b 5 − m + k = 3 − k = 2
Giả sử (d ) tiếp xúc với ( ;
O 4 2 ) tại K và vuông góc với ( AB) tại H . Dễ thấy AOKH là hình
chữ nhật. Suy ra OH = OK = 4 2 . Tọa độ H là nghiệm của hệ phương trình y = x + 2 b − 2 b + 2 x = ; y = .
y = −x + b 2 2
b − 2 b + 2 b Suy ra H ; AH = 2 2 2 b 4 2 =
b = 8 b = 8 . 2 Vậy ( ; a b) ( 1 − ; 8 − );( 1
− ;8) là giá trị cần tìm.
CHUYÊN ĐỀ 3: PHƯƠNG TRÌNH Câu 1.
(HSG 9 Tỉnh Bắc Kạn 2023-2024) Giải phương trình 1
4 x + 3 = 1+ 4x − . x Lời giải
Điều kiện: x −3; x 0 1 Ta có 2 2
4 x + 3 = 1+ 4x −
4x x + 3 = x + 4x −1 4x − 4x x + 3 + x + 3 = 4 x x − x + =
Ta có phương trình ( x − x + )2 2 3 2 (*) 2 3
= 4 2x− x+3 =−2 (**) 9 + 65 x = Từ (*) ta có 2 2 8 (*)
x + 3 = 2x − 2 x + 3 = 4x − 8x + 4 4x − 9x +1 = 0 9 − 65 x = 8 9 + 65
Thay vào (*) và đối chiếu điều kiện ta thấy x =
là nghiệm phương trình đã cho 8 Từ (**) ta có 7 − + 33 x = 2 2 8 (**)
x + 3 = 2x + 2 x + 3 = 4x + 8x + 4 4x + 7x +1 = 0 7 − − 33 x = 8 7 − + 33
Thay vào (**) và đối chiếu điều kiện ta thấy x =
là nghiệm phương trình đã cho 8 7 − + 33 9 + 65
Vậy tập nghiệm của phương trình là T = ; . 8 8 Câu 2.
(HSG 9 Tỉnh Hà Nam 2023-2024) Giải phương trình: ( 3 2
x + x + x) = 7 ( 2 x + ) 4 21 4 1 x +1. Lời giải
Điều kiện: x Phương trình tương đương: x ( 2 x + x + ) = 7 ( 2 x + ) 4 21 1 4 1 x +1 2 1 3 3 Vì 2 2 4
x + x +1 = x +
+ 0; x +1 0; x +1 0 với mọi x 2 4 4
Suy ra x 0 Chia cả hai vế của phương trình cho 2 x ta được: 2 1 1 1 21 x + +1 = 4 7 x + x + − 2 x x x Đặ 1 1 1 t: t = x +
, vì x 0 suy ra: t = x + 2 . x = 2 x x x Phương trình: 2
21(t +1) = 4 7t t − 2 2 t t − − t + t − = t ( 2 4 7 2 28 7 21 0 4 7
t − 2 − 7 ) + 7(t −3) = 0 7t ( 2 4 t − 9) 4 7t(t + 3)
+ 7(t − 3) = 0 (t − 3) + 7 = 0 2 2 t − 2 + 7 t − 2 + 7 t = 3 4 7t(t + 3) + 7 = 0(1) 2 t − 2 + 7
TH1: với t − 3 = 0 t = 3 ( thỏa mãn đk t 2 ) Khi đó 3 − 5 x = 1 2 2 x +
= 3 x − 3x +1 = 0 thỏa mãn x 0 x 3 + 5 x = 2 4 7t(t + 3) 4 7t(t + 3) TH2:
+ 7 = 0(1),Do t 2
0 VT(1) 7 0. 2 2 t − 2 + 7 t − 2 + 7 Nên pt(1) vô nghiệm. 3 − 5 3 + 5
Vậy phương trình có 2 nghiệm x = ; x = 2 2 Câu 3.
(HSG 9 Tỉnh Bắc Ninh 2023-2024) Phương trình 2
x − 3x − 5 = 0 có hai nghiệm là x , x . Đặt 2
g(x) = x − 4 . Tính giá trị của biểu thức 1 2
T = g ( x g x . 1 ) ( 2 ) Lời giải Vì phương trình 2
x − 3x − 5 = 0 oó hai nghiệm là x , x nên 1 2 2 2
x −3x −5 = 0
x − 4 = 3x +1 1 1 1 1 2 2
x − 3x − 5 = 0 x − 4 = 3x +1 2 2 2 2 x + x = 3
Đồng thời theo Viét có 1 2 . Từ đó x .x = 5 − 1 2
g ( x ) g ( x ) = ( 2 x − 4)( 2
x − 4 = 3x +1 3x +1 1 2 1 2 ) ( 1 )( 2 )
= 3(x + x + 9x x +1 1 2 ) 1 2 = 3.3+ 9.( 5 − ) +1 = −35.
Vậy g ( x g x = 35 − . 1 ) ( 2 ) Câu 4.
(HSG 9 Tỉnh Bắc Ninh 2023-2024) Giải phương trình: 2
3x − 5 + 7 − 3x = 9x − 36x + 38 . Lời giải Điề 5 7 u kiện x . 3 3