




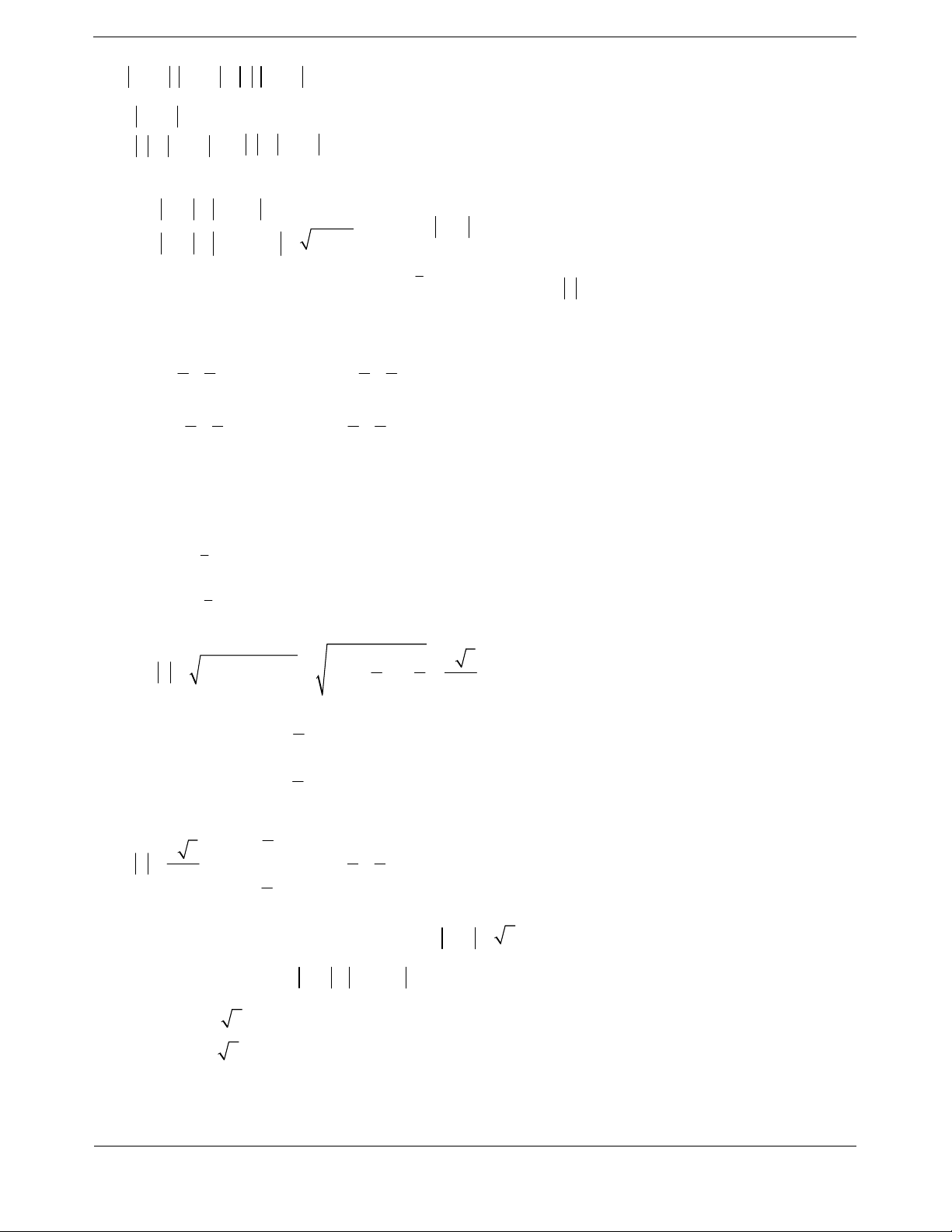


Preview text:
BÀI 4. CỰC TRỊ SỐ PHỨC
A. LÍ THUYẾT TRỌNG TÂM
1. Các bất đẳng thức thường dùng
a. Cho các số phức z , z ta có: 1 2
+) z z z z (1). 1 2 1 2 z 0
Đẳng thức xảy ra khi và chỉ khi 1 . z 0, k
, k 0, z kz 1 2 1
+) z z z z (2). 1 2 1 2 z 0
Đẳng thức xảy ra khi và chỉ khi 1 . z 0, k
, k 0, z kz 1 2 1
b. Bất đẳng thức Cauchy – Schwarz
Cho các số thực a, , b x, y ta có: 2 2 2 2 ax by a b x y
Đẳng thức xảy ra khi và chỉ khi ay bx .
2. Một số kết quả đã biết a. Cho hai điểm ,
A B cố định. Với điểm M bất kỳ luôn có bất đẳng thức tam giác:
+) MA MB AB , dấu “=” xảy ra M nằm giữa hai điểm , A B .
+) MA MB AB , dấu “=” xảy ra B nằm giữa hai điểm , A M . b. Cho hai điểm ,
A B nằm cùng phía đối với đường thẳng d và M là điểm di động trên d . Ta có:
+) MA MB AB , dấu “=” xảy ra Ba điểm ,
A M , B thẳng hàng.
+) Gọi A là điểm đối xứng với A qua d , khi đó ta có
MA MB MA MB AB , dấu “=” xảy ra Ba điểm A , M , B thẳng hàng. c. Cho hai điểm ,
A B nằm khác phía đối với đường thẳng d và M là điểm di động trên d . Ta có:
+) MA MB AB , dấu “=” xảy ra M nằm giữa hai điểm , A B .
+) Gọi A là điểm đối xứng với A qua d , khi đó ta có
MA MB MA MB AB , dấu “=” xảy ra Ba điểm A , M , B thẳng hàng.
d. Cho đoạn thẳng PQ và điểm A không thuộc PQ , M là điểm di động trên đoạn thẳng PQ , khi đó
max AM maxAP, A
Q . Để tìm giá trị nhỏ nhất của AM ta xét các trường hợp sau:
+) Nếu hình chiếu vuông góc H của A trên đường thẳng PQ nằm trên đoạn PQ thì min AM AH .
+) Nếu hình chiếu vuông góc H của A trên đường thẳng PQ không nằm trên đoạn PQ thì
min AM minAP; A Q .
e. Cho đường thẳng và điểm A không nằm trên . Điểm M trên có khoảng cách đến A nhỏ nhất
chính là hình chiếu vuông góc của A trên . f. Cho ,
x y là các tọa độ của các điểm thuộc miền đa giác A A ...A . Khi đó giá trị lớn nhất (nhỏ nhất) của 1 2 n
biểu thức F ax by ( a,b là hai số thực đã cho không đồng thời bằng 0 ) đạt được tại một trong các
đỉnh của miền đa giác.
SƠ ĐỒ HỆ THỐNG HÓA
Bất đẳng thức Cauchy – Schwarz
Với các số thực a, , b x, y ta có 2 2 2 2 ax by a b x y . a b Dấu “=” xảy ra khi . x y
Các bất đẳng thức thường dùng
Bất đẳng thức tam giác
z z z z . Dấu “=” xảy ra khi z kz k 0 . 1 2 1 2 1 2
z z z z . Dấu. “=” xảy ra khi z kz k 0 . 1 2 1 2 1 2
z z z z . Dấu. “=” xảy ra khi z kz k 0 . 1 2 1 2 1 2 z z z
z Dấu “=” xảy ra khi z kz k 0 . 1 2 1 2 1 2
B. CÁC DẠNG BÀI TẬP
Dạng 1: Phương pháp hình học
1. Phương pháp giải
Vi dụ: Cho số phức z thỏa mãn 2 2 z z
i z z . Giá trị nhỏ nhất của z 3i bằng A. 3. B. 3 . C. 2 3 . D. 2. Hướng dẫn giải
Bước 1: Chuyển đổi ngôn ngữ bài toán số phức Giả sử z x yix, y z x yi . Khi đó sang ngôn ngữ hình học.
z z iz z2 yi 2 2 2 2 2
4x i y x . Gọi M ;
x y; A0;3 lần lượt là điểm biểu diễn cho số phức z; 3
i thì z 3i MA .
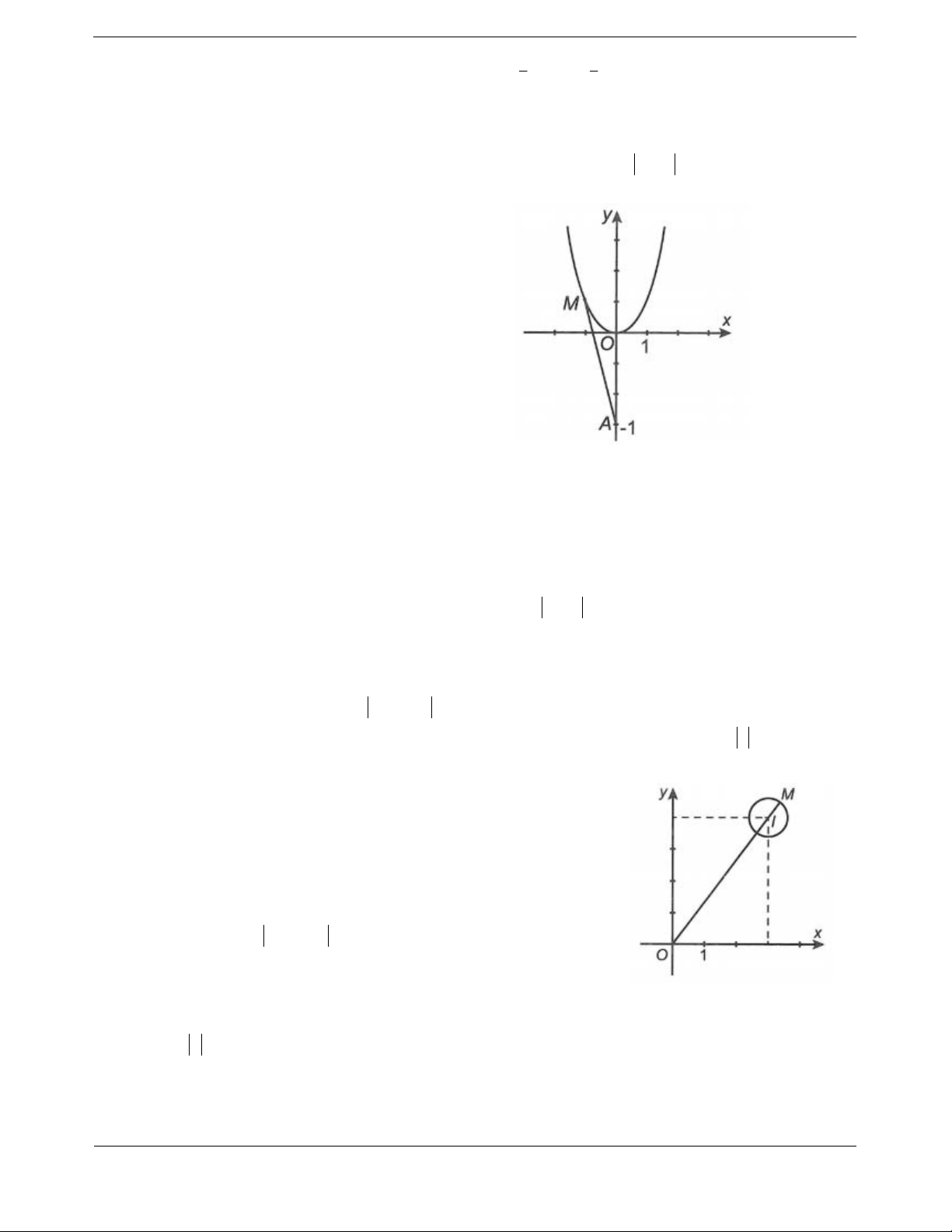
Bước 2: Sử dụng một số kết quả đã biết để giải bài toán hình học. Parabol 2
y x có đỉnh tại điểm O 0;0 , trục đối
xứng là đường thẳng x 0 . Hơn nữa, điểm A
thuộc trục đối xứng của parabol, nên ta có:
MA OA 3. Suy ra, min MA 3 khi M O .
Bước 3: Kết luận cho bài toán số phức.
Vậy min z 3i 3 , khi z 0 . Chọn A. 2. Bài tập mẫu
Bài tập 1: Cho số phức z thỏa mãn z 3 4i 1. Môđun lớn nhất của Nhận xét: số phức z bằng
OI r OM z OI r A. 7. B. 6. C. 5. D. 4. Hướng dẫn giải Chọn B Gọi M ;
x y, I 3;4 là các điểm biểu diễn lần lượt cho các số phức
z;3 4i . Từ giả thiết z 3 4i 1 MI 1.
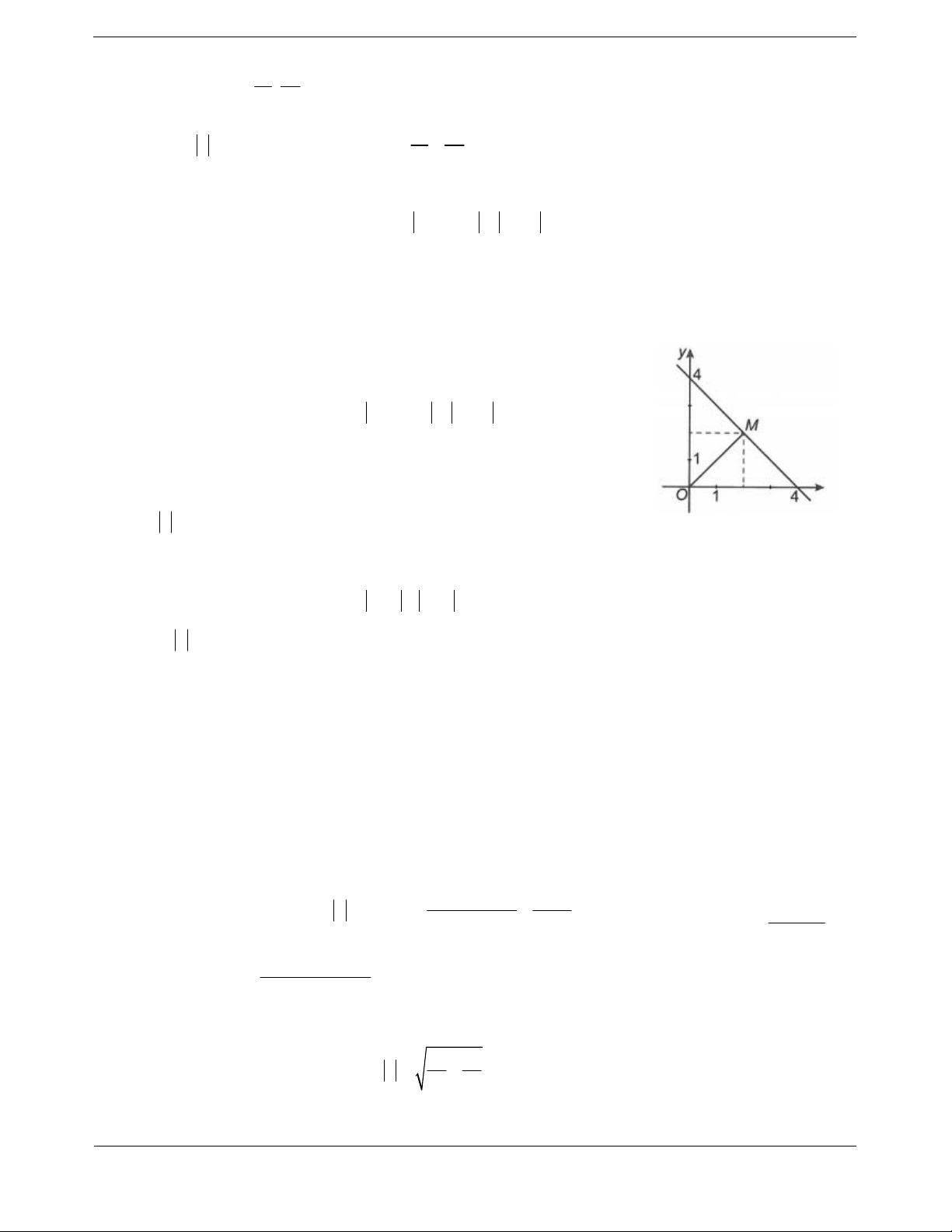
Tập hợp các điểm M biểu diễn số phức z thỏa mãn giả thiết là đường
tròn tâm I 3;4 , bán kính r 1.
Mặt khác z OM . Mà OM đạt giá trị lớn nhất bằng OI r , khi
M là giao điểm của đường thẳng OM với đường tròn tâm I 3;4 , bán 18 24
kính r 1. Hay M ; . 5 5 18 24
Do đó, max z OI r 5 1 6 , khi z i . 5 5
Bài tập 2: Trong các số phức z thỏa mãn z 2 4i z 2i , số phức Nhận xét: Trong tất cả các đoạn
z có môđun nhỏ nhất là
thẳng kẻ từ điểm O đến đường
thẳng d , đoạn vuông góc OM
A. z 2 2i .
B. z 1 i . ngắn nhất.
C. z 2 2i .
D. z 1 i . Hướng dẫn giải Chọn C
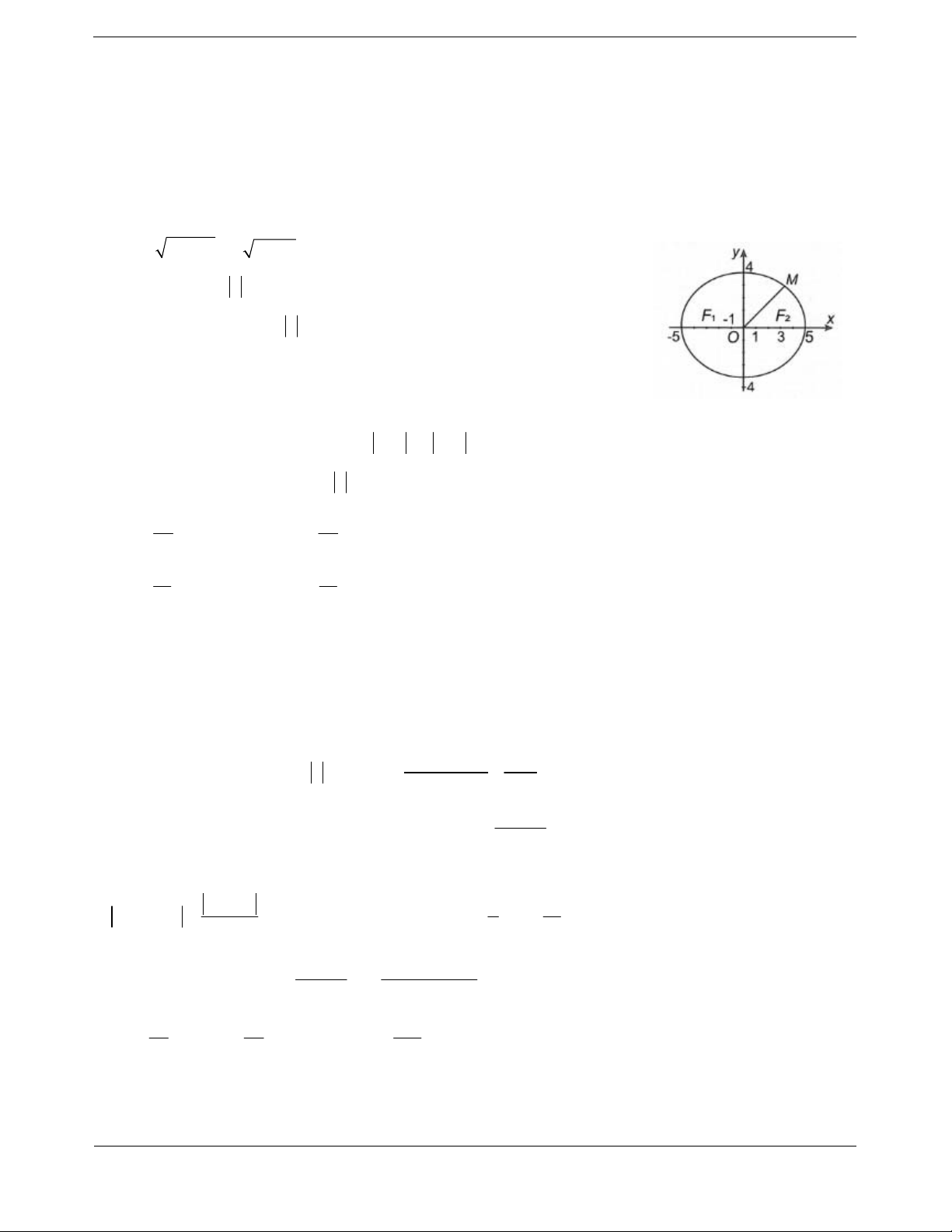
Đặt z x yi x, y . Khi đó z 2 4i z 2i x y 4 0 d .
Vậy tập hợp điểm M biểu diễn số phức z là đường thẳng d .
Do đó z OM nhỏ nhất khi M là hình chiếu của O trên d .
Suy ra M 2;2 hay z 2 2i .
Bài tập 3: Cho số phức z thỏa mãn z 3 z 3 10 . Giá trị nhỏ nhất của z là A. 3. B. 4. C. 5. D. 6. Hướng dẫn giải Chọn B Cách 1:
Gọi F 3;0 , F 3;0 , có trung điểm là O 0;0 . Điểm M biểu diễn 1 2 số phức z .
Với mọi số thực a,b ta có bất 2 2 2 MF MF F F
Theo công thức trung tuyến thì 2 2 1 2 1 2 z OM . a b 2 2 2 2 4
đẳng thức: a b 2 MF MF 1 2 2 2 2 2 2
Ta có MF MF 50 . 1 2 2 Đẳng thức xảy ra khi MF MF M 4; 0 1 2 50 36 min z 4 , MF MF 10 M 4;0 2 4 1 2
Khi z 4i hoặc z 4 i . Cách 2:.
Gọi F 3;0 , F 3;0 , M ;
x y; x, y lần lượt là các điểm biểu
Với mọi điểm M nằm trên elip, 1 2 diễn các số phức 3; 3; z .
đoạn OM ngắn nhất là đoạn nối
O với giao điểm của trục bé với
Ta có F F 2c 6 c 3 . Theo giả thiết ta có MF MF 10 , tập 1 2 1 2 elip.
hợp điểm M là đường elip có trục lớn 2a 10 a 5 ; trục bé 2 2
2b 2 a c 2 25 9 8 .
Mặt khác OM z nhỏ nhất bằng 4 khi z 4i hoặc z 4 i .
Vậy giá trị nhỏ nhất của z bằng 4.
Bài tập 4: Xét số phức z thỏa mãn 4 z i 3 z i 10 . Tổng giá trị
lớn nhất và giá trị nhỏ nhất của z là 60 58 A. . B. . 49 49 18 16 C. . D. . 7 7 Hướng dẫn giải Chọn D Gọi A0; 1 , B 0;
1 , đoạn thẳng AB có trung điểm O 0;0 . Điểm
M biểu diễn số phức z . 2 2 2 MA MB AB
Theo công thức trung tuyến 2 2 z OM . 2 4 10 4a
Theo giả thiết 4MA 3MB 10 . Đặt MA a MB . 3 Khi đó 10 7a 4 16 MA MB AB 2 6
10 7a 6 a . 3 7 7 2 10 4a 5a 8 36 2 2 2 2
Ta có MA MB a . 3 9 36 24 576 Do 5a 8
0 5a 82 nên 7 7 49 2 2
MA MB 4 z 1 260 . 2 2 2 81 9 MA MB z z 49 49 7 24 7 9 9
Đẳng thức z 1khi z
i . Đẳng thức z khi z i . 25 25 7 7 16
Vậy tổng giá trị lớn nhất và giá trị nhỏ nhất của z là . 7
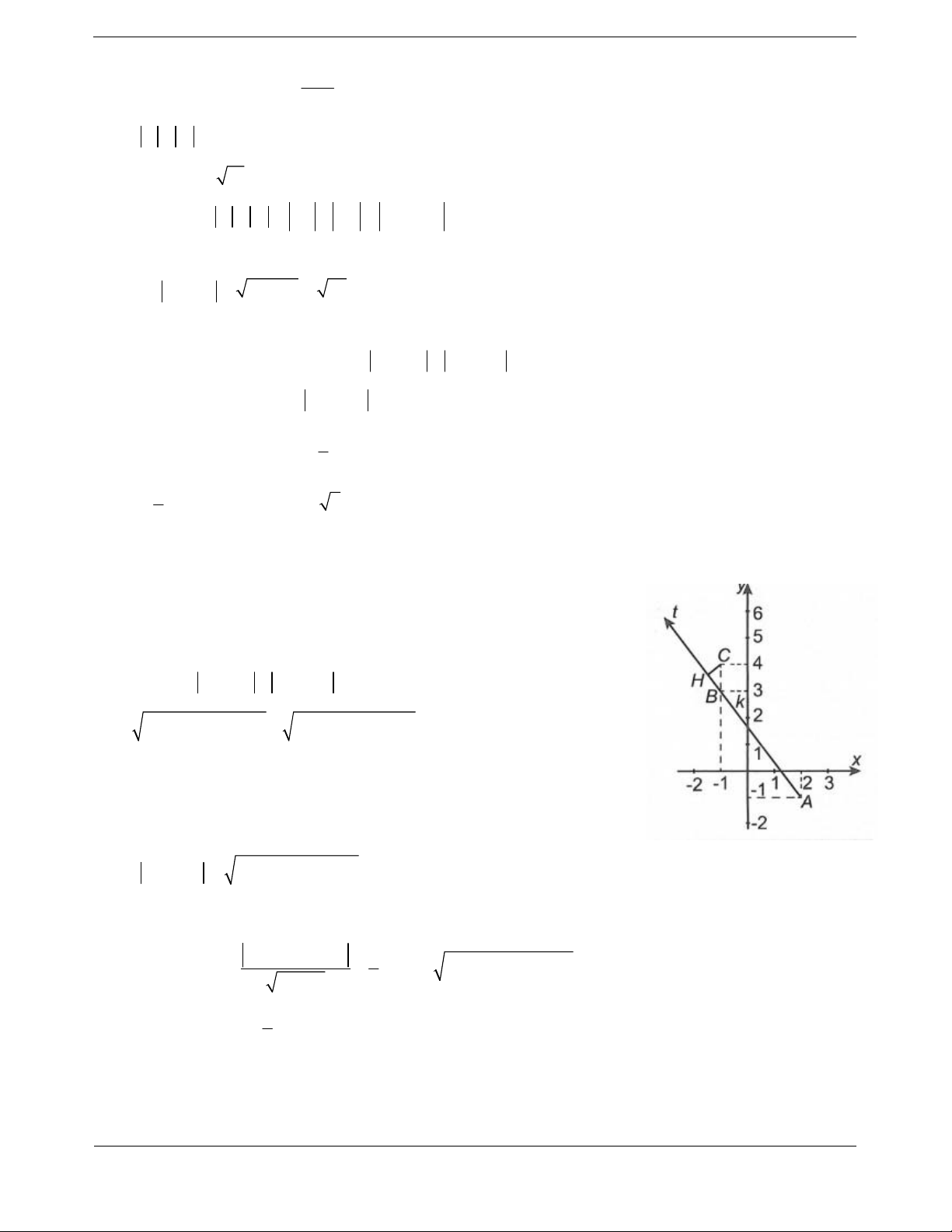
Bài tập 5: Cho z là số phức thay đổi thỏa mãn z 2 z 2 4 2 .
Trong mặt phẳng tọa độ gọi M , N là điểm biểu diễn số phức z và z .
Giá trị lớn nhất của diện tích tam giác OMN là A. 1. B. 2 . C. 4 2 . D. 2 2 . Hướng dẫn giải Chọn D
Đặt z x yi x, y z x yi .
Gọi F 2;0 , F 2;0 , M ; x y, N ;
x y lần lượt là các điểm biểu 1 2 diễn các số phức 2; 2; z; z . Do ,
M N là điểm biểu diễn số phức z và z nên suy ra M , N đối xứng nhau qua Ox . Khi đó S xy . OMN
Ta có F F 2c 4 c 2 . Theo giả thiết ta có MF MF 4 2 , 1 2 1 2
tập hợp điểm M thỏa điều kiện trên là elip có trục lớn
2a 4 2 a 2 2 ; trục bé 2 2
2b 2 a c 2 8 4 4 b 2 . 2 2 x y
Nên elip có phương trình E : 1 . 8 4 2 2 2 2 x y x y xy Do đó 1 2 . S xy 2 2 . 8 4 8 4 2 2 OMN x 2
Đẳng thức xảy ra khi . y 2
Bài tập 6: Cho số phức z thỏa mãn z i z 2 i . Giá trị nhỏ nhất
của P i
1 z 4 2i là 3 A. 1. B. . 2 3 2 C. 3. D. . 2 Hướng dẫn giải Chọn C
Gọi z x yi x, y ; M ;
x y là điểm biểu diễn số phức z .
Ta có z i z 2 i x y
1 i x 2 y 1 i
x y 2 x 2 y 2 2 1 2 1
x y 1 0 . 4 2i
Ta có P i
1 z 4 2i i
1 z 2 z 3i i 1
x 2 y 2 2 3
1 2MA , với A 3; 1 . 3 11
P 2MA 2d , A 2 3. min min 2 2 1 1
Đẳng thức xảy ra khi M là hình chiếu vuông góc của A trên đường 3 5 3 5 thẳng hay M ; z i . 2 2 2 2
Bài tập 7: Cho hai số phức z , z thỏa mãn z z 6 và z z 2 . 1 2 1 2 1 2 Gọi ,
M m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
P z z . Khi đó môđun của số phức M mi là 1 2 A. 76 . B. 76. C. 2 10 . D. 2 11 . Hướng dẫn giải Chọn A Ta gọi ,
A B lần lượt là các điểm biểu diễn của các số phức z , z . 1 2
Từ giả thiết z z 6 OA OB 6 OI 3 với I là trung 1 2
điểm của đoạn thẳng AB .
z z 2 OA OB 2 AB 2 . 1 2 2 AB Ta có 2 2 2
OA OB 2OI 20. 2
P z z 2
OA OB P 2 2 2 2 1 1
OA OB 40. 1 2
Vậy max P 2 10 M .
Mặt khác, P z z OA OB OA OB 6 . 1 2
Vậy min P 6 m .
Suy ra M mi 40 36 76 .
Bài tập 8: Cho số phức z thỏa mãn z 2 i z 1 3i 5 . Giá trị
nhỏ nhất của biểu thức P z 1 4i bằng 3 A. 1. B. . 5 1 C. . D. 2 . 5 Hướng dẫn giải Chọn B Gọi M ;
x y là điểm biểu diễn số phức z ; gọi A2; 1 , B 1 ;3 là
điểm biểu diễn số phức 2 i; 1
3i . Ta có AB 5 .
Từ giả thiết z 2 i z 1 3i 5
x 2 y 2 x 2 y 2 2 1 1 3 5
MA MB 5 MA MB AB MA MB AB . Suy ra M , ,
A B thẳng hàng ( B nằm giữa M và A ). Do đó quỹ tích
điểm M là tia Bt ngược hướng với tia BA .
P z 1 4i x 2 y 2 1 4 , với C 1;
4 P MC . Ta có AB 3;
4phương trình đường thẳng :
AB 4x 3y 5 0 .
CH d C AB 4 1 3.4 5 3 ,
, CB 2 2 1 1 3 4 1 . 2 2 4 3 5 3
Do đó min P CH khi H là giao điểm của đường thẳng AB và 5
đường thẳng đi qua điểm C và vuông góc với AB .
Dạng 2: Phương pháp đại số
1. Phương pháp giải
Các bất đẳng thức thường dùng:
1. Cho các số phức z , z ta có: 1 2
a. z z z z (1) 1 2 1 2 z 0
Đẳng thức xảy ra khi và chỉ khi 1 z 0, k
, k 0, z kz 1 2 1
b. z z z z .(2) 1 2 1 2 z 0
Đẳng thức xảy ra khi và chỉ khi 1 z 0, k
, k 0, z kz 1 2 1
2. Bất đẳng thức Cauchy - Schwarz
Cho các số thực a, , b x, y ta có 2 2 2 2 ax by a b x y
Đẳng thức xảy ra khi và chỉ khi ay bx . 2. Bài tập
Bài tập 1: Cho số phức z a a 3i,a . Giá trị của a để
Nhận xét: Lời giải có sử
khoảng cách từ điểm biểu diễn số phức z đến gốc tọa độ là nhỏ nhất dụng đánh giá 2 bằng x 0, x 3 1 A. a . B. a . 2 2 C. a 1. D. a 2 . Hướng dẫn giải Chọn A 2
z a a 32 3 9 3 2 2 2 a . 2 2 2 3 3 3
Đẳng thức xảy ra khi a . Hay z i . 2 2 2
Bài tập 2: Trong các số phức z thỏa mãn điều kiện z 2 4i z 2i ,
số phức z có môđun nhỏ nhất là
A. z 1 2i .
B. z 1 i .
C. z 2 2i .
D. z 1 i . Hướng dẫn giải Chọn C
Gọi z a bi a,b .
z 2 4i z 2i a 2 b 4i a b 2i a b 4 0 .
z b bi z b2 b b 2 2 4 4 2 2 8 2 2 .
Suy ra min z 2 2 b 2 a 2 z 2 2i . z 1 3
Bài tập 3: Cho số phức z thỏa mãn
1, biết z 5i đạt giá z 2i 2
trị nhỏ nhất. Giá trị của z bằng 2 A. 2 . B. . 2 5 17 C. . D. . 2 2 Hướng dẫn giải Chọn C.
Gọi z a bi z 2ia,b .
z 1 1 z 1 z 2i 2a 4b3 0 2a 3 4b z 2i 3
z 5i 2b2 b 52 5b 2 1 20 2 5 2 1 3 a 1
Suy ra min z 5i 2 5
2 z i 2 2 b 1 5 Vậy z . 2
Bài tập 4: Cho hai số phức z , z thỏa mãn z z 3 4i và
Nhận xét: Lời giải sử dụng 1 2 1 2
z z 5 . Giá trị lớn nhất của biểu thức z z là
bất đẳng thức Cauchy – 1 2 1 2 Schwarz. A. 5. B. 5 3 . C. 12 5 . D. 5 2 . Hướng dẫn giải Chọn D. Ta có 2 2 2 z z 2 2 2 2 2
z z z z 5 3 4 50 . 1 2 1 2 1 2
Sử dụng bất đẳng thức Cauchy – Schwarz, ta có
z z 2 2 2 z z 50 5 2 . 1 2 1 2
Gọi z x yi, z a bi;a, , b x, y 1 2
z z 3 4i 1 2
z z 5 1 2
Đẳng thức xảy ra khi và chỉ khi 2 2 z z 25 1 2 z z 1 2 7 1 x a 2 2 7 1 1 7 và
. Hay z i; z i . 1 1 2 7 2 2 2 2 y b 2 2
Thay z , z vào giả thiết thỏa mãn. 1 2
Vậy, giá trị lớn nhất của biểu thức z z bằng 5 2 . 1 2
Bài tập 5: Cho số phức z thỏa mãn z 1. Giá trị lớn nhất của biểu
Nhận xét: Lời giải sử dụng
bất đẳng thức Cauchy –
thức P 1 z 3 1 z bằng Schwarz. A. 2 10 . B. 6 5 . C. 3 15 . D. 2 5 . Hướng dẫn giải Chọn A.
Ta có P 2 2
z z 2 2 2 2 1 3 1 1 20 1 z 2 10 Đẳng thức xảy ra khi 4 2 2 z 1 x y 1 x 5 4 3 1 z 5
z i x . 2 2 1 z x y 1 0 3 5 5 3 2 y 5 Vậy max P 2 10 .
Bài tập 6: Cho số phức z thỏa mãn z 1 2i 2 . Giá trị lớn nhất của
Nhận xét: Lời giải sử dụng bất đẳng thức
z 3 i bằng
z z z z . 1 2 1 2 A. 6. B. 7. C. 8. D. 9. Hướng dẫn giải Chọn B.
Ta có z 3 i z 1 2i 4 3i z 1 2i 4 3i 7 .
z 1 2i k
43i,k 0 13 16
Đẳng thức xảy ra khi z i .
z 1 2i 2 5 5
Vậy giá trị lớn nhất của z 3 i bằng 7.
Bài tập 7: Cho số phức z thỏa mãn điều kiện z 3 4i 4 . Gọi M và Nhận xét: Lời giải sử dụng
m là giá trị lớn nhất và nhỏ nhất của môđun số phức z . Giá trị của bất đẳng thức M .m bằng
z z z z và 1 2 1 2 A. 9. B. 10.
z z z z . 1 2 1 2 C. 11. D. 12. Hướng dẫn giải Chọn A.
Ta có z z 3 4i 3 4i z 3 4i 3 4i 4 5 9 M . 4 3 4 3 4 , 0 k z i k i k Đẳng thức xảy ra khi 5 .
z 3 4i 4 27 36 z i 5 5 Mặt khác
z z 3 4i 3 4i z 3 4i 3 4i 4 5 1 m . 4 3 4 3 4 , 0 k z i k i k Đẳng thức xảy ra khi 5
z 3 4i 4 3 4 z i 5 5
Bài tập 8: Cho số phức z thỏa mãn 2
z 4 z z 2i . Giá trị nhỏ
Chú ý: Với mọi số phức z , z :
nhất của z i bằng 1 2
z .z z . z . 1 2 1 2 A. 2. B. 2 . 1 C. 1. D. . 2 Hướng dẫn giải Chọn C. Ta có 2
z 4 z z 2i z 2i z 2i z z 2i
z 2i . z 2i z . z 2i
z 2i 0 z 2 i z 2 i
z z 2i
z z 2i
z a i, a
z i 2 i i 1 Do đó min z 1 1.
z i a i 2
i a 4 2
Bài tập 9: Tìm số phức z thỏa mãn z
1 z 2i là số thực và z đạt giá trị nhỏ nhất. 4 2 4 2
A. z i . B. z i . 5 5 5 5 4 2 4 2
C. z i .
D. z i . 5 5 5 5 Hướng dẫn giải Chọn D. Gọi ;
z a bi a,b . Ta có z
1 z 2i a
1 a b2 b
2a b 2i Do đó z
1 z 2i là số thực 2a b 2 0 b 2 2a 2 4 4 2 5
Khi đó z a 2 2a2 2 5 a . 5 5 5 4 a Đẳng thức xảy ra khi 5 2 b 5 4 a 2 5 5 4 2 min z
. Vậy z i . 5 2 5 5 b 5
Bài tập 10: Cho số phức z thỏa mãn điều kiện z 1 2 . Tìm giá trị
lớn nhất của biểu thức T z i z 2 i .
A. max T 8 2 . B. max T 4 .
C. max T 4 2 . D. max T 8 . Hướng dẫn giải Chọn B.
Đặt z x yi x, y , ta có z
x yi x 2 2 1 2 1 2 1 y 2 x 2 2 2 2
1 y 2 x y 2x 1 (*). Lại có
T z i z 2 i x y
1 i x 2 y 1 i 2 2 2 2
x y 2y 1 x y 4x 2y 5
Kết hợp với (*) ta được
T 2x 2 y 2 6 2x 2y 2 x y 2 6 2 x y
Đặt T x y , khi đó T f t 2t 2 6 2t với t 1; 3 .
Cách 1: Sử dụng phương pháp hàm số 1 1
Ta có f 't
; f t 0 t 1. 2t 2 6 2t Mà f 1 4, f
1 2 2, f 3 2 2 . Vậy max f t f 1 4 .
Cách 2: Sử dụng phương pháp đại số
Áp dụng bất đẳng thức Cauchy – Schwarz ta có
T 2t 2 6 2t 1 1 .8 4 .
Đẳng thức xảy ra khi t 1 .
Bài tập 11: Cho số phức z thỏa mãn z 1. Gọi M và m lần lượt là
giá trị lớn nhất và giá trị nhỏ nhất của 2
z 1 z z 1 . Khi đó giá trị
của M m bằng A. 5. B. 6. 5 9 C. . D. . 4 4 Hướng dẫn giải Chọn B.
Đặt z a bi a,b và t z 1 . Khi đó t t z 1 z 2 2 2 2
1 z 1 z z 2 2a a . 2 Ta có 2 2 2 2
z z a b abi a bi a 2 1 2 1
1 b a b2a 1 i
a a2 b a 2 a a 2 a a 2 2 2 2 2 2 2 1 2 1 1 2 1 2
2a 1 t 1 2 2
z 1 z z 1 t t 1 (với 0 t 2 , do 2 a 1).
Xét hàm số f t 2
t t 1 với t 0;2 . 1 5
Trường hợp 1: t 0; 1 f t 2 2
t 1 t t
t 1 f 2 4 f t 5 max
và có f 0 f 1 1 nên 0; 1 4 .
min f t 1 0; 1 Trường hợp 2:
t f t 2 2 1; 2
t t 1 t t 1, f t 2t 1 0, t 1;2
max f t f 2 5 1;2
Do đó hàm số luôn đồng biến trên 1;2 . min f
t f 1 1 1;2
M max f t 5 0;2 Vậy . m f t M m 6 min 1 0;2




