Thông tin
Quiz

Các dạng bài tập VDC nguyên hàm, tích phân và ứng dụng Toán 12

Các dạng bài tập VDC nguyên hàm, tích phân và ứng dụng Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Chủ đề:

Chương 3: Nguyên hàm - Tích phân và ứng dụng 199 tài liệu

Môn:

Toán 12 3.8 K tài liệu

Thông tin:

138 trang 1 năm trước

Tác giả:

Mai Nguyệt

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Các dạng bài tập VDC nguyên hàm, tích phân và ứng dụng Toán 12

86 43 lượt tải Tải xuống

CHƯƠNG 3: N

GUYÊN HÀM – TÍCH PHÂN VÀ ỨNG DỤNG

BÀI 1: NGUYÊN HÀM VÀ PHƯƠNG PHÁP TÌM NGUYÊN HÀM

IẾN THỨC CƠ BẢN CẦN NẮ

NGUY

N HÀM VÀ TÍNH CHẤT

Nguyên hàm

Định nghĩa: Cho hàm

số



xác định trên

(

là khoảng hoặc đoạn hoặc nửa đoạn của

). Hàm số



được gọi là nguyên hàm của hàm số





trên K nếu









Fʹ xfx

với mọi xK.



Định lý 1: Nếu



là một nguyên hàm của hàm số





trên

thì với mỗi hằng số C, hàm số

 

Gx Fx C

cũng là một nguyên hàm của





trên

Định lý 2: Nếu



là một nguyên hàm của hàm số





trên

thì mọi nguyên hàm của





đều có dạng



Fx C,

với

là một hằng số.

Hai định lý trên cho thấy:

Nếu



là một nguyên hàm của hàm số





trên

thì





Fx C,C





là họ tất cả các nguyên

hàm của



trên K. Kí hiệu

 

fxdx Fx C.



Chú ý: Biểu t

hức





fxdx

chính là vi phân của nguyên hàm



của





fx,

vì

  

dFx F xdx fxdx.

2. Tính

chất của nguyên hàm

Tính chất 1

 

fʹ xdx fx C







Tính chấ

t 2

 

kf x dx k f x dx



, k là hằng số khác 0.

Tính chất 3

   

fx gx dx fxdx gxdx.









3. Sự tồn tại của nguyên

hàm

Định lý 3: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.

4. Bảng nguyên hàm

Nguyên hàm của hàm số

sơ cấp

Nguyên hàm của hàm số

hợp









u=u x

Nguy

ên hàm của hàm số hợp





u=ax+b;a 0

dx x C



du u C











dax b ax b C









xdx C





























ax b

ax b dx C













lndx x C





lndu u C







lndx ax b C

ax b a







dx C

 



du C









111

.dx C

aax b

ax b

 





xdx x x C



udu u u C









ax bdx ax b ax b C







2dx x C





2du u C







.2dx ax b C

ax b







edx e C



edu e C







ax b ax b

edx e C









0, 1

adx C a a







0, 1

adu C a a









.0,1

mx n

adx Ca a









sin cosxdx x C 



sin cosudu u C







 

sin cos

ax b dx ax b C



  



cos sinxdx x C



cos sinudu u C







 

cos sin

ax b dx ax b C







tan ln cosxdx x C 



tan ln cosudu u C







 

tan ln cos

ax b dx ax b



  



cot ln sinxdx x C



cot ln sinudu u C







 

cot ln sin

ax b dx ax b C







cot

sin

dx x C

 



cot

sin

du u C









cot

sin

dx ax b C

ax b a

  





tan

cos

dx x C





tan

cos

du u C









tan

cos

dx ax b C

ax b a







ln tan

sin 2

dx C





ln tan

sin 2

du C









ln tan

sin 2

dx ax b

ax b a









ln tan

cos 2 4













ln tan

cos 2 4

















cos

ln tan

ax b

















II. PHƯƠNG PHÁP TÍNH NGUYÊN HÀM

1. Phương pháp đổi biến số

Định lý 1: Nếu

f(u)du F(u) C



và uu(x)



có đạo hàm liên tục thì:

fu(x).uʹ(x)dx F u(x) C

 





 



Hệ quả: Với



uaxba0 

ta có

 

faxbdx Faxb C.

 



2. Phương pháp tín

h nguyên hàm từng phần:

Định lý 2: Nếu hai hàm số



uux

và





vvx

có đạo hàm liên tục trên K thì:

   

uxvʹ xdx uxvx uʹ xv x dx.



B. PHÂN LOẠI VÀ P

HƯƠNG PHÁP GIẢI BÀI TẬP

Dạng 1: Tìm nguyên hàm bằng các phép biến đổi sơ cấp

1. Phương pháp giải

 Biến đổ

i các

hàm số dưới dấu nguyên hàm về dạng tổng, hiệu của các biểu thức chứa x,

trong đó mỗi biểu thức chứa x là những dạng cơ bản có trong bảng nguyên hàm.

 Áp dụng các công thức nguyên hàm trong bảng nguyên hàm cơ bản để tìm nguyên hàm.

2. Bài tập

Bài tậ

p 1.

Nguyên hàm của hàm số







là

ln 2



 B.



ln 2 1









ln 2 1









ln 2 1





Hướng dẫn giải

Chọn C.

Ta có:



21 2 2

ln 2 1

dx dx e dx e C

ee e







 









Bài tập 2. Nguyên hàm của hàm số









2019

2fx xx

là









2021 2020

2021 1010













2020 2018

2021 1009















2021 2020

2021 1010











2021 2020

2021 1010







Hướng dẫn giải

Chọn D.

Ta có













 



2019 2019

2021 2020

2020 2019

2222

222

2021 1010

x x dx x x dx

xdxxdx C









     



Bài tập 3.

Nguyên hàm của hàm số







là

ln 1

xe C B.



ln 1

xe C









ln 1

eC





ln 1

xe C





Hướng dẫn giải

Chọn B.

Ta c

ó:





22 2

11 1

xx x

ee e





 

Do đó







22 2

111

1ln1

11212

xx x

dx dx dx x e C

ee e





    



 



 

Bài tập 4.

Nguyên hàm của hàm số









là:









xxC



  





xxC











222

xxxC  



22 2

xx xC



 

Hướng dẫn giải

Chọn A.

Ta c

ó:

   

122

12 2 1 1

22 22 22 22

43 3 6 6

dx dx

xx xx Cxx xxC

 



 











Chú ý: Sử

dụng kĩ thuật nhân liên hợp:







Lưu ý:



ax bdx ax b ax b C

  



Bài tập 5. Nguyên hàm của hàm số



513









là:

2ln 3 3ln 2xxC  B. 3ln 3 2 ln 2xxC





2ln 3 3ln 2xxC  D. 2ln 3 3ln 2xxC





Hướng dẫn giải

Chọn D.

Ta c

ó:



513 513

56 2 3

xx x x





  

Ta sẽ phân tí

ch:













513 2 31xAxBx  

Thế

2x 

và

3x 

lần lượt vào (1) ta có



và



Khi đó











2233

513 2 3

56 2 3 3 2

2ln 3 3ln 2

dx dx dx dx

xx x x x x

xxC

 





    



 

Bài tập 6.

Nguyên hàm của hàm số



1 x







là:



ln ln 1

xxC





ln ln 1xx C







ln ln 1

xxC



ln ln 1

xxC





Hướng dẫn giải

Chọn C.

Ta có:







1121

ln ln 1

dx dx dx dx x x C

xx x x











 

Bài tập 7. Nguyên hàm của hàm số



333









là:

ln 2 2 ln 1

xx C

  



ln 2 2 ln 1

xx C







2ln 2 ln 1

xx C

  



2ln 2 ln 1

xx C



 



Hướng dẫn giải

Chọn A.

Ta có:

 

333 333

xx xx

dx dx

 







Ta phân tích

















333 1 1 2 2xx Ax Bx x Cx     .

Ta có thể dùng các giá trị riêng, tính ngay

1, 3AC



 và



(thay

21;13xAxC      và 02xB



).

Khi đó

  

333 1 1 1 3

2 3 ln 2 2 ln 1

21 1

12 1

dx dx dx dx x x C

xx x



 

 

 



Lưu ý: Ta có kiến t

hức tổng quát dùng cho các nguyên hàm hữu tỉ







Idx





, với





và



Qx là các đa thức, cụ thể như sau:

 Nếu

















deg deg

xQx

thì ta thực hiện phép chia





cho



(ở đây, kí hiệu









deg

x là bậc của đa thức





x ).

 Khi

















deg deg

xQx

thì ta quan sát mẫu số





ta tiến hành phân tích thành các

nhân tử

, sau đ

ó, tách





x theo các tổ hợp của các nhân tử đó. Đến đây, ta sẽ sử dụng đồng

nhất thức (hoặc giá trị riêng) để đưa về dạng tổng của các phân thức.

Mộ

t số trường hợp đồng nhấ

t thức thường gặp

Trường hợp 1:



11ac

ax b cx d ad bc ax b cx d







   



Trường hợp 2:









Ax Ba x Ad Bb

mx n A B

ax b cx d ax b cx d ax b cx d







   

Ta đồng nhất thức









1mx n Ax Ba x Ad Bb    .

Cách 1. Phương pháp đồng nhất hệ số.

Đồng nhất đẳng thức, ta được

Ac Ba m

Ad Bb n











. Suy ra A, B.

Cách 2. Phương pháp giá trị riêng.

Lần lượt thay

;

 

vào hai vế của (1), tìm được A, B.

Trường hợp 3:

 

mx n A B

ax b

ax b ax b









Trường hợp 4:





mx n A B C

cx d ax b

ax b cx d ax b

mx n A cx d B ax b C ax b cx d







 

    

Lần lượt th

;;0

xxx

   vào hai vế của (*) để tìm A, B, C.

Trường hợp 5:



1 ABxC

x m ax bx c











với

40bac



 

Trường hợp 6:

  

22 2 2

1 ABCD

xa xb

xa xb xa xb

 



  

Bài tập 8. Cho hà

m số





xác định trên













thỏa mãn

 

';01

fx f





và



12f  . Giá trị của biểu thức









ff là:

3ln5 ln2 B. 3ln2 ln5 C. 32ln5



D. 3ln15

Hướng dẫn giải

Chọn D.

 



ln 2 1

'ln21

21 1

ln 1 2

xCkhix

f x f x dx dx x C

xCkhix



























Vì



























Suy ra



ln 2 1 2

ln 1 2 1

xkhix



 









 





Do đó









1 3 3 ln 3 ln 5 3 ln15Pf f   

Bài tập 9.

Cho hàm số





xác định trên





\1;1

, thỏa mãn

  

';332ln2

fx f f





và











. Giá trị của biểu thức













204Pf f f 

là:

2ln2 ln5 B. 6ln2 2ln3 ln5 C. 2ln2 2ln3 ln5



 D. 6ln2 2ln5

Hướng dẫn giải

Chọn C.

 

211 1

'ln

111 1

f x f x dx dx dx C

xxxx









 





Hay



ln 1

ln ln 1 1

ln 1

Ckhix

fx C Ckhi x

Ckhix





















 

























Theo bài ra, ta có:









332ln2

2ln2



 















 











  

32 1

2 0 4 ln3 ln 2ln2 2ln3 ln5

fff CC C         

Bài tập 10. Nguyên hàm

xx dx



là:



xxC 



xxC





xC D.



xxC





Hướng dẫn giải

Chọn A.

Ta c

ó:



2222

.1 1 1 1

xx dx x dx x C   



Bài tậ

p 11.

Nguyên hàm của hàm số





sin cos sinxxxdx



là:

11 1

sin 2 cos 2

24 4

xx xC

11 1

sin 2 cos2

24 4

xx xC





sin 2 cos2

xx xC 

11 1

sin 2 cos 2

24 4

xx xC





Hướng dẫn giải

Chọn B.

Ta có:









sin cos sin sin sin cos

1cos2 sin2 1 1 1

sin 2 cos 2

22 222

xxxdx xxxdx

dx x x x C





 



 

 





Bài tập 12.

Nguyên hàm của hàm số

sin cos



là:

tan cotxxC

tan cotxxC

tan cotxxC



cot tanxxC

Hướng dẫn giải

Chọn B.

Ta c

ó:

22 2 2 2 2

1sincos 11

tan cot

sin cos sin .cos cos sin

dx dx dx x x C

xx x x x x











 

Bài tập 13. Nguyên hàm của hàm số

4cos 4cos 1







là:

cot 2

C

B. tan 2xC C. cot 2xC



tan 2

C

Hướng dẫn giải

Chọn D.

Ta c

ó:



 



42 22 2 2

11111tan2

(2 )

4 cos 4 cos 1 (2 cos 1) cos 2 2 cos 2 2

dx dx dx d x C

xx x x x

Bài tập 14.

Nguyên hàm của hàm số

tan xdx



là:

tan

ln cos

xC

tan

ln sin





tan

ln cos

xC

tan

4cos



Hướng dẫn giải

Chọn A.

Từ





tan tan 1 tan tanxx x x

Suy ra







cos

tan

tan tan tan ln cos

cos 2

xdx xd x x C



 

Bài tập 15. Gọi





Fx là nguyên hàm của hàm số





sin 2 tanfx x x thỏa mãn











. Giá

trị của









là:

212







212







212





212





Hướng dẫn giải

Chọn D.

Ta c

ó:



sin

sin 2 . tan 2 sin .cos . 2 sin

cos

F x x xdx x x dx xdx

 

 

Suy ra

  

sin 2

1cos2

xxdxxC  



Theo giả thiết, ta có:

312 3 3

sin

34323 4 23

FCC



 



 





Vậy



sin 2 3

223

Fx x



   .

Do đó

1331

sin 2

442 4 23 2 12



 



 

   

 

 

Bài tập 16. Gọi





là nguyên hàm của hàm số





cos 2fx x

thỏa mãn





0 2019F 

. Giá trị

của









là:

3 16153





3 129224





3 129224





3 129224





Hướng dẫn giải

Chọn C.

Ta có



1cos4 1

cos 2 1 2 cos 4 cos 4

11cos81

1 2cos4 3 4cos4 cos8

428

xxx















   





Do đ

 

111

3 4 cos 4 cos8 3 sin 4 sin 8

888

Fx x xdx x x x C



    







Mà





0 2019F 

nên ta có

2019C 

Vậy



3 sin 4 sin 8 2019

Fx x x x



 





Do đó

3 129224

864













Bài tập 17. Gọ



Fx là nguyên hàm của hàm số



cos

1sin





, với

xkk







và thỏa

mãn





 . Giá trị của











là:

B. 0. C.

Hướng dẫn giải

Chọn D.

Ta t

hấy:



  

323

cos

cos 1 sin 1 sin cos cos .sin

1sin

sin cos

1 sin sin cos cos sin

xx xxxx

Fx xd x xd x x C

 



    



Theo giả thiết, ta có





 nên 1C



Vậy



sin cos

sin

Fx x C  

Do đ











Chú ý:

Với

n   , ta có:



cos

cos .sin cos cos

xxdx xd x C











và



sin

sin .cos sin sin

xxdx xdx C









Bài tập 18. Biết





cosx a

dx ln 5sin x 9 C , a,b

5sinx 9 b









 ,

là phân số tối giản. Giá trị 2a b



là

10.



Hướng dẫn giải

CHỌN D



d5sinx 9

cosx 1

5sinx 9 5 5sinx 9









ln 5sin x 9 C



Vậy

a1,b5.

Nên 2a b 3.

Bài tập 19. Tìm một nguyên hàm



của hàm số

  

fx 1 sinx biết











Fx x 2cosx sin2x.

 



Fx x 2cosx sin2x.

 



Fx x 2cosx sin2x.

 



Fx x 2cosx sin2x.

 

Hướng dẫn giải

CHỌN B

Ta c



1cos2x

1 sin x dx 1 2sin x sin x dx 1 2sin x dx

x2cosx sin2xc









  

 

33 1 3

F2cossincc0

2422 24 4



   

   





Vậy



Fx x 2cosx sin2x

 

Bài tập 20. Cho



cos2x

dx F x C

sin x cosx







và





Fab.





Tính



Aab.

2. B. 2. C. 1. D. 1.

Hướng dẫn giải

CHỌN C

Ta c

ó:



cos2 x cos x sin x

F x dx dx

sinx cosx sinx cosx













cosx sinx cosx sinx

dx cosx sin x dx sin x cosx.

sin x cos x











F1abA1.

Bài tập 21.

Cho tích phân

dx a.

sin xcos x





Tính

A12cot2x theo a.

4a . B.

2a . C.

3a . D.

a .

Hướng dẫn giả

CHỌN C

Ta c

ó:



22 22 2 2

1sinxcosx11

F x dx dx dx

sinxcosx sinxcosx cosx sinx





 





 

tan x cot x .

Theo đề:

sin x cos x sin x cos x 2 cos 2x

tan x cot x a

cosx sinx sinxcos x sin 2x

cos2x a

sin 2x 2

cos 2x a

A 12. 12. 3a .

sin 2x



    











Bài tập 22

. Cho





là một nguyên hàm của hàm số

sin 2

cos 4sin

x



và



02 1











. Tính













. B.



. C.

. D.

Lời giải

CHỌN B

Ta có





cos 4sindx x





2sin cos 8sin cos

xxxdx 

6sin cos

xdx



3sin2







sin 2 cos 4sin

dx d x x 

Do đó :

sin 2

cos 4sin

x







cos 4sin

dx x













cos 4sin

2cos 4sin

dx x









cos 4sin







24 7

02 2. 3 1

23 3 9

FF CC











Vậy



24 7

20 2. 2

23 3 9

FF CCC











Bài tập 23. Gọi





là nguyên hàm của hàm số







trên khoảng





22;22

thỏa

mãn





20F  . Khi đó phương trình





Fx x



có nghiệm là:

A. 0x  B. 1x  C. 1x



 D. 13x 

Hướng dẫn giải

Chọn D.

Ta có:



828

Fx dx d x x C

 





Mặt khác



20 8 0 2FxCC    

Vậy



82Fx x  

Xét phương trình



82 82

13 13

2440

Fx x x x x x







    























  



















Bài tập 24. Cho





Fx là một nguyên hàm của hàm số



432

xxx







trên khoảng









và



F 

. Tổng

















1 2 3 ... 2019SF F F F

là

2019

2020

2019.2021

2020

2018

2020

2019

2020



Hướng dẫn giải

Chọn C.

Phân tích



432

21 21 21

xxx









Khi

đó



 



21 1 1x

Fx dx dx x C

xx xx



 







Mặt khác



11 1

22 2

FCC

Vậy



1111

11 1

xx xx xx



      



 



Do đ

     

11111 1 1

1 2 3 ... 2019 1 ... 2019

2 2 3 3 4 2019 2020

111

1 2019 2018 2018

2020 2020 2020

SF F F F



   







     





Bài tập 25. Cho hàm số





fx có đạo hàm xác định trên  thỏa mãn



 

022, 0ffx và

    

.' 2 1 1 ,fx f x x f x x   . Giá trị





1f là:

A. 62 B. 10 C. 53 D. 26

Hướng dẫn giải

Chọn D.

Ta có:

    











.' 2 1 1 2 1

fx f x

fx f x x f x x

   



Suy ra

 













 

21 21 1

121

dfx

fx f x

dx x dx x dx f x x x C

fx fx



  





Theo giả thiết





022f  , suy ra



122 3CC





Với

3C  thì

 



22 2

13 31fx xx fx xx

Vậy



12426f 

Bài tập 26. Cho hàm số



yfx

có đạo hàm liên tục trên đoạn





2;1

thỏa mãn





03f



và









.' 3 4 2fx f x x x. Giá trị lớn nhất của hàm số





yfx trên đoạn





2;1 là:

242

215

Hướng dẫn giải

Chọn C.

Ta có:







 

.' 3 4 2 *fx f x x x

Lấy ngu

yên hàm hai vế của đẳng thức (*) ta được:



 

2332332

.' 3 4 2 2 2 3 6 6 3

f x f x dx x x dx f x x x x C f x x x x C 



Theo giả thiết, ta có





03f 

nên













32 3 32

0 3 0 2.0 2.0 27 3 9 3 6 6 27fCCCfxxxx 

Ta tìm giá trị lớn nhất của hàm số





36627gx x x x



 trên đoạn





2;1 .

Ta có









'91260, 2;1gx x x x

nên đồng biến trên đoạn





2;1 .

Vậy













2;1 2;1

max max 42fx gx





Dạng 2: Phương pháp đổi biến dạng 1, đặt





u=u x

1. Phương pháp giải

Định lí:

Cho









fudu Fu C



và





uux

là hàm số có đạo hàm liên tục thì













'fux uxdx Fux C

 



 



Các bước thực hiện đổi biến:

Xét













'Ifuxuxdx



Bước 1: Đặt





uux

, suy ra





'du u x dx

Bước 2: Ch

uyển nguyên hàm ban đầu về ẩn u ta được









IfuduFuC







, trong đó





Fu là

một nguyên hàm của hàm số





fu.

Bước 3: Trả về biến x ban đầu, ta có nguyên hàm cần tìm là









IFux C





Hệ quả: nếu





Fx là một nguyên hàm của hàm số





fx trên K và ,;0ab a ta có:

 

faxbdx Faxb C

 



2. Bài tập

Bài tậ

p 1.

Nguyên hàm





Fx của hàm số





fx xe





, biết





 là:



Fx e C



 B.



2019

Fx e



 C.



Fx e





 D.



Fx e





Hướng dẫn giải

Chọn D.

Đặt

1ux ta có

du x dx x dx du

Suy ra



fxdx e du e C



Do đ



xeC





Mặt khác



F 

nên 0C  . Vậy



fxdx e







Lưu ý: Ta có thể viết như sau:



33 3

21 1 3 1

xx x

f x dx x e dx e d x e C

 





 

Chú ý: Với các viết



xdx d x

, ta có thể tính nguyên hàm đã cho một cách đơn giản và

nhanh gọn.

Bài tập 2. Nguyên hàm

2sin

13cos







là:



ln 1 3cos

xC  B.

ln 1 3cos





ln 1 3cos

xC  

ln 1 3cos



 

Hướng dẫn giải

Chọn C.

Đặt 13cosux , ta có 3sindu xdx hay

2sin

xdx du

Khi đó

21 2

du u C

  



Vậy

2sin 2

ln 1 3cos

13cos 3

dx x C







Bài tập 3.



sin x

43a

Idx,a,b.

sin 2x 2 1 sin x cos x



















 





Tìm tỉ lệ

Hướng dẫn giải

CHỌN B

Đặt



dt cosx sin x dx 2 sin x dx

tsinxcosx

sin 2x t 1







  

















và

x:0





thì t:1 2 .



1dt 2dt21432

22t14

t121t



   



 





Bài tập 4. Cho



cos xsinxdx F x C



và



F0 a b .





Tính

A a b 2018.

A. 2018. B. 2016. C. 2022. D. 2020.

Hướng dẫn giải

CHỌN A

cos xsin xdx



Đặt

ucosx dusinxdx .



 

ucosx

cos xsinxdx u du C C

F0 ab ab0.

A a b 2018 a b 2ab a b 2018 2018.

    



    



Chú ý: chú ý rằng với

0a 

và

,;0mn n

ta luôn có:

aa .

Bài tập 5. Nguyên hàm







là:

111







111



















Hướng dẫn giải

Chọn D.

Đặt

11ux ux

. Suy ra

1xu





và 2dx udu



Khi đó



2211 1

111 1

du du du C

uuu u









 







Vậy







Bài tập 6. Nguyên hàm

9Sxx dx



là:







39 9

xxC











39 9

xxC











39 9

xxC













Hướng dẫn giải

Chọn A.

Xét

32 22

xx dx xx xdx



Đặt

222

99ux ux. Suy ra

9xu



 và xdx udu



Khi đó

  

2423

9. 9 3

u u udu u u du u C  



Vậy







39 9

xxC





Bài tập 7. Nguyên hàm

ln 1

Tdx







là:

2ln 1





B. 2ln 1TxC







ln 1 ln 1

Tx xC 

ln 1TxC





Hướng dẫn giải

Chọn B.

Ta có:



ln 1 2 ln 1

ln 1 ln 1

TdxdxxC

xx x

 





Bài tập 8. Nguyên hàm







2020

2022

Udx









là:

2021













2020

6060 1















2021

6063 1













2023

6069 1















Hướng dẫn giải

Chọn C.

Xét





 

2020

2022 2

Udx dx

















Đặt

 

2311

ududxdudx



 





Suy ra.

2020 2021

3 6063

Uudu uC



. Vậy

2021

6063 1















Lưu ý:







ax b

dx C

nadbdcxd

cx d









 







Bài tập 9. Xét nguyên hàm



1ln1

Vdx







. Đặt

11lnux 

, khẳng định nào sau đây

sai?



udu









.2 2

Vudu







54 32

2516

52 3

Vu u uuC 

523

VuuC



  

Hướng dẫn giải

Chọn C.

Đặt

 

1 1 ln 1 1 ln ln 2 2 2

uxu xxuuudu

          

Khi đó









432 5 4 32

.2 2

1ln1

2516

2584 4

52 3

Vdxudu

uuuuduu u uuC













Bài tập 10. Gọi





là nguyên hàm của hàm số





sin 2 .cos 2fx x x

thỏa 0











. Giá trị



2019F



là:



2019



 B.





2019 0F







2019





 D.



2019





Hướng dẫn giải

Chọn A.

Đặt

sin 2 2 cos2 cos 2

u x du xdx du xdx 

Ta có



 

23 22 24

35 3 5

sin 2 . cos 2 . 1

11 1 1

sin 2 sin 2

610 6 10

F x x xdx u u du u u du

uuC x xC



   



11 1

0sin sin 0

462102 15

FCC





    





Vậy



11 1

sin 2 sin 2

61015

Fx x x 

Do đ



2019





Bài tập 11. Biết rằng





  

1231

xdx

xx x x gx







 



(với C là hằng số). Gọi S là tập

nghiệm của phương trình





0gx . Tổng các phần tử của S bằng:

A. 0. B.

35

C. 3



35

Hướng dẫn giải

Chọn C.

Vì

 

22 2

1231 3 321 31xx x x xxxx xx





  





nên ta đặt

3ux x,

khi đó



23du x dx

uyên hàm ban đầu trở thành











Suy ra





 

1231 31

xdx

xx x x x x



 

  



Vậy

 

31; 0 310

gx x x gx x x









 











Do đó

3535

;



 











Tổng giá trị các phần tử của S bằng

3 .

Bài tập 12.



3cos2x sin 4x

IdxFxC.

2sinxcosx









Tính





F1,

biết rằng





không chứa hệ số tự do.

Hướng dẫn giải

CHỌN A



  



32sin2xcos2x

3cos2x sin4x

Idx dx

2sinxcosx 2sinxcosx

32sin2xcosxsinxcosxsinx

2sinxcosx





 











Đặt



dt cos x sin x dx

tsinxcosx

sin 2x t 1



















32t 1.t

2t 5t 6

Idtdt2t4t3dt

2t t2 t2

t2t3t6lnt2 C.











    



 













Dạng 3: Tìm nguyên hàm bằng cách đổi biến dạng 2

1. Phương pháp giải

Kiến thức cần nhớ:

Ta đã biết các đẳng thức sau:

sin cos 1tt

, với mọi t  .



1tan ,

cos 2

1cot ,

sin

ttkk



 

 



Với các bà

i toán sau đây thì ta không thể giải quyết

ngay bằng nguyên hàm cơ bản cũng như đổi biến số ở

dạng 1, đòi hỏi người học phải trang bị tư duy đổi

biến theo kiểu “

lượng giác hóa” dựa vào các hằng

đẳng thức lượng giác cơ bản và một số biến đổi thích

hợp, cụ thể ta xem xét các nguyên hàm sau đây:

Các kĩ thuật đổi biến dạng 2 thường gặp và

cách xử lí.

Bài toán 1: Tính







Bài toán 1:

Tính







Đặt

sinxa t , với

;













hoặc

cosxa t với





0;t





Bài toán 2: Tính







Bài toán 2: Tính







Đặt

tanxa t , với ;













Bài toán 3: Tính

Adx









Bài toán 3: Tính

Adx









Đặt

cos 2xa t



với











Bài toán 4: Tính









Axaxbdx



Bài toán 4: Tính









Axaxbdx



Đặt





sinxa ba t  với











Bài toán 5: Tính

Axadx



Bài toán 5: Tính

Axadx



Đặt

sin



với ;













2. Bài tập

Bài tậ

p 1.

Nguyên hàm

Idx







là:

arcsin

xx x





2arccos

xx x





arccos

xx x





2arcsin

xx x





Hướng dẫn giải

Chọn D.

Đặt 2sinxt với ;













. Ta có cos 0t  và 2cosdx tdt



Khi đó

4sin

2cos 4sin

44sin

Itdttdt







(vì cos 0 , ;













Suy ra





21cos2 2 sin2ItdtttC  



Từ

2 sin arcsin

xtt

và

sin 2 2 sin .cos

ttt





Vậy

2arcsin

xxxx

Idx C









Bài tập 2. Nguyên hàm



Idx







là:



1 xC











1 x





Hướng dẫn giải

Chọn B.

Đặt cos , 0 sin .xtt dx tdt



.

Khi đó

sin .

cot

sin sin

tdt dt

Idt tC

   



hay







Vậy



dx C







Ví dụ 3. Nguyên hàm

Idx







là:

arctan xC B. arccot xC



C. arcsin xC



D. arccos xC



Hướng dẫn giải

Chọn A.

Đặt tanxt với

;













, ta có





1tandx t dt

Khi đó



1tan

ItdtdttC







Vậy

arctan

IdxxC







Dạng 4: Tìm nguyên hàm bằng phương pháp nguyên hàm từng phần

1. Phương pháp giải

Với



uux

và





vvx

là các hàm số có đạo hàm trên khoảng K thì ta có:





.' '.'uv u vv u

Viết dưới dạng vi phân





d uv vdu udv

Khi đó lấy nguyên hàm hai vế ta được:





d uv vdu udv





Từ đó suy





1udv uv vdu



Công thức (

1) là công thức nguyên hàm từng phần.

Dấu hiệu nhận biết phải sử dụng phương pháp nguyên hàm từng phần.

Bài toán: Tìm









.Iuxvxdx



, trong đó





ux và





vx là hai hàm có tính chất khác nhau,

chẳng hạn:



ux là hàm số đa thức,



vx là hàm số lượng giác.



ux là hàm số đa thức,



vx là hàm số mũ.





ux là hàm số logarit,





vx là hàm số đa thức.



là hàm số mũ,



là hàm số lượng giác.

Phương pháp nguyên hàm từng phần

Bước 1: Đặt









'du u x dx

uux

dv v x dx v v x dx























Bước 2: Áp dụ

ng công thức (1), ta được:

udv uv vdu



Lưu ý: Đặt



uux (ưu tiên) theo thứ tự: “Nhất lốc, nhì đa, tam lượng, tứ mũ”. Tức là, nếu có

logarit thì ưu tiên đặt u là logarit, không có logarit thì ưu tiên u là đa thức,… thứ tự ưu tiên sắp xếp

như thế.

Còn đối với nguyên hàm





vvxdx



ta chỉ cần Chọn một hằng số thích hợp. Điều này sẽ được

làm rõ qua các Bài tập minh họa ở cột bên phải.

2. Bài tập

Bài tậ

p 1.

Kết quả nguyên hàm





ln 2Ix xdx



là:



ln 2



 



2ln 2

xx C



 









222

2ln 2xxxC D.



ln 2





Hướng dẫn giải

Chọn D.

Đặt



ln 2

du dx

dv xdx

































Khi

đó

 

222

ln 2 ln 2

222

xxx

IxxdxxC







Chú ý: Thông thường thì với

dv xdx v

Tuy

nhiên trong trường hợp này, ta để ý



 mang lại sự hiệu quả.

Bài tập 2. Kết quả nguyên hàm





ln sin 2cos

cos

Idx







là:









tan 2 .ln sin 2 cos 2 ln cosxxxxxC









tan 2 .ln sin 2 cos 2 ln cosxxxxxC













tan 2 .ln sin 2 cos 2 ln cosxxxxxC









cot 2 .ln sin 2cos 2 ln cosxxxxxC

Hướng dẫn giải

Chọn B.

Đặt



cos 2 sin

ln sin 2cos

sin 2 cos

tan 2

cos

uxx

du dx

































Khi

đó

 

cos 2sin

tan 2 ln sin 2cos

cos

tan 2 ln sin 2cos 2 ln cos

Ix x x dx

xxxxxC



  

   



Chú ý:

Ở Bài tập này, Chọn tan 2vx có thể rút gọn được ngay tử và mẫu trong nguyên hàm

vdu



Bài tập 3. Kết quả nguyên hàm

sin 5Ix xdx



là:

122

cos 5 sin 5 cos 5

525125

xxxx xC

122

cos 5 sin 5 cos 5

525125

xxxx xC





122

cos 5 sin 5 cos 5

525125

xxxx xC

122

cos5 sin5 cos5

5 25 125

xxxx xC





Hướng dẫn giải

Chọn D.

Phân tích: Ở đây ta sẽ ưu tiên

ux là đa thức, tuy nhiên vì bậc của u là 2 nên ta sẽ từng phần hai

lần mới thu được kết quả. Nhằm tiết kiệm thời gian, tôi gợi ý với phương pháp “sơ đồ đường chéo”

cụ thể như sau:

Bước 1: Chia thành 3 cột:

+ Cột 1: Cột u luôn lấy đạo hàm đến 0.

+ Cột 2: Dùng để ghi rõ dấu của các phép toán đường chéo.

+ Cột 3: Cột dv luôn lấy nguyên hàm đến khi tương ứng với cột 1.

Bước 2: Nhân chéo kết quả của 2 cột với nhau. Dấu của phép nhân đầu tiên sẽ có dấu (+), sau đó

đan dấu (-), (+), (-),… rồi cộng các tích lại với nhau.

Khi

đó

122

cos 5 sin 5 cos5

5 25 125

Ixxxx xC   

Chú ý:

Kĩ thuật này rất đơn giản và tiết kiệm nhiều thời gian.

Trong kĩ thuật tìm nguyên hàm theo sơ đồ đường chéo, yêu cầu độc giả cần tính toán chính xác đạo

hàm

và nguyên hàm ở hai cột 1 và 3. Nếu nhầm lẫn thì rất đáng tiếc.

Bài tập 4. Nguyên hàm

43x

Ixedx



là:

43 2

2345

4122424

33 3 3 3

xx x x

IeC



  









43 2

2345

412 2424

33 3 3 3

xx x x

IeC



  





43 2

412

33 3

xx x

IeC





 





Hướng dẫn giải

Chọn A.

Nếu làm thông thường thì từng phần 4 lần ta mới thu được kết quả. Ở đây, chúng tôi trình bày theo

sơ đồ đường chéo cho kết quả và nhanh chóng hơn.

Vậy

43 2

2345

4122424

33 3 3 3

xx x x

IeC



  





Bài tập 5. Nguyên hàm sin

Ie xdx



là:





2sin cos

ex xC B.





2sin cos

exxC







sin cos

exxC



sin cos

ex xC



Hướng dẫn giải

Chọn C.

Phân tích: Sự tồn tại của hàm số mũ và lượng giác trong cùng một nguyên hàm sẽ rất dễ gây cho

người học sự nhầm lẫn, nếu ta sẽ không biết điểm dừng thì có thể sẽ bị lạc vào vòng luẩn quẩn. Ở

đây, để tìm được kết quả thì ta phải từng phần hai lần như trong Bài tập 3. Tuy nhiên, với sơ đồ

đường chéo thì sao? Khi nào sẽ dừng lại?

Khi

đó, ta sẽ có thể kết luận

sin cos sin

xx x

Ie xe x e xdx



Hay

2sin.cos

Ie xe x

. Vậy



sin cos

Ie x xC

Chú ý: Chỉ dừng lại khi đạo hàm của nó có dạng giống dòng đầu tiên. Dòng cuối thu được

sin

xe dx I



Bài tập 6. Tìm









Iaxbvxdx



, trong đó





vx là hàm đa thức,

n   và ,;0ab a

Hướng dẫn giải

Phân tích: Vì ưu tiên









ux ax b nên





.ln

na ax b

du dx

ax b









và tiếp tục đạo hàm thì cột 1

sẽ không về 0 được, vì vậy phải chuyển lượng



ax b





từ cột 1 sang nhân với





vx ở cột 3 để

rút gọn bớt; tiếp tục quá trình như thế cho đến khi đạo hàm cột 1 về 0, và chú ý sử dụng quy tắc đan

dấu bình thường.

Bài tập 6.1. Kết quả nguyên hàm .lnIxxdx



là:

.ln2

C

.ln2



 C.

.ln2



 D.

.ln2

C

Hướng dẫn giải

Chọn A.

Vậy

.ln .ln2

Ixxdx C



Chú ý: chuyển lượng





bên cột 1 sang nhân với



vx

ta thu được kết quả

. Khi đó

bên cột 1 còn lại 1, đạo hàm của nó bằng 0; bên cột 3 có nguyên hàm của

là

Bài tập 6.2. Kết quả nguyên hàm









41.ln2Ix xdx



là:



23 2 2 2

2ln233ln236ln2 6

xx x x x x x x x xC 



23 2 2 2

2ln233ln236ln2 6

xx x x x x x x x xC 



23 2 2 2

2ln233ln236ln2 6

xx x x x x x x x xC 



23 2 2 2

2ln233ln236ln2 6

xx x x x x x x x xC 

Hướng dẫn giải

Chọn B.

Vậy



23 2 2 2

2ln233ln236ln2 6

Ixx x xx x xx x xC   

Chú ý:

Chuyển

, nhân với



2xx thu được





63x



Chuyển

, nhân với





33xx thu được





66x



Chuyển

, nhân với



36xx thu được





36x



Bài tập 7. Cho









xxe là một nguyên hàm của hàm số





fxe. Biết rằng hàm số





có đạo hàm liên tục trên

 . Nguyên hàm của hàm số





fxe là:





xe C





xe C





xe C







xe C

Hướng dẫn giải

Chọn A.

Ta có





















222

'1...

xx x x x x

Fx fxe e x e fxe fxe xe  .

Xét





fxedx



Đặt

 

ue du edx

dv f x dx v f x

















Do đ













.2 21

xxxx

Ifxe fxedxxe x eC 



Vậy









I f xe dx xe C



Dạng 5: Các bài toán thực tế ứng dụng nguyên hàm

1. Phương pháp giải

Ý nghĩa vật lí của đạo hàm:

Một chất điểm chuyển động theo phương trình





SSt

, với





là quãng đường mà chất điểm đó

đi được trong thời gian t, kể từ thời điểm ban đầu.

Gọi





vt và





at lần lượt là vận tốc tức thời và gia tốc tức thời của chất điểm tại thời điểm t, ta có:

 

'vt S t và









'at v t .

Từ đó ta có:









St vtdt



và









vt atdt



2. Bài tập

Bài tậ

p 1.

Một vật chuyển động với gia tốc



at m s





, trong đó t là khoảng thời gian tính

từ thời điểm ban đầu. Vận tốc ban đầu của vật là. Hỏi vận tốc cảu vật tại giây thứ 10 bằng bao

nhiêu?

A. 10 m/s. B. 15,2 m/s. C. 13,2 m/s. D. 12 m/s.

Hướng dẫn giải

Chọn C.

Vận tốc của vật tại thời điểm t

được tính theo công thức:

 

3ln 1

v t a t dt dt t C









Vì vận tốc b

an đầu (lúc

0t  ) của vật là

6/vms



nên:









03ln01 6 6 3ln16vCCvtt

Vận tốc c

ủa vật chuyển

động tại giây thứ 10 là:









10 3ln 10 1 6 13, 2 /vms .

Bài tập 2. Một vận động viên điền kinh chạy với gia tốc



322

24 16

at t t m s 

, trong đó t là

khoảng thời gian tính từ lúc xuất phát. Hỏi vào thời điểm 5 (s) sau khi xuất phát thì vận tốc của vận

động viên là bao nhiêu?

A. 5,6 m/s. B. 6,51 m/s. C. 7,26 m/s. D. 6,8 m/s.

Hướng dẫn giải

Chọn B.

Vận tốc





chính là nguyên hàm của gia tốc





nên ta có:

 

32 4 3

15 15

24 16 96 48

v t a t dt t t dt t t C











Tại thời điểm

ban đầu





0t 

thì vận động viên ở tại vị trí xuất phát nên vận tốc lúc đó là:



000 .0 .0 0 0

96 48

vv CC     

Vậy công thức vận tốc là



96 48

vt t t 

Vận tốc của vận động viên tại giây

thứ 5 là





56,51/vms .

Chú ý: Gia tốc của vật chuyển động là



at m s





. Ta tính









vt atdt



, kết hợp với

điều kiện vận tốc ban đầu

6/vms . Suy ra công thức tính vận tốc





vt tại thời điểm t và tính

được





10v

Bài tập 3. Một nhà khoa học tự chế tên lửa và phóng tên lửa từ mặt đất với vận tốc ban đầu là 20

m/s. Giả sử bỏ qua sức cản của gió, tên lửa chỉ chịu tác động của trọng lực. Hỏi sau 2s thì tên lửa

đạt đến tốc độ là bao nhiêu?

A. 0,45 m/s. B. 0,4 m/s. C. 0,6 m/s. D. 0,8 m/s.

Hướng dẫn giải

Chọn B.

Xem như tại thời điểm

0t  thì nhà khoa học phóng tên lửa với vận tốc đầu 20 m/s. Ta có





00s 

và





020v 

Vì t

ên lửa chuyển động thẳng đứng nên gia tốc trọng trường tại mọi thời điểm t là





9,8 /

st ms .

Nguyên hàm của gia tốc là vận tốc nên ta có vận tốc của tên lửa tại thời điểm t là



9,8 9,8vt dt t C  







020v 

nên





9,8 20 20 9,8 20tC C vt t 

Vậy vận tốc của tên lửa sau 2s là







29,8.2200,4/vms   .

BÀ

I 2: T

ÍCH PHÂN

KIẾN THỨC CƠ BẢN CẦN NẮM

I. ĐỊNH NGHĨA VÀ TÍNH CHẤT CỦA TÍCH PHÂN

1. Định nghĩa tích phân

Định nghĩa

Cho hàm số





x liên tục trên đoạn





;ab , với

.ab

Nếu





Fx là nguyên hàm của hàm số





x trên

đoạn



;ab thì giá trị









Fb Fa được gọi là tích

phân của hàm số





trên đoạn



;ab

Kí hiệu

   

xdx F x Fb Fa



(1)

Công thức (1) còn được gọi là công thức Newton –

Leibnitz; a và b được gọi là cận dưới và cận trên của

tích phân.

Ý nghĩa hình học của tích phân

Giả sử hàm số



yfx là hàm số liên tục và không

âm trên đoạn



;ab . Khi đó, tích phân



xdx



chính l

à diện tích hình phẳng giới hạn bởi đường

cong



yfx , trục hoành Ox và hai đường thẳng

ax b với

.ab



Sfxdx



Chẳng hạ





Fx x C



 là một nguyên

hàm của hàm số





xx nên tích phân

    

10fxdx Fx F F











101.CC



 

Lưu ý: Giá tr

ị của tích phân không phụ

thuộc vào hằng số C.

Trong tính toán, ta thường chọn

0.C 

Chẳng hạn: Hàm số





xx x có

đồ thị





C và

  

10fx x 

, với





Diện tíc

h “tam giác cong” giới hạn bởi





, trục Ox và hai đường thẳng

1x 

và



là



21Sfxdx xxdx













 





Lưu ý: Ta còn gọi hình phẳng trên là “hình

thang cong”.

2. Tính chất cơ bản của tích phân

Cho hàm số





x và



x là hai hàm số liên tục

trên khoảng K, trong đó K có thể là khoảng, nửa

khoảng hoặc đoạn và

,, ,abc K khi đó:

a. Nếu ba thì



fxdx



b. Nếu





x có đạo hàm liên tục trên đoạn





;ab

thì ta có:

   

xdx f x f b f a







c. Tính chất tuyến tính

   

.. .

bbb

aaa

kf x hgx dx k f xdx h gxdx





Với mọi

,.kh

d. Tính chất trung cận

  

bcb

aac

xdx f xdx f xdx



, với





;cab

e. Đảo cận tích phân

 

xdx f xdx



f. Nếu





0,fx



;

ab thì



fxdx



và



fxdx



khi



0fx .

g. Nếu

 





xgxxab thì

Chẳng hạn: Cho hàm số





x liên tục, có

đạo hàm trên đoạn





1; 2 thỏa mãn





18f



 và





21.f





Khi đó

    

219fxdx fx f f











Lưu ý: Từ đó ta cũng có

  

bfa fxdx







và

  

afb fxdx







 

xdx g xdx



h. Nếu







;

min

mfx và







;

max

fx thì

  

mb a f xdx M b a  



i. Tích phân không phụ thuộc vào biến, tức là ta luôn

có

   

...

bbb b

aaa a

f x dx f t dt f u du f y dy  



II. CÁC PHƯƠNG PHÁP TÍNH TÍCH PHÂN

1. Phương pháp đổi biến số

Đổi biến dạng 1

Bài toán:

Giả sử ta cần tính tích phân



fxdx



, trong

đó ta có thể phân tích

















xguxux





thì ta thực hiện

phép đổi biến số.

Phương pháp:

+ Đặt





uux , suy ra



.du u x dx





+ Đổi cận:

x a b









+ Khi đó

 



aua

Ifxdx guduGu 



, với





Gu là nguyên hàm của





Đổi biến dạng 2

Dấu hiệu Cách đặt

ax

sin ; ;

xa tt

















a

sin



;



;\0













ax

tan ; ;

xa tt











Lưu ý:

Phương pháp đổi biến số

trong tích phân cơ bản giống như

đổi biến số trong nguyên hàm, ở

đây chỉ thêm bước

đổi cận.





.cos2 ; 0;

xa tt

















.cos2 ; 0;

xa tt



















abx



sin ; 0;

xa ba tt







  









2. Phương pháp tích phân từng phần

Bài toán:

Tính tích phân

 

Iuxvxdx







Hướng dẫn giải

Đặt



uux duuxdx

dv v x dx v v x



















Khi đó



Iuv vdu



(công thức tích phân từng

phần)

Chú ý: Cần phải lựa chọn u và dv hợp lí

sao cho ta dễ dàng tìm được v và tích phân

vdu



dễ tính hơn

udv



III. TÍCH PHÂN CÁC HÀM SỐ ĐẶC BIỆT

Cho hàm số





x liên tục trên



;aa . Khi đó

Đặc biệt

   

xdx f x f x dx









(1)

+ Nếu





x là hàm số lẻ thì ta có



fxdx







(1.1)

+ Nếu





x là hàm số chẵn thì ta có

 

xdx f xdx







(1.2)

và



dx f x dx











01b (1.3)

2. Nếu





x liên tục trên đoạn



;ab thì

  

xdx f a b xdx



Hệ quả: Hàm số





x liên tục trên





0;1 , khi đó:

 

sin cos

xdx f xdx







3. Nếu





x liên tục trên đoạn



;ab và









abx fx  thì

 

f x dx f x dx







B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP

Dạng 1: Tính tích phân bằng cách sử dụng định nghĩa, tính chất

1. Phương pháp giải

Sử dụng các tính chất của tích phân.

Sử dụng bảng nguyên hàm và định nghĩa tích phân để tính tích phân.

2. Bài tập

Bài tập 1: Biết tích phân



abc

xxxx







, với ,,abc . Giá trị biểu thức

abc là

8.P 

0.P 

2.P



6.P 

Hướng dẫn giải

Chọn B.

Ta có





10,1;2xxx  

nên



222

111

221

.1 1

Idxdxdxxx

xx x x









42 23 2.

Suy ra 4, 2abc nên

0.P abc





Nhân liên hợp

x

Bài tập 2: Cho hàm số





x thỏa mãn







và

 

xxfx













với mọi

x 

. Giá trị





bằng



f 



f 









f 

Hướng dẫn giải

Chọn C.

Từ

 

xxfx









(1), suy ra





0fx



 với mọi





1; 2x  .

Suy ra





x là hàm không giảm trên đoạn





1; 2 nên









20fx f



 ,



1; 2x .

Chia 2 vế hệ thức (1) cho







ta được









,1;2.









(2)

Lấy tích phân 2 vế trên đoạn



1; 2

hệ thức (2), ta được







  

1113

2122

dx xdx

fx f f









   















f 

nên suy ra



f 

Chú ý rằng đề bài cho



, yêu cầu tính





, ta có thể sử dụng nguyên hàm để tìm hằng số C.

Tuy nhiên ta cũng có thể dựa vào định nghĩa của tích phân để xử lí.

Bài tập 3: Cho hàm số



xác định trên













thỏa mãn









và







01,1 2ff

. Khi đó









13ff bằng

1ln15.

3ln5.

2ln3.





1ln15.

Hướng dẫn giải

Chọn A.

Ta có

   

01fxdx f f









nên suy ra

  

10 .

ffxdx





 





xdx









Tương tự ta cũng có

  

ffxdx









xdx



 



Vậy

    

1 3 1 1 ln 2 1 ln 2 1 .f f f x dx f x dx x x





         



Vậy









1 3 1 ln15.ff 

Bài tập 4: Cho hàm số



x có đạo hàm liên tục trên đoạn





0;1 thỏa mãn





10f





7fx dx











và



.1.xf xdx







Giá trị



xdx



là

A. 1. B.

D. 4.

Hướng dẫn giải

Chọn C.

Ta có



7fx dx











(1).

49 7

xdx xdx 



(2).

và



14 . 14xf xdx







(3).

Cộng hai vế (1), (2) và (3) suy ra



70fx x dx











mà



70fx x

















Hay



xC 



10 0 .

fCC  

Do đó



fx 

Vậy



77 7

44 5

f x dx dx



  







Bài tập 5: Cho

 

xgx là hai hàm số liên tục trên đoạn





1;1 và





x là hàm số chẵn,





là hà

m số lẻ. Biết

 

5; 7f x dx g x dx



. Giá trị của

 

f x dx g x dx







là

A. 12. B. 24. C. 0. D. 10.

Hướng dẫn giải

Chọn D.

Vì





x là hàm số chẵn nên

 

22.510f x dx f x dx









Vì



x là hàm số lẻ nên



0gxdx







Vậy

10.A 

Bài tập 6: Cho



ln 3

xdx







với a, b là các số hữu tỉ. Giá trị của ab



bằng



Hướng dẫn giải

Chọn D.

Ta có

  

11 1

22 2

00 0

12 11 1 1 1

2221

21 21 21

xdx x

dx dx

xx x











 



 



11 11

ln 2 1 ln 3.

42 1 4 6 4











Vậy

11 1

64 12

ab ab    

Bài tập 7: Cho

ln 2 ln 3,

dx a b









với

,ab





. Giá trị biểu thức

aabb



là

A. 11. B. 21. C. 31. D. 41.

Hướng dẫn giải

Ta có

33 3

22 22

22 2

23 212 21 2xx x

dx dx dx

xx xx xxxx

 







 



 



212 2

ln 2ln 2ln 1 5ln 2 4ln 3

dx x x x x

xxxx















41.

aabb













Chọn D.

Bài tập 8.

Biết rằng tích phân

ln 2 ln 3 ln 5,

dx a b c









với

,,abc

là các số nguyên. Giá

trị biểu thức

Sabc

là bao nhiêu?

A. 62.S  B. 10.S  C. 20.S



D. 10.S 

Hướng dẫn giải

Chọn B.

Ta có



22 2

11 1

56 56 9 4

56 2 3 3 2

dx dx dx

xx x x x x









    



 



9ln 3 4ln 2 9ln5 4ln3 26ln2.xx

Suy ra

26, 4, 9.abc   Vậy

26 4.9 10.Sabc   

Bài tập 9: Cho



cos sin .cos 1

ln 2 ln 1 3

cos sin .cos

xxx

dx a b c

xxx





  





, với

,,abc

là các số hữu tỉ. Giá

trị abc bằng

A. 0. B.

2.



6.

Hướng dẫn giải

Chọn C.

Ta có



222

cos sin .cos 1 2cos sin .cos sin

cos sin .cos

cos cos sin .cos

xx x xx x

dx dx

xxx

xxxx



 







 



2 tan tan 2 tan tan

tan

cos 1 tan 1 tan

xx xx

dx d x

xx x



 









2tan

tan tan 2ln tan 1

1tan 2

xdx x





   













1 2ln 2 2ln 3 1 .  

Suy ra 1, 2, 2ab c nên

4.abc





Bài tập 10: Cho hàm số



23 , 0

em khix

xxkhix





















liên tục trên



Biết

 

3,,f x dx ae b c abc



  



 . Tổng 3Tab c



 bằng

A. 15. B. 10. C. 19.



D. 17.

Hướng dẫn giải

Chọn C.

Do hàm số liên tục trên



nên hàm số liên tục tại















lim lim 0 1 0 1.

fx fx f m m







Ta có

  

101

110

xdx f xdx f xdx I I









22222

216

23 3 3 3 3 23 .

Ixxdx xdx xx





 



 

12.

Iedxexe



Suy ra



23 .

fxdx I I e



 



Suy ra

1; 2; .

ab c 

Vậy

31222 19.Tab c  

Bài tập 11: Biết

cos

dx m











. Giá trị của

cos









bằng

A. .m



 B.













Hướng dẫn giải

Chọn A.

Ta c



cos cos 1

cos 1 cos 2 .

13 13 2

dx dx xdx x dx

 





 





 

Suy ra

cos

dx m











Dạng 2: Tính tích phân bằng phương pháp đổi biến

1. Phương pháp giải

Nắm vững phương pháp đổi biến số dạng 1 và dạng 2, cụ thể:

Đổi biến dạng 1

Bài toán:

Giả sử ta cần tính



xdx



trong đó ta có thể phân tích







xguxux





Bước 1: Đặt





,uux suy ra





.du u x dx





Bước 2: Đổi cận

x a B









Bước 3: Tính

 



aua

Ifxdx guduGu 



Với



Gu là một nguyên hàm của





u .

Đổi biến dạng 2

Bài toán:

Giả sử ta cần tính



xdx



, ta có thể đổi biến như sau:

Bước 1: Đặt





 ta có





.dx t dt







Bước 2: Đổi cận

x a b





Bước 3:

Tính



  

.I f t t dt g t dt G t

















Với



Gt là một nguyên hàm của





Dấu hiệu Cách đặt

ax

sin , ;

xa tt

















a



,;\0

sin 2 2













ax

tan , ;

xa tt















.cos2 , 0;

xa tt

















.cos2 , 0;

xa tt



















abx



sin , 0;

xa ba tt







  









2. Bài tập mẫu

Bài tập 1: Biết

cos

ln 2 ln 3,

sin 3sin 2

dx a b









với ,ab là các số nguyên.

Giá trị của

ab là

A. 3. B. 7. C. 5. D. 1.

Hướng dẫn giải

Chọn A.

Ta có

 



cos 1

sin

sin 3sin 2 sin 1 sin 2

dx d x

xx x x





  





sin lnsin 1 lnsin 2

sin 1 sin 2

dx x x





 











ln 2 ln1 ln 3 ln 2 2ln 2 ln 3   

Suy ra

2, 1 2 3.ab ab

Bài tập 2: Biết



ln 2

ln ln ln

Iabc

ee c









, với ,,abc là các số nguyên tố.

Giá trị của

abc

là

3.P 

1.P 

4.P



3.P 

Hướng dẫn giải

Chọn D.

Ta có

ln 2 ln 2

34 43

xx xx

dx e dx

ee e e





 



Đặt

te dtedx

Đổi cận 01,ln22.xtx t  

Khi đó



1111111

ln ln 3 ln 5 ln 2 .

43 2 1 3 2 3 2

Idt dt

tt t t t









   





Suy ra

3, 5, 2abc. Vậy

23.Pabc

Bài tập 3: Biết

1sin

dx a b











, với

,,ab c





và a, b, c là các số nguyên tố cùng nhau.

Giá trị của tổng

abc

bằng

A. 5. B. 12. C. 7. D.

1.

Hướng dẫn giải

Chọn A.

Ta có

66 6 6

22 2

00 0 0

1tan

cos

1sin

cos sin 1 tan 1 tan

22 2 2

dx dx

Idxdx

xx x x

  









  



 

 

 

 

  

Đặt

1tan 2 1tan .

tdtdx



   





Đổi cận

01; 33.

xtx t



  

22 33









Suy ra

1, 3, 3abc   nên

5.abc

Lưu ý:

1sin sin cos .



 





Chia tử và mẫu cho

cos .







Bài tập 4: Cho hàm số





yfx liên tục trên



và



28.fxdx





Giá trị của



Ixfxdx



là

A. 4. B. 8. C. 16. D. 64.

Hướng dẫn giải

Chọn B.

Đặt

22 2 .

u xdx du xdx du   

Đổi cận

00,21.xux u  

Khi đó

 

228.Ifudufxdx



Bài tập 5: Cho hàm số



yfx xác định và liên tục trên







 sao cho









xxfe fe

với mọi





0;x  . Giá trị của





.ln





là

I 

I 

Hướng dẫn giải

Chọn C.

Với





0;x  ta có

  

11.

xx x

xf e f e f e x







Đặt

ln .

xt xe dt

   

Đổi cận

;1.

xet xet 

Khi đó



.1.

I t f e dt t t dt



Bài tập 6: Biết



3sin cos 11

ln 2 ln 3 , ,

2sin 3cos 13

dx b c b c











 . Giá trị của

là



Hướng dẫn giải

Chọn A.

Phân tích









2sin 3cos 2cos 3sin

3sin cos

2sin 3cos 2sin 3cos

mx xn x x

xx xx

 













23sin 32cos

2sin 3cos

mn x mn x







Đồng nhất hệ số ta

có

233

311

;

32 1

13 13















Suy ra



311

2sin 3cos 2cos 3sin

3sin cos

13 13

2sin 3cos 2sin 3cos

xx xx

dx dx

xx xx



 











3 11 2cos 3sin 3 11 2cos 3sin

13 13 2sin 3cos 13 13 2sin 3cos

xx xx

dx x dx

xxx









  











2sin 3cos

311 311

ln 2sin 3cos

26 13 2sin 3cos 26 13

dx x

dx x x







  





311 11

ln 2 ln 3.

26 13 13

 



Do đó

11 26 22

13 3 3







 











Bài tập 7: Cho hàm số



x liên tục trên



và thỏa mãn



tan . cos 2xf x dx







và









. Giá trị của





2fx

Idx





là

A. 0. B. 1. C. 4. D. 8.

Hướng dẫn giải

Chọn D.

Đặt

 

00.

sin .cos

tan . cos 2 . cos 2.

cos

A xfxdx fxdx



 



Đặt

cos 2sin cos sin cos .

t x dt x xdx dt x xdx 

Đổi cận

t

và



 Khi đó





Adt





Đặt









ln ln . ln

22.

ln ln

fx xfx

Bdx dx

xx x x

 



Tương tự ta có





Bdt





Giá trị của



Idx





Đặt

t x dx dt

Đổi cận

xt và

24.xt

Khi đó













414

448



ft ft ft

Idtdtdt

ttt

Bài tập 8: Cho



;

dx a b







với ,ab là các số nguyên. Giá trị của biểu thức

ab

bằng

A. 17. B. 57. C. 145. D. 32.

Hướng dẫn giải

Chọn A.

Giá trị của





Idx











Đặt

 

xdx

t tdt dx tdt



  





Đổi cận

03,12.xtxt 

Ta có



123

32.

I t dt dt t







Mà



dx a b







nên suy ra 3, 2.ab



Từ đó ta có giá trị

3217.

ab

Bài tập 9: Cho

dx b

xab













, với ,ab là các số nguyên tố. Giá trị của biểu thức





ab bằng

A. 12. B. 10. C. 18. D. 15.

Hướng dẫn giải

Chọn B.

Biến đổi

11 1 1

3 4

11 1 1

22 2 2

.1 1

xx x

Idx dx dx dx

  













  

Đặt

33 4

11 3

112u u udu dx

xx x

 

và





Đổi cận

3; 1 2.

xuxu 

Ta có



21113

ln ln 2 .

313132

udu

du u





 











Suy ra

3, 2.ab

Vậy



2 10.Pab

Dạng 3: Tính tích phân bằng phương pháp tích phân từng phần

Bài tập 1. Cho tích phân

ln 2

Idxa





với a là số thực b và c là các số dương, đồng thời

là phân số tối giản. Giá trị của biểu thức

abc





là

6.P 

5.P 

6.P





4.P 

Hướng dẫn giải

Chọn D.

Đặt





























Khi đó

ln 1 ln 1 1 ln 2

Idx

xx xx













Suy ra

1, 2, .

bc a



  Do đó

23 4.Pabc

+ Ưu tiên logarit.

+ Đặt















Bài tập 2: Biết

ln 2,

1cos2

dx a b









với ,ab là các số hũu tỉ. Giá trị của

16 8Tab

là

4.T 

5.T 

2.T



2.T 

Hướng dẫn giải

Chọn A.

Đặt

444

000

1cos2 2cos 2cos

xxx

dx dx dx









Đặt

tan

cos

ux dudx

dv dx v x

 













Khi

đó



tan tan tan ln cos

Axx xdx xx x





















1211 1

ln ln 2 ln 2.

24 2 24 2 8 4





  





Vậy



 do đó

16 8 2 2 4.ab

+ Biến đổi

1cos2 2cos .

x

+ Ưu tiên đa thức.

+ Đặt

cos

dv dx















Bài tập 3: Cho

Ixedxaeb



với ,ab



 . Giá trị của tổng



là

D. 1.

Hướng dẫn giải

Sử dụng phương pháp từng phần.

Đặt

du dx

dv e dx























Khi đó

11 11

22 222

00 00

11 1111

.. . . .

22 2444

xx xx

Iuv vdu xe edx xe e e



Suy ra

ae b e 

Đồng nhất hệ số hai vế ta có

ab Vậy





Chọn A.

+ Ưu tiên đa thức.

+ Đặt

dv e dx











Bài tập 4: Cho hàm số





x liên tục, có đạo hàm trên







216f



và



4.fxdx



Tích phân











bằng

A. 112. B. 12. C. 56. D. 144.

Hướng dẫn giải

Chọn A.

Đặt 22.

txtdxdt  

Đổi cận











Do đó

  

422

000

44.

fdxtftdtxfxdx













Đặt

 

ux dudx

dv f x dx v f x



















Suy ra

    

222

000

4 4 4 8 2 4 8.16 4.4 112.xf xdx xfx fxdx f fxdx









Bài tập 5. Cho



ln sin 2cos

ln 3 ln 2

cos

dx a b c









với ,,abc là các số hữu tỉ.

Giá trị của abc bằng

Hướng dẫn giải

Chọn A.

Đặt





ln sin 2cos

cos 2sin

sin 2cos

tan 2

cos

uxx

du dx

























Khi đó



 

4 4

0 0

ln sin 2cos

cos 2sin

tan2lnsin2cos

cos cos

dx x x x dx

 







  





3ln 2ln2 1 2tan















3ln3 ln2 2ln cos



 

725

3ln 3 ln 2 2ln 3ln 3 ln 2 .

24 2 24



   

Suy ra

3, , .

ab c  Vậy

18.abc



Bài tập 6. Biết



edxme n







trong đó

,,,mn pq

là các số nguyên dương và

là phân

số tối giản. Giá trị của

Tmnpq

là

11.T 

10.T 

7.T



8.T 

Hướng dẫn giải

Chọn B.

Ta có





22 22

1111

11 11

12112.

xxxx

I x e dx x x e dx x e dx xe dx



     

 

Xét



22 2 2

11 1 1

22 2 2

11 1 1

1.. .

  







   





  

xx x x

xx x

I x edxxe dxxedx xde



11 1 1

222

xx x x

eedxxe xedx

  

 



11 1

241

xx x

Ixedxxe Ixe e

 

    



4, 1, 3, 2.mnpq   

Khi đó

413210.Tmnpq

Bài tập 7. Tìm số thực

m1

thỏa mãn



ln x 1 dx m.







A. m2e. B.

me.



me.



D. me1.

Hướng dẫn giải

Chọn B



mmm

111

Alnx1dxlnxdxdx 



I ln xdx



Đặt

ulnx

du dx

dv dx























Ixlnx dx 



A x ln x m ln m m .













Bài tập 8. Đặt

ln d ,



k nguyên dương. Ta có





khi:





1; 2 .k  B.





2;3 .k  C.





4;1 .k  D.





3; 4 .k 

Hướng dẫn giải

Chọn A

Đặt

ududx

dv dx v x



















.ln + d 1 ln 1

Ix xe k



  







Ie



1ln 1 2 ln ln 1

eke k k



    



nguyên dương nên





1; 2 .k 

Bài tập 9.

Tìm m để







exmdxe

m0.

me.



m1.



me.

Hướng dẫn giải

Chọn C

Đặt

  

xxxx

uxm dudx

dv e dx v e

I e x m dx e x m e dx e x m 1 me m 1

 











          



Mặt khác:





I e mem1e me1 e1 m1.     

Dạng 4: Tích phân chứa dấu giá trị tuyệt đối

1. Phương pháp

Bài toán: Tính tích phân



Igxx



( với

()

là biểu thức chứa ẩn trong dấu giá trị tuyệt đối)

PP chung:

Xét dấu của biểu thức trong dấu giá trị tuyệt đối trên





;ab

Dựa vào dấu để tách

tích phân trên mỗi đoạn tương ứng ( sử dụng tính chất 3 để tách)

Tính mỗi tích phân thành phần.

Đặc biệt: Tính tích phân

()d

Ifxx



Cách giải

Cách 1:

+) Cho

() 0fx

tìm nghiệm trên



;ab

+) Xét dấu của

()

trên



;ab

, dựa vào dấu của

()

để tách tích phân trên mỗi đoạn tương ứng

( sử dụng tính chất 3 để tách)

+) Tính mỗi tích phân thành phần.

Cách 2:

+) Cho () 0fx tìm nghiệm trên





;ab giả sử các nghiệm đó là

; ;...

( với

...

Khi đó

()d ()d ()d ... ()d

 

ax x x

()d ()d ()d ... ()d   

 

ax x x

I fxx fxx fxx fxx

+) Tính mỗi tích phân thành phần

2. Bài tập

Bài tập 1:



Sxx2dx,a,b ,





 





là phân số tối giản. Giá trị

ab

bằng

A. 11. B. 25. C. 100. D. 50.

Hướng dẫn giải

Chọn A



Sxx2dx xx2dx 2x

84 11 9

32 32 2















 

   



 

 





Bài tập 2:



I1sin2xdxaa,a .



  





Hỏi

là bao nhiêu?

A. 27. B. 64. C. 125. D. 8.

Hướng dẫn giải

Chọn D

Ta có:



1 sin2x sinx cosx sinx cosx 2 sin x .



   





Với

x0; x ; .

444



    





+ Với

x;0









thì

sin x 0









+ Với

x0;

 







thì

sin x 0









I2sinxdx2sinxdx22.



 

    

 

 



Chọn 3: Biết

221

d4ln2ln5,







Ixab

với

là các số nguyên. Giá trị

Sab

bằng

11.

3.

Hướng dẫn giải

Chọn B

Ta có:

525

112

221 221 221

ddd

xxx

Ixxx

xxx

  





 

22 1 2 2 1

52 2 3

dx dx dx dx

xxxx

 









25 2 5

2 5ln 2 3ln

dx dx x x x x

 

 

 

 



8ln2 3ln5 4

11.













Bài tập 4: Cho tích phân







1cos2xdxab

và

ab222.

Giá trị của a và b lần lượt là













a22















a22

2b22











 





a22

2b22

















Hướng dẫn giải

Chọn D









  

  



22 2

000

1cos2xdx 2 sinxdx 2sinxdx 2 sinxdx

2cosx 2cosx 4 2.



ab 4 2

a22

X222X420 .

2b22

ab222

























Bài tập 5: Tính tích phân

-d, 0Ixxaxa



ta được kết quả

()Ifa



. Khi đó tổng

(8)









có giá trị bằng:

. B.

. C.

. D.

Hướng dẫn giải

Chọn B

TH1:

Nếu

1a 

khi đó



18111

d(8)

32 23 233

xax a

Ixxax f





         







TH 2: Nếu 01a khi đó

 

I xxa x xxa x   



32 32 3

111111

32 32 323 224438

xax xax aa







   









Khi đó

111191

(8)

23824









Bài tập 6:

Cho hàm số





x liên tục trên



thỏa



2d 2





fxx

và



6d 14



fxx

. Giá trị



52d







bằng

A. 30. B. 32. C. 34. D. 36.

Lời giải

Chọn B

+ Xét



2d 2fxx



Đặt

2d2dux u x

;

00xu

;

12xu





Nên



22d

xx





uu





d4fu u



+ Xét



6d 14fxx



Đặt

6d6dvx v x

;

00xv

;

212xv





Nên



14 6 d

xx





vv





d84fv v



+ Xét



52d







 

52d 52d

xxfxx







 Tính



52dIfx x







Đặt

52tx

Khi

20x  , 52tx  d5dtx ; 212xt



 ; 02



.



Iftt







 

12 2

tt ftt













84 4 16





 Tính



52dIfx x



Đặt

52tx

Khi

02x

52tx d5dtx

;

212xt





;







Iftt



 

12 2

tt ftt













84 4 16





Vậy



52d32fx x







Bài tập 7: Cho hàm số



yfx liên tục trên





0; 4 và







;



d3



fx x

. Giá trị



31d





bằng

. B.

. C.

. D.

Hướng dẫn giải

Chọn C



 

11/31

111/3

31d 13d 31d

xxf xxfxx



   



 

1/3 1

11/3

13d13 3 1d3 1

fx x fx x



     



 

tt ft t 





114

3.1

333

   

Bài tập 8.

24 3

43 .







Syydy

Giá tị



bằng

A. 80. B. 83. C. 142. D. 79.

Hướng dẫn giải

Chọn C



42 2 2

y4y3 y1y3 

Xét

dấu



y1y3

, ta có:





24 42

113

42 42 42

S 4 4y 1 y dy y 4y 3 dy

y4y3dy y4y3dy y4y3dy





  

      





11 3

53 53 53

311

y4y y4y y4y

3y 3y 3y

53 53 53

112 24 3









  









Bài tập 9.



S4x4x1dx,a,b ,



 





là phân số tối giản. Giá trị

a4b

bằng



35.

Hướng dẫn giải

Chọn D

Ta có:



I2x1dx2x1dx



 

11 1

00 0

I 2 x 1 dx 2x 1 dx 2 x 1 dx 1 2x dx 2x 1 dx

          

 

Suy ra:

a1,b2.

Bài tập 10.

I1sinxdxAB



 



, biết

A2B



Giá trị



bằng

A. 72. B. 8. C. 65. D. 35.

Hướng dẫn giải

Chọn A

Ta có:

xx xx x

1 sin x sin cos sin cos 2 sin

22 22 24

 

     

 

 

‐‐‐

‐

+++

∞

1‐1‐ 3

‐∞

‐1)(y

‐3)

‐3

‐1

Với

xx5

x0;2 0; ;

22444



     





 





+ Với

;

24 4



 





thì

sin 0









+ Với

;

24 4

 







thì

sin 0









I 2 sin dx 2 sin dx 4 2

24 24



 

    

 

 



Bài tập 11. Cho tích phân

13sin22cos 3. 



xdx a b



Giá trị 4



Aab bằng

A. 2. B. 5



. C. 5. D. 8 .

Hướng dẫn giải

Chọn D





     



000

I 1 3sin2x 2cos xdx sinx 3cosx dx sinx 3cosxdx



sin x 3 cos x 0 tan x 3 x k









x0;

nên



x







     

           

  

I sin x 3 cos x dx sin x 3 cos x dx sin x 3 cos x dx sin x 3 cos x dx

13 13

cosx 3 sinx cosx 3 sinx 1 3 3 3 .

22 22

  a1;b3A8

Dạng 5: Tính tích phân các hàm đặc biệt, hàm ẩn

1. Phương pháp giải

a. Cho hàm số





x liên tục trên



;aa .

Khi đó

Bài tập 1: Tích phân

cos .ln

Ixdx











bằng

   

xdx f x f x dx









(1)

Chứng minh

Ta có

  

xdx f xdx f xdx







Xét



Ifxdx







Đổi biến

tdx dt  

Đổi cận

;0 0

atax t     

Khi đó

    

Iftdt ftdtfxdx



Do đó (1) được chứng minh.

Đặc biệt

+ Nếu





là hàm số lẻ thì ta có



fxdx







(1.1).

+ Nếu





x là hàm số chẵn thì ta có

 

xdx f xdx







(1.2)

+ Nếu





x là hàm số chẵn thì ta cũng có



dx f x dx













01b

(1.3).

Chứng minh (1.3):

Đặt













(*).

Đổi biến

tdx dt  

Đổi cận

;

ataxat a     

Khi đó







fbft

dt dt











0. D. 1.

Hướng dẫn giải

Hàm số



cos .ln

fx x







xác định và liên tục

trên đoạn





1; 1 .

Mặt khác, với





1;1 1;1xx 

và

  

cos .ln cos .ln .

xx x fx





   





Do đó hàm số



cos .ln

fx x







là hàm số lẻ.

Vậy

cos .ln 0

Ixdx











Chọn C.

Bài tập 2:

Cho





yfx là hàm số chẵn, liên tục

trên đoạn





6;6 .

Biết rằng



8fxdx







và



23.fxdx



Tính



xdx





11.I



5.I 

2.I



14.I 

Hướng dẫn giải

Gọi





Fx là một nguyên hàm của hàm số





x trên

đoạn





6;6 ta có

 

23 23fxdx fxdx



 





23.





Do đó









626FF



 hay



6.fxdx



Vậy

  

626

112

14.









I f xdx f xdx f xdx

Hay





bfx









(**).

Suy ra

 

fxdx A fxdx







Chọn D.

Bài tập 3:

Tích phân

2020

Idx









có giá trị là

0.I



2020

2019

I 

2021

I 

2019

I 

Hướng dẫn giải

Áp dụng bài toán (1.3) ở cột bên trái cho hàm số





2020

xx và



ta có

Ta có

2021 2021 2021

2020

12.22

2 2021 2021 2021

Ixdx I







Chọn C.

Nếu





x liên tục trên đoạn





;ab thì

  

xdx f a b xdx



Hệ quả: hàm số





x liên tục trên





0;1 , khi đó:

 

sin cos

xdx f xdx







Bài tập 4: Cho hàm số





x liên tục trên



thỏa điều

kiện









2cos ,

xfx x với

x

Giá trị của



Nfxdx









là

1.N





0.N 

1.N



2.N 

Hướng dẫn giải

Ta có

 

N f xdx f xdx









Suy ra

  

22cos.Nfxfxdx xdx













Vậy

2 cos 2sin 2.Nxdxx









Chọn D.

c. Nếu





liên tục trên đoạn





;ab

và



abx fx  thì

 

fxdx fxdx







d. Nếu





x liên tục trên đoạn





;ab và





0fx với



;

ab thì



fxdx



và



fxdx



khi





0.fx

Bài tập 5: Cho hàm số



liên tục trên



và thỏa

mãn













22,.fx f x x x x



  

Giá trị tích phân



Gfxdx



là

2.G



G 



G 

Hướng dẫn giải

Ta có

  

2Gfxdxf xdx



Suy ra

    

22Gfxfxdxxxdx





Vậy



Gxxdx







Chọn C.

Bài tập 6:

Cho hàm số





x có đạo hàm liên tục trên

đoạn





0;1 thỏa mãn





10,f 



7fx dx











và



xf xdx





Tích phân



xdx



bằng

B. 1.

D. 4.

Hướng dẫn giải

Đặt



du f x dx

ufx

dv x dx

















Ta có















xf x

fxdx xf xdx

 

..x1.

xf xdx xf xd



   



Cách 1: Ta có



7fx dx











(1).

49 .49 7

77 7

xdx xdx



  



(2).

 

.114.14xf xdx xf xdx





 



(3).

Cộng hai vế (1), (2) và (3) suy ra

 

111

000

'4914.0fx dx xdx xfxdx













70.fx x dx



 





 

70 7 0fx x fx x dx







  





. Mà

 

70 7.

xxdx fx x

















Mà



10 0 .

fCC



    

Do đó







Vậy



77 7

44 5

fxdx dx





 







Một số kĩ thu

ật giải tích phân hàm ẩn

Loại 1: Biểu thức tích phân đưa về dạng:

(

)

(

)

(

)

(

)

(

)

''ux f x u x f x hx+=

Cách giải:

+ Ta có

() () () () () ()

''uxf x uxfx uxfx

éù

ëû

+ D

đó

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

''ux f x u x f x hx ux f x hx

+= =

Suy ra

() () ()

ux f x hxdx=

Suy ra được

()

Loại 2: Biểu thức tích phân đưa về dạng:

() () ()

xfxhx+=

Cách giải:

+ N

ân hai vế với

() () () () ()

.' . . . .

xx x x x x

e ef x efx ehx efx ehx

éù

+= =

Suy ra

() ()

efx ehxdx=

Suy ra được

()

Loại 3: Biểu thức tích phân đưa về dạng:

() () ()

xfxhx-=

Cách giải:

+ Nhân hai vế với

() () () () ()

.' . . . .

xx x x x x

e e f x e f x e hx e f x e hx

-- - - - -

éù

+= =

Suy ra

() ()

efx ehxdx

Suy ra được

()

Loại 4: Biểu thức tích phân đưa về dạng:

(

)

(

)

(

)

(

)

xpxfxhx+=

Cách giải:

+ Nhân hai vế với

()

() ()

()

'. . . .

pxdx pxdx pxdx pxdx

pxdx pxdx

e f xe pxe f x hxe

fxe hxe

òòò ò

+ =

éù

òò

êú

=

êú

ëû

Suy ra

()

() ()

()

pxdx pxdx

xe e hxdx

òò

Suy ra được

()

Công thức

() ( )

xdx f a b xdx



2. Bài tập

Bài tập 1: Cho số thực

0.a 

Giả sử hàm số





x liên tục và luôn dương trên đoạn





0; a thỏa mãn

  

.1.fxfa x Giá trị tích phân



Idx







là

I 

B. .

I  C. .



a

Hướng dẫn giải

Chọn B.

Đặt

.tax dt dx 

Đổi cận 0; 0.xtaxat 

Khi đó

 









00 00

111

11 1

 

  



 

aa aa

Idt dxdxdx

fa t fa x fx









00 0

21..

aa a

Idxdxdxa

fx fx

   





Vậy .



Ta có thể chọn hàm số





1fx , với mọi





a thỏa mãn yêu cầu đề bài.

Khi đó



122

Idxdx







Bài tập 2: Cho hàm số





liên tục trên





1;1

và













2019 , 1;1 .

fx fxex  

Tích phân



fxdx







bằng

2019



2020



Hướng dẫn giải

Chọn C.

Ta có

  

f x dx f x dx







Do đó

   

11 1

2020 2019 2019 .

f x dx f x dx f x f x dx

 











 

Suy ra

2020 2020

Medx







Nếu





x liên tục trên đoạn





;ab thì



xdx







abxdx



Bài tập 3. Cho





x là một hàm số liên tục trên



thỏa mãn









22cos2

xfx x 

Giá trị tích phân



fxdx









là

3.P 

4.P 

6.P



8.P 

Hướng dẫn giải

Chọn C.

Ta có

 







f x dx f x dx



  

333

222

222cos24sin.

f x f x dx xdx x dx







    





2 sin 2 sin 2cosx 2cos 6. 



Pxdx xdx x



Bài tập 4: Cho





x là hàm số liên tục trên



thỏa mãn









sin

xfx x



 với mọi

và





01.f 

Tích phân





.ef



bằng

















Hướng dẫn giải

Chọn C.

Ta có









sin

xfx x



 nên









.sin , .

xx x

ef x ef x e x x









.sin

ef x e x









hay



.sin

ef x dx e xdx













  



sin cos 0 1

ef x e x x ef f e





 



 









Để ý rằng





 nên nếu nhân thêm hai vế của









sin

xfx x



 với

e thì ta sẽ có ngay



..sin.

efx e x





Bài tập 5: Cho hàm số





x tuần hoàn với chu kì



và có đạo hàm liên tục thỏa mãn













fx dx











và



.cos .

fx xdx







Giá trị của





2019f



1.

B. 0. C.

D. 1.

Hướng dẫn giải

Chọn A.

Bằng phương pháp tích phân từng phần ta có

  

.cos .sin .sin .

x xdx f x x f x xdx















Suy ra



.sin .

fx xdx











Mặt khác

1cos2 2 sin2

sin .

244

xxx

xdx dx













 







Suy ra

  

2222

2 2

0000

2 sin sin 0 sin 0.f x dx xf x dx xdx f x x dx



 

  

  







sin .



 Do đó





cos .

xxC Vì











nên

0.C



Ta được













cos 2019 cos 2019 1.fx x f



  

Bài tập 6: Cho hàm số





x có đạo hàm liên tục trên





0;1 , thoả mãn





2018

xxfxx



 với

mọi





0;1 .x  Tính



dIfxx



2018 2021

I 



2019 2020

I 



2019 2021

I 



2018 2019

I 



Hướng dẫn giải

Chọn C

Từ giả thiết









2018

3,fx xf x x





nhân hai vế cho

ta được

  

2 3 2020 3 2020

3.xf x xf x x xf x x





 



Suy ra



2021

32020

2021

fx x x C



Thay

0x  vào hai vế ta được



2018

2021

Cfx 

Vậy



2018 2019

111 1

dd. .

2021 2021 2019 2021 2019

fx x x x x 





Bài tập 7: Cho hàm số





x có đạo hàm liên tục trên





0; 4 , thỏa mãn









xfxe x





 

với mọi



0; 4 .x 

Khẳng định nào sau đây là đúng?

 

40 .

ef f









403.ef f e













40 1.ef f e D.









403.ef f





Lời giải

Chọn A

Nhân hai vế cho

e để thu được đạo hàm đúng, ta được

  

'21 21.

xx x

ef x ef x x ef x x



 



Suy ra

 

21d 2121 .

ef x x x x x C 



Vậy

 

40 .

ef f

Bài tập 8: Cho hàm số



x có đạo hàm trên , thỏa mãn









2017 2018

' 2018 2018

fx fx x e với

mọi

x 

và





0 2018.f  Giá trị





bằng

2018

2018 .



2018

2017 .e

2018

2018 .e

2018

2019 .e

Lời giải

Chọn D

Nhân hai vế cho

2018



để thu được đạo hàm đúng, ta được

  

2018 2018 2017 2018 2017

2018 2018 2018 .

xx x

f xe f xe x f xe x

 









Suy ra



2018 2017 2018

2018 d .

xe x x x C







Thay

0x 

vào hai vế ta được









2018 2018

2018 2018 .

Cfxxe  

Vậy





2018

1 2019 .fe

Bài tập 9: Cho hàm số





x có đạo hàm và liên tục trên , thỏa mãn

 

xxfx xe







và





02.f  Giá trị



bằng

.

Hướng dẫn giải

Chọn C

Nhân hai vế cho

e để thu được đạo hàm đúng, ta được

  

2222 2

22.

xxx x

xe f xxe xe e f x xe









 





Suy ra



222

2d2 .

xxx

efx xe x e C







Thay

0x  vào hai vế ta được



02.

Cfxe



 

Vậy



12 .fe



 

Bài tập 10: Xét hàm số ()

x liên tục trên đoạn





0;1 và thỏa mãn

2() 3(1 ) 1

xfx x





. Tích

phân

()d



bằng

. B.

. C.

. D.

Hướng dẫn giải

Chọn C

Ta có:

2() 3(1 ) 1

xfx x

(1)

Đặt

1tx

, thay vào

(1)

, ta được: 2(1 ) 3()

tft t



 hay 2(1 ) 3()

xfx x 

(2)

Từ

(1) & (2), ta được:

() 1

xx x

Do đó, ta có:

()d



d1d

xxx



515







Cách 2. Công thức

() ( )

xdx

abxdx



Lấy t

ích phân 2 vế ta được

11 1

00 0

2()d3(1)d 1d

xx xx

 

Chú ý: Ta có thể dùng công thức . Khi đó:

Từ suy ra:

Bài tập 11: Cho là hàm số chẵn, có đạo hàm trên đoạn . Biết rằng và

Giá trị bằng

A. B. C. D.

Hướng dẫn giải

Chọn D

Ta có là hàm số chẵn nên suy ra

Mặt khác:

5()d ()d

315

fx x fx x 



 

xaxb

ax b x f x x















231 1

xfx x

  

11 1

00 0

2d31d1d

xx f xx xx

 

 

101

010

2d3d1d

xx fxx xx



 

5d d

315

fx x fx x



 



 

11 a

Iftdtfxdx.

22 2

 







yfx





6;6



fxdx 8









f2xdx3.





1



xdx



14.



yfx









f2x f 2x

 

f2xdx f2xdx3.







   

33 6 6

11 2 2

f2xdx f2xd2x fxdx 3 fxdx 6.



  

Vậy

Bài tập 12: Tìm tất cả các giá trị thực của tham số k để

A. B. C. D.

Hướng dẫn giải

Chọn D

Ta có

Mà

Khi đó

Bài tập 13: Cho là hàm liên tục trên đoạn thỏa mãn và

, trong đó b, c là hai số nguyên dương và là phân số tối giản. Khi đó có giá

trị thuộc khoảng nào dưới đây?

A. B. C. D.

Hướng dẫn giải

ĐÁP ÁN B

Đặt

Đổi cận

Lúc đó

Suy ra

Do đ

  

626

112

I fxdx fxdx f xdx 8 6 14.









x11

2x 1 dx 4lim .























































 



2x 1 2k 1

2x1dx 2x1d2x1

2444



    













x0 x0 x0

x11 x11

x11 1

4lim 4lim 4lim 2

x11

xx11

 

 



  





2k 1 1

x11

2x 1 dx 4lim 2 2k 1 9 .











  















0;a













fx.fa x 1

fx 0, x 0;a















dx ba

1fx c







c





11;22 .





0;9 .





7;21 .





2017;2020 .

tax dt dx 

x0 ta;xa t0 

  









a0 a a a

0a 0 0 0

fxdx

dx dt dx dx

1 fx 1 fa t 1 fa x 1 fx



   

 



  



aa a

00 0

fxdx

2I I I 1dx a

1fx 1fx

   





Iab1;c2bc3.



Cách 2: Chọn là một hàm thỏa các giả thiết. Dễ dàng tính được

Bài tập 14: Cho hàm số liên tục trên và Giá trị của

tích phân bằng

A. . B. . C. . D. .

Hướng dẫn giải

ĐÁP ÁN C

 Xét Đặt suy ra

Đổi cận

Suy ra

 Xét Đặt suy ra

Đổi cận Suy ra

Vậy

Bài tập 15: Cho hàm số liên tục trên và Giá trị của

tích phân bằng

. B. . C. . D. .

Hướng dẫn giải

ĐÁP ÁN A

Xét



fx 1

Iab1;c2bc3.















d4, sincosd2.





xfxxx











d4.





,txtx

2d d .tt x

















 

933

111

4d22dd2.

xfttftt







sin cos d 2.fxxx







sin ,ux



dcosd.uxx



















 

2sincosd d.

xxx







  

313

001

ddd4.I fxx fxx fxx











tan d 4, d 2.

xf x

fxx x











d



Ifxx

6I 





tan d 4.fxx







Đặt suy

Đổi cận: Khi đó

Từ đó suy ra

Bài tập 16: Cho hàm số liên tục trên và thỏa mãn

Giá trị của tích phân bằng

. B. . C. . D. .

Hướng dẫn giải

ĐÁP ÁN D

● Xét .

Đặt

Suy ra

Đổi cận:

Khi

đó

● Xét Đặt

Suy ra

Đổi cận:

Khi đó

tan ,

tx



ddtan1dd.

cos 1

txxxx























 

000

4tand d d.

ft fx

xx t x















11 1

00 0

dd d426.

fx xfx

Ifxx x x

 













tan . cos d 1,xf x x











d1.









d





tan . cos d 1







cos .tx

d 2sin cos d 2cos tan d 2 .tan d tan d .

t x xx x xx t xx xx

   

















   

111

222

111

1dddd2.

222

ft ft fx fx

Attxx

ttxx

    







d1.





ln .ux

2ln 2ln 2 d du

dd dd .

ln ln ln 2

xxux

ux xx

xx xx xx u

 

xe u











 





444

111

1ddd2.

fu fx fx

Buxx

uxx

   



● Xét t

ích phân cần tính

Đặt suy ra Đổi cận:

Khi đó

Bài tập 17: Cho hàm số nhận giá trị dương, có đạo hàm liên tục trên Biết và

với mọi Giá trị tích phân bằng

A. . B. . C. . D. .

Hướng dẫn giải

ĐÁP ÁN D

Từ giả thiết

Ta có Đặt

Khi đó

Ta có

Suy ra









2,vx



















































44 1 4

11 1

22 2

dddd224.

fv fx fx fx

Iv x xx

vx xx

   

 









0; 2 .





01f



  

fxf x e









0; 2 .x 



















xxfx



   

224

221.

xxx

fxf x e f



  











xxfx









d36d

ux x

uxxx

vfx























32 2

3ln 3 6ln d

32lnd3.



  

  



Ix x fx x x fxx

xxfxx J



  

2ln d 2 22 ln 2 d2

xxfxx t t f t t





    





 



222ln2d2 2ln2d.

xfx x xxfxx



   







  

2 2 ln d 2 ln 2 d

2ln 2 d

  

 





xxfxxxxf xx

xxfxf xx

  

22422

32 16

2ln d 2 2 4d .

15 15

xxe x xxxxx J



   



Vậy

Bài tập 18: Cho hàm số liên tục trên và thỏa mãn Giá

trị của tích phân bằng

. B. . C. . D. .

Hướng dẫn giải

ĐÁN ÁN B

Từ giả thiết, thay bằng ta được

Do đó ta có hệ

Khi đó

Bài tập 19: Cho hàm số liên tục trên và thỏa mãn Giá trị của

tích phân bằng

. B. . C. . D. .

Hướng dẫn giải

ĐÁP ÁN B

Từ giả thiết, thay bằng ta được

Do đó ta có hệ

Khi đ

IJ 





x

;

























2cos.

xx









Ifxx

















2cos.

xx 









 









  



2 cos 4 2 2cos

cos .

2 cos 2 cos

fx f x x fx f x x

fx fx x fx fx x

  









   







112

dcosdsin .

333

Ifxx xx x











 





















23.

xf x













d





2.ffx













23 23

13 16

242

fxfxfxfx

ffx fxf

xx xx



 

 

 









 



  

 



 







223

Idx dxx

xx x

 



 

 



Cách khác. Từ

Khi đó

Xét Đặt , suy ra

Đổi cận:

Khi đó

Vậy .

Bài tập 20: Cho hàm số thỏa mãn với mọi và

Giá trị của bằng

A. B. C.

Hướng dẫn giải

ĐÁP ÁN C

Nhận thấy được

đó giả thiết tương đương vớ

Suy ra

Thay vào hai vế ta đượ

 

23 32.fx f x fx x f

 



 

 



22 22

11 11

22 22

d32 d3d2 d.

Ix xx x

xx x



 

 



 



 





 













ddddd.

txtxxt

   



















 

ddtd.

ft fx

tf t t x I

ttx



  







3d 2 d .

IxIIx







  

.1512

xfxfxxx



















001.ff









8. 10.

    

...f x fxf x fxf x





  

  

 

.1512.

xf x x x









 



 

001.

452

.1512d36 1

fxf x x x x x x C C







     



 

.361fxf x x x





 







52 3

.d361d 2 '.

xf x x x x x x xC







0x 





''.





Vậy

Bài tập 22: Cho hàm số liên tục trên thỏa mãn . Giá trị

bằng

A. B. 1. C. D.

Hướng dẫn giải

ĐAP ÁN A

 

263 2

421 18.fx x x x f  











tan cos ,fx xx











Ifxdx









 



ftanx cosx ftanx

tan x 1

fx fxdx



 









  





Dạng 8: Bất đẳng thức tích phân

1. Phương pháp

Áp dụng các bất đẳng thức:

+ Nếu liên tục trên thì

+ Nếu liên tục trên và thì

+ Nếu liên tục trên thì dấu xẩy

ra khi và chỉ khi .

+ Bất đẳng thức AM-GM

2. Bài tập

Bài tập 1: Cho hàm số có đạo hàm liên tục trên thỏa mãn ,

và Giá trị phân bằng

A. . B. . C. . D. .

Hướng dẫn giải

Chọn B

Dùng tích phân từng phần ta có Kết hợp với giả thiết

, ta suy ra

Theo Holder

Vậy đẳng thức xảy ra nên ta có thay vào ta được

Suy ra









;ab

 

xdx f xdx











;ab







  

mb a f xdx M b a



















;ab

   

bbb

aaa

xgxdx f xdx g xdx





















xkgx









0;1 ,





10f











fx x







xf x x





  

d'd.

fx x fx xf x x







10f 



'd 1.xf x x



  

111

000

1'dd.'d.71.

xf x x x x f x x



   













xkx



'd 1xf x x







7.k 



xx







'7,0;1

xxx fx xC



 

777 7

444 5

Cfxx fxx





   



Bài tập 2: Cho hàm số có đạo hàm liên tục trên thỏa mãn ,

và Giá trị bằng

A. B. C. D.

Hướng dẫn giải

Chọn D

Theo Holder

Vậ

Bài tập 3: Cho hàm số có đạo hàm liên tục trên thỏa mãn và

Tích phân bằng

A. B. C. D.

Hướng dẫn giải

Chọn B

Theo Holder

Vậy

Bài tập 4: Cho hàm số nhận giá trị dương và có đạo hàm liên tục trên thỏa mãn

và Mệnh đề nào sau đây đúng?

A. B.

C. D.

Hướng dẫn giải









0;1 ,





11f







xf x x

 









fx fx





251

256

261

 

111

612

000

2144

d.d..

13 13 13 169

xf x x xdx f x x





 









 



fx x fx x C C







 

25 261

77 7

fx x f 









0;1 ,









12, 00ff



d4.











fx x



2018 d .









xxx

0. 1011. 2018. 2022.

 

111

000

2'dd.'d1.44.fxx x fx x



 



















'2 2 0.

fx fx xC C





 

2 2018 d 1011.fx x f x x x



  

















0;1 ,

  

10fef



d2.











fx x

































Chọn C

Ta có

Mà nên dấu xảy ra, tức là

Theo giả thiết nên ta có

Bài tập 5: Cho hàm số nhận giá trị dương trên có đạo hàm dương và liên tục trên

thỏa mãn và Giá trị bằng

A. B. C. D.

Hướng dẫn giải

Chọn A

Áp dụng bất đẳng thức cho ba số dương ta có

Suy ra

Mà nên dấu xảy ra, tức là









11 1 1

AM GM

00 0 0

'd ' d 2 d

xx fx x x

fx fx fx





  



 



  

  







2ln 2ln 1 2 ln 0 2ln 2 ln 2.

fx f f e





'd2

fx x







'' ''





 

''1fx fxfx





 







'd d 22.

xf x x xx x C fx x C











10fef

22 2 22 2

CeC CeC C

  



 

222

212 .

111

fx x f

eee













0;1 ,





0;1 ,





01f

   

4d3 d.

















xfxxfxfxx



d



Ifxx





21.e





21.



e

AM GM

  











 

4' 4'

34 ' . . 3 ' .









f x fx fx

fxfx

fx fxf x

   

4' d 3' d.

xfxxfxfxx









   

4' d3' d

xfxxfxfxx









'' ''













 

4' '

22 2

fx fx

xfxfx

















 

11 1

ddln .

22 2

fx fx

x x fx xC fx e

fx fx



  



Theo giả thiết

Bài tập 6: Cho hàm số có đạo hàm liên tục trên thỏa mãn và

Giá trị tích phân bằng

A. B. C. D.

Hướng dẫn giải

ĐÁP ÁN B

Theo Holder

Bài tập 7: Cho hàm số có đạo hàm liên tục trên thỏa t và

Giá trị của ích phân bằng

A. B. C. D.

Hướng dẫn giải

ĐÁP ÁN B

Theo Holder

Vậ

Bài tập 8: Cho hàm số nhận giá trị dương trên có đạo hàm dương liên và tục trên

thỏa mãn và Giá trị của bằng

A. B. C. D.

  



01 0 d 2 1.

fCfxefxxe      











0; ,





sin d 1









fx xx





d.



fxx







fx x











  

000

1cosd dcosd.1.

fx xx f x x xx





 



 

22cos4

cos d d .

fx x xfx x x







   











0;1 ,

  

10, d











ffxx





cos d .











fx x









 

111

000

sin ' d sin d . ' d . .

42 2 28

fxx x fx x



 



   

  



   



   





 



'sin cos 0.

22 2

fx fx C C

 



 

  

 

 

 

cos d .

fx fx x





















0;1 ,





0;1 ,









xf x





01,f













1. 4.

Hướng dẫn giải

ĐÁP ÁN C

Hàm dưới dấu tích phân là Điều này làm ta liên tưởng đến đạo

hàm đúng , muốn vậy ta phải đánh giá theo như sau:

với và

Do đó ta cần tìm tham số sao cho

hay

Để dấu xảy ra thì ta cần có

Với thì đẳng thức xảy ra nên

Theo giả thiết

Cách 2. Theo Holder

Vậy đẳng thức xảy ra nên ta có thay vào ta được

Suy ra (làm tiếp như trên)





., 0;1.

xf x f x

fx fx









AM GM





xxfx

mx m

xfx



0m 





0;1 .x 

0m 



d2. d

fx xfx

mx x m x

fx fx











  

ln 2 .1 ln 1 ln 0

2202.

  



fx m m f f

'' ''

20 2 4.

mm   

4m 











 

d4dln 2 .

xxx fxxCfxe













Cfxef e









   















11 11

00 00

'''1

1d.dd.d.ln1.

xf x f x f x f

xx xxx x

fx fx fx f

 

 

 

 

 

 











xf x





4.k 





Bài tập 9: Cho hàm số có đạo hàm liên tục trên thỏa mãn và

Giá trị của bằng

A. B. C. D.

Lời giải

ĐÁP ÁN A

Hàm dưới dấu tích phân là Điều này làm ta liên tưởng đến đạo hàm đúng

, muốn vậy ta phải đánh giá theo như sau:

với

Do đó ta cần tìm tham số sao cho

hay

Để dấu xảy ra thì ta cần có

Với thì đẳng thức xảy ra nên

 (vô lý)



Theo giả thiết

Cách 2. Ta có

Theo Holder

Vậy đẳng thức xảy ra nên ta có thay vào ta được Suy ra

(làm tiếp như trên)









0;1 ,

 









xf x x





01,f





13.f







2. 3.

 

'.fxf x













AM GM



   

'2.'

xf x m mfxf x





0.m 

0m 

 





 

'd2 'd.

xf x m x m fxf x x









12. 12.

mm mm 

'' ''

12 1.mmm 

1m 

 









 

'1 .

fxf x



















   





'1 'dd 11.

fxf x fxf x x x x      



   







'1 'dd 22.

xf x fxf x x x x C fx x C       





21 2.

Cfxxf







   













 





  

'd 1 0 1.

fxf x x f f









   

111

000

11. 'd 1d. 'd1.11.fxf x x x fxf x x



 

















xfx k



 

'd1

xf x x





1.k 









'1.fxfx

Bài tập 10: Cho hàm số nhận giá trị dương và có đạo hàm liên tục trên thỏa

mãn và Giá trị của bằng

A. B. C. D.

Hướng dẫn giải

ĐÁP ÁN D

Hàm dưới dấu tích phân là Điều này làm ta liên tưởng đến đạo hàm đúng

, muốn vậy ta phải đánh giá theo như sau:

với và

Do đó ta cần tìm tham số sao cho

hay

Để dấu xảy ra thì ta cần có

Với thì đẳng thức xảy ra nên

Theo giả thiết

Cách 2. Ta có

Theo Holder













1; 2 ,



d24











xf x





11,f





2 16.f





2. 4.



fx fx

xf x x f x

 

 









AM GM





mx m

xf x







0m 





1; 2 .x 

0m 



d2 d

mx x m x

xf x

















  

22 2

24 4 24 4 2 1 24 12 16.

33 3

mm m

mfx m f f m m



    



'' ''

24 12 16.

mm 

16m 



16 2

xf x















 



d2d .

xx fx x C fx x C











024.

216

Cfxxf





   





















  

d2. d2 2 2 1 6.

fx fx

xxfxff

fx fx











21 22

11 11

6 d . d d . d .24 36.

fx fx

xx xxx x

xf x

fx xfx

 





 

  

 

 

 

Vậy đẳng thức xảy ra

nên ta có thay vào ta được

Suy ra (làm tiếp như trên)

Bài tập 11: Cho hàm số





x có đạo hàm liên tục trên đoạn





0;1 , và

  

10 .

ff

Biết

rằng







022,0;1



fx x x

. Khi đó, giá trị của tích phân



xdx









thuộc khoảng nào

sau đây?





2; 4 . B.

13 14







10 13









1; 3 .

Hướng dẫn giải

Chọn C.







022,0;1fx x x





nên









08,0;1.fx xx





Suy ra



xdx xdx











hay



4fx dx











(1).

Mặt khác, áp dụng BĐT Cauchy-Schwarz, ta có:

    

111 1

222

000 0

1. 1 0

xdx dxfxdx f f fxdx



 



  



  



 



xdx











Vậy



fx dx





















fx fx

kx kx

xf x f x

 











4.k 









BÀI 3. ỨNG DỤNG

HÌNH HỌC TÍCH PHÂN

A. KIẾN THỨC SÁCH GIÁO KHOA CẦN NẮM

I. DIỆN TÍCH HÌNH PHẲNG

1. Định lý 1: Cho hàm số

()yfx

liên tục, không âm trên



;ab

. Khi đó diện tích S của hình thang

cong giới hạn bởi đồ thị hàm số

()yfx

, trục hoành và 2 đường thẳng

,xaxb

là:

()

Sfxdx



2. Bài toán liên quan

Bài toán 1: Diện tích

hình phẳng giới hạn bởi đồ thị hàm số

()yfx

liên tục trên đoạn



;ab

, trục

hoành và hai đường thẳng

xa

xb

được xác định:

()

Sfxdx



Bài toán 2: Diện tích hình phẳng giới hạn bởi đồ thị hàm số

()yfx

()ygx

liên tục trên đoạn



;ab

và hai đường thẳng

xa

xb

được xác định:

() ()

Sfxgxdx



Chú ý:

Nếu trên đoạn

[;]ab

, hàm số

()fx

không đổi dấu thì:

() ()

fxdx fxdx



Bài toán 3: Diện tích của h

ình phẳng giới hạn bởi các đường

()xgy

()xhy

và hai đường thẳng

yc

yd

được xác định:

() ()

Sgyhydy



Bài toán 4: Diện

tích hình phẳng giới hạn bởi 2 đồ thị

():()Cfx

là:

() ()



Sfxgxdx

. Trong đó:

,xx

tương ứng là nghiệm của phương trình



() (),fx gx x x

II. THỂ TÍCH CỦA K

HỐI TRÒN XOAY





















(): ()

()

Cyfx

()C





Sfxfxdx

() ()

1. Thể tích

vật thể

Gọi

là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b;

()Sx là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm

()axb . Giả sử ()Sx là hàm số liên tục trên đoạn [;]ab .

2. Thể tích khối tròn xoay

Bài toán 1: Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường

()yfx , trục hoành và hai đường thẳng



quanh trục Ox:

Bài toán 2: Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường

()

gy , trục hoành và hai đường thẳng



, yd



quanh trục Oy:

Bài toán 3: Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường

()yfx

()ygx

và hai đường thẳng



quanh trục Ox:

() ()

xdx







B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP

Dạng 1: Tính diện tích giới hạn bởi 1 đồ thị

1. Phương pháp:

a/ Phương pháp 1:

|()|

Sfxdx



* Xé

t dấu biểu thức

()

;

[;]

ab

, phá dấu trị tuyệt đối và tính tích phân.

b/ Phương pháp 2:

* Giải phương trình

() 0fx ; chọn nghiệm trong [;]ab. Giả sử các nghiệm là ;





với





 .

* Áp dụng tính chất liên tục của hàm số

()

x trên [;]ab; ta có:

|()d||()d||()d|

Sfxx fxx fxx



 

2. Các Bài tập mẫu:

Bài tập 1: Tính diện tích S của hình phẳng giới hạn bởi đồ thị



, trục hoành và đường thẳng

x2



S16.



Hướng dẫn giải

CHỌN D

Nhận thấy rằng, để tính diện tích ta cần phải tìm được 2 cận. Để tìm thêm cận còn lại ta giải phương

trình hoành độ giao điểm của đồ thị



P:y x



với trục hoành.

Phương trình hoành độ giao điểm của đồ thị



P:y x



với trục hoành:

x0x0





Áp dụng công thức ta có

Sxdx.





Nhận xét: Nếu ta vẽ đồ thị hàm số



và đường thẳng



ta dễ dàng xác định được hình

phẳng giới hạn bởi các đường này. Từ đó ta dễ dàng tính được diện tích S.

Bài tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số

yx.e

, trục hoành và đường

thẳng

x1

A. e2. B. 2e.



C. 2e.



D. 1.

Hướng dẫn giải

CHỌN A

Phương trình hoành độ giao điểm

xe 0 x 0





Ta có:

 



11 1

2x 2 x 2x x 2

00 0

11 1

xxxx

00 0

S xedx xd e xe ed x

e 2 xe dx e 2 xd e e 2xe 2 e dx

 

   

 

e 2e 2e e 2e 2 e 2.   

Lời bình: Bài toán trên đã có 1 cận, ta chỉ cần tìm thêm 1 cận nữa bằng

cách giải phương trình hoành độ giao điểm. Sau đó áp dụng công thức.

Nếu vẽ đồ thị bài này để tìm hình phẳng giới hạn bởi các đường là không

nên vì đồ thị hàm số hơi phức tạp. Việc tìm được công thức

Sxedx



và tín

h tích phân này ta có thể dùng MTCT để tính và chọn Chọn.

Bài tập 3: Tính diện tích hình phẳng giới hạn bởi đồ thị

y1x



 và trục hoành:

2.

B. .



C. 1. D. .



Hướng dẫn giải

CHỌN D

Phương trình hoành độ giao điểm của, Ox là

1x 0 x 1





Khi đó, diện tích hình phẳng cần tìm là

S 1 x dx.







Đặt

x sin t dx cos tdt

và

x1 t

x1t















  





Suy ra

22 2

S 1 x dx 1 sin t.cos tdt cos tdt









    

 

Lời bình: Bài toán trên chưa có cận, ta phải giải phương trình hoành độ

giao điểm để tìm cận. Sau đó áp dụng công thức. Việc tìm được công

thức

S1xdx







và tính tích phân này tương đối phức tạp, do đó ta

có thể dùng MTCT để tính và chọn Chọn.

Nếu vẽ được đồ thị thì ta xác định được hình phẳng và diện tích của nó

dễ dàng, đó chính là diện tích của nữa đường tròn bán kính bằng 1. Do

đó:

SR.



 

Bài tập 4: Tính diện tích S hình phẳng giới hạn bởi các đường

y lnx, x e, x



 và trục hoành

S2 .



S1 .



 C.

S2 .



 D.

S1 .



Hướng dẫn giải

CHỌN A

Phương trình hoành độ giao điểm của đồ thị

ylnx



và trụ hoành là

ln x 0 x 1.



e1e

S ln x dx ln xdx ln x.dx x x ln x x ln x x 2 .





Bài tập 5: Diện tích tam giác được cắt ra bởi các trục tọa độ và tiếp tuyến của đồ thị ylnx tại giao

điểm của đồ thị hàm số với trục Ox là:



Hướng dẫn giải

Chọn D

Phương trình hoành độ giao điểm:

ln x 0 x 1





Ta có:

 

y' lnx ' .y' 1 1

 

Phương trình tiếp tuyến của đồ thị

ylnx



tại giao điểm của đồ thị hàm số với trục Ox

là:





y1x1 0 hay yx1

Đường thẳng

yx1 cắt Ox tại điểm





A1;0 và cắt Oy tại điểm





B0; 1 .

Tam giác vuông OAB có

OAB

OA 1,OB 1 S OA.OB





  

Bài tập 6: Diện tích hình phẳng giới hạn bởi đường cong





y2axa0



 , trục hoành và đường

thẳng

xa bằng

ka . Tính giá trị của tham số k.



Hướng dẫn giải

    

b0 b 0b

aa 0 a0

S f xdx f x dx f xdx f xdx f xdx

 

Chọn B

Có

24 4

S2axdx2a..x aka k

33 3

 



Bài tập 7: Cho hình cong giới hạn bởi các đường

ye,y0,x0





và

xln4



. Đường thẳng



với

0kln4

chia thành hai phần có diện tích là S

và S

như hình vẽ

bên. Tìm k để

S2S

kln4



kln2

kln



D. kln3

Hướng dẫn giải

Chọn D

ln 4

ln 4 ln 4

xxx

121

22 2 2

S2S S S edx edx e 2

33 3 3

   



Do đó:

xk k

Sedxe12e3kln3



Dạng 2: Tính diện tích giới hạn bởi 2 hai đồ thị

1. Phương pháp:

Công th

ức tính

|() ()|

Sfxgxdx



. Tính như dạng 1.

2. Một số bài tập mẫu

Bài tậ

p 1:

Tính diện tích hình phẳng giới hạn bởi đồ thị

;;;

cos sin 6 3

yyxx





Lời giải

Ta có:

cos sin

Sdx







Trong trường hợp này nếu chọn cách xét dấu biểu thức

;;

cos sin





 





hoặc vẽ đồ thị hàm số

;;

cos sin







 









là khá khó khăn.

Vì vậy ta chọn cách sau:

+ Xét phương trình:

cos sin



0

;

















cos sin 0xx





;











cos 2 0x

;















Từ đó suy ra:

/4 /3

22 22

64/4

11 11

cos sin cos sin

Sdx dx

xx xx





 







/4 4 3

/6 3

Sxx xx





     





Bài tập 2 : Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số

;





Lời giải

Xét phương trình hoành độ giao điểm của hai đồ thị trên:





42 2

20 1

xx x















Vì vậy

hình phẳng đã cho có diện tích là:

Sdx









Do trên

(1;1) phương trình





vô nghiệm nên ta có:

111

22 2

222

111

ddd

12 12 1 2

xx x

Sdx xxx

xxx







 







 

Tính









+/ Đặt

tan

t

;











cos

dx dt



+/ Đổi cận:





  









/4 /4

cos

1tan 2

Idtt







  













Thay thế v

ào ta được:

S 







.

Bài tập 3: Tính diện tích hình phẳng giới hạn bởi đồ thị

43yx x





và 3y  .

Hướng dẫn giải

Xét phương trình hoành độ giao điểm của hai đồ thị trên:

43xx

3

433



















Khi đ

ó:

S 





242

43|3| | 43|3 |

xdxxxdx  



‖







222

433 433 433Sxx dxxxdxxxdx     















22 2

4464|Sxxdx xxdxxxdx      



33 3

22 2

22628

33 3

xx x

SS x x x x

 

       

 

 

Bài tập 4: Tính diện tích hình phẳng giới hạn bởi đồ thị: sin | |



yx;





Hướng dẫn giải

Xét phương trình hoành độ: sin | | | |xx





Đặt

t

Khi đó trở thành:

sin tt



sin 0tt





Xét hàm số

()

t 

sin tt





; [0, )t .

() cost 1 0 [0, )ft t





BBT của hàm số

()

t như sau:



phương trình có nghiệm duy nhất







phương trình có 2 nghiệm phân biệt:







và







|sin | | | | | (sin | | | | )Sxxdx xxdx





 



3. Bài tập

Bài tậ

p 1:

Diện tích hình phẳng giới hạn bởi parabol





P:y x 3x 3



  và đường thẳng



d:y 2x 1 là:

D. 11

Hướng dẫn giải

Chọn B

Xét phương trình

x3x32x1 xx20







  







Gọi S là diện tích hình phẳng giới hạn bởi parabol





P:y x 3x 3



 

và đường thẳng



d:y 2x 1

là



xx 13

S x 3x 3 2x 1 dx 2 x x dx 2x

23 3





       







Vậy

 .

Bài tập 2: Parabol chia hình tròn có tâm tại gốc tọa độ, bán kính thành 2 phần. Tỉ số

diện tích của chúng thuộc khoảng nào:

A. B. C. D.





0,7; 0,8

Hướng dẫn giải

Chọn A

Phương trình đường tròn:

22 2 2

xy8x8y



 

Thế vào phương trình parabol, ta được

yy2y80









x4x2

y4l













Diện tích phần được tạo bởi phần đường tròn phía trên với Parabol là:

222

1 12

222

S8xdx8xdxdxII





  







;

xx8

Idx

263











Tính

I8xdx28xdx



  



Đặt

x22sint dx22costdt;x0 t0 

; x2 t







444

000

cos 2t 1

I 2 2 2 cos t2 2 cos tdt 16 cos tdt 16 dt 4 2









y 



0, 4;0,5





0,5;0,6





0,6;0,7

112

SII 42 2



Diện tích hình tròn:

SR8 SSS8 2 6



          







0, 435 0,4;0,5



 





Bài tập 3:

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số

 và đồ thị hàm số



A. 24 B.









Hướng dẫn giải

Chọn B

Phương trình hoành độ giao điểm:





x16l

4x22





  









. Khi đó

xx 4

S4 2





 



Bài tập 4: Gọi S là diện tích hình phẳng giới hạn bởi các đường

my x



mx y

(với

0m 

Tìm giá trị của

m để

3S 

1m 

. B.

2m 

. C.



. D.

4m 

Hướng dẫn giải

Chọn C.

Vì

0m 

nên từ

my x

ta suy





;

Từ

mx y

nên

0x 

và

ymx

Xét phương trình

mx x m x













Khi đó diện tích hình phẳng cần tìm là:

Smxdx mx dx



 







211

3333

xmm









Yêu cầu bài toán

3393

Smmm   

(vì 0m  ).

Bài tập 5: Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm



và





là

ln 2Sab

với a, b là những số hữu tỷ. Giá trị của



là



. B. 2. C.



. D. 1.

Hướng dẫn giải

Chọn A.

Phương trình hoành độ giao điểm của





C :



và





C :





là



232

1201

xxxxxx



















Diện tích hình phẳng cần tìm là:

111

22 5

2 2 2ln 1 2ln2

11 33

Sxdx xdxxx





 





 



 





Suy ra

a 

và

2b 

Vậy

ab

Bài tập 6:

Cho





H là hình phẳng giới hạn bởi parabol

3yx ,

cung tròn có phương trình

x

(với 02x



 ) và trục hoành

(phần tô đậm trong hình vẽ). Diện tích của





là





. B.





4233





. D.

53 2





Hướng dẫn giải

Phương trình hoành độ giao điểm của parabol

3yx

và cung tròn



 (với

02x



) lả

22 24

4343 1

xxxx  .

Diện tích của



là

223

Sxdx xdxxI I



với

4Ixdx



Đặt

2sin

t

;2cos.

tdxtdt





  





Đổi cận











222

666

4 4sin .2cos . 4cos . 2 1 cos2 . 2 sin 2Ittdttdttdtxt









    







Vậy

332343

33326







Chọn B.

Bài tập 7:

Hình phẳng





được giới hạn bởi đồ thị





C của hàm đa thức bậc ba và parabol





có trục đối xứng vuông góc với trục hoành. Phần

tô đậm của hình vẽ có diện tích bằng

. B.

. C.

. D.

Hướng dẫn giải

Chọn A.

Vì đồ thị hàm bậc ba và đồ thị hàm bậc hai cắt trục tung tại các điểm có tung độ lần lượt là

2y  và 0y  nên ta xét hai hàm số là

2yax bx cx





mx nx





(với a,

0m 

Suy ra





C :





2yfx axbxcx và









ygx mx nx



.

Phương trình hoành độ giao điểm của





C và





là:







32 2 32 2

220ax bx cx mx nx ax bx cx mx nx   

Đặt





32 2

2P x ax bx cx mx nx .

Theo giả thiết,



C và



cắt nhau tại các điểm có hoành độ lần lượt là

1x 



nên

















112Px ax x x.

Ta có



a .

Mặt khác, ta có

  

0002 1Pfg a.

Vậy diện tích phần tô đậm là

 

112

Sxxxdx



 



Dạng 3: Tính thể tích vật thể tròn xoay dựa vào định nghĩa

1. Phương pháp:

Gọi

là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b; ()Sx là

diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục

Ox tại điểm

()axb



Giả sử

()Sx

là hàm số liên tục trên đoạn





,ab .

2. Các Bài tập mẫu:

Bài tập 1:

Cho phần vật thể

giới hạn bởi hai mặt phẳng có phương trình



và

2x 

. Cắt phần

vật thể

bởi mặt phẳng vuông góc trục

tại điểm có hoành độ





02xx



 , ta được diện tích là

một tam giác đều có độ dài cạnh bằng



Tính thể tích

của phần vật thể

Lời giải

Một tam giác đều cạnh a có diện tích





Do tam giác đều cạnh

x có diện tích là





()







Suy ra thể tích







22 2

00 0

3343

() 2

44 433

Ca sio

SSxdx dx x xdx



   

 

Bài tập 2: Trong không gian Oxyz , cho vật thể nằm giữa hai mặt phẳng



và



 , biết rằng

thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục

tại điểm có hoành độ bằng





,0xx





là một tam giác đều cạnh là 2sin

.Tính thể tích của vật thể đó.

Lời giải

Một tam giác đều cạnh a có diện tích



Do đó tam

giác đều cạnh

2sin

có diện tích là



4sin . 3

3sin

Sx x



Suy ra t

hể tíc



d3sind23VSxx xx 



Bài tập 3: Một bồn trụ đang chứa dầu được đặt nằm ngang có chiều dài bồn là 5m, bán kính đáy 1m

. Người ta rút dầu ra trong bồn tương ứng với 0,5m của đường kính đáy. Tính thể tích gần đúng của

dầu còn lại trong bồn

Lời giải

* Thể tích cả khối trụ





22 3

.1 .5 5VRh m

 

* Tính thể tích phần khối trụ bị mất đi

+ Cách 1:

2



viên ph

ân

SRxdx

21 0,61



xdx

.21 53,07



viên phân

VS h xdx

Suy ra thể tích khối trụ còn lại



5 2 1 5 12,637   



VVV xdx m



+ Cách 2: Tính góc ở tâm

cos

















1122

sin . sin 0,614

2233









viên phân





12 2

.. sin 5

23 3









viên phân

VS h



-x



12 2

5 . sin 5 12,637

23 3



   





VVV m





Bài tập 4: Bạn A có một cốc thủy tinh hình trụ, đường kính trong lòng đáy cốc là chiều cao

trong lòng cốc là đang đựng một lượng nước. Bạn A nghiêng cốc nước, vừa lúc khi nước chạm

miệng cốc thì ở đáy mực nước trùng với đường kính đáy. Tính thể tích lượng nước trong cốc

Lời giải

Phân tích: Thể tích nước có hình dạng “cái nêm”; có 2 phương pháp tính thể tích này

+ Cách 1 – Chứng minh công thức bằng PP tích phân: Xét thiết diện cắt cốc thuỷ tinh tại vị trí

bất kỳ; ta có diện tích thiết diện là

; thể tích.

Cách 2:

Gọi S là diện tích thiết diện do mặt phẳng có phương vuông góc với trục Ox với khối nước, mặt

phẳng này cắt trục Ox tại điểm có hoành độ . Ta có

, vì thiết diện này là nửa hình tròn bán kính

Thể tích lượng nước chứa trong bình là.

Bài giải

+ Cách 1: Áp dụng công thức tính thể tích cái nêm biết góc giữa mặt cắt và mặt đáy bằng là

với ta được

6,cm

10cm



RxR









22 22 22

.. .tan tan

  Sx Rx Rx Rx





22 3

dtan d tan



 



VSxx RxxR



0hx

()



rhx hxR

Rh h

1()

()



 

hxR

Sx r





.tan



VRhR



tan 





32 3

. .3 .10 60



VR cm

+ Cách 2: Tính trực tiếp bài toán bằng PP tích phân. ; thể tích

Bài tập 5:

Cắt một khối trụ bởi một mặt phẳng ta được một khối như hình vẽ bên. Biết rằng thiết diện

là một hình elip có độ dài trục lớn bằng 10, khoảng cách từ điểm thuộc thiết diện gần mặt đáy nhất

và điểm thuộc thiết diện xa mặt đáy nhất lần lượt là 8 và 14. Tính thể tích của.

Lời

giải

Tính các số đo: ; suy ra bán kính khối trụ là

 Cách 1: Thể tích khối bằng thể tích “khối trụ trung bình”:

 Cách 2: Áp dụng công thức tính thể tích “cái nêm”: Lấy mặt phẳng vuông góc với đường

sinh của hình trụ và đi qua điểm , khi đó chia khối thành hai khối:

+ Khối 1: là khối trụ chiều cao , bán kính



nên thể tích

+ Khối 2: là phân nửa một khối trụ có chiều cao và bán kính nên thể tích

+ Vậy

1()

()



 

hxR

Sx r



() (10 ) 60( ).

200





VSxdx xdx cm



()



VSxdx

14 8 6

















8  AD AE DE





. .4 .11 176











AB CE

VR đvtt











8h

128Vrh





.. ..4.648



VrAD











12848176  

VvVV đ tt

 

3. Bài tập

Câu 1

Cho





T là vật thể nằm giữa hai mặt phẳng



. Tính thể tích

của





T biết

rằng khi cắt





T bởi mặt phẳng vuông góc với trục

tại điểm có hoành độ bằng



, ta được thiết diện là tam giác đều có cạnh bằng



V 



. B.





. C.

V 

. D.





Lời giải

Chọn C

Ta có diện tích tam giác đều cạnh bằng 1



là





















Thể tíc

h của vật thể





T là



dVSxx





















Câu 2: Cho vật thể





giới hạn bởi hai mặt phẳng 0; 2xx



 . Cắt vật thể





bởi mặt phẳng

vuông góc với trục

tại





02xx



ta thu được thiết diện là một hình vuông có cạnh

bằng





e

. Thể tích vật thể





bằng





13 1





. B.

13 1



. C.

. D.

2 e



Lời giải

Chọn B

Diện tích thiết diện là

  

Sx x e

Thể tích của vật thể





là

  

VSxdx x edx



 

22 22

19111

2222

xx xx

V x e x edx e edx





    







44 4

244

91311 1 1131

224 444

ee e

eee

 



Dạng 4: Tính thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi 1 đồ thị

1. Phương pháp:

Vật thể tròn xoay sinh bởi miền hình phẳng được giới hạn: Đồ thị ; trục ;

; quay xung quanh .

- Nếu t

hiếu cận thì giải phương trìn

để bổ sung cận.

- Tính thể tích theo công thức:

()



(0)Ox y



ax b

() 0fx=

()

xdx







2. Cá

c Bài tập mẫu:

Bài tập 1:

Kí hiệu là hình phẳng giới hạn bởi đồ thị hàm số và trục hoành. Tính thể

tích của vật thể tròn xoay được sinh ra bởi hình phẳng đó khi nó quay quanh trục .

Lời giải

Phương trình hoành độ giao điểm .

Thể tích của vật thể tròn xoay cần tìm .

Bài tập 2: Cho miền hình phẳng giới hạn bởi: quay xung quanh . Tính thể

tích của vật thể tạo thành.

Lời giải

Xét phương trình hoành độ giao điểm của đồ thị hàm số: và trục

Vậy vật thể tròn xoay có thể tích là:

Bài tập 3: Cho miền hình phẳng giới hạn bởi: ; quay xung quanh . tính thể

tích của vật thể tạo thành.

Lời giải

Hoành độ giao điểm của đồ thị hàm số: và đường thẳng là nghiệm của phương

trình:

Vật thể tạo thành có thể tích là:

Bài tập 4: Gọi là thể tích khối tròn xoay tạo thành khi quanh hình phẳng giới hạn bởi các đường

và trục

. Đường thẳng cắt đồ thị hàm số tại





2yxx





VOx















Vxxx







, Ox 1

yxe x



yxe

xe 

0x









Vxedxxedx







22 2 2

xx x

V xe xedx xedx





   











22 2

22 2 4 4

xx x

Vxeedxe











    







4, 0yx xy





4yx x







40xx





















2432

4816Vxxdxxxxdx







16 512

5315





 





;0;4yxy x





04xa a





x

Gọi là thể tí

ch khối tròn xoay tạo thành khi quay tam giác quanh trục . Biết rằng

2VV



. Tính

Lời giải

Ta có .

Tam giác

OH quanh trục tạo nên hai khối nón chung đáy. Gọi là hình chiếu vuông góc của

trên trục . Suy ra .

Suy ra .

Bài tập 5: Cho là hình phẳng giới hạn bởi độ thị hàm số ; trục và đường thẳng

Tính thể tích khối tròn xoay thu được khi quay quanh hình xung quanh trục .

Lời giải

Phương trình hoành độ giao điểm

Theo bài toán thì thể tích của vật thể tròn xoay cần tìm

OH Ox



dd8 4

VxxxxV



 





Ox N





rMN y ya a 



11 4

.. .4.

33 3

VOHr a





  











1.x 





00.







ln 4 ln ln .

42 232

Vdx x











Do đó

3. Bài tập

Câu 1:

Cho hình phẳng





giới hạn bởi các đường

3, 0, 0, 2yx y x x





. Gọi

là thể

tích khối tròn xoay được tạo thành khi quay





xung quanh trục

. Mệnh đề nào sau

đây đúng?



3dVx x







. B.



3dVx x





3dVx x



. D.



3dVxx







Lời giải

Thể tích của vật thể được tạo nên là



3d.Vx x







Câu 2: Gọi

là thể tích khối tròn xoay tạo thành do quay xung quanh trục hoành một elip có

phương trình

25 16



có giá trị gần nhất với giá trị nào sau đây?

550

400

670

335

Lời giải

Chọn D

Quay elip đã cho xung quanh trục hoành chính là quay hình phẳng:

41 , 0, 5, 5

Hy y x x





   







Vậy thể tích khối tròn xoay sinh ra bởi

khi quay xung quanh trục hoành là:

16 16 320

16 16 335,1

25 75 3

Vdxx







 

  

 



 





4, 3 7.ab ab

Câu 3

Cho hình phẳng

()H

được giới hạn bởi đường cong

ymx





(

là tham số khác 0

) và trục hoành. Khi

()H

quay xung quanh trục hoành được khối tròn xoay có thể tích V .

Có bao nhiêu giá trị nguyên của

để 1000V





A. 18. B. 20. C. 19. D. 21.

Lời giải

Chọn A

Phương trình hoành độ giao điểm của đường cong và trục hoành là:

0mx x m

Thể tíc

h vật thể tròn xoay cần tính là:

22 2 3

()( )|

Vmxdxmxx











Ta có:

1000V





1000





750m

750 750m  

Ta có

750 9,08

và

0m 

. Vậy có 18 giá trị nguyên của m.

Câu 8 : Cho hình phẳng

giới hạn bởi các đường cong







, trục hoành và trục tung. Khối

tròn xoay tạo thành khi quay

quanh trục hoành có thể tích

(ln2)





Vab

với

,ab

là

các số nguyên. Tính

.Tab

3.T B. 6.



T C. 10.



T D. 1.T

Lời giải

Dựa vào đồ thị hàm số trên ta có:

33 3

00 0

34 816

111(1)

8ln( 1) (15 16ln 2) 15;b 16.

 







  





  



  





   







 

Vdx dx dx

xxxx

xx a

Vậy

1.Tab

Câu 4: Cho hình





trong hình vẽ dưới đây quay quanh trục

tạo thành một khối tròn xoay

có thể tích bằng bao nhiêu?



. B.



. C.



. D.



Lời giải

Thể tích khối tròn xoay nhận được khi quay hình



quanh trục

là



1c 1

sd d sin2

os 2

Vx xxxx











 







Câu 5:

Vật thể parabolide tròn xoay như hình vẽ bên dưới có đáy có diện tích

3B 

chiều cao

4h 

. Thể tích của vật thể trên là





. B.

6V 

. C.





. D.

8V 

Lời giải

Đường cong para

bol có dạng:

yax

và đi qua điểm có tọa độ



;Rh

nên ta có:





Thể tích của khối tròn xoay trên là:

Vyy y









 .

Áp dụng công thức ta có:

VRh





.3.4

Bh



Câu 6: Cho hàm số









,,,, , 0yfx axbxcxdabcd a 

có đồ thị



. Biết rằng đồ

thị



C tiếp xúc với đường thẳng 4y



tại điểm có hoành độ âm và đồ thị của hàm số





'yfx cho bởi hình vẽ dưới đây. Tính thể tích vật thể tròn xoay được tạo thành khi

quay hình phẳng H giới hạn bởi đồ thị





C và trục hoành khi quay xung quanh trục

725



. B.



. C. 6



. D. Chọn khác.

Lời giải

Chọn D

Dựa vào đồ thị hàm số





'yfx









'31fx x

i đó

 

xfxdxxxC



Điều kiện

đồ thị hàm số





x tiếp xúc với đường thẳng 4y



là:



310

xxC

















 













suy ra









xx x C  .



COx hoành độ giao điểm là 2; 1



.

+Khi đó



729

Vxxdx









Dạng 5: Tính thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi 2 đồ thị

1. Phương pháp:

Nếu hình phẳng được giới hạn bởi các đường thì thể tích khối

tròn xoay sinh bởi khi quay quanh trục

được tính bởi công thức:

2. Các Bài tập mẫu:

Bài tập 1:

Cho hình phẳng giới hạn bởi các đường quay xung quanh trục

. Thể tích của khối tròn xoay tạo thành bằng:











. B. .

C. . D.

Hướng dẫn giải

Chọn D

Tọa độ giao điểm của hai đường và là các điểm và . Vậy thể

tích của khối tròn xoay cần tính là: .

Bài tập 2: Cho hình phẳng giới hạn bởi các đường quay xung quanh trục Ox.

Thể tích của khối tròn xoay tạo thành bằng:









,,,yfxygxxaxb





 

Vfxgxdx











., , , 0yaxybxab

























.yax



(0; 0)O

;







22 24

V bxdx axdx













 

. B. .

C. . D.

Hướng dẫn giải

Chọn B

Tọa độ giao điểm của hai đường và là các điểm và . Vậy

thể tích của khối tròn xoay cần tính là:

Bài tập 3: Cho hình phẳng giới hạn bởi các đường quay xung quanh trục Ox. Thể

tích của khối tròn xoay tạo thành bằng:

. B. . C. . D. .

Hướng dẫn g

iải

Chọn D

Với thì

Tọa độ giao điểm của đường với là các điểm và . Vậy thể tích của

khối tròn xoay cần tính là:

Bài tập 4: Thể tích khối tròn xoay khi quay hình phẳng D giới hạn bởi các đường elip

quay quanh Ox bằng:

. B. . C. . D.

Hướng dẫn giải

Chọn D

24 3





28 3





28 2





24 2





4yx

yx





3;1A 



3;1B



1283

Vxdxxdx



  



2, 4



yxy x























0; 2x



44yxy x

2yx

4yx (0; 0)O (1; 2)A

.4 .4 . .

Vxdxxdx



 



99xy



Ta có: .

Bài tập 5: Thể tích của khối tròn xoay khi quay hình phẳng D giới hạn bởi các đường

quanh trục Ox bằng:

. B. .

C. . D.

Hướng dẫn giải

Chọn D

Xét phương trình .

Và .

3. Bài tập

Câu 1:

Quay hình phẳng như hình được tô đậm trong hình vẽ bên quanh trục Ox ta được khối tròn

xoay có thể tích là:

. B. . C. . D.

Hướng dẫn giải

Chọn A

Xét hệ phương trình:

22 2

xy x



 













Do đối xứng nhau qua Oy nên:

22 2 2

99 4

xy y V ydx dx







   



x



xdx









xdx









xdx









xdx







0; 1

xxx





  











22 2

0;1 ( )

xx V x xdx xxdx



     



43V



 63V



 53V



 23V





Câu 2: Quay hình phẳng như hình được tô đậm trong hình vẽ bên quanh trục Ox ta được khối tròn

xoay có thể tích:

. B. . C. . D. .

Hướng dẫn giải

Chọn B

Xé

hệ phương trình: .

Do đối xứng nhau qua Oy nên

Câu 3: Quay hình phẳng như hình được tô đậm trong hình vẽ bên quanh trục Ox ta được khối tròn

xoay có thể tích là:

. B. . C.





. D.

 

22 2

24 1 23 23 43

Vxdxxdxx



 



























13V























224

24 3 24 3Vxxdxxxdx





 







346

35 15





 

















Hướng dẫn giải

Chọn D

Ta có:

Đặt ;

Câu 4: Cho hình giới hạn bởi các đường cong tiếp tuyến của tại điểm

và trục Thể tích của khối tròn xoay khi quay quanh trục bằng:

. B. . C. . D.

Lời giải

Chọn D

Ta có

Phương trình tiếp tuyến của tại là

Diện tích của bằng: .

Câu 5: Cho hình phẳng giới hạn bởi các đường . Thể tích

của khối tròn xoay được tạo thành khi quay xung quanh trục bằng:

. B. . C. . D. .

Lời giải

Chọn D

 

11 11

xy y x









  

















22 2

211 11 81Vxxdxxdx





 







sin

t

;



















2 2

sin 2

8cos 4 1cos2 4 2

Vtsdt tdtt









     













Cye













-1 1 2

e 





e 

















ex e

ex







222 2 3

23 6

Veexxex







  









4, 2 4, 0, 2yx y x x x



















Suy ra thể tích cần tìm là .

Dạng 6: Tính thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi nhiều đồ thị

1. Phương pháp:

2. Các Bài tậ

p mẫu:

Bài tập 1:

Gọi là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường

, và quanh trục . Đường thẳng cắt đồ thị hàm tại

Gọi là thể tí

ch khối tròn xoay tạo thành khi quay tam giác quanh trục . Biết rằng

. Khi đó

. B. . C. . D. .

Hướng dẫn giải

Chọn

Ta có . Khi đó

Ta có

Khi quay tam giác quanh trục tạo thành hai hình nón có chung đáy:

 Hình nón có đỉnh là , chiều cao , bán kính đáy ;

 Hình nón thứ 2 có đỉnh là , chiều cao , bán kính đáy

Khi đó

Theo đề bài .

Bài tập 2: Cho hình thang cong giới hạn bởi các đường . Đường thẳng x

= k chia thành hai hình phẳng là S

và S

như hình vẽ bên. Quay quanh trục Ox

được khối tròn xoay có thể tích lần lượt là . Với giá trị nào của k thì

A. . B. . C.

111

k 

. D.



4d 2 4d

Vx x xx









x

0y 

4x  Ox





04xa a





x

OMH Ox

2VV



2a 

22a 



3a 

00xx

d8Vxx











;

OMH Ox





N O



hOKa



MK a







hHK a 

MK a

112

11 4

33 3





VRhRha

282. 3



 VV aa

,0,0,ln4

yey x x 





0ln4k

,SS

,VV

2VV



132

k 

ln11

k 

Hướng dẫn g

iải

Chọn

Ta có:

Theo giả thiết:

228 11ln11

22 2 2

VV e k

 





   





Bài tập 3: Cho hình phẳng D giới hạn bởi các đường

4yx

và đường thẳng

4x

. Thể tích của

khối tròn xoay sinh ra khi

D xoay quanh trục Ox là:

32

. B.

64

16

. D.

4

Hướng dẫn giải :

Chọn A

Giao điểm của hai đường

4yx

và

4x 

là



4; 4D 

và



4; 4E

. Phần phía trên

của đường

4yx

có phương trình

2yx

. Từ hình vẽ suy ra thể tích của khối tròn xoay cần tính là:



232Vxdx  



Bài tập 4: Cho hình phẳng giới hạn bởi các đường

3, , 0, 1yxyxx x

quay xung quanh trục

Ox. Thể tích của khối tròn xoay tạo thành bằng:

 

ln 4

22 2 2

ln 4

222 2 2

kxk

ee e e

V e dx V e dx

 

   

 

  

 

 















D. V.

Hướng dẫn giải

Chọn A

Tọa độ giao điểm của đường



với



và 3yx



là các điểm





1; 1C và





3;1B . Tọa độ giao

điểm của đường

3yx với

yx

là





0;0O . Vậy thể tích của khối tròn xoay cần tính là:

.9 .

Vxdxxdx  



Bài tập 5: Trên mặt phẳng Oxy, cho hình phẳng giới hạn bởi các đường

   

:;':y4;:4PyxP xdy . Thể tích của khối tròn xoay khi quay quanh trục Ox bằng:



. B.



. C.



. D. 2



Hướng dẫn giải

Chọn B

Đặt V là thể tí

ch cần tìm

Xét phương trình hoành độ giao điểm của và:















Xét

phương trình hoành độ giao điểm của và:















OAC

là thể tích khối tròn xoay sinh bởi khi quay:













quanh Ox

OAB

là thể tích khối tròn xoay sinh bởi khi quay:













quanh Ox

Lúc đó:

      

22 21

2224

00 00

4444416

OAC OAB

VV V x dx x dx xdx xdx

 

 

       

 

 

 

32 16 4

441684

55555



 

 



 

 





 

3. Bài tập trắ

c nghiệm:

Câ

u 1:

Cho



là hình phẳng giới hạn bởi đồ thị của các hàm số





:y , 0, 2

xy y x

Thể tích của khối tròn xoay thu được khi quay hình





xung quanh trục

là:

42 1





. B.

82 3





. D.



Lời giải

Chọn D

02 02

(2 ) 5 4 0

xxxx

 



  



 





(2 )

Vxdx xdx









Câu 2: Cho hình



H giới hạn bởi các đường

1yx





;



;



. Quay hình



H quanh

trục

ta được khối tròn xoay có thể tích là:



. B.

125



. C.



. D.

18

Lời giải

Chọn

Phương trình hoành

độ giao điểm:



1600

xxxx





      







Vì

10x



với





1; 2x 

nên thể tích cần tính là



635

d1d

Vxxx















Câu 3: Gọi





là hình phẳng giới hạn bởi các đường:

3; ; 1yxyxx





. Quay





xung

quanh trục

ta được khối tròn xoay có thể tích là:



. B.



. C.



. D.

8

Lời giải

Chọn A

Phương trình hoành độ giao điểm:

30xx x





và

30xx

với





0;1x 

Thể tích cần tính là



3d d

Vxxxx









Câu 4: Cho hình phẳng



H giới hạn bởi các đường

,2yxy x

. Thể tích của khối tròn xoay

được tạo thành khi quay



H xung quanh trục

bằng:



. B.



. C.



. D.



Lời giải

Chọn D

Hoành độ giao điểm của đồ thị 2 hàm số



và 2yx



là nghiệm của phương trình













Thể tíc

h của khối tròn xoay tạo thành là



π 2dπ dVxxxx



464π

ππ

3515









Câu 5: Cho hình phẳng giới hạn bởi các đường

yxyx 

quay xung quanh trục

Thể tích của khối tròn xoay tạo thành bằng:

28 2





. B.

28 3





. C.

24 2





. D.

24 3





Lời giải

Chọn B

Giải phương trình

xxx 

Thể tích cần tìm là





28 3

4d d

Vxx x









 







Dạng 7: Một số bài toán thực tế ứng dụng tích phân

1. Phương pháp

giải

Một vật chuyển động có phương trình vận

tốc trong khoảng thời gian từ đến

sẽ di chuyển được quãng đường

là:

Ví dụ 1: Một vật chuyển động chậm dần đều với

vận tốc . Quãng đường

mà vật chuyển động từ thời điểm đến

thời điểm mà vật dừng lại là

A. 1028m. B. 1280m.

C. 1308m. D. 1380m.

Hướng dẫn giải

Khi vật dừng lại thì

Do đó

Chọn B.

Một vật chuyển động có phương trình

gia tốc thì vận tốc của vật đó sau

khoảng thời gian là:

Ví dụ 2: Một chiếc ô tô chuyển động với vận tốc

, có gia tốc

Vận tốc của ô tô sau 10 giây (làm tròn đến hàng đơn

vị) là

A. 4,6 m/s. B. 7,2 m/s.

1,5 m/s. D. 2,2 m/s.

Hướng dẫn giải

Vận tốc của ô tô sau 10 giây là











tbab



Svtdt











160 10 /vt tm s





0ts





160 10 0 16vt t t





  

16 16

160 10Svtdt tdt





160 5 1280tt m 







;tt



vatdt











/ms

 



at v t m s









33 3

ln 2 1 ln 21 4, 6 /

21 2 2

vdtt ms







Chọn A.

Điện lượng chuyển qua tiết diện của dây dẫn

của đoạn mạch trong thời gian từ đến là:

2. Bài tập

Bài tậ

p 1: Một vật chuyển động với vận tốc 10 m/s thì tăng tốc với gia tốc . Tính

quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc.

A. B. 4300 m. C. 430 m. D.

Hướng d

ẫn giải

Chọn A.

Hàm vận tốc

Lấy mốc thời gian lúc tăng tốc

Ta được

Sau 10 giây, quãng đường vật đi được là

Bài tập 2: Dòng điện xoay chiều hình sin chạy qua một đoạn mạch LC có biểu thức cường độ là

. Biết với

q là điện tích tức thời ở tụ điện. Tính từ lúc , điện lượng

chuyển qua tiết diện thẳng của dây dẫn của đoạn mạch đó trong thời gian từ 0 đến là

A. B. 0. C. D.

Hướng dẫn giải



QItdt







3at t t

4300

430

 



v t a t dt t t dt C







0 10 10.vC



10.

vt 



23 34

3 4300

10 10

23 212 3

tt tt

Sdttm



 















vt atdt





cos

it I t

















0t 













Chọn C.

Điện lượng chuyển qua tiết diện của dây dẫn của đoạn mạch trong thời gian từ 0 đến là

Bài tập 3: Gọi là mức nước trong bồn chứa sau khi bơm được t giây. Biết rằng

và lúc đầu bồn không có nước. Tìm mức nước ở bồn sau khi bơm nước được 6 giây

(chính xác đến 0,01

cm)

A. 2,67 cm. B. 2,66 cm. C. 2,65 cm. D. 2,68 cm.

Hướng dẫn giải

Chọn B.

Mức nước ở bồn sau khi bơm nước được 6 giây là

Bài tập 3: Một viên đá được bắn thẳng đứng lên trên với vận tốc ban đầu là

m/s từ một điểm cao

5 m cách mặt đất. Vận tốc của viên đá sau

giây được cho bởi công thức





40 10vt t m/s. Tính

độ cao lớn nhất viên đá có thể lên tới so với mặt đất.

m. B.

m. C.

m. D.

Lời giải

Chọn

Gọi

là quãng đường lên cao của viên đá.





















'dt4010dt405vt h t ht vt t t t c  



Tại thời điểm

0t 

thì

5h 

. Suy ra



Vậy





40 5 5ht t t





lớn nhất khi





040100 4vt t t  

. Khi đó





485mh 

Bài tập 4: Một ô tô chạy với vận tốc

m/s thì người lái đạp phanh còn được gọi là “thắng”. Sau khi

đạp phanh, ô tô chuyển động chậm dần đều với vận tốc





40 20vt t



 trong đó

là khoảng thời

gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Quãng đường ô tô di chuyển từ lúc đạp phanh đến

khi dừng hẳn là bao nhiêu?







cos sin .

QItdtI t dt t















 

  

 

 















Qt Itdt









ht cm



ht t





  

8882,66

520

htdt t dt t t cm













m. B.

m. C.

m. D.

Lời giải

Chọn

Lấy mốc thời gian là lúc ô tô bắt đầu đạp phanh







Gọi

là thời điểm ô tô dừng lại. Khi đó vận tốc lúc dừng là





0vT



Vậy thời gian từ lúc đạp phanh đến lúc dừng là



040200

vT T T



    

Gọi





t là quãng đường ô tô đi được trong khoảng thời gian

Ta có









vt s t





suy ra





t là nguyên hàm của





Vậy trong



ô tô đi được quãng đường là:

  



d 40 20 d 20 20 5

vt t t t t t



   



Bài tập 5: Một ô tô xuất phát từ A chuyển dộng với vận tốc nhanh dần đều,

giây sau, ô tô đạt vận

tốc

và từ thời điểm đó ô tô chuyển động đều. Ô tô thứ hai cũng xuất phát từ A nhưng sau ô tô thứ

nhất là 10 giây, chuyển động nhanh dần đều và đuổi kịp ô tô thứ nhất sau

giây. Vận tốc ô tô thứ

hai tại thời điểm đó là

. B.

. C.

. D.

Lời giải

Chọn

Ta có gia tốc trong

s đầu của ô tô thứ nhất là



0,5 m/s







Trong

s đầu, ô tô thứ nhất chuyển động nhanh dần với vận tốc





0,5vt t



Quãng đường ô tô thứ nhất đi được trong

s là



0,5 dt 25 mt 



Trong

s tiếp theo, ô tô thứ nhất đi được

5.25 125



Vậy quãng đường ô tô thứ nhất đi được đến khi bị đuổi kịp là





25 125 150 m

Mặt khác

SS at



Gia tốc của ô tô thứ hai là







2.150

0, 48 m/s





Vậy kh

i đuổi kịp ô tô thứ nhất, vận tốc của ô tô thứ hai là

vvat





Bài tập 6: Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc





7vt t



đi được

, người lái

xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc





70 m/sa 

. Tính quãng đường





mS đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi

dừng h

ẳn.





95,70 mS 

. B.





87,50 mS  . C.





94,00 mS  . D.





96,25 mS  .

Lời giải

Chọn D

Quãng đường ô tô đi được từ lúc xe lăn bánh đến khi được phanh.

 

dt 7 dt 7 87,5 m .

Svt t



Vận tốc









m/svt của ô tô từ lúc được phanh đến khi dừng hẳn thỏa mãn









70 dt 70vt tC  









5535 385vv C. Vậy





70 385vt t  .

Thời điểm xe dừng hẳn tương ứng với

thỏa mãn









05,5svt t .

Quãng đường ô tô đi được từ lúc xe được phanh đến khi dừng hẳn.

    

5,5 5,5

dt 70 385 dt 8,75 mSvt t



ãng đường cần tính





96,25 mSS S .

Bài tập 7: Một vật di chuyển với gia tốc

  





20 1 2 /at t m s



 

. Khi

0t 

thì vận tốc của vật

là



30 /ms. Tính quãng đường vật đó di chuyển sau

giây.

46Sm

. B.

47Sm



. C.

48Sm



. D.

49Sm

Lời giải :

Chọn C

Vận tốc vật là :

     

20 1 2 10 1 2vt atdt t dt t C







Khi

0t 

thì

 

0 10. 1 30 20vCC





Nên

    

10 1 2 20 /vt t m s



 

Suy ra :



10 1 2 20 48Stdtm







Bài tập 8: Vật chuyển động với vận tốc ban đầu

5/ms

và có gia tốc được xác định bởi công thức



ams





. Vận tốc của vật sau 10s đầu tiên là

10 /ms

. B.

9/ms

. C.

11 /ms

. D.

12 /ms

Hướng dẫn giải:

Chọn A

Ta có

 

2ln 1

vt dt t c







Mà vận tốc ban đầu 5m/s tức là :









05 2ln01 5 5vcc





Nên

  

2ln 1 5vt t

Vận tốc của vật sau 10s đầu tiên là :









10 2ln 11 5 9,8v 

Chọn Chọn

Bài tập 9:

Trong giờ thực hành môn Vật Lí. Một nhóm sinh viên đã nghiên cứu về sự chuyển động

của các hạt. Trong quá trình thực hành thì nhóm sinh viên này đã phát hiện một hạt prôton di chuyển

trong điện trường với biểu thức gia tốc là:



20 1 2at



 

.Với

của ta được tính bằng giây. Nhóm

sinh viên đã tìm hàm vận tốc

v theo

, biết rằng khi



thì

30 /vms . Hỏi biểu thức đúng là?

25 /

vcms











. B.

20 /

vcms











10 /

vcms











. D.

20 /

vcms











Hướng dẫn giải :

Chọn D

Trước hết để giải bài toán này ta cũng chú ý. Biểu thức vận tốc

theo thời gian

có gia

tốc

a là:

.vadt



Áp dụng công th

ức trên, ta có :



v adt dt









Đến đây t

a đặt :

12 2

u t du dt dt    

10 10 10

vduuduK K

uut









Với

0, 30 20tv K

Vậy biểu thức vận tốc theo thời gian là :

20 / .

vcms











Bài tập 10: Người ta tổ chức thực hành nghiên cứu thí nghiệm bằng cách như sau. Họ tiến hành quan

sát một tia lửa điện bắn từ mặt đất bắn lên với vận tốc 15

m / s. Hỏi biểu thức vận tốc của tia lửa điện

là?

9,8 15vt 

9,8 13vt





9,8 15vt





9,8 13vt 

Hướng dẫn giải

Chọn A

Tia lửa chịu sự tác động của trọng lực hướng xuống nên ta có gia tốc





9,8 /ams

Ta có biểu thức vận tốc

v theo thời gian

có gia tốc a là :

9,8 9,8v adt dt t C



Ở đây,

với :

0, 15 / 15tvmsC 

Vậy ta được biểu thức vận tốc có dạng :

9,8 15vt





Bài tập 11: Người ta tổ chức thực hành nghiên cứu thí nghiệm bằng cách như sau. Họ tiến hành quan

sát một tia lửa điện bắn từ mặt đất bắn lên với vận tốc 15

m / s. Hỏi sau 2, 5 giây thì tia lửa điện đấy có

chiều cao là bao nhiêu?





6.235 m . B.





5.635 m . C.





4.235 m . D.





6.875 m

Hướng dẫn giải

Chọn D

Tia lửa chịu sự tác động của trọng lực hướng xuống nên ta có gia tốc





9,8 /ams

Ta có biểu thức vận tốc

v theo thời gian

có gia tốc a là :

9,8 9,8v adt dt t C



Ở đây,

với

0, 15 / 15tvmsC 

Vậy ta được biểu thức vận tốc có dạng:

9,8 15vt 

Lấy tích phân biểu thức vận tốc, ta sẽ có được bểu thức quãng đường:



9,8 15 4,9 t 15

vdt t dt t K 



Theo đề bài,

ta được khi

00 0.tsK 

Vậy biểu thức tọa độ của quảng đường là :

4,9 15 .

tt 

Khi





2,5ts , ta sẽ được





6,875

m .

Dạng 8: Bài toán thực tế

1. Phương pháp: Vận dụng các kiến thức về tích phân và bài toán ứng dụng.

2. Các Bài tập mẫu:

Bài tập 1:

Tính thể tích hình xuyến tạo thành do quay hình tròn

  

:21Cx y





quanh trục

Hướng dẫn giải:

Hình tròn



có tâm



0; 2I

, bán kính

1R

là



21 xy

Ta có

  

11 1 1



 







 



yxx

Thể tíc

cần tính:









222

21 21 4







 







Vxxdx

Bài tập 2: Thành phố định xây cây cầu bắc ngang con sông dài

500m

, biết rằng người ta định xây

cầu có 10 nhịp cầu hình dạng parabol,mỗi nhịp cách nhau

40m

,biết 2 bên đầu cầu và giữa mối nhịp

nối người ta xây 1 chân trụ rộng

. Bề dày nhịp cầu không đổi là

20cm

. Biết 1 nhịp cầu như hình

vẽ. Hỏi lượng bê tông để xây các nhịp cầu là bao nhiêu

20m

. B.

50m

40m

. D.

100m

Hướng dẫn giải:

Chọn C

Chọn hệ trục tọa độ như hình vẽ với gốc



0;0O

là chân cầu,

đỉnh



25;2I

, điểm



50;0A

Gọi Parabol trê

n có phương trình:

 



11 1

:P y ax bx c ax bx O P 

20 1

100 2

yaxbx axaxbx    là phương trình parabol dưới

Ta có

 

111 2

24 241

625 25 625 25 5

IA P P y x x y x x       

Khi đó diện tích mỗi nhịp cầu là

SS

với

là phần giới hạn bởi

;yy

trong khoảng



0; 25

0,2

00,2

24 1

20,9

625 25 5

Sxxdxdxm



   







Vì bề dày

nhịp cầu không đổi nên coi thể tích là tích diện tích và bề dày

.0,2 1,98VS m 

số

lượng bê tông cần cho mỗi nhịp cầu

2m

Vậy mười nhịp cầu hai bên cần

40m

bê tông

Chọn Chọn.

Bài tập 3:

Trong Công viên Toán học có những mảnh đất mang hình dáng khác nhau. Mỗi mảnh

được trồng một loài hoa và nó được tạo thành bởi một trong những đường cong đẹp trong toán học.

Ở đó có một mảnh đất mang tên Bernoulli, nó được tạo thành từ đường Lemmiscate có phương trình

trong hệ tọa độ

Oxy

là



22 2

16 25yx x

như hình vẽ bên.

Tính diện tích

của mảnh đất Bernoulli biết rằng mỗi đơn vị trong hệ tọa độ

Oxy

tương ứng với

chiều dài

mét.



125

Sm

. B.



125

Sm



250

Sm . D.



125

Sm

Hướng dẫn g

iải

Chọn

Vì tính đối xứng trụ nên diện tích của mảnh đất tương ứng với 4 lần diện tích của mảnh đất thuộc

góc phần tư thứ nhất của hệ trục tọa độ

Oxy .

Từ giả thuyết bài toán, ta có

yxx 

Góc phần tư thứ nhất



25 ; 0;5

yx xx

Nên

()

1 125 125

25 d ( )

4123

Sxxx Sm



Bài tập 4: Một Bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình

phẳng giới hạn bởi các đường

1yx

và trục Ox quay quanh trục Ox biết đáy lọ và miệng lọ có

đường kính lần lượt là

2dm

và

4dm

, khi đó thể tích của lọ là:

8 .dm



. B.



. D.

Lời giải

Chọn B



11 1

10ry x



22 2

23ry x

Suy ra:



d1d

Vyx xx x



 











Bài tập 5: Để kéo căng một lò xo có độ dài tự nhiên từ

10cm

đến

15cm

cần lực

40N

. Tính công (

) sinh ra khi kéo lò xo có độ dài từ

15cm

đến

18cm

A. 1, 56 ( )

J . B. 1 ( )



C. 2,5 ( )

J . D. 2 ( )



Lời giải

Chọn A

Theo Định luật Hooke, lực cần dùng để giữ lò xo giãn thêm

mét từ độ dài tự nhiên là



fx kx

, với



/kNm

là độ cứng của lò xo. Khi lò xo được kéo giãn từ độ dài

10cm

đến

15cm

, lượng kéo giãn

là

5 0.05 cm m

. Điều này có nghĩa



0.05 40f 

, do đó:



0,05 40 800 /

0,05

kk Nm 

Vậy



800fx x

và công cần để kéo dãn lò xo từ đến

18cm

là:

 

0,08

0,05

800d 400 400 0,08 0,05 1,56Axx J



 





Góc phần tư thứ nhất



25 ; 0;5

yx xx

Nên

()

1 125 125

25 d ( )

4123

Sxxx Sm



3. Bài tập trắc nghiệm:

Câu 1:

Trong chương trình nông thôn mới, tại một xã X có xây một cây cầu bằng bê tông như hình

vẽ. Tính thể tích khối bê tông để đổ đủ cây cầu.

19m

. B.

21m

. C.

18m

. D.

40m

Hướng dẫn giải

Chọn D

Chọn hệ trục

Oxy

như hình vẽ.

15cm

0,5m 0,5m19m

5 m

2 m

0,5m





xkx

Ta có

Gọ



:Pyax c

là Parabol đi qua hai điểm



;0 , 0;2







Nên ta có hệ ph

ương trình sau:



0. 2

361

Py x

























Gọi



:Pyaxc

là Parabol đi qua hai điểm



10;0 , 0;







Nên ta có hệ ph

ương trình sau:

Ta có thể tích của bê tông là:

223

15 8

5.2 2 40

40 2 361

Vxdxxdxm



 





 

 





Câu 2: Cho hai mặt cầu



có cùng bán kính

thỏa mãn tính chất: tâm của



thuộc



và ngược lại. Tính thể tích phần chung

của hai khối cầu tạo bởi

()S

và

()S





. B.





. C.





. D.





Hướng dẫn giải

Chọn C



0.10

40 2

Py x

























22 2

():Cx y R

O x

Gắn hệ trục

Oxy

như hình vẽ

Khối cầu



,SOR

chứa một đường tròn lớn là



22 2

:Cx y R

Dựa vào hình vẽ, thể tích cần tính là

Câu 3: Một thùng rượu có bán kính các đáy là 30cm, thiết diện vuông góc với trục và cách đều hai

đáy có bán kính là 40cm, chiều cao thùng rượu là 1m. Biết rằng mặt phẳng chứa trục và

cắt mặt xung quanh thùng rượu là các đường parabol, hỏi thể tích của thùng rượu

là bao nhiêu?

425,2

lit. B.

425162

lit. C.

212581

lit. D.

212,6

lit.

Hướng dẫn giải

Chọn A



Gọi



:Pyax bxc

là parabol đi qua điểm



0,5;0,3A

và có đỉnh



0;0, 4S

. Khi

đó, thể tích thùng rượu bằng thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi



trụ

c ho

ành và hai đường thẳng

0,5x 

quay quanh trục

 Dễ dàng tìm được



:0,4

Py x 

 Thể tích thùng rượu là:

0,5 0,5

0,5 0

2 2 203

0,4 2 0, 4 425,5 (l)

5 5 1500

Vxdxxdx





   











Câu 4: Bác Năm làm một cái cửa nhà hình parabol có chiều cao từ mặt đất đến đỉnh là 2,25 mét,

chiều rộng tiếp giáp với mặt đất là 3 mét. Giá thuê mỗi mét vuông là 1500000 đồng. Vậy

số tiền bác Năm phải trả là:



22 2

2d2

312

VRxxRx















0,4m

0,3m

0,5m

33750000 đồng. B. 12750000 đồng. C. 6750000 đồng. D. 3750000

đồng.

Hướng dẫn giải

Chọn C



Gắn parabol



và hệ trục tọa độ sao cho



đi qua

(0;0)O

 Gọi phương trình của parbol là:



: Pyaxbxc

Theo đề ra,



đi qua ba điểm

(0;0)O

(3;0)A

(1, 5; 2, 25)B

Từ

đó, suy



: 3Py x x 

 Diện tích phần Bác Năm xây dựng:

Sxxdx  



 Vậy số tiền bác Năm phải trả là: 1500000 675 0

000 .

Câu 5: Ông An có một mảnh vườn hình Elip có độ dài trục lớn bằng

16m

và độ dài trục bé bằng

10m

. Ông muốn trồng hoa trên một dải đất rộng

và nhận trục bé của elip làm trục đối

xứng. Biết kinh phí để trồng hoa là

100.000

đồng/

. Hỏi ông An cần bao nhiêu tiền để

trồng hoa trên dải đất đó?

7.862.000

đồng. B.

7.653.000

đồng. C.

7.128.000

đồng. D.

7.826.000

đồng.

Hướng dẫn giải

Chọn B

Giả sử elip có phương trình



Từ giả thiết ta có

216 8aa

và

210 5bb

Vậy phương trình của elip là

64 ( )

64 25

64 ( )

yyE



 













Khi đó diện tích dải vườn được giới hạn bởi các đường

();(); 4; 4EEx x 

và diện

tích của dải vườn là

264d 64d

Sxxxx







Tính tích phân này bằng phép đổi biến

8sin



, ta được











Khi đó số tiền là

80 .100000 7652891,82 7.653.000





 







Câu 6: Người ta dựng một cái lều vải có dạng hình “chóp lục giác cong đều” như hình vẽ bên. Đáy

của là một hình lục giác đều cạnh

3.m

Chiều cao

6SO m



. Các cạnh bên của là các sợi

dây

123456

,,,,,cccccc

nằm trên các đường parabol có trục đối xứng song song với SO. Giả

sử giao tuyến của với mặt phẳng vuông góc với SO là một lục giác đều và khi qua trung

điểm của SO thì lục giác đều có cạnh bằng

1.m

Tính thể tích phần không gian nằm bên

trong cái lều đó.

135 3

()

. B.

96 3

()

. C.

135 3

()

. D.

135 3

()

Hướng dẫn giải

Chọn D

Đặt hệ tọa độ như hình vẽ, ta có parabol cần tìm đi qua 3 điểm có tọa độ lần lượt là

(0;6), (1;3), (3;0)ABC

nên có phương trình là

yx x





Theo hình vẽ ta có cạnh của thiết diện là

Nếu ta đặt

tOM

thì

BM t





Khi

đó diện tích của thiết diện lục giác:

3337 1

() 6. 2 ,

422 4

St t









với





0; 6t 

Vậy thể tí

ch của túp lều theo đề bài là:

3 3 7 1 135 3

() 2 .

22 4 8

VStdt t dt



 







Câu 7: Một vật có kích thước và hình dáng như hình vẽ dưới đây. Đáy là hình tròn giới hạn bởi

đường tròn , cắt vật bởi các mặt phẳng vuông góc với trục Ox ta được thiết diện

là tam giác đều. Thể tích của vật thể là:

32 3



. B.

256 3



16xy

256

V 

Hướng dẫn giải

Chọn B

Giải phương trình

22 2 2 2

16 16 16

yyxy x 

Diện tíc

thiết diện là



() 216 .sin 16 3

Sx x x



 

Thể tích cần tìm là



256 3

() 3 16

VSxdx xdx







Dạng 9: Các bài toán bản chất đặt sắc của tích phân

Bài tập 1: Cho hàm số



yfx

có đồ thị trên





2;6

như hình vẽ bên. Biết các miền A, B, 2x



có diện tí

ch lần lượt là 32; 2; 3. Tích phân



221

xdx















bằng

. B. 41. C. 37. D.

Hướng dẫn giải

Chọn D.

Ta có

 

221 22 4

xdxfxdx



   







Xét



22Ifxdx







Đặt

22 2

t x dt dx dx 

Đổi cận:

22xt  

;

t

Suy ra



Iftdt







Gọi

;

là các hoành độ giao điểm của đồ thị hàm số





yfx với trực hoành





26xx   . Ta có

   



133

32 2 3

I f tdf f tdf f tdf S S S















Vậy



33 41

221 4 4

fx dxI



  







Bài tập 2: Cho hàm số





yfx có đồ thị của hàm số





yfx



 như hình bên. Đặt

   

21gx f x x

. Mệnh đề nào dưới đây đúng?













331

gg . B.













331

gg  .













133gg g . D.













13 3gg g.

Hướng dẫn giải

Chọn D.

Ta có

   

221gx f x x













xfxx



 . Đây là phương trình hoành độ giao điểm của đồ thị hàm số







và

đường thẳng d:

1yx

Dựa vào đồ thị ta thấy:

 

gx f x x







 









Bảng biến thiên:



–3 1 3











–

0 + 0 – 0 +























Suy ra

 

g và









g

Gọi

lần lượt là diện tích các hình phẳng giới hạn bởi đồ thị hàm số







, đường thẳng

1yx trên các đoạn





3;1 và



1; 3 ta có:

+) Trên đoạn





3;1 ta có





 nên

   

Sgxdx fxxdx

















+) Trên đoạn



1; 3

ta có







nên

 

Sgxdx xfxdx















Dựa vào

đồ thị ta thấy

SS

nên ta có:

         

13 313 3gx gx g g g g g g



        

Vậy













13 3ggg.

Lưu ý:

- Hoành độ giao điểm của đồ thị hàm số







và đường thẳng d:

1yx





chính là nghiệm của

phương trình





0gx



 .

- Lập b

ảng biến thịên ta

thấy



lớn hơn







. Ta chỉ cần so sánh





3g và





3g  .

- So sánh diện tích dựa vào đồ

thị.

Ví dụ 4: Hình phẳng



H được giới hạn bởi đồ thị





C của hàm đa thức bậc ba và parabol





có

trục đối xứng vuông góc với trục hoành. Phần

tô đậm của hình vẽ có diện tích bằng

. B.

. C.

. D.

Hướng dẫn giải

Chọn A.

Vì đồ thị hàm bậc ba và đồ thị hàm bậc hai cắt trục tung tại các điểm có tung độ lần lượt là

2y  và 0y  nên ta xét hai hàm số là

2yax bx cx





ymx nx





(với a,

0m 

Suy ra



C :





2yfx axbxcx và









ygx mx nx



.

Phương trình hoành độ giao điểm của





C và





là:







32 2 32 2

220ax bx cx mx nx ax bx cx mx nx   

Đặt





32 2

2P x ax bx cx mx nx 

Theo giả thiết,



C và



cắt nhau tại các điểm có hoành độ lần lượt là

1x 



nên

















112Px ax x x.

Ta có





a .

Mặt khác, ta có

  

0002 1Pfg a

Vậy diện tích phần tô đậm là

 

112

Sxxxdx



 



Bấm Tải xuống để xem toàn bộ.

| 1/138

| | Tải xuống

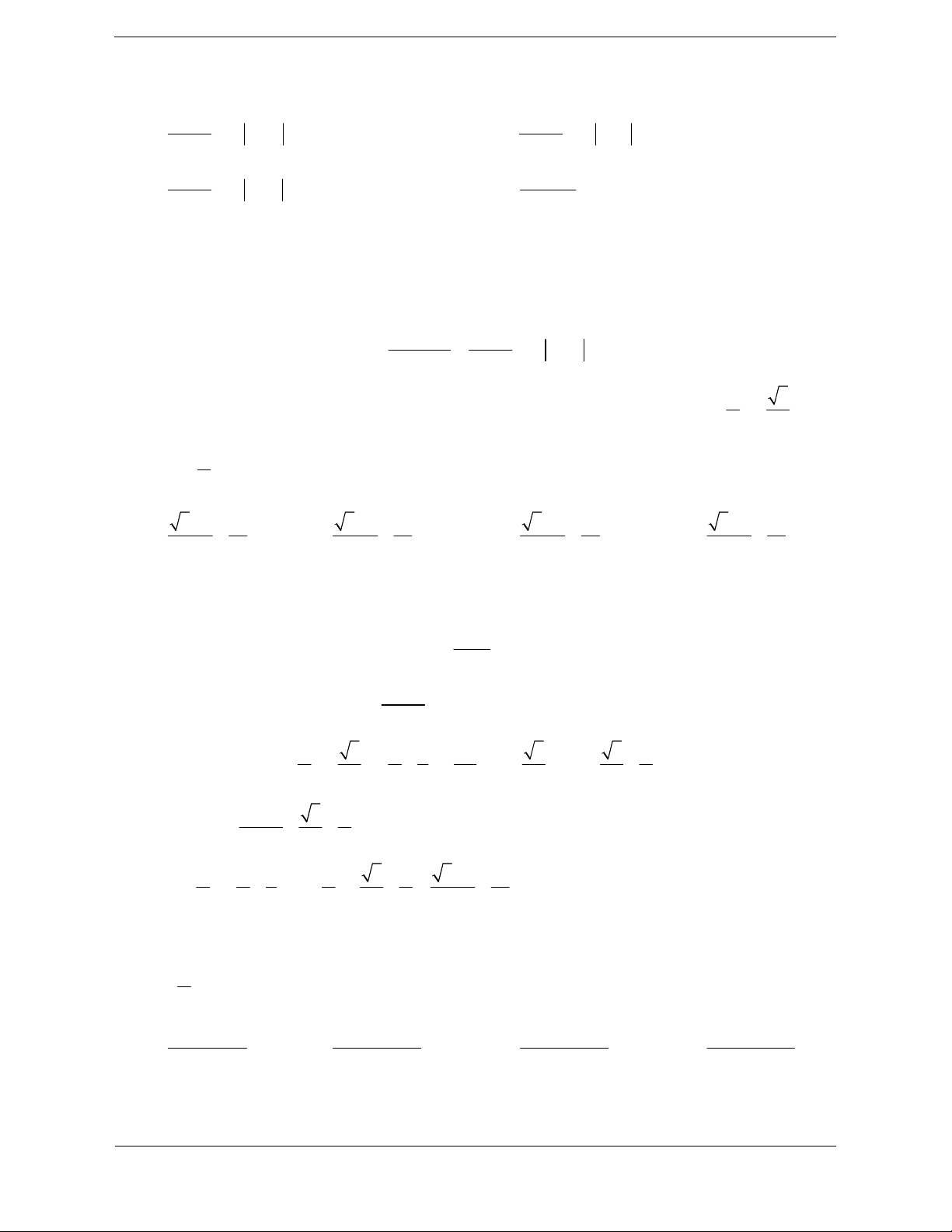
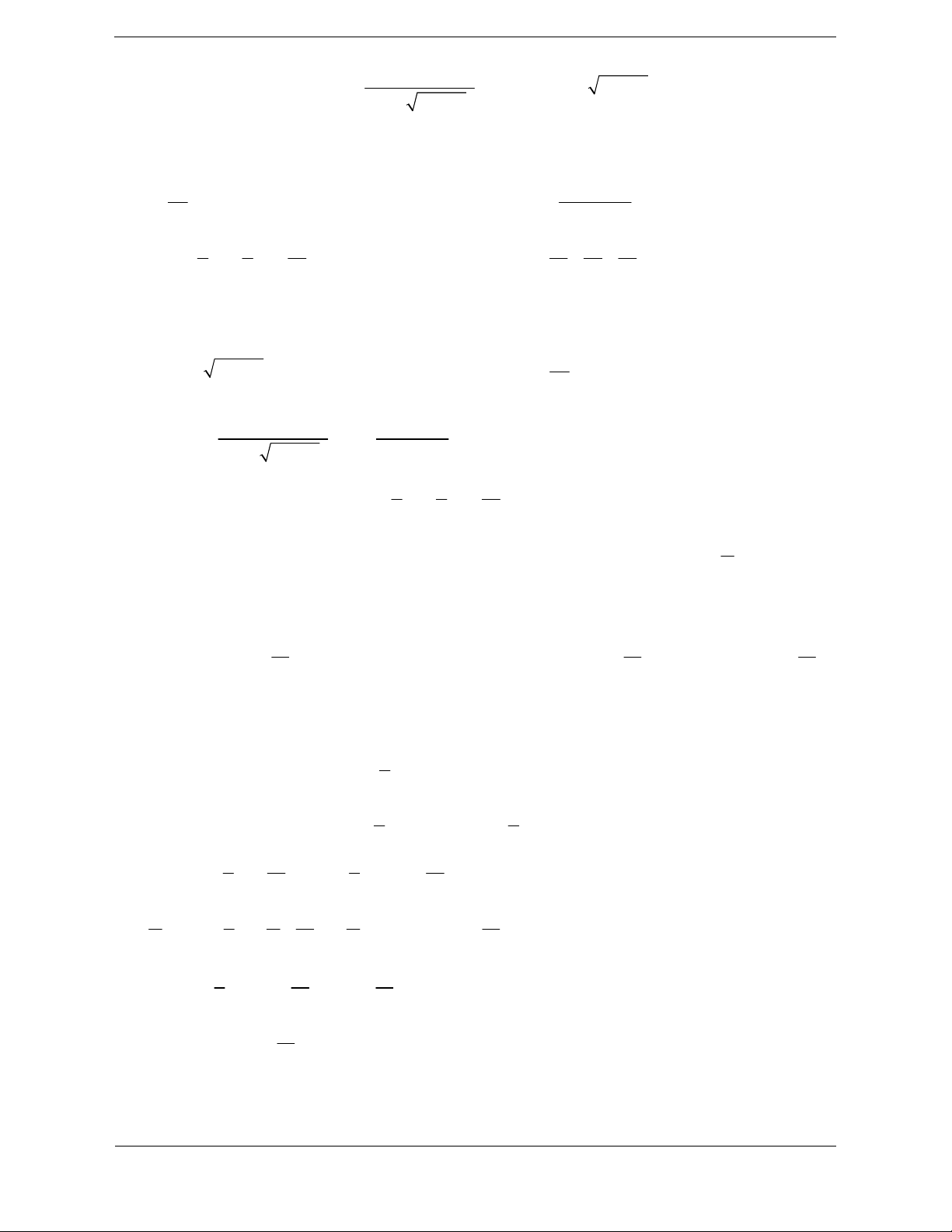
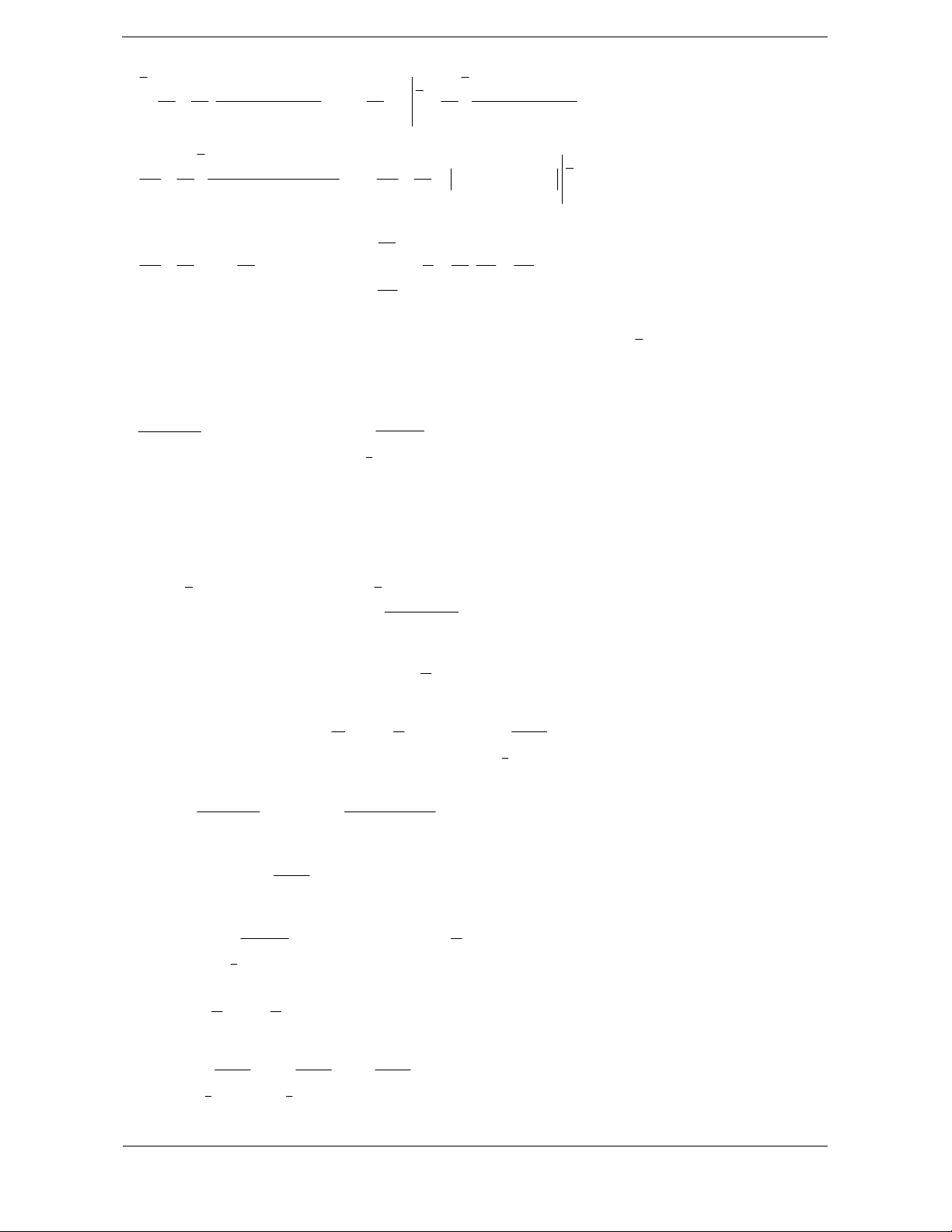
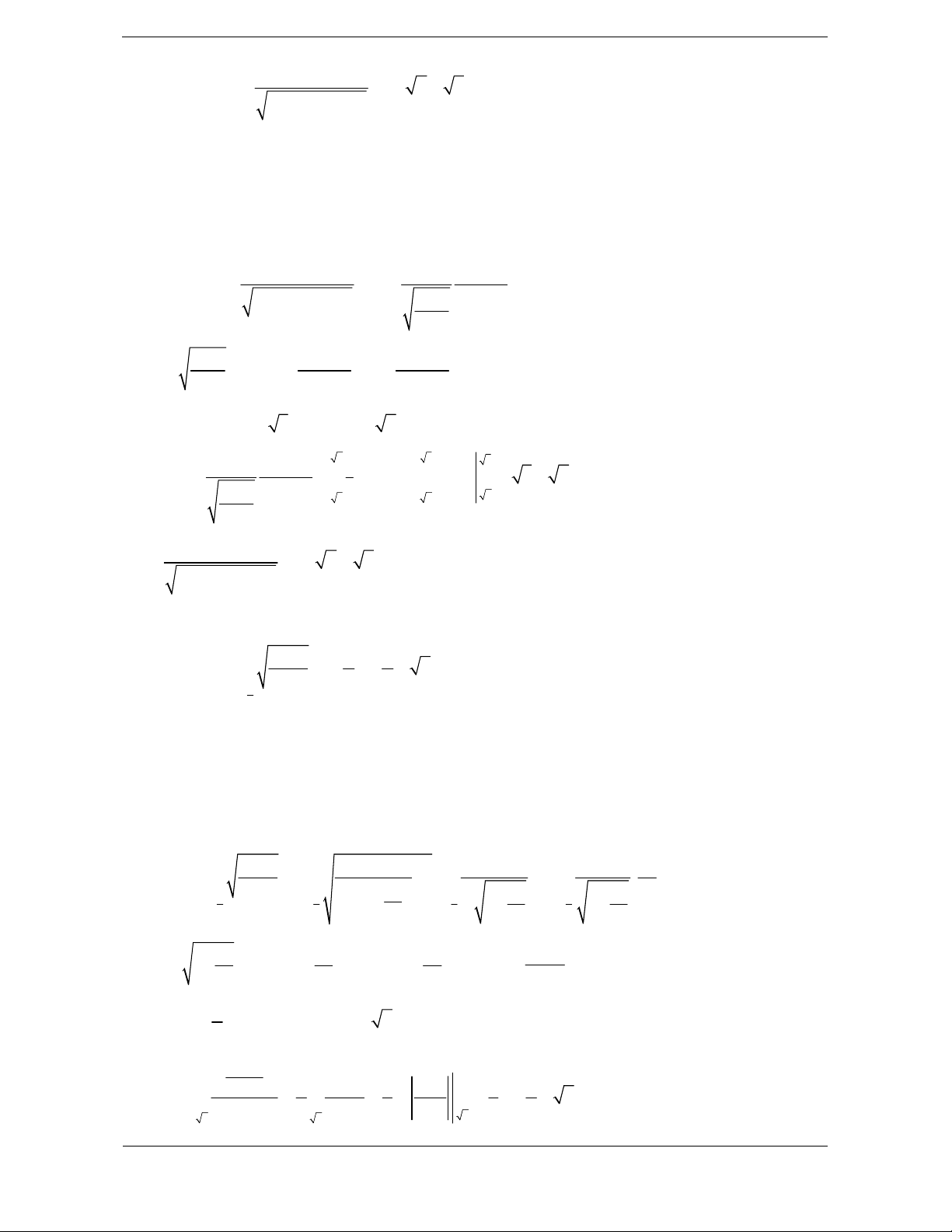
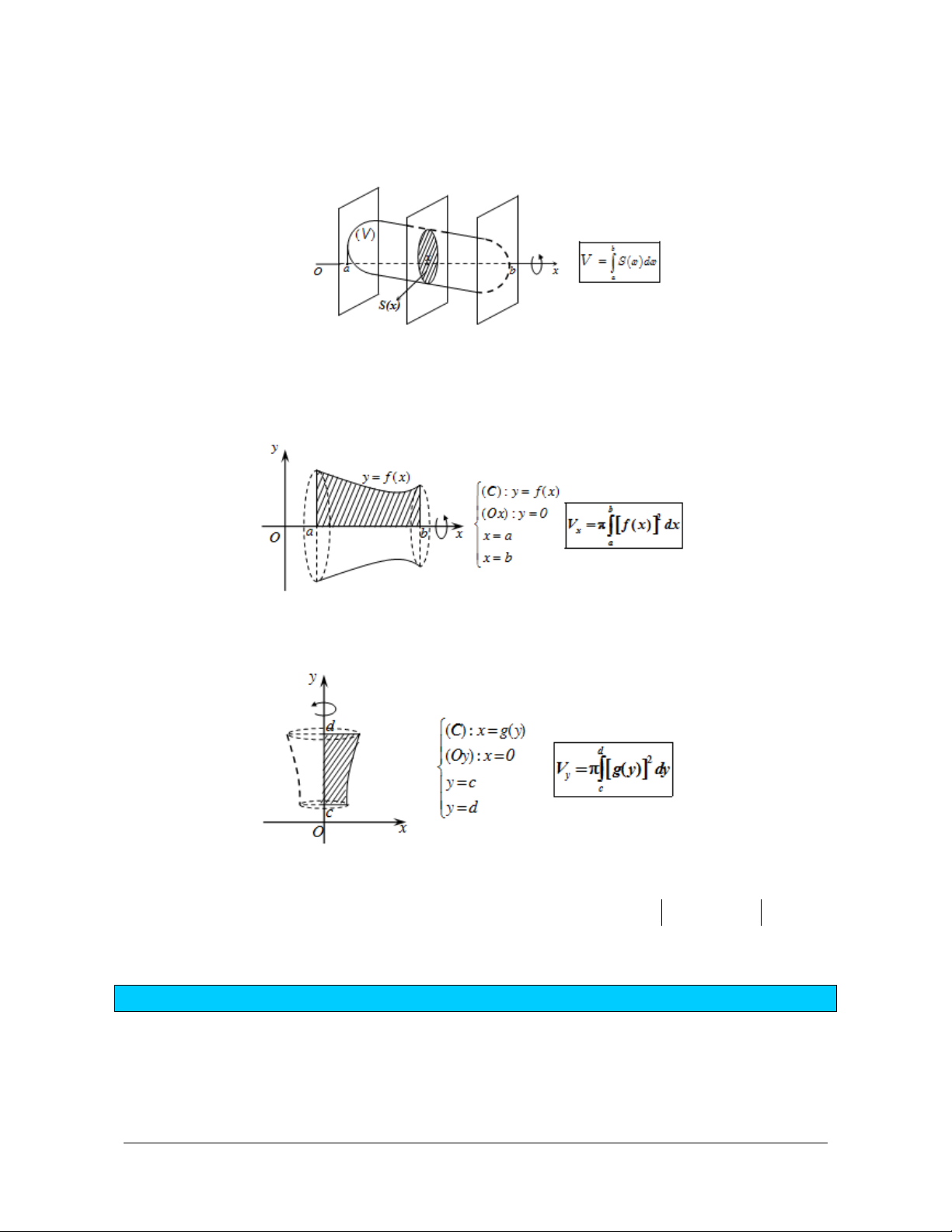
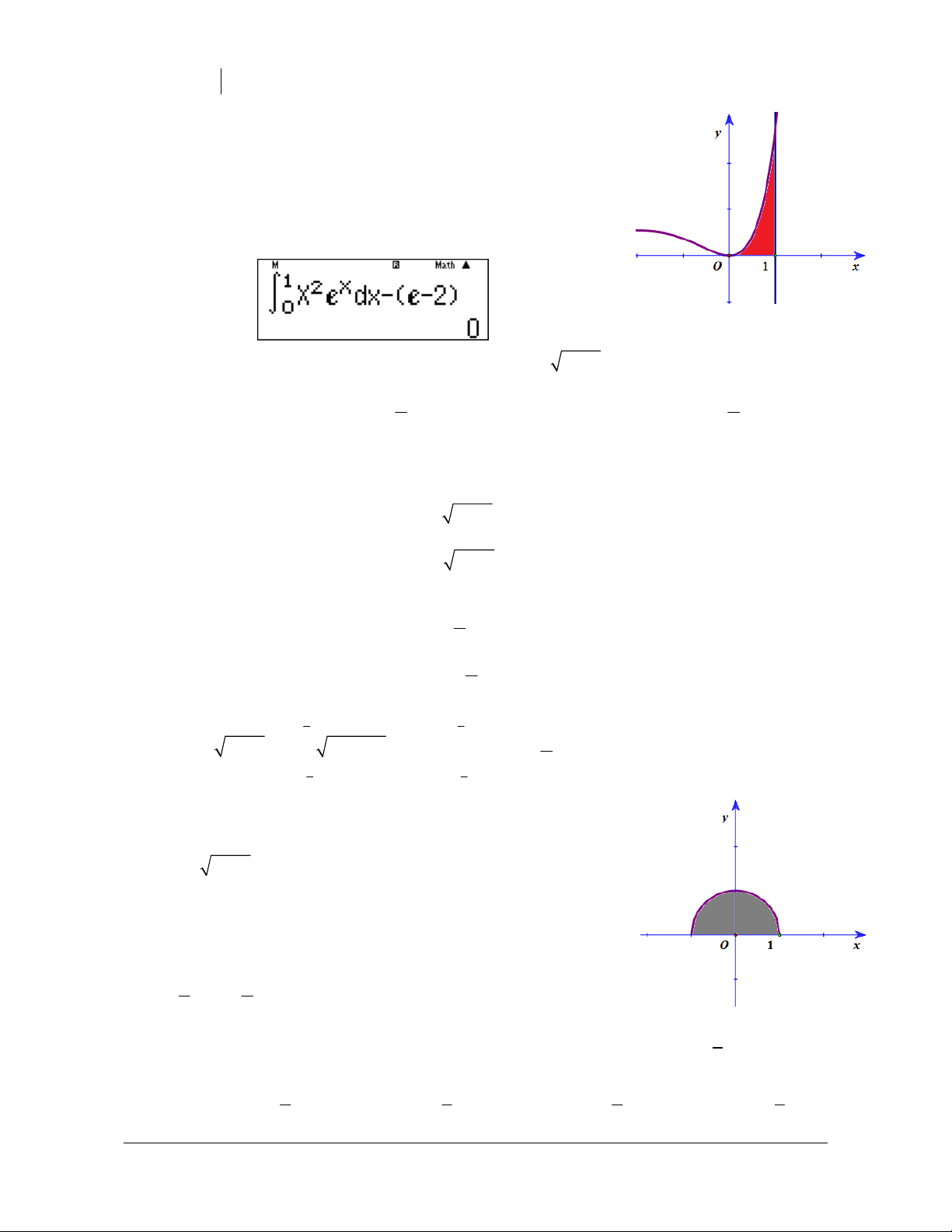
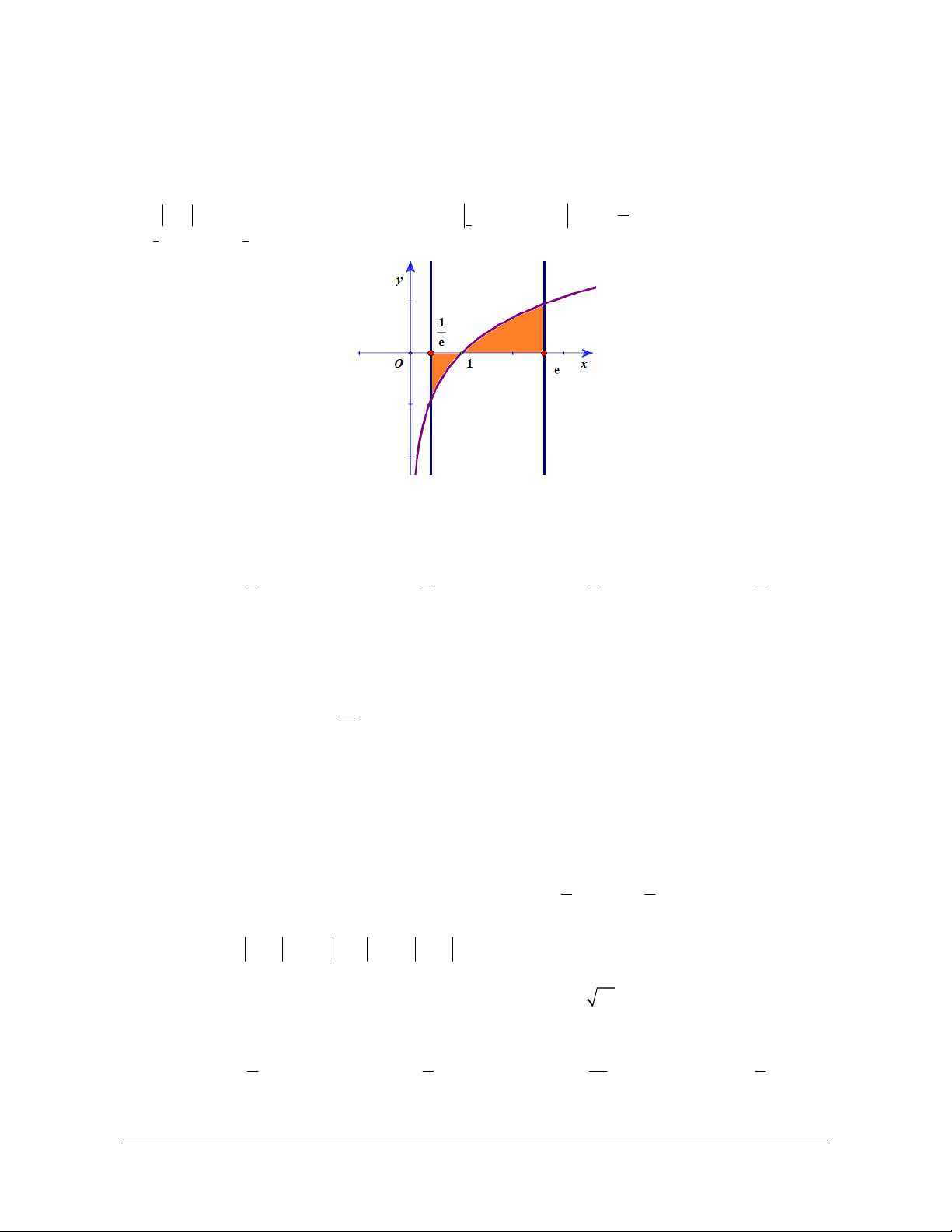
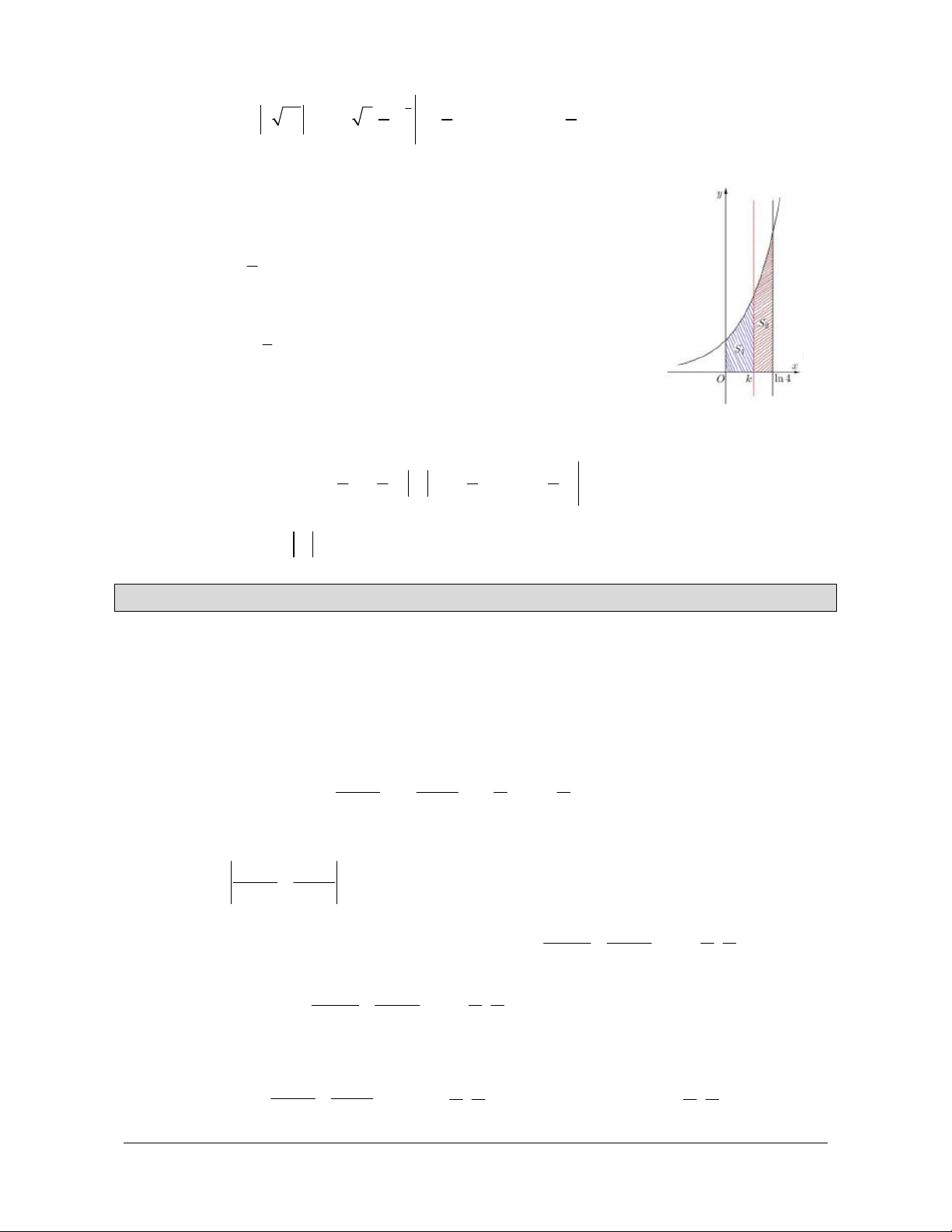
Preview text:

CHƯƠNG 3: NGUYÊN HÀM – TÍCH PHÂN VÀ ỨNG DỤNG
BÀI 1: NGUYÊN HÀM VÀ PHƯƠNG PHÁP TÌM NGUYÊN HÀM
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I. NGUYÊN HÀM VÀ TÍNH CHẤT 1. Nguyên hàm
Định nghĩa: Cho hàm số f x xác định trên K ( K là khoảng hoặc đoạn hoặc nửa đoạn của
). Hàm số Fx được gọi là nguyên hàm của hàm số f x trên K nếu Fʹx  f x với mọi xK.
Định lý 1: Nếu Fx là một nguyên hàm của hàm số f x trên K thì với mỗi hằng số C, hàm số
G x  Fx  C cũng là một nguyên hàm của f x trên K.
Định lý 2: Nếu Fx là một nguyên hàm của hàm số f x trên K thì mọi nguyên hàm của f x
đều có dạng Fx  C, với C là một hằng số.
Hai định lý trên cho thấy:
Nếu Fx là một nguyên hàm của hàm số f x trên K thì Fx  C,C là họ tất cả các nguyên
hàm của f x trên K. Kí hiệu f
 xdx  Fx  C.
Chú ý: Biểu thức f xdx chính là vi phân của nguyên hàm Fx của f x, vì   ʹ
dF x  F xdx  f xdx.
2. Tính chất của nguyên hàm Tính chất 1 f ʹ
 xdx  fx C Tính chất 2 kf
 xdx  k fxdx , k là hằng số khác 0. Tính chất 3 f
 xgxdx  f   xdx  g  xdx.
3. Sự tồn tại của nguyên hàm
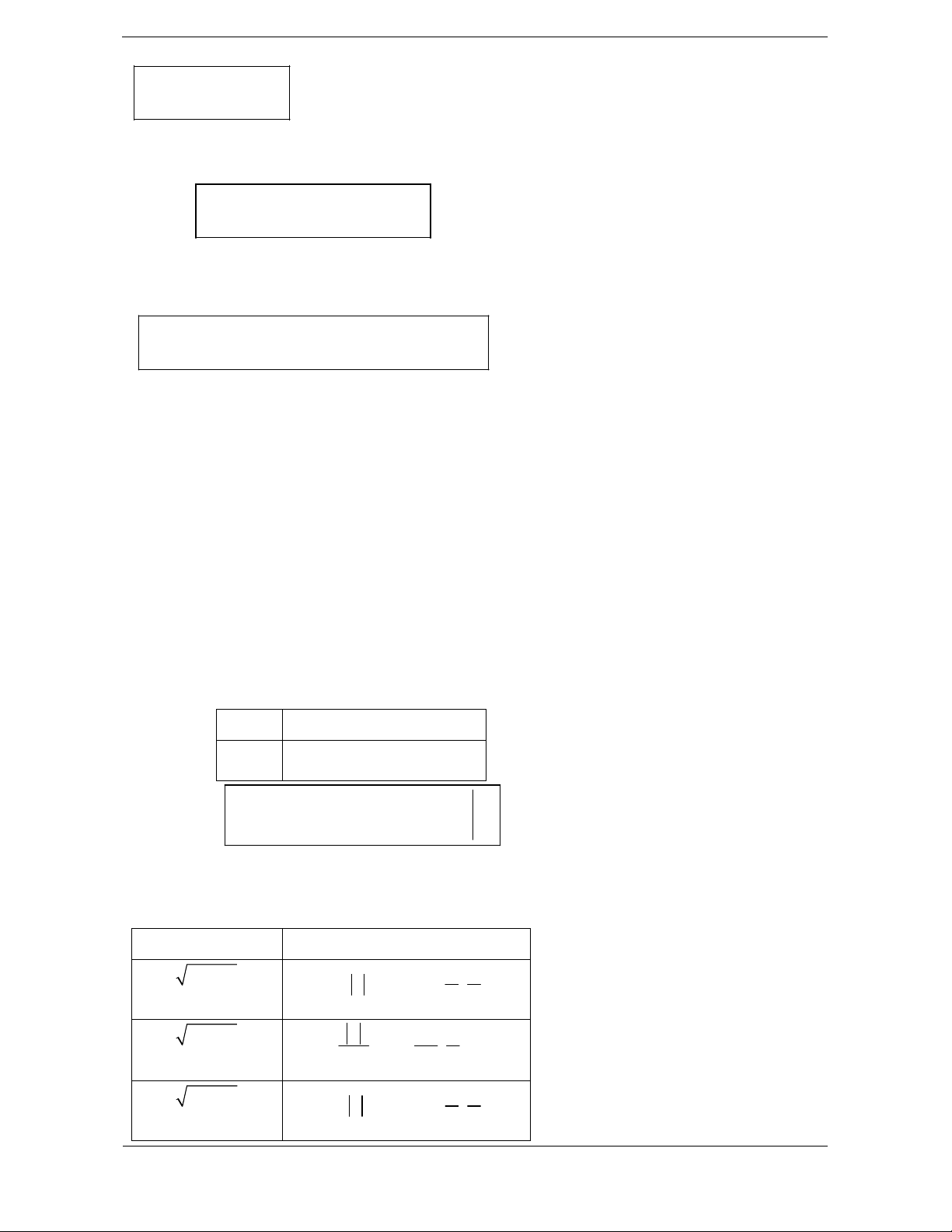
Định lý 3: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K. 4. Bảng nguyên hàm
Nguyên hàm của hàm số
Nguyên hàm của hàm số
Nguyên hàm của hàm số hợp sơ cấp
hợp u = ux
u = ax+b;a  0
dx  x  C 
du  u  C  d
 ax b  ax bC  1    1   1   1 ax b  x u
ax  b   dx   C   x dx   C     1 u   C     1    1  1 a 1
1 dx  ln x  C 
1 du  ln u  C  1 1 dx 
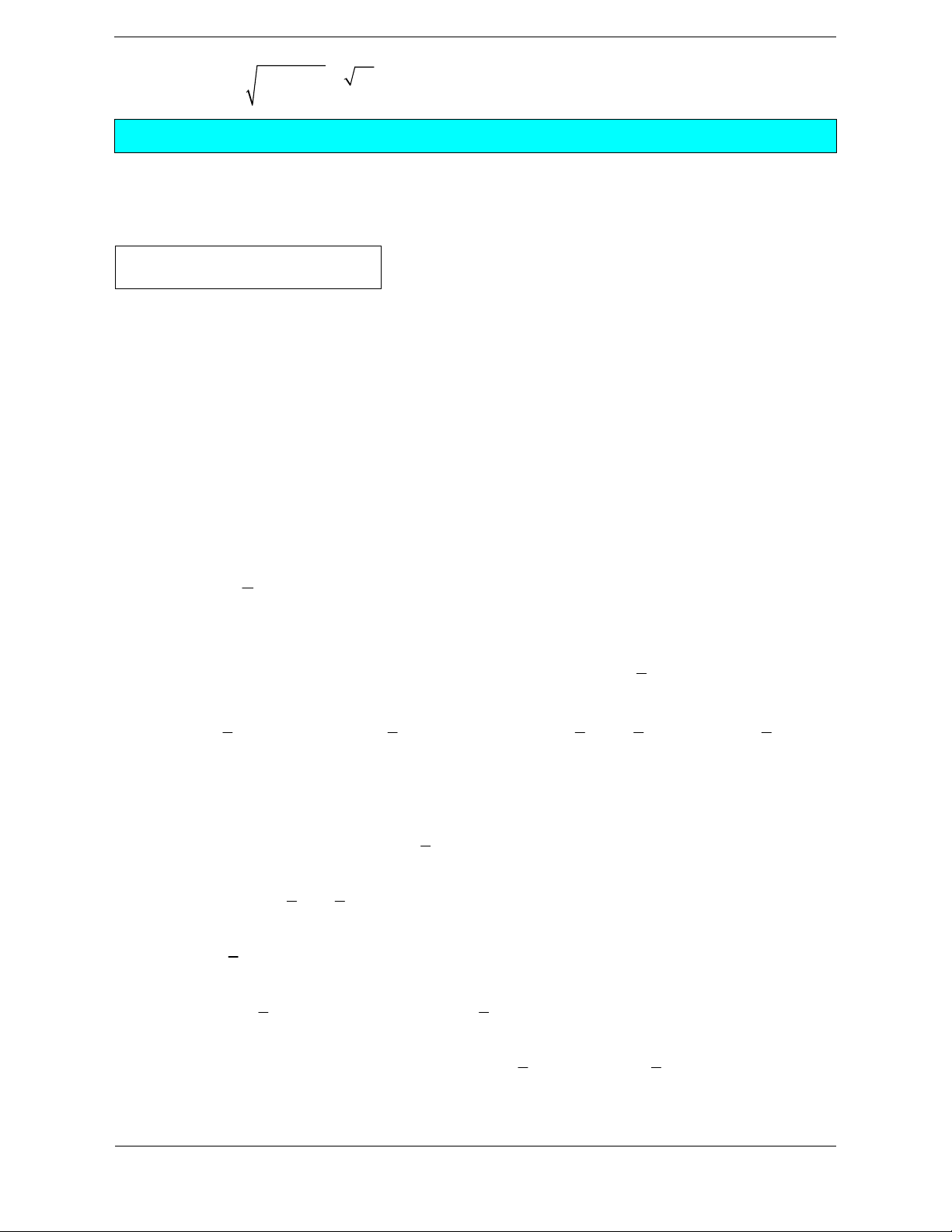
ln ax  b  C  x u ax  b a 1 1 1 1 1 1 1 dx    C  du    C  dx   .  C  2 x x 2 u u ax  b2 a ax  b 1 2 2 ax  bdx  . ax  b
ax  b  C  xdx  x x  C  2 udu  u u  C    a 3 3 3
1 dx  2 x  C 
1 du  2 u  C  1 1 dx 
.2 ax  b  C  x u ax  b a x x
e dx  e  C  u u
e du  e  C  ax b 2 axb e dx  e  C  a x a u a x  a dx 
 Ca  0,a    1 u a du 
 C a  0,a    1  1 mx n a mx n ln a ln a a dx  .
 Ca  0,a   1 m ln a 1
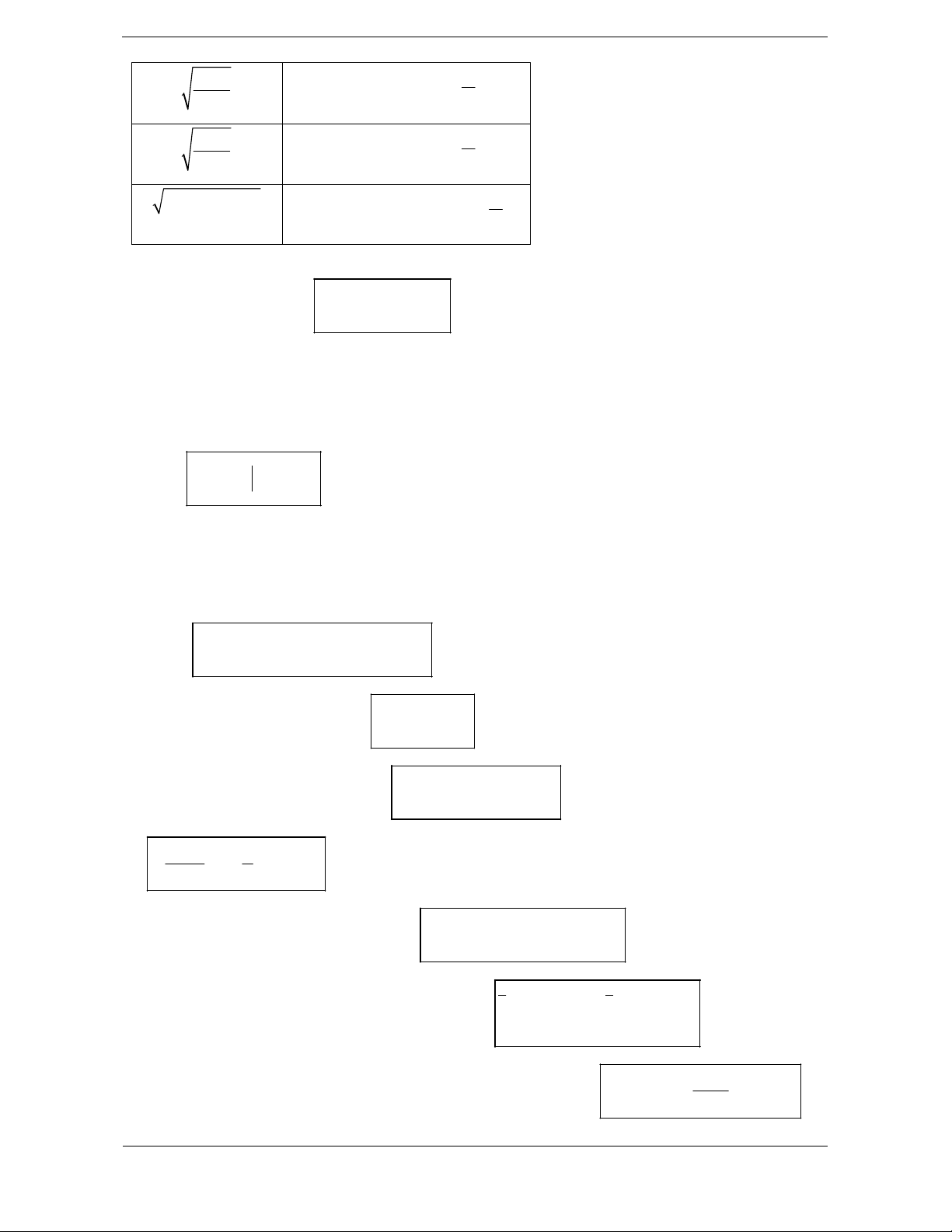
sin xdx   cos x  C 
sin udu   cos u  C  sin
 ax  bdx   cosax  bC a 1
cos xdx  sin x  C 
cos udu  sin u  C  cos
 ax  bdx  sinax  bC a 1
tan ax  b dx  
ln cos ax  b  C 
tan xdx   ln cos x  C 
tan udu   ln cos u  C      a 1
cot ax  b dx 
ln sin ax  b  C 
cot xdx  ln sin x  C 
cot udu  ln sin u  C      a 1 1 1 1 dx  
cot ax  b  C 
dx   cot x  C 
du   cot u  C  2
sin ax  b   a 2 sin x 2 sin u 1 1 1 1
dx  tan x  C 
du  tan u  C  dx 
tan ax  b  C  2 2 cos x 2 cos u
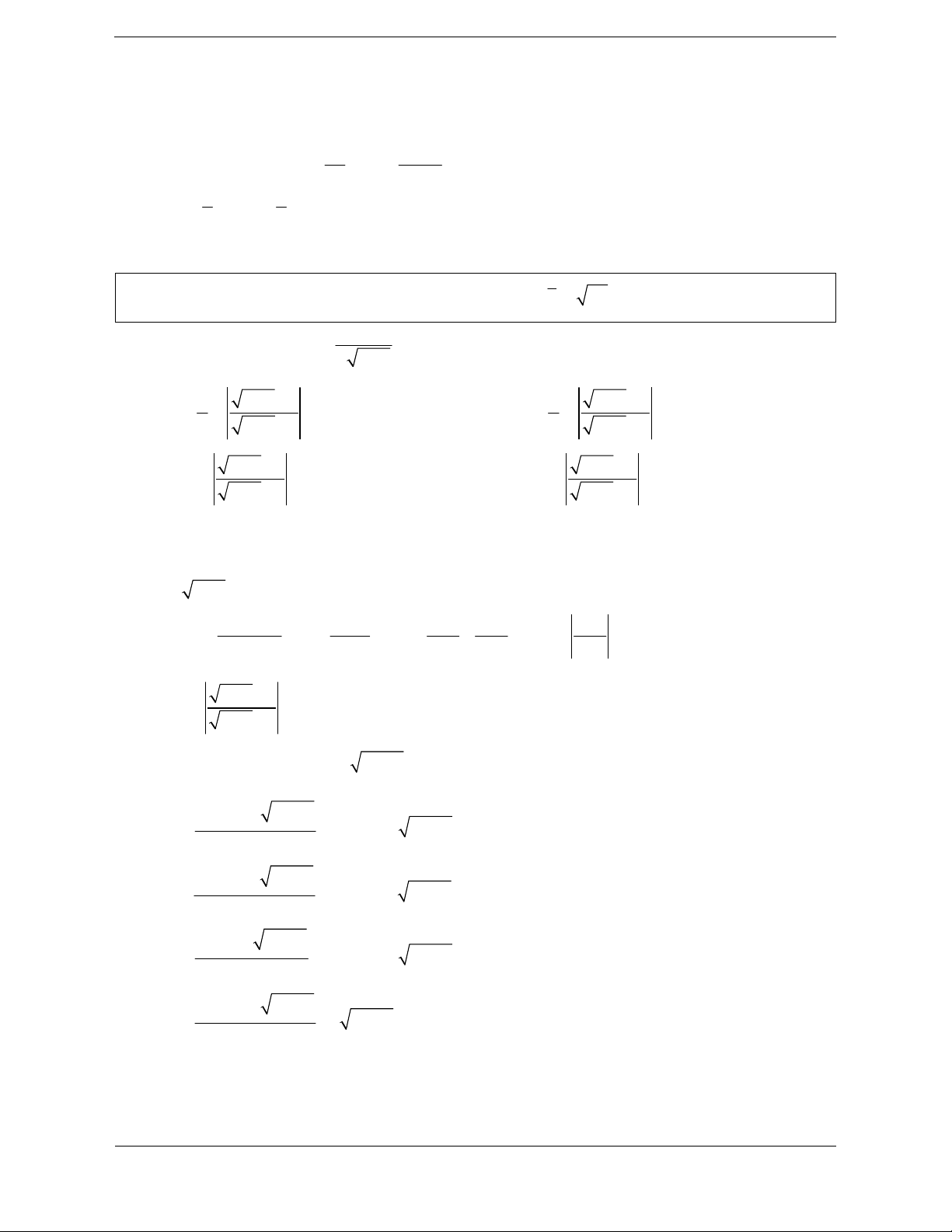
cos ax  b   a 1 x u dx 1 ax  b dx  ln tan  C 
1 du  ln tan  C   ln tan  C  sin x 2 sin u 2
sin ax  b a 2 1 dx  1  x    u    dx  ln tan   C  1   du  ln tan   C  cos ax b   cos x  2 4  cos u  2 4  1
 ax  b    ln tan   C   a  2 4 
II. PHƯƠNG PHÁP TÍNH NGUYÊN HÀM
1. Phương pháp đổi biến số
Định lý 1: Nếu f(u)du  F(u)  C 
và u  u(x) có đạo hàm liên tục thì: f u 
  (x) .uʹ(x)dx  F u  (x) C
Hệ quả: Với u  ax  ba  0 ta có     1
f ax b dx  Fax  b  C. a
2. Phương pháp tính nguyên hàm từng phần:
Định lý 2: Nếu hai hàm số u  ux và v  vx có đạo hàm liên tục trên K thì: u
 xvʹxdx  uxvx uʹ  xvxdx.
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Tìm nguyên hàm bằng các phép biến đổi sơ cấp
1. Phương pháp giải
 Biến đổi các hàm số dưới dấu nguyên hàm về dạng tổng, hiệu của các biểu thức chứa x,
trong đó mỗi biểu thức chứa x là những dạng cơ bản có trong bảng nguyên hàm.
 Áp dụng các công thức nguyên hàm trong bảng nguyên hàm cơ bản để tìm nguyên hàm. 2. Bài tập x 
Bài tập 1. Nguyên hàm của hàm số f  x 2 1  là x e x x A. 2  2 x  e  C B.  x
 e  C x e ln 2 x e ln 2   1 x x C. 2  2 x  e  C D. x  e  C x e ln 2   1 x e ln 2   1 Hướng dẫn giải Chọn C. x x x    Ta có: 2 1 2  x 2  x dx  dx  e dx   e  C     . x x e  e  e ln 2   1
Bài tập 2. Nguyên hàm của hàm số f  x  x  x  2019 2 là  2020 2018 x  2021 x  2020 2 2 x  2 x  2 A.    C B.   C 2021 1010 2021 1009  2021 2020 x  2021 x  2020 2 2 x  2 x  2 C.   C D.   C 2021 1010 2021 1010 Hướng dẫn giải Chọn D. Ta có: x
 x 22019 dx  
x 22x 22019 dx 2021 2020  x  x  
x  22020 dx  2x  22019  2  2 dx    C 2021 1010
Bài tập 3. Nguyên hàm của hàm số f  x 1  là 2 x e 1 A. 1 2  ln x x e 1  C B.  ln  2x x e   1  C 2 C.  2 ln x e   1  C D.   2 ln x x e   1  C Hướng dẫn giải Chọn B. x x 1  2e   2 2 1 x  e Ta có: e   1 . 2 x 2 x 2 e 1 e 1 x e 1 x 1 x   1 d  2 2 e e   1 Do đó 1 dx   1
 dx  dx 
 x  ln e   C   x x x  2x 1 2 2 2  e 1 e 1 2 e    1 2
Bài tập 4. Nguyên hàm của hàm số f  x 1  là:
x  2  x  2 3 3 A. 1        
x  2    x  2   C B. 1 x 2 x 2  C 6    6   C. 1 1 1 1 x  2 
x 2 x 2  C D.
x  2 x  2  x  2  C 6 6 6 6 Hướng dẫn giải Chọn A.    Ta có: 1 x 2 x 2 dx  dx  
x  2  x  2 4 1  2     x   2 x   x   1 x   C   x   1 2 2 2 2 2
x  2   x  2 x  2  C 4  3 3  6 6 
Chú ý: Sử dụng kĩ thuật nhân liên hợp: a b a  b  . a  b Lưu ý: 2 ax  bdx  
ax  b ax  b  C. 3a 
Bài tập 5. Nguyên hàm của hàm số f  x 5x 13  là: 2 x  5x  6
A. 2 ln x  3  3ln x  2  C
B. 3ln x  3  2 ln x  2  C
C. 2 ln x  3  3ln x  2  C
D. 2 ln x  3  3ln x  2  C Hướng dẫn giải Chọn D.   Ta có: 5x 13 5x 13  2 x  5x  6
x 2x 3
Ta sẽ phân tích: 5x 13  A x  2  B x  3   1
Thế x  2 và x  3 lần lượt vào (1) ta có B  3 và A  2 . 5x 13
2  x  2  3 x  3 Khi đó 2 3 dx  dx  dx  dx     2 x  5x  6
x 2x 3 x  3 x  2
 2 ln x  3  3ln x  2  C 
Bài tập 6. Nguyên hàm của hàm số   4 1 x f x  là: 5 x  x A. 1 ln x  ln  4 x   1  C B. x   4 ln ln x   1  C 2 C. 1 1 ln x  ln  4 x   1  C
D. ln x  ln  4 x   1  C 2 2 Hướng dẫn giải Chọn C. 1  x  4 1  x  4 4 3  2x Ta có: 1 2x 1 dx            x  x x  dx dx dx ln x ln x 1 C 4 x    4 5 4  1 x x  1 2  
Bài tập 7. Nguyên hàm của hàm số f  x 2 3x 3x 3  là: 3 x  3x  2 A. 3
ln x  2  2 ln x 1   C B. 3
ln x  2  2 ln x 1   C x 1 x 1 C. 3
2 ln x  2  ln x 1   C D. 3
2 ln x  2  ln x 1   C x 1 x 1 Hướng dẫn giải Chọn A. 2 2     Ta có: 3x 3x 3 3x 3x 3 dx  dx   . 3 x  3x  2 x  2 1  x  2
Ta phân tích x  x   A x  2 2 3 3 3
1  B  x  
1  x  2  C  x  2 .
Ta có thể dùng các giá trị riêng, tính ngay A  1,C  3 và B  2 . (thay x  2
  A  1; x  1 C  3 và x  0  B  2 ). 2   Khi đó 3x 3x 3 1 1 1 3               . x   dx dx 2 dx 3 dx ln x 2 2 ln x 1 C 2 1  x  2 x  2 x 1 x  2 1 x 1 P  x 
Lưu ý: Ta có kiến thức tổng quát dùng cho các nguyên hàm hữu tỉ I    dx , với Px và Q x
Q  x  là các đa thức, cụ thể như sau:
 Nếu degPx  degQx thì ta thực hiện phép chia Px cho Qx (ở đây, kí hiệu
deg P x là bậc của đa thức P x ).
 Khi degPx  degQx thì ta quan sát mẫu số Qx ta tiến hành phân tích thành các
nhân tử, sau đó, tách P  x theo các tổ hợp của các nhân tử đó. Đến đây, ta sẽ sử dụng đồng
nhất thức (hoặc giá trị riêng) để đưa về dạng tổng của các phân thức.
Một số trường hợp đồng nhất thức thường gặp   Trường hợp 1: 1 1 a c      .
ax  bcx  d 
ad  bc  ax  b cx  d  mx  n A B
Ax  Ba x  Ad  Bb Trường hợp 2:     .
ax  bcx  d  ax  b cx  d
ax  bcx  d
Ta đồng nhất thức mx  n   Ax  Ba x  Ad  Bb   1 .
Cách 1. Phương pháp đồng nhất hệ số.
Ac  Ba  m
Đồng nhất đẳng thức, ta được  . Suy ra A, B.
Ad  Bb  n
Cách 2. Phương pháp giá trị riêng. Lần lượt thay b d
x   ; x  
vào hai vế của (1), tìm được A, B. a c  Trường hợp 3: mx n A B   .
ax  b2 ax  b ax  b2  Trường hợp 4: mx n A B C   
ax  b2 cx  d ax  b2 cx  d ax  b
 mx  n  Acx  d  Bax  b2  Cax  bcx  d * Lần lượt thay b d
x   ; x  
; x  0 vào hai vế của (*) để tìm A, B, C. a c  Trường hợp 5: 1 A Bx C    với 2
  b  4ac  0 . x  m 2
ax  bx  c 2 x  m
ax  bx  c Trường hợp 6: 1 A B C D     .
x  a2 x  b2 x  a x  a2 x  b x  b2  
Bài tập 8. Cho hàm số 2
f  x  xác định trên 1
 \   thỏa mãn f ' x  ; f 0  1 và 2  2x 1 f  
1  2 . Giá trị của biểu thức P  f   1  f 3 là: A. 3ln 5  ln 2 B. 3ln 2  ln 5 C. 3  2 ln 5 D. 3  ln15 Hướng dẫn giải Chọn D.   x   1 ln 2 1  C khi x  
f  x   f  x 1 2 2 ' dx 
dx  ln 2x 1  C    2x 1    x 1 ln 1 2  C khi x  2  2  f  0  1 C  1 Vì 2    .  f    1  2 C  2  1   x   1 ln 2 1  2 khi x  
Suy ra f  x 2   .    x 1 ln 1 2 1 khi x   2
Do đó P  f  
1  f 3  3  ln 3  ln 5  3  ln15
Bài tập 9. Cho hàm số
f  x  xác định trên  \ 1;  1 , thỏa mãn     f  x  2 '  ; f 3
  f 3  2 ln 2 và 1 1 f   f  0    
. Giá trị của biểu thức 2     x 1  2   2 
P  f 2  f 0  f 4 là: A. 2 ln 2  ln 5
B. 6 ln 2  2 ln 3  ln 5
C. 2 ln 2  2 ln 3  ln 5 D. 6 ln 2  2 ln 5 Hướng dẫn giải Chọn C.   
f  x   f  x 2 1 1 x 1 ' dx  dx   dx  ln  C    2 x 1
 x 1 x 1 x  1   x 1 ln  C khi x  1    1  x 1     Hay   x 1 1 x f x  ln  C  ln
 C khi 1  x  1 2 x  1 1 x    x 1 ln  C khi x  1     3   x 1  f  3
   f 3  2 ln 2 
C  C  2 ln 2 Theo bài ra, ta có: 1 3   1   1    f   f  0 C  0       2   2   2 
Do đó f    f    f   3 2 0
4  ln 3  C  C  ln
 C  2 ln 2  2 ln 3  ln 5. 3 2 1 5
Bài tập 10. Nguyên hàm 3 2
P  x. x 1dx  là: A. 3 3 P   2x   3 2 1 x 1  C B. P   2 x   2 1 x  1  C 8 8 C. 3 3 3 2 P  x  1  C D. P   2 x   3 2 1 x  1  C 8 4 Hướng dẫn giải Chọn A. 1 4 Ta có: 1 3 3 2
x. x 1dx  
 2x  1 d 2x  1   2 3 x  3 1  C . 2 8
Bài tập 11. Nguyên hàm của hàm số sin x cos xsin xdx là: A. 1 1 1 x  sin 2x  cos 2x  C B. 1 1 1 x  sin 2x  cos 2x  C 2 4 4 2 4 4 C. 1 1 x  sin 2x  cos 2x  C D. 1 1 1 x  sin 2x  cos 2x  C 2 2 2 4 4 Hướng dẫn giải Chọn B. Ta có:  x  x  xdx   2 sin cos sin
sin x  sin x cos x  dx
1 cos2x sin 2x  1  1 1    dx  x  sin 2x  cos 2x  C      2 2  2  2 2 
Bài tập 12. Nguyên hàm của hàm số 1 dx  là: 2 2 sin x cos x
A.  tan x  cot x  C B. tan x  cot x  C
C. tan x  cot x  C
D. cot x  tan x  C Hướng dẫn giải Chọn B. 2 2    Ta có: 1 sin x cos x 1 1 dx  dx  
dx  tan x  cot x  C     . 2 2 2 2 2 2 sin x cos x sin x. cos x
 cos x sin x 
Bài tập 13. Nguyên hàm của hàm số 1 dx  là: 4 2
4 cos x  4 cos x 1 A. cot 2x  x
C B. tan 2x  C
C. cot 2x  C D. tan 2  C 2 2 Hướng dẫn giải Chọn D. Ta có: 1  1  1  1 1 x  tan 2x dx dx dx d(2 )   C 4 2  2 2  2 
4 cos x  4 cos x  1 (2 cos x  2 1) cos 2x 2 cos 2x 2
Bài tập 14. Nguyên hàm của hàm số 3 tan xdx  là: 2 2 A. tan x  tan x ln cos x  C B.
 ln sin x  C 2 2 2 4 C. tan x  tan x ln cos x  C D.  C 2 2 4 cos x Hướng dẫn giải Chọn A. Từ 3 x  x  2 tan tan
1  tan x   tan x d cos x Suy ra x
tan xdx  tan xd   tan x   2 tan 3  
 ln cos x  C  . cos x 2   
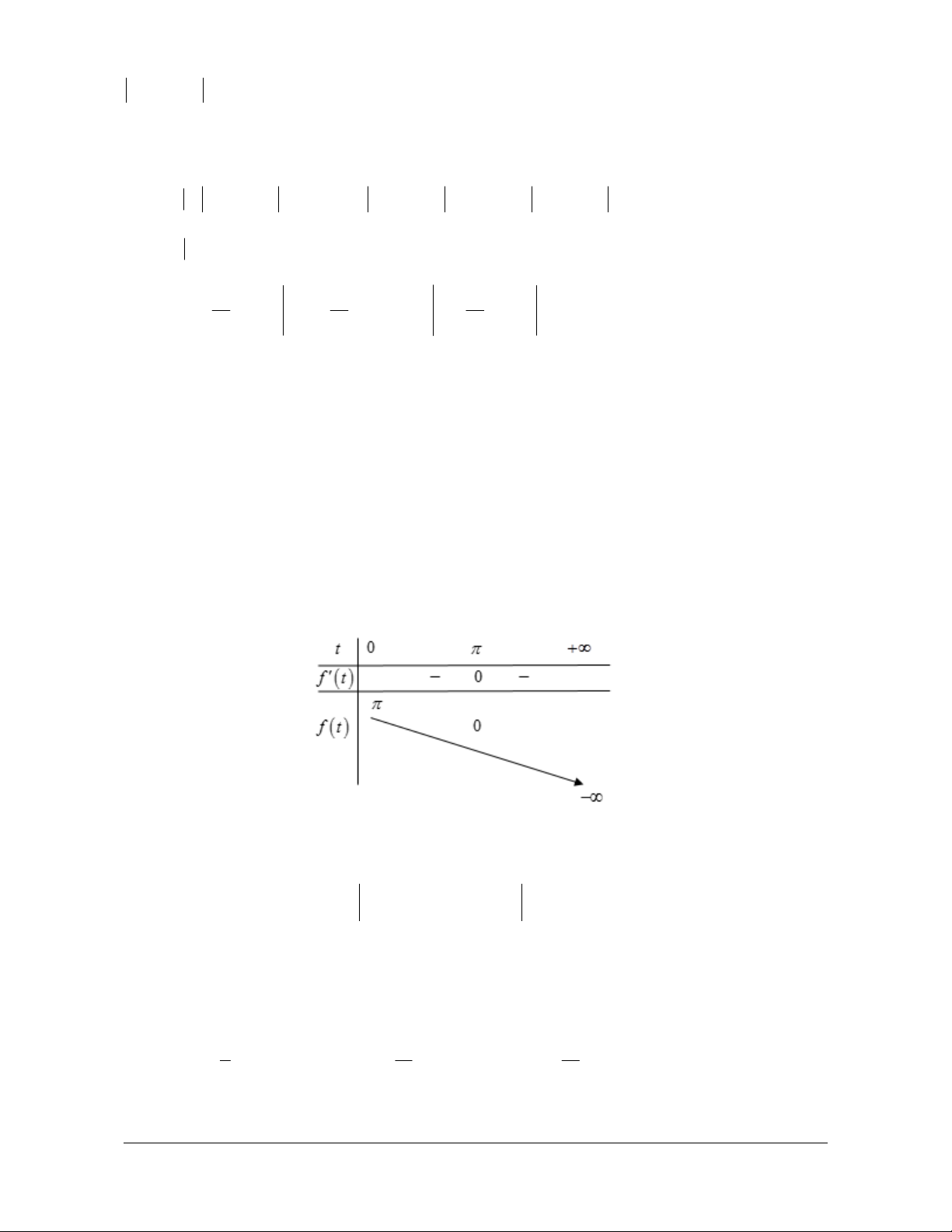
Bài tập 15. Gọi F  x là nguyên hàm của hàm số f  x  sin 2x tan x thỏa mãn 3 F    . Giá  3  4   
trị của F   là:  4          A. 3 1  B. 3 1  C. 3 1  D. 3 1  2 12 2 12 2 12 2 12 Hướng dẫn giải Chọn D.
Ta có: F  x sin x 2
 sin 2x.tan xdx  2sin x.cos x. dx  2 sin xdx    . cos x Suy ra      x  sin 2x F x 1 cos 2 dx  x   C . 2       Theo giả thiết, ta có: 3 1 2 3 3 F    sin  C   C     .  3  4 3 2 3 4 2 3  Vậy F  x sin 2x 3  x    . 2 2 3           Do đó 1 3 3 1 F   sin 2         .  4  4 2  4  2 3 2 12
Bài tập 16. Gọi F  x là nguyên hàm của hàm số f  x 4
 cos 2x thỏa mãn F 0  2019 . Giá trị    của F   là:  8          A. 3 16153 B. 3 129224 C. 3 129224 D. 3 129224 64 8 64 32 Hướng dẫn giải Chọn C. 2    Ta có: 1 cos 4x 1 4 cos 2x      2
1  2 cos 4x  cos 4x   2  4 1  1  cos8x  1  1  2 cos 4x    
3 4cos4x  cos8x 4  2  8  
Do đó F  x 1    x  x  1 1 3 4 cos 4 cos8 dx 
3x  sin 4x  sin 8x  C   8 8  8 
Mà F 0  2019 nên ta có C  2019 .  
Vậy F  x 1 1 
3x  sin 4x  sin 8x  2019   . 8  8       Do đó 3 129224 F     8  64  Bài tập 17. Gọi x
F  x  là nguyên hàm của hàm số f  x  5 cos  , với x 
 k2,k  và thỏa 1  sin x 2    mãn F   3
 . Giá trị của F    là: 4  2  A. 2 B. 0. C. 5 D. 1 3 3 3 Hướng dẫn giải Chọn D. 5 Ta thấy: cos x 3
 cos x 1 sin x   2 1  sin x  3
cos x  cos x.sin x 1 sin x      x x F x
1  sin x  d sin x  cos xd  cos x 3 4 sin cos 2 3  sin x    C 3 4
Theo giả thiết, ta có F   3  nên C  1. 4 Vậy   3 4 sin x cos x
F x  sin x    C 3 4    Do đó 1 F     .  2  3 Chú ý: n Với x * n   , ta có: n n x xdx   xd    x 1 cos cos .sin cos cos    C và n  1  x n n x xdx  xd    x n 1 sin sin .cos sin sin   C . n 1 Bài tập 18. Biết cos x a  dx  ln 5sin x  9  C, 
a,b , a là phân số tối giản. Giá trị 2ab 5sin x  9 b b là A. 10. B. 4. C. 7. D. 3. Hướng dẫn giải CHỌN D cos x 1 d5sin x  9 dx    1  ln 5sin x  9  C 5sin x  9 5 5sin x  9 5
Vậy a  1,b  5. Nên 2a  b  3.    
Bài tập 19. Tìm một nguyên hàm Fx của hàm số      2 f x 1 sin x biết 3 F    .  2  4 A.   3 1
F x  x  2 cos x  sin 2x. 2 4 B.   3 1
F x  x  2 cos x  sin 2x. 2 4 C.   3 1
F x  x  2 cos x  sin 2x. 2 4 D.   3 1
F x  x  2 cos x  sin 2x. 2 4 Hướng dẫn giải CHỌN B Ta có   2      2    1 cos 2x 1 sin x dx 1 2 sin x sin x dx  1  2 sin x   d  x  2  3 1
 x  2cosx  sin 2x  c 2 4    3 3   1 3 F    2cos  sin   c   c    0 .  2  4 2 2 2 4 4 Vậy   3 1
F x  x  2 cos x  sin 2x . 2 4 Bài tập 20. Cho cos 2x dx  F 
x  C và F  a  b. Tính    6 A a b . sin x  cos x A. 2. B. 2. C. 1. D. 1. Hướng dẫn giải CHỌN C  Ta có:   2 2 cos 2x cos x sin x F x  dx  dx   sin x  cos x sin x  cos x
cosx sinxcosx sinx  dx  
cosx sinxdx  sinx cosx. sin x  cos x
 F  1  a  b  A  1.
Bài tập 21. Cho tích phân 1 dx  a.  Tính 2 A  12 cot 2x theo a. 2 2 sin x cos x A. 2 4a . B. 2 2a . C. 2 3a . D. 2 a . Hướng dẫn giải CHỌN C    Ta có:   2 2 1 sin x cos x 1 1 F x  dx  dx      dx 2 2 2 2 2 2 sin xcos x sin x cos x  cos x sin x   tanx  cot x. Theo đề: 2 2 sin x cos x sin x  cos x 2  cos2x tan x  cot x      a cos x sin x sin x cos x sin 2x cos 2x a    sin 2x 2 2 2 cos 2x  a  2 A  12.  12.     3a . 2 sin 2x  2  sin 2x
Bài tập 22. Cho F x là một nguyên hàm của hàm số dx  và 2 2 cos x  4sin x     F    0  2 f 1  
. Tính 2F 0  F   .  2   2  7 7 A. . B.  . C. 0. D. 1 9 9 Lời giải CHỌN B Ta có d  2 2
cos x  4 sin x  2s
 in xcos x8sin xcos xdx  6sin xcos xdx 3sin 2xdx 1
 sin 2xdx  d  2 2
cos x  4 sin x . 3 Do đó : d  2 2 cos x  4sin 2 2 1 x
d cos x  4sin 2 x sin 2x 2 dx      2 2 
cos x4sin x C 2 2
cos x  4 sin x 3 2 2 cos x  4sin x 3 2 2
2 cos x  4sin x 3   F   2 4 7 0  2F
  2. 3C 1 C     .  2  3 3 9   Vậy F   2 4 7 2 0  F
 2.  2C  C  C      2  3 3 9 Bài tập 23. Gọi x
F  x  là nguyên hàm của hàm số f  x   trên khoảng  2  2;2 2  thỏa 2 8  x
mãn F 2  0 . Khi đó phương trình F  x  x có nghiệm là: A. x  0 B. x  1 C. x  1  D. x  1 3 Hướng dẫn giải Chọn D.
Ta có: F  x x 1  dx   d    2 8  x  2
  8  x  C 2 2 8  x 2 8  x Mặt khác F   2
2  0   8  x  C  0  C  2 Vậy F  x 2
  8  x  2 . 2  x  0 
Xét phương trình F  x 2 2
 x   8  x  2  x  8  x  2  x  8x   2  x2 2 x  2 x  2     
 x  1 3  x  1 3 2
2x  4x  4  0  x 1 3  Bài tập 24. Cho 2x 1
F  x là một nguyên hàm của hàm số f  x   trên khoảng 0; 4 3 2
x  2x  x và F   1 1 
. Tổng S  F  
1  F 2  F 3  ...  F 2019 là 2 A. 2019 B. 2019.2021 C. 1 2018 D. 2019  2020 2020 2020 2020 Hướng dẫn giải Chọn C.   
Phân tích f  x 2x 1 2x 1 2x 1    4 3 2 2
x  2x  x x  x  2 1  2x  x2 
Khi đó F  x 2x 1 1  dx  d    1 2 x  x    C . 2 2        2 2 2 x  x x x x x Mặt khác F   1 1 1 1 
   C   C  1 . 2 2 2   Vậy F  x 1 1 1 1   1   1    1   . 2 x  x x  x   1  x x 1  
Do đó S  F    F    F     F   1 1 1 1 1 1 1 1 2 3 ... 2019   1       ...    2019    2 2 3 3 4 2019 2020   1  1 1   1  2019  2018   2018    2020  2020 2020
Bài tập 25. Cho hàm số f  x có đạo hàm xác định trên  thỏa mãn f 0  2 2, f  x  0 và
f  x  f  x    x   2 . ' 2 1
1  f  x, x
   . Giá trị f   1 là: A. 6 2 B. 10 C. 5 3 D. 2 6 Hướng dẫn giải Chọn D.
f x . f ' x
Ta có: f  x. f ' x  2x   2 1
1  f  x        2x 1. 2
1  f  x 
f  x . f ' x  d  2
1  f  x  Suy ra dx  
2x  1dx    2x   2
1 dx  1  f  x  2
 x  x  C 2
1  f  x  2
2 1  f  x 
Theo giả thiết f 0  2 2 , suy ra   2 1 2 2
 C  C  3 Với C  3 thì
 f x  x  x   f x  x  x  2 2 2 2 1 3 3 1 Vậy f   1  24  2 6
Bài tập 26. Cho hàm số y  f  x có đạo hàm liên tục trên đoạn   2;1 
thỏa mãn f 0  3 và
 f x2 f x 2 . '
 3x  4x  2 . Giá trị lớn nhất của hàm số y  f x trên đoạn   2;1 là: A. 3 2 42 B. 3 2 15 C. 3 42 D. 3 15 Hướng dẫn giải Chọn C.
Ta có:  f x2 f x 2 . '
 3x  4x  2 *
Lấy nguyên hàm hai vế của đẳng thức (*) ta được:
 f x2 .f 'xdx   1 2
3x  4x  2 3 dx  f  x  3 2 3
 x  2x  2x  C  f x 3 2
 3x  6x  6x  3C 3
Theo giả thiết, ta có f 0  3 nên
 f  3   3 2    C 3 
 C  C   f x 3 2 0 3 0 2.0 2.0 27 3 9
 3x  6x  6x  27
Ta tìm giá trị lớn nhất của hàm số g  x 3 2
 3x  6x  6x  27 trên đoạn   2;1 .
Ta có g  x 2 '
 9x 12x  6  0, x  2; 
1 nên đồng biến trên đoạn   2;1 .
Vậy max f  x  max g  x 3  42 . 3 2; 1  2  ;  1
Dạng 2: Phương pháp đổi biến dạng 1, đặt u = ux
1. Phương pháp giải
Định lí: Cho f
 udu  FuC và u  ux là hàm số có đạo hàm liên tục thì f u
  xu'
  x dx  F u
  x  C 
Các bước thực hiện đổi biến: Xét I  f
 uxu'xdx
Bước 1: Đặt u  u x , suy ra du  u' xdx
Bước 2: Chuyển nguyên hàm ban đầu về ẩn u ta được I  f
 udu  FuC , trong đó Fu là
một nguyên hàm của hàm số f u .
Bước 3: Trả về biến x ban đầu, ta có nguyên hàm cần tìm là I  F ux  C
Hệ quả: nếu F  x là một nguyên hàm của hàm số f  x trên K và , a b  ;  a  0 ta có:     1 f ax b dx 
F ax  b  C . a 2. Bài tập
Bài tập 1. Nguyên hàm F  x của hàm số   3 2 1 . x f x x e   , biết F   1 1  là: 3 A. 1 1 1 x 1 F  x  3 1 x 1 e  
 C B. F x 3 x 1 e  
 2019 C. F x 3 1 e   
D. F  x 3 x 1 e   3 3 3 3 3 Hướng dẫn giải Chọn D. Đặt 1 3
u  x  1 ta có 2 2
du  3x dx  x dx  du 3 Suy ra    u 1 1 u f x dx  e du  e  C  3 3
Do đó F  x 3 1 x 1 e    C . 3 Mặt khác 1 F   1 1 
nên C  0 . Vậy f  x 3 x 1 dx e    . 3 3
Lưu ý: Ta có thể viết như sau: f  x 3 3 x  1 x dx x e dx e  d   x  3 1 2 1 1 3 x 1 1 e       C 3 3
Chú ý: Với các viết 1 2 x dx  d  3 x  
1 , ta có thể tính nguyên hàm đã cho một cách đơn giản và 3 nhanh gọn.
Bài tập 2. Nguyên hàm 2 sin x M  dx  là: 1  3cos x A. 1 M 
ln 1 3cos x   C B. 2 M 
ln 1  3cos x  C 3 3 C. 2 M  
ln 1  3cos x  C D. 1
M   ln 1  3cos x  C 3 3 Hướng dẫn giải Chọn C.
Đặt u  1 3cos x , ta có du  3s  in xdx hay 2 2 sin xdx   du . 3 Khi đó 2 1 2 M   du   ln u  C  3 u 3 Vậy 2 sin x 2 M  dx  
ln 1 3cos x  C 13cosx 3     sin  x  4     Bài tập 3. 4 4 3 a  I      Tìm tỉ lệ a .
sin 2x  21  sin x  cos x dx ,a,b . b b 0 A. 1 . B. 1 . C. 2 . D. 3 . 3 2 1 1 Hướng dẫn giải CHỌN B     dt
  cosx  sin xdx   2 sin x  dx
Đặt t  sin x  cosx    4   2 sin 2x  t   1 
và x : 0  thì t : 1  2 . 4 2 2 2 1 dt 2 dt 2 1 4  3 2  I      .    . 2 2 2 t  1  2 1  t 2 2 t  1 4 1   1 t  12 1 Bài tập 4. Cho 3 cos x sin xdx  F  x C và   1 F 0  a  b  . 4 Tính 2 2 A  a  b  2018. A. 2018. B. 2016. C. 2022. D. 2020. Hướng dẫn giải CHỌN A 3 cos x sin xdx 
Đặt u  cos x  du  sin xdx . 4 4 3 3 u cos x
cos x sin xdx   u du    C    C   4 4    1 1 F 0    a  b   a  b  0. 4 4
A  a  b  2018  a  b2 3 3
 2aba  b  2018  2018. m
Chú ý: chú ý rằng với a  0 và , m n  ;
 n  0 ta luôn có: n m n a  a .
Bài tập 5. Nguyên hàm 1 R  dx  là: x x  1     A. 1 x 1 1 x R  ln  C B. 1 1 1 R  ln  C 2 x  1 1 2 x 1 1     C. x 1 1 x R  ln  C D. 1 1 R  ln  C x 1 1 x 1 1 Hướng dẫn giải Chọn D. Đặt 2 u 
x  1  u  x 1 . Suy ra 2
x  u 1 và dx  2udu .    Khi đó 2u 2 1 1 u 1 R    du  du   du  ln  C    . 2 u   2 1 u u 1
 u 1 u 1 u  1   Vậy x 1 1 R  ln  C x  1  1
Bài tập 6. Nguyên hàm 3 2 S  x x  9dx  là: x 92 2 2 x  9 A. S   3 2 x  9 2
x  9  C 5 x 94 2 2 x  9 B. S   3 2 x  9 2 x  9  C 5
 2x 9 2x 9 C. S   3x  92 2 2 x  9  C 5 x 92 2 2 x  9 D. 2 S 
 3 x  9  C 5 Hướng dẫn giải Chọn A. Xét 3 2 2 2 S  x
x  9dx  x x  9xdx   . Đặt 2 2 2 u 
x  9  u  x  9 . Suy ra 2 2
x  u  9 và xdx  udu .
Khi đó S  u  u udu  u  u  5 u 2 4 2 3 9 . 9 du   3u  C . 5 x 92 2 2 x  9 Vậy S   3 2 x  9 2 x  9  C 5
Bài tập 7. Nguyên hàm 1 T  dx  là: x ln x 1 A. 1 T   C
B. T  2 ln x 1  C 2 ln x 1 C. 2 T 
ln x  1 ln x 1  C
D. T  ln x 1  C 3 Hướng dẫn giải Chọn B. Ta có: 1 1 T  dx  d  
ln x  1  2 ln x 1  C . x ln x 1 ln x 1 x 22020
Bài tập 8. Nguyên hàm U   là: x   dx 2022 1 2021    2020    A. 1 x 2 1 x 2 U   C   B. U   C   3  x 1  6060  x 1  2021    2023    C. 1 x 2 1 x 2 U   C   D. U   C   6063  x 1  6069  x 1  Hướng dẫn giải Chọn C. x 22020 2020    Xét x 2 1 U       x   dx dx 2022 1  x 1  x  2 1  Đặt x 2 3 1 1 u   du  dx  du  dx . x 1 x  2 1 3 x  2 1 2021    Suy ra. 1 1 1 x 2 2020 2021 U  u du  u  C  . Vậy U   C   3 6063 6063  x 1  Lưu ý:  
ax  bn n 1 1 1  ax  b         cx  d  dx C n 2
n  1 ad  bd  cx  d  2
Bài tập 9. Xét nguyên hàm ln x V   
dx . Đặt u  1  1 ln x , khẳng định nào sau đây
x 1  ln x 1 sai? u  u2 2 2
A. dx  2u  2 du B. V  .  2u 2du x u 5 4 C. 2 5 16 u u 16 5 4 3 2 V  u  u 
u  4u  C D. 3 2 V   
u  4u  C 5 2 3 5 2 3 Hướng dẫn giải Chọn C. Đặt u  
 x  u  2 dx 2 1 1 ln 1
 1 ln x  ln x  u  2u 
 2u  2du . x u 2 ln u x 2 2 2 Khi đó V      x  dx u du 1  ln x  1 .2 2 u  2 2 5 16 4 3 2
u  5u  8u  4u 5 4 3 2 du  u  u 
u  4u  C 5 2 3   
Bài tập 10. Gọi F  x là nguyên hàm của hàm số f  x 2 3
 sin 2x.cos 2x thỏa F  0   . Giá trị  4  F 2019  là: A. F    1 2019  
B. F 2019   0 C. F    2 2019   D. F    1 2019  15 15 15 Hướng dẫn giải Chọn A. Đặt 1
u  sin 2x  du  2 cos 2xdx  du  cos 2xdx 2
Ta có F  x 1 1 2 3 2
 sin 2x.cos 2xdx  u .    2
1  u  du   2 4
u  u  du 2 2 1 1 1 1 3 5 3 5  u  u  C  sin 2x  sin 2x  C 6 10 6 10    1  1  1 3 5 F  0  sin  sin
 C  0  C      4  6 2 10 2 15
Vậy F  x 1 1 1 3 5  sin 2x  sin 2x  6 10 15 Do đó F    1 2019   15 2x 3dx
Bài tập 11. Biết rằng 1  
(với C là hằng số). Gọi S là tập      C
x x 1  x  2 x  3 1 g  x 
nghiệm của phương trình g  x  0 . Tổng các phần tử của S bằng: A. 0. B. 3   5 C. 3  D. 3   5 Hướng dẫn giải Chọn C.
Vì x  x   x   x     x  xx  x     x  x 2 2 2 2 1 2 3 1 3 3 2 1 3 1 nên ta đặt 2
u  x  3x ,
khi đó du  2x  3 dx
Nguyên hàm ban đầu trở thành du 1     . u   C 2 1 u  1 2x 3dx Suy ra 1        C
x x 1  x  2 x  3 2 1 x  3x 1  3   5 x  Vậy g  x 2
 x  x  g x 2 2 3 1;
 0  x  3x 1  0   .  3   5 x   2      Do đó 3 5 3 5 S   ;  .  2 2  
Tổng giá trị các phần tử của S bằng 3  .  Bài tập 12. 3cos 2x sin 4x I  dx  F 
x C. Tính F1, biết rằng Fx không chứa hệ số tự do. 2  sin x  cos x A. 17 . B. 2 . C. 15 . D. 9 . 3 3 3 3 Hướng dẫn giải CHỌN A 3cos 2x  sin 4x 3 2sin2xcos2x I  dx  dx   2  sin x  cos x 2  sin x  cos x
3 2sin2xcosx  sinxcosx sinx       dx 2 sin x cos x dt   cosx   sin xdx
Đặt t  sin x  cosx   2 sin2x  t 1 3 2   2t 1   .t 3  2t  5t   2 6  I  dt  dt  2t  4t  3     dt 2  t t  2  t  2   2  3 2 
t  2t  3t  6 ln t  2    C.  3 
Dạng 3: Tìm nguyên hàm bằng cách đổi biến dạng 2
1. Phương pháp giải
Kiến thức cần nhớ:
Các kĩ thuật đổi biến dạng 2 thường gặp và
Ta đã biết các đẳng thức sau: cách xử lí. 2 2
sin t  cos t  1, với mọi t   . 1  2 1  tan t  , t
   k k  2   cos t 2 1 2 1  cot t  , t
  k k  2   sin t
Với các bài toán sau đây thì ta không thể giải quyết
ngay bằng nguyên hàm cơ bản cũng như đổi biến số ở
dạng 1, đòi hỏi người học phải trang bị tư duy đổi
biến theo kiểu “lượng giác hóa” dựa vào các hằng
đẳng thức lượng giác cơ bản và một số biến đổi thích
hợp, cụ thể ta xem xét các nguyên hàm sau đây: Bài toán 1: Tính dx dx A  
Bài toán 1: Tính A   1 1 2 2 a  x 2 2 a  x     
Đặt x  a sin t , với t  ;   hoặc  2 2 
x  a cos t với t  0;  Bài toán 2: Tính dx dx A  
Bài toán 2: Tính A   2 2 2 a  x 2 2 2 a  x     
Đặt x  a tan t , với t  ;   .  2 2    Bài toán 3: Tính a x a x A  dx 
Bài toán 3: Tính A  dx  3 a  x 3 a  x   
Đặt x  a cos2t với t  0;    2 
Bài toán 4: Tính A  x  a x  b dx 
Bài toán 4: Tính A  x  a x  b dx  4    4      
Đặt x  a  b  a 2
sin t với t  0;    2  Bài toán 5: Tính 2 2 A  x  a dx  Bài toán 5: Tính 2 2 A  x  a dx  5 5 a      Đặt x  với t  ;   sin t  2 2  2. Bài tập 2
Bài tập 1. Nguyên hàm x I  dx  là: 2 4  x 2  2  A. x x 4 x x x 4 x arcsin   C B. 2arccos   C 2 4 2 2 2  2  C. x x 4 x x x 4 x arccos   C D. 2arcsin   C 2 4 2 2 Hướng dẫn giải Chọn D.     
Đặt x  2sin t với t  ; 
 . Ta có cost  0 và dx  2 costdt .  2 2  2      Khi đó 4 sin t 2 I 
2 cos tdt  4 sin tdt  
(vì cost  0, t   ;   ). 2 4  4 sin t  2 2 
Suy ra I  21cos2tdt  2t sin2t  C 2  Từ x x 4 x
x  2 sin t  t  arcsin
và sin 2t  2sin t.cost  2 2 2 2  Vậy x x x 4 x I  dx  2 arcsin   C  2  2 2 4 x
Bài tập 2. Nguyên hàm 1 I  dx  là: 1 x 3 2 2  A.   2 x x 1 x 2 3 1 x  C B.  C C.  C D.  C 2 1  x   x x 3 2 1 Hướng dẫn giải Chọn B.
Đặt x  cost,t  0    dx  sin t.dt . Khi đó sin t.dt dt x I   dt    cot t  C   hay I   C 3 2 sin t sin t 2 1  x Vậy 1 x dx   C    3 2 2 1  1 x x
Ví dụ 3. Nguyên hàm 1 I  dx  là: 2 1  x
A. arctan x  C
B. arccot x  C
C. arcsin x  C
D. arccos x  C Hướng dẫn giải Chọn A.     
Đặt x  tan t với t  ;   , ta có dx   2
1  tan t  dt .  2 2  Khi đó 1 I    2
1  tan t dt  dt  t  C  2  1  tan t Vậy 1 I 
dx  arctan x  C  2 1  x
Dạng 4: Tìm nguyên hàm bằng phương pháp nguyên hàm từng phần
1. Phương pháp giải
Với u  u x và v  v x là các hàm số có đạo hàm trên khoảng K thì ta có:  .
u v'  u ' . v v ' u
Viết dưới dạng vi phân d uv  vdu  udv
Khi đó lấy nguyên hàm hai vế ta được: d
 uv  vdu udv  
Từ đó suy ra udv  uv  vdu    1
Công thức (1) là công thức nguyên hàm từng phần.
Dấu hiệu nhận biết phải sử dụng phương pháp nguyên hàm từng phần.
Bài toán: Tìm I  u
 x.vxdx , trong đó ux và vx là hai hàm có tính chất khác nhau, chẳng hạn:
u  x  là hàm số đa thức, v  x  là hàm số lượng giác.
u  x  là hàm số đa thức, v  x  là hàm số mũ.
u  x  là hàm số logarit, v  x là hàm số đa thức.
u  x  là hàm số mũ, v  x  là hàm số lượng giác.
Phương pháp nguyên hàm từng phần u  u  x
du  u'xdx  Bước 1: Đặt    dv  v  xdx v  v  xdx  
Bước 2: Áp dụng công thức (1), ta được: udv  uv  vdu  
Lưu ý: Đặt u  u  x (ưu tiên) theo thứ tự: “Nhất lốc, nhì đa, tam lượng, tứ mũ”. Tức là, nếu có
logarit thì ưu tiên đặt u là logarit, không có logarit thì ưu tiên u là đa thức,… thứ tự ưu tiên sắp xếp như thế.
Còn đối với nguyên hàm v  v
 xdx ta chỉ cần Chọn một hằng số thích hợp. Điều này sẽ được
làm rõ qua các Bài tập minh họa ở cột bên phải. 2. Bài tập
Bài tập 1. Kết quả nguyên hàm I  x   2
ln 2  x  dx là: 2 2  A. x 2 x x ln  2 x  2   C
B. x   x   2 2 2 2 ln 2   C 2 2 2 2 2  C.  x 2 x 2 x    2 x   2 2 ln 2  x  C D. ln  2 x  2   C 2 2 Hướng dẫn giải Chọn D.  x du  dx u  ln 2 2 2  x   2   Đặt x 2    2 dv  xdx x  2 v   2 2 2 2   Khi đó x 2 x x I  ln  2 2
x  2  xdx  ln 
 2x 2 C 2 2 2 2
Chú ý: Thông thường thì với x
dv  xdx  v  2 2 
Tuy nhiên trong trường hợp này, ta để ý x 2 v 
mang lại sự hiệu quả. 2
ln sin x  2 cos x 
Bài tập 2. Kết quả nguyên hàm I  dx  là: 2 cos x
A. tan x  2.lnsin x  2 cos x  x  2 ln cos x  C
B. tan x  2.lnsin x  2cos x  x  2 ln cos x  C
C. tan x  2.lnsin x  2cos x  x  2 lncos x  C
D. cot x  2.ln sin x  2 cos x  x  2 ln cos x  C Hướng dẫn giải Chọn B.      x  x  cos x 2 sin x u ln sin 2 cos du  dx     Đặt sin x 2 cos x   dx  dv 
sin x  2 cos x  2
v  tan x  2   cos x  cos x  Khi đó   x    x  x  cos x 2 sin x I tan 2 ln sin 2 cos  dx  cos x
 tan x  2lnsin x  2cos x  x  2 ln cos x  C
Chú ý: Ở Bài tập này, Chọn v  tan x  2 có thể rút gọn được ngay tử và mẫu trong nguyên hàm vdu  .
Bài tập 3. Kết quả nguyên hàm 2
I  x sin 5xdx  là: A. 1 2 2 1 2 2 2  x cos5x  x sin 5x 
cos 5x  C B. 2  x cos5x  x sin 5x  cos 5x  C 5 25 125 5 25 125 C. 1 2 2 1 2 2 2 x cos 5x  x sin 5x 
cos 5x  C D. 2  x cos5x  x sin 5x  cos 5x  C 5 25 125 5 25 125 Hướng dẫn giải Chọn D.
Phân tích: Ở đây ta sẽ ưu tiên 2
u  x là đa thức, tuy nhiên vì bậc của u là 2 nên ta sẽ từng phần hai
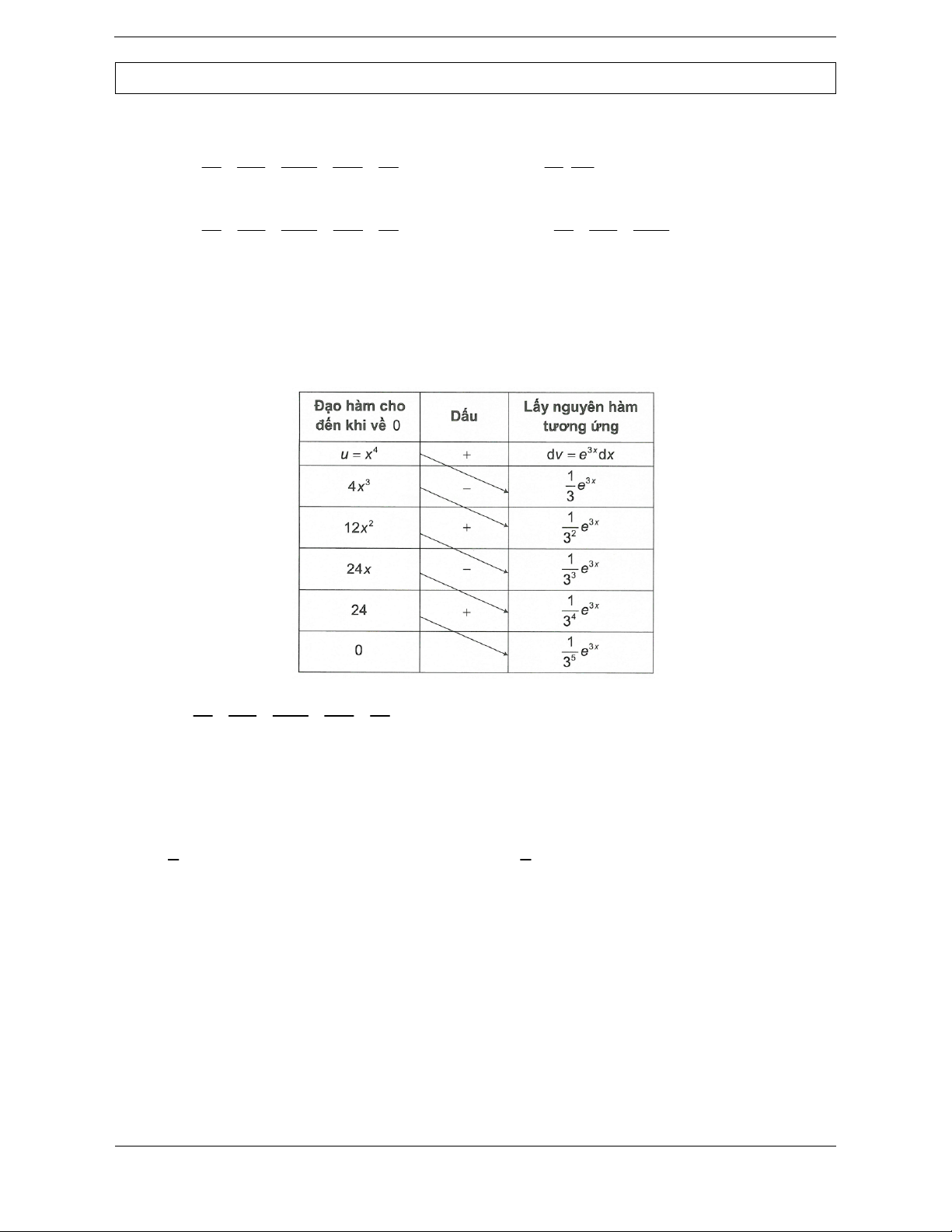
lần mới thu được kết quả. Nhằm tiết kiệm thời gian, tôi gợi ý với phương pháp “sơ đồ đường chéo” cụ thể như sau:
Bước 1: Chia thành 3 cột:
+ Cột 1: Cột u luôn lấy đạo hàm đến 0.
+ Cột 2: Dùng để ghi rõ dấu của các phép toán đường chéo.
+ Cột 3: Cột dv luôn lấy nguyên hàm đến khi tương ứng với cột 1.
Bước 2: Nhân chéo kết quả của 2 cột với nhau. Dấu của phép nhân đầu tiên sẽ có dấu (+), sau đó
đan dấu (-), (+), (-),… rồi cộng các tích lại với nhau. Khi đó 1 2 2 2 I   x cos 5x  x sin 5x  cos 5x  C 5 25 125 Chú ý:
Kĩ thuật này rất đơn giản và tiết kiệm nhiều thời gian.
Trong kĩ thuật tìm nguyên hàm theo sơ đồ đường chéo, yêu cầu độc giả cần tính toán chính xác đạo
hàm và nguyên hàm ở hai cột 1 và 3. Nếu nhầm lẫn thì rất đáng tiếc.
Bài tập 4. Nguyên hàm 4 3x I  x e dx  là: 4 3 2   5 3x A. x 4x 12x 24x 24 x e 3x I      
e  C B. I  .  C 2 3 4 5  3 3 3 3 3  5 3 4 3 2   4 3 2   C. x 4x 12x 24x 24 x 4x 12x 3x I      
e  C D. 3x I     e  C 2 3 4 5  3 3 3 3 3  2 3  3 3 3  Hướng dẫn giải Chọn A.
Nếu làm thông thường thì từng phần 4 lần ta mới thu được kết quả. Ở đây, chúng tôi trình bày theo
sơ đồ đường chéo cho kết quả và nhanh chóng hơn. 4 3 2   Vậy x 4x 12x 24x 24 3x I       e  C . 2 3 4 5  3 3 3 3 3 
Bài tập 5. Nguyên hàm x
I  e sin xdx  là: A. 2 x
e sin x  cos x   C B. 2 x
e sin x  cos x   C C. 1 1 x
e sin x  cos x   C D. x
e sin x  cos x   C 2 2 Hướng dẫn giải Chọn C.
Phân tích: Sự tồn tại của hàm số mũ và lượng giác trong cùng một nguyên hàm sẽ rất dễ gây cho
người học sự nhầm lẫn, nếu ta sẽ không biết điểm dừng thì có thể sẽ bị lạc vào vòng luẩn quẩn. Ở
đây, để tìm được kết quả thì ta phải từng phần hai lần như trong Bài tập 3. Tuy nhiên, với sơ đồ
đường chéo thì sao? Khi nào sẽ dừng lại?
Khi đó, ta sẽ có thể kết luận x  sin x  cos x I e x e
x  e sin xdx  . Hay 1 2 x  sin x I e
x  e . cos x . Vậy x I 
e sin x  cos x   C 2
Chú ý: Chỉ dừng lại khi đạo hàm của nó có dạng giống dòng đầu tiên. Dòng cuối thu được  sin x xe dx  I  .
Bài tập 6. Tìm  lnn I
 ax bvxdx , trong đó vx là hàm đa thức, * n   và ,
a b  ;a  0 Hướng dẫn giải 1 . lnn na
 ax  b
Phân tích: Vì ưu tiên    lnn u x
ax  b nên du 
dx và tiếp tục đạo hàm thì cột 1 ax  b
sẽ không về 0 được, vì vậy phải chuyển lượng   na t x 
từ cột 1 sang nhân với v  x ở cột 3 để ax  b
rút gọn bớt; tiếp tục quá trình như thế cho đến khi đạo hàm cột 1 về 0, và chú ý sử dụng quy tắc đan dấu bình thường.
Bài tập 6.1. Kết quả nguyên hàm I  x.ln xdx  là: 2 2 2 2 2 2 2 2 A. x x x x x x x x . ln 2   C B. . ln 2   C C. . ln 2   C D. . ln 2   C 2 4 2 4 4 2 4 2 Hướng dẫn giải Chọn A. 2 2 Vậy x x
I  x. ln xdx  . ln 2   C  2 4
Chú ý: chuyển lượng   1 x x t x 
bên cột 1 sang nhân với v  x 2 
ta thu được kết quả . Khi đó x 2 2 2
bên cột 1 còn lại 1, đạo hàm của nó bằng 0; bên cột 3 có nguyên hàm của x là x . 2 4
Bài tập 6.2. Kết quả nguyên hàm I   x    3 4
1 . ln 2x  dx là: A.  x
2x  x  ln 2x  3x  3x ln 2x  3x  6x ln 2x 2 3 2 3 2 2 2 
 6x  C 2 B.  x
2x  x  ln 2x  3x  3x ln 2x  3x  6x ln 2x 2 3 2 3 2 2 2 
 6x  C 2 C.  x
2x  x  ln 2x  3x  3x ln 2x  3x  6x ln 2x 2 3 2 3 2 2 2   6x  C 2 D.  x
2x  x  ln 2x  3x  3x ln 2x  3x  6x ln 2x 2 3 2 3 2 2 2   6x  C 2 Hướng dẫn giải Chọn B. Vậy   x I
2x  x  ln 2x  3x  3x ln 2x  3x  6x ln 2x 2 3 2 3 2 2 2   6x  C 2 Chú ý: Chuyển 3 , nhân với  2
2x  x  thu được 6x  3 x Chuyển 2 , nhân với  2
3x  3x  thu được 6x  6 . x Chuyển 1 , nhân với  2
3x  6x  thu được 3x  6 . x
Bài tập 7. Cho       1 x F x x
e là một nguyên hàm của hàm số   2x
f x e . Biết rằng hàm số f  x 
có đạo hàm liên tục trên  . Nguyên hàm của hàm số   2 ' x f x e là:
A. 2   x x e  C
B. 2   x x e  C C. 1  x x e  C D. 1  x x e  C Hướng dẫn giải Chọn A. Ta có      2x x 
    x    2x    2 ' 1 . . x  . x F x f x e e x e f x e f x e x e . Xét   2 ' x f x e dx  2 x 2     2 x u e du e dx Đặt    dv  f ' 
xdx v  f  x Do đó    2
. x  2   x x   2   1 x I f x e f x e dx xe x e  C Vậy     2 ' x  2   x I f x e dx x e  C
Dạng 5: Các bài toán thực tế ứng dụng nguyên hàm
1. Phương pháp giải
Ý nghĩa vật lí của đạo hàm:
Một chất điểm chuyển động theo phương trình S  S t , với S t là quãng đường mà chất điểm đó
đi được trong thời gian t, kể từ thời điểm ban đầu.
Gọi v t và at lần lượt là vận tốc tức thời và gia tốc tức thời của chất điểm tại thời điểm t, ta có:
v t  S 't và a t  v 't .
Từ đó ta có: S t  v
 tdt và vt  a  tdt . 2. Bài tập
Bài tập 1. Một vật chuyển động với gia tốc at 3   2
m / s  , trong đó t là khoảng thời gian tính t 1
từ thời điểm ban đầu. Vận tốc ban đầu của vật là. Hỏi vận tốc cảu vật tại giây thứ 10 bằng bao nhiêu? A. 10 m/s. B. 15,2 m/s. C. 13,2 m/s. D. 12 m/s. Hướng dẫn giải Chọn C.
Vận tốc của vật tại thời điểm t được tính theo công thức: v t  a  t 3 dt 
dt  3 ln t 1  C  t1
Vì vận tốc ban đầu (lúc t  0 ) của vật là v  6m / s nên: 0
v 0  3ln 0 1  C  6  C  6  v t  3ln t 1  6 .
Vận tốc của vật chuyển động tại giây thứ 10 là: v 10  3ln 10 1  6  13,2m / s .
Bài tập 2. Một vận động viên điền kinh chạy với gia tốc at 1 5 3 2   t  t  2
m / s  , trong đó t là 24 16
khoảng thời gian tính từ lúc xuất phát. Hỏi vào thời điểm 5 (s) sau khi xuất phát thì vận tốc của vận động viên là bao nhiêu? A. 5,6 m/s. B. 6,51 m/s. C. 7,26 m/s. D. 6,8 m/s. Hướng dẫn giải Chọn B.
Vận tốc v t chính là nguyên hàm của gia tốc at nên ta có:  
v t  a  t 1 5 1 5 3 2 4 3 dt   t  t dt   t  t  C    24 16  96 48
Tại thời điểm ban đầu t  0 thì vận động viên ở tại vị trí xuất phát nên vận tốc lúc đó là:
v  0  v 0 1 5 4 3  0   .0 
.0  C  0  C  0 . 0 96 48
Vậy công thức vận tốc là v t 1 5 4 3   t  t 96 48
Vận tốc của vận động viên tại giây thứ 5 là v 5  6,51 m / s .
Chú ý: Gia tốc của vật chuyển động là at 3   2
m / s  . Ta tính vt  a
 tdt , kết hợp với t 1
điều kiện vận tốc ban đầu v  6m / s . Suy ra công thức tính vận tốc v t tại thời điểm t và tính 0 được v 10 .
Bài tập 3. Một nhà khoa học tự chế tên lửa và phóng tên lửa từ mặt đất với vận tốc ban đầu là 20
m/s. Giả sử bỏ qua sức cản của gió, tên lửa chỉ chịu tác động của trọng lực. Hỏi sau 2s thì tên lửa
đạt đến tốc độ là bao nhiêu? A. 0,45 m/s. B. 0,4 m/s. C. 0,6 m/s. D. 0,8 m/s. Hướng dẫn giải Chọn B.
Xem như tại thời điểm t  0 thì nhà khoa học phóng tên lửa với vận tốc đầu 20 m/s. Ta có 0
s 0  0 và v 0  20 .
Vì tên lửa chuyển động thẳng đứng nên gia tốc trọng trường tại mọi thời điểm t là n s t 2  9,  8 m / s .
Nguyên hàm của gia tốc là vận tốc nên ta có vận tốc của tên lửa tại thời điểm t là v t  9,  8dt  9  ,8t  C  . 1
Do v 0  20 nên 9,
 8t  C  20  C  20  v t  9  ,8t  20 . 1 1  
Vậy vận tốc của tên lửa sau 2s là v 2  9
 ,8.2  20  0,4m / s . BÀI 2: TÍCH PHÂN
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I. ĐỊNH NGHĨA VÀ TÍNH CHẤT CỦA TÍCH PHÂN
1. Định nghĩa tích phân Định nghĩa
Chẳng hạn:   3
F x  x  C là một nguyên
Cho hàm số f  x liên tục trên đoạn a;b , với hàm của hàm số f x 2
 3x nên tích phân a  . b 1 f
 xdx  F x 1  F  1 F 0
Nếu F  x là nguyên hàm của hàm số f  x trên 0 0
đoạn a;b thì giá trị F b  F a được gọi là tích   3 C 3 1 0  C  1.
phân của hàm số f  x trên đoạn a;b .
Lưu ý: Giá trị của tích phân không phụ b
thuộc vào hằng số C. b Kí hiệu f
 xdx  F x  F b F a (1)
Trong tính toán, ta thường chọn C  0. a a
Công thức (1) còn được gọi là công thức Newton –
Leibnitz; a và b được gọi là cận dưới và cận trên của tích phân.
Chẳng hạn: Hàm số f  x 2
 x  2x 1 có
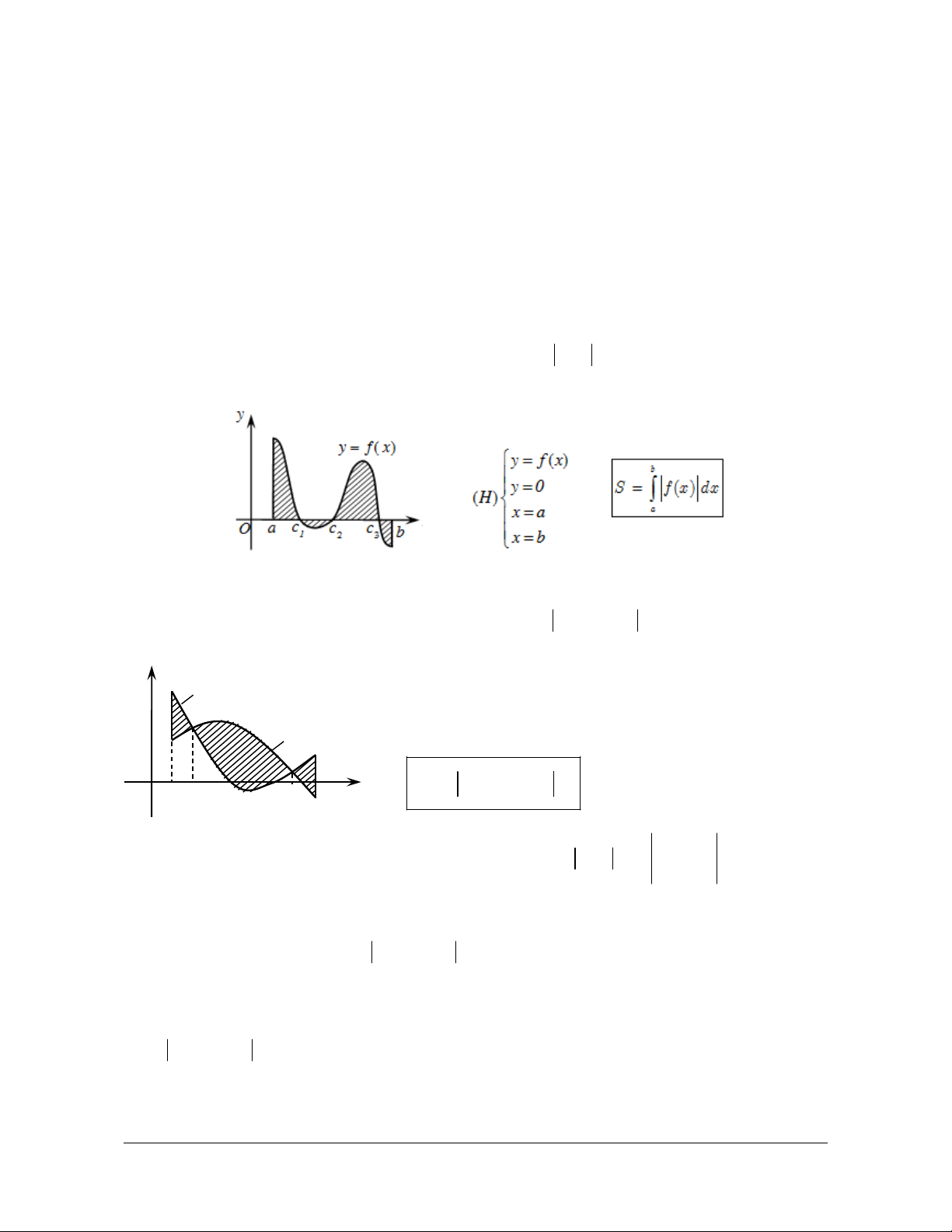
Ý nghĩa hình học của tích phân
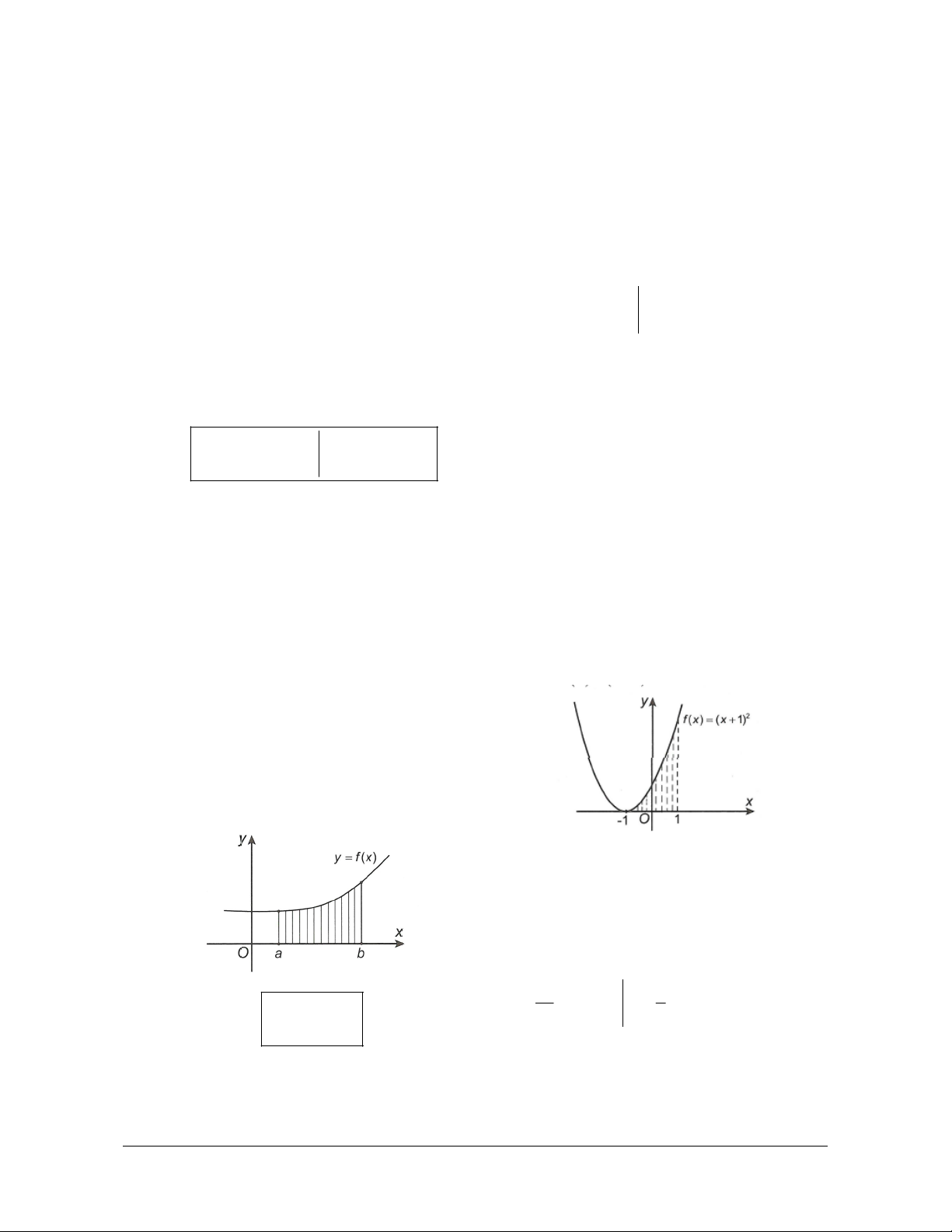
Giả sử hàm số y  f  x là hàm số liên tục và không đồ thị C và f  x   x  2 1  0 , với b x    .
âm trên đoạn a;b . Khi đó, tích phân f  xdx a
chính là diện tích hình phẳng giới hạn bởi đường
cong y  f  x , trục hoành Ox và hai đường thẳng
x  a, x  b, với a  . b
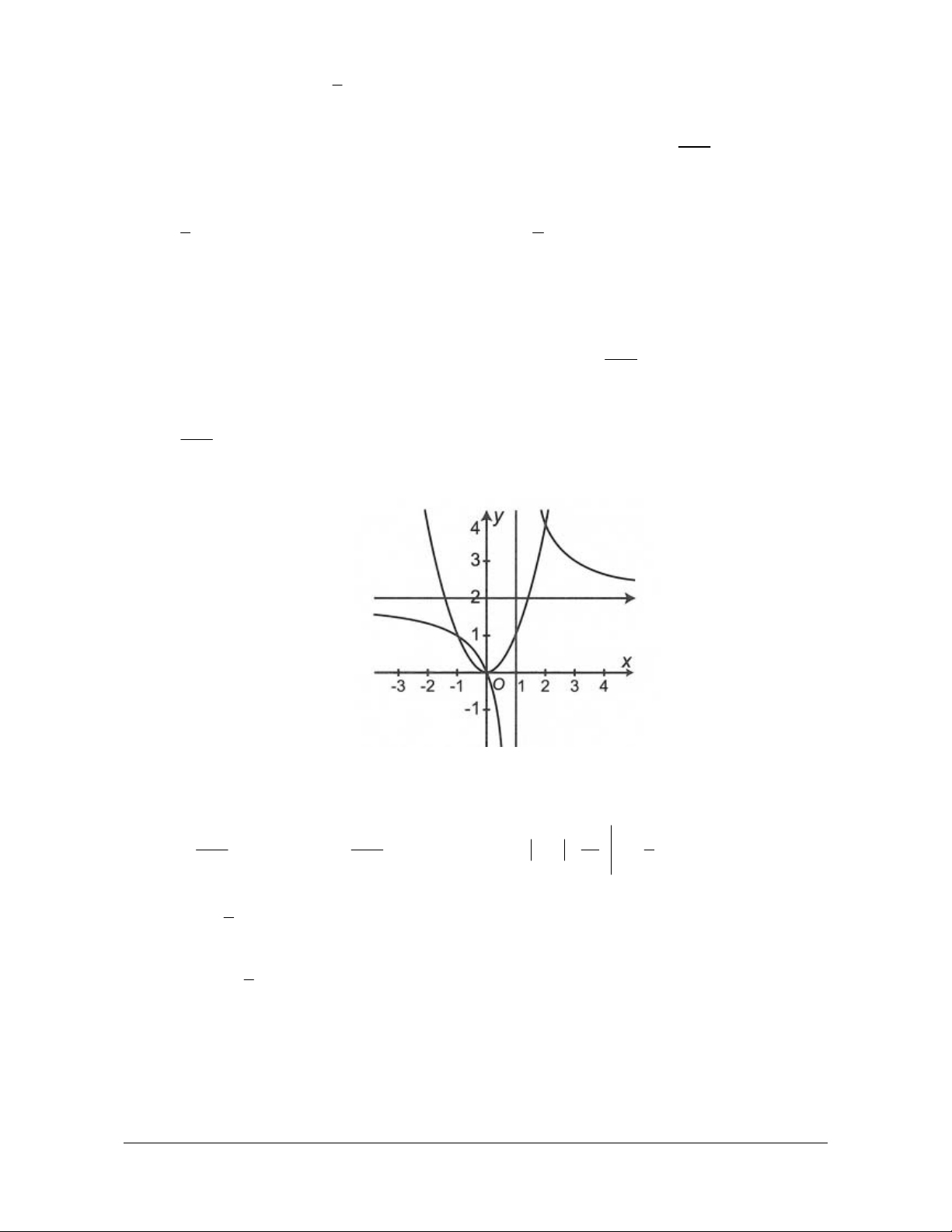
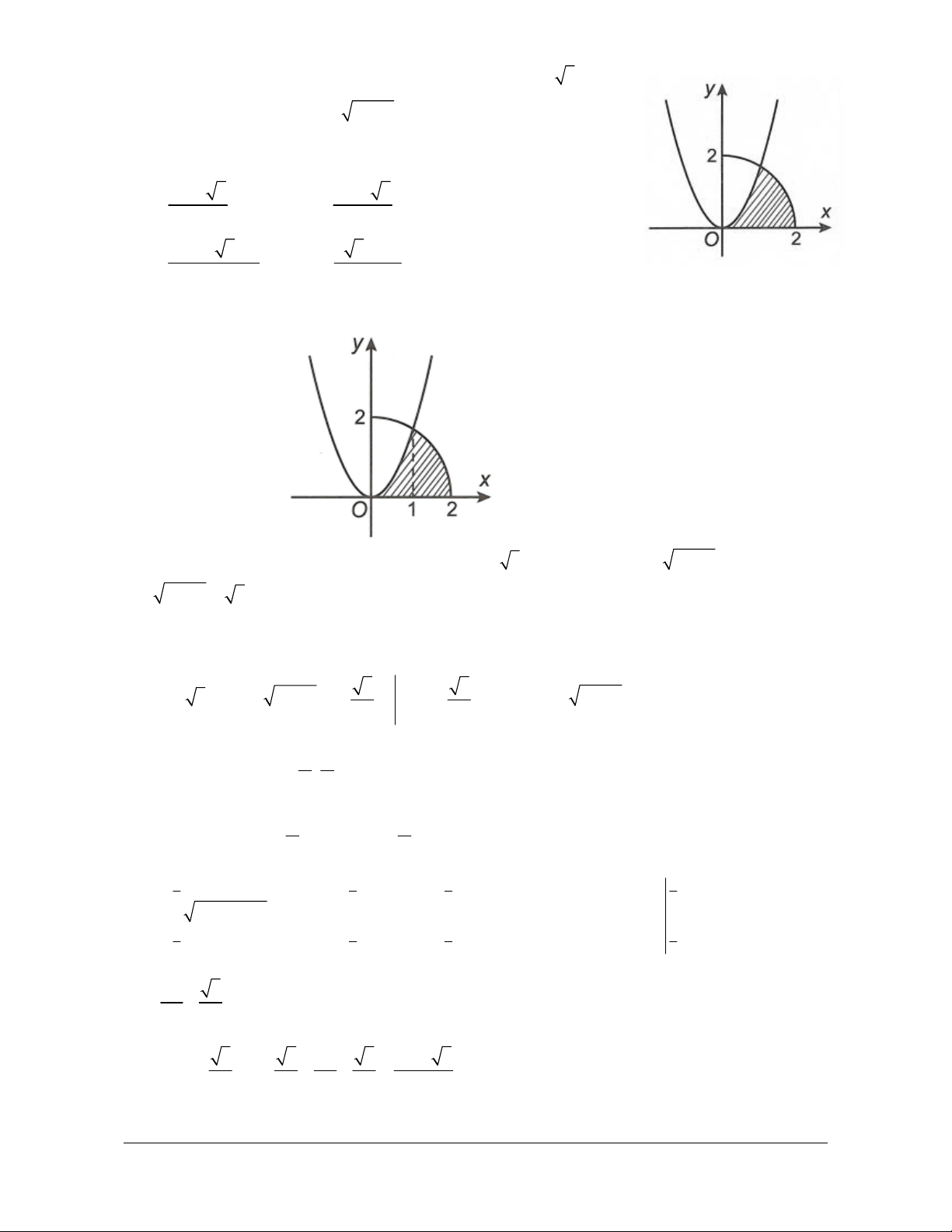
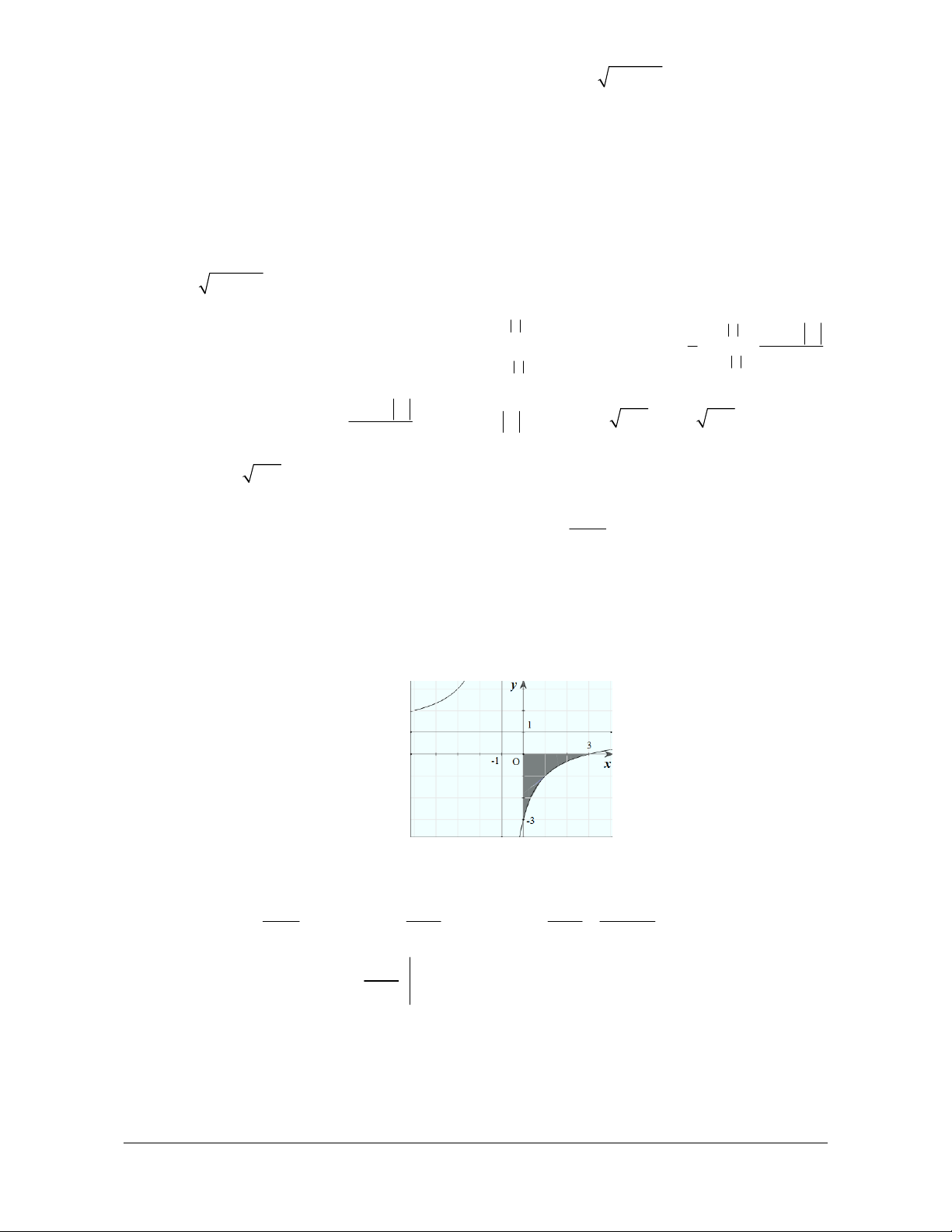
Diện tích “tam giác cong” giới hạn bởi C
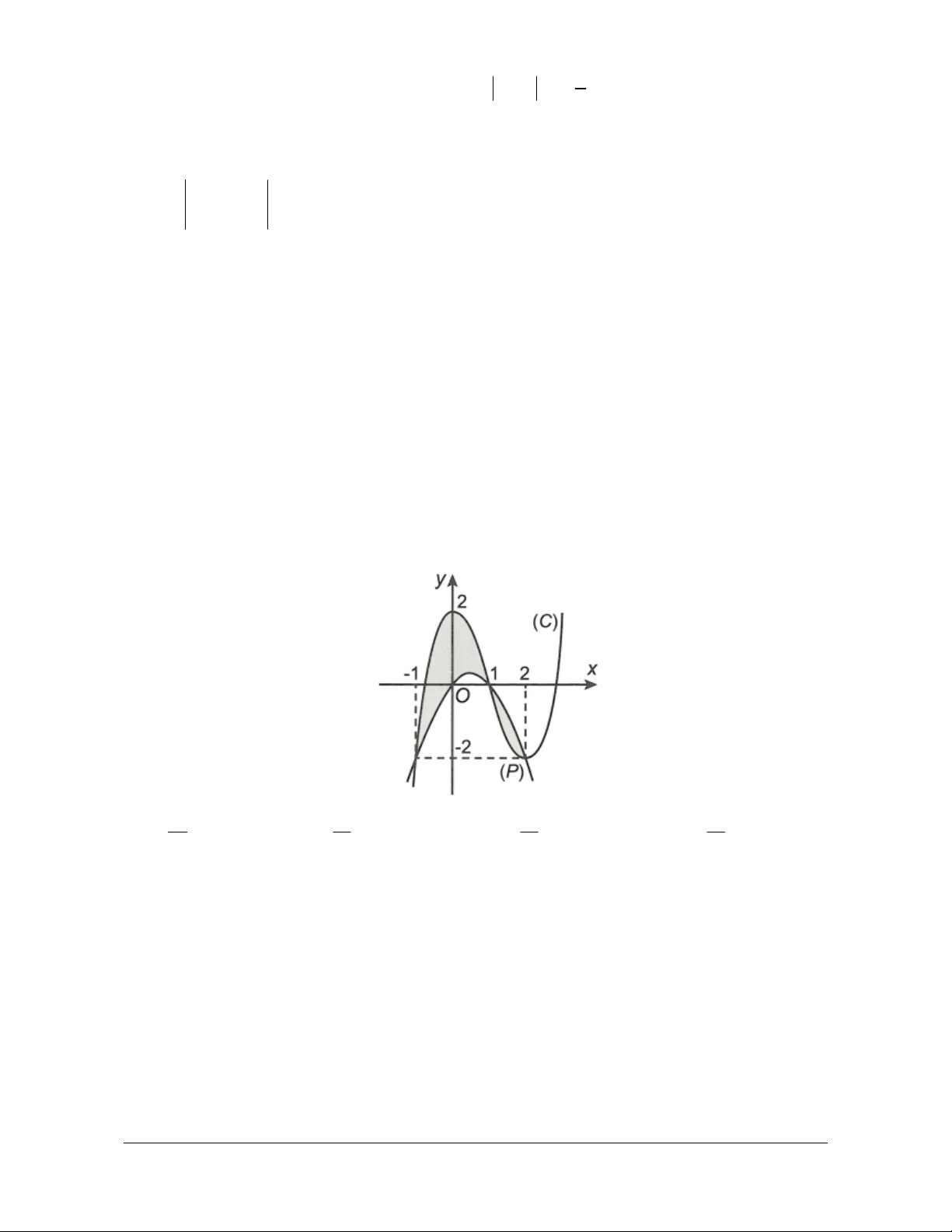
, trục Ox và hai đường thẳng x  1  và 1 1
x  1 là S 
f  x dx   2 x  2x    1dx 1  1  3 1  x  8 b 2
   x  x  . S  f  xdx  3 1   3 a
Lưu ý: Ta còn gọi hình phẳng trên là “hình thang cong”.
2. Tính chất cơ bản của tích phân
Cho hàm số f  x và g  x là hai hàm số liên tục
trên khoảng K, trong đó K có thể là khoảng, nửa
khoảng hoặc đoạn và a,b, c  K, khi đó: a
a. Nếu b  a thì f
 xdx  0
Chẳng hạn: Cho hàm số f  x liên tục, có a
đạo hàm trên đoạn  1  ;2 thỏa mãn
b. Nếu f  x có đạo hàm liên tục trên đoạn a;b f  
1  8 và f 2  1  . thì ta có: Khi đó b f 
 xdx  f x b f b f a 2 2 a a
f  x dx  f  x
 f 2  f   1  9   1 1  
Lưu ý: Từ đó ta cũng có b
f b  f a  f   xdx a b
và f a  f b  f   xdx a
c. Tính chất tuyến tính b b b k. f
 x .hgxdx  k f 
 xdx  .h g  xdx a a a
Với mọi k, h  . 
d. Tính chất trung cận b c b f
 xdx  f
 xdx  f
 xdx , với c ;ab a a c
e. Đảo cận tích phân a b f
 xdx   f  xdx b a b
f. Nếu f  x  0, x
 a;b thì f
 xdx  0 và a b f
 xdx  0 khi f x  0. a
g. Nếu f  x  g  x, x   ; a b thì b b f
 xdx  g  xdx a a
h. Nếu m  min f  x và M  max f  x thì a;b a;b b
mb  a  f
 xdx  M ba a
i. Tích phân không phụ thuộc vào biến, tức là ta luôn có b b b b f
 xdx  f
 tdt  f
 udu  f
  ydy ... a a a a
II. CÁC PHƯƠNG PHÁP TÍNH TÍCH PHÂN
1. Phương pháp đổi biến số Đổi biến dạng 1 b
Bài toán: Giả sử ta cần tính tích phân I  f
 xdx, trong a
đó ta có thể phân tích f  x  g u  xu x thì ta thực hiện Lưu ý: Phương pháp đổi biến số phép đổi biến số.
trong tích phân cơ bản giống như Phương pháp:
đổi biến số trong nguyên hàm, ở
+ Đặt u  u  x , suy ra du  u x . dx
đây chỉ thêm bước đổi cận. + Đổi cận: x a b u
u a u b b ub ub
+ Khi đó I  f
 xdx  g
 udu  Gu , với   ua a u a 
G u là nguyên hàm của g u. Đổi biến dạng 2 Dấu hiệu Cách đặt 2 2 a  x    
x  a sin t;t   ;  2 2    2 2 x  a a      x  ; t  ; \  0 sin t  2 2    2 2 a  x    
x  a tan t;t   ;    2 2  a  x    x  .c
a os 2t;t  0;   a  x  2  a  x    x  .c
a os 2t;t  0;   a  x  2 
x  ab  x   
x  a  b  a 2 sin t;t  0;  2   
2. Phương pháp tích phân từng phần b
Chú ý: Cần phải lựa chọn u và dv hợp lí
Bài toán: Tính tích phân I  u
 x.vxdx
sao cho ta dễ dàng tìm được v và tích phân a b b
Hướng dẫn giải vdu
 dễ tính hơn udv  . u   u a a  x du  u  xdx Đặt    dv  v 
xdx v  v  x b
Khi đó I  u.v b  . v du a 
(công thức tích phân từng a phần)
III. TÍCH PHÂN CÁC HÀM SỐ ĐẶC BIỆT
1. Cho hàm số f  x liên tục trên  ; a a. Khi đó a a Đặc biệt f
 xdx   f
 x f xdx  (1) a 0 a
+ Nếu f  x là hàm số lẻ thì ta có f
 xdx  0 (1.1) a a a
+ Nếu f  x là hàm số chẵn thì ta có f
 xdx  2 f
 xdx (1.2) a 0 a f  x 1 a và dx  f x dx   0  b   1 (1.3) x   1 b 2 a 0 b b
2. Nếu f  x liên tục trên đoạn a;b thì f
 xdx  f
 a b xdx a a   2 2
Hệ quả: Hàm số f  x liên tục trên 0;  1 , khi đó: f
 sin xdx  f
 cos xdx 0 0 b b a  b
3. Nếu f  x liên tục trên đoạn a;b và f a  b  x  f  x thì xf
 xdx  f  xdx 2 a a
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Tính tích phân bằng cách sử dụng định nghĩa, tính chất
1. Phương pháp giải
Sử dụng các tính chất của tích phân.
Sử dụng bảng nguyên hàm và định nghĩa tích phân để tính tích phân. 2. Bài tập 2 dx
Bài tập 1: Biết tích phân I 
 a 2  b 3  c 
, với a,b, c   . Giá trị biểu thức x 1 x  x x 1 1  
P  a  b  c là A. P  8. B. P  0. C. P  2. D. P  6.
Hướng dẫn giải Chọn B.
Ta có x 1  x  0, x  1;2 nên 2 2 2 x 1  x 1 1 I  dx  dx  dx    
2 x 2 x1 2 x. x 1 x x 1 1 1 1 1
 4 2  2 3  2. Suy ra a  4,b  c  2
 nên P  a  b  c  0.
Nhân liên hợp x 1  x.
Bài tập 2: Cho hàm số f  x thỏa mãn f   1
2   và       2 f x x f x  3
 với mọi x  . Giá trị f   1 bằng A. f   2 1  . B. f   3 1  . C. f   2 1   . D. f   1 1  . 3 2 3 3
Hướng dẫn giải Chọn C.
Từ       2 f x x f x  
 (1), suy ra f  x  0 với mọi x1;2.
Suy ra f  x là hàm không giảm trên đoạn 1;2 nên f  x  f 2  0 , x  1;2 . f  x
Chia 2 vế hệ thức (1) cho    2 f x    ta được  x, x   1;2 . (2) 2    f x  
Lấy tích phân 2 vế trên đoạn 1;2 hệ thức (2), ta được 2 f  x 2 2 2 2  1   x  1 1 3 dx  xdx          .    f   x 2  f    x 1   2 1  f 1 f 2 2 1 1     Do f   1
2   nên suy ra f   2 1   . 3 3
Chú ý rằng đề bài cho f 2 , yêu cầu tính f  
1 , ta có thể sử dụng nguyên hàm để tìm hằng số C.
Tuy nhiên ta cũng có thể dựa vào định nghĩa của tích phân để xử lí. 1 
Bài tập 3: Cho hàm số f  x xác định trên  \   thỏa mãn f x 2 
và f 0  1, f   1  2 2 2x 1 . Khi đó f   1  f 3 bằng A. 1   ln15. B. 3  ln 5. C. 2   ln 3. D. 1   ln15.
Hướng dẫn giải
Chọn A. 0 0
Ta có f  x dx  f 0  f   
1 nên suy ra f  
1  f 0  f 
 xd .x 1 1  0 1 f 
 xd .x 1  Tương tự ta cũng có 3
f 3  f   1  f   xdx 1 3  2   f   xdx. 1 0 3 0 3 Vậy f   1  f 3  1   f 
 xdx  f 
 xdx  1   ln 2x 1  ln 2x 1 . 1  1 1  1 Vậy f   1  f 3  1   ln15.
Bài tập 4: Cho hàm số f  x có đạo hàm liên tục trên đoạn 0;  1 thỏa mãn f   1  0 , 1 1 1  f 
 x 2 dx  7  và 3 x . f   xdx  1
 . Giá trị I  f
 xdx là 0 0 0 7 7 A. 1. B. . C. . D. 4. 4 5
Hướng dẫn giải
Chọn C. 1 2 Ta có  f 
 x dx  7  (1). 0 1 1 1 6 6
x dx   49x dx  7   (2). 7 0 0 1 và 3 14x . f   xdx  1  4 (3). 0
Cộng hai vế (1), (2) và (3) suy ra 1  f   x 2 3
 7x  dx  0  
mà  f  x 2 3  7x   0   0  f x 3  7  x . 4 7x
Hay f  x    C. 4 f   7 7
1  0    C  0  C  . 4 4 4 7x 7
Do đó f  x    . 4 4 1 1 4  7x 7  7 Vậy f
 xdx    dx  .  4 4  5 0 0
Bài tập 5: Cho f  x, g  x là hai hàm số liên tục trên đoạn  1;  
1 và f  x là hàm số chẵn, g  x 1 1 1 1
là hàm số lẻ. Biết f
 xdx  5; g
 xdx  7. Giá trị của A  f
 xdx g
 xdx là 0 0 1 1  A. 12. B. 24. C. 0. D. 10.
Hướng dẫn giải
Chọn D. 1 1
Vì f  x là hàm số chẵn nên f
 xdx  2 f
 xdx  2.5 10 1  0 1
Vì g  x là hàm số lẻ nên g
 xdx  0 . 1 Vậy A  10. 1 xdx Bài tập 6: Cho  a  bln 3   
với a, b là các số hữu tỉ. Giá trị của a b bằng 2x  2 0 1 5 1 1 1 A. . B.  . C. . D. . 12 3 4 12
Hướng dẫn giải
Chọn D. 1 1 1 xdx 1 2x 1 1 1  1 1    Ta có  dx     dx     2x  2 1 2 2x  2 1
2  2x 1 2x   2  0 0 0 1   1 1  1 1          x  ln 2x  1 1 ln 3. 4 2 1 4   0 6 4  1 1 1
Vậy a   ,b   a  b  . 6 4 12 3 2x  3 Bài tập 7: Cho
dx  a ln 2  b ln 3, 
với a,b  . Giá trị biểu thức 2
a  ab  b là 2 x  x 2 A. 11. B. 21. C. 31. D. 41.
Hướng dẫn giải 3 3 3 2x  3 2x 1 2  2x 1 2  Ta có dx  dx   dx    2 2  2 2  x  x x  x
 x  x x  x  2 2 2 3  2x 1 2 2     dx   
ln x  x 2ln x 2ln x1 3 2  5  ln 2  4ln 3 2
 x  x x x 1 2 2 a  5  2  
 a  ab  b  41. b   4
Chọn D. 2 5x  6
Bài tập 8. Biết rằng tích phân
dx  a ln 2  b ln 3  c ln 5, 
với a,b, c là các số nguyên. Giá 2 x  5x  6 1
trị biểu thức S  a  bc là bao nhiêu? A. S  62.  B. S 10. C. S  20. D. S  10. 
Hướng dẫn giải
Chọn B. 2 2 2 5x  6 5x  6  9 4  Ta có dx  dx   dx    2   x  5x  6 x  2 x  3
 x  3 x  2  1 1    1
 9ln x  3  4ln x  2  2  9ln 5  4ln3 26ln 2. 1
Suy ra a  26,b  4, c  9. Vậy S  a  bc  26   4.9 10.  3 2 cos x  sin . x cos x 1 Bài tập 9: Cho
dx  a  b ln 2  c ln 1 3 
, với a,b, c là các số hữu tỉ. Giá 4 3     cos x sin . x cos x 4 trị abc bằng A. 0. B. 2.  C. 4.  D. 6. 
Hướng dẫn giải
Chọn C.   3 2 3 2 2 cos x  sin . x cos x 1 2cos x  sin .
x cos x  sin x Ta có dx  dx   4 3 2   cos x sin . x cos x  cos x  2 cos x  sin . x cos x 4 4   3 2 3 2
2  tan x  tan x
2  tan x  tan x  dx  d tan x   2    cos x 1 tan x  1 tan x   4 4   3 2   3 2 tan x  3  tan x        
x d tan x 2ln tan x 1 1 tan   2     4 4 4
1 2ln 2  2ln 3  1. Suy ra a 1,b  2,c  2 nên abc  4.  x e  m, khi x  0 
Bài tập 10: Cho hàm số f  x   liên tục trên  . 2
2x 3 x , khi x  0 1 Biết
f  xdx  ae  b 3  ca,b,c  
 . Tổng T  a  b  3c bằng 1  A. 15. B. 10.  C. 19  . D. 17  .
Hướng dẫn giải
Chọn C.
Do hàm số liên tục trên  nên hàm số liên tục tại x  0
 lim f x  lim f x  f 0  1 m  0  m  1. x 0 x 0   1 0 1 Ta có f
 xdx  f
 xdx f
 xdx  I  I 1 2 1  1  0 I 
2x 3  x dx  
 3 x 1 d 3 x  2  3 x  0 0 0 16 2 2 2 2 2 2 3  x  2 3  . 1 1  1  3 1  3
   x  1   x I e dx e  x 1 1  e  2. 2 0 0 1 22 22 Suy ra f
 xdx  I  I  e2 3  . Suy ra a 1;b  2;c   . 1 2 1 3 3
Vậy T  a  b  3c 1 2  22  1  9.  2 cos x  2 cos x Bài tập 11: Biết dx  m  . Giá trị của dx  bằng 1 3x 1 3x     A.   . m B.  . m C.   m. D.  . m 4 4
Hướng dẫn giải
Chọn A.  2  2 cos x cos x  1  Ta có 2 dx 
dx  cos xdx   x dx        x x 1 cos2  . 1 3 1 3 2      2 cos x Suy ra dx    . m  1 3x 
Dạng 2: Tính tích phân bằng phương pháp đổi biến
1. Phương pháp giải
Nắm vững phương pháp đổi biến số dạng 1 và dạng 2, cụ thể: Đổi biến dạng 1 b
Bài toán: Giả sử ta cần tính I  f
 xd ,x trong đó ta có thể phân tích f x  guxux. a
Bước 1: Đặt u  u  x, suy ra du  u x . dx
Bước 2: Đổi cận x a B u
u a u b Bước 3: Tính b ub ub
I  f  x dx 
g u du G    u   ua a u a 
Với G u là một nguyên hàm của g u . Đổi biến dạng 2 b
Bài toán: Giả sử ta cần tính I  f
 xdx, ta có thể đổi biến như sau: a
Bước 1: Đặt x   t, ta có dx  t dt.
Bước 2: Đổi cận x a b t  
Bước 3:    Tính I  f
 t.tdt  g
 tdt  Gt   
Với G t là một nguyên hàm của g t. Dấu hiệu Cách đặt 2 2 a  x    
x  a sin t,t   ;  2 2    2 2 x  a a      x  ,t  ; \   0 sin t  2 2    2 2 a  x    
x  a tan t,t   ;    2 2  a  x    x  .c
a os 2t,t  0;   a  x  2  a  x    x  .c
a os 2t,t  0;   a  x  2 
x  ab  x   
x  a  b  a 2 sin t,t  0;  2    2. Bài tập mẫu  2 cos x Bài tập 1: Biết
dx  a ln 2  b ln 3, 
với a,b là các số nguyên. 2
sin x  3sin x  2 0
Giá trị của P  2a  b là A. 3. B. 7. C. 5. D. 1.
Hướng dẫn giải
Chọn A.   2 2 cos x 1 Ta có dx  d sin x   2
sin x  3sin x  2
sin x 1 sin x  2 0 0       2 1 1      d 
 sin x  ln sin x 1  ln sin x  2  2
 sin x 1 sin x  2  0 0
 ln 2  ln1 ln 3 ln 2  2ln 2  ln 3
Suy ra a  2,b  1
  2a  b  3. ln 2 dx 1
Bài tập 2: Biết I  
a  b  c 
, với a,b, c là các số nguyên tố. x  x ln ln ln  0 e  3e  4 c
Giá trị của P  2a  b  c là A. P  3.  B. P  1.  C. P  4. D. P  3.
Hướng dẫn giải
Chọn D. x ln 2 dx ln 2 e dx Ta có I   .   x  x 2 0 0 e  3e  4 x e  4 x e  3 Đặt x x
t  e  dt  e d . x
Đổi cận x  0  t  1, x  ln 2  t  2. Khi đó 2 2 1 1 2  1 1  1 t 1 1 I  dt   dt  ln  ln 3  ln 5  ln 2 .   2     1 1 t  4t  3 2
 t 1 t  3  2 t  3 1 2
Suy ra a  3,b  5, c  2 . Vậy P  2a  b  c  3.  6 dx a 3  b Bài tập 3: Biết   , với a,b ,  c  
 và a, b, c là các số nguyên tố cùng nhau. 1 sin x c 0
Giá trị của tổng a  b  c bằng A. 5. B. 12. C. 7. D. 1. 
Hướng dẫn giải Chọn A. 1    x   2 x  2 cos 1 tan 6 6 6 6 dx dx   Ta có 2  2 I dx      d . x     2 2 2 1 sin x 0 0  x x  0  x  0  x  cos  sin 1 tan 1 tan        2 2   2   2  x  x  Đặt 2
t  1 tan  2dt  1 tan d . x   2  2  
Đổi cận x  0  t  1; x   t  3 3. 6 3 3 3 3 2dt 2  3  3 I     .  2 t t 1 3 1
Suy ra a  1,b  3,c  3 nên a  b  c  5. Lưu ý: 2  x x   x
1 sin x  sin  cos .  
 Chia tử và mẫu cho 2 cos .  2 2     2  1 2
Bài tập 4: Cho hàm số y  f  x liên tục trên  và f
 2xdx 8. Giá trị của I  xf
  2xdx là 0 0 A. 4. B. 8. C. 16. D. 64.
Hướng dẫn giải
Chọn B. Đặt 2
x  2u  2xdx  2du  xdx  du.
Đổi cận x  0  u  0, x  2  u  1. 1 1 Khi đó I  f
 2udu  f
 2xdx 8. 0 0
Bài tập 5: Cho hàm số y  f  x xác định và liên tục trên 0; sao cho 2 
 x  x x xf e f e  1;
e f  x.ln x
với mọi x 0; . Giá trị của I  dx  là x e 1 2 1 3 A. I   . B. I   . C. I  . D. I  . 8 3 12 8
Hướng dẫn giải
Chọn C.  x x x x 1
Với x 0; ta có x  xf e   f e  1 f e  2 2   1 . x 1 x dx Đặt ln t
x  t  x  e  dt  . x 1
Đổi cận x  e  t  ; x  e  t  1. 2 1 1 t 1
Khi đó I  t. f
 e dt  t1tdt  . 12 1 1 2 2 
2 3sin x  cos x 1  1 b Bài tập 6: Biết dx 
ln 2  b ln 3  c , 
 ,bc. Giá trị của là
2sin x  3cos x 13 c 0 22 22 22 22 A. . B. . C. . D. . 3 3 3 13
Hướng dẫn giải
Chọn A. 3sin x  cos x
m 2sin x  3cos x  n2cos x  3sin x Phân tích 
2sin x  3cos x
2sin x  3cos x
2m 3nsin x 3m  2ncos x 
2sin x  3cos x
2m  3n  3 3 11
Đồng nhất hệ số ta có   m  ;n   . 3
 m  2n  1  13 13   3 11 2 2
2sin x 3cos x 2cos x 3sin x 3sin x  cos x Suy ra 13 13 dx  . dx  
2sin x  3cos x
2sin x  3cos x 0 0   2  2
 3 11 2cos x  3sin x  3 x  x   . dx   x 11 2cos 3sin 2  . dx  
13 13 2sin x 3cos x    13 0
13 2sin x  3cos x 0 0  2 3
11 d 2sin x  3cos x 3 11    2   dx  
ln 2sin x  3cos x  26 13
2sin x  3cos x 26 13 0 0  11 b  3 11 11     13 b 11 26 22 ln 2  ln 3. Do đó    .  26 13 13 3 c 13 3 3 c   26  4
Bài tập 7: Cho hàm số f  x liên tục trên  và thỏa mãn tan . x f   2
cos xdx  2 và 0 2 e f  2 ln x 2 f 2x dx  2 
. Giá trị của I  dx  là x ln x x e 1 4 A. 0. B. 1. C. 4. D. 8.
Hướng dẫn giải
Chọn D.   4 4 sin . x cos x Đặt A  tan . x f   2
cos xdx  2  .f   2 cos x dx  2. 2  cos x 0 0. 1 Đặt 2
t  cos x  dt  2
 sin x cos xdx   dt  sin x cos x . dx 2  1 1 f t
Đổi cận x  0  t  1 và x 
 t  . Khi đó A  dt  4.  4 2 t 1 2 2 e f ln x 2 2 e ln . x f  2 ln x Đặt B  dx  2  dx  2.   2 x ln x x ln x e e 4 f t
Tương tự ta có B  dt  4.  t 1 2 f 2x 1 Giá trị của I  d . x 
Đặt t  2x  dx  dt. x 2 1 4 1 1
Đổi cận x   t  và x  2  t  4. 4 2 4 f t 1 f t 4 f t Khi đó I  dt  dt  dt  4  4  8    t t t 1 1 1 2 2 1 1 Bài tập 8: Cho
dx  a  b; 
với a,b là các số nguyên. Giá trị của biểu thức
x 3x  3 0 1 b a a  b bằng A. 17. B. 57. C. 145. D. 32.
Hướng dẫn giải
Chọn A. 1 1 1 1 dx Giá trị của I  dx  .  
x 3x   x  3 1 x  2 3 0 0 1 x 1 x  3 2 dx Đặt t   2tdt  dx   tdt. x 1 x  2 1 x  2 1
Đổi cận x  0  t  3, x  1  t  2. 1 2 3 3 1 dx 1 Ta có I   t
 dt  dt  t  3  2.    2   x  3 x  t 0  1 2 3 2 x 1 1 1 Mà
dx  a  b 
nên suy ra a  3,b  2.
x 3x  3 0 1
Từ đó ta có giá trị b a 2 3
a  b  3  2  17. 1 x 1  a  Bài tập 9: Cho dx  ln  b 
, với a,b là các số nguyên tố. Giá trị của biểu thức 3   x 1 a  b 1  2
P  2a  b bằng A. 12. B. 10. C. 18. D. 15.
Hướng dẫn giải Chọn B. 1 1 1 1 3 x x 1 x 1 Biến đổi I  dx  dx  dx  . dx     . 3 4 x 1  1  x 1 1 3 1 1 1 1 x 1   . x 1 1 3 2 2 2 3 2 3  x  x x 1 1 3 1 Đặt 2 u  1  u  1  2udu   dx và 3 x  . 3 3 4 x x x 2 u 1 1
Đổi cận x   u  3; x  1 u  2. 2 2udu 3 3 3 2 du 1 u 1 1  3  Ta có 3 I      ln  ln  2 .    2 u   2 1 .u 3 u 1 3 u 1 2 3  2  2 2
Suy ra a  3,b  2. Vậy P  2a  b 10.
Dạng 3: Tính tích phân bằng phương pháp tích phân từng phần 2 ln x b
Bài tập 1. Cho tích phân I 
dx   a ln 2 
với a là số thực b và c là các số dương, đồng thời x c 1
b là phân số tối giản. Giá trị của biểu thức P  2a 3bc là c A. P  6. B. P  5. C. P  6.  D. P  4.
Hướng dẫn giải Chọn D.  dx u   ln x du     Đặt x  dx   . dv  1  2  x v   x 2 2 2 ln x 1  ln x 1   1 ln 2 Khi đó I   dx     .  2   x 1 x  x x  1 2 2 1 1 
Suy ra b  1,c  2, a 
. Do đó P  2a  3b  c  4. 2 + Ưu tiên logarit. u   ln x  + Đặt  dx . dv   2  x  4 x Bài tập 2: Biết
dx  a  b ln 2, 
với a,b là các số hũu tỉ. Giá trị của T 16a  8b là 1 cos 2x 0 A. T  4. B. T  5. C. T  2. D. T  2. 
Hướng dẫn giải Chọn A.    4 4 4 x x 1 x Đặt A  dx  dx  . dx    2 2 1 cos 2x 2cos x 2 cos x 0 0 0 u
  x  du  dx  Đặt  1 dv 
dx  v  tan x  2  cos x Khi đó     4 1 1      4 A  x tan x  tan xdx     
xtan xln cos x  4  2 0 2  0 0       1   2  1   1   1    ln    ln 2   ln 2.     2 4 2 2    4 2  8 4 1 1 
Vậy a  ,b 
do đó 16a  8b  2  2  4. 8 4 + Biến đổi 2 1 cos 2x  2cos . x + Ưu tiên đa thức. u  x  + Đặt  1 . dv  dx  2  cos x 1 Bài tập 3: Cho 2x 2
I  xe dx  . a e  b 
với a,b   . Giá trị của tổng a  b là 0 1 1 A. . B. . C. 0. D. 1. 2 4
Hướng dẫn giải
Sử dụng phương pháp từng phần. du  dx u   x  Đặt    x 1 . 2 2 x dv  e dx v  e  2 1 1 1 1 1 1 1 x 1 x 1 x 1 x 1 1 Khi đó 2 2 2 2 2 I  . u v  . v du  . x e  e dx  . x e  e  e  .   0 2 0 2 2 0 4 0 4 4 0 0 1 1 Suy ra 2 2 .
a e  b  e  . 4 4 1 1 1
Đồng nhất hệ số hai vế ta có a  ,b  . Vậy a  b  . 4 4 2
Chọn A. + Ưu tiên đa thức. u   x + Đặt  . 2x dv  e dx 2
Bài tập 4: Cho hàm số f  x liên tục, có đạo hàm trên  , f 2 16 và f
 xdx  4. Tích phân 0 4  x  xf  dx    bằng  2  0 A. 112. B. 12. C. 56. D. 144.
Hướng dẫn giải
Chọn A. x
Đặt t   x  2t  dx  2dt. 2
x  0  t  0 4 2 2  x  Đổi cận  . Do đó xf  dx  4tf    
 tdt  4xf  
xd .x
x  4  t  2  2  0 0 0 u  4x  du  4dx  Đặt    dv  f  
xdx v  f  x. Suy ra 2 2 2 2 4xf  
xdx  4xf 
x  4 f 
 xdx 8f 24 f
 xdx 8.164.4 112. 0 0 0 0 
4 ln sin x  2cos x Bài tập 5. Cho
dx  a ln 3  b ln 2  c 
với a,b, c là các số hữu tỉ. 2 cos x 0
Giá trị của abc bằng 15 5 5 17 A. . B. . C. . D. . 8 8 4 8
Hướng dẫn giải
Chọn A. u
  ln sin x  2cos x  cos x  2sin x  du  dx Đặt  dx   sin x  2cos x . dv   2  
v  tan x  2 cos x Khi đó  
4 ln sin x  2cos x  4    x  x dx
tan x  2ln sin x  2cos x cos 2sin 4  dx  2 cos x 0 cos x 0 0  4  3 2   3ln 
  2ln 2  1 2tan xdx  2    0 7 
 3ln 3 ln 2  x  2ln cos x  4 2 0 7  2 5   3ln 3  ln 2   2ln  3ln 3  ln 2  . 2 4 2 2 4 5 1
Suy ra a  3,b   , c   . Vậy abc  18. 2 4 2 1 p x p
Bài tập 6. Biết x  2 1 x q e dx  me  , n trong đó , m ,
n p, q là các số nguyên dương và là phân q 1
số tối giản. Giá trị của T  m  n  p  q là A. T  11. B. T 10. C. T  7. D. T  8.
Hướng dẫn giải
Chọn B. Ta có 2 1 2 1 2 1 2 1  2 x x x x  1 x
  2  2  1 x  2  1 x  2 x I x e dx x x e dx x e dx xe . dx  1 1 1 1 2 1 2 1 2 2 1 2 1 x x x 1 x  1   x  Xét I   2 x   2 2 2 1 x e dx  x . x e . dx  x . x e d x   x x d e 1        2 x  x  1 1 1 1   1 2 2 1     2 x x     2 1 2 2 1 2 x x x x x   2 x x e e d x x e xe dx  1 1 1 1 2 1 1 2 1 2 3 x   2 x 2 x x x x 2
 I  2xe dx  x e  I  x e  4e 1 1  1 1 1
 m  4, n  1, p  3, q  2.
Khi đó T  m  n  p  q  4 1 3  2  10. m
Bài tập 7. Tìm số thực m  1 thỏa mãn ln x   1 dx  m. 1 A. m  2e. B. m  e. C. 2 m  e . D. m  e 1. Hướng dẫn giải Chọn B m m m A  ln x   1 dx  ln xdx  dx   1 1 1 m I  ln xdx 1  1 u  ln x du  dx Đặt    x dv  dx v  x m m  I  x ln x  dx  1 1   m m e
A  x ln x  m ln m  m  . 1  m  0 k
Bài tập 8. Đặt I  ln dx, e
k nguyên dương. Ta có I  e  2 khi: k 1 x k
A. k 1;  2 .
B. k 2;  3 . C. k 4;  1 . D. k 3;  4 . Hướng dẫn giải Chọn A  k  1 u   ln du   dx e  k e  Đặt  x   x  I  .l x n + dx  e 
k   I  e  2 k      1 ln 1 k  1  x  dv  dx v  x 1    e   e 3 2
1 ln k 1  e  2  ln k   ln k  1 e 1 e 1
Do k nguyên dương nên k 1;  2 . 1
Bài tập 9. Tìm m để      xe x m dx e. 0 A. m  0. B. m  e. C. m  1. D. m  e. Hướng dẫn giải Chọn C Đặt u  x  m du  dx    x x dv  e dx v  e 1 1  I  e
 x mdx  e x m1  e dx  e  x  m  1 x x x x 1  me  m 1 0 0 0 0
Mặt khác: I  e  me  m 1  e  me   1  e 1  m  1.
Dạng 4: Tích phân chứa dấu giá trị tuyệt đối 1. Phương pháp b
Bài toán: Tính tích phân I  g  xdx a
( với g ( x ) là biểu thức chứa ẩn trong dấu giá trị tuyệt đối) PP chung:
Xét dấu của biểu thức trong dấu giá trị tuyệt đối trên  ; a b
Dựa vào dấu để tách tích phân trên mỗi đoạn tương ứng ( sử dụng tính chất 3 để tách)
Tính mỗi tích phân thành phần. b
Đặc biệt: Tính tích phân I  f (x) dx  a Cách giải Cách 1:
+) Cho f (x)  0 tìm nghiệm trên  ; a b
+) Xét dấu của f ( x) trên  ;
a b, dựa vào dấu của f (x) để tách tích phân trên mỗi đoạn tương ứng
( sử dụng tính chất 3 để tách)
+) Tính mỗi tích phân thành phần. Cách 2:
+) Cho f (x)  0 tìm nghiệm trên  ;
a b giả sử các nghiệm đó là x ; x ;...x 1 2 n
( với x  x  ...  x ). 1 2 n 1 x 2 x 3 x b Khi đó I 
f (x) dx 
f (x) dx 
f (x) dx  ...  f (x) d     x a 1 x 2 x n x 1 x 2 x 3 x b
 I  f (x)dx 
f (x)dx 
f (x)dx  ...  f (x)d     x a 1 x 2 x n x
+) Tính mỗi tích phân thành phần 2. Bài tập 2 Bài tập 1: 2 a           a S x x 2 dx , a, b
, là phân số tối giản. Giá trị a  b bằng b b 1  A. 11. B. 25. C. 100. D. 50. Hướng dẫn giải Chọn A            2 2 2  3 2  2 2 x x S x x 2 dx x x 2 dx     2x  3 2  1  1    1   8 4   1 1  9       4       2    3 2   3 2  2  Bài tập 2: I  1  sin 2xdx  a a , * a    . Hỏi 3 a là bao nhiêu? 0 A. 27. B. 64. C. 125. D. 8. Hướng dẫn giải Chọn D    Ta có:     2 1 sin 2x sin x cos x
 sin x  cos x  2 sin x    .  4      Với 3 x  0;   x    ; .     4  4 4         + Với x    ;0   thì sin x     0 4  4   4        + Với 3 x   0;   thì sin x     0 4  4   4   4         I   2 sin x  dx  2 sin x  dx        2 2.  4   4  0  4 5 2  2 1 Chọn 3: Biết  d  4  ln 2  ln 5,  x I x a b
với a, b là các số nguyên. Giá trị S  a  b bằng x 1 A. 9. B. 11. C. 5. D. 3.  Hướng dẫn giải Chọn B 5 2 5 2 x  2 1 2 x  2 1 2 x  2 1 Ta có: I  dx  dx  dx    x x x 1 1 2 2 22  x 5 1 2 x  2 1 2 5  2x 5 2x  3  dx  dx  dx  dx     1 2 x x x x 1 2 2  5 5   3    x dx  2  dx       
5ln x  x2 2x3ln x 5 1 2 1 2  x   x  a  8
 8ln 2 3ln5  4  
 a  b  11. b   3  2
Bài tập 4: Cho tích phân 1  cos 2xdx  
ab và a  b  2  2 2. Giá trị của a và b lần lượt là 0 a   2  A.    . B. a 2 2  . b  2 2 b  2   a  2   a  2 C. a 2 2 a 2 2    . D.    . b  2 b  2 2 b  2 b  2 2 Hướng dẫn giải Chọn D 2 2  2 1  cos 2xdx  2 sin x dx  2 sin xdx     2  sin xdx 0 0 0   2   2 cos x  2 cos x  4 2. 0  ab  4 2   a  2 2        a 2 2 X 2 2 2 X  4 2  0     . a  b  2  2 2 b  2 b  2 2 1  1 
Bài tập 5: Tính tích phân I  x x - a dx, a  0 
ta được kết quả I  f (a) . Khi đó tổng f (8)  f    2  0 có giá trị bằng: A. 2 4 . B. 9 1 . C. 17 . D. 2 9 1 2 4 2 17 Hướng dẫn giải Chọn B 1 1 3 2  x ax  a 1 8 1 11
TH1: Nếu a  1 khi đó I   x
 xadx  
    f (8)     3 2  2 3 2 3 3 0 0 a 1
TH 2: Nếu 0  a  1 khi đó I   x
 x  adx  x
 x  adx 0 a a 1 3 2 3 2 3  x ax   x ax  a a 1  1  1 1 1 1         f            3 2   3 2  3 2 3  2  24 4 3 8 0 a  1  11 1 91
Khi đó f (8)  f      .  2 3 8 24 1 2
Bài tập 6: Cho hàm số f  x liên tục trên  thỏa  f 2xdx  2 và  f 6xdx 14 . Giá trị 0 0 2
 f 5 x  2dx bằng 2  A. 30. B. 32. C. 34. D. 36. Lời giải Chọn B 1 + Xét f
 2xdx  2. 0
Đặt u  2x  du  2dx ; x  0  u  0 ; x 1 u  2 . 1 2 1 2 Nên 2  f
 2xdx  f
 udu  f
 udu  4. 2 0 0 0 2 + Xét f
 6xdx 14 . 0
Đặt v  6x  dv  6dx ; x  0  v  0 ; x  2  v 12 . 2 12 1 12 Nên 14  f
 6xdx  f
 vdv  f
 vdv  84. 6 0 0 0 2 0 2 + Xét f
 5 x  2dx  f
 5 x  2dx  f
 5 x  2dx . 2 2 0 0 Tính I 
f 5 x  2 dx . 1    2
Đặt t  5 x 2. Khi 2
  x  0 , t  5x  2  dt  5  dx ; x  2
  t 12 ; x  0  t  2. 2 1  12 2   I  f t dt 1  1  f
 tdt  f  t  84  4  . 1    dt 16 5  5 5 12  0 0  2
Tính I  f 5 x  2 dx . 1    0
Đặt t  5 x 2.
Khi 0  x  2, t  5x  2  dt  5dx ; x  2  t  12 ; x  0  t  2. 12 1 12 2   I  f t dt 1  1  f
 tdt  f  t  84  4  . 2    dt 16 5  5 5 2  0 0  2 Vậy f
 5 x 2dx  32. 2  2 4
Bài tập 7: Cho hàm số y  f  x liên tục trên 0;4 và  f xdx 1;  f xdx  3. Giá trị 0 0 1
 f  3x1dx bằng 1 A. 4. B. 2. C. 4 . D. 1. 3 Hướng dẫn giải Chọn C 1
f  3x 1  1/3 1 dx 
f 1 3xdx  f 3x      1 dx . 1  1 1/3 1/3 1 1  
f   x   x 1 1 3 d 1 3  f 3x   1 d 3x     1 . 3 3 1 1/3 0 2 1   f  t 1 dt  f
 tdt 1     1 4 3  .1  . 3 3 3 3 3 4 0 3  24 3 Bài tập 8. 4 2   4  3  .  a S y y dy
Giá tị A  2B bằng b  3 A. 80. B. 83. C. 142. D. 79. Hướng dẫn giải Chọn C 4 2     2   2 y 4y 3 y 1 y  3 Xét dấu  2   2 y 1 y  3 , ta có: y ‐∞ ‐ 3 ‐1 1 3 +∞ y2‐1 + + 0 ‐ + + y2‐3 + 0 ‐ ‐ 0 ‐ 0 + (y2‐1)(y2‐3) + 0 ‐ 0 ‐ 0 ‐ 0 + 3
S   4  4y   1  y  3 2 4 4 2 dy  y  4y  3 dy   3  3 1     y  4y  3 1
dy   y  4y  3 3 4 2 4 2 dy     4 2 y  4y  3dy  3 1  1 1 1 3  5 3   5 3   5 3 y 4y y 4y y 4y      3y     3y     3y  5 3   5 3   5 3         3 1 1 112  24 3  . 15 1 Bài tập 9. 2 a           a S 4x 4x 1dx , a, b
, là phân số tối giản. Giá trị a  4b bằng b b 0 A. 1. B. 3. C. 35. D. 3. Hướng dẫn giải Chọn D 1 1
Ta có: I   2x  2   7 1 dx 2x 1 dx  0 0 1 1 1 2 1 2 1  I            . 7 2x 1 dx 2x 1 dx 2x 1 dx    1 2x 1 dx 2x 1dx 2 0 0 1 0 1 2 2 Suy ra: a  1,b  2. 2 Bài tập 10. I  1  sin xdx  A B  , biết A  2B Giá trị 3 3 A  B bằng 0 A. 72. B. 8. C. 65. D. 35. Hướng dẫn giải Chọn A 2      Ta có: x x x x x 1  sin x  sin  cos  sin  cos  2 sin       2 2  2 2  2 4      Với x x 5 x  0; 2   0;     ;       . 2 2 4  4 4         + Với x   ;    thì x sin     0 2 4  4   2 4         + Với x 5   ;   thì x sin     0 2 4  4   2 4  3 2 2  x    x    I  2 sin  dx  2 sin  dx        4 2 .  2 4   2 4  0 3 2  2
Bài tập 11. Cho tích phân 2 1 3 sin 2  2cos  3  .  x xdx a
b Giá trị A  a  b  4 bằng 0 A. 2. B. 5 . C. 5. D. 8 . Hướng dẫn giải Chọn D   2 4 2 2 I  1  3 sin 2x  2 2 cos xdx 
sinx 3cosx dx sinx    3 cos x dx . 0 0 0 
sin x  3 cos x  0  tan x  3  x    k . 3     Do x0;  nên x  .  2  3     3 2 3 2 I  sin x  3 cos x dx  sin x  3 cos x dx   
sinx  3cosxdx  sinx  3cosxdx 0  0  3 3     3   
 2  1  3     1  3 cos x 3 sin x cos x 3 sin x 1 3  3   3. 0 2 2 2 2 3
 a  1; b  3  A  8
Dạng 5: Tính tích phân các hàm đặc biệt, hàm ẩn
1. Phương pháp giải
a. Cho hàm số f  x liên tục trên  ; a a. 1 2  x
Bài tập 1: Tích phân I  cos . x ln dx  bằng 2  x Khi đó 1  a a A. 1.  B. f
 xdx   f
 x f xdx  (1) 2. a 0 C. 0. D. 1. Chứng minh
Hướng dẫn giải a 0 a Ta có f
 xdx  f
 xdx  f
 xd .x  x
Hàm số f  x 2  cos . x ln xác định và liên tục a a 0 2  x 0 Xét I  f
 xd .x
Đổi biến trên đoạn  1  ;  1 . a Mặt khác, với x   1;   1  x  1;   1 và x  t
  dx  dt. 2  x 2  x
Đổi cận x  a  t  a; x  0  t  0
f x  cosx.ln  cos . x ln
  f x. 2  x 2  x Khi đó  x
Do đó hàm số f  x 2  cos . x ln là hàm số lẻ. 0 a a 2  x I  f
 tdt  f
 tdt  f  xdx a 0 0 1 2  x Vậy I  cos . x ln dx  0  .
Do đó (1) được chứng minh. 2  x 1  Đặc biệt
Chọn C.
+ Nếu f  x là hàm số lẻ thì ta có
Bài tập 2: Cho y  f  x là hàm số chẵn, liên tục a trên đoạn  6;  6. f
 xdx  0 (1.1). a 2 3 Biết rằng f
 xdx  8 và f   2
 xdx  3.
+ Nếu f  x là hàm số chẵn thì ta có 1 1 6 a a f
 xdx  2 f
 xdx (1.2) Tính f
 xd .x 1 a 0 A. I  11. B. I  5.
+ Nếu f  x là hàm số chẵn thì ta cũng có C. I  2. D. I  14. a f  x 1 a
Hướng dẫn giải dx  f x dx   0  b  1 x   1 b 2 a a
Gọi F  x là một nguyên hàm của hàm số f  x trên (1.3). đoạn  6;  6 ta có Chứng minh (1.3): 3 3 a f x f   2
 xdx  3  f
 2xdx  3 Đặt A  dx  (*). 1 x  b 1 1 a 1
Đổi biến x  t
  dx  dt.
 F 2x 3 3. 2 1
Đổi cận x  a  t  ;
a x  a  t  a 6 a f   1 a t b . f t
Do đó F 6  F 2  6 hay f
 xdx  6. Khi đó A  dt  dt  2   t     . 1 b 1 t  b a a 6 2 6
Vậy I   f xdx   f xdx   f xdx 14. 1  1  2 a x
b . f  x
Chọn D. Hay A  dx  (**). 1 x  b 1 2020 a x
Bài tập 3: Tích phân I  dx  có giá trị là x Suy ra e 1 1 a a 2020 2 A  f  x 1 2 dx  A  f
 xd .x A. I  0. B. I  . 2 2019 a a 2021 2 2019 2 C. I  . D. I  . 2021 2019
Hướng dẫn giải
Áp dụng bài toán (1.3) ở cột bên trái cho hàm số   2020 f x  x
và b  e ta có Ta có 1 2021 1 2021 2021 1 x 2.2 2 2020 I  x dx    I  .  2 2021 1 2021 2021 1 
Chọn C.
b. Nếu f  x liên tục trên đoạn  ; a b thì
Bài tập 4: Cho hàm số f  x liên tục trên  thỏa điều b b
kiện f  x  f x  2cos x, với x    . f
 xdx  f
 a b xdx a a  2
Hệ quả: hàm số f  x liên tục trên 0; 
1 , khi đó: Giá trị của N  f
 xdx là   2   2 2 A. N  1.  B. N  0. f
 sin xdx f
 cos xdx 0 0 C. N 1. D. N  2.
Hướng dẫn giải   2 2 Ta có N  f
 xdx  f  xdx     2 2   2 2 Suy ra 2N   f
  x f xdx  2cos xd .x       2 2  2  Vậy 2
N  2 cos xdx  2sin x  2.  0 0
Chọn D.
Bài tập 5: Cho hàm số f  x liên tục trên  và thỏa
mãn f  x  f 2  x  x2  x, x   .  2
Giá trị tích phân G  f
 xdx là 0 1 A. G  2. B. G  . 2 2 1
c. Nếu f  x liên tục trên đoạn  ; a b và C. G  . D. G  . 3 3
f a  b  x  f  x thì
Hướng dẫn giải 2 2 b b    a  b Ta có G  f
 xdx  f
 2 xdx xf x dx  f  xdx 2 0 0 a a 2 2
Suy ra 2G   f
 x f xdx  x 
 2 xdx 0 0 2 1 2 Vậy G  x
 2 xdx  . 2 3 0
Chọn C.
Bài tập 6: Cho hàm số f  x có đạo hàm liên tục trên 1 đoạn 0;  1 thỏa mãn f   1  0,  f 
 x 2 dx  7  và 0 1 1 1 2 x f 
xdx  . Tích phân f xdx  bằng 3 0 0 7 A. . B. 1. 5 7 C. . D. 4. 4
d. Nếu f  x liên tục trên đoạn  ;
a b và Hướng dẫn giải
du  f  x dx b u
  f x   
f  x  0 với x
 a;b thì f
 xdx  0 và Đặt   3  2 x     a dv x dx v  3 b f
 xdx  0 khi f x  0. 1 3 1 1 x f x 1 Ta có 2  x f x   3 dx   x f   xdx a 3 0 3 0 0 1 1 1 1 3   x . f   x 3
dx   x . f  
xdx  1. 3 3 0 0 1
Cách 1: Ta có  f 
 x 2 dx  7  (1). 0 1 7 1 1 x 1 1 6 6 x dx 
  49x dx  .49  7   (2). 7 0 7 7 0 0 1 1 3 x . f   x 3
dx  1 14x . f  
xdx  14 (3). 0 0
Cộng hai vế (1), (2) và (3) suy ra 1 1 1  f '  x 2 6 3
 dx  49x dx  14x . f     xdx  0 0 0 0 1   f  x 2 3
 7x  dx  0.   0 1 2 2
Do  f  x 3
 7x   0   f   x 3
 7x  dx  0     . Mà 0 1  f   x 2 3
 7x  dx  0  f x 3  7x .   0 4   7x f x    C. 4 Mà f   7 7
1  0    C  0  C  . 4 4 4 7x 7
Do đó f  x    . 4 4 1 1 4  7x 7  7 Vậy f
 xdx    dx   .  4 4  5 0 0
Một số kĩ thuật giải tích phân hàm ẩn
Loại 1: Biểu thức tích phân đưa về dạng: u(x) f '(x)+u '(x) f (x)= h(x) Cách giải:
+ Ta có u(x) f (x)+ u (x) f (x)= éu(x) f (x) ' ' ' ù ë û
+ Do đó u(x) f (x)+ u (x) f (x)= h(x)  éu(x) f (x) ' ' ' ù = h(x) ë û
Suy ra u(x) f (x)= ò h(x)dx
Suy ra được f (x)
Loại 2: Biểu thức tích phân đưa về dạng: f '(x)+ f (x)= h(x) Cách giải: '
+ Nhân hai vế với x x  . '( ) x + . ( ) x = . ( ) é x  . ( )ù x e e f x e f x e h x
e f x = e .h(x) êë úû Suy ra x. ( ) x
e f x = ò e h(x)dx
Suy ra được f (x)
Loại 3: Biểu thức tích phân đưa về dạng: f '(x)- f (x)= h(x) Cách giải: '
+ Nhân hai vế với -x -x  . '( ) -x + . ( ) -x = . ( ) é -x  . ( )ù -x e e f x e f x e h x e
f x = e .h(x) êë úû Suy ra -x. ( ) -x e
f x = ò e h(x)dx
Suy ra được f (x)
Loại 4: Biểu thức tích phân đưa về dạng: f '(x)+ p(x) f (x)= h(x) Cách giải: ( p x)dx eò f '(x) ( p x) . dx eò p(x) ( p x) . dx eò
. f (x) h(x) ( p x) . dx eò  + = + Nhân hai vế với ' é ù  f (x) ( p x)dx p x dx .eò = h(x) ( ) .eò ê ú ê ú ë û Suy ra ( ) ( p x)dx ( p x)dx f x .eò eò = ò .h(x)dx
Suy ra được f (x) b b
Công thức f (x)dx  f (a  b  x)dx   a a 2. Bài tập
Bài tập 1: Cho số thực a  0. Giả sử hàm số f  x liên tục và luôn dương trên đoạn 0;a thỏa mãn a 1
f  x. f a  x 1. Giá trị tích phân I  dx  là 1 f x 0   2a a a A. I  . B. I  . C. I  . D. I  . a 3 2 3
Hướng dẫn giải Chọn B.
Đặt t  a  x  dt  d .
x Đổi cận x  0  t  a; x  a  t  0. a 1 a 1 a 1 a f  x Khi đó I  dt  dx  dx  d .     x 1 f a  t 1 f a  x 1 1 f x 0   0   0 0   1 f x a 1 a   a f x  a 2I  dx 
dx  1.dx  . a    Vậy I  . 1 f x 1 f x 2 0   0   0
Ta có thể chọn hàm số f  x 1, với mọi x 0;a thỏa mãn yêu cầu đề bài. a 1 a 1 a Khi đó I  dx  dx  .   1 f x 2 2 0   0
Bài tập 2: Cho hàm số f  x liên tục trên  1;  
1 và    2019   x f x
f x  e , x   1   ;1 . Tích phân 1 M  f
 xdx bằng 1  2 e 1 2 e 1 2 e 1 A. . B. . C. . D. 0. 2019e e 2020e
Hướng dẫn giải
Chọn C. 1 1 Ta có M  f
 xdx  f  x . dx 1  1 1 1 1
Do đó 2020M  2019 f
 xdx f
 xdx   f
  x2019 f x . dx  1  1  1  1 2 1 e  x 1 Suy ra M  e dx  .  2020 2020e 1 b b
Nếu f  x liên tục trên đoạn  ;
a b thì f  xdx    f
 a b xdx a a
Bài tập 3. Cho f  x là một hàm số liên tục trên  thỏa mãn f  x  f x  2  2cos 2x . 3 2
Giá trị tích phân P  f
 xdx là 3  2 A. P  3. B. P  4. C. P  6. D. P  8.
Hướng dẫn giải
Chọn C. 3 3 2 2 Ta có P 
f  x dx  f    x dx 3 3   2 2 3 3 3 2 2 2  2P   f
  x f xdx 
2  2cos 2xdx  4 sin x . dx    3 3 0   2 2 3  2  3 Hay 2
P  2 sin xdx  2 sin xdx  2  cosx  2cos x  6.   0 0  
Bài tập 4: Cho f  x là hàm số liên tục trên  thỏa mãn f  x  f  x  sin x với mọi x và
f 0 1. Tích phân e . f   bằng e 1 e 1 e  3  1 A. . B. . C. . D. . 2 2 2 2
Hướng dẫn giải
Chọn C.
Ta có f  x  f  x  sin x nên x   x    x e f x
e f x  e .sin x, x   .    x      x
e f x   e .sin x x  x   hay e f 
x dx  e .sin xdx    0 0   x     1 x e f x   e  x 
x  e f    f   1 sin cos 0  e       1 0 2 0 2  
 e f   e 3  . 2
Để ý rằng  x  x e
 e nên nếu nhân thêm hai vế của f x  f x  sin x với x e thì ta sẽ có ngay
 x.   x e f x  e .sin . x    
Bài tập 5: Cho hàm số f  x tuần hoàn với chu kì và có đạo hàm liên tục thỏa mãn f  0 , 2    2       f 
  x 2 dx   và f
 x.cos xdx  . Giá trị của f 2019 .  4  4 2 2 1 A. 1.  B. 0. C. . D. 1. 2
Hướng dẫn giải
Chọn A.
Bằng phương pháp tích phân từng phần ta có      f
 x.cos xdx   f x.sin x  f      
 x.sin x . dx Suy ra f
 x.sin xdx .   4 2  2 2 2   1 cos 2x
2x  sin 2x    Mặt khác 2 sin xdx  dx   .   2  4      4 2 2 2 Suy ra     2 2 2 2  f 
 x 2 dx 2 sin xf   
xdx  sin xdx  0   f    x 2 2
 sin x dx  0.  0 0 0 0    
f  x  sin .
x Do đó f  x  cos x  C. Vì f  0   nên C  0.  2 
Ta được f  x  cos x  f 2019   cos2019   1. 
Bài tập 6: Cho hàm số f  x có đạo hàm liên tục trên 0;  1 , thoả mãn     2018 3 f x xf x  x với 1 mọi x 0; 
1 . Tính I  f  xdx . 0 1 1 A. I  . B. I  . 2018 2021 2019  2020 1 1 C. I  . D. I  . 2019  2021 2018 2019 Hướng dẫn giải Chọn C
Từ giả thiết f  x  xf  x 2018 3  x , nhân hai vế cho 2 x ta được 2 x f  x 3
 x f x 2020 3  x
 x f x  2020 3   x .   2021 x Suy ra 3 x f  x 2020  x dx   C.  2021 2018 x
Thay x  0 vào hai vế ta được C  0  f  x  . 2021 1 1 1 1 1 1 1 Vậy f  x 2018 2019 dx  x dx  . x  .  2021 2021 2019 2021 2019 0 0 0
Bài tập 7: Cho hàm số f  x có đạo hàm liên tục trên 0;4, thỏa mãn       x f x f x  e 2x 1
với mọi x 0;4. Khẳng định nào sau đây là đúng? 26 A. 4
e f 4  f 0  . B. 4
e f 4  f 0  3 . e 3 C. 4
e f    f   4 4 0  e 1. D. 4
e f 4  f 0  3. Lời giải Chọn A Nhân hai vế cho x
e để thu được đạo hàm đúng, ta được x   x    x e f x e f x 
x   e f  x / ' 2 1   2x 1.   x 1
Suy ra e f  x  2x 1dx  
2x  1 2x 1C. 3 26 Vậy 4
e f 4  f 0  . 3
Bài tập 8: Cho hàm số f  x có đạo hàm trên , thỏa mãn      2017 2018 ' 2018  2018 x f x f x x e với
mọi x   và f 0  2018. Giá trị f   1 bằng A. 201  8 2018e . B. 2018 2017e . C. 2018 2018e . D. 2018 2019e . Lời giải Chọn D
Nhân hai vế cho 2018x e
để thu được đạo hàm đúng, ta được 
f  x 2018x e 
f  x 2018x 2017 e  x
  f x 2018x 2017 2018 2018 e   2018x .  
Suy ra f  x 2018x 2017 2018 e
 2018x dx  x  C. 
Thay x  0 vào hai vế ta được       2018   2018 2018 2018 x C f x x e . Vậy f   2018 1  2019e .
Bài tập 9: Cho hàm số f  x có đạo hàm và liên tục trên , thỏa mãn     2 2 x f x xf x xe    và f 0  2
 . Giá trị f   1 bằng 1 2 2 A. . e B. . C. . D.  . e e e Hướng dẫn giải Chọn C 2 x Nhân hai vế cho 2
e để thu được đạo hàm đúng, ta được 2 2 2 2  2 x x x x x     f  x 2
e  f  x 2 2 2 xe  xe
 e f x 2 2   2xe .   2 2 2 x x x   Suy ra 2 e f  x 2 2
 2xe dx  2e  C. 
Thay x  0 vào hai vế ta được   2 0 2 x C f x e     .  2 Vậy f   1 1  2e   . e
Bài tập 10: Xét hàm số f (x) liên tục trên đoạn 0; 
1 và thỏa mãn 2 f (x)  3 f (1 x)  1 x . Tích 1
phân f (x)dx  bằng 0 2 1 2 3 A. . B. . C. . D. . 3 6 15 5 Hướng dẫn giải Chọn C
Ta có: 2 f (x)  3 f (1 x)  1 x (1) .
Đặt t  1 x , thay vào (1) , ta được: 2 f (1 t)  3 f (t)  t hay 2 f (1 x)  3 f (x)  x (2) . 3 2
Từ (1) & (2) , ta được: f (x)  x  1 x . 5 5 1 1 1 3 2
Do đó, ta có: f (x) dx   x dx  1 x dx   2 4   2  . 5 5 5 15 15 0 0 0 b b
Cách 2. Công thức f (x)dx  f (a  b  x)dx   a a 1 1 1
Lấy tích phân 2 vế ta được 2 f (x)dx  3 f (1 x)dx  1 x dx    0 0 0 1 1 2 2
5 f (x)dx   f (x)dx  .   3 15 0 0 x ax b
Chú ý: Ta có thể dùng công thức . 2 f
 ax b 2 dx  f 
xdx Khi đó:  1 x a 1 x b 1 1 1
Từ 2 f  x  3 f 1 x  1 x suy ra: 2 f
 xdx 3 f
 1 xdx  1 xdx  0 0 0 1 1 2 1 2  2 f  x 0 dx  3 f  x 1 dx 
1 xdx  5 f x dx   f x dx  .        0 1 0 0 0 3 15 2 2 1     1     a I f t dt f x dx  . 2 2 2 1 1 2
Bài tập 11: Cho y  f x là hàm số chẵn, có đạo hàm trên đoạn .  6;  6 Biết rằng f  xdx 8 và 1  3 6 f   2
 xdx  3. Giá trị  f xdx bằng 1 1 A. 1. B. e. C. 1.  D. 14. Hướng dẫn giải Chọn D 3 3
Ta có y  f x là hàm số chẵn nên f 2x  f 2x suy ra f   2  xdx  f  2xdx  3. 1 1 3 3 6 6 Mặt khác:    1       1 f 2x dx f 2x d 2x  f
 xdx  3 fxdx  6. 2 2 1 1 2 2 6 2 6 Vậy I  f  xdx  f
 xdx  f xdx  86 14. 1  1  2 k x 1 1
Bài tập 12: Tìm tất cả các giá trị thực của tham số k để 2x   1 dx  4 lim . x0 x 1 k 1 k 1 k  1  k  1  A. . B. . C. . D. .     k  2 k  2  k  2  k  2 Hướng dẫn giải Chọn D 2 2 k k k 1 2x 1 2k 1 1 Ta có 2x   1 dx  2x   1 d 2x       1      2 4 1 4 4 1 1  x1 1 x1   1 x 1 1 1 Mà 4 lim   4lim  4lim  2 x0 x0 x x  x 1   x0 1 x 1 1 2 k x 1 1 2k 1 1 k  2 Khi đó 2x     1 dx  4lim   2  2k  2 1  9  .  x0 x 4 k  1  1 f
 x.f a  x  1
Bài tập 13: Cho f x là hàm liên tục trên đoạn 0;a thỏa mãn  và f  x  0, x  0;a a dx ba 
, trong đó b, c là hai số nguyên dương và là phân số tối giản. Khi đó b  c có giá  b 1 f x c c 0  
trị thuộc khoảng nào dưới đây? A. 11;22. B. 0;9. C. 7;2  1 . D. 2017;2020. Hướng dẫn giải ĐÁP ÁN B Đặt t  a  x  dt  dx Đổi cận
x  0  t  a; x  a  t  0 a 0 a a a dx dt dx dx f xdx Lúc đó I           1 f x 1 f a  t 1 f a  x 1 1 f x 0   a   0   0 0   1 f x a a dx f x a dx Suy ra 2I  I  I    1dx  a    1 f x 1 f x 0   0   0 1 Do đó
I  a  b 1; c  2  b  c  3. 2 Cách 2: Chọn f x  1 là
một hàm thỏa các giả thiết. Dễ dàng tính được 1
I  a  b  1; c  2  b  c  3. 2  9 f  x  2
Bài tập 14: Cho hàm số f  x liên tục trên  và dx  4, 
 f sin xcos d
x x  2. Giá trị của x 1 0 3
tích phân  f xdx bằng 0 A. 2 . B. 6 . C. 4 . D. . 10 Hướng dẫn giải ĐÁP ÁN C 9 f  x   Xét dx  4. Đặt
t  x  t  x suy ra  2 , 2 d t t  d . x x 1
x 1 t 1 Đổi cận  .
x  9  t  3 9 f  x  3 3 Suy ra 4  dx  2 f 
 t2dt  f
 tdt  2. x 1 1 1  2  Xét f  sin xcos d
x x  2. Đặt u  sin x, suy ra du  cos d x . x 0
x  0  u  0   2 1 Đổi cận   . Suy ra 2  f  sin xcos d x x  f  tdt. x   u 1  2 0 0 3 1 3 Vậy I  f
 xdx  f
 xdx  f
 xdx  4.. 0 0 1  4 1 2 x f x
Bài tập 15: Cho hàm số
f  x liên tục trên  và f  tan x   dx  4,
dx  2. Giá trị của  2x 1 0 0 1
tích phân I   f xdx bằng 0 A. I  6 . B. I  2 . C. I  3 . D. . I 1 Hướng dẫn giải ĐÁP ÁN A  4 Xét f
 tan xdx  4. 0 1 dt Đặt
t  tan x, suy ra dt  dx   2
tan x 1 dx  dx  . 2  2 cos x 1 t
x  0  t  0   4 1 1 f t f x Đổi cận:   . Khi đó 4  f  tan x     dx  dt  d . x   x   t 1  2 2 t 1 x 1  4 0 0 0 1 1 1 2 f x x f x
Từ đó suy ra I  f  x     dx  dx  dx  4  2  6.   2 2 x 1 x 1 0 0 0  4
Bài tập 16: Cho hàm số f  x liên tục trên  và thỏa mãn tan . x f   2 cos xdx 1, 0 2 e f  2 ln x 2 2 
dx  1. Giá trị của tích phân  d bằng   f x I x x ln x x e 1 4 A. 1. B. 2 . C. 3 . D. . 4 Hướng dẫn giải ĐÁP ÁN D  4 ● Xét A  tan . x f   2
cos xdx 1. Đặt 2 t  cos . x 0 Suy ra dt 2
dt  2sin x cos d
x x  2cos x tan d x x  2  t.tan d x x   tan d x x   . 2t
x  0  t 1  Đổi cận:   1 . x   t   4 2 1 2 1 f t  1 1 f t 1 1 f  x 1 f x Khi đó 1  A   dt  dt  dx  dx  2.     2 t 2 t 2 x x 1 1 1 1 2 2 2 2 e f  2 ln x ● Xét B  dx  1. Đặt  2 u  ln . x x ln x e 2 2 ln x 2ln x 2u dx du Suy ra du  dx  dx  dx   . x x ln x x ln x x ln x 2u
x  e  u 1 Đổi cận:  . 2
x  e  u  4 4 1 f u 4 1 f  x 4 f  x Khi đó 1  B  du  dx  dx  2.    2 u 2 x x 1 1 1 2 f 2x
● Xét tích phân cần tính I  d . x  x 1 2  1 dx  dv   1 1 
x   v  Đặt v  2x, suy ra 2  . Đổi cận:  4 2 . v x 
x  2  v  4  2 4 f v 4 f  x 1 f x 4 f x Khi đó I  dv  dx  dx  dx  2  2  4.     v x x x 1 1 1 1 2 2 2
Bài tập 17: Cho hàm số
f  x nhận giá trị dương, có đạo hàm liên tục trên 0;2. Biết f 0 1 và  3 2 2
x  3x  f x     2 2 4 2 x x f x f x e   
với mọi x 0;2. Giá trị tích phân I  dx bằng  f x 0   14 A.  32 . B.  16 . C.  16 . D. .  3 5 3 5 Hướng dẫn giải ĐÁP ÁN D Từ giả thiết
f  x f 2  x 2 2 x 4 x x2  e
 f 2  1.  3 2 u   x  3x 3 2 2
x  3x  f 'x du     2
3x  6xdx Ta có I  d . x Đặt   f ' x   . f x dv  dx 
v  ln f  x 0   f  x   Khi đó I   3 2 x  3x  2 2
ln f  x   2
3x  6xln f x dx 0 0 f 2 1  2
  3 2x  2xln f x dx  3  J. 0 2 0 x2t
Ta có J  x  2xln f x dx    2t2 2
 22  t ln f 2  t d2  t   0 2 0 2  
 2 x2 22 xln f 2 x d2 x   2x 2xln f 2 x d .x   2 0 Suy ra 2
2J  x  2x 2 2
ln f  x dx   2x  2xln f 2 x dx 0 0 2
  2x  2xln f x f 2 x dx 0 2   x  x 32 16 2 x  2x 2 2 2 4 ln e
dx   2x  2x 2
2x  4xdx   J  . 15 15 0 0 16 Vậy
I  3J   . 5    
Bài tập 18: Cho hàm số y  f  x liên tục trên  ;
và thỏa mãn 2 f  x  f x  cos . x Giá  2 2     2
trị của tích phân I   f xdx bằng   2 A. I  2  2 . B. I  3 . C. I  . D. I  2 . 3 2 Hướng dẫn giải ĐÁN ÁN B
Từ giả thiết, thay x bằng  x ta được
2 f x  f  x  cos . x Do đó ta có hệ 2 f 
x  f x  cos x 4 f 
x 2 f x  2cos x     f x 1  x 2 f 
x f x  cos x  f
  x  2 f x cos .  cos x 3   2 2 1 1  2 Khi đó I  f  x 2 dx  cos d x x  sin x  .  3 3     3 2   2 2 1   
Bài tập 19: Cho hàm số f  x liên tục trên
; 2 và thỏa mãn f  x 1  2 f  3 . x   Giá trị của 2     x  2   tích phân  d bằng  f x I x x 1 2 1 3 5 7 A. . B. . C. . D. . 2 2 2 2 Hướng dẫn giải ĐÁP ÁN B 1  1  3
Từ giả thiết, thay x bằng ta được f  2 f   x  . x  x  x Do đó ta có hệ       f   x 1  f  x f     x 1 2 3  2 f  3x     x    x       f x 2   . x   1      f x 3  f  x 1 6 x f 2 4  2 f       x x      x  x 2 f  x 2 2  2   2  3 Khi đó I  dx 
1 dx    x  .   2    1 x  x   x  2 1 1 2 2 2  1   1 
Cách khác. Từ f  x  2 f  3x  f  
x  3x  2 f .    x   x    1    1  f f 2 f x 2     2 2    x   x  Khi đó I  dx  3  2
dx  3 dx  2 d . x     x  x  x 1 1 1 1   2 2 2 2    1  f 2    x  1 1 Xét J  d . x Đặt  , suy ra  1 t 2 dt   dx  t
 dx  dx   dt. x x 2 2 x t 1 2  1
x   t  2  Đổi cận: 2  . 1
x  2  t   2 1 2 2 2  1  f t f x Khi đó J  tf  t      dt  dt  dx  I.    2   t  t x 2 1 1 2 2 2 2 3 Vậy .
I  3 dx  2I  I  dx  .   2 1 1 2 2
Bài tập 20: Cho hàm số
f  x thỏa mãn  f    x 2   f 
x f  x 4 .
 15x 12x với mọi x   và
f 0  f 0 1. Giá trị của 2 f   1 bằng 5 9 A. . B. . C. 8. D. 10. 2 2 Hướng dẫn giải ĐÁP ÁN C Nhận thấy được  f   x 2   f 
x.f x   f
  x. f  x      . 
Do đó giả thiết tương đương với  f
  x f  x  4 .  15x 12 . x 
Suy ra f  x. f  x   4 15x 12x 5 2
f 0 f 0 1  .
dx  3x  6x  C  C 1
 f x f x 5 2 .
 3x  6x 1 2 6  f
 x f x x   f x x 5 2 x  x     3 . d 3 6 1 dx  
 2x  x  C '. 2 2 2 f 0 1
Thay x  0 vào hai vế ta được
 C '  C '  . 2 2 Vậy 2 f  x 6 3 2
 x  4x  2x 1 f   1  8.
Bài tập 22: Cho hàm số f  x liên tục trên  thỏa mãn f  x 4 tan  cos x, x   . Giá trị 1
I   f xdx bằng 0 2   2    A. . B. 1. C. . D. . 8 4 4 Hướng dẫn giải ĐAP ÁN A 2   f tan x 1 4
 cos x  f tan x   2   tan x 1 1   1 2    f x   f x dx   2    2   8 x 1 0
Dạng 8: Bất đẳng thức tích phân 1. Phương pháp
Áp dụng các bất đẳng thức: b b
+ Nếu f  x liên tục trên  ; a b thì f
 xdx  f  xdx a a b
+ Nếu f  x liên tục trên  ;
a b và m  f  x  M thì mb  a  f
 xdx  M ba a 2 b b b   + Nếu
f  x, g  x liên tục trên  ;
a b thì  f
 xgx 2 dx   f  x 2 d . x g
 xdx dấu "  " xẩy  a  a a
ra khi và chỉ khi f  x  k.g  x . + Bất đẳng thức AM-GM 2. Bài tập 1 2
Bài tập 1: Cho hàm số f  x có
đạo hàm liên tục trên 0; 
1 , thỏa mãn f   1  0 ,  f 
 x dx  7  0 1 1 1 và 2
 x f xdx  . Giá trị phân  f xdx bằng 3 0 0 7 7 A. 1. B. . C. . D. 4 . 5 4 Hướng dẫn giải Chọn B 1 3 1 1 x 1
Dùng tích phân từng phần ta có 2 x f  xdx  f  x 3  x f ' 
xd .x Kết hợp với giả thiết 3 0 3 0 0 1 f   1  0 , ta suy ra 3 x f ' 
xdx  1. 0 2 1 1 1 7 1   2 2 x Theo Holder   3 1   x f '  x 6 dx   x d . x  f ' 
 x dx  .7  1.  7 0  0  0 0 1
Vậy đẳng thức xảy ra nên ta có f  x 3 '  kx , thay vào 3 x f ' 
xdx  1 ta được k  7.  0 7
Suy ra f  x 3 '  7
 x  f 'x 3  7x , x  0;  1  f  x 4   x  C 4 1 f   1 0 7
C   f x 7 7 7 4
  x   f
 xdx  . 4 4 4 5 0 1 11
Bài tập 2: Cho hàm số f  x có
đạo hàm liên tục trên 0; 
1 , thỏa mãn f   1  1, 5  d   x f x x 78 0 1 
 f x  f x 4 d  . f 2 và Giá trị bằng 13 0 251 256 261 A. 2. B. . C. . D. . 7 7 7 Hướng dẫn giải Chọn D 2 2 1 1 1  2    2 1 4 4 Theo Holder 6     x f   x 12 dx   x d . x  f  
 x dx  .  . 13    13 13 169  0  0 0  f x 6
 x  f x 2 7 f   1 1  5 2
 x  C C  . 7 7 2 5 261 Vậy f  x 7
 x   f 2  . 7 7 7
Bài tập 3: Cho hàm số f  x có
đạo hàm liên tục trên 0; 
1 , thỏa mãn f  
1  2, f 0  0 và 1 1  f 
 x 2 dx  4.Tích phân 3 
 f x2018xd .x bằng    0 0 A. 0. B. 1011. C. 2018. D. 2022. Hướng dẫn giải Chọn B 2 1 1 1   2 Theo Holder 2 2   f '
 xdx  d .x  f '
  x dx 1.4  4.   0  0 0
 f x   f x f 00 ' 2
 2x  C C  0. 1 Vậy f  x 3  2x   f
 x 2018xdx 1011.   0
Bài tập 4: Cho hàm số
f  x nhận giá trị dương và có đạo hàm f  x liên tục trên 0;  1 , thỏa mãn 1 1 dx 2 f   1  ef 0 và
  f  x  dx  2. Mệnh đề nào sau đây đúng?   2   f x 0     0 e 2 e  2 A. f   2 1  . B. f     1  . e 1 e 1 2 2e 2 e  2 C. f   1  . D. f     1  . 2 e 1 e 1 Hướng dẫn giải Chọn C 1 1 1 1   AMGM dx 2 1 2 f ' x Ta có
  f ' x  dx     
  f ' x     dx  2 dx  2 f  x   2 f x f x 0 0 0         0   1  f  x  f    f   f   1 2 ln 2 ln 1 2ln 0  2ln  2ln e  2. f 0 0   1 1 dx 2 1 Mà
  f ' x  dx  2 nên dấu
 xảy ra, tức là f ' x 
 f x f ' x 1   '' '' 2 f x   f  x     0     0 2     f x f x f ' x   dx  d x x 
 x  C  f 
x  2x  2C. 2 1
Theo giả thiết f  
1  ef 0 nên ta có 2
2  2C  e 2C  2  2C  e 2C  C  2 e 1 2    2 2 2e f x  2x   f 1  2   . 2   2 2 e 1 e 1 e 1
Bài tập 5: Cho hàm số
f  x nhận giá trị dương trên 0; 
1 , có đạo hàm dương và liên tục trên 0;  1 , 1 1 1 3
thỏa mãn f 0  1 và  3
 f x4 f     x 
 dx  3 f  
 x 2f xd .x Giá trị I   f xdx bằng   0 0 0 e 1 2 e 1
A. 2 e   1 . B.  2 2 e   1 . C. . D. . 2 2 Hướng dẫn giải Chọn A
Áp dụng bất đẳng thức AM  GM cho ba số dương ta có 3 3   f x f x f x  4  f '   x 3   4  f '    x 3 3         2 2 3 3 f x f x  3 4  f '   x 3      . .  3 f '  x 2 3 f  x. 2 2 1 1 3 Suy ra 3  f
 x 4 f '   x    dx  3 f ' 
 x 2f xd .x   0 0 1 1 3 Mà 3  f
 x 4 f '   x    dx  3 f ' 
 x 2f xdx nên dấu ''  '' xảy ra, tức là   0 0 3 3  f   x 3 f  x f  x     f  x 1 4 ' '  f x 2 2 2 f ' x 1 f ' x 1 1 1 xC 2    dx 
dx  ln f x  x  C  f x  e .   f  x 2 f  x     2 2 1 1 x Theo giả thiết
f 0 1 C  0  f  x 2
 e  f  xdx  2 e   1. 0 
Bài tập 6: Cho hàm số f  x có
đạo hàm liên tục trên 0; , thỏa mãn 
 f xsin d x x  1  và 0  2  2
 f xdx  . Giá trị tích phân  xf xdx bằng  0 0 6 4 A.  4 . B.  2 . C. . D. .     Hướng dẫn giải ĐÁP ÁN B 2    2  Theo Holder  2 1  f  x 2 cos d x x  f  x 2 dx cos d x x  .  1.   2 0 0 0    f x 2  x  xf  x 2x cos x 4 cos dx  dx   .     0 0 1 2 2 
Bài tập 7: Cho hàm số f  x có
đạo hàm liên tục trên 0;  1 , thỏa t f   1  0,  f   x  dx  và  8 0 1    1  x   f  x 1 cos
dx  . Giá trị của ích phân  f xdx bằng  2  2 0 0 1 2  A. . B. . C. . D.  .   2 Hướng dẫn giải ĐÁP ÁN B Theo Holder 2 2 1 1 1 2       x     x        sin f '
   xdx  sin d . x  f '     x 2 1 2  dx  . . 4 2 2          2 8 0 0 0         f x x    f   x x f   1 0 ' sin  cos
 C C  0.   2  2   2  1   x  2 Vậy
f  x  cos  f  
 xdx  .  2   0
Bài tập 8: Cho hàm số
f  x nhận giá trị dương trên 0; 
1 , có đạo hàm dương liên và tục trên 0;  1 , 1    1  thỏa mãn
d  1 và f 0  1, f   2
1  e . Giá trị của f   bằng  xf x x f x  2  0   A. 1. B. 4. C. e. D. . e Hướng dẫn giải ĐÁP ÁN C xf ' x f ' x
Hàm dưới dấu tích phân là  x. , x
  0;1 . Điều này làm ta liên tưởng đến đạo f  x f  x   f ' x hàm đúng ,
muốn vậy ta phải đánh giá theo AM  GM như sau: f  x f ' x xf ' x  mx  2 m. với m  0 và x 0;  1 . f  x f  x
Do đó ta cần tìm tham số m  0 sao cho
1  f ' x 1  xf ' x 
 mx dx  2 m. dx  f x f x 0     0   hay 1 2 x m ln f  x 1  m
 2 m.1  ln f   1  ln f 0  0 2 0 2  m 2 m  2  0   2 m. 2 m Để dấu
''  '' xảy ra thì ta cần có 2  0 
 2 m  m  4. 2 f ' x Với m  4 thì đẳng thức xảy ra nên    4x f x f ' x  dx  4 d
x x  ln f x  2 x C
x  C  f x  e .   f  x     2 2 2  f  0  1 x  1  Theo giả thiết 
 C  0  f x 2 2       f    e f e. 2 1  e  2  Cách 2. Theo Holder  xf ' x 2   f ' x 2 1 1 1 1  f ' x 1 f 1 2     1   dx    x. dx   d x . x dx  .ln 1.      f x   f x  f x 2 f 0 0   0   0 0         f ' x 1 xf ' x
Vậy đẳng thức xảy ra nên ta có  kx, thay vào dx  1 ta được  k  4. f  x f x 0   f ' x Suy ra  4 .
x (làm tiếp như trên) f  x 1 2
Bài tập 9: Cho hàm số f  x có
đạo hàm liên tục trên 0;  1 , thỏa mãn 
 f x f x dx 1 và  0  1 
f 0  1, f    1 3. Giá trị của f   bằng  2  A. 2. B. 3. C. e. D. . e Lời giải ĐÁP ÁN A
Hàm dưới dấu tích phân là  f
  x f  x 2 '
 . Điều này làm ta liên tưởng đến đạo hàm đúng 
f  x f ' x
, muốn vậy ta phải đánh giá theo AM  GM như sau:  f
  x f  x 2 '
  m  2 m. f 
x f 'x với m  0.
Do đó ta cần tìm tham số m  0 sao cho 1  1  f
  x f ' x 2   m 
dx2 m f x f 'xd .x 0 0 hay 2 f  x 1 1 m  2 m.
 1 m  2 m. 2 0 Để dấu
''  '' xảy ra thì ta cần có 1 m  2 m  m  1.   2
f  x f ' x 1 Với m 1 thì
đẳng thức xảy ra nên  f
  x f ' x 1    .  f
  x f ' x  1  1 1 2 1 1 f x
 f  x f ' x  1   f
 x f 'x  
dx   dx   x  1  1  . (vô lý)  2 0 0 0 0 2 f x
 f  x f ' x  1 f
 x f 'x   dx  dx 
 x  C  f 
x  2x  2C. 2  f  0 1 1  1  Theo giả thiết 
 C   f x  2x 1  f  2.    f    1  3 2  2  1 2 1 f x 1
Cách 2. Ta có f
 x f 'x   2 dx    f   2
1  f 0 1. 2   0 2 0 2 1 1 1   2 Theo Holder 2 1   1. f
 x f 'x 2 dx   1 d . x  f 
 x f 'x dx 1.11.   0  0 0 1
Vậy đẳng thức xảy ra nên ta có f ' x f  x  k, thay vào f
 x f 'xdx 1 ta được k  1. Suy ra 0
f ' x f  x 1.(làm tiếp như trên)
Bài tập 10: Cho hàm số
f  x nhận giá trị dương và có đạo hàm f  x liên tục trên 1;2, thỏa
 f x 2 2    f   f 2 f  2 mãn dx  24  và 1  1,  16. Giá trị của bằng xf x 1   A. 1. B. 2. C. 2. D. 4. Hướng dẫn giải ĐÁP ÁN D  f x 2 
1  f  x 2 ' '     
Hàm dưới dấu tích phân là  .
. Điều này làm ta liên tưởng đến đạo hàm đúng xf  x x f  x
f ' x , muốn vậy ta phải đánh giá theo AMGM như sau: f  x  f   x 2 '  f '  x  mx  2 m với m  0 và x 1;2. xf  x f  x
Do đó ta cần tìm tham số m  0 sao cho   f '   x 2 2  2  f '  x 
 mxdx  2 m dx    xf x  1   1 f  x   hay 2m   m f  x 2 2m   
m  f    f   2m 24 4 24 4 2 1   24 
12 m  m 16. 3   1 3 3 m Để dấu ''  2
'' xảy ra thì ta cần có 24 
 12 m  m  16. 3  f   x 2 '  f '  x Với m  16 thì đẳng thức xảy ra nên   16x   2x xf x 2 f  x f ' x  dx  2 d x x  f  
x  x C  f x  x C2 2 2 . 2 f  x  f    1  1 Theo giả thiết 
 C  0  f x 4
 x  f  2   f    4. 2  16 2 f ' x 2 f ' x 2 Cách 2. Ta có dx  2. dx  2 f  
x  2 f 2  f   1   6. f  x 2 f  x   1 1 1  f ' x   f ' x   f ' x    x 2   2   2   2 2 1 2 2 2 2 Theo Holder 6   dx    x. dx   d x . x dx  .24  36.      f  x   xf  x  xf  x 2 1 1 1 1 1     f ' x f ' x 2 f ' x
Vậy đẳng thức xảy ra nên ta có  k x   kx, thay vào dx  6 ta được  xf  x f  x 1 f  x f ' x k  4. Suy ra  4 .
x (làm tiếp như trên) f  x
Bài tập 11: Cho hàm số f  x có đạo hàm liên tục trên đoạn 0; 
1 , và f    f   14 1 0  . Biết 2 1
rằng 0  f  x  2 2x,x 0; 
1 . Khi đó, giá trị của tích phân  f 
 x 2 dx  thuộc khoảng nào 0 sau đây? 13 14  10 13  A. 2;4 . B. ; .   C. ; .   D. 1;3.  3 3   3 3 
Hướng dẫn giải
Chọn C. 2
Do 0  f  x  2 2x, x  0; 
1 nên 0   f  x  8 , x x  0;  1 . 1 1 1 Suy ra  f   2   x 2  dx  8xdx   hay  f 
 x dx  4  (1). 0 0 0
Mặt khác, áp dụng BĐT Cauchy-Schwarz, ta có: 2 1 1 1 1    f 
 xdx  1 d .x  f  
 x 2 dx   f     1  f 0 2    f    x 2 2  dx   0  0 0 0 1 7    f 
 x 2 dx 2  0 1 7 Vậy   f 
 x 2 dx  4. 2  0
BÀI 3. ỨNG DỤNG HÌNH HỌC TÍCH PHÂN
A. KIẾN THỨC SÁCH GIÁO KHOA CẦN NẮM
I. DIỆN TÍCH HÌNH PHẲNG
1. Định lý 1: Cho hàm số y  f (x) liên tục, không âm trêna;b . Khi đó diện tích S của hình thang b
cong giới hạn bởi đồ thị hàm số y  f (x) , trục hoành và 2 đường thẳng x  a, x  b là: S  f (x)dx a
2. Bài toán liên quan
Bài toán 1: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y  f (x) liên tục trên đoạn a;b , trục b
hoành và hai đường thẳng x  a , x  b được xác định: S  f (x) dx  a
Bài toán 2: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y  f (x) , y  g(x) liên tục trên đoạn b
a;b và hai đường thẳng x  a, x  b được xác định: S  f (x)  g(x) dx a y
(C ) : y  f (x) (C ) 1  1 1
(C ) : y  f ( x) (H )  2 2  x  a (C ) 2 x  b b S  f (x )  a c O c 1 b x 2  f (x ) dx 1 2 a b b
Chú ý: Nếu trên đoạn [a;b] , hàm số f (x) không đổi dấu thì: f (x) dx  f (x)dx   a a
Bài toán 3: Diện tích của hình phẳng giới hạn bởi các đường x  g( y) , x  h( y) và hai đường thẳng d
y  c , y  d được xác định: S  g( y)  h( y) dy c
Bài toán 4: Diện tích hình phẳng giới hạn bởi 2 đồ thị (C ) : f (x) , (C ) : f (x) là: 1 1 2 2 2 x S 
f (x)  g(x) 
dx . Trong đó: x , x tương ứng là nghiệm của phương trình f (x)  g(x), x  x 1 2  1 2 1 x
II. THỂ TÍCH CỦA KHỐI TRÒN XOAY
1. Thể tích vật thể
Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b;
S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm x ,
(a  x  b) . Giả sử S(x) là hàm số liên tục trên đoạn [ ; a b] .
2. Thể tích khối tròn xoay
Bài toán 1: Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường
y  f (x) , trục hoành và hai đường thẳng x  a , x  b quanh trục Ox:
Bài toán 2: Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường
x  g( y) , trục hoành và hai đường thẳng y  c , y  d quanh trục Oy:
Bài toán 3: Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường b
y  f (x) , y  g(x) và hai đường thẳng x  a , x  b quanh trục Ox: 2 2
V   f (x)  g (x) dx  . a
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Tính diện tích giới hạn bởi 1 đồ thị 1. Phương pháp:
a/ Phương pháp 1: b S 
|f (x) | dx a
* Xét dấu biểu thức f (x) ; x [a;b] , phá dấu trị tuyệt đối và tính tích phân.
b/ Phương pháp 2:
* Giải phương trình f (x)  0 ; chọn nghiệm trong [a;b]. Giả sử các nghiệm là ;  với    .
* Áp dụng tính chất liên tục của hàm số f (x) trên [a;b]; ta có: S |
 f (x)dx |  | f (x)dx |  |b f (x)dx | a  
2. Các Bài tập mẫu:
Bài tập 1: Tính diện tích S của hình phẳng giới hạn bởi đồ thị 2
y  x , trục hoành và đường thẳng x  2 . 8 16 8 A. S  . B. S  . C. S  16. D. S  . 9 3 3 Hướng dẫn giải CHỌN D
Nhận thấy rằng, để tính diện tích ta cần phải tìm được 2 cận. Để tìm thêm cận còn lại ta giải phương
trình hoành độ giao điểm của đồ thị   2
P : y  x với trục hoành.
Phương trình hoành độ giao điểm của đồ thị   2
P : y  x với trục hoành: 2 x  0  x  0 2 8
Áp dụng công thức ta có 2 S  x dx  .  3 0
Nhận xét: Nếu ta vẽ đồ thị hàm số 2
y  x và đường thẳng x  2 ta dễ dàng xác định được hình
phẳng giới hạn bởi các đường này. Từ đó ta dễ dàng tính được diện tích S.
Bài tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số 2 x
y  x .e , trục hoành và đường thẳng x  1 A. e  2. B. 2  e. C. 2  e. D. 1. Hướng dẫn giải CHỌN A
Phương trình hoành độ giao điểm 2 x x e  0  x  0 Ta có: 1 1 S  x e dx  x d   e  1 1 2 x 2 x 2 x x  x e  e d   2x 0 0 0 0 1 1
 e  2 xe dx  e  2 xd   e  1 1 x x x x  e  2xe  2 e dx  0 0 0 0 1 x  e  2e  2e
 e  2e  2  e  2. 0
Lời bình: Bài toán trên đã có 1 cận, ta chỉ cần tìm thêm 1 cận nữa bằng
cách giải phương trình hoành độ giao điểm. Sau đó áp dụng công thức.
Nếu vẽ đồ thị bài này để tìm hình phẳng giới hạn bởi các đường là không 1
nên vì đồ thị hàm số hơi phức tạp. Việc tìm được công thức 2 x S  x e dx 0
và tính tích phân này ta có thể dùng MTCT để tính và chọn Chọn.
Bài tập 3: Tính diện tích hình phẳng giới hạn bởi đồ thị 2
y  1 x và trục hoành:   A.   2. B. . C. 1. D. . 4 2 Hướng dẫn giải CHỌN D
Phương trình hoành độ giao điểm của, Ox là 2 1 x  0  x  1 1
Khi đó, diện tích hình phẳng cần tìm là 2 S  1 x dx.  1    x  1  t  
Đặt x  sin t  dx  cos tdt và 2   x  1   t    2   1 2 2  Suy ra 2 2 2 S  1 x dx  1 sin t.cos tdt  cos tdt        2 1   2 2
Lời bình: Bài toán trên chưa có cận, ta phải giải phương trình hoành độ
giao điểm để tìm cận. Sau đó áp dụng công thức. Việc tìm được công 1 thức 2 S  1 x dx 
và tính tích phân này tương đối phức tạp, do đó ta 1 
có thể dùng MTCT để tính và chọn Chọn.
Nếu vẽ được đồ thị thì ta xác định được hình phẳng và diện tích của nó
dễ dàng, đó chính là diện tích của nữa đường tròn bán kính bằng 1. Do 1  đó: 2 S  R   . 2 2 1
Bài tập 4: Tính diện tích S hình phẳng giới hạn bởi các đường
y  lnx, x  e, x  và trục hoành e 2 1 2 1 A. S  2  . B. S  1 . C. S  2  . D. S  1 . e e e e Hướng dẫn giải CHỌN A
Phương trình hoành độ giao điểm của đồ thị y  lnx và trụ hoành là ln x  0  x 1. e 1 e           1 xln x  x e 2 S ln x dx ln xdx ln x.dx x x ln x 1  2  . 1 e 1 1 e 1 e e
Bài tập 5: Diện tích tam giác được cắt ra bởi các trục tọa độ và tiếp tuyến của đồ thị y  ln x tại giao
điểm của đồ thị hàm số với trục Ox là: 2 1 2 1 A. S  B. S  C. S  D. S  3 4 5 2 Hướng dẫn giải Chọn D
Phương trình hoành độ giao điểm: ln x  0  x  1 1
Ta có: y '  ln x'  .y '  1  1 x '
Phương trình tiếp tuyến của đồ thị y  ln x tại giao điểm của đồ thị hàm số với trục Ox là: y  1x   1  0 hay y  x 1
Đường thẳng y  x 1 cắt Ox tại điểm A 1;0 và cắt Oy tại điểm B0;  1 . 1 1
Tam giác vuông OAB có OA  1,OB  1 S  OA.OB  OA  B 2 2 b 0 b 0 b
S  f x dx  f x dx  f x dx   f x dx  f x dx D                a a 0 a 0
Bài tập 6: Diện tích hình phẳng giới hạn bởi đường cong y  2 ax a  0, trục hoành và đường thẳng x  a bằng 2
ka . Tính giá trị của tham số k. 7 4 12 6 A. k  B. k  C. k  D. k  3 3 5 5 Hướng dẫn giải Chọn B a a 3 2 4 4 Có 2 2 2 S  2 ax dx  2 a. .x  a  ka  k   3 3 3 0 0
Bài tập 7: Cho hình cong giới hạn bởi các đường x
y  e , y  0, x  0 và x  ln 4 . Đường thẳng x  k
với 0  k  ln 4 chia thành hai phần có diện tích là S1 và S2 như hình vẽ bên. Tìm k để S  2S . 1 2 2 A. k  ln 4 3 B. k  ln 2 8 C. k  ln 3 D. k  ln 3 Hướng dẫn giải Chọn D ln 4 ln 4 ln 4 2 2 2 2 Do x x x S  2S  S  S  e dx  e dx  e  2 1 2 1   3 3 3 3 0 0 0 k Do đó: x k k
S  e dx  e 1  2  e  3  k  ln 3 1  0
Dạng 2: Tính diện tích giới hạn bởi 2 hai đồ thị 1. Phương pháp: b
Công thức tính S 
|f (x)  g(x) | dx  . Tính như dạng 1. a
2. Một số bài tập mẫu
Bài tập 1: Tính diện tích hình phẳng giới hạn bởi đồ thị 1 1   y  ; y  ; x  ; x  2 2 cos x sin x 6 3 Lời giải  /3 1 1 Ta có: S   dx  2 2
 /6 cos x sin x 1 1   
Trong trường hợp này nếu chọn cách xét dấu biểu thức y   ; x  ; 2 2  6 3  cos x sin x  1 1   
hoặc vẽ đồ thị hàm số y   ; x  ; là khá khó khăn. 2 2  6 3  cos x sin x 
Vì vậy ta chọn cách sau: 1 1       + Xét phương trình:   0 ; x  ; 2 2
 cos x  sin x  0 x  ; 2 2 cos x sin x  6 3     6 3        cos 2x  0  ; x  ;   x  6 3    4  /4  1 1  /3   1 1  Từ đó suy ra: S   dx  |  dx    2 2   2 2  6 4/4
 cos x sin x 
 cos x sin x   / 4   4 3   S |
 (tan x  cot x) |
|  | (tan x  cot x) | 2  2 .   / 6   3  4   2 1 x
Bài tập 2 : Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y  ; y  . 2 x 1 2 Lời giải
Xét phương trình hoành độ giao điểm của hai đồ thị trên: 2 1 x x  1   4 2 2
 x  x  2  0  x 1  2  x 1 2  x 1 2 1 1 x
Vì vậy hình phẳng đã cho có diện tích là: S   dx  2 1 x 1 2 2 1 x
Do trên (1;1) phương trình  vô nghiệm nên ta có: 2 x 1 2 2 1 2 1 1 2 1 1 x  1 x  1 x S   dx      d  x  dx  dx   2 2 2 1 x 1 2 x 1 2 x 1 2 1   1  1 1 1 Tính I  dx 1  . 2 1  x 1     1
+/ Đặt x  tan t ; t   ;    dx  dt  2 2  2 cos t   x  1   t   1   /4 2  /4  +/ Đổi cận: 4  cos t  I  dt  dt      1 2  /4  /4 1 tan t 2
x  1  t   4 2 1 x 1 I  dx  2 1 2 3  1 
Thay thế vào ta được: S   1   . 2 3 2 3
Bài tập 3: Tính diện tích hình phẳng giới hạn bởi đồ thị 2
y  x  4x  3 và y  3 . Hướng dẫn giải
Xét phương trình hoành độ giao điểm của hai đồ thị trên: 2
x  4x  3  3 x  0 2
x  4x  3  3    2  x
  4x  3  3 x   4 4 Khi đó: S  2 4
x  4x  3 | 3  | dx |   ‖
 2x 4x3| 3  dx | 0  0  S 
 x 4x3 3 3
dx    x  4x 3 3 4 1 2 2
dx    2x  4x 3 3 dx 0 1 3   S  x 4x 3
dx   x  4x 6 4 1 2 2
dx    2x  4x dx | 0  1 3 3 3 1 3 3 4  x   x   x  2 2 2
 S  S    2x     2x  6x    2x   8. 3 3 3   0     3 1
Bài tập 4: Tính diện tích hình phẳng giới hạn bởi đồ thị: y  sin | x | ; y  | x | - . Hướng dẫn giải
Xét phương trình hoành độ: sin | x | |  x |  
Đặt | x |  t
Khi đó trở thành: sin t  t    sin t  t    0
Xét hàm số f (t)  sin t  t  ; t [0, ) . f 
 (t)  cost 1 0 t  [0,) .
BBT của hàm số f (t) như sau:
 phương trình có nghiệm duy nhất t   .
 phương trình có 2 nghiệm phân biệt: x    và x   .    S 
|sin | x |  | x |   | dx 
(sin | x |  | x |   )dx   .   3. Bài tập
Bài tập 1: Diện tích hình phẳng giới hạn bởi parabol   2
P : y  x  3x  3 và đường thẳng d: y  2x 1 là: 7 13 19 A. B. C. D. 11 3 3 6 Hướng dẫn giải Chọn B x  1  Xét phương trình 2 2
x  3x  3  2x 1  x  x  2  0  x  2
Gọi S là diện tích hình phẳng giới hạn bởi parabol   2
P : y  x  3x  3 và đường thẳng d: y  2x 1 là 2 2  
S   x 3x 3 2 2 3 x x 13 2  2x   1 dx    2
2  x  x dx   2x      2 3  3 1 1  1  13 Vậy S  . 3 2 x
Bài tập 2: Parabol y 
chia hình tròn có tâm tại gốc tọa độ, bán kính 2 2 thành 2 phần. Tỉ số 2
diện tích của chúng thuộc khoảng nào: A. 0,4;0,5 B. 0,5;0,6 C. 0,6;0,7 D. 0,7;0,8 Hướng dẫn giải Chọn A
Phương trình đường tròn: 2 2 2 2
x  y  8  x  8  y 2 8  y
Thế vào phương trình parabol, ta được 2 y   y  2y  8  0 2  y  2 2    
   x  4  x  2  y 4 l
Diện tích phần được tạo bởi phần đường tròn phía trên với Parabol là: 2 2 2 2 2  x  x 2 2 3 x x 2 2 2 8 S    8 x  d  x  8  x dx  dx  I  I I  dx   1   ; 1 2   2  2 2 2 6 2  3 2  2  2  2  2 2 Tính 2 2 I  8  x dx  2 8  x dx 1   2 0 
Đặt x  2 2 sin t  dx  2 2 cos tdt; x  0  t  0 ; x  2  t  4    4 4 4 cos 2t 1 2
I  2 2 2 cos t2 2 cos tdt  16 cos tdt  16 dt  4  2 1    2 0 0 0 8 4
S  I  I  4  2    2 1 1 2 3 3  4  4 Diện tích hình tròn: 2 S  R 
 8  S  S  S  8   2  6  2 1    3  3 4  2 S1 3  
 0, 4350,4;0,5 . S 4 2 6  3 2 x
Bài tập 3: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y  4  và đồ thị hàm số 4 2 x y  4 2 4 4 8 A. 2  4 B. 2  C. 2  D. 3 3 3 Hướng dẫn giải Chọn B
Phương trình hoành độ giao điểm: 2 2 2 x x x  1  6l 2 2 2 2 x x 4 4      x  2  2 . Khi đó S  4    2   2 4 4 2 x  8 4 4 2 3 2  2
Bài tập 4: Gọi S là diện tích hình phẳng giới hạn bởi các đường 2 my  x , 2
mx  y (với m  0 ).
Tìm giá trị của m để S  3. A. m 1. B. m  2 . C. m  3 . D. m  4 .
Hướng dẫn giải Chọn C. 2 x Vì m  0 nên từ 2
my  x ta suy y   0 ; m Từ 2
mx  y nên x  0 và y  mx . 2 x x  0 Xét phương trình 4 3
 mx  x  m x  m  x  m
Khi đó diện tích hình phẳng cần tìm là: m 2 m 2 x  x  S  mx  dx  mx    dx  m  m 0 0  3  2 m m x  1 1 2 2   .x x    m  m  3 3m  3 3   0 1 Yêu cầu bài toán 2 2
S  3  m  3  m  9  m  3 (vì m  0 ). 3 2x
Bài tập 5: Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm 2
y  x và y  là x 1
S  a  bln 2 với a, b là những số hữu tỷ. Giá trị của a  b là 1 2 A.  . B. 2. C.  . D. 1. 3 3
Hướng dẫn giải Chọn A. 2x
Phương trình hoành độ giao điểm của C : 2
y  x và C : y  là 2  1  x 1 x  0 2x 2 x x  3 2 1 x x 2x 0         x  1  x 1   x  2 
Diện tích hình phẳng cần tìm là: 0 0 3 0  2x   2   x  5 2 2 S   x dx  2   x dx       
 2x  2ln x 1     2ln 2  x 1   x 1   3  3 1 1  1  5
Suy ra a  và b  2  3 1
Vậy a  b   3
Bài tập 6: Cho H  là hình phẳng giới hạn bởi parabol 2 y  3x ,
cung tròn có phương trình 2
y  4  x (với 0  x  2 ) và trục hoành
(phần tô đậm trong hình vẽ). Diện tích của H  là 4  3 4  3 A. . B. . 12 6 4  2 3  3 5 3  2 C. . D. . 6 3
Hướng dẫn giải
Phương trình hoành độ giao điểm của parabol 2
y  3x và cung tròn 2
y  4  x (với 0  x  2 ) lả 2 2 2 4
4  x  3x  4  x  3x  x  1.
Diện tích của H  là 1 2 1 3 3 2 2 2 3 S  3x dx  4  x dx  x  I   I   với 2 I  4  x dx  . 3 3 0 1 0 1    
Đặt x  2sin t , t   ;
 dx  2cost.dt  2 2     
Đổi cận x  1  t 
, x  2  t  . 6 2     2 2 2 2 2 2 I 
4  4sin t.2cos t.dt  4cos t.dt  2  
 1cos2t.dt  2xsin2t     6 6 6 6 2 3   3 2 3 3 2 3 4  3 Vậy S   I     3 3 3 2 6 Chọn B.
Bài tập 7: Hình phẳng H  được giới hạn bởi đồ thị C của hàm đa thức bậc ba và parabol P
có trục đối xứng vuông góc với trục hoành. Phần tô đậm của hình vẽ có diện tích bằng 37 7 11 5 A. . B. . C. . D. . 12 12 12 12
Hướng dẫn giải Chọn A.
Vì đồ thị hàm bậc ba và đồ thị hàm bậc hai cắt trục tung tại các điểm có tung độ lần lượt là
y  2 và y  0 nên ta xét hai hàm số là 3 2
y  ax  bx  cx  2 , 2
y  mx  nx (với a, m  0 ).
Suy ra C : y  f  x 3 2
 ax  bx  cx  2 và P :    2
y g x  mx  nx .
Phương trình hoành độ giao điểm của C và P là: 3 2 2
ax  bx  cx   mx  nx   3 2
ax  bx  cx     2 2 2
mx  nx  0 .
Đặt P  x   3 2
ax  bx  cx     2 2 mx  nx.
Theo giả thiết, C và P cắt nhau tại các điểm có hoành độ lần lượt là x  1
 , x  1, x  2
nên P  x  a x   1  x   1  x  2 .
Ta có P 0  2a .
Mặt khác, ta có P 0  f 0  g 0  2  a 1. 2 37
Vậy diện tích phần tô đậm là S   x   1  x  
1  x  2 dx   12 1 
Dạng 3: Tính thể tích vật thể tròn xoay dựa vào định nghĩa 1. Phương pháp:
Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b; S(x) là
diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm x , (a  x  b) .
Giả sử S(x) là hàm số liên tục trên đoạn a,b .
2. Các Bài tập mẫu:
Bài tập 1: Cho phần vật thể B giới hạn bởi hai mặt phẳng có phương trình x  0 và x  2 . Cắt phần
vật thể B bởi mặt phẳng vuông góc trục Ox tại điểm có hoành độ x 0  x  2, ta được diện tích là
một tam giác đều có độ dài cạnh bằng x 2  x. Tính thể tích V của phần vật thể B . Lời giải 2 a 3
Một tam giác đều cạnh a có diện tích S   4 2
x 2  x 3
Do tam giác đều cạnh x 2  x có diện tích là S(x)   4 2 2 2 x 2  x 2 3 3 Ca sio 3 4 3 Suy ra thể tích 2
S  S(x)dx  dx 
x 2  xdx         4 4 4 3 3 0 0 0
Bài tập 2: Trong không gian Oxyz , cho vật thể nằm giữa hai mặt phẳng x  0 và x   , biết rằng
thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ bằng
x,0  x    là một tam giác đều cạnh là 2 sin x .Tính thể tích của vật thể đó. Lời giải 2 a 3
Một tam giác đều cạnh a có diện tích S  4 x
Do đó tam giác đều cạnh 2 sin x có diện tích là S  x 4sin . 3   3 sin x 4 2 2
Suy ra thể tích V  S
 xdx  3sin d x x  2 3  0 0
Bài tập 3: Một bồn trụ đang chứa dầu được đặt nằm ngang có chiều dài bồn là 5m, bán kính đáy 1m
. Người ta rút dầu ra trong bồn tương ứng với 0,5 m của đường kính đáy. Tính thể tích gần đúng của dầu còn lại trong bồn Lời giải
* Thể tích cả khối trụ 2 2
V   R h  .1 .5  5  3 m  1
* Tính thể tích phần khối trụ bị mất đi y y= R2-x2 2 d x O d R 2 R 1 + Cách 1: 2 2 S  2 R  x dx 2  2 1  0,61 viên phân   x dx d 1 2 1 2 V  S .h  2
1 x dx 5  3,07 2 viên phân 1 2 1
Suy ra thể tích khối trụ còn lại 2
V  V V  5  2
1 x dx5  12,637  3 m  1 2 1 2  OH 1   2
+ Cách 2: Tính góc ở tâm cos        2 R 2 2 3 3 y 2 A x O H R 2 B 1 1  2 2 2 S R      sin   . viên phân   sin   0,614 2 2  3 3  1  2 2  V  S .h  . viên phân   sin 5 2 2  3 3  1  2 2 
V  V V  5  .  sin 5  12,637  3 m  1 2 2  3 3 
Bài tập 4: Bạn A có một cốc thủy tinh hình trụ, đường kính trong lòng đáy cốc là 6 cm, chiều cao
trong lòng cốc là 10 cm đang đựng một lượng nước. Bạn A nghiêng cốc nước, vừa lúc khi nước chạm
miệng cốc thì ở đáy mực nước trùng với đường kính đáy. Tính thể tích lượng nước trong cốc Lời giải
Phân tích: Thể tích nước có hình dạng “cái nêm”; có 2 phương pháp tính thể tích này
+ Cách 1 – Chứng minh công thức bằng PP tích phân: Xét thiết diện cắt cốc thuỷ tinh tại vị trí x
R  x  R bất kỳ; ta có diện tích thiết diện là S  x 1 1 2 2
 . R  x . 2 2
R  x .tan    2 2
R  x  tan ; thể tích. 2 2 R R
V  S  x 1 dx  tan  2 2 2 R  x  3
dx  R tan .   2 3 R R Cách 2:
Gọi S là diện tích thiết diện do mặt phẳng có phương vuông góc với trục Ox với khối nước, mặt
phẳng này cắt trục Ox tại điểm có hoành độ .
h  x  0 Ta có: r h  x (h  x)    R r
, vì thiết diện này là nửa hình tròn bán kính r R h h 2 2 1  (  ) 2  ( )    h x R S x r 2 2 2h
Thể tích lượng nước chứa trong bình là. Bài giải
+ Cách 1: Áp dụng công thức tính thể tích cái nêm biết góc giữa mặt cắt và mặt đáy bằng  là 2 2 2 3 2 h 2
V  R h  R .tan với tan  h ta được 3 2 V  R .  .3 .10  60 3 cm  3 3 R 3 R 3 2 2 1  (  )
+ Cách 2: Tính trực tiếp bài toán bằng PP tích phân. 2  ( )    h x R S x r ; thể tích 2 2 2h h 10 9 h 2 3
V  S(x)dx 
(10  x) dx  60 (cm ).  
V  S(x)  dx 200 0 0 0
Bài tập 5: Cắt một khối trụ bởi một mặt phẳng ta được một khối như hình vẽ bên. Biết rằng thiết diện
là một hình elip có độ dài trục lớn bằng 10, khoảng cách từ điểm thuộc thiết diện gần mặt đáy nhất
và điểm thuộc thiết diện xa mặt đáy nhất lần lượt là 8 và 14. Tính thể tích của. Lời giải AB  8 
Tính các số đo: AE  10 2 2
 AD  AE  DE  8 ; suy ra bán kính khối trụ là 
DE  14  8  6  AD R  4 . 2
 Cách 1: Thể tích khối bằng thể tích “khối trụ trung bình”:  AB  CE 2  2 V   R .   đvtt H    .4 .11 176      2 
 Cách 2: Áp dụng công thức tính thể tích “cái nêm”: Lấy mặt phẳng P vuông góc với đường
sinh của hình trụ và đi qua điểm , A khi
đó chia khối  H  thành hai khối:
+ Khối 1: là khối trụ chiều cao h  8 , bán kính r  4 nên thể tích 2
V   r h  128 1
+ Khối 2: là phân nửa một khối trụ có chiều cao DE  6 và bán kính r  4 nên thể tích 1 1 2 2
V  . r .AD  ..4 .6  48 2 2 2 + Vậy V
 V V 128  48 176  v đ tt  H  1 2 3. Bài tập
Câu 1: Cho T  là vật thể nằm giữa hai mặt phẳng x  0 , x 1. Tính thể tích V của T  biết
rằng khi cắt T  bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ bằng x ,
0  x 1, ta được thiết diện là tam giác đều có cạnh bằng 1 x . 3 3 3 3 3 3 A. V   . B. V   . C. V  . D. V   . 2 8 8 2 Lời giải Chọn C   x2 1 3 3 1 x
Ta có diện tích tam giác đều cạnh bằng 1 x là S  x    4 4 1 1 3 1 x 3
Thể tích của vật thể T  là V  S
 xdx  dx   1 3 3 x 1 2   . 4 8 0 8 0 0
Câu 2: Cho vật thể T  giới hạn bởi hai mặt phẳng x  0; x  2 . Cắt vật thể T  bởi mặt phẳng
vuông góc với trục Ox tại x 0  x  2 ta thu được thiết diện là một hình vuông có cạnh bằng    1 x x
e . Thể tích vật thể T  bằng   4 13e   1 4 13e 1 A. . B. . C. 2 2e . D. 2 2 e . 4 4 Lời giải Chọn B
Diện tích thiết diện là      2 2 1 x S x x e . 2 2
Thể tích của vật thể T  là         2 2 1 x V S x dx x e dx . 0 0 2 2 2 4 2 1    
V   x  2 e x x x 9 1 1 x 1 2 1 e  x  2 2 2 1 x e dx    e  e dx  2 2  2 2  0 0 0  0  2 4 4 4
9e 1 3e 1 1 e  x 1 1 13 1 2 4 4    e
 3e  e   . 2 2 4 4 4 4 0
Dạng 4: Tính thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi 1 đồ thị 1. Phương pháp:
Vật thể tròn xoay sinh bởi miền hình phẳng được giới hạn: Đồ thị ;
y  f (x) trục ; Ox( y  0)
x  a, x  b ; quay xung quanh Ox .
- Nếu thiếu cận thì giải phương trình f (x) = 0 để bổ sung cận. b
- Tính thể tích theo công thức: 2 V   f (x)dx Ox a
2. Các Bài tập mẫu:
Bài tập 1: Kí hiệu H  là hình phẳng giới hạn bởi đồ thị hàm số 2
y  2x  x và trục hoành. Tính thể tích
V của vật thể tròn xoay được sinh ra bởi hình phẳng đó khi nó quay quanh trục . Ox Lời giải x  0
Phương trình hoành độ giao điểm . 2
2x  x  0  x 2 2 16
Thể tích của vật thể tròn xoay cần tìm V   2x  x 2 2 dx  . 15 0
Bài tập 2: Cho miền hình phẳng giới hạn bởi: x
y  xe , Ox x  1 quay xung quanh Ox . Tính thể
tích của vật thể tạo thành. Lời giải
Xét phương trình hoành độ giao điểm của đồ thị hàm số: x
y  xe và trục Ox x
xe  0  x  0 1 2 1
Vậy vật thể tròn xoay có thể tích là:     x      2 2x V xe dx x e dx 0 0 1 2  1 1  e 1 2 2 x 2 x 2 x  V   x e  xe dx    xe dx     0 0  2  2 0       1 e e x 1 1 1 1 2 2 x 2 x  2 2 1   V   x e  e dx  e  .    0 0 0 2  2 2  4 4
Bài tập 3: Cho miền hình phẳng giới hạn bởi: 2
y  x  4x, y  0 ; quay xung quanh Ox . tính thể
tích của vật thể tạo thành. Lời giải
Hoành độ giao điểm của đồ thị hàm số: 2
y  x  4x và đường thẳng y  0 là nghiệm của phương x  0 trình: 2
x  4x  0  x  4
Vật thể tạo thành có thể tích là: 4 4 5 3   
V     2x  4x2 4 dx     4 3 2
x  8x 16x dx x 4 16x 512     2x    0 0 5 3 15   0 Bài tập 4: Gọi V là
thể tích khối tròn xoay tạo thành khi quanh hình phẳng giới hạn bởi các đường
y  x; y  0; x  4 và trục Ox . Đường thẳng c
x  a 0  a  4 ắt đồ thị hàm số y  x tại M .
Gọi V là thể tích khối tròn xoay tạo thành khi quay tam giác MOH quanh trục . Ox
Biết rằng V  2V 1 1 . Tính a Lời giải 4 4 2 V
Ta có V    x  dx   d
x x  8  V   4  1 . 2 0 0
Tam giác MOH quanh trục
Ox tạo nên hai khối nón chung đáy. Gọi N là hình chiếu vuông góc của
M trên trục Ox . Suy ra r  MN  y  y a  a M   . 1 1  a
 V  OH..r  .4. a 2 4 2  1 . 3 3 3 4 a Suy ra 4   a  3 . 3 x
Bài tập 5: Cho H  là hình phẳng giới hạn bởi độ thị hàm số ; y  trục Ox và đường thẳng 2 4  x
x 1. Tính thể tích khối tròn xoay thu được khi quay quanh hình H  xung quanh trục . Ox Lời giải x
Phương trình hoành độ giao điểm  0  x  0. 2 4  x
Theo bài toán thì thể tích của vật thể tròn xoay cần tìm 1 1 x    2 4 a V  
dx   ln 4  x  ln  ln .  2 4  x 2 2 3 2 b 0 0 Do đó
a  4,b  3  a  b  7. 3. Bài tập
Câu 1: Cho hình phẳng H  giới hạn bởi các đường 2
y  x  3, 0, y  x  0, 2
x  . Gọi V là thể
tích khối tròn xoay được tạo thành khi quay H  xung quanh trục Ox . Mệnh đề nào sau đây đúng? 2 2 2
A. V    2x 3 dx .
B. V   2x  3dx . 0 0 2 2 2
C. V   2x 3 dx .
D. V    2x 3dx . 0 0 Lời giải 2 2
Thể tích của vật thể được tạo nên là V    2x  3 d .x 0
Câu 2: Gọi V là thể tích khối tròn xoay tạo thành do quay xung quanh trục hoành một elip có 2 2 x y phương trình 
 1. V có giá trị gần nhất với giá trị nào sau đây? 25 16 A. 550 B. 400 C. 670 D. 335 Lời giải Chọn D
Quay elip đã cho xung quanh trục hoành chính là quay hình phẳng: 2  x   
H  y  4 1
, y  0, x  5  , x  5 . 25  
Vậy thể tích khối tròn xoay sinh ra bởi H khi quay xung quanh trục hoành là: 2 3 5  16x   16x  5 320 V    16 d
 x   16x     335,1 5  25 75 5      3
Câu 3: Cho hình phẳng (H ) được giới hạn bởi đường cong 2 2
y  m  x ( m là tham số khác 0
) và trục hoành. Khi (H ) quay xung quanh trục hoành được khối tròn xoay có thể tích V .
Có bao nhiêu giá trị nguyên của m để V 1000 . A. 18. B. 20. C. 19. D. 21. Lời giải Chọn A
Phương trình hoành độ giao điểm của đường cong và trục hoành là: 2 2
m  x  0  x  m m 2 1 m 4 m m
Thể tích vật thể tròn xoay cần tính là: 2 2 2 3 V  
(m  x )dx   (m x  x ) |   3  m 3  m 2 4 m m
Ta có: V 1000   1000 3  m  750 3 3
  750  m  750 . 3
Ta có 3 750  9, 08 và m  0 . Vậy có 18 giá trị nguyên của m. x  3
Câu 8 : Cho hình phẳng D giới hạn bởi các đường cong y 
, trục hoành và trục tung. Khối x  1
tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V   (a  b ln 2) với a, b là
các số nguyên. Tính T  a  . b A. T  3. B. T  6. C. T 10. D. T  1. Lời giải
Dựa vào đồ thị hàm số trên ta có: 3 2 3 2 3  x  3   4   8 16 V   dx    1 dx   1       dx 2   x 1   x 1   x 1 (x 1) 0 0 0  3  16   
x  8 ln(x 1) 
  (15 16 ln 2)  a  15; b  16.    x 1  0
Vậy T  a  b  1.
Câu 4: Cho hình H  trong hình vẽ dưới đây quay quanh trục Ox tạo thành một khối tròn xoay
có thể tích bằng bao nhiêu? 2   A. . B. . C. 2 . D. 2 2 . 2 2 Lời giải
Thể tích khối tròn xoay nhận được khi quay hình H  quanh trục Ox là   2 x   
V   in x2 1 cos 2 1 s dx       dx  x  sin 2x      2 2  2  0 2 0 0
Câu 5: Vật thể parabolide tròn xoay như hình vẽ bên dưới có đáy có diện tích B  3 chiều cao
h  4 . Thể tích của vật thể trên là h B 1 1 A. V   . B. V  6 . C. V   . D. V  8 . 3 4 Lời giải y h x O R
Đường cong parabol có dạng: 2
y  ax và đi qua điểm có tọa độ  ; R h nên ta có: h 2 y  x 2 R R y  x   h h 2 2 R R 1 h 1
Thể tích của khối tròn xoay trên là: 2 V   d y y   . y  2   R h . 0 h h 2 2 0 1 1 1
Áp dụng công thức ta có: 2
V   R h  Bh  .3.4  6 . 2 2 2
Câu 6: Cho hàm số y  f  x 3 2
 ax  bx  cx  d,a, ,
b c, d  , a  0 có đồ thị C . Biết rằng đồ
thị C tiếp xúc với đường thẳng y  4 tại điểm có hoành độ âm và đồ thị của hàm số
y  f ' x cho bởi hình vẽ dưới đây. Tính thể tích vật thể tròn xoay được tạo thành khi
quay hình phẳng H giới hạn bởi đồ thị C và trục hoành khi quay xung quanh trục Ox . 725 1 A.  . B.  . C. 6 . D. Chọn khác. 35 35 Lời giải Chọn D
Dựa vào đồ thị hàm số y  f ' x  f  x   2 ' 3 x   1 .
Khi đó f  x  f  x 3 '
dx  x  3x  C  .
Điều kiện đồ thị hàm số f  x tiếp xúc với đường thẳng y  4 là:  f   x 3  4
x  3x  C  4  x  1     
suy ra f  x 3 2
 x  3x  2C .  f '   x  0 3   2 x   1  0 C  2
+ C Ox  hoành độ giao điểm là x  2; x  1. 1 2 729
+Khi đó V    3 2
x  3x  2 dx   . 35 2 
Dạng 5: Tính thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi 2 đồ thị 1. Phương pháp: Nếu hình phẳng
D được giới hạn bởi các đường y  f  x, y  g  x, x  a, x  b thì thể tích khối b
tròn xoay sinh bởi khi quay D quanh trục Ox được tính bởi công thức: 2 V   f  x 2
 g x dx a
2. Các Bài tập mẫu:
Bài tập 1: Cho hình phẳng giới hạn bởi các đường 2 y  .
a x , y  bx, a,b  0 quay xung quanh trục
Ox . Thể tích của khối tròn xoay tạo thành bằng: 3 b 1 1 5 b A. V     .  . B. V   . . 3   a  3 5  3 5a 5 b 5 b 1 1 C. V  . . D. V     .  3   3a 3 a  3 5  Hướng dẫn giải Chọn D 2  b b 
Tọa độ giao điểm của hai đường 2 y  . a x và y  .
b x là các điểm O(0; 0) và A ;   . Vậy thể  a a  b b a a 5 b  1 1 
tích của khối tròn xoay cần tính là: 2 2 2 4 V  b  x dx  a  x dx        . 3 a  3 5  0 0 1
Bài tập 2: Cho hình phẳng giới hạn bởi các đường 2 2
y  4  x , y  x quay xung quanh trục Ox. 3
Thể tích của khối tròn xoay tạo thành bằng: 24 3  A. V  28 3 . B. V  . 5 5 28 2  C. V  24 2 . D. V  5 5 Hướng dẫn giải Chọn B 1
Tọa độ giao điểm của hai đường 2
y  4  x và 2
y  x là các điểm A 3;  1 và B  3;  1 . Vậy 3
thể tích của khối tròn xoay cần tính là: 3 V    4 x  3 1 28 3 2 4 dx  .  x dx   .  9 5  3  3
Bài tập 3: Cho hình phẳng giới hạn bởi các đường 2 2
y  2x , y  4x quay xung quanh trục Ox. Thể
tích của khối tròn xoay tạo thành bằng: 88    A. V  9 . B. V  4 . C. . V  6 D. . V  5 70 3 5 Hướng dẫn giải Chọn D Với x  0;2 thì 2  
y  4x  y  4x
Tọa độ giao điểm của đường 2 y  2x với 2 y  4x là các điểm O(0; 0) và (1 A ;2) . Vậy thể tích của 1 1 6
khối tròn xoay cần tính là: 4
V  .4xdx  .4x dx  . .   5 0 0
Bài tập 4: Thể tích khối tròn xoay khi quay hình phẳng D giới hạn bởi các đường elip 2 2 x  9y  9 quay quanh Ox bằng: A.  . B. 2 . C. 3 . D. 4 Hướng dẫn giải Chọn D 2 3 3 2 9  x 9  x Ta có: 2 2 2 2
x  9 y  9  y 
 V   y dx   dx  4 .   9 9 3  3 
Bài tập 5: Thể tích của khối tròn xoay khi quay hình phẳng D giới hạn bởi các đường y  x, y  x
quanh trục Ox bằng: 1 1 A.
  x  xdx.
B.  x  x dx. 0 0 1 1 C.   2
x  x dx . D.   2
x  xdx 0 0 Hướng dẫn giải Chọn D  x  0
Xét phương trình x  x  
 x  0; x 1. 2 x  x 1 1 Và . x  x x  0;  1  V    2 2
( x)  x dx    2
x  x dx 0 0 3. Bài tập
Câu 1: Quay hình phẳng như hình được tô đậm trong hình vẽ bên quanh trục Ox ta được khối tròn xoay có thể tích là:
A. V  4 3 .
B. V  6 3 .
C. V  5 3 . D. V  2 3 Hướng dẫn giải Chọn A 2 2 2
x  y  4 x  3 Xét hệ phương trình:     x   3 .  y  1   y  1
Do đối xứng nhau qua Oy nên: 3   V       x  3   dx       x  3 x 2 2 2 3 2 4 1 2 3
dx  2 3x    4 3 .  3  0 0 0
Câu 2: Quay hình phẳng như hình được tô đậm trong hình vẽ bên quanh trục Ox ta được khối tròn xoay có thể tích: 46   A. V  46 . B. V  23 . C. V  . D. V 13 . 9 15 9 Hướng dẫn giải Chọn B 2 2
x  y  4 Xét hệ phương trình:   x  1  .  y  3x
Do đối xứng nhau qua Oy nên 3 V 2   4 x    3x 3 2 2     dx  2   2 4
4  x  3x dx   0 0 5 5  x 3x  3 46  2 4x      .  3 5  0 15
Câu 3: Quay hình phẳng như hình được tô đậm trong hình vẽ bên quanh trục Ox ta được khối tròn xoay có thể tích là: 2 2 V  A. 2 V  3 . B. 2 V   . C. 3 . D. 2 V  2 Hướng dẫn giải Chọn D 2
 y 1 1 x
Ta có: x   y  2
1 1   y  2 2 2 1 1 x   2
y 1 1 x 1 1 2 2  
Ta có: V  2   2 1 1 x   2 1 1 x  2 dx  8 1 x dx     0 0       Đặt ; x  sin t t   ;     2 2        2 2 2  t 
 V  8 cos tsdt  4  1cos2t sin 2 2
dt  4 t    2  2 .  2  0 0 0 Câu 4: x
Cho hình H  giới hạn bởi các đường cong C : y  e , tiếp tuyến của C tại điểm
M 1;e và trục
Oy. Thể tích của khối tròn xoay khi quay H  quanh trục Ox bằng: 3 y 2 1 x -1 O 1 2 e  2 2 e 1 2 e 1 2 e  3 A. . B. . C. . D. 2 3 2 6 Lời giải Chọn D Ta có x y  e
Phương trình tiếp tuyến của C tại M 1;e là
y  e x  
1  e  y  . ex 1 2 1 2  e  e  x 1 x 3 Diện tích của
H  bằng: V    2 2 2 e  e x  2 3 dx  e   x   .  2 3  6 0 0 Câu 5: 2 Cho hình phẳng
H  giới hạn bởi các đường .
y  x  4, y  2x  4, x  0, x  2 Thể tích
của khối tròn xoay được tạo thành khi quay  H  xung quanh trục Ox bằng: 32 32 A.  . B. 6 . C. 6 . D. . 5 5 Lời giải Chọn D 2 2 2 32
Suy ra thể tích cần tìm là V   x  4 dx  2x  42 2 dx  . 5 0 0
Dạng 6: Tính thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi nhiều đồ thị 1. Phương pháp:
2. Các Bài tập mẫu:
Bài tập 1: Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
y  x , y  0 và x  4 quanh trục . Ox Đường thẳng
x  a 0  a  4 cắt đồ thị hàm y  x tại M . y M a H O K 4 x
Gọi V là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục . Ox
Biết rằng V  2V 1 1 . Khi đó A. a  2 . B. a  5 2 2 . C. a  . D. a  3 . 2 Hướng dẫn giải Chọn D 4
Ta có x  0  x  0 . Khi đó V   d x x  8 0
Ta có M a; a 
Khi quay tam giác OMH quanh trục
Ox tạo thành hai hình nón có chung đáy: Hình nón  N O
h  OK  a
R  MK  a 1  có đỉnh là , chiều cao , bán kính đáy ; 1 Hình nón  N H
h  HK  4  a
R  MK  a 2  thứ 2 có đỉnh là , chiều cao , bán kính đáy 2 1 1 4 Khi đó 2 2
V   R h   R h   a 1 1 2 3 3 3 4
Theo đề bài V  2V  8  2.  a  a  3 1 . 3
Bài tập 2: Cho hình thang cong giới hạn bởi các đường . x
y  e , y  0, x  0, x  ln 4 Đường thẳng x
= k 0  k  ln 4 chia thành hai hình phẳng là S1 và S2 như hình vẽ bên. Quay S , S quanh trục Ox 1 2
được khối tròn xoay có thể tích lần lượt là V ,V . Với giá trị nào của k thì V  2V 1 2 1 2 1 32 1 11 k  1 ln k  32 ln11 k  ln k  ln A. 2 3 . B. 2 . C. 2 3 . D. 3 Hướng dẫn giải Chọn B Ta có: k        V    e k e e e x e  2 x 2k ln 4 dx      
V     xe  2 x 2k 2 2 ln 4 ; dx      8  1 2  2 0  2 2  2 k  2 0 k 2k 2k e   e  k 1 Theo giả thiết: 2 V  2V    2 8   
 e 11  k  ln11 1 2  2 2  2  2
Bài tập 3: Cho hình phẳng D giới hạn bởi các đường 2
y  4x và đường thẳng x  4 . Thể tích của
khối tròn xoay sinh ra khi D xoay quanh trục Ox là: A. 32. B. 64. C. 16 . D. 4.
Hướng dẫn giải : Chọn A
Giao điểm của hai đường 2
y  4x và x  4 là D 4; 4
  và E 4;4 . Phần phía trên Ox của đường 2
y  4x có phương trình y  2 x . Từ hình vẽ suy ra thể tích của khối tròn xoay cần tính là: 4
V  2 x 2 dx  32  . 0
Bài tập 4: Cho hình phẳng giới hạn bởi các đường y  3x, y  x, x  0, x  1 quay xung quanh trục
Ox. Thể tích của khối tròn xoay tạo thành bằng: 8 4 2 A. V  . B. V  . C. V  . D. V  .  3 3 3 Hướng dẫn giải Chọn A
Tọa độ giao điểm của đường x 1 với y  x và y  3x là các điểm C 1;  1 và B 3;  1 . Tọa độ giao
điểm của đường y  3x với y  x là O 0;0 . Vậy thể tích của khối tròn xoay cần tính là: 1 1 8 2 2 V  .9  x dx  .  x dx     . 3 0 0
Bài tập 5: Trên mặt phẳng Oxy, cho hình phẳng giới hạn bởi các đường P 2
y  x P  2 : ;
' : y  4x ;d  : y  4 . Thể tích của khối tròn xoay khi quay quanh trục Ox bằng: 9 4 7 A. . B. . C. . D. 2 . 5 5 5 Hướng dẫn giải Chọn B
Đặt V là thể tích cần tìm  x  2
Xét phương trình hoành độ giao điểm của và: 2
x  4  x  2  x 1
Xét phương trình hoành độ giao điểm của và: 2
4x  4  x  1 2  y  x  V
là thể tích khối tròn xoay sinh bởi khi quay: y  4 quanh Ox OAC   Oy  2  y  4x  V
là thể tích khối tròn xoay sinh bởi khi quay: y  4 quanh Ox OAB   Oy  2 2 2 1 2 2 Lúc đó: V V V  4
  2x dx  4     2 4x         dx      2
4  x dx   4 4 16x dx OAC OAB   0 0 0 0 5 5  x  2  x  1  32 16  4   4x   4x 16   8   4          5 0   5 0   5 5  5
3. Bài tập trắc nghiệm:
Câu 1: Cho H  là hình phẳng giới hạn bởi đồ thị của các hàm sốP : y  x, y  0, y  2  x .
Thể tích của khối tròn xoay thu được khi quay hình H  xung quanh trục Ox là: 4 2 1 7 8 2  3 5 A.  . B. . C.  . D.  . 3 6 6 6 Lời giải Chọn D 0  x  2 0  x  2
x  2  x      x 1 2 2
x  (2  x)
x  5x  4  0 1
V    x  2 2 5 2
dx   (2  x) dx    . 6 0 1 6
Câu 2: Cho hình H  giới hạn bởi các đường y  x 1; y  ; x  1. Quay hình H  quanh x
trục Ox ta được khối tròn xoay có thể tích là: 13 125 35 A. . B. . C. . D. 18 . 6 6 3 Lời giải Chọn C y x 1 6 x  2
Phương trình hoành độ giao điểm: 2 x 1 
 x  x  6  0x  0   x x  3  l 6
Vì  x 1  0 với x 1;2 nên thể tích cần tính là x 2 2  6 2   V   x    x 2 35 d 1 dx    . 1 1  x  3
Câu 3: Gọi H  là hình phẳng giới hạn bởi các đường: y  3x; y  x ;x 1. Quay H  xung
quanh trục Ox ta được khối tròn xoay có thể tích là: 8 2 8 A. . B. . C. 2 8 . D. 8 . 3 3 Lời giải Chọn A
Phương trình hoành độ giao điểm: 3x  x  x  0 và 3x  x  0 với x 0;  1 . 1 1 8
Thể tích cần tính là V   3x2 2
dx  x dx    . 0 0 3
Câu 4: Cho hình phẳng H  giới hạn bởi các đường 2
y  x , y  2x . Thể tích của khối tròn xoay
được tạo thành khi quay H  xung quanh trục Ox bằng: 16 21 32 64 A. . B. . C. . D. . 15 15 15 15 Lời giải Chọn D
Hoành độ giao điểm của đồ thị 2 hàm số 2
y  x và y  2x là nghiệm của phương trình x  0 2
x  2x  x  2
Thể tích của khối tròn xoay tạo thành là 2 2 2 2 5  4   x  64π
V  π2x2 dx  π 2x 2 dx 3  π x  π       3   5  15 0 0 0 0 . 1
Câu 5: Cho hình phẳng giới hạn bởi các đường 2 2
y  4  x , y  x quay xung quanh trục Ox . 3
Thể tích của khối tròn xoay tạo thành bằng:     A. 28 2 V  . B. 28 3 V  . C. 24 2 V  . D. 24 3 V  . 5 5 5 5 Lời giải Chọn B 1 Giải phương trình 2 2
4  x  x  x   3 3  x  28 3
Thể tích cần tìm là V     4  x  2 3 3 2 2 2
dx      dx  .  3  5  3  3
Dạng 7: Một số bài toán thực tế ứng dụng tích phân
1. Phương pháp giải
* Một vật chuyển động có phương trình vận
Ví dụ 1: Một vật chuyển động chậm dần đều với
tốc v t trong khoảng thời gian từ t  a đến vận tốc .
v t 160 10t m / s Quãng đường
t  ba  b sẽ di chuyển được quãng đường
mà vật chuyển động từ thời điểm
t  0s đến là:
thời điểm mà vật dừng lại là b A. 1028m. B. 1280m. S  v  tdt C. 1308m. D. 1380m. a
Hướng dẫn giải Khi vật dừng lại thì
v t 160 10t  0  t 16 16 16 Do đó S  v
 tdt  16010tdt 0 0
 160t 5t  16 2  1280m . 0
Chọn B.
* Một vật chuyển động có phương trình
Ví dụ 2: Một chiếc ô tô chuyển động với vận tốc
gia tốc a t thì vận tốc của vật đó sau
v t m / s , có gia tốc
khoảng thời gian t ;t 3 1 2  là:
a t  vt   2 m / s . 2t 1 t2
Vận tốc của ô tô sau 10 giây (làm tròn đến hàng đơn v  a  tdt 1 t vị) là A. 4,6 m/s. B. 7,2 m/s. C. 1,5 m/s. D. 2,2 m/s.
Hướng dẫn giải
Vận tốc của ô tô sau 10 giây là 10 10 3 3 3 v 
dt  ln 2t 1  ln 21  4,6  m / s . 2t 1 2 0 2 0
Chọn A.
* Điện lượng chuyển qua tiết diện của dây dẫn
của đoạn mạch trong thời gian từ t t 1 đến 2 là: t2 Q  I  tdt 1 t 2. Bài tập
Bài tập 1: Một vật chuyển động với vận tốc 10 m/s thì tăng tốc với gia tốc . a t 2
 3t  t Tính
quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc. 4300 430 A. . m B. 4300 m. C. 430 m. D. . m 3 3
Hướng dẫn giải
Chọn A. 3t t Hàm vận tốc
v t  a
 tdt  3t t  2 3 2 dt    C. 2 3
Lấy mốc thời gian lúc tăng tốc
 v0 10  C 10. 2 3 3t t Ta được v t   10. 2 3
Sau 10 giây, quãng đường vật đi được là 10 2 3 3 4 10  3t t   t t  4300 S     10 dt     10t   m  2 3   2 12 0  3 0
v t   a  tdt
Bài tập 2: Dòng điện xoay chiều hình sin chạy qua một đoạn mạch LC có biểu thức cường độ là   
i t  I cos t  i  q t  0 0   . Biết
với q là điện tích tức thời ở tụ điện. Tính từ lúc , điện lượng  2  
chuyển qua tiết diện thẳng của dây dẫn của đoạn mạch đó trong thời gian từ 0 đến là   2I 2I  I A. 0 . B. 0. C. 0 . D. 0 .    2
Hướng dẫn giải
Chọn C. 
Điện lượng chuyển qua tiết diện của dây dẫn của đoạn mạch trong thời gian từ 0 đến là             Q  I  t I 2I 0  0
dt  I cos t  dt  sin t   .  0      2    2  0  0 0
Q t    I tdt Bài tập 3: Gọi
htcm là
mức nước trong bồn chứa sau khi bơm được t giây. Biết rằng ht 1 3 
t  8 và lúc đầu bồn không có nước. Tìm mức nước ở bồn sau khi bơm nước được 6 giây 5
(chính xác đến 0,01cm) A. 2,67 cm. B. 2,66 cm. C. 2,65 cm. D. 2,68 cm.
Hướng dẫn giải
Chọn B.
Mức nước ở bồn sau khi bơm nước được 6 giây là 6 6   h  t 1 3 dt  t  8dt   t 8 6 3 3 t  8  2,66cm 5  20    0 0 0
Bài tập 3: Một viên đá được bắn thẳng đứng lên trên với vận tốc ban đầu là 40 m/s từ một điểm cao
5 m cách mặt đất. Vận tốc của viên đá sau t giây được cho bởi công thức v t  40 10t m/s. Tính
độ cao lớn nhất viên đá có thể lên tới so với mặt đất. A. 85 m. B. 80 m. C. 90 m. D. 75 m. Lời giải Chọn A
Gọi h là quãng đường lên cao của viên đá.
v t   h t   h t   v
 t    t 2 ' dt
40 10 dt  40t  5t  c
Tại thời điểm t  0 thì h  5 . Suy ra c  5. Vậy ht 2
 40t  5t  5
h t lớn nhất khi vt  0  40 10t  0  t  4 . Khi đó h4  85m .
Bài tập 4: Một ô tô chạy với vận tốc 20 m/s thì người lái đạp phanh còn được gọi là “thắng”. Sau khi
đạp phanh, ô tô chuyển động chậm dần đều với vận tốc v t  40
 t  20 trong đó t là khoảng thời
gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Quãng đường ô tô di chuyển từ lúc đạp phanh đến
khi dừng hẳn là bao nhiêu? A. 2 m. B. 3 m. C. 4 m. D. 5 m. Lời giải Chọn D
Lấy mốc thời gian là lúc ô tô bắt đầu đạp phanh t  0
Gọi T là thời điểm ô tô dừng lại. Khi đó vận tốc lúc dừng là v T   0
Vậy thời gian từ lúc đạp phanh đến lúc dừng là v T  1  0  4
 0T  20  0  T  2
Gọi s t là quãng đường ô tô đi được trong khoảng thời gian T .
Ta có v t  st suy ra s t là nguyên hàm của vt 1 1 T 2 1
Vậy trong s ô tô đi được quãng đường là: v
 tdt   40
 t  20dt   2 20
 t  20t 2  5 2 0 t 0
Bài tập 5: Một ô tô xuất phát từ A chuyển dộng với vận tốc nhanh dần đều, 10 giây sau, ô tô đạt vận
tốc 5 và từ thời điểm đó ô tô chuyển động đều. Ô tô thứ hai cũng xuất phát từ A nhưng sau ô tô thứ
nhất là 10 giây, chuyển động nhanh dần đều và đuổi kịp ô tô thứ nhất sau 25 giây. Vận tốc ô tô thứ
hai tại thời điểm đó là A. 12 . B. 8 . C. 10 . D. 7 . Lời giải Chọn A v  v 5
Ta có gia tốc trong 10 s đầu của ô tô thứ nhất là 0 a    0,5 2 m/s  t  t 10 0
Trong 10 s đầu, ô tô thứ nhất chuyển động nhanh dần với vận tốc v t  0,5t 10
 Quãng đường ô tô thứ nhất đi được trong 10 s là 0,5tdt  25  m. 0
Trong 25 s tiếp theo, ô tô thứ nhất đi được 5.25  125
Vậy quãng đường ô tô thứ nhất đi được đến khi bị đuổi kịp là 25 125  150m 1 Mặt khác 2
S  S  at 0 2 2S  S0   2.150
Gia tốc của ô tô thứ hai là a    0, 48 2 m/s 2 2  t 25
Vậy khi đuổi kịp ô tô thứ nhất, vận tốc của ô tô thứ hai là v  v  at  12 . t 0
Bài tập 6: Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc v t  7t đi được 5 , người lái 1  
xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc a    2
70 m/s  . Tính quãng đường S m đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn.
A. S  95, 70 m .
B. S  87,50m .
C. S  94,00m . D. S  96, 25m . Lời giải Chọn D
Quãng đường ô tô đi được từ lúc xe lăn bánh đến khi được phanh. 5 5 5 2 t
S  v t dt  7tdt  7  87,5 m . 1  1      2 0 0 0
Vận tốc v t m/s của ô tô từ lúc được phanh đến khi dừng hẳn thỏa mãn 2     v t 
70 dt  70t  C , v 5  v 5  35  C  385. Vậy v t  70  t  385 . 2   2   1   2    
Thời điểm xe dừng hẳn tương ứng với t thỏa mãn v t  0  t  5,5 s . 2    
Quãng đường ô tô đi được từ lúc xe được phanh đến khi dừng hẳn. 5,5 5,5 S  v t dt  70
 t  385 dt  8,75 m . 2  1        5 5
Quãng đường cần tính S  S  S  96, 25 m . 1 2  
Bài tập 7: Một vật di chuyển với gia tốc at  t 2     2 20 1 2
m / s  . Khi t  0 thì vận tốc của vật
là 30m / s . Tính quãng đường vật đó di chuyển sau 2 giây.
A. S  46m .
B. S  47m .
C. S  48m .
D. S  49m . Lời giải : Chọn C
Vận tốc vật là : vt a
 tdt   t 2 dt  t 1 20 1 2 10 1 2         C .
Khi t  0 thì v     1 0 10. 1
 C  30  C  20 . Nên vt  t 1 10 1 2   
 20m / s . 2
Suy ra : S  101 2t1  20dt  48m 0
Bài tập 8: Vật chuyển động với vận tốc ban đầu 5m / s và có gia tốc được xác định bởi công thức 2 a   2
m / s  . Vận tốc của vật sau 10s đầu tiên là t 1
A. 10m / s .
B. 9m / s .
C. 11m / s .
D. 12m / s Hướng dẫn giải: Chọn A 2
Ta có vt  dt  2ln 
t  1c t 1
Mà vận tốc ban đầu 5m/s tức là : v 0  5  2ln 0  
1  c  5  c  5 .
Nên v t  2ln t   1  5
Vận tốc của vật sau 10s đầu tiên là : v 10  2ln   11  5  9,8 Chọn Chọn A.
Bài tập 9: Trong giờ thực hành môn Vật Lí. Một nhóm sinh viên đã nghiên cứu về sự chuyển động
của các hạt. Trong quá trình thực hành thì nhóm sinh viên này đã phát hiện một hạt prôton di chuyển
trong điện trường với biểu thức gia tốc là: a     t 2 20 1 2
.Với t của ta được tính bằng giây. Nhóm
sinh viên đã tìm hàm vận tốc v theo t , biết rằng khi t  0 thì 2
v  30m / s . Hỏi biểu thức đúng là?  10   10  A. 2 v   25 / cm s   . B. 2 v   20 / cm s   . 1 2t  1 t   10   10  C. 2 v  10 / cm s   . D. 2 v   20 / cm s   1 2t  1 2t 
Hướng dẫn giải : Chọn D
Trước hết để giải bài toán này ta cũng chú ý. Biểu thức vận tốc v theo thời gian t có gia
tốc a là: v  . a dt  20 
Áp dụng công thức trên, ta có : v  adt  dt   12t2 Đến đây ta đặt : du
u  1 2t  du  2dt  dt  2 10   10 10 2 v  du  10  u du   K   K   u u 1 2t
Với t  0,v  30  K  20  10 
Vậy biểu thức vận tốc theo thời gian là : 2 v   20 / cm s .   1 2t 
Bài tập 10: Người ta tổ chức thực hành nghiên cứu thí nghiệm bằng cách như sau. Họ tiến hành quan
sát một tia lửa điện bắn từ mặt đất bắn lên với vận tốc 15m / s. Hỏi biểu thức vận tốc của tia lửa điện là?
A. v  9,8t 15.
B. v  9,8t 13.
C. v  9,8t 15.
D. v  9,8t 13 Hướng dẫn giải Chọn A
Tia lửa chịu sự tác động của trọng lực hướng xuống nên ta có gia tốc a    2 9,8 m / s 
Ta có biểu thức vận tốc v theo thời gian t có gia tốc a là : v  adt  9,  8dt  9,  8t  C  
Ở đây, với : t  0,v  15m / s  C  15
Vậy ta được biểu thức vận tốc có dạng : v  9,8t 15
Bài tập 11: Người ta tổ chức thực hành nghiên cứu thí nghiệm bằng cách như sau. Họ tiến hành quan
sát một tia lửa điện bắn từ mặt đất bắn lên với vận tốc 15m / s. Hỏi sau 2, 5 giây thì tia lửa điện đấy có
chiều cao là bao nhiêu?
A. 6.235m .
B. 5.635m .
C. 4.235m . D. 6.875m Hướng dẫn giải Chọn D
Tia lửa chịu sự tác động của trọng lực hướng xuống nên ta có gia tốc a    2 9,8 m / s 
Ta có biểu thức vận tốc v theo thời gian t có gia tốc a là : v  adt  9,  8dt  9,  8t  C  
Ở đây, với t  0,v  15m / s  C  15
Vậy ta được biểu thức vận tốc có dạng:
v  9,8t 15
Lấy tích phân biểu thức vận tốc, ta sẽ có được bểu thức quãng đường: s  vdt    t   2 9,8 15 dt  4,
 9 t 15t  K
Theo đề bài, ta được khi t  0  s  0  K  0.
Vậy biểu thức tọa độ của quảng đường là : 2 s  4,  9t 15t.
Khi t  2,5s , ta sẽ được s  6,875m .
Dạng 8: Bài toán thực tế
1. Phương pháp: Vận dụng các kiến thức về tích phân và bài toán ứng dụng.
2. Các Bài tập mẫu:
Bài tập 1: Tính thể tích hình xuyến tạo thành do quay hình tròn C  x   y  2 2 : 2  1 quanh trục Ox . Hướng dẫn giải:
Hình tròn C có tâm I 0;2 , bán kính R 1 là x   y  2 2 2  1 2
 y  2  1 x Ta có  y  2 2 1  1 x  1   x   1   2
y  2 1 x Thể tích cần tính: 1 V      
2  1 x 2 2 1 x 2 2 2 2 dx  4    1 
Bài tập 2: Thành phố định xây cây cầu bắc ngang con sông dài 500m , biết rằng người ta định xây
cầu có 10 nhịp cầu hình dạng parabol,mỗi nhịp cách nhau 40m ,biết 2 bên đầu cầu và giữa mối nhịp
nối người ta xây 1 chân trụ rộng 5m . Bề dày nhịp cầu không đổi là 20cm . Biết 1 nhịp cầu như hình
vẽ. Hỏi lượng bê tông để xây các nhịp cầu là bao nhiêu A. 3 20m . B. 3 50m . C. 3 40m . D. 3 100m . Hướng dẫn giải: Chọn C
Chọn hệ trục tọa độ như hình vẽ với gốc O0;0 là chân cầu,
đỉnh I 25;2 , điểm A50;0
Gọi Parabol trên có phương trình: P  2 2
: y  ax  bx  c  ax  bx O  P 1 1   1 20 1 2 2
 y  ax  bx 
ax  ax  bx  là phương trình parabol dưới 2 100 2 2 4 2 4 1
Ta có I, AP   P  2 2 : y   x  x  y   x  x  1 1 1 2 625 25 625 25 5
Khi đó diện tích mỗi nhịp cầu là S  S với S là phần giới hạn bởi y ; y trong khoảng 0;25 1 1 1 2 0,2 15  2 4  1   2 2 S  2  x  x dx  dx      0,9m   625 25 5     0 0,2 
Vì bề dày nhịp cầu không đổi nên coi thể tích là tích diện tích và bề dày 3
V  S.0, 2 1,98m  số
lượng bê tông cần cho mỗi nhịp cầu 3  2m
Vậy mười nhịp cầu hai bên cần 3  40m bê tông Chọn Chọn. C.
Bài tập 3: Trong Công viên Toán học có những mảnh đất mang hình dáng khác nhau. Mỗi mảnh
được trồng một loài hoa và nó được tạo thành bởi một trong những đường cong đẹp trong toán học.
Ở đó có một mảnh đất mang tên Bernoulli, nó được tạo thành từ đường Lemmiscate có phương trình
trong hệ tọa độ Oxy là 2 2 y  x  2 16
25  x  như hình vẽ bên. y x
Tính diện tích S của mảnh đất Bernoulli biết rằng mỗi đơn vị trong hệ tọa độ Oxy tương ứng với chiều dài 1 mét. 125 125 A. S   2 m  . B. S   2 m  . 6 4 250 125 C. S   2 m  . D. S   2 m  3 3 Hướng dẫn giải Chọn D
Vì tính đối xứng trụ nên diện tích của mảnh đất tương ứng với 4 lần diện tích của mảnh đất thuộc
góc phần tư thứ nhất của hệ trục tọa độ Oxy . 1
Từ giả thuyết bài toán, ta có 2
y   x 5  x . 4 1 Góc phần tư thứ nhất 2
y  x 25  x ; x 0;5 4 5 1 125 125 Nên 2 3 S 
x 25  x dx   S  (m ) (I )  4 12 3 0
Bài tập 4: Một Bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình
phẳng giới hạn bởi các đường y  x 1 và trục Ox quay quanh trục Ox biết đáy lọ và miệng lọ có
đường kính lần lượt là 2dm và 4dm , khi đó thể tích của lọ là: 15 A. 2 8 dm .. B. 3  dm .. 2 14 15 C. 2  dm . . D. 2 dm . 3 2 Lời giải Chọn B
 r  y 1 x  0 1 1 1 y x O 3
 r  y  2  x  3 2 2 2 3 3 2  x  15 Suy ra: 2
V   y dx    x  3 1 dx     x   0  2  2 0 0
Bài tập 5: Để kéo căng một lò xo có độ dài tự nhiên từ 10cm đến 15cm cần lực 40N . Tính công (
A ) sinh ra khi kéo lò xo có độ dài từ 15cm đến 18cm .
A. A  1,56 (J ) .
B. A  1 (J ) .
C. A  2,5 (J ) .
D. A  2 (J ) . Lời giải Chọn A x
f  x  k.x O M x x
Theo Định luật Hooke, lực cần dùng để giữ lò xo giãn thêm x mét từ độ dài tự nhiên là f  x  kx , với
k  N /m là độ cứng của lò xo. Khi lò xo được kéo giãn từ độ dài 10cm đến 15cm , lượng kéo giãn là 5 0 cm  .05
m . Điều này có nghĩa f 0.05  40, do đó: 40
0,05k  40  k   800N/m 0,05
Vậy f  x  800x và công cần để kéo dãn lò xo từ 15cm đến 18cm là: 0,08 0,08 A  800 dx  400x  400   0,082 0,052 2  1,56J  0,05   0,05 1 Góc phần tư thứ nhất 2
y  x 25  x ; x 0;5 4 5 1 125 125 Nên 2 3 S 
x 25  x dx   S  (m ) ( I )  4 12 3 0
3. Bài tập trắc nghiệm:
Câu 1: Trong chương trình nông thôn mới, tại một xã X có xây một cây cầu bằng bê tông như hình
vẽ. Tính thể tích khối bê tông để đổ đủ cây cầu. 0 , 5 m 2 m 5 m 0 , 5 m 1 9 m 0 , 5 m A. 3 19m . B. 3 21m . C. 3 18m . D. 3 40m . Hướng dẫn giải Chọn D
Chọn hệ trục Oxy như hình vẽ. y O x Ta có 19  Gọi P  2
: y  ax  c là Parabol đi qua hai điểm A ;0 , B   0;2 1  2  2  19   8 0  . a  2   a   8
Nên ta có hệ phương trình sau:   2    361   P  2 : y   x  2 1 361    b   2 2 b   Gọi P  2
: y  ax  c là Parabol đi qua hai điểm C   5 10;0 , D 0; 2    2    0  . a 102 5 1  a    2  40 1 5
Nên ta có hệ phương trình sau:     P  2 : y   x  2 5 5 40 2  b b    2  2 19  10 1 5   8  
Ta có thể tích của bê tông là: 2 2 3 2 V  5.2  x  dx  
x  2 dx  40m        . 0 0   40 2   361  
Câu 2: Cho hai mặt cầu S , S có cùng bán kính R thỏa mãn tính chất: tâm của S thuộc 1  2  1 
S và ngược lại. Tính thể tích phần chung V của hai khối cầu tạo bởi (S )và (S ). 2  1 2 3  R 3 5 R 3 2 R A. 3 V   R . B. V  . C. V  . D. V  . 2 12 5 Hướng dẫn giải Chọn C y 2 2 2
(C) : x  y  R O R R x 2
Gắn hệ trục Oxy như hình vẽ
Khối cầu S O, R chứa một đường tròn lớn là C 2 2 2
: x  y  R
Dựa vào hình vẽ, thể tích cần tính là R R       R  x  3 3 2 2 2 x 5 R V 2
dx  2  R x    . 3 R 12 R   2 2
Câu 3: Một thùng rượu có bán kính các đáy là 30cm, thiết diện vuông góc với trục và cách đều hai
đáy có bán kính là 40cm, chiều cao thùng rượu là 1m. Biết rằng mặt phẳng chứa trục và
cắt mặt xung quanh thùng rượu là các đường parabol, hỏi thể tích của thùng rượu là bao nhiêu? A. 425, 2 lit. B. 425162 lit. C. 212581 lit. D. 212,6 lit. Hướng dẫn giải Chọn A y S A 0,4m 0,3m x O 0,5m  Gọi P 2
: y  ax  bx  c là parabol đi qua điểm A0,5;0,3 và có đỉnh S 0;0, 4 . Khi
đó, thể tích thùng rượu bằng thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi P ,
trục hoành và hai đường thẳng x  0,5 quay quanh trục Ox . 2
 Dễ dàng tìm được P 2
: y   x  0, 4 5
 Thể tích thùng rượu là: 0,5 2 0,5 2  2   2  203 2 2 V 
 x  0,4 dx  2
 x  0,4 dx   425,5 (l)          .  5   5  1500 0,  5 0
Câu 4: Bác Năm làm một cái cửa nhà hình parabol có chiều cao từ mặt đất đến đỉnh là 2,25 mét,
chiều rộng tiếp giáp với mặt đất là 3 mét. Giá thuê mỗi mét vuông là 1500000 đồng. Vậy
số tiền bác Năm phải trả là: A. 33750000 đồng. B. 12750000 đồng. C. 6750000 đồng. D. 3750000 đồng. Hướng dẫn giải Chọn C y B x O A
 Gắn parabol P và hệ trục tọa độ sao cho P đi qua O(0;0)
 Gọi phương trình của parbol là: P 2
: y  ax  bx  c
Theo đề ra, P đi qua ba điểm O(0;0) , A(3;0) , B(1,5;2, 25) .
Từ đó, suy ra P 2 :
y  x  3x 3 9
 Diện tích phần Bác Năm xây dựng: 2
S  x  3x dx   2 0 9
 Vậy số tiền bác Năm phải trả là: .1500000  67500 0 0 . 2
Câu 5: Ông An có một mảnh vườn hình Elip có độ dài trục lớn bằng 16m và độ dài trục bé bằng
10m. Ông muốn trồng hoa trên một dải đất rộng 8m và nhận trục bé của elip làm trục đối
xứng. Biết kinh phí để trồng hoa là 100.000 đồng/ 2
1m . Hỏi ông An cần bao nhiêu tiền để
trồng hoa trên dải đất đó? 8m A. 7.862.000 đồng. B. 7.653.000 đồng. C. 7.128.000 đồng. D. 7.826.000 đồng. Hướng dẫn giải Chọn B 2 2 x y
Giả sử elip có phương trình  1. 2 2 a b
Từ giả thiết ta có 2a 16  a  8 và 2b 10  b  5  5 2 y   64  y (E ) 2 2  1 x y
Vậy phương trình của elip là 8  1  64 25 5  2 y  64  y (E ) 1  8
Khi đó diện tích dải vườn được giới hạn bởi các đường (E ); (E ); x  4
 ; x  4 và diện 1 2 4 4 5 5 tích của dải vườn là 2 2 S  2 64  x dx  64  x dx   8 2 4  0   3 
Tính tích phân này bằng phép đổi biến x  8sint , ta được S  80    6 4    3 
Khi đó số tiền là T  80 
.100000  7652891,82  7.653.000 .  6 4 
Câu 6: Người ta dựng một cái lều vải có dạng hình “chóp lục giác cong đều” như hình vẽ bên. Đáy
của là một hình lục giác đều cạnh 3 .
m Chiều cao SO  6m . Các cạnh bên của là các sợi
dây c ,c ,c ,c ,c ,c nằm trên các đường parabol có trục đối xứng song song với SO. Giả 1 2 3 4 5 6
sử giao tuyến của với mặt phẳng vuông góc với SO là một lục giác đều và khi qua trung
điểm của SO thì lục giác đều có cạnh bằng 1m. Tính thể tích phần không gian nằm bên trong cái lều đó. S c6 c c 1 5 1m c4 c2 c3 O 3m 135 3 96 3 135 3 135 3 A. 3 (m ) . B. 3 (m ) . C. 3 (m ) . D. 3 (m ) 5 5 4 8 Hướng dẫn giải Chọn D
Đặt hệ tọa độ như hình vẽ, ta có parabol cần tìm đi qua 3 điểm có tọa độ lần lượt là 1 7 (
A 0;6), B(1;3), C(3;0) nên có phương trình là 2
y  x  x  6 2 2
Theo hình vẽ ta có cạnh của thiết diện là BM 7 1
Nếu ta đặt t  OM thì BM   2t  2 4
Khi đó diện tích của thiết diện lục giác: 2 2 BM 3 3 3  7 1  S(t)  6. 
  2t   , với t 0;6 4 2  2 4    2 6 6 3 3  7 1  135 3
Vậy thể tích của túp lều theo đề bài là: V  S(t)dt   
  2t   dt  .. 2  2 4  8 0 0  
Câu 7: Một vật có kích thước và hình dáng như hình vẽ dưới đây. Đáy là hình tròn giới hạn bởi đường tròn 2 2
x  y  16 , cắt vật bởi các mặt phẳng vuông góc với trục Ox ta được thiết diện
là tam giác đều. Thể tích của vật thể là: y x O 32 3 256 3 A. V  . . B. V  .. 3 3 256 32 C. V  . . D. V  . 3 3 Hướng dẫn giải Chọn B Giải phương trình 2 2 2 2 2
x  y  16  y  16  x  y   16  x 2 1 
Diện tích thiết diện là 2 S(x)  2 16  x .sin   2 16  x  3 2 3 4 4 256 3
Thể tích cần tìm là V  S(x)dx  3  2
16  x dx    . 3 4  4 
Dạng 9: Các bài toán bản chất đặt sắc của tích phân
Bài tập 1: Cho hàm số y  f  x có đồ thị trên  2;
 6 như hình vẽ bên. Biết các miền A, B, x  2 2
có diện tích lần lượt là 32; 2; 3. Tích phân  f
  2x 21dx  bằng 2  45 41 A. . B. 41. C. 37. D. . 2 2
Hướng dẫn giải Chọn D. 2 2 Ta có  f
  2x 21dx  f 
 2x 2dx  4 2 2  2 Xét I 
f 2x  2 dx . 1    2  dt
Đặt t  2x  2  dt  2dx  dx  2 Đổi cận: x  2   t  2
 ; x  2  t  6. 6 1 Suy ra I  f t dt . 1    2 2
Gọi x ; x là các hoành độ giao điểm của đồ thị hàm số y  f  x với trực hoành 1 2  2
  x  x  6 . Ta có 1 2  1 x x 6 1   1
I   f t df  f t df  f t df  
S  S  S 1    2        A B C  2   2  2  1 x 2 x 1      33 32 2 3  2 2 2 33 41 Vậy  f
  2x 21dx  I  4  4   1 2 2 2 
Bài tập 2: Cho hàm số y  f  x có đồ thị của hàm số y  f  x như hình bên. Đặt
g  x  f  x   x  2 2
1 . Mệnh đề nào dưới đây đúng?
A. g 3  g  3    g   1 . B. g  3
   g 3  g   1 . C. g   1  g  3    g 3. D. g  
1  g 3  g  3  .
Hướng dẫn giải Chọn D.
Ta có g x  2 f  x  2 x   1
g x  0  f  x  x 1. Đây là phương trình hoành độ giao điểm của đồ thị hàm số f  x và
đường thẳng d: y  x 1. x 
Dựa vào đồ thị ta thấy: g x   f  x 1 0
 x 1  x  3 Bảng biến thiên: x  –3 1 3  g x – 0 + 0 – 0 +  g   1  g  x g  3   g 3 Suy ra g  3    g  
1 và g 3  g   1
Gọi S , S lần lượt là diện tích các hình phẳng giới hạn bởi đồ thị hàm số f  x , đường thẳng 1 2
d: y  x 1 trên các đoạn  3;   1 và 1;  3 ta có: 1 1 1 +) Trên đoạn  3;  
1 ta có f  x  x 1 nên S  g x dx 
 f  x  x 1  dx . 1          2  3 3  3 3 1 +) Trên đoạn 1; 
3 ta có f  x  x 1 nên S  g x dx 
 x 1 f  x  dx . 2        2  1 1
Dựa vào đồ thị ta thấy S  S nên ta có: 1 2 1 3 g  x
 g x  g  
1  g 3  g 3  g  
1  g 3  g 3 . 3 1 Vậy g  
1  g 3  g  3  . Lưu ý:
- Hoành độ giao điểm của đồ thị hàm số f  x và đường thẳng d: y  x 1 chính là nghiệm của
phương trình g x  0 .
- Lập bảng biến thịên ta thấy g   1 lớn hơn g  3
  . Ta chỉ cần so sánh g 3 và g  3   .
- So sánh diện tích dựa vào đồ thị.
Ví dụ 4: Hình phẳng H  được giới hạn bởi đồ thị C của hàm đa thức bậc ba và parabol P có
trục đối xứng vuông góc với trục hoành. Phần tô đậm của hình vẽ có diện tích bằng 37 7 11 5 A. . B. . C. . D. . 12 12 12 12
Hướng dẫn giải Chọn A.
Vì đồ thị hàm bậc ba và đồ thị hàm bậc hai cắt trục tung tại các điểm có tung độ lần lượt là
y  2 và y  0 nên ta xét hai hàm số là 3 2
y  ax  bx  cx  2 , 2
y  mx  nx (với a, m  0 ).
Suy ra C : y  f  x 3 2
 ax  bx  cx  2 và P :    2
y g x  mx  nx .
Phương trình hoành độ giao điểm của C và P là: 3 2 2
ax  bx  cx   mx  nx   3 2
ax  bx  cx     2 2 2
mx  nx  0 .
Đặt P  x   3 2
ax  bx  cx     2 2 mx  nx.
Theo giả thiết, C và P cắt nhau tại các điểm có hoành độ lần lượt là x  1
 , x  1, x  2
nên P  x  a x   1  x   1  x  2 .
Ta có P 0  2a .
Mặt khác, ta có P 0  f 0  g 0  2  a 1. 2 37
Vậy diện tích phần tô đậm là S   x   1  x  
1  x  2 dx   12 1 