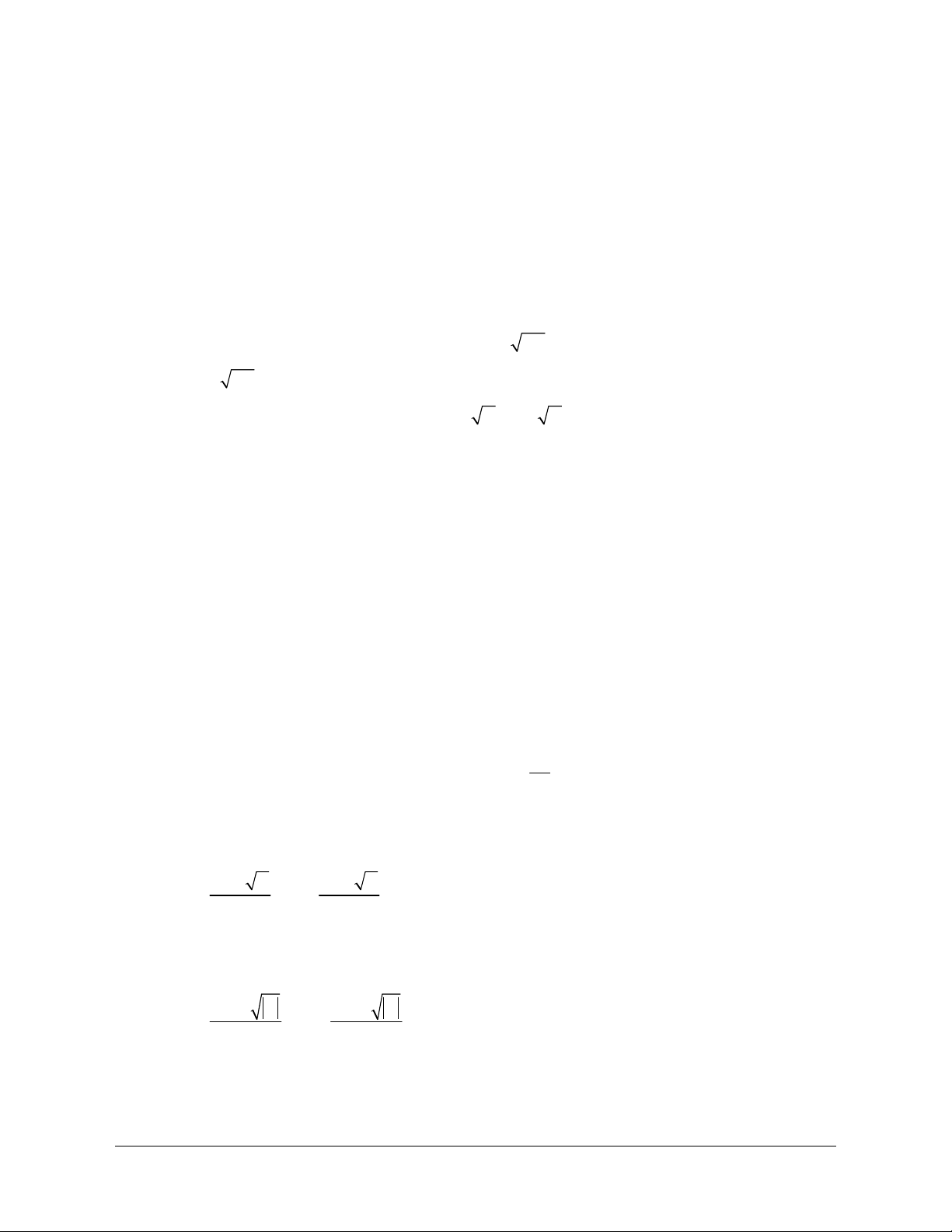

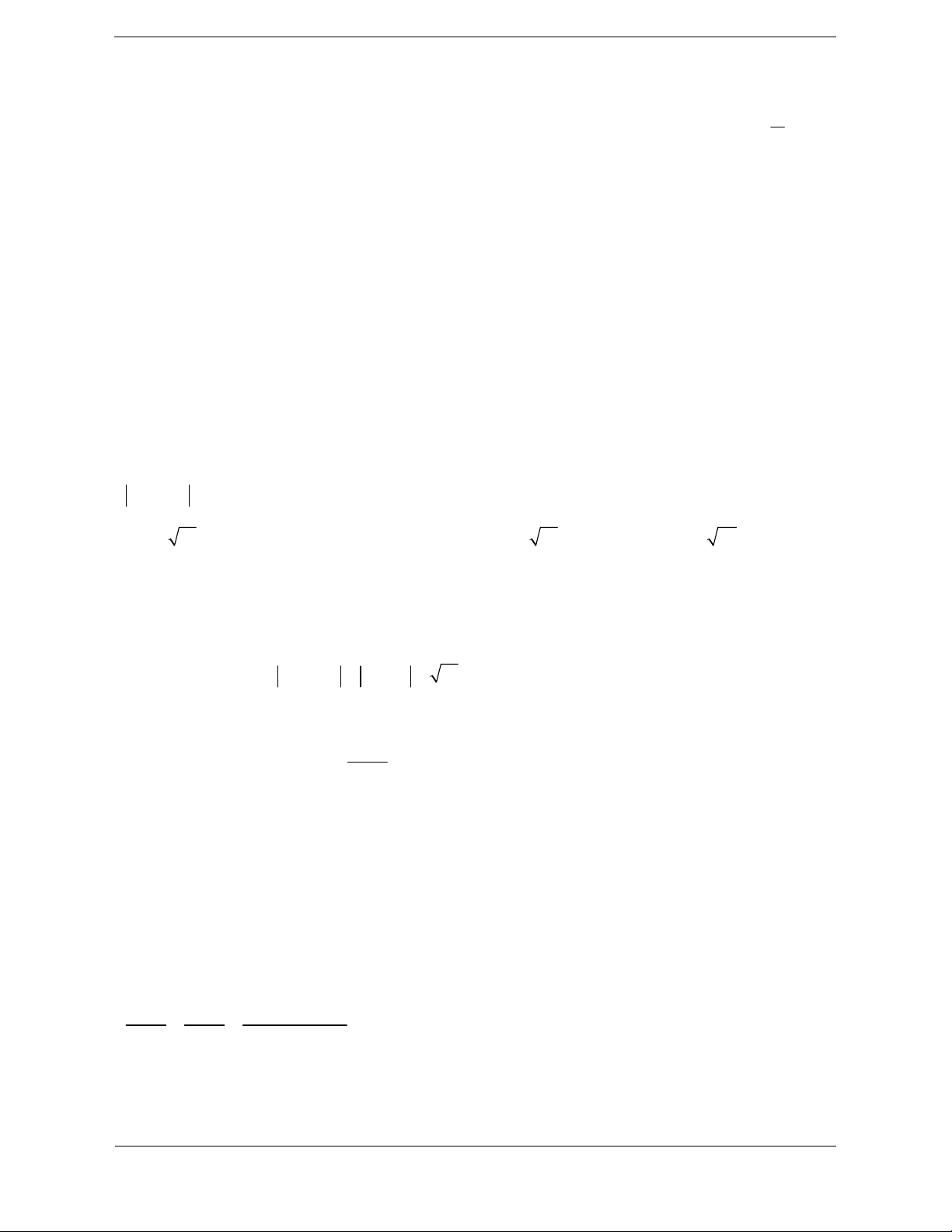





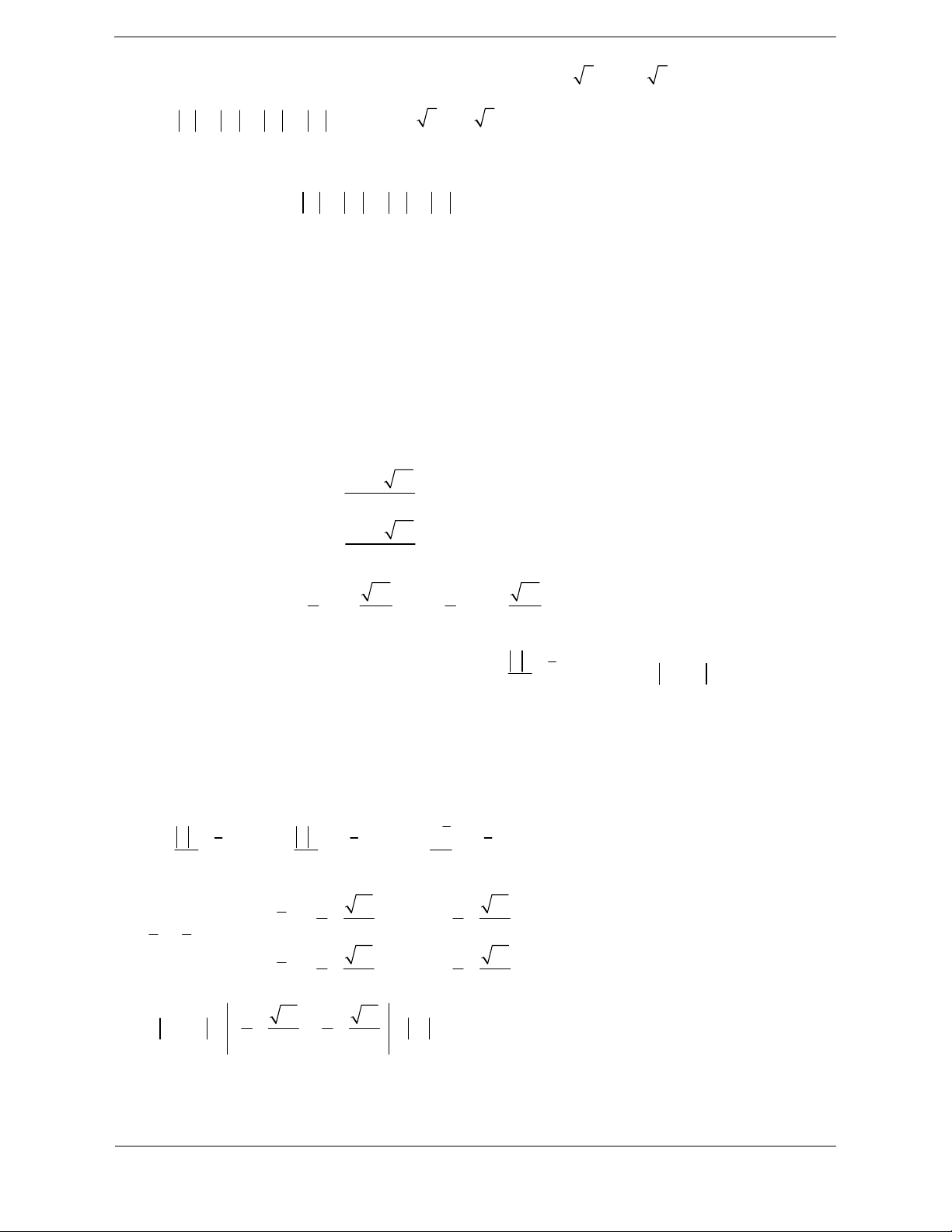
Preview text:
BÀI 3. PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC A. LÍ THUYẾT
1. Căn bậc hai của một phức Định nghĩa
Cho số phức w. Mỗi số phức z thỏa mãn 2
z w được gọi là
một căn bậc hai của w
Tìm căn bậc hai của số phức w Nhận xét: w là số thực.
+) Số 0 có đúng một căn bậc hai
+ Nếu w 0 thì w có hai căn bậc hai là i w và là 0
+) Mỗi số phức khác 0 có hai căn i w
bậc hai là hai số đối nhau (khác
+ Nếu w 0 thì w có hai căn bậc hai là w và w 0)
w a bi a,b , b 0
Nếu z x iy là căn bậc hai của w thì x iy2 a bi 2 2
x y a
Do đó ta có hệ phương trình: 2xy b
Mỗi nghiệm của hệ phương trình cho ta một căn bậc hai Chú ý: của w
Mọi phương trình bậc n:
2. Giải phương trình bậc hai với hệ số thực n n 1 A z A z
... A z A 0 0 1 n 1 n Xét phương trình 2
az bz c 0 a, , b c ; a 0
luôn có n nghiệm phức (không Ta có 2
b 4ac
nhất thiết phân biệt) với n nguyên
Nếu 0 thì phương trình có nghiệm thực b x dương. 2a
Nếu 0 thì phương trình có hai nghiệm thực phân biệt: b x ; b x 1 2a 2 2a
Nếu 0 thì phương trình có hai nghiệm thực phân biệt: b i b i x ; x 1 2a 2 2a
Hệ thức Vi-ét đối với phương trình bậc hai với hệ số thực Phương trình bậc hai 2
ax bx c 0 a 0 có hai nghiệm
phân biệt x , x (thực hoặc phức) thì 1 2
S x x b 1 2 a c P x x 1 2 a
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Giải phương trình. Tính toán biểu thức nghiệm
1. Phương pháp giải
Ví dụ: Xét phương trình 2
z 2z 5 0 Cho phương trình:
a) Giải phương trình trên tập số phức 2
az bz c 0 a,b,c ; a 0 b) Tính z z 1 2
Giải pương trình bậc hai với hệ số thực
Hướng dẫn giải
Áp dụng các phép toán trên tập số phức a) Ta có: i2 ' 1 5 4 2
để biến đổi biểu thức
Phương trình có hai nghiệm là:
z 2 2i ; z 2 2i 1 2 b) Ta có 2 2
z z 2 2 2 2 1 2
Suy ra z z 2 2 2 2 4 2 1 2 2. Bài tậ
Bài tập 1. Trong các số sau, số nào là nghiệm của phương trình 2
z 1 z z ? 1 3i 1 3 1 3 1 2i A. B. C. D. 2 2 2 2
Hướng dẫn giải Chọn A 2 2 1 1 3 1 3i Ta có 2
z 1 z z 2 z 2. . z z 2 4 4 2 4 1 3i 1 3i z z 2 2 2 1 3i 1 3i z z 2 2 2
Bài tập 2. Phương trình 2
z az b 0 a,b có nghiệm phức là 3 4i . Giá trị của a b bằng A. 31 B. 5 C. 19 D. 29
Hướng dẫn giải Chọn C
Chú ý: Nếu z là 0
Cách 1: Do z 3 4i là nghiệm của phương trình 2
z az b 0 nên ta có: nghiệm của phương i2 3 4
a3 4i b 0 3a b 7 4a 24i 0 trình bậc hai với hệ
số thực thì z cũng 3
a b 7 0 a 6 0 4a 24 0 b 25 là nghiệm của
Do đó a b 19 phương trình
Cách 2: Vì z 3 4i là nghiệm của phương trình 2
z az b 0 nên 1
z 3 4i cũng là nghiệm của phương trình đã cho 2
z z a
Áp dụng hệ thức Vi-ét vào phương trình trên ta có 1 2 z .z b 1 2 3 4
i 3 4i a a 6 a b
3 4i3 4i 19 b b 25
Bài tập 3. Gọi z là nghiệm phức có phần ảo dương của phương trình 2
z 6z 34 0 . Giá trị của 0
z 2 i là 0 A. 17 B. 17 C. 2 17 D. 37
Hướng dẫn giải Chọn A ra có i2 ' 25 5
. Phương trình có hai nghiệm là z 3
5i ; z 3 5i Do đó z 3
5i z 2 i 1 4i 17 0 0
Bài tập 4. Gọi z là nghiệm phức có phần ảo âm của phương trình 2
z 2z 5 0 1 7 4i
Tọa độ điểm biểu diễn số phức
trên mặt phẳng phức là z1 A. P 3;2
B. N 1;2
C. Q 3;2 D. M 1;2
Hướng dẫn giải Chọn A z 1 2i Ta có 2
z 2z 5 0 z 12i
Theo yêu cầu của bài toán ta chọn z 1 2i . Khi đó: 1 7 4i 7 4i
7 4i1 2i 3 2i 2 2 z 1 2i 1 2 1
Vậy điểm biểu diễn của số phức là P 3;2
Bài tập 5. Gọi z , z là hai nghiệm phức của phương trình 2
z 4z 5 0 . Giá trị của biểu thức 1 2 z 2019 1 z 2019 1 bằng 1 2 A. 1009 2 B. 1010 2 C. 0 D. 1010 2
Hướng dẫn giải Chọn D z 2 i Xét phương trình 2
z 4z 5 0 z 22 1 1 z 2 i 2
Khi đó ta có: z 2019 1 z 2019 1
1 i2019 1i2019 1 2
i i 1009 i i 1009 2 2 1 . 1 1 . 1
i i1009 i i1009 1 . 2 1 . 2
i1009 i i i1010 2i 505 1010 1010 2 1 1 2 .2 2
Dạng 2: Định lí Vi-ét và ứng dụng
1. Phương pháp giải
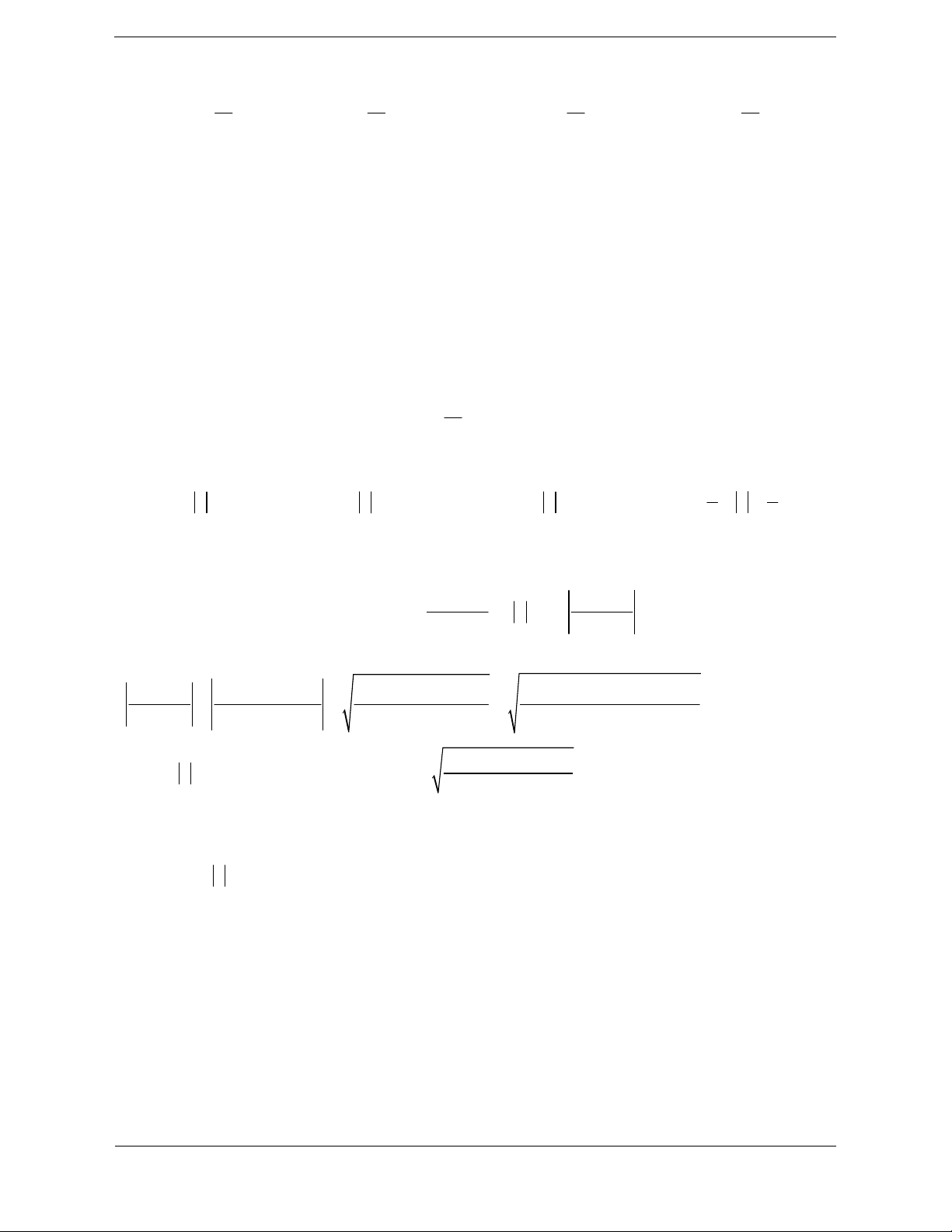
Ví dụ: Phương trình 2
z 4z 24 0 có hai
Định lí Vi-ét: Cho phương trình:
nghiệm phức z , z nên 1 2 2
az bz c 0 ; a, ,
b c ; a 0
z z 4 ; z .z 24 1 2 1 2 b z z b 1 2
Chú ý: Học sinh hay nhầm lẫn: z z
có hai nghiệm phức z , z thì a 1 2 a 1 2 c z .z 1 2 a 2. Bài tập
Bài tập 1: Gọi z , z là hai nghiệm phức của phương trình 2
z 2z 5 0 . Giá trị của biểu thức 1 2 2 2 z z bằng 1 2 A. 14 B. –9 C. –6 D. 7
Hướng dẫn giải Chọn C
Gọi z , z là nghiệm của phương trình 2
z 2z 5 0 1 2 z z 2
Theo định lí Vi-ét ta có: 1 2 z .z 5 1 2
Suy ra z z z z 2 2 2 2
2z z 2 2.5 6 1 2 1 2 1 2
Bài tập 2: Phương trình bậc hai nào sau đây có nghiệm là 1 2i ?
Chúng ta có thể giải từng A. 2
z 2z 3 0 B. 2
z 2z 5 0 phương trình: C. 2
z 2z 5 0 D. 2
z 2z 3 0 +) 2
z 2z 3 0
Hướng dẫn giải z 2 2 1 2i Chọn C
z 1 i 2
Phương trình bậc hai có hai nghiệm phức là liên hợp của nhau nên z 1i 2
phương trình bậc hai có nghiệm 1 2i thì nghiệm còn lại là 1 2i
Khi đó tổng và tích của hai nghiệm lần lượt là 2; 5 +) 2
z 2z 5 0
Vậy số phức 1 2i là nghiệm của phương trình 2
z 2z 5 0 z 2 2 1 4i z 1 2 i
z 1 2i +) 2
z 2z 5 0 z 2 2 1 4i z 1 2 i
z 1 2i +) 2
z 2z 3 0 z 2 2 1 2i
z 1 i 2
z 1 i 2
Bài tập 3: Kí hiệu z , z là nghiệm phức của phương trình 2
2z 4z 3 0 . Tính giá trị biểu thức 1 2
P z z i z z 1 2 1 2 7 5 A. P 1 B. P C. P 3 D. P 2 2
Hướng dẫn giải Chọn D
Ta có z , z là hai nghiệm của phương trình 2
2z 4z 3 0 1 2 z z 2 1 2
Theo định lý Vi-ét ta có 3 z .z 1 2 2 2 3 3 3 5
Ta có P z z i z z i 2 2i 2 2 1 2 1 2 2 2 2 2
Bài tập 4: Gọi z , z là hai nghiệm phức của phương trình Cách khác: 1 2 Ta có: 2
z 4z 7 0 . Giá tị của 3 3
P z z bằng 2
z 4z 7 0 1 2 A. –20 B. 20 z 2 2 2 3i C. 14 7 D. 28 7
z 2 3i 1
Hướng dẫn giải
z 2 3i 2 Chọn A Do đó: z z 4
Theo định lý Vi-ét ta có 1 2 3 3 z z z .z 7 1 2 1 2
2 3i3 2 3i3 Suy ra 3 3
z z z z 2 2
z z z z 1 2 1 2 1 1 2 2 20
z z z z 2 3z z 1 2 1 2 1 2 2 4. 4 3.7 20
Bài tập 5: Gọi z và z là hai nghiệm phức của phương trình 2
3z 2z 27 0 . Giá trị của 1 2
z z z z bằng 1 2 2 1 A. 2 B. 6 C. 3 6 D. 6
Hướng dẫn giải Chọn A 2
Áp dụng định lý Vi-ét, ta có z z và z .z 9 1 2 3 1 2 Mà z z z z
z .z 9 3 1 2 1 2 1 2 2
Do đó z z z z z .3 z .3 3 z z 3. 2 1 2 2 1 1 2 1 2 3
Bài tập 6: Cho số thực a 2 và gọi z , z là hai nghiệm phức của phương trình 2
z 2z a 0 . 1 2
Mệnh đề nào sau đây sai?
A. z z là số thực
B. z z là số ảo 1 2 1 2 z z z z C. 1 2 là số ảo D. 1 2 là số thực z z z z 2 1 2 1
Hướng dẫn giải Chọn C b
Ta có z z 2 . Đáp án A đúng 1 2 a
Phương trình bậc hai với hệ số thực có hai nghiệm là số phức liên hợp. Gọi z x yi ; x, y là 1
một nghiệm, nghiệm còn lại là z x yi 2
Suy ra z z 2yi là số ảo. Đáp án B đúng 1 2 z z z z z z 2z z 4 2a 1 2 1 2 2 2 2 1 2 1 2 z z z .z z .z a 2 1 1 2 1 2
Vậy C là đáp án sai và D đúng
Dạng 3: Phương trình quy về phương trình bậc hai
1. Phương pháp giải
Ví dụ: Giải phương trình: 4 2
z z 6 0 trên tập
Nắm vững cách giải phương trình bậc số phức.
hai với hệ số thực trên tập số phức
Hướng dẫn giải
Nắm vững cách giải một số phương trình Đặt 2
z t , ta có phương trình:
quy về bậc hai, hệ phương trình đại số t 3 2 bậc cao;…
t t 6 0 t 2 Với t 3 ta có 2
z 3 z 3 Với t 2 ta có 2 z 2
z i 2
Vậy phương trình đã cho có bốn nghiệm
z 3 ; z i 2 2. Bài tậpmẫu
Bài tập 1: Tổng môđun bốn nghiệm phức của phương trình 4 2
2z 3z 2 0 là A. 3 2 B. 5 2 C. 2 5 D. 2 3
Hướng dẫn giải Chọn A z 2 z 2 2 z 2 Ta có: 4 2 2z 3z 2 0 2 1 1 2 2 . z i z i 2 2 2 2 z i 2
Khi đó, tổng môđun bốn nghiệm phức của phương trình đã cho bằng 2 2 2 2 i i 3 2 2 2
Bài tập 2: Kí hiệu z , z , z , z là bốn nghiệm phức của phương trình 4 2
z 4z 5 0 . Giá trị của 1 2 3 4 2 2 2 2 z z
z z bằng 1 2 3 4 A. 2 2 5 B. 12 C. 0 D. 2 5
Hướng dẫn giải Chọn B z 1 2 z 1 z 1 Ta có: 4 2 z 4z 5 0 2 z 5 z 5i
z 5i
Phương trình có bốn nghiệm lần lượt là: z 1, z 1 , z i
5 , z i 5 1 2 3 4 2 2 Do đó: 2 2 2 2 2 2 z z z z 1 1 5 5 12 1 2 3 4 2
Bài tập 3: Gọi z , z , z , z là các nghiệm phức của phương trình 2
z z 2
4 z z 12 0 . 1 2 3 4
Giá trị của biểu thức 2 2 2 2
S z z
z z là 1 2 3 4 A. S 18 B. S 16 C. S 17 D. S 15
Hướng dẫn giải Chọn C 2 Ta có: 2
z z 2
4 z z 12 0 t 2 Đặt 2
t z z , ta có 2
t 4t 12 0 t 6 z 1 1 z 2 2 2
z z 2 0 Suy ra: 1 i 23 z 2 3
z z 6 0 2 1 i 23 z 4 2 2 2 2 2 1 23 1 23
Suy ra S 1 2 2 2 17 2 2 2 2 4 z
Bài tập 4: Gọi z , z là hai nghiệm của phương trình z 4
. Khi đó z z bằng 1 2 2 z 1 2 A. 1 B. 4 C. 8 D. 2
Hướng dẫn giải Chọn A
Điều kiện: z 0 2 4 2 2 z z z.z Ta có: z 4 z 4 z 4 2 z z z 1 15 1 15 z i z i 2 2 2 2 2
z z 4 0 1 15 1 15 z i z i 2 2 2 2 1 15 1 15
Vậy z z i i 1 1 1 2 2 2 2 2
Bài tập 5: Cho số thực a, biết rằng phương trình 4 2
z az 1 0 có bốn nghiệm z , z , z , z thỏa 1 2 3 4 mãn 2 z 4 2 z 4 2 z 4 2
z 4 441. Tìm a 1 2 3 4 a 1 a 1 a 1 a 1 A. 19 B. C. D. 19 19 19 a a a a 2 2 2 2
Hướng dẫn giải Chọn B
Nhận xét: z z i2 2 2 4 2
z 2iz 2i
Đặt f x 4 2
z az 1, ta có:
z 4z 4z 4z 4 4
z 2i z i f i f i k 4 2 2 2 2 . 2 2 . 2 1 2 3 4 k k 1 k 1
i ai i ai a2 4 2 4 2 16 4 1 16 4 1 17 4 a 1
Theo giả thiết, ta có 17 4a2 441 19 a 2
Bài tập 6: Cho số phức z thỏa mãn 2018 2017 11z 10iz
10iz 11 0 . Mệnh đề nào dưới đây đúng? 1 3
A. 2 z 3 B. 0 z 1 C. 1 z 2 D. z 2 2
Hướng dẫn giải Chọn D 1110iz 1110iz Ta có z 11z 10i 2017 2017 2017
1110iz z z 11z 10i 11z 10i Đặt
z a bi có 1110iz
1110i a bi 10b 2 2 11 100a 100 2 2
a b 220b 121 11z 10i 11a bi 2 10i
121a 11b 102 121 2 2
a b 220b 100 2
100t 220b 121
Đặt t z t 0 ta có phương trình 2017 t 2
121t 220b 100
Nếu t 1 VT 1; VP 1
Nếu t 1 VT 1; VP 1
Nếu t 1 z 1




