

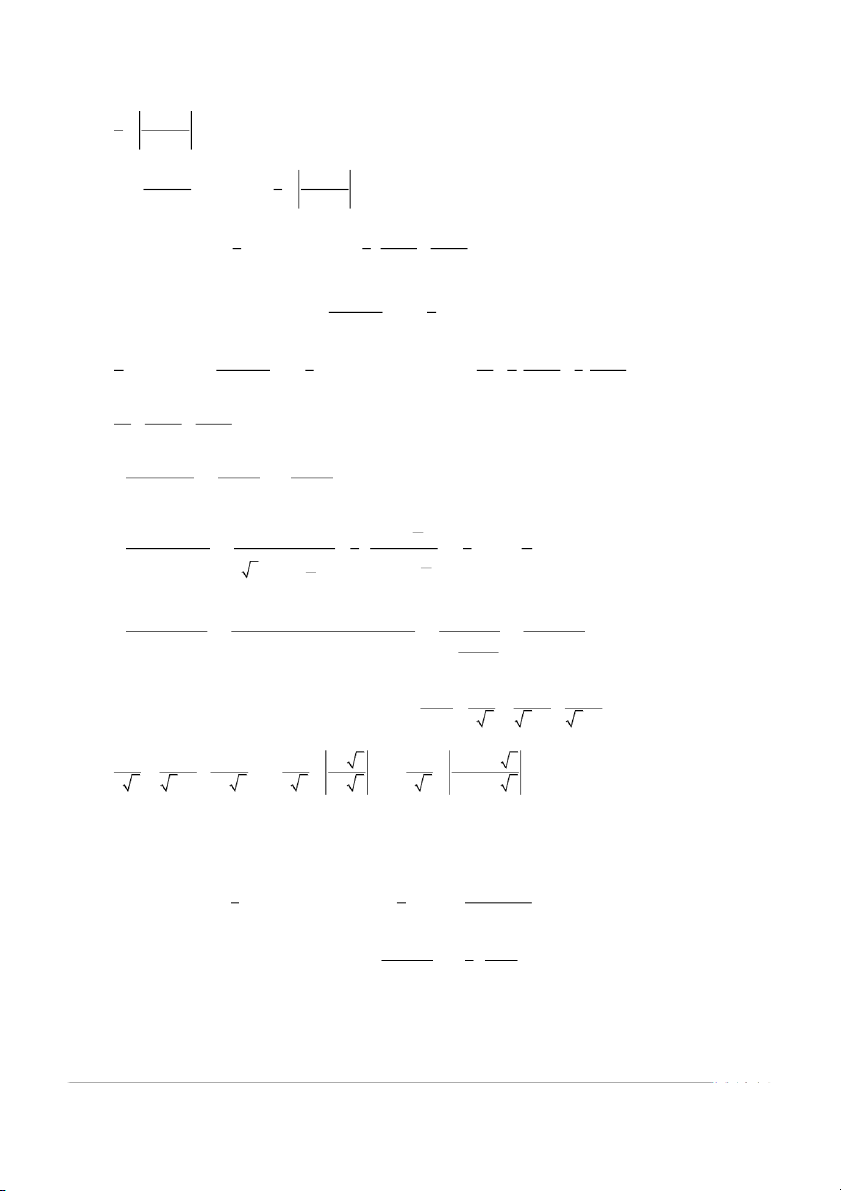

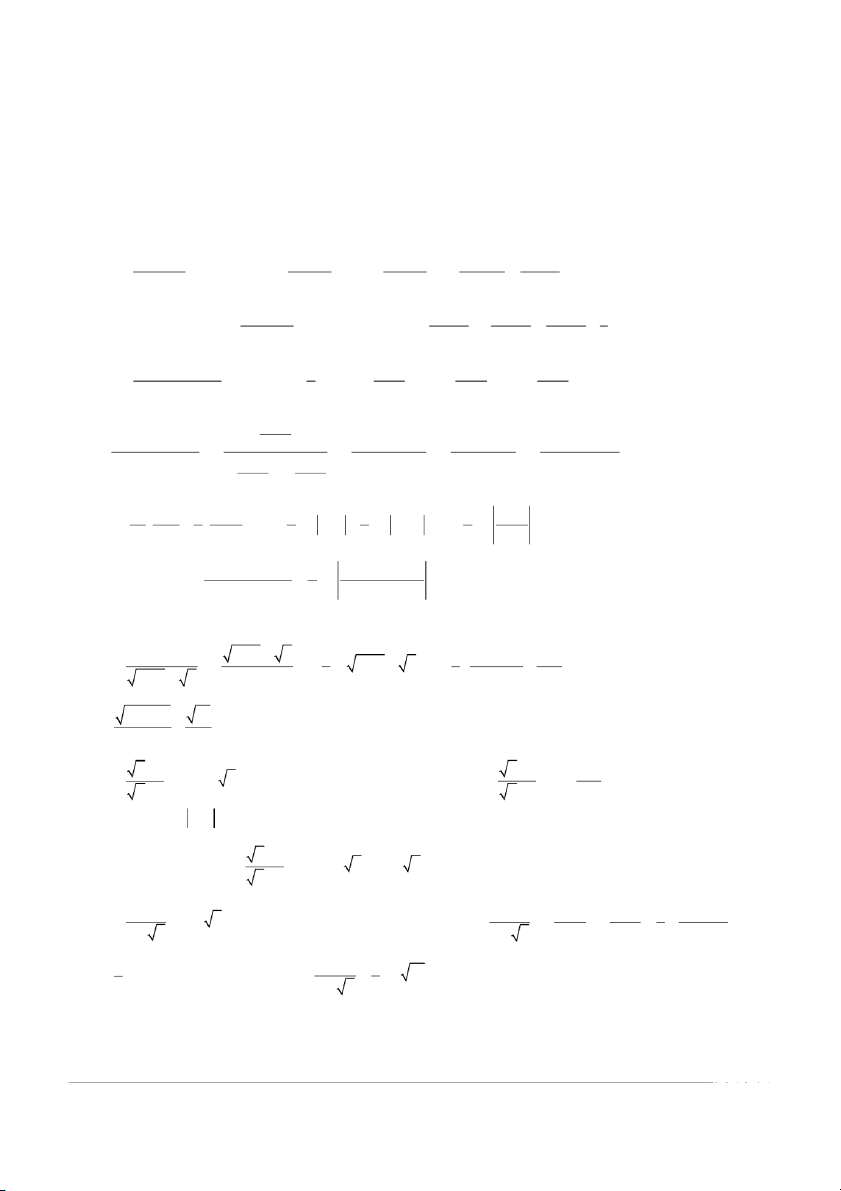



Preview text:
Anh Long Fanpage: https://www.facebook.com/chinhphuctcc/
KHÓA HỌC: TOÁN CAO CẤP - GIẢI TÍCH I
BÀI 9: CÁC DẠNG TÍCH PHÂN THƯỜNG GẶP - LỜI GIẢI Bài 1: 1. xdx −2 1 5 1 −2 5 = . + . dx = ln x+ 2 + ln x + 5 + C .
(x + 2)(x + 5)
3 x + 2 3 x + 5 3 3 2 2. dx 1 1 1 1 1 2 1 = − dx = − + dx 2 2 2 2 2 2
(x − a) (x − b) (a − b)
x − a x − b (a − b) (x − a)
(x − a)(x − b) (x − b) 1 1 2 1 1 1 = − − + dx 2 2 2 (a − b) (x − a)
a −b x − a
x −b (x − b) 1 1 − 2 x − a 1 1 − 1 2 x − a 1 = − .ln − +C = + .ln + +C . 2 2 (a − b) x − a a − b x − b x − b (a −
b) x − a a − b x − b x − b + + 3. 6x 3 6x 3 3 1 1 dx = dx = + − dx 3 2 2
x − 3x + 2
(x −1) (x + 2) ( x −1)
x − 1 x + 2 − 3 x− 1 = + ln +C . x − 1 x + 2 2 2 + + 4. x 2 x 2 1 1 dx = dx = + dx 3 2 2 x +1
(x +1)(x −x +1)
x+ 1 x −x +1 1 d x − dx dx 2 2 2x −1 Có: =
ln x+ 1 + C ; = = arc tan + C . x +1 2 2 − + 2 x x 1 3 3 1 3 x − + 2 2 2 x + 2 2 2x − 1 Vậy:
dx = ln x + 1 + arc tan + C . 3 x + 1 3 3 2 2 2 x dx x 1 1 1 5. = dx = + dx 2 2 2 (1− x ) x − 1
4 x −1 x + 1 1 1 2 1 = + + dx 2 2
4 (x −1)
(x −1)(x +1) (x +1) 1 1 1 1 1 = + − + dx 2 2
4 (x −1)
x −1 x +1 (x +1) Trang 1
Anh Long Fanpage: https://www.facebook.com/chinhphuctcc/ 1 1 − x −1 1 = + ln − + C . 4 x − 1 x + 1 x + 1 + + 6. (3x 2)dx (3x 3)dx dx = − = I − I 2 2 2 2 2 2 1 2
(x + 2x + 2)
(x + 2x + 2)
(x + 2x + 2) 2 3 (2x + 2)dx
3 d(x + 2x + 2) −3 1 Có: I = . = = . + C . 1 2 2 2 2 2
2 (x + 2x + 2)
2 (x + 2x + 2)
2 x + 2x + 2 dx dt Lại có: I = . Đặt 2
x + 1 = tant dx =
= (1+ tan t)dt , thay vào ta được: 2 2 2
((x + 1) + 1) 2 cos t 2 dx (1+ tan t)dt dt 1+ cos2t t sin 2t 2 = = = cos tdt = dt = + + C . 2 2 2 2 2
((x+ 1) + 1) (1+ tan t) 1+ tan t 2 2 4 arctan(x + 1) 1
Thay lại biến cũ: I = +
sin 2arctan(x+ 1) + C . 2 2 4 (3x + 2)dx 3 − 1 arc tan(x +1) 1 Vậy: = . − −
sin2arc tan(x + 1) + C . 2 2 2
(x + 2x+ 2)
2 x + 2x+ 2 2 4 2 x + 1 5 − 1 5 1 3 1 1 1 7. dx = . + . + . + . dx 3 2 3
(x + 3)(x − 1)
32 x + 3 32 x −1 8 (x −1) 2 (x −1) 5 x −1 3 1 1 = ln − . − C + . 2 32 x + 3
8 x − 1 4(x −1) 2 2 + + 2 1 1 + 2 2 8*. x 2 = x = x dx dx dx = I 4 2 x +4 2 4 2 x + 2 x − + 4 x x 2 2
Đặt t = x − dt = 1+
dx. Thay vào ta có: 2 x x 2 x − 2 dt 1 t 1 1 x − 2 = = + = x I arc tan C arc tan + C = arctan + C . 2 t +4 2 2 2 2 2 2x
Nhận xét: bài toán này khá khó ở chỗ làm sao để biết chia cả tử và mẫu cho 2
x , sau đó lại nhận ra nhóm mẫu s t
ố hành hẳng đẳng thức và đặt ẩn ph . N ụ
ói chung bài khó làm nhiều m c ới quen đượ :D. Bài 2: + 1. 1 sin x 1 1 sinxdx d(cos x) dx = dx + dx = − cot x + = − cot x+ 2 2 2 2 sin x sin x sin x 1 −cos x 1 −cos x − Đặ d(cos x) dt 1 1 1 1 t 1
t t = cos x dt = − sin xdx. Thay vào ta có: = = − dt = ln + C 2 2 1− cos x t − 1
2 t − 1 t + 1 2 t + 1 Trang 2
Anh Long Fanpage: https://www.facebook.com/chinhphuctcc/ 1 cos x − 1 = ln +C . 2 cos x + 1 1+ sin x 1 cos x − 1 Vậy:
dx = − cot x+ ln + C . 2 sin x 2 cos x +1 1 1 sin8x sin 4x
2. cos6x.cos2xdx = (cos8x +cos4x)dx = + + C . 2 2 8 4 2 2 + 3. 4 2 1 cos4x 1 2 cos (2x)dx =
cos (2x) dx =
dx = (1+ 2cos4x + cos 4x)dx 2 4 1 1 +cos8x 1 3x 4 sin 4x 1 sin8x = (1 + 2cos 4x + )dx =
(3 + 4 cos 4x +cos8x)dx = + . + . + C 4 2 8 8 8 4 8 8 3x sin 4x sin8x = + + +C . 8 8 64 4. dx 4dx d(2x) = = 2 = 2 − cot 2x + C . 2 2 2 2 sin x.cos x sin 2x sin 2x π d(x + ) 5. dx dx 1 1 π = = 4 = −
.cot(x + ) +C . 2 2 (sin x +cos x) 2 π 2 2 4 π sin (x + + ) 2 sin(x ) 4 4 6. cos2x dx cos2x dx cos2x dx 2cos2x dx = = = = I . 4 4 2 2 2 2 2 2 2 sin x +cos x
(sin x +cos x) −2sin x.cos x sin 2x 2 −sin 2x 1− 2 Đặ dt 1 1 1
t t = sin 2x dt = 2cos2xdx . Thay vào ta có: I = = + dt 2 2 −t
2 2 2 − t 2 + t 1 1 1 1 t + 2 1 sin 2x+ 2 = − dt = ln + C = ln + C .
2 2 2 +t t − 2 2 2 t − 2 2 2 sin 2x − 2
7. Chú ý tích phân với dx thì x là biến s c
ố òn y là hằng s . V ố ậy ta có: 1 1 sin(2x + y)
sinx.sin(x+ y)dx =
cosy− cos(2x+ y) dx = x cos y − + C . 2 2 2 8. Đặ 1 1 1
t t = 2x dt = 2dx. Thay vào cho g n: ọ dx = dt . 4 4 sin (2x) 2 sin t Trang 3
Anh Long Fanpage: https://www.facebook.com/chinhphuctcc/ 3 1 1 dt cot t Lại có: 2 dt = − . −
= − (1+ cot t).d(cott)= − cott− + C . 4 2 2 sin t
sin t sin t 3 1 1 1 Vậy: 3 dx= − cot 2x− cot 2x+ C . 4 sin (2x) 2 6 3 2 − 9. 3 sin x 1 cos x tan xdx = dx = .sin xdx = I . 3 3 cos x cos x
Đặt t = cos x dt = −sin xdx. Thay vào ta được: 2 t − 1 1 1 1 1 I = dt = − dt = ln t + + C = ln cosx + + C . 3 3 2 2 t t t 2t 2cos x cos x − 2 3 3 10. dx = 1− dx = 1− dx cos x +1 cos x + 1 x 2 2cos 2 x d 2 x = x −3. = x −3tan + C . 2 x 2 cos 2 11. 1 = 1 dx dx . = I . 4 2 2 sin (2x) sin (2x) sin ( 2x) Đặ 2 1
t t = cot 2x dt = − dx. Mặt khác: = 1+ 2
cot 2x = 1 + 2
t .Thay vào ta được: 2 sin 2x 2 sin (2x) −1 − 3 1 t − 3 I = (1+ 1 cot 2x 2 t )dt = (t + ) + C = (cot 2x+ )+ C . 2 2 3 2 3 12. dx = 1 dx . = I . 2 2
5cos x − 8 sin xcosx+ 3sin x 5 − 8tan x + 2 2 3tan x cos x Đặ dx
t t = tan x dt = . Thay vào ta có: 2 cos x 1 dx dt dt 1 1 3 1 I = . = = = − . + . dt 2 2 2
5 − 8tan x + 3tan x cos x
5 − 8t + 3t
(t −1)(3t − 5)
2 t −1 2 3t − 5 1 1 1 3t − = − − + − + = 5 .ln t 1 .ln 3t 5 C .ln + C . 2 2 2 t −1 1 3tan x− 5
Thay lại biến cũ: I = ln + C . 2 tan x − 1 Trang 4
Anh Long Fanpage: https://www.facebook.com/chinhphuctcc/ 13. sinx = sinx e .sin2xdx 2 e .sin x.(cos xdx) = I .
Đặt t = sinx dt = cos xdx. Thay vào ta có: = = = − + t t I 2 te dt ... 2(t 1)e C ( các em t t ự ích phân từng phần nhé). Thay lại biến cũ: = − sinx + I 2(sin x 1)e C . 14. x sinxdx . Đặ sin xdx sinxdx d(cos x) 1 t u= x,dv= v= = − = . 3 3 3 cos x 3 2 cos x cos x cos x 2cos x x sin xdx x dx x 1 Tích phân t ng ph ừ ần:
= udv = uv − vdu = − = − tanx + C . 3 2 2 2 cos x 2cos x 2cos x 2cos x 2 x 2dt 2t 1 − 2 15. dx . Đặ t t t = tan dx = ,sin x = ,cos x = . Thay vào ta có:
3sin x − 4 cos x 2 2 t + 2 1 t + 2 1 t + 1 2dt 2 dx + = = 2dt = dt = dt t 1 2 2 2
3sin x − 4 cos x 2t 1 −t
6t − 4(1 −t )
2t + 3t − 2 (t + 2)(2t − 3. − 1) 4. 2 t + 1 1+ 2 t − − = . + .
dt = − .ln t + 2 +
.ln 2t − 1 + C = .ln + 1 1 2 1 1 1 1 2t 1 C .
5 t + 2 5 2t −1 5 5 5 t + 2 − Trả lại biến cũ: = + dx 1 2tan(x / 2) 1 .ln C .
3sin x− 4 cos x 5 tan(x / 2)+ 2 Bài 3: dx x + 2 − x 1 1 (x + 3/2 3/2 1. = = + − = 2) − x + dx ( x 2 x)dx C x + 2 + x
(x + 2) − x 2 2 3 / 2 3 / 2 (x + 3 3 =
2) − x +C. 3 3 − x −1 t − 2. x 1 1 dx . Đặt = = 2 x t
x t dx =2tdt . Thay vào ta có: = = dx .2tdt ... x + 1 + x 1 t +1 = 2
t −4t + 4ln t +1 +C (tích phân hữu tỉ đơn giản, các em tự tính nhé). − Thay lại biến cũ ta có: = − + + +
x 1 dx x 4 x 4ln( x 1) C . x + 1 2 2 dx 3t dt 3tdt 3 d(t + 3. dx . Đặ 1)
t 3 x =t x = 3
t dx = 2
3t dt . Thay vào ta có: = = = . 3 2 3 x + x x + x t + t t + 2 3 1 2 t + 1 dx 3 = 3 2
ln(t +1) +C . Trả lại biến cũ: = ln( x + 1)+ 3 2 C . 2 x + 3 x 2 Trang 5
Anh Long Fanpage: https://www.facebook.com/chinhphuctcc/ 4. dx . Đặt
− = = 2 + 2 = 2 + x 2 t x (t 2) dx 2(t
2).2tdt . Thay vào ta có: x − 2 2 + 3 dx = 4t(t 2)dt = 2 + = t 4(t 2)dt 4( + 2t) + C . − t 3 x 2 − 3 dx ( x 2) Trả lại biến cũ: = 4( + 2 x − 2)+ C . − 3 x 2 5. dx 3 4 x − x
Khi có cả m x và n x thì ta đặt = p t
x , với p = BCNN(m,n) .
Vậy với bài toán trên ta đặt = 12 = 12 = 11 3 = 4 4 t x x t dx 12t dt, x t , x = 3 t . Thay vào ta có: 11 8 8 − dx = 12t dt = t dt = 1 t 1 1 12. 12. dt 12. t t ... t 1 dt 4 3 + = + 7 + 6 + + + 3 − 4 x x t − − − − − t t 1 t 1 t 1 t 1 8 7 2 = t t t 12 − + + + + + ln t 1 ... t +C . 8 7 2 3 2 12 7 6 dx x x x Thay lại biến cũ: = 12 − + + + + + 12 + 12 ln x 1 ... x C . 3 4 − x x 8 7 2 3− 2x dx 2xdx d(1− 2 6. = − = + x ) = + − 2 + dx 3 . 3arc sin x 3arc sin x 2 1 x C . 1 − 2 x 1 − 2 x 1 − 2 x 1 − 2 x 1 .(2x − 2)+ x + 2 2 1 1 d(x − 2x − 7. = = 1) + dx 2 = + dx dx . 2. I I . − − − − 2 x 2x 1 x 2x 1
x − 2x − 1 x − 2x − 1 2 2 2 2 2 1 2 − − 1 d(x 2x 1) − dx d(x 1) Ta có: I = . = 2
x − 2x − 1 + C ; I = 2. = 2. 2 1 2 2 − − x 2x 1 2 − − − 2 − x 2x 1 (x 1) 2 = − + 2 − − + 2ln x 1 x 2x 1 C . x + 1 Vậy:
dx = I + I = x − 2x − 1 + 2ln x − 1+ x − 2x − 1 + 2 2 C . x − 2x − 1 2 2 1 − 8. − 2 + − = 1 x x 4x 1dx
( −2x + 4) − 2
x + 4x −1dx + 2 − 2
x + 4x −1dx = I + I . 1 2 2 −1 1 Ta có: I =
(−2x + 4) − 2
x + 4x − 1dx = − . − 2
x + 4x − 1d(− 2
x + 4x − 1) 1 2 2 −1 (− 2
x + 4x − 3/2 1) − = + = 1 . C . ( − 2
x +4x − 3 1) +C . 2 3 / 2 3 Trang 6
Anh Long Fanpage: https://www.facebook.com/chinhphuctcc/ 1 3 x − 2 Lại có: I = 2 − 2
x + 4x − 1dx = 2 3 − (x − 2
2) d(x − 2) = ( x − 2) − 2
x + 4x −1 + arc sin + C . 2 2 2 3 − 1 1 3 x− 2
Vậy: x −x + 4x − 1dx = I + I =
. (−x + 4x − 1) + ( x − 2) −x + 4x − 1 + arc sin + 2 2 3 2 C . 1 2 3 2 2 3 2 9*. x x x 2 2u 4u dx . Đặt u= 2 u = = − + 1 x= dx= du. Thay vào tích 2− x − − − 2 x 2 x 2 x + 2 + 2 2 1 u (1 u ) 2 x 4u 1 1 phân ta được: dx = du = 4 − du = 4.(I − I ) . 2 2 2 2 2 − 2 x + (1 u ) + + 1 u (1 u ) 1 2 1 1 Xét I =
du = arctanu + C . Với tích phân = I du ta đặt 2 1 1+ 2u + 2 2 (1 u ) 1 + 2 tan t dt = = dt u tant du = ( + 2
1 tan t)dt , thay vào ta có: I = .dt = 2 2 2 2 cos t (1 +tan t) 1 + 2 tan t = = = 1 + u cos tdt ... (arc tanu ) + 2 C . 2 1 + 2 u x 2 x 2u x Tóm lạ − i: = − + = − 2 x + dx 2arc tanu C 2arc tan C − + 2 − 2 x 1 u 2 x + x 1 − 2 x = x 2arc tan
− x(2− x) + C. 2 −x 10*. dx . 2
(1+ x) x + 6x + 3 1 1 − Đặ 1 t u =
x= − 1 dx=
du. Thay vào tích phân ban đầu: 1+ 2 x u u dx u 1 = − du = − 1 du 2 (1+ 2 x) x + 6x + 2 3 u 1 1 1 u + 4 − − + − + 2 1 6 1 3 2 u u u u = − 1 = − 1 = − 1 1 du du . d(u − 1) − 2
2u + 4u +1
3 − 2(u − 2 1) 2
3 −(u − 2 1) 2 1 u − = − 1 arc sin + C . 2 3 / 2 dx 1 −x Trả lại biến cũ: = − arc sin + C . (1+ 2
x) x + 6x + 3 2 ( + 1 x) 3 / 2 11*. dx = dx = I . 1 + 2 x +4x +5 1 + (x + 2 2) +1 Trang 7
Anh Long Fanpage: https://www.facebook.com/chinhphuctcc/ π π dt
Cách 1: Đặt x + 2 = tant với t −
; . Ta có dx = . Thay vào ta được: 2 2 2 cos t 2 2 t = dt / cos t = dt / cos t = dt I
. Đến đây ta đặt tiếp u = ta n
, tích phân trở thành : + + 2 2 1 cos t + + cos t 1 1 tan t 2 1 cost 1+ 2 u du. Các em t l ự àm tiếp nhé. 1− 2 u
Cách 2: Sử dụng phép đặt Euler. Đặt + = 2 + + 2 + + 2 = 2 + + x t x 4x 5 x 2xt t x 4x 5 5 − 2 t − 2 t + 4t − − 2 t + 4t − = = 5 5 x dx
dt . Thay vào tích phân ta được: I = dt . 2t − 4 2(t − 2 2) 5 − 2 − 2 + t 2(t 2) 1 + t 2t − 4 − 2 5 t (Chú ý là 2
x + 4x + 5 = x + t = + t ). 2t − 4 Các em t r ự út g n ọ và làm n t ố nhé.
Nhận xét: Dù làm theo cách nào thì câu này cũng rất khoai. Trang 8




