
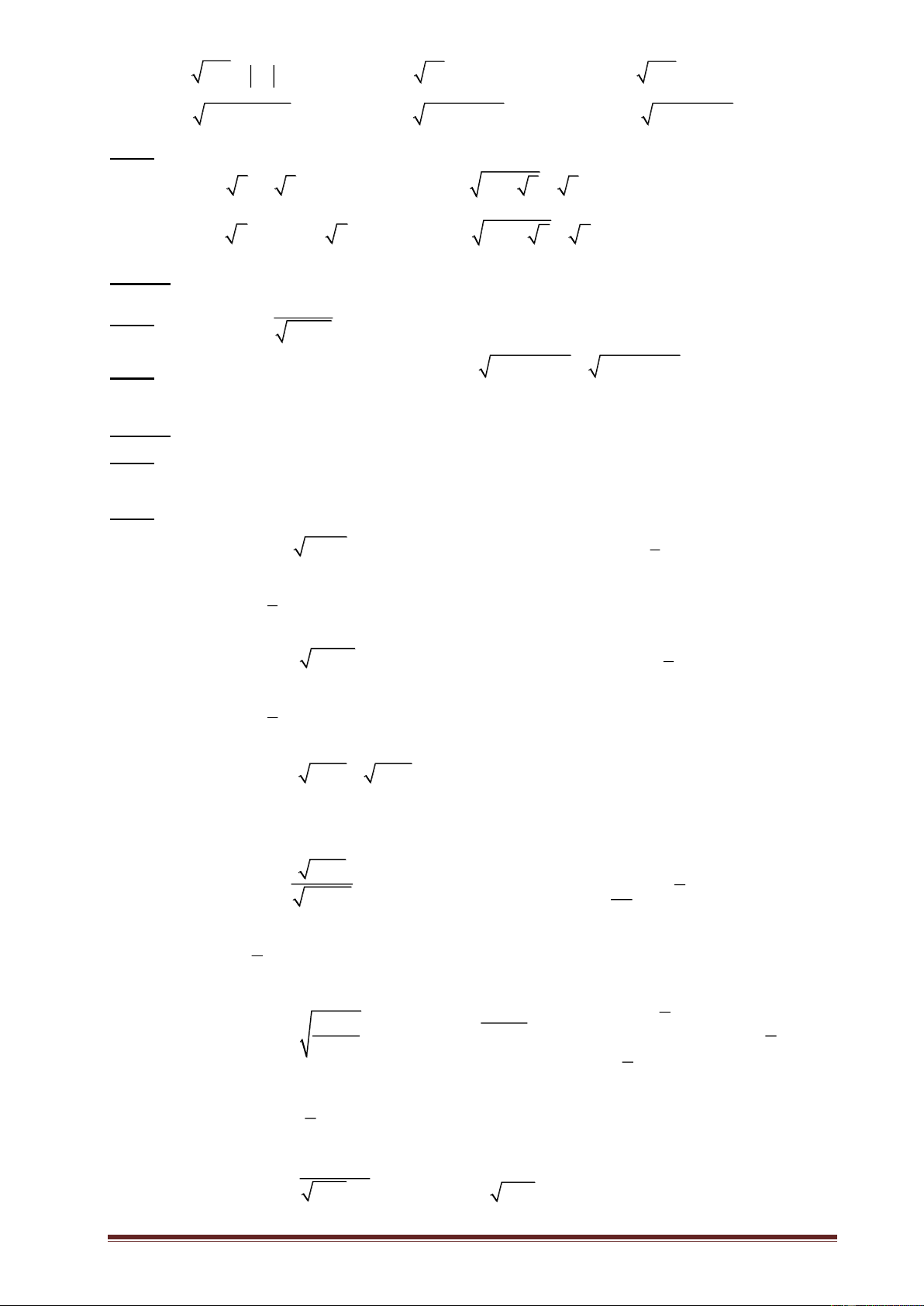

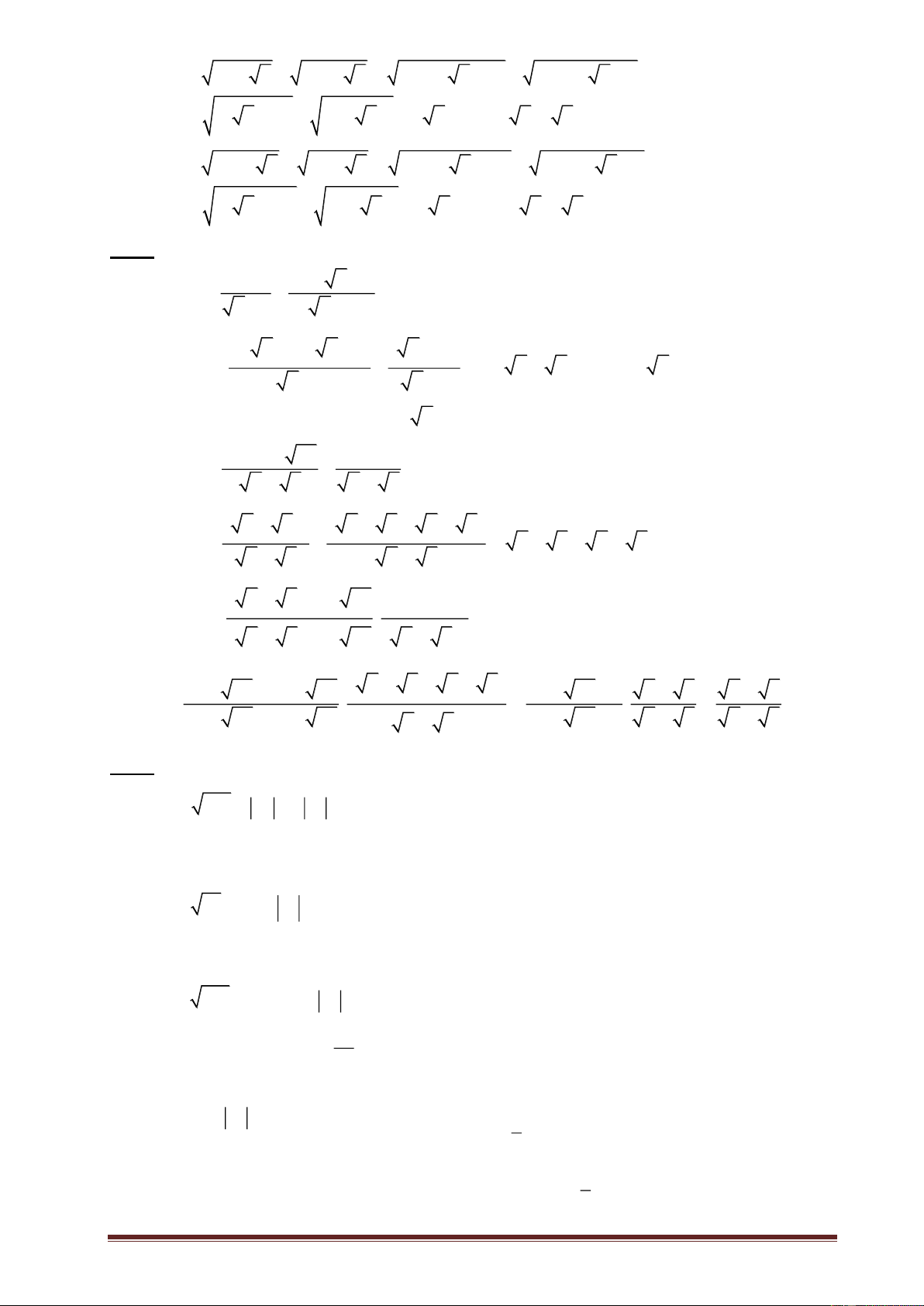
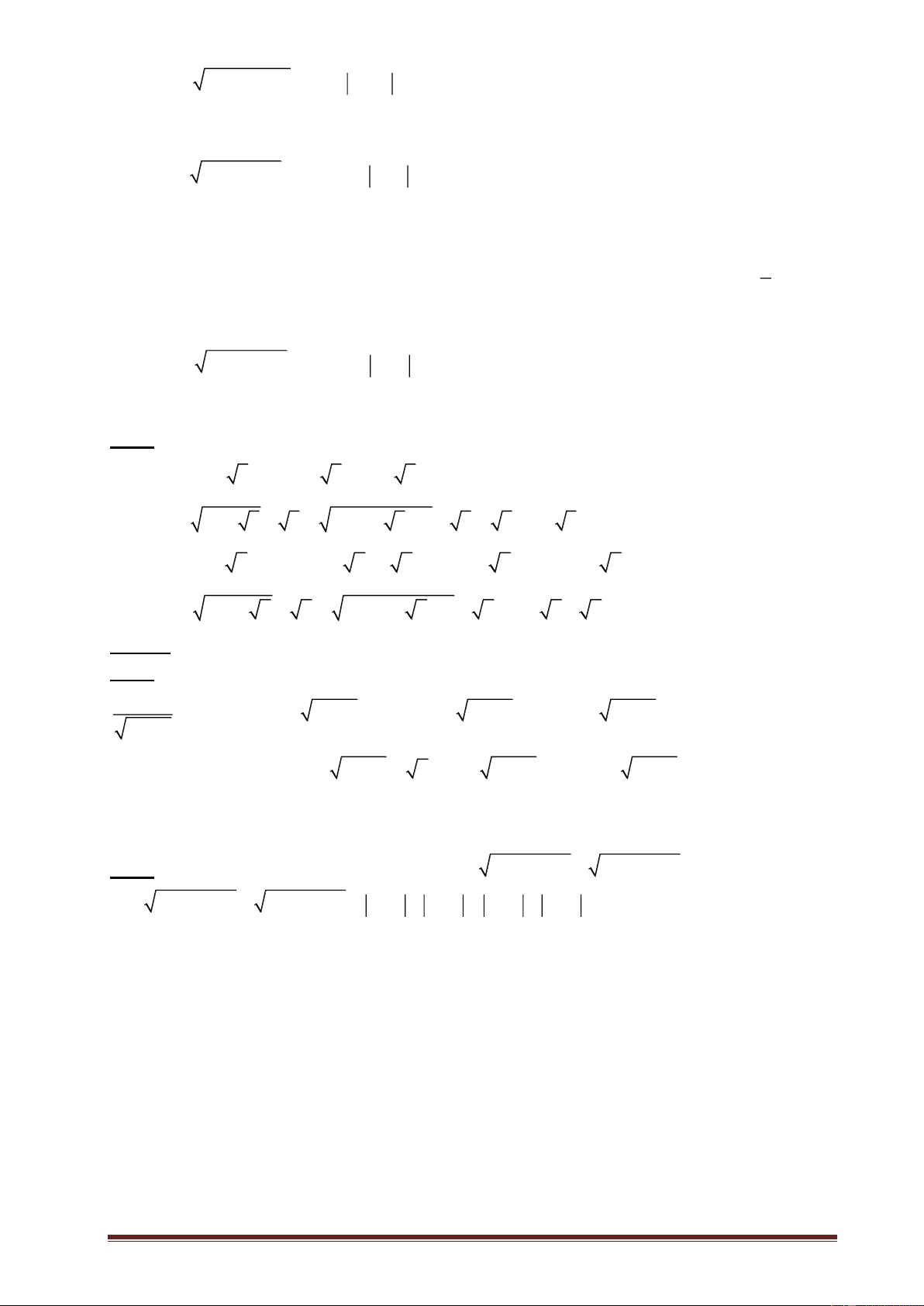
Preview text:
CÁC DẠNG TOÁN 9 BÀI 2: CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC
Dạng 1: Tìm điều kiện để biểu thức có nghĩa (được xác định)
Bài 1: Chọn đáp án đúng
1. Điều kiện xác định của biểu thức 2 ab là: A. b 0 B. a < 0 C. a 0 D. a = 0 2. Biểu thức 2
( 5 3) có giá trị là: A. 2 B. 5 3 C. 3 5 D. 2 1
3. Với x y 0 , biểu thức 6 2
x (x y) có kết quả rút gọn là: x y A. 3 x B. - 3 x C. 3 | x | D. Kết quả khác 4. Phương trình 2
(x 1) 3 có nghiệm là: A. x = 4 B. x 4 C. x = - 2 D. x = 4 và x = - 2
Bài 2: Tìm điều kiện để biểu thức sau có nghĩa 1
a) 3x 1 b) 5 3x c) x 2 4 x d) x 2 + 2 x 4 1 3 x x 2 1 3 e) f ) g) h) i) 7x 14 7x 2 7 2x x 1 1 x 1 2 2 2
j) x 2 k) x 3 l) 25 4x 1 1 1 3x 2
n) 2x 5x 3 p) q) r) 2 2 2x x x 5x 6 x 3 5 x Dạng 2: Rút gọn
Bài 1: Rút gọn rồi tính a) 4 5 ( 2 ) b) 6 4 ( 3 ) c) 8 ( 5 ) d) 6 8 2 ( 5 ) 3 ( 2 ) Bài 2: Tính
A 8 5 32 3 72
B 20 2 45 3 80 125
C 3 2 2 3 2 2
D 8 2 15 8 2 15
E 9 4 5 6 2 5 ; F 9 4 2 11 6 2 ; G 12 8 2 6 4 2
Bài 3: Rút gọn biểu thức sau: 9 a 9 6 a a a) A
, với a 0, a 9 a 3 a 3
a b 2 ab a b b) B
với a 0,b 0, a b a b a b
a b2 4 ab ab c) C
với a 0, b 0, a b a b .
2 4 ab a b2
Bài 4: Giải các phương trình sau Trang 1 2 a) 9x 9 4 b) x 9 2
c) 9x 2x 1 2
d ) 1 4x 4x 5 2
e) x 6x 9 3x 1 2
f ) x 4x 4 2 x Bài 5: Chứng minh a 2 ) 9 4 5 5 2 )
b 9 4 5 5 2 c 2 ) 4 7 238 7
d) 23 8 7 7 4
Dạng 3: Bài tập nâng cao 2 a 3 Bài 1: Chứng minh
2 với mọi giá trị của a 2 a 2
Bài 2: Tìm giá trị nhỏ nhất của biểu thức 2 2 A
x 4x 4 x 4x 4
ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI
Dạng 1: Tìm điều kiện để biểu thức có nghĩa (được xác định)
Bài 1: Chọn đáp án đúng 1 - C 2 - C 3 - A 4 - D
Bài 2: Tìm điều kiện để biểu thức sau có nghĩa
a) Để biểu thức 3x 1 có nghĩa 1
3x 1 0 3x 1 x 3 1 Vậy với x
thì biểu thức đã cho có nghĩa 3 b) Để 5
biểu thức 5 3x có nghĩa 5 3x 0 3x 5 x 3 5 Vậy với x
thì biểu thức đã cho có nghĩa 3 x 2 0 x 2
c) Để biểu thức x 2 4 x có nghĩa 2 x 4 4 x 0 x 4
Vậy với 2 x 4 thì biểu thức đã cho có nghĩa x 3 f) Để 3 x 3 x 0 2 biểu thức có nghĩa 2
x 3 7 x 2 7x 2 0 x 7 7 2 Vậy với
x 3 thì biểu thức đã cho có nghĩa 7 7 x 2 2 x g) Để x 2 0 2 7 biểu thức
có nghĩa 7 2x 2 x 7 2x 7 2
7 2x 0 x 2 7
Vậy với 2 x
thì biểu thức đã cho có nghĩa 2 x 1 0 h) Để 1 x 1 x 1 biểu thức có nghĩa x 1 1 x 1 1 0 x 1 1 x 0 Trang 2 Vậy với 1
x 0thì biểu thức đã cho có nghĩa j) Để x 2 biểu thức 2 x 2 có nghĩa 2
x 2 0 (x 2)(x 2) 0 x 2
Vậy với x 2 hoặc x 2 thì biểu thức đã cho có nghĩa k) Để biểu thức 2 x 3 có nghĩa 2
x 3 0 (luôn đúng) Vậy với x
thì biểu thức đã cho có nghĩa l) Để 5 5 biểu thức 2 25 4x có nghĩa 2
25 4x 0 x 2 2 3 x n) Biểu thức 2
2x 5x 3 có nghĩa 2 2x 5x 3 0 (x 1)(2x 3) 0 2 x 1 p) Để 1 biểu thức có nghĩa 2
2x x 0 x(2 x) 0 0 x 2 2 2x x q) Để 1 biểu thức có nghĩa 2 x 5x 6 x 3 2
x 5x 6 0 (x 2)(x 3) 0 x 2 r) Để 1 3x x 3 0 x 3 biểu thức có nghĩa 3 x 5 x 3 5 x 5 x 0 x 5 Dạng 2: Rút gọn
Bài 1: Rút gọn rồi tính a) 4 2 2 2 5 ( 2
) 5 (2 ) 5.2 20 b) 6 3 4 ( 3 ) 4 .3 1 08 c) 8 4 2 ( 5 ) 5 5 25 d) 6 8 3 4 2 ( 5 ) 3 ( 2 ) 2.5 3.2 298 Bài 2: Tính
A 8 5 32 3 72
4.2 5 16.2 3 36.2 2 2 5.4 2 3.6 2
2 2 20 2 18 2 0
B 20 2 45 3 80 125 4.5 2 9.5 3 16.5 25.5
2 5 2.3 5 3.4 5 5 5 2 5 6 5 12 5 5 5 (2 6 12 5) 5 1 1 5
C 3 2 2 3 2 2
2 2 2 1 2 2 2 1 2 2 1 2 2 1 2 1 2 1 2 2
D 8 2 15 8 2 15 5 2. 5. 3 3 5 2 5. 3 3
5 32 5 32 5 3 5 3 2 3
E 9 4 5 6 2 5 5 2.2. 5 4 5 2. 5.11
5 22 5 2 1
5 2 5 1 3 Trang 3
F 9 4 2 11 6 2 8 2.2 2.11 9 2.3. 2 2 2 2 2 1
3 22 2 2 13 2 2 4
G 12 8 2 6 4 2 8 2.2 2.2 4 4 2.2. 2 2
2 2 22 2 2 2 2 2 2 2 2 2
Bài 3: Rút gọn biểu thức sau: 9 a 9 6 a a a) A
, với a 0, a 9 a 3 a 3
a a a 2 3 3 3
3 a a 3 6 2 a a 3 a 3
Vậy với 0, a 9 thì A 6 2 a
a b 2 ab a b b) B
với a 0,b 0, a b a b a b
a b2 a b a b B
a b a b 0 a b a b
a b2 4 ab ab c) C
với a 0, b 0, a b a b .
2 4 ab a b2 2 4
a b a b a ab b ab
a2 ab b a b a b .
a 2 ab b 4 ab . 2
a 2 ab b a b a b a b
Bài 4: Giải các phương trình sau 3x 9 x 3 2 a) 9x 9 3x 9 3x 9 x 3
Vậy phương trình đã cho có tập nghiệm là S 3; 3 x 3 4 2 2
b) x 9 x 9 x 9 x 3
Vậy phương trình đã cho có tập nghiệm là S 3; 3 2
c) 9x 2x 1 3x 2x 1 ĐK: 1
2x 1 0 x 2 x 1
3x 2x 1 Ta có:
3x 2x 1 1 ( thỏa mãn) 3x 2 x 1 x 5 1
Vậy phương trình đã cho có tập nghiệm là S 1 ; 5 Trang 4 1 2x 5 x 2 2
d ) 1 4x 4x 5 1 2x 5 1 2x 5 x 3
Vậy phương trình đã cho có tập nghiệm là S 3; 2 2
e) x 6x 9 3x 1 x 3 3x 1
- Nếu x 3 0 x 3
, khi đó ta có phương trình: x 3 3x 1 x 2 (thỏa mãn)
- Nếu x 3 0 x 3
, khi đó ta có phương trình: 1
x 3 3x 1 x (loại) 2
Vậy phương trình đã cho có tập nghiệm là S 2 2
f ) x 4x 4 2 x x 2 x 2 x 2 0 x 2
Vậy phương trình đã cho có tập nghiệm là S x
R / x 2 Bài 5: Chứng minh a 2 ) 9 4 5 5 2.2. 5 4 5 2 (đpcm) )
b 9 4 5 5 5 2.2. 5 4 5 5 2 5 2 (đpcm) c 2 2 2 ) 4 7 4 2.4. 7 7
16 8 7 7 238 7 (đpcm)
d) 23 8 7 7 16 2.4. 7 7 7 4 7 7 4 (đpcm)
Dạng 3: Bài tập nâng cao
Bài 1: Chứng minh với mọi giá trị của a 2
a 3 2 a 3 2 a 2 a 2 2 a 2 1 0 a 2 2 2 2 2 2 2 1 0 2 a 2 Có 2
a 2 2 với a
R a
a a 2 2 2 2 2 2 1 2 1 0 2 1 0 với a R
Từ đó suy ra điều phải chứng minh
Bài 2: Tìm giá trị nhỏ nhất của biểu thức 2 2 A
x 4x 4 x 4x 4 2 2 A
x 4x 4 x 4x 4 x 2 x 2 x 2 2 x + Nếu x 2
A x 2 2 x 2
x > 4 hay A > 4 + Nếu 2
x 2 A x 2 2 x 4
+ Nếu x 2 A x 2 ( 2
x) 2x 4 > 4 hay A > 4
A 4 với mọi a nên A 4 khi 2 x 2 min Trang 5




