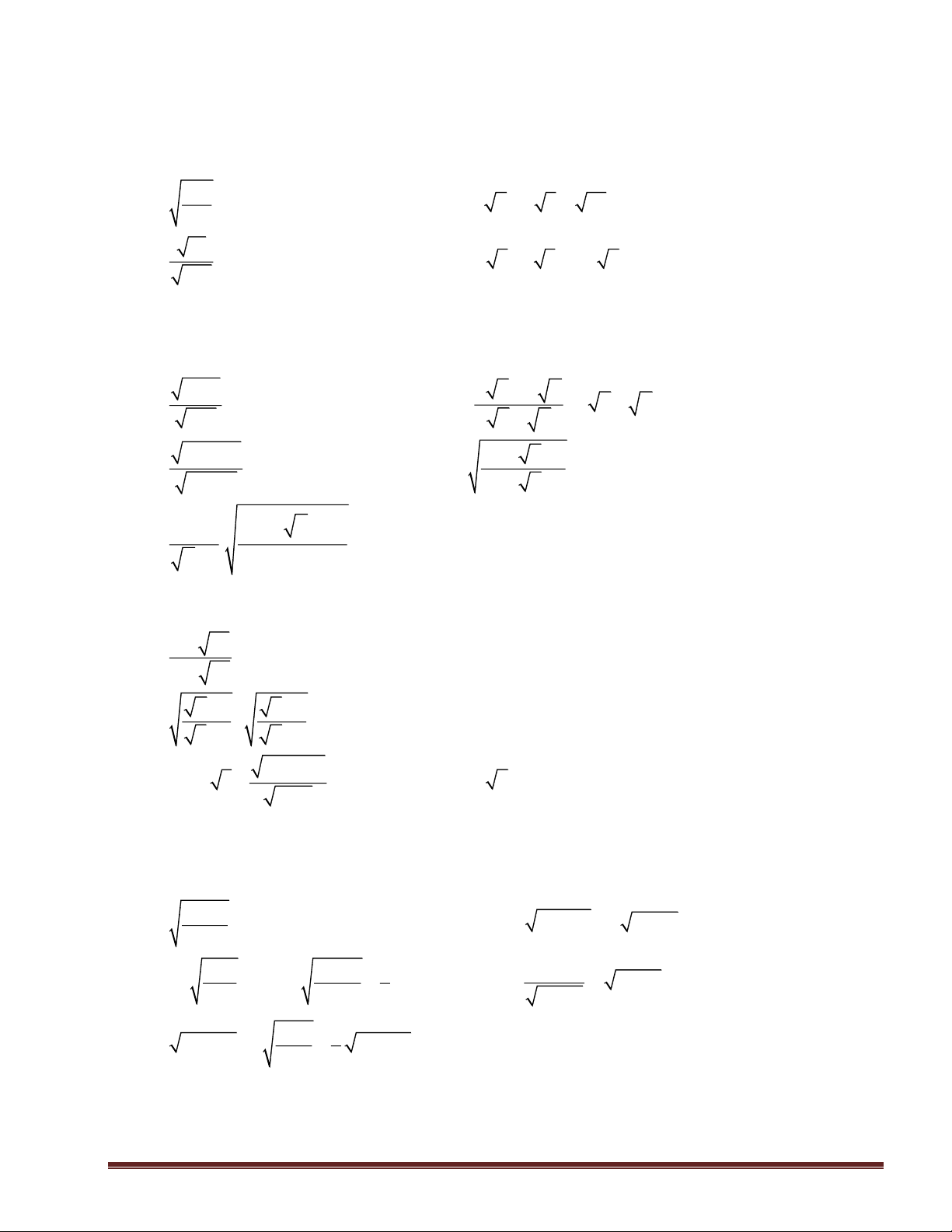


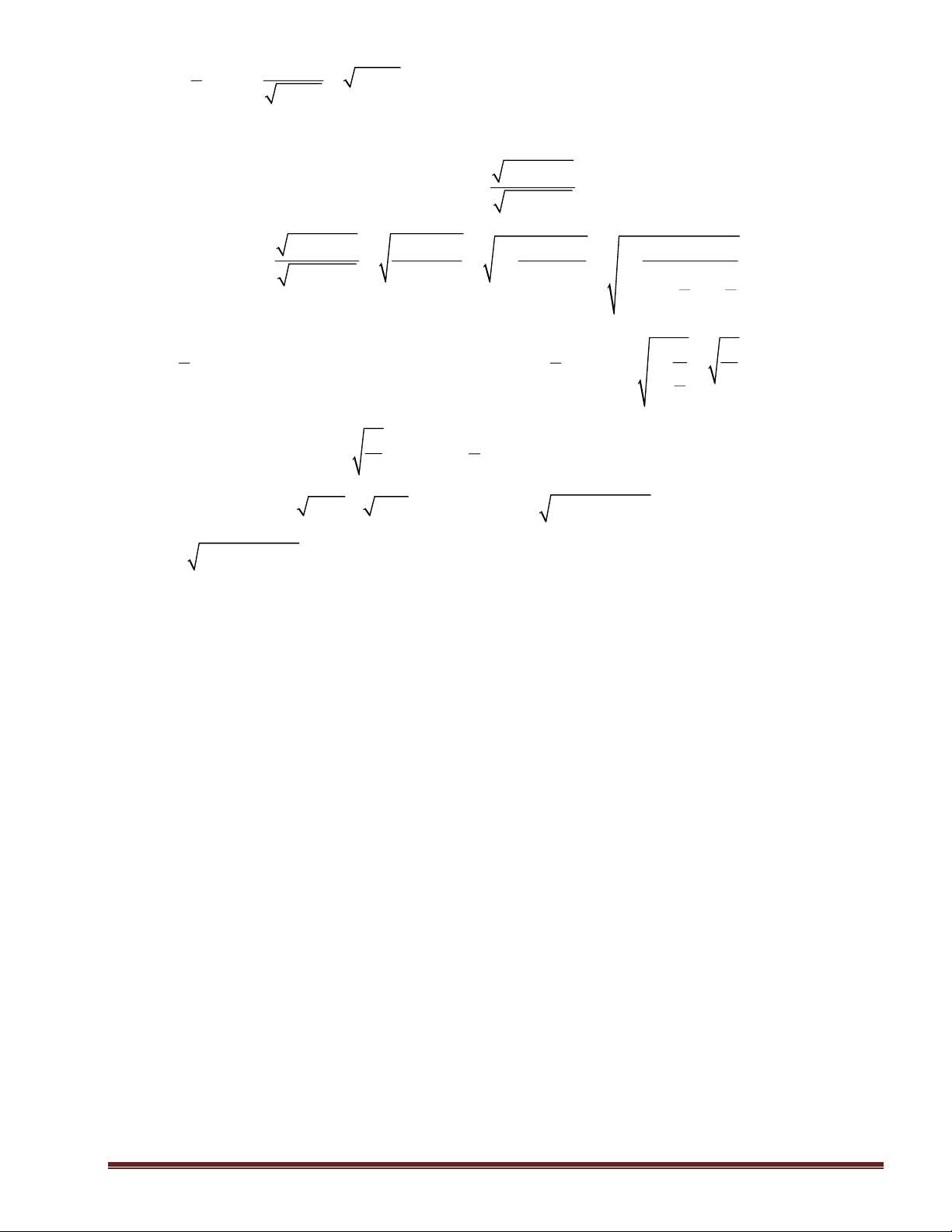
Preview text:
CÁC DẠNG TOÁN 9 BÀI 4: LIÊN HỆ GIỮA PHÉP CHIA VÀ PHÉP KHAI PHƯƠNG
Dạng 1. Thực hiện phép tính
Bài 1: Thực hiện phép tính a. 169 ; c. (5 7 + 7 5): 35; 225 b. 13 ; d. (2 8 −3 3 + ) 1 : 6. 208
Dạng 2. Rút gọn biểu thức
Bài 2: Rút gọn các biểu thức sau: 3 x x + y y a. 27a (a 0); d.
− ( x − y )2 ; 48a x + y 2 − + b. 150mn ( x 2 x 1
m 0;n 0); e. (x 0); 3 294m x + 2 x +1 1 (y−2 y x + − )2 1 c. .
x 1; y 1; y 0 . 4 ( ) y −1 (x − ) 1 Bài 3: Rút gọn và tính: x + xy a.
(x 0; y 0) tại x = 3; y = 27; y + xy − − b. a 1 b 1 :
với a = 7, 25; b = 3, 25; b +1 a +1 3 2 x + 2x c. 4x − 8 + (x 2 − ) tại x = − 2. x + 2 Dạng 3. Tìm x:
Bài 4: Tìm x biết: x − a. 2 3 = 2; d. 2
4x − 9 = 2 2x + 3; x −1 x − x − 9x − 7 b. 1 4 4 1 2 − 3 = 2 − ; e. = 7x + 5; 4 9 3 7x + 5 x − c. 5 1 4x − 20 + 3 − 9x − 45 = 4. 9 3 a.
Dạng 4. Tìm GTLN – GTNN: Trang 1 2 + +
Bài 5: Tìm giá trị lớn nhất của các biểu thức biểu thức: x x 3 A = ; 2 x + x +1
B = 9 − a + a −1. Hướng dẫn giải:
Dạng 1. Thực hiện phép tính
Bài 1: Thực hiện phép tính a. 169 169 13 = = ; 225 225 15 b. 13 13 1 1 = = = ; 208 208 16 4 c. (5 7 + 7 5): 35 = 5 + 7; d. ( − + ) 4 3 3 2 6 2 8 3 3 1 : 6 = − + . 3 2 6
Dạng 2. Rút gọn biểu thức
Bài 2: Rút gọn các biểu thức sau: 3 3 2 a. Với 27a 27a 9a 3a a 0 ta có = = = ; 48a 48a 16 4 2 2 2 b. Với 150mn 150mn 25n 5n
m 0; n 0 ta có = = = ; 3 2 3 294m 294m 49m 7m x −1 (y−2 y + )2 1 x −1 ( y − )2 1 y −1 − c. Với x 1
x 1; y 1; y 0 ta có . = . = . y −1 (x − )4 1 y −1 (x − )4 1 y −1 (x − )2 1 1 (y )1 1− x = 1 ( y ) 1 x −1 3 3 + 2 x + y x x y y d.
− ( x − y ) ( ) ( ) =
− (x − 2 xy + y) x + y x + y
( x + y)(x− xy + y) −x+2 xy −y= xy; x + y x − x + ( x − )2 1 x −1 2 1
e. Với x 0 ta có = = x + 2 x +1 ( x + ) . 2 x +1 1 Trang 2 Bài 3: Rút gọn và tính: x + ( x + y x xy ) x
a. Với x 0; y 0 ta có = = y + xy
y ( x + y ) y
Thay x = 3; y = 27 vào x ta được: 3 3 1 1 = = = . y 27 27 9 3 1 1 1 1 ( a − )1( a a b a b + − − − − )1 − b. Ta có: a 1 : = : = = b +1 a +1 b +1 a +1
( b − )1( b + )1 b−1 − − Thay a
a = 7, 25; b = 3, 25 vào 1 ta được: 7,25 1 6, 25 25 5 = = = . b −1 3, 25 −1 2, 25 9 3 3 2 x + 2x x x + 2
c. Với x −2 ta có 4x − 8 + = 4x − 2 2 +
= 4x − 2 2 + x = x + 2 x + 2 5 x − 2 2 (x 0) = 3 x − 2 2 ( 2 − x 0)
Thay x = − 2 vào 3x − 2 2 ta được 3 − 2 − 2 2 = 5 − 2.
Dạng 3. Tìm x:
Bài 4: Tìm x biết: 3 2x − 3 2x − 3 1
a. Với x 1; x ta có = 2
= 4 2x − 3 = 4(x − )
1 2x = 1 x = (tm). 2 x −1 x −1 2 x −1 4x − 4 1 4 1
b. Với x 1 ta có: 2 − 3 = 2 − x −1 − 6 = x −1 − 4 9 3 3 3 1 17 x −1 = − x −1 = 1 − 7 (Vô nghiệm) 3 3 x − 5 1
c. Với x 5 ta có: 4x − 20 + 3 −
9x − 45 = 4 2 x − 5 + x − 5 − x − 5 = 4 9 3
x − 5 = 2 x = 9(tm). 3
d. Với x − ta có: 2
4x − 9 = 2 2x + 3 (2x − 3)(2x + 3) − 2 2x + 3 2 3 3 = − 2 + 3 = 0 = − ( ) x x x tm
2x + 3 ( 2x −3 − 2) = 0 2 2 2x 3 2 0 − − = 7 2x − 3 = 4 x = (tm) 2 3 7
Vậy x − ; . 2 2 Trang 3 5 9x − 7
Với x − ta có:
= 7x + 5 9x − 7 = 7x + 5 2x =12 x = 6(tm). 7 7x + 5
Dạng 4. Tìm GTLN – GTNN: 2 + +
Bài 5: Tìm giá trị lớn nhất của biểu thức: x x 3 A = . 2 x + x +1 2 2 x + x + 3 x + x + 3 2 2
Bài giải: Ta có: A = = = 1+ = 1+ 2 2 2 2 x + x +1 x + x +1 x + x +1 1 3 x + + 2 4 2 2 11 Do 1 x + 0
với mọi x , dấu “ = “ xảy ra khi 1
x = − nên A 1+ = . 2 2 3 3 4 11
Vậy giá trị lớn nhất của A là khi 1 x = − . 3 2
Với 1 a 9 ta có 2
B = 9 − a + a −1 B = 9 − a + 2 (9 − a)(a − ) 1 + a −1 2
B = 8 + 2 (9 − a)(a − )
1 8 + 9 − a + a −1 = 16 B 4.
Dấu bằng xảy ra khi 9 − a = a −1 a = 5(tm).
Vậy GTLN của B là 4 khi a = 5. Trang 4




