Các dạng toán 9 bài: Luyện tập bài tập căn thức bậc hai và hằng đẳng thức

Tổng hợp Các dạng toán 9 bài: Bìa tập căn thức bậc hai và hằng đẳng thức rất hay và bổ ích giúp bạn đạt điểm cao. Các bạn tham khảo và ôn tập để chuẩn bị thật tốt cho kỳ thi tốt nghiệp sắp đến nhé. Mời bạn đọc đón xem.

45 23 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 9

Môn: Toán 9

Thông tin:

4 trang 9 tháng trước

Tác giả:

Profile Minh Thư
Trang 1
CÁC DẠNG TOÁN 9 BÀI : LUYỆN TẬP CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG
THỨC
Dạng 1. So sánh các căn bậc hai số học
Bài 1. So snh
a. 5 và
17 1.
b. 3 và
15 1.
Bài 2. Tìm giá trị của
x
biết
a.
1 6.x
b.
2
2.xx
Dạng 2. Tính giá trị của biểu thức chứa căn bậc hai
Bài 3. Thực hiện các phép tính sau:
a.
5 2 6 5 2 6.
b.
c.
31 12 3 31 12 3.
d.
21 12 3 21 12 3.
Dạng 3. Rút gọn biểu thức chứa căn bậc hai
Bài 4. Rút gọn các biểu thức sau:
a.
2
4 4 4x x x
với
2.x
b.
2
3 9 6x x x
với
3.x 
c.
2
6 9 3
4 4 4
9
x x x
x x x
x
với
0 9.x
Dạng 4. Tìm điều kiện để biểu thức chứa căn bậc hai có nghĩa
Bài 5. Với giá trị nào của x thì cc căn thức sau có nghĩa
a.
3 5 6 .xx
b.
24
.
5
x
x
c.
2
8 9.xx
d.
2
16 .x
Dạng 5. Giải phương trình chứa căn bậc hai
Bài 6. Giải cc phương trình sau
a.
2
412 .xxx
b.
2
4 1.xxx 
c.
2 1 2.xx
d.
2 2 2 2 3 2 13 8 2 3 5.x x x x
Bài 7*. Tìm cc s thực
,,x y z
tha mn
8 2 1 4 2 6 3.x y z x y z
LỜI GIẢI
Dạng 1. So sánh các căn bậc hai số học
Bài 1.
Trang 2
a. Ta có
16 1 17 1
5 17 1.
b. Ta có
16 1 15 1
3 15 1.
Bài 2.
a. Điu kiện
1 0 1xx
. Ta có
1 36 35xx
(tha mn điu kiện).
b. Điu kiện
0x
. Ta có
2
2
2 2 0
0
x
x x x x
x
Kết hp điu kiện ta có
0x
hoc
2x
.
Dạng 2. Tính giá trị của biểu thức chứa căn bậc hai
Bài 3.
a.
5 2 6 5 2 6
22
3 2 3 2
3 2 3 2
3 2 3 2 2 2
.
b.
49 12 5 49 12 5
22
3 5 2 3 5 2
3 5 2 3 5 2
6 5.
c.
31 12 3 31 12 3
22
3 3 2 3 3 2
4.

d.
21 12 3 21 12 3
22
2 3 3 2 3 3
4 3.
Dạng 3. Rút gọn biểu thức chứa căn bậc hai
Bài 4.
a.
2
4 4 4x x x
2
42xx
42xx
42xx
(do
2x
)
32x
b.
2
3 9 6x x x
2
33xx
33xx
33xx
do 3x 
23x
c.
6 9 3
4
9
x x x
x
x
2
33
4 4 3 3 3.
33
xx
x x x x
xx


Dạng 4. Tìm điều kiện để biểu thức chứa căn bậc hai có nghĩa
Bài 5.
a. Điu kiện:
( )( )
3 5 6 0- - ³xx
Trang 3
TH1:
3
3 5 0
5
60
6
x
x
x
x



không tha mãn.
TH2:
3
3 5 0
3
6
5
60
5
6
x
x
x
x
x



Vậy
3
6.
5
x
b. Điu kiện:
24
0
5
x
x
TH1:
2 4 0 2
25
5 0 5
xx
x
xx



TH2:
2 4 0 2
5 0 5
xx
xx



Vậy
2 5.x
c. Điu kiện:
2
1
8 9 0 1 9 0 .
9
x
x x x x
x

d. Điu kiện:
2
16 0 4 4.- ³ Û - £ £xx
Dạng 5. Giải phương trình chứa căn bậc hai.
Bài 6.
a.
2
412 xxx
Phương trình tương đương với
22
1
2 4 2 1
x
x x x x
Suy ra phương trình vô nghiệm.
b.
2
4 1xxx
Phương trình tương đương với
2
2
1
2 3 0 3; 1
41
ì
³
ï
ï
Û - - = Û = = -
í
ï
- - = -
ï
î
x
x x x x
x x x
Đi chiếu với điu kiện ta suy ra phương trình có nghiệm
3.=x
c.
2 1 2xx
Điu kiện
1x
.
Phương trình tr thnh
2
1 2 1 1 2 1 1 2x x x
Trang 4
1 1 2 1 1 2 1 1 2x x x x
(Tha mn).
d.
2 2 2 2 3 2 13 8 2 3 5x x x x
Điu kiện
3
2
x
Phương trình tr thnh
22
2 3 1 2 3 4 5xx
2 3 1 2 3 4 5xx
3
2 3 1 2 3 4 5 2 2 3 0
2
x x x x
(Tha mn).
Bài 7. Biến đi đng thức v dng
2 2 2
1 1 2 2 3 3 0x y z
T đó tìm đưc
2, 6, 12.x y z
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

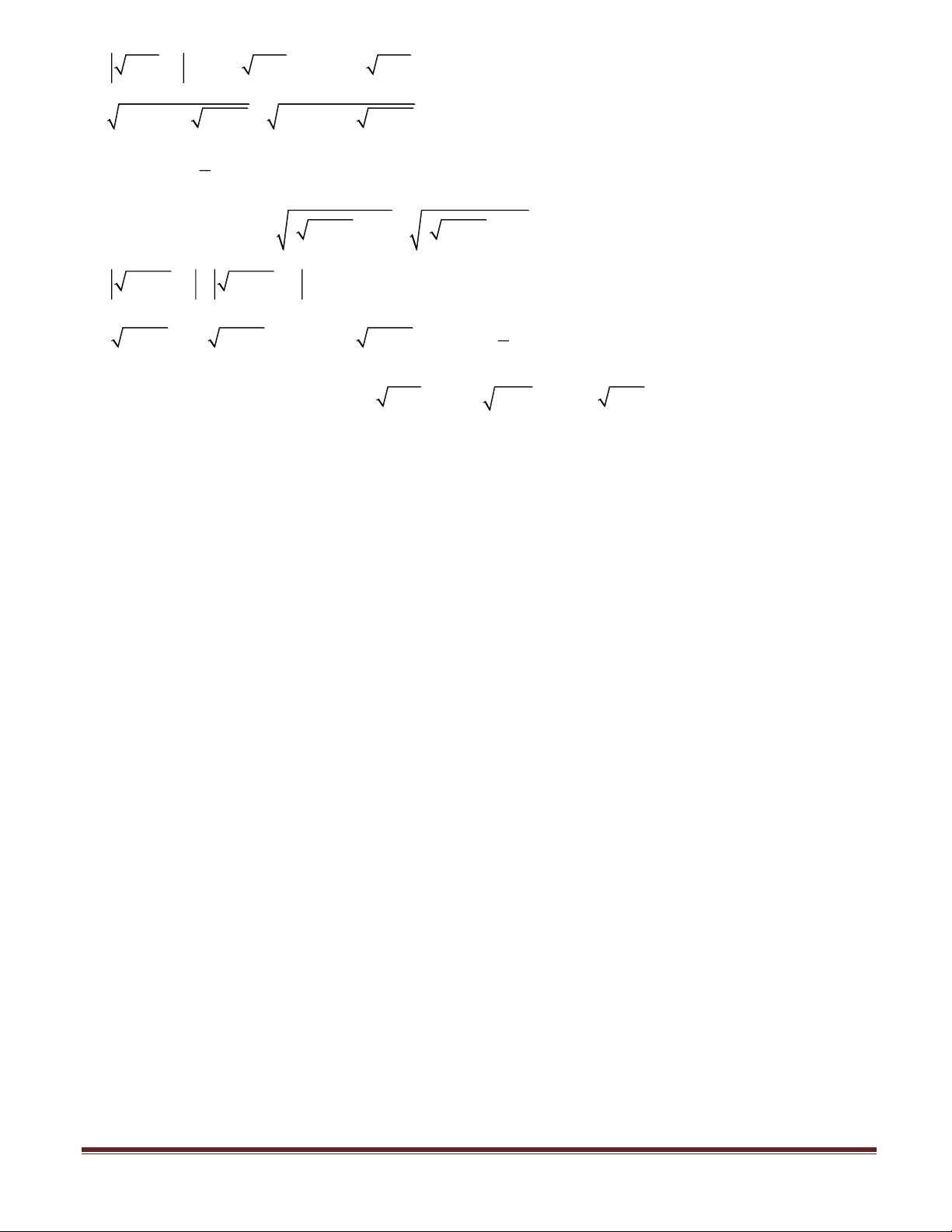
Preview text:

CÁC DẠNG TOÁN 9 BÀI : LUYỆN TẬP CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC
Dạng 1. So sánh các căn bậc hai số học Bài 1. So sánh a. 5 và 17 1. b. 3 và 15 1.
Bài 2. Tìm giá trị của x biết a. x 1  6. b. 2 2x x .
Dạng 2. Tính giá trị của biểu thức chứa căn bậc hai
Bài 3. Thực hiện các phép tính sau: a. 5  2 6  5  2 6. b. 49 12 5  49 12 5. c. 3112 3  3112 3. d. 2112 3  2112 3.
Dạng 3. Rút gọn biểu thức chứa căn bậc hai
Bài 4. Rút gọn các biểu thức sau: a. 2 4x
x  4x  4 với x  2. b. 2
3x  9  6x x với x  3. 
x6 x 9 x 3 c. 2 4 x
x  4x  4 với 0  x  9. x  9
Dạng 4. Tìm điều kiện để biểu thức chứa căn bậc hai có nghĩa
Bài 5. Với giá trị nào của x thì các căn thức sau có nghĩa
a. 3  5x x  6. 2x  4 b. . 5  x c. 2 x  8x  9. d. 2 16  x .
Dạng 5. Giải phương trình chứa căn bậc hai
Bài 6. Giải các phương trình sau a. 2
x  2x  4  x 1. b. 2
x x  4  x 1.
c. x  2 x 1  2.
d. 2x  2  2 2x  3  2x 13 8 2x  3  5.
Bài 7*. Tìm các số thực ,
x y, z thỏa mãn x y z  8  2 x 1  4 y  2  6 z  3. LỜI GIẢI
Dạng 1. So sánh các căn bậc hai số học Bài 1. Trang 1
a. Ta có 16 1  17 1
b. Ta có 16 1  15 1  5  17 1.  3  15 1. Bài 2.
a. Điều kiện x 1 0  x 1. Ta có x 1 36  x  3
 5 (thỏa mãn điều kiện). x  2
b. Điều kiện x  0 . Ta có 2
2x x x x  2  0   x  0
Kết hợp điều kiện ta có x  0 hoặc x  2 .
Dạng 2. Tính giá trị của biểu thức chứa căn bậc hai Bài 3. a. 5  2 6  5  2 6 b. 49 12 5  49 12 5
   2    2 2 2 3 2 3 2
 3 5  2  3 5  2  3  2  3  2  3 5  2  3 5  2
 3  2  3  2  2 2 .  6 5. c. 3112 3  3112 3 d. 2112 3  2112 3   2 2
3 3  22  3 3  22
 2 3 3  2 3 3  4.   4 3.
Dạng 3. Rút gọn biểu thức chứa căn bậc hai Bài 4. a. 2 4x x  4x  4 b. 2
3x  9  6x x
x   x  2 4 2
x    x2 3 3
 4x x  2
 3x  3 x
 4x  x  2 (do x  2 )
 3x 3 x do x  3    3x  2  2x 3
x6 x 9 x 3 c. 4 x x  9  x  2 3  x  3  4 x       
x   x   4 x x 3 3 x 3. 3 3
Dạng 4. Tìm điều kiện để biểu thức chứa căn bậc hai có nghĩa Bài 5.
a. Điều kiện: (3- 5x)(x- ) 6 ³ 0 Trang 2  3 3   5x  0 x  TH1:    5 không thỏa mãn. x  6  0 x  6  3 3   5x  0 x  3 TH2:    5   x  6 x  6  0 5 x  6 3 Vậy  x  6. 5 2x  4 b. Điều kiện:  0 5  x 2x  4  0 x  2 TH1:     2  x  5 5   x  0 x  5 2x  4  0 x  2 TH2:    5   x  0 x  5 Vậy 2  x  5. x  1  c. Điều kiện: 2
x  8x  9  0   x  
1  x  9  0  .  x  9 d. Điều kiện: 2
16- x ³ 0 Û - 4 £ x £ 4.
Dạng 5. Giải phương trình chứa căn bậc hai. Bài 6. a. 2
x  2x  4  x 1 x 1
Phương trình tương đương với  2 2
x  2x  4  x  2x 1
Suy ra phương trình vô nghiệm. b. 2
x x  4  x 1 ìï x ³ 1
Phương trình tương đương vớ ï i 2 í
Û x - 2x - 3 = 0 Û x = 3; x = - 1 2
ï x - x- 4 = x- 1 ïî
Đối chiếu với điều kiện ta suy ra phương trình có nghiệm x = 3.
c. x  2 x 1  2
Điều kiện x 1.
Phương trình trở thành x   x      x   2 1 2 1 1 2 1 1  2 Trang 3
x 1 1  2  x 1 1  2  x 1  1  x  2 (Thỏa mãn).
d. 2x  2  2 2x  3  2x 13  8 2x  3  5 Điề 3 u kiện x  2 2 2
Phương trình trở thành  2x 3   1
  2x 3  4  5
 2x  3 1  2x  3  4  5 3
 2x  3 1 2x  3  4  5  2 2x  3  0  x  (Thỏa mãn). 2 2 2 2
Bài 7. Biến đổi đẳng thức về dạng  x 1  
1   y  2  2   z 3 3  0
Từ đó tìm được x  2, y  6, z  12. Trang 4