












Preview text:
CÁC DẠNG TOÁN CÓ YẾU TỐ MAX- MIN TRONG SỐ PHỨC
Giáo viên: Trương Đức Thịnh – Nguyễn Thu Hằng
Nhóm giáo viên tiếp sức Chinh phục kỳ thi THPT 2021
Bài toán có yếu tố max-min trong số phức là một trong những dạng toán khó ở trong chương
trình môn Toán THPT và thường được lựa chọn ở các câu VD-VDC mang tính phân loại thí sinh.
Trong đề tham khảo của bộ năm 2021 cũng có một câu ở mức độ như vậy. Chúng ta cùng phân
tích câu 49 dưới những góc nhìn khác nhau để tìm ra các hướng xử lý cho dạng toán này.
A. Phân tích bài toán số phức trong đề tham khảo 2021
Ví dụ 1. (Câu 49-Đề tham khảo 2021) Xét hai số phức z ,z thỏa mãn z 1, z 2 1 2 1 2
và z z 3 . Giá trị lớn nhất 3z z 5i bằng 1 2 1 2 A. 5 19 . B. 5 19 . C. 5 2 19 . D. 5 2 19 . Phân tích hướng giải
Đối với dạng toán có yếu tố max-min trong số phức ta có 2 hướng tiếp cận chính như sau:
+) Hướng 1: Sử dụng các phép toán số phức liên quan tới môđun để đưa bài toán về
hàm số một biến rồi khảo sát hoặc dùng các bất đẳng thức để đánh giá.
+) Hướng 2: Đưa về bài toán cực trị hình học quen thuộc
Căn cứ vào yêu cầu bài toán tìm giá trị lớn nhất của biểu thức 3z z 5i có dạng 1 2
môđun của một tổng, bài toán có thể được giải quyết nếu 3z z là một hằng số, từ đó 1 2
ta mạnh dạn đi tính 3z z từ các giả thiết của bài toán. Sau đó ta sẽ sử dụng một trong 1 2
2 hướng kể trên hoặc tổng hợp các hướng để kết thúc bài toán. Lời giải tham khảo
+ Trước hết ta tính 3z z ta có một vài cách tính như sau 1 2
Cách 1: Tính toán trực tiếp
Đây là cách tiếp cận đơn giản nhất cho bài toán chỉ sử sụng những kiến thức cơ bản
của số phức để biến đổi.
Đặt z a b ,iz c di với a, ,b ,cd và 2i 1.Theo giả thiết ta suy ra 1 2 z 1 2 a 2 b 1 1 z 2 2 c 2 d 4 2 z z = 3 (a 2 c) (b 2 d) 3. 1 2 Khai triển và rút gọn 2 a ac 2 c 2 b bd 2 2 2 d 3 ac bd 1.
Ta có 3z z (3a c) (3b d)i nên 1 2 3z 2 z (3a 2 c) (3b 2 d) 2 9(a 2 b ) 2 (c 2 d ) 6(ac bd) 19. 1 2 Suy ra 3z z 19 . 1 2
Cách 2: Sử dụng các đẳng thức môđun
Để sử dụng cách này đòi hỏi các em phải có kỹ năng biến đổi phép toán trên số phức
ở dạng hình thức. Ta có đẳng thức mz 2 nz 2 m z 2 2 2 m z mn z z z .z . 1 2 1 2 1 2 1 2
Đẳng thức này ta được chứng minh nhờ hai tính chất cơ bản 2
z z.z và z z z z 1 2 1 2 Thật vậy 2
mz nz mz nz . mz nz mz nz mz nz 1 2 1 2 1 2 1 2 1 2 2 2 2 2
m z m z mn z z z z (điều phải chứng minh). 1 2 1 2 1 2
Áp dụng đẳng thức trên ta được: 3z 2 z 2 9 z 2 z 3 z z z .z 13 3 z z z .z . 1 2 1 2 1 2 1 2 1 2 1 2 Lại có 3 z 2 z 2 z 2 z z z z .z z z z .z 2 . Thay lại ta được 1 2 1 2 1 2 1 2 1 2 1 2 3z z 19 . 1 2
Cách 3: Sử dụng hình học
Để sử dụng được pháp pháp này các em cần phải vận dụng linh hoạt về biểu diễn
hình học của số phức, kết hợp với kiến thức về véctơ hay hệ thức lượng trong tam giác…để giải quyết bài toán. Gọi ,
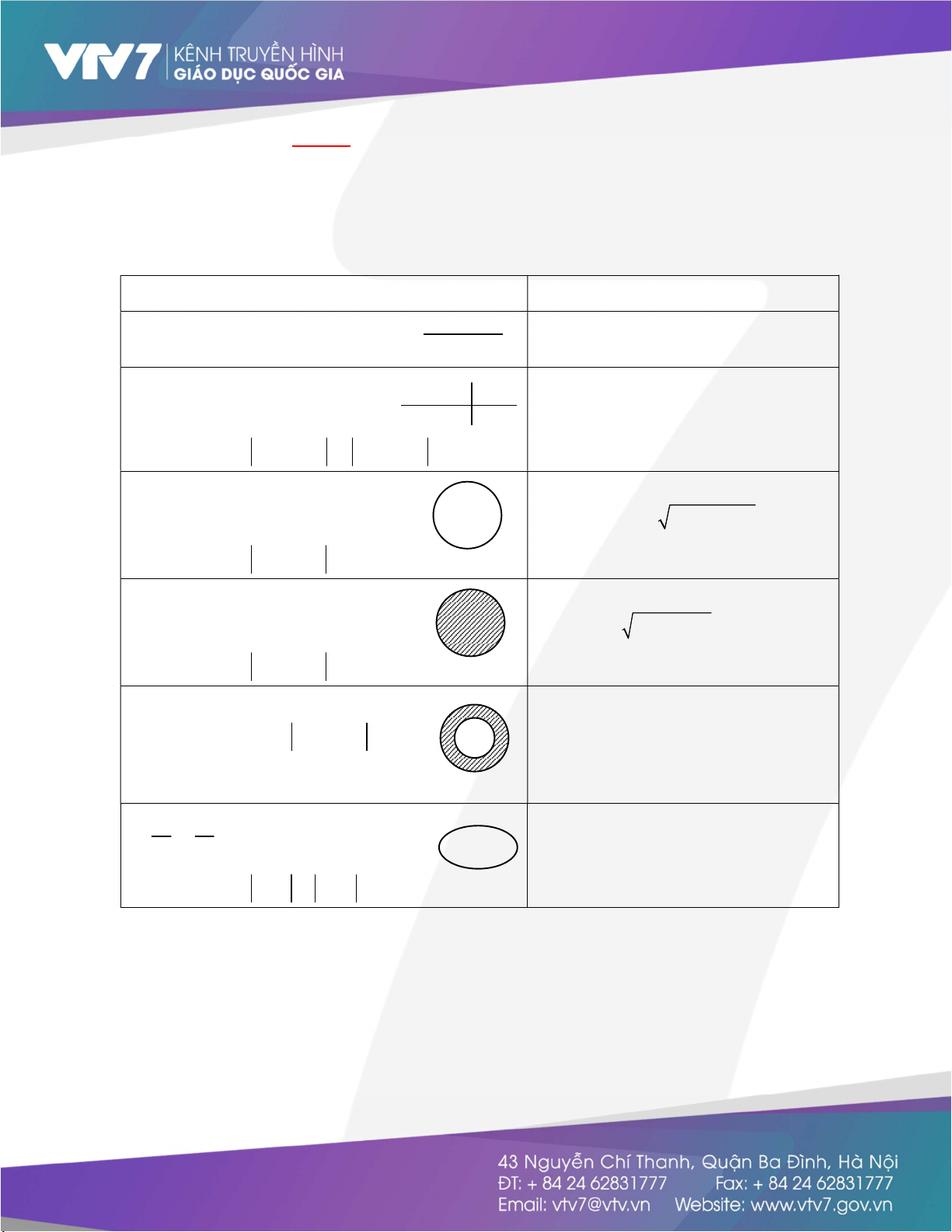
A B,C,D là các điểm biểu diễn của z ,z , 3z , z giả thiết trở thành 1 2 1 2
z 1 OA 1; z 2 OB 2; z z 3 AB 3 . 1 2 1 2 Khi đó 3z z CD . 1 2
Sử dụng định lý Cosin trong tam giác OCD và để ý COD AOB o 180 ta được 2 2 2
CD OC OD 2OC.OD.cosCOD 13 12cosCOD 13 12cosAOB 2 OA 2 OB 2 13 12
AB 19. Suy ra 3z z CD 19. 2OAOB 1 2
Tiếp theo ta tìm giá trị lớn nhất của biểu thức 3z z 5i 1 2
Cách 1: Sử dụng bất đẳng thức tam giác ở dạng môđun z 0
+ z z z z . Đẳng thức xảy ra khi và chỉ khi 2 . 1 2 1 2
z 0,k ,k 0 : z kz 2 1 2 z 0
+ z z z z . Đẳng thức xảy ra khi và chỉ khi 2 . 1 2 1 2
z 0,k ,k 0 : z kz 2 1 2
Áp dụng bất đẳng thức tam giác ở dạng môđun ta có
3z z 5i 3z z 5i 19 5. 1 2 1 2
Dấu bằng xảy ra khi 3z z k 5i , k 0 3z z 19i . 1 2 1 2
Cách 2: Sử dụng hình học
Gọi M,N lần lượt là điểm biểu diễn của 3z z , 5i suy ra OM 19 như vậy M thuộc 1 2
đường tròn tâm O bán kính R 19 và cần tìm giá trị lớn nhất MN .
Sử dụng kết quả quen thuộc ta được MN MO ON 5 19 .
Dấu bằng xảy ra khi M,O,N theo thứ tự thẳng hàng hay M 0; 19.
Một cách tổng quát ta có thể xây dựng bài toán Max-min liên quan các
yếu tố của số phức theo các dạng sau:
B. Các dạng toán thường gặp Dang 1:
Sử dụng biến đổi đại số kết hợp với các bất đẳng thức quen thuộc để đánh giá
1.Kiến thức cần chuẩn bị: 1.1. Đẳng thức Môđun:
Cho số phức z a bi 2
a, b &i 1 môđun củaz ký hiệu là z và 2 2 z a b z z + 2 z z.z; z .z z . z ; 1 ; z z ; n n z z n * ; 1 2 1 2 1 z 2 z2 + 2 2 2 2 2
mz nz m z n z mn z z z z với m,n và z , z . 1 2 1 2 1 2 1 2 1 2 2 2 + 2 2 z z z z 1 2 1 2 z z z z 2 z với z, z , z . 1 2 2 2 1 2 z z
+ z z 2 z 1 z với z , z là các số phức khác 0 1 2 1 2 z z 1 2 . 1 2
1.2. Bất đẳng thức thường dùng
+ Bất đẳng thức tam giác ở dạng môđun z 0
z z z z . Đẳng thức xảy ra khi và chỉ khi 2 . 1 2 1 2
z 0,k ,k 0 : z kz 2 1 2 z 0
z z z z . Đẳng thức xảy ra khi và chỉ khi 2 . 1 2 1 2
z 0,k ,k 0 : z kz 2 1 2
+ Bất đẳng thức Bunhiacopxky 2 2 2 2 2 ax by a b x
y dấu " " xảy ra a x . b y
Ví dụ 2. Xét các số phức z ,z thỏa mãn 2z z 35 và 3z 2z 7. Giá trị lớn nhất 1 2 1 2 1 2
của biểu thức T z z bằng 1 2 A. 4. B. 5. C. 2 3 D. 5.
Phân tích tìm lời giải : Tương tự như đề minh họa khi biết 2z z 35 và 3z 2z 7 ta có 1 2 1 2 thể tính được 2 2 2 2 m z n z
p , đến đây dùng bất đẳng thức Bunhiacopxky là có thể đánh 1 2 giá được T z z . 1 2 Lời giải Nhận xét z z 2 . z và z z z z 1 2 1 2
35 2z z 2z z 4 z z 2 z z z z 1 2 1 2 2 2 1 2 1 2 1 2 49 2 2
3z 2z 3z 2z 9 z 4 z 6 z z z z 1 2 1 2 1 2 1 2 1 2 2 21 z 2 7 z 84 2 3 z 2 z 12. 1 2 1 2 1
Ta có T 1 . 3 z 1. z 2 2 1 3 z z 4. 1 2 1 2 3 3 z 3 z z 1
Đẳng thức xảy ra khi và chỉ khi 2 1 1 2 2 . 3 z z z 3 12 1 2 2
Vậy giá trị lớn nhất của T bằng 4 .
Ví dụ 3. Cho số phức z thỏa mãn z 1i 5. Biết biểu thức T 2 z 8i z 7 9i đạt giá trị
lớn nhất khi z x yi ,
x y . Khi đó giá trị x 2y bằng A. 9 B. 8 C. 7 D. 6
Phân tích tìm lời giải : Để đơn giản ta đặt u z 1 i, khi đó u 5và cần tìm giá trị lớn nhất
của T 2 u 17i u 68i . Ta nghĩ đến bất đẳng thức tam giác ở dạng môđun, tuy nhiên có
một trở ngại ở đây là hệ số của z không giống nhau do vậy ta sẽ tìm cách để đưa về hệ số giống nhau. Lời giải Gọi 2
u a bi; a,b ,i 1 , giả thiết suy ra 2 2 a b 25 0 .
T u i a 2 b 2 2 2 a b 2 2 2 1 7 6 8 3
25 2 u 1 7i 4a 4b 12a 16b 25 2 3 u i a b 2 3 2 1 7 2 2
2 u 1 7i u 2i . 2 2 Từ đó 3 3
T 2 1 7i u u 2i 2 1
7i u u 2i 5 5. 2 2 k ,k 0 3 u 2i 0 k 2
Đẳng thức xảy ra khi và chỉ khi 2 . i u 3 1 7 k u 2 u 4 3i i 2 u 5
Từ u 4 3i z 5 2 .i Vậy x 2y 9.
Ngoài ra ta có thể sử dụng công thức cân hệ số để biến đổi, tuy nhiên công thức này không thực
sự phổ biến. Áp dụng công thức z z 2 1 z z z
z với z , z là các số phức khác 0 1 2 1 2 . z z 1 2 1 2 Ta có 3 i 6 8i u u 6 8 u
68i 2 u 2i . u 6 8i 2
Ví dụ 4. (Đề thi thử sở GD&ĐT Hải phòng 2021) Xét hai số phức z ,z thỏa mãn 1 2
z 6 8i 7 z và z z 3 . Gọi M,n lần lượt là giá trị lớn nhất và nhỏ nhất của 1 2 1 2
biểu thức P z 2z 21 3i . Khi đó 2 2 M n bằng 1 2 A. 220. B. 124. C. 144 . D. 225.
Phân tích tìm lời giải : Biểu thức cần đánh giá của bài này tương tự như đề tham
khảo tuy nhiên giả thiết cho rất khó để tính được z 2z . Tinh ý một chút các em sẽ 1 2
phát hiện ra 6 8i 10 7 3 và như vậy ta lại có thể dùng bất đẳng thức tam giác ở dạng môđun. Lời giải
Giả thiết suy ra 7 z 6 8i z z z 6 8i z z 6 8i 7 . 1 2 1 2 1 2 z 0 2
Suy đẳng thức tương đương
z 0, z 6 8i kz , k 0 . 2 1 2
z z m 68i , m 0 1 2 Do z z z z 3 3 68i . 1 2 1 2 10 + ) Nếu z 0 suy ra 3 6 8i P 3 41 . 1 2 10
+) Trường hợp z 0, z 6 8i kz , k 0 thay vào ta được 2 1 2 3k 10 7 z 6 8i ; z 6 8i . 1 10k 2 1 10k 1 Khi đó 3k z z 24 2 6 8i . Đặt 3k 24 12 3 x , k 0 x . 1 2 10k 1 10k 1 5 10
Thay vào ta được P x i i 2 6 8 21 3 100x 300x 450 .
Khảo sát hàm số theo biến x ta được 15 P 3 41 .
Như vậy ta được 15 P 3 41 do đó 2 M 2 n 144 .
Ví dụ 5. Xét số phức z thoả mãn z i 2 z iz 2 3 3 3
z 9 . Gọi M, m lần lượt là giá trị
lớn nhất và giá trị nhỏ nhất của z 1 5i . Khi đó 2 2 M 2m thuộc khoảng A. 0;13. B. 13;40 . C. 40;55 . D. 55;70 .
Phân tích tìm lời giải : Giả thiết bài toán sẽ trở nên quen thuộc nếu các em để ý 2 2 2
z 3i z 3i z 3i ; z 9 z 9i z 3i z 3i . Lời giải
Khai thác giả thiết, ta có: 2 z 2 9
z 3iz 3 z 3i z 3i z 3i z z 3i 3 z 3i z 3i 0 . z 3i z 3
+ Trường hợp 1: z 3i 0 z 3i z 1 5i 1 2i 5 .
+ Trường hợp 2: z 3i z 3 .
Đặt z x yix,y và 2i 1, khi đó z 3i z 3
x2 2 2x 2 3 y y 3 1.
Ta có VT 2 2 1 3 y
y 3 y y 3 VP 1. x 0
Do đó từ suy ra 1 . 0 y 3
Vậy z 1 5i 1 y 5i 2y 10y 26 .
Khảo sát hàm số f y 2y 10y 26 với 0 y 3.
Ta được m 5 , M 65 . Suy ra 2 2 M 2m 55 .
Dạng 2: Sử dụng biểu diễn hình học của số phức
đưa về các bài toán cực trị quen thuộc
2.1 Các quỹ tích cơ bản
Gọi M(x;y) là điểm biểu diễn số phức z x yi (x, y ) và 2i 1.
Mối liên hệ giữa x và y
Kết luận tập hợp điểm M(x;y) Ax By C 0. Là đường thẳng d : Ax By C 0.
Là đường trung trực của đoạn thẳng AB. o MA MB.
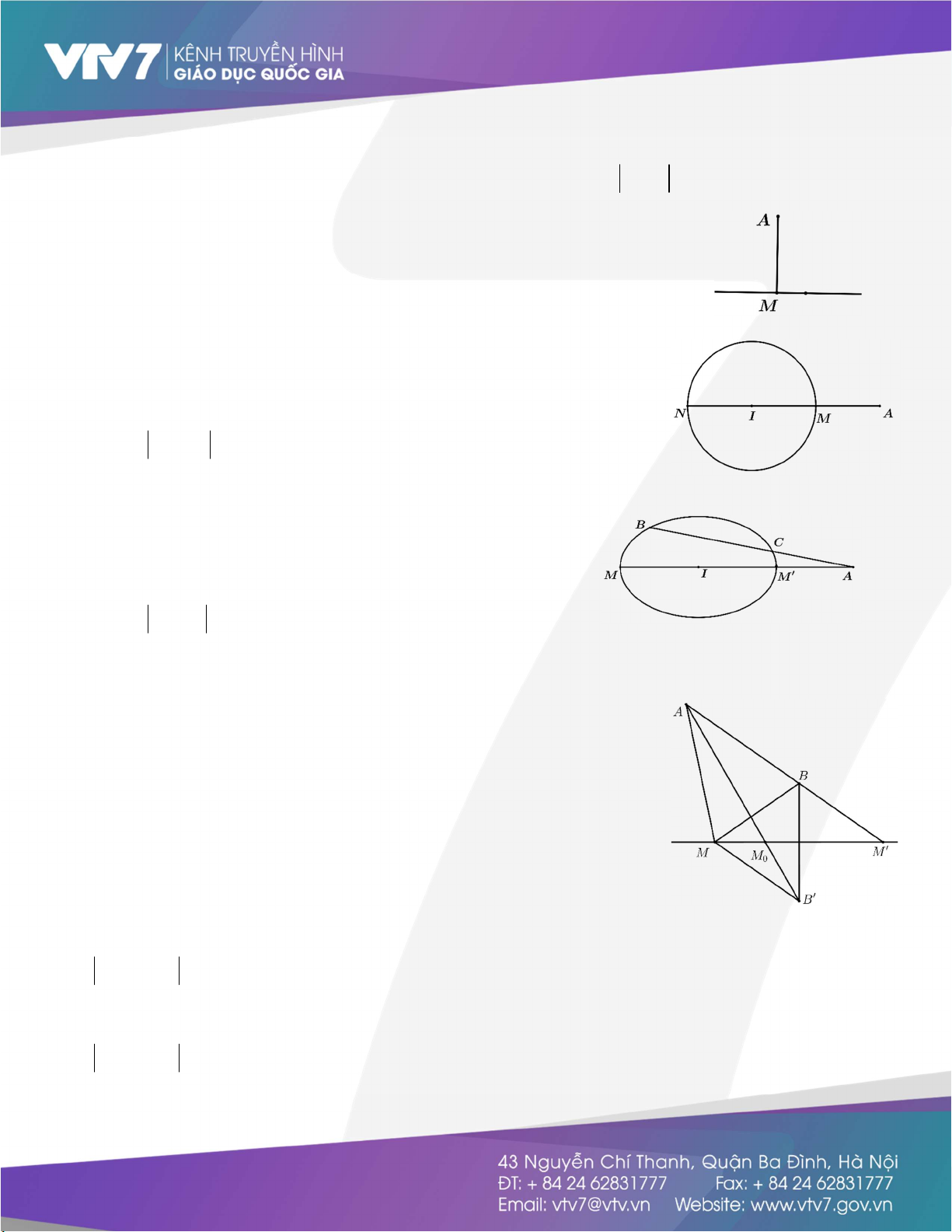
Dạng số phức z a bi z c di 2 2 2 (x a) (y b) R
Là đường tròn (C) có tâm I( ; a b) và 2 2
x y 2ax 2by c 0 bán kính 2 2 R a b c.
Dạng số phức z a bi R 2 2 2 (x a) (y b) R
Là hình tròn (C) có tâm I( ; a b) và bán 2 2
x y 2ax 2by c 0 kính 2 2
R a b c (đường tròn kể
Dạng số phức z a bi R cả bên trong) 2 2 2 2
R (x a) (y b) R .
Là những điểm thuộc miền có hình 1 2
Dạng số phức R z a bi R
vành khăn tạo bởi hai đường tròn 1 2 đồng tâm I( ;
a b) và bán kính lần lượt R và R . 1 2 2 2 M F MF 2a
Là một elíp có trục lớn 2 , a trục bé 2b x y 1 với 1 2 2 2 a b F F 2c 2a
và tiêu cự là 2c trong đó 1 2
Dạng số phức z c z c 2a 2 2 2
a b c , (a b 0).
2.2 Một số kết quả quan trọng cần nhớ:
Gọi điểm biểu diễn của số phức z , z lần lượt là M , A . Khi đó z z MA . 0 0
Một số bất đẳng thức hình học thường dùng:
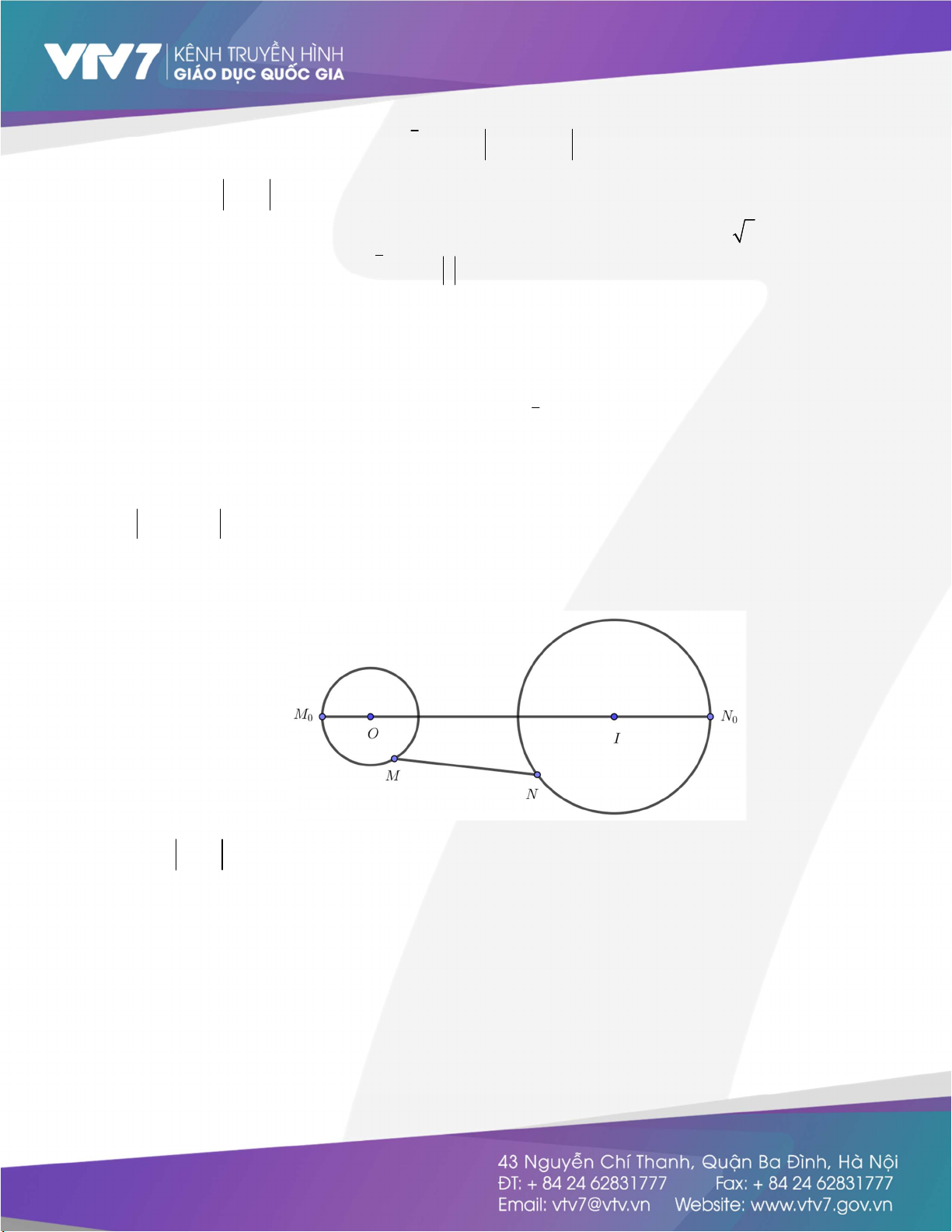
1. Cho M di động trên đường thẳng , A là điểm cố định. MA d ;
A , dấu đẳng thức xảy ra khi và chỉ khi AM .
2. Cho M di động trên đường tròn I;R, A là điểm cố định.
MA AI R , dấu " " xảy ra AI IM M N .
MA AI R , dấu " " xảy ra AI IM
3. Cho M di động trên Elip E có trục lớn , độ dài 2a , tâm I , A là
điểm cố định trên trục lớn
MA AI a , dấu " " xảy ra AI IM .
MA AI a , dấu " " xảy ra AI IM .
4. Cho M di động trên đường thẳng . ,
A B là hai điểm cố định khác phía với
MA MB AB dấu " " xảy ra M AB .
5. Cho M di động trên đường thẳng Và ,
A B là hai điểm cố định cùng phía với
MA MB AB ' dấu " " xảy ra M AB ' trong đó B '
đối xứng với B qua .
6. Cho M di động trên đường thẳng ,
A B là hai điểm cố định cùng phía với
MA MB AB dấu " " xảy ra M AB .
7. Cho M di động trên đường thẳng và ,
A B là hai điểm cố định khác phía với
MA MB AB ' dấu " " xảy ra M AB
' trong đó B ' đối xứng với B qua .
Ví dụ 6. Xét hai số phức z, w thoả mãn z.z 1 và w 3 4i 2. Giá trị lớn nhất của biểu thức P z w bằng A. 5. B. 8 . C. 10 . D. 5 2 .
Phân tích tìm lời giải: Ta thấyz.z 1 z 1 như vậy điểm biểu diễn của hai số phức đều nằm
trên đường tròn và ta đưa về bài toán hình học quen thuộc: Tìm hai điểm trên hai đường tròn
sao cho khoảng cách giữa chúng là lớn nhất. Lời giải
Gọi M x;y là điểm biểu diễn của số phức z , z.z 1 2 2
x y 1 M C có tâm 1
O0; 0, bán kính R 1. Gọi N là điểm biểu diễn của số phức w. 1
w 3 4i 2 N C : x 32 y 42 4 , có tâm I3; , bán kính . 2 4 R 2 2
Do OI 5 R R C ; C nằm ngoài nhau. 1 2 1 2
P z w MN . Ta có P R R MN OM IN ON IN OI 5 P 8 . 1 2
Dấu bằng xảy ra M , O, I, N theo thứ tự thẳng hàng.
Vậy giá trị lớn nhất của P bằng 8 .
Ví dụ 7. (Đề tham khảo 2018) Xét số phức z a bi ,ab
thỏa mãn z 4 3i 5 .
Khi z 1 3i z 1 i đạt giá trị lớn nhất thì giá trị P a b bằng A. P 8 . B. P 10 . C. P 4 . D. P 6 .
Phân tích tìm lời giải: Ta thấy điểm biểu diễn của số phức M ;
a b đường tròn. Với biểu
thức cần đánh giá có dạng MA MB thì ta có thể nghĩ đến bất đẳng thức
Bunhiacopxky để đưa về bình phương độ dài và dùng công thức đường trung tuyến hay
sử dụng tâm tỷ cự của một họ điểm để đánh giá tiếp. Lời giải
Goi M ;ab là điểm biểu diễn của số phức z.
Theo giả thiết ta có: z i
a 2 b 2 4 3 5 4
3 5 Tập hợp điểm biểu diễn
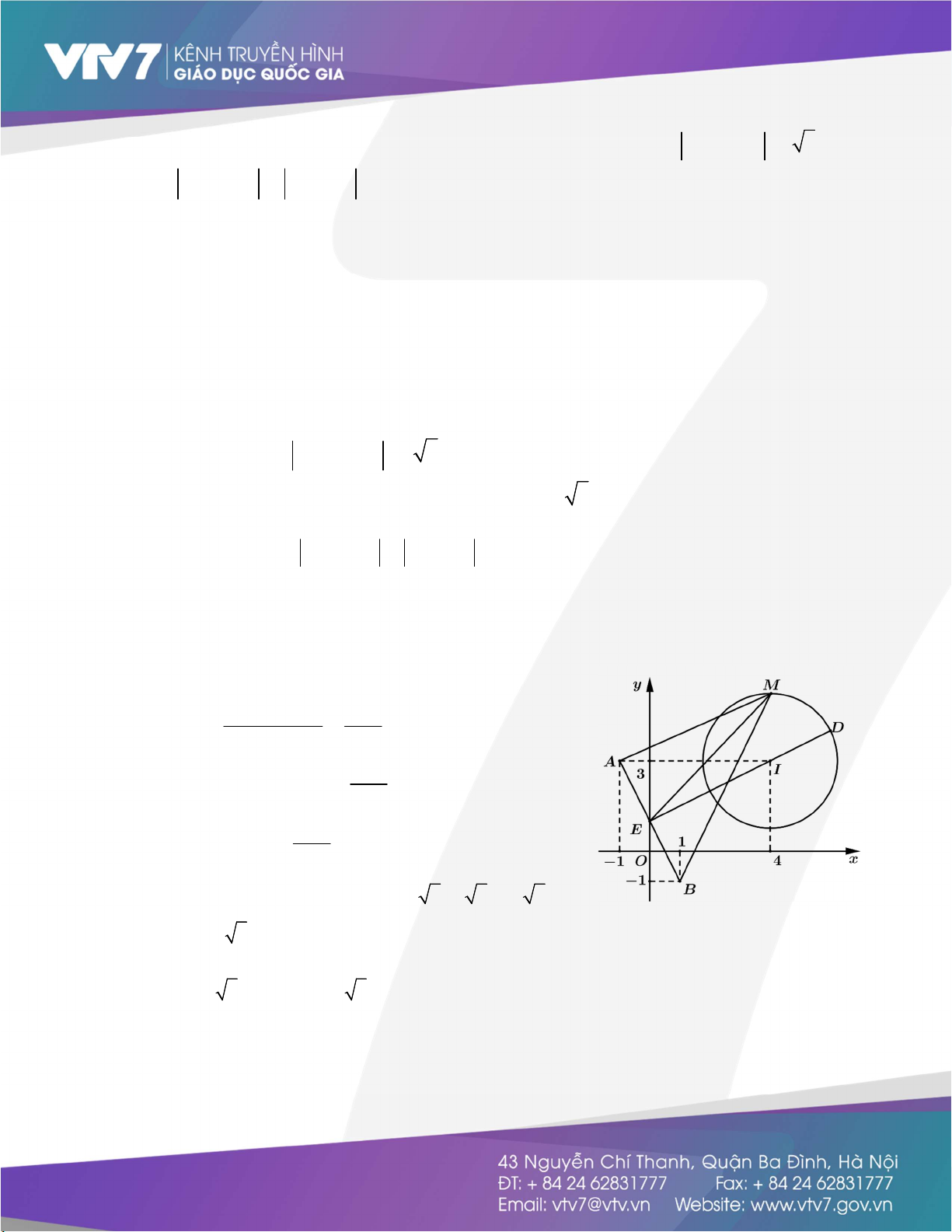
số phức z là đường tròn tâm I 4; 3 bán kính R 5 . Gọi A 1;3
Q z 1 3i z 1 i MA MB B 1; 1
Gọi E là trung điểm của AB, kéo dài EI cắt đường tròn tại D Q MA MB2 2 2 2 2 MA MB
Vì ME là trung tuyến trong MAB 2 2 MA 2 2 MB AB ME 2 4 2 2 2 2 2 AB MA MB ME 2 2 2 2 AB 2 2 Q 2 2 ME 4ME AB . 2
Mặt khác ME DE EI ID 2 5 5 3 5 Q 2 2 4. 3 5 20 200 M A MB Q 10 2 Q 10 2 max M D 4 2(x 4) x 6 EI 2 D D ID
M 6;4 P a b 10. 2 2(y 3) y 4 D D Ví dụ 8.
(Đề thi thử THPT Trần Nhân Tông-Quảng Ninh 2019) Xét số phức z thỏa mãn
z 1 i 4 z 2 5i 4 1 i z 4 2i . Giá trị lớn nhất của z 13i bằng A. 4 3 . B. 4 5 . C. 3 5 . D. 3 6 .
Phân tích tìm lời giải: Trước hết ta biến đổi các biểu thức môđun để đưa về dạng quen thuộc.
Nhận xét với mọi số phức u, v ta có u u ; uv u v
Giả thiết z 1 i 4 z 2 5i 4 1 i z 4 2i 4 2i
z 1 i 4 z 2 5i 4 1 i z
z 1 i 4 z 2 5i 4 2 z 1 3i 1 i
Gọi M là điểm biểu diễn của số phức z , A 1 ; 1 , B2; 5 , I 1; 3 .
Giả thiết trở thành MA 4MB 4 2MI . Giá trị cần đánh giá nằm ở vế phải tương tự như
Ví dụ 7 ta nghĩ đến bất đẳng thức Bunhiacopxky để đưa về bình phương độ dài, tuy nhiên
cần lựa chọ hệ số thích hợp để đánh giá được vế phải. Rất may ta có được IA 2IB 0 nên 2 2 2 2 2
MA 2MB 3MI IA 2IB . Từ đó ta chọn được hệ số cho bất đẳng thức Bunhiacopxky. Lời giải:
Giả thiết z 1 i 4 z 2 5i 4 1 i z 4 2i z 1 i 4 z 2 5i 4 2 z 13i
Gọi M là điểm biểu diễn của số phức z , A 1 ; 1 , B2; 5 , I 1; 3 .
Giả thiết trở thành MA 4MB 4 2MI . Ta thấy IA 2IB 0 từ đó ta có đánh giá sau MI MA MB 2 2 2 4 2 1. 2 2. 2 1 2 2 MA 2MB
MI MI IA2 MI IB2 MI 2 MI MI IA IB 2 2 2 2 32 9 2 32 9 3 2 2 IA 2IB 2 MI 2 2 2 MI MI IA IB 2 32 9 3 2 .0 2
5MI 920 2.5 MI 3 6. 8 3 1 MA MB 2 MA MA Dấu bằng xảy ra 8 3 3 M ; A I;3 6 . 2 2 2MB MI 3 6 3 MI 3 6 Mà 8 3 IA 20
3 6 nên hai đường tròn luôn cắt nhau hay luôn tồn tại M. 3
Vậy giá trị lớn nhất của MI 3 6.
Ví dụ 9. (Đề thi thử Chuyên Hà Tĩnh Lần 2- 2021)
Xét số phức z thay đổi thỏa mãn 3z i 2. Giá trị nhỏ nhất của biểu thức
S z 1 z 1 z 3i bằng A. 4 . B. 16 . C. 2 . D. 8 . 3 3 3 3
Phân tích tìm lời giải: Làm đẹp lại giả thiết ta thấy rằng điểm M biểu diễn của số
phức z thuộc đường tròn tâm 1 2 I 0; ;R
. Biểu thức cần đánh giá là 3 3
S MAMB MC thấy rằng , A , B C I;
R hơn nữa ABC đều, đến đây ta sử
dụng một kết quả quen thuộc nếuM thuộc cung nhỏ AB thì MC MA MB từ đó ta chỉ việc đánh giá MC . Lời giải
Gọi M là điểm biểu diễn của số phức z. i 2 3z i 2 z
M thuộc đường tròn tâm 1 2 I 0; ;R . 3 3 3 3 Gọi A 1; 0,B 1
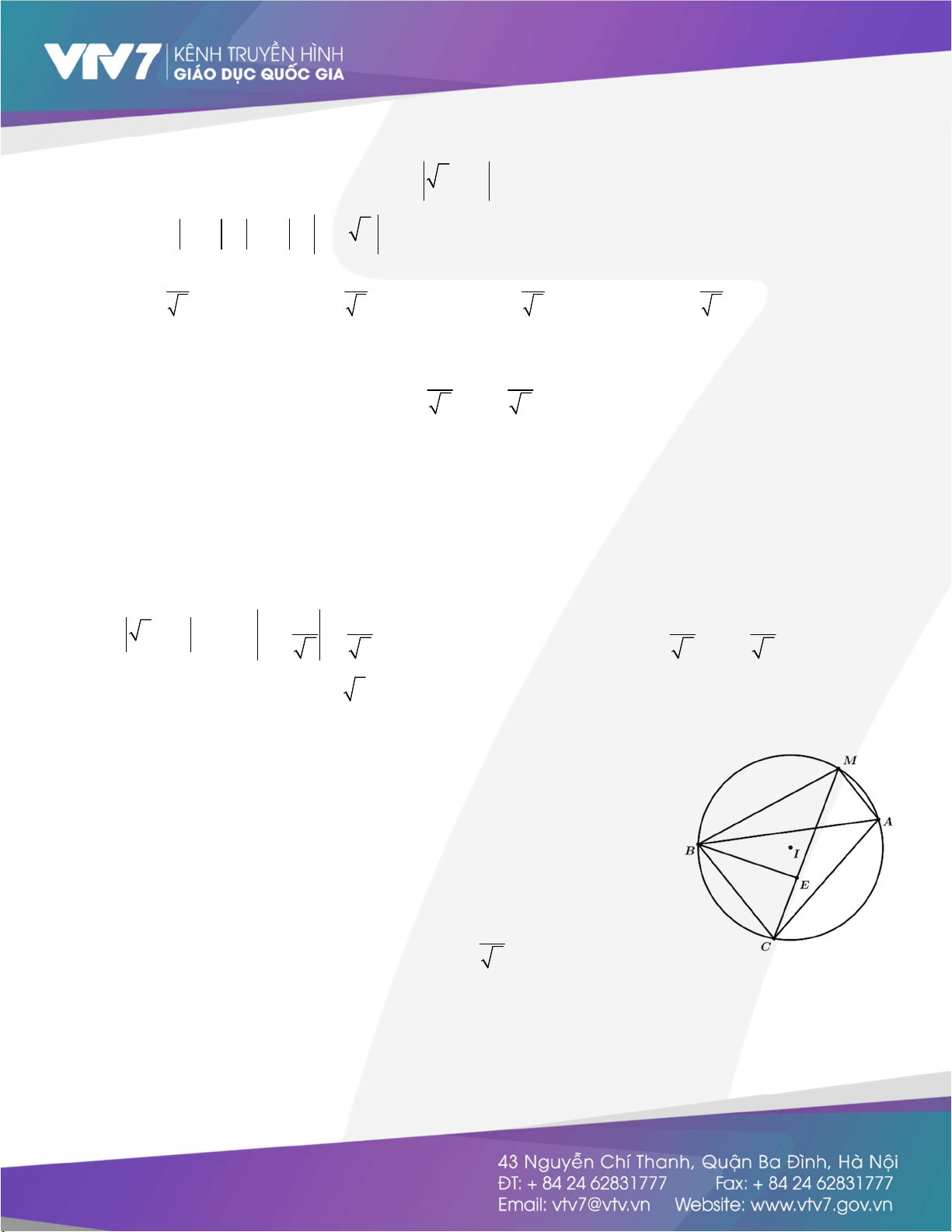
; 0,C0; 3. Ta thấy ,A ,BC I; R và ABC đều.
Không mất tính tổng quát, giả sử M thuộc cung nhỏ AB.
Lấy điểm E MC sao cho MB MC do o BMC BMC 60 nên MB MC BE . Từ đó suy ra được B
CE BAM .c .gc MA EC và do đó MC MA MB 8
S MA MB MC 2MC 2.2R . 3 Dấu “=” xảy ra khi , M ,IC thẳng hàng.
Chú ý: Bạn nào chuyên sâu hơn có thể sử dụng định lý Ptoleme cho tứ giác nôi tiếp AMBC
AB.MC AC .MB BC .MA cũng suy ra được MC MA MB (do ABC đều).
Ví dụ 10. Xét số phức z thỏa mãn z 1 i z 3 i 6 . Giá trị lớn nhất của T z 2i bằng A. 10 . B. 2 10 . C. 3 2 . D. 2 5 . 3 3
Phân tích tìm lời giải: Nhìn vào giả thiết ta thấy rằng tập hợp các điểm biểu diễn của z số là đường
Elíp, do đó ta đưa về bài toán đánh giá khoảng cách từ một điểm cụ thể đến một điểm thay
đổi trên đường Elíp. Khó khăn gặp phải ở đây là ta phải đưa phương trình đường Elíp về
dạng chính tắc để thuận tiện cho việc tính toán. Ta xét cách đổi biến sau
Đặt z u a bi;a,b . Khi đó u a 1 (b 1)i u a 3 b 1i 6. a 1 a 3 a 1 Ta chọn , a b sao cho
ta được u 2 i u 2 i . b 1 b 1 b 0 6
Đến đây chỉ việc chia 2 vế cho 2 i ta sẽ đưa được Elíp về dạng chính tắc. Lời giải
Ta có z 1 i z 3 i 6 z 1 2 i z 12 i 6 z 1 z 1 6 1 1
, đặt z 1 t ta sẽ đưa về 6 t 1 t 1 . 2 i 2 i 5 2 i 5
Như vậy ta được tập hợp điểm biểu diễn của t là một đường Elíp có trục lớn 6 2a , tiêu 5 2 2 cự 2c 2 , do đó 2 2 2 4
b a c suy ra phương trình đường Elíp : 5x 5y 1, E. 5 9 4
Từ cách đặt z 1 t z 2 it 1 thay vào T 2 it 1 2i 5 t i . 2 i
Gọi M x;ylà điểm biểu diễn của t , M x;y E và A0; 1 khi đó T 5MA.
Lại có MA x y 2 9 5 y y 2 2 2 2 5 2 14 1 1 1 y 2y . 5 4 4 5
Khảo sát hàm số f y 5 2 14 2 2
y 2y ,y ;
ta được giá trị lớn nhất của f ylà 18 . 4 5 5 5 5
Thay vào ta được giá trị lớn nhất của T là 3 2 .
Dạng 3 : Một vài cách hỏi khác cho bài toán số phức ở mức độ VD-VDC
Quan sát đề tham khảo và đề thi chính thức qua các năm gần đây chúng ta thấy rằng các
câu ở mức độ vận dụng cao thường không dập khuôn theo đề tham khảo mà chỉ liên quan
đến đề tham khảo ở mảng kiến thức nhất định, vì vậy ngoài việc nắm chắc kiến thức cơ
bản, thành thạo các bài toán gốc các em còn phải rèn luyện thêm tư duy nhạy bén để xử lý
được các bài toán một cách nhanh nhất. Dưới đây là một vài dạng toán khác liên quan tới
câu số phức mức độ vận dụng cao.
Ví dụ 11. (Đề thi thử sở GD&ĐT Hà nội 2021)
Xét hai số phức z , z thỏa mãn z z z 3 và z z 3 3 . Giá trị của biểu thức 1 2 1 1 2 1 2
z z 3 z z 3 bằng 1 2 1 2 A. 1458. B. 324. C. 729 . D. 6561. Lời giải Giả thiết 2 2 z z 3 z z z z z z 9 . 1 2 1 2 1 2 1 2 2 2 z z 3 3 z z z z z z 27 . 1 2 1 2 1 2 1 2 Từ đó suy ra 2 2 z z
18 z z z z 9 và z 3. 1 2 1 2 1 2 2 Biểu thức cần tính
z z 3 z z 3 z z z z 3 3z z z z z z z z 2 2 3 9 27 z z 1458. 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2
Ví dụ 12. Có bao nhiêu số phức z thoả mãn z 6i z 4i z 3i z i và z 2021 ? A. 4032 B. 4034 C. 2021 D. 2020 Lời giải
Đặt u z i giả thiết trở thành u 5i u 5i u 2i u 2i 2b .
Nhận xét được 2b u 5i u 5i b 5 . Ta xét 2 trường hợp
+Trường hợp 1 : b 5 u 5 i thỏa mãn.
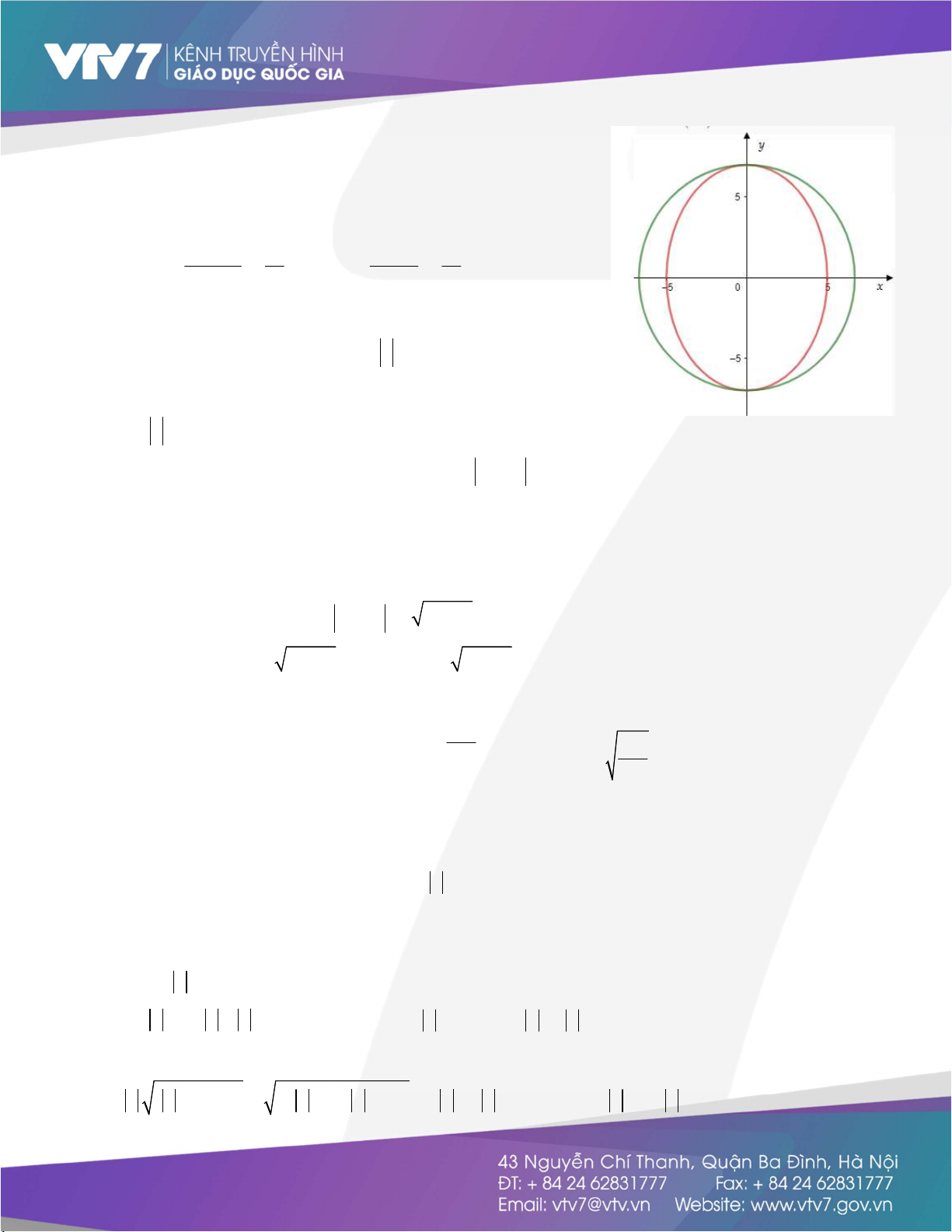
+ Trường hợp 2: b 5 gọi M x;ylà điểm biểu diễn
của u khi đó M x;ythuộc 2 Elíp 2 2 : x y 1; : x y E E 1 dễ thấy 2 2 2 2 1 2 2 2 b 25 b b 4 b E E 0; b u b i . 1 2
Với u bi z b 1i do z 2021 5 b 2020. Với u b i z b 1i do
z 2021 5 b 2022. Vậy có 4034 số z thỏa mãn.
Ví dụ 13 . Có bao nhiêu số phức z thỏa mãn 2
4z z 3i z 84 0 ? A. 1. B. 2. C. 3. D. 4. Lời giải
Ta có phương trình bậc 2 theo z có a.c 4.(84) 0 nên phương trình luôn có nghiệm
thực. Do đó z , nên 2 z 3i z 9 Vậy ta có 2 2 2 2
4z z z 9 84 0 z z 9 84 4z 2 z 16 4 2 1
5z 681z 7056 0 z 4 2 147 . z z 147 2 84 4z 0 z z 5 5 2 84 4z 0
Vậy có 2 số phức z thỏa mãn.
Ví dụ 14. (Đề thi THPT NĂM 2018)
Có bao nhiêu số phức z thỏa mãn z z 4 i 2i 5 i z ? A. 2 B. 3 C. 1 D. 4 Lời giải
Ta có z z 4 i 2i 5 i z
z z 4 z z i 2i 5 i z z z 5 i 4 z z 2i .
Lấy môđun 2 vế ta được z z
2 1 z 2 z 2 2 5 4 2 z z 52 1
4 z 2 z 22 1 .
Đặt t z , t 0 . Phương trình 1 trở thành
t t 2 1 t2 t 2 2 5 4 2 2 2 2
t t 10t 26 17t 4t 4 t 1 t 1 t 8,95 4 3 2
t 10t 9t 4t 4 0 t 3 2
1 t 9t 4 0 . 3 2 t 9t 4 0 t 0,69 t 0,64 4 t 2 ti
Ứng với mỗi giá trị t 0 ta được z
là 1 số phức thoả yêu cầu bài toán. 5 i t
Vậy có 3 số phức z thỏa mãn. z z z 1 2 3 3 4 5
Ví dụ 15. Xét các số phức z ,z ,z 0 thoả mãn 2
5z z 9z z 16z z . Giá trị z z bằng 1 2 3 1 2 2 3 1 3 1 3 z z 10 1 2 A. 2 13 . B. 4 43 . C. 2 10 . D. 8 10 . 3 Lời giải z z z Đặt 1 2 3
t 0 suy ra z 3t; z 4t; z 5t 3 4 5 1 2 3 2 2 2
25z z 9z z 16z z 25t z z 9t z z 16t z z z z z z z z z z z z z z 1 2 2 3 1 3 1 2 2 3 1 3 3 3 1 2 1 1 2 3 2 2 1 3
z z z z z z . 3 1 2 3 1 2 Suy ra z z z 2 z z 2 z 3 1 2 3 1 2 2 z 2 z 2
z z z z z z z z z 0 . 3 1 2 1 2 1 2 1 2 1 2 Xét giả thiết 2 2
z z 10 z z z z z z 2
100 25t 100 t 4. 1 2 1 2 1 2 1 2 Ta có z z = 2 2
2z z 4 z z 2 z z z z 4 13 . 1 2 1 2 1 2 1 2 1 3 CÁC BÀI TOÁN LUYỆN TẬP
Câu 1: Xét số phức z thỏa mãn z 3 4i 5 . Gọi M,m lần lượt là giá trị lớn nhất và giá trị 2 2
nhỏ nhất của P z 2 z i . Tính giá trị 2 2 A M m . A. A 1258. B. A 1758. C. A 1268. D. A 1287.
Câu 2: Xét các số phức z , z , z z z 2, z z 2 2 1 2 thỏa mãn 1 2 1 2 . Giá trị nhỏ
nhất của biểu thức P z z z z z 1 2 bằng A. P 2 2 2 B. P 2 2 3 . C. P 2 3 . D. P 4 3 .
Câu 3: Xét số phức z thỏa mãn 2 z z z z
z . Giá trị lớn nhất của z 4 3i bằng A. 41 2. B. 41 2. C. 5 2. D. 29 2. Câu 4:
Xét các số phức z , z thoả mãn 1 2
z 1 2i 3; z 2021 6i z 2021 4i và số phức z 1 2 2
thoả mãn rằng biểu thứcP z z z z đạt giá trị nhỏ nhất. Giá trị lớn nhất của z là 1 2 A. 2021 B. 5 C. 34 D. 26
Câu 5: Xét số phức z thỏa mãn điều kiện 5 z i z 1 3i 3 z 1 i . Giá trị lớn nhất của biểu thức z 2 3i bằng A. 3 5. B. 80. C. 2 5. D. 4 5.
Câu 6: Xét các số phức z ,z thỏa mãn | z 54i
| | z 14i |và 1i|z
| 2z 2z i . Giá trị 2 2 2 1 2 1 1 nhỏ nhất của P 2 z 2i z z z z bằng 1 1 2 1 2 4 1 1 A. . B. P . C. . D. . 3 3 P 0 9
Câu 7: Cho các số phức w , z thỏa mãn 3 5 w i
và 5w 2 iz 4. Giá trị lớn nhất của 5
biểu thức P z 12i z 5 2i bằng A. 6 7 . B. 42 13 . C. 2 53. D. 4 13. Câu 8:
Xét hai số phức z ,z thỏa mãn
. Giá trị nhỏ nhất của 1 2
2 z i z z 2i và z i 10 1 1 1 1 2 biểu thức z z bằng 1 2 A. 3 5 1. B. 101 1. C. 101 1 . D. 10 1. Câu 9:
[THPT Chuyên Lương Văn Chánh-Phú Yên 2021] Biết rằng hai số phức z , z thỏa mãn 1 2 i 1
z 3 4i 3 và z 1
. Số phức z có phần thực là a và phần ảo là b thỏa mãn 1 2 4 2
a 2b 5 . Giá trị nhỏ nhất của P z z z 4z bằng: 1 2 A. 130 . B. 130 2 . C. 130 3. D. 130 5.
Câu 10: Xét hai số phức z thỏa mãn z 2 z 2 2 3 . Giá trị nhỏ nhất của
P z 2 3 i z 3 3 2i z 3i là A. 12. B. 6. C. 8 . D. 10.
Câu 11: Xét z , z là các số phức thỏa mãn z 3 2i z 3 2i 2 và z z 2 3 . Gọi m, n lần lượt là 1 2 1 2 1 2
giá trị lớn nhất và giá trị nhỏ nhất của z z 3 5i . Giá trị của biểu thức T m 2n bằng 1 2 A. T 3 10 2 . B. T 6 10 . C. 6 34 . D. 3 34 2 .
Câu 12: Xét số phức z thỏa mãn z 2 . Giá trị nhỏ nhất của biểu thức P 2 z 1 2 z 1 z z 4i bằng A. 4 2 3 . B. 2 3 . C. 14 4 . D. 7 2 . 15 15
Câu 13: [Trường chuyên ĐH Vinh lần 2 năm 2021] Cho các số thực b , c sao cho phương trình 2
z bz c 0 có hai nghiệm phức z , z z 43i 1 z 86i 4 1 2 thỏa mãn và . Mệnh đề 1 2 nào sau đây đúng? A. 5b c 4 . B. 5b c 12 . C. 5b c 12 . D. 5b c 4 .
Câu 14: Xét số phức z,w thỏa mãn z 1 i z 3 i 6 và 1 w 2 4i . Giá trị lớn nhất 5
của T z w 2i là 3 a b . Khi đó giá trị a b thuộc khoảng A. 9 0 ; . B. 11 13 ; . C. 14 19 ; . D. 29 4 ; . 5 6 5 5 6 6 Câu 15: Xét số phức z ,z
1 2 là hai trong các số phức thỏa mãn các điều kiện
z i z 1, z z 4 2 . Số phức w thỏa mãn 2 w 2 i 3 w 1 2i 6 2 . Giá trị 2 1
nhỏ nhất của T w z w z bằng 1 2 A. 3 3 . B. 4 2 . C. 5 2 . D. 3 5 .




