Các dạng toán góc và khoảng cách thường gặp trong kỳ thi THPTQG Toán 12

Giới thiệu đến quý thầy, cô giáo cùng các em học sinh khối 12 tài liệu tuyển tập các dạng câu hỏi và bài tập trắc nghiệm góc và khoảng cách trong không gian thường gặp trong đề thi THPT Quốc gia môn Toán.Mời bạn đọc đón xem.

Chủ đề:

Chương 1: Khối đa diện 172 tài liệu

Môn:

Toán 12 3.9 K tài liệu

Thông tin:
72 trang 1 năm trước
Tác giả:
L
Lan Tường
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Các dạng toán góc và khoảng cách thường gặp trong kỳ thi THPTQG Toán 12

Giới thiệu đến quý thầy, cô giáo cùng các em học sinh khối 12 tài liệu tuyển tập các dạng câu hỏi và bài tập trắc nghiệm góc và khoảng cách trong không gian thường gặp trong đề thi THPT Quốc gia môn Toán.Mời bạn đọc đón xem.

61 31 lượt tải Tải xuống

Chủ đề: Chương 1: Khối đa diện 172 tài liệu

Môn: Toán 12 3.9 K tài liệu

Thông tin:

72 trang 1 năm trước

Tác giả:

Profile Lan Tường
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CHUYÊN
ĐỀ 6
GÓC VÀ KHOẢNG CÁCH
MỤC LỤC
PHẦN A. CÂU HỎI ....................................................................................................................................................... 1
Dạng 1. Góc ..................................................................................................................................................................... 1
Dạng 1.1 Góc của đường thẳng với mặt phẳng ........................................................................................................ 1
Dạng 1.2 Góc của đường thẳng với đường thẳng .................................................................................................... 4
Dạng 1.3 Góc của mặt với mặt .................................................................................................................................. 5
Dạng 2. Khoảng cách...................................................................................................................................................... 8
Dạng 2.1 Khoảng cách từ điểm đến mặt phẳng ....................................................................................................... 8
Dạng 2.2 Khoảng cách của đường thẳng với đường thẳng ................................................................................... 11
Dạng 2.3 Khoảng cách của đường với mặt ............................................................................................................. 15
PHẦN B. LỜI GIẢI THAM KHẢO ...................................................................................................................................... 15
Dạng 1. Góc ................................................................................................................................................................... 15
Dạng 1.1 Góc của đường thẳng với mặt phẳng ...................................................................................................... 15
Dạng 1.2 Góc của đường thẳng với đường thẳng .................................................................................................. 25
Dạng 1.3 Góc của mặt với mặt ................................................................................................................................ 27
Dạng 2. Khoảng cách.................................................................................................................................................... 39
Dạng 2.1 Khoảng cách từ điểm đến mặt phẳng ..................................................................................................... 39
Dạng 2.2 Khoảng cách của đường thẳng với đường thẳng ................................................................................... 51
Dạng 2.3 Khoảng cách của đường với mặt ............................................................................................................. 71
PHẦN A. CÂU HỎI
Dạng 1. Góc
Dạng 1.1 Góc của đường thẳng với mặt phẳng
Câu 1. (MĐ 103 BGD&ĐT NĂM 2017-2018) Cho hình chóp
.
S ABC
có đáy là tam giác vuông tại
C
,
AC a
,
2BC a
,
SA
vuông góc với mặt phẳng đáy và
SA a
. Góc giữa đường thẳng
SB
và mặt phẳng
đáy bằng
A.
60
B.
90
C.
30
D.
45
Câu 2. (Mã đề 102 BGD&ĐT NĂM 2018) Cho hình chóp
.
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng đáy và
2SA a
. Góc giữa đường thẳng
SC
và mặt phẳng đáy bằng
A.
45
B.
60
C.
30
D.
90
Câu 3. (Mã 102 - BGD - 2019) Cho hình chóp
.
S ABC
có
SA
vuông góc với mặt phẳng
ABC
,
2SA a
, tam giác
ABC
vuông tại
B
,
AB a
và
3BC a
(minh họa như hình vẽ bên).
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
Góc giữa đường thẳng
SC
và mặt phẳng
ABC
bằng
A.
30
. B.
60
. C.
45
. D.
90
.
Câu 4. (Mã đề 101 BGD&ĐT NĂM 2018) Cho hình chóp
.
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng đáy và
2SB a
. Góc giữa đường thẳng
SB
và mặt phẳng đáy bằng
A.
45
B.
60
C.
90
D.
30
Câu 5. (Mã 103 - BGD - 2019) Cho hình chóp
.
S ABC
có
SA
vuông góc với mặt phẳng
ABC
.
2SA a
. Tam giác
ABC
vuông cân tại B và
AB a
( minh họa như hình vẽ bên).
Góc giữa đường thẳng
SC
và mặt phẳng
ABC
bằng
A.
0
45
. B.
0
60
. C.
0
30
. D.
0
90
.
Câu 6. (Mã đề 101 - BGD - 2019) Cho hình chóp
.
S ABC
có
SA
vuông góc với mặt phẳng
ABC
,
2SA a
, tam giác
ABC
vuông tại
,B
3AB a
và
BC a
(minh họa như hình vẽ bên). Góc giữa đường thẳng
SC
và mặt phẳng
ABC
bằng:
A.
0
45
. B.
0
30
. C.
0
60
. D.
0
90
.
Câu 7. (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho hình chóp tứ giác đều
.
S ABCD
có tất cả các cạnh bằng
a
. Gọi
M
là trung điểm của
SD
(tham khảo hình vẽ bên). Tang của góc giữa đường thẳng
BM
và mặt
phẳng
ABCD
bằng
A
C
B
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
A.
2
2
B.
3
3
C.
2
3
D.
1
3
Câu 8. (Mã đề 104 - BGD - 2019) Cho hình chóp
.
S ABC
có
SA
vuông góc với mặt phẳng
ABC
,
2SA a
, tam giác
ABC
vuông cân tại
B
và
2
AB a
(minh họa như hình vẽ bên). Góc giữa đường thẳng
SC
và
mặt phẳng
ABC
bằng
A.
30
o
. B.
90
o
. C.
60
o
. D.
45
o
.
Câu 9. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
a
,
SA ABCD
và
6
3
a
SA
. Tính góc giữa
SC
và mặt phẳng
?
A.
30
. B.
45
. C.
60
. D.
90
.
Câu 10. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
và
SA ABCD
. Biết
6
3
a
SA
. Tính góc giữa
SC
và
ABCD
.
A.
30
B.
60
C.
75
D.
45
Câu 11. (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho hình chóp
.
, đáy
ABCD
là hình vuông cạnh bằng
a
và
SA ABCD
. Biết
2SA a
. Tính góc giữa
SC
và
.
A.
45
B.
30
C.
60
D.
75
Câu 12. (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Cho hình chóp tứ giác đều
.
có tất cả các cạnh bằng
2a
. Gọi
M
là trung điểm của
SD
Tính
tan
của góc giữa đường thẳng
BM
và mặt phẳng
.
A.
2
2
. B.
3
3
. C.
2
3
. D.
1
3
.
Câu 13. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019) Cho khối chóp
.
S ABC
có
SA ABC
, tam giác
ABC
vuông tại
B
,
2AC a
,
BC a
,
2 3SB a
. Tính góc giữa
SA
và mặt phẳng
SBC
.
A.
45
. B.
30
. C.
60
. D.
90
.
A
B
C
D
S
M
A
C
B
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
Câu 14. (CHUYÊN HÙNG VƯƠNG GIA LAI NĂM 2018-2019 LẦN 01) Cho hình chóp
.
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với đáy và
3SA a
. Gọi
là góc giữa
SD
và
SAC
. Giá
trị
sin
bằng
A.
2
4
. B.
2
2
. C.
3
2
. D.
2
3
.
Câu 15. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hình chóp tam giác
.
S ABC
có đáy là
tam giác đều cạnh
a
. Tam giác
SAB
cân tại
S
và thuộc mặt phẳng vuông góc với đáy. Biết
SC
tạo với mặt
phẳng đáy một góc
60
, gọi
M
là trung điểm của
BC
. Gọi
là góc giữa đường thẳng
SM
và mặt phẳng
ABC
. Tính
cos
.
A.
6
cos
3
. B.
3
cos
3
. C.
3
cos
10
. D.
1
cos
10
.
Câu 16. (THPT CHUYÊN BẮC NINH LẦN 01 NĂM 2018-2019) Cho hình chóp
SABCD
có đáy là hình
thang vuông tại
1
và
B
.
, 2AB BC a AD a
. Biết
SA
vuông góc với đáy
( )ABCD
và
SA a
. Gọi
,M N
lần lượt là trung điểm
,SB CD
. Tính sin góc giữa đường thẳng
MN
và mặt phẳng
( )SAC
A.
5
5
B.
55
10
C.
3 5
10
D.
2 5
5
Câu 17. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho hình chóp tứ giác đều
.
S ABCD
có
AB a
,
O
là trung điểm
AC
và
SO b
. Gọi
là đường thẳng đi qua
C
,
chứa trong mặt
phẳng
ABCD
và khoảng cách từ
O
đến
là
14
6
a
. Giá trị lượng giác
cos ,SA
bằng
A.
2 2
2
3 4 2
a
b a
. B.
2 2
2
3 2 4
a
a b
. C.
2 2
3 2 4
a
a b
. D.
2 2
3 4 2
a
b a
.
Câu 18. (HSG BẮC NINH NĂM 2018-2019) Cho hình chóp
.
có đáy
ABCD
là hình chữ nhật,
, 3AB a AD a
. Mặt bên
SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Cosin
của góc giữa đường thẳng
SD
và mặt phẳng
SBC
bằng
A.
13
4
B.
3
4
C.
2 5
5
D.
1
4
Câu 19. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho hình chóp
.
S ABC
có đáy là tam giác vuông tại
C
,
CH
vuông góc với
AB
tại
H
,
I
là trung điểm của đoạn
HC
. Biết
SI
vuông góc với mặt phẳng đáy,
90
ASB
. Gọi
O
là trung điểm của đoạn
AB
,
O
là tâm mặt cầu ngoại tiếp tứ diện
SABI
. Góc tạo bởi
đường thẳng
OO
và mặt phẳng
ABC
bằng
A.
60
. B.
30
. C.
90
. D.
45
.
Câu 20. (SỞ GD&ĐT BẮC NINH NĂM 2018-2019 LẦN 01) Cho hình chóp
.
có đáy
ABCD
là
hình thoi cạnh
a
và
60
ABC . Hình chiếu vuông góc của điểm
S
lên mặt phẳng
trùng với trọng
tâm của tam giác
ABC
, gọi
là góc giữa đường thẳng
SB
và mặt phẳng
SCD
, tính
sin
biết rằng
SB a
.
A.
sin
3
2
. B.
sin
1
4
. C.
sin
1
2
. D.
sin
2
2
.
Dạng 1.2 Góc của đường thẳng với đường thẳng
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
Câu 21. (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho tứ diện
OABC
có
, , OA OB OC
đôi một vuông góc
với nhau và
OA OB OC
. Gọi
M
là trung điểm của
BC
( tham khảo hình vẽ bên dưới). Góc giữa hai
đường thẳng
OM
và
AB
bằng
A.
0
45
B.
0
90
C.
0
30
D.
0
60
Câu 22. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Cho tứ diện
ABCD
với
0
3
, 60 ,
2
AC AD CAB DAB CD AD
. Gọi
là góc giữa hai đường thẳng
AB
và
CD
. Chọn khẳng định
đúng về góc
.
A.
3
4
cos
B.
0
30
C.
0
60
D.
1
4
cos
Câu 23. (TRƯƠNG THPT HOANG HOA THAM HƯNG YÊN NĂM 2018-2019) Cho hình hộp chữ nhật
.
ABCD A B C D
, biết đáy
ABCD
là hình vuông. Tính góc giữa
A C
và
BD
.
A.
90
. B.
30
. C.
60
. D.
45
.
Câu 24. (CHUYÊN KHTN NĂM 2018-2019 LẦN 01) Cho tứ diện
ABCD
có
2AB CD a
. Gọi
M
,
N
lần lượt là trung điểm
AD
và
BC
. Biết
3MN a
, góc giữa hai đường thẳng
AB
và
CD
bằng.
A.
0
45
. B.
0
90
. C.
0
60
. D.
0
30
.
Câu 25. (CHUYÊN LƯƠNG VĂN CHÁNH PHÚ YÊN NĂM 2018-2019 LẦN 01) Cho hình lập phương
.
ABCD A B C D
; gọi
M
là trung điểm của
B C
. Góc giữa hai đường thẳng
AM
và
BC
bằng
A.
45
. B.
90
. C.
30
. D.
60
.
Dạng 1.3 Góc của mặt với mặt
Câu 26. (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho hình lăng trụ tam giác đều
.
ABC A B C
có
2 3
AB
và
2.
AA
Gọi
, ,M N P
lần lượt là trung điểm các cạnh
,
A B A C
và
BC
(tham khảo hình vẽ bên). Côsin
của góc tạo bởi hai mặt phẳng
AB C
và
MNP
bằng
A
D
C
B
A'
D'
C'
B'
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
A.
17 13
65
B.
18 13
65
C.
6 13
65
D.
13
65
Câu 27. (Mã đề 102 BGD&ĐT NĂM 2018) Cho hình lập phương
.ABCD A B C D
có tâm
.O
Gọi
I
là tâm
của hình vuông
A B C D
và
M
là điểm thuộc đoạn thẳng
OI
sao cho
1
2
MO MI
(tham khảo hình vẽ). Khi
đó cosin của góc tạo bởi hai mặt phẳng
( )MC D
và
( )MAB
bằng
A.
7 85
85
B.
6 85
85
C.
17 13
65
D.
6 13
65
Câu 28. (Mã đề 101 BGD&ĐT NĂM 2018) Cho hình lập phương
.ABCD A B C D
có tâm
O
. Gọi
I
là tâm
của hình vuông
A B C D
và
M
là điểm thuộc đoạn thẳng
OI
sao cho
2MO MI
(tham khảo hình vẽ). Khi
đó côsin của góc tạo bởi hai mặt phẳng
( )MC D
và
( )MAB
bằng
A.
7 85
85
B.
17 13
65
C.
6 13
65
D.
6 85
85
Câu 29. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hình chóp
.S ABCD
có đáy
ABCD
là
hình chữ nhật,
AB a
,
2AD SA a
,
SA ABCD
. Tính tang của góc giữa hai mặt phẳng
SBD
và
( )ABCD
.
A.
5
2
. B.
5
. C.
1
5
. D.
2
5
.
Câu 30. Cho hình hộp chữ nhật
.ABCD A B C D
có các cạnh
2, 3; 4AB AD AA
. Góc giữa hai mặt
phẳng
AB D
và
A C D
là
. Tính giá trị gần đúng của góc
?
P
N
M
C'
B'
A'
C
B
A
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
A.
45, 2
. B.
38,1
. C.
53, 4
. D.
61, 6
.
Câu 31. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Cho hình chóp
SABCD
có đáy
ABCD
là hình thoi tâm
O
, đường thẳng
SO
vuông góc với mặt phẳng
. Biết
AB SB a
,
6
3
a
SO
. Tìm số đo của góc giữa hai mặt phẳng
SAB
và
.SAD
A.
30
B.
45
C.
60
D.
90
Câu 32. (TRƯỜNG THPT LƯƠNG TÀI SỐ 2 NĂM 2018-2019) Cho lăng trụ tam giác đều
.
ABC A B C
có diện tích đáy bằng
2
3a
(đvdt), diện tích tam giác
A BC
bằng
2
2a
(đvdt). Tính góc giữa hai mặt phẳng
A BC
và
ABC
?
A.
120
B.
60
C.
30
D.
45
Câu 33. (SỞ GD&ĐT QUẢNG NINH NĂM 2018-2019 LẦN 01) Cho hình chóp
.
có đáy
ABCD
là hình vuông có độ dài đường chéo bằng
2a
và
SA
vuông góc với mặt phẳng
. Gọi
là góc
giữa hai mặt phẳng
SBD
và
ABCD
. Nếu
tan 2
thì góc giữa
SAC
và
SBC
bằng.
A.
0
30
. B.
0
90
C.
0
60
. D.
0
45
.
Câu 34.
(THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01)
Cho hình chóp
SABCD
có đáy là hình
thang vuông
ABCD
tại
A
và
D
, cạnh bên
A
vuông góc với mặt phẳng đáy và
2SA a
. Cho biết
2 2 2AB AD DC a
. Tính góc giữa hai mặt phẳng
SBA
và
SBC
A.
0
30
. B.
0
60
. C.
0
45
D.
1
arcsin
4
.
Câu 35. (CHUYEN PHAN BỘI CHÂU NGHỆ AN NĂM 2018-2019 LẦN 02) Cho hình hộp chữ nhật
. ' ' ' 'ABCD A B C D
có mặt
ABCD
là hình vuông,
6
'
2
AB
AA
. Xác định góc giữa hai mặt phẳng
'
A BD
và
'
C BD
.
A.
0
30
. B.
0
45
. C.
0
60
. D.
0
90
.
Câu 36. (THPT GANG THÉP THÁI NGUYÊN NĂM 2018-2019) Cho hình lập phương
.
ABCD A B C D
. Góc giữa hai mặt phẳng
( )ADC B
và
( )BCD A
là
A.
30
. B.
45
. C.
90
. D.
60
.
Câu 37. (ĐỀ 01 ĐỀ PHÁT TRIỂN ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hình hộp chữ
nhật
.
ABCD A B C D
có đáy
ABCD
là hình vuông,
2AC a
. Gọi
P
là
mặt phẳng qua
AC
cắt
,
BB DD
lần lượt tại
,M N
sao cho tam giác
AMN
cân tại
A
có
MN a
. Tính
cos
với
,
P ABCD
.
A.
2
2
. B.
1
2
. C.
1
3
. D.
3
3
.
Câu 38. (THPT HÀM RỒNG THANH HÓA NĂM 2018-2019 LẦN 1) Cho lặng trụ đứng
.
ABC A B C
có
diện tích tam giác
ABC
bằng
2 3
. Gọi
M
,
N
,
P
lần lượt thuộc các cạnh
AA
,
BB
,
CC
, diện tích tam giác
MNP
bằng
4
. Tính góc giữa hai mặt phẳng
ABC
và
MNP
A.
120
. B.
45
. C.
30
. D.
90
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
Dạng 2. Khoảng cách
Dạng 2.1 Khoảng cách từ điểm đến mặt phẳng
Câu 39. (Mã đề 101 BGD&ĐT NĂM 2018) Cho hình chóp
.S ABC
có đáy là tam giác vuông đỉnh
B
,
AB a
,
SA
vuông góc với mặt phẳng đáy và
2SA a
. Khoảng cách từ
A
đến mặt phẳng
SBC
bằng
A.
2 5
5
a
B.
5
3
a
C.
2 2
3
a
D.
5
5
a
Câu 40. (Mã đề 102 BGD&ĐT NĂM 2018) Cho hình chóp
.S ABC
có đáy là tam giác vuông đỉnh
B
,
AB a
,
SA
vuông góc với mặt phẳng đáy và
SA a
. Khoảng cách từ điểm
A
đến mặt phẳng
SBC
bằng
A.
6
3
a
B.
2
2
a
C.
2
a
D.
a
Câu 41. (Mã 103 - BGD - 2019) Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
, mặt bên
SAB
là tam
giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (minh họa như hình vẽ bên). Khoảng cách từ
D
đến mặt phẳng
SAC
bằng
A.
2
2
a
. B.
21
7
a
. C.
21
14
a
. D.
21
28
a
.
Câu 42. (Mã đề 101 - BGD - 2019) Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a
mặt bên
SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (minh họa như hình vẽ bên). Khoảng
cách từ
A
đến mặt phẳng
SBD
bằng
A
B
D
C
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
A.
21
14
a
. B.
21
7
a
. C.
2
2
a
D.
21
28
a
.
Câu 43. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hình chóp
.S ABCD
có đáy là hình thoi
cạnh
a
,
o
60BAD ,
SA a
và
SA
vuông góc với mặt phẳng đáy. Khoảng cách tứ
B
đến
SCD
bằng?
A.
21
3
a
. B.
15
3
a
. C.
21
7
a
. D.
15
7
a
.
Câu 44. (Mã 102 - BGD - 2019) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên
SAB
là tam
giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy ( minh họa như hình vẽ bên). Khoảng cách
từ
C
đến mặt phẳng
( )SBD
bằng
A.
21
.
14
a
B.
2
.
2
a
C.
21
.
7
a
D.
21
.
28
a
Câu 45. (MĐ 103 BGD&ĐT NĂM 2017-2018) Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh 3a ,
SA
vuông góc với mặt phẳng đáy và
SA a
. Khoảng cách từ A đến mặt phẳng
SBC
bằng
A.
6
6
a
B.
3
3
a
C.
5
3
a
D.
3
2
a
Câu 46. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho tứ diện đều
ABCD
có cạnh bằng
a
. Tính khoảng cách từ
A
đến mặt phẳng
.BCD
A.
6
2
a
. B.
6
3
a
. C.
3
2
a
. D.
2a
.
Câu 47. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho hình chóp
DSABC
có
DSA ABC
, đáy
DABC
là hình chữ nhật. Biết
D 2aA
,
SA a
. Khoảng cách từ
A
đến
DSC
bằng:
A.
3a
7
B.
3a 2
2
C.
2a
5
D.
2a 3
3
Câu 48. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho hình chop
.S ABC
có đáy là tam giác vuông tại
A
,
AB a
, 3AC a ,
SA
vuông góc với mặt phẳng đáy và
2SA a
. Khoảng
cách từ điểm
A
đến mặt phẳng
( )SBC
bằng:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
A.
57
19
a
B.
2 57
19
a
C.
2 3
19
a
D.
2 38
19
a
Câu 49. (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hình chóp tứ giác đều
.
có cạnh đáy bằng
a
và chiều cao bằng
2a
. Tính khoảng cách
d
từ tâm
O
của đáy
ABCD
đến
một mặt bên theo
a
.
A.
2 5
3
a
d
. B.
3
2
a
d
. C.
5
2
a
d
. D.
2
3
a
d
.
Câu 50. (CHUYÊN TRẦN PHÚ HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho khối chóp
.
có đáy
ABCD
là hình vuông cạnh
a
,
SA ABCD
và
2SA a
. Gọi
M
là trung điểm cạnh
SC
. Khoảng cách từ
điểm
M
đến mặt phẳng
SBD
bằng
A.
2
4
a
B.
10
10
a
C.
2
2
a
D.
10
5
a
Câu 51. (THPT GANG THÉP THÁI NGUYÊN NĂM 2018-2019) Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
A
,
AB a
,
3AC a
;
SA
vuông góc với đáy,
2SA a
. Khoảng cách từ điểm
A
đến
mặt phẳng
SBC
bằng
A.
2 3
7
a
. B.
3
7
a
. C.
3
19
a
. D.
2 3
19
a
.
Câu 52. (THPT CHUYÊN SƠN LA NĂM 2018-2019 LẦN 01) Cho hình chóp
.
S ABC
có đáy
ABC
là tam
giác đều cạnh
a
,
SA a
và
SA
vuông góc với mặt phẳng đáy. Khoảng cách từ điểm
A
đến mặt phẳng
SBC
bằng:
A.
2
2
a
. B.
3
7
a
. C.
21
7
a
. D.
15
5
a
.
Câu 53. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho hình chóp đều
.
, cạnh đáy
bằng
a
, góc giữa mặt bên và mặt đáy là
60
. Tính khoảng cách từ điểm
B
đến mặt phẳng
SCD
.
A.
4
a
B.
3
4
a
C.
3
2
a
D.
2
a
Câu 54. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hinh chop
.
co đay la
nưa luc giac đêu
ABCD
nôi tiêp trong đương tron đương kinh
va co canh
SA
vuông goc vơi măt
phăng đay
vơi
6SA a
. Tính khoang cach tư
B
đên măt phăng
SCD
.
A.
2
a
. B.
3a
. C.
2
2
a
. D.
3
2
a
.
Câu 55. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
,
,AB BC a
2 .AD a
Hình chiếu của
S
lên mặt phẳng đáy trùng với
trung điểm
H
của
AD
và
6
.
2
a
SH
Tính khoảng cách
d
từ
B
đến mặt phẳng
SCD
.
A.
6
8
a
d
B.
d a
C.
6
4
a
d
D.
15
5
a
d
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
Câu 56. (THPT CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho tứ diện
.
O ABC
có
, ,OA OB OC
đôi một vuông góc với nhau
3.
OA OB OC Khoảng cách từ
O
đến
( )mp ABC
là
A.
1
3
B.
1
C.
1
2
D.
1
3
Câu 57. (THPT CẨM GIÀNG 2 NĂM 2018-2019) Cho hình chóp
.
có đáy
ABCD
là hình thoi
cạnh
a
,
60
ABC
. Cạnh bên
SA
vuông góc với đáy,
2SC a
. Khoảng cách từ
B
đến mặt phẳng
SCD
là
A.
15
5
a
. B.
2
2
a
. C.
2
5
a
. D.
5 30
3
a
.
Câu 58. (ĐỀ 01 ĐỀ PHÁT TRIỂN ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hình chóp
.
có đáy là hình thoi cạnh
2a
, góc
60
BAD
,
SAB
là tam giác đều nằm trên mặt phẳng vuông góc
với mặt phẳng đáy. Khoảng cách từ
B
đến mặt phẳng
SCD
là
A.
3
2
a
.
B.
3
2
a
.
C.
6
2
a
.
D.
6a
Câu 59. (KTNL GV THUẬN THÀNH 2 BẮC NINH NĂM 2018-2019) Cho hình chóp tứ giác
.
có đáy
ABCD
là hình bình hành tâm
;O
mặt phẳng
SAC
vuông góc với mặt phẳng
SBD
. Biết khoảng
cách từ
O
đến các mặt phẳng
, ,
SAB SBC SCD
lần lượt là
1;2; 5
. Tính khoảng cách
d
từ
O
đến mặt
phẳng
SAD
.
A.
d
. B.
d
. C.
2
d
. D.
2
2
d
.
Dạng 2.2 Khoảng cách của đường thẳng với đường thẳng
Câu 60. (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho lập phương
.
ABCD A B C D
có cạnh bằng
a
( tham
khảo hình vẽ bên ).Khoảng cách giữa hai đường thẳng
BD
và
A C
bằng
A.
3
2
a
B.
2a
C.
3a
D.
a
Câu 61. (Mã đề 101 BGD&ĐT NĂM 2018) Cho hình chóp
.
có đáy là ình chữ nhật,
, 2 ,AB a BC a
SA
vuông góc với mặt phẳng đáy và
.SA a
Khoảng cách giữa hai đường thẳng
AC
và
SB
bằng
A.
6
2
a
B.
2
3
a
C.
2
a
D.
3
a
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
Câu 62. (Mã đề 102 BGD&ĐT NĂM 2018) Cho hình chóp
.
có đáy là hình chữ nhật,
AB a
,
,
SA
vuông góc với mặt phẳng đáy và
SA a
. Khoảng cách giữa hai đường thẳng
BD
,
SC
bằng
A.
4 21
21
a
B.
2 21
21
a
C.
30
12
a
D.
30
6
a
Câu 63. (Mã đề 104 BGD&ĐT NĂM 2018) Cho tứ diện
.
O ABC
có
, ,OA OB OC
đôi một vuông góc với
nhau,
OA a
và
2OB OC a
. Gọi
M
là trung điểm của
BC
. Khoảng cách giữa hai đường thẳng
OM
và
AB
bằng
A.
6
3
a
B.
a
C.
2 5
5
a
D.
2
2
a
Câu 64. (MĐ 103 BGD&ĐT NĂM 2017-2018) Cho tứ diện
OABC
có
OA
,
OB
,
OC
đôi một vuông góc
với nhau, và
OA OB a
,
2OC a
. Gọi
M
là trung điểm của
AB
. Khoảng cách giữa hai đường thẳng
OM
và
AC
bằng
A.
2 5
5
a
B.
2
2
a
C.
2
3
a
D.
2
3
a
Câu 65. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
A
với
3AC a
. Biết
BC
hợp với mặt phẳng
AA C C
một góc
30
o
và hợp với
mặt phẳng đáy góc
sao cho
6
sin
4
. Gọi
,M N
lần lượt là trung điểm cạnh
BB
và
A C
. Khoảng cách
giữa
MN
và
AC
là:
A.
6
4
a
B.
3
6
a
C.
5
4
a
D.
3
a
Câu 66. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho hình chóp
.
S ABC
,
có
SA SB SC
, đáy là tam giác đều cạnh
a
. Biết thể tích khối chóp .
S ABC
bằng
3
3
3
a
. Khoảng cách
giữa hai đường thẳng
SA
và
BC
bằng:
A.
4
7
a
B.
3 13
13
a
C.
6
7
a
D.
3
4
a
Câu 67. (THPT CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hình lập
phương
. ' ' ' 'ABCD A B C D
có cạnh bằng
a
(tham khảo hình vẽ).
Khoảng cách giữa hai đường thẳng
BD
và
' 'A C
bằng
D
A
C
B
D'
B'
C'
A'
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
A.
a
B.
2a
C.
3
2
a
D.
3a
Câu 68. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Cho hình chóp
.
có
SA ABCD
, đáy
ABCD
là hình chữ nhật với
5AC a
và
2BC a
. Tính khoảng cách giữa
SD
và
BC
.
A.
3
2
a
. B.
3a
. C.
2
3
a
. D.
3
4
a
.
Câu 69. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho hình chóp
.
có đáy
ABCD
là hình vuông tâm
O
cạnh
a
,
SO
vuông góc với mặt phẳng
và
.SO a
Khoảng cách giữa
SC
và
AB
bằng
A.
3
15
a
B.
5
5
a
C.
2 3
15
a
D.
2 5
5
a
Câu 70. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho lăng trụ tam giác đều
.
ABC A B C
có tất cả các cạnh đều bằng
a
. Khoảng cách giữa hai đường thẳng
BC
và
AB
bằng
A.
21
7
a
B.
3
2
a
C.
7
4
a
D.
2
2
a
Câu 71. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hình chóp
.
có đáy
ABCD
là hình thoi cạnh
a
,
AC a
. Tam giác
SAB
cân tại
S
và nằm trong mặt phẳng vuông góc với mặt
phẳng đáy. Tính khoảng cách giữa hai đường thẳng
AD
và
SC
, biết góc giữa đường thẳng
SD
và mặt đáy
bằng
60
.
A.
906
29
a
B.
609
29
a
C.
609
19
a
D.
600
29
a
Câu 72. (KTNL GIA BÌNH NĂM 2018-2019) Cho hình chóp , đáy là hình bình hành có
4, 3
AB BC
,
6
SA SB SC SD
. là hình chiếu vuông góc của xuống . Tính độ dài
d
đoạn
vuông góc chung của và .
A.
119
11
B.
4 229
13
C.
259
5
D.
4 119
15
Câu 73. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Cho hình lăng trụ tam giác đều
.
ABC A B C
có
,AB a
2 .AA a
Tính khoảng cách giữa hai đường thẳng
AB
và
.A C
A.
3
2
a
B.
2 5
5
a
C.
5a
D.
2 17
17
a
Câu 74. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Cho hình chóp
.S ABC
có đáy là
tam giác đều cạnh bẳng
4
, góc giữa
SC
và mặt phẳng
ABC
là
45
. Hình chiếu của
S
lên mặt phẳng
ABC
là điểm
H
thuộc cạnh
AB
sao cho
2HA HB
. Tính khoảng cách giữa hai đường thẳng
SA
và
BC
.
.
S ABCD
ABCD
K
B
AC
SA
BK
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
A.
4 210
45
d
. B.
210
5
d
. C.
4 210
15
d
. D.
2 210
15
d
.
Câu 75. (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Cho hình chóp
.
S ABC
có tam giác
ABC
vuông tại
B
,
60
C
,
2
AC
,
SA
ABC
,
1
SA
. Gọi
M
là trung điểm của
AB
. Khoảng cách
d
giữa
SM
và
BC
là
A.
21
7
d
. B.
1
2
7
2
d
. C.
1
3
2
d
. D.
1
2
3
2
d
.
Câu 76. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho khối chóp tứ giác đều
.
S ABCD
có thể tích bằng
2
3
a b
với
AB a
. Gọi
G
là trọng tâm của tam giác
SCD
, trên các cạnh
,AB SD
lần lượt lấy các điểm
,E F
sao cho
EF
song song
BG
. Khoảng cách giữa hai đường thẳng
DG
và
EF
bằng
A.
2 2
2
3 2
ab
b a
. B.
2 2
2
ab
b a
. C.
2
2 2
3 2
a b
b a
. D.
2 2
3 2
ab
b a
.
Câu 77. (TRƯƠNG THPT HOANG HOA THAM HƯNG YÊN NĂM 2018-2019) Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
2 3a
, mặt bên
SAB
là tam giác cân với
120
ASB
và nằm trong mặt
phẳng vuông góc với đáy. Gọi
M
là trung điểm của
SC
và
N
là trung điểm của
MC
. Tính khoảng cách
giữa hai đường thẳng
AM
,
BN
.
A.
2 327
79
a
. B.
237
79
a
. C.
2 237
79
a
. D.
5 237
316
a
.
Câu 78. (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Cho tứ diện đều
ABCD
có cạnh bằng
3
cm. Gọi
M
là trung điểm của
CD
. Khoảng cách giữa
AC
và
BM
là:
N
M
C
B
A
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
A.
2 11
. B.
3 22
11
cm
. C.
3 2
11
cm
D.
2
11
cm
.
Câu 79. (TRƯỜNG THPT LƯƠNG TÀI SỐ 2 NĂM 2018-2019) Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành và
11
SA SB SC
,
30
SAB
,
60
SBC
và
45
SCA
. Tính khoảng cách
d
giữa
hai đường thẳng
AB
và
SD
?
A.
4 11
d
B.
2 22
d
C.
d
D.
22
d
Câu 80. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho tứ diện
ABCD
có các cạnh
, ,
AB AC AD
vuông góc với nhau đôi một và
2 3 .AD AC AB a
Gọi
là đường thẳng chứa trong mặt
( )BCD
sao cho khoảng cách từ điểm
A
đến
là nhỏ nhất và khoảng cách lớn nhất giữa hai đường thẳng
và
AD
là
.d
Khẳng định nào sau đây là đúng?.
A.
14
.
14
d a
B.
3 4 .a d a
C.
3 4
.
14 7
a a
d
D.
4 .d a
Câu 81. (THPT NGÔ GIA TỰ VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hình chóp
.
S ABCD
có đáy
là hình bình hành và
11,
SA SB SC
0
30 ,
SAB
0
60
SBC và
0
45 .
SCA Tính khoảng cách
d
giữa
hai đường thẳng
AB
và
?SD
A.
4 11.
d
B.
2 22.
d
C.
22
.
2
d
D.
22.
d
Câu 82. (THPT NĂM 2018-2019 LẦN 04) Cho hình hộp
ABCDA B C D
có tất cả các cạnh đều bằng 1 và
các góc phẳng ở đỉnh
A
đều bằng
60
. Tính khoảng cách giữa hai đường thẳng
AB
và
A C
.
A.
22
11
. B.
2
11
. C.
2
11
. D.
3
11
.
Dạng 2.3 Khoảng cách của đường với mặt
Câu 83. (THPT LÊ XOAY VĨNH PHÚC LẦN 1 NĂM 2018-2019) Cho hình chóp
.
S ABCD
có đáy là
hình thang vuông tại
A
và
D
,
SD
vuông góc với mặt đáy
ABCD
,
2 , 2AD a SD a
. Tính khoảng
cách giữa đường thẳng
CD
và mặt phẳng
SAB
A.
a
.
2
B.
a 2.
C.
2a
.
3
D.
a 3
.
2
Câu 84. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với đáy và
2SA a
. Gọi
M
là trung điểm của
SD
. Tính khoảng cách
d
giữa đường thẳng
SB
và mặt phẳng
ACM
A.
3
2
a
d
B.
d a
C.
2
3
a
d
D.
3
a
d
PHẦN B. LỜI GIẢI THAM KHẢO
Dạng 1. Góc
Dạng 1.1 Góc của đường thẳng với mặt phẳng
Câu 1. Chọn C
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
Có
SA ABC
nên
AB
là hình chiếu của
SA
trên mặt phẳng
ABC
.
, ,
SB ABC SB AB SBA
.
Mặt khác có
ABC
vuông tại
C
nên
2 2
3AB AC BC a
.
Khi đó
1
tan
3
SA
SBA
AB
nên
, 30
SB ABC
.
Câu 2. Chọn A
Do
SA ABCD
nên góc giữa đường thẳng
SC
và mặt phẳng đáy bằng góc
SCA
.
Ta có
2SA a
,
2AC a
tan
SA
SCA
AC
1
45
SCA
.
Vậy góc giữa đường thẳng
SC
và và mặt phẳng đáy bằng bằng
45
.
Câu 3. Chọn C
Vì
SA
vuông góc với mặt phẳng
ABC
, suy ra góc giữa đường thẳng
SC
và mặt phẳng
ABC
bằng
SCA
.
Mà
2 2
2
tan 1
3
SA a
SCA
AC
a a
.
Vậy
45
SCA
.
Câu 4. Chọn B
D
A
B
C
S
D
A
B
C
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
Do
SA ABCD
nên góc giữa đường thẳng
SB
và mặt phẳng đáy bằng góc
SBA
.
Ta có
cos
AB
SBA
SB
1
2
60
SBA
.
Vậy góc giữa đường thẳng
SB
và và mặt phẳng đáy bằng bằng
60
.
Câu 5. Chọn A
Ta có
AC
là hình chiếu vuông góc của
SC
trên mặt phẳng
ABC
.
Suy ra góc giữa đường thẳng
SC
và mặt phẳng
ABC
bằng
SCA
.
Ta có
2, 2AC a SA a
nên tam giác
SAC
vuông cân tại
A
0
45
.
Câu 6. Chọn A
Ta có
SA
ABC
nên
AC
là hình chiếu của
SC
lên mặt phẳng
ABC
.
Do đó
, ,
SC ABC SC AC SCA
.
Tam giác
ABC
vuông tại
,B
3AB a
và
BC a
nên
2 2 2
4 2AC AB BC a a
.
Do đó tam giác
SAC
vuông cân tại
A
nên
0
45
SCA .
Vậy
0
, 45
SC ABC
.
Câu 7. Chọn D
Gọi
O
là tâm của hình vuông. Ta có
SO ABCD
và
2
2
2
2 2
a a
SO a
Gọi
M
là trung điểm của
OD
ta có
/ /MH SO
nên
H
là hình chiếu của
M
lên mặt phẳng
ABCD
và
1 2
2 4
a
MH SO
.
Do đó góc giữa đường thẳng
BM
và mặt phẳng
( )ABCD
là
MBH
.
O
A
B
C
D
S
M
H
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
Khi đó ta có
2
1
4
tan
3
3 2
4
a
MH
MBH
BH
a
.
Vậy tang của góc giữa đường thẳng
BM
và mặt phẳng
ABCD
bằng
1
3
Câu 8. Chọn D
Ta có
SA ABC
nên đường thẳng
AC
là hình chiếu vuông góc của đường thẳng
SC
lên mặt phẳng
ABC
.
Do đó,
, ,
SC ABC SC AC SCA
(tam giác
SAC
vuông tại
A
).
Tam giác
ABC
vuông cân tại
B
nên
2 2
AC AB a
.
Suy ra
tan 1
SA
SCA
AC
nên
45
o
.
Câu 9.
2AC a
,
AC
là hình chiếu vuông góc của
SC
trên
, ;ABCD SC ABCD SC AC SCA
6 3
: tan : 2 30
3 3
SA a
SAC SCA a SCA
AC
.
Câu 10. Chọn A
Ta có
2AC a
Vì
AC
là hình chiếu của SC lên
ABCD
nên góc giữa
SC
và
ABCD
là góc giữa
SC
và
AC
a 2
C
B
a
a
a 6
3
D
A
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
Xét
SAC
vuông tại A, ta có:
6
3
3
tan
3
2
a
SCA
a
. Suy ra
0
30
SCA
Câu 11. Chọn A
Vì
; ;
SA ABCD SC ABCD SC AC SCA
.
Ta có
2 2
2.
AC AB BC a
0
2
tan 1 45 .
2
SA a
SAC SCA
AC
a
Câu 12.
Trong tam giác
SOD
dựng
// ,
MH SO H OD
ta có
MH ABCD
.
Vậy góc tạo bởi
BM
và mặt phẳng
là
MBH
.
Ta có
2 2 2 2
1 1 1 2
4 2
2 2 2 2
a
MH SO SD OD a a
.
3 3 3 2
2 2
4 4 2
a
BH BD a
.
Vậy
1
tan
3
MH
MBH
BH
.
H
M
O
C
A
D
B
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
Câu 13.
Trong
SAB
kẻ
AH SB
H SB
.
Vì
SA BC
BC SAB BC AH
AB BC
.
Mà
SB AH
do cách dựng nên
AH SBC
, hay
H
là hình chiếu của
A
lên
SBC
suy ra góc giữa
SA
và
SBC
là góc
ASH
hay góc
ASB
.
Tam giác
ABC
vuông ở
B
2 2
3AB AC BC a
Tam giác
SAB
vuông ở
A
1
sin 30
2
AB
ASB ASB
SB
Câu 14.
Gọi
O AC BD
. Ta có:
DO AC
DO ABCD
DO SA SA ABCD
.
SO
là hình chiếu của
SD
lên mặt phẳng
SAC
; ;SD SAC SD SO DSO
.
Xét
SAD
vuông tại
A
:
2 2
3 2SD a a a
.
Xét
SOD
vuông tại
O
: có
2SD a
,
2 2
sin sin
2 4
a DO
OD DSO
SD
.
A
B
C
S
H
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
Câu 15.
Gọi
H
là trung điểm
AB
dễ thấy
SH ABC
.
SC
tạo với mặt phẳng đáy một góc
60
suy ra
60
SCH
.
Có
3 3
.tan
2 2
a a
HC SH HC SCH
.
Dễ thấy
SMH
,
1 10 1
cos
2 2 2
10
a a HM
HM AC SM
SM
.
Câu 16. Chọn C
Ta gọi
,E F
lần lượt là trung điểm của
SC AB
.
Ta có
/ /ME NF
( do cùng song song với
BC
. Nên tứ giác
MENF
là hình thang,
và
/
( )
( )
MF ISA
MF ABCD
SA ABCD
hay tứ giác
MENF
là hình thang vuông tại
,M F
Gọi
,
K NF AC I EK M
thì
( )I MN SAC
Ta có:
( )
NC AC
NC SAC
NC SA
hay
E
là hình chiếu vuông góc của
N
lên
( )SAC
Từ đó ta có được, góc giữa
MN
và
( )SAC
là góc giữa
MN
và
CI
Suy ra, gọi
Q
là góc giữa
MN
và
( )SAC
thì
sin
CN
IN
1 2
D
2 2
a
NC C
;
2
2
3
IN KN
IN MN
M ME
2 2
2 10
3 3
a
MF FN
Vậy
3 5
sin
10
CN
IN
.
M
H
A
C
B
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
Câu 17.
Gọi
là đường thẳng đi qua
A
và song song với
. Hạ
' '
OH H
. Do
O
là trung điểm
của
AC
và
// '
nên
, ' ,d O d O
hay
14
6
a
OH
.
Do
.S ABCD
là hình chóp tứ giác đều nên đáy
ABCD
là hình vuông và
SO ABCD
.
Do
AH OH
và
AH SO
nên, suy ra
AH SH
.
Do
ABCD
là hình vuông cạnh
a
nên
2AC a
, suy ra
2
2
a
OA
.
Áp dụng Định lí Pitago vào tam giác vuông
AHO
ta có
2 2 2
OA OH AH
, suy ra
2 2
2 2
2 14
2 6 3
a a a
AH OA OH
.
Áp dụng Định lí Pitago vào tam giác vuông
SAO
ta có
2 2 2
SA OA SO
, suy ra
2
2 2
2 2 2
2 2 4
2 2
a a b
SA OA SO b
.
Do
// '
nên
2 2
2
cos , cos , cos
3 2 4
AH a
SA SA SAH
SA
a b
.
Câu 18.
Gọi
,H M
lần lượt là trung điểm của
,AB SB
;
O
là tâm của hình chữ nhật
ABCD
.
Ta có
/ /MO SD
.
Dễ thấy
BC SAB BC AM
, mà
SB AM
nên
AM SBC
.
O
M
H
A
D
C
B
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
Xét tam giác
AMO
, có:
3
2
a
AM
;
2 2
1 1
3
2 2
AO AC a a a
;
2
2
2 2 2 2 2 2
1 1 1 1 3
3
2 2 2 2 2 2
a a
MO SD SH HD SH HA AD a a
.
AMO
cân tại
O
2
2
2
2
3
;
13
16
4
sin
4
a
AM
a
MO
d O AM
AMO
OM OM a
.
13
cos ; sin
4
SD SBC AMO
Câu 19.
Do
90
ASB
nên tâm
O
của mặt cầu ngoại tiếp tứ diện
SABI
nằm trên đường thẳng
d
đi qua trung điểm
O
của đoạn thẳng
AB
và
d SAB
.
1
Trong mặt phẳng
SCH
kẻ
IK SH
tại
K
.
Theo giả thiết
SI ABC
suy ra
SI AB
. Từ
SI AB
và
AB CH
suy ra
AB SCH AB IK
.
Từ
IK SH
và
AB IK
ta có
IK SAB
.
2
Từ
1
và
2
ta có
IK d
. Bởi vậy
'; ; ;
OO ABC d ABC IK ABC
.
Vì
SCH ABC
nên
IH
là hình chiếu vuông góc của
IK
trên mặt phẳng
ABC
. Bởi vậy
; ,
IK ABC IK IH HIK HSI
.
Do tam giác
ABC
vuông tại
C
và
SAB
vuông tại
S
nên
2
AB
CO SO
.
d
O
I
C
B
A
S
H
K
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
Xét hai tam giác vuông
CHO
và
SHO
có
CO SO
, cạnh
OH
chung nên
c.g.c
CHO SHO
, bởi vậy
CH SH
.
Xét tam giác
SIH
vuông tại
I
có
2 2
CH SH
IH
, ta có
1
sin 30
2
IH
HSI HSI
SH
.
Vậy
'; 30
OO ABC
.
Câu 20.
Cách 1:
● Gọi
O
là trọng tâm của tam giác
ABC
. Dựng đường thẳng
d
qua
O
và
//d SB
,
d
cắt
SD
tại
K
. Khi đó
góc giữa
SB
và
SCD
chính là góc giữa
OK
và
SCD
.
● Vì
( )SO ABCD
SO CD
.
Ta lại có:
ABC
đều (
ABC
cân tại
B
và
60
BAC ).
AB CO CD CO
( ) ( ) ( ) CD SCO SCD SCO
.
Gọi
H
là hình chiếu của
O
trên
SC
, khi đó ta có:
OH SC
OH SCD
OH CD
. Do đó góc giữa
SB
và mặt phẳng
SCD
là:
OKH
.
Ta có:
sin sin
OH
OKH
OK
.
● Tứ diện
.
S ABC
là tứ diện đều cạnh
a
nên ta tính được:
3
3
a
OC
,
6
3
a
SO
2
3
a
OH
.
Vì
2
//
3
OK DO
OK SB
SB DB
2 2
3 3
OK SB a
.
Vậy:
2
sin
2
OH
OK
.
Cách 2:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
Trước hết ta chứng minh được
sin ( ;
))
(
( ,(
))
d B SC
SCD
D
SB
SB
(như hình trên).
Gọi
O
là trọng tâm tam giác
ABC
. Khi đó ta có
CO CD
.
Dựng
OH SC
suy ra
( )OH SCD
. Ta tính được
3 6 2
,
3 3 3
a a a
OC SO OH
.
Khi đó
3 3 3
( ,( )) ( ,( ))
a 2 a
32 2
2
2 2
d B SCD d O SCD OH
.
Vậy
2
2
2
sin ( ;( ))
2
SB SCD
a
a
.
Dạng 1.2 Góc của đường thẳng với đường thẳng
Câu 21. Chọn D
Đặt
OA a
suy ra
OB OC a
và
2AB BC AC a
Gọi
N
là trung điểm
AC
ta có
/ /MN AB
và
2
2
a
MN
Suy ra góc
, ,
OM AB OM MN
. Xét
OMN
Trong tam giác
OMN
có
2
2
a
ON OM MN
nên
OMN
là tam giác đều
Suy ra
0
60
OMN
. Vậy
0
, , 60
OM AB OM MN
Câu 22. Chọn D
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
Ta có
0 0
. . . . . . 60 . . 60
AB CD AB AD AC AB AD AB AC AB AD cos AB AC cos

0 0
3 1
. . 60 . . 60 .
2 4
AB AD cos AB AD cos AB AD
. 1 1
,
. 4 4
AB CD
cos AB CD cos
AB CD

Câu 23. Vì
ABCD
là hình vuông nên
BD AC
.
Mặt khác
AA ABCD BD AA
.
Ta có
'
BD AC
BD AA C BD A C
BD AA
.
Do đó góc giữa
A C
và
BD
bằng
90
.
Câu 24.
Gọi
P
là trung điểm
AC
, ta có
//PM CD
và
//PN AB
, suy ra
, ,
AB CD PM PN
.
Dễ thấy
PM PN a
.
Xét
PMN
ta có
2 2 2 2 2 2
3 1
cos
2 . 2. . 2
PM PN MN a a a
MPN
PM PN a a
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
0 0 0 0
120 , 180 120 60
MPN AB CD
.
Câu 25.
Giả sử cạnh của hình lập phương là
0
a
.
Gọi
N
là trung điểm đoạn thẳng
BB
. Khi đó,
//MN BC
nên
, ,
AM BC AM MN
.
Xét tam giác
A B M
vuông tại
B
ta có:
A M
2 2
A B B M
2
2
4
a
a
5
2
a
.
Xét tam giác
AA M
vuông tại
A
ta có:
2 2
AM AA A M
2
2
5
4
a
a
3
2
a
.
Có
5
2
a
AN A M
;
2
2 2
BC a
MN
.
Trong tam giác
AMN
ta có:
cos
AMN
2 2 2
2. .
MA MN AN
MA MN
2 2 2
9 2 5
4 4 4
3 2
2. .
2 2
a a a
a a
2
2
6 4
.
4
6 2
a
a
1
2
.
Suy ra
45
AMN
.
Vậy
, ,
AM BC AM MN
45
AMN
.
Dạng 1.3 Góc của mặt với mặt
Câu 26. Chọn D
Gọi
,P Q
lần lượt là trung điểm của
BC
và
;B C
, , .I BM AB J CN AC E MN A Q
Suy ra,
MNP AB C MNCB AB C IJ
và gọi
K IJ PE K AQ
với
E
là trung điểm
M N
(hình vẽ).
, , ,AA QP IJ AQ IJ PE IJ MNP AB C AQ PE
Ta có
13
3, 2 13 ;
3
AP PQ AQ QK
5 5
.
2 3
PE PK
2 2 2
13
cos cos .
2 . 65
KQ KP PQ
QKP
KQ KP
N
M
C
D
A
D'
B'
C'
A'
B
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
Cách 2
Gắn hệ trục tọa độ
Oxyz
như hình vẽ
0;0;0 , 3;0;0 , 0; 3;0 , 0; 3;0 , 3;0;2 , 0; 3;2 , 0; 3;2
P A B C A B C
nên
3 3 3 3
; ;2 , ; ;2
2 2 2 2
M N
Ta có vtpt của mp
AB C
là
1
1
, 2;0;3
2 3
n AB AC

và vtpt của mp
MNP
là
2
4;0; 3
n
Gọi
là góc giữa hai mặt phẳng
AB C
và mp
MNP
1 2
8 9
13
os os ,
65
13 25
c c n n
Cách 3
K
E
Q
J
I
P
N
M
C'
B'
A'
C
B
A
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
Gọi
Q
là trung điểm của
'AA
, khi đó mặt phẳng
' 'AB C
song song với mặt phẳng
MNQ
nên góc giữa
hai mặt phẳng
' 'AB C
và
MNP
cũng bằng góc giữa hai mặt phẳng
MNQ
và
MNP
.
Ta có:
; ;
;
MNP MNQ MN
PE MNP PE MN MNP MNQ PEQ
QE MNQ QE MN
hoặc
0
; 180MNP MNQ PEQ
Tam giác
ABC
đều có cạnh
2 3 3AP
.
Tam giác
APQ
vuông tại
A
nên ta có:
2 2 2 2
3 1 10PQ AP AQ
Tam giác
'A QE
vuông tại
'A
nên ta có:
2
2 2 2
3 13
' ' 1
2 2
QE A E A Q
Tam giác
PEF
vuông tại
F
nên ta có:
2
2 2 2
3 5
2
2 2
PE FP FE
Áp dụng định lý hàm số côsin vào tam giác
PQE
ta có:
2 2 2
25 13
10
13
4 4
cos
2. . 65
5 13
2. .
2 2
EP EQ PQ
PEQ
EP EQ
Do đó:
0
13
cos ; ' ' cos 180 cos
65
MNP AB C PEQ PEQ
.
Câu 27. Chọn C
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
Không mất tính tổng quát ta đặt cạnh của khối lập phương là 1.
Chọn hệ trục tọa độ sao cho
(0;0;0),A
(1;0;0),B
(0;1;0)D
và
(0;0;1)A
(như hình vẽ).
Khi đó ta có:
1 1 1
; ; .
2 2 3
M
Suy ra:
1 1 2
(1;0;0), ; ;
2 2 3
AB MA
1
2 1
, 0; ; (0; 4;3)
3 2
AB MA n
là VTPT của mặt phẳng
( ).MAB
2
1 1 1 1 1
(1;0;0), ; ; , 0; ; (0;2; 3)
2 2 3 3 2
D C MD D C MD n

là VTPT của mặt phẳng
( )MC D
.
cosin của góc giữa hai mặt phẳng
( )MAB
và
( )MC D
bằng:
1 2
1 2
2 2 2 2 2 2
1 2
. 0.0 4.2 3.( 3)
17 13
cos( , ) .
. 65
0 ( 4) 3 . 0 2 ( 3)
n n
n n
n n
Câu 28. Chọn A
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
Giao tuyến của
( )MAB
và
( )MC D
là đường thẳng
KH
như hình vẽ.
Gọi
J
là tâm hình vuông
ABCD
.
,L N
lần lượt là trung điểm của
C D
và
AB
.
Ta có:
( )
C D LIM C D LM LM KH
.
Tương tự
( )
AB NJM AB MN MN KH
.
Suy ra góc giữa hai mặt phẳng
( )MAB
và
( )MC D
chính là góc giữa 2 đường thẳng
( , )MN ML
.
Gọi cạnh hình lập phương là
1
. Ta có
10
6
LM
,
34
6
MN
,
NL
.
Ta có:
2 2 2
7 85
cos
2 . 85
MN ML NL
LMN
MN ML
.
Suy ra cosin của góc giữa hai mặt phẳng
( )MAB
và
( )MC D
là
7 85
85
.
Câu 29.
Ta có:
( )
SBD ABCD BD
.
Hạ
AH BD
tại
H
.
Ta có ( )
AH BD
BD SAH BD SH
BD SA
.
;( ) ,
SBD ABCD HA HS
.
SAH
vuông tại A
0
90 ,
SHA HA HS SHA
B'
A'
N
J
O
K
H
M
I
L
C'
D'
D
C
B
A
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
tan
SA
SHA
AH
.
Xét
ABD
vuông tại
A
có:
2 2 2
1 1 1
.
2 5
.
5
AH AB AD
AH
2
tan 5.
2 5
5
SA a
SHA
AH
a
Câu 30. Cách 1: Hai mặt phẳng
AB D
và
A C D
có giao tuyến là
EF
như hình vẽ.
Do
//EF AB
mà
A D A ABB
nên
AD AB
' '
/ /EF A D
Từ
A
kẻ vuông góc lên giao tuyến
EF
tại
H
thì
'
A H EF
EF ADH
EF D H
. Khi đó, góc
giữa hai mặt phẳng cần tìm chính là góc giữa hai đường thẳng
AH
và
D H
.
Tam giác
'
D EF
lần lượt có
13
2 2
D B
D E
,
5
2 2
D A
D F
,
5
2
B A
EF
.
Theo Hê-rông ta có:
'
61
4
DEF
S
. Suy ra
2 305
10
DEF
S
D H
EF
.
Dễ thấy
' '
A EF D EF
' '
A H D H
.
Tam giác
DA H
có:
2 2 2
29
cos
2 . 61
HA HD A D
A HD
HA HD
.
Do đó
118,4A HD
hay
, 180 118,4 61,6
A H DH
.
Cách 2: Gắn hình hộp chữ nhật
.ABCD A B C D
vào hệ trục tọa độ như hình vẽ. Khi đó
0;0;0 ,A
2;0;0 ,B
0;3;0 ,D
2;3;0 ,C
0;0;4 ,A
2;0;4 ,B
0;3;4 ,D
2;3;4C
.
Gọi
1
n
là véc tơ pháp tuyến của
AB D
. Có
1
; 12; 8;6n AB AD
 
.
Gọi
2
n
là véc tơ pháp tuyến của
A C D
. Có
2
; 12;8; 6n A C A D
 
.
Gọi
là góc giữa hai mặt phẳng
AB D
và
A C D
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
1 2
1 2
29
cos
61
n n
n n
. Vậy giá trị gần đúng của góc
là
61, 6
.
Cách 3.
Do hai mặt phẳng
AB D
và
A C D
chứa hai đường
AB
và
C D
song song với nhau nên giao tuyến của
chúng song song hai đường đó.
Kẻ
A H AB
,
H AB
, dựng hình bình hành
A HKD
có tâm
I
như hình vẽ.
Do
A D A ABB
nên
AD AB
suy ra
AB A HKD
góc giữa hai mặt phẳng
AB D
và
A C D
là góc giữa
AK
và
D H
.
Trong tam giác vuông
AAB
có
AH
là đường cao nên
2 2 2
1 1 1 1 1 5
4 16 16A H A B AA
.
Vậy
4
5
AH
.
Xét tam giác
AIH
có
cos cosI A H
29
cos cos sin sin
61
A H A H
.
Vậy góc giữa hai mặt phẳng
AB D
và
A C D
gần đúng bằng
61, 6
.
Câu 31. Chọn D
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
Gọi
M
trung điểm
SA
. Ta có
SAB
cân tại
(1)
B BM SA
Vì
SO ABCD SO BD
, lại có
O
trung điểm
BD
SBD
cân tại
S
nên
SD SB a
SAD
cân tại
D
nên
(2)
DM SA
Lại có
(3)
SAB SAD SA
Từ
(1);(2);(3) ,
SAB SAD BMD
hoặc
, 180
SAB SAD BMD
.
Xét
3 2 3
3 3
a a
SOB OB BD
.
Xét
6
3
a
AOB OA OC
. Xét
2 3 1 3 1
3 2 3 2
a a
SOC SC OM SC BD
Do đó
BMD
vuông tại
M
, vậy
, 90
SAB SAD BMD
, do đó chọn D.
Câu 32. Chọn C
Ta có
A BC
cân tại
A
. Gọi I là trung điểm của
BC
' ; ;A BC ABC AI A I A IA
.
Theo đề bài ta suy ra
2
2
2 3
2
BC a
A I a
a
AI
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
Xét tam giác vuông
A AI
có
3
cos 30 .
' 2
AI
A I
Vậy
' ; 30
A BC ABC
.
Câu 33.
Gọi
O
là tâm đáy, và
K
là hình chiếu vuông góc của
O
trên
.SC
Do
BD AC
BD SAC BD SO
BD SA
, suy ra góc giữa hai mặt phẳng
SBD
và
ABCD
là góc
SOA
. Ta có
tan 2 . 2 .
SA
SA OA a
OA
Do
.
SC BD
SC BK
SC OK
nên góc giữa hai mặt phẳng
SAC
và
SBC
là
.BKO
Ta có
2
2
2 2
2
2. . 1 2
2
2
tan 3
1 .
1. 2
,
2
BO BO BO
BKO
SA AC
OK
d A SC
SA AC
suy ra
0
60
BKO
.
Câu 34.
Ta có tam giác
ABC
vuông tại
C
nên
1
BC AC
.
Vì
2
SA ABCD
BC SA
BC ABCD
.
Từ
1 , 2
BC SAC
Trong
SAC
vẽ
AH SC
tại
H
Ta có:
,AH BC BC SAC AH SAC
AH SBC
AH SC
O
C
B
A
S
D
K
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 36
AH SBC
SB AH
SB SBC
Trong
SAB
vẽ
AK SB
tại
K
SB AH
SB AHK
SB AK
mà
HK AHK
nên
SB HK
Ta có:
; ;
SB AK
SB HK
AK SAB SBA SBC AK HK AKH
HK SBC
SB SAB SBC
SAC
vuông tại
A
có đường cao
:AH
2 2
2 2 2 2
1 1 1 1 1 1
2 2
AH SA AC AH
a a
2 2
1 1
AH a
AH a
.
SAB
vuông tại
A
có đường cao
:AK
2 2
2 2 2 2
1 1 1 1 1 1
2
2
AK SA AB AK
a
a
2 2
1 3 2
4
3
a
AK
AK a
.
AHK
vuông tại
:H
2 2
2 2 2 2 2 2
4
3 3
3
a a a
AK AH HK Pytago a HK HK HK
.
AHK
vuông tại
H
0
1
3
cos 60
2
2
3
a
HK
AKH AKH
a
AK
.
Câu 35.
+ Gọi
O
là giao điểm của hai đường chéo hình vuông
ABCD
.
Đặt
6
; '
2
x
AB x BC x AA
.
O
D'
C'
A'
B'
D
C
B
A
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 37
2
2
6 10
' ' '
2 2
x x
A B A D x A BD
cân
' A O BD
.
2
2
6 10
' ' '
2 2
x x
C B C D x C BD
cân
' C O BD
.
+
' ' A BD C BD BD
' , ' ' A O BD A O A BD
' , ' '
C O BD C O C BD
góc giữa hai mặt phẳng
'A BD
và
'C BD
bằng góc giữa
'A O
và
'C O
.
+ Tính
' 'A OC
.
2 2
2 2
10 2
' ' ' 2
2 2
x x
A O C O A B BO x
.
' ' 2A C x
.
' 'A OC
đều
0
' ' 60A OC
.
Vậy góc giữa hai mặt phẳng
'A BD
và
'C BD
bằng
0
60
.
Cách khác: Gắn hệ trục tọa độ
Oxyz
vào hình hộp chữ nhật
. ' ' ' 'ABCD A B C D
để tìm góc giữa hai mặt phẳng
'A BD
và
'C BD
.
Câu 36.
Cách 1: Gọi
I A B B A
;
J C D D C
. Ta có
IJ ( ) ( )ADB C BCD A
(1).
Theo giả thiết, ta có:
IJ ( )DCC D
IJC D
(2).
Từ (1) và (2)
( )C D BCD A
( ) ( )ADC B BCD A
.
Vậy góc giữa hai mặt phẳng
( )ADC B
và
( )BCD A
là
90
.
Cách 2: Mặt phẳng
( )DCC D
vuông góc và cắt hai mặt phẳng
( )ADC B
và
( )BCD A
lần lượt theo hai
giao tuyến
DC
và
D C
.
Góc giữa hai mp
( )ADC B
và
( )BCD A
là góc giữa hai đường thẳng
DC
và
D C
.
Vì
.ABCD A B C D
là hình lập phương nên tứ giác
DCC D
là hình vuông
DC D C
.
Vậy góc giữa hai mặt phẳng
( )ADC B
và
( )BCD A
là
90
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 38
Câu 37.
Ta có
AMC N
là hình bình hành, mà tam giác
AMN
cân tại
A
nên
MN AC
.
Ta có
' '
BDD B
cắt ba mặt phẳng
,
' ' ' '
A B C D
,
'
AMC N
lần lượt theo ba giao tuyến
' '
/ / / /
BD B D MN
.
Hai mặt phẳng
P
và
có điểm chung
A
và lần lượt chứa hai đường thẳng song song
MN
,
BD
nên giao tuyến của chúng là đường thẳng
d
đi qua
A
và song song với
,MN BD
.
Trên hai mặt phẳng
P
và
lần lượt có hai đường thẳng
AC
và
AC
cùng vuông góc với
d
nên
góc giữa hai mặt phẳng
P
và
chính là góc giữa
AC
và
AC
, bằng góc
CAC
. Xét tam giác
'
C CA
vuông tại
C
có:
2
cos
2
2
AC BD MN a
AC AC AC
a
Cách 2:
Theo chứng minh ở trên thì
//MN BD
và
MN BD a
.
Đa giác
AMC N
nằm trên mặt phẳng
P
có hình chiếu trên mặt
là hình vuông
ABCD
nên:
2
2
2
2
cos
1 1
2
. .
2 2
ABCD
AMC N
BD
S
AB
S
AC MN AC MN
.
Câu 38.
Do
. ' ' 'ABC A B C
là hình lăng trụ đứng nên ta có:
.cos ,
ABC MNP
S S MNP ABC
2 3 3
cos ,
4 2
ABC
MNP
S
MNP ABC
S
0
, 30
MNP ABC
N
P
M
B
C
A
C'
B'
A'
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 39
Dạng 2. Khoảng cách
Dạng 2.1 Khoảng cách từ điểm đến mặt phẳng
Câu 39. Chọn A
Ta có
BC AB
BC SAB
BC SA
.
Kẻ
AH SB
. Khi đó
AH BC
AH SBC
AH
là khoảng cách từ
A
đến mặt phẳng
SBC
.
Ta có
2 2 2 2 2 2
1 1 1 1 1 5
4 4AH SA AB a a a
2
2
4 2 5
5 5
a a
AH AH
.
Câu 40. Chọn B
S
A
B
C
H
Kẻ
AH SB
trong mặt phẳng
SBC
Ta có:
BC AB
BC SAB
BC SA
BC AH
Vậy
AH BC
AH SBC
AH SB
1 2
,
2 2
a
d A SBC AH SB
.
Câu 41. Chọn B
a
2a
A
C
B
S
H
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 40
* Gọi
O AC BD
và
G
là trọng tâm tam giác
ABD
,
I
là trung điểm của
AB
ta có
SI ABCD
và
;
2 ; 2. ;
;
d D SAC
DG
d D SAC d I SAC
IG
d I SAC
.
* Gọi
K
là trung điểm của
AO
,
H
là hình chiếu của
I
lên
SK
ta có
;
IK AC IH SAC
; 2. ; 2.d D SAC d I SAC IH
* Xét tam giác
SIK
vuông tại I ta có:
3 2
;
2 2 4
a BO a
SI IK
2 2 2 2 2 2
1 1 1 4 16 28 3
3 2 3
2 7
a
IH
IH SI IK a a a
21
; 2. ; 2.
7
a
d D SAC d I SAC IH
.
Câu 42. Chọn B
Gọi
H
là trung điểm của
.AB
Khi đó,
.SH ABCD
Gọi
O
là giao điểm của
AC
và
BD
suy ra
AC BD
. Kẻ
HK BD
tại
K
(
K
là trung điểm
BO
).
Kẻ
HI SH
tại I. Khi đó:
, 2 , 2 .d A SBD d H SBD HI
Xét tam giác
,SHK
có:
3
,
2
a
SH
1 2
2 4
a
HK AO
.
Khi đó:
2 2 2 2
1 1 1 28 21
.
3 14
a
HI
HI SH HK a
O
G
I
A
B
D
C
S
O
A
C
S
I
K
H
O
C
D
S
A
B
K
I
H
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 41
Suy ra:
21
, 2 .
7
a
d A SBD HI
Câu 43. Chọn C
CÁCH 1:
Ta có
/ / ; A;AB CD d B SCD d SCD
.
Kẽ
MA CD M CD
,kẽ
,
AH SM SH SCD d A SCD SH
.
SA a
;
2
3
2
ACD ABCD
S S
a
AM
CD CD
2 2 2
1 1 1 21
7
SM a
SH SA AM
CÁCH 2: Ta có
. .A
3 3
21
/ / ; A;
2 7
S BCD S BCD
SCD SCD
V V
a
AB CD d B SCD d SCD
S S
.
(
; 2; 2 ;CD aSCD SD a SC a
)
Câu 44. Chọn C
Gọi
H
là trung điểm của
( ).AB SH AB SH ABCD
Từ
H
kẻ
HM BD
,
M
là trung điểm của
BI
và
I
là tâm của hình vuông.
Ta có: (SHM)
BD HM
BD
BD SH
D
B
C
S
A
M
H
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 42
Từ
H
kẻ
HK SM HK BD
( Vì
(SHM)
BD
)
( ) d(H;(SBD)) HK.
HK SBD
Ta có:
2
.
2 4 4
AI AC a
HM
3
2
a
SH
.
2 2 2 2
2 3
.
. 21
4 2
.
14
2 3
4 2
a a
HM HS a
HK
HM HS
a a
21 21
( ;( )) ( ;( )) 2 ( ;( )) 2 2. .
14 7
a a
d C SBD d A SBD d H SBD HK
Vậy:
( ;( ))d C SBD
21
.
7
a
Câu 45. Chọn D
Ta có:
BC AB
BC SA
BC SAB
SAB SBC
SAB SBC SB
Trong mặt phẳng
SAB
: Kẻ
AH SB
;
AH d A SBC
2 2 2
1 1 1
AH SA AB
2 2
1 1
3a a
2
4
3a
.
3
;
2
a
d A SBC AH
. Chọn D
Câu 46. Chọn B
Gọi
, ,E F G
lần lượt là trung điểm của
,BD CD
và trọng tâm tam giác
BCD
Tam giác
BCD
đều nên suy ra
3 3
2 2
BC a
CE
2 3
3 3
a
CG CE
Tam giác
ACG
vuông tại
G
nên ta có
2 2
2 2 2 2
2 6
3 3 3
a a a
AG AC CG a AG
Vậy
6
,
3
a
d A BCD AG
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 43
Câu 47.
Chọn C
Gọi
H
là hình chiếu của
A
lên
DS
ta chứng minh được
DAH SC
2 2 2
1 1 1 2a
D
5
AH
AH SA A
Câu 48. Chọn B
Ta có
2 2 2 2 2 2 2 2 2 2
1 1 1 1 1 1 1 1 1 19
3 4 12AK AH AS AB AC AS a a a a
.
Suy ra
2 3
19
a
AK
hay
2 57
( ,( ))
19
a
d A SBC
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 44
Câu 49.
.
là hình chóp tứ giác đều nên
ABCD
là hình vuông và
SO ABCD
.
Vẽ
OH
vuông góc với
CD
tại
H
thì
H
là trung điểm
CD
,
2
a
OH
.
Dễ thấy
CD SOH SCD SOH
nên kẻ
OK
vuông góc với
SH
tại
K
thì
OK SCD
.
,
d O SCD
OK
.
Tam giác vuông
SOH
có
OK
là đường cao nên
2 2 2
2
2.
. 2
2
3
2
4
a
a
OS OH a
OK
OS OH a
a
.
Vậy
2
,
3
a
d O SCD
.
Câu 50.
Do
M
là trung điểm
SC
nên
1 1
; ; ;
2 2
d M SBD d C SBD d A SBD
Gọi
H
là hình chiếu của
A
lên
;
mp SBD d A SBD AH
H
O
D
S
B
C
A
K
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 45
Lại có
, ,AS AB AD
đôi một vuông góc nên
2
2 2 2 2 2 2 2
1 1 1 1 1 1 1 5
2
2
AH AS AB AD a a a
a
10 10
;
5 10
a a
AH d M SBD
.
Câu 51.
Ta có
SA ABC
SA BC
BC ABC
.
Trong
ABC
, kẻ
AH BC
, mà
BC SA BC SAH BC SH
.
Trong
SAH
, kẻ
AK SH
, mà
SH BC
AK SBC
hay
;
d A SBC AK
.
Vì
ABC
vuông tại
A
nên
2 2
2BC AB AC a
.
Mặt khác có
AH
là đường cao nên
. 3
2
AB AC a
AH
BC
.
Vì
SAH
vuông tại
A
nên
2 2
19
2
a
SH SA AH
.
Vậy có
AK
là đường cao
. 2 3
19
SA AH a
AK
SH
.
Nhận xét. Trong thực hành làm toán trắc nghiệm ta nên áp dụng bài toán sau:
Cho tứ diện
OABC
có
, ,
OA OB OC
đôi một vuông góc với nhau và
H
là hình chiếu của
O
lên mặt phẳng
ABC
. Khi đó
2 2 2 2
1 1 1 1
OH OA OB OC
.
Câu 52.
Gọi
M
là trung điểm
BC
. Kẻ
AH SM
tại
H
.
Ta có
AM BC
và
SA BC
nên
BC SAM
BC AH
1
.
A
C
B
S
H
K
M
A
C
B
S
H
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 46
Mà
AH SM
2
.
Từ
1
và
2
suy ra
AH SBC
.
Do đó
,
d A SBC AH
.
Xét tam giác
SAM
vuông tại
A
, có
2 2 2
1 1 1
AH AM AS
2
2
1 1
3
2
a
a
2
7
3a
3
7
AH a
21
7
a
.
Câu 53. Chọn C
* Ta có:
;
2
;
d B SCD
BD
OD
d O SCD
; 2. ; 2
d B SCD d O SCD OH
. Trong đó
H
là hình chiếu
vuông góc của
O
lên
SCD
.
* Gọi
I
là trung điểm của
CD
ta có:
; ; 60
SI CD SCD ABCD OI SI S
SCD ABCD C
D
D
IO
OI C
.
Xét tam giác
SOI
vuông tại
O
ta có:
3
.tan 60
2
a
SO OI
.
Xét
SOI
, ta có
2 2 2 2 2 2
1 1 1 4 4 16
3 3OH OI OS a a a
3 3
;
4 2
a a
OH d B SCD
.
Câu 54. Chọn C
60
O
I
A
B
C
D
S
H
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 47
Từ giả thiết suy ra:
2
AD
AB BC CD a
, 3AC a .
Gọi
E AB CD
, suy ra tam giác
ADE
đều.
Khi đó
C
là trung điểm của
ED
và
AC ED
.
Dựng
AH SC
thì
AH SCD
, suy ra
,d A SCD AH
.
Xét tam giác
SAC
vuông tại
A
, có
AH
là đường cao
Suy ra:
2 2 2
1 1 1
2AH a
AH SA AC
Mà
1 1 2
, ,
2 2 2
a
d B SCD d A SCD AH
.
Câu 55. Chọn C
Gọi
M
là trung điểm của
CD
,
K
là hình chiếu của
H
lên
SM
Tam giác
HCD
vuông tại
H
có
2CD a
và
2
2
a
HM
Ta có
/ / , ,BH CD d B SCD d H SCD HK
Tam giác
SHM
vuông tại
H
có
2 2
. 6
4
HM HS a
HK
HM HS
Vậy
6
,
4
a
d B SCD
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 48
Câu 56. Chọn B
Gọi
'A
là chân đường cao kẻ từ
A
lên
,BC
'C
là chân đường cao kẻ từ
C
lên
.AB
Gọi
H
là giao của AA’ với CC’ suy ra H là trực tâm của tam giác
.ABC
Ta dễ dàng chứng
minh được
( ).OH ABC
Do đó:
( ;( )) .d O ABC OH
Tính
.OH
Ta có: Tam giác
'OAA
vuông tại
,O
có
OH
là đường cao. Suy ra :
2 2 2
1 1 1
'
OH OA OA
(1)
Lại có: Tam giác
OBC
vuông tại
,B
có
'OA
là đường cao. Suy ra:
2 2 2
1 1 1
'
OA OB OC
(2)
Từ (1) và (2) suy ra:
2 2 2 2
1 1 1 1
.
OH OA OB OC
Thay 3 OA OB OC vào, ta được:
2
1 1 1 1
1 1.
3 3 3
OH
OH
Vậy
( ;( )) 1. d O ABC OH
Câu 57.
Cách 1: Sử dụng kiến thức ở lớp 11.
ABCD
là hình thoi cạnh
a
,
60ABC
,ABC
ACD
là các tam giác đều cạnh
a
.
Xét
SAC
vuông tại
A
có:
2 2
SA SC AC
2 2
4
a a
3a .
Vì
//AB CD
nên
//AB SCD
. Do đó
, ,d B SCD d A SCD
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 49
Kẻ
AH CD
H CD
. Suy ra
H
là trung điểm của cạnh
CD
,
3
2
a
AH
.
Kẻ
AK SH
K SH
1
Ta có:
CD AH
CD SA
CD SAH
CD AK
2
Từ (1) và (2) suy ra:
AK SCD
,
d A SCD AK
.
Xét
SAH
vuông ở
A
:
2 2 2
1 1 1
AK AH SA
2 2
4 1
3 3a a
2
5
3a
15
5
a
AK
.
Vậy
15
,
5
a
d B SCD
.
Cách 2: Tính khoảng cách thông qua tính thể tích.
ABCD
là hình thoi cạnh
a
,
60
ABC
,ABC
ACD
là các tam giác đều cạnh
a
.
Xét
SAC
vuông tại
A
có:
2 2
SA SC AC
2 2
4
a a
3a
.
Vì
//
AB DC
nên
//
AB SDC
. Do đó
3
, ,
SACD
SCD
V
d B SCD d A SCD
S
.
1
.
3
SACD ACD
V SA S
2
1 3
3.
3 4
a
a
3
4
a
.
Xét
SAC
và
SAD
có:
AD AC a
,
SA
chung,
90
SAC SAD
.
Do đó
SAC SAD
SC SD
SCD
cân tại
S
.
Gọi
H
là trung điểm
CD
SH CD
.
Xét
SHC
vuông ở
H
:
2 2
SH SC CH
2
2
4
4
a
a
15
2
a
.
1
.
2
SCD
S SH CD
1 15
. .
2 2
a
a
2
a
.
,
d A SCD
3
2
3.
4
15
4
a
a
15
5
a
.
Vậy
15
,
5
a
d B SCD
.
Câu 58.
Gọi
O
là trung điểm của
AB
( )SO ABCD
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 50
2 . 3
3
2
a
SO a
do
SO
là đường cao của tam giác đều cạnh
2a
Từ giả thiết suy ra tam giác
BCD
và tam giác
ABD
là tam giác đều
CD OD
Ta có:
CD OD
CD SOD
CD SO
Trong tam giác
SOD
kẻ
OH SD
tại
H
OH SD
OH SCD
OH CD
Do
AB SCD
suy ra
, ,
d B SCD d O SCD OH
Nhận thấy tam giác
SOD
là tam giác vuông cân tại
O
với
3OD a
2 2
1 1 6
3 3
2 2 2
a
OH SD a a
.
Câu 59. Chọn B
Gọi
, , ,p q u v
lần lượt là các khoảng cách từ
O
đến các mặt phẳng
, , , .SAB SBC SCD SDA
Trong mặt phẳng
SAC
dựng đường thẳng qua
O
vuông góc với đường thẳng
SO
cắt hai đường thẳng
,SA SC
lần lượt tại
', 'A C
Trong mặt phẳng
SBD
dựng đường thẳng qua
O
vuông góc với đường thẳng
SO
cắt hai đường thẳng
,SB SD
lần lượt tại
', 'B D
.
Do
, , ' '
SAC SBD SAC SBD SO A C SO
nên
' '
A C SBD
' ' ' 'A C B D
.
Khi đó tứ diện
' 'OSA B
có
, ', 'OS OA OB
đôi một vuông góc nên ta chứng minh được
2 2 2 2
1 1 1 1
1
' '
p OS OA OB
Chứng minh tương tự:
2 2 2 2
1 1 1 1
2
' 'q OS OB OC
;
2 2 2 2
1 1 1 1
3
' 'u OS OC OD
2 2 2 2
1 1 1 1
4
' 'v OS OD OA
O
D'
C'
B'
A'
D
C
B
A
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 51
Từ
1 , 2 , 3 , 4
ta có
2 2 2 2
1 1 1 1
.
p u q v
Với
2
2 2 2 2
1 1 1 1 1 19 20
1; 2; 5
1 2 20 19
5
p q u d v
v v
.
Dựng mặt phẳng qua O, vuông góc với
SO
, cắt các đường thẳng
, , ,SA SB SC SD
lần lượt tại
, , ,A B C D
SO A B C D
.
Vì
SAC SBD
A C B D
.
Ta có:
2 2 2
1 1 1 1
1
,d O SA B
SO OA OB
.
1
2 2 2
1 1 1 1 1
4
,d O SB C
SO OB OC
.
2
2 2 2
1 1 1 1 1
5
,d O SC D
SO OC OD
.
3
2 2 2 2
1 1 1 1 1
,d O SD A
SO OD OA d
.
4
2
1 1 1
1 , 2 , 3 , 4 1
5 4
d
20
19
d
.
Dạng 2.2 Khoảng cách của đường thẳng với đường thẳng
Câu 60. Chọn D
Ta có khoảng cách giữa hai đường thẳng chéo nhau
BD
và
A C
bằng khoảng cách giữa mặt phẳng song
song
ABCD
và
A B C D
thứ tự chứa
BD
và
A C
. Do đó khoảng cách giữa hai đường thẳng
BD
và
A C
bằng
a
.
Câu 61. Chọn B
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 52
Từ
B
kẻ
// // ,
Bx AC AC SB Bx
Suy ra
, , , , ,
d AC SB d AC SB Bx d A SB Bx
Từ
A
kẻ
AK Bx K Bx
và
AH SK
Do
AK Bx
Bx SAK Bx AH
SA Bx
Nên
, , ,
AH SB Bx d A SB Bx AH
Ta có
BKA
đồng dạng với
ABC
vì hai tam giác vuông có
KBA BAC
(so le trong
Suy ra
. .2 2 5
.
5
5
AK AB AB CB a a a
AK
CB CA CA
a
Trong tam giác
SAK
có
2 2 2 2 2 2
1 1 1 1 5 9 2
.
4 4 3
a
AH
AH AS AK a a a
Vậy
2
, .
3
a
d AC SB
Câu 62. Chọn B
Gọi
O
là tâm hình chữ nhật và M là trung điểm
SA
, ta có:
//
SC BMD
.
Do đó
,
d SC BD
,
d SC BMD
,
d S BMD
,
d A BMD h
Ta có:
, ,AM AB AD
đôi một vuông góc nên
x
O
CD
B
A
S
K
H
O
M
D
C
B
A
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 53
2 2 2 2 2 2 2
1 1 1 1 4 1 1
4h AM AB AD a a a
Suy ra:
2 21
21
a
h
.
Câu 63. Chọn A
Ta có
OBC
vuông cân tại
O
,
M
là trung điểm của
BC
OM BC
Dựng hình chữ nhật
OMBN
, ta có
/ /
/ /
OM BN
OM ABN
BN ABN
, , ,
d AB OM d OM ABN d O ABN
Gọi
H
là hình chiếu vuông góc của
O
trên
AN
ta có:
BN ON
BN OAN
BN OA
OH BN
mà
OH AN
OH ABN
,
d O ABN OH
OAN
vuông tại
O
, đường cao
OH
2 2 2
1 1 1
OH OA ON
2 2
1 1
OA BM
2 2
1 4
OA BC
2 2 2
1 4
OA OB OC
2 2 2 2
1 4 3
4 4 2a a a a
2
2
2
3
a
OH
6
3
a
OH
6
,
3
a
d AB OM OH
Nhận xét:
M
A
O
B
C
N
H
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 54
Chọn hệ trục tọa độ
Oxyz
như hình vẽ, khi đó
0;0;0
O
,
2 ;0;0
B a
,
0;2 ;0C a
,
0;0;A a
M
là trung điểm của
BC
; ;0M a a
Ta có
; ;0OM a a
;
0;2 ;0OB a
;
2 ;0;
AB a a
2 2 2
, ; ; 2
OM AB a a a
, .
,
,
OM AB OB
d AB OM
OM AB
3
4 4 4
2 6
3
4
a a
a a a
Câu 64.
Chọn C
Gọi
N
là trung điểm của
BC
suy ra
//AC
MN
AC//
OMN
;
d OM AC
;
d C OMN
;
d B OMN
.
3
.
1 1 1
. . .2
3 2 3
A OBC
V a a a a
.
.
.
;
.
;
M OBC OBN
A OBC OBC
d M ABC
V S
V S
d A ABC
1 1 1
.
2 2 4
3
.
1
12
M OBC
V a
.
Xét tam giác vuông cân
AOB
:
1 2
2 2
OM AB a
.
M
A
O
B
C
H
N
M
O
A
C
B
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 55
Xét tam giác vuông
BOC
:
2
2
1 1 5
2
2 2 2
ON BC a a a
.
Xét tam giác
BAC
:
2
2
1 1 5
2
2 2 2
MN AC a a a
.
Trong tam giác cân
OMN
, gọi
H
là trung điểm của
OM
ta có
2 2
3 2
NH
4
NM HM a
.
Suy ra
2
1 3
.
2 8
OMN
S OM NH a
.
Vậy
.
3
2
;
3
M OBN
OMN
V
d B OMN a
S
.
Câu 65. Chọn A
+) Ta có:
A
, 30
A
o
C CBC BC A
+) Mặt khác
, ABCBC C BC
+) Gọi
2 2
3
AB x BC a x
2 2
3 3
.tan
5
a x
CC BC
.cot30 3
o
AC AB x
+) Mặt khác ta có:
2 2 2
2 3 ' 6AC CC AC x a CC a AC a
+) Gọi
P
là trung điểm của
B C
, ta có: Do mặt phẳng
/ /
MNP ABC
nên
1
, , , ,
2
d MN AC d MN ABC d N ABC d A ABC
+) Kẻ
A H AC A H ABC
1 6
,
2 2
a
d A ABC A H
,
6
4
d MN
a
AC
Câu 66. Chọn C
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 56
Do hình chóp
.
S ABC
đều nên
SG
là đường cao của hình chóp (
G
là trọng tâm tam giác đều
ABC
). Kẻ
MH SA
tại
H
thì
MH
là đoạn vuông góc chung của
SA
và
BC
.
Vậy khoảng cách giữa hai đường thẳng
SA
và
BC
bằng
MH
.
Ta có
2 3
.
1 3 3
4
3 4 3
S ABC
a a
V SG SG a
,
3
3
a
AG
,
2
2 2 2
3 7 3
16
9 3
a a
SA AG SG a . Ta
có
. 3.4 . 3 6
. .
7
2.7 3
SG AM a a a
SA MH SG AM MH
SA
a
Câu 67. Chọn A
Ta có:
/ / ' ' ' '
; ' ' [ ; ' ' ' ' ] '
' ' ' ' ' '
ABCD A B C D
BD ABCD d BD A C d ABCD A B C D AA a
A C A B C D
Câu 68.
Ta có
/ /
/ / , , ,
BC AD
BC SAD d BC SD d BC SAD d B SAD
BC SAD
.
Có
SA ABCD SA AB
.
A
S
C
B
M
G
H
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 57
Ta có
,
BA AD
BA SA BA SAD d B SAD BA
SA AD A
.
Xét tam giác vuông
2 2 2 2
, 5 2 3BAC BA AC BC a a a
.
Vậy
, 3 , 3d B SAD a d BC SD a
.
Câu 69. Chọn D
Gọi
,M N
lần lượt là trung điểm của các cạnh
,AB CD
;
H
là hình chiếu vuông góc của
O
trên
.SN
Vì
//AB CD
nên
,SC ,( ) ,( ) 2 ,( )d AB d AB SCD d M SCD d O SCD
(vì
O
là trung điểm đoạn
MN
)
Ta có ( )
CD SO
CD SON CD OH
CD ON
Khi đó
( ) ;( ) .
CD OH
OH SCD d O SCD OH
OH SN
Tam giác
SON
vuông tại
O
nên
2
2 2 2 2 2
1 1 1 1 1 5
5
4
a
OH
a
OH ON OS a a
Vậy
2 5
,SC 2
5
a
d AB OH
.
Câu 70. Chọn A
Ta có
//
BC B C
//
BC AB C
suy ra
,
d BC AB
,
d BC AB C
,
d B AB C
,
d A AB C
.
I
A
C
B
C'
B'
A'
H
S
B
A
D
C
O
M
N
H
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 58
Gọi
I
và
H
lần lượt là hình chiếu vuông góc của
A
trên
B C
và
AI
.
Ta có
B C A I
và
B C A A
nên
B C A AI
B C A H
mà
AI A H
. Do đó
AB C A H
Khi đó
,
d A AB C
A H
2 2
.
A A A I
A A A I
2
2
3
.
2
3
2
a
a
a
a
21
7
a
.
Vậy khoảng cách cần tìm là
21
7
a
.
Câu 71. Chọn B
Không mất tính tổng quát, giả sử
1
a
.
Gọi
H
là trung điểm của
AB
. Kẻ
HM BC M BC
;
HN SM N SM
.
Tam giác
SAB
cân tại
S
và nằm trong mặt phẳng vuông góc với đáy nên
SH ABCD
.
Áp dụng định lý hàm số
cos
:
2 2 2
1 1 1 7
2 . .cos120 1 2.1.
4 2 2 4
DH DA AH DA AH
7
2
DH
Theo đề bài:
60
SDH
7 21
.tan 60 . 3
2 2
SH DH
Lại có:
1 3 3
.sin 60 .
2 2 4
HM HB
.
Ngoài ra:
BC SHM BC HN
HN SBC
;
2 2 2
1 1 1 116
21HN SH HM
609
58
HN
.
Chú ý rằng
//
AD SCB
nên khoảng cách giữa
AD
và
SC
là khoảng cách giữa
A
và mặt phẳng
SBC
,
bằng 2 lần khoảng cách từ
H
(theo định lý Ta-let),
609
2
29
d HN
Câu 72. Chọn D
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 59
Gọi là hình chiếu của trên mặt đáy. Vì nên
HA HB HC HD
. Suy ra hình
bình hành nội tiếp trong đường tròn tâm . Vì vậy là hình chữ nhật.
Kẻ vuông góc với tại (1).
Ta có (2).
Từ (1) và (2) ta có: .
Kẻ vuông góc với tại .
Ta có:
.
Ta có: .
.
Câu 73. Chọn D
Gọi
' 'I AB A B
;
H
là trung điểm của
BC
.
// ' ' // ( ' )IH A C A C B AH
' ; ' ';( ' ) ;( ' )
.
A C AB A B AH B B AH
d d d
Kẻ
'BK B H
, với
'K B H
.
H
S
6
SA SB SC SD
ABCD
H
ABCD
KP
SA
P
BK AC
BK SAC BK KP
BK SH
( , )
d SA BK KP
HQ
SA
Q
2 2 2 2
1 1 5 119
,
2 2 2 2
AH AC AB BC SH SA AH
. 5 119
24
SH HA
HQ
SA
2
2 2
. 32
. .2 2.
25
KP KA KA AC KA AC AB
HQ HA AC HA AC AC
32 4 119
( , )
25 15
d SA BK KP HQ
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 60
Chứng minh:
;( ' )
2 2 2
2
2 .
' . 2
2
( ' )
17
'
(2 )
2
B B AH
a
a
B B BH a
BK B AH d BK
B B BH
a
a
Vậy
( ' ; ')
2
17
A C AB
a
d .
Câu 74. Chọn B
; 45
SC ABC SCH
Ta có:
1 4
3 3
BH AB
2
2 2 2
4 4 4 7
2 . .cos 4 2. .4.cos 60
3 3 3
CH BH BC BH BC HBC
2 34
.tan 45
3
SH CH
Dựng hình thoi
ACBD
(với
D
là đỉnh thứ 4 của hình thoi)
/ / / /
AD BC BC SAD
Vậy
3
; ; ; ;
2
d SA BC d BC SAD d B SAD d H SAD
Gọi
M
là trung điểm của
AD
BM AD
(
ΔDAB
đều).
Từ
H
dựng
/ /HI BM HI AD
Ta có:
AD HI
AD SIH SAD SIH
AD SH
Từ
H
dựng
HK SI HK SAD
Vậy
;
d H SAD HK
Ta có:
8
2 3.
. 4 3
3
/ /
4 3
AH HI BM AH
HI BM HI
AB BM AB
2 2 2 2
4 7 4 3
.
. . 2 210
3 3
15
4 7 4 3
3 3
SH IH SH IH
HK
SI
SH HI
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 61
3 210
; BC
2 5
d SA HK
Câu 75.
Ta có
,
SA
AB
SAB
SA AB SAB
SA A
BC
BC
B
B
C
A
.
Trong
SAB
, dựng
BH SM
và cắt
SM
ở
H
.
Ta có
, .
BH SM
d SM BC BH d BH
BH BC
Ta có
1
BH BM SA BM
BMH SMA BH
SA SM SM
∽
.
Xét
ABC
vuông tại
B
có
0
sin sin 60 2 3
AB
AA BB
AC
C
.
3
2
AM BM
.
Xét
SAM
vuông ở
A
có
2
2 2 2 2
3 7
2
7
.
4 2
1S SM SA AM M
Thế vào
1
, ta có
3
1
3 21
2
.
7
7 7
2
SA BM
BH
SM
Cách 2: (Nguyễn Văn Thịnh)
Nhận xét: Các dạng toán về khoảng cách nếu có thể thì nên sử dụng các quan hệ song song và tỉ lệ để đưa
về tính khoảng cách từ chân đường cao của hình chóp.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 62
Gọi
N
là trung điểm của
AC
.
Ta có
// , , , ,BC SMN d BC SM d BC SMN d B SMN d A SMN
.
Kẻ
AH SM
,
H SM
, ta có
AH SMN
,
d A SMN AH
.
Ta có
.sin 2.sin 60 3AB AC C
3
2
AM
.
Xét tam giác
SAM
vuông tại
A
có
AH
là đường cao, suy ra
2 2
. 21
7
SA AM
AH
SA AM
.
Vậy
21
,
7
d BC SM
.
Câu 76.
Gọi
M
là trung điểm
CD
,
O
là trung điểm
BD
. Do
.S ABCD
là khối chóp tứ giác đều nên
ABCD
là hình
vuông và
SO ABCD
.
Do
2 2
.
.
.
3 3 3
ABCD
S ABCD
S SO
a SO a b
V SO b
.
Ta có
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 63
BE// CD BE// SCD
BE// GF
BEFG SCD GF
mà
BE// CD GF // CD
.
Do
G
là trọng tâm
SCD
nên
2
3
SG
SM
mà
//GF CD
nên
2
3
GF SF SG
DM SD SM
.
Trên tia đối của tia
DC
lấy điểm
N
sao cho
2
3
DN GF DM
. Từ đó ta có
DNFG
và
BEND
là hai hình
bình hành và
//
BDG NEF
.
Trên đoạn thẳng
OD
lấy điểm
K
sao cho
1
3
KD DF
OD SD
, từ đó ta có
//FK SO
mà
SO ABCD
suy ra
( )FK ABCD
.
Hạ
KP EN
và
KH PF
, do
( )FK ABCD
nên
FK KP
.
Do
EN KP
EN FKP EN KH
EN FK
mà
KH PF
suy ra
KH NEF
.
Khi đó:
,EF , , ,
d DG d DG NEF d BDG NEF d K NEF KH
.
Ta có:
2 2
.
3 3 2 3 3
CD CD a
BE GF MD
Do
//FK SO
nên
1
3
FK DF
SO DS
, suy ra
1
3 3
b
FK SO
.
Hạ
EJ BD
. Do
2 2
// , ,EJ BD KP .sin 45 .
3 2 6
a a
EN BD KP EN EJ BE
.
Áp dụng hệ thức lượng vào tam giác vuông
FKP
với đường cao
KH
ta có:
2 2
2 2
2 2 2 2 2
2 2
9 2
1 1 1 1 1
3 2
2
3
6
b a
ab
KH
KH KF KP a b
b
b a
a
Vậy
2 2
,EF
3 2
ab
d DG
b a
.
Câu 77. Cách 1:
Gọi
H
là trung điểm
AB
.
Vì
SAB ABC
nên
SH ABC
.
Chọn hệ trục tọa độ
Oxyz
, với
O H
,
,
HC Oy
,
HS Oz
.
z
y
x
H
B
S
A
C
M
N
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 64
Ta có:
2 2
3HC AC AH a
;
tan
AH
SH a
ASH
.
Khi đó:
0;0;0
H
,
0;0;S a
,
3;0;0
A a ,
3;0;0
B a ,
0;3 ;0
C a
,
3
0; ;
2 2
a a
M
,
9
0; ;
4 4
a a
N
.
Suy ra:
3
3; ;
2 2
a a
AM a
,
9
3; ;
4 4
a a
BN a
,
2 3;0;0
AB a
,
2 2 2
3 3 3 15 3
, ; ;
4 4 4
a a a
AM BN
.
Khoảng cách giữa hai đường thẳng
,AM BN
là
3
2
3 3
, .
2 237
2
,
79
711
,
4
a
AM BN AB
a
d AM BN
a
AM BN
.
Cách 2:
Gọi
P
là trung điểm của
AC
,
G
là trọng tâm tam giác
ABC
.
Kẻ
/ /NK SH
,
K HC
;
/ /
EK AC
,
E BP
.
Suy ra:
/ / / / , , ,
NP AM AM NPB d AM BN d M NPB d C NPB
.
Ta có:
/ /NK SH
nên
1
1
4 4
5
4
8
a
NK SH
NK KC CN
GK
SH CH CS
GC
.
/ /
EK AC
nên
5 5 5 3
8 8 8
EK GK a
EK PC
PC GC
.
2 2
79
8
a
NE NK EK
;
3BP HC a
.
Vì:
KN BP
BO NPB BP EN
KE BP
.
Diện tích tam giác
NBP
là:
1 3 79
.
2 16
NBP
a
S NE BP
.
Thể tích tứ diện
.
N CPB
là:
3
.
1 1 1 1 1 3
, . . .SH. . .PC .a.3a.a 3
3 3 4 2 24 8
N CPB CBP
a
V d N ABC S BP
.
I
E
G
K
P
H
S
A
B
C
M
N
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 65
Khoảng cách từ
C
đến
NBP
là:
.
3
2 237
,
79
N CPB
NBP
V
a
d C NBP
S
.
Vậy khoảng cách giữa hai đường thẳng
,AM BN
là
2 237
79
a
.
Cách 3:
Kẻ
KI NE
,
I NE
.
Khi đó:
8
/ / / / , , , ,
5
NP AM AM NPB d AM BN d M NPB d C NPB d K NPB
.
Ta có:
,
KI NE
KI NPB d K NPB KI
KI BP
.
Suy ra:
8
/ / / / ,
5
NP AM AM NPB d AM BN KI
.
Trong tam giác vuông
NKE
ta có:
2 2 2 2
1 1 1 1264 5 237 2 237
,
75 316 79
a a
KI d AM BN
KI KN KE a
.
Câu 78.
Gọi
,I G
lần lượt là trung điểm của
AC
và trọng tâm của tam giác
ABC
.
Ta có
DG ABC
và
1 9 2
.
3 4
ABCD ABC
V DG S
.
Gọi
N
là trung điểm của
AD
||MN AC
||AC BMN
.
, , , ,
d AC BM d AC BMN d A BMN d N BMN h
.
Gọi
K
là trung điểm của
MN
, ta có
2 2
1 1 9 11
. . .
2 2 16
BMN
S BK MN BM MK MN
.
Ta có:
. . 2.2.1 4
DACB
DNMB
V
DA DC DB
V DN DM DB
1
4
DACB DBMN
V V
9 2 1
. .
16 3
BMN
h S
.
9 2 1 9 11 3 22
. .
16 3 16 11
h h
.
Câu 79.
Chọn D
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 66
Gọi
H
là trung điểm của
AB
, vẽ
HE CD
tại
E
,
HK SE
tại
K
.
Ta có
SBC
đều nên
11
BC
,
SAC
vuông cân tại
S
nên
11 2
AC
.
Trong
SAB
,
2 2 2
2 . .cos120
AB SA SB SASB
11 3
AB .
ABC
có
2 2 2
AB AC BC
nên
ABC
vuông tại
C
, từ đó
H
là tâm đường tròn
ABC
SH ABCD
CD SHE
CD HK
HK SCD
.
Ta có
, ,
d AB SD AB SCD
,
H SCD HK
.
Ta có
,
HE d A CD
2 2
.AC AD
AC AD
2 2
11 2.11 11 6
3
2.11 11
,
11
2 2
SA
SH
.
2 2
.SH HE
HK
SH HE
11 11 6
.
2 3
22
121 121.2
4 3
.
Vậy
, 22
d AB SD .
Câu 80.
Gọi
H
là hình chiếu vuông góc của
A
lên
( ).BCD
Khi đó ta có
H
là trực tâm của tam giác
.BCD
Với mọi đường thẳng
nằm trong
( )BCD
thì
( ; ) .d A AH
Do đó đường thẳng
thỏa mãn phải đi qua
điểm
.H
Kẻ
( )HK AD K AD
khi đó
,H K
là hai điểm cố định lần lượt nằm trên
& .AD
A
B
C
D
H
K
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 67
Hiển nhiên, khoảng cách giữa
&
AD
là độ dài đoạn vuông góc chung của chúng nên
( ; ) .d AD HK
Dấu
bằng xảy ra khi
.
HK
Ta có
2 2 2 2 2 2
2 2
1 1 1 1 1 1 1 14
( ) ( )
3 2
a a
AH AB AC AD a a
.
14
a
AH
Ta có:
1 13 13
cos sin .sin .
14
14 14
AH a
HAK HAK HK HA HAK
AD
3 4
.
14 7
a a
d
Câu 81. Chọn D
Do
11
SB SC
và
0
60
SBC nên
SBC
đều, do
đó
BC
Ta lại có,
11
SA SC
và
0
45
SCA
nên
SAC
vuông cân tại
,S
hay
11 2.
AC
Mặt khác,
11
SA SB
và
0
30
SAB nên
11 3.
AB
Từ đó, ta có
2 2 2
AB BC AC
suy ra
ABC
vuông
tại
.C
Gọi
H
là trung điểm của
.AB
Khi đó,
H
là tâm
đường tròn ngoại tiếp
.ABC
Vì
SA SB SC
nên
( ).SH ABC
Gọi
M
là điểm trên
CD
sao cho
,HM AB
suy ra
.HM CD
Gọi
N
là chân đường vuông góc hạ từ
C
xuống
.AB
Khi đó,
/ /HM CN
và
.HM CN
Do
ABC
vuông tại
C
nên theo công thức tính diện tích ta có:
2 2
. 11 6
3
CACB
HM CN
CA CB
Ta lại có,
1 11 3
2 2
CH AB
nên
2 2
11
.
2
SH SC CH
Trong tam giác vuông
,SHM
dựng đường cao
HI
( ),I SM
suy ra
( ).HI SCD
Khi đó,
2 2
.
( , ) ( ,( )) ( ,( )) 22.
SH HM
d AB SD d AB SCD d H SCD HI
SH HM
Vậy
( , ) 22.
d AB SD
Câu 82.
A. Phân tích bài toán:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 68
1. Vẽ hình hộp, yếu tố vẽ hình quan trọng, giúp bạn tư duy “nét” nhất cho bài toán. Các cạnh của hình hộp
bằng 1 và góc phẳng tại đỉnh
A
bằng
60
cho ta thêm dữ kiện hình hộp xiên có đáy là hình thoi.
2. Kiến thức khoảng cách giữa hai đường thẳng chéo nhau
a
và
b
.
Cách 1: Là độ dài đoạn vuông góc chung giữa
a
và
b
.
HK a
;
HK b
( , )d a b HK a
.
Cách 2: Là khoảng cách từ đường thẳng này đến mặt phẳng song song với nó chứa đường thẳng còn lại.
/ / a
,
b I
,
,P b
, , ,d a b d a P d A P AH
.
Cách 3: Là khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đã cho.
, , ,d a b d P Q d A Q AH
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 69
Trong quá trình dẫn dắt ra lời giải bài toán ta giới thiệu cả 3 cách xác định khoảng cách.
Cách sử dụng trong bài toán này là cách 2. Tính khoảng cách từ đường thẳng tới mặt phẳng song song với
đường thẳng ấy.
3. Kiến thức khoảng cách từ 1 điểm đến đến một mặt phẳng. Không xác định trưc tiếp khoảng cách từ điểm
đó tới mặt phẳng mà xác định gián tiếp từ điểm khác mà ta nhìn được khoảng cách dễ dàng hơn, còn gọi là
đổi điểm.
; ;d A C AB d A C ACB
;d C ACB
;d B ACB
.
.
4. Thu gọn bài toán tính các yêu tố trong hình hộp xiên sang tính các yếu tố trong hình tứ diện. Hay ta có bài
toán mới đơn giản hơn và có nhiều cách giải hơn.
Tính chiều cao hạ từ đỉnh
B
của tứ diện
BACB
biết các góc tại đỉnh
B
là
60CBB
,
120B BA ABC
và các cạnh bên
BA BC BB a
.
Vậy bài toàn phức tạp đã đưa về một bài toán đơn giản mà ta đã biết cách giải.
Ở bài toán mới học sinh cần vận dụng kiến thức về hình học phẳng như
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 70
Định lí hàm số cosin:
Cho
ABC
có
AB c
,
AC b
,
BC a
với các góc của tam giác là
A
,
B
,
C
ta có:
2 2 2
2 cosa b c bc A
Các công thức tính diện tích tam giác:
1
.
4 2
ABC a
abc
S h a
R
(
a
h chiều cao của tam giác hạ từ đỉnh
A
;
R
là bán kính đường tròn ngoại tiếp
ABC
), từ đó tính ra chiều cao của tứ diện.
Sau khi phân tích bài toán, học sinh sẽ tự trình bày lời giải như sau:
Có
/ /AC A C
/ /A C AB C
; ;d A C AB d A C ACB
;d C ACB
;d B ACB
Xét tứ diện
.B ACB
có
+)
1BA BC BB
nên điểm
B
nằm trên trục của đường tròn ngoại tiếp
ACB
. Suy ra
BO ACB
tại tâm
O
của đường tròn ngoại tiếp
ACB
.
+)
60CBB
,
120B BA ABC
nên áp dụng định lý hàm số cosin trong tam giác
B BA
và
ABC
ta
có 3AB AC
.
;d B ACB BO
2 2
BA R
với
R
là bán kính của đường tròn ngoại tiếp tam giác
ACB
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 71
. . .
4 2
ACB
AB CB AC AH B C
S
R
1
3
3 3
4
4 2R
3
11
R
9 2
1
11 11
BO
22
11
BO
.
;d A C AB OB
.
Vậy khoảng cách giữa hai đường thẳng
AB
và
A C
là
22
11
.
Đáp án cần chọn là A.
Nhận xét
Bài toán này đã giúp người học ôn lại
+) Kiến thức về khoảng cách trong không gian.
+) Hệ thức lượng trong tam giác và giải tam giác.
Và quan trọng biết chuyển từ bài toán hình hộp xiên sang hình tứ diện, biết độ dài các cạnh.
Khai thác bài toán
Vẫn với hình vẽ và một phần lời giải của bài toán ban đầu, một số bài toán tương tự với các hướng dẫn kèm
theo cho học sinh ôn luyện.
Dạng 2.3 Khoảng cách của đường với mặt
Câu 83.
Ta có:
AB AD
AB SD
nên
AB SAD
.
Kẻ
DH SA
tại
H
. Do
DH SAD
nên
AB DH
.
Ta có:
DH SA
DH SAB
DH AB
.
Do
/ /DC AB
nên
/ /DC SAB
.
Vậy khoảng cách giữa đường thẳng
CD
và mặt phẳng
SAB
là
DH
.
Xét
SAD
vuông tại
D
có:
2 2 2
1 1 1
DH SD AD
2 2
2
1 1 3
4
2
2
a
a
a
.
2
3
a
DH . Khoảng cách giữa đường thẳng
CD
và mặt phẳng
SAB
là
2
3
a
.
Câu 84. Chọn C
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 72
Gọi
O
là tâm hình vuông. Ta có:
/ / / /( )MO SB SB ACM
( ,( )) ( ,( )) ( ,( ))d SB ACM d B ACM d D ACM
( vì
O
là trung điểm
BD
)
Gọi I là trung điểm AD
/ / ( )
( ,( )) 2 ( ,( ))
MI SA MI ABCD
d D ACM d I ACM
Trong
kẻ
IK AC
tại K
Trong
( )MIK
kẻ
IH MK
tại H (1)
Ta có:
, ( ) (2)
AC MI AC IK AC MIK AC IH
Từ
(1) & (2) ( ) ( ,( ))
IH ACM d I ACM IH
Trong tam giác
MIK
ta có:
2 2
IM.IK
IH=
IM +IK
Biết
2
2
2
2
4
,
2 2 4 4 3
8
a
a
SA OD BD a a
MI a IK IH
a
a
Vậy:
2
( ,( ))
3
a
d SB ACM
| 1/72

Tài liệu khác của Toán 12

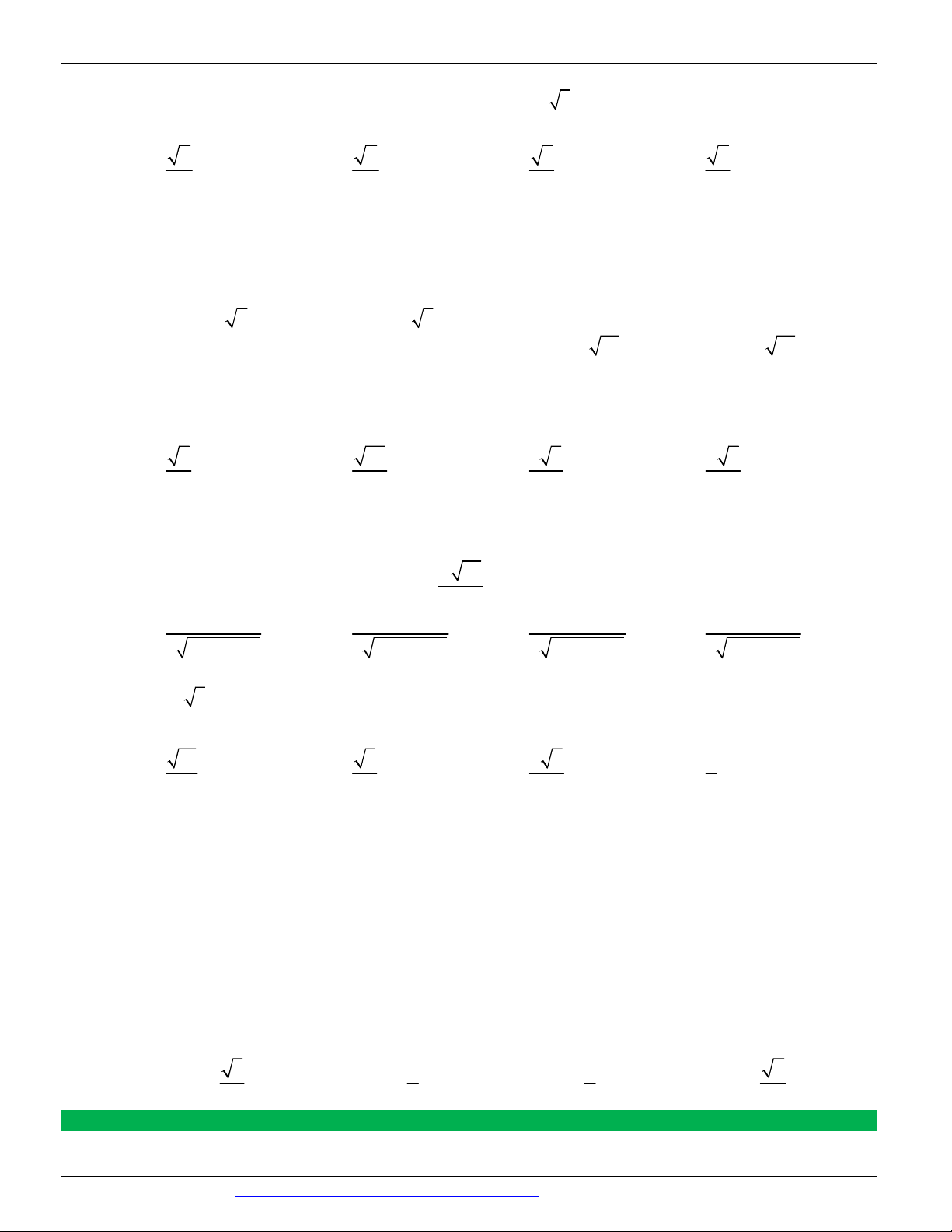
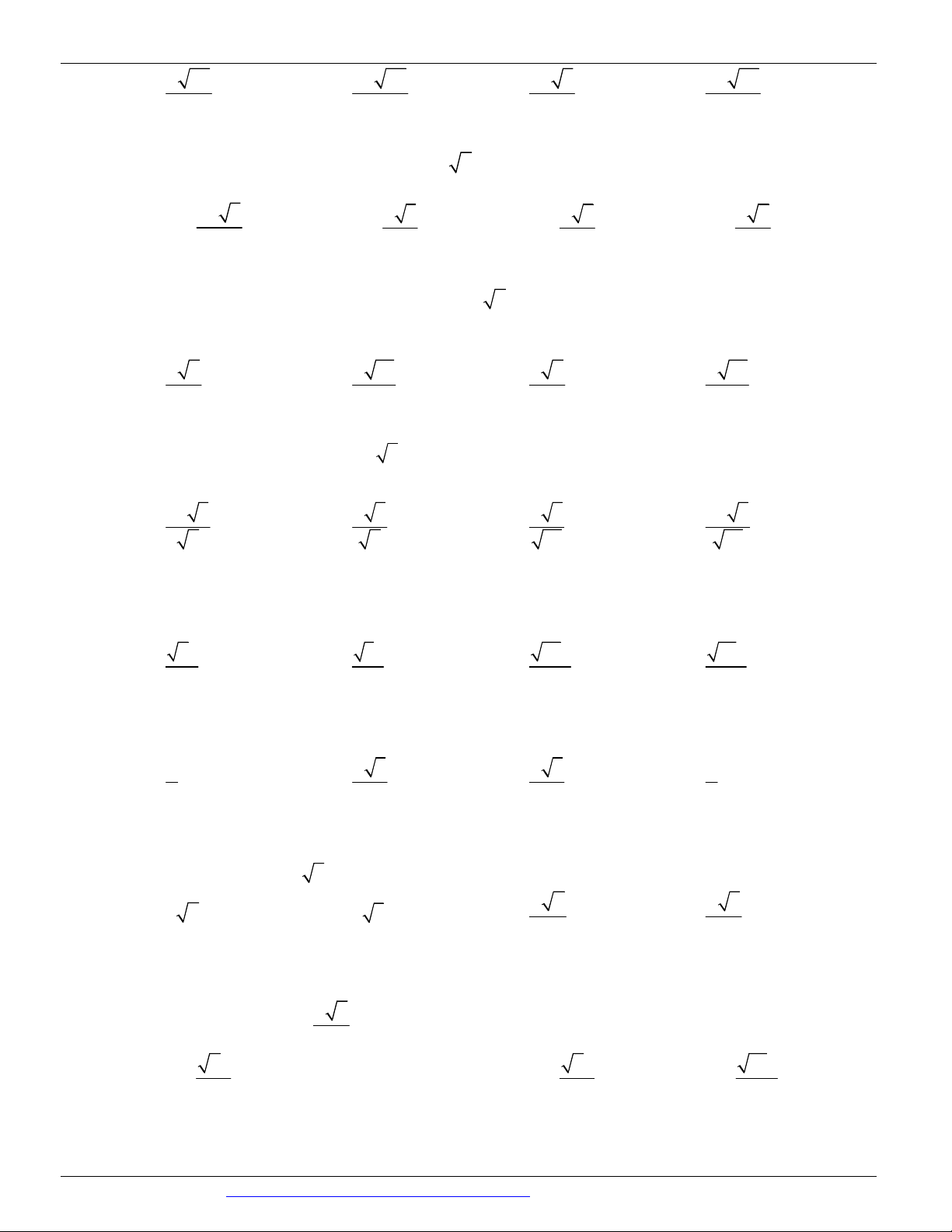
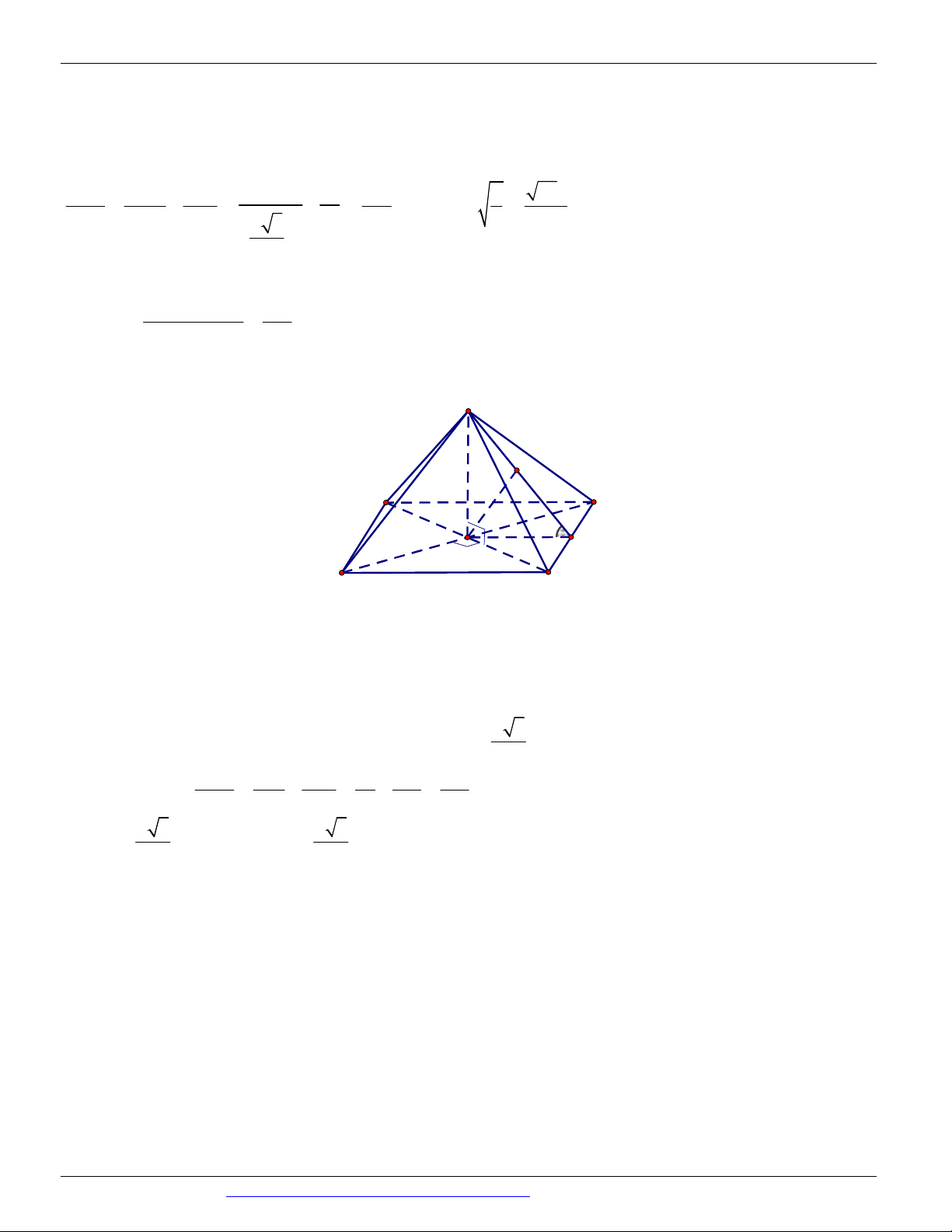
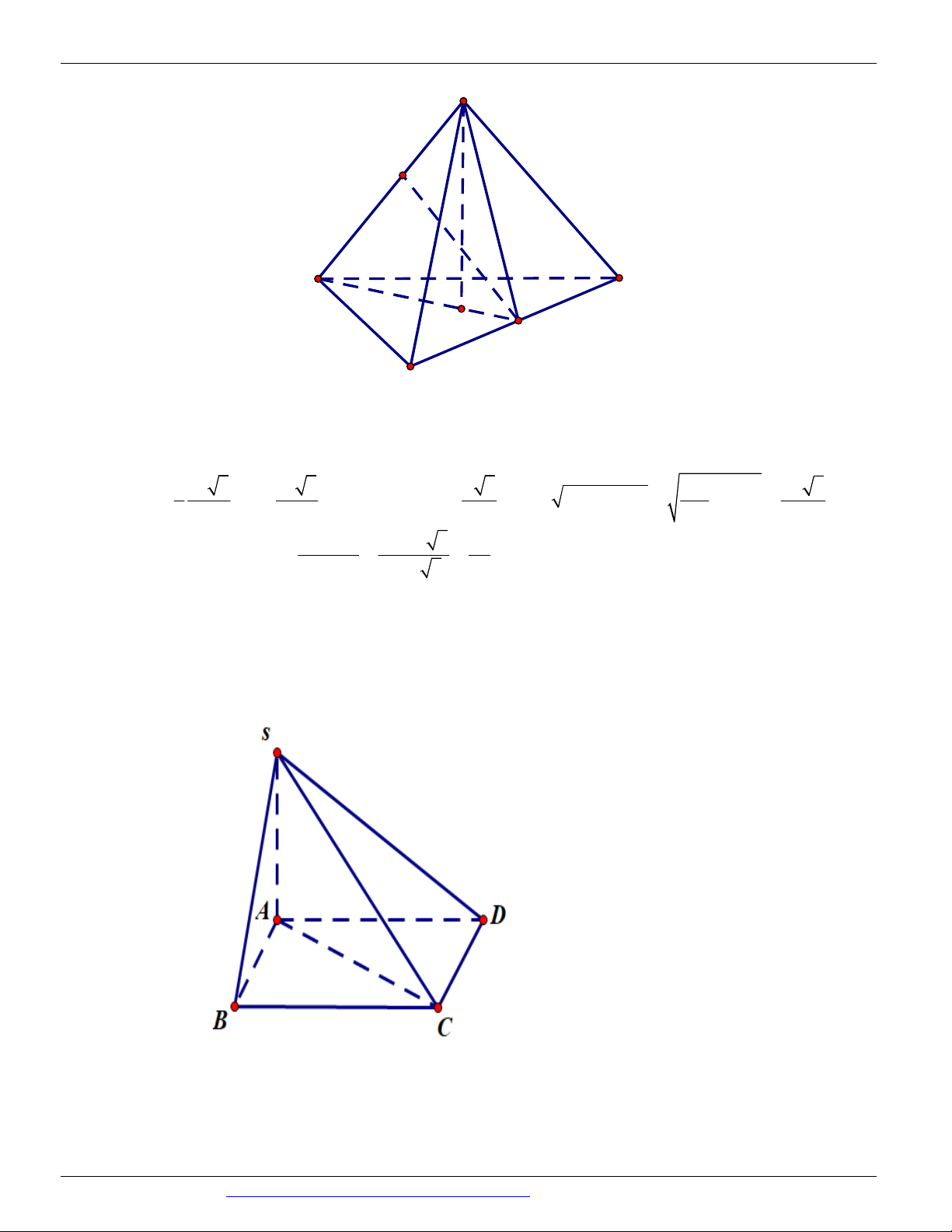
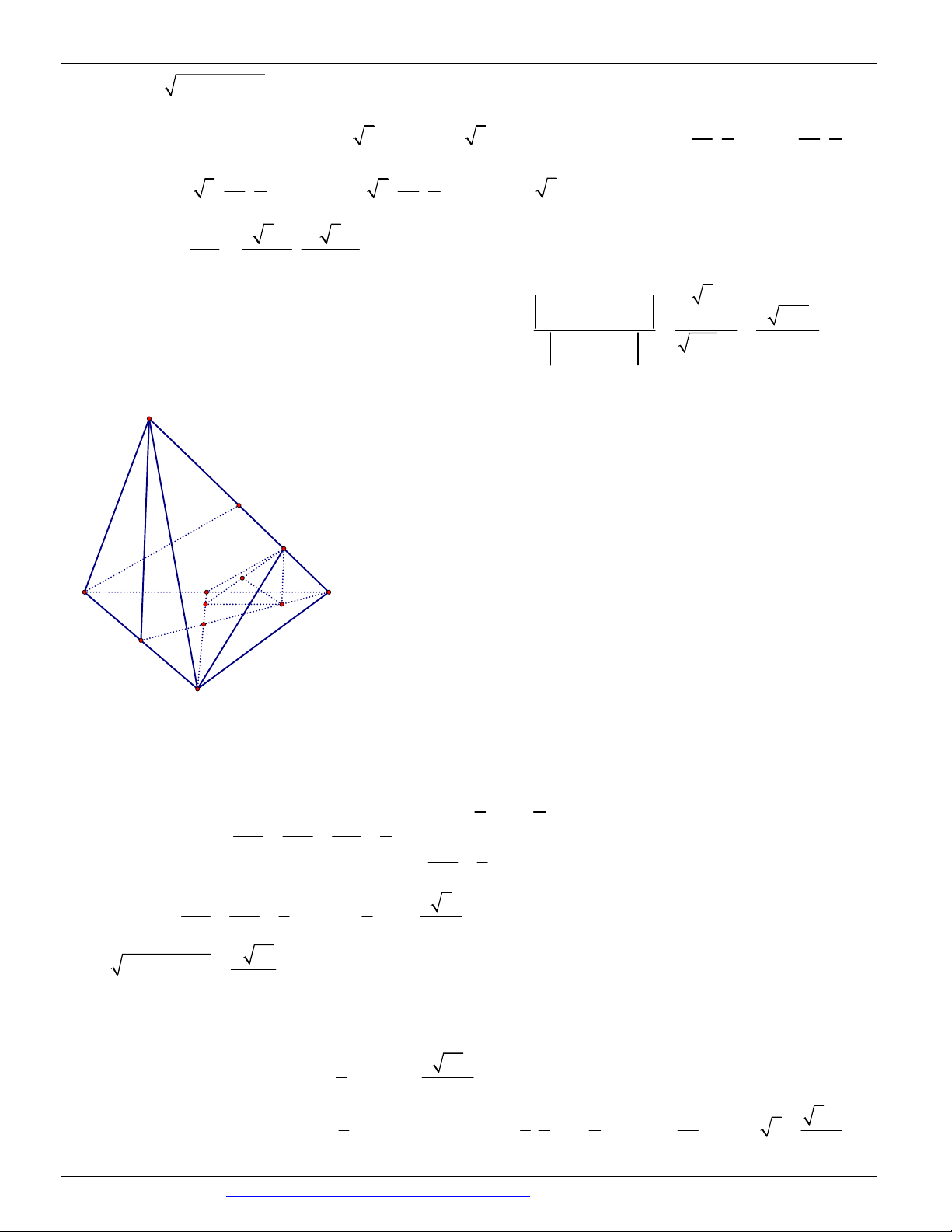
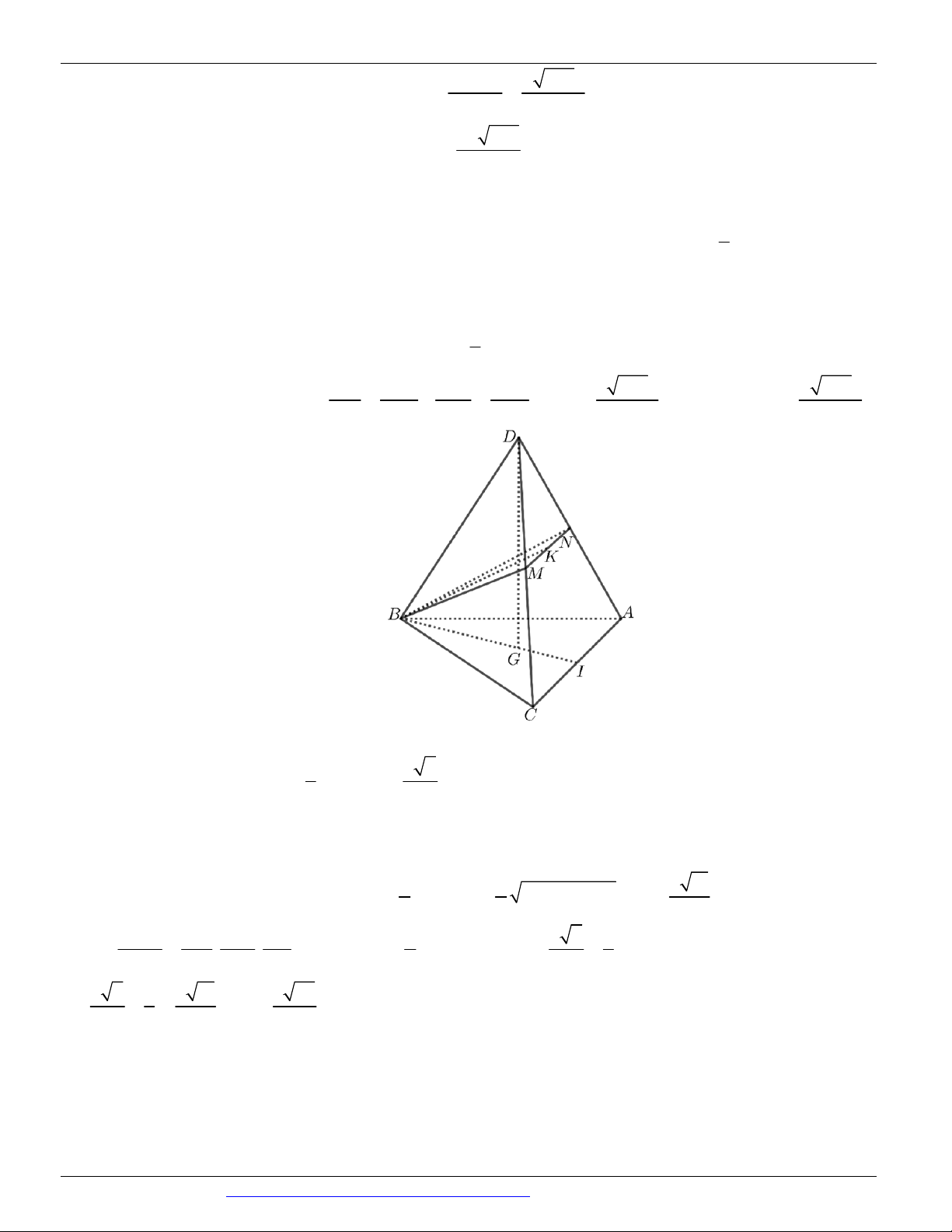
Preview text:

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 CHUYÊN
GÓC VÀ KHOẢNG CÁCH ĐỀ 6 MỤC LỤC
PHẦN A. CÂU HỎI ....................................................................................................................................................... 1
Dạng 1. Góc ..................................................................................................................................................................... 1
Dạng 1.1 Góc của đường thẳng với mặt phẳng ........................................................................................................ 1
Dạng 1.2 Góc của đường thẳng với đường thẳng .................................................................................................... 4
Dạng 1.3 Góc của mặt với mặt .................................................................................................................................. 5
Dạng 2. Khoảng cách...................................................................................................................................................... 8
Dạng 2.1 Khoảng cách từ điểm đến mặt phẳng ....................................................................................................... 8
Dạng 2.2 Khoảng cách của đường thẳng với đường thẳng ................................................................................... 11
Dạng 2.3 Khoảng cách của đường với mặt ............................................................................................................. 15
PHẦN B. LỜI GIẢI THAM KHẢO ...................................................................................................................................... 15
Dạng 1. Góc ................................................................................................................................................................... 15
Dạng 1.1 Góc của đường thẳng với mặt phẳng ...................................................................................................... 15
Dạng 1.2 Góc của đường thẳng với đường thẳng .................................................................................................. 25
Dạng 1.3 Góc của mặt với mặt ................................................................................................................................ 27
Dạng 2. Khoảng cách.................................................................................................................................................... 39
Dạng 2.1 Khoảng cách từ điểm đến mặt phẳng ..................................................................................................... 39
Dạng 2.2 Khoảng cách của đường thẳng với đường thẳng ................................................................................... 51
Dạng 2.3 Khoảng cách của đường với mặt ............................................................................................................. 71 PHẦN A. CÂU HỎI Dạng 1. Góc
Dạng 1.1 Góc của đường thẳng với mặt phẳng
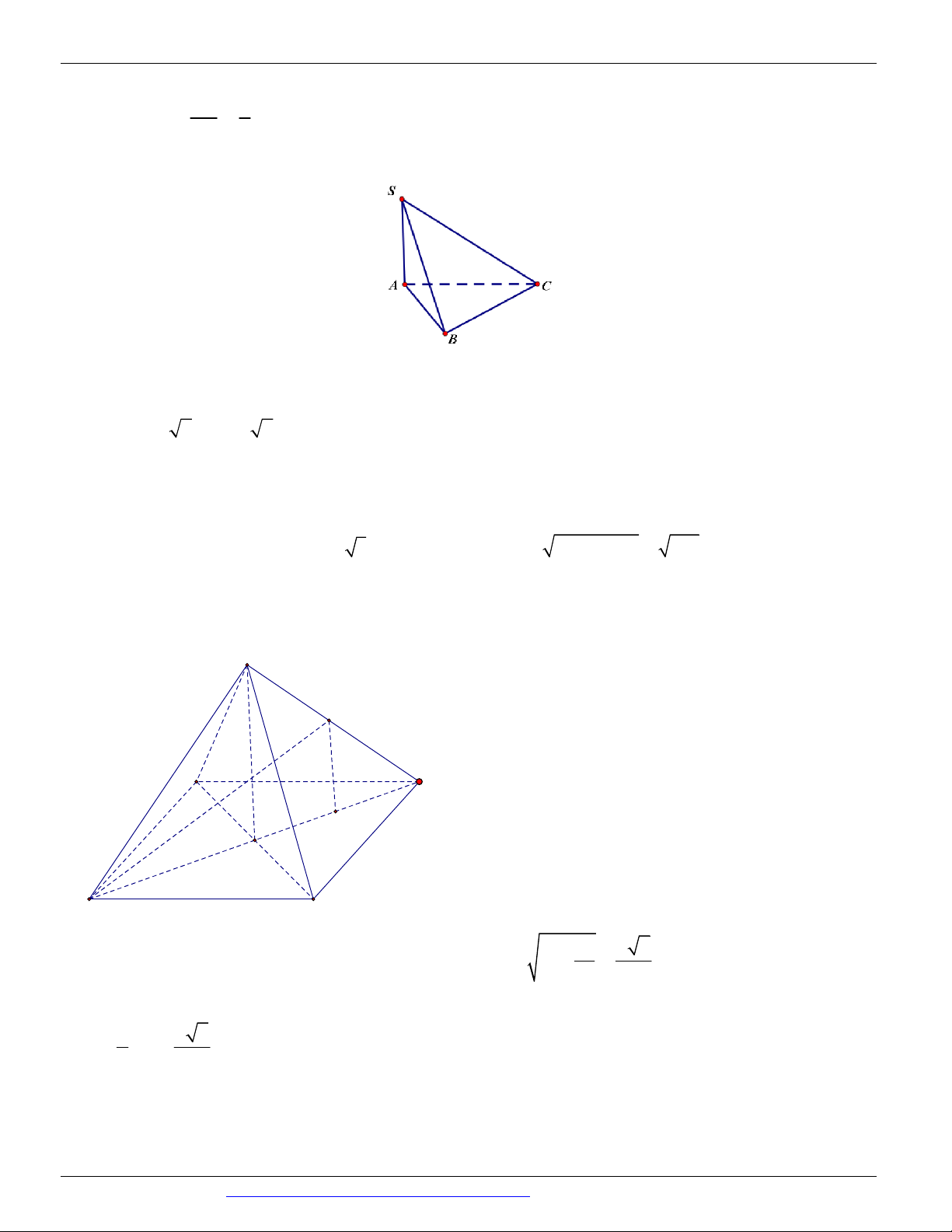
Câu 1. (MĐ 103 BGD&ĐT NĂM 2017-2018) Cho hình chóp S.ABC có đáy là tam giác vuông tại C ,
AC a , BC  2a , SA vuông góc với mặt phẳng đáy và SA a . Góc giữa đường thẳng SB và mặt phẳng đáy bằng A. 60 B. 90 C. 30 D. 45
Câu 2. (Mã đề 102 BGD&ĐT NĂM 2018) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA
vuông góc với mặt phẳng đáy và SA
2a . Góc giữa đường thẳng SC và mặt phẳng đáy bằng A. 45 B. 60 C. 30 D. 90
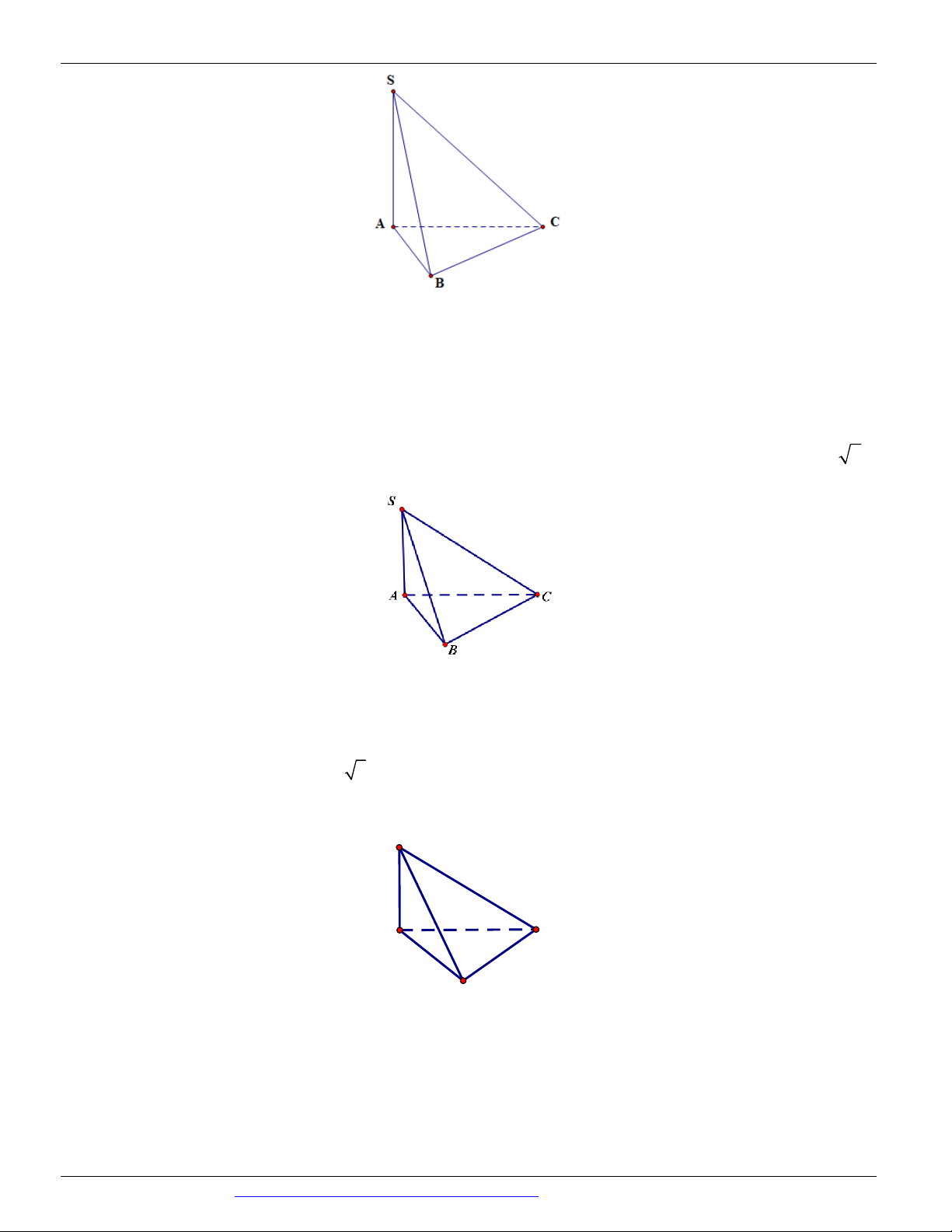
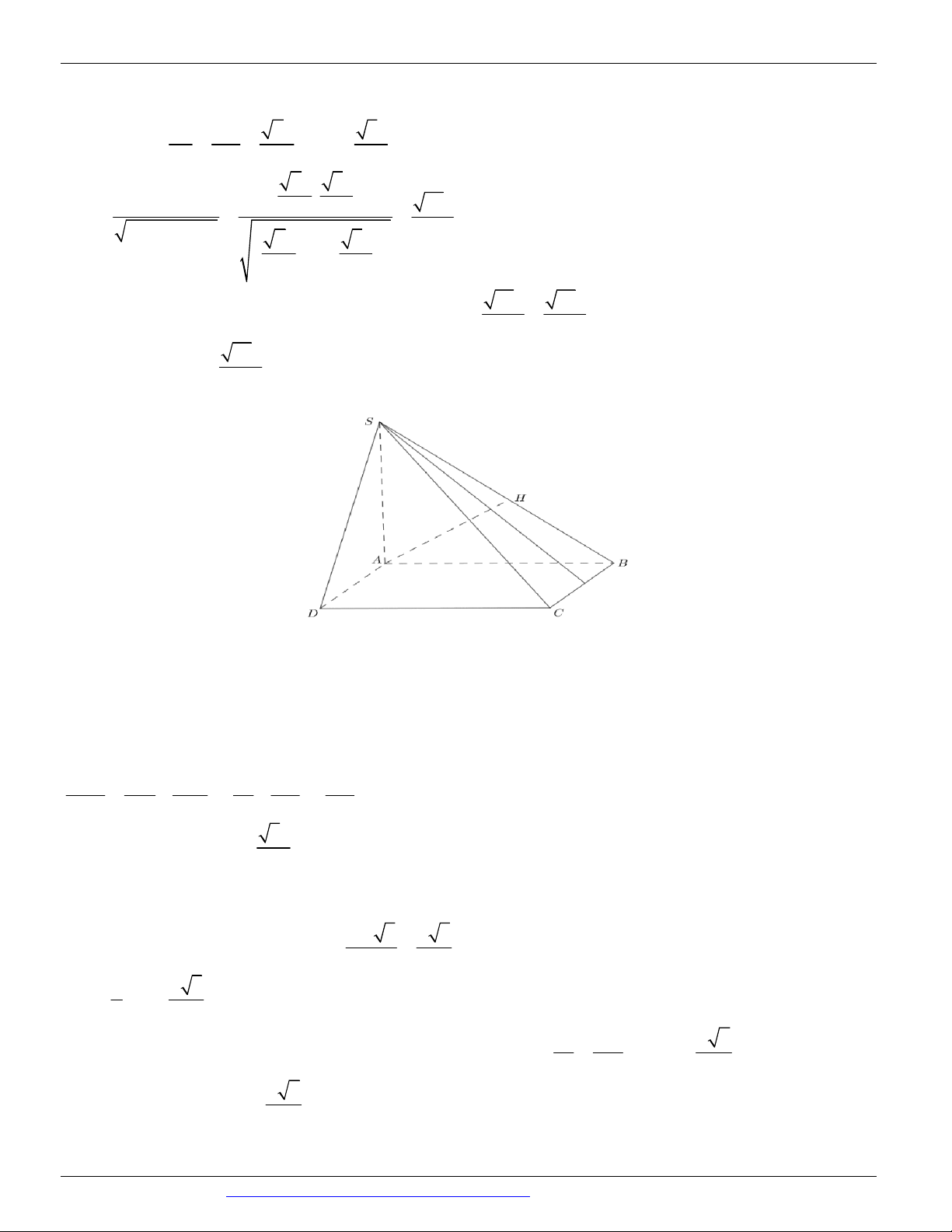
Câu 3. (Mã 102 - BGD - 2019) Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC  , SA  2a
, tam giác ABC vuông tại B , AB a và BC  3a (minh họa như hình vẽ bên).
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Góc giữa đường thẳng SC và mặt phẳng  ABC  bằng A. 30 . B. 60 . C. 45 . D. 90 .
Câu 4. (Mã đề 101 BGD&ĐT NĂM 2018) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA
vuông góc với mặt phẳng đáy và SB  2a . Góc giữa đường thẳng SB và mặt phẳng đáy bằng A. 45 B. 60 C. 90 D. 30
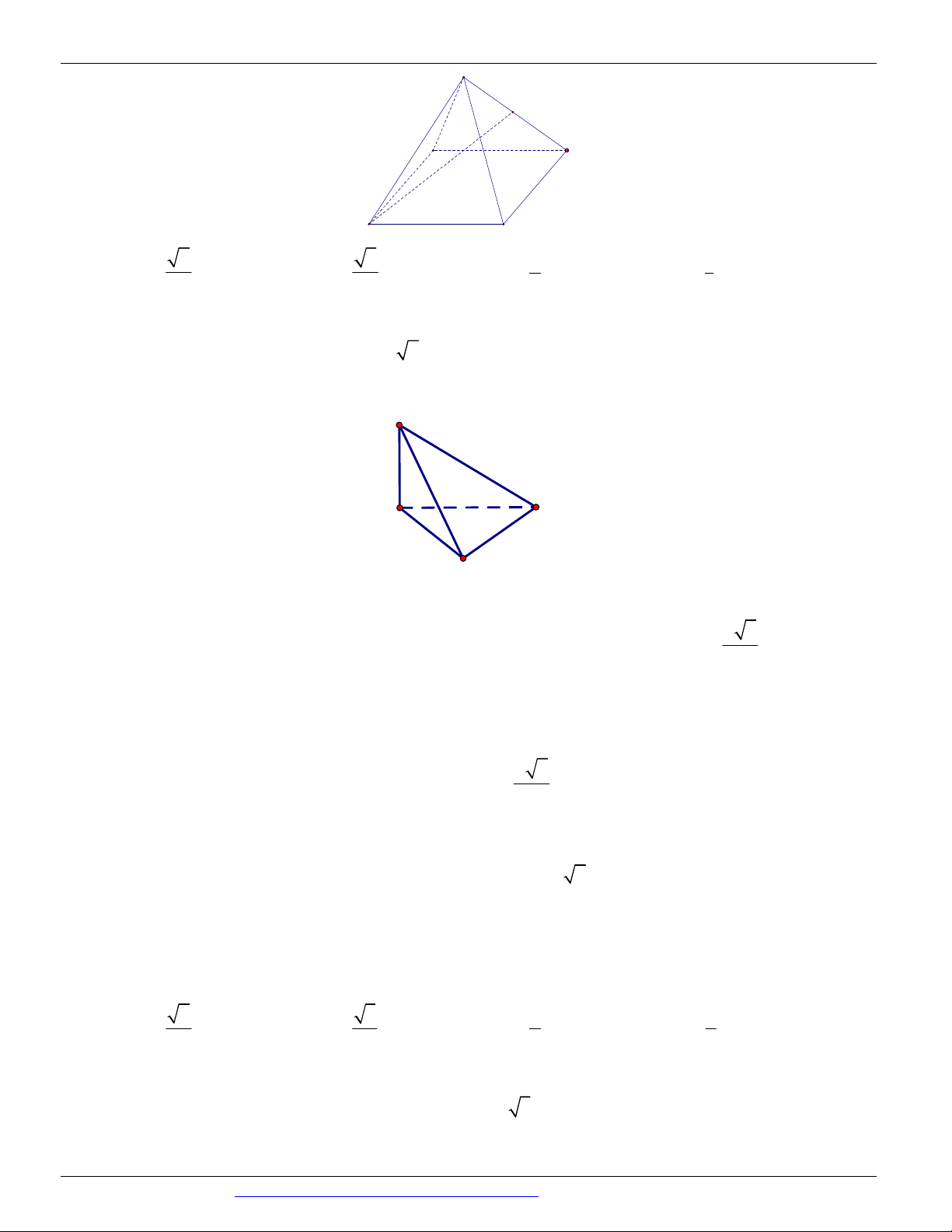
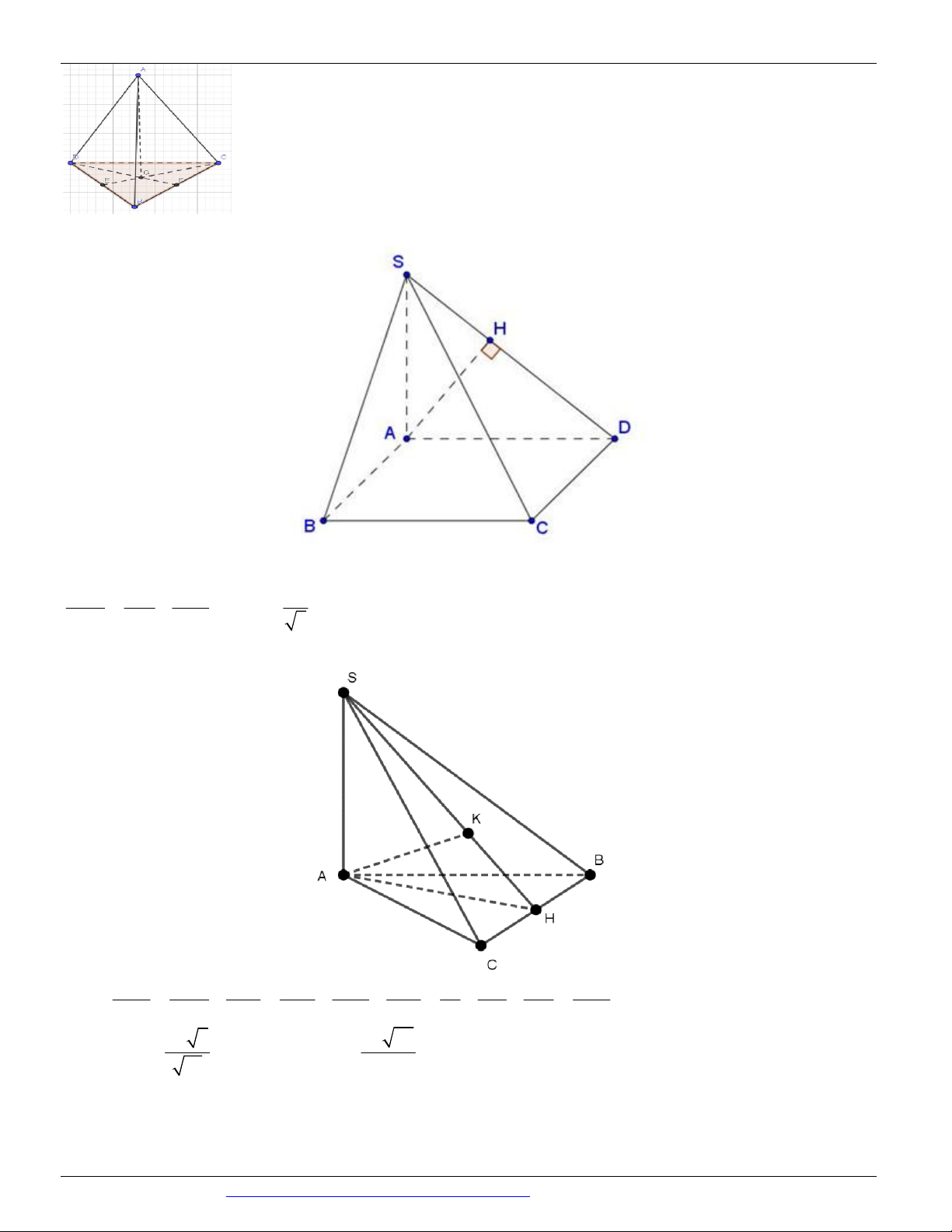
Câu 5. (Mã 103 - BGD - 2019) Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC . SA  2a
. Tam giác ABC vuông cân tại B và AB a ( minh họa như hình vẽ bên).
Góc giữa đường thẳng SC và mặt phẳng  ABC bằng A. 0 45 . B. 0 60 . C. 0 30 . D. 0 90 .
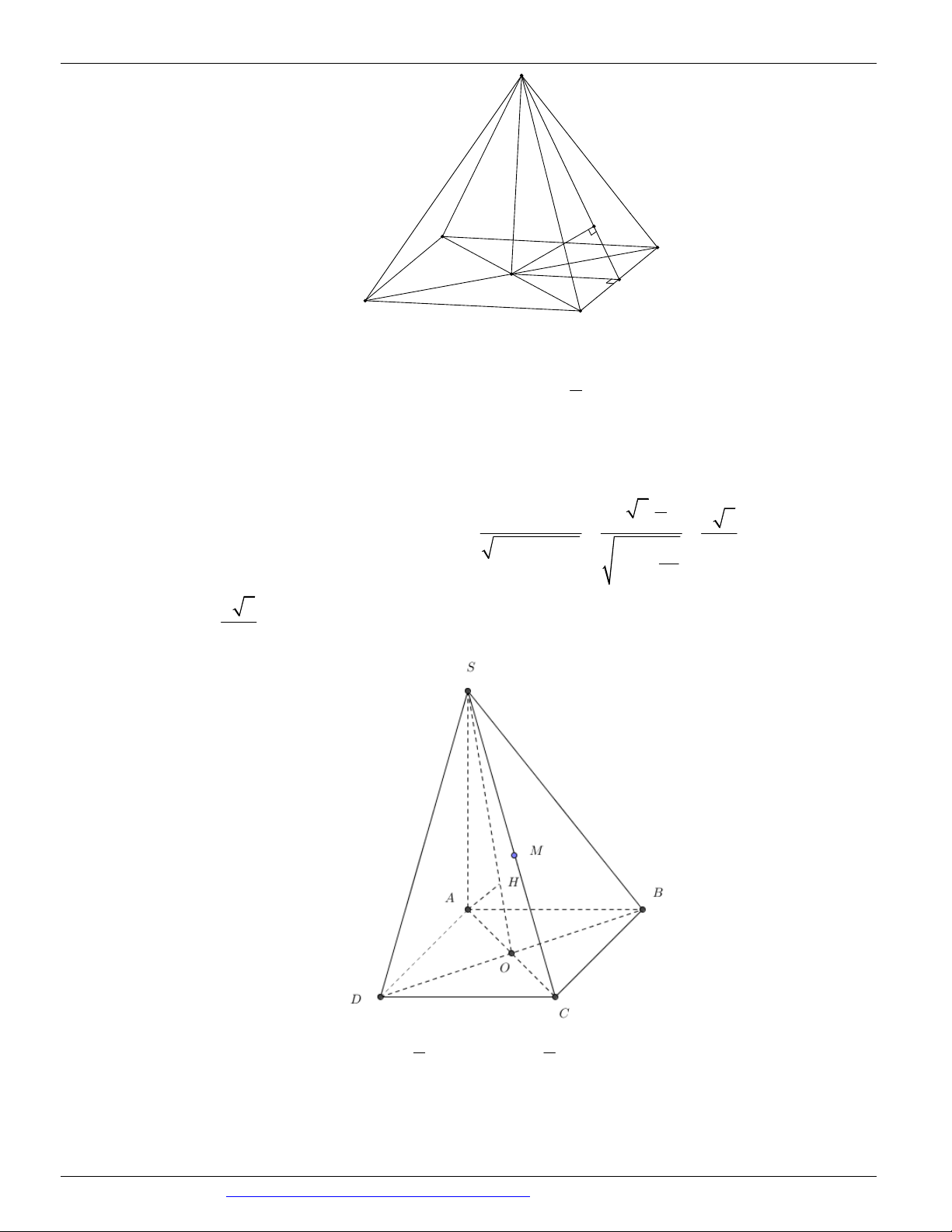
Câu 6. (Mã đề 101 - BGD - 2019) Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC  , SA  2a
, tam giác ABC vuông tại B, AB a 3 và BC a (minh họa như hình vẽ bên). Góc giữa đường thẳng SC
và mặt phẳng  ABC  bằng: S A C B A. 0 45 . B. 0 30 . C. 0 60 . D. 0 90 .
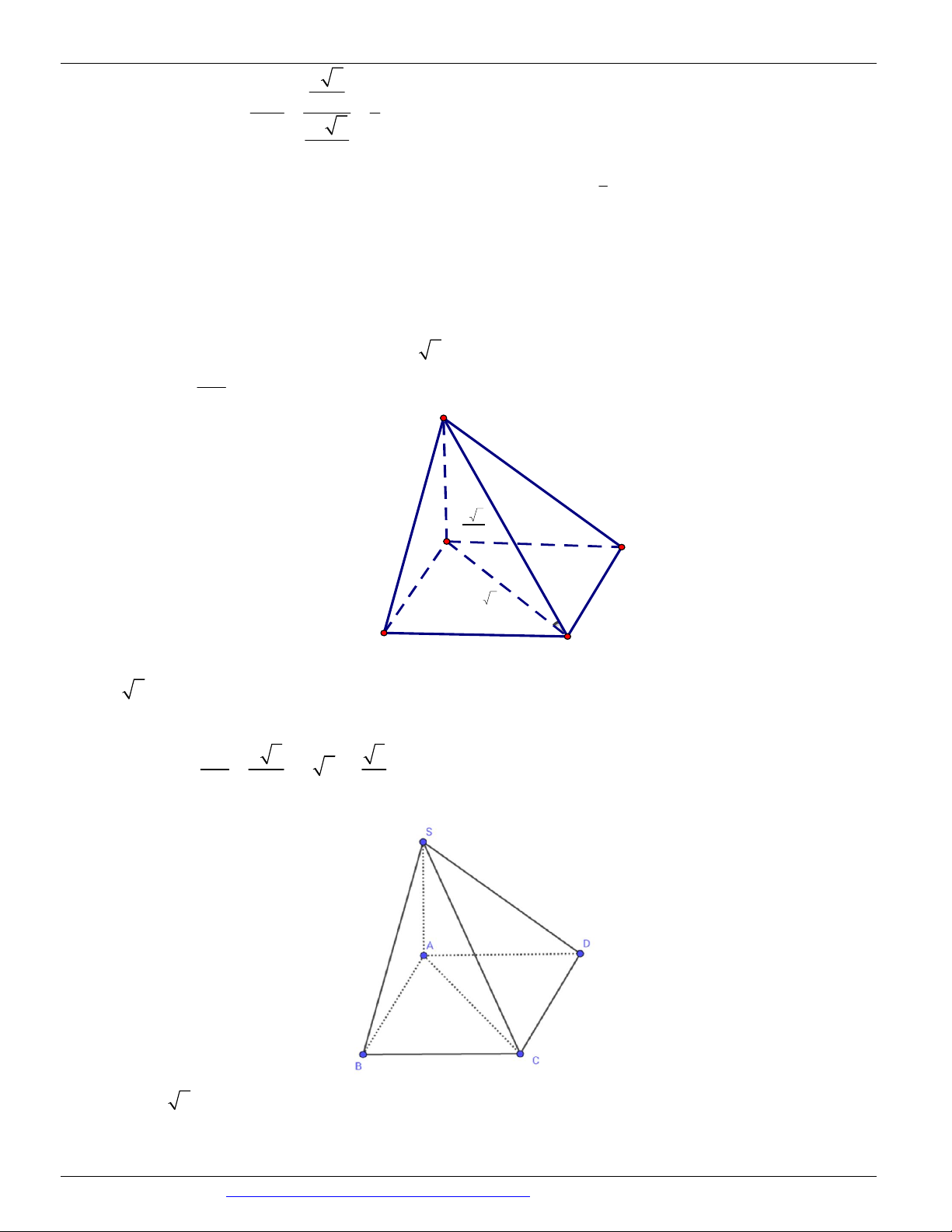
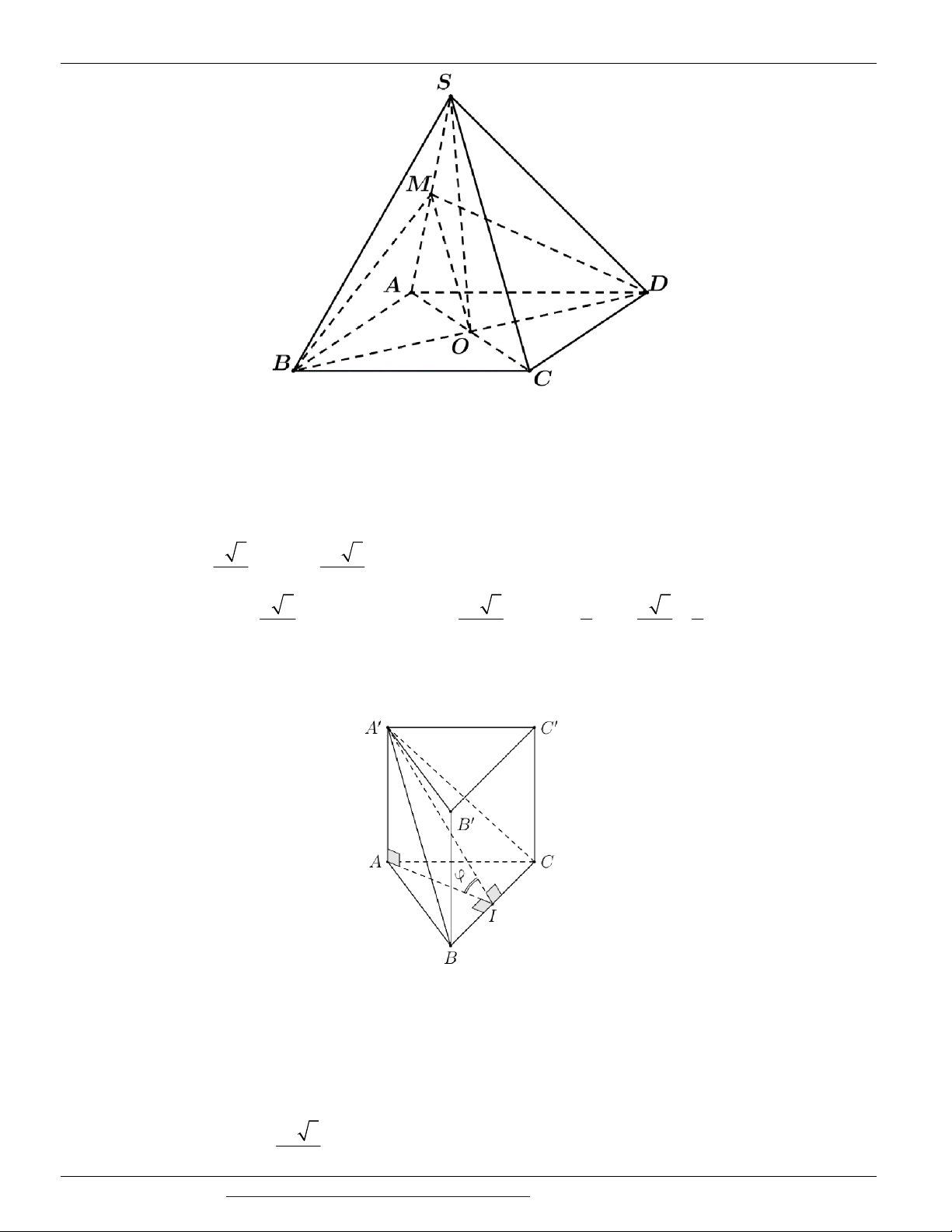
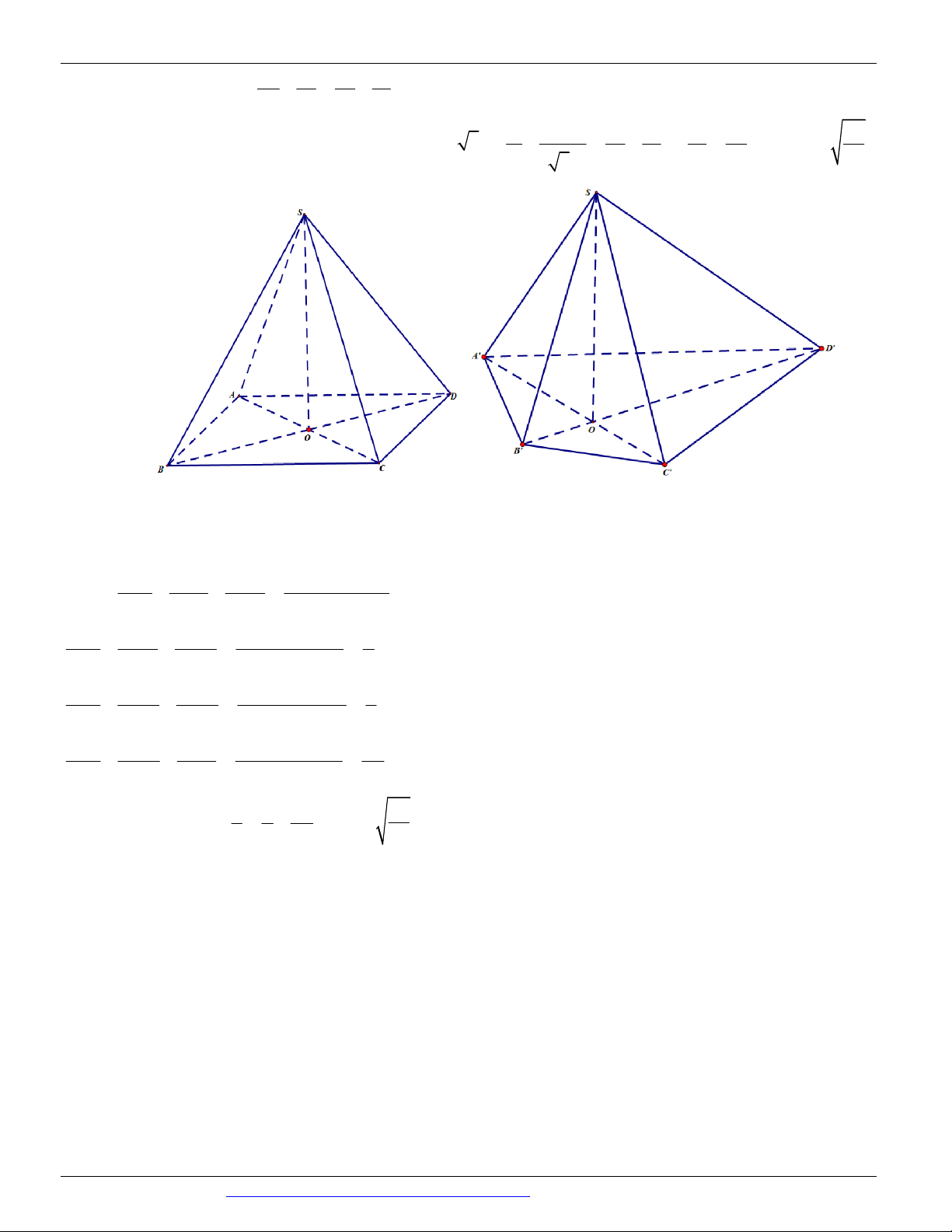
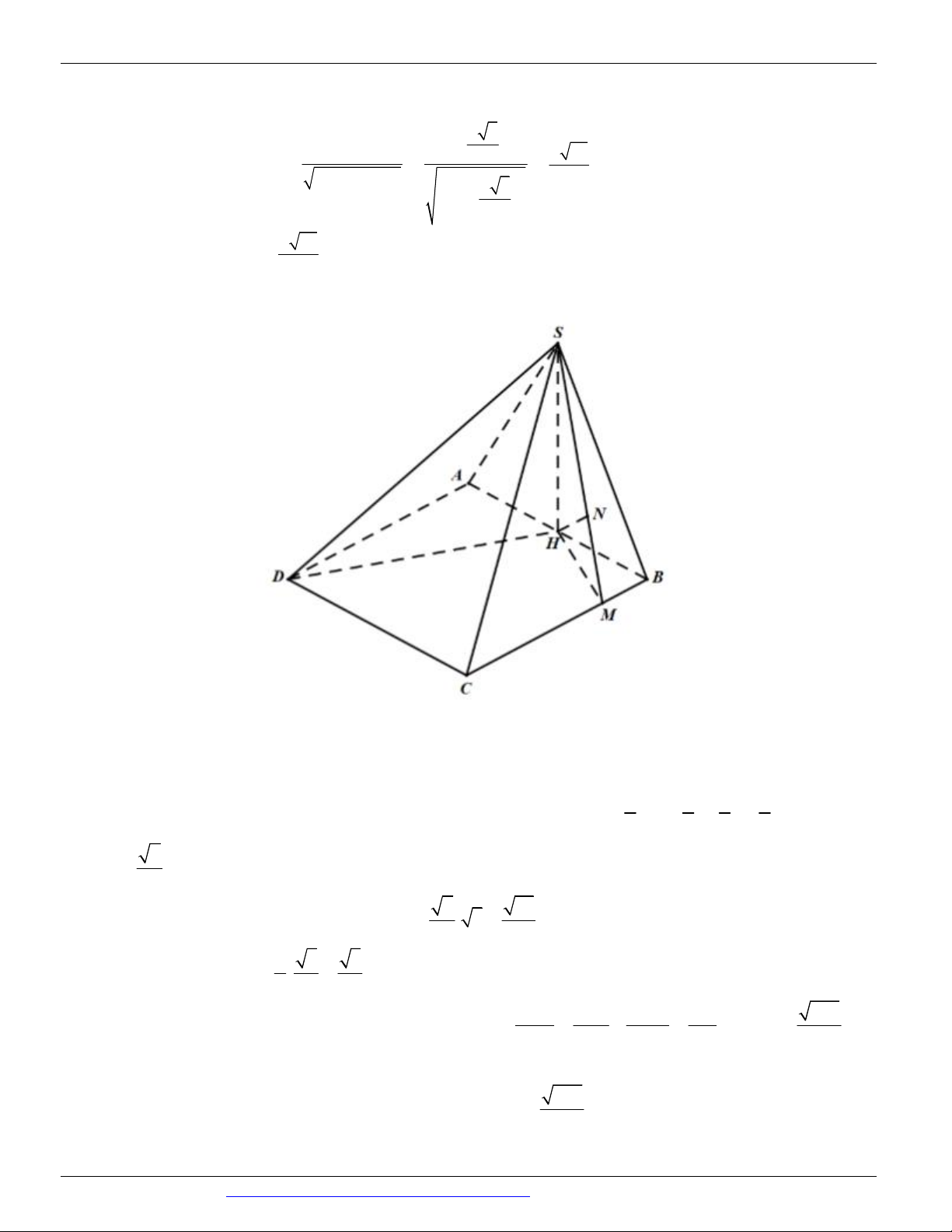
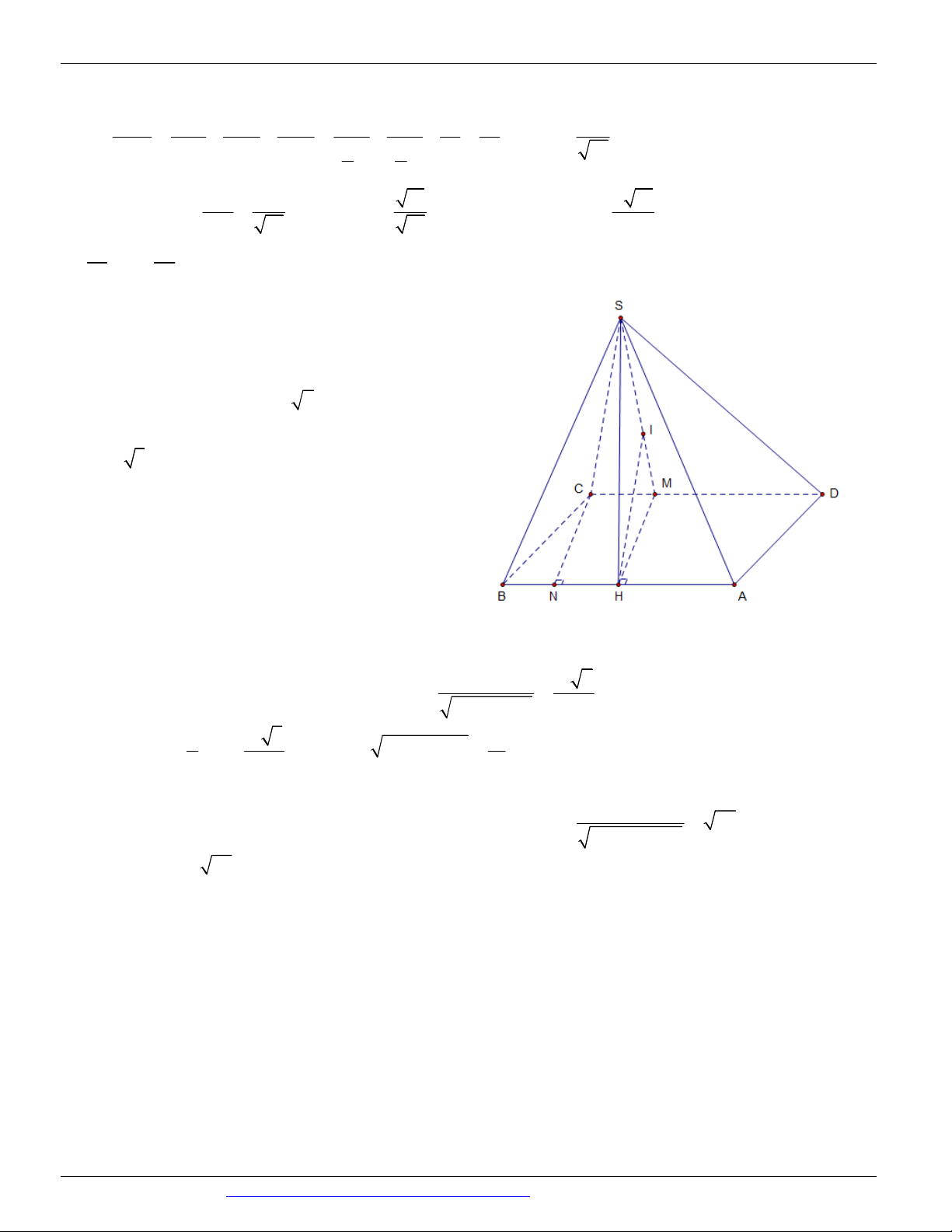
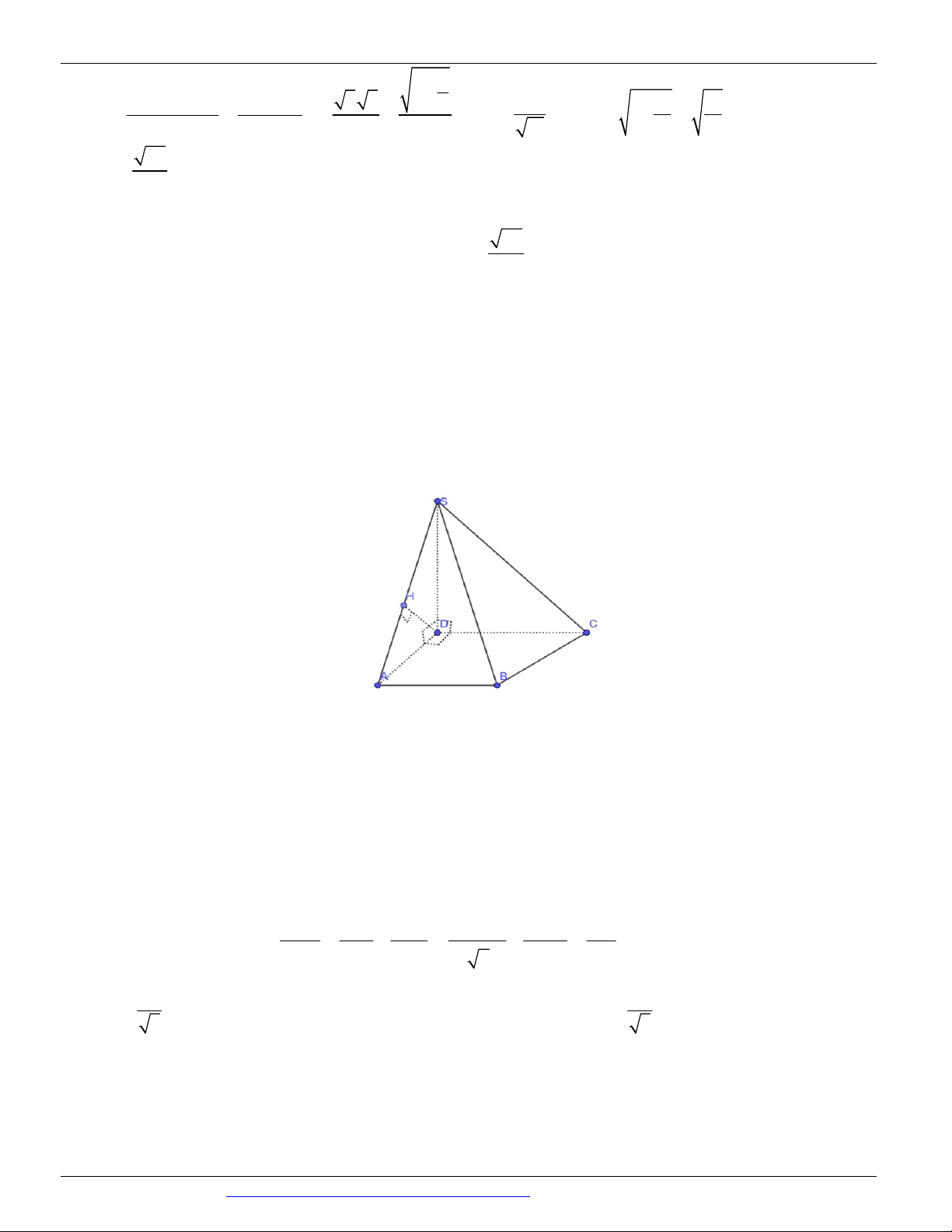
Câu 7. (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng
a . Gọi M là trung điểm của SD (tham khảo hình vẽ bên). Tang của góc giữa đường thẳng B M và mặt
phẳng  ABCD bằng
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 S M A D B C 2 3 2 1 A. B. C. D. 2 3 3 3
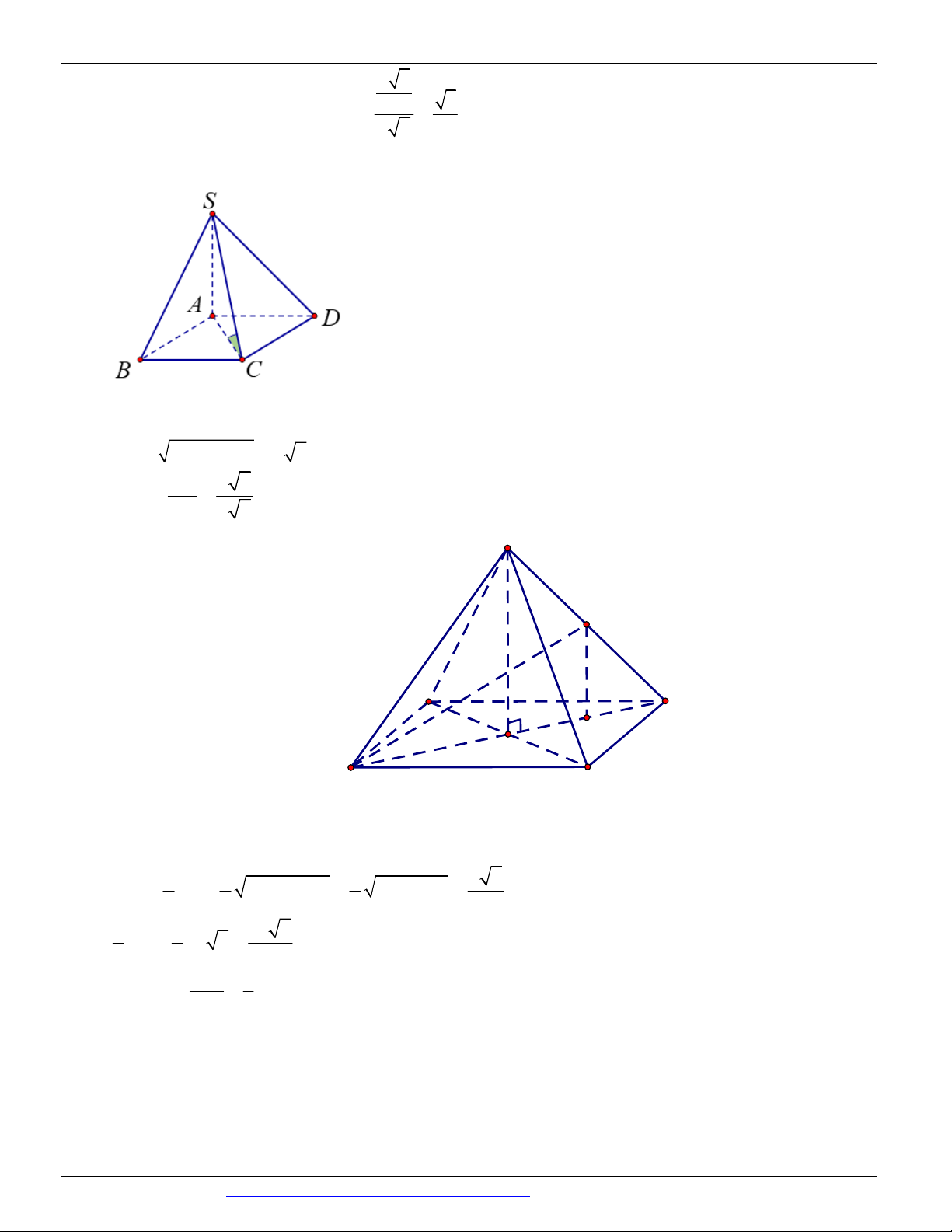
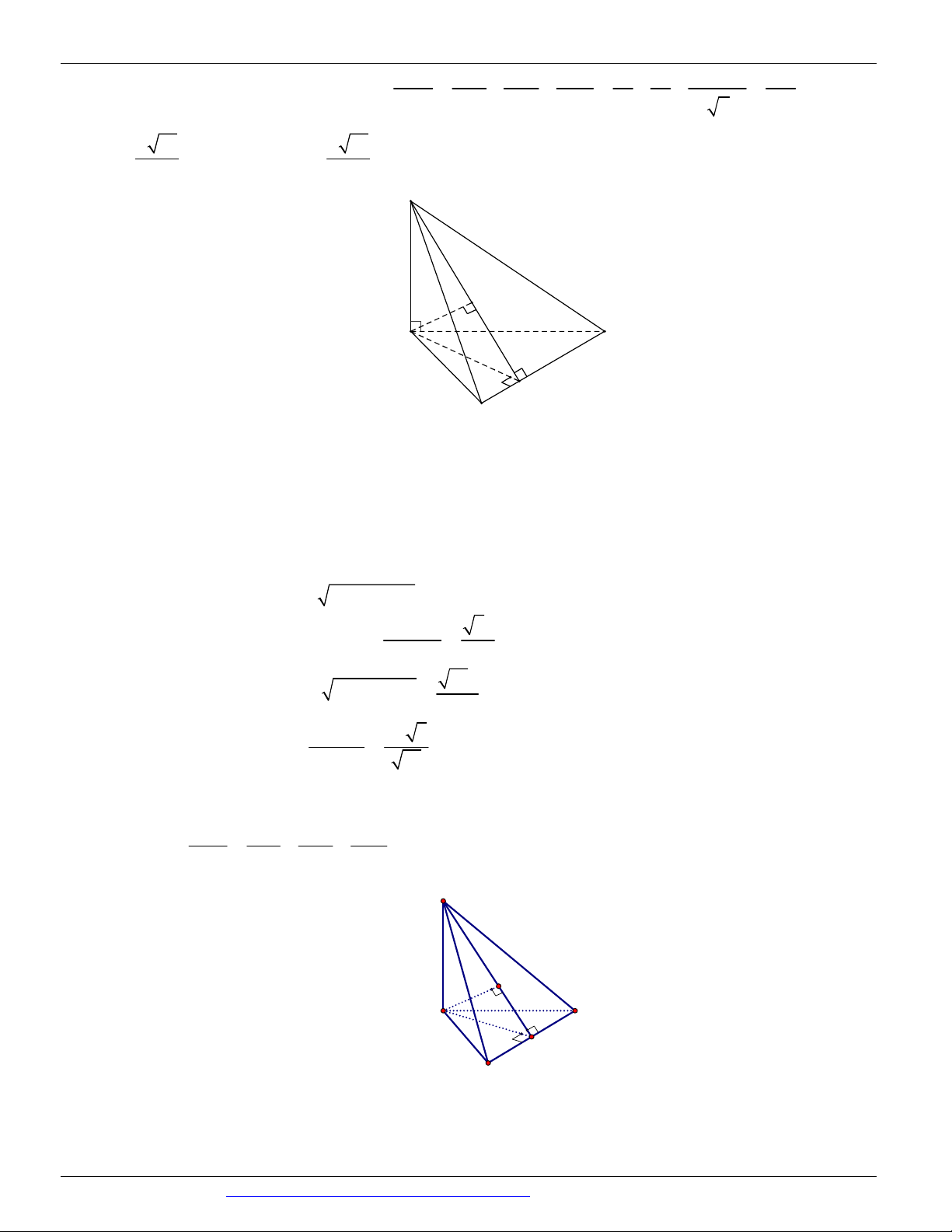
Câu 8. (Mã đề 104 - BGD - 2019) Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC  , SA  2a
, tam giác ABC vuông cân tại B và AB a 2 (minh họa như hình vẽ bên). Góc giữa đường thẳng SC và
mặt phẳng  ABC bằng S A C B A. 30o . B. 90o . C. 60o . D. 45o . a 6
Câu 9. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA   ABCD và SA  . Tính góc giữa 3
SC và mặt phẳng  ABCD ? A. 30 . B. 45 . C. 60 . D. 90 .
Câu 10. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho hình chóp S.ABCD có đáy a 6
ABCD là hình vuông cạnh a và SA   ABCD . Biết SA
. Tính góc giữa SC và  ABCD  . 3 A. 30 B. 60 C. 75 D. 45
Câu 11. (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho hình chóp S.ABCD , đáy
ABCD là hình vuông cạnh bằng a và SA   ABCD . Biết SA a 2 . Tính góc giữa SC và  ABCD . A. 45 B. 30 C. 60 D. 75
Câu 12. (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Cho hình chóp tứ giác đều
S.ABCD có tất cả các cạnh bằng 2a . Gọi M là trung điểm của SD Tính tan của góc giữa đường thẳng BM
và mặt phẳng  ABCD . 2 3 2 1 A. . B. . C. . D. . 2 3 3 3
Câu 13. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019) Cho khối chóp S.ABC có SA   ABC
, tam giác ABC vuông tại B , AC  2a , BC a , SB  2a 3 . Tính góc giữa SA và mặt phẳng SBC. A. 45 . B. 30 . C. 60 . D. 90 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 14. (CHUYÊN HÙNG VƯƠNG GIA LAI NĂM 2018-2019 LẦN 01) Cho hình chóp S.ABCD có đáy
ABCD là hình vuông cạnh a , SA vuông góc với đáy và SA a 3 . Gọi  là góc giữa SD và SAC  . Giá trị sin bằng 2 2 3 2 A. . B. . C. . D. . 4 2 2 3
Câu 15. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hình chóp tam giác S.ABC có đáy là
tam giác đều cạnh a . Tam giác SAB cân tại S và thuộc mặt phẳng vuông góc với đáy. Biết SC tạo với mặt
phẳng đáy một góc 60 , gọi M là trung điểm của BC . Gọi  là góc giữa đường thẳng SM và mặt phẳng
ABC . Tính cos . 6 3 3 1 A. cos  . B. cos  . C. cos  . D. cos  . 3 3 10 10
Câu 16. (THPT CHUYÊN BẮC NINH LẦN 01 NĂM 2018-2019) Cho hình chóp SABCD có đáy là hình
thang vuông tại 1và B . AB BC a, AD  2a . Biết SA vuông góc với đáy ( ABCD) và SA a . Gọi M , N
lần lượt là trung điểm SB, CD . Tính sin góc giữa đường thẳng MN và mặt phẳng (SAC) 5 55 3 5 2 5 A. B. C. D. 5 10 10 5
Câu 17. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho hình chóp tứ giác đều
S.ABCD có AB a , O là trung điểm AC và SO b . Gọi  là đường thẳng đi qua C ,  chứa trong mặt a 14
phẳng  ABCD và khoảng cách từ O đến  là
. Giá trị lượng giác cos SA, bằng 6 2a 2a a a A. . B. . C. . D. . 2 2 3 4b  2a 2 2 3 2a  4b 2 2 3 2a  4b 2 2 3 4b  2a
Câu 18. (HSG BẮC NINH NĂM 2018-2019) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
AB a, AD a 3 . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Cosin
của góc giữa đường thẳng SD và mặt phẳng SBC  bằng 13 3 2 5 1 A. B. C. D. 4 4 5 4
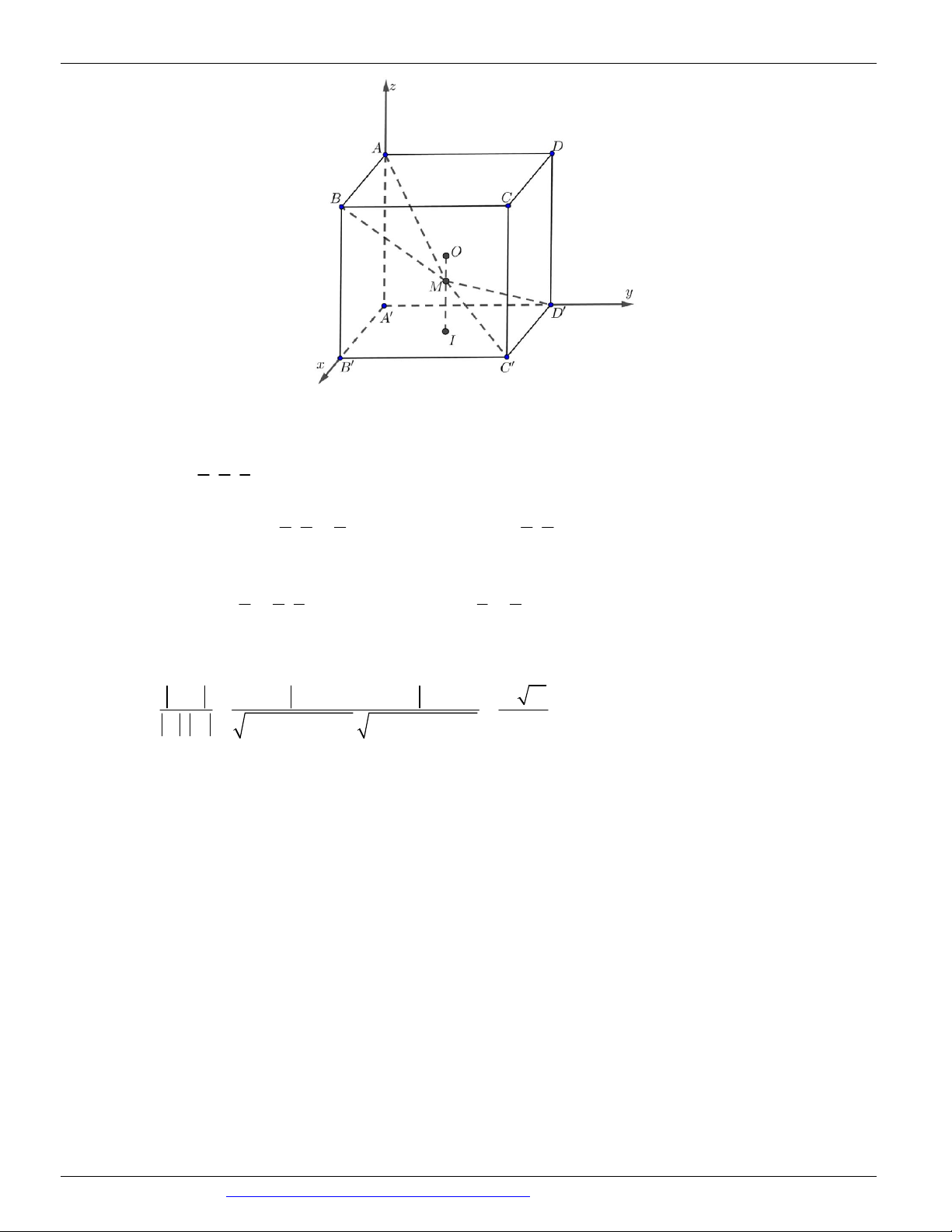
Câu 19. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho hình chóp S.ABC có đáy là tam giác vuông tại C ,
CH vuông góc với AB tại H , I là trung điểm của đoạn HC . Biết SI vuông góc với mặt phẳng đáy, 
ASB  90 . Gọi O là trung điểm của đoạn AB , O là tâm mặt cầu ngoại tiếp tứ diện SABI . Góc tạo bởi
đường thẳng OO và mặt phẳng  ABC  bằng A. 60 . B. 30 . C. 90 . D. 45 .
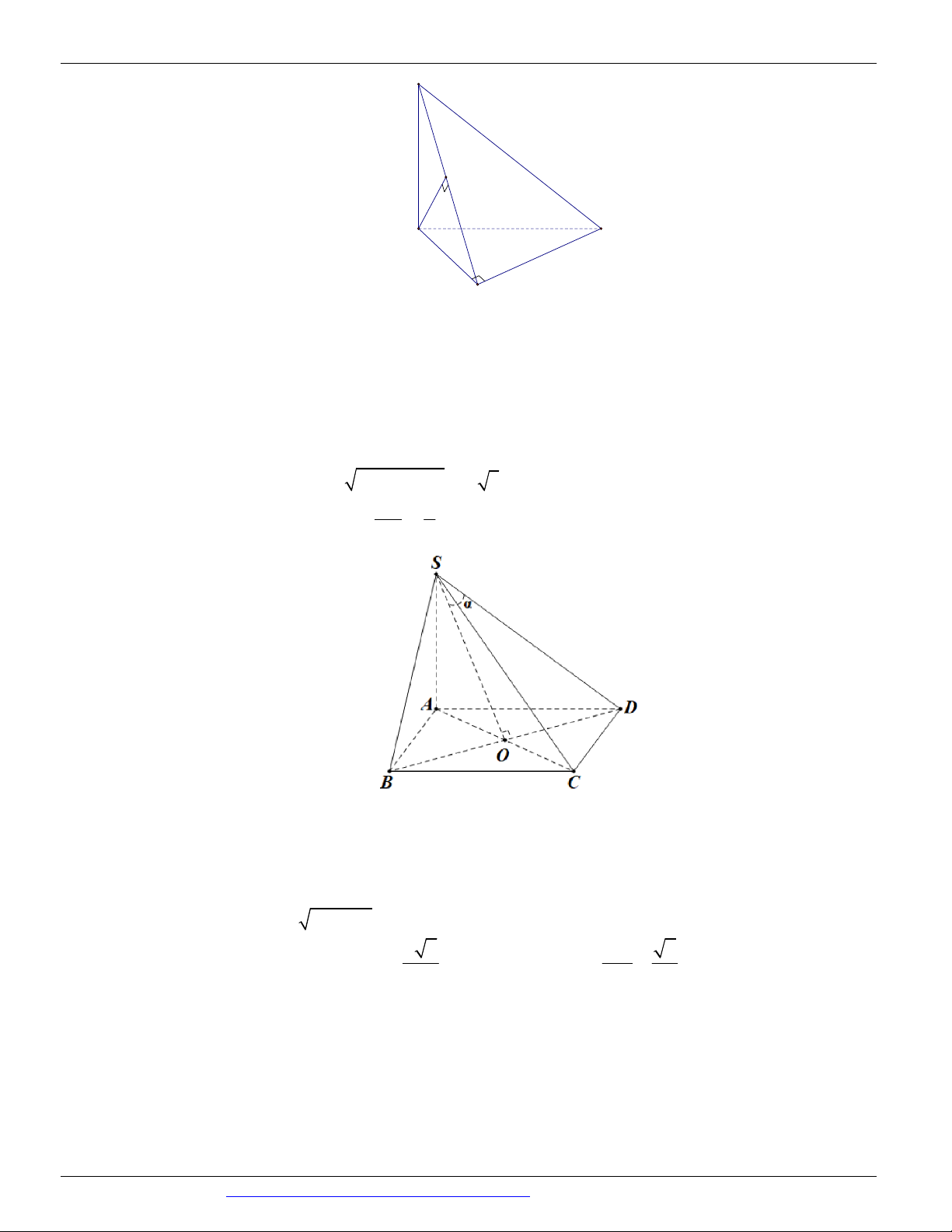
Câu 20. (SỞ GD&ĐT BẮC NINH NĂM 2018-2019 LẦN 01) Cho hình chóp S.ABCD có đáy ABCD là
hình thoi cạnh a và 
ABC  60 . Hình chiếu vuông góc của điểm S lên mặt phẳng  ABCD trùng với trọng
tâm của tam giác ABC , gọi  là góc giữa đường thẳng SB và mặt phẳng SCD , tính sin  biết rằng SB a . 3 1 1 2 A. sin   . B. sin   . C. sin   . D. sin   . 2 4 2 2
Dạng 1.2 Góc của đường thẳng với đường thẳng
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
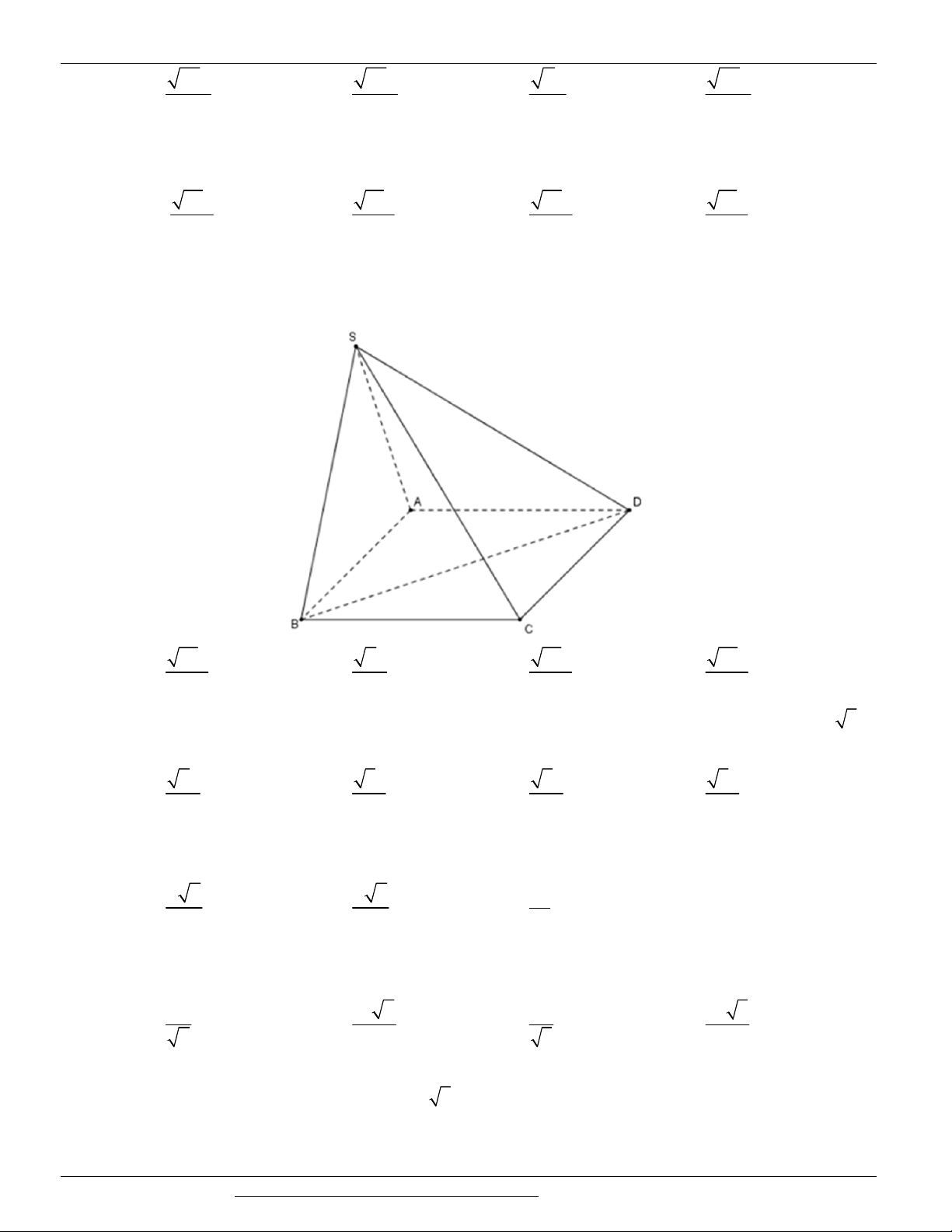
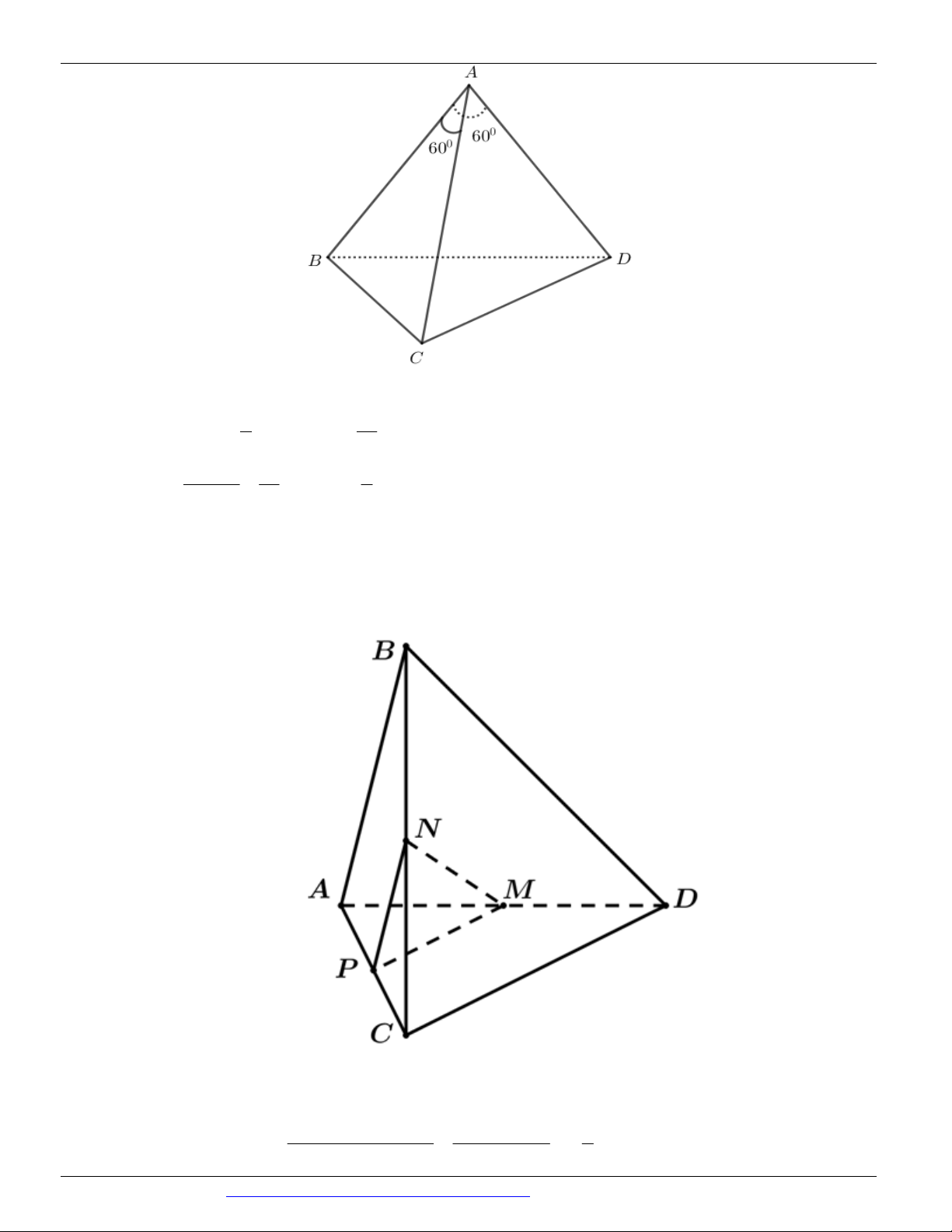
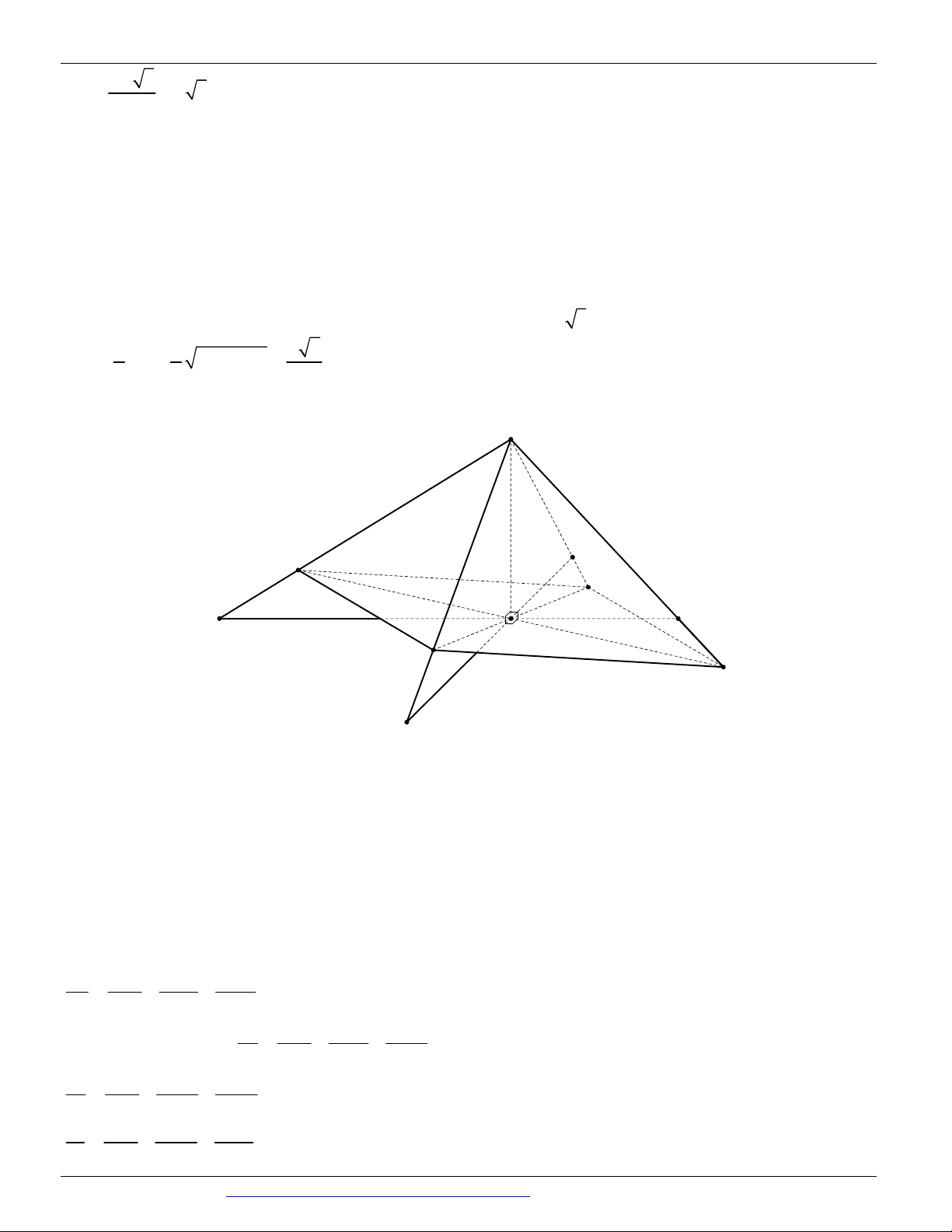
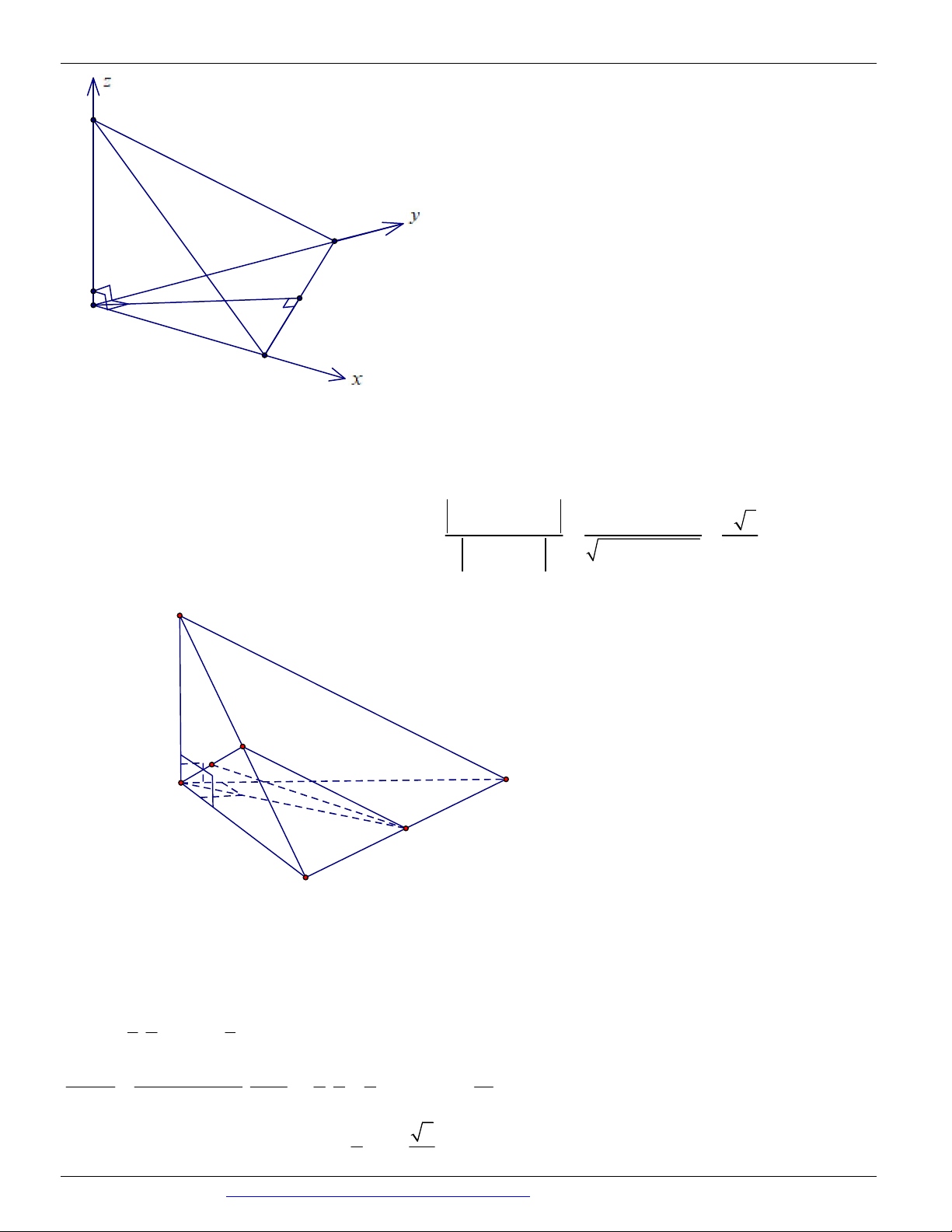
Câu 21. (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho tứ diện OABC có O , A O ,
B OC đôi một vuông góc
với nhau và OA OB OC . Gọi M là trung điểm của BC ( tham khảo hình vẽ bên dưới). Góc giữa hai
đường thẳng OM và AB bằng A. 0 45 B. 0 90 C. 0 30 D. 0 60
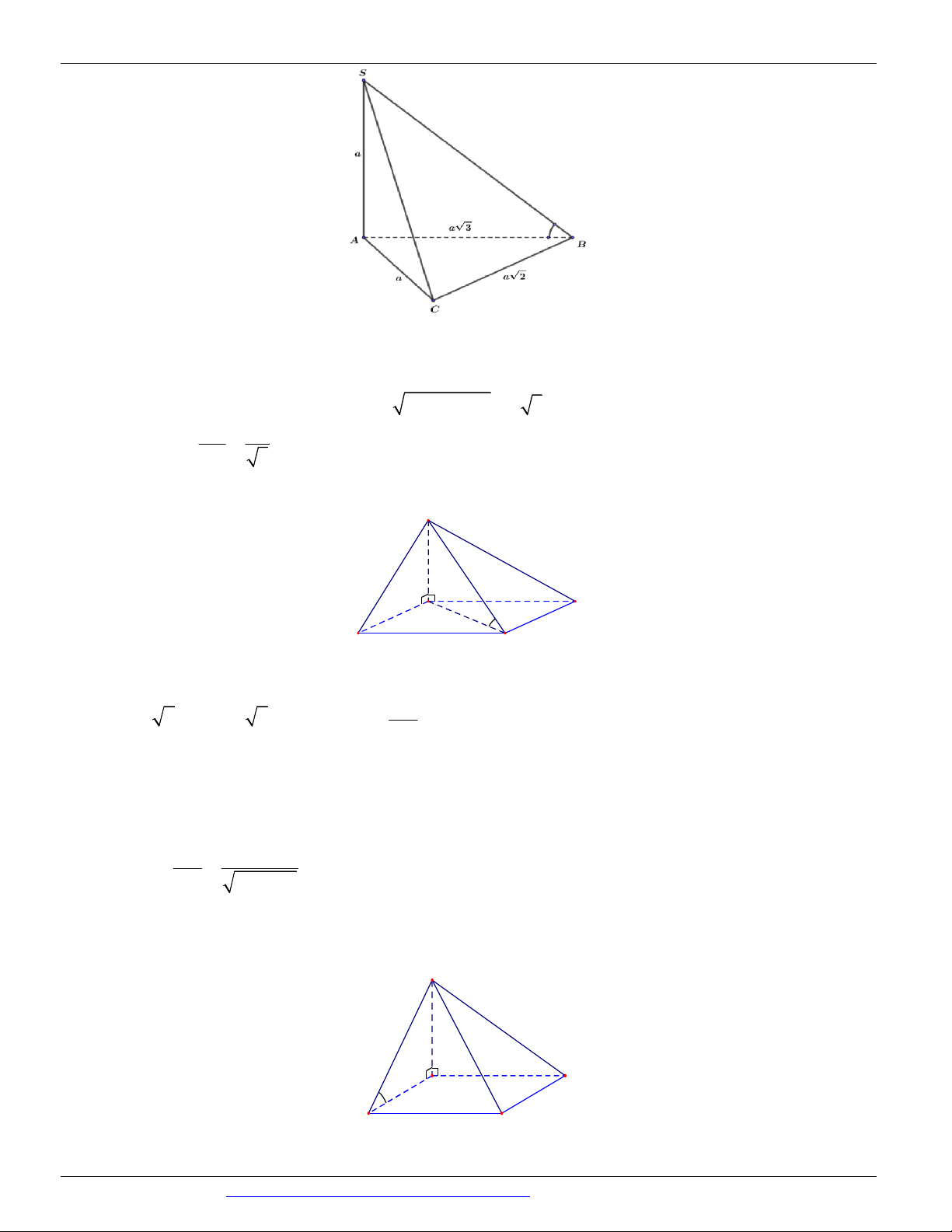
Câu 22. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Cho tứ diện ABCD với 3   0 AC
AD,CAB DAB  60 ,CD AD . Gọi  là góc giữa hai đường thẳng AB và CD . Chọn khẳng định 2 đúng về góc  . 3 1 A. cos  B. 0 30 C. 0 60 D. cos  4 4
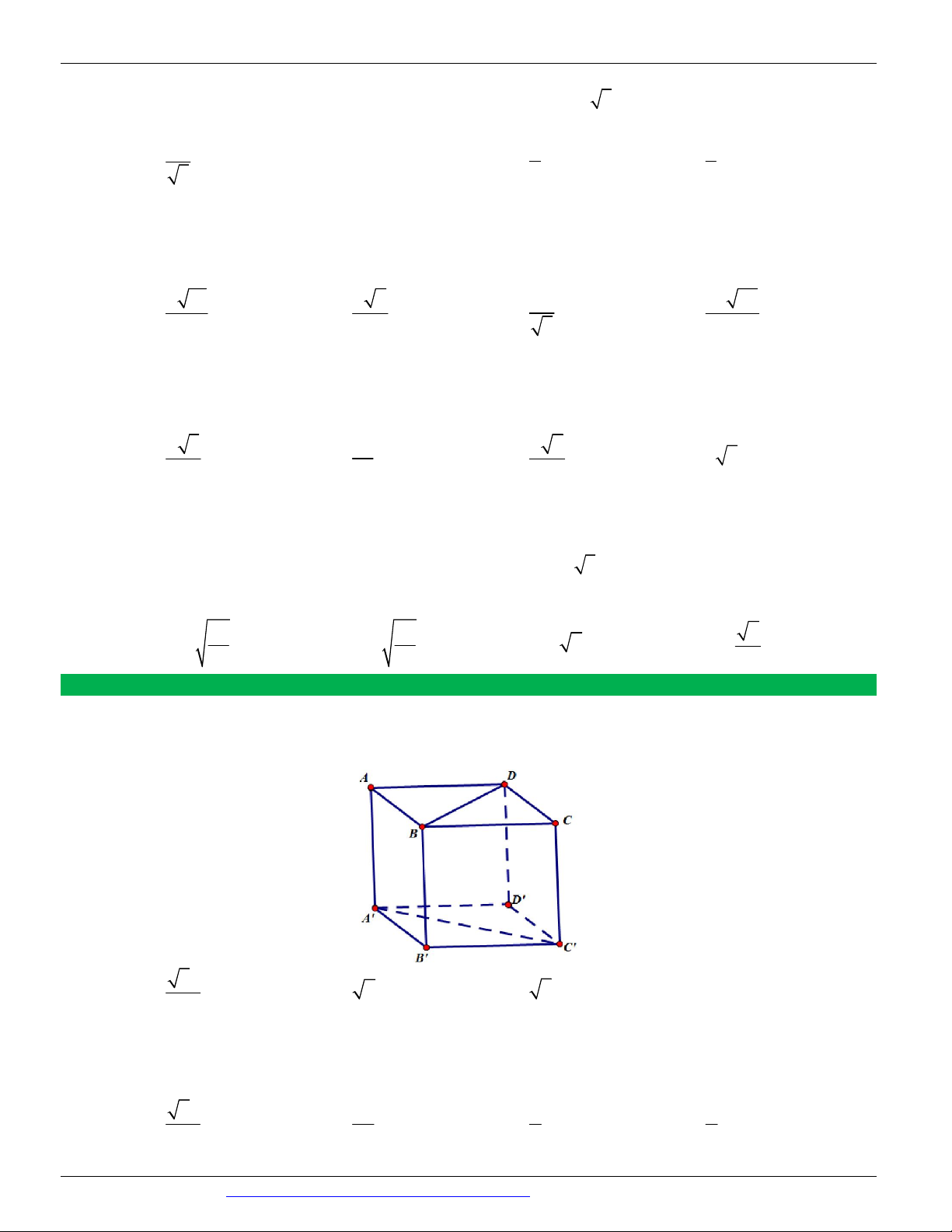
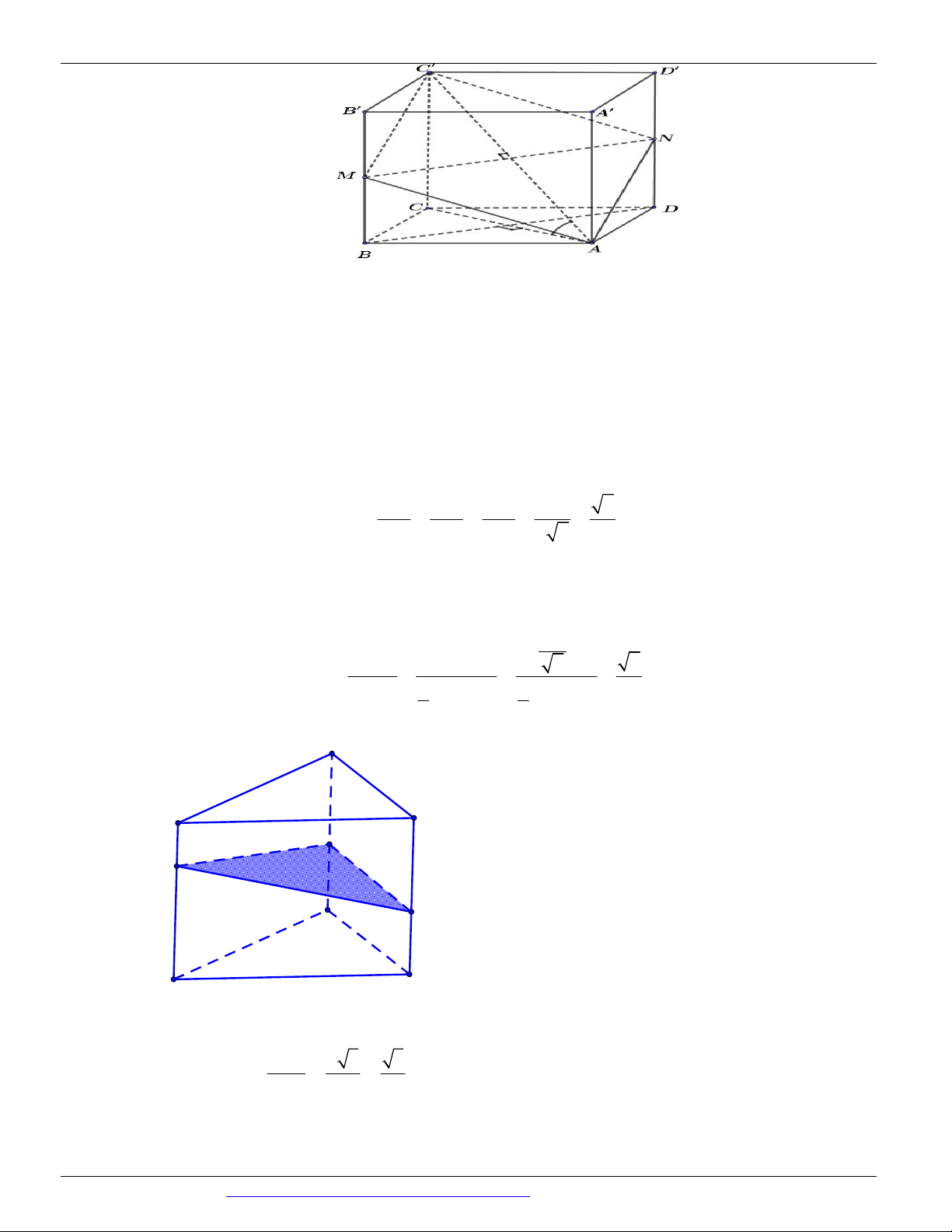
Câu 23. (TRƯỜNG THPT HOÀNG HOA THÁM HƯNG YÊN NĂM 2018-2019) Cho hình hộp chữ nhật ABC . D AB CD
  , biết đáy ABCD là hình vuông. Tính góc giữa A C  và BD . B' C' A' D' C B A D A. 90 . B. 30 . C. 60 . D. 45 .
Câu 24. (CHUYÊN KHTN NĂM 2018-2019 LẦN 01) Cho tứ diện ABCD có AB CD  2a . Gọi M , N
lần lượt là trung điểm AD và BC . Biết MN a 3 , góc giữa hai đường thẳng AB và CD bằng. A. 0 45 . B. 0 90 . C. 0 60 . D. 0 30 .
Câu 25. (CHUYÊN LƯƠNG VĂN CHÁNH PHÚ YÊN NĂM 2018-2019 LẦN 01) Cho hình lập phương
ABCD.AB CD
  ; gọi M là trung điểm của B C
  . Góc giữa hai đường thẳng AM và BC bằng A. 45 . B. 90 . C. 30 . D. 60 .
Dạng 1.3 Góc của mặt với mặt
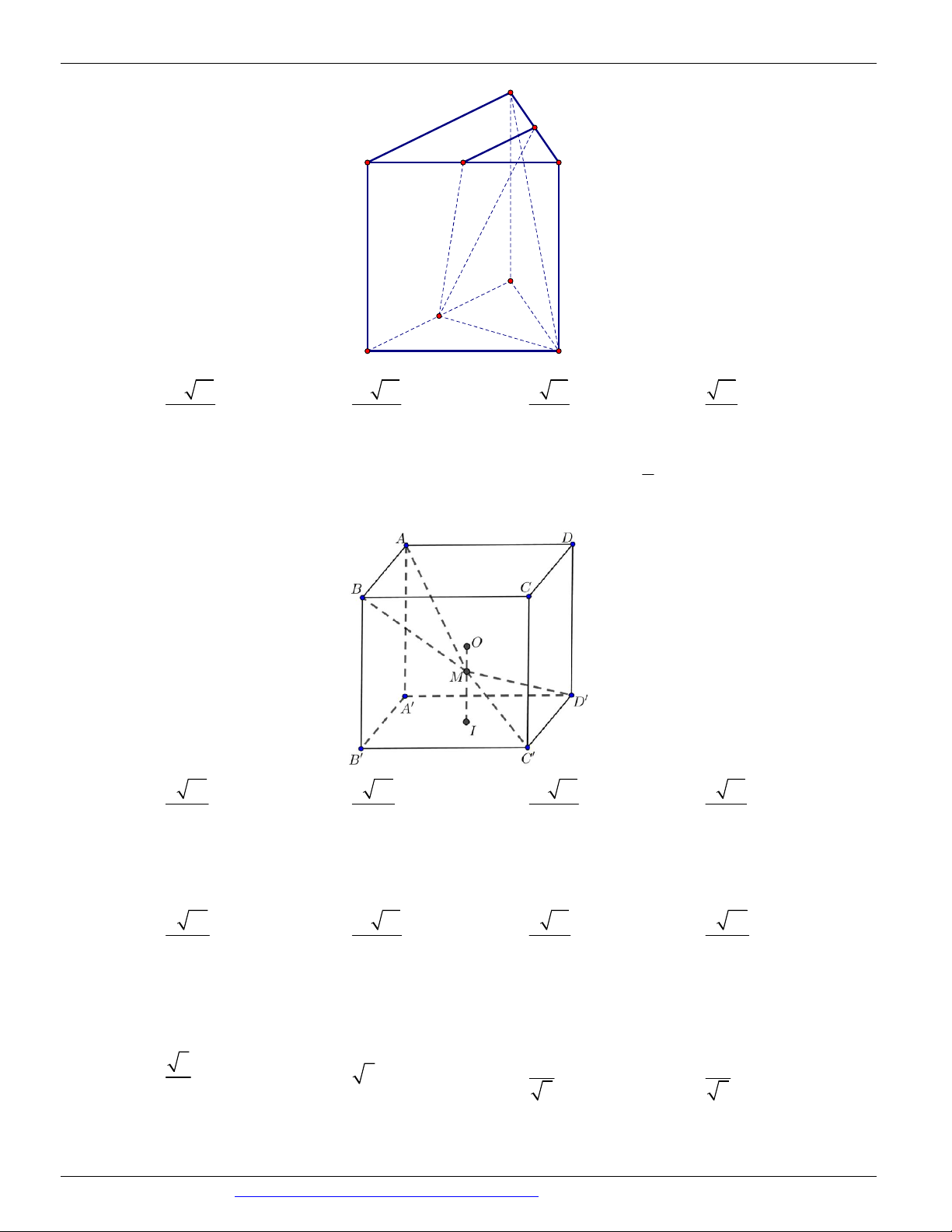
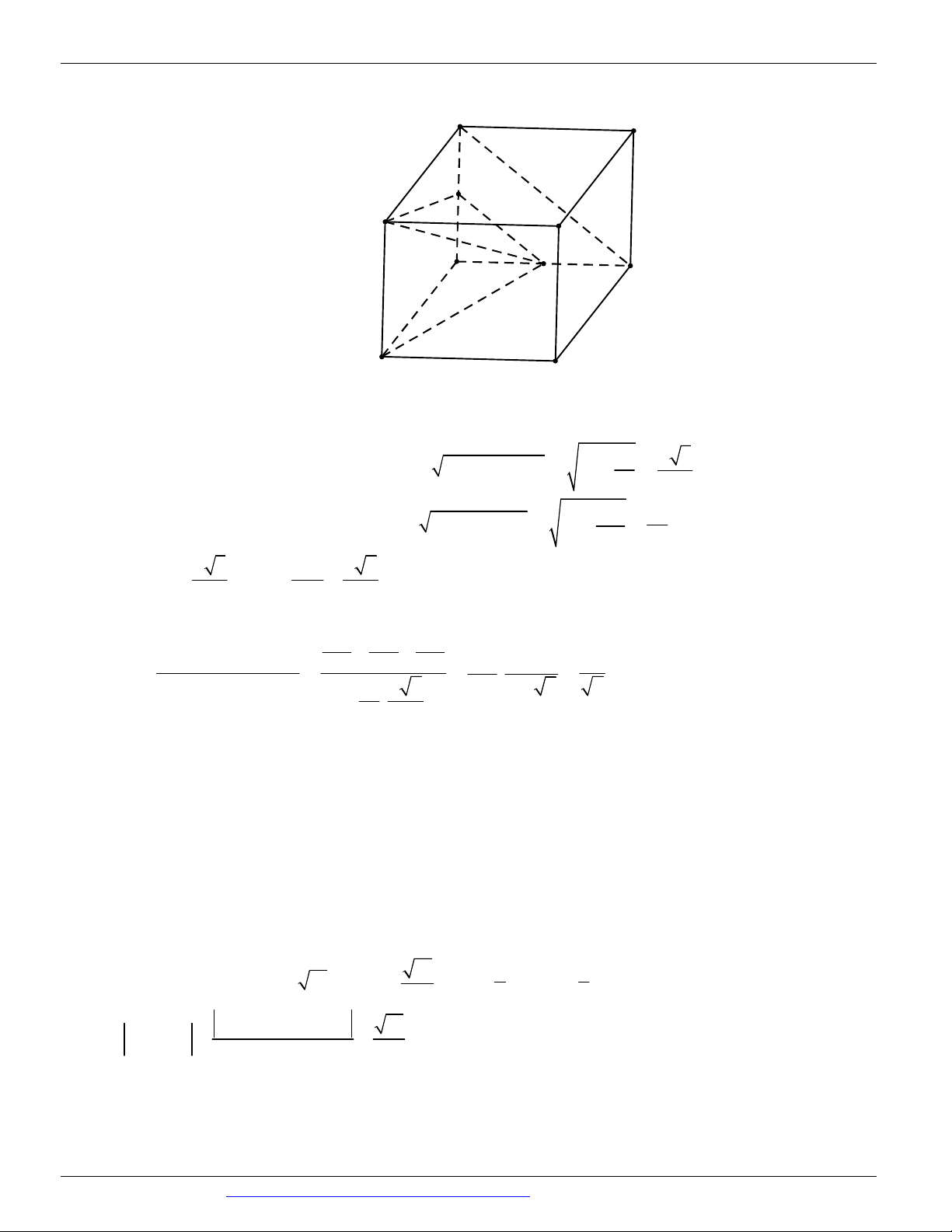
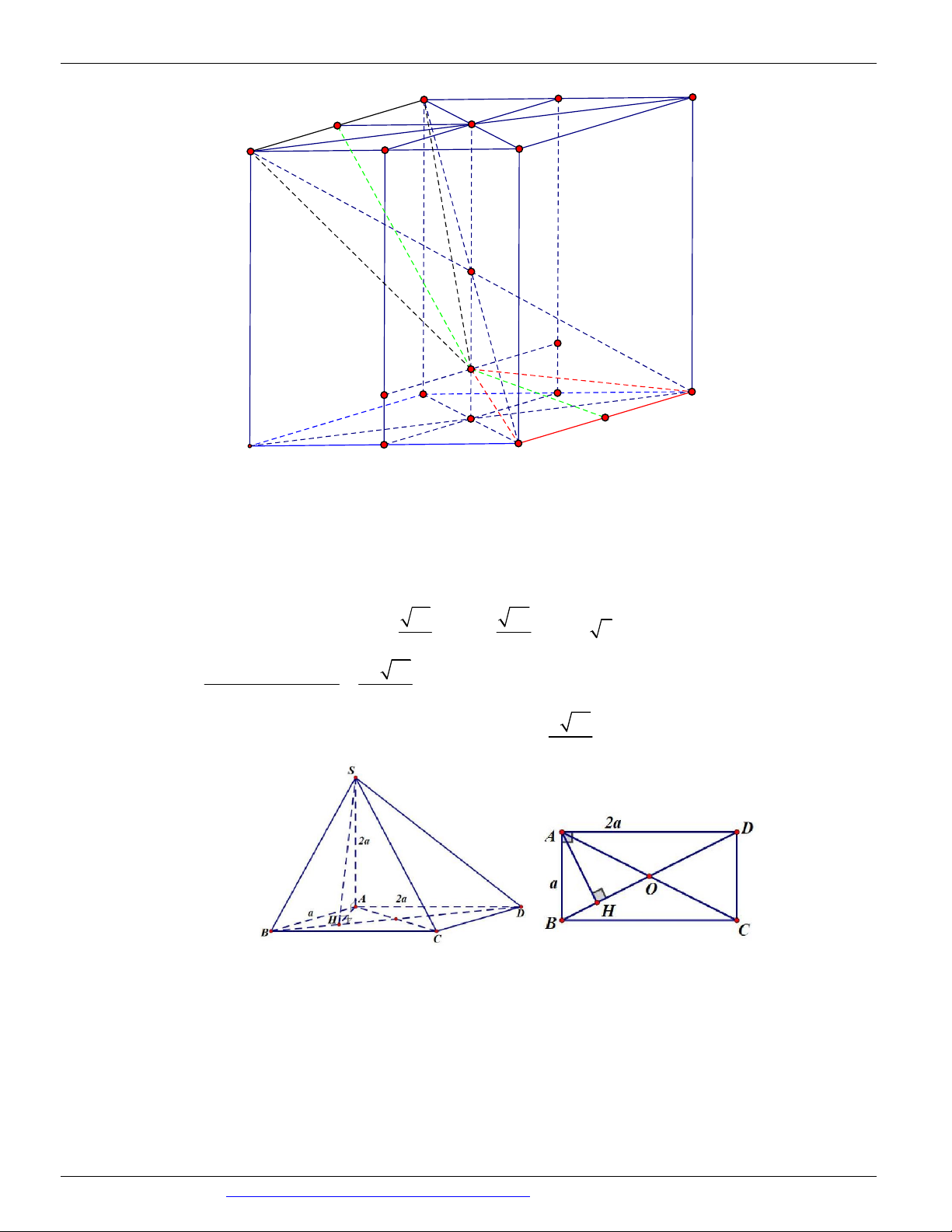
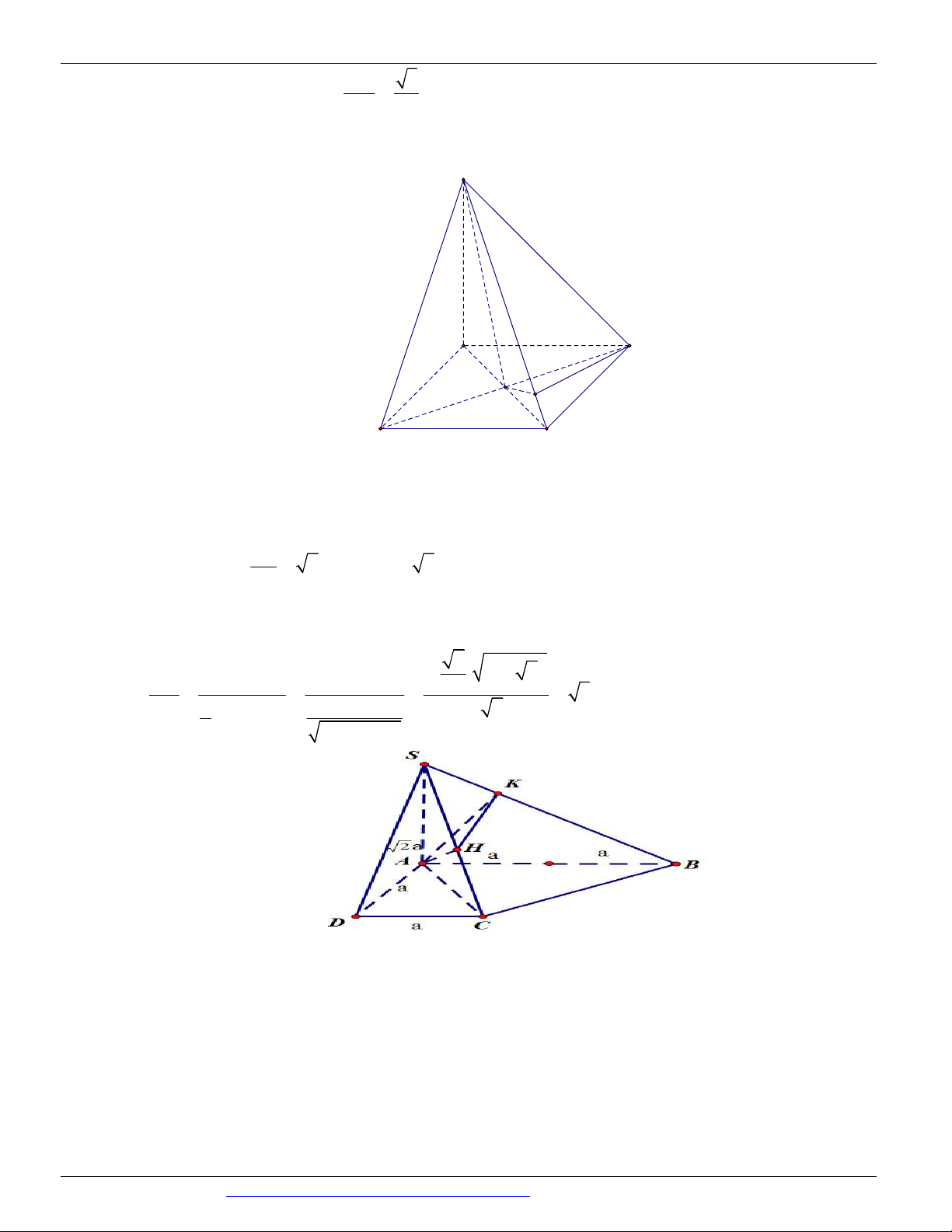
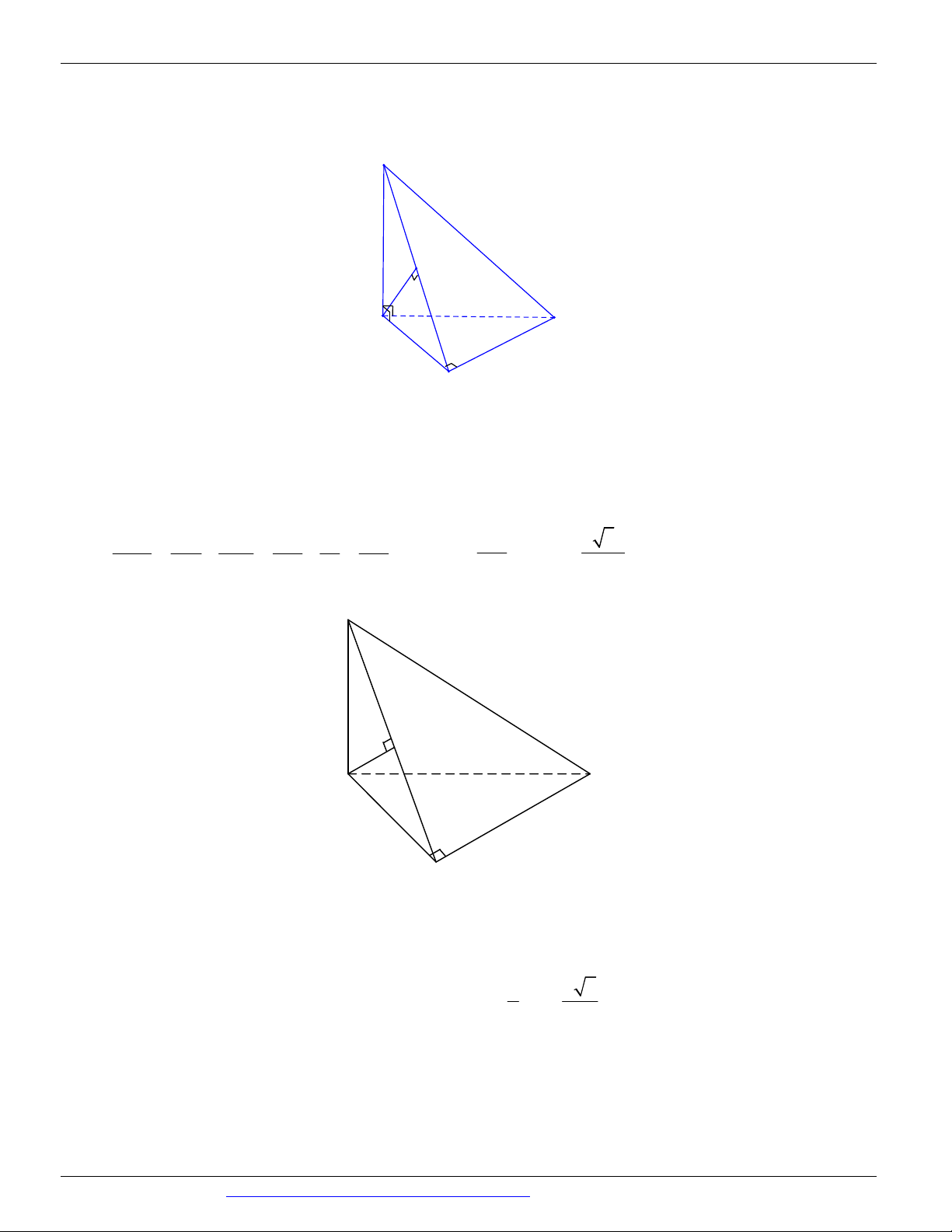
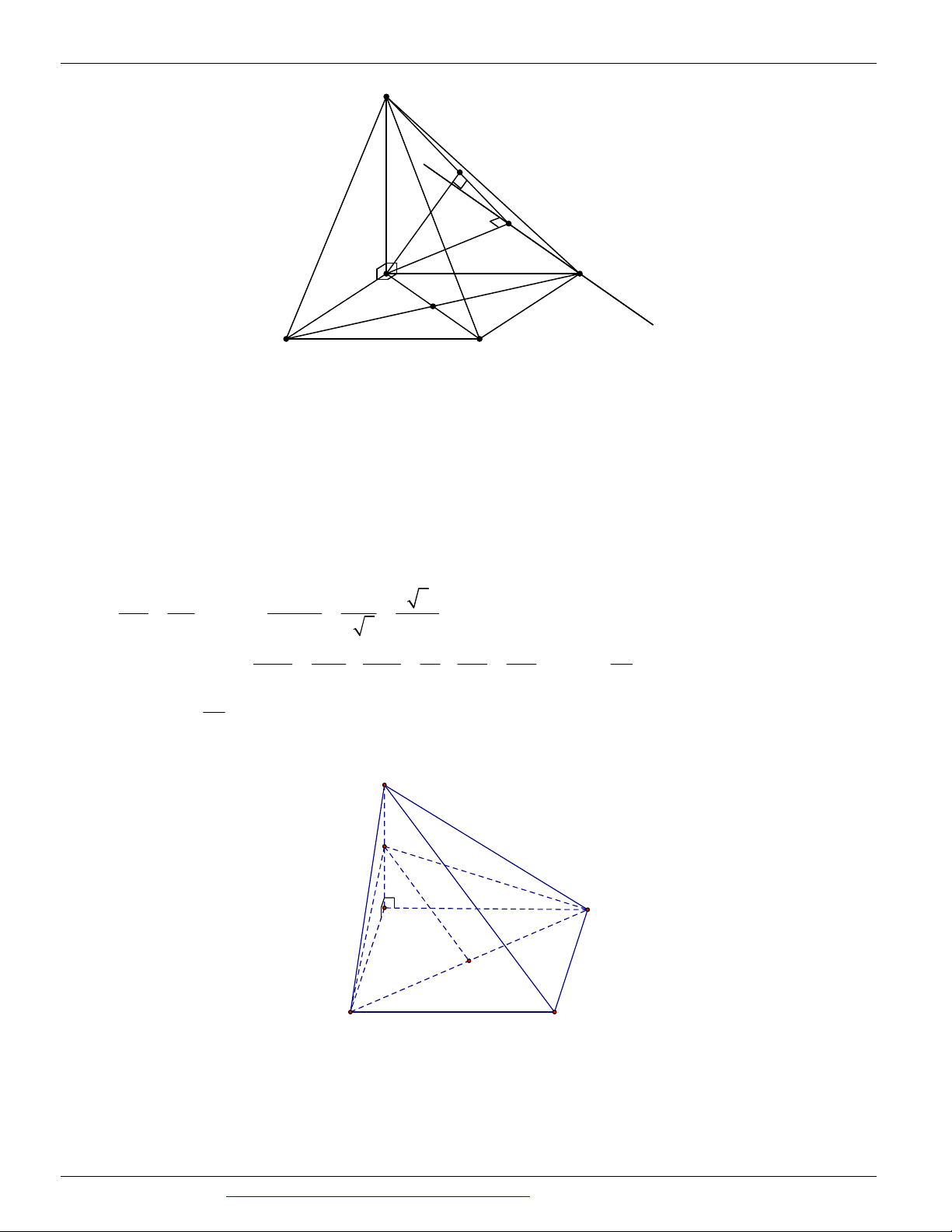
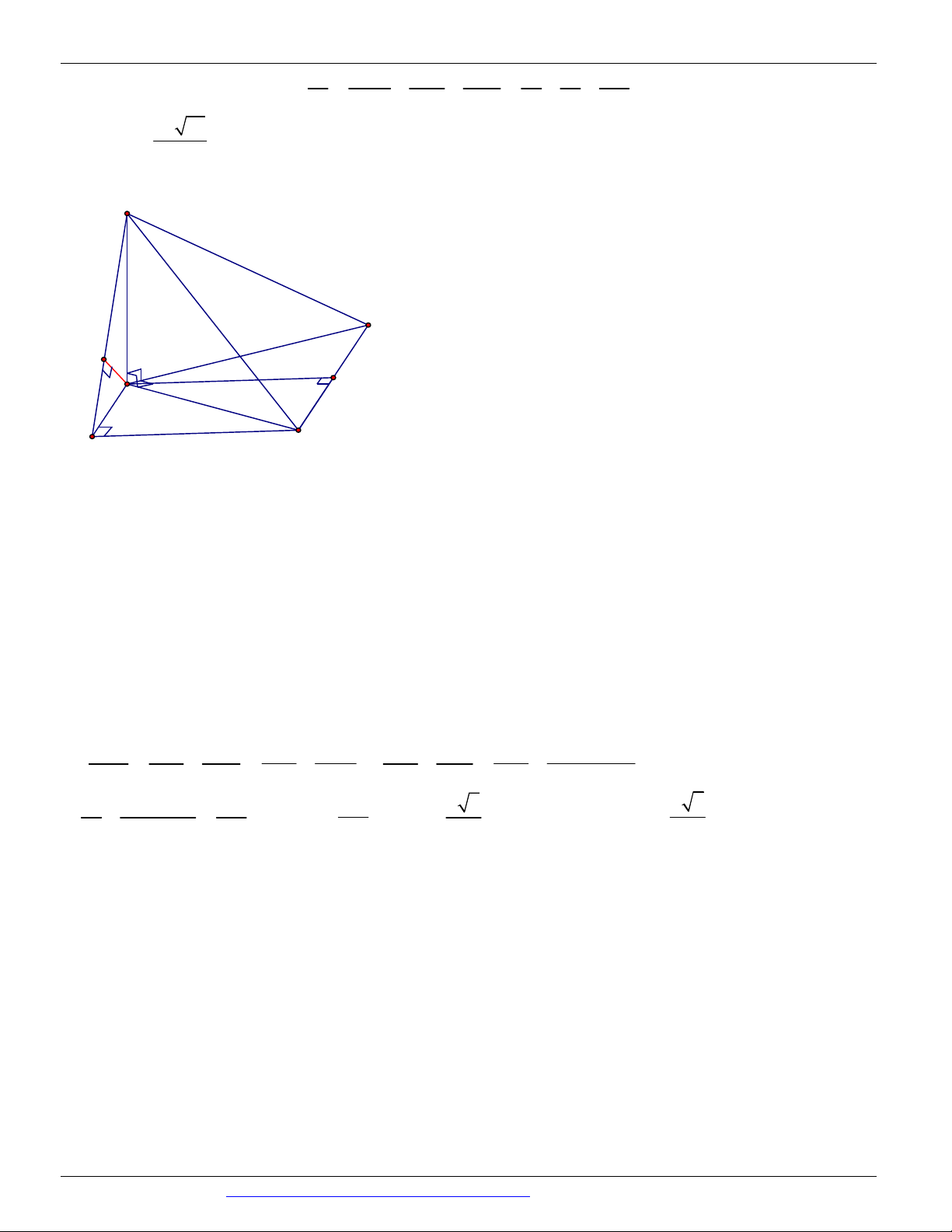
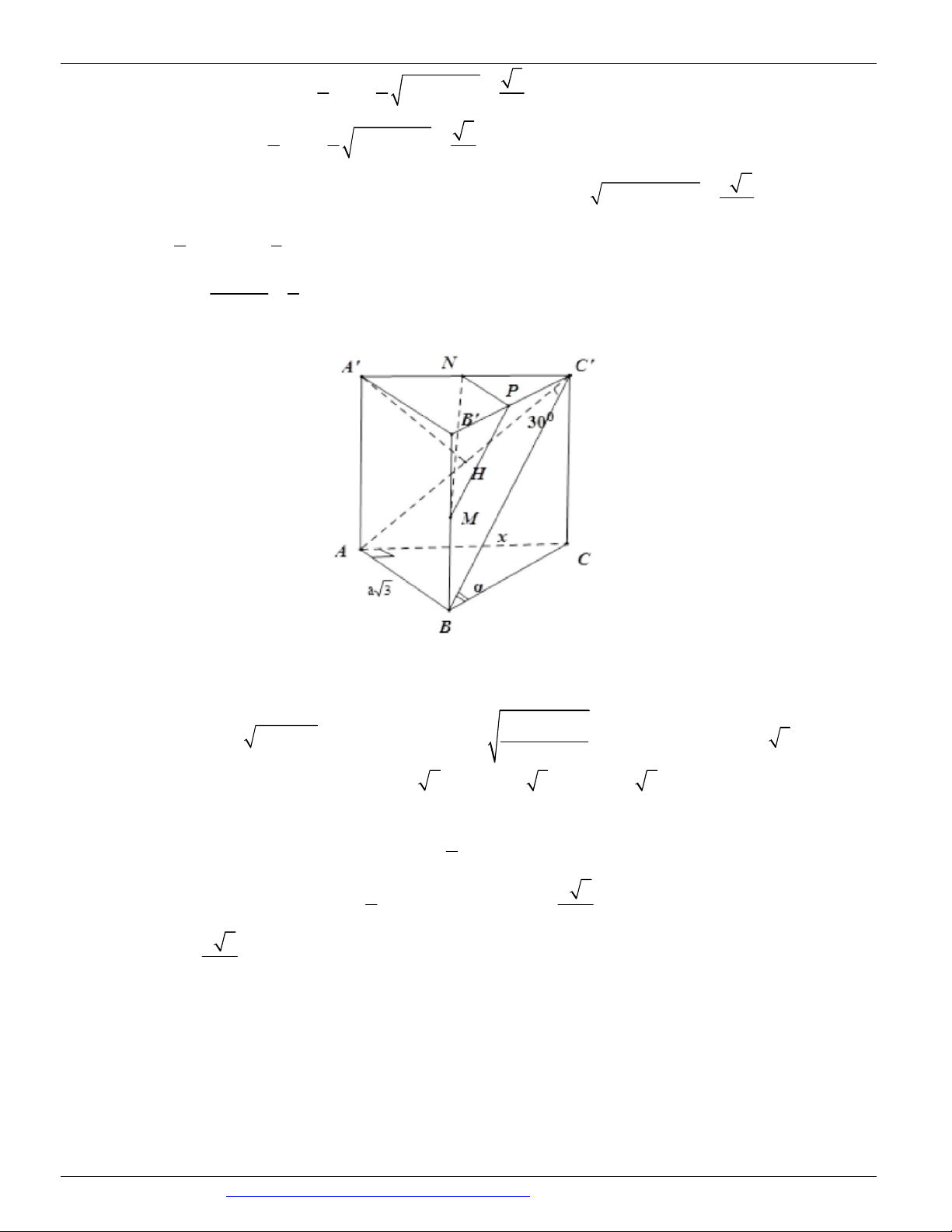
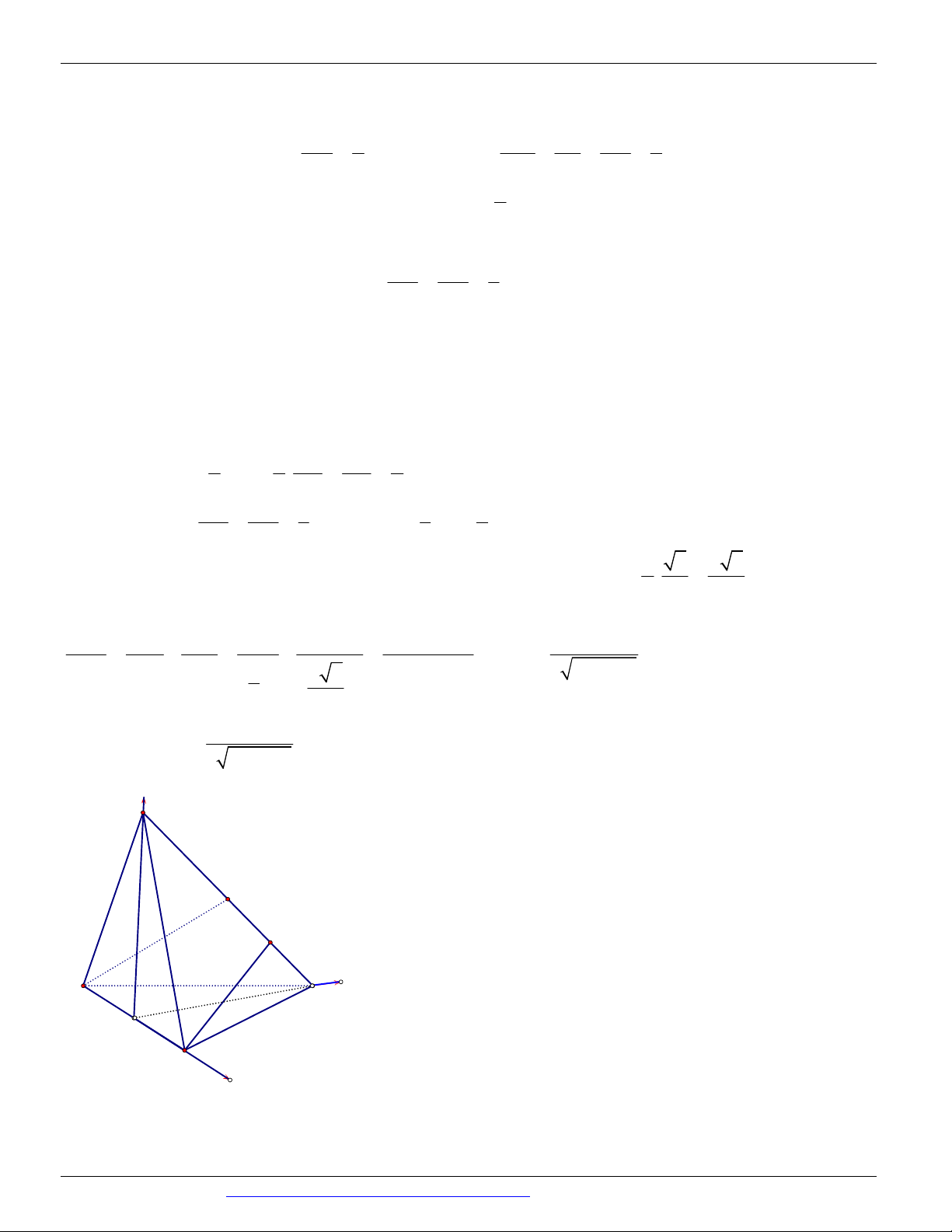
Câu 26. (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho hình lăng trụ tam giác đều ABC .AB C   có AB  2 3
và AA  2. Gọi M , N , P lần lượt là trung điểm các cạnh A B  , A C
  và BC (tham khảo hình vẽ bên). Côsin
của góc tạo bởi hai mặt phẳng  AB C
  và MNP bằng
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 C' N M B' A' C P B A 17 13 18 13 6 13 13 A. B. C. D. 65 65 65 65
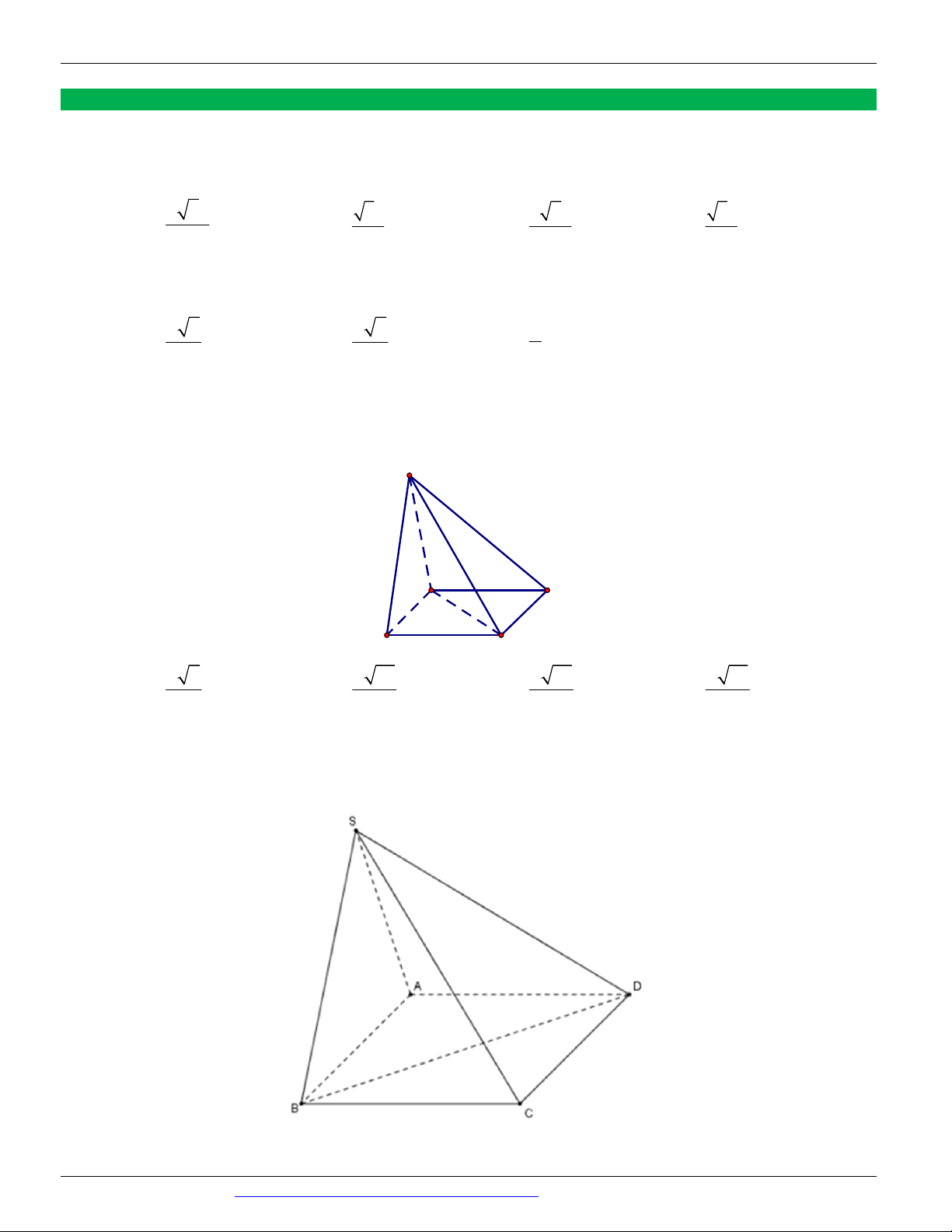
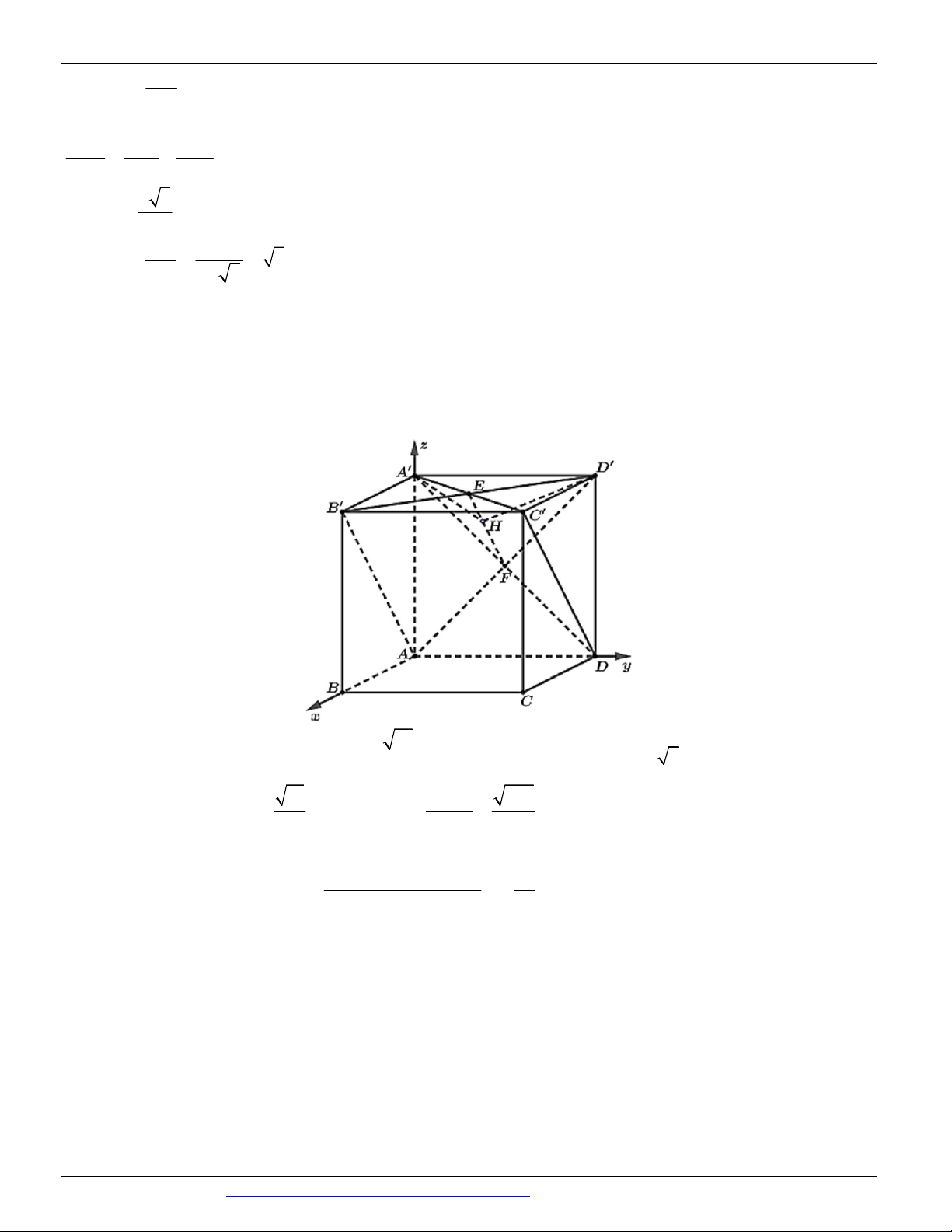
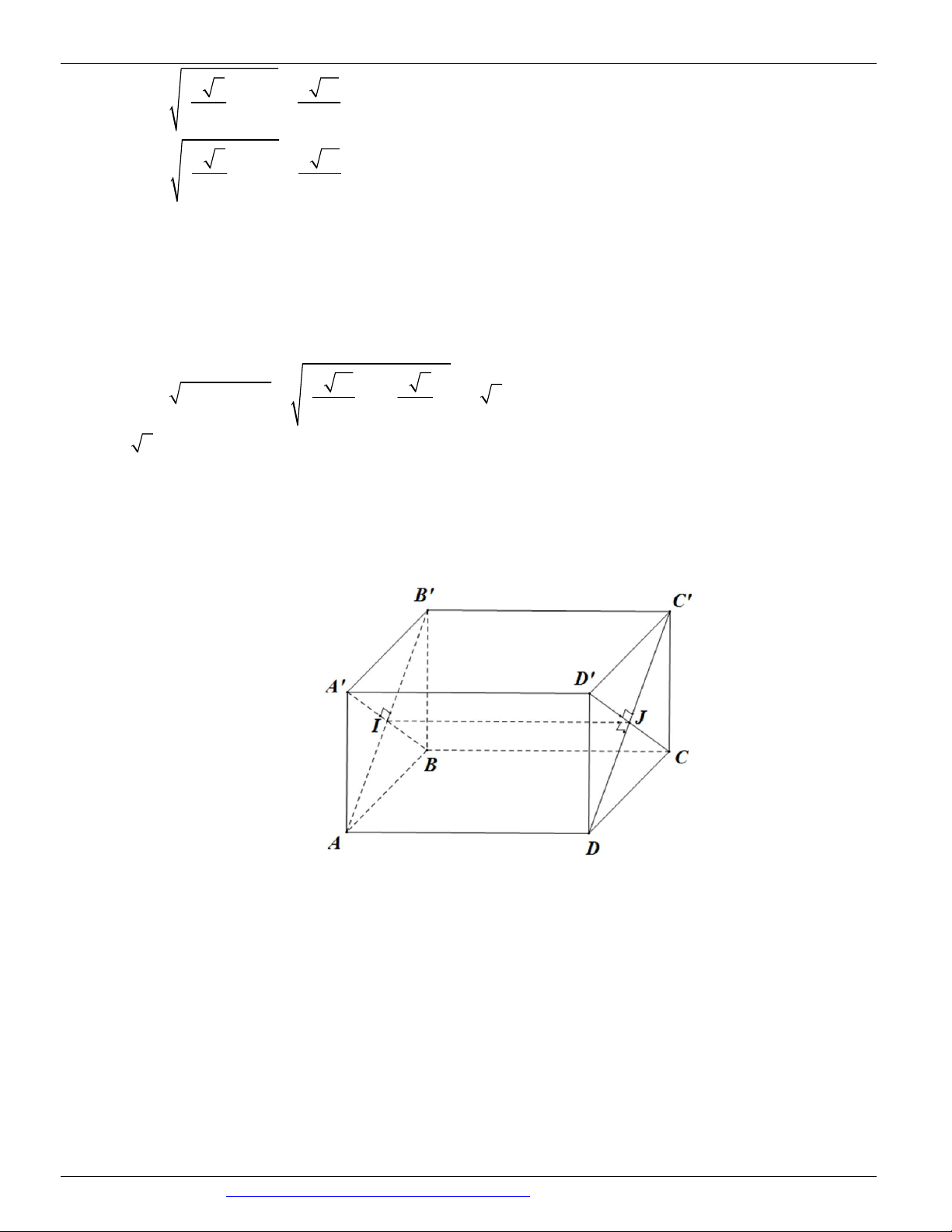
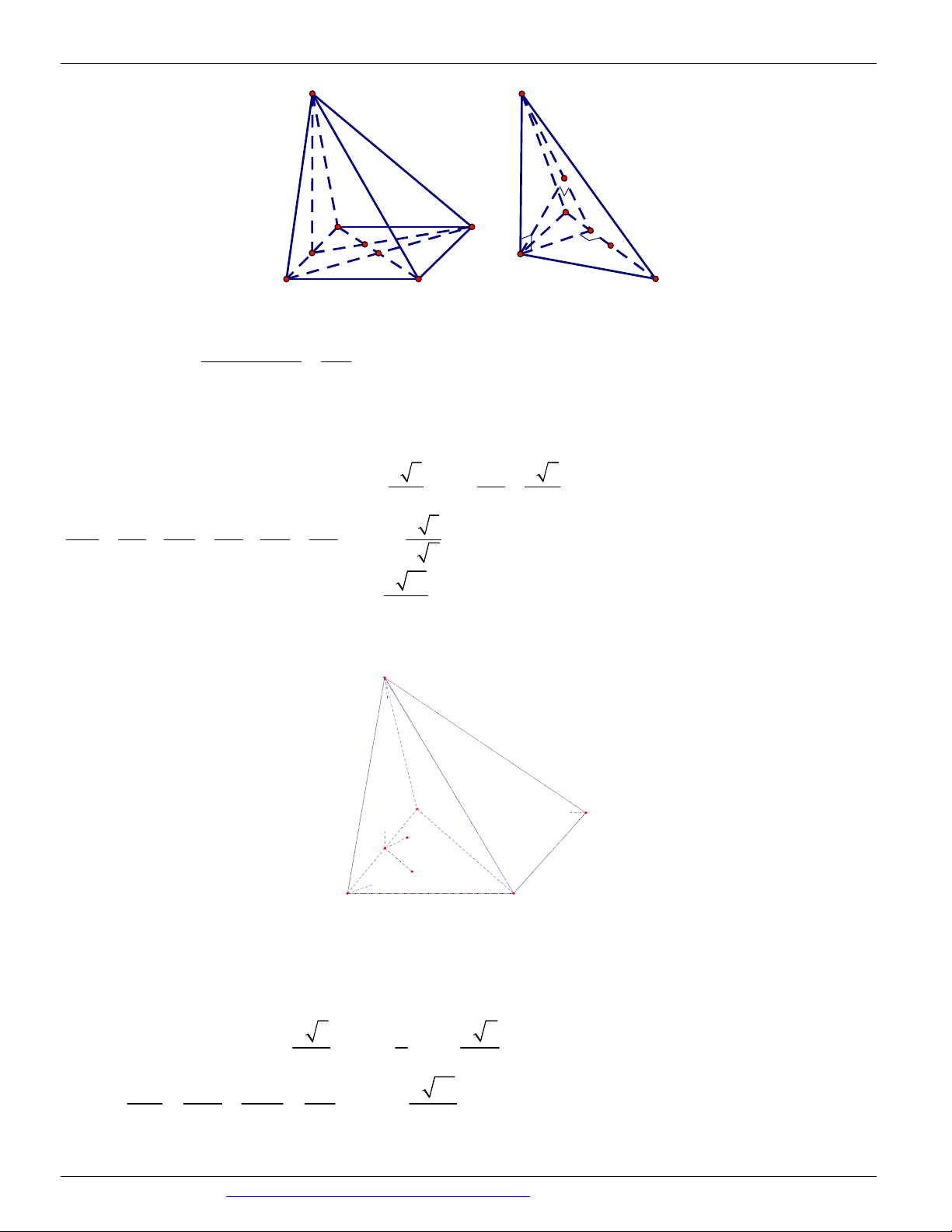
Câu 27. (Mã đề 102 BGD&ĐT NĂM 2018) Cho hình lập phương ABC . D AB CD   có tâm .
O Gọi I là tâm 1
của hình vuông AB CD
  và M là điểm thuộc đoạn thẳng OI sao cho MO
MI (tham khảo hình vẽ). Khi 2
đó cosin của góc tạo bởi hai mặt phẳng (MC D  )  và (MAB) bằng 7 85 6 85 17 13 6 13 A. B. C. D. 85 85 65 65
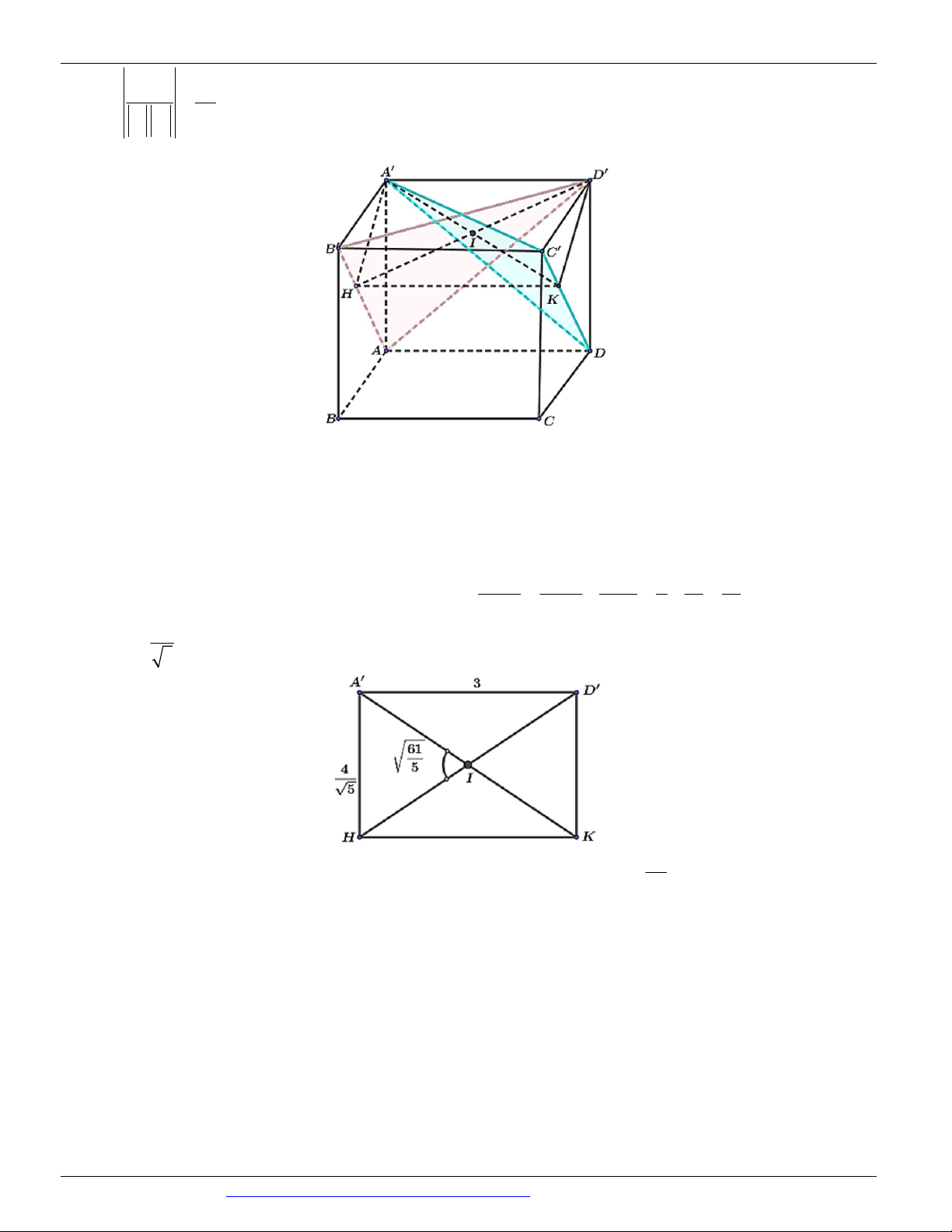
Câu 28. (Mã đề 101 BGD&ĐT NĂM 2018) Cho hình lập phương ABC . D AB CD
  có tâm O . Gọi I là tâm
của hình vuông AB CD
  và M là điểm thuộc đoạn thẳng OI sao cho MO  2MI (tham khảo hình vẽ). Khi
đó côsin của góc tạo bởi hai mặt phẳng (MC D  )
 và (MAB) bằng 7 85 17 13 6 13 6 85 A. B. C. D. 85 65 65 85
Câu 29. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hình chóp S.ABCD có đáy ABCD là
hình chữ nhật, AB a , AD SA  2a , SA   ABCD . Tính tang của góc giữa hai mặt phẳng SBD và ( ABCD) . 5 1 2 A. . B. 5 . C. . D. . 2 5 5
Câu 30. Cho hình hộp chữ nhật ABC . D AB CD
  có các cạnh AB  2, AD  3; AA  4 . Góc giữa hai mặt phẳng  AB D   và  A CD
  là  . Tính giá trị gần đúng của góc  ?
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. 45, 2 . B. 38,1 . C. 53, 4 . D. 61, 6 .
Câu 31. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Cho hình chóp SABCD có đáy
ABCD là hình thoi tâm O , đường thẳng SO vuông góc với mặt phẳng  ABCD . Biết AB SB a , a 6 SO
. Tìm số đo của góc giữa hai mặt phẳng SAB và SAD. 3 A. 30 B. 45 C. 60 D. 90
Câu 32. (TRƯỜNG THPT LƯƠNG TÀI SỐ 2 NĂM 2018-2019) Cho lăng trụ tam giác đều ABC.A BC   có diện tích đáy bằng 2
3a (đvdt), diện tích tam giác A BC bằng 2
2a (đvdt). Tính góc giữa hai mặt phẳng
ABC  và  ABC  ? A. 120 B. 60 C. 30 D. 45
Câu 33. (SỞ GD&ĐT QUẢNG NINH NĂM 2018-2019 LẦN 01) Cho hình chóp S.ABCD có đáy ABCD
là hình vuông có độ dài đường chéo bằng a 2 và SA vuông góc với mặt phẳng  ABCD . Gọi  là góc
giữa hai mặt phẳng SBD và  ABCD . Nếu tan  2 thì góc giữa  S AC  và SBC  bằng. A. 0 30 . B. 0 90 C. 0 60 . D. 0 45 .
Câu 34. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Cho hình chóp SABCD có đáy là hình
thang vuông ABCD tại A và D , cạnh bên A vuông góc với mặt phẳng đáy và SA a 2 . Cho biết
AB  2AD  2DC  2a . Tính góc giữa hai mặt phẳng SBA và SBC  1  A. 0 30 . B. 0 60 . C. 0 45 D. arcsin   .  4 
Câu 35. (CHUYEN PHAN BỘI CHÂU NGHỆ AN NĂM 2018-2019 LẦN 02) Cho hình hộp chữ nhật AB 6
ABCD.A ' B ' C ' D ' có mặt ABCD là hình vuông, AA ' 
. Xác định góc giữa hai mặt phẳng  A' BD 2
và C ' BD . A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 .
Câu 36. (THPT GANG THÉP THÁI NGUYÊN NĂM 2018-2019) Cho hình lập phương ABCD.AB CD  
. Góc giữa hai mặt phẳng ( ADC B  )  và (BCD A  )  là A. 30 . B. 45 . C. 90 . D. 60 .
Câu 37. (ĐỀ 01 ĐỀ PHÁT TRIỂN ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hình hộp chữ
nhật ABCD.AB CD
  có đáy ABCD là hình vuông, AC  a 2 . Gọi  P là
mặt phẳng qua AC cắt BB ,
DD lần lượt tại M , N sao cho tam giác AMN cân tại A có
MN a . Tính cos với    P, ABCD   . 2 1 1 3 A. . B. . C. . D. . 2 2 3 3
Câu 38. (THPT HÀM RỒNG THANH HÓA NĂM 2018-2019 LẦN 1) Cho lặng trụ đứng AB . C A BC   có
diện tích tam giác ABC bằng 2 3 . Gọi M , N , P lần lượt thuộc các cạnh AA , BB , CC , diện tích tam giác
MNP bằng 4 . Tính góc giữa hai mặt phẳng  ABC và MNPA. 120 . B. 45 . C. 30 . D. 90 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Dạng 2. Khoảng cách
Dạng 2.1 Khoảng cách từ điểm đến mặt phẳng
Câu 39. (Mã đề 101 BGD&ĐT NĂM 2018) Cho hình chóp S.ABC có đáy là tam giác vuông đỉnh B ,
AB a , SA vuông góc với mặt phẳng đáy và SA  2a . Khoảng cách từ A đến mặt phẳng SBC  bằng 2 5a 5a 2 2a 5a A. B. C. D. 5 3 3 5
Câu 40. (Mã đề 102 BGD&ĐT NĂM 2018) Cho hình chóp S.ABC có đáy là tam giác vuông đỉnh B ,
AB a , SA vuông góc với mặt phẳng đáy và SA a . Khoảng cách từ điểm A đến mặt phẳng SBC  bằng a 6 a 2 a A. B. C. D. a 3 2 2
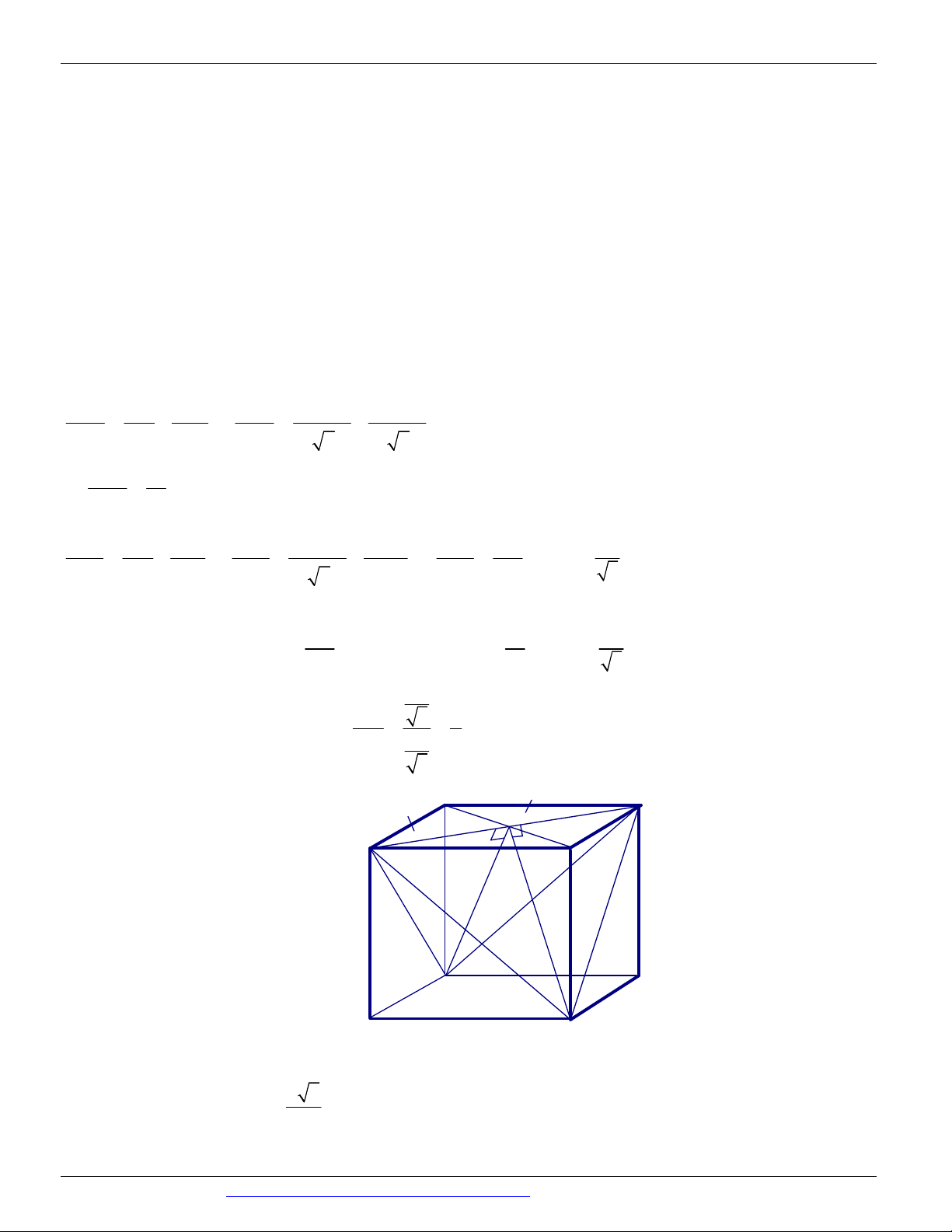
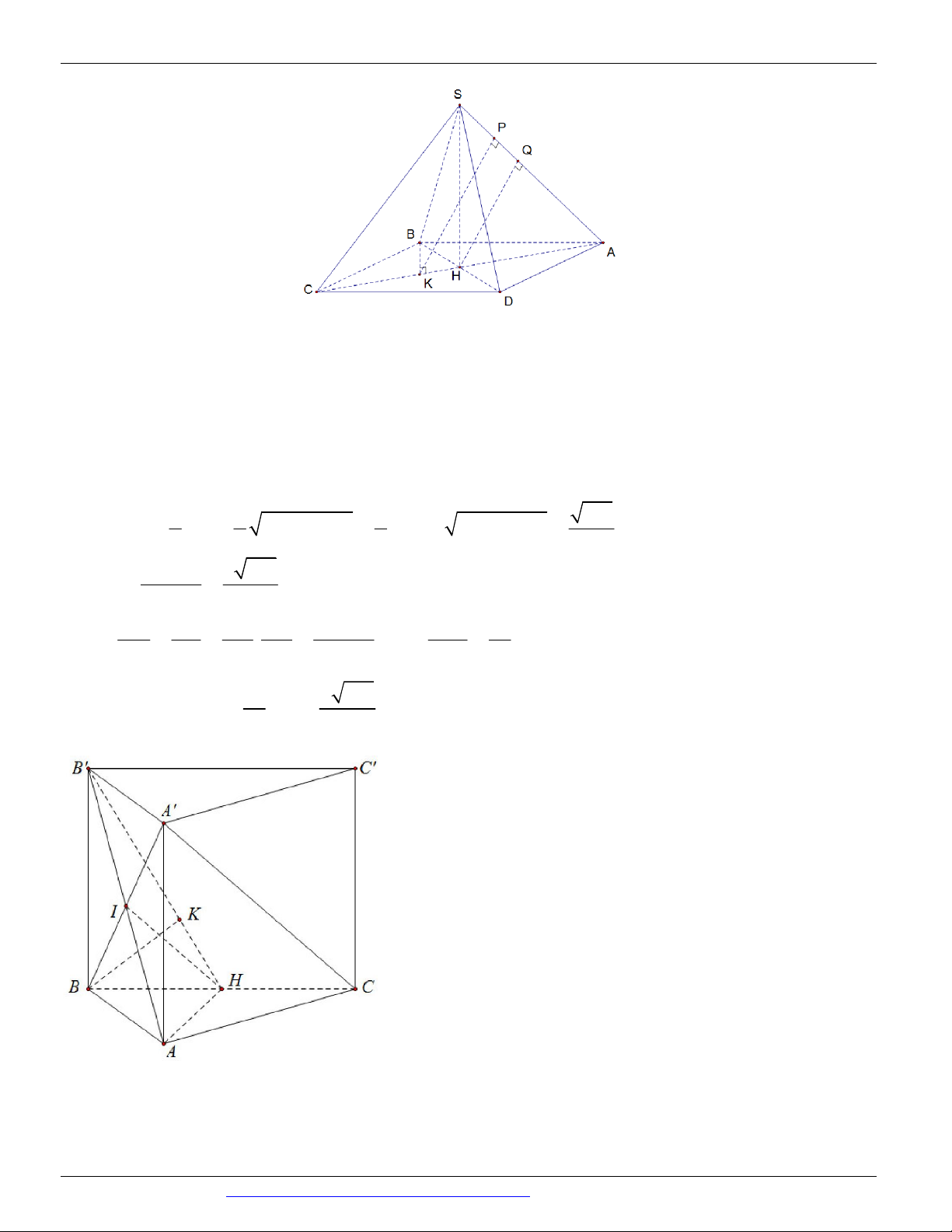
Câu 41. (Mã 103 - BGD - 2019) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , mặt bên SAB là tam
giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (minh họa như hình vẽ bên). Khoảng cách từ
D đến mặt phẳng SAC  bằng S A D B C a 2 a 21 a 21 a 21 A. . B. . C. . D. . 2 7 14 28
Câu 42. (Mã đề 101 - BGD - 2019) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (minh họa như hình vẽ bên). Khoảng
cách từ A đến mặt phẳng  SBD bằng
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 21a 21a 2a 21a A. . B. . C. D. . 14 7 2 28
Câu 43. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hình chóp S.ABCD có đáy là hình thoi cạnh a ,  o
BAD  60 , SA a và SA vuông góc với mặt phẳng đáy. Khoảng cách tứ B đến SCD bằng? 21a 15a 21a 15a A. . B. . C. . D. . 3 3 7 7
Câu 44. (Mã 102 - BGD - 2019) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam
giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy ( minh họa như hình vẽ bên). Khoảng cách
từ C đến mặt phẳng (SB ) D bằng 21a 2a 21a 21a A. . B. . C. . D. . 14 2 7 28
Câu 45. (MĐ 103 BGD&ĐT NĂM 2017-2018) Cho hình chóp S.ABCD có đáy là hình vuông cạnh 3a ,
SA vuông góc với mặt phẳng đáy và SA a . Khoảng cách từ A đến mặt phẳng SBC  bằng 6a 3a 5a 3a A. B. C. D. 6 3 3 2
Câu 46. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho tứ diện đều ABCD có cạnh bằng
a . Tính khoảng cách từ A đến mặt phẳng  BCD. a 6 a 6 3a A. . B. . C. . D. 2a . 2 3 2
Câu 47. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho hình chóp SAB D C có SA   AB D
C  , đáy AB D
C là hình chữ nhật. Biết D A
 2a , SA a . Khoảng cách từ A đến S D C  bằng: 3a 3a 2 2a 2a 3 A. B. C. D. 7 2 5 3
Câu 48. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho hình chop S.ABC
có đáy là tam giác vuông tại A , AB a , AC a 3 , SA vuông góc với mặt phẳng đáy và SA  2a . Khoảng
cách từ điểm A đến mặt phẳng (SBC) bằng:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 a 57 2a 57 2a 3 2a 38 A. B. C. D. 19 19 19 19
Câu 49. (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hình chóp tứ giác đều
S.ABCD có cạnh đáy bằng a và chiều cao bằng a 2 . Tính khoảng cách d từ tâm O của đáy ABCD đến
một mặt bên theo a . 2a 5 a 3 a 5 a 2 A. d  . B. d  . C. d  . D. d  . 3 2 2 3
Câu 50. (CHUYÊN TRẦN PHÚ HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho khối chóp S.ABCD có đáy
ABCD là hình vuông cạnh a , SA   ABCD và SA a 2 . Gọi M là trung điểm cạnh SC . Khoảng cách từ
điểm M đến mặt phẳng  SBD bằng a 2 a 10 a 2 a 10 A. B. C. D. 4 10 2 5
Câu 51. (THPT GANG THÉP THÁI NGUYÊN NĂM 2018-2019) Cho hình chóp S.ABC có đáy ABC
là tam giác vuông tại A , AB a , AC a 3 ; SA vuông góc với đáy, SA  2a . Khoảng cách từ điểm A đến
mặt phẳng SBC  bằng 2a 3 a 3 a 3 2a 3 A. . B. . C. . D. . 7 7 19 19
Câu 52. (THPT CHUYÊN SƠN LA NĂM 2018-2019 LẦN 01) Cho hình chóp S.ABC có đáy ABC là tam
giác đều cạnh a , SA a và SA vuông góc với mặt phẳng đáy. Khoảng cách từ điểm A đến mặt phẳng SBC  bằng: 2a 3a 21a 15a A. . B. . C. . D. . 2 7 7 5
Câu 53. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho hình chóp đều S.ABCD , cạnh đáy
bằng a , góc giữa mặt bên và mặt đáy là 60 . Tính khoảng cách từ điểm B đến mặt phẳng  SCD . a a 3 a 3 a A. B. C. D. 4 4 2 2
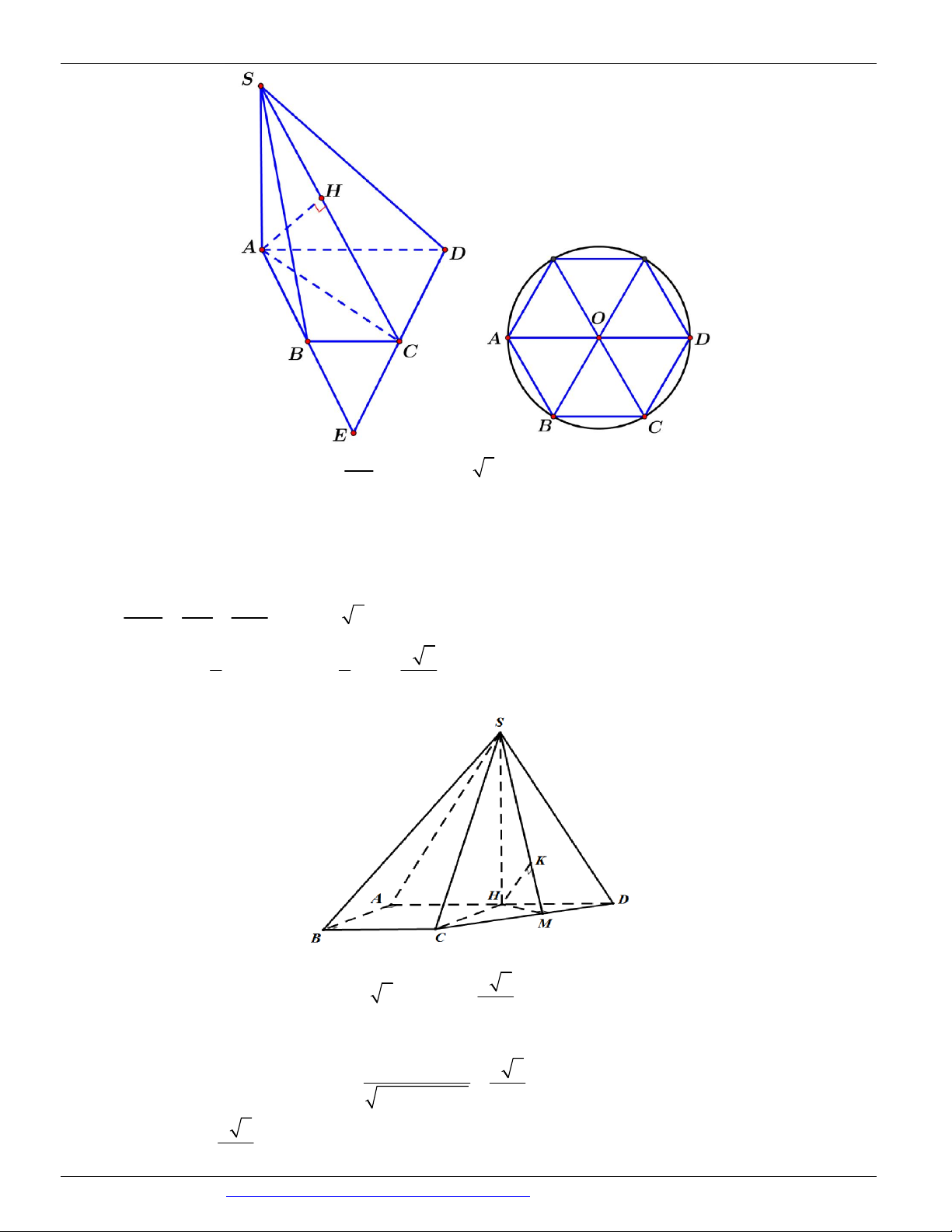
Câu 54. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hình chóp S.ABCD có đáy là
nửa lục giác đều ABCD nội tiếp trong đường tròn đường kính AD  2a và có cạnh SA vuông góc với mặt
phẳng đáy  ABCD với SA a 6 . Tính khoảng cách từ B đến mặt phẳng  SCD . a 2 a 3 A. a 2 . B. a 3 . C. . D. . 2 2
Câu 55. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Cho khối chóp S.ABCD có đáy ABCD
là hình thang vuông tại A và B , AB BC a, AD  2 .
a Hình chiếu của S lên mặt phẳng đáy trùng với a 6
trung điểm H của AD và SH
. Tính khoảng cách d từ B đến mặt phẳng SCD . 2 6a 6a 15a A. d
B. d a C. d D. d  8 4 5
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
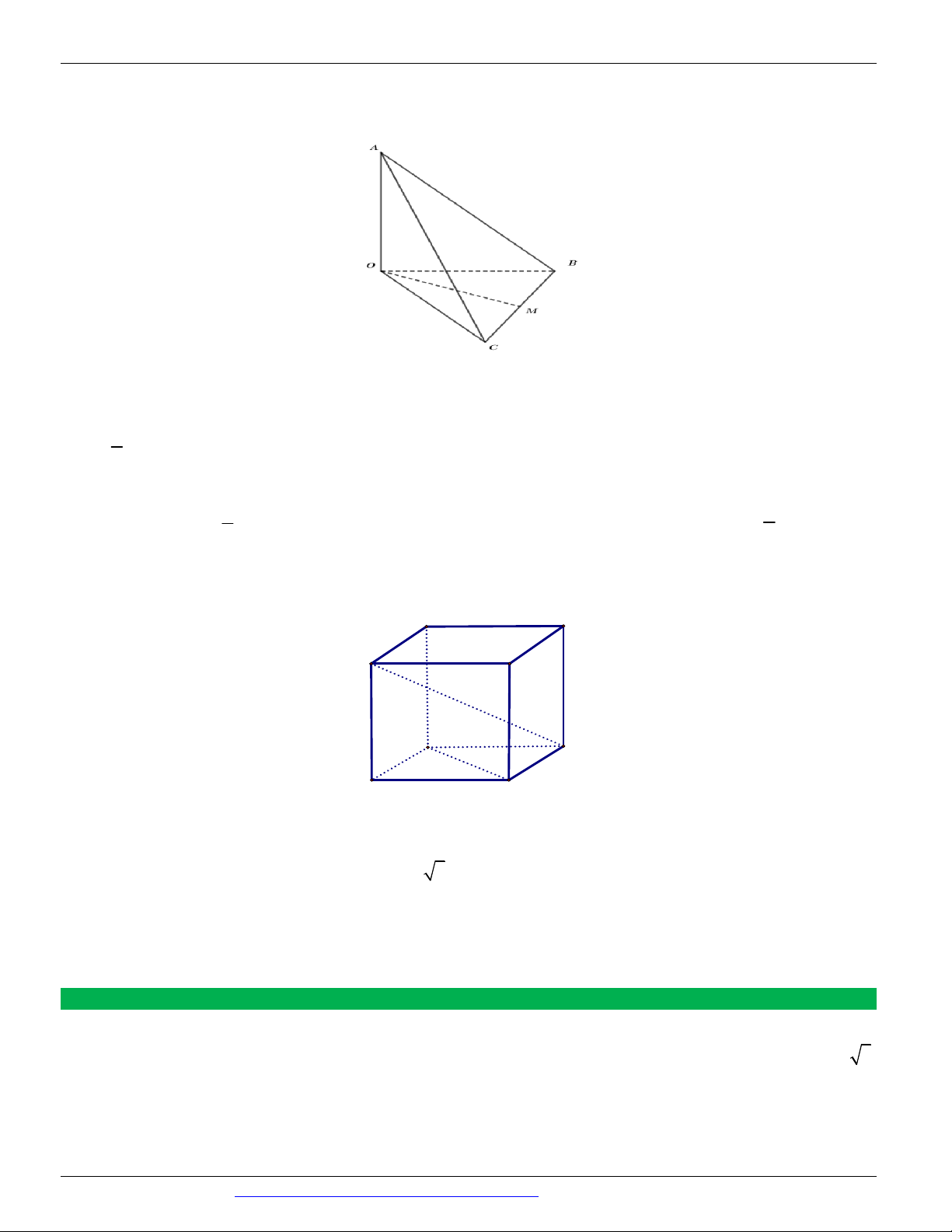
Câu 56. (THPT CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho tứ diện . O ABC có O ,
A OB, OC đôi một vuông góc với nhau OA OB OC  3. Khoảng cách từ O đến mp( ABC) là 1 1 1 A. B. 1 C. D. 3 2 3
Câu 57. (THPT CẨM GIÀNG 2 NĂM 2018-2019) Cho hình chóp S.ABCD có đáy ABCD là hình thoi 
cạnh a , ABC  60 . Cạnh bên SA SC a vuông góc với đáy,
2 . Khoảng cách từ B đến mặt phẳng SCD là a 15 a 2 2a 5a 30 A. . B. . C. . D. . 5 2 5 3
Câu 58. (ĐỀ 01 ĐỀ PHÁT TRIỂN ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hình chóp
S.ABCD có đáy là hình thoi cạnh 2a , góc 
BAD  60 , SAB là tam giác đều nằm trên mặt phẳng vuông góc
với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng SCD là a 3 3a a 6 A. B. C. D. a 6 2 . 2 . 2 .
Câu 59. (KTNL GV THUẬN THÀNH 2 BẮC NINH NĂM 2018-2019) Cho hình chóp tứ giác S.ABCD
có đáy ABCD là hình bình hành tâm O; mặt phẳng  SAC  vuông góc với mặt phẳng  SBD . Biết khoảng
cách từ O đến các mặt phẳng SAB, SBC ,SCD lần lượt là 1; 2; 5 . Tính khoảng cách d từ O đến mặt phẳng  SAD . 19 20 2 A. d  . B. d  . C. d  2 . D. d  . 20 19 2
Dạng 2.2 Khoảng cách của đường thẳng với đường thẳng
Câu 60. (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho lập phương ABCD.AB CD
  có cạnh bằng a ( tham
khảo hình vẽ bên ).Khoảng cách giữa hai đường thẳng BD và AC  bằng 3a A. B. 2a C. 3a D. a 2
Câu 61. (Mã đề 101 BGD&ĐT NĂM 2018) Cho hình chóp S.ABCD có đáy là ình chữ nhật,
AB a, BC  2a, SA vuông góc với mặt phẳng đáy và SA  .
a Khoảng cách giữa hai đường thẳng AC và SB bằng 6a 2a a a A. B. C. D. 2 3 2 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 62. (Mã đề 102 BGD&ĐT NĂM 2018) Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB a ,
BC  2a , SA vuông góc với mặt phẳng đáy và SA a . Khoảng cách giữa hai đường thẳng BD , SC bằng 4 21a 2 21a a 30 a 30 A. B. C. D. 21 21 12 6
Câu 63. (Mã đề 104 BGD&ĐT NĂM 2018) Cho tứ diện . O ABC có O ,
A OB, OC đôi một vuông góc với
nhau, OA a và OB OC  2a . Gọi M là trung điểm của BC . Khoảng cách giữa hai đường thẳng OM và AB bằng 6a 2 5a 2a A. B. a C. D. 3 5 2
Câu 64. (MĐ 103 BGD&ĐT NĂM 2017-2018) Cho tứ diện OABC có OA , OB , OC đôi một vuông góc
với nhau, và OA OB a , OC  2a . Gọi M là trung điểm của AB . Khoảng cách giữa hai đường thẳng
OM và AC bằng 2 5a 2a 2a 2a A. B. C. D. 5 2 3 3
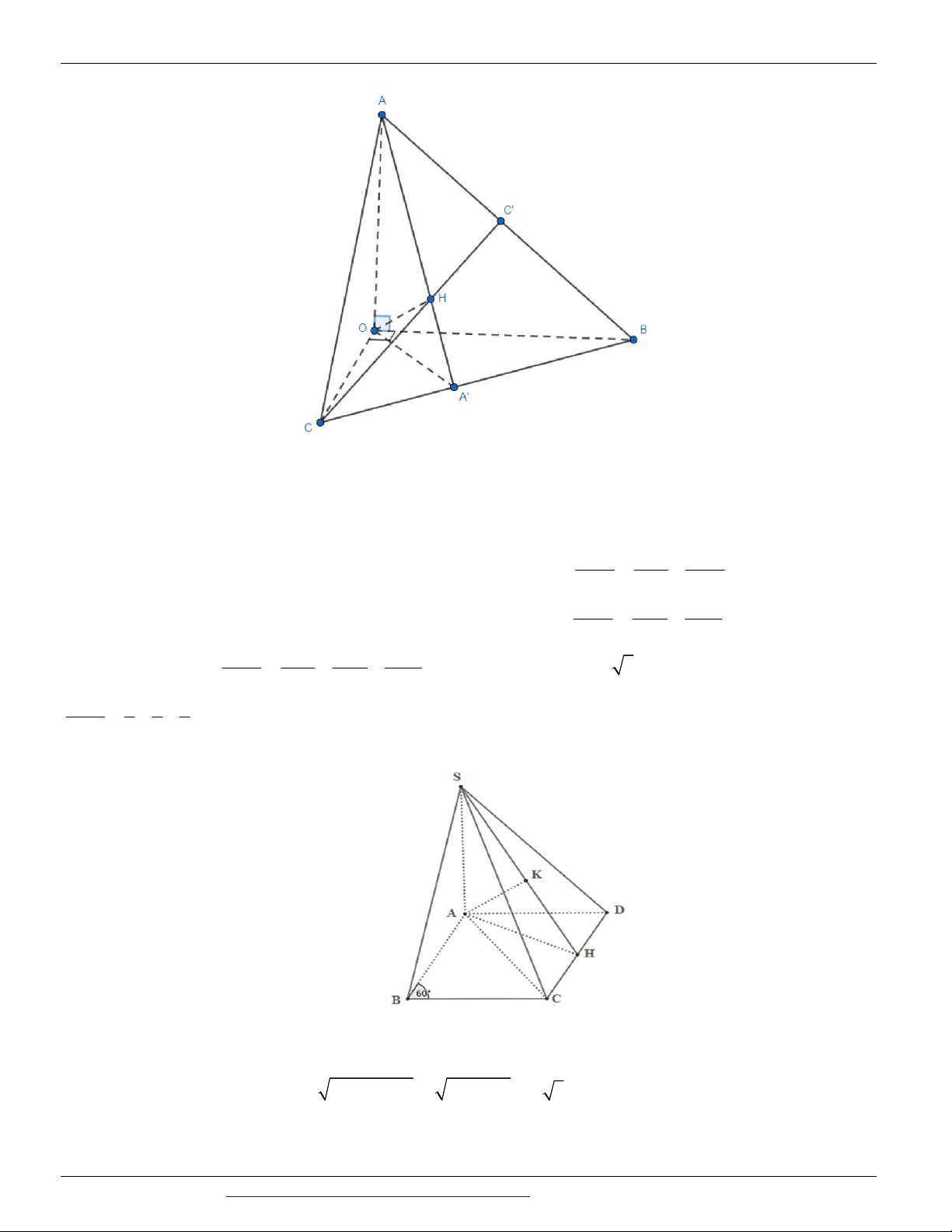
Câu 65. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho lăng trụ đứng ABC.AB C   có đáy ABC
là tam giác vuông tại A với AC a 3 . Biết BC hợp với mặt phẳng  AA CC
  một góc 30o và hợp với 6
mặt phẳng đáy góc  sao cho sin 
. Gọi M , N lần lượt là trung điểm cạnh BB và A C   . Khoảng cách 4
giữa MN và AC là: a 6 a 3 a 5 a A. B. C. D. 4 6 4 3
Câu 66. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho hình chóp S.ABC , 3 a 3
có SA SB SC , đáy là tam giác đều cạnh a . Biết thể tích khối chóp S.ABC bằng . Khoảng cách 3
giữa hai đường thẳng SA và BC bằng: 4a 3 13a 6a a 3 A. B. C. D. 7 13 7 4
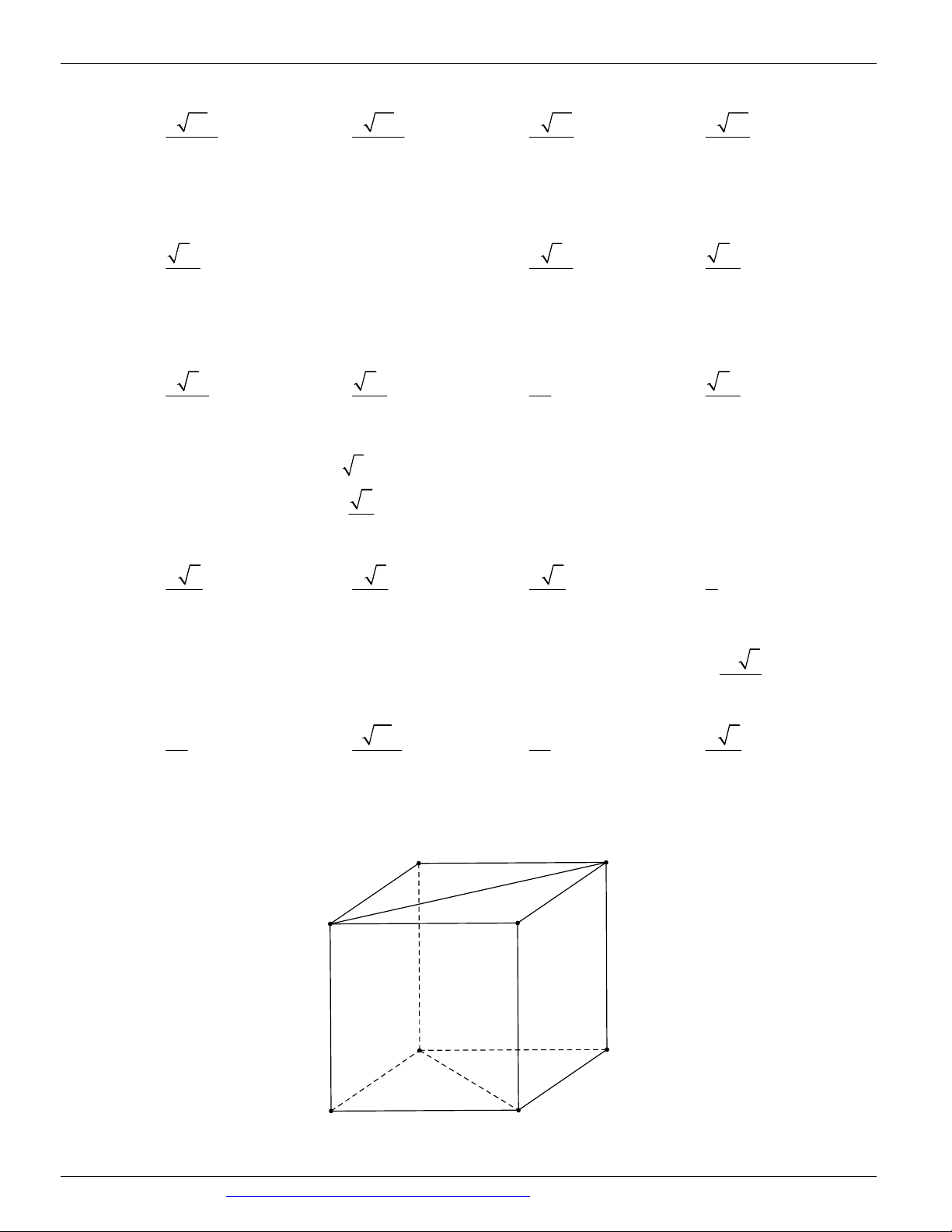
Câu 67. (THPT CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hình lập phương ABC .
D A' B 'C ' D ' có cạnh bằng a (tham khảo hình vẽ). A D B C A' D' B' C'
Khoảng cách giữa hai đường thẳng BD và A 'C ' bằng
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 3 A. a B. 2a C. a D. 3a 2
Câu 68. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Cho hình chóp S.ABCD có
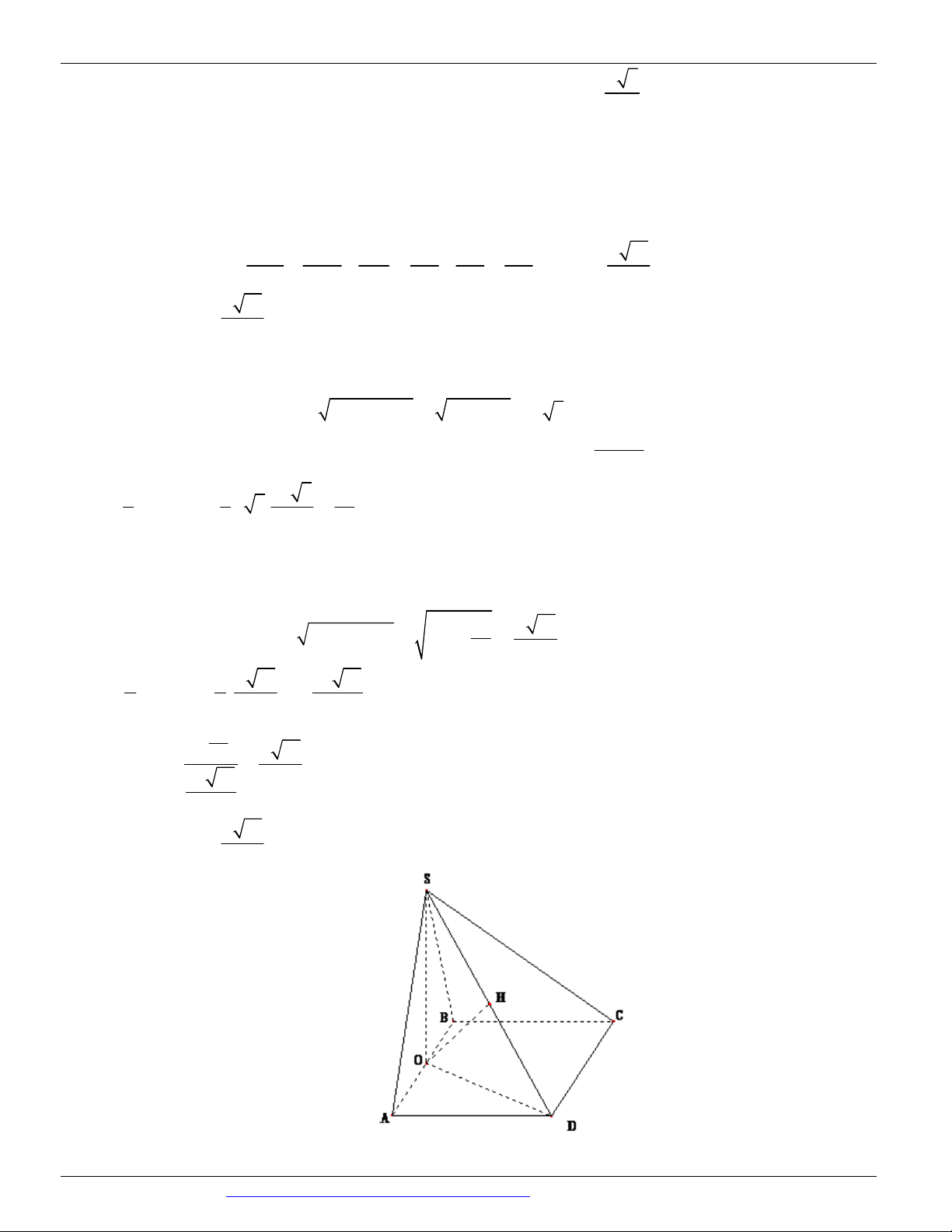
SA   ABCD , đáy ABCD là hình chữ nhật với AC a 5 và BC a 2 . Tính khoảng cách giữa SD và BC . a 3 2a 3a A. . B. a 3 . C. . D. . 2 3 4
Câu 69. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho hình chóp S.ABCD có đáy ABCD
là hình vuông tâm O cạnh a , SO vuông góc với mặt phẳng  ABCD và SO  .
a Khoảng cách giữa SC và AB bằng a 3 a 5 2a 3 2a 5 A. B. C. D. 15 5 15 5
Câu 70. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho lăng trụ tam giác đều ABC.AB C  
có tất cả các cạnh đều bằng a . Khoảng cách giữa hai đường thẳng BC và AB bằng a 21 a 3 a 7 a 2 A. B. C. D. 7 2 4 2
Câu 71. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hình chóp S.ABCD có đáy
ABCD là hình thoi cạnh a , AC a . Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt
phẳng đáy. Tính khoảng cách giữa hai đường thẳng AD và SC , biết góc giữa đường thẳng SD và mặt đáy bằng 60 . a 906 a 609 a 609 a 600 A. B. C. D. 29 29 19 29
Câu 72. (KTNL GIA BÌNH NĂM 2018-2019) Cho hình chóp S.ABCD , đáy ABCD là hình bình hành có
AB  4, BC  3 , SA SB SC SD  6 . K là hình chiếu vuông góc của B xuống AC . Tính độ dài d đoạn
vuông góc chung của SA và BK . 119 4 229 259 4 119 A. B. C. D. 11 13 5 15
Câu 73. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Cho hình lăng trụ tam giác đều ABC.A BC
  có AB a, AA  2 .
a Tính khoảng cách giữa hai đường thẳng AB và A . Ca 3 2 5 2 17 A. B. a C. a 5 D. a 2 5 17
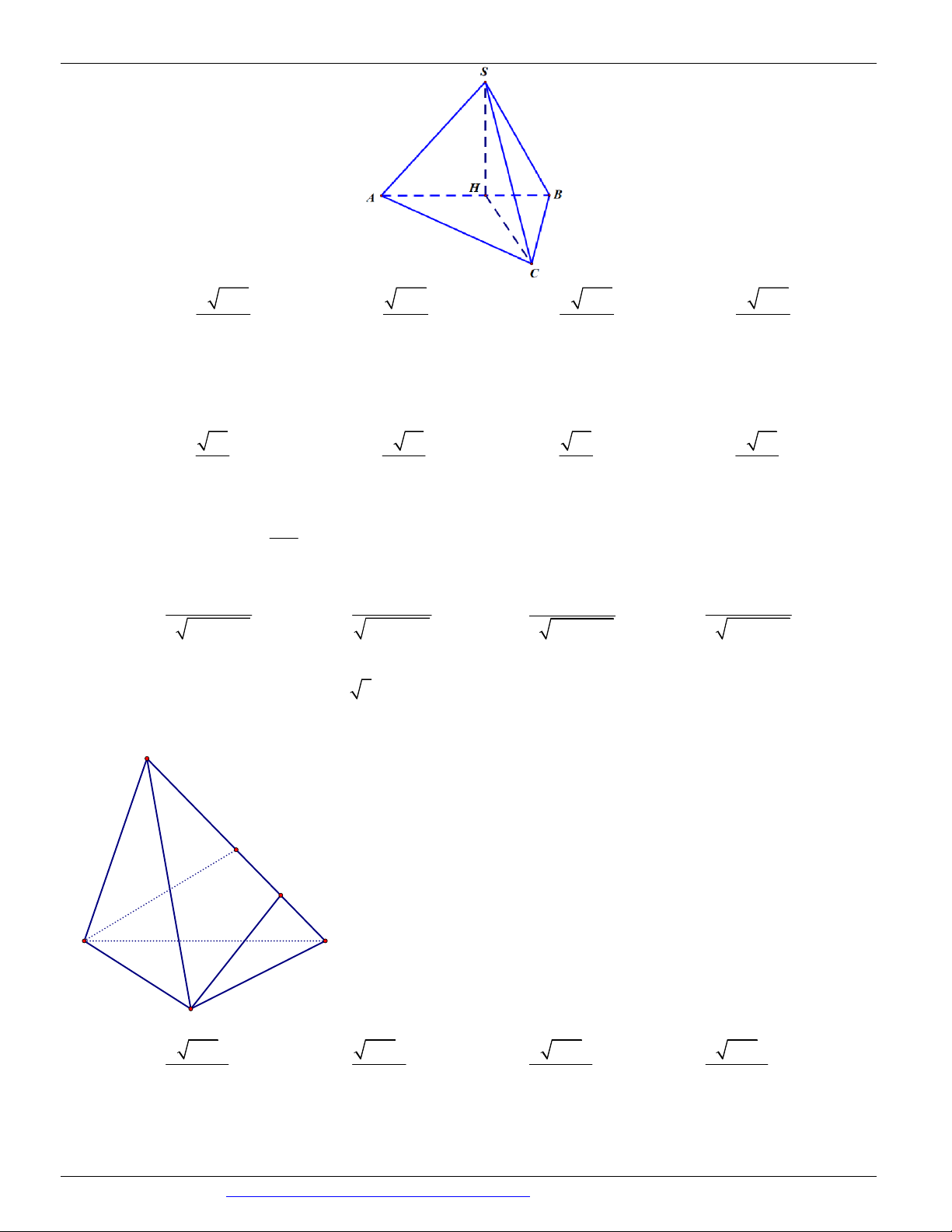
Câu 74. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Cho hình chóp . S ABC có đáy là
tam giác đều cạnh bẳng 4 , góc giữa SC và mặt phẳng ABC là 45 . Hình chiếu của S lên mặt phẳng
ABC là điểm H thuộc cạnh AB sao cho HA  2HB. Tính khoảng cách giữa hai đường thẳng SA và BC .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 4 210 210 4 210 2 210 A. d  . B. d  . C. d  . D. d  . 45 5 15 15
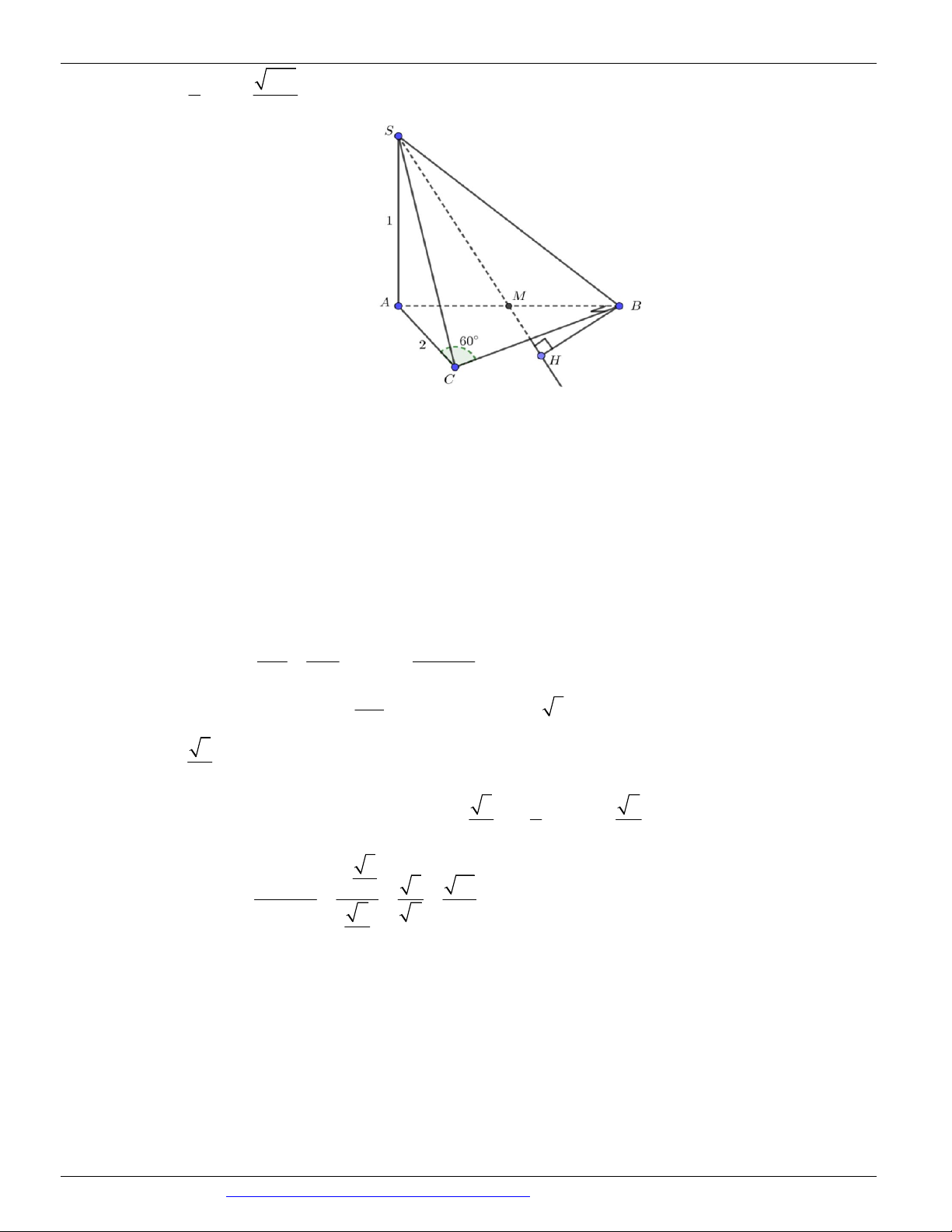
Câu 75. (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Cho hình chóp S.ABC có tam giác ABC
vuông tại B , C  60 , AC  2 , SA   ABC  , SA  1 . Gọi M là trung điểm của AB . Khoảng cách d giữa SM và BC là 21 2 21 21 2 21 A. d  . B. d  . C. d  . D. d  . 7 7 3 3
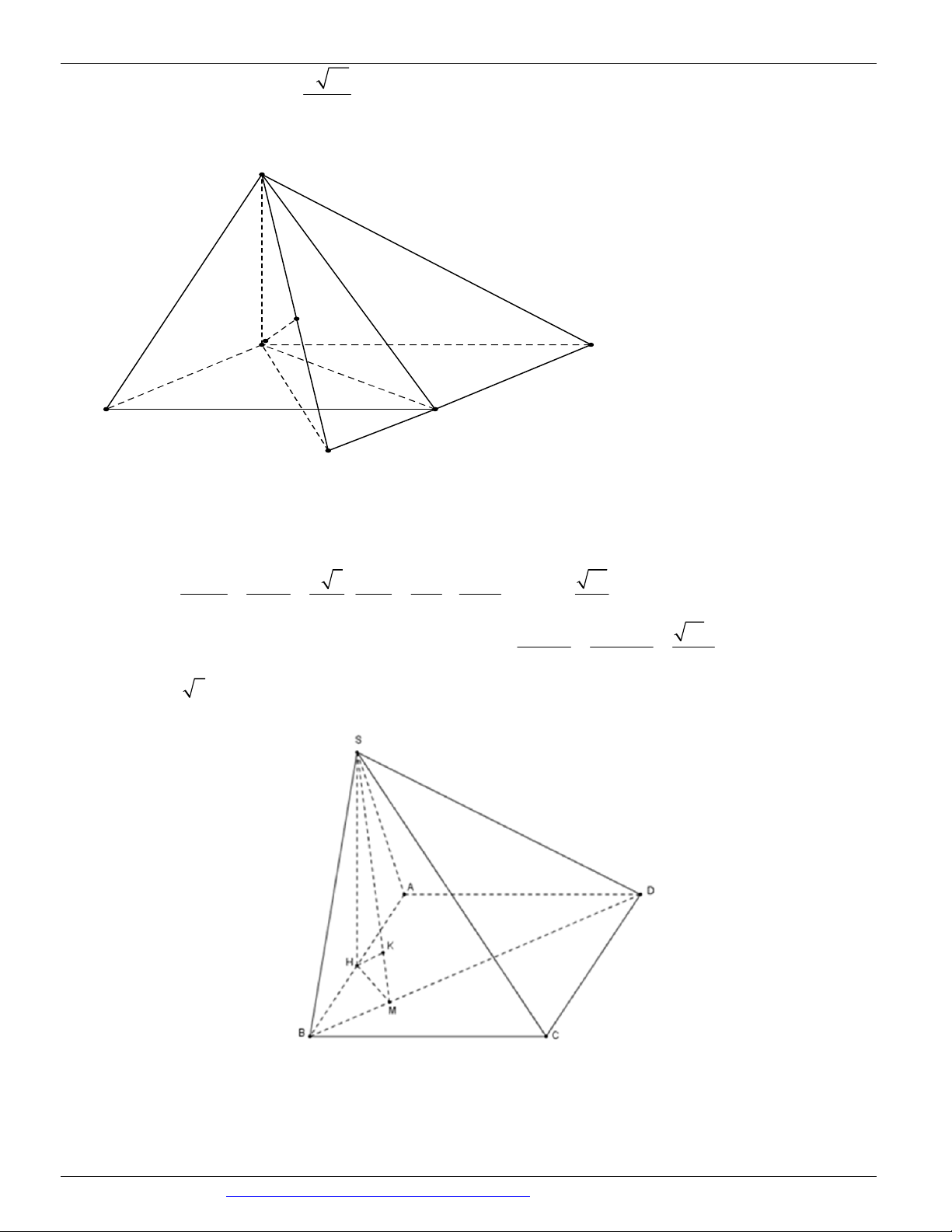
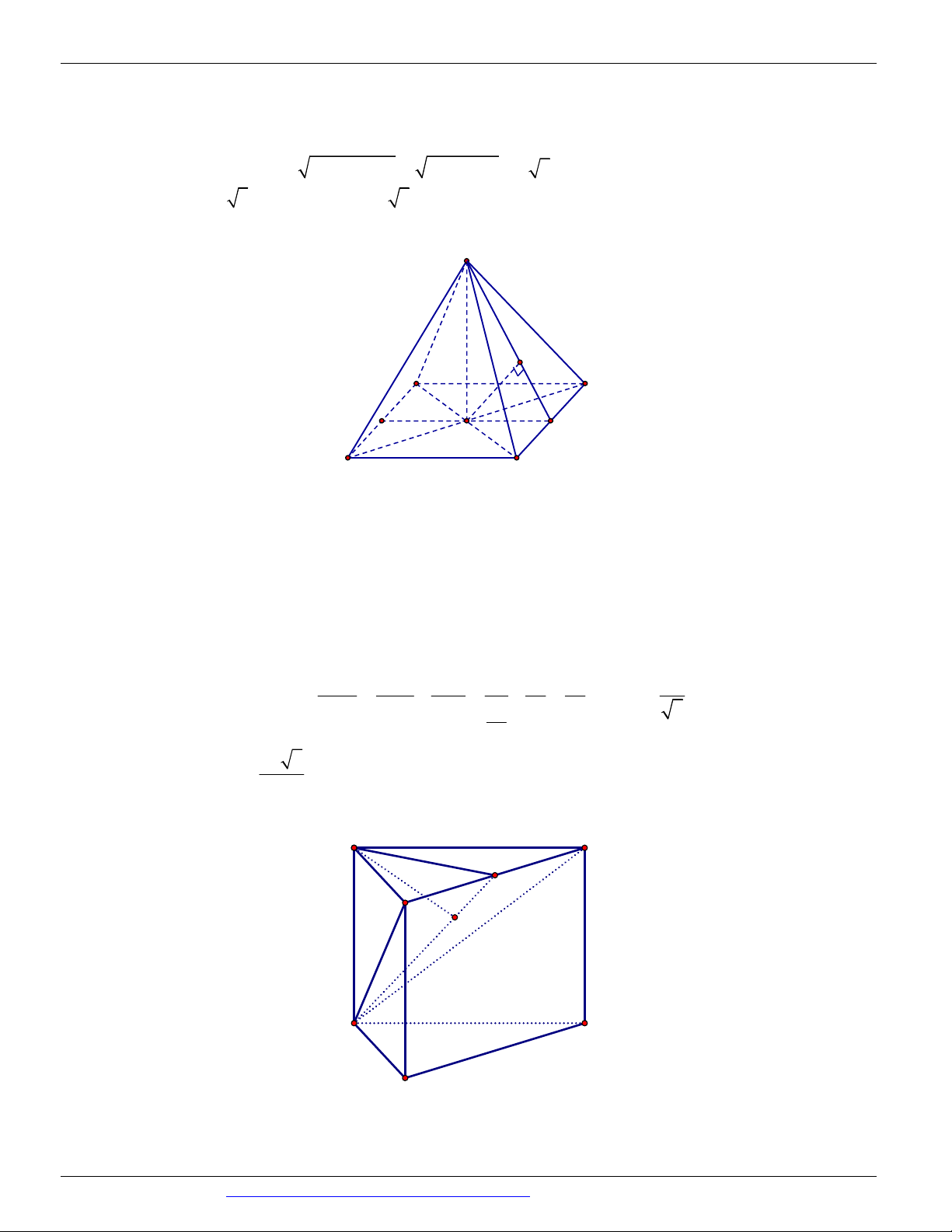
Câu 76. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho khối chóp tứ giác đều 2 a b
S.ABCD có thể tích bằng
với AB a . Gọi G là trọng tâm của tam giác SCD , trên các cạnh A , B SD 3
lần lượt lấy các điểm E, F sao cho EF song song BG . Khoảng cách giữa hai đường thẳng DG và EF bằng 2ab ab 2 a b ab A. . B. . C. . D. . 2 2 3 2b a 2 2 2b a 2 2 3 2b a 2 2 3 2b a
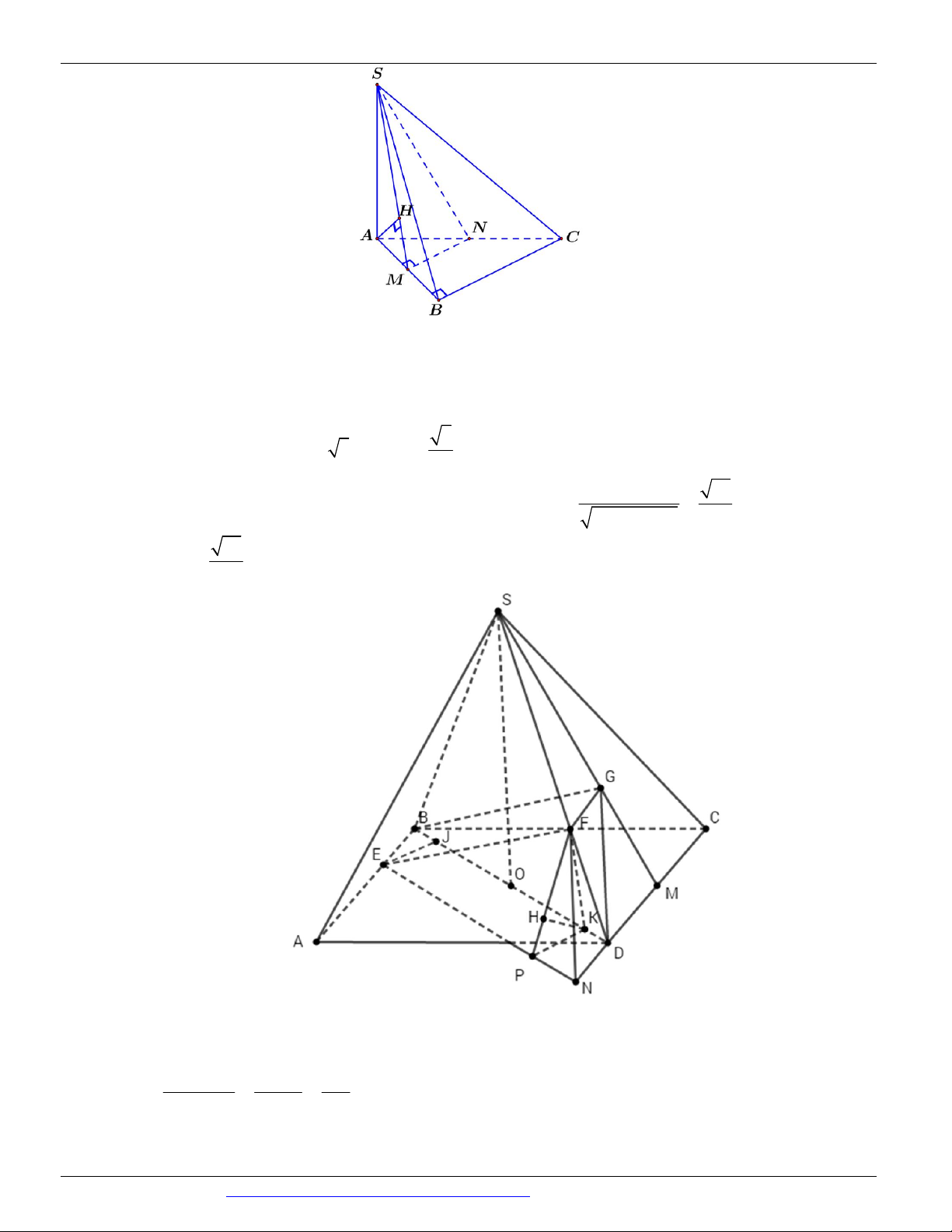
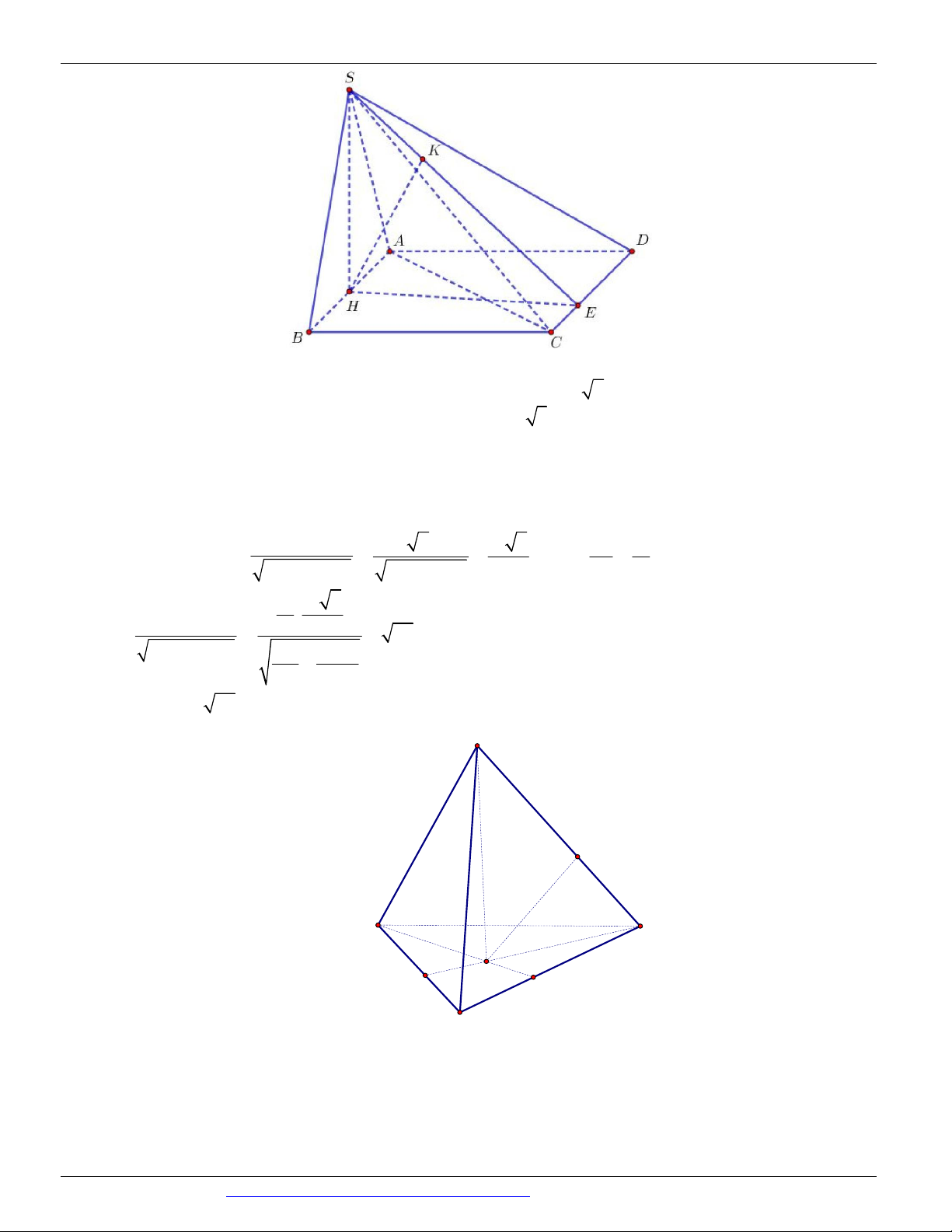
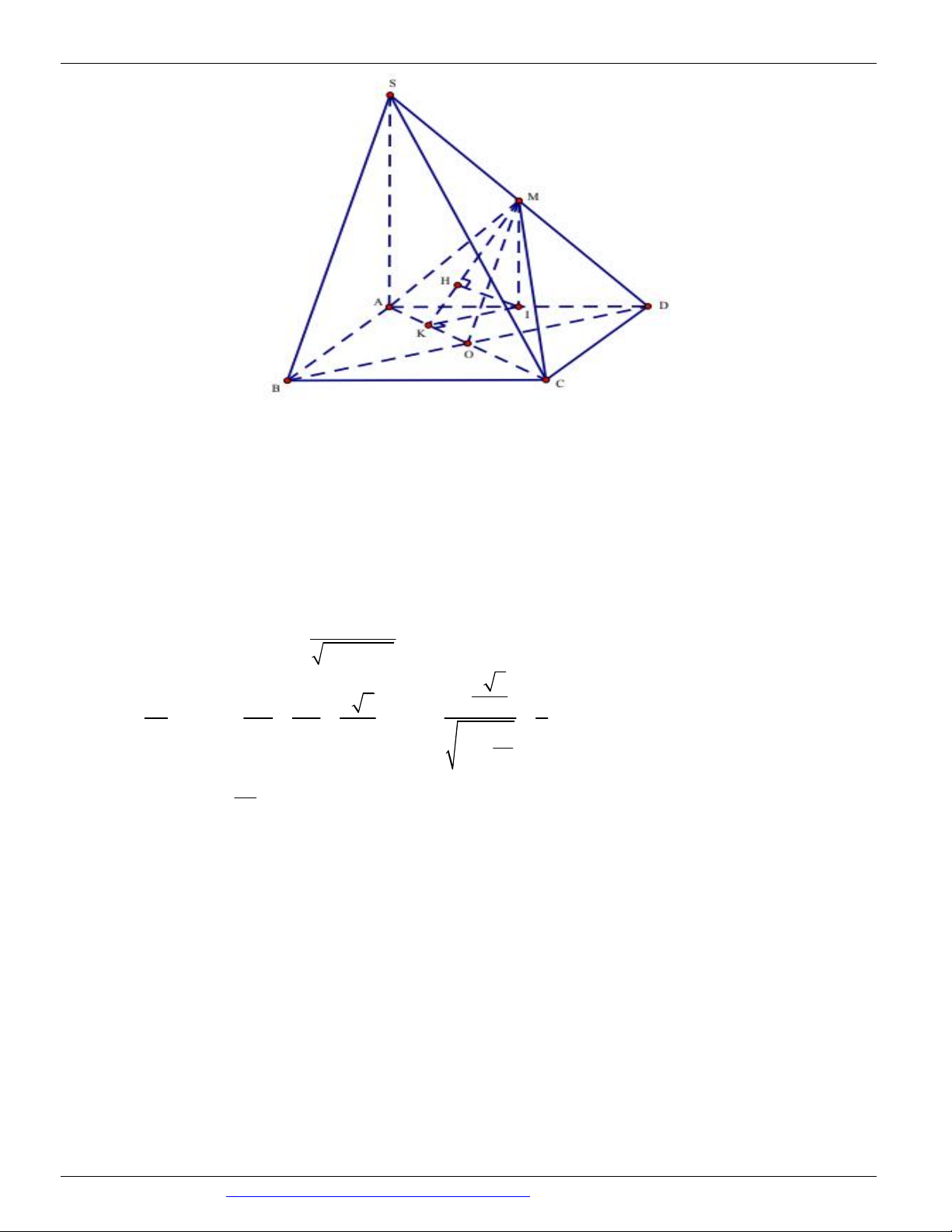
Câu 77. (TRƯỜNG THPT HOÀNG HOA THÁM HƯNG YÊN NĂM 2018-2019) Cho hình chóp S.ABC
có đáy ABC là tam giác đều cạnh 2a 3 , mặt bên SAB là tam giác cân với 
ASB  120 và nằm trong mặt
phẳng vuông góc với đáy. Gọi M là trung điểm của SC và N là trung điểm của MC . Tính khoảng cách
giữa hai đường thẳng AM , BN . S M N A C B 2 327a 237a 2 237a 5 237a A. . B. . C. . D. . 79 79 79 316
Câu 78. (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Cho tứ diện đều ABCD có cạnh bằng 3 cm. Gọi
M là trung điểm của CD . Khoảng cách giữa AC và BM là:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 11 3 22 3 2 2 A. cm . B. cm . C. cm D. cm . 11 11 11 11
Câu 79. (TRƯỜNG THPT LƯƠNG TÀI SỐ 2 NĂM 2018-2019) Cho hình chóp S.ABCD có đáy ABCD   
là hình bình hành và SA SB SC  11 , SAB  30 , SBC  60 và SCA  45 . Tính khoảng cách d giữa
hai đường thẳng AB và SD ? 22 A. d  4 11 B. d  2 22 C. d D. d  22 2
Câu 80. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho tứ diện ABCD có các cạnh A ,
B AC, AD vuông góc với nhau đôi một và AD  2 AC  3AB a. Gọi  là đường thẳng chứa trong mặt
(BCD) sao cho khoảng cách từ điểm A đến  là nhỏ nhất và khoảng cách lớn nhất giữa hai đường thẳng 
và AD là d. Khẳng định nào sau đây là đúng?. 14 3a 4a
A. d a .
B. 3a d  4a. C.d  .
D. d  4a. 14 14 7
Câu 81. (THPT NGÔ GIA TỰ VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hình chóp S.ABCD có đáy 
là hình bình hành và SA SB SC  11, 0 SAB  30 ,  0 SBC  60 và  0
SCA  45 . Tính khoảng cách d giữa
hai đường thẳng AB và SD? 22 A. d  4 11. B. d  2 22. C. d  . D. d  22. 2
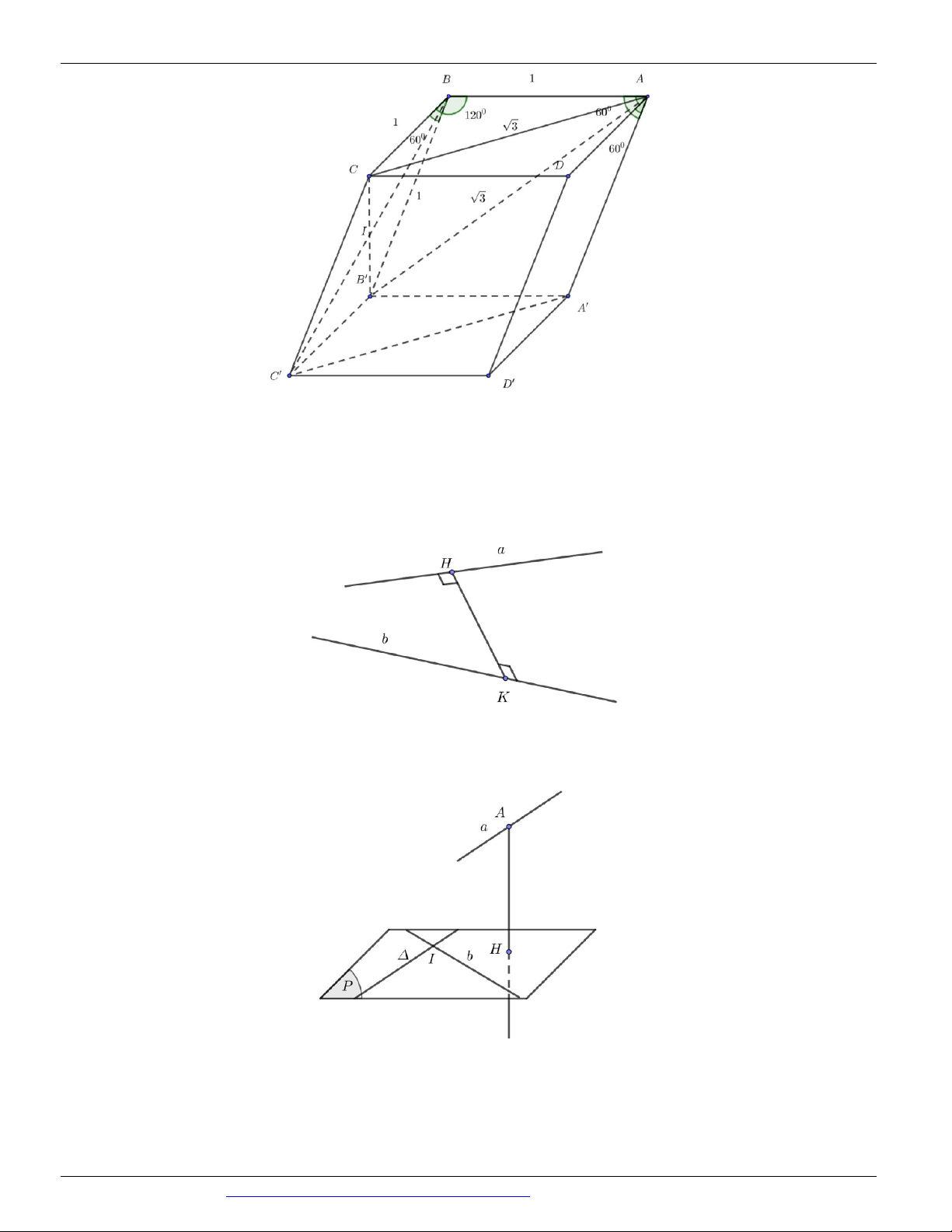
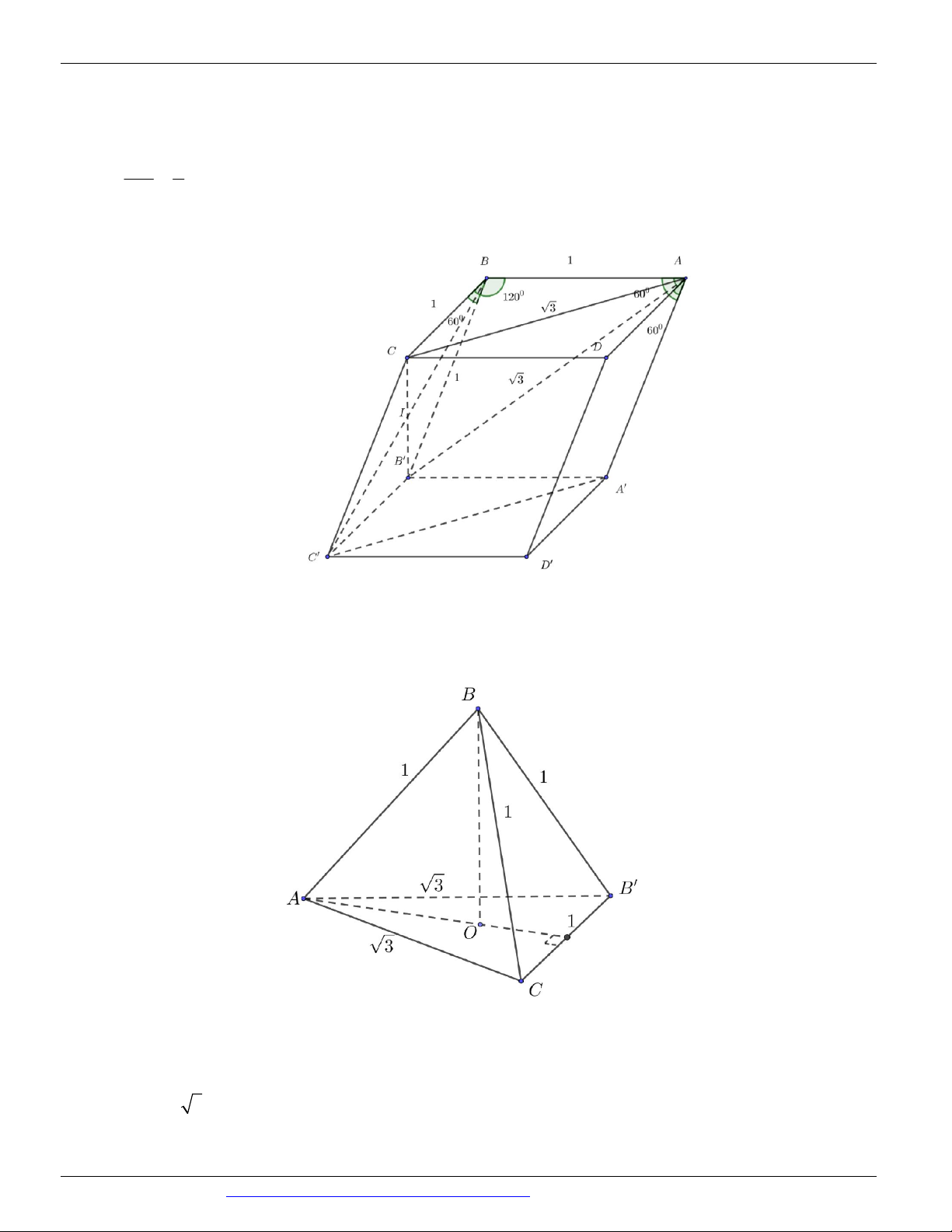
Câu 82. (THPT NĂM 2018-2019 LẦN 04) Cho hình hộp ABCDAB CD
  có tất cả các cạnh đều bằng 1 và
các góc phẳng ở đỉnh A đều bằng 60 . Tính khoảng cách giữa hai đường thẳng AB và AC . 22 2 2 3 A. . B. . C. . D. . 11 11 11 11
Dạng 2.3 Khoảng cách của đường với mặt
Câu 83. (THPT LÊ XOAY VĨNH PHÚC LẦN 1 NĂM 2018-2019) Cho hình chóp S.ABCD có đáy là
hình thang vuông tại A và D , SD vuông góc với mặt đáy  ABCD , AD  2 ,
a SD a 2 . Tính khoảng
cách giữa đường thẳng CD và mặt phẳng SAB a 2a a 3 A. . B. a 2. C. . D. . 2 3 2
Câu 84. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy và SA  2a
. Gọi M là trung điểm của SD . Tính khoảng cách d giữa đường thẳng SB và mặt phẳng  ACM  3a 2a a A. d
B. d a C. d D. d  2 3 3
PHẦN B. LỜI GIẢI THAM KHẢO Dạng 1. Góc
Dạng 1.1 Góc của đường thẳng với mặt phẳng Câu 1. Chọn C
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Có SA   ABC  nên AB là hình chiếu của SA trên mặt phẳng  ABC  .
SB ABC       SB AB  , ,  SBA . Mặt khác có A
BC vuông tại C nên 2 2 AB
AC BC a 3 . SA Khi đó  1 tan SBA  
nên SB,  ABC      30. AB 3 Câu 2. Chọn A S D A B C
Do SA   ABCD nên góc giữa đường thẳng SC và mặt phẳng đáy bằng góc  SCA . SA Ta có SA
2a , AC  2a    tan SCA
 1  SCA  45 . AC
Vậy góc giữa đường thẳng SC và và mặt phẳng đáy bằng bằng 45 . Câu 3. Chọn C
Vì SA vuông góc với mặt phẳng  ABC  , suy ra góc giữa đường thẳng SC và mặt phẳng  ABC  bằng SCA . SA 2a Mà  tan SCA    1 . 2 2 AC a  3a
Vậy SCA  45 . Câu 4. Chọn B S D A B C
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Do SA   ABCD nên góc giữa đường thẳng SB và mặt phẳng đáy bằng góc  SBA . AB 1 Ta có   cos SBA    SBA  60 . SB 2
Vậy góc giữa đường thẳng SB và và mặt phẳng đáy bằng bằng 60 . Câu 5. Chọn A
Ta có AC là hình chiếu vuông góc của SC trên mặt phẳng  ABC . 
Suy ra góc giữa đường thẳng SC và mặt phẳng  ABC bằng SCA   .
Ta có AC a 2 , SA a 2 nên tam giác SAC vuông cân tại A 0    45 . Câu 6. Chọn A
Ta có SA   ABC  nên AC là hình chiếu của SC lên mặt phẳng  ABC  .
Do đó SC ABC   SC AC   , ,  SCA .
Tam giác ABC vuông tại B, AB a 3 và BC a nên 2 2 2 AC
AB BC  4a  2a .
Do đó tam giác SAC vuông cân tại A nên  0 SCA  45 .
Vậy SC ABC  0 ,  45 . Câu 7. Chọn D S M A D H O B C 2 a a 2
Gọi O là tâm của hình vuông. Ta có SO   ABCD và 2 SO a   2 2
Gọi M là trung điểm của OD ta có MH / / SO nên H là hình chiếu của M lên mặt phẳng  ABCD và 1 a 2 MH SO  . 2 4 
Do đó góc giữa đường thẳng BM và mặt phẳng ( ABCD) là MBH .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 a 2 MH 1 Khi đó ta có  4 tan MBH    . BH 3a 2 3 4 1
Vậy tang của góc giữa đường thẳng BM và mặt phẳng  ABCD bằng 3 Câu 8. Chọn D
Ta có SA   ABC  nên đường thẳng AC là hình chiếu vuông góc của đường thẳng SC lên mặt phẳng  ABC .
Do đó,   SC ABC       SC AC  , ,
SCA (tam giác SAC vuông tại A ).
Tam giác ABC vuông cân tại B nên AC AB 2  2a . SA Suy ra  tan SCA
 1 nên   45o . AC S a 6 3 A D a 2 Câu 9. a B a C AC a 2 ,
AC là hình chiếu vuông góc của SC trên  ABCD  SC ABCD   SC AC   , ;  SCA SA a 6 S
AC : tan SCA   : a 2 3    SCA  30 . AC 3 3
Câu 10. Chọn A
Ta có AC a 2
Vì AC là hình chiếu của SC lên  ABCD  nên góc giữa SC và  ABCD  là góc giữa SC và AC
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 a 6 3
Xét SAC vuông tại A, ta có:  3 tan SCA   . Suy ra  0 SCA  30 a 2 3
Câu 11. Chọn A
Vì SA   ABCD  SC ABCD   SC AC   ; ;  SCA . Ta có 2 2 AC
AB BC a 2.  SA a 2  0  tan SAC    1  SCA  45 . AC a 2 S M A D H O B C Câu 12.
Trong tam giác SOD dựng MH //SO, H OD ta có MH   ABCD . 
Vậy góc tạo bởi BM và mặt phẳng  ABCD là MBH . 1 1 1 a 2 Ta có 2 2 2 2 MH SO SD OD  4a  2a  . 2 2 2 2 3 3 3a 2 BH BD  2a 2  . 4 4 2 MH Vậy  1 tan MBH   . BH 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 S H A C Câu 13. B
Trong SAB kẻ AH SB H SB. SA BC  Vì 
BC  SAB BC AH  . AB BC 
Mà SB AH do cách dựng nên AH  SBC , hay H là hình chiếu của A lên SBC suy ra góc giữa SA  
và SBC là góc ASH hay góc ASB .
Tam giác ABC vuông ở B 2 2
AB AC BC a 3 AB 1
Tam giác SAB vuông ở A    sin ASB
  ASB  30 SB 2 Câu 14. DO AC
Gọi O AC BD . Ta có: 
DO   ABCD .
DO SASA    ABCD 
SO là hình chiếu của SD lên mặt phẳng SAC   SD SAC    SD SO   ; ;  DSO   . Xét S
AD vuông tại A : 2 2
SD  3a a  2a . a 2 DO 2 Xét S
OD vuông tại O : có SD  2a ,  OD
 sin   sin DSO   . 2 SD 4
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 S A C H M B Câu 15.
Gọi H là trung điểm AB dễ thấy SH   ABC  .
SC tạo với mặt phẳng đáy một góc 60 suy ra  SCH  60 . a 3 3a Có  HC
SH HC. tan SCH  . 2 2 1 a a 10 HM 1 Dễ thấy 
  SMH , HM AC   SM   cos   . 2 2 2 SM 10
Câu 16. Chọn C
Ta gọi E, F lần lượt là trung điểm của SC AB . 
Ta có ME / / NF ( do cùng song song với BC . Nên tứ giác MENF là hình thang, MF / ISA và 
MF  ( ABCD) hay tứ giác MENF là hình thang vuông tại M , F SA  ( ABCD) 
Gọi K NF AC, I EK M thì I MN  (SAC) NC AC Ta có: 
NC  (SAC) hay E là hình chiếu vuông góc của N lên (SAC) NC SA
Từ đó ta có được, góc giữa MN và (SAC) là góc giữa MN và CI CN
Suy ra, gọi Q là góc giữa MN và (SAC) thì sin   IN 1 a 2 IN KN 2 2 a 10 NC CD  ;   2  IN MN 2 2  MF FN  2 2 M ME 3 3 3 CN 3 5 Vậy sin    . IN 10
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Câu 17.
Gọi  là đường thẳng đi qua A và song song với  . Hạ OH   ' H  ' . Do O là trung điểm a 14
của AC và  //  ' nên d  ,
O  '  d  ,
O  hay OH  . 6
Do S.ABCD là hình chóp tứ giác đều nên đáy ABCD là hình vuông và SO   ABCD .
Do AH OH và AH SO nên, suy ra AH SH . a 2
Do ABCD là hình vuông cạnh a nên AC a 2 , suy ra OA  . 2
Áp dụng Định lí Pitago vào tam giác vuông AHO ta có 2 2 2
OA OH AH , suy ra 2 2  a 2   a 14  a 2 2
AH OA OH        .  2   6  3    
Áp dụng Định lí Pitago vào tam giác vuông SAO ta có 2 2 2
SA OA SO , suy ra 2 2 2  a 2  2a  4b 2 2 2
SA OA SO     b  .  2  2   AH 2a
Do  //  ' nên cos SA,  cosSA,   cos SAH   . 2 2 SA 3 2a  4b S A M D H O B C Câu 18.
Gọi H , M lần lượt là trung điểm của AB, SB ; O là tâm của hình chữ nhật ABCD .
Ta có MO / / SD .
Dễ thấy BC  SAB  BC AM , mà SB AM nên AM  SBC .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Xét tam giác AMO , có: a 3 AM  ; 2 1 1 2 2 AO AC
a  3a a ; 2 2 2 2 1 1 1 1  a 3   a 2 2 2 2 2  2 MO SD SH HD
SH HA AD      3a a   . 2 2 2 2  2   2     A
MO cân tại O 2 2 AM 3a 2 2 MO a   d  ; O AM  4 16 13  sin AMO     . OM OM a 4  SD SBC      13 cos ;  sin AMO  4 S K C B I O H d A Câu 19.
Do ASB  90 nên tâm O của mặt cầu ngoại tiếp tứ diện SABI nằm trên đường thẳng d đi qua trung điểm
O của đoạn thẳng AB và d  SAB .   1
Trong mặt phẳng  SCH  kẻ IK SH tại K .
Theo giả thiết SI   ABC  suy ra SI AB . Từ SI AB và AB CH suy ra AB  SCH   AB IK .
Từ IK SH và AB IK ta có IK  SAB . 2 Từ  
1 và 2 ta có IK d . Bởi vậy OO ABC 
  d ABC
  IK ABC  '; ; ; .
Vì SCH    ABC  nên IH là hình chiếu vuông góc của IK trên mặt phẳng  ABC  . Bởi vậy
IK ABC   IK IH     ; ,
HIK HSI . AB
Do tam giác ABC vuông tại C và SAB vuông tại S nên CO SO  . 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Xét hai tam giác vuông CHO và SHO có CO SO , cạnh OH chung nên CHO SHO c.g.  c , bởi vậy CH SH . CH SH IH 1
Xét tam giác SIH vuông tại I có IH   , ta có   sin HSI    HSI  30 . 2 2 SH 2
Vậy OO ABC  ';  30 . Câu 20. Cách 1:
● Gọi O là trọng tâm của tam giác ABC . Dựng đường thẳng d qua O và d // SB , d cắt SD tại K . Khi đó
góc giữa SB và SCD chính là góc giữa OK và SCD .
● Vì SO  ( ABCD)  SO CD .
Ta lại có: ABC đều ( ABC cân tại B và  BAC  60 ).
AB CO CD CO
CD  (SCO)  (SCD)  (SCO) .
Gọi H là hình chiếu của O trên SC , khi đó ta có: OH SC  
  OH   SCD  . Do đó góc giữa SB và mặt phẳng  SCD là: OKH   . OH CDOH Ta có:  sin   sin OKH  . OK
● Tứ diện S.ABC là tứ diện đều cạnh a nên ta tính được: a 3 a 6 a 2 OC  , SO   OH  . 3 3 3 OK DO 2 2 2
Vì OK // SB     OK SB a . SB DB 3 3 3 OH 2 Vậy: sin    . OK 2 Cách 2:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
d (B, (SCD))
Trước hết ta chứng minh được sin (SB; (SCD))  (như hình trên). SB
Gọi O là trọng tâm tam giác ABC . Khi đó ta có CO CD . a 3 a 6 a 2
Dựng OH SC suy ra OH  (SCD) . Ta tính được OC  , SO   OH  . 3 3 3 3 3 3 a 2 a 2
Khi đó d (B, (SCD)) 
d (O, (SCD))  OH   . 2 2 2 3 2 a 2 2 Vậy 2 sin ( ; SB (SCD))   . a 2
Dạng 1.2 Góc của đường thẳng với đường thẳng Câu 21. Chọn D
Đặt OA a suy ra OB OC a và AB BC AC a 2 a 2
Gọi N là trung điểm AC ta có MN / / AB và MN  2  Suy ra góc OM AB   OM MN  , , . Xét OMN a 2
Trong tam giác OM N có ON OM MN
nên OM N là tam giác đều 2  Suy ra 0
OMN  60 . Vậy OM AB   OM MN  0 , ,  60
Câu 22. Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
    
  
Ta có AB CD AB AD AC 0 0 . .  . AB AD  . AB AC  . AB . AD cos 60  . AB AC.cos 60 3 1  0 0  A . B A . D cos 60  A . B A . D cos 60  A . B AD 2 4      cos AB CD . AB CD 1 1 ,    cos  . AB CD 4 4
Câu 23. Vì ABCD là hình vuông nên BD AC .
Mặt khác AA   ABCD  BD AA . BD AC Ta có 
BD   AAC   BD AC . BD AA'  Do đó góc giữa A C
 và BD bằng 90 . Câu 24.
Gọi P là trung điểm AC , ta có PM //CD và PN //AB , suy ra  AB,CD 
 PM , PN  .
Dễ thấy PM PN a .
PM PN MN
a a a Xét PMN ta có  2 2 2 2 2 2 3 1 cosMPN     2PM .PN 2. . a a 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  0   MPN    AB CD 0 0 0 120 ,  180 120  60 . B C N A D B' M C' A' Câu 25. D'
Giả sử cạnh của hình lập phương là a  0 .
Gọi N là trung điểm đoạn thẳng BB . Khi đó, MN //BC nên  AM , BC   AM , MN  . 2 a a 5 Xét tam giác A BM
vuông tại B ta có: A M  2 2 
AB  B M  2  a   . 4 2 2 5a 3a Xét tam giác AA M
vuông tại A ta có: 2 2 AM
AA  AM 2  a   . 4 2 a 5 BCa 2
Có AN AM  ; MN   . 2 2 2
Trong tam giác AMN ta có: 2 2 2 9a 2a 5a    2 2 2
MA MN AN 2 6a 4 1 cos AMN  4 4 4   .  . 2.M . A MN 3a a 2 2 4 6a 2 2 2. . 2 2 Suy ra  AMN  45 .
Vậy  AM , BC   AM , MN    AMN  45 .
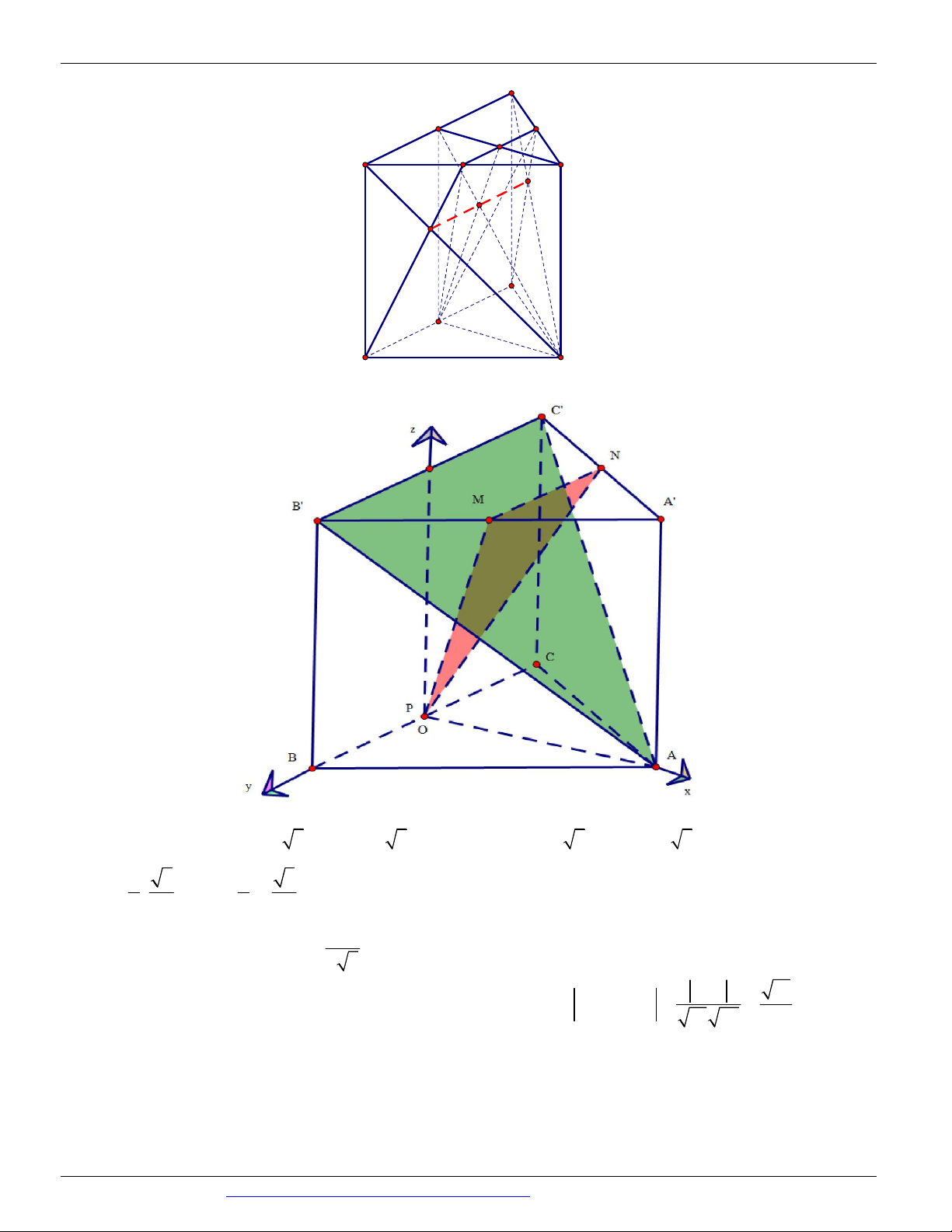
Dạng 1.3 Góc của mặt với mặt Câu 26. Chọn D Gọi ,
P Q lần lượt là trung điểm của BC và B C
 ; I BM AB , J CN AC , E MN A . Q
Suy ra, MNP  AB C
   MNCB  AB C
   IJ và gọi K IJ PE K AQ với E là trung điểm M N (hình vẽ).
AAQP  IJ AQ IJ , PE IJ  MNP, AB C      
  AQ, PE    13 5 5
Ta có AP  3, PQ  2  AQ  13  QK  ; PE   PK  . 3 2 3 2 2 2 
KQ KP PQ 13 cos  cos QKP   . 2 . KQ KP 65
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 C' Q N E M B' A' J K I C P B A Cách 2
Gắn hệ trục tọa độ Oxyz như hình vẽ
P 0;0;0, A3;0;0, B 0; 3;0,C 0; 3;0, A3;0;2, B0; 3;2,C0; 3;2  3 3   3 3  nên M  ; ; 2  , N  ;  ; 2   2 2   2 2       1   
Ta có vtpt của mp  AB C   là n
AB , AC  2;0;3 và vtpt của mp MNP là n  4;0;3 2   1   2 3     8  9 13
Gọi  là góc giữa hai mặt phẳng  AB C
  và mp MNP  o c s  o
c s n ,n   1 2  13 25 65 Cách 3
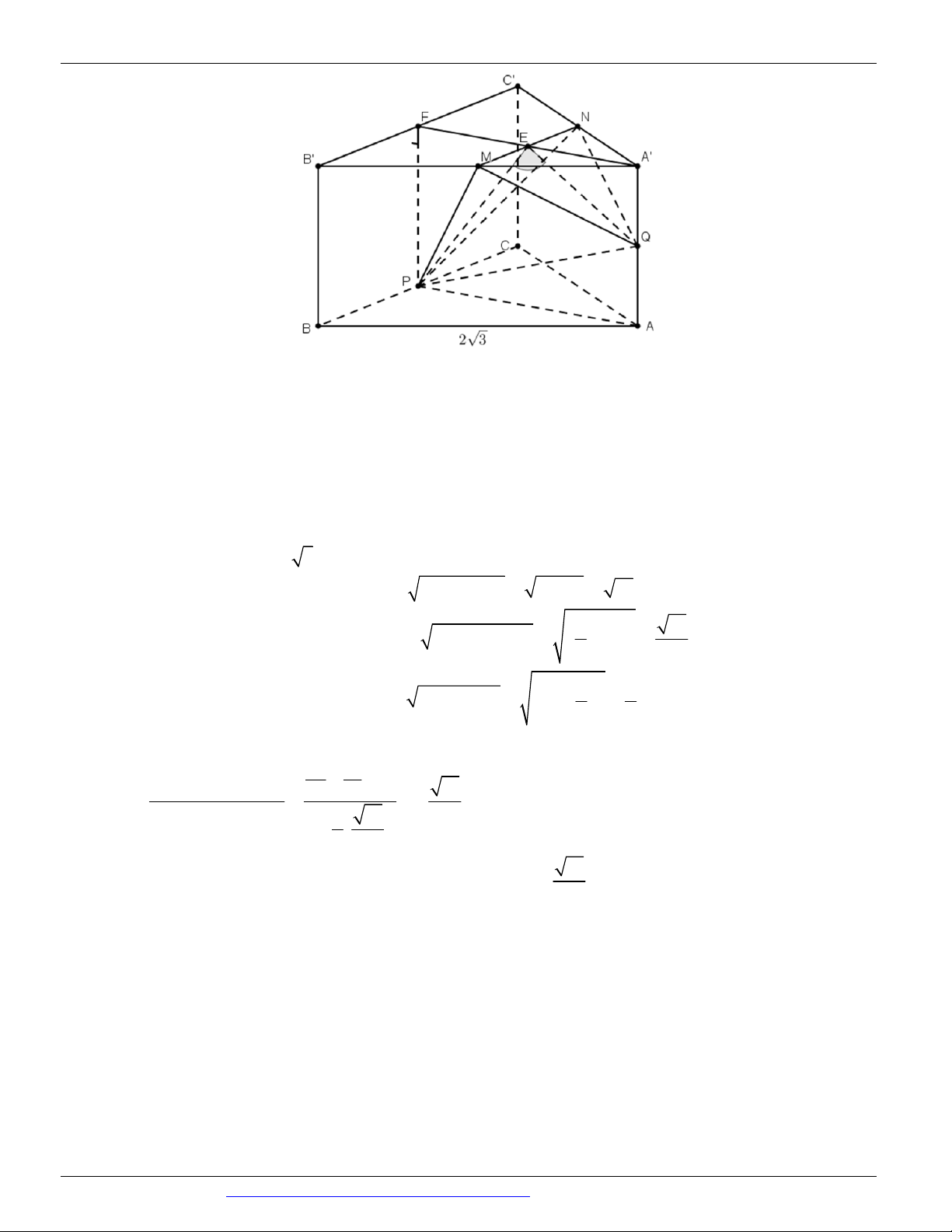
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Gọi Q là trung điểm của AA ' , khi đó mặt phẳng  AB 'C ' song song với mặt phẳng  MNQ nên góc giữa
hai mặt phẳng  AB 'C ' và  MNP cũng bằng góc giữa hai mặt phẳng  MNQ và  MNP . Ta có: 
MNP  MNQ  MN  0
PE   MNPPE MN   MNP  MNQ   ; ;
PEQ hoặc MNP;MNQ    180  PEQ
QE  MNQ; QE MN
Tam giác ABC đều có cạnh 2 3  AP  3.
Tam giác APQ vuông tại A nên ta có: 2 2 2 2 PQ
AP AQ  3 1  10 2  3  13
Tam giác A 'QE vuông tại A ' nên ta có: 2 2 2 QE
A ' E A 'Q  1     2  2 2  3  5
Tam giác PEF vuông tại F nên ta có: 2 2 2 PE FP FE  2      2  2
Áp dụng định lý hàm số côsin vào tam giác PQE ta có: 25 13  10  2 2 2
EP EQ PQ 13 4 4 cos PEQ     2.E . P EQ 5 13 65 2. . 2 2 13
Do đó: cos MNP; AB 'C '  0 
 cos 180  PEQ    cos PEQ  . 65
Câu 27. Chọn C
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Không mất tính tổng quát ta đặt cạnh của khối lập phương là 1.
Chọn hệ trục tọa độ sao cho A (  0; 0; 0), B (  1; 0; 0), D (  0;1; 0) và (
A 0; 0;1) (như hình vẽ).  1 1 1  Khi đó ta có: M ; ; .    2 2 3     1 1 2     2 1  
Suy ra: AB  (1; 0; 0), MA  ; ;    
AB, MA  0;  ;  n  (0; 4;3)   là VTPT của mặt phẳng 1  2 2 3     3 2  (MAB).    1 1 1 
   1 1   D C
   (1; 0;0), MD  ;  ;  D C  ,
MD  0; ;   n  (0; 2; 3)     là VTPT của mặt phẳng 2 2 2 3      3 2  (MC D  )  .
cosin của góc giữa hai mặt phẳng (MAB) và (MC D  )  bằng:     n .n 0.0  4.2  3.(3) 1 2 17 13
cos(n , n )      . 1 2 2 2 2 2 2 2 n . n 65 1 2 0  ( 4)   3 . 0  2  ( 3  ) Câu 28. Chọn A
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 B C N J A D O H M K B' C' I L A' D'
Giao tuyến của (MAB) và (MC D  )
 là đường thẳng KH như hình vẽ.
Gọi J là tâm hình vuông ABCD . L, N lần lượt là trung điểm của C D   và AB . Ta có: C D
   (LIM )  C D
   LM LM KH .
Tương tự AB  (NJM )  AB MN MN KH .
Suy ra góc giữa hai mặt phẳng (MAB) và (MC D  )
 chính là góc giữa 2 đường thẳng (MN , ML) . 10 34
Gọi cạnh hình lập phương là 1. Ta có LM  , MN  , NL  2 . 6 6
MN ML NL  Ta có:  2 2 2 7 85 cos LMN   . 2MN.ML 85 7 85
Suy ra cosin của góc giữa hai mặt phẳng (MAB) và (MC D  )  là . 85 Câu 29. Ta có:
SBD  (ABCD)  BD .
Hạ AH BD tại H . AH BD Ta có
  BD  (SAH )  BD SH . BD SA
 SBD;(ABCD)    H , A HS  .  0 
SAH vuông tại A  SHA  90  H , A HS    SHA
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 SA tan SHA  . AH
Xét ABD vuông tại A có: 1 1 1   . 2 2 2 AH AB AD 2 5  AH  . 5  SA 2a tan SHA    5. AH 2a 5 5
Câu 30. Cách 1: Hai mặt phẳng  AB D   và  A CD
  có giao tuyến là EF như hình vẽ.
Do EF //AB mà A D     A A
BB nên A D    AB ' '  EF / / A D
Từ A kẻ vuông góc lên giao tuyến EF tại H thì '
A H EF EF   A DH
   EF D H  . Khi đó, góc
giữa hai mặt phẳng cần tìm chính là góc giữa hai đường thẳng AH  và D H  . D B   13 D A  5 B A  Tam giác '
D EF lần lượt có D E    , D F    , EF   5 . 2 2 2 2 2 61 2S 305
Theo Hê-rông ta có: S  . Suy ra DEF D H    . ' D EF 4 EF 10 Dễ thấy ' '
A EF  D EF ' '
A H D H .  2 2 2
HA  HD  A D   29 Tam giác D AH  có: cos A HD    . 2HA .HD 61   Do đó A H
D 118, 4 hay  A H  , D H
  180118,4  61,6.
Cách 2: Gắn hình hộp chữ nhật ABC . D A BCD
  vào hệ trục tọa độ như hình vẽ. Khi đó  A 0;0;  0 , B2;0;  0 , D0;3;  0 , C2;3; 
0 , A0;0;4, B2;0;4, D0;3;4, C2;3;4 .    
Gọi n là véc tơ pháp tuyến của  AB D   . Có     . 1 n AB ; AD  12;  8; 6 1      
 
Gọi n là véc tơ pháp tuyến của  A CD   . Có       . 2 n
A C ; A D  12; 8; 6 2    
Gọi  là góc giữa hai mặt phẳng  AB D   và  A CD  
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  n n 29 1 2
cos    
. Vậy giá trị gần đúng của góc  là 61, 6 . n n 61 1 2 Cách 3.
Do hai mặt phẳng  AB D   và  A CD
  chứa hai đường AB và C D
 song song với nhau nên giao tuyến của
chúng song song hai đường đó. Kẻ A H
AB , H AB, dựng hình bình hành A H
KD có tâm I như hình vẽ. Do A D     A A
BB nên A D
   AB suy ra AB   A H
KD góc giữa hai mặt phẳng  AB D   và  A CD
  là góc giữa AK  và D H  . 1 1 1 1 1 5
Trong tam giác vuông AAB   có AH  là đường cao nên      . 2 2 2 AH ABAA 4 16 16 4 Vậy A H   . 5 29 Xét tam giác A I
H có cos I  cos A  H    cos Acos H  sin Asin H  . 61
Vậy góc giữa hai mặt phẳng  AB D   và  A CD
  gần đúng bằng 61, 6 .
Câu 31. Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Gọi M trung điểm SA . Ta có S
AB cân tại B BM SA (1)
Vì SO   ABCD  SO BD , lại có O trung điểm BD S
BD cân tại S nên SD SB a SAD
cân tại D nên DM SA (2)
Lại có SAB  SAD  SA (3) Từ
 SAB SAD   (1); (2); (3) ,
BMD hoặc SAB SAD   ,  180  BMD . a 3 2a 3
Xét SOB OB   BD  . 3 3 a 6 2a 3 1 a 3 1
Xét AOB OA OC
. Xét SOC SC   OM SC   BD 3 3 2 3 2
Do đó BMD vuông tại M , vậy SAB SAD   ,
BMD  90 , do đó chọn D.
Câu 32. Chọn C Ta có AB
C cân tại A . Gọi I là trung điểm của BC
  A BC   ABC  
  AI AI   ' ; ;
AIA   .   BC  2a  
Theo đề bài ta suy ra  AI  2a  2a 3  AI     2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 AI 3
Xét tam giác vuông AAI có cos       30 .  A' I 2
Vậy  A' BC ; ABC   30 . S A B O K D C Câu 33.
Gọi O là tâm đáy, và K là hình chiếu vuông góc của O trên S . C BD AC Do 
BD  SAC   BD SO , suy ra góc giữa hai mặt phẳng SBD và  ABCD là góc BD S A   SA
SOA   . Ta có tan    2  SA  . OA 2  . a OASC BD  Do 
SC BK. nên góc giữa hai mặt phẳng  S AC  và SBC  là BK . O Ta có SC OK  2 2 2 2. . 1  2  BO BO 2BO 2  tan BKO      3 suy ra 0 BKO  60 . OK 1 . SA AC d A SC  1. 2 , 2 2 2 SA AC Câu 34.
Ta có tam giác ABC vuông tại C nên BC AC   1 . SA ABCD Vì 
BC SA2 . BC ABCD  Từ  
1 ,2 BC  SAC
Trong SAC vẽ AH SC tại H
AH BC BC   SAC , AH   SAC  Ta có: 
AH   SBC AH SC
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 AH   SBC 
SB AH SB   SBC  
Trong  SAB vẽ AK SB tại K SB AH
SB   AHK mà HK   AHK  nên SB HK SB AK  SB AK  SB HK
Ta có:  AK   SAB
 SBA SBC    AK HK   ; ;  AKH  
HK  SBC 
SB  SAB SBC  S
AC vuông tại A có đường cao AH : 1 1 1 1 1 1      2 2 2 2 AH SA AC AH
a 22 a 22 1 1    AH a . 2 2 AH a S
AB vuông tại A có đường cao AK : 1 1 1 1 1 1 1 3 2a         AK  . 2 2 2 2 AK SA AB AK  2  2 2 2 2 a a 2 AK 4a 3
AHK vuông tại H : 2 2 4a a a 2 2 2
AK AH HK Pytago 2 2 2 
a HK HK   HK  3 3 3 . aHK 3 1
AHK vuông tại H  cos AKH   0     AKH  60 . AK 2a 2 3 A D O B C A' D' B' C' Câu 35.
+ Gọi O là giao điểm của hai đường chéo hình vuông ABCD . x 6
Đặt AB x BC  ; x A A '  . 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 36
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2  x 6  x 10 2
A ' B A ' D     x
  A ' BD cân  A'O BD .  2  2   2  x 6  x 10 2
C ' B C ' D     x
 C ' BD cân  C 'O BD .  2  2  
+  A' BD  C ' BD  BD
A'O B ,
D A'O   A' BD
C 'O B ,
D C 'O  C ' BD
 góc giữa hai mặt phẳng  A' BD và C ' BD bằng góc giữa A'O và C 'O . 
+ Tính A'OC ' . 2 2  x 10   x 2  2 2
A'O C 'O
A ' B BO        x 2 .  2   2     
A'C '  x 2 . 
  A 'OC ' đều  0 A'OC '  60 .
Vậy góc giữa hai mặt phẳng  A' BD và C ' BD bằng 0 60 .
Cách khác: Gắn hệ trục tọa độ Oxyz vào hình hộp chữ nhật ABCD.A ' B 'C ' D ' để tìm góc giữa hai mặt phẳng
A' BD và C ' BD . Câu 36.
Cách 1: Gọi I A B   B A  ; J C D   D C
 . Ta có IJ  ( ADB C  )   (BCD A  )  (1).
Theo giả thiết, ta có: IJ  (DCC D  )   C D   IJ (2).
Từ (1) và (2)  C D   (BCD A  )   ( ADC B  )   (BCD A  )  .
Vậy góc giữa hai mặt phẳng ( ADC B  )  và (BCD A  )  là 90 .
Cách 2: Mặt phẳng (DCC D  )
 vuông góc và cắt hai mặt phẳng ( ADC B  )  và (BCD A  )  lần lượt theo hai
giao tuyến DC và D C  .
 Góc giữa hai mp ( ADC B  )  và (BCD A  )
 là góc giữa hai đường thẳng DC và D C  .
Vì ABCD.AB CD
  là hình lập phương nên tứ giác DCC D
  là hình vuông  DC  D C  .
Vậy góc giữa hai mặt phẳng ( ADC B  )  và (BCD A  )  là 90 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 37
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Câu 37. Ta có AMC N
 là hình bình hành, mà tam giác AMN cân tại A nên MN AC . Ta có  ' '
BDD B  cắt ba mặt phẳng  ABCD ,  ' ' ' ' A B C D  ,  '
AMC N  lần lượt theo ba giao tuyến ' '
BD / /B D / /MN .
Hai mặt phẳng  P và  ABCD có điểm chung A và lần lượt chứa hai đường thẳng song song MN , BD
nên giao tuyến của chúng là đường thẳng d đi qua A và song song với MN, BD .
Trên hai mặt phẳng  P và  ABCD lần lượt có hai đường thẳng AC và AC cùng vuông góc với d nên
góc giữa hai mặt phẳng  P và  ABCD chính là góc giữa AC và AC , bằng góc 
CAC . Xét tam giác ' C CA vuông tại C có: AC BD MN a 2 cos      ACACACa 2 2 Cách 2:
Theo chứng minh ở trên thì MN //BD và MN BD a . Đa giác AMC N
 nằm trên mặt phẳng  P có hình chiếu trên mặt  ABCD là hình vuông ABCD nên: 2  BD  2 S AB   ABCD  2  2 cos     . S 1 1 2 AMC NAC .MN AC .MN 2 2 B' C' A' N M B P C A Câu 38.
Do ABC.A' B 'C ' là hình lăng trụ đứng nên ta có: SS
.cos MNP, ABC ABC MNP     S
MNP  ABC  2 3 3 cos , ABC   
 MNP  ABC  0 ,  30 S 4 2 MNP
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 38
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Dạng 2. Khoảng cách
Dạng 2.1 Khoảng cách từ điểm đến mặt phẳng Câu 39. Chọn A S 2a H A C a BBC AB Ta có 
BC  SAB . BC SA
Kẻ AH SB . Khi đó AH BC AH  SBC
AH là khoảng cách từ A đến mặt phẳng  SBC  . 1 1 1 1 1 5 2 4a 2 5a Ta có      2  AH   AH  . 2 2 2 2 2 2 AH SA AB 4a a 4a 5 5 Câu 40. Chọn B S H A C B
Kẻ AH SB trong mặt phẳng SBC  BC AB Ta có: 
BC  SAB  BC AH BC SA   AH BC a Vậy 
AH  SBC   d A SBC  1 2 ,  AH SB  . AH SB  2 2
Câu 41. Chọn B
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 39
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 S S H A A D K G I O O I B C C
* Gọi O AC BD và G là trọng tâm tam giác ABD , I là trung điểm của AB ta có
d D;SAC  DG
SI   ABCD và 
 2  d D;SAC   2.d I;SAC  .
d I;SAC  IG
* Gọi K là trung điểm của AO , H là hình chiếu của I lên SK ta có IK AC; IH  SAC
d D;SAC   2.d I;SAC   2.IH a 3 BO a 2
* Xét tam giác SIK vuông tại I ta có: SI  ; IK   2 2 4 1 1 1 4 16 28 a 3       IH  2 2 2 2 2 2 IH SI IK 3a 2a 3a 2 7   a
d D SAC   d I SAC  21 ; 2. ;  2.IH  . 7 Câu 42. Chọn B S A D I H O K B C
Gọi H là trung điểm của A .
B Khi đó, SH   ABCD.
Gọi O là giao điểm của AC và BD suy ra AC BD . Kẻ HK BD tại K ( K là trung điểm BO ).
Kẻ HI SH tại I. Khi đó: d  ,
A SBD  2d H ,SBD  2HI. a 3 1 a 2
Xét tam giác SHK , có: SH  , HK AO . 2 2 4 1 1 1 28 a 21 Khi đó:     HI  . 2 2 2 2 HI SH HK 3a 14
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 40
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 a
Suy ra: d A SBD 21 ,  2HI  . 7
Câu 43. Chọn C S H A D B C M CÁCH 1:
Ta có AB / /CD d B;SCD  d A;SCD .
Kẽ MA CD M CD ,kẽ AH SM SH  SCD  d  ,
A SCD  SH . 2S S a 3 1 1 1 21 SA a ; ACD ABCD AM       SM a CD CD 2 2 2 2 SH SA AM 7 3V 3V 21a
CÁCH 2: Ta có AB / /CD d B;SCD  d A;SCD S .BCD S .A BCD    . S 2S 7 SCD SCD
( SCD; SD a 2; SC  2a; CD  a ) Câu 44. Chọn C
Gọi H là trung điểm của AB SH AB SH  (ABCD).
Từ H kẻ HM BD , M là trung điểm của BI và I là tâm của hình vuông. BD HM Ta có:   BD  (SHM) BD SH
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 41
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Từ H kẻ HK SM HK BD ( Vì BD  (SHM) )
HK  (SBD)  d(H;(SBD))  HK. AI AC 2a 3a Ta có: HM    . SH  . 2 4 4 2 2a 3a . HM .HS 21 4 2 a HK    . 2 2 2 2 14 HM HS  2a   3a       4 2     21a 21a
d (C; (SBD))  d ( ;
A (SBD))  2d (H ; (SBD))  2HK  2.  . 14 7 21a
Vậy: d (C; (SBD))  . 7 Câu 45. Chọn D BC AB Ta có: 
BC  SABBC SA   
SAB  SBC     SAB
  SBC   SB
Trong mặt phẳng  SAB : Kẻ AH SB AH d  ; A SBC  1 1 1 1 1 4      . 2 2 2 AH SA AB 2 2 a 3a 2 3a a
d A SBC  3 ;  AH  . Chọn D 2 Câu 46. Chọn B
Gọi E, F,G lần lượt là trung điểm của B ,
D CD và trọng tâm tam giác BCD BC 3 a 3
Tam giác BCD đều nên suy ra CE   2 2 2 a 3 CG CE  3 3 2 2 a 2a a 6
Tam giác ACG vuông tại G nên ta có 2 2 2 2
AG AC CG a    AG  3 3 3 a
Vậy d A BCD 6 ,  AG  3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 42
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Câu 47. Chọn C
Gọi H là hình chiếu của A lên D
S ta chứng minh được AH  SCD 1 1 1 2a    AH  2 2 2 AH SA D A 5
Câu 48. Chọn B 1 1 1 1 1 1 1 1 1 19 Ta có          . 2 2 2 2 2 2 2 2 2 2 AK AH AS AB AC AS a 3a 4a 12a 2a 3 2a 57 Suy ra AK  hay d ( , A (SBC))  . 19 19
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 43
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 S A K D O H Câu 49. B C
S.ABCD là hình chóp tứ giác đều nên ABCD là hình vuông và SO   ABCD . a
Vẽ OH vuông góc với CD tại H thì H là trung điểm CD , OH  . 2
Dễ thấy CD  SOH   SCD   SOH  nên kẻ OK vuông góc với SH tại K thì OK  SCD .  d  , O SCD    OK . a a 2. OS.OH a 2
Tam giác vuông SOH có OK là đường cao nên 2 OK    . 2 2 2 3 OS OH a 2 2a  4 a 2 Vậy d  ,
O SCD    . 3 Câu 50. 1 1
Do M là trung điểm SC nên d M ;SBD  d C;SBD  d  ; A SBD 2 2
Gọi H là hình chiếu của A lên mp SBD  d  ;
A SBD  AH
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 44
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1 1 1 1 1 1 1 5
Lại có AS, AB, AD đôi một vuông góc nên        2 2 2 2 2 2 AH AS AB AD a a  2 2 2 2 a a a 10  AH   d a 10
M ;SBD  . 5 10 S K A C H Câu 51. B Ta có
SA   ABC    SA BC .
BC   ABC
Trong  ABC  , kẻ AH BC , mà BC SA BC  SAH   BC SH .
Trong SAH  , kẻ AK SH , mà SH BC AK  SBC  hay d  ;
A SBC  AK .
Vì ABC vuông tại A nên 2 2 BC
AB AC  2a . A . B AC 3a
Mặt khác có AH là đường cao nên AH   . BC 2 19a
Vì SAH vuông tại A nên 2 2
SH SA AH  . 2 . SA AH 2a 3
Vậy có AK là đường cao AK   . SH 19
Nhận xét. Trong thực hành làm toán trắc nghiệm ta nên áp dụng bài toán sau:
Cho tứ diện OABC có O ,
A OB, OC đôi một vuông góc với nhau và H là hình chiếu của O lên mặt phẳng 1 1 1 1
ABC . Khi đó    . 2 2 2 2 OH OA OB OC S H A C M B Câu 52.
Gọi M là trung điểm BC . Kẻ AH SM tại H .
Ta có AM BC và SA BC nên BC  SAM   BC AH   1 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 45
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Mà AH SM 2 . Từ  
1 và 2 suy ra AH   SBC  . Do đó d  ,
A SBC   AH .
Xét tam giác SAM vuông tại A , có 1 1 1 1 1 7 3 21a       AH a  . 2 2 2 AH AM AS 2 2 2  3 a a  3a 7 7   2  
Câu 53. Chọn C d  ; B SCD BD * Ta có:   2  d  ;
B SCD  2.d  ;
O SCD  2OH . Trong đó H là hình chiếu
d O;SCD OD
vuông góc của O lên  SCD . S H A D 60 O I B C
* Gọi I là trung điểm của CD ta có: 
SCD   ABCD  CD  SI CD
 SCD  ABCD  OI SI   ; ;  SIO  60 . OI   CDa 3
Xét tam giác SOI vuông tại O ta có: SO OI. tan 60  . 2 1 1 1 4 4 16 Xét SOI , ta có      2 2 2 2 2 2 OH OI OS a 3a 3a a 3  OH   d a 3
B;SCD  . 4 2
Câu 54. Chọn C
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 46
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 AD
Từ giả thiết suy ra: AB BC CD
a , AC a 3 . 2
Gọi E AB CD , suy ra tam giác ADE đều.
Khi đó C là trung điểm của ED và AC ED .
Dựng AH SC thì AH   SCD , suy ra d  ,
A SCD  AH .
Xét tam giác SAC vuông tại A , có AH là đường cao 1 1 1 Suy ra:    AH  2a 2 2 2 AH SA AC 1 1 a 2
Mà d B, SCD  d  ,
A SCD   AH  . 2 2 2
Câu 55. Chọn C
Gọi M là trung điểm của CD , K là hình chiếu của H lên SM a 2
Tam giác HCD vuông tại H có CD a 2 và HM  2
Ta có BH / /CD d B,SCD  d H ,SCD  HK HM .HS a 6
Tam giác SHM vuông tại H có HK   2 2 4 HM HS a
Vậy d B SCD 6 ,  4
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 47
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 56. Chọn B
Gọi A' là chân đường cao kẻ từ A lên BC, C ' là chân đường cao kẻ từ C lên A . B
Gọi H là giao của AA’ với CC’ suy ra H là trực tâm của tam giác ABC. Ta dễ dàng chứng
minh được OH  ( ABC). Do đó: d ( ;
O ( ABC))  OH . Tính OH. 1 1 1
Ta có: Tam giác OAA' vuông tại O, có OH là đường cao. Suy ra :   (1) 2 2 2 OH OA OA' 1 1 1
Lại có: Tam giác OBC vuông tại B, có OA' là đường cao. Suy ra:   (2) 2 2 2 OA' OB OC 1 1 1 1 Từ (1) và (2) suy ra:   
. Thay OA OB OC  3 vào, ta được: 2 2 2 2 OH OA OB OC 1 1 1 1     1  OH  1. 2 OH 3 3 3 Vậy d ( ;
O ( ABC))  OH  1. Câu 57.
Cách 1: Sử dụng kiến thức ở lớp 11.
ABCD là hình thoi cạnh a , 
ABC  60  ABC, A
CD là các tam giác đều cạnh a . Xét S
AC vuông tại A có: 2 2
SA SC AC 2 2 
4a a a 3 .
Vì AB // CD nên AB // SCD . Do đó d  ,
B SCD  d  ,
A SCD .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 48
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 a 3
Kẻ AH CD H CD . Suy ra H là trung điểm của cạnh CD , AH  . 2
Kẻ AK SH K SH    1 CD   AH Ta có: 
CD  SAH   CD AK 2 CD SA
Từ (1) và (2) suy ra: AK  SCD  d  ,
A SCD  AK . 1 1 1 4 1 5 a 15 Xét S
AH vuông ở A :       AK  . 2 2 2 AK AH SA 2 2 3a 3a 2 3a 5 a
Vậy d B SCD 15 ,  . 5
Cách 2: Tính khoảng cách thông qua tính thể tích.
ABCD là hình thoi cạnh a , 
ABC  60  ABC, A
CD là các tam giác đều cạnh a . Xét S
AC vuông tại A có: 2 2
SA SC AC 2 2 
4a a a 3 . V
Vì AB // DC nên AB // SDC  . Do đó d B SCD  d A SCD 3 , , SACD  . S SCD 1 2 1 a 3 3 a V  . SA Sa 3.  . SACD 3 ACD 3 4 4 Xét SAC và S
AD có: AD AC a , SA chung,  
SAC SAD  90 . Do đó SAC S
AD SC SD S
CD cân tại S .
Gọi H là trung điểm CD SH CD . 2 a a 15 Xét S
HC vuông ở H : 2 2
SH SC CH 2  4a   . 4 2 1 1 a 15 2 a 15 SSH .CD  . .a  . SCD 2 2 2 4 3 a 3. a 15 d  , A SCD 4   . 2 a 15 5 4 a
Vậy d B SCD 15 ,  . 5 Câu 58.
Gọi O là trung điểm của AB SO  (ABCD) .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 49
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 . a 3 SO
a 3 do SO là đường cao của tam giác đều cạnh 2a 2
Từ giả thiết suy ra tam giác BCD và tam giác ABD là tam giác đều  CD OD CD OD Ta có: 
CD  SODCD SO
Trong tam giác SOD kẻ OH SD tại H OH   SD
OH  SCDOH CD
Do AB  SCD suy ra d B,SCD  d  ,
O SCD  OH
Nhận thấy tam giác SOD là tam giác vuông cân tại O với OD a 3 1 1 a 6 2 2 OH SD  3a  3a  . 2 2 2
Câu 59. Chọn B S D' A D C' A' O B C B'
Gọi p, q, u, v lần lượt là các khoảng cách từ O đến các mặt phẳng SAB,SBC ,SCD,SDA.
Trong mặt phẳng  SAC  dựng đường thẳng qua O vuông góc với đường thẳng SO cắt hai đường thẳng S ,
A SC lần lượt tại A ', C '
Trong mặt phẳng  SBD dựng đường thẳng qua O vuông góc với đường thẳng SO cắt hai đường thẳng
SB, SD lần lượt tại B ', D ' .
Do SAC   SBD,SAC   SBD  S ,
O A'C '  SO nên A'C '  SBD
A'C '  B ' D ' .
Khi đó tứ diện OSA' B ' có OS, OA ', OB ' đôi một vuông góc nên ta chứng minh được 1 1 1 1    1 2 2 2 2   p OS OA' OB ' 1 1 1 1 Chứng minh tương tự:    2 ; 2 2 2 2   q OS OB ' OC ' 1 1 1 1    3 2 2 2 2 u OS OC ' OD ' 1 1 1 1    4 2 2 2 2 v OS OD ' OA '
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 50
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1 1 1 1 Từ  
1 ,2,3,4 ta có    . 2 2 2 2 p u q v 1 1 1 1 1 19 20 Với
p  1; q  2;u  5        d v  . 2 1  2 2 2 2 2 v v 20 19 5
Dựng mặt phẳng qua O, vuông góc với SO , cắt các đường thẳng S , A S ,
B SC, SD lần lượt tại A ,
B , C , D
SO   AB CD   .
Vì SAC   SBD  A C    B D   . 1 1 1 1 Ta có:     1.   1 2 2 2 SO OAOB
d O,SAB 1 1 1 1 1     . 2 2 2 2 SO OBOC
d O,SB C   4 1 1 1 1 1     . 3 2 2 2 SO OCOD
d O,SC D   5 1 1 1 1 1     . 4 2 2 2 SO ODOA
d O,SD A   2 d 1 1 1 20  
1 , 2,3,4  1    d  . 2 5 4 d 19
Dạng 2.2 Khoảng cách của đường thẳng với đường thẳng Câu 60. Chọn D
Ta có khoảng cách giữa hai đường thẳng chéo nhau BD và AC  bằng khoảng cách giữa mặt phẳng song
song  ABCD và  A BCD
  thứ tự chứa BD và AC  . Do đó khoảng cách giữa hai đường thẳng BD và
AC  bằng a .
Câu 61. Chọn B
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 51
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 S H K B A O x D C
Từ B kẻ Bx//AC AC// SB, Bx
Suy ra d AC, SB  d AC,SB, Bx  d  ,
A SB, Bx
Từ A kẻ AK Bx K Bx và AH SK AK Bx Do 
Bx  SAK   Bx AH SA Bx
Nên AH  SB, Bx  d  ,
A SB, Bx  AH
Ta có BKA đồng dạng với A
BC vì hai tam giác vuông có  
KBA BAC (so le trong AK AB . AB CB .2 a a 2 5a Suy ra   AK    . CB CA CA a 5 5 1 1 1 1 5 9 2a
Trong tam giác SAK có       AH  . 2 2 2 2 2 2 AH AS AK a 4a 4a 3 2a
Vậy d AC, SB  . 3 Câu 62. Chọn B S M D A O B C
Gọi O là tâm hình chữ nhật và M là trung điểm SA , ta có: SC //  BMD .
Do đó d SC, BD  d SC, BMD  d S, BMD  d  ,
A BMD  h
Ta có: AM , AB, AD đôi một vuông góc nên
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 52
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1 1 1 1 4 1 1       2 2 2 2 2 2 2 h AM AB AD a a 4a 2a 21 Suy ra: h  . 21
Câu 63. Chọn A A C H M O B N Ta có O
BC vuông cân tại O , M là trung điểm của BC OM BC OM  / / BN
Dựng hình chữ nhật OMBN , ta có 
OM / /  ABN BN    ABN  
d AB,OM   d OM , ABN   d  ,
O ABN 
Gọi H là hình chiếu vuông góc của O trên AN ta có: BN ON
BN  OAN   OH BN mà OH AN BN OA
OH   ABN   d  ,
O ABN   OH
OAN vuông tại O , đường cao OH 1 1 1 1 1 1 4 1 4          2 2 2 OH OA ON 2 2 OA BM 2 2 OA BC 2 2 2 OA OB OC 1 4 3 2 2a a 6 a 6    2  OH   OH   d A ,
B OM   OH  2 2 2 2 a 4a  4a 2a 3 3 3 Nhận xét:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 53
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A C M O B
Chọn hệ trục tọa độ Oxyz như hình vẽ, khi đó O 0;0;0 , B 2 ;
a 0; 0 , C 0; 2 ;
a 0 , A0;0; a
M là trung điểm của BC M  ; a ; a 0   
Ta có OM  a; a;0 ; OB  0; 2a;0 ; AB  2 ; a 0; a
    
OM , AB.OB   3 2a a 6  OM AB   2 2 2 ,
a ; a ; 2a   d AB,OM         OM , AB 4 4 4 3
a a  4a   A M H C O N B Câu 64. Chọn C
Gọi N là trung điểm của BC suy ra MN //AC  AC// OMN
d OM ; AC   d C;OMN   d  ;
B OMN  . 1 1 1 3 V  . . a .2 a a a . . A OBC 3 2 3 V
d M ; ABC  S 1 1 1 1 M .OBC  . OBN  .  3  Va . V d ; A ABC S 2 2 4 M .OBC 12 . A OBC    OBC 1 2
Xét tam giác vuông cân AOB : OM AB a . 2 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 54
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1 1 5
Xét tam giác vuông BOC : ON BC  2a2 2  a a . 2 2 2 1 1 5
Xét tam giác BAC : MN AC a  2a2 2  a . 2 2 2 3 2
Trong tam giác cân OMN , gọi H là trung điểm của OM ta có 2 2 NH  NM HM a . 4 1 3 Suy ra 2 SOM .NH a . OMN 2 8 3V 2
Vậy d B;OMN M .OBN   a . S 3 OMN
Câu 65. Chọn A
+) Ta có: BC ,A     A  BC A   30o C C
+) Mặt khác BC    , ABCC BC    2 2 3 3a x  +) Gọi 2 2
AB x BC  3a x CC  BC. tan      .cot 30o AC AB  3x 5 +) Mặt khác ta có: 2 2 2
AC CC  AC  x a 2  CC  a 3  AC '  a 6
+) Gọi P là trung điểm của B C
  , ta có: Do mặt phẳng MNP / /  ABC nên 1
d MN , AC  d MN , ABC  d N, ABC  d A , ABC 2 1 a 6 +) Kẻ A H
AC  A H
  ABC  d A , ABC  AH  2 2 a 6
d MN , AC  4
Câu 66. Chọn C
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 55
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 S H A C G M B
Do hình chóp S.ABC đều nên SG là đường cao của hình chóp ( G là trọng tâm tam giác đều ABC ). Kẻ
MH SA tại H thì MH là đoạn vuông góc chung của SA và BC .
Vậy khoảng cách giữa hai đường thẳng SA và BC bằng MH . 2 3 1 a 3 a 3 a 3 2 3a 7a 3 Ta có VSG
SG  4a , AG  , 2 2 2 SA AG SG  16a  . Ta S . ABC 3 4 3 3 9 3 . SG AM 3.4 . a a 3 6a có . SA MH  . SG AM MH    SA 2.7a 3 7
Câu 67. Chọn A
ABCD / /  A' B 'C ' D ' 
Ta có: BD   ABCD  d  ;
BD A'C '  d[ ABCD; A' B 'C ' D ' ]  AA'  a
A'C '   A'B'C 'D'  Câu 68. BC / / AD  Ta có 
BC / / SAD  d BC, SD  d BC,SAD  d B,SAD . BC   SAD 
Có SA   ABCD  SA AB .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 56
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 BA AD
Ta có BA SA
BA  SAD  d B,SAD  BA .
SAAD A  Xét tam giác vuông 2 2 2 2 BAC, BA
AC BC  5a  2a a 3 .
Vậy d B,SAD  a 3  d BC, SD  a 3 . Câu 69. Chọn D S H A D M O N B C
Gọi M , N lần lượt là trung điểm của các cạnh AB, CD ; H là hình chiếu vuông góc của O trên SN.
Vì AB//CD nên d A ,
B SC  d AB, (SCD)  d M , (SCD)  2d O, (SCD) (vì O là trung điểm đoạn MN ) CD   SO Ta có 
CD  (SON )  CD OH CD ONCD   OH Khi đó 
OH  (SCD)  d  ;
O (SCD)  OH. OH SN  1 1 1 1 1 5 a
Tam giác SON vuông tại O nên       OH  2 2 2 2 2 2 OH ON OS a a a 5 4 2a 5
Vậy d AB,SC  2OH  . 5
Câu 70. Chọn A A' C' I B' H A C B Ta có BC //B C
   BC//AB C  
suy ra d BC, AB  d BC,AB C
   dB,AB C
   dA,AB C   .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 57
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Gọi I và H lần lượt là hình chiếu vuông góc của A trên B C   và AI . Ta có B C
   AI và B C
   AA nên B C
   AAI  B C
   AH mà AI AH . Do đó AB C
   AH a 3 . a A . A AI a 21
Khi đó d A,AB C
   AH  2   . 2 2
AA AI 2   7 2 a 3  a       2  a 21
Vậy khoảng cách cần tìm là . 7
Câu 71. Chọn B
Không mất tính tổng quát, giả sử a  1.
Gọi H là trung điểm của AB . Kẻ HM BC M BC  ; HN SM N SM  .
Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy nên SH   ABCD . 1 1  1  7
Áp dụng định lý hàm số cos : 2 2 2
DH DA AH  2 .
DA AH .cos120  1  2.1.     4 2  2  4 7  DH  2 7 21 Theo đề bài: 
SDH  60  SH DH . tan 60  . 3  2 2 1 3 3 Lại có: HM  . HB sin 60  .  . 2 2 4 1 1 1 116 609
Ngoài ra: BC  SHM   BC HN HN   SBC  ;      HN  . 2 2 2 HN SH HM 21 58
Chú ý rằng AD// SCB nên khoảng cách giữa AD và SC là khoảng cách giữa A và mặt phẳng SBC  , 609
bằng 2 lần khoảng cách từ H (theo định lý Ta-let), d  2HN  29
Câu 72. Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 58
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Gọi H là hình chiếu của S trên mặt đáy. Vì SA SB SC SD  6 nên HA HB HC HD . Suy ra hình
bình hành ABCD nội tiếp trong đường tròn tâm H . Vì vậy ABCD là hình chữ nhật.
Kẻ KP vuông góc với SA tại P (1). BK AC Ta có 
BK  SAC  BK KP (2). BK SH
Từ (1) và (2) ta có: d ( ,
SA BK )  KP .
Kẻ HQ vuông góc với SA tại Q . 1 1 5 119 Ta có: 2 2 2 2 AH AC AB BC  , SH SA AH  2 2 2 2 SH.HA 5 119  HQ   . SA 24 2 KP KA KA AC K . A AC AB 32 Ta có:   .  .2  2.  . 2 2 HQ HA AC HA AC AC 25 32 4 119  d ( ,
SA BK )  KP HQ  . 25 15
Câu 73. Chọn D
 Gọi I AB ' A' B ; H là trung điểm của BC .
IH // A'C A'C // (B ' AH )  ddd .
A'C;AB'
A';(B' AH )
B;(B' AH )
 Kẻ BK B ' H , với K B ' H .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 59
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 a 2 . a B ' . B BH 2a Chứng minh: 2
BK  (B ' AH )  dBK   
B;(B' AH ) 2 2 2
B ' B BH 17  a 2  (2a)     2  2a Vậy d  .
( A'C ;AB ') 17
Câu 74. Chọn B
SC ABC  ;  SCH  45 1 4 Ta có: BH AB  3 3 2   2 2  4   2 4 4 7
CH BH BC  2BH.BC.cos HBC     4  2. .4.cos 60    3   3 3 2 34
SH CH.tan 45  3
Dựng hình thoi ACBD (với D là đỉnh thứ 4 của hình thoi)
AD / /BC BC / /SAD 3
Vậy dSA; BC  dBC;SAD  d ;
B SAD dH;SA D  2
Gọi M là trung điểm của AD BM AD ( ΔDAB đều).
Từ H dựng HI / /BM HI AD AD HI  Ta có: 
AD  SIHSAD SIH  AD SH 
Từ H dựng HK SI HK  SAD
Vậy dH;SAD HK 8 2 3. AH HI BM.AH 4 3 Ta có: 3 HI / /BM    HI    AB BM AB 4 3 4 7 4 3 . SH.IH SH.IH 2 210 3 3  HK     2 2 2 2 SI      15 SH HI 4 7  4 3             3   3 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 60
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 dSA  3 210 ; BC  HK  2 5 Câu 75. Ta có BC SA   BC AB
  BC   SAB . ,
SA AB  SAB
SA AB A  
Trong SAB , dựng BH SM và cắt SM ở H . Ta có BH SM
  d SM , BC   BH d BH. BH BC BH BM SABM Ta có BMH  ∽ SMA    BH    1 . SA SM SM AB
Xét ABC vuông tại B có  0 sin BCA
AB  sin 60  2  3 . AC 3
AM BM  . 2 2  3  7 7
Xét SAM vuông ở A có 2 2 2 2
SM SA AM  1      SM  .  2  4 2   3 1 SA BM 3 21 Thế vào   1 , ta có 2 BH     . SM 7 7 7 2
Cách 2: (Nguyễn Văn Thịnh)
Nhận xét: Các dạng toán về khoảng cách nếu có thể thì nên sử dụng các quan hệ song song và tỉ lệ để đưa
về tính khoảng cách từ chân đường cao của hình chóp.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 61
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Gọi N là trung điểm của AC .
Ta có BC // SMN   d BC, SM   d BC,SMN   d B,SMN   d  ,
A SMN  .
Kẻ AH SM , H SM , ta có AH  SMN   d  ,
A SMN   AH . 3 Ta có 
AB AC.sin C  2.sin 60  3  AM  . 2 . SA AM 21
Xét tam giác SAM vuông tại A có AH là đường cao, suy ra AH   . 2 2 7 SA AM 21
Vậy d BC, SM   . 7 Câu 76.
Gọi M là trung điểm CD , O là trung điểm BD . Do S.ABCD là khối chóp tứ giác đều nên ABCD là hình
vuông và SO   ABCD . 2 2 S .SO a .SO a b Do ABCD V     SO b . S .ABCD 3 3 3 Ta có
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 62
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
BE // CD BE // SCD     
BE // GF mà BE// CD GF // CD . BEFG SCD GF   SG 2 GF SF SG 2
Do G là trọng tâm SCD nên 
mà GF //CD nên    . SM 3 DM SD SM 3 2
Trên tia đối của tia DC lấy điểm N sao cho DN GF
DM . Từ đó ta có DNFG và BEND là hai hình 3
bình hành và  BDG //  NEF  . KD DF 1
Trên đoạn thẳng OD lấy điểm K sao cho  
, từ đó ta có FK //SO mà SO   ABCD suy ra OD SD 3
FK  ( ABCD) .
Hạ KP EN và KH PF , do FK  ( ABCD) nên FK KP . EN KP Do
  EN   FKP  EN KH mà KH PF suy ra KH   NEF  . EN FK
Khi đó: d DG, EF  d DG, NEF   d  BDG, NEF   d K, NEF   KH . 2 2 CD CD a
Ta có: BE GF MD  .   3 3 2 3 3 FK DF 1 1 b
Do FK //SO nên   , suy ra FK SO  . SO DS 3 3 3  a 2 a 2
Hạ EJ BD . Do EN //BD, KP EN , EJ  BD  KP  EJ BE.sin 45  .  . 3 2 6
Áp dụng hệ thức lượng vào tam giác vuông FKP với đường cao KH ta có: 9  2 2 2 1 1 1 1 1 b a ab       KH  2 2 2 2 2 2 2 2 2 KH KF KPb   a 2 a b  3 2b a   3     6   ab
Vậy d DG, EF  . 2 2 3 2b a
Câu 77. Cách 1: z S M N C A y H B x
Gọi H là trung điểm AB .
Vì SAB   ABC  nên SH   ABC  .
Chọn hệ trục tọa độ Oxyz , với O H , HB Ox , HC Oy , HS Oz .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 63
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 AH Ta có: 2 2 HC
AC AH  3a ; SH   a . tan ASH  3a a   9a a
Khi đó: H 0; 0; 0 , S 0; 0; a , Aa 3;0;0 , B a 3 ;0;0 , C 0;3a;0 , M 0; ;   , N 0; ;   .  2 2   4 4     3a a    9a a
Suy ra: AM a 3 ; ; 
 , BN  a 3 ; ; 
 , AB  2a 3 ;0;0 ,  2 2   4 4  2 2 2    3a 3 3a 15 3a
AM , BN     ;  ;    .  4 4 4    3
   3 3a
AM , BN .AB   2 237a
Khoảng cách giữa hai đường thẳng AM , BN là d AM BN  2 ,      . 2  AM , BN  711a 79   4 Cách 2: S M N P I A C E K G H B
Gọi P là trung điểm của AC , G là trọng tâm tam giác ABC .
Kẻ NK / / SH , K HC ; EK / / AC , E BP .
Suy ra: NP / / AM AM / /  NPB  d AM , BN   d M , NPB  d C , NPB .  1 a NK SH NK KC CN 1   4 4
Ta có: NK / / SH nên      . SH CH CS 4 GK 5     GC 8 EK GK 5 5 5 3a EK / / AC nên    EK PC  . PC GC 8 8 8 a 79 2 2 NE NK EK
; BP HC  3a . 8 KN BP Vì: 
BO   NPB  BP EN . KE BP  1 3 79a
Diện tích tam giác NBP là: SNE.BP  . NBP 2 16 3 1 1 1 1 1 3a
Thể tích tứ diện N.CPB là: Vd N , ABC .S  . .SH . . . BP PC  .a .3a .a 3  . N .CPB    CBP 3 3 4 2 24 8
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 64
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 3V 2 237a
Khoảng cách từ C đến  NBP là: d C , NBP N .CPB   . S 79 NBP 2a 237
Vậy khoảng cách giữa hai đường thẳng AM , BN là . 79 Cách 3:
Kẻ KI NE , I NE . 8
Khi đó: NP / / AM AM / /  NPB  d AM , BN   d M , NPB  d C , NPB  d K , NPB . 5 KI NE Ta có: 
KI   NPB  d K , NPB  KI . KI BP  8
Suy ra: NP / / AM AM / /  NPB  d AM , BN   KI . 5 1 1 1 1264 5 237a 2 237a
Trong tam giác vuông NKE ta có:     KI
d AM , BN   . 2 2 2 2 KI KN KE 75a 316 79 Câu 78.
Gọi I , G lần lượt là trung điểm của AC và trọng tâm của tam giác ABC . 1 9 2
Ta có DG   ABC và VDG.S  . ABCD 3 ABC 4
Gọi N là trung điểm của AD MN || AC AC ||  BMN  .
d AC, BM   d AC,BMN   d  ,
A BMN   d N,BMN   h . 1 1 9 11
Gọi K là trung điểm của MN , ta có 2 2 S  .BK.MN
BM MK .MN  . BMN 2 2 16 V DA DC DB 1 9 2 1 Ta có: DACB  . .  2.2.1  4  VV   . . h S . V DN DM DB 4 DACB DBMN 16 3 BMN DNMB 9 2 1 9 11 3 22   . . hh  . 16 3 16 11
Câu 79. Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 65
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Gọi H là trung điểm của AB , vẽ HE CD tại E , HK SE tại K . Ta có S
BC đều nên BC  11, S
AC vuông cân tại S nên AC  11 2 . Trong SAB , 2 2 2
AB SA SB  2S . A S .
B cos120  AB  11 3 . ABC có 2 2 2
AB AC BC nên AB
C vuông tại C , từ đó H là tâm đường tròn  ABC
SH   ABCD  CD  SHE  CD HK HK  SCD .
Ta có d AB, SD   AB,SCD  H ,SCD  HK . AC.AD 11 2.11 11 6 SA 11
Ta có HE d  , A CD    , SH   . 2 2 AC AD 2 2 3 2.11 11 2 2 11 11 6 . SH.HEHK  2 3   22 . 2 2 SH HE 121 121.2  4 3
Vậy d AB, SD  22 . A K B D H Câu 80. C
Gọi H là hình chiếu vuông góc của A
BCD Khi đó ta có H BCD lên ( ).
là trực tâm của tam giác .
Với mọi đường thẳng  nằm trong (BCD) thì d ( ;
A )  AH. Do đó đường thẳng  thỏa mãn phải đi qua điểm H .
Kẻ HK AD(K AD) khi đó H , K là hai điểm cố định lần lượt nằm trên  & AD.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 66
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Hiển nhiên, khoảng cách giữa  & AD là độ dài đoạn vuông góc chung của chúng nên d ( ;
AD)  HK. Dấu
bằng xảy ra khi HK  . 1 1 1 1 1 1 1 14 a Ta có         AH  . 2 2 2 2 2 2 AH AB AC AD a a 2 2 a a ( ) ( ) 14 3 2 AH 1 13 a 13 Ta có:    cos HAK    sin HAK   HK H . A sin HAK  . AD 14 14 14 3a 4a   d  . 14 7
Câu 81. Chọn D
Do SB SC  11 và  0
SBC  60 nên SBC đều, do đó BC  11.
Ta lại có, SA SC  11 và  0
SCA  45 nên SAC
vuông cân tại S , hay AC  11 2.
Mặt khác, SA SB  11 và  0 SAB  30 nên AB  11 3. Từ đó, ta có 2 2 2
AB BC AC suy ra ABC vuông tại C.
Gọi H là trung điểm của A .
B Khi đó, H là tâm
đường tròn ngoại tiếp AB .
C Vì SA SB SC nên SH  ( ABC).
Gọi M là điểm trên CD sao cho HM AB, suy ra HM C .
D Gọi N là chân đường vuông góc hạ từ C xuống A .
B Khi đó, HM / /CN và HM CN. Do A
BC vuông tại C nên theo công thức tính diện tích ta có: C . A CB 11 6 HM CN   2 2 3 CA CB 1 11 3 11 Ta lại có, CH AB  nên 2 2 SH SC CH  . 2 2 2
Trong tam giác vuông SHM , dựng đường cao HI (I SM ), suy ra HI  (SCD). Khi đó, SH .HM
d ( AB, SD)  d ( AB, (SCD))  d (H , (SCD))  HI   22. 2 2 SH HM
Vậy d ( AB, SD)  22. Câu 82.
A. Phân tích bài toán:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 67
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
1. Vẽ hình hộp, yếu tố vẽ hình quan trọng, giúp bạn tư duy “nét” nhất cho bài toán. Các cạnh của hình hộp
bằng 1 và góc phẳng tại đỉnh A bằng 60 cho ta thêm dữ kiện hình hộp xiên có đáy là hình thoi.
2. Kiến thức khoảng cách giữa hai đường thẳng chéo nhau a và b .
Cách 1: Là độ dài đoạn vuông góc chung giữa a và b .
HK a ; HK b d (a, )
b HK a .
Cách 2: Là khoảng cách từ đường thẳng này đến mặt phẳng song song với nó chứa đường thẳng còn lại.
 / / a ,   b I ,  P  b, 
  d a, b  d a, P  d  ,
A P  AH .
Cách 3: Là khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đã cho.
d a,b  d  P,Q  d  ,
A Q  AH .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 68
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Trong quá trình dẫn dắt ra lời giải bài toán ta giới thiệu cả 3 cách xác định khoảng cách.
Cách sử dụng trong bài toán này là cách 2. Tính khoảng cách từ đường thẳng tới mặt phẳng song song với đường thẳng ấy.
3. Kiến thức khoảng cách từ 1 điểm đến đến một mặt phẳng. Không xác định trưc tiếp khoảng cách từ điểm
đó tới mặt phẳng mà xác định gián tiếp từ điểm khác mà ta nhìn được khoảng cách dễ dàng hơn, còn gọi là đổi điểm.
d AC ; AB  d AC ; ACB  d C ; ACB  d B; ACB . .
4. Thu gọn bài toán tính các yêu tố trong hình hộp xiên sang tính các yếu tố trong hình tứ diện. Hay ta có bài
toán mới đơn giản hơn và có nhiều cách giải hơn.
Tính chiều cao hạ từ đỉnh B của tứ diện BACB biết các góc tại đỉnh B là
CBB  60 ,   B B
A ABC  120 và các cạnh bên BA BC BB  a .
Vậy bài toàn phức tạp đã đưa về một bài toán đơn giản mà ta đã biết cách giải.
Ở bài toán mới học sinh cần vận dụng kiến thức về hình học phẳng như
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 69
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Định lí hàm số cosin:
Cho ABC có AB c , AC b , BC a với các góc của tam giác là A , B , C ta có: 2 2 2
a b c  2bc cos A
Các công thức tính diện tích tam giác: abc 1 S  
h .a ( h chiều cao của tam giác hạ từ đỉnh A ; R là bán kính đường tròn ngoại tiếp ABC ABC  4R 2 a a
), từ đó tính ra chiều cao của tứ diện.
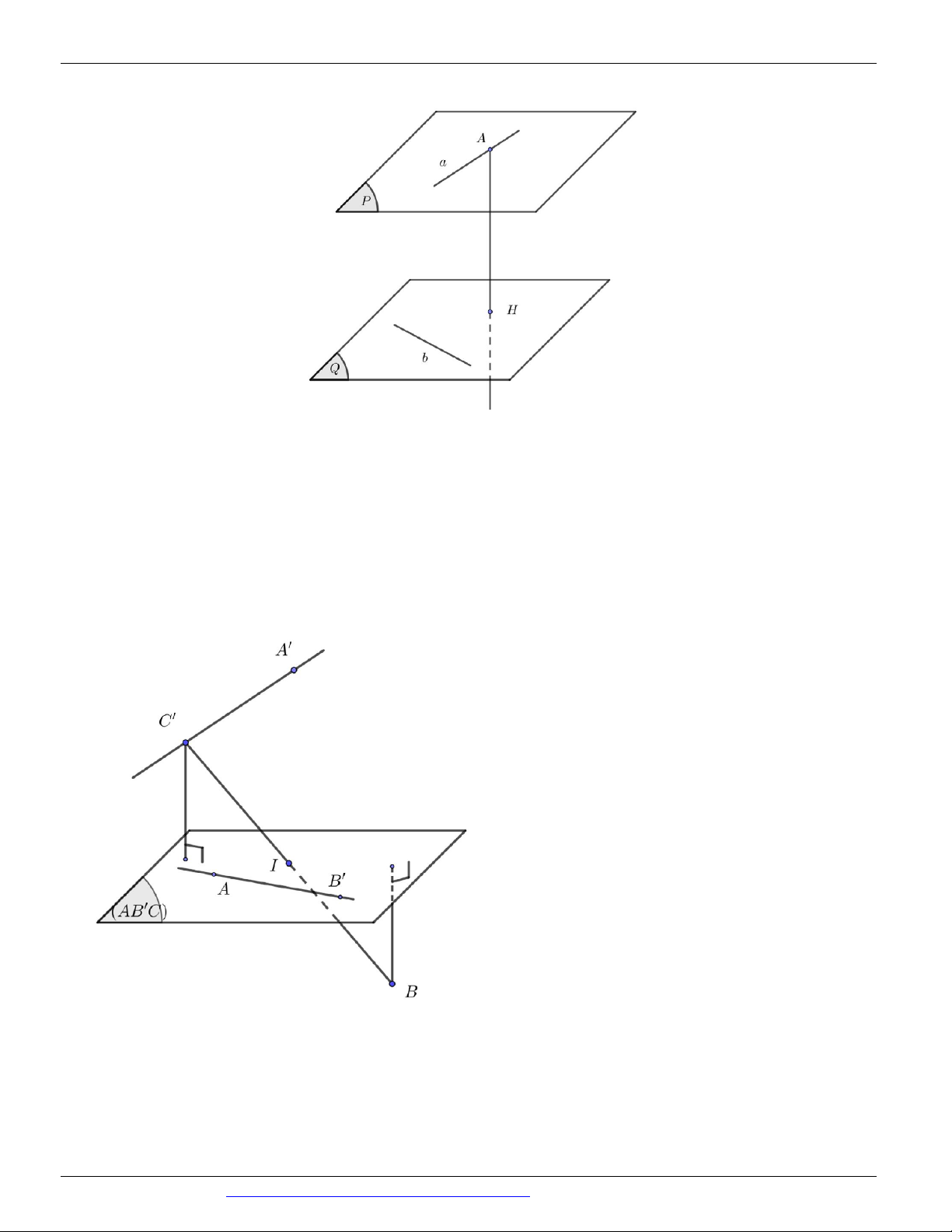
Sau khi phân tích bài toán, học sinh sẽ tự trình bày lời giải như sau: Có AC / / A C
   AC / /  AB C  
d AC ; AB  d AC ; ACB  d C ; ACB  d B; ACB
Xét tứ diện B.ACB có
+) BA BC BB  1 nên điểm B nằm trên trục của đường tròn ngoại tiếp ACB . Suy ra BO   ACB
tại tâm O của đường tròn ngoại tiếp ACB . +)  CBB  60 ,   B B
A ABC  120 nên áp dụng định lý hàm số cosin trong tam giác B B
A và ABC ta
có AB  AC  3 .
d B; ACB  BO 2 2
BA R với R là bán kính của đường tròn ngoại tiếp tam giác ACB .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 70
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1 3 
AB .CB .AC AH .B C  3 3 4 3 9 2 S      R   BO  1  ACB 4R 2 4R 2 11 11 11 22  BO  . 11
d AC ; AB  OB . 22
Vậy khoảng cách giữa hai đường thẳng AB và AC là . 11 Đáp án cần chọn là A. Nhận xét
Bài toán này đã giúp người học ôn lại
+) Kiến thức về khoảng cách trong không gian.
+) Hệ thức lượng trong tam giác và giải tam giác.
Và quan trọng biết chuyển từ bài toán hình hộp xiên sang hình tứ diện, biết độ dài các cạnh. Khai thác bài toán
Vẫn với hình vẽ và một phần lời giải của bài toán ban đầu, một số bài toán tương tự với các hướng dẫn kèm
theo cho học sinh ôn luyện.
Dạng 2.3 Khoảng cách của đường với mặt Câu 83. AB AD Ta có: 
nên AB  SAD . AB SD
Kẻ DH SA tại H . Do DH  SAD nên AB DH . DH SA Ta có: 
DH  SAB . DH AB
Do DC / / AB nên DC / / SAB .
Vậy khoảng cách giữa đường thẳng CD và mặt phẳng SAB là DH . 1 1 1 1 1 3 Xét S
AD vuông tại D có:      . 2 2 2 DH SD AD  2 2 2 a a 2 2 4a 2a 2aDH
. Khoảng cách giữa đường thẳng CD và mặt phẳng SAB là . 3 3
Câu 84. Chọn C
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 71
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Gọi O là tâm hình vuông. Ta có: MO / /SB SB / /( ACM )
d (SB, ( ACM ))  d (B, ( ACM ))  d (D, ( ACM )) ( vì O là trung điểm BD )
MI / /SA MI  ( ABCD)
Gọi I là trung điểm AD  
d (D, ( ACM ))  2d (I , ( ACM )) 
Trong ( ABCD) kẻ IK AC tại K
Trong (MIK ) kẻ IH MK tại H (1)
Ta có: AC MI , AC IK AC  (MIK )  AC IH (2)
Từ (1) & (2)  IH  ( ACM )  d (I , ( ACM ))  IH IM.IK
Trong tam giác MIK ta có: IH= 2 2 IM +IK a 2 a SA OD BD a 2 a Biết 4 MI   a, IK     IH   2 2 2 4 4 3 2 a a  8 2a
Vậy: d (SB, ( ACM ))  3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 72