Các dạng toán hệ trục tọa độ Oxyz và phương trình mặt cầu thường gặp Toán 12

Các dạng toán hệ trục tọa độ Oxyz và phương trình mặt cầu thường gặp Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

72 36 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễ

n Bảo Vương: https://www.facebook.com/phong.baovuong 1

CHUYÊN

ĐỀ 21

MỤC LỤC

PHẦN A. C

ÂU HỎI ......................................................................................................................................................... 1

Dạng 1. Tìm tọa độ điểm, véc tơ liên quan đến hệ trục tọa dộ OXYZ ............................................................................. 1

Dạng 2. Tích vô hướng, tích có hướng và ứng dụng ........................................................................................................ 8

Dạng 2.1 Tích vô hướng và ứng dụng .......................................................................................................................... 8

Dạng 2.2 Tích có hướng và ứng dụng .......................................................................................................................... 9

Dạng 3. Mặt cầu ............................................................................................................................................................. 10

Dạng 3. Xác định tâm, bán kính của mặt cầu ............................................................................................................. 10

Dạng 3. Viết phương trình mặt cầu ............................................................................................................................ 13

Dạng 3. Một số bài toán khác ..................................................................................................................................... 16

Dạng 4. Bài toán cực trị .................................................................................................................................................. 17

PHẦN B. LỜI GIẢI THAM KHẢO .............................................................................................................................. 19

Dạng 1. Tìm tọa độ điểm, véc tơ liên quan đến hệ trục tọa dộ OXYZ ........................................................................... 19

Dạng 2. Tích vô hướng, tích có hướng và ứng dụng ...................................................................................................... 27

Dạng 2.1 Tích vô hướng và ứng dụng ........................................................................................................................ 27

Dạng 2.2 Tích có hướng và ứng dụng ........................................................................................................................ 28

Dạng 3. Mặt cầu ............................................................................................................................................................. 31

Dạng 3. Xác định tâm, bán kính của mặt cầu ............................................................................................................. 31

Dạng 3. Viết phương trình mặt cầu ............................................................................................................................ 34

Dạng 3. Một số bài toán khác ..................................................................................................................................... 37

Dạng 4. Bài toán cực trị .................................................................................................................................................. 42

PHẦN A. CÂU HỎI

Dạng 1. Tìm tọa độ điểm, véc tơ liên quan đến hệ trục tọa dộ OXYZ

Câu 1. (Mã đề 102 BGD&ĐT NĂM 2018) Trong không gian

Oxyz

, cho hai điểm

 

1;1; 2



và

 

2;2;1

Vectơ



có tọa độ là

 

1; 1; 3  

 

3;1;1

 

1;1;3

 

3;3; 1

Câu 2. (Mã đề 104 - BGD - 2019) Trong không gian

Oxyz

, hình chiếu vuông góc của điểm

 

3;1

; 1



trên

trục

có tọa độ là

 

0; 1

. B.

 

1;0

. C.

 

0;0

. D.

 

0; 1

HỆ TRỤC TỌA ĐỘ OXYZ, PHƯƠNG TRÌNH MẶT CẦU

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2

Câu 3. (Mã đề 101 BGD&ĐT NĂM 2018) Trong không gian

Oxyz

, cho hai điểm

 

2; 4;3

A 

và

 

2;2;7

Trung điểm của đoạn thẳng

có tọa độ là

 

4; 2;10



 

1;3;2

 

2;6;4

 

2; 1;5



Câu 4. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Trong không gian với hệ tọa độ

Oxyz

, cho các điểm

 

3; 4;0

A 

 

1;1;3

B 

 

3,1,0

. Tìm tọa độ điểm

trên trục hoành sao cho

AD BC

 

6;0;0

 

12;0;0

 

0;0;0

 

6;0;0

 

2;1;0

D 

 

4;0;0

D 

 

0;0;0

 

6;0;0

D 

Câu 5. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Trong không gian

,Oxyz

cho hai điểm

 

1;1; 1



và

 

2;3;2

. Vectơ



có tọa độ là

 

1; 2; 3

 

1; 2; 3

 

 

3;5;1

 

3;4;1

Câu 6. (Mã 103 - BGD - 2019) Trong không gian

Oxyz

, hình chiếu vuông góc của điểm

 

2;1; 1



trên

trục

có tọa độ là

 

0;0; 1

. B.

 

2;0; 1

. C.

 

0;1;0

. D.

 

2;0;0

Câu 7. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Trong không gian với hệ toạ độ

Oxyz

, cho điểm

 

2;2;1

Tính độ dài đoạn thẳng

OA 



Câu 8. (Mã 102 - BGD - 2019) Trong không gian

Oxyz

, hình chiếu vuông góc của điểm

 

3; 1;1

M 

trên trục

có tọa độ là

 

3; 1;0



. B.

 

0;0;1

. C.

 

0; 1;0



. D.

 

3;0;0

Câu 9. Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

3; 2;3

A

và

 

1;2;5

B

. Tìm tọa độ trung điểm

của đoạn thẳng

 

1;0;4

. B.

 

2;0;8

. C.

 

2; 2; 1 

. D.

 

2;2;1

I

Câu 10. (Mã đề 101 - BGD - 2019) Trong không gian

Oxyz

, hình chiếu vuông góc của điểm

 

2;1; 1



trên trục

có tọa độ là

 

2;0;0

. B.

 

0;1;0

. C.

 

2;1;0

. D.

 

0;0; 1

Câu 11. Trong không gian với hệ tọa độ Oxyz, cho hai điểm

 

2;3;1

A 

và

 

5; 6; 2

. Đường thẳng

cắt

mặt phẳng

 

Oxz

tại điểm

. Tính tỉ số



Câu 12. (ĐỀ THAM KHẢO BGD & ĐT 2018) Trong không gian

Oxyz

, cho điểm

 

3; 1;1

A 

. Hình chiếu

vuông góc của điểm

trên mặt phẳng

 

Oyz

là điểm

 

3;0;0

 

0; 1;1

N 

 

0; 1;0

P 

 

0;0;1

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3

Câu 13. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Trong không gian với hệ trục tọa

độ

Oxyz

, cho ba vecto

     

1;2;3 ; 2;2; 1 ; 4;0; 4

a b c

 



 

. Tọa độ của vecto

2d a b c  

 

là

 

7;0; 4

 



 

7;0;4

d 



 

7;0; 4





 

7;0;4



Câu 14. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Trong không gian

,Oxyz

cho vectơ

   

2; 2; 4 , 1; 1;1 .

a b    



Mệnh đề nào dưới đây sai?

 

3; 3; 3

a b

   



và



cùng phương

b 



a b



Câu 15. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Trong không gian

Oxyz

, cho hai điêm

 

0;1; 1



 

2;3;2

. Vectơ



co toa đô la

 

2;2;3

. B.

 

1;2;3

. C.

 

3;5;1

. D.

 

3;4;1

Câu 16. (THPT CẨM GIÀNG 2 NĂM 2018-2019) Trong không gian với hệ tọa độ

Oxyz

cho hai điểm

 

3; 2;3

A 

và

 

1;2;5

B 

. Tìm tọa độ trung điểm

của đoạn thẳng

la :

 

2;2;1

I 

. B.

 

1;0;4

. C.

 

2;0;8

. D.

 

2; 2; 1

 

Câu 17. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Trong không gian

Oxyz

cho

 

2;3;2

a 



và

 

1;1; 1

 



. Vectơ

a b



có tọa độ là

 

3;4;1

. B.

 

1; 2;3

 

. C.

 

3;5;1

. D.

 

1;2;3

Câu 18. (TRƯƠNG THPT HOANG HOA THAM HƯNG YÊN NĂM 2018-2019) Trong không gian với hệ

trục tọa độ

Oxyz

, cho

 

2; 3;3

a  



 

0;2; 1

 



 

3; 1;5

c  



. Tìm tọa độ của vectơ

2 3 2u a b c  



  

 

10; 2;13



. B.

 

2;2; 7 

. C.

 

2; 2;7

 

. D.

 

2;2;7



Câu 19. (TRƯƠNG THPT HOANG HOA THAM HƯNG YÊN NĂM 2018-2019) Trong không gian với hệ

tọa độ

Oxyz

, cho

 

1;3;2

 

3; 1;4

B 

. Tìm tọa độ trung điểm

của

.AB

 

2; 4;2

I 

. B.

 

4;2;6

. C.

 

2; 1; 3

  

. D.

 

2;1;3

Câu 20. (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Trong không gian với hệ trục

Oxyz

cho ba điểm

     

1;2; 3 , 1;0;2 , ; ; 2

A B C x y

  

thẳng hàng. Khi đó

x y

bằng

x y

 

. B.

x y

 

. C.

x y

  

. D.

x y 

Câu 21. (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Trong không gian với hệ trục

tọa độ

Oxyz

, cho

2 3a i j k   

  



. Tọa độ của vectơ



là

 

1; 2; 3 

. B.

 

2; 3; 1 

. C.

 

2; 1; 3 

. D.

 

3;2; 1 

Câu 22. (ĐỀ 15 LOVE BOOK NĂM 2018-2019) Trong không gian cho hệ trục toạ độ

Oxyz

, cho ba điểm

     

1; 2;3 , 1; 2;5 , 0;0;1

A B C 

. Tìm toạ độ trọng tâm

của tam giác

ABC

 

0;0;3

. B.

 

0;0;9

. C.

 

1;0;3

G 

. D.

 

0;0;1

Câu 23. (TT HOÀNG HOA THÁM - 2018-2019) Trong không gian với hệ tọa độ

Oxyz

, cho

 

2; 3; 3

a  



 

0; 2; 1

 



 

3; 1; 5

c  



. Tìm tọa độ của vectơ

2 3 2u a b c  

   

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4

 

10; 2;13



. B.

 

2; 2; 7 

. C.

 

2; 2; 7

 

. D.

 

2; 2; 7



Câu 24. (TT HOÀNG HOA THÁM - 2018-2019) Trong không gian với hệ trục tọa độ

Oxyz

cho

 

1;3;2

 

3; 1;4

B 

. Tìm tọa độ trung điểm

của

 

2; 4;2

I 

. B.

 

4;2;6

. C.

 

2; 1;3

I  

. D.

 

2;1;3

Câu 25. (LIÊN TRƯỜNG THPT TP VINH NGHỆ AN NĂM 2018-2019) Trong không gian

Oxyz

, cho hai

điểm

 

1;5;2

A 

và

 

3; 3;2

B 

. Tọa độ trung điểm

của đoạn thẳng

là

 

1;1;2

 

2;2;4

 

2; 4;0

M 

 

4; 8;0

M 

Câu 26. (THPT MINH KHAI HÀ TĨNH NĂM 2018-2019) Trong không gian với hệ tọa độ

Oxyz

, cho hai

vectơ

 

2;1; 3

 



và

 

1;0; 1

 



. Tìm tọa độ của vectơ

2a x y 

  

 

4;1; 1

 



. B.

 

3;1; 4

 



. C.

 

0;1; 1

 



. D.

 

4;1; 5

 



Câu 27. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Trong không gian

Oxyz

, cho hai điểm

 

2; 4;3

A 

và

 

2;2;7

. Trung điểm của đoạn thẳng

có tọa độ là

 

1;3;2

. B.

 

2; 1;5



. C.

 

2; 1; 5 

. D.

 

2;6;4

Câu 28. (THPT CÙ HUY CẬN NĂM 2018-2019 LẦN 01) Trong không gian với hệ tọa độ

Oxyz

, cho các

điểm

 

1;0;3

 

2;3; 4



 

3;1;2

C 

. Tìm tọa độ điểm

sao cho

ABCD

là hình bình hành.

 

4; 2;9

D  

. B.

 

4;2;9

D 

. C.

 

4; 2;9

D 

. D.

 

4;2; 9



Câu 29. (THPT CÙ HUY CẬN NĂM 2018-2019 LẦN 01) Trong không gian với hệ tọa độ

Oxyz

, cho tam

giác

ABC

với

     

1;3;4 , 2; 1;0 , 3;1;2

A B C

. Tọa độ trọng tâm

của tam giác

ABC

là

 

2;1;2

. B.

 

6;3;6

. C.

3; ;3

 

 

 

. D.

 

2; 1;2

G 

Câu 30. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Trong không gian với hệ tọa độ

Oxyz

cho tam giác

ABC

biết

   

5; 2;0 , 2;3;0

A B 

 

0;2;3

. Trọng tâm

của tam giác

ABC

có tọa

độ:

 

1;2;1

. B.

 

2;0; 1

. C.

 

1;1;1

. D.

 

1;1; 2

Câu 31. (THPT - YÊN ĐỊNH THANH HÓA 2018 2019- LẦN 2) Trong không gian

O xyz

, cho

 

2; 1;0

A

và

 

1;1; 3

. Vectơ



có tọa độ là

 

3;0; 3

. B.

 

1;2; 3 

. C.

 

1; 2;3

 

. D.

 

1; 2;3



Câu 32. (THPT - YÊN ĐỊNH THANH HÓA 2018 2019- LẦN 2) Trong không gian

Oxyz

, cho ba điểm

     

1;0;0 , 1;1;0 , 0;1;1

A B C

. Tìm tọa độ điểm

sao cho tứ giác

ABCD

(theo thứ tự các đỉnh) là hình bình

hành?

 

2;0;0

. B.

 

1;1;1

. C.

 

0;0;1

. D.

 

0;2;1

Câu 33. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Trong không gian

Oxyz

cho

   

2; 2;1 , 1; 1;3 .

A B 

Tọa

độ vecto



là:

( 1;1; 2).

. B.

( 3;3; 4). 

. C.

(3; 3;4).

. D.

(1; 1; 2) 

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5

Câu 34. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Trong không gian với hệ

tọa độ

Oxyz

, điểm nào sau đây nằm trên mặt phẳng tọa độ

 

Oyz

 

3;4;0

. B.

 

2;0;3

P 

. C.

 

2;0;0

. D.

 

0;4; 1



Câu 35. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Trong không gian

Oxyz

với

, ,i j k

  

lần lượt là các vecto đơn vị trên các trục

, , .Ox Oy Oz

Tính tọa độ của vecto

.i j k 

  

( 1; 1;1).

i j k    

  

( 1;1;1).

i j k   

  

(1;1; 1).

i j k

   

  

(1; 1;1).

i j k   

  

Câu 36. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Trong không gian với hệ trục tọa độ

Oxyz

cho

 

4;5;6

. Hình chiếu của

xuống mặt phẳng

 

Oyz

là



. Xác định tọa độ



 

4;5;0



. B.

 

4;0;6



. C.

 

4;0;0



. D.

 

0;5;6



Câu 37. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Trong không gian với hệ trục tọa độ

Oxyz

cho

điểm

 

; ;M x y z

. Trong các mệnh đề sau, mệnh đề nào đúng?

A. Nếu



đối xứng với

qua mặt phẳng

 

Oxz

thì

 

; ;M x y z





B. Nếu



đối xứng với

qua

thì

 

; ;M x y z





C. Nếu



đối xứng với

qua mặt phẳng

 

Oxy

thì

 

; ;M x y z





D. Nếu



đối xứng với

qua gốc tọa độ

thì

 

2 ;2 ;0M x y



Câu 38. (THPT GANG THÉP THÁI NGUYÊN NĂM 2018-2019) Trong không gian với hệ tọa độ

Oxyz

giả

sử

2 3

u i j k  

   

, khi đó tọa độ véc tơ



là

 

2;3;1



. B.

 

2;3; 1

. C.

 

2; 3; 1 

. D.

 

2;3;1

Câu 39. (THPT CHUYÊN SƠN LA NĂM 2018-2019 LẦN 01) Trong không gian

Oxyz

, cho 2 điểm

 

1; 2;2

M 

và

 

1;0;4

. Toạ độ trung điểm của đoạn thẳng

là:

 

1; 1;3



. B.

 

0;2;2

. C.

 

2; 2;6



. D.

 

1;0;3

Câu 40. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Trong không gian

Oxyz

, cho

 

1;2;1

a 



và

 

1;3;0

b  



. Vectơ

c a b 



 

có tọa độ là

 

1; 7;2

. B.

 

1; 5; 2

. C.

 

3; 7; 2

. D.

 

1; 7;3

Câu 41. (KTNL GV BẮC GIANG NĂM 2018-2019) Trong mặt phẳng với hệ trục tọa độ

Oxy

, cho hai điểm

 

3;4

A 

và

 

5;6

. Trung điểm của đoạn thẳng

có tọa độ là

 

1;5

. B.

 

4;1

. C.

 

5;1

. D.

 

8;2

Câu 42. (KTNL GV BẮC GIANG NĂM 2018-2019) Trong không gian với hệ tọa độ

Oxyz

, cho hai vectơ

 

2;1; 2

 



và vectơ

 

1;0;2

b 



. Tìm tọa độ vectơ



là tích có hướng của



và



 

2;6; 1

 



. B.

 

4;6; 1

 



. C.

 

4; 6; 1

  



. D.

 

2; 6; 1

  



Câu 43. (KTNL GV THUẬN THÀNH 2 BẮC NINH NĂM 2018-2019) Trong không gian với trục hệ tọa độ

Oxyz

, cho

2 3 .a i j k

   

   

Tọa độ của vectơ



là:

 

1;2; 3

 



. B.

 

2; 3; 1

 



. C.

 

3;2; 1

 



. D.

 

2; 1; 3

 



CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6

Câu 44. (THPT CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019 LẦN 01) Trong không gian

Oxyz

, cho hai điểm

 

2; 4;3

A 

và

 

2;2;9

. Trung điểm của đoạn

có tọa độ là

 

0;3;3

. B.

 

4; 2;12



. C.

 

2; 1;6



. D.

3 3

0; ;

2 2

 

 

 

Câu 45. (SỞ GD&ĐT THANH HÓA NĂM 2018 - 2019) Trong không gian với hệ tọa độ Oxyz, cho hai điểm

 

1; 3;1



, B

 

3;0; 2

. Tính độ dài

A. 26. B. 22. C.

. D.

22.

Câu 46. (LIÊN TRƯỜNG THPT TP VINH NGHỆ AN NĂM 2018-2019) Trong không gian

Oxyz

, cho hai

điểm

 

1;5;2

A 

và

 

3; 3;2

B 

. Tọa độ trung điểm

của đoạn thẳng

là

 

1;1;2

 

2;2;4

 

2; 4;0

M 

 

4; 8;0

M 

Câu 47. (ĐỀ HỌC SINH GIỎI TỈNH BẮC NINH NĂM 2018-2019) Trong không gian với hệ tọa độ

Oxyz

cho các vectơ

   

2; 1;3 , 1;3; 2a m b n

   

 

. Tìm

,m n

để các vectơ

,a b

 

cùng hướng.

m n

  

. B.

4; 3

m n

  

. C.

1; 0

m n

 

. D.

m n

  

Câu 48. (THPT NGHĨA HƯNG NĐ- GK2 - 2018 - 2019) Trong không gian với hệ tọa độ

Oxyz

cho hai điểm

 

1;5;3

A 

và

 

2;1; 2



. Tọa độ điểm

biết

là trung điểm của

là

1 1

;3;

2 2

 

 

 

. B.

 

4;9;8

B 

 

5;3; 7



. D.

 

5; 3; 7

 

Câu 49. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Trong không gian với hệ trục tọa

độ

Oxyz

, cho ba điểm

(1;2; 1), (2; 1;3)

A B

 

và

( 3;5;1)



. Tìm tọa độ điểm

sao cho tứ giác

ABCD

là

hình bình hành.

( 2;8; 3)

 

( 4;8; 5)

 

( 2;2;5)



( 4;8; 3)

 

Câu 50. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Trong không gian với hệ tọa độ

Oxyz

, cho

điểm

 

1;2; 3



 

7;4; 2



Nếu điểm

thỏa nãm đẳng thức



 

thì tọa độ điẻm

là:

8 8

3; ;

3 3

 



 

 

8 8

;3;

3 3

 



 

 

. C.

3;3;

 



 

 

1; 2;

 

 

 

Câu 51. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Trong mặt phẳng với hệ tọa độ

Oxyz

, Tam giác

ABC

với

 

1; 3;3

A 

;

 

2; 4;5

B 

 

; 2;C a b



nhận điểm

 

1; ;3G c

làm trọng tâm của nó

thì giá trị của tổng

a b c 

bằng.

5

2

Câu 52. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

     

A 2; 1;5 , 5; 5;7 , ; ;1

 

B M x y

. Với giá trị nào của

,x y

thì

, ,A B M

thẳng hàng.

4; 7 

x y

4; 7   

x y

4; 7  

x y

4; 7  

x y

Câu 53. (KTNL GIA BÌNH NĂM 2018-2019) Trong không gian với hệ tọa độ

Oxyz

, cho tam giác

ABC

với

 

1;2; 3



 

2;5;7

 

3;1;4

C 

. Điểm

để tứ giác

ABCD

là hình bình hành là

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7

 

6;6;0

8 8

0; ;

3 3

 

 

 

 

0;8;8

 

4; 2; 6

  

Câu 54. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Trong không gian

Oxyz

, tọa độ

điểm đối xứng của

 

M ; ;1 2 3

qua mặt phẳng

 

Oyz

là

 

0 2 3; ;

. B.

 

1 2 3; ;  

. C.

 

1 2 3; ;



. D.

 

1 2 3; ;

Câu 55. (THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019 LẦN 1) Cho tam giác

ABC

có

 

1; 2;0

A 

 

2;1; 2



 

0;3; 4

. Tìm tọa độ điểm

để tứ giác

ABCD

là hình bình hành.

 

1;0; 6

. B.

 

1;6;2

. C.

 

1;0;6



. D.

 

1;6; 2

Câu 56. (LIÊN TRƯỜNG THPT TP VINH NGHỆ AN NĂM 2018-2019) Trong không gian

Oxyz

, cho hai

điểm

 

3;1; 2

 

2; 3;5

B

. Điểm

thuộc đoạn

sao cho

2MA MB

, tọa độ điểm

là

7 5 8

; ;

3 3 3

 



 

 

. B.

 

4;5; 9

. C.

3 17

; 5;

2 2

 



 

 

. D.

 

1; 7;12



Câu 57. (THPT MINH KHAI HÀ TĨNH NĂM 2018-2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho

hai điểm

 

0;1; 2



và

 

3; 1;1

B 

. Tìm tọa độ điểm M sao cho

3AM AB



 

 

9; 5;7

M 

. B.

 

9;5;7

 

9;5; 7

 

. D.

 

9; 5; 5

 

Câu 58. (THPT QUỲNH LƯU 3 NGHỆ AN NĂM 2018-2019) Trong không gian

Oxyz

, cho hai điểm

 

2; 2;1

A 

 

0;1;2

. Tọa độ điểm

thuộc mặt phẳng

 

Oxy

sao cho ba điểm

thẳng hàng là

 

4; 5;0

M 

. B.

 

2; 3;0

M 

. C.

 

0;0;1

. D.

 

4;5;0

Câu 59. (THPT YÊN KHÁNH - NINH BÌNH - 2018 - 2019) Trong không gian với hệ tọa độ

Oxyz

cho các

véc tơ

2 2

u i j k  

   

 

;2; 1

v m m

 



với

là tham số thực. Có bao nhiêu giá trị của

để

u v

 

. B.

. C.

. D.

Câu 60. (CHUYÊN PHAN BỘI CHÂU NĂM 2018-2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho

hai điểm

   

1;2; 1 , 1;3;1

A AB 



thì tọa độ của điểm

là:

 

2;5;0

. B.

 

0; 1; 2

 

. C.

 

0;1;2

. D.

 

2; 5;0

B  

Câu 61. (CHUYÊN ĐHSP HÀ NỘI NĂM 2018-2019 LẦN 01) Trong không gian với hệ tọa độ

Oxyz

, cho

hình hộp

ABCD A B C D

   

có

 

0;0;0

 

;0;0

B a

;

 

0;2 ;0D a

 

0;0;2A a



với



. Độ dài đoạn thẳng



là

. B.

2 a

. C.

3 a

. D.

Câu 62. (CHUYÊN KHTN LẦN 2 NĂM 2018-2019) Trong không gian

Oxyz

, cho

 

3;1;2

A 

, tọa độ điểm

đối xứng với điểm

qua trục

là

 

3; 1; 2 

. B.

 

3; 1;2



. C.

 

3;1; 2

. D.

 

3; 1;2

 

Câu 63. Trong không gian

Oxyz

, cho ba điểm

 

3;1;0

 

0; 1;0

B 

 

0;0; 6



. Nếu tam giác

A B C

  

có

các đỉnh thỏa mãn hệ thức

A A B B C C

  

  

  



thì tam giác

A B C

  

có tọa độ trọng tâm là

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8

 

3; 2;0



. B.

 

2; 3;0



. C.

 

1;0; 2

. D.

 

3; 2;1



Câu 64. (ĐỀ THI CÔNG BẰNG KHTN LẦN 02 NĂM 2018-2019) Trong không gian

Oxyz

, cho hình bình

hành

ABCD

. Biết

 

1;0;1

A 

 

2;1;2

B 

và

 

1; 1;1

D  

. Tọa độ điểm

là

 

2;0;2

. B.

 

2;2;2

. C.

 

2; 2;2



. D.

 

0; 2;0



Câu 65. (SỞ GD&ĐT PHÚ THỌ NĂM 2018-2019 LẦN 01) Trong không gian với hệ tọa độ

,Oxyz

cho hai

điểm

 

1; 2; 2

và

8 4 8

; ;

3 3 3

 

 

 

. Biết

 

; ;I a b c

là tâm của đường tròn nội tiếp tam giác

OAB

. Giá trị

 a b c

bằng

Câu 66. (CHUYÊN ĐHSP HÀ NỘI NĂM 2018-2019 LẦN 01) Trong không gian tọa độ

Oxyz

, cho

     

2;0;0 , 0;2;0 , 0;0;2

A B C

. Có tất cả bao nhiêu điểm

trong không gian thỏa mãn

không trùng với

các điểm

, ,A B C

và



AMB BMC CMA

   

. B.

. C.

. D.

Dạng 2. Tích vô hướng, tích có hướng và ứng dụng

Dạng 2.1 Tích vô hướng và ứng dụng

Câu 67. (MĐ 105 BGD&ĐT NĂM 2017) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai vectơ

 





2;1; 0

a và

 

  



1; 0; 2

b . Tính

 

 

cos ,a b

 

 

 

cos ,

a b

 

 

 

cos ,

a b

 



 

cos ,

a b

 



 

cos ,

a b

Câu 68. (MĐ 104 BGD&DT NĂM 2017) Trong không gian với hệ tọa độ

Oxyz

cho ba điểm

 

2;3; 1



 

1;1;1

N 

và

 

1; 1;2

P m 

. Tìm

để tam giác

MNP

vuông tại

A. B. C. D.

Câu 69. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Trên mặt phẳng toạ độ

Oxy

, cho tam giác

ABC

biết

 

1;3

 

2; 2

 

 

3;1

. Tính cosin góc

của tam giác.

cos

A  B.

cos

A  C.

cos

A   D.

cos

A  

Câu 70. (THPT QUỲNH LƯU 3 NGHỆ AN NĂM 2018-2019) Trong không gian

Oxyz

, góc giữa hai vectơ



và

 

3; 0;1

u  



là

120

. B.

60

. C.

150

. D.

30

Câu 71. (THPT CHUYÊN ĐẠI HỌC VINH NĂM 2018-2019 LẦN 01) Trong không gian

Oxyz

, cho

 

3;4;0

a  



 

5;0;12

b 



. Côsin của góc giữa



và



bằng

. B.

. C.



. D.



Câu 72. (CHUYÊN ĐHSP HÀ NỘI NĂM 2018-2019 LẦN 01) Trong không gian tọa độ

Oxyz

góc giữa hai

vectơ



và

 

3;0;1

u  



là

120

. B.

30

. C.

60

. D.

150



 



 

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9

Câu 73. (CHUYÊN NGUYỄN TẤT THÀNH YÊN BÁI LẦN 01 NĂM 2018-2019) Trong không gian với

hệ tọa độ

xyz

, cho vectơ

 

3;0;1

u 



và

 

2;1;0

v 



. Tính tích vô hướng

.u v

 

. 8

u v



 

. B.

. 6

u v



 

. C.

. 0

u v



 

. D.

. 6

u v

 

 

Câu 74. (CHUYÊN HƯNG YÊN NĂM 2018-2019 LẦN 03) Trong không gian toa đô

Oxyz

, goc giưa hai

vectơ



va

 

3;0;1

u  



la

. B.

120

. C.

. D.

150

Câu 75. (CHUYÊN TRẦN PHÚ HẢI PHÒNG NĂM 2018-2019 LẦN 02) Trong không gian

,Oxyz

cho ba

điểm

( 1; 2;3)

 

(0;3;1)

(4;2;2)

. Cosin của góc



BAC

là

. B.

 . C.

2 35

 . D.

2 35

Câu 76. (THPT YÊN KHÁNH - NINH BÌNH - 2018 - 2019) Trong không gian

Oxyz

cho các điểm

     

5;1;5 ; 4;3;2 ; 3; 2;1

A B C  

. Điểm

 

; ;I a b c

là tâm đường tròn ngoại tiếp tam giác

ABC

. Tính

a b c 

. B.

9.

Câu 77. (THPT NGÔ SĨ LIÊN BẮC GIANG NĂM 2018-2019 LẦN 01) Trong không gian với hệ tọa độ

Oxyz

, cho tam giác

ABC

có

 

1;0;0

 

0;0;1

 

2;1;1

. Diện tích của tam giác

ABC

bằng:

Câu 78. (ĐỀ HỌC SINH GIỎI TỈNH BẮC NINH NĂM 2018-2019) Trong không gian với hệ tọa độ

Oxyz

cho véc tơ

   

1;1; 2 , 1;0;u v m

  

 

. Tìm tất cả giá trị của

để góc giữa



bằng





. B.

2 6

m   . C.

2 6

m   . D.

2 6

m   .

Dạng 2.2 Tích có hướng và ứng dụng

Câu 79. (ĐỀ GK2 VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Trong hệ trục tọa độ

Oxyz

, cho tứ diện

ABCD

biết

 

3; 2;A m



 

2;0;0

 

0;4;0

 

0;0;3

. Tìm giá trị dương của tham số

để thể tích tứ diện

bằng 8.



. B.



. C.



. D.



Câu 80. (ĐỀ GK2 VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Trong hệ trục tọa độ

Oxyz

, cho bốn điểm

(1; 2;0)



(2;0;3)

( 2;1;3)



và

(0;1;1)

. Thể tích khối tứ diện

ABCD

bằng:

. B.

. C.

. D.

Câu 81. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Trong không gian với hệ tọa độ

Oxyz

, cho

   

1;1;2 , 1; ; 2

u v m m

   

 

. Khi

, 14

u v

 



 

 

thì



hoặc

 

hoặc

 



hoặc

 

Câu 82. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Trong không gian với hệ trục tọa

độ

Oxyz

, cho tứ diện

ABCD

có

 

2; 1;1

A ,

 

3;0; 1

B ,

 

2; 1;3

C ,

D Oy

và có thể tích bằng

. Tính

tổng tung độ của các điểm

6

4

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10

Câu 83. (HỌC MÃI NĂM 2018-2019-LẦN 02) Trong không gian với hệ toạ độ

Oxyz

, cho

 

1; 2;3

a  



và

 

1;1; 1

 



. Khẳng định nào sau đây sai?

a b

 

 

. B.

. 4

a b

 

 

. C.

a b

 

 

. D.

 

, 1; 4;3

a b

 

  

 

 

Câu 84. (TOÁN HỌC TUỔI TRẺ NĂM 2018 - 2019 LẦN 01) Trong không gian với hệ tọa độ

Oxyz

, cho

điểm

 

1; 2;0



 

1;0; 1



 

0; 1;2



 

2; ;D m n

. Trong các hệ thức liên hệ giữa

và

dưới đây,

hệ thức nào để bốn điểm

đồng phẳng?

2 13

m n

 

. B.

2 13

m n

 

. C.

2 13

m n

 

. D.

2 3 10

m n

 

Câu 85. (CHUYÊN TRẦN PHÚ HẢI PHÒNG NĂM 2018-2019 LẦN 02) Trong không gian

,Oxyz

cho hai

điểm

   

1;0; 1 , 1; 1;2

 A B

. Diện tích tam giác

OAB

bằng

11.

Câu 86. Trong không gian

Oxyz

, cho hai véc tơ

 

4 ; 3 ;1

m 



và

 

0 ; 0 ; 1

n 



. Gọi



là véc tơ cùng hướng

với

,m n

 

 

 

và





. Tọa độ của véc tơ



là

 

9 ; 12 ; 0



. B.

 

0 ; 9 ; 12



. C.

 

9 ; 12 ; 0



. D.

 

0 ; 9 ; 12



Câu 87. (ĐỀ THI GIỮA KỲ II YÊN PHONG 1 - 2018) Trong không gian

Oxyz

, cho 4 điểm

 

2;0;2

 

1; 1; 2

 

 

1;1;0

C 

 

2;1;2

D 

. Thể tích của khối tứ diện

ABCD

bằng

. B.

. C.

. D.

Câu 88. (ĐỀ GK2 VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Trong hệ trục tọa độ

Oxyz

, cho bốn điểm

       

0; 2;1 ; 1;0; 2 ; 3;1; 2 ; 2; 2; 1

A B C D

     

. Câu nào sau đây sai?

A. Bốn điểm

, , ,A B C D

không đồng phẳng. B. Tam giác

ACD

là tam giác vuông tại

C. Góc giữa hai véctơ



và



là góc tù. D. Tam giác

ABD

là tam giác cân tại

Câu 89. (THPT LƯƠNG THẾ VINH - HN - LẦN 1 - 2018) Trong không gian

Oxyz

, cho ba điểm

 

2;3;1

A 

 

2;1;0

 

3; 1;1

C  

. Tìm tất cả các điểm

sao cho

ABCD

là hình thang có đáy

và 3

ABCD ABC

S S



 

8;7; 1



. B.

 

8; 7;1

12;1; 3

 









. C.

 

8;7; 1

12; 1;3





 





. D.

 

12; 1;3

D  

Dạng 3. Mặt cầu

Dạng 3. Xác định tâm, bán kính của mặt cầu

Câu 90. (MĐ 104 BGD&DT NĂM 2017) Trong không gian với hệ toạ độ

Oxyz

, cho mặt cầu

     

2 2

: 2 2 8

S x y z

    

. Tính bán kính

của

 

2 2

R 



4R 

Câu 91. (Mã đề 104 BGD&ĐT NĂM 2018) Trong không gian

Oxyz

, mặt cầu

       

2 2 2

: 5 1 2 3

S x y z

     

có bán kính bằng

2 3

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11

Câu 92. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Trong không gian hệ tọa độ

Oxyz

, tìm tất cả các giá trị của

để phương trình

2 2 2

2 2 4 0

x y z x y z m

      

là phương trình của một mặt cầu.









Câu 93. (MĐ 105 BGD&ĐT NĂM 2017) Trong không gian với hệ toạ độ

Oxyz

, cho mặt cầu

       

     

2 2 2

:  5 1 2 9

S x y z . Tính bán kính

của

 

 6R

 3R

 18R

 9R

Câu 94. (MĐ 103 BGD&ĐT NĂM 2017-2018) Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 3 1 1 2

S x y z

     

. Tâm của

 

có tọa độ là

 

3; 1;1



 

3; 1;1

 

 

3;1; 1 

 

3;1; 1

Câu 95. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Trong không gian với hệ trục tọa độ

Oxyz

, tìm tọa độ

tâm

và bán kính

của mặt cầu

     

2 2 2

1 2 4 20

x y z

     

 

1;2; 4 , 2 5

I R   B.

 

1; 2;4 , 20

I R

 

 

1; 2;4 , 2 5

I R  D.

 

1;2; 4 , 5 2

I R  

Câu 96. (Mã đề 101 - BGD - 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 2 7 0

S x y z x z

     

. Bán kính của mặt cầu

đã cho bằng

. B.

. C.

. D.

Câu 97. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Trong không gian

Oxyz

cho hai điểm

 

1;1;1

và

 

1;2;3

. Phương trình mặt cầu có tâm I và đi qua A là

     

2 2 2

1 1 1 5

x y z

     

     

2 2 2

1 1 1 29

x y z

     

     

2 2 2

1 1 1 5

x y z

     

     

2 2 2

1 1 1 25

x y z

     

Câu 98. (Mã đề 104 - BGD - 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 2 7 0     

S x y z y z

. Bán kính của mặt cầu đã cho bằng

. B.

. C.

. D.

Câu 99. (Mã 102 - BGD - 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 2 7 0.

S x y z x y

     

Bán kính của mặt cầu đã cho bằng

. B.

. C.

. D.

Câu 100. (Mã 103 - BGD - 2019) Trong không gian

Oxyz

, cho mặt cầu

2 2 2

( ) : 2 2 7 0.

S x y z y z

     

Bán kính của mặt cầu đã cho bằng

. B.

. C. 9. D.

Câu 101. (TRƯƠNG THPT HOANG HOA THAM HƯNG YÊN NĂM 2018-2019) Trong không gian với

hệ tọa độ

Oxyz

, cho mặt cầu

 

2 2 2

: 8 2 1 0

S x y z x y

     

. Tìm tọa độ tâm và bán kính của mặt cầu

 

–4;1;0 .

I R



 

–4;1;0 .

I R



 

4; –1;0 , 2.

I R



 

4; –1;0 , 4.

I R



CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12

Câu 102. (THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019 LẦN 1) Cho mặt cầu

 

2 2 2

: 2 4 2 3 0

S x y z x y z

      

. Tính bán kính

của mặt cầu

 

R 

. B.



. C.



. D.

3 3

R 

Câu 103. (TT HOÀNG HOA THÁM - 2018-2019) Trong không gian vơi hệ tọa độ

Oxyz

, cho mặt cầu

 

2 2 2

: 8 2 1 0

S x y z x y

     

. Tìm tọa độ tâm và bán kính mặt cầu

 

4;1;0 , 2

I R

 

. B.

 

4;1;0 , 4

I R

 

. C.

 

4; 1;0 , 2

I R

 

. D.

 

4; 1;0 , 4

I R

 

Câu 104. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 3 1 1 2

S x y z

     

. Xác định tọa độ tâm của mặt cầu

 

3;1; 1

 

. B.

 

3;1; 1



. C.

 

3; 1;1

I  

. D.

 

3; 1;1

I 

Câu 105. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 4 2 3 0

S x y z x y z

      

. Tọa độ tâm

của mặt cầu

 

là:

 

1; 2; 1



. B.

 

2; 4; 2 

. C.

 

1; 2; 1 

. D.

 

2;4;2



Câu 106. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Trong không gian

Oxyz

, cho

mặt cầu

 

2 2 2

: 8 10 6 49 0

S x y z x y z

      

. Tính bán kính

của mặt cầu

 

1R 

. B.



. C.

151

R 

. D.

R 

Câu 107. (ĐÊ 04 VTED NĂM 2018-2019) Trong không gian

Oxyz

, mặt cầu

 

2 2 2

: 4 2 6 1 0

S x y z x y z

      

có tâm là

 

4;2; 6 

 

2; 1;3



 

2;1; 3 

 

4; 2;6



Câu 108. (THPT GANG THÉP THÁI NGUYÊN NĂM 2018-2019) Trong không gian với hệ tọa độ

Oxyz

cho mặt cầu có phương trình

     

2 2 2

1 2 3 4

x y z

     

. Tìm tọa độ tâm

và bán kính

của mặt cầu

đó.

 

1;2; 3

 

;

2R 

. B.

 

1;2; 3

 

;

4R 

 

1; 2;3

I 

;

2R 

. D.

 

1; 2;3

I 

;

4R 

Câu 109. (KTNL GV BẮC GIANG NĂM 2018-2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

( )S

có phương trình

2 2 2

4 2 4 0

x y z x y

     

.Tính bán kính

của

( ).S

. B.

. C.

. D.

Câu 110. (THPT CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019 LẦN 01) Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 3 1 1 4

S x y z

     

. Tâm của

 

có tọa độ là

 

3;1; 1 

. B.

 

3; 1;1

. C.

 

3; 1; 1 

. D.

 

3;1; 1

Câu 111. (SỞ GD&ĐT PHÚ THỌ NĂM 2018-2019 LẦN 01) Trong không gian

Oxyz

, có tất cả bao nhiêu

giá nguyên của

để

   

2 2 2 2

2 2 2 1 3 5 0        

x y z m x m z m

là phương trình một mặt cầu?

Câu 112. (ĐỀ 15 LOVE BOOK NĂM 2018-2019) Trong không gian với hệ trục tọa độ

Oxyz

, tìm tất cả các

giá trị của

để phương trình

 

2 2 2

2 2 4 19 6 0       

x y z m x my m

là phương trình mặt cầu.

1 2 

. B.

1

hoặc

2

. C.

2 1  

. D.

2 

hoặc

1

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13

Câu 113. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Trong không gian

Oxyz

có tất

cả bao nhiêu giá trị nguyên

để phương trình

2 2 2 2

4 2 2 9 28 0

x y z mx my mz m

       

là phương trình mặt cầu?

. B.

. C.

. D.

Câu 114. Trong không gian

Oxyz

, xét mặt cầu

 

có phương trình dạng

2 2 2

4 2 2 10 0

x y z x y az a

      

. Tập hợp các giá trị thực của

để

 

có chu vi đường tròn lớn bằng

8

là

 

1;10

. B.

 

2; 10



. C.

 

1;11



. D.

 

1; 11



Câu 115. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Trong không gian với hệ tọa độ

Oxyz

cho

 

1;0;0

A 

 

0;0;2

 

0; 3;0

C 

. Tính bán kính mặt cầu ngoại tiếp tứ diện

OABC

là

Câu 116. (THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019 LẦN 1) Gọi

 

là mặt cầu đi qua

điểm

       

2;0;0 , 1;3;0 , 1;0;3 , 1;2;3

A B C D

. Tính bán kính

của

 

2 2

R 



. C.



R 

Lời giải

Câu 117. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho hai điểm

,A B

cố định trong không gian có độ dài

là

. Biết rằng tập hợp các điểm

trong không gian sao cho

MA MB

là một mặt cầu. Bán kính mặt

cầu đó bằng

. B.

. C.

. D.

Câu 118. (SỞ GD&ĐT BÌNH PHƯỚC - LẦN 1 - 2018) Trong không gian với hệ trục

Oxyz

, cho phương

trình

 

2 2 2 2

2 2 4 2 5 9 0

x y z m x my mz m

        

. Tìm các giá trị của

để phương trình trên là

phương trình của một mặt cầu.

 

hoặc



. B.

5 1

  

. C.

 

. D.



Câu 119. (ĐỀ THI GIỮA KỲ II YÊN PHONG 1 - 2018) Trong không gian

Oxyz

. Cho tứ diện đều

ABCD

có

 

0;1;2

và hình chiếu vuông góc của

trên mặt phẳng

 

BCD

là

 

4; 3; 2

 

. Tìm tọa độ tâm

của

mặt cầu ngoại tiếp tứ diện

ABCD

 

3; 2; 1

 

. B.

 

2; 1;0

I 

. C.

 

3; 2;1

I 

. D.

 

3; 2;1

I  

Dạng 3. Viết phương trình mặt cầu

Câu 120. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Trong không gian

Oxyz

cho hai điểm

 

1;1;1

và

 

1;2;3

. Phương trình mặt cầu có tâm I và đi qua A là

     

2 2 2

1 1 1 5

x y z

     

     

2 2 2

1 1 1 29

x y z

     

     

2 2 2

1 1 1 5

x y z

     

     

2 2 2

1 1 1 25

x y z

     

Câu 121. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 



1; 2; 3

. Gọi

là hình chiếu vuông góc của

trên trục

. Phương trình nào dưới đây là phương trình mặt cầu tâm

bán kính

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14

 

   

2 2

1 13

x y z B.

 

   

2 2

1 17

x y z

 

   

2 2

1 13

x y z D.

 

   

2 2

1 13

x y z

Câu 122. (THPT CÙ HUY CẬN NĂM 2018-2019 LẦN 01) Trong không gian với hệ tọa độ

Oxyz

, cho hai

điểm

   

1; 2;7 , 3;8; 1

A B

  

. Mặt cầu đường kính

có phương trình là

     

2 2 2

1 3 3 45

x y z     

. B.

     

2 2 2

1 3 3 45

x y z

     

     

2 2 2

1 3 3 45

x y z     

. D.

     

2 2 2

1 3 3 45

x y z

     

Câu 123. (THPT - YÊN ĐỊNH THANH HÓA 2018 2019- LẦN 2) Trong không gian với hệ tọa độ

Oxyz

viết phương trình mặt cầu có tâm

 

1; 4;3

I 

và đi qua điểm

 

5; 3;2

A 

     

2 2 2

1 4 3 18

x y z

     

. B.

     

2 2 2

1 4 3 16

x y z

     

     

2 2 2

1 4 3 16

x y z

     

. D.

     

2 2 2

1 4 3 18

x y z

     

Câu 124. (THPT CHUYÊN SƠN LA NĂM 2018-2019 LẦN 01) Trong không gian

Oxyz

, cho hai điểm

 

1;1;1

và

 

1; 1;3

B 

. Phương trình mặt cầu có đường kính

là

   

2 2

1 2 8

x y z

    

. B.

   

2 2

1 2 2

x y z

    

   

2 2

1 2 2

x y z

    

. D.

   

2 2

1 2 8

x y z

    

Câu 125. (SỞ GD&ĐT THANH HÓA NĂM 2018 - 2019) Trong không gian Oxyz, cho hai điểm A(2;4;1), B

 

2;2; 3 

. Phương trình mặt cầu đường kính AB là

   

2 2

3 1 36.

x y z    

   

2 2

3 1 9.

x y z

    

   

2 2

3 1 9.

x y z

    

   

2 2

3 1 36.

x y z    

Câu 126. (CHUYÊN BẮC GIANG NĂM 2018-2019 LẦN 02) Trong không gian với hệ tọa độ Oxyz, hỏi

trong các phương trình sau phương trình nào là phương trình của mặt cầu?

2 2 2

2 4 1 0

x y z x z

     

2 2

3 2 4 1 0

x z x y z

     

2 2 2

2 4 4 1 0

x y z xy y z

      

2 2 2

2 2 4 8 0

x y z x y z

      

Câu 19 : Trong không gian

Oxyz

, cho hai điểm

 

2; 1; 3 

;

 

0;3; 1

. Phương trình của mặt cầu đường

kính

là :

     

2 2 2

1 1 2 6     

x y z

     

2 2 2

1 1 2 24     

x y z

     

2 2 2

1 1 2 24     

x y z

     

2 2 2

1 1 2 6     

x y z

Câu 127. (CHUYÊN KHTN LẦN 2 NĂM 2018-2019) Trong không gian với hệ tọa độ

Oxyz

phương trình

nào sau đây không phải là phương trình của một mặt cầu?

2 2 2

2 4 3 0

x y z x y z

      

. B.

2 2 2

2 2 2 0

x y z x y z

     

2 2 2

2 2 2 4 8 6 3 0

x y z x y z

      

. D.

2 2 2

2 4 4 10 0

x y z x y z

      

Câu 128. (CHUYÊN PHAN BỘI CHÂU NGHỆ AN LẦN 1 NĂM 2018-2019) Trong không gian với hệ trục

tọ độ

Oxyz

, cho hai điểm

   

1;2;3 , 5;4; 1

A B



. Phương trình mặt cầu đường kính

là

     

2 2 2

3 3 1 36

x y z

     

. B.

     

2 2 2

3 3 1 9

x y z

     

     

2 2 2

3 3 1 6

x y z

     

. D.

     

2 2 2

3 3 1 9

x y z

     

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15

Câu 129. (ĐỀ GK2 VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Trong hệ trục tọa độ

Oxyz

, phương trình mặt

cầu tâm

 

2;1; 2



bán kính

2R 

là:

     

2 2 2

2 1 2 2

x y z

     

. B.

2 2 2

4 2 4 5 0

x y z x y z

      

2 2 2

4 2 4 5 0

x y z x y z

      

. D.

     

2 2 2

2 1 2 2

x y z

     

Câu 130. (ĐỀ GK2 VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Phương trình nào sau đây là phương trình mặt

cầu

 

tâm

 

2;1;0

, đi qua điểm

 

0;1;2

     

2 2

: 2 1 8

S x y z

    

. B.

     

2 2

: 2 1 8

S x y z

    

     

2 2

: 2 1 64

S x y z

    

. D.

     

2 2

: 2 1 64

S x y z

    

Câu 131. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Trong không gian

Oxyz

cho hai điểm

 

1;1;1

và

 

1;2;3

. Phương trình mặt cầu có tâm I và đi qua A là

     

2 2 2

1 1 1 29

x y z

     

     

2 2 2

1 1 1 5

x y z

     

     

2 2 2

1 1 1 25

x y z

     

     

2 2 2

1 1 1 5

x y z

     

Câu 132. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Trong không gian Oxyz, cho điểm

(1; 2;3)



. Viết phương trình mặt cầu tâm I, cắt trục

tại hai điểm

và

sao cho

2 3

AB 

2 2 2

( 1) ( 2) ( 3) 16.

x y z     

2 2 2

( 1) ( 2) ( 3) 20.

x y z     

2 2 2

( 1) ( 2) ( 3) 25.

x y z     

2 2 2

( 1) ( 2) ( 3) 9.

x y z

     

Câu 133. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Trong không gian

Oxyz

, cho điểm

 

1; 2;3

M 

. Gọi

là hình chiếu vuông góc của

trên trục

. Phương trình nào sau đây là phương trình

mặt cầu tâm

bán kính

 

2 2

1 13

x y z   

. B.

 

2 2

1 13

x y z

   

 

2 2

1 13

x y z

   

. D.

 

2 2

1 17

x y z

   

Câu 134. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Trong không gian với hệ tọa độ

Oxyz

, trong

các mặt cầu dưới đây, mặt cầu nào có bán kính

2R 

 

2 2 2

: 4 2 2 3 0

S x y z x y z

      

. B.

 

2 2 2

: 4 2 2 10 0

S x y z x y z

      

 

2 2 2

: 4 2 2 2 0

S x y z x y z

      

. D.

 

2 2 2

: 4 2 2 5 0

S x y z x y z

      

Câu 135. (THPT GANG THÉP THÁI NGUYÊN NĂM 2018-2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho điểm

   

1;1;2 , 3;2; 3

A B



. Mặt cầu

 

có tâm

thuộc

và đi qua hai điểm

,A B

có phương

trình.

2 2 2

8 2 0

x y z x

    

. B.

2 2 2

8 2 0

x y z x

    

2 2 2

4 2 0

x y z x

    

. D.

2 2 2

8 2 0

x y z x

    

Câu 136. (ĐỀ THI THỬ VTED 02 NĂM HỌC 2018 - 2019) Trong không gian

Oxyz

, mặt cầu có tâm

 

1;1;1

và diện tích bằng



có phương trình là

     

2 2 2

1 1 1 4

x y z

     

     

2 2 2

1 1 1 1

x y z

     

     

2 2 2

1 1 1 4

x y z

     

     

2 2 2

1 1 1 1

x y z

     

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16

Câu 137. (ĐỀ GK2 VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Trong không gian với hệ tọa độ

Oxyz

, mặt cầu

 

qua bốn điểm

 

3;3;0

 

3;0;3

 

0;3;3

 

3;3;3

. Phương trình mặt cầu

 

là

2 2 2

3 3 3 3 3

2 2 2 2

x y z

     

     

     

     

2 2 2

3 3 3 27

2 2 2 4

x y z

     

     

     

     

2 2 2

3 3 3 27

2 2 2 4

x y z

     

     

     

     

2 2 2

3 3 3 27

2 2 2 4

x y z

     

     

     

     

Câu 138. (THPT CHUYÊN NGUYỄN ĐÌNH TRIỂU - ĐỒNG THÁP - LẦN 1 - 2018) Trong không gian

Oxyz

, cho mặt cầu

     

2 2

: 1 1 4.

S x y z

    

Một mặt cầu

 



có tâm

 

9;1;6



và tiếp xúc ngoài với

mặt cầu

 

Phương trình mặt cầu

 



là

     

2 2 2

9 1 6 64

x y z

     

. B.

     

2 2 2

9 1 6 144

x y z     

     

2 2 2

9 1 6 36

x y z

     

. D.

     

2 2 2

9 1 6 25

x y z

     

Câu 139. (THPT HAI BÀ TRƯNG - HUẾ - 2018) Trong không gian

Oxyz

, viết phương trình mặt cầu đi qua

điểm

 

1; 1;4

A 

và tiếp xúc với các mặt phẳng tọa độ.

     

2 2 2

3 3 3 16

x y z

     

. B.

     

2 2 2

3 3 3 9

x y z

     

     

2 2 2

3 3 3 36

x y z

     

. D.

     

2 2 2

3 3 3 49

x y z

     

Câu 140. [KIM LIÊN - HÀ NỘI - LẦN 1 - 2018] Trong không gian

Oxyz

, cho hai điểm

 

2;2;1

8 4 8

; ;

3 3 3



 

 

 

. Viết phương trình mặt cầu có tâm là tâm của đường tròn nội tiếp tam giác

OMN

và tiếp xúc

với mặt phẳng

 

Oxz

   

2 2

1 1 1

x y z

    

. B.

   

2 2

1 1 1

x y z

    

   

2 2

1 1 1

x y z

    

. D.

   

2 2

1 1 1

x y z

    

Câu 141. (CHUYÊN HÀ TĨNH - LẦN 1 - 2018) Trong không gian

Oxyz

, gọi

 

; ;I a b c

là tâm mặt cầu đi

qua điểm

 

1; 1;4

A 

và tiếp xúc với tất cả các mặt phẳng tọa độ. Tính

P a b c  



. B.



. C.



. D.



Dạng 3. Một số bài toán khác

Câu 142. (Mã 102 - BGD - 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2

: 2 3

S x y z

   

. Có tất

cả bao nhiêu điểm

 

; ;A a b c

(

, ,a b c

là các số nguyên) thuộc mặt phẳng

 

Oxy

sao cho có ít nhất hai tiếp

tuyến của

 

đi qua

và hai tiếp tuyến đó vuông góc với nhau?

. B.

. C.

. D.

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17

Câu 143. (Mã đề 104 - BGD - 2019) Trong không gian

Oxyz

, cho mặt cầu

   

2 2

: 1 5

S x y z

   

. Có tất

cả bao nhiêu điểm

 

, ,A a b c

(

, ,a b c

là các số nguyên) thuộc mặt phẳng

 

Oxy

sao cho có ít nhất hai tiếp tuyến

của

 

đi qua

và hai tiếp tuyến đó vuông góc với nhau?

A. 20 B. 8 C. 12 D. 16

Câu 144. (Mã 103 - BGD - 2019) Trong không gian

Oxyz

, cho mặt cầu:

   

2 2

: 1 5

S x y z

   

. Có tất cả

bao nhiêu điểm

 

; ;A a b c

( , , a b c

là các số nguyên) thuộc mặt phẳng

 

Oxy

sao cho có ít nhất hai tiếp tuyến

của

 

đi qua

và hai tiếp tuyến đó vuông góc nhau?

. B.

. C.

. D.

Câu 145. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

  

2 2 2

( ) : 9

S x y z

, điểm

(1;1 ); 2M

và mặt phẳng

   ( ) : 4 0P x y z

. Gọi



là đường thẳng đi qua

, thuộc (P) và cắt

( )S

tại 2 điểm

,A B

sao cho

nhỏ nhất. Biết rằng



có một vectơ chỉ phương là



(1; ; )u a b

, tính

 T a b

 2T

 1T

 0T

 1T

Câu 146. (TOÁN HỌC TUỔI TRẺ NĂM 2018 - 2019 LẦN 01) Trong không gian với hệ tọa độ Oxyz, cho

hai điểm

 

9, 3,4



 

, ,B a b c

. Gọi

, ,M N P

lần lượt là giao của đường thẳng AB với mặt phẳng

, ,

Oxy Oxz Oyz

. Biết các điểm

, ,M N P

đều nằm trên đoạn AB sao cho

AM MN NP PB  

. Tính giá trị

ab bc ac 

bằng

17

. B.

. C.

9

. D.

Câu 147. (THPT CHUYÊN NGỮ - HÀ NỘI - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

     

2 2

: 1 1 4

S x y z

    

và một điểm

 

2;3;1

. Từ

kẻ được vô số các tiếp tuyến tới

 

, biết tập

hợp các tiếp điểm là đường tròn

 

. Tính bán kính

của đường tròn

 

2 3

r 

. B.

r 

. C.

r 

. D.

 

Câu 148. (THPT MỘ ĐỨC - QUẢNG NGÃI - 2018) Trong mặt phẳng tọa độ

Oxyz

, cho bốn điểm

 

0; 1;2

A 

 

2; 3;0

B 

 

2;1;1

C 

 

0; 1;3

D 

. Gọi

 

là tập hợp tất cả các điểm

trong không gian

thỏa mãn đẳng thức

. . 1

MA MB MC MD

 

   

. Biết rằng

 

là một đường tròn, đường tròn đó có bán kính

bằng bao nhiêu?

r 

. B.

r 

. C.

r 

. D.

r 

Câu 149. (THPT CHUYÊN HẠ LONG - LẦN 2 - 2018) Trong không gian, cho bốn mặt cầu có bán kính lần

lượt là

(đơn vị độ dài) tiếp xúc ngoài với nhau. Mặt cầu nhỏ nhất tiếp xúc ngoài với cả bốn mặt cầu

nói trên có bán kính bằng

. B.

. C.

. D.

Dạng 4. Bài toán cực trị

Câu 150. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Trong không gian với hệ trục

Oxyz

, cho các điểm

   

1;2;3 , 6; 5;8

A B 

và

. .OM a i b k

 

  

trong đó

,a b

là cá số thực luôn thay đổi. Nếu

MA MB



 

đạt giác trị nhỏ nhất thì giá trị

a b

bằng

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18

25

13

Câu 151. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Trong không gian

Oxyz

, cho hai điểm

 

1;2;1

;

 

2; 1;3

B 

và điểm

 

; ;0

M a b

sao cho

2 2

MA MB

nhỏ nhất. Giá trị của

a b

là

. B.

2

. C.

. D.

Câu 152. (CHUYEN PHAN BỘI CHÂU NGHỆ AN NĂM 2018-2019 LẦN 02) Trong không gian với hệ

trục tọa độ

Oxyz

, cho mặt cầu

2 2 2

( ) :( 1) ( 2) ( 1) 9

S x y z

     

và

hai điểm

(4;3;1)

(3;1;3)

;

là điểm thay đổi trên

( )S

. Gọi

,m n

lần lượt là giá trị lớn

nhất và giá trị nhỏ nhất của biểu thức

2 2

2P MA MB 

. Xác định

( )m n

. B.

. C.

. D.

Câu 153. (THPT GANG THÉP THÁI NGUYÊN NĂM 2018-2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho

điểm

 

2;4; 1



 

1;4; 1



 

2;4;3

 

2;2; 1



, biết

 

; ;M x y z

để

2 2 2 2

MA MB MC MD

  

đạt giá trị nhỏ nhất thì

x y z 

bằng

. B.

. C.

. D.

Câu 154. Trong không gian

Oxyz

, cho hai điểm

 

1;2;1

 

2; 1; 3



 

3;1; 5



. Tìm điểm

trên mặt phẳng

 

Oyz

sao cho

2 2

2MA MB MC 

lớn nhất.

3 1

; ; 0

2 2

 

















 

. B.

1 3

; ;0

2 2

 



















 

. C.

 

0; 0;5

. D.

 

3; 4; 0



Câu 155. (CHUYÊN PHAN BỘI CHÂU NĂM 2018-2019) Trong không gian với hệ trục tọa độ

Ox ,yz

cho

mặt cầu

       

2 2 2

: 1 2 1 9

S x y z

     

và hai điểm

 

4;3;1

 

3;1;3

; M là điểm thay đổi trên

 

Gọi

,m n

là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức

2 2

2P MA MB 

. Xác định

 

.m n



. B.

. C.

. D.

Câu 156. (THPT NGHĨA HƯNG NĐ- GK2 - 2018 - 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho

tam giác

ABC

với

 

2;1;3

 

1; 1;2

B 

 

3; 6;1

C 

. Điểm

 

; ;M x y z

thuộc mặt phẳng

 

Oyz

sao cho

2 2 2

MA MB MC

 

đạt giá trị nhỏ nhất. Tính giá trị biểu thức

P x y z  



. B.

2P 

. C.



. D.

2P  

Câu 157. Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

     

4;2;2 , 1;1; 1 , 2; 2; 2

A B C

  

. Tìm tọa

độ điểm

thuộc mặt phẳng

 

Oyz

sao cho 2

MA MB MC

 

  

nhỏ nhất

 

2;3;1

. B.

 

0;3;1

. C.

 

0; 3;1

M 

. D.

 

0;1;2

Câu 158. (THPT CHUYÊN LÊ QUÝ ĐÔN - ĐÀ NẴNG - LẦN 1 - 2018) Trong không gian với hệ trục tọa

độ

Oxyz

, cho bốn điểm

 

2; 3;7

A 

 

0;4;1

 

3;0;5

và

 

3;3;3

. Gọi

là điểm nằm trên mặt phẳng

 

Oyz

sao cho biểu thức

MA MB MC MD

  

   

đạt giá trị nhỏ nhất. Khi đó tọa độ của

là:

 

0;1; 4



. B.

 

2;1;0

. C.

 

0;1; 2



. D.

 

0;1;4

Câu 159. (TOÁN HỌC TUỔI TRẺ - THÁNG 4 - 2018) Trong không gian cho ba điểm

 

1;1;1

 

1;2;1

B 

 

3;6; 5



. Điểm

thuộc mặt phẳng

Oxy

sao cho

2 2 2

MA MB MC

 

đạt giá trị nhỏ nhất là

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19

 

1;2;0

. B.

 

0;0; 1



. C.

 

1;3; 1



. D.

 

1;3;0

Câu 160. (LÊ QUÝ ĐÔN - HẢI PHÒNG - LẦN 1 - 2018) Trong không gian với hệ tọa độ

Oxyz

cho

 

3;2;1

 

2;3;6

B 

. Điểm

 

; ;

M M M

M x y z

thay đổi thuộc mặt phẳng

 

Oxy

. Tìm giá trị của biểu thức

M M M

T x y z  

khi 3

MA MB



 

nhỏ nhất.



. B.

. C.

. D.

2

Câu 161. (THPT CHUYÊN VĨNH PHÚC - LẦN 3 - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho

mặt cầu

 

có phương trình là

2 2 2

2 2 6 7 0

x y z x y z

      

. Cho ba điểm

nằm trên mặt cầu

 

sao cho



AMB

 

. Diện tích tam giác

AMB

có giá trị lớn nhất bằng?

. B.

. C.

4

. D. Không tồn tại.

Câu 162. (THPT PHAN ĐÌNH PHÙNG - HÀ TĨNH - LẦN 1 - 2018) Cho

, , , , ,a b c d e f

là các số thực thỏa

mãn

     

   

2 2 2

2 2

1 2 3 1

3 2 9

d e f

a b c



     





    





Gọi giá trị lớn nhất, giá trị nhỏ nhất của biểu thức

     

2 2 2

F a d b e c f

     

lần lượt là

, .M m

Khi đó,

M m

bằng

. B.

. C.

. D.

2 2

Câu 163. (THPT LÊ XOAY - LẦN 3 - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

2;2; 2

 

;

 

3; 3;3

B 

. Điểm

trong không gian thỏa mãn



. Khi đó độ dài

lớn nhất bằng

6 3

. B.

12 3

. C.

5 3

. D.

5 3

Câu 164. (THPT NGUYỄN TẤT THÀNH - YÊN BÁI - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho

các điểm

 

0; 1;3

A 

 

2; 8; 4

  

 

2; 1;1

C 

và mặt cầu

       

2 2 2

: 1 2 3 14

S x y z

     

. Gọi

 

; ;

M M M

M x y z

là điểm trên

 

sao cho biểu thức 3 2

MA MB MC

 

  

đạt giá trị nhỏ nhất. Tính

M M

P x y

 



. B.

P 

. C.



. D.

3 14

P 

PHẦN B. LỜI GIẢI THAM KHẢO

Dạng 1. Tìm tọa độ điểm, véc tơ liên quan đến hệ trục tọa dộ OXYZ

Câu 1. Chọn C

 

2 1;2 1;1 2

    



hay

 

1;1;3

AB 



Câu 2. Chọn B

Hình chiếu vuông góc của điểm

 

3;1; 1



trên trục

có tọa độ là

 

0;1;0

Câu 3. Chọn D

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20

Gọi

là trung điểm của

, ta có tọa độ điểm

là

A B

x x

y y

z z





 







  









 





Vậy

 

2; 1;5

I 

Câu 4. Chọn B

Gọi

 

;0;0

D x Ox



 

3 16 5

AD BC x





     







Câu 5. Chọn A

   

; ; 1;2;3

B A B A B A

AB x x y y z z    



Câu 6. Chọn C

Hình chiếu vuông góc của điểm

 

2;1; 1



trên trục

có tọa độ là

 

0;1;0

Câu 7. Chọn C

2 2 2

2 2 1 3

   

Câu 8.

Lơi giải

Chọn B

Hình chiếu vuông góc của điểm

 

3; 1;1

M 

trên trục

có tọa độ là

 

0;0;1

Câu 9. Chọn A

Tọa độ trung điểm

của đoạn

với

 

3; 2;3

A

và

 

1;2;5

B

được tính bởi

 

0 1;0;4



















 











A B

Câu 10. Chọn D

Hình chiếu vuông góc của điểm

 

2;1; 1



trên trục

có tọa độ là:

 

0;0; 1

Câu 11. Chọn D

   

;0;M Oxz M x z

 

;

 

7;3;1 59

AB AB  



;

 

2; 3; 1

AM x z

   



và

, ,A B M

thẳng hàng

 

. AM k AB k  

 



2 7 9

3 3 1

1 0

x k x

k k

z k z

   

 

 

     

 

 

  

 

 

9;0;0 .

M 

   

14; 6; 2 ; 7; 3; 1 2 .

         

 

BM BMA

Câu 12.

Lơi giai

Chọn B

Khi chiếu vuông góc một điểm trong không gian lên mặt phẳng

 

Oyz

, ta giữ lại các thành phần tung độ và

cao độ nên hình chiếu của

 

3; 1;1

A 

lên

 

Oyz

là điểm

 

0; 1;1

N 

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21

Câu 13. Chọn B

Ta có:

   

2 1 2 2.4;2 2 2.0;3 1 2.( 4) 7;0; 4

d a b c

            

 

Câu 14. Chọn B

 Xét đáp án A:

 

3; 3; 3

a b

   



đúng.

 Xét đáp án B:

   

2 1; 1; 2 1; 1;1

a b     



. Suy ra



và



không cùng phương.

Đáp án B sai.

Câu 15. Hai điêm

 

0;1; 1



 

2;3;2

. Vectơ



co toa đô la

 

2;2;3

Câu 16. Chon B

Cho hai điểm

 

3; 2;3

A 

và

 

1;2;5

B 

Trung điêm

co toa đô:

 

3 1

2 2

3 5

2 2

A B

x x

y y

z z

 



 



 





 





 



 





 

1;0;4

I

Câu 17. Ta có:

   

2 1;3 1;2 1 1;2;3

a b     



Câu 18. Ta có:

 

2 4; 6;6

a  



 

3 0;6; 3

 



 

2 6;2; 10

c   



 

2 3 2 2;2; 7

u a b c

      



  

Câu 19. Ta có

 

1 2;1;3

A B

x x

y y

y I

z z





 







  









 





Câu 20. Có

   

2; 2;5 , 1; 2;1

AB AC x y

 

    

, , A B C

thẳng hàng

, AB AC

 



cùng phương

1 2 1

2 2 5

x y





 



 



      















Câu 21.

 

2 3 1;2; 3      

  

 

a i j k a

Câu 22. Toạ độ trong tâm

của tam giác

ABC

bằng

 

1 1 0

3 3

2 2 0

0 0;0;3

3 3

3 5 1

3 3

A B C

x x x

y y y

y G

z z z

 

 



  



 

  



   





 



  





Câu 23. Có

     

2 4; 6;6 ; 3 0;6; 3 ; 2 6;2; 10

a b c       

  

Khi đó:

 

2 3 2 2; 2; 7

u a b c

     

   

Câu 24. Tọa độ trung điểm

của

là

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22

 

1 3

3 1

1 2;1;3 .

2 4

y I





 







  









 





Câu 25. Trung điểm

có tọa độ là

 

1 3

2 2

5 3

1 1;1;2

2 2

A B

x x

y y

y M

z z

  



  



 



   





 



  





Câu 26. Ta có:

 

2 2;0; 2

 



   

2 2 2;1 0; 3 2 4;1; 5

a x y

        

  

Câu 27. Gọi

là trung điểm của đoạn thẳng

, ta có:

2 2

4 2

2 2

3 7

2 2

A B

x x

y y

z z

 



  



  



   





 



  







 

2; 1;5

M 

Câu 28. Gọi

 

; ;D x y z

. Để

ABCD

là hình bình hành

     

1;3; 7 3 ;1 ;2 2 4; 2;9

AB DC x y z y D

 





              









 

Câu 29. Tọa độ trọng tâm

là

 

1 2 3

3 1 1

1 2;1;2 .

4 0 2

y G

 



 



 



  





 



 





Câu 30. Giả sử

 

, ,G x y z

Vì

là trọng tâm của tam giác

ABC

suy ra

 

5 2 0

2 3 2

1 1;1;1

3 3

0 0 3

A B C

x x x

y y y

y y G

z z z

  

 





 



 

  

 

    

 

 

   

 

 



 



Câu 31.

 

2; 1;0

A

 

1;1; 3

   

1 2;1 1; 3 0 1;2; 3        



AB .

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23

Câu 32. Gọi

 

; ;D x y z

Tứ giác

ABCD

là hình bình hành khi và chỉ

AD BC



 

Ta có

 

1; ;AD x y z

 



và

 

1;0;1

BC  



Suy ra

0; 0; 1x y z  

Vậy

 

0;0;1

Câu 33. Ta có:

 

1;1;2

AB  



Câu 34. Mặt phẳng tọa độ

 

Oyz

có phương trình là

   

0 0;4; 1

x N Oyz

   

Câu 35. Ta có

(1;0;0), (0;1;0), (0;0;1).

i j k  

  

Do đó,

(1;1; 1).

i j k

   

  

Câu 36. Hình chiếu của

 

4;5;6

xuống mặt phẳng

 

Oyz

là

 

0;5;6



Câu 37. Nếu



đối xứng với

qua mặt phẳng

 

Oxz

thì

 

; ;M x y z





. Do đó phương án

sai.

Nếu



đối xứng với

qua

thì

 

;y;M x z



 

. Do đó phương án

sai.

Nếu



đối xứng với

qua gốc tọa độ

thì

 

; y; z

M x



  

. Do đó phương án

sai.

Câu 38. Theo định nghĩa ta có

 

1;0;0

i 



 

0;1;0

j 



và

 

0;0;1

k 



Do đó,

 

2 3 2;3; 1

u i j k u

     

    

Câu 39. Gọi

là trung điểm

. Ta có:

1 1

2 2

2 0

2 2

2 4

2 2

M N

x x

y y

z z





  





 



   









  





Vậy

 

1; 1;3

I 

Câu 40. Có

c a b 



 

, gọi

 

1 2 3

; ;c c c c





 

2.1 1 1

2.2 3 7

2.1 0 2

   





   





  



Vậy

 

1;7;2

c 



Câu 41. Chọn A.

Gọi

là trung điểm của đoạn thẳng

. Khi đó ta có:

3 5

2 2

4 6

2 2

A B

x x

y y

  



  





 



  





 

1;5

I

Câu 42. Chọn D.

Áp dụng công thức tính tích có hướng trong hệ trục tọa độ

Oxyz

ta được:

 

, 2; 6; 1

c a b

 

   

 

  

Vậy chọn đáp án D

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24

Câu 43. Chọn A

+) Ta có

 

; ;a xi y j zk a x y z

   

    

nên

 

1;2; 3 .

 



Do đó Chọn A

Câu 44. Chọn C

Gọi

là trung điểm của đoạn

. Ta có

2 2

4 2

2 2

3 9

2 2

A B

x x

y y

z z

 



  



  



   





 



  





 

2; 1;6

I 

Câu 45.

2 2 2

(2;3; 3) 2 3 ( 3) 22.

AB AB       



Câu 46. Chọn A

Trung điểm

có tọa độ là

 

1 3

2 2

5 3

1 1;1;2

2 2

A B

x x

y y

y M

z z

  



  









   





 



  





Câu 47.



và



cùng hướng

a kb

 

 

 

2 2

0 1 3 7

3 2

k k

k m k m

k n







 



     

 

 

 





 



. Vậy

m n

  

Câu 48. Giả sử

 

; ;

B B B

B x y z

Vì

là trung điểm của

nên ta có:

2 2

1 3

2 2

A B B

M B

A B M

x x x

y y y

y y

z z z

  

 

 

 





 

 

  

     

  

  

 



 

 

  

 

 

. Vậy

 

5; 3; 7

 

Câu 49. Chọn D

Gọi

( ; ; )

D D D

D x y z

cần tìm

Tứ giác

ABCD

là hình bình hành

AB DC

 

 

2 1 3 4

1 2 5 8

3 ( 1) 1 3

B A C D

D D

B A C D D D

D DB A C D

x x x x

x x

y y y y y y

z zz z z z

  

     



 

  

          

  

  

     

  

 



Suy ra:

( 4;8; 3)

 

Câu 50. Chọn A

Gọi

 

; ;E x y z

Ta có:

 

7; 4; 2

CE x y z

   



;

 

2 2 2 ;4 2 ; 6 2EB x y z

    



CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25

7 2 2x

E 4 4 2

2 6 2z

B y yC y







  





 

     

 

 

   





 







 

Câu 51. Chọn D

1 2

3 4 2

3 5

c b

 













  

 

  

 

 

 



 









Vậy

a b c

   

Câu 52. Chọn A

Ta có

   

3; 4;2 , 2; 1; 4     

AB AM x y

 

, ,A B M

thẳng hàng

,

AB AM

 

cùng phương

2 1 4

3 4 2

 



  

   









x y

Câu 53. Chọn D

Tứ giác

ABCD

là hình bình hành

1 3 4

3 1 2

10 4 6

D D

x x

AB DC y y

z z

    

 

 

       

 

 

   

 

 

Vậy

 

4; 2; 6

  

Câu 54. Gọi

là hình chiếu của

lên mặt phẳng

   

Oyz H ; ;



0 2 3

Gọi

M '

là điểm đối xứng với

 

M ; ;1 2 3

qua mặt phẳng

 

Oyz

H

là trung điểm của

 

MM ' M ' ; ;

 

1 2 3

Câu 55. Ta có:

ABCD

là hình bình hành

OA OC OB OD

   

   

OD OA OC OB

   

   

D A C B

x x x x

y y y y

z z z z

  





   





  



1 0 2

2 3 1

0 4 2

  





    





  



 

1;0;6

D 

Câu 56. Gọi

 

;y;z

M x

. Vì M thuộc đoạn AB nên:

 

3 2 2

2 1 2 3

2 2 5

x x

MA MB y y y

z z







    



          

 

 

    











 

Câu 57. Gọi

 

; ;M x y z

. Ta có:

   

; 1; 2 ; 3; 2;3

AM x y z AB    

 

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26

9 9

3 1 6 5

2 9 7

x x

AM AB y y

z z

 

 

 

       

 

 

  

 

 

. Vậy

 

9; 5;7M 

Câu 58. Ta có

   

; ;0M Oxy M x y 

;

   

2;3;1 ; 2; 2; 1AB AM x y     

 

Để

thẳng hàng thì



và



cùng phương, khi đó:

2 2 1

2 3 1

x y  

 











 



Vậy

 

4; 5;0M 

Câu 59. Ta có

 

2; 2;1u  



Khi đó

 

2 2

2 2 1 3u     



và

 

2 2 2

2 1 2 2 5v m m m m      



Do đó

9 2 2 5u v m m    

 

2 0

m m





    



 



Vậy có 2 giá trị của

thỏa yêu cầu bài toán.

Câu 60. Gọi

 

; ;B x y z

Có

 

1;2; 1A 

 

1;3;1AB 



 

1; 2; 1x y z   

 

5 2;5;0

y B







  









Câu 61.

Ta có

 

;0;0AB a



;

 

0;2 ;0AD a



;

 

0;0;2AA a







Theo quy tắc hình hộp ta có

AB AD AA AC

 

  

   

 

;2 ;2AC a a a



 



Suy ra AC AC



   

2 2

2 2 3a a a a   

Vậy độ dài đoạn thẳng

3AC a





Câu 62. Gọi

 

; ; , '( ; ; )A x y z A x y z

  

là điểm đối xứng với điểm A qua trục

Điểm

đối xứng với điểm

qua trục

nên

x x

y y

z z

 











 



. Do đó

 

' 3;1; 2A  

Câu 63. Gọi

là trọng tâm của tam giác

ABC

. Ta có

 

1;0; 2G 

và

0GA GB GC  

  



Ta có:

0A A B B C C

  

  

  



0GA GA GB GB GC GC

  

      

     



GA GB GC GA GB GC

  

     

     

0GA GB GC

  

   

  





là trọng tâm của tam giác

A B C

  

Vậy tọa độ trọng tâm của tam giác

A B C

  

là

 

1;0; 2

Câu 64. Gọi tọa độ điểm

là

 

; ;x y z

Vì

ABCD

là hình bình hành nên

DC AB

 

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27

Ta có

 

1; 1; 1

DC x y z

   



và

 

1;1;1

AB 



Suy ra

1 1 2

1 1 0

1 1 2

x x

y y

z z

  

 

 

   

 

 

  

 

Vậy tọa độ điểm

là

 

2;0;2

Câu 65. Chọn D

Ta có

 

1; 2; 2 



8 4 8

; ;

3 3 3

 



 

 



, do đó

3, 4 

OA OB

Gọi

là chân đường phân giác trong kẻ từ

, ta có

. .

   

DA OA

DA DB DB

DB OB

  

, suy ra

3 4. 3.

4 7



   

OA OB

DA DB OD

 

  

. Do đó

12 12

; ; 0

7 7

 

 

 

Ta có

5 2 15

; ; 2

7 7 7

 

   

 

 

AD AD



   

ID IO IO

  

 

1; 1; 0

  OI OD D

 

Do đó

0  

a b c

Câu 66. Gọi

, ,I J K

lần lượt là trung điểm của

, ,AB BC CA



AMB BMC CMA

   

nên các tam giác

, ,

AMB BMC CMA  

vuông tại

Khi đó

; ;

2 2 2

AB BC AC

IM JM KM  

. Mặt khác

2 2

AB BC AC  

Vậy

MI MJ MK  

. Khi đó

thuộc trục của đường tròn ngoại tiếp đáy

IJK

và cách

 

IJK

một

khoảng không đổi là

. Khi đó có hai điểm

thỏa mãn điều kiện trên.

Dạng 2. Tích vô hướng, tích có hướng và ứng dụng

Dạng 2.1 Tích vô hướng và ứng dụng

Câu 67. Chọn B

Ta có:

 



   

 

. 2 2

cos ,

5. 5

a b

Câu 68. Chọn C

   

3; 2;2 ; 2; 2;1

MN NP m  

 

Tam giác

MNP

vuông tại

 

. 0 6 2 2 2 0 2 2 0

N MN NP m m m

             

 

Câu 69. Chọn B

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28

Ta có:

 

3; 5

  



 

2; 2

 



Khi đó:

 

. 3.2 5.2 1

cos cos ;

34.2 2 17

AB AC

A AB AC

AB AC

 

   

 

Câu 70. Ta có

 

1; 0; 0

i 



Vậy:

 

cos ,i u

 

i u



 

 

2 2

1. 3 0.0 0.1

1. 3 0 1

  



  



 

, 150

i u

  

 

Câu 71. Chọn D

Ta có:

 

2 2 2 2 2

. 3.5 4.0 0.12 3

os ;

3 4 0 . 5 0 12

a b

c a b

a b

   

  

    

 

Câu 72. Ta có

 

1;0;0

i 





 

. 3

cos ,

u i



 

 

. Vậy

 

, 150

u i

 

 

Câu 73. Ta có

. 3.2 0.1 1.0 6

u v

   

 

Câu 74. Goi



la goc giưa hai vectơ



va

 

3;0;1

u  



, ta co:

. 3

cos 150

i u

 



   

 

Câu 75. Ta có

 

1;5; 2





;

 

5;4; 1







. 5 20 2 9

30. 42 2 35

AB AC

cosBAC

AB AC

 

  

 

Câu 76. Ta có

 

1;2; 3

. 0

7; 5; 1

AB BC



  



  



   







 



tam giác

ABC

vuông tại



tâm

của đường tròn ngoại tiếp tam giác

ABC

là trung điểm của cạnh huyền



1; ;3

 



 

 

. Vậy

2 3.

a b c

  

Câu 77. Chọn C

Ta có:

   

1; 0;1 , 1;1;1

  

 

AB AC

 

1 .1 0.1 1.1 0      

AB AC

Nên diện tích tam giác

ABC

là

1 6

2 2

 S AB AC

Câu 78. +

   

, 45 cos ,

u v u v   

   

. 2

u v

 

 

1 2 1

6. 1



 



 

3 1 1 2m m

   

2 2

1 2 0

3 3 1 4 4

m m m

 







   



4 2 0

m m













  



2 6

m   .

Dạng 2.2 Tích có hướng và ứng dụng

Câu 79. Ta có:

     

3; 2; 3 , 2;0; 3 , 0;4; 3      

  

DA m DB DC

Thể tích tứ diện:

 

1 1

, . 8 24 8 3

6 6

 



 

     



 





  

V DB DC DA m

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29

Vì

dương nên



Do đó chọn D.

Câu 80. Ta có:

(1;2;3)

AB 



;

( 3;3;3)

AC  



;

( 1;3;1)

AD  



, ( 3; 12;9)

AB AC

 

  

 

 

;

, . ( 3).( 1) ( 12).3 9.1 24

AB AC AD

 

       

 

  

1 1

, . 24 4

6 6

ABCD

V AB AC AD

 

   

 

  

Câu 81. Chọn C

     

2 2

, 2; ; 1 , 2 1 3 6 5

u v m m m u v m m m m m

   

             

   

   

 

2 2

, 14 3 6 5 14 3 6 9 0

u v m m m m





         



 



 

Câu 82. Chọn A.

 

0; ;0

 

D Oy D y

, khi đó:

 

2; 1 ;1

  

DA y



 

3; ; 1  

DB y



 

2; 1 ;3

  

DC y



Khi đó

 

, 1 2 ;5; 3

 

  

 

DA DB y y

 

Và

2 6 30 12

, . 5

2 6 30 18

  

 

 

   

 

 

    

 

ABCD

y y

V DA DB DC

y y

  

Vậy

1 2

12 18 6    

y y .

Câu 83. Ta có



     

2 2 2

1 1 2 1 3 1 4 1 4 3

a b u

            

  

(đúng).



   

. 1.1 2 .1 3. 1 1 2 3 4

a b

         

 

(đúng).



     

2 2 2

1 1 2 1 3 1 0 9 16 5

a b u

            

  

(đúng).



 

2 3 3 1 1 2

, ; ; 1;4;3

1 1 1 1 1 1

a b

   

 

  

 

 

 

 

 

(sai).

Câu 84. Ta tính

 

0;2; 1 ;

 



 

1;1;2 ;

 



 

3; 2;AD m n  



;

 

, 5;1;2

AB AC

 



 

 

 

Bốn điểm

đồng phẳng

, . 0 2 13

AB AC AD m n

 

    

 

 

  

Câu 85.

 

, 1; 3; 1

 

   

 

 

OA OB

1 1 11

, 1 9 1

2 2 2



 

    

 

 

OAB

S OA OB

Câu 86. Ta có:

 

, 3 ; 4 ; 0

m n

 

 

 

 

Vì



là véc tơ cùng hướng với

,m n

 

 

 

nên

 

. , 3 ; 4 ;0 , 0

p k m n k k k

 

   

 

  

Ta có:

2 2

15 9 16 15

p k k

 



    









So sánh với điều kiện

0 3

k k

  

 

9 ; 12 ; 0

p  



Câu 87.

     

3;1; 2 ; 1; 1; 4 ; 4;1;0

AC AB AD        

  

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30

 

, 6; 10;4

AB AC

 

  

 

 

Thể tích khối tứ diện là:

1 1 7

. , . 14

6 6 3

V AB AC AD

 

  

 

  

Câu 88.

   

 

1; 2; 3 ; 5; 3;1

3;3; 3 ; 3; 2;1

2;0; 2

AB CD

AC BD

    

  

 



Ta có:

 

, 3; 6; 3

AB AC

 

  

 

 

    

, . 2 .3 0.6 2 3 0

AB AC AD

 

       

 

  

, ,AB AC AD



  

đồng phẳng hay bốn điểm

, , ,A B C D

đồng phẳng. Vậy đáp án A sai.

Lại có

     

. 3. 2 3.0 3 . 2 0

AC AD AC AD

        

 



tam giác

ACD

là tam giác vuông tại

. Vậy đáp án B đúng.

Mặt khác:

     

   

. 1. 5 2. 3 3 .1 14 0 , 0 ,

ABCD cos AB CD AB CD

           

     

là góc tù. Vậy đáp

án C đúng.

AB BD hay AB BD

  

 



tam giác

ABD

là tam giác cân tại

. Vậy đáp án D đúng.

Câu 89. Ta có

AD BC AD

nhận

 

5;2; 1

 



là một VTCP.

Kết hợp với

qua

 

2;3;1

A 

2 5

: 3 2

x t

AD y t

z t

  





  





 



 

t 



 

5 2;2 3;1

D t t t   

Biến đổi 3

ABCD ABC

S S

 2

ACD ABC

S S

 

 

Ta có

 

4; 2; 1

; 4;1; 18

1; 4;0

; 4 ; ;18

5 ;2 ;

AB AC

AC AD t t t

AD t t t



  



 

  



  

   

 

 

 

 

 



 







 



 



   

     

2 2

2 2 2

1 1 341

; 4 1 18

2 2 2

341

1 1

; 4 18

2 2 2

ABC

ACD

S AB AC

S AC AD t t t



 

      



 









 

     



 



 

Kết hợp với

 

ta được

 

2 8;7; 1

341

2 12; 1;3

t D

  

 



    





Với

   

8;7; 1 10;4; 2 2 2

D AD CB BC

      

  

Với

   

12; 1;3 10; 4;2 2 2

D AD CB BC

        

  

Hình thang

ABCD

có đáy

thì

AD kBC



 

với



Do đó chỉ có

 

12; 1;3

D  

thỏa mãn.

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31

Dạng 3. Mặt cầu

Dạng 3. Xác định tâm, bán kính của mặt cầu

Câu 90. Chọn A

Phương trình mặt cầu tổng quát:

     

2 2 2

2 2

x a y b z c R R       

Câu 91. Chọn D

Câu 92. Chọn A

Phương trình

2 2 2

2 2 4 0

x y z x y z m

      

là một phương trình mặt cầu

2 2 2

1 1 2 0

    





Câu 93. Chọn B

Phương trình mặt cầu tâm

 

; ;I a b c

, bán kính

có dạng:

     

       

2 2 2

x a y b z c R R .

Câu 94. Chọn B

Tâm của

 

có tọa độ là

 

3; 1;1

 

Câu 95. Chọn C

Trong không gian với hệ trục tọa độ

Oxyz

, mặt cầu

       

2 2 2

S x a y b z c R     

có tâm

 

; ;I a b c

và bán kính

Nên mặt cầu

     

2 2 2

1 2 4 20

x y z

     

có tâm và bán kính là

 

1; 2;4 , 2 5.

I R 

Câu 96. Chọn A

2 2 2 2 2 2

2 2 7 0 2.( 1). 2.0. 2.1. 7 0

x y z x z x y z x y z

              

1, 0, 1, -7

a b c d

     



Tâm mặt cầu

 

1;0;1

I 

bán kính

 

2 2 2 2 2

1 0 1 7 3

R a b c d

         

Câu 97.

lời giải

Chọn C

Ta có

     

2 2 2

1 1 2 1 3 1 5

R IA       

vậy phương trình mặt cầu tâm

và đi qua điểm

có phương trình là

           

2 2 2 2 2 2

1 1 1 5

I I I

x x y y z z R x y z

            

Câu 98. Chọn D

Ta có

   

1 1 7 3     

Câu 99. Chọn D

Ta có

     

2 2

2 2 2 2

: 2 2 7 0 1 1 9

S x y z x y x y z

           

Vậy bán kính của mặt cầu bằng

Câu 100. Chọn B

Mặt cầu đã cho có phương trình dạng

2 2 2

2 2 2 0

x y z ax by cz d

      

có bán kính là

2 2 2 2 2

1 1 7 3

a b c d

      

Câu 101. Ta có:

   

2 2

2 2 2 2

8 2 1 0 4 1 16.

x y z x y x y z           

Vậy mặt cầu

 

có tâm

 

4; –1;0

và bán kính



Câu 102.

 

2 2 2

: 2 4 2 3 0

S x y z x y z

      

     

2 2 2

1 2 1 9

x y z

      

Vậy bán kính của mặt cầu

 

là



Câu 103.

 

2 2 2

: 8 2 1 0

S x y z x y

     

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32

 

4; 1;0

I 

4R 

Câu 104. Mặt cầu

 

có tâm là

 

3; 1;1

I  

Câu 105. Ta có:

     

2 2 2

2 4 2 3 0 1 2 1 9

x y z x y z x y z

             

Từ đó suy ra mặt cầu

 

có tâm là:

 

1;2;1



Câu 106. Phương trình mặt cầu:

2 2 2

2 2 2 0

x y z ax by cz d

      

 

2 2 2

a b c d

   

có tâm

 

; ;I a b c

, bán kính

2 2 2

R a b c d   

Ta có



 



. Do đó

2 2 2

R a b c d

    

Câu 107. Chọn B

Từ phương trình mặt cầu suy ra tâm của mặt cầu là

 

2; 1;3



Câu 108. Mặt cầu đã cho có tâm

 

1; 2;3

I 

và bán kính

2R 

Câu 109. Chọn D.

Giả sử phương trình mặt cầu

2 2 2 2 2 2

( ) : 2 2 2 0 ( 0)

S x y z ax by cz d a b c d

          

Ta có:

2, 1, 0, 4

a b c d

      

Bán kính

2 2 2

R a b c d

    

Câu 110. Chọn B

Tâm của

 

có tọa độ là

 

3; 1;1

Câu 111. Chọn D

Phương trình đã cho là phương trình mặt cầu khi và chỉ khi

   

2 2

2 1 3 5 0

2 10 0

1 11 1 11

     

   

     

m m m

m m

Theo bài ra





2; 1;0;1;2;3;4

     

m m



có

giá trị của

nguyên thỏa mãn bài toán.

Câu 112. Điều kiện để phương trình

 

2 2 2

2 2 4 19 6 0       

x y z m x my m

là phương trình mặt cầu

là:

 

2 2

2 4 19 6 0 5 15 10 0        

m m m m m

1 

hoặc

2

Câu 113. Ta có

2 2 2 2

4 2 2 9 28 0

x y z mx my mz m

       

     

2 2 2

2 28 3x m y m z m m

       

 

là phương trình mặt cầu

28 28

28 3 0

3 3

m m      

nguyên nên

 

3; 2; 1;0;1;2;3

m   

Vậy có

giá trị của

thỏa mãn yêu cầu bài toán.

Câu 114. Đường tròn lớn có chu vi bằng

8

nên bán kính của

 

là







Từ phương trình của

 

suy ra bán kính của

 

là

2 2 2

2 1 10a a

  

Do đó:

2 2 2

2 1 10 4

a a

 



    







Câu 115. Cách 1: Tìm tọa độ tâm mặt cầu suy ra bán kính.

Gọi

 

; ;I x y z

và

lần lượt là tâm và bán kính mặt cầu ngoại tiếp tứ diện

OABC

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33

Ta có:

IO IA IB IC R   

2 2

IO IA

IO IB

IO IC







 









 

2 2 2 2 2

x y z x y z



     



      





     







 



  











1 3

; ;1

2 2

 

 

 

 

R IO  

Cách 2: Tìm phương trình mặt cầu suy ra bán kính.

Gọi phương trình mặt cầu

 

ngoại tiếp tứ diện

OABC

là:

2 2 2

2 2 2 0

x y z ax by cz d

      

 

đi qua bốn điểm

, , ,A B C O

nên ta có:

1 2 0

4 4 0

9 6 0

a d

c d

b d

  





  





  









 



 

















bán kính của

 

là:

2 2 2

R a b c d    

Cách 3: Sử dụng công thức tính bán kính mặt cầu ngoại tiếp của tứ diện vuông.

Do tứ diện

OABC

có ba cạnh

, ,OA OB OC

đôi một vuông góc nên bán kính mặt cầu ngoại tiếp tứ diện

OABC

là

2 2 2

R OA OB OC

  

1 14

1 4 9

2 2

   

Câu 116.

Gọi

 

; ;I a b c

là tâm mặt cầu đi qua bốn điểm

, , ,A B C D

. Khi đó:

     

       

2 2 2

2 2

2 2 2

2 2 2 2 2

2 2

2 2 2 2

2 2

2 1 3

2 1 2 3

a b c a b c

AI BI

AI CI a b c a b c

AI DI

a b c a b c



       







         

 

 



        







 

3 3 0

1 1 0;1;1

2 3 5 1

a b a

a c b I

a b c c

   

 

 

      

 

 

    

 

Bán kính:

2 2 2

2 1 1 6

R IA    

Câu 117.

Ta có:

2 2

3 9

MA MB MA MB

  

 

   

2 2

MI IA MI IB

   

   

 

2 2 2

9 2 9 8 1

IA IB MI IA IB MI    

  

Gọi

thỏa mãn

9 0

IA IB BI AB

   

    

nên

1 9

;

2 2

IB IA

 

Từ

 

suy ra

8 18

MI MI

   

suy ra

; .

M S I

 



 

 

Câu 118. Ta có điều kiện xác định mặt cầu là

2 2 2

a b c 

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34



 

2 2 2

2 4 5 9 0

m m m m

     

4 5 0

m m

   

 











Câu 119. Gọi

     

; ; ;1 ;2 ; 4 ; 3 ; 2

I a b c IA a b c IH a b c          

 

ABCD

là tứ diện đều nên tâm

của mặt cầu ngoại tiếp trùng với trọng tâm tứ diện

3IA IH

  

 

 

3 4

1 3 3 2

2 3 2

a a

b b b

c c



   







        

 

 

 

    



 

3; 2; 1

  

Dạng 3. Viết phương trình mặt cầu

Câu 120.

lời giải

Chọn C

Ta có

     

2 2 2

1 1 2 1 3 1 5

R IA       

vậy phương trình mặt cầu tâm

và đi qua điểm

có phương trình là

           

2 2 2 2 2 2

1 1 1 5

I I I

x x y y z z R x y z

            

Câu 121. Chọn A

Hình chiếu vuông góc của

trên trục

là

 

 

1; 0; 0 13

I IM

.Suy ra phương trình mặt cầu tâm

bán kính

là:

 

   

2 2

1 13

x y z .

Câu 122. Gọi

là trung điểm

ta có

 

1;3;3

I 

là tâm mặt cầu.

Bán kính

     

2 2 2

1 1 2 3 7 3 45.

R IA        

Vậy phương trình mặt cầu cần tìm là

     

2 2 2

1 3 3 45

x y z

     

Câu 123. Mặt cầu có tâm

 

1; 4;3

I 

và đi qua điểm

 

5; 3;2

A 

nên có bán kính

3 2

R IA 

Vậy phương trình mặt cầu cần tìm là:

     

2 2 2

1 4 3 18

x y z

     

Câu 124. Gọi

là tâm của mặt cầu đường kính

Khi đó

 

1;0;2

Bán kính của mặt cầu là:

     

2 2 2

1 1

1 1 1 1 3 1 2

2 2

R AB        

Vậy phương trình mặt cầu là:

   

2 2

1 2 2

x y z

    

Câu 125. Gọi I là trung điểm của AB

(0;3; 1).

 

2 2 2

(2;1;2) 2 1 2 3.

IA IA

     



Mặt cầu đã cho có tâm I, đường kính AB nên có phương trình là

   

2 2

3 1 9.

x y z

    

Câu 126. Chọn A

Đáp án B vì không có số hạng

. Đáp án C loại vì có số hạng

2xy

. Đáp án D loại vì

2 2 2

1 1 4 8 2 0

a b c d

         

Đáp án A thỏa mãn vì

2 2 2

1 0 4 1 6 0

a b c d

        

Câu 19 : [2H3-1.3-1] Trong không gian

Oxyz

, cho hai điểm

 

2; 1; 3 

;

 

0;3; 1

. Phương trình của mặt

cầu đường kính

là :

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35

     

2 2 2

1 1 2 6     

x y z

     

2 2 2

1 1 2 24     

x y z

     

2 2 2

1 1 2 24     

x y z

     

2 2 2

1 1 2 6     

x y z

Lờigiải

Chọn D

Tâm

mặt cầu là trung điểm của

 

1;1; 2

bán kính

1 1 1

4 16 4 24

2 2 2

    R AB

     

2 2 2

1 1 2 6     

x y z

Câu 127. Phương trình

2 2 2

2 2 2 0

x y z ax by cz d

      

là phương trình của một mặt cầu nếu

2 2 2

a b c d

   

Câu 128. Tọa độ tâm mặt cầu là

 

3;3;1

, bán kính

R IA

 

Câu 129. Phương trình mặt cầu tâm

 

2;1; 2



bán kính

2R 

có hai dạng:

Chính tắc:

     

2 2 2

2 1 2 2

x y z

     

Tổng quát:

2 2 2

4 2 4 5 0

x y z x y z

      

Vậy đáp án đúng là B.

Câu 130. Vì mặt cầu

 

có tâm

 

2;1;0

, đi qua điểm

 

0;1;2

nên mặt cầu

 

có tâm

 

2;1;0

và

nhận độ dài đoạn thẳng

là bán kính.

Ta có:

 

2 :0;2

AB  



 

2 2

2 0 2 2 2

AB AB     



. Suy ra:

2 2

R 

Vậy:

     

2 2

: 2 1 8

S x y z

    

Vậy chọn đáp án B

Câu 131.

lời giải

Chọn B

Ta có

     

2 2 2

1 1 2 1 3 1 5

R IA       

vậy phương trình mặt cầu tâm

và đi qua điểm

có phương trình là

           

2 2 2 2 2 2

1 1 1 5

I I I

x x y y z z R x y z

            

Câu 132.

Gọi

là trung điểm

suy ra

là hình chiếu vuông góc của

lên

nên

 

1;0;0

2 2

13 4

IH R IA IH AH

     

Phương trình mặt cầu là:

     

2 2 2

1 2 3 16

x y z

     

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 36

Câu 133. Với điểm

 

1; 2;3

M 

thì hình chiếu vuông góc của

trên trục

là

 

1;0;0

Có

IM 

vậy phương trình mặt cầu tâm

 

1;0;0

bán kính

là:

 

2 2

1 13

x y z

   

Câu 134. Ta có mặt cầu

 

2 2 2

: 2 2 2 0

S x y z ax by cz d

      

có bán kính là

2 2 2

R a b c d   

Trong đáp án C ta có:

2 2 2

4 2

R a b c d







 



      



 







Câu 135. Gọi

 

;0;0

I a Ox



   

1 ;1;2 ; 3 ;2; 3

IA a IB a

   

 

 

đi qua hai điểm

,A B

nên

   

2 2

1 5 3 13

IA IB a a

      

4 16 4

a a

   

 



có tâm

 

4;0;0

, bán kính

R IA 

   

2 2 2 2 2

: 4 14 8 2 0.

S x y z x y z x

          

Câu 136. Ta có:

4 4 1

S R R

 

   

Vậy

 

tâm

 

1;1;1

bán kính

1R 

có pt:

     

2 2 2

1 1 1 1

x y z

     

Câu 137. Gọi phương trình mặt cầu

 

2 2 2 2 2 2

: 2 2 2 0 0

S x y z ax by cz d a b c d

          

Vì mặt cầu đi qua 4 điểm nên:

18 6 6 0

27 6 6 6 0

a b d

a c d

b c d

a b c d

   





   





   



    



6 6 18

6 6 6 27

a b d

a c d

b c d

a b c d

    





    







    



     



























Suy ra tâm

3 3 3

; ;

2 2 2

 

 

 

bán kính

2 2 2

3 3 3 3 3

2 2 2 2

     

   

     

     

Vậy phương trình mặt cầu

2 2 2

3 3 3 27

2 2 2 4

x y z

     

     

     

     

Câu 138. Chọn A

Gọi

 

1;1;0 , 2.

I R







Gọi



là bán kính của mặt cầu

 



. Theo giả thiết, ta có

R R II R II R

   

     

Khi đó phương trình mặt cầu

 



     

2 2 2

9 1 6 64

x y z

     

Câu 139. Gọi

 

; ;I a b c

là tâm của mặt cầu

 

. Mặt cầu

 

tiếp xúc với các mặt phẳng tọa độ

 

, , ,

d I Oxy d I Oyz d I Oxz

 

a b c R   

 

Mặt cầu

 

đi qua

 

1; 1;4

A 

0; 0; 0

IA R

a c b









  



2 2

0; 0; 0

IA R

a c b









  



     

 

2 2 2

1 1 4

0 ( 1 )

a b c R

a c b R do



     







    





CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 37

     

2 2 2

1 1 4

a a a a

a c b R



      







    





2 12 18 0

a a

a c b R



  





    



6 9 0

a a

a c b R



  





    



a c

 





  









       

2 2 2

: 3 3 3 9

S x y z

      

Câu 140. Gọi

là tâm đường tròn nội tiếp tam giác

OMN

Ta áp dụng tính chất sau : “Cho tam giác

OMN

với

là tâm đường tròn nội tiếp, ta có

. . . 0

a IO b IM c IN

  

   

, với

a MN

b ON

c OM

”.

Ta có

2 2 2

2 2 1 3

   

2 2 2

8 4 8

3 3 3



     

   

     

     

2 2 2

8 4 8

2 2 1 5

3 3 3



     

      

     

     

5.0 4.2 3.

3 4 5

5.0 4.2 3.

5. 4. 3. 0 1

3 4 5

5.0 4.2 3.

3 4 5

IO IM IN y

 

 

 

 



 



 

 



 

 



 



 

     



 



 

 

 



 



 

 





   

Mặt phẳng

 

Oxz

có phương trình



Mặt cầu tiếp xúc với mặt phẳng

 

Oxz

nên mặt cầu có bán kính

 

, 1

R d I Oxz

 

Vậy phương trình mặt cầu là:

   

2 2

1 1 1

x y z

    

Câu 141. Vì mặt cầu tâm

tiếp xúc với các mặt phẳng tọa độ nên

 

, , ,

d I Oyz d I Ozx d I Oxy

 

a b c  

a b c

 





  







  



   



Nhận thấy chỉ có trường hợp

a b c  

thì phương trình

 

AI d I Oxy



có nghiệm, các trường hợp còn

lại vô nghiệm.

Thật vậy:

Với

a b c  

thì

 

; ;I a a a



 

AI d I Oyx



     

2 2 2

1 1 4

a a a a      

6 9 0

a a

   

 

Khi đó

P a b c

   

Dạng 3. Một số bài toán khác

Câu 142. Chọn C

Mặt cầu

 

có tâm

 

0;0; 2

I và bán kính

R 

;

 

A Oxy



 

; ;0

A a b

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 38

* Xét trường hợp

 

A S

, ta có

2 2

1a b 

. Lúc này các tiếp tuyến của

 

thuộc tiếp diện của

 

tại

nên có vô số các tiếp tuyến vuông góc nhau.

Trường hợp này ta có 4 cặp giá trị của

 

;a b

là

0 0 1 1

; ; ;

1 1 0 0

a a a a

b b b b

     

   

   

    

   

* Xét trường hợp

ở ngoài

 

. Khi đó, các tiếp tuyến của

 

đi qua

thuộc mặt nón đỉnh

. Nên các

tiếp tuyến này chỉ có thể vuông góc với nhau tại

Điều kiện để có ít nhất 2 tiếp tuyến vuông góc là góc ở đỉnh của mặt nón lớn hơn hoặc bằng

90

Giả sử

;A N A M

 

là các tiếp tuyến của

 

thỏa mãn

AN AM

(

;N M

là các tiếp điểm)

Dễ thấy

A NIM



là hình vuông có cạnh 3IN R  và 3. 2 6IA



  .

Điều kiện phải tìm là

IA R

IA IA











 





2 2

a b



 







 





Vì

,a b

là các số nguyên nên ta có các cặp nghiệm

 

;a b

là

               

0;2 , 0; 2 , 2;0 , 2;0 , 1;1 , 1; 1 , 1;1 , 1; 1     

Vậy có

điểm

thỏa mãn yêu cầu.

Câu 143. Chọn A

Mặt cầu có tâm

 

0;0;1I

, bán kính

5R 

Vì

 

A Oxy

nên

0c 

. Các giao tuyến của

đến mặt cầu (nếu

IA R

) tạo nên một mặt nón tâm

, để

mặt nón này có hai đường sinh vuông góc thì góc của mặt nón này phải

90 

hay

2IA R

Vậy

2 2 2 2

2 5 1 10 4 9R IA R a b a b          

Ta có các bộ số thõa mãn

             

0; 2 ; 0; 3 ; 1; 2 ; 2; 2 ; 2; 1 ; 2;0 ; 3;0         

, 20 bộ số.

Câu 144. Chọn A

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 39

Mặt cầu

 

2 2 2

: ( 1) 5

S x y z

   

có tâm

 

0;0; 1



và có bán kính

R 

   

; ;0A a b

Oxy



, Gọi



là trung điểm của

; ;

2 2 2

a b

AI I

 



 

 

 

Gọi

,E F

lần lượt là hai tiếp điểm của tiếp tuyến đi qua

sao cho

AE AF

Ta có:

,E F

cùng thuộc mặt cầu

 



đường kính

có tâm

; ;

2 2 2

a b

 





 

 

, bán kính

2 2

R a b



  

Đề tồn tại

,E F

thì hai mặt cầu

 

và

 



phải cắt nhau suy ra

R R II R R

  

   

2 2 2 2 2 2

1 1 1

5 1 1 5 1

2 2 2

a b a b a b

          

 

2 2 2 2

5 1 4 1

a b a b      

Gọi

là hình chiếu của

trên

 

AEF

khi đó tứ giác

AEHF

là hình vuông có cạnh

AE HF AI

  

Ta có

 

2 2 2 2 2 2 2 2 2

5 5 10 0 1 10 9 2

IH R HF AI AI a b a b              

Từ

 

và

 

ta có

2 2

4 9

a b

  

mà

, , a b c



nên có

điểm thỏa bài toán.

Cách khác:

Mặt cầu

 

có tâm

 

0,0, 1



bán kính

R  . Ta có

 

I Oxy

d R

  

mặt cầu

 

cắt mặt phẳng

 

Oxy

. Để có tiếp tuyến của

 

đi qua

 

A AI R 

Có

     

2 2

, , , ,0 , 1

A a b c Oxy A a b IA a b

    

Quỹ tích các tiếp tuyến đi qua

của

 

là một mặt nón nếu

AI R

và là một mặt phẳng nếu

AI R

Trong trường hợp quỹ tích các tiếp tuyến đi qua

của

 

là một mặt nón gọi

AM AN

là hai tiếp tuyến

sao cho

, , ,A M I N

đồng phẳng.

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 40

Tồn tại ít nhất hai tiếp tuyến của

 

đi qua

và hai tiếp tuyến đó vuông góc với nhau khi và chỉ khi



 

90 2 2

MAN IA R  

Từ

   

2 2

1 , 2 4 9

a b

   

. Vì

,a b



















hoặc















hoặc















hoặc















hoặc















hoặc















hoặc















Bốn hệ phương trình đầu tiên có hai nghiệm, ba hệ sau có 4 nghiệm suy ra số điểm

thỏa mãn là

4.2 3.4 20 

Câu 145. Chọn D

Nhận thấy điểm

nằm bên trong mặt cầu

 

. Để

  

2 2

( , )

AB R d O

nhỏ nhất khi

 

,

d O

lớn nhất.

Ta thấy

 

  

, std O OM con

. Dấu ‘=’ xảy ra khi

  OM

Suy ra







. 0u OM

và



 

. 0

u n

nên

      



 

   

 

1 0 1

1 2 0 0

a b a

a b b

Suy ra

   1T a b

Câu 146. Vì các điểm

, ,M N P

đều nằm trên đoạn AB sao cho

AM MN NP PB  

Do đó ta có

   

3 , 3 A, 3.4

, A, 3

3 3 , A, 3. 9

BM MA d B Oxy d Oxy c

BN NA d B Oxz d Oxz b

BP PA d B Oyz d Oyz a

 



  

 



 



 



  

     

  

  

  

  





 

 

Để

, ,M N P

đều nằm trên đoạn AB thì hai điểm A và B không nằm về cùng 1 phía so với lần lượt các mặt

phẳng

, ,

Oxy Oxz Oyz

Do đó

 

12,3, 3

 

Vậy

ab bc ac

   

Câu 147.

Mặt cầu

 

có tâm

 

1;1;0

và bán kính

2R 

Ta có

 

1;2;1

IM 



và

IM  .

Gọi

là một tiếp điểm tùy ý khi kẻ tiếp tuyến từ

Oxyz

đến mặt cầu, khi đó

2 2

MH IM R  

. Gọi

là tâm của đường tròn

 

khi đó

IM HO

và

HO r

Ta có

. .HI HM HO IM

. 2 2 2 3

HI HM

    .

Câu 148. Gọi

 

; ;M x y z

là tập hợp các điểm thỏa mãn yêu cầu bài toán. Ta có

 

; 1; 2

AM x y z

  



 

2; 3;BM x y z

  



 

2; 1; 1

CM x y z

   



 

; 1; 3

DM x y z

  



CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 41

Từ giả thiết:

. 1

. . 1

. 1

MA MB

MA MB MC MD

MC MD







  









 

   

 

      

       

2 1 3 2 1

2 1 1 1 3 1

x x y y z z

      







       





2 2 2

2 4 2 2 0

2 4 1 0

x y z x y z

x y z x z



      







     





Suy ra quỹ tích điểm

là đường tròn giao tuyến của mặt cầu tâm

 

1; 2;1

I 



và mặt cầu tâm

 

1;0;2

I 



Ta có:

1 2

I I 

Dễ thấy:

1 2

5 11

2 4 2

I I

r R

 

    

 

 

Câu 149. Cách 1:

Gọi

, , ,A B C D

là tâm bốn mặt cầu, không mất tính tổng quát ta giả sử

4AB 

AC BD AD BC

   

Gọi

,M N

lần lượt là trung điểm của

AB CD

. Dễ dàng tính được

2 3

MN  . Gọi

là tâm mặt cầu nhỏ

nhất với bán kính

tiếp xúc với bốn mặt cầu trên. Vì

IA IB IC ID 

nên

nằm trên đoạn

Đặt

IN x

, ta có

2 2

3 3

IC x r   

 

2 2 3 2

IA x r    

Từ đó suy ra

 

2 2 2

12 3

3 2 2 2 1

x x x      

, suy ra

12 3 6

3 3

11 11

 

   

 

 

Cách 2

Gọi

,A B

là tâm quả cầu bán kính bằng

,C D

là tâm quả cầu bán kính bằng

là tâm quả cầu bán kính

Mặt cầu

 

tiếp xúc ngoài với

mặt cầu tâm

, , ,A B C D

nên

2, 3IA IB x IC ID x     

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 42

Gọi

 

lần lượt là các mặt phẳng trung trực đoạn

và

 

     

IA IB I P

I P Q

IC ID I Q

  



  



  





Tứ diện

ABCD

có

DA DB CA CB

   

suy ra

là đường vuông góc chung của

và

, suy ra

   

MN P Q

 

(2).

Từ

 

và

 

suy ra

I MN

Tam giác

IAM

có

 

2 2

2 4

IM IA AM x

    

Tam giác

CIN

có

 

2 2

3 9

IN IC CN x

    

Tam giác

ABN

có

2 2

NM NA AM  

Suy ra

   

2 2

3 9 2 4 12

x x x

       

Dạng 4. Bài toán cực trị

Câu 150. Chọn C

Ta có:

 

. . ;0;OM a i b k M a b

  

  

     

1 a;2;3 ; 6 ; 5;8 2 12 2 ;10; 16 2MA b MB a b MB a b

              

  

 

2 13;12; 13

MA MB a b    

 

   

2 2

2 13 12 13 12

MA MB a b

       

 

Vậy

min

2 12

MA MB





  







 

. Do đó

a b

 

Câu 151. Ta thấy

   

; ;0

M a b Oxy



Gọi

3 1

; ;2

2 2

 

 

 

là trung điểm của đoạn thẳng

, ta có

2 2

MA MB MA MB  

 

   

2 2

IA IM IB IM

   

   









2 2 2 2

2 . 2 .

IA IM IA IM IB IM IB IM

     

       

 

2 2 2 2

2 2 7

IM IA IM IA IB IM IM

       

  

Bởi vậy

2 2

MA MB

nhỏ nhất



ngắn nhất



là hình chiếu vuông góc của

trên mặt phẳng

 

Oxy

. Bởi vậy

3 1

; ;0

2 2

 

 

 

. Như vậy

3 1 3 1

, 2

2 2 2 2

a b a b

      

Câu 152.

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 43

Gọi

là điểm thỏa mãn

2 0

IA IB

 

  

(2 ;2 ;2 )

A B A B A B

I x x y y z z   

(5;5; 1)

 

Suy ra

là điểm cố định.

Suy ra P đạt giá trị nhỏ nhất khi

đạt giá trị nhỏ nhất, P đạt giá trị lớn nhất khi

đạt giá trị lớn nhất.

2 2 2

( ) :( 1) ( 2) ( 1) 9

S x y z

     

có tâm

(1;2; 1)



và bán kính



Suy ra



Mà

là điểm thay đổi trên

( )S

Do đó:

min

5 3 2

MI IM JI R

     

max

5 3 8

MI IM JI R

     

Suy ra

2 2

8 2 60

m n

   

Câu 153. Xét điểm

 

; ;I a b c

thỏa mãn

IA IB IC ID

   

    

. Khi đó

7 7

; ;0

4 2

 

 

 

Ta có

2 2 2 2

MA MB MC MD

  

       

2 2 2 2

MI IA MI IB MI IC MI ID

       

       

 

2 2 2 2 2

4 2

MI MI IA IB IC ID IA IB IC ID

        

    

2 2 2 2 2 2 2 2 2

MI IA IB IC ID IA IB IC ID

        

( vì



với mọi điểm

)

Dấu

" "

xảy ra

M I 

tức là

7 7 7 7

; ;0

4 2 4 2

M x y z

 

    

 

 



Câu 154. Gọi điểm

thỏa

2 0EA EB 

 



. Suy ra

là trung điểm của

, suy ra

 

3; 4; 5



Khi đó:

2 2

2MA MB 

   

2 2

ME EA ME EB

  

   

2 2 2

2ME EA EB   

Do đó

2 2

2MA MB

lớn nhất



nhỏ nhất



là hình chiếu của

 

3; 4; 5



lên

 

Oxy

 

3; 4; 0

 

Chú ý: Ta có thể làm trắc nghiệm như sau

+ Loại C vì

 

0; 0;5

không thuộc

 

Oxy

+ Lần lượt thay

3 1

; ; 0

2 2

 

















 

1 3

; ;0

2 2

 



















 

 

3; 4; 0



vào biểu thức

2 2

2MA MB

thì

 

3; 4; 0



cho

giá trị lớn nhất nên ta chọn

 

3; 4; 0



Câu 155. Xét điểm I sao cho:

2 0.

IA IB

 

  

Giả sử

 

; ; ,I x y z

ta có:

   

4 ;3 ;1 , 3 ;1 ;3 .IA x y z IB x y z

     

 

Do đó:

 

2 4 3

2 0 2 3 1 5;5; 1 .

2 1 3

x x

IA IB y y I

z z

  



       





  



  

Do đó:

2 2

2P MA MB 

   

2 2

MI IA MI IB

   

   





2 2 2 2

2 2 4 . 2 .MI IA MI IA MI IB MI IB

     

       

 

2 2 2

MI IA IB MI IA IB

    

     

 

2 2 2

MI IA IB MI IA IB

    

  

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 44

2 2 2

2 .MI IA IB

  

Do I cố định nên

2 2

,IA IB

không đổi. Vậy

lớn nhất (nhỏ nhất)



lớn nhất (nhỏ nhất).

MI

lớn

nhất (nhỏ nhất)

M

là giao điểm của đường thẳng IK (với

 

1;2; 1



là tâm của mặt cầu (S)) với mặt cầu

(S).

Ta có: MI đi qua

 

5;5; 1



và có vectơ chỉ phương là

 

4;3;0 .



Phương trình của MI là:

1 4

2 3

x t

y t

 





 





 



Tọa độ điểm M cần tìm ứng với giá trị t là nghiệm của phương trình:

     

2 2 2

1 4 1 2 3 2 1 1 9 25 9

t t t







           



 





Với

1 1

3 17 19

; ; 1 2 (min).

5 5 5

t M M I

 

    

 

 

Với

1 2

3 7 1

; ; 1 8 (max).

5 5 5

t M M I

 

      

 

 

Vậy

max

min

60.

m P

m n

n P

 



  



  



Câu 156. Gọi

là điểm thỏa

IA IB IC

  

   

 

2; 2;2

I 

2 2 2

MA MB MC

 

     

2 2 2

MI IA MI IB MI IC

     

     

 

2 2 2 2

3 2 .

MI IA IB IC MI IA IB IC

      

   

2 2 2 2

MI IA IB IC

   

Mà

 

M Oyz



2 2 2

MA MB MC

  

đạt giá trị nhỏ nhất



là hình chiếu của

lên

 

Oyz

 

0; 2;2

M 

Vậy

0 2 2 0

   

Câu 157. Gọi

 

; ;I x y z

là điểm thỏa

2 0

IA IB IC

  

   

Khi đó

     

2 0 2 0

IA IB IC OA OI OB OI OC OI

         

          

 

   

2 2;3;1 2;3;1

OI OA OB OC I     

   

Ta có

     

2 2

MA MB MC MI IA MI IB MI IC

       

        

2 2 2 2MI IA IB IC MI MI

     

    

MA MB MC

 

  

nhỏ nhất khi và chỉ khi

ngắn nhất, khi đó

là hình chiếu của

 

2;3;1

lên mặt

phẳng

 

Oyz

. Suy ra

 

0;3;1

Câu 158. Ta có:

 

2;7; 6

  



 

1;3; 2

 



 

1;6; 4

 



nên

, . 4 0

AB AC AD

 

  

 

  

Suy ra:



không đồng phẳng.

Gọi

là trọng tâm tứ diện

ABCD

. Khi đó

 

2;1;4

Ta có: 4 4

MA MB MC MD MG MG

    

    

Do đó

MA MB MC MD

  

   

nhỏ nhất khi và chỉ khi

ngắn nhất.

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 45

Vậy

là hình chiếu vuông góc của

lên mặt phẳng

 

Oyz

nên

 

0;1;4

Câu 159. Lấy

 

1;3; 1



là trọng tâm của tam giác

ABC

Ta có:

2 2 2

MA MB MC

 

     

2 2 2

MG GA MG GB MG GC

     

     

2 2 2 2

MG GA GB GC

   

Do đó

2 2 2

MA MB MC

 

bé nhất khi

bé nhất.

Hay

là hình chiếu của điểm

lên mặt phẳng

Oxy

Vậy

 

1;3;0

Câu 160. Gọi điểm

thỏa mãn

3 0

HA HB

 

  

khi đó:

1 3

A B

x x

y y

z z





































3 11 19

; ;

4 4 4

 

 

 

 

Phương trình mặt phẳng

 

Oxy

là



Xét

1 4

T  

do đó tọa độ điểm

cần tìm là:

M H

x x aT

y y bT

z z cT

 





 





 



3 11

; ;0

4 4

 

 

 

 

Vậy

M M M

T x y z  

3 11

0 2

4 4

    

Câu 161. Ta có

       

2 2 2

: 1 1 3 4

S x y z

     

 



có tâm

 

1;1;3

và bán kính

2R 

Bài ra

nằm trên mặt cầu

 

và



AMB

 

AB

qua

2 4

I AB R

  

Ta có

AMB

S MA MB



2 2

MA MB





 

Dấu

" "

xảy ra

2 2

MA MB    và

4AB 

Do đó diện tích tam giác

AMB

có giá trị lớn nhất bằng

Câu 162. Gọi

 

, ,A d e f

thì

thuộc mặt cầu

       

2 2 2

: 1 2 3 1

S x y z

     

có tâm

 

1;2;3

, bán

kính



 

, ,B a b c

thì

thuộc mặt cầu

     

2 2

: 3 2 9

S x y z

    

có tâm

 

3;2;0

I 

bán kính



. Ta có

1 2 1 2

I I R R  

 



và

 

không cắt nhau và ở ngoài nhau.

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489

guyễn Bảo Vương: https://www.facebook.com/phong.baovuong 46

Dễ thấy

F AB

max khi

,A A B B   Giá trị lớn nhất bằng

2 1 2

9I I R R   .

min khi

,A A B B   Giá trị nhỏ nhất bằng

2 1 2

1I I R R   .

Vậy

m 

Câu 163. Gọi

 

;

;M x y z

Ta có



3 2MA MB 

9 4MA MB 

           

2 2 2 2 2

2 2 2 4 3 3 3x y z x y z

   

           

   

2 2

12 12 12 0x y z x y z      

     

2 2

6 6 108x y z      

Như vậy, điểm

thuộc mặt cầu

 

tâm

 

;6; 6I  

và bán kính 108 6 3R   .

Do đó

lớn nhất bằng

   

6 6 6 6 3 12 3OI R       

Câu 164. Gọi

 

; ;E x y z

là điểm thỏa mãn

0EA EB EC  

   

Ta có

     

2 ;12 2 ;18 2 0;0;0 3;6;9x y z E    

3 2 2MA MB MC ME  

   

Mặt cầu

 

có tâm

 

1;2;3I

Đường thẳng

có PTTS

3 3

x t

y t

z t

 





 





 



   

;2 2 ;3 3M IE M t t t    

 

14 1M S t t     

 

1 1

1 2;4;6 , 14t M EM   .

 

2 2 1

1 0;0;0 , 3 14t M EM EM     .

Vậy 2 4 6

x y    .

Bấm Tải xuống để xem toàn bộ.

| 1/46

| | Tải xuống

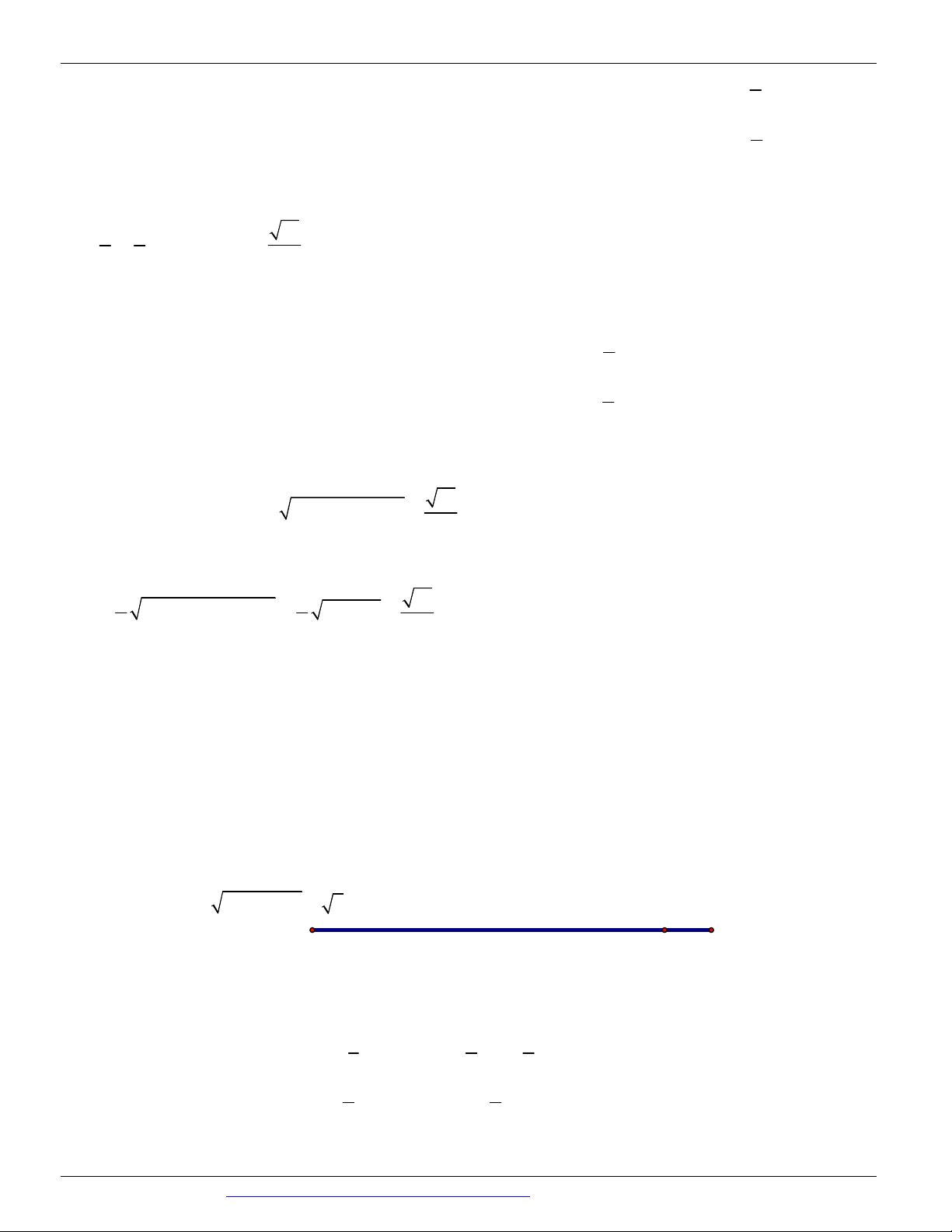
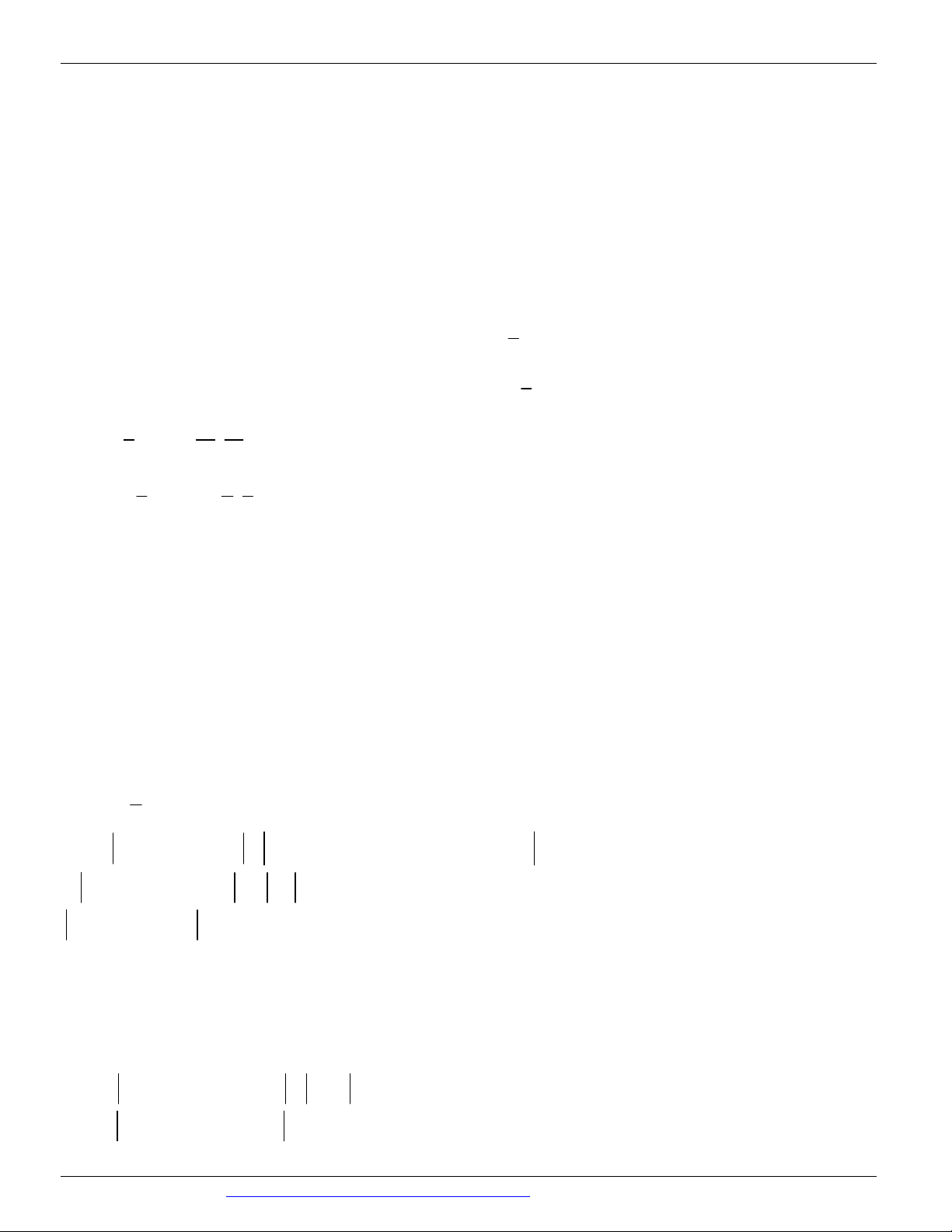
Preview text:

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 CHUYÊN
HỆ TRỤC TỌA ĐỘ OXYZ, PHƯƠNG TRÌNH MẶT CẦU ĐỀ 21 MỤC LỤC
PHẦN A. CÂU HỎI ......................................................................................................................................................... 1
Dạng 1. Tìm tọa độ điểm, véc tơ liên quan đến hệ trục tọa dộ OXYZ ............................................................................. 1
Dạng 2. Tích vô hướng, tích có hướng và ứng dụng ........................................................................................................ 8
Dạng 2.1 Tích vô hướng và ứng dụng .......................................................................................................................... 8
Dạng 2.2 Tích có hướng và ứng dụng .......................................................................................................................... 9
Dạng 3. Mặt cầu ............................................................................................................................................................. 10
Dạng 3. Xác định tâm, bán kính của mặt cầu ............................................................................................................. 10
Dạng 3. Viết phương trình mặt cầu ............................................................................................................................ 13
Dạng 3. Một số bài toán khác ..................................................................................................................................... 16
Dạng 4. Bài toán cực trị .................................................................................................................................................. 17
PHẦN B. LỜI GIẢI THAM KHẢO .............................................................................................................................. 19
Dạng 1. Tìm tọa độ điểm, véc tơ liên quan đến hệ trục tọa dộ OXYZ ........................................................................... 19
Dạng 2. Tích vô hướng, tích có hướng và ứng dụng ...................................................................................................... 27
Dạng 2.1 Tích vô hướng và ứng dụng ........................................................................................................................ 27
Dạng 2.2 Tích có hướng và ứng dụng ........................................................................................................................ 28
Dạng 3. Mặt cầu ............................................................................................................................................................. 31
Dạng 3. Xác định tâm, bán kính của mặt cầu ............................................................................................................. 31
Dạng 3. Viết phương trình mặt cầu ............................................................................................................................ 34
Dạng 3. Một số bài toán khác ..................................................................................................................................... 37
Dạng 4. Bài toán cực trị .................................................................................................................................................. 42 PHẦN A. CÂU HỎI
Dạng 1. Tìm tọa độ điểm, véc tơ liên quan đến hệ trục tọa dộ OXYZ
Câu 1. (Mã đề 102 BGD&ĐT NĂM 2018) Trong không gian Oxyz , cho hai điểm A1;1;  2 và B 2; 2;  1 . 
Vectơ AB có tọa độ là A.  1  ; 1;  3 B. 3;1  ;1 C. 1;1;3 D. 3;3;   1
Câu 2. (Mã đề 104 - BGD - 2019) Trong không gian Oxyz , hình chiếu vuông góc của điểm M 3;1;   1 trên
trục Oy có tọa độ là A. 3;0;  1 . B. 0;1; 0 . C. 3;0;0 . D. 0;0;   1 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 3. (Mã đề 101 BGD&ĐT NĂM 2018) Trong không gian Oxyz , cho hai điểm A2; 4
 ;3 và B2;2;7 .
Trung điểm của đoạn thẳng AB có tọa độ là A. 4; 2  ;10 B. 1;3; 2 C. 2;6; 4 D. 2; 1  ;5
Câu 4. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Trong không gian với hệ tọa độ Oxyz , cho các điểm A3; 4  ;0 , B  1
 ;1;3 , C 3,1,0 . Tìm tọa độ điểm D trên trục hoành sao cho AD  BC .
A. D 6;0;0 , D12;0;0
B. D 0;0;0 , D 6;0;0 C. D  2  ;1;0 , D  4  ; 0;0
D. D 0;0;0 , D  6  ; 0;0
Câu 5. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Trong không gian Oxyz, cho hai điểm A1;1;   1 
và B 2;3; 2 . Vectơ AB có tọa độ là A. 1; 2; 3 B.  1  ;  2; 3 C. 3;5  ;1 D. 3; 4  ;1
Câu 6. (Mã 103 - BGD - 2019) Trong không gian Oxyz , hình chiếu vuông góc của điểm M 2;1;   1 trên
trục Oy có tọa độ là A. 0;0;   1 . B. 2;0;   1 . C. 0;1;0 . D. 2;0;0 .
Câu 7. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Trong không gian với hệ toạ độ Oxyz , cho điểm A2; 2  ;1 .
Tính độ dài đoạn thẳng OA . A. OA  5 B. OA  5 C. OA  3 D. OA  9
Câu 8. (Mã 102 - BGD - 2019) Trong không gian Oxyz , hình chiếu vuông góc của điểm M 3; 1   ;1 trên trục
Oz có tọa độ là A. 3; 1  ;0 . B. 0;0  ;1 . C. 0; 1  ;0 . D. 3;0;0 .
Câu 9. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A3; 2  ;3 và B  1
 ; 2;5 . Tìm tọa độ trung điểm
I của đoạn thẳng AB . A. I 1;0; 4 . B. I 2;0;8 . C. I 2; 2  ;   1 . D. I  2  ; 2  ;1 .
Câu 10. (Mã đề 101 - BGD - 2019) Trong không gian Oxyz , hình chiếu vuông góc của điểm M 2;1;   1
trên trục Oz có tọa độ là A. 2;0;0 . B. 0;1; 0 . C. 2;1;0 . D. 0;0;  1 .
Câu 11. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A 2  ;3; 
1 và B 5; 6; 2 . Đường thẳng AB cắt AM
mặt phẳng Oxz tại điểm M . Tính tỉ số . BM AM AM AM 1 AM 1 A.  3 B.  2 C.  D.  BM BM BM 3 BM 2
Câu 12. (ĐỀ THAM KHẢO BGD & ĐT 2018) Trong không gian Oxyz , cho điểm A3; 1  ;  1 . Hình chiếu
vuông góc của điểm A trên mặt phẳng Oyz là điểm A. M 3;0;0 B. N 0; 1  ;  1 C. P0; 1  ;  0 D. Q 0;0;  1
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 13. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Trong không gian với hệ trục tọa       
độ Oxyz , cho ba vecto a 1; 2;3;b 2; 2;   1 ; c 4;0; 4
  . Tọa độ của vecto d  a  b  2c là    
A. d 7;0; 4 B. d 7;0; 4 C. d 7;0; 4 D. d 7;0; 4
Câu 14. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Trong không gian Oxyz, cho vectơ  a  2;2; 4
 , b  1; 1 
;1 . Mệnh đề nào dưới đây sai?    
A. a  b  3; 3; 3
B. a và b cùng phương    C. b  3 D. a  b
Câu 15. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Trong không gian Oxyz , cho hai điểm A0;1; 1  , 
B 2;3;2 . Vectơ AB có tọa độ là A. 2; 2;3 . B. 1; 2;3 . C. 3;5  ;1 . D. 3; 4  ;1 .
Câu 16. (THPT CẨM GIÀNG 2 NĂM 2018-2019) Trong không gian với hệ tọa độ Oxyz cho hai điểm A3; 2  ;3 và B  1
 ; 2;5 . Tìm tọa độ trung điểm I của đoạn thẳng AB là : A. I  2  ; 2;  1 . B. I 1;0; 4 . C. I 2;0;8 . D. I 2; 2  ;   1 .
Câu 17. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Trong không gian Oxyz cho    
a  2;3;2 và b  1;1; 
1 . Vectơ a  b có tọa độ là A. 3;4;  1 . B.  1  ;  2;3 . C. 3;5;  1 . D. 1;2;3 .
Câu 18. (TRƯỜNG THPT HOÀNG HOA THÁM HƯNG YÊN NĂM 2018-2019) Trong không gian với hệ       
trục tọa độ Oxyz , cho a  2; 3;3 , b  0;2;  
1 , c  3; 1;5 . Tìm tọa độ của vectơ u  2a  3b  2c . A. 10; 2;13 . B. 2; 2; 7   . C. 2; 2;7 . D. 2; 2;7 .
Câu 19. (TRƯỜNG THPT HOÀNG HOA THÁM HƯNG YÊN NĂM 2018-2019) Trong không gian với hệ
tọa độ Oxyz , cho A1;3; 2 , B 3; 1; 4 . Tìm tọa độ trung điểm I của A . B A. I 2; 4  ; 2 . B. I 4; 2;6 .
C. I 2; 1; 3 . D. I 2;1;3 .
Câu 20. (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Trong không gian với hệ trục
Oxyz cho ba điểm A 1  ;2;  3 , B1;0;  2 , C  ; x y; 
2 thẳng hàng. Khi đó x  y bằng 11 11
A. x  y  1 .
B. x  y  17 .
C. x  y   . D. x  y  . 5 5
Câu 21. (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Trong không gian với hệ trục     
tọa độ Oxyz , cho a  i  2 j  3k . Tọa độ của vectơ a là A. 1; 2; 3 . B. 2; 3; 1 . C. 2; 1; 3 . D. 3; 2; 1 .
Câu 22. (ĐỀ 15 LOVE BOOK NĂM 2018-2019) Trong không gian cho hệ trục toạ độ Oxyz , cho ba điểm A1; 2  ;3, B  1
 ; 2;5,C 0;0 
;1 . Tìm toạ độ trọng tâm G của tam giác ABC . A. G 0;0;3 . B. G 0;0;9 . C. G  1  ; 0;3 . D. G 0;0;  1 . 
Câu 23. (TT HOÀNG HOA THÁM - 2018-2019) Trong không gian với hệ tọa độ Oxyz , cho a  2;  3; 3      
, b  0; 2;  
1 , c  3; 1; 5 . Tìm tọa độ của vectơ u  2a  3b  2c .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. 10;  2;13 . B.  2  ; 2;  7 . C.  2  ;  2; 7 . D.  2  ; 2; 7 .
Câu 24. (TT HOÀNG HOA THÁM - 2018-2019) Trong không gian với hệ trục tọa độ Oxyz cho A1;3; 2
, B 3; 1; 4 . Tìm tọa độ trung điểm I của AB . A. I 2; 4  ; 2 . B. I 4;2;6 . C. I  2  ; 1  ;3 . D. I 2;1;3 .
Câu 25. (LIÊN TRƯỜNG THPT TP VINH NGHỆ AN NĂM 2018-2019) Trong không gian Oxyz , cho hai điểm A 1
 ;5; 2 và B 3; 3; 2 . Tọa độ trung điểm M của đoạn thẳng AB là A. M 1;1; 2 B. M 2; 2; 4 C. M 2;  4;0 D. M 4; 8;0
Câu 26. (THPT MINH KHAI HÀ TĨNH NĂM 2018-2019) Trong không gian với hệ tọa độ Oxyz , cho hai      vectơ x  2;1; 3
  và y  1;0;  
1 . Tìm tọa độ của vectơ a  x  2 y .    
A. a  4;1;   1 .
B. a  3;1; 4 .
C. a  0;1;   1 . D. a  4;1; 5   .
Câu 27. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Trong không gian Oxyz , cho hai điểm A2; 4
 ;3 và B 2;2;7 . Trung điểm của đoạn thẳng AB có tọa độ là A. 1;3; 2 . B. 2; 1  ;5 . C. 2; 1  ; 5   . D. 2;6; 4 .
Câu 28. (THPT CÙ HUY CẬN NĂM 2018-2019 LẦN 01) Trong không gian với hệ tọa độ Oxyz , cho các
điểm A1;0;3 , B 2;3;  4 , C  3
 ;1; 2 . Tìm tọa độ điểm D sao cho ABCD là hình bình hành. A. D  4  ;  2;9 . B. D 4; 2;9 .
C. D 4;  2;9 .
D. D 4; 2;  9 .
Câu 29. (THPT CÙ HUY CẬN NĂM 2018-2019 LẦN 01) Trong không gian với hệ tọa độ Oxyz , cho tam
giác ABC với A1;3; 4, B 2; 1;0,C 3;1; 2 . Tọa độ trọng tâm G của tam giác ABC là  2  A. G 2;1; 2 . B. G 6;3;6 . C. G 3; ;3   .
D. G 2; 1; 2 .  3 
Câu 30. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Trong không gian với hệ tọa độ
Oxyz cho tam giác ABC biết A5; 2  ;0, B  2
 ;3;0 , C 0; 2;3 . Trọng tâm G của tam giác ABC có tọa độ: A. 1; 2;  1 . B. 2;0;  1  . C. 1;1  ;1 . D. 1;1; 2   .
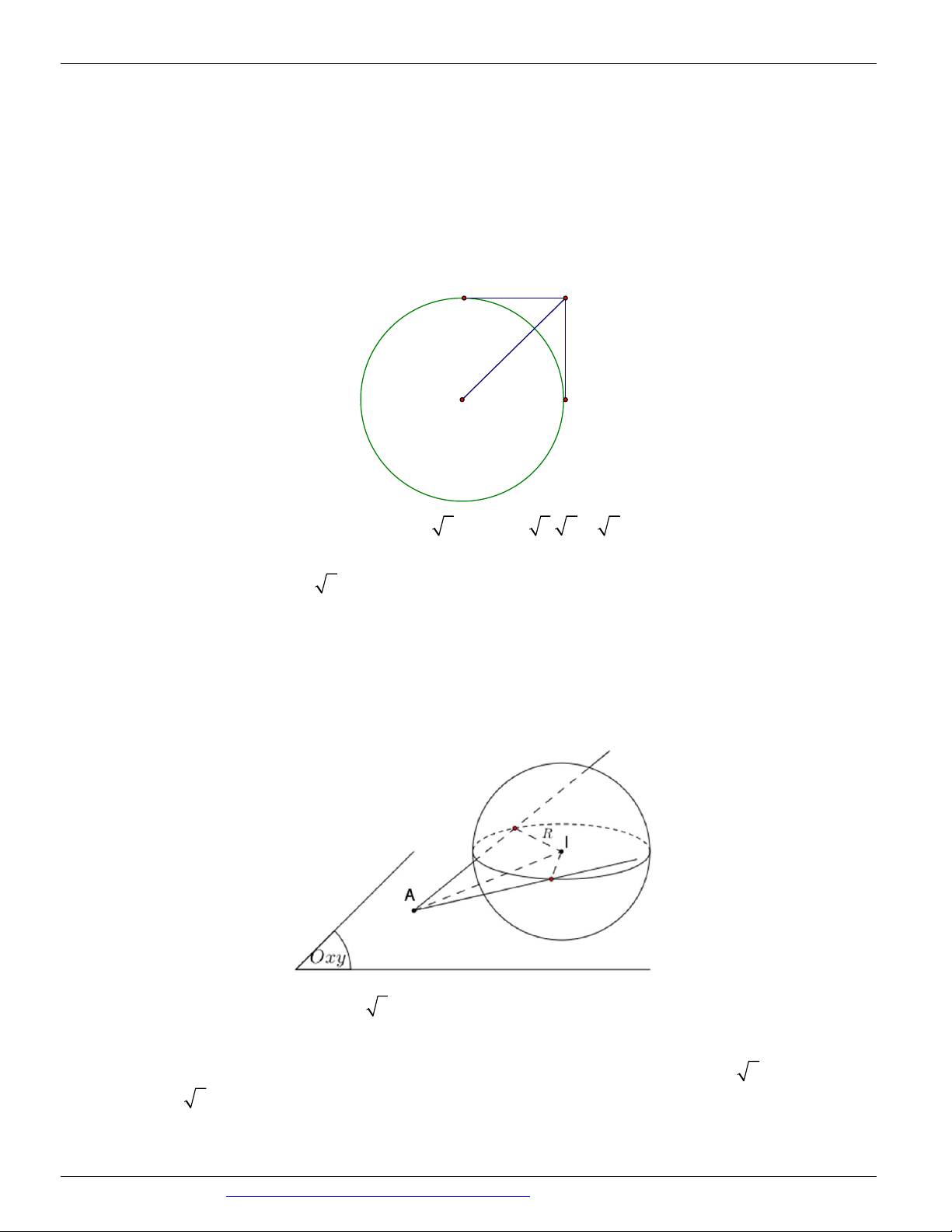
Câu 31. (THPT - YÊN ĐỊNH THANH HÓA 2018 2019- LẦN 2) Trong không gian O xyz , cho A2; 1  ;0  và B 1;1;  3 
. Vectơ AB có tọa độ là A. 3;0; 3   . B.  1  ; 2;   3 . C.  1  ; 2  ;  3 . D. 1; 2  ;3 .
Câu 32. (THPT - YÊN ĐỊNH THANH HÓA 2018 2019- LẦN 2) Trong không gian Oxyz , cho ba điểm
A1;0;0, B1;1;0,C 0;1; 
1 . Tìm tọa độ điểm D sao cho tứ giác ABCD (theo thứ tự các đỉnh) là hình bình hành? A. D 2;0;0 . B. D1;1;  1 . C. D 0;0;  1 . D. D 0;2;  1 .
Câu 33. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Trong không gian Oxyz cho A2; 2  ;1 , B 1; 1  ;3. Tọa  độ vecto AB là: A. (1;1; 2). . B. (3;3; 4). . C. (3; 3; 4).. D. (1; 1; 2)
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 34. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Trong không gian với hệ
tọa độ Oxyz , điểm nào sau đây nằm trên mặt phẳng tọa độ Oyz ? A. M 3;4;0 . B. P  2  ;0;3 . C. Q 2;0;0 . D. N 0; 4;   1 .
Câu 35. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Trong không gian Oxyz      
với i, j, k lần lượt là các vecto đơn vị trên các trục Ox, Oy, Oz. Tính tọa độ của vecto i  j  k.            
A. i  j  k  ( 1  ; 1
 ;1). B. i  j  k  (1;1;1). C. i  j  k  (1;1; 1). D. i  j  k  (1; 1;1).
Câu 36. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Trong không gian với hệ trục tọa độ Oxyz cho
M 4;5;6 . Hình chiếu của M xuống mặt phẳng Oyz là M. Xác định tọa độ M. A. M 4;5;0 . B. M 4;0;6 . C. M 4;0;0 . D. M 0;5;6 .
Câu 37. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Trong không gian với hệ trục tọa độ Oxyz cho
điểm M  x; y; z  . Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu M đối xứng với M qua mặt phẳng Oxz thì M  x; y; z .
B. Nếu M đối xứng với M qua Oy thì M  x; y; z .
C. Nếu M đối xứng với M qua mặt phẳng Oxy thì M  x; y; z .
D. Nếu M đối xứng với M qua gốc tọa độ O thì M 2x;2 y;0 .
Câu 38. (THPT GANG THÉP THÁI NGUYÊN NĂM 2018-2019) Trong không gian với hệ tọa độ Oxyz giả     
sử u  2i  3 j  k , khi đó tọa độ véc tơ u là A. 2;3;  1 . B. 2;3;  1  . C. 2; 3;   1 . D. 2;3;  1 .
Câu 39. (THPT CHUYÊN SƠN LA NĂM 2018-2019 LẦN 01) Trong không gian Oxyz , cho 2 điểm
M 1; 2;2 và N 1;0;4 . Toạ độ trung điểm của đoạn thẳng MN là: A. 1;1;3 . B. 0; 2; 2 . C. 2;  2;6 . D. 1;0;3 . 
Câu 40. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Trong không gian Oxyz , cho a  1; 2  ;1 và    
b  1;3;0 . Vectơ c  2a  b có tọa độ là A. 1; 7;2 . B. 1;5;2 . C. 3; 7;2 . D. 1; 7;  3 .
Câu 41. (KTNL GV BẮC GIANG NĂM 2018-2019) Trong mặt phẳng với hệ trục tọa độ Oxy , cho hai điểm A 3
 ; 4 và B 5;6 . Trung điểm của đoạn thẳng AB có tọa độ là A. 1;5 . B. 4  ;1 . C. 5  ;1 . D. 8; 2 .
Câu 42. (KTNL GV BẮC GIANG NĂM 2018-2019) Trong không gian với hệ tọa độ Oxyz , cho hai vectơ     
a  2;1;2 và vectơ b  1;0;2 . Tìm tọa độ vectơ c là tích có hướng của a và b .     A. c  2;6;  1 . B. c  4;6;  1 .
C. c  4;6;  1 .
D. c  2;6;  1 .
Câu 43. (KTNL GV THUẬN THÀNH 2 BẮC NINH NĂM 2018-2019) Trong không gian với trục hệ tọa độ     
Oxyz , cho a  i  2 j  3k. Tọa độ của vectơ a là:    
A. a 1; 2; 3 .
B. a 2; 3;   1 .
C. a 3; 2;   1 .
D. a 2; 1; 3 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 44. (THPT CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019 LẦN 01) Trong không gian
Oxyz , cho hai điểm A2; 4
 ;3 và B2;2;9 . Trung điểm của đoạn AB có tọa độ là  3 3  A. 0;3;3 . B. 4; 2  ;12 . C. 2; 1  ; 6 . D. 0; ;   .  2 2 
Câu 45. (SỞ GD&ĐT THANH HÓA NĂM 2018 - 2019) Trong không gian với hệ tọa độ Oxyz, cho hai điểm A 1; 3  ;  1 , B 3;0; 2
  . Tính độ dài AB . A. 26. B. 22. C. 26 . D. 22.
Câu 46. (LIÊN TRƯỜNG THPT TP VINH NGHỆ AN NĂM 2018-2019) Trong không gian Oxyz , cho hai điểm A 1
 ;5; 2 và B 3; 3; 2 . Tọa độ trung điểm M của đoạn thẳng AB là A. M 1;1; 2 B. M 2; 2; 4 C. M 2;  4;0 D. M 4; 8;0
Câu 47. (ĐỀ HỌC SINH GIỎI TỈNH BẮC NINH NĂM 2018-2019) Trong không gian với hệ tọa độ Oxyz ,    
cho các vectơ a  2; m 1;3,b  1;3; 2
 n . Tìm m, n để các vectơ a,b cùng hướng. 3 4
A. m  7; n   .
B. m  4; n  3  .
C. m  1; n  0 .
D. m  7; n   . 4 3
Câu 48. (THPT NGHĨA HƯNG NĐ- GK2 - 2018 - 2019) Trong không gian với hệ tọa độ Oxyz cho hai điểm
A1;5;3 và M 2;1;  2 . Tọa độ điểm B biết M là trung điểm của AB là  1 1  A. B ;3;   . B. B 4;9;8 .  2 2  C. B 5;3; 7 . D. B 5; 3  ; 7   .
Câu 49. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Trong không gian với hệ trục tọa
độ Oxyz , cho ba điểm (
A 1; 2; 1), B(2; 1;3) và C(3; 5;1) . Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành. A. D(2;8; 3) B. D(4;8; 5) C. D(2; 2;5) D. D(4;8; 3)
Câu 50. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Trong không gian với hệ tọa độ  
Oxyz , cho 2 điểm B 1; 2; 3   , C 7; 4; 2
  Nếu điểm E thỏa nãm đẳng thức CE  2EB thì tọa độ điẻm E là:  8 8   8 8   8   1  A. 3; ;    B. ;3;    . C. 3;3;    D. 1; 2;    3 3   3 3   3   3 
Câu 51. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Trong mặt phẳng với hệ tọa độ
Oxyz , Tam giác ABC với A1; 3  ;3 ; B 2; 4
 ;5 , C a; 2
 ;b nhận điểm G 1; ;
c 3 làm trọng tâm của nó
thì giá trị của tổng a  b  c bằng. A. 5  B. 3 C. 1 D. 2 
Câu 52. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Trong không gian với hệ tọa độ
Oxyz , cho ba điểm A 2; 1;5, B 5; 5;7, M  x; y 
;1 . Với giá trị nào của , x y thì ,
A B, M thẳng hàng.
A. x  4; y  7 B. x  4  ; y  7 
C. x  4; y  7  D. x  4  ; y  7
Câu 53. (KTNL GIA BÌNH NĂM 2018-2019) Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC với A1; 2; 3
  , B 2;5;7 , C  3
 ;1; 4 . Điểm D để tứ giác ABCD là hình bình hành là
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  8 8  A. D 6;6;0 B. D 0; ;   C. D 0;8;8 D. D  4  ; 2  ; 6    3 3 
Câu 54. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Trong không gian Oxyz , tọa độ
điểm đối xứng của M  ; 1 ; 2 
3 qua mặt phẳng Oyz  là
A. 0;2;3 . B. 1; 2  ; 3 . C.  1  ;2;3 . D. 1;2; 3   .
Câu 55. (THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019 LẦN 1) Cho tam giác ABC có A1; 2  ; 0
, B 2;1; 2 , C 0;3; 4 . Tìm tọa độ điểm D để tứ giác ABCD là hình bình hành. A. 1;0; 6   . B. 1;6; 2 . C.  1  ; 0;6 . D. 1;6; 2   .
Câu 56. (LIÊN TRƯỜNG THPT TP VINH NGHỆ AN NĂM 2018-2019) Trong không gian Oxyz , cho hai
điểm A3;1;  2 , B 2;  3;5 . Điểm M thuộc đoạn AB sao cho MA  2MB , tọa độ điểm M là  7 5 8   3 17  A. ;  ;   . B. 4;5;  9 . C. ;  5;   . D. 1; 7  ;12 .  3 3 3   2 2 
Câu 57. (THPT MINH KHAI HÀ TĨNH NĂM 2018-2019) Trong không gian với hệ trục tọa độ Oxyz , cho   hai điểm A0;1; 2   và B3; 1  
;1 . Tìm tọa độ điểm M sao cho AM  3AB . A. M 9; 5  ;7 . B. M 9;5;7 . C. M  9  ;5; 7   . D. M 9; 5  ; 5   .
Câu 58. (THPT QUỲNH LƯU 3 NGHỆ AN NĂM 2018-2019) Trong không gian Oxyz , cho hai điểm A2; 2 
;1 , B 0;1;2 . Tọa độ điểm M thuộc mặt phẳng Oxy sao cho ba điểm A , B , M thẳng hàng là
A. M 4;  5;0 .
B. M 2;  3;0 . C. M 0;0;  1 . D. M 4;5;0 .
Câu 59. (THPT YÊN KHÁNH - NINH BÌNH - 2018 - 2019) Trong không gian với hệ tọa độ Oxyz cho các       
véc tơ u  2i  2 j  k , v   ; m 2; m  
1 với m là tham số thực. Có bao nhiêu giá trị của m để u  v . A. 0 . B. 1. C. 2 . D. 3 .
Câu 60. (CHUYÊN PHAN BỘI CHÂU NĂM 2018-2019) Trong không gian với hệ trục tọa độ Oxyz , cho 
hai điểm A1; 2;   1 , AB  1;3 
;1 thì tọa độ của điểm B là: A. B 2;5;0 . B. B 0; 1  ; 2   . C. B 0;1; 2 . D. B  2  ; 5  ; 0
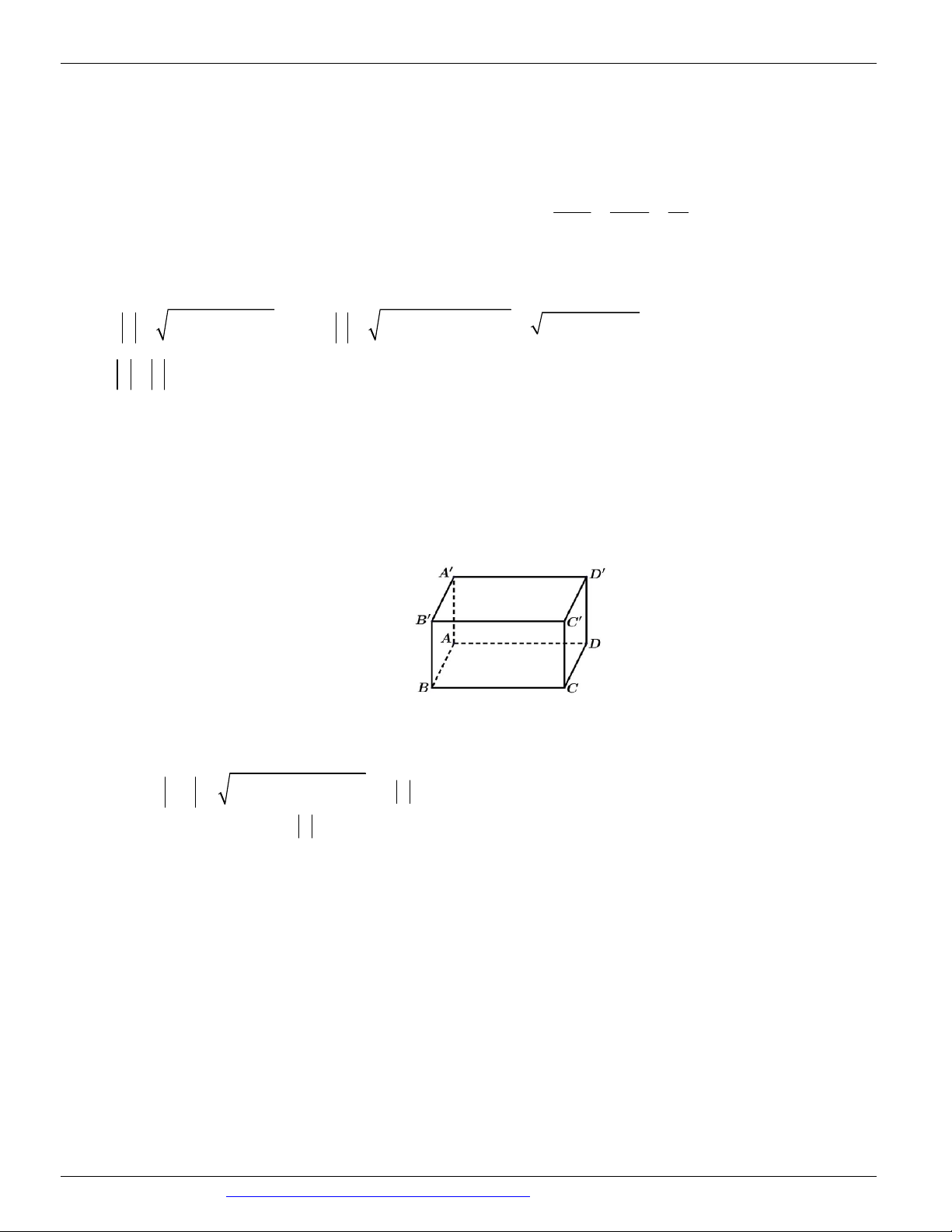
Câu 61. (CHUYÊN ĐHSP HÀ NỘI NĂM 2018-2019 LẦN 01) Trong không gian với hệ tọa độ Oxyz , cho hình hộp ABC . D A B  C  D
  có A0;0;0 , B a;0;0 ; D 0; 2a;0 , A0;0; 2a với a  0 . Độ dài đoạn thẳng AC là 3 A. a . B. 2 a . C. 3 a . D. a . 2
Câu 62. (CHUYÊN KHTN LẦN 2 NĂM 2018-2019) Trong không gian Oxyz , cho A3;1; 2 , tọa độ điểm
A ' đối xứng với điểm A qua trục Oy là A. 3; 1; 2 . B. 3; 1; 2 . C. 3;1; 2 . D. 3; 1; 2 .
Câu 63. Trong không gian Oxyz , cho ba điểm A3;1;0 , B 0; 1
 ; 0 , C 0;0; 6
  . Nếu tam giác A B  C   có
   
các đỉnh thỏa mãn hệ thức A A   B B   C C
  0 thì tam giác A B  C
  có tọa độ trọng tâm là
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. 3; 2  ;0 . B. 2; 3  ;0 . C. 1;0; 2   . D. 3; 2  ;  1 .
Câu 64. (ĐỀ THI CÔNG BẰNG KHTN LẦN 02 NĂM 2018-2019) Trong không gian Oxyz , cho hình bình
hành ABCD . Biết A  1;0 
;1 , B  2;1; 2 và D  1; 1 
;1 . Tọa độ điểm C là A. 2;0; 2 . B. 2; 2; 2 . C. 2;  2; 2 . D. 0;  2;0 .
Câu 65. (SỞ GD&ĐT PHÚ THỌ NĂM 2018-2019 LẦN 01) Trong không gian với hệ tọa độ Oxyz, cho hai  8 4 8 
điểm A1; 2;  2 và B ; ;   . Biết I  ; a ;
b c là tâm của đường tròn nội tiếp tam giác OAB . Giá trị  3 3 3 
a  b  c bằng A. 1 B. 3 C. 2 D. 0
Câu 66. (CHUYÊN ĐHSP HÀ NỘI NĂM 2018-2019 LẦN 01) Trong không gian tọa độ Oxyz , cho
A2;0;0, B 0;2;0,C 0;0;2 . Có tất cả bao nhiêu điểm M trong không gian thỏa mãn M không trùng với    các điểm ,
A B,C và AMB  BMC  CMA  90 ? A. 0 . B. 1. C. 2 . D. 3 .
Dạng 2. Tích vô hướng, tích có hướng và ứng dụng
Dạng 2.1 Tích vô hướng và ứng dụng
Câu 67. (MĐ 105 BGD&ĐT NĂM 2017) Trong không gian với hệ trục tọa độ Oxyz , cho hai vectơ    
a  2;1; 0 và b  1; 0; 2 . Tính cos a, b .   2   2   2   2
A. cos a, b  
B. cos a,b  
C. cos a,b 
D. cos a,b  25 5 25 5
Câu 68. (MĐ 104 BGD&DT NĂM 2017) Trong không gian với hệ tọa độ Oxyz cho ba điểm M 2;3;   1 , N 1;1; 
1 và P 1; m 1; 2 . Tìm m để tam giác MNP vuông tại N . A. m  2 B. m  6  C. m  0 D. m  4 
Câu 69. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Trên mặt phẳng toạ độ Oxy , cho tam giác
ABC biết A1; 3 , B 2; 2 , C 3;1 . Tính cosin góc A của tam giác. 2 1 2 1 A. cos A  B. cos A  C. cos A   D. cos A   17 17 17 17
Câu 70. (THPT QUỲNH LƯU 3 NGHỆ AN NĂM 2018-2019) Trong không gian Oxyz , góc giữa hai vectơ  
i và u   3; 0;  1 là A. 120 . B. 60 . C. 150 . D. 30 .
Câu 71. (THPT CHUYÊN ĐẠI HỌC VINH NĂM 2018-2019 LẦN 01) Trong không gian Oxyz , cho    
a  3; 4;0 , b  5;0;12 . Côsin của góc giữa a và b bằng 3 5 5 3 A. . B. . C.  . D.  . 13 6 6 13
Câu 72. (CHUYÊN ĐHSP HÀ NỘI NĂM 2018-2019 LẦN 01) Trong không gian tọa độ Oxyz góc giữa hai  
vectơ i và u   3;0;  1 là A. 120 . B. 30 . C. 60 . D. 150 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 73. (CHUYÊN NGUYỄN TẤT THÀNH YÊN BÁI LẦN 01 NĂM 2018-2019) Trong không gian với    
hệ tọa độ Oxyz , cho vectơ u  3;0; 
1 và v  2;1;0 . Tính tích vô hướng u.v .         A. . u v  8 . B. . u v  6 . C. . u v  0 . D. . u v  6  .
Câu 74. (CHUYÊN HƯNG YÊN NĂM 2018-2019 LẦN 03) Trong không gian tọa độ Oxyz , góc giữa hai  
vectơ i và u   3;0;  1 là A. 0 30 . B. 0 120 . C. 0 60 . D. 0 150 .
Câu 75. (CHUYÊN TRẦN PHÚ HẢI PHÒNG NĂM 2018-2019 LẦN 02) Trong không gian Oxyz, cho ba điểm ( A 1  ; 2
 ;3) B(0;3;1) , C(4; 2; 2) . Cosin của góc  BAC là 9 9 9 9 A. . B.  . C.  . D. . 35 35 2 35 2 35
Câu 76. (THPT YÊN KHÁNH - NINH BÌNH - 2018 - 2019) Trong không gian Oxyz cho các điểm
A5;1;5; B 4;3; 2; C 3; 2  
;1 . Điểm I a; ;
b c  là tâm đường tròn ngoại tiếp tam giác ABC . Tính
a  2b  c ? A. 1. B. 3. C. 6. D. 9.
Câu 77. (THPT NGÔ SĨ LIÊN BẮC GIANG NĂM 2018-2019 LẦN 01) Trong không gian với hệ tọa độ
Oxyz , cho tam giác ABC có A1;0;0 , B 0;0;  1 , C 2;1 
;1 . Diện tích của tam giác ABC bằng: 11 7 6 5 A. B. C. D. 2 2 2 2
Câu 78. (ĐỀ HỌC SINH GIỎI TỈNH BẮC NINH NĂM 2018-2019) Trong không gian với hệ tọa độ Oxyz ,    
cho véc tơ u  1;1; 2
 , v  1;0;m . Tìm tất cả giá trị của m để góc giữa u , v bằng 45 . A. m  2 . B. m  2  6 . C. m  2  6 . D. m  2  6 .
Dạng 2.2 Tích có hướng và ứng dụng
Câu 79. (ĐỀ GK2 VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Trong hệ trục tọa độ Oxyz , cho tứ diện ABCD
biết A3;  2; m , B 2;0;0 , C 0; 4;0 , D 0;0;3 . Tìm giá trị dương của tham số m để thể tích tứ diện bằng 8. A. m  8 . B. m  4 . C. m  12 . D. m  6 .
Câu 80. (ĐỀ GK2 VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Trong hệ trục tọa độ Oxyz , cho bốn điểm (
A 1;  2;0) , B(2;0;3) , C( 2
 ;1;3) và D(0;1;1) . Thể tích khối tứ diện ABCD bằng: A. 6 . B. 8 . C. 12 . D. 4 .
Câu 81. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Trong không gian với hệ tọa độ    
Oxyz , cho u  1;1; 2, v  1; ;
m m  2 . Khi u  ,v  14   thì 11 11
A. m  1 hoặc m   B. m  1  hoặc m   5 3
C. m  1 hoặc m  3  D. m  1 
Câu 82. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Trong không gian với hệ trục tọa
độ Oxyz , cho tứ diện ABCD có A2; 1; 
1 , B 3;0; 1 , C  2; 1; 3 , D  Oy và có thể tích bằng 5 . Tính
tổng tung độ của các điểm D . A. 6  B. 2 C. 7 D. 4
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 
Câu 83. (HỌC MÃI NĂM 2018-2019-LẦN 02) Trong không gian với hệ toạ độ Oxyz , cho a  1; 2  ; 3 và
b  1;1; 1. Khẳng định nào sau đây sai?        
A. a  b  3 . B. . a b  4  .
C. a  b  5 .
D. a,b   1  ; 4  ;3   .
Câu 84. (TOÁN HỌC TUỔI TRẺ NĂM 2018 - 2019 LẦN 01) Trong không gian với hệ tọa độ Oxyz , cho điểm A1; 2  ;  0 , B1;0;  1 , C 0; 1  ;  2 , D 2  ; ;
m n . Trong các hệ thức liên hệ giữa m và n dưới đây,
hệ thức nào để bốn điểm , A ,
B C, D đồng phẳng?
A. 2m  n  13 .
B. 2m  n  13 .
C. m  2n  13 .
D. 2m 3n  10 .
Câu 85. (CHUYÊN TRẦN PHÚ HẢI PHÒNG NĂM 2018-2019 LẦN 02) Trong không gian Oxyz, cho hai
điểm A1;0;   1 , B 1; 1
 ; 2 . Diện tích tam giác OAB bằng 6 11 A. 11. B. . C. . D. 6. 2 2   
Câu 86. Trong không gian Oxyz , cho hai véc tơ m  4 ; 3 ; 
1 và n  0 ; 0 ; 
1 . Gọi p là véc tơ cùng hướng    
với m , n và p  15 . Tọa độ của véc tơ p là   A. 9 ; 12 ; 0 . B. 0 ; 9 ; 12   . C.  9  ; 12 ; 0 . D. 0 ; 9 ; 12 .
Câu 87. (ĐỀ THI GIỮA KỲ II YÊN PHONG 1 - 2018) Trong không gian Oxyz , cho 4 điểm A2;0; 2 , B 1; 1  ; 2 , C  1  ;1; 0 , D  2
 ;1; 2 . Thể tích của khối tứ diện ABCD bằng 42 14 21 7 A. . B. . C. . D. . 3 3 3 3
Câu 88. (ĐỀ GK2 VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Trong hệ trục tọa độ Oxyz , cho bốn điểm A0;  2; 
1 ; B 1; 0;  2;C 3;1;  2; D 2;  2;   1 . Câu nào sau đây sai? A. Bốn điểm ,
A B, C, D không đồng phẳng.
B. Tam giác ACD là tam giác vuông tại A .  
C. Góc giữa hai véctơ AB và CD là góc tù.
D. Tam giác ABD là tam giác cân tại B .
Câu 89. (THPT LƯƠNG THẾ VINH - HN - LẦN 1 - 2018) Trong không gian Oxyz , cho ba điểm A 2  ;3  ;1
, B 2;1;0 , C  3  ; 1  
;1 . Tìm tất cả các điểm D sao cho ABCD là hình thang có đáy AD và S  3S ABCD ABC . D 8; 7  ;1 D 8;7;   1 A. D 8;7;   1 . B.  . C.  . D. D  1  2; 1  ;3 . D 12;1; 3   
D  12; 1;3  Dạng 3. Mặt cầu
Dạng 3. Xác định tâm, bán kính của mặt cầu
Câu 90. (MĐ 104 BGD&DT NĂM 2017) Trong không gian với hệ toạ độ Oxyz , cho mặt cầu
S  x   y  2   z  2 2 : 2 2
 8 . Tính bán kính R của S  . A. R  2 2 B. R  64 C. R  8 D. R  4 Câu 91. (Mã đề 104 BGD&ĐT NĂM 2018) Trong không gian Oxyz , mặt cầu
S   x  2   y  2   z  2 : 5 1 2  3 có bán kính bằng A. 9 B. 2 3 C. 3 D. 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 92. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Trong không gian hệ tọa độ Oxyz , tìm tất cả các giá trị của m để phương trình 2 2 2
x  y  z  2x  2y  4z  m  0 là phương trình của một mặt cầu. A. m  6 B. m  6 C. m  6 D. m  6
Câu 93. (MĐ 105 BGD&ĐT NĂM 2017) Trong không gian với hệ toạ độ Oxyz , cho mặt cầu S  2 2 2
: x  5   y  1  z  2  9 . Tính bán kính R của S . A. R  6 B. R  3 C. R  18 D. R  9
Câu 94. (MĐ 103 BGD&ĐT NĂM 2017-2018) Trong không gian Oxyz , cho mặt cầu
S   x  2   y  2   z  2 : 3 1 1
 2 . Tâm của  S  có tọa độ là A. 3; 1   ;1 B.  3  ; 1   ;1 C.  3  ;1;   1 D. 3;1;  1 
Câu 95. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Trong không gian với hệ trục tọa độ Oxyz , tìm tọa độ 2 2 2
tâm I và bán kính R của mặt cầu  x   1
  y  2   z  4  20 .
A. I 1; 2; 4, R  2 5 B. I 1; 2  ; 4, R  20
C. I 1; 2; 4, R  2 5 D. I 1; 2; 4, R  5 2
Câu 96. (Mã đề 101 - BGD - 2019) Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x  y  z  2x  2z  7  0
. Bán kính của mặt cầu đã cho bằng A. 3 . B. 15 . C. 7 . D. 9 .
Câu 97. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Trong không gian Oxyz cho hai điểm I 1;1  ;1 và
A1; 2;3 . Phương trình mặt cầu có tâm I và đi qua A là 2 2 2 2 2 2 A.  x   1   y   1   z   1  5 B.  x   1   y   1   z   1  29 2 2 2 2 2 2 C.  x   1   y   1   z   1  5 D.  x   1   y   1   z   1  25
Câu 98. (Mã đề 104 - BGD - 2019) Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x  y  z  2 y  2z  7  0
. Bán kính của mặt cầu đã cho bằng A. 15 . B. 7 . C. 9 . D. 3 .
Câu 99. (Mã 102 - BGD - 2019) Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x  y  z  2x  2 y  7  0.
Bán kính của mặt cầu đã cho bằng A. 7 . B. 9 . C. 15 . D. 3 .
Câu 100. (Mã 103 - BGD - 2019) Trong không gian Oxyz , cho mặt cầu 2 2 2
(S) : x  y  z  2 y  2z  7  0.
Bán kính của mặt cầu đã cho bằng A. 7 . B. 3 . C. 9. D. 15 .
Câu 101. (TRƯỜNG THPT HOÀNG HOA THÁM HƯNG YÊN NĂM 2018-2019) Trong không gian với
hệ tọa độ Oxyz , cho mặt cầu S  2 2 2
: x  y  z  8x  2 y 1  0 . Tìm tọa độ tâm và bán kính của mặt cầu S  .
A. I  –4;1;0, R  2.
B. I  –4;1;0, R  4.
C. I 4; –1;0, R  2.
D. I 4; –1;0, R  4.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 102. (THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019 LẦN 1) Cho mặt cầu S  2 2 2
: x  y  z  2x  4 y  2z  3  0 . Tính bán kính R của mặt cầu S  . A. R  3 . B. R  3 . C. R  9 . D. R  3 3 .
Câu 103. (TT HOÀNG HOA THÁM - 2018-2019) Trong không gian vơi hệ tọa độ Oxyz , cho mặt cầu S  2 2 2
: x  y  z  8x  2 y 1  0 . Tìm tọa độ tâm và bán kính mặt cầu S  :
A. I 4;1;0, R  2 .
B. I 4;1;0, R  4 . C. I 4; 1;0, R  2 . D. I 4; 1;0, R  4 .
Câu 104. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Trong không gian Oxyz , cho mặt cầu
S   x  2   y  2   z  2 : 3 1 1
 2 . Xác định tọa độ tâm của mặt cầu  S  A. I  3  ;1;   1 . B. I 3;1;   1 . C. I  3  ; 1   ;1 . D. I 3; 1   ;1 .
Câu 105. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x  y  z  2x  4 y  2z  3  0 . Tọa độ tâm I của mặt cầu  S  là: A. 1; 2;  1 . B. 2;  4;  2 . C. 1;  2;   1 . D.  2  ; 4; 2 .
Câu 106. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x  y  z  8x 10 y  6z  49  0 . Tính bán kính R của mặt cầu  S  . A. R  1 . B. R  7 . C. R  151 . D. R  99 . Câu 107. (ĐỀ 04 VTED NĂM 2018-2019) Trong không gian Oxyz , mặt cầu S  2 2 2
: x  y  z  4x  2 y  6z  1  0 có tâm là A. 4; 2;  6 B. 2; 1;3 C. 2;1;  3 D. 4;  2;6
Câu 108. (THPT GANG THÉP THÁI NGUYÊN NĂM 2018-2019) Trong không gian với hệ tọa độ Oxyz , 2 2 2
cho mặt cầu có phương trình  x  
1   y  2   z   3
 4 . Tìm tọa độ tâm I và bán kính R của mặt cầu đó. A. I 1;2; 3
  ; R  2 . B. I 1;2; 3   ; R  4 . C. I 1; 2;  3 ; R  2 . D. I 1; 2;  3 ; R  4 .
Câu 109. (KTNL GV BẮC GIANG NĂM 2018-2019) Trong không gian với hệ tọa độ Oxyz , cho mặt cầu
(S ) có phương trình 2 2 2
x  y  z  4x  2 y  4  0 .Tính bán kính R của (S ). A. 1. B. 9 . C. 2 . D. 3 .
Câu 110. (THPT CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019 LẦN 01) Trong không gian 2 2 2
Oxyz , cho mặt cầu S   : x   3  y   1 z  
1  4 . Tâm của S có tọa độ là A.  3  ;1;  1 . B. 3; 1   ;1 . C. 3; 1  ;  1 . D. 3;1;  1  .
Câu 111. (SỞ GD&ĐT PHÚ THỌ NĂM 2018-2019 LẦN 01) Trong không gian Oxyz , có tất cả bao nhiêu
giá nguyên của m để 2 2 2
x  y  z  m   x  m   2 2 2 2
1 z  3m  5  0 là phương trình một mặt cầu? A. 4 B. 6 C. 5 D. 7
Câu 112. (ĐỀ 15 LOVE BOOK NĂM 2018-2019) Trong không gian với hệ trục tọa độ Oxyz , tìm tất cả các
giá trị của m để phương trình 2 2 2
x  y  z  2 m  2 x  4my 19m  6  0 là phương trình mặt cầu. A. 1  m  2 .
B. m  1 hoặc m  2 . C. 2   m  1. D. m  2  hoặc m  1.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 113. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Trong không gian Oxyz có tất
cả bao nhiêu giá trị nguyên m để phương trình 2 2 2 2
x  y  z  4mx  2my  2mz  9m  28  0 là phương trình mặt cầu? A. 7 . B. 8 . C. 9 . D. 6 . Câu 114. Trong không gian Oxyz , xét mặt cầu S  có phương trình dạng 2 2 2
x  y  z  4x  2y  2az 10a  0 . Tập hợp các giá trị thực của a để S  có chu vi đường tròn lớn bằng 8 là A. 1  ;10 . B. 2;   10 . C. 1;1  1 . D. 1; 1  1 .
Câu 115. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Trong không gian với hệ tọa độ Oxyz ,
cho A1;0;0 , B 0;0; 2 , C 0; 3;0 . Tính bán kính mặt cầu ngoại tiếp tứ diện OABC là 14 14 14 A. B. C. D. 14 3 4 2
Câu 116. (THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019 LẦN 1) Gọi S  là mặt cầu đi qua 4 điểm
A2; 0;0, B 1;3; 0,C 1; 0;3, D 1; 2;3 . Tính bán kính R của S  . A. R  2 2 . B. R  3 . C. R  6 . D. R  6 . Lời giải
Câu 117. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho hai điểm ,
A B cố định trong không gian có độ dài
AB là 4 . Biết rằng tập hợp các điểm M trong không gian sao cho MA  3MB là một mặt cầu. Bán kính mặt cầu đó bằng 9 3 A. 3 . B. . C. 1. D. . 2 2
Câu 118. (SỞ GD&ĐT BÌNH PHƯỚC - LẦN 1 - 2018) Trong không gian với hệ trục Oxyz , cho phương trình 2 2 2
x  y  z  m   2 2
2 x  4my  2mz  5m  9  0 . Tìm các giá trị của m để phương trình trên là
phương trình của một mặt cầu. A. m  5
 hoặc m  1 . B. 5  m  1 . C. m  5  . D. m  1 .
Câu 119. (ĐỀ THI GIỮA KỲ II YÊN PHONG 1 - 2018) Trong không gian Oxyz . Cho tứ diện đều ABCD
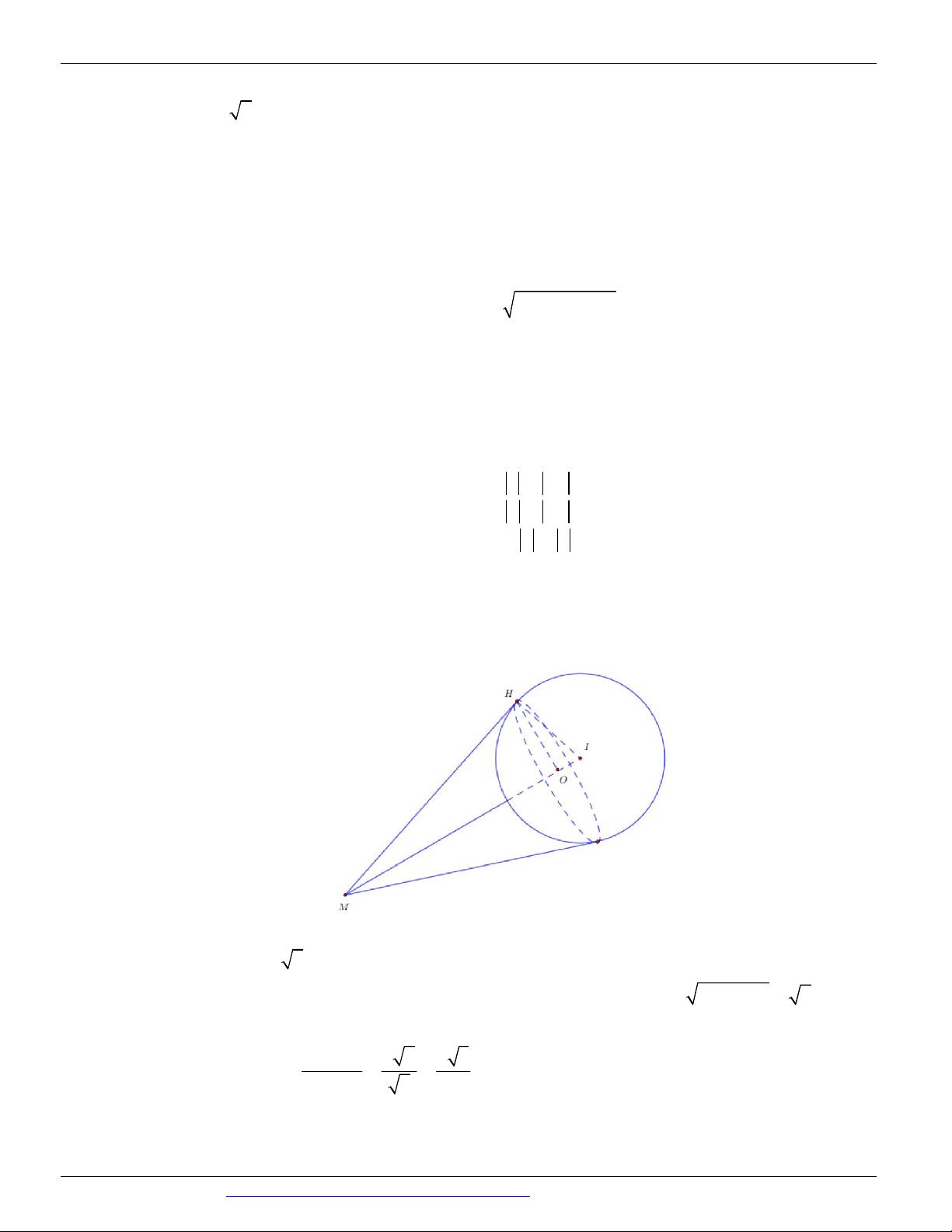
có A0;1; 2 và hình chiếu vuông góc của A trên mặt phẳng  BCD là H 4;  3;  2 . Tìm tọa độ tâm I của
mặt cầu ngoại tiếp tứ diện ABCD .
A. I 3;  2;   1 . B. I 2; 1;0 . C. I 3;  2  ;1 . D. I  3  ;  2  ;1 .
Dạng 3. Viết phương trình mặt cầu
Câu 120. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Trong không gian Oxyz cho hai điểm I 1;1  ;1
và A1; 2;3 . Phương trình mặt cầu có tâm I và đi qua A là 2 2 2 2 2 2 A.  x   1   y   1   z   1  5 B.  x   1   y   1   z   1  29 2 2 2 2 2 2 C.  x   1   y   1   z   1  5 D.  x   1   y   1   z   1  25
Câu 121. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Trong không gian với hệ tọa độ Oxyz , cho điểm M 1; 2; 3
. Gọi I là hình chiếu vuông góc của M trên trục Ox . Phương trình nào dưới đây là phương trình mặt cầu tâm
I bán kính IM ?
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 2 A. x    2 y  2 1 z  13 B. x    2 y  2 1 z  17 2 2 C. x    2 y  2 1 z  13 D. x    2 y  2 1 z  13
Câu 122. (THPT CÙ HUY CẬN NĂM 2018-2019 LẦN 01) Trong không gian với hệ tọa độ Oxyz , cho hai điểm A1; 2
 ; 7, B 3;8;  
1 . Mặt cầu đường kính AB có phương trình là 2 2 2 2 2 2 A.  x  
1   y  3   z  3  45 . B.  x  
1   y  3   z  3  45 . 2 2 2 2 2 2 C.  x  
1   y  3   z  3  45 . D.  x  
1   y  3   z  3  45 .
Câu 123. (THPT - YÊN ĐỊNH THANH HÓA 2018 2019- LẦN 2) Trong không gian với hệ tọa độ Oxyz ,
viết phương trình mặt cầu có tâm I 1; 4; 
3 và đi qua điểm A5;3;2 . A.  2 2 2
x  2   y  2   z  2 1 4 3  18 . B.  x   1
  y  4   z  3  16 . C.  2 2 2
x  2   y  2   z  2 1 4 3  16 . D.  x   1
  y  4   z  3  18 .
Câu 124. (THPT CHUYÊN SƠN LA NĂM 2018-2019 LẦN 01) Trong không gian Oxyz , cho hai điểm A1;1 
;1 và B 1; 1;3 . Phương trình mặt cầu có đường kính AB là 2 2 2 2 A.  x   2 1
 y   z  2  8 . B.  x   2 1
 y   z  2  2 . 2 2 2 2 C.  x   2 1
 y   z  2  2 . D.  x   2 1
 y   z  2  8 .
Câu 125. (SỞ GD&ĐT THANH HÓA NĂM 2018 - 2019) Trong không gian Oxyz, cho hai điểm A(2;4;1), B  2  ; 2; 3
  . Phương trình mặt cầu đường kính AB là 2 2 2 2 A. 2
x   y  3   z   1  36. B. 2
x   y  3   z   1  9. 2 2 2 2 C. 2
x   y  3   z   1  9. D. 2
x   y  3   z   1  36.
Câu 126. (CHUYÊN BẮC GIANG NĂM 2018-2019 LẦN 02) Trong không gian với hệ tọa độ Oxyz, hỏi
trong các phương trình sau phương trình nào là phương trình của mặt cầu? A. 2 2 2
x  y  z  2x  4z 1  0 B. 2 2
x  z  3x  2 y  4z 1  0 C. 2 2 2
x  y  z  2xy  4 y  4z 1  0 D. 2 2 2
x  y  z  2x  2 y  4z  8  0
Câu 19 : Trong không gian Oxyz , cho hai điểm A2; 1  ; 3   ; B 0;3;  1 
. Phương trình của mặt cầu đường kính AB là : 2 2 2 2 2 2 A.  x   1   y   1
  z  2  6 B.  x   1   y   1
  z  2  24 2 2 2 2 2 2 C.  x   1   y   1
  z  2  24 D.  x   1   y   1
  z  2  6
Câu 127. (CHUYÊN KHTN LẦN 2 NĂM 2018-2019) Trong không gian với hệ tọa độ Oxyz phương trình
nào sau đây không phải là phương trình của một mặt cầu? A. 2 2 2
x  y  z  x  2 y  4z  3  0 . B. 2 2 2
2x  2 y  2z  x  y  z  0 . C. 2 2 2
2x  2 y  2z  4x  8y  6z  3  0 . D. 2 2 2
x  y  z  2x  4 y  4z 10  0 .
Câu 128. (CHUYÊN PHAN BỘI CHÂU NGHỆ AN LẦN 1 NĂM 2018-2019) Trong không gian với hệ trục
tọ độ Oxyz , cho hai điểm A1;2;  3 , B 5;4;  
1 . Phương trình mặt cầu đường kính AB là 2 2 2 2 2 2 A.  x   3   y   3   z   1  36 . B.  x   3   y   3   z   1  9 . 2 2 2 2 2 2 C.  x   3   y   3   z   1  6 . D.  x   3   y   3   z   1  9 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 129. (ĐỀ GK2 VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Trong hệ trục tọa độ Oxyz , phương trình mặt
cầu tâm I 2;1;  2 bán kính R  2 là: 2 2 2
A.  x     y     z   2 2 1 2  2 . B. 2 2 2
x  y  z  4x  2y  4z  5  0 . 2 2 2 C. 2 2 2
x  y  z  4x  2y  4z  5  0 .
D.  x  2   y   1
  z  2  2 .
Câu 130. (ĐỀ GK2 VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Phương trình nào sau đây là phương trình mặt
cầu S  tâm A2;1;0 , đi qua điểm B 0;1;2 ? 2 2 2 2
A. S   x     y   2 : 2 1  z  8 .
B.  S   x     y   2 : 2 1  z  8 . 2 2 2 2
C. S   x     y   2 : 2 1  z  64 .
D. S   x     y   2 : 2 1  z  64 .
Câu 131. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Trong không gian Oxyz cho hai điểm I 1;1;  1
và A1; 2;3 . Phương trình mặt cầu có tâm I và đi qua A là 2 2 2 2 2 2 A.  x   1   y   1   z   1  29 B.  x   1   y   1   z   1  5 2 2 2 2 2 2 C.  x   1   y   1   z   1  25 D.  x   1   y   1   z   1  5
Câu 132. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Trong không gian Oxyz, cho điểm
I (1; 2; 3) . Viết phương trình mặt cầu tâm I, cắt trục Ox tại hai điểm A và B sao cho AB  2 3 A. 2 2 2
(x 1)  ( y  2)  (z  3)  16. B. 2 2 2
(x 1)  ( y  2)  (z  3)  20. C. 2 2 2
(x 1)  ( y  2)  (z  3)  25. D. 2 2 2
(x 1)  ( y  2)  (z  3)  9.
Câu 133. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Trong không gian Oxyz , cho điểm M 1; 2
 ;3 . Gọi I là hình chiếu vuông góc của M trên trục Ox . Phương trình nào sau đây là phương trình
mặt cầu tâm I bán kính IM ? A.  x  2 2 2
1  y  z  13 . B.  x  2 2 2 1
 y  z  13 . C.  x  2 2 2
1  y  z  13 . D.  x  2 2 2
1  y  z  17 .
Câu 134. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Trong không gian với hệ tọa độ Oxyz , trong
các mặt cầu dưới đây, mặt cầu nào có bán kính R  2 ? A. S  2 2 2
: x  y  z  4x  2 y  2z  3  0 . B. S  2 2 2
: x  y  z  4x  2 y  2z 10  0 . C. S  2 2 2
: x  y  z  4x  2 y  2z  2  0 . D. S  2 2 2
: x  y  z  4x  2 y  2z  5  0 .
Câu 135. (THPT GANG THÉP THÁI NGUYÊN NĂM 2018-2019) Trong không gian với hệ trục tọa độ
Oxyz , cho điểm A1;1;2 , B 3;2; 3 . Mặt cầu S  có tâm I thuộc Ox và đi qua hai điểm , A B có phương trình. A. 2 2 2
x  y  z  8x  2  0 . B. 2 2 2
x  y  z  8x  2  0 . C. 2 2 2
x  y  z  4x  2  0 . D. 2 2 2
x  y  z  8x  2  0 .
Câu 136. (ĐỀ THI THỬ VTED 02 NĂM HỌC 2018 - 2019) Trong không gian Oxyz , mặt cầu có tâm I 1;1;  1
và diện tích bằng 4 có phương trình là 2 2 2 2 2 2 A.  x   1   y   1   z   1  4 B.  x   1   y   1   z   1  1 2 2 2 2 2 2 C.  x   1   y   1   z   1  4 D.  x   1   y   1   z   1  1
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 137. (ĐỀ GK2 VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Trong không gian với hệ tọa độ Oxyz , mặt cầu
S  qua bốn điểm A3;3;0 , B 3;0;3 , C 0;3;3 , D 3;3;3 . Phương trình mặt cầu S  là 2 2 2  3   3   3  3 3 A. x   y   z         .  2   2   2  2 2 2 2  3   3   3  27 B. x   y   z         .  2   2   2  4 2 2 2  3   3   3  27 C. x   y   z         .  2   2   2  4 2 2 2  3   3   3  27 D. x   y   z         .  2   2   2  4
Câu 138. (THPT CHUYÊN NGUYỄN ĐÌNH TRIỂU - ĐỒNG THÁP - LẦN 1 - 2018) Trong không gian 2 2
Oxyz , cho mặt cầu S   x     y   2 : 1
1  z  4. Một mặt cầu S có tâm I 9;1;6 và tiếp xúc ngoài với
mặt cầu S . Phương trình mặt cầu  S là 2 2 2 2 2 2
A.  x  9   y  
1   z  6  64 .
B.  x  9   y  
1   z  6  144 . 2 2 2 2 2 2
C.  x  9   y  
1   z  6  36 .
D.  x  9   y  
1   z  6  25 .
Câu 139. (THPT HAI BÀ TRƯNG - HUẾ - 2018) Trong không gian Oxyz , viết phương trình mặt cầu đi qua điểm A1; 1
 ; 4 và tiếp xúc với các mặt phẳng tọa độ. 2 2 2 2 2 2
A.  x  3   y  3   z  3  16 .
B.  x  3   y  3   z  3  9 . 2 2 2 2 2 2
C.  x  3   y  3   z  3  36 .
D.  x  3   y  3   z  3  49 .
Câu 140. [KIM LIÊN - HÀ NỘI - LẦN 1 - 2018] Trong không gian Oxyz , cho hai điểm M 2; 2  ;1 ,  8  4 8  N ; ; 
 . Viết phương trình mặt cầu có tâm là tâm của đường tròn nội tiếp tam giác OMN và tiếp xúc  3 3 3 
với mặt phẳng Oxz . 2 2 2 2 A. 2
x   y   1   z   1  1. B. 2
x   y   1   z   1  1. 2 2 2 2
C.  x     y   2 1 1  z  1. D.  x   2
1  y   z   1  1.
Câu 141. (CHUYÊN HÀ TĨNH - LẦN 1 - 2018) Trong không gian Oxyz , gọi I a; ;
b c là tâm mặt cầu đi
qua điểm A1; 1; 4 và tiếp xúc với tất cả các mặt phẳng tọa độ. Tính P  a  b  c . A. P  6 . B. P  0 . C. P  3 . D. P  9 .
Dạng 3. Một số bài toán khác
Câu 142. (Mã 102 - BGD - 2019) Trong không gian Oxyz , cho mặt cầu S  x  y   z  2 2 2 : 2  3 . Có tất
cả bao nhiêu điểm Aa;b;c ( , a ,
b c là các số nguyên) thuộc mặt phẳng Oxy sao cho có ít nhất hai tiếp
tuyến của  S  đi qua A và hai tiếp tuyến đó vuông góc với nhau? A. 8 . B. 16 . C. 12 . D. 4 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 143. (Mã đề 104 - BGD - 2019) Trong không gian Oxyz , cho mặt cầu S  x  y   z  2 2 2 : 1  5 . Có tất
cả bao nhiêu điểm Aa, , b c ( , a ,
b c là các số nguyên) thuộc mặt phẳng Oxy sao cho có ít nhất hai tiếp tuyến
của  S  đi qua A và hai tiếp tuyến đó vuông góc với nhau? A. 20 B. 8 C. 12 D. 16
Câu 144. (Mã 103 - BGD - 2019) Trong không gian Oxyz , cho mặt cầu: S  x  y   z  2 2 2 : 1  5 . Có tất cả
bao nhiêu điểm Aa;b;c (a, b, c là các số nguyên) thuộc mặt phẳng Oxy sao cho có ít nhất hai tiếp tuyến
của  S  đi qua A và hai tiếp tuyến đó vuông góc nhau? A. 20 . B. 8 . C. 12 . D. 16 .
Câu 145. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Trong không gian với hệ tọa độ Oxyz , cho mặt cầu 2 S x  2 y  2 ( ) :
z  9 , điểm M(1; 1 ; 2) và mặt phẳng (P) : x  y  z  4  0 . Gọi  là đường thẳng đi qua M 
, thuộc (P) và cắt (S) tại 2 điểm A, B sao cho AB nhỏ nhất. Biết rằng  có một vectơ chỉ phương là ( u 1; a; ) b
, tính T  a  b . A. T  2 B. T  1 C. T  0 D. T  1
Câu 146. (TOÁN HỌC TUỔI TRẺ NĂM 2018 - 2019 LẦN 01) Trong không gian với hệ tọa độ Oxyz, cho hai điểm A9, 3  ,  4 , Ba, ,
b c . Gọi M , N, P lần lượt là giao của đường thẳng AB với mặt phẳng
Oxy,Oxz,Oyz . Biết các điểm M , N, P đều nằm trên đoạn AB sao cho AM  MN  NP  PB . Tính giá trị
ab  bc  ac bằng A. 17 . B. 17 . C. 9 . D. 12.
Câu 147. (THPT CHUYÊN NGỮ - HÀ NỘI - 2018) Trong không gian với hệ tọa độ Oxyz , cho mặt cầu
S   x  2   y  2 2 : 1
1  z  4 và một điểm M 2;3 
;1 . Từ M kẻ được vô số các tiếp tuyến tới S  , biết tập
hợp các tiếp điểm là đường tròn C  . Tính bán kính r của đường tròn C  . 2 3 3 2 A. r  . B. r  . C. r  . D. 2 . 3 3 3
Câu 148. (THPT MỘ ĐỨC - QUẢNG NGÃI - 2018) Trong mặt phẳng tọa độ Oxyz , cho bốn điểm
A0;1;2 , B 2;3;0 , C 2;1; 
1 , D 0;1;3 . Gọi  L là tập hợp tất cả các điểm M trong không gian
   
thỏa mãn đẳng thức M .
A MB  MC.MD  1. Biết rằng  L là một đường tròn, đường tròn đó có bán kính r bằng bao nhiêu? 11 7 3 5 A. r  . B. r  . C. r  . D. r  . 2 2 2 2
Câu 149. (THPT CHUYÊN HẠ LONG - LẦN 2 - 2018) Trong không gian, cho bốn mặt cầu có bán kính lần
lượt là 2 , 3 , 3 , 2 (đơn vị độ dài) tiếp xúc ngoài với nhau. Mặt cầu nhỏ nhất tiếp xúc ngoài với cả bốn mặt cầu
nói trên có bán kính bằng 5 3 7 6 A. . B. . C. . D. . 9 7 15 11
Dạng 4. Bài toán cực trị
Câu 150. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Trong không gian với hệ trục Oxyz   
, cho các điểm A 1  ; 2;3, B6; 5  ;8 và OM  . a i  .
b k trong đó a, b là cá số thực luôn thay đổi. Nếu  
MA  2MB đạt giác trị nhỏ nhất thì giá trị a  b bằng
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. 25  B. 13  C. 0 D. 26
Câu 151. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Trong không gian Oxyz , cho hai điểm A1; 2;  1 ; B 2; 1
 ;3 và điểm M  ; a ; b 0 sao cho 2 2
MA  MB nhỏ nhất. Giá trị của a  b là A. 2 . B. 2  . C. 3 . D. 1.
Câu 152. (CHUYEN PHAN BỘI CHÂU NGHỆ AN NĂM 2018-2019 LẦN 02) Trong không gian với hệ
trục tọa độ Oxyz , cho mặt cầu 2 2 2
(S) :(x 1)  ( y  2) (z 1)  9 và hai điểm (4 A ;3;1) , (
B 3;1;3) ; M là điểm thay đổi trên (S) . Gọi m, n lần lượt là giá trị lớn
nhất và giá trị nhỏ nhất của biểu thức 2 2
P  2MA  MB . Xác định (m  ) n . A. 64 . B. 68 . C. 60 . D. 48 .
Câu 153. (THPT GANG THÉP THÁI NGUYÊN NĂM 2018-2019) Trong không gian với hệ trục tọa độ Oxyz , cho 4 điểm A 2;4;   1 , B 1;4;   1 , C 2;4;  3 , D 2;2;   1 , biết
M  x; y; z  để 2 2 2 2
MA  MB  MC  MD đạt giá trị nhỏ nhất thì x  y  z bằng 21 A. 6 . B. . C. 8 . D. 9 . 4 A1;2;  1 B 2;1;3
Câu 154. Trong không gian Oxyz , cho hai điểm , ,C 3;1;  5 . Tìm điểm M
trên mặt phẳng Oyz  sao cho 2 2 2
MA  2MB  MC lớn nhất. 3 1    1 3    A. M  ; ; 0  M  ; ;0 M 0; 0;5 M 3;4; 0  . B. . C.  . D.  . 2 2  2 2 
Câu 155. (CHUYÊN PHAN BỘI CHÂU NĂM 2018-2019) Trong không gian với hệ trục tọa độ Oxyz, cho 2 2 2
mặt cầu S  :  x   1
  y  2   z   1
 9 và hai điểm A4;3 
;1 , B 3;1;3 ; M là điểm thay đổi trên  S  .
Gọi m, n là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 2
P  2MA  MB . Xác định m  n. A. 64 . B. 68 . C. 60 . D. 48 .
Câu 156. (THPT NGHĨA HƯNG NĐ- GK2 - 2018 - 2019) Trong không gian với hệ trục tọa độ Oxyz , cho
A 2;1;3 B 1; 1; 2 C 3; 6  ;1
M  x; y; z  Oyz tam giác ABC với , , . Điểm thuộc mặt phẳng sao cho 2 2 2
MA  MB  MC đạt giá trị nhỏ nhất. Tính giá trị biểu thức P  x  y  z . A. P  0 . B. P  2 . C. P  6 . D. P  2 .
Câu 157. Trong không gian với hệ tọa độ Oxyz , cho ba điểm A4; 2; 2, B 1;1;  
1 , C 2; 2; 2 . Tìm tọa   
độ điểm M thuộc mặt phẳng Oyz sao cho MA  2MB  MC nhỏ nhất A. M 2;3  ;1 . B. M 0;3  ;1 . C. M 0;  3  ;1 . D. M 0;1; 2 .
Câu 158. (THPT CHUYÊN LÊ QUÝ ĐÔN - ĐÀ NẴNG - LẦN 1 - 2018) Trong không gian với hệ trục tọa
độ Oxyz , cho bốn điểm A2; 3;7 , B 0; 4 
;1 , C 3;0;5 và D 3;3;3 . Gọi M là điểm nằm trên mặt phẳng
   
Oyz sao cho biểu thức MA  MB  MC  MD đạt giá trị nhỏ nhất. Khi đó tọa độ của M là: A. M 0;1; 4 . B. M 2;1;0 . C. M 0;1; 2 . D. M 0;1; 4 .
Câu 159. (TOÁN HỌC TUỔI TRẺ - THÁNG 4 - 2018) Trong không gian cho ba điểm A1;1;  1 , B 1; 2  ;1
, C 3;6; 5 . Điểm M thuộc mặt phẳng Oxy sao cho 2 2 2
MA  MB  MC đạt giá trị nhỏ nhất là
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. M 1; 2;0 . B. M 0;0;   1 . C. M 1;3;   1 . D. M 1;3;0 .
Câu 160. (LÊ QUÝ ĐÔN - HẢI PHÒNG - LẦN 1 - 2018) Trong không gian với hệ tọa độ Oxyz cho A3; 2  ;1 , B  2
 ;3; 6 . Điểm M  x ; y ; z
thay đổi thuộc mặt phẳng Oxy . Tìm giá trị của biểu thức M M M   
T  x  y  z khi MA  3MB nhỏ nhất. M M M 7 7 A.  . B. . C. 2 . D. 2 . 2 2
Câu 161. (THPT CHUYÊN VĨNH PHÚC - LẦN 3 - 2018) Trong không gian với hệ trục tọa độ Oxyz , cho
mặt cầu S  có phương trình là 2 2 2
x  y  z  2x  2 y  6z  7  0 . Cho ba điểm A , M , B nằm trên mặt cầu S  sao cho 
AMB  90 . Diện tích tam giác AMB có giá trị lớn nhất bằng? A. 4 . B. 2 . C. 4 . D. Không tồn tại.
Câu 162. (THPT PHAN ĐÌNH PHÙNG - HÀ TĨNH - LẦN 1 - 2018) Cho a, b, c, d , e, f là các số thực thỏa   d   2
1  e  22   f  32  1 mãn 
. Gọi giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 
 a  32  b  22 2  c  9 
   2    2    2 F a d b e c f
lần lượt là M , m. Khi đó, M  m bằng A. 10 . B. 10 . C. 8. D. 2 2 .
Câu 163. (THPT LÊ XOAY - LẦN 3 - 2018) Trong không gian với hệ tọa độ Oxyz , cho hai điểm MA 2 A 2
 ; 2; 2 ; B 3; 3
 ;3 . Điểm M trong không gian thỏa mãn 
. Khi đó độ dài OM lớn nhất bằng MB 3 5 3 A. 6 3 . B. 12 3 . C. . D. 5 3 . 2
Câu 164. (THPT NGUYỄN TẤT THÀNH - YÊN BÁI - 2018) Trong không gian với hệ tọa độ Oxyz , cho 2 2 2
các điểm A0;1;3 , B 2
 ; 8; 4 C 2;1; 
1 và mặt cầu S  :  x  
1   y  2   z  3 14 . Gọi   
M  x ; y ; z
là điểm trên  S  sao cho biểu thức 3MA  2MB  MC đạt giá trị nhỏ nhất. Tính P  x  y M M M  M M . A. P  0 . B. P  14 . C. P  6 . D. P  3 14 .
PHẦN B. LỜI GIẢI THAM KHẢO
Dạng 1. Tìm tọa độ điểm, véc tơ liên quan đến hệ trục tọa dộ OXYZ Câu 1. Chọn C  
AB  2 1; 2 1;1 2 hay AB  1;1;3 . Câu 2. Chọn B
Hình chiếu vuông góc của điểm M 3;1;  
1 trên trục Oy có tọa độ là 0;1;0 . Câu 3. Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  x  x A B x   2 I  2   y  y
Gọi I là trung điểm của AB , ta có tọa độ điểm I là A B  y   1  . I 2   z  z A B z   5 I   2
Vậy I 2; 1;5 . Câu 4. Chọn B Gọi D  ; x 0;0 Ox  x 
AD  BC   x  2 0 3 16  5   . x  6  Câu 5. Chọn A 
AB   x  x ; y  y ; z  z   1; 2;3 B A B A B A  Câu 6. Chọn C
Hình chiếu vuông góc của điểm M 2;1;  
1 trên trục Oy có tọa độ là 0;1;0 . Câu 7. Chọn C 2 2 2 OA  2  2 1  3 . Câu 8. Lời giải Chọn B
Hình chiếu vuông góc của điểm M 3; 1  
;1 trên trục Oz có tọa độ là 0;0  ;1 Câu 9. Chọn A
Tọa độ trung điểm I của đoạn AB với A3; 2  ;3 và B  1
 ; 2;5 được tính bởi  x  x x  A B  1  I 2   y  y  y  A B  0  I I 1;0;4 2   z  z z  A B  4   I 2 Câu 10. Chọn D
Hình chiếu vuông góc của điểm M 2;1;  
1 trên trục Oz có tọa độ là: 0;0;   1 . Câu 11. Chọn D  
M Oxz  M  ;0
x ;z  ; AB  7;3; 
1  AB  59 ; AM   x  2;  3;z   1 và  
x  2  7k x  9    , A ,
B M thẳng hàng  AM  k.AB k     3   3k   1
  k  M  9  ;0;0. z 1 k    z  0     BM   14 
;  6;  2 ;AM  7;  3;   1  BM  2 . AB Câu 12. Lời giải Chọn B
Khi chiếu vuông góc một điểm trong không gian lên mặt phẳng Oyz , ta giữ lại các thành phần tung độ và
cao độ nên hình chiếu của A3; 1  ; 
1 lên Oyz là điểm N 0; 1  ;  1 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Câu 13. Chọn B    
Ta có: d  a  b  2c  1 2  2.4; 2  2  2.0;3 1 2.( 4)    7;0; 4   .
Câu 14. Chọn B  
 Xét đáp án A: a  b  3;3;3 đúng.    
 Xét đáp án B: a  21; 1  ; 2
   b  1; 1 
;1 . Suy ra a và b không cùng phương. Đáp án B sai. 
Câu 15. Hai điểm A0;1;  
1 , B 2;3; 2 . Vectơ AB có tọa độ là 2; 2;3 . Câu 16. Chọn B
Cho hai điểm A3; 2  ;3 và B  1  ; 2;5 .  x  x 3    1 A B   1  2 2   y  y  2    2
Trung điểm I có tọa độ: A B  
 0  I 1;0; 4 . 2 2   z  z 3  5 A B   4  2 2   
Câu 17. Ta có: a  b  2 1;3 1; 2   1  1; 2;3 .       
Câu 18. Ta có: 2a  4; 6;6 , 3b  0;6; 3 , 2c  6; 2; 10  u  2a  3b  2c   2  ; 2; 7   .  x  x A B x   2 I  2   y  y Câu 19. Ta có A B  y   1  I . I 2;1;3 2   z  z A B z   3 I   2  
Câu 20. Có AB  2;2;5, AC  x 1; y  2;  1 .  3      x  x 1 y  2 1  5 ,
A B, C thẳng hàng  AB, AC cùng phương     
 x  y 1. 2 2 5  8 y   5     
Câu 21. a  i  2 j  3k  a 1; 2; 3 .
Câu 22. Toạ độ trong tâm G của tam giác ABC bằng 
x  x  x 11 0 A B C x    0 G  3 3  
y  y  y 2   2  0 A B C  y    0  G G 0;0;3 3 3  
z  z  z 3  5 1 A B C z    3  G  3 3   
Câu 23. Có 2a  4; 6;6; 3b  0;6; 3
 ;  2c   6  ; 2; 10 .    
Khi đó: u  2a  3b  2c  2; 2;  7 .
Câu 24. Tọa độ trung điểm I của AB là
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  1 3 x   2 I  2   3 1  y   1  I I 2;1;3. 2   2  4 z   3 I   2  x  x 1   3 A B x    1 M  2 2   y  y 5  3
Câu 25. Trung điểm M có tọa độ là A B  y    1  M . M 1;1;2 2 2   z  z 2  2 A B z    2 M   2 2 
Câu 26. Ta có: 2 y  2;0; 2 .   
a  x  2 y  2  2;1 0; 3  2  4;1; 5 .  x  x 2  2 A B x    2 M  2 2   y  y 4   2
Câu 27. Gọi M là trung điểm của đoạn thẳng AB , ta có: A B  y    1   M 2; 1  ;5 . M 2 2   z  z 3  7 A B z    5 M   2 2
Câu 28. Gọi D  ;
x y; z  . Để ABCD là hình bình hành x  4    
 AB  DC  1;3;  7  3  ;
x 1 y; 2  z    y  2  D  4  ;  2;9 . z  9 
Câu 29. Tọa độ trọng tâm G là  1 2  3 x   2 G  3   3 11  y   1  G G 2;1;2. 3   4  0  2 z   2 G   3
Câu 30. Giả sử G  , x y, z  .
Vì G là trọng tâm của tam giác ABC suy ra 
x  x  x  5    A B C  2 0 x  x   1   3 3   
y  y  y  2   3  2 A B C  y    y   1  G 1;1  ;1 . 3 3   
z  z  z  0  0  3 A B C z  z   1  3   3 
Câu 31. A2; 1  ;0 , B1;1;  3  
 AB  1 2;11;3  0   1  ; 2; 3 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 32. Gọi D  x; y ; z .  
Tứ giác ABCD là hình bình hành khi và chỉ AD  BC .  
Ta có AD   x 1; y ; z và BC   1  ; 0  ;1 .
Suy ra x  0; y  0; z  1 . Vậy D 0;0;  1 . 
Câu 33. Ta có: AB  1;1; 2 .
Câu 34. Mặt phẳng tọa độ Oyz có phương trình là x  0  N 0; 4;   1 Oyz .   
Câu 35. Ta có i  (1; 0; 0), j  (0;1; 0), k  (0; 0;1).   
Do đó, i  j  k  (1;1; 1).
Câu 36. Hình chiếu của M 4;5;6 xuống mặt phẳng Oyz là M 0;5;6 .
Câu 37. Nếu M đối xứng với M qua mặt phẳng Oxz thì M  x;  y; z . Do đó phương án A sai.
Nếu M đối xứng với M qua Oy thì M  x; y; z . Do đó phương án B sai.
Nếu M đối xứng với M qua gốc tọa độ O thì M x;  y;  z . Do đó phương án D sai.   
Câu 38. Theo định nghĩa ta có i  1;0;0 , j  0;1;0 và k  0;0  ;1 .     
Do đó, u  2i  3 j  k  u  2;3;  1 .
Câu 39. Gọi I là trung điểm MN . Ta có:  x  x 11 M N x    1 I  2 2   y  y 2   0 M N  y    1  I 2 2   z  z 2  4 M N z    3 I   2 2
Vậy I 1; 1;3 .    
Câu 40. Có c  2a  b , gọi c  c ;c ;c 1 2 3 
c  2.1 1  1 1   
 c  2.2  3  7 2 c  2.1 0  2 3  
Vậy c  1;7; 2 Câu 41. Chọn A.  x  x 3  5 A B x    1 I   2 2
Gọi I là trung điểm của đoạn thẳng AB . Khi đó ta có:   I 1;5 . y  y 4  6 A B  y    5 I   2 2 Câu 42. Chọn D.
Áp dụng công thức tính tích có hướng trong hệ trục tọa độ Oxyz ta được:   
c  a,b  2; 6;  1   Vậy chọn đáp án D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Câu 43. Chọn A      
+) Ta có a  xi  y j  zk  a  ;
x y; z  nên a  1  ; 2; 3  .Do đó Chọn A Câu 44. Chọn C  x  x 2  2 A B x    2 I  2 2   y  y 4   2
Gọi I là trung điểm của đoạn AB . Ta có A B  y    1   I 2; 1  ; 6 . I 2 2   z  z 3  9 A B z    6 I   2 2  Câu 45. 2 2 2
AB  (2;3; 3)  AB  2  3  (3)  22. Câu 46. Chọn A  x  x 1 3 A B x    1 M  2 2   y  y 5  3
Trung điểm M có tọa độ là A B  y    1  M . M 1;1;2 2 2   z  z 2  2 A B z    2 M   2 2       2 k k  2     3
Câu 47. a và b cùng hướng  a  kb k  0  m 1  3k  m  7 . Vậy m  7;n   4 3  k  2n    3  n    4
Câu 48. Giả sử B  x ; y ; z . B B B 
Vì M là trung điểm của AB nên ta có:  x  x  1 x A B x  2 B  M  2  2   x  5 B  y  y  5  y  A B  y   1 B  
  y  3 . Vậy B 5; 3  ; 7   . M 2 2 B   z  7  z  z  3  B  z A B z  2 M  M  2    2 Câu 49. Chọn D
Gọi D(x ; y ; z ) cần tìm D D D  
Tứ giác ABCD là hình bình hành  AB  DC
x  x  x  x 2 1  3   x x  4  B A C D D D   
  y  y  y  y   1   2  5  y   y  8 . B A C D D D
z  z  z  z 3  ( 1) 1 z      z  3   B A C D  D  D
Suy ra: D(4;8; 3) . Câu 50. Chọn A
Gọi E  x; y; z  
Ta có: CE   x  7; y  4; z  2 ; 2EB  2  2 ;
x 4  2 y; 6  2z 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  x  3 x  7  2  2x      8
CE  2EB   y  4  4  2y   y  3 z 2 6 2z        8 z     3 Câu 51. Chọn D  1 2  a 1   3  a  0  3   4  2  c   b   1 3  c  3   3 5 b    3    3
Vậy a  b  c  2  Câu 52. Chọn A  
Ta có AB  3; 4; 2, AM   x  2; y  1; 4   x  2 y  1 4 x  4 ,
A B, M thẳng hàng  AB, AM cùng phương      . 3 4 2 y  7  Câu 53. Chọn D 1   3   x x  4  D D    
Tứ giác ABCD là hình bình hành  AB  DC  3   1 y   y  2  D D 10  4 z    z  6   D  D Vậy D  4  ; 2  ; 6   .
Câu 54. Gọi H là hình chiếu của M lên mặt phẳng Oyz  H  ; 0 ; 2  3
Gọi M ' là điểm đối xứng với M  ; 1 ; 2 
3 qua mặt phẳng Oyz 
 H là trung điểm của MM '  M '  ; 1 ; 2 
3 .        
Câu 55. Ta có: ABCD là hình bình hành  OA  OC  OB  OD  OD  OA  OC  OB
x  x  x  x x  1 0  2 D A C B D  
  y  y  y  y   y  2
  3 1  D  1  ;0; 6 . D A C B D
z  z  z  z   z  0  4  2 D A C B  D
Câu 56. Gọi M  x; y;z . Vì M thuộc đoạn AB nên:  7 x  
  x     x 3 3 2 2      5 MA  2  MB  1   y  2   3
  y    y   3   2
  z  25  z   8 z    3  
Câu 57. Gọi M  ;
x y; z  . Ta có: AM   ;
x y 1; z  2; AB  3; 2;3 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 x  9 x  9    
AM  3AB   y 1  6    y  5  . Vậy M 9; 5  ;7 . z 2 9    z  7    
Câu 58. Ta có M Oxy  M  x; y ;0 ; AB   2  ;3; 
1 ; AM   x  2; y  2;   1 .   x  2 y  2 1 x  4
Để A , B , M thẳng hàng thì AB và AM cùng phương, khi đó:     . 2  3 1 y  5  
Vậy M 4;  5;0 . 
Câu 59. Ta có u  2; 2;  1   Khi đó u    2 2 2 2 2
1  3 và v  m   m  2 2 2 2 2 1  2m  2m  5   m  1 Do đó 2
u  v  9  2m  2m  5 2
 m  m  2  0   m  2 
Vậy có 2 giá trị của m thỏa yêu cầu bài toán.
Câu 60. Gọi B  ; x y; z  x  2  Có A1; 2;   1 AB  1;3 
;1   x 1; y  2; z  
1   y  5  B 2;5;0 z  0  Câu 61.    Ta có AB   ;
a 0;0 ; AD  0;2 ;
a 0 ; AA  0;0;2a .
    
Theo quy tắc hình hộp ta có AB  AD  AA  AC  AC  a;2a;2a .  2 2 Suy ra AC  AC 2
 a  2a  2a  3 a .
Vậy độ dài đoạn thẳng AC  3 a .
Câu 62. Gọi A  ;
x y; z , A'(x ; y ; z )
 là điểm đối xứng với điểm A qua trục Oy . x '  x 
Điểm A ' đối xứng với điểm A qua trục Oy nên  y '  y . Do đó A'  3;1; 2 . z '  z 
   
Câu 63. Gọi G là trọng tâm của tam giác ABC . Ta có G 1;0; 2
  và GA  GB  GC  0 .
   
       Ta có: A A   B B   C C
  0  GA  GA  GB  GB  GC  GC  0
     
   
 GA  GB  GC  GA  GB  GC  GA  GB  GC  0 .
 G là trọng tâm của tam giác A B  C   .
Vậy tọa độ trọng tâm của tam giác A B  C   là 1;0; 2   .
Câu 64. Gọi tọa độ điểm C là  x ; y ; z   
Vì ABCD là hình bình hành nên DC  AB
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  
Ta có DC   x 1; y 1; z 1  và AB  1;1;  1 x 1  1 x  2  
Suy ra  y 1  1  y  0 z 1 1    z  2  
Vậy tọa độ điểm C là 2;0; 2 . Câu 65. Chọn D O I A B D    8 4 8 
Ta có OA  1; 2;  2 , OB  ; ; 
 , do đó OA  3, OB  4 .  3 3 3   DA  OA 
Gọi D là chân đường phân giác trong kẻ từ O , ta có DA   .DB   .DB , suy ra DB OB    3   4.OA  3.OB  12 12  DA   DB  OD  . Do đó D ; ; 0   . 4 7  7 7    5 2  15 Ta có AD  ;  ; 2  AD    .  7 7  7  AD  5   7  ID   .IO   IO  OI 
OD  D 1; 1; 0 AO 7 12
Do đó a  b  c  0 .
Câu 66. Gọi I , J , K lần lượt là trung điểm của AB, BC,CA .   
Do AMB  BMC  CMA  90 nên các tam giác AMB, BM  C, CMA  vuông tại M . AB BC AC Khi đó IM  ; JM  ; KM 
. Mặt khác AB  BC  AC  2 2 . 2 2 2
Vậy MI  MJ  MK 
2 . Khi đó M thuộc trục của đường tròn ngoại tiếp đáy IJK và cách  IJK  một
khoảng không đổi là 2 . Khi đó có hai điểm M thỏa mãn điều kiện trên.
Dạng 2. Tích vô hướng, tích có hướng và ứng dụng
Dạng 2.1 Tích vô hướng và ứng dụng
Câu 67. Chọn B     . a b 2 2
Ta có: cos a, b        . a . b 5. 5 5 Câu 68. Chọn C  
MN 3; 2; 2; NP 2; m  2; 
1 .  
Tam giác MNP vuông tại N  MN.NP  0  6  2 m  2  2  0  m  2  2  m  0 . Câu 69. Chọn B
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489   Ta có: AB   3
 ;  5 , AC  2;  2 .     AB AC   Khi đó: A  AB AC . 3.2 5.2 1 cos cos ;    . . AB AC 34.2 2 17 
Câu 70. Ta có i  1; 0; 0 .     . i u
1. 3  0.0  0.1  3  
Vậy: cos i, u     =
 i, u 150. i . u 2 1.  32 2 2  0 1
Câu 71. Chọn D     . a b 3.  5  4.0  0.12 3 Ta có: os c
a; b      . a . b 32 2 2 2 2 2 13  4  0 . 5  0 12 
Câu 72. Ta có i  1;0;0     u i     u i . 3 cos ,    
. Vậy u,i 150 . u . i 2   Câu 73. Ta có .
u v  3.2  0.11.0  6 .  
Câu 74. Gọi  là góc giữa hai vectơ i và u   3;0;  1 , ta có:   i .u  3 0 cos      150 . i . u 2     AB AC  
Câu 75. Ta có AB 1;5; 2
  ; AC 5;4;  1 .  . 5 20 2 9
cosBAC      . AB . AC 30. 42 2 35   AB   1;2;3  
Câu 76. Ta có   .
AB BC  0  tam giác ABC vuông tại B . BC   7  ; 5  ;   1 
 tâm I của đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh huyền AC .  1   I 1;  ;3 
 . Vậy a  2b  c  3.  2  Câu 77. Chọn C  
Ta có: AB  1; 0;  1 , AC  1;1;  1   
1 .1 0.11.1  0  AB  AC . 1 6
Nên diện tích tam giác ABC là S  A . B AC  . 2 2       . u v 2 1 2m 1
Câu 78. + u v    u v 2 , 45 cos ,          2 3 m   1  1 2m 2 u . v 2 2 6. 1 m 2  1 1   2m  0 m      2  m  2  6 . 2 2
3m  3  1 4m  4m  2
m  4m  2  0 
Dạng 2.2 Tích có hướng và ứng dụng   
Câu 79. Ta có: DA  3;  2; m  3, DB  2; 0;  3, DC  0; 4;  3 .
1    1 m  6 
Thể tích tứ diện: V 
DB , DC.DA  8 
24  8m  3     . 6 6 m  6 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Vì m dương nên m  6. Do đó chọn D.   
Câu 80. Ta có: AB  (1; 2;3) ; AC  (3;3;3) ; AD  (1;3;1) .    A , B AC  ( 3  ; 12;9)   ;
    A ,
B AC . AD  ( 3  ).( 1  )  ( 12  ).3  9.1  24    . 1    1 V 
 AB, AC . AD  24  4 . ABCD 6   6 Câu 81. Chọn C    
u v  m  m m    u v  m  2  m  m  2 2 2 , 2; ; 1 , 2 1
 3m  6m  5       m  1 u,v 2 2
 14  3m  6m  5  14  3m  6m  9  0   . m  3   Câu 82. Chọn A.   
Do D Oy  D0; ;
y 0 , khi đó: DA  2; 1   y;  1 , DB  3;  ; y   1 , DC  2; 1   ; y  3 .   Khi đó  ,
DA DB  1  2 y;5; y   3
1    2 y  6  30  y  12 Và V  DA DB DC . ABCD  , .  5     6 2 y  6  30 y  18  
Vậy y  y  12  18  6 . 1 2 Câu 83. Ta có    2 2 2
 a  b  u  1  1  2   1  3   1
 4 1 4  3 (đúng).    . a b  1.1  2  .1 3. 
1  1 2  3  4 (đúng).    2 2 2
 a  b  u  1  1  2   1  3   1
 0  9 16  5 (đúng).    2 3 3 1 1 2 
 a, b  ; ;    1;4;3 (sai).   1 1 1 1 1 1   Câu 84. Ta tính      AB  0; 2;  1 ; AC   1
 ;1;2; AD  3;m  2;n; AB, AC  5;1;2  
   Bốn điểm , A ,
B C, D đồng phẳng  AB, AC 
.AD  0  m  2n  13     Câu 85.  , OA OB   1  ; 3  ;   1   1   1 11 S  O , A OB  1 9 1  OAB . 2   2 2  
Câu 86. Ta có: m , n  3 ;  4 ; 0 .        
Vì p là véc tơ cùng hướng với m , n nên p  k.m , n  3k ;  4k ;0, k  0 .      k  3  Ta có: 2 2
p  15  9k 16k  15   . k  3 
So sánh với điều kiện k  0  k  3  p  9 ; 12 ; 0 .   
Câu 87. AC  3;1; 2
 ; AB  1; 1; 4; AD  4;1;0 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  
 AB, AC    6  ; 10; 4 .   1
   1 7
Thể tích khối tứ diện là: V 
.  AB, AC  .AD  14  . 6   6 3  
AB  1; 2;  3 ; CD  5;  3  ;1  
Câu 88. AC  3;3; 3 ; BD  3;  2;  1 
AD  2;0;  2  
   Ta có:  A ,
B AC  3; 6;  3   A , B AC .AD  2  .3  0.6  2  3   0          .
  
 AB, AC, AD đồng phẳng hay bốn điểm ,
A B, C, D đồng phẳng. Vậy đáp án A sai.  
Lại có AC.AD  3.2  3.0  3.2  0  AC  AD .
 tam giác ACD là tam giác vuông tại A . Vậy đáp án B đúng.       Mặt khác: A . B CD  1. 5    2. 3     3  .1  1
 4  0  cos  AB,CD  0   A ,
B CD là góc tù. Vậy đáp án C đúng.  
AB  BD  14 hay AB  BD  tam giác ABD là tam giác cân tại B . Vậy đáp án D đúng. 
Câu 89. Ta có AD//BC  AD nhận CB  5; 2;   1 là một VTCP.
x  2  5t 
Kết hợp với AD qua A 2  ;3 
;1  AD :  y  3  2t t    D 5t  2; 2t  3;1 t  . z 1 t  Biến đổi S  3S  S  2S   1 ABCD ABC ACD ABC 
 AB  4;2;  1    
AB; AC   4;1; 18     
Ta có AC  1; 4;0       
 AC; AD  4t; t  ;18t 
AD  5t; 2t; t        1   1 341 S   ; AB AC         ABC  42 1  182 2 2    2 2      1 1 t 341 S 
 AC; AD  t  t  t  ACD 4 2  2 18 2  2    2 2 t 341
t  2  D 8;7;   1 Kết hợp với   1 ta được  341   2
t  2  D  12  ; 1;3     Với D 8;7;  
1  AD  10; 4; 2  2CB  2  BC .   
Với D 12; 1;3  AD  10; 4
 ; 2  2CB  2BC .  
Hình thang ABCD có đáy AD thì AD  k BC với k  0 .
Do đó chỉ có D  1  2; 1  ;3 thỏa mãn.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Dạng 3. Mặt cầu
Dạng 3. Xác định tâm, bán kính của mặt cầu Câu 90. Chọn A 2 2 2
Phương trình mặt cầu tổng quát:  x  a   y  b   z  c 2
 R  R  2 2 . Câu 91. Chọn D Câu 92. Chọn A Phương trình 2 2 2
x  y  z  2x  2y  4z  m  0 là một phương trình mặt cầu 2 2 2
 1  1  2  m  0  m  6 . Câu 93. Chọn B
Phương trình mặt cầu tâm I a; b; c , bán kính R có dạng:  2 2 2
x  a  y  b  z  c  2 R  R  3 . Câu 94. Chọn B
Tâm của  S  có tọa độ là  3  ; 1   ;1 . Câu 95. Chọn C 2 2 2
Trong không gian với hệ trục tọa độ Oxyz , mặt cầu S   x  a   y  b   z  c 2 :
 R có tâm I  ; a ; b c và bán kính R . 2 2 2
Nên mặt cầu  x   1
  y  2   z  4  20 có tâm và bán kính là I 1; 2  ; 4, R  2 5. Câu 96. Chọn A 2 2 2 2 2 2
x  y  z  2x  2z  7  0  x  y  z  2.(1).x  2.0.y  2.1.z  7  0 .
 a  1, b  0, c  1, d  -7 .
 Tâm mặt cầu I  1  ; 0 
;1 bán kính R  a  b  c  d   2 2 2 2 2 2 1  0 1  7  3 . Câu 97. lời giải Chọn C 2 2 2
Ta có R  IA  1  1  2   1  3   1  5
vậy phương trình mặt cầu tâm I và đi qua điểm A có phương trình là
 x  x 2   y  y 2   z  z 2  R   x  2   y  2   z  2 2 1 1 1  5 I I I Câu 98. Chọn D 2 Ta có 2 R  1    1   7    3 . Câu 99. Chọn D 2 2 Ta có S  2 2 2
x  y  z  x  y  
  x     y   2 : 2 2 7 0 1 1  z  9
Vậy bán kính của mặt cầu bằng 3. Câu 100. Chọn B
Mặt cầu đã cho có phương trình dạng 2 2 2
x  y  z  2ax  2by  2cz  d  0 có bán kính là 2 2 2 2 2
a  b  c  d  1  1  7  3 2 2 Câu 101. Ta có: 2 2 2
x  y  z  x  y  
  x     y   2 8 2 1 0 4 1  z  16.
Vậy mặt cầu S  có tâm I 4; –1;0 và bán kính R  4. 2 2 2
Câu 102. S  2 2 2
: x  y  z  2x  4 y  2z  3  0   x  
1   y  2   z   1  9 .
Vậy bán kính của mặt cầu S  là R  3 .
Câu 103. S  2 2 2
: x  y  z  8x  2 y 1  0
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  I 4; 1; 0 R  4 .
Câu 104. Mặt cầu  S  có tâm là I  3  ; 1   ;1 . 2 2 2 Câu 105. Ta có: 2 2 2
x  y  z  2x  4 y  2z  3  0   x  
1   y  2   z   1  9 .
Từ đó suy ra mặt cầu  S  có tâm là:  1  ; 2  ;1 .
Câu 106. Phương trình mặt cầu: 2 2 2
x  y  z  2ax  2by  2cz  d  0  2 2 2
a  b  c  d  0 có tâm
I a;b;c , bán kính 2 2 2
R  a  b  c  d .
Ta có a  4 , b  5
 , c  3, d  49 . Do đó 2 2 2
R  a  b  c  d  1. Câu 107. Chọn B
Từ phương trình mặt cầu suy ra tâm của mặt cầu là 2; 1;3 .
Câu 108. Mặt cầu đã cho có tâm I 1; 2; 
3 và bán kính R  2 . Câu 109. Chọn D.
Giả sử phương trình mặt cầu 2 2 2 2 2 2
(S) : x  y  z  2ax  2by  2cz  d  0 (a  b  c  d  0)
Ta có: a  2, b  1, c  0, d  4  Bán kính 2 2 2
R  a  b  c  d  3. Câu 110. Chọn B
Tâm của S có tọa độ là 3; 1   ;1 . Câu 111. Chọn D
Phương trình đã cho là phương trình mặt cầu khi và chỉ khi
m  22  m  2 2 1  3m  5  0 2
 m  2m 10  0
 1 11  m  1 11
Theo bài ra m    m   2  ; 1; 0;1; 2;3; 
4  có 7 giá trị của m nguyên thỏa mãn bài toán.
Câu 112. Điều kiện để phương trình 2 2 2
x  y  z  2 m  2 x  4my 19m  6  0 là phương trình mặt cầu là: m  2 2 2 2
 4m 19m  6  0  5m 15m 10  0  m  1 hoặc m  2 . Câu 113. Ta có 2 2 2 2
x  y  z  4mx  2my  2mz  9m  28  0
  x  m 2   y  m 2   z  m 2 2 2  28  3m   1 . 28 28  
1 là phương trình mặt cầu 2
 28  3m  0    m  . 3 3
Do m nguyên nên m 3;  2; 1; 0;1; 2;  3 .
Vậy có 7 giá trị của m thỏa mãn yêu cầu bài toán. 8
Câu 114. Đường tròn lớn có chu vi bằng 8 nên bán kính của  S  là  4 . 2
Từ phương trình của  S  suy ra bán kính của  S  là 2 2 2 2 1   a 10a . a  1  Do đó: 2 2 2 2 1 
 a 10a  4   . a  11 
Câu 115. Cách 1: Tìm tọa độ tâm mặt cầu suy ra bán kính.
Gọi I  x; y ; z và R lần lượt là tâm và bán kính mặt cầu ngoại tiếp tứ diện OABC .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  1 x   2 2 2 2 2 2  2 2   IO  IA
x  y  z   x   1  y  z 2     2  3
Ta có: IO  IA  IB  IC  R 2 2  2 2 2 2 2
IO  IB  x  y  z  x  y   z  2   y   .  2 2 2   IO  IC 2 2 2 2 2 2 
x  y  z  x  
 y  3  z  z  1    1 3  14 I  ;  ;1 
  R  IO  .  2 2  2
Cách 2: Tìm phương trình mặt cầu suy ra bán kính.
Gọi phương trình mặt cầu S  ngoại tiếp tứ diện OABC là: 2 2 2
x  y  z  2ax  2by  2cz  d  0 .  1 a   1
  2a  d  0  2  
4  4c  d  0  3
Do S  đi qua bốn điểm ,
A B,C,O nên ta có:   b    .
9  6b  d  0  2  d  0 c  1  d  0  14
 bán kính của S  là: 2 2 2
R  a  b  c  d  . 2
Cách 3: Sử dụng công thức tính bán kính mặt cầu ngoại tiếp của tứ diện vuông.
Do tứ diện OABC có ba cạnh O ,
A OB, OC đôi một vuông góc nên bán kính mặt cầu ngoại tiếp tứ diện OABC 1 1 14 là 2 2 2 R 
OA  OB  OC  1 4  9  . 2 2 2 Câu 116. Gọi I  ; a ;
b c là tâm mặt cầu đi qua bốn điểm ,
A B, C, D . Khi đó:   
 a  22  b  c  a  2 1  b  32 2 2 2 2 2  c AI BI   
 AI  CI  
 a  22  b  c  a  2
1  b  c  32 2 2 2 2 2  2 2  AI  DI  a  2 
2  b  c  a  2
1  b  22  c  32 2 2 
a  3b  3  a  0  
 a  c  1   b
  1  I 0;1  ;1
a 2b 3c 5      c  1   Bán kính: 2 2 2
R  IA  2 1 1  6 . A B I Câu 117.          2 2 2 2
Ta có: MA  3MB  MA  9MB  MI  IA  9MI  IB 2 2
 IA  IB  MI IA  IB 2 9 2 9  8MI   1     1  1 9
Gọi I thỏa mãn IA  9IB  0  BI  AB nên IB  ; IA  . 8 2 2 3  3  Từ   1 suy ra 2
 8MI  18  MI 
suy ra M  S I; .   2  2 
Câu 118. Ta có điều kiện xác định mặt cầu là 2 2 2
a  b  c
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 m  5  m  2 2 2 2 2
 4m  m  5m  9  0 2
 m  4m  5  0   . m  1   
Câu 119. Gọi I a; ;
b c  IA  a;1 ;
b 2  c; IH  4  a;  3  ;
b  2  c  
ABCD là tứ diện đều nên tâm I của mặt cầu ngoại tiếp trùng với trọng tâm tứ diện  IA  3  IH a  3  4  a a  3    1   b  3   3
  b  b   2
  I 3;  2;   1 .   c  c c  1 2 3 2        
Dạng 3. Viết phương trình mặt cầu Câu 120. lời giải Chọn C 2 2 2
Ta có R  IA  1  1  2   1  3   1  5
vậy phương trình mặt cầu tâm I và đi qua điểm A có phương trình là
 x  x 2   y  y 2   z  z 2  R   x  2   y  2   z  2 2 1 1 1  5 I I I Câu 121. Chọn A
Hình chiếu vuông góc của M trên trục Ox là I 1; 0; 0  IM  13 .Suy ra phương trình mặt cầu tâm I 2
bán kính IM là: x    2 y  2 1 z  13 .
Câu 122. Gọi I là trung điểm AB ta có I 1;3;3 là tâm mặt cầu. 2 2 2
Bán kính R  IA  1 
1  2  3  7  3  45. 2 2 2
Vậy phương trình mặt cầu cần tìm là  x  
1   y  3   z  3  45 .
Câu 123. Mặt cầu có tâm I 1; 4; 
3 và đi qua điểm A5;3;2 nên có bán kính R  IA  3 2
Vậy phương trình mặt cầu cần tìm là:  x  2   y  2   z  2 1 4 3  18 .
Câu 124. Gọi I là tâm của mặt cầu đường kính AB .
Khi đó I 1;0; 2 . 1 1 2 2 2
Bán kính của mặt cầu là: R  AB  1  1  1   1  3   1  2 . 2 2 2 2
Vậy phương trình mặt cầu là:  x   2 1
 y   z  2  2 .
Câu 125. Gọi I là trung điểm của AB  I (0;3; 1).  2 2 2
IA  (2;1; 2)  IA  2 1  2  3. 2 2
Mặt cầu đã cho có tâm I, đường kính AB nên có phương trình là 2
x   y  3   z   1  9. Câu 126. Chọn A
Đáp án B vì không có số hạng 2
y . Đáp án C loại vì có số hạng 2xy . Đáp án D loại vì 2 2 2
a  b  c  d  1 1  4  8  2  0 . Đáp án A thỏa mãn vì 2 2 2
a  b  c  d  1  0  4 1  6  0 .
Câu 19 : [2H3-1.3-1] Trong không gian Oxyz , cho hai điểm A2; 1  ; 3   ; B 0;3;  1  . Phương trình của mặt
cầu đường kính AB là :
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 2 2 2 2 2 A.  x   1   y   1
  z  2  6 B.  x   1   y   1
  z  2  24 2 2 2 2 2 2 C.  x   1   y   1
  z  2  24 D.  x   1   y   1
  z  2  6 Lờigiải Chọn D
Tâm I mặt cầu là trung điểm của AB 1 1 1 I 1;1; 2
  bán kính R  AB  4 16  4  24 2 2 2
 x  2   y  2   z  2 1 1 2  6
Câu 127. Phương trình 2 2 2
x  y  z  2ax  2by  2cz  d  0 là phương trình của một mặt cầu nếu 2 2 2
a  b  c  d  0 .
Câu 128. Tọa độ tâm mặt cầu là I 3;3 
;1 , bán kính R  IA  3 .
Câu 129. Phương trình mặt cầu tâm I 2;1;  2 bán kính R  2 có hai dạng: 2 2 2
Chính tắc:  x     y     z   2 2 1 2  2 Tổng quát: 2 2 2
x  y  z  4x  2y  4z  5  0 . Vậy đáp án đúng là B.
Câu 130. Vì mặt cầu S  có tâm A2;1;0 , đi qua điểm B 0;1;2 nên mặt cầu S  có tâm A2;1;0 và
nhận độ dài đoạn thẳng AB là bán kính.  
Ta có: AB  2 :0; 2 . AB  AB   2 2 2 2
 0  2  2 2 . Suy ra: R  2 2 . 2 2
Vậy:  S   x     y   2 : 2 1  z  8 . Vậy chọn đáp án B Câu 131. lời giải Chọn B 2 2 2
Ta có R  IA  1  1  2   1  3   1  5
vậy phương trình mặt cầu tâm I và đi qua điểm A có phương trình là
 x  x 2   y  y 2   z  z 2  R   x  2   y  2   z  2 2 1 1 1  5 I I I Câu 132.
Gọi H là trung điểm AB suy ra H là hình chiếu vuông góc của I lên Ox nên H 1;0;0 . 2 2
IH  13  R  IA  IH  AH  4 . 2 2 2
Phương trình mặt cầu là:  x  
1   y  2   z  3  16 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 133. Với điểm M 1; 2
 ;3 thì hình chiếu vuông góc của M trên trục Ox là I 1;0;0
Có IM  13 vậy phương trình mặt cầu tâm I 1;0;0 bán kính IM là:  x  2 2 2 1
 y  z  13
Câu 134. Ta có mặt cầu S  2 2 2
: x  y  z  2ax  2by  2cz  d  0 có bán kính là 2 2 2
R  a  b  c  d a  2 b   1 Trong đáp án C ta có: 2 2 2   R 
a  b  c  d  4  2 . c  1  d  2   
Câu 135. Gọi I a ;0;0 Ox  IA1  a ;1;2; IB 3  a ;2; 3 . 2 2
Do S  đi qua hai điểm ,
A B nên IA  IB  1 a  5  3  a 13  4a  16  a  4
 S  có tâm I 4;0;0 , bán kính R  IA  14 .
 S  x  2 2 2 2 2 2 : 4
 y  z  14  x  y  z  8x  2  0. Câu 136. Ta có: 2
S  4 R  4  R  1 2 2 2
Vậy  S  tâm I 1;1; 
1 bán kính R  1 có pt:  x   1   y   1   z   1  1
Câu 137. Gọi phương trình mặt cầu S  2 2 2
x  y  z  ax  by  cz  d   2 2 2 : 2 2 2
0 a  b  c  d  0
Vì mặt cầu đi qua 4 điểm nên:  3 a   1
 8  6a  6b  d  0  6
 a  6b  d  18 2    3 1 
 8  6a  6c  d  0  6
 a  6c  d  18 b        2
18  6b  6c  d  0  6
 b  6c  d  18   3
27  6a  6b  6c  d  0 c    6
 a  6b  6c  d  27  2  d  0  2 2 2  3 3 3   3   3   3  3 3 Suy ra tâm I ; ;   bán kính R           .  2 2 2   2   2   2  2 2 2 2  3   3   3  27
Vậy phương trình mặt cầu x   y   z         .  2   2   2  4 Câu 138. Chọn A
Gọi I 1;1;0, R  2. II   10 .
Gọi R là bán kính của mặt cầu S . Theo giả thiết, ta có R  R  II   R  II   R  8 . 2 2 2
Khi đó phương trình mặt cầu S :  x  9   y  
1   z  6  64 .
Câu 139. Gọi I  ; a ;
b c là tâm của mặt cầu S  . Mặt cầu S  tiếp xúc với các mặt phẳng tọa độ
d I,Oxy  d  I,Oyz  d I,Oxz  a  b  c  R   1
Mặt cầu  S  đi qua A1; 1  ; 4 2 2 2 2 IA  R 2 2 IA  R    a   1  b  
1  c  4  R      
a  0; c  0; b  0 
a  0; c  0;b  0 
a  c  b
  R  0 (do    1 ) 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 36
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489   2 2
 a  2  a  2  a  2 2 1 1 4  a
2a 12a 18  0
a  6a  9  0      
a  c  b  R  0 
a  c  b   R  0 
a  c  b   R  0  a  c  3   b 2 2 2   3 
 S  :  x  3   y  3   z  3  9 . R  3 
Câu 140. Gọi I là tâm đường tròn nội tiếp tam giác OMN .    
Ta áp dụng tính chất sau : “Cho tam giác OMN với I là tâm đường tròn nội tiếp, ta có . a IO  . b IM  . c IN  0
, với a  MN , b  ON , c  OM ”. 2 2 2  8    4   8  Ta có 2 2 2
OM  2  2 1  3 , ON     4       .  3   3   3  2 2 2  8    4   8  MN   2   2  1  5       .  3   3   3    8  5.0  4.2  3.     3 x     0 I  3  4  5   4   5.0  4.2  3.         3 
5.IO  4.IM  3.IN  0   y   1 . I 3  4  5    8  5.0  4.2  3.     3 z     1 I  3  4  5  
Mặt phẳng Oxz có phương trình y  0 .
Mặt cầu tiếp xúc với mặt phẳng Oxz nên mặt cầu có bán kính R  d  I,Oxz  1 . 2 2
Vậy phương trình mặt cầu là: 2
x   y   1   z   1  1.
Câu 141. Vì mặt cầu tâm I tiếp xúc với các mặt phẳng tọa độ nên
a  b  c
a  b  c
d  I,Oyz  d  I,Ozx  d  I,Oxy  a  b  c  
a  b  c
a  b  c 
Nhận thấy chỉ có trường hợp a  b  c thì phương trình AI  d I,Oxy có nghiệm, các trường hợp còn lại vô nghiệm. Thật vậy:
Với a  b  c thì I a;  a; a 2 2 2
AI  d  I,Oyx  a    a    a   2 1 1 4  a 2
 a  6a  9  0  a  3
Khi đó P  a  b  c  9 .
Dạng 3. Một số bài toán khác Câu 142. Chọn C
Mặt cầu  S  có tâm I 0;0; 2  và bán kính R  3 ; AOxy  Aa;b;0 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 37
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
* Xét trường hợp AS  , ta có 2 2
a  b  1 . Lúc này các tiếp tuyến của  S  thuộc tiếp diện của  S  tại A
nên có vô số các tiếp tuyến vuông góc nhau.
a  0 a  0 a  1  a  1 
Trường hợp này ta có 4 cặp giá trị của  ; a b là  ;  ;  ;  . b  1 b  1  b  0 b  0    
* Xét trường hợp A ở ngoài  S  . Khi đó, các tiếp tuyến của  S  đi qua A thuộc mặt nón đỉnh A . Nên các
tiếp tuyến này chỉ có thể vuông góc với nhau tại A .
Điều kiện để có ít nhất 2 tiếp tuyến vuông góc là góc ở đỉnh của mặt nón lớn hơn hoặc bằng 90 . Giả sử A N  ; A M 
là các tiếp tuyến của  S  thỏa mãn AN  AM ( N; M là các tiếp điểm) N A I M Dễ thấy A N
 IM là hình vuông có cạnh IN  R  3 và IA  3. 2  6 . IA  R 2 2   a  b  1
Điều kiện phải tìm là   
IA  IA  6 2 2  a  b  4 
Vì a ,b là các số nguyên nên ta có các cặp nghiệm  ; a b là
0;2,0; 2,2;0, 2  ;0,1;  1 , 1  ;   1 , 1  ;  1 ,1;  1 .
Vậy có 12 điểm A thỏa mãn yêu cầu. Câu 143. Chọn A
Mặt cầu có tâm I 0;0; 
1 , bán kính R  5 .
Vì A  Oxy nên c  0 . Các giao tuyến của A đến mặt cầu (nếu IA  R ) tạo nên một mặt nón tâm A , để
mặt nón này có hai đường sinh vuông góc thì góc của mặt nón này phải  90 hay IA  R 2 . Vậy 2 2 2 2
R  IA  R 2  5  a  b  1  10  4  a  b  9
Ta có các bộ số thõa mãn 0; 2  ;0; 3  ; 1  ; 2  ; 2  ; 2  ; 2  ;   1 ; 2  ; 0; 3  ;0 , 20 bộ số. Câu 144. Chọn A
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 38
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Mặt cầu S  2 2 2
: x  y  (z 1)  5 có tâm I 0;0; 
1 và có bán kính R  5  a b 1 
Aa;b;0 Oxy , Gọi I  là trung điểm của AI  I  ; ;     2 2 2 
Gọi E, F lần lượt là hai tiếp điểm của tiếp tuyến đi qua A sao cho AE  AF .  a b 1  1
Ta có: E, F cùng thuộc mặt cầu  S đường kính IA có tâm I  ; ;    , bán kính 2 2 R  a  b 1 .  2 2 2  2
Đề tồn tại E, F thì hai mặt cầu  S  và  S phải cắt nhau suy ra R  R  II  R  R 1 1 1 2 2 2 2 2 2  5  a  b 1 
a  b 1  5  a  b 1 2 2 2 2 2 2 2
 5  a  b 1  a  b  4  1
Gọi H là hình chiếu của I trên  AEF  khi đó tứ giác AEHF là hình vuông có cạnh 2 AE  HF  AI  5 . Ta có 2 2 2
IH  R  HF    2 AI   2 2 2 2 2 5
5  10  AI  0  a  b  1  10  a  b  9 2 Từ   1 và 2 ta có 2 2
4  a  b  9 mà a, b, c   nên có 20 điểm thỏa bài toán. Cách khác:
Mặt cầu  S  có tâm I 0, 0,  
1 bán kính R  5 . Ta có d
 1  R  mặt cầu  S  cắt mặt phẳng
I Oxy
Oxy . Để có tiếp tuyến của S  đi qua A  AI  R   1 .
Có Aa b c Oxy  Aa b  2 2 , ,
, , 0 , IA  a  b 1.
Quỹ tích các tiếp tuyến đi qua A của  S  là một mặt nón nếu AI  R và là một mặt phẳng nếu AI  R .
Trong trường hợp quỹ tích các tiếp tuyến đi qua A của  S  là một mặt nón gọi AM , AN là hai tiếp tuyến sao cho ,
A M , I , N đồng phẳng. M A I N
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 39
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Tồn tại ít nhất hai tiếp tuyến của  S  đi qua A và hai tiếp tuyến đó vuông góc với nhau khi và chỉ khi   90o MAN  IA  R 2 2 . Từ     2 2
1 , 2  4  a  b  9 . Vì a, b   2  2 2 2 2 2 2 a  0  a  9  a  4  a  0  a  1  a  4  a  4   hoặc  hoặc  hoặc  hoặc  hoặc  hoặc  . 2 b  9 2 2 2 2 2 2  b  0  b  0  b  4  b  4  b  1  b  4 
Bốn hệ phương trình đầu tiên có hai nghiệm, ba hệ sau có 4 nghiệm suy ra số điểm A thỏa mãn là 4.2  3.4  20 . Câu 145. Chọn D
Nhận thấy điểm M nằm bên trong mặt cầu S . Để AB  2 R  2
d (O, ) nhỏ nhất khi d O,  lớn nhất.
Ta thấy d O,   OM  const . Dấu ‘=’ xảy ra khi   OM .    
1  a  b  0 a  1 Suy ra . u OM  0 và . u n  0 nên   P 
1  a  2b  0 b    0
Suy ra T  a  b  1 .
Câu 146. Vì các điểm M , N, P đều nằm trên đoạn AB sao cho AM  MN  NP  PB BM  3MA d
 B,Oxy 3d A,Oxy  c  3.4         
Do đó ta có  BN  NA   d B,Oxz  d A,Oxz   b  3         3BP  PA
3d B,Oyz d A,Oyz 3  . a  9   
Để M , N, P đều nằm trên đoạn AB thì hai điểm A và B không nằm về cùng 1 phía so với lần lượt các mặt
phẳng Oxy,Oxz,Oyz Do đó B 12  ,3,  3
Vậy ab  bc  ac  9 Câu 147.
Mặt cầu S  có tâm I 1;1;0 và bán kính R  2 . 
Ta có IM  1; 2;  1 và IM  6 .
Gọi H là một tiếp điểm tùy ý khi kẻ tiếp tuyến từ Oxyz đến mặt cầu, khi đó 2 2 MH 
IM  R  2 . Gọi O
là tâm của đường tròn C  khi đó IM  HO và HO  r . HI.HM 2 2 2 3
Ta có HI.HM  H . O IM  r    . IM 6 3
Câu 148. Gọi M  x; y; z là tập hợp các điểm thỏa mãn yêu cầu bài toán. Ta có     AM   ;
x y  1; z  2 , BM   x  2; y  3; z , CM   x  2; y 1; z   1 , DM   ;
x y  1; z  3 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 40
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  
      . MA MB  1 Từ giả thiết: .
MA MB  MC.MD  1    MC.MD  1  x 2 2 2
  x  2   y  
1  y  3  z  z  2  1 
x  y  z  2x  4 y  2z  2  0     x 2 2 2
  x  2   y   1  y   1   z   1  z  3  1 
x  y  z  2x  4z 1  0 
Suy ra quỹ tích điểm M là đường tròn giao tuyến của mặt cầu tâm I 1; 2
 ;1 , R  2 và mặt cầu tâm 1   1 I 1  ;0; 2 , R  2 . 2   2 M I1 I2 Ta có: I I  5 . 1 2 2  I I  5 11 Dễ thấy: 2 1 2 r  R   4   . 1    2  4 2 Câu 149. Cách 1: Gọi ,
A B,C, D là tâm bốn mặt cầu, không mất tính tổng quát ta giả sử AB  4 , AC  BD  AD  BC  5 .
Gọi M , N lần lượt là trung điểm của AB, CD . Dễ dàng tính được MN  2 3 . Gọi I là tâm mặt cầu nhỏ
nhất với bán kính r tiếp xúc với bốn mặt cầu trên. Vì IA  IB, IC  ID nên I nằm trên đoạn MN .
Đặt IN  x , ta có 2 2
IC  3  x  3  r , IA     x2 2 2 2 3  2  r 2 12 3  12 3  6
Từ đó suy ra 3  x  2  2 2  x2 2 2 2  1  x  , suy ra 2 r  3     3  11  11  11   Cách 2 Gọi ,
A B là tâm quả cầu bán kính bằng 2 . C, D là tâm quả cầu bán kính bằng 3 . I là tâm quả cầu bán kính x .
Mặt cầu  I  tiếp xúc ngoài với 4 mặt cầu tâm ,
A B,C, D nên IA  IB  x  2, IC  ID  x  3 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 41
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Gọi  P , Q lần lượt là các mặt phẳng trung trực đoạn AB và CD .
IA  IB  I   P 
 I   P  Q   1 .
IC  ID  I   Q 
Tứ diện ABCD có DA  DB  CA  CB  5 suy ra MN là đường vuông góc chung của AB và CD , suy ra
MN   P  Q (2). Từ  
1 và 2 suy ra I  MN
Tam giác IAM có IM 
IA  AM   x  2 2 2 2  4 .
Tam giác CIN có IN 
IC  CN   x  2 2 2 3  9 . Tam giác ABN có 2 2 NM 
NA  AM  12 . 2 2 6
Suy ra  x  3  9   x  2  4  12  x  . 11
Dạng 4. Bài toán cực trị Câu 150. Chọn C    Ta có: OM  . a i  . b k  M  ; a 0;b   
MA  1 a; 2;3  b; MB  6  ;
a 5;8  b  2MB  12  2a;10; 16  2b  
 MA  2MB  a 13;12;b 13  
 MA  MB  a  2   b  2 2 2 13 12 13  12   a  13 Vậy MA  2MB  12  
. Do đó a  b  0 min b  13 
Câu 151. Ta thấy M  ; a ;
b 0 Oxy .  3 1  Gọi I ; ; 2 
 là trung điểm của đoạn thẳng AB , ta có  2 2       2 2 2 2 2 2
MA  MB  MA  MB  IA  IM   IB  IM            2 2
IA  IM  IA IM    2 2 2 . IB  IM  2 . IB IM  2
   AB 2 2
 IM  IA  IM IA  IB 2 2 2 2  IM   IM  7 . 2 Bởi vậy 2 2
MA  MB nhỏ nhất  IM ngắn nhất  M là hình chiếu vuông góc của I trên mặt phẳng   3 1  3 1 3 1
Oxy . Bởi vậy M ; ; 0   . Như vậy a  , b   a  b    2 .  2 2  2 2 2 2 Câu 152.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 42
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489   
Gọi I là điểm thỏa mãn 2IA  IB  0
 I (2x  x ; 2y  y ; 2z  z ) A B A B A B  I (5;5; 1) .
Suy ra I là điểm cố định.
Suy ra P đạt giá trị nhỏ nhất khi MI đạt giá trị nhỏ nhất, P đạt giá trị lớn nhất khi MI đạt giá trị lớn nhất. 2 2 2
(S) :(x 1)  ( y  2) (z 1)  9 có tâm J (1; 2; 1) và bán kính R  3 Suy ra IJ  5
Mà M là điểm thay đổi trên (S) Do đó:
min MI  IM  JI  R  5  3  2 1
max MI  IM  JI  R  5  3  8 2 Suy ra 2 2
m  n  8  2  60
      7 7 
Câu 153. Xét điểm I a; ;
b c thỏa mãn IA  IB  IC  ID  0 . Khi đó I ; ;0   .  4 2          2 2 2 2 Ta có 2 2 2 2
MA  MB  MC  MD  MI  IA  MI  IB  MI  IC  MI  ID
     2
 MI  MI IA  IB  IC  ID 2 2 2 2 4 2
 IA  IB  IC  ID 2 2 2 2 2 2 2 2 2
 4MI  IA  IB  IC  ID  IA  IB  IC  ID ( vì 2
MI  0 với mọi điểm M )  7 7  7 7 21
Dấu "  " xảy ra  M  I tức là M
; ;0  x  y  z      .  4 2  4 2 4   
Câu 154. Gọi điểm E thỏa EA  2EB  0 . Suy ra B là trung điểm của AE , suy ra E 3;4;5.   2   2 Khi đó: 2 2
MA  2MB  ME  
EA  2ME  EB 2 2 2  M
 E  EA  2EB . Do đó 2 2
MA  2MB lớn nhất  ME nhỏ nhất  M là hình chiếu của E 3;4;5 lên Oxy  M 3;4;0.
Chú ý: Ta có thể làm trắc nghiệm như sau
+ Loại C vì M 0; 0;5 không thuộc Oxy . 3 1    1 3   
+ Lần lượt thay M  ; ; 0 
M  ; ;0 M 3;4;0 MA  MB M 3;4; 0  , ,   vào biểu thức 2 2 2 thì   cho 2 2  2 2 
giá trị lớn nhất nên ta chọn M 3;4; 0.   
Câu 155. Xét điểm I sao cho: 2IA  IB  0. Giả sử I  ; x ; y z, ta có:   IA4  ;
x 3  y;1 z , IB 3  ;1
x  y;3  z .
24  x  3  x    
Do đó: 2IA  IB  0  23  y  1 y  I 5;5;   1 .
21 z  3 z      2 2 Do đó: 2 2
P  2MA  MB  2MI  IA  MI  IB         2 2
 MI  IA  MI IA   2 2 2 2 4 .
MI  IB  2MI.IB      
   2 2 2
 MI  2IA  IB  2MI 2IA  IB 2 2 2
 MI  2IA  IB  2MI 2IA  IB
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 43
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 2 2
 MI  2IA  IB . Do I cố định nên 2 2
IA , IB không đổi. Vậy P lớn nhất (nhỏ nhất) 2
 MI lớn nhất (nhỏ nhất).  MI lớn
nhất (nhỏ nhất)  M là giao điểm của đường thẳng IK (với K 1; 2;  
1 là tâm của mặt cầu (S)) với mặt cầu (S). 
Ta có: MI đi qua I 5;5;  
1 và có vectơ chỉ phương là KI 4;3;0. x  1 4t 
Phương trình của MI là:  y  2  3t z  1.  
Tọa độ điểm M cần tìm ứng với giá trị t là nghiệm của phương trình:  3 t  
  t  2    t  2    2 2 5 1 4 1 2 3 2 1 1
 9  25t  9   3 t   .  5 3  17 19  Với t   M ;
; 1  M I  2 (min). 1   1 5  5 5  3  7 1  m  P  48 Với t    M
 ; ; 1  M I  8 (max). Vậy max 
 m  n  60. 1   2 5  5 5  n  P  12   min
   
Câu 156. Gọi I là điểm thỏa IA  IB  IC  0  I 2; 2; 2 .      
    2 2 2 2 2 2
MA  MB  MC  MI  IA  MI  IB  MI  IC 2 2 2 2
 3MI  IA  IB  IC  2MI.IA  IB  IC 2 2 2 2
 3MI  IA  IB  IC .
Mà M  Oyz  2 2 2
 MA  MB  MC đạt giá trị nhỏ nhất  M là hình chiếu của I lên Oyz  M 0; 2  ; 2 .
Vậy P  0  2  2  0 .    
Câu 157. Gọi I  ;
x y; z  là điểm thỏa IA  2IB  IC  0 .           
Khi đó IA  2IB  IC  0  OA  OI   2OB  OI   OC  OI   0  1     OI 
OA 2OB OC  2;3;  1  I 2;3;  1 . 2         
Ta có MA  2MB  MC  MI  IA  2MI  IB  MI  IC     
 2MI  IA  2IB  IC  2 MI  2MI .   
MA  2MB  MC nhỏ nhất khi và chỉ khi MI ngắn nhất, khi đó M là hình chiếu của I 2;3;  1 lên mặt
phẳng Oyz . Suy ra M 0;3  ;1 .   
  
Câu 158. Ta có: AB  2;7; 6
  , AC  1;3; 2
  , AD  1;6; 4 nên  AB, AC .AD  4  0 .  
  
Suy ra: AB , AC , AD không đồng phẳng.
Gọi G là trọng tâm tứ diện ABCD . Khi đó G 2;1; 4 .
    
Ta có: MA  MB  MC  MD  4MG  4MG .
   
Do đó MA  MB  MC  MD nhỏ nhất khi và chỉ khi MG ngắn nhất.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 44
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Vậy M là hình chiếu vuông góc của G lên mặt phẳng Oyz nên M 0;1; 4 .
Câu 159. Lấy G 1;3;  
1 là trọng tâm của tam giác ABC . Ta có:       2 2 2 2 2 2
MA  MB  MC  MG  GA  MG  GB  MG  GC 2 2 2 2
 3MG  GA  GB  GC . Do đó 2 2 2
MA  MB  MC bé nhất khi MG bé nhất.
Hay M là hình chiếu của điểm G lên mặt phẳng Oxy . Vậy M 1;3;0 .  x  3x A B x  H  1 3      y  3y  3 11 19 
Câu 160. Gọi điểm H thỏa mãn HA  3HB  0 khi đó: A B  y   H  ; ; . H   1 3   4 4 4   z  3z A B z  H   1 3
Phương trình mặt phẳng Oxy là z  0 . x  x  aT M H z 19   3 11  Xét H T  
do đó tọa độ điểm M cần tìm là:  y  y  bT  M  ; ; 0   . 1 4 M H   4 4  z  z  cT  M H 3 11
Vậy T  x  y  z     0  2 . M M M 4 4 2 2 2
Câu 161. Ta có S  :  x   1   y  
1   z  3  4  S  có tâm I 1;1;3 và bán kính R  2 .
Bài ra A , M , B nằm trên mặt cầu S  và 
AMB  90  AB qua I  AB  2R  4 . 1 2 2 MA  MB 2 AB Ta có S  M . A MB    4 . AMB 2 4 4 AB
Dấu "  " xảy ra  MA  MB   2 2 và AB  4 . 2
Do đó diện tích tam giác AMB có giá trị lớn nhất bằng 4 . 2 2 2
Câu 162. Gọi Ad, ,
e f  thì A thuộc mặt cầu S : x 1  y  2  z  3  1 có tâm I 1;2;3 , bán 1   1        2 2
kính R  1, B a, ,
b c thì B thuộc mặt cầu S : x  3  y  2  z  9 có tâm I 3  ; 2; 0 , 2   2      2 1
bán kính R  3 . Ta có I I  5  R  R   S và S không cắt nhau và ở ngoài nhau. 2  1  2 1 2 1 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 45
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Dễ thấy F  AB , AB max khi A  A , B  B  Giá trị lớn nhất bằng I I  R  R  9 . 1 1 1 2 1 2
AB min khi A  A , B  B  Giá trị nhỏ nhất bằng I I  R  R  1. 2 2 1 2 1 2
Vậy M  m  8
Câu 163. Gọi M  ; x y; z  . MA 2 Ta có   3MA  2MB 2 2  9MA  4MB MB 3  x 2  y 2  z 2   x 2  y 2  z 2 9 2 2 2 4 3 3 3                  2 2 2
 x  y  z 12x 12 y 12z  0
  x  2   y  2   z  2 6 6 6  108 .
Như vậy, điểm M thuộc mặt cầu S  tâm I 6;6; 6 và bán kính R  108  6 3 . 2 2
Do đó OM lớn nhất bằng OI  R    2 6
 6  6  6 3  12 3 .    
Câu 164. Gọi E  ;
x y; z là điểm thỏa mãn EA  2EB  EC  0 Ta có 6  2 ; x 12  2 ;
y 18  2z   0;0;0  E 3;6;9 .    
3MA  2MB  MC  2ME
Mặt cầu  S  có tâm I 1;2;3 x  1 t 
Đường thẳng EI có PTTS  y  2  2t z  3 3t 
M  IE  M 1 t;2  2t;3  3t M S  2
14t  14  t  1 
t  1  M 2; 4;6 , EM  14 . 1   1 t  1   M
0;0;0 , EM  3 14  EM . 2   2 1
Vậy x  y  2  4  6 . M M
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 46

Các dạng toán hệ trục tọa độ Oxyz và phương trình mặt cầu thường gặp Toán 12

Thông tin :

Tài liệu liên quan:

Bài giảng vectơ và hệ trục tọa độ trong không gian Toán 12 KNTTVCS

Toán ứng dụng thực tế vectơ và hệ trục toạ độ trong không gian

Chuyên đề hình học giải tích không gian – Lưu Huy Thưởng Toán 12

Chuyên đề HH giải tích không gian – Trung tâm LTĐH Vĩnh Viễn Toán 12

Bài tập tọa độ không gian phân theo dạng có lời giải chi tiết – Trần Sĩ Tùng Toán 12