Các dạng toán số phức thường gặp trong kỳ thi THPTQG

Các dạng toán số phức thường gặp trong kỳ thi THPTQG được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

78 39 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Số phức

Môn: Toán 12

Thông tin:

97 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễ
n Bảo Vương: https://www.facebook.com/phong.baovuong 1
CHUYÊN
ĐỀ 25
MỤC LỤC
Ph
ần A. CÂU HỎI .......................................................................................................................................................... 1
Dạng 1. Xác định các yếu tố cơ bản của số phức ......................................................................................................... 1
Dạng 1.1 Xác định phần thực, phần ảo của số phức .................................................................................................... 1
Dạng 1.2 Xác định số phức liên hợp, số phức đối, môđun của số phức ....................................................................... 2
Dạng 2. Biểu diễn hình học cơ bản của số phức .......................................................................................................... 3
Dạng 3. Thực hiện các phép tính cộng, trừ, nhân, chia cơ bản của số phức ............................................................. 6
Dạng 3.1 Phép tính cộng trừ 2 số phức ........................................................................................................................ 6
Dạng 3.2 Phép tính nhân, chia 2 số phức ..................................................................................................................... 7
Dạng 4. Tìm số phức thỏa mãn điều kiện cho trước ................................................................................................. 10
Dạng 4.1 Điều kiện cho trước không chứa yếu tố môđun .......................................................................................... 10
Dạng 4.2 Điều kiện cho trước chứa yếu tố môđun ..................................................................................................... 12
Phần B. LỜI GIẢI THAM KHẢO ............................................................................................................................. 16
Dạng 1. Xác định các yếu tố cơ bản của số phức ....................................................................................................... 16
Dạng 1.1 Xác định phần thực, phần ảo của số phức .................................................................................................. 16
Dạng 1.2 Xác định số phức liên hợp, số phức đối, môđun của số phức ..................................................................... 16
Dạng 2. Biểu diễn hình học cơ bản của số phức ........................................................................................................ 17
Dạng 3. Thực hiện các phép tính cộng, trừ, nhân, chia cơ bản của số phức ........................................................... 18
Dạng 3.1 Phép tính cộng trừ 2 số phức ...................................................................................................................... 18
Dạng 3.2 Phép tính nhân, chia 2 số phức ................................................................................................................... 18
Dạng 4. Tìm số phức thỏa mãn điều kiện cho trước ................................................................................................. 21
Dạng 4.1 Điều kiện cho trước không chứa yếu tố môđun .......................................................................................... 21
Dạng 4.2 Điều kiện cho trước chứa yếu tố môđun ..................................................................................................... 25
Phần A. CÂU HỎI
Dạng 1. Xác định các yếu tố cơ bản của số phức
Dạng 1.1 Xác định phần thực, phần ảo của số phức
Câu 1. (Mã đề 104 BGD&ĐT NĂM 2018) Số phức có phần thực bằng
1
và phần ảo bằng
3
là
A.
1 3i
B.
1 3i
C.
1 3i
D.
1 3i
Câu 2. (MĐ 103 BGD&ĐT NĂM 2017-2018) Số phức
5 6i
có phần thực bằng
A.
6
. B.
6
. C.
5
. D.
5
Câu 3. (Mã đề 102 BGD&ĐT NĂM 2018) Số phức có phần thực bằng
3
và phần ảo bằng
4
là
KHÁI NIỆM SỐ PHỨC, CÁC PHÉP TOÁN SỐ PHỨC
VÀ MỘT SỐ BÀI TOÁN LIÊN QUAN
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
A.
3 4i
B.
4 3i
C.
3 4i
D.
4 3i
Câu 4. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Kí hiệu
,a b
lần lượt là phần thực và phần ảo của số phức
. Tìm
a
,
b
.
A.
3; 2
a b
B.
3; 2 2
a b
C.
3; 2
a b
D.
3; 2 2
a b
Câu 5. (Mã đề 101 BGD&ĐT NĂM 2018) Số phức
3 7i
có phần ảo bằng:
A.
7
B.
7
C.
3
D.
3
Câu 6. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Số phức nào dưới đây là số thuần ảo.
A.
3z i
B.
2z
C.
2 3z i
D.
3z i
Câu 7. (MĐ 105 BGD&ĐT NĂM 2017) Cho số phức
2 3z i
. Tìm phần thực
a
của
z
?
A.
2a
B.
3a
C.
2a
D.
3a
Câu 8. (THPT CẨM GIÀNG 2 NĂM 2018-2019) Cho số phức
3 4z i
. Tìm phần thực và phần ảo của số
phức
z
.
A. Phần thực là
4
và phần ảo là
3i
. B. Phần thực là
3
và phần ảo là
4
.
C. Phần thực là
4
và phần ảo là
3
. D. Phần thực là
3
và phần ảo là
4i
.
Câu 9. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho sô phưc
3 2z i
. Tim phân thưc va phân ao cua sô
phưc
z
:
A. Phân thưc băng
3
va Phân ao băng
2i
B. Phân thưc băng
3
va Phân ao băng
2
C. Phân thưc băng
3
va Phân ao băng
2i
D. Phân thưc băng
3
va Phân ao băng
2
Dạng 1.2 Xác định số phức liên hợp, số phức đối, môđun của số phức
Câu 10. (Mã đề 104 - BGD - 2019) Số phức liên hợp của số phức
3 2z i
là.
A.
3 2i
. B.
3 2i
. C.
2 3i
. D.
3 2i
.
Câu 11. (Mã 103 - BGD - 2019) Số phức liên hợp của số phức
1 2i
là:
A.
1 2i
. B.
1 2i
. C.
2 i
. D.
1 2i
.
Câu 12. (MĐ 104 BGD&DT NĂM 2017) Cho số phức
2z i
. Tính
z
.
A.
5
z
B.
5
z
C.
2
z
D.
3
z
Câu 13. (Mã 102 - BGD - 2019) Số phức liên hợp của số phức
5 3i
là
A.
3 5i
. B.
5 3i
. C.
5 3i
. D.
5 3i
.
Câu 14. (Mã đề 101 - BGD - 2019) Số phức liên hợp của số phức
3 4i
là
A.
3 4i
. B.
4 3i
. C.
3 4i
. D.
3 4i
.
Câu 15. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Cho số phức
3 2z i
. Tìm phần
thực và phần ảo của số phức
z
.
A. Phần thực bằng
3
và phần ảo bằng
2
.
B. Phần thực bằng
3
và phần ảo bằng
2
.
C. Phần thực bằng
3
và phần ảo bằng
2i
.
D. Phần thực bằng
3
và phần ảo bằng
2
.
Câu 21 Cho số phức
3 2z i
. Tìm phần thực và phần ảo của số phức
z
.
A. Phần thực bằng
3
và phần ảo bằng
2i
. B. Phần thực bằng
3
và phần ảo bằng
2
.
C. Phần thực bằng
3
và phần ảo bằng
2i
. D. Phần thực bằng
3
và phần ảo bằng
2
.
Câu 16. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Số phức đối của
5 7z i
là?
A.
5 7z i
. B.
5 7z i
. C.
5 7z i
. D.
5 7z i
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
Câu 17. (THPT CHUYÊN SƠN LA NĂM 2018-2019 LẦN 01) Số phức liên hợp của số phức
1 2z i
là
A.
1 2z i
. B.
2z i
. C.
1 2z i
. D.
1 2z i
.
Câu 18. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Số phức liên hợp của số
phức
5 6z i
là
A.
5 6z i
. B.
5 6z i
. C.
6 5z i
. D.
5 6z i
.
Câu 19. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Cho số phức
2 3z i
. Số phức
liên hợp của số phức
z
là:
A.
3 2z i
. B.
3 2z i
. C.
2 3z i
. D.
2 3z i
.
Dạng 2. Biểu diễn hình học cơ bản của số phức
Câu 20. (ĐỀ THAM KHẢO BGD & ĐT 2018) Điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
A.
1 2z i
B.
1 2z i
C.
2z i
D.
2z i
Câu 21. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Điểm nào trong hình vẽ bên là điểm biểu diễn
của số phức
1 2z i
?
A.
P
B.
M
C.
Q
D.
N
Câu 22. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là
điểm
M
như hình bên?
A.
1
1 2z i
B.
2
1 2z i
C.
3
2z i
D.
4
2z i
Câu 23. Điểm
M
trong hình vẽ bên là điểm biểu diễn của số phức
z
. Tìm phần thực và phần ảo của số
phức
z
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
A. Phần thực là
3
và phần ảo là
4 i
B. Phần thực là
3
và phần ảo là
4
C. Phần thực là
4
và phần ảo là
3i
D. Phần thực là
4
và phần ảo là
3
Câu 24. (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Trong hình vẽ bên, điểm M
biểu diễn số phức
z
. Số phức
z
là:
A.
1 2i
. B.
2 i
. C.
1 2i
. D.
2 i
.
Câu 25. (HỌC MÃI NĂM 2018-2019-LẦN 02) Điểm nào ở hình vẽ bên biểu diễn số phức
3 2z i
?
A.
M
. B.
N
. C.
P
. D.
Q
.
Câu 26. (THPT QUỲNH LƯU 3 NGHỆ AN NĂM 2018-2019) Điểm biểu diễn hình học của số phức
2 3z i
là điểm nào trong các điểm sau đây?
A.
2;3
M
. B.
2; 3
Q
. C.
2; 3
N
. D.
2;3
P
.
Câu 27. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Số phức nào dưới đây có điểm biểu diễn trên
mặt phẳng tọa độ là điểm M như hình vẽ bên?
A.
1 2 .i
B.
2.i
C.
2.i
D.
1 2 .i
Câu 28. (SỞ GD&ĐT THANH HÓA NĂM 2018 - 2019) Điểm
M
trong hình vẽ bên dưới biểu thị cho số
phức
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
A.
3 2 .i
B.
2 3 .i
C.
2 3 .i
D.
3 2 .i
Câu 29. (CHUYÊN LAM SƠN THANH HÓA LẦN 2 NĂM 2018-2019) Điểm
M
trong hình vẽ bên biểu
diễn số phức
z
. Chọn kết luận đúng về số phức
z
.
A.
3 5z i
. B.
3 5z i
. C.
3 5z i
. D.
3 5z i
.
Câu 30. (ĐỀ THI CÔNG BẰNG KHTN LẦN 02 NĂM 2018-2019) Điểm
M
trong hình vẽ là biểu diễn hình
học của số phức nào dưới đây?
A.
2z i
. B.
2z i
. C.
1 2z i
. D.
1 2z i
.
Câu 31. (SỞ GD&ĐT BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Số phức nào sau đây có điểm biểu diễn
là
(1; 2)
M
?
A.
1 2i
B.
1 2i
C.
1 2i
D.
2 i
Câu 32. Trong mặt phẳng tọa độ
Oxy
, điểm biểu diễn của hai số phức đối nhau là
A. hai điểm đối xứng nhau qua gốc tọa độ
O
.
B. hai điểm đối xứng nhau qua trục hoành.
C. hai điểm đối xứng nhau qua trục tung.
D. hai điểm đối xứng nhau qua đường thẳng
y x
.
Câu 33. (TT THANH TƯỜNG NGHỆ AN NĂM 2018-2019 LẦN 02) Điểm nào trong hình vẽ dưới đây là
điểm biểu diễn số phức liên hợp của số phức
3 2z i
?
x
y
2
M
3
O
2
-1
O
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
A.
M
. B.
N
. C.
Q
. D.
P
.
Câu 34. (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Trong hình vẽ bên, điểm M
biểu diễn số phức
z
. Số phức
z
là:
A.
1 2i
. B.
2 i
. C.
1 2i
. D.
2 i
.
Câu 35. (ĐỀ 01 ĐỀ PHÁT TRIỂN ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Trong mặt phẳng tọa
độ
Oxy
, 3 điểm
, ,A B C
lần lượt là điểm biểu diễn của ba số phức
1 2
3 7 , 9 5z i z i
và
3
5 9z i
. Khi đó, trọng tâm
G
là điểm biểu diễn của số phức nào
sau đây?
A.
1 9z i
. B.
3 3z i
. C.
7
3
z i
. D.
2 2z i
.
Dạng 3. Thực hiện các phép tính cộng, trừ, nhân, chia cơ bản của số phức
Dạng 3.1 Phép tính cộng trừ 2 số phức
Câu 36. (Mã đề 104 - BGD - 2019) Cho hai số phức
1
2 z i
và
2
1 z i
. Trên mặt phẳng tọa độ
Oxy
,
điểm biểu diễn của số phức
1 2
2
z z
có tọa độ là
A.
0; 5
. B.
5; 1
. C.
1; 5
. D.
5; 0
.
Câu 37. (Mã 103 - BGD - 2019) Cho hai số phức
1
1z i
và
2
2z i
. Trên mặt phẳng tọa độ
Oxy
, điểm
biểu diễn số phức
1 2
2z z
có tọa độ là
A.
(3;5)
. B.
(5;2)
. C.
(5;3)
. D.
(2;5)
.
Câu 38. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho 2 số phức
1
5 7z i
và
2
2 3z i
. Tìm số phức
1 2
z z z
.
A.
3 10z i
B.
14
C.
7 4z i
D.
2 5z i
Câu 39. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hai số phức
1
và
2
2 3z i
. Tính môđun
của số phức
1 2
.z z
A.
1 2
5
z z
. B.
1 2
5
z z . C.
1 2
1
z z
. D.
1 2
13
z z .
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
Câu 40. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho hai số phức
1
4 3z i
và
2
7 3z i
. Tìm số phức
1 2
z z z
.
A.
3 6z i
B.
11z
C.
1 10z i
D.
3 6z i
Câu 41. (MĐ 104 BGD&DT NĂM 2017) Cho số phức
1
1 2z i
,
2
3z i
. Tìm điểm biểu diễn của số
phức
1 2
z z z
trên mặt phẳng tọa độ.
A.
2; 5
M
B.
2; 1
P
C.
1;7
Q
D.
4; 3
N
Câu 42. (MĐ 104 BGD&DT NĂM 2017) Tìm số phức
z
thỏa mãn
2 3 3 2z i i
.
A.
5 5z i
B.
1z i
C.
1 5z i
D.
1z i
Câu 43. (MĐ 105 BGD&ĐT NĂM 2017) Cho hai số phức
1
1 3z i
và
2
2 5z i
. Tìm phần ảo
b
của
số phức
1 2
z z z
.
A.
3b
B.
2b
C.
2b
D.
3b
Câu 44. (CHUYEN PHAN BỘI CHÂU NGHỆ AN NĂM 2018-2019 LẦN 02) Cho hai số phức
1
1z i
và
2
2 3z i
. Tính môđun của số phức
1 2
z z
.
A.
1 2
1
z z
. B.
1 2
5
z z
. C.
1 2
13
z z
. D.
1 2
5
z z
.
Câu 45. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Gọi
1
z
,
2
z
lần lượt có điểm
biểu diễn là
M
và
N
trên mặt phẳng phức ở hình bên. Tính
1 2
z z
.
A.
2 29
. B.
20
. C.
2 5
. D.
116
.
Dạng 3.2 Phép tính nhân, chia 2 số phức
Câu 46. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho số phức
2 5 .z i
Tìm số phức
w iz z
A.
3 3w i
. B.
3 7 .w i
. C.
7 7w i
D.
7 3w i
.
Câu 47. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Tính môđun của số phức
z
biết
4 3 1
z i i
.
A.
5 2
z B.
2
z C.
25 2
z D.
7 2
z
Câu 48. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho số phức
3
1
z i i
. Tìm phần thực
a
và phần ảo
b
của
z
.
A.
1, 0
a b
B.
0, 1
a b
C.
1, 2
a b
D.
2, 1
a b
Câu 49. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho số phước
1 2 .z i
Điểm nào dưới đây là điểm biểu
diễn số phức
w iz
trên mặt phẳng tọa độ
x
y
-4
3
2
O
1
M
N
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
A.
1; 2
Q
B.
2; 1
N
C.
2;1
P
D.
1; 2
M
Câu 50. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Trong mặt phẳng tọa độ, điểm
M
là điểm biểu diễn
của số phức
z
. Điểm nào trong hình vẽ là điểm biểu diễn của số phức
2z
?
A. Điểm
Q
B. Điểm
E
C. Điểm
P
D. Điểm
N
Câu 51. (Mã đề 101 - BGD - 2019) Cho hai số phức
1
1z i
và
2
1 2z i
. Trên mặt phẳng tọa độ
Oxy
,
điểm biểu diễn số phức
1 2
3
z z
có tọa độ là:
A.
1;4
. B.
1;4
. C.
4;1
. D.
4; 1
.
Câu 52. (Mã 102 - BGD - 2019) Cho hai số phức
1
2z i
và
2
1 .z i
Trên mặt phẳng tọa độ
,Oxy
điểm biểu diễn số phức
1 2
2
z z
có tọa độ là
A.
3;3
. B.
3;2
. C.
3; 3
. D.
2; 3
.
Câu 53. Tìm số phức liên hợp của số phức
3 1
z i i
.
A.
3 z i
. B.
3 z i
. C.
3 z i
. D.
3 z i
.
Câu 54. (THPT CẨM GIÀNG 2 NĂM 2018-2019) Cho số phức
z
thỏa mãn
1 2 4 3z i i
. Tìm số phức
liên hợp
z
của
z
.
A.
2 11
5 5
z i
. B.
2 11
z i
5 5
. C.
2 11
z
5 5
= i
. D.
2 11
z
5 5
= i
.
Câu 55. (ĐỀ 15 LOVE BOOK NĂM 2018-2019) Cho số phức
z
thỏa mãn
1 3 5z i i
. Tính môđun
của
z
A.
17
z . B.
16
z
. C.
17
z
. D.
4
z
.
Câu 56. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Cho số phức
2
1 2z i
.
Tính mô đun của số phức
1
z
.
A.
1
5
. B.
5
. C.
1
25
. D.
1
5
.
Câu 57. (KTNL GV THPT LÝ THÁI TỔ NĂM 2018-2019) Cho số phức
2
1 1 2z i i
. Số phức
z
có phần ảo là:
A.
2
. B.
2
. C.
4
. D.
2i
.
Câu 58. (KTNL GV THUẬN THÀNH 2 BẮC NINH NĂM 2018-2019) Cho số phức
1
1
3
z i
. Tìm số
phức
w 3iz z
.
A.
8
w
3
. B.
8
w
3
i
. C.
10
w
3
. D.
10
w
3
i
.
O
x
y
Q
E
P
N
M
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
Câu 59. (THPT YÊN PHONG SỐ 1 BẮC NINH NĂM 2018-2019 LẦN 01) Cho số phức
2z i
. Điểm
nào dưới đây là biểu diễn của số phức
w iz
trên mặt phẳng toạ độ?
A.
1; 2 .
M
B.
2;1 .
P
C.
2;1 .
N
D.
1;2 .
Q
Câu 60. (CHUYÊN BẮC GIANG NĂM 2018-2019 LẦN 02) Cho số phức
1 2z i
. Tìm tổng phần thực
và phần ảo của số phức
2
w z z
.
A.
3
B.
5
C.
1
D.
2
Câu 61. (CHUYÊN KHTN LẦN 2 NĂM 2018-2019) Cho số phức
z
khác
0
. Khẳng định nào sau đây là
sai?
A.
z
z
là số thuần ảo. B.
.z z
là số thực. C.
z z
là số thực. D.
z z
là số ảo.
Câu 62. (CHUYÊN LAM SƠN THANH HÓA LẦN 2 NĂM 2018-2019) Cho hai số phức
1
1 2z i
và
2
3 4z i
. Số phức
1 2 1 2
2 3
z z z z
là số phức nào sau đây?
A.
10i
. B.
10i
. C.
11 8i
. D.
11 10i
.
Câu 63. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Tìm tọa độ điểm
M
là điểm biểu diễn
số phức
z
biết
z
thỏa mãn phương trình
1 3 5i z i
.
A.
1;4
M
. B.
1; 4
M
. C.
1;4
M
. D.
1; 4
M
.
Câu 64. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Cho số phức
z
thỏa mãn
1 3 5 7 .i z i
Mệnh đề nào sau đây đúng?
A.
13 4
5 5
z i
. B.
13 4
5 5
z i
. C.
13 4
5 5
z i
. D.
13 4
5 5
z i
.
Câu 65. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Cho số phức
2019
1z i
. Phần thực của
z
bằng
A.
1009
2
. B.
2019
2
. C.
2019
2
. D.
1009
2
.
Câu 66. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Cho số phức
2 3 4
3 2
i i
z
i
. Tìm tọa độ điểm biểu diễn của số phức
z
trên mặt phẳng
Oxy
.
A.
1;4
. B.
1;4
. C.
. D.
1; 4
.
Câu 67. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Cho
1 2
2 4 , 3 5z i z i
. Xác định phần thực
của
2
1 2
.w z z
A.
120
. B.
32
. C.
88
. D.
152
.
Câu 68. (CHUYÊN BẮC GIANG NĂM 2018-2019 LẦN 02) Cho số phức z thỏa mãn phương trình
2
(3 2 ) (2 ) 4i z i i
. Tìm tọa độ điểm M biểu diễn số phức z.
A.
1;1
M
B.
1; 1
M
C.
1;1
M
D.
1; 1
M
Câu 69. (THPT CHUYÊN ĐẠI HỌC VINH NĂM 2018-2019 LẦN 01) Cho số phức
z
thỏa mãn
2
1 3 4 3i z i
. Môđun của
z
bằng
A.
5
4
B.
5
2
C.
2
5
D.
4
5
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
Câu 70. (THPT CHU VĂN AN - HÀ NỘI - 2018) Số phức
2 2018
1 1 ... 1z i i i
có phần ảo
bằng
A.
1009
2 1
. B.
1009
1 2
. C.
1009
2 1
. D.
1009
2 1
.
Câu 71. (THPT NGÔ QUYỀN - QUẢNG NINH - HKII - 2018) Tìm tất cả các giá trị thực của tham số
m
để số phức
2
2
m i
z
m i
có phần thực dương
A.
2
m
. B.
2
2
m
m
. C.
2 2
m
. D.
2
m
.
Câu 72. (THPT NGÔ QUYỀN - QUẢNG NINH - HKII - 2018) Cho
3 i
z
x i
. Tổng phần thực và phần
ảo của
z
là
A.
2 4
2
x
. B.
4 2
2
x
. C.
2
4 2
1
x
x
. D.
2
2 6
1
x
x
.
Câu 73. (THCS&THPT NGUYỄN KHUYẾN - BÌNH DƯƠNG - 2018) Gọi
T
là tổng phần thực, phần ảo
của số phức
2 3 2018
2 3 ... 2018
w i i i i
. Tính giá trị của T.
A.
0.
T
B.
1.
T
C.
2.
T
D.
2.
T
Dạng 4. Tìm số phức thỏa mãn điều kiện cho trước
Dạng 4.1 Điều kiện cho trước không chứa yếu tố môđun
Câu 74. (Mã đề 104 BGD&ĐT NĂM 2018) Tìm hai số thực
x
và
y
thỏa mãn
2 3 3 5 4x yi i x i
với
i
là đơn vị ảo.
A.
1; 1
x y
. B.
1; 1x y
. C.
1; 1
x y
. D.
1; 1x y
.
Câu 75. (MĐ 105 BGD&ĐT NĂM 2017) Tìm tất cả các số thực
,x y
sao cho
2
1 1 2x yi i
.
A.
2 , 2
x y B.
2, 2
x y C.
0, 2x y
D.
2 , 2
x y
Câu 76. (Mã đề 101 BGD&ĐT NĂM 2018) Tìm hai số thực
x
và
y
thỏa mãn
2 3 1 3 6x yi i x i
với
i
là đơn vị ảo.
A.
1; 1
x y
B.
1; 3
x y
C.
1; 3
x y
D.
1; 1
x y
Câu 77. (Mã đề 104 - BGD - 2019) Cho số phức
z
thỏa mãn
2 3 16 2
i z i z i
. Môđun của
z
bằng
A.
13
. B.
5
. C.
5
. D.
13
.
Câu 78. (Mã 103 - BGD - 2019) Cho số
z
thỏa mãn
2 4 8 19i z z i i
. Môđun của
z
bằng
A.
13
. B.
5
. C.
13
. D.
5
.
Câu 79. (Mã đề 102 BGD&ĐT NĂM 2018) Tim hai sô thưc
x
va
y
thoa man
3 2 2 2 3x yi i x i
vơi
i
la đơn vi ao.
A.
2; 2
x y
B.
2; 1
x y
C.
2; 2
x y
D.
2; 1
x y
Câu 80. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Tìm các số thực
,a b
thỏa mãn
2 ( ) 1 2a b i i i
với
i
là đơn vị ảo.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
A.
0, 1.
a b
B.
1, 2.
a b
C.
0, 2.
a b
D.
1
, 1.
2
a b
Câu 81. (MĐ 103 BGD&ĐT NĂM 2017-2018) Tìm hai số thực
x
và
y
thỏa mãn
3 4 2 5 2x yi i x i
với
i
là đơn vị ảo.
A.
2
x
;
4
y
B.
2
x
;
0
y
C.
2
x
;
0
y
D.
2
x
;
4
y
Câu 82. (Mã 102 - BGD - 2019) Cho số phức
z
thoả mãn
3 2 3 7 16 .z i i z i
Môđun của
z
bằng
A.
3.
B.
5.
C.
5.
D.
3.
Câu 83. (Mã đề 101 - BGD - 2019) Cho số phức
z
thỏa mãn
3 2 3 10z i i z i
. Môđun của
z
bằng
A.
3
. B.
3
. C.
5
. D.
5
.
Câu 84. (THPT CẨM GIÀNG 2 NĂM 2018-2019) Tìm hai số thực
x
và
y
thỏa mãn
2 3 1 3 1 6x yi i i
với
i
là đơn vị ảo.
A.
1x
;
3
y
. B.
1
x
;
3
y
. C.
1
x
;
1
y
. D.
1x
;
1
y
.
Câu 85. (ĐÊ 04 VTED NĂM 2018-2019) Tìm hai số thực
x
và
y
thỏa mãn
2 3 3 5 4x yi i x i
với
i
là đơn vị ảo.
A.
1, 1
x y
B.
1, 1x y
C.
1, 1x y
D.
1, 1
x y
Câu 86. (THPT CHUYÊN SƠN LA NĂM 2018-2019 LẦN 01) Tìm các số thực
x
và
y
thỏa mãn
3 2 2 1 1 5
x y i x y i
, với
i
là đơn vị ảo.
A.
3
, 2
2
x y
. B.
3 4
,
2 3
x y
. C.
4
1,
3
x y
. D.
3 4
,
2 3
x y
.
Câu 87. (CHUYÊN PHAN BỘI CHÂU NĂM 2018-2019) Cho số phức
,z a bi a b
thỏa mãn
1 2 3 2i z z i
. Tính
P a b
A.
1P
B.
1
2
P
C.
1
2
P
D.
1P
Câu 88. (CHUYÊN KHTN NĂM 2018-2019 LẦN 01) Cho số phức
z
thỏa mãn
2 3 4 3 13 4i z i i
. Môđun của
z
bằng
A.
2
. B.
4
. C.
2 2
. D.
10
.
Câu 89. (HSG BẮC NINH NĂM 2018-2019) Cho số phức
,z x yi x y
thỏa mãn
1 2 3 4i z z i
. Tính giá trị của biểu thức
3 2S x y
.
A.
12
S
B.
11
S
C.
13
S
D.
10
S
Câu 90. (SỞ GD&ĐT BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Tổng phần thực và phần ảo của số phức
z
thoả mãn
1 2iz i z i
bằng
A.
6
B.
2
C.
2
D.
6
Câu 91. (SỞ GD&ĐT BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho
,a b
và thỏa mãn
2 1 3a bi i a i
, với
i
là đơn vị ảo. Giá trị
a b
bằng
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
A.
4
B.
10
C.
4
D.
10
Câu 92. (CHUYEN PHAN BỘI CHÂU NGHỆ AN NĂM 2018-2019 LẦN 02) Cho số phức
( , )
z a bi a b
thoả mãn
(1 ) 2 3 2i z z i
. Tính
P a b
A.
1P
. B.
1
2
P
. C.
1
2
P
. D.
1P
Câu 93. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Tìm số phức
z
biết
4 5 27 7z z i
.
A.
3 7z i
. B.
3 7z i
. C.
3 7z i
. D.
3 7z i
.
Câu 94. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Cho số phức
z
thỏa mãn
2
3 2 2 4i z i i
. Mô đun của số phức
1w z z
bằng.
A.
2
. B.
10
. C.
5
. D.
4
.
Câu 95. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Tìm các số thực
,a b
thỏa mãn
2 4 2 2a b a b i a b bi
với
i
là đơn vị ảo.
A.
3, 1a b
. B.
3, 1
a b
. C.
3, 1
a b
. D.
3, 1a b
.
Câu 96. Cho hai số phức
1
1 2z m i
và
1
2 1z m i
. Có bao nhiêu giá trị thực của tham số
m
để
1 2
. 8 8z z i
là một số thực.
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 97. (CHUYÊN BẮC GIANG NĂM 2018-2019 LẦN 02) Tìm mô đun của số phức
z
biết
2 1 1 1 1 2 2z i z i i
.
A.
1
9
B.
2
3
C.
2
9
D.
1
3
Câu 98. (TT THANH TƯỜNG NGHỆ AN NĂM 2018-2019 LẦN 02) Tính mô đun của số phức
z
thỏa
mãn
1 2 1 4 0z i z i i
với
i
là đơn vị ảo.
A.
6
. B.
5
. C.
2
. D.
3
.
Câu 99. (CHUYÊN TRẦN ĐẠI NGHĨA - TPHCM - HK2 - 2018) Tìm số phức thỏa mãn
.
A. . B. . C. . D. .
Dạng 4.2 Điều kiện cho trước chứa yếu tố môđun
Câu 100. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Hỏi có bao nhiêu số phức z thỏa mãn đồng thời các
điều kiện
5
z i
và
2
z
là số thuần ảo?
A.
4
B.
0
C.
2
D.
3
Câu 101. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho số phức
, z a bi a b
thoả mãn
2
z i z
.
Tính
4
S a b
.
A.
4
S
B.
2
S
C.
2
S
D.
4
S
Câu 102. (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho số phức
,z a bi a b
thỏa mãn
2 1 0
z i z i
và
1
z
. Tính
P a b
.
A.
1P
B.
5
P
C.
3
P
D.
7
P
z
2 3 1 9z i z i
2z i
2z i
2z i
2 i
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
Câu 103. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Có bao nhiêu số phức
z
thỏa mãn
| 2 | 2 2
z i
và
2
1
z
là số thuần ảo?
A.
0
B.
2
C.
4
D.
3
Câu 104. (Mã đề 104 BGD&ĐT NĂM 2018) Có bao nhiêu số phức
z
thỏa mãn
5 2 6
z z i i i z
?
A.
1
B.
3
C.
4
D.
2
Câu 105. (MĐ 103 BGD&ĐT NĂM 2017-2018) Có bao nhiêu số phức thỏa mãn
6 2 7
z z i i i z
?
A.
1
B.
4
C.
2
D.
3
Câu 106. (Mã đề 102 BGD&ĐT NĂM 2018) Có bao nhiêu số phức
z
thỏa mãn
3 2 4
z z i i i z
?
A.
1
B.
3
C.
2
D.
4
Câu 107. (MĐ 105 BGD&ĐT NĂM 2017) Cho số phức
z
thỏa mãn
3 5
z
và
2 2 2z i z i
. Tính
z
.
A.
17
z
B.
17
z
C.
10
z
D.
10
z
Câu 108. (MĐ 105 BGD&ĐT NĂM 2017) Có bao nhiêu số phức
z
thỏa mãn
3 13
z i
và
2
z
z
là số
thuần ảo?
A.
0
B.
2
C. Vô số D.
1
Câu 109. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Có bao nhiêu số phức
z
thỏa mãn điều kiện
. 2
z z z
và
2
z
?
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 110. (CHUYÊN BẮC GIANG NĂM 2018-2019 LẦN 02) Có bao nhiêu số phức
z
thỏa mãn điều kiện
5 5 6
z i z i
, biết
z
có môđun bằng
5
?
A.
3
B.
4
C.
2
D.
0
Câu 111. (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Cho hai số phức
1
z
,
2
z
thỏa mãn các điều kiện
1 2
2
z z
và
1 2
2 4
z z
. Giá trị của
1 2
2
z z
bằng
A.
2 6
. B.
6
. C.
3 6
. D.
8
.
Câu 19 Cho số phức
z
có phần thực là số nguyên và
z
thỏa mãn
2 7 3
z z i z
. Môđun của số phức
2
1
w z z
bằng
A.
445
w
. B.
425
w
. C.
37
w
. D.
457
w
Câu 112. (HỌC MÃI NĂM 2018-2019-LẦN 02) Cho sô phưc
z a bi
,a b
thoa man
4 2 5 1
z i z i i
. Tinh gia tri cua biêu thưc
T a b
.
A.
2T
. B.
3
T
. C.
1T
. D.
1T
.
Câu 113. (ĐÊ 04 VTED NĂM 2018-2019) Có bao nhiêu số phức
z
thỏa mãn
2
3
2 0
z i z
.
A.
4
B.
3
C.
2
D.
6
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
Câu 114. (ĐỀ 01 ĐỀ PHÁT TRIỂN ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Có bao nhiêu số phức
z
thỏa
1 2 3 4z i z i
và
2z i
z i
là một số thuần ảo
A.
0
. B. Vô số. C.
1
. D.
2
.
Câu 115. Có bao nhiêu số phức
z
thỏa mãn
(2 ) 10
z i và
. 25
z z
.
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 116. (THPT CHUYÊN ĐẠI HỌC VINH NĂM 2018-2019 LẦN 01) Có bao nhiêu số phức
z
thỏa mãn
2
2019
1 1
z z z i z z i
?
A. 4 B. C. 1 D. 3
Câu 117. (ĐỀ THI THỬ VTED 02 NĂM HỌC 2018 - 2019) Có bao nhiêu số phức
z
thỏa mãn
2
z z z z
z
và
2
z
là số thuần ảo
A.
4
B.
2
C.
3
D.
5
Câu 118. Có bao nhiêu số phức
z
thỏa mãn
2
3
2 0
z i z
.
A.
4
B.
3
C.
2
D.
6
Câu 119. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Cho số phức
z a bi
,a b
thỏa mãn
3 1z z
và
2
z z i
là số thực. Tính
a b
.
A.
2
. B. 0. C. 2. D. 4.
Câu 120. (CHUYÊN NGUYỄN TẤT THÀNH YÊN BÁI LẦN 01 NĂM 2018-2019) Cho số phức
z a bi
, a b
thỏa mãn
1 3 0z i z i
. Tính
2 3S a b
.
A.
6
S
. B.
6
S
. C.
5
S
. D.
5
S
.
Câu 121. (THPT NĂM 2018-2019 LẦN 04) Cho ba số phức
1 2 3
; ;z z z
thỏa mãn
1 2 3
1 2 3
0
2 2
3
z z z
z z z
.
Tính
2 2 2
1 2 2 3 3 1
A z z z z z z
A.
2 2
3
. B.
2 2
. C.
8
3
. D.
3
8
.
Câu 122. (THPT CHUYÊN HẠ LONG - LẦN 2 - 2018) Cho số phức
,z a bi a b
thỏa mãn
2 5 5
z i
và
. 82
z z
. Tính giá trị của biểu thức
P a b
.
A.
10
. B.
8
. C.
35
. D.
7
.
Câu 123. (SGD&ĐT ĐỒNG THÁP - 2018) Cho
M
la tâp hơp cac sô phưc
z
thoa
2 2
z i iz
. Goi
1
z
,
2
z
la hai sô phưc thuôc tâp hơp
M
sao cho
1 2
1
z z
. Tinh gia tri cua biêu thưc
1 2
P z z
.
A.
3
P
. B.
3
2
P
. C.
2
P
. D.
2P
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
Câu 124. (THPT CHUYÊN QUANG TRUNG - BP - LẦN 1 - 2018) Cho số phức
z
thoả mãn
1 i
z
là số
thực và
2
z m
với
m
. Gọi
0
m
là một giá trị của
m
để có đúng một số phức thoả mãn bài toán. Khi
đó:
A.
0
1
0;
2
m
. B.
0
1
;1
2
m
. C.
0
3
;2
2
m
. D.
0
3
1;
2
m
.
Câu 125. (THPT CHUYÊN QUANG TRUNG - BP - LẦN 1 - 2018) Gọi
S
là tập hợp các số thực
m
sao
cho với mỗi
m S
có đúng một số phức thỏa mãn
6
z m
và
4
z
z
là số thuần ảo. Tính tổng của các phần
tử của tập
S
.
A.
10.
B.
0.
C.
16.
D.
8.
Câu 126. (SGD&ĐT CẦN THƠ - HKII - 2018) Cho số phức
z
thỏa mãn
4 1 4 3z i z z i
. Môđun
của số phức
z
bằng
A.
2
. B.
1
. C.
16
. D.
4
.
Câu 127. (THPT CHUYÊN LÊ HỒNG PHONG - TPHCM - 2018) Cho số phức
z a bi
, , 0
a b a
thỏa
. 12 13 10z z z z z i
. Tính
S a b
.
A.
17
S
. B.
5
S
. C.
7
S
. D.
17
S
.
Câu 128. (HỒNG LĨNH - HÀ TĨNH - LẦN 1 - 2018) Cho số phức
0
z
thỏa mãn
2
3 1
1
iz i z
z
i
. Số
phức
13
3
w iz
có môđun bằng
A.
26
. B.
26
. C.
3 26
2
. D.
13
.
Câu 129. (TOÁN HỌC TUỔI TRẺ - THÁNG 4 - 2018) Cho hai số phức
1
z
,
2
z
thỏa mãn
1
1
z
,
2
2
z
và
1 2
3
z z
. Giá trị của
1 2
z z
là
A.
0
. B.
1
. C.
2
. D. một giá trị khác.
Câu 130. [HỒNG LĨNH - HÀ TĨNH - LẦN 1 - 2018] Cho số phức
0
z
thỏa mãn
2
3 1
1
iz i z
z
i
. Số
phức
13
3
w iz
có môđun bằng
A.
26
. B.
26
. C.
3 26
2
. D.
13
.
Câu 131. (THPT CHUYÊN NGUYỄN THỊ MINH KHAI - SÓC TRĂNG - 2018) Cho số phức
,
z a bi a b R
thỏa mãn
7 2 0
z i z i
và
3.
z
Tính
.P a b
A.
5
. B.
1
2
. C.
7
. D.
5
2
.
Câu 132. (THCS&THPT NGUYỄN KHUYẾN - BÌNH DƯƠNG - 2018) Cho hai số phức
1 2
,z z
thoả mãn:
1
2 3
z ,
2
3 2
z . Hãy tính giá trị biểu thức
2 2
1 2 1 2
.P z z z z
A.
60.
P
B.
20 3
P . C.
30 2
P
. D.
50
P
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
Câu 133. (HỒNG LĨNH - HÀ TĨNH - LẦN 1 - 2018) Cho số phức
w x yi
,
,x y
thỏa mãn điều
kiện
2
4 2w w
. Đặt
2 2
8 12
P x y
. Khẳng định nào dưới đây đúng?
A.
2
2
2
P w
. B.
2
2
2
P w
. C.
2
4
P w
. D.
2
2
4
P w
.
Phần B. LỜI GIẢI THAM KHẢO
Dạng 1. Xác định các yếu tố cơ bản của số phức
Dạng 1.1 Xác định phần thực, phần ảo của số phức
Câu 1. Chọn C
Câu 2. Chọn D
Số phức
5 6i
có phần thực bằng 5, phần ảo bằng
6
.
Câu 3. Chọn A
Số phức có phần thực bằng
3
và phần ảo bằng
4
là:
3 4z i
.
Câu 4. Chọn B
Số phức
có phần thực là
3
a
và phần ảo là
2 2
b
.
Câu 5. Chọn A
Câu 6. Chọn D
Số phức
z
được gọi là số thuần ảo nếu phần thực của nó bằng
0
.
Câu 7. Chọn A
Số phức
2 3z i
có phần thực
2a
.
Câu 8. Số phức
3 4z i
có phần thực là
3
và phần ảo là
4
.
Câu 9.
Lơi giai
Chọn B
3 2 3 2z i z i
. Vây phân thưc băng
3
va Phân ao băng
2
.
Dạng 1.2 Xác định số phức liên hợp, số phức đối, môđun của số phức
Câu 10. Chọn A
Số phức liên hợp của số phức
z a bi
là số phức
z a bi
từ đó suy ra chọn đáp án B.
Câu 11. Chọn B
Theo định nghĩa số phức liên hợp của số phức
, ,z a bi a b
là số phức
, ,z a bi a b
.
Câu 12. Chọn A
Ta có
2
2 1 5
z
.
Câu 13.
Lơi giải
Chọn C
Số phức liên hợp của số phức
5 3i
là
5 3i
Câu 14. Chọn A
Số phức liên hợp của số phức
a bi
là số phức
a bi
.
Vậy số phức liên hợp của số phức
3 4i
là số phức
3 4i
.
Câu 15.
3 2z i
3 2z i
. Nên số phức
z
có phần thực bằng
3
và phần ảo bằng
2
.
Câu 21 [2D4-1.1-1] Cho số phức
3 2z i
. Tìm phần thực và phần ảo của số phức
z
.
A. Phần thực bằng
3
và phần ảo bằng
2i
. B. Phần thực bằng
3
và phần ảo bằng
2
.
C. Phần thực bằng
3
và phần ảo bằng
2i
. D. Phần thực bằng
3
và phần ảo bằng
2
.
3 2z i
.
Phần thực bằng
3
và phần ảo bằng
2
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
Câu 16. Số phức đối của
z
là
z
. Suy ra
5 7z i
.
Câu 17. Số phức liên hợp của số phức
z a bi
là số phức
z a bi
.
Câu 18. Số phức liên hợp của số phức
z x yi
,
,x y
là số phức
z x yi
. Do đó số phức liên hợp
của số phức
5 6z i
là
5 6z i
.
Câu 19. Số phức liên hợp của số phức
2 3z i
là
2 3z i
.
Dạng 2. Biểu diễn hình học cơ bản của số phức
Câu 20. Chọn D
Theo hình vẽ
2;1 2M z i
Câu 21. Chọn C
Ta có điểm biểu diễn của số phức
1 2z i
trên hệ trục tọa độ
Oxy
là điểm
1 2Q ;
Câu 22. Chọn C
Điểm
2;1
M
là điểm biểu diễn số phức
1
2z i
Câu 23. Chọn B
Nhắc lại:Trên mặt phẳng phức, số phức
z x yi
được biểu diễn bởi điểm
( ; )M x y
.
Điểm
M
trong hệ trục
Oxy
có hoành độ
3
x
và tung độ
4
y
.
Vậy số phức
z
có phần thực là
3
và phần ảo là
4
.
Câu 24. Điểm
2;1
M
trong hệ tọa độ vuông góc cuả mặt phẳng được gọi là điểm biểu diễn số phức
suy ra
2z i
.
Câu 25.
Lời giai
Chọn D.
Câu 26. Điểm biểu diễn hình học của số phức
z a bi
,a b
là
;a b
.
Với
2 3z i
ta có
2
a
và
3
b
. Do đó điểm biểu diễn tương ứng là
2; 3
N
.
Câu 27. Tọa độ điểm
( 1;2)
M
là điểm biểu diễn của số phức
1 2z i
.
Câu 28. Điểm
2;3
M
biểu thị cho số phức
2 3 .z i
Câu 29. Tọa độ điểm
3;5 3 5 3 5M z i z i
.
Câu 30. Điểm
(2; 1)
M
nên nó biểu diễn cho số phức
2z i
.
Câu 31. Chọn C
(1; 2)
M
là điểm biểu diễn cho số phức có phần thực bằng
1
và phần ảo bằng
2
, tức là
1 2i
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
Câu 32. Điểm biểu diễn của số phức
z a bi
trong mặt phẳng tọa độ
Oxy
là điểm
;M a b
Điểm biểu diễn của số phức
z a bi
trong mặt phẳng tọa độ
Oxy
là điểm
;
N a b
Do đó: điểm biểu diễn của hai số phức đối nhau là hai điểm đối xứng nhau qua gốc tọa độ
Câu 33. Số phức liên hợp của số phức
3 2z i
là
2 3 z i
. Điểm biểu diễn số phức
z
là
2 ; 3
N
.
Vậy điểm biểu diễn số phức liên hợp của số phức
3 2z i
là
N
.
Câu 34. Điểm
2;1
M
trong hệ tọa độ vuông góc cuả mặt phẳng được gọi là điểm biểu diễn số phức
suy ra
2z i
.
Câu 35. Ta có:
3; 7 , 9; 5 , 5;9
A B C
Trọng tâm của tam giác
ABC
là
7
; 1
3
G
Vậy trọng tâm
G
là điểm biểu diễn của số phức
7
3
z i
.
Dạng 3. Thực hiện các phép tính cộng, trừ, nhân, chia cơ bản của số phức
Dạng 3.1 Phép tính cộng trừ 2 số phức
Câu 36. Chọn B
Ta có
1 2
2 5 z z i
. Nên ta chọn A.
Câu 37. Chọn C
Ta có
1 2
2 (1 ) 2(2 ) 5 3z z i i i
.
Do đó điểm biểu diễn số phức
1 2
2z z
có tọa độ là
(5;3)
.
Câu 38. Chọn C
5 7 2 3 7 4z i i i
.
Câu 39. Chọn D
1 2
1 2 3 3 2z z i i i
nên ta có:
2
2
1 2
3 2 3 2 13
z z i
.
Câu 40. Chọn A
Ta có
1 2
z z z
4 3 7 3i i
3 6i
.
Câu 41. Chọn B
1 2
2z z z i
.
Câu 42.
Lơi giai
Chọn D
2 3 3 2z i i
3 2 2 3 1z i i i
.
Câu 43. Chọn B
Ta có
1 2
3 2 2
z z z i b
Câu 44. Ta có
1 2 1 2
1 2 3 3 2 3 2 13
z z i i i z z i
.
Câu 45. Từ hình bên ta có tọa độ
3;2
M
biểu diễn số phức
1
3 2z i
.
Tọa độ
1; 4
N
biểu diễn
2
1 4z i
.
Ta có
1 2
4 2z z i
2 2
1 2
4 2 2 5
z z
.
Dạng 3.2 Phép tính nhân, chia 2 số phức
Câu 46. Chọn A
Ta có
(2 5 ) (2 5 ) 2 5 2 5 3 3w iz z i i i i i i
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
Câu 47. Chọn A
4 3 1
z i i
7 i
7z i
5 2
z
Câu 48. Chọn C
Ta có:
3 2
1 1 . 1 1 2z i i i i i i i i
(vì
2
1
i
)
Suy ra phần thực của
z
là
1
a
, phần ảo của
z
là
2
b
.
Câu 49. Chọn B
1 2 2w iz i i i
Câu 50. Chọn B
Gọi
,z a bi a b
. Điểm biểu diễn của
z
là điểm
;M a b
2 2 2z a bi
có điểm biểu diễn trên mặt phẳng
Oxy
là
1
2 ;2M a b
.
Ta có
1
2
OM OM
suy ra
1
M E
.
Câu 51. Chọn D
1 2
3 3 1 1 2 4z z i i i
. Suy ra: Tọa độ điểm biểu diễn là:
4; 1 .
Câu 52. Chọn A
Ta có:
1 2
2 4 2 1 3 3 .z z i i i
Vậy điểm biểu diễn số phức
1 2
2
z z
có tọa độ là
3;3
.
Câu 53. Chọn B
3 1 3z i i i
nên suy ra
3z i
.
Câu 54. Vì
1 2 4 3z i i
nên
4 3
1 2
i
z =
i
2 2
4 3 1 2
1 2
i i
2 11
5
i
2 11
5 5
= i
.
Vậy nên
2 11
z
5 5
= i
.
Câu 55.
3 5
1 3 5 1 4
1
i
z i i z i
i
2 2
1 4 17
z
.
Câu 56. Cách 1:
Ta có
2
2
1 2 1 4 4 3 4z i i i i
1 1 3 4
3 4 25 25
i
z i
.
Do đó
2 2
1 3 4 1
25 25 5
z
.
Câu 57. Chọn B
Ta có:
2
2 2
1 1 2 1 2 1 2 2 1 2 2 4 4 2z i i i i i i i i i i
.
Suy ra số phức
z
có phần ảo là:
2
.
Câu 58. Chọn A
Ta có
1 1
1 1
3 3
z i z i
Khi đó:
1 1 8
w 3 (1 ) 3(1 )
3 3 3
iz z i i i
Câu 59. Chọn A
Ta có:
2 1 2w iz i i i
.
Vậy điểm biểu diễn số phức
w iz
là điểm
1; 2 .
M
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
Câu 60. Chọn B
Ta có
1 2 1 2z i z i
2 2(1 2 ) 1 2 3 2w z z i i i
Vậy tổng phần thực và phần ảo của số phức
w
là
5
Câu 61. Đặt
1 1
, ,
z a bi a b z a bi
.
2
2 2
2 2
2 2 2 2 2 2
2 .
2
.
a b ab i
a bi
z a bi a b ab
i
z a bi a bi a bi a b a b a b
chỉ là số thuần ảo
a b
.
Câu 62. Ta có
1 2 1 2
2 3
z z z z
2 1 2 3 3 4 1 2 3 4i i i i
11 8 11 2 10i i i
.
Câu 63. Ta có
1 3 5i z i
3 5
1
i
z
i
1 4z i
.
Suy ra
1 4z i
. Vậy
1;4
M
.
Câu 64.
5 7 13 4 13 4
1 3 5 7 .
1 3 5 5 5 5
i
i z i z z i z i
i
Câu 65. Cách 1: Phương pháp lượng giác
Xét số phức
1
1 1
1 2 2 sin
4 4
2 2
z i i cos i
Ta có số phức
2019
2019
2019
1
2019 2019
1 2 sin
4 4
z z i cos i
2019 2019
1009 1009
3 3 2 2
2 sin 2 2 2
4 4 2 2
cos i i i
Phần thực của
z
bằng
1009
2
.
Cách 2:
Ta có
2020 505
2019
505 1009 1009
(1 ) ( 4) 1 1
1 ( 4) ( ) 2 2
1 (1 ) 2 2
i
z i i i
i i
Phần thực của
z
bằng
1009
2
.
Câu 66. Ta có
2 3 4
3 2
i i
z
i
8 3 2 12
3 2
i
i
5 14
3 2
i
i
5 14 3 2
3 2 3 2
i i
i i
15 28 10 42
9 4
i
13 52
13
i
1 4i
.
Vậy điểm biểu diễn số phức
z
trên mặt phẳng
Oxy
là
1; 4
M
.
Câu 67. Ta có
2
2 2
3 5 16 30z i z i
2
1 2
. 2 4 16 30 152 4w z z i i i
.
Vậy phần thực của
w
là
152
.
Câu 68. Chọn C
Ta có
2
4 2
1
3 2
i i
z i
i
nên
1;1
M
.
Câu 69. Chọn A
Ta có
2
4 3
1 3
i
z
i
2
4 3
5
4
1 3
i
z
i
.
Câu 70.
2 2018
1 1 ... 1z i i i
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
2018
1009
1 1
2 1
1 1
1 1
i
i
i i
i i
1009 1009 1009
1 2 2 1 2 1i i i
.
z
có phần ảo bằng
1009
2 1
.
Câu 71.
2
2
m i
z
m i
2
2 2
4
m i m i
m
2
2 2
4 4
4 4
m m
i
m m
.
Vì
z
có phần thực dương
2
2
4 0
2
m
m
m
.
Câu 72. Ta có:
2 2 2
3
3 3 3 1 3 1 ( 3)
( )( ) 1 1 1
i x i
i x i xi x x i
z
x i x i x i x x x
.
Suy ra tổng phần thực và phần ảo của số phức
z
là:
2 2 2
3 1 3 4 2
1 1 1
x x x
x x x
.
Câu 73.
2 2017
1 2 3 ... 2018w i i i i
Xét
2018 2019
2 3 2018
1
( ) ...
1 1
x x x
f x x x x x x
x x
2018 2019
2 2017
2
2019 1 ( 1)
'( ) 1 2 3 ... 2018
( 1)
x x x x
f x x x x
x
2018 2019
2 2017
2
2019 1 ( 1)
1 2 3 ... 2018 . ( )
( 1)
i i i i
w i i i i i f i i
i
2020( 1) 2
1010 1009
2
i i
i i
i
1010 1009 1
T
.
Dạng 4. Tìm số phức thỏa mãn điều kiện cho trước
Dạng 4.1 Điều kiện cho trước không chứa yếu tố môđun
Câu 74. Chọn D
2 3 5 1
2 3 3 5 4 2 3 3 1 5 4
3 1 4 1
x x x
x yi i x i x y i x i
y y
Câu 75. Chọn C
Từ
2
1 1 2x yi i
2
0
1 1
2
2
x
x
y
y
Câu 76. Chọn C
Ta có
2 3 1 3 6x yi i x i
1 3 9 0x y i
1 0
3 9 0
x
y
1
3
x
y
.
Câu 77. Chọn A
Gọi
z x yi
.
2 3 16 2
i z i z i
2 3 16 2
i x yi i x yi i
2 2 3 16 2 2 2x yi xi y i x yi i
2 3 2
2 16 2 2
x y x
y x y
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
3 0
4 14
y
x y
2
3
x
y
Suy ra
2 3z i
. Vậy
13
z .
Câu 78. Chọn A
Gọi
; , .
z a bi z a bi a b
Ta có:
2 4 8 19
2 4 8 19
2 6 4 8 19
2 8 3
6 4 19 2
i z z i i
i a bi a bi i i
a b a b i
a b a
a b b
Vậy
3 2 13.
z i z
Câu 79. Chọn C
Ta có:
3 2 2 2 3x yi i x i
3 2 2 1 2 3x y x i
3 2 2 2
2 1 3 2
x x x
y y
.
Câu 80. Chọn B
2 ( ) 1 2a b i i i
2
2 1 2a bi i i
(2 1) 1 2a bi i
2 1 1
2
a
b
1
2
a
b
Câu 81. Chọn A
3 4 2 5 2x yi i x i
2 4 4 0x y i
2 4 0
4 0
x
y
2
4
x
y
.
Câu 82. Chọn B
Đặt
;z a bi a b
.
Theo đề ta có

3 2 3 7 16a bi i i a bi i
3 3 3 2 2 3 3 7 16a bi i a bi ai b i
3 3 5 3 7 16a b a b i
3 7 3 7 1
3 5 3 16 3 5 13 2
a b a b a
a b a b b
.
Vậy
2 2
1 2 5
z
.
Câu 83. Chọn D
Đặt
, ,z x yi x y
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
3 2 3 10
3 2 3 10
5 3 3 10
3
5 3 10
2
1
z i i z i
x yi i i x yi i
x y x y i i
x y
x y
x
y
2z i
Vậy
5
z
Câu 84. Ta có:
2 3 1 3 1 6x yi i i
2 1 3 3 1 6x y i i
.
Suy ra
2 1 1
3 3 6
x
y
1
3
x
y
.
Câu 85. Chọn B
Từ
2 3 3 5 4 2 3 3 1 5 4x yi i x i x y i x i
2 3 5 1
3 1 4 1
x x
y y
Vậy
1, 1x y
.
Câu 86. Ta có
3 2 2 1 1 5 3 2 2 1 1 5
x y i x y i x y i x y i
3
3 2 1
2
4
2 1 5
3
x
x x
y y
y
.
Câu 87. Ta có
1 2 3 2 1 2 3 2
3 3 2
1
3 3
2
2 3
2
i z z i i a bi a bi i
a b a b i i
a
a b
a b
b
Vậy
1
P a b
.
Câu 88.
2 3 4 3 13 4i z i i
9 7
2 3 9 7
2 3
i
i z i z
i
9 7 2 3
4 9
i i
z
39 13
3
13
i
z z i
.
Vậy
9 1 10
z .
Câu 89. Có
2
2 2 3
1 2 3 4 13
7
2 4
3
x
x y
i z z i S
x
y
.
Câu 90. Chọn A
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
Giả sử số phức
z
có dạng:
, ,z x yi x y
.
Ta có:
1 2iz i z i
1 2i x yi i x yi i
2 2x y yi i
.
2 0 4
2 2
x y x
y y
6
x y
.
Tổng phần thực và phần ảo của số phức
z
bằng
6
.
Câu 91. Chọn D
Ta có
2 1 3
2 1 3 2 1 3
3 7
b a a
a bi i a i b a ai i
a b
Vậy
10
a b
.
Câu 92.
(1 ) 2 3 2 (1 )( ) 2( ) 3 2 (3 ) ( ) 3 2i z z i i a bi a bi i a b a b i i
1
3 3
2
2 3
2
a
a b
a b
b
. Suy ra:
1
P a b
.
Câu 93. Giả sử
,
z a bi a b R
, khi đó
4( ) 5( ) 27 7 9 27 7a bi a bi i a bi i
9 27 3
3 7
7 7
a a
z i
b b
.
Câu 94. Ta có:
2
3 2 2 4 3 2 1 5 1i z i i i z i z i
.
Do đó:
1 1 1 1 2 1 3w z z zz z i i i i i
.
2
3 1 10
w
.
Câu 95. Ta có:
2 4 2 2a b a b i a b bi
.
2 2 3 0 3
4 2 4 1
a b a b a b a
a b b a b b
.
Câu 96. Ta có:
2
1 2
. 8 8 1 2 2 1 8 8 8 2 3z z i m i m i i m m i
.
Để
1 2
. 8z z i
là một số thực thì
2
1
2 3 0
3
m
m m
m
.
Vậy có hai giá trị của tham số
m
để
1 2
. 8z z i
là một số thực.
Câu 97. Chọn B
Giả sử
z a bi z a bi
Do đó
2 1 1 1 1 2 2z i z i i
2 2 1 1 1 1 2 2a bi i a bi i i
2 2 1 2 2 1 1 1 2 2a b a b i a b a b i i
1
2 2 1 1 2
3 3 2
3
0 1
2 2 1 1 2
3
a
a b a b
a b
a b
a b a b
b
Khi đó
2 2
2
3
z a b
.
Câu 98. Giả sử:
z x yi
,
,x y
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
Ta có:
1 2 1 4 0z i z i i
1 2 1 4 0x yi i x yi i i
2 3 4 1 0x y x i
2 3 4 0
1 0
x y
x
2
1
y
x
1 2 5
z i z
.
Câu 99. Giả sử . Ta có:
.
Vậy .
Dạng 4.2 Điều kiện cho trước chứa yếu tố môđun
Câu 100. Chọn A
Giả sử
2 2 2
2z a bi z a b abi
Vì
5
z i
và
2
z
là số thuần ảo ta có hệ phương trình
2 2
2 2
2 2
2 2
4
1 25
1 25 3
4
0
3
1 25
( )
( )
( )
a b
a b
b b
a b a b
b a
a b
a b
b a
b b
.
Câu 101. Chọn A
Ta có
2 2
2 2
2 (1)
2 2 1
1 0 (2)
a a b
z i z a b i a b
b
Từ (2) ta có:
1
b
. Thay vào (1):
2
2 2
2 0
3
1 2
4
1 ( 2)
a
a a a
a a
Vậy
4 4
S a b
Câu 102. Chọn D
Ta có:
2 1 0
z i z i
2 2
2 1 0
a bi i a b i
2 2
2 2 2 2
2 2
2 0 1
2 1 0
1 0 2
a a b
a a b b a b i
b a b
Lấy
1
trừ
2
ta được:
1 0 1a b b a
. Thế vào
1
ta được:
2
2 2
2 2 2
2 1 0 2 2 2 1
2
2 2
3
4 4 2 2 1 2 3 0
1
a a a a a a
a
a a
a tm
a a a a a a
a tm
Với
3 4
a b
;
1 0
a b
.
Vì
3
1 3 4 3 4 7
4
a
z z i P a b
b
.
Câu 103. Chọn D
z a bi
,a b
2 3 1 9z i z i
2 3 1 9a bi i a bi i
3 3 3 1 9a b a b i i
3 1
3 3 9
a b
a b
2
1
a
b
2z i
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
Gọi số phức
z x yi
,x y
, vì
2
2
2
1 1 2 1x x y
y
z i
là số thuần ảo nên theo
đề bài ta có hệ phương trình:
2 2
2
2
2 1 8 (1)
1 (2)
x y
x y
Từ
(2)
suy ra:
( 1)
y x
Với
, thay vào
(1)
, ta được:
2 2
2
8 0 0.
2 2 xx x x
Suy ra:
z i
.
Với
( 1)
y x
, thay vào
(1)
, ta được:
2 2
2
8 22 4 4
0 1 3.
x xx x x
Suy ra:
1 3 2 3z i
;
1 3 2 3z i
Vậy có 3 số phức thỏa mãn.
Câu 104. Chọn B
Ta có
5 2 z z i i
6
i z
6
z i z
5 2
z z i
1
Lây môđun hai vế của
1
ta có:
2
6 1.
z z
2
2
25 2
z z
Bình phương và rút gọn ta được:
4 3 2
12 11 4 4 0
z z z z
3 2
1 11 4 0
z z z
3 2
1
11 4 0
z
z z
1
10,9667...
0,62...
0,587...
z
z
z
z
Do
0
z
, nên ta có
1
z
,
10,9667...
z
,
0,62...
z
. Thay vào
1
ta có
3
số phức thỏa mãn
đề bài.
Câu 105. Chọn D
Đặt
0,z a a
, khi đó ta có
6 2 7
z z i i i z
6 2 7
a z i i i z
7 6 2a i z a ai i
7 6 2a i z a a i
7 6 2a i z a a i
2 2
2 2
7 1 36 2
a a a a
4 3 2
14 13 4 4 0
a a a a
3 2
3 2
1
1 13 4 0
12 4 0
a
a a a
a a
Xét hàm số
3 2
13 0
f a a a a
, có bảng biến thiên là
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
Đường thẳng
4
y
cắt đồ thị hàm số
f a
tại hai điểm nên phương trình
3 2
12 4 0
a a
có
hai nghiệm khác
1
(do
1 0
f
). Mỗi giá trị của
a
cho ta một số phức
z
.
Vậy có
3
số phức thỏa mãn điều kiện.
Câu 106. Chọn B
3 2 4
z z i i i z
4 3 2z i z z z i
(*)
2 2
2
4 1. 9 2
z z z z (1).
Đặt
0
m z
ta có
2 2
2 2
1 4 1 . 9 2
m m m m
4 3 2
8 7 4 4 0
m m m m
3 2
1 7 4 0
m m m
3 2
1
7 4 0
m
m m
1
6,91638
0.80344
0.71982 L
m
m
m
m
.
Từ (*) ta suy ra ứng với mỗi
z m
sẽ có một số phức
3 2
4
m m i
z
m i
thỏa mãn đề bài.
Vậy có
3
số phức
z
thỏa mãn yêu cầu bài toán.
Câu 107. Chọn C
Đặt
; ,z x yi x y
Theo bài ra ta có
2
2
2
2
2 2 2
2
3 25
3 25
4 4 0
2 2 2
x y
x y
x
x y x y
2
3
9
1
1
y
y
x
x
. Vậy
10
z
Câu 108. Chọn B
Gọi số phức
, ,z a bi a b
Ta có
3 13 3 13
z i a bi i
2
2
3 13
a b
2 2 2 2
6 4 0 4 6 1a b b a b b
2
2
2 2
2 2
1 1 1
2 2 2
2
a bi
z
z z a bi
a b
.
2
2
2 2
2 2
2 2 4
2
2 2
a b a
b
i
a b a b
2 2
2 2
2 2
2 2
2 2
a b a b
i
a b a b
Do
2
z
z
là số thuần ảo nên
2 2
2 2
2
2
2 0 2
2
0 2
2
0
a b a
a b a
a
a b
b
Thay
1
vào
2
ta có
4 6 2 0 3 2b a a b
thay vào
1
ta có
2
2 2
3 2 4 6 0 10 6 0
b b b b b
0( )
3 1
5 5
b L
b a
Vậy có một số phức cần tìm.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
Câu 109. Đặt
z x yi
(
x
;
y
;
2
1
i
).
Theo bài ra ta có:
2 2
2 2
2 2
2
4 2
4
2
x y x yi
x yi
x y
x y
2
2
2 2
4 4
4
x y
x y
2
0
x
y
Vậy có
1
số phức thỏa yêu cầu bài toán là
2z
.
Câu 110. Chọn B
Gọi
2
, , 1
z a bi a b i
Ta có
2 2
2 2
2 2
2
2 2
2 2
2
5 5 6
5 5 6
5
5
4
16
36 16 144
5
5
9 3
5
5
5
z i z i
a b a b
z
a b
a
a
a b
a b
b b
Vậy có
4
số phức thỏa mãn.
Câu 111. Giả sử
1
z a bi
, (
a
,
b
);
2
z c di
, (
c
,
d
).
Theo giả thiết ta có:
1
2
1 2
2
2
2 4
z
z
z z
2 2
2 2
2 2
4
4
2 2 16
a b
c d
a c b d
2 2
2 2
2 2 2 2
4 1
4 2
4 4 16 3
a b
c d
a b c d ac bd
Thay
1
,
2
vào
3
ta được
1
ac bd
4
.
Ta có
1 2
2
z z
2 2
2 2
a c b d
2 2 2 2
4 4
a b c d ac bd
5
.
Thay
1
,
2
,
4
vào
5
ta có
1 2
2 2 6
z z .
Câu 19 [2D4-1.6-2] Cho số phức
z
có phần thực là số nguyên và
z
thỏa mãn
2 7 3
z z i z
. Môđun
của số phức
2
1
w z z
bằng
A.
445
w
. B.
425
w
. C.
37
w
. D.
457
w
Đặt
,z a bi a b
.
Khi đó:
2 7 3
z z i z
2 2
2 2 7 3
a b a bi i a bi
2 2
3 7 3 0
a b a b i
3
5
7
( )
4
3
3
4
b
a
a
b
a
.
Do
a
nên
4 4 3 4 21 457
a z i w i w
Câu 112.
4 2 5 1 4 2 5 1
z i z i i a bi i a bi i i
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
4 5 1
2 5 2
a bi
a b i
Tư
1
va
2
, ta co
2 2
2 2
4 2 4 2 2 3
a bi a b i a b a b b a
.
Kêt hơp vơi
1
, ta đươc:
2
2
2
4 5
1
2 3
a
a b
b
b a
Vây
3
T a b
.
Câu 113. Chọn A
2
3 3 2
2
0
2 0 2 z 0 2 0
2 0 2
z
z i z z iz z z iz
z iz
Gọi
z x yi z x yi
với
,x y
thay vào
2
có:
2 2
2
2 2
2 2
2
0
2 0
2 0
2 0
2 2x 1 0
0
2 1 0
1
1
3 0
x
x y y
y y
x y y
x y y y i
x
x y
y
y
x
0
0
2
3
1
3
1
x y
x
y
x
y
x
y
0
2
3
3
z
z i
z i
z i
Vậy phương trình có 4 nghiệm
Câu 114. Đặt
( ,
)
z x yi x y
Theo bài ra ta có
2 2 2 2
1 2 3 4
1 2 3 4 5
x y i x y i
x y x y y x
Số phức
2
2
2
2 2 1 2 3
2
w
1
1
x y i x y y x y i
z i
x y i
z i
x y
w
là một số ảo khi và chỉ khi
2
2
2
12
2 1 0
7
1 0
23
5
7
x y y
x
x y
y
y x
Vậy
12 23
7 7
z i
.Vậy chỉ có
1
số phức
z
thỏa mãn.
Câu 115. Gọi số phức cần tìm là
,z a bi a b
.
Ta có:
2
2 2
. 25 (1)
z z z a b
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
Lại có:
(2 ) 10 2 ( 1) 10
z i a b i
2 2
2 2
2 2
( 2) ( 1) 10
( 2) ( 1) 10
4 2 5 10 (2)
a b
a b
a b a b
Thay (1) vào (2) ta được:
25 4 2 5 10 2 10
a b b a
.
Nên
2 2 2 2
25 ( 2 10) 25
a b a a
2
5 0
5 40 75 0
3 4
a b
a a
a b
Vậy Vậy có 2 số phức
z
thoả mãn là
5
z
và
3 4z i
.
Câu 116. Chọn D
Gọi
z a bi
;
,a b
z a bi
.
Ta có:
2 2
2
2
1 1 1
z a bi a b
,
2
2 2
z z i a bi a bi i b i b i
,
2019
i i
,
2019
2z z i i a bi a bi ai
.
Suy ra phương trình đã cho tương đương với:
2
2
1 2 2 1a b b i ai
2
2
2 2
2
0
0
0
2 0
1 1 2 2 0
1
1
1
2 2 0
1
1
a
b
b
a a b
a b b b
a
b
b
a b
b a a b
a b
a
b
Vậy có 3 số phức
z
thỏa mãn.
Câu 117. Gọi số phức
z a bi
,
,a b
.
Ta có
2
2
2
2 2
z z z z a az
b bi
2 2
2 2 1
a b a b
.
Lại có
22
2
2
2
a bi az
b abi
là số thuần ảo, suy ra
2 2
0
a b a b
Trường hợp 1:
a b
thay vào
1
ta được:
2
0
0
2 4
2
2
a
a
a a
a
a
0
2
a b
a b
.
Trường hợp 2:
a b
thay vào
1
ta được:
2
0
0
2 4
2
2
a
a
a a
a
a
0
2
b
b
.
Vậy có
5
số phức thỏa mãn bài toán là
0
z
,
2 2z i
,
2 2z i
.
Câu 118. Chọn A
2
3 3 2
2
0
2 0 2 z 0 2 0
2 0 2
z
z i z z iz z z iz
z iz
Gọi
z x yi z x yi
với
,x y
thay vào
2
có:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
2 2
2
2 2
2 2
2
0
2 0
2 0
2 0
2 2x 1 0
0
2 1 0
1
1
3 0
x
x y y
y y
x y y
x y y y i
x
x y
y
y
x
0
0
2
3
1
3
1
x y
x
y
x
y
x
y
0
2
3
3
z
z i
z i
z i
Vậy phương trình có 4 nghiệm
Câu 119. Ta có
z a bi
,a b
.
+)
3 1z z
3 1
a bi a bi
2 2
2 2
3 1
a b a b
2 2
2 2
3 1
a b a b
4 8 0
a
2
a
.
+)
2 2 2 1z z i a bi a bi i a bi a b i
2 1 2 2a a b b a b i
.
2
z z i
là số thực
2 2 0
a b
.
Thay
2
a
tìm được
2
b
. Vậy
0
a b
.
Câu 120. Ta có
1 3 0z i z i
2 2
1 3 0a b a b i
.
2 2
1 0
3 0
a
b a b
2
1
1 3 *
a
b b
.
2
2
3
*
1 3
b
b b
3
4
3
b
b
4
3
b
.
Vậy
1
4
3
a
b
2 3 6
S a b
.
Câu 121.
1 2 3
1 2 3 1 3 2
3 2 1
0
z z z
z z z z z z
z z z
.
2
2 2 2 2 2 2 2 2 2
1 2 2 3 3 1 1 2 3 1 2 3
2 2 8
3.
3 3
A z z z z z z z z z z z z
.
Câu 122. Theo giả thiết ta có
2 2
2 2
2 2
5 43
1
2 5 5
2
82
82 2
b
a
a b
a b
a b
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
Thay
1
vào
2
ta được
2
9
29 430 1521 0
169
29
b
b b
b
Vì
b
nên
9 1b a
. Do đó
8
P a b
.
Câu 123. Đăt
z x yi
vơi
x
,
y
.
Ta co:
2 2
2 2 2 2 1 2 1
z i iz x y i y xi x y
.
Suy ra tâp hơp cac điêm biêu diên sô phưc
z
trên mặt phẳng phưc la đương tron
;1
O
1 2
1
z z
.
Ta co:
2 2 2 2
2
1 2 1 2 1 2
2 3 3
z z z z z z P P
.
Câu 124. Giả sử
,z a bi
,a b
.
Đặt:
1
i
w
z
1
i
a bi
2 2
1
a b a b i
a b
2 2 2 2
a b a b
i
a b a b
.
w
là số thực nên:
1
a b
.
Mặt khác:
2
a bi m
2
2 2
2 2
a b m
.
Thay
1
vào
2
được:
2
2 2
2
a a m
2 2
2 4 4 0 3
a a m
.
Để có đúng một số phức thoả mãn bài toán thì PT
3
phải có nghiệm
a
duy nhất.
0
2
4 2 4 0
m
2
2
m
3
1;
2
2m
(Vì
m
là mô-đun).
Trình bày lại
Giả sử
,z a bi
vì
0
z
nên
2 2
0
a b
*
.
Đặt:
1
i
w
z
1
i
a bi
2 2
1
a b a b i
a b
2 2 2 2
a b a b
i
a b a b
.
w
là số thực nên:
1
a b
.Kết hợp
*
suy ra
0
a b
.
Mặt khác:
2
a bi m
2
2 2
2 2
a b m
.(Vì
m
là mô-đun nên
0
m
).
Thay
1
vào
2
được:
2
2 2
2
a a m
2 2
2 4 4 0
g a a a m
3
.
Để có đúng một số phức thoả mãn bài toán thì PT
3
phải có nghiệm
0
a
duy nhất.
Có các khả năng sau :
KN1 : PT
3
có nghiệm kép
0
a
ĐK:
2
2
0
2 0
2
0 0
4 0
m
m
g
m
.
KN2: PT
3
có hai nghiệm phân biệt trong đó có một nghiệm
0
a
ĐK:
2
2
0
2 0
2
0 0
4 0
m
m
g
m
.
Từ đó suy ra
0
3
2 1;
2
m
.
Câu 125. Cách 1:
Gọi
z x iy
với
,x y
ta có
2
2 2
2 2
4 4 4
4 4
4 4
x iy x iy x x y iy
z x iy
z x iy
x y x y
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
là số thuần ảo khi
2
2 2
4 0 2 4
x x y x y
Mà
2
2
6 36
z m x m y
Ta được hệ phương trình
2
2
2
2
2
2
2
2
2
2
2
36
4 2 36
36
4 2
36
4 2
2 4
4 2
4 2
m
x
m x m
x m y
m
m
y x
x y
y
m
Ycbt
2
2
36
4 2 0
4 2
m
m
2
36
2 2
4 2
m
m
hoặc
2
36
2 2
4 2
m
m
10
m
hoặc
2
m
hoặc
6
m
Vậy tổng là
10 2 6 6 8
.
Câu 126. Giả sử
,z a bi a b
.
Ta có:
4 1 4 3z i z z i
1 3 4 4 1
z i i i z
2 2
1 3 4 4 1
a bi i i i a b
2 2 2 2
3 4 3 4
a b a b i a b a b i
2 2
2 2
3 4
3 4
a b a b
a b a b
2 2
3 4
2 4
a b a b
a b
2
5 8 5 16 16
2 4
b b b
a b
2
5 8 0
20 64 48 0
2 4
b
b b
a b
8
5
2
6
5
2 4
b
b N
b L
a b
2
0
b
a
.
Vậy
2
z
.
Câu 127. Ta có:
. 12 13 10z z z z z i
2 2 2 2
12 2 13 10a b a b bi i
2 2 2 2
12 13
2 10
a b a b
b
2 2
25 12 25 13
5
a a
b
2
2
25 13
25 1
5
a
a VN
b
12
5
a
b
12
5
a
b
, vì
0
a
.
Vậy
7
S a b
.
Câu 128. Gọi
,z a bi a b
. Suy ra
z a bi
.
Ta có
2
2 2
3 1 3 1
1 1
iz i z i a bi i a bi
z a b
i i
2 2 2 2
3 3
ai b ai b a bi a b a i b i
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
2 2 2 2
2 4 0
a b a b i a b b a
2 2
2 2
2 0
4 0
a b a b
a b a b
2
0, 0 0
26 9 0
9 45 45 9
,
5
26 26 26 26
b a z
b b
b a z i
a b
45 9
26 26
z i
(Vì
0
z
).
Với
45 9 15 3 3 26
w w
26 26 2 2 2
z i i
.
Câu 129. Giả sử
1 1 1 1 1
, ,z a b i a b
,
2 2 2 2 2
, ,z a b i a b
.
Theo bài ra ta có:
1
2
1 2
1
2
3
z
z
z z
2 2
1 1
2 2
2 2
2 2
1 2 1 2
1
4
9
a b
a b
a a b b
2 2
1 1
2 2
2 2
1 2 1 2
1
4
2 2 4
a b
a b
a a b b
.
Khi đó, ta có:
2 2
1 2 1 2 1 2
z z a a b b
2 2 2 2
1 1 2 2 1 2 1 2
2 2
a b a b a a b b
1
.
Vậy
1 2
1
z z
.
Câu 130. Gọi
,z a bi a b
. Suy ra
z a bi
.
Ta có
2
2 2
3 1 3 1
1 1
iz i z i a bi i a bi
z a b
i i
2 2 2 2
3 3
ai b ai b a bi a b a i b i
2 2 2 2
2 4 0
a b a b i a b b a
2 2
2 2
2 0
4 0
a b a b
a b a b
2
0, 0 0
26 9 0
9 45 45 9
,
5
26 26 26 26
b a z
b b
b a z i
a b
45 9
26 26
z i
(Vì
0
z
).
Với
45 9 15 3 3 26
w w
26 26 2 2 2
z i i
.
Câu 131.
2 2 2 2
7 1 2 0a b i a b a b i
2 2
2 2
7 2 1
1 2
a a b
a b b
7 2 1 2 5a b a b
thế vào (2).
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
2
2
2
1
1
4
2 5 1
4 22 24 0
3
2
b
b
b
b b b
b b
b
TH1:
4 3 5 3.
b a z
(loại)
TH2:
3 5
2 3.
2 2
b a z
(nhận).
1
.
2
P a b
Câu 132. Đặt
1 2
, , , ,z a bi z c di a b c d
Theo đề:
2 2
1
2 2
2
2 3
12
18
3 2
z
a b
c d
z
Vậy
2 2
1 2 1 2
2 2 2 2
2 2 2 2
2 60
P z z z z
a c b d a c b d a b c d
Câu 133. Ta có
2
4
w
2
4
x yi
2 2
2 4x y xyi
2
2 2 2 2 2
4 4 4
w x y x y
.
Do đó
2
4 2w w
2
2 2 2 2 2 2
4 4 2
x y x y x y
2
2 2 2 2 2 2
4 4 4
x y x y x y
4 4 2 2 2 2 2 2 2 2
2 8 16 4 4
x y x y x y x y x y
4 4 2 2 2 2 2 2
2 4 4 8 12 0
x y x y x y x y
2
2 2 2 2 2 2
4 4 8 12 0
x y x y x y
2
2 2 2 2
2 8 12 0
x y x y
2
2 2 2 2
8 12 2
x y x y
2
2
2
P w
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ngu
yễn Bảo Vương:https://www.facebook.com/phong.baovuong 1
CHUYÊN
ĐỀ 26
MỤC LỤC
PhầnA.C
ÂUHỎI ........................................................................................................................................................... 1
Dạng1.Tậphợpđiểmbiểudiễnlàđườngtròn ................................................................................................................ 1
Dạng2.Tậphợpđiểmbiểudiễnlàđườngthẳng ............................................................................................................. 6
Dạng3.Tậphợpđiểmbiểudiễnlàđườngconic ............................................................................................................. 7
Dạng4.Tậphợpđiểmbiểudiễnlàmộtmiền .................................................................................................................. 8
PhầnB.LỜIGIẢITHAMKHẢO ................................................................................................................................. 10
Dạng1.Tậphợpđiểmbiểudiễnlàđườngtròn .............................................................................................................. 10
Dạng2.Tậphợpđiểmbiểudiễnlàđườngthẳng ........................................................................................................... 19
Dạng3.Tậphợpđiểmbiểudiễnlàđườngconic ........................................................................................................... 21
Dạng4.Tậphợpđiểmbiểudiễnlàmộtmiền ................................................................................................................ 23
PhầnA.CÂUHỎI
Dạng1.Tậphợpđiểmbiểudiễnlàđườngtròn
Câu1. (Mãđề102BGD&ĐTNĂM2018)Xétcácsốphức
z
thỏamãn
3
i 3
z
z
làsốthuầnảo.
Trênmặtphẳngtọađộ,tậphợptấtcảcácđiểmbiểudiễncácsốphức
z
làmộtđườngtròncóbán
kínhbằng:
A.
9
2
B.
3 2
C.
3
D.
3 2
2
Câu2. (MĐ103BGD&ĐTNĂM2017-2018)Xétcácsốphức
z
thỏamãn
2
2
z
i z
làsốthuần
ảo.Trênmặtphẳngtọađộ,tậphợptấtcảcácđiểmbiểudiễncácsốphức
z
làmộtđườngtròncó
bánkínhbằng
A.
2
2
B.
4
C.
2
D.
2
Câu3. (Mãđề104-BGD-2019)Xétcácsốphức
z
thỏamãn
2
z .Trênmặtphẳngtọađộ
Oxy
tập
hợpcácđiểmbiểudiễncácsốphức
5
1
i
z
w
z
làmộtđườngtròncóbánkínhbằng
A.
4
4
. B.
5
2
. C.
2 13
. D.
2
11
.
Câu4. (Mãđề104BGD&ĐTNĂM2018)Xétcácsốphức
z
thỏamãn
2 2
z i z
làsốthuầnảo.
Trênmặtphẳngtọađộ,tậphợptấtcảcácđiểmbiểudiễncácsốphức
z
làmộtđườngtròncóbán
kínhbằng?
A.
2
B.
2
C.
4
D.
2
2
BÀI TOÁN TÌM TẬP HỢP ĐIỂM BIỂU DIỄN SỐ PHỨC
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 2
Câu5. (ĐỀMINHHỌAGBD&ĐTNĂM2017)Chocácsốphức
z
thỏamãn
4
z
.Biếtrằngtậphợp
cácđiểmbiểudiễncácsốphức
(3 4 )
w i z i
làmộtđườngtròn.Tínhbánkính
r
củađườngtròn
đó
A.
22r
B.
4r
C.
5
r
D.
20
r
Câu6. (ĐỀTHAMKHẢOBGD&ĐTNĂM2018-2019)Xétcácsốphức
z
thỏamãn
2 2
z i z
là
sốthuầnảo.Biếtrằngtậphợptấtcảcácđiểmbiểudiễncủa
z
làmộtđườngtròn,tâmcủađường
trònđócótọađộlà
A.
1;1
B.
1;1
C.
1; 1
D.
1; 1
Câu7. (Mãđề101BGD&ĐTNĂM2018)Xétcácsốphức
z
thỏamãn
2
z i z
làsốthuầnảo.Trên
mặtphẳngtọađộ,tậphợptấtcảcácđiểmbiểudiễnsốphức
z
làmộtđườngtròncóbánkínhbằng
A.
3
2
B.
1
C.
5
4
D.
5
2
Câu8. (Mãđề101-BGD-2019)Xétsốphức
z
thỏamãn
2
z
.Trênmặtphẳngtọađộ
Oxy
,tập
hợpđiểmbiểudiễncácsốphức
4
1
iz
w
z
làmộtđườngtròncóbánkínhbằng
A.
26
. B.
34
. C.
26
. D.
34
.
Câu9. (Mã102-BGD-2019)Xétsốphức
z
thỏamãn
2
z
.Trênmặtphẳngtọađộ
Oxy
,tậphợp
điểmbiểudiễncácsốphức
3
1
iz
w
z
làmộtđườngtròncóbánkínhbằng
A.
2 5
. B.
20
. C.
12
. D.
2 3
.
Câu10. (Mã103-BGD-2019)Xétcácsốphức
z
thỏamãn
2
z .Trênmặtphẳngtọađộ
Oxy
,tập
hợpcácđiểmbiểudiễnsốphức
2
1
iz
w
z
làmộtđườngtròncóbánkínhbằng
A.
10
. B.
2
. C.
2
. D.
10
.
Câu11. (THPTGIALỘCHẢIDƯƠNGNĂM2018-2019LẦN01) Chosốphức
z
thỏamãn
2
z
.Biết
rằngtậphợpcácđiểmbiểudiễnsốphức
w 3 2 2
i i z
làmộtđườngtròn.Tìmtọađộtâm
I
củađườngtrònđó?
A.
3; 2
I
. B.
3;2
I
. C.
3;2
I
. D.
3; 2
I
.
Câu12. (ĐỀMẪUKSNLĐHQGTPHCMNĂM2018-2019)Trongmặtphẳngphức,tậphợpcácđiểm
biểudiễnsốphức
z
thoảmãn
. 1z z
là
A.mộtđườngthẳng. B.mộtđườngtròn. C.mộtelip. D.mộtđiểm.
Câu13. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Cho số phức
z
thỏa
1 2 3
z i
.Biếtrằngtậphợpcácđiểmbiểudiễncủasốphức
2
w z i
trênmặtphẳng
Oxy
làmộtđườngtròn.Tìmtâmcủađườngtrònđó.
A.
I
. B.
1;1
I
. C.
0;1
I
. D.
1;0
I
.
Câu14. (THPTCHUYÊNSƠNLANĂM2018-2019LẦN01)Tậphợpcácđiểmbiểudiễnsốphức
z
thỏa
mãn
1
z i i z
làmộtđườngtròn,tâmcủađườngtrònđócótọađộlà
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ngu
yễn Bảo Vương:https://www.facebook.com/phong.baovuong 3
A.
1;1
. B.
0
; 1
. C.
0
;1
. D.
1
; 0
.
Câu15. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Cho số phức
z
thỏa mãn
1
2
z
i
.Biếtrằngtậphợpcácđiểmbiểudiễnsốphức
z
làmộtđườngtròn
C
.Tínhbánkính
r
củađườngtròn
C
.
A.
1
.
r
B.
5.
r C.
2
.
r
. D.
3.
r .
Câu16. (KTNLGVBẮCGIANGNĂM2018-2019)Trongmặtphẳngtọađộđiểmbiểudiễnsốphức
z
thỏamãn
1
2 3
z
i
là
A. đườngtròntâm
(
1;2)
I
,bánkính
9
R
. B. đườngtròntâm
(
1;2)
I
,bánkính
3
R
.
C. đườngtròntâm
( 1; 2)
I
,bánkính
3
R
. D.
đườngthẳngcóphươngtrình
2 3 0
x y
.
Câu17. (SỞGD&ĐTTHANHHÓANĂM2018-2019)Xétcácsốphức
z
thỏamãn
(
2 )( )z z i
làsố
thuầnảo.Tậphợpcácđiểmbiểudiễncủa
z
trongmặtphẳngtọađộlà:
A. Đườngtròntâm
1
1
;
2
I
,bánkính
5
2
R
.
B. Đườngtròntâm
1
1;
2
I
,bánkính
5
2
R
.
C. Đườngtròntâm
2;1
I
,bánkính
5
R
.
D. Đườngtròntâm
1
1;
2
I
,bánkính
5
2
R
nhưngbỏđiểm
(2;0); (0;1)
A B
.
Câu18. (CHUYÊNBẮCGIANGNĂM2018-2019LẦN02)Tìmtậphợpđiểmbiểudiễnsốphứczthỏa
mãn
(1 )z i i z
.
A. ĐườngtròntâmI(0;1),bánkính
2
R
. B.ĐườngtròntâmI(1;0),bánkính
2
R
.
C. ĐườngtròntâmI(-1;0),bánkính
2
R
. D.ĐườngtròntâmI(0;-1),bánkính
2
R
.
Câu19. (ĐỀTHITHỬVTED02NĂMHỌC2018-2019)Tâphợptấtcảcácđiểmbiểudiễnsốphức
,z
x yi x y
thỏamãn
4
z
i
làđườngcongcóphươngtrình
A.
2
2
1
4
x
y
B.
2
2
1
4
x
y
C.
2
2
1
16
x
y
D.
2
2
1
16
x
y
Câu20. (CHUYÊNNGUYỄNTẤTTHÀNHYÊNBÁILẦN01NĂM2018-2019)Tậphợptấtcảcác
điểmbiểudiễncácsốphức
z
thỏamãn
2 4
z i
làđườngtròncótâmvàbánkínhlầnlượtlà
A.
2
; 1
I
;
4R
. B.
2
; 1
I
;
2R
. C.
2
; 1
I
;
4R
. D.
2
; 1
I
;
2R
.
Câu21. (ĐỀTHICÔNGBẰNGKHTNLẦN02NĂM2018-2019)Tậphợpđiểmbiểudiễnsốphức
z
thỏamãn
1
2
z
i
làđườngtròncótâmvàbánkínhlầnlượtlà:
A.
1
;1 , 4
I
R
. B.
1
;1 , 2
I
R
. C.
1
; 1 , 2
I
R
. D.
1
; 1 , 4
I
R
.
Câu22. (CHUYÊNKHTNNĂM2018-2019LẦN01)Tậphợptấtcảcácđiểmbiểudiễncácsốphức
z
thỏamãn
1
5 2
i
z i
làmộtđườngtròntâm
I
vàbánkính
R
lầnlượtlà
A.
2; 3 , 2
I R
. B.
2
; 3 , 2
I
R
. C.
2;3 , 2
I R
. D.
2
;3 , 2
I
R
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ngu
yễn Bảo Vương:https://www.facebook.com/phong.baovuong 4
Câu23. (CHUYÊNKHTNNĂM2018-2019LẦN01)Xétcácsốphức
z
thỏamãn
2
2
z
z i
làsốthuầnảo.
Biếtrằngtậphợpcácđiểmbiểudiễncácsốphức
z
luônthuộcmộtđườngtròncốđịnh.Bánkính
củađườngtrònđóbằng
A.
1
. B.
2
. C.
2
2
. D.
2
.
Câu24. (CHUYÊNLÊQUÝĐÔNQUẢNGTRỊNĂM2018-2019LẦN01)Tínhtổngcủatấtcảcácgiá
trịcủathamsố
m
đểtồntạiduynhấtsốphức
z
thoảmãnđồngthời
z
m
và
2
4
3
z
m mi m
.
A.
4
. B.
6
. C.
9
. D.
1
0
.
Câu25. (THPTYÊNKHÁNH-NINHBÌNH-2018-2019)Chosốphức
z
thỏamãn:
2 3
z i
.Tập
hợpcácđiểmtrongmặtphẳngtọađộ
Oxy
biểudiễnsốphức
1w
z
là
A. Đườngtròntâm
2
;1
I
bánkính
3
R
.
B. Đườngtròntâm
2
; 1
I
bánkính
3
R
.
C. Đườngtròntâm
1
; 1
I
bánkính
9
R
.
D. Đườngtròntâm
1
; 1
I
bánkính
3
R
.
Câu26. (KTNLGVBẮCGIANGNĂM2018-2019)Chocácsốphức
z
thỏamãn
2 5
z .Biếtrằng
trongmặtphẳngtọađộcácđiểmbiểudiễncủasốphức
2
w i i z
cùngthuộcmộtđườngtròn
cốđịnh.Tínhbánkính
r
củađườngtrònđó?
A.
5
r
. B.
10
r
. C.
2
0
r
. D.
2 5
r
.
Câu27. (ĐỀTHITHỬVTED03NĂMHỌC2018-2019)Xétcácsốphức
z
thỏamãn
2
3
z
i z
là
sốthuầnảo.Trênmặtphẳngtọađộ,tậphợptấtcảcácđiểmbiểudiễnsốphức
z
làmộtđườngtròn
cóbánkínhbằng
A.
13
B.
11
C.
1
1
2
D.
1
3
2
Câu28. Cho các số phức
z
thỏa mãn
1
2
z
. Biết rằng tập hợp các điểm biểu diễn các số phức
1 8
w i z i
làmộtđườngtròn.Bánkính
r
củađườngtrònđólà
A.
9
. B.
3
6
. C.
6
. D.
3
.
Câu29. Cho
1
2
,z z
làhaisốphứcthỏamãnđiềukiện
|
z 5 3i | 5
đồngthời
1
2
| | 8
z z
.Tậphợpcácđiểm
biểudiễnsốphức
1
2
w z z
trongmặtphẳngtọađộ
O
xy
làđườngtròncóphươngtrình
A.
2
2
( 10) ( 6) 36
x y
. B.
2
2
( 10) ( 6) 16
x y
.
C.
2
2
5 3
(
) ( ) 9
2 2
x
y
. D.
2
2
5 3 9
(
) ( )
2
2 4
x
y
.
Câu30. (CHUYÊNKHTN-LẦN1-2018).Tậphợptấtcảcácđiểmbiểudiễncácsốphức
z
thỏamãn:
2 4
z i
làđườngtròncótâm
I
vàbánkính
R
lầnlượtlà:
A.
2
; 1
I
;
4R
. B.
2
; 1
I
;
2R
. C.
2
; 1
I
;
4R
. D.
2
; 1
I
;
2
; 1
I
.
Câu31. (TOÁNHỌCTUỔITRẺ-THÁNG4-2018)Chosốphức
z
thỏamãn
2
z
.Tậphợpđiểmbiểu
diễnsốphức
1 2w i z i
là
A. Mộtđườngtròn. B. Mộtđườngthẳng.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ngu
yễn Bảo Vương:https://www.facebook.com/phong.baovuong 5
C. MộtElip. D. Mộtparabolhoặchyperbol.
Câu32. (SGD&ĐT ĐỒNG THÁP - HKII - 2018) Tập hợp điểm biểu diễn của số phức
z
thỏa mãn
1
1 2z i z
làđườngtròn
C
.Tínhbánkính
R
củađườngtròn
C
A.
1
0
9
R
. B.
2 3
R . C.
7
3
R
. D.
10
3
R
.
Câu33. (SGD-HÀTĨNH-HK2-2018)Tậphợptấtcảcácđiểmbiểudiễnsốphức
z
thỏamãn
2
6
z
i
làmộtđườngtròncóbánkínhbằng:
A.
3
. B.
6
2
. C.
6
. D.
3
2
.
Câu34. (THPTCHUYÊNTHĂNGLONG-ĐÀLẠT-2018)Chosốphức
z
thỏamãn
1 3 2
z i
.
Biếttậphợpđiểmbiểudiễnsốphức
2
3 5w i z i
làmộtđườngtròn.Xácđịnhtâm
I
và
bánkínhcủađườngtròntrên.
A.
6; 4 , 2 5
I R .B.
6;4 , 10
I R
.
C.
6;4 , 2 5
I R . D.
6;4 , 2 5
I R .
Câu35. (THPTCHUYÊNHOÀNGVĂNTHỤ-HÒABÌNH-2018)Chosốphức
z
thỏamãn
2
z
.
Biếtrằngtậphợpcácđiểmbiểudiễnsốphức
3
2 2
w
i i z
làmộtđườngtròn.Bánkính
R
củađườngtrònđóbằng?
A.
7
. B.
2
0
. C.
2 5
. D.
7
.
Câu36. (SGDTHANHHÓA-LẦN1-2018)Cho
1
z
,
2
z
làhaitrongcácsốphức
z
thỏamãnđiềukiện
5
3 5
z
i
,đồngthời
1
2
8
z
z
.Tậphợpcácđiểmbiểudiễncủasốphức
1
2
w z z
trong
mặtphẳngtọađộ
O
xy
làđườngtròncóphươngtrìnhnàodướiđây?
A.
2 2
5
3 9
2 2 4
x
y
. B.
2
2
10
6 36
x
y
.
C.
2
2
10
6 16
x
y
. D.
2
2
5
3
9
2 2
x y
.
Câu37. (THPTTHÁIPHIÊN-HẢIPHÒNG-LẦN1-2018)Xétsốphứczthỏamãn
3 4 3
z i
,biết
rằngtậphợpcácđiểmbiểudiễnsốphức
(
12 5 ) 4w i z i
làmộtđườngtròn.Tìmbánkínhrcủa
đườngtrònđó.
A.
1
3
r
. B.
3
9
r
. C.
17
r
D.
3
r
.
Câu38. (THPTTHỰCHÀNH-TPHCM-2018)Chosốphức
z
thỏamãn
3
1
z
.Biếtrằngtậphợp
cácđiểmbiểudiễncácsốphức
1 3 1 2w i z i
làmộtđườngtròn.Tínhbánkính
r
của
đườngtrònđó.
A.
2r
. B.
1r
. C.
4r
. D.
2
r
.
Câu39. [THPT Lệ Thủy-Quảng Bình] Gọi
M
là điểm biểu diễn của số phức
z
thỏa mãn
1 3 4
z m i
.Tìmtấtcảcácsốthực
m
saochotậphợpcácđiểm
M
làđườngtròntiếpxúc
vớitrục
Oy
.
A.
5
; 3
m
m
. B.
5
; 3
m
m
. C.
3
m
. D.
5m
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ngu
yễn Bảo Vương:https://www.facebook.com/phong.baovuong 6
Câu40. [Cụm4HCM]Chosốphức
z
thỏamãn
2 2
z
.Biếtrằngtậphợpcácđiểmbiểudiễncácsố
phức
1
w
i z i
làmộtđườngtròn.Tínhbánkính
r
củađườngtrònđó.
A.
2r
. B.
4r
. C.
2
r
. D.
2
2
r
.
Câu41. (Chuyên Lương Thế Vinh – Hà Nội – Lần 2 – 2018 – BTN) Cho số phức
z
thỏa mãn
2 2 25
z i z i
.Biếttậphợpcácđiểm
M
biểudiễnsốphức
2
2 3w z i
làđường
tròntâm
;I a b
vàbánkính
c
.Giátrịcủa
bằng
A.
1
8
. B.
2
0
. C.
1
0
. D.
1
7
.
Dạng2.Tậphợpđiểmbiểudiễnlàđườngthẳng
Câu42. (THPTHÙNGVƯƠNGBÌNHPHƯỚCNĂM2018-2019LẦN01)Chosốphức
z
thỏamãn
1
2
z
i z
.Trongmặtphẳngphức,quỹtíchđiểmbiểudiễncácsốphức
z
.
A. làđườngthẳng
3 1 0
x y
. B. làđườngthẳng
3 1 0
x y
.
C. làđườngthẳng
3 1 0
x y
. D. làđườngthẳng
3 1 0
x y
.
Câu43. (ĐỀ 15 LOVE BOOK NĂM 2018-2019) Trên mặt phẳng phức, tập hợp các số phức
,z x yi x y
thỏamãn
2 3z i z i
làđườngthẳngcóphươngtrình
A.
1y
x
. B.
1y
x
. C.
1y
x
. D.
.
Câu44. (CHUYÊNLÊQUÝĐÔNQUẢNGTRỊNĂM2018-2019LẦN01)Trongmặtphẳngtọađộ
Oxy
,tậphợpcácđiểmbiểubiễncácsốphức
z
thỏamãn
1 2 1 2z i z i
làđườngthẳngcó
phươngtrình
A.
2 1 0
x y
. B.
2 0
x y
. C.
2 0
x y
. D.
2 1 0
x y
.
Câu45. Xétcácsốphức
z
thỏamãn
2 4 1z z i i
làsốthực.Biếtrằngtậphợpcácđiểmbiểudiễn
củasốphức
z
làđườngthẳng
d
.Diệntíchtamgiácgiớihạnbởiđườngthẳng
d
vàhaitrụctọa
độbằng
A.
8
. B.
4
. C.
2
. D.
1
0
.
Câu46. (ĐỀTHICÔNGBẰNGKHTNLẦN02NĂM2018-2019)Tậphợpcácđiểmbiểudiễncácsố
phức
z
thỏamãn
2
z
z i
làmộtđườngthẳngcóphươngtrình
A.
4 2 3 0
x y
. B.
2 4 13 0
x y
. C.
4 2 3 0
x y
. D.
2 4 13 0
x y
.
Câu47. (LIÊNTRƯỜNG-NGHỆAN-LẦN2-2018)Chosốphức
z
thỏamãn:
1
2 3z z i
.Tập
hợpcácđiểmbiểudiễnsốphức
z
là
A. Đườngtròntâm
1
;2
I
,bánkính
1R
.
B. Đườngthẳngcóphươngtrình
2 6 12 0
x y
.
C. Đườngthẳngcóphươngtrình
3
6 0
x
y
.
D. Đườngthẳngcóphươngtrình
5 6 0
x y
.
Câu48. (THPTCHUYÊNLÊHỒNGPHONG-TPHCM-2018)Tìmtậphợpđiểmbiểudiễncácsốphức
z
thỏa
12 5 17 7
13
2
i
z i
z i
.
A.
:
6 4 3 0
d
x y
. B.
:
2 1 0
d
x y
.
C.
2
2
:
2 2 1 0
C
x y x y
. D.
2
2
:
4 2 4 0
C
x y x y
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ngu
yễn Bảo Vương:https://www.facebook.com/phong.baovuong 7
Câu49. (CHUYÊNTRẦNĐẠINGHĨA-TPHCM-HK2-2018)Trênmặtphẳngtạođộ ,tậphợp
điểmbiểudiễnsốphức thỏamãn là
A. Đườngthẳng . B.Đườngthẳng .
C. Đườngthẳng . D.Đườngtròntâm .
Câu50. (SGD&ĐTBRVT-2018)Chosốphức
z x yi
,x
y
thỏamãn
2
1 0
z
i z i
.
Trongmặtphẳngtọađộ
O
xy
,điểm
M
làđiểmbiểudiễncủasốphức
z
.Hỏi
M
thuộcđường
thẳngnàosauđây?
A.
5 0
x y
. B.
2 0
x y
. C.
2 0
x y
. D.
1 0
x y
.
Câu51. Trongmặtphẳngphức
Oxy
,tậphợpcácđiểmbiểudiễnsốphức
Z
thỏamãn
2
2
2
2 16
z z z
làhaiđườngthẳng
1
2
,d d
.Khoảngcáchgiữa2đườngthẳng
1
2
,d d
làbaonhiêu?
A.
1
2
, 1
d d d
. B.
1
2
, 6
d d d
. C.
1
2
, 2
d d d
. D.
1
2
, 4
d d d
.
Câu52. [BTN166-2017]Trongmặtphẳngphức,tậphợpcácđiểm
M
biểudiễnsốphức
z
thỏamãn
điềukiện
3
4z z i
là?
A. Parabol
2
4y x
. B. Đườngthẳng
6
8 25 0
x
y
.
C. Đườngtròn
2
2
4 0
x y
. D. Elip
2
2
1
4
2
x
y
.
Câu53. [TTLTĐHDiệuHiền-2017]Chosốphức
z
thỏa:
2
2 3 2 1 2z i i z
.Tậphợpđiểmbiểu
diễnchosốphức
z
là.
A. Môtđươngthăngcophươngtrinh:
2
0 32 47 0
x
y
.
B. Môtđươngcophươngtrinh:
2
3 20 2 20 0
y x y
.
C. Môtđươngthăngcophươngtrinh:
20 16 47 0
x y
.
D. Môtđươngthăngcophươngtrinh:
2
0 16 47 0
x
y
.
Dạng3.Tậphợpđiểmbiểudiễnlàđườngconic
Câu54. (SỞGD&ĐTBÌNHPHƯỚCNĂM2018-2019LẦN01)Tậphợpcácđiểmbiểudiễncácsốphức
z
thỏamãn
2 2z i z z i
là
A. Mộtđiểm B. Mộtđườngtròn C. Mộtđườngthẳng D.MộtParabol
Câu55. (CHUYÊNLƯƠNGTHẾVINHĐỒNGNAINĂM2018-2019LẦN01)Chosốphức
z
thỏamãn
2
2 4
z
z
.Tậphợpđiểmbiểudiễncủasốphức
z
trênmặtphẳngtọađộlà
A. Mộtđườngelip. B. Mộtđườngparabol.
C. Mộtđoạnthẳng. D. Mộtđườngtròn.
Câu56. (ĐỀ01ĐỀPHÁTTRIỂNĐỀTHAMKHẢOBGD&ĐTNĂM2018-2019)Xétcácsốphức
z
thoả
mãn
1
1
z i
z z i
làsốthực.Tậphợpcácđiểmbiểudiễncủasốphức
2
z
là
parabolcótoạđộđỉnh
A.
1 3
;
4
4
I
. B.
1 1
;
4 4
I
. C.
1 3
;
2
2
I
. D.
1 1
;
2 2
I
.
Oxy
z
z
i iz
2
y
1
2
y
1
2
y
0
;1
I
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ngu
yễn Bảo Vương:https://www.facebook.com/phong.baovuong 8
Câu57. (CHUYÊNKHTNLẦN2NĂM2018-2019)Tínhdiệntíchhìnhphẳnggiớihạnbởicácđiểmbiểu
diễncácsốphứcthỏamãn
2 4 10
z i z i
.
A.
1
5
. B.
1
2
. C.
2
0
. D. Đápánkhác.
Câu58. (SGD-BÌNHDƯƠNG-HK2-2018)Tậphợpcácđiểmbiểudiễncácsốphức
z
thỏamãn
2
2z i z z i
là
A. Mộtđườngthẳng. B.Mộtđườngtròn. C.MộtParabol. D. Mộtđiểm
Câu59. [THPTCHUYÊNVINH]Gọi
M
làđiểmbiểudiễncủasốphức
z
thỏamãn
3
2 3z i z z i
.Tìmtậphợptấtcảnhữngđiểm
M
nhưvậy.
A. Mộtđườngthẳng. B.Mộtparabol. C. Mộtelip. D. Mộtđườngtròn.
Câu60. [SởBìnhPhước]Chosốphức
z
thỏamãn
2 2 8
z z
.Trongmặtphẳngphứctậphợpnhững
điểm
M
biểudiễnchosốphức
z
là?
A.
2 2
: 2 2 64
C x y
. B.
2
2
:
1
16 12
x
y
E
.
C.
2 2
:
1
12 16
x
y
E
. D.
2
2
: 2 2 8
C x y
.
Câu61. [THPTNguyễnTrãiLần1]Tậphợpcácđiểmtrongmặtphẳngtọađộbiểudiễnsốphức
z
thỏa
mãnđiềukiện
2
2z i z z i
làhìnhgì?
A. Mộtđườngtròn. B. MộtđườngParabol.
C. MộtđườngElip. D. Mộtđườngthẳng.
Câu62. [THPTHaiBàTrưng-Huế]Tìmtậphợpcácđiểm
M
biểudiễnhìnhhọcsốphức
z
trongmặt
phẳngphức,biếtsốphức
z
thỏamãnđiềukiện:
4
4 10.
z
z
.
A. Tậphợpcácđiểmcầntìmlàđườngelipcóphươngtrình
2
2
1
9
25
x
y
.
B. Tậphợpcácđiểmcầntìmlànhữngđiểm
;M x y
trongmặtphẳng
Oxy
thỏamãnphươngtrình
2 2
2 2
4
4 12
x
y x y
.
C. Tậphợpcácđiểmcầntìmlàđườngtròncótâm
0; 0
O
vàcóbánkính
4R
.
D. Tậphợpcácđiểmcầntìmlàđườngelipcóphươngtrình
2
2
1
2
5 9
x
y
.
Câu63. [THPTCHUYÊNBẾNTRE]Chosốphức
z
thỏamãnđiềukiện:
4 4 10
z
z
.Tậphợp
cácđiểm
M
biểudiễnchosốphức
z
làđườngcóphươngtrình.
A.
2
2
1
9
25
x y
. B.
2
2
1
25
9
x y
. C.
2
2
1
9
25
x y
. D.
2
2
1
25
9
x y
.
Dạng4.Tậphợpđiểmbiểudiễnlàmộtmiền
Câu64. (THPTNĂM2018-2019LẦN04)Phầngạchtronghìnhvẽdướilàhìnhbiểudiễncủatậpcácsố
phứcthỏamãnđiềukiệnnàosauđây?
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 9
A.
6 8
z
. B.
2 4 4 4
z i
. C.
2 4 4 4
z i
. D.
4 4 4 16
z i
.
Câu65.
(CHUYÊNLÊQUÝĐÔNĐIỆNBIÊNLẦN3NĂM2018-2019)
Trongmặtphẳngtọađộ
Oxy
,
tìmtậphợpcácđiểmbiểudiễnsốphức
z
biết
2 3 2
z i
.
A.Mộtđườngthẳng. B.Mộthìnhtròn. C.Mộtđườngtròn. D.MộtđườngElip.
Câu66. Trongmặtphẳngphức,tậphợpđiểmbiểudiễnchosốphức
z
thỏa
4 4 2
z i
là
A.Hìnhtròntâm
I
,bánkính
4R
. B.Hìnhtròntâm
I
,bánkính
2R
.
C.Hìnhtròntâm
I
,bánkính
2R
. D.Hìnhtròntâm
I
,bánkính
4R
.
Câu67. (THPTQUANGTRUNGĐỐNGĐAHÀNỘINĂM2018-2019)Chosốphức
z
thỏamãnđiều
kiện
3 3 1 5
z i
.Tậphợpcácđiểmbiểudiễncủa
z
tạothànhmộthìnhphẳng.Tínhdiệntích
củahìnhphẳngđó.
A.
25
S
. B.
8
S
. C.
4
S
. D.
16
S
.
Câu68. (THPTTHỰCHÀNH-TPHCM-2018)Trongmặtphẳng
Oxy
chosốphức
z
cóđiểmbiểudiến
nằmtrongcungphầntưthứ
I
.Hỏiđiểmbiểudiễnsốphức
1
w
iz
nằmtrongcungphầntưthứ
mấy?
A.Cung
IV
. B.Cung
II
. C.Cung
III
. D.Cung
I
.
Câu69. (SỞGD&ĐTNAMĐỊNH-HKII-2018)Trongmặtphẳngtọađộ
Oxy
,gọi
H
làphầnmặtphẳng
chứacácđiểmbiểudiễncácsốphức
z
thỏamãn
16
z
và
16
z
cóphầnthựcvàphầnảođềuthuộcđoạn
0;1
.Tínhdiệntích
S
của
H
A.
32 6 .
S
B.
16 4 .
S
C.
S
. D.
64 .
S
.
Câu70. (SỞGD&ĐTYÊNBÁI-2018)Chosốphức
z
thỏamãnđiềukiện
3 3 1 5
z i
.Tậphợpcác
điểmbiểudiễncủa
z
tạothànhmộthìnhphẳng.Tínhdiệntích
S
củahìnhphẳngđó.
A.
4
S
. B.
25
S
. C.
8
S
. D.
S
.
Câu71. [SỞGD-ĐTHÀTĨNHL2]Biếtsốphức
z
thõamãn
z
và
z z
cóphầnảokhôngâm.
Phầnmặtphẳngbiểudiễnsốphức
z
códiệntíchlà:
A.
2
. B.
2
. C.
2
. D.
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ngu
yễn Bảo Vương:https://www.facebook.com/phong.baovuong 10
Câu72. [CHUYÊNVÕNGUYÊNGIÁP]Gọi
H
làhìnhbiểudiễntậphợpcácsốphức
z
trongmặtphẳng
tọađộ
0xy
saocho
2 3
z z
,vàsốphức
z
cóphầnảokhôngâm.Tínhdiệntíchhình
H
.
A.
3
2
. B.
3
4
. C.
6
. D.
3
.
Câu73. [THPTChuyênTháiNguyên]Tậphợpcácsốphức
1
1w i z
với
z
làsốphứcthỏamãn
1
1
z
làhìnhtròn.Tínhdiệntíchhìnhtrònđó.
A.
2
. B.
. C.
3
. D.
4
.
Câu74. [2017] Gọi
M
là điểm biểu diễn số phức
2
2
3
2
z z i
z
, trong đó
z
là số phức thỏa mãn
2
3
i
z i i z
. Gọi
N
là điểm trong mặt phẳng sao cho
,
2
O
x ON
, trong đó
,
O
x OM
làgóclượnggiáctạothànhkhiquaytia
Ox
tớivịtrítia
OM
.Điểm
N
nằmtrong
gócphầntưnào?
A. Gócphầntưthứ(IV).B.Gócphầntưthứ(I).
C. Gócphầntưthứ(II). D.Gócphầntưthứ(III).
Câu75. [TRẦNHƯNGĐẠO–NB-2017]Chosốphức
z
thỏamãnđiềukiện
3 4 2.
z i
Trongmặt
phẳng
Oxy
tậphợpđiểmbiểudiễnsốphức
2
1w z i
làhìnhtròncódiệntích
A.
9
S
. B.
1
2
S
. C.
1
6
S
. D.
2
5
S
.
Câu76. [THPTHoàngHoaThám-KhánhHòa-2017]Biếtsốphức
z
thỏađiềukiện
3
3 1 5
z
i
.
Tậphợpcácđiểmbiểudiễncủa
z
tạothành
1
hìnhphẳng.Diệntíchcủahìnhphẳngđóbằng:
A.
9
. B.
1
6
. C.
25
. D.
4
.
PhầnB.LỜIGIẢITHAMKHẢO
Dạng1.Tậphợpđiểmbiểudiễnlàđườngtròn
Câu1. ChọnD
Gọi
iz x y
,với
,x y
.
Theogiảthiết,tacó
3
i 3
z
z
2
3
3i 9i
z
z z
làsốthuầnảokhi
2
2
3 3 0
x y x y
.Đâylàphươngtrìnhđườngtròntâm
3 3
;
2 2
I
,bánkính
3 2
2
R
.
Câu2. ChọnC
Giảsử
z x yi
với
,x y
.
Vì
2
2 2 2
z
i z x y i x yi
2 2 2 2
x x y y xy x y i
là
sốthuầnảonêncóphầnthựcbằngkhôngdođó
2
2 0
x
x y y
2
2
1
1 2
x
y
.
Suyratậphợpcácđiểmbiểudiễncácsốphức
z
làmộtđườngtròncóbánkínhbằng
2
.
Câu3. ChọnC
Gọi
w x yi
với
,x
y
làcácsốthực.
Tacó
5
5
1
i
z w
w z
z i w
.
Lạicó
5
2
2
w
z
i w
2
2
2 2
5
2 5 2 1
w
w i x y x y
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 11
2 2
5 4 52
x y
.
Vậytậphợpcácđiểmbiểudiễncácsốphức
w
làmộtđườngtròncóbánkínhbằng
52 2 13
.
Câu4. ChọnA
Gọi
z a bi
,
,a b
Tacó:
2 2
2 2 2 2 2 2 2 2z i z a bi i a bi a a b b a b i
Vì
2 2
z i z
làsốthuầnảonêntacó
2 2
2 2
2 2 0 1 1 2
a a b b a b
.
Trênmặtphẳngtọađộ,tậphợptấtcảcácđiểmbiểudiễncácsốphức
z
làmộtđườngtròncóbán
kínhbằng
2
.
Câu5. ChọnD
Giasư
; ; , , ,z a bi w x yi a b x y
Theođê
3 4 3 4
w i z i x yi i a bi i
3 4 3 4
3 4 3 4 1
3 4 1 1 3 4
x a b x a b
x yi a b b a i
y b a y b a
Taco
2 2 2
2 2 2 2 2
1 3 4 4 3 25 25 25
x y a b a b a b a b
Ma
2 2
4 16
z a b
.Vây
2
2
1 25.16 400
x y
Bankinhđươngtronla
400 20
r
.
Câu6. ChọnC
Gọi
z x yi
z x yi
2 2
z i z
. 2 2 4z z z iz i
2 2
2 2 4x y x yi i x yi i
2 2
2 2 2 2 4x y x y x y i
2 2
z i z
làsốthuầnảo
2 2
2 2 0
x y x y
Vậytậphợpcácđiểmbiểudiễncủa
z
làmộtđườngtròncótâmlà
1; 1
I
.
Câu7. ChọnD
Đặt
,z x yi x y
.
2 1 2
z i z x y i x yi
làsốthuầnảo
2 1 0
x x y y
2 2
2 0
x y x y
.
Vậytậphợpcácđiểmbiểudiễnsốphức
z
làmộtđườngtròncótâm
1 5
1; ,
2 2
I R
.
Câu8. ChọnB
4
1 4
1
iz
w z w iz
z
4
z w i w
. 4
z w i w
2. 4
w i w
(*)
Gọi
, ,w x yi x y
khiđóthayvào(*)tacó:
2. 4
x yi i x yi
2 2
2 2
2 1 4
x y x y
2 2
2 2
8 4 14 0 4 2 34
x y x y x y
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 12
Vậytậphợpđiểmbiểudiễncácsốphức
4
1
iz
w
z
làmộtđườngtròncóbánkínhbằng
34
.
Câu9. ChọnA
Tacó:
3
3 3
1
iz
w w wz iz w i w z
z
.
3 3
w i w z w i w z
.
Gọi
, ,w x yi x y
.
Dođó,
2 2
2 2
3 3 1 . 2
w i w z x y x y
2 2
2 2 2 2
3 2 2 1 6 4 7 0
x y x y x y x y
.
Vậytậphợpđiểmbiểudiễnsốphức
w
thỏamãn
2
z
làđườngtròncótâm
3;2
I
vàbán
kínhbằng
2 5
.
Câu10. ChọnA
Gọisốphức
; ,w x yi x y
.Khiđó:
2
1
iz
w
z
1 2 2
w z iz w z i w
2 2
w z i w w z z i w
2 2 2 2
2 2
2 2 1 2 2 10 *
x y x y x y
Từ
*
suyrađiểmbiểudiễnsốphức
w
làmộtđườngtròncóbánkínhbằng
10
.
Câu11. Cách1.
Đặt
w x yi
.Tacó
w 3 2 2
i i z
.
3 2 2
x yi i i z
.
2 3 2i z x y i
.
2
4 3 2 . 2
i z x y i i
.
2 8 2 1
5 5
x y x y
z i
.
Vì
2
z
nên
2 2
2 8 2 1
4
5 5
x y x y
.
2 2
6 4 13 20
x y x y
.
2 2
3 2 20
x y
.
Vâytậphợpbiểudiễnsốphức
w
làđườngtròntâm
3; 2
I
.
Cách2.
Đặt
;w
z a bi x yi
.
Vì
2
z
nên
2 2
4
a b
.
Tacó
w 3 2 2
i i z
.
2 3 2
x yi i i a bi
.
3 2 2 2
x y i a b b a i
.
2 2 2 2
3 2 2 2
x y a b b a
.
2 2
2 2
3 2 5
x y a b
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ngu
yễn Bảo Vương:https://www.facebook.com/phong.baovuong 13
2
2
3
2 20
x
y
.
Vâytậphợpbiểudiễnsốphức
w
làđườngtròntâm
3; 2
I
.
Câu12. Đặt
z x yi
;
,x y
.Khiđó
z x yi
.
Vì
2
2
.
1 1 1
z
z x yi x yi x y
.
Vậytậphợpcácđiểmbiểudiễnsốphức
z
cầntìmlàđườngtrònđơnvị.
Câu13. Cách1:
Gọi
M
làđiểmbiểudiễnsốphức
w
.
Tacó
2
2
w
i
w
z i z
.
Dođó
1
2 3
z
i
1
2 3
2
w i
i
2
3 6
w
i
6
M
I
,với
2
; 3
I
.
Dođótậphợpđiểm
M
làđườngtròntâm
I
vàbánkính
6
R
.
Câu14. Đặt
,z
x yi x y
.
Tacó
1
z
i i z
.
1 1
x y i i x yi
1
x y i x y x y i
2
2 2
2
1
x
y x y x y
2 2
2 1 0
x y y
2
2
1
2
x
y
.
Vậytậphợpcácđiểmbiểudiễnsốphức
z
làđườngtròncótâm
0
; 1
.
Câu15. Tacó:
1
2 5
2
z
z
i
i
.
Suyratậphợpcácđiểmbiểudiễnsốphức
z
làmộtđườngtròncóbánkính
5.
r
Câu16. ChọnC
Giảsửđiểm
M
(x;y)
làđiểmbiểudiễnsốphức
z
.Tacó:
2
2
1
2 3 ( 1) ( 2)i 3 ( 1) ( 2) 9
z
i x y x y
Vậyđiểm
M
(x;y)
thuộcđườngtròn
2
2
( 1) ( 2) 9
x y
cótâm
(
1;2)
I
,bánkính
3
R
.
Câu17. Gọisốphức
,
.z x yi x y z x yi
Thayvàođiềukiệntađược:
(
2 )( ).
(2 )( ).
2 1 .
(
2 ) (1 ) (2 )(1 ) .
z
z i
x yi x yi i
x yi x y i
x
x y y x y xy i
(
2 )( )z z i
làsốthuầnảokhivàchỉkhi:
(2 ) (1 ) 0
x x y y
.
2
2
2 0
x y x y
.
Vậysốphức
z x yi
thuộcđườngtròntâm
1
1
;
2
I
,bánkính
5
2
R
.
Câu18. ChọnD
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 14
2
2
(1 ) 1 2
z i i z a b
nêntậpđiểm
M
làĐườngtròntâmI(0;-1),bánkính
2
R
.
Câu19.
lờigiải:
Tacó
2 2
2 2
4 1 4 1 16
z i x y x y
Câu20. Giảsửsốphứcthỏamãnbàitoáncódạng
z x yi
,x y
.
Suyra
2 2 2 ( 1)z i x yi i x y i
.
Dođó:
2 2
2 4 2 ( 1) 4 ( 2) ( 1) 16
z i x y i x y
.
Vậytậphợptấtcảcácđiểmbiểudiễnsốphức
z
làđườngtròntâm
2; 1
I
,bánkính
4R
.
Câu21. Gọi
z a bi
,với
,x y
,tacó:
1 2
z i
1 2 1 1 2
x yi i x y i
2 2
1 1 4
x y
.
Vậytậphợpcácđiểmbiểudiễnsốphức
z
làđườngtròntâm
1; 1
I
,bánkính
2R
.
Câu22. Gọi
, ,z x yi x y
.Tacó:
1 5 2 1 5 2
i z i i x yi i
5 1 2
x y x y i
2 2
5 1 4
x y x y
2 2
2 2 8 12 22 0
x y x y
2 2
4 6 11 0
x y x y
.
Vậytậphợptấtcảcácđiểmbiểudiễncácsốphức
z
làđườngtròntâm
2; 3
I
và
2
R
.
Câu23. Đặt
, ,z a bi a b
.Gọi
làđiểmbiểudiễnchosốphức
z
.
Có
2 2
w
2 2
z a bi
z i a b i
2
2
2 2
2
a bi a b i
a b
2
2
2 2 2 2
2
a a b b a b ab i
a b
w
làsốthuầnảo
2
2
2 2 0 1
2 0
a a b b
a b
Có
2 2
1 2 2 0
a b a b
.
Suyra
M
thuộcđườngtròntâm
1;1
I
,bánkính
2
R
.
Câu24. Đặt
,z x yi x y
.Tacóđiểmbiểudiễn
z
là
;M x y
.
Với
0
m
,tacó
0
z
,thoảmãnyêucầubàitoán.
Với
0
m
,tacó:
+
z m
M
thuộcđườngtròn
1
C
tâm
0;0 ,
I
bánkính
R m
+
2 2
2 4
4 3 4 3
z m mi m x m y m m
M
thuộcđườngtròn
2
C
tâm
4 ; 3 ,I m m
bánkính
2
R m
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 15
+)Códuynhấtmộtsốphức
z
thoảmãnyêucầubàitoánkhivàchỉkhi
1
C
và
2
C
tiếpxúcnhau
2
2
5
4
.
5
6
0
m m m
II R R
m
m m m
II R R
m
m
Kếthợpvới
0
m
,suyra
0;4;6
m
.Vậytổngtấtcảcácgiátrịcủa
m
là
10
.
Câu25. Gọi
w x yi
,
x
,
y
.Sốphức
w
đượcbiểudiễnbởiđiểm
;M x y
.
Từ
1w z
suyra
1x yi z
1
z x yi
1
z x yi
.
Mà
2 3
z i
nêntacó:
1 2 3
x yi i
1 1 3
x y i
2 2
1 1 3
x y
2 2
2
1 1 3
x y
.
Vậytậphợpđiểmbiểudiễnsốphức
w
làđườngtròntâm
1; 1
I
bánkính
3
R
.
Câu26. ChọnB
Tacó
2 2
w i i z w i i z
.Suyra
2 2 . 10
w i i z i z
.
Vậytậphợpđiểmbiểudiễncủasốphức
w
trênmặtphẳngtọađộnằmtrênđườngtròncóbán
kính
10
r
.
Câu27. ChọnD
Gọi
,z x yi x y
.
Khiđó:
2 3
w z i z
( 2) ( 3)
x y i x yi
( 3) ( 2) ( 3)( 2)x x y y xy x y i
Do
w
làsốthuầnảo
( 3) ( 2) 0
x x y y
2 2
3 2 0
x y x y
2
2
3 13
1
2 4
x y
.
Vậytậphợpcácđiểmbiểudiễnsốphức
z
làđườngtròntâm
3
; 1
2
I
,bánkính
13
2
R
.
Câu28. Gọi
,w x yi x y
Theođềbàitacó:
1 8 1 8 1 8 1 1 8
w i z i w i i z w i i z i
1 8 1 8 1 1 1 8 1 8 1
w i i i z x y i i z
2 2 2
2 2
2
1 1 8 1 8 .2 1 1 8 36
x y x y
Vậytậphợpcácđiểmbiểudiễnsốphức
1 8
w i z i
làmộtđườngtròncóbánkính
6.
r
Câu29. +)Đặt
z x yi
Khiđó
2 2
| z 5 3i | 5 | x 5 (y 3)i | 5 ( 5) ( 3) 25
x y
( )C
GọiA,Blầnlượtlà2điểmbiểudiễnsốphức
1 2
,z z
A,Bthuộcđườngtròn
( )C
cótâmI(5;3),bánkínhR=5và
1 2
| | 8 8
z z AB
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ngu
yễn Bảo Vương:https://www.facebook.com/phong.baovuong 16
+)GọiHlàđiểmbiểudiễnsốphức
1
2
w =
2
z z
HlàtrungđiểmAB
4
2
A
B
AH
XéttamgiácAIHvuôngtạiHcóAH=4,AI=5nên
2
2 2 2
5
4 3
I
H IA AH
Hthuộcđườngtròn
(
)C
cótâmI(5;3),bánkính
3
R
(*)
+)GọiMlàđiểmbiểudiễnsốphức
1
2
w=
z z
2
OM OH
 
MlàảnhcủaHquaphépvịtựtâmO,tỉsốk=2vớiOlàgốctọađộ(**)
Từ(*)và(**)
tậphợpMlàđườngtròn
(
)C
làảnhcủa
(
)C
phépvịtựtâmO,tỉsốk=2
+)Giảsửđườngtròn
( )C
cótâmJ(a;b)vàbánkính
R
2.5
10
2.3 6
2.R 6
a
b
R
Phươngtrìnhđườngtròn
(
)C
là
2
2
( 10) ( 6) 36
x y
Câu30. Gọisốphức
,z x iy x y
Tacó:
2 4 2 1 4
z i x y i
2
2
2 1 16
x y
Vậytậphợptấtcảcácđiểmbiểudiễncácsốphức
z
thỏamãn:
2 4
z i
làđườngtròncótâm
2
; 1
I
vàcóbánkính
4R
.
Câu31. Tacó:
1 2w i z i
2 1
w i i z
2 1
w i i z
2 2 2
w i .
Dođó,tậphợpđiểmbiểudiễnsốphức
w
làđườngtròntâm
0
;2
I
vàbánkính
2
2
.
Câu32. Gọisốphức
z
a bi
,
,a
b
1 1 2
a bi i a bi
2
2 2
2
1 1 2 1 2
a b a b
2
2 2 2
2
1 1 4 4 1 4 4a a b a a b b
2
2
4
1
2
0
3 3
a
b a b
Tậphợpcácđiểmbiểudiễnsốphức
z
làmộtđườngtròncótâm
2
1
;
3
I
,
Bánkính
2
2
1
1
3 3
R
10
3
.
Câu33. Cách1:Đặt
z
a bi
tacó
2
6
z
i
2
2 6
a
bi i
2
2
4 2 1 6
a b
.
2
2
4
4 4 35 0
a
b b
2 2
35
0
4
a b b
2
2
1
9
2
a b
.
Vậytậphợptấtcảcácđiểmbiểudiễnsốphức
z
làđườngtròntâm
1
0;
2
I
bánkính
3
R
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ngu
yễn Bảo Vương:https://www.facebook.com/phong.baovuong 17
Cách2:
2
6
z
i
1
0 3
2
z i
.Gọi
I
làđiểmbiểudiễnsốphức
1
0
2
i
,
M
làđiểmbiểu
diễnsốphức
z
.Tacó
3
MI
.Vậytậphợptấtcảcácđiểmbiểudiễnsốphức
z
làđườngtròntâm
1
0
;
2
I
bánkính
3
R
.
Câu34. Tacó:
2
3 5 2 1 3 6 4w i z i w i z i i
6
4 2 1 3w i i z i
6 4 2 1 3 2 5
w i i z i
Gọi
;M
x y
làđiểmbiểudiễnsốphức
;w
x yi x y
6
4 2 5 6 4 2 5
w
i x y i
2
2
2
6 4 2 5
x y
Vậytậphợpđiểmbiểudiễnsố
w
làđườngtròntâm
6
;4
I
,bánkính
2 5
R .
Câu35. Tacó
3
2 2
w
i i z
3
2
2
w i
z
i
.Đặt
w x yi
,x
y
.
Khiđó
3
2
2
x yi i
z
i
.
Tacó
2
z
3
2
2
2
x yi i
i
3 2
2
2
x y i
i
3 2
2
2
x y i
i
3
2 2 2
x
y i i
3
2 2 5
x
y i
2
2
2
3
2 2 5
x
y
.
Vậytậphợpcácđiểmbiểudiễnsốphức
3
2 2
w
i i z
làmộtđườngtròncóbánkính
2 5
R .
Câu36.
Gọi
A
,
B
,
M
là các điểm biểu diễn của
1
z
,
2
z
,
w
. Khi đó
A
,
B
thuộc đường tròn
2
2
:
5 3 25
C
x y
và
1
2
8
A
B z z
.
C
cótâm
5
;3
I
vàbánkính
5
R
,gọi
T
làtrungđiểmcủa
A
B
khiđó
T
làtrungđiểmcủa
O
M
và
2
2
3
I
T IA TA
.
Gọi
J
làđiểmđốixứngcủa
O
qua
I
suyra
10;6
J
và
IT
làđườngtrungbìnhcủatamgiác
OJM
,dođó
2
6
JM
IT
.
Vậy
M
thuộcđườngtròntâm
J
bánkínhbằng
6
vàcóphươngtrình
2
2
10
6 36
x
y
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 18
Câu37. Gọisốphức
,w x yi
với
,
x y R
,biểudiễnbởi
( ; )M x y
(12 5 ) 4w i z i
(12 5 ) 4x yi i z i
( 4)
12 5
x y i
z
i
( 4)
12 5
x y i
z
i
Tacó:
3 4 3
z i
( 4)
3 4 3
12 5
x y i
i
i
63 ( 12)
3
12 5
x y i
i
2 2
2 2
( 63) ( 12)
3
12 5
x y
2 2 2
( 63) ( 12) 39
x y
Vậy
39
r
.
Câu38. Gọi
w x yi
.
1 3 1 2w i z i
1 3 1 2 x yi i z i
1 2
1 3
x y i
z
i
1 3
1 2
4 4
z x y i i
1 3 2 2 1 3
4 4
x y y x
i
3
z
13 3 2 2 1 3
4 4
x y y x
i
3 1
z
2 2
13 3 2 2 1 3
1
4 4
x y y x
2 2 2 2
13 2 3 13 2 3 2 2 2 2 1 3 3 1 16
x x y y y y x x
2 2
8 4 6 3 12 3 43 0
x y x y
Bánkính
2
2
4 2 3 3 12 3 43 2
r .
Câu39. ChọnB
Đặt
, ,z x yi x y
.Khiđó.
1 3 4 1 3 4
z m i x yi m i
.
2
2
1 3 4 1 3 4
x m y i x m y .
2
2
1 3 16
x m y .
Dođótậphợpcácđiểm
M
biểudiễncủasốphức
z
làđườngtròntâm
1 ; 3
I m
vàbánkính
4R
.Đểđườngtrònnàytiếpxúcvớitrục
Oy
thì
1 4 3
1 4
1 4 5
m m
m
m m
.
Vậy
5; 3
m m
.
Câu40. ChọnD
1
1
w i
w i z i z
i
;đặt
; ,w x yi x y
.
1
x yi i
z
i
.Tacó
1
2 2 2 2 2 2
1 2
x yi i i
x yi i
z
i

.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ngu
yễn Bảo Vương:https://www.facebook.com/phong.baovuong 19
2
2
2 2 2 2
2 2 2 2
1
2
2 1 4 4 3 1 4
2
3
1 16 9 2 6 6 1 2 2 2 16
2
2 8 4 6 0 4 2 3 0
x yi i i
x xi yi y i x y x y i
x y x y x y xy y x x y xy y x
x y x y x y x y
.
Đườngtròncóbánkínhlà
2 2
2 1 3 2 2
R
.
Câu41. ChọnA
Giảsử
z
a bi
;a
b
và
w x yi
;x
y
.
2 2 25 2 1 2 1 25
z i z i a b i a b i
2
2
2
1 25
a
b
1
Theogiảthiết:
2 2 3 2 2 3 2 2 3 2w z i x yi a bi i x yi a b i
.
2
2 2
2
3 2 3
2
x
a
x a
y b y
b
2
.
Thay
2
vào
1
tađược:
2
2
2 2
2 3
2 1 25 2 5 100
2
2
x y
x y
.
Suyra,tậphợpđiểmbiểudiễncủasốphức
w
làđườngtròntâm
2
;5
I
vàbánkính
10
R
.
Vậy
1
7
a
b c
.
Dạng2.Tậphợpđiểmbiểudiễnlàđườngthẳng
Câu42. Giảsửsốphức
z
códạng:
z
x yi x,y
Tacó:
1 2 1 2 1 1 2
z i z x yi i x yi x y i x yi
2
2 2
2
1
1 2
x
y x y
2
2 2
2
1 1 2
x y x y
2
2 2 2
2 1 2 1 4 4
x x y y x x y
6 2 2 0 3 1 0
x y x y
Vậytậphợpđiểmbiểudiễnsốphức
z
làđườngthẳng
3 1 0
x y
.
Câu43.
2
2 2
2
2 3 2 1 3 4 4 4 0 1z i z i x y x y x y y x
.
Câu44. Đặt
,
z x yi x y z x yi
và
;M
x y
làđiểmbiểudiễncủasốphức
z
.
Tacó:
1 2 1 2 1 2 1 2z i z i x yi i x yi i
1
2 1 2
x
y i x y i
2 2 2 2
1
2 1 2
x
y x y
2
2 2 2
2 1 4 4 2 1 4 4 4 8 0 2 0
x x y y x x y y x y x y
.
Vậytậphợpcácđiểmbiểubiễncácsốphức
z
thỏamãnyêucầubàitoánlàđườngthẳngcóphương
trìnhlà
2 0
x y
.
Câu45. Giảsử
z
a bi
,
a
b R
.
Khiđó
2 4 1 2 4 1 . 2 1 4 1z z i i a bi a bi i i a bi a b i i
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ngu
yễn Bảo Vương:https://www.facebook.com/phong.baovuong 20
2
1 1 2 4 1a a b b a b b a i i
2
1 1 2 4a a b b a b i
.
+
2 4 1z z i i
làsốthựcsuyra
2 4 0.
a b
+ Sốphức
z
cóđiểmbiểudiễn
;
: 2 4 0
M
a b M d x y
.
+ Đườngthẳng
d
cắttrục
Ox
,
Oy
lầnlượttại
4
;0
A
và
1
0
;2 . . 4
2
OAB
B
S OAOB
.
Câu46. Gọisốphức
z
a bi
,với
,a
b
thuộc
.Khiđo,
(
a;b)
M
lađiêmbiểudiễnsốphức
z
.
Tacó:
2
z
z i
2
(b 1)a bi a i
2 2 2 2
(a 2) (b 1)
b a
2
2 2 2
(a 2) (b 1)
b a
4 2 3 0
a b
điêm
(a;b)
M
thuôcđươngthăng
4 2 3 0
x y
Vây,tâphơpcacđiêm
M
thoamanbairalađươngthăng
4
2 3 0
x
y
.
Câu47. Gọi
z x yi
;(
x
,
y
).
Tacó:
1
2 3z z i
2
2 2
2
1 2 3
x y x y
3 6 0
x y
.
Vậytậphợpcácđiểmbiểudiễnsốphức
z
làđườngthẳngcóphươngtrình
3
6 0
x
y
.
Câu48. Đặt
,
2
z
x yi x y
z i
,tacó:
12
5 17 7
13
2
i z i
z i
12 5 17 7 13 2
i z i z i
12 5 1 13 2i z i z i
1
2 5 1 13 2i z i z i
1
3 1 13 2z i z i
1
2
z
i z i
1
2x yi i x yi i
2
2 2 2
1 1 2 1
x y x y
6
4 3 0
x
y
.(thỏađiềukiện
2z i
)
Vậytậphợpđiểmbiểudiễnsốphức
z
làđườngthẳng
6 4 3 0
x y
.
Câu49. Gọisốphức .
Tacó:
.
Vậytậphợpđiểmbiểudiễnsốphức thỏamãnđiềukiệnbàitoánlàđườngthẳng .
Câu50. Tacó
2
1 0
z
i z i
2 2
2 1 0
x yi i i x y
2 2 2 2
2 1 0x x y y x y i
2
2
2 2
2 0
1 0
x x y
y x y
2
2 2 2
2
1 0
x
x y y x y
1 0
x y
.
Dođó
M
thuộcđườngthẳng
1
0
x
y
.
Câu51. ChọnD
Gọi
,M x y
làđiểmbiểudiễnsốphức
,
z x yi x y R
Tacó:
2
2
2
2 2 2 2 2 2
2 16 2 2 2 2 16
z z z x xyi y x xyi y x y
2
4 16 2
x x
1
2
, 4
d d d
z
a bi
,a
b
z
i iz
a
bi i i a bi
1
a
b i b ai
2
2
2 2
1
a
b b a
2
1 0
b
z
1
2
y
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 21
Ở đây lưu ý hai đường thẳng x = 2 và x = -2 song song với nhau.
Câu52. ChọnB
Đặt
,z x yi x y
và
;M x y
làđiểmbiểudiễncủaz.
Tacó
2 2
3 4 3 4 3 4
z x y
z i x iy i x y i
.
2 2
3 4 3 4
z i x y
.
Vậy
2 2
2 2
3 4 3 4 6 8 25 0
z z i x y x y x y
.
Câu53. ChọnD
Gọi
;M x y
làđiểmbiểudiễnsốphức
z x yi
.
Tacó.
2 2 3 2 1 2
2 2 3 1 2 2 2
z i i z
x y i x y i
.
2 2 2 2
2 2 2 2
2 2 3 1 2 2 2
4 4 6 13 4 4 4 8 5
20 16 47 0
x y x y
x y x y x y x y
x y
.
Vậytậphợpđiểm
;M x y
làđườngthẳng
20 16 47 0
x y
.
Dạng3.Tậphợpđiểmbiểudiễnlàđườngconic
Câu54. ChọnD
Đặt
,z x yi x y
z x yi
.
Khiđó
2 2z i z z i
2 1 2 2x y i y i
2 2
2
4 1 2 2
x y y
2 2 2
4 4 8 4 4 8 4
x y y y y
2
4
x
y
làmộtParabol.
Câu55. Gọi
;M x y
làđiểmbiểudiễnsốphức
z x yi
.
Xéthaiđiểm
1
2;0
F
,
2
F
,khiđótheogiảthiết:
2 2
2 2
1 2
2 2 4 2 2 4 4
z z x y x y MF MF
.
Mà
1 2
F F
,nên
1 2 1 2
MF MF F F
.
Dođótậphợpcácđiểmbiểudiễncủa
z
chínhlàđoạnthẳng
1 2
F F
.
Câu56. Giảsử
z a bi
,
a b R
.
Khiđó
2
1 1 1 2
1 1
1
1 2 1 4
1
a b i ai
a b i
z i
ai a
z z i
2
1 2 1 2 1 1
1 4
a a b a a b i
a
.
1
1
z i
z z i
làsốthựcsuyra
2
2
1
2 1 1 0 2 2 1 4. 2.
2 2 2 2
b a a
a a b b a a
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 22
Sốphức
2
z
cóđiểmbiểudiễn
;
2 2
a b
M
quỹtích
M
làparabolcóphươngtrình
2
1
4 2
2
y x x
Tậphợpcácđiểmbiểudiễncủasốphức
2
z
làparabolcótoạđộđỉnh
1 3
;
4 4
I
.
Câu57. Gọi
;M x y
làđiểmbiểudiễncủasốphức
, .
z x yi x y
Tacó:
2 4 10
z i z i
2 1 4 1 10.
x y i x y i
2 2 2 2
2 1 4 1 10
x y x y
(*)
Đặt
2
2
2;1 , 4;1 4 2 0 6.
A B AB
Khiđóphươngtrình(*)trởthành:
10.
MA MB
Khiđótậphợpnhữngđiểm
M
thỏamãnphươngtrình(*)làmộtelipvới.
+Độdàitrụclớn
10
2 10 5.
2
a a
+Tiêucự
6
2 6 3.
2
c AB c
+Độdàitrụcbé
2b
với
2 2 2 2 2
5 3 16 4.
b a c b
Vậydiệntíchhìnhphẳnggiớihạnbởicácđiểmbiểudiễncácsốphứcthỏamãn
2 4 10
z i z i
làdiệntíchEliptrên:
4.5 20
S ab
.
Câu58. Gọi
z x yi
z x yi
,
,x y
.
2 2z i z z i
2 1 2 2x y i y i
2 2
2 2
2 1 0 2 2
x y y
2 2 2
4 2 1 4 8 4
x y y y y
2
4 16x y
2
1
4
y x
Vậytậphợpcácđiểmbiểudiễncácsốphức
z
thỏamãn
2 2z i z z i
làmộtParabol
P
cóphươngtrình:
2
1
4
y x
.
Câu59. ChọnB
Gọisốphức
z x yi
cóđiểmbiểudiễnlà
,M x y
trênmặtphẳngtọađộ:
Theođềbàitacó:
3 2 3 3( ) 3 2( ) ( ) 3
z i z z i x yi i x yi x yi i
.
2 2 2 2
3 (3 3) (3 3 ) 9 (3 3) (3 3 )x y i x y x y x y
.
2 2 2 2 2 2
2
9 (3 3) (3 3 ) 8 36 0
9
x y x y x y y x
.
Vậytậphợpcácđiểm
,M x y
biểudiễnsốphứcztheoyêucầucủađềbàilàMộtparabol
2
2
9
y x
.
Câu60. ChọnB
Gọi
;M x y
,
1
( 2;0)
F
,
2
(2;0)
F
.
Tacó
2 2 2 2
2 2 8 ( 2) ( 2) 8
z z x y x y
1 2
8
MF MF
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ngu
yễn Bảo Vương:https://www.facebook.com/phong.baovuong 23
Dođóđiểm
;M x y
nằmtrênelip
E
có
2
8 4,
a
a
tacó
1 2
2 4 2 2
F F c c c
.
Tacó
2
2 2
1
6 4 12
b
a c
.VậytậphợpcácđiểmMlàelip
2
2
: 1
16 12
x
y
E
.
Câu61. ChọnB
Đặt
z x yi z x yi
điểmbiểudiễncủa
z
là
;M x y
.Tacó:
2
2
2
2
2 2 2
1
2
1 2 1 2 1 2 1
4
z
i z z i x yi i x yi x yi i
x
y i y i x y y y x
.
Vậytậphợpcácđiểmbiểudiễnsốphức
z
làmộtđườngParabol.
Câu62. ChọnD
Tacó:Gọi
;M
x y
làđiểmbiểudiễncủasốphức
.z x yi
.
Gọi
4
; 0
A
làđiểmbiểudiễncủasốphức
4
.z
.
Gọi
4
; 0
B
làđiểmbiểudiễncủasốphức
.
Khiđó:
4
4 10 10.
z
z MA MB
(*).
Hệthứctrênchứngtỏtậphợpcácđiểm
M
làelipnhận
,A
B
làcáctiêuđiểm.
Gọiphươngtrìnhcủaeliplà
2 2
2
2 2
2
2
1
, 0,
x y
a
b a b c
a b
.
Từ(*)tacó:
2
10 5.a a
.
2
2 2
2
8 2 4 9AB c c c b a c
.
Vậyquỹtíchcácđiểm
M
làelip:
2 2
:
1.
25 9
x y
E
Câu63. ChọnB
Gọi
;M x y
biểudiễnsốphức
,
z x yi x y R
.
Từgiảthiếttacó
2
2
2 2
1 2
4
4 10 10
x
y x y MF MF
với
1 2
4
;0 , 4;0
F
F
.
Vậytậphợpcácđiểm
M
biểudiễnchosốphức
z
làđườngElipcóphươngtrình
2
2
1
25 9
x
y
.
Dạng4.Tậphợpđiểmbiểudiễnlàmộtmiền
Câu64. Dễthấyđiểm
4
;4
I
làtâmcủahaiđườngtròn.
Đườngtrònnhỏcóphươngtrìnhlà:
2
2
4
4 4
x
y
.
Đườngtròntocóphươngtrìnhlà:
2
2
4
4 16
x
y
.
Vậytậphợpđiểmbiểudiễnsốphứcthỏamãnđềbàilà
2
4 4 4
z
i
.
Câu65.
Cách1:
Đặt
z
x yi
với
, yx
.
Theobàira:
2
3 2
z
i
2
3 2
x
yi i
2
( 3) 2
x
y i
2 2
2 3 2
x y
2
2
2
3 4
x
y
.
Vậytậphợpcácđiểmbiểudiễnsốphức
z
trongmặtphẳngtọađộ
Oxy
làhìnhtròntâm
2
; 3
I
,bánkính
2R
.
Câu66. Gọi
;M
x y
làđiểmbiểudiễnchosốphức
;
;
z
x yi x y
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 24
4 4 2
z i
.
4 4 2x yi i
4 4 2
x y i
2 2
4 4 2
x y
2 2
4 4 4
x y
.
Vậytậphợpđiểmbiểudiễnchosốphức
z
thỏa
4 4 2
z i
làhìnhtròntâm
I
,bánkính
2R
.
Câu67. Gọi
;M a b
làđiểmbiểudiễncủasốphức
z
;
1;3
A
làđiểmbiểudiễnsốphức
1 3i
.
Khiđó,
2 2
3 1 1 3
AM z i a b
2 2
2
3 1 3 25
a b
,tậphợpcácđiểmbiểudiễncủa
z
làhìnhvànhkhăngiớihạnbởi
haiđườngtròn
;3A
và
;5A
,kểcảcácđiểmnằmtrênhaiđườngtrònnày.
25 9 16
S dvdt
.
Câu68. Vìsốphức
z
cóđiểmbiểudiếnnằmtrongcungphầntưthứ
I
nêngọi
, 0, 0
z a bi a b
.
2 2 2 2 2 2
1 1 1 b ai b a
w i
iz i a bi b ai a b a b a b
Do
2 2 2 2
0, 0 0, 0
b a
a b
a b a b
.
Vậyđiểmbiểudiễn
w
nằmtrongcungphầntưthứ
III
.
Câu69.
Gọi
, ,z x yi x y R
khiđóđiểmbiểudiễncủa
z
là
; .M x y
16 16 16 16
z x yi x y
i
theogiảthiết
0 1
0 16
16
0 16
0 1
16
x
x
y y
(I)
2 2 2 2 2 2
16
16 16 16 16
x yi
x y
i
x yi
z
x y x y x y
20
18
16
14
12
10
8
6
4
2
2
4
6
8
10
5 5 10 15
I
B
A
O
E
C
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 25
Theogiảthiết
2 2
2 2
2 2
2 2
16
0 1
0 16
16
0 16
0 1
x
x x y
x y
y
y x y
x y
2 2
2 2
0, 0
16 0
16 0
x y
x y x
x y y
2
2
2
2
0, 0
8 64
8 64
x y
x y
x y
(II)
Gọi
1
S
làdiệntíchhìnhvuôngOABCcócạnhbằng16,
2
1
16 256S
.
2
S
làdiệntíchhìnhtròncóbánkínhbằng8.
3
S
làdiệntíchphầngiaocủahainửađườngtrònnhưhìnhvẽ.
2 2
1 2 3
1 1
256 64 2 8 8
4 2
S S S S
Vậy
256 64 32 64 32 6S
.
Câu70. Gọi
z a bi
;a b
.
Tacó
3 3 1 5z i 3 3 1 5a bi i
2 2
9 3 1 25a b
.
Dođótậphợpcácđiểmbiểudiễncủa
z
làhìnhvànhkhăngiớihạnbởihaiđườngtròncótâm
3; 1I
bánkínhlầnlượtlà3và5.
Vìvậy
2 2
5 3S
16
.
Câu71. ChọnC
.
Đặt
z x yi z x yi
khiđótacó:
1 1 1 1z x yi
.
2
2
1 1 1 1 1x yi x y
.
2z z x yi x yi yi cóphầnảokhôngâmsuyra
0 2y
.
x
y
O
-1
-1
1
2
2
1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ngu
yễn Bảo Vương:https://www.facebook.com/phong.baovuong 26
Từ(1)và(2)tasuyraphầnmặtphẳngbiểudiễnsốphức
z
lànửahìnhtròntâm
1;0
I
bánkính
1r
,diệntíchcủanóbằng
2
1
2
2
r
(đvdt).
Câu72. ChọnB
Gọi
,
,z x yi x y
.
Tacó
2
2
2 2 2 2
2 3 9 3 9 9 1
9 1
x
y
x yi x yi x y x y
.
Suyratậphợpđiểmbiểudiễnsốphức
z
làmiềntrongcủaElip
2
2
1
9 1
x
y
.
Tacó
3, 1a b
,nêndiệntíchhình
H
cầntìmbằng
1
4
diệntíchElip.
Vậy
1
3
.
. .
4 4
S
a b
.
Câu73. ChọnA
Gọi
; ;w x yi x y
.
Tacó
1
1 1
1
w
w i z z
i
.
Dođó
2 1
1 2
1 1 1 1 1 1
1
1 1
x y i
w w i
z
i i i
.
2
2
2 1
1
2 1 2
1
x
y i
x y
i
.
Vậydiệntíchhìnhtrònđólà
2
S
.
Câu74. ChọnB
Tacó:
5 1 5 1 1
2 3 1 ; tan .
4 4 4 4 5
i z i i z z i w i M
Lúcđó:
2
2
2
2 tan 5 1 tan 12
sin 2 0; cos 2 0
13 13
1 tan 1 tan
.
Câu75. ChọnC
1
2 1
2
w i
w z i z
1
3
4 2 3 4 2 1 6 8 4 7 9 4 1
2
w
i
z i i w i i w i
Giảsử
,w
x yi x y
,khiđó
2
2
1 7 9 16
x y
Suyratậphợpđiểmbiểudiễnsốphức
w
làhìnhtròntâm
7
; 9
I
,bánkính
4.
r
Vậydiệntíchcầntìmlà
2
.4 16 .
S
Câu76. ChọnB
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
N
guyễn Bảo Vương:https://www.facebook.com/phong.baovuong 27
.
Gọi z x yi .
(với
,x y
)
2
2
3
3 1 5 9 1 3 25z i x y
.
Vậytậphợpcácđiểmbiểudiễnsốphức
z
trênmặtphẳngphứclàhìnhvànhkhăngiớihạnbởi
haiđườngtrònbánkính
5R
và
3.r
Diệntích
2 2
16S R r
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ngu
yễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CHUYÊN
ĐỀ 27
MỤC LỤC
PHẦN
A. CÂU HỎI ......................................................................................................................................................... 1
Phương trình bậc 2 với hệ số thực .................................................................................................................................... 1
Bài toán MIN-MAX ......................................................................................................................................................... 4
PHẦN B. LỜI GIẢI THAM KHẢO ................................................................................................................................ 8
Phương trình bậc 2 với hệ số thực .................................................................................................................................... 8
Bài toán MIN-MAX ....................................................................................................................................................... 14
PHẦN A. CÂU HỎI
Phương trình bậc 2 với hệ số thực
Câu 1. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Kí hiệu
1 2 3
,
,z z z
và
4
z
là bốn nghiệm phức của phương
trình
4
2
1
2 0
z
z
. Tính tổng
1
2 3 4
T
z z z z
A.
2 2 3
T
B.
4T
C.
2 3
T
D.
4 2 3
T
Câu 2. (ĐỀ THAM KHẢO BGD & ĐT 2018) Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình
2
4 4 3 0
z z
. Giá trị của biểu thức
1 2
z z
bằng:
A.
3
2
B.
2
3
C.
3
D.
3
Câu 3. (MĐ 104 BGD&DT NĂM 2017) Kí hiệu
1
z
,
2
z
là hai nghiệm của phương trình
2
4
0
z
. Gọi
M
,
N
lần lượt là điểm biểu diễn của
1
z
,
2
z
trên mặt phẳng tọa độ. Tính
T
OM ON
với
O
là gốc tọa độ.
A.
8
T
B.
4
C.
2
T
D.
2T
Câu 4. (Mã đề 101 - BGD - 2019) Gọi
1
2
,z z
là hai nghiệm phức của phương trình
2
6
10 0
z
z
. Giá trị
của
2
2
1 2
z z
bằng:
A.
16.
B.
5
6
. C.
2
0.
D.
26
.
Câu 5. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Phương trình nào dưới đây nhận hai số phức
1 2i
và
1 2i
là nghiệm.
A.
2
2
3 0z z
B.
2
2
3 0z z
C.
2
2
3 0z z
D.
2
2
3 0z z
Câu 6. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Kí hiệu
1
2
,z
z
là hai nghiệm phức của phương trình
2
3
1 0
z
z
. Tính
1 2
P z z
.
A.
2
3
P
B.
3
3
P
C.
2
3
3
P
D.
14
3
P
PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC, BÀI TOÁN MIN-MAX
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
Câu 7. (Mã 102 - BGD - 2019) Kí hiệu
1 2
,z z
là hai nghiệm phức của phương trình
2
6z 14 0
z
. Giá trị
của
2 2
1 2
z z
bằng
A.
36
. B.
8
. C.
28
. D.
18
.
Câu 8. (Mã đề 104 - BGD - 2019) Gọi
1 2
,z z
là hai nghiệm phức của phương trình
2
4 7 0.
z z
Giá trị
của
2 2
1 2
z z
bằng
Hàm số đã cho đạt cực tiểu tại
A. 2. B. 8. C. 16. D. 10.
Câu 9. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Kí hiệu
1 2
;z z
là hai nghiệm của phương trình
2
1 0
z z
. Tính
2 2
1 2 1 2
P z z z z
.
A.
2P
B.
1P
C.
0
P
D.
1P
Câu 10. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Kí hiệu
1
z
và
2
z
là hai nghiệm phức của phương
trình
2
3 5 0
z z
. Giá trị của
1 2
z z
bằng:
A.
10
B.
2 5
. C.
5
. D.
3
.
Câu 11. (MĐ 105 BGD&ĐT NĂM 2017) Kí hiệu
1 2
,z z
là hai nghiệm phức của phương trình
2
6 0z z
. Tính
1 2
1 1
P
z z
.
A.
1
6
B.
1
6
C.
6
D.
1
12
Câu 12. (Mã 103 - BGD - 2019) Gọi
1 2
,z z
là 2 nghiệm phức của phương trình
2
4z 5 0
z
. Giá trị của
2 2
1 2
z z
bằng
A. 16. B. 26. C. 6. D. 8.
Câu 13. (CHUYEN PHAN BỘI CHÂU NGHỆ AN NĂM 2018-2019 LẦN 02) Gọi
1
z
;
2
z
là hai nghiệm của
phương trình
2
2 10 0
z z
. Tính giá trị biểu thức
2 2
1 2
A z z
.
A.
10 3
. B.
5 2
. C.
2 10
. D.
20
.
Câu 14. (THPT CHUYÊN SƠN LA NĂM 2018-2019 LẦN 01) Ký hiệu
1
z
,
2
z
là nghiệm của phương trình
2
2 10 0
z z
. Giá trị của
1 2
.z z
bằng
A.
5
. B.
5
2
. C.
10
. D.
20
.
Câu 15. (ĐỀ THI THỬ VTED 02 NĂM HỌC 2018 - 2019) Kí hiệu
1
z
,
2
z
là hai nghiệm phức của phương
trình
2
3
z
. Giá trị của
1 2
z z
bằng
A.
6
. B.
2 3
. C.
3
. D.
3
.
Câu 16. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Gọi
1
z
,
2
z
là các nghiệm phức của
phương trình
2
8 25 0
z z
. Giá trị
1 2
z z
bằng
A.
5
. B.
3
. C.
8
. D.
6
.
Câu 17. (HỌC MÃI NĂM 2018-2019-LẦN 02) Biết
z
là số phức có phần ảo âm và là nghiệm của phương
trình
2
6 10 0
z z
. Tính tổng phần thực và phẩn ảo của số phức
w
z
z
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
A.
7
5
. B.
1
5
. C.
2
5
. D.
4
5
.
Câu 18. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Gọi
1
z
,
2
z
là hai nghiệm phức
của phương trình
2
4 5 0
z z
. Tính
2 2
1 2 2 1
1 2
1 1
w i z z z z
z z
.
A.
4
20
5
w i
. B.
4
20
5
w i
. C.
4 20w i
. D.
4
20
5
w i
.
Câu 19. (ĐÊ 04 VTED NĂM 2018-2019) Với các số thực
,a b
biết phương trình
2
8 64 0
z az b
có nghiệm
phức
0
8 16z i
. Tính môđun của số phức
w
a bi
A.
w 19
B.
w 3
C.
w 7
D.
w 29
Câu 20. (THPT YÊN KHÁNH - NINH BÌNH - 2018 - 2019) Phương trình
2
. 0
z a z b
, với
,a b
là các
số thực nhận số phức
1 i
là một nghiệm.
Tính
?a b
.
A.
2
. B.
4
. C.
4
. D.
0
.
Câu 21. (KTNL GV THPT LÝ THÁI TỔ NĂM 2018-2019) Tính modun của số phức
w b ci
,
,b c
biết số phức
8
7
1 2
1
i i
i
là nghiệm của phương trình
2
0
z bz c
.
A.
2
. B.
3
. C.
2 2
. D.
3 2
.
Câu 22. (THPT CHUYÊN ĐẠI HỌC VINH NĂM 2018-2019 LẦN 01) Gọi
1 2
,z z
là các nghiệm phức của
phương trình
2
4 7 0z z
. Số phức
1 2 2 1
. .z z z z
bằng
A.
2
B.
10
C.
2i
D.
10i
Câu 23. (ĐỀ THI THỬ VTED 03 NĂM HỌC 2018 - 2019) Gọi
1 2
;z z
là hai nghiệm phức của phương trình
2
3 2 27 0
z z
. Giá trị của
1 2 1
2
z z z z
bằng:
A.
2
B.
6
C.
3 6
D.
6
Câu 24. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Gọi
1
z
và
2
z
là hai nghiệm
phức của phương trình
2
4 29 0
z z
.Tính giá trị của biểu thức
4 4
1 2
z z
.
A.
841
. B.
1682
. C.
1282
. D.
58
.
Câu 25. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Kí hiệu
1
;z
2
z
là hai nghiệm phức
của phương trình
2
3 1 0
z z
. Tính
1 2
P z z
.
A.
14
3
P
. B.
2
3
P
. C.
3
3
P
. D.
2 3
3
P
.
Câu 26. (CHUYÊN NGUYỄN TẤT THÀNH YÊN BÁI LẦN 01 NĂM 2018-2019) Gọi
1
z
,
2
z
là hai nghiệm
phức của phương trình
2
3 2 0
z z
. Tính giá trị biểu thức
2 2
1 2
zT
z
.
A.
2
3
T
. B.
8
3
T
. C.
4
3
T
. D.
11
9
T
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
Câu 27. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Gọi
,A B
là hai điểm trong mặt
phẳng phức theo thứ tự biểu diễn cho các số phức
1 2
, z
z khác
0
thỏa mãn đẳng thức
2 2
1 2 1 2
0,
z z z z
khi
đó tam giác
OAB
(
O
là gốc tọa độ):
A. Là tam giác đều. B. Là tam giác vuông.
C. Là tam giác cân, không đều. D. Là tam giác tù.
Câu 28. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Cho hai số phức và khác ,
thỏa mãn và . Hỏi mệnh đề nào dưới đây đúng?
A. . B. . C. . D. .
Câu 29. (KTNL GV THUẬN THÀNH 2 BẮC NINH NĂM 2018-2019) Cho phương trình
2
0
bz caz
,
với
, , , 0
a b c a
có các nghiệm
1 2
,z z
đều không là số thực. Tính
2 2
1 2 1 2
z
z z
P z
theo
, , .a b c
A.
2
2
2
b
a
P
ac
. B.
2
P
a
c
. C.
4
P
a
c
. D.
2
2
2 4
b
a
P
ac
.
Câu 30. (THPT YÊN PHONG SỐ 1 BẮC NINH NĂM 2018-2019 LẦN 01) Gọi
S
là tổng các số thực
m
để phương trình
2
2 1 0
z z m
có nghiệm phức thỏa mãn
2.
z
Tính
.S
A.
6.
S
B.
10.
S
C.
3.
S
D.
7.
S
Câu 31. (CHUYÊN NGUYỄN TẤT THÀNH YÊN BÁI LẦN 01 NĂM 2018-2019) Cho số phức
z a bi
, a b
thỏa mãn
1 3 0z i z i
. Tính
2 3S a b
.
A.
6
S
. B.
6
S
. C.
5
S
. D.
5
S
.
Câu 32. (TT THANH TƯỜNG NGHỆ AN NĂM 2018-2019 LẦN 02) Gọi
S
là tổng các giá trị thực của
m
để phương trình
2
9 6 1 0
z z m
có nghiệm phức thỏa mãn
1
z
. Tính
S
.
A.
20
. B.
12
. C.
14
. D.
8
.
Bài toán MIN-MAX
Câu 33. (ĐỀ THAM KHẢO BGD & ĐT 2018) Xét số phức
z a bi
,a b
thỏa mãn
4 3 5
z i
. Tính
P a b
khi
1 3 1z i z i
đạt giá trị lớn nhất.
A.
8
P
B.
10
P
C.
4P
D.
6
P
Câu 34. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Xét số phức
z
thỏa mãn
2 4 7 6 2.
z i z i
Gọi
, m M
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của
1 .z i
Tính
.P m M
A.
5 2 2 73
2
P
B.
5 2 73
P
C.
5 2 73
2
P
D.
13 73
P
Câu 35. (KTNL GIA BÌNH NĂM 2018-2019) Cho hai số phức
1 2
,z z
thỏa mãn đồng thời hai điều kiện sau
1 34, 1 2z z mi z m i
(trong đó
m
là số thực) và sao cho
1 2
z z
là lớn nhất. Khi đó giá trị
1 2
z z
bằng
A.
2
B.
10
C.
2
D.
130
z
w
0
3 4 5
z w z w
1
w
2 3
z
2 3
3
z
3
z
3
2
z
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
Câu 36. (THPT CẨM GIÀNG 2 NĂM 2018-2019) Cho số phức
z
thỏa mãn
2 2 1z i
. Số phức
z i
có môđun nhỏ nhất là:
A.
5 2
. B.
5 1
. C.
5 1
. D.
5 2
.
Câu 37. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Gọi
M
và
m
lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của
2
z i
P
z
với
z
là số phức khác
0
và thỏa mãn
2
z
. Tính tỉ số
M
m
.
A.
3
M
m
. B.
4
3
M
m
. C.
5
3
M
m
. D.
2
M
m
.
Câu 38. Cho số phức
z
thoả mãn
2 3 1z i
. Tìm giá trị lớn nhất của
1z i
.
A.
13 3
. B.
13 5
. C.
13 1
. D.
13 6
.
Câu 39. Xét tất cả các số phức
z
thỏa mãn
3 4 1
z i
. Giá trị nhỏ nhất của
2
7 24z i
nằm trong khoảng
nào?
A.
0;1009
. B.
1009;2018
. C.
2018;4036
. D.
4036;

.
Câu 40. (CHUYEN PHAN BỘI CHÂU NGHỆ AN NĂM 2018-2019 LẦN 02) Cho số phức z thỏa mãn
4
z z z z
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
2 2P z i
. Đặt
A M m
. Mệnh đề nào sau đây là đúng?
A.
34;6
A
. B.
6; 42
A
. C.
2 7; 33
A
. D.
4;3 3
A
.
Câu 41. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Cho số phức
z
thỏa mãn
6 6 20
z z
. Gọi
M
,
n
lần lượt là môđun lớn nhất và nhỏ nhất của z. Tính
M n
A.
2
M n
. B.
4
M n
. C.
7M n
. D.
14
M n
.
Câu 42. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Cho số phức
z
thỏa mãn
3 4 2
z i
và
w 2 1z i
. Khi đó
w
có giá trị lớn nhất bằng
A.
4 74
. B.
2 130
. C.
4 130
. D.
16 74
.
Câu 43. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Xét số phức
z
và số phức liên
hợp của nó có điểm biểu diễn là
M
và
M
. Số phức
4 3z i
và số phức liên hợp của nó có điểm biểu diễn
là
N
và
N
. Biết rằng
M
,
M
,
N
,
N
là bốn đỉnh của hình chữ nhật. Tìm giá trị nhỏ nhất của
4 5z i
.
A.
5
34
. B.
2
5
. C.
1
2
. D.
4
13
.
Câu 44. Biết số phức
z
thỏa mãn
3 2iz z i
và
z
có giá trị nhỏ nhất. Phần thực của số phức
z
bằng:
A.
2
5
. B.
1
5
. C.
2
5
. D.
1
5
.
Câu 45. (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Xét các số phức
z
thỏa mãn
1 3 2
z i
. Số phức
z
mà
1z
nhỏ nhất là
A.
1 5z i
. B.
1z i
. C.
1 3z i
. D.
1z i
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
Câu 46. (CHUYÊN PHAN BỘI CHÂU NĂM 2018-2019) Cho số phức
z
thỏa mãn
4.
z z z z
Gọi
,M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
2 2 .P z i
Đặt
.A M m
Mệnh đề nào sau đây
là đúng?
A.
34;6
A . B.
6; 42
A . C.
2 7; 33
A . D.
4;3 3
A
.
Câu 47. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Trong các số phức
z
thỏa mãn
1 1 2z i z i
, số phức
z
có mô đun nhỏ nhất có phần ảo là
A.
3
10
. B.
3
5
. C.
3
5
. D.
3
10
.
Câu 48. Cho hai số phức
1 2
,z z
thỏa mãn
1 2
1 2
1; 2
2 3 1
z i z i
z i z i
. Giá trị nhỏ nhất của
1 2
z z
là
A.
2 2
. B.
2
. C.
1
. D.
2 1
.
Câu 49. (SỞ GD&ĐT BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Gọi
S
là tập hợp các số phức
z
thỏa mãn
1 34
z và
1 2z mi z m i
, (trong đó
m
). Gọi
1
z
,
2
z
là hai số phức thuộc
S
sao cho
1 2
z z
lớn nhất, khi đó giá trị của
1 2
z z
bằng
A.
2
B.
10
C.
2
D.
130
Câu 50. Cho hai số phức
,z w
thỏa mãn
3 2 2
z ,
4 2 2 2
w i . Biết rằng
z w
đạt giá trị nhỏ
nhất khi
0
z z
,
0
w w
. Tính
0 0
3
z w
.
A.
2 2
. B.
4 2
. C. 1. D.
6 2
.
Câu 51. (ĐÊ 04 VTED NĂM 2018-2019) Cho hai số phức
z
và
w
thỏa mãn
2 8 6z w i
và
4.
z w
Giá trị lớn nhất của biểu thức
z w
bằng
A.
4 6.
B.
2 26.
C.
66.
D.
3 6.
Câu 52. Cho số phức
z
thoả mãn
1
z
. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
biểu thức
2
1 1P z z z
. Tính
.M m
A.
13 3
4
. B.
39
4
. C.
3 3
. D.
13
4
.
Câu 53. (THPT YÊN KHÁNH - NINH BÌNH - 2018 - 2019) Cho hai số phức
z
và
a bi
thỏa mãn
5 5 6
z z
;
5 4 20 0
a b
. Giá trị nhỏ nhất của
z
là
A.
3
41
. B.
5
41
. C.
4
41
. D.
3
41
.
Câu 54. (KTNL GV THPT LÝ THÁI TỔ NĂM 2018-2019) Gọi
z a bi
,a b
là số phức thỏa mãn
điều kiện
1 2 2 3 10
z i z i
và
có mô đun nhỏ nhất. Tính
7 ?S a b
A.
7
. B.
0
. C.
5
. D.
12
.
Câu 55. (KTNL GV THUẬN THÀNH 2 BẮC NINH NĂM 2018-2019) Cho số phức thỏa mãn
z
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
. Gọi lần lượt là giá trị lớn nhất, nhỏ nhất của biểu thức . Tính
.
A. . B. . C. . D. .
Câu 56. (CHUYÊN BẮC GIANG NĂM 2018-2019 LẦN 02) Cho số phức z có
1
z
. Tìm giá trị lớn nhất
của biểu thức
2 2
1P z z z z
.
A.
13
4
B. 3 C.
3
D.
11
4
Câu 57. (THPT CHUYÊN ĐẠI HỌC VINH NĂM 2018-2019 LẦN 01) Giả sử
1 2
,z z
là hai trong các số phức
thỏa mãn
6 8
z zi
là số thực. Biết rằng
1 2
4
z z
, giá trị nhỏ nhất của
1 2
3z z
bằng
A.
5 21
B.
20 4 21
C.
20 4 22
D.
5 22
Câu 58. (ĐỀ THI THỬ VTED 03 NĂM HỌC 2018 - 2019) Trong các số phức
z
thỏa mãn
3 4 2
z i
có
hai số phức
1 2
,z z
thỏa mãn
1 2
1
z z
. Giá trị nhỏ nhất của
2 2
1 2
z z
bằng
A.
10
B.
4 3 5
C.
5
D.
6 2 5
Câu 59. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Cho hai số phức
1 2
,z z
thoả
mãn
1 1
2 4 7 6 2
z i z i
và
2
1 2 1iz i
. Tìm giá trị nhỏ nhất của biểu thức
1 2
T z z
.
A.
2 1
. B.
2 1
. C.
2 2 1
. D.
2 2 1
.
Câu 60. (CHUYÊN NGUYỄN TẤT THÀNH YÊN BÁI LẦN 01 NĂM 2018-2019) Cho
z
là số phức thỏa
mãn
2z z i
. Giá trị nhỏ nhất của
1 2 1 3z i z i
là
A.
5 2
. B.
13
. C.
29
. D.
5
.
Câu 61. (THPT CHUYÊN HẠ LONG - LẦN 2 - 2018) Cho các số phức
1
2z i
,
2
2z i
và số phức
z
thay đổi thỏa mãn
2 2
1 2
16
z z z z
. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
z
. Giá trị biểu thức
2 2
M m
bằng
A.
15
. B.
7
. C.
11
. D.
8
.
Câu 62. (THPT CHUYÊN QUANG TRUNG - BP - LẦN 1 - 2018) Cho số phức
z
thỏa mãn
2 4z i z i
và
3 3 1z i
. Giá trị lớn nhất của biểu thức
2
P z
là:
A.
13 1
. B.
10 1
. C.
13
. D.
10
.
Câu 63. (TT DIỆU HIỀN - CẦN THƠ - 2018) Xét số phức
z
thỏa mãn
2 2 2
z i
. Giá trị nhỏ nhất của
biểu thức
1 5 2P z i z i
bằng
A.
1 10
. B.
4
. C.
17
D.
5
.
Câu 64. (SGD&ĐT CẦN THƠ - HKII - 2018) Cho số phức
z
thỏa mãn
3 4 5
z i . Gọi
M
và
m
lần
lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
2 2
2
P z z i
. Môđun của số phức
w M mi
là
A.
3 137
w . B.
1258
w . C.
2 309
w . D.
2 314
w .
2 8
z z z z
,M m
3 3P z i
M m
10 34
2 10
10 58
5 58
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
Câu 65. (THPT HẬU LỘC 2 - TH - 2018) Cho hai số phức
1 2
,z z
thỏa mãn
1
1 2
z i
và
2 1
z iz
. Tìm giá
trị nhỏ nhất
m
của biểu thức
1 2
z z
?
A.
2 1
m
. B.
2 2
m
. C.
2
m
. D.
2 2 2
m
.
Câu 66. (SGD&ĐT BẮC GIANG - LẦN 1 - 2018) Hcho hai số phức
, wz
thỏa mãn
3 2 1
w 1 2 w 2
z i
i i
. Tìm giá trị nhỏ nhất
min
P
của biểu thức
w
P z
.
A.
min
3 2 2
2
P
. B.
min
2 1
P
. C.
min
5 2 2
2
P
. D.
min
3 2 2
2
P
.
Câu 67. (THPT CHUYÊN LÊ HỒNG PHONG - TPHCM - 2018) Cho số phức
z
thỏa
1
z
. Gọi
m
,
M
lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của biểu thức
5 3 4
6 2 1
P z z z z
. Tính
M m
.
A.
4
m
,
3
n
. B.
4
m
,
3
n
C.
4
m
,
4
n
. D.
4
m
,
4
n
.
Câu 68. (THPT CHUYÊN ĐH VINH - LẦN 3 - 2018) Cho các số phức
w
,
z
thỏa mãn
3 5
w i
5
và
5w 2 i 4
z
. Giá trị lớn nhất của biểu thức
1 2i 5 2i
P z z
bằng
A.
6 7
. B.
4 2 13
. C.
2 53
. D.
4 13
.
Câu 69. (KIM LIÊN - HÀ NỘI - LẦN 1 - 2018) Xét các số phức
z a bi
(
,a b
) thỏa mãn
3 2 2
z i
. Tính
a b
khi
1 2 2 2 5z i z i
đạt giá trị nhỏ nhất.
A.
4 3
. B.
2 3
. C.
3
. D.
4 3
.
Câu 70. (LIÊN TRƯỜNG - NGHỆ AN - LẦN 2 - 2018) Biết rằng hai số phức
1
z
,
2
z
thỏa mãn
1
3 4i 1
z
và
2
1
3 4i
2
z
. Số phức
z
có phần thực là
a
và phần ảo là
b
thỏa mãn
3 2 12
a b
. Giá trị nhỏ nhất của
1 2
2 2
P z z z z
bằng:
A.
min
9945
11
P
. B.
min
5 2 3
P
. C.
min
9945
13
P
. D.
min
5 2 5
P
.
PHẦN B. LỜI GIẢI THAM KHẢO
Phương trình bậc 2 với hệ số thực
Câu 1. Chọn D
2
4 2
2
3
3
12 0
2
4
z
z i
z z
z
z
1 2 3 4
3 3 2 2 2 3 4
T z z z z i i
Câu 2.
Lơi giai
Chọn D
Xét phương trình
2
4 4 3 0
z z
ta có hai nghiệm là:
1
2
1 2
2 2
1 2
2 2
z i
z i
V
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
1 2
3
2
z z
1 2
3
z z
Câu 3. Chọn B
Ta có:
1
2
2
2
4 0
2
z i
z
i
z
.
Suy ra
0; 2
M
;
0;2
N
nên
2
2
2 2 4
T OM ON
.
Câu 4. Chọn A
Áp dụng định lý Viet áp dụng cho phương trình trên ta được:
1 2
1 2
6
10
z z
z z
.
Khi đó ta có
2
2 2
1 2 1 2 1 2
2 36 20 16
z z z z z z
.
Câu 5. Chọn B
Theo định lý Viet ta có
1 2
1 2
2
. 3
z z
z z
, do đó
1 2
,z z
là hai nghiệm của phương trình
2
2 3 0z z
Câu 6. Chọn C
Xét phương trình
2
3 1 0
z z
có
2
1 4.3.1 11 0
.
Phương trình đã cho có 2 nghiệm phức phân biệt
1
1 11 1 11
;
6 6 6
i
z i
2
1 11 1 11
6 6 6
i
z i
Suy ra
1 2
P z z
1 11 1 11
6 6 6 6
i i
2 2
2 2
1 11 1 11
6 6 6 6
3 3
3 3
2 3
3
Câu 7.
Ta có :
2 2
2 2 2
1 2
3 5
6z 14 0 3 5 3 5 8.
3 5
z i
z z z i i
z i
Câu 8. Chọn A
Ta có
2
4 7 3 3 .
i
Do đó phương trình có hai nghiệm phức là
1 2
2 3 , 2 3 .
z i z i
Suy ra
2 2
2 2
1 2
2 3 2 3 4 4 3 3 4 4 3 3 2.
z z i i i i
Câu 9. Chọn C
Cách 1
2
1 3
2 2
1 0
1 3
2 2
z i
z z
z i
2 2
2 2
1 2 1 2
1 3 1 3 1 3 1 3
2 2 2 2 2 2 2
0
2
i i iP z z z z i
Cách 2: Theo định lí Vi-et:
1 2
1
z z
;
1 2
. 1
z z
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
Khi đó
2
2 2 2
1 2 1 2 1 2 1 2 1 2
2 1 1 0
P z z z z z z z z z z
.
Câu 10. Chọn B
Xét phương trình
2
3 5 0
z z
ta có hai nghiệm là:
1
2
3 11
3 11
2 2
2 2
z i
z i
1 2
5
z z
1 2
2 5
z z .
Câu 11. Chọn A
Theo định lí Vi-et, ta có
1 2
1 2
1
6
z z
z z
nên
1 2
1 2 1 2
1 1 1
. 6
z z
P
z z z z
Câu 12. Chọn C
2
' b' 4 5 1
ac
Phương trình có 2 nghiệm phức
1 2
2 , 2z i z i
nên
2 2
2 2 2 2 2
1 2
2 2 4 4 4 4 8 2 8 2 6
z z i i i i i i i
Câu 13.
1
2
2
1 3
2 10 0
1 3
z i
z z
z i
.
Do đó:
2 2 2 2
1 2
1 3 1 3 20
A z z i i
.
Câu 14. Phương trình
2
1 3
2 10 0
1 3
z i
z z
z i
. Vậy
1
1 3 z i
,
2
1 3 z i
.
Suy ra
1 2
. 10. 10 10
z z
.
Câu 15. Ta có:
2
3
3
3
z i
z
z i
1 2
3 3 2 3
z z i i .
Câu 16. Phương trình
2
8 25 0
z z
1
2
4 3
4 3
z i
z i
.
Suy ra:
1 2
6 6
z z i
.
Câu 17. Ta có:
2
6 10 0
z z
3
3
z i
z i
. Vì
z
là số phức có phần ảo âm nên
3z i
Suy ra
3 4 3
w
3 5 5
z i
i
i
z
Tổng phần thực và phần ảo:
4 3 1
5 5 5
.
Câu 18. Theo hệ thức Vi-et, ta có
1 2
1 2
4
5
z z
z z
.
Suy ra
2 1
1 2 1 2
1 2
z z
w i z z z z
z z
4
20
5
i
.
Câu 19. Chọn D
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
Theo Viet ta có
1 2
1 2
8 16
2
. 64 64.5 5
z z a
a
z z b b
. Vậy
w 29
.
Câu 20. Do số phức
1 i
là một nghiệm của phương trình
2
. 0
z a z b
.
Nên ta có:
2
1 1 0 2 0i a i b a b a i
0 2
2 0 2
a b a
a b
.
Vậy:
4
a b
.
Câu 21. Chọn C
+) Đặt
8
7
1 2
1
o
i i
z
i
, ta có
4
4
8 2
3
7 2
1 1
.
i i
i i i i
2
2 1
1 1 2 2
1
1 1 1
o
i i
i i
z i
i i i
.
+)
o
z
là nghiệm của đa thức
2
P z z bz c
o
z
là nghiệm còn lại của
P z
.
+) Ta có:
2 2
o o
b
z z b b
a
.
. 1 1 2
o o
c
z z i i c c
a
2 2
2 2 2 2 2 2
w i w
.
Câu 22. Chọn A
Ta có
2 2
1
1 2 2 1
2
2 3
. . 2 3 2 3 2
2 3
z i
z z z z i i
z i
Câu 23.
Lờigiải
Chọn A
2
3 2 27 0
z z
1 2
1 80 1 80
;
3 3
i i
z z
vậy
1 2 1
2
z z z z
=2
Câu 24. Phương trình
2 2 2
1
2
2
2 5
4 29 0 2 25 2 5
2 5
z i
z z z z i
z i
.
Suy ra
2
2
1 2
2 5 29
z z
.
Vậy
4 4
4 4
1 2
29 29 1682
z z .
Câu 25. Cách 1:
Ta có
2 2 2
1 1 1 11
3 1 0 0
3 3 6 36
z z z z z
2 2
1 11
1 11
6 6
6 36
1 11
6 6
z i
z i
z i
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
Khi đó
2 2
2 2
1 11 1 11 2 3
6 6 6 6 3
P
.
Cách 2:
Theo tính chất phương trình bậc 2 với hệ số thực, ta có
1
;z
2
z
là hai số phức liên hợp nên
2 2
1 2 1 2
.
z z z z
.
Mà
1 2
1
.
3
z z
suy ra
1 2
3
3
z z
.
Vậy
1 2
2 3
3
P z z
.
Câu 26. Phương trình
2
3 2 0
z z
có
1
2
2
1 23
6
( 1) 4.3.2 23
1 23
6
i
z
i
z
.
2
1
2
2
2
2
1 23 2 2 2 4
6 6 3 3 3 3
zz T
.
Câu 27. Cách 1:
+ Gọi
2 2
1
( , : b 0)
z a bi a b a
.
;A a b
.
Khi đó
2
z
là nghiệm phương trình:
2
2
2 2
0
z a bi z a bi
+ Ta có:
2 2
2 2 2
4 3 3 3
a bi a bi a bi a bi i b ai
Phương trình có hai nghiệm phân biệt:
2
3 3
2 2
a b a b
z i
nên
3 3
;
2 2
a b a b
B
.
Hoặc
2
3 3
2 2
a b a b
z i
nên
3 3
;
2 2
a b a b
B
.
+ Tính
2 2 2
b ,
OA a
2 2 2
b ,
OB a
2 2 2
b .
AB a
Vậy tam giác
OAB
đều.
Cách 2:
Theo giả thiết:
2 2 2 2
1 2 1 2 1 2 1 2 1 2
0 0
z z z z z z z z z z
3 3 3 3
1 2 1 2 1 2
0
z z z z z z OA OB
.
Mặt khác:
2
1 2
2 2 1 2 1 2 1 2
0
z z z z z z z z
2
2
2
1 2 1 2 1 2 1 2
.z z z z z z z z AB OAOB
.
Mà
OA OB
nên
AB OA OB
.
Vậy tam giác
OAB
đều.
Cách 3:
+
2
2 2
1 1
1 2 1 2
2 2
0 1 0
z z
z z z z
z z
2
1 1 1 1
1 2
2 2 2 2
1 3
1 0 1
2
z z z z
i
z z
z z z z
Vậy
OA OB
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
Mặt khác:
1 2 2 2 2
1 3
2
i
z z z z z AB OB
Vậy tam giác
OAB
đều.
Câu 28. Ta xét phương trình với điều kiện .
Ta có .
Vì nên ta được phương trình .
Giải phương trình được kết quả .
Suy ra . Mà nên .
Câu 29. Chọn C
Cách 1: Tự luận.
Ta có phương trình
2
0
bz caz
có các nghiệm
1 2
,z z
đều không là số thực, do đó
2
4 0
b ac
. Ta
có
2 2
4
i ac b
.
*
2
1
2
2
4
2
4
2
b i ac b
z
a
b i ac b
z
a
Khi đó:
2
2
1 2
2
2 2
1 2 1 2
2
2
1 2
2
4
4
z
c
P z z
a
ac b
z
b
z
a
a
z z
z
. Vậy
4c
P
a
.
Cách 2: Trắc nghệm.
Cho
1, 0, 1a b c
, ta có phương trình
2
1 0
z
có 2 nghệm phức là
1 2
,
z i z i
. Khi đó
2 2
1 2 1 2
4
P z zz z
.
Thế
1, 0, 1a b c
lên các đáp án, ta thấy chỉ có đáp án C cho kết quả giống.
Câu 30. Chọn D
Ta có:
2
2
2 1 0 1
z z m z m
1
+) Với
0
m
thì
1 1
z m
. Do
1
2 1 2
9
m
z m
m
(thỏa mãn).
+) Với
0
m
thì
1 1 .z i m
Do
2 1 2 1 4 3
z i m m m
(thỏa mãn).
Vậy
1 9 3 7
S
.
3 4 5
z w z w
0
z w
2 2
3 4 5
3 4 2 0
w z wz
z w z w
0
z
2
3 2 4 0
w w
z z
1 11
3 3
1 11
3 3
w
i
z
w
i
z
2 3
3
w
z
1
w
3
2
z
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
Câu 31. Ta có
1 3 0z i z i
2 2
1 3 0a b a b i
.
2 2
1 0
3 0
a
b a b
2
1
1 3 *
a
b b
.
2
2
3
*
1 3
b
b b
3
4
3
b
b
4
3
b
.
Vậy
1
4
3
a
b
2 3 6
S a b
.
Câu 32.
2
9 6 1 0
z z m
*
.
Trường hợp 1:
*
có nghiệm thực
0 9 9 1 0 1
m m
.
1
1
1
z
z
z
.
1 16
z m
(thỏa mãn).
1 4
z m
(thỏa mãn).
Trường hợp 2:
*
có nghiệm phức
0
z a bi b
0 9 9 1 0 1
m m
.
Nếu
z
là một nghiệm của phương trình
2
9 6 1 0
z z m
thì
z
cũng là một nghiệm của phương trình
2
9 6 1 0
z z m
.
Ta có
2
1
1 1 .z 1 1 1 8
9
c m
z z z m
a
(thỏa mãn).
Vậy tổng các giá trị thực của
m
bằng
12
.
Bài toán MIN-MAX
Câu 33.
Lơi giai
Chọn B
Goi
;M a b
là điểm biểu diễn của số phức z.
Theo giả thiết ta có:
2 2
4 3 5 4 3 5
z i a b
Tập hợp điểm biểu diễn số phức
z
là
đường tròn tâm
4;3
I
bán kính
5
R
Gọi:
1;3
1 3 1
1; 1
A
Q z i z i MA MB
B
Gọi E là trung điểm của AB, kéo dài EI cắt đường tròn tại D
Ta có:
2 2 2
2 .
MA MBQ
MA MB
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
2 2 2 2 2 2 2
2
Q MA MB MA MB MA MB
Vì
ME
là trung tuyến trong
MAB
2 2 2 2
2 2 2 2
2
2 4 2
MA MB AB AB
ME MA MB ME
2
2 2 2 2
2 2 4
2
AB
Q ME ME AB
. Mặt khác
2 5 5 3 5
ME DE EI ID
2
2
4. 3 5 20 200
Q
10 2 10 2
4 2( 4) 6
2 6;4 10
2 2( 3) 4
max
D D
D D
MA MB
Q Q
M D
x x
EI ID M P a b
y y

Cách 2:Đặt
.z a bi
Theo giả thiết ta có:
2 2
4 5 5.
a b
Đặt
4 5 sin
3 5 cos
a t
b t
. Khi đó:
2 2 2 2
1 3 1 1 3 1 1
Q z i z i a b a b
2 2 2
2
5 sin 5 5cos 5 sin 3 5 cos 4
t t t t
30 10 5 sin 30 2 5 3sin 4cost t t
Áp dụng BĐT Bunhiacopski ta có:
2 60 8 5 2sin cos 2 60 8 5. 5 200 10 2
Q t t
10 2 10 2
max
Q Q
Dấu bằng xảy ra khi
2
sin
6
5
10.
1 4
cos
5
t
a
P a b
b
t
Câu 34.
Lời giai
Chọn A
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
Gọi
A
là điểm biểu diễn số phức
z
,
2;1 , 4;7
E F
và
1; 1 .
N
Từ
2 4 7 6 2
AE A F z i z i và
6 2
EF
nên ta có
A
thuộc đoạn thẳng
EF
. Gọi
H
là
hình chiếu của
N
lên
EF
, ta có
3 3
;
2 2
H
. Suy ra
5 2 2 73
.
2
P NH NF
Câu 35. Chọn C
Gọi
,M N
lần lượt là điểm biểu diễn của số phức
1 2
,z z
Gọi
, ,z x iy x y
Ta có
1 34 ,z M N
thuộc đường tròn
C
có tâm
1;0
I
, bán kính
34
R
Mà
1 2 1 2z mi z m i x yi mi x yi m i
2 2 2 2
1 2
x y m x m y
2 1 2 2 3 0
m x m y
Suy ra
,M N
thuộc đường thẳng
: 2 1 2 2 3 0
d m x m y
Do đó
,M N
là giao điểm của đường thẳng
d
và đường tròn
C
Ta có
1 2
z z MN
nên
1 2
z z
lớn nhất khi và chỉ khi
MN
lớn nhất
5
8
6
4
2
2
H
E
N
D
A
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
MN
đường kính của
C
. Khi đó
1 2
2 2
z z OI
Câu 36. Cách 1:
Đặt
w z i z w i
.
Gọi
;M x y
là điểm biểu diễn hình học của số phức
.w
Từ giả thiết
2 2 1z i
ta được:
2 2 1w i i
2 1w i
2 1 1x y i
2 2
2 1 1
x y
.
Suy ra tập hợp những điểm
;M x y
biểu diễn cho số phức
w
là đường tròn
C
có tâm
2;1
I
bán kính
1R
.
Giả sử
OI
cắt đường tròn
C
tại hai điểm
,A B
với
A
nằm trong đoạn thẳng
OI
.
Ta có
w OM
Mà
OM MI OI
OM MI OA AI
OM OA
Nên
w
nhỏ nhất bằng
5 1
OA OI IA
khi
.M A
Cách 2:
Từ
2 2 1z i
2 2
2 2 1
a b
với
,z a bi a b
2 sin ; 2 cosa x b x
2 sin , 2 cosa x b x
Khi đó:
2 sin 2 cos
z i x x i i
2 2
2 sin 1 cos
x x
6 4sin 2cosx x
2 2 2 2
6 4 2 sin cos
x x
2
6 2 5 5 1 5 1
Nên
z i
nhỏ nhất bằng
5 1
khi
4cos 2sin
4sin 2cos 2 5
x x
x x
2 5
sin
5
5
cos
5
x
x
Ta được
2 5 5
2 2
5 5
z i
Cách 3:
Sử dụng bất đẳng thức
1 2 1 2 1 2
z z z z z z
2 2 2 2 2 2 5 1
z i z i i z i i
Câu 37. Ta có
2 2 2
2 1 1 3 5
2 2
2 2
z i z i z i
z i
P P P P
z z z z z z
.
Vậy
5
3
M
m
.
Câu 38. Chọn C
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
Ta có
2
1 2 3 2 3 . 2 3 2 3 2 3z i z i z i z i z i
1 2 3 2 3 2 3 1` 1 3 2 1(*)
z i z i z i z i i
.
+Đặt
w 1z i
, khi đó
w 3 2 1i
.
Tập hợp các điểm biểu diễn số phức
w 1z i
là đường tròn
;1I
và
w
là khoảng cách từ gốc tọa độ
đến 1 điểm trên đường tròn. Do đó giá trị lớn nhất của
w
chính là đoạn
OQ
.
2 2
max
w 1 3 2 1 13
.
Câu 39. Ta có
1 3 4 3 4 5 1 5 1 4 6
z i z i z z z
.
Đặt
2
0 0 0
4 3 5, 7 24z i z z i
.
Ta có
2 2
2 2
2 2 2 2 2
7 24
o o o
A z i z z z z z z
2
4 4 2
. . 2 .
o o o o
z z z z z z z z
Mà
2 2
1 . . 1
o o o o o
z z z z z z z z z z
Suy ra
2
2
4 4 2 2 4 2
1 2 . 2 2 1201
o o o
A z z z z z z z z
.
Hàm số
4 2
2 2 1201
y t t đồng biến trên
4;6
nên
4 2
2.4 2.4 1201 1681
A
.
Dấu bằng xảy ra khi và chỉ khi
4
4 3 1
z
z i
.
Do đó
2
7 24z i
nằm trong khoảng
1009;2018
.
Câu 40. Giả sử:
, , ;z x yi x y N x y
: điểm biểu diễn của số phức z trên mặt phẳng tọa độ
Oxy
.
Ta có:
•
4 2
z z z z x y N
thuộc các cạnh của hình vuông BCDF (hình vẽ).
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
•
2 2
2 2 2 2 ;P z i P x y P d I N
với
2;2
I
Từ hình ta có:
1;1
E
2 2
max
4 2 2 5
M P ID
và
2 2
min
2 1 2 1 2
m P IE
Vậy,
2 2 5 34;6
A M m
.
Câu 41. Gọi , . Theo giả thiết, ta có
6 6 20
z z
.
6 6 20
x yi x yi
2 2
2 2
6 6 20x y x y
.
Gọi
;M x y
,
1
6;0
F
và
2
6;0
F
.
Khi đó
1 2 1 2
20 12
MF MF F F
nên tập hợp các điểm
E
là đường elip có hai tiêu điểm
1
F
và
2
F
. Và độ dài trục lớn bằng
20
.
Ta có
6
c
;
2 20 10
a a
và
2 2 2
64 8
b a c b
.
Do đó, phương trình chính tắc của là
2 2
1
100 64
x y
.
Suy ra
'
max 10
z OA OA
khi
10
z
và
'
min 8
z OB OB
khi
8z i
.
Vậy
2
M n
.
Câu 42. Theo bất đẳng thức tam giác ta có
w 2 1 2 6 8 7 9 2 6 8 7 9 4 130
z i z i i z i i
.
Vậy giá trị lớn nhất của
w
là
4 130
.
Câu 43.
Gọi
z x yi
, trong đó
,x y
. Khi đó
z x yi
,
;M x y
,
;
M x y
.
x
y
1
1
-2 2
-2
2
O
D
F
C
I
B
E
z x yi
,x y
E
E
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
Ta đặt
4 3 4 3 4 3 3 4 4 3 ;3 4w z i x yi i x y x y i N x y x y
. Khi đó
4 3 4 3 3 4 4 3 ; 3 4w z i x y x y i N x y x y
.
Ta có
M
và
M
;
N
và
N
từng cặp đối xứng nhau qua trục
Ox
. Do đó, để chúng tạo thành một hình chữ
nhật thì
M N
y y
hoặc
M N
y y
. Suy ra
3 4y x y
hoặc
3 4y x y
. Vậy tập hợp các điểm
M
là hai
đường thẳng:
1
: 0
d x y
và
2
:3 5 0
d x y
.
Đặt
2 2
4 5 5 4
P z i x y
. Ta có
P MA
với
5; 4
A
.
min min 1
;P MA MA d A d
hoặc
2
;MA d A d
. Mà
1
1
;
2
d A d
,
2
5
;
34
d A d
, vậy
min 1
1
;
2
P d A d
.
Câu 44. Đặt
z x yi
(
x
,
y
).
Khi đó
3 2iz z i
2 2 2
2
3 2 1
x y x y
2 1 0
x y
2 1x y
1
.
Lại có
2 2
z x y
2
.
Thay
1
vào
2
ta được:
2 2
z x y
2
2
2 1
y y
2
5 4 1y y
2
2 1 5
5
5 5 5
y
Dấu đẳng thức xảy ra khi
2
0
5
y
2
5
y
.
Thay
2
5
y
vào
1
suy ra
1
5
x
.
Vậy phần thực của số phức
z
là
1
5
.
Câu 45. Gọi
z x yi
,
,x y
. Khi đó
; M x y
là điểm biểu diễn của số phức
z
.
Theo bài ra ta có
2 2
1 3 2 1 3 4
z i x y
.
Suy ra tập hợp điểm
M
là đường tròn tâm
1; 3
I
bán kính
2R
.
Khi đó
2
2
1 1
z x y I M
với
1; 0
I
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
1z
nhỏ nhất khi
I M
ngắn nhất hay
I
,
M
,
I
thẳng hàng,
M
nằm giữa
I
và
I
.
Phương trình đường thẳng
II
là
1x
.
Tọa độ giao điểm của đường thẳng
II
với đường tròn tâm
I
bán kính
2R
là
1
1; 1M
và
1
1; 5M
.
Thử lại ta thấy
1
1; 1M
thỏa mãn. Vậy
1z i
.
Câu 46. Đặt z x iy và gọi
;M x y
là điểm biểu diễn của z x iy
ta có: 4 2z z z z x y
Gọi
2;2A
và
P MA
* Theo hình vẽ,
min , ,P d A
với
: 2x y
và
2 2 2
min 2
2
P
2 2
max 2 4 2 5,P AE với
0; 2E
Vậy
2 2 5 5,88M m
Câu 47. Gọi z x yi ,
,x y
được biểu diễn bởi điểm
;M x y
.
1 1 2 1 1 1 2z i z i x y i x y i
2 2 2 2
3
1 1 1 2 4 2 3 0 2
2
x y x y x y y x
.
Cách 1:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
2 2
2 2 2 2
3 9 3 9 3 5
2 5 6 5 ,
2 4 5 20 10
z x y x x x x x x
.
Suy ra
3 5
10
min z
khi
3 3
;
5 10
x y
.
Vậy phần ảo của số phức
z
có mô đun nhỏ nhất là
3
10
.
Cách 2:
Trên mặt phẳng tọa độ
Oxy
, tập hợp điểm biểu diễn số phức
z
là đường thẳng
: 4 2 3 0
d x y
.
Ta có
z OM
.
z
nhỏ nhất
OM
nhỏ nhất
M
là hình chiếu của
O
trên
d
.
Phương trình đường thẳng
OM
đi qua
O
và vuông góc với
d
là:
2 0
x y
.
Tọa độ của
M
là nghiệm của hệ phương trình:
3
4 2 3 0
5
2 0 3
10
x
x y
x y
y
3 3
;
5 10
M
. Hay
3 3
5 10
z i
.
Vậy phần ảo của số phức
z
có mô đun nhỏ nhất là
3
10
.
Nhận xét: Ta có thể tìm tập hợp điểm biểu diễn số phức
z
như sau:
1 1 2 1 1 2z i z i z i z i
*
Gọi
M
biểu diễn số phức
z
, điểm
1; 1
A
biểu diễn số phức
1 i
, điểm
1; 2
B
biểu diễn số phức
1 2i
.
Khi đó
*
MA MB
. Suy ra tập hợp điểm biểu diễn số phức
z
là đường trung trực của đoạn thẳng
AB
có phương trình
: 4 2 3 0
d x y
.
Câu 48. Giả sử
1 1 1
z x y i
với
1 1
;x y
. Khi đó:
1
1 1 1 1 1 1
1
1 2 3 1 2 3
2 3
z i
z i z i x y i x y i
z i
1
2 2 2
2
1 1 1 1 2
1 2 3 3 0
x y x y x y
.
Quỹ tích điểm
M
biểu diễn số phức
1
z
là đường thẳng
: 3 0
x y
.
Giả sử
2 2 2
z x y i
với
2 2
;x y
. Ta có:
2
2 2 2 2 2 2
2
2 2 1 1 2 1 1
1
z i
z i z i x y i x y i
z i
2 2 2
2 2 2
2 2 2 2 2 2 2 2
1 2 1 1 4 2 3 0
x y x y x y x y
.
Quỹ tích điểm
N
biểu diễn số phức
2
z
là đường tròn
2 2
: 4 2 3 0
C x y x y
có tâm
2; 1
I
và
bán kính
2
2
2 1 3 2
R
.
Khoảng cách từ
I
đến
là:
2
2
2 1 3
; 3 2
1 1
d I R
đường thẳng
và đường tròn
C
không
có điểm chung.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
Quỹ tích các điểm biểu diễn số phức
1 2
z z
là đoạn thẳng
MN
.
1 2
z z
nhỏ nhất khi và chỉ khi
MN
nhỏ
nhất.
Dễ thấy
min
3 2 2 2 2
MN
.
Câu 49. Chọn A
Đặt
z x yi
,
,x y
. Khi đó
1 34
z
2
2
1 34
x y
;
1 2z mi z m i
2 1 2 2 3 0
m x m y
.
Do đó tập hợp các điểm
M
biểu diễn số phức
z
là giao điểm của đường tròn
2
2
: 1 34
C x y
và
đường thẳng
: 2 1 2 2 3 0
d m x m y
.
Gọi
A
,
B
là hai điểm biểu diễn
1
z
và
2
z
. Suy ra
,C d A B
.
Mặt khác
1 2
2 2 34
z z AB R do đó
1 2
max 2 34 2 1;0
z z AB R I d
.
Từ đó ta có
1
2
m
nên
:3 5 3 0
d x y
1
2
6 3
4 3
z i
z i
.
Vậy
1 2
2
z z
.
Câu 50. Ta có: +
3 2 2
z , suy ra tập hợp điểm biểu diễn
M
biểu diễn số phức
z
là đường tròn có tâm
3 2 ;0
I , bán kính
2
r
.
+
4 2 2 2
w i , suy ra tập hợp điểm biểu diễn
N
biểu diễn số phức
w
là đường tròn có tâm
0;4 2
J
, bán kính
2 2
R
.
Ta có
min min
z w MN
.
+
5 2; 2; 2 2
IJ IM r NJ R
.
N
M
I
N'
M'
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
Mặt khác
IM MN NJ IJ
MN IJ IM NJ
hay
5 2 2 2 2 2 2
MN
.
Suy ra
min 2 2
MN
khi
, , ,I M N J
thẳng hàng và
,M N
nằm giữa
,I J
(Hình vẽ).
Cách 1:
Khi đó ta có:
0 0
3 3
z w OM ON

và
3 2
IN
1 3
;
5 5
IM IJ IN IJ
.
Mặt khác
ON OI IN
3
5
OI IJ
;
3 3OM OI IM
1 3
3 3
5 5
OI IJ OI IJ

.
Suy ra
0 0
3 3
z w OM ON

3 3
3 2
5 5
OI IJ OI IJ OI
6 2
.
Cách 2:
Ta có
3 3 0
IN IM IM IN
.
Do đó
0 0
3 3 3 2 2. 2.3 2 6 2.
z w OM ON OI IM OI IN OI OI
Cách 3:
+)
0
12 2
1 12 2 4 2
5
5 5 5
4 2
5
M
M
x
IM
IM IJ IM IJ z i
IJ
y
.
+)
0
6 2
3 6 2 12 2
5
5 5 5
12 2
5
N
N
x
IN
IN IJ IN IJ w i
IJ
y
.
Suy ra
0 0
3 6 2 6 2
z w .
Câu 51. Chọn C
Giả sử
,M N
lần lượt là các điểm biểu diễn cho
z
và
.w
Suy ra
2 ,OM ON OF OI
  
4
z w MN
và
2 10.
OF OI
Đặt
; .
2
a
z ON w OM b
Dựng hình bình hành
OMFE
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
Ta có
2 2 2
2 2
2 2 2
25
264
2 4
2
3
16
2 4
a b ME
a b
b ME a
2
2
2 2
1 1
2 66
2 4 2
a
z w b a b
Suy ra
66,
a b
dấu “=” xảy ra khi
2 66
.
3
a b
Vậy
max
66.
a b
Câu 52. Thay
2
1
z
vào
P
ta có
2
1 1P z z z
2
2
1
z z z z
2
1 .z z z z z
1 1z z z z
1 1z z z
.
Mặt khác
2
1 1 1 2
z z z z z
.
Đặt
t z z
do
1
z
nên điều kiện
2;2
t
.
Suy ra
2 1P t t
.
Xét hàm số
2 1f t t t
với
2;2
t
.
1
1
2 2
f t
t
với
1t
. Suy ra
0
f t
với
1t
.
1
1
2 2
f t
t
với
1t
. Suy ra
0
f x
7
4
x
.
Ta có bảng biến thiên
Từ bảng biến thiên suy ra
13
4
M
tại
7
4
t
và
3
m tại
2t
.
Vậy
13 3
.
4
M m
.
a
b
I
F
E
N
M
O
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
Câu 53. Đặt
1
5 ;0
F
,
2
5 ;0
F
, vì
5 3
nên tập hợp các điểm
M
biểu diễn số phức
z
thuộc elip có
2 2 2
3
4
5
a
b a c
c
suy ra
2 2
: 1
9 4
x y
E
.
Tập hợp các điểm
N
biểu diễn số phức
thuộc đường thẳng
: 5 4 20 0
x y
.
Yêu cầu bài toán trở thành tìm điểm
M E
và
N
sao cho
MN
nhỏ nhất.
Đường thẳng
d
song song với
có dạng
: 5 4 0
d x y c
,
20
c
.
d
tiếp xúc với
E
khi và chỉ khi
2
2 2
17
5 .9 4 .4 289
17
c
c
c
.
Với
17
c
2
2
20 17
37
,
41
5 4
d d
.
Với
17
c
2
2
20 17
3
,
41
5 4
d d
.
Vậy
3
min
41
MN
.
Câu 54. Chọn A
Gọi
;M a b
là điểm biểu diễn số phức
z a bi
1;2
A
là điểm biểu diễn số phức
1 2i
2;3
B
là điểm biểu diễn số phức
2 3i
,
10
AB
1 2 2 3 10
z i z i trở thành
MA MB AB
, ,M A B
thẳng hàng và M ở giữa A và B
4
2
2
4
O
M
H
B
A
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
Gọi H là điểm chiếu của
O
lên AB, phương trình
: 3 7 0AB x y
,
: 3 0OH x y
Tọa độ điểm
7 21
;
10 10
H
, Có
3 1
;
10 10
AH
,
27 9
;
10 10
BH
và
9BH AH
Nên H thuộc đoạn AB
z
nhỏ nhất
OM
nhỏ nhât, mà M thuộc đoạn AB
7 21
;
10 10
M H
Lúc đó
49 21
7 7
10 10
S a b
. Chọn A
Câu 55.
Giải:
Chọn D
Gọi
, ,z x yi x y
, ta có
4
2 8 2 4
2
x
z z z z x y
y
, tập hợp
;K x y
biểu
diễn số phức
z
thuộc cạnh các cạnh của trong hình thoi
ABCD
như hình vẽ.
đạt giá trị lớn nhất khi
KM
lớn nhất, theo hình vẽ ta có
KM
lớn nhất khi
K D
hay
4;0K
suy ra
49 9 58M
đạt giá trị nhỏ nhất khi
KM
nhỏ nhất, theo hình vẽ ta có
KM
nhỏ nhất khi
K F
(
F
là
hình chiếu của
E
trên
AB
.
Suy ra
2;1
F
do
AE AB
nên
F
là trung điểm của
AB
.
Suy ra
1 4 5m
. Vậy
58 5M m
Câu 56. Chọn A
2 2 2 2
1 1 1 1 1P z z z z z z z z z z z
Do
1z
nên ta đặt
cos .sinz x i x
. Khi đó
3 3P z i
3 3P z i
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
2
2 2 2
2
2
1 1 cos .sin 1 cos 2 sin 2 cos sin 1
cos 1 sin cos2 cos 1 sin 2 sin
2 2cos 3 4cos 2cos 2
2 2cos 4cos 4cos 1
2 2cos 2cos 1
P z z z x i x x i x x i x
x x x x x x
x x x
x x x
x x
Đặt
cos , 1;1t x t
. Xét hàm 2 2 2 1y t t
Với
1
2
t
thì
1
2 2 2 1, ' 2
2 2
y t t y
t
1 7
' 0 2 0
8
2 2
y t
t
7 13
1 3;
8 4
y y
;
1
3
2
y
Với
1
2
t
thì
1
2 2 2 1, ' 2
2 2
y t t y
t
1 1
' 0 2 0 2 2
2
2 2
y t
t
(phương trình vô nghiệm)
1 3y
;
1
3
2
y
Vậy
1;1
13
max
4
y
. Do đó giá trị lớn nhất của
2 2
1P z z z z
là
13
4
.
Câu 57. Chọn C
Giả sử z x yi ,
,x y
.Gọi
,A B
lần lượt là điểm biểu diễn cho các số phức
1 2
,z z
. Suy ra
1 2
4AB z z
.
* Ta có
6 8z zi
6 . 8x yi y xi
2 2
8 6 48 6 8x y x y x y i
. Theo giả thiết
6 8z zi
là số thực nên ta suy ra
2 2
6 8 0x y x y
. Tức là các điểm
,A B
thuộc đường tròn
C
tâm
3;4I
, bán kính
5R
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
* Xét điểm
M
thuộc đoạn
AB
thỏa
3 0 3 4
MA MB OA OB OM
.Gọi
H
là trung điểm
AB
. Ta tính
được
2 2 2 2 2
21; 22
HI R HB IM HI HM
, suy ra điểm
M
thuộc đường tròn
C
tâm
3;4
I
,
bán kính
22
r
.
* Ta có
1 2
3 3 4 4
z z OA OB OM OM
, do đó
1 2
3z z
nhỏ nhất khi
OM
nhỏ nhất.
Ta có
0
min
5 22
OM OM OI r
.
Vậy
1 2 0
min
3 4 20 4 22
z z OM
.
Câu 58. Chọn A
Đặt
1 1 1 1 1
, ,z x y i x y
và
2 2 2 2 2
, ,z x y i x y
.
Khi đó
2 2
1 1
2 2
2 2
3 4 4
3 4 4
x y
x y
và
2 2
1 2 1 2
1
x x y y
.
Ta có
2 2 2 2
1 1 2 2
3 4 3 3
x y x y
2 2 2 2
1 1 2 2 1 2 1 2
6 8
x y x y x x y y
.
Suy ra
2 2 2 2
2 2
1 2 1 2 1 2 1 2 1 2
2 3 4 2. 3 4 10
z z x x y y x x y y
.
Do đó
2 2
1 2
10 10
z z
.
Câu 59.
Gọi
M
là điểm biểu diễn số phức
1
z
và
2;1
A
;
4;7
B
lần lượt là hai điểm biểu diễn hai số phức
2 i
,
4 7i
. Ta có
6 2
AB
. Phương trình đường thẳng
AB
là
: 3 0
d x y
.
+)
1 1
2 4 7 6 2
z i z i
6 2
MA MB
MA MB AB
. Do đó tập hợp các điểm biểu diễn
số phức
1
z
là đoạn thẳng
AB
.
+)
2 2 2
1 2 1 1 2 1 2 1iz i iz i i z i
.
Gọi
N
là điểm biểu diễn số phức
2
z
và
2;1
I
là điểm biểu diễn số phức
2 i
. Ta có
1
IN
Suy ra tập
hợp các điểm biểu diễn số phức
2
z
là đường tròn
C
có phương trình:
2 2
2 1 1
x y
.
, 2 2 1
d I AB
, suy ra
AB
không cắt đường tròn.
Gọi
K
là hình chiếu của
2;1
I
lên
AB
. Dễ thấy
K
nằm trên đoạn thẳng
AB
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
Gọi
H
là giao điểm của đoạn
IK
với đường tròn
C
.
Ta có
1 2
, 2 2 1
z z MN KH d I AB R
.
Suy ra
1 2
2 2 1.
min z z
Câu 60. Đặt
,z a bi a b
.
Ta có:
2
2 2 2
2 2
z z i a b a b
4 4 0 1
b b
z a i
.
Xét:
1 2 1 3 1 1 2z i z i a i a i
2 2
2 2
1 1 1 2
a a
.
Áp dụng BĐT Mincôpxki:
2 2 2 2
2 2
1 1 1 2 1 1 1 2
a a a a
4 9 13
.
Suy ra:
1 2 1 3z i z i
đạt GTNN là
13
khi
1
2 1 1
3
a a a
.
Nhận xét : Bài toán trên có thể được giải quyết bằng cách đưa về bài toán hình học phẳng.
Câu 61. Giả sử
,z x yi x y
.
Ta có:
2 2
1 2
16
z z z z
2 2
2 2 16
x yi i x yi i
2
2
1 4
x y
.
Suy ra tập hợp điểm biểu diễn của số phức
z
là đường tròn tâm số phức
0;1
I
bán kính
2R
.
Do đó
1
m
,
3
M
.
Vậy
2 2
8
M m
.
Câu 62.
Gọi
;M x y
là điểm biểu diễn số phức
z
ta có:
2 4z i z i
2 2
2 2
2 4
x y x y
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
3y
;
3 3 1z i
điểm M nằm trên đường tròn tâm
3;3I
và bán kính bằng 1. Biểu thức
2P z AM
trong đó
2;0A
, theo hình vẽ thì giá trị lớn nhất của
2P z
đạt được khi
4;3M
nên
2 2
max 4 2 3 0 13P
.
Câu 63.
Gọi
;M x y
là điểm biểu diễn số phức
z
. Do
2 2 2z i
nên tập hợp điểm
M
là đường tròn
2 2
: 2 2 4C x y
.
Các điểm
1;1A
,
5;2B
là điểm biểu diễn các số phức
1 i
và
5 2i
. Khi đó,
P MA MB
.
Nhận thấy, điểm
A
nằm trong đường tròn
C
còn điểm
B
nằm ngoài đường tròn
C
, mà
17MA MB AB . Đẳng thức xảy ra khi
M
là giao điểm của đoạn
AB
với
C
.
Ta có, phương trình đường thẳng
: 4 3 0AB x y
.
Tọa độ giao điểm của đường thẳng
AB
và đường tròn
C
là nghiệm của hệ với
1 5y
2 2 2 2
2 2 4 4 5 2 4
4 3 0 4 3
x y y y
x y x y
Ta có
2 2
2
22 59
17
4 5 2 4 17 44 25 0
22 59
17
y N
y y y y
y L
Vậy min 17P khi
37 4 59 22 59
17 17
z i
Câu 64. - Đặt z x yi , với
,x y
.
Ta có: 3 4 5z i
3 4 5x y i
2 2
3 4 5x y
, hay tập hợp các điểm biểu diễn
số phức
z
là đường tròn
C
có tâm
3;4I
, bán kính 5r .
- Khi đó :
2 2
2P z z i
2 2
2 2
2 1x y x y
4 2 3x y
4 2 3 0x y P
, kí hiệu là đường thẳng
.
- Số phức
z
tồn tại khi và chỉ khi đường thẳng
cắt đường tròn
C
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
;
d I r
23
5
2 5
P
23 10
P
13 33
P
Suy ra
33
M
và
13
m
33 13w i
.
Vậy
1258
w .
Câu 65. Chọn D
Đặt
1
; ,z a bi a b
2
z b ai
1 2
z z a b b a i
.
Nên
2 2
1 2 1
2.z z a b b a z
Ta lại có
1 1 1
2 1 1 2
z i z i z
1
2 2
z . Suy ra
1 2 1
2. 2 2 2
z z z
.
Dấu
" "
xảy ra khi
0
1 1
a b
.
Vậy
1 2
min 2 2 2
m z z
.
Câu 66. Giả sử
z a bi
,a b
,
w x yi
,x y
.
3 2 1z i
2 2
3 2 1
a b
(1)
w 1 2 w 2i i
2 2 2 2
1 2 2 1
x y x y
.
Suy ra
0
x y
.
2 2 2 2
w
P z a x b y a x b x
.
Từ (1) ta có
3;2
I
, bán kính
1r
. Gọi
H
là hình chiếu của
I
trên
:
d y x
.
Đường thẳng
HI
có PTTS
3
2
x t
y t
.
3 ;2
M HI M t t
2
2 1
M C t
1
2
1
2
t
t
1 1
2 3 ;2
2 2
t M
,
5 2
2
MH
1 1
3 3 ;2
2 2
t M
,
5 2
2
MH
Vậy
min
5 2 2
2
P
.
Câu 67. Vì
1
z
và
2
.
z z z
nên ta có
1
z
z
.
Từ đó,
5 3 4
6 2 1
P z z z z
4 4 4
6 2 1
z z z z
4 4 4
6 2 1
z z z
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
Đặt
4
z x iy
, với
,x y
. Do
1
z
nên
4 2 2
1
z x y
và
1 , 1x y
.
Khi đó
6 2 1
P x iy x iy x iy
2
2
2 6 2 1
x x y
2 6 2 2 2
x x
2
2 2 1 3
x
.
Do đó
3
P
. Lại có
1 1x
0 2 2 2
x
1 2 2 1 1
x
4
P
.
Vậy
4M
khi
4
1z
và
3
m
khi
4
1 3
i
2 2
z
. Suy ra
1
M m
.
Câu 68. Gọi
iz x y
, với
,x y
. Khi đó
;M x y
là điểm biểu diễn cho số phức
z
.
Theo giả thiết,
5w 2 i 4
z
5 w i 2 i 4 5i
z
2 i w i 3 2i
z
3 2i 3
z
. Suy ra
;M x y
thuộc đường tròn
2 2
: 3 2 9
C x y
.
Ta có
1 2i 5 2i
P z z
MA MB
, với
1;2
A
và
5;2
B
.
Gọi
H
là trung điểm của
AB
, ta có
3;2
H
và khi đó:
P MA MB
2 2
2
MA MB
hay
2 2
4
P MH AB
.
Mặt khác,
MH KH
với mọi
M C
nên
2 2
4
P KH AB
2
2
4
IH R AB
2 53
.
Vậy
max
2 53
P
khi
M K
MA MB
hay
3 5i
z
và
3 11
w i
5 5
.
Câu 69. Cách 1:
Đặt
3 2
z i w
với
w x yi
,x y
. Theo bài ra ta có
2 2
2 4
w x y
.
Ta có
2 2 2
2
1 2 2 2 5 4 2 1 3 4 2 1 3
P z i z i w w i x y x y
2 2 2 2
20 8 2 1 3 2 5 2 2 1 3
x x y x x y
2 2 2 2 2
2 2 2
2 2 1 1 3 2 1 1 3
x y x x y x y x y
2 3 2 3 6
y y y y
.
2 2
1
1
6 3 0
3
4
x
x
P y y
y
x y
.
Vậy GTNN của
P
là bằng
6
đạt được khi
2 2 3z i
.
Cách 2:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
3 2 2
z i
2
MI
;2M I
với
3;2
I
.
1 2 2 2 5 2
P z i z i MA MB
với
1;2
A
,
2;5
B
.
Ta có
2IM
;
4IA
. Chọn
2;2
K
thì
1IK
. Do đó ta có
2
.
IA IK IM
IA IM
IM IK
IAM
và
IMK
đồng dạng với nhau
2
AM IM
MK IK
2
AM MK
.
Từ đó
2P MA MB
2
MK MB
2BK
.
Dấu bằng xảy ra khi và chỉ khi
M
,
K
,
B
thẳng hàng và
M
thuộc đoạn thẳng
BK
.
Từ đó tìm được
2;2 3
M .
Cách 3:
Gọi
;M a b
là điểm biểu diễn số phức
.z a bi
Đặt
3;2
I
,
1;2
A
và
2;5
B
.
Ta xét bài toán: Tìm điểm M thuộc đường tròn
C
có tâm
I
, bán kính
2R
sao cho biểu thức
2P MA MB
đạt giá trị nhỏ nhất.
Trước tiên, ta tìm điểm
;K x y
sao cho
2MA MK
M C
.
Ta có
2 2
2 2
2 4 4
MA MK MA MK MI IA MI IK

2 2 2 2 2 2 2
2 . 4 2 . 2 4 3 4
MI IA MI IA MI IK MI IK MI IA IK R IK IA
*
.
*
luôn đúng
2 2 2
4 0
3 4 0
IA IK
M C
R IK IA
.
4 3 4
2
4 0
2
4 2 0
x
x
IA IK
y
y
.
Thử trực tiếp ta thấy
2;2
K
thỏa mãn
2 2 2
3 4 0
R IK IA
.
Vì
2 2 2 2
1 3 10 4
BI R
nên
B
nằm ngoài
C
.
Vì
2 2
1 4KI R
nên
K
nằm trong
C
.
Ta có
2 2 2 2 2
MA MB MK MB MK MB KB
.
Dấu bằng trong bất đẳng thức trên xảy ra khi và chỉ khi
M
thuộc đoạn thẳng
BK
.
Do đó
2MA MB
nhỏ nhất khi và chỉ khi M là giao điểm của
C
và đoạn thẳng
.BK
Phương trình đường thẳng
: 2
BK x
.
Phương trình đường tròn
2 2
: 3 2 4
C x y
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
Tọa độ điểm
M
là nghiệm của hệ
2 2
2
2
3 2 4
2 3
x
x
x y
y
hoặc
2
2 3
x
y
.
Thử lại thấy
2;2 3
M thuộc đoạn
BK
.
Vậy
2
a
,
2 3
b
4 3
a b .
Câu 70. Gọi
1
M
,
2
M
,
M
lần lượt là điểm biểu diễn cho số phức
1
z
,
2
2z
,
z
trên hệ trục tọa độ
Oxy
. Khi
đó quỹ tích của điểm
1
M
là đường tròn
1
C
tâm
3;4
I
, bán kính
1R
;
quỹ tích của điểm
2
M
là đường
2
C
tròn tâm
6;8
I
, bán kính
1R
;
quỹ tích của điểm
M
là đường thẳng
:3 2 12 0
d x y
.
Bài toán trở thành tìm giá trị nhỏ nhất của
1 2
2
MM MM
.
Gọi
3
C
có tâm
3
138 64
;
13 13
I
,
1R
là đường tròn đối xứng với
2
C
qua
d
. Khi đó
1 2 1 3
min 2 min 2
MM MM MM MM
với
3 3
M C
.
Gọi
A
,
B
lần lượt là giao điểm của đoạn thẳng
1 3
I I
với
1
C
,
3
C
. Khi đó với mọi điểm
1 1
M C
,
3 3
M C
,
M d
ta có
1 3
2 2
MM MM AB
, dấu "=" xảy ra khi
1 3
,
M A M B
. Do đó
min 1 3
2 2 2
P AB I I
1 3
9945
13
I I
.
I
3
I
2
I
1
M
8
6
4
3O
y
x
B
A
| 1/97
| | Tải xuống

Có thể bạn quan tâm:

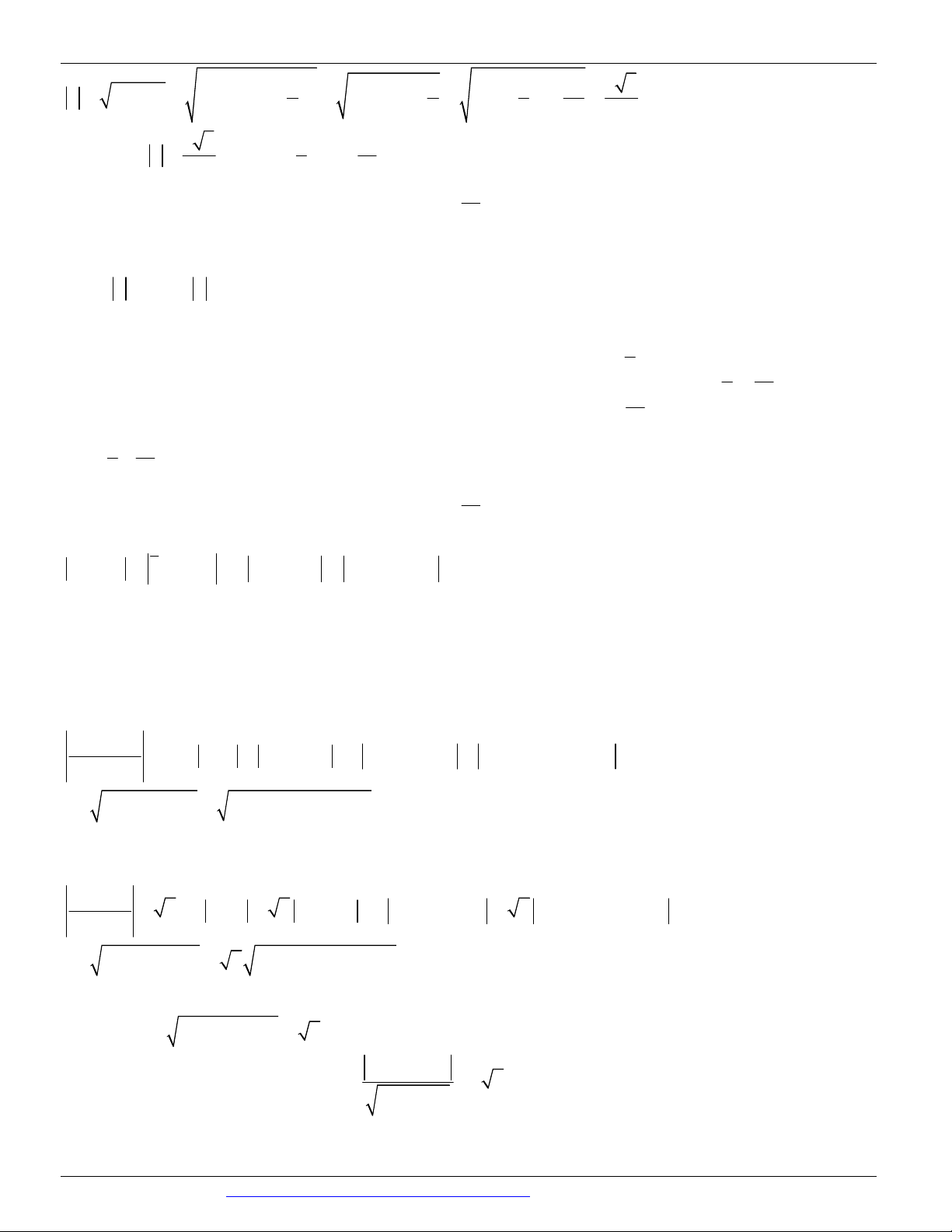
Preview text:

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 CHUYÊN
KHÁI NIỆM SỐ PHỨC, CÁC PHÉP TOÁN SỐ PHỨC ĐỀ 25
VÀ MỘT SỐ BÀI TOÁN LIÊN QUAN MỤC LỤC
Phần A. CÂU HỎI .......................................................................................................................................................... 1
Dạng 1. Xác định các yếu tố cơ bản của số phức ......................................................................................................... 1
Dạng 1.1 Xác định phần thực, phần ảo của số phức .................................................................................................... 1
Dạng 1.2 Xác định số phức liên hợp, số phức đối, môđun của số phức ....................................................................... 2
Dạng 2. Biểu diễn hình học cơ bản của số phức .......................................................................................................... 3
Dạng 3. Thực hiện các phép tính cộng, trừ, nhân, chia cơ bản của số phức ............................................................. 6
Dạng 3.1 Phép tính cộng trừ 2 số phức ........................................................................................................................ 6
Dạng 3.2 Phép tính nhân, chia 2 số phức ..................................................................................................................... 7
Dạng 4. Tìm số phức thỏa mãn điều kiện cho trước ................................................................................................. 10
Dạng 4.1 Điều kiện cho trước không chứa yếu tố môđun .......................................................................................... 10
Dạng 4.2 Điều kiện cho trước chứa yếu tố môđun ..................................................................................................... 12
Phần B. LỜI GIẢI THAM KHẢO ............................................................................................................................. 16
Dạng 1. Xác định các yếu tố cơ bản của số phức ....................................................................................................... 16
Dạng 1.1 Xác định phần thực, phần ảo của số phức .................................................................................................. 16
Dạng 1.2 Xác định số phức liên hợp, số phức đối, môđun của số phức ..................................................................... 16
Dạng 2. Biểu diễn hình học cơ bản của số phức ........................................................................................................ 17
Dạng 3. Thực hiện các phép tính cộng, trừ, nhân, chia cơ bản của số phức ........................................................... 18
Dạng 3.1 Phép tính cộng trừ 2 số phức ...................................................................................................................... 18
Dạng 3.2 Phép tính nhân, chia 2 số phức ................................................................................................................... 18
Dạng 4. Tìm số phức thỏa mãn điều kiện cho trước ................................................................................................. 21
Dạng 4.1 Điều kiện cho trước không chứa yếu tố môđun .......................................................................................... 21
Dạng 4.2 Điều kiện cho trước chứa yếu tố môđun ..................................................................................................... 25 Phần A. CÂU HỎI
Dạng 1. Xác định các yếu tố cơ bản của số phức
Dạng 1.1 Xác định phần thực, phần ảo của số phức
Câu 1. (Mã đề 104 BGD&ĐT NĂM 2018) Số phức có phần thực bằng 1 và phần ảo bằng 3 là A. 1 3i B. 1   3i C. 1 3i D. 1   3i
Câu 2. (MĐ 103 BGD&ĐT NĂM 2017-2018) Số phức 5  6i có phần thực bằng A. 6  . B. 6 . C. 5  . D. 5
Câu 3. (Mã đề 102 BGD&ĐT NĂM 2018) Số phức có phần thực bằng 3 và phần ảo bằng 4 là
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. 3  4i B. 4  3i C. 3  4i D. 4  3i
Câu 4. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Kí hiệu a, b lần lượt là phần thực và phần ảo của số phức
3  2 2i . Tìm a , b . A. a  3;b  2
B. a  3;b  2 2
C. a  3;b  2
D. a  3;b  2 2
Câu 5. (Mã đề 101 BGD&ĐT NĂM 2018) Số phức 3
  7i có phần ảo bằng: A. 7 B. 7  C. 3  D. 3
Câu 6. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Số phức nào dưới đây là số thuần ảo.
A. z  3  i B. z  2
C. z  2  3i D. z  3i
Câu 7. (MĐ 105 BGD&ĐT NĂM 2017) Cho số phức z  2  3i . Tìm phần thực a của z ? A. a  2 B. a  3 C. a  2 D. a  3
Câu 8. (THPT CẨM GIÀNG 2 NĂM 2018-2019) Cho số phức z  3  4i . Tìm phần thực và phần ảo của số phức z .
A. Phần thực là  4 và phần ảo là 3i .
B. Phần thực là 3 và phần ảo là  4 .
C. Phần thực là  4 và phần ảo là 3 .
D. Phần thực là 3 và phần ảo là  4i .
Câu 9. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho số phức z  3  2i . Tìm phần thực và phần ảo của số phức z :
A. Phần thực bằng 3 và Phần ảo bằng 2i
B. Phần thực bằng 3 và Phần ảo bằng 2 C. Phần thực bằng 3
 và Phần ảo bằng 2  i D. Phần thực bằng 3
 và Phần ảo bằng 2 
Dạng 1.2 Xác định số phức liên hợp, số phức đối, môđun của số phức
Câu 10. (Mã đề 104 - BGD - 2019) Số phức liên hợp của số phức z  3  2i là. A. 3  2i . B. 3   2i . C. 2   3i . D. 3   2i .
Câu 11. (Mã 103 - BGD - 2019) Số phức liên hợp của số phức 1 2i là: A. 1  2i . B. 1 2i . C. 2  i . D. 1   2i .
Câu 12. (MĐ 104 BGD&DT NĂM 2017) Cho số phức z  2  i . Tính z . A. z  5 B. z  5 C. z  2 D. z  3
Câu 13. (Mã 102 - BGD - 2019) Số phức liên hợp của số phức 5  3i là A. 3   5i . B. 5   3i . C. 5  3i . D. 5   3i .
Câu 14. (Mã đề 101 - BGD - 2019) Số phức liên hợp của số phức 3  4i là A. 3  4i . B. 4   3i . C. 3   4i . D. 3   4i .
Câu 15. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Cho số phức z  3  2i . Tìm phần
thực và phần ảo của số phức z . A. Phần thực bằng 3  và phần ảo bằng 2  .
B. Phần thực bằng 3 và phần ảo bằng 2  .
C. Phần thực bằng 3 và phần ảo bằng 2i .
D. Phần thực bằng 3 và phần ảo bằng 2 .
Câu 21 Cho số phức z  3 2i . Tìm phần thực và phần ảo của số phức z .
A. Phần thực bằng 3 và phần ảo bằng 2i . B. Phần thực bằng 3  và phần ảo bằng 2  . C. Phần thực bằng 3  và phần ảo bằng 2  i .
D. Phần thực bằng 3 và phần ảo bằng 2 .
Câu 16. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Số phức đối của z  5  7i là?
A. z  5  7i . B. z  5   7i . C. z  5   7i .
D. z  5  7i .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 17. (THPT CHUYÊN SƠN LA NĂM 2018-2019 LẦN 01) Số phức liên hợp của số phức z  1  2i là
A. z  1 2i .
B. z  2  i . C. z  1   2i . D. z  1   2i .
Câu 18. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Số phức liên hợp của số
phức z  5  6i là A. z  5   6i . B. z  5   6i .
C. z  6  5i .
D. z  5  6i .
Câu 19. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Cho số phức z  2  3i . Số phức
liên hợp của số phức z là:
A. z  3  2i .
B. z  3  2i . C. z  2   3i .
D. z  2  3i .
Dạng 2. Biểu diễn hình học cơ bản của số phức
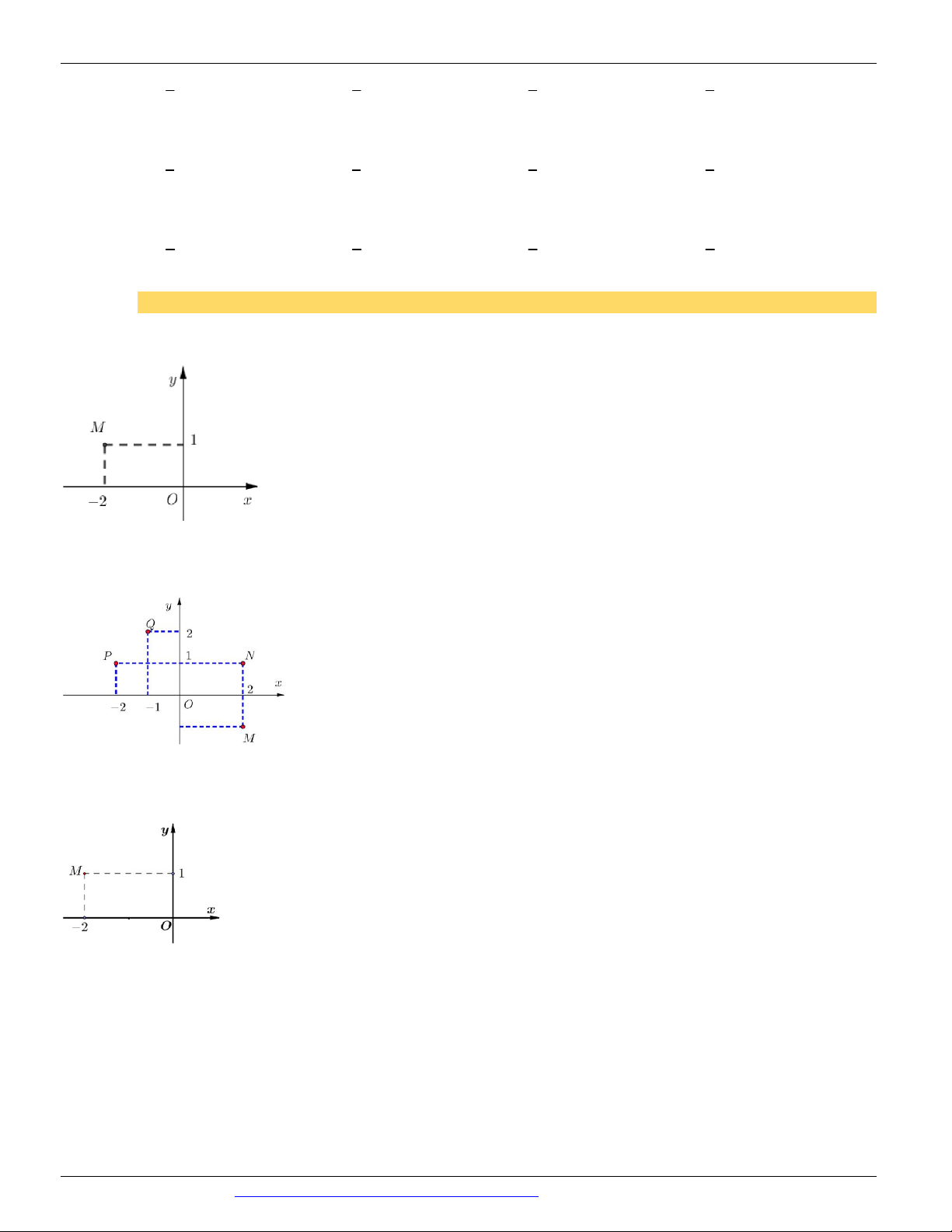
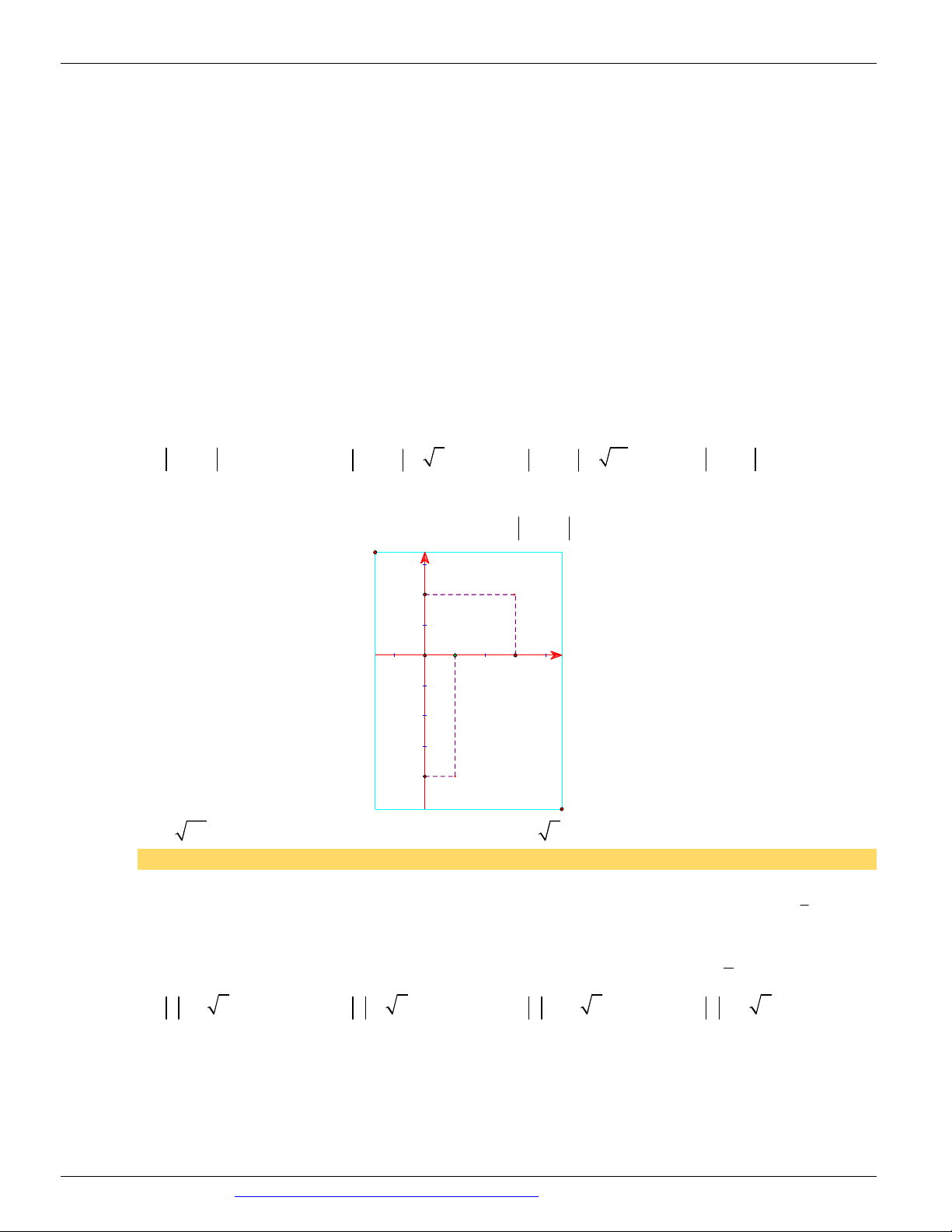
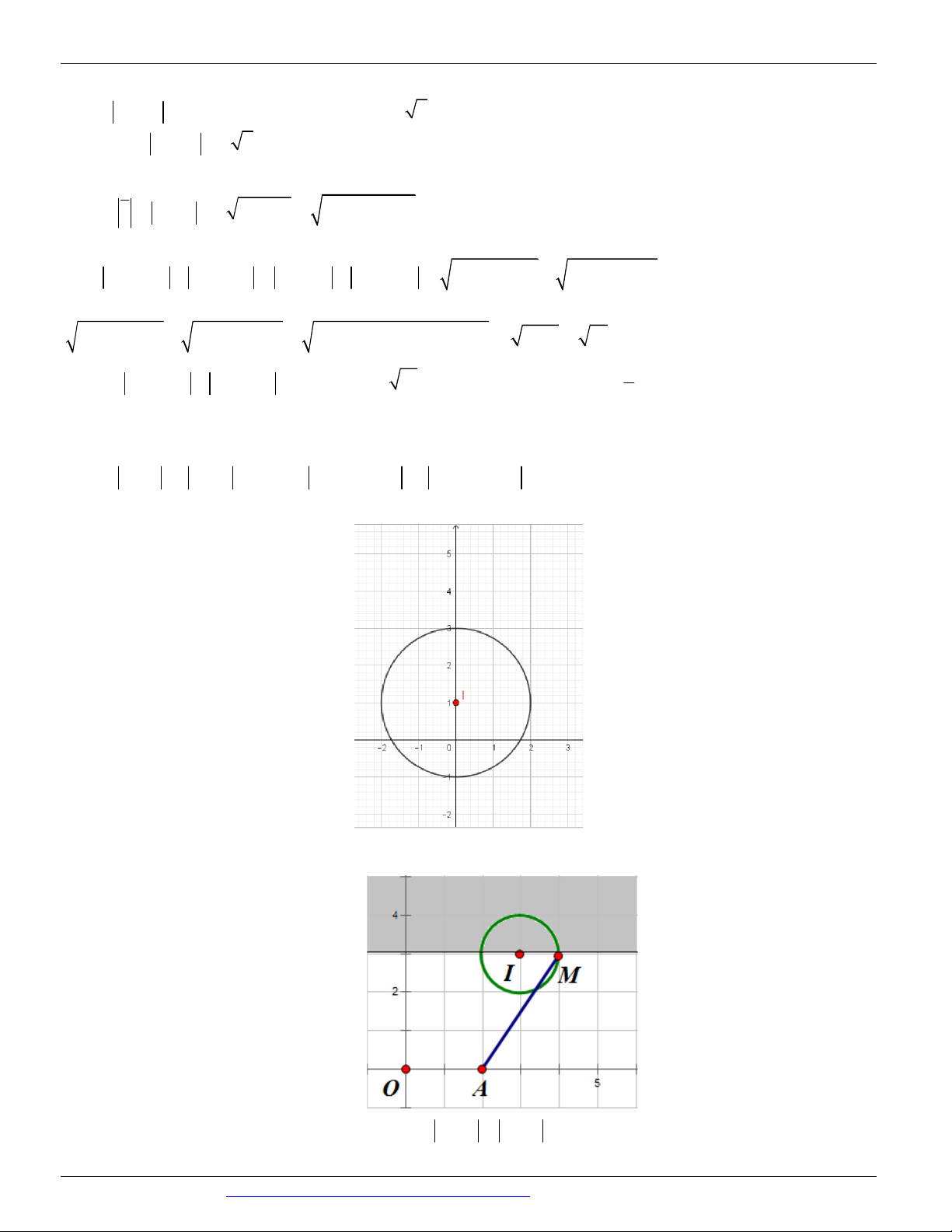
Câu 20. (ĐỀ THAM KHẢO BGD & ĐT 2018) Điểm M trong hình vẽ bên là điểm biểu diễn số phức
A. z  1  2i
B. z  1  2i
C. z  2  i
D. z  2  i
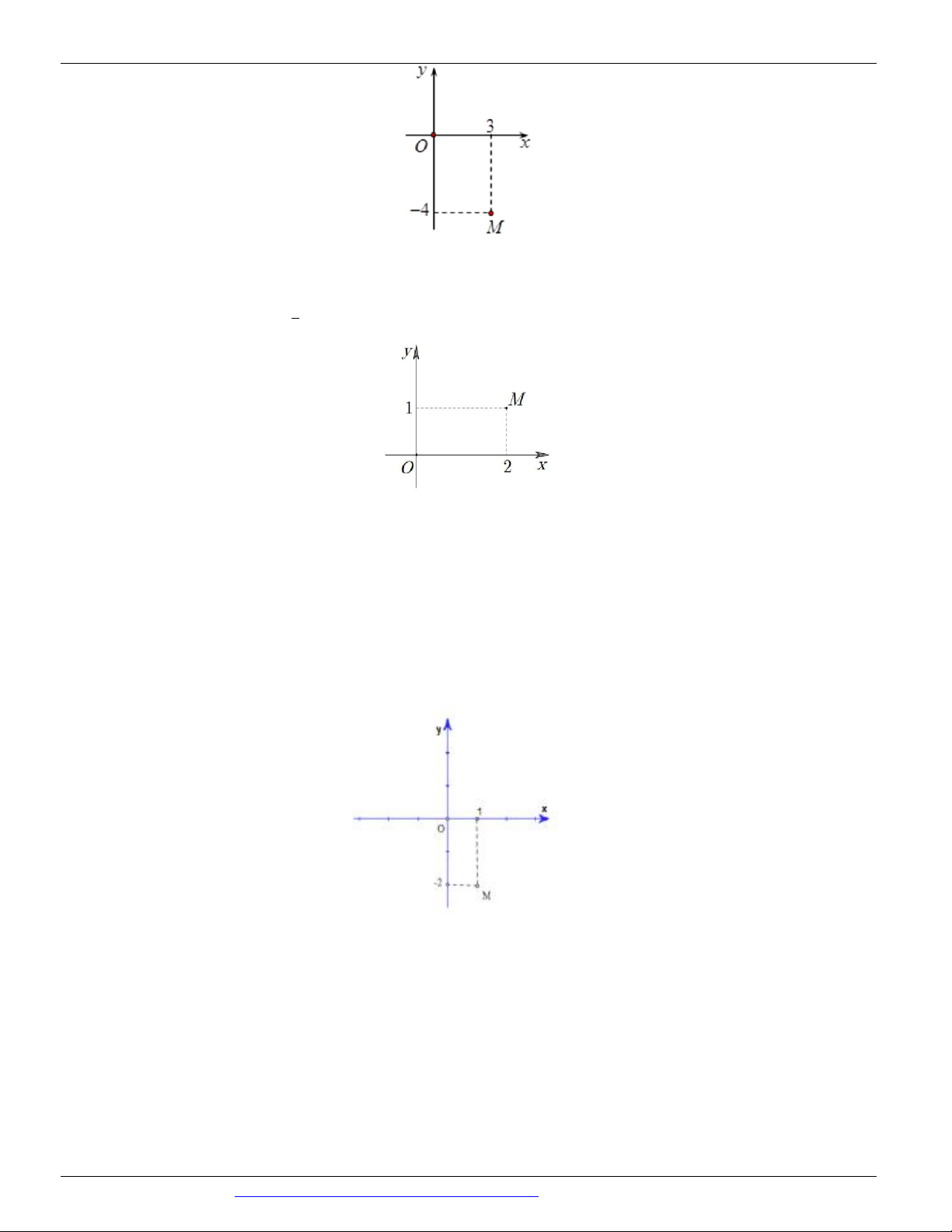
Câu 21. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Điểm nào trong hình vẽ bên là điểm biểu diễn
của số phức z  1   2i ? A. P B. M C. Q D. N
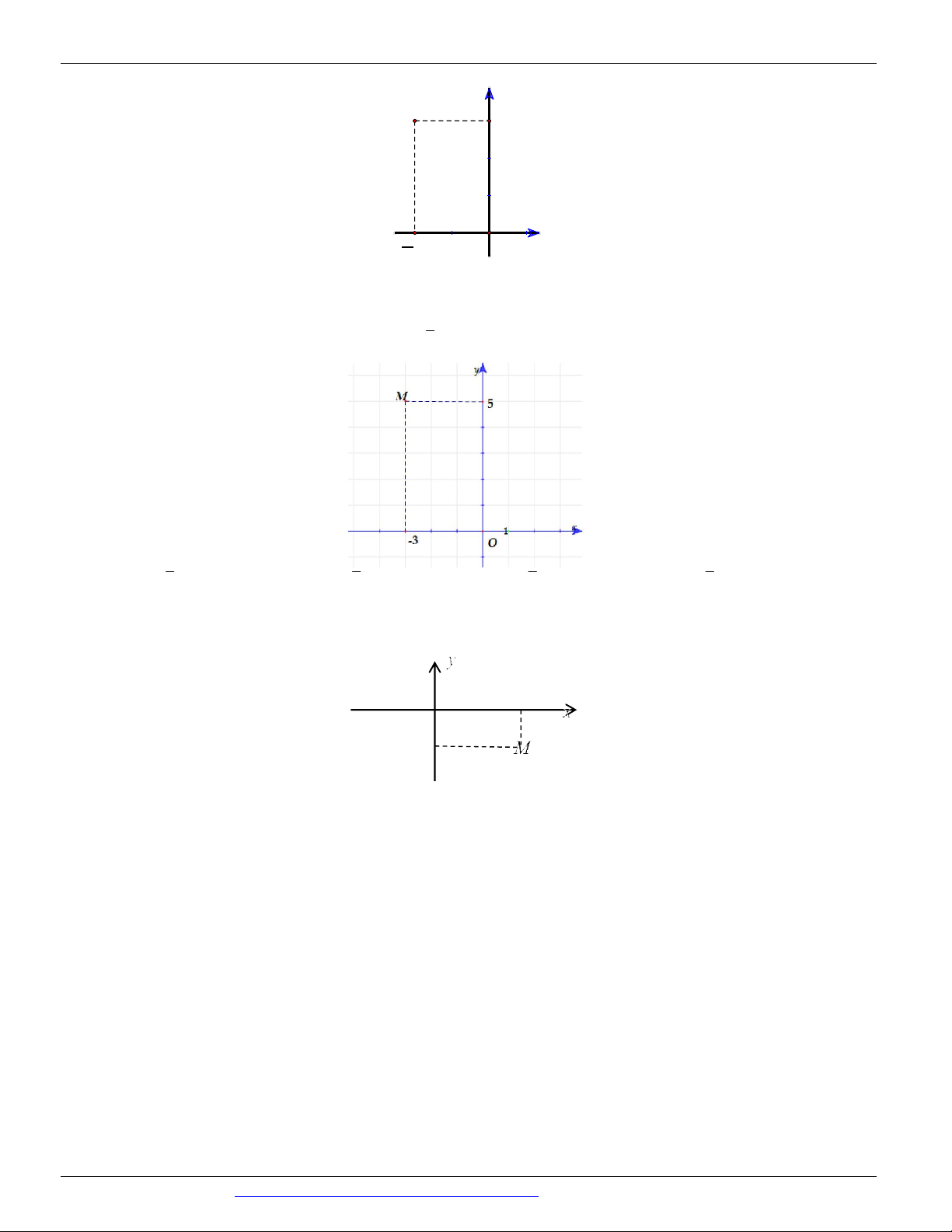
Câu 22. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là
điểm M như hình bên?
A. z  1 2i
B. z  1 2i C. z  2   i
D. z  2  i 1 2 3 4
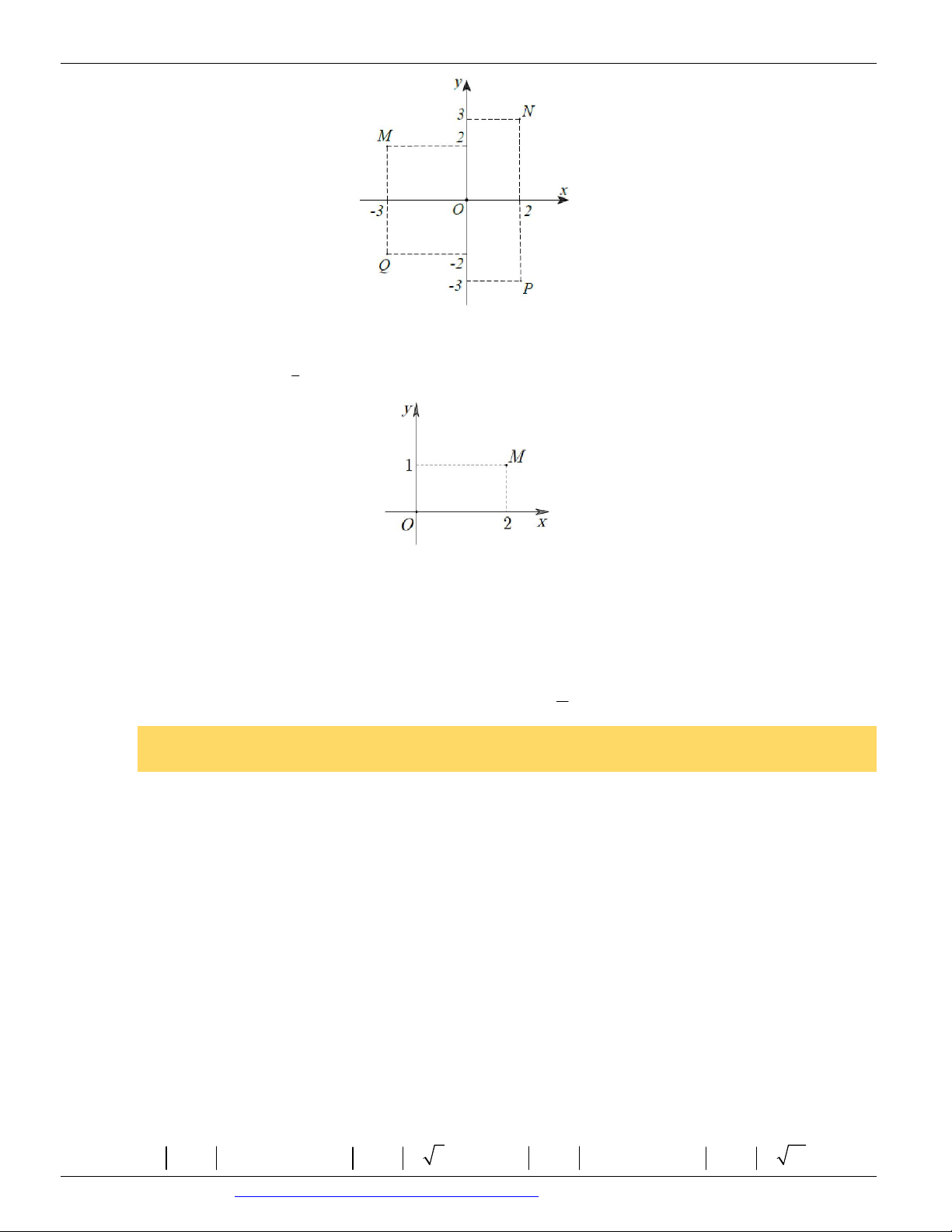
Câu 23. Điểm M trong hình vẽ bên là điểm biểu diễn của số phức z . Tìm phần thực và phần ảo của số phức z .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
A. Phần thực là 3 và phần ảo là 4  i
B. Phần thực là 3 và phần ảo là 4  C. Phần thực là 4
 và phần ảo là 3i D. Phần thực là 4  và phần ảo là 3
Câu 24. (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Trong hình vẽ bên, điểm M
biểu diễn số phức z . Số phức z là: A. 1 2i . B. 2  i . C. 1 2i . D. 2  i .
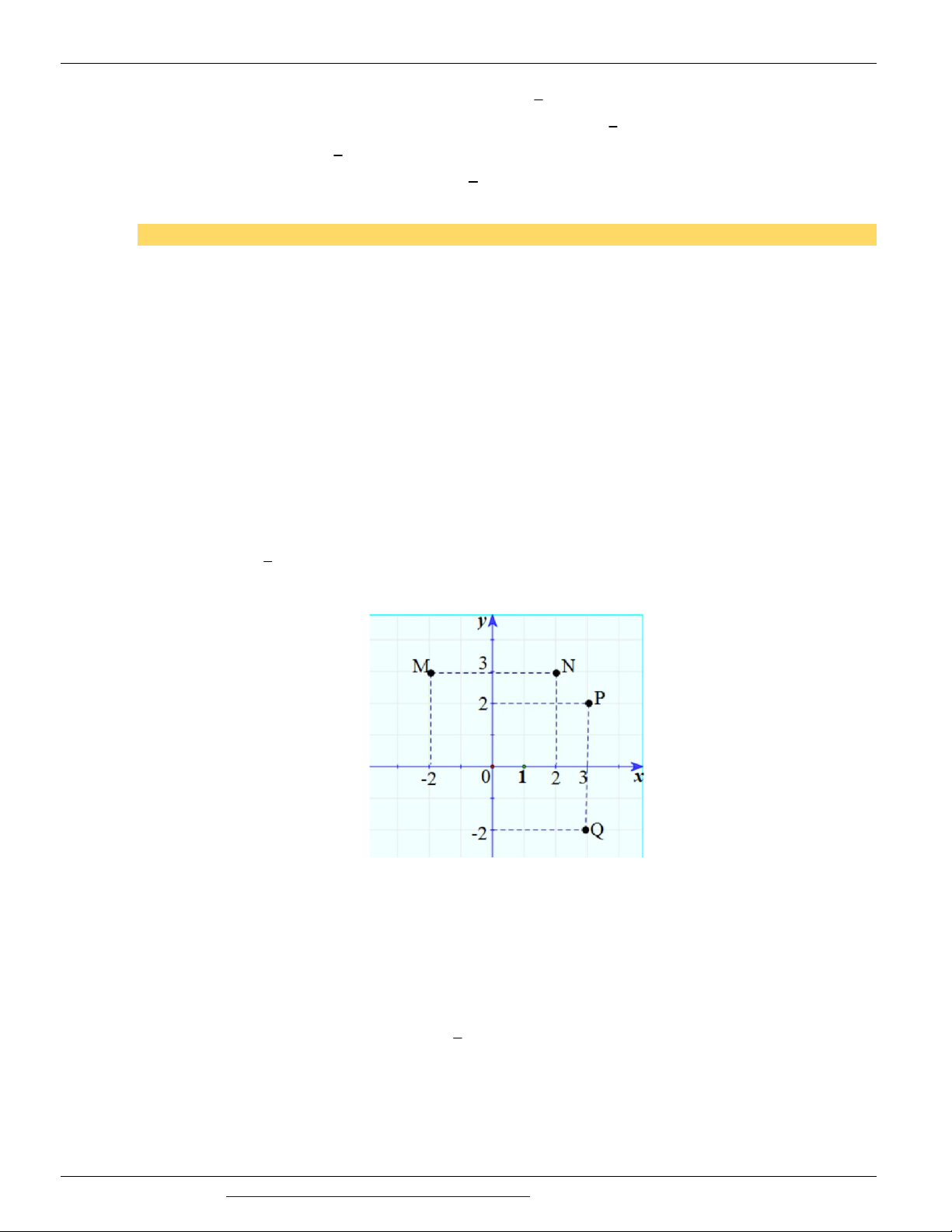
Câu 25. (HỌC MÃI NĂM 2018-2019-LẦN 02) Điểm nào ở hình vẽ bên biểu diễn số phức z  3  2i ? A. M . B. N . C. P . D. Q .
Câu 26. (THPT QUỲNH LƯU 3 NGHỆ AN NĂM 2018-2019) Điểm biểu diễn hình học của số phức
z  2  3i là điểm nào trong các điểm sau đây? A. M  2  ;3 . B. Q  2  ;   3 . C. N 2;  3 . D. P 2;3 .
Câu 27. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Số phức nào dưới đây có điểm biểu diễn trên
mặt phẳng tọa độ là điểm M như hình vẽ bên? A. 1 2 . i B. i  2. C. i  2. D. 1 2 . i
Câu 28. (SỞ GD&ĐT THANH HÓA NĂM 2018 - 2019) Điểm M trong hình vẽ bên dưới biểu thị cho số phức
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 y M 3 x O 2 A. 3  2 . i B. 2  3 . i C. 2   3 . i D. 3  2 . i
Câu 29. (CHUYÊN LAM SƠN THANH HÓA LẦN 2 NĂM 2018-2019) Điểm M trong hình vẽ bên biểu
diễn số phức z . Chọn kết luận đúng về số phức z .
A. z  3  5i .
B. z  3  5i .
C. z  3  5i .
D. z  3  5i .
Câu 30. (ĐỀ THI CÔNG BẰNG KHTN LẦN 02 NĂM 2018-2019) Điểm M trong hình vẽ là biểu diễn hình
học của số phức nào dưới đây? 2 O -1
A. z  2  i .
B. z  2  i . C. z  1   2i . D. z  1   2i .
Câu 31. (SỞ GD&ĐT BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Số phức nào sau đây có điểm biểu diễn là M (1; 2) ? A. 1   2i B. 1 2i C. 1 2i D. 2   i
Câu 32. Trong mặt phẳng tọa độ Oxy , điểm biểu diễn của hai số phức đối nhau là
A. hai điểm đối xứng nhau qua gốc tọa độ O .
B. hai điểm đối xứng nhau qua trục hoành.
C. hai điểm đối xứng nhau qua trục tung.
D. hai điểm đối xứng nhau qua đường thẳng y x .
Câu 33. (TT THANH TƯỜNG NGHỆ AN NĂM 2018-2019 LẦN 02) Điểm nào trong hình vẽ dưới đây là
điểm biểu diễn số phức liên hợp của số phức z  3  i  2 ?
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. M . B. N . C. Q . D. P .
Câu 34. (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Trong hình vẽ bên, điểm M
biểu diễn số phức z . Số phức z là: A. 1 2i . B. 2  i . C. 1 2i . D. 2  i .
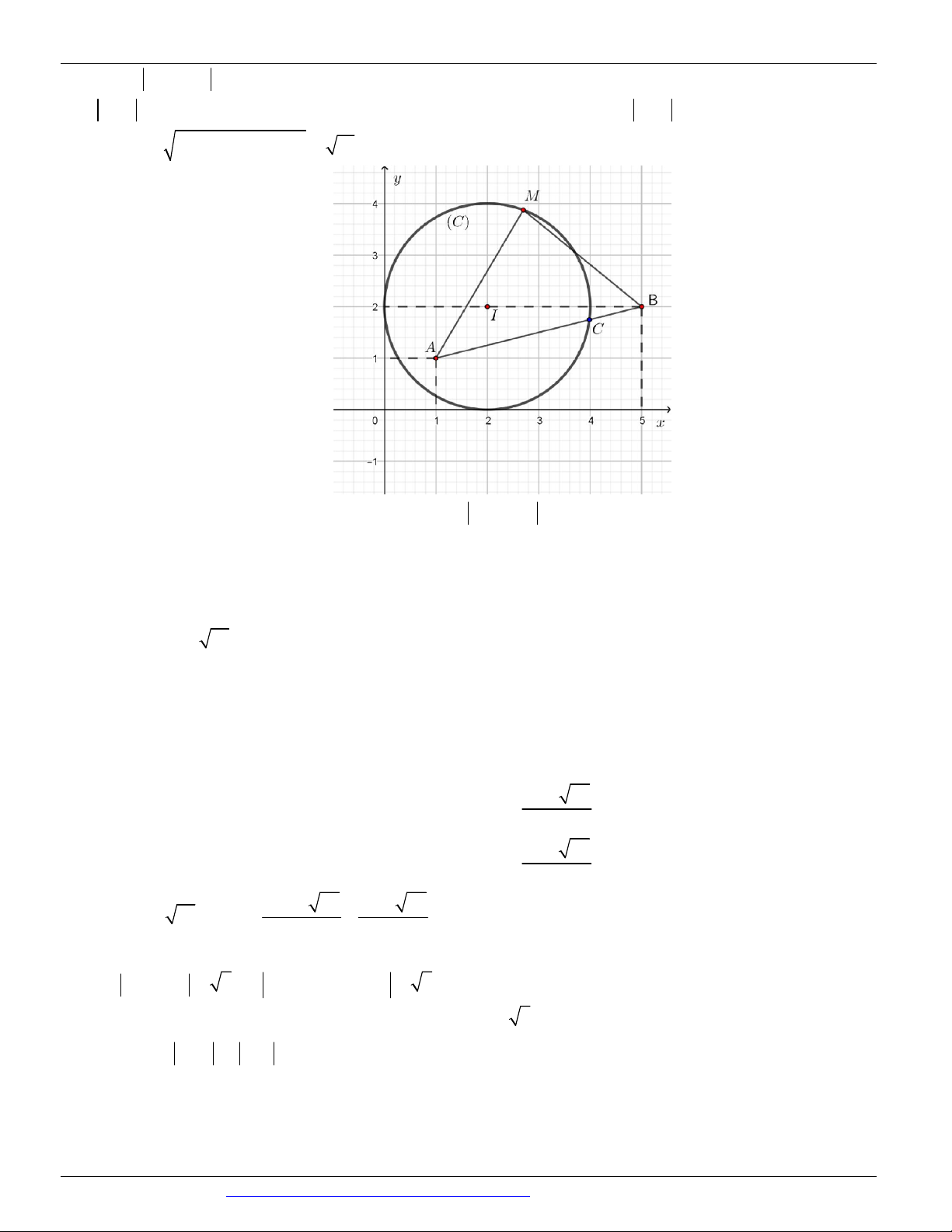
Câu 35. (ĐỀ 01 ĐỀ PHÁT TRIỂN ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Trong mặt phẳng tọa độ Oxy , 3 điểm , A ,
B C lần lượt là điểm biểu diễn của ba số phức
z  3  7i, z  9  5i và z  5  9i . Khi đó, trọng tâm G 1 2 3
là điểm biểu diễn của số phức nào sau đây? 7
A. z  1 9i .
B. z  3  3i . C. z   i .
D. z  2  2i . 3
Dạng 3. Thực hiện các phép tính cộng, trừ, nhân, chia cơ bản của số phức
Dạng 3.1 Phép tính cộng trừ 2 số phức
Câu 36. (Mã đề 104 - BGD - 2019) Cho hai số phức z  2  i và z  1 i . Trên mặt phẳng tọa độ Oxy , 1 2
điểm biểu diễn của số phức 2z z có tọa độ là 1 2 A. 0; 5 . B. 5;  1  . C.  1  ; 5 . D. 5; 0 .
Câu 37. (Mã 103 - BGD - 2019) Cho hai số phức z  1 i và z  2  i . Trên mặt phẳng tọa độ Oxy , điểm 1 2
biểu diễn số phức z  2z có tọa độ là 1 2 A. (3; 5) . B. (5; 2) . C. (5;3) . D. (2; 5) .
Câu 38. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho 2 số phức z  5  7i và z  2  3i . Tìm số phức 1 2
z z z 1 2 .
A. z  3  10i B. 14
C. z  7  4i
D. z  2  5i
Câu 39. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hai số phức z  1 i và z  2  3i . Tính môđun 1 2
của số phức z z . 1 2
A. z z  5 .
B. z z  5 .
C. z z  1.
D. z z  13 . 1 2 1 2 1 2 1 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 40. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho hai số phức z  4  3i và z  7  3i . Tìm số phức 1 2
z z z . 1 2 A. z  3   6i B. z  11 C. z  1  10i
D. z  3  6i
Câu 41. (MĐ 104 BGD&DT NĂM 2017) Cho số phức z  1 2i , z  3  i . Tìm điểm biểu diễn của số 1 2
phức z z z trên mặt phẳng tọa độ. 1 2 A. M 2; 5 B. P 2;   1 C. Q  1  ; 7 D. N 4; 3
Câu 42. (MĐ 104 BGD&DT NĂM 2017) Tìm số phức z thỏa mãn z  2 3i  3  2i .
A. z  5  5i
B. z  1 i
C. z  1 5i
D. z  1 i
Câu 43. (MĐ 105 BGD&ĐT NĂM 2017) Cho hai số phức z  1  3i và z  2  5i . Tìm phần ảo b của 1 2
số phức z z z . 1 2 A. b  3 B. b  2 C. b  2 D. b  3
Câu 44. (CHUYEN PHAN BỘI CHÂU NGHỆ AN NĂM 2018-2019 LẦN 02) Cho hai số phức z  1 i 1
và z  2  3i . Tính môđun của số phức z z . 2 1 2
A. z z  1.
B. z z  5 .
C. z z  13 .
D. z z  5 . 1 2 1 2 1 2 1 2
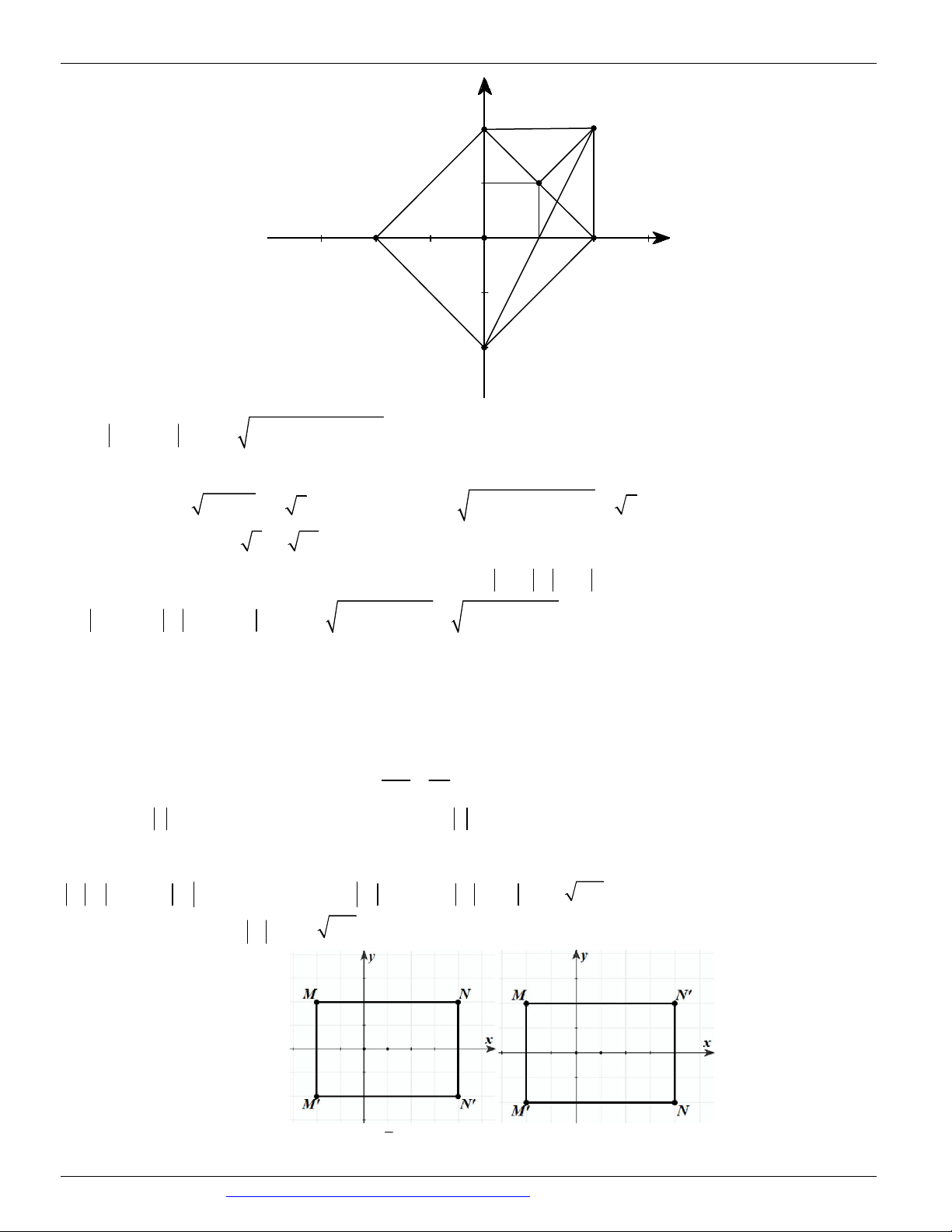
Câu 45. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Gọi z , z lần lượt có điểm 1 2
biểu diễn là M và N trên mặt phẳng phức ở hình bên. Tính z z . 1 2 y 2 M O 1 3 x -4 N A. 2 29 . B. 20 . C. 2 5 . D. 116 .
Dạng 3.2 Phép tính nhân, chia 2 số phức
Câu 46. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho số phức z  2  5 .
i Tìm số phức w iz z A. w  3   3i . B. w  3  7 . i . C. w  7   7i
D. w  7  3i .
Câu 47. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Tính môđun của số phức z biết z  4  3i1 i . A. z  5 2 B. z  2 C. z  25 2 D. z  7 2
Câu 48. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho số phức 3
z  1 i i . Tìm phần thực a và phần ảo b của z .
A. a  1, b  0
B. a  0, b  1
C. a  1, b  2
D. a  2, b  1
Câu 49. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho số phước z  1 2 .
i Điểm nào dưới đây là điểm biểu
diễn số phức w iz trên mặt phẳng tọa độ
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. Q 1; 2 B. N 2;1 C. P 2;1 D. M 1; 2
Câu 50. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Trong mặt phẳng tọa độ, điểm M là điểm biểu diễn
của số phức z . Điểm nào trong hình vẽ là điểm biểu diễn của số phức 2z ? y Q E M O x N P A. Điểm Q B. Điểm E C. Điểm P D. Điểm N
Câu 51. (Mã đề 101 - BGD - 2019) Cho hai số phức z  1 i và z  1 2i . Trên mặt phẳng tọa độ Oxy , 1 2
điểm biểu diễn số phức 3z z có tọa độ là: 1 2 A. 1; 4 . B.  1  ; 4 . C. 4  ;1 . D. 4;  1  .
Câu 52. (Mã 102 - BGD - 2019) Cho hai số phức z  2
  i và z  1 .
i Trên mặt phẳng tọa độ Oxy, 1 2
điểm biểu diễn số phức 2z z có tọa độ là 1 2 A.  3  ;3 . B.  3  ; 2 . C. 3; 3   . D. 2; 3   .
Câu 53. Tìm số phức liên hợp của số phức z i 3i   1 .
A. z  3  i . B. z  3   i .
C. z  3  i . D. z  3   i .
Câu 54. (THPT CẨM GIÀNG 2 NĂM 2018-2019) Cho số phức z thỏa mãn z 1 2i  4  3i . Tìm số phức
liên hợp z của z . 2  11 2 11 2  11 2 11 A. z   i . B. z   i . C. z =i . D. z =i . 5 5 5 5 5 5 5 5
Câu 55. (ĐỀ 15 LOVE BOOK NĂM 2018-2019) Cho số phức z thỏa mãn z 1 i  3  5i . Tính môđun của z A. z  17 . B. z  16 . C. z  17 . D. z  4 .
Câu 56. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Cho số phức z    i2 1 2 . 1
Tính mô đun của số phức . z 1 1 1 A. . B. 5 . C. . D. . 5 25 5 2
Câu 57. (KTNL GV THPT LÝ THÁI TỔ NĂM 2018-2019) Cho số phức z  1 i 1 2i . Số phức z có phần ảo là: A. 2 . B. 2 . C. 4 . D. 2  i . 1
Câu 58. (KTNL GV THUẬN THÀNH 2 BẮC NINH NĂM 2018-2019) Cho số phức z  1 i . Tìm số 3
phức w  iz  3z . 8 8 10 10 A. w  . B. w   i . C. w  . D. w   i . 3 3 3 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 59. (THPT YÊN PHONG SỐ 1 BẮC NINH NĂM 2018-2019 LẦN 01) Cho số phức z  2   i . Điểm
nào dưới đây là biểu diễn của số phức w iz trên mặt phẳng toạ độ? A. M  1  ; 2  . B. P  2   ;1 . C. N 2  ;1 . D. Q 1; 2.
Câu 60. (CHUYÊN BẮC GIANG NĂM 2018-2019 LẦN 02) Cho số phức z  1 2i . Tìm tổng phần thực
và phần ảo của số phức w  2z z . A. 3 B. 5 C. 1 D. 2
Câu 61. (CHUYÊN KHTN LẦN 2 NĂM 2018-2019) Cho số phức z khác 0 . Khẳng định nào sau đây là sai? z A. là số thuần ảo.
B. z.z là số thực.
C. z z là số thực.
D. z z là số ảo. z
Câu 62. (CHUYÊN LAM SƠN THANH HÓA LẦN 2 NĂM 2018-2019) Cho hai số phức z  1 2i và 1
z  3  4i . Số phức 2z  3z z z là số phức nào sau đây? 2 1 2 1 2 A. 10i . B. 1  0i . C. 11 8i . D. 1110i .
Câu 63. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Tìm tọa độ điểm M là điểm biểu diễn
số phức z biết z thỏa mãn phương trình 1 iz  3  5i . A. M  1  ; 4 .
B. M 1;  4 . C. M 1; 4 . D. M 1;  4 .
Câu 64. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Cho số phức z thỏa mãn
1 3iz  5  7 .i Mệnh đề nào sau đây đúng? 13 4 13 4 13 4 13 4 A. z   i . B. z    i . C. z    i . D. z   i . 5 5 5 5 5 5 5 5
Câu 65. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Cho số phức
z    i2019 1
. Phần thực của z bằng A. 1009 2 . B. 2019 2 . C. 2019 2 . D. 1009 2 .
Câu 66. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Cho số phức
2  3i4  iz
. Tìm tọa độ điểm biểu diễn của số phức z trên mặt phẳng Oxy . 3  2i A. 1; 4 . B.  1  ; 4 . C.  1  ;  4 . D. 1;  4 .
Câu 67. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Cho z  2  4i, z  3 5i . Xác định phần thực 1 2 2
của w z .z 1 2 A. 120 . B. 32 . C. 88 . D. 152 .
Câu 68. (CHUYÊN BẮC GIANG NĂM 2018-2019 LẦN 02) Cho số phức z thỏa mãn phương trình 2
(3  2i)z  (2  i)  4  i . Tìm tọa độ điểm M biểu diễn số phức z. A. M  1   ;1 B. M  1  ;   1 C. M 1  ;1 D. M 1;   1
Câu 69. (THPT CHUYÊN ĐẠI HỌC VINH NĂM 2018-2019 LẦN 01) Cho số phức z thỏa mãn   i2 1 3
z  4  3i . Môđun của z bằng 5 5 2 4 A. B. C. D. 4 2 5 5
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 2018
Câu 70. (THPT CHU VĂN AN - HÀ NỘI - 2018) Số phức z  1 i  1 i  ...  1 i có phần ảo bằng A. 1009 2 1. B. 1009 1 2 . C. 1009 2 1 . D.   1009 2   1 .
Câu 71. (THPT NGÔ QUYỀN - QUẢNG NINH - HKII - 2018) Tìm tất cả các giá trị thực của tham số m m  2i để số phức z  có phần thực dương m  2im  2 A. m  2 . B.  . C. 2  m  2 . D. m  2 . m  2  3  i
Câu 72. (THPT NGÔ QUYỀN - QUẢNG NINH - HKII - 2018) Cho z
. Tổng phần thực và phần x i ảo của z là 2x  4 4x  2 4x  2 2x  6 A. . B. . C. . D. . 2 2 2 x 1 2 x 1
Câu 73. (THCS&THPT NGUYỄN KHUYẾN - BÌNH DƯƠNG - 2018) Gọi T là tổng phần thực, phần ảo của số phức 2 3 2018
w i  2i  3i  ...  2018i
. Tính giá trị của T. A. T  0. B. T  1  . C. T  2. D. T  2  .
Dạng 4. Tìm số phức thỏa mãn điều kiện cho trước
Dạng 4.1 Điều kiện cho trước không chứa yếu tố môđun
Câu 74. (Mã đề 104 BGD&ĐT NĂM 2018) Tìm hai số thực x và y thỏa mãn 2x  3yi  3  i  5x  4i
với i là đơn vị ảo.
A. x  1; y  1.
B. x  1; y  1 .
C. x  1; y  1 .
D. x  1; y  1 .
Câu 75. (MĐ 105 BGD&ĐT NĂM 2017) Tìm tất cả các số thực x, y sao cho 2
x  1 yi  1 2i .
A. x  2 , y  2
B. x   2 , y  2
C. x  0, y  2
D. x  2 , y  2
Câu 76. (Mã đề 101 BGD&ĐT NĂM 2018) Tìm hai số thực x và y thỏa mãn 2x  3yi  1 3i  x  6i
với i là đơn vị ảo.
A. x  1; y  1
B. x  1; y  3
C. x  1; y  3
D. x  1; y  1
Câu 77. (Mã đề 104 - BGD - 2019) Cho số phức z thỏa mãn 2  iz  3 16i  2 z i . Môđun của z bằng A. 13 . B. 5 . C. 5 . D. 13 .
Câu 78. (Mã 103 - BGD - 2019) Cho số z thỏa mãn 2  iz  4 z i  8
 19i . Môđun của z bằng A. 13 . B. 5 . C. 13 . D. 5 .
Câu 79. (Mã đề 102 BGD&ĐT NĂM 2018) Tìm hai số thực x và y thỏa mãn 3x  2yi  2  i  2x  3i
với i là đơn vị ảo.
A. x  2; y  2
B. x  2; y  1
C. x  2; y  2
D. x  2; y  1
Câu 80. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Tìm các số thực , a b thỏa mãn
2a  (b i )i  1 2i với i là đơn vị ảo.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1
A. a  0,b  1.
B. a  1,b  2.
C. a  0,b  2. D. a  ,b  1. 2
Câu 81. (MĐ 103 BGD&ĐT NĂM 2017-2018) Tìm hai số thực x và y thỏa mãn
3x yi  4  2i  5x  2i với i là đơn vị ảo.
A. x  2 ; y  4 B. x  2  ; y  0
C. x  2 ; y  0 D. x  2  ; y  4
Câu 82. (Mã 102 - BGD - 2019) Cho số phức z thoả mãn 3z i2 3iz  7 16  .
i Môđun của z bằng A. 3. B. 5. C. 5. D. 3.
Câu 83. (Mã đề 101 - BGD - 2019) Cho số phức z thỏa mãn 3 z i  2  iz  3 10i . Môđun của z bằng A. 3 . B. 3 . C. 5 . D. 5 .
Câu 84. (THPT CẨM GIÀNG 2 NĂM 2018-2019) Tìm hai số thực x và y thỏa mãn
2x  3yi  1 3i  1
  6i với i là đơn vị ảo.
A. x  1 ; y  3  . B. x  1  ; y  3  . C. x  1  ; y  1  .
D. x  1 ; y  1  .
Câu 85. (ĐỀ 04 VTED NĂM 2018-2019) Tìm hai số thực x và y thỏa mãn 2x  3yi  3 i  5x  4i
với i là đơn vị ảo. A. x  1  , y  1 
B. x  1, y  1 C. x  1  , y  1
D. x  1, y  1 
Câu 86. (THPT CHUYÊN SƠN LA NĂM 2018-2019 LẦN 01) Tìm các số thực x và y thỏa mãn
3x  2  2y  
1 i   x  
1   y  5i , với i là đơn vị ảo. 3 3 4 4 3 4 A. x  , y  2  .
B. x   , y   .
C. x  1, y  . D. x  , y  . 2 2 3 3 2 3
z a bi a,b  
Câu 87. (CHUYÊN PHAN BỘI CHÂU NĂM 2018-2019) Cho số phức thỏa mãn
1 iz  2z  3  2i . Tính P a b 1 1 A. P  1 B. P   C. P  D. P  1 2 2
Câu 88. (CHUYÊN KHTN NĂM 2018-2019 LẦN 01) Cho số phức z thỏa mãn 2  3iz  4  3i  13  4i
. Môđun của z bằng A. 2 . B. 4 . C. 2 2 . D. 10 .
Câu 89. (HSG BẮC NINH NĂM 2018-2019) Cho số phức z x yi x, y   thỏa mãn
1 2iz z  3  4i . Tính giá trị của biểu thức S  3x  2y . A. S  12 B. S  11 C. S  13 D. S  10
Câu 90. (SỞ GD&ĐT BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Tổng phần thực và phần ảo của số phức
z thoả mãn iz  1 iz  2  i bằng A. 6 B. 2  C. 2 D. 6 
Câu 91. (SỞ GD&ĐT BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho a, b   và thỏa mãn
a bii  2a 1 3i , với i là đơn vị ảo. Giá trị a b bằng
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. 4 B. 10  C. 4  D. 10
Câu 92. (CHUYEN PHAN BỘI CHÂU NGHỆ AN NĂM 2018-2019 LẦN 02) Cho số phức
z a bi (a, b  ) thoả mãn (1 i)z  2z  3  2i . Tính P a b 1 1 A. P  1 . B. P   . C. P  . D. P  1 2 2
Câu 93. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Tìm số phức z biết 4z  5z  27  7i .
A. z  3  7i .
B. z  3  7i .
C. z  3  7i .
D. z  3  7i .
Câu 94. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Cho số phức z thỏa mãn
  iz    i2 3 2 2
 4  i . Mô đun của số phức w   z   1 z bằng. A. 2 . B. 10 . C. 5 . D. 4 .
Câu 95. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Tìm các số thực a, b thỏa mãn
a  2b  a b  4i  2a b  2bi với i là đơn vị ảo.
A. a  3, b  1 .
B. a  3, b  1 .
C. a  3, b  1 .
D. a  3, b  1 .
Câu 96. Cho hai số phức z m 1 2i và z  2  m 1 i . Có bao nhiêu giá trị thực của tham số m để 1   1
z . z  8  8i là một số thực. 1 2 A. 1. B. 2 . C. 3 . D. 4 .
Câu 97. (CHUYÊN BẮC GIANG NĂM 2018-2019 LẦN 02) Tìm mô đun của số phức z biết 2z  
1 1 i   z  
1 1 i  2  2i . 1 2 2 1 A. B. C. D. 9 3 9 3
Câu 98. (TT THANH TƯỜNG NGHỆ AN NĂM 2018-2019 LẦN 02) Tính mô đun của số phức z thỏa
mãn z 1 2i  z 1 i  4  i  0 với i là đơn vị ảo. A. 6 . B. 5 . C. 2 . D. 3 .
Câu 99. (CHUYÊN TRẦN ĐẠI NGHĨA - TPHCM - HK2 - 2018) Tìm số phức z thỏa mãn
z  2  3iz  1 9i . A. z  2   i . B. z  2   i .
C. z  2  i . D. 2  i .
Dạng 4.2 Điều kiện cho trước chứa yếu tố môđun
Câu 100. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Hỏi có bao nhiêu số phức z thỏa mãn đồng thời các
điều kiện z i  5 và 2
z là số thuần ảo? A. 4 B. 0 C. 2 D. 3
Câu 101. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho số phức z a bi  ,
a b thoả mãn z  2  i z .
Tính S  4a b . A. S  4  B. S  2 C. S  2  D. S  4
Câu 102. (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho số phức z a bi  ,
a b   thỏa mãn
z  2  i z 1 i  0 và z 1. Tính P a b . A. P  1 B. P  5 C. P  3 D. P  7
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 103. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Có bao nhiêu số phức z thỏa mãn | z  2  i | 2 2 và  z  2 1 là số thuần ảo? A. 0 B. 2 C. 4 D. 3
Câu 104. (Mã đề 104 BGD&ĐT NĂM 2018) Có bao nhiêu số phức z thỏa mãn z z  5  i  2i  6  iz ? A. 1 B. 3 C. 4 D. 2
Câu 105. (MĐ 103 BGD&ĐT NĂM 2017-2018) Có bao nhiêu số phức thỏa mãn z z  6  i  2i  7  iz ? A. 1 B. 4 C. 2 D. 3
Câu 106. (Mã đề 102 BGD&ĐT NĂM 2018) Có bao nhiêu số phức z thỏa mãn z z  3  i  2i  4  iz ? A. 1 B. 3 C. 2 D. 4
Câu 107. (MĐ 105 BGD&ĐT NĂM 2017) Cho số phức z thỏa mãn z  3  5 và z  2i z  2  2i . Tính z . A. z  17 B. z  17 C. z  10 D. z  10 z
Câu 108. (MĐ 105 BGD&ĐT NĂM 2017) Có bao nhiêu số phức z thỏa mãn z  3i  13 và là số z  2 thuần ảo? A. 0 B. 2 C. Vô số D. 1
Câu 109. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Có bao nhiêu số phức z thỏa mãn điều kiện
z.z z  2 và z  2 ? A. 2 . B. 3 . C. 1. D. 4 .
Câu 110. (CHUYÊN BẮC GIANG NĂM 2018-2019 LẦN 02) Có bao nhiêu số phức z thỏa mãn điều kiện
z i 5  z i 5  6 , biết z có môđun bằng 5 ? A. 3 B. 4 C. 2 D. 0
Câu 111. (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Cho hai số phức z , z 1 2
thỏa mãn các điều kiện z z  2 và z  2z  4 . Giá trị của 2z z bằng 1 2 1 2 1 2 A. 2 6 . B. 6 . C. 3 6 . D. 8 .
Câu 19 Cho số phức z có phần thực là số nguyên và z thỏa mãn z  2z  7
  3i z . Môđun của số phức 2
w  1  z z bằng A. w  445 . B. w  425 . C. w  37 . D. w  457
Câu 112. (HỌC MÃI NĂM 2018-2019-LẦN 02) Cho số phức z a bi a,b   thoả mãn
z  4 i z  2i
5 1 i . Tính giá trị của biểu thức T a b . A. T  2 . B. T  3. C. T  1. D. T  1  . 2
Câu 113. (ĐỀ 04 VTED NĂM 2018-2019) Có bao nhiêu số phức z thỏa mãn 3
z  2i z  0 . A. 4 B. 3 C. 2 D. 6
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 114. (ĐỀ 01 ĐỀ PHÁT TRIỂN ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Có bao nhiêu số phức z  2i
z thỏa z 1 2i z  3  4i và là một số thuần ảo z i A. 0 . B. Vô số. C. 1. D. 2 .
Câu 115. Có bao nhiêu số phức z thỏa mãn z  (2  i)  10 và . z z  25 . A. 2 . B. 3 . C. 1. D. 4 .
Câu 116. (THPT CHUYÊN ĐẠI HỌC VINH NĂM 2018-2019 LẦN 01) Có bao nhiêu số phức z thỏa mãn 2 z
z z i   z z 2019 1 i  1 ? A. 4 B. C. 1 D. 3
Câu 117. (ĐỀ THI THỬ VTED 02 NĂM HỌC 2018 - 2019) Có bao nhiêu số phức z thỏa mãn 2
z z z z z và 2
z là số thuần ảo A. 4 B. 2 C. 3 D. 5 2
Câu 118. Có bao nhiêu số phức z thỏa mãn 3
z  2i z  0 . A. 4 B. 3 C. 2 D. 6
Câu 119. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Cho số phức z a bi
a,b  thỏa mãn z  3  z 1 và  z  2z i là số thực. Tính a b . A. 2 . B. 0. C. 2. D. 4.
Câu 120. (CHUYÊN NGUYỄN TẤT THÀNH YÊN BÁI LẦN 01 NĂM 2018-2019) Cho số phức z a bi
a, b  thỏa mãn z 1  3i z i  0 . Tính S  2a  3b . A. S  6  . B. S  6 . C. S  5  . D. S  5.
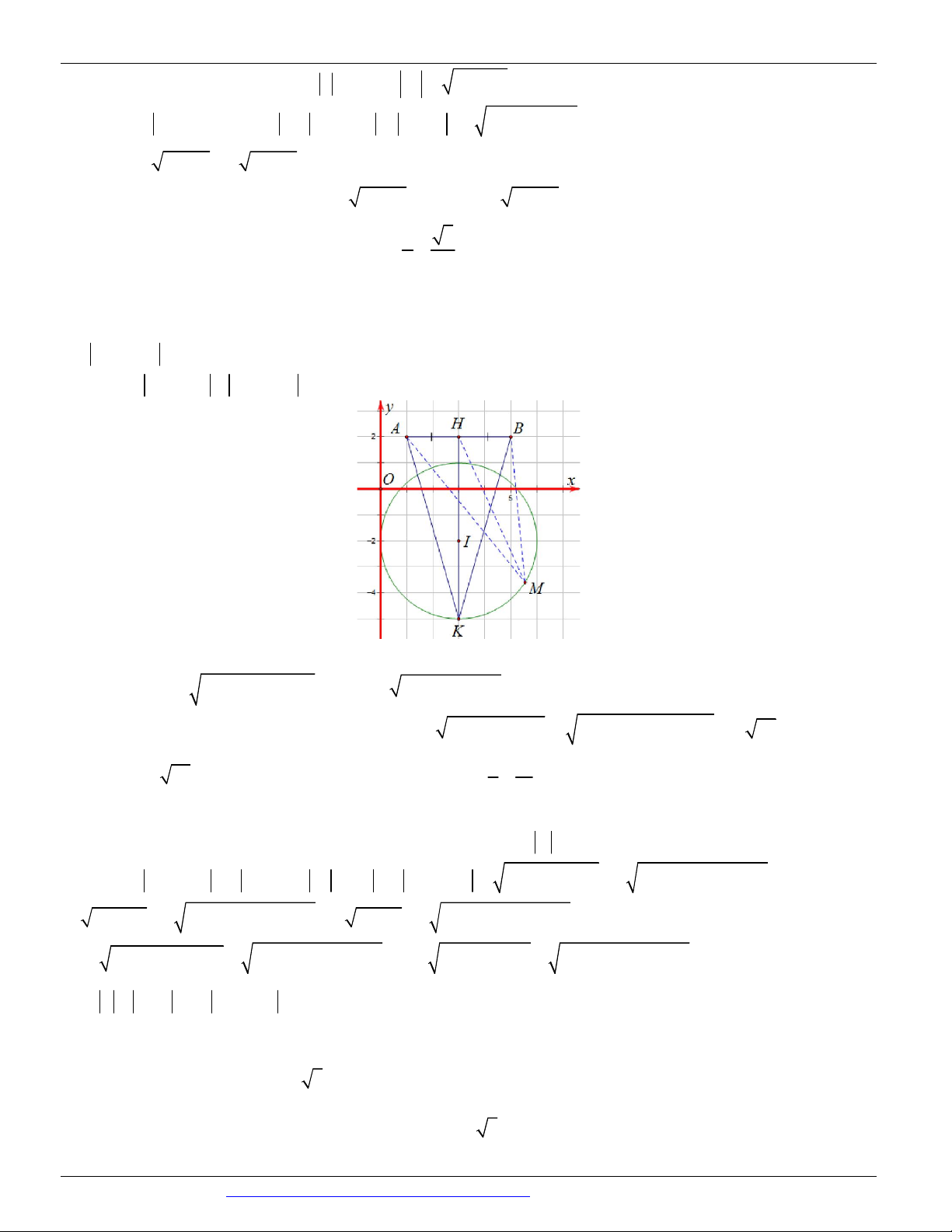
z z z  0 1 2 3 
Câu 121. (THPT NĂM 2018-2019 LẦN 04) Cho ba số phức z ; z ; z thỏa mãn . 1 2 3  2 2
z z z   1 2 3  3 Tính 2 2 2
A z zz zz z 1 2 2 3 3 1 2 2 8 3 A. . B. 2 2 . C. . D. . 3 3 8
Câu 122. (THPT CHUYÊN HẠ LONG - LẦN 2 - 2018) Cho số phức z a bi a,b   thỏa mãn
z  2  5i  5 và z.z  82 . Tính giá trị của biểu thức P a b . A. 10 . B. 8 . C. 35 . D. 7 .
Câu 123. (SGD&ĐT ĐỒNG THÁP - 2018) Cho M là tập hợp các số phức z thỏa 2z i  2  iz . Gọi z1
, z là hai số phức thuộc tập hợp M sao cho z z  1. Tính giá trị của biểu thức P z z . 2 1 2 1 2 3 A. P  3 . B. P  . C. P  2 . D. P  2 . 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1 i
Câu 124. (THPT CHUYÊN QUANG TRUNG - BP - LẦN 1 - 2018) Cho số phức z thoả mãn là số z
thực và z  2  m với m   . Gọi m là một giá trị của m để có đúng một số phức thoả mãn bài toán. Khi 0 đó:  1   1   3   3  A. m  0; . B. m  ;1 . C. m  ; 2 . D. m  1; . 0   0   0   0    2   2   2   2 
Câu 125. (THPT CHUYÊN QUANG TRUNG - BP - LẦN 1 - 2018) Gọi S là tập hợp các số thực m sao z
cho với mỗi m S có đúng một số phức thỏa mãn z m  6 và
là số thuần ảo. Tính tổng của các phần z  4 tử của tập S . A. 10. B. 0. C. 16. D. 8.
Câu 126. (SGD&ĐT CẦN THƠ - HKII - 2018) Cho số phức z thỏa mãn z  4  1 iz  4  3z i . Môđun
của số phức z bằng A. 2 . B. 1. C. 16 . D. 4 .
Câu 127. (THPT CHUYÊN LÊ HỒNG PHONG - TPHCM - 2018) Cho số phức z a bi a,b  , a  0
thỏa z.z 12 z   z z   13 10i . Tính S a b . A. S  17 . B. S  5 . C. S  7 . D. S  17 .
iz  3i   1 z 2
Câu 128. (HỒNG LĨNH - HÀ TĨNH - LẦN 1 - 2018) Cho số phức z  0 thỏa mãn  z . Số 1 i 13 phức w iz có môđun bằng 3 3 26 A. 26 . B. 26 . C. . D. 13. 2
Câu 129. (TOÁN HỌC TUỔI TRẺ - THÁNG 4 - 2018) Cho hai số phức z , z thỏa mãn z  1, z  2 1 2 1 2
và z z  3 . Giá trị của z z là 1 2 1 2 A. 0 . B. 1. C. 2 . D. một giá trị khác.
iz  3i   1 z 2
Câu 130. [HỒNG LĨNH - HÀ TĨNH - LẦN 1 - 2018] Cho số phức z  0 thỏa mãn  z . Số 1 i 13 phức w iz có môđun bằng 3 3 26 A. 26 . B. 26 . C. . D. 13. 2
Câu 131. (THPT CHUYÊN NGUYỄN THỊ MINH KHAI - SÓC TRĂNG - 2018) Cho số phức
z a bi a,b R thỏa mãn z  7  i z 2  i  0 và z  3. Tính P a  . b 1 5 A. 5 . B.  . C. 7 . D. . 2 2
Câu 132. (THCS&THPT NGUYỄN KHUYẾN - BÌNH DƯƠNG - 2018) Cho hai số phức z , z thoả mãn: 1 2 2 2
z  2 3 , z  3 2 . Hãy tính giá trị biểu thức P z zz z . 1 2 1 2 1 2 A. P  60. B. P  20 3 . C. P  30 2 . D. P  50 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 133. (HỒNG LĨNH - HÀ TĨNH - LẦN 1 - 2018) Cho số phức w x yi ,  x , y   thỏa mãn điều kiện 2
w  4  2 w . Đặt P   2 2
8 x y  12 . Khẳng định nào dưới đây đúng?
A. P   w  2 2 2 .
B. P   w  2 2 2 .
C. P    w  2 4 .
D. P    w  2 2 4 .
Phần B. LỜI GIẢI THAM KHẢO
Dạng 1. Xác định các yếu tố cơ bản của số phức
Dạng 1.1 Xác định phần thực, phần ảo của số phức Câu 1. Chọn C Câu 2. Chọn D
Số phức 5  6i có phần thực bằng 5, phần ảo bằng 6 . Câu 3. Chọn A
Số phức có phần thực bằng 3 và phần ảo bằng 4 là: z  3  4i . Câu 4. Chọn B
Số phức 3  2 2i có phần thực là a  3 và phần ảo là b  2  2 . Câu 5. Chọn A Câu 6. Chọn D
Số phức z được gọi là số thuần ảo nếu phần thực của nó bằng 0 . Câu 7. Chọn A
Số phức z  2  3i có phần thực a  2 .
Câu 8. Số phức z  3  4i có phần thực là 3 và phần ảo là  4 . Câu 9. Lời giải Chọn B
z  3  2i z  3  2i . Vậy phần thực bằng 3 và Phần ảo bằng 2 .
Dạng 1.2 Xác định số phức liên hợp, số phức đối, môđun của số phức Câu 10. Chọn A
Số phức liên hợp của số phức z a bi là số phức z a bi từ đó suy ra chọn đáp án B. Câu 11. Chọn B
Theo định nghĩa số phức liên hợp của số phức z a bi, a, b   là số phức z a bi, a, b   . Câu 12. Chọn A Ta có 2 z  2 1  5 . Câu 13. Lời giải Chọn C
Số phức liên hợp của số phức 5  3i là 5  3i Câu 14. Chọn A
Số phức liên hợp của số phức a bi là số phức a bi .
Vậy số phức liên hợp của số phức 3  4i là số phức 3  4i .
Câu 15. z  3  2i z  3  2i . Nên số phức z có phần thực bằng 3 và phần ảo bằng 2  .
Câu 21 [2D4-1.1-1] Cho số phức z  3 2i . Tìm phần thực và phần ảo của số phức z .
A. Phần thực bằng 3 và phần ảo bằng 2i . B. Phần thực bằng 3  và phần ảo bằng 2  . C. Phần thực bằng 3  và phần ảo bằng 2  i .
D. Phần thực bằng 3 và phần ảo bằng 2 . z  3 2i .
Phần thực bằng 3 và phần ảo bằng 2 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 16. Số phức đối của z là z . Suy ra z  5   7i .
Câu 17. Số phức liên hợp của số phức z a bi là số phức z a bi .
Câu 18. Số phức liên hợp của số phức z x yi , x, y   là số phức z x yi . Do đó số phức liên hợp
của số phức z  5  6i là z  5  6i .
Câu 19. Số phức liên hợp của số phức z  2  3i là z  2  3i .
Dạng 2. Biểu diễn hình học cơ bản của số phức Câu 20. Chọn D Theo hình vẽ M  2  ;  1  z  2   i Câu 21. Chọn C
Ta có điểm biểu diễn của số phức z  1
  2i trên hệ trục tọa độ Oxy là điểm Q 1;2 Câu 22. Chọn C Điểm M  2  
;1 là điểm biểu diễn số phức z  2   i 1 Câu 23. Chọn B
Nhắc lại:Trên mặt phẳng phức, số phức z x yi được biểu diễn bởi điểm M (x; y) .
Điểm M trong hệ trục Oxy có hoành độ x  3 và tung độ y  4 .
Vậy số phức z có phần thực là 3 và phần ảo là 4  .
Câu 24. Điểm M 2; 
1 trong hệ tọa độ vuông góc cuả mặt phẳng được gọi là điểm biểu diễn số phức
z  2  i suy ra z  2  i . Câu 25. Lời giải Chọn D.
Câu 26. Điểm biểu diễn hình học của số phức z a bi a,b   là a; b .
Với z  2  3i ta có a  2 và b  3
 . Do đó điểm biểu diễn tương ứng là N 2;  3 .
Câu 27. Tọa độ điểm M (1; 2) là điểm biểu diễn của số phức z  1 2i .
Câu 28. Điểm M  2  ; 
3 biểu thị cho số phức z  2   3 . i
Câu 29. Tọa độ điểm M 3;5  z  3  5i z  3  5i .
Câu 30. Điểm M (2; 1
 ) nên nó biểu diễn cho số phức z  2  i . Câu 31. Chọn C
M (1; 2) là điểm biểu diễn cho số phức có phần thực bằng 1 và phần ảo bằng 2 , tức là 1 2i .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 32. Điểm biểu diễn của số phức z a bi trong mặt phẳng tọa độ Oxy là điểm M a;b
Điểm biểu diễn của số phức z  a bi trong mặt phẳng tọa độ Oxy là điểm N  ; a b  
Do đó: điểm biểu diễn của hai số phức đối nhau là hai điểm đối xứng nhau qua gốc tọa độ
Câu 33. Số phức liên hợp của số phức z  3
i  2 là z  2  3i . Điểm biểu diễn số phức z là N 2 ; 3 .
Vậy điểm biểu diễn số phức liên hợp của số phức z  3
i  2 là N .
Câu 34. Điểm M 2; 
1 trong hệ tọa độ vuông góc cuả mặt phẳng được gọi là điểm biểu diễn số phức
z  2  i suy ra z  2  i .
Câu 35. Ta có: A3; 7  , B 9; 5  ,C  5  ;9  7 
Trọng tâm của tam giác ABC là G ; 1     3  7
Vậy trọng tâm G là điểm biểu diễn của số phức z   i . 3
Dạng 3. Thực hiện các phép tính cộng, trừ, nhân, chia cơ bản của số phức
Dạng 3.1 Phép tính cộng trừ 2 số phức Câu 36. Chọn B
Ta có 2z z  5  i . Nên ta chọn A. 1 2 Câu 37. Chọn C
Ta có z  2z  (1 i)  2(2  i)  5  3i . 1 2
Do đó điểm biểu diễn số phức z  2z có tọa độ là (5;3) . 1 2 Câu 38. Chọn C
z  5  7i  2  3i  7  4i . Câu 39. Chọn D
z z  1 i  2  3i  3  2i nên ta có: z z  3  2i  3  2   13 . 1 2  2 2 1 2   Câu 40. Chọn A
Ta có z z z  4  3i  7  3i  3   6i . 1 2 Câu 41. Chọn B
z z z  2   i . 1 2 Câu 42. Lời giải Chọn D
z  2 3i  3 2i z  3 2i  2  3i 1 i . Câu 43. Chọn B
Ta có z z z  3  2i b  2 1 2
Câu 44. Ta có z z  1  i  2  3i  3  2i z z  3  2i  13 . 1 2 1 2
Câu 45. Từ hình bên ta có tọa độ M  3;2  biểu diễn số phức z  3  2i . 1
Tọa độ N  1; 4  biểu diễn z  1 4i . 2 2 2
Ta có z z  4  2i z z  4  2   2 5 . 1 2     1 2
Dạng 3.2 Phép tính nhân, chia 2 số phức Câu 46. Chọn A
Ta có w iz z i(2  5i)  (2  5i)  2i  5  2  5i  3  3i
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Câu 47. Chọn A
z  4  3i1 i  7  i z  7  i z  5 2 Câu 48. Chọn C Ta có: 3 2
z  1  i i  1  i i .i  1  i i  1  2i (vì 2 i  1 )
Suy ra phần thực của z là a  1, phần ảo của z là b  2  . Câu 49. Chọn B
w iz i 1  2i  2  i Câu 50. Chọn B
Gọi z a bi a,b   . Điểm biểu diễn của z là điểm M  ; a b
 2z  2a  2bi có điểm biểu diễn trên mặt phẳng Oxy là M 2 ; a 2b . 1    
Ta có OM  2OM suy ra M E . 1 1 Câu 51. Chọn D
3z z  3 1 i  1 2i  4  i . Suy ra: Tọa độ điểm biểu diễn là: 4;   1 . 1 2     Câu 52. Chọn A
Ta có: 2z z  4
  2i 1 i  3   3 . i 1 2
Vậy điểm biểu diễn số phức 2z z có tọa độ là  3  ;3 . 1 2 Câu 53. Chọn B
z i 3i   1  3
  i nên suy ra z  3   i . 4  3i
4  3i1 2i 2 11i 2 11
Câu 54. Vì z 1 2i  4  3i nên z =   =i . 1 2i 2 2 1  2 5 5 5 2  11 Vậy nên z =i . 5 5 3  5i 2 2
Câu 55. z 1 i  3  5i z   1
  4i z    1   4    17 . 1 i Câu 56. Cách 1: 1 1 3 4
Ta có z    i2 2 1 2
 1 4i  4i  3  4i      i . z 3   4i 25 25 2 2 1  3   4  1 Do đó         . z  25   25  5 Câu 57. Chọn B 2
Ta có: z    i   i   2
i i   i   i   i 2 1 1 2 1 2 1 2 2 1 2  2
i  4i  4  2i .
Suy ra số phức z có phần ảo là: 2 . Câu 58. Chọn A 1 1
Ta có z  1 i z  1 i 3 3 1 1 8
Khi đó: w  i z  3z i(1 i)  3(1 i)  3 3 3 Câu 59. Chọn A
Ta có: w iz i  2   i  1   2i .
Vậy điểm biểu diễn số phức w iz là điểm M  1  ; 2  .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Câu 60. Chọn B
Ta có z  1 2i z  1 2i
w  2z z  2(1  2i) 1  2i  3  2i
Vậy tổng phần thực và phần ảo của số phức w là 5
Câu 61. Đặt z a bi, a ,b    z a bi . 1 1  z a bia bi2  2 2 a b  2 2  2 . ab i a b 2ab     
.i chỉ là số thuần ảo z a bi
a bia bi 2 2 2 2 2 2 a b a b a ba b  .
Câu 62. Ta có 2z  3z z z  2 1 2i  33  4i  1 2i3  4i  11 8i  11 2i  10i . 1 2 1 2 3  5i
Câu 63. Ta có 1 iz  3  5i z
z  1  4i . 1 i
Suy ra z  1  4i . Vậy M  1  ; 4 . 5  7i 13 4 13 4
Câu 64. 1 3iz  5  7i z   z   i z   . i 1 3i 5 5 5 5
Câu 65. Cách 1: Phương pháp lượng giác  1 1      Xét số phức 1
z  1 i  2  i  2 cosi sin      2 2   4 4  2019 2019 2019  2019 2019 
Ta có số phức z  1 z  1 i  2 cosi sin    4 4  2019 3 3 2019  2 2    1009 1009  2 cosi sin  2      i   2   2 i 4 4  2 2     
Phần thực của z bằng 1009 2 . Cách 2: 2020 505 2019 (1 i) ( 4)  1 1
Ta có z  1 i 505 1009 1009    ( 4)  (  i)  2   2 i 1 i (1 i) 2 2
Phần thực của z bằng 1009 2 .
2  3i4  i
8  3  2 12i 5 14i
5 14i3  2i
Câu 66. Ta có z     3  2i 3  2i 3  2i
3  2i3  2i
15  28  10  42i 13  52i    1   4i . 9  4 13
Vậy điểm biểu diễn số phức z trên mặt phẳng Oxy là M  1  ;  4 . 2 2
Câu 67. Ta có z  3 5i z
 16  30i w z .z  2  4i 16 
 30i   152  4i . 1 2    2 2
Vậy phần thực của w là 152 . Câu 68. Chọn C
i    i2 4 2 Ta có z
 1 i nên M 1  ;1 . 3  2i Câu 69. Chọn A 4  3i 4  3i 5 Ta có z   z   .  2 1 3i2 4 1  3i 2 2018
Câu 70. z  1 i  1 i  ...  1 i
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489   i2018 1009 1 1 2 i 1  1 i  1 i 1 i 1 i
   i 1009  i 1009     1009 1 2 2 1 2   1 i .
z có phần ảo bằng 1009 2 1. m  2i
m  2im  2i 2 m  4 4m Câu 71. z     i . m  2i 2 m  4 2 2 m  4 m  4 m  2
Vì z có phần thực dương 2
m  4  0   . m  2  3  i
3  i x i 3x  3i xi 1 3x 1 (x  3)i
Câu 72. Ta có: z      . 2 2 2 x i
(x i)(x i) x 1 x 1 x 1 3x 1 x  3 4x  2
Suy ra tổng phần thực và phần ảo của số phức z là:   . 2 2 2 x 1 x 1 x 1
Câu 73. w i  2 2017
1 2i  3i  ...  2018i  2018 2019 x 1 xx Xét 2 3 2018
f (x)  x x x  ...  xxx 1 x 1  2018 2019x   1 (x 1)   2019 xx 2 2017 
f '(x)  1 2x  3x  ...  2018x  2 (x 1)  2018 2019i   1 (i 1)   2019 ii 2 2017 
w i 1 2i  3i  ... 2018i
  .i f (i)  i 2 (i 1) 20 
20(i 1)  2ii  10  10 1009i 2  i T  1  010 1009  1 .
Dạng 4. Tìm số phức thỏa mãn điều kiện cho trước
Dạng 4.1 Điều kiện cho trước không chứa yếu tố môđun Câu 74. Chọn D
2x  3  5xx  1
2x  3yi  3  i  5x  4i  2x  3  3y  
1 i  5x  4i     3y 1  4 y  1   Câu 75. Chọn C   2 x  1  1 x  0 Từ 2
x  1 yi  1 2i     y  2 y    2 Câu 76. Chọn C x 1  0 x  1
Ta có 2x  3yi  1 3i  x  6i x 1  3
y  9i  0     . 3  y  9  0  y  3   Câu 77. Chọn A
Gọi z x yi .
2  iz  3 16i  2z i
 2  i x yi  316i  2 x yi i
 2x  2 yi xi y  3 16i  2x  2 yi  2i
2x y  3  2x
 2y x 16  2y  2 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 y  3  0
 x  4y  14   x  2   y  3  
Suy ra z  2  3i . Vậy z  13 . Câu 78. Chọn A
Gọi z a bi ; z a bi a,b  . Ta có:
2  iz  4z i  8  19i
 2  ia bi  4a bi i  8  19i  2
a b  a  6b  4  8  19i  2
a b  8  a  3    
a  6b  4  19 b  2  
Vậy z  3  2i z  13 . Câu 79. Chọn C
Ta có: 3x  2yi  2  i  2x  3i
 3x  2  2y  
1  2x  3i 3
x  2  2xx  2     . 2 y 1  3 y  2   Câu 80. Chọn B
2a  (b i )i  1 2i 2
 2a bi i  1 2i
 (2a  1)  bi  1 2i 2a  1 1   b  2  a  1   b  2  Câu 81. Chọn A 2x  4  0 x  2
3x yi  4  2i  5x  2i  2x  4  4  yi  0     . 4  y  0  y  4  Câu 82. Chọn B
Đặt z a bi  ; a b   . Theo đề ta có
3a bi i2 3ia bi  7 1
 6i  3a3bi 3i 2a2bi 3ai 3b  7 1  6i           a b a b a   
a 3b 3
a5b  3  7 1  3 7 3 7 1 6i        .
3a 5b3  16 
3a5b  13 b   2    Vậy 2 2 z  1  2  5 . Câu 83. Chọn D
Đặt z x yi,  x, y  
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
3 z i  2  iz  3 10i
 3 x yi i  2  i x yi  3 10i
x y   x  5y  3i  3 10ix y  3
 x 5y  3 10  x  2   y  1  z  2  i Vậy z  5
Câu 84. Ta có: 2x  3yi  1 3i  1
  6i  2x 1 3y  3i  1   6i . 2x 1  1  x  1  Suy ra    . 3  y  3  6  y  3   Câu 85. Chọn B
2x  3yi  3  i  5x  4i  2x  3  3y  
1 i  5x  4i Từ 2x  3  5 x  1    
Vậy x  1, y  1. 3y 1  4 y  1  
Câu 86. Ta có 3x  2  2y  
1 i   x  
1   y  5i  3x  2  2y  
1 i   x  
1  5  yi  3 x  3
x  2  x 1   2     .
2 y 1  5  y 4   y    3 Câu 87. Ta có
1 iz  2z  3  2i  1 ia bi  2a bi  3  2i
 3a b  a bi  3  2i  1 a  3
a b  3   2     a b  2 3  b      2
Vậy P a b  1  . 9  7i
Câu 88. 2  3iz  4  3i  13  4i  2  3iz  9  7i z  2  3i
9  7i 2  3i 39 13iz   z
z  3  i . 4  9 13
Vậy z  9 1  10 . x  2 
2x  2 y  3 
Câu 89. Có 1 2iz z  3  4i     7  S  13  . 2x  4  y      3 Câu 90. Chọn A
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Giả sử số phức z có dạng: z x yi , x , y   .
Ta có: iz  1 iz  2
i i x yi  1 i x yi  2
i x  2 y yi  2i .
x  2 y  0 x  4    
x y  6 .  y  2  y  2  
Tổng phần thực và phần ảo của số phức z bằng 6 . Câu 91. Chọn D  b   2a  1 a  3
Ta có a bii  2a  1 3i  b  2a ai  1 3i     a  3 b  7   
Vậy a b  10 .
Câu 92. (1 i)z  2z  3  2i  (1 i)(a bi)  2(a bi)  3  2i  (3a b)  (a b)i  3  2i  1 a  3
a b  3   2    
. Suy ra: P a b  1  . a b  2 3  b      2
Câu 93. Giả sử z a bi a, b R , khi đó 4(a bi)  5(a bi)  27  7i  9a bi  27  7i 9a  27 a  3    
z  3  7i . b  7 b  7   2
Câu 94. Ta có: 3  2iz  2  i  4  i  3  2iz  1 5i z  1 i .
Do đó: w   z  
1 z z z z  1 i1 i 1 i  2 1 i  3  i . 2
w  3 1  10 .
Câu 95. Ta có: a  2b  a b  4i  2a b  2bi .
a  2b  2a b
a  3b  0 a  3        .
a b  4  2b a b  4  b  1   
Câu 96. Ta có: z . z  8  8i  m 1 2i 2  m  
1 i  8  8i  8      2
m  2m  3 i . 1 2  m  1
Để z . z  8  i là một số thực thì 2
m  2m  3  0  . 1 2 m  3  
Vậy có hai giá trị của tham số m để z . z  8  i là một số thực. 1 2 Câu 97. Chọn B
Giả sử z a bi z a bi Do đó 2z  
1 1 i   z  
1 1 i  2  2i
 2a  2bi  
1 1 i  a bi  
1 1 i  2  2i
 2a  2b  
1  2a  2b  
1 i  a b  
1  a b  
1 i  2  2i  1  a
 2a  2b   
1  a b   1  2 3
a  3b  2   3       2a  2b   
1  a b   1  2 a b  0 1   b      3 2 Khi đó 2 2 z a b  . 3
Câu 98. Giả sử: z x yi , , x y   .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ta có: z 1 2i  z 1 i  4  i  0   x yi1 2i   x yi1 i  4  i  0
2x  3y  4  0  y  2
 2x  3y  4   x   1 i  0     x 1  0  x  1 
z  1 2i z  5 .
Câu 99. Giả sử z a bi a,b   . Ta có:
z  2  3iz  1 9i a bi  2  3ia bi  1 9i  a  3b   3
a  3bi  1 9i
a  3b  1 a  2     . 3
a  3b  9  b  1  
Vậy z  2  i .
Dạng 4.2 Điều kiện cho trước chứa yếu tố môđun Câu 100. Chọn A Giả sử 2 2 2
z a bi z a b  2abi
Vì z i  5 và 2
z là số thuần ảo ta có hệ phương trình a   ba b  4  2 2 2 2  
a  (b 1)  25
b  (b 1)  25 a b  3        . 2 2  a b  0  a  b b  a  4      2 2
b  (b 1)  25
b  a  3    Câu 101. Chọn A 2 2  a   a b
Ta có z   i z  a    b   2 2 2 (1) 2 2 1 i a b   b 1  0 (2)  a  2  0 3 
Từ (2) ta có: b  1  . Thay vào (1): 2
a 1  a  2    a  2 2
a 1  (a  2) 4 
Vậy S  4a b  4  Câu 102. Chọn D
Ta có: z  2  i z 1 i  0 2 2
a bi  2  i a b 1 i  0  2 2
a  2  a b  0 1 2 2 
a  2  a b   2 2
b 1 a b    i  0   2 2 b
 1 a b  0 2  Lấy  
1 trừ 2 ta được: a b  1  0  b a  1. Thế vào   1 ta được: 2
a  2  a  a  2 2 1  0  a  2  2a  2a 1 a  2  a  2 a  2         a  3  tm 2 2 2
a  4a  4  2a  2a 1 
a  2a  3  0   a  1  tm 
Với a  3  b  4 ; a  1  b  0 . a  3
Vì z  1  z  3  4i  
P a b  3  4  7 . b  4  Câu 103. Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 2
Gọi số phức z x yi  ,
x y  , vì  z  1  x  2 1  y      2  x  
1 yi là số thuần ảo nên theo     x  2  2   y  2 1  8 (1)
đề bài ta có hệ phương trình:    x  2 2 1  y (2) 
Từ (2) suy ra: y   (x 1)  2 2
Với y x 1, thay vào (1) , ta được:  x  2   x  2 2
 8  x  0  x  0.
Suy ra: z  i .  Với y  (
x 1) , thay vào (1) , ta được:
x  22  x2 2
 8  2x  4x  4  0  x  1 3. Suy ra: z   1
  3  2  3i ; z   1
  3  2  3i
Vậy có 3 số phức thỏa mãn. Câu 104. Chọn B
Ta có z z  5  i  2i  6  iz   z  6  iz  5 z   z  2i   1
Lây môđun hai vế của   1 ta có:  2 z  2 6 1. z
25 z   z  22
Bình phương và rút gọn ta được: 4 3 2 3 2
z 12 z  11 z  4 z  4  0   z  
1  z 11 z  4  0  z  1   z  1 z  10, 9667...     3 2 
z 11 z  4  0  z  0, 62...   z  0,587... 
Do z  0 , nên ta có z  1, z  10, 9667..., z  0, 62... . Thay vào  
1 ta có 3 số phức thỏa mãn đề bài. Câu 105. Chọn D
Đặt z a  0, a   , khi đó ta có
z z  6  i  2i  7  iz a z  6  i  2i  7  iz  a  7  iz  6a ai  2i
 a  7  iz  6a  a  2i  a  7  iz  6a  a  2i a 2     a
a  a  2 2 2 7 1 36 2 4 3 2
a 14a  13a  4a  4  0   a  1  a   1  3 2
a 13a  4  0   3 2
a 12a  4  0 
Xét hàm số f a 3 2
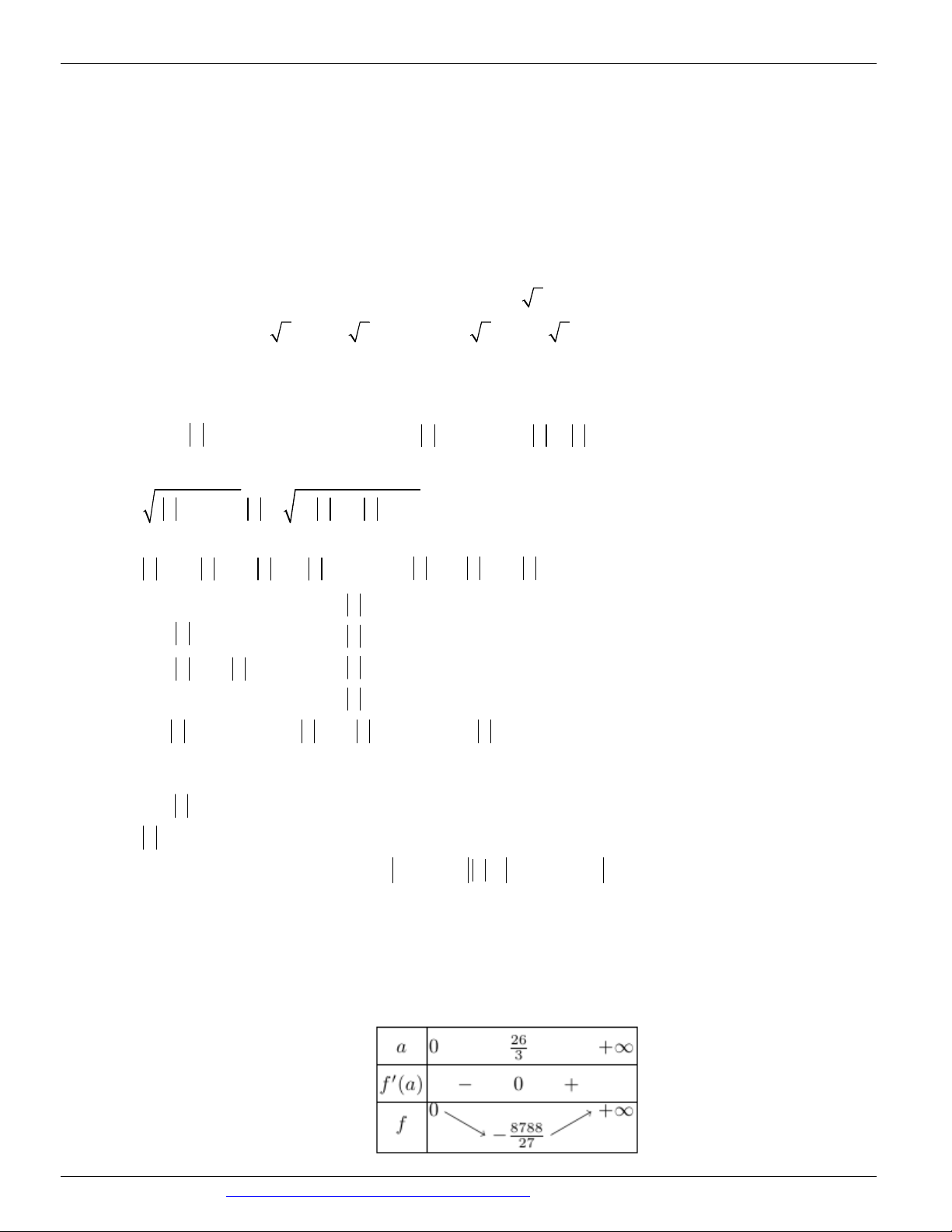
a 13a a  0 , có bảng biến thiên là
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Đường thẳng y  4 cắt đồ thị hàm số f a tại hai điểm nên phương trình 3 2
a 12a  4  0 có
hai nghiệm khác 1 (do f  
1  0 ). Mỗi giá trị của a cho ta một số phức z .
Vậy có 3 số phức thỏa mãn điều kiện. Câu 106. Chọn B
z z  3  i  2i  4  iz   z  4  iz  3 z   z  2i (*)   z  2 2 4
1. z  9 z   z  22 (1). 2 2
Đặt m z  0 ta có    m     2 2 1 4
1 .m  9m  m  2 4 3 2
m  8m  7m  4m  4  0 m  1  m  1 m  6, 91638  m   3 2
1 m  7m  4  0     . 3 2
m  7m  4  0  m  0.80344  m  0.7  1982 L 
3m  m  2i
Từ (*) ta suy ra ứng với mỗi z m sẽ có một số phức z  thỏa mãn đề bài. m  4  i
Vậy có 3 số phức z thỏa mãn yêu cầu bài toán. Câu 107. Chọn C
Đặt z x yi; x, y     2 x  2 2  3  y  25    x  3  2 y  25    Theo bài ra ta có 2 2 2  2
x   y  2  x  2  y  2 4x  4   0    2 y  9 y  3     . Vậy z  10 x  1 x    1 Câu 108. Chọn B
Gọi số phức z a bi,a,b   2
Ta có z  3i  13  a bi  3i  13  2
a  b  3  13  2 a  2
b b    2 a  2 6 4 0
b  4  6b 1 z 2 2
2 a  2  bi  1   1   1  . z  2 z  2 a  2  bi  2 a  2  2 b  2 a  2  2 b  2a  4 2b 2 a  2 b  2a 2b   i   i  2 2 2 2 a  2  2 ba  2  2 ba  2  2 ba  2  2 b  2 a  2
b  2a  0 2 z 2 a  2 b  2a  Do là số thuần ảo nên  0  a  2 z  2  2 a  2  2 bb  0 
Thay 1 vào 2 ta có 4  6b  2a  0  a  3b  2 thay vào 1 ta có b  0(L)  2 b    2
b   b   2 3 2 4 6 0
10b  6b  0   3   1 b   a   5 5
Vậy có một số phức cần tìm.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 109. Đặt z x yi ( x ; y   ; 2 i  1 ). 2 2
x y x yi  2 
 4  x yi  2 Theo bài ra ta có:    2 2 2 2 x y  4  x y  2      4  x2 2  y  4 x  2      2 2
x y  4  y  0 
Vậy có 1 số phức thỏa yêu cầu bài toán là z  2  . Câu 110. Chọn B
Gọi z a bi  2
a, b  , i    1 Ta có 
z i 5  z i 5  6 
a  b  5 2  a  b  5 2 2 2  6     z  5  2 2  a b  5   16  4 2 a a   2 2 36   a 16b  144    5  5       2 2 a b  5 9 3 2  bb       5   5
Vậy có 4 số phức thỏa mãn.
Câu 111. Giả sử z a bi , ( a , b   ); z c di , ( c , d   ). 1 2 Theo giả thiết ta có:  z  2 2 2  2 2 a b  4   1 1 a b  4      2 2 2 2  z  2
 c d  4
 c d  4 2 2    z  2z  4 2 2 2 2 2 2  1 2 a  2c
  b  2d   16  a b  4 
c d   4ac bd  16 3  Thay  
1 , 2 vào 3 ta được ac bd  1  4 . 2 2
Ta có 2z z
2a c  2b d    2 2
a b    2 2 4
c d   4ac bd  5 . 1 2 Thay  
1 , 2 , 4 vào 5 ta có 2z z  2 6 . 1 2
Câu 19 [2D4-1.6-2] Cho số phức z có phần thực là số nguyên và z thỏa mãn z  2z  7
  3i z . Môđun của số phức 2
w  1  z z bằng A. w  445 . B. w  425 . C. w
37 . D. w  457 Đặt z a bi a  , b   .
Khi đó: z  2z  7
  3i z  2 2
a b  2a  2bi  7
 3i a bib   3   5   a   7 2 2
a b  3a  7   b  3i  0   4 (a  )  . 3  b   3  a4  
Do a   nên a  4  z  4  3i w  4  21i w  457
Câu 112. z  4 i z  2i  5 1 i  a bi  4 i a bi  2i  5 1 i
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
a  4  bi  5    1   a  
b  2i  5 2  2 2 Từ  
1 và 2 , ta có a   bi a  b  i  a   2 2 4 2 4
b a  b  2  b  2a  3 .    a  42 2  b  5 a  2 Kết hợp với   1 , ta được:    b  1 b   2a  3  
Vậy T a b  3 . Câu 113. Chọn A  z  0 2 3 3
z  2i z  0  z  2izz  0  z  2
z  2iz   0   2 z  2iz  0 2 
Gọi z x yi z x yi với ,
x y   thay vào 2 có: x  0 2 2
x y  2 y  0  2 2 2
x y  2 y  0
y  2 y  0 2 2   
x y  2 y  2x  y   1 i  0    x  0  2x   y  1 0     y  1    y  1    2  x  3  0 
x y  0 x  0   z  0  y  2    z  2i    x   3  
z   3  iy  1   
z  3  i   x  3   y  1 
Vậy phương trình có 4 nghiệm
Câu 114. Đặt z x yi (x, y  ) Theo bài ra ta có
x 1  y  2i x  3  4  yi   x  2
1   y  22   x  32   y  42  y x  5 z  2i
x   y  2 2 i
x   y  2 y  
1  x 2 y  3i Số phức w    z i
x  1 yi
x   y  2 2 1 2
x   y  2 y   1  0  12 x       7 w 2
là một số ảo khi và chỉ khi 2
x   y   1  0   23   5 y y x        7 12 23 Vậy z   
i .Vậy chỉ có 1 số phức z thỏa mãn. 7 7
Câu 115. Gọi số phức cần tìm là z a bia,b   . 2 Ta có: 2 2
z.z z a b  25 (1) .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Lại có: z  (2  i)  10  a  2  (b 1)i  10 2 2 
(a  2)  (b 1)  10 2 2
 (a  2)  (b 1)  10 2 2
a b  4a  2b  5  10 (2)
Thay (1) vào (2) ta được: 25  4a  2b  5  10  b  2  a 10 . Nên 2 2 2 2
a b  25  a  (2a 10)  25 a  5 b  0 2
 5a  40a  75  0     a  3 b  4  
Vậy Vậy có 2 số phức z thoả mãn là z  5 và z  3  4i . Câu 116. Chọn D
Gọi z a bi ; a,b    z a bi . 2 2 2 Ta có: z   a bi   a   2 1 1
1  b , z z i a bi a bi i   b2 2 i  2 b i , 2019 ii
 ,  z z 2019 i
 i a bi a bi  2ai .
Suy ra phương trình đã cho tương đương với: a  2 2
1  b  2 b i  2ai  1  a  0  b  0    b  0    a  2 2 2 2 2 1  b  1
a  2a b  0  
2 b  2 b  0    a  1      
  b  1     2 b  2a  0 a    b a bb  1       a   b    a  1   b  1  
Vậy có 3 số phức z thỏa mãn.
Câu 117. Gọi số phức z a bi , a, b   . 2 Ta có 2 2
z z z z z a b  2a  2bi 2 2
a b  2 a  2 b   1 . 2 Lại có 2
z  a bi 2 2
a b  2abi là số thuần ảo, suy ra 2 2
a b  0  a  b
Trường hợp 1: a b thay vào   1 ta được:  a  0 a  0 a b  0 2
 2a  4 a       .  a  2 a  2   a b  2  
Trường hợp 2: a b  thay vào   1 ta được:  a  0 a  0 b  0 2
 2a  4 a       .  a  2 a  2   b  2  
Vậy có 5 số phức thỏa mãn bài toán là z  0 , z  2  2i , z  2   2i . Câu 118. Chọn A  z  0 2 3 3
z  2i z  0  z  2izz  0  z  2
z  2iz   0   2 z  2iz  0 2 
Gọi z x yi z x yi với ,
x y   thay vào 2 có:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 x  0 2 2
x y  2 y  0  2 2 2
x y  2 y  0
y  2 y  0 2 2   
x y  2 y  2x  y   1 i  0    x  0  2x   y  1 0     y  1    y  1    2  x  3  0 
x y  0 x  0   z  0  y  2    z  2i    x   3  
z   3  iy  1   
z  3  i   x  3   y  1 
Vậy phương trình có 4 nghiệm
Câu 119. Ta có z a bi a,b   . 2 2
+) z  3  z 1  a  3  bi a 1 bi  a   2
b  a   2 3 1  b
 a  2  b  a  2 2 2 3 1
b  4a  8  0  a  2 .
+)  z  2 z i  a bi  2a bi i  a  2  bi a  b   1 i    
a a  2  bb  
1  a  2b  2i .
z  2z i là số thực  a  2b  2  0 .
Thay a  2 tìm được b  2
 . Vậy a b  0 .
Câu 120. Ta có z  1  3i z i  0  a     2 2 1
b  3  a b i  0 . a 1  0  a  1       . 2 2 2
b  3  a b  0 
1  b b  3    *  bb  3    3  4     *     4  b   . 1 b   b  32 2  b    3  3 a  1  Vậy 
4  S  2a  3b  6  . b     3
z z  z 1 2 3 
Câu 121. z z z  0  z z  z . 1 2 3 1 3 2
z z  z  3 2 1 2   2 2 2 2 2 2 2 2 2 2 2 8
A z zz zz z  z  z  zzzz  3.   . 1 2 2 3 3 1 1 2 3 1 2 3  3  3    5  b  43 
 a  22  b  52  5 a     1
Câu 122. Theo giả thiết ta có   2  2 2 2 2
a b  82  
a b  82 2 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 b  9  Thay   1 vào 2 ta được 2 29b 430b 1521 0      169  b   29
Vì b   nên b  9  a  1. Do đó P a b  8  .
Câu 123. Đặt z x yi với x , y   .
Ta có: z i   iz
x   y   2 2 2 2 2 2
1 i  2  y xi x y  1.
Suy ra tập hợp các điểm biểu diễn số phức z trên mặt phẳng phức là đường tròn   ;1 O
z z  1. 1 2 2 2 2 2 Ta có: z zz z
 2  z z  2
P  3  P  3 . 1 2 1 2 1 2
Câu 124. Giả sử z a bi, a,b   . 1 i 1 i 1 a b a b Đặt: w   
a b a b i   i . 2 2   z a bi a b    2 2 2 2 a b a b
w là số thực nên: a b   1 . 2
Mặt khác: a  2  bi m  a   2 2 2
b m 2 . Thay  
1 vào 2 được: a  2 2 2 2  a m 2 2
 2a  4a  4  m  0 3 .
Để có đúng một số phức thoả mãn bài toán thì PT 3 phải có nghiệm a duy nhất.  3     0    2 4 2 4  m   0 2
m  2  m  2  1; 
 (Vì m là mô-đun).  2  Trình bày lại
Giả sử z a bi, vì z  0 nên 2 2
a b  0 * . 1 i 1 i 1 a b a b Đặt: w   
a b a b i   i . 2 2   z a bi a b    2 2 2 2 a b a b
w là số thực nên: a b  
1 .Kết hợp * suy ra a b  0 . 2
Mặt khác: a  2  bi m  a   2 2 2
b m 2 .(Vì m là mô-đun nên m  0 ). Thay  
1 vào 2 được: a  2 2 2 2
a m g a 2 2
 2a  4a  4  m  0 3 .
Để có đúng một số phức thoả mãn bài toán thì PT 3 phải có nghiệm a  0 duy nhất. Có các khả năng sau :
KN1 : PT 3 có nghiệm kép a  0 2   0   m  2  0 ĐK:     m  2 . g  0 2  0  4  m  0 
KN2: PT 3 có hai nghiệm phân biệt trong đó có một nghiệm a  0 2   0   m  2  0 ĐK:     m  2 . g  0 2  0  4  m  0   3  Từ đó suy ra m   2  1; . 0    2  Câu 125. Cách 1: z x iy
x iy x  4  iyx x  4 2  y  4iy
Gọi z x iy với , x y   ta có    z  4 x  4  iy
x  42  yx  42 2 2  y
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
là số thuần ảo khi x x    y    x  2 2 2 4 0 2  y  4 Mà z m
  x m2 2 6  y  36
Ta được hệ phương trình 2  36  m x     x m  2 2  y  36   4  2m 2 x  36  m 4  2m        2   x  22 2 2  y  4
y  4   x  22 2  36  m     2 y  4   2    4  2m    2 2  36  m  2 36  m 2 36  m Ycbt  4   2  0    2   2 hoặc 2   2 4  2m   4  2m 4  2m
m  10 hoặc m  2 hoặc m  6
Vậy tổng là 10  2  6  6  8 .
Câu 126. Giả sử z a bi a,b   .
Ta có: z  4  1 iz  4  3z i z 1 3i  4  4i  1 iz
 a bi  i   i    i 2 2 1 3 4 4 1
a b a b    a b   2 2 2 2 3 4 3 4 i
a b a b i 2 2 
a  3b  4  a b 2 2 
a  3b  4  a b 2   5
b  8  5b 16b 16       2 2 3
a b  4  a b  a  2  b  4  a  2  b  4   8 b    5  5b  8  0 b  2   N   b   2 2   
20b  64b  48  0   6  .    b    La  0  a  2  b  4   5 
a  2b  4   Vậy z  2 . Câu 127. Ta có:
z.z 12 z   z z   13 10i 2 2 2 2
a b 12 a b  2bi  13 10i 2  a  25 13 2 2 2 2 
a b 12 a b  13 2 2 
a  25 12 a  25  13       2
  a  25  1VN  2b  10    b   5   b   5  a  12  a  12     , vì a  0 . b  5  b  5 
Vậy S a b  7 .
Câu 128. Gọi z a bi a,b   . Suy ra z a bi .
iz  3i   1 z 2
i a bi  3i   1 a bi Ta có 2 2  z   a b 1 i 1 i 2 2 2 2
ai b  3ai  3b a bi a b a i b i
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489   2 2
a b a bi   2 2 2
a b  4b a  0 2 2 
a b  2a b  0   2 2
a b a  4b  0 
b  0, a  0  z  0 2
26b  9b  0   45  9    9  4  5  45  9  z i  (Vì z  0 ). a  5bb  , a   z i   26 26  26 26  26 26 45  9 15 3 3 26 Với z i   w   i  w  . 26 26 2 2 2
Câu 129. Giả sử z a b i,
a , b   , z a b i, a , b   . 2 2 2  2 2  1 1 1  1 1  Theo bài ra ta có:  z  1 2 2 a b  1 2 2 a b  1 1 1 1 1 1     2 2 2 2  z  2
 a b  4
 a b  4 . 2 2 2 2 2    z z  3 2 2
2a a  2b b  4 1 2  a ab b  9   1 2 1 2 1 2   1 2   Khi đó, ta có:
z z  a a 2  b b 2   2 2
a b    2 2 a b
 2a a  2b b  1. 1 1 2 2   1 2 1 2  1 2 1 2 1 2
Vậy z z  1. 1 2
Câu 130. Gọi z a bi a,b   . Suy ra z a bi .
iz  3i   1 z 2
i a bi  3i   1 a bi Ta có 2 2  z   a b 1 i 1 i 2 2 2 2
ai b  3ai  3b a bi a b a i b i   2 2
a b a bi   2 2 2
a b  4b a  0 2 2 
a b  2a b  0   2 2
a b a  4b  0 
b  0, a  0  z  0 2
26b  9b  0   45  9    9  4  5  45  9  z i  (Vì z  0 ). a  5bb  , a   z i   26 26  26 26  26 26 45  9 15 3 3 26 Với z i   w   i  w  . 26 26 2 2 2
Câu 131. a   b   2 2 2 2 7
1 i  2 a b a b i  0 2 2
a  7  2 a b    1  2 2
a b b 1 2 
a  7  2 b  
1  a  2b  5 thế vào (2).
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 b   1 b  1       b  2 2 b 4 2 5
b b 1     2 4b 22b 24 0      3 b    2
TH1: b  4  a  3  z  5  3. (loại) 3 5 TH2: b   a  2   z   3. (nhận). 2 2 1
P a b   . 2
Câu 132. Đặt z a bi , z c di a,b, c, d   1 2   2 2  z  2 3   1
a b  12 Theo đề:    2 2  z  3 2
c d  18 2   Vậy 2 2
P z zz z 1 2 1 2
 a c2  b d 2  a c2  b d 2   2 2 2 2
2 a b c d   60 Câu 133. Ta có 2
w  4   x yi2  4 2 2
x y  2xyi  4  w
  x y  2 2 2 2 2 2 4 4  4x y . Do đó 2
w  4  2 w
x y  2 2 2 2 2 2 2 4
 4x y  2 x y
  x y  2 2 2 2 2  x y   2 2 4 4 4 x y  4 4 2 2
x y x y   2 2 x y  2 2   x y   2 2 2 8 16 4 4 x y  4 4 2 2
x y x y   2 2
x y     2 2 2 4
4 8 x y  12  0 2
  x y 2 2 2   2 2
x y     2 2 4
4 8 x y  12  0   2 2
x y     2 2 2
8 x y  12  0
  x y  
   x y  2 2 2 2 2 8 12 2
P    w  2 2 2 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 CHUYÊN ĐỀ 26
BÀI TOÁN TÌM TẬP HỢP ĐIỂM BIỂU DIỄN SỐ PHỨC MỤC LỤC
Phần A. CÂU HỎI ........................................................................................................................................................... 1
Dạng 1. Tập hợp điểm biểu diễn là đường tròn ................................................................................................................ 1
Dạng 2. Tập hợp điểm biểu diễn là đường thẳng ............................................................................................................. 6
Dạng 3. Tập hợp điểm biểu diễn là đường conic ............................................................................................................. 7
Dạng 4. Tập hợp điểm biểu diễn là một miền .................................................................................................................. 8
Phần B. LỜI GIẢI THAM KHẢO ................................................................................................................................. 10
Dạng 1. Tập hợp điểm biểu diễn là đường tròn .............................................................................................................. 10
Dạng 2. Tập hợp điểm biểu diễn là đường thẳng ........................................................................................................... 19
Dạng 3. Tập hợp điểm biểu diễn là đường conic ........................................................................................................... 21
Dạng 4. Tập hợp điểm biểu diễn là một miền ................................................................................................................ 23 Phần A. CÂU HỎI
Dạng 1. Tập hợp điểm biểu diễn là đường tròn Câu 1.
(Mã đề 102 BGD&ĐT NĂM 2018) Xét các số phức z thỏa mãn  z  3i z  3 là số thuần ảo.
Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng: 9 3 2 A. B. 3 2 C. 3 D. 2 2 Câu 2.
(MĐ 103 BGD&ĐT NĂM 2017-2018) Xét các số phức z thỏa mãn  z  2i z  2 là số thuần
ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng A. 2 2 B. 4 C. 2 D. 2 Câu 3.
(Mã đề 104 - BGD - 2019) Xét các số phức z thỏa mãn z
2 . Trên mặt phẳng tọa độ Oxy tập 5  iz
hợp các điểm biểu diễn các số phức w
là một đường tròn có bán kính bằng 1 z A. 44 . B. 52 . C. 2 13 . D. 2 11 . Câu 4.
(Mã đề 104 BGD&ĐT NĂM 2018) Xét các số phức z thỏa mãn  z  2i z  2 là số thuần ảo.
Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng? A. 2 B. 2 C. 4 D. 2 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Câu 5.
(ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho các số phức z thỏa mãn z  4 . Biết rằng tập hợp
các điểm biểu diễn các số phức w  (3  4i)z i là một đường tròn. Tính bán kính r của đường tròn đó A. r  22 B. r  4 C. r  5 D. r  20 Câu 6.
(ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Xét các số phức z thỏa mãn  z  2i z  2 là
số thuần ảo. Biết rằng tập hợp tất cả các điểm biểu diễn của z là một đường tròn, tâm của đường
tròn đó có tọa độ là A. 1  ;1 B. 1  ;1 C.  1  ;   1 D. 1;  1  Câu 7.
(Mã đề 101 BGD&ĐT NĂM 2018) Xét các số phức z thỏa mãn  z i z  2 là số thuần ảo. Trên
mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn số phức z là một đường tròn có bán kính bằng 3 5 5 A. B. 1 C. D. 2 4 2 Câu 8.
(Mã đề 101 - BGD - 2019) Xét số phức z thỏa mãn z
2 . Trên mặt phẳng tọa độ Oxy , tập 4  iz
hợp điểm biểu diễn các số phức w
là một đường tròn có bán kính bằng 1 z A. 26 . B. 34 . C. 26 . D. 34 . Câu 9.
(Mã 102 - BGD - 2019) Xét số phức z thỏa mãn z  2 . Trên mặt phẳng tọa độ Oxy , tập hợp 3  iz
điểm biểu diễn các số phức w
là một đường tròn có bán kính bằng 1 z A. 2 5 . B. 20 . C. 12 . D. 2 3 .
Câu 10. (Mã 103 - BGD - 2019) Xét các số phức z thỏa mãn z  2 . Trên mặt phẳng tọa độ Oxy , tập 2  iz
hợp các điểm biểu diễn số phức w
là một đường tròn có bán kính bằng 1 z A. 10 . B. 2 . C. 2 . D. 10 .
Câu 11. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Cho số phức z thỏa mãn z  2. Biết
rằng tập hợp các điểm biểu diễn số phức w  3  2i  2  iz là một đường tròn. Tìm tọa độ tâm
I của đường tròn đó? A. I 3;  2 . B. I  3;  2 . C. I 3;  2 .
D. I 3;  2 .
Câu 12. (ĐỀ MẪU KSNL ĐHQG TPHCM NĂM 2018-2019) Trong mặt phẳng phức, tập hợp các điểm
biểu diễn số phức z thoả mãn z.z  1 là A. một đường thẳng. B. một đường tròn. C. một elip. D. một điểm.
Câu 13. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Cho số phức z thỏa
z 1 2i  3 . Biết rằng tập hợp các điểm biểu diễn của số phức w  2z i trên mặt phẳng Oxy
là một đường tròn. Tìm tâm của đường tròn đó. A. I 2;  3 . B. I 1;  1 . C. I 0  ;1 . D. I 1;0 .
Câu 14. (THPT CHUYÊN SƠN LA NĂM 2018-2019 LẦN 01) Tập hợp các điểm biểu diễn số phức z thỏa
mãn z i  1  i z là một đường tròn, tâm của đường tròn đó có tọa độ là
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A.   1;1 . B. 0;  1 . C. 0;  1 . D. 1; 0  .
Câu 15. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Cho số phức z thỏa mãn z
 1. Biết rằng tập hợp các điểm biểu diễn số phức z là một đường tròn C  . Tính bán kính i  2
r của đường tròn C  . A. r  1. B. r  5. C. r  2. . D. r  3..
Câu 16. (KTNL GV BẮC GIANG NĂM 2018-2019) Trong mặt phẳng tọa độ điểm biểu diễn số phức z
thỏa mãn z 1 2i  3 là
A. đường tròn tâm I (1; 2) , bán kính R  9 .
B. đường tròn tâm I (1; 2) , bán kính R  3 .
C. đường tròn tâm I ( 1  ; 2
 ) , bán kính R  3 . D. đường thẳng có phương trình x  2y  3  0 .
Câu 17. (SỞ GD&ĐT THANH HÓA NĂM 2018 - 2019) Xét các số phức z thỏa mãn (2  z)(z i) là số
thuần ảo. Tập hợp các điểm biểu diễn của z trong mặt phẳng tọa độ là:  1  5
A. Đường tròn tâm I 1;   ,bán kính R  .  2  2  1  5
B. Đường tròn tâm I 1  ;    ,bán kính R  .  2  2
C. Đường tròn tâm I 2 
;1 ,bán kính R  5 .  1  5
D. Đường tròn tâm I 1;   ,bán kính R  nhưng bỏ điểm (
A 2;0); B(0;1) .  2  2
Câu 18. (CHUYÊN BẮC GIANG NĂM 2018-2019 LẦN 02) Tìm tập hợp điểm biểu diễn số phức z thỏa
mãn z i  (1 i)z .
A. Đường tròn tâm I(0; 1), bán kính R  2 .
B. Đường tròn tâm I(1; 0), bán kính R  2 .
C. Đường tròn tâm I(-1; 0), bán kính R  2 . D. Đường tròn tâm I(0; -1), bán kính R  2 .
Câu 19. (ĐỀ THI THỬ VTED 02 NĂM HỌC 2018 - 2019) Tâp hợp tất cả các điểm biểu diễn số phức
z x yi  ,
x y   thỏa mãn z i  4 là đường cong có phương trình A.  x  2 2 1  y  4
B. x   y  2 2 1  4 C.  x  2 2 1  y  16
D. x   y  2 2 1  16
Câu 20. (CHUYÊN NGUYỄN TẤT THÀNH YÊN BÁI LẦN 01 NĂM 2018-2019) Tập hợp tất cả các
điểm biểu diễn các số phức z thỏa mãn z  2  i  4 là đường tròn có tâm và bán kính lần lượt là A. I 2;   1 ; R  4 . B. I 2;   1 ; R  2 . C. I 2;  
1 ; R  4 . D. I 2;   1 ; R  2 .
Câu 21. (ĐỀ THI CÔNG BẰNG KHTN LẦN 02 NĂM 2018-2019) Tập hợp điểm biểu diễn số phức z
thỏa mãn z 1 i  2 là đường tròn có tâm và bán kính lần lượt là: A. I 1  ;1 , R  4 . B. I 1  ;1 , R  2 . C. I 1;   1 , R  2 . D. I 1;   1 , R  4 .
Câu 22. (CHUYÊN KHTN NĂM 2018-2019 LẦN 01) Tập hợp tất cả các điểm biểu diễn các số phức z
thỏa mãn 1 iz  5  i  2 là một đường tròn tâm I và bán kính R lần lượt là
A. I 2; 3, R  2 . B. I 2; 3  , R  2 .
C. I 2;3, R  2 . D. I 2;3, R  2 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 z  2
Câu 23. (CHUYÊN KHTN NĂM 2018-2019 LẦN 01) Xét các số phức z thỏa mãn là số thuần ảo. z  2i
Biết rằng tập hợp các điểm biểu diễn các số phức z luôn thuộc một đường tròn cố định. Bán kính
của đường tròn đó bằng A. 1. B. 2 . C. 2 2 . D. 2 .
Câu 24. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Tính tổng của tất cả các giá
trị của tham số m để tồn tại duy nhất số phức z thoả mãn đồng thời z m và 2
z  4m  3mi m . A. 4 . B. 6 . C. 9 . D. 10 .
Câu 25. (THPT YÊN KHÁNH - NINH BÌNH - 2018 - 2019) Cho số phức z thỏa mãn: z  2  i  3 . Tập
hợp các điểm trong mặt phẳng tọa độ Oxy biểu diễn số phức w  1 z là
A. Đường tròn tâm I  2   ;1 bán kính R  3 .
B. Đường tròn tâm I 2;   1 bán kính R  3 .
C. Đường tròn tâm I 1;   1 bán kính R  9 .
D. Đường tròn tâm I 1;   1 bán kính R  3 .
Câu 26. (KTNL GV BẮC GIANG NĂM 2018-2019) Cho các số phức z thỏa mãn z  2 5 . Biết rằng
trong mặt phẳng tọa độ các điểm biểu diễn của số phức w i  2  iz cùng thuộc một đường tròn
cố định. Tính bán kính r của đường tròn đó? A. r  5 . B. r  10 . C. r  20 . D. r  2 5 .
Câu 27. (ĐỀ THI THỬ VTED 03 NĂM HỌC 2018 - 2019) Xét các số phức z thỏa mãn  z  2i z  3 là
số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn số phức z là một đường tròn có bán kính bằng 11 13 A. 13 B. 11 C. D. 2 2
Câu 28. Cho các số phức z thỏa mãn z 1  2 . Biết rằng tập hợp các điểm biểu diễn các số phức
w  1 i 8 z i là một đường tròn. Bán kính r của đường tròn đó là A. 9 . B. 36 . C. 6 . D. 3 .
Câu 29. Cho z , z là hai số phức thỏa mãn điều kiện | z 5  3i | 5 đồng thời | z z | 8 . Tập hợp các điểm 1 2 1 2
biểu diễn số phức w z z trong mặt phẳng tọa độ Oxy là đường tròn có phương trình 1 2 A. 2 2
( x  10)  ( y  6)  36 . B. 2 2
(x 10)  ( y  6)  16 . 5 3 5 3 9 C. 2 2
(x  )  ( y  )  9 . D. 2 2
(x  )  ( y  )  . 2 2 2 2 4
Câu 30. (CHUYÊN KHTN - LẦN 1 - 2018). Tập hợp tất cả các điểm biểu diễn các số phức z thỏa mãn:
z  2  i  4 là đường tròn có tâm I và bán kính R lần lượt là: A. I 2;   1 ; R  4 . B. I 2;  
1 ; R  2 . C. I 2;   1 ; R  4 . D. I 2;   1 ; I 2;   1 .
Câu 31. (TOÁN HỌC TUỔI TRẺ - THÁNG 4 - 2018) Cho số phức z thỏa mãn z  2 . Tập hợp điểm biểu
diễn số phức w  1 iz  2i là A. Một đường tròn. B. Một đường thẳng.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 C. Một Elip.
D. Một parabol hoặc hyperbol.
Câu 32. (SGD&ĐT ĐỒNG THÁP - HKII - 2018) Tập hợp điểm biểu diễn của số phức z thỏa mãn
z 1  1 i  2z là đường tròn C  . Tính bán kính R của đường tròn C  10 7 10 A. R  . B. R  2 3 . C. R  . D. R  . 9 3 3
Câu 33. (SGD - HÀ TĨNH - HK 2 - 2018) Tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn 2z i  6
là một đường tròn có bán kính bằng: A. 3 . B. 6 2 . C. 6 . D. 3 2 .
Câu 34. (THPT CHUYÊN THĂNG LONG - ĐÀ LẠT - 2018) Cho số phức z thỏa mãn z 1 3i  2 .
Biết tập hợp điểm biểu diễn số phức w  2  iz  3i  5 là một đường tròn. Xác định tâm I và
bán kính của đường tròn trên.
A. I 6;  4, R  2 5 . B. I 6; 4, R 10 .
C. I 6; 4, R  2 5 .
D. I 6; 4, R  2 5 .
Câu 35. (THPT CHUYÊN HOÀNG VĂN THỤ - HÒA BÌNH - 2018) Cho số phức z thỏa mãn z  2 .
Biết rằng tập hợp các điểm biểu diễn số phức w  3  2i  2  iz là một đường tròn. Bán kính R
của đường tròn đó bằng? A. 7 . B. 20 . C. 2 5 . D. 7 .
Câu 36. (SGD THANH HÓA - LẦN 1 - 2018) Cho z , z là hai trong các số phức z thỏa mãn điều kiện 1 2
z  5  3i  5 , đồng thời z z  8 . Tập hợp các điểm biểu diễn của số phức w z z trong 1 2 1 2
mặt phẳng tọa độ Oxy là đường tròn có phương trình nào dưới đây? 2 2  5   3  9 2 2 A. x   y       .
B.  x 10   y  6  36 .  2   2  4 2 2 2 2  5   3 
C.  x 10   y  6  16 . D. x   y   9     .  2   2 
Câu 37. (THPT THÁI PHIÊN - HẢI PHÒNG - LẦN 1 - 2018) Xét số phức z thỏa mãn z  3i  4  3 , biết
rằng tập hợp các điểm biểu diễn số phức w  (12  5i)z  4i là một đường tròn. Tìm bán kính r của đường tròn đó. A. r  13 . B. r  39 . C. r  17 D. r  3 .
Câu 38. (THPT THỰC HÀNH - TPHCM - 2018) Cho số phức z thỏa mãn z  3  1 . Biết rằng tập hợp
các điểm biểu diễn các số phức w  1 3iz 1 2i là một đường tròn. Tính bán kính r của đường tròn đó. A. r  2 . B. r  1. C. r  4 . D. r  2 .
Câu 39. [THPT Lệ Thủy-Quảng Bình] Gọi M là điểm biểu diễn của số phức z thỏa mãn
z m 1  3i  4 . Tìm tất cả các số thực m sao cho tập hợp các điểm M là đường tròn tiếp xúc với trục Oy . A. m  5  ; m  3 .
B. m  5; m  3  . C. m  3  . D. m  5 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 40. [Cụm 4 HCM] Cho số phức z thỏa mãn z  2  2 . Biết rằng tập hợp các điểm biểu diễn các số
phức w  1 iz i là một đường tròn. Tính bán kính r của đường tròn đó. A. r  2 . B. r  4 . C. r  2 . D. r  2 2 .
Câu 41. (Chuyên Lương Thế Vinh – Hà Nội – Lần 2 – 2018 – BTN) Cho số phức z thỏa mãn
z  2  iz  2  i  25 . Biết tập hợp các điểm M biểu diễn số phức w  2z  2  3i là đường tròn tâm I  ;
a b và bán kính c . Giá trị của a b c bằng A. 18 . B. 20 . C. 10 . D. 17 .
Dạng 2. Tập hợp điểm biểu diễn là đường thẳng
Câu 42. (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho số phức z thỏa mãn
z  1  i z  2 . Trong mặt phẳng phức, quỹ tích điểm biểu diễn các số phức z .
A. là đường thẳng 3x y  1  0 .
B. là đường thẳng 3x y  1  0 .
C. là đường thẳng 3x y 1  0 .
D. là đường thẳng 3x y 1  0 .
Câu 43. (ĐỀ 15 LOVE BOOK NĂM 2018-2019) Trên mặt phẳng phức, tập hợp các số phức
z x yi x, y   thỏa mãn z  2  i z  3i là đường thẳng có phương trình A. y x 1.
B. y  x 1.
C. y  x 1. D. y x 1.
Câu 44. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Trong mặt phẳng tọa độ Oxy
, tập hợp các điểm biểu biễn các số phức z thỏa mãn z 1 2i z 1 2i là đường thẳng có phương trình
A. x  2 y  1  0 .
B. x  2 y  0 .
C. x  2 y  0 .
D. x  2 y 1  0 .
Câu 45. Xét các số phức z thỏa mãn z z  2  i  4i 1 là số thực. Biết rằng tập hợp các điểm biểu diễn
của số phức z là đường thẳng d . Diện tích tam giác giới hạn bởi đường thẳng d và hai trục tọa độ bằng A. 8 . B. 4 . C. 2 . D. 10 .
Câu 46. (ĐỀ THI CÔNG BẰNG KHTN LẦN 02 NĂM 2018-2019) Tập hợp các điểm biểu diễn các số
phức z thỏa mãn z  2  z i là một đường thẳng có phương trình
A. 4x  2 y  3  0 .
B. 2x  4 y 13  0 .
C. 4x  2 y  3  0 .
D. 2x  4 y 13  0 .
Câu 47. (LIÊN TRƯỜNG - NGHỆ AN - LẦN 2 - 2018) Cho số phức z thỏa mãn: z 1  z  2  3i . Tập
hợp các điểm biểu diễn số phức z là
A. Đường tròn tâm I 1; 2 , bán kính R  1 .
B. Đường thẳng có phương trình 2x  6 y 12  0 .
C. Đường thẳng có phương trình x  3y  6  0 .
D. Đường thẳng có phương trình x  5y  6  0 .
Câu 48. (THPT CHUYÊN LÊ HỒNG PHONG - TPHCM - 2018) Tìm tập hợp điểm biểu diễn các số phức
12  5iz 17  7i z thỏa  13 . z  2  i
A. d :6x  4 y  3  0 .
B. d : x  2 y 1  0 . C. C  2 2
: x y  2x  2 y 1  0 . D. C  2 2
: x y  4x  2 y  4  0 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 49. (CHUYÊN TRẦN ĐẠI NGHĨA - TPHCM - HK2 - 2018) Trên mặt phẳng tạo độ Oxy , tập hợp
điểm biểu diễn số phức z thỏa mãn z i iz là 1
A. Đường thẳng y  2 . B. Đường thẳng y   . 2 1
C. Đường thẳng y
. D. Đường tròn tâm I 0;  1 . 2
Câu 50. (SGD&ĐT BRVT - 2018) Cho số phức z x yi x, y   thỏa mãn z  2  i z 1 i  0 .
Trong mặt phẳng tọa độ Oxy , điểm M là điểm biểu diễn của số phức z . Hỏi M thuộc đường thẳng nào sau đây?
A. x y  5  0 .
B. x y  2  0 .
C. x y  2  0 .
D. x y 1  0 .
Câu 51. Trong mặt phẳng phức Oxy , tập hợp các điểm biểu diễn số phức Z thỏa mãn z   z2 2 2  2 z  16
là hai đường thẳng d ,d . Khoảng cách giữa 2 đường thẳng d ,d là bao nhiêu? 1 2 1 2
A. d d , d  1.
B. d d , d  6 .
C. d d , d  2 .
D. d d , d  4 . 1 2  1 2  1 2  1 2 
Câu 52. [BTN 166 - 2017] Trong mặt phẳng phức, tập hợp các điểm M biểu diễn số phức z thỏa mãn
điều kiện z z  3  4i là? A. Parabol 2 y  4x .
B. Đường thẳng 6x  8y  25  0 . 2 2 x y C. Đường tròn 2 2
x y  4  0 . D. Elip   1 . 4 2
Câu 53. [TTLTĐH Diệu Hiền - 2017] Cho số phức z thỏa: 2 z  2  3i  2i 1 2z . Tập hợp điểm biểu
diễn cho số phức z là.
A. Một đường thẳng có phương trình: 2
 0x  32 y  47  0 .
B. Một đường có phương trình: 2
3y  20x  2y  20  0 .
C. Một đường thẳng có phương trình: 20x 16 y  47  0 .
D. Một đường thẳng có phương trình: 20x 16 y  47  0 .
Dạng 3. Tập hợp điểm biểu diễn là đường conic
Câu 54. (SỞ GD&ĐT BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Tập hợp các điểm biểu diễn các số phức
z thỏa mãn 2 z i z z  2i là A. Một điểm B. Một đường tròn C. Một đường thẳng D. Một Parabol
Câu 55. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Cho số phức z thỏa mãn
z  2  z  2  4 . Tập hợp điểm biểu diễn của số phức z trên mặt phẳng tọa độ là A. Một đường elip. B. Một đường parabol. C. Một đoạn thẳng. D. Một đường tròn.
Câu 56. (ĐỀ 01 ĐỀ PHÁT TRIỂN ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Xét các số phức z thoả z 1 i z mãn
là số thực. Tập hợp các điểm biểu diễn của số phức là
z zi 1 2
parabol có toạ độ đỉnh  1 3   1 1   1 3   1 1  A. I ;    . B. I  ;   . C. I ;    . D. I  ;   .  4 4   4 4   2 2   2 2 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 57. (CHUYÊN KHTN LẦN 2 NĂM 2018-2019) Tính diện tích hình phẳng giới hạn bởi các điểm biểu
diễn các số phức thỏa mãn z  2  i z  4  i  10 . A. 15 . B. 12 . C. 20 . D. Đáp án khác.
Câu 58. (SGD - BÌNH DƯƠNG - HK 2 - 2018) Tập hợp các điểm biểu diễn các số phức z thỏa mãn
2 z i z z  2i là A. Một đường thẳng. B. Một đường tròn. C. Một Parabol. D. Một điểm
Câu 59. [THPT CHUYÊN VINH] Gọi M là điểm biểu diễn của số phức z thỏa mãn 3 z i  2z  z  3i
. Tìm tập hợp tất cả những điểm M như vậy. A. Một đường thẳng. B. Một parabol. C. Một elip. D. Một đường tròn.
Câu 60. [Sở Bình Phước] Cho số phức z thỏa mãn z  2  z  2  8 . Trong mặt phẳng phức tập hợp những
điểm M biểu diễn cho số phức z là? 2 2 2 2 x y
A. C  :  x  2   y  2  64 . B.  E  :   1 . 16 12 2 2 x y 2 2 C.  E  :   1 .
D. C  :  x  2   y  2  8 . 12 16
Câu 61. [THPT Nguyễn Trãi Lần 1] Tập hợp các điểm trong mặt phẳng tọa độ biểu diễn số phức z thỏa
mãn điều kiện 2 z i z z  2i là hình gì? A. Một đường tròn. B. Một đường Parabol. C. Một đường Elip. D. Một đường thẳng.
Câu 62. [THPT Hai Bà Trưng- Huế] Tìm tập hợp các điểm M biểu diễn hình học số phức z trong mặt
phẳng phức, biết số phức z thỏa mãn điều kiện: z  4  z  4  10.. 2 2 x y
A. Tập hợp các điểm cần tìm là đường elip có phương trình   1 . 9 25
B. Tập hợp các điểm cần tìm là những điểm M x;y trong mặt phẳng Oxy thỏa mãn phương trình
x  2 y  x  2 2 2 4 4  y  12 .
C. Tập hợp các điểm cần tìm là đường tròn có tâm O 0; 0 và có bán kính R  4 . 2 2 x y
D. Tập hợp các điểm cần tìm là đường elip có phương trình   1. 25 9
Câu 63. [THPT CHUYÊN BẾN TRE] Cho số phức z thỏa mãn điều kiện: z  4  z  4  10 . Tập hợp
các điểm M biểu diễn cho số phức z là đường có phương trình. 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1 . C.   1. D.   1 . 9 25 25 9 9 25 25 9
Dạng 4. Tập hợp điểm biểu diễn là một miền
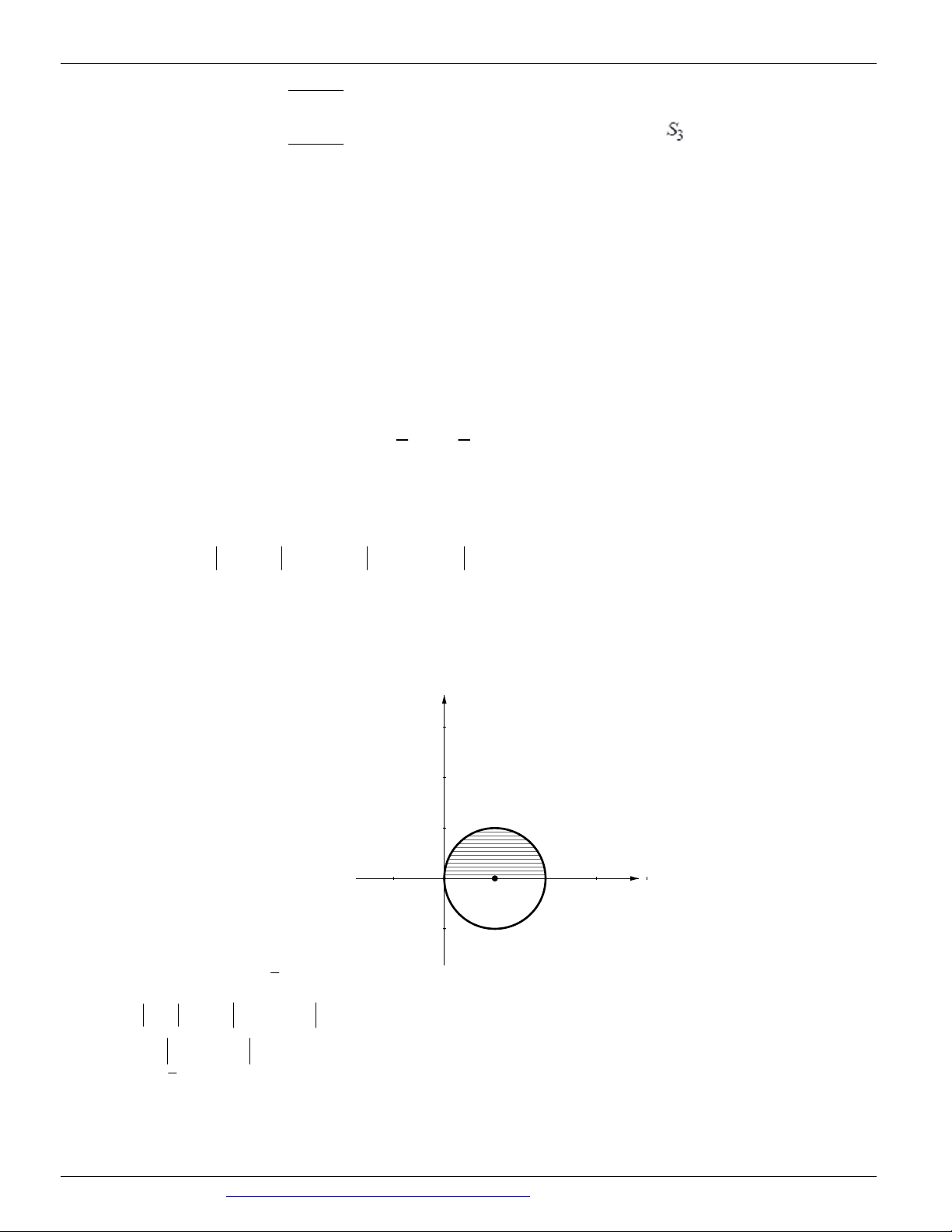
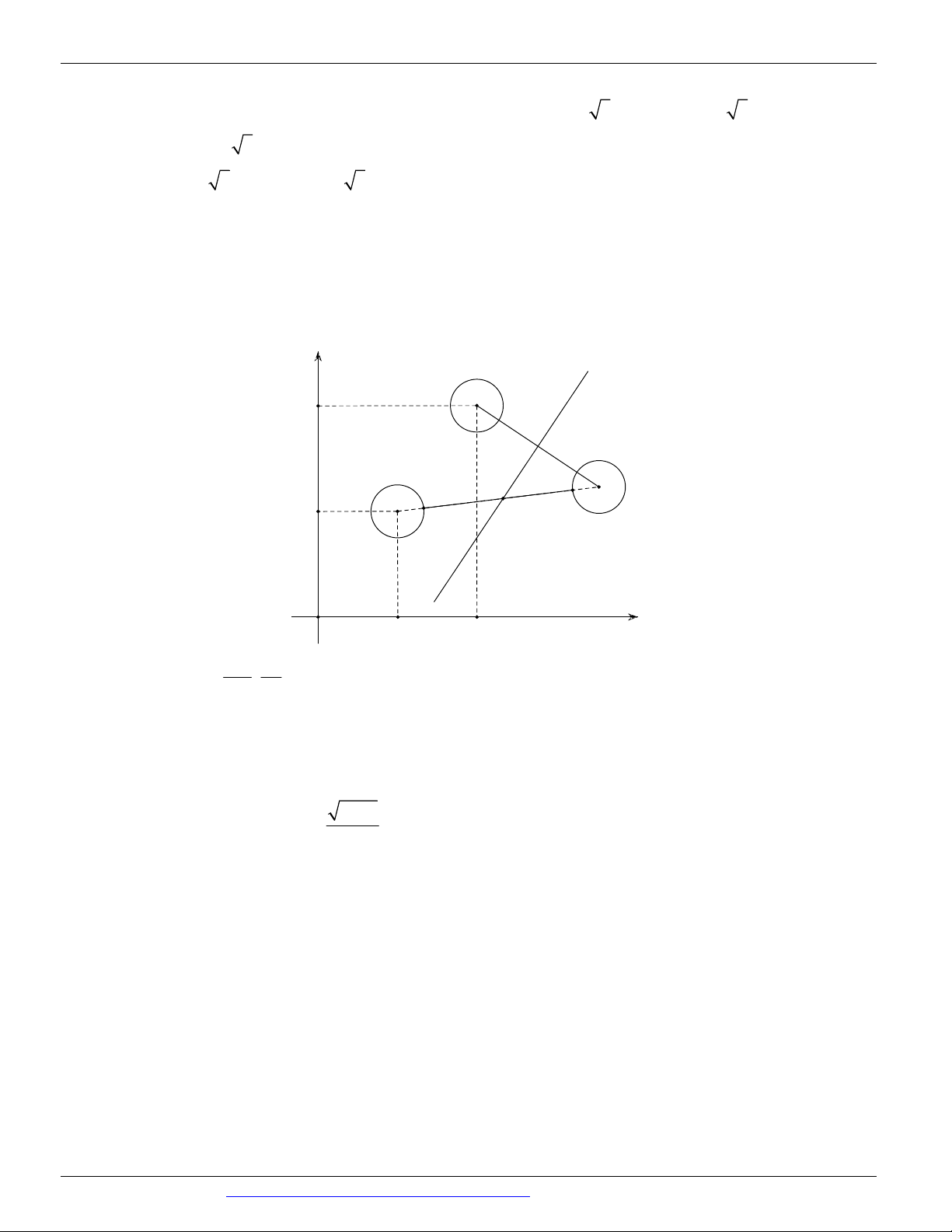
Câu 64. (THPT NĂM 2018-2019 LẦN 04) Phần gạch trong hình vẽ dưới là hình biểu diễn của tập các số
phức thỏa mãn điều kiện nào sau đây?
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. 6  z  8 .
B. 2  z  4  4i  4 . C. 2  z  4  4i  4 . D. 4  z  4  4i  16 .
Câu 65. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Trong mặt phẳng tọa độ Oxy ,
tìm tập hợp các điểm biểu diễn số phức z biết z  2  3i  2 . A. Một đường thẳng. B. Một hình tròn. C. Một đường tròn. D. Một đường Elip.
Câu 66. Trong mặt phẳng phức, tập hợp điểm biểu diễn cho số phức z thỏa z  4  4i  2 là
A. Hình tròn tâm I 4; 4
  , bán kính R  4 .
B. Hình tròn tâm I 4; 4
  , bán kính R  2 .
C. Hình tròn tâm I  4
 ; 4 , bán kính R  2 .
D. Hình tròn tâm I  4
 ; 4 , bán kính R  4 .
Câu 67. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Cho số phức z thỏa mãn điều
kiện 3  z  3i 1  5. Tập hợp các điểm biểu diễn của z tạo thành một hình phẳng. Tính diện tích của hình phẳng đó. A. S  25 . B. S  8 . C. S  4 . D. S 16 .
Câu 68. (THPT THỰC HÀNH - TPHCM - 2018) Trong mặt phẳng Oxy cho số phức z có điểm biểu diến 1
nằm trong cung phần tư thứ  I  . Hỏi điểm biểu diễn số phức w
nằm trong cung phần tư thứ iz mấy? A. Cung  IV  . B. Cung  II  . C. Cung  III  . D. Cung  I  .
Câu 69. (SỞ GD&ĐT NAM ĐỊNH - HKII - 2018) Trong mặt phẳng tọa độ Oxy ,gọi  H  là phần mặt phẳng z 16
chứa các điểm biểu diễn các số phức z thỏa mãn và
có phần thực và phần ảo đều thuộc đoạn 16 z 0 
;1 .Tính diện tích S của  H
A. S  326  .
B. S  164  . C. S  256.. D. S  64. .
Câu 70. (SỞ GD&ĐT YÊN BÁI - 2018) Cho số phức z thỏa mãn điều kiện 3  z  3i 1  5. Tập hợp các
điểm biểu diễn của z tạo thành một hình phẳng. Tính diện tích S của hình phẳng đó. A. S  4 . B. S  25 . C. S  8 . D. S  16 .
Câu 71. [SỞ GD-ĐT HÀ TĨNH L2] Biết số phức z thõa mãn z 1  1 và z z có phần ảo không âm.
Phần mặt phẳng biểu diễn số phức z có diện tích là:  A. 2 . B. 2  . C. . D.  . 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 72. [CHUYÊN VÕ NGUYÊN GIÁP] Gọi H là hình biểu diễn tập hợp các số phức z trong mặt phẳng
tọa độ 0xy sao cho 2z z  3 , và số phức z có phần ảo không âm. Tính diện tích hình H . 3 3 A. . B. . C. 6 . D. 3 . 2 4
Câu 73. [THPT Chuyên Thái Nguyên] Tập hợp các số phức w  1 iz 1 với z là số phức thỏa mãn
z 1  1 là hình tròn. Tính diện tích hình tròn đó. A. 2 . B.  . C. 3 . D. 4 .
z  2z  3i
Câu 74. [2017] Gọi M là điểm biểu diễn số phức  
, trong đó z là số phức thỏa mãn 2 z  2  
2  iz i  3  i z . Gọi N là điểm trong mặt phẳng sao cho Ox,ON  2 , trong đó  
  Ox,OM là góc lượng giác tạo thành khi quay tia Ox tới vị trí tia OM . Điểm N nằm trong góc phần tư nào?
A. Góc phần tư thứ (IV). B. Góc phần tư thứ (I).
C. Góc phần tư thứ (II). D. Góc phần tư thứ (III).
Câu 75. [TRẦN HƯNG ĐẠO – NB-2017] Cho số phức z thỏa mãn điều kiện z  3  4i  2. Trong mặt
phẳng Oxy tập hợp điểm biểu diễn số phức w  2z  1  i là hình tròn có diện tích A. S  9 . B. S  12 . C. S  16 . D. S  25 .
Câu 76. [THPT Hoàng Hoa Thám - Khánh Hòa - 2017] Biết số phức z thỏa điều kiện 3  z  3i 1  5.
Tập hợp các điểm biểu diễn của z tạo thành 1 hình phẳng. Diện tích của hình phẳng đó bằng: A. 9 . B. 16 . C. 25 . D. 4 .
Phần B. LỜI GIẢI THAM KHẢO
Dạng 1. Tập hợp điểm biểu diễn là đường tròn Câu 1. Chọn D
Gọi z x  i
y , với x, y . 2
Theo giả thiết, ta có  z  3i z  3  z  3z  3iz  9i là số thuần ảo khi  3 3 3 2 2 2 
x y  3x  3y  0 . Đây là phương trình đường tròn tâm I ;   , bán kính R  .  2 2  2 Câu 2. Chọn C
Giả sử z x yi với x, y   .
Vì  z  2i z  2  x  2  yi 
x  2  yi     
x x  2  y 2  y   xy   x  22  y  i     là 2 2
số thuần ảo nên có phần thực bằng không do đó x x  2  y 2  y  0   x   1   y   1  2 .
Suy ra tập hợp các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng 2 . Câu 3. Chọn C
Gọi w x yi với ,
x y là các số thực. 5  iz w  5 Ta có w   z  . 1 z i w w  5 Lại có z  2   2 i w w w ix 2  y xy 2 2 2 5 2 5 2 1             
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
  x  2   y  2 5 4  52 .
Vậy tập hợp các điểm biểu diễn các số phức w là một đường tròn có bán kính bằng 52  2 13 . Câu 4. Chọn A
Gọi z a bi , a, b  
Ta có:  z i z    a bi ia bi   2 2 2 2 2
2  a  2a b  2b  2a b  2i 2 2
Vì  z  2i z  2 là số thuần ảo nên ta có 2 2
a  2a b  2b  0  a   1  b   1  2 .
Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng 2 . Câu 5. Chọn D
Giả sử z a bi ; w x yi ;a, , b , x y  
Theo đề w  3  4iz i x yi  3  4ia bi  i
x  3a  4b
x  3a  4b
x yi  3a  4b  3b  4a   1 i     Ta có
y  3b  4a 1
y 1  3b  4a  
x   y  2   a b2   a b2 2 2 2  a b   2 2 1 3 4 4 3 25 25 25 a b  Mà 2 2
z  4  a b  16 . Vậy x   y  2 2 1  25.16  400
Bán kính đường tròn là r  400  20 . Câu 6. Chọn C
Gọi z x yi z x yi
z  2iz  2  .
z z  2z  2iz  4i 2 2
x y  2  x yi  2i x yi  4i 2 2
x y  2x  2 y  2x  2 y  4i
z  2iz  2 là số thuần ảo 2 2
x y  2x  2 y  0
Vậy tập hợp các điểm biểu diễn của z là một đường tròn có tâm là I 1;   1 . Câu 7. Chọn D
Đặt z x yi  , x y   .
z iz  2  x  1 yi x  2 yi   
 là số thuần ảo  x x  2  y y   1  0 2 2
x y  2x y  0 .  1  5
Vậy tập hợp các điểm biểu diễn số phức z là một đường tròn có tâm I 1  ; , R    .  2  2 Câu 8. Chọn B 4  iz w
 1 zw  4  iz z w i  4  w 1 z
z . w i  4  w
2. w i  4  w (*)
Gọi w x yi,  ,
x y   khi đó thay vào (*) ta có: 2 2
2. x yi i  4  x yi 2 xy        x   2 2 1 4  y  
x y x y  
  x  2   y  2 2 2 8 4 14 0 4 2  34 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 4  iz
Vậy tập hợp điểm biểu diễn các số phức w
là một đường tròn có bán kính bằng 34 . 1 z Câu 9. Chọn A 3  iz Ta có: w
w wz  3  iz w  3  i wz . 1 z
w  3  i wz w  3  i wz .
Gọi w x yi,  , x y  . 2 2 Do đó, w
 i wz   x   2 2 3 3  y
x  1 y . 2
  x  2  y x    y 2 2 2 2 2 3 2 2 1
x y  6x  4 y  7  0 .
Vậy tập hợp điểm biểu diễn số phức w thỏa mãn z  2 là đường tròn có tâm I 3; 2 và bán kính bằng 2 5 . Câu 10. Chọn A
Gọi số phức w x yi; x, y   . Khi đó: 2  iz w
w1 z  2  iz w  2  z i w
w  2  z i w  w  2  z z i w 1 z
  x  2  y  x    y2   x  2   y  2 2 2 2 2 1 2 2  10*
Từ * suy ra điểm biểu diễn số phức w là một đường tròn có bán kính bằng 10 . Câu 11. Cách 1.
Đặt w  x yi .Ta có w  3  2i  2  iz .
x yi  3 2i  2iz .
 2iz   x  
3  y  2i .   2
4  i z   x  3   y  2i.2  i   . 2 x y  8 x  2 y  1  z   i . 5 5 2 2
 2x y  8 
x  2 y 1  Vì z  2 nên   4     .  5   5  2 2
x y 6x4y 1  3 20.
  x  2   y  2 3 2  20 .
Vây tập hợp biểu diễn số phức w là đường tròn tâm I 3;  2 . Cách 2.
Đặt z a b ;
i w  x yi . Vì z  2 nên 2 2 a b  4 .
Ta có w  3  2i  2  iz .
x yi  2i  3  2  ia bi .
  x  3   y  2i  2a b  2b ai .
  x  2   y  2   a b2   b a2 3 2 2 2 .
  x  2   y  2   2 2 3 2 5 a b  .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
  x  2   y  2 3 2  20 .
Vây tập hợp biểu diễn số phức w là đường tròn tâm I 3;  2 .
Câu 12. Đặt z x yi ; x, y   . Khi đó z x yi .
Vì z z    x yi x yi 2 2 . 1
 1  x y  1.
Vậy tập hợp các điểm biểu diễn số phức z cần tìm là đường tròn đơn vị. Câu 13. Cách 1:
Gọi M là điểm biểu diễn số phức w . w i
Ta có w  2z i z  . 2 w i
Do đó z 1 2i  3 
1 2i  3  w  2  3i  6  MI  6 , với I 2; 3   . 2
Do đó tập hợp điểm M là đường tròn tâm I 2; 
3 và bán kính R  6 .
Câu 14. Đặt z x yi x, y   .
Ta có z i  1  i z .
x   y  
1 i  1 i x yi  x   y  
1 i   x y    x y i
x   y  2   x y 2   x y 2 2 1 2 2
x y  2 y  1  0  x   y  2 2 1  2 .
Vậy tập hợp các điểm biểu diễn số phức z là đường tròn có tâm 0;  1 . z Câu 15. Ta có:
 1  z i  2  5 . i  2
Suy ra tập hợp các điểm biểu diễn số phức z là một đường tròn có bán kính r  5. Câu 16. Chọn C
Giả sử điểm M(x; y) là điểm biểu diễn số phức z . Ta có: 2 2
z 1 2i  3  (x 1)  ( y  2) i  3  (x 1)  ( y  2)  9 2 2
Vậy điểm M(x; y) thuộc đường tròn (x 1)  ( y  2)  9 có tâm I(1; 2) , bán kính R  3 .
Câu 17. Gọi số phức z x yi x, y    z x y .i
Thay vào điều kiện ta được:
(2  z)(z i).
 (2  x yi)(x yi i).
 2  x  yi x  1 yi.    
 (2  x)x y(1 y)  (2  x)(1 y)  xy .i
(2  z)(z i) là số thuần ảo khi và chỉ khi:
(2  x)x y(1 y)  0 . 2 2
x y  2x y  0 .  1  5
Vậy số phức z x yi thuộc đường tròn tâm I 1;   ,bán kính R  .  2  2 Câu 18. Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 z i
i z a  b  2 2 (1 ) 1
 2 nên tập điểm M là Đường tròn tâm I(0; -1), bán kính R  2 . Câu 19. lời giải: 2 2 Ta có 2 z i  
x   y   2 4 1
 4  x   y   1  16
Câu 20. Giả sử số phức thỏa mãn bài toán có dạng z x yi x, y  .
Suy ra z  2  i x yi  2  i x  2  ( y 1)i . Do đó: 2 2
z  2  i  4  x  2  ( y 1)i  4  (x  2)  ( y 1)  16 .
Vậy tập hợp tất cả các điểm biểu diễn số phức z là đường tròn tâm I  2  ;  
1 , bán kính R  4 .
Câu 21. Gọi z a bi , với x, y   , ta có: 2 2
z 1 i  2  x yi 1 i  2   x   1   y  
1 i  2   x   1   y   1  4 .
Vậy tập hợp các điểm biểu diễn số phức z là đường tròn tâm I 1;  
1 , bán kính R  2 .
Câu 22. Gọi z x yi, x , y   . Ta có:
1 iz  5  i  2  1 i x yi  5  i  2   x y  5   x y   1 i  2
  x y  2   x y  2 5 1  4 2 2
 2x  2 y  8x 12 y  22  0 2 2
x y  4x  6 y 11  0 .
Vậy tập hợp tất cả các điểm biểu diễn các số phức z là đường tròn tâm I 2;  3 và R  2 .
Câu 23. Đặt z a bi, a, b   . Gọi M  ;
a b là điểm biểu diễn cho số phức z . z  2 a  2  bi
a  2  bi a  b  2i   Có w    z  2i
a  b  2i
a  b  22 2
a a  2  bb  2  a  2b  2  abi   
a  b  22 2
a a  2  b b  2  0   1 
w là số thuần ảo   a   b  22 2  0  Có   2 2
1  a b  2a  2b  0 .
Suy ra M thuộc đường tròn tâm I  1  
;1 , bán kính R  2 .
Câu 24. Đặt z x yi x, y   . Ta có điểm biểu diễn z là M  ; x y .
Với m  0 , ta có z  0 , thoả mãn yêu cầu bài toán.
Với m  0 , ta có:
+ z m M thuộc đường tròn C tâm I 0;0 , bán kính R m 1  2 2 + 2
z m mi m   x m   y m 4 4 3 4 3  m
M thuộc đường tròn C tâm I4 ; m 3  m, bán kính 2 R  m . 2 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
+) Có duy nhất một số phức z thoả mãn yêu cầu bài toán khi và chỉ khi C và C tiếp xúc nhau 2  1  2
5m m m
II   R R   m  4 2   
5m m m  .
II   R R    m  6    m  0 
Kết hợp với m  0 , suy ra m 0; 4; 
6 . Vậy tổng tất cả các giá trị của m là 10 .
Câu 25. Gọi w x yi , x , y   . Số phức w được biểu diễn bởi điểm M x; y .
Từ w  1 z suy ra x yi  1 z z   x  
1  yi z   x   1  yi .
Mà z  2  i  3 nên ta có:  x  
1  yi  2  i  3   x   1   y  
1 i  3   x  2   y  2 1 1  3
  x  2   y  2 2 1 1  3 .
Vậy tập hợp điểm biểu diễn số phức w là đường tròn tâm I 1;   1 bán kính R  3 . Câu 26. Chọn B
Ta có w i  2  iz w i  2  iz . Suy ra w i  2  iz  2  i . z  10 .
Vậy tập hợp điểm biểu diễn của số phức w trên mặt phẳng tọa độ nằm trên đường tròn có bán kính r  10 . Câu 27. Chọn D
Gọi z x y i  , x y    .
Khi đó: w   z  2i z  3  x  ( y  2)i(x  3)  y i
x(x  3)  y( y  2)  xy  (x  3)( y  2) i
Do w là số thuần ảo  x(x  3)  y( y  2)  0 2 2
x y  3x  2 y  0 2  3  13  x    y  2 1    .  2  4  3  13
Vậy tập hợp các điểm biểu diễn số phức z là đường tròn tâm I  ; 1   , bán kính R  .  2  2
Câu 28. Gọi w x yi  , x y   Theo đề bài ta có:
w  1 i 8 z i wi  1 i 8 z wi  1 i 8 z   1  1 i 8
w i 1 i 8  1 i 8 z   1   x  
1   y 1 8i  1 i 8 z   1 2 2 2
  x  2   y         x  2 2 1 1 8 1 8 .2
1   y 1 8  36
Vậy tập hợp các điểm biểu diễn số phức w  1 i 8 z i là một đường tròn có bán kính r  6.
Câu 29. +)Đặt z x yi Khi đó 2 2 | z 5  3i | 5 |
 x 5  (y 3) i | 5  (x  5)  ( y  3)  25 (C)
Gọi A, B lần lượt là 2 điểm biểu diễn số phức z , z 1 2
 A, B thuộc đường tròn (C) có tâm I (5; 3), bán kính R = 5 và | z z | 8  AB  8 1 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 z z
+) Gọi H là điểm biểu diễn số phức 1 2 w =  2 AB
 H là trung điểm AB  AH   4 2
Xét tam giác AIH vuông tại H có AH = 4, AI = 5 nên 2 2 2 2 IH
IA AH  5  4  3
 H thuộc đường tròn (C) có tâm I (5; 3), bán kính R  3 (*)
+) Gọi M là điểm biểu diễn số phức w=z z 1 2    OM  2OH
 M là ảnh của H qua phép vị tự tâm O, tỉ số k = 2 với O là gốc tọa độ (**)
Từ (*)và (**)  tập hợp M là đường tròn (C )
 là ảnh của (C) phép vị tự tâm O, tỉ số k = 2
+) Giả sử đường tròn (C )
 có tâm J (a; b) và bán kính R a  2.5  10   b  2.3  6
R  2.R  6 
 Phương trình đường tròn (C )  là 2 2
( x  10)  ( y  6)  36
Câu 30. Gọi số phức z x iy x, y   Ta có: 2 2
z  2  i  4   x  2   y  
1 i  4   x  2   y   1  16
Vậy tập hợp tất cả các điểm biểu diễn các số phức z thỏa mãn: z  2  i  4 là đường tròn có tâm I 2;  
1 và có bán kính R  4 .
Câu 31. Ta có: w  1 iz  2i w  2i  1 iz w  2i  1 iz w  2i  2 2 .
Do đó, tập hợp điểm biểu diễn số phức w là đường tròn tâm I 0; 2 và bán kính 2 2 .
Câu 32. Gọi số phức z a bi , a,b  2 2 2
a bi 1  1 i  2a bi  a   2
1  b  1 2a   1   2b 4 1 2 2 2 2
a  2a 1 b  1 4a  4a 1 4b  4b 2 2
a b  2a b   0 3 3  2 
Tập hợp các điểm biểu diễn số phức z là một đường tròn có tâm I 1;    ,  3  2  2  1 10
Bán kính R  1      .  3  3 3
Câu 33. Cách 1: Đặt z a bi ta có 2z i  6  2a  2bi i  6 
a   b  2 2 4 2 1  6 . 2 35  1 2 2 
4a  4b  4b  35  0 2 2
a b b   0 2  a b   9   . 4  2   1 
Vậy tập hợp tất cả các điểm biểu diễn số phức z là đường tròn tâm I 0; 
 bán kính R  3 .  2 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  1  1
Cách 2: 2z i  6  z  0  i  3  
. Gọi I là điểm biểu diễn số phức 0 
i , M là điểm biểu  2  2
diễn số phức z . Ta có MI  3 . Vậy tập hợp tất cả các điểm biểu diễn số phức z là đường tròn tâm  1  I 0; 
 bán kính R  3 .  2 
Câu 34. Ta có: w  2  iz  3i  5  w  2  i z 1 3i  6  4i
w  6  4i  2  i z 1 3i
w  6  4i  2  i z 1 3i  2 5 Gọi M  ;
x y là điểm biểu diễn số phức w x yi  ; x y  
w  6  4i  2 5   x  6   y  4i  2 5
  x     y     2 2 2 6 4 2 5
Vậy tập hợp điểm biểu diễn số w là đường tròn tâm I 6; 4 , bán kính R  2 5 . w  3  2i
Câu 35. Ta có w  3  2i  2  iz z
. Đặt w x yi x, y   . 2  i
x yi  3  2i Khi đó z  . 2  i
x yi  3  2i
x  3   y  2i
x  3   y  2i Ta có z  2   2   2   2 2  i 2  i 2  i
x  3   y  2 i  2 2  i x  3   y  2i  2 5   x     y     2 2 2 3 2 2 5 .
Vậy tập hợp các điểm biểu diễn số phức w  3  2i  2  iz là một đường tròn có bán kính R  2 5 . Câu 36.
Gọi A , B , M là các điểm biểu diễn của z , z , w . Khi đó A , B thuộc đường tròn 1 2
C  x  2   y  2 : 5 3
 25 và AB z z  8 . 1 2
C  có tâm I 5;3 và bán kính R  5 , gọi T là trung điểm của AB khi đó T là trung điểm của OM và 2 2 IT
IA TA  3 .
Gọi J là điểm đối xứng của O qua I suy ra J 10;6 và IT là đường trung bình của tam giác
OJM , do đó JM  2IT  6 . 2 2
Vậy M thuộc đường tròn tâm J bán kính bằng 6 và có phương trình  x 10   y  6  36 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 37. Gọi số phức w x yi, với ,
x y R , biểu diễn bởi M ( ; x y)
x  ( y  4)i
w  (12  5i)z  4i x yi  (12  5i)z  4i z  12  5i
x  ( y  4)iz  12  5i
x  ( y  4)i
Ta có : z  3i  4  3   3i  4  3 12  5i
x  63  ( y 12)i 2 2
(x  63)  ( y 12)   3   3 2 2 2
 (x  63)  ( y 12)  39 12  5i 2 2 12  5 Vậy r  39 .
Câu 38. Gọi w x yi .
x 1  y  2i
w  1 3iz 1 2i x yi  1 3iz 1 2i z  1 3i  1 3   x  
1  3  y  2  y  2   x   1 3
z   x 1  y  2i   i      i  4 4    4 4
x 13  3  y  2  y  2   x   1 3  z  3   i 4 4 2 2
  x 13  3  y  2 
  y  2   x   1 3  z  3  1        1  4   4        x  2 
x   y     y  2   y  2   y   x     x  2 13 2 3 13 2 3 2 2 2 2 1 3 3 1  16 2 2
x y  8x  4  6 3 y 12 3  43  0 Bán kính r     2 2 4 2 3 3 12 3  43  2 . Câu 39. Chọn B
Đặt z x yi ,  x, y   . Khi đó.
z m 1 3i  4  x yi m 1 3i  4 .
  x m     y
i   x m    y  2 2 1 3 4 1 3  4 .
  x m     y  2 2 1 3  16 .
Do đó tập hợp các điểm M biểu diễn của số phức z là đường tròn tâm I 1 ;
m  3 và bán kính 1   m  4 m  3
R  4 . Để đường tròn này tiếp xúc với trục Oy thì 1  m  4   . 1  m 4     m  5  
Vậy m  5; m  3  . Câu 40. Chọn D w i
w  1 iz i z
; đặt w x yi ; , x y  . 1 i
x yi i
x yi i
x yi i1 i  z
. Ta có z  2  2   2  2   2  2 . 1 i 1 i 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
x yi i1 i 
 2  2  x xi yi y i 1 4  4  x y  3   x y   1 i  4 2
  x y  32   x y  2 2 2 2 2 1
 16  x y  9  2xy  6 y  6x x y 1 2xy  2 y  2x  16 . 2 2 2 2
 2x  2 y  8x  4 y  6  0  x y  4x  2 y  3  0
Đường tròn có bán kính là 2 2
R  2 1  3  2 2 . Câu 41. Chọn A
Giả sử z a bi  ;
a b   và w x yi  ; x y   .
z  2  iz  2  i  25  a  2  b  
1 i a  2  b   1 i  25    
 a  2  b  2 2 1  25   1
Theo giả thiết: w  2z  2  3i x yi  2 a bi  2  3i x yi  2a  2  3  2bi .  x  2 a
x  2a  2   2     2 . y  3  2b 3  yb     2 2 2  x  2   3  y  2 2 Thay 2 vào   1 ta được:  2  1  25     
x  2   y  5  100 .  2   2 
Suy ra, tập hợp điểm biểu diễn của số phức w là đường tròn tâm I 2;5 và bán kính R 10.
Vậy a b c  17 .
Dạng 2. Tập hợp điểm biểu diễn là đường thẳng
Câu 42. Giả sử số phức z có dạng: z x yix, y  
Ta có: z 1 i z  2  x yi 1 i x yi  2   x   1   y  
1 i   x  2  yi
x  2   y  2   x  2 2 1 1 2  y
  x  2   y  2   x  2 2 1 1 2  y 2 2 2 2
x  2x 1 y  2 y 1  x  4x  4  y
 6x  2 y  2  0  3x y 1  0
Vậy tập hợp điểm biểu diễn số phức z là đường thẳng 3x y  1  0 . 2 2 2
Câu 43. z   i z i   x     y   2 2 3 2 1
x   y  3  4x  4 y  4  0  y x 1.
Câu 44. Đặt z x yi x, y    z x yi và M  ;
x y là điểm biểu diễn của số phức z .
Ta có: z 1 2i z 1 2i x yi 1 2i x yi 1 2i   x  
1   y  2i   x  
1  2  y i
  x  2   y  2   x  2    y2 1 2 1 2 2 2 2 2
x  2x 1 y  4 y  4  x  2x 1 y  4 y  4  4x  8y  0  x  2 y  0 .
Vậy tập hợp các điểm biểu biễn các số phức z thỏa mãn yêu cầu bài toán là đường thẳng có phương
trình là x  2 y  0 .
Câu 45. Giả sử z a bi a,b R .
Khi đó z z  2  i  4i 1  a bia bi  2  i  4i 1  a bi.a  2  1 bi  4i 1  
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
a a  2  b 1 b  a 1 b  b a  2 i  4i 1  
a a  2  b 1 b 1 a  2b  4i .
+ z z  2  i  4i 1 là số thực suy ra a  2b  4  0.
+ Số phức z có điểm biểu diễn M  ;
a b  M d : x  2 y  4  0 . 1
+ Đường thẳng d cắt trục Ox , Oy lần lượt tại A4;0 và B 0;2  S  .O . A OB  4 . OAB 2
Câu 46. Gọi số phức z a bi , với a,b thuộc  . Khi đó, M (a; b) là điểm biểu diễn số phức z .
Ta có: z  2  z i a  2  bi a  (b1)i 2 2 2 2
 (a 2)  b a  (b1) 2 2 2 2
 (a 2)  b a  (b1)  4a  2b  3  0  điểm M (a; b) thuộc đường thẳng
4x  2 y  3  0
Vậy, tập hợp các điểm M thỏa mãn bài ra là đường thẳng 4x  2 y  3  0 .
Câu 47. Gọi z x yi ; ( x , y   ). 2 2 2
Ta có: z 1  z  2  3i   x   2
1  y   x  2   y  3  x  3y  6  0 .
Vậy tập hợp các điểm biểu diễn số phức z là đường thẳng có phương trình x  3y  6  0 . 
z x yi x, y  
12  5iz 17  7i Câu 48. Đặt  , ta có:
 13  12  5iz 17  7i  13 z  2  iz  2  iz  2  i
 12  5i z 1 i  13 z  2  i  12  5i z 1 i  13 z  2  i  13 z 1 i  13 z  2  i 2 2 2 2
z 1 i z  2  i x yi 1 i x yi  2  i   x   1   y   1
  x  2   y   1
 6x  4 y  3  0 .(thỏa điều kiện z  2  i )
Vậy tập hợp điểm biểu diễn số phức z là đường thẳng 6x  4 y  3  0 .
Câu 49. Gọi số phức z a bi a,b   .
Ta có: z i iz a bi i i a bi  a  b  
1 i  b ai
a  b  2 2 2 2 1
b a  2  b 1  0 . 1
Vậy tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện bài toán là đường thẳng y  . 2
Câu 50. Ta có z  2  i z 1 i  0  x yi   i    i 2 2 2 1 x y  0 2 2
x   x y   2 2 2
y 1 x y i  0 2 2
x  2  x y  0    2 2 2 2
x  2  x y y 1 x y  0  x y 1  0 . 2 2
y 1 x y  0 
Do đó M thuộc đường thẳng x y 1  0 . Câu 51. Chọn D Gọi M  ,
x y là điểm biểu diễn số phức z x yi , x y R
Ta có: z  z2 2 2 2 2 2 2 2 2  2 z
 16  x  2xyi y x  2xyi y  2x  2 y  16 2
 4x  16  x  2  d d , d  4 1 2 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ở đây lưu ý hai đường thẳng x = 2 và x = -2 song song với nhau. Câu 52. Chọn B
Đặt z x yi  ,
x y   và M  ;
x y  là điểm biểu diễn của z. 2 2   z x y Ta có  .
z  3  4i x iy  3  4i   x  3  y  4 i
z   i   x  2   y  2 3 4 3 4 . 2 2 Vậy 2 2
z z  3  4i x y   x  3   y  4  6x  8 y  25  0 . Câu 53. Chọn D Gọi M  ;
x y  là điểm biểu diễn số phức z x yi . Ta có.
2 z  2  3i  2i 1 2z .
 2  x  2   y  3i  1 2x  2 y  2i
 2  x  22   y  32   1
  2x2  2 y  22  4 2 2
x y  4x  6 y 13 2 2
 4x  4 y  4x  8 y  5 .
 20x 16 y  47  0
Vậy tập hợp điểm M  ;
x y  là đường thẳng 20x 16 y  47  0 .
Dạng 3. Tập hợp điểm biểu diễn là đường conic Câu 54. Chọn D
Đặt z x yi  ,
x y    z x yi .
Khi đó 2 z i z z  2i  2 x   y  
1 i  2 y  2i xy 2       y  2 2 4 1 2 2   2 2 2
 4x  4y  8y  4  4y  8y  4 2 xy  là một Parabol. 4
Câu 55. Gọi M x; y là điểm biểu diễn số phức z x yi . Xét hai điểm F 2
 ; 0 , F 2;0 , khi đó theo giả thiết: 2   1  
z  2  z  2  4 
x  22  y   x  22 2 2
y  4  MF MF  4 . 1 2
Mà F F  4 , nên MF MF F F . 1 2 1 2 1 2
Do đó tập hợp các điểm biểu diễn của z chính là đoạn thẳng F F . 1 2
Câu 56. Giả sử z a bi a,b R . z 1 i
a 1 b   1 i
a 1 b  
1 i 1 2ai Khi đó     z z 2 i 1 1 2ai 1 4a
a 1 2a b  
1  2a a  
1  b 1 i    . 2 1 4a 2 z 1 i ba a 1
là số thực suy ra 2a a   2
1  b 1  0  b  2a  2a 1   4.  2.  .   
z z i 1 2  2  2 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 za b  Số phức
có điểm biểu diễn M ; 
  quỹ tích M là parabol có phương trình 2  2 2  1 2
y  4x  2x  2 z  1 3 
Tập hợp các điểm biểu diễn của số phức
là parabol có toạ độ đỉnh I ;    . 2  4 4 
Câu 57. Gọi M x; y là điểm biểu diễn của số phức z x yi x, y  .
Ta có: z  2  i z  4  i  10  x  2   y  
1 i x  4   y   1 i  10.
  x  2   y  2   x  2   y  2 2 1 4 1  10 (*) Đặt A  B
  AB    2 2 2;1 , 4;1 4 2  0  6.
Khi đó phương trình (*) trở thành: MAMB 10.
Khi đó tập hợp những điểm M thỏa mãn phương trình (*) là một elip với. 10
+ Độ dài trục lớn 2a  10  a   5. 2 6
+ Tiêu cự 2c AB  6  c   3. 2
+ Độ dài trục bé 2b với 2 2 2 2 2
b a c  5  3 16  b  4.
Vậy diện tích hình phẳng giới hạn bởi các điểm biểu diễn các số phức thỏa mãn
z  2  i z  4  i  10 là diện tích Elip trên: S   ab   4.5  20 .
Câu 58. Gọi z x yi z x yi , x, y   . 2 2
2 z i z z  2i  2 x   y  
1 i  2y  2i 2 
x   y   2 2 1
 0  2 y  2 1   2 2
x y y   2 4 2
1  4 y  8 y  4 2  4x  16 y 2  y x 4
Vậy tập hợp các điểm biểu diễn các số phức z thỏa mãn 2 z i z z  2i là một Parabol  P 1 có phương trình: 2 y x . 4 Câu 59. Chọn B
Gọi số phức z x yi có điểm biểu diễn là M  ,
x y trên mặt phẳng tọa độ:
Theo đề bài ta có: 3 z i  2z z  3i  3(x yi)  3i  2(x yi)  (x yi)  3i  . 2 2 2 2
3x  (3y  3)i x  (3  3y)  9x  (3y  3) 
x  (3  3y)  . 2 2 2 2 2 2 2
9x  (3y  3)  x  (3  3y)  8x  36 y  0  y   x . 9
Vậy tập hợp các điểm M  ,
x y biểu diễn số phức z theo yêu cầu của đề bài là Một parabol 2 2 y   x . 9 Câu 60. Chọn B Gọi M  ; x y , F ( 2  ;0) , F (2;0) . 1 2 Ta có 2 2 2 2
z  2  z  2  8 
x  ( y  2)  x  ( y  2)  8  MF MF  8 . 1 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Do đó điểm M  ;
x y nằm trên elip  E có 2a  8  a  4, ta có F F  2c  4  2c c  2 . 1 2 2 2 x y Ta có 2 2 2
b a c  16  4  12 . Vậy tập hợp các điểm M là elip  E  :   1 . 16 12 Câu 61. Chọn B
 Đặt z x yi z x yi điểm biểu diễn của z là M  ; x y . Ta có:
2 z i z z  2i  2 x yi i   x yi   x yi  2i 1 .
 2 x   y  
1 i  2  y  
1 i  2 x   y  2 2 2 1
 2 y  1  y x 4
Vậy tập hợp các điểm biểu diễn số phức z là một đường Parabol. Câu 62. Chọn D
Ta có: Gọi M x;y là điểm biểu diễn của số phức z x  . yi .
Gọi A4; 0 là điểm biểu diễn của số phức z  4..
Gọi B 4; 0 là điểm biểu diễn của số phức z  4. .
Khi đó: z  4  z  4  10  MA MB  10. (*).
Hệ thức trên chứng tỏ tập hợp các điểm M là elip nhận ,
A B là các tiêu điểm. 2 2 x y
Gọi phương trình của elip là   1, 2 2 2
a b  0,a b c . 2 2  a b
Từ (*) ta có: 2a  10  a  5. . 2 2 2
AB  2c  8  2c c  4  b a c  9 . x y
Vậy quỹ tích các điểm M là elip: E  2 2 :   1. 25 9 Câu 63. Chọn B Gọi M  ;
x y biểu diễn số phức z x yi x, y R . 2 2
Từ giả thiết ta có  x  4 2
y   x  4 2
y  10  MF MF  10 với F 4  ;0 , F 4;0 . 1   2   1 2 2 2 x y
Vậy tập hợp các điểm M biểu diễn cho số phức z là đường Elip có phương trình   1 . 25 9
Dạng 4. Tập hợp điểm biểu diễn là một miền
Câu 64. Dễ thấy điểm I 4; 4 là tâm của hai đường tròn. 2 2
Đường tròn nhỏ có phương trình là:  x  4   y  4  4 . 2 2
Đường tròn to có phương trình là:  x  4   y  4  16 .
Vậy tập hợp điểm biểu diễn số phức thỏa mãn đề bài là 2  z  4  4i  4 . Câu 65. Cách 1:
Đặt z x yi với , x y   .
Theo bài ra: z  2  3i  2  x yi  2  3i  2  x  2  ( y  3)i  2
  x  2   y  2 2 3
 2   x  2   y  2 2 3  4 .
Vậy tập hợp các điểm biểu diễn số phức z trong mặt phẳng tọa độ Oxy là hình tròn tâm
I 2 ;  3 , bán kính R  2 .
Câu 66. Gọi M  ;
x y là điểm biểu diễn cho số phức z x y ; i  ; x y   .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
z  4  4i  2 .
x yi  4  4i  2
x  4   y  4i  2
  x  2   y  2 4 4  2
  x  2   y  2 4 4  4 .
Vậy tập hợp điểm biểu diễn cho số phức z thỏa z  4  4i  2 là hình tròn tâm I  4  ; 4 , bán kính R  2 .
Câu 67. Gọi M a;b là điểm biểu diễn của số phức z ; A 1
 ;3 là điểm biểu diễn số phức 1   3i . 2 2
Khi đó, AM z  3i 1  a   1  b  3 
 a  2  b  2 2 3 1 3
 25 , tập hợp các điểm biểu diễn của z là hình vành khăn giới hạn bởi hai đường tròn  ; A 3 và  ;
A 5 , kể cả các điểm nằm trên hai đường tròn này.
S  25  9  16 dvdt  .
Câu 68. Vì số phức z có điểm biểu diến nằm trong cung phần tư thứ  I  nên gọi z a bi,a  0,b  0 . 1 1 1 b   ai baw       i iz
i a bi 2 2 2 2 2 2 b   ai a b a b a bb a
Do a  0, b  0   0,   0 . 2 2 2 2 a b a b
Vậy điểm biểu diễn w nằm trong cung phần tư thứ  III  . 20 18 A B 16 14 12 10 8 6 4 2 O 10 5 5 E I 10 15 C 2 4 6 Câu 69. 8
Gọi z x yi, ,
x y R khi đó điểm biểu diễn của z là M  ; x y.  x 0   1 z x yi x y   0  x  16 16   
i theo giả thiết    (I) 16 16 16 16 y 0  y  16 0   1    16 16 16
16  x yi 16x 16 y     i 2 2 2 2 2 2 z x yi x y x y x y
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  16x 0   1  2 2 2 2  x y
0  16x x y Theo giả thiết    2 2 16 y
0  16 y x y 0   1  2 2  x y
x  0, y  0
x  0, y  0   2 2  2  2
x y 16x  0  
x  8  y  64 (II)  2 2 
x y 16 y  0 2  2 x    y  8  64  Gọi 1
S là diện tích hình vuông OABC có cạnh bằng 16, 2 1 S  16  256 .
S2 là diện tích hình tròn có bán kính bằng 8.
S3 là diện tích phần giao của hai nửa đường tròn như hình vẽ.  1 2 1 2  S  1 S S2  3
S  256  64  2  8  8    4 2 
Vậy S  256  64  32  64  326    .
Câu 70. Gọi z a bi a ;b   . 2 2
Ta có 3  z  3i 1  5  3  a bi  3i 1  5  9  a  3  b   1  25 .
Do đó tập hợp các điểm biểu diễn của z là hình vành khăn giới hạn bởi hai đường tròn có tâm I 3;  
1 bán kính lần lượt là 3 và 5.
Vì vậy S    2 2 5  3   16 . Câu 71. Chọn C y 2 1 -1 O 1 2 x -1 .
Đặt z x yi z x yi khi đó ta có:
z 1  1   x yi 1  1.
  x    yi    x  2 2 1 1 1  y  1   1 .
z z   x yi   x yi  2 yi có phần ảo không âm suy ra y  0 2 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Từ (1) và (2) ta suy ra phần mặt phẳng biểu diễn số phức z là nửa hình tròn tâm I 1;0 bán kính 1 
r  1 , diện tích của nó bằng 2  r   (đvdt). 2 2 Câu 72. Chọn B
Gọi z x yi,  x, y   . 2 2 x y Ta có
x yi   x yi 2 2 2 2 2  3 
x  9 y  3  x  9 y  9    1 . 9 1 2 2 x y
Suy ra tập hợp điểm biểu diễn số phức z là miền trong của Elip   1. 9 1 1
Ta có a  3, b  1, nên diện tích hình H cần tìm bằng diện tích Elip. 4 1 3 Vậy S  . . . a b  . 4 4 Câu 73. Chọn A
Gọi w x y ; i ; x y . w 1
Ta có w  1 iz 1  z  . 1 i w 1 w  2  i
x  2   y   1 i
Do đó z 1  1  1  1   1   1 . 1 i 1 i 1 i
x  2   y   1 i
 1   x  22   y  2 1  2 . 1 i
Vậy diện tích hình tròn đó là S  2 . Câu 74. Chọn B  
Ta có:   iz i 5 1 5 1 1 2
 3  i z z  1  i w   i M ;  tan  . 4 4  4 4    5 2 2 tan 5 1 tan  12 Lúc đó: sin 2    0; cos 2    0 . 2 2 1  tan  13 1  tan  13 Câu 75. Chọn C w 1 i
w  2z 1  i z  2 w 1 i
z  3  4i  2 
 3  4i  2  w 1 i  6  8i  4  w  7  9i  4   1 2 2 2
Giả sử w x yi x, y   , khi đó  
1   x  7   y  9  16
Suy ra tập hợp điểm biểu diễn số phức w là hình tròn tâm I 7;  9 , bán kính r  4.
Vậy diện tích cần tìm là 2
S   .4  16 . Câu 76. Chọn B
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 .
Gọi z x yi . 2 2 (với ,
x y   )  3  z  3i 1  5  9   x   1
  y  3  25 .
Vậy tập hợp các điểm biểu diễn số phức z trên mặt phẳng phức là hình vành khăn giới hạn bởi
hai đường tròn bán kính R  5 và r  3. Diện tích S    2 2
R r  16 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 CHUYÊN ĐỀ 27
PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC, BÀI TOÁN MIN-MAX MỤC LỤC
PHẦN A. CÂU HỎI ......................................................................................................................................................... 1
Phương trình bậc 2 với hệ số thực .................................................................................................................................... 1
Bài toán MIN-MAX ......................................................................................................................................................... 4
PHẦN B. LỜI GIẢI THAM KHẢO ................................................................................................................................ 8
Phương trình bậc 2 với hệ số thực .................................................................................................................................... 8
Bài toán MIN-MAX ....................................................................................................................................................... 14 PHẦN A. CÂU HỎI
Phương trình bậc 2 với hệ số thực
Câu 1. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Kí hiệu z , z , z và z là bốn nghiệm phức của phương 1 2 3 4 trình 4 2
z z 12  0 . Tính tổngT z z z z 1 2 3 4 A. T  2  2 3 B. T  4 C. T  2 3 D. T  4  2 3
Câu 2. (ĐỀ THAM KHẢO BGD & ĐT 2018) Gọi z và z là hai nghiệm phức của phương trình 1 2 2
4z  4z  3  0 . Giá trị của biểu thức z z bằng: 1 2 A. 3 2 B. 2 3 C. 3 D. 3
Câu 3. (MĐ 104 BGD&DT NĂM 2017) Kí hiệu z , z là hai nghiệm của phương trình 2
z  4  0 . Gọi M 1 2
, N lần lượt là điểm biểu diễn của z , z trên mặt phẳng tọa độ. Tính T OM ON với O là gốc tọa độ. 1 2 A. T  8 B. 4 C. T  2 D. T  2
Câu 4. (Mã đề 101 - BGD - 2019) Gọi z , z là hai nghiệm phức của phương trình 2
z  6z  10  0 . Giá trị 1 2 của 2 2
z z bằng: 1 2 A. 16. B. 56 . C. 20. D. 26 .
Câu 5. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Phương trình nào dưới đây nhận hai số phức 1  2i và 1  2i là nghiệm. A. 2
z  2z  3  0 B. 2
z  2z  3  0 C. 2
z  2z  3  0 D. 2
z  2z  3  0
Câu 6. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Kí hiệu z , z là hai nghiệm phức của phương trình 1 2 2
3z z 1  0 . Tính P z z . 1 2 2 3 2 3 14 A. P  B. P  C. P  D. P  3 3 3 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 7. (Mã 102 - BGD - 2019) Kí hiệu z , z là hai nghiệm phức của phương trình 2
z  6z 14  0 . Giá trị 1 2 của 2 2 z z bằng 1 2 A. 36 . B. 8 . C. 28 . D. 18 .
Câu 8. (Mã đề 104 - BGD - 2019) Gọi z , z là hai nghiệm phức của phương trình 2
z  4z  7  0. Giá trị 1 2 của 2 2 z z bằng 1 2
Hàm số đã cho đạt cực tiểu tại A. 2. B. 8. C. 16. D. 10.
Câu 9. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Kí hiệu z ; z là hai nghiệm của phương trình 1 2 2
z z  1  0 . Tính 2 2
P z z z z . 1 2 1 2 A. P  2 B. P  1  C. P  0 D. P  1
Câu 10. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Kí hiệu z và z là hai nghiệm phức của phương 1 2 trình 2
z  3z  5  0 . Giá trị của z z bằng: 1 2 A. 10 B. 2 5 . C. 5 . D. 3 .
Câu 11. (MĐ 105 BGD&ĐT NĂM 2017) Kí hiệu z , z là hai nghiệm phức của phương trình 2
z z  6  0 1 2 1 1 . Tính P   . z z 1 2 1 1 1 A. B.  C. 6 D. 6 6 12
Câu 12. (Mã 103 - BGD - 2019) Gọi z , z là 2 nghiệm phức của phương trình 2
z  4z  5  0 . Giá trị của 1 2 2 2 z z bằng 1 2 A. 16. B. 26. C. 6. D. 8.
Câu 13. (CHUYEN PHAN BỘI CHÂU NGHỆ AN NĂM 2018-2019 LẦN 02) Gọi z ; z là hai nghiệm của 1 2 2 2 phương trình 2
z  2z 10  0 . Tính giá trị biểu thức A zz . 1 2 A. 10 3 . B. 5 2 . C. 2 10 . D. 20 .
Câu 14. (THPT CHUYÊN SƠN LA NĂM 2018-2019 LẦN 01) Ký hiệu z , z là nghiệm của phương trình 1 2 2
z  2z 10  0 . Giá trị của z . z bằng 1 2 5 A. 5 . B. . C. 10 . D. 20 . 2
Câu 15. (ĐỀ THI THỬ VTED 02 NĂM HỌC 2018 - 2019) Kí hiệu z , z là hai nghiệm phức của phương 1 2 trình 2
z  3 . Giá trị của z z bằng 1 2 A. 6 . B. 2 3 . C. 3 . D. 3 .
Câu 16. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Gọi z , z là các nghiệm phức của 1 2 phương trình 2
z  8z  25  0 . Giá trị z z bằng 1 2 A. 5 . B. 3 . C. 8 . D. 6 .
Câu 17. (HỌC MÃI NĂM 2018-2019-LẦN 02) Biết z là số phức có phần ảo âm và là nghiệm của phương z trình 2
z  6z 10  0 . Tính tổng phần thực và phẩn ảo của số phức w  . z
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 7 1 2 4 A. . B. . C. . D. . 5 5 5 5
Câu 18. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Gọi z , z là hai nghiệm phức 1 2 của phương trình 2
z  4z  5  0 . Tính 1 1 w    i  2 2 z z z z . 1 2 2 1  z z 1 2 4 4 4 A. w    20i . B. w   20i .
C. w  4  20i . D. w  20  i . 5 5 5
Câu 19. (ĐỀ 04 VTED NĂM 2018-2019) Với các số thực ,
a b biết phương trình 2
z  8az  64b  0 có nghiệm
phức z  8 16i . Tính môđun của số phức w  a bi 0 A. w  19 B. w  3 C. w  7 D. w  29
Câu 20. (THPT YÊN KHÁNH - NINH BÌNH - 2018 - 2019) Phương trình 2
z a. z b  0 , với a ,b là các
số thực nhận số phức 1  i là một nghiệm.
Tính a b ? . A. 2  . B. 4  . C. 4 . D. 0 .
Câu 21. (KTNL GV THPT LÝ THÁI TỔ NĂM 2018-2019) Tính modun của số phức w b ci , , b c   8 i 1 2i biết số phức
là nghiệm của phương trình 2
z bz c  0 . 7 1 i A. 2 . B. 3 . C. 2 2 . D. 3 2 .
Câu 22. (THPT CHUYÊN ĐẠI HỌC VINH NĂM 2018-2019 LẦN 01) Gọi z , z là các nghiệm phức của 1 2 phương trình 2
z  4z  7  0 . Số phức z .z z .z bằng 1 2 2 1 A. 2 B. 10 C. 2i D. 10i
Câu 23. (ĐỀ THI THỬ VTED 03 NĂM HỌC 2018 - 2019) Gọi z ; z là hai nghiệm phức của phương trình 1 2 2
3z  2z  27  0 . Giá trị của z z z z bằng: 1 2 1 2 A. 2 B. 6 C. 3 6 D. 6
Câu 24. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Gọi z và z là hai nghiệm 1 2 4 4 phức của phương trình 2
z  4z  29  0 .Tính giá trị của biểu thức zz . 1 2 A. 841. B. 1682 . C. 1282 . D. 58 .
Câu 25. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Kí hiệu z ; z là hai nghiệm phức 1 2 của phương trình 2
3z z 1  0 . Tính P z z . 1 2 14 2 3 2 3 A. P  . B. P  . C. P  . D. P  . 3 3 3 3
Câu 26. (CHUYÊN NGUYỄN TẤT THÀNH YÊN BÁI LẦN 01 NĂM 2018-2019) Gọi z , z là hai nghiệm 1 2 2 2 phức của phương trình 2
3z z  2  0 . Tính giá trị biểu thức T zz . 1 2 2 8 4 11 A. T  . B. T  . C. T  . D. T   . 3 3 3 9
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 27. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Gọi ,
A B là hai điểm trong mặt
phẳng phức theo thứ tự biểu diễn cho các số phức z , z khác 0 thỏa mãn đẳng thức 2 2
z z z z  0, khi 1 2 1 2 1 2
đó tam giác OAB ( O là gốc tọa độ): A. Là tam giác đều. B. Là tam giác vuông.
C. Là tam giác cân, không đều. D. Là tam giác tù.
Câu 28. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Cho hai số phức z và w khác 0 , 3 4 5 thỏa mãn  
và w  1. Hỏi mệnh đề nào dưới đây đúng? z w z w 2 3 3 A. z  2 3 . B. z  . C. z  3 . D. z  . 3 2
Câu 29. (KTNL GV THUẬN THÀNH 2 BẮC NINH NĂM 2018-2019) Cho phương trình 2
az bz c  0 , 2 2
với a, b, c  , a  0 có các nghiệm 1 z , 2
z đều không là số thực. Tính P  1 z z2  1
z z2 theo a,b, . c 2 b  2ac 2 2c 4c 2b  4ac A. P  . B. P  . C. P  . D. P  . 2 a a a 2 a
Câu 30. (THPT YÊN PHONG SỐ 1 BẮC NINH NĂM 2018-2019 LẦN 01) Gọi S là tổng các số thực m để phương trình 2
z  2z 1 m  0 có nghiệm phức thỏa mãn z  2. Tính S. A. S  6. B. S  10. C. S  3. D. S  7.
Câu 31. (CHUYÊN NGUYỄN TẤT THÀNH YÊN BÁI LẦN 01 NĂM 2018-2019) Cho số phức z a bi
a, b   thỏa mãn z  1  3i z i  0 . Tính S  2a  3b . A. S  6  . B. S  6 . C. S  5  . D. S  5.
Câu 32. (TT THANH TƯỜNG NGHỆ AN NĂM 2018-2019 LẦN 02) Gọi S là tổng các giá trị thực của m 2
để phương trình 9z  6z 1 m  0 có nghiệm phức thỏa mãn z  1. Tính S . A. 20 . B. 12. C. 14 . D. 8 . Bài toán MIN-MAX
Câu 33. (ĐỀ THAM KHẢO BGD & ĐT 2018) Xét số phức z a bi  ,
a b   thỏa mãn z  4  3i  5
. Tính P a b khi z 1 3i z 1 i đạt giá trị lớn nhất. A. P  8 B. P  10 C. P  4 D. P  6
Câu 34. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Xét số phức z thỏa mãn z  2  i z  4  7i  6 2.
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của z 1 i . Tính P m M . 5 2  2 73 5 2  73 A. P  B. P  5 2  73 C. P  D. P  13  73 2 2
Câu 35. (KTNL GIA BÌNH NĂM 2018-2019) Cho hai số phức z , z thỏa mãn đồng thời hai điều kiện sau 1 2
z 1  34, z 1 mi z m  2i (trong đó m là số thực) và sao cho z z là lớn nhất. Khi đó giá trị 1 2 z z bằng 1 2 A. 2 B. 10 C. 2 D. 130
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 36. (THPT CẨM GIÀNG 2 NĂM 2018-2019) Cho số phức z thỏa mãn z  2  2i  1 . Số phức z i có môđun nhỏ nhất là: A. 5  2 . B. 5 1. C. 5 1 . D. 5  2 .
Câu 37. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Gọi M và m lần lượt là giá trị lớn nhất 2z i M
và giá trị nhỏ nhất của P  với z
z  . Tính tỉ số . z
là số phức khác 0 và thỏa mãn 2 m M M 4 M 5 M A.  3 . B.  . C.  . D.  2 . m m 3 m 3 m
Câu 38. Cho số phức z thoả mãn z  2  3i  1. Tìm giá trị lớn nhất của z 1 i . A. 13  3 . B. 13  5 . C. 13 1 . D. 13  6 .
Câu 39. Xét tất cả các số phức z thỏa mãn z  3i  4  1. Giá trị nhỏ nhất của 2
z  7  24i nằm trong khoảng nào? A. 0;1009 . B. 1009; 2018 . C. 2018; 4036 . D. 4036;  .
Câu 40. (CHUYEN PHAN BỘI CHÂU NGHỆ AN NĂM 2018-2019 LẦN 02) Cho số phức z thỏa mãn
z z z z  4 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P z  2  2i . Đặt A M m
. Mệnh đề nào sau đây là đúng? A. A 34;6 . B. A 6; 42  . C. A2 7; 33 . D. A4;3 3.
Câu 41. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Cho số phức z thỏa mãn z  6  z  6  20 . Gọi
M , n lần lượt là môđun lớn nhất và nhỏ nhất của z. Tính M n
A. M n  2 .
B. M n  4 .
C. M n  7 .
D. M n  14 .
Câu 42. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Cho số phức z thỏa mãn
z  3  4i  2 và w  2z 1 i . Khi đó w có giá trị lớn nhất bằng A. 4  74 . B. 2  130 . C. 4  130 . D. 16  74 .
Câu 43. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Xét số phức z và số phức liên
hợp của nó có điểm biểu diễn là M và M . Số phức z 4  3i và số phức liên hợp của nó có điểm biểu diễn
là N và N. Biết rằng M , M , N , N là bốn đỉnh của hình chữ nhật. Tìm giá trị nhỏ nhất của z  4i  5 . 5 2 1 4 A. . B. . C. . D. . 34 5 2 13
Câu 44. Biết số phức z thỏa mãn iz  3  z  2  i và z có giá trị nhỏ nhất. Phần thực của số phức z bằng: 2 1 2 1 A. . B. . C.  . D.  . 5 5 5 5
Câu 45. (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Xét các số phức z thỏa mãn
z 1 3i  2 . Số phức z mà z 1 nhỏ nhất là
A. z  1 5i .
B. z  1 i .
C. z  1 3i .
D. z  1 i .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 46. (CHUYÊN PHAN BỘI CHÂU NĂM 2018-2019) Cho số phức z thỏa mãn z z z z  4. Gọi
M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P z  2  2i . Đặt A M  .
m Mệnh đề nào sau đây là đúng? A. A  34;6 . B. A 6; 42  .
C. A 2 7; 33 . D. A 4;3 3 .  
Câu 47. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Trong các số phức z thỏa mãn
z 1  i z  1  2i , số phức z có mô đun nhỏ nhất có phần ảo là 3 3 3 3 A. . B. . C.  . D.  . 10 5 5 10 z i z i
Câu 48. Cho hai số phức z , z thỏa mãn 1 2  1; 
2 . Giá trị nhỏ nhất của z z là 1 2 z  2  3i z 1 i 1 2 1 2 A. 2 2 . B. 2 . C. 1. D. 2 1.
Câu 49. (SỞ GD&ĐT BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Gọi S là tập hợp các số phức z thỏa mãn
z 1  34 và z 1 mi z m  2i , (trong đó m   ). Gọi z , z là hai số phức thuộc S sao cho z z 1 2 1 2
lớn nhất, khi đó giá trị của z z bằng 1 2 A. 2 B. 10 C. 2 D. 130
Câu 50. Cho hai số phức z , w thỏa mãn z  3 2  2 , w  4 2i  2 2 . Biết rằng z w đạt giá trị nhỏ
nhất khi z z , w w . Tính 3z w . 0 0 0 0 A. 2 2 . B. 4 2 . C. 1. D. 6 2 .
Câu 51. (ĐỀ 04 VTED NĂM 2018-2019) Cho hai số phức z và w thỏa mãn z  2w  8  6i và z w  4.
Giá trị lớn nhất của biểu thức z w bằng A. 4 6. B. 2 26. C. 66. D. 3 6.
Câu 52. Cho số phức z thoả mãn z  1 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2
P z 1  z z 1 . Tính M .m 13 3 39 13 A. . B. . C. 3 3 . D. . 4 4 4
Câu 53. (THPT YÊN KHÁNH - NINH BÌNH - 2018 - 2019) Cho hai số phức z và   a bi thỏa mãn
z  5  z  5  6 ; 5a  4b  20  0 . Giá trị nhỏ nhất của z   là 3 5 4 3 A. . B. . C. . D. . 41 41 41 41
Câu 54. (KTNL GV THPT LÝ THÁI TỔ NĂM 2018-2019) Gọi z a bi  ,
a b là số phức thỏa mãn
điều kiện z  1  2i z  2  3i  10 và
có mô đun nhỏ nhất. Tính S  7a b ? A. 7 . B. 0 . C. 5. D. 12 .
Câu 55. (KTNL GV THUẬN THÀNH 2 BẮC NINH NĂM 2018-2019) Cho số phức z thỏa mãn
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
z z  2 z z  8 . Gọi M,m lần lượt là giá trị lớn nhất, nhỏ nhất của biểu thức P z  3  3i . Tính M m . A. 10  34 . B. 2 10 . C. 10  58 . D. 5  58 .
Câu 56. (CHUYÊN BẮC GIANG NĂM 2018-2019 LẦN 02) Cho số phức z có z  1. Tìm giá trị lớn nhất của biểu thức 2 2
P z z z z 1 . 13 11 A. B. 3 C. 3 D. 4 4
Câu 57. (THPT CHUYÊN ĐẠI HỌC VINH NĂM 2018-2019 LẦN 01) Giả sử z , z là hai trong các số phức 1 2
thỏa mãn  z  68  zi là số thực. Biết rằng z z  4, giá trị nhỏ nhất của z  3z bằng 1 2 1 2 A. 5  21 B. 20  4 21 C. 20  4 22 D. 5  22
Câu 58. (ĐỀ THI THỬ VTED 03 NĂM HỌC 2018 - 2019) Trong các số phức z thỏa mãn z  3  4i  2 có 2 2
hai số phức z , z thỏa mãn z z  1. Giá trị nhỏ nhất của zz bằng 1 2 1 2 1 2 A. 1  0 B. 4  3 5 C. 5  D. 6  2 5
Câu 59. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Cho hai số phức z , z thoả 1 2
mãn z  2  i z  4  7i  6 2 và iz 1 2i  1 . Tìm giá trị nhỏ nhất của biểu thức T z z . 1 1 2 1 2 A. 2 1. B. 2 1. C. 2 2 1. D. 2 2 1.
Câu 60. (CHUYÊN NGUYỄN TẤT THÀNH YÊN BÁI LẦN 01 NĂM 2018-2019) Cho z là số phức thỏa
mãn z z  2i . Giá trị nhỏ nhất của z 1 2i z 1 3i là A. 5 2 . B. 13 . C. 29 . D. 5 .
Câu 61. (THPT CHUYÊN HẠ LONG - LẦN 2 - 2018) Cho các số phức z  2  i , z  2  i và số phức z 1 2 2 2
thay đổi thỏa mãn z zz z
 16 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của z 1 2 . Giá trị biểu thức 2 2 M m bằng A. 15 . B. 7 . C. 11. D. 8 .
Câu 62. (THPT CHUYÊN QUANG TRUNG - BP - LẦN 1 - 2018) Cho số phức z thỏa mãn z  2i z  4i
và z  3  3i  1. Giá trị lớn nhất của biểu thức P z  2 là: A. 13 1 . B. 10 1. C. 13 . D. 10 .
Câu 63. (TT DIỆU HIỀN - CẦN THƠ - 2018) Xét số phức z thỏa mãn z  2  2i  2 . Giá trị nhỏ nhất của
biểu thức P z 1 i z  5  2i bằng A. 1 10 . B. 4 . C. 17 D. 5 .
Câu 64. (SGD&ĐT CẦN THƠ - HKII - 2018) Cho số phức z thỏa mãn z  3  4i  5 . Gọi M và m lần 2 2
lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P z  2  z i . Môđun của số phức w M mi là A. w  3 137 . B. w  1258 . C. w  2 309 . D. w  2 314 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 65. (THPT HẬU LỘC 2 - TH - 2018) Cho hai số phức z , z thỏa mãn z 1 i  2 và z iz . Tìm giá 1 2 1 2 1
trị nhỏ nhất m của biểu thức z z ? 1 2 A. m  2 1. B. m  2 2 . C. m  2 . D. m  2 2  2 .
z  3  2i  1 
Câu 66. (SGD&ĐT BẮC GIANG - LẦN 1 - 2018) Hcho hai số phức z, w thỏa mãn  w 1 2i  w 2i  
. Tìm giá trị nhỏ nhất P
của biểu thức P z  w . min 3 2  2 5 2  2 3 2  2 A. P  . B. P  2 1. C. P  . D. P  . min 2 min min 2 min 2
Câu 67. (THPT CHUYÊN LÊ HỒNG PHONG - TPHCM - 2018) Cho số phức z thỏa z  1. Gọi m , M
lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của biểu thức 5 3 4
P z z  6z  2 z 1 . Tính M m .
A. m  4 , n  3 .
B. m  4 , n  3
C. m  4 , n  4 .
D. m  4 , n  4  . 3 5
Câu 68. (THPT CHUYÊN ĐH VINH - LẦN 3 - 2018) Cho các số phức w , z thỏa mãn w  i  và 5
5w  2  i z  4 . Giá trị lớn nhất của biểu thức P z 1 2i  z  5  2i bằng A. 6 7 . B. 4  2 13 . C. 2 53 . D. 4 13 .
Câu 69. (KIM LIÊN - HÀ NỘI - LẦN 1 - 2018) Xét các số phức z a bi ( a, b   ) thỏa mãn V
z  3  2i  2 . Tính a b khi z 1 2i  2 z  2  5i đạt giá trị nhỏ nhất. A. 4  3 . B. 2  3 . C. 3 . D. 4  3 .
Câu 70. (LIÊN TRƯỜNG - NGHỆ AN - LẦN 2 - 2018) Biết rằng hai số phức z , z thỏa mãn z  3  4i  1 1 2 1 1 và z  3  4i 
. Số phức z có phần thực là a và phần ảo là b thỏa mãn 3a  2b  12 . Giá trị nhỏ nhất của 2 2
P z z z  2z  2 bằng: 1 2 9945 9945 A. P  . B. P  5  2 3 . C. P  . D. P  5  2 5 . min 11 min min 13 min
PHẦN B. LỜI GIẢI THAM KHẢO
Phương trình bậc 2 với hệ số thực Câu 1. Chọn D 2 z  3  z i  3 4 2
z z 12  0     2 z  4 z  2   
T z z z z i 3  i 3  2  2  2 3  4 1 2 3 4 Câu 2. Lời giải Chọn D  1 2 z   i 1 2 2 Xét phương trình 2
4z  4z  3  0 ta có hai nghiệm là:   1 2 z   i 2  2 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 3  z z
z z  3 1 2 2 1 2 Câu 3. Chọn B  z  2i Ta có: 2 1 z  4  0   . z  2i  2 Suy ra M 0; 2
  ; N 0;2 nên T OM ON   2 2 2  2  4 . Câu 4. Chọn A z z  6
Áp dụng định lý Viet áp dụng cho phương trình trên ta được: 1 2  . z z  10  1 2
Khi đó ta có z z   z z 2 2 2
 2z z  36  20  16 . 1 2 1 2 1 2 Câu 5. Chọn B z z  2 Theo định lý Viet ta có 1 2 2 
, do đó z , z là hai nghiệm của phương trình z  2z  3  0 z .z  1 2  3 1 2 Câu 6. Chọn C Xét phương trình 2
3z z 1  0 có    2 1  4.3.1  11  0 .
Phương trình đã cho có 2 nghiệm phức phân biệt 1 i 11 1 11 1 i 11 1 11 z    i; z    i 1 6 6 6 2 6 6 6 Suy ra 2 2 2 2 1 11 1 11 1  11  1  11      3 3 2 3
P z z   i   i                1 2  6 6 6 6 6  6  6  6          3 3 3 Câu 7.  2 2 z  3  5i Ta có : 2 2 2
z  6z 14  0    z z  3  5i  3  5i  8. 1 2    
z  3  5i  Câu 8. Chọn A Ta có        i2 4 7 3 3 .
Do đó phương trình có hai nghiệm phức là z  2  3i, z  2  3 . i 1 2 2 2 Suy ra 2 2
z z  2  3i  2  3i
 4  4 3i  3  4  4 3i  3  2. 1 2     Câu 9. Chọn C Cách 1  1 3 z    i 2 2 2
z z 1  0    1 3 z    i  2 2 2 2  1 3   1 3   1 3   1 3  2 2
P z z z z     i      i      i    i   0 1 2 1 2  2 2   2 2   2 2   2 2         
Cách 2: Theo định lí Vi-et: z z  1
 ; z .z  1. 1 2 1 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Khi đó P z z z z   z z 2 2 2 2
 2z z z z  1 1  0 . 1 2 1 2 1 2 1 2 1 2 Câu 10. Chọn B  3 11 z   i  1 2 2 Xét phương trình 2
z  3z  5  0 ta có hai nghiệm là:   3 11 z   i 2  2 2
z z  5  z z  2 5 . 1 2 1 2 Câu 11. Chọn A z z  1 1 1 z z 1
Theo định lí Vi-et, ta có 1 2  nên P    1 2  z z   6 z z z .z 6 1 2 1 2 1 2 Câu 12. Chọn C 2
'  b'  ac  4  5  1
Phương trình có 2 nghiệm phức z  2  i, z  2   i 1 2 2 2 nên 2 2
z z  2  i  2  i 2 2 2
 4  4i i  4  4i i  8  2i  8  2  6 1 2  z  1   3i Câu 13. 2 1
z  2z 10  0   . z  1   3i  2 2 2 2 2 Do đó: A zz
 1 3i  1 3i  20 . 1 2 z  1   3i
Câu 14. Phương trình 2
z  2z 10  0   . Vậy z  1
  3i , z  1   3i . z  1   3 1 2  i
Suy ra z . z  10. 10  10 . 1 2 z i 3 Câu 15. Ta có: 2 z  3  
z z i 3  i 3  2 3 . 1 2 z  i 3 
z  4  3i
Câu 16. Phương trình 2
z  8z  25  0  1  . z  4  3i  2
Suy ra: z z  6i  6 . 1 2 Câu 17. Ta có: 2
z  6z 10  0 z  3  i  
. Vì z là số phức có phần ảo âm nên  z  3  i z  3  iz 3  i 4 3 Suy ra w     i z 3  i 5 5 4  3  1
Tổng phần thực và phần ảo:      . 5  5  5 z z  4
Câu 18. Theo hệ thức Vi-et, ta có 1 2  . z z  5  1 2 z z 4 Suy ra 2 1 w
i z z z z   20i . 1 2  1 2 z z 5 1 2 Câu 19. Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
z z  8a  16 a  2 Theo Viet ta có 1 2    . Vậy w  29 .
z .z  64b  64.5 b  5  1 2 
Câu 20. Do số phức 1  i là một nghiệm của phương trình 2
z a. z b  0 . 2 a b  0 a  2 
Nên ta có: 1 i  a1 i  b  0  a b  a  2i  0     . a  2  0 b  2  
Vậy: a b  4 . Câu 21. Chọn C 4 4 8 2  8 i 1 2i i   i     1  1 +) Đặt z  , ta có o  7 1 i
i  i 3 7 2 .i  i  11 2i 2i
2i 1 i  z     1 i . o 2 1 i 1 i 1 i
+) z là nghiệm của đa thức P z  2
z bz c z là nghiệm còn lại của P z . o o b
+) Ta có: z z    b  2   b  2 . o o a c z .z    1   i 1
  i  c c  2 o o a 2 2
w  2  2i w  2  2  2 2 . Câu 22. Chọn A  2 2 z  2   3i Ta có 1 
z .z z .z  2   3i  2   3i  2 1 2 2 1     z  2   3i  2 Câu 23. Lờigiải Chọn A 2
3z  2z  27  0 1 80i 1 80i z  ; z  vậy z z z z =2 1 2 3 3 1 2 1 2 2 2 2  z  2   5i
Câu 24. Phương trình 2
z  4z  29  0   z  2  2
 5   z  2  5i 1   . z  2   5i  2
Suy ra z z   2  2 2  5  29 . 1 2 4 4 4 4 Vậy zz  29  29  1682 . 1 2     Câu 25. Cách 1: 1 1  1  11 Ta có 2 2 2
3z z 1  0  z z   0  z      3 3  6  36  1 11 z   i  1  2 11 2 6 6  z   i     .  6  36  1 11 z   i  6 6
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 2 2 2 1  11  1  11      2 3 Khi đó P               . 6  6  6  6      3     Cách 2:
Theo tính chất phương trình bậc 2 với hệ số thực, ta có z ; z là hai số phức liên hợp nên 2 2
z .z z z . 1 2 1 2 1 2 1 3 Mà z .z
suy ra z z  . 1 2 3 1 2 3 2 3
Vậy P z z  . 1 2 3  1 23iz  1 6
Câu 26. Phương trình 2
3z z  2  0 có 2   ( 1  )  4.3.2  23    .  1 23iz  2  6 2 2   2 2  1  23 2 2 2 4 zz         T    . 2 1 6  6    3 3 3 3  
Câu 27. Cách 1: + Gọi 2 2
z a bi ( ,
a b   : a  b  0) . A ; a b . 1
Khi đó z là nghiệm phương trình: z a bi z a bi  0 2   2  2 2 2 2 2 2 2 2
+ Ta có:   a bi  4a bi  3
 a bi   3 a bii   3  b   ai    
Phương trình có hai nghiệm phân biệt: a  3b 3a ba  3b 3a b z   i nên B  ; . 2  2 2  2 2    a  3b  3a b
a  3b  3a b  Hoặc z   i nên B  ; . 2  2 2  2 2    + Tính 2 2 2 OA a  b , 2 2 2 OB a  b , 2 2 2
AB a  b . Vậy tam giác OAB đều. Cách 2: Theo giả thiết: 2 2
z z z z  0   z z  2 2
z z z z  0 1 2 1 2 1 2 1 2 1 2  3 3 3 3  z z
 0  z  z
z z OA OB . 1 2 1 2 1 2
Mặt khác: z z z z  0   z z 2 1 2  z z 2 2 1 2 1 2 1 2
  z z 2 2 2
 z z z z
z z AB O . A OB . 1 2 1 2 1 2 1 2
Mà OA OB nên AB OA OB .
Vậy tam giác OAB đều. Cách 3: 2  z z + 2 2 1 1
z z z z  0    1  0 1 2 1 2   z z  2  2 2  z z z 1  3i z 1 1 1 1    1  0   
 1  z z   1 2 z z z 2 z  2  2 2 2
Vậy OA OB .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1  3i
Mặt khác: z z
z z z AB OB 1 2 2 2 2 2
Vậy tam giác OAB đều. 3 4 5
Câu 28. Ta xét phương trình  
với điều kiện z w  0. z w z w 3 4 5 Ta có 2 2  
 3w  4z  2wz  0 . z w z w 2  w   w
Vì z  0 nên ta được phương trình 3  2  4  0 .      z   z   w 1 11    iz 3 3
Giải phương trình được kết quả  .  w 1 11     iz 3 3 w 2 3 3 Suy ra 
. Mà w  1 nên z  . z 3 2 Câu 29. Chọn C Cách 1: Tự luận. Ta có phương trình 2
az bz c  0 có các nghiệm 1 z , 2
z đều không là số thực, do đó 2
  b  4ac  0 . Ta có 2   i  2 4ac b  .  2 b
  i 4ac b  1 z   2a *  2  b
  i 4ac b z2    2a 2  2 b  1 z z2  2  a 2 2 4c 4c Khi đó:   P  1 z z2  1 z z2  . Vậy P  . 2 aa 2 4ac b 1 z z2   2  a Cách 2: Trắc nghệm.
Cho a  1, b  0, c  1, ta có phương trình 2
z 1  0 có 2 nghệm phức là 1
z i, z2  i  . Khi đó 2 2 P  1 z z2  1
z z2  4 .
Thế a  1, b  0, c  1 lên các đáp án, ta thấy chỉ có đáp án C cho kết quả giống. Câu 30. Chọn D
Ta có: z z   m    z  2 2 2 1 0 1  m   1 m  1
+) Với m  0 thì  
1  z  1 m . Do z  2  1 m  2   (thỏa mãn). m  9 
+) Với m  0 thì  
1  z  1 i m.
Do z  2  1 i m  2  1 m  4  m  3 (thỏa mãn).
Vậy S  1 9  3  7 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 31. Ta có z  1  3i z i  0  a     2 2 1
b  3  a b i  0 . a 1  0  a  1       . 2 2 2
b  3  a b  0 
1  b b  3    *  bb  3    3  4     *     4  b   . 1 b   b  32 2  b    3  3 a  1  Vậy 
4  S  2a  3b  6  . b     3 Câu 32. 2
9z  6z 1 m  0 * .
Trường hợp 1: * có nghiệm thực    0  9  91 m  0  m  1. z  1 z  1   . z  1  
z  1  m  16 (thỏa mãn).
z  1  m  4 (thỏa mãn).
Trường hợp 2: * có nghiệm phức z a bi b  0    0  9  91 m  0  m  1.
Nếu z là một nghiệm của phương trình 2
9z  6z 1 m  0 thì z cũng là một nghiệm của phương trình 2
9z  6z 1 m  0 . cm Ta có 2 1
z  1  z  1  z. z  1   1 
 1  m  8 (thỏa mãn). a 9
Vậy tổng các giá trị thực của m bằng 12 . Bài toán MIN-MAX Câu 33. Lời giải Chọn B Goi M  ;
a b là điểm biểu diễn của số phức z. 2 2
Theo giả thiết ta có: z  4  3i  5  a  4  b  3  5  Tập hợp điểm biểu diễn số phức z là
đường tròn tâm I 4;  3 bán kính R  5  A  1;3 Gọi: 
Q z 1 3i z 1 i MA MB B 1;    1 
Gọi E là trung điểm của AB, kéo dài EI cắt đường tròn tại D Ta có: 2 2 2
Q MA MB  2M . A MB
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 2 2 2 2
Q MA MB MA MB   2 2 2 MA MB  2 2 2 2 MA MB AB AB
Vì ME là trung tuyến trong MAB 2 2 2 2  ME  
MA MB  2ME  2 4 2 2  AB  2 2 2 2
Q  2 2ME   4ME AB  
. Mặt khác ME DE EI ID  2 5  5  3 5 2   MA MB
Q  10 2  Q  10 2  maxM D   Q   2 2 4. 3 5  20  200   4  2(x  4) x  6  EI  2 D D ID    
 M 6; 4  P a b  10 2  2( y  3) y  4  DD 2 2
Cách 2:Đặt z a b .
i Theo giả thiết ta có: a  4  b  5  5. 
a  4  5 sin t Đặt  . Khi đó: b   3  5 cos t
Q z   i z   i  a  2  b  2  a  2  b  2 1 3 1 1 3 1 1   t  2  t   t  2   t  2 2 5 sin 5 5cos 5 sin 3 5 cos 4
 30 10 5 sin t  30  2 5 3sin t  4 cos t
Áp dụng BĐT Bunhiacopski ta có: Q
2 60  8 5 2sin t  cost   260  8 5. 5  200  10 2
Q 10 2  Q 10 2 max  2 sin t    5 a  6 Dấu bằng xảy ra khi   
P a b  10. 1 b  4 cost     5 Câu 34. Lời giải Chọn A
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 8 D 6 4 A 2 H E 5 N 2
Gọi A là điểm biểu diễn số phức z , E 2 
;1 , F 4;7 và N 1;   1 .
Từ AE A F z  2  i z  4  7i  6 2 và EF  6 2 nên ta có A thuộc đoạn thẳng EF . Gọi H là  3 3  5 2  2 73
hình chiếu của N lên EF , ta có H  ; 
 . Suy ra P NH NF  .  2 2  2 Câu 35. Chọn C
Gọi M , N lần lượt là điểm biểu diễn của số phức z , z 1 2
Gọi z x iy,  x, y  
Ta có z 1  34  M , N thuộc đường tròn C  có tâm I 1;0 , bán kính R  34
Mà z 1 mi z m  2i x yi 1 mi x yi m  2i
  x  2   y m2   x m2   y  2 1 2  2m  
1 x  2m  2 y  3  0
Suy ra M , N thuộc đường thẳng d : 2m  
1 x  2m  2 y  3  0
Do đó M , N là giao điểm của đường thẳng d và đường tròn C
Ta có z z MN nên z z lớn nhất khi và chỉ khi MN lớn nhất 1 2 1 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
MN đường kính của C  . Khi đó z z  2OI  2 1 2
Câu 36. Cách 1:
Đặt w z i z w i . Gọi M  ;
x y là điểm biểu diễn hình học của số phức . w
Từ giả thiết z  2  2i  1 ta được:
w i  2  2i  1  w  2  i  1 2 2
  x  2   y  
1 i  1   x  2   y   1  1.
Suy ra tập hợp những điểm M  ;
x y biểu diễn cho số phức w là đường tròn C có tâm I 2  ;1 bán kính R  1 .
Giả sử OI cắt đường tròn C tại hai điểm ,
A B với A nằm trong đoạn thẳng OI .
Ta có w OM
Mà OM MI OI OM MI OA AI OM OA
Nên w nhỏ nhất bằng OA OI IA  5 1 khi M  . A Cách 2: 2 2
Từ z  2  2i  1  a  2  b  2  1 với z a bi a,b   a  2  sin ;
x b  2  cos x a  2  sin x, b  2  cos x 2 2
Khi đó: z i  2  sin x  2  cos xi i  2  sin x  1 cos x  6  4sin x  2cos x    2 2   2 2 6 4 2
sin x  cos x      2 6 2 5 5 1  5 1  2 5 sin  x  
4 cos x  2sin x   5
Nên z i nhỏ nhất bằng 5 1 khi   
4 sin x  2 cos x  2  5    5 cos x    5  2 5   5 
Ta được z   2     2   i  5   5      Cách 3:
Sử dụng bất đẳng thức z z
z z z z 1 2 1 2 1 2
z i   z  2  2i  2  i  z  2  2i  2  i  5 1 2z i 2z i 2z i 2z i 1 1 3 5
Câu 37. Ta có P     P   2   P  2    P  . z z z z z z 2 2 M 5 Vậy  . m 3 Câu 38. Chọn C
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2
Ta có 1  z  2  3i   z  2  3i . z  2  3i   z  2  3i z  2  3i
 1   z  2  3i z  2  3i  z  2  3i  1` z 1 i  3  2i  1(*) .
+Đặt w  z 1 i , khi đó  w  3  2i  1.
Tập hợp các điểm biểu diễn số phức w  z 1 i là đường tròn  I
;1 và w là khoảng cách từ gốc tọa độ
đến 1 điểm trên đường tròn. Do đó giá trị lớn nhất của w chính là đoạn OQ . 2 2  w
 1 3  2  1 13 . max
Câu 39. Ta có 1  z  3i  4  z  3i  4  z  5  1
  z  5  1  4  z  6 . Đặt 2
z  4  3i z  5, z  7  24i . 0 0 0 2 2 2 2 Ta có 2 2 2 A z  
i z z   2 2 7 24 z z z zz zz z z zz z oo o 2 4 4 2 . . 2 . o o   oo
Mà  z z z z  2 2
 1  z.z z .z  1 z z o o o o o
Suy ra A z z
   z z 2 2 4 4 2 2 4 2 1  2 . z z
 2 z  2 z 1201 . o o o Hàm số 4 2
y  2t  2t 1201 đồng biến trên 4;6 nên 4 2
A  2.4  2.4 1201  1681.  z  4 
Dấu bằng xảy ra khi và chỉ khi  .
z  4  3i  1   Do đó 2
z  7  24i nằm trong khoảng 1009; 2018 .
Câu 40. Giả sử: z x yi, ,
x y    N  ;
x y : điểm biểu diễn của số phức z trên mặt phẳng tọa độ Oxy . Ta có:
• z z z z  4  x y  2 N thuộc các cạnh của hình vuông BCDF (hình vẽ).
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 y 2 I B 1 E C F x O 1 -2 2 D -2 2 2
• P z  2  2i P   x  2   y  2  P d I; N  với I 2; 2
Từ hình ta có: E 1  ;1 2 2 2 2 M PID
4  2  2 5 và m PIE  2 1  2 1  2 min     max
Vậy, A M m  2  2 5  34;6 .
Câu 41. Gọi z x yi ,  ,
x y   . Theo giả thiết, ta có z  6  z  6  20 . 2 2
x  6  yi x  6  yi  20   x   2
y   x   2 6 6  y  20    .
Gọi M x; y , F 6;0 và F 6;0 . 2   1   Khi đó  
  MF MF  20  F F  12 nên tập hợp các điểm E là đường elip  E có hai tiêu điểm F và 1 2 1 2 1
F . Và độ dài trục lớn bằng 20 . 2
Ta có c  6 ; 2a  20  a  10 và 2 2 2
b a c  64  b  8 . 2 2 x y
Do đó, phương trình chính tắc của  E là   1 . 100 64 Suy ra '
max z OA OA  10 khi z  10 và '
min z OB OB  8 khi z  8i .
Vậy M n  2 .
Câu 42. Theo bất đẳng thức tam giác ta có
w  2z  1 i  2z  6  8i  7  9i  2z  6  8i  7  9i  4  130 .
Vậy giá trị lớn nhất của w là 4 130 . Câu 43.
Gọi z x yi , trong đó x, y   . Khi đó z x yi , M x; y  , M  ; x y  .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ta đặt w z 4  3i   x yi4  3i  4x  3y  3x  4yi N 4x  3 ;
y 3x  4 y . Khi đó
w z 4  3i   4x  3 y   3x  4 y i N  4x  3 y; 3x  4 y  .
Ta có M và M ; N và N từng cặp đối xứng nhau qua trục Ox . Do đó, để chúng tạo thành một hình chữ
nhật thì y y hoặc y y . Suy ra hoặc
. Vậy tập hợp các điểm M là hai M N M N
y  3x  4 y
y  3x  4 y
đường thẳng: d : x y  0 và d : 3x  5y  0 . 1 2 2 2
Đặt P z  4i  5   x  5   y  4 . Ta có P MA với A5; 4   . 1 5 PMAMA d ;
A d hoặc MA d  ; A d . Mà d  ; A d d ; A d  1  ,  2  , vậy 2  min min  1  2 34 1 Pd ; A d  min  1  . 2
Câu 44. Đặt z x yi ( x , y ). Khi đó 2 2 2
iz  3  z  2  i 2
x  y  3   x  2   y   1
x  2 y 1  0  x  2  y 1   1 . Lại có 2 2
z x y 2 . Thay   1 vào 2 ta được: 2  2  1 5 2 2
z x y   y  2 2 2 1  y 2
 5y  4y 1  5 y       5  5 5 2 2
Dấu đẳng thức xảy ra khi y   0  y   . 5 5 2 1
Thay y   vào   1 suy ra x   . 5 5 1
Vậy phần thực của số phức z là  . 5
Câu 45. Gọi z x yi , x, y . Khi đó M  ;
x y là điểm biểu diễn của số phức z . 2 2
Theo bài ra ta có z 1 3i  2   x  
1   y  3  4 .
Suy ra tập hợp điểm M là đường tròn tâm I 1; 3 bán kính R  2 .
Khi đó z    x  2 2 1 1  y I M
với I1; 0 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
z 1 nhỏ nhất khi I M
ngắn nhất hay I , M , I  thẳng hàng, M nằm giữa I và I  .
Phương trình đường thẳng II  là x  1 .
Tọa độ giao điểm của đường thẳng II  với đường tròn tâm I bán kính R  2 là M 1; 1 và 1   M 1; 5 . 1  
Thử lại ta thấy M 1; 1 thỏa mãn. Vậy z  1 i . 1  
Câu 46. Đặt z x iy và gọi M  ;
x y là điểm biểu diễn của z x iy
ta có: z z z z  4  x y  2
Gọi A2; 2 và P MA
* Theo hình vẽ, min P d  ,
A , với  : x y  2 2  2  2 và min P   2 2 2 2 max P AE
2  4  2 5, với E 0; 2  
Vậy M m  2  2 5  5,88
Câu 47. Gọi z x yi ,  x , y   được biểu diễn bởi điểm M x; y .
z 1  i z  1  2i   x   1   y  
1 i   x  
1   y  2i
x  2   y  2   x  2   y  2 3 1 1 1 2
 4x  2 y  3  0  y  2  x  . 2 Cách 1:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 2  3  9  3  9 3 5 2 2 2 2 z x y x  2  x
 5x  6x   5 x    , x      .  2  4  5  20 10 3 5 3 3 Suy ra min z
khi x   ; y   . 10 5 10 3
Vậy phần ảo của số phức z có mô đun nhỏ nhất là  . 10 Cách 2:
Trên mặt phẳng tọa độ Oxy , tập hợp điểm biểu diễn số phức z là đường thẳng d : 4x  2 y  3  0 .
Ta có z OM . z nhỏ nhất  OM nhỏ nhất  M là hình chiếu của O trên d .
Phương trình đường thẳng OM đi qua O và vuông góc với d là: x  2 y  0 .  3 x  
4x  2 y  3  0   5  3 3 
Tọa độ của M là nghiệm của hệ phương trình:     M  ;    . Hay x  2 y  0 3    5 10  y     10 3 3 z    i . 5 10 3
Vậy phần ảo của số phức z có mô đun nhỏ nhất là  . 10
Nhận xét: Ta có thể tìm tập hợp điểm biểu diễn số phức z như sau:
z 1  i z 1  2i z  1 i  z   1   2i *
Gọi M biểu diễn số phức z , điểm A1;  
1 biểu diễn số phức 1  i , điểm B  1;
  2 biểu diễn số phức 1  2i . Khi đó  
*  MA MB . Suy ra tập hợp điểm biểu diễn số phức z là đường trung trực của đoạn thẳng AB
có phương trình d : 4x  2 y  3  0 .
Câu 48. Giả sử z x y i với x ; y   . Khi đó: 1 1 1 1 1 z i 1
 1  z i z  2  3i x y 1 i x  2  y  3 i 1 1 1  1   1   1  z  2  3i 1 
x   y 1  x  2  y  3
x y  3  0 . 1 2  1 2  1 2 2 1 1 2
 Quỹ tích điểm M biểu diễn số phức z là đường thẳng  : x y  3  0 . 1
Giả sử z x y i với x ; y   . Ta có: 2 2 2 2 2 z i 2 
2  z i
2 z 1 i x y 1 i
2 x 1  y 1 i 2 2 2  2   2   2  z 1 i 2 
x   y  2 1  2  x  2 1   y  2 2 2 2 1
x y  4x  2 y  3  0 . 2 2 2 2 2 2 2 2
 Quỹ tích điểm N biểu diễn số phức z là đường tròn C  2 2
: x y  4x  2 y  3  0 có tâm I 2;   1 và 2 bán kính R    2 2 2 1  3  2 . 2    1  3
Khoảng cách từ I đến  là: d I;  
 3 2  R  đường thẳng  và đường tròn C không 1   2 2 1 có điểm chung.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Quỹ tích các điểm biểu diễn số phức z z là đoạn thẳng MN .  z z nhỏ nhất khi và chỉ khi MN nhỏ 1 2 1 2 nhất. I N' N M M' Dễ thấy MN  3 2  2  2 2 . min Câu 49. Chọn A
Đặt z x yi ,  x, y   . Khi đó
z 1  34   x  2 2 1
y  34 ; z 1 mi z m  2i  2 m  
1 x  22  my  3  0 .
Do đó tập hợp các điểm M biểu diễn số phức z là giao điểm của đường tròn C   x  2 2 : 1  y  34 và
đường thẳng d : 2m  
1 x  22  my  3  0 .
Gọi A, B là hai điểm biểu diễn z và z . Suy ra C   d   , AB . 1 2
Mặt khác z z AB  2R  2 34 do đó max z z  2 34  AB  2R I 1; 0  d . 1 2   1 2 1
z  6  3i
Từ đó ta có m  
nên d : 3x  5y  3  0 1   . 2 z  4   3i  2
Vậy z z  2 . 1 2
Câu 50. Ta có: + z  3 2 
2 , suy ra tập hợp điểm biểu diễn M biểu diễn số phức z là đường tròn có tâm
I 3 2 ;0 , bán kính r  2 .
+ w  4 2i  2 2 , suy ra tập hợp điểm biểu diễn N biểu diễn số phức w là đường tròn có tâm J 0;4 2 
, bán kính R  2 2 .
Ta có min z w  min MN .
+ IJ  5 2; IM r
2; NJ R  2 2 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Mặt khác IM MN NJ IJ MN IJ IM NJ hay MN  5 2  2  2 2  2 2 .
Suy ra min MN  2 2 khi I , M , N , J thẳng hàng và M , N nằm giữa I , J (Hình vẽ). Cách 1:    1   3 
Khi đó ta có: 3z w  3OM ON và IN  3 2  IM IJ ; IN IJ . 0 0 5 5
    3       1    3 
Mặt khác ON OI IN OI
IJ ; 3OM  3OI IM   3 OI IJ  3OI IJ   . 5  5  5  
 3    3  
Suy ra 3z w  3OM ON  3OI IJ OI IJ  2OI  6 2 . 0 0   5  5  Cách 2:     
Ta có IN  3IM  3IM IN  0 .       
Do đó 3z w  3OM ON  3 OI IM OI IN  2OI  2.OI  2.3 2  6 2. 0 0     Cách 3:  12 2 x       IM 1 M  5 12 2 4 2 +) IM IJ IM IJ    z   i . 0 IJ 5 5 5  4 2 y M   5  6 2 x       IN 3 N  5 6 2 12 2 +) IN IJ IN IJ    w   i . 0 IJ 5 5 5  12 2 y N   5
Suy ra 3z w  6 2  6 2 . 0 0 Câu 51. Chọn C
   
Giả sử M , N lần lượt là các điểm biểu diễn cho z và .
w Suy ra OM ON OF  2OI , z w MN  4
và OF  2OI  10. a
Đặt z ON  ; w OM  .
b Dựng hình bình hành OMFE 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 E F I N a O b M 2 2 2  a b ME   25   2 4 264 Ta có 2 2   a  2b  2 2 2 b ME a 3    16   2 4 2   2  a    z w   b     1 1 2 2 a  2b    66    2   4 2  2 66
Suy ra a b  66, dấu “=” xảy ra khi a b  . 3
Vậy a b  66. max 2
Câu 52. Thay z  1 vào P ta có 2 2
P z 1  z z 1 2
z 1  z z z 2
z 1  z z  .
z z z 1  z z z 1
z 1  z z 1 . 2
Mặt khác z 1   z   1  z  
1  2  z z .
Đặt t z z do z  1 nên điều kiện t 2; 2.
Suy ra P t  2  t 1 .
Xét hàm số f t   t  2  t 1 với t 2; 2. 1
f t  
1 với t  1. Suy ra f  t   0 với t  1. 2 t  2 1 7
f t  
1 với t  1. Suy ra f  x  0  x  . 2 t  2 4 Ta có bảng biến thiên 13 7 
Từ bảng biến thiên suy ra M  tại t
và m  3 tại t  2 . 4 4 13 3 Vậy M .m  . 4
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 53. Đặt F  5 ; 0 , F
5 ; 0 , vì 5  3 nên tập hợp các điểm M biểu diễn số phức z thuộc elip có 2   1   a  3  2 2 x y 2 2 2 
b a c  4 suy ra  E :   1. c  5  9 4
Tập hợp các điểm N biểu diễn số phức  thuộc đường thẳng  : 5x  4 y  20  0 .
Yêu cầu bài toán trở thành tìm điểm M  E  và N   sao cho MN nhỏ nhất.
Đường thẳng d song song với  có dạng d : 5x  4 y c  0 , c  20   . c  17
d tiếp xúc với  E khi và chỉ khi c  5 .9  42 2 2 .4  289   . c  17  20 17 37
Với c  17  d d,    .   2 2 41 5 4 20 17 3 Với c  17 
d d,    .   2 2 41 5 4 3 Vậy min MN   . 41 Câu 54. Chọn A 4 B M H 2 A O 2 4 Gọi M  ; a
b là điểm biểu diễn số phức z a bi A1; 
2 là điểm biểu diễn số phức 1  2iB 2  ; 
3 là điểm biểu diễn số phức  2
  3i, AB  10
z1 2i z 2  3i  10 trở thành MAMB AB M, ,
A B thẳng hàng và M ở giữa A và B
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Gọi H là điểm chiếu của O lên AB, phương trình  AB : x  3y  7  0, OH  : 3x y  0    7 21
  3 1    27 9  Tọa độ điểm H ;   , Có AH   ;   , BH  ;    và BH  9  AH 10 10   10 10   10 10  
Nên H thuộc đoạn AB
z nhỏ nhất  OM nhỏ nhât, mà M thuộc đoạn AB  7 21  M H ;   10 10   49 21
Lúc đó S 7a b    7 . Chọn A 10 10 Câu 55. Giải: Chọn D x  4 
Gọi z x yi, ,
x y   , ta có z z  2 z z  8  x  2 y  4   , tập hợp K  ; x y biểu y  2 
diễn số phức z thuộc cạnh các cạnh của trong hình thoi ABCD như hình vẽ.
P z  3  3i đạt giá trị lớn nhất khi KM lớn nhất, theo hình vẽ ta có KM lớn nhất khi K D hay K  4
 ;0 suy ra M  49  9  58
P z  3  3i đạt giá trị nhỏ nhất khi KM nhỏ nhất, theo hình vẽ ta có KM nhỏ nhất khi K F ( F là
hình chiếu của E trên AB . Suy ra F 2; 
1 do AE AB nên F là trung điểm của AB .
Suy ra m  1 4  5 . Vậy M m  58  5 Câu 56. Chọn A 2 2 2 2
P z z z z 1  z z 1  z z 1  z 1  z z 1
Do z  1 nên ta đặt z  cos x  .
i sin x . Khi đó
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2
P z 1  z z 1  cos x  .
i sin x 1  cos 2x i sin 2x  cos x i sin x 1  cos x  2
1  sin x  cos 2x  cos x  2
1  sin 2x  sin x2 2
 2  2 cos x  3  4 cos x  2 cos 2x 2
 2  2 cos x  4 cos x  4 cos x 1
 2  2 cos x  2 cos x 1 Đặt t  cos , x t  1  
;1 . Xét hàm y  2  2t  2t 1 1 1  Với t   thì y
2  2t  2t 1, y '   2 2 2  2t 1  7 y '  0   2  0  t  2  2t 8  7  13  1  y   1  3; y    ; y   3    8  4  2  1 1  Với t  
thì y  2  2t  2t 1, y '   2 2 2  2t 1  1  y '  0   2  0  2  2t
(phương trình vô nghiệm) 2  2t 2  1  y   1  3 ; y   3    2  13 13 Vậy max y
. Do đó giá trị lớn nhất của 2 2
P z z z z 1 là . 1;  1 4 4 Câu 57. Chọn C
Giả sử z x yi , , x y   .Gọi ,
A B lần lượt là điểm biểu diễn cho các số phức z , z . Suy ra 1 2
AB z z  4 . 1 2
* Ta có  z  68  zi   x  6  yi.8  y  xi 2 2   
  8x  6 y  48   x y  6x  8 y i . Theo giả thiết
z  68 zi là số thực nên ta suy ra 2 2
x y  6x 8y  0 . Tức là các điểm ,
A B thuộc đường tròn C
tâm I 3; 4 , bán kính R  5 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489      
* Xét điểm M thuộc đoạn AB thỏa MA  3MB  0  OA  3OB  4OM .Gọi H là trung điểm AB . Ta tính được 2 2 2 2 2
HI R HB  21; IM HI HM  22 , suy ra điểm M thuộc đường tròn C tâm I 3;4 , bán kính r  22 .   
* Ta có z  3z OA  3OB  4OM  4OM , do đó z  3z nhỏ nhất khi OM nhỏ nhất. 1 2 1 2 Ta có OM
OM OI r  5  22 . 0 min Vậy z  3z
 4OM  20  4 22 . 1 2 0 min Câu 58. Chọn A
Đặt z x y i, x , y   và z x y i, x , y   . 2 2 2  2 2  1 1 1  1 1  
 x  32   y  42  4 1 1 2 2 Khi đó  và  x xy y  1. 1 2   1 2 
 x  32   y  42  4  2 2 2 2 2 2
Ta có  x  3  y  4  x  3  y  3 2 2
x y   2 2 x y  6 x x  8 y y . 1 1 2 2   1 2   1 2  1   1   2   2  2 2 2 2 Suy ra z z 2 3 x x  4 y y  2.  2 2 3 4  x x y y             10 . 1 2 1 2 1 2   1 2   1 2    2 2 Do đó 10  zz  10 . 1 2 Câu 59.
Gọi M là điểm biểu diễn số phức z và A 2  
;1 ; B 4;7 lần lượt là hai điểm biểu diễn hai số phức 2  i 1
, 4  7i . Ta có AB  6 2 . Phương trình đường thẳng AB là d : x y  3  0 .
+) z  2  i z  4  7i  6 2  MA MB  6 2  MA MB AB . Do đó tập hợp các điểm biểu diễn 1 1
số phức z là đoạn thẳng AB . 1
+) iz 1 2i  1  iz 1 2i i  1  z  2  i  1 . 2 2 2
Gọi N là điểm biểu diễn số phức  z và I 2 
;1 là điểm biểu diễn số phức 2  i . Ta có IN  1 Suy ra tập 2 2 2
hợp các điểm biểu diễn số phức  z là đường tròn C có phương trình:  x  2   y   1  1 . 2
d I , AB  2 2  1 , suy ra AB không cắt đường tròn.
Gọi K là hình chiếu của I 2 
;1 lên AB . Dễ thấy K nằm trên đoạn thẳng AB .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Gọi H là giao điểm của đoạn IK với đường tròn C .
Ta có z z MN KH d I , AB R  2 2 1 . 1 2  
Suy ra min z z  2 2 1. 1 2
Câu 60. Đặt z a bi a, b   .
Ta có: z z i a b
a  b  2 2 2 2 2 2
 4b  4  0  b  1 
z a i . 2 2
Xét: z 1 2i z 1 3i a 1 i a 1 2i    a 2     a 2 1 1 1  2 . Áp dụng BĐT Mincôpxki:
  a2     a2 
   a   a2    2 2 2 1 1 1 2 1 1 1 2  4  9  13 . 1
Suy ra: z 1 2i z 1 3i đạt GTNN là 13 khi 21 a  1 a a  . 3
Nhận xét : Bài toán trên có thể được giải quyết bằng cách đưa về bài toán hình học phẳng.
Câu 61. Giả sử z x yi x, y   . 2 2 2 2 Ta có: z zz z
 16  x yi  2  i x yi  2  i  16  x   y  2 2 1  4 . 1 2
Suy ra tập hợp điểm biểu diễn của số phức z là đường tròn tâm số phức I 0 
;1 bán kính R  2 .
Do đó m  1, M  3 . Vậy 2 2 M m  8 . Câu 62. 2 2
Gọi M x; y là điểm biểu diễn số phức z ta có: z  2i z  4i 2
x   y   2 2
x   y  4
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
y  3 ; z  3  3i  1  điểm M nằm trên đường tròn tâm I 3;3 và bán kính bằng 1. Biểu thức
P z  2  AM trong đó A2;0 , theo hình vẽ thì giá trị lớn nhất của P z  2 đạt được khi M 4;3 2 2
nên max P  4  2  3  0  13 . Câu 63. Gọi M  ;
x y  là điểm biểu diễn số phức z . Do z  2  2i  2 nên tập hợp điểm M là đường tròn
C  x  2   y  2 : 2 2  4 . Các điểm A1; 
1 , B 5; 2 là điểm biểu diễn các số phức 1 i và 5  2i . Khi đó, P MA MB .
Nhận thấy, điểm A nằm trong đường tròn C  còn điểm B nằm ngoài đường tròn C  , mà
MA MB AB  17 . Đẳng thức xảy ra khi M là giao điểm của đoạn AB với C  .
Ta có, phương trình đường thẳng AB : x  4 y  3  0 .
Tọa độ giao điểm của đường thẳng AB và đường tròn C  là nghiệm của hệ với 1  y  5    x 2  y 2       
y  2   y  2 2 2 4 4 5 2  4   
x  4 y  3  0 
x  4 y  3   22  59  y   N  2 2 17
Ta có 4 y  5   y  2 2
 4  17 y  44 y  25  0    22  59  y   L  17 37  4 59 22  59
Vậy min P  17 khi z   i 17 17
Câu 64. - Đặt z x yi , với , x y   . 2 2
Ta có: z  3  4i  5   x  3   y  4i  5   x  3   y  4  5 , hay tập hợp các điểm biểu diễn
số phức z là đường tròn C  có tâm I 3; 4 , bán kính r  5 . 2 2 2 2
- Khi đó : P z  2  z i   x   2 2 2
y x   y   1
 4x  2 y  3
 4x  2 y  3  P  0 , kí hiệu là đường thẳng  .
- Số phức z tồn tại khi và chỉ khi đường thẳng  cắt đường tròn C
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 23  P
d I;   r
 5  P  23  10  13  P  33 2 5
Suy ra M  33 và m  13  w  33 13i . Vậy w  1258 . Câu 65. Chọn D
Đặt z a b ; i ,
a b    z b   ai 1 2
z z a b b a i . 1 2     2 2 Nên z z a bb a  2. z 1 2     1
Ta lại có 2  z 1 i z  1 i z  2 1 1 1
z  2  2 . Suy ra z z  2. z  2 2  2 . 1 1 2 1 a b Dấu "  " xảy ra khi   0 . 1 1 
Vậy m  min z z  2 2  2 . 1 2
Câu 66. Giả sử z a bi a,b   , w  x yi x, y   . 2 2
z  3  2i  1  a  3  b  2  1 (1) 2 2 2 2
w 1 2i  w  2  i   x  
1   y  2   x  2   y   1 .
Suy ra x y  0 . P z
 a x2  b y2  a x2  b x2 w .
Từ (1) ta có I 3; 2 , bán kính r  1. Gọi H là hình chiếu của I trên d : y  x . x  3  t
Đường thẳng HI có PTTS  . y  2  t
M HI M 3  t; 2  t   1 t   2 M  C  2  2t  1    1 t     2  1 1  5  2
t  2  M 3  ; 2    , MH   2 2  2  1 1  5  2
t  3  M 3  ; 2    , MH   2 2  2 5 2  2 Vậy P  . min 2 2 1
Câu 67. Vì z  1 và .
z z z nên ta có z  . z Từ đó, 5 3 4
P z z  6z  2 z 1 4 4 4
z z z  6  2 z 1 4 4 4
z z  6  2 z 1 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Đặt 4
z x iy , với x, y   . Do z  1 nên 4 2 2 z
x y  1 và 1
  x, y  1.
Khi đó P x iy x iy  6  2 x iy 1  x    x  2 2 2 6 2 1  y
 2x  6  2 2x  2   x   2 2 2 1  3 .
Do đó P  3 . Lại có 1  x  1  0 
2x  2  2  1 
2x  2 1  1  P  4 . 1 3 Vậy M  4 khi 4 z  1  và m  3 khi 4 z   
i . Suy ra M m  1. 2 2
Câu 68. Gọi z x  i y , với ,
x y . Khi đó M x; y là điểm biểu diễn cho số phức z .
Theo giả thiết, 5w  2  i z  4  5w  i  2  i z  4  5i  2  iw  i  z  3  2i 2 2
z  3  2i  3 . Suy ra M x; y thuộc đường tròn C  :  x  3   y  2  9 .
Ta có P z 1 2i  z  5  2i  MA MB , với A1; 2 và B 5; 2 .
Gọi H là trung điểm của AB , ta có H 3; 2 và khi đó:
P MA MB   2 2
2 MA MB  hay 2 2
P  4MH AB .
Mặt khác, MH KH với mọi M  C  nên 2 2
P  4KH AB    2 2 4 IH RAB  2 53 . M K 3 11 Vậy P  2 53 khi
hay z  3  5i và w   i . max MA MB  5 5 Câu 69. Cách 1:
Đặt z  3  2i w với w x yi x, y   . Theo bài ra ta có 2 2
w  2  x y  4 . 2 2 2
Ta có P z   i
z   i w  
w   i   x   2 1 2 2 2 5 4 2 1 3 4
y  2  x   1   y  3   x
x  2   y  2   x
x  2   y  2 20 8 2 1 3 2 5 2 2 1 3 
x y x    x  2   y    2  
x  2  y   x  2   y    2 2 2 2 2 2 1 1 3 2 1 1 3 
 2 y y  3   2 y  3  y  6 . x  1  x  1 
P  6   y 3  y  0   .   y  3  2 2 x y  4 
Vậy GTNN của P là bằng 6 đạt được khi z  2  2  3i . Cách 2:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
z  3  2i  2  MI  2  M   I; 2 với I  3; 2 .
P z 1 2i  2 z  2  5i MA  2MB với A  1; 2 , B  2;5 . IA IM
Ta có IM  2 ; IA  4 . Chọn K 2; 2 thì IK  1. Do đó ta có 2 I . A IK IM   IM IK AM IM
 IAM và I
MK đồng dạng với nhau  
 2  AM  2MK . MK IK
Từ đó P MA  2MB  2 MK MB  2BK .
Dấu bằng xảy ra khi và chỉ khi M , K , B thẳng hàng và M thuộc đoạn thẳng BK .
Từ đó tìm được M  2;2  3 . Cách 3:
Gọi M a;b là điểm biểu diễn số phức z a b .i Đặt I  3; 2 , A1; 2 và B 2;5 .
Ta xét bài toán: Tìm điểm M thuộc đường tròn C  có tâm I , bán kính R  2 sao cho biểu thức
P MA  2MB đạt giá trị nhỏ nhất.
Trước tiên, ta tìm điểm K x; y sao cho MA  2MK M   C  .     2 2 Ta có 2 2
MA  2MK MA  4MK  MI IA  4MI IK         2 2
MI IA MI IA   2 2
MI IK MI IK   MI IA IK  2 2 2 2 . 4 2 . 2 4
 3R  4IK IA * .    
IA  4IK  0 * luôn đúng M   C    . 2 2 2 3
R  4IK IA  0     4
  x  3  4 x  2
IA  4IK  0     . 4
  y  2  0 y  2  
Thử trực tiếp ta thấy K 2; 2 thỏa mãn 2 2 2
3R  4IK IA  0 . Vì 2 2 2 2
BI  1  3  10  R  4 nên B nằm ngoài C  . Vì 2 2
KI  1  R  4 nên K nằm trong C  .
Ta có MA  2MB  2MK  2MB  2 MK MB  2KB .
Dấu bằng trong bất đẳng thức trên xảy ra khi và chỉ khi M thuộc đoạn thẳng BK .
Do đó MA  2MB nhỏ nhất khi và chỉ khi M là giao điểm của C  và đoạn thẳng BK.
Phương trình đường thẳng BK : x  2 . 2 2
Phương trình đường tròn C  :  x  3   y  2  4 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 x  2 x  2   x  2 
Tọa độ điểm M là nghiệm của hệ    hoặc  .  x  3 
2   y  22  4  y  2  3    y  2  3 
Thử lại thấy M 2;2  3 thuộc đoạn BK .
Vậy a  2 , b  2  3  a b  4  3 .
Câu 70. Gọi M , M , M lần lượt là điểm biểu diễn cho số phức z , 2z , z trên hệ trục tọa độ Oxy . Khi 1 2 1 2
đó quỹ tích của điểm M là đường tròn C tâm I 3; 4 , bán kính R  1 ; 1  1
quỹ tích của điểm M là đường C tròn tâm I 6;8 , bán kính R  1 ; 2  2
quỹ tích của điểm M là đường thẳng d : 3x  2 y 12  0 .
Bài toán trở thành tìm giá trị nhỏ nhất của MM MM  2 . 1 2 y I2 8 I3 B I A 1 M 4 O 3 6 x  138 64 
Gọi C có tâm I ;
, R  1 là đường tròn đối xứng với C qua d . Khi đó 2  3  3    13 13 
min MM MM  2  min MM MM  2 với M C . 3  3  1 2   1 3 
Gọi A , B lần lượt là giao điểm của đoạn thẳng I I với C , C . Khi đó với mọi điểm M C , 1  1  3  1  1 3 M C
, M d ta có MM MM  2  AB  2 , dấu "=" xảy ra khi M  ,
A M B . Do đó 3  3  1 3 1 3 9945 P
AB  2  I I  2  2  I I  . min 1 3 1 3 13
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
Document Outline

  • [NBV]-CHUYÊN ĐỀ 25. KHÁI NIỆM SỐ PHỨC, CÁC PHÉP TOÁN SỐ PHỨC VÀ MỘT SỐ BÀI TOÁN LIÊN QUAN (1)
  • [NBV]-CHUYÊN ĐỀ 26. MỘT SỐ BÀI TOÁN TÌM TẬP HỢP ĐIỂM BIỂU DIỄN SỐ PHỨC
  • [NBV]-CHUYÊN ĐỀ 27. PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC, BÀI TOÁN MIN-MAX
    • Untitled