Các dạng toán thể tích khối đa diện thường gặp trong kỳ thi THPTQG Toán 12

Giới thiệu đến quý thầy, cô giáo cùng các em học sinh khối 12 tài liệu tuyển tập các dạng câu hỏi và bài tập trắc nghiệm thể tích khối đa diện thường gặp trong đề thi THPT Quốc gia môn Toán.Mời bạn đọc đón xem.

Chủ đề:

Chương 1: Khối đa diện 172 tài liệu

Môn:

Toán 12 3.9 K tài liệu

Thông tin:
95 trang 1 năm trước
Tác giả:
L
Lan Tường
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Các dạng toán thể tích khối đa diện thường gặp trong kỳ thi THPTQG Toán 12

Giới thiệu đến quý thầy, cô giáo cùng các em học sinh khối 12 tài liệu tuyển tập các dạng câu hỏi và bài tập trắc nghiệm thể tích khối đa diện thường gặp trong đề thi THPT Quốc gia môn Toán.Mời bạn đọc đón xem.

41 21 lượt tải Tải xuống

Chủ đề: Chương 1: Khối đa diện 172 tài liệu

Môn: Toán 12 3.9 K tài liệu

Thông tin:

95 trang 1 năm trước

Tác giả:

Profile Lan Tường
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CHUYÊN
ĐỀ 8
THỂ TÍCH KHỐI ĐA DIỆN
MỤC LỤC
PHẦN A. CÂU HỎI ....................................................................................................................................................... 2
Dạng 1.THỂ TÍCH KHỐI CHÓP ................................................................................................................................. 2
Dạng 1.1 Biết chiều cao và diện tích đáy ..................................................................................................................... 2
Dạng 1.2 Cạnh bên vuông góc với đáy ........................................................................................................................ 2
Dạng 1.3 Mặt bên vuông góc với đáy .......................................................................................................................... 5
Dạng 1.4 Biết hình chiếu của đỉnh lên đáy ................................................................................................................... 6
Dạng 1.5 Thể tích khối chóp đều ................................................................................................................................. 7
Dạng 1.6 Thể tích khối chóp khác ................................................................................................................................ 8
Dạng 2. THỂ TÍCH KHỐI LĂNG TRỤ ...................................................................................................................... 9
Dạng 2.1 Biết chiều cao và diện tích đáy ..................................................................................................................... 9
Dạng 2.2 Thể tích khối lăng trụ đứng......................................................................................................................... 10
Dạng 2.3 Thể tích khối lăng trụ xiên .......................................................................................................................... 12
Dạng 3. THỂ TÍCH KHỐI ĐA DIỆN KHÁC ............................................................................................................ 14
Dạng 4. TỈ SỐ THỂ TÍCH ........................................................................................................................................... 16
Dạng 4.1 Tỉ số thể tích của khối chóp ........................................................................................................................ 16
Dạng 4.2 Tỉ số thể tích các khối đa diện .................................................................................................................... 16
Dạng 4.3 Ứng dụng tỉ số thể tích để tìm thể tích ........................................................................................................ 18
Dạng 5. BÀI TOÁN THỰC TẾ VÀ BÀI TOÁN CỰC TRỊ ...................................................................................... 20
PHẦN B. LỜI GIẢI THAM KHẢO ........................................................................................................................... 23
Dạng 1.THỂ TÍCH KHỐI CHÓP ............................................................................................................................... 23
Dạng 1.1 Biết chiều cao và diện tích đáy ................................................................................................................... 23
Dạng 1.2 Cạnh bên vuông góc với đáy ...................................................................................................................... 23
Dạng 1.3 Mặt bên vuông góc với đáy ........................................................................................................................ 31
Dạng 1.4 Biết hình chiếu của đỉnh lên đáy ................................................................................................................. 36
Dạng 1.5 Thể tích khối chóp đều ............................................................................................................................... 38
Dạng 1.6 Thể tích khối chóp khác .............................................................................................................................. 43
Dạng 2. THỂ TÍCH KHỐI LĂNG TRỤ .................................................................................................................... 48
Dạng 2.1 Biết chiều cao và diện tích đáy ................................................................................................................... 48
Dạng 2.2 Thể tích khối lăng trụ đứng......................................................................................................................... 48
Dạng 2.3 Thể tích khối lăng trụ xiên .......................................................................................................................... 53
Dạng 3. THỂ TÍCH KHỐI ĐA DIỆN KHÁC ............................................................................................................ 62
Dạng 4. TỈ SỐ THỂ TÍCH ........................................................................................................................................... 68
Dạng 4.1 Tỉ số thể tích của khối chóp ........................................................................................................................ 68
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
Dạng 4.2 Tỉ số thể tích các khối đa diện .................................................................................................................... 70
Dạng 4.3 Ứng dụng tỉ số thể tích để tìm thể tích ........................................................................................................ 78
Dạng 5. BÀI TOÁN THỰC TẾ VÀ BÀI TOÁN CỰC TRỊ ...................................................................................... 85
PHẦN A. CÂU HỎI
Dạng 1.THỂ TÍCH KHỐI CHÓP
Dạng 1.1 Biết chiều cao và diện tích đáy
Câu 1. (ĐỀ THAM KHẢO BGD & ĐT 2018) Thể tích của khối chóp có chiều cao bằng
h
và diện tích đáy
bằng
B
là:
A.
V Bh
1
2
B.
V Bh
1
6
C.
V Bh
D.
V Bh
1
3
Câu 2. (Mã đề 101 BGD&ĐT NĂM 2018) Cho khối chóp có đáy là hình vuông cạnh
a
và chiều cao bằng
2a
. Thể tích của khối chóp đã cho bằng
A.
3
4a
B.
3
2
3
a
C.
3
2a
D.
3
4
3
a
Câu 3. (Mã đề 102 BGD&ĐT NĂM 2018) Cho khối chóp có đáy là hình vuông cạnh
a
và chiều cao bằng
. Thể tích khối chóp đã cho bằng
A.
3
16a
B.
3
16
3
a
C.
3
4a
D.
3
4
3
a
Câu 4. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hình chóp tứ giác
.
S ABCD
có đáy
ABCD
là hình
vuông cạnh
a
, cạnh bên
SA
vuông góc với mặt phẳng đáy và
2SA a
. Tính thể tích
V
của khối chóp
.
S ABCD
A.
3
2
6
a
V
B.
3
2
4
a
V
C.
3
2V a
D.
3
2
3
a
V
Dạng 1.2 Cạnh bên vuông góc với đáy
Câu 5. (MĐ 105 BGD&ĐT NĂM 2017) Cho khối chóp
.S ABC
có
SA
vuông góc với đáy,
4SA
,
6AB
,
10BC
và
8CA
. Tính thể tích
V
của khối chóp
.S ABC
.
A.
32V
B.
192V
C.
40V
D.
24V
Câu 6. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Cho hình chóp tứ giác
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
SA
vuông góc với mặt phẳng đáy và
2SA a
. Tính thể tích
khối chóp
.
S ABCD
.
A.
3
2
6
a
B.
3
2
4
a
C.
3
2a
D.
3
2
3
a
Câu 7. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Cho hình chóp
.
S ABC
có đáy là tam giác
đều cạnh
a
, cạnh bên
SA
vuông góc với đáy và thể tích của khối chóp đó bằng
3
4
a
. Tính cạnh bên
SA
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
A. B. C. D.
Câu 8. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Cho hình chóp
.
S ABC
có đáy
ABC
là
tam giác đều cạnh
a
. Biết
SA ABC
và
3SA a
. Tính thể tích khối chóp
.
S ABC
.
A.
4
a
B.
3
2
a
C.
3
4
a
D.
3
3
4
a
Câu 9. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt đáy,
SD
tạo với mặt phẳng
SAB
một góc bằng
30
. Tính thể tích
V
của khối
chóp
.
S ABCD
.
A.
3
3V a
B.
3
6
3
a
V
C.
3
3
3
a
V
D.
3
6
18
a
V
Câu 10. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hình chóp
.
S ABC
có đáy là tam giác
đều cạnh
a
. Cạnh bên
SC
vuông góc với mặt phẳng
ABC
,
SC a
. Thể tích khối chóp
.
S ABC
bằng
A.
3
3
3
a
B.
3
2
12
a
C.
3
3
9
a
D.
3
3
12
a
Câu 11. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho tứ diện
ABCD
có
AD
vuông góc
với mặt phẳng
ABC
biết đáy
ABC
là tam giác vuông tại
B
và
10, 10, 24
AD AB BC
. Tính thể tích của
tứ diện
ABCD
.
A.
1200
V
B.
960
V
C.
400
V
D.
1300
3
V
Câu 12. (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hình chóp
.
S ABC
có
cạnh bên
SA
vuông góc với mặt phẳng đáy
ABC
. Biết
SA a
, tam giác
ABC
là tam giác vuông cân tại
A
,
2AB a
. Tính theo
a
thể tích
V
của khối chóp
.
S ABC
.
A.
3
6
a
V
. B.
3
2
a
V
. C.
3
2
3
a
V
. D.
3
2V a
.
Câu 13. (CHUYÊN KHTN NĂM 2018-2019 LẦN 01) Cho khối chóp
.
S ABC
có đáy
ABC
là tam giác
vuông tại
B
,
, 2 ,
AB a AC a SA ABC
và
SA a
. Thể tích của khối chóp đã cho bằng
A.
3
3
3
a
. B.
3
3
6
a
. C.
3
3
a
. D.
3
2
3
a
.
Câu 14. (MĐ 105 BGD&ĐT NĂM 2017) Cho khối chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông
góc với đáy và khoảng cách từ
A
đến mặt phẳng
SBC
bằng
2
2
a
. Tính thể tích của khối chóp đã cho.
A.
B.
3
a
C.
3
3
9
a
D.
Câu 15. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
AB a
,
3AD a
,
SA
vuông góc với mặt phẳng đáy và mặt phẳng
SBC
tạo với đáy một góc
60
o
. Tính
thể tích
V
của khối chóp
.
S ABCD
.
A.
3
3V a
B.
3
3
3
a
V
C.
3
V a
D.
3
3
a
V
3
.
2
a
3
.
3
a
3.
a
2 3.
a
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
Câu 16. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với đáy,
SC
tạo với mặt phẳng
SAB
một góc
0
30
. Tính thể tích khối chóp
.
S ABCD
A.
3
2
3
a
B.
3
2
3
a
C.
3
6
3
a
D.
3
2a
Câu 17. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hình chóp
.
S ABC
có đáy là tam
giác vuông cân tại
,C
cạnh bên
SA
vuông góc với mặt đáy, biết
4a, 6a.
AB SB
Thể tích khối chóp
.
S ABC
là
.V
Tỷ số
3
3
a
V
là
A.
5
80
B.
5
40
C.
5
20
D.
3 5
80
Câu 18. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho hình chóp tam giác
.
S ABC
có
đáy
ABC
là tam giác vuông tại
B
,
AB a
,
60
ACB
, cạnh bên
SA
vuông góc với mặt đáy và
SB
hợp
với mặt đáy một góc
45
. Tính thể tích
V
của khối chóp
.
S ABC
.
A.
3
3
18
a
V
B.
3
3
12
a
V
C.
3
2 3
a
V
D.
3
3
9
a
V
Câu 19. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật
AB a
và
2AD a
, cạnh bên
SA
vuông góc với đáy. Tính thể tích
V
của khối chóp
.
S ABCD
biết góc giữa hai mặt phẳng
SBD
và
ABCD
bằng
0
60
.
A.
3
15
15
a
V
B.
3
15
6
a
V
C.
3
4 15
15
a
V
D.
3
15
3
a
V
Câu 20. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Cho hình chóp
.
S ABC
có
AC a
,
2BC a
,
0
120
ACB
, cạnh bên
SA
vuông góc với đáy. Đường thẳng
SC
tạo với mặt phẳng
SAB
góc
0
30
. Tính thể tích của khối chóp
.
S ABC
A.
3
105
28
a
. B.
3
105
21
a
. C.
3
105
42
a
. D.
3
105
7
a
.
Câu 21. (TT HOÀNG HOA THÁM - 2018-2019) Cho hình chóp
.
S ABCD
có
5 3, 3 3
AB BC
, góc
90
BAD BCD
,
9
SA
và
SA
vuông góc với đáy. Biết thể tích khối chóp
.
S ABCD
bằng
66 3
, tính
cotang của góc giữa mặt phẳng
SBD
và mặt đáy.
A
B
C
D
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
Câu 22. A.
20 273
819
. B.
91
9
. C.
3 273
20
. D.
9 91
9
Câu 23. (THPT YÊN KHÁNH - NINH BÌNH - 2018 - 2019) Cho hình chóp
.
S ABC
có đáy
ABC
là tam
giác đều,
SA ABC
. Mặt phẳng
SBC
cách
A
một khoảng bằng
a
và hợp với mặt phẳng
ABC
góc
0
30
. Thể tích của khối chóp
.
S ABC
bằng
A.
3
8
9
a
. B.
3
8
3
a
. C.
3
3
12
a
. D.
3
4
9
a
.
Dạng 1.3 Mặt bên vuông góc với đáy
Câu 24. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hình chóp
.
S ABCD
có đáy
ABCD
là
hình vuông cạnh
a
, mặt bên
SAB
là tam giác cân tại
S
và nằm trong mặt phẳng vuông góc với đáy; góc giữa
SC
và mặt phẳng đáy bằng
45
o
. Tính thể tích khối chóp
.
S ABCD
bằng:
A.
3
3
12
a
B.
3
3
9
a
C.
3
5
24
a
D.
3
5
6
a
Câu 25. (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho hình chóp
.
S ABCD
có
đáy
ABCD
là hình chữ nhật, tam giác
SAB
là tam giác đều cạnh
a
và nằm trong mặt phẳng vuông góc với
đáy. Mặt phẳng
SCD
tạo với đáy góc
30
. Thể tích khối chóp
.
S ABCD
là?
A.
3
3
4
a
B.
3
3
2
a
C.
3
3
36
a
D.
3
5 3
36
a
Câu 26. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông cân tại
B
và
2AB a
. Tam giác
SAB
đều và nằm trong mặt phẳng vuông góc với
đáy. Tính thể tích
V
của khối chóp
.
S ABC
A.
3
3
4
a
V
B.
3
3
3
a
V
C.
3
3
12
a
V
D.
3
2 3
3
a
V
Câu 27. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Cho hình chóp tứ giác
.
S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
2a
. Tam giác
SAD
cân tại
S
và mặt bên
SAD
vuông góc với
mặt phẳng đáy. Biết thể tích khối chóp
.
S ABCD
bằng
3
4
3
a
. Tính khoảng cách
h
từ
B
đến mặt phẳng
SCD
.
A.
4
3
h a
B.
3
2
h a
C.
2 5
5
h a
D.
6
3
h a
Câu 28. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hình chóp tứ giác
.
S ABCD
có đáy là hình vuông
cạnh bằng
2a
. Tam giác
SAD
cân tại
S
và mặt bên
SAD
vuông góc với mặt phẳng đáy. Biết thể tích
khối chóp
.
S ABCD
bằng
3
4
3
a
. Tính khoảng cách
h
từ
B
đến mặt phẳng
SCD
A.
3
4
h a
B.
2
3
h a
C.
4
3
h a
D.
8
3
h a
Câu 29. (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Cho khối chóp
.
S ABCD
có đáy là hình vuông
cạnh
2a
, tam giác
SAC
vuông tại
S
và nằm trong mặt phẳng vuông góc với đáy, cạnh bên
SA
tạo với đáy
góc
60
. Tính thể tích
V
của khối chóp
.
S ABCD
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
A.
3
3
12
a
V
. B.
3
3
3
a
V
. C.
3
6
12
a
V
. D.
3
2
12
a
V
.
Câu 30. (KTNL GIA BÌNH NĂM 2018-2019) Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông và
tam giác
SAB
đều nằm trong mặt phẳng vuông góc với đáy. Biết khoảng cách giữa hai đường thẳng
SA
và
BD
bằng
21
. Hãy cho biết cạnh đáy bằng bao nhiêu?
A.
21
B.
21
C.
7 3
D.
7
Câu 31. (THPT MINH KHAI HÀ TĨNH NĂM 2018-2019) Cho hình chóp
.
S ABCD
có đáy
ABCD
là
hình thang vuông tại
A
và
B
,
1
2
BC AD a
. Tam giác
SAB
đều và nằm trong mặt phẳng vuông góc với
đáy, góc giữa
SC
và mặt phẳng
ABCD
bằng
sao cho
15
tan
5
. Tính thể tích khối chóp
.
S ACD
theo
a
.
A.
3
.
2
S ACD
a
V . B.
3
.
3
S ACD
a
V . C.
3
.
2
6
S ACD
a
V
. D.
3
.
3
6
S ACD
a
V
.
Câu 32. (THPT GANG THÉP THÁI NGUYÊN NĂM 2018-2019) Cho hinh chop
.
S ABCD
co đay la hinh
chư nhât;
; 2AB a AD a
. Tam giac
SAB
cân tai
S
va năm trong măt phăng vuông goc vơi đay. Goc giưa
đương thăng
SC
va mp
ABCD
băng
45
. Goi
M
la trung điêm cua
SD
. Tinh theo
a
khoang cach
d
tư
điêm
M
đên
SAC
.
A.
1513
89
a
d
. B.
2 1315
89
a
d
. C.
1315
89
a
d
. D.
2 1513
89
a
d
.
Dạng 1.4 Biết hình chiếu của đỉnh lên đáy
Câu 33. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hình chóp
.
S ABC
có đáy
ABC
là
tam giác vuông tại
A
. Hình chiếu của
S
lên mặt phẳng
ABC
là trung điểm
H
của
BC
,
AB a
,
3AC a
,
2SB a
. Thể tích của khối chóp
.
S ABC
bằng
A.
3
3
2
a
. B.
3
6
2
a
. C.
3
3
6
a
. D.
3
6
6
a
.
Câu 34. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019) Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật, mặt bên
SAD
là tam giác vuông tại
S
. Hình chiếu vuông góc của
S
trên mặt phẳng đáy là
điểm
H
thuộc cạnh
AD
sao cho
3
HA HD
. Biết rằng
2 3SA a
và
SC
tạo với đáy một góc bằng
30
.
Tính theo
a
thể tích
V
của khối chóp
.
S ABCD
.
A.
3
8 6V a
. B.
3
8 6
3
a
V
. C.
3
8 2V a
. D.
3
8 6
9
a
V
.
Câu 35. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hình chóp
.
S ABCD
có đáy là hình thang
vuông tại
A
và
D
,
AB AD a
,
2CD a
. Hình chiếu của đỉnh
S
lên mặt
ABCD
trùng với trung điểm
của
BD
. Biết thể tích tứ diện
SBCD
bằng
3
6
a
. Khoảng cách từ đỉnh
A
đến mặt phẳng
SBC
là?
A.
3
2
a
B.
2
6
a
C.
3
6
a
D.
6
4
a
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
Câu 36. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Hình chóp
.
S ABCD
có đáy
ABCD
là vuông cạnh
a
, hình chiếu vuông góc của
S
trên mặt phẳng
ABCD
trùng với trung điểm của
cạnh
;AD
gọi
M
là trung điểm của
;CD
cạnh bên
SB
hợp với đáy góc
60
. Tính theo
a
thể tích của khối
chóp
.
S ABM
.
A.
3
15
3
a
B.
3
15
6
a
C.
3
15
4
a
D.
3
15
12
a
Câu 37. (HSG BẮC NINH NĂM 2018-2019) Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
. Hình chiếu vuông góc của
S
trên đáy là điểm
H
trên cạnh
AC
sao cho
2
3
AH AC
; mặt phẳng
SBC
tạo với đáy một góc
60
o
. Thể tích khối chóp
.
S ABC
là?
A.
3
3
12
a
B.
3
3
48
a
C.
3
3
36
a
D.
3
3
24
a
Dạng 1.5 Thể tích khối chóp đều
Câu 38. (CHUYÊN HÙNG VƯƠNG GIA LAI NĂM 2018-2019 LẦN 01) Thể tích của khối chóp tứ giác
đều có tất cả các cạnh bằng
a
là
A.
3
2
6
a
. B.
3
2
3
a
. C.
3
a
. D.
3
2
2
a
.
Câu 39. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho khối chóp tứ giác đều có tất cả các cạnh
bằng
2a
. Thể tích của khối chóp đã cho bằng
A.
3
2 2
3
a
B.
3
8a
3
C.
3
8 2
3
a
D.
3
4 2
3
a
Câu 40. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho khối chóp tứ giác đều có cạnh đáy bằng
,a
cạnh bên gấp
hai lần cạnh đáy. Tính thể tích
V
của khối chóp đã cho.
A.
3
2
2
a
V
B.
3
14
2
a
V
C.
3
2
6
a
V
D.
3
14
6
a
V
Câu 41. (LIÊN TRƯỜNG THPT TP VINH NGHỆ AN NĂM 2018-2019) Cho khối chóp tứ giác đều có
cạnh đáy bằng
2a
cạnh bên bằng
5a
. Thể tích của khối chóp đã cho bằng
A.
3
4 5a
. B.
3
4 3a
. C.
3
4 5
3
a
. D.
3
4 3
3
a
.
Câu 42. (MĐ 104 BGD&DT NĂM 2017) Cho khối chóp tam giác đều
.
S ABC
có cạnh đáy bằng
a
và cạnh
bên bằng
. Tính thể tích
V
của khối chóp
.
S ABC
.
A.
3
11
6
a
V
B.
3
11
4
a
V
C.
3
13
12
a
V
D.
3
11
12
a
V
Câu 43. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho một hình chóp tam giác đều có
cạnh đáy bằng
a
, góc giữa cạnh bên và mặt phẳng đáy bằng
0
45 .
Thể tích khối chóp đó là
A.
3
3
12
a
.
B.
3
12
a
.
C.
3
36
a
.
D.
3
3
36
a
.
Câu 44. (TRƯỜNG THPT LƯƠNG TÀI SỐ 2 NĂM 2018-2019) Cho hình chóp tứ giác đều S.ABCD có
cạnh đáy bằng
6a
, góc giữa cạnh bên và mặt đáy bằng
0
60
. Tính thể tích V của khối chóp S.ABC?
A.
3
9V a
B.
3
2V a
C.
3
3V a
D.
3
6V a
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
Câu 45. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Cho hình chóp tam giác đều
.
S ABC
có độ dài cạnh đáy bằng
a
, góc hợp bởi cạnh bên và mặt đáy bằng
60
. Thể tích của khối chóp đã cho bằng
A.
3
3
12
a
. B.
3
3
3
a
. C.
3
3
6
a
. D.
3
3
4
a
.
Câu 46. (CHUYÊN TRẦN PHÚ HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho khối chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
, góc giữa mặt bên và mặt đáy bằng
0
60
. Thể tích
V
của khối chóp
.
S ABCD
bằng
A.
3
3
2
a
V
B.
3
2
2
a
V
C.
3
3
6
a
V
D.
3
2
6
a
V
Câu 47. (HSG BẮC NINH NĂM 2018-2019) Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
,
tâm của đáy là
O
. Gọi
và
N
lần lượt là trung điểm của
SA
và
BC
. Biết góc giữa đường thẳng
MN
và
mặt phẳng
ABCD
bằng
0
60
. Tính thể tích khối chóp
.
S ABCD
.
A.
3
10
6
a
B.
3
30
2
a
C.
3
30
6
a
D.
3
10
3
a
Câu 48. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho tứ diện
DABC
có các cạnh
AB
,
AC
và
DA
đôi
một vuông góc với nhau;
6AB a
,
7AC a
và
4AD a
. Gọi
M
,
N
,
P
tương ứng là trung điểm các cạnh
BC
,
DC
,
DB
. Tính thể tích
V
của tứ diện
AMNP
.
A.
3
7V a
B.
3
14V a
C.
3
28
3
V a
D.
3
7
2
V a
Dạng 1.6 Thể tích khối chóp khác
Câu 49. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hình chóp
.
S ABCD
có đáy là hình
bình hành. Gọi
V
là thể tích của khối chóp
.
S ABCD
và
M
,
N
,
P
lần lượt là trung điểm của các đoạn thẳng
SC
,
SD
,
AD
. Thể tích của khối tứ diện
AMNP
bằng
A.
1
8
V
. B.
1
4
V
. C.
1
16
V
. D.
1
32
V
.
Câu 50. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Cho tứ diện
ABCD
có các cạnh
, ,
AB AC AD
đôi một vuông góc nhau;
6AB a
,
7AC a
và
4AD a
. Gọi
, ,M N P
tương ứng là trung
điểm các cạnh
, ,BC CD DB
. Tính thể tích
V
của khối tứ diện
AMNP
.
A.
3
7V a
. B.
3
28
3
a
V . C.
3
7
2
a
V . D.
3
14V a
.
Câu 51. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho hình chóp
.
S ABC
có
6
SA SB SC
,
4
AC
;
ABC
là tam giác vuông cân tại
B
. Tính thể tích
V
của khối chóp
.
S ABC
.
A.
16 7
V B.
16 7
3
V
C.
16 2
V
D.
16 2
3
V
Câu 52. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Cho tứ diện
ABCD
có các cạnh
,AB AC
và
AD
đôi một vuông góc với nhau. Gọi
1 2 3
, ,G G G
và
4
G
lần lượt là trọng tâm các tam giác
, ,
ABC ABD ACD
và
BCD
. Biết
6 ,AB a
9AC a
,
12AD a
. Tính theo a thể tích khối tứ diện
1 2 3 4
G G G G
.
A.
3
4a
. B.
3
a
. C.
3
108a
. D.
3
36a
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
Câu 53. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019) Cho hình chóp
.
S ABC
có đáy là tam
giác đều cạnh
.a
90 .
SAB SCB
Gọi
là trung điểm của
.SA
Khoảng cách từ
A
đến mặt phẳng
( )MBC
bằng
6
.
7
a
Tính thể tích
V
của khối chóp
. .S ABC
A.
3
5 3
.
12
a
V
B.
3
5 3
.
6
a
V
C.
3
4 3
.
3
a
V
D.
3
7 3
.
12
a
V
Câu 54. (THPT QUỲNH LƯU 3 NGHỆ AN NĂM 2018-2019) Cho hình chóp
.
S ABC
biết rằng
SA SB SC a
,
120
ASB
,
60
BSC
và
90
ASC
. Thể tích khối chóp
.
S ABC
là
A.
3
2
12
a
. B.
3
2
6
a
. C.
3
3
4
a
. D.
3
3
8
a
.
Câu 55. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
1
, biết khoảng cách từ
A
đến
SBC
là
6
4
, từ
B
đến
SCA
là
15
10
, từ
C
đến
SAB
là
30
20
và hình chiếu vuông góc của
S
xuống đáy nằm trong tam giác
ABC
. Tính thể tích khối chóp
.
S ABC
V
.
A.
1
36
B.
1
48
C.
1
12
D.
1
24
Câu 56. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019 LẦN 01) Cho hình chóp
.
S ABC
có đáy
là tam giác đều cạnh
a
.
0
90
SAB SCB
. Gọi
là trung điểm của
SA
. Khoảng cách từ
A
đến mặt phẳng
MBC
bằng
6
7
a
. Tính thể tích
V
của khối chóp
.
S ABC
.
A.
3
5 3
12
a
V
B.
3
5 3
6
a
V
C.
3
4 3
3
a
V
D.
3
7 3
12
a
V
Câu 57. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Cho hình chóp
.
S ABC
có các cạnh
3
SA BC
;
4
SB AC
;
2 5
SC AB . Tính thể tích khối chóp
.
S ABC
.
A.
390
12
B.
390
4
C.
390
6
D.
390
8
Dạng 2. THỂ TÍCH KHỐI LĂNG TRỤ
Dạng 2.1 Biết chiều cao và diện tích đáy
Câu 58. (Mã đề 101 - BGD - 2019) Thể tích khối lăng trụ có diện tích đáy
B
và có chiều cao
h
là
A.
Bh
. B.
4
3
Bh
. C.
1
3
Bh
. D.
3Bh
.
Câu 59. (MĐ 103 BGD&ĐT NĂM 2017-2018) Cho khối lăng trụ có đáy là hình vuông cạnh
a
và chiều cao
bằng
. Thể tích của khối lăng trụ đã cho bằng
A.
3
16a
B.
3
4a
C.
3
16
3
a
D.
3
4
3
a
Câu 60. (Mã 103 - BGD - 2019) Thể tích khối lăng trụ có diện tích đáy
B
và chiều cao
h
là:
A.
1
3
Bh
. B.
Bh
. C.
4
3
Bh
. D.
3Bh
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
Câu 61. (Mã đề 104 BGD&ĐT NĂM 2018) Cho khối lăng trụ có đáy là hình vuông cạnh
a
và chiều cao
bằng
. Thể tích của khối lăng trụ đã cho bằng
A.
3
2
3
a
B.
3
4
3
a
C.
3
2a
D.
3
4a
Câu 62. (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho khối lăng trụ có diện tích
đáy bằng
2
3
a , khoảng cách giữa hai đáy của lăng trụ bằng
6a
. Tính thể tích
V
của khối lăng trụ
A.
3
3 2
V a
B.
3
2
V a
C.
3
2
3
a
V
D.
3
3 2
4
a
V
Dạng 2.2 Thể tích khối lăng trụ đứng
Câu 63. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Thể tích của khối lập phương cạnh
2a
bằng
A.
3
8a
B.
3
2a
C.
3
a
D.
3
6a
Câu 64. (Mã đề 104 - BGD - 2019) Cho khối lăng trụ đứng
.
ABC A B C
có đáy là tam giác đều cạnh
a
và
' 2AA a
(minh họa như hình vẽ bên dưới).
Thể tích của khối lăng trụ đã cho bằng
A.
3
6
2
a
. B.
3
6
4
a
. C.
3
6
6
a
. D.
3
6
12
a
.
Câu 65. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Thể tích của khối lăng trụ tam giác đều có tất cả các
cạnh bằng
a
.
A.
3
3
12
a
V
B.
3
3
2
a
V
C.
3
3
4
a
V
D.
3
3
6
a
V
Câu 66. (Mã 102 - BGD - 2019) Cho khối lăng trụ đứng .
ABC A B C
có đáy là tam giác đều cạnh
a
và
2AA a
(minh họa như hình vẽ bên).
Thể tích của khối lăng trụ đã cho bằng
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
A.
3
3
2
a
. B.
3
3
6
a
. C.
3
3 .a
D.
3
3
3
a
.
Câu 67. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho khối lăng trụ đứng
.
ABC A B C
có
BB a
, đáy
ABC
là tam giác vuông cân tại
B
và
2AC a
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
3
a
V B.
3
2
a
V C.
3
V a
D.
3
6
a
V
Câu 68. (Mã 103 - BGD - 2019) Cho khối lăng trụ đứng
. ' ' 'ABC A B C
có đáy là tam giác đều cạnh
2a
và
' 3AA a
(minh họa như hình vẽ bên).
Thể tích của khối lăng trụ đã cho bằng
A.
3
6 3a
. B.
3
3 3a
. C.
3
2 3 .a
D.
3
3a
.
Câu 69. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tính thể tích
V
của khối lập phương
.
ABCD A B C D
,
biết
3AC a
.
A.
3
V a
B.
3
3 6
4
a
V
C.
3
3 3V a
D.
3
1
3
V a
Câu 70. (TRƯƠNG THPT HOANG HOA THAM HƯNG YÊN NĂM 2018-2019) Hình lập phương có
đường chéo bằng
a
thì có thể tích bằng
A.
3
3 3a
. B.
3
2
4
a
. C.
3
3
9
a
. D.
3
a
.
Câu 71. (Mã đề 101 - BGD - 2019) Cho khối lăng trụ đứng
. ' ' 'ABC A B C
có đáy là tam giác đều
cạnh
a
và
' 3AA a
(minh họa hình vẽ bên). Thể tích khối lăng trụ đã cho bằng.
A.
3
4
a
. B.
3
2
a
. C.
3
3
4
a
. D.
3
3
2
a
.
Câu 72. (MĐ 104 BGD&DT NĂM 2017) Cho khối lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác cân
với
AB AC a
,
120
BAC
. Mặt phẳng
( )AB C
tạo với đáy một góc
60
. Tính thể tích
V
của khối lăng
trụ đã cho.
A.
3
3
8
a
V B.
3
9
8
a
V C.
3
8
a
V D.
3
3
4
a
V
A'
C'
B'
B
C
A
A'
C'
B'
B
C
A
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
Câu 73. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hình lăng trụ đứng .
ABC A B C
có đáy
là tam giác vuông cân tại
B
,
AB a
và
3A B a
. Thể tích khối lăng trụ .
ABC A B C
là
A.
3
3
2
a
B.
3
6
a
C.
3
2
a
D.
3
2
2
a
Câu 74. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho lăng trụ đều
.ABC A B C
. Biết
rằng góc giữa
A BC
và
ABC
là
30
, tam giác
A BC
có diện tích bằng
8
. Tính thể tích khối lăng
trụ
.ABC A B C
.
A.
8 3
. B.
8
. C.
3 3
. D.
8 2
.
Câu 75. (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho lăng trụ tam giác đều
. ' ' 'ABC A B C
có diện tích đáy bằng
2
3
4
a
. Mặt phẳng
'
A BC
hợp với mặt phẳng đáy một góc
0
60
. Tính
thể tích khối lăng trụ
. ' ' 'ABC A B C
.
A.
3
3 3
8
a
B.
3
3
8
a
C.
3
5 3
12
a
D.
3
3 2
8
a
Câu 76. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho khối lăng trụ đều
. ' ' 'ABC A B C
có cạnh đáy bằng
a
. Khoảng cách từ điểm
'A
đến mặt phẳng
' 'AB C
bằng
2 3
19
a
. Thể tích
của khối lăng trụ đã cho là
A.
3
3
4
a
B.
3
3
6
a
C.
3
3
2
a
D.
3
3
2
a
Dạng 2.3 Thể tích khối lăng trụ xiên
Câu 77. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho lăng trụ
. ' ' 'ABC A B C
có đáy
ABC
là tam giác
vuông tại
B
, đường cao
BH
. Biết
'
A H ABC
và
1, 2, ' 2
AB AC AA
. Thể tích của khối lăng trụ
đã cho bằng
A.
21
12
. B.
7
4
. C.
21
4
. D.
3 7
4
.
Câu 78. (SỞ GD&ĐT BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hình lăng trụ
.
ABC A B C
có tất cả
các cạnh bằng
a
, các cạnh bên tạo với đáy góc
60
. Tính thể tích khối lăng trụ
.
ABC A B C
bằng
A.
3
3
24
a
B.
3
3
8
a
C.
3
3
8
a
D.
3
8
a
Câu 79. (HSG BẮC NINH NĂM 2018-2019) Cho hình lăng trụ
.
ABC A B C
có đáy
ABC
là tam giác
vuông cân tại
, 2 2
A AC
, biết góc giữa
AC
và
ABC
bằng
0
60
và
4
AC
. Tính thể tích
V
của khối
lăng trụ
.
ABC A B C
.
A.
8
3
V
B.
16
3
V
C.
8 3
3
V
D.
8 3
Câu 80. (KTNL GIA BÌNH NĂM 2018-2019) Cho lăng trụ tam giác
. ' ' 'ABC A B C
có đáy là tam giác đều
cạnh
a
, góc giữa cạnh bên và mặt đáy bằng
0
30
. Hình chiếu của
'A
lên
ABC
là trung điểm
I
của
BC
.
Tính thể tích khối lăng trụ
A.
3
3
2
a
B.
3
13
12
a
C.
3
3
8
a
D.
3
3
6
a
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
Câu 81. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Một khối lăng trụ tam giác có
đáy là tam giác đều cạnh bằng
3
, cạnh bên bằng
2 3
tạo với mặt phẳng đáy một góc
30
. Khi đó thể tích
khối lăng trụ là:
A.
9
4
B.
27
4
C.
27 3
4
D.
9 3
4
Câu 82. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Cho hình lăng trụ
. ' ' 'ABC A B C
có đáy là tam giác đều cạnh
a
, góc giữa cạnh bên và mặt phẳng đáy bằng
0
30
. Hình chiếu của
'A
xuống
ABC
là trung điểm
BC
. Tính thể tích khối lăng trụ
. ' ' 'ABC A B C
.
A.
3
3
8
a
B.
3
8
a
C.
3
3
24
a
D.
3
3
4
a
Câu 83. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho hình lăng trụ
.
ABC A B C
có đáy
ABC
là tam giác đều cạnh
a
,
3
2
a
AA
. Biết rằng hình chiếu vuông góc của
A
lên
ABC
là trung điểm
BC
. Tính thể tích
V
của khối lăng trụ đó.
A.
3
V a
B.
3
2
3
a
V C.
3
3
4 2
a
V
D.
3
3
2
V a
Câu 84. (MĐ 103 BGD&ĐT NĂM 2017-2018) Cho khối lăng trụ
. ' ' 'ABC A B C
, khoảng cách từ
C
đến
đường thẳng
'BB
bằng 2, khoảng cách từ
A
đến các đường thẳng
'BB
và
'CC
lần lượt bằng 1 và
3
, hình
chiếu vuông góc của
A
lên mặt phẳng
( ' ' ')A B C
là trung điểm
của
' 'B C
và
' 2A M
. Thể tích của khối
lăng trụ đã cho bằng
A.
2 3
3
B.
1
C.
3
D.
2
Câu 85. (Mã đề 102 BGD&ĐT NĂM 2018) Cho khối lăng trụ
.
ABC A'B'C'
, khoảng cách từ
C
đến
'BB
là
5
, khoảng cách từ
A
đến
'BB
và
'CC
lần lượt là
1; 2
. Hình chiếu vuông góc của
A
lên mặt phẳng
' ' 'A B C
là trung điểm
của
' 'B C
,
15
'
3
A M
. Thể tích của khối lăng trụ đã cho bằng
A.
2 5
3
. B.
5
C.
2 15
3
D.
15
3
Câu 86. (Mã đề 101 BGD&ĐT NĂM 2018) Cho khối lăng trụ
.
ABC A B C
, khoảng cách từ
C
đến đường
thẳng
BB
bằng
2
, khoảng cách từ
A
đến các đường thẳng
BB
và
CC
lần lượt bằng
1
và
3
, hình chiếu
vuông góc của
A
lên mặt phẳng
A B C
là trung điểm
của
B C
và
2 3
3
A M
. Thể tích của khối lăng
trụ đã cho bằng
A.
2
B.
1
C.
3
D.
2 3
3
Câu 87. (Mã đề 104 BGD&ĐT NĂM 2018) Cho khối lăng trụ
.
ABC A B C
. Khoảng cách từ
C
đến đường
thẳng
BB
bằng
5
, khoảng cách từ
A
đến các đường thẳng
BB
và
CC
lần lượt bằng
1
và
2
, hình chiếu
vuông góc của
A
lên mặt phẳng
A B C
là trung điểm
M
của
B C
và
5
A M
. Thể tích của khối lăng
trụ đã cho bằng
A.
5
B.
15
3
C.
2 5
3
D.
2 15
3
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
Câu 88. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hình lăng trụ
.
ABCD A B C D
có đáy
ABCD
là hình thoi cạnh
a
,
60
ABC
. Chân đường cao hạ từ
B
trùng với tâm
O
của đáy
ABCD
; góc
giữa mặt phẳng
BB C C
với đáy bằng
60
. Thể tích lăng trụ bằng:
A.
3
3 3
8
a
B.
3
2 3
9
a
C.
3
3 2
8
a
D.
3
3
4
a
Câu 89. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Cho lăng trụ
.
ABC A B C
có đáy
là tam giác đều cạnh
a
, hình chiếu vuông góc của điểm
’A
lên mặt phẳng
ABC
trùng với trọng tâm tam
giác
.ABC
Biết khoảng cách giữa hai đường thẳng
’AA
và
BC
bằng
3
4
a
. Tính theo
a
thể tích của khối
lăng trụ đã cho.
A.
3
3
3
a
B.
3
3
24
a
C.
3
3
6
a
D.
3
3
12
a
Câu 90. (TOÁN HỌC TUỔI TRẺ NĂM 2018 - 2019 LẦN 01) Cho hình lăng trụ .
ABC A B C
có
2AA a
, tam giác
ABC
vuông tại
C
và
60
BAC
, góc giữa cạnh bên
BB
và mặt đáy
ABC
bằng
60
. Hình chiếu vuông góc của
B
lên mặt phẳng
ABC
trùng với trọng tâm của tam giác
ABC
. Thể tích của
khối tứ diện .
A ABC
theo
a
bằng
A.
3
9
208
a
. B.
3
3
26
a
. C.
3
9
26
a
. D.
3
27
208
a
.
Câu 91. (CHUYÊN HÙNG VƯƠNG GIA LAI NĂM 2018-2019 LẦN 01) Cho khôi lăng tru
. ,ABC A B C
tam giac
A BC
co diên tich băng 1 va khoang cach tư
A
đên
mặt phẳng
A BC
băng 2. Thê tich khôi lăng tru đã cho băng
A. 6. B. 3. C. 2. D. 1.
Câu 92. (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho lăng trụ tam giác
. ' ' 'ABC A B C
có đáy
ABC
là tam giác đều cạnh
a
. Hình chiếu của điểm
'A
trên mặt phẳng
ABC
trùng
vào trọng tâm
G
của tam giác
ABC
. Biết tam giác
' 'A BB
có diện tích bằng
2
2 3
3
a
. Tính thể tích khối lăng
trụ
. ' ' 'ABC A B C
.
A.
3
6 2
7
a
B.
3
3 7
8
a
C.
3
3 5
8
a
D.
3
3 3
8
a
Dạng 3. THỂ TÍCH KHỐI ĐA DIỆN KHÁC
Câu 93. (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho hình vuông
ABCD
và
ABEF
có cạnh bằng
1
, lần lượt
nằm trên hai mặt phẳng vuông góc với nhau. Gọi
S
là điểm đối xứng của
B
qua đường thẳng
DE
. Thể tích
của khối đa diện
ABCDSEF
bằng
A.
7
6
B.
C.
2
3
D.
5
6
Câu 94. (Mã đề 104 - BGD - 2019) Cho lăng trụ
.
ABC A B C
có chiều cao bằng 4 và đáy là tam giác đều
cạnh bằng 4. Gọi
,M N
và
P
lần lượt là tâm của các mặt bên
,
ABB A ACC A
và
BCC B
. Thể tích của khối
đa diện lồi có các đỉnh là các điểm
, , , , ,A B C M N P
bằng
A.
8 3
. B.
6 3
. C.
20 3
3
. D.
14 3
3
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
Câu 95. (Mã 103 - BGD - 2019) Cho lăng trụ
.
ABC A B C
có chiều cao bằng 6 và đáy là tam giác đều cạnh
bằng 4. Gọi
, ,M N P
lần lượt là tâm các mặt bên
, ,
ABB A ACC A BCC B
. Thể tích khối đa diện lồi có các
đỉnh là các điểm
, , , , ,A B C M N P
bằng
A.
9 3
. B.
10 3
. C.
7 3
. D.
12 3
.
Câu 96. (Mã 102 - BGD - 2019) Cho lăng trụ
. ' ' 'ABC A B C
có chiều cao bằng
8
và đáy là tam giác đều
cạnh bằng
4
. Gọi
,M N
và
P
lần lượt là tâm các mặt bên
' ', ' 'ABB A ACC A
và
' 'BCC B
. Thể tích của khối
đa diện lồi có các đỉnh là các điểm
, , , , ,A B C M N P
bằng
A.
40 3
3
. B.
16 3
. C.
28 3
3
. D.
12 3
.
Câu 97. (Mã đề 101 - BGD - 2019) Cho lăng trụ
. ' ' 'ABC A B C
có chiều cao bằng
8
và đáy là tam giác đều
cạnh bằng
6
. Gọi
,M N
và
P
lần lượt là tâm của các mặt bên
' ', ' 'ABB A ACC A
và
' 'BCC B
. Thể tích của
khối đa diện lồi có các đỉnh là các điểm
, , , , ,A B C M N P
bằng
A.
30 3
. B.
36 3
. C.
27 3
. D.
21 3
.
Câu 98. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Thể tích của bát diện đều cạnh bằng
3a
là.
A.
3
6a
. B.
3
6a
. C.
3
4
3
a
. D.
3
a
.
Câu 99. (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho hình lập phương
cạnh . Gọi là trung điểm của , thuộc cạnh thỏa . Mặt phẳng
chia khối lập phương thành hai khối, gọi là khối chứa điểm . Thể tích của khối theo
là?
A.
3
53
137
a
B.
3
55
144
a
C.
3
47
154
a
D.
3
65
113
a
Câu 100. Cho một hình lập phương có cạnh bằng
a
. Tính theo
a
thể tích của khối bát diện đều có các đỉnh
là tâm các mặt của hình lập phương.
A.
3
1
4
a
. B.
3
1
6
a
. C.
3
1
12
a
. D.
3
1
8
a
.
Câu 101. (THPT YÊN KHÁNH - NINH BÌNH - 2018 - 2019) Cho hình hộp chữ nhật
ABCDA B C D
.
Khoảng cách giữa
AB
và
B C
là
2 5
5
a
, giữa
BC
và
AB
là
2 5
5
a
, giữa
AC
và
BD
là
3
3
a
. Thể tích
của khối hộp đó là
A.
3
8a
. B.
3
4a
. C.
3
2a
. D.
3
a
.
Câu 102. (THPT NGÔ GIA TỰ VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hình hộp chữ nhật
. ' ' ' 'ABCD A B C D
có
, 2 , ' 3AB a BC a AC a
. Điểm
N
thuộc cạnh
'BB
sao cho
2 'BN NB
, điểm
M
thuộc cạnh
'DD
sao cho
' 2D M MD
. Mặt phẳng
'
A MN
chia hình hộp chữ nhật làm hai phần, tính thể
tích phần chứa điểm
'C
.
A.
3
4a
. B.
3
a
. C.
3
2a
. D.
3
3a
.
Câu 103. (SỞ GD&ĐT THANH HÓA NĂM 2018 - 2019) Cho hình chóp đều
.
S ABC
có đáy cạnh bằng
a
, góc giữa đường thẳng
SA
và mặt phẳng
ABC
bằng
60
. Gọi
A
,
B
,
C
tương ứng là các điểm đối xứng
của
A
,
B
,
C
qua
S
. Thể tích
V
của khối bát diện có các mặt
,ABC
A B C
,
A BC
,
B CA
,
C AB
,
AB C
,
BA C
,
CA B
là
. ' ' ' 'ABCD A B C D
a
M
BC
N
CD
1
3
CN
CD
( ' )A MN
( )H
A
( )H
a
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
A.
3
2 3
3
a
V
. B.
3
2 3V a
. C.
3
3
2
a
V
. D.
3
4 3
3
a
V
.
Dạng 4. TỈ SỐ THỂ TÍCH
Dạng 4.1 Tỉ số thể tích của khối chóp
Câu 104. (THPT QUỲNH LƯU 3 NGHỆ AN NĂM 2018-2019) Cho hình chóp
.
S ABC
. Gọi
, ,M N P
lần lượt là trung điểm của
, ,SA SB SC
. Tỉ số thể tích
.
.
S ABC
S MNP
V
V
bằng
A.
12
. B.
2
. C.
8
. D.
3
.
Câu 105. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho tứ diện
MNPQ
. Gọi
I
;
J
;
K
lần lượt là trung điểm của các cạnh
MN
;
MP
;
MQ
. Tỉ số thể tích
MIJK
MNPQ
V
V
bằng
A.
1
3
B.
1
4
C.
1
6
D.
1
8
Câu 106. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho hình chóp
.S ABCD
. Gọi
A
,
B
,
C
,
D
theo thứ tự là trung điểm của
SA
,
SB
,
SC
,
SD
. Tính tỉ số thể tích của hai khối chóp
.S A B C D
và
.S ABCD
.
A.
1
16
B.
1
4
C.
1
8
D.
1
2
Câu 107. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Cho hình chóp
.
S ABC
có thể
tích bằng
V
. Gọi
G
là trọng tâm tam giác
SBC
. Mặt phẳng
( )
đi qua hai điểm
,A G
và song song với
BC
. Mặt phẳng
( )
cắt các cạnh
,SB SC
lần lượt tại các điểm
M
và
N
. Thể tích khối chóp
.
S AMN
bằng
A.
9
V
B.
2
V
C.
4
9
V
D.
4
V
Dạng 4.2 Tỉ số thể tích các khối đa diện
Câu 108. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Cho khối tứ diện có thể tích bằng
V
. Gọi
V
là thể
tích của khối đa diện có các đỉnh là các trung điểm của các cạnh của khối tứ diện đã cho, tính tỉ số
.
A.
2
3
V
V
. B.
5
8
V
V
. C.
1
2
V
V
. D.
1
4
V
V
.
Câu 109. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hình chóp
.
S ABCDE
có đáy là hình
ngũ giác và có thể tích là
V
. Nếu tăng chiều cao của chóp lên
3
lần đồng thời giảm độ dài cạnh đáy đi
3
lần
ta được khối chóp mới
.
S A B C D E
có thể tích
V
. Tỉ số
V
V
là
A.
3
B.
1
5
C.
1
D.
1
3
Câu 110. (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Cho khối chóp tam giác
.
S ABC
có đỉnh
S
và đáy là tam giác
ABC
. Gọi
V
là thể tích của khối chóp. Mặt phẳng đi qua trọng tâm của ba mặt bên của
khối chóp chia khối chóp thành hai phần. Tính theo
V
thể tích của phần chứa đáy của khối chóp.
A.
37
64
V
. B.
27
64
V
. C.
19
27
V
. D.
8
27
V
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
Câu 111. (CHUYÊN LÊ THÁNH TÔNG NĂM 2018-2019 LẦN 01) Cho lăng trụ
.
ABC A B C
,
là
trung điểm
CC
. Mặt phẳng
ABM
chia khối lăng trụ thành hai khối đa diện. Gọi
1
V
là thể tích khối lăng
trụ chứa đỉnh
C
và
2
V
là thể tích khối đa diện còn lại. Tính tỉ số
.
A.
1
5
. B.
1
6
. C.
1
2
.
D.
2
5
Câu 112. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Cho hình hộp
.
ABCD A B C D
có
I
là giao điểm của
AC
và
BD
. Gọi
1
V
và
2
V
lần lượt là thể tích của các khối
.
ABCD A B C D
và
.
I A B C
. Tính tỉ số
1
2
V
V
A.
1
2
6
V
V
. B.
1
2
3
2
V
V
. C.
1
2
2
V
V
. D.
1
2
3
V
V
.
Câu 113. (HSG BẮC NINH NĂM 2018-2019) Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành.
Gọi
,M N
lần lượt là trung điểm của
;AD SC
.
I
là giao điểm của
BM
và
AC
. Tính tỷ số thể tích của hai
khối chóp
ANIB
và
.
S ABCD
A.
B.
1
8
C.
D.
1
24
Câu 114. (ĐỀ MẪU KSNL ĐHQG TPHCM NĂM 2018-2019) Cho khối lăng trụ
.
ABC A B C
. Gọi
E
,
F
lần lượt là trung điểm của
AA
,
CC
. Mặt phẳng
BEF
chia khối lăng trụ thành hai phần. Tỉ số thể tích
của hai phần đó là
A.
1
3
. B.
1
. C.
1
2
. D.
2
3
.
Câu 115. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Cho hình chop
.
S ABCD
có
đáy là hình vuông
ABCD
cạnh
a
, góc giữa mặt bên và mặt phẳng đáy là
thoả mãn
1
cos
3
. Mặt phẳng
P
qua
AC
và vuông góc với mặt phẳng
SAD
chia khối chóp
.
S ABCD
thành hai khối đa diện là khối
chop
.
N ACD
và đa diện chứa đỉnh
S
. Tỉ số hai khối đa diện đó gần nhất với giá trị nào trong các giá trị sau?
A.
0.11
B.
0.13
C.
0.7
D.
0.9
Câu 116. (THPT HÀM RỒNG THANH HÓA NĂM 2018-2019 LẦN 1) Cho tứ diện
ABCD
, trên các
cạnh
BC
,
BD
,
AC
lần lượt lấy các điểm
,
N
,
P
sao cho
3
BC BM
,
3
2
BD BN
,
2
AC AP
. Mặt
phẳng
MNP
chia khối tứ diện
ABCD
thành hai phần có thể tích là
1
V
,
2
V
. Tính tỉ số
A.
1
2
26
19
V
V
. B.
1
2
3
19
V
V
. C.
1
2
15
19
V
V
. D.
1
2
26
13
V
V
.
Câu 117. (THPT MINH KHAI HÀ TĨNH NĂM 2018-2019) Cho hình chóp
.
S ABCD
có đáy
ABCD
là
hình thoi cạnh
a
,
o
60
BAD
và
SA
vuông góc với mặt phẳng
ABCD
. Góc giữa hai mặt phẳng
SBD
và
ABCD
bằng
o
45
. Gọi
M
là điểm đối xứng của
C
qua
B
và
N
là trung điểm của
SC
. Mặt phẳng
MND
chia khối chóp
.
S ABCD
thành hai khối đa diện, trong đó khối đa diện chứa đỉnh
S
có thể tích là
1
V
, khối
còn lại có thể tích là
2
V
(tham khảo hình vẽ bên). Tính tỉ số
1
2
V
V
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
A.
1
2
1
5
V
V
. B.
1
2
5
3
V
V
. C.
1
2
12
7
V
V
. D.
1
2
7
5
V
V
.
Câu 118. (CHUYÊN TRẦN PHÚ HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho khối chóp
.
S ABCD
có
đáy
ABCD
là hình vuông cạnh bằng
,a
2 .SA a
Hai mặt phẳng
( )SAB
và
( )SAD
cùng vuông góc với
( ).ABCD
Một mặt phẳng
( )P
qua
A
và vuông góc
,SC
cắt các cạnh
, ,SB SC SD
lần lượt tại
, ,B C D
. Gọi
1
V
và
2
V
lần lượt là thể tích của khối chóp
.
S AB C D
và khối đa diện
.
ABCD D C B
. Tỉ số
1
2
V
V
bằng
A.
8
.
15
B.
8
.
7
C.
32
.
13
D.
1
.
2
Câu 119. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Cho hình lập phương
.
ABCD A B C D
có
cạnh bằng
1
. Gọi
1
V
là thể tích phần không gian bên trong chung của hai hình tứ diện
ACB D
và
A C BD
,
2
V
là phần không gian bên trong hình lập phương đã cho mà không bị chiếm chỗ bởi hai khối tứ diện nêu
trên. Tính tỉ số
?
A.
3
. B.
1
2
. C.
3
2
. D.
2
.
Câu 120. Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
,a
2 .SA a
Hai mặt phẳng
( )SAB
và
( )SAD
cùng vuông góc với
( ).ABCD
Một mặt phẳng
( )P
qua
A
và vuông góc
,SC
cắt các cạnh
, ,SB SC SD
lần lượt tại
, ,B C D
. Gọi
1
V
và
2
V
lần lượt là thể tích của khối chóp
.
S AB C D
và khối đa diện
.
ABCD D C B
. Tỉ số
1
2
V
V
bằng
A.
8
.
15
B.
8
.
7
C.
32
.
13
D.
1
.
2
Câu 121. Cho hình chóp
SABCD
có đáy là hình bình hành. Gọi
, , ,M N P Q
lần lượt là trọng tâm của các
tam giác
, , ,
SAB SBC SCD SDA
. Gọi
O
là điểm bất kỳ trên mặt phẳng đáy
ABCD
. Biết thể tích khối chóp
OMNPQ
bằng
V
. Tính thể tích khối chóp
SABCD
.
A.
27
8
V
. B.
27
2
V
. C.
9
4
V
. D.
27
4
V
.
Câu 122. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình bình hành, gọi
M
là trung điểm của
SC
. Mặt phẳng chứa
AM
và song song với
BD
cắt
,SB SD
lần
lượt tại
,P Q
. Biết thể tích khối chóp
.
S ABCD
bằng
.V
Tính thể tích khối chóp
. .S APMQ
A.
4
V
B.
8
V
C.
3
V
D.
6
V
Dạng 4.3 Ứng dụng tỉ số thể tích để tìm thể tích
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
Câu 123. (ĐỀ 01 ĐỀ PHÁT TRIỂN ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho khối lăng trụ
.
ABC A B C
có thể tích bằng
2
. Gọi
M
là trung điểm của đoạn thẳng
AA
và
N
là điểm nằm trên cạnh
'BB
sao cho
2 'BN B N
. Đường thẳng
CM
cắt đường thẳng
C A
tại
P
,
đường thẳng
CN
cắt đường thẳng
C B
tại
Q
. Thể tích của khối đa diện lồi
A MPB NQ
bằng
A.
7
9
. B.
5
9
. C.
2
3
. D.
13
9
.
Câu 124. (THPT YÊN KHÁNH - NINH BÌNH - 2018 - 2019) Cho hình chóp
.S ABCD
, đáy
ABCD
là
hình vuông cạnh
a
;
3; ( )SA a SA ABCD
. Gọi
,M N
lần lượt là trung điểm của
;SB SD
, mặt phẳng
( )AMN
cắt
SC
tại
I
. Tính thể tích của khối đa diện
ABCDMIN
A.
3
5 3
.
18
a
V
B.
3
3
.
18
a
V
C.
3
5 3
.
6
a
V
D.
3
13 3
.
36
a
V
Câu 125. (THPT CHUYÊN BẮC NINH LẦN 01 NĂM 2018-2019) Cho khối hộp
ABCDA B C D
có thể
tích bằng
2018
. Gọi
M
là trung điểm của cạnh
AB
. Mặt phẳng
MB D
chia khối chóp
ABCDA B C D
thành hai khối đa diện. Tính thể tích phần khối đa diện chứa đỉnh
A
.
A.
5045
6
B.
7063
6
C.
10090
17
D.
7063
12
Câu 126. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Cho hình chóp
.S ABCD
có
đáy là hình bình hành và thể tích
270V
. Lấy điểm
S
trong không gian thỏa mãn 2SS CB
. Tính thể
tích
v
của phần chung của hai khối chóp
.S ABCD
và
.S ABCD
. (tham khảo hình vẽ sau)
A.
120.v
B.
150.v
C.
180.v
D.
90.v
Câu 127. (THPT CHUYÊN BẮC NINH LẦN 01 NĂM 2018-2019) Cho hình chóp
SABC
có
1, 2, 3SA SB SC
và
60 , 120 , 90ASB BSC CSA
. Tính thể tích khối chóp
.S ABC
.
A.
2
2
B.
2
C.
2
6
D.
2
4
Câu 128. (ĐÊ 04 VTED NĂM 2018-2019) Cho khối chóp
.S ABCD
có đáy là hình bình hành thể tích bằng
1
. Gọi M là điểm đối xứng của
C
qua
;B N
là trung điểm cạnh
SC
. Mặt phẳng
MDN
chia khối chóp
.S ABCD
thành hai khối đa diện,thể tích của khối đa diện chứa đỉnh
S
bằng
A.
5
6
B.
5
8
C.
12
19
D.
7
12
Câu 129. (TRƯỜNG THPT LƯƠNG TÀI SỐ 2 NĂM 2018-2019) Cho hình chóp
.S ABCD
có đáy là
hình vuông, mặt bên
SAB
là một tam giác đều nằm trong mặt phẳng vuông góc với mặt đáy
ABCD
và
có diện tích bằng
27 3
4
(đvdt). Một mặt phẳng đi qua trọng tâm tam giác
SAB
và song song với mặt đáy
ABCD
chia khối chóp
.S ABCD
thành hai phần, tính thể tích
V
của phần chứa điểm
S
?
A.
24V
B.
8V
C.
12V
D.
36V
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
Câu 130. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019). Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
,M N
lần lượt là trung điểm các cạnh
,SB SC
. Tính thể tích khối chóp
.
S AMND
, biết rằng khối chóp
.
S ABCD
có thể tích bằng
3
.a
A.
3
4
a
B.
3
8
a
C.
3
2
a
D.
3
3
8
a
Câu 131. (THPT-THANG-LONG-HA-NOI-NAM-2018-2019 LẦN 01) Cho hình chóp
.
S ABCD
, gọi
, , ,I J K H
lần lượt là trung điểm của các cạnh
, , ,SA SB SC SD
. Tính thể tích khối chóp
.
S ABCD
biết rằng
thể tích khối chóp
.
S IJKH
là
1
A.
16
. B.
8
. C.
2
. D.
4
.
Câu 132. (CHUYÊN LÊ THÁNH TÔNG NĂM 2018-2019 LẦN 01) Cho hình chóp
.
S ABC
có đáy là
tam giác
ABC
vuông cân ở
B
,
2AC a
.
SA
vuông góc với mặt phẳng
ABC
và
SA a
. Gọi
G
là trọng
tâm của tam giác
SBC
. Một mặt phẳng đi qua hai điểm
A
,
G
và song song với
BC
cắt
SB
,
SC
lần lượt tại
B
và
C
. Thể tích khối chóp
.
S AB C
bằng:
A.
3
2
27
a
. B.
3
9
a
. C.
3
4
27
a
. D.
3
2
9
a
.
Câu 133. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Cho hình chóp
.
S ABCD
có đáy là hình bình hành và có thể tích bằng
. Trên cạnh
,SB SD
lấy điểm
,M N
sao cho
SM MB
,
3SD SN
. Mặt phẳng
AMN
cắt
SC
tại
P
. Tính thể tích
V
của khối tứ diện
SMNP
.
A.
1
2
V
. B.
1
3
V
. C.
2
V
. D.
1
V
.
Câu 134. (TT THANH TƯỜNG NGHỆ AN NĂM 2018-2019 LẦN 02) Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
N
là trung điểm
,SB
P
thuộc đoạn
SC
sao cho
2 ,SP PC M
thuộc đoạn
SA
sao cho
4
.
5
SM MA
Mặt phẳng
MNP
cắt
SD
tại
.Q
NP
cắt
BC
tại
,E CQ
cắt
DP
tại
.R
Biết rằng thể
tích khối chóp
EPQR
bằng
3
18 .cm
Thể tích khối chóp
SMNPQ
bằng
A.
3
65
cm
. B.
3
260
9
cm
. C.
3
75
cm
. D.
3
70
cm
.
Dạng 5. BÀI TOÁN THỰC TẾ VÀ BÀI TOÁN CỰC TRỊ
Câu 135. (Mã đề 102 BGD&ĐT NĂM 2018) Ông A dự định sử dụng hết
2
6,7m
kính để làm một bể cá
bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước
không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm).
A.
3
1,23m
B.
3
2,48m
C.
3
1,57m
D.
3
1,11m
Câu 136. (Mã đề 104 BGD&ĐT NĂM 2018) Ông A dự định sử dụng hết
2
5,5 m
kính để làm một bể cá có
dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể).
Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?:
A.
3
1,40 m
B.
3
1,01 m
C.
3
1,51 m
D.
3
1,17 m
Câu 137. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Người ta cần xây dựng một bể
bơi có dạng hình hộp chữ nhật có thể tích là
3
125m
. Đáy bể bơi là hình chữ nhật có chiều dài gấp ba lần chiều
rộng. Tính chiều rộng của đáy bể bơi để khi thi công tiết kiệm nguyên vật liệu nhất (kết quả làm tròn đến hai
chữ số thập phân)?
A.
3,12 m
B.
3,82m
C.
3,62m
D
3,42m
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
Câu 138. (THPT CẨM GIÀNG 2 NĂM 2018-2019) Người ta muốn thiết kế một bể cá bằng kính không
có nắp với thể tích
3
72dm
, chiều cao là
3dm
. Một vách ngăn (cùng bằng kính) ở giữa, chia bể cá thành hai
ngăn, với các kích thước
,a b
(đơn vị
dm
) như hình vẽ. Tính
,a b
để bể cá tốn ít nguyên liệu nhất (tính cả
tấm kính ở giữa), coi bề dày các tấm kính như nhau và không ảnh hưởng đến thể tích của bể.
A.
24 dm
a
;
24 dm
b
. B.
6dm
a
;
4dm
b
.
C.
3 2 dm
a
;
4 2 dm
b
. D.
4dm
a
;
6dm
b
.
Câu 139. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Xét khối tứ diện
ABCD
có cạnh
AB x
và các cạnh còn
lại đều bằng
2 3
. Tìm
x
để thể tích khối tứ diện
ABCD
đạt giá trị lớn nhất.
A.
14
x
B.
3 2
x
C.
6
x
D.
2 3
x
Câu 140. (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Xét khối chóp
.
S ABC
có đáy là tam giác vuông cân tại
A
,
SA
vuông góc với mặt phẳng đáy, khoảng cách từ
A
đến mặt phẳng
SBC
bằng 3. Gọi
là góc giữa hai mặt phẳng
SBC
và
ABC
, giá trị
cos
khi thể tích khối chóp
.
S ABC
nhỏ nhất là
A.
2
2
. B.
2
3
. C.
3
3
. D.
6
3
.
Câu 141. (CHUYÊN LÊ THÁNH TÔNG NĂM 2018-2019 LẦN 01) Cho hình hộp chữ nhật
.
ABCD A B C D
có
AB x
,
1AD
. Biết rằng góc giữa đường thẳng
A C
và mặt phẳng
ABB A
bằng
30
. Tìm giá trị lớn nhất
max
V
của thể tích khối hộp
.
ABCD A B C D
.
A.
3 3
4
max
V
. B.
3
4
max
V
. C.
1
2
max
V
. D.
3
2
max
V
.
Câu 142. (THPT QUỲNH LƯU 3 NGHỆ AN NĂM 2018-2019) Nhân ngày quốc tế Phụ nữ 8 – 3 năm
2019. Ông A đã mua tặng vợ một món quà và đặt nó trong một chiếc hộp chữ nhật có thể tích là 32 (đvtt) có
đáy là hình vuông và không nắp. Để món quà trở nên đặc biệt và xứng tầm với giá trị của nó, ông quyết định
mạ vàng chiếc hộp, biết rằng độ dày của lớp mạ trên mọi điểm của chiếc hộp là không đổi và như nhau. Gọi
chiều cao và cạnh đáy của chiếc hộp lần lượt là
h
và
x
. Để lượng vàng trên hộp là nhỏ nhất thì giá trị của
h
và
x
là?
A.
2
h
,
4
x
. B.
3
2
h
,
4
x
. C.
2
h
,
1x
. D.
4
h
,
2
x
.
Câu 143. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Xét tứ diện
ABCD
có các cạnh
1
AB BC CD DA
và
AC
,
BD
thay đổi. Giá trị lớn nhất của thể tích khối tứ diện
ABCD
bằng
A.
2 3
27
B.
4 3
27
C.
2 3
9
D.
4 3
9
Câu 144. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hình chóp
SABC
có
, , 1.
SA x SB y AB AC SB SC
Thể tích khối chóp
SABC
đạt giá trị lớn nhất khi tổng
x y
bằng
A.
2
3
B.
3
C.
4
3
D.
4 3
b dm
a dm
3 dm
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
Câu 145. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Cho hình hộp chữ nhật
. ' ' ' 'ABCD A B C D
có tổng diện tích tất cả các mặt là 36, độ dài đường chéo
'AC
bằng 6. Hỏi thể tích của
khối hộp lớn nhất là bao nhiêu?
A.
8 2
B.
6 6
C.
24 3
D.
16 2
Câu 146. (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Cho hình chóp
.
S ABCD
có
SC x
0 3
x a , các cạnh còn lại đều bằng
a
. Biết rằng thể tích khối chóp
.
S ABCD
lớn nhất khi và chỉ khi
a m
x
n
*
,m n
. Mệnh đề nào sau đây đúng?
A.
2 10
m n
. B.
2
30
m n
. C.
2
2 3 15
n m
. D.
2
4 20
m n
.
Câu 147. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Cho tứ diện
ABCD
có
AB x
,
CD y
, tất
cả các cạnh còn lại bằng
2
. Khi thể tích tứ diện
ABCD
là lớn nhất tính
xy
.
A.
2
3
. B.
4
3
. C.
16
3
. D.
1
3
.
Câu 148. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Cho hình chóp
.
S ABCD
có
đáy
ABCD
là hình bình hành và có thể tích
V
. Điểm
P
là trung điểm của
SC
, một mặt phẳng qua
AP
cắt
hai cạnh
SD
và
SB
lần lượt tại
và
. Gọi
1
V
là thể tích khối chóp
.
S AMPN
. Giá trị lớn nhất của
thuộc khoảng nào sau đây?
A.
1
0;
5
. B.
1 1
;
5 3
. C.
1 1
;
3 2
. D.
1
;1
2
.
Câu 149. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Trong một cuộc thi làm đồ
dùng học tập do trường phát động, bạn An nhờ bố làm một hình chóp tứ giác đều bằng cách lấy một mảnh tôn
hình vuông
ABCD
có cạnh bằng
5cm
(tham khảo hình vẽ).
Cắt mảnh tôn theo các tam giác cân
AEB
,
BFC
,
CGD
,
DHA
và sau đó gò các tam giác
AEH
,
BEF
,
CFG
,
DGH
sao cho bốn đỉnh
A
,
B
,
C
,
trùng nhau tạo thành khối chóp tứ giác đều. Thể tích lớn nhất của khối
chóp tứ giác đều tạo thành bằng
A.
4 10
3
. B.
4 10
5
. C. . D. .
Câu 150. Cho khối lập phương
.
ABCD A B C D
cạnh
a
. Các điểm
,M N
lần lượt di động trên các tia
,
AC B D
sao cho
2AM B N a
.Thể tích khối tứ diện
AMNB
có giá trị lớn nhất là
A.
3
12
a
B.
3
6
a
C.
3
3
6
a
D.
3
2
12
a
8 10
3
8 10
5
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
Câu 151. (SỞ GD&ĐT BẮC NINH NĂM 2018-2019 LẦN 01) Cho tứ diện
SABC
có
G
là trọng tâm tứ
diện, mặt phẳng quay quanh
AG
cắt các cạnh
,SB SC
lần lượt tại
,M N
. Giá trị nhỏ nhất của tỉ số
.
.
S AMN
S ABC
V
V
là?
A.
4
9
. B.
3
8
. C.
1
3
. D.
1
2
.
PHẦN B. LỜI GIẢI THAM KHẢO
Dạng 1.THỂ TÍCH KHỐI CHÓP
Dạng 1.1 Biết chiều cao và diện tích đáy
Câu 1.
Lơi giai
Chon A
Thể tích của khối chóp có chiều cao bằng
h
và diện tích đáy bằng
B
là:
V Bh
1
3
Câu 2. Chọn B
Khối chóp có đáy là hình vuông cạnh
a
nên có diện tích đáy:
2
đáy
S a
.
Chiều cao
2h a
.
Vậy thể tích khối chóp đã cho là
1
. .
3
đáy
V S h
2
1
. .2
3
a a
3
2
3
a
.
Câu 3. Chọn D
Thể tích khối chóp:
1
.
3
V B h
2
1
.4
3
a a
3
4
3
a
.
Dạng 1.2 Cạnh bên vuông góc với đáy
Câu 4. Chọn D
Ta co
SA ABCD SA
la đương cao cua hinh chop
Thê tich khôi chop
.
S ABCD
:
3
2
1 1 2
. . 2.
3 3 3
ABCD
a
V SA S a a
.
Câu 5. Chọn A
A
B
D
C
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
Ta có
2 2 2
BC AB AC
suy ra
ABC
vuông tại
A
.
24
ABC
S
,
1
. 32
3
ABC
V S SA
Câu 6. Chọn D
Ta có
2
ABCD
S a
.
3
. D
1 2
.
3 3
S ABCD ABC
a
V SA S
.
Câu 7.
3
.
.
2
3.
1 3
4
. . 3
3
3
4
S ABC
S ABC ABC
ABC
a
V
V S SA SA a
S
a
.
Câu 8. Chọn C
S
A
B
C
A
C
B
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
Ta có
SA
là đường cao hình chóp
Tam giác
ABC
đều cạnh
a
nên
2
3
4
ABC
a
S
Vậy thể tích cần tìm là:
2 3
.
1 3
. . 3
3 4 4
S ABC
a a
V a
.
Câu 9. Chọn C
Góc giữa SD và mp là
0
30DSA
.
Ta có
0
3
tan30
AD
SA a
.
3
2
1 3
. 3
3 3
a
V a a
.
Câu 10. Chọn D
a 3
a
a
a
A
C
B
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
2
3
4
ABC
a
S
2 3
.
1 3 3
. .
3 4 12
S ABC
a a
V a
.
Câu 11. Chọn C
Ta có
1 1 1
. . 10.10.24 400
3 2 6
ABCD
V AD AB BC
Câu 12. Diện tích tam giác
ABC
vuông cân tại
A
là:
2
1 1
. 2 .2 2
2 2
ABC
S AB AC a a a
.
Thể tích khối chóp
.
S ABC
là:
3
2
.
1 1 2
. . .2
3 3 3
S ABC ABC
a
V SA S a a
.
Câu 13.
Ta có
2 2 2 2
3 3BC AC AB a BC a
.
Vậy
3
.
1 1 1 1 3
. . . . . . 3.
3 3 2 6 6
S ABC ABC
a
V S SA AB BC SA a a a
.
Câu 14. Chọn A
A
C
B
S
A
B
D
C
S
H
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
Ta có
,BC AB BC SA BC AH
. Kẻ
AH SB AH SBC
.
Suy ra
2
;
2
a
d A SBC AH
.
Tam giác
SAB
vuông tại
A
có:
2 2 2
1 1 1
SA a
AH SA AB
.
Vậy
3
1
. .
3 3
SABCD ABCD
a
V SA S
Câu 15. Chọn.C
Ta có
2
3
ABCD
S a
.
Vì
, ;
SBC ABCD BC
BC SB SBC SBC ABCD SB AB SBA
BC AB ABCD
.
Vậy
60
o
SBA
Xét tam giác vuông
SAB
có:
tan 60 .tan 60 3
o o
SA
SA AB a
AB
Vậy
2 3
.
1 1
. 3. 3
3 3
S ABCD ABCD
V S SA a a a
.
Câu 16. Chọn B
+) Do ABCD là hình vuông cạnh a nên:
2
ABCD
S a
60
a
a 3
D
A
B
C
S
30
0
C
A
D
B
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
+) Chứng minh được
BC SAB
góc giữa SC và (SAB) là
0
30CSB
.
+) Đặt
SA x
2 2
SB x a
. Tam giác SBC vuông tại B nên
0
1
tan tan 30
3
BC
CSA
SB
Ta được:
2 2
3 3 2SB BC x a a x a
.
Vậy
3
2
1 1 2
. . . 2.a
3 3 3
SABCD ABCD
a
V SA S a
(Đvtt)
Câu 17. Chọn B
Ta có:
+
ABC
vuông cân tại
, 4aC AB
suy ra
2a 2.AC BC
Do đó:
2
1
. 4a .
2
ABC
S AC BC
+
SA ABC SA AB ABC
vuông tại
A
2 2
2 2
6a 4a 2a 5.SA SB AB
+ Khối chóp
.S ABC
có
SA ABC
3
2
1 1 8a 5
. 4a .2a 5
3 3 3
ABC
V S SA
Vậy tỷ số:
3 3
3
5
.
3 40
3.8a 5
3
a a
V
Câu 18. Chọn A
B
C
A
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
ABC
là tam giác vuông tại
B
,
AB a
,
60
ACB
0
3
tan 60 3
AB
BC a
0
, , 45
SB ABC SB AB
nên tam giác
SAB
vuông cân tại
S
SA AB a
3
.
1 1 1 1 3 3
. . . . .
3 3 2 6 3 18
S ABC ABC
a
V S SA BA BC SA a a a
Câu 19. Chọn C
Kẻ
AE BD
0
, 60
SBD ABCD SEA
Xét
ABD
vuông tại
A
2
2 2
. 2 2 5
5
5
AD AB a a
AE
a
AD AB
Xét
SAE
vuông tại
A
0
2 5 2 15
.tan 60 . 3
5 5
a a
SA AE
Khi đó thể tích
.
S ABCD
3
2
1 1 2 15 4 15
. . .2
3 3 5 15
ABCD
a a
V SA S a
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
Câu 20. Chọn C
Theo giả thiết ta có đường thẳng
SC
tạo với mặt phẳng
SAB
góc
0
30
.
Nên
0
30
ASC
.
Ta
2
1 1 3 3
. .sin . .2 .
2 2 2 2
ABC
a
S AC BC ACB a a
Xét tam giác
ABC
ta có
2 2 2 2
2 . .cos 7AB AC BC AC BC ACB a
Gọi
H
là hình chiếu vuông góc của
C
trên
AB
khi đó do đường thẳng
SC
tạo
với mặt phẳng
SAB
góc
0
30
nên
0
30
CSH
.
Xét
ABC
ta có
2
1 3 21
. .
2 2 7
a a
CH AB CH
.
Xét
SCH
vuông tại
H
ta có
0
21
sin30 7
CH a
SC
.
Xét
SAC
vuông tại
A
ta có
2 2
35
7
a
SA SC AC
.
Vậy
2 3
1 1 35 3 105
. . . .
3 3 7 2 42
SABC ABC
a a a
V SA S
.
Câu 21.
Có:
.
1 1
. . 66 3 .9. 44 3
3 3
S ABCD ABCD ABCD ABCD
V SA S S S
Suy ra
1 1
. . 44 3 5 3 44
2 2
AB AD BC CD AD CD
. (1)
Áp dụng định lí Pitago trong 2 tam giác vuông
;
ABD BCD
, ta có:
2 2 2 2 2 2 2
48
AB AD BD BC CD CD AD
(2)
Từ (1) và (2) suy ra
4
47
2
AD
AD
47
2
AD
không thỏa mãn do từ (1) ta có:
44
4
5
AD AD
.
Trong tam giác
ABD
, dựng
AH BD
lại có
SA BD BD SH
.
Vậy góc giữa
SBD
và đáy là góc
SHA
.
A
B
C
D
S
H
S
A
B
C
H
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
Dễ tính
. 20 273
91,
91
AB AD
BD AH
BD
,
20 273
cot
819
AH
SHA
SA
.
Câu 23.
Gọi
I
là trung điểm sủa
BC
suy ra góc giữa mp
SBC
và mp
ABC
là
0
30
SIA .
H
là hình chiếu vuông góc của
A
trên
SI
suy ra
,
d A SBC AH a
.
Xét tam giác
AHI
vuông tại
H
suy ra
0
2
sin30
AH
AI a
.
Giả sử tam giác đều
ABC
có cạnh bằng
x
, mà
AI
là đường cao suy ra
3 4
2
2
3
a
a x x
.
Diện tích tam giác đều
ABC
là
2
2
4 3 4 3
.
4 3
3
ABC
a a
S
.
Xét tam giác
SAI
vuông tại
A
suy ra
0
2
.tan30
3
a
SA AI .
Vậy
2 3
.
1 1 4 3 2 8
. . . .
3 3 3 9
3
S ABC ABC
a a a
V S SA
.
Dạng 1.3 Mặt bên vuông góc với đáy
Câu 24. Chọn D
Gọi
H
là trung điểm của
AB
,
SAB
cân tại
S SH AB
;
SAB ABCD
SAB ABCD AB SH ABCD
SH SAB SH AB
H
30
0
I
C
B
A
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
; 45
o
SC ABCD SCH
SHC
vuông cân tại
H
2
2 2 2
5
4 2
a a
SH HC BC BH a ;
2 2
ABCD
S AB a
3
2
.
1 1 5 5
. . .
3 3 2 6
S ABCD ABCD
a a
V S SH a
Câu 25. Chọn A
Gọi
H
,
K
lần lượt là trung điểm
AB
và
CD
.
Suy ra
SH ABCD
và
, 30
SCD ABCD SKH
.
Xét
SHK
vuông tại
H
, có
3 1 3
:
tan30 2 2
3
SH a a
HK
.
Vậy
3
.
1 1 3 3 3
. . . .
3 3 2 2 4
S ABCD ABCD
a a a
V SH S a
.
Câu 26. Chọn D
Gọi
H
là trung điểm của
AB
suy ra
3SH a
2
2
1
2 2 2 2
2
ABC
AB a BC a S a a
3
2
.
1 1 2 3
. . 2 3
3 3 3
S ABC ABC
a
V S SH a a
Câu 27. Chọn A
30°
K
H
D
A
B
C
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
Gọi
H
là trung điểm của
AD
. Nên
SH AD
SAD ABCD
SAD ABCD AD SH ABCD
AD SH
Ta có:
2
2
ABCD
S a
3
2
4
3.
3
3
2
2
ABCD
a
V
SH a
S a
Gọi
I
là hình chiếu của
H
lên
SD
; ; 2 ; 2d B SCD d A SCD d H SCD IH
Mà
2 2 2
2
2
2 .
. . 2
2
3
2
2
2
a
a
SH HD SH HD
IH a
SD
SH HD
a
a
Vậy
4
;
3
d B SCD a
Câu 28.
Lơi giai
Chọn C
Goi
I
la trung điêm cua
AD
. Tam giac
SAD
cân tai
S
SI AD
Ta co
SI AD
SI ABCD
SAD ABCD
SI
la đương cao cua hinh chop.
Theo gia thiêt
3 2
.
1 4 1
. . .2 2
3 3 3
S ABCD ABCD
V SI S a SI a SI a
Vi
AB
song song vơi
SCD
, , 2 ,
d B SCD d A SCD d I SCD
Goi
H
la hinh chiêu vuông goc cua
I
lên
SD
.
Măt khac
SI DC
IH DC
ID DC
. Ta co
,
IH SD
IH SCD d I SCD IH
IH DC
Xet tam giac
SID
vuông tai
2 2 2 2 2
1 1 1 1 4 2
:
4 2 3
a
I IH
IH SI ID a a
4
, , 2 ,
3
d B SCD d A SCD d I SCD a
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
Câu 29.
Kẻ
SH AC
,
H AC
H suy ra
SH ABCD
.
2AC a
, tam giác
SAC
vuông ở
S
, góc
60
SAC
nên
3
, 3,
2
a
SA a SC a SH
.
Thể tích hình chóp là
3
2
1 3 3
2 .
3 2 3
a a
V a
.
Câu 30. Chọn D
Giả sử
AB a
. Gọi
H
là trung điểm của
AB SH AB SH ABCD
Ta có
2
1
. .
2
SA BD SH HA BA BC HA BA a

2 2
1 1 7
2. , , sin ,
2 8
2 2
a cos SA BD a cos SA BD SA BD

2 3 3
1 1 3 3 3
. . .
3 3 2 6 12
SABCD SABD
a
V SH AB AD a a V a
3 3
,
1 3 1 7 3
. . .sin , . 2. 21. 7
6 12 6 8 12
SA BD
SA BD d SA BD a a a a a
D
B
C
A
S
H
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
Câu 31.
Gọi
H
là trung điểm
AB
, từ giả thiết ta có:
SH ABCD
,
,SC ABCD SCH
.
Đặt
AB x
, ta có:
2
2 2 2
4
x
HC BH BC a
,
2
2
15
.tan .
4 5
x
SH HC a
.
Mặt khác
3
2
x
SH
. Vậy ta có:
2
2
15 3
.
4 5 2
x x
a
x a
.
2
.
3
2 2
ABCD
AD BC AB
a
S
;
2
2
3
ACD ABCD
S S a
;
3
.
1 3
.
3 6
S ACD ACD
a
V SH S
.
Câu 32.
Goi
H
la trung điêm đoan
AB
SH ABCD
.
Xet
BCH
vuông tai
B
, co:
2
2
17
4
4 2
a a
CH a .
Xet
SHC
vuông cân tai
H
, co:
17 34
;
2 2
a a
SH SC
.
Xet
SAH
vuông tai
H
, co:
2 2
17 3 2
4 4 2
a a
SA a
.
Xet
ABC
vuông tai
B
, co:
2 2
4 5AC a a a
.
2
89
4
SAC
S a
.
Ta co:
3
.
1 17
. .
3 3
S ABCD ABCD
a
V V SH S
;
3
.
1 17
2 6
S ACD
a
V V
.
3
. .
1 17
2 12
S ACM S ACD
a
V V
. Ma
2
.
1 89
. . .
3 12
S MAC SAC
V d S a d
1513
89
a
d
.
H
C
A
B
D
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 36
Dạng 1.4 Biết hình chiếu của đỉnh lên đáy
Câu 33.
Xét tam giác
ABC
vuông tại
A
có:
2
2 2 2
3 2BC AB AC a a a
.
H
là trung điểm của
BC
nên
BH a
.
Xét tam giác
SBH
vuông tại
H
có:
2
2 2 2
2
SH SB HB a a a
.
Diện tích đáy
ABC
là:
2
1 1
. 3
2 2
ABC
S AB AC a
.
Thể tích của khối chóp
.
S ABC
là:
3
2
1 1 1 3
. . . . 3
3 3 2 6
ABC
a
V SH S a a
.
Câu 34.
2 2
. 3 3
SH HD HA HD SH HD
Có:
2 2
tan 3
3 2 4
3
tan
SH
SDH
SA SA
DH
SD a DA SD SA a
SA
SD
SDH
SD
.
1
4
DH DA a
.
Tam giác
SHC
có
tan tan 30 3
tan 30
SH SH SH
SCH HC a
HC HC
.
Tam giác
DHC
có
2 2
2 2DC DH HC a
H
C
B
A
S
2a 3
30°
B
A
D
C
S
H
H
D
A
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 37
Vậy
3
.
1 1 8 6
. . . 3 .4 .2 2
3 3 3
S ABCD
a
V SH AD DC a a a
Câu 35. Chọn D
Gọi
M
là trung điểm của
CD
thì ta có
ABMD
là hình vuông cạnh
a
do đó
2
BC BD a
2 2 2 2
4
CD a BC BD
do đó tam giác
BCD
vuông cân tại
B
.
Gọi
H
là trung điểm của
BD
thì
SH ABCD
.
Khi đó
.
1 1
. .
3 2
S BCD
V SH BD BC
3
2
6.
6
6
2 2
a
a
SH
a
.
Hạ
HI SB
.
Vì
ABMD
là hình vuông nên
H
là trung điểm của
AM
và ta có
AMCB
là hình bình hành do đó
//AH BC
; ;
d A SBC d H SBC HI
.
Khi đó
2 2 2
1 1 1
HI SH HB
2 2 2
4 2 8
6 3a a a
6
4
a
HI
hay
6
;
4
a
d A SBC
.
Câu 36. Chọn D
Ta có
2
D
1 1
.
2 2
ABM ABC
S S a
Gọi
I
là hình chiếu vuông góc của
S
trên mặt phẳng
ABCD
2
2 2 2
5
2 2
a a
IB IA AB a
M
H
D
C
A
B
S
I
M
I
A
B
D
C
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 38
Ta có
IB
là hình chiếu vuông góc của
SB
lên
, D , 60
mp ABCD SB ABC SB IB
Ta có
15
.tan 60
2
a
SI IB
2 3
.
1 1 15 15
. . . .
3 3 2 2 12
S ABM ABM
a a a
V SI S
.
Câu 37.
Gọi
M
là trung điểm của
BC
.
1
:
3
CN CH
N CM
CM CA
//HN AM
. Mà
ABC
đều nên
AM BC HN BC BC SHN
.
Nên
; ; 60
o
SBC ABC SN HN SNH
.
Do
ABC
đều nên
3 1 3
2 3 6
a a
AM HN AM
.
SHN
vuông tại
H
có
3
.sin .sin 60
6 4
o
a a
SH HN SNH
.
2 3
.
1 1 3 3
. . .
3 3 4 4 48
S ABC ABC
a a a
V SH S
.
Dạng 1.5 Thể tích khối chóp đều
Câu 38.
Giả sử khối chóp tứ giác đều đã cho là
.S ABCD
. Khi đó
ABCD
là hình vuông cạnh
a
và
SA SB SC SD a
.
Gọi
H
là tâm của hình vuông
ABCD
thì
SH ABCD
nên
SH
là chiều cao của khối chóp
.S ABCD
.
Tính
SH
:
Xét tam giác
ABC
vuông tại
B
ta có:
2 2
AC AB BC
2 2
a a
2a
.
H
C
A
B
D
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 39
Nhận thấy
2 2 2
AC SA SC
nên tam giác
SAC
vuông tại
S
. Suy ra
2
AC
SH
2
a
.
Diện tích đáy của khối chóp
.
S ABCD
là
2
ABCD
S a
.
Vậy thể tích khối chóp
.
S ABCD
là:
1
. .
3
ABCD
V S SH
2
1
. .
3
2
a
a
3
2
6
a
.
Câu 39. Chọn D
Gọi hình chóp tứ giác đều có tất cả các cạnh bằng
2a
là
.
S ABCD
và
I
tâm của đáy ta có:
SA SC BA BC DA DC
SAC BAC DBC
; ;
SAC BAC DAC
lần lượt vuông tại
, ,S B D
.
I
là trung điểm của
AC
suy ra
1 1
2a. 2 2
2 2
SI AC a
3
2
.
1 1 4 2
. 2 . 2
3 3 3
S ABCD ABCD
a
V S SI a a
Câu 40.
Lơi giai
Chọn D
Chiều cao của khối chóp:
2
2 2 2
2 14
4
2 2
a a
SI SA AI a
Thể tích khối chóp:
3
2
1 1 14 14
. .
3 3 2 6
ABCD
a a
V SI S a
I
A
B
C
D
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 40
Câu 41.
Ta có
2
4
ABCD
S a
;
2 2 2 2
5 2 3SO SB OB a a a
Vậy
2 3
.
1 3.4 4 3
.
3 3 3
S ABCD ABCD
a a a
V SO S
Câu 42. Chọn D
Do đáy là tam giác đều nên gọi
I
là trung điểm cạnh
BC
, khi đó
AI
là đường cao của tam giác đáy. Theo
định lý Pitago ta có
2
2
3
4 2
a a
AI a
, và
2 2 3 3
3 3.2 3
a a
AO AI
.
Trong tam giác
SOA
vuông tại
O
ta có
2
2
11
4
3
3
a a
SO a
.
Vậy thể tích khối chóp
.
S ABC
là
3
1 1 3 11 11
. .
3 2 2 12
3
a a a
V a
.
Câu 43. Chọn B
O
I
A
C
B
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 41
+
; 45SA ABC SAO
+
3
.tan 45
3
a
SO AO
+
2 3
1 1 3 3
. . . .
3 3 3 4 12
ABC
a a a
V SO S
Câu 44. Chọn D
Diện tích đáy là:
2
2 2
6 6 .
ABCD
S AB a a
Góc giữa cạnh bên
SB
và mặt đáy
ABCD
là
0
, 60SD ABCD SDO SDO
ABCD
là hình vuông suy ra
1 1 1
2 6. 2 3.
2 2 2
DO BD AB a a
Xét tam giác vuông
0
: .tan 3.tan60 3 .SOD SO DO SDO a a
Vậy
2 3
.
1 1
. . .3 .6 6 .
3 3
S ABCD ABCD
V SO S a a a
Câu 45.
Gọi
H
là tâm của tam giác đều
ABC
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 42
Khi đó
SH ABC
,
3
3
a
BH
.
Theo đề bài ta có:
, 60
SB ABC SBH
.
Xét
SBH
vuông tại
H
.
Có
3
.tan 60 . 3
3
a
SH BH a
.
Thể tích
2 3
.
1 1 3 3
. .
3 3 4 12
S ABC ABC
a a
V SH S a
.
Câu 46.
Gọi
O
là tâm của đáy, gọi
M
là trung điểm của
BC
.
Ta có
SO BC
OM BC
nên
SOM BC
, suy ra
0
, , 60
SCD ABCD SM OM SMO
.
Có
1
2 2
a
OM BC
,
0
3
tan 60
2
a
SO OM
.
Thể tích khối chóp
.
S ABCD
là
3
2
.
1 1 3 3
. . .
3 3 2 6
S ABCD ABCD
a a
V SO S a
.
Câu 47.
Gọi
H
là trung điểm
AO
. Khi đó góc giữa
MN
và
ABCD
là
MNH
.
Ta có
2 2 0
2 . .cos 45
HN CN CH CN CH
10
4
a
.
Suy ra
0
10 30
.tan 60 . 3
4 4
a a
MH HN
.
Do đó
30
2
2
a
SO MH
.
H
N
M
O
C
A
B
D
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 43
3
2
.
1 30 30
.
3 2 6
S ABCD
a
V a a
.
Dạng 1.6 Thể tích khối chóp khác
Câu 48. Chọn A
Ta co
3
1 1 1
. . 6 .7 .4 28
3 2 6
ABCD
V AB AD AC a a a a
Ta nhân thây
3
1 1 1
7
2 4 4
MNP MNPD BCD AMNP ABCD
S S S V V a
.
Câu 49.
Do
N
,
P
lần lượt là trung điểm của
SD
,
AD
nên
1
4
ANP
SAD
S
S
.
Lại có,
M
là trung điểm của
SC
nên
,
1
2
,
d M SAD
MS
CS
d C SAD
.
.
.
1
. , .
1 1 1
3
.
1
2 4 8
. , .
3
A
M ANP
C SAD
NP
SAD
d M SAD S
V
V
d C SAD S
.
Mặt khác,
. . .
1 1
2 2
C SAD S ACD S ABCD
V V V V
.
1
16
M ANP
V V
.
Câu 50. Chọn A
P
N
M
D
C
B
A
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 44
AB AC
AB ACD
AB AD
3
1 1 7 .4 .6
. . . 28
3 2 6
ABCD
a a a
V AC AD AB a
Gọi H là hình chiếu của A lên
BCD
h AH
là 1 đường cao của hình chóp
ABCD
.
, ,M N P
tương ứng là trung điểm các cạnh
, ,BC CD DB
, ,MN NP PM
tương ứng là đường trung bình của
BCD
MNP
đồng dạng với
BCD
với tỉ số
1
2
k
2
1
4
MNP
BCD
S
k
S
3
1
. .
1 1
3
. 7 .
1
4 4
. .
3
MNP
AMNP MNP
AMNP ABCD
ABCD BCD
BCD
S h
V S
V V a
V S
S h
Câu 51. Chọn D
Gọi
H
là hình chiếu của
S
trên mặt phẳng
( )ABC
.
Do
SA SB SC
nên
SHA SHB SHC
(cạnh huyền-cạnh góc vuông)
HA HB HC
H
là tâm đường tròn ngoại tiếp tam giác
ABC
.
Tam giác
ABC
vuông cân tại
B
nên
H
là trung điểm
AC
.
Suy ra
1
2
2
HA HC AC
2 2
4 2SH SA HA
Ta có:
2
2 2
2
AC
BA BC
Vậy
.
1 1 1 16 2
. . . 2 2 2 2 .4 2 .
3 3 2 3
S ABC ABC
V S SH
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 45
Câu 52.
1 2 3
GG G
đồng dạng với
ACD
theo tỉ số
1
3
và nằm trong hai mặt phẳng song song.
1 2 3
2
1
6 .
9
G G G ABD
S S a
và .
1 2 3 4 1 2 3
3
3 4
1
. 4 .
3
G G G G G G G
V G G S a
Câu 53.
Gọi
I
là trung điểm của
.SB
Do
90
SAB SCB
nên
I
là tâm mặt cầu ngoại tiếp hình chóp
. .S ABC
Gọi
O
là tâm của đáy
ABC
( )OI ABC
.
Gọi
H
là hình chiếu của
S
lên mặt phẳng
.ABC
Ta có
( ) .AB SAH AB AH
Tương tự,
.BC CH
Suy ra
H
thuộc đường tròn ngoại tiếp tam giác
,ABC
có tâm là
O
nên
O
là trung điểm của
.BH
Do đó,
2 .SH OI
Gọi
N
là trung điểm của
//BC IN SC
nên
(*)
BC IN BC AIN
Gọi
G
là trọng tâm của tam giác
SAB
và
K
là hình chiếu của
G
lên mặt phẳng
ABC
K AO
và
2 4 5
// .
3 9 9
GK OI AK AO AN KN AN
5 10
, , .
9 21
a
d K MBC d A MBC
Kẻ
(*)
10
, .
21
a
KE GN KE BC KE MBC d K MBC KE
Tam giác
GKN
vuông tại
K
có
2 2 2
1 1 1 10
2 3 10 .
3
a
GK SH OI GK a
KE GK KN
Vậy thể tích khối chóp
.
S ABC
là
2 3
1 3 5 3
. .10 .
3 4 6
a a
V a
G2
A
D
C
B
E
G4
G3
F
G1
3 4
/ /G G AB
3 4
1
2
3
G G AB a
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 46
Câu 54.
Ta có
SB SC a
,
60BSC suy ra tam giác
BSC
đều
BC a
.
Lại có
SA SC a
,
90ASC suy ra tam giác
ASC
vuông cân tại
S
2AC a
.
Mặt khác,
SA SB a
,
120ASB , áp dụng định lí cosin cho tam giác
ASB
, ta được:
2 2 2 2
2 . . 3 3AB SA SB SA SB cos ASB a AB a
.
Xét tam giác
ABC
có
2 2 2 2 2 2
2 3BC AC a a a AB
suy ra tam giác
ABC
vuông tại
C
.
Vậy diện tích tam giác
ABC
là:
2
1 2
.
2 2
ABC
a
S AC BC
.
Gọi
O
là trung điểm của cạnh
AB
suy ra
O
là tâm đường tròn ngoại tiếp tam giác
ABC
.
Mà
SA SB SC
SO ABC
.
Xét tam giác vuông
ASO
vuông tại
O
có
2
2 2 2
3
2 2
a a
SO SA AO a
.
Vậy thể tích khối chóp
.S ABC
là:
2 3
.
1 1 2 2
. . . .
3 3 2 2 12
S ABC ABC
a a a
V S SO
.
Câu 55. Chọn B
Gọi
, ,M N P
lần lượt là hình chiếu của
H
lên các cạnh
, ,AC BC AB
.
Đặt
.
1 3 3
. .
3 4 12
S ABC
h
SH h V h
.
Ta có
.
2 6
3 30
2 : 10
2 20
;
SAB S ABC
SAB
S V
h
AP S h
AB
d C SAB
Tương tự, tính được
2 ,HM h HN h
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 47
2 2
3PH SP SH h
Ta có
1
2
ABC HAB HAC HBC
S S S S HP HM HN
3 3
3
4 12
h h
Vậy
.
3 3 1
.
12 12 48
S ABC
V
.
Câu 56. Chọn B
Vì
0
90SAB SCB
, , ,S A B C
cùng thuộc mặt cầu đường kính
SB
.
Gọi
D
là trung điểm
BC
,
I
là trung điểm
SB
và
O
là tâm đường tròn ngoại tiếp
ABC
, ta có
OI ABC
.
Gọi
H
là điểm đối xứng với
B
qua
O
SH ABC
(vì
OI
là đường trung bình
SHB
).
Gọi
BM AI J
, ta có
J
trọng tâm
SAB
.
Trong
AID
, kẻ
/ /JN IO
. Khi đó, vì
BC JND
nên
JND MBC
.
Kẻ
NE JD
, ta có
NE MBC
. Do đó
;d N MBC NE
.
Ta có
,
,
d A MBC
AD AD
ND AD AN
d N MBC
9
2 4
5
3 9
AD AD
AD AO AD AD
.
Suy ra,
5 10
, ,
9 21
a
d N MBC d A MBC
.
Xét
JND
có
2 2 2
1 1 1
NE ND NJ
nên
10
3
a
NJ
3
5
2
OI NJ a
10SH a
.
Vậy
2 3
1 1 3 5 3
. .10 .
3 3 4 6
SABC ABC
a a
V SH S a
.
Câu 57.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 48
+ Dựng hình chóp
. ' ' 'S A B C
sao cho A là trung điểm
' 'B C
,
B
là trung điểm
' 'A C
,
C
là trung điểm
' 'A B
.
+ Khi đó
' ' 4
SB AC BA BC
nên
' 'SA C
vuông tại
S
và
2
2 2
' ' 2. 64 (1)
SA SC SB
.
+ Tương tự
' 'SB C
,
' 'SA B
vuông tại
S
và
2 2
2 2
' ' 80 (2)
' ' 36 (3)
SA SB
SB SC
.
+ Từ
1 ; 2 ; 3
ta suy ra
' 10
SC ;
' 26
SB ;
' 54
SA .
+ Ta tính được
. ' ' '
1 1
'. . '. ' 390
3 2
S A B C
V SC SA SB
và
. . ' ' '
1 390
4 4
S ABC S A B C
V V
(đvtt).
Dạng 2. THỂ TÍCH KHỐI LĂNG TRỤ
Dạng 2.1 Biết chiều cao và diện tích đáy
Câu 58. Chọn A
Thể tích khối lăng trụ có diện tích đáy
B
và có chiều cao
h
là:
.V B h
.
Câu 59. Chọn B
2 3
. .4 4
day
V S h a a a
.
Câu 60. Chọn B
Theo công thức tính thể tích lăng trụ.
Câu 61. Chọn C
Ta có:
.
langtru day
V S h
2
.2a a
3
2a
.
Câu 62. Chọn A
Thể tích khối lăng trụ là
2 3
. 3. 6 3 2
V B h a a a
Dạng 2.2 Thể tích khối lăng trụ đứng
Câu 63. Chọn A
Thể tích của khối lập phương cạnh
2a
bằng:
3
3
2 8V a a
Câu 64. Chọn B
Ta có:
2
3
4
ABC
a
S
.
Vậy thể tích của khối lăng trụ đã cho là
2 3
.
3 6
. . 2
4 4
ABC A B C ABC
a a
V S AA a
.
Câu 65.
Lơi giai
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 49
Chọn C
3
2
3
.
3
4
4
h a
a
V h S
a
S
.
Câu 66. Chọn A
Tam giác
ABC
đều cạnh
a
nên
2
3
4
ABC
a
S
Do khối lăng trụ .
ABC A B C
là lăng trụ đứng nên đường cao của lăng trụ là
2AA a
Thể tích khối lăng trụ là
2 3
3 3
. 2 . .
4 2
ABC
a a
V AA S a
Câu 67. Chọn B
Tam giác
ABC
vuông cân tại
B
2
AC
AB BC a
. Suy ra:
2
1
2
ABC
S a
.
Khi đó:
3
2
.
1
. .
2 2
ABC A B C ABC
a
V S BB a a
Câu 68. Chọn B
Khối lăng trụ đã cho có đáy là tam giác đều có diện tích là
2
(2 ) 3
4
a
và chiều cao là
' 3AA a
(do là lăng
trụ đứng) nên có thể tích là
2
3
(2 ) 3
.3 3 3
4
a
a a
Câu 69. Chọn A
a
a 2
C'
B'
A
B
C
A'
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 50
Gia sư khôi lâp phương co canh băng
; 0
x x
Xet tam giac
' ' 'A B C
vuông cân tai
'B
ta có:
2 2 2
' ' ' ' ' 'A C A B B C
2 2 2
2x x x
' ' 2A C x
Xet tam giac
' 'A AC
vuông tai
'A
ta co
2 2 2
' ' ' 'AC A A A C
2 2 2
3 2a x x
x a
Thê tich cua khôi lâp phương
.
ABCD A B C D
la
3
V a
.
Câu 70.
Xét hình lập phương
.
ABCD A B C D
ta có:
2 2 2 2 2 2
AC AA A C AA A B A D
2 2
3
AA a
3
a
AA
3
3
.
3
9
3
ABCD A B C D
a
V a
.
Câu 71. Chọn C
Ta có
2
3
4
ABC
a
S
;
' 3AA a
.
Từ đó suy ra
3
2
3 3
3.
4 4
a
V a a
.
Câu 72. Chọn A
120°
60°
H
C
B
A'
B'
C'
A
C
B
A
D
D
A
C
B
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 51
Gọi
H
là trung điểm của
B C
, khi đó góc giữa mp
AB C
và đáy là góc
60
AHA
.
Ta có
2
1 3
. .sin120
2 4
ABC
a
S AC AB
.
2 2 2 2
1
2 . .cos120 2. . . 3
2
B C BC AB AC AB AC a a a a a
2
2
ABC
S
a
A H
B C
.tan 6
3
2
0AA
a
A H
.
Vậy
3
3
.
8
ACB
a
V S AA
.
Câu 73. Chọn D
Ta có
2 2
2AA A B AB a
,
2
2
1
2 2
ABC
a
S AB .
Thể tích khối lăng trụ là
3
2
.
2
ABC
a
V AA S
.
Câu 74. Chọn A
Đặt
, 0
AB x x
, gọi
M
là trung điểm
BC
.
Ta có
, 30
A BC ABC BC
AM BC A BC ABC A MA
A M BC
.
Xét
A AM
, có
3 2
.
cos30 2
3
AM x
A M x
.
a 3
a
C'
B'
A
B
C
A'
x
30°
M
C
B
A'
B'
C'
A
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 52
2
1
8 . 8 16 4
2
A BC
S A M BC x x
Suy ra
4. 3 1
.tan30 . 2
2
3
A A AM
;
16. 3
4 3
4
ABC
S
.
Vậy
.
. 2.4 3 8 3
ABC A B C ABC
V A A S
.
Câu 75. Chọn A
Vì đáy
ABC
là tam giác đều có diện tích bằng
2
3
4
a
cạnh đáy bằng
a
.
Gọi
M
trung điểm
BC
, ta có '
'
BC AM
BC A M
BC AA
Từ đó ta có
0
' , ' , ' 60A BC ABC A M AM A MA
.
Xét
'A AM
ta có
0
3
' .tan60
2
a
AA AM
Thể tích lăng trụ
. ' ' 'ABC A B C
là
3
. ' ' '
3 3
'.
8
ABC A B C ABC
a
V AA S
Câu 76. Chọn C
Gọi
M
là trung điểm của
' 'B C
.
Ta có
' ' '
' ' '
AA B C
A M B C
' ' 'B C AA M
' ' 'AB C AA M
theo giao tuyến
AM
.
Kẻ
'A H AM
trong mặt phẳng
'AA M
, suy ra
' ' 'A H AB C
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 53
Vậy khoảng cách từ
'A
đến mặt phẳng
' 'AB C
là
2 3
'
19
a
A H .
Ta có
2 2 2 2 2 2 2
1 1 1 1 1 1 1
' ' ' ' ' ' 4A H A A A M A A A H A M a
' 2A A a
.
Vậy thể tích khối lăng trụ là
2 3
' ' '
3 3
'. 2 .
4 2
A B C
a a
V AA S a
.
Dạng 2.3 Thể tích khối lăng trụ xiên
Câu 77.
Tam giác
ABC
vuông tại
B
có
1; 2AB AC
nên
2
2 1 3BC
.
Độ dài của đường cao
BH
:
. 3
2
AB BC
BH
AC
. Suy ra
3 1
: 3
2 2
AH
.
Khi đó độ dài đường cao
'A H
của hình lăng trụ bằng :
2 2
1 7
' ' 2
4 2
A H AA AH
.
Thể tích khối lăng trụ đã cho bằng :
1 1 7 21
. . ' .1. 3
2 2 2 4
V AB BC A H
.
Câu 78. Chọn B
Kẻ
, 60 .AH ABC A A ABC A AH
Xét
3
:sin 60 .sin 60 .
2
A H a
AHA A H AA
AA
Thể tích khối lăng trụ
2 3
3 3 3
. : . . .
4 2 8
ABC
a a a
ABC A B C V S A H
60
o
H
C'
B'
A'
C
B
A
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 54
Câu 79.
Gọi
H
là hình chiếu của
C
lên mặt phẳng
ABC
, khi đó
C H
là đường cao
0
, 60
AC ABC C AH
Xét tam giác vuông
AC H
ta có
0
.sin 60 2 3
C H C A
Khi đó
2
.
1
. 2 2 .2 3 8 3
2
ABC A B C d
V S C H
Câu 80. Chọn C
Ta có
'
A I ABC AI
là hình chiếu vuông góc của
'AA
lên
ABC
Nên
0
', ',
' 30
ABC AIA A AA AIA
Ta có
2
0
3 3
' tan 30 ,
2 2 4
ABC
a a a
AI A I AI S
Vậy
2 3
. ' ' '
3 3
.
4 2 8
ABC A B C
a a a
V
Câu 81. Chọn B
A'
C'
B'
C
B
A
H
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 55
Gọi
H
là hình chiếu của
A
lên mặt đáy. Suy ra góc
30
A AH
1
sin 30 .sin 30 2 3. 3
2
A H
A H A A
A A
Khi đó:
2
.
3 27
3 . . 3
4 4
ABC A B C
V
.
Câu 82. Chọn A
Gọi
H
là trung điểm
BC
suy ra
'
A H ABC
Ta có
0
' , ' , ' 30
A A ABC A A AH A AH
Ta có
3
2
a
AH
Ta có
0
' .tan 30
2
a
A H AH
và
2
3
4
ABC
a
S
Vậy
3
3
' .
8
ABC
a
V A H S
Câu 83. Chọn C
Gọi
H
là trung điểm
BC
.
Theo giả thiết,
A H
là đường cao hình lăng trụ và
2 2
6
.
2
a
A H AA AH
Vậy thể tích khối lăng trụ là
2 3
Δ
3 6 3 2
. .
4 2 8
ABC
a a a
V S A H
.
Câu 84. Chọn D
A
B
C
A
B
C
H
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 56
Gọi
1 2
,A A
lần lượt là hình chiếu của
A
trên
'BB
,
'CC
. Theo đề ra
1 2 1 2
1; 3; 2.
AA AA A A
Do
2 2 2
1 2 1 2
AA AA A A
nên tam giác
1 2
AA A
vuông tại
A
.
Gọi
H
là trung điểm
1 2
A A
thì
1 2
1
2
A A
AH
.
Lại có
1 2
' ( )
MH BB MH AA A MH AH
suy ra
2 2
3
MH AM AH
.
nên
1 2
3
cos(( ),( )) cos( , ) cos .
2
MH
ABC AA A MH AM HMA
AM
Suy ra
1 2
1 2
1.
cos(( ),( ))
AA A
ABC
S
S
ABC AA A
Thể tích lăng trụ là
2
ABC
V AM S
.
Nhận xét. Ý tưởng câu này là dùng diện tích hình chiếu
' cos
S S
.
Câu 85. Chọn C
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 57
Kẻ
'AI BB
,
'AK CC
( hình vẽ ).
Khoảng cách từ
A
đến
'BB
và
'CC
lần lượt là
1; 2
1 AI
,
2AK
.
Gọi
F
là trung điểm của
BC
.
15
'
3
A M
15
3
AF
Ta có
'
'
'
AI BB
BB AIK
BB AK
'
BB IK
.
Vì
' 'CC BB
( , ') d C BB
( , ') d K BB
IK
5
AIK
vuông tại
A
.
Gọi
E
là trung điểm của
IK
' EF BB
EF AIK
EF AE
.
Lại có
AM ABC
. Do đó góc giữa hai mặt phẳng
ABC
và
AIK
là góc giữa
EF
và
AM
bằng góc
AME FAE
. Ta có
cos
AE
FAE
AF
5
2
15
3
3
2
30
FAE
.
Hình chiếu vuông góc của tam giác
ABC
lên mặt phẳng
AIK
là
AIK
nên ta có:
cos
AIK ABC
S S EAF
3
1
2
ABC
S
2
3
ABC
S
.
Xét
AMF
vuông tại
A
:
tan
AF
AMF
AM
15
3
3
3
AM
5
AM
.
Vậy
. ' ' '
2
5.
3
ABC A B C
V
2 15
3
.
F
E
K
I
A'
B'
M
C
B
A
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 58
Câu 86. Chọn A
Cắt lăng trụ bởi một mặt phẳng qua
A
và vuông góc với
AA
ta được thiết diện là tam giác
1 1
A B C
có các
cạnh
1
1
A B
;
1
3
A C
;
1 1
2
B C
.
Suy ra tam giác
1 1
A B C
vuông tại
A
và trung tuyến
A H
của tam giác đó bằng
1
.
Gọi giao điểm của
AM
và
A H
là
T
.
Ta có:
2 3
3
A M
;
1A H
1
3
MH . Suy ra
30
MA H
.
Do đó
60
MA A
4
3
cos
A M
AA
MA A
.
Thể tích khối lăng trụ
.
ABC A B C
bằng thể tích khối lăng trụ
1 1 2 2
.
A B C AB C
và bằng
1 1
4 3
. 2
2
3
A B C
V AA S
.
Câu 87. Chọn D
Gọi
J
,
K
lần lượt là hình chiếu vuông góc của
A
lên
BB
và
CC
,
H
là hình chiếu vuông góc của
C
lên
BB
Ta có
1
AJ BB
.
2
AK CC AK BB
.
T
M
B
2
H
C
2
A'
C
1
A
B
1
A
A'
T
B'
C'
M
H
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 59
Từ
1
và
2
suy ra
BB AJK
BB JK
//JK CH
5
JK CH .
Xét
AJK
có
2 2 2
5
JK AJ AK
suy ra
AJK
vuông tại
A
.
Gọi
F
là trung điểm
JK
khi đó ta có
5
2
AF JF FK
.
Gọi
N
là trung điểm
BC
, xét tam giác vuông
ANF
ta có:
cos
AF
NAF
AN
5
2
5
1
2
60
NAF
. (
5
AN AM vì
//
AN AM
và
AN AM
).
Vậy ta có
1
.
2
AJK
S AJ AK
1
.1.2 1
2
.cos60
AJK ABC
S S
1
2
1
cos60
2
AJK
ABC
S
S
.
Xét tam giác
AMA
vuông tại
M
ta có
30
MAA AMF
hay
.tan30
AM A M
15
3
.
Vậy thể tích khối lăng trụ là .
ABC
V AM S
15 2 15
.2
3 3
.
Câu 88. Chọn D
ABCD
là hình thoi nên
AB BC
. Lại có
60
ABC
nên
ABC
là tam giác đều.
OH BC
. Góc giữa
mặt phẳng
BB C C
với đáy khi đó là
60
B HO
.
Ta có
2 2
2 2 2 2 2 2
1 1 1 1 1 4 4 16
3
3 3
4 4
a a
OH OB OC a a a
.
3
4
a
OH
Theo giả thiết,
B O
là đường cao lăng trụ
.
ABCD A B C D
.
3 3
.tan tan60
4 4
a a
B O OH B HO
.
2 3
.
3 3 3 3
. .
2 4 8
ABCD A B C D day
a a a
V S h
Câu 89. Chọn D
H
O
D'
D
C'
A'
B'
B
A
C
H
O
B
A
C
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 60
Ta có
'
'G
BC AM
BC AA
BC A
Kẻ
'MH AA
tại
H
, suy ra
MH
là đoạn vuông góc chung của giữa hai đường thẳng
’AA
và
BC
Tam giác
MHA
vuông tại
H
có
2 2
3
4
AH AM AH a
Tam giác
'A GA
đồng dạng tam giác
MHA
nên
' .
'
3
A G GA MH GA a
A G
MH HA HA
Thể tích khối lăng trụ là
3
3
. '
12
ABC
a
V S A G
Câu 90.
Ta có
3
sin 60 2 . 3
2
1 3 3
cos60 2 .
2 2 2
B G BB a a
a
BG BB a a BI BG
.
Đặt
2 0 ; .tan 60 2 3AC x x CI x BC AC x
.
Khi đó
2
2
2
2
3 3 13 1 1 3 13 3 13 9 3
2 3 . .2. .2. . 3 .
2 26 2 2 26 26 26
ABC
a a a a a
x x x S AC BC
Vậy
2 3
.
1 9 3 9
. . 3
3 26 26
A ABC
a a
V a
60
o
60
o
2a
I
A'
C'
G
A
C
B
B'
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 61
Câu 91.
Gọi
H
là hình chiếu vuông góc của
trên mp
ABC
suy ra
A'H
là chiều cao của lăng trụ.
Xét khối chóp
A.A' BC
có diện tích đáy
1
A' BC
B S
, chiều cao
2
h d A, A' BC
suy ra thể
tích của khối chóp
A.A' BC
là
1 1 2
1 2
3 3 3
A.A' BC
V Bh . .
.
Mặt khác
1 2
2
3 3 2
3 3
3
A.A' BC A' .ABC ABC
ABC.A' B' C' A.A' BC
ABC.A' B' C' ABC
V V S . A'H
V V .
V S . A'H
.
* Cách khác.
Ta thấy lăng trụ
ABC.A' B' C'
được chia thành ba khối chóp có thể thích bằng nhau là
A' .ABC, A' .BCB', A' .B' C' C
.
Mà
1 1 2
1 2
3 3 3
A' .ABC A.A' BC
V V Bh . .
suy ra
2
3 3 2
3
ABC .A' B' C' A.A' BC
V V .
.
Câu 92.
Chọn B
+ Ta có
AB CM
AB A CM AB A M
AB A M
Nên
2
1 2 3 4 3
.
2 3 3
A AB
a a
S A M AB A M
Do
ABC
đều cạnh bằng
a
nên
1 3
3 6
a
GM CM
H
C'
B'
A'
C
B
A
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 62
+ Trong
A GM
vuông tại
G
ta có
2 2
21
2
a
A G A M GM
Vậy
2 3
.
21 3 3 7
.dt .
2 4 8
ABC A B C
a a a
V A G ABC
Dạng 3. THỂ TÍCH KHỐI ĐA DIỆN KHÁC
Câu 93. Chọn D
Ta có:ADF.BCE là hình lăng trụ đứng có đáy là tam giác vuông cân
Dựa vào hình vẽ ta có:
. . .. .
2
ABCDSEF ADF BCE ADFS CDFE B CDFEBCE AD E
B DE
F ABC
V V V V V V V
.
1 1 1 1 1 5
. ; . 2.
2 3 6 2 6 6
ADF BCE BCE BADE ABE ABCDSEF
V AB S V AD S V
Câu 94. Chọn B
Thể tích khối lăng trụ
.
ABC A B C
là
2
4 . 3
4. 16 3
4
V
.
Gọi thể tích của khối đa diện lồi có các đỉnh là các điểm
, , , , ,A B C M N P
là
1
V
.
Ta có:
1
AMNCB BMNP BNPC
V V V V
.
Dễ thấy
1
3
A ABC
V V
và
3
4
AMNCB A ABC
V V
nên
1
4
AMNCB
V V
.
S
F
E
D
C
B
A
N
P
M
A'
C'
B'
B
C
A
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 63
1
3
BA B C
V V
và
1
8
BMNP BA B C
V V
nên
1
24
BMNP
V V
.
1
3
A BCB A B CC
V V V
và
1
4
BNPC BA B C
V V
nên
1
12
BNPC
V V
.
Vậy
1
3
6 3
8
AMNCB BMNP BNPC
V V V V V
.
Câu 95. Chọn A
Gọi
DEF
là thiết diện của lăng trụ cắt bởi mặt phẳng
MNP
.
Dễ chứng minh được
/ /
DEF ABC
và
, ,D E F
lần lượt là trung điểm của các đoạn
thẳng
, ,
AA BB CC
suy ra
. .
1
12 3
2
ABC DEF ABC A B C
V V
.
Ta có
.
ABCPNM ABC DEF ADMN BMPE CPMF
V V V V V .
Mặt khác
. .
1 3
9 3
12 4
ADMN BMPE CPMF ABC DEF ABCPNM ABC DEF
V V V V V V
.
Câu 96.
Lơi giải
Chọn D
Ta có:
2
. ' ' '
3
8. .4 32 3;
4
ABC A B C
V
'. . ' ' '
1
;
3
C ABC ABC A B C
V V
. ' ' . ' ' '
1
3
A BC B ABC A B C
V V
P
N
M
C
B
A'
C'
B'
F
E
D
P
N
M
C'
B'
A'
C
B
A
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 64
Khối đa diện cần tìm
. . .C ABPN P AMN P ABM
V V V V
Ta có
. '. . ' ' '
3 1
4 4
C ABPN C ABC ABC A B C
V V V
Ta có
' ' . ' ' '
1 1
8 24
PAMN ABC B ABC A B C
V V V
Ta có
' ' . ' ' '
1 1
4 12
PABM ABC B ABC A B C
V V V
Vậy thể tích khối cần tìm
. ' ' ' . ' ' ' . ' ' '
1 1 1
4 24 12
ABC A B C ABC A B C ABC A B C
V V V V
. ' ' '
3
12 3
8
ABC A B C
V
.
Câu 97. Chọn C
Gọi
h
là chiều cao của hình lăng trụ
. ' ' 'ABC A B C
.
Vì
ABC
đều có độ dài cạnh bằng
6
nên
2
3
6 . 9 3
4
ABC
S
.
Thể tích lặng trụ
. ' ' 'ABC A B C
là
. 8.9 3 72 3
ABC
V h S
.
Gọi
E
là trung điểm của cạnh
'AA
.
Thể tích khối chóp
.A EMN
là
.
1 1 1 1 1
, . . .
3 3 2 4 24
A EMN EMN ABC
V d A EMN S h S V
.
Thể tích khổi đa diện
ABCMNP
là:
.
1 1 1 3
3 3. 27 3
2 2 24 8
ABCMNP A EMN
V V V V V V
.
Câu 98.
Ta có khối bát diện đều cạnh 3a được tạo từ 2 khối chóp tứ giác đều có cạnh đáy và cạnh bên bằng 3a .
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 65
Chiều cao của khối chóp là:
2
2
6 6
3
2 2
a a
h a
.
Thể tích của khối chóp:
3
2
1 6 6
3 .
3 2 2
chop
a a
V a
(đvtt).
Vậy thể tích khối bát diện là:
3
2 6
chop
V V a (đvtt).
Câu 99. Chọn B
Ta có:
MN
cắt
AB
và
AD
lần lượt tại
I
và
J
.
'A I
cắt
'BB
tại
.P
'A J
cắt
'DD
tại
.Q
Do
//MC JD
nên
1
2
MC NC
JD ND
2 .JD MC a
Do
// 'DQ AA
nên
1
' 2
DQ JD
AA JA
'
.
2 2
AA a
DQ
Do
//BI NC
nên
1
BI BM
NC CM
.
3
a
BI NC
Do
// 'PB AA
nên
1
' 4
PB IB
AA IA
'
.
4 4
AA a
PB
Ta có:
'
A AIJ JDNQ IBMP
H
V V V V
1 1 1
'. . . . . .
6 6 6
AA AI AJ DN DQ DJ BM BP BI
3
1 4 1 2 1 55
. .2 . . . . . . .
6 3 6 3 2 6 2 4 3 144
a a a a a a
a a a a
Câu 100. Chọn B
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 66
Giả sử hình lập phương
.
ABCD A B C D
có cạnh bằng
a
và tâm các mặt là
, , , , ,P Q R S O O
như hình vẽ.
Ta có
PQ
là đường trung bình của tam giác đều
B CD
cạnh
2a
nên
2
2
a
PQ
.
Do đó
2 2
1
2
PQRS
S PQ a
và
OO a
.
Vậy thể tích bát diện cần tìm là
3
1 1
.
3 6
PQRS
V S OO a
(đvtt).
Câu 101.
Đặt
AB x
,
AD y
,
AA z
.
Gọi
H
là hình chiếu vuông góc của
B
trên
B C
, ta có
BH
là đoạn vuông góc chung của
AB
và
B C
nên
2 2 2 2
2 5 1 1 1 5
,
5 4
a
d AB B C BH
BH z y a
. (1)
Gọi
I
là hình chiếu vuông góc của
B
trên
AB
, ta có
BI
là đoạn vuông góc chung của
BC
và
AB
nên
2 2 2 2
1 1 1 5
,
4
d BC AB BI
BI x z a
. (2)
Gọi
là trung điểm của
DD
,
O
là giao điểm của
AC
và
BD
, ta có mặt phẳng
ACM
chứa
AC
và song
song với
BD
nên
, , ,
d AC BD d BD ACM d D ACM
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 67
Gọi
J
là hình chiếu vuông góc của
D
trên
AC
,
K
là hình chiếu vuông góc của
D
trên
MJ
, ta có
2 2 2 2 2
1 1 1 4 3
, ,d D ACM d D ACM DK
DK x y z a
. (3)
Từ (1), (2) và (3) ta có
2 2
2 1
2
2
z a x y a
z a
.
Thể tích khối hộp là
3
2V xyz a
.
Câu 102. Chọn C
Nhận xét:
'B NDM
là hình bình hành
' , ' //B N DM B N DM
'MN B D O là trung điểm của mỗi đoạn nên
O
cũng là trung điểm của đường chéo
'A C
.
Vậy thiết diện tạo bởi mặt
'A MN
và hình chóp là hình bình hành
'A NCM
.
Ta có:
2 2 2 2
' ' 'C A B B BA BC B B
2a
.
Cách 1:
Thể tích phần chứa
'C
là
'. ' ' '. ' ' ' ' '
1 1
. ' '. . ' '.
3 3
A B C CN A C CMD B C CN C D MC
V V V A B S A D S
3
2 4
2 2
1 1
3 3
. .2 .2 . 2
3 2 3 2
a a
a a
a a a a a
.
Cách 2: Áp dụng công thức tính nhanh
Gọi thể tích phần chứa
'C
là
'V
.
Ta có:
3 3
. ' ' ' '
' '
' 1 1
' '
' .4 2
2 2 2
ABCD A B C D
B N D M
V
B B D D
V a a
V
.
Cách 3: Nhận xét nhanh do đa diện chứa
'C
đối xứng với đa diện không chứa
'C
qua
O
nên thể tích của
hai phần này bằng nhau, suy ra
3
. ' ' ' '
1
' . 2
2
ABCD A B C D
V V a
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 68
Câu 103.
Gọi
,D D
theo thứ tự là đỉnh thứ tư của hình thoi
,
ABCD A B C D
.
Thể tích của bát diện cần tìm:
. . . .
1 1
6 6
ABCD C D A B BC D A B ACD ABCD C D A B ABCD C D A B ABCD C D A B
V V V V V V V
.
2 2
.2 .2
3 3
ABCD C D A B ABC
V SO S
.(*)
Ta có:
2
3
4
ABC
a
S
.
Ta có:
2 3
, 60 .tan 60 . . 3
3 2
a
SA ABC SAO SO OA a
.
Do đó:
2 3
8 3 2 3
. .
3 4 3
a a
V a
.
Dạng 4. TỈ SỐ THỂ TÍCH
Dạng 4.1 Tỉ số thể tích của khối chóp
Câu 104.
Ta có
.
.
. . 2.2.2 8
S ABC
S MNP
V
SA SB SC
V SM SN SP
, suy ra đáp án C.
Câu 105. Chọn D
A
C
B
S
B'
A'
C'
D'
D
M
O
N
M
P
A
C
B
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 69
Ta có:
.
.
1 1 1 1
. . . .
2 2 2 8
M IJK
M NPQ
V
MI MJ MK
V MN MP MQ
.
Câu 106. Chọn C
Ta có
.
.
1
. .
8
S A B D
S ABD
V
SA SB SD
V SA SB SD
.
.
1
16
S A B D
S ABCD
V
V
.
Và
.
.
1
. .
8
S B D C
S BDC
V
SB SD SC
V SB SD SC
.
.
1
16
S B D C
S ABCD
V
V
.
Suy ra
. .
. .
1 1 1
16 1
6 8
S A B D S B D C
S ABCD S ABCD
V V
V V
.
.
1
8
S A B C D
S ABCD
V
V
.
Câu 107. Chọn D
K
J
I
N
Q
P
M
D'
C'
B'
A'
D
C
B
A
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 70
Ta có
( ) ( )
( ) ( ) //
// ( )
SBC G
SBC MM BC
BC
(
MN
đi qua
; ;
G M SB N SC
).
Vì
G
là trọng tâm
2
3
SM SN SG
SBC
SB SC SE
.
Ta có
2 2 4 4
. .
3 3 9 9
SAMN
SAMN
SABC
V
SM SN V
V
V SB SC
.
Dạng 4.2 Tỉ số thể tích các khối đa diện
Câu 108. Chọn C
Cách 1. Đặc biệt hóa tứ diện cho là tứ diện đều cạnh
a
. Hình đa diện cần tính có được bằng cách cắt
4
góc
của tứ diện, mỗi góc cũng là một tứ diện đều có cạnh bằng
2
a
.
Do đó thể tích phần cắt bỏ là
4.
8 2
V V
V
.
Vậy
1
2 2
V V
V
V
.
Q
P
N
M
D
C
B
A
E
F
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 71
Cách 2. Khối đa diện là hai khối chóp tứ giác có cùng đáy là hình bình hành úp lại. Suy ra:
. . .
1 1 1
2 4. 4. 4. .
2 4 2
N MEPF N MEP P MNE
V V V V V V
Cách 3. Ta có
. . . .
'
A QEP B QMF C MNE D NPF
V V V V V
V
V V
. .
. .
1
A QEP B QMF
C MNE D NPF
V V
V V
V V V V
1 1 1 1 1 1 1 1 1 1 1 1 1
1 . . . . . . . .
2 2 2 2 2 2 2 2 2 2 2 2 2
.
Câu 109. Chọn D
Hai đa giác đáy đồng dạng nên Sau khi giảm độ dài cạnh đáy đi
3
lần thì diện tích đáy giảm đi
9
lần
1
9
A B C D E ABCDE
S S
.
Do đó
1
.3 .
1
3 9
1
3
.
3
B
h
V
V
Bh
.
Câu 110.
Gọi
1 2 3
; ;G G G
lần lượt là trọng tâm tam giác
SAC
;
SBC
;
SAB
Khi đó
1 2 3
G G G SAB MN
với
1 2
/ / / /
MN AB G G
,
3
G MN
1 2 3
G G G SAC MP
với
2 3
/ / / /
MP AC G G
,
1
G MP
1 2 3
G G G SBC NP
với
1 3
/ / / /
NP BC G G
,
2
G NP
Do đó
1 2 3
G G G
chia khối chóp thành 2 phần:
SMNP
và
MNPABC
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 72
Ta có:
2 2 2 8
. . . .
3 3 3 27
SMNP
SABC
V SM SN SP
V SA SB SC
8 19 19
27 27 27
MNPABC SABC SMNP SABC SABC SABC
V V V V V V V
.
Câu 111.
1
V
là thể tích khối lăng trụ chứa đỉnh
C
tức là
1 .
1
.
3
M ABC ABC
V V S MC
2
V
là thể tích khối đa diện còn lại
2 . 1
1 5
. . .
6 6
ABC A B C ABC ABC ABC
V V V S CC S CC S CC
Khi đó ta có tỉ số
1
2
1 1
.
1
3 6
5 5
5
. .
6 6
ABC ABC
ABC ABC
S MC S CC
V
V
S CC S CC
.
Câu 112.
1 .
. .
ABCD A B C D A B C D
V V h S
2 . ' '
1 1 1 1
, . . . h.
3 3 2 6
I A B C A B C A B C D A B C D
V V d I A B C S h S S
.
1
2
.
6
1
.
6
A B C D
A B C D
h S
V
V
h S
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 73
Câu 113.
Ta có
.
.
ANIB N
AIB
S ABCD ABCD S
V h
S
V S h
.
Trong đó
;
N S
h h
lần lượt là chiều cao kẻ từ đỉnh
;N S
nên
1
2
N
S
h
NC
h SC
(1)
Ta có
;
AO BM
lần lượt là các trung tuyến của tam giác
ABD
nên
I
là trọng tâm từ đó
2 1
3 2
AI AO AC
từ đó
1
2 2 6
AIB AIB
ABCD ABC
S S AI
S S AC
(2)
Từ (1) và (2) ta có
.
1 1 1
. .
6 2 12
ANIB N
AIB
S ABCD ABCD S
V h
S
V S h
Câu 114.
Gọi
V
là thể tích khối lăng trụ
.
ABC A B C
;
1
V
là thể tích khối chóp
.
B AEFC
;
2
V
là thể tích khối đa diện
BB EFC A
;
I
là trung điểm của cạnh
BB
và
h
là chiều cao của khối lăng trụ
.
ABC A B C
.
Ta có:
//
EIF ABC
nên
,
2
h
d B EIF
.
.
1 1 1
. . .
3 2 6 6
B IEF ABC ABC
h
V S h S V
.
Do đó
1 . .
1 1 1
2 6 3
ABC EIF B EIF
V V V V V V
.
2 1
1 2
3 3
V V V V V V
.
Vậy
1
2
1
2
V
V
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 74
Câu 115.
Gọi
là trung điểm
,CD H
là hình chiếu vuông góc của
0
lên
S
, trong mặt phẳng
( )SCD
kẻ
CH SD
tại
N
ta có:
CD SO
CD SM
CD OM
.
, ( )
, ( )
( ) ( )
CD SM SM SCD
CD OM OM ABCD SMO
SCD ABCD CD
.
SOM
vuông tại
O
cos 3
OM
SMO SM OM
SM
;
2 2
2SO SM OM a
.
SOD
vuông tại
0
,
2 10
2, 5
2 2
a a SD
SO a OD SD
OD
.
Có:
( )
CD SOM CD OH
mà
( ) ( ) ( )OH SM OH SCD ACN SCD
hay
( ) ( )P ACN
.
Khi đó hình chóp
S. DABC
được chia thành hai khối đa diện
S.ABCN
và
N.ACD
, gọi
N.ACD 1 S.ABCN 2
V ;V
V V
.
Có
DSO
vuông tại
O
,
ON
là đường cao nên
2
2
D
D D. D ND
D
O
O N S
S
.
2
. D . D . D
1 2
. D 1
2
. D
D D
5
D D 5 10 10
S AC S AC S ABC
N AC
N AC
V V V
V V
S S
V V
V N O
.
Vậy:
1
2
1
0.11
9
V
V
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 75
Câu 116.
Gọi
I
là giao điểm của
MN
và
CD
,
Q
là giao điểm của
và
AD
. Khi đó thiết diện của tứ diện
ABCD
là tứ giác
ABC
.
Ta có:
. . 1
NB ID MC
ND IC MB
1
4
ID
IC
và
. . 1
ID PC QA
IC PA QD
4
QA
QD
.
2
.
5
ANPQ
ANCD
V
AP AQ
V AC AD
2 2
5 15
ANPQ ANCD
V V V
.
1 2 1
3 15 5
N PQDC
V V V V
.
Và
1
.
3
CMNP
ABCD
V
CM CP
V CB CA
1 2
3 9
CMND CBNA
V V V
.
Suy ra
2
19
45
NPQDC CMNP
V V V V
.
Do đó,
1 2
V V V
26
45
V
.
Vậy
1
2
26
19
V
V
.
Câu 117.
Q
I
N
P
M
A
D
B
C
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 76
Trong tam giác
SMC
,
SB
và
MN
là hai trung tuyến cắt nhau tại trọng tâm
K
2
3
SK
SB
.
BI
là đường trung bình của tam giác
MCD I
là trung điểm
AB
.
1 . . .S AID S IKN S IND
V V V V
Đặt:
.S ABCD
V V
.
1
.
4
S AID
V V
;
. .
2 1 1 1
. . . .
3 2 4 12
S IKN S IBC
SK SN
V V V V
SB SC
;
. .
1 1 1
. . .
2 2 4
S IND S ICD
SN
V V V V
SC
1
1 1 1 7
. .
4 12 4 12
V V V
2
5
.
12
V V
1
2
7
5
V
V
.
Câu 118.
Gọi
, , ,O AC BD I SO AC B I D
thẳng hàng và
.B D BD
2 3 2 6
2 6 ,
3 3
a a
AC a SC a AC SC
Ta có
4
. . 1 4
5
AO C C IS IS SI SB SD
AC C S IO IO SO SB SD
.
1 1
. . 2
2
. . 8 8
.
2 . . 15 7
S AB I
S ABCD S ABC
V
V VSA SB SC
V V SA SB SC V
Câu 119.
Gọi
I
,
I
,
M
,
N
,
P
,
Q
lần lượt là tâm các hình vuông
ABCD
,
A B C D
,
AA D D
,
ABB A
,
BB C C
,
CDD C
. Ta được
1
V là thể tích khối bát diện đều với 6 đỉnh
I
,
I
,
M
,
N
,
P
,
Q
cạnh
2
2
MN
1 .
2
I MNPQ
V V
1
2. , .
3
MNPQ
d I MNPQ S
2 1 1 1
. .
3 2 2 6
.
I
O
D'
C'
B'
C
D
B
A
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 77
1 1 1
. .
2 2 4
ABIN
ABCB
V
AI AN
V AC AB
.
2
8
ABIN
V V
1
8.
4
ABCB
V
=
1 1 1
8. .
4 6 3
. Vậy
2
1
2
V
V
Câu 120. Chọn B
Gọi
, , ,O AC BD I SO AC B I D
thẳng hàng và
.B D BD
2 3 2 6
2 6 ,
3 3
a a
AC a SC a AC SC
Ta có
4
. . 1 4
5
AO C C IS IS SI SB SD
AC C S IO IO SO SB SD
.
1 1
. . 2
2
. . 8 8
.
2 . . 15 7
S AB I
S ABCD S ABC
V
V VSA SB SC
V V SA SB SC V
Câu 121.
Ta có
// , 2 , 2 2
SMNPQ OMNPQ
MNPQ ABCD d S MNPQ d O MNPQ V V V
2 2 2 8 8
. . . .
3 3 3 27 27
SMNQ
SMNQ SEFK
SEFK
V
SM SN SQ
V V
V SE SF SK
.
2 2 2 8 8
. . . .
3 3 3 27 27
SNPQ
SNPQ SFGK
SFGK
V
SN SP SQ
V V
V SF SG SK
.
8 8 8 27 27
27 27 27 8 4
SMNQ SNPQ SEFK SFGK SMNPQ SEFGK SEFGK SMNPQ
V V V V V V V V V
.
I
O
D'
C'
B'
C
D
B
A
S
O
N
P
Q
M
F
K
G
E
D
B
C
A
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 78
Ta có:
1
. .sin
1 1 1
2
1
4 4 8
. .sin
2
EBF
EBF ABC ABCD
ABC
BE BF B
S
S S S
S
BA BC B
.
Khi đó,
4
EFGK ABCD ABF FCG GDK KAE ABCD EBF
S S S S S S S S
1
2
EFGK ABCD
S S
Nên
1
,
1 27
3
2
1
2 2
,
3
EFGK
SEFGK
SABCD SEFGK
SABCD
ABCD
d S EFGK S
V
V V V
V
d S ABCD S
.
Câu 122. Chọn C
Gọi
O AC BD; I SO AM
Do
P
chứa
AM
và song song
BD
nên
P
qua
I
và song song
BD
. Kẻ đường thẳng qua
I
song song
BD
cắt
SB
tai
P
, cắt
SD
tại
Q
vậy
P (APMQ)
; Ta có
I
là trọng tâm tam giác
SAC
nên
SI 2 SP SQ
SO 3 SB SD
;
Ta có
S.AMQ
SAMQ
S.ACD
V
SM SQ 1 2 1 1 V V
. . V .
V SC SD 2 3 3 3 2 6
S.AMP
SAMP
S.ACB
V
1 1 V V
V .
V 3 3 2 6
; Vậy
SAPMQ
V V
V 2.
6 3
Dạng 4.3 Ứng dụng tỉ số thể tích để tìm thể tích
Câu 123.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 79
Ta có:
. '
. '
. ' ' '
1 ' 13 13
3 ' ' ' 18 9
ABC MNC
ABC MNC
ABC A B C
V
AM BN CC
V
V AA BB CC
.
Lại có:
.
.
. ' ' '
1 7 7
3 ' ' ' 18 9
ABC MNC
ABC MNC
ABC A B C
V
AM BN CC
V
V AA BB CC
.
Suy ra:
. ' . ' .
2
3
C MNC ABC MNC ABC MNC
V V V
.
Mà:
. '
. '
'
. . *
'
C MNC
C PQC
V
CM CN CC
V CP CQ CC
Ta có:
1
1
'
2
'
2
'
2
'
3
CMCM AM
CMA PMA
CP
PM A M
CN BN
CN
CNB QNB
QN B N
CQ
.
Thay vào
*
ta có:
. '
. ' . '
. '
1 2 1
. .1 3 2
2 3 3
C MNC
C PQC C MNC
C PQC
V
V V
V
.
Có:
' ' '. .
11
9
A B C MNC LT ABC MNC
V V V
.
' ' . ' ' ' '.
7
9
A MPB NQ C PQC A B C MNC
V V V
.
Câu 124.
Gọi
O
là tâm hình vuông
ABCD
,
SO
cắt
MN
tại
K
I
là giao điểm của
AK
với
SC
.
Vì
MN
là đường trung bình của tam giác
SBD
nên
K
là trung điểm của
.SO
Gọi
'A
là điểm đối xứng của
A
qua
S
,
H
là giao điểm của
AK
với
SC
.
Vì
'SO A C
và
K
là trung điểm của
SO
H
là trung điểm của
'A C
I
là trọng tâm của tam giác
'AA C
1
3
SI SC
.
Ta có
3
. . . .
1 3 1
. , .
3 3 2
S ABCD ABCD S ABC S BCD S ABCD
a
V SA S V V V
. . . . . . .
1 1 1 1 1 1 1 1 1 1
. . . . . .
1 2 2 2 2 3 4 12 2 6
S AMIN S AMN S MIN S ABC S BCD S ABCD S ABCD
V V V V V V V
Do đó
3
. . .
5 5 3
.
6 18
ABCDMIN S ABCD S AMIN S ABCD
a
V V V V
Câu 125.
Chọn D
I
K
N
M
O
D
C
A
B
S
H
A'
I
K
C
O
A
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 80
+) Gọi BM AA E
;
ED AD N
.
Ta có M là trung điểm của AB
M
là trung điểm là EB
N
là trung điểm của ED
và
AD
+) Ta có
.
.
1
. .
8
E AMN
E A B D
V
EA EM EN
V EA EB ED
. . . .
7 7 1 7 7063
.2. .
8 8 2 24 12
AMN A B D E A B D A A B D ABCD A B C D
V V V V
Câu 126. Chọn A.
Gọi
,H I
lần lượt là giao điểm của các cặp đường thẳng
SC
và
S B
,
SD
và
S A
.
Vì 2SS CB
nên
||BC SS
và 2
SS
BC
.
Suy ra 2
SI SS
IC BC
. Tương tự, ta cũng có 2
SH
HD
.
Do đó
2
3
SI SH
SC SD
.
Dễ thấy hai khối chóp
.S ACB
và
.S ACD
có diện tích đáy bằng nhau và chiều cao bằng nhau nên thể tích
của chúng bằng nhau và bằng
1
135
2
V .
Mà:
2 2 2
135 90
3 3 3
.
. .
.
. .
S AIB
S AIB S ACB
S ACB
V
SI
V V
V SC
.
Và
2 2 4 4
135 60
3 3 9 9
.
. .
.
. . . .
S AIH
S AIB S ACD
S ACD
V
SI SH
V V
V SC SD
.
Suy ra thể tích của khối đa diện là phần chung của hai khối chóp
.S ABCD
và
.S ABCD
bằng:
N
M
E
D
C
B
A
D'
C'
B'
A'
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 81
270 90 60 120
. . .
.
S ABCD S AIB S AIH
V V V
Câu 127. Chọn A
Trên cạnh
SB
,
SC
lần lượt lấy các điểm
,M N
thỏa mãn
1
SM SN
Ta có
1, 2, 3
AM AN MN
tam giác
AMN
vuông tại
A
Hình chóp
.
S AMN
có
1
SA SM SN
hình chiếu của
S
trên
( )AMN
là tâm
I
của đường tròn ngoại tiếp tam giác
AMN
, ta có
I
là trung
điểm của
MN
Trong
2 2
1
,
2
SIM SI SN IN
.
1 1 2 2
3 2 2 12
S AMN
V
Ta có
.
,
1
6
S AMN
S ABC
V
SM SN
V SB SC
.
2
2
S ABC
V
.
Câu 128. Chọn D
+) Gọi
P MN SB P
là trọng tâm của
SCM
vì là giao của hai đường trung tuyến ,
SB MN
+) Gọi
D
Q M AB Q
là trung điểm của
DM
+) Ta có
D . D . D . D . D . D . D
1 1 2 5
. . 1 . .
D 2 2 3 6
BC QNP M C N M C N M C N M C N M C N M C N
MB MQ MP
V V V V V V V
MC M MN
+) Mặt khác
D
. D . D . D . D . D
D
1
D.
, D
1 1 1
2
. .
,( D) D. 2 2 2
MC
M C N N MC S ABC S ABC S ABC
ABC
C CM
d N ABC
S
V V V V V
S d S ABC C CB
+) Vậy
DQNP D . D D
5 5 7
1
12 12 12
BC SANPQ S ABC BC QNP
V V V V
Câu 129.
Chọn C
Q
A
D
B
C
M
S
Q
P
N
M
G
H
A
B
D
C
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 82
Gọi
G
là trọng tâm tam giác
SAB
,
H
là trung điểm của
AB
SH ABCD
Ta có
2
3 27 3
3 3
4 4
ABC
AB
S AB
.
Qua
G
kẻ đường thẳng song song với
AB
cắt
SB
tại
N
, qua
N
kẻ song song với
BC
cắt
SC
tại
P
, qua
P
kẻ đường thẳng song song với
CD
cắt
SD
tại
Q
.
Ta có:
. . . .
2
S MNPQ S MNP S MPQ S MNP
V V V V
.
3
.
.
2 8
. .
3 27
S MNP
S ABC
V
SM SN SP
V SA SB SC
.
2
. .
8 8 1 8 1 3 3. 3 1
. . . . . . 3 3 6
27 27 3 27 3 2 2
S MNP S ABC ABC
V V SH S
.
.
12
S MNPQ
V
.
Câu 130.
Chọn D
Ta có
3
. . .
1
2 2
S ABD S BCD S ABCD
a
V V V
3
.
.
.
1
2 4
S AMD
S AMD
S ABD
V
SM a
V
V SB
,
3
.
.
.
1
.
4 8
S MND
S AMD
S BCD
V
SM SN a
V
V SB SC
.
Từ đó suy ra
3 3 3
. . .
3
4 8 8
S AMND S AMD S MND
a a a
V V V .
A
D
B
C
S
M
N
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 83
Câu 131.
Ta có :
.
.
1
. .
8
S IJK
S ABC
V
SI SJ SK
V SA SB SC
. .
8
S ABC S IJK
V V .
Tương tự :
.
. .
.
1
8
8
S IKH
S ACD S IKH
S ACD
V
V V
V
.
Suy ra :
. . . . . .
8 8 8
S ABCD S ABC S ACD S IJK S IKH S IJKH
V V V V V V
.
Câu 132.
Xét tam giác vuông cân
ABC
có
2 2 2
AB BC AC
2
2
2 2
AB a
2 2
AB a
AB a
.
Ta có
1
.
2
ABC
S AB BC
2
2
a
.
1
. .
3
S ABC ABC
V SA S
3
3
a
.
Gọi
I
là trung điểm của
BC
. Ta có
2
3
SB SC SG
SB SC SI
.
Ta có
.
.
. .
. .
S AB C
S ABC
V
SA SB SC
V SA SB SC
2 2
.
3 3
4
9
.
3
.
4
.
9 3
S AB C
a
V
3
4
27
a
.
Câu 133. Gọi
O
là tâm
ABCD
,
I
là giao điểm của
MN
và
SO
. Khi đó
P
là giao điểm của
AI
và
SC
.
H
K
J
I
A
D
B
C
S
C'
B'
G
I
A
C
B
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 84
+) Mặt phẳng
AMN
cắt hình chóp
.S ABCD
có đáy là hình bình hành theo thiết diện là tứ giác
AMPN
nên
ta có
1
4
4
SA SC SB SD SC SP
SA SP SM SN SP SC
.
+) Xét hình chóp
.S ABCD
có:
. .
1
. 24
2
S BCD S ABCD
V V
.
Ta có
.
.
.
1 1 1 1
. . . . 1
2 3 4 24
S MNP
S MNP
S BDC
V SM SN SP
V
V SB SD SC
.
Câu 134.
Gọi
,O AC BD I MP SO Q NI SD
ÁP dụng định lí Menelauyt cho tam giác
SBC
với cát tuyết
NPE
, ta được
. . 1
NB PS EC
NS PC EB
CE CB
(1)
Do
MIP
nên
2 4
(1 ) (1 )
3 9
SI xSP x SM x SC x SA
  
1 1 3 8
,
2 2 5 15
SI k SO k SC SA x k
. Tương tự với ba điểm thẳng hàng
, ,N I Q
ta có
4
7
SQ SD
(2)
ÁP dụng định lí Menelauyt cho tam giác
SCQ
với cát tuyết
PRD
, ta được
6
3
7
RQ
RC
Từ (1), (2) và (3) ta có
6 6 1 2 4 8
. . .
13 13 3 13 7 91
PRQ PQC SQC SDC SDC
S S S S S
8 8 4
91 91 91
EPQR ESDC SBDC SABCD
V V V V
18.91
4
SABCD
V
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 85
Do đó
. . . .
2
SABCD
SMNPQ SMNP SMPQ
V
SM SN SP SM SP SQ
V V V
SA SB SC SA SC SD
3
4 2 1 2 4 4
. . . . . 65cm
9 3 2 3 9 7 2
SABCD
V
Dạng 5. BÀI TOÁN THỰC TẾ VÀ BÀI TOÁN CỰC TRỊ
Câu 135. Chọn C
Gọi
x
là chiều rộng, ta có chiều dài là
Do diện tích đáy và các mặt bên là
2
6,7m
nên có chiều cao
2
6,7 2
6
x
h
x
,
ta có
0
h
nên
6,7
2
x
.
Thể tích bể cá là
3
6,7 2
3
x x
V x
và
2
6,7 6
0
3
x
V x
6,7
6
x
Bảng biến thiên
Bể cá có dung tích lớn nhất bằng
3
1,57m
.
Câu 136. Chọn D
Gọi
,2 ,x x h
lần lượt là chiều rộng, dài, cao của bể cá.
Ta có
2
2 2 2 5,5
x xh xh
2
5,5 2
6
x
h
x
( Điều kiện
5,5
0
2
x
).
Thể tích bể cá
2
2 3
5,5 2 1
2 . (5,5 2 )
6 3
x
V x x x
x
.
/ 2
1
(5,5 6 )
3
V x
.
/
5,5
0
6
V x
.
Lập BBT suy ra
3
max
11 33
1,17
54
V m
.
Câu 137. Thể tích của bế cá:
3
72 24
3 72dm
3
V ab b
a a
, với
, 0
a b
.
Diện tích kính để làm bể cá như hình vẽ:
24 24
3.3 2.3 9 6. .
S a b ab a a
a a
144 144
9 24 2 9 . 24
a a
a a
96
S
.
144
96 9 4 6
S a a b
a
.
Vậy để bể cá tốn ít nguyên liệu nhất thì
4dm
a
;
6dm
b
.
Câu 139. Chọn B
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 86
Gọi
,M N
lần lượt là trung điểm của
CD
và
AB
.
Ta có
CD MB CD MN
CD MAB
CD MA CD AB
.
Tam giác
MAB
cân tại
nên
MN AB
.
1 1
. . , .sin , .2 3. .sin 90
6 6
ABCD
V AB CD d AB CD AB CD x MN
2 2
2
2 2
36
1 3 3
.2 3. 3 . 36 . 3 3
6 2 6 6 2
x x
x
x x x
.
Dấu
" "
xảy ra
2
36 3 2
x x x
.
Câu 140.
Đặt
,
SA h AB AC a
. Ta có
2
3
2 2 2 2 2 2 2 4 2
1 1 1 1 1 1 1 1 1
; 3; 3 6
9
d A SBC AH a h
AH SA AB AC a a h a h
.
,SBC ABC SMA
.
2
.
1
1
6
S ABC
V a h
. Thể tích nhỏ nhất bằng 1 khi
3
2
a h SM a
2 2 3
os
2 3
3
AM a
c
SM
a
.
2 3
2 3
2 3
2 3
2 3
x
M
N
A
D
C
B
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 87
Câu 141.
Ta có
BC BB
CB ABB A
BC AB
A B
là hình chiếu vuông góc của
A C
trên mặt phẳng
ABB A
góc giữa đường thẳng
A C
và mặt phẳng
ABB A
là góc
,
A B A C BA C
(vì
BA C
nhọn do
BA C
vuông tại
B
). Vậy
30
BA C .
Ta có
1
3
tan30
tan
BC
A B
BA C
;
2 2 2
3
A A A B AB x
.
2 2
2
.
3
3
. . 3
2 2
ABCD A B C D
x x
V AB AD AA x x .
Dấu
xảy ra
2 2 2
3
3 3
2
x x x x x
(vì
0
x
).
Vậy
3
2
max
V
.
Câu 142. Ta có thể tích chiếc hộp:
2
32
V x h
(đvtt), với
, 0
x h
. Suy ra
2
32
h
x
.
Phần mạ vàng của chiếc hộp:
2
2 8S x xh
2
2
32
2 8 .
x x
x
2
256
2x
x
.
Cách 1
Ta có
2
256
2x
x
2 2
3
128 128 128 128
2 3 2 . . 96
x x
x x x x
(BĐT AM-GM).
Đẳng thức xảy ra khi
2
128
2x
x
hay
4
x
, khi đó
2
h
.
Cách 2.
Xét hàm số
2
256
2f x x
x
với
0
x
.
D'
C'
A'
D
B
C
A
B'
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 88
Ta có
3
2 2
256 4 256
4
x
f x x
x x
,
3
0 4 256 4f x x x
;
4 96f
.
BBT
x
0
4
f x
0
f x
96
Dựa vào BBT ta thấy hàm số đạt GTNN tại
4
x
, khi đó
2
h
.
Vậy phương án A đúng.
Câu 143. Chọn A
Gọi
,M N
lần lượt là trung điểm của
BD
,
AC
. Đặt
2BD x
,
2AC y
, 0x y
.
Ta có
,CM BD AM BD
BD AMC
.
Ta có
2
1MA MC x
,
2 2
1MN x y
,
1
.
2
AMC
S MN AC
2 2
1
. 1
2
y x y
.
1
. .
3
ABCD AMC
V DB S
2 2
1
.2 . 1
3
x y x y
2 2 2 2
2
. . 1
3
x y x y
3
2 2 2 2
1
2
3 27
x y x y
2 3
27
ABCD
V
. Dấu đẳng thức xảy ra khi
1
3
x y .
Vậy giá trị lớn nhất của thể tích khối tứ diện
ABCD
là
2 3
27
.
Câu 144. Chọn C
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 89
Gọi
,M N
lần lượt là trung điểm của
,SA BC
và đặt
2 ,2 .a x b y
,
1
2 .
3
SABC BSAN CSAN BSAN SAN
BC AN BC SN BC SAN
V V V V BC S
2 2 2
2 2 2 2 2 2 2
2 2
3
2 2 2 2
2 2 2 2 2 2 2
2
1 1
2 4
1
. 1
2
1 1 4 1
2 1 .4 . 1 .
3 9 9 3
4
243
SAN
SABC SABC
SABC
AB AC BC
AN b MN AN MA b a
S SA NM a a b
a b a b
V ab a b V a b a b
V
Dấu bằng xảy ra
2 2 2 2
1 2 4
1
3 3 3
a b a b a b x y x y .
Câu 145. Chọn A
+) Gọi độ dài
,
AB a AD b
và
AA c
Ta có tổng diện tích tất cả các mặt là 36 nên
2 2 2 36 18 1
ab bc ca ab bc ca
Do độ dài đường chéo
'AC
bằng 6 nên
2 2 2
36 2
a b c
+) Thể tích khối hộp là
V abc
Ta có
2
2 2 2
2 72 6 2
a b c a b c ab bc ca a b c
Từ
2
1 18 18 6 2 6 2 18
ab c a b c c c c
Nên
3 2
6 2 18 , 0;6 2
V abc c c c f c c
Ta có
2
3 2
3 12 2 18 0
2
c
f c c c
c
Lập bảng biến thiên ta được
0;6 2
2 8 2
Max V f
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 90
Câu 146.
 Gọi
I
là trung điểm
SC
,
O AC BD
.
Ta có
BI SC
BD SC
DI SC
Mà
ABCD
là hình thoi nên
BD AC
Khi đó,
BD SAC
.
. . .
2 2
S ABCD S ABC B SAC
V V V .
2 2 2 2 2 2
AO AB BO AB BI OI
2 2
2 2 2 2
4
x a
AB SB SI OI
2 2 2 2 2 2
4
AC AO x a SA SC
SAC
vuông tại
S
.
2 2
2 2
3
2
a x
BO AB AO
.
. .
1 1
2 2
3 2
S ABCD B SAC
V V BO SA SC
2 2 2 2
1 3 3
3 2 6
a x ax a x
a x
.
 Ta có
2 2 2
2
2 2 2 2 2
3
3
3 . 3
2 2
x a x
a
x a x x a x
3
.
4
S ABCD
a
V
. Dấu “=” xảy ra
2 2 2
6
3
2
a
x a x x
.
Vậy, thể tích khối chóp
.
S ABCD
lớn nhất khi và chỉ khi
6
2
a
x
6; 2
m n
2 10
m n
.
Câu 147.
Gọi
,M N
lần lượt là trung điểm của
,AB CD
.
Tam giác ,
ADB CAB
là hai tam giác cân cạnh đáy
AB
nên
DM AB
và
CM AB
. Suy ra
AB MCD
.
a
a
a
a
x
a
I
O
C
B
A
D
S
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 91
. .
1 1
. . . .
3 3
ABCD B MCD A MCD MCD MCD
V V V BM S AM S .
3
MCD
x
S
.
Tam giác
. .ABC ABD c c c
nên
CM DM
MN CD
.
2 2 2 2 2
1 1 1
. . . .
2 2 2
MCD
S CD MN y MC CN y BC BM CN
2 2
1
4
2 4 4
x y
y
2 2
1
16
4
y x y
.
2 2
1
16 16 2 . . 16 2
12 12 12
ABCD
xy xy
V x y xy xy xy xy
3
3
16 2
1 1 16
12 3 12 3
xy xy xy
.
Dấu bằng xảy ra khi
16
16 2
3
x y
x y
xy xy
xy
.
Vậy thể tích
ABCD
đạt giá trị lớn nhất khi
16
3
xy
.
Câu 148.
Gọi
O AC BD
,
G AP SO
, suy ra
là trọng tâm tam giác
SAC
.
Gọi
P
là mặt phẳng qua
AP
cắt hai cạnh
SD
và
SB
lần lượt tại
và
.
Dễ thấy:
P SBD MN
P SAC AP
SBD SAC SO
MN
,
AP
,
SO
đồng quy hay
,
,
thẳng hàng.
Đặt:
SM
x
SD
0 1
x
và
SN
y
SB
0 1
y
.
. .
1
. .
1 1 1
. . . .
2 2 4
S AMP S ANP
S ADC S ABP
V V
V SA SM SP SA SN SP
x y
V V V SA SD SC SA SB SC
.
Từ tỷ lệ:
1 1 1
. . .
2 2 3
SMN SMG SNG
SBD SDO SBO
S S S
SM SN SM SG SN SG SM SN
S S S SD SB SD SO SB SO SD SB
.
1
3
xy x y
. Lại có:
1 1 0 1 0
x y xy x y
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 92
Từ đó suy ra:
2
1 0
3
x y
hay
3
2
x y
. Vậy
lớn nhất bằng
3
8
.
Câu 149.
Gọi là trung điểm , đặt .
Ta có ; .
Suy ra .
Ta có .
, .
Bảng biến thiên
Dựa vào bảng biến thiên, ta có khi .
Câu 150. Chọn A
K
AD
5
,0
2
HK x x
5
2
2
EF FG GH HE x
2
2
5
2
HD x
2 2
2 2 2 2 2
5 5
2 2
SO SH OH HD OH x x
2 2 2 2
2
1 5 5 5 2 5
.2. . . 5
3 2 2 2 3 2
V x x x x x
2
2 5 5 5
2 5
3 2 2
2 5
V x x x
x
5
2
0
1
2
x
V
x
max
4 10
3
V
1
2
x
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 93
Ta có
1
, .
3
AB MN AB M
V d N AB M S
Do
ACB D
là tứ diện đều nên
6
sin ,
3
B D AB M
,
3
sin
2
B AM
Suy ra
1 1
.sin , . . .sin . .
3 2 6
AB MN
a
V B N B D AB M AB AM B AM AM B N
2
3
6 2 12
a AM B N a
Vậy
3
max
12
AB MN
a
V
Câu 151.
Gọi
, ,E F G
lần lượt là trung điểm
, ,BC SA EF
suy ra
G
là trọng tâm tứ diện
SABC
. Điểm
I
là giao điểm
của
AG
và
SE
. Qua
I
dựng đường thẳng cắt các cạnh
,SB SC
lần lượt tại
,M N
. Suy ra
AMN
là mặt
phẳng quay quanh
AG
thỏa mãn yêu cầu bài toán.
N
M
D'
C'
B'
A'
D
C
B
A
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 94
Kẻ
// , GK SE K SA
suy ra
K
là trung điểm
FS
.
3
4
KG AK
SI AS
. Mà
1 2
2 3
KG SI
SE SE
.
Cách 1:
Kẻ
// , // BP MN CQ MN
;
, P Q SE
.
Ta có:
;
SM SI SN SI
SB SP SC SQ
.
BEP CEQ
E
là trung điểm
PQ 2 SP SQ SE
(đúng cả trong trường hợp
P Q E
).
Ta có:
2
2 2
.
2
2
.
4
. . 1. .
9
4
AM GM
S AMN
S ABC
V
SA SM SN SI SI SI SI SI
V SA SB SC SP SQ SE SE
SP SQ
.
Dấu
" "
xảy ra khi và chỉ khi
SP SQ SE
. Hay
// P Q E MN BC
.
Cách 2:
Ta chứng minh được
3
SB SC
SM SN
.
Thật vậy, qua
I
kẻ các đường thẳng lần lượt song song
,SB SC
cắt
,SC SB
tương ứng tại
,D L
.
Ta có:
3
3
. 3.
SB DB
SB IQ NI SB NI
IQ DI
IQ SM NM SM NM
IQ NI
SM NM
,
1
.
Lại có:
3
3
. 3.
SC LC
SC IP MI SC MI
IP LI
IP MI
IP SN MN SN MN
SN MN
,
2
.
Từ
1
và
2
ta có:
3 3
SB SC NI MI
SM SN NM MN
.
Đặt
;
SB SC
x y
SM SN
. Suy ra
3 x y
.
Ta có:
.
2
.
1 1 4
. .
9
4
AM GM
S AMN
S ABC
V
SA SM SN
V SA SB SC xy
x y
.
Dấu
" "
xảy ra khi và chỉ khi
3
//
2
x y MN BC
.
Cách 3:
Đặt
SB
x
SM
;
SC
y
SN
, với
0x
,
0y
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 95
Ta có
2 1 1
( ) ( )
3 3 3 3 3
x y
SI SE SB SC xSM ySN SM SN
.
Do
I
,
,
N
thẳng hàng nên
1 3
3 3
x y
x y
.
Ta có
.
2
.
1 1 1 1 4
. .
9
( )
2
S AMN
S ABC
V
SM SN
x y
V SB SC x y xy
.
Vậy
.
.
S AMN
S ABC
V
V
đạt giá trị nhỏ nhất bằng
4
9
khi
x y
, hay
MN
đi qua
I
và song song với
BC
.
| 1/95

Tài liệu khác của Toán 12

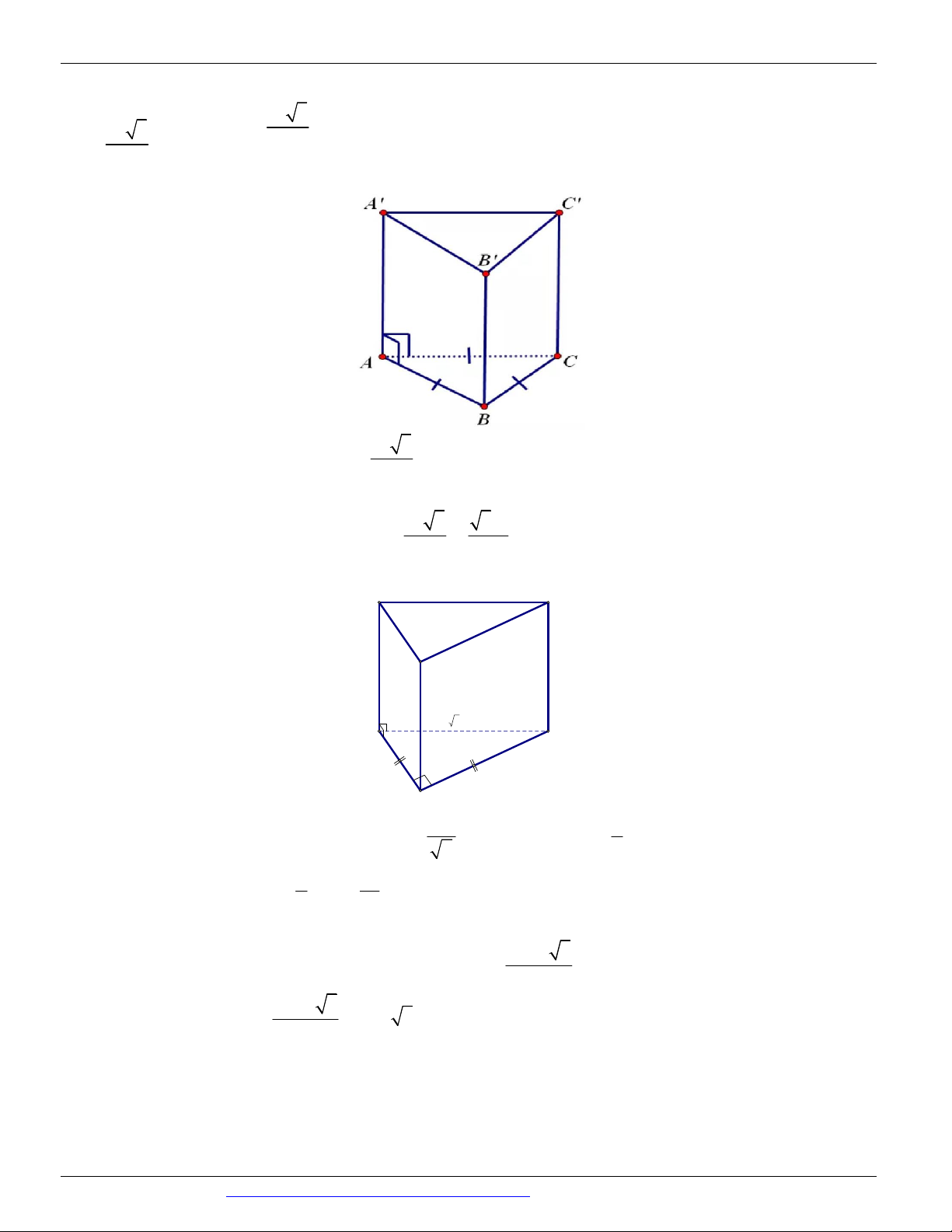
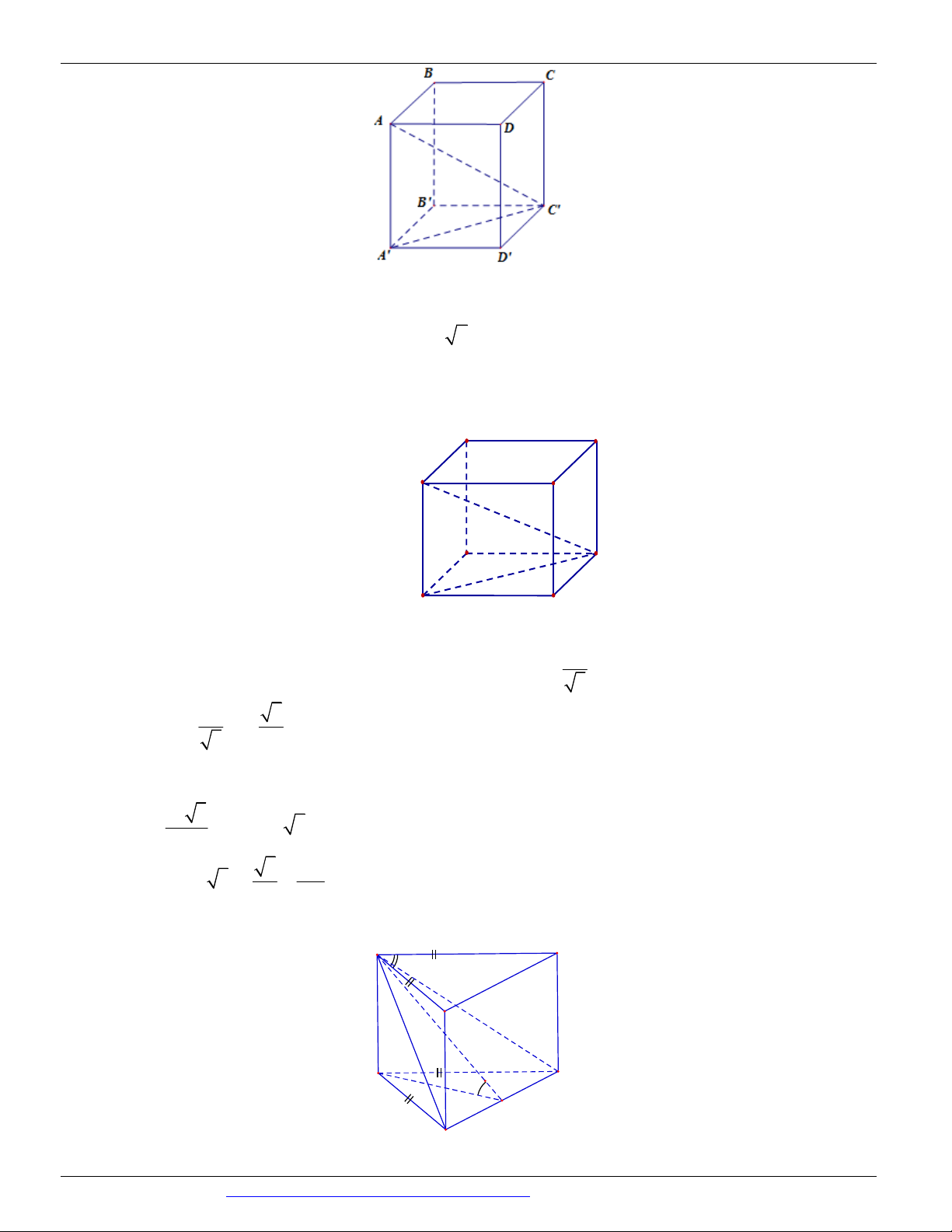
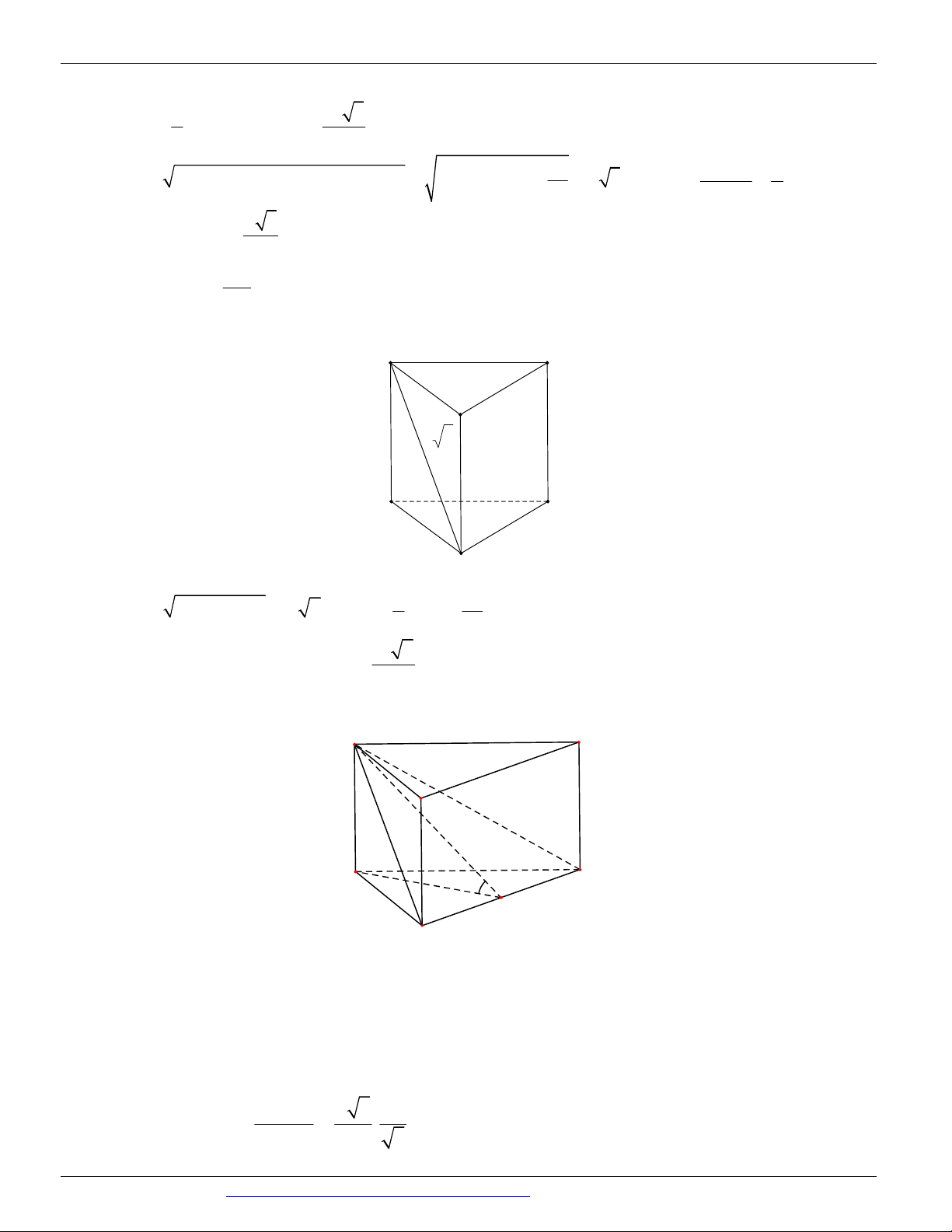
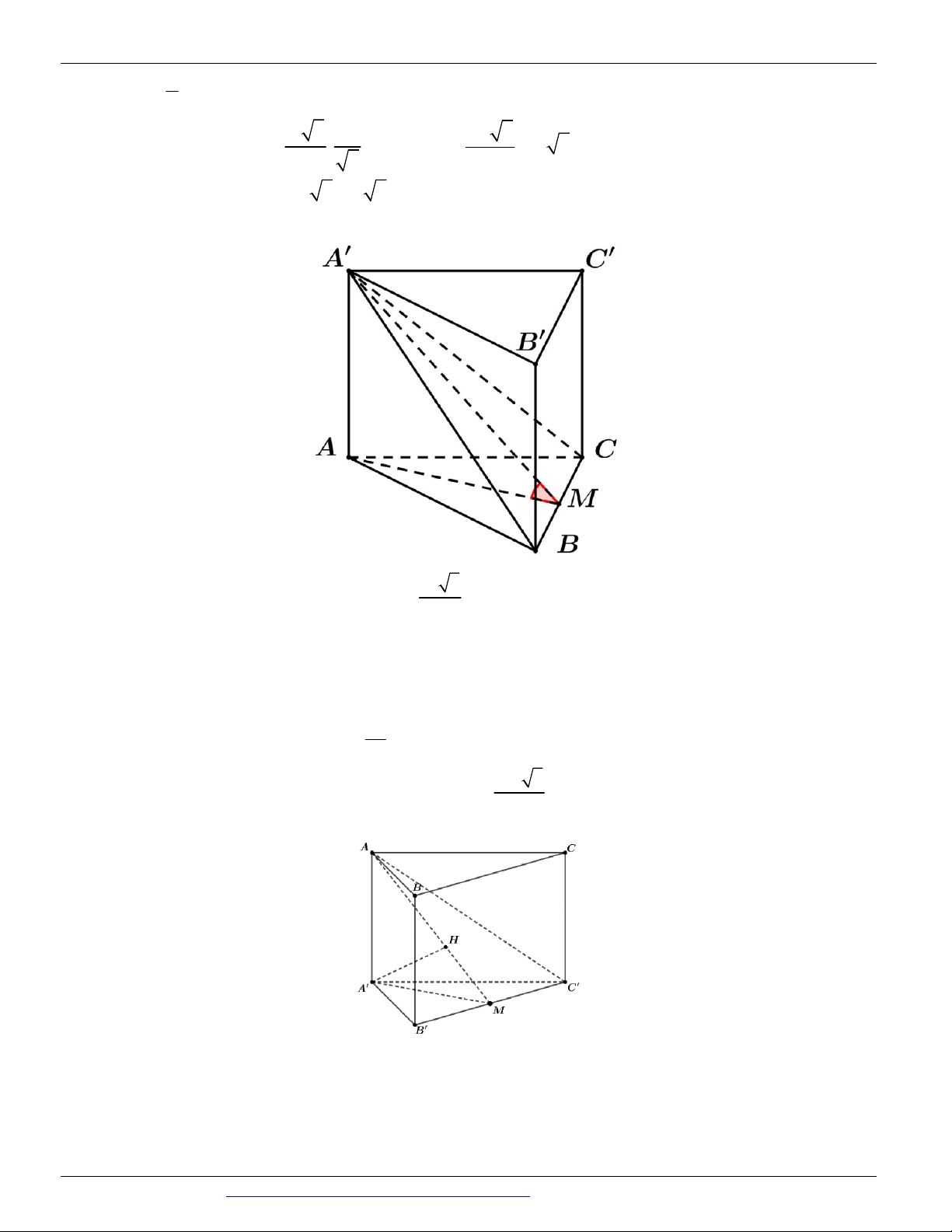
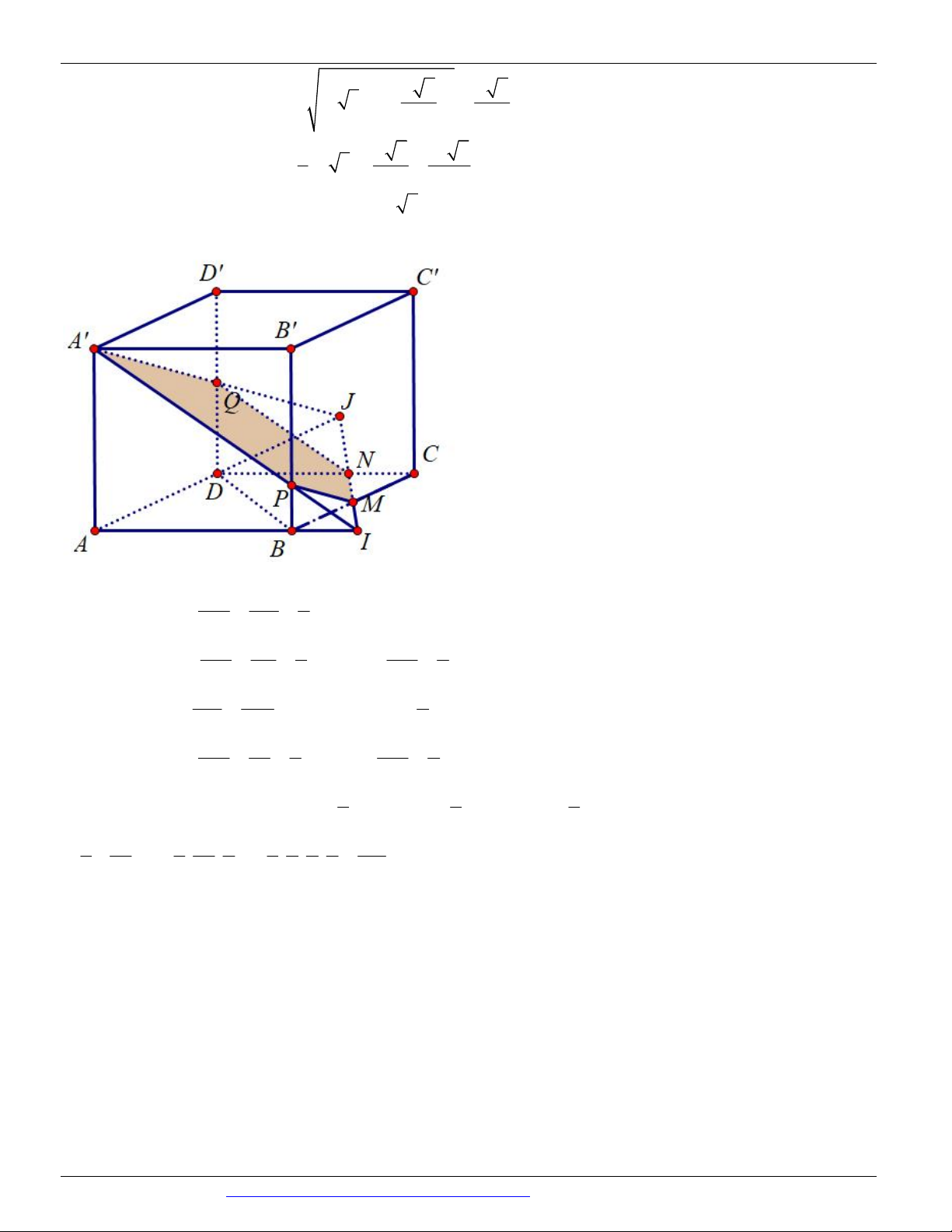
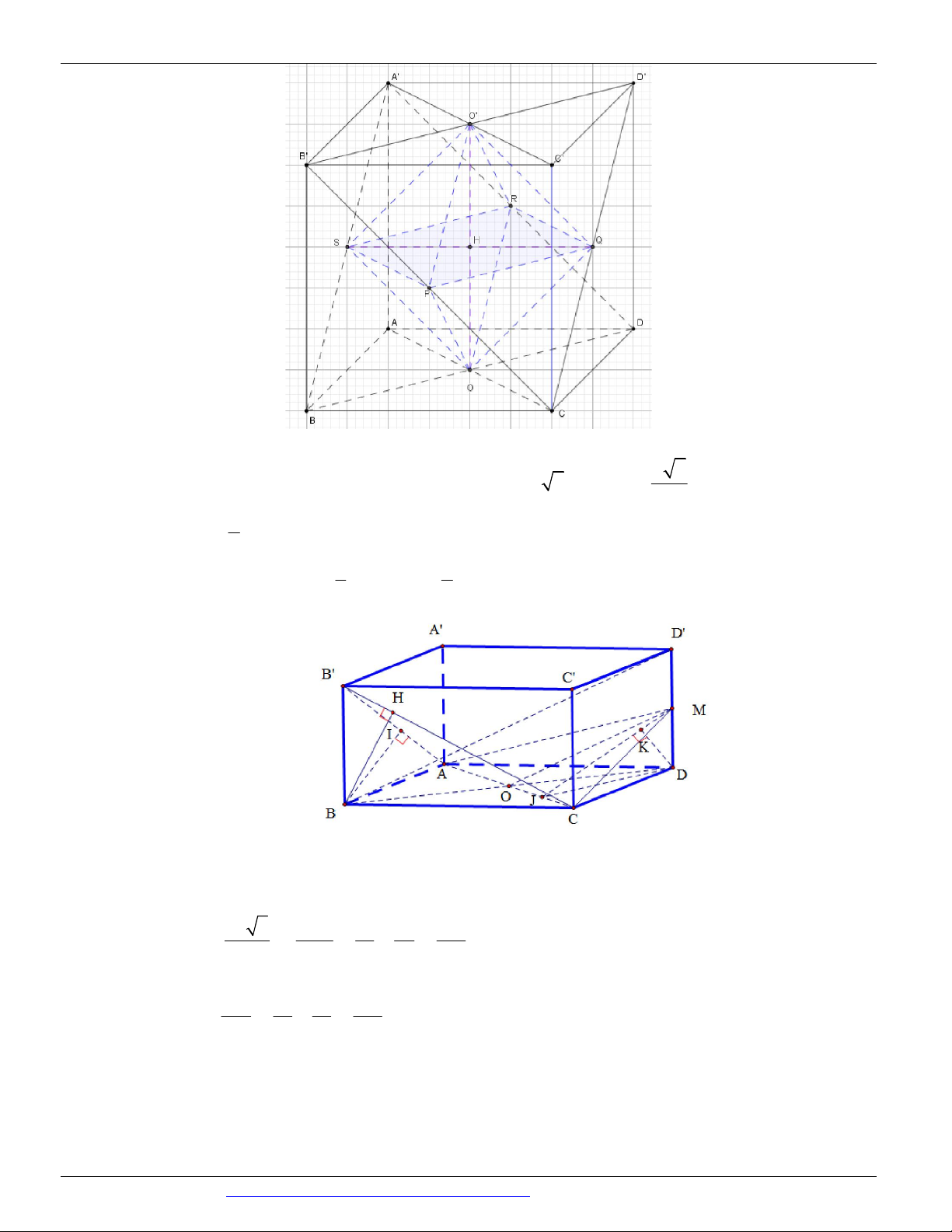
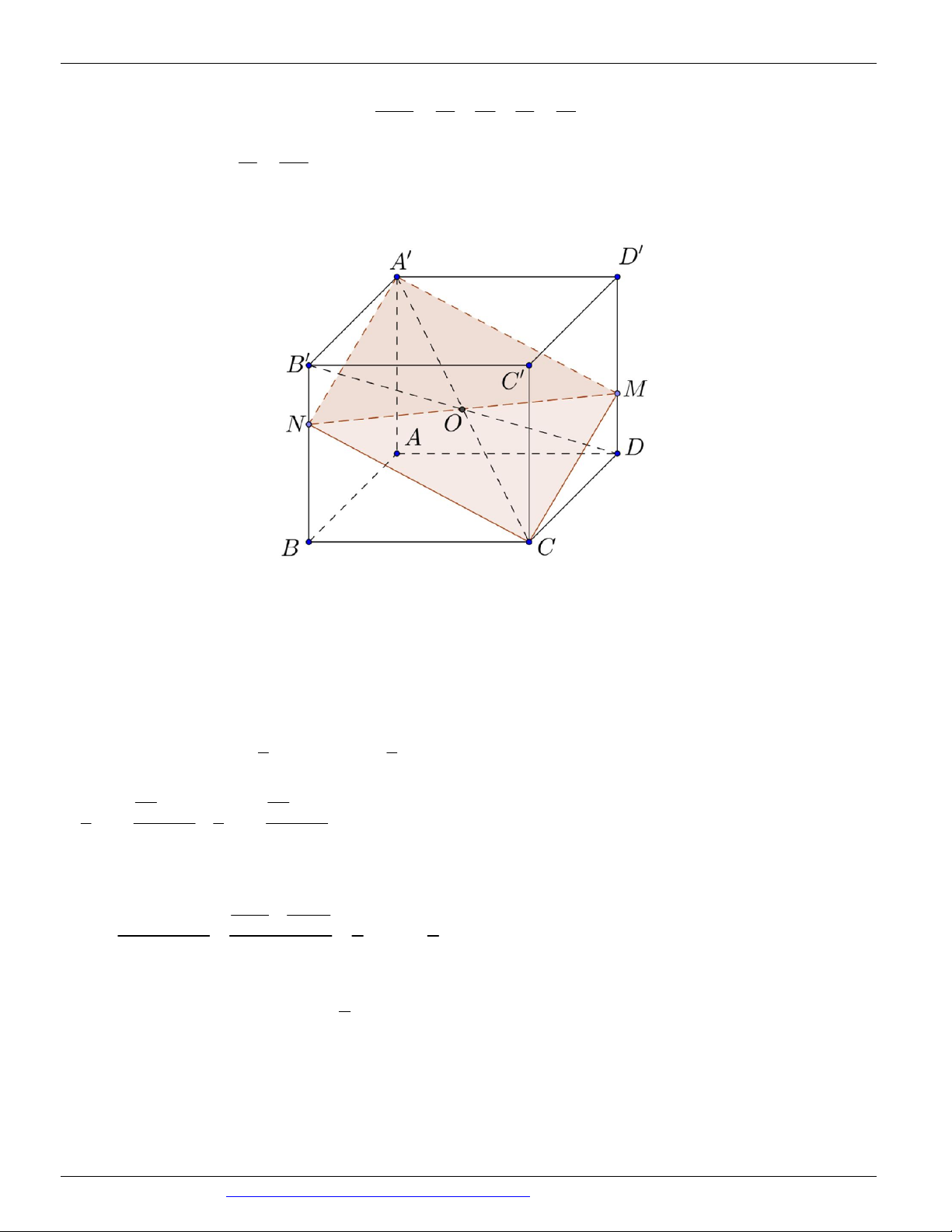
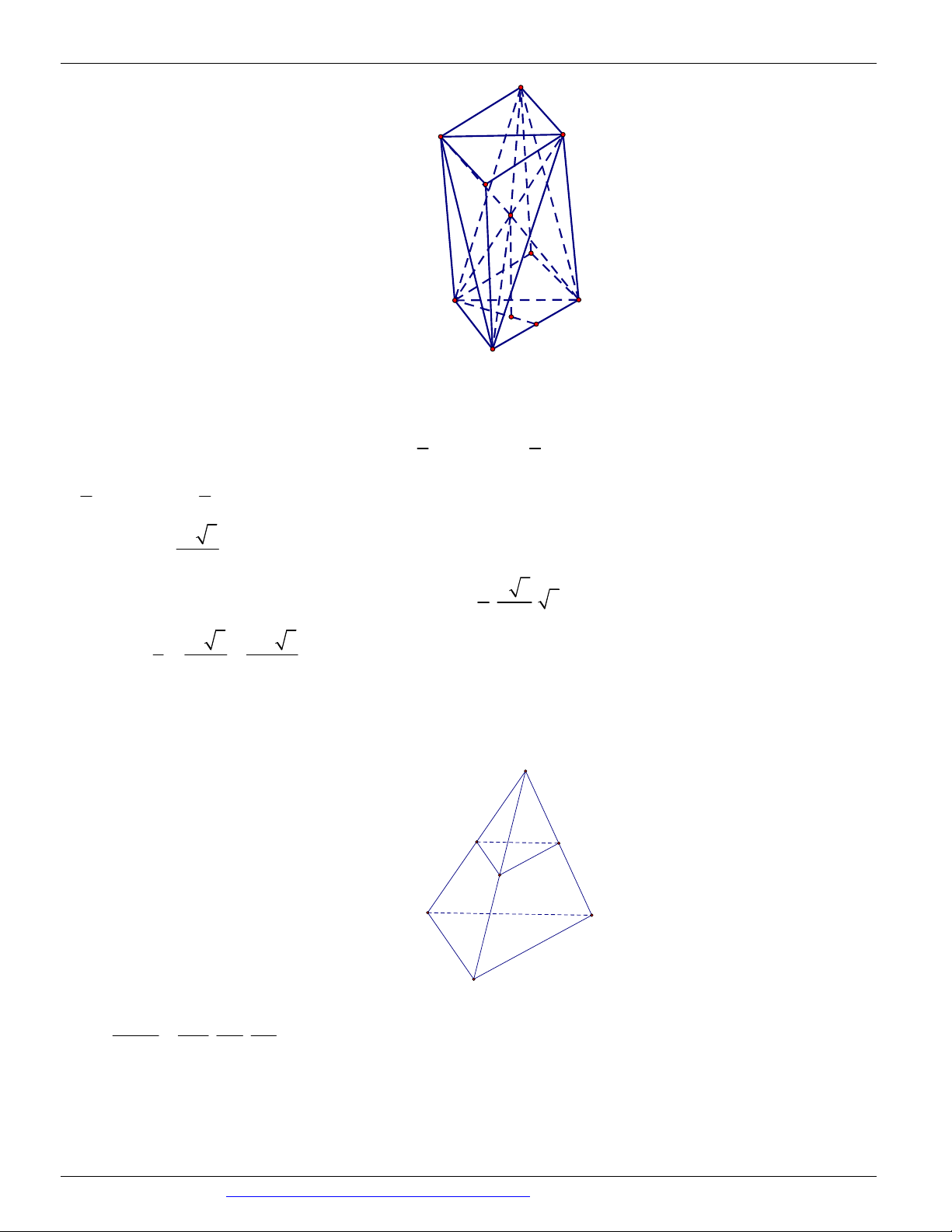
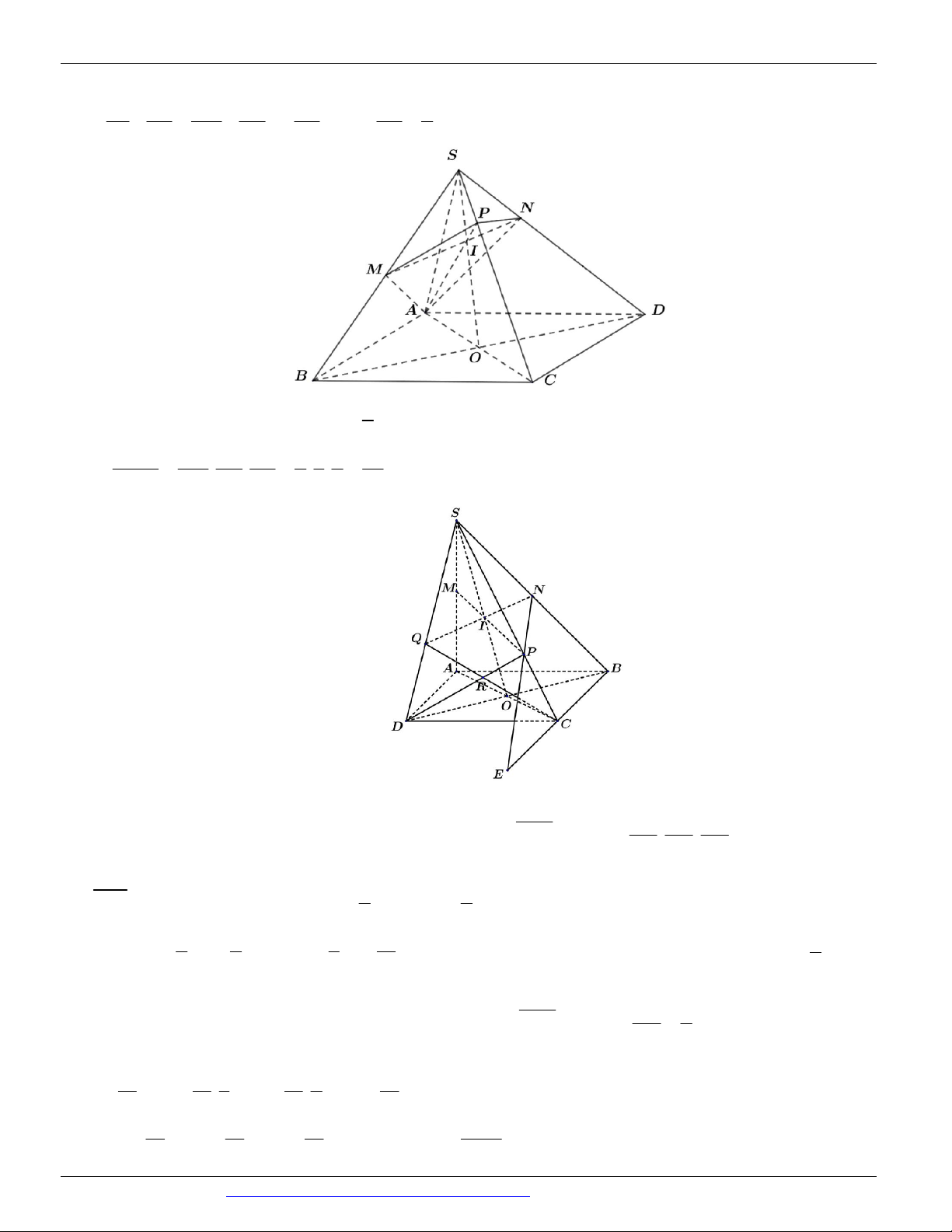
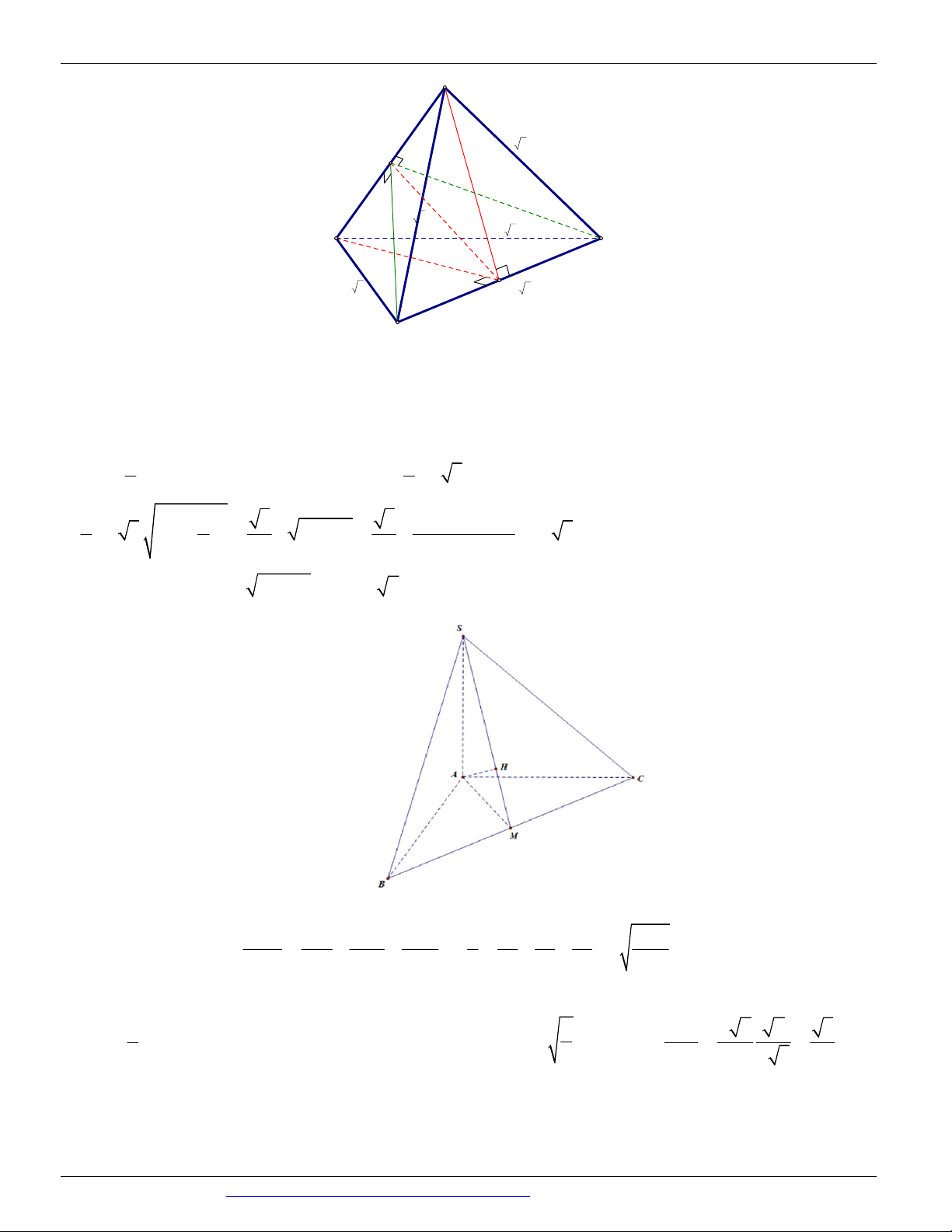
Preview text:

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 CHUYÊN
THỂ TÍCH KHỐI ĐA DIỆN ĐỀ 8 MỤC LỤC
PHẦN A. CÂU HỎI ....................................................................................................................................................... 2
Dạng 1.THỂ TÍCH KHỐI CHÓP ................................................................................................................................. 2
Dạng 1.1 Biết chiều cao và diện tích đáy ..................................................................................................................... 2
Dạng 1.2 Cạnh bên vuông góc với đáy ........................................................................................................................ 2
Dạng 1.3 Mặt bên vuông góc với đáy .......................................................................................................................... 5
Dạng 1.4 Biết hình chiếu của đỉnh lên đáy ................................................................................................................... 6
Dạng 1.5 Thể tích khối chóp đều ................................................................................................................................. 7
Dạng 1.6 Thể tích khối chóp khác ................................................................................................................................ 8
Dạng 2. THỂ TÍCH KHỐI LĂNG TRỤ ...................................................................................................................... 9
Dạng 2.1 Biết chiều cao và diện tích đáy ..................................................................................................................... 9
Dạng 2.2 Thể tích khối lăng trụ đứng......................................................................................................................... 10
Dạng 2.3 Thể tích khối lăng trụ xiên .......................................................................................................................... 12
Dạng 3. THỂ TÍCH KHỐI ĐA DIỆN KHÁC ............................................................................................................ 14
Dạng 4. TỈ SỐ THỂ TÍCH ........................................................................................................................................... 16
Dạng 4.1 Tỉ số thể tích của khối chóp ........................................................................................................................ 16
Dạng 4.2 Tỉ số thể tích các khối đa diện .................................................................................................................... 16
Dạng 4.3 Ứng dụng tỉ số thể tích để tìm thể tích ........................................................................................................ 18
Dạng 5. BÀI TOÁN THỰC TẾ VÀ BÀI TOÁN CỰC TRỊ ...................................................................................... 20
PHẦN B. LỜI GIẢI THAM KHẢO ........................................................................................................................... 23
Dạng 1.THỂ TÍCH KHỐI CHÓP ............................................................................................................................... 23
Dạng 1.1 Biết chiều cao và diện tích đáy ................................................................................................................... 23
Dạng 1.2 Cạnh bên vuông góc với đáy ...................................................................................................................... 23
Dạng 1.3 Mặt bên vuông góc với đáy ........................................................................................................................ 31
Dạng 1.4 Biết hình chiếu của đỉnh lên đáy ................................................................................................................. 36
Dạng 1.5 Thể tích khối chóp đều ............................................................................................................................... 38
Dạng 1.6 Thể tích khối chóp khác .............................................................................................................................. 43
Dạng 2. THỂ TÍCH KHỐI LĂNG TRỤ .................................................................................................................... 48
Dạng 2.1 Biết chiều cao và diện tích đáy ................................................................................................................... 48
Dạng 2.2 Thể tích khối lăng trụ đứng......................................................................................................................... 48
Dạng 2.3 Thể tích khối lăng trụ xiên .......................................................................................................................... 53
Dạng 3. THỂ TÍCH KHỐI ĐA DIỆN KHÁC ............................................................................................................ 62
Dạng 4. TỈ SỐ THỂ TÍCH ........................................................................................................................................... 68
Dạng 4.1 Tỉ số thể tích của khối chóp ........................................................................................................................ 68
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Dạng 4.2 Tỉ số thể tích các khối đa diện .................................................................................................................... 70
Dạng 4.3 Ứng dụng tỉ số thể tích để tìm thể tích ........................................................................................................ 78
Dạng 5. BÀI TOÁN THỰC TẾ VÀ BÀI TOÁN CỰC TRỊ ...................................................................................... 85 PHẦN A. CÂU HỎI
Dạng 1.THỂ TÍCH KHỐI CHÓP
Dạng 1.1 Biết chiều cao và diện tích đáy
Câu 1. (ĐỀ THAM KHẢO BGD & ĐT 2018) Thể tích của khối chóp có chiều cao bằng h và diện tích đáy bằng B là: 1 1 1 A. V Bh B. V Bh
C. V Bh D. V Bh 2 6 3
Câu 2. (Mã đề 101 BGD&ĐT NĂM 2018) Cho khối chóp có đáy là hình vuông cạnh a và chiều cao bằng
2a . Thể tích của khối chóp đã cho bằng 2 4 A. 3 4a B. 3 a C. 3 2a D. 3 a 3 3
Câu 3. (Mã đề 102 BGD&ĐT NĂM 2018) Cho khối chóp có đáy là hình vuông cạnh a và chiều cao bằng
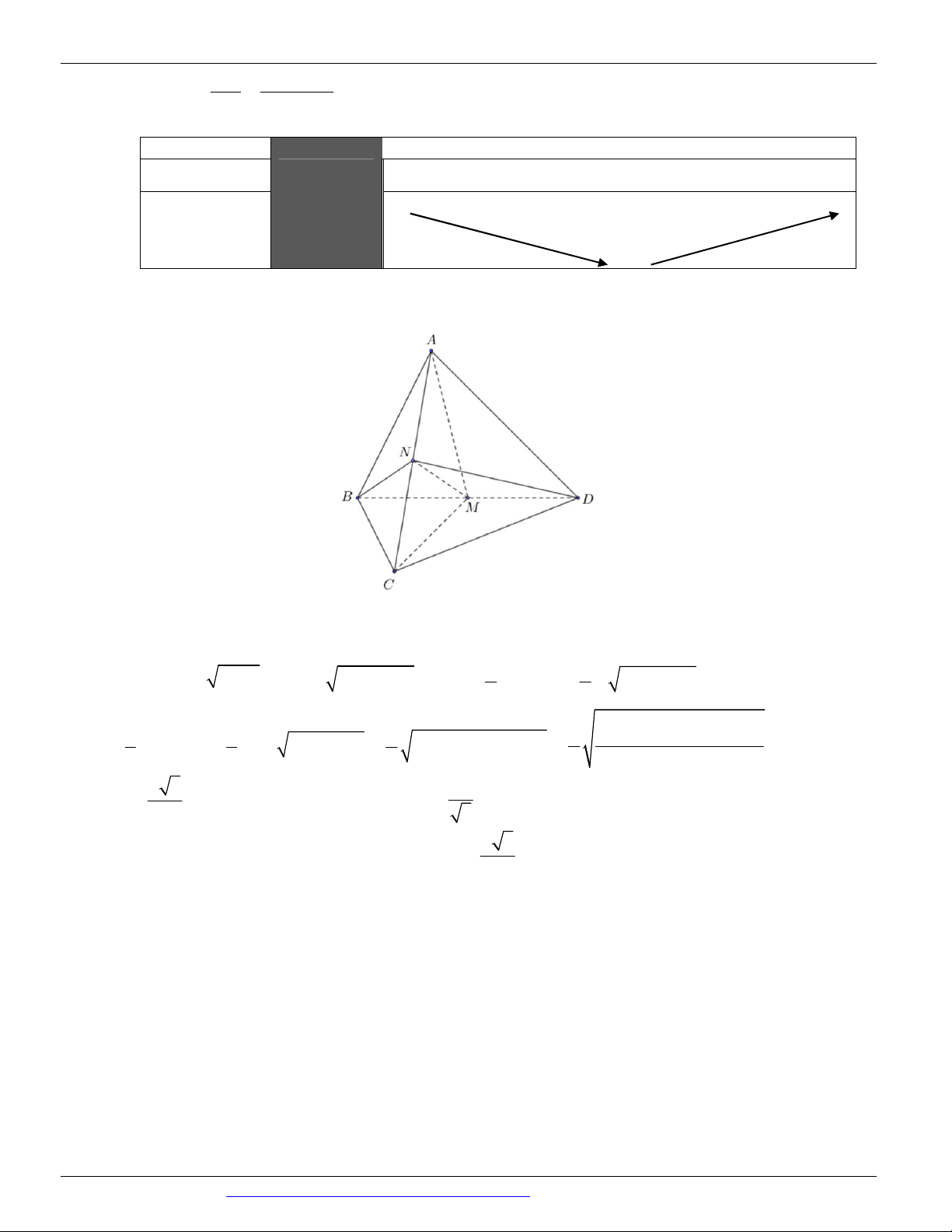
4a . Thể tích khối chóp đã cho bằng 16 4 A. 3 16a B. 3 a C. 3 4a D. 3 a 3 3
Câu 4. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình
vuông cạnh a , cạnh bên SA vuông góc với mặt phẳng đáy và SA a 2 . Tính thể tích V của khối chóp S.ABCD 3 2a 3 2a 3 2a A. V B. V C. 3
V  2a D. V  6 4 3
Dạng 1.2 Cạnh bên vuông góc với đáy
Câu 5. (MĐ 105 BGD&ĐT NĂM 2017) Cho khối chóp .
S ABC có SA vuông góc với đáy, SA  4 , AB  6
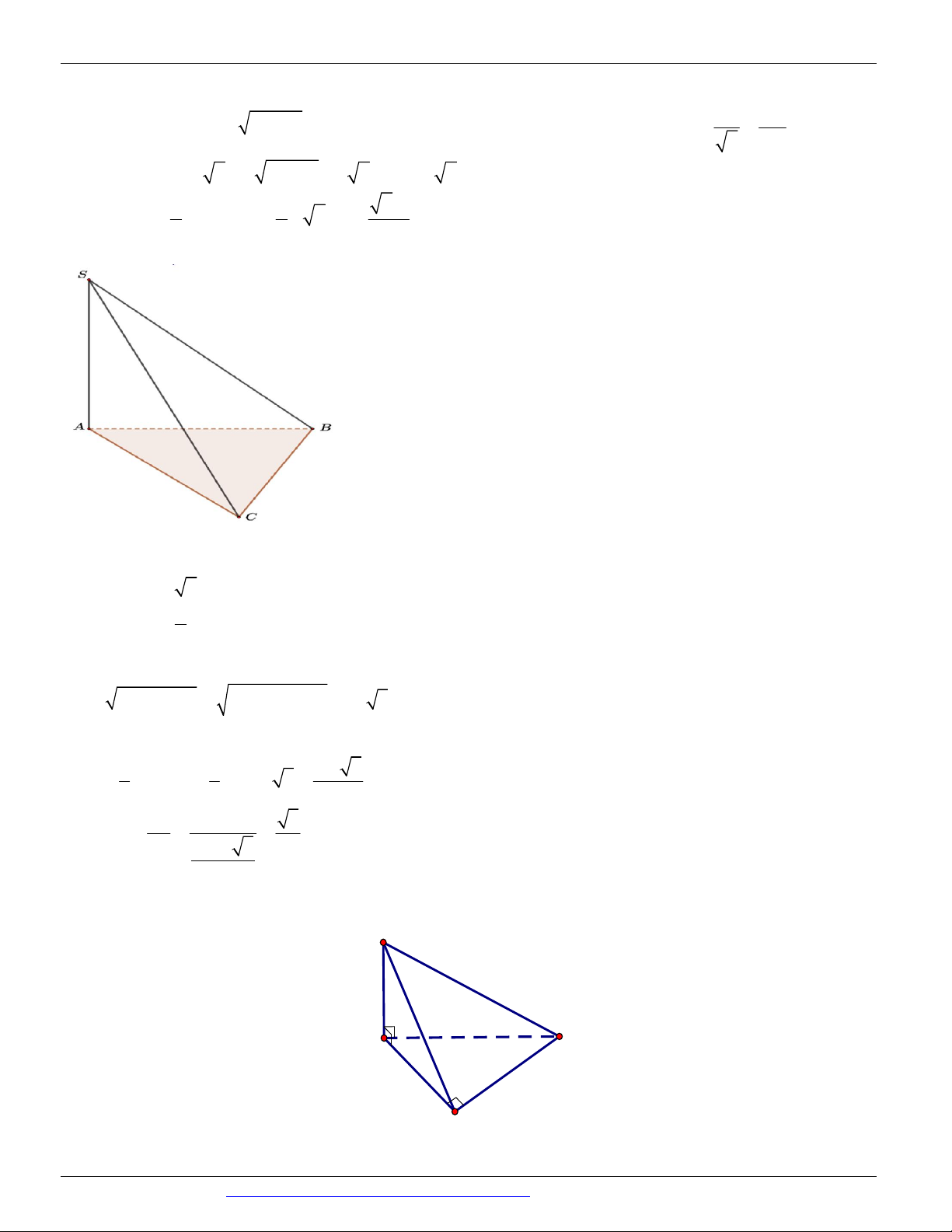
, BC  10 và CA  8 . Tính thể tích V của khối chóp . S ABC .
A. V  32
B. V  192
C. V  40 D. V  24
Câu 6. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Cho hình chóp tứ giác S.ABCD
có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với mặt phẳng đáy và SA  2a . Tính thể tích
khối chóp S.ABCD . 3 2a 3 2a 3 2a A. B. C. 3 2a D. 6 4 3
Câu 7. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Cho hình chóp S.ABC có đáy là tam giác 3 a
đều cạnh a , cạnh bên SA vuông góc với đáy và thể tích của khối chóp đó bằng
. Tính cạnh bên SA . 4
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 a 3 a 3 A. . B. . C. a 3. D. 2a 3. 2 3
Câu 8. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Cho hình chóp S.ABC có đáy ABC là
tam giác đều cạnh a . Biết SA   ABC và SA a 3 . Tính thể tích khối chóp S.ABC . a 3 a 3 a 3 3a A. B. C. D. 4 2 4 4
Câu 9. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a
, SA vuông góc với mặt đáy, SD tạo với mặt phẳng SAB một góc bằng 30 . Tính thể tích V của khối
chóp S.ABCD . 3 6a 3 3a 3 6a A. 3
V  3a B. V C. V D. V  3 3 18
Câu 10. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hình chóp S.ABC có đáy là tam giác
đều cạnh a . Cạnh bên SC vuông góc với mặt phẳng  ABC , SC a . Thể tích khối chóp S.ABC bằng 3 a 3 3 a 2 3 a 3 3 a 3 A. B. C. D. 3 12 9 12
Câu 11. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho tứ diện ABCD có AD vuông góc
với mặt phẳng  ABC  biết đáy ABC là tam giác vuông tại B và AD  10, AB  10, BC  24 . Tính thể tích của tứ diện ABCD . 1300 A. V  1200 B. V  960 C. V  400 D. V  3
Câu 12. (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hình chóp S.ABC có
cạnh bên SA vuông góc với mặt phẳng đáy  ABC  . Biết SA a , tam giác ABC là tam giác vuông cân tại
A , AB  2a . Tính theo a thể tích V của khối chóp S.ABC . 3 a 3 a 3 2a A. V  . B. V  . C. V  . D. 3 V  2a . 6 2 3
Câu 13. (CHUYÊN KHTN NĂM 2018-2019 LẦN 01) Cho khối chóp S.ABC có đáy ABC là tam giác
vuông tại B , AB a, AC  2a, SA   ABC  và SA a . Thể tích của khối chóp đã cho bằng 3 a 3 3 a 3 3 a 3 2a A. . B. . C. . D. . 3 6 3 3
Câu 14. (MĐ 105 BGD&ĐT NĂM 2017) Cho khối chóp .
S ABCD có đáy là hình vuông cạnh a , SA vuông a 2
góc với đáy và khoảng cách từ A đến mặt phẳng SBC  bằng
. Tính thể tích của khối chóp đã cho. 2 3 a 3 3a 3 a A. B. 3 a C. D. 3 9 2
Câu 15. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật,
AB a , AD a 3 , SA vuông góc với mặt phẳng đáy và mặt phẳng  SBC  tạo với đáy một góc 60o . Tính
thể tích V của khối chóp S.ABCD . 3 3a 3 a A. 3
V  3a B. V C. 3 V a D. V 3 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 16. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA
vuông góc với đáy, SC tạo với mặt phẳng SAB một góc 0
30 . Tính thể tích khối chóp S.ABCD 3 2a 3 2a 3 6a A. B. C. D. 3 2a 3 3 3
Câu 17. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hình chóp S.ABC có đáy là tam
giác vuông cân tại C, cạnh bên SA vuông góc với mặt đáy, biết AB  4a, SB  6a. Thể tích khối chóp S.ABC 3 a là V . Tỷ số là 3V 5 5 5 3 5 A. B. C. D. 80 40 20 80
Câu 18. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho hình chóp tam giác S.ABC có 
đáy ABC là tam giác vuông tại B , AB a , ACB  60 , cạnh bên SA vuông góc với mặt đáy và SB hợp
với mặt đáy một góc 45 . Tính thể tích V của khối chóp S.ABC . 3 a 3 3 a 3 3 a 3 a 3 A. V B. V C. V D. V  18 12 2 3 9
Câu 19. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Cho hình chóp S.ABCD có đáy
ABCD là hình chữ nhật AB a và AD  2a , cạnh bên SA vuông góc với đáy. Tính thể tích V của khối chóp S.ABCD 0
biết góc giữa hai mặt phẳng SBD và  ABCD bằng 60 . 3 a 15 3 a 15 3 4a 15 3 a 15 A. V B. V C. V D. V  15 6 15 3
Câu 20. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Cho hình chóp S.ABC có AC a  0
, BC  2a , ACB  120 , cạnh bên SA vuông góc với đáy. Đường thẳng SC tạo với mặt phẳng  SAB góc 0
30 . Tính thể tích của khối chóp S.ABC 3 a 105 3 a 105 3 a 105 3 a 105 A. . B. . C. . D. . 28 21 42 7
Câu 21. (TT HOÀNG HOA THÁM - 2018-2019) Cho hình chóp S.ABCD có AB  5 3, BC  3 3 , góc  
BAD BCD  90 , SA  9 và SA vuông góc với đáy. Biết thể tích khối chóp S.ABCD bằng 66 3 , tính
cotang của góc giữa mặt phẳng SBD và mặt đáy. S A D B C
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 20 273 91 3 273 9 91 Câu 22. A. . B. . C. . D. 819 9 20 9
Câu 23. (THPT YÊN KHÁNH - NINH BÌNH - 2018 - 2019) Cho hình chóp S.ABC có đáy ABC là tam
giác đều, SA   ABC . Mặt phẳng SBC cách A một khoảng bằng a và hợp với mặt phẳng  ABC  góc 0
30 . Thể tích của khối chóp S.ABC bằng 3 8a 3 8a 3 3a 3 4a A. . B. . C. . D. . 9 3 12 9
Dạng 1.3 Mặt bên vuông góc với đáy
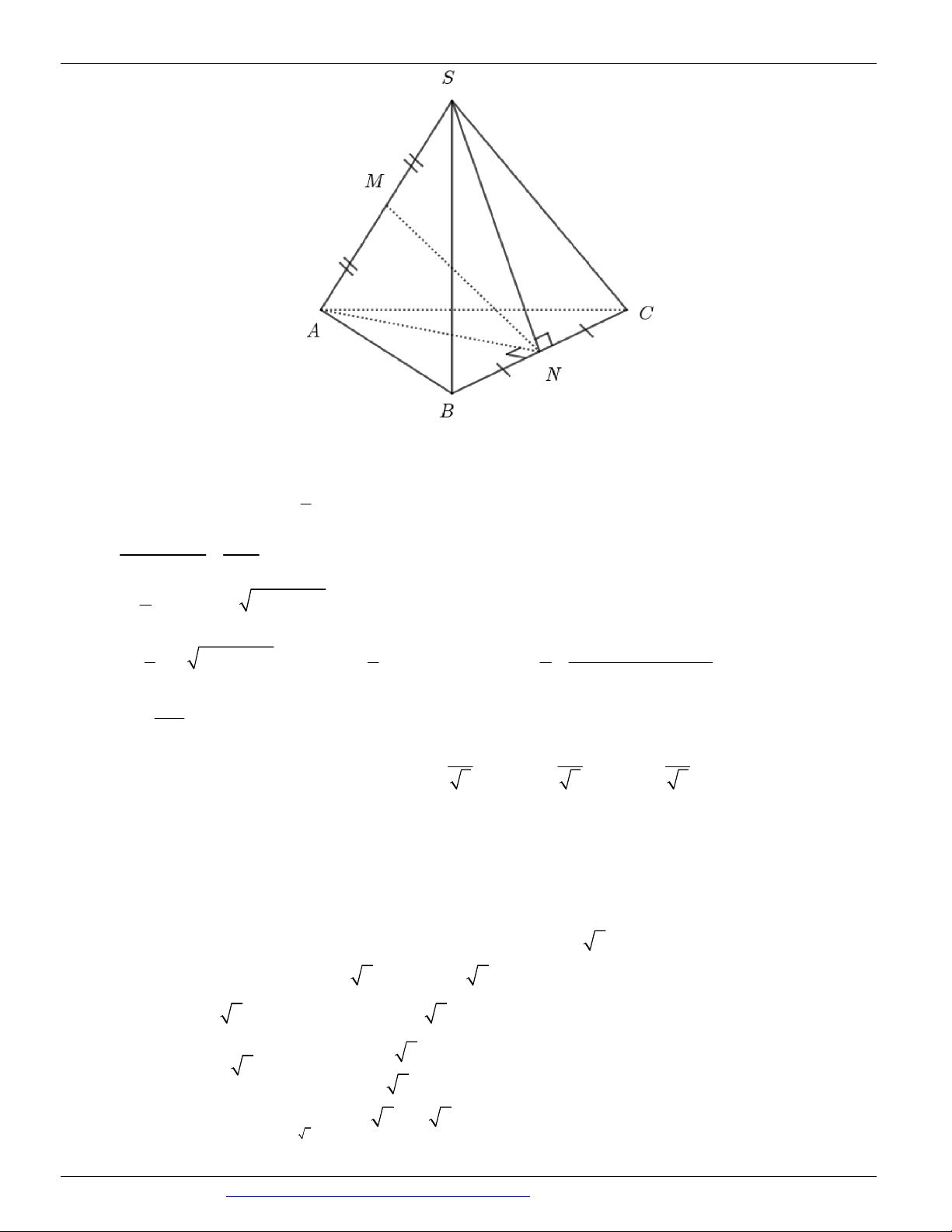
Câu 24. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hình chóp S.ABCD có đáy ABCD là
hình vuông cạnh a , mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy; góc giữa
SC và mặt phẳng đáy bằng 45o . Tính thể tích khối chóp S.ABCD bằng: 3 a 3 3 a 3 3 a 5 3 a 5 A. B. C. D. 12 9 24 6
Câu 25. (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho hình chóp S.ABCD có
đáy ABCD là hình chữ nhật, tam giác SAB là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với
đáy. Mặt phẳng SCD tạo với đáy góc 30 . Thể tích khối chóp S.ABCD là? 3 a 3 3 a 3 3 a 3 3 5a 3 A. B. C. D. 4 2 36 36
Câu 26. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Cho hình chóp S.ABC có đáy
ABC là tam giác vuông cân tại B và AB  2a . Tam giác SAB đều và nằm trong mặt phẳng vuông góc với
đáy. Tính thể tích V của khối chóp S.ABC 3 a 3 3 a 3 3 a 3 3 2a 3 A. V B. V C. V D. V  4 3 12 3
Câu 27. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Cho hình chóp tứ giác S.ABCD
có đáy ABCD là hình vuông cạnh bằng 2a . Tam giác SAD cân tại S và mặt bên SAD vuông góc với 4
mặt phẳng đáy. Biết thể tích khối chóp S.ABCD bằng 3
a . Tính khoảng cách h từ B đến mặt phẳng SCD 3 . 4 3 2 5 6 A. h a B. h a C. h a D. h a 3 2 5 3
Câu 28. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hình chóp tứ giác S.ABCD có đáy là hình vuông
cạnh bằng 2a . Tam giác SAD cân tại S và mặt bên SAD vuông góc với mặt phẳng đáy. Biết thể tích 4
khối chóp S.ABCD bằng 3
a . Tính khoảng cách h từ B đến mặt phẳng SCD 3 3 2 4 8 A. h a B. h a C. h a D. h a 4 3 3 3
Câu 29. (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Cho khối chóp S.ABCD có đáy là hình vuông
cạnh a 2 , tam giác SAC vuông tại S và nằm trong mặt phẳng vuông góc với đáy, cạnh bên SA tạo với đáy
góc 60 . Tính thể tích V của khối chóp S.ABCD .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 3 a 3 3 a 3 3 a 6 3 a 2 A. V  . B. V  . C. V  . D. V  . 12 3 12 12
Câu 30. (KTNL GIA BÌNH NĂM 2018-2019) Cho hình chóp S.ABCD có đáy ABCD là hình vuông và
tam giác SAB đều nằm trong mặt phẳng vuông góc với đáy. Biết khoảng cách giữa hai đường thẳng SA và
BD bằng 21 . Hãy cho biết cạnh đáy bằng bao nhiêu? A. 21 B. 21 C. 7 3 D. 7
Câu 31. (THPT MINH KHAI HÀ TĨNH NĂM 2018-2019) Cho hình chóp S.ABCD có đáy ABCD là 1
hình thang vuông tại A và B , BC
AD a . Tam giác SAB đều và nằm trong mặt phẳng vuông góc với 2 15
đáy, góc giữa SC và mặt phẳng  ABCD bằng  sao cho tan 
. Tính thể tích khối chóp S.ACD 5 theo a . 3 a 3 a 3 a 2 3 a 3 A. V  . B. V  . C. V  . D. V  . S . ACD 2 S . ACD 3 S . ACD 6 S . ACD 6
Câu 32. (THPT GANG THÉP THÁI NGUYÊN NĂM 2018-2019) Cho hình chóp S. ABCD có đáy là hình
chữ nhật; AB a; AD  2a . Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa
đường thẳng SC và mp  ABCD bằng 45 . Gọi M là trung điểm của SD . Tính theo a khoảng cách d từ
điểm M đến SAC  . a 1513 2a 1315 a 1315 2a 1513 A. d  . B. d  . C. d  . D. d  . 89 89 89 89
Dạng 1.4 Biết hình chiếu của đỉnh lên đáy
Câu 33. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hình chóp S.ABC có đáy ABC là
tam giác vuông tại A . Hình chiếu của S lên mặt phẳng  ABC là trung điểm H của BC , AB a ,
AC a 3 , SB a 2 . Thể tích của khối chóp S.ABC bằng 3 a 3 3 a 6 3 a 3 3 a 6 A. . B. . C. . D. . 2 2 6 6
Câu 34. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019) Cho hình chóp S.ABCD có đáy ABCD
là hình chữ nhật, mặt bên SAD là tam giác vuông tại S . Hình chiếu vuông góc của S trên mặt phẳng đáy là
điểm H thuộc cạnh AD sao cho HA  3HD . Biết rằng SA  2a 3 và SC tạo với đáy một góc bằng 30 .
Tính theo a thể tích V của khối chóp S.ABCD . 3 8 6a 3 8 6a A. 3
V  8 6a . B. V  . C. 3
V  8 2a . D. V  . 3 9
Câu 35. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hình chóp S.ABCD có đáy là hình thang
vuông tại A và D , AB AD a , CD  2a . Hình chiếu của đỉnh S lên mặt  ABCD trùng với trung điểm 3 a
của BD . Biết thể tích tứ diện SBCD bằng
. Khoảng cách từ đỉnh A đến mặt phẳng SBC  là? 6 a 3 a 2 a 3 a 6 A. B. C. D. 2 6 6 4
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
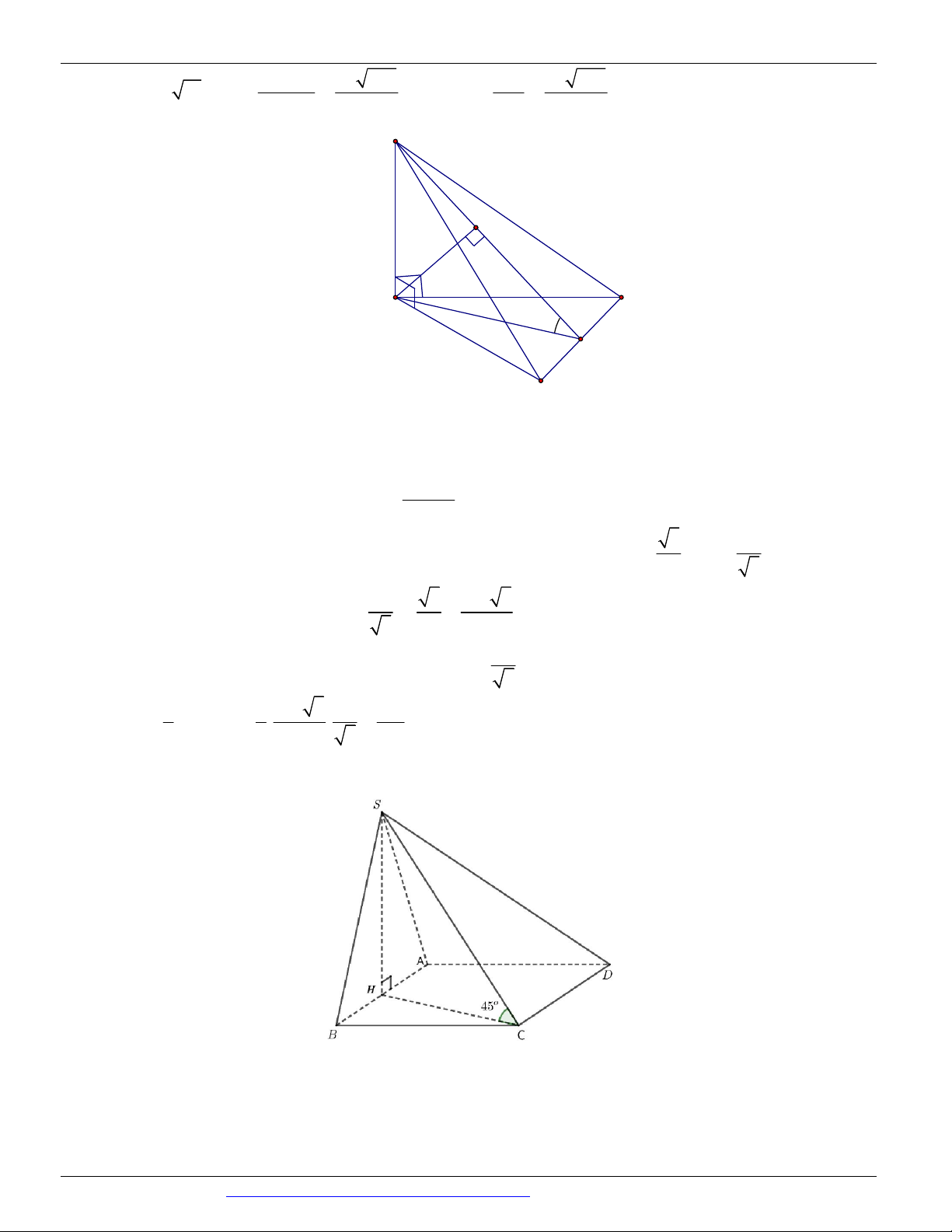
Câu 36. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Hình chóp S.ABCD có đáy
ABCD là vuông cạnh a , hình chiếu vuông góc của S trên mặt phẳng  ABCD trùng với trung điểm của
cạnh AD; gọi M là trung điểm của CD; cạnh bên SB hợp với đáy góc 60 . Tính theo a thể tích của khối chóp S.ABM . 3 a 15 3 a 15 3 a 15 3 a 15 A. B. C. D. 3 6 4 12
Câu 37. (HSG BẮC NINH NĂM 2018-2019) Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a 2
. Hình chiếu vuông góc của S trên đáy là điểm H trên cạnh AC sao cho AH
AC ; mặt phẳng SBC  3
tạo với đáy một góc 60o . Thể tích khối chóp S.ABC là? 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 12 48 36 24
Dạng 1.5 Thể tích khối chóp đều
Câu 38. (CHUYÊN HÙNG VƯƠNG GIA LAI NĂM 2018-2019 LẦN 01) Thể tích của khối chóp tứ giác
đều có tất cả các cạnh bằng a là 3 a 2 3 a 2 3 a 2 A. . B. . C. 3 a . D. . 6 3 2
Câu 39. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho khối chóp tứ giác đều có tất cả các cạnh
bằng 2a . Thể tích của khối chóp đã cho bằng 3 2 2a 3 8a 3 8 2a 3 4 2a A. B. C. D. 3 3 3 3
Câu 40. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho khối chóp tứ giác đều có cạnh đáy bằng a, cạnh bên gấp
hai lần cạnh đáy. Tính thể tích V của khối chóp đã cho. 3 2a 3 14a 3 2a 3 14a A. V B. V C. V D. V  2 2 6 6
Câu 41. (LIÊN TRƯỜNG THPT TP VINH NGHỆ AN NĂM 2018-2019) Cho khối chóp tứ giác đều có
cạnh đáy bằng 2a cạnh bên bằng a 5 . Thể tích của khối chóp đã cho bằng 3 4 5a 3 4 3a A. 3 4 5a . B. 3 4 3a . C. . D. . 3 3
Câu 42. (MĐ 104 BGD&DT NĂM 2017) Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh
bên bằng 2a . Tính thể tích V của khối chóp S.ABC . 3 11a 3 11a 3 13a 3 11a A. V B. V C. V D. V  6 4 12 12
Câu 43. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho một hình chóp tam giác đều có
cạnh đáy bằng a , góc giữa cạnh bên và mặt phẳng đáy bằng 0
45 . Thể tích khối chóp đó là 3 a 3 3 a 3 a 3 a 3 A. . B. . C. . D. . 12 12 36 36
Câu 44. (TRƯỜNG THPT LƯƠNG TÀI SỐ 2 NĂM 2018-2019) Cho hình chóp tứ giác đều S.ABCD có
cạnh đáy bằng a 6 , góc giữa cạnh bên và mặt đáy bằng 0
60 . Tính thể tích V của khối chóp S.ABC? A. 3 V  9a B. 3 V  2a C. 3 V  3a D. 3 V  6a
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 45. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Cho hình chóp tam giác đều S.ABC
có độ dài cạnh đáy bằng a , góc hợp bởi cạnh bên và mặt đáy bằng 60 . Thể tích của khối chóp đã cho bằng 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 12 3 6 4
Câu 46. (CHUYÊN TRẦN PHÚ HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho khối chóp tứ giác đều S.ABCD 0
có cạnh đáy bằng a , góc giữa mặt bên và mặt đáy bằng 60 . Thể tích V của khối chóp S.ABCD bằng 3 a 3 3 a 2 3 a 3 3 a 2 A. V B. V C. V D. V  2 2 6 6
Câu 47. (HSG BẮC NINH NĂM 2018-2019) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a ,
tâm của đáy là O . Gọi M và N lần lượt là trung điểm của SA và BC . Biết góc giữa đường thẳng MN và
mặt phẳng  ABCD bằng 0
60 . Tính thể tích khối chóp S.ABCD . 3 a 10 3 a 30 3 a 30 3 a 10 A. B. C. D. 6 2 6 3
Câu 48. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho tứ diện ABCD có các cạnh AB , AC và D A đôi
một vuông góc với nhau; AB  6a , AC  7a và AD  4a . Gọi M , N , P tương ứng là trung điểm các cạnh
BC , CD , DB . Tính thể tích V của tứ diện AMNP . 28 7 A. 3
V  7a B. 3
V  14a C. 3 V a D. 3 V a 3 2
Dạng 1.6 Thể tích khối chóp khác
Câu 49. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Cho hình chóp S.ABCD có đáy là hình
bình hành. Gọi V là thể tích của khối chóp S.ABCD và M , N , P lần lượt là trung điểm của các đoạn thẳng
SC , SD , AD . Thể tích của khối tứ diện AMNP bằng 1 1 1 1 A. V . B. V . C. V . D. V . 8 4 16 32
Câu 50. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Cho tứ diện ABCD có các cạnh
AB, AC, AD đôi một vuông góc nhau; AB  6a , AC  7a và AD  4a . Gọi M , N , P tương ứng là trung
điểm các cạnh BC, CD, DB . Tính thể tích V của khối tứ diện AMNP . 3 28a 3 7a A. 3 V  7a . B. V  . C. V  . D. 3 V  14a . 3 2
Câu 51. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho hình chóp S.ABC có
SA SB SC  6 , AC  4 ; ABC là tam giác vuông cân tại B . Tính thể tích V của khối chóp S.ABC . 16 7 16 2 A. V  16 7 B. V C. V  16 2 D. V  3 3
Câu 52. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Cho tứ diện ABCD có các cạnh A , B AC
và AD đôi một vuông góc với nhau. Gọi G ,G ,G và G lần lượt là trọng tâm các tam giác ABC, AB , D ACD 1 2 3 4
và BCD . Biết AB  6a, AC  9a , AD  12a . Tính theo a thể tích khối tứ diện G G G G . 1 2 3 4 A. 3 4a . B. 3 a . C. 3 108a . D. 3 36a .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
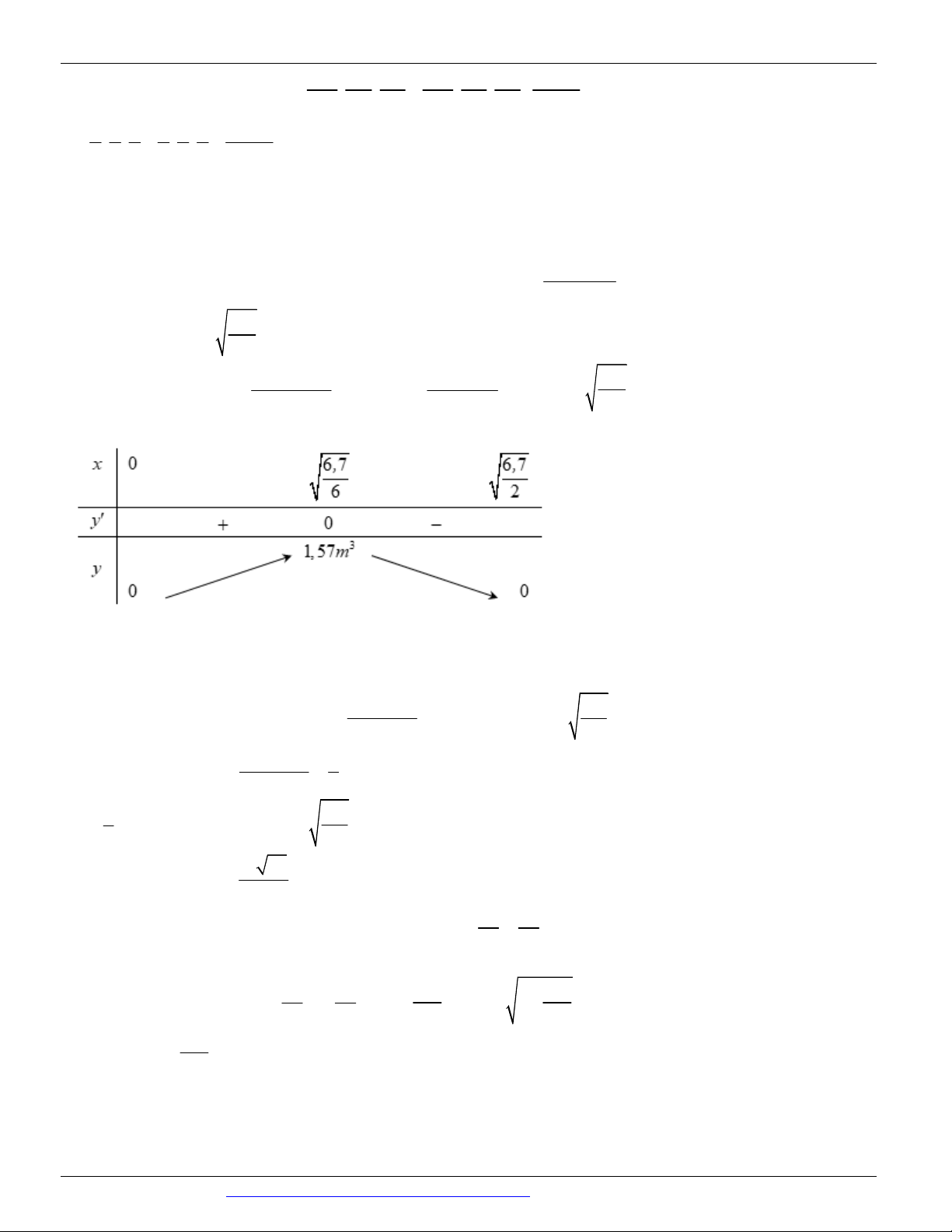
Câu 53. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019) Cho hình chóp S.ABC có đáy là tam   giác đều cạnh .
a SAB SCB  90 .
 Gọi M là trung điểm của S .
A Khoảng cách từ A đến mặt phẳng (MBC) 6a bằng
. Tính thể tích V của khối chóp S.AB . C 7 3 5 3a 3 5 3a 3 4 3a 3 7 3a A. V  . B. V  . C. V  . D. V  . 12 6 3 12
Câu 54. (THPT QUỲNH LƯU 3 NGHỆ AN NĂM 2018-2019) Cho hình chóp S.ABC biết rằng
SA SB SC a ,  ASB  120 ,  BSC  60 và 
ASC  90 . Thể tích khối chóp S.ABC là 3 a 2 3 a 2 3 a 3 3 a 3 A. . B. . C. . D. . 12 6 4 8
Câu 55. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Cho hình chóp S.ABC có đáy 6 15
ABC là tam giác đều cạnh 1, biết khoảng cách từ A đến SBC  là
, từ B đến  SCA là , từ C đến 4 10 30 SAB là
và hình chiếu vuông góc của S xuống đáy nằm trong tam giác ABC . Tính thể tích khối chóp 20 V . S.ABC 1 1 1 1 A. B. C. D. 36 48 12 24
Câu 56. (CỤM LIÊN TRƯỜNG HẢI PHÒNG NĂM 2018-2019 LẦN 01) Cho hình chóp S.ABC có đáy  
là tam giác đều cạnh a . 0
SAB SCB  90 . Gọi M là trung điểm của SA . Khoảng cách từ A đến mặt phẳng  6a MBC  bằng
. Tính thể tích V của khối chóp S.ABC . 7 3 5 3a 3 5 3a 3 4 3a 3 7 3a A. V B. V C. V D. V  12 6 3 12
Câu 57. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Cho hình chóp S.ABC có các cạnh
SA BC  3; SB AC  4 ; SC AB  2 5 . Tính thể tích khối chóp S.ABC . 390 390 390 390 A. B. C. D. 12 4 6 8
Dạng 2. THỂ TÍCH KHỐI LĂNG TRỤ
Dạng 2.1 Biết chiều cao và diện tích đáy
Câu 58. (Mã đề 101 - BGD - 2019) Thể tích khối lăng trụ có diện tích đáy B và có chiều cao h là 4 1 A. Bh . B. Bh . C. Bh . D. 3Bh . 3 3
Câu 59. (MĐ 103 BGD&ĐT NĂM 2017-2018) Cho khối lăng trụ có đáy là hình vuông cạnh a và chiều cao
bằng 4a . Thể tích của khối lăng trụ đã cho bằng 16 4 A. 3 16a B. 3 4a C. 3 a D. 3 a 3 3
Câu 60. (Mã 103 - BGD - 2019) Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là: 1 4 A. Bh . B. Bh . C. Bh . D. 3Bh . 3 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 61. (Mã đề 104 BGD&ĐT NĂM 2018) Cho khối lăng trụ có đáy là hình vuông cạnh a và chiều cao
bằng 2a . Thể tích của khối lăng trụ đã cho bằng 2 4 A. 3 a B. 3 a C. 3 2a D. 3 4a 3 3
Câu 62. (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho khối lăng trụ có diện tích đáy bằng 2 a
3 , khoảng cách giữa hai đáy của lăng trụ bằng a 6 . Tính thể tích V của khối lăng trụ 3 a 2 3 3a 2 A. 3 V  3a 2 B. 3 V a 2 C. V D. V 3 4
Dạng 2.2 Thể tích khối lăng trụ đứng
Câu 63. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Thể tích của khối lập phương cạnh 2a bằng A. 3 8a B. 3 2a C. 3 a D. 3 6a
Câu 64. (Mã đề 104 - BGD - 2019) Cho khối lăng trụ đứng ABC.AB C
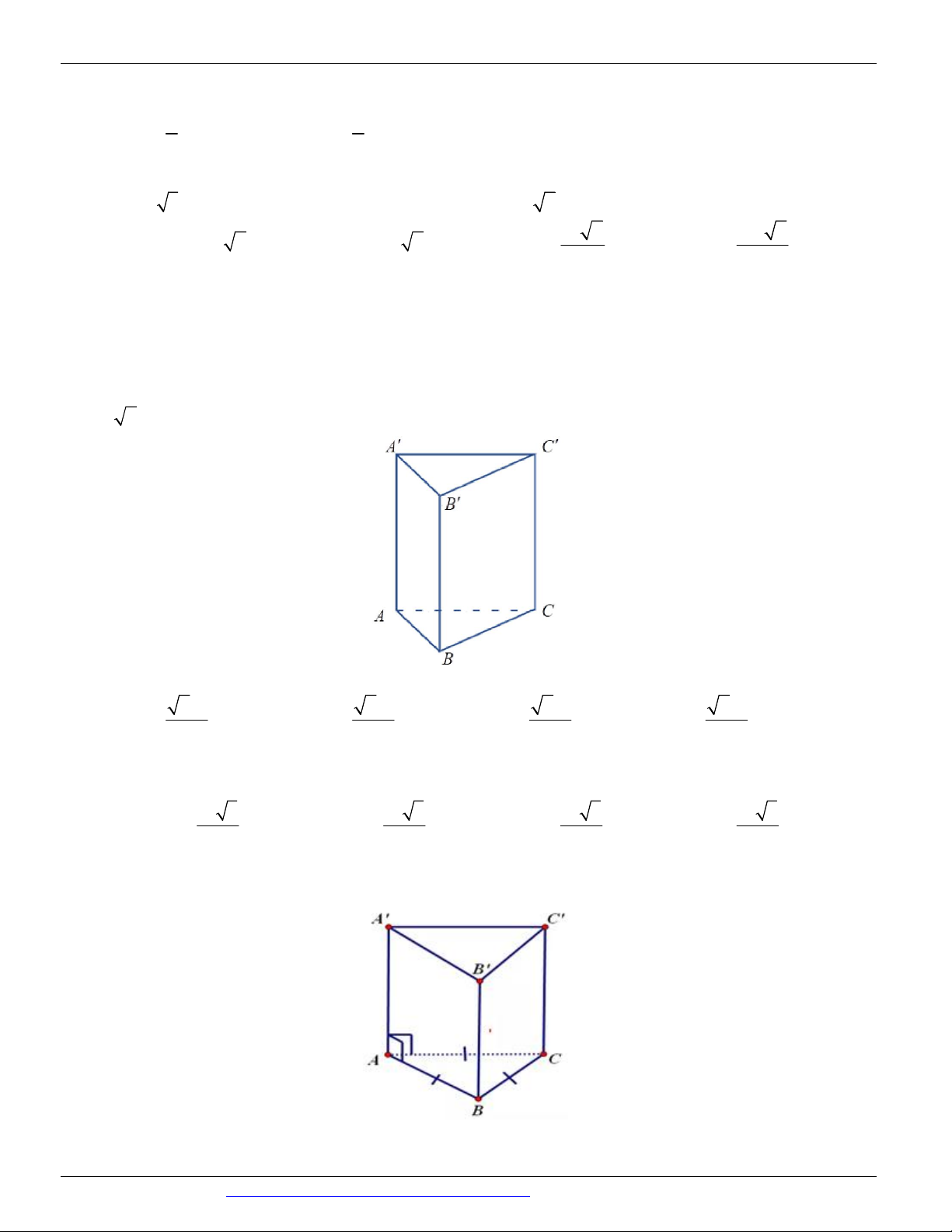
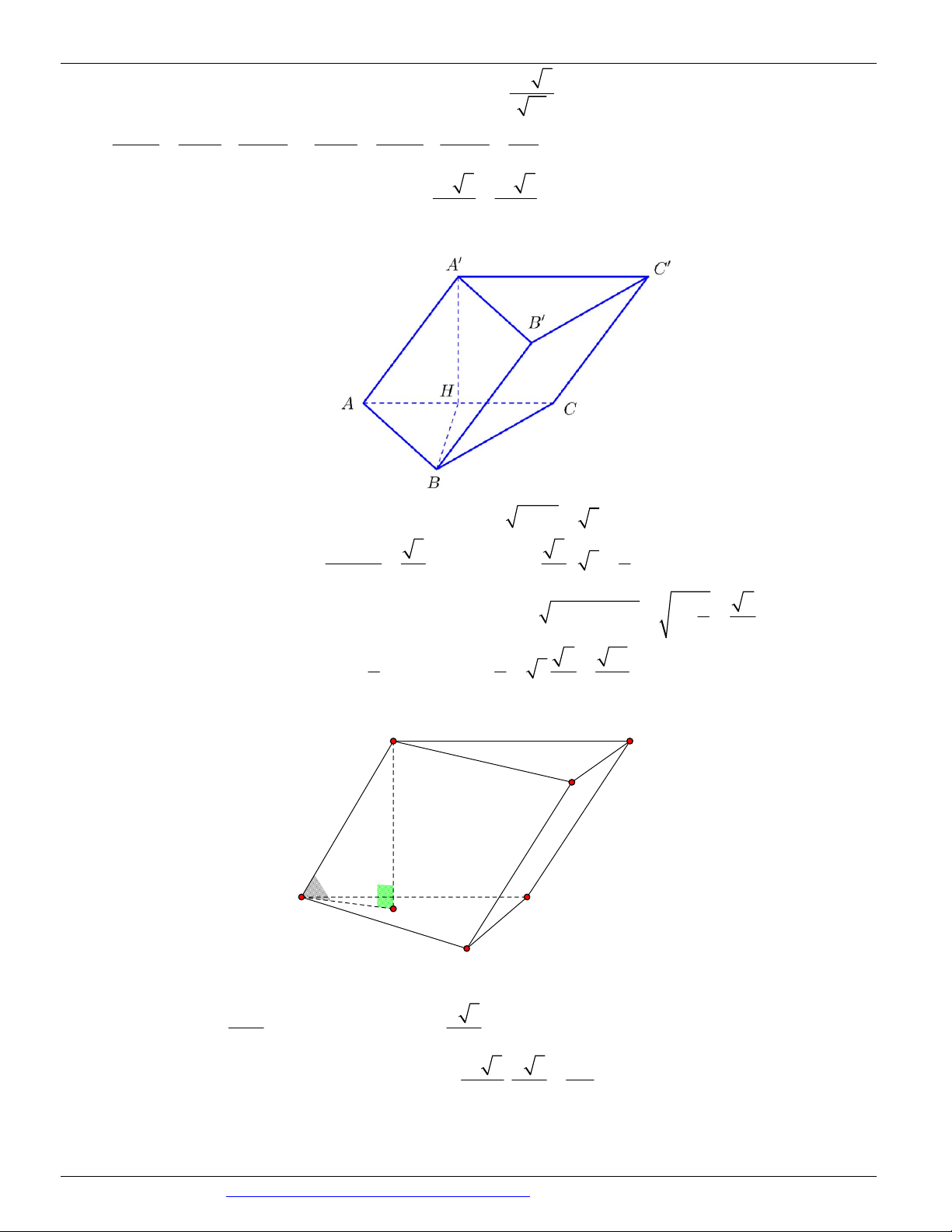
  có đáy là tam giác đều cạnh a và AA ' 
2a (minh họa như hình vẽ bên dưới).
Thể tích của khối lăng trụ đã cho bằng 3 6a 3 6a 3 6a 3 6a A. . B. . C. . D. . 2 4 6 12
Câu 65. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Thể tích của khối lăng trụ tam giác đều có tất cả các
cạnh bằng a . 3 a 3 3 a 3 3 a 3 3 a 3 A. V B. V C. V D. V  12 2 4 6
Câu 66. (Mã 102 - BGD - 2019) Cho khối lăng trụ đứng ABC.AB C
  có đáy là tam giác đều cạnh a và
AA  2a (minh họa như hình vẽ bên).
Thể tích của khối lăng trụ đã cho bằng
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 3 3a 3 3a 3 3a A. . B. . C. 3 3a . D. . 2 6 3
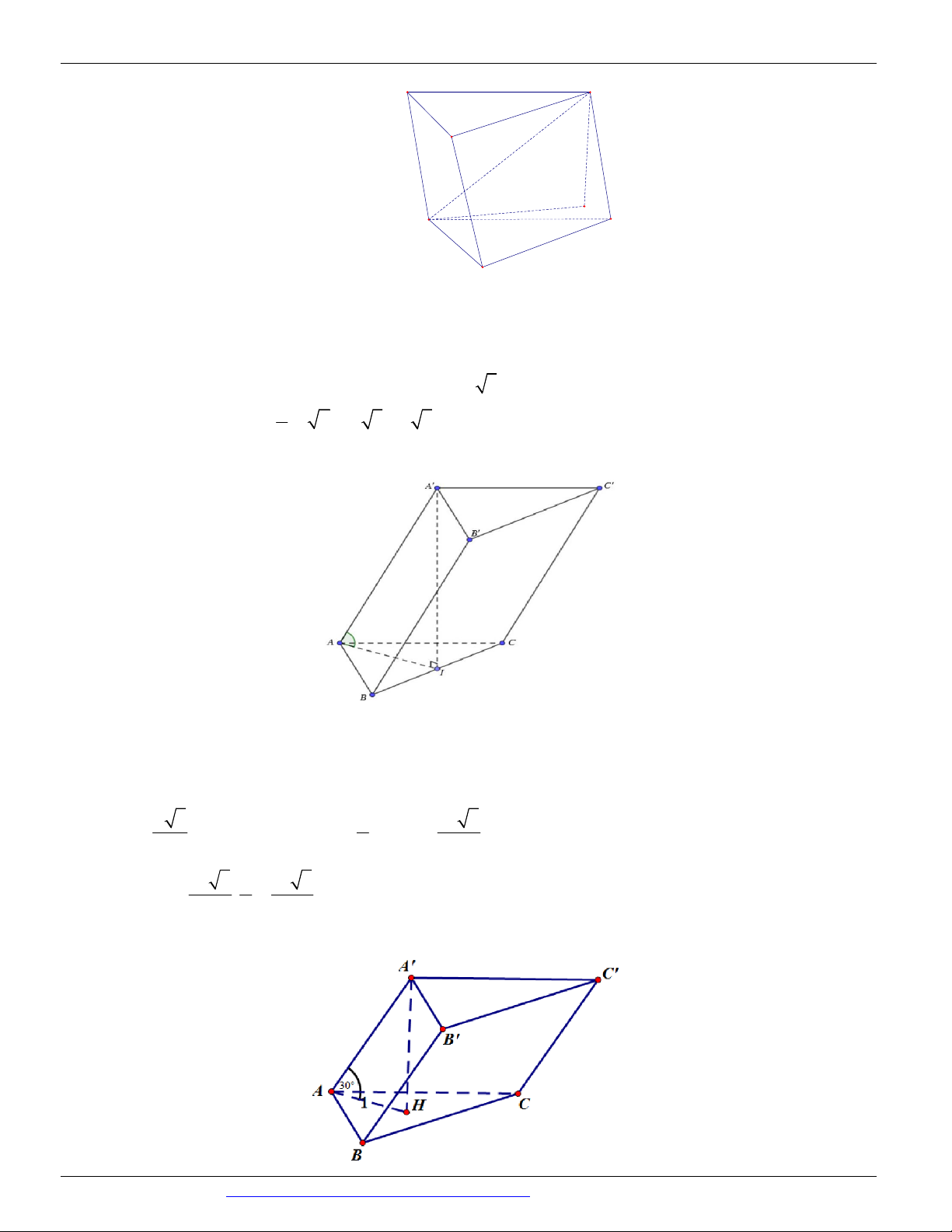
Câu 67. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho khối lăng trụ đứng AB . C A BC
  có BB  a , đáy ABC
là tam giác vuông cân tại B và AC a 2 . Tính thể tích V của khối lăng trụ đã cho. 3 a 3 a 3 a A. V B. V C. 3 V a D. V 3 2 6
Câu 68. (Mã 103 - BGD - 2019) Cho khối lăng trụ đứng ABC. A' B 'C ' có đáy là tam giác đều cạnh 2a và
AA'  3a (minh họa như hình vẽ bên). A' C' B' C A B
Thể tích của khối lăng trụ đã cho bằng A. 3 6 3a . B. 3 3 3a . C. 3 2 3a . D. 3 3a .
Câu 69. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tính thể tích V của khối lập phương ABC . D A BCD   ,
biết AC  a 3 . 3 3 6a 1 A. 3 V a B. V C. 3
V  3 3a D. 3 V a 4 3
Câu 70. (TRƯỜNG THPT HOÀNG HOA THÁM HƯNG YÊN NĂM 2018-2019) Hình lập phương có
đường chéo bằng a thì có thể tích bằng 2 3 A. 3 3 3a . B. 3 a . C. 3 a . D. 3 a . 4 9
Câu 71. (Mã đề 101 - BGD - 2019) Cho khối lăng trụ đứng ABC.A ' B 'C ' có đáy là tam giác đều
cạnh a và AA '  3a (minh họa hình vẽ bên). Thể tích khối lăng trụ đã cho bằng. A' C' B' C A B 3 a 3 a 3 3a 3 3a A. . B. . C. . D. . 4 2 4 2
Câu 72. (MĐ 104 BGD&DT NĂM 2017) Cho khối lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác cân
với AB AC a , 
BAC  120 . Mặt phẳng ( AB C  )
 tạo với đáy một góc 60 . Tính thể tích V của khối lăng trụ đã cho. 3 3a 3 9a 3 a 3 3a A. V B. V C. V D. V  8 8 8 4
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 73. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hình lăng trụ đứng ABC.AB C   có đáy
là tam giác vuông cân tại B , AB a và AB a 3 . Thể tích khối lăng trụ ABC.AB C   là 3 a 3 3 a 3 a 3 a 2 A. B. C. D. 2 6 2 2
Câu 74. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho lăng trụ đều ABC.AB C   . Biết
rằng góc giữa  ABC  và  ABC  là 30 , tam giác ABC có diện tích bằng 8 . Tính thể tích khối lăng
trụ ABC.AB C   . A. 8 3 . B. 8 . C. 3 3 . D. 8 2 .
Câu 75. (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho lăng trụ tam giác đều 2 a 3
ABC.A' B 'C ' có diện tích đáy bằng
. Mặt phẳng  A' BC  hợp với mặt phẳng đáy một góc 0 60 . Tính 4
thể tích khối lăng trụ ABC.A' B 'C ' . 3 3a 3 3 a 3 3 5a 3 3 3a 2 A. B. C. D. 8 8 12 8
Câu 76. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho khối lăng trụ đều 2a 3
ABC.A' B 'C ' có cạnh đáy bằng a . Khoảng cách từ điểm A' đến mặt phẳng  AB 'C ' bằng . Thể tích 19
của khối lăng trụ đã cho là 3 a 3 3 a 3 3 a 3 3 3a A. B. C. D. 4 6 2 2
Dạng 2.3 Thể tích khối lăng trụ xiên
Câu 77. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho lăng trụ AB .
C A' B 'C ' có đáy ABC là tam giác
vuông tại B , đường cao BH . Biết A' H   ABC  và AB  1, AC  2, AA'  2 . Thể tích của khối lăng trụ đã cho bằng 21 7 21 3 7 A. . B. . C. . D. . 12 4 4 4
Câu 78. (SỞ GD&ĐT BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hình lăng trụ AB . C A BC   có tất cả
các cạnh bằng a , các cạnh bên tạo với đáy góc 60 . Tính thể tích khối lăng trụ AB . C A BC   bằng 3 a 3 3 3a 3 a 3 3 a A. B. C. D. 24 8 8 8
Câu 79. (HSG BẮC NINH NĂM 2018-2019) Cho hình lăng trụ AB . C A BC
  có đáy ABC là tam giác vuông cân tại ,
A AC  2 2 , biết góc giữa AC và  ABC  bằng 0
60 và AC  4 . Tính thể tích V của khối lăng trụ AB . C A BC   . 8 16 8 3 A. V B. V C. V D. 8 3 3 3 3
Câu 80. (KTNL GIA BÌNH NĂM 2018-2019) Cho lăng trụ tam giác ABC.A' B 'C ' có đáy là tam giác đều
cạnh a , góc giữa cạnh bên và mặt đáy bằng 0
30 . Hình chiếu của A ' lên  ABC  là trung điểm I của BC .
Tính thể tích khối lăng trụ 3 a 3 3 a 13 3 a 3 3 a 3 A. B. C. D. 2 12 8 6
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 81. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Một khối lăng trụ tam giác có
đáy là tam giác đều cạnh bằng 3 , cạnh bên bằng 2 3 tạo với mặt phẳng đáy một góc 30 . Khi đó thể tích khối lăng trụ là: 9 27 27 3 9 3 A. B. C. D. 4 4 4 4
Câu 82. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Cho hình lăng trụ ABC.A' B 'C '
có đáy là tam giác đều cạnh a , góc giữa cạnh bên và mặt phẳng đáy bằng 0
30 . Hình chiếu của A ' xuống
ABC là trung điểm BC . Tính thể tích khối lăng trụ ABC.A'B'C '. 3 a 3 3 a 3 a 3 3 a 3 A. B. C. D. 8 8 24 4
Câu 83. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho hình lăng trụ ABC.AB C   có đáy 3a
ABC là tam giác đều cạnh a , AA 
. Biết rằng hình chiếu vuông góc của A lên  ABC  là trung điểm 2
BC . Tính thể tích V của khối lăng trụ đó. 3 2a 3 3a 3 A. 3 V a B. V C. V D. 3 V a 3 4 2 2
Câu 84. (MĐ 103 BGD&ĐT NĂM 2017-2018) Cho khối lăng trụ AB .
C A' B 'C ' , khoảng cách từ C đến
đường thẳng BB ' bằng 2, khoảng cách từ A đến các đường thẳng BB ' và CC ' lần lượt bằng 1 và 3 , hình
chiếu vuông góc của A lên mặt phẳng ( A ' B 'C ') là trung điểm M của B 'C ' và A ' M  2 . Thể tích của khối
lăng trụ đã cho bằng 2 3 A. B. 1 C. 3 D. 2 3
Câu 85. (Mã đề 102 BGD&ĐT NĂM 2018) Cho khối lăng trụ AB .
C A'B'C' , khoảng cách từ C đến BB ' là
5 , khoảng cách từ A đến BB ' và CC ' lần lượt là 1; 2 . Hình chiếu vuông góc của A lên mặt phẳng A' B 'C ' 15
là trung điểm M của B 'C ' , A' M
. Thể tích của khối lăng trụ đã cho bằng 3 2 5 2 15 15 A. . B. 5 C. D. 3 3 3
Câu 86. (Mã đề 101 BGD&ĐT NĂM 2018) Cho khối lăng trụ AB . C A BC
  , khoảng cách từ C đến đường
thẳng BB bằng 2 , khoảng cách từ A đến các đường thẳng BB và CC lần lượt bằng 1 và 3 , hình chiếu 2 3
vuông góc của A lên mặt phẳng  A BC
  là trung điểm M của B C
  và AM
. Thể tích của khối lăng 3 trụ đã cho bằng 2 3 A. 2 B. 1 C. 3 D. 3
Câu 87. (Mã đề 104 BGD&ĐT NĂM 2018) Cho khối lăng trụ ABC.AB C
  . Khoảng cách từ C đến đường
thẳng BB bằng 5 , khoảng cách từ A đến các đường thẳng BB và CC lần lượt bằng 1 và 2 , hình chiếu
vuông góc của A lên mặt phẳng  A BC
  là trung điểm M của B C
  và AM  5 . Thể tích của khối lăng trụ đã cho bằng 15 2 5 2 15 A. 5 B. C. D. 3 3 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 88. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hình lăng trụ A . BCD AB CD   có đáy 
ABCD là hình thoi cạnh a , ABC  60 . Chân đường cao hạ từ B trùng với tâm O của đáy ABCD ; góc
giữa mặt phẳng  BB CC
  với đáy bằng 60 . Thể tích lăng trụ bằng: 3 3a 3 3 2a 3 3 3a 2 3 3a A. B. C. D. 8 9 8 4
Câu 89. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Cho lăng trụ ABC.AB C   có đáy
là tam giác đều cạnh a , hình chiếu vuông góc của điểm ’
A lên mặt phẳng  ABC trùng với trọng tâm tam a 3
giác ABC. Biết khoảng cách giữa hai đường thẳng A ’
A và BC bằng
. Tính theo a thể tích của khối 4 lăng trụ đã cho. 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 3 24 6 12
Câu 90. (TOÁN HỌC TUỔI TRẺ NĂM 2018 - 2019 LẦN 01) Cho hình lăng trụ ABC.AB C   có
AA  2a , tam giác ABC vuông tại C và 
BAC  60 , góc giữa cạnh bên BB và mặt đáy  ABC bằng 60
. Hình chiếu vuông góc của B lên mặt phẳng  ABC trùng với trọng tâm của tam giác ABC . Thể tích của khối tứ diện A .
ABC theo a bằng 3 9a 3 3a 3 9a 3 27a A. . B. . C. . D. . 208 26 26 208
Câu 91. (CHUYÊN HÙNG VƯƠNG GIA LAI NĂM 2018-2019 LẦN 01) Cho khối lăng trụ ABC.AB C  , tam giác A B
C có diện tích bằng 1 và khoảng cách từ A đến
mặt phẳng  ABC  bằng 2. Thể tích khối lăng trụ đã cho bằng A. 6. B. 3. C. 2. D. 1.
Câu 92. (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho lăng trụ tam giác
ABC.A ' B 'C ' có đáy ABC là tam giác đều cạnh a . Hình chiếu của điểm A ' trên mặt phẳng  ABC  trùng 2 2a 3
vào trọng tâm G của tam giác ABC . Biết tam giác A ' BB ' có diện tích bằng
. Tính thể tích khối lăng 3
trụ ABC.A ' B 'C ' . 3 6a 2 3 3a 7 3 3a 5 3 3a 3 A. B. C. D. 7 8 8 8
Dạng 3. THỂ TÍCH KHỐI ĐA DIỆN KHÁC
Câu 93. (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho hình vuông ABCD và ABEF có cạnh bằng 1 , lần lượt
nằm trên hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng của B qua đường thẳng DE . Thể tích
của khối đa diện ABCDSEF bằng 7 11 2 5 A. B. C. D. 6 12 3 6
Câu 94. (Mã đề 104 - BGD - 2019) Cho lăng trụ AB . C A BC
  có chiều cao bằng 4 và đáy là tam giác đều
cạnh bằng 4. Gọi M , N và P lần lượt là tâm của các mặt bên ABB A  , ACC A   và BCC B
  . Thể tích của khối
đa diện lồi có các đỉnh là các điểm ,
A B, C, M , N , P bằng 20 3 14 3 A. 8 3 . B. 6 3 . C. . D. . 3 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 95. (Mã 103 - BGD - 2019) Cho lăng trụ AB . C A BC
  có chiều cao bằng 6 và đáy là tam giác đều cạnh
bằng 4. Gọi M , N , P lần lượt là tâm các mặt bên ABB A  , ACC A  , BCC B
  . Thể tích khối đa diện lồi có các đỉnh là các điểm ,
A B, C, M , N , P bằng A. 9 3 . B. 10 3 . C. 7 3 . D. 12 3 .
Câu 96. (Mã 102 - BGD - 2019) Cho lăng trụ ABC.A ' B 'C ' có chiều cao bằng 8 và đáy là tam giác đều
cạnh bằng 4 . Gọi M , N và P lần lượt là tâm các mặt bên ABB ' A', ACC ' A' và BCC ' B ' . Thể tích của khối
đa diện lồi có các đỉnh là các điểm , A ,
B C, M , N, P bằng 40 3 28 3 A. . B. 16 3 . C. . D. 12 3 . 3 3
Câu 97. (Mã đề 101 - BGD - 2019) Cho lăng trụ AB .
C A' B 'C ' có chiều cao bằng 8 và đáy là tam giác đều
cạnh bằng 6 . Gọi M , N và P lần lượt là tâm của các mặt bên ABB ' A', ACC ' A ' và BCC ' B ' . Thể tích của
khối đa diện lồi có các đỉnh là các điểm ,
A B, C, M , N , P bằng A. 30 3 . B. 36 3 . C. 27 3 . D. 21 3 .
Câu 98. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Thể tích của bát diện đều cạnh bằng a 3 là. 4 A. 3 6a . B. 3 6a . C. 3 a . D. 3 a . 3
Câu 99. (THPT THIỆU HÓA – THANH HÓA NĂM 2018-2019 LẦN 01) Cho hình lập phương CN 1 ABC .
D A ' B ' C ' D ' cạnh a . Gọi M là trung điểm của BC , N thuộc cạnh CD thỏa  . Mặt phẳng CD 3
(A ' MN) chia khối lập phương thành hai khối, gọi (H) là khối chứa điểm A . Thể tích của khối (H) theo a là? 3 53a 3 55a 3 47a 3 65a A. B. C. D. 137 144 154 113
Câu 100. Cho một hình lập phương có cạnh bằng a . Tính theo a thể tích của khối bát diện đều có các đỉnh
là tâm các mặt của hình lập phương. 1 1 1 1 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 4 6 12 8
Câu 101. (THPT YÊN KHÁNH - NINH BÌNH - 2018 - 2019) Cho hình hộp chữ nhật ABCDAB CD   . 2a 5 2a 5 a 3
Khoảng cách giữa AB và B C  là
, giữa BC và AB là
, giữa AC và BD là . Thể tích 5 5 3 của khối hộp đó là A. 3 8a . B. 3 4a . C. 3 2a . D. 3 a .
Câu 102. (THPT NGÔ GIA TỰ VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' có AB a, BC  2a, AC '  3a . Điểm N thuộc cạnh BB ' sao cho BN  2NB ' , điểm M
thuộc cạnh DD ' sao cho D ' M  2MD . Mặt phẳng  A' MN  chia hình hộp chữ nhật làm hai phần, tính thể
tích phần chứa điểm C ' . A. 3 4a . B. 3 a . C. 3 2a . D. 3 3a .
Câu 103. (SỞ GD&ĐT THANH HÓA NĂM 2018 - 2019) Cho hình chóp đều S.ABC có đáy cạnh bằng
a , góc giữa đường thẳng SA và mặt phẳng  ABC bằng 60 . Gọi A , B , C tương ứng là các điểm đối xứng
của A , B , C qua S . Thể tích V của khối bát diện có các mặt ABC, AB C   , A BC , B CA , C AB , AB C   , BA C  , CA B   là
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 3 2 3a 3 3a 3 4 3a A. V  . B. 3 V  2 3a . C. V  . D. V  . 3 2 3
Dạng 4. TỈ SỐ THỂ TÍCH
Dạng 4.1 Tỉ số thể tích của khối chóp
Câu 104. (THPT QUỲNH LƯU 3 NGHỆ AN NĂM 2018-2019) Cho hình chóp S.ABC . Gọi M , N , P V
lần lượt là trung điểm của ,
SA SB, SC . Tỉ số thể tích S.ABC bằng VS.MNP A. 12 . B. 2 . C. 8 . D. 3 .
Câu 105. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho tứ diện MNPQ . Gọi I ; J ; K V
lần lượt là trung điểm của các cạnh MN ; MP ; MQ . Tỉ số thể tích MIJK bằng VMNPQ 1 1 1 1 A. B. C. D. 3 4 6 8
Câu 106. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Cho hình chóp S.ABCD . Gọi A , B ,
C , D theo thứ tự là trung điểm của SA , SB , SC , SD . Tính tỉ số thể tích của hai khối chóp S.A BCD   và S.ABCD . 1 1 1 1 A. B. C. D. 16 4 8 2
Câu 107. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Cho hình chóp S.ABC có thể
tích bằng V . Gọi G là trọng tâm tam giác SBC . Mặt phẳng ( ) đi qua hai điểm ,
A G và song song với BC
. Mặt phẳng ( ) cắt các cạnh SB, SC lần lượt tại các điểm M và N . Thể tích khối chóp S.AMN bằng V V 4V V A. B. C. D. 9 2 9 4
Dạng 4.2 Tỉ số thể tích các khối đa diện
Câu 108. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Cho khối tứ diện có thể tích bằng V . Gọi V  là thể V
tích của khối đa diện có các đỉnh là các trung điểm của các cạnh của khối tứ diện đã cho, tính tỉ số . V V  2 V  5 V  1 V  1 A.  . B.  . C.  . D.  . V 3 V 8 V 2 V 4
Câu 109. (GKI THPT VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Cho hình chóp S.ABCDE có đáy là hình
ngũ giác và có thể tích là V . Nếu tăng chiều cao của chóp lên 3 lần đồng thời giảm độ dài cạnh đáy đi 3 lần V
ta được khối chóp mới S .AB CDE
  có thể tích V  . Tỉ số là V 1 1 A. 3 B. C. 1 D. 5 3
Câu 110. (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Cho khối chóp tam giác S.ABC có đỉnh
S và đáy là tam giác ABC . Gọi V là thể tích của khối chóp. Mặt phẳng đi qua trọng tâm của ba mặt bên của
khối chóp chia khối chóp thành hai phần. Tính theo V thể tích của phần chứa đáy của khối chóp. 37 27 19 8 A. V . B. V . C. V . D. V . 64 64 27 27
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 111. (CHUYÊN LÊ THÁNH TÔNG NĂM 2018-2019 LẦN 01) Cho lăng trụ ABC.AB C   , M là
trung điểm CC . Mặt phẳng  ABM  chia khối lăng trụ thành hai khối đa diện. Gọi V là thể tích khối lăng 1 V
trụ chứa đỉnh C và V là thể tích khối đa diện còn lại. Tính tỉ số 1 . 2 V2 1 1 1 2 A. . B. . C. 5 6 2 . D. 5
Câu 112. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Cho hình hộp AB . CD AB CD
  có I là giao điểm của AC và BD . Gọi V và V lần lượt là thể tích của các khối 1 2 V AB . CD AB CD
  và I.AB C   . Tính tỉ số 1 V2 V V 3 V V A. 1  6 . B. 1  . C. 1  2 . D. 1  3. V V 2 V V 2 2 2 2
Câu 113. (HSG BẮC NINH NĂM 2018-2019) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
Gọi M , N lần lượt là trung điểm của AD; SC . I là giao điểm của BM và AC . Tính tỷ số thể tích của hai
khối chóp ANIB và S.ABCD 1 1 1 1 A. B. C. D. 16 8 12 24
Câu 114. (ĐỀ MẪU KSNL ĐHQG TPHCM NĂM 2018-2019) Cho khối lăng trụ ABC.AB C   . Gọi E ,
F lần lượt là trung điểm của AA , CC . Mặt phẳng  BEF  chia khối lăng trụ thành hai phần. Tỉ số thể tích của hai phần đó là 1 1 2 A. . B. 1. C. . D. . 3 2 3
Câu 115. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Cho hình chop S.ABCD có 1
đáy là hình vuông ABCD cạnh a , góc giữa mặt bên và mặt phẳng đáy là  thoả mãn cos  . Mặt phẳng 3
P qua AC và vuông góc với mặt phẳng SAD chia khối chóp S.ABCD thành hai khối đa diện là khối
chop N.ACD và đa diện chứa đỉnh S . Tỉ số hai khối đa diện đó gần nhất với giá trị nào trong các giá trị sau? A. 0.11 B. 0.13 C. 0.7 D. 0.9
Câu 116. (THPT HÀM RỒNG THANH HÓA NĂM 2018-2019 LẦN 1) Cho tứ diện ABCD , trên các 3
cạnh BC , BD , AC lần lượt lấy các điểm M , N , P sao cho BC  3BM , BD
BN , AC  2AP . Mặt 2 V
phẳng MNP chia khối tứ diện ABCD thành hai phần có thể tích là V , V . Tính tỉ số 1 1 2 V2 V 26 V 3 V 15 V 26 A. 1  . B. 1  . C. 1  . D. 1  . V 19 V 19 V 19 V 13 2 2 2 2
Câu 117. (THPT MINH KHAI HÀ TĨNH NĂM 2018-2019) Cho hình chóp S.ABCD có đáy ABCD là  o
hình thoi cạnh a , BAD  60 và SA vuông góc với mặt phẳng  ABCD . Góc giữa hai mặt phẳng  SBD  và o
ABCD bằng 45 . Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC . Mặt phẳng MND
chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích là V , khối 1 V
còn lại có thể tích là V (tham khảo hình vẽ bên). Tính tỉ số 1 . 2 V2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 V 1 V 5 V 12 V 7 A. 1  . B. 1  . C. 1  . D. 1  . V 5 V 3 V 7 V 5 2 2 2 2
Câu 118. (CHUYÊN TRẦN PHÚ HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho khối chóp S.ABCD có
đáy ABCD là hình vuông cạnh bằng a, SA  2 .
a Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với
(ABCD). Một mặt phẳng (P) qua A và vuông góc SC, cắt các cạnh S ,
B SC,SD lần lượt tại B ,
C ,D . Gọi V
V và V lần lượt là thể tích của khối chóp S.AB CD
  và khối đa diện ABC . D D CB   . Tỉ số 1 bằng 1 2 V2 8 8 32 1 A. . B. . C. . D. . 15 7 13 2
Câu 119. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Cho hình lập phương ABC . D A BCD   có
cạnh bằng 1. Gọi V là thể tích phần không gian bên trong chung của hai hình tứ diện ACB D   và A CBD , 1
V là phần không gian bên trong hình lập phương đã cho mà không bị chiếm chỗ bởi hai khối tứ diện nêu 2 V trên. Tính tỉ số 2 ? V1 1 3 A. 3 . B. . C. . D. 2 . 2 2
Câu 120. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, SA  2 . a Hai mặt phẳng
(SAB) và (SAD) cùng vuông góc với (ABCD). Một mặt phẳng (P) qua A và vuông góc SC, cắt các cạnh S ,
B SC,SD lần lượt tại B ,
C ,D . Gọi V và V lần lượt là thể tích của khối chóp S.AB CD   và khối đa diện 1 2 V ABC . D D CB   . Tỉ số 1 bằng V2 8 8 32 1 A. . B. . C. . D. . 15 7 13 2
Câu 121. Cho hình chóp SABCD có đáy là hình bình hành. Gọi M , N , P, Q lần lượt là trọng tâm của các
tam giác SAB, SBC, SCD, SDA . Gọi O là điểm bất kỳ trên mặt phẳng đáy ABCD . Biết thể tích khối chóp
OMNPQ bằng V . Tính thể tích khối chóp SABCD . 27 27 9 27 A. V . B. V . C. V . D. V . 8 2 4 4
Câu 122. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Cho khối chóp S.ABCD có đáy ABCD
là hình bình hành, gọi M là trung điểm của SC . Mặt phẳng chứa AM và song song với BD cắt SB, SD lần
lượt tại P, Q . Biết thể tích khối chóp S.ABCD bằng V . Tính thể tích khối chóp S.APM . Q V V V V A. B. C. D. 4 8 3 6
Dạng 4.3 Ứng dụng tỉ số thể tích để tìm thể tích
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 123. (ĐỀ 01 ĐỀ PHÁT TRIỂN ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho khối lăng trụ AB . C A
B C có thể tích bằng 2 . Gọi M là trung điểm của đoạn thẳng  AA và
N là điểm nằm trên cạnh BB ' sao cho BN  2B ' N . Đường thẳng CM cắt đường thẳng C  A tại P ,
đường thẳng CN cắt đường thẳng C 
B tại Q . Thể tích của khối đa diện lồi  A MP B NQ bằng 7 5 2 13 A. . B. . C. . D. . 9 9 3 9
Câu 124. (THPT YÊN KHÁNH - NINH BÌNH - 2018 - 2019) Cho hình chóp S.ABCD , đáy ABCD là
hình vuông cạnh a ; SA a 3 ; SA  ( ABCD) . Gọi M , N lần lượt là trung điểm của ; SB SD , mặt phẳng
( AMN ) cắt SC tại I . Tính thể tích của khối đa diện ABCDMIN 3 5 3a 3 3a 3 5 3a 3 13 3a A. V  . B. V  . C. V  . D. V  . 18 18 6 36
Câu 125. (THPT CHUYÊN BẮC NINH LẦN 01 NĂM 2018-2019) Cho khối hộp ABCDABCD có thể
tích bằng 2018 . Gọi M là trung điểm của cạnh AB . Mặt phẳng MBD  chia khối chóp ABCDABCD
thành hai khối đa diện. Tính thể tích phần khối đa diện chứa đỉnh A . 5045 7063 10090 7063 A. B. C. D. 6 6 17 12
Câu 126. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Cho hình chóp S.ABCD có  
đáy là hình bình hành và thể tích V  270 . Lấy điểm S  trong không gian thỏa mãn SS   2  CB . Tính thể
tích v của phần chung của hai khối chóp S.ABCD và S .ABCD . (tham khảo hình vẽ sau) A. v  120. B. v  150. C. v  180. D. v  90.
Câu 127. (THPT CHUYÊN BẮC NINH LẦN 01 NĂM 2018-2019) Cho hình chóp SABC có
SA  1, SB  2, SC  3 và    ASB  60 ,  BSC  120 ,
CSA  90 . Tính thể tích khối chóp S.ABC . 2 2 2 A. B. 2 C. D. 2 6 4
Câu 128. (ĐỀ 04 VTED NĂM 2018-2019) Cho khối chóp S.ABCD có đáy là hình bình hành thể tích bằng
1 . Gọi M là điểm đối xứng của C qua ;
B N là trung điểm cạnh SC . Mặt phẳng  MDN  chia khối chóp
S.ABCD thành hai khối đa diện,thể tích của khối đa diện chứa đỉnh S bằng 5 5 12 7 A. B. C. D. 6 8 19 12
Câu 129. (TRƯỜNG THPT LƯƠNG TÀI SỐ 2 NĂM 2018-2019) Cho hình chóp S.ABCD có đáy là
hình vuông, mặt bên SAB là một tam giác đều nằm trong mặt phẳng vuông góc với mặt đáy  ABCD và 27 3 có diện tích bằng
(đvdt). Một mặt phẳng đi qua trọng tâm tam giác SAB và song song với mặt đáy 4
ABCD chia khối chóp S.ABCD thành hai phần, tính thể tích V của phần chứa điểm S ? A. V  24 B. V  8 C. V  12 D. V  36
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 130. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019). Cho hình chóp S.ABCD có đáy
ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm các cạnh SB, SC . Tính thể tích khối chóp
S.AMND , biết rằng khối chóp S.ABCD có thể tích bằng 3 a . 3 a 3 a 3 a 3 3a A. B. C. D. 4 8 2 8
Câu 131. (THPT-THANG-LONG-HA-NOI-NAM-2018-2019 LẦN 01) Cho hình chóp S.ABCD , gọi
I , J , K , H lần lượt là trung điểm của các cạnh ,
SA SB, SC, SD . Tính thể tích khối chóp S.ABCD biết rằng
thể tích khối chóp S.IJKH là 1 A. 16 . B. 8 . C. 2 . D. 4 .
Câu 132. (CHUYÊN LÊ THÁNH TÔNG NĂM 2018-2019 LẦN 01) Cho hình chóp S.ABC có đáy là
tam giác ABC vuông cân ở B , AC a 2 . SA vuông góc với mặt phẳng  ABC  và SA a . Gọi G là trọng
tâm của tam giác SBC . Một mặt phẳng đi qua hai điểm A , G và song song với BC cắt SB , SC lần lượt tại
B và C . Thể tích khối chóp S.AB C   bằng: 3 2a 3 a 3 4a 3 2a A. . B. . C. . D. . 27 9 27 9
Câu 133. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Cho hình chóp S.ABCD
có đáy là hình bình hành và có thể tích bằng 48 . Trên cạnh SB, SD lấy điểm M , N sao cho SM MB ,
SD  3SN . Mặt phẳng  AMN  cắt SC tại P . Tính thể tích V của khối tứ diện SMNP . 1 1 A. V  . B. V  . C. V  2 . D. V  1 . 2 3
Câu 134. (TT THANH TƯỜNG NGHỆ AN NĂM 2018-2019 LẦN 02) Cho hình chóp S.ABCD có đáy
ABCD là hình bình hành. Gọi N là trung điểm S ,
B P thuộc đoạn SC sao cho SP  2PC, M thuộc đoạn SA 4 sao cho SM M .
A Mặt phẳng  MNP  cắt SD tại .
Q NP cắt BC tại E,CQ cắt DPtại . R Biết rằng thể 5 3
tích khối chóp EPQR bằng 18cm . Thể tích khối chóp SMNPQ bằng 260 A. 3 65cm . B. 3 cm . C. 3 75cm . D. 3 70cm . 9
Dạng 5. BÀI TOÁN THỰC TẾ VÀ BÀI TOÁN CỰC TRỊ
Câu 135. (Mã đề 102 BGD&ĐT NĂM 2018) Ông A dự định sử dụng hết 2
6, 7m kính để làm một bể cá
bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước
không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm). A. 3 1, 23m B. 3 2, 48m C. 3 1,57m D. 3 1,11m
Câu 136. (Mã đề 104 BGD&ĐT NĂM 2018) Ông A dự định sử dụng hết 2
5, 5 m kính để làm một bể cá có
dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể).
Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?: A. 3 1, 40 m B. 3 1, 01 m C. 3 1, 51 m D. 3 1,17 m
Câu 137. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Người ta cần xây dựng một bể
bơi có dạng hình hộp chữ nhật có thể tích là 3
125m . Đáy bể bơi là hình chữ nhật có chiều dài gấp ba lần chiều
rộng. Tính chiều rộng của đáy bể bơi để khi thi công tiết kiệm nguyên vật liệu nhất (kết quả làm tròn đến hai chữ số thập phân)? A. 3,12 m B. 3,82m
C. 3, 62m D 3, 42m
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 138. (THPT CẨM GIÀNG 2 NĂM 2018-2019) Người ta muốn thiết kế một bể cá bằng kính không có nắp với thể tích 3
72 dm , chiều cao là 3dm . Một vách ngăn (cùng bằng kính) ở giữa, chia bể cá thành hai
ngăn, với các kích thước a, b (đơn vị dm ) như hình vẽ. Tính a, b để bể cá tốn ít nguyên liệu nhất (tính cả
tấm kính ở giữa), coi bề dày các tấm kính như nhau và không ảnh hưởng đến thể tích của bể. 3 dm b dm a dm A. a  24 dm ; b  24 dm .
B. a  6 dm ; b  4 dm .
C. a  3 2 dm ; b  4 2 dm .
D. a  4 dm ; b  6 dm .
Câu 139. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Xét khối tứ diện ABCD có cạnh AB x và các cạnh còn
lại đều bằng 2 3 . Tìm x để thể tích khối tứ diện ABCD đạt giá trị lớn nhất.
A. x  14
B. x  3 2
C. x  6
D. x  2 3
Câu 140. (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Xét khối chóp S.ABC
có đáy là tam giác vuông cân tại A , SA vuông góc với mặt phẳng đáy, khoảng cách từ A đến mặt phẳng
SBC bằng 3. Gọi  là góc giữa hai mặt phẳng SBC và  ABC , giá trị cos khi thể tích khối chóp
S.ABC nhỏ nhất là 2 2 3 6 A. . B. . C. . D. . 2 3 3 3
Câu 141. (CHUYÊN LÊ THÁNH TÔNG NĂM 2018-2019 LẦN 01) Cho hình hộp chữ nhật AB . CD
A BCD có AB x , AD  1 . Biết rằng góc giữa đường thẳng 
A C và mặt phẳng  ABB  A  bằng
30 . Tìm giá trị lớn nhất V
của thể tích khối hộp AB . CD
A BCD . max 3 3 3 1 3 A. V  . B. V  . C. V  . D. V  . max 4 max 4 max 2 max 2
Câu 142. (THPT QUỲNH LƯU 3 NGHỆ AN NĂM 2018-2019) Nhân ngày quốc tế Phụ nữ 8 – 3 năm
2019. Ông A đã mua tặng vợ một món quà và đặt nó trong một chiếc hộp chữ nhật có thể tích là 32 (đvtt) có
đáy là hình vuông và không nắp. Để món quà trở nên đặc biệt và xứng tầm với giá trị của nó, ông quyết định
mạ vàng chiếc hộp, biết rằng độ dày của lớp mạ trên mọi điểm của chiếc hộp là không đổi và như nhau. Gọi
chiều cao và cạnh đáy của chiếc hộp lần lượt là h và x . Để lượng vàng trên hộp là nhỏ nhất thì giá trị của h và x là? 3
A. h  2 , x  4 . B. h  , x  4 .
C. h  2 , x  1 .
D. h  4 , x  2 . 2
Câu 143. (THPT LÊ VĂN THỊNH BẮC NINH NĂM 2018-2019) Xét tứ diện ABCD có các cạnh
AB BC CD DA  1 và AC , BD thay đổi. Giá trị lớn nhất của thể tích khối tứ diện ABCD bằng 2 3 4 3 2 3 4 3 A. B. C. D. 27 27 9 9
Câu 144. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 01) Cho hình chóp SABC có
SA x, SB y, AB AC SB SC  1. Thể tích khối chóp SABC đạt giá trị lớn nhất khi tổng x y bằng 2 4 A. B. 3 C. D. 4 3 3 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 145. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Cho hình hộp chữ nhật AB .
CD A' B 'C ' D ' có tổng diện tích tất cả các mặt là 36, độ dài đường chéo AC ' bằng 6. Hỏi thể tích của
khối hộp lớn nhất là bao nhiêu? A. 8 2 B. 6 6 C. 24 3 D. 16 2
Câu 146. (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Cho hình chóp S.ABCD có SC x
0  x a 3, các cạnh còn lại đều bằng a . Biết rằng thể tích khối chóp S.ABCD lớn nhất khi và chỉ khi a m x   * ,
m n    . Mệnh đề nào sau đây đúng? n
A. m  2n  10 . B. 2
m n  30 . C. 2
2n  3m  15 . D. 2
4m n  20 .
Câu 147. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Cho tứ diện ABCD có AB x , CD y , tất
cả các cạnh còn lại bằng 2 . Khi thể tích tứ diện ABCD là lớn nhất tính xy . 2 4 16 1 A. . B. . C. . D. . 3 3 3 3
Câu 148. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Cho hình chóp . S ABCD có
đáy ABCD là hình bình hành và có thể tích V. Điểm P là trung điểm của SC , một mặt phẳng qua AP cắt V
hai cạnh SD và SB lần lượt tại M và N . Gọi V là thể tích khối chóp .
S AMPN . Giá trị lớn nhất của 1 1 V
thuộc khoảng nào sau đây?  1   1 1   1 1   1  A. 0;   . B. ;   . C. ;   . D. ;1   .  5   5 3   3 2   2 
Câu 149. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Trong một cuộc thi làm đồ
dùng học tập do trường phát động, bạn An nhờ bố làm một hình chóp tứ giác đều bằng cách lấy một mảnh tôn
hình vuông ABCD có cạnh bằng 5cm (tham khảo hình vẽ).
Cắt mảnh tôn theo các tam giác cân AEB, BFC , CGD , DHA và sau đó gò các tam giác AEH , BEF, CFG
, DGH sao cho bốn đỉnh A, B, C, D trùng nhau tạo thành khối chóp tứ giác đều. Thể tích lớn nhất của khối
chóp tứ giác đều tạo thành bằng 4 10 4 10 8 10 8 10 A. . B. . C. . D. . 3 5 3 5
Câu 150. Cho khối lập phương ABCD.AB CD
  cạnh a . Các điểm M , N lần lượt di động trên các tia AC, B D
  sao cho AM B N
a 2 .Thể tích khối tứ diện AMNB có giá trị lớn nhất là 3 a 3 a 3 a 3 3 a 2 A. B. C. D. 12 6 6 12
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 151. (SỞ GD&ĐT BẮC NINH NĂM 2018-2019 LẦN 01) Cho tứ diện SABC có G là trọng tâm tứ V
diện, mặt phẳng quay quanh AG cắt các cạnh SB, SC lần lượt tại M , N . Giá trị nhỏ nhất của tỉ số S.AMN VS.ABC là? 4 3 1 1 A. . B. . C. . D. . 9 8 3 2
PHẦN B. LỜI GIẢI THAM KHẢO
Dạng 1.THỂ TÍCH KHỐI CHÓP
Dạng 1.1 Biết chiều cao và diện tích đáy Câu 1. Lời giải Chọn A 1
Thể tích của khối chóp có chiều cao bằng h và diện tích đáy bằng B là: V Bh 3 Câu 2. Chọn B
Khối chóp có đáy là hình vuông cạnh a nên có diện tích đáy: 2 Sa . đáy
Chiều cao h  2a . 1 1 2
Vậy thể tích khối chóp đã cho là V  .S .h 2  .a .2a 3  a . 3 đáy 3 3 Câu 3. Chọn D 1 1 4
Thể tích khối chóp: V  . B h 2  a .4a 3  a . 3 3 3
Dạng 1.2 Cạnh bên vuông góc với đáy Câu 4. Chọn D S B A D C
Ta có SA   ABCD  SA là đường cao của hình chóp 3 1 1 a 2
Thể tích khối chóp S.ABCD : 2 V S . A S  .a 2.a  . 3 ABCD 3 3 Câu 5. Chọn A
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 S C A B 1 Ta có 2  2  2 BC AB
AC suy ra ABC vuông tại A . S  24 , V S .SA  32 ABC 3 ABC Câu 6. Chọn D 3 1 2a Ta có 2 Sa . VS . A S  . ABCD S . ABCD ABCD 3 3 S C A B Câu 7. 3 a 3. 1 3VS.ABC 4 V  .S .SA SA    a 3 . S. ABC ABC  2 3 S a 3 ABC 4 Câu 8. Chọn C
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 S a 3 a A C a a B
Ta có SA là đường cao hình chóp 2 a 3
Tam giác ABC đều cạnh a nên S  ABC 4 2 3 1 a 3 a
Vậy thể tích cần tìm là: V  . .a 3  . S . ABC 3 4 4 Câu 9. Chọn C
Góc giữa SD và mp là 0 DSA  30 . AD Ta có SA   a 3 . 0 tan 30 3 1 a 3 2 V a .a 3  . 3 3
Câu 10. Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 a 3 2 3 1 a 3 a 3 S   V  . . a  . ABC 4 S . ABC 3 4 12
Câu 11. Chọn C 1 1 1 Ta có V  . AD .
AB BC  10.10.24  400 ABCD 3 2 6 1 1
Câu 12. Diện tích tam giác ABC vuông cân tại A là: 2 S  . AB AC  2 .
a 2a  2a . ABC 2 2 3 1 1 2a
Thể tích khối chóp S.ABC là: 2 VS . A S  . .2 a a  . S . ABC 3 ABC 3 3 S A C B Câu 13. Ta có 2 2 2 2
BC AC AB  3a BC a 3 . 3 1 1 1 1 a 3 Vậy VS .SA  . . AB BC.SA  . . a a 3.a  . S . ABC 3 ABC 3 2 6 6 Câu 14. Chọn A S H A B D C
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ta có BC AB, BC SA BC AH . Kẻ AH SB AH  SBC . a 2
Suy ra d A;SBC  AH  . 2 1 1 1
Tam giác SAB vuông tại A có:    SA a . 2 2 2 AH SA AB 3 1 a Vậy V  . SA S  . SABCD 3 ABCD 3
Câu 15. Chọn.C S a 60 B A a 3 D C Ta có 2 S  3a . ABCD
SBC    ABCD  BC
Vì BC SB  SBC
 SBC  ABCD   SB AB   , ;  SBA .
BC AB   ABCD   Vậy 60o SBA SA
Xét tam giác vuông SAB có: tan 60o   SA  .
AB tan 60o a 3 AB 1 1 Vậy 2 3 VS .SA a
3.a 3  a . S . ABCD 3 ABCD 3 Câu 16. Chọn B S 300 A D B C
+) Do ABCD là hình vuông cạnh a nên: S  2 a ABCD
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
+) Chứng minh được BC  SAB  góc giữa SC và (SAB) là CSB  0 30 .  BC
+) Đặt SA x   2  2 SB x
a . Tam giác SBC vuông tại B nên CSA  0 1 tan tan 30   3 SB
Ta được: SB BC  2 x  2 3
a a 3  x a 2 . 3 1 1 2a Vậy V  .S . A S  2 .a 2.a  (Đvtt) SABCD 3 ABCD 3 3 Câu 17. Chọn B Ta có:
+ ABC vuông cân tại C, AB  4a suy ra
AC BC  2a 2. 1 Do đó: 2 SAC.BC  4a . ABC 2
+ SA   ABC  SA AB A
BC vuông tại A
SA SB AB   2   2 2 2 6a 4a  2a 5.
+ Khối chóp S.ABC có SA   ABC 3 1 1 8a 5 2  V S .SA  4a .2a 5  3 ABC 3 3 3 3 a a 5 Vậy tỷ số:   . 3 3V 3.8a 5 40 3
Câu 18. Chọn A S A C B
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 AB 3
ABC là tam giác vuông tại B , AB a , 
ACB  60  BC   a 0 tan 60 3
SB ABC   SB AB  0 , ,
 45 nên tam giác SAB vuông cân tại S SA AB a 3 1 1 1 1 3 a 3 VS .SA  . B . A BC.SA  . a a a S . ABC 3 ABC 3 2 6 3 18
Câu 19. Chọn C Kẻ AE BD
SBD  ABCD     0 ,  SEA  60
Xét ABD vuông tại A 2 . AD AB 2a 2a 5 AE    2 2 a 5 5 AD AB
Xét SAE vuông tại A 0 2a 5 2a 15
SA AE.tan 60  . 3  5 5
Khi đó thể tích S.ABCD 3 1 1 2a 15 2 4a 15 V S . A S  . .2 ABCD a  3 3 5 15
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Câu 20. Chọn C
Theo giả thiết ta có đường thẳng SC tạo với mặt phẳng  SAB góc 0 30 . S  Nên 0 ASC  30 .  2 1 1 3 a 3 Ta S
AC.BC.sin ACB  . .2 a . aH ABC 2 2 2 2 A B 2 2 2 
Xét tam giác ABC ta có 2
AB AC BC  2A . C B .
C cos ACB  7a
Gọi H là hình chiếu vuông góc của C trên AB khi đó do đường thẳng SC tạo C
với mặt phẳng  SAB góc 0 30 nên 0 CSH  30 . 2 1 a 3 a 21
Xét ABC ta có .CH.AB   CH  . 2 2 7 CH a 21 Xét SCH
vuông tại H ta có SC   . 0 sin 30 7 a 35 Xét SAC
vuông tại A ta có 2 2 SA SC AC  . 7 2 3 1 1 a 35 a 3 a 105 Vậy V  .S . A S  . .  . SABC 3 ABC 3 7 2 42 S A D H B C Câu 21. 1 1 Có: V  . . SA S  66 3  .9.SS  44 3 S . ABCD 3 ABCD 3 ABCD ABCD 1 1 Suy ra . AB AD
BC.CD  44 3  5AD  3CD  44 . (1) 2 2
Áp dụng định lí Pitago trong 2 tam giác vuông ABD; BCD , ta có: 2 2 2 2 2 2 2
AB AD BD BC CD CD AD  48 (2)  AD  4 Từ (1) và (2) suy ra  47  AD   2 47 44 AD
không thỏa mãn do từ (1) ta có: AD   AD  4 . 2 5
Trong tam giác ABD , dựng AH BD lại có SA BD BD SH . 
Vậy góc giữa SBD và đáy là góc SHA .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A . B AD 20 273 AH
Dễ tính BD  91, AH   ,  20 273 cot SHA   . BD 91 SA 819 S H A C 300 I B Câu 23.
Gọi I là trung điểm sủa BC suy ra góc giữa mp SBC và mp  ABC  là  0 SIA  30 .
H là hình chiếu vuông góc của A trên SI suy ra d  ,
A SBC  AH a . AH
Xét tam giác AHI vuông tại H suy ra AI   2a . 0 sin 30 3 4a
Giả sử tam giác đều ABC có cạnh bằng x , mà AI là đường cao suy ra 2a xx  . 2 3 2 2  4a  3 4a 3
Diện tích tam giác đều ABC là S  .  . ABC    3  4 3 2a
Xét tam giác SAI vuông tại A suy ra 0
SA AI.tan 30  . 3 2 3 1 1 4a 3 2a 8a Vậy V  .S .SA  . .  . S.ABC 3 ABC 3 3 3 9
Dạng 1.3 Mặt bên vuông góc với đáy
Câu 24. Chọn D
Gọi H là trung điểm của AB , S
AB cân tại S SH AB
SAB   ABCD  
SAB  ABCD  AB  SH   ABCD 
SH  SAB; SH AB
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489      ;   45o SC ABCD SCH
 SHC vuông cân tại H 2 a a 5 2 2 2
SH HC
BC BH a   ; 2 2 SAB a 4 2 ABCD 3 1 1 a 5 a 5 2  V  .S .SH a .  S . ABCD 3 ABCD 3 2 6
Câu 25. Chọn A S A D 30° H K B C
Gọi H , K lần lượt là trung điểm AB và CD .
Suy ra SH   ABCD và SCD  ABCD     ,  SKH  30 . SH a 3 1 3a Xét SH
K vuông tại H , có HK   :  . tan 30 2 3 2 3 1 1 a 3 3a a 3 Vậy VSH .S  . . . a  . S . ABCD 3 ABCD 3 2 2 4
Câu 26. Chọn D
Gọi H là trung điểm của AB suy ra SH a 3 1
AB  2a BC  2a Saa ABC 2 2 2 2 2 3 1 1 2a 3 2 V  .S .SH  2a a 3  S . ABC 3 ABC 3 3
Câu 27. Chọn A
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Gọi H là trung điểm của AD . Nên SH AD
SAD   ABCD
SADABCD  AD SH  ABCD  AD SH  Ta có: 2 S  2a ABCD 3 4 3. a 3V 3  SH    2a 2 S 2a ABCD
Gọi I là hình chiếu của H lên SD d  ;
B SCD  d  ;
A SCD  2d H;SCD  2IH a 2 2 . a SH.HD SH.HD 2 Mà 2 IH     a 2 2 2 SD 3 SH HDa 2  2a2    2  
Vậy d B SCD 4 ;  a 3 Câu 28. Lời giải Chọn C
Gọi I là trung điểm của AD . Tam giác SAD cân tại S SI AD SI AD  Ta có 
SI   ABCD SAD    ABCD 
SI là đường cao của hình chóp. 1 4 1 Theo giả thiết 3 2 V  .SI.Sa
SI.2a SI  2a S . ABCD 3 ABCD 3 3
Vì AB song song với SCD
d B,SCD  d  ,
A SCD  2d I,SCD
Gọi H là hình chiếu vuông góc của I lên SD . SI DCIH SD Mặt khác 
IH DC . Ta có 
IH  SCD  d I,SCD  IH ID DCIH DC  1 1 1 1 4 2a
Xét tam giác SID vuông tại I :      IH  2 2 2 2 2 IH SI ID 4a 2a 3
d B SCD  d A SCD  d I SCD 4 , , 2 ,  a . 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 S A D H B Câu 29. C
Kẻ SH AC , H AC H suy ra SH   ABCD . a 3
AC  2a , tam giác SAC vuông ở S , góc SAC  60 nên SA a, SC a 3, SH  . 2 3 2 1 a 3 a 3
Thể tích hình chóp là V  a 2 .  . 3 2 3
Câu 30. Chọn D
Giả sử AB a . Gọi H là trung điểm của AB SH AB SH   ABCD  
      1 Ta có S .
A BD  SH HABA BC  2  H . A BA a 2   1   1 7 2  a 2.cos  , SA BD 2  a cos  , SA BD   sin  , SA BD  2 2 2 8 1 1 a 3 3 3 2 3 3 VSH. . AB AD  .a a Va SABCD 3 3 2 6 SABD 12 1 3 1 7 3  . SA . BD d .sin S , A BD a  . a a 2. 21.  a a  7 SA,BD   3 3   6 12 6 8 12
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 S A D H B C Câu 31.
Gọi H là trung điểm AB , từ giả thiết ta có: SH   ABCD , SC ABCD  ,  SCH   . 2 x 2 x 15
Đặt AB x , ta có: 2 2 2 HC BH BC   a , 2
SH HC.tan   a . . 4 4 5 x 3 2 x 15 x 3 Mặt khác SH  . Vậy ta có: 2  a .   x a . 2 4 5 2
AD BC  2 .AB 3a 2 3 1 a 3 S   ; 2 SSa ; VSH.S  . ABCD 2 2 ACD 3 ABCD S . ACD 3 ACD 6 Câu 32.
Gọi H là trung điểm đoạn AB SH   ABCD. 2 a a 17
Xét BCH vuông tại B , có: 2 CH  4a   . 4 2 a 17 a 34
Xét SHC vuông cân tại H , có: SH  ; SC  . 2 2 2 2 17a a 3 2
Xét SAH vuông tại H , có: SA    a . 4 4 2
Xét  ABC vuông tại B , có: 2 2 AC
a  4a a 5 . 89 2  Sa  . SAC 4 3 1 a 17 3 1 a 17 Ta có: V
V  .SH.S  ; VV  . S. ABCD 3 ABCD 3 S . ACD 2 6 3 1 a 17 1 89 a 1513 VV  . Mà 2 V  .d.Sa .d d  . S. ACM S .   2 ACD 12 S.MAC 3 SAC 12 89
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Dạng 1.4 Biết hình chiếu của đỉnh lên đáy S A C H B Câu 33.
Xét tam giác ABC vuông tại A có: BC AB AC a  a 2 2 2 2 3  2a .
H là trung điểm của BC nên BH a .
Xét tam giác SBH vuông tại H có: SH
SB HB  a 2 2 2 2 2  a a . 1 1
Diện tích đáy ABC là: 2 SA . B AC a 3 . ABC 2 2 3 1 1 1 a 3
Thể tích của khối chóp S.ABC là: 2 V SH .S  . . a .a 3  . 3 ABC 3 2 6 S 2a 3 S A B H 30° D A D H Câu 34. C 2 2 SH H .
D HA  3HD SH  3HD   SH tan SDH   3  DH SA SA Có: 2 2    3  SD
 2a DA SD SA  4a  .   SA SD 3 tan SDH   SD 1 DH DA a . 4 SH SH SH Tam giác SHC có  tan SCH   tan 30   HC   3a . HC HC tan 30 Tam giác DHC có 2 2
DC DH HC  2 2a
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 36
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 3 1 1 8 6a Vậy VSH. . AD DC  . 3 .4 a .2 a 2a S . ABCD 3 3 3 Câu 35. Chọn D S I M D C H A B
Gọi M là trung điểm của CD thì ta có ABMD là hình vuông cạnh a do đó BC BD a 2 2 2 2 2
CD  4a BC BD do đó tam giác BCD vuông cân tại B .
Gọi H là trung điểm của BD thì SH   ABCD . 3 a 6. 1 1 6 a 6 Khi đó VSH . B . D BC SH   . S .BCD 3 2 2 2a 2
Hạ HI SB .
Vì ABMD là hình vuông nên H là trung điểm của AM và ta có AMCB là hình bình hành do đó AH //BCd  ;
A SBC  d H;SBC  HI . 1 1 1 4 2 8 a 6 a Khi đó       HI
hay d A SBC  6 ;  . 2 2 2 HI SH HB 2 2 2 6a a 3a 4 4 Câu 36. Chọn D S D M C I A B 1 1 Ta có 2 SSa . ABM ABCD 2 2
Gọi I là hình chiếu vuông góc của S trên mặt phẳng  ABCD 2  a a 5 2 2 2 IB IA AB   a     2  2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 37
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ta có IB là hình chiếu vuông góc của SB lên mp ABCD
SB, ABCD SB, IB 60    a  15 Ta có SI  . IB tan 60  2 2 3 1 1 a 15 a a 15  V  .SI.S  . .  . S . ABM 3 ABM 3 2 2 12 Câu 37.
Gọi M là trung điểm của BC . CN CH 1 N CM :  
HN //AM . Mà CM CA 3 AB
C đều nên AM BC HN BC BC  SHN  . Nên        ;  ;   60o SBC ABC SN HN SNH . a 3 1 a 3 Do AB
C đều nên AM   HN AM  . 2 3 6 a a SH
N vuông tại H có  3
SH HN.sin SNH  .sin 60o  . 6 4 2 3 1 1 a a 3 a 3 VSH.S  . .  . S . ABC 3 ABC 3 4 4 48
Dạng 1.5 Thể tích khối chóp đều S A B H D Câu 38. C
Giả sử khối chóp tứ giác đều đã cho là S.ABCD . Khi đó ABCD là hình vuông cạnh a và
SA SB SC SD a .
Gọi H là tâm của hình vuông ABCD thì SH   ABCD nên SH là chiều cao của khối chóp S.ABCD . Tính SH :
Xét tam giác ABC vuông tại B ta có: 2 2 AC AB BC 2 2 
a a a 2 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 38
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 AC a Nhận thấy 2 2 2
AC SA SC nên tam giác SAC vuông tại S . Suy ra SH   . 2 2
Diện tích đáy của khối chóp S.ABCD là 2 Sa . ABCD 1 1 a 3 a 2
Vậy thể tích khối chóp S.ABCD là: V  .S .SH 2  .a .  . 3 ABCD 3 2 6
Câu 39. Chọn D
Gọi hình chóp tứ giác đều có tất cả các cạnh bằng 2a là S.ABCD và I tâm của đáy ta có:
SA SC BA BC DA DC SAC BAC DBC SAC; BAC; D
AC lần lượt vuông tại S, , B D . 1 1
I là trung điểm của AC suy ra SI AC  2a. 2  a 2 2 2 3 1 1 4 2a VS .SI a a S ABCD ABCD 2 2 . 2 . 3 3 3 Câu 40. Lời giải Chọn D S A D I B C 2   a a
Chiều cao của khối chóp: SI  2 SA  2 AI  2 2 14 4a        2  2 3 1 1 a 14 14a
Thể tích khối chóp: V SI.S  2 . a  3 ABCD 3 2 6
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 39
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Câu 41. Ta có 2 S  4a ; 2 2 2 2
SO SB OB  5a  2a a 3 ABCD 2 3 1 a 3.4a 4 3a Vậy V  . SO S   S . ABCD 3 ABCD 3 3 Câu 42. Chọn D S A C O I B
Do đáy là tam giác đều nên gọi I là trung điểm cạnh BC , khi đó AI là đường cao của tam giác đáy. Theo 2 a a 3 2 2a 3 a 3 định lý Pitago ta có 2 AI a   , và AO AI   . 4 2 3 3.2 3 2 a 11a
Trong tam giác SOA vuông tại O ta có 2 SO  4a   . 3 3 3 1 1 a 3 11a 11a
Vậy thể tích khối chóp S.ABC là V  . a .  . 3 2 2 3 12
Câu 43. Chọn B
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 40
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
+ SA ABC   ;  SAO  45 a 3 + SO A . O tan 45  3 2 3 1 1 a 3 a 3 a + V  . . SO S  . .  3 ABC 3 3 4 12
Câu 44. Chọn D
Diện tích đáy là: SAB  a 2 2 2 6  6a . ABCD
Góc giữa cạnh bên SB và mặt đáy  ABCD là SD ABCD    0 ,
SDO SDO  60 1 1 1
ABCD là hình vuông suy ra DO BD AB 2  a 6. 2  a 3. 2 2 2  Xét tam giác vuông 0
SOD :SO D .
O tan SDO a 3.tan 60  3 . a 1 1 Vậy 2 3 V  .S . O S  .3 .6 a a  6a . S .ABCD 3 ABCD 3 Câu 45.
Gọi H là tâm của tam giác đều ABC .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 41
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 a 3
Khi đó SH   ABC , BH  . 3
Theo đề bài ta có: SB ABC   ,  SBH  60 . a 3
Xét SBH vuông tại H . Có SH BH.tan 60  . 3  a . 3 2 3 1 1 a 3 a 3 Thể tích VSH .S  . a  . S . ABC 3 ABC 3 4 12 Câu 46.
Gọi O là tâm của đáy, gọi M là trung điểm của BC . SO BC Ta có 
nên  SOM   BC , suy ra SCD  ABCD   SM OM   0 , ,  SMO  60 OM BC   .  1 a a 3 Có OM BC  , 0
SO OM tan 60  . 2 2 2 3 1 1 a 3 a 3
Thể tích khối chóp S.ABCD là 2 VS . O S  . .a  . S . ABCD 3 ABCD 3 2 6 S M D C O N H A B Câu 47.
Gọi H là trung điểm AO . Khi đó góc giữa MN và  ABCD là MNH . a 10 Ta có 2 2 0
HN CN CH  2CN.CH.cos 45  . 4 a 10 a 30 Suy ra 0
MH HN.tan 60  . 3  . 4 4 a 30
Do đó SO  2MH  . 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 42
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 3 1 30 a 30 2 Va .a  . S . ABCD 3 2 6
Dạng 1.6 Thể tích khối chóp khác Câu 48. Chọn A 1 1 1 Ta có 3 V  . AB . AD AC  6 .7 a .4 a a  28a ABCD 3 2 6 1 1 1 Ta nhận thấy 3 SSSVV  7a . MNP 2 MNPD 4 BCD AMNP 4 ABCD S N M A D P B C Câu 49. S 1
Do N , P lần lượt là trung điểm của SD , AD nên ANP   . S 4 SAD
d M ,SAD MS 1
Lại có, M là trung điểm của SC nên   .
d C,SAD CS 2
1 .d M,SAD.S ANP V 1 1 1 M .ANP 3    .  . V 1 2 4 8 C.SAD
.d C,SAD.S 3 SAD 1 1 1 Mặt khác, VVVV VV . C.SAD S . ACD S . 2 ABCD 2 M .ANP 16
Câu 50. Chọn A
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 43
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 AB AC
  AB   ACD AB AD 1 1 7 .4 a .6 a a 3 V  . AC.A . D AB   28a ABCD 3 2 6
Gọi H là hình chiếu của A lên  BCD  h AH là 1 đường cao của hình chóp ABCD .
M , N , P tương ứng là trung điểm các cạnh BC, CD, DB MN , NP, PM tương ứng là đường trung bình của 1 S 1 BCD M
NP đồng dạng với BC
D với tỉ số k  MNP 2   k  2 S 4 BCD 1 .S .h MNP V S 1 1 AMNP 3 MNP 3     V  .V  7a . V 1 S 4 AMNP 4 ABCD ABCD .S . BCD h 3 BCD
Câu 51. Chọn D
 Gọi H là hình chiếu của S trên mặt phẳng (ABC) .
Do SA SB SC nên SHA SHB SH
C (cạnh huyền-cạnh góc vuông)
HA HB HC H là tâm đường tròn ngoại tiếp tam giác ABC .
Tam giác ABC vuông cân tại B nên H là trung điểm AC . 1
Suy ra HA HC AC  2 2 2
SH SA HA  4 2 2 AC 2
 Ta có: BA BC   2 2 2 1 1 1 16 2 Vậy V  .S .SH  . 2 2 2 2 .4 2  . S. ABC ABC    3 3 2 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 44
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 B G2 G4 G1 A D F G3 E
Câu 52. C 1
G G G đồng dạng với ACD theo tỉ số và nằm trong hai mặt phẳng song song. 1 2 3 3 1 1 1 2 SS
 6a . G G / / AB và G G AB  2a . 3 VG G .S  4a .  3 4 1 G 2 G 3 G 9 ABD 3 4 1 G 2 G 3 G 4 G 3 4 1 G 2 G 3 3 3  G Câu 53.
Gọi I là trung điểm của S . B  
Do SAB SCB  90 nên I là tâm mặt cầu ngoại tiếp hình chóp S.AB . C
Gọi O là tâm của đáy ABC OI  ( ABC) .
Gọi H là hình chiếu của S lên mặt phẳng  ABC. Ta có AB  (SAH )  AB AH. Tương tự, BC CH.
Suy ra H thuộc đường tròn ngoại tiếp tam giác ABC, có tâm là O nên O là trung điểm của BH. Do đó, SH  2OI.
Gọi N là trung điểm của BC IN // SC nên BC IN BC   AIN (*)
Gọi G là trọng tâm của tam giác SAB và K là hình chiếu của G lên mặt phẳng  ABC  K AO và 2 4 5
GK // OI AK AO AN KN AN. 3 9 9   MBC 5
  d A MBC 10a d K , ,   .     9 21 (*) 10a
Kẻ KE GN KE BC KE  MBC  d K ,MBC  KE  .   21 1 1 1 10a
Tam giác GKN vuông tại K có    GK
SH  2OI  3GK 10 . a 2 2 2 KE GK KN 3 2 3 1 a 3 5a 3
Vậy thể tích khối chóp S.ABC là V  . .10a  . 3 4 6
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 45
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Câu 54.
Ta có SB SC a , 
BSC  60 suy ra tam giác BSC đều  BC a .
Lại có SA SC a , 
ASC  90 suy ra tam giác ASC vuông cân tại S AC a 2 .
Mặt khác, SA SB a , 
ASB  120 , áp dụng định lí cosin cho tam giác ASB , ta được: 2 2 2  2
AB SA SB  2 . SA .
SB cos ASB  3a AB a 3 .
Xét tam giác ABC có 2 2 2 2 2 2
BC AC a  2a  3a AB suy ra tam giác ABC vuông tại C . 2 1 a 2
Vậy diện tích tam giác ABC là: SAC.BC  . ABC 2 2
Gọi O là trung điểm của cạnh AB suy ra O là tâm đường tròn ngoại tiếp tam giác ABC .
Mà SA SB SC SO   ABC . 2  3a a
Xét tam giác vuông ASO vuông tại O có 2 2 2 SO SA AO a     .  2  2   2 3 1 1 a 2 a a 2
Vậy thể tích khối chóp S.ABC là: V  .S .SO  . .  . S . ABC 3 ABC 3 2 2 12
Câu 55. Chọn B
Gọi M , N , P lần lượt là hình chiếu của H lên các cạnh AC, BC, AB . 1 3 h 3
Đặt SH h V  . . h  . S .ABC 3 4 12 2S 6V h 3 30 Ta có SAB S . AP   2 ABC S   :  h 10 SAB AB
d C;SAB 2 20
Tương tự, tính được HM  2h, HN h
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 46
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 2
PH SP SH  3h 1 3 3 Ta có SSSS
HP HM HN  3h   h ABC HAB HAC HBC   2 4 12 3 3 1 Vậy V  .  . S .ABC 12 12 48
Câu 56. Chọn B   Vì 0
SAB SCB  90  S, ,
A B,C cùng thuộc mặt cầu đường kính SB .
Gọi D là trung điểm BC , I là trung điểm SB và O là tâm đường tròn ngoại tiếp ABC , ta có
OI   ABC  .
Gọi H là điểm đối xứng với B qua O SH   ABC  (vì OI là đường trung bình SHB ).
Gọi BM AI J , ta có J trọng tâm SAB . Trong A
ID , kẻ JN / / IO . Khi đó, vì BC   JND  nên  JND  MBC .
Kẻ NE JD , ta có NE  MBC  . Do đó d N;MBC   NE . d  , A MBC  AD AD AD AD 9 Ta có      .
d N,MBC  ND AD AN 2 4 5 AD AO AD AD 3 9 5 10a
Suy ra, d N,MBC   d  ,
A MBC   . 9 21 1 1 1 10a 3 Xét JND có   nên NJ   OI
NJ  5a SH  10a . 2 2 2 NE ND NJ 3 2 2 3 1 1 a 3 5 3a Vậy VSH .S  .10 . a  . SABC 3 ABC 3 4 6 Câu 57.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 47
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
+ Dựng hình chóp S.A ' B 'C ' sao cho A là trung điểm B 'C ' , B là trung điểm A'C ' , C là trung điểm A' B ' .
+ Khi đó SB AC BA'  BC '  4 nên SA
'C ' vuông tại S và SA SC   SB2 2 2 ' ' 2.  64 (1) . 2 2 
SA'  SB '  80 (2) + Tương tự SB  'C ' , SA
' B ' vuông tại S và  . 2 2
SB '  SC '  36 (3)  + Từ  
1 ;2;3 ta suy ra SC '  10 ; SB '  26 ; SA'  54 . 1 1 1 390 + Ta tính được V
SC '. .SA'.SB '  390 và VV  (đvtt).
S . A' B 'C ' 3 2 S . ABC
S . A' B 'C ' 4 4
Dạng 2. THỂ TÍCH KHỐI LĂNG TRỤ
Dạng 2.1 Biết chiều cao và diện tích đáy Câu 58. Chọn A
Thể tích khối lăng trụ có diện tích đáy B và có chiều cao h là: V  . B h .
Câu 59. Chọn B 2 3 V S
.h a .4a  4a . day Câu 60. Chọn B
Theo công thức tính thể tích lăng trụ. Câu 61. Chọn C Ta có: VS .h 2  a .2a 3  2a . langtru day
Câu 62. Chọn A
Thể tích khối lăng trụ là 2 3 V  . B h a 3.a 6  3a 2
Dạng 2.2 Thể tích khối lăng trụ đứng Câu 63. Chọn A
Thể tích của khối lập phương cạnh 2a bằng: V   a3 3 2  8a
Câu 64. Chọn B 2 a 3 Ta có: S  . ABC 4
Vậy thể tích của khối lăng trụ đã cho là 2 3 a 3 a 6 VS .AA  .a 2  .
ABC. AB C   ABC 4 4 Câu 65. Lời giải
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 48
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Chọn C h a 3  a 3 2   V  . 3 h S a  . S  4   4
Câu 66. Chọn A 2 a 3
Tam giác ABC đều cạnh a nên SABC  4
Do khối lăng trụ ABC.AB C
  là lăng trụ đứng nên đường cao của lăng trụ là AA  2a 2 3 a 3 3a
Thể tích khối lăng trụ là V AA .  S  2 . a  . ABC 4 2 Câu 67. Chọn B A' C' a B' a 2 A C B AC 1
Tam giác ABC vuông cân tại B AB BC   a . Suy ra: 2 Sa . ABC 2 2 3 1 a Khi đó: 2 VS .BB  a .a
ABC. AB C   ABC 2 2
Câu 68. Chọn B 2 (2a) 3
Khối lăng trụ đã cho có đáy là tam giác đều có diện tích là
và chiều cao là AA'  3a (do là lăng 4 2 (2a) 3
trụ đứng) nên có thể tích là 3
.3a  3 3a 4
Câu 69. Chọn A
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 49
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Giả sử khối lập phương có cạnh bằng ;
x x  0
Xét tam giác A' B 'C ' vuông cân tại B ' ta có: 2 2 2
A 'C '  A ' B '  B 'C ' 2 2 2
x x  2x A'C '  x 2
Xét tam giác A' AC ' vuông tại A' ta có 2 2 2
AC '  A ' A A 'C ' 2 2 2
 3a x  2x x a
Thể tích của khối lập phương ABC . D A BCD   là 3 V a . B C A D BCCâu 70. AD
Xét hình lập phương ABC . D A BCD   ta có: a 2 2 2 2 2 2
AC  AA  A C
   AA  A B    A D   2 2
 3AA  a AA  3 3  a  3 3  V   a . ABCD. A BCD      3  9 Câu 71. Chọn C 2 a 3 Ta có S  ; AA'  a 3 . ABC 4 3 3 3a Từ đó suy ra 2
V a 3.a  . 4 4
Câu 72. Chọn A A C 120° B A' 60° C' H B'
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 50
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Gọi H là trung điểm của B C
 , khi đó góc giữa mp  AB C
  và đáy là góc  AHA  60 . 2 1 a 3 Ta có SAC.A . B sin120  . ABC 2 4 1  2S 2 2 2 2 a B C    BC
AB AC  2A .
B AC.cos120  a a  2. . a . aa 3 ABCAH   2 B C   2 a 3
AA  A H  .tan 60  . 2 3 3a Vậy V S .AA  . ACB 8
Câu 73. Chọn D C' A' B' a 3 A C a B 2 1 a Ta có 2 2 AA 
AB AB a 2 , 2 SAB  . ABC 2 2 3 a 2
Thể tích khối lăng trụ là V AA .  S  . ABC 2
Câu 74. Chọn A A' C' B' A 30° C x M B
Đặt AB x, x  0 , gọi M là trung điểm BC . 
ABC    ABC   BC
Ta có  AM BC
  ABC   ABC    ,
AMA  30 .
AM BCAM x 3 2 Xét A
 AM , có A M    .  x . cos 30 2 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 51
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1 2 S  8 
AM .BC  8  x  16  x  4 A BC  2 4. 3 1 16. 3 Suy ra A A
  AM .tan 30  .  2 ; S   4 3 . 2 ABC 3 4 Vậy VA . A S  2.4 3  8 3 .
ABC. AB C   ABC
Câu 75. Chọn A 2 a 3
Vì đáy ABC là tam giác đều có diện tích bằng
 cạnh đáy bằng a . 4 BC AM
Gọi M trung điểm BC , ta có 
BC A' M BC AA' 
Từ đó ta có  A BC  ABC   A M AM    0 ' , ' ,
A' MA  60 . 3a
Xét A ' AM ta có 0
AA'  AM .tan 60  2 3 3a 3
Thể tích lăng trụ ABC.A' B 'C ' là VAA '.S
ABC . A' B 'C ' ABC 8
Câu 76. Chọn C
Gọi M là trung điểm của B 'C ' .
AA '  B 'C ' Ta có 
B 'C '   AA' M    AB 'C '   AA' M  theo giao tuyến AM .
A' M B 'C ' 
Kẻ A' H AM trong mặt phẳng  AA' M  , suy ra  A' H   AB 'C ' .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 52
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2a 3
Vậy khoảng cách từ A' đến mặt phẳng  AB 'C ' là A' H  . 19 1 1 1 1 1 1 1 Ta có      
A ' A  2a . 2 2 2 2 2 2 2 A' H A' A A' M A' A A' H A' M 4a 2 3 a 3 a 3
Vậy thể tích khối lăng trụ là V AA'.S  2 . a  . A' B 'C ' 4 2
Dạng 2.3 Thể tích khối lăng trụ xiên Câu 77.
Tam giác ABC vuông tại B có AB  1; AC  2 nên 2 BC  2 1  3 . A . B BC 3 3 1
Độ dài của đường cao BH : BH   . Suy ra AH  : 3  . AC 2 2 2 1 7
Khi đó độ dài đường cao A' H của hình lăng trụ bằng : 2 2 A' H
AA'  AH  2   . 4 2 1 1 7 21
Thể tích khối lăng trụ đã cho bằng : V  .
AB BC.A' H  .1. 3  . 2 2 2 4
Câu 78. Chọn B A' B' C' 60o A B H C
Kẻ AH    ABC    AA ABC   ,
AAH  60 .  AH a 3
Xét AHA : sin 60 
AH AA .sin 60  . AA 2 2 3 a 3 a 3 3a
Thể tích khối lăng trụ ABC.AB C   :V S .AH  .  . ABC 4 2 8
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 53
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A' C' B' H A C B Câu 79.
Gọi H là hình chiếu của C lên mặt phẳng  ABC  , khi đó C H  là đường cao
AC  ABC    0 ,  C AH  60
Xét tam giác vuông AC H  ta có 0 C H   C . A sin 60  2 3 1 Khi đó VS .C H    ABC AB Cd 2 22 .2 3 8 3 . 2
Câu 80. Chọn C
Ta có A' I   ABC   AI là hình chiếu vuông góc của AA ' lên  ABC
Nên AA ABC        A A AI   0 ', ',
A ' AI  30 2 a 3 a a 3 Ta có 0 AI
A ' I AI tan 30  , S  2 2 ABC 4 2 3 a 3 a a 3 Vậy V  . 
ABC. A' B 'C ' 4 2 8
Câu 81. Chọn B
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 54
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Gọi H là hình chiếu của A lên mặt đáy. Suy ra góc 
AAH  30 AH 1 sin 30 
AH A . A sin 30  2 3.  3 AA 2 3 27 Khi đó: 2 V  3 . . 3  .
ABC . AB C  4 4
Câu 82. Chọn A
Gọi H là trung điểm BC suy ra A' H   ABC
Ta có A A ABC  A A AH   0 ' , ' ,
A' AH  30 a 3 Ta có AH  2 a 2 a 3 Ta có 0
A ' H AH . tan 30  và S  2 ABC 4 3 a 3
Vậy V A' H.SABC 8
Câu 83. Chọn C BC AH C B A
Gọi H là trung điểm BC . a 6
Theo giả thiết, AH là đường cao hình lăng trụ và 2 2 AH AA  AH  . 2 2 3 a 3 a 6 3a 2
Vậy thể tích khối lăng trụ là V S .AH  .  . ΔABC 4 2 8
Câu 84. Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 55
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Gọi A , A lần lượt là hình chiếu của A trên BB ' , CC ' . Theo đề ra AA  1; AA  3; A A  2. 1 2 1 2 1 2 Do 2 2 2
AA AA A A nên tam giác AA A vuông tại A . 1 2 1 2 1 2 A A
Gọi H là trung điểm A A thì 1 2 AH   1. 1 2 2
Lại có MH BB '  MH  ( AA A )  MH AH suy ra 2 2 MH
AM AH  3 . 1 2 MH 3
nên cos(( ABC), ( AA A ))  cos(MH , AM )  cos HMA   . 1 2 AM 2 S Suy ra AA A 1 2 S
 1. Thể tích lăng trụ là V AM S  2 . ABC
cos(( ABC), ( AA A )) ABC 1 2
Nhận xét. Ý tưởng câu này là dùng diện tích hình chiếu S '  S cos . Câu 85. Chọn C
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 56
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A B F I E C B' A' K M
Kẻ AI BB ' , AK CC ' ( hình vẽ ).
Khoảng cách từ A đến BB ' và CC ' lần lượt là 1; 2  AI  1, AK  2 . 15 15
Gọi F là trung điểm của BC . A' M   AF  3 3 AI BB '  Ta có
  BB '   AIK   BB '  IK . BB '  AK
Vì CC '  BB '  d (C, BB ')  d (K , BB ')  IK  5  AIK vuông tại A .
Gọi E là trung điểm của IK EF BB '  EF   AIK   EF AE .
Lại có AM   ABC  . Do đó góc giữa hai mặt phẳng  ABC và  AIK  là góc giữa EF và AM bằng góc 5    AE 3  AME FAE 2 . Ta có cos FAE     FAE  30 . AF 15 2 3 
Hình chiếu vuông góc của tam giác ABC lên mặt phẳng  AIK  là AIK nên ta có: SS cos EAF AIK ABC 3 2 1  S   S . ABC 2 ABC 3 15  AF 3
Xét AMF vuông tại A : tan AMF   AM   AM  5 . AM 3 3 2 2 15 Vậy V  5.  .
ABC.A'B 'C ' 3 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 57
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 86. Chọn A A C2 B2 C' A M M B' A' C A' 1 H T H B1 T
Cắt lăng trụ bởi một mặt phẳng qua A và vuông góc với AA ta được thiết diện là tam giác AB C có các 1 1
cạnh AB  1 ; A C   3 ; B C  2 . 1 1 1 1
Suy ra tam giác AB C vuông tại A và trung tuyến AH của tam giác đó bằng 1. 1 1
Gọi giao điểm của AM và AH là T . 2 3 1
Ta có: AM
; AH  1  MH  . Suy ra 
MAH  30 . 3 3 AM 4 Do đó 
MAA  60  AA    . cos MAA 3
Thể tích khối lăng trụ AB . C A BC
  bằng thể tích khối lăng trụ AB C .AB C và bằng 1 1 2 2 4 3
V AA .S    2 . A 1 B 1 C 3 2 Câu 87. Chọn D
Gọi J , K lần lượt là hình chiếu vuông góc của A lên BB và CC , H là hình chiếu vuông góc của C lên BB
Ta có AJ BB   1 .
AK CC  AK BB 2 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 58
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Từ  
1 và 2 suy ra BB   AJK   BB  JK JK //CH JK CH  5 . Xét AJK có 2 2 2
JK AJ AK  5 suy ra AJK vuông tại A . 5
Gọi F là trung điểm JK khi đó ta có AF JF FK  . 2
Gọi N là trung điểm BC , xét tam giác vuông ANF ta có: 5  AF 1 cos NAF  2   
NAF  60 . ( AN AM  5 vì AN //AM và AN AM ). AN 5 2 1 1 S Vậy ta có SAJ.AK  .1.2  1  SS .cos 60 1 AJKS     2 . AJK 2 2 AJKABC ABC cos 60 1 2
Xét tam giác AMA vuông tại M ta có  
MAA  AMF  30 hay AM A M  .tan 30 15  . 3 15 2 15
Vậy thể tích khối lăng trụ là V AM .S  .2  . ABC 3 3 Câu 88. Chọn D B' C' A' B D' H C B H O A O C A D
ABCD là hình thoi nên AB BC . Lại có ABC  60 nên ABC là tam giác đều. OH BC . Góc giữa  mặt phẳng  BB CC
  với đáy khi đó là B HO  60 . 1 1 1 1 1 4 4 16 a 3 Ta có        .  OH  2 2 2 2 2 2 2 2 OH OB OC 3a a 3a a 3a 4 4 4 Theo giả thiết, B O
 là đường cao lăng trụ A . BCD AB CD   .  a 3 3a B O
  OH.tan B HO  tan 60  . 4 4 2 3 a 3 3a 3a 3 VS .h  .  ABCD. A BCD   day 2 4 8
Câu 89. Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 59
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 BC AM  Ta có
  BC AA' BC A'G
Kẻ MH AA' tại H , suy ra MH là đoạn vuông góc chung của giữa hai đường thẳng A ’ A và BC 3
Tam giác MHA vuông tại H có 2 2 AH AM AH a 4 A'G GA MH.GA a
Tam giác A'GA đồng dạng tam giác MHA nên   A'G   MH HA HA 3 3 a 3
Thể tích khối lăng trụ là V S .A 'G ABC 12 C' A' B' 2a I C A 60o G 60o B Câu 90. Ta có 3 B G
  BBsin 60  2 . aa 3 2 . 1 3 3a
BG BB cos 60  2 . a
a BI BG  2 2 2
Đặt AC  2x x   0  CI  ;
x BC AC.tan 60  2x 3 . Khi đó   aa a a a x 2x 3 2 2 2 3 3 13 1 1 3 13 3 13 9 3 2       x   S
AC.BC  .2. .2. . 3  .     2  26 ABC 2 2 26 26 26 2 3 1 9a 3 9a Vậy V  . .a 3  A. ABC 3 26 26
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 60
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A' C' B' A C H B Câu 91.
Gọi H là hình chiếu vuông góc của A' trên mp  ABC  suy ra A'H là chiều cao của lăng trụ.
Xét khối chóp A.A' BC có diện tích đáy B S
 1, chiều cao h d A,A' BC   2 suy ra thể A' BC 1 1 2
tích của khối chóp A.A' BC là VBh  1 . 2 .  . A.A' BC 3 3 3  1 2 V   VS . A'H A.A' BC A' .ABC ABC 2 Mặt khác  3 3  V  3V  3.  2 . ABC .A' B' C' A.A' BC 3 V   S . A'HABC.A' B'C' ABC * Cách khác.
Ta thấy lăng trụ ABC.A' B' C' được chia thành ba khối chóp có thể thích bằng nhau là
A' . ABC, A' .BCB', A' .B' C' C . 1 1 2 2 Mà VVBh .1.2  suy ra V  3V  3.  2 . A' .ABC A.A' BC 3 3 3 ABC .A' B' C' A.A' BC 3
Câu 92. Chọn BAB CM + Ta có 
AB   A C
M   AB A MAB A M   2 1 2a 3 4a 3 Nên SA M  .AB   A M   A AB 2 3 3 1 a 3 Do A
BC đều cạnh bằng a nên GM CM  3 6
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 61
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 a 21 + Trong A G
M vuông tại G ta có 2 2 A G   A M   GM  2 2 3 a 21 a 3 3a 7 Vậy VA . G dt ABC  .  AB . C A BC     2 4 8
Dạng 3. THỂ TÍCH KHỐI ĐA DIỆN KHÁC Câu 93. Chọn D S F E D A C B
Ta có:ADF.BCE là hình lăng trụ đứng có đáy là tam giác vuông cân Dựa vào hình vẽ ta có: VVVVV  2VV ABCDSEF ADF .BCE S.CDFE ADF .BCE B.CDFE ADF . E BC B D A E 1 1 1 1 1 5 VA . B S  ;VAD.S   V  2.   ADF .BCEBCE 2 BADE 3 ABE 6 ABCDSEF 2 6 6
Câu 94. Chọn B A' C' B' N P M A C B 2 4 . 3
Thể tích khối lăng trụ AB . C A BC   là V  4.  16 3 . 4
Gọi thể tích của khối đa diện lồi có các đỉnh là các điểm ,
A B, C, M , N , P là V . 1 Ta có: V VVV . 1 AMNCB BMNP BNPC 1 3 1 Dễ thấy VV và VV nên VV . AABC 3 AMNCB 4 AABC AMNCB 4
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 62
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1 1 1 VV và VV nên VV . BAB C   3 BMNP 8 BAB C   BMNP 24 1 1 1 VVV và VV nên VV . A BCBAB CC   3 BNPC 4 BAB CBNPC 12 3 Vậy V VVVV  6 3 . 1 AMNCB BMNP BNPC 8
Câu 95. Chọn A A' C' B' N D F M P E A C B
Gọi DEF là thiết diện của lăng trụ cắt bởi mặt phẳng MNP .
Dễ chứng minh được  DEF  / /  ABC và D, E, F lần lượt là trung điểm của các đoạn 1 thẳng AA ,
BB ,CC suy ra VV  12 3 . ABC.DEF ABC. 2 A BC   Ta có VVVVV . ABCPNM ABC.DEF ADMN BMPE CPMF 1 3 Mặt khác VVVVVV  9 3 . ADMN BMPE CPMF ABC.DEF ABCPNM ABC. 12 4 DEF Câu 96. Lời giải Chọn D A' C' B' N M P C A B 3 1 1 Ta có: 2 V  8. .4  32 3; VV ; VV
ABC. A' B 'C ' 4 C '. ABC
ABC . A' B 'C ' 3 . A BC ' B '
ABC. A' B 'C ' 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 63
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Khối đa diện cần tìm V VVV C.ABPN . P AMN . P ABM 3 1 Ta có VVV C.ABPN C '. ABC
ABC.A' B'C ' 4 4 1 1 Ta có VVV PAMN ABC ' B '
ABC.A' B 'C ' 8 24 1 1 Ta có VVV PABM ABC ' B '
ABC.A' B 'C ' 4 12 1 1 1 3
Vậy thể tích khối cần tìm V VVVV  12 3 .
ABC.A' B 'C '
ABC.A' B 'C '
ABC.A' B 'C ' 4 24 12 . ' ' ' 8 ABC A B C
Câu 97. Chọn C
Gọi h là chiều cao của hình lăng trụ AB .
C A' B 'C ' . 3 Vì A
BC đều có độ dài cạnh bằng 6 nên 2 S  6 .  9 3 . ABC 4
Thể tích lặng trụ AB .
C A' B 'C ' là V  . h S  8.9 3  72 3 . ABC
Gọi E là trung điểm của cạnh AA ' . 1 1 1 1 1 Thể tích khối chóp . A EMN là Vd , A EMN .S  . . h SV . . A EMN    3 EMN 3 2 4 ABC 24
Thể tích khổi đa diện ABCMNP là: 1 1 1 3 VV  3VV  3. V V  27 3 . ABCMNP . 2 A EMN 2 24 8 Câu 98.
Ta có khối bát diện đều cạnh a 3 được tạo từ 2 khối chóp tứ giác đều có cạnh đáy và cạnh bên bằng a 3 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 64
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 2  a 6  a 6
Chiều cao của khối chóp là: h  a 3     . 2 2   3 2 1 a 6 a 6
Thể tích của khối chóp: Va  (đvtt). chop  3 . 3 2 2
Vậy thể tích khối bát diện là: 3 V  2Va 6 (đvtt). chop
Câu 99. Chọn B
Ta có: MN cắt AB và AD lần lượt tại I và J . A ' I cắt BB ' tại .
P A ' J cắt DD ' tại Q. MC NC 1 Do MC//JD nên  
JD  2MC  . a JD ND 2 DQ JD 1 AA' a Do DQ//AA' nên    DQ   . AA' JA 2 2 2 BI BM a
Do BI //NC nên 
 1  BI NC  . NC CM 3 PB IB 1 AA' a Do PB//AA' nên    PB   . AA' IA 4 4 4 1 1 1 Ta có: VVVV
AA'.AI.AJ DN.D . Q DJ BM .B . P BI H A' AIJ JDNQ IBMP 6 6 6 1 4a 1 2a a 1 a a a 55 3  . a .2a  . . .a  . . .  a . 6 3 6 3 2 6 2 4 3 144
Câu 100. Chọn B
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 65
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Giả sử hình lập phương A . BCD AB CD
  có cạnh bằng a và tâm các mặt là P, Q, R, S, O, O như hình vẽ. a 2
Ta có PQ là đường trung bình của tam giác đều B C
D cạnh a 2 nên PQ  . 2 1 Do đó 2 2 SPQ
a và OO  a . PQRS 2 1 1
Vậy thể tích bát diện cần tìm là 3 V S .OO  a (đvtt). 3 PQRS 6 Câu 101.
Đặt AB x , AD y , AA  z .
Gọi H là hình chiếu vuông góc của B trên B C
 , ta có BH là đoạn vuông góc chung của AB và B C  nên d AB B C   2a 5 1 1 1 5 ,  BH      . (1) 2 2 2 2 5 BH z y 4a
Gọi I là hình chiếu vuông góc của B trên AB , ta có BI là đoạn vuông góc chung của BC và AB nên d BC AB 1 1 1 5 ,  BI     . (2) 2 2 2 2 BI x z 4a
Gọi M là trung điểm của DD , O là giao điểm của AC và BD , ta có mặt phẳng  ACM  chứa AC và song
song với BD nên d AC, BD  d BD,ACM   d D,ACM  .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 66
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Gọi J là hình chiếu vuông góc của D trên AC , K là hình chiếu vuông góc của D trên MJ , ta có
d D ACM   d D ACM  1 1 1 4 3 , ,  DK      . (3) 2 2 2 2 2 DK x y z a 2 1 Từ (1), (2) và (3) ta có 
z  2a x y a . 2 2 z 2a Thể tích khối hộp là 3
V xyz  2a .
Câu 102. Chọn C
Nhận xét: B ' NDM là hình bình hành  B ' N DM , B ' N //DM
MN B ' D O là trung điểm của mỗi đoạn nên O cũng là trung điểm của đường chéo A'C .
Vậy thiết diện tạo bởi mặt  A' MN  và hình chóp là hình bình hành A' NCM . Ta có: 2 2 2 2
C ' A B ' B BA BC B ' B  2a . Cách 1:
Thể tích phần chứa C ' là 1 1 V VV
 .A' B '.S
 .A' D '.S
A'.B 'C ' CN
A'.C ' CMD B 'C ' CN C ' D ' 3 3 MC 2a 4a  2a  2a 1 1 3 3 3  .a.2a  .2a.a  2a . 3 2 3 2
Cách 2: Áp dụng công thức tính nhanh
Gọi thể tích phần chứa C ' là V ' . B ' N D ' MV ' 1 1 Ta có: B ' B D ' D 3 3    V '  .4a  2a . V 2 2 2
ABCD. A' B 'C ' D '
Cách 3: Nhận xét nhanh do đa diện chứa C ' đối xứng với đa diện không chứa C ' qua O nên thể tích của 1
hai phần này bằng nhau, suy ra 3 V '  .V  2a . . ' ' ' ' 2 ABCD A B C D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 67
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 B' C' A' D' S D A C O M Câu 103. B
Gọi D , D theo thứ tự là đỉnh thứ tư của hình thoi ABCD , A BCD   .
Thể tích của bát diện cần tìm: 1 1 V VVVVVV ABCD.C DAB   BC DA   B ACDABCD.C DAB   ABCD.C DAB   ABCD. 6 6 C DA  B 2 2 V    .2 .2 SO S .(*) ABCD. 3 C DAB   3 ABC 2 a 3 Ta có: S  . ABC 4 a
Ta có: SA ABC      2 3 ,
SAO  60  SO  . OA tan 60  . . 3  a . 3 2 2 3 8 a 3 2a 3 Do đó: V  . . a  . 3 4 3
Dạng 4. TỈ SỐ THỂ TÍCH
Dạng 4.1 Tỉ số thể tích của khối chóp S M P N A C B Câu 104. V SA SB SC Ta có S.ABC  . .
 2.2.2  8 , suy ra đáp án C. V SM SN SP S .MNP
Câu 105. Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 68
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 M I K J N Q P VM.IJK MI MJ MK 1 1 1 1 Ta có:  . .  . .  . V MN MP MQ 2 2 2 8 M .NPQ
Câu 106. Chọn C S D' C' A' B' D C A B V   
VS A BD 1    SA SB SD S A B D 1 Ta có .  . .  .   . V SA SB SD 8 V 16 S.ABD S.ABCD V   
VS B DC 1    SB SD SC S B D C 1 Và .  . .  .   . V SB SD SC 8 V 16 S.BDC S.ABCD V V
VS A BCD 1 S A BD   S B DC   1 1 1 Suy ra . .     .   . V V 16 16 8 V 8 S.ABCD S.ABCD S.ABCD
Câu 107. Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 69
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
( )  (SBC)  G Ta có 
 ( )  (SBC)  MM //BC ( MN đi qua G; M SB; N SC ). BC // ( )  SM SN SG 2
Vì G là trọng tâm SBC     . SB SC SE 3 V SM SN 2 2 4 4V Ta có SAMN  .  .   V  . V SB SC 3 3 9 SAMN 9 SABC
Dạng 4.2 Tỉ số thể tích các khối đa diện
Câu 108. Chọn C A Q P B E F D M N C
Cách 1. Đặc biệt hóa tứ diện cho là tứ diện đều cạnh a . Hình đa diện cần tính có được bằng cách cắt 4 góc a
của tứ diện, mỗi góc cũng là một tứ diện đều có cạnh bằng . 2 V V
Do đó thể tích phần cắt bỏ là V   4.  . 8 2 V V  1 Vậy V     . 2 V 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 70
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Cách 2. Khối đa diện là hai khối chóp tứ giác có cùng đáy là hình bình hành úp lại. Suy ra: 1 1 1 V   2V  4.V  4.V
 4. . V V N .MEPF N .MEP P.MNE 2 4 2 V ' V V . A QEP B
V .QMF C
V .MNE D V .NPF Cách 3. Ta có  V V V . A QEP B V .QMF C V .MNE D V . 1 1 1 1 1 1 1 1 1 1 1 1 1  1 NPF      1  . .  . .  . .  . .  . V V V V 2 2 2 2 2 2 2 2 2 2 2 2 2
Câu 109. Chọn D
Hai đa giác đáy đồng dạng nên Sau khi giảm độ dài cạnh đáy đi 3 lần thì diện tích đáy giảm đi 9 lần 1 SS . AB CDE   9 ABCDE 1 B .3 . h V  1 Do đó 3 9   . V 1 3 .Bh 3 Câu 110.
Gọi G ;G ;G lần lượt là trọng tâm tam giác SAC ; SBC ; SAB 1 2 3
Khi đó G G G SAB MN với MN / / AB / / G G , G MN 1 2 3    1 2 3
G G G SAC MP với MP / / AC / / G G , G MP 1 2 3    2 3 1
G G G SBC NP với NP / / BC / /G G , G NP 1 2 3    1 3 2
Do đó G G G chia khối chóp thành 2 phần: SMNP và MNPABC 1 2 3 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 71
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 V SM SN SP 2 2 2 8 8 19 19 Ta có: SMNP  . .  . .   VVVVVVV . V SA SB SC 3 3 3 27 MNPABC SABC SMNP SABC 27 SABC 27 SABC 27 SABC Câu 111. 1
V là thể tích khối lăng trụ chứa đỉnh C tức là V VS .MC 1 1 M . ABC 3 ABC 1 5
V là thể tích khối đa diện còn lại  V VV S .CC  S .CC  S .CC 2 2
ABC. AB C   1 ABC 6 ABC 6 ABC Khi đó ta có tỉ số 1 1 S MC S .CCABC ABC V 1 1 3 6    . V 5 5 5 2 S .CCS .CC 6 ABC 6 ABC Câu 112. V V  . h S . 1
ABCD. AB CD   A BCD   1 1 1 1 V Vd I , A BC   .S  . h .S  h.S . 2 I .A BC    
 ABC A BCD  ' A BCD  ' 3 3 2 6 V . h S 1 A BCD     6 . V 1 2 . h S 6 A BCD  
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 72
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Câu 113. V S h Ta có ANIB AIB  . N . V S h S . ABCD ABCD S h NC 1
Trong đó h ; h lần lượt là chiều cao kẻ từ đỉnh N; S nên N   (1) N S h SC 2 S 2 1
Ta có AO; BM lần lượt là các trung tuyến của tam giác ABD nên I là trọng tâm từ đó AI AO AC 3 2 S S AI 1 từ đó AIB AIB    (2) S 2S 2 AC 6 ABCD ABC V S h 1 1 1 Từ (1) và (2) ta có ANIB AIB  . N  .  V S h 6 2 12 S . ABCD ABCD S Câu 114.
Gọi V là thể tích khối lăng trụ ABC.AB C
  ; V là thể tích khối chóp .
B AEFC ; V là thể tích khối đa diện 1 2 BB EFC A
  ; I là trung điểm của cạnh BB và h là chiều cao của khối lăng trụ ABC.AB C   . h
Ta có:  EIF  //  ABC  nên d B, EIF   . 2 1 h 1 1 V  . .S  . h SV . B.IEF 3 2 ABC 6 ABC 6 1 1 1 Do đó V VV
V V V . 1 ABC.EIF B.EIF 2 6 3 1 2
V V V V V V . 2 1 3 3 V 1 Vậy 1  . V 2 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 73
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Câu 115.
Gọi M là trung điểm CD, H là hình chiếu vuông góc của 0 lên S , trong mặt phẳng (SCD) kẻ CH SD tại N ta có: CD SO
  CD SM . CD OM
CD SM , SM  (SCD)  
CD OM , OM  ( ABCD)  SMO   . (SCD) ( ABCD) CD     OM S
OM vuông tại O   cos SMO
SM  3OM ; 2 2
SO SM OM a 2 . SM a 2 a 10 SD S
OD vuông tại 0 , SO a 2,OD   SD    5 . 2 2 OD
Có: CD  (SOM )  CD OH mà OH SM OH  (SCD)  ( ACN )  (SCD) hay (P)  ( ACN ) .
Khi đó hình chóp S.AB D
C được chia thành hai khối đa diện S.ABCN và N.ACD , gọi V  V ; V  V . N.ACD 1 S.ABCN 2 2 D O Có S D
O vuông tại O , ON là đường cao nên 2 D O
ND.SD  ND  . D S 2 V D S D S V V V V S . A D C S . ACD S . D ABC 1 2    5   VV   . 2 N . ACD 1 V ND D O 5 10 10 N . ACD V 1 Vậy: 1   0.11 . V 9 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 74
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 C P M B A N Q D I Câu 116.
Gọi I là giao điểm của MN và CD , Q là giao điểm của IP và AD . Khi đó thiết diện của tứ diện ABCD là tứ giác ABC . Ta có: NB ID MC ID 1 ID PC QA QA . .  1   và . .  1   4 . ND IC MB IC 4 IC PA QD QD VANPQ AP AQ 2 2 2 1 2 1  .   VVV VV V V . V AC AD 5 ANPQ 5 ANCD 15 N .PQDC 3 15 5 ANCD V CM CP 1 1 2 Và CMNP  .   VVV . V CB CA 3 CMND 3 CBNA 9 ABCD 19 Suy ra V VVV . 2 NPQDC CMNP 45 26
Do đó, V V V V . 1 2 45 V 26 Vậy 1  . V 19 2 Câu 117.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 75
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 SK 2
Trong tam giác SMC , SB và MN là hai trung tuyến cắt nhau tại trọng tâm K   . SB 3
BI là đường trung bình của tam giác MCD I là trung điểm AB . V VVV 1 S . AID S .IKN S .IND Đặt:VV S .ABCD 1 SK SN 2 1 1 1 SN 1 1 1  V  .V ; V  . .V  . . V V ; V  .V  . V  .V S . AID 4 S .IKN S .IBC SB SC 3 2 4 12 S .IND S .ICD SC 2 2 4  1 1 1  7 5 V 7  V    .V  .V V  .V 1   . 1   2  4 12 4  12 12 V 5 2 S D' C' I B' A D O B C Câu 118.
Gọi O AC B ,
D I SO AC  B ,
I, D thẳng hàng và B D    B . D 2a 3 2a 6
AC a 2  SC a 6  AC  , SC  3 3 AO C CIS IS SI SBSD 4 Ta có . .  1   4     AC C SIO IO SO SB SD 5 V 2V . SA SB .SC 8 V 8 1 S . AB I  1      . V 2V . SA . SB SC 15 V 7 S . ABCD S. ABC 2 Câu 119.
Gọi I , I  , M , N , P , Q lần lượt là tâm các hình vuông ABCD , A BCD
  , AAD D  , ABB A   , BB CC  , 2 CDD C
  . Ta được V là thể tích khối bát diện đều với 6 đỉnh I , I  , M , N , P , Q cạnh MN  1 2 1 2 1 1 1  V  2V
 2. d I,MNPQ.S  . .  . 1 I .MNPQ 3 MNPQ 3 2 2 6
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 76
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 V AI AN 1 1 1 ABIN  .  .  . V AC AB 2 2 4 ABCB 1 1 1 1 V V  8V  8. V =  8. .  . Vậy 2  2 2 ABIN 4 ABCB 4 6 3 V1
Câu 120. Chọn B S D' C' I B' A D O B C
Gọi O AC B ,
D I SO AC  B ,
I, D thẳng hàng và B D    B . D 2a 3 2a 6
AC a 2  SC a 6  AC  , SC  3 3 AO C CIS IS SI SBSD 4 Ta có . .  1   4     AC C SIO IO SO SB SD 5 V 2V . SA SB .SC 8 V 8 1 S . AB I  1      . V 2V . SA . SB SC 15 V 7 S . ABCD S . ABC 2 S Q M P N A K D E O G B F C Câu 121.
Ta có MNPQ //  ABCD  d S,MNPQ  2d O,MNPQ  V  2V  2V SMNPQ OMNPQ VSMNQ SM SN SQ 2 2 2 8 8  . .  . .   VV . V SE SF SK 3 3 3 27 SMNQ 27 SEFK SEFK VSNPQ SN SP SQ 2 2 2 8 8  . .  . .   VV . V SF SG SK 3 3 3 27 SNPQ 27 SFGK SFGK 8 8 8 27 27  VVVVVVV VV . SMNQ SNPQ 27 SEFK 27 SFGK SMNPQ 27 SEFGK SEFGK 8 SMNPQ 4
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 77
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1 
BE.BF.sin B S 1 1 1 Ta có: EBF 2    SSS . S 1  4 EBF 4 ABC 8 ABCD ABC . BA BC.sin B 2 Khi đó, SS  SSSS   S  4S EFGK ABCD ABF FCG GDK KAE ABCD EBF 1  SS EFGK 2 ABCD
1 d S,EFGKSEFGK V 1 27 Nên SEFGK 3    V  2VV . V 1 SABCD SEFGK SABCD
d S ABCD 2 2 , S 3 ABCD
Câu 122. Chọn C
Gọi O  AC  BD; I  SO  AM
Do P chứa AM và song song BD nên P qua I và song song BD . Kẻ đường thẳng qua I song song BD
cắt SB tai P , cắt SD tại Q vậy P  (APMQ) ; Ta có I là trọng tâm tam giác SAC nên SI 2 SP SQ    ; SO 3 SB SD V SM SQ 1 2 1 1 V V Ta có S.AMQ  .  .   V  .  SAMQ V SC SD 2 3 3 3 2 6 S.ACD V 1 1 V V V V S.AMP   V  .  ; Vậy V  2.  SAMP V 3 3 2 6 SAPMQ 6 3 S.ACB
Dạng 4.3 Ứng dụng tỉ số thể tích để tìm thể tích Câu 123.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 78
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 V 1 AM BN CC ABC MNC  '  13 13 Ta có: . '      V    . ABC.MNC ' V 3 AA BB CC ABC A B C  ' ' '  18 9 . ' ' ' V 1 AM BN CC ABC MNC   7 7 Lại có: .      V    . ABC. V 3 MNC AA BB CC ABC A B C  ' ' '  18 9 . ' ' ' 2 Suy ra: VVV  . C.MNC ' ABC.MNC ' ABC.MNC 3 V CM CN CC ' Mà: C.MNC'  . .   * V CP CQ CC ' C.PQC ' CM AMCM 1   1   CMA PMA'     PM A'  MCP 2 Ta có:      .
CNB  QNB ' CN BN CN 2     2   QN B ' NCQ 3   V 1 2 1
Thay vào * ta có: C.MNC'  . .1   V  3V  2 . C.PQC ' C.MNC ' V 2 3 3 C.PQC ' 11 Có: VVV  .
A' B 'C '.MNC LT ABC.MNC 9 7  VVV  .
A'MPB ' NQ C.PQC '
A' B 'C '.MNC 9 S A' I N M K S H I D K A O A C Câu 124. B C O
Gọi O là tâm hình vuông ABCD , SO cắt MN tại K I là giao điểm của AK với SC .
Vì MN là đường trung bình của tam giác SBD nên K là trung điểm của SO.
Gọi A' là điểm đối xứng của A qua S , H là giao điểm của AK với SC .
Vì SO A'C và K là trung điểm của SO H là trung điểm của A 'C I là trọng tâm của tam giác AA 'C 1  SI SC . 3 3 1 a 3 1 Ta có VS . A S  , VVV . S .ABCD ABCD S .ABC S .BCD S . 3 3 2 ABCD 1 1 1 1 1 1  1 1  1 1 VVV  . . V  . . V   . VV . S . AMIN S . AMN S .MIN S . ABC S .BCD   S . ABCD S . 1 2 2 2 2 3  4 12  2 6 ABCD 3 5 5a 3 Do đó VVVV  . ABCDMIN S . ABCD S . AMIN S . 6 ABCD 18 Câu 125. Chọn D
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 79
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 E N A D M C B A' D' B' C' +) Gọi BM AA 
E ; ED  AD N .
Ta có M là trung điểm của AB
M là trung điểm là EB
N là trung điểm của ED và AD V EA EM EN 1
+) Ta có E.AMN  . .    E V . EA EB ED 8 AB D   7 7 1 7 7063
VAMN.A B D E V .  .2. . A B D V . A A B D V         
ABCD.AB CD    8 8 2 24 12
Câu 126. Chọn A.
Gọi H , I lần lượt là giao điểm của các cặp đường thẳng SC và S B
 , SD và S A  .   SS  Vì SS   2
CB nên BC || SS  và  2 . BC SI SSSH Suy ra 
 2 . Tương tự, ta cũng có  2 . IC BC HD SI SH 2 Do đó   . SC SD 3
Dễ thấy hai khối chóp S.ACB và S.ACD có diện tích đáy bằng nhau và chiều cao bằng nhau nên thể tích 1
của chúng bằng nhau và bằng V  135 . 2 V SI 2 2 2 Mà: S.AIB    V  .V  .135  90 . V SC 3 S .AIB 3 S .ACB 3 S .ACB V SI SH 2 2 4 4 Và S.AIH  .  .  V  .V  .135  60 . V SC SD 3 3 S .AIB 9 S .ACD 9 S .ACD
Suy ra thể tích của khối đa diện là phần chung của hai khối chóp S.ABCD và S .ABCD bằng:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 80
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 VVV     ABCDS AIB S AIH  270 90 60 120. S. . . Câu 127. Chọn A
Trên cạnh SB , SC lần lượt lấy các điểm M , N thỏa mãn SM SN  1
Ta có AM  1, AN  2, MN  3  tam giác AMN vuông tại A
Hình chóp S.AMN có SA SM SN  1
 hình chiếu của S trên ( AMN ) là tâm I của đường tròn ngoại tiếp tam giác AMN , ta có I là trung điểm của MN 1 Trong 2 2 SIM  , SI SN IN  2 1 1 2 2 V     S . AMN 3 2 2 12 V SM SN 1 2 Ta có S.AMN     V  . V SB SC 6 S . ABC 2 S , ABC
Câu 128. Chọn D S D A Q M B C
+) Gọi P MN SB P là trọng tâm của S
CM vì là giao của hai đường trung tuyến SB, MN
+) Gọi Q MD  AB Q là trung điểm của MD MB MQ MP  1 1 2  5 +) Ta có VVVV  . . V  1  . . VV D BC QNP M . D C N M . D C N M . D C N M . D C N   M. D C N M . D MC D M MN  2 2 3  6 C N 1 S    CD. , D CM d N ABC 1 1 1 +) Mặt khác D MC 2 VV  . V  . VVM . D C N N .MCD S d S ABC C CB ABC  , ( D) S.ABCD S . ABCD S . ABCD D. 2 2 2 D 5 5 7 +) Vậy V   VVV  1   B DQ C NP SANP D Q S . D ABC D 12 BC QNP 12 12 Câu 129. Chọn C S M Q A G D N P H B C
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 81
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Gọi G là trọng tâm tam giác SAB , H là trung điểm của AB SH   ABCD 2 AB 3 27 3 Ta có S    AB  3 3 ABC . 4 4
Qua G kẻ đường thẳng song song với AB cắt SB tại N , qua N kẻ song song với BC
cắt SC tại P , qua P kẻ đường thẳng song song với CD cắt SD tại Q . Ta có: V .  V . V .  2 S MNPQ S MNP S MPQ S V .MNP . 3 S V . SM SN SP  2  8 MNP  . .     . S V . SA SB SC  3  27 ABC 8 8 1 8 1 3 3. 3 1  VV  . .SH .S  . . . S MNP S ABC ABC 3 32 . .  6 . 27 27 3 27 3 2 2  V .  12 S MNPQ . Câu 130. Chọn D S N M D A B C 3 1 a Ta có VVVS . ABD S .BCD S. 2 ABCD 2 3 V SM 1 a 3 V SM SN 1 a S . AMD   V  , S.MND  .  V  . S . V SB 2 AMD 4 S . V SB SC 4 AMD 8 S . ABD S .BCD 3 3 3 a a 3a Từ đó suy ra VVV    . S . AMND S . AMD S .MND 4 8 8
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 82
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 S I H K J A D C B Câu 131. V SI SJ SK 1
Ta có : S.IJK  . .   V  8V . V SA SB SC 8 S . ABC S .IJK S . ABC V 1
Tương tự : S.IKH   V  8V . S . ACD S . V 8 IKH S . ACD Suy ra : VVV  8 VV  8V  8 . S . ABCD S . ABC S. ACDS.IJK S .IKH S .IJKH S C' G B' A C I B Câu 132.
Xét tam giác vuông cân ABC có 2 2 2
AB BC AC AB  a 2 2 2 2 2 2
AB a AB a . 1 2 a Ta có S  . AB BC ABC 2 2 1 3 a V  . . SA S  . S . ABC 3 ABC 3 SBSCSG 2
Gọi I là trung điểm của BC . Ta có    . SB SC SI 3 V . SA SB .SC 2 2 4 Ta có S.AB C     .  . V . SA . SB SC 3 3 9 S . ABC 3 4 a 3 4aV  .  . S . AB C   9 3 27
Câu 133. Gọi O là tâm ABCD , I là giao điểm của MN và SO . Khi đó P là giao điểm của AI và SC .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 83
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
+) Mặt phẳng  AMN  cắt hình chóp S.ABCD có đáy là hình bình hành theo thiết diện là tứ giác AMPN nên SA SC SB SD SC SP 1 ta có      4   . SA SP SM SN SP SC 4 1
+) Xét hình chóp S.ABCD có: V  .V  24 . S .BCD S. 2 ABCD V SM SN SP 1 1 1 1 Ta có S.MNP  . .  . .   V  1 . S . V SB SD SC 2 3 4 24 MNP S .BDC Câu 134.
Gọi O AC BD, I MP SO Q NI SD NB PS EC
ÁP dụng định lí Menelauyt cho tam giác SBC với cát tuyết NPE , ta được . .
 1  CE CB NS PC EB (1)    2  4 
Do MIP nên SI xSP  (1  x)SM x SC  (1  x) SA 3 9      1 1  3 8  4 
SI k SO k SC SA x  , k   
. Tương tự với ba điểm thẳng hàng N, I ,Q ta có SQ SD  2 2  5 15 7 (2) RQ 6
ÁP dụng định lí Menelauyt cho tam giác SCQ với cát tuyết PRD , ta được  3 RC 7 Từ (1), (2) và (3) ta có 6 6 1 2 4 8 SS  . S  . .SS PRQ 13 PQC 13 3 SQC 13 7 SDC 91 SDC 8 8 4 18.91  VVVVVEPQR 91 ESDC 91 SBDC 91 SABCD SABCD 4
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 84
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 SM SN SP SM SP SQ V Do đó VVV  . .  . . SABCD SMNPQ SMNP SMPQ    SA SB SC SA SC SD  2  4 2 1 2 4 4  VSABCD 3  . .  . . .  65cm    9 3 2 3 9 7  2
Dạng 5. BÀI TOÁN THỰC TẾ VÀ BÀI TOÁN CỰC TRỊ Câu 135. Chọn C
Gọi x là chiều rộng, ta có chiều dài là 2x 2 6, 7  2x
Do diện tích đáy và các mặt bên là 2
6, 7m nên có chiều cao h  , 6x 6, 7
ta có h  0 nên x  . 2 3 6, 7x  2x 2 6, 7  6x 6, 7
Thể tích bể cá là V x 
và V  x   0  x  3 3 6 Bảng biến thiên
Bể cá có dung tích lớn nhất bằng 3 1,57m . Câu 136. Chọn D
Gọi x, 2x, h lần lượt là chiều rộng, dài, cao của bể cá. 2 5,5  2x 5,5 Ta có 2
2x  2 xh  2xh  5,5  h
( Điều kiện 0  x  ). 6x 2 2 5,5  2x 1 Thể tích bể cá 2 3 V  2x . 
(5, 5x  2x ) . 6x 3 1 5,5 / 2 V  (5,5  6x ) . /
V  0  x  . 3 6 11 33 Lập BBT suy ra 3 V   1,17 m . max 54 72 24
Câu 137. Thể tích của bế cá: 3
V  3ab  72 dm  b  
, với a,b  0 . 3a a
Diện tích kính để làm bể cá như hình vẽ: 24 24 144 144
S  3.3a  2.3b ab  9a  6.  . a  9a   24  2 9 . a  24  S  96 . a a a a 144
S  96  9a
a  4  b  6 . a
Vậy để bể cá tốn ít nguyên liệu nhất thì a  4 dm ; b  6 dm . Câu 139. Chọn B
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 85
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A 2 3 N x 2 3 2 3 B C 2 3 2 3 M D
Gọi M , N lần lượt là trung điểm của CD và AB . CD MBCD   MN Ta có
  CD   MAB   . CD MA CD AB  
Tam giác MAB cân tại M nên MN AB . 1 1 V  . AB . CD d AB CD AB CD x MNABCD  , .sin  ,  .2 3. .sin 90 6 6 2 2  x  36 1   3 3  x x  2 2  2   .2 x 3. 3   . x 36  x  .   3 3   . 6  2  6 6  2    Dấu "  " xảy ra 2
x  36  x x  3 2 . Câu 140.
Đặt SA h, AB AC a . Ta có d  1 1 1 1 1 1 1 1 1 ; A SBC 2 3  AH  3;         3  a h  6 . 2 2 2 2 2 2 2 4 2 AH SA AB AC 9 a a h a h
SBC  ABC   ,  SMA   . 1 3 AM a 2 2 3 2 V
a h  1 . Thể tích nhỏ nhất bằng 1 khi a h SM a  os c     . S . ABC 6 2 SM 2 a 3 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 86
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 B' C' D' A' B C A D Câu 141. BC BB Ta có
  CB   ABB  A   
A B là hình chiếu vuông góc của 
A C trên mặt phẳng  ABB  A   BC AB
góc giữa đường thẳng 
A C và mặt phẳng  ABB  A  là góc   A BA C   ,   BA C (vì   BA C nhọn do   BA C
vuông tại B ). Vậy   BA C  30 . BC 1 Ta có  A B     3 ; 2 2 2  A A  
A B AB  3  x . tan  BA C tan 30 2 x   2 3  x 3 2  V  . AB . AD
AA x 3  x   . ABCD. 
A BCD 2 2 3 Dấu  xảy ra 2 2 2
x  3  x x  3  x x  (vì x  0 ). 2 3 Vậy V. max 2 32
Câu 142. Ta có thể tích chiếc hộp: 2
V x h  32 (đvtt), với x, h  0 . Suy ra h  . 2 x 32 256
Phần mạ vàng của chiếc hộp: 2
S  2x  8xh 2  2x  8 . x 2  2x  . 2 x x Cách 1 256 128 128 128 128 Ta có 2 2x  2 2 3  2x    3 2x . .  96 (BĐT AM-GM). x x x x x 128 Đẳng thức xảy ra khi 2 2x
hay x  4 , khi đó h  2 . x Cách 2. 256
Xét hàm số f x 2  2x  với x  0 . x
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 87
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 3 256 4x  256
Ta có f  x  4x   , f  x 3
 0  4x  256  x  4 ; f 4  96. 2 2 x x BBT x 0 4  f  x  0  f x   96
Dựa vào BBT ta thấy hàm số đạt GTNN tại x  4 , khi đó h  2 . Vậy phương án A đúng.
Câu 143. Chọn A
Gọi M , N lần lượt là trung điểm của BD , AC . Đặt BD  2x , AC  2 y  , x y  0 .
Ta có CM BD, AM BD BD   AMC . 1 1 Ta có 2
MA MC  1 x , 2 2
MN  1 x y , SMN.AC 2 2 
y. 1 x y . AMC 2 2 1 1 2
x y   x y 3 2 2 2 2 1 2 V  .D . B S 2 2  .2 .
x y 1 x y 2 2  x .y . 2 2
1 x y   ABCD 3 AMC 3 3 3 27 2 3 1  V
. Dấu đẳng thức xảy ra khi x y  . ABCD 27 3 2 3
Vậy giá trị lớn nhất của thể tích khối tứ diện ABCD là . 27
Câu 144. Chọn C
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 88
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Gọi M , N lần lượt là trung điểm của S ,
A BC và đặt 2a x, 2b y.
BC AN , BC SN BC  SAN  1 VVV  2VBC.S SABC BSAN CSAN BSAN 3 SAN 2 2 2 AB AC BC 2 2 2 2 2 2 2 AN  
 1 b MN AN MA  1 b a 2 4 1 2 2  S  .
SA NM a 1 a b SAN 2 3 2 2 2 2 1 1
4  a b 1 a b  2 2 2 2 2  V
2ab 1 a b V  .4a b .  a bSABC SABC  2 2 1  .  3 9 9 3   4 2  VSABC 243 1 2 4 Dấu bằng xảy ra 2 2 2 2
a b  1 a b a b   x y   x y  . 3 3 3 Câu 145. Chọn A
+) Gọi độ dài AB  ,
a AD b và AA   c
Ta có tổng diện tích tất cả các mặt là 36 nên 2ab  2bc  2ca  36  ab bc ca  18   1
Do độ dài đường chéo AC ' bằng 6 nên 2 2 2
a b c  36 2
+) Thể tích khối hộp là V abc 2
Ta có a b c 2 2 2
a b c  2ab bc ca  72  a b c  6 2 Từ    ab   ca  b   c  c 2 1 18 18 6 2
c  6 2c 18 Nên 3 2
V abc c  6 2c 18c f c, c0;6 2 c  3 2
Ta có f c 2
 3c 12 2c  18  0   c  2 
Lập bảng biến thiên ta được Max V f  2  8 2 0;6 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 89
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 S x a a I a A D O a B Câu 146. a C
Gọi I là trung điểm SC , O AC BD . BI SC Ta có   BD SC DI SC
Mà ABCD là hình thoi nên BD AC
Khi đó, BD  SAC  . V  2V  2V . S . ABCD S . ABC B.SAC 2 2 x a 2 2 2 2      2 2 AO AB BO AB BI OI  2  AB   2 2 SB SI  2  OI  4 2 2 2 2 2 2
AC  4 AO x a SA SC  SAC vuông tại S . 2 2 3a x 2 2 BO AB AO  . 2 1 1 2 2 2 2 1 3a x
ax 3a xV  2V  2  BO SA SC   a x  . S . ABCD B.SAC 3 2 3 2 6 2
x  3a x 3a 2 2 2 2 2  2 2  2
Ta có x 3a x
x .3a x    2 2 3 a a 6  V  . Dấu “=” xảy ra 2 2 2
x  3a x x  . S . ABCD 4 2 a 6
Vậy, thể tích khối chóp S.ABCD lớn nhất khi và chỉ khi x
m  6; n  2 2
m  2n  10 . Câu 147.
Gọi M , N lần lượt là trung điểm của AB,CD .
Tam giác ADB,CAB là hai tam giác cân cạnh đáy AB nên DM AB và CM AB . Suy ra
AB   MCD .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 90
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1 1 x VVV  .BM .S  .AM .S  .S . ABCD B.MCD . A MCD 3 MCD 3 MCD 3 MCD
Tam giác ABC  ABD  . c .
c c nên CM DM MN CD . 1 1 1 2 2 2 2 1 x y S  .C . D MN  . y MC CN  . y BC BMCN y 4   MCD  2 2  2 2 2 2 2 4 4 1  y 16   2 2 x y  . 4 xy xy V  16  x y   xy xy xyxy ABCD  1 2 2  16 2 . .16 2  12 12 12 1
xy xy    xy  3 3 16 2  1  16        . 12 3 12    3   x yx y  Dấu bằng xảy ra khi    16 .
xy  16  2xy xy     3 16
Vậy thể tích ABCD đạt giá trị lớn nhất khi xy  . 3 Câu 148.
Gọi O AC BD , G APSO, suy ra G là trọng tâm tam giác SAC .
Gọi  P là mặt phẳng qua AP cắt hai cạnh SD và SB lần lượt tại M và N . 
P  SBD  MN  Dễ thấy: 
P   SAC   AP
MN , AP , SO đồng quy hay M , N , G thẳng hàng. 
SBDSAC  SOSM SN Đặt: x  0  x   1 và y  0  y   1 . SD SB V 1  V V  1  SA SM SP SA SN SP  1 1 S . AMP S . ANP     . .  . .     
x y  . V 2 V V 2    SA SD SC SA SB SC  4 S . ADC S . ABP S 1  S SSM SN 1  SM SG SN SG  1  SM SN Từ tỷ lệ:  SMNSMGSNG    .  .  .         . S 2 S S SD SB 2    SD SO SB SO  3  SD SBSBDSDOSBO  1  xy
x y . Lại có:  x   1  y  
1  0  xy   x y 1 0 . 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 91
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 3 V 3 Từ đó suy ra: 
x y 1  0 hay x y  . Vậy 1 lớn nhất bằng . 3 2 V 8 Câu 149.
Gọi K là trung điểm AD 5
, đặt HK x, 0  x  . 2 2  5   5 
Ta có EF FG GH HE   x 2 ; 2 HD   x .      2   2  2 2  5   5  Suy ra 2 2 2 2 2
SO SH OH HD OH   x   x .      2   2  2 2 2 2 1  5   5   5  2  5  Ta có 2 V  .2.  xx   x  .  x . 5x .         3  2   2   2  3  2   5 2 x  2  5 5 5       2  V    2   x 5x   x    
 , V   0   . 3   2   2  2 5x   1 x   2 Bảng biến thiên 4 10 1
Dựa vào bảng biến thiên, ta có V  khi x  . max 3 2
Câu 150. Chọn A
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 92
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A' B' N D' C' A B M D C 1 Ta có Vd N AB MS AB MN  , .   3 AB M  3 Do ACB D
  là tứ diện đều nên B D    AB M      6 sin ,  , sin B AM  3 2 1 1 a Suy ra VB N  .sin B D  ,  AB MABAM B AM   AM B NAB MN         . . .sin . . 3 2 6 2 3
a AM B N   a     6  2  12 3 a Vậy VAB MN  max 12 Câu 151.
Gọi E, F , G lần lượt là trung điểm BC, ,
SA EF suy ra G là trọng tâm tứ diện SABC . Điểm I là giao điểm
của AG và SE . Qua I dựng đường thẳng cắt các cạnh SB, SC lần lượt tại M , N . Suy ra  AMN  là mặt
phẳng quay quanh AG thỏa mãn yêu cầu bài toán.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 93
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Kẻ GK // SE,  K SA suy ra K là trung điểm FS . KG AK 3 KG 1 SI 2    . Mà    . SI AS 4 SE 2 SE 3 Cách 1:
Kẻ BP // MN,CQ // MN ;  P,Q SE  . SM SI SN SI Ta có:  ;  . SB SP SC SQ
 BEP  CEQ E là trung điểm PQ SP SQ  2SE (đúng cả trong trường hợp P Q E ). 2 2 2 AM GM V SA SM SN SI SI SI SI SI S AMN   4 Ta có: .  . .  1. .       . V SA SB SC SP SQ SP SQ SE SE S ABC   2 2   9 . 4
Dấu "  " xảy ra khi và chỉ khi SP SQ SE . Hay P Q E MN // BC . Cách 2: SB SC Ta chứng minh được   3 . SM SN
Thật vậy, qua I kẻ các đường thẳng lần lượt song song SB, SC cắt SC, SB tương ứng tại D, L . SB DB    3 IQ DISB IQ NI SB 3NI Ta có:   .  3.   ,   1 . IQ NIIQ SM NM SM NM   SM NMSC LC    3 IP LISC IP MI SC 3MI Lại có:   .  3.   , 2 . IP MIIP SN MN SN MNSN MN   SB SCNI MI  Từ   1 và 2 ta có:   3   3   . SM SNNM MN SB SC Đặt x  ; y
. Suy ra x y  3 . SM SN V SA SM SN 1 AM GM 1 4
Ta có: S.AMN  . .    . V SA SB SC xy S ABCx y2 9 . 4 3
Dấu "  " xảy ra khi và chỉ khi x y   MN // BC . 2 Cách 3: SB SC Đặt  x ;
y , với x  0 , y  0 . SM SN
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 94
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  2  1   1     x y Ta có SI SE  (SB SC) 
(xSM ySN )  SM SN . 3 3 3 3 3 x y
Do I , M , N thẳng hàng nên 
 1  x y  3 . 3 3 V SM SN 1 1 1 1 4 Ta có S.AMN  .  .    . V SB SC x y xy x y 2 9 S . ABC ( ) 2 V 4
Vậy S.AMN đạt giá trị nhỏ nhất bằng
khi x y , hay MN đi qua I và song song với BC . V 9 S . ABC
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 95