























































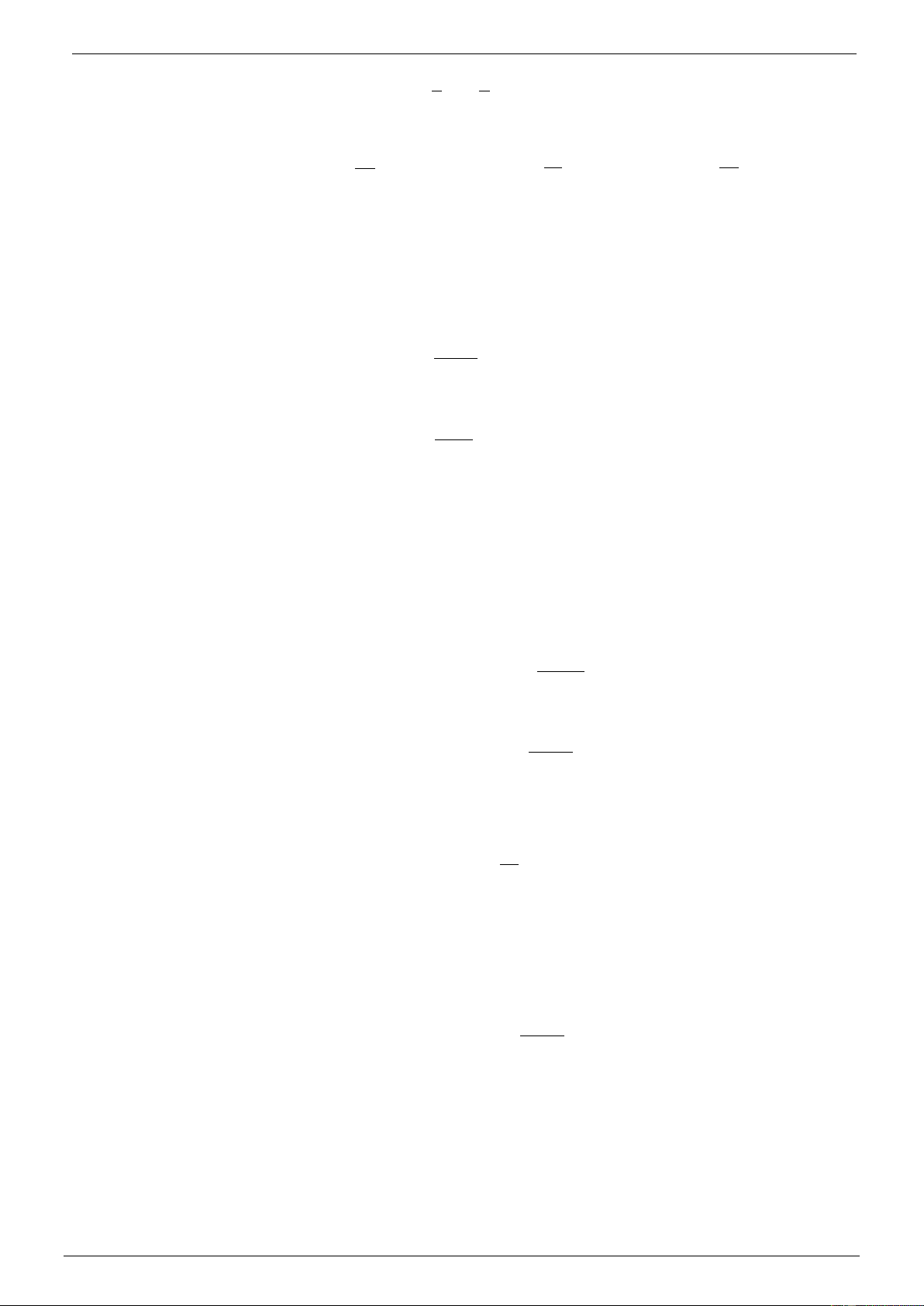











































Preview text:
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM CHƯƠNG 5 ĐẠO HÀM
BÀI 1. ĐỊNH NGHĨA – QUY TẮC TÍNH ĐẠO HÀM _____________________________________________ 2
A. TÓM TẮT LÝ THUYẾT ______________________________________________________________ 1
B. DẠNG TOÁN VÀ BÀI TẬP ___________________________________________________________ 2
_ DẠNG 1. TÍNH ĐẠO HÀM BẰNG ĐỊNH NGHĨA _________________________________________ 2
_ DẠNG 2. CÁC QUY TẮC TÍNH ĐẠO HÀM VÀ BẢNG ĐẠO HÀM _____________________________ 3
_ DẠNG 3. BÀI TOÁN CHỨNG MINH, GIẢI PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH _____________ 16
_ DẠNG 4. ĐẠO HÀM CỦA HÀM SỐ LƯỢNG GIÁC ______________________________________ 20
_ DẠNG 5. CHÚNG MINH ĐẲNG THỨC, GIẢI PHƯƠNG TRÌNH CHỨA ĐẠO HÀM _______________ 26
C. BÀI TẬP RÈN LUYỆN _____________________________________________________________ 27
D. LỜI GIẢI BÀI TẬP RÈN LUYỆN ______________________________________________________ 32
BÀI 2. PHƯƠNG TRÌNH TIẾP TUYẾN _____________________________________________________ 41
A. TÓM TẮT LÝ THUYẾT _____________________________________________________________ 41
B. DẠNG TOÁN VÀ BÀI TẬP __________________________________________________________ 41
_ DẠNG 1. VIẾT PTTT KHI BIẾT TIẾP ĐIỂM (TẠI ĐIỂM M ) HOẶC BIẾT HOÀNH ĐỘ, TUNG ĐỘ _____ 41
_ DẠNG 2. VIẾT PTTT KHI BIẾT HỆ SỐ GÓC HOẶC SONG SONG, VUÔNG GÓC VỚI MỘT ĐƯỜNG
THẲNG. ____________________________________________________________________________ 48
_DẠNG 3. BÀI TOÁN VỀ XÁC ĐỊNH HỆ SỐ GÓC NHỎ NHẤT, LỚN NHẤT CỦA TIẾP TUYẾN ________ 54
_ DẠNG 4. VIẾT PTTT KHI BIẾT ĐIỂM MÀ TIẾP TUYẾN ĐI QUA _____________________________ 57
_ DẠNG 5. TÌM THAM SỐ m ĐỂ TỪ 1 ĐIỂM TA KẺ ĐƯỢC ĐÚNG MỘT TIẾP TUYẾN ĐẾN ĐỒ THỊ
HÀM SỐ ____________________________________________________________________________ 62
TỔNG HỢP KIẾN THỨC CẦN NHỚ VỀ TIẾP TUYẾN ________________________________________ 64
C. BÀI TẬP RÈN LUYỆN _____________________________________________________________ 65
D. LỜI GIẢI BÀI TẬP RÈN LUYỆN ______________________________________________________ 71
BÀI 3. ĐẠO HÀM CẤP CAO VÀ VI PHÂN __________________________________________________ 92
A. TÓM TẮT LÝ THUYẾT _____________________________________________________________ 92
B. DẠNG TOÁN VÀ BÀI TẬP __________________________________________________________ 92
_ DẠNG 1. TÍNH ĐẠO HÀM CẤP CAO CỦA MỘT HÀM SỐ _________________________________ 92
_ DẠNG 2. TÌM VI PHÂN CỦA MỘT HÀM SỐ ___________________________________________ 94
BÀI 4. ÔN TẬP CHƯƠNG V _____________________________________________________________ 96 1 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
BÀI 1. ĐỊNH NGHĨA – QUY TẮC TÍNH ĐẠO HÀM
A. TÓM TẮT LÝ THUYẾT
1. Định nghĩa đạo hàm: Cho hàm số y = f ( x) các định trên khoảng ( ; a b) và x ; a b . 0 ( )
f ( x) − f ( x0 )
Giới hạn hữu hạn nếu có của tỉ số
x → x được gọi là đạo hàm của hàm số đã cho tại x − khi x 0 0
x , kí hiệu f '( x hay y '( x . Như vậy, ta có: 0 ) 0 ) 0 f x − f x f '( x = lim 0 ) ( ) ( 0 ) x→ x − 0 x x0
2. Quan hệ giữa sự tồn tại của đạo hàm và tính liên tục của hàm số
Định lí 1. Nếu hàm số y = f ( x) có đạo hàm tại x thì nó liên tục tại điểm đó. 0
3. Ý nghĩa của đạo hàm
a) Ý nghĩa hình học: Phương trình tiếp tuyến của đồ thị hàm số y = f ( x) tại điểm M ( x ; f x có 0 ( 0 ))
dạng: y = k ( x − x + f x với k = f '( x là hệ số góc của tiếp tuyến. 0 ) 0 ) ( 0)
b) Ý nghĩa vật lý:
– Vận tóc tức thời: v (t) = s '(t) .
– Gia tốc tức thời: a (t) = v '(t).
– Cường độ dòng điện tức thời: I (t) = Q '(t) .
4. Đạo hàm trên khoảng: Hàm số y = f ( x) được gọi là có đạo hàm trên khoảng ( ;
a b) nếu nó có đạo
hàm tại mọi điểm x trên khoảng đó.
B. DẠNG TOÁN VÀ BÀI TẬP
_ DẠNG 1. TÍNH ĐẠO HÀM BẰNG ĐỊNH NGHĨA PHƯƠNG PHÁP: f x − f x
Cần nhớ công thức: f '( x) ( ) ( 0 ) = lim x→x − 0 x x0
Phương pháp tính giới hạn của hàm số
_VÍ DỤ MINH HỌA
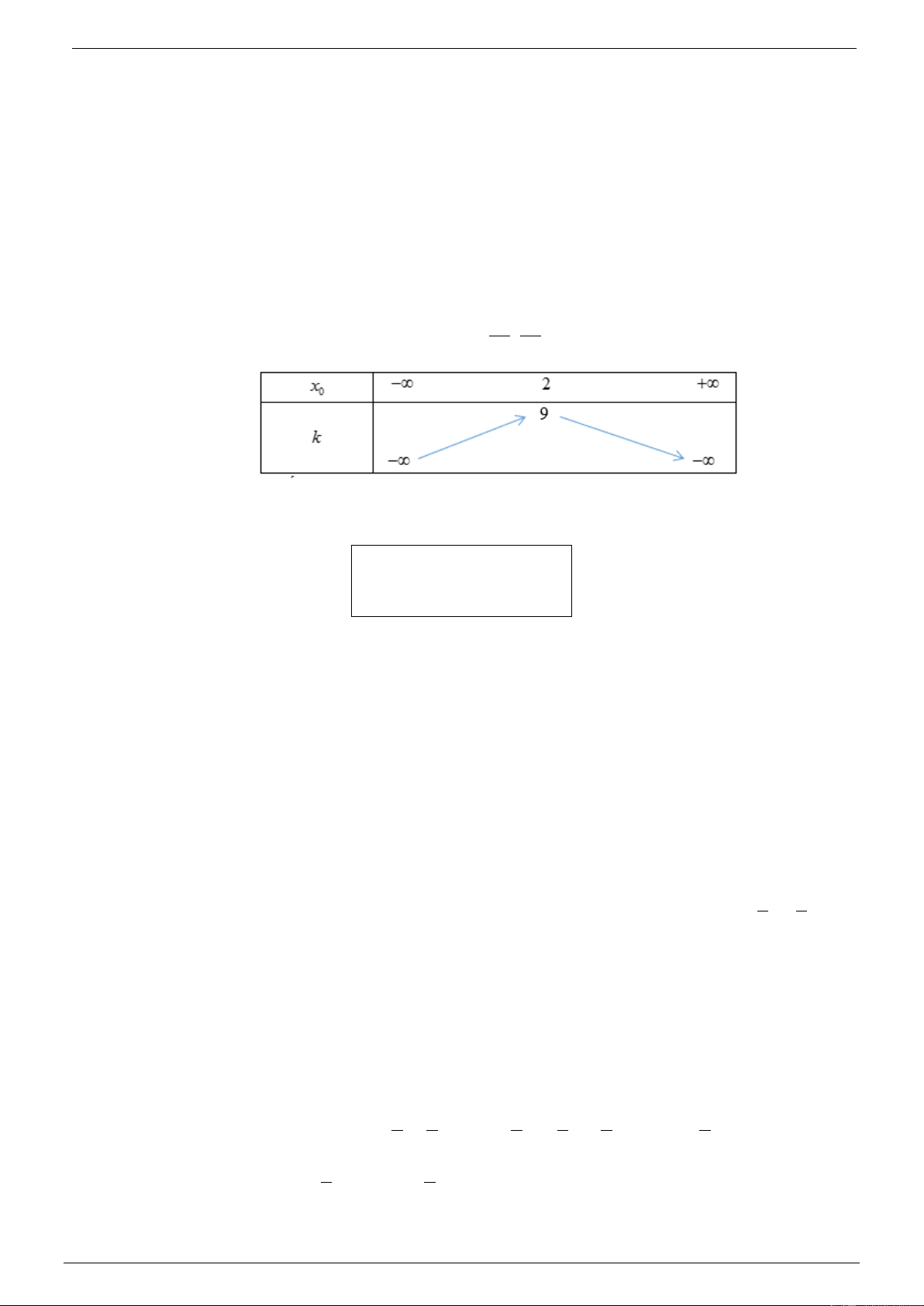
Ví dụ 1. Cho hàm số f ( x) 2
= 2x + x +1. Tính f '(2) ? Lời giải f x − f 2 2x + x +1−11 (x −2)(2x +5) Ta có f '(2) ( ) ( ) 2 = lim = lim = lim = lim(2x +5) = 9 . x→2 x→2 x − 2 x − 2 x→2 x→2 x − 2
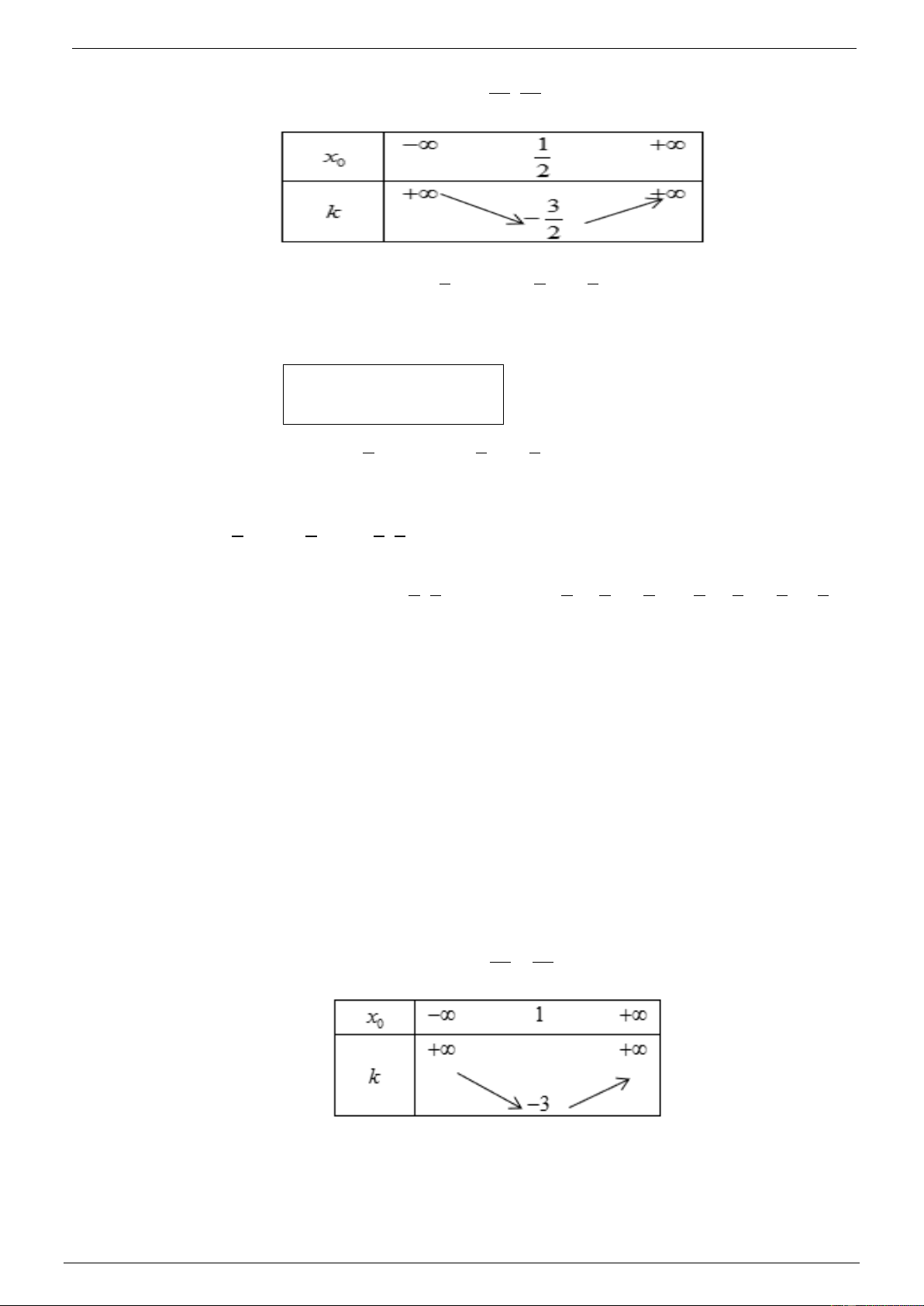
Ví dụ 2. Cho hàm số 3
y = x − 2x +1. Tính y '(2) ? Lời giải y x − y 1 x − 2x +1− 0 Ta có y '(2) ( ) ( ) 3 = lim = lim x 1 → x 1 x −1 → x −1
(x − )1( 2x + x− )1 = lim = lim( 2 x + x − ) 1 = 1. x 1 → x 1 x −1 →
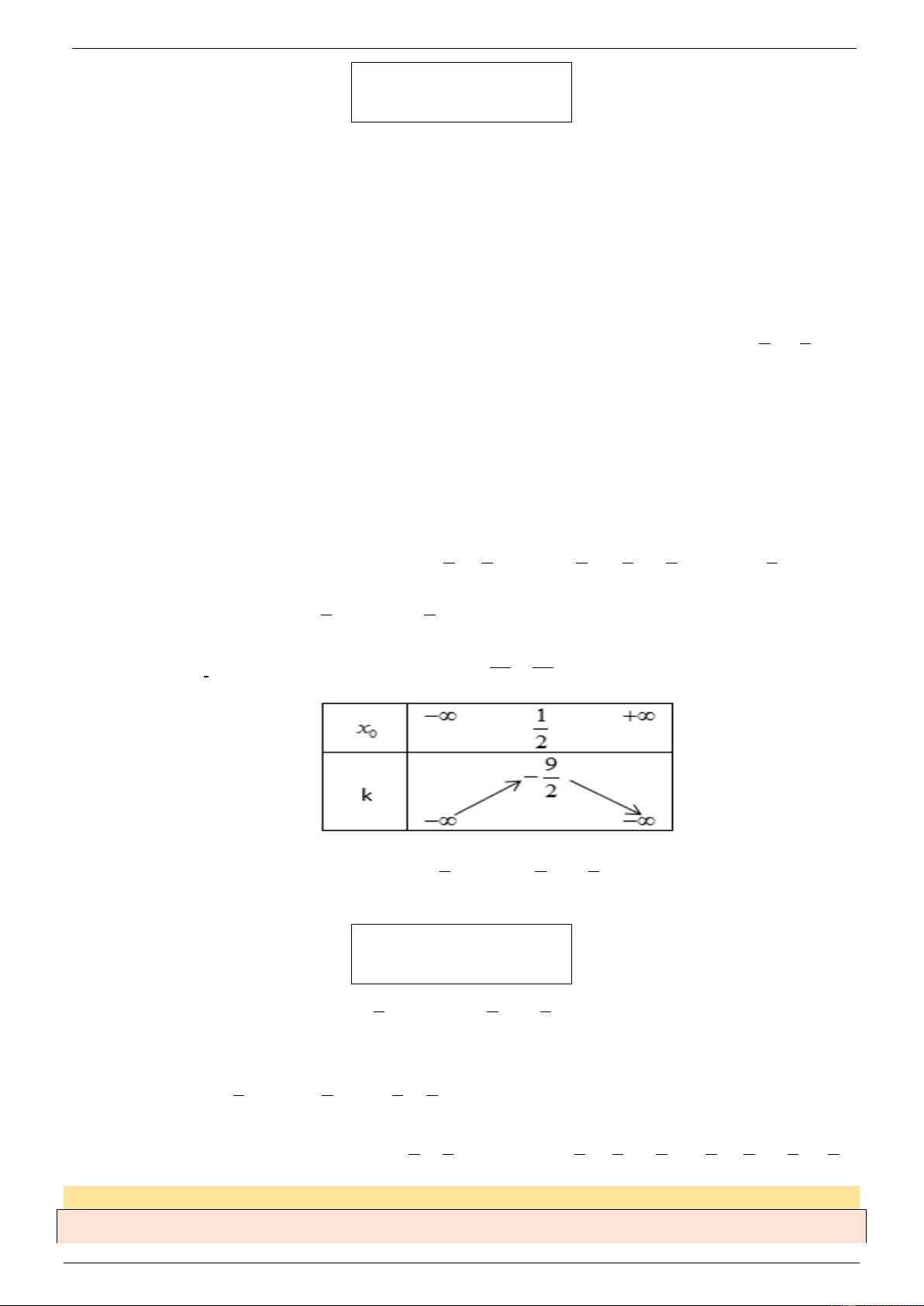
Ví dụ 3. Cho hàm số f ( x) = 2x +1 . Tính f '( ) 1 ? Lời giải 2 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM f x − f 1 2x +1 − 3 Ta có f '( ) ( ) ( ) 1 = lim = lim x 1 → x 1 x −1 → x −1 2x − 2 2 3 = lim = lim = . x 1 → (x − )
1 ( 2x +1 + 3) x 1 → 2x +1 + 3 3 2x −1
Ví dụ 4. Cho hàm số y = . Tính y '(3) ? x + 3 Lời giải 2x −1 5 − y x − y 3 + 7x − 21 7 7 Ta có y ( ) ( ) ( ) x 3 6 ' 3 = lim = lim = lim = lim = x→3 x→3 x − 3 x − 3 x 3
→ 6( x + 3)( x − 3) x 3 → 6( x + . 3) 36 _BÀI TẬP ÁP DỤNG
Bài 1. Tính đạo hàm của các hàm số sau tại các điểm được chỉ ra:
1. Cho f ( x) 3
= x + x − 2 . Tính f '(−2) ? ĐS: f '( 2 − ) =13
2. Cho y = 3 − 2x . Tính y '(−3) ? ĐS: y (− ) 1 ' 3 = − 3 x +
3. Cho f ( x) 2 1 = . Tính f '(2) ? ĐS: f '(2) = 3 − x −1 _LỜI GIẢI 3 f x − f 2 − x + x − 2 − 1 − 2 1. Ta có f '( 2 − ) ( ) ( ) ( ) = lim = lim x→ 2 − x→ 2 x + 2 − x + 2
(x + 2)( 2x −2x+5) = lim = lim ( 2
x − 2x + 5) =13 . x→ 2 − x→ 2 x + 2 − y x − y 1 3 − 2x − 3 2. Ta có y '( 3 − ) ( ) ( ) = lim = lim x→ 3 − x→ 3 x + 3 − x + 3 6 − − 2x 2 − 1 = lim = lim = − . x→ 3
− (x + 3)( 3−2x +3) x→ 3− 3−2x +3 3 2x +1 −5 f x − f 3 − 3 − x + 6 3 − 3. Ta có f ( ) ( ) ( ) x 1 ' 2 = lim = lim = lim = lim = 3 − . x→2 x→2 x→2 x − 2 x − 2
(x − )1(x −2) x→2 2(x − )1
_ DẠNG 2. CÁC QUY TẮC TÍNH ĐẠO HÀM VÀ BẢNG ĐẠO HÀM
Quy tắc tính đạo hàm
(u + v − w)' = u '+ v '− w' ( .
u v)' = u 'v + v 'u − u u 'v v 'u = 2 v v
(k.u)' = k.u ' (k ) Bảng đạo hàm Hàm sơ cấp Hàm hợp
(C)' = 0 (C ) n n− − (u ) 1 * . n u .u ' (n ) ( n x ) n 1 * = . n x (n ) 3 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM u ( x ) 1 = (x 0) ( u ) ' = (u 0) 2 x 2 u 1 1 1 u ' = − (x 0) = − (u 0) 2 x x 2 u u o Công thức nhanh ax + b ad − bc = cx + d (cx + d )2 2 2
ax + bx + c
adx + 2aex + (be − cd ) = dx + e (dx + e)2 a b 2 a c b c 1 1 1 1 1 1 + + 2 x 2 x
a x + b x + c a b a c b c 1 1 1 2 2 2 2 2 2 =
(Tích huyền trừ tích sắc) 2
a x + b x + c ( 2 2 2 2
a x + b x + c 2 2 2 )2
Loại 1. Làm quen nhóm công thức ( n x ) n 1 = . n x − và ( .
u v) = u 'v + v 'u 1. Ví dụ minh họa
Ví dụ 1. Tìm đạo hàm của hàm số 4 2
y = x − 2x +1. Lời giải 3 3
y ' = 4x − 2.2x = 4x − 4x
Ví dụ 2. Tìm đạo hàm của hàm số 2
y = 5x (3x − ) 1 . Lời giải 2
y = x ( x − ) = ( 2x) ( x− ) 2
+ x ( x − ) = x ( x − ) 2 2 ' 5 3 1 5 . 3 1 ' 5 . 3 1 ' 10 . 3
1 + 5x .3 = 45x −10x 2. Bài tập áp dụng Bài 1.
Tính đạo hàm của các hàm số sau 1. 4 2 y = 2
− x + 4x − 3x +1. ĐS: 3 8
− x +8x −3. 2. 3 2
y = x − 3x + x −1 . ĐS: 2
3x − 6x +1 . 1 3 5 3. 5 4 3 2 y =
x + x − x −
x + 4x − 5 . ĐS: 4 3 2
x + 4x − 3x − 3x + 4 . 2 2 2 1 1 1 1 4. 2 4 y =
− x + x − x . ĐS: 3
− + 2x − 2x . 4 3 2 3 Bài 2.
Tính đạo hàm của các hàm số sau 1 1 1. 5 4 3 2 y = mx − 2x +
x + m −1. ĐS: 4 3 2
mx − 8x + x . 5 3 4 3 x x 1 2. 2 y = −
+ x + m −1. ĐS: 3 2
x − x + x . 4 3 3 3. 3
y = x + (m − ) 2 2 3 2
1 x + x + m −1 . ĐS: 2 9x + 4(m − ) 1 x +1. Bài 3.
Tính đạo hàm của các hàm số sau 1. y = ( 2 x + x)( 2 3 − x ) . ĐS: 3 2 4
− x −3x + 6x + 3. 2 2
2. y = (2x − ) 1 (2x + ) 1 . ĐS: 2 16x + 4 .
3. y = x (2x − ) 1 (3x + 2) . ĐS: 2
18x + 2x − 2 . 4 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 3. Lời giải Bài 1. 1. 3 3 y ' = 2
− .4x + 4.2x − 3 = 8
− x + 8x − 3 . 2. 2 2
y ' = 3x − 3.2x +1 = 3x − 6x +1. 1 3 5 3. 4 3 2 4 3 2 y ' =
.5x + 4x − 3x − .2x + 4 =
x + 4x − 3x − 3x + 4 . 2 2 2 1 1 1 4. 3 3
y ' = − + 2x − .4x = − + 2x − 2x . 3 2 3 1 1 Bài 2. 1. 4 3 2 4 3 2
y ' = .5mx − 2.4x + .3x = mx − 8x + x . 5 3 1 1 1 2. 3 2 3 2 y ' =
.4x − .3x + .2x = x − x + x . 4 3 2 3. 2 y = x + (m− ) 2 ' 3.3 2.2
1 x +1 = 9x + 4 (m − ) 1 x +1 . Bài 3. 1. y = ( 2 x + x)( 2 − x ) = ( 2x + x) ( 2 − x )+ ( 2 x + x) ( 2 ' 3 3 . 3 − x ) = ( x + )( 2 − x ) + ( 2
x + x)(− x) 3 2 2 1 3 2 = 4
− x − 3x + 6x + 3 = − + 2 2 2 2 2 2. y '
(2x )1 (2x )1 = (2x− ) 1 (2x + ) 1 + (2x − ) 1 . ( 2x + ) 1
= ( x + )2 + ( x − )2 2 2. 2 1 2
1 .2 = 16x + 4 .
3. y ' = x (2x − )
1 (3x + 2) = x '.(2x − ) 1 (3x + 2) + . x (2x − ) 1 (3x + 2) =1.(2x − ) 1 (3x + 2) + . x (2x − )
1 '.(3x + 2) + (2x − ) 1 .(3x + 2)' 2
=1.6x + x − 2 + .
x 2.(3x + 2) + (2x − ) 1 .3 2
= x + x − + x x + 2 2 2 6 2 12
1 = 6x + x − 2 +12x = 18x + 2x − 2 . −
Loại 2. Làm quen nhóm công thức ( n u ) n 1 = . n u .u 1. Ví dụ minh họa
Ví dụ 1. Tìm đạo hàm của hàm số = ( + )2 7 y x x . Lời giải y = ( 7 x + x) ( 6 x + ) = ( 13 7
x + x + x) 13 7 2 . 7 1 2 7 8 =14x +16x + 2 . x
Ví dụ 2. Tìm đạo hàm của hàm số y = ( x − x + )( x + )3 2 2 3 2 1 Lời giải y = (
x − x + )( x+ )3 = (x − x+ ) ( x+ )3 +(x − x+ ) ( x+ )3 2 2 2 2 3 2 1 2 3 . 2 1 2 3 . 2 1
= ( x − ) ( x + )3 +(x − x + ) ( x + )2 = ( x − ) ( x + )3 + (x − x + )( x + )2 2 2 2 2 . 2 1 2 3 . 3 2 1 .2 2 2 . 2 1 6 2 3 2 1 . 2. Bài tập áp dụng Bài 1.
Tìm đạo hàm của hàm số sau
1. y = ( x − x − x + )2 3 2 2 3 6 1 . ĐS: 5 4 3 2
25x − 60x − 60x +120x + 60x −12 9
2. y = ( x + x + )10 7 4 3 2 . ĐS: ( 7 4 x + x + ) ( 6 3 10 3 2 . 7x +12x ) 5
3. y = ( x − x + x − )2 4 2 2 1 . ĐS: 7 5 4 3 2
8x − 24x +10x + 8x −12x +10x − 2 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 10 5 4. y = ( 2 3
3x − 5x + 4x ) ( x + 3) . ĐS:
( x − x+ )(x+ ) ( x− x + x )9 + (x+ ) ( x− x + x )10 5 4 2 2 3 2 3 10 12 10 3 5 3 5 4 5 3 3 5 4 3. Lời giải Bài 1. 1. y = ( 3 2
x − x − x + ) ( 2 x − x − ) ( 5 4 3 2 2 2 3 6 1 . 6 6
6 = 2 12x − 30x − 30x + 60x + 30x − 6) 5 4 3 2
= 24x − 60x − 60x +120x + 60x −12 . 9 2. y = ( 7 4 x + x + ) ( 6 3 10 3 2 . 7x +12x ). 3. y = ( 4 2
x − x + x − ) ( 3 x − x + ) ( 7 5 4 3 2 2 2 1 . 4 4
1 = 2 4x −12x + 5x + 4x − 6x + 5x − ) 1 7 5 4 3 2
= 8x − 24x +10x + 8x −12x +10x − 2 . 4.
y = ( x − x + x )10 (x + )
( x− x + x )10 (x+ ) +( x− x + x )10 5 5 (x + )5 2 3 2 3 2 3 3 5 4 . 3 = 3 5 4 . 3 3 5 4 . 3 (
x − x + x )9 ( − x + x ) (x + ) + ( x − x + x )10 5 (x + )4 2 3 2 2 3 = 10 3 5 4 . 3 10 12 . 3 3 5 4 . 5 3 .1
( x − x+ )(x+ ) ( x− x + x )9 + (x+ ) ( x− x + x )10 5 4 2 2 3 2 3 = 10 12 10 3 3 3 5 4 5 3 3 5 4 . u u v − v u ax + b ad − bc
Loại 3. Làm quen nhóm công thức = và = 2 v v cx + d (cx + d )2 1. Ví dụ minh họa 2x +1
Ví dụ 1. Tính đạo hàm của hàm số y = . x +1 Lời giải u u v − v u
- Cách 1. Sử dụng công thức = ta được 2 v v ( 2x + ) 1 ( x + ) 1 − ( x + ) 1 (2x + ) 1 2 ( x + ) 1 − (2x + ) 1 1 y = = = ( x + ) . 2 1 (x + )2 1 (x + )2 1 ax + b ad − bc
- Cách 2. Sử dụng công thức nhanh =
(rèn luyên cho lớp 12 trong trắc cx + d (cx + d )2 nghiệm) 2.1−1.1 1 y = = ( x + ) . 2 1 (x + )2 1 2mx +1
Ví dụ 2. Tính đạo hàm của hàm số y = . x + m Lời giải u u v − v u
- Cách 1. Sử dụng công thức = ta được 2 v v ( 2mx + )
1 ( x + m) − ( x + m) (2mx + ) 1
2m ( x + m) −1.(2mx + ) 2 1 2m −1 y = = = ( x + m) . 2 (x + m)2 (x + m)2 6 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM ax + b ad − bc
- Cách 2. Sử dụng công thức nhanh =
(rèn luyên cho lớp 12 trong trắc cx + d (cx + d )2 nghiệm) 2 2 . m m −1.1 2m −1 y = = ( x + m) . 2 (x + m)2 2. Bài tập áp dụng Bài 1.
Tính đạo hàm của các hàm số sau 2x −1 2 − 1. y = . ĐS: . 4x − 3 (4x −3)2 3 6 − 2. y = . ĐS: . 2x +1 (2x + )2 1 2x +1 5 3. y = . ĐS: . 1− 3x (1−3x)2 1− 2x 11 − 4. y = . ĐS: . x + 5 (x +5)2 Bài 2.
Tính đạo hàm của các hàm số sau mx + 4 2 m − 4 1. y = . ĐS: . x + m (x + m)2
(2m+ )1x −2(m+ )1 3 2 2m + 3m −1 2. y = . ĐS: . 2 mx + m −1 (mx+m − )2 2 1 3. Lời giải u u v − v u Bài 1.
1. - Cách 1. Sử dụng công thức = ta được 2 v v ( 2x − )
1 (4x − 3) − (4x − 3) (2x − ) 1
2 (4x − 3) − 4.(2x − ) 1 2 − y = = = ( 4x − 3) . 2 (4x −3)2 (4x −3)2 ax + b ad − bc
- Cách 2. Sử dụng công thức nhanh =
(rèn luyên cho lớp 12 trong trắc cx + d (cx + d )2 nghiệm) 2.( 3 − ) − 4.(− ) 1 2 − y = = ( 4x − 3) . 2 (4x −3)2 u u v − v u
2. - Cách 1. Sử dụng công thức = ta được 2 v v ( 3) .(2x + ) 1 − (2x + ) 1 .3 0.(2x + ) 1 − 2.3 6 − y = = = ( 2x + ) . 2 1 (2x + )2 1 (2x + )2 1 ax + b ad − bc
- Cách 2. Sử dụng công thức nhanh =
(rèn luyên cho lớp 12 trong trắc cx + d (cx + d )2 7 nghiệm) Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 0.1− 2.3 6 − y = = ( 2x + ) . 2 1 (2x + )2 1 u u v − v u
3. - Cách 1. Sử dụng công thức = ta được 2 v v ( 2x + )
1 .(1− 3x) − (1− 3x) .(2x + ) 1
2.(1− 3x) + 3.(2x + ) 1 5 y = = = ( 1− 3x) . 2 (1−3x)2 (1−3x)2 ax + b ad − bc
- Cách 2. Sử dụng công thức nhanh =
(rèn luyên cho lớp 12 trong trắc cx + d (cx + d )2 nghiệm) 2.1+ 3.1 5 y = = ( 1− 3x) . 2 (1−3x)2 u u v − v u
4. - Cách 1. Sử dụng công thức = ta được 2 v v (
1− 2x) .( x + 5) − ( x + 5) .(1− 2x) 2.
− (x + 5) −1.(1− 2x) 11 − y = = = ( x + 5) . 2 (x +5)2 (x +5)2 ax + b ad − bc
- Cách 2. Sử dụng công thức nhanh =
(rèn luyên cho lớp 12 trong trắc cx + d (cx + d )2 nghiệm) 2 − .5 −1.1 1 − 1 y = = ( 1− 3x) . 2 (x +5)2 u u v − v u Bài 2.
1. - Cách 1. Sử dụng công thức = ta được 2 v v (
mx + 4) .( x + m) − ( x + m) .(mx + 4) .
m ( x + m) −1.(mx + 4) 2 m − 4 y = = = ( x + m) . 2 (x + m)2 (x + m)2 ax + b ad − bc
- Cách 2. Sử dụng công thức nhanh =
(rèn luyên cho lớp 12 trong trắc cx + d (cx + d )2 nghiệm) 2 . m m − 4.1 m − 4 y = = ( x + m) . 2 (x + m)2 u u v − v u
2. - Cách 1. Sử dụng công thức = ta được 2 v v ( 2m + ) 1 x − 2(m + ) 1 .( 2 mx + m − ) 1 − ( 2 mx + m − ) 1 . (2m + ) 1 x − 2 (m + ) 1 y = (mx+m − )2 2 1 (2m+ ) 1 .( 2 mx + m − ) 1 − . m (2m + ) 1 x − 2 (m + ) 3 2 1 2m + 3m −1 = = . 2 2 2 2 mx + m −1 mx + m −1 8 ( ) ( ) Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM ax + b ad − bc
- Cách 2: Sử dụng công thức nhanh: =
(Rèn luyện cho lớp 12 trong trắc cx + d (cx + d )2 nghiệm) (2m+ ) 1 ( 2 m − ) 1 + 2(m + ) 3 2 1 m 2m + 3m −1 y = ( = . mx + m − )2 1 (mx+m − )2 2 2 1 u u v − uv
Loại 4. Làm quen với nhóm công thức = và 2 v v a b 2 a c b c 1 1 1 1 1 1 + + 2 x 2 x
a x + b x + c a b a c b c 1 1 1 2 2 2 2 2 2 = 2
a x + b x + c ( 2 2 2 2
a x + b x + c 2 2 2 )2 1. Ví dụ minh họa 2 x + x +1
Ví dụ 1. Tính đạo hàm của hàm số y = . 2 2x − x + 4 Lời giải u u v − uv
- Cách 1: Sử dụng công thức: = ta được 2 v v ( 2 x + x + ) 1 '( 2
2x − x + 4) − ( 2
2x − x + 4) ( 2 x + x + ) 1 y = (2x − x+4)2 2 (2x + ) 1 ( 2
2x − x + 4) − (4x − ) 1 ( 2 x + x + ) 2 1 3 − x + 4x + 5 = ( = 2x − x + 4) . 2 (2x − x+4)2 2 2
- Cách 2. Sử dụng công thức nhanh (Rèn luyện cho lớp 12 trong trắc nghiệm): = (1 1 − − x + − x + + − x + x + y = = . 2 −1 4) 1 ( 1.1 2 ) 2 .1 2 (1.4 2 ) .1 (1.4 1 ) 2 .1 3 4 5 (2x − x+4)2 (2x − x+4)2 2 2 2 x − 2(m − ) 1 x + m + 3
Ví dụ 2. Tính đạo hàm của hàm số y = . x −1 Lời giải u u v − uv
- Cách 1: Sử dụng công thức: = ta được 2 v v ( 2 x − 2(m − )
1 x + m + 3) ( x − ) 1 − ( x − ) 1 ( 2 x − 2 (m − ) 1 x + m + 3) y = ( x − )2 1
(2x−2(m− )1)(x− )1−( 2x −2(m− )1x+m+3) 2x −2x+m−5 = = ( x − ) . 2 1 (x − )2 1
- Cách 2. Sử dụng công thức nhanh (Rèn luyện cho lớp 12 trong trắc nghiệm): 1 − 2(m − ) 2 1 m + 3
x − 2x + m − 5 y = = 0 1 −1 (x − ) . 2 1
2. Bài tập áp dụng 9 Bài 1.
Tính đạo hàm của các hàm số sau Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 2 1+ x − x 4 − x + 2 1. y = . ĐS: . 2 1− x + x (2x − x+4)2 2 2 x − 3x + 7 2 2x −10x +1 2. y = . ĐS: . 2 x− 5 (2x −5)2 2x − 5 2 2 − x +10x + 9 3. y = . ĐS: . 2 x + x + 2 (x + x+2)2 2 2
2x + (m + 2) x − 3m +1 2
2x − 4x + 2m − 3 Bài 2.
Tính đạo hàm của hàm số y = . ĐS: . x −1 (x − )2 1 3. Lời giải u u v − uv Bài 1.
1. - Cách 1: Sử dụng công thức: = ta được 2 v v ( 2 1+ x − x ) ( 2
1− x + x ) − ( 2 1− x + x ) ( 2 1+ x − x ) y = (1− x+ x )2 2 (1−2x)( 2
1− x + x ) − ( 1 − + 2x)( 2 1+ x − x ) 4 − x + 2 = ( = 1− x + x ) . 2 (1− x+ x )2 2 2
- Cách 2. Sử dụng công thức nhanh (Rèn luyện cho lớp 12 trong trắc nghiệm) = ( − − − x − − x + + − y = 1 −1 1 ) ( 1.( )1 1. ) 2 1 2(1.1 1. ) 1 (1.1 1. ) 1 1 1 1 (2x − x+4) . 2 2 u u v − uv
2. - Cách 1: Sử dụng công thức: = ta được 2 v v ( 2
x − 3x + 7) (2x − 5) − (2x − 5) ( 2 x − 3x + 7) y = (2x −5)2
(2x −3)(2x −5)−2( 2x −3x +7) 2 2x −10x +1 = = ( 2x − 5) . 2 (2x −5)2
- Cách 2. Sử dụng công thức nhanh (Rèn luyện cho lớp 12 trong trắc nghiệm) = (1 −3 7 x − x + y = . 0 −1 − 5) 2 2 10 1 (2x −5)2 u u v − uv
3. - Cách 1: Sử dụng công thức: = ta được 2 v v ( 2x − 5) ( 2
x + x + 2) − ( 2
x + x + 2) (2x − 5) 2 2 − x +10x + 9 y = ( = x + x + 2) . 2 (x + x+2)2 2 2
- Cách 2. Sử dụng công thức nhanh (Rèn luyện cho lớp 12 trong trắc nghiệm) 2 0 2 − 5 2 − x +10x + 9 y = ( = 1 1 2 ) (x + x+2) . 2 2 10 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM u u v − uv Bài 2.
- Cách 1: Sử dụng công thức: = ta được 2 v v ( 2
2x + (m + 2) x − 3m + ) 1 ( x − ) 1 − ( x − ) 1 ( 2
2x + (m + 2) x − 3m + ) 1 y = (x − )2 1
(4x + m + 2)(x − )1−( 2
2x + (m + 2) x − 3m + ) 2 1
2x − 4x + 2m − 3. = = ( x − )2 1 (x − )2 1
- Cách 2. Sử dụng công thức nhanh (Rèn luyện cho lớp 12 trong trắc nghiệm) + − + − + − y = (2 m 2 m x x m = 0 1 −1 ) 2 1 2 4 2 3 (x − ) . 2 1 ' ' 1 1 1 u '
Loại 5. Làm quen nhóm công thức = − và = − 2 x x 2 u u 1. Ví dụ minh họa
Ví dụ 1. Tính đạo hàm của các hàm số sau: 1 9 2 1 1. y = +1.
2. y = x − + . 3. y = . x −1 4 3 x x + 6x −1 2 3x + 2x Lời giải ( x − ) 1 1 1. y = − + = − ( . x − ) 0 2 1 (x − )2 1 ( 4 3 x + 6x − ) 1 ( 3 2 4x +18 9 9 x ) 2. y = 1+ + 2. =1+ + 2. . 2 x ( +6 − )2 2 4 3 1 x x x ( 4 3 x + 6x − )2 1 ( 2 3x + 2x) 6x + 2 3. y = − ( = − . 3x + 2x)2 (3x +2x)2 2 2
Ví dụ 2. Tính đạo hàm của các hàm số sau: 1 4 1 2 1. y = = = − ( . 2. y . 3. y . 2x − 5)2 (x −2x+5)2 2 x (3x− x )5 2 Lời giải (2x −5) ' 2 2
(2x −5).(2x −5)' 4 1. y ' = − = − = − ( . 2x − 5)4 (2x −5)4 (2x −5)3 ( 2 x − 2x + 5) ' 2 2
( 2x −2x+5).( 2x −2x+5)' 2. y ' = 4 − . ( = − x − 2x + 5) 4. 4 (x −2x+5)4 2 2 16( x − ) 1 16(1− x) = − ( = x − 2x + 5)3 (x −2x+5)3 2 2 ( 2 3x − x ) ' 5 4 ' 2 2 − − 5 1 1
(3x x ) .(3x x ) 10(3−2x) 1 3. y ' = − 2. = − + 2 = − 2 10 2 10 6 2 2 2 2 x x x 11 (3x− x ) (3x− x ) (3x− x ) Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM Ví dụ 3. 3 5
Tính đạo hàm của hàm số: y = + . x −1 2(2x − )6 1 Lời giải ' ( − ) 2(2x − x )6 ' 1 1 1 2.6(2x − )5 1 .(2x − )' 1 3 30 y ' = 3 − . − = − − = − − ( x − ) 5. 3. 5. 2 1 4(2x − )12 1 (x − )2 1 4(2x − )12 1 (x − )2 1 (2x − )7 1 2. Bài tập áp dụng Bài 1.
Tính đạo hàm của các hàm số sau 1 1 1. y = − 2x . ĐS: − − 2 . x +1 (x + )2 1 1 2 2. y = . ĐS: − . 2 x − 2x +1 (x − )3 1 1 3 − 2x 3. y = . ĐS: . 2 x − 3x +1 (x −3x+ )2 2 1 Bài 2.
Tính đạo hàm củ các hàm số sau 1 5(5 − 2x) 1. y = ( . ĐS: . x − x + )5 2 1 (x − x+ )6 2 1 3 3(2 − x) 2. 2 y = ( − x . ĐS: − 4x . 2x − 8x) 2 4 2 (x −4x)5 2 3 30(2x − 3)
3. y = x − ( . ĐS: 1− . x − 3x)10 2 (x −3x)11 2 1 1 1 1 2 10 4. − + . ĐS: − + − . 2 x x ( 2 2 2x + 5)5 x x (2x − )6 1 3. Lời giải ( x + ) 1 1
Bài 1. 1. y ' = − − = − − ( . x + ) 2 2 2 1 (x + )2 1 ( x − )2 1 1
2(x −1).(x −1) 2 2. y ' = = − = − = − . (x − )2 1 (x − )4 4 1 (x −1) (x − )3 1 ( 2 x − 3x + ) 1 2x − 3 3 − 2x 3. y ' = − ( = − = x − 3x + )2 1 (x −3x+ )2 1 (x −3x+ )2 2 2 2 1 ( 2 x − x + )5 1 5 ( 2x − x+ )4 1 .( 2 x − x + ) 1 5(2x −1) 5(1− 2x)
Bài 2. 1. y ' = ( = − = − = . x − x + )10 1 (x − x+ )10 1 (x − x+ )6 1 (x − x+ )6 2 2 2 2 1 ( 2 2x − 8x) ' 4 4 ( 2 2x − 8x)3 .( 2 2x − 8x) 3(2 − x) 2. y ' = 3 − − 4x = 3 − . = − 4x 8 8 5 2 2 2 (2x −8x) (2x −8x) (x −4x) 12 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM ( 2 x − 3x)10 10
( 2x −3x)9.( 2x −3x) 30(2x − 3)
3. y ' = 1− 3 ( = − = − . x − 3x) 1 3. 1 20 (x −3x)20 (x −3x)11 2 2 2 ( − x ) (2x )5 2 1 1 1 2 10 4. y ' = − + − = − + − 2 4 x x (2x − )10 2 3 1 x x (2x − )6 1 u
Loại 6. Làm quen nhóm công thức ( ) 1 x = , ( u ) ' =
và kết hợp một số công thức khác x x 2 u 1. Ví dụ minh họa
Ví dụ 1. Tính đạo hàm của các hàm số sau: 1 2 1. 4 3 y = 2x − x + 2 x − 5. 2. 2
y = 3x − 4 x + −1. 3. 2 y = x + 6x + 7 . 3 x Lời giải 1 1. 3 2
y ' = 8x − x + . x 1 1 2 2
2. y ' = 6x − 4. − 2. = 6x − − . 2 2 2 x x x x (x +6x+7)' 2 2x + 6 x + 3 3. y ' = = = . 2 2 2 2 x + 6x + 7 2 x + 6x + 7 x + 6x + 7 2. Bài tập áp dụng Bài 1.
Tính đạo hàm của các hàm số sau: 3 1. 5 3
y = x − 4x + 2x − 3 x . ĐS: 4 2
5x −12x + 2 − . x x −1 2. 2 y =
x − 2x − 8 . ĐS: . 2 x − 2x − 8 2 − x 3. 2
y = 4x − x . ĐS: 2 4x − x Bài 2.
Tính đạo hàm của các hàm số sau: 1 1 1. y =
x + 4 − 4 − x . ĐS: y ' = + 2 x + 4 2 4 − x 2
x + 3x + 3 − 2x − 3 2. 2
y = x − 2 x + 3x + 3 . ĐS: y ' = 2 x + 3x + 3 2 2 x − 3 − x 3. 2
y = 2x − x − 3 . ĐS: y ' = . 2 x − 3 2 2x +1 + 2x 4. 2
y = x + 2x +1 . ĐS: y ' = 2 2x +1 1 1 2 12 − 3x + 3x 5. 2 y = x − 12 − 3x . ĐS: y ' = . 2 2 2 2 12 − 3x Bài 3.
Tính đạo hàm của các hàm số sau: 2 15x + 3x −1 2 13
1. y = (3x − x) 2x +1 . ĐS: y ' = . 2x +1 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 2 2 − x + 4x − 6
2. y = ( − x) 2 1 x − 2x + 5 . ĐS: y ' = . 2 x − 2x + 5 3 2 6 1 3. y = − x + x x . ĐS: y ' = − − + x . 2 x 3 3 x 2 x 2 16 − 2x 3 1 4. 2
y = x 16 − x + ( x − ) 1 x . ĐS: y ' = + x − . 2 − 2 16 x 2 x x +1 3 5. 2 y =
x + 2x + 5 − ( x + ) 1 x +1 . ĐS: y ' = − x +1 . 2 + + 2 x 2x 5 Bài 4.
Tính đạo hàm của các hàm số sau: 3
1. y = ( x − )3 2 . ĐS: y ' = x − 2 . 2 1+ x 3 − x 2. y = . ĐS: y ' = . 1− x
2 1− x (1− x) 3 x 4 2 2x −18x 3. y = . ĐS: y ' = . 2 x − 6
( 2x −6) 2x −6 x +1 1 4. y = . ĐS: y ' = . 2 1− x (1− x) 2 1− x 2 2x − x + 3 11x − 20 5. y = . ĐS: y ' = . 3x + 2 2 (3x + 2)2 2 2x − x + 3 3. Lời giải 1 3 Bài 1. 1. 4 2 4 2
y ' = 5x −12x + 2 − 3.
= 5x −12x + 2 − . 2 x 2 x (x −2x−8)' 2 2x − 2 x −1 2. y ' = = = . 2 2 2 2 x − 2x − 8 2 x − 2x − 8 x − 2x − 8 (4x− x )'2 4 − 2x 2 − x 3. y ' = = = 2 2 2 2 4x − x 2 4x − x 4x − x
Bài 2. 1. Tập xác định: D = [ 4 − ;4].
(x + )' ( − x)' 4 4 1 1 Ta có y ' = − = + 2 x + 4 2 4 − x 2 x + 4 2 4 − x
2. Tập xác định: D = R . 2.( x + 3x + 3)' 2 2 2x + 3
x + 3x + 3 − 2x − 3 Ta có y ' = 1− =1− = . 2 2 2 2 x + 3x + 3 x + 3x + 3 x + 3x + 3
3. Tập xác định: D = (− ; − 3 3;+ ). (x −3)' 2 2 2x 2 x − 3 − x Ta có y ' = 2 − = 2 − = . 2 2 2 2 x − 3 2 x − 3 x − 3
4. Tập xác định: D = R . (2x + )' 2 2 1 4x 2x +1 + 2x 14 Ta có y ' = 1+ =1+ = . 2 2 2 2 2x +1 2 2x +1 2x +1 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
5. Tập xác định: D = [ 2 − ;2]. (12−3 1 1 x )' 2 2 1 3x 12 − 3x + 3x Ta có y ' = − . = 1+ = . 2 2 2 2 2 − 2 2 12 3x 12 − 3x 2 12 − 3x 1
Bài 3. 1. Tập xác định: D = − ; + . 2 1 15x + 3x −1
Ta có: y ' = (6x − ) 1
2x +1 + (3x − x) 2 2 . = . 2x +1 2x +1
2. Tập xác định: D = R . x −1 2 − x + 4x − 6
Ta có y ' = − x − 2x + 5 + (1− x) 2 2 . = 2 2 x − 2x + 5 x − 2x + 5
3. Tập xác định: D = (0; +) . 3( x )' 2 1 2 1 6 1 Ta có y ' = − − + x + . x = − − + x 4 3 x 2 x 3 2 x x 2 x
4. Tập xác định: D = [0; 4] . 2 − x 1 2 ( )
Ta có: y ' = 16 − x + . x + x + (x − ) 1 . . 2 2 16 − x 2 x 2 16 − 2x 3 1 = + x − . 2 − 2 16 x 2 x
5. Tập xác định: D = 1 − ;+) . 2x + 2 1 x +1 3 Ta có: y ' =
− x +1 − (x + ) 1 = − x +1 . 2 2 2 x + 2x + 5 2 x +1 + + 2 x 2x 5
Bài 4. 1. Tập xác định: D = 2; +) . 3( x − 2)2 3 Ta có y ' = = x − 2 . (x − )3 2 2 2
2. Tập xác định: D = (− ) ;1 . − − x − ( + x) 1 1 1 . 2 1− x 3 − x Ta có y ' = = . 1− x
2 1− x (1− x)
3. Tập xác định: D = (− ; − 6)( 6;+). 2x 2 2 3 3x x − 6 − x . 4 2 2 2 x − 6 2x −18x Ta có y ' = = . 2 x − 6
( 2x −6) 2x −6
4. Tập xác định: D = ( 1 − ) ;1 . 2 − x 2
1− x − ( x + ) 1 . 2 2 1− x 1 Ta có y ' = = . 2 1− x (1− x) 2 1− x 15 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 2
5. Tập xác định: D = R \ − . 3
(4x − )1(3x + 2) 2
− 3 2x − x + 3 2 2 2x − x + 3 11x − 20 Ta có y ' = = ( . 3x + 2)2 2(3x + 2)2 2 2x − x + 3
_ DẠNG 3. BÀI TOÁN CHỨNG MINH, GIẢI PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH PHƯƠNG PHÁP: Tính y .
Dùng các kiến thức đã học để rút gọn, biến đổi về phương trình hoặc bất phương trình đã biết cách
giải như phương trình bậc nhất, bậc hai, bậc ba (sử dụng máy tính cầm tay).
Đối với bài toán chứng minh bất đẳng thức thì ta biến đổi vế phức tạp thành vế đơn giản hoặc biến
đổi cả hai vế cùng bằng một biểu thức trung gian.
Một số bài toán tìm nghiệm của phương trình bậc hai thỏa mãn điều kiện cho trước. Cho phương trình 2
ax + bx + c = 0 (*) với a 0 . b
S = x + x = − 1 2
1. Nếu phương trình (*) có hai nghiệm x , x thì a . 1 2 c P = x x = 1 2 a
2. Phương trình (*) có hai nghiệm trái dấu khi và chỉ khi ac 0 . 0 b
3. Phương trình (*) có hai nghiệm dương phân biệt khi và chỉ khi S = − 0 . a c P = 0 a 0 b
4. Phương trình (*) có hai nghiệm âm phân biệt khi và chỉ khi S = − 0 . a c P = 0 a
Một số bài toán về bất phương trình bậc hai thường gặp.
Cho tam thức bậc hai f ( x) 2
= ax + bx + c = 0 với a 0. a 1. f ( x) x 0 0, . 0 a 2. f ( x) x 0 0, . 0 a 3. f ( x) x 0 0, . 0 a 4. f ( x) x 0 0, 16 . 0 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
_VÍ DỤ MINH HỌA
Ví dụ 1. Cho hàm số 2 y =
x + 1+ x . Chứng minh rằng 2
2y . 1+ x − y = 0 . Lời giải ( x 2 + x + + x u ) 1 1 2 2 2 1+ x x + 1+ x x + 1+ x Ta có: y = = = = = . 2 2 2 2 2 2 u + + + + + + + 2 1 2 1 2 1 2 1 1 + x x x x x x x x 2 + + Do đó: 1 1 x 2 2 2 2 2
2 y . 1+ x − y = 2
. 1+ x − 1+ 1+ x = 1+ 1+ x − 1+ 1+ x = 0 . 2 2 1+ x Vậy 2
2y . 1+ x − y = 0 .
Ví dụ 2. Cho hàm số 2
y = 3x + 10 − x . Giải phương trình y = 0 . Lời giải Điề x
u kiện: − 10 x 10 (*). Ta có y = 3 − . Khi đó, 2 10 − x x x 0 2 y = 0 3 −
= 0 3 10 − x = x 9 − ( 2 10 − x ) 2 = 2 x 10 x x 0 x 0 = 2 x 10x − 90 = . 0 3 x = 3
Vậy phương trình y = 0 có nghiệm duy nhất x = 3 . B 0
! Cần nhớ: A = B 2 A = . B
Ví dụ 3. Cho hàm số f ( x) 3 2
= x − x + 3mx + 2019 . Tìm tham số m để phương trình f (x) = 0 có hai
nghiệm dương phân biệt. Lời giải Ta có f ( x) 2
= 3x − 2x + 3m và f (x) 2
= 0 3x − 2x + 3m = 0 (*) .
Phương trình (*) có hai nghiệm dương phân biệt khi và chỉ khi 3 0 a 0 1 − 9m 0 1 0 1 2 m 0 9 m S 0 0 9 m 0 3 P 0 m 0 1
Vậy giá trị m là m 0; . 9
Ví dụ 4. Cho hàm số 3 2
y = x − mx + ( 2 3 3 m − )
1 x . Tìm tham số m để phương trình y = 0 có hai nghiệm
phân biệt x , x phân biệt thỏa mãn 2 2
x + x − x x = 10. 1 2 1 2 1 2 Lời giải Ta có 2
y = x − mx + ( 2 3 6 3 m − ) 1 và 2 y =
x − mx + ( 2 m − ) 2
= x − mx + ( 2 0 3 6 3 1 0 2 m − ) 1 = 0 (*) .
Ta biến đổi được x + x − x x = 10 ( x + x )2 2 2 − 3x x =10 . 1 2 1 2 1 2 1 2
Khi đó, yêu cần bài toán tương đương với 17 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 2 m − ( 2 m − ) 1 0 0 2 = = 2 m m . S − 3P = 10 (2m )2 −3 ( 7 7 2 m − ) 1 = 10
Vậy giá trị m cần tìm là m = 7 .
Ví dụ 5. Cho hàm số 4 y = mx + ( 2 m − ) 2
9 x +10 . Tìm m để phương trình y = 0 có 3 nghiệm phân biệt. Lời giải x = 0 Ta có 3 y = mx + ( 2 4
2 m − 9) x và 3
y = 0 4mx + 2 ( 2
m − 9) x = 0 2 2
2mx + m − 9 = 0 (*)
Phương trình y = 0 có 3 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm phân biệt
khác 0. Điều kiện tương đương là m 0 2m 0 − − = − m( 2 m − ) m 3 m 3 0 2 9 0 . 0 m 3 0 m 3 2 2 2 . m 0 m 9 0 + − m 3
Vậy giá trị m cần tìm là m 3
− hoặc 0 m 3. 2 x + 5x − 2
Ví dụ 6. Cho hàm số y =
. Giải bất phương trình y 0 . x −1 Lời giải 2 x − 2x − 3 Ta có y = . Điề . Khi đó 2 − − − ( u kiện x 1 (*) y 0 x 2x 3 0 1 x 3 . x − )2 1
Đối chiếu với điều kiện (*), bất phương trình y 0 có tập nghiệm là S = ( 1 − ;3) \ 1 . 1
Ví dụ 7. Cho hàm số f ( x) = ( 2 m − m − 6) 3 x − (m + 2) 2
x − 4x + m . Tìm tham số m sao cho 3
f ( x) 0, x . Lời giải
Ta có f ( x) = ( 2 m − m − ) 2
6 x − 2 (m + 2) x − 4 . m = − - TH1: 2 2
m − m − 6 = 0 . m = 3 Nếu m = 2
− thì f (x) = 4 − 0, x
. Do đó, m = 2 − thỏa mãn bài toán.
Nếu m = 3 thì f ( x) = 10
− x − 4 0 là nhị thức bậc nhất nên f (x) không lớn hơn 0 với mọi x
. Do đó, m = 3 không thỏa mãn bài toán. m 2 − - TH2: 2
m − m − 6 0 m . Khi đó, 3 f ( x) x ( 2 m − m − ) 2 0,
6 x − 2 (m + 2) x − 4 0, x 2 2
m − m − 6 0 a 0
m − m − 6 0 2 − m 3 − m . 0 (m+ 2 )2 + 4 ( 2 m − m − 6) 2 2 2 0 5 m − 20 0 2−m2
Vậy, giá trị m cần tìm là 2 − m 2 . _BÀI TẬP ÁP DỤNG Bài 1.
1. Cho hàm số f ( x) 3 2
= x − 3x + 2 . Giải phương trình f (x) = 0 .
ĐS: x = 2, x = 0 . 2 x + 3x + 3 2. Cho hàm số y =
. Giải phương trình y = 0 . ĐS: x = 2 − , x = 0 . + 18 x 1 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
3. Cho hàm số f ( x) = ( x − ) 1
2x +1 . Giải phương trình y = 0 . ĐS: x = 0 . 1 Bài 2. 1. Cho hàm số 3 2 y =
x − 2x − 6x − 8 . Giải bất phương trình y 0 . ĐS: S = 2 − 10; 2 + 10 3
2. Cho hàm số f ( x) 4 2
= −x + 8x +1. Giải bất phương trình f (x) 0 . ĐS: S = ( 2 − ;0)(2;+) Bài 3. Cho hàm số 3 2
y = 3mx − 2x + (3 − m) x . Tìm tham số m để phương trình y 0 có hai nghiệm trái dấu.
ĐS: m 0 hoặc m 3 . 1 Bài 4.
Cho hàm số f ( x) 3 2
= x + mx + (m+ 6) x +1. Tìm tham số m sao cho f (x) 0, x . 3 ĐS: 2 − m 3. 1 Bài 5. Cho hàm số 3
y = − mx + (m − ) 2
1 x + mx + 3. Tìm tham số m để phương trình y = 0 có 3
1. hai nghiệm phân biệt cùng âm,
ĐS: không có giá trị m . 2
2. hai nghiệm x , x thỏa mãn 2 2 x + x = 3 .
ĐS: m = 2, m = . 1 2 1 2 3 _LỜI GIẢI x = Bài 1.
1. Ta có: f ( x) 2
= 3x − 6x . Khi đó, f (x) 2 0
= 0 3x − 6x = 0 . x = 2
Vậy phương trình f ( x) = 0 có hai nghiệm x = 2, x = 0 . 2 x + 2x x = − 2. Ta có y = . Điề − . Khi đó, 2 2 = + = ( u kiện x 1 ( ) * y 0 x 2x 0 = . x + )2 1 x 0
Đối chiếu với điều kiện (*), phương trình y = 0 có hai nghiệm x = 2 − , x = 0 . x − x 3. Ta có y = x + + ( x − ) 2 1 3 1. 2 1 1 . = 2x +1 + = . 2 2x +1 2x +1 2x +1 Điề 1 u kiện x − ( )
* . Khi đó, y = 0 x = 0 . Đối chiếu với điều kiện (*), phương trình y = 0 2 có nghiệm x = 0 . Bài 2. 1. Ta có 2 2
y = x − 4x − 6 . Khi đó, 2 2
y 0 x − 4x − 6 0 2 − 10 x 2 + 10 .
Vậy bất phương trình y 0 có tập nghiệm là S = 2 − 10; 2 + 10 . − x
2. Ta có f ( x) 3 = 4
− x +16x . Khi đó f (x) 3 2 0 0 4
− x +16x 0 . x 2
Vậy bất phương trình f ( x) 0 có tập nghiệm là S = ( 2 − ;0)(2;+). Bài 3. Ta có 2
y = 9mx − 4x + (3 − m) và 2
y = 0 9mx − 4x + (3 − m) = 0 (*) .
Phương trình (*) có hai nghiệ a 0 m m 0
m trái dấu khi và chỉ khi ac 0 9 0
9m (3 − m) 0 . m 3
Vậy giá trị m cần tìm là m 0 hoặc m 3 . Bài 4. Ta có f ( x) 2
= x + 2mx + (m + 6) . Khi đó f (x) 2 0, x
x + 2mx + (m + 6) 0, x a 0 10 − 2 2 m 3 0
m − n − 6 . 0
Vậy giá trị m cần tìm là 2 − m 3. Bài 5. Ta có 2
y = −mx + 2(m − )
1 x + mx + 3 và 2
y = 0 −mx + 2(m − )
1 x + mx + 3 = 0 (*) . 19
1. Phương trình (*) có hai nghiệm phân biệt cùng âm khi và chỉ khi Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM −m 0 a 0 ( m − )2 2 1 + m 0 0 2(m − ) 1
(vô lý). Vậy không có giá trị m thỏa mãn. S 0 0 P 0 m 1 − 0
2. Ta có x + x = 3 ( x + x )2 2 2
− 2x x = 3. Yêu cầu bài toán tương đương với 1 2 1 2 1 2 m 0 m 0 a 0 m = 2 m m = 0 ( m − )2 2 0 2 1 + m 0 2 .
3m − 8m + 4 = 0 2 m = 2 2 2
S − 2P = 3 = 2(m − ) 1 m 3 3 + 2 = 3 m 2
Vậy giá trị m cần tìm là m = 2, m = . 3
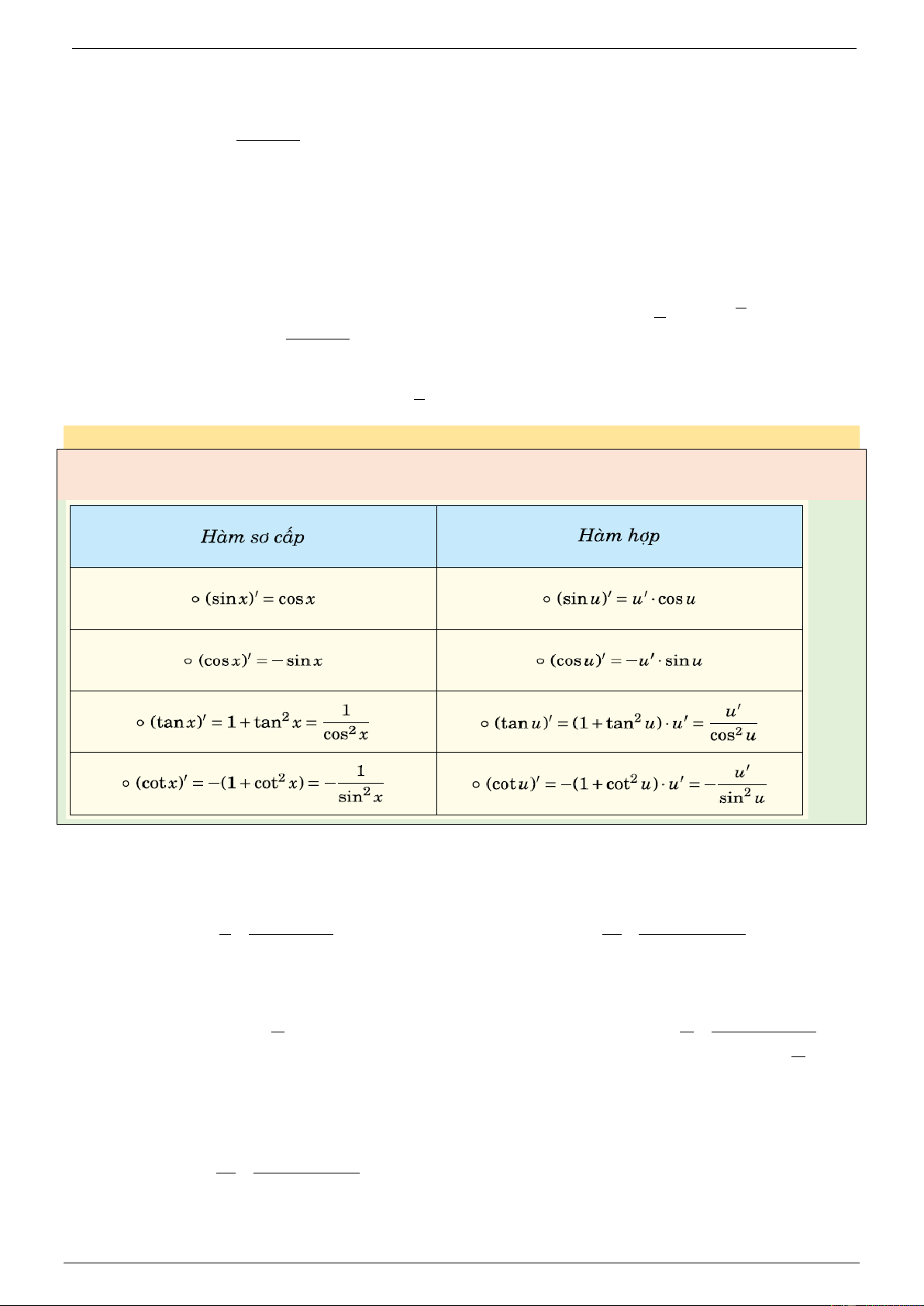
_ DẠNG 4. ĐẠO HÀM CỦA HÀM SỐ LƯỢNG GIÁC PHƯƠNG PHÁP:
Bảng công thức đạo hàm _VÍ DỤ MINH HỌA
Ví dụ 1. Tính đạo hàm của các hàm số sau:
1. y = 5sin x − 3cos x .
ĐS: y = 5cos x + 3sin x . 2( 3 2 4x +18 9 x ) 9 2
2. y = x − + . ĐS: y = 1+ − . 4 3 x x + 6x −1 2 x ( 4 3 x + 6x − )2 1 3. 2 y = cos 5x . ĐS: y = 5 − sin10x . 1 4. 3 y = tan 5x + . ĐS: 2 y = 15.tan 5x + . . 3 3 2 cos 5x + 3 Lời giải
1. y = 5cos x + 3sin x . 2( 3 2 4x +18 9 x ) 2. y = 1+ − . 2 x ( 4 3 x + 6x − )2 1 20 3. y = 5 − sin10x . Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 1 4. 2 y = 15.tan 5x + . . 3 2 cos 5x + 3
Ví dụ 2. Tính đạo hàm của các hàm số sau: 1. 4 4
y = sin x + cos x .
ĐS: y = −sin 4x . cos 2x
2. y = 1+ sin 2x . ĐS: y = . 1+ sin 2x Lời giải 1 3 1
1. Ta có y = (sin x + cos x)2 2 2 2 2 2
− 2sin xcos x =1− sin 2x = + cos 4x . 2 4 4
Suy ra y = − sin 4x cos 2x 2. y = . 1+ sin 2x
Ví dụ 3. Tính đạo hàm của các hàm số sau:
2sin x − 3cos x 1. y = . ĐS: 5 y = . sin x + cos x sin 2x +1 2 1+ cos 2x
8sin 2x (1+ cos 2x) 2. y = . ĐS: y = − . 1− cos 2x (1−cos2x)3 Lời giải
1. Điều kiện xác định của hàm số là x −
+ k,k . Ta có 4 (
2 sin x − 3cos x) (sin x + cos x) − (2sin x − 3cos x)(sin x + cos x) 5 y = = ( . sin x + cos x)2 sin 2x +1
2. Điều kiện xác định của hàm số là x k , k . Ta có 1+ cos 2x 2
− sin 2x(1− cos2x) −(1+ cos2x).2sin 2x
8sin 2x (1+ cos 2x) y = 2 . = − . 1− cos 2x (1−cos2x)2 (1−cos2x)3 _BÀI TẬP ÁP DỤNG Bài 1.
Tính đạo hàm của các hàm số sau:
1. y = 2sin x + cos 2x .
ĐS: y = 2cos x − 2sin 2x . 2x + 2 2. y = x + ( 2 cos 3 tan x + 2x) . ĐS: y = 3 − sin 3x + . 2 cos ( 2 x + 2x)
3. y = (2cos x + ) 1 (3sin x + ) 1 .
ĐS: y = 6cos 2x − 2sin x + 3cos x . 1 2
4. y = sin x − cos 3x + 2 tan x + .
ĐS: y = cos x + sin 3x + . 3 2 cos x 3 1 4x +1 5. 4 2 y = x +
sin 2x + 2x + x . ĐS: 3
y = 3x + cos 2x + . 4 2 2 2 2x + x
6. y = 7sin 4x − 2cos 5x .
ĐS: y = 28cos 4x +10sin 5x . 2 7. y = ( 7
cos 3x + 2) + cot 2x . ĐS: 6 y = 2 − 1x .sin ( 7 3x + 2) − . 2 sin 2x 1
9. y = sin 2x − cot x − .
ĐS: y = 2cos 2x + . 21 3 2 sin x − 3 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 10. y = ( 2
cos 2x − 5x +14).
ĐS: y = ( − x) ( 2 5 4
.sin 2x − 5x +14). 11. 2
y = cos 2x − sin 2x . ĐS: y = 2
− sin 4x − 2cos 2x . 12. 2
y = sin 3x + cos x .
ĐS: y = 3sin 6x − sin x . 1 13. 3
y = cos 2x − tan x . ĐS: 2 y ' = 6 − cos 2 . x sin 2x − . 2 cos x 14. 3
y = sin (2x +1). ĐS: 2
y ' = 6sin (2x +1).co s(2x +1) . 15. 4
y = cos (3x −1). ĐS: 3 y ' = 1
− 2cos (3x −1).sin(3x −1) . 16. 2
y = cos (sin 2x).
ĐS: y ' = −sin(2sin 2x).cos 2x . 17. 2 2 y = sin(cos . x tan x). ĐS: 2 y ' = − sin 2 . x cos(sin x) . 18. 2 3
y = 2sin 4x − 3cos 5 . x ĐS: 2
y ' = 8sin 8x + 45cos 5 . x sin 5x . x +1 1 x +1 19. 2 y = cos . ĐS: y ' = .sin 2. . x −1 − x ( x − )2 x 1 1 20. 2017 3 y = cos x + . ĐS: 2 2016 3 3 y = 6 − 015x .cos x + .sin x + . 7 7 7 2 2 − 2 tan 2x 4 21. 3 y = tan − 2x .
ĐS: y ' = 12 2x − . . 4 2 4 2 cos − 2x 4 22. y = ( − x)3 3 sin . ĐS: y = − x ( − x)2 ' 3cos . 3 sin . Bài 2.
Tính đạo hàm của các hàm số sau 1. y = ( x + x)8 sin cos . ĐS: 7 y ' = 128cos x + .sin x + . 4 4 2. 4
y = (2sin x − cos x) . ĐS: 3
y ' = 4(2 cos x + sin x)(2sin x − cos x) . 3. 2 8
y = (2 + sin 2x) . ĐS: 2 7
y ' = 16sin 4x(2 + sin 2x) . 4. 4 4 5
y = (cos x − sin x) . ĐS: y = 5 − sin 4x . cos x
5. y = sin x . ĐS: y ' = . 2 x sin 2x
6. y = cos 2x . ĐS: y ' = − . cos 2x cos x + 2
7. y = sin x + 2x . ĐS: y ' = . 2 sin x + 2x 2 x sin 2 + x 8. 2 y = cos 2 + x . ĐS: y ' = . 2 2 + x 2 x cos x +1 9. 2 y = sin x +1 . ĐS: y ' = . 2 x +1 2 6x + 5cos 5x 10. 3 y = 2x + sin 5x . ĐS: y ' = . 3 2 2x + sin 5x Bài 3.
Tìm đạo hàm của các hàm số sau 22 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM x
cos x + x sin x 1. y = . ĐS: y ' = . cos x 2 cos x 2x + sin 2x 4x sin 2x 2. y = . ĐS: y ' = . 1− cos 2x 2 (1− cos 2x) sin x x cos x sin x 1− x cot x 3. y = + . ĐS: y ' = − + . x sin x 2 x x sin x 3 3 cos x + sin x 4. y = .
ĐS: y ' = −cos 2x . sin x + cos x 2 5x +1 2
10x(4 + 3sin x) − 3cos x(5x +1) 5. y = . ĐS: y ' = . 4 + 3sin x 2 (4 + 3sin x) sin 2x + cos 2x 4 6. y = . ĐS: y ' = − .
sin 2x − cos 2x 2
(sin 2x − cos 2x) x + sin x
2(x cos x − sin x) 7. y = . ĐS: y ' = . x − sin x 2 (x − sin x) 3 sin x 2 3sin x 8. y = . ĐS: y ' = . 1+ cos x 3 (1+ cos x) x Bài 4.
Cho hàm số f ( x) cos =
. Tính f '(0), f '( ), f ' , f ' . 1+ sin x 2 4
ĐS : f ( ) = − f ( ) 1 ' 0 1, ' = 1 − , f ' = − , f ' = 2 − 2 2 2 4 _LỜI GIẢI
Bài 1. 1. y = 2(sin x) − (2x) .sin 2x = 2cos x − 2sin 2x . ( 2 x + 2x) 2x + 2 2. y = 3 − sin 3x + = 3 − sin 3x + . 2 cos ( 2 x + 2x) 2 cos ( 2 x + 2x) 3. y = 2
− sin x(3sin x + ) 1 + (2cos x + )
1 .3cos x = 6 cos 2x − 2sin x + 3cos x . 2
4. y = cos x + sin 3x + . 2 cos x ( 2 2x + x 4x +1 3 ) 5. 3
y = 3x + cos 2x + = 3x + cos 2x + . 2 2 2 2x + x 2 2x + x
6. y = 28cos 4x +10sin 5x . 2 2 7. y = −( 7 3x + 2).sin ( 7 3x + 2) 6 − = 2 − 1x .sin ( 7 3x + 2 − . 2 ) 2 sin 2x sin 2x x − 3 1
8. y = 2 cos 2x + = 2cos 2x + . 2 2 sin x − sin x − 3 3 2
9. y = cos x − 3sin x − . 2 cos x
10. y = − ( 2 x − x + )
( 2x − x+ ) = ( − x) ( 2 2 5 14 .sin 2 5 14 5 4
.sin 2x − 5x +14) . 23 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
11. y = 2 cos 2 .
x (cos 2x) − 2cos 2x = 4
− sin 2xcos 2x − 2cos 2x = 2
− sin 4x − 2cos 2x .
12. y = 2sin 3 .
x (sin 3x) − sin x = 6sin 3x cos3x − sin x = 3sin 6x − sin x . 1 1 13. 2 2 y ' = 3cos 2 . x (cos 2 ) x '− = 6 − cos 2 . x sin 2x − . 2 2 cos x cos x 14. 2 2
y ' = 3sin (2x +1).(sin(2x +1)) ' = 6sin (2x +1).co s(2x +1) . 15. 3 3
y ' = 4 cos (3x −1).(cos(3x −1)) ' = 1
− 2cos (3x −1).sin(3x −1) .
16. y ' = 2cos(sin 2x).(cos(sin 2x)) ' = 2
− cos(sin 2x).sin(2sin 2x).cos 2x = −sin(2sin 2x).cos 2x . 17. Ta có: 2
y = sin(sin x) . Suy ra 2 2 2 2
y ' = (sin x) '.cos(sin x) = 2sin . x cos .
x cos(sin x) = sin 2 . x cos(sin x) . 18. 2 y ' = 4sin 4 .
x (sin 4x) '− 9 cos 5 . x (cos 5x) ' 2 2
=16sin 4xcos 4x + 45cos 5xsin5x = 8sin8x + 45cos 5xsin5x . ' ' x +1 x +1 x +1
x +1 x +1
19. y ' = 2 cos .cos = 2 − cos .sin . x −1 x −1 x −1 x −1 x −1 1 1 ( x −1) − ( x +1) + x 1 + 2 x 2 x 1 x 1 = −sin 2. . = .sin 2. . 2 x −1 ( x −1) − x ( x − )2 x 1 1 ' 20. 2016 3 3 2 2016 3 3 y ' = 2017.cos x + . cos x + = −6015x .cos x + .sin x + . 7 7 7 7 2 2 21. 2 2 y ' = 3 tan − 2x . tan − 2x . 4 4 2 2 − 2x 2 − 2 tan 2x 4 2 = 4 3 tan − 2x . =12 2x − . . 2 4 2 4 2 cos − 2x 2 cos − 2x 4 4 2 2
22. y ' = 3.(3 − sin x) .(3 − sin x) ' = 3 − cos .
x (3 − sin x) . 8 Bài 2. 1. Ta có: 8 y = 2 sin x + =16.sin x + . 4 4 Suy ra: 7 7
y ' = 16.8.cos x + sin x + =128cos x + .sin x + . 4 4 4 4 2. 3 3
y ' = 4(2sin x − cos x) '.(2sin x − cos x) = 4(2 cos x + sin x)(2sin x − cos x) . 3. 2 2 7 2 7 2 7
y ' = 8(2 + sin 2x) '.(2 + sin 2x) = 16(sin 2 ) x '.sin 2 . x (2 + sin 2 ) x =16sin 4 .
x (2 + sin 2x) . 4. Ta có: 2 2 2 2 5 5
y = ((cos x − sin x)(cos x + sin x)) = cos 2x . Suy ra: 4
y ' = 5(cos 2x) '.cos 2x = 5 − sin 4x . cos x 5. y ' = x 'cos x = . 2 x 24 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM (cos 2x) ' sin 2x 6. y ' = = − . 2 cos 2x cos 2x (sin x + 2x)' cos x + 2 7. y ' = = . 2 sin x + 2x 2 sin x + 2x (2 + x ) ' x sin 2 + x
8. y ' = ( 2 + x ) 2 2 2 2 2 '.sin 2 + x = sin 2 + x = . 2 2 2 2 + x 2 + x x cos x +1
9. y ' = ( x +1) 2 2 2 '.cos x +1 = . 2 x +1 3 2 (2x + sin 5x) ' 6x + 5cos 5x 10. y ' = = . 3 3 2 2x + sin 5x 2 2x + sin 5x
Bài 3. 1. Điều kiện xác định của hàm số là x
+ k,k . 2
x '.cos x − x(cos x) '
cos x + x sin x Ta có y ' = = . 2 2 cos x cos x
2. Điều kiện xác định của hàm số là x k , k .
(2 + 2cos 2x)(1− cos 2x) − (2x + sin 2x).2sin 2x Ta có y ' = 2 (1− cos 2x) 2 2
2 − 2 cos 2x + 2 cos 2x − 2 cos 2x − 4x sin 2x − 2sin 2x 4x sin 2x = = . 2 2 (1− cos 2x) (1− cos 2x)
3. Điều kiện xác định của hàm số là x k , k .
x cos x − sin x
sin x − x cos x cos x sin x 1− x cot x Ta có y ' = + = − + . 2 2 2 x sin x x x sin x
4. Điều kiện xác định của hàm số là x + k,k . 4 3 3 2 2 cos x + sin x
(cos x + sin x)(cos x − cos x sin x + sin x) 1 Ta có y = = =1− sin 2x . sin x + cos x sin x + cos x 2 ' Khi đó: 1 y ' = 1− sin 2x = −cos 2x . 2 2 2 2
(5x +1) '.(4 + 3sin x) − (5x +1)(4 + 3sin ) x ' 10 ( x 4 + 3sin ) x − 3cos ( x 5x +1) 5. Ta có y ' = = . 2 2 (4 + 3sin x) (4 + 3sin x)
6. Điều kiện xác định của hàm số là x + k ,k . 8 2
(2cos 2x − 2sin 2x)(sin 2x − cos 2x) − (sin 2x + cos 2x)(2cos 2x + 2sin 2x) Ta có y ' = 2
(sin 2x − cos 2x) 2 2 2
− (sin 2x − cos 2x) + (sin 2x + cos 2x) 2 −
1− 2sin 2xcos2x +1+ 2sin 2xcos2x = = 2 2
(sin 2x − cos 2x)
(sin 2x − cos 2x) 4 = − . 2
(sin 2x − cos 2x)
7. Điều kiện xác định của hàm số là x 0 .
(1+ cos x)(x − sin x) − (x + sin x)(1− cos x) Ta có y ' = 2 25 (x − sin x) Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
x − sin x + x cos x − sin x cos x − x + x cos x − sin x + sin x cos x
2(x cos x − sin x) = = . 2 2 (x − sin x) (x − sin x)
8. Điều kiện xác định của hàm số là x + k2 , k . 2 2 2 2 3sin x
cos x(1+ cos x) + sin x 3sin x(1+ cos x) 3sin x Ta có y ' = . = = . 2 2 4 3 (1+ cos x) (1+ cos x) (1+ cos x) (1+ cos ) x
Bài 4. Điều kiện xác định của hàm số là x + k2,k . 2
−sin x(1+ sin x) − cos x −sin x −sin x − cos x 1 Ta có f '( x) 2 2 2 = = = − 2 2 (1+ sin x) (1+ sin x) sin x +1
Vậy : f ( ) = − f ( ) 1 ' 0 1, ' = 1 − , f ' = − , f ' = 2 − 2 . 2 2 4
_ DẠNG 5. CHÚNG MINH ĐẲNG THỨC, GIẢI PHƯƠNG TRÌNH CHỨA ĐẠO HÀM PHƯƠNG PHÁP:
Tính đạo hàm của hàm số đã cho
Thay y, y vào biểu thức để biến đổi chứng minh hoặc giải phương trình liên quan. _VÍ DỤ MINH HỌA
Ví dụ 1. Cho hàm số y = tan x . Chứng minh 2
y '− y −1 = 0 . Lời giải
Điều kiện xác định của hàm số là x
+ k,k Z 2 1 Ta có 2 y ' = =1+ tan x 2 cos x Khi đó 2 2 2
y '− y −1 = 1+ tan x − tan x −1 = 0
Ta có điều phải chứng minh.
Ví dụ 2. Cho hàm số f ( x) = sin 2x − 2 cos x . Giải phương trình f '( x) = 0 . Lời giải
Ta có f '( x) = 2cos 2x + 2sin x . Khi đó f ( x) 2 '
= 0 2cos 2x + 2sin x = 0 2
− sin x + sin x +1 = 0 x =
+ k2 ,k Z 2 sin x =1
1 x = − + k2 , k Z . sin x = − 6 2 7 x =
+ k2 ,k Z 6 7
Vậy phương trình f '( x) = 0 có các nghiệm x =
+ k2, x = − + k2, x = + k2 với 2 6 6 k Z . _BÀI TẬP ÁP DỤNG Bài 1. Cho hàm số y = .
x sin x . Chứng minh
1. xy + x (2 cos x − y) = 2( y '− sin x) 2. y '− . x cos x = cos .
x tan x với x
+ k,k Z 26 2 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM cos x Bài 2.
Cho hàm số f ( x) 2 = . f − 3. f ' = 3 2 1+ sin x 4 4 Bài 3. Cho hàm số 2
y = cos x + sin x . Giải phương trình y ' = 0 5 ĐS: x =
+ k; x = + k2 , x =
+ k2;k Z 2 6 6 _LỜI GIẢI
Bài 1. Ta có y ' = sin x + . x cos x
1. xy + x (2 cos x − y) = 2( y '− sin x) xy + 2 .
x cos x − xy = 2 (sin x + .
x cos x − sin x) 2 . x cos x = 2 .
x cos x (luôn đúng)
2. Với mọi x
+ k,k Z , ta có 2 sin x y '− .
x cos x = sin x + . x cos x − .
x cos x = sin x = cos . x = cos . x tan x cos x 2 − cos . x sin x ( 2 1+ sin x) 2 − cos . x 2sin . x cos x
Bài 2. Ta có f '( x) = ( 1+ sin x)2 2 2 − sin . x cos x ( 2 2
1+ sin x + cos x) = ( 1+ sin x)2 2 2sin 2x = − ( 1+ sin x)2 2 1 8 Lại có f = ; f ' = − 4 3 4 9 Do đó, 1 8 f − 3. f ' = − 3. − = 3 . 4 4 3 9
Bài 3. Ta có y ' = 2 − cos .
x sin x + cos x = − cos x (2sin x − ) 1 x =
+ k;k Z 2 cos x = 0
Khi đó y ' = 0 − cos x (2sin x − ) 1 = 0 1 x =
+ k2;k Z sin x = 6 2 5 x =
+ k2;k Z 6 5
Vậy phương trình y ' = 0 có các nghiệm x =
+ k; x = + k2; x =
+ k2;k Z . 2 6 6
C. BÀI TẬP RÈN LUYỆN Bài 1. 1. Cho 2
y = 2x − x + 2 . Tính y '( ) 1 ? ĐS: y '( ) 1 = 3 .
2. Cho f ( x) = 2x + 7 . Tính f '( ) 1 ? ĐS: f ( ) 1 ' 1 = . 3 3. Cho 2 y =
x + 5 . Tính y '(2) ? ĐS: y ( ) 2 ' 2 = . 3 Bài 2.
Tính đạo hàm của các hàm số sau 1. 6 3 2
y = x − 2x − 5x + 3 ĐS: 5 2
6x − 6x −10x . 2 1 x 27 2. 4 y = x − − 2 ĐS: 3 x − x . 4 2 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 1 3. 4 2 y = − x − 2x − 5 ĐS: 3 −x − 4x. 4 Bài 3.
Tính đạo hàm của các hàm số sau 1. 2 4
y = m x − (m − ) 2 2
1 x + m − 5m + 4 ĐS: 2 3
4m x − 2(m − ) 1 x . 2. 5 4 2
y = 3x − 6mx − 2mx + m −1 ĐS: 4 3
15x − 24mx − 2m . Bài 4.
Tính đạo hàm của các hàm số sau
1. y = ( x − )( 5 2 3 x − 2x) ĐS: 5 4
12x −15x − 8x + 6 . 2. y = ( 2 x − x + )( 2 2 3 2x + 3) ĐS: 3 2
8x −12x +18x − 6 . 3. y = ( 2 x + )( 2 1 5 − 3x ) ĐS: 3 1 − 2x + 4x . Bài 5.
Tìm đạo hàm của hàm số sau
1. y = ( − x )3 2 1 2 . ĐS: 5 3 4
− 8x + 48x −12x .
2. y = ( x + x + )4 2 1 .
ĐS: ( x + )(x + x + )3 2 4 2 1 1 . 3. = ( − )32 2 y x x . ĐS: ( − )( − )31 2 32 1 2x x x .
4. y = ( x − x + )3 2 1
ĐS: ( x − )(x − x + )2 2 3 2 1 1 . Bài 6.
Tính đạo hàm của hàm số sau 5x 5 1. y = . ĐS: y = . 1− 4x (1− 4x)2 x −1 3 2. y = . ĐS: . x + 2 (x + 2)2 6x −1 13 3. y = . ĐS: . x + 2 (x + 2)2 mx − 2 2 −m + m + 2 4. y = . ĐS: . x − m +1 (x − m+ )2 1 ( m + ) 2 3
1 x − m + m 2 4m 5. y = . ĐS: . x + m (x + m)2 Bài 7.
Tính đạo hàm của hàm số sau 2 x + 5x − 2 2 x − 2x − 3 1. y = . ĐS: . x −1 (x − )2 1 2 2x + 4x +1 2 2x −12x +11 2. y = . ĐS: . x − 3 (x −3)2 x −1 2 −x + 2x 3. y = . . 2 x − 3x + ĐS: 3 (x −3x+3)2 2 2
2x + mx − 3m +1 2 2
2mx − 4x + 3m − 2m 4. y = . ĐS: . mx −1 (mx − )2 1 Bài 8.
Tính đạo hàm của các hàm số sau: 28 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 1 1
1. y = −x +1− . ĐS: 1 − + . x + 2 (x + 2)2 3 18 2. y = − ( . ĐS: . 3x + 5)2 (3x +5)3 2 6x(2 − x) 3. y = ĐS: 3 2 x − 3x +1 (x −3x + )2 3 2 1 2 1 1 33(1− x ) 1 4. y = ( − .ĐS: + − 12 2 3 )11 3 x x x ( 3 −3 ) x x x Bài 9.
Tính đạo hàm của các hàm số sau: 2 1 2 2 1. 4 y = + 4 x − x +1. ĐS: 3 − + − 2x . x 2 2 x x 1− x 2. 2
y = 1+ 2x − x . ĐS: . 2 1+ 2x − x 4x − 5 3. 2
y = 2x − 5x + 2 . ĐS: . 2 2 2x − 5x + 2 Bài 10.
Tính đạo hàm của các hàm số sau: 1 (x − 2) 2
4x − x + 2x − 4 1. 2 2 y =
x − x − 4x − x . ĐS: y ' = . 4 2 2 4x − x 5 2. 2 y = x x .
ĐS: y ' = x x . 2 3 3. 2
y = x + x x +1.
ĐS: y ' = 2x + x . 2 9x +1
4. y = ( x − ) 1 3x + 2 . ĐS: y ' = . 2 3x + 2 2 1− 2x 5. 2
y = x 1− x . ĐS: y ' = . 2 1− x Bài 11.
Tính đạo hàm của các hàm số sau: x 100 − x 1. y = . ĐS: y ' = . x +100 2( x +100)2 x x 16 2. y = . ĐS: y ' = . 2 16 − x ( 2 16 − x ) 2 16 − x x + 2 5 − x + 8 3. y = . ĐS: y ' = 2 x − x + 3 2( 2 x − x + 3) 2 x − x + 3 2 4 + x 4 − 4. . ĐS: y ' = . x 2 2 x 4 + x 2 x x +1 3 2 2x − 2x −1 5. y = y ' = . 2x − . ĐS: 1 (2x − )2 2 1 x +1 Bài 12.
Tính đạo hàm của các hàm số sau: 29 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 1 3 2 − x x − x x x 1. y = . ĐS: 2 2 y ' = . 2 x −1 (x − )2 2 1 2 x +1 2 x −1 2. y = . ĐS: y ' = . x 2 2x x x +1 3. y = ( − − x )3 1 1 2 .
ĐS: y = ( − − x)2 1 ' 3 1 1 2 . . 1− 2x 1− x 1 4. y = . ĐS: y ' = . 1+ x x (1+ x )2 1+ x + 3
−x − 7 − 2 x + 3 5. y = . ĐS: y ' = . x −1
2 x + 3 ( x − )2 1 Bài 13.
1. Cho hàm số f ( x) 4 2 = 2
− x − x + 4 . Giải phương trình f (x) = 0 . ĐS: x = 0 . 2 2x + 2
2. Cho hàm số y =
. Giải phương trình y = 0 .
ĐS: x =1 2 . 1− x 4
3. Cho hàm số y = x − 2 +
. Giải phương trình y = 0 . ĐS: x = 2 . 2 x Bài 14. Cho hàm số 4 2 2
y = x − 2mx + 2m . Tìm m để phương trình y = 0 có ba nghiệm phân biệt. ĐS: m 0. Bài 15.
Cho hàm số f ( x) 3 2
= x + 3x − 9x +1. Giải bất phương trình f (x) 0 . Bài 16.
Cho hàm số f ( x) 3 2
= x + mx + (4m −9) x . Tìm tham số m sao cho f (x) 0, x .
ĐS: 3 m 9 . 1 Bài 17. Cho hàm số 3 2 y =
x − mx − x + m +1. Tìm tham số m để phương trình y = 0 có hai nghiệm 3
phân biệt x , x thỏa mãn 2 2
x + x + 4x x = 2 . ĐS: m = 1 . 1 2 1 2 1 2 Bài 18.
Tính đạo hàm của các hàm số sau 2 2(1+ tan 4x)
1. y = tan 4x . ĐS: y ' = . tan 4x 2 1+ tan x
2. y = 1+ 2 tan x . ĐS: y ' = . 1+ 2 tan x 2 2 3(2x −1) cot x − x +1 3. 3 2 y = cot x − x +1 . ĐS: y ' = . 2 2 2 2 x − x +1.sin x − x +1 3 4sin 2x +1) cos 2x +1 4. 4 y = cos 2x +1 . ĐS: y ' = . 2x +1 cot x ( 2 1+ cot x) 5. 2
y = 1− cot x . ĐS: y ' = . 2 1− cot x 4sin 2x 6. 2
y = 2sin x − 3cos 2x + 5 . ĐS: y ' = . 2
2sin x − 3cos 2x + 5 30 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 2x cot ( 2 x + ) 1 7. 2 y = ( 2 cot x + ) 1 . ĐS: y ' = . 2 −sin ( 2 x + ) 2 1 cot ( 2 x + ) 1 3 − ( 2 1+ cot 2x) 8. 3 y = cot 2x . ĐS: y ' = . 3 cot 2x Bài 19.
Tính đạo hàm của các hàm số sau 1. y = . x cos x .
ĐS: y ' = cos x − . x sin x . 2. y = . x sin x .
ĐS: y ' = sin x − . x cos x .
3. y = (2x + ) 1 .sin x .
ĐS: y ' = 2sin x + (2x + ) 1 .cos x .
4. y = (5 − x).cos 5x . ĐS: y ' = 5
− (5− x)sin5x y ' = 2sin x + (2x + ) 1 .cos x . 5. y = ( 2
4 − x ).cos 2x .
ĐS: y = − x x − ( 2 ' 2 cos 2
2 4 − x )sin 2x . 6. y = ( 2
2 − x ).sin 3x .
ĐS: y = − x x + ( 2 ' 2 sin 3
3 2 − x )cos3x .
7. y = ( x − sin x).( − x − sin x) .
ĐS: y ' = (1− cos x) − 2x + sin 2x .
8. y = x cot 2x . ĐS: y = x − x ( 2 ' cot 2 2 1+ cot 2x) . sin x − cos x 9. y = . ĐS: 2 y ' = 1+ tan x − . sin x + cos x 4 s inx + cos x 10. y = . ĐS: 2 y ' = 1 − − cot x − . s inx − cos x 4 Bài 20.
Tìm đạo hàm của các hàm số sau: cos x 2sin x 1. y = . ĐS: y ' = − 2 1+ s in x ( 2 1+ sin x) 2 1+ sin x 4 ( 4 cos 3x − ) cos 3x −1 3 1 sin 2x 12sin 3 . x cos 3x 2. y = . ĐS: y ' = − cos 2x − 2 ( x − )2 cos 2x − 2 cos 2 2 cos 2x 2 sin x 2sin 2x 3. y = . ĐS: y ' = 2 1+ cos x (1+cos x)2 2 2 1+ tan 3x 6sin 6x 4. y = . ĐS: y ' = 2 1− tan 3x 2 cos 6x sin x − . x cos x 2 x 5. y = . ĐS: y ' = cos x + . x sin x
(cos x+ xsin x)2 2 4x − 2 6. y = . ĐS:
4cot x − sin x + x ( − + − x − x + x ) 4( 2 1 cot x) − ( x − ) cos x 1 4 4 cot sin 4 2 + 2 4cot x − sinx 2 x y ' = ( .
4 cot x − sin x + x )2 cos x 1 7. y = y ' = cos x − . ĐS: sin x 1− . sin 2x 31 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM sin x 1 8. y = . ĐS: y ' = . cos x + sin x sin 2x +1 2 − sin 2x
2(cos x − sin x) 9. y = . ĐS: y ' = − . 3 3 cos x + sin x sin 2x +1 2 cos x 2sin 2x 10. y = . ĐS: y ' = − . 2 1+ sin x (1+sin x)2 2 Bài 21.
Cho hàm số y = cot 2x . Chứng minh 2
y '+ 2 y + 2 = 0 . Bài 22.
Cho các hàm số f ( x) 4 4
= sin x + cos x và g (x) 6 6
= sin x + cos x .
Chứng minh 3 f '( x) − 2g '( x) = 0 . Bài 23.
Cho hàm số y = 3sin 2x + 4cos 2x +10x . Giải phương trình y ' = 0 .
ĐS: x = arctan 2 + k;k Z .
D. LỜI GIẢI BÀI TẬP RÈN LUYỆN Bài 2. 1. 5 2 5 2
y = 6.x − 2.3x − 5.2x = 6x − 6x −10 . x 2 1 x 1 1 2. 4 3 3 y = x −
− 2 = .4x − .2x = x − .x 4 2 4 2 1 1 3. 4 2 3 3 y = − x − 2x − 5
= − .4x − 2.2x = −x − 4 . x 4 4 Bài 3. 1. 2 3 y = m x − (m− ) 2 3 4. 2.
1 x = 4m x − 2 (m − ) 1 . x 2. 4 3 4 3
y = 3.5x − 6.4mx − 2m = 15x − 24mx − 2 . m = − − Bài 4. 1. y ( x )
( 5x x) = ( x− )
( 5x − x)+( x− ) ( 5 2 3 2 2 3 . 2 2 3 . x − 2x) = ( 5
x − x) + ( x − ) ( 4 x − ) 5 5 4 5 4 2. 2 2 3 . 5
2 = 2x − 4x +10x −15x − 4x + 6 = 12x −15x − 8x + 6.
2. y = ( 2 x − x + )( 2 x + ) =
( 2x − x+ ) ( 2x + )+( 2x − x+ ) ( 2 2 3 2 3 2 3 . 2 3 2 3 . 2x + 3) = ( x − ) ( 2 x + ) + ( 2
x − x + ) ( x) 3 2 3 2 2 2 . 2 3 2 3 . 4
= 4x − 4x + 6x − 6 + 4x −8x +12x 3 2
= 8x −12x +18x − 6
3. y = ( 2 x + )( 2 − x ) = ( 2x + ) ( 2 − x ) + ( 2 x + ) ( 2 1 5 3 1 . 5 3 1 . 5 − 3x ) = ( x) ( 2 − x ) + ( 2 x + ) (− x) 3 3 3 2 . 5 3 1 . 6
=10x − 6x − 6x − 6x = 12 − x + 4 . x 2
Bài 5. 1. y = ( 2
− x ) (− x) = − x( 4 2 x − x + ) 5 3 3 1 2 . 4 12 4 4 1 = 4
− 8x + 48x −12 . x 3 3 2. y = ( 2
x + x + ) ( x + ) ( x + )( 2 4 1 . 2 1 =4 2 1 x + x + ) 1 . 31 31 3. y = ( 2
x − x ) ( − x) = ( − x)( 2 32. . 1 2 32 1 2 x − x ) . 2 2 4. y = ( 2
x − x + ) ( x − ) = ( x − )( 2 3 1 . 2 1 3 2 1 x − x + ) 1 . u u v − uv Bài 6.
1. - Cách 1: Sử dụng công thức: = ta được: 2 v v (
5x) (1− 4x) − 5x (1− 4x)
5(1− 4x) + 4.5x 5 32 y = = = ( 1− 4x)2 (1− 4x)2 (1− 4x)2 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM ax + b ad − bc
- Cách 2: Sử dụng công thức nhanh: =
(Rèn luyện cho lớp 12 trong trắc cx + d (cx + d )2 nghiệm) 5.1+ 4.0 5 y = = ( 1− 4x)2 (1−4x)2 u u v − uv
2. - Cách 1: Sử dụng công thức: = ta được 2 v v ( x − )
1 ( x + 2) − ( x − ) 1 ( x + 2)
1.( x + 2) − ( x − ) 1 .1 3 y = = = ( . x + 2)2 (x + 2)2 (x + 2)2 ax + b ad − bc
- Cách 2: Sử dụng công thức nhanh: =
(Rèn luyện cho lớp 12 trong trắc cx + d (cx + d )2 nghiệm) 1.2 +1.1 3 y = = ( . x + 2)2 (x + 2)2 u u v − uv
3. - Cách 1: Sử dụng công thức: = ta được 2 v v ( 6x − )
1 ( x + 2) − (6x − ) 1 ( x + 2)
6.( x + 2) − (6x − ) 1 .1 13 y = = = ( . x + 2)2 (x + 2)2 (x + 2)2 ax + b ad − bc
- Cách 2: Sử dụng công thức nhanh: =
(Rèn luyện cho lớp 12 trong trắc cx + d (cx + d )2 nghiệm) 6.2 +1.1 13 y = = ( . x + 2)2 (x + 2)2 u u v − uv
4. - Cách 1: Sử dụng công thức: = ta được 2 v v (
mx − 2) ( x − m + )
1 − (mx − 2)( x − m + ) 1
m ( x − m + ) 1 − (mx − 2) 2 .1 −m + m + 2 y = = = ( . 2 2 x − m + )2 1 (x −m+ ) 1 (x −m+ ) 1 ax + b ad − bc
- Cách 2: Sử dụng công thức nhanh: =
(Rèn luyện cho lớp 12 trong trắc cx + d (cx + d )2 nghiệm) m (−m + ) 2 1 + 2.1 −m + m + 2 y = = ( . x − m + )2 1 (x − m+ )2 1 u u v − uv
5. - Cách 1: Sử dụng công thức: = ta được 2 v v 33 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM ( 3m + ) 2
1 x − m + m) ( x + m) − ( 3m + ) 2
1 x − m + m)( x + m) y = (x + m)2 ( . 3m + )
1 .( x + m) − ( 3m + ) 2
1 x − m + m) 2 .1 4m = = (x + m)2 (x + m)2 ax + b ad − bc
- Cách 2: Sử dụng công thức nhanh: =
(Rèn luyện cho lớp 12 trong trắc cx + d (cx + d )2 nghiệm)
(3m + )1.m −1.( 2 −m + m) 2 4m y = = ( . x + m)2 (x + m)2 u u v − uv Bài 7.
1. - Cách 1: Sử dụng công thức: = ta được 2 v v ( 2
x + 5x − 2) ( x − ) 1 − ( x − ) 1 ( 2 x + 5x − 2) (2x +5)(x − ) 1 − ( 2 x + 5x − 2) 2 x − 2x − 3 y = = = ( 2 2 x − )2 1 (x − )1 (x − )1
- Cách 2. Sử dụng công thức nhanh (Rèn luyện cho lớp 12 trong trắc nghiệm):
= (1 5 −2 x − x− y = 0 1 −1 ) 2 2 3 (x − ) . 2 1 u u v − uv
2. - Cách 1: Sử dụng công thức: = ta được 2 v v ( 2 2x − 4x + )
1 ( x − 3) − ( x − 3) ( 2 2x − 4x + ) 1 y = (x −3)2
(4x − 4)(x −3)−( 2 2x − 4x + ) 2 1 2x −12x +11 = = ( x − 3) . 2 (x −3)2
- Cách 2. Sử dụng công thức nhanh (Rèn luyện cho lớp 12 trong trắc nghiệm): = (2 −4 1 x − x + y = 0 1 − 3) 2 2 12 11 (x −3) . 2 ' u
u 'v − v 'u
3. - Cách 1. Sử dụng công thức = ta được: 2 v v (x − )
1 ( x − 3x + 3) − ( x − 3x + 3)' ' 2 2 (x − ) 1 1.( 2
x − 3x + 3) − (2x − 3)( x − ) 1 y ' = ( = = 2 x − 3x + 3)2 2 ( 2x −3x+3) 2 −x + 2x ( x − 3x + 3)2 2
- Cách 2. Sử dụng công thức nhan (rèn luyện cho lớp 12 trong trắc nghiệm) 2 0 1 1 − −x + 2x y ' = = 2 − 2 1 3 3 (x −3x +3) 34 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM ' u
u 'v − v 'u
4. - Cách 1. Sử dụng công thức = ta được: 2 v v
(2x +mx−3m+ )'1(mx− )1−(mx− )' 2 1 ( 2
2x + mx − 3m + ) 1 y ' = ( x − )2 1
(4x + m)(x −1) − m ( 2 2x − 3m + ) 1 = 2 (mx −1) 2 2
2mx − 4x + 3m − 2m = ( mx − )2 1
- Cách 2. Sử dụng công thức nhanh (rèn luyện cho lớp 12 trong trắc nghiệm) 2 2 2 m 3
− m +1 2mx − 4x + 3m − 2m ' y = = 0 m 1 − (mx − )2 1 (x + 2)' 1 Bài 8. 1. y ' = 1 − + 0 + = − + ( x + 2) 1 2 (x + 2)2 (3x +5) ' 2 '
2(3x + 5).(3x + 5) 18 2. y ' = 3 − . = − = − ( . 3x + 4) 3. 4 4 3 (3x + 5) (3x + 5) (x −3x + )' 3 2 2 1 3x − 6x 6x(2 − x) 3. y ' = 2 − . ( = − = x − 3x + ) 2. 2 1 (x −3x + )2 1 (x −3x + )2 3 2 3 2 3 2 1 ( x − 3x) ' 11 3 10 ' 11( 3 x − 3x) .( 3 x − 3x) 33( 2 1− x ) 1 1 1 y ' = − ( + = − + = + 22 2 12 2 x − 3x)22 2 3 x ( 3x −3x) x
( 3x −3x) x 4. 1 1 1 2 2 Bài 9. 1. 3 3 y ' = 2 − . + 4. − .4x = − + − 2x . 2 2 x 2 x 2 x x (1+2x− x )'2 2 − 2x 1− x 2. y ' = = = . 2 2 2 2 1+ 2x − x 2 1+ 2x − x 1+ 2x − x (2x −5x+2)' 2 4x − 5 3. y ' = = . 2 2 2 2x − 5x + 2 2 2x − 5x + 2 Bài 10.
1. Tập xác định: D = 0; 4 . 1 (4x− x )'2 1 2 − x (x − 2) 2
4x − x + 2x − 4 Ta có y ' = x −1− = x −1− = . 2 2 2 2 − 2 2 4x x 4x − x 2 4x − x
2. Tập xác định: D = 0; +) . ' 1 5 Ta có y ' = ( 2 x ) 2
. x + x .( x )' = 2x x + x x = x x . 2 2
3. Tập xác định: D = 0; +) .
Ta có y = x + ( x) x + x( x )' ' 3 ' 2 = 2x + x . 2 35 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 2
4. Tập xác định: D = − ; + . 3 ' + ' 3 9x 1
Ta có y ' = ( x − ) 1
3x + 2 + ( x − )
1 ( 3x + 2) = 3x + 2 + (x − ) 1 . = . 2 3x + 2 2 3x + 2
5. Tập xác định: D = 1 − ;1 . 1− x x 1− 2x 2 ( )'2 2 2 Ta có 2 y ' = 1− x + . x = 1− x − = . 2 2 2 2 1− x 1− x 1− x Bài 11.
1. Tập xác định: D = 0; +) . 2 x 100 − x Ta có y ' = = ( . x +100)2 2( x +100)2 x
2. Tập xác định: D = ( 4 − ;4) . −x 2 ( ) 16 − x − . x 2 16 − x 16 Ta có y ' = = . 2 16 − x ( 2 16 − x ) 2 16 − x
3. Tập xác định: D = R . 2x −1 2
x − x + 3 − ( x + 2). 2 2 x − x + 3 5 − x + 8 Ta có y ' = = . 2 x − x + 3 2( 2 x − x + 3) 2 x − x + 3
4. Tập xác định: D = R \ 0 . x 2 .x − 4 + x 2 4 + x 4 − Ta có y ' = = 2 2 2 x x 4 + x 1
5. Tập xác định: D = R \ . 2 (2x − ) 1 (x x +1)' 2 2 − 2x x +1 Ta có y ' = ( 2x − )2 1 ( x 2x − ) 1 x +1 + (2x − ) 2 2 2 1 . − 2x x +1 2 x +1 = ( 2x − )2 1 3 2 2x − 2x −1 = ( . 2x − )2 2 1 x +1 Bài 12.
1. Tập xác định: D = 0; +) \ 1 . ( )'( − ) 3 − x ( 1 3 2 x − ) 2 2 2 2 1 − 2 1 2 x x − x x − x x x x x x Ta có 2 2 2 y ' ( = = . x − )2 1 (x − )2 1 (x − )2 2 2 2 1
2. Tập xác định: D = (0; +) . 36 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM ' 2 x +1 1 1− 2 2 x x −1 Ta có ' x y = = = . 2 2 2 x +1 x +1 2x x x +1 2 2 x x 1
3. Tập xác định: D = ; − . 2 2 ' 2 1
Ta có y ' = 3(1− 1− 2x ) (1− 1− 2x ) = 3(1− 1− 2x ) . . 1− 2x
4. Tập xác định: D = 0; +) . ' 2 − 1 − Ta có y ' = . x = . 2 ( ) (1+ x) x (1+ x )2
5. Tập xác định: D = 3 − ;+) \ 1 . 1 .( x − ) 1 − (1+ x + 3) 2 x + 3
(x − )1− 2 x +3 − 2(x +3) −x −7 −2 x +3 Ta có y ' = = = ( . x − )2 1
2 x + 3 ( x − )2 1
2 x + 3 ( x − )2 1 Bài 13.
1. Ta có f ( x) 3 = 8
− x − 2x . Khi đó f (x) 3
= − x − x = − x( 2 0 8 2 0 2 4x + ) 1 = 0 x = 0 .
Vậy phương trình f ( x) = 0 có một nghiệm x = 0 . 2 2 − x + 4x + 2 2. Ta có y = . Điề . Khi đó ( u kiện x 1 (*) 1− x)2 2 y = 0 2
− x + 4x + 2 = 0 x =1 2 .
Kết hợp với điều kiện (*), phương trình y = 0 có hai nghiệm x =1 2 . 4( 2 x ) 3 8 x − 8
3. Điều kiện x 0 (*) . Ta có y = 1− ( ) =1− = . 2 3 3 2 x x x Khi đó 3
y = 0 x − 8 = 0 x = 2 .
Kết hợp với điều kiện (*), phương trình y = 0 có một nghiệm x = 2 . x = 0 Bài 14. Ta có 3
y = 4x − 4mx . Khi đó 3
y = 0 4x − 4mx = 0 4x ( 2 x − m) = 0 2 . x − m = 0 ( ) *
Phương trình y = 0 có ba nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm phân m 0
biệt khác 0. Điều kiện tương đương là 2 m 0 0 − m . 0
Vậy giá trị m cần tìm là m 0 . x − Bài 15. Ta có f ( x) 3
= 3x + 6x − 9 . Khi đó, f (x) 3 3
0 3x + 6x − 9 0 . x 1
Vậy bất phương trình f ( x) 0 có tập nghiệm là S = (− ; 3 − )(1;+). Bài 16. Ta có f ( x) 2
= 3x + 2mx + (4m −9) . Khi đó f ( x) 2 0, x
3x + 2mx + (4m −9) 0, x a 0 3 0 − + 37 . m − ( m− ) 2 2 m 12m 27 0 3 m 9 0 3 4 9 0 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
Vậy giá trị m cần tìm là 3 m 9 . Bài 17. Ta có 2
y = x − 2mx −1 và 2
y = 0 x − 2mx −1 = 0 (*) .
Phương trình (*) có ac = 1
− 0 nên luôn có 2 nghiệm phân biệt x , x . Khi đó 1 2
x + x + 4x x = 2 ( x + x )2 + 2x x = 2 (2m)2 2 2
− 2 = 2 m = 1. 1 2 1 2 1 2 1 2
Vậy giá trị m cần tìm là m = 1 . 2sin . x cos . x cos x 2 −sinx 1+ sin x − −sin x + ( 2
1+ sin x) − sin x( 2 2 1− sin 2 1 sin x x ) Bài 20. 1. Ta có y ' = = 2 1+ sin x ( 2 1+ sin x) 2 1+ sin x 2sin x = − ( 2 1+ sin x) 2 1+ sin x
2. Điều kiện xác định −
+ k x + k,k Z 4 4 2 − sin 2x 3 4 cos 3x ( 3
− sin 3x)( cos2x −2)−( 4 cos 3x − ) 1 2 cos2x Ta có y ' = ( cos 2x − 2)2 ( 4 cos 3x − ) 3 1 sin 2x 12sin 3 . x cos 3x = ( − x − )2 cos 2x − 2 cos 2 2 cos 2x 2sin . x cos x ( 2 1+ cos x) 2 + 2cos . x sin . x sin x 2sin . x cos x ( 2 2
1+ cos x + sin x) 3. Ta có y ' = ( = 1+ cos x)2 (1+cos x)2 2 2 4sin . x cos x 2sin 2x = ( = 1+ cos x)2 (1+cos x)2 2 2 k k
4. Điều kiện xác định của hàm số là x + , x + , k Z 12 3 6 3 2 1+ tan 3x 1 1 1 Ta có y = = = = 2 2 1− tan 3x cos 3x ( 2 1− tan 3x) 2 2
cos 3x − sin 3x cos 6x (cos6x)' Khi đó 6sin 6x y ' = − = 2 2 cos 6x cos 6x
5. Điều kiện xác định của hàm số là cos x + x sin x 0 cos x −
(cos x − .xsin x)(cos x+ xsin x)−(sin x− xcosx)−sin x+
(sin x + xcos x) Ta có y ' = (
cos x + x sin x)2
x sin x (cos x + x sin x) − x cos x (sin x − x cos x) 2 2 2 2
x sin x cos x + x sin x − x sin x cos x + x cos x = = (
cos x + x sin x)2
(cos x + xsin x)2 2 x = ( x + x x)2 cos sin 38 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 6. Với điều kiện xác định của hàm số ta có ( − + − x − x + x ) 4( 2 1 cot x) − ( x − ) cos x 1 4 4 cot sin 4 2 +
2 4cot x − sin x 2 x y ' = (
4 cot x − sin x + x )2
7. Điều kiện xác định của hàm số là x
+ k,k Z 4 Ta có
−sin x(cos x −sin x) − cos x(−sin x − cos x) 2 2
−sin x cos x + sin x + sin x cos x + cos x y ' = = (
cos x − sin x)2 1− sin 2x 1 = 1− sin 2x
8. Điều kiện xác định của hàm số là x −
+ k,k Z 4
cos x (cos x + sin x) − sin x (cos x − sin x) 2 2
sin x cos x + cos x − sin x cos x + sin x Ta có y ' = = ( cos x + sin x)2 1+ sin 2x 1 = 1+ sin 2x
9. Điều kiện xác định của hàm số là x −
+ k,k Z 4 2 − 2sin 2x
2(1− sin x cos x) 2 Ta có y ' = = = 3 3 sin x + cos x
(sin x +cos x)( 2 2
sin x − sin x cos x + cos x ) sin x + cos x
s (sin x + cos x)'
2(cos x − sin x) Khi đó y ' = − = − ( sin x + cos x)2 sin 2x +1 10. Ta có 2 − cos xsin x( 2 1+ sin x) 2 − cos .
x 2 cos x sin x 2 − cos xsin x( 2 2
1+ sin x + cos x) y ' = ( = 1+ sin x)2 (1+sin x)2 2 2 2sin 2x = − ( 1+ sin x)2 2 Bài 21.
Điều kiện xác định của hàm số là x k , k Z 2 Ta có y = − ( 2 ' 2 1+ cot 2x) Khi đó 2 y + y + = − ( 2 + x) 2 2 2 ' 2 2 2 1 cot 2 + 2cot 2x + 2 = 2
− − 2cot 2x + 2cot 2x + 2 = 0
Ta có điều phải chứng minh Bài 22. Ta có
f ( x) = (sin x + cos x)2 1 2 2 2 2 2 − 2sin .
x cos x = 1− sin 2x 2
g ( x) = (sin x + cos x)2 3 2 2 2 2 −3sin . x cos x ( 2 2 sin x + cos x) 2 2 2
=1−3sin xcos x =1− sin 2x 4 Khi đó 39 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM f ( x) 1 ' = − .2sin 2 .
x 2cos 2x = −sin 4x và g ( x) 3 3 ' = − .2.sin 2 .
x 2.cos 2x = − sin 4x 2 4 2
Vì vậy, f ( x) − g ( x) 3 3 ' 2 ' = 3
− sin 4x − 2. − sin 4x = 0 2
Ta có điều phải chứng minh Bài 23.
Ta có y ' = 6 cos 2x − 8sin 2x +10
Khi đó y ' = 0 6cos 2x − 8sin 2x +10 = 0(*) Ta thấy x =
+ k,k Z không là nghiệm của phương trình (*) 2 − Đặ 1 t 2t
t t = tan x , phương trình (*) trở thành 2 6. −8.
+10 = 0 4t −16t +16 = 0 t = 2 2 2 1+ t 1+ t
Với t = 2 thì tan x = 2 x = arctan 2 + k ; k Z
Vậy phương trình y ' = 0 có nghiệm x = arctan 2 + k ; k Z . 40 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
BÀI 2. PHƯƠNG TRÌNH TIẾP TUYẾN
A. TÓM TẮT LÝ THUYẾT
Cho đồ thị (C) : y = f ( x) , M ( x ; y C (C) M 0 0 )
( ) . Phương trình tiếp tuyến với tại là
: y = y '(x x − x + y 0 ) ( 0 ) 0
Trong đó M ( x ; y (y = f x 0 ( 0 )) 0
0 ) là tọa độ tiếp điểm .
f '( x = k
(k = y'(x = f ' x 0 ) ( 0 )) 0 )
là hệ số góc của tiếp tuyến .
B. DẠNG TOÁN VÀ BÀI TẬP
_ DẠNG 1. VIẾT PTTT KHI BIẾT TIẾP ĐIỂM (TẠI ĐIỂM M ) HOẶC BIẾT HOÀNH ĐỘ, TUNG ĐỘ PHƯƠNG PHÁP:
Bước 1. Tính y ' = f '( x) và tính hệ số góc k = f '( x0 )
Bước 2. Phương trình tiếp tuyến dạng: y − y = f ' x x − x 0 ( 0)( 0 ) . _VÍ DỤ MINH HỌA
Ví dụ 1. Viết phương trình tiếp tuyến tại M (0 )
;1 thuộc đồ thị (C ) 3
: y = 2x − 6x +1. Lời giải
- Tập xác định D = . - Ta có, 2
y = 6x − 6 hệ số góc là k = y(0) = 6 −
- Phương trình tiếp tuyến cần tìm là : y = y(0)( x − 0) +1 : y = 6 − x +1.
Ví dụ 2. Viết phương trình tiếp tuyến tại điểm M (1;− ) 1 thuộc (C ) 3 2
: y = 3x − 5x +1. Lời giải
- Tập xác định D = - Ta có, 2
y = 9x −10x hệ số góc là k = y( ) 1 = 1 −
- Phương trình tiếp tuyến cần tìm là : y = 1 − (x − )
1 −1 : y = −x .
Ví dụ 3. Viết phương trình tiếp tuyến tại điểm M (1 ) ;1 thuộc (C ) 3
: y = 2x − 6x +1 . Lời giải
- Tập xác định D = - Ta có, 2
y = 6x − 6 hệ số góc là k = y( ) 1 = 0
- Phương trình tiếp tuyến cần tìm là : y = 1 . x +
Ví dụ 4. Viết phương trình tiếp tuyến tại điểm M ( 2 − ;5) thuộc (C) 3 1 : y = . x +1 Lời giải
- Tập xác định D = \ − 1 2 - Ta có, y =
hệ số góc là k = y( 2 − ) = 2 (x + )2 1
- Phương trình tiếp tuyến cần tìm là : y = 2( x + 2) + 5 = 2x + 9 . − + Ví dụ 5. x x M (2; 4) = 41
Viết phương trình tiếp tuyến tại điểm thuộc (C ) 2 2 : y . x −1 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM Lời giải 2 x − 2x −1 - Ta có, y =
hệ số góc là k = y(2) = 1 − (x − )2 1
- Phương trình tiếp tuyến cần tìm là : y = − ( x − 2) + 4 = −x + 6 .
Ví dụ 6. Viết phương trình tiếp tuyến tại điểm M (0;3) thuộc (C) 2 : y = x +1− . 2x −1 Lời giải 1
- Tập xác định D = \ 2 4 - Ta có, y = 1+
hệ số góc là k = y(0) = 5 (2x − )2 1
- Phương trình tiếp tuyến cần tìm là : y = 5( x − 0) + 3 = 5x + 3 .
_BÀI TẬP ÁP DỤNG Bài 1.
1. Viết phương trình tiếp tuyến tại điểm M (1;0) thuộc (C ) 4 2
: y = x − 2x +1 .
ĐS: : y = 0 .
2. Viết phương trình tiếp tuyến tại điểm M (1; 2) thuộc (C ) 4 2
: y = −x + 3x .
ĐS: : y = 2x . Bài 2. 1. Cho hàm số 3 2
y = x − x + 2 . Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M có hoành độ x = 1 − .
ĐS: : y = 5x + 5 . 0 2x −1
2. Cho hàm số y =
. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M có x +1 hoành độ x = 3 1 1.
ĐS: : y = x − . 0 4 4 2x +1
3. Cho hàm số y =
. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M có x −1 hoành độ x = 1 − 3 1 .
ĐS: : y = − x − . 0 4 4 2x − 2
4. Cho hàm số y =
. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M có x − 2 5 hoành độ x = . ĐS: : y = 8 − x + 26 . 0 2 x − 3 Bài 3.
1. Cho hàm số y =
. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M có tung x +1 độ y = 1 − .
ĐS: : y = x − 2 . 0 2x − 2
2. Cho hàm số y =
. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M có x − 2 tung độ y = 1 3 .
ĐS: : y = − x + 5 . 0 2 3. Cho hàm số 3 2
y = 2x + 3x −1. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M có tung độ y = 4 .
ĐS: : y =12x −8 . 0 42 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 4. Cho hàm số 3 2
y = x + 3x +1. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M có tung độ y = 1 .
ĐS: : y = 9x + 28, y =1. 0
5. Cho hàm số y =
x + 2 . Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M có 1 3 tung độ bằng 2 .
ĐS: : y = x + . 4 2 6. Cho hàm số 4 2
y = x − 2x +1. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M có tung độ y = 0 .
ĐS: : y = 0 . 0 x + Bài 4.
1. Viết phương trình tiếp tuyến của (C ) 2 1 : y =
tại giao điểm của nó với trục tung. x −1 ĐS: : y = 3 − x −1 . x +
2. Viết phương trình tiếp tuyến của (C ) 3 : y =
tại giao điểm của nó với trục tung. x −1 ĐS: : y = 4 − x −3 . x + Bài 5.
1. Viết phương trình tiếp tuyến của (C ) 2 1 : y =
tại giao điểm của nó với trục hoành. x +1
ĐS: : y = 4x + 2 .
2. Viết phương trình tiếp tuyến của (C ) 2
: y = 2x − 2x +1 tại giao điểm của nó với trục hoành. 1
ĐS: : y = x − . 2 x + Bài 6.
1. Viết phương trình tiếp tuyến của (C) 2 : y =
tại giao điểm của nó với đường thẳng x +1
d : y − 2 = 0 .
ĐS: : y = 4x + 2 . 1
2. Viết phương trình tiếp tuyến của (C) 3 2 : y =
x + 2x + 3x −1 tại giao điểm của nó với đường 3
thẳng d : y +1 = 0 . ĐS: : y = 1
− , y = 3x −1 . − x 3. Cho (C) 3 2 : y =
. Viết phương trình tiếp tuyến của (C ) tại giao điểm của (C ) và đường x −1
thẳng d : y = x − 3
ĐS: : y = −x +1−1, y = −x − 3 . 4. Cho (C ) 3 2
: y = x − 3x + 2 . Viết phương trình tiếp tuyến của (C ) tại giao điểm của (C ) và
đường thẳng d : x + y + 3 = 0
ĐS: : y = 9x + 7 . 3 9 11 5. Cho (C) 3 2 : y = x − x − x +
. Viết phương trình tiếp tuyến của (C ) tại giao điểm của (C ) 2 4 8
và đường thẳng d : y = 4x + 4 có hoành độ dương.
ĐS: : y = 24x − 66 . x + 6. Cho (C ) 2 1 : y =
. Viết phương trình tiếp tuyến của (C ) tại giao điểm của (C ) và đường x −1
thẳng d : y = x + 1 1 3 . ĐS: y = 3
− x +11, y = − x + . 3 3 _LỜI GIẢI Bài 1. 1. Ta có, 3
y = 4x − 4x hệ số góc là k = y( ) 1 = 0
Phương trình tiếp tuyến cần tìm là : y = 0 . 43 2. Ta có, 3 y = 4
− x + 6x hệ số góc là k = y( ) 1 = 2 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
Phương trình tiếp tuyến cần tìm là : y = 2( x − ) 1 + 2 = 2x . Bài 2. 1. Với x = 1
− y = 0 M 1 − ;0 0 0 ( ) Ta có, 2
y = 3x − 2x hệ số góc là k = y(− ) 1 = 5
Phương trình tiếp tuyến cần tìm là : y = 5( x + ) 1 + 0 = 5x + 5 . 1 1 2. Với x = 1
− y = M 1; 0 0 2 2 3 Ta có, y =
hệ số góc là k = y( ) 3 1 = (x + )2 1 4 3 1 3 1
Phương trình tiếp tuyến cần tìm là : y = (x − ) 1 + = x − . 4 2 4 4 1 1 3. Với x = 1
− y = M 1 − ; 0 0 2 2 3 − Ta có, y =
hệ số góc là k = y(− ) 3 1 = − (x + )2 1 4 3 1 3 1
Phương trình tiếp tuyến cần tìm là : y = − (x + ) 1 + = − x − . 4 2 4 4 5 5 4. Với x = y = 6 M ; 6 0 0 2 2 2 5 Ta có, y =
hệ số góc là k = y = 8 − (x − 2)2 2 5
Phương trình tiếp tuyến cần tìm là : y = 8 − x − + 6 = 8 − x + 26 . 2 Bài 3. 1. D = \ − 1
Gọi M ( x ; y C 0 0 ) ( ) là tiếp điểm x − 3 Với 0 y = 1 − = 1
− x =1 M 1; 1 − 0 0 ( ) . x +1 0 4 Ta có, y =
hệ số góc là k = y( ) 1 = 1 (x + )2 1
Phương trình tiếp tuyến cần tìm là : y = 1( x − ) 1 −1 = x − 2 . 2. D = \ 2
Gọi M ( x ; y C 0 0 ) ( ) là tiếp điểm 2x − 2 Với 0 y = 3
= 3 x = 4 M 4;3 0 0 ( ) x − 2 0 2 − Ta có, y =
hệ số góc là k = y( ) 1 4 = − (x − 2)2 2 1
y = − ( x − 4) 1 + = − +
Phương trình tiếp tuyến cần tìm là : 3 x 5 . 2 2 44 3. D = Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
Gọi M ( x ; y C 0 0 ) ( ) là tiếp điểm Với 3 2
y = 4 2x + 3x −1 = 4 x = 1 M 1; 4 0 0 0 0 ( ) Ta có, 2
y = 6x + 6x hệ số góc là k = y( ) 1 = 12
Phương trình tiếp tuyến cần tìm là : y = 12( x − ) 1 + 4 = 12x + 8 . 4. D =
Gọi M ( x ; y C 0 0 ) ( ) là tiếp điểm x = 3 − 3 2 0
Với y = 1 x + 3x +1 = 1
M 1;4 , M 0;1 0 0 0 1 ( ) 2 ( ) . x = 0 0 Ta có, 2
y = 6x + 6x
Tại M hệ số góc là k = y( 3 − ) = 9 1
Phương trình tiếp tuyến tại M là : y = 9 x + 3 +1 = 9x + 28 1 ( ) . 1
Tại M hệ số góc là k = y(0) = 0 2
Phương trình tiếp tuyến tại M là : y = 0 x + 0 +1 = 1 2 ( ) . 2 5. D = 2; − +)
Gọi M ( x ; y C 0 0 ) ( ) là tiếp điểm
Với y = 2 x = 2 M 2; 2 0 0 ( ) . 1 Ta có, y =
hệ số góc là k = y( ) 1 2 = 2 x + 2 4 1 1 1 3
Phương trình tiếp tuyến cần tìm là : y = (x − 2) + 2 = (x − 2) + 2 = x + . 4 4 4 2 6. D =
Gọi M ( x ; y C 0 0 ) ( ) là tiếp điểm x = 1 − 4 2 0
Với y = 0 x − 2x +1 = 1
M −1;0 , M 1;0 0 0 0 1 ( ) 2 ( ) . x = 1 0 Ta có, 3
y = 4x − 4x
Tại M hệ số góc là k = y(− ) 1 = 0 1
Phương trình tiếp tuyến tại M là : y = 0 x +1 + 0 = 0 1 ( ) . 1
Tại M hệ số góc là k = y( ) 1 = 0 2
Phương trình tiếp tuyến tại M là : y = 0 x +1 + 0 = 0 2 ( ) . 2 Bài 4. 1. D = \ 1
Giao điểm của đồ thị với trục tung là M (0;− ) 1 3 − Ta có, y =
hệ số góc là k = y(0) = 3 − (x − )2 1
Phương trình tiếp tuyến cần tìm là : y = 3 − (x − 0) −1= 3 − x −1 . 45 2. D = \ 1 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
Giao điểm của đồ thị với trục tung là M (0; 3 − ) 4 − Ta có, y =
k = y 0 = 4 − 2 ( ) (x − ) 1
Phương trình tiếp tuyến cần tìm là : y = 4 − (x − 0) −3 = 4 − x − 3 . Bài 5. 1. D = \ − 1 2x +1 1 1
Tại giao điểm với trục hoành 0 y = 0
= 0 x = − M − ;0 0 0 x +1 2 2 0 1 1 Ta có, y = k = y − = 4 (x + )2 1 2 1
Phương trình tiếp tuyến cần tìm là : y = 4 x + + 0 = 4x + 2 . 2 2. D = 1 1
Tại giao điểm với trục hoành 2
y = 0 2x − 2x +1 = 0 x = M ; 0 0 2 2 2x 1 Ta có, y = 2 − k = y =1 2 2x +1 2 1 1
Phương trình tiếp tuyến cần tìm là : y = 1 x − + 0 = x − . 2 2 Bài 6. 1. D = \ − 1
Gọi M ( x ; y (C) d : y − 2 = 0 0 0 ) là giao điểm của với x + 2
Phương trình hoành độ giao điểm
= 2 x = 0 M (0;2) x +1 1 − Ta có, y =
k = y 0 = 1 − 2 ( ) (x + ) 1
Phương trình tiếp tuyến cần tìm là : y = 1
− (x − 0) + 2 = −x + 2 . 2. D =
Gọi M ( x ; y (C) d : y +1 = 0 0 0 ) là giao điểm của với 1 x = 3 −
Phương trình hoành độ giao điểm 3 2
x + 2x + 3x −1 = 1 − M 3 − ; 1 − 1 ( ) và 3 x = 0 M 0; 1 − 2 ( ) Ta có, 2
y = x + 4x + 3
Tại M hệ số góc là k = y( 3 − ) = 0 1
Phương trình tiếp tuyến tại M là : y = 0 x + 3 −1 = 1 − 1 ( ) . 1
Tại M hệ số góc là k = y(0) = 3 2
Phương trình tiếp tuyến tại M là : y = 3 x − 0 −1 = 3x −1 2 ( ) . 2
3. Gọi M ( x ; y (C) d 0 0 ) là giao điểm của với
. Ta có phương trình hoành độ giao điểm: 46 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 3 − 2x x = 0 0 0 = x − 3 M 0; 3 − , M 2; 1 − . 1 ( ) 2 ( ) 0 (nhận) x −1 x = 2 0 0 1 − Ta có, y = (x − )2 1
Tại M hệ số góc là k = y(0) = 1 − 1
Phương trình tiếp tuyến tại M là : y = 1
− x − 0 − 3 y = −x − 3 1 ( ) . 1
Tại M hệ số góc là k = y(2) = 1 − 2
Phương trình tiếp tuyến tại M là : y = 1
− x − 2 −1 = −x +1 2 ( ) . 2
4. - Gọi M ( x ; y (C) d 0 0 ) là giao điểm của với
. Ta có phương trình hoành độ giao điểm:
x − 3x + 2 = −x − 3 x +1 x − 2 +1 = 0 x = 1 − M (−1;−2) 0 0 0 ( 0 ) ( 0 )2 3 2 0 - Ta có, 2
y = 3x − 6x k = y( ) 1 = 9
- Phương trình tiếp tuyến tại M là : y = 9 x +1 − 2 y = 9x + 7 1 ( ) .
5. Gọi M ( x ; y (C) d 0 0 ) là giao điểm của với
. Ta có phương trình hoành độ giao điểm: 7 x = 2 3 9 11 1 3 2 7 x − x − x +
= 4x + 4 x = − (L) M ;18 2 4 8 2 2 3 x = − (L) 2 9 7 Ta có, 2
y = 3x − 3x − k = y = 24 4 2 7
Phương trình tiếp tuyến tại M là : y = 24 x −
+18 y = 24x − 66 1 . 2
6. Gọi M ( x ; y (C) d 0 0 ) là giao điểm của với
. Ta có phương trình hoành độ giao điểm: 2x +1 x = 2 = x + 3 M 2;5 , M 2 − ;1 1 ( ) 2 ( ) x −1 x = 2 − 3 − Ta có, y = (x − )2 1 7
Phương trình tiếp tuyến tại M là : y = 24 x −
+18 y = 24x − 66 1 . 2
Tại M hệ số góc là k = y 2 = 3 − 1 ( ) 1
Phương trình tiếp tuyến tại M là : y = 3
− x − 2 + 5 y = 3 − x +11 1 ( ) . 1 1
Tại M hệ số góc là k = y 2 − = − 2 ( ) 2 3 1 1 1
Phương trình tiếp tuyến tại M là : y = −
x + 2 +1 = − x + 2 ( ) . 2 3 3 3 47 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
_ DẠNG 2. VIẾT PTTT KHI BIẾT HỆ SỐ GÓC HOẶC SONG SONG, VUÔNG GÓC VỚI MỘT ĐƯỜNG THẲNG. PHƯƠNG PHÁP:
Gọi M ( x ; y C 0 0 ) ( ) là tiếp điểm.
Ta có k = y( x = a
y( x = a x y 0 ) 0 ) , giải phương trình 0 0 . Nhắc lại:
o d : y = a x + b k = a 1 1 1 d 1 1
o d : y = a x + b k = a 1 1 1 d 1 1
o d / /d k = k a = a 1 2 d d 1 2 1 2
o d ⊥ d k .k = 1 − a .a = 1 − 1 2 d d 1 2 1 2
_VÍ DỤ MINH HỌA x
Ví dụ 1. Cho hàm số y =
có đồ thị (C ) . Viết phương trình tiếp tuyến với (C ) biết hệ số góc x +1 k =1 . Lời giải Tập xác định D =
Gọi M ( x ; y
y(x = k 0 ) 0 0 ) là tiếp điểm
x = 0 y = 0 M 0;0 1 1 0 0 1 ( ) Ta có: y = k = =1 (x + )2 1 (x +1 x = 2
− y = 2 M 2 − ;2 0 )2 0 0 2 ( )
Phương trình tiếp tuyến tại M là : y = 1( x − 0) + 0 y = x 1 1
Phương trình tiếp tuyến tại M là : y = 1( x + 2) + 2 y = x + 4 . 1 2
Ví dụ 2. Viết phương trình tiếp tuyến ( ) của đồ thị (C ) 3
: y = x − 3x + 2 , biết tiếp tuyến song song với
(d): y = 3x −2 . Lời giải
Gọi M ( x ; y C () (C) 0 0 )
( ) là tọa độ tiếp điểm của với . = −
() (d) y(x = 3 2x −3 = 3 x = 3 y = 2 M 3;2 0 ) 0 0 0 ( ) Ta có y 2x 3 . Vì .
Phương trình tiếp tuyến ()
(): y = 3(x −3)+ = − tại điểm M là 2 3x 7 .
Ví dụ 3. Viết phương trình tiếp tuyến của đồ thị (C ) 2
: y = x − x + 2 , biết vuông góc với
(d):5y = −x +300. Lời giải 1 = − + = − + Ta có 5y x 300 y x 600 5 1
hệ số góc của đường thẳng (d ) là k = − d . 5 = − M ( x ; y 0 0 ) Ta có y 2x 1 . Gọi
là tiếp điểm của tiếp tuyến . 48 ⊥ (d ) '
f (x .k = 1
− k . 2x −1 = 1
− 2x −1 = 5 x = 3 0 ) d d ( 0 ) Vì 0 0 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM y = 8 0 ' f
(x = 2x −1 = 5 0 ) 0
Phương trình tiếp tuyến () : y = 5( x − 3) + 8 = 5x − 7 .
_BÀI TẬP ÁP DỤNG x −1 Bài 1.
1. Cho hàm số y =
có đồ thị (C ) . Viết phương trình tiếp tuyến với (C ) biết hệ số góc x +1 k = 2 .
ĐS: : y = 2x −1; : y = 2x + 7. 1 2 2x +1
2. Cho hàm số y =
có đồ thị (C ) . Viết phương trình tiếp tuyến với (C ) biết hệ số góc x −1 k = 3 − . ĐS: : y = 3
− x +11; : y = 3 − x −1. 1 2 2x −1
3. Cho hàm số y =
có đồ thị (C ) . Viết phương trình tiếp tuyến với (C ) biết hệ số góc x +1 k = 3.
ĐS: : y = 3x −1; : y = 3x +11. 1 2 4. Cho hàm số 3 2
y = x − x + 2 có đồ thị (C ) . Viết phương trình tiếp tuyến với (C ) biết hệ số 59 góc k =1 .
ĐS: : y = x +1; : y = x + 1 2 27 5. Cho hàm số 3 2
y = −x + 5x − 3 có đồ thị (C ) . Viết phương trình tiếp tuyến với (C ) biết hệ 94 số góc k = 3.
ĐS: : y = 3x + 6; : y = 3x − . 1 2 27 2 x − x + 2
6. Cho hàm số y =
(C ) . Viết phương trình tiếp tuyến (d ) với (C ) , biết hệ số góc của x −1
tiếp tuyến là k = 1 − .
ĐS: y = −x − 2 và y = −x + 6 . x − x + 7. Với (C) 2 3 4 : y =
. Viết phương trình tiếp tuyến () với (C ) , biết k = 1 − . x −1
ĐS: y = −x + 4 và y = −x − 4 .
8. Cho hàm số y = 2x +1 có đồ thị (C ) . Viết phương trình tiếp tuyến của đồ thị (C ) biết 1
hệ số góc của tiếp tuyến là k = 1 5 .
ĐS: y = x + . 3 3 3 1 1 4 Bài 2.
1. Viết phương trình tiếp tuyến của đồ thị (C) 3 2 : y = x + x − 2x − , biết tiếp tuyến song 3 2 3
song với (d ) : y = 4x − y + 2 = 26 0 .
ĐS: y = 4x − 73 và y = 4x + . 3 6 x +
2. Viết phương trình tiếp tuyến của đồ thị (C ) 2 1 : y =
, biết song song với đường thẳng 1− 2x
(d): y = 4x − y −8 = 0 .
ĐS: : y = 4x − 7 , : y = 4x +1. 1 2 3. Cho hàm số 3 2
y = x − 3x + 6x +10 có đồ thị (C ) . Viết phương trình tiếp tuyến với đồ thị (C )
, biết tiếp tuyến song song với đường thẳng (d ) : 3x − y −10 = 0 .
ĐS: : y = 3x +11. x −
4. Viết phương trình tiếp tuyến của đồ thị (C) 3 1 : y =
, biết tiếp tuyến song song với x + 2
đường thẳng d : y = x − 7y + 3 = 0 49 . Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
ĐS: x − 7y + 9 = 0 , x − 7y + 37 = 0 . 5. Cho hàm số 2
y = 1− x − x có đồ thị (C ) . Viết phương trình tiếp tuyến của đồ thị (C ) ,
biết tiếp tuyến song song với đường thẳng d : x + 2y = 0 .
ĐS: : x + 2y − 2 = 0 . Bài 3. 1. Cho hàm số 3 2
y = x + 3x − 2 của đồ thị (C ) . Viết phương trình tiếp tuyến của đồ thị (C ) ,
biết vuông góc với đường thẳng (d ) : x + 9 y = 0 .
ĐS: y = 9x − 7 và y = 9x + 25 . 2. Cho hàm số 4 2
y = −x − x + 6 có đồ thị (C ) . Viết phương trình tiếp tuyến của đồ thị (C ) ,
biết tiếp tuyến vuông góc với đường thẳng d : 6x − y −1 = 0 .
ĐS: : y = 6x +10 . x −
3. Viết phương trình tiếp tuyến của đồ thị (C) 1 : y =
, biết vuông góc với đường thẳng x +1
d : x + 2 y −1 = 0 .
ĐS: : y = 2x −1 , : y = 2x + 7 . 1 2 x −
4. Viết phương trình tiếp tuyến của đồ thị (C ) 2 1 : y =
, biết vuông góc với đường thẳng 1− 4x
d : x − 2 y +10 = 0 . ĐS: : y = 2
− x −1 hoặc : y = 2 − x +1 . _LỜI GIẢI
Bài 1. 1. Tập xác định D = \ − 1
Gọi M ( x ; y
y(x = k 0 ) 0 0 ) là tiếp điểm
x = 0 y = 1 − M 0; 1 2 2 − 0 0 1 ( ) Ta có: y = k = = 2 (x + )2 1 (x +1 x = 2
− y = 3 M 2 − ;3 0 )2 0 0 2 ( )
Phương trình tiếp tuyến tại M là : y = 2( x − 0) −1 y = 2x −1 1 1
Phương trình tiếp tuyến tại M là : y = 2( x + 2) + 3 y = 2x + 7 . 1 2
2. Tập xác định D = \ 1
Gọi M ( x ; y
y(x = k 0 ) 0 0 ) là tiếp điểm − −
x = 0 y = 1 − M 0; 1 3 3 − 0 0 1 ( ) Ta có: y = k = = 3 − (x + )2 1 (x +1
x = 2 y = 5 M 2;5 0 )2 0 0 2 ( )
Phương trình tiếp tuyến tại M là : y = 3
− .(x − 0) −1 y = 3 − x −1 1 1
Phương trình tiếp tuyến tại M là : y = 3
− .(x − 2) + 5 y = 3 − x +11 . 1 2
3. Tập xác định D = \ − 1
Gọi M ( x ; y
y(x = k 0 ) 0 0 ) là tiếp điểm
x = 0 y = 1 − M 0; 1 3 3 − 0 0 1 ( ) Ta có: y = k = = 3 (x + )2 1 (x +1 x = 2
− y = 5 M 2 − ;5 0 )2 0 0 2 ( )
Phương trình tiếp tuyến tại M là : y = 3.( x − 0) −1 y = 3x −1 1 1
Phương trình tiếp tuyến tại M là : y = 3.( x + 2) + 5 y = 3x +11 . 1 2
4. Tập xác định D =
Gọi M ( x ; y
y(x = k 0 ) 0 0 ) là tiếp điểm 50 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
x =1 y = 2 M 1;2 0 0 1 ( ) Ta có: 2 2
y = 3x − 2x k = 3x − 2x −1 = 0 1 50 1 50 0 0 x = − y = M − ; 0 0 2 3 27 3 27
Phương trình tiếp tuyến tại M là : y = 1.( x − )
1 + 2 y = x +1 1 1
Phương trình tiếp tuyến tại M là 1 50 59 : y = 1. x + + y = x + . 1 2 3 27 27
5. - Tập xác định D =
- Gọi M ( x ; y
y(x = k 0 ) 0 0 ) là tiếp điểm x = 3 0 - Ta có: 2 2 y = 3
− x +10x k = 3
− x +10x = 3 0 0 1 x = 0 3
Với x = 3 y = 15 : y = 3 x − 3 +15 = 3x + 6. 0 0 ( ) ( ) 1 67 1 67 94 Với x = y =
: y = 3 x − + = 3x − 0 0 ( ) . 3 27 3 27 27
6. Tập xác định: D = \ 1 . 2 x − 2x −1 Ta có y = 2 . (x − )1
Gọi M ( x ; y C () (C) (d ) 0 0 )
( ) là tọa độ tiếp điểm của với
. Vì hệ số góc của tiếp tuyến có
giá trị là k =1 nên ta có phương trình sau 2 x − 2x −1 x = 0 0 0 2 2 2 0 = 1
− x − 2x −1 = −x + 2x −1 2x − 4x = 0 2 0 0 0 0 0 0 (x − ) 1 x = 2 0 0
- Khi x = 0 y = 2
− d : y = −x − 2. 0 0 ( )
- Khi x = 2 y = 4 d : y = − x − 2 + 4 = −x + 6. 0 0 ( ) ( ) .
7. Tập xác định: D = \ 1 .
(2x −3)(x − )
1 − x − 3x + 4
2x − 5x + 3 − x − 3x + 4 x − 2x −1 ' ( 2 ) 2 ( 2 ) 2 Ta có y = = = . . (x − )2 1 (x − )2 1 (x − )2 1
Gọi M ( x ; y C () (C) 0 0 )
( ) là tọa độ tiếp điểm của với
. Vì hệ số góc của tiếp tuyến bằng 1 − nên 2 x − 2x −1 x = 0 0 0 2 2 2 0 = − − − = − + − − = ( x − ) 1 x 2x 1 x 2x 1 2x 4x 0 2 0 0 0 0 0 0 1 x = 2 0 0
- Khi x = 0 y = 4
− d : y = −x − 4 0 0 ( )
- Khi x = 2 y = 2 d : y = − x − 2 + 2 = −x + 4 0 0 ( ) ( ) . 1
8. Tập xác định: D = − ; + . 2 1 Ta có: y = . 2x +1 51 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 1
Gọi M ( x ; y C () (C) 0 0 )
( ) là tọa độ tiếp điểm của với
. Vì hệ số góc của tiếp tuyến bằng 3 1 1 nên = x = 4 . 0 2x +1 3 0 1 1 5
Khi x = 4 y = 3 , khi đó phương trình tiếp tuyến cần tìm là () : y = ( x − 4) + 3 = x + . 0 0 3 3 3
Bài 2. 1. Ta có (d ) : y = 4x + 2 hệ số góc của (d ) là k = 4 . d
Gọi M ( x ; y () (C) 0
0 ) là tiếp điểm của tiếp tuyến với đồ thị hàm số . Ta có ' 2 ' 2
y = x + x − 2 . Hệ số góc của tiếp tuyến là y ( x = x + x − 2 0 ) 0 0 . x = 3 −
Vì tiếp tuyến ( ) vuông góc với (d ) nên '
f ( x = k x + x − 2 = 4 0 ) 2 0 d 0 0 . x = 2 0 2 2 26
- Với x = 2 y = −
: y = 4 x − 2 − = 4x − 0 0 ( ) ( ) . 3 3 3 1 1 73 - Với x = 3
− y = : y = 4 x + 3 + = 4x + 0 0 ( ) ( ) . 6 6 6 2x +1 2. Gọi 0 M x ; 0
là tọa độ của tiếp điểm. 1− 2x 0 4
Hệ số góc của phương trình tiếp tuyến tại M là: y( x = 0 ) . (1− 2x )2 0
Vì tiếp tuyến song song với đường thẳng d nên 4 x = 0 ' y ( x = 4 = 4 1− 2x =1 0 ) 2 ( 0 )2 0 . (1−2x ) x = 1. 0 0
Phương trình tiếp tuyến tại điểm có hoành độ x = 0 là y = 4( x − 0) +1 y = 4x +1. 0
Phương trình tiếp tuyến tại điểm có hoành độ x = 1 là y = 4( x − ) 1 + ( 3
− ) y = 4x − 7 . 0 3. Gọi M ( 3 2
x ; x − 3x + 6x +10 0 0 0 0
) là tọa độ của tiếp điểm.
Hệ số góc của phương trình tiếp tuyến tại M là: y( x ) 2 = 3x − 6x + 6. 0 0 0
Vì tiếp tuyến song song với đường thẳng d nên y( x ) 2
= 3 3x − 6x + 6 = 3 x =1. 0 0 0 0
Phương trình tiếp tuyến tại điểm có hoành độ x = 1 là y = 3( x − )
1 +14 y = 3x +11 . 0 3x −1 4. Gọi 0 M x ; 0
là tọa độ của tiếp điểm. x + 2 0 7 '
Hệ số góc của phương trình tiếp tuyến tại M là: y ( x = 0 ) 2 . (x + 2 0 )
Vì tiếp tuyến song song với đường thẳng d nên 1 7 1 x = 5 ' y ( x = = x + 2 = 49 0 ) 2 ( 0 )2 0 . 7 (x +2) 7 x = 9. − 0 0
Phương trình tiếp tuyến tại điểm có hoành độ x = 5 0 là 52 1 y = (x − ) 1 9 5 + 2 y = x +
x − 7y + 9 = 0. 7 7 7 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM Phương trình tiế 1
p tuyến tại điểm có hoành độ x = 9 − 0 là y =
(x +9)+ 4 x −7y +37 = 0.. 7 3 2
Cho hàm số y = x + 3x − 2 của đồ thị (C ) . 5. Gọi M ( 2
x ; 1− x − x 0 0
0 ) là tọa độ của tiếp điểm. −1− 2x
Hệ số góc của phương trình tiếp tuyến tại M là: y( x = 0 ) 0 2 2 1− x − x 0 0
Vì tiếp tuyến song song với đường thẳng d nên − − = y( 1 1 2x 1 x 0 x = −
= − 1+ 2x = 1− x − x 1+ 2x
=1− x − x 0 ) 0 2 0 0 0 ( 0 )2 2 0 0 0 2 2 − − 2 x = 1 2 1 x x − 0 0 0
Thử lại chỉ có x = 0 x = 0. 0
thỏa mãn. Vậy nghiệm của phương trình là 0 Phương trình tiế 1
p tuyến tại điểm có hoành độ x = 0 0
là y = − ( x − 0) +1 x + 2y − 2 = 0.. 2 Bài 3. 1. Ta có ( (d ) − d ) 1 : y = −
x hệ số góc của là k = 9 d . 9
Gọi M ( x ; y () (C) 0
0 ) là tiếp điểm của tiếp tuyến với đồ thị hàm số . 2
Ta có y = 3x + 6x . Hệ số góc của tiếp tuyến là y( x = 3x + 6x 0 ) 2 . 0 0
Vì tiếp tuyến ( ) vuông góc với (d ) nên ( ) x = f x .k = 1 − x + x − = − d ( 1 1 2 3 6 1 0 0 0 ) 0 . 9 x = 3 − 0 '
- Với x = 1 y = 2
f ( x = 9 : y = 9 x −1 + 2 = 9x − 7 0 ) ( ) ( ) 0 0 và . ' - Với x = 3 − y = 2 −
f ( x = 9 : y = 9 x + 3 − 2 = 9x + 25 0 ) ( ) ( ) 0 0 và . 2. Gọi M ( 4 2
x ; −x − x + 6 0 0 0
) là tọa độ của tiếp điểm.
Hệ số góc của phương trình tiếp tuyến tại M là: y( x = 4 − x − 2x . 0 ) 3 0 0
Vì tiếp tuyến song song với đường thẳng d nên y( x = 6 4
− x − 2x = 6 x = 1 − . 0 ) 3 0 0 0
Phương trình tiếp tuyến tại điểm có hoành độ x = 1 −
y = 6( x + ) + = + 0 là 1 4 y 6x 10 . x −1 3. Gọi 0 M x ;
là tọa độ của tiếp điểm. 0 x +1 0 2
Hệ số góc của phương trình tiếp tuyến tại M là: y( x = 0 ) . (x + )2 1 0
Vì tiếp tuyến vuông góc với đường thẳng d nên ( ) 1 x = y x . − = 1 − y (x ) 2 0 = 2 = 2 x +1 =1 2 ( )2 0 0 0 0 . 2 (x + )1 x = 2. − 0 0
Phương trình tiếp tuyến tại điểm có hoành độ x = 0
y = 2( x − 0) − = − 0 là 1 y 2x 1. −
Phương trình tiếp tuyến tại điểm có hoành độ x = 2
y = 2( x + 2) + = + 0 là 3 y 2x 7 . 53 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 2x −1 4. Gọi 0 M x ;
là tọa độ của tiếp điểm. 0 1− 4x 0 2 −
Hệ số góc của phương trình tiếp tuyến tại M là: y( x = 0 ) . (1− 4x )2 0
Vì tiếp tuyến vuông góc với đường thẳng d nên x = 0 − y( 1 2 x . = 1
− y x = −2 = −2 1− 4x = 1 0 ) ( 0 ) 2 ( 0 ) 0 2 1 . 2 (1− 4x ) x = . 0 0 2
Phương trình tiếp tuyến tại điểm có hoành độ x = 0 y = 2
− (x − 0) − = − − 0 là 1 y 2x 1. 1 Phương trình tiế 1
p tuyến tại điểm có hoành độ x = là y = 2 − x −
+ 0 y = −2x +1 . 0 2 2
_DẠNG 3. BÀI TOÁN VỀ XÁC ĐỊNH HỆ SỐ GÓC NHỎ NHẤT, LỚN NHẤT CỦA TIẾP TUYẾN Bài 1.
Viết phương trình tiếp tuyến của đồ thị (C ) 3 2
: y = x + 6x − 9x + 5 , biết có hệ số góc nhỏ nhất. Lời giải
Gọi M ( x ; y C 0 0 ) ( ) là tiếp điểm. ' 2 ' 2
Ta có: y = 3x +12x − 9. . Suy ra hệ số góc k = y ( x = 3x +12x − 9. 0 ) 0 0
Xác định hệ số góc nhỏ nhất:
Cách 1: Áp dụng (a b)2 + c c k = c min
Ta có k = 3x +12x − 9 = 3 x + 4x + 4 − 21 = 3 x + 2 − 21 2 − 1 k = 2 − 1. 0 0 ( 0 0 ) ( 0 )2 2 2 min
Dấu “=” xảy ra x + 2 = x = 2 − . 0 0 b
Cách 2: Áp dụng công thức đỉnh parabol I − ; 2a 4a
Từ bảng biến thiên của parabol x = 2 − ,k = y 2 − = 2 − 1 0 min ( )
Cách 3: Sử dụng công thức k
= y (x ), y x = 0 min 0 ( 0) k
= y (x ), y x = 0 max 0 ( 0)
y ( x = 6x +12 = 0 x = 2
− k = y 2 − = 2 − 1. 0 ) 0 0 min ( )
Phương trình tiếp tuyến: Ta có: x = 2
− y = 39 M 2 − ;39 . 0 0 ( )
Phương trình tiếp tuyến tại M ( 2
− ;39): y = k . x + 2 +39 = 2 − 1 x + 2 + 39 = 2 − 1x −3 min ( ) ( ) . Bài 2.
Viết phương trình tiếp tuyến của đồ thị (C ) 3 2
: y = −x + 6x − 3x + 2 , biết có hệ số góc 54 lớn nhất. Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM Lời giải
Gọi M ( x ; y C 0 0 ) ( ) là tiếp điểm. ' 2 Ta có: y = 3
− x +12x −3. . Suy ra hệ số góc k = y(x = 3 − x +12x − 3 0 ) 2 0 0
Xác định hệ số góc lớn nhất:
Cách 1: Áp dụng − (a b)2 + c c k = c max Ta có k = 3
− x +12x − 3 = 3
− x − 4x + 4 + 9 = 3
− x − 2 + 9 9 k = 9 0 0 ( 0 0 ) ( 0 )2 2 2 max
Dấu “=” xảy ra x − 2 = x = 2 0 0 b
Cách 2: Áp dụng công thức đỉnh parabol I − ; 2a 4a = =
Từ bảng biến thiên của parabol x 2, k y (2) = 9 0 max
Cách 3: Sử dụng công thức k
= y (x ), y x = 0 min 0 ( 0) k
= y (x ), y x = 0 max 0 ( 0) y ( x ) = 6
− x +12 = 0 x = 2 k = y (2) = 9 0 0 0 max
Phương trình tiếp tuyến:
Ta có: x = 2 y = 8 M (2;8) 0 0
Phương trình tiếp tuyến tại = − + = − + = − M (2,8) : y k
.(x 2) 8 9(x 2) 8 9x 10 max
Nhận xét: Thông thường ta dùng cách 1. Cách 2, cách 3 thường dùng trong trắc nghiệm hoặc
Câu toán chứa tham số m. Bài 3.
Viết phương trình tiếp tuyến 3 2
của đồ thị (C) : y = 2x − 3x +1, biết có hệ số góc nhỏ nhất. ĐS 3 5
: y = − x + . 2 4 Lời giải
Gọi M (x , y ) (C) 0 0 là tiếp điểm. 2 2
Ta có: y ' = 6x − 6 .
x Suy ra hệ số góc k = y '(x ) = 6x − 6x . 0 0 0
Xác định hệ số góc nhỏ nhất: 2
Cách 1: Áp dụng (a )
b + c c k = c min 2 1 3 1 3 3 3 Ta có 2 2
k = 6x − 6x = 6(x − x + ) − = 6 x − − − k = − 0 0 0 0 0 min 4 2 2 2 2 2 1 1
Dấu “=” xảy ra x − = 0 x = 0 0 2 2 55 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM b
Cách 2: Áp dụng công thức đỉnh parabol I − ; 2a 4a 1 1 3
Từ bảng biến thiên của parabol x = , k = y ' = − 0 min 2 2 2 Cách 3: Sử dụng công thức k
= y (x ), y (x ) = 0 min 0 0
k = y (x ), y (x ) = 0 max 0 0 1 1 3 y (
x ) =12x − 6 = 0 x = k = y = − 0 0 0 min 2 2 2
Phương trình tiếp tuyến: 1 1 1 1 Ta có: x = y = M , 0 0 2 2 2 2 1 1 1 1 3 1 1 3 5
Phương trình tiếp tuyến tại M , : y = k . x − + = − x − + = − x + . min 2 2 2 2 2 2 2 2 4 Bài 4.
Viết phương trình tiếp tuyến 3 2
của đồ thị (C) : y = x − 3x +1, biết có hệ số góc nhỏ nhất. ĐS: y = 3 − x + 2. Lời giải
Gọi M (x , y ) (C) 0 0 là tiếp điểm. 2 2
Ta có: y = 3x − 6x . Suy ra hệ số góc k = y (
x ) = 3x −6x 0 0 0
Xác định hệ số góc nhỏ nhất: 2
Cách 1: Áp dụng (a )
b + c c k = c min 2 2 2
Ta có k = 3x − 6x = 3(x − 2x +1) − 3 = 3(x −1) − 3 3 − k = 3 − 0 0 0 0 0 min
Dấu “=” xảy ra x −1 = 0 x = 1. 0 0 b
Cách 2: Áp dụng công thức đỉnh parabol I − ; − 2a 4a = =
Từ bảng biến thiên của parabol x 1, k y (1) = 3 − 0 min
Cách 3: Sử dụng công thức 56 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM k
= y (x ), y (x )=0 min 0 0
k = y (x ), y(x ) = 0 max 0 0 y (
x ) = 6x − 6 = 0 x =1 k = y 1 = 3 − 0 0 0 min ( ) .
Phương trình tiếp tuyến:
Ta có: x = 1 y = 1 − M 1, 1 − 0 0 ( )
Phương trình tiếp tuyến tại M (1,− ) 1 : y = k . x −1 −1 = 3 − x −1 −1= 3 − x + 2 min ( ) ( ) . Bài 5.
Viết phương trình tiếp tuyến 3 2
của đồ thị (C) : y = 2
− x +3x −6x +1, biết có hệ số góc lớn nhất. ĐS: 9 3 y = − x + 2 4 Lời giải
Gọi M (x , y ) (C) 0 0 là tiếp điểm. 2 2 Ta có: y ' = 6
− x + 6x −6. Suy ra hệ số góc k = y'(x ) = 6 − x +6x −6 0 0 0
Xác định hệ số góc lớn nhất: 2
Cách 1: Áp dụng ( − a )
b + c c k = c max 2 1 9 1 9 9 9 Ta có 2 2 k = 6
− x + 6x − 6 = 6 − x − x + − = 3 − x − − − k = − 0 0 0 0 0 max 4 2 2 2 2 2 1 1
Dấu “=” xảy ra x − = 0 x = 0 0 2 2 b
Cách 2: Áp dụng công thức đỉnh parabol I − ; − 2a 4a 1 1 9
Từ bảng biến thiên của parabol x = , k = y = − 0 max 2 2 2
Cách 3: Sử dụng công thức k
= y (x ), y (x )=0 min 0 0
k = y (x ), y(x ) = 0. max 0 0 1 1 9 y ( x ) = 1
− 2x + 6 = 0 x = k = y = − 0 0 0 max 2 2 2
Phương trình tiếp tuyến: 1 3 1 3 Ta có: x =
y = − M , − 0 0 2 2 2 2 1 3 1 3 9 1 3 9 3
Phương trình tiếp tuyến tại M , − : y = k . x − − = − x − − = − x + max . 2 2 2 2 2 2 2 2 4
_ DẠNG 4. VIẾT PTTT KHI BIẾT ĐIỂM MÀ TIẾP TUYẾN ĐI QUA 57 PHƯƠNG PHÁP: Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
Bước 1: Gọi x0 là hoành độ tiếp điểm
Bước 2: Ta có PTTT y = y( x
x − x + y x 0 ) ( 0 ) ( 0)
Bước 3: Vì TT đi qua điểm A( x ; y
y = y x
x − x + y x A ( 0)( A 0) ( 0) A A ) nên ta có:
Bước 4: Giải phương trình ta tìm được x0
_VÍ DỤ MINH HỌA Bài 1.
Viết phương trình tiếp tuyến 3 2
của đồ thị (C) : y = x + 3x − 6x +1 biết tiếp tuyến đi qua điểm M (0;1). Lời giải 3 2
y = x +3x −6x +1 0 0 0 0
Gọi hoành độ tiếp điểm là x . 0 . Suy ra 2
y '(x ) = 3x + 6x − 6 0 0 0
Phương trình tiếp tuyến
y = y '(x )(x − x ) + y 2 3 2
y = (3x + 6x − 6)(x − x ) + x + 3x − 6x +1. 0 0 0 hay 0 0 0 0 0 0 Mà M (0 ) ;1 nên ( 2
3x + 6x − 6)(0 − x ) 3 2
+ x + 3x − 6x +1 =1 0 0 0 0 0 0 x = 0 0 3 2 2
− x − 3x = 0 3 0 0 x = − 2 3 33
Thế x = 0, x = − vào phương trình tiếp tuyến ta được : y = 6 − , x : y = − x +1 . 0 2 1 2 4 Bài 2.
Viết phương trình tiếp tuyến của đồ thị (C ) 4 2
: y = 2x − 4x −1 biết tiếp tuyến đi qua điểm M (1; 3 − ) . Lời giải 4 2
y = 2x −4x −1 0 0 0
- Gọi hoành độ tiếp điểm là x0 . Suy ra ' y (x ) 3 = 8x −8x 0 0 0
- Phương trình tiếp tuyến ' y = y ( x
x − x + y y = ( 3 8x − 8x x − x + 2x − 4x −1 0 0 ) ( 0 ) 4 2 0 ) ( 0 ) hay 0 0 0 y = ( 3
8x − 8x )( x − x ) 4 2 + 2x − 4x −1 0 0 0 0 0 . Mà M (1; 3 − ) nên ( 3
8x − 8x )(1− x ) 4 2 4 3 2
+ 2x − 4x −1 = 3 − 6
− x + 8x + 4x + 2 = 0 0 0 0 0 0 0 0 0 1 x = 0 3 x = 1 − 0 x =1 0 1 64 17 - Thế x = 1
− , x = , x =1 vào phương trình tiếp tuyến ta được. : y = 3 − , : y = − x − 0 0 0 3 1 2 27 27 58 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM x + Bài 3.
Viết phương trình tiếp tuyến của đồ thị (C) 2 1 : y =
biết tiếp tuyến đi qua điểm x +1 M ( 1 − ;3) . Lời giải 2x +1 0 y = 0 x +1
Gọi hoành độ tiếp điểm là x 0 0 . Suy ra y( 1 x = 0 ) (x + )2 1 0
Phương trình tiếp tuyến 1 2x +1
y = y( x
x − x + y y = x − x + 2 ( 0 ) 0 0 ) ( 0 ) hay . 0 (x + ) 1 x +1 0 0 Mà M ( 1 − ;3) nên 1 2x +1 2x0 1 − − x + = 3 3 = x = 3 − 2 ( 0 ) 0 0 (x + ) 1 x +1 x +1 0 0 0 Thế x = 3 − 1 13 0
vào phương trình tiếp tuyến ta được : y = x + . 4 4
_BÀI TẬP ÁP DỤNG Bài 1.
Viết phương trình tiếp tuyến của đồ thị (C ) 3 2
: y = x − 3x − 9x +1 biết tiếp tuyến đi qua điểm M ( 1 − ;6) . ĐS: : y = 6 : y = 9 − x −3 1 và 2 . Bài 2.
Viết phương trình tiếp tuyến của đồ thị (C ) 3 2
: y = x − 2x + x + 4 biết tiếp tuyến đi qua điểm M ( 4 − ; 24 − ).
ĐS: : y = 133x + 508, : y = 8x + 8
: y = 5x − 4 1 2 và 3 . Bài 3.
Viết phương trình tiếp tuyến của đồ thị (C ) 4 2
: y = x + x +1 biết tiếp tuyến đi qua điểm M ( 1 − ;3) . ĐS: : y = 6 − x − 3 . x + Bài 4.
Viết phương trình tiếp tuyến của đồ thị (C) 2 1 : y =
biết tiếp tuyến đi qua điểm x −1 M ( 7 − ;5) 3 1 3 59 .
ĐS: : y = − x − và : y = − x + . 1 4 4 2 16 16 x − Bài 5.
Viết phương trình tiếp tuyến của đồ thị (C) 2 1 : y =
biết tiếp tuyến đi qua điểm x +1 M ( 1 − ;4) 1 13 .
ĐS: : y = x + . 3 3 Bài 6.
Viết phương trình tiếp tuyến của đồ thị (C ) 3 2
: y = x + 3x − 6x +1 biết tiếp tuyến đi qua điểm M (0 ) ;1 .
ĐS: : y = 6, : y = 9 − x −3 1 2 . Bài 7.
Viết phương trình tiếp tuyến của đồ thị (C ) 3 2
: y = x − 3x − 9x +1 biết tiếp tuyến đi qua điểm M ( 1 − ;6) .
ĐS: : y = 6, : y = 9 − x −3 1 2 . _LỜI GIẢI 3 2
y = x −3x −9x +1 0 0 0 0 Bài 1.
Gọi hoành độ tiếp điểm là x0 . Suy ra y (x ) 2
= 3x − 6x − 9 0 0 0 59 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
Phương trình tiếp tuyến y = y( x
x − x + y 0 ) ( 0 ) hay 0 ( = − 2 x 1
3x − 6x − 9)( 1 − − x ) 3 2
+ x − 3x − 9x +1 = 3 6 2
− x +6x + 4 = 0 0 0 0 0 0 0 0 0 0 x = 2 0 y = ( 2
3x − 6x − 9)( x − x ) 3 2
+ x − 3x − 9x +1 0 0 0 0 0 0 . Mà M ( 1 − ;6) nên ( 2
3x − 6x − 9)( 1 − − x ) 3 2
+ x − 3x − 9x +1 = 6 0 0 0 0 0 0 x = 1 − 3 0 2
− x + 6x + 4 = 0 0 0 x = 2 0 Thế x = 1 − , x = 2 : y = 6 : y = 9 − x −3 0 0
vào phương trình tiếp tuyến ta được 1 và 2 . 3 2
y = x − 2x + x + 4 0 0 0 0 Bài 2.
Gọi hoành độ tiếp điểm là x0 . Suy ra ' y (x ) 2 = 3x − 4x +1 0 0 0
Phương trình tiếp tuyến
y = y( x
x − x + y y = ( 2
3x − 4x +1 x − x
+ x − 2x + x + 4 0 0 )( 0 ) 3 2 0 ) ( 0 ) hay 0 0 0 . 0 Mà M ( 4 − ; 2 − 4) nên ( 2
3x + 6x − 6)(0 − x ) 3 2 3 2
+ x + 3x − 6x +1 = 1 −2x − 3x = 0 0 0 0 0 0 0 0 0 x = 0 0 3 x = − 0 2 3 Thế = + = + x = 0, x = −
vào phương trình tiếp tuyến ta được : y 133x 508, : y 8x 8 1 2 và 0 0 2
: y = 5x − 4 3 . 2x +1 0 y = 0 x +1 Bài 3.
Gọi hoành độ tiếp điểm là x 0 0 . Suy ra y( 1 x = 0 ) (x + )2 1 0
Phương trình tiếp tuyến ' y = y ( x
x − x + y y = ( 3 4x + 2x x − x + x + x +1 0 0 ) ( 0 ) 4 2 0 ) ( 0 ) hay 0 0 . 0 Mà M ( 1 − ;3) nên ( 3 4x + 2x )( 1 − − x ) 4 2 + x + x +1 = 3 4 3 2 3
− x − 4x − x − 2x − 2 = 0 x = 1 − 0 0 0 0 0 0 0 0 0 0 Thế x = 1 − = − − 0
vào phương trình tiếp tuyến ta được : y 6x 3 . 2x +1 0 y = 0 x −1 Bài 4.
Gọi hoành độ tiếp điểm là x 0 0 . Suy ra 3 − ' y (x = 0 ) (x − )2 1 0
Phương trình tiếp tuyến 3 − 2x +1
y = y( x
x − x + y y = x − x + 2 ( 0 ) 0 0 ) ( 0 ) hay . 0 (x − ) 1 x −1 0 0 Mà M ( 7 − ;5) nên 60 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 3 − 2x +1 7 − − x + = 5 2 ( 0 ) 0 (x − ) 1 x −1 0 0 2
3x −12x −15 = 0 0 0 x = 1 − 0 x = 5 0 3 1 Thế x = 1 − , x = 5 0 0
vào phương trình tiếp tuyến ta được : y = − x − và 1 4 4 3 59 : y = − x + . 2 16 16 2x +1 0 y = 0 x +1 Bài 5.
Gọi hoành độ tiếp điểm là x 0 0 . Suy ra y( 1 x = 0 ) (x + )2 1 0
Phương trình tiếp tuyến 3 2x −1
y = y( x
x − x + y y = x − x + 2 ( 0 ) 0 0 ) ( 0 ) hay . 0 (x + ) 1 x +1 0 0 Mà M ( 1 − ;4) nên 3 2x −1 1 − − x + = 4 2 ( 0 ) 0 (x + ) 1 x +1 0 0 2x = 8 − 0 x = 4 − 0 Thế x = 4 − 1 13 0
vào phương trình tiếp tuyến ta được : y = x + . 3 3 3 2
y = x +3x −6x +1 0 0 0 0 Bài 6.
Gọi hoành độ tiếp điểm là x0 . Suy ra y (x ) 2 = 3x + 6x − 6 0 0 0
Phương trình tiếp tuyến ' y = y ( x
x − x + y y = ( 2 3x − 6x − 9 x − x
+ x − 3x − 9x +1 0 0 )( 0 ) 3 2 0 ) ( 0 ) hay 0 0 0 . 0 Mà M (0 ) ;1 nên ( 2
3x + 6x − 6)(0 − x ) 3 2
+ x + 3x − 6x +1 =1 0 0 0 0 0 0 3 2 2 − x − 3x = 0 0 0 x = 0 0 3 x = − 0 2 3 Thế x = 1 − , x = 2 0 0
x = 0, x = − vào phương trình tiếp tuyến ta được 0 0 2
: y = 6, : y = 9 − x −3 1 2 . 3 2
y = x −3x −9x +1 0 0 0 0 Bài 7.
Gọi hoành độ tiếp điểm là x0 . Suy ra 2 y
(x = 3x − 6x −9 0 ) 0 0 61
Phương trình tiếp tuyến Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
y = y( x
x − x + y y = ( 2 3x − 6x − 9 x − x
+ x − 3x − 9x +1 0 0 )( 0 ) 3 2 0 ) ( 0 ) hay 0 0 0 0 y = ( 2
3x − 6x − 9)( x − x ) 3 2
+ x − 3x − 9x +1 0 0 0 0 0 0 . Mà M ( 1 − ;6) nên ( 2
3x − 6x − 9)(0 − x ) 3 2
+ x − 3x − 9x +1 = 6 0 0 0 0 0 0 3 2
− x +6x + 4 = 0 0 0 x = −1 0 x = 2 0 Thế x = 1 − , x = 2
: y = 6, : y = 9 − x −3 0 0
vào phương trình tiếp tuyến ta được 1 2 .
_ DẠNG 5. TÌM THAM SỐ m ĐỂ TỪ 1 ĐIỂM TA KẺ ĐƯỢC ĐÚNG MỘT TIẾP TUYẾN ĐẾN ĐỒ THỊ HÀM SỐ Bài 1.
Tìm tổng tất cả các giá trị của a để từ điểm A(a )
;1 kẻ được đúng 1 tiếp tuyến đến đồ thị hàm số −x + 2 5 y = . ĐS: . x −1 2 Lời giải
Điều kiện x 1.
Tiếp tuyến qua A(a )
;1 là y = k ( x − a) +1. − +
k ( x − a) x 2 +1 = x −1 − − + Điều kiện tiếp x a x x 2 úc +1 = 2
2x − 6x + 3+ a = 0 (*) . 1 − − k = − (x )2 1 x 1 (x − )2 1
Để từ A kẻ đúng 1 tiếp tuyến đến đồ thị thì (*) phải có nghiệm kép 1 hoặc có 2 nghiệm
phân biệt trong đó có 1 nghiệm bằng 1.
= 3− 2a = 0 b 3 − = 1 3 a = 2a 2 2 .
= 3− 2a 0 a = 1 2−6+3+ a = 0
Tổng các giá trị của a 5 là . 2 x + Bài 2.
Tìm m để từ A( 2; − m) kẻ đúng 1 2 1
tiếp tuyến đến đồ thị hàm số y =
. ĐS: m = 1, m = 2 . x −1 Lời giải
Điều kiện x 1.
Tiếp tuyến qua A( 2;
− m) là y = k (x + 2) + m. + k ( x + ) 2x 1 2 + m = x −1 + + Điều kiện tiếp xúc x 2 2x 1 3. − + m = 3 − − k = − (x )2 1 x 1 (x − )2 1 62
− x − + m( 2 3 6 x − 2x + ) 1 = (2x + ) 1 ( x − ) 1 (m − ) 2 2 x + ( 2
− − 2m) x + m −5 = 0 (*) . Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM (*) 2
có = (−m − ) 1
− (m − 5)(m − 2) = 9m − 9 .
Để từ A kẻ đúng 1 tiếp tuyến đến đồ thị thì (*) phải có nghiệm kép 1 hoặc có 2 nghiệm
phân biệt trong đó có 1 nghiệm bằng 1 hoặc có 1 nghiệm khác 1.
- Nếu (*) có 1 nghiệm. Khi đó m = 2 . 1
Thế m = 2 vào (*) , ta được 6
− x −3 = 0 x = − (thoả x 1) nên nhận m = 2 . 2
- Nếu (*) có nghiệm kép thì
= 9m −9 = 0 m =1. b 2 + 2
Khi đó nghiệm của phương trình là − = = 2
− 1 nên nhận m =1. 2a 2(1− 2)
- Nếu (*) có 2 nghiệm phân biệt thì 0 m 1.
Để phương trình có 1 nghiệm bằng 1 và 1 nghiệm khác 1 thì m − 2 − 2 − 2m + m −5 = 0 9 − = 0 (vô lý).
Vậy m = 1 và m = 2 thoả mãn yêu cầu câu toán. x − m Bài 3.
Tìm m để từ A(−1; 2) kẻ đúng 1 tiếp tuyến đến đồ thị hàm số y = . ĐS: m = 3. x −1 Lời giải
Điều kiện x 1.
Tiếp tuyến qua A(−1;2) là y = k ( x + ) 1 + 2 . ( + ) x − m k x 1 + 2 = x −1 (x + ) 1 (m − ) Điều kiện tiếp xúc 1
+ 2 = x − m x −1 2 ( )( ) 1 − + m k = − (x − ) 1 (x − )2 1 2
x + (2m − 4) x +1= 0 (*) .
(*) có = (m− )2 2 2
−1 = m − 4m + 3.
Để từ A kẻ đúng 1 tiếp tuyến đến đồ thị thì (*) phải có nghiệm kép 1 hoặc có 2 nghiệm
phân biệt trong đó có 1 nghiệm bằng 1. m =
- Nếu (*) có nghiệm kép thì = 1 0 . m = 3 b
Với m = 1 thì nghiệm phương trình là − =1 (loại). 2a b
Với m = 3 thì nghiệm phương trình là − = 1
− 1 (nhận m = 3). 2a m
- Nếu (*) có 2 nghiệm phân biệt thì 3 0 . m 1
Để phương trình có 1 nghiệm bằng 1 và 1 nghiệm khác 1 thì 1+ 2m − 4 +1 = 0 m =1 (không thoả m 1).
Vậy m = 3 thoả mãn yêu cầu Câu toán. x + Bài 4.
Tìm m để từ A(0; m) kẻ đúng 1 2
tiếp tuyến đến đồ thị hàm số y =
. ĐS: m = 1, m = 2 − . x −1 63 Lời giải
Điều kiện x 1. Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
Tiếp tuyến qua A(0; m) là y = kx + m . x + 2 kx + m = x −1 Điều kiện tiếp xúc
− x + m(x − )2 3 1
= (x − 2)(x − ) 1 3 k = − (x − )2 1 (m − ) 2 1 x + ( 2
− m − 4) x + m + 2 = 0 (*) . (*) 2
có = (m + 2) − (m − )
1 (m + 2) = 3m + 6.
Để từ A kẻ đúng 1 tiếp tuyến đến đồ thị thì (*) phải có nghiệm kép 1 hoặc có 2 nghiệm
phân biệt trong đó có 1 nghiệm bằng 1 hoặc có 1 nghiệm khác 1. 1
- Nếu m = 1 thì (*) trở thành 6
− x + 3 = 0 x = 1 nên nhận m =1. 2 - Nếu m 1 và
= 3m+ 6 = 0 m = 2 − .
Khi đó phương trình có nghiệ b m kép là −
= 0 1 nên nhận m = 2 − . 2a - Nếu m 1 và 0 m 2
− thì phương trình có 2 nghiệm phân biệt.
Để phương trình có 1 nghiệm bằng 1 và 1 nghiệm khác 1 thì m −1− 2m − 4 + m + 2 = 0 3 − = 0 ( vô lý).
Vậy m = 1 và m = 2
− thoả mãn yêu cầu câu toán.
TỔNG HỢP KIẾN THỨC CẦN NHỚ VỀ TIẾP TUYẾN
1. Viết phương trình tiếp tuyến của đồ thị hàm số y = f ( x) tại điểm M ( x , y 0 0 ) .
Bước 1: Tính đạo hàm y = f ( x) . Suy ra hệ số góc tiếp tuyến k = y( x = f x 0 ) ( 0) .
Bước 2: Phương trình tiếp tuyến của đồ thị hàm số tại M ( x , y
d : y = k ( x − x + y 0 ) 0 0 ) có dạng . 0
Nếu đề bài yêu cầu viết phương trình tiếp tuyến tại điểm có hoành độ x y 0 thì khi đó ta tìm 0 bằng
cách thế vào hàm số ban đầu, tức y = f x y 0
( 0) . Tương tự khi đề cho 0 .
Nếu đề bài yêu cầu viết phương trình tiếp tuyến tại các giao điểm đồ thị (C) : y = f ( x) và đường
thẳng d : y = ax + b . Khi đó các hoành độ tiếp điểm là nghiệm của phương trình hoành độ giao điểm giữa
d và (C ) . Đặc biệt Ox : y = 0 , trục tung Oy : x = 0.
Nếu đề bài cho hệ số góc tiếp tuyến là k , ta làm theo các bước sau:
- Bước 1: Gọi M ( x ; y
y ' = f '( x) 0
0 ) là tiếp điểm và tính .
- Bước 2: Ta có: k = f '( x x y
0 ) và giải phương trình này ta sẽ tìm được 0 , suy ra 0 .
- Bước 3: Ứng với mỗi tiếp điểm, ta tìm được một tiếp tuyến d : y = k ( x − x + y 0 ) 0.
Ngoài ra đề bài thường cho hệ số góc tiếp tuyến dưới dạng sau:
- Nếu tiếp tuyến d // : y = ax + b k = a 64 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 1
- Nếu tiếp tuyến d ⊥ : y = ax + b k = − . a
- Nếu tiếp tuyến tạo với trục hoành Ox một góc
thì k = tan ( hoặc k = − tan ). k − a
- Nếu tiếp tuyến tạo với d : y = ax + b một góc thì
= tan (hoặc − tan ). 1+ ka
2. Viết phương trình tiếp tuyến của đồ thị hàm số y = f ( x) kẻ từ A( x ; y A
A ) (qua A ).
Bước 1: Gọi M ( ;
a f (a)) là tiếp điểm và tính hệ số góc tiếp tuyến k = y(a) = f (a) theo a
Bước 2: Tiếp tuyến dạng d : y = f (a)( x − a) + y (a)() .
Vì điểm A( x ; y d y = f ' a x − a + y a và giải được a . A ( )( A ) ( ) A A )
Bước 3: Thế a vào () ta được tiếp tuyến cần tìm.
3. Điều kiện tiếp xúc của hai đường cong.
Cho hai đồ thị hàm số (C) : y = f ( x) và (C) : y = g (x) . Tọa độ giao điểm (nếu có) của (C ) và (C) là y = f (x)
nghiệm của hệ phương trình
f (x) = g (x).() . y = g (x)
- Phương trình () được gọi là phương trình hoành độ giao điểm chung của (C ) và (C) .
- Số nghiệm của () chính là số điểm chung của hai đồthị hàm số.
- Trục hoành Ox có phương trình y = 0 , trục tung Oy có phương trình x = 0 . f
(x) = g (x)
- Điều kiện tiếp xúc: (C ) tiếp xúc với (C) có nghiệm. f
(x) = g(x)
- Từ điểm A kẻ được n tiếp tuyến đến (C ) khi hệ tiếp xúc có n nghiệm phân biệt.
C. BÀI TẬP RÈN LUYỆN 4 2 x x Câu 1.
Hệ số góc tiếp tuyến của đồ thị hàm số y = +
−1 tại điểm có hoành độ x = 1 − 0 bằng 4 2 A. −2 . B. 1 − . C. 2 . D. 0 . x +1 Câu 2.
Tiếp tuyến của đò thị hàm số A(−1;0) y = tại điểm
có hệ số góc bằng x − 5 1 1 6 6 A. . B. − . C. . D. − . 6 6 25 25 3 2 Câu 3.
Phương trình tiếp tuyến của đồ thị hàm số y = x − 3x + 2 tại điểm M ( 1 − ; 2 − ) là
A. y = 9x +11.
B. y = 9x −11.
C. y = 9x − 7 .
D. y = 9x + 7 . 4 2 Câu 4.
Phương trình tiếp tuyến của đồ thị hàm số y = x − 3x + 4 tại điểm A(1;2) là
A. y = 3x + 5 .
B. y = 2x + 4 . C. y = 2 − x + 4 . D. y = 2 − . x 65 2x −1 Câu 5.
Phương trình tiếp tuyến của đồ thị hàm số M (0; − ) y = tại điểm 1 là x +1 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
A. y = 3x +1 .
B. y = 3x −1 . C. y = 3 − x −1. D. y = 3 − x +1. 2 x − 2x 1 Câu 6.
Phương trình tiếp tuyến của đồ thị hàm số y = A 1; − x + tại điểm 1 2 là 1 1 3 1 3 1 1 A. y = x . B. y = x + . C. y − x − . D. y = x + . 2 4 4 4 4 2 2 Câu 7.
Phương trình tiếp tuyến của đồ thị hàm số 2
y = x + x +1 tại điểm M (0 ) ;1 là 1 1 A. y = x +1.
B. y = − x +1.
C. y = −x +1.
D. y = x +1. 2 2 3 2 Câu 8.
Phương trình tiếp tuyến của đồ thị hàm số y = x + 3x − 2 tại điểm có hoành độ bằng x = 3 − 0
A. y = 30x + 25 .
B. y = 9x − 25 .
C. y = 30x − 25 .
D. y = 9x + 25. 4 2 Câu 9.
Phương trình tiếp tuyến của đồ thị hàm số y = x + 2x −1 tại điểm có hoành độ bằng 1 là A. y = 8 − x − 6 .
B. y = 8x − 6 . C. y = 8 − x +10 .
D. y = 8x +10. 4
Câu 10. Tiếp tuyến của đồthị hàm số y =
tại điểm có hoành độ x = 1 − là x −1 0
A. y = −x − 3 .
B. y = x −1 .
C. y = −x + 2 .
D. y = −x −1.
Câu 11. Phương trình tiếp tuyến của đồ thị hàm số 3 2
y = x − 3x + 2 tại điểm thuộc đồ thị hàm số có hoành
độ x thỏa mãn y( x = 0 0 ) là 0 A. y = 3 − x + 3.
B. y = 9x + 7 .
C. y = 9x − 7 . D. y = 3 − x −3.
Câu 12. Phương trình tiếp tuyến của đồ thị hàm số 3 2
y = x − 3x +1 tại điểm thuộc đồ thị hàm số có
hoành độ x thỏa mãn 2y ' ( x + y ' x +15 = 0 0 ) ( 0) là 0
A. y = 9x + 7 .
B. y = 9x + 6 .
C. y = 9x .
D. y = 9x +1.
Câu 13. Phương trình tiếp tuyến của đồ thị hàm số 3 2
y = x − x + x +1 tại điểm có tung độ bằng 2
A. y = 2x . B. y = 9x −11 .
C. y = 54x + 32 . D. y = 3 − x −3.
Câu 14. Phương trình tiếp tuyến của đồ thị hàm số 4 2
y = x − 3x +1 tại điểm có tung độ bằng 5 là
A. y = 20x − 35 . B. y = 2
− 0x − 35 và y = 20x + 35.
C. y = 20x − 35 và y = 2 − 0x − 35 . D. y = 2 − 0x + 35. 2x − 4
Câu 15. Phương trình tiếp tuyến của đồthị hàm số y =
tại điểm có tung độ bằng 3 là x − 4
A. x + 4 y − 20 = 0 .
B. x + 4y − 5 = 0 . C.
4x + y − 2 = 0 .
D. 4x + y − 5 = 0 . 3
Câu 16. Viết phương trình tiếp tuyến của đường cong 4 2 (C) : y =
x + x −1, biết tiếp tuyến vuông góc 2
với đường thẳng d : x + 8y +16 = 0 . 13 A. y = 8 − x + 13 .
B. y = 8x + 13 . C. y = 8 − x − 13 .
D. y = 8x − . 2 2 2 2
Câu 17. Phương trình tiếp tuyến với đồ thị 3 2
(C) : y = 2x − 6x + 3 có hệ số góc nhỏ nhất là 6x + y − 5 = 0 6x + y + 5 = 0 6x − y + 3 = 0 6x + y − 7 = 0 A. . B. . C. . D. .
Câu 18. Phương trình tiếp tuyến với đồ thị 3 2
y = −x + 3x − 5x +1 có hệ số góc lớn nhất là 66 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
A. 2x − y = 0 .
B. x − 2 y +1 = 0 .
C. 2x + y = 0 .
D. x + 2 y +1 = 0. Câu 19. Cho hàm số 3 2
y = x + x −1 có đồ thị (C), phương trình tiếp tuyến của (C) tại (
A 1;1) cắt (C) tại điểm .
B Tính độ dài đoạn . AB A. 4 26 . B. 10 . C. 105 . D. 2 . Câu 20. Cho hàm số 2
f (x) = 2x − 4. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành
độ tiếp điểm bằng tung độ tiếp điểm.
A. y = 2x + 2 . B. y = 2 − x − 2 .
C. y = 2x − 2 . D. y = 2 − x + 2 . 2x −1
Câu 21. Tiếp tuyến của đồ thị hàm số y = đi qua điểm ( A 1
− ;4) có phương trình là x +1 1 13 1 1 1 1 13 A. y = x + . B. y = x + . C. y = x + 4 . D. y = x − . 3 3 3 3 3 3 3 Câu 22. Cho hàm số 3 2
y = x + mx + x +1. Gọi k là hệ số góc tiếp tuyến của đồ thịa àm số tại M có hoành
độ x =1. Tìm tham số m để thỏa mãn k f ( 1 − ) 0. A. m 2 . B. m 2 − . C. 2 − m 1. D. m 1. 1 1
Câu 23. Gọi d , d là hai tiếp tuyến của đồ thị hàm số 3 2 y = x +
x − 6x −1 tại hai điểm lần lượt có 1 2 3 2
hoành độ là x và x . Biết x , x là hai nghiệm phương trình 2
x + mx − 3 = 0. Tìm tham số m để 1 2 1 2
d song song d . 1 2 A. m = 1 − . B. 10m = 2 . C. m = 1. D. m = 2 − .
Câu 24. Tìm tham số m để tiếp tuyến của đồ thị hàm số 3 2
y = x − 2x + 3mx +1 tại điểm có hoành độ bằng 1 đi qua điểm ( A 1;3). A. m = 2 . B. m = 2 − . C. m = 1 − . D. m = 1.
Câu 25. Tìm tham số m để tiếp tuyến của đồ thị hàm số 4 2
y = x − mx + 3m +1 tại điểm có hoành độ bằng 1 − đi qua điểm ( A 0; 2). A. m = 1. B. m = 2 . C. m = 1 − . D. m = 2 − .
Câu 26. Gọi M là điểm thuộc đồ thị hàm số 4 2
y = x − (2m +1)x + m + 2 có hoành độ bằng 1. Hỏi giá trị
của tham số m thuộc khoảng nào thì tiếp tuyến tại điểm M sẽ vuông góc với đường thẳng d
có phương trình y = x − 4y − 2018 = 0. A. (− ; 3 − ) . B. [ − 3; 0) . C. [0;5) . D. [5; ) + . x − m
Câu 27. Cho hàm số y = có đồ thị C và điểm ( A 1
− ;2) . Gọi S là tập hợp tất cả các giá trị thực x − ( ) 1 m
của m để có đúng một tiếp tuyến của (Cm ) đi qua .
A Tổng tất cả các phần tử của S bằng. A. 1. B. 2 . C. 3 . D. 4 . 1
Câu 28. Tiếp tuyến tại điểm là nghiệm y ' = 0 của đồ thị hàm số 3 2 y =
x − 2x + 3x − 5 thì 3
A. Song song với đường thẳng.
B. Song song với trục hoành.
C. Có hệ số góc dương. D. Có hệ số góc bằng 1. −
Câu 29. Hệ số góc tiếp tuyến của đồ thị hàm số (C ) 4 2
: y = x − 8x + 2 tại điểm có hoành độ x = 2 bằng 0 A. 6 − 2 . B. 7 − 2 . C. 8 − 2 . D. 9 − 2.
Câu 30. Hệ số góc của tiếp tuyến với đồ thị (C ) 3
: y = x − 2x +1 tại điểm M ( 1 − ;2) bằng 67 A. 3 . B. 5 − . C. 25 . D. 1. Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 1 1
Câu 31. Tiếp tuyến của đồ thị hàm số 3 2 f (x) = x −
x − 4x + 6 tại điểm có hoành độ là nghiệm của 3 2 phương trình f (
x) = 0 có hệ số góc bằng 47 13 17 A. −4 . B. . C. − . D. − . 12 4 4
Câu 32. Trong các tiếp tuyến tại các điểm trên đồ thị hàm số 3 2
y = x − 3x + 2, tiếp tuyến có hệ số góc nhỏ nhất bằng A. 3 − . B. 3 . C. −4 . D. 0 .
Câu 33. Phương trình tiếp tuyến của đồ thị hàm số 3 2
y = x − 3x + 2 tại điểm ( A 1; 0) là A. y = 3 − x + 3. B. y = 3 − x +1 .
C. y = 3x +1 .
D. y = 3x + 3 . 2x −1
Câu 34. Phương trình tiếp tuyến của đồ thị y = tại điểm ( A 2;3) là x −1 A. y = 3 − x + 9 .
B. y = −x + 5 .
C. y = 3x − 5 .
D. y = x +1 . x −1
Câu 35. Phương trình tiếp tuyến của đồ thị y =
tại điểm có hoành độ bằng 3 − là x + 2 A. y = 3 − x − 5.
B. y = 3x +13 .
C. y = 3x + 5 . D. y = 3 − x +13 .
Câu 36. Tiếp tuyến của đồ thị hàm số 3 2
y = 2x + 3x tại điểm M có tung độ bằng 5 là A. y = 1 − 2x − 7 .
B. y = 12x − 7 . C. y = 1 − 2x +17 .
D. y = 12x +17 .
Câu 37. Phương trình tiếp tuyến của (C ) 3 2
: y = x − 3x + 9 tại điểm có hoành độ bằng 9 là A. y = 1 = − = − và y 9x 1 .
B. y = 19 và y 9x 8. C. y = 9 y = 9x −18 y = 9x −1 và . D. y = 0 và . 2x − 4
Câu 38. Phương trình tiếp tuyến tại giao điểm của đồ thị y =
với trục hoành là x − 3
A. y = 2x . B. y = 2 − x + 4 . C. y = 2 − x − 4 .
D. y = 2x − 4 . 2x +1
Câu 39. Viết phương trình tiếp tuyến của đồ thị hàm số y =
, biết tiếp tuyến có hệ số góc bằng 5. x − 2 A. y = 5 − x + 2 y = 5 − x + 22 y = 5 − x + 2 y − 5x − 22 và . B. và .
C. y = 5x + 2 y = 5 − x + 22 y = 5 − x − 2 y = 5 − x + 22 và . D. và . x
Câu 40. Viết phương trình tiếp tuyến với đồ thị (C ) 3 2 : y =
+ 3x − 2, biết tiếp tuyến có hệ số góc k = 9 − 3 A. y = 9 − x − 43 . B. y = 9 − x + 43 . C. y = 9 − x − 27 . D. y = 9 − x −11 .
Câu 41. Viết phương trình tiếp tuyến của đồ thị (C ) 3 2
: y = −x + 3x +1, biết tiếp tuyến song song với
đường thẳng d : y = 3x + 2.
A. y = 3x .
B. y = 3x − 6 . C. y = 3 − x + 3.
D. y = 3x + 6 . x +
Câu 42. Viết phương trình tiếp tuyến của đồ thị (C ) 2 1 : y =
, biết tiếp tuyến song song với đường x + 2
thẳng : 3x − y + 2 = 0.
A. y = 3x +14 = + = + và y 3x 2 . B. y 3x 14 .
C. y = 3x + 5 = − = − và y 3x 8 . D. y 3x 8 .
Câu 43. Viết phương trình tiếp tuyến với đồ thị hàm số 3 2
y = x − 2x −1, biết tiếp tuyến vuông góc với
đường thẳng d : y = x . 68 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 23
A. y = x −1.
B. y = −x − . 27 23
C. y = −x −1.
D. y = −x −1, y = −x − . 27
Câu 44. Viết phương trình tiếp tuyến với đồ thị hàm số (C ) 3
: y = x − 3x + 2, biết tiếp tuyến vuông góc
với đường thẳng x + 9 y − 9 = 0. 1 1 A. y = x +18 và y = x−14 . B. y = 9 − x +18 y = − x + . 9 và 9 5 9
C. y = 9x +18 = + = + = − và y 9x 5 . D. y
9x 18 và y 9x 14 .
Câu 45. Tiếp tuyến của đồ thị hàm số 3 y = 4
− x + 3x +1 đi qua ( A 1
− ;2) có phương trình là A. y = 9
− x + 7 hoặc y = −x + 2. B. y = 9
− x −11 hoặc y = −x + 2. C. y = 9
− x +11 hoặc y = 2 . D. y = 9
− x − 7 hoặc y = 2 .
Câu 46. Tiếp tuyến của đồ thị hàm số 3 2
y = x + 4x + 4x +1 tại điểm ( A 3 − ; 2
− ) cắt đồ thị hàm số tại điểm thứ hai là . B Điể
m B có tọa độ là A. B( 1 − ;0) . B. B(1;10) . C. B(2;33) . D. B( 2 − ;1) . Câu 47. Cho hàm số 3 2
y = x + 3x +1 có đồ thị (C ). Gọi là tiếp tuyến của (C ) tại điểm ( A 1;5) và B
là giao điểm thứ hai của với (C ). Diện tích tam giác AOB bằng A. 12 . B. 6 . C. 15 . D. 24 . ( + C ) 2x 1 : y = M O , x Oy
Câu 48. Tiếp tuyến của đồ thị tại điểm
cắt các trục tọa độ lần lượt tại x − (2;5) 1 A và .
B Diện tích tam giác AOB O (với
là gốc tọa độ) bằng 121 119 123 125 A. . B. . C. . D. . 6 6 6 6 2x +1 y = 0 A
Câu 49. Tiếp tuyến của đồ thị hàm số
tại điểm có hoành độ bằng
cắt các trục tọa độ tại x +1 và .
B Diện tích tam giác AOB O (với
là gốc tọa độ) bằng 1 1 A. . B. 1 . C. . D. 2 . 2 4 mx 1
Câu 50. Tìm tham số m để tiếp tuyến của đồ thị hàm số y
tại điểm có hoành độ bằng 1 đi qua x 2 điểm ( A 1; 2) . A. m 1. B. m 3 . C. m 3 . D. m 1. x b
Câu 51. Cho hàm số y
có hàm số (C) . Biết a,b là các giá trị thực sao cho tiếp tuyến của (C) ax 2
tại điểm M (1; 2) song song với đường thẳng d : 3x y 4 0 . Tính a b . A. a b 0 . B. a b 1. C. a b 2 . D. a b 1. 3 2
Câu 52. Cho hàm số y x 3x (2m 1)x 2m 3 có đồ thị (C ) m m . Tìm
để tiếp tuyến có hệ số
góc lớn nhất của đồ thị (C ) d : x 2 y 4 0 m vuông góc với . A. m 2 . B. m 1. C. m 0 . D. m 4 .
Câu 53. Hỏi m thuộc khoảng nào sau đây thì tiếp tuyến có hệ số góc nhỏ nhất của đồ thị hàm số 3 2 y x 3x (m 2)x
3m vuông góc với đường thẳng d : x y 2 0 . 69 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM A. ( ; 4) . B. 4;3 . C. 3;5 . D. 5; . 1 Câu 54. Cho hàm số 3 2 2 y x 2mx m x
1 . Tìm m để tiếp tuyến của đồ thị hàm số tại điểm có 3 hoành độ x 2 d :15x 3y 2 0 0
song song với đường thẳng . A. m 9 . B. m 1, m 9 . C. m 1. D. m 1, m 9 .
Câu 55. Tìm tổng các giá trị của tham số m để từ điểm ( A ;1
m ) kẻ đúng một tiếp tuyến đến đồ thị hàm 2 x số y . x 1 3 5 1 A. 1. B. . C. . D. . 2 2 2
Câu 56. Tìm tổng các giá trị của tham số m để từ điểm ( A 1; )
m kẻ đúng hai tiếp tuyến đến đồ thị hàm 3 2 số y x 3x 2. A. 1. B. 4 . C. 3 . D. 2 . x m
Câu 57. Cho hàm số y có đồ thị (C ) ( A 1; 2) S m và điểm . Gọi
là tập hợp tất cả các giá trị thực x 1
của m để có một tiếp tuyến của (C ) A m đi qua
tạo với hai trục tọa độ một tam giác cân. Tổng
tất cả các phần tử của S bằng A. 1. B. 4 . C. 3 . D. 5 .
Câu 58. Tìm tổng các giá trị của tham số m để từ điểm ( A ;
m 0) kẻ đúng hai tiếp tuyến đến đồ thị hàm 3 2 số y x
3x và hai tiếp tuyến đó vuông góc với nhau. 1 15 217 217 A. . B. . C. . D. 27 18 9 18
Câu 59. Tìm tổng các giá trị của tham số m để tiếp tuyến có hệ số góc nhỏ nhất của đồ thị hàm số 3 2 2 y x 3x (m 2)x m đi qua điểm ( A 1; 4) . A. 3 . B. 1. C. 1. D. 0 . x 1
Câu 60. Tìm m để đường thẳng d : y m
x cắt đồ thị hàm số (C) : y
tại hai điểm phân biệt x 1 ,
A B sao cho các tiếp tuyến của (C) tại A và B song song nhau. A. m 0 . B. m 1. C. m 2 . D. m 3 . 3 2
Câu 61. Tìm m để đường thẳng d : y ( m x 2)
2 cắt đồ thị hàm số (C) : y x 3x 2 tại ba điểm (
A 2; 2), B, D để tích các hệ số góc tiếp tuyến tại B, D của (C) là 27. A. m 0 . B. m 1. C. m 2 . D. m 3 . 70 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
D. LỜI GIẢI BÀI TẬP RÈN LUYỆN 4 2 x x Câu 1.
Hệ số góc tiếp tuyến của đồ thị hàm số y = +
−1 tại điểm có hoành độ x = 1 − bằng 0 4 2 A. −2 . B. 1 − . C. 2 . D. 0 . Lời giải
Tập xác định D = R . Ta có 3
y ' = x + x
Gọi M ( x ; y là tiếp điểm x = 1 − . 0 0 ) 0
Suy ra hệ số góc của tiếp tuyến với đồ thị hàm số tại M là k = y '(− ) 1 = 2 − . Chọn A x +1 Câu 2.
Tiếp tuyến của đò thị hàm số y =
tại điểm A(−1;0) có hệ số góc bằng x − 5 1 1 6 6 A. . B. − . C. . D. − . 6 6 25 25 Lời giải
Tập xác định D = R \ 5 . 6 −
Ta có y ' = (x − . 5)2
Vì A(−1;0) là tiếp điểm nên hệ số góc của tiếp tuyến với đồ thị hàm số tại A là k = y (− ) 1 ' 1 = − 6 Chọn B Câu 3.
Phương trình tiếp tuyến của đồ thị hàm số 3 2
y = x − 3x + 2 tại điểm M ( 1 − ; 2 − ) là
A. y = 9x +11.
B. y = 9x −11.
C. y = 9x − 7 .
D. y = 9x + 7 . Lời giải
Tập xác định D = R . Ta có 2
y ' = 3x − 6x .
Vì M là tiếp điểm nên hệ số góc của tiếp tuyến với đồ thị hàm số tại M là k = y '(− ) 1 = 9 .
Phương trình tiếp tuyến với đồ thị hàm số tại M là y = 9( x + )
1 − 2 y = 9x + 7 Chọn D Câu 4.
Phương trình tiếp tuyến của đồ thị hàm số 4 2
y = x − 3x + 4 tại điểm A(1; 2) là
A. y = 3x + 5 .
B. y = 2x + 4 . C. y = 2 − x + 4 . D. y = 2 − . x Lời giải
Tập xác định D = R . Ta có 3
y ' = 4x − 6x .
Vì A là tiếp điểm nên hệ số góc của tiếp tuyến với đồ thị hàm số tại A là k = y '( ) 1 = 2 − .
Phương trình tiếp tuyến với đồthị hàm số tại A là y = 2 − (x − ) 1 + 2 y = 2 − x + 4 . Chọn C 2x −1 Câu 5.
Phương trình tiếp tuyến của đồ thị hàm số y =
tại điểm M (0; − ) 1 là 71 x +1 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
A. y = 3x +1 .
B. y = 3x −1 . C. y = 3 − x −1. D. y = 3 − x +1. Lời giải
Tập xác định D = R \ − 1 3 Ta có y ' = ( . x + )2 1
Vì M là tiếp điểm nên hệ số góc của tiếp tuyến với đồ thị hàm số tại M là k = y '(0) = 3
Phương trình tiếp tuyến với đồ thị hàm số tại M là y = 3(x − 0) −1 y = 3x −1. Chọn B 2 x − 2x 1 Câu 6.
Phương trình tiếp tuyến của đồ thị hàm số y = tại điểm A 1; − là x +1 2 1 1 3 1 3 1 1 A. y = x . B. y = x + . C. y − x − . D. y = x + . 2 4 4 4 4 2 2 Lời giải
Tập xác định D = R \ − 1 . 1 Ta có y ' = 5 − 2( x − ) . 2 1 1
Vì A là tiếp điểm nên hệ số góc của tiếp tuyến với đồthị hàm số tại A là k = y ' = 3 . 2
Phương trình tiếp tuyến với đồ thị hàm số tại A là 1 5 y = 3 x − + y = 3x +1 . 2 2 Chọn D Câu 7.
Phương trình tiếp tuyến của đồ thị hàm số 2 y = x + x + M (0 ) 1 tại điểm ;1 là 1 1 A. y = x +1. B. y = − x +1.
C. y = −x +1.
D. y = x +1. 2 2 Lời giải
Tập xác định D = R . 2x +1 Ta có y ' = . 2 2 x + x +1
Vì M là tiếp điểm nên hệ số góc của tiếp tuyến với đồ thị hàm số tại M là k = y ( ) 1 ' 0 = . 2
Phương trình tiếp tuyến với đồ thị hàm số tại M là 1 y = (x − ) 1 0 +1 y = x +1. 2 2 Chọn A Câu 8.
Phương trình tiếp tuyến của đồ thị hàm số 3 2
y = x + 3x − 2 tại điểm có hoành độ bằng x = 3 − 0
A. y = 30x + 25 .
B. y = 9x − 25 .
C. y = 30x − 25 .
D. y = 9x + 25. Lời giải
Tập xác định D = R . Ta có 2 y ' = 3x + 6 . x
Gọi M ( x ; y là tiếp điểm x = 3 − ; y = 2 − . 0 0 ) 0 0
Hệ số góc của tiếp tuyến với đồthị hàm số tại M là 72
y = 9( x + 3) − 2 y = 9x + 25. Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM Chọn D Câu 9.
Phương trình tiếp tuyến của đồ thị hàm số 4 2
y = x + 2x −1 tại điểm có hoành độ bằng 1 là A. y = 8 − x − 6..
B. y = 8x − 6.. C. y = 8 − x +10..
D. y = 8x +10. Lời giải
Tập xác định D = R . Ta có 3 y ' = 4x + 4 . x
Gọi M ( x ; y là tiếp điểm x = 1; y = 2. 0 0 ) 0 0
Hệ số góc của tiếp tuyến với đồ thị hàm số tại M là k = y '( ) 1 = 8 .
Phương trình tiếp tuyến với đồthị hàm số tại M là y = 8( x − )
1 + 2 y = 8x − 6. Chọn B 4
Câu 10. Tiếp tuyến của đồthị hàm số y =
tại điểm có hoành độ x = 1 − là x −1 0
A. y = −x − 3 .
B. y = x −1.
C. y = −x + 2 .
D. y = −x −1. Lời giải
Tập xác định D = R \ 1 4 − Ta có y ' = ( x − )2 1 .
Gọi M ( x ; y là tiếp điểm x = 1 − ; y = 2 − . 0 0 ) 0 0
Hệ số góc của tiếp tuyến với đồ thị hàm số tại M là k = y '(− ) 1 = 1 − .
Phương trình tiếp tuyến với đồthị hàm số tại M là y = 1 − (x + )
1 − 2 y = −x − 3. Chọn A
Câu 11. Phương trình tiếp tuyến của đồ thị hàm số 3 2
y = x − 3x + 2 tại điểm thuộc đồ thị hàm số có hoành
độ x thỏa mãn y ' ( x = 0 0 ) là 0 A. y = 3 − x + 3.
B. y = 9x + 7 .
C. y = 9x − 7 . D. y = 3 − x − 3. Lời giải
Tập xác định D = R . 2
Ta có y ' = 3x − 6 ;
x y ' = 6x − 6.
Theo đề y ' ( x = 0 6x − 6 = 0 x =1. 0 ) 0 0
Gọi M ( x ; y là tiếp điểm x = 1; y = 0. 0 0 ) 0 0
Hệ số góc cuả tiếp tuyến với đồ thị hàm số tại M là k = y '( ) 1 = 3 − .
Phương trình tiếp tuyến với đồ thị hàm số tại M là y = 3 − (x − ) 1 + 0 y = 3 − x + 3. Chọn A
Câu 12. Phương trình tiếp tuyến của đồ thị hàm số 3 2
y = x − 3x +1 tại điểm thuộc đồ thị hàm số có
hoành độ x thỏa mãn 2y ' ( x + y ' x +15 = 0 0 ) ( 0) là 0 = +
A. y = 9x + 7 .
B. y = 9x + 6 .
C. y = 9x . D. y 9x 1. Lời giải 73
Tập xác định D = R . Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 2
Ta có y ' = 3x − 6 ;
x y ' = 6x − 6. Theo đề
2 y ' ( x ) + y '( x ) +15 = 0 2(6x − 6) 2 2
+ 3x − 6x +15 = 0 3x + 6x + 3 = 0 x = 1 − 0 0 0 0 0 0 0 0
6x −6 = 0 x =1. 0 0
Gọi M ( x ; y là tiếp điểm x = 1 − ; y = 3 − . 0 0 ) 0 0
Hệ số góc cuả tiếp tuyến với đồ thị hàm số tại M là k = y '(− ) 1 = 9.
Phương trình tiếp tuyến với đồ thị hàm số tại M là y = 9( x + )
1 − 3 y = 9x + 6. Chọn B
Câu 13. Phương trình tiếp tuyến của đồ thị hàm số 3 2
y = x − x + x +1 tại điểm có tung độ bằng 2 là
A. y = 2x .
B. y = 9x −11.
C. y = 54x + 32 . D. y = 3 − x − 3. 74 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM Lời giải
Tập xác định D = R . 2
Ta có y ' = 3x − 2x +1.
M ( x ; y là tiếp điểm y = 2. và x là nghiệm của phương trình 0 0 ) 0 0 3 2 3 2
x − x + x +1 = 2 x − x + x −1 = 0 x =1. 0 0 0 0 0 0 0
Hệ số góc cuả tiếp tuyến với đồ thị hàm số tại M là k = y '( ) 1 = 2.
Phương trình tiếp tuyến với đồ thị hàm số tại M là y = 2( x − ) 1 + 2 y = 2 . x Chọn A
Câu 14. Phương trình tiếp tuyến của đồ thị hàm số 4 2
y = x − 3x +1 tại điểm có tung độ bằng 5 là
A. y = 20x − 35 . B. y = 2
− 0x − 35 và y = 20x + 35 .
C. y = 20x − 35 và y = 2 − 0x − 35 . D. y = 2 − 0x + 35. Lời giải
Tập xác định D = R . Ta có 3 y ' = 4x − 6 . x M ( x ; y y = 5. x 0 0 ) là tiếp điểm và
là nghiệm của phương trình 0 0 2 x = 1 − vn 4 2 4 2 0 ( ) 2
x − 3x +1 = 5 x − 3x − 4 = 0 x = 4 0 2 x = 4 0 x = 2 0 - Với M 2;5 M k = y ' 2 = 2. 1 ( ) 1 (
) hệ số góc cuả tiếp tuyến với đồ thị hàm số tại là 1
Phương trình tiếp tuyến với đồ thị hàm số tại M là 1
y = 20( x − 2) + 5 y = 20x − 35. - Với M 2 − ;5 M k = y ' 2 − = 2 − 0. 2 ( ) 2 (
) hệ số góc cuả tiếp tuyến với đồ thị hàm số tại là 2
Phương trình tiếp tuyến với đồ thị hàm số tại M là 2 y = 2
− 0(x + 2) + 5 y = 2 − 0x − 35. Chọn C 2x − 4
Câu 15. Phương trình tiếp tuyến của đồthị hàm số y =
tại điểm có tung độ bằng 3 là x − 4
A. x + 4 y − 20 = 0 .
B. x + 4y − 5 = 0 .
C. 4x + y − 2 = 0 .
D. 4x + y − 5 = 0 . Lời giải
Tập xác định D = R \ 4 . 4 − = Ta có y '
Gọi M ( x ; y y = 3 x 0 0 ) là tiếp điểm và
là nghiệm của phương trình (x − 4)2 . 0 0 2x − 4 0
= 3 2x − 4 = 3 x − 4 x = 8. 0 ( 0 ) 0 x − 4 0
Hệ số góc của tiếp tuyến với đồ thị hàm số tại M là k = y ( ) 1 ' 8 = − . . 4 1
Phương trình tiếp tuyến với đồthị hàm số tại M là y = − (x −8) + 3 x + 4y − 20 = 0. 4 75 Chọn A Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 3
Câu 16. Viết phương trình tiếp tuyến của đường cong 4 2 (C) : y =
x + x −1, biết tiếp tuyến vuông góc 2
với đường thẳng d : x + 8y +16 = 0 . 13 13 13 13 A. y = 8 − x + .
B. y = 8x + . C. y = 8 − x − .
D. y = 8x − . 2 2 2 2 Lời giải
Tập xác định D = . Ta có 3 y ' = 6x + 2 . x
Gọi M (x ; y ) là tiếp tuyến hệ số góc của tiếp tuyến là k = y '(x ). 0 0 0 1
Vì tiếp tuyến vuông góc với đường thẳng d : y = − x − 2 nên 8 1 3 3 y '(x ). − = 1
− y '(x ) = 8 6x + 2x = 8 6x + 2x −8 = 0 x =1 0 0 0 0 0 0 0 , 8 3
Với x = 1 M 1; . 0
Phương trình tiếp tuyến với đồ thị hàm số tại là 2 M 3 13 y = 8(x −1) + y = 8x − . 2 2 Chọn D
Câu 17. Phương trình tiếp tuyến với đồ thị 3 2
(C) : y = 2x − 6x + 3 có hệ số góc nhỏ nhất là
A. 6x + y − 5 = 0 .
B. 6x + y + 5 = 0 .
C. 6x − y + 3 = 0 .
D. 6x + y − 7 = 0. Lời giải
Tập xác định D = . Ta có 2
y ' = 6x −12x .
Gọi M (x ; y ) là tiếp điểm hệ số góc của tiếp tuyến tại M là 0 0 2 2
k = y '(x ) = 6x −12x = 6 (x −1) −1 6. − 0 0 0 0
Dấu " = " xảy ra khi x = 1. 0 Do đó, tại M (1; 1
− ) thì tiếp tuyến với đồ thị hàm số có hệ số góc nhỏ nhất là k = 6. −
Vậy phương trình tiếp tuyến với đồ thị hàm số tại M là y = 6
− (x −1) −1 6x + y − 5 = 0 . Chọn A
Câu 18. Phương trình tiếp tuyến với đồ thị 3 2
y = −x + 3x − 5x +1 có hệ số góc lớn nhất là
A. 2x − y = 0 .
B. x − 2 y +1 = 0 .
C. 2x + y = 0 .
D. x + 2 y +1 = 0. Lời giải
Tập xác định D = . Ta có 2 y ' = 3
− x + 6x − 5.
Gọi M (x ; y ) là tiếp điểm hệ số góc của tiếp tuyến tại M là 0 0 2 2
k = y '(x ) = 3
− x + 6x −5 = 3
− (x −1) − 2 2 − . 0 0 0 0
Dấu " = " xảy ra khi x = 1. 0 Do đó, tại M (1; 2
− ) thì tiếp tuyến với đồ thị hàm số có hệ số góc nhỏ nhất là k = 2. −
Vậy, phương trình tiếp tuyến với đồ thị hàm số tại M là y = 2
− (x −1) − 2 2x + y = 0. Chọn C 3 2
Câu 19. Cho hàm số y = x + x −1 có đồ thị (C), phương trình tiếp tuyến của (C) tại (
A 1;1) cắt (C) tại điểm .
B Tính độ dài đoạn . AB 76 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM A. 4 26 . B. 10 . C. 105 . D. 2 Lời giải 2 y ' = 3x + 2 ; x y '(1) = 5.
Phương trình tiếp tuyến của (C) tại (
A 1;1) là d : y = 5(x −1) +1 = 5x − 4
Phương trình hoành độ giao điểm của (C) và d : x =1 3 2 3 2
x + x −1 = 5x − 4 x + x − 5x + 3 = 0 x = 3 − Tọa độ B( 3 − ; 1
− 9). Độ dài AB = 4 26. Chọn A Câu 20. Cho hàm số 2
f (x) = 2x − 4. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành
độ tiếp điểm bằng tung độ tiếp điểm.
A. y = 2x + 2 . B. y = 2 − x − 2 .
C. y = 2x − 2 . D. y = 2 − x + 2 . Lời giải A( 2 x ; 2x − 4 2 − = = 0 0 ) Gọi
thuộc đồ thị hàm số. Ta có 2x 4 x x 2. 0 0 0 2x y ' = ; y '(2) = 2. 2 2x − 4
Phương trình tiếp tuyến của đồ thị hàm số tại (
A 2; 2) là d : y = 2(x − 2) + 2 = 2x − 2. Chọn C 2x −1
Câu 21. Tiếp tuyến của đồ thị hàm số y = đi qua điểm ( A 1
− ;4) có phương trình là x +1 1 13 1 1 1 1 13
A. y = x + . B. y = x + . C. y = x + 4 . D. y = x − . 3 3 3 3 3 3 3 Lời giải 2x −1 3 3 Gọi 0 M x ; y ' = ; y '(x ) = . 0
thuộc đồ thị hàm số. Ta có 2 0 2 x +1 (x +1) (x +1) 0 0 3 2x −1 Phương trình tiế 0
p tuyến của đồ thị hàm số tại = − + M là y (x x ) . 2 0 (x +1) x +1 0 0 3( 1
− − x ) 2x −1 0 0 Do tiếp tuyến đi qua ( A 1
− ;4) nên ta có phương trình: + = 4 x = 4 − . 2 0 (x +1) x +1 0 0
Vậy phương trình tiếp tuyến của đồ thị hàm số tại M ( 4 − 1 13 ;3) là y = x + . 3 3 Chọn A Câu 22. Cho hàm số 3 2
y = x + mx + x +1. Gọi k là hệ số góc tiếp tuyến của đồ thịa àm số tại M có hoành
độ x =1. Tìm tham số m để thỏa mãn k f ( 1 − ) 0. A. m 2 . B. m 2 − . C. 2 − m 1. D. m 1. Lời giải 2
y ' = 3x + 2mx +1; k = y '(1) = 2m + 4.
Điều kiện Câu toán k f ( 1
− ) 0 (2m + 4)(m −1) 0 2 − m 1. Chọn C 77 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 1 1
Câu 23. Gọi d , d là hai tiếp tuyến của đồ thị hàm số 3 2 y = x +
x − 6x −1 tại hai điểm lần lượt có 1 2 3 2
hoành độ là x và x . Biết x , x là hai nghiệm phương trình 2
x + mx − 3 = 0. Tìm tham số m để 1 2 1 2
d song song d . 1 2 A. m = 1 − . B. 10m = 2 . C. m = 1. D. m = 2. − Lời giải 2
y ' = x + x − 6.
Hệ số góc của d , d lần lượt là 2
y '(x ) = x + x − 6 và 2
y '(x ) = x + x − 6. 1 2 1 1 1 2 2 2 Ta có d
d y '(x ) = y '(x ) (x − x ) (x + x +1) = 0 x + x +1 = 0(x x ). 1 2 1 2 1 2 1 2 1 2 1 2
Vì x , x là hai nghiệm phương trình 2
x + mx − 3 = 0 nên x + x = − .
m Suy ra m = 1. 1 2 1 2 Chọn C
Câu 24. Tìm tham số m để tiếp tuyến của đồ thị hàm số 3 2
y = x − 2x + 3mx +1 tại điểm có hoành độ bằng 1 đi qua điểm ( A 1;3). A. m = 2 . B. m = 2 − . C. m = 1 − . D. m = 1. Lời giải Gọi M (1;3 )
m thuộc đồ thị hàm số. 2
y ' = 3x − 4x + 3 ;
m y '(1) = 3m −1.
Phương trình tiếp tuyến của đồ thị hàm số tại M : y = (3m −1)x +1. Vì tiếp tuyến đi qua điểm (
A 1;3) nên suy ra m =1. Chọn D
Câu 25. Tìm tham số m để tiếp tuyến của đồ thị hàm số 4 2
y = x − mx + 3m +1 tại điểm có hoành độ bằng 1 − đi qua điểm ( A 0; 2). A. m = 1. B. m = 2 . C. m = 1 − . D. m = 2. − Lời giải Gọi M ( 1
− ;2m + 2) thuộc đồ thị hàm số. 3
y ' = 4x − 2m ; x y '( 1 − ) = 2m − 4.
Phương trình tiếp tuyến của đồ thị hàm số tại M : y = (2m − 4)x + 4m − 2.
Vì tiếp tuyến đi qua điểm (0
A ; 2) nên suy ra m =1. Chọn A
Câu 26. Gọi M là điểm thuộc đồ thị hàm số 4 2
y = x − (2m +1)x + m + 2 có hoành độ bằng 1. Hỏi giá trị
của tham số m thuộc khoảng nào thì tiếp tuyến tại điểm M sẽ vuông góc với đường thẳng d
có phương trình y = x − 4y − 2018 = 0. A. (− ; 3 − ) . B. [ − 3; 0) . C. [0;5) . D. [5; +). Lời giải Gọi M (1;1− )
m thuộc đồ thị hàm số. 3
y ' = 4x − 2(m +1) ; x y '(1) = 2 − 2 . m 1
Đường thẳng d có hệ số góc k = . d 4
Vì tiếp tuyến tại điểm M vuông góc với đường thẳng d nên y '(1) = 2 − 2m = 4 − m = 3. Chọn C x − m
Câu 27. Cho hàm số y = có đồ thị C và điểm ( A 1
− ;2) . Gọi S là tập hợp tất cả các giá trị thực x − ( ) 1 m
của m để có đúng một tiếp tuyến của (Cm ) đi qua .
A Tổng tất cả các phần tử của S bằng. A. 1. B. 2 . C. 3 . D. 4. 78 Lời giải Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM Điều kiện m 1. x − m Gọi 0 M x ; 0
thuộc đồ thị hàm số. x −1 0 m −1 m −1 y ' = ; y '(x ) = . 2 0 2 (x −1) (x −1) 0 m −1 x − m Phương trình tiế 0
p tuyến của đồ thị hàm số tại = − + M là y (x x ) . 2 0 (x −1) x −1 0 0 Do tiếp tuyến đi qua ( A 1
− ;2) nên ta có phương trình: m −1 x − m 0 ( 1 − − x ) + = 2. 2 0 (x −1) x −1 0 0
Biến đổi phương trình ta được: 2
x + (2m − 4)x +1 = 0(x 1). 0 0 0
Phương trình có nghiệm duy nhất khi và chỉ khi m =1 2 2
(2m − 4) − 4 = 0 4m −16m +12 = 0 m = 3.
Do điều kiện m 1 nên chỉ có m = 3 thỏa mãn điều kiện Câu toán.
Tổng tất cả các giá trị thực của m bằng 3. Chọn C 1
Câu 28. Tiếp tuyến tại điểm là nghiệm y ' = 0 của đồ thị hàm số 3 2 y =
x − 2x + 3x − 5 thì 3
A. Song song với đường thẳng.
B. Song song với trục hoành.
C. Có hệ số góc dương. D. Có hệ số góc bằng 1. − Lời giải
Gọi x là nghiệm phương trình y ' = 0 : y '(x ) = 0. Khi đó tiếp tuyến tại điểm có hoành độ x 0 0 0
sẽ có hệ số góc k = y '(x ) = 0 nên tiếp tuyến song song với trục hoành. 0 Chọn B
Câu 29. Hệ số góc tiếp tuyến của đồ thị hàm số (C ) 4 2
: y = x − 8x + 2 tại điểm có hoành độ x = 2 bằng 0 A. 6 − 2 . B. 7 − 2 . C. 8 − 2 . D. 9 − 2. Lời giải 3 y '( 2) y ' = 4x −16 .
x Hệ số góc của tiếp tuyến tại điểm có hoành độ x = 2 là = 8 − 2. 0 Chọn C
Câu 30. Hệ số góc của tiếp tuyến với đồ thị (C ) 3
: y = x − 2x +1 tại điểm M ( 1 − ;2) bằng A. 3 . B. 5 − . C. 25 . D. 1. Lời giải 2
y ' = 3x − 2. Hệ số góc của tiếp tuyến tại điểm M ( 1 − ;2) bằng y '( 1 − ) =1. Chọn D 1 1
Câu 31. Tiếp tuyến của đồ thị hàm số 3 2 f (x) = x −
x − 4x + 6 tại điểm có hoành độ là nghiệm của 3 2
phương trình f "(x) = 0 có hệ số góc bằng 47 13 17 A. −4 . B. . C. − . D. − . 12 4 4 Lời giải 2
f '(x) = x − x − 4; f "(x) = 2x −1. 79 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 1
f "(x) = 2x −1 = 0 x = . 2 1
Hệ số góc của tiếp tuyến tại điểm có hoành độ x = 1 17 bằng f ' = − . 2 2 4 Chọn D
Câu 32. Trong các tiếp tuyến tại các điểm trên đồ thị hàm số 3 2
y = x − 3x + 2, tiếp tuyến có hệ số góc nhỏ nhất bằng A. 3 − . B. 3 . C. −4 . D. 0 . Lời giải 2 2
y ' = 3x − 6x = 3(x −1) − 3 3 − ; x .
Tiếp tuyến có hệ số góc nhỏ nhất bằng 3
− tại điểm có hoành độ bằng 1. Chọn A
Câu 33. Phương trình tiếp tuyến của đồ thị hàm số 3 2
y = x − 3x + 2 tại điểm ( A 1; 0) là A. y = 3 − x + 3. B. y = 3 − x +1 .
C. y = 3x +1 .
D. y = 3x + 3 . Lời giải 2 y ' = 3x − 6 ; x y '(1) = 3 − .
Phương trình tiếp tuyến của đồ thị hàm số 3 2
y = x − 3x + 2 tại điểm ( A 1; 0) là y = 3 − (x −1) = 3 − x + 3. Chọn A 2x −1
Câu 34. Phương trình tiếp tuyến của đồ thị y = tại điểm ( A 2;3) là x −1 A. y = 3 − x + 9 .
B. y = −x + 5 .
C. y = 3x − 5 .
D. y = x +1 . Lời giải 1 − y ' = ; y '(2) = 1 − . 2 (x −1) 2x −1
Phương trình tiếp tuyến của đồ thị y = tại điểm ( A 2;3) là y = (
− x − 2) + 3 = −x + 5. x −1 Chọn B x −1
Câu 35. Phương trình tiếp tuyến của đồ thị y =
tại điểm có hoành độ bằng 3 − là x + 2 A. y = 3 − x − 5.
B. y = 3x +13 .
C. y = 3x + 5 . D. y = 3 − x +13 . Lời giải 3 y ' = ; y '( 3 − ) = 3 và y − = 2 (x + ( 3) 4. 2)
Phương trình tiếp tuyến của đồ thị tại điểm có hoành độ bằng 3
− là y = 3(x + 3) + 4 = 3x +13. Chọn B
Câu 36. Tiếp tuyến của đồ thị hàm số 3 2
y = 2x + 3x tại điểm M có tung độ bằng 5 là A. y = 1 − 2x − 7 .
B. y = 12x − 7 . C. y = 1 − 2x +17 .
D. y = 12x +17 . Lời giải
Gọi M (x ; y ) là điểm thuộc đồ thị hàm số. Theo đề Câu 3 2
y = 2x + 3x = 5 x 0 = 1. 0 0 0 0 0
Phương trình tiếp tuyến cần tìm là y = y '(1) (x −1) + y = 12(x −1) + 5 = 12x − 7. 0 Chọn B 80
Câu 37. Phương trình tiếp tuyến của (C ) 3 2
: y = x − 3x + 9 tại điểm có hoành độ bằng 9 là Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM A. y = 1 = − = − và y 9x 1 .
B. y = 19 và y 9x 8. C. y = 9 = − = − và y 9x 18 .
D. y = 0 và y 9x 1 . Lời giải x = 0
Gọi M (x ; y ) là điểm thuộc đồ thị hàm số. Theo đề Câu 3 2 0
y = x − 3x + 9 = 9 0 0 0 0 0 x = 3. 0 x = 0 :
y = y '(0) (x − 0) + y = 0(x − 0) + 9 = 9. 0
Phương trình tiếp tuyến cần tìm là 0 x = 3 :
y = y '(3) (x − 3) + y = 9(x − 3) + 9 = 9x −18. 0
Phương trình tiếp tuyến cần tìm là 0 Chọn C 2x − 4
Câu 38. Phương trình tiếp tuyến tại giao điểm của đồ thị y =
với trục hoành là x − 3
A. y = 2x . B. y = 2 − x + 4 . C. y = 2 − x − 4 .
D. y = 2x − 4 . Lời giải − Phương trình hoành độ 2x 4
giao điểm của đồ thị với trục hoành là = 0 x = 2 x − 3 2 y ' = − ; y '(2) = 2 − . 2 (x − 3)
Phương trình tiếp tuyến cần tìm là y = 2 − (x − 2) = 2 − x + 4. Chọn B 2x +1
Câu 39. Viết phương trình tiếp tuyến của đồ thị hàm số y =
, biết tiếp tuyến có hệ số góc bằng 5. x − 2 A. y = 5 − x + 2 y = 5 − x + 22 y = 5 − x + 2 y − 5x − 22 và . B. và .
C. y = 5x + 2 = − + = − − = − + và y 5x 22 . D. y 5x 2 và y 5x 22 . Lời giải 5 x = y ' = −
. Giải y = − ( x − )2 3 ' 5 2 =1 2 (x − 2) x =1. x = 3: = − − + = − +
Phương trình tiếp tuyến cần tìm là y 5(x 3) 7 5x 22. x = 1: = − − − = − +
Phương trình tiếp tuyến cần tìm là y 5(x 1) 3 5x 2. Chọn A x
Câu 40. Viết phương trình tiếp tuyến với đồ thị (C ) 3 2 : y =
+ 3x − 2, biết tiếp tuyến có hệ số góc k = 9 − 3 A. y = 9 − x − 43 . B. y = 9 − x + 43 . C. y = 9 − x − 27 . D. y = 9 − x −11 . Lời giải Tập xác định D = .
M (x ; y ) C 0 0 ( ) Gọi là tiếp điểm. 2
Ta có y ' = x + 6 .
x Mà theo giả thiết, tiếp tuyến có hệ số góc k = 9 − nên 2 2 y '(x ) = 9
− x + 6x = 9
− (x + 3) = 0 x = 3 − . 0 0 0 0 0 3 ( 3 − ) Do đó 2 y = + 3( 3
− ) − 2 =16 M ( 3 − ;16). 0 3
Vậy phương trình tiếp tuyến là y = 9
− (x − x ) + y = 9 − (x + 3) +16 = 9 − x −11 0 0 . Chọn D
Câu 41. Viết phương trình tiếp tuyến của đồ thị (C ) 3 2
: y = −x + 3x +1, biết tiếp tuyến song song với 81
đường thẳng d : y = 3x + 2. Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
A. y = 3x .
B. y = 3x − 6 . C. y = 3 − x + 3.
D. y = 3x + 6 . Lời giải Tập xác định D = .
M (x ; y ) C 0 0 ( ) Gọi là tiếp điểm. 2 Ta có y ' = 3 − x + 6 .
x Mà tiếp tuyến song song với d : y = 3x + 2 nên có hệ số góc k = 3. Do đó 2 2
y '(x ) = 3 3
− x + 6x = 3 3
− (x −1) = 0 x =1. 0 0 0 0
Do đó y = 3 M (1;3). 0
Vậy phương trình tiếp tuyến là y = 3 (x − x ) + y = 3(x −1) + 3 = 3 . x 0 0 Chọn A x +
Câu 42. Viết phương trình tiếp tuyến của đồ thị (C ) 2 1 : y =
, biết tiếp tuyến song song với đường x + 2
thẳng : 3x − y + 2 = 0.
A. y = 3x +14 = + = + và y 3x 2 . B. y 3x 14 .
C. y = 3x + 5 = − = − và y 3x 8 . D. y 3x 8 . Lời giải Tập xác định D = \ − 2 .
M (x ; y ) C 0 0 ( ) Gọi là tiếp điểm. 3 Ta có y ' =
. Mà tiếp tuyến song song với x − y + = k = 3. 2 nên có hệ số góc (x + : 3 2 0 2) Do đó 3 x + 2 = 1 x = 1 − 2 0 0 y '(x ) = 3 = 3 (x + 2) = 1 . 0 2 0 (x + 2) x + 2 = 1 − x = 3 − 0 0 0 x = 1 − y = 1 − M ( 1 − ; 1 − ). Với 0 0
Do đó phương trình tiếp tuyến là y = 3(x +1) −1 = 3x + 2.(loại vì trùng với ) x = 3
− y = 5 M ( 3 − ;5). Với 0 0
Do đó phương trình tiếp tuyến là y = 3(x + 3) + 5 = 3x +14. (nhận) Chọn B 3 2
Câu 43. Viết phương trình tiếp tuyến với đồ thị hàm số y = x − 2x −1, biết tiếp tuyến vuông góc với
đường thẳng d : y = x . 23
A. y = x −1.
B. y = −x − . 27 23
C. y = −x −1.
D. y = −x −1, y = −x − . 27 Lời giải Tập xác định D = .
M (x ; y ) C 0 0 ( ) Gọi là tiếp điểm. 2
Ta có y ' = 3x − 4 .
x Mà tiếp tuyến vuông góc với d : y = x −
nên có hệ số góc k = 1. Do đó x = 1 0 2 2 y '(x ) = 1
− 3x − 4x = 1
− 3x − 4x +1 = 0 0 0 0 0 0 1 x = 0 3
Với x = 1 y = 2 − M (1; 2 − ) 0 0
Do đó phương trình tiếp tuyến là y = 1
− (x −1) − 2 = −x −1 82 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 1 32 1 32 Với x = y = − M ( ;− ) 0 0 3 27 3 27 Do đó phương trình tiế 1 32 23 p tuyến là y = 1 − (x − ) − = −x − . 3 27 27 Chọn D
Câu 44. Viết phương trình tiếp tuyến với đồ thị hàm số (C ) 3
: y = x − 3x + 2, biết tiếp tuyến vuông góc
với đường thẳng x + 9 y − 9 = 0. 1 1
A. y = x +18 và y = x−14 . B. y = 9 − x +18 = − + và y 9x 5 . 9 9
C. y = 9x +18 = + = + = − và y 9x 5 . D. y
9x 18 và y 9x 14 . Lời giải Tập xác định D = .
M (x ; y ) C 0 0 ( ) Gọi là tiếp điểm. 2
Ta có y ' = 3x − 3. Mà tiếp tuyến vuông góc với x + 9 y − 9 = 0 nên có hệ số góc k = 9. Do đó 2 2 y x
) = 9 3x −3 = 9 x = 4 x = 2 . 0 0 0 0
Với x = 2 y = 4 M (2; 4). Do đó phương trình tiếp tuyến là y = 9 (x − 2) + 4 = 9x −14. 0 0 Với x = 2
− y = 0 M ( 2
− ;0). Do đó phương trình tiếp tuyến là y = 9(x + 2) = 9x +18. 0 0 Chọn D
Câu 45. Tiếp tuyến của đồ thị hàm số 3 y = 4
− x + 3x +1 đi qua ( A 1
− ;2) có phương trình là A. y = 9
− x + 7 hoặc y = −x + 2. B. y = 9
− x −11 hoặc y = −x + 2. C. y = 9
− x +11 hoặc y = 2 . D. y = 9
− x − 7 hoặc y = 2 . Lời giải Tập xác định D = .
Gọi d là tiếp tuyến cần tìm. Gọi M (x ; y ) C 0 0
( ) là tiếp điểm. Khi đó ta có 3 y = 4 − x + 3x +1 0 0 0 2 y '(x ) = 1 − 2x + 3. 0 0
Do đó phương trình tiếp tuyến d là 2 3
y = y '(x ) (x − x ) + y = ( 1
− 2x + 3)(x − x ) − 4x + 3x +1. 0 0 0 0 0 0 0 Mà ( A 1
− ;2)d nên ta có 2 3 3 2 2 = ( 1 − 2x + 3)( 1
− − x ) − 4x + 3x +1 8x −12x − 4 = 0 0 0 0 0 0 0 1 2x −1 = 0 x = 0 2
4(2x −1)(x +1) = 0 0 2 0 0 2 (x +1) = 0 0 x = −1 0 1 Với x =
ta có d : y = 2. 0 2 Với x = 1 − d : y = 9 − x − 7. 0 ta có Chọn D 3 2
Câu 46. Tiếp tuyến của đồ thị hàm số y = x + 4x + 4x +1 tại điểm ( A 3 − ; 2
− ) cắt đồ thị hàm số tại điểm thứ hai là . B Điể
m B có tọa độ là A. B( 1 − ;0) . B. B(1;10) . C. B(2;33) . D. B( 2 − ;1) . Lời giải 83 Tập xác định D = . Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 2
Ta có y ' = 3x + 8x + 4. Phương trình tiếp tuyến của đồ thị tại ( A 3 − ; 2 − ) là
d : y = y '( 3
− )(x + 3) − 2 = 7x +19.
Phương trình hoành độ giao điểm của (C ) và d là x = 2 3 2 3 2
x + 4x + 4x +1 = 7x +19 x + 4x − 3x −18 = 0 x = 3. −
Do đó điểm B có tọa độ (2;33) . Chọn C Câu 47. Cho hàm số 3 2
y = x + 3x +1 có đồ thị (C ). Gọi là tiếp tuyến của (C ) tại điểm ( A 1;5) và B
là giao điểm thứ hai của với (C ). Diện tích tam giác AOB bằng A. 12 . B. 6 . C. 15 . D. 24 . Lời giải Tập xác định D = . 2
Ta có y ' = 3x + 6 .
x Phương trình tiếp tuyến của đồ thị tại a(1;5) là
d : y = y '(1) (x −1) + 5 = 9x − 4.
Phương trình hoành độ giao điểm của (C ) và d là x = 5 − 3 2 3 2
x + 3x +1 = 9x −14 x = 3x − 9x + 5 = 0 x = 1.
Do đó, điểm B có tọa độ ( 5 − ; 4
− 9). Suy ra AB = 6 82. 4 Mà d ( ; O AB) = d ( ; O d ) =
nên diện tích tam giác AOB bằng 82 1 1 4 AB d ( ; O AB) = 6 82 =12. 2 2 82 Chọn A ( + C ) 2x 1 : y = M O , x Oy
Câu 48. Tiếp tuyến của đồ thị tại điểm
cắt các trục tọa độ lần lượt tại x − (2;5) 1 A và .
B Diện tích tam giác AOB O (với
là gốc tọa độ) bằng 121 119 123 125 A. . B. . C. . D. . 6 6 6 6 Lời giải Tập xác định D = \ 1 . 3 − Ta có y ' =
. Phương trình tiếp tuyến của đồ thị tại M 2 là (x − (2;5) 1)
d : y = y '(2) (x − 2) + 5 = 3 − x +11. 11 11
Do A là giao điểm của d với Ox nên có tọa độ ; 0 OA = . 3 3
Do B là giao điểm của d với Oy nên có tọa độ (0 ) ;11 OB = 11. 1 1 11 121
Ta có tam giác AOB vuông tại O nên có diện tích bằng OAOB = 11 = . 2 2 3 6 Chọn A 84 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 2x +1 y = 0 A
Câu 49. Tiếp tuyến của đồ thị hàm số
tại điểm có hoành độ bằng cắt các trục tọa độ tại x +1 và .
B Diện tích tam giác AOB O (với
là gốc tọa độ) bằng 1 1 A. . B. 1 . C. . D. 2 . 2 4 Lời giải Tập xác định D = \ −
1 . Gọi M (0; y ) là tiếp điểm. 0 2 0 +1 1 Ta có y = =1 M (0;1) y = . 0 và 2
Phương trình tiếp tuyến của đồ thị tại 0 +1 (x +1) M (0;1) là
d : y = y (0
) x +1= x +1
Do A là giao điểm của d và Ox nên có tọa độ ( 1; 0) OA 1 .
Do B là giao điểm của d và Oy nên có tọa độ (0;1) OB 1. 1 1 1
Ta có tam giác AOB vuông tại O nên có diện tích bằng .O . A OB .1.1 . 2 2 2 Chọn A mx 1
Câu 50. Tìm tham số m để tiếp tuyến của đồ thị hàm số y
tại điểm có hoành độ bằng 1 đi qua x 2 điểm ( A 1; 2) . A. m 1. B. m 3 . C. m 3 . D. m 1. Lời giải Tập xác định D
\ 2 . Gọi M (1; y ) 0 là tiếp điểm. m 1 1 2m Ta có y 1 m M (1;1 ) m và y ' . 0 1 2 2 (x 2)
Phương trình tiếp tuyến của đồ thị tại M (1;1 ) m là: d : y y ' (x 1) 1 m (1 2 m).x m (1) Mà d đi qua ( A 1; 2) nên ta có: 2 (1 2 ) m .1 m m 3 . Chọn B x b
Câu 51. Cho hàm số y
có hàm số (C) . Biết a, b là các giá trị thực sao cho tiếp tuyến của (C) ax 2
tại điểm M (1; 2) song song với đường thẳng d : 3x y 4 0 . Tính a b . A. a b 0 . B. a b 1. C. a b 2 . D. a b 1. Lời giải 2 Tập xác định D \ . a 2 ab Ta có y ' . Do M (1; 2)
(C) và tiếp tuyến tại M song song với d có hệ số góc 2 (ax 2) 1 b b 3 2a 2 b 3 2a k
3 nên ta có hệ phương trình a 2 2 ab 2 3 3a 12a 10 ab 0 2 y ' 3 (1) (a 2)
Giải hệ trên ta được ( ; a b) (1;1), (2; 1) . 85 Ta loại đi đáp án ( ; a b)
(2; 1) vì khi đó tập xác định là D \ 1 nên M (1; 2) (C) . Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM Vậy ( ; a ) b (1;1) a b 2 . Chọn C 3 2
Câu 52. Cho hàm số y x 3x (2m 1)x 2m 3 có đồ thị (C ) m m . Tìm
để tiếp tuyến có hệ số
góc lớn nhất của đồ thị (C ) d : x 2 y 4 0 m vuông góc với . A. m 2 . B. m 1. C. m 0 . D. m 4. Lời giải Tập xác định D 2 . Ta có y ' 3x 6x 2m 1.
Gọi k là hệ số góc của tiếp tuyến
của đồ thị tại M (x ; y ) 0 0 . Khi đó 2 k y ' 3x 6x 2m 1. ( 0 x ) 0 0 Ta có 2 2 k 3(x 2x 1) 2m 2 3(x 1) 2m 2 2m 2 . Do đó k 2m 2 max 0 0 0 khi x 1 0 . 1 Mặt khác ta có
vuông góc với d : y x
2 nên có hệ số góc bằng 2 , suy ra 2 2m 2 2 m 2 . Chọn A
Câu 53. Hỏi m thuộc khoảng nào sau đây thì tiếp tuyến có hệ số góc nhỏ nhất của đồ thị hàm số 3 2 y x 3x (m 2)x
3m vuông góc với đường thẳng d : x y 2 0 . A. ( ; 4) . B. 4;3 . C. 3; 5 . D. 5; . Lời giải Tập xác định D 2 . Ta có y ' 3x 6x m 2 .
Gọi k là hệ số góc của tiếp tuyến
của đồ thị tại M (x ; y ) 0 0 . Khi đó 2 k y ' 3x 6x m 2 . ( 0 x ) 0 0 Ta có 2 2 k 3(x 2x 1) m 5 3(x 1) m 5 m 5 . Do đó k m 5 x 1 min khi 0 . 0 0 0 Mặt khác ta có
vuông góc với nên ta có hệ số góc bằng 1 , suy ra m 5 1 m 4. Chọn C 1 Câu 54. Cho hàm số 3 2 2 y x 2mx m x
1 . Tìm m để tiếp tuyến của đồ thị hàm số tại điểm có 3 hoành độ x 2 d :15x 3y 2 0 0
song song với đường thẳng . A. m 9 . B. m 1, m 9 . C. m 1. D. m 1, m 9 . Lời giải Tập xác định D 2 2 . Ta có y ' x 4mx m .
Gọi k là hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x 2 0 nên 2 k y '(2) 4 8m m . 2
Mặt khác tiếp tuyến lại song song với d : y 5x nên k 5 2 4 8m m 5 3 m 1 . m 9 19 11 Với m
1 thì tiếp tuyến lúc đó có phương trình y 5(x 2) 5x . 86 3 3 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 259 229 Với m
9 thì tiếp tuyến lúc đó có phương trình y 5(x 2) 5x . 3 3 Chọn D
Câu 55. Tìm tổng các giá trị của tham số m để từ điểm ( A ;1
m ) kẻ đúng một tiếp tuyến đến đồ thị hàm 2 x số y . x 1 3 5 1 A. 1. B. . C. . D. . 2 2 2 Lời giải Tập xác định D \ 1 .
Tiếp tuyến của đồ thị hàm số qua M ( ;
m 1) có dạng y k(x ) m 1. 2 x k(x m) 1 (1) Để x 1
từ A kẻ được đúng một tiếp tuyến đến đồ thị thì hệ 1 k (2) 2 (x 1)
Có duy nhất một nghiệm. Thay (2) vào (1) ta được 2 x m x 1 2 2x 6x 3 m 0 (*) 2 x 1 (x 1)
Để hệ trên có một nghiệm duy nhất thì phương trình (*) phải có nghiệm kép khác 1 hoặc có 2
nghiệm phân biệt trong đó có 1 nghiệm bằng 1 . Do đó ta có ' 3 2m 0 b 3 3 1 m 2a 2 2 . ' 3 2m 0 m 1 2 6 3 m 0 Chọn C
Câu 56. Tìm tổng các giá trị của tham số m để từ điểm ( A 1; )
m kẻ đúng hai tiếp tuyến đến đồ thị hàm 3 2 số y x 3x 2. A. 1. B. 4 . C. 3 . D. 2 . Lời giải Tập xác định D .
Tiếp tuyến của đồ thị hàm số qua ( A 1; ) m có dạng y k(x 1) m . 3 2 x 3x 2 k(x 1) m (1)
Để từ A kẻ được đúng hai tiếp tuyến đến đồ thị thì hệ 2 3x 6x k (2)
Có đúng hai nghiệm. thay (2) vào (1) ta được 3 2 2 x 3x 2 (3x 6x)(x 1) m 3 2x 6x 2 . m (*)
Để hệ trên có đúng hai nghiệm thì phương trình (*) có đúng hai nghiệm phân biệt, điều này tương đương với đồ 3 thị hàm số y f (x) 2x 6x
2 và đường thẳng y m có đúng hai giao điểm.
Vẽ đồ thị hàm số y
f (x) ta thấy để đồ thị hàm số và đường thẳng y m có đúng hai giao điểm thì m 2 hoặc m 6 . 87 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
Vậy tổng các giá trị của tham số m thỏa yêu cầu câu toán là 2 6 4 . Chọn B x m
Câu 57. Cho hàm số y có đồ thị (C ) ( A 1; 2) S m và điểm . Gọi
là tập hợp tất cả các giá trị thực x 1
của m để có một tiếp tuyến của (C ) A m đi qua
tạo với hai trục tọa độ một tam giác cân. Tổng
tất cả các phần tử của S bằng A. 1. B. 4 . C. 3 . D. 5 . Lời giải b m Tập xác định D \ 1 . Gọi B( ; b )
(C ) là tiếp điểm (b 1) . b 1 m m 1 Ta có y ' . 2 (x 1)
Phương trình tiếp tuyến của (C ) B m tại là b m m 1 b m d : y y '(b).(x b) .(x b) . 2 b 1 (b 1) b 1 Mà d đi qua ( A 1; 2) nên ta có m 1 b m 2 .( 1 ) b 2 2(b 1) (m 1)( 1 b) (b ) m (b 1) 2 (b 1) b 1 2 2 2b 4b 2 b(1 ) m 1 m b b( 1 ) m m 2 2 2b 4b 2 b 2mb 1 2 b b(2m 4) 1 0 (*) m 1
Mặt khác d tạo với hai trục tọa độ một tam giác cân nên y '( ) b 1 hay 1. 2 (b 1) m 1 TH1: 1 2 m 1 b 2b 1 2 m b 2b 2 . Thay vào (*) ta được 2 (b 1) 1 b (tm) 2 2 b b(2b 4b) 1 0 3 2 2b 3b 1 0 2 b 1 (l) 1 13 Với b m . 2 4 m 1 TH2: 1 2 m 1 b 2b 1 2 m b
2b . Thay vào (*) ta được 2 (b 1) 88 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 1 b (tm) 2 2 b b( 2b 4b 4) 1 0 3 2 2b 5b 4b 1 0 2 b 1 (l) 1 3 Với b m . 2 4 3 13 Vậy S , . 4 4 Chọn B
Câu 58. Tìm tổng các giá trị của tham số m để từ điểm ( A ;
m 0) kẻ đúng hai tiếp tuyến đến đồ thị hàm 3 2 số y x
3x và hai tiếp tuyến đó vuông góc với nhau. 1 15 217 217 A. . B. . C. . D. 27 18 9 18 Lời giải Tập xác định D
. Đường thẳng đi qua A có dạng d : y k(x ) m .
Để từ A kẻ được đúng hai tiếp tuyến đến đồ thị thì hệ 3 2 x 3x k(x m) (1) 2 3 x 6x k (2)
Có đúng 2 nghiệm phân biệt. Thay (2) vào (1) ta được 3 2 2 x 3x (3x 6x)(x ) m 2 x(x 3x) x(3x 6)(x m) 0 x 0 2 2 x(x 3x 3x 6x 3mx 6 ) m 0 2 2x x(3m 3) 6m 0 (*) Ta thấy với x
0 thì tiếp tuyến qua A là d : y
0 , khi đó không có tiếp tuyến nào của đồ thị vuông góc với d .
Vậy để từ A kẻ được đúng hai tiếp tuyến vuông góc với nhau thì phương trình (*) phải có hai nghiệm x , x 0 2 2 (3x 6x )(3x 6x ) 1 1 2 phân biệt khác và thỏa , suy ra 1 1 2 2 0 2 (3m 3) 48m 0 m 0 m 0 2 2 (3x 6x )(3 x 6x ) 1 2 2 9x x 18x x (x x ) 36x x 1 1 1 2 2 1 2 1 2 1 2 1 2 2 9m 30m 9 0 m 0 2 9P 18PS 36P 1 3m 3 Với S x x , P x x 3m 1 2
(hệ thức vi-et). Khi đó hệ tương đương với 1 2 2 1 m ( ; 3) ( ; ) 1 3 m ( ; 3) ( ; ) 1 m 0 3 m . 1 27 2 81m 27m(3m 3) 108m 1 m 27 Chọn A 89 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
Câu 59. Tìm tổng các giá trị của tham số m để tiếp tuyến có hệ số góc nhỏ nhất của đồ thị hàm số 3 2 2 y x 3x (m 2)x m đi qua điểm ( A 1; 4) . A. 3 . B. 1. C. 1. D. 0 . Lời giải Tập xác định D 2 . Ta có y ' 3x 6x (m 2).
Gọi k là hệ số góc của tiếp tuyến của đồ thị tại M (x , y ) 0 0 , khi đó 2 k y '(x ) 3x 6x m 2. 0 0 0 Ta có 2 k 3(x 2x 1) m 5 2 3(x 1) m 5 m 5 . Do đó k m 5 x 1. min khi 0 0 0 0 Khi đó tiế 2
p tuyến có dạng d : y (m 5)(x 1) m m 4. Mà d đi qua ( A 1; 4) nên ta có m 1 2 4 2(m 5) m m 4 2 m m 2 0 m 2.
Vậy tổng các giá trị m thỏa yêu cầu câu toán là 2 1 1. Chọn B x 1
Câu 60. Tìm m để đường thẳng d : y m
x cắt đồ thị hàm số (C) : y
tại hai điểm phân biệt x 1 ,
A B sao cho các tiếp tuyến của (C) tại A và B song song nhau. A. m 0 . B. m 1. C. m 2. D. m 3 . Lời giải 2 Tập xác định D \ 1 . Ta có y ' . 2 (x 1) Phương trình hoành độ x 1
giao điểm của (C) và d là m x (m x)(x 1) x 1 x 1 2 x (2 ) m x 1 m 0 (*) .
Để d cắt (C) tại hai điểm phân biệt sao cho tiếp tuyến tại chúng song song với nhau thì
phương trình (*) phải có hai nghiệm x , x y '(x ) y '(x ) 1 2 phân biệt thỏa mãn 1 2 . Do đó ta có hệ 2 (2 m) 4(1 ) m 0 2 m 8 0 x 1 x 1 x x (L) 1 2 1 2 2 2 2 2 (x 1) (x 1) x 1 x 1 x x 2 2 2 1 2 1 2 (x 1) (x 1) 1 2 1 2
Áp dụng hệ thức vi – et cho phương trình (*) ta có x x m 2 m 2 2 1 2 . Do đó m 0. Chọn A 3 2
Câu 61. Tìm m để đường thẳng d : y ( m x 2)
2 cắt đồ thị hàm số (C) : y x 3x 2 tại ba điểm (
A 2; 2), B, D để tích các hệ số góc tiếp tuyến tại B, D của (C) là 27. A. m 0 . B. m 1. C. m 2. D. m 3 . Lời giải Tập xác định D 2 . Ta có y ' 3x 6 . x
Phương trình hoành độ giao điểm của (C) và d là 90 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 3 2 x 3x 2 m(x 2) 2 3 2 x 3x 4 ( m x 2) 0 2 (x 2)(x x 2) m(x 2) 0 2 (x 2)(x x 2 ) m 0 x 2 2 x x 2 m 0 (*)
Để d cắt (C) tại ba điểm , A ,
B D và tích các hệ số góc tiếp tuyến tại ,
B D là 27 thì phương
trình (*) phải có hai nghiệm x , x 2
y '(x ).y '(x ) 27. 1 2 phân biệt khác thỏa 1 2 Do đó ta có hệ 1 4(2 ) m 0 9 4m 0 2 2 2 2 m 0 m 0 2 2 2 2 (3x 6x ).(3x 6x ) 27 9x x 18x x (x x ) 36x x 27 1 1 2 2 1 2 1 2 1 2 1 2 9 m 4 m 0 2 9P 18SP 36P 27 Với S x x 1 P x x 2 m 1 2 , 1 2
. Khi đó hệ tương đương với 9 9 9 m m m 4 4 4 m 0 m 0 m 0 m 1. 2 9(2 ) m 18(2 ) m 36(2 ) m 27 2 9m 18m 27 0 m 1 m 3 Chọn B 91 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
BÀI 3. ĐẠO HÀM CẤP CAO VÀ VI PHÂN A. TÓM TẮT LÝ THUYẾT
1. Đạo hàm cấp hai. Cho hàm số y = f (x) có đạo hàm tại mọi điểm trên (a;b). Khi đó, hệ thức y ' = f '(x)
xác định một hàm số mới trên (a;b). Nếu hàm số y ' = f '(x) lại có đạo hàm tại x thì ta gọi đạo hàm của
y ' là đạo hàm cấp hai của hàm số y = f (x) tại x , và ký hiệu là y '' hay f ' (x) . Ta có
f ' (x) = [f '(x)]'.
2. Đạo hàm cấp 3 của hàm số y = f (x) được định nghĩa tương tự và kí hiệu là y ''' hay f ' '(x) hoặc (3) f (x)
3. Tổng quát. Cho hàm số y = f (x) có đạo hàm cấp − n −1, ký hiệu là (n 1) f
(x) (n 2, n ) . Nếu (n 1 − ) f
(x) có đạo hàm thì đạo hàm của nó được gọi là đạo hàm cấp n của hàm số y = f (x) , kí hiệu (n) y hay (n) f (x) . Ta có (n) (n 1 − ) f (x) = [f (x)]' .
4. Ý nghĩa của đạo hàm cấp hai. Đạo hàm cấp hai f '(t) là gia tốc tức thời của chuyển động s(t) tại thời điểm t.
5. Vi phân. Cho hàm số y = f (x) xác định trên (a;b) và có đạo hàm tại x ( ; a ) b . Giả sử x là số gia
của x . Khi đó, ta gọi tích f '(x) x
là vi phân của hàm số y = f (x) tại x ứng với số gia x , kí hiệu là
df (x) hoặc là dy . Tức là dy = df (x) = f ' x). x .
B. DẠNG TOÁN VÀ BÀI TẬP
_ DẠNG 1. TÍNH ĐẠO HÀM CẤP CAO CỦA MỘT HÀM SỐ PHƯƠNG PHÁP.
- Tính đạo hàm cấp một y '.
- Lần lượt tính các đạo hàm cấp 2, 3,., n của hàm số y = f (x) . _VÍ DỤ MINH HỌA
Ví dụ 1. Tính đạo hàm cấp n của các hàm số sau đây a) 5 2
y = x − 2x 1 + , n = 3.
b) y = sin 2x + cos 2 , x n = 5 . Lời giải a) 5 2
y = x − 2x 1 + , n = 3. Ta có 4
y ' = 5x − 4x 4 3
y ' = (5x − 4x)' = 20x − 4 (3) 3 2
y = (20x − 4)' = 60x .
b) y = sin 2x + cos 2 , x n = 5.
Ta có y ' = 2 cos 2x − 2sin 2x y ' = (2 cos 2x − 2sin 2x) ' = 4
− sin 2x − 4cos 2x
y ''(x) = ( 4
− sin 2x − 4cos 2x)' = 8 − cos 2x +8sin 2 . x (4) y = ( 8
− cos 2x + 8sin 2x)' =16sin 2x +16cos 2x (5)
y = (16sin 2x +16cos 2x)' = 32cos 2x −32sin 2 . x _BÀI TẬP ÁP DỤNG Bài 1.
Tính đạo hàm cấp hai của hàm số 3 2
y = 2x − 3x + 4x −1.
ĐS. y ' =12x − 6. Bài 2.
Tính đạo hàm cấp bốn của hàm số 4 3
y = 5x + 4x − 7x + 2019. ĐS. (4) y =120. 1 2 Bài 3.
Tính đạo hàm cấp hai của hàm số y = . ĐS. y ' = . 3 1− x (1− x) = + + + = + 92 Bài 4.
Tính đạo hàm cấp năm của hàm số 3 y sin(2x 1) x 5. ĐS. (5) y 32 cos(2x 1). Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM Bài 5. Cho hàm số 5 4 2
y = f (x) = 2x + 4x − 3x + x − 2020 . Tính giá trị của (4) (4) f ( 1 − ); f (0) ĐS. (4) (4) f ( 1 − ) = 1 − 44; f (0) = 96 . 1 Bài 6. Cho hàm số 2
y = f (x) = sin 2x +
x − x . Tính giá trị của ' (3) f ( ); f ( ) 2 6 ĐS. ' (3)
f ( ) = 1− 2 3; f ( ) = 8 − . 6 Bài 7.
Cho chuyển động thẳng xác định bởi phương trình 3 2
s(t) = t − 3t − 9t . Trong đó, t được tính bằng
giây và s được tính bằng mét. Tính gia tốc của chuyển động khi t = 3s . ĐS. 2
a(3) = 12m / s Bài 8.
Cho chuyển động thẳng xác định bởi phương trình 3 2
s(t) = t − 3t − 9t . Trong đó, t được tính bằng
giây và s được tính bằng mét. Tính vận tốc của chuyển động khi gia tốc bị triệt tiêu. ĐS. 2 v(1) = 1
− 2m / s x − 3 Bài 9.
Chứng minh rằng hàm số y = thỏa 2
2( y ') = ( y −1).y ' . x + 4 Bài 10.
Chứng minh rằng hàm số y = x sin x thỏa xy − 2( y '− sin x) + x y' = 0 . 3 3 sin x + cos x Bài 11.
Chứng minh rằng hàm số y = thỏa 2 2 ( y ') + (y' ) = 2 . 1− sin x cos x Bài 12. Chứng minh rằng hàm số 2
y = tan 2x thỏa 2
y ' − 32 y − 24 y = 8 . _LỜI GIẢI Bài 1. Ta có 3 2 2
y ' = (2x − 3x + 4x −1) ' = 6x − 6x + 4 . Suy ra 2
y ' = (6x − 6x + 4) ' = 12x − 6 . Bài 2. Ta có 3 2
y ' = 20x +12x − 7 2
y ' = 60x + 24x (3) y =120x + 24 (4) y =120. 1 2 Bài 3. Ta có y ' = y '' = . 2 (1− x) 3 (1− x) Bài 4. Ta có 2
y ' = 2 cos(2x +1) + 3x y ' = 4
− sin(2x +1) + 6x (3) y = 8 − cos(2x +1) + 6 (4)
y =16sin(2x +1) (5)
y = 32cos(2x +1) . Bài 5. Ta có 4 3
y ' = 10x +16x − 6x +1 3 2
y ' = 40x + 48x − 6 (3) 2
y =120x + 96x (4)
y = 240x + 96 Suy ra (4) (4) f ( 1 − ) = 240.( 1 − ) + 96 = 1
− 44; f (0) = 240.0 + 96 = 96. Bài 6.
Ta có y ' = 2 cos 2x + x −1 y ' = 4 − sin 2x +1 (3) y = 8 − cos 2x . Suy ra (3) f ' ( ) = 4
− sin( ) +1=1− 2 3; f () = 8 − cos(2) = 8 − . 6 3 Bài 7.
Ta có vận tốc của chuyển động tại thời điểm t là 2
v(t) = s '(t) = 3t − 6t − 9.
Suy ra gia tốc của chuyển động tại thời điểm t là a(t) = v '(t) = 6t − 6 = 0 Vậy 2
a(3) = 6.3 − 6 = 12 m / s . Bài 8.
Ta có vận tốc của chuyển động tại thời điểm t là 2
v(t) = s '(t) = 3t − 6t − 9.
Suy ra gia tốc của chuyển động tại thời điểm t là a(t) = v '(t) = 6t − 6 = 0 93
Gia tốc bị triệt tiêu khi a(t) = 0 6t − 6 = 0 t =1. Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM Suy ra v(1) = 1 − 2m / s . 7 14 − Bài 9. Ta có y ' = y '(x) = . 2 (x + 4) 3 (x + 4) x − 3 14 49 Suy ra 2
( y −1) y ' = ( − −1). = 2. = 2(y ') 3 4 x + 4 (x + 4) (x + 4)
Ta có điều phải chứng minh. Bài 10.
Ta có y ' = (x sin x) ' = sin x + x cos x y ' = cos x + (cos x − x sin x) = 2cos x − x sin . x Suy ra 2
xy − 2( y '− sin x) + xy ' = x sin x − 2x cos x + x(2 cos x − x sin x) = 0
Ta có điều phải chứng minh. 3 3 sin x + cos x
(sin x + cos x)(1− sin x cos x) Bài 11. Ta có y = = = sin x + cos . x 1− sin x cos x 1− sin x cos x
y ' = cos x − sin x y ' = −sin x − cos x Suy ra 2 2 2 2
( y ') + ( y ' ) = (cos x − sin x) = (− sin x − cos x) = (1− 2sin x cos x) = (1+ 2sin x cos x) = 2
Ta có điều phải chứng minh. Bài 12. Ta có 2 3
y ' = 2 tan 2x(tan 2x) ' = 4 tan 2x(1+ tan 2x) = 4 tan 2x + 4 tan 2 . x 2 2 2 4 2
y ' = 8(1+ tan 2x) + 24 tan 2x(1+ tan 2x) = 24 tan 2x + 32 tan 2x +8 Suy ra 2 4 2 2 4
y ' − 32 y − 24 y = 24 tan 2x + 32 tan 2x + 8 − 32 tan 2x − 24 tan 2x = 8 .
Ta có điều phải chứng minh.
_ DẠNG 2. TÌM VI PHÂN CỦA MỘT HÀM SỐ PHƯƠNG PHÁP. - Tính f '( x)
- Áp dụng công thức dy = f '( x) dx _VÍ DỤ MINH HỌA
Ví dụ 1. Tìm vi phân của các hàm số a) 3
y = x − 5x +1. b) 3 y = sin x . Lời giải a) 3
y = x − 5x +1. Ta có. 2
y = 3x − 5 . Suy ra y = ( 2 d 3x − 5)dx b) 3
y = sin x Ta có. 2 y = x ( x) 2 ' 3sin sin = 3sin . x cos x . Suy ra 2
dy = 3sin x cos d x x _BÀI TẬP ÁP DỤNG Bài 1. Tìm vi phân của hàm số 3 2 y = 2
− x + 3x +1. ĐS. 2 dy = ( 6
− x + 6x)d . x 2x +1 5 Bài 2.
Tìm vi phân của hàm số y = . ĐS. dy = d . x 2 94 x + 3 (x + 3) Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM Bài 3. Tìm vi phân của hàm số 2
y = sin x − sin x cos x .
ĐS. dy = (sin 2x − cos 2x)d . x Bài 4.
Tìm vi phân của hàm số y = 2x +1 . ĐS. 1 dy = d . x 2x +1 _LỜI GIẢI Bài 1. Ta có 2 y ' = 6
− x + 6x . Suy ra 2
dy = y ' dx = ( 6 − x + 6 x)d . x . 5 5 Bài 2. Ta có y ' =
. Suy ra dy = y ' dx = dx . 2 (x + 3) 2 (x + 3) Bài 3.
Ta có y ' = 2sin x cos x − cos 2x = sin 2x − cos 2x . Suy ra dy = y ' dx = (sin 2x − cos 2x)d . x . 1 1 Bài 4. Ta có y ' =
. Suy ra dy = y ' dx = d . x 2x +1 2x +1 95 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
BÀI 4. ÔN TẬP CHƯƠNG V Bài 1.
Dùng định nghĩa, tìm đạo hàm của hàm số 2
y = f (x) =
x + 5 −1 tại điểm x = 2. 0 Đ 2 S. f '(2) = . 3 Lời giải Tập xác định D = . Giả sử x
là số gia đối số tại x = 2. 0 Ta có 2 2 y = (x + x
) + 5 −1− x + 5 +1 2 2 = (x + x ) + 5 − x + 5 . 0 0 0 0 2 2 y (x + x ) + 5 − x + 5 Khi đó 0 0 = x x 2 2 (x + x ) − x 0 0 = 2 2 x ( (x + x ) + 5 + x + 5) 0 0 2 2x x + x 0 = 2 2 (x + x ) + 5 + x + 5 0 0 2x + x 0 = 2 2 (x + x ) + 5 + x + 5 0 0 y 2x + x 4 2 Nên 0 lim = lim = = . x →0 x →0 2 2 x (x + x ) + 5 + x + 5 6 3 0 0 2 Vậy f '(2) = . 3 Bài 2.
Tính đạo hàm của hàm số 2 2
y = (x + x)(5 − 3x ). ĐS. 3 2 y ' = 1
− 2x − 9x +10x + 5. Lời giải Ta có 2 2 4 3 2
y = (x + x)(5 − 3x ) = 3 − x − 3x + 5x + 5x. Suy ra 3 2 y ' = 1
− 2x − 9x +10x + 5. x + 7 Bài 3.
Tính đạo hàm của hàm số 4 y = . ĐS. y ' = . 3 − x 2 (3 − x) Lời giải x + 4 x + 4 7 Ta có y = = . Suy ra y ' = . 3 − x −x + 3 2 (3 − x) 2 2 1 Bài 4.
Tính đạo hàm của hàm số 3
y = 4x + 3x − + x ĐS. 2 y ' = 12x + 3 + + . x 2 x 2 x Lời giải 2 Ta có 3
y = 4x + 3x − + x x 2 1 Suy ra 2 y ' = 12x + 3 + + . 2 x 2 x 2 15x − 6x Bài 5.
Tính đạo hàm của hàm số 3 2
y = 5x − 3x +1. ĐS. y ' = . 3 2 2 5x − 3x +1 Lời giải 96 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 2 15x − 6x Ta có y ' = . 3 2 2 5x − 3x +1 4 x 5 5 Bài 6.
Tính đạo hàm của hàm số 3 2 y = + 3x + x + 5 ĐS. 3 2
y ' = x + 9x + x 4 4 2 Lời giải 5
Với mọi giá trị thực của x . 3 2 y ' = x + 9 x + x 2 Bài 7.
Tính đạo hàm của hàm số 2
y = (2x −1)(3x + 5) ĐS. 2
y ' = 18x + 20x − 3 Lời giải
Với mọi giá trị thực của x . 2 2
y ' = 4x(3x + 5) + 3(2x −1) = 18x + 20x − 3 3 x −1 4 2
2x + 3x + x Bài 8.
Tính đạo hàm của hàm số y = . ĐS. y ' = . 2 x +1 2 2 (x +1) x +1 Lời giải x 2 2 3x x +1 − ( 3x − )1 4 2 2 x +1
2x + 3x + x
Với mọi x , y ' = = . 2 x +1 ( 2x + ) 2 1 x +1 2 2x + 4x + 4 Bài 9.
Tính đạo hàm của hàm số y = (x + ) 2 4 x + 4. ĐS. y' = 2 x + 4 Lời giải x x + 4 2x + 4x + 4 2 ( ) 2
Với mọi x , y ' = x + 4 + = . 2 2 x + 4 x + 4 5 1 10x Bài 10.
Tính đạo hàm hàm số y = 3x +1 − . ĐS. y ' = + 2 x + 2 2 3x +1 (x +2)2 2 Lời giải Với mọi 1 1 5.( 2 − x) 1 10x
x − , y ' = − = + 3 2 3x +1 (x + ) . 2 2 3x +1 2 (x +2)2 2 2 Bài 11.
Cho hàm số g ( x) = (− x + )2015 2 6 96 . Tính g '(0).
ĐS. g '(0) = 0. Lời giải 2014 Với mọi x g ( x) = ( 2 , ' 2015 6 − x + 96) ( 1
− 2x). Suy ra g '(0) = 0. 2 2x − 2x +1 Bài 12.
Tính đạo hàm của hàm số y = (x − ) 2 2 x +1. ĐS. y ' = . 2 x +1 Lời giải x − 2x 2x − 2x +1 Ta có y '
(x 2)' x 1 (x 2) 2 2 2 2 2 x 1 = − + + − + ' = x +1 + = . 2 2 x +1 x +1 Bài 13.
Tính đạo hàm y ' của hàm số 2 y =
x − 6x + 8 và giải phương trình y ' = 0. − Đ x 3 S. y ' = . 2 x − 6x + 8 97 Lời giải Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM Điề x u kiện. 2 2
x − 6x + 8 0 x 4. 2x − 6 x − 3 Ta có y ' = = . 2 2 2 x − 6x + 8 x − 6x + 8 − Khi đó x 3 y ' = 0
= 0 x = 3 (loại). 2 x − 6x + 8
Vậy Phương trình y ' = 0 vô nghiệm. Bài 14. Cho f ( x) 3 2
= x − 2x − 6x + 2. Giải bất phương trình. f '(x) 2. Đ 2 S. S = − ; − 2;+ ). 3 Lời giải
Tập xác định D = . Ta có f ( x) 2 '
= 3x − 4x − 6. 2 Khi đó − '( ) 2 2 3 − 4 − 4 0 x f x x x 3 x 2. 2
Vậy bất phương trình có tập nghiệm là S = − ; − 2;+ ). 3 4 Bài 15.
Tính đạo hàm của hàm số sau. y = ( 3
x + 7x) 2x − . ĐS. 3
y ' = 8x + 20x x Lời giải 4 4 Ta có y ' = ( 2 3x + 7) 2x − + ( 3 x + 7x) 3 2 + = 8x + 20 . x 2 x x 2 −x − 3 4 2
x + 5x − 4x +12 Bài 16.
Tính đạo hàm của hàm số sau. y = . ĐS. y ' = . 3 x + 4x + 2 (x +4x+2)2 3 Lời giải 2 − x( 3
x + 4x + 2) − ( 2 −x − 3)( 2 3x + 4) 4 2
x + 5x − 4x +12 Ta có. y ' = ( = x + 4x + 2)2 (x +4x+2)2 3 3 2 3( 2 x +10x − 2) 3x − x +1 Bài 17.
Tính đạo hàm của hàm số sau. y = . ĐS. y ' = . x + 5 (x +5)2 Lời giải Tập xác định. D = \ − 5 .
(6x − )1(x +5)−( 2 3x − x + ) 1 3( 2 x +10x − 2) Ta có y ' = = ( x + 5) . 2 (x +5)2 Bài 18.
Tính đạo hàm của hàm số sau. y = (4 − 5x)( 2 − x + ) 1 .
ĐS. y ' = 20x −13 Lời giải Ta có 2
y = 10x −13x + 4.
Khi đó y ' = 20x −13. 98 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM x +1 2 − x Bài 19.
Tính đạo hàm của hàm số y = . ĐS. y ' = 2 x + 2 ( 2x +2) 2x +2 Lời giải x 2
x + 2 − ( x + ) 1 . 2 x + 2 − + x + 2 ( 2 2 x x) 2 − x y ' = = = 2 x + 2
( 2x +2) 2x +2 ( 2x +2) 2x +2 2 − 3x Bài 20. Cho hàm số y = . Tính y '( ) 1 . 2 x − x +1 Lời giải 3 − ( 2 x − x + )
1 − (2 − 3x)(2x − ) 2 1 3x − 4x −1 Ta có y ' = ( = x − x + ) . 2 1 (x − x+ )2 2 2 1 − Khi đó, y ( ) 2 ' 1 = = 2 − . 1 Vậy y '( ) 1 = 2. − Bài 21.
Tính đạo hàm của hàm số f ( x) = ( x − x + )( x + )13 2 2 3 2 1 . Đ 2
S. y = ( x + ) ( 2 ' 2 1
10x −14x +16). Lời giải
f ( x) = ( x − )( x + )3 + (x − x + ) ( x + )2 2 ' 2 2 2 1 2 3 .3 2 1 .2 = ( x + )2 (
x − )( x + )+ ( 2 2 1 2 2 2 1
6 x − 2x + 3) = ( x + )2 ( 2 2 1
10x −14x +16). 2 x + 3x + 2 Bài 22.
Tính đạo hàm của hàm số y = . ĐS. y ' =1. x +1 Lời giải Với x = 1.
− Hàm số đã cho không có đạo hàm. Với x 1
− , y = x + 2. Khi đố, y ' =1. x + f '(39) 1 Bài 23.
Cho hàm số f ( x) 50 15 = . Tính A = − . f "(4 ) 1 . 40 − x 2015 2 ĐS. A = 2014 − Lời giải 2015
Ta có. y '( x) = f ' 39 = 2015. 2 ( ) (4− x) − f ( x) 4030 " = f " 41 = 4030. 3 ( ) (40− x)
Khi đó, A =1− 2015 = 2 − 014. 4 2 12x 2x +1 Bài 24.
Tính đạo hàm của hàm số 5 y = 3x − + 2x +1 x ĐS. 4 15x + + 2 x + 3 ( ) x 6 x 2 x Lời giải Ta có. 99 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM y ' = (3x ) ' ' 4 5 − + ( 2x + )1 x )' 3 4 =15x +
.( x )' + (2x + )' 4 3 1 x + 2x +1 x 6 ( )( )' x 2 12x 2x +1 4 ( ) =15x + + 2 x + . 6 x 2 x Bài 25.
Tính đạo hàm của hàm số sau. 3 4 3 1. 3
y = 2x − 4 x − −1 ĐS. 2 6x − + x 2 2 x x 2 x − 2x − 3 2 x +10x − 7 2. y = ĐS. x + 5 (x +5)2 Lời giải 4 3 1. 2 y ' = 6x − + . 2 2 x x 2.
(x −2x−3)'(x+5)−(x+5)' 2
( 2x −2x−3) (2x−2)(x+5)−( 2x −2x−3) 2x +10x−7 y ' = = = ( x + 5) . 2 (x +5)2 (x +5)2 Bài 26.
Tính đạo hàm của các hàm số sau. 1. y = ( 3 x + )( 2 2 2 x + ) 1 . ĐS. 4 2
10x + 6x + 4x 2 5 − 3x − x 2 −x + 4x +1 2. y = . ĐS. x − 2 (x − 2)2 Lời giải ' ' 1. y = ( 3 x + ) ( 2 x + ) + ( 2 x + ) ( 3 x + ) 2 = x ( 2 x + ) + x( 3 ' 2 2 1 1 2 2 6 1 2 2x + 2) 4 2 4 4 2
= 6x + 6x + 4x + 4x =10x + 6x + 4x
(5−3x− x )'(x−2)−(x−2)' 2 ( 2
5 − 3x − x ) ( 3
− − 2x)(x − 2) − ( 2 5 − 3x − x ) 2. y ' = = ( x − 2)2 (x − 2)2 2 −x + 4x +1 = ( x − 2)2 x x 2 −x x + 3 x Bài 27.
Tính đạo hàm của các hàm số sau y = . ĐS. . 2 x −1 (x − )2 2 1 Lời giải Ta có. (x x)'(x − ) x x x
1 − (x x )(x − )' 3 1 ( 3 2 x − ) 2 2 2 1 − 2x x − − x 2 −x x + 3 2 2 2 x y ' = ( = = = x − ) . 2 1 (x − )2 1 (x − )2 1 (x − )2 2 2 2 2 1 Bài 28.
Tính đạo hàm của các hàm số sau. 2015 2014 2x +1 2x +1 1 1. y = . ĐS. 2015 . 3x +1 3x +1 (3x + )2 1 100 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM 2 2x − 4x + 6
2. y = ( − x) 2 1
x − 2x + 5. ĐS. − 2 x − 2x + 5 Lời giải 2014 ' 2014 2x +1 2x +1 2x +1 1 − 1. y ' = 2015 = 2015 3x +1 3x +1 3x +1 (3x + ) .2 1
2. y = ( − x)
x − x + − ( − x) ' ' 2 2 ' 1 2 5 1 x − 2x + 5 x − x − x +
= − x − 2x + 5 + (1− x) 2 1 2 4 6 2 = − 2 2 x − 2x + 5 x − 2x + 5 Bài 29.
Tính đạo hàm của các hàm số sau. 5 4 1. 4 3 y = x +
x − x − 5. ĐS. 3 2
5x + 4x −1 4 3 2 2x − 5x +1 2 2x + 8x −11 2. y = . ĐS. x + 2 (x + 2)2
3. y = (− x + x − )15 2 3 3 7 .
ĐS. − ( x − )(− x + x − )14 2 45 2 1 3 3 7 2 2x − 2x − 6
4. y = ( x − ) 2 5
x + 2x −1. ĐS. 2 x + 2x −1 Lời giải 1. 3 2
y ' = 5x + 4x −1.
(2x −5x+ )'1(x+2)−(2x −5x+ )1(x+2)' 2 2 2. y ' = ( x + 2)2
(4x −5)(x + 2)−( 2 2x − 5x + ) 2 1 2x + 8x −11 = = ( x + 2)2 (x + 2)2 14 ' 14 3. y = ( 2
− x + x − ) ( 2
− x + x − ) = − ( x − )( 2 ' 15 3 3 7 . 3 3 7 45 2 1 3
− x + 3x − 7) . x +1 2x − 2x − 6 4. y ' =
x + 2x −1 + ( x − 5) 2 2 . = . 2 2 x + 2x −1 x + 2x −1 Bài 30. Cho hàm số 3 2
y = x − 4x + 5 .
x Tìm tất cả các giá trị của x thỏa mãn y ' 0. ĐS 5 . x hoặc x 1 3 Lời giải Ta có. 2
y ' = 3x − 8x + 5. Khi đó 5 2
y ' 0 3x − 8x + 5 x
hoặc x 1. 3 3x + 2 1 − 1x + 21 Bài 31.
Tính đạo hàm của hàm số y = . ĐS. y ' = 2 x − 6x + 5
( 2x −6x+5) 2x −6x+5 Lời giải 101 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM Với mọi 2x − 6 2 ( )
3 x − 6x + 5 − .(3x + 2) − + − + x (− ) x x x ;1 (5;+) 2 2 6 5 11 21 , y ' = ( = x − x + )2 ( 2x −6x+5) 2 2 x − 6x + 5 6 5 2 3 Bài 32.
Cho hàm số f ( x) 2 = x −1 − 2 .
x Giải phương trình f '( x) = 0. ĐS. S = 3 Lời giải x 1 − x 1 − x 1 x 2 3
Ta có f '( x) = 0 − 2 = 0 x 1 x 0 x = . 2 2 − 3 x 1
2 x −1 = x 2 3 x = 3 4 Bài 33.
Giải bất phương trình y ' 0 biết y = x − 2 + . ĐS. S = (− ; 0)2;+) 2 x Lời giải 8 Ta có y ' = 1− . 3 x
Điều kiện x 0. 3 − Do đó 8 x 8 y ' 0 1− 0 0. 3 3 x x Bảng xét dấu
Dựa vào bảng xét dấu ta có. x (− ; 0)2;+). Vậy S = (− ; 0)2;+) 1 2 Bài 34.
Giải bất phương trình y ' 0 biết y = ( x − ) 1 2x +1. ĐS. S = ; 2 3 Lời giải ' − − ' x 1 3x 2
Ta có y ' = ( x − ) 1
2x +1 + ( x − ) ( )
1 2x +1 = 2x +1 + = . 2x +1 2x +1 x − − Khi đó x y + 2 3 2 3x 2 0 1 2 3 ' 0 0 x ; . 2x −1 0 1 2x 1 2 3 x 2 1 2 Vậy S = ; 2 3 Bài 35.
Tính đạo hàm của hàm số sau. y = ( − x )(x + )2 3 2 1 . ĐS. 4 3 2 y ' = 5
− x −8x − 3x + 4x + 4. Lời giải 102 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
Ta có y = ( − x )( x + )2 3 5 4 3 2 2 1
= −x − 2x − x + 2x + 4x + 2. 3 2
2x + x − 3x +1 4 3 2
2x + 4x +10x − 4 Bài 36.
Tính đạo hàm của hàm số sau. y = . ĐS. y ' = . 2 x + x +1 (x + x+ )2 2 1 Lời giải
Tập xác định. D = . ( 2
6x + 2x − 3)( 2 x + x + ) 1 + ( 3 2
2x + x − 3x + ) 1 (2x + ) 4 3 2 1
2x + 4x +10x − 4 Ta có y ' = ( = x + x + ) . 2 1 (x + x+ )2 2 2 1 1 Bài 37. Cho hàm số 3 3 y =
x − 2x − 12x − x . Tính y ' và giải phương trình y ' = 0 . 3 2 2 − − Đ 12 6x 6 3x S. 2 2
y ' = x − 2 − = x − 2 − , x = 2, x = − 2. 3 3 2 12x − 2x 12x − 2x Lời giải 2 2 12 − 6x 6 − 3x 2 2
y ' = x − 2 − = x − 2 − . 3 3 2 12x − 2x 12x − 2x Điều kiện. 3
12x − 2x 0. 2 6 − 3x x = 2 Ta có 2 2
y ' = 0 x − 2 −
= 0 x − 2 = 0 3 − x = − 2. 12x 2x
So sánh điều kiện, hai giá trị x đều thỏa mãn.
Vậy x = 2, x = − 2 Bài 38.
Viết phương trình tiếp tuyến của (C ) 4 2
: y = x − x + 3 tại điểm có hoành độ là 1 − . ĐS. y = 2 − x +1 Lời giải Ta có. 3 y ' = 4x − 2 . x x = 1
− y = 3; y x = y 1 − = 2 − 0 0 ( 0) ( ) Suy ra PTTT: y = 2 − (x + ) 1 + 3 = 2 − x +1. 2x +1 Bài 39.
Gọi (C ) là đồ thị của hàm số y =
. Viết phương trình tiếp tuyến của đồ thị (C ) , biết tiếp 2x −1
tuyến song song với đường thẳng d : y = 4 − x + 3 . ĐS. y = 4
− x −1; y = 4 − x + 7 Lời giải 1 4 − Với mọi x , y = . 2 (2x − )2 1 2a +1 Gọi A a ; là tiếp điểm. 2a −1 a =
Ta có. y(a) = − ( a − )2 0 4 2 1 =1 . a = 1
- a = 0 . Suy ra A(0; − )
1 và phương trình tiếp tuyến tương ứng là y − (− ) 1 = 4
− (x − 0) y = 4 − x −1(nhận).
- a =1. Suy ra A(1;3) và phương trình tiếp tuyến tương ứng là y − 3 = 4 − (x − ) 1 y = 4 − x + 7 103 (nhận). Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM x + 2 Bài 40. Cho hàm số y =
có đồ thị là (C ) . Viết phương trình tiếp tuyến của đồ thị (C ) , biết tiếp x −1 1 2 1 10
tuyến vuông góc với đường thẳng d : y = 3x + 2 . ĐS. y = − x − ; y = − x + 3 3 3 3 Lời giải 3 − Ta có y = ( , x 1. x − )2 1 a + 2 Gọi A a ; là tiếp điểm. a −1 Tiếp tuyến của
(C) tại A vuông góc với d khi và chỉ khi − = y(a) 3 a 4 .3 = 1 − .3 = 1 − a −1 = 9 . 2 ( )2 ( − = − a ) a 2 1 1 2 a = 2
− . Khi đó, A(−2;0) và phương trình tiếp tuyến tương ứng là y = − x − . 3 3 1 10
a = 4 . Khi đó, A(4; 2) và phương trình tiếp tuyến tương ứng là y = − x + . 3 3 Bài 41.
Cho đường cong (C) y = f (x) 3 2 : = 4
− x − 3x + 5x − 7 . Viết phương trình tiếp tuyến của (C ) biết 21
tiếp tuyến song song với d : y = −x .
ĐS. y = −x −12 ; y = −x − . 4 Lời giải Ta có 2 y = 1
− 2x − 6x + 5.
Gọi M (a ;b) (C ) . Suy ra hệ số góc của tiếp tuyến với (C ) tại tiếp điểm M là 2 k = 1
− 2a − 6a + 5. Do tiếp tuyến của (C ) song song với d : y = −x nên ta có a = 1 − b = 1 − 1 2 1
− 2a − 6a + 5 = 1 − 1 23 . a = b = − 2 4 Tại M ( 1; − − )
11 phương trình tiếp tuyến của (C ) là y = − ( x + )
1 −11 y = −x −12 . 1 23 Tại M ; −
phương trình tiếp tuyến của (C ) là 2 4 1 23 21 y = − x − − y = −x − . 2 4 4 21
Kết luận. Có hai tiếp tuyến là y = −x −11 và y = −x − . 4 Bài 42.
Cho hàm số y = f ( x) 3 2
= x − 5x + 2 có đồ thị (C ). Viết phương trình tiếp tuyến của đồ thị (C ) 67
biết tiếp tuyến song song với d : y = 3 − x − 7 . ĐS. y = 3 − x + . 27 Lời giải Ta có 2
y = 3x −10x .
Gọi M (a ;b) (C ) . Suy ra hệ số góc của tiếp tuyến với (C ) tại tiếp điểm M là 2
k = 3a −10a . 104
Do tiếp tuyến của (C ) song song với d : y = 3
− x − 7 nên ta có Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
a = 3 b = 1 − 6 2 3a −10a = 3 − 1 40 . a = b = 3 27
Tại M (3;−16) phương trình tiếp tuyến của (C ) là y = 3
− (x −3) −16 y = 3 − x − 7 (loại). 1 40 Tại M ;
phương trình tiếp tuyến của (C ) là 3 27 1 40 67 y = 3 − x − + y = 3 − x + . 3 27 27 67
Kết luận. Phương trình tiếp tuyến cần tìm là y = 3 − x + . 27 2x +1 Bài 43.
Viết phương trình tiếp tuyến của đồ thị hàm số y =
biết tiếp tuyến song song với đường x −1 1 13 1 1
thẳng () : x + 3y +1 = 0 .
ĐS. y = − x + ; y = − x + . 3 3 3 3 Lời giải 3 − Ta có y = ( . x − )2 1
Gọi M (a ;b) (C ) với a 1. Suy ra hệ số góc của tiếp tuyến với (C ) tại tiếp điểm M là 3 − k = ( . a − )2 1
Do tiếp tuyến của (C ) song song với () : x + 3y +1 = 0 nên ta có 3 − 1
a = 4 b = 3
= − a −1 = 9 . 2 ( )2 ( − = − = a ) a 2 b 1 1 3
Tại M (4;3) phương trình tiếp tuyến của (C ) là 1
y = − ( x − ) 1 13
4 + 3 y = − x + . 3 3 3 Tại M ( 2 − ; )
1 phương trình tiếp tuyến của (C ) là 1 y = − ( x + ) 1 1
2 +1 y = − x + . 3 3 3 1 13 1 1
Kết luận. Có hai tiếp tuyến là y = − x + và y = − x + . 3 3 3 3 Bài 44.
Viết phương trình tiếp tuyến của đồ thị hàm số 3 2
y = x − 5x + 2 , biết tiếp tuyến song song với
đường thẳng 3x + y + 7 = 0 . Đ 67 S. y = 3 − x + . 27 Lời giải 2
y = 3x −10x .
Gọi M ( x ; y là tiếp điểm. 0 0 )
Vì tiếp tuyến song song với đường thẳng 3x + y + 7 = 0 hay y = 3
− x − 7 nên hệ số góc của tiếp 105
tuyến tại M bằng 3 − . Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM x = 3
Ta có. y( x ) 0 2 = 3
− 3x −10x = 3 − 1 . 0 0 0 x = 0 3
Với x = 3 thì y = 16
− . Phương trình tiếp tuyến tại điểm M (3;−16) là. y = 3
− (x − 3) −16 hay 0 0 y = 3 − x − 7 (loại). 1 40 1 40 1 40 Với x = thì y =
. Phương trình tiếp tuyến tại điểm M ; là. y = 3 − x − + 0 2 0 27 3 27 3 27 67 hay y = 3 − x + . 27 67 Vậy y = 3 − x + . 27 2x −1 Bài 45. Cho hàm số y =
(C) . Viết phuwong trình tiếp tuyến của (C) biết tiếp tuyến song song −x + 2
với đường thẳng 3x − y −14 = 0 .
ĐS. y = 3x − 2 . Lời giải 3 y = ( . −x + 2)2
Gọi M ( x ; y là tiếp điểm. 0 0 )
Vì tiếp tuyến song song với đường thẳng 3x − y −14 = 0 hay y = 3x −14 nên hệ số góc của tiếp
tuyến tại M bằng 3 . 3 −x + 2 =1 x =1
Ta có. y( x ) = 3 = 3 −x + 2 =1 . 2 ( 0 )2 0 0 0 ( − + = − = −x + 2) x 2 1 x 3 0 0 0
Với x = 1 thì y = 1 . Phương trình tiếp tuyến tại điểm M (1 )
;1 là. y = 3( x − )
1 +1 hay y = 3x − 2 0 0 .
Với x = 3 thì y = 5
− . Phương trình tiếp tuyến tại điểm M (3;−5) là. y = 3(x − 3) − 5 hay 0 0
y = 3x −14 (loại).
Vậy y = 3x − 2 . Bài 46. Cho hàm số 3 2
y = −x + 3x − 3x + 2 có đồ thị (C ) . Viết phương trình tiếp tuyến d của đồ thị (C )
biết d vuông góc với đường thẳng : x − 3y − 3 = 0 . ĐS. y = 3
− x + 2 , y = 3 − x + 6 . Lời giải 1
Vì tiếp tuyến d vuông góc với : x − 3y − 3 = 0 hay y =
x −1 nên hệ số góc của tiếp tuyến 3 bằng 3 − .
Gọi M ( x ; y là tiếp điểm. 0 0 ) x = 2
Ta có. y( x ) 2 0 = 3
− 3x + 6x = 3 − . 0 0 0 x = 0 0
Với x = 0 thì y = 2 . Phương trình tiếp tuyến của đồ thị (C ) tại điểm A(0; 2) là. y = 3 − x + 2 0 0 . . Phương trình tiế = − −
Với x = 2 thì y = 0
p tuyến của đồ thị (C ) tại điểm A(2;0) là. y 3( x 2) 0 0 hay y = 3 − x + 6 . 106
Vậy có hai tiếp tuyến thỏa mãn yêu cầu đề Câu là y = 3
− x + 2 , y = 3 − x + 6 . Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM Bài 47. Cho hàm số 3 2
y = x + 2x −1 có đồ thị (C ) . Viết phương trình tiếp tuyến của đồ thị (C ) biết tiếp 31
tuyến song song với đường thẳng d : x + y − 3 = 0 .
ĐS. y = −x −1, y = −x − . 27 Lời giải
Vì tiếp tuyến song song với d : x + y − 3 = 0 hay y = −x + 3 nên hệ số góc của tiếp tuyến bằng 1 − .
Gọi M ( x ; y là tiếp điểm. 0 0 ) x = 1 −
Ta có. y( x ) 0 2 = 1
− 3x + 4x +1 = 0 1 . 0 0 0 x = − 0 3 Với x = 1
− thì y = 0 . Phương trình tiếp tuyến của đồ thị (C ) tại điểm A( 1; − 0) là. 0 0 y = − ( x + ) 1 . 1 22 1 22
Với x = − thì y = −
. Phương trình tiếp tuyến của đồ thị (C ) tại điểm A − ;− là. 0 3 0 27 3 27 1 22 31 y = − x + −
hay y = −x − . 3 27 27 31
Vậy có hai tiếp tuyến thỏa mãn yêu cầu đề Câu là y = −x −1, y = −x − . 27 − x Bài 48.
Cho hàm số y = f ( x) 1 3 =
có đồ thị (C ) . Viết phương trình tiếp tuyến của đồ thị (C ) biết x + 2
tiếp tuyến vuông góc với đường thẳng d : x − 7 y −1 = 0 . ĐS. y = 7
− x −3 và y = 7 − x −31. Lời giải 7 Ta có. y = − ( . x + 2)2 1 1
Vì tiếp tuyến vuông góc với d : x − 7 y −1 = 0 hay y = x −
nên hệ số góc của tiếp tuyến bằng 7 7 7 − .
Gọi M ( x ; y là tiếp điểm. 0 0 ) 7 x = 1 −
Ta có. y( x ) = 7 − − = 7 − x + 2 =1 . 2 ( 0 )2 0 0 ( = − x + 2) x 3 0 0 Với x = 1
− thì y = 4 . Phương trình tiếp tuyến của đồ thị (C ) tại điểm A(−1;4) là. 0 0 y = 7 − (x + ) 1 + 4 hay y = 7 − x −3 . Với x = 3 − thì y = 10
− . Phương trình tiếp tuyến của đồ thị (C ) tại điểm B( 3 − ;−10) là. 0 0 y = 7
− (x + 3) −10 hay y = 7
− x −31. Vậy có hai tiếp tuyến thỏa mãn yêu cầu đề Câu là y = 7
− x −3 và y = 7 − x −31. x − Bài 49.
Lập phương trình tiếp tuyến của đồ thị C y = f ( x) 2 : =
, biết tiếp tuyến song song với đường x −1
thẳng d : y = x + 2 .
ĐS. y = x − 2 . Lời giải 1
Ta có. f ( x) = . 107 (x − )2 1 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
Vì tiếp tuyến song song với d : y = x + 2 nên hệ số góc của tiếp tuyến bằng 1.
Gọi M ( x ; y là tiếp điểm. 0 0 ) 7 1 x = 2
Ta có. y( x ) = 7 − − =1 =1 x −1 =1 . 2 2 ( 0 )2 0 0 ( = x + 2) (x − ) x 0 0 1 0 0
Với x = 2 thì y = 0 . Phương trình tiếp tuyến của đồ thị (C ) tại điểm A(2;0) là. y = x − 2 . 0 0
Với x = 0 thì y = 2 . Phương trình tiếp tuyến của đồ thị (C ) tại điểm B (0; 2) là. y = x + 2 0 0 (loại).
Vậy y = x − 2 . Bài 50.
Viết phương trình tiếp tuyến của đồ thị hàm số (C ) 3 2
: y = x + x − 4x − 2 tại giao điểm của đồ thị
với đường thẳng x =1 .
ĐS. y = x − 5 . Lời giải Ta có 2
y = 3x + 2x − 4 .
Gọi M là giao điểm của đồ thị (C ) với đường thẳng x =1 . Suy ra tọa độ M (1; − 4) .
Hệ số góc của tiếp tuyến với (C ) tại tiếp điểm M là k = y( ) 1 = 1.
Vậy phương trình tiếp tuyến của (C ) tại điểm M là
y = x −1− 4 y = x − 5 .
Kết luận. Phương trình tiếp tuyến cần tìm là y = x − 5 . x −1 Bài 51. Cho hàm số y =
có đồ thị (C ) . Tiếp tuyến của đồ thị (C ) tạo với trục Ox , Oy tam giác x +1
vuông cân tại O . Viết phương trình tiếp tuyến đó. ĐS. y = x + 2 − 2 2 ; y = x + 2 + 2 2 . Lời giải 2 Ta có y = ( . x + )2 1 a −1 Gọi M a ;
(C) với a 1 − . a +1 a −1 Vì O
AB vuông cân tại O nên tiếp tuyến tại điểm M a;
(C) phải song song với đường a +1
phân giác y = x hoặc y = −x . Suy ra hệ số góc của tiếp tuyến của (C ) tại M bằng 1 hoặc 1 − . Khi đó 2 = (a+ ) 1 2 1 ( = − + a + )2 a 1 2 1 = 2 . 2 = − a = 1 − − 2 (a + ) 1 2 1 Với a = 1
− + 2 phương trình tiếp tuyến là y = x + 2 − 2 2 . Với a = 1
− − 2 phương trình tiếp tuyến là y = x + 2 + 2 2 .
Kết luận. Có hai tiếp tuyến là y = x + 2 − 2 2 và y = x + 2 + 2 2 . 2 Bài 52.
Tính đạo hàm của hàm số y = (x − 2)sin x + 2xcos x . ĐS. 2
y = x cos x Lời giải 108 Ta có y = ( 2
x − 2)sin x + 2x cos x Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM Suy ra y = ( 2 x − ) x + ( 2 2 .sin
x − 2)(sin x) + (2x) .cos x + 2 . x (cos x) = x x + ( 2 x − ) 2 2 sin
2 cos x + 2 cos x − 2x sin x = x cos x . Bài 53.
Tính đạo hàm của hàm số y = xsin 2x .
ĐS. y = sin 2x + 2x cos 2x Lời giải
Với mọi giá trị thực của x , y = sin 2x + 2x cos 2x . 1 1 Bài 54. Tính đạo hàm hàm số 2 y = sin 2x − cos 4x .
ĐS. y = 2sin 4x 2 4 Lời giải Với mọi x , 1 y = x ( x) 1 − (− x) 1 1 .2.sin 2 . sin 2 .4. sin 4 = .2.sin 2 .
x 2.cos 2x − .4.(−sin 4x) 2 4 2 4
sin 4x + sin 4x = 2sin 4x . Bài 55.
Tính đạo hàm của hàm số y = ( − x)3 2 3 2 tan . ĐS. y = − x ( 2 − x)( 2 12 tan 3 2 tan 1+ tan x) Lời giải 2 Ta có . y = ( 2 − x) ( 2 − x) = − x ( 2 − x)( 2 3 3 2 tan 3 2 tan 12 tan 3 2 tan 1+ tan x) .. Bài 56.
Tính đạo hàm của hàm số 3 y = tan 2x − . ĐS. 2 2 y = 6 tan 2x − 1+ tan 2x − 4 4 4 Lời giải Ta có 3 y = tan 2x − 4 Suy ra 2 2 2 y = 3 tan 2x − tan 2x − = 6 tan 2x − 1+ tan 2x − . 4 4 4 4 sin x
x cos x − 2 cos x Bài 57.
Tính đạo hàm y của hàm số y = . ĐS. y = . 2 x 3 x Lời giải Tập xác định D = \ 0 . 2 cos .
x x − 2x cos x
x cos x − 2cos x Ta có y = = . 4 3 x x x +1 2 Bài 58.
Tính đạo hàm của hàm số sau. y = tan . ĐS. y = x + 3 ( x + x + 3)2 1 2 cos x + 3 Lời giải x 3 −
Điều kiện. x +1 .
+ k (k ) x + 3 2 2 x +1 x + 3 (x +3)2 2 Ta có y = = = . x +1 x +1 x + cos cos ( x + 3)2 1 2 2 2 cos x + 3 x + 3 x + 3 109 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM x Bài 59.
Tính đạo hàm của hàm số sau. 2
y = sin 1+ x . ĐS. 2 y = cos 1+ x 2 1+ x Lời giải Tập xác định. D = . x Ta có y = ( 2 1+ x ) 2 2 cos 1+ x = cos 1+ x . 2 1+ x sin x 1 − Bài 60.
Tính đạo hàm của hàm số sau. y = . ĐS. y = . sin x − cos x
(sin x −cos x)2 Lời giải
cos x (sin x − cos x) − sin x (cos x + sin x) 1 − Ta có y = = ( .
sin x − cos x)2
(sin x −cos x)2 x 2 1 1− x Bài 61.
Tính đạo hàm của hàm số tan . ĐS. y = . . 2 x +1 x (x + )2 2 2 1 cos 2 x +1 Lời giải 2 2 2 1 x 1 x +1− 2x 1 1− x y = . = . = . . 2 x x +1 x ( 2x + )2 1 x ( 2 2 2 2 x + )2 1 cos cos cos 2 2 2 x +1 x +1 x +1 Bài 62.
Cho hàm số y = f ( x) 3 2
= cos 3x − 2 x . Tính f ( ) .
ĐS. f ( ) = 0 . Lời giải f ( x) 2 2 2 = − x − x x − x ( 2 3cos 3 2 .sin 3 2 . 3x − 2 x ) 6x − 2 2 2 2 = 3
− cos 3x − 2 x.sin 3x − 2 x. 2 2 3x − 2 x 4 Vậy f ( ) 2 = 3 − cos .sin. = 0 . 2 1 Bài 63.
Cho hàm số y = sin 2x − cot x − . Tính y − . ĐS. y − = . 3 3 3 3 Lời giải 1
Ta có y = 2 cos 2x + . 2 sin x − 3 Khi đó, 2 1 1 y − = 2cos − + = . 3 3 2 2 3 sin − 3 x Bài 64.
Tính đạo hàm của hàm số 2
y = sin x +1 . ĐS. 2 y = cos x +1. . 2 x +1 Lời giải 2x x 2 2 y = cos x +1. = cos x +1. . 2 2 2 x +1 x +1 3sin 2 1− 3x Bài 65.
Tính đạo hàm của hàm số 2 y = cos 1− 3x . ĐS. − 110 2 1− 3x Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM Lời giải Ta có y = ( 2 cos
1− 3x ) = 2cos 1−3x.(cos 1−3x ) = 2
− cos 1−3x.sin 1−3x.( 1−3x) 1 − = − − x − x ( − x) 3sin 2 1 3x 2 cos 1 3 .sin 1 3 . 1 3 = − 2 1− 3x 2 1− 3x Bài 66.
Tính đạo hàm của các hàm số sau 1. y = ( 2 4x − 3)cos x ĐS. x x − ( 2 8 cos 4x − 3)sin x 2. y = ( − x)5 2 4 sin 3 ĐS. − ( − x)4 2 15 4 sin 3 .sin 6x Lời giải 1. y = ( 2 x − ) x + ( 2 x − )( x) = x x − ( 2 4 3 cos 4 3 cos 8 cos
4x − 3)sin x . 2. y = ( − x)4 ( − x) = − ( − x)4 x x = − ( − x)4 2 2 2 2 5 4 sin 3 . 4 sin 3 5 4 sin 3 .2.sin 3 .3cos 3 15 4 sin 3 .sin 6x 2x + sin 2x 4 − xsin 2x Bài 67.
Tính đạo hàm của hàm số y = . ĐS. 1− cos 2x (1−cos2x)2 Lời giải Ta có (
2x + sin 2x) (1− cos 2x) − (2x + sin 2x)(1− cos 2x) y = (1−cos2x)2
(2+ 2cos2x)(1−cos2x)−2sin 2x(2x +sin 2x) − = 4x sin 2x = ( . 1− cos 2x)2 (1−cos2x)2 Bài 68.
Tính đạo hàm của các hàm số sau
1. y = (5sin x − 3)(3cos x − ) 1 .
ĐS. 15cos 2x −5cos x + 9sin x 3 3 cos x − sin x 2. y = ĐS. cos 2x cos x − sin x Lời giải
1. y = 5cos x (3cos x − )
1 − 3sin x (5sin x − 3) = 15cos 2x − 5cos x + 9sin x . 3 3 cos x − sin x 1 2. 2 2 y =
= cos x + cos xsin x + sin x =1+ sin 2x y = cos 2x . cos x − sin x 2 1 Bài 69.
Tính đạo hàm của hàm số y = x ( 2 tan
cos x + cot x) .
ĐS. y = cos x − 2 sin x Lời giải k Với mọi x
(k ), ta có y = sin x +cot x. 2 Do đó, 1 y = cos x − . 2 sin x sin x − cos x 2 Bài 70.
Tính đạo hàm của hàm số y = . ĐS. y = sin x + cos x (sin x + cos x)2 Lời giải 111 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM
(sin x +cos x)2 +(sin x −cos x)2 2 Với mọi x −
+ k (k ), y = = . 4 (sin x +cos x)2 (sin x +cos x)2 2 sin x 2sin 2x Bài 71.
Tính đạo hàm của hàm số y = . ĐS. y = 2 1+ cos x (1+cos x)2 2 Lời giải Với mọi x , 2 sin x cos x ( 2 1+ cos x) 2 + 2cos xsin . x sin x 2 sin x cos x ( 2 2
1+ sin x + cos x) 2 sin 2x y = ( = = 1+ cos x)2 (1+cos x)2 (1+cos x)2 2 2 2 cos x 2 − sin x Bài 72.
Tính đạo hàm của hàm số y = . ĐS. y = . 2 1+ sin x ( 2 1+ sin x) 2 1+ sin x Lời giải sin x cos x 2 −sin .
x 1+ sin x − cos . x −sin x( 2 1+ sin x) 2 2 − 1+ sin x cos x sin x y = = 2 1+ sin x ( 2 1+ sin x) 2 1+ sin x −sin x( 2 1+ sin x) − ( 2 1− sin x)sin x − = 2sin x ( = . 2 1+ sin x) 2 1+ sin x ( 2 1+ sin x) 2 1+ sin x Bài 73.
Tính đạo hàm của hàm số sau. 3
y = x sin (2x + ) 1 . ĐS. 2
y = sin (2x + ) 1 (sin (2x + )
1 + 6x cos (2x + ) 1 ) . Lời giải Ta có 3 y = ( x + ) 2 + x ( x + ) ( x + ) 2 sin 2 1 6 sin 2 1 cos 2 1 = sin (2x + ) 1 (sin (2x + )
1 + 6x cos (2x + ) 1 ) . 2 3 Bài 74.
Tính đạo hàm của hàm số sau. y = (x + )3 cos 1 . ĐS. y = 3 − (x + ) 1 sin ( x + ) 1 . Lời giải 3 3 2 3
Ta có y = −( x + ) 1 ) sin(x + ) 1 = 3 − (x + ) 1 sin ( x + ) 1 . 2 (1+ tan 2x)2 2 tan 2x Bài 75.
Tính đạo hàm của hàm số. y = . ĐS. y = . 2 1− tan 2x (1−tan 2x)2 2 Lời giải ( tan 2x)'( 2
1− tan 2x) − tan 2x ( 2 1− tan 2x) Ta có y = ( 1− tan 2x)2 2 2 ( 2 2
1− tan 2x − tan 2x 2 − tan 2x 2 ) 2 cos 2x cos 2x = (1−tan 2x)2 2 2 ( 2 1+ tan 2x)( 2 1− tan 2x) 2 + 4 tan 2x( 2 1+ tan 2x) 4 2 4 − + + =
2 2 tan 2x 4 tan 2x 4 tan 2x ( = 2 1− tan 2x)2 2 ( 2 1− tan 2x) 2 (1+ tan 2x)2 2 = . 112 (1−tan 2x)2 2 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM sin x − cos x Bài 76. Cho hàm số y =
. Tính y và chứng minh 2 y − tan x − =1 . cos x + sin x 4 ĐS. 2 y = 1+ tan x − . 4 Lời giải
(cos x +sin x)(cos x +sin x)−(sin x −cos x)(−sin x +cos x) y = (cos x +sin x)2 2 2 2 2
cos x + 2sin x cos x + sin x + sin x − 2sin x cos x + cos x = ( cos x + sin x)2 2 2 1 2 = = = = + − ( x cos x + sin x) 1 tan 2 2 2 4 cos 2 cos x x − − 4 4 Từ đó suy ra, 2 y − tan x − =1 (đpcm). 4 Bài 77.
Cho hàm số y = sin 2x + cos 2x +12 . Tính y và giải phương tình y = 2 . ĐS. y = 2 − 2 sin 2x − và x = k 4 2 Lời giải
Ta có y = 2 cos 2x − 2sin 2x = 2 − 2 sin 2x − . 4 Lại có 2x − = − + k2 x = k 1 4 4
y = 2 sin 2x − = −
x = k (k ) 4 2 x = + k 2 2x − = − + k2 2 4 4 3 sin x Bài 78. Cho hàm số y =
. Chứng minh rằng y = cos x − cos 2x . 1+ cos x Lời giải
Với mọi x + k 2 (k ) ,
3sin x cos x (1+ cos x) 2 + sin . x sin x
sin x 3cos x (1+ cos x) 2 2 3 + sin x y = = ( 1+ cos x)2 (1+cos x)2 Bài 79.
Cho hàm số y = f ( x) = (x + + x )10 2 1 . Chứng minh. y = y ( 2 100 1+ x ) + y x . Lời giải 10(x + 1+ x )10 2 x + + x
y = 10 (x + 1+ x ) (x + 1+ x ) =10(x + 1+ x ) 2 9 9 1 2 2 2 . = 2 1+ x 2 1+ x
(1+cos x)(1−cos x)( 2
2 cos x + 3cos x + ) 1
(1−cos x)(1+cos x)2 (2cos x + ) 1 = = (1+cos x)2 (1+cos x)2 = ( − x)( x + ) = x − ( 2 1 cos 2 cos 1 cos 2 cos x − )
1 = cos x − cos 2x y
+ x = (x+ + x )10 2 2 1 10 1 113 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM + + Đạ x x 1 x
o hàm hai vế, ta được y 1+ x + y =100(x + 1+ x ) 2 9 2 2 . 2 2 1+ x 1+ x y ( 2 1+ x ) + y x =100y (đpcm). x − 3 2 Bài 80. Cho hàm số y =
. Chứng minh. 2 ( y) = ( y − ) 1 .y . x + 4 Lời giải 7 y = ( x + 4)2 14( x + 4) 14 y = − = − ( . x + 4)4 (x + 4)3 2 98 Ta có. 2( y) = ( . x + 4)4 ( − − − − y − ) x 3 14 7 14 98 1 y = −1 . = = . x + 4 (x + 4) . 3 x + 4 ( x + 4)3 (x + 4)4
Từ đó suy ra điều phải chứng minh. Bài 81. Cho hàm số 2
y = sin x . Chứng minh rằng 2 y + y tan x + y − 2 = 0 . Lời giải
Ta có y = 2sin x (sin x) = 2sin x cos x = sin 2x Và y = ( x) 2 2 sin 2
= 2cos 2x = 2cos x − 2sin x . Do đó sin x 2 2 2
2y + y tan x + y − 2 = 2sin x + 2sin x cos . x
+ 2cos x − 2sin x − 2 cos x 2 2
= 2sin x + 2cos x − 2 = 0 Bài 82.
Cho hàm số y = x sin x . Chứng minh rằng xy − 2( y − sin x) + xy = 0 . Lời giải
Ta có y = sin x + x cos x y = cos x + cos x − x sin x = 2 cos x − x sin x .
Khi đó xy − ( y − x) 2 + xy = x x − ( x + x x − x) 2 2 sin sin 2 sin cos sin
+ 2x cos x − x sin x = 0 . Bài 83. Cho hàm số 2 y =
x + 2x . Chứng minh rằng 3 .
y y + y .y = x . Lời giải
Tập xác định. D = (−; − 2 0; + ) . x +1 Ta có y = . 2 x + 2x x +1 x +1 2 ( )( ) x + 2x − 2 + − Khi đó x 2x 1 y = = . 2 2 x + 2x x + 2x ( 2 x + 2x) 3 x +1 1 − Vậy 3 2 .
y y + y .y = x + 2x. + ( 2x + 2x .
= x +1−1 = x . 2 ) 2 x + 2x x + 2x ( 2 x + 2x) m Bài 84. Cho hàm số 2 2
y = sin x + (m +1)sin x + x + 2019
với m là tham số thuộc . Chứng minh 114
phương trình y ' = 0 luôn có nghiệm với mọi m . Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL
ĐẠI SỐ VÀ GIẢI TÍCH 11 – CHƯƠNG 5 - ĐẠO HÀM Lời giải Tập xác định. D = . 2mx
Ta có y ' = 2sin x o
c sx + (m +1) o
c sx + là hàm số liên tục trên .
Trường hợp 1. m = 0 ta có x = + k 2 c s o x = 0
y ' = 0 2sin x o c sx + o c sx = 0
1 x = − + k2 (k ) . sin x = − 6 2 7 x = + k2 6
Trường hợp 2. m 0 ta có y '(− ) = −m ; y '( ) = m . 2 2 Khi đó 2 y '(−
).y '( ) = −m 0 , m
0 nên phương trình y ' = 0 luôn có nghiệm trên 2 2 − ;
với mọi m 0 . 2 2
Kết luận. Vậy phương trình y ' = 0 luôn có nghiệm với mọi m . 115 Page
Tài liệu biên soạn và sưu tầm! Fb: ThayTrongDGL




