Cal1 Mid S22 - Calculus 1 | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố HCM
Cal1 Mid S22 - Calculus 1 | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố HCM được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Calculus 1 (MA001IU)
Trường: Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Thông tin :
Môn:
Trường:
Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh
Tác giả:
Tài liệu liên quan:
Preview text:
Calculus 1 Answer key for the Midterm Page 1 of 5
PART 1: MULTIPLE CHOICE QUESTIONS
No calculator is allowed in this part. x2023 − 1 1. The limit lim is x→1 x − 1 (A) ∞ (B) 2023 (C) 2021 (D) 2022 Answer: (B) xn − 1 f (x) − f (1) Generally, the limit lim = lim
= f ′(1) = n by the definition of derivative. The x→1 x − 1 x→1 x − 1
value of n can be n = 2021, n = 2023 or n = 2024 in some exam versions.
2. A bacteria culture initially contains 100 cells and grows at a rate proportional to its size, that is,
dP = kP, where k is a positive constant. After an hour the population has increased to 400. The dt
number of bacteria after t hours is (A) P(t) = 100e(ln4)t (C) P(t) = 300tet−1 + 100 (B) P(t) = 100 + 300t (D) P(t) = 300t2 + 100 Answer: (A)
3. If the point (−1,2) lies on the graph of y = f (x) then which point must lie on the graph of y = f −1(x)? 1 1 (A) (−1 1, −2) (D) (2, −1 . , ) (B) ( , −1) (C) ( ) 2 2 Answer: (D)
4. Which of the following is the inverse of f (x) = ln(x − 2) for x > 2? (A) f −1(x) = ex−2 1 (B) y = (C) f −1(x) = ex + 2 (D) f −1(x) = ex − 2 ln(x − 2) Answer: (C)
5. If x6 − 2 f f (x) f x2 − 2 for −1 f x f 1, then lim f (x) is x→0 (A) undefined (B) 2 (C) 0 (D) −2 Answer: (D)
6. Given a curve with equation 2x2 + xy − 4y3 = 10. The slope of the tangent line to this curve at the point (2, −1) is 1 7 (A) (B) 1 (C) (D) 2 2 10 Answer: (C)
7. The displacement s of a particle (in meters) at time t seconds is given by s(t) = t4 − 3t3 + 4t2 + 2t − 1.
The acceleration of the particle (in m/s2) at time t = 1 (s) is Calculus 1 Answer key for the Midterm Page 2 of 5 (A) 2 (B) 3 (C) 4 (D) None of the above Answer: (A)
8. If the side x of a cube (a cubical box) is increased by 3%, then the volume is increased approximately by (A) 0.03x (B) 0.09x3 (C) 0.06x (D) 8% Answer: (B)
(Note: V (x) = x3. Thus, dV = V ′(x)dx = 3x2dx = 0.09x3 with dx = 0.03x.) √
9. The cost C in dollars of producing x units of a product is C(x) = 4000 + 20 x + 10x + 0.01x2. At a
production level of 100 units, the marginal cost is (A) $4000 /unit (B) $12 /unit (C) $4300 /unit (D) $13 /unit Answer: (D)
(the marginal cost is C′(x) at x = 100 units).
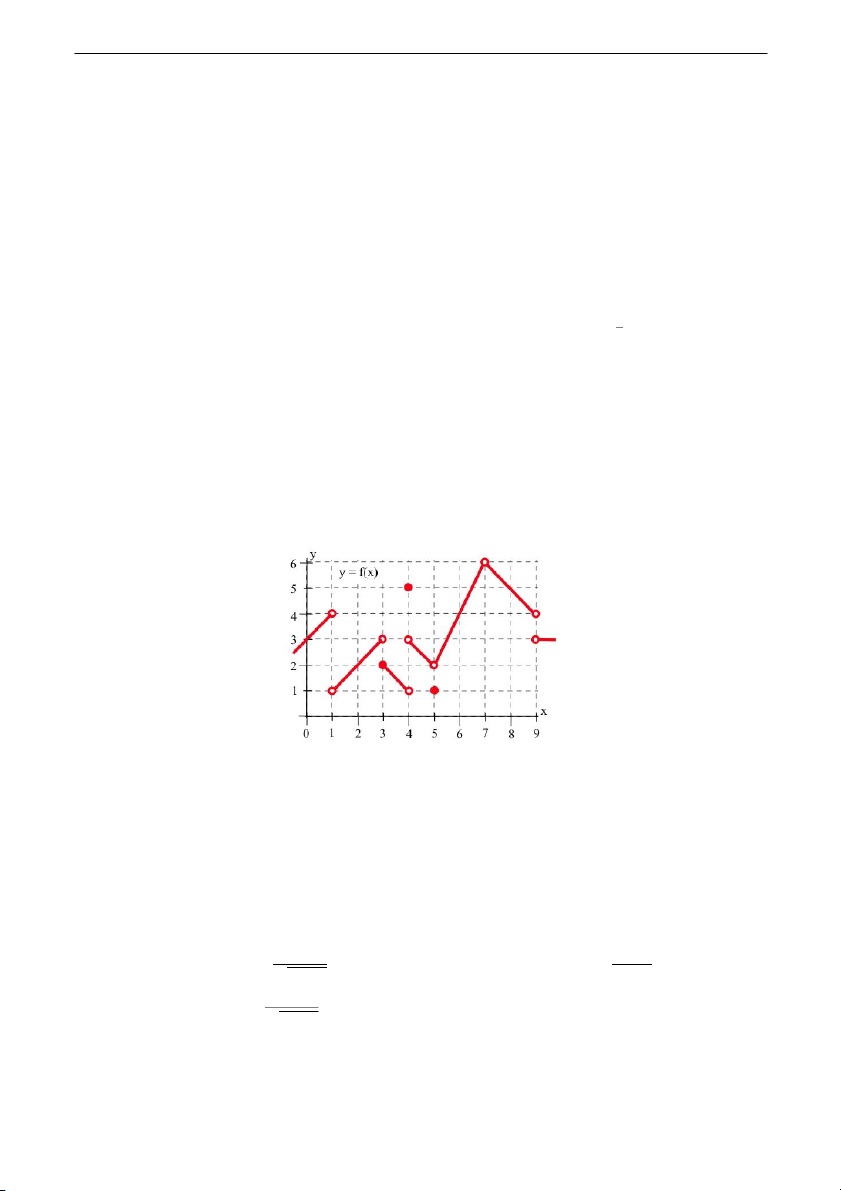
10. For the function f whose graph is given below. Find lim f (x) and lim f (x) x→1 x→5
(A) lim f (x) = 1 and lim f (x) = 2
(C) lim f (x) is undefined and lim f (x) = 2 x→1 x→5 x→1 x→5
(B) lim f (x) is undefined and lim f (x) = 1
(D) lim f (x) = 4 and lim f (x) = 2 x→1 x→5 x→1 x→5 Answer: (C)
11. The derivative of f (x) = x2 sin−1 x is x2 x2
(A) f ′(x) = 2x sin−1 x + √ (C) f ′(x) = 2x sin−1 x + 1 − x2 1 + x2 2x
(B) f ′(x) = x sin−1 x + √1−x2 (D) None of them Ans: (A) Calculus 1 Answer key for the Midterm Page 3 of 5
12. Consider the following piecewise function: x + 2 if x f 1 f (x) = x2 − 2x + 4 if 1 < x f 2 4 − x if x > 2.
(A) f is discontinuous at x = 1
(C) f is continuous at both x = 1 and x = 2
(B) f is discontinuous at x = 2 (D) None of these. Ans: (B) 13. Let g(x) = 6 + 4 f (x),
f (1) = 5 and f ′(1) = 1. Find g′(1). 1 1 2 (A) √ (B) √ (C) 0 (D) √ 2 26 2 26 26 Ans: (D) 4 (An answer in form of √
is also correct. Additionally, (A) and (B) are the same but the answer of 2 26 1 √ is incorrect). 2 26 |x + 2| 14. The value of lim is x→−2− x + 2 (A) 0 (B) 1 (C) −1 (D) undefined Ans: (C) |x + 2|
(Note: |x + 2| = −(x + 2) if x < −2. Therefore, = −1 if x < −2.) x + 2
15. A particle moves along a horizontal line with its displacement s(t) given by s = 1 + 10t − 5t2, where
s is measured in meters and t in seconds. At which time below is the particle moving forward? (A) t = 0.5 (B) t = 2 (C) t = 3 (D) t = 4 Ans: (A) √ √ 16. Let f (x) = 3 x and g(x) = x + 14. Find (g ◦ f )(8). √ (A) 3 (B) 2 (C) 4 (D) 14 Ans: C
17. Let f (x) = 1 + x + e3x. Find f −1(2). (A) −1 (B) 2 (C) 4 (D) 0 Ans: (D) (clearly, f (0) = 2.)
18. Suppose that f is continuous on [0,5] and the only solutions of the equation f (x) = 5 are x = 1 and x = 2. If f (3) = 4 then Calculus 1 Answer key for the Midterm Page 4 of 5 (A) f (4) < 5 (B) f (4) > 6 (C) f (4) > 5 (D) f (4) > 7 Answer: (A)
19. Let f (x) = x3 + 3x . Find f −1′ (4). 1 1 1 (A) (B) (C) (D) None of them 2 3 6 Ans: (C) 1 1 1
(By derivative of the inverse, f −1′ (4) = = = .) f ′( f −1(4)) f ′(1) 6
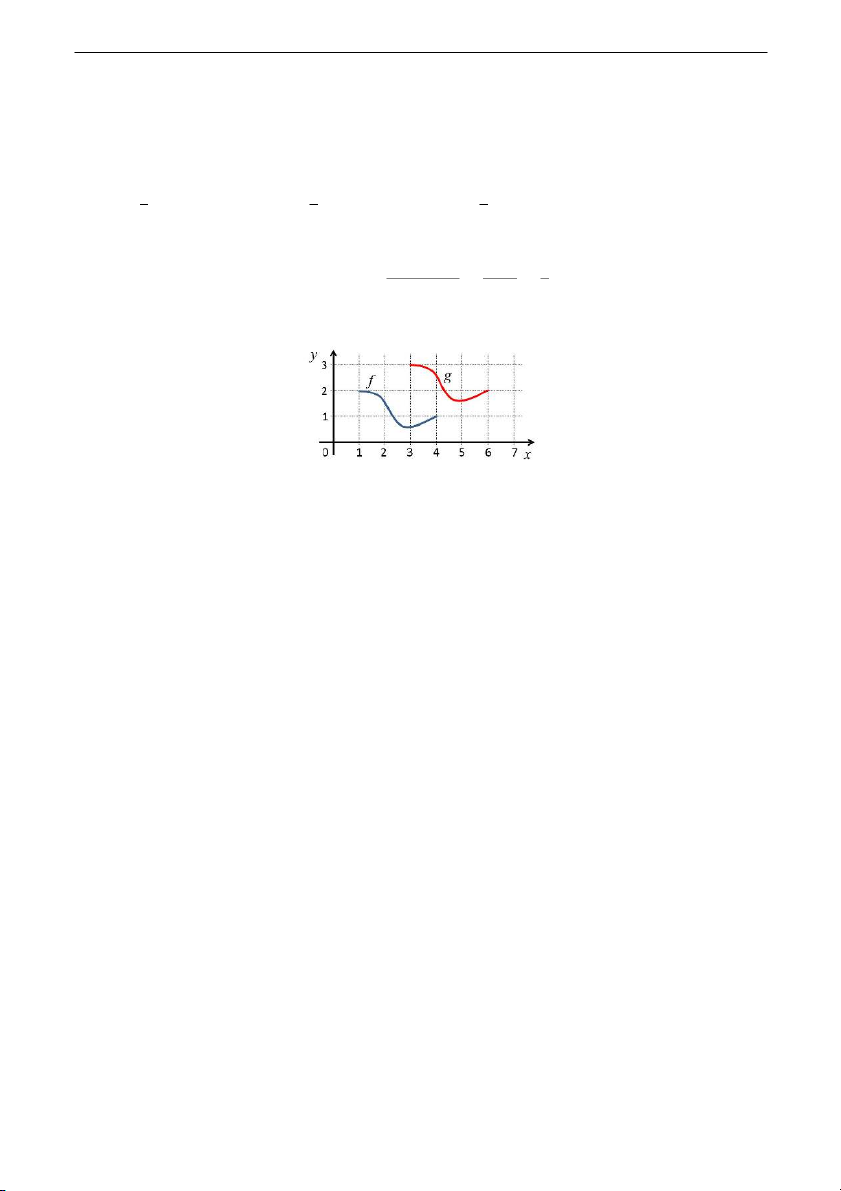
20. Consider the functions f and g shown in the figure. The relationship between these functions is: (A) g(x) = f (x + 1) − 2 (C) g(x) = f (x − 1) + 2 (B) g(x) = f (x + 2) + 1 (D) g(x) = f (x − 2) + 1 Ans: (D) —END OF PART 1— Calculus 1 Answer key for the Midterm Page 5 of 5 Answer key for Part 2 1 √ 1
1. Since f ′(x) = √ , the linearization of the function f (x) =
x at x = 16 is L(x) = 4 + (x − 16). 2 x 8 2. Given (x2 + 1) x4 − x2 + 15 f (x) = √ for x > −4. x + 4 2x 4x3 − 2x 1 1
(a) Use logarithmic differentiation: f ′(x) = f (x) × ( + 5 − ). x2 + 1 x4 − x2 + 1 2 x + 4 1 1 1
(b) The tangent line at (0, ) is y − = − (x − 0). 2 2 16 4x
3. (a) Differentiate 4x2 + y2 = 4 with respect to x, to obtain 8x + 2yy′ = 0 so y′ = − . y 4x y − xy′
(b) To obtain y′′, differentiating both sides of y′ = −
with respect to x, it yields: y′′ = −4 . y y2
Hence, at (0, −2) we have y′ = 0 and, therefore, y′′ = 2. -The end-