Cẩm nang tra cứu công thức, dạng toán và phương pháp giải Toán 9

Tài liệu “Cẩm nang tra cứu công thức, dạng toán và phương pháp giải Toán 9” gồm 59 trang. Mời bạn đọc đón xem!

33 17 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 9

Môn: Toán 9

Thông tin:

59 trang 2 tháng trước

Tác giả:

Profile Lê Phương
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Page 1
MỤC LỤC
PHẦN 1: SỔ TAY TRA CỨU KIẾN THỨC VÀ CÁC DẠNG BÀI .................................................... 3
Dạng 1: Tìm điều kiện xác định của biểu thức chứa dấu căn ............................................................... 3
Dạng 2: Tìm x, giải phương trình ............................................................................................................... 3
Dạng 3: Thực hiện các phép toán căn thức ............................................................................................... 4
Dạng 4: Tìm x nguyên để biểu thức sau rút gọn nguyên ....................................................................... 5
Dạng 5: Tìm giá trị lớn nhất, giá trị nhỏ nhất ......................................................................................... 5
Dạng 6: Hàm số bậc nhất và tính chất hàm số bậc nhất ....................................................................... 6
Dạng 7: Vẽ đồ thị hàm số bậc nhất ............................................................................................................ 6
Dạng 8: Vị trí tương đối của hai đường thẳng ......................................................................................... 7
Dạng 9: Lập phương trình đường thẳng ..................................................................................................... 7
Dạng 10: Tìm điểm cố định của hàm số
y f m
. Chứng minh đồ thị luôn đi qua một điểm cố định
(hay tìm điểm mà đồ thị luôn đi qua) ........................................................................................................ 9
Dạng 11: Tìm tham số m để ba đường thẳng đồng quy ........................................................................ 9
Dạng 12: Khoảng cách từ gốc tọa độ đến đường thẳng ....................................................................... 10
Dạng 13: Các tính chất của hàm số bậc hai
2
y ax
........................................................................... 11
Dạng 14: Vẽ đồ thị hàm số
2
y ax
.......................................................................................................... 12
Dạng 15: Bài toán tương giao của đường thẳng
y mx n
và Parabol
2
y ax
,
a
................. 13
Dạng 16: Giải bài toán bằng cách lập phương trình, hệ phương trình .............................................. 14
Dạng 17: Dự đoán số nghiệm của hệ phương trình .............................................................................. 19
Dạng 18: Giải hệ phương trình bằng phương pháp cộng, phương pháp thế .................................... 20
Dạng 19: Tìm hệ số
,
a b
biết hệ
1 1 1
2 2 2
a x b y c
a x b y c
có nghiệm là
0 0
;
x y
......................................... 21
Dạng 20: Tìm điều kiện để hệ phương trình có nghiệm duy nhất ...................................................... 22
Dạng 21: Giải phương trình bậc hai
2
0
ax bx c
............................................................................ 23
Dạng 22: Tìm
m
để phương trình có nghiệm
0
x
. ................................................................................. 24
Dạng 23: Tìm tham số m để phương trình bậc hai
2
0
ax bx c
có nghiệm, vô nghiệm, có hai
nghiệm phân biệt .......................................................................................................................................... 25
Dạng 24: Các bài toán liên quan đến các hệ thức Vi-et ....................................................................... 26
Dạng 25: Giải phương trình trùng phương
4 2
0
ax bx c
............................................................... 33
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Page 2
Dạng 26: Hệ thức lượng trong tam giác vuông ....................................................................................... 33
Dạng 27. Tỉ số lượng giác của góc nhọn .................................................................................................. 35
Dạng 28. Đường tròn ................................................................................................................................... 36
Dạng 29. Góc với Đường tròn .................................................................................................................... 39
Dạng 30: Các mô hình mẫu thường gặp trong đề thi tuyển sinh 9 lên 10 ........................................ 42
Dạng 31. Hình Học Không Gian ................................................................................................................ 47
PHỤ LỤC LỚP 8 ......................................................................................................................................... 51
1. Hình bình hành .................................................................................................................................... 51
2. Hình chữ nhật ....................................................................................................................................... 51
3. Hình thoi ............................................................................................................................................... 52
4. Hình vuông ............................................................................................................................................ 52
5. Công thức tính diện tích đa giác ...................................................................................................... 53
6. Các trường hợp đồng dạng của tam giác ......................................................................................... 53
7. Chứng minh hai góc bằng nhau ........................................................................................................ 54
8. Chứng minh hai đoạn thẳng bằng nhau .......................................................................................... 54
9. Chứng minh hai đường thẳng song song ......................................................................................... 55
10. Chứng minh hai đường thẳng vuông góc....................................................................................... 55
11. Chứng minh ba đường thẳng đồng quy ......................................................................................... 55
12. Chứng minh hai tam giác bằng nhau ............................................................................................. 56
13. Chứng minh đẳng thức hình học .................................................................................................... 56
14. Các bài toán tính toán độ dài cạnh, độ lớn góc ........................................................................... 56
15. Phương pháp chứng minh ba điểm thẳng hàng. .......................................................................... 56
16. Bảy hằng đẳng thức đáng nhớ ........................................................................................................ 57
16. Cách giải t phương trình bậc nhất 1 ẩn { Học sinh mất gốc tối thiểu phải nắm được cái này
trước khi học toán} .................................................................................................................................. 57
17. Cách giải bất phương trình bậc nhất 1 ẩn { Học sinh mất gốc tối thiểu phải nắm được cái này
trước khi học toán} .................................................................................................................................. 58
18. Nhân đơn thức với đa thức .............................................................................................................. 59
19. Nhân đa thức với đa thức ................................................................................................................ 59
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Page 3
PHẦN 1: SỔ TAY TRA CỨU KIẾN THỨC VÀ CÁC DẠNG BÀI
Dạng 1: Tìm điều kiện xác định của biểu thức chứa dấu căn
Phương pháp Ví dụ và lời giải
A
có nghĩa (xác định) khi
0
A
Ví dụ 1: Tìm điều kiện để
3 2
x
có nghĩa (xác
định).
Lời giải
2
x
xác định khi
2
3 2 0 3 2
3
x x x
1
A
có nghĩa (xác định) khi
0
A
Ví dụ 2: Tìm điều kiện để
1
5 2
x
có nghĩa (xác
định).
Lời giải
1
5 2
x
xác định khi
5
5 2 0 2 5
2
x x x
A
B
có nghĩa (xác định) khi
0
B
Ví dụ 3: Tìm điều kiện để
4 1
3 6
x
x
xác định.
Lời giải
4 1
3 6
x
x
xác định khi
3 6 0 3 6 2
x x x
Dạng 2: Tìm x, giải phương trình
Phương pháp Ví dụ và lời giải
2 2
A B A B
Hệ quả:
2
, 0
x a x a a
Ví dụ 1: Tìm
x
biết
2
1 16
x
Lời giải
2
1 4 5
1 16
31 4
x x
x
xx
Ví dụ 2: Tìm
x
biết
2
9.
x
Lời giải
2
9 3
x x
2
0
B
A B
A B
Ví dụ 3: Tìm
x
biết
a)
2
x
; b)
3 1 2
x
Lời giải
a)
2 4
x x
b)
2
5
1 2 3 1 2 3 5
3
x x x x
0B
BA
A B hay A B
Ví dụ 4: Giải phương trình
2
4 4 5
x x
Lời giải
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Page 4
2
2
524 4 5 2 5
xx x x
72 5
32 5
xx
xx
Dạng 3: Thực hiện các phép toán căn thức
2
nÕu A 0
nÕu A < 0
A
AA
A
Ví dụ 1: Tính
2
81 9 9
Ví dụ 2: Tính
2
3 1313131
Ví dụ 3: Tính
2
3 13 14 2 3
.
AB A B
(Với
0; 0
A B
)
Ví dụ 1: Tính
49.25 49 25 7.5 35
.
Ví dụ 2: Tính
810 40 81 4 100 81 4 100 9 2 10 180
.
A A
B
B
(Với
0; 0
A B
)
Ví dụ 1: Tính
25 25 5
121 11
121
.
Ví dụ 2: Tính
80 80
16 4
5
5
.
2
BAA B
(Với
0
B
)
Ví dụ 1: Tính
2
20 4 5 2 5 2 5
2
A BBA
(Với
0; 0
A B
)
Ví dụ 1:
2
3 7 3 7 63
2
A BBA
(Với
0; 0
A B
)
Ví dụ 1: Tính
2
2 3 2 3 12
.
1
A
AB
B B
(Với
0; 0
A B
)
Ví dụ 1:
2
2 2.3 2.3 6
3 3.3 3
3
.
A A B
B
B
(Với
0
B
)
Ví dụ 1:
5 5 3 5 3
3
3 3 3
.
2
A
C
A B
A B
(Với
2
0; A B
A
)
Ví dụ 1:
10 10( 3 1) 10( 3 1)
5( 3 1)
3 1
3 1 ( 3 1)( 3 1)
.
Ví dụ 2:
20.( 1)20( 1)20
5( 1)
5 1
11 ( 1)(5 5 )
55
5
5
.
BAC
C
A B
A B
(Với
0; 0; A B
A B
)
Ví dụ 1:
6 6( 5 3) 6( 5 3)
3( 5 3)
5 3
5 3 ( 5 3)( 5 3)
.
Ví dụ 2:
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Page 5
)
7 7( ) 7( )
7(
3 2
( )( )2
3 2 3 2
3 2
3 2 3 2 3
.
3
3
3
3
A A A
Ví dụ :
3 3
3
27 3 3
Dạng 4: Tìm x nguyên để biểu thức sau rút gọn nguyên
Phương pháp Ví dụ và lời giải
Bước 1: Tìm điều kiện xác định (thường đề bài
đã cho hoặc đã được xác định ở câu trước)
Bước 2: Thực hiện phép chia biểu thức về dạng
a
A f x
g x
(Bước này quan sát dưới mẫu, phân tích tử
theo mẫu các em nhé!!!)
Ví dụ 1: Tìm
x
nguyên để
4
1
x
A
x
nguyên
Lời giải
Điều kiện:
x
Ta có:
34 1 3
1
1 1 1
x x
A
x x x
A nguyên khi
1
x
là ước của 3
1 1 0
1 1 2( ) 0
4
1 3 4( )
1 3 2
xx
x
x
x loaix
xx
Dạng 5: Tìm giá trị lớn nhất, giá trị nhỏ nhất
Phương pháp Ví dụ và lời giải
Giả sử cho
2
A ax bx c
ta cần biến đổi về
dạng
2
A a x m n
Lúc đó:
*
A n
nếu
0
a
. Lúc đó
A
nhỏ nhất bằng
n
khi
x m
*
A n
nếu
0
a
Lúc đó
A
lớn nhất bằng
n
khi
x m
Ví dụ 1: Tìm giá trị nhỏ nhất của
A x x
Lời giải
Điều kiện:
x
Ta có
2
2
2
1 1 3
2. .
2 2 4
1 3 3
2 4 4
A x x x x
x
Vậy,
A
nhỏ nhất bằng
3
4
khi
1 1 1
0
2 2 4
x xx
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Page 6
Ví dụ 2: Tìm giá trị lớn nhất của
2
2 4 9
A x x
Lời giải
Ta có
2 2
2
2 4 9 2 2 1 11
2 1 11 11
A x x x x
x
Vậy,
A
lớn nhất bằng
11
khi
1
x
Dạng 6: Hàm số bậc nhất và tính chất hàm số bậc nhất
Phương pháp Ví dụ và lời giải
Hàm số
y ax b
là hàm số
bậc nhất nếu
0
a
Ví dụ 1: Tìm m để hàm số
2 1 5
y m x
là hàm số bậc nhất.
Lời giải
Hàm số
2 1 5
y m x
là hàm số bậc nhất khi
1
2 1 0
2
m m
.
Cho hàm số bậc nhất:
y ax b
* Hàm số đồng biến trên
khi
0
a
* Hàm số nghịch biến trên
khi
0
a
.
Ví dụ 2: Cho hàm số bậc nhất
2 6 9
y m x
. Tìm m để
hàm số đồng biến và nghịch biến trên
.
Lời giải
* Hàm số đồng biến khi
2 6 0 2 6 3
m m m
{chia số
âm nhớ đổi dấu bất phương trình các em nhé}
* Hàm số nghịch biến khi
2 6 0 2 6 3
m m m
2 6 0 2 6 3
m m m
{chia số âm nhớ đổi dấu bất phương trình các em nhé}
Dạng 7: Vẽ đồ thị hàm số bậc nhất
Phương pháp Ví dụ và lời giải
Để vẽ đồ thị hàm số bậc nhất
, 0
y ax b a
ta
lấy 2 điểm mà đồ thị đi qua, rồi vẽ đường thẳng đi
qua hai điểm đó ( thường lấy giao của đồ thị với hai
trục
, )
Ox Oy
Bảng giá trị
0
0
x y b
b
y x
a
Ví dụ 1: Vẽ đồ thị hàm số
2 4
y x
Lời giải
Bảng giá trị
Đồ thị
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Page 7
Chú ý:
* Đồ thi
y ax
đi qua hai điểm có toạ độ
(0;0)
và
(1; )
a
.
* Đường thằng
x a
song song với
Oy
cắt
Ox
tại
a
.
* Đường thằng
y b
song song với
Ox
cắt
Oy
tai
b
.
Dạng 8: Vị trí tương đối của hai đường thẳng
Nếu bài toán cho hàm bậc nhất, các em phải tìm điều kiện cho
a
Nếu bài toán không cho hàm số bậc nhất, ta không phải tìm điều kiện
a
Phương pháp Ví dụ và lời giải
Nếu hai đường thẳng biểu diễn dưới dạng
1 1
y a x b
và
2 2
y a x b
* Cắt nhau khi
1 2
a a
* Song song khi
1 2
1 2
a a
b b
* Vuông góc khi
1 2
1
a a
* Trùng nhau khi
1 2
1 2
a a
b b
Ví dụ 1: Cho hai đường thẳng có phương trình
1
: 2 1 5
d y m x
và
2
: 3 4
d y x m
Tìm giá trị m trong các trường hợp sau
1
)
a d
cắt
2
d
;
b)
1
d
song song
2
d
;
c)
1
d
vuông góc
2
d
;
Lời giải
1
)
a d
cắt
2
d
khi
4
2 1 3 3 3 1
3
m m m
1
)
b d
song song
2
d
khi
2
2 1 3
2
5
5 4
4
m
m
m
m
m
c)
1
d
vuông góc
2
d
khi
1 1
2 1 . 3 1 2 1
3 3
m m m
Dạng 9: Lập phương trình đường thẳng
Phương pháp Ví dụ và lời giải
Bài toán 1: Lập phương trình đường thẳng
:
d y ax b
đi qua
1 1
,
A x y
và có hệ số góc
k
.
Ví dụ 1: Lập phương trình đường thẳng
:
d y ax b
đi qua điểm
3; 4
A
và có hệ
số góc
5
k
Lời giải
Đường thẳng
:
d y ax b
đi qua điểm
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Page 8
Vì đường thẳng là
y ax b
có hệ số góc
k
nên
.
a k
Mặt
khác, đường thẳng
d
đi qua
1 1
,
A x y
nên thay tọa độ A
vào đường thẳng để tìm b.
3; 4
A
nên
. 3 4 3 4
a b a b
(*)
Mặt khác, đường thẳng
:
d y ax b
có hệ số
góc
5
k
nên nên
5
a
. Thay
5
a
vào
phương trình (*) ta được
3.5 4 11
b b
Vậy
: 5 11
d y x
Bài toán 2: Lập phương trình đường thẳng
:
d y ax b
đi qua
1 1
,
A x y
và song song
1
:
d y mx n
.
Đường thẳng
:
d y ax b
đi qua điểm
1 1
;
A x y
nên
1 1
ax b y
(*)
Mặt khác, đường thẳng
:
d y ax b
song song với
đường thẳng
1
:
d y mx n
nên
,
a m b n
.
Thay
a m
vào phương trình (*) ta tìm được b
Ví dụ 2: Lập phương trình đường thẳng
:
d y ax b
đi qua điểm
3; 4
A
và song
song với đường thẳng
1
: 4 5
d y x
Lời giải
Đường thẳng
:
d y ax b
đi qua điểm
3; 4
A
nên
. 3 4 3 4
a b a b
(*)
Mặt khác, đường thẳng
:
d y ax b
song
song với đường thẳng
1
: 4 5
d y x
nên
4, 5
a b
. Thay
4
a
vào phương
trình (*) ta được
3.4 4 8
b b
Vậy
: 4 8
d y x
Bài toán 3: Lập phương trình đường thẳng
:
d y ax b
đi qua
1 1
,
A x y
và vuông góc
1
:
d y mx n
.
Đường thẳng
:
d y ax b
đi qua
điểm
1 1
;
A x y
nên
1 1
ax b y
(*)
Mặt khác, đường
thẳng
:
d y ax b
vuông góc với đường
thẳng
1
:
d y mx n
nên
1
. 1a m a
m
. Thay
1
a
m
vào phương trình (*) ta tìm được b
Ví dụ 3: Lập phương trình đường thẳng
:
d y ax b
đi qua điểm
3; 4
A
và vuông
góc với đường thẳng
1
: 4 5
d y x
Lời giải
Đường thẳng
:
d y ax b
đi qua điểm
3; 4
A
nên
. 3 4 3 4
a b a b
(*)
Mặt khác, đường thẳng
:
d y ax b
vuông
góc với đường thẳng
1
: 4 5
d y x
nên
1
.4 1
4
a a
. Thay
1
4
a
vào
phương trình (*) ta được
1 3 21
3. 4 4
4 4 4
b b
Vậy
1 21
:
4 4
d y x
Bài toán 4: Lập phương trình đường thẳng
Ví dụ 4: Lập phương trình đường thẳng
:
d y ax b
đi qua điểm
3; 4
A
và
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Page 9
:
d y ax b
đi qua hai điểm
1 1 2 2
, ; ,
A x y B x y
Vì đường thẳng
:
d y ax b
đi qua điểm
1 1
,
A x y
nên
1 1
ax b y
Vì đường thẳng
:
d y ax b
đi qua điểm
2 2
,
B x y
nên
1 2
ax b y
Ta có hệ phương trình:
1 1
2 2
ax b y
ax b y
Giải hệ ta được
,
a b
1;2
B
Lời giải
Đường thẳng
:
d y ax b
đi qua điểm
3; 4
A
nên
. 3 4 3 4
a b a b
Đường thẳng
:
d y ax b
đi qua điểm
1;2
B
nên
. 1 2 2
a b a b
Ta có hệ phương trình:
3 4 3
2 5
a b a
a b b
.
Vậy
: 3 5
d y x
Dạng 10: Tìm điểm cố định của hàm số
y f m
. Chứng minh đồ thị luôn đi qua một điểm
cố định (hay tìm điểm mà đồ thị luôn đi qua)
Phương pháp Ví dụ và lời giải
Bước 1. Chuyển
( , )
y f x m
về dạng
( , ) - 0
f x m y
.
Bước 2. Nhóm các số chứa m lại với nhau:
. ( ) ( , ) 0
m f x g x y
.
Bước 3: Gọi
0 0
I(x , y )
là điểm cố định , suy
ra
00
00 0
?( ) 0
?( , ) 0
xf x
yg x y
.
Suy ra điểm cố định là I.
Ví dụ 1: Chứng minh rằng hàm số
3 1 2 6
y m x m
luôn đi qua một điểm cố đinh
Lời giải
Ta có:
3 1 2 6 3 1 2 6 0
3 2 6 0 3 2 6 0
3 2 6 0
y m x m m x m y
mx x m y mx m x y
m x x y
Gọi
0 0
I(x , y )
là điểm cố định mà hàm số đi qua
Lúc đó:
0 0 0
3 2 6 0
m x x y
với mọi m
0
0
0 0
0
2
2 03
3
206 0
3
x
x
x y
y
Vậy, hàm số luôn đi qua điểm cố định
2 20
;
3 3
I
Dạng 11: Tìm tham số m để ba đường thẳng đồng quy
Phương pháp Ví dụ và lời giải
Bước 1: Gọi
;
I x y
là giao điểm của 2 đường
Ví dụ 1: Tìm tham số m để ba đường thẳng sau
đồng quy
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Page 10
thẳng (2 đường thẳng không chứa m). Tọa độ
I là nghiệm của hệ phương trình.
Bước 2: Vì 3 đường thẳng đồng quy nên thay
tọa độ I vào đường thẳng còn lại, ta sẽ tìm
được m
1 2 3
: 2 3; : 1; : 2 1
d y x d y x d y m x m
Lời giải
Gọi
;
I x y
là giao điểm của 2 đường thẳng. Tọa
độ của I là nghiệm của hệ phương trình
2
2 32 3
2 5
3
;
3 3
511
3
x
x yy x
I
x yy x
y
Vì 3 đường thẳng đồng quy nên
5 2
2 1 . 7
3 3
m mm
Dạng 12: Khoảng cách từ gốc tọa độ đến đường thẳng
Phương pháp Ví dụ và lời giải
Để tính khoảng cách từ điểm
0;0
O
đến một
đường thẳng, ta tìm giao điểm của đường thẳng
với hai trục
,
Ox Oy
là A,B. Từ
O
kẻ
OH AB
rồi tính
OH
dựa vào tam giác vuông
OAB
:
2 2 2
1 1 1
OH OA OB
.
Ví dụ 1: Cho hàm số :
1
y x 1
2
(d).
Tính khoảng cách từ gốc
O
của hệ trục tọa độ
đến đường thẳng (d).
Lời giải
Kẻ
OH
vuông góc với (d) tại
H
. Khi đó
OH
là khoảng cách từ
O
đến đường thẳng (d) (hình
9).
Trong tam giác vuông
OAB
, ta có :
2 2 2 2 2
1 1 1 1 1 5
OH OA OB 1 2 4
Từ đó suy ra:
2
2 54
OHOH
55
.
Vậy khoảng cách từ
O
đến
(d)
là
2 5
5
.
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Page 11
Với các bài toán tìm điều kiện để khoảng cách
lớn nhất, nhỏ nhất:
Xét
0
a
. Tìm giao điểm của đồ thị với 2 trục
tọa độ và tính khoảng cách.
Xét
0
a
. Tìm giao điểm của đồ thị với 2 trục
tọa đô và tính khoảng cách. Sau khi tính được
khoảng cách ta đi tìm m MIN, MAX của biểu
thức khoảng cách.
Ví dụ 2. Cho hàm số
y mx 3( d)
. Tìm
m
để
khoảng cách từ gốc tọa độ
O
đến đường thẳng
(d)
là lớn nhất.
Giải
Trường hơp 1. Xét
m 0
.
Khi
m 0
thì
(d)
có phương trình
0. 3 3 hay 3.
y x y
Đồ thị hàm số
y 3
là đường thẳng song song
với trục hoành và cắt trục tung tại điểm có
tung độ bằng 3 nên khoảng cách từ
O
đến (d)
bằng 3 .
Trường hợp 2. Xét
m 0
.
Khi đó
(d)
:
y mx 3
luôn đi qua điểm
A(0;3)
nằm trên trục tung. Kẻ
OH
vuông góc với
(d)
tại
H
.
Khi đó
OH
là khoảng cách từ
O
đến đường
thẩng
(d)
.
Ta có
OH OA
hay
OH 3
(dấu " = " không
xảy ra vì
m 0
nền
H
không trùng A).
Do đó
OH 3
.
Kết hợp hai trường hợp ta có khi
m 0
thì
khoảng cách từ
O
đến đường thẳng
(d) là lớn nhất.
Dạng 13: Các tính chất của hàm số bậc hai
2
y ax
Phương pháp Ví dụ và lời giải
Hàm số
2
0
y ax a
xác định với mọi
x
.
* Nếu
0
a
thì hàm số đồng biến khi
0
x
,
nghịch biến khi
0
x
.
* Nếu
0
a
thì hàm số đồng biến khi
x
và
nghịch biến khi
0
x
Ví dụ 1. Cho hàm số
2
y (3 m 2)x
với
2
m
3
.
a) Tìm điều kiện của
m
để hàm số đồng biến
khi
0
x
;
b) Tìm điều kiện của
m
để hàm số nghịch biền
khi
0
x .
Lời giải
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Page 12
* Hàm số đạt GTNN bằng 0 khi
0
a
.
* Hàm số đạt GTLN bằng 0 khi
0
a
.
a)
2
y (3 m 2)x
đồng biến khi
x 0
có điều
kiện là
3 m 2 0
2
3
m
.
b)
2
y (3 m 2)x
nghịch biến khi
x 0
có điều
kiện là
2
3 m 2 0 m
3
.
* Để tính
0
f x
thay
0
x x
vào
y f x
.
* Để kiểm tra điểm
;
M a b
có thuộc đồ thị
hàm số
y f x
ta thay
,
x a y b
vào đồ thị
nếu thõa mãn thì
;
M a b
thuộc đồ thị và
ngược lại.
Ví dụ 2: Cho hàm số
2
y 2x
a) Tính giá trị của hàm số tại
0 0
2, 1
x x
b) Điểm
4;2
M
có thuộc đồ thị hàm số hay
không?
Lời giải
a) Khi
2
0
2
0
2 2.2 8,
1 2. 1 2
x y
x y
b) Với
2
4 2. 4 32 2
x y
nên điểm
4;2
M
không thuộc đồ thị hàm số đã cho
Tìm m để điểm
;
A A
A x y
thuộc đồ thị hàm số
2
y ax
Ta cần thay tọa độ điểm A vào hàm số, giải
phương trình (hoặc tính) để tìm giá trị m
Ví dụ 3. Cho Parabol
2
1
y x
4
. Xác định giá
trị của
m
để điểm
A( 2; m)
thuộc Parabol
Lời giải
Điểm
A
thuộc Parabol thì ta
có
2
1 1
: m ( 2)
4 2
.
Dạng 14: Vẽ đồ thị hàm số
2
y ax
Phương pháp Ví dụ và lời giải
Bước 1: Kẻ bảng giá trị (lấy ít nhất 5 điểm)
Bước 2: Nhận xét đồ thị hàm số là parabol nhận
trục
Oy
là trục đối xứng, đi qua 5 điểm (ở bước
1) rồi vẽ
Ví dụ 1: Vẽ đồ thị hàm số
2
1
y x
3
.
Lời giải
Bảng giá trị
Đồ thị
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Page 13
Dạng 15: Bài toán tương giao của đường thẳng
y mx n
và Parabol
2
y ax
,
a
Phương pháp Ví dụ và lời giải
Xét hoành độ giao điểm của 2 đồ thị thỏa mãn
phương trình:
2
ax mx n
Đưa phương trình về dạng:
2
0 1
ax mx n
a) Để hai đồ thị tiếp xúc nhau (có duy nhất 1
điểm chung):
Để hai đồ thị tiếp xúc nhau thì phương trình
(1) có nghiệm kép:
0
hoặc
' 0
Từ đó tìm được m.
Ví dụ 1: Cho hàm số
2
1
2
y x
có đồ thị
( )
P
và đường thẳng
( ) : 2 5.
d y x
Tìm
,
m n
để
đường thẳng
( ) :
y mx n
song song với
đường thẳng
( )
d
và có duy nhất một điểm
chung với đồ thị
( ).
P
Lời giải
( )
và
( )
d
song song nhau khi và chỉ khi
2
m
và
5
n
Hoành độ giao điểm của
( )
và
( )
P
là nghiệm
của phương trình
2 2
1 1
2 2 0 (*).
2 2
x x n x x n
( )
và
( )
P
có duy nhất một điểm chung khi và
chỉ khi
(*)
có nghiệm
kép
' 0 4 2 0 2
x n
thỏa mãn
điều kiện
5.
n
Vậy
2
m
và
2.
n
b) Để hai đồ cắt nhau tại hai điểm phân biệt
Để hai đồ cắt nhau tại hai điểm phân biệt thì
phương trình (1) có hai nghiệm phân biệt
0
hoặc
' 0
.
Từ đó tìm được m.
c) Để hai đồ thị không cắt nhau
Để hai đồ thị không cắt nhau thì phương trình
Ví dụ 2: Cho Parabol
2
:
P y x
và đường
thẳng
: 1.
d y mx m
Tìm
m
để
d
cắt
P
tại
hai điểm phân biệt có hoành độ
1 2
,
x x
.
Lời giải
Xét phương trình hoành độ giao điểm của
d
và
:
P
2 2
1 1 0 *
x mx m x mx m
Có
2 2
2
4.1. 1 4 4 2
m m m m m
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Page 14
(1) vô nghiệm
0
hoặc
' 0
. Từ đó tìm
được m.
D
cắt
P
tại hai điểm phân biệt
phương
trình
*
có hai nghiệm phân biệt
2
0 2 0 2
m m
Dạng 16: Giải bài toán bằng cách lập phương trình, hệ phương trình
PHƯƠNG PHÁP CHUNG
Bước 1: Lập phương trình - Hệ phương trình.
- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
- Biểu diễn các đại lượng chưa biết khác theo ẩn và các đại lượng đã biết.
- Lập phương trình, hệ phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình - Hệ phương trình.
Bước 3: Kết luận.
Kiểm tra xem trong các nghiệm của phương trình, hệ phương trình, nghiệm nào thỏa mãn điều
kiện của ẩn, nghiệm nào không, rồi kết luận.
Phương pháp Ví dụ và lời giải
Bài toán 1: Dạng toán cấu tạo số
* Gọi số có hai chữ số cần tìm là:
xy
.
Điều kiện:
, ,0 9;0 9.
x y N x y
* Gọi số có ba chữ số cần tìm là:
xyz
.
Điều kiện:
, , ,0 9;0 , 9.
x y z N x y z
Sau đó sử dụng các chú ý sau để lập
phương trình:
Số có hai chữ số có dạng:
10
xy x y
.
Số có ba chữ số có dạng:
100 10
xyz x y z
.
Ví dụ: Tìm hai số biết rằng tổng của hai số đó bằng 17
đơn vị. Nếu số thứ nhất tăng thêm 3 đơn vị, số thứ hai
tăng thêm 2 đơn vị thì tích của chúng bằng 105 đơn vị.
Lời giải
Gọi số thứ nhất là
x
, số thứ hai là
y
.
Theo để bài, tổng của hai số đó bằng 17 đơn vị ta có
phương trình :
17
x y
(1)
Só thứ nhất tăng thêm 3 đơn vị, số thứ hai tăng thêm 2
đơn vị thì tích của chúng bằng 105 đơn vị ta có phương
trình
( 3)( 2) 105
x y
Từ (1), (2) ta có hệ phương trình :
17
( 3)( 2) 105
x y
x y
2
16 48 0.
x x
$
Giải phương trình ta được
1
12
x (thoả mãn),
2
4
x
(thoả mãn).
Vậy nếu số thứ nhất là 12 thì số thứ hai là 5 ; nếu số thứ
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Page 15
nhất là 4 thì số thứ hai là 13 .
Bài toán 2: Dạng toán làm chung -
làm riêng
Gọi thời gian người thứ nhất làm
một mình xong công việc là
x
, thời
gian người thứ hai làm một mình
xong công việc là
y
thì :
1 giờ người thứ nhất làm được
1
x
(công việc),
1 giờ người thứ hai làm được
1
y
công
việc
1 giờ cả hai người làm được
1 1
x y
(công việc)
Ví dụ 1: Hai công nhân cùng làm một công việc trong
18 h
thì xong. Nếu người thứ nhất là
6 h
và người thứ hai
làm
12 h
thì chỉ hoàn thành
50%
công việc. Hỏi nếu làm
riêng thì mổi người hoàn thành công viêc đó trong bao
lâu?
Lời giải
Gọi thời gian người thứ nhất làm một mình hoàn thành
công việc là
x
(giờ,
0
x
); người thứ hai làm một mình
hoàn thành công việc là
(giờ,
y 0
).
Trong
1 h
người thứ nhầt làm được
1
x
công việc, người
thứ hai làm được
1
y
công việc.
Hai người làm chung
18 h
thì xong, ta có phương trình :
1 1 1
18
x y
Nếu người thứ nhât làm trong
6 h
và người thứ hai làm
trong
12 h
thì hoàn thành
50%
công việc, ta có phương
trình :
6 12
50%
x y
Ta được hệ phương trình:
1 1 1
18
6 12
50%.
x y
x y
Giải hệ phương trình ta được
x 36
:
y 36
thoả mãn
điều kiện.
Vậy nếu làm riêng thì người thứ nhất hoàn thành công
việc trong
36 h
và người thứ hai hoàn thành công việc
trong 36h.
Bài toán 3: Dạng Toán Chuyển
Động
Gọi S là quãng đường đi, v là vận
tốc, t là thời gian đi, ta có:
S v t
.
Ví dụ 1: Hai ô tô cùng khởi hành từ
A
đến
B
cách nhau
560 km
. Vận tốc ô tô (II) hơn vận tốc ồ tô (I) là
10 km / h
nên đã đến B sớm hơn ô tô (I) là 1 giờ. Tính vận tốc mỗi
xe.
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Page 16
Vận tốc ca nô xuôi dòng nước =
Vận tốc thực của ca nô + Vận tốc
dòng nước
Vận tốc ca nô ngược dòng nước =
Vận tốc thực của ca nô - Vận tốc
dòng nước.
Vận tốc ca nô xuôi - vận tốc ca nô
ngược = 2 vận tốc dòng nước
Vận tốc bèo trôi chính là vận tốc
dòng nước.
Lời giải
Gọi vận tôc ô tô (I) là
( / , 0)
x km h x
.
Khi đó vận tốc ô tô (II) là
10( km / h)
x
.
Thời gian ô tô (
I)
đi từ
A
đển
B
là
560
x
(giờ).
Thời gian ô tô (II) đi từ
A
đến
B
là
560
x 10
(giờ).
Theo để bài, xe ô tô (II) đến
B
sớm hơn xe ô tô (I) là 1
giờ nên ta có phương trình
2
560 560
1
10
560( 10) 560 ( 10)
10 5600 0
x x
x x x x
x x
Phương trình có nghiệm:
1
5 75 80
x (loại) ;
2
5 75 70 (chon).
x
Vậy vận tốc ô tô (I) là
70( km / h)
.
Vận tốc ô tô (II) là
70 10 80( km / h)
.
Ví dụ 3. Một tàu thuỷ chạy trên khúc sông dài
120 km
.
Cả đi lẫn về mát 6 giờ 45 phút. Tính vận tốc tàu thuỷ khi
nước yên lạng biết vận tốc của dòng nước là
4 km / h
.
Giải.
Gọi vận tốc của tàu thuỷ khi nước yên lặng là
( / , 4)
x km h x
.
Suy ra: Vạn tóc của tàu thuỷ khi xuôi dòng là
4( km / h)
x .
Vận tốc của tàu thuỷ khi ngược dòng là
4( km / h)
x
.
Thời gian tàu thuỷ đi xuôi dòng
120 km
là
120
4
x
(giờ).
Thời gian tàu thuỷ đi ngược dòng
120 km
là
120
4
x
(giờ).
Theo đề bài, thời gian cả đi lẫn vể mất 6 giờ 45 phút (
3
6
4
giờ).
Ta có phương trình
120 120 3
6
4 4 4
x x
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Page 17
2
27
1449 3204)4)(4) (4) 120(120(
4
x x x x x x
Phương trình có nghiệm là:
1
160 164 4
9 9
x
(loại) ;
2
160 164
36
9
x
.
Vậy, vận tốc tàu thuỷ khi nước yên lặng là
36 km / h
.
Bài toán 4:
Hai vật chuyển động
trên 1 đường tròn:
- Nếu chuyển động ngược chiều, khi
gặp nhau thì
1 2
Chu vi 2
S S R
- Nếu chuyển động cùng chiều, khi
gặp nhau thì
1 2
S S
Chu vi 2
R
Ví dụ: Hai vật chuyển động đều trên một con đường tròn
đường kính
20 cm
, xuất phát cùng một lúc, từ cùng một
điểm. Nếu chuyển động cùng chiều thì cứ 20 giây chúng
lại gặp nhau. Nếu chuyển động ngược chiểu thì cứ sau 4
giây chúng lại gặp nhau. Tính vận tốc của mỗi vật.
Lời giải
Gọi vận tốc của vật thứ nhất là
( cm / s)
x
, vận tốc của vật
thứ hai là
( cm / s)
y
Giả sử vật thứ nhất đi nhanh hơn vật thứ hai.
Điều kiện
0
x y
.
Chu vi vòng tròn là : 20.π (cm)
Quãng đường vật thứ nhất đi được trong 20 s là
20 (cm)
Quãng đường vật thứ hai đi được trong 20s là
20y(cm)
Khi chuyển động cùng chiều, cứ 20 giây chúng lại gặp
nhau, nghĩa là quãng đường 2 vật đi được trong 20 giây
chênh lệch nhau đúng bằng 1 vòng tròn. Nên ta có phương
trình:
20 20 20x y
(1).
Quãng đường vật thứ nhất đi được trong
4 s
là
4 (cm)
Quãng đường vật thứ hai đi được trong
4 s
là
4y(cm)
Khi chuyển động ngược chiều, cứ 4 giây chúng lại gặp
nhau, nghĩa là tổng quãng đường hai vật đi được trong 4
giây là đúng 1 vòng tròn nên ta có phương trình:
4 4 20x y
(2)
Từ (1) và (2) ta có hệ phương trình
20 20 20 3
4 4 20 2
x y x
x y y
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Page 18
Vậy vận tốc của hai vật lần lượt là
3
và
2
.
Bài toán 5 : Hai vật chuyển động
trên một đường thẳng AB:
Chuyển động ngược chiều, xuất
phát cùng lúc khi gặp nhau thì
quãng đường hai vật đi được là AB,
tức là
1 2
t v t v AB
.
Ví dụ 1: Hai khách du lịch xuất phát đồng thời từ hai
thành phố A và B cách nhau
53
km
. Họ đi ngược chiều và
gặp nhau sau
2
h
. Hỏi vận tốc của mỗi người, biết rằng
khi gặp nhau người thứ hai đi được nhiều hơn người thứ
nhất
3
km
.
Lời giải
Gọi
( / )
x km h
là vận tốc của người thứ nhất đi từ thành
phố A đến thành phố B
( 0)
x
( / )
y km h
là vận tốc của người thứ hai đi từ thành phố B
đến thành phố A
( 0)
y
Quãng đường đi được của người thứ nhất trong
2
h
:
2 ( )
x km
Quãng đường đi được của người thứ hai trong
2
h
:
2 ( )
y km
Người thứ hai đi nhiều hơn người thứ nhất
3
km
2 2 3
y x
Hai người đi ngược chiều nhau trên quãng đường
53
km
,
gặp nhau sau
2
h
2 2 53
x y
Giải hệ phương trình:
2.14 3
2 2 32 2 3
12,5
2
4 562 2 53
14
y xy x
x
yx y
y
Vậy vận tốc của người thứ nhất là
12,5 ( / )
km h
, vận tốc
của người thứ hai là
14 ( / )
km h
Bài toán 6 : Bài toán có liên quan
yếu tố hình học
Sau khi gọi ẩn số, các em cần sử
dụng các kiến thức cơ bản sau để
thiết lập phương trình hoặc hệ
phương trình :
Diện tích hình chữ nhật có hai kích
thước a ; b là S =ab
Chu vi hình chữ nhật là :
2( )
P a b
Diện tích tam giác là
1
2
S
. đáy.
Ví dụ 1: Một thửa ruộng hình chữ nhật, nếu tăng chiểu
dài thêm
2 m
, chiều rộng thêm
3 m
thì diện tích tăng
thêm
2
100 m
. Nếu giảm chiều dài và chiều rộng đi
2 m
thì
diện tích giảm đi
2
68 m
. Tính diện tích của thửa ruộng đó.
Lời giải
Gọi chiếu dài thửa ruộng là
( , 0)
x m x
và chiều rộng là
( , 0)
y m y .
Nếu tăng chiểu dài thêm
2 m
, chiều rộng thêm
3 m
thì
diện tích tăng thêm
2
100 m
.
Ta có phương trình:
( 2) ( 3) 100
x y xy
(1).
Nếu giảm chiều dài và chiểu rộng đi
2 m
thì diện tích
giảm đi
2
68 m
.
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Page 19
chiều cao
Diện tích tam giác vuông có hai cạnh
góc vuông a ;b là :
2
ab
S
Thể tích hình lập phương :
3
a
Thể tích hình hộp : a.b.c
Diện tích hình thang :
(daylon+day be)
2
S Chieucao
Diện tích hình vuông :
2
a
.
Chu vi hình vuông :
4
a
Ta có phương trình:
( 2) ( 2) 68
x y xy
(2).
Từ (1), (2) ta có hệ phương trình :
3 2 94( 2)( 3) 100
2 2 72.( 2)( 2) 68
x yx y xy
x yx y xy
Giải hệ phương trình ta được :
22
14
x
y
(thoả mãn điểu
kiện).
Vạy diện tích thửa ruộng là
2
22 14 308 m
.
Bài toán 7 : Bài toán năng suất
làm việc
Lập
bảng
Năng
suất
Khối
lượng
công
việc
Thời
gian
Theo kế
hoạch
Thực tế
Công thức sử dụng :
Khối lượng = năng suất lao động x
thời gian
Ví dụ 1: Một công nhân dự định làm 70 sản phẩm trong
thời gian quy định. Nhưng do áp dụng kĩ thuật nên đã
tăng năng suất thêm 5 sản phẩm mỗi giờ. Do đó không
những hoàn thành kế hoạch trước thời hạn 40 phút mà
còn vượt mức 10 sản phảm. Tính năng suất dự định.
Lời giải
Gọi năng suấ dự định là x (sản phảm/ giờ,
*
x
N
) ;
Thời gian dự định làm 70 sản phẩm là
70
x
(giờ);
Thời gian thực tế làm 80 sản phảm với năng suất
5
x
(sản phẩm/ giờ) là
80
5
x
(giờ).
Theo để bài, cóng nhân hoàn thành trước kể hoạch 40
phút (=
2
3
giờ). Ta có phương trình
2
70 80 2
20 525 0
5 3
x x
x x
.
Giải ra, ta có :
1
15
x (thoả mãn),
2
35
x (không thoả
mãn). Vậy năng suât dự định là 15 sản phẩm/giờ.
Dạng 17: Dự đoán số nghiệm của hệ phương trình
Phương pháp Ví dụ và lời giải
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Page 20
Để dự đoán số nghiệm của hệ
1 1 1
2 2 2
1
2
a x b y c
a x b y c
+ Bước 1: Chuyển phương trình (1) về dạng
y ax b
+ Bước 1: Chuyển phương trình (2) về dạng
y mx n
+ Bước 3: Xét vị trí tương đối của hai đường thẳng
(Xem lại dạng 7)
Ví dụ 1: Đoán nhận số nghiệm của
mỗi hệ phương trình sau, giải thích vì
sao:
a)
2
3 3 2
x y
x y
;b)
3 2 1
6 4 0
x y
x y
Lời giải
a) (I):
2
3 3 2
x y
x y
Xét (d):
2
x y
hay (d):
2
y x
có
1; 2
a b
.
(d')
3 3 2
x y
hay
2
:
3
d y x
có
2
1;
3
a b
Ta có: ;a a b b
(d) // (d')
Hệ (I) vô nghiệm.
b) (II):
3 2 1
6 4 0
x y
x y
Xét: (d):
3 2 1
x y
hay (d):
3 1 3 1
y x có a ; b
2 2 2 2
: 6 4 0
d x y
hay
:
d
3 3
y x có a ; b 0
2 2
Ta có: ;a a b b
(d)
/ /
d
Hệ (II) vô nghiệm.
Dạng 18: Giải hệ phương trình bằng phương pháp cộng, phương pháp thế
Phương pháp Ví dụ và lời giải
Bài toán 1: Giải hệ phương trình
1 1 1
2 2 2
a x b y c
a x b y c
bằng phương pháp thế
Rút
x
hoặc
y
từ một phương trình rồi thế vào
Ví dụ: Giải hệ phương trình
3 2 4
2 5
x y
x y
Lời giải
| 1/59
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9 MỤC LỤC
PHẦN 1: SỔ TAY TRA CỨU KIẾN THỨC VÀ CÁC DẠNG BÀI .................................................... 3
Dạng 1: Tìm điều kiện xác định của biểu thức chứa dấu căn ............................................................... 3
Dạng 2: Tìm x, giải phương trình ............................................................................................................... 3
Dạng 3: Thực hiện các phép toán căn thức ............................................................................................... 4
Dạng 4: Tìm x nguyên để biểu thức sau rút gọn nguyên ....................................................................... 5
Dạng 5: Tìm giá trị lớn nhất, giá trị nhỏ nhất ......................................................................................... 5
Dạng 6: Hàm số bậc nhất và tính chất hàm số bậc nhất ....................................................................... 6
Dạng 7: Vẽ đồ thị hàm số bậc nhất ............................................................................................................ 6
Dạng 8: Vị trí tương đối của hai đường thẳng ......................................................................................... 7
Dạng 9: Lập phương trình đường thẳng ..................................................................................................... 7
Dạng 10: Tìm điểm cố định của hàm số y f m . Chứng minh đồ thị luôn đi qua một điểm cố định
(hay tìm điểm mà đồ thị luôn đi qua) ........................................................................................................ 9
Dạng 11: Tìm tham số m để ba đường thẳng đồng quy ........................................................................ 9
Dạng 12: Khoảng cách từ gốc tọa độ đến đường thẳng ....................................................................... 10
Dạng 13: Các tính chất của hàm số bậc hai 2
y ax ........................................................................... 11
Dạng 14: Vẽ đồ thị hàm số 2
y ax .......................................................................................................... 12
Dạng 15: Bài toán tương giao của đường thẳng y mx n và Parabol 2
y ax , a  0 ................. 13
Dạng 16: Giải bài toán bằng cách lập phương trình, hệ phương trình .............................................. 14
Dạng 17: Dự đoán số nghiệm của hệ phương trình .............................................................................. 19
Dạng 18: Giải hệ phương trình bằng phương pháp cộng, phương pháp thế .................................... 20
a x b y c
Dạng 19: Tìm hệ số a, b biết hệ 1 1 1 
có nghiệm là  x ; y ......................................... 21 0 0  a x   b y c  2 2 2
Dạng 20: Tìm điều kiện để hệ phương trình có nghiệm duy nhất ...................................................... 22
Dạng 21: Giải phương trình bậc hai 2
ax bx c  0 ............................................................................ 23
Dạng 22: Tìm m để phương trình có nghiệm x . ................................................................................. 24 0
Dạng 23: Tìm tham số m để phương trình bậc hai 2
ax bx c  0 có nghiệm, vô nghiệm, có hai
nghiệm phân biệt .......................................................................................................................................... 25
Dạng 24: Các bài toán liên quan đến các hệ thức Vi-et ....................................................................... 26
Dạng 25: Giải phương trình trùng phương 4 2
ax bx c  0 ............................................................... 33 Page 1
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Dạng 26: Hệ thức lượng trong tam giác vuông ....................................................................................... 33
Dạng 27. Tỉ số lượng giác của góc nhọn .................................................................................................. 35
Dạng 28. Đường tròn ................................................................................................................................... 36
Dạng 29. Góc với Đường tròn .................................................................................................................... 39
Dạng 30: Các mô hình mẫu thường gặp trong đề thi tuyển sinh 9 lên 10 ........................................ 42
Dạng 31. Hình Học Không Gian ................................................................................................................ 47
PHỤ LỤC LỚP 8 ......................................................................................................................................... 51
1. Hình bình hành .................................................................................................................................... 51
2. Hình chữ nhật ....................................................................................................................................... 51
3. Hình thoi ............................................................................................................................................... 52
4. Hình vuông ............................................................................................................................................ 52
5. Công thức tính diện tích đa giác ...................................................................................................... 53
6. Các trường hợp đồng dạng của tam giác ......................................................................................... 53
7. Chứng minh hai góc bằng nhau ........................................................................................................ 54
8. Chứng minh hai đoạn thẳng bằng nhau .......................................................................................... 54
9. Chứng minh hai đường thẳng song song ......................................................................................... 55
10. Chứng minh hai đường thẳng vuông góc....................................................................................... 55
11. Chứng minh ba đường thẳng đồng quy ......................................................................................... 55
12. Chứng minh hai tam giác bằng nhau ............................................................................................. 56
13. Chứng minh đẳng thức hình học .................................................................................................... 56
14. Các bài toán tính toán độ dài cạnh, độ lớn góc ........................................................................... 56
15. Phương pháp chứng minh ba điểm thẳng hàng. .......................................................................... 56
16. Bảy hằng đẳng thức đáng nhớ ........................................................................................................ 57
16. Cách giải t phương trình bậc nhất 1 ẩn { Học sinh mất gốc tối thiểu phải nắm được cái này
trước khi học toán} .................................................................................................................................. 57
17. Cách giải bất phương trình bậc nhất 1 ẩn { Học sinh mất gốc tối thiểu phải nắm được cái này
trước khi học toán} .................................................................................................................................. 58
18. Nhân đơn thức với đa thức .............................................................................................................. 59
19. Nhân đa thức với đa thức ................................................................................................................ 59 Page 2
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
PHẦN 1: SỔ TAY TRA CỨU KIẾN THỨC VÀ CÁC DẠNG BÀI
Dạng 1: Tìm điều kiện xác định của biểu thức chứa dấu căn Phương pháp Ví dụ và lời giải 
A có nghĩa (xác định) khi A  0
Ví dụ 1: Tìm điều kiện để 3x  2 có nghĩa (xác định). Lời giải 2
x  2 xác định khi 3x  2  0  3x  2  x  3 1 1 
có nghĩa (xác định) khi A  0
Ví dụ 2: Tìm điều kiện để có nghĩa (xác A 5  2x định). Lời giải 1 5
xác định khi 5  2x  0  2
x  5  x  5  2x 2 A 4x 1 
có nghĩa (xác định) khi B  0
Ví dụ 3: Tìm điều kiện để xác định. B 3x  6 Lời giải
4x 1 xác định khi 3x  6  0  3x  6  x  2 3x  6
Dạng 2: Tìm x, giải phương trình Phương pháp Ví dụ và lời giải 2 2
A B A  B
Ví dụ 1: Tìm x biết  x  2 1  16 Lời giải Hệ quả: 2
x a x   a, a  0  x   x   x  2 1 4 5 1  16     x 1  4  x  3  
Ví dụ 2: Tìm x biết 2 x  9. Lời giải 2
x  9  x  3   B  0
Ví dụ 3: Tìm x biết A B   2  A B
a) x  2 ; b) 3x 1  2 Lời giải
a) x  2  x  4 5 b) 2
x 1  2  3x 1  2  3x  5  x  3 B  0
Ví dụ 4: Giải phương trình 2
x  4x  4  5 A B  
A B hay A  B Lời giải  Page 3
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
x  4x  4  5   x  22 2
 5  x  2  5  x  2  5 x  7     x  2  5 x  3  
Dạng 3: Thực hiện các phép toán căn thức  A nÕu A  0 2 A A     Ví dụ 1: Tính 2 81 9 9   A nÕu A < 0 2
Ví dụ 2: Tính 1 3  1 3  1 3  3 1
Ví dụ 3: Tính 4  2 3   3  2 1  3 1 AB
A. B (Với A  0; B  0 )
Ví dụ 1: Tính 49.25  49  25  7.5  35 . Ví dụ 2: Tính
810  40  81 4 100  81  4  100  9  2 10  180 . A A 25 25 5 
(Với A  0; B  0 ) Ví dụ 1: Tính   . B B 121 121 11 80 80 Ví dụ 2: Tính   16  4 . 5 5 2 A B A
B (Với B  0 ) Ví dụ 1: Tính 2
20  4 5  2 5  2 5 2 A B
A B (Với A  0; B  0 ) Ví dụ 1: 2 3 7  3  7  63 2 A B  
A B (Với A  0; B  0 ) Ví dụ 1: Tính 2 2 
3   2  3   12 . A 1 2 2.3 2.3 6 
AB (Với A  0; B  0 ) Ví dụ 1:    . B B 2 3 3.3 3 3 A A B 5 5 3 5 3  (Với B  0 ) Ví dụ 1:   . B B 3 3  3 3 CA   10 10( 3 1) 10( 3 1)  Ví dụ 1:    5( 3 1) . 2 A B A B 3 1 ( 3 1)( 3 1) 3 1 (Với 2 A  0; A  B ) 20 20( 5 1) 20.( 5 1) Ví dụ 2:    5( 5 1) . 5 1 ( 5 1)( 5 1) 5 1 C Ví dụ 1: CA B   A B A B 6 6( 5  3) 6( 5  3)    3( 5  3) . 5  3 ( 5  3)( 5  3) 5  3
(Với A  0; B  0; A  B ) Ví dụ 2: Page 4
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9 7 7( 3  2) 7( 3  2)    7( 3  2) . 3  2 ( 3  2)( 3  2) 3  2  3 3 A 3 3 3  A A Ví dụ : 3 3 27  3  3
Dạng 4: Tìm x nguyên để biểu thức sau rút gọn nguyên Phương pháp Ví dụ và lời giải
Bước 1: Tìm điều kiện xác định (thường đề bài x  4
Ví dụ 1: Tìm x nguyên để A  nguyên
đã cho hoặc đã được xác định ở câu trước) x 1 Lời giải
Bước 2: Thực hiện phép chia biểu thức về dạng Điều kiện: x  0    a A f x x  4 x 1 3 3 g x Ta có: A    1 x  1 x 1 x 1
(Bước này quan sát dưới mẫu, phân tích tử
A nguyên khi x 1 là ước của 3 theo mẫu các em nhé!!!)  x 1 1    x  0     1  1   x  2  ( )   0       x  4  x  1  3   x  4  (loai)    x 1  3 x  2  
Dạng 5: Tìm giá trị lớn nhất, giá trị nhỏ nhất Phương pháp Ví dụ và lời giải Giả sử cho 2
A ax bx c ta cần biến đổi về
Ví dụ 1: Tìm giá trị nhỏ nhất của A x x Lời giải dạng    2 A a x m n
Điều kiện: x  0 Lúc đó: Ta có 2 2 1  1  3
* A n nếu a  0 . Lúc đó A nhỏ nhất bằng n A x x x  2. . x     2  2  4 khi x m 2  1  3 3
* A n nếu a  0 Lúc đó A lớn nhất bằng n x       2  4 4 khi x m 3
Vậy, A nhỏ nhất bằng khi 4 1 1 1 x   0  x   x  2 2 4 Page 5
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Ví dụ 2: Tìm giá trị lớn nhất của 2 A  2
x  4x  9 Lời giải Ta có 2 A  2
x  4x  9  2   2 x  2x   1  11  2   x  2 1  11  11
Vậy, A lớn nhất bằng 11 khi x  1
Dạng 6: Hàm số bậc nhất và tính chất hàm số bậc nhất Phương pháp Ví dụ và lời giải Hàm số y
Ví dụ 1: Tìm m để hàm số y  2m  
1 x  5 là hàm số bậc nhất.
ax b là hàm số
bậc nhất nếu a  0 Lời giải
Hàm số y  2m  
1 x  5 là hàm số bậc nhất khi 1
2m 1  0  m  . 2 Cho hàm số bậc nhất:
Ví dụ 2: Cho hàm số bậc nhất y   2
m  6 x  9 . Tìm m để
y ax b
hàm số đồng biến và nghịch biến trên  . Lời giải
* Hàm số đồng biến trên 
* Hàm số đồng biến khi 2m  6  0  2m  6  m  3 {chia số khi a  0
âm nhớ đổi dấu bất phương trình các em nhé}
* Hàm số nghịch biến trên 
* Hàm số nghịch biến khi 2m  6  0  2
m  6  m  3 2m  6  0  2m  6  m  3 khi a  0 .
{chia số âm nhớ đổi dấu bất phương trình các em nhé}
Dạng 7: Vẽ đồ thị hàm số bậc nhất Phương pháp Ví dụ và lời giải
Ví dụ 1: Vẽ đồ thị hàm số
Để vẽ đồ thị hàm số bậc nhất y  2x  4 y ax  ,
b a  0 ta Lời giải
lấy 2 điểm mà đồ thị đi qua, rồi vẽ đường thẳng đi Bảng giá trị
qua hai điểm đó ( thường lấy giao của đồ thị với hai trục Ox,Oy) Bảng giá trị Đồ thị
x  0  y b b
y  0  x   a Page 6
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9 Chú ý:
* Đồ thi y ax đi qua hai điểm có toạ độ (0; 0) và (1; a) .
* Đường thằng x a song song với Oy cắt Ox tại a .
* Đường thằng y b song song với Ox cắt Oy tai b .
Dạng 8: Vị trí tương đối của hai đường thẳng
Nếu bài toán cho hàm bậc nhất, các em phải tìm điều kiện cho a  0
Nếu bài toán không cho hàm số bậc nhất, ta không phải tìm điều kiện a  0 Phương pháp Ví dụ và lời giải
Ví dụ 1: Cho hai đường thẳng có phương trình
Nếu hai đường thẳng biểu diễn dưới dạng
d : y  2m 1 x  5 và d : y  3x  4m 1  
y a x b và y a x b 2 1 1 2 2
Tìm giá trị m trong các trường hợp sau
* Cắt nhau khi a a 1 2
a) d cắt d ; 1 2
b) d song song d ; 1 2 a a
c) d vuông góc d ;  1 2 * Song song khi 1 2  b   b Lời giải  1 2
a) d cắt d khi
* Vuông góc khi a a  1 1 2 1 2 4 2m 1  3
  3m  3 1  m    a a * Trùng nhau khi 1 2 3  b b  1 2
b) d song song d khi 1 2 m  2 2m 1  3      m  2 5  5  4m m     4
c) d vuông góc d khi 1 2
m     1 1 2 1 . 3  1   2m 1   m   3 3
Dạng 9: Lập phương trình đường thẳng Phương pháp Ví dụ và lời giải
Ví dụ 1: Lập phương trình đường thẳng
Bài toán 1: Lập phương trình đường thẳng
d : y ax b đi qua điểm A 3; 4   và có hệ
d : y ax b đi qua A x , y và có hệ số góc k . 1 1  số góc k  5 Lời giải
Đường thẳng d : y ax b đi qua điểm Page 7
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Vì đường thẳng là y ax b A 3; 4   nên .
a 3  b  4  3
a b  4 
có hệ số góc k nên ak. Mặt (*)
khác, đường thẳng d đi qua
Mặt khác, đường thẳng d : y ax b có hệ số
A x , y nên thay tọa độ A 1 1 
góc k  5 nên nên a  5 . Thay a  5 vào
vào đường thẳng để tìm b.
phương trình (*) ta được
3.5  b  4  b  11
Vậy d : y  5x 11
Ví dụ 2: Lập phương trình đường thẳng
Bài toán 2: Lập phương trình đường thẳng
d : y ax b đi qua điểm A 3; 4   và song
d : y ax b đi qua A x , y và song song 1 1 
song với đường thẳng d : y  4x  5
d : y mx n . 1 1 Lời giải
Đường thẳng d : y ax b đi qua điểm A x ; y
Đường thẳng d : y ax b đi qua điểm 1 1 
nên ax b y (*) A 3; 4   nên .
a 3  b  4  3
a b  4  1 1
Mặt khác, đường thẳng d : y ax b song song với (*)
đường thẳng d : y mx n nên a m, b n .
Mặt khác, đường thẳng d : y ax b song 1 song với đường thẳng Thay a
d : y  4x  5
m vào phương trình (*) ta tìm được b 1
nên a  4, b  5
  . Thay a  4 vào phương
trình (*) ta được 3.4  b  4  b  8
Vậy d : y  4x  8
Ví dụ 3: Lập phương trình đường thẳng
Bài toán 3: Lập phương trình đường thẳng
d : y ax b đi qua điểm A 3; 4   và vuông
d : y ax b đi qua A x , y và vuông góc 1 1 
góc với đường thẳng d : y  4x  5
d : y mx n . 1 1 Lời giải Đường thẳng
Đường thẳng d : y ax b đi qua điểm
d : y ax b đi qua A 3; 4   nên .
a 3  b  4  3
a b  4 
điểm A x ; y nên 1 1  (*)
ax b y (*)
Mặt khác, đường thẳng d : y ax b vuông 1 1 Mặt khác, đường
góc với đường thẳng d : y  4x  5 1
thẳng d : y ax b 1 1 nên .4
a  1  a   . Thay a   vào vuông góc với đường 4 4 1
phương trình (*) ta được
thẳng d : y mx n nên .
a m  1  a  . Thay 1 m  1  3 21 3. 
b  4  b  4     1  4 4 4 a   
vào phương trình (*) ta tìm được b m 1 21
Vậy d : y   x  4 4
Ví dụ 4: Lập phương trình đường thẳng
Bài toán 4: Lập phương trình đường thẳng
d : y ax b đi qua điểm A 3; 4   và Page 8
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
d : y ax b đi qua hai điểm A x , y ; B x , y B 1;2 1 1   2 2  Lời giải
Vì đường thẳng d : y ax b đi qua điểm
Đường thẳng d : y ax b đi qua điểm
A x , y nên ax b y 1 1  1 1 A 3; 4   nên .
a 3  b  4  3
a b  4 
Vì đường thẳng d : y ax b đi qua điểm
Đường thẳng d : y ax b đi qua điểm
B x , y nên ax b y B 1;2 nên . a  
1  b  2  a b  2 2 2  1 2 Ta có hệ phương trình:
ax b y  Ta có hệ phương trình: 1 1   3
a b  4  a  3 ax .   b y     2 2 a b  2 b  5   Giải hệ ta được , a b
Vậy d : y  3x  5
Dạng 10: Tìm điểm cố định của hàm số y f m . Chứng minh đồ thị luôn đi qua một điểm
cố định (hay tìm điểm mà đồ thị luôn đi qua) Phương pháp Ví dụ và lời giải
Ví dụ 1: Chứng minh rằng hàm số
Bước 1. Chuyển y f (x, m) về dạng
y  3m  
1 x  2m  6 luôn đi qua một điểm cố đinh
f (x, m) - y  0 . Lời giải
Bước 2. Nhóm các số chứa m lại với nhau: Ta có: . m f (x)  ( g x, y)  0 .
y  3m  
1 x  2m  6  3m  
1 x  2m  6  y  0
Bước 3: Gọi I(x , y ) là điểm cố định , suy
 3mx x  2m  6  y  0  3mx  2m x y  6  0 0 0
m 3x  2  x y  6  0 ra   f (x )  0  x  ?
Gọi I(x , y ) là điểm cố định mà hàm số đi qua 0 0 0 0    . ( g x , y )  0 y  ?   0 0   0
Lúc đó: m 3x  2  x y  6  0 với mọi m 0  0 0
Suy ra điểm cố định là I.  2 x       0 3x 2 0  0  3     x   y  6  0 20  0 0 y   0   3
Vậy, hàm số luôn đi qua điểm cố định  2 20  I  ;   3 3   
Dạng 11: Tìm tham số m để ba đường thẳng đồng quy Phương pháp Ví dụ và lời giải
Ví dụ 1: Tìm tham số m để ba đường thẳng sau
Bước 1: Gọi I x; y là giao điểm của 2 đường đồng quy Page 9
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
thẳng (2 đường thẳng không chứa m). Tọa độ d : y  2x  3; d : y  x 1; d : y  2m 1 x m 1 2 3  
I là nghiệm của hệ phương trình. Lời giải
Bước 2: Vì 3 đường thẳng đồng quy nên thay Gọi I x; y là giao điểm của 2 đường thẳng. Tọa
tọa độ I vào đường thẳng còn lại, ta sẽ tìm
độ của I là nghiệm của hệ phương trình được m  2 x   y  2x  3
2x y  3     3  2 5        I  ;   y  x 1 x y  1 5 3 3   y      3
Vì 3 đường thẳng đồng quy nên 5     m   2 2 1 . 
m m  7 3  3   
Dạng 12: Khoảng cách từ gốc tọa độ đến đường thẳng Phương pháp Ví dụ và lời giải 1
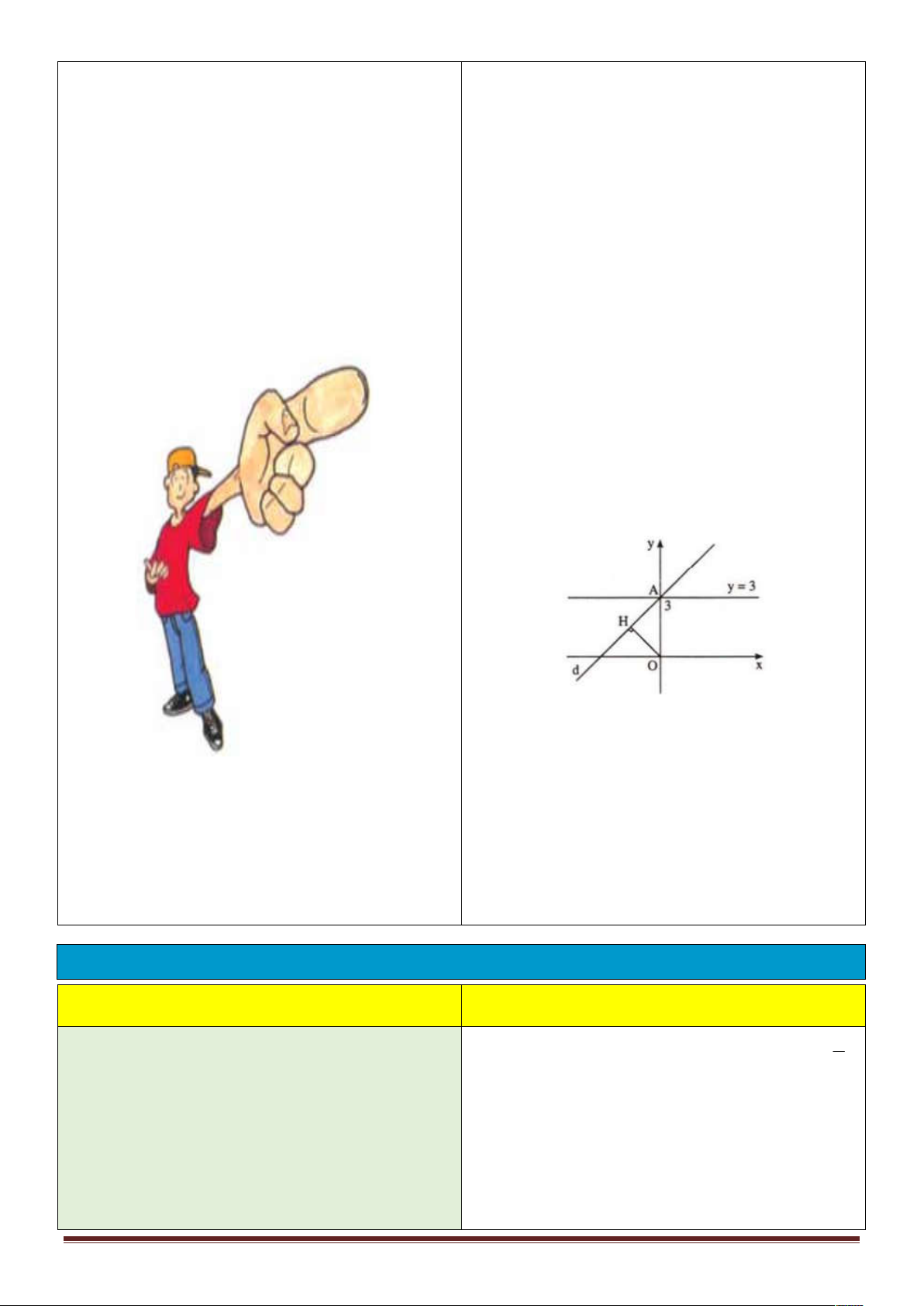
Để tính khoảng cách từ điểm O 0;0 đến một
Ví dụ 1: Cho hàm số : y  x 1 (d). 2
đường thẳng, ta tìm giao điểm của đường thẳng Tính khoảng cách từ gốc O của hệ trục tọa độ
với hai trục Ox,Oy là A,B. Từ O kẻ OH AB đến đường thẳng (d).
rồi tính OH dựa vào tam giác vuông OAB : Lời giải
Kẻ OH vuông góc với (d) tại H . Khi đó OH 1 1 1   . 2 2 2 là khoảng cách từ OH OA OB
O đến đường thẳng (d) (hình 9).
Trong tam giác vuông OAB , ta có : 1 1 1 1 1 5      2 2 2 2 2 OH OA OB 1 2 4 4 2 5 Từ đó suy ra: 2 OH   OH  . 5 5 2 5
Vậy khoảng cách từ O đến (d) là . 5 Page 10
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9 Ví dụ 2. Cho hàm số . Tìm
Với các bài toán tìm điều kiện để khoảng cách y  mx  3( d) m để
khoảng cách từ gốc tọa độ lớn nhất, nhỏ nhất: O đến đường thẳng (d) là lớn nhất.
Xét a  0 . Tìm giao điểm của đồ thị với 2 trục Giải
tọa độ và tính khoảng cách.
Trường hơp 1. Xét m  0 . Xét a Khi thì
 0 . Tìm giao điểm của đồ thị với 2 trục m  0 (d) có phương trình
tọa đô và tính khoảng cách. Sau khi tính được
y  0.x  3  3 hay y  3.
Đồ thị hàm số y  3 là đường thẳng song song
khoảng cách ta đi tìm m MIN, MAX của biểu
với trục hoành và cắt trục tung tại điểm có thức khoảng cách.
tung độ bằng 3 nên khoảng cách từ O đến (d) bằng 3 .
Trường hợp 2. Xét m  0 .
Khi đó (d) : y  mx  3 luôn đi qua điểm A(0;3)
nằm trên trục tung. Kẻ OH vuông góc với (d) tại H .
Khi đó OH là khoảng cách từ O đến đường thẩng (d) .
Ta có OH  OA hay OH  3 (dấu " = " không
xảy ra vì m  0 nền H không trùng A). Do đó OH  3 .
Kết hợp hai trường hợp ta có khi m  0 thì
khoảng cách từ O đến đường thẳng (d) là lớn nhất.
Dạng 13: Các tính chất của hàm số bậc hai 2 y ax Phương pháp Ví dụ và lời giải 2 Hàm số 2
y ax a  0 xác định với mọi x   . Ví dụ 1. Cho hàm số 2 y  (3 m  2)x với m  . 3 * Nếu a a) Tìm điều kiện của
 0 thì hàm số đồng biến khi x  0 ,
m để hàm số đồng biến khi x  0 ;
nghịch biến khi x  0 .
b) Tìm điều kiện của m để hàm số nghịch biền
* Nếu a  0 thì hàm số đồng biến khi x  0 và khi x  0 .
nghịch biến khi x  0 Lời giải Page 11
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
* Hàm số đạt GTNN bằng 0 khi a  0 . a) 2
y  (3 m  2)x đồng biến khi x  0 có điều 2
* Hàm số đạt GTLN bằng 0 khi a  0 .
kiện là 3 m  2  0  m  . 3 b) 2
y  (3 m  2)x nghịch biến khi x  0 có điều 2
kiện là 3 m  2  0  m  . 3 Ví dụ 2: Cho hàm số 2
* Để tính f x thay x y  2x
x vào y f x . 0  0
a) Tính giá trị của hàm số tại x  2, x  1 0 0
* Để kiểm tra điểm M  ;
a b có thuộc đồ thị
b) Điểm M 4;2 có thuộc đồ thị hàm số hay
hàm số y f x ta thay x a, y b vào đồ thị không? Lời giải
nếu thõa mãn thì M  ;
a b thuộc đồ thị và a) Khi ngược lại. 2
x  2  y  2.2  8, 0 x  1
  y  2. 2 1  2 0
b) Với x   y   2 4 2. 4  32  2 nên điểm
M 4;2 không thuộc đồ thị hàm số đã cho 1
Tìm m để điểm Ax ; y thuộc đồ thị hàm số Ví dụ 3. Cho Parabol 2 y   x . Xác định giá A A  4 2 y ax
trị của m để điểm A( 2; m) thuộc Parabol
Ta cần thay tọa độ điểm A vào hàm số, giải Lời giải Điểm
phương trình (hoặc tính) để tìm giá trị m A thuộc Parabol thì ta 1 1 có 2 : m   ( 2)  . 4 2
Dạng 14: Vẽ đồ thị hàm số 2 y ax Phương pháp Ví dụ và lời giải 1
Bước 1: Kẻ bảng giá trị (lấy ít nhất 5 điểm)
Ví dụ 1: Vẽ đồ thị hàm số 2 y  x . 3
Bước 2: Nhận xét đồ thị hàm số là parabol nhận Lời giải
trục Oy là trục đối xứng, đi qua 5 điểm (ở bước Bảng giá trị 1) rồi vẽ Đồ thị Page 12
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Dạng 15: Bài toán tương giao của đường thẳng y mx n và Parabol 2
y ax , a  0 Phương pháp Ví dụ và lời giải 1
Xét hoành độ giao điểm của 2 đồ thị thỏa mãn Ví dụ 1: Cho hàm số 2 y  
x có đồ thị (P) 2 phương trình: 2
ax mx n
và đường thẳng (d) : y  2  x  5. Tìm , m n để
Đưa phương trình về dạng: 2
ax mx n  0   1
đường thẳng () : y mx n song song với
đường thẳng (d) và có duy nhất một điểm
a) Để hai đồ thị tiếp xúc nhau (có duy nhất 1 chung với đồ thị (P). điểm chung): Lời giải
() và (d) song song nhau khi và chỉ khi
Để hai đồ thị tiếp xúc nhau thì phương trình
m  2 và n  5
(1) có nghiệm kép:   0 hoặc  '  0
Hoành độ giao điểm của () và (P) là nghiệm Từ đó tìm được m. của phương trình 1 1 2 2 
x  2x n  
x  2x n  0 (* ). 2 2
() và (P) có duy nhất một điểm chung khi và chỉ khi (*) có nghiệm
kép   '  0  4  2x  0  n  2 thỏa mãn
điều kiện n  5.
Vậy m  2 và n  2. Ví dụ 2: Cho Parabol và đường
b) Để hai đồ cắt nhau tại hai điểm phân biệt  P 2 : y x
thẳng d : y mx m 1. Tìm m để d cắt P tại
Để hai đồ cắt nhau tại hai điểm phân biệt thì
hai điểm phân biệt có hoành độ x , x . 1 2
phương trình (1) có hai nghiệm phân biệt Lời giải
   0 hoặc  '  0 .
Xét phương trình hoành độ giao điểm của d và 2 2 Từ đó tìm được m.
P : x mx m 1 x mx m 1  0 *
c) Để hai đồ thị không cắt nhau Có   m2 
m    m m   m  2 2 4.1. 1 4 4 2
Để hai đồ thị không cắt nhau thì phương trình Page 13
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
(1) vô nghiệm   0 hoặc  '  0 . Từ đó tìm
D cắt P tại hai điểm phân biệt  phương được m.
trình * có hai nghiệm phân biệt     m  2 0 2  0  m  2 
Dạng 16: Giải bài toán bằng cách lập phương trình, hệ phương trình PHƯƠNG PHÁP CHUNG
Bước 1: Lập phương trình - Hệ phương trình.
- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
- Biểu diễn các đại lượng chưa biết khác theo ẩn và các đại lượng đã biết.
- Lập phương trình, hệ phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình - Hệ phương trình. Bước 3: Kết luận.
Kiểm tra xem trong các nghiệm của phương trình, hệ phương trình, nghiệm nào thỏa mãn điều
kiện của ẩn, nghiệm nào không, rồi kết luận. Phương pháp Ví dụ và lời giải
Bài toán 1: Dạng toán cấu tạo số
Ví dụ: Tìm hai số biết rằng tổng của hai số đó bằng 17
đơn vị. Nếu số thứ nhất tăng thêm 3 đơn vị, số thứ hai
* Gọi số có hai chữ số cần tìm là: xy tăng thêm 2 đơn vị thì tích của chúng bằng 105 đơn vị. . Lời giải
Điều kiện: x, y N,0  x  9; 0  y  9.
Gọi số thứ nhất là x , số thứ hai là y .
* Gọi số có ba chữ số cần tìm là: xyz .
Theo để bài, tổng của hai số đó bằng 17 đơn vị ta có
phương trình : x y  17 (1) Điều kiện:
x, y, z N, 0  x  9; 0  y, z  9.
Só thứ nhất tăng thêm 3 đơn vị, số thứ hai tăng thêm 2
đơn vị thì tích của chúng bằng 105 đơn vị ta có phương
Sau đó sử dụng các chú ý sau để lập
trình (x  3)( y  2)  105 phương trình:
Từ (1), (2) ta có hệ phương trình :
Số có hai chữ số có dạng: xy
x y  17  10x y . 2 
x 16x  48  0.$
(x  3)( y  2)  105 
Số có ba chữ số có dạng:
Giải phương trình ta được (thoả mãn), xyz x  12 x  4
 100x 10y z . 1 2 (thoả mãn).
Vậy nếu số thứ nhất là 12 thì số thứ hai là 5 ; nếu số thứ Page 14
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
nhất là 4 thì số thứ hai là 13 .
Bài toán 2: Dạng toán làm chung - Ví dụ 1: Hai công nhân cùng làm một công việc trong làm riêng
18 h thì xong. Nếu người thứ nhất là 6 h và người thứ hai
làm 12 h thì chỉ hoàn thành 50% công việc. Hỏi nếu làm
Gọi thời gian người thứ nhất làm
riêng thì mổi người hoàn thành công viêc đó trong bao
một mình xong công việc là x , thời lâu?
gian người thứ hai làm một mình
xong công việc là y thì : Lời giải
1 giờ người thứ nhất làm được
Gọi thời gian người thứ nhất làm một mình hoàn thành 1
công việc là x (giờ, x  0 ); người thứ hai làm một mình (công việc), x
hoàn thành công việc là y (giờ, y  0 ). 1 1
1 giờ người thứ hai làm được
công Trong 1 h người thứ nhầt làm được công việc, người y x 1 việc thứ hai làm được công việc. y
1 giờ cả hai người làm được
Hai người làm chung 18 h thì xong, ta có phương trình : 1 1  (công việc) x y 1 1 1   x y 18
Nếu người thứ nhât làm trong 6 h và người thứ hai làm
trong 12 h thì hoàn thành 50% công việc, ta có phương trình : 6 12   50% x y  1 1 1     x y 18
Ta được hệ phương trình:  6 12    50%.   x y
Giải hệ phương trình ta được x  36 : y  36 thoả mãn điều kiện.
Vậy nếu làm riêng thì người thứ nhất hoàn thành công
việc trong 36 h và người thứ hai hoàn thành công việc trong 36h.
Bài toán 3: Dạng Toán Chuyển
Ví dụ 1: Hai ô tô cùng khởi hành từ A đến B cách nhau Động
560 km . Vận tốc ô tô (II) hơn vận tốc ồ tô (I) là 10 km / h
nên đã đến B sớm hơn ô tô (I) là 1 giờ. Tính vận tốc mỗi
Gọi S là quãng đường đi, v là vận xe.
tốc, t là thời gian đi, ta có: S v t . Page 15
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
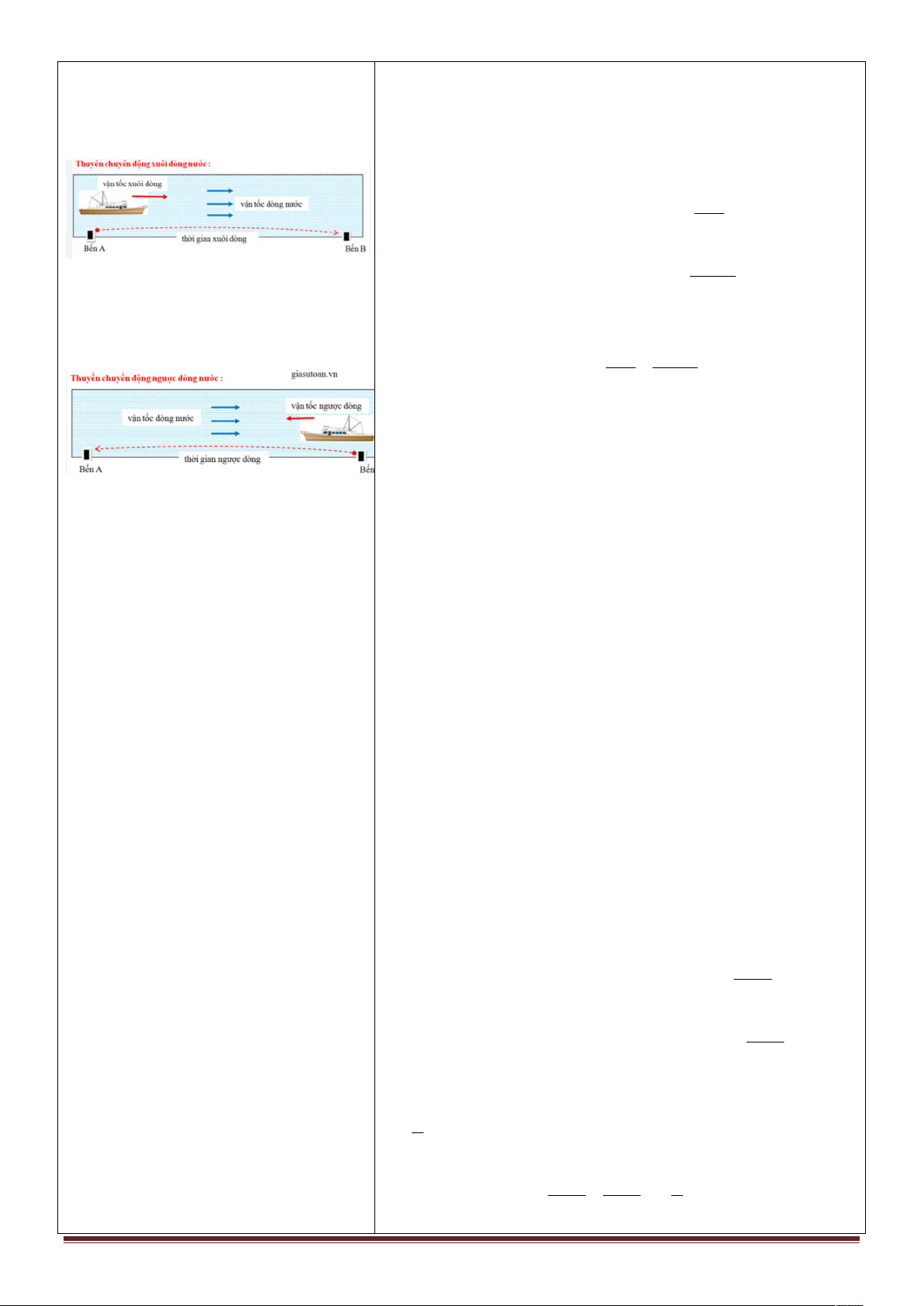
Vận tốc ca nô xuôi dòng nước = Lời giải
Vận tốc thực của ca nô + Vận tốc
Gọi vận tôc ô tô (I) là x(km / h, x  0) . dòng nước
Khi đó vận tốc ô tô (II) là x 10( km / h) . 560
Thời gian ô tô ( I) đi từ A đển B là (giờ). x 560
Thời gian ô tô (II) đi từ A đến B là (giờ).
Vận tốc ca nô ngược dòng nước = x 10
Vận tốc thực của ca nô - Vận tốc
Theo để bài, xe ô tô (II) đến B sớm hơn xe ô tô (I) là 1 dòng nước. 560 560   1 x x 10
giờ nên ta có phương trình  560(x 10)  560x x(x 10) 2
x 10x  5600  0 Phương trình có nghiệm:
Vận tốc ca nô xuôi - vận tốc ca nô x  5
  75  80 (loại) ; x  5   75  70 (chon). 1 2
ngược = 2 vận tốc dòng nước
Vậy vận tốc ô tô (I) là 70( km / h) .
Vận tốc bèo trôi chính là vận tốc dòng nước.
Vận tốc ô tô (II) là 70 10  80( km / h) .
Ví dụ 3. Một tàu thuỷ chạy trên khúc sông dài 120 km .
Cả đi lẫn về mát 6 giờ 45 phút. Tính vận tốc tàu thuỷ khi
nước yên lạng biết vận tốc của dòng nước là 4 km / h . Giải.
Gọi vận tốc của tàu thuỷ khi nước yên lặng là
x(km / h, x  4) .
Suy ra: Vạn tóc của tàu thuỷ khi xuôi dòng là x  4( km / h) .
Vận tốc của tàu thuỷ khi ngược dòng là x  4( km / h) . 120
Thời gian tàu thuỷ đi xuôi dòng 120 km là (giờ). x  4 120
Thời gian tàu thuỷ đi ngược dòng 120 km là (giờ). x  4
Theo đề bài, thời gian cả đi lẫn vể mất 6 giờ 45 phút ( 3  6 giờ). 4 120 120 3 Ta có phương trình   6 x  4 x  4 4 Page 16
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9 27 2
 120(x  4) 120(x  4) 
(x  4)(x  4)  9x  320x 144  4
Phương trình có nghiệm là: 160 164 4 160 164 x    (loại) ; x   36 . 1 9 9 2 9
Vậy, vận tốc tàu thuỷ khi nước yên lặng là 36 km / h .
Bài toán 4: Hai vật chuyển động
Ví dụ: Hai vật chuyển động đều trên một con đường tròn trên 1 đường tròn:
đường kính 20 cm , xuất phát cùng một lúc, từ cùng một
điểm. Nếu chuyển động cùng chiều thì cứ 20 giây chúng
- Nếu chuyển động ngược chiều, khi
lại gặp nhau. Nếu chuyển động ngược chiểu thì cứ sau 4
gặp nhau thì S S  Chu vi  2 R 1 2
giây chúng lại gặp nhau. Tính vận tốc của mỗi vật.
- Nếu chuyển động cùng chiều, khi Lời giải
gặp nhau thì S S  Chu vi  2 R 1 2
Gọi vận tốc của vật thứ nhất là x( cm / s) , vận tốc của vật
thứ hai là y( cm / s)
Giả sử vật thứ nhất đi nhanh hơn vật thứ hai.
Điều kiện x y  0 .
Chu vi vòng tròn là : 20.π (cm)
Quãng đường vật thứ nhất đi được trong 20 s là 20 (cm)
Quãng đường vật thứ hai đi được trong 20s là 20y(cm)
Khi chuyển động cùng chiều, cứ 20 giây chúng lại gặp
nhau, nghĩa là quãng đường 2 vật đi được trong 20 giây
chênh lệch nhau đúng bằng 1 vòng tròn. Nên ta có phương
trình: 20x  20 y  20 (1).
Quãng đường vật thứ nhất đi được trong 4 s là 4 (cm)
Quãng đường vật thứ hai đi được trong 4 s là 4y(cm)
Khi chuyển động ngược chiều, cứ 4 giây chúng lại gặp
nhau, nghĩa là tổng quãng đường hai vật đi được trong 4
giây là đúng 1 vòng tròn nên ta có phương trình:
4x  4 y  20 (2)
Từ (1) và (2) ta có hệ phương trình
20x  20 y  20 x  3   
4x  4 y  20 y  2   Page 17
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Vậy vận tốc của hai vật lần lượt là 3 và 2 .
Bài toán 5 : Hai vật chuyển động
Ví dụ 1: Hai khách du lịch xuất phát đồng thời từ hai
trên một đường thẳng AB:
thành phố A và B cách nhau 53km . Họ đi ngược chiều và
gặp nhau sau 2h . Hỏi vận tốc của mỗi người, biết rằng
Chuyển động ngược chiều, xuất
khi gặp nhau người thứ hai đi được nhiều hơn người thứ
phát cùng lúc khi gặp nhau thì nhất 3km .
quãng đường hai vật đi được là AB,
tức là t v t v AB . Lời giải 1 2
Gọi x (km/h) là vận tốc của người thứ nhất đi từ thành
phố A đến thành phố B (x  0)
y (km/h) là vận tốc của người thứ hai đi từ thành phố B
đến thành phố A ( y  0)
Quãng đường đi được của người thứ nhất trong 2h : 2x (km)
Quãng đường đi được của người thứ hai trong 2h : 2 y (km)
Người thứ hai đi nhiều hơn người thứ nhất
3km  2 y  2x  3
Hai người đi ngược chiều nhau trên quãng đường 53km ,
gặp nhau sau 2h  2x  2 y  53 Giải hệ phương trình:  2.14  3
 2 y  2x  3
2 y  2x  3 x   12,5      2
2x  2 y  53 4 y  56    y  14 
Vậy vận tốc của người thứ nhất là 12,5 (km/h) , vận tốc
của người thứ hai là 14 (km/h)
Bài toán 6 : Bài toán có liên quan
Ví dụ 1: Một thửa ruộng hình chữ nhật, nếu tăng chiểu yếu tố hình học
dài thêm 2 m , chiều rộng thêm 3 m thì diện tích tăng thêm 2
100 m . Nếu giảm chiều dài và chiều rộng đi 2 m thì
Sau khi gọi ẩn số, các em cần sử diện tích giảm đi 2
68 m . Tính diện tích của thửa ruộng đó.
dụng các kiến thức cơ bản sau để
thiết lập phương trình hoặc hệ Lời giải phương trình :
Gọi chiếu dài thửa ruộng là x( ,
m x  0) và chiều rộng là
Diện tích hình chữ nhật có hai kích y( , m y  0) . thước a ; b là S =ab
Nếu tăng chiểu dài thêm 2 m , chiều rộng thêm 3 m thì
Chu vi hình chữ nhật là : diện tích tăng thêm 2 100 m .
P  2(a b)
Ta có phương trình: (x  2)  ( y  3)  xy 100 (1). 1
Diện tích tam giác là S  . đáy. 2
Nếu giảm chiều dài và chiểu rộng đi 2 m thì diện tích giảm đi 2 68 m . Page 18
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9 chiều cao
Ta có phương trình: (x  2)  ( y  2)  xy  68 (2).
Diện tích tam giác vuông có hai cạnh Từ (1), (2) ta có hệ phương trình : ab
góc vuông a ;b là : S
(x  2)( y  3)  xy 100 3
x  2 y  94 2   
(x  2)( y  2)  xy  68
2x  2 y  72.  
Thể tích hình lập phương : 3 a x  22
Thể tích hình hộp : a.b.c
Giải hệ phương trình ta được :  (thoả mãn điểu y  14  Diện tích hình thang : kiện). (day lon +day be) S   Chieu cao
Vạy diện tích thửa ruộng là    2 22 14 308 m  . 2 Diện tích hình vuông : 2 a .
Chu vi hình vuông : 4a
Bài toán 7 : Bài toán năng suất
Ví dụ 1: Một công nhân dự định làm 70 sản phẩm trong làm việc
thời gian quy định. Nhưng do áp dụng kĩ thuật nên đã
tăng năng suất thêm 5 sản phẩm mỗi giờ. Do đó không Khối
những hoàn thành kế hoạch trước thời hạn 40 phút mà Lập Năng lượng Thời
còn vượt mức 10 sản phảm. Tính năng suất dự định. bảng suất công gian Lời giải việc
Gọi năng suấ dự định là x (sản phảm/ giờ, * x N ) ; 70 Theo kế
Thời gian dự định làm 70 sản phẩm là (giờ); x hoạch
Thời gian thực tế làm 80 sản phảm với năng suất x  5 80 Thực tế (sản phẩm/ giờ) là (giờ). x  5
Theo để bài, cóng nhân hoàn thành trước kể hoạch 40 Công thức sử dụng : 2 phút (= giờ). Ta có phương trình
Khối lượng = năng suất lao động x 3 thời gian 70 80 2 2  
x  20x  525  0 . x x  5 3
Giải ra, ta có : x  15 (thoả mãn), x  35  (không thoả 1 2
mãn). Vậy năng suât dự định là 15 sản phẩm/giờ.
Dạng 17: Dự đoán số nghiệm của hệ phương trình Phương pháp Ví dụ và lời giải Page 19
CẨM NANG TRA CỨU CÔNG THỨC, DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN 9
Ví dụ 1: Đoán nhận số nghiệm của
a x b y   c 1 1 1 1  
Để dự đoán số nghiệm của hệ 
mỗi hệ phương trình sau, giải thích vì a x b y   c 2 2 2 2    sao: x y  2 3
x  2 y  1
+ Bước 1: Chuyển phương trình (1) về dạng y ax b a)  ;b)  3x  3y  2 
6x  4 y  0 
+ Bước 1: Chuyển phương trình (2) về dạng y mx n Lời giải x y  2
+ Bước 3: Xét vị trí tương đối của hai đường thẳng a) (I):  3x  3y  2  (Xem lại dạng 7)
Xét (d): x y  2 hay (d): y  x  2
có a  1;b  2 .
(d') 3x  3y  2 hay d  2 : y  x  3   2 có a  1  ;b  3 Ta có: a a;b b    (d) // (d')  Hệ (I) vô nghiệm. 3
x  2 y  1 b) (II): 
6x  4 y  0 
Xét: (d): 3x  2 y  1 hay (d): 3 1 3 1 y  x  có a  ; b  2 2 2 2
d : 6x  4y  0 hay d : 3  3 y  x có a  ; b  0 2 2 Ta có: a a;b b  
 (d) / / d   Hệ (II) vô nghiệm.
Dạng 18: Giải hệ phương trình bằng phương pháp cộng, phương pháp thế Phương pháp Ví dụ và lời giải
Bài toán 1: Giải hệ phương trình 3
x  2y  4
Ví dụ: Giải hệ phương trình  2x y  5 a x   b y c  1 1 1  bằng phương pháp thế Lời giải a x   b y c  2 2 2
Rút x hoặc y từ một phương trình rồi thế vào Page 20