Các trường hợp bằng nhau của tam giác vuông kèm ví dụ minh họa

Các trường hợp bằng nhau của tam giác vuông kèm ví dụ minh họa
1. Khái niệm hai tam giác bằng nhau
Hai tam giác bằng nhau là hai tam giác có các
cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Để kí hiệu sự bằng nhau của tam giác ABC và tam giác A’B’C".
2. Các trường hợp bằng nhau của tam giác vuông
Trường hợp 1: Hai cạnh góc vuông
Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc
vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (cạnh – góc – cạnh). Ví dụ:
Xét tam giác vuông ABC và tam giác DEF ta có: AB = DE BC = EF
=> ∆ABC = ∆DEF (cạnh – góc – cạnh)
Trường hợp 2: Cạnh góc vuông và góc nhọn kề cạnh đó
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông
này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác
vuông kia thì hai tam giác vuông đó bằng nhau (góc– cạnh – góc) Ví dụ:
Xét tam giác vuông ABC và tam giác vuông FHI ta có: ABC = FHI = {90^0}
BC = HI => ∆ABC = ∆FHI (góc – cạnh – góc)
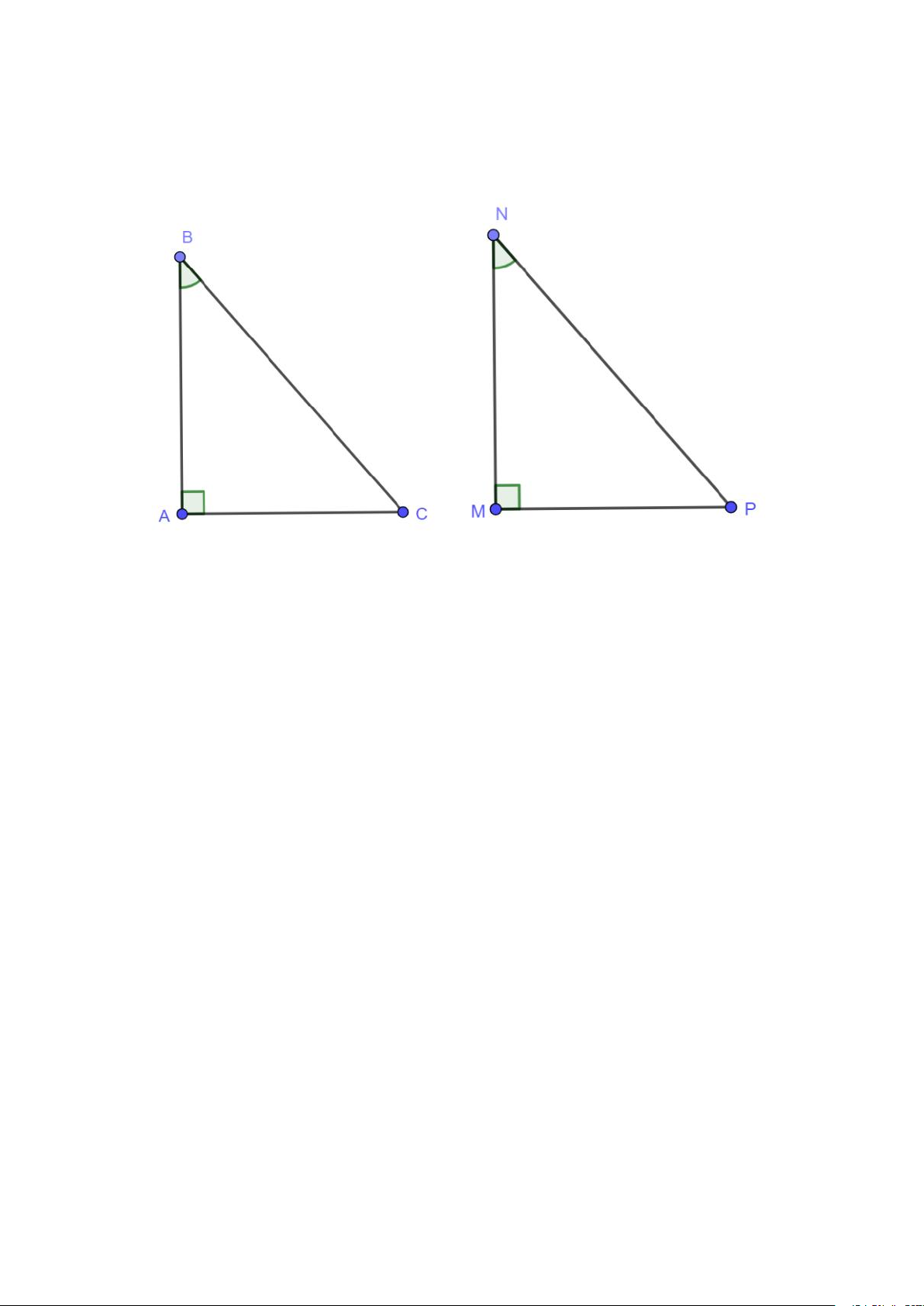
Trường hợp 3: Cạnh Huyền và góc nhọn
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền
và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau
(cạnh huyền – góc nhọn) Ví dụ minh họa:
Hai tam giác vuông bằng nhau theo cạnh huyền và góc nhọn
Trường hợp 4: Cạnh huyền và cạnh góc vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh
huyền và một cạnh góc vuông kia thì hai tam giác vuông đó bằng nhau (cạnh
huyền – cạnh góc vuông) Ví dụ minh họa:
3. Các dạng bài về các trường hợp bằng nhau của tam giác vuông
Ở mục 2 phía trên, Luật Minh Khuê đã giới thiệu về các trường hợp bằng
nhau của tam giác vuông. Tuy nhiên, để các em học sinh có thể hiểu và nắm
rõ hơn về những khái niệm này chúng ta sẽ cùng tìm hiểu qua các ví dụ sau đây:
Dạng 1: Chứng minh các tam giác vuông bằng nhau
Ở dạng này chúng ta sẽ xét hai tam giác vuông, rồi kiểm tra các điều kiện
bằng nhau: cạnh - góc - cạnh, góc - cạnh - góc, cạnh huyền - góc nhọn hoặc
cạnh huyền - cạnh góc vuông. Từ đó, xác định xem hai tam giác đó bằng
nhau theo trường hợp nào và đưa ra kết luận hai tam giác bằng nhau.
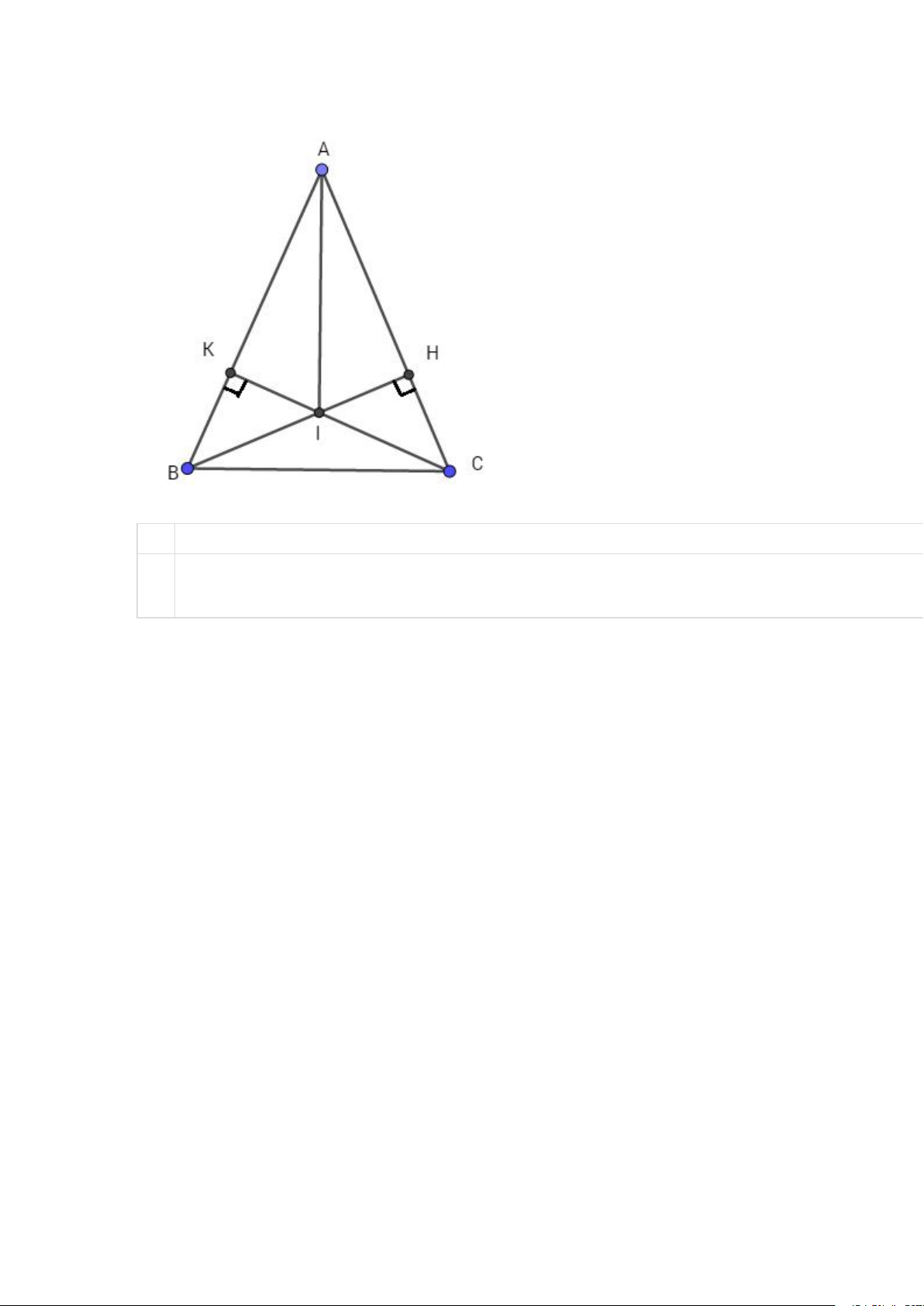
Ví dụ: Cho ΔABC , BE và CD là đường cao của ΔABC . Chứng minh rằng: ΔBCD =ΔCBE , biết BD = EC. Giải: ΔABC , CD ⊥ AB , CE ⊥ AB GT (D ∈ AB , E ∈ AC) BD = EC KL ΔBCD = ΔCBE
Xét ΔBCD vuông tại D và ΔCBE vuông tại E có: BD = CE (gt) Cạnh BC chung.
Nên ΔBCD = ΔCBE (cạnh huyền - cạnh góc vuông).
Dạng 2: Chứng minh góc và đoạn thẳng bằng nhau
Với dạng bài này cũng sẽ vận dụng những kiến thức về các trường hợp bằng
nhau của hai tam giác vuông. Từ đó, chứng minh hai tam giác bằng nhau thì
các đoạn thẳng và các góc cũng bằng nhau. Nếu bạn thấy tam giác vuông thì
cần tìm thêm hai điều kiện bằng nhau, trong đó có ít nhất một điều kiện về
cạnh để chứng minh hai tam giác đó là bằng nhau vậy mới có thể chứng
minh hai cạnh hay góc tương ứng bằng nhau.
Ví dụ: Các tam giác ABC cân tại A ( < ). Vẽ BH ⊥
AC (H ∈ AC), CK ⊥ AB (K ∈ AB).
a) Chứng minh rằng AH = AK.
b) Gọi I là giao điểm của BH và CK. Chứng minh rằng tia AI là tia phân giác của Giải:
GT ΔABC ( ˆ A < 90o ) , AB = ACBH ⊥ AC , CK ⊥ AB ( H ∈ AC , K ∈ AB) BH ∩ CK = I
KL a) Chứng minh rằng AH = AK.
b) Tia AI là tia phân giác của ˆ BAC .
a) Xét ΔABH vuông tại H và ΔACK vuông tại K có: AB = AC (ΔABC cân tại A) ˆ A chung.
Nên ∆ABH = ∆ACK (cạnh huyền - góc nhọn)
⇒ AH = AK (hai cạnh tương ứng)
b) Xét ΔAIH vuông tại H và ΔAIK vuông tại K có: AK = AH (cmt) AI cạnh chung
Nên ∆AIK = ∆AIH (cạnh huyền - cạnh góc vuông)
⇒ ˆ IAK = ˆ IAH (hai góc tương ứng)
Vậy AI là tia phân giác của ˆBAC.
Dạng 3: Tìm thêm các điều kiện để hai tam giác vuông bằng nhau
Với dạng bài này trước tiên bạn cần đọc kĩ đề bài và vẽ hình để có thể xem
hai tam giác vuông đã có những yếu tố nào bằng nhau. Từ đó, bạn tính toán
thêm xem cần phải bổ sung thêm điều kiện nào để hai tam giác vuông đó có thể bằng nhau.
Ví dụ: Các tam giác ABC và MNP có ˆA = ˆM = 90o , ˆB = ˆN . Hãy bổ sung
thêm một điều kiện bằng nhau để ∆ABC = ∆MNP. Giải:
* Trường hợp 1: ΔABC = ΔMNP theo trường hợp cạnh góc vuông - góc nhọn kề.
Xét hai tam giác vuông ABC và MNP có: +) ˆB = ˆN (giả thiết)
Bổ sung AB = MN thì ΔABC = ΔMNP (cạnh góc vuông - góc nhọn kề).
* Trường hợp 2: ΔABC = ΔMNP theo trường hợp hai cạnh huyền – góc nhọn.
Xét hai tam giác vuông ABC và MNP có: +) ˆ B = ˆ N (giả thiết)
Bổ sung BC = NP thì ΔABC = ΔMNP (cạnh huyền - góc nhọn). 4. Bài Tập Vận Dụng 4.1 Bài tập trắc nghiệm
Bài 1: Cho tam giác ABC và tam giác NPM có BC = PM, ∠B = ∠P = 90°.Cần
điều kiện gì để tam giác ABC bằng tam giác NPM theo trường hợp cạnh
huyền – cạnh góc vuông? A. BA = PM B. BA = PN C. CA = MN D. ∠A = ∠N
Ta có hai tam giác ABC và tam giác NPM có BC = PM, ∠B = ∠P = 90° mà
BC, PM là hai cạnh góc vuông của tam giác ABC và NPM nên để hai tam giác
bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông thì ta cần thêm điều kiện CA = MN Chọn đáp án C.
Bài 2: Cho tam giác ABC và tam giác MNP có ∠A = ∠M = 90°, ∠C = ∠P.
Cần điều kiện gì để hai tam giác ABC và tam giác MNP bằng nhau theo
trường hợp cạnh góc vuông – góc nhọn kề? A. AC = MP B. AB = MN C. BC = NP D. AC = MN
Ta có: ∠C = ∠P mà góc C và góc P là hai góc nhọn kề của tam giác ABC và tam giác MNP
Do đó để tam giác ABC và tam giác MNP bằng nhau theo trường hợp cạnh
hóc vuông – góc nhọn kề thì cần thêm điều kiện AC = MP Chọn đáp án A.
Bài 3: Cho tam giác ABC và tam giác DEF có: ∠B = ∠E = 90°, AC = DF, ∠A
= ∠F. Phát biểu nào sau đây đúng? A. ΔABC = ΔFED B. ΔABC = ΔFDE C. ΔBAC = ΔFED D. ΔABC = ΔDEF
Xét tam giác ABC và tam giác FED có: = = , AC = DF, = Suy ra ΔABC = ΔFED Chọn đáp án A.
Bài 4: Cho tam giác ABC và tam giác KHI có: ∠A = ∠K = 90°, AB = KH, BC
= HI. Phát biểu nào sau đây đúng? A. ΔABC = ΔKHI B. ΔABC = ΔHKI C. ΔABC = ΔKIH D. ΔACB = ΔKHI
Xét tam giác ABC và tam giác KHI có:
∠A = ∠K = 90°, AB = KH, BC = HI ⇒ ΔABC = ΔKHI Chọn đáp án A
4.2 Bài Tập tự luận
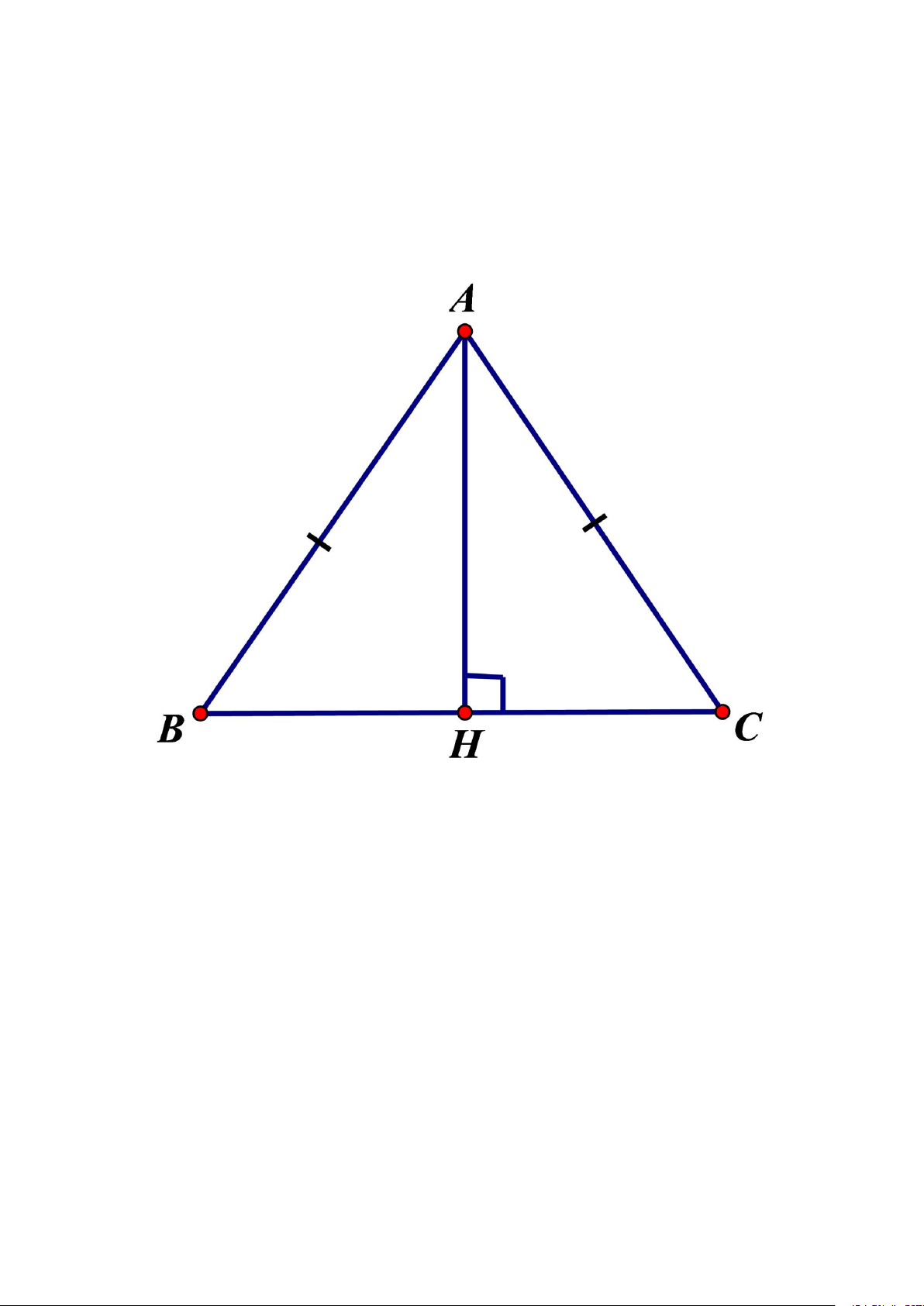
Bài 1: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (H ∈ BC). Chứng minh rằng: a) HB = HC
b) AH là tia phân giác của góc BAC. Giải:
a) ΔABH = ΔACH (cạnh huyền - góc nhọn) ⇒ H B = H C
b) Từ câu a ta có: ˆ BAH = ˆCAH
Bài 2: Cho góc xOy khác góc bẹt. Lấy điểm A thuộc tia Ox, B thuộc tia Oy
sao cho OA = OB. Kẻ đường vuông góc với Ox tại A, đường vuông góc với
Oy tại B, chúng cắt nhau tại C.
a) Chứng minh: OC là tia phân giác của góc xOy.
b) Gọi I là điểm bất kì thuộc OC. Gọi M, N theo thứ tự là chân đường vuông
góc kẻ từ I đến Ox, Oy. Chứng minh: IM = IN. Giải:
a) ΔOAC = ΔOBC (cạnh huyền - cạnh góc vuông)
⇒ ˆAOC = ˆBOC nên OC là tia phân giác góc xOy.
b) ΔOMI = ΔONI (cạnh huyền - góc nhọn) ⇒ IM = IN
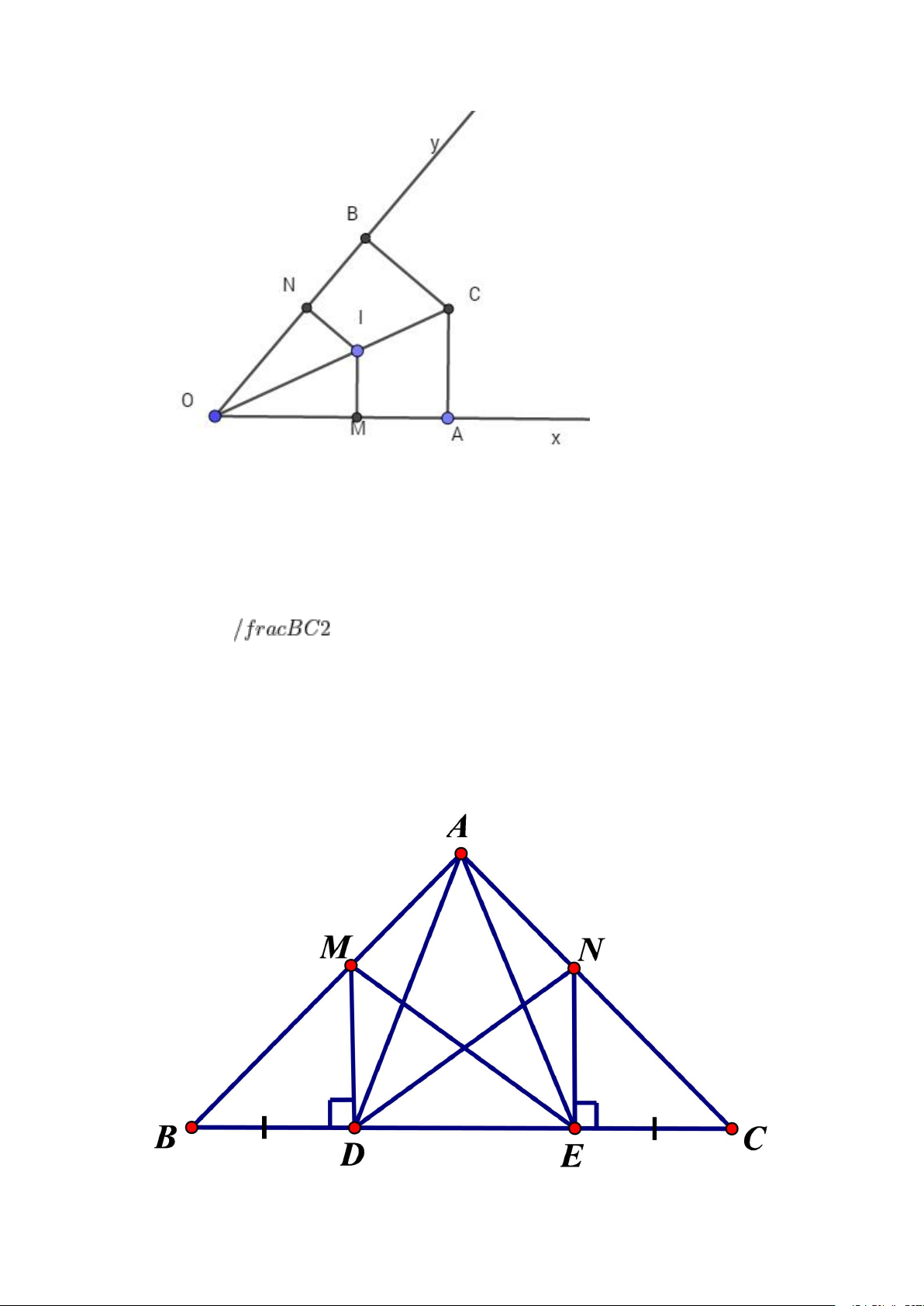
Bài 3: Cho tam giác ABC cân tại A, trên cạnh BC lấy hai điểm D và E sao cho BD = CE <
. Đường thẳng kẻ từ D vuông góc với BC cắt AB tại M,
đường thẳng kẻ từ E vuông góc với BC cắt AC tại N. Chứng minh rằng: a) DM = EN b) EM = DN c) Tam giác ADE cân. Giải:
a) ΔMDB = ΔNEC (cạnh góc vuông - góc nhọn) suy ra MD = NE
b) ΔMDE = ΔNED (hai cạnh góc vuông) suy ra ME = ND
c) ΔABD = ΔACE ( cạnh . góc . cạnh ) suy ra AD = AE. Vậy ΔADE cân tại A.
Document Outline

• Các trường hợp bằng nhau của tam giác vuông kèm ví
  • 1. Khái niệm hai tam giác bằng nhau
  • 2. Các trường hợp bằng nhau của tam giác vuông
    • Trường hợp 1: Hai cạnh góc vuông
    • Trường hợp 2: Cạnh góc vuông và góc nhọn kề cạnh đ
    • Trường hợp 3: Cạnh Huyền và góc nhọn
    • Trường hợp 4: Cạnh huyền và cạnh góc vuông
  • 3. Các dạng bài về các trường hợp bằng nhau của ta
    • Dạng 1: Chứng minh các tam giác vuông bằng nhau
    • Dạng 2: Chứng minh góc và đoạn thẳng bằng nhau
    • Dạng 3: Tìm thêm các điều kiện để hai tam giác vuô
  • 4. Bài Tập Vận Dụng
    • 4.1 Bài tập trắc nghiệm
    • 4.2 Bài Tập tự luận