Câu hỏi ôn quản trị học căn bản | Trường đại học kinh tế - luật đại học quốc gia thành phố Hồ Chí Minh
1.4. Mỗi quan hệ giữa các cấp QT và chức năng QT, cấp QT và kỹnăng QT 1.5. Những thách thức của hoạt động QT gần đây (Tái cấu trúc,thuê ngoài, trao quyền, xu hướng công nghệ, sự đa dạng lực lượng lđ) 1.8.Một vài đặc điểm/tính cách/ văn hoá con người trong Quản trị. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!
Môn: Quản trị học căn bản (K22503C)
Trường: Trường Đại học Kinh Tế - Luật, Đại học Quốc gia Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Thông tin :
Môn:
Quản trị học căn bản (K22503C)
Trường:
Trường Đại học Kinh Tế - Luật, Đại học Quốc gia Thành phố Hồ Chí Minh
Tác giả:
Tài liệu liên quan:
Preview text:
lOMoAR cPSD| 47167580
Các loại rủi ro và các hàm lợi ích của chúng:
Từ quan điểm lý thuyết E (U), chúng ta có thể phân loại tất cả các tác nhân kinh tế thành
một trong ba loại như đã nêu trong Chương 1 "Bản chất của Rủi ro: Tổn thất và Cơ hội": • Không thích rủi ro • Trung lập rủi ro •
Tìm kiếm rủi ro (thích rủi ro) * Không thích rủi ro:
Xét hàm công thức: E(U) =
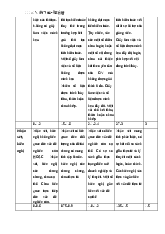
Với hàm số này ta thấy mỗi đơn vị của cải bổ sung sẽ làm tăng lợi ích với tỷ lệ giảm dần. Ta có đồ thị:
Hình 3.2 Một hàm lợi ích cho một người không thích rủi ro
Xét về độ nhạy của biểu đồ Hình 3.2, ta thấy mức độ thỏa dụng luôn tăng lên mặc dù với
tốc độ giảm dần. Đặc điểm của hàm lợi ích này được gọi là mức độ thỏa dụng cận biên
giảm dần. Có thể được viết dưới dạng kết hợp của các hạn chế đối với đạo hàm thứ nhất và
thứ hai (tốc độ thay đổi độ dốc) của hàm lợi ích, u'(W) > 0, u"(W) < 0. Một số hàm thỏa
mãn tính chất này là u (W) = .LN (W), .
Người có sở thích đặc trưng được thể hiện như biểu đồ Hình 3.2 là những người không
thích may rủi, họ sẽ từ bỏ trò chơi may rủi nếu giá của nó bằng AFP (actuarially fair price:
giá cả hợp lý về mặt tính toán). Một người như vậy sẽ cần động lực để sẵn sàng chơi trò
chơi. Nó có thể là một khoản giảm giá khi chơi xổ số, hoặc như một khoản phí bảo hiểm
để bù đắp rủi ro cho cá nhân. Cũng giống như vậy, các công ty bảo hiểm thu phí bảo hiểm
cá nhân để chuyển rủi ro thông qua bảo hiểm.
Ví dụ: Với trò chơi ở Bảng 3.1 Bảng 3.1 "Hàm lợi ích với Khoản tài trợ ban đầu là 10 đô
la" dựa trên việc tung một đồng xu. AFP cho trò chơi là $ 4. Giả sử rằng một người tên là
Terry trả trước chi phí này và thắng; thì tài sản cuối cùng của anh ta là $10- $4 + $10= $16 lOMoAR cPSD| 47167580
(tài sản ban đầu trừ chi phí của trò chơi, cộng với số tiền thắng là $10), hoặc nếu không thì
nó bằng $10- $4 - $2 = $4 (tài sản ban đầu trừ đi chi phí của trò chơi, trừ đi khoản lỗ $ 2)
trong trường hợp anh ta thua cuộc. Giả sử hàm lợi ích của cá nhân này được cho bởi . Sau
đó, lợi ích mong đợi khi trò chơi có giá AFP bằng 0.5 + 0.5 = 3. Mặt khác, giả sử Terry
không chơi trò chơi; lợi ích của anh ta vẫn ở = 3,162. Vì lợi ích khi không chơi trò chơi
cao hơn, nên có thể kết luận rằng bất kỳ cá nhân nào có sở thích được mô tả trong Hình 3.2
sẽ từ bỏ trò chơi may rủi nếu giá của nó bằng AFP. Đây là một kết quả quan trọng đối với
một hàm lợi ích lõm như trong Hình 3.2.
Trong một nghiên cứu thử nghiệm, Holt và Laury (2002) nhận thấy rằng phần lớn các đối
tượng được nghiên cứu của họ đã đưa ra "những lựa chọn an toàn", tức là thể hiện sự không
thích rủi ro. * Tìm kiếm rủi ro:
Chúng ta biết rằng hầu hết chúng ta không phải lúc nào cũng cư xử như những người
không thích rủi ro. Thuật ngữ “phóng đại phi lý” ra đời mô tả sự lệch lạc của mọi người
so với sở thích binh thường. Chúng ta có thể xem xét điều kiện thị trường bên ngoài và
“tâm lý bầy đàn” là những yếu tố góp phần đáng kể vào việc thay đổi các đặc điểm sợ rủi ro hợp lý.
Những người có hành vi tìm kiếm rủi ro thể hiện các sở thích dường như ngược lại với
không thích rủi ro, nên biểu diễn hàm toán học cũng có thể cho thấy hành vi ngược lại.
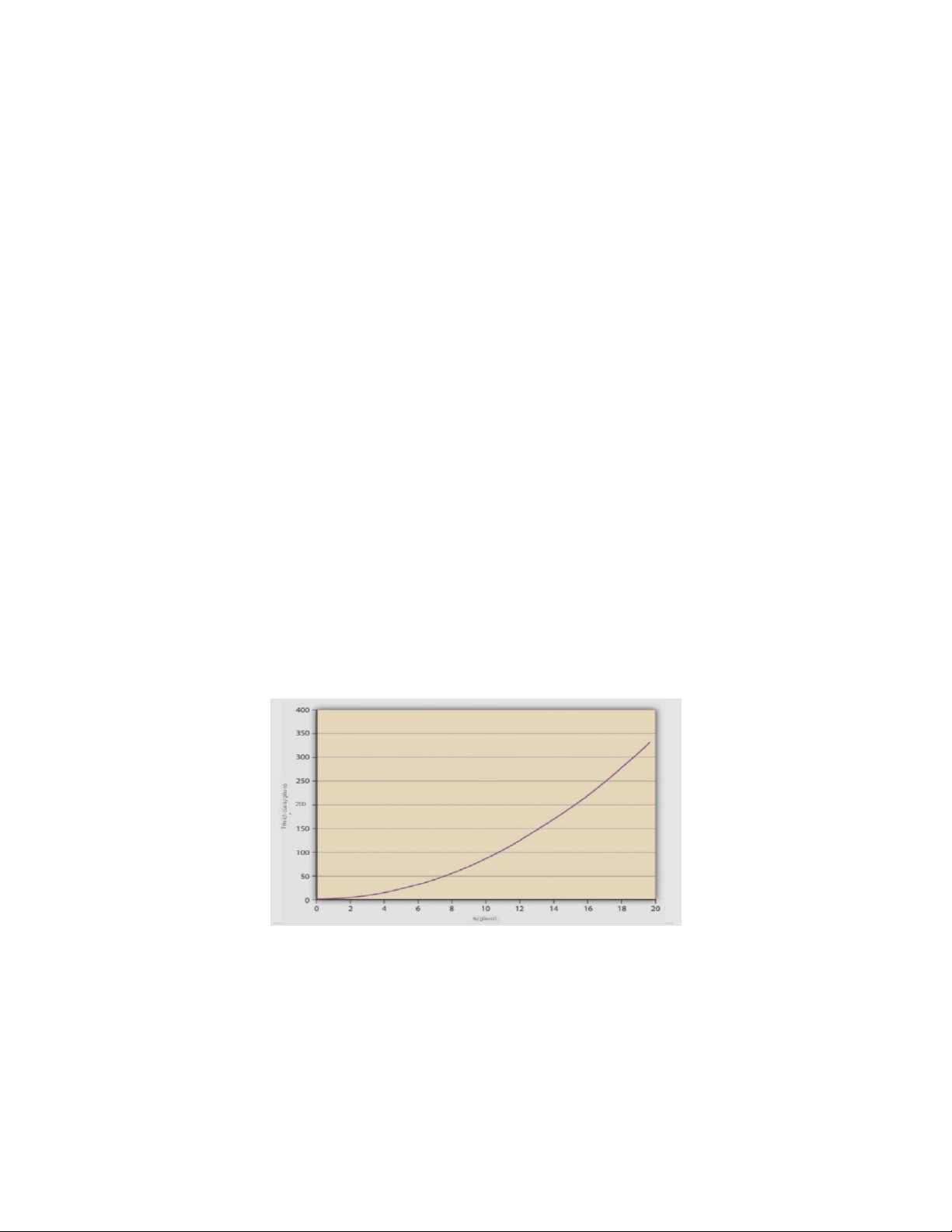
Hình 3.3 “Hàm lợi ích cho cá nhân tìm kiếm rủi ro” Nó cho thấy rằng mức độ giàu có của
cá nhân càng lớn thì mức độ lợi ích càng cao khi người đó cho thêm một đô la, đây là đặc
điểm của hàm, trong đó lợi ích luôn tăng với tốc độ ngày càng lớn, lợi ích cận biên ngày càng tăng.
Hình 3.2 Một hàm lợi ích cho một người tìm kiếm rủi ro
Một cá nhân thích mạo hiểm sẽ luôn chọn chơi một canh bạc tại AFP của họ, giả sử rằng
sở thích của cá nhân được đưa ra bởi u (W) = W². Như trước đây, cá nhân sở hữu 10 đô la
và phải quyết định có chơi xổ số hay không dựa trên việc tung đồng xu. Phần thưởng nếu
phần đầu quay lên là 10 đô la và – 2 đô la nếu là phần đuôi, AFP để chơi xổ số này là 4 lOMoAR cPSD| 47167580
đô la. Sau khi trả trước chi phí xổ số, tài sản là 6 đô la. Nếu đầu quay lên, tài sản cuối
cùng trở thành 16$ (10$+6$). Trong trường hợp sấp ngửa, thì tài sản cuối cùng bằng 4 đô
la (6$- 2$) Lợi ích mong đợi của mọi người nếu họ chơi xổ số là u (W) = 0,5 x 16² +0,5 x
4² = 136 utils. Mặt khác, nếu một cá nhân tên Ray quyết định không chơi xổ số, thì E (U)
= 10² = 100. Vì E (U) cao hơn nếu Ray chơi xổ số tại AFP của nó, anh ta sẽ chơi xổ số =>
Sự đối lập giữa lựa chọn của những người không thích rủi ro và những người thích mạo
hiểm là hoàn toàn rõ ràng. Đối với người không thích rủi ro E(U[W]) ≤ U[E(W)] ; với
người tìm kiếm rủi ro E(U[W)] ≥ U[E(W)] ( bất đẳng thức Jensen) * Trung lập rủi ro:
Cuối cùng, thái độ rủi ro thứ ba gọi là trung lập rủi ro. Sở thích của một cá nhân như vậy
có thể được nắm bắt trong lý thuyết E (U) bởi một hàm thỏa dụng tuyến tính có dạng u
(W) = aW, trong đó a là một số thực > 0. Một cá nhân như vậy đạt được mức thỏa dụng
biên không đổi của của cải, nghĩa là, mỗi đô la bổ sung sẽ bổ sung cùng một tiện ích cho
người đó bất kể cá nhân đó được ưu đãi với 10 đô la hay 10.000 đô la. Hàm lợi ích của
một cá nhân như vậy được mô tả trong Hình 3.4 “ Hàm lợi ích cho cá nhân trung lập với rủi ro”
Hình 3.4 Hàm lợi ích cho một cá nhân trung lập rủi ro