Câu hỏi trắc nghiệmToán 12 Bài 3: Phương trình đường thẳng trong không gian (có đáp án)

Tổng hợp câu hỏi trắc nghiệm Bài 3: Phương trình đường thẳng trong không gian kèm lời giải chi tiết giúp bạn ôn tập và đạt kết quả cao trong kỳ thi sắp tới.

54 27 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Phương pháp tọa độ trong không gian

Môn: Toán 12

Thông tin:

10 trang 10 tháng trước

Tác giả:

Profile VietJack
Trang 1/10
BÀI TẬP PHƯƠNG TRÌNH ĐƯỜNG THẲNG
Câu 1 Viết phương trình đường thẳng d đi qua 2 điểm A(2; 1; 0), B(0; 1; 2)
A. (d):
0
xt
y
zt
B. (d):
2
1
xt
y
zt
C. (d):
2
1
xt
y
zt
D. (d):
0
2
xt
y
zt
Câu 2. Vi ết phương trình đường thẳngd đi qua điểm A(4; –2; 2), song song với Δ:
2 5 2
4 2 3
x y z
.
A. (d):
4 2 2
4 2 3
x y z
B. (d):
4 2 2
4 2 3
x y z
C. (d):
4 2 2
423
x y z
D. (d):
Câu 3. Viết phương trình đường thẳng(d) đi qua điểm A(–1; 0; 2), vuông góc với (P): 2x – 3y +
6z + 4 = 0.
A. (d):
12
2 3 6
x y z
B. (d):
12
2 3 6
x y z
C. (d):
12
2 3 6
x y z
D. (d):
12
2 3 6
x y z
Câu 4. Viết phương trình giao tuyến của 2 mặt phẳng (P): 2x + y – z + 3 = 0; (Q): x + y + z – 1
= 0
A. (d):
12
2 3 1
x y z
B. (d):
12
2 3 1
x y z
C. (d):
21
2 3 1
x y z
D. (d):
11
2 3 1
x y z
Câu 5. Viết phương trình đường thẳng(d) đi qua điểm A(1; 0; 5), đồng thời vuông góc với hai
đường thẳng (d
1
):
1 3 1
2 2 1
x y z
và (d
2
):
1 2 3
1 1 3
x y z
A. (d):
15
5
54
xt
yt
zt
B. (d):
1
5
xt
yt
z
C. (d):
1
5
xt
yt
z
D. (d):
1
5
xt
yt
z
Trang 2/10
Câu 6 Viết phương trình đường thẳng(d) đi qua điểm A(1; 2; –2), đồng thời vuông góc và cắt
đường thẳng Δ:
1
1 1 2
x y z
A.
1 2 2
1 1 1
x y z
B.
C.
1 2 2
1 1 1
x y z
D.
1 2 2
1 1 1
x y z
Câu 7. Lập phương trình tổng quát của đường thẳng
d
đi qua điểm
(1;0;3)A
và
(4;2; 1)B
?
A.
2 3 2 0
4 3 13 0
xy
xz
B.
2 3 2 0
4 3 13 0
xy
xz
C.
2 3 2 0
4 3 13 0
xy
xz
D.
2 3 2 0
4 3 13 0
xy
xz
Câu 8. Phương trình chính tắc của đường thẳng
d
đi qua điểm
(1; 2;5)M
và vuông góc với
mặt phẳng
( ) : 4 3 2 5 0x y z
là:
A.
1 2 5
4 3 2
x y z
B.
1 2 5
4 3 2
x y z
C.
1 2 5
4 3 2
x y z
D.
1 2 5
4 3 2
x y z
Câu 9: Phương trình của mp(P) đi qua điểm A(1;-1;-1) và vuông góc với đường thẳng
2
:1
12
xt
d y t
zt
l:
A. x - y - 2z + 4=0 B. x - y + 2z - 4=0
C. x - y + 2z + 4=0 D.x – y – 2z – 4 = 0
Câu 10: Lập phương trình của mặt phẳng (P) đi qua điểm A(1;-1;-1) và vuông góc với đường
thẳng
d :
x+3 1-y z+2
= =
2 3 4
A. 2x-3y +4z -1=0 B. 2x-3y +4z +1=0
C. 2x-3y -4z -1=0 D. 2x-3y -4z +1=0
Trang 3/10
Câu 11: Phương trình tham số của đường thẳng đi qua điểm A(1; 2;3) v c VTCP
( 2;0;1)u
l:
A.
12
:2
3
xt
dy
zt
B.
12
:2
3
xt
dy
zt
C.
1
:2
3
xt
dy
zt
D.
1
:2
3
xt
dy
zt
Câu 12: Lập phương trình tham số của đường thẳng d đi qua hai điểm A(1;2;3) và B(2;1;1)
A.
1
:2
32
xt
d y t
zt
B.
1
:2
32
xt
d y t
zt
C.
1
:2
3
xt
d y t
zt
D.
1
:2
3
xt
d y t
zt
Câu 13:Lập phương trình tham số của đường thẳng d đi qua điểm M(1;-2;3) và song song với
đường thẳng Δ
12
:2
3
xt
yt
zt
A.
12
:2
3
xt
d y t
zt
B.
12
:2
3
xt
d y t
zt
C.
12
:2
3
xt
d y t
zt
D.
12
:2
3
xt
d y t
zt
Câu 15: Cho đường thẳng d :
22
3
35
xt
yt
zt
. Phương trình chính tắc của d là:
A.
23
2 3 5
x y z
B.
23
2 3 5
x y z
C. x -2 = y = z+3 D. x+2 = y = z - 3
Câu 16: Cho đường thẳng d :
22
3
35
xt
yt
zt
. Một véc tơ chỉ phương của d là :
A.
(2; 0; 3)u
B.
(2; 3;5)u
C.
(2; 3; 5)u
D.
2;0;5u
Trang 4/10
Câu 17. Cho hai đường thẳng d
1
:
6 6 2
2 2 1
x y z
, d
2
:
1 2 3
2 3 1
x y z
. Viết
phương trình đường thẳng đồng thời cắt và vuông góc với cả hai đường thẳng d
1
, d
2
.
A. d:
3
8
12
xt
y
zt
B. d:
35
8
1 10
xt
yt
zt
C. d:
35
8
1 10
xt
yt
zt
D. d:
3
8
12
xt
y
zt
Câu18. Hãy tìm một vectơ chỉ phương của đường thẳng là giao tuyến của hai mặt phẳng
2 3 5 8 0, 2 1 0x y z x y z
?
A.
(11; 1; 5)u
B.
( 11;1;5)u
C.
(11; 1;5)u
D.
(11;1;5)u
Câu19. Tìm toạ độ giao điểm
M
của đường thẳng
12
:2
1
xt
d y t
zt
và mặt phẳng
( ) : 4 5 0P x y z
?
A.
(1;1;2)M
B.
(1; 1;2)M
C.
(1;1; 2)M
D.
( 1; 1;2)M
Câu 20: Trong không gian Oxyz, cho mp(P) :x+ y +z -1 =0 v đường thẳng d c phương
trình:
1
:
1
x
d y t
z
.Tìm giao điểm A của d v mp(P)
A. A(1;1;-1) B. A(1;1;1) C. A(1;-1;-1) D. A(1;-1;1)
Câu 21: Cho điểm A(2;3;5) và mp (P): 2x +3y+z -17=0 , gọi d l đường thẳng đi qua A v vuông
góc với mp(P) . Xác định giao điểm M của d và trục Oz.
A. M(0;0;2) B. M(0;0;3) C. M(0;0;4) D. M(0;0;-4)
Câu 22: Tìm giao điểm M của đường thẳng
x=4+3t
: y=-6-3t
z=t
và mặt phẳng (P) : 2x+ 4y - 3z - 1 =0
A. M(-1;1;-1) B. M(-1;-1;1) C. M(1;-1;-1) D.M(1;1;1)
Câu 23. Góc giữa đường thẳng
5
:2
42
xt
yt
zt
và mặt phẳng
( ) : 2 7 0x y z
bằng:
A.
4
B.
6
C.
3
D.
2
Trang 5/10
Câu 24. Tính góc giữa 2 đường thẳng
1
12
: 2 2
3
xt
d y t
z
và
2
3 1 2
:
2 1 2
x y z
d
?
A.
6
B.
3
C.
4
D.
2
Câu 25. Toạ độ giao điểm
M
của 2 đường thẳng
1
18
: 1 3
25
xt
d y t
zt
và
2
7 3 5
:
2 5 2
x y z
d
là:
A.
(9;2;7)M
B.
(9;2; 7)M
C.
(9; 2; 7)M
D.
(9; 2;7)M
Câu 26: Tìm hình chiếu H của điểm A(2;-1;3) trên đường thẳng (D):
x=3t
y=-7 +5t
z=2 +2t
A. H(3;-2;-4) B. H(3;2;4) C. H(-3;-2;4) D. Một điểm khác.
Câu 27: Tính khoảng cách d từ A (2;-1;3) đến đường thẳng (D):
x=3t
y=-7 +5t
z=2 +2t
A. d=
2
B. d=
3
C. d=
23
D. d=
32
Câu 28: Xác định điểm A' đối xứng của điểm A(2;-1;3) qua đường thẳng d:
x=3t
y=-7 +5t
z=2 +2t
A. A'(4;3;5) B. A'(4;3;-5) C. A'(4;-3;5) D. A'(4;-3;-5)
Câu 29: Cho mặt phẳng (P) 2x+y+3z+1=0 v đuờng thẳng d c phương trình tham số:
3
22
1
xt
yt
z
, trong các mệnh đề sau, mệnh đề no đúng:
A. d vuông góc với (P); B. d cắt (P);
C. d song song với (P); D. d thuộc (P)
Trang 6/10
Câu 30: Góc giữa 2 đuờng thẳng
12
2 2 3
: : 1
1 1 1
13
xt
x y z
va d y t
zt
là :
A. 0
0
; B.30
0
; C. 90
0
; D.60
0
Câu 31: Giao điểm của hai đường thẳng d :
32
23
64
xt
yt
zt
v d’ :
5'
1 4 '
20 '
xt
yt
zt
là :
A. (-3;-2;6) B. (5;-1;20) C. (3;7;18) D.(3;-2;1)
Câu 32:Khoảng cách giữa hai đường thẳng d:
12
1
1
xt
yt
z
v d’ :
2 2 3
1 1 1
x y z
là
:
A.
6
B.
6
2
C.
1
6
D.
2
Câu 33: Cho hai đường thẳng d1:
21
4 6 8
x y z
và d2:
72
6 9 12
x y z
. Vị trí
tương đối giữa d1 và d2 là:
A. Trùng nhau B. Song song C. Cắt nhau D. Chéo
nhau
Câu 34: Khoảng cách giữa hai đường thẳng d1:
21
4 6 8
x y z
và d2:
72
6 9 12
x y z
là:
A.
35
17
B.
35
17
C.
854
29
D.
854
29
Câu 35. Tìm
m
để 2 đường thẳng
1
:
23
x y z
d
m
và
cắt nhau?
A.
m=1
B.
m=2
C.
m=3
D.
m=4
Trang 7/10
Câu 36. Xác định toạ độ hình chiếu
'M
của điểm
(1;2;6)M
lên đường thẳng
2 1 3
:
2 1 1
x y z
d
?
A.
'(0;2;4)M
B.
'(0; 2; 4)M
C.
'(0; 2;4)M
D.
(0;2; 4)M
Câu 37. Khoảng cách từ điểm
(2;3;1)A
đến đường thẳng
14
: 2 2
14
xt
d y t
zt
bằng :
A.
3
B.
5
C.
6
D.
7
Câu 38. Khoảng cách giữa 2 đường thẳng song song
1
32
:
1 2 1
x y z
d
và
2
3 1 2
:
1 2 1
x y z
d
bằng:
A.
56
6
B.
53
6
C.
5 30
6
D.
55
6
Câu 39. Xét vị trí tương đối giữa 2 đường thẳng
12
1 3 2 2 1 4
: , :
2 2 3 3 2 4
x y z x y z
dd
ta được kết quả nào?
A. Cắt nhau
B. Song song
C. Chéo nhau
D. Trùng nhau
Câu 40. Cho mặt phẳng
( ) : 2 3 1 0x y z
v đường thẳng
3
: 2 2
1
xt
d y t
z
. Tìm mệnh
đề đúng trong các mệnh đề sau?
A.
d ( )
B.
d ( )
C.
d ( )=M
D.
d ( )
Câu 41. Trong không gian với hệ trục toạ độ Oxyz cho đường thẳng
2 2 0
:
2 5 0
x y z
d
xz
.
Gọi
Md
và
u
l vectơ chỉ phương của đường thẳng . Tìm nhận định đúng?
A.
(3; 1;1)M
và
(1; 1;2)u
B.
(3;1; 1)M
và
(1;1; 2)u
C.
(3;1; 1)M
và
(1;1;2)u
D. Cả 3 đáp án trên đều sai
Câu 42. Xét vị trí tương đối của 2 đường thẳng
1
:2
3
xt
d y t
zt
và
12
' : 1 2
22
xu
d y u
zu
?
A.
d
và
'd
chéo nhau
B.
d'd
C.
d '=Md
D.
d'd
Trang 8/10
Câu 43.Cho 2 đường thẳng chéo nhau
1
1
:1
1
xt
d y t
zt
và
2
32
:
3 3 3
x y z
d
. Độ dài
đường vuông góc chung của 2 đường thẳng trên bằng bao nhiêu?
A.
112
3
B.
104
3
C.
114
3
D. Đáp số A, B, C sai
Câu 44. Cho điểm
(0;1;1)M
v 2 đường thẳng
12
20
12
: , :
10
3 1 1
x y z
x y z
dd
x
. Gọi l đường thẳng đi qua điểm
M
vuông
góc với
1
d
, cắt
2
d
. Tính góc giữa 2 đường thẳng
2
d
và ?
A.
0
120
B.
0
30
C.
0
60
D.
0
45
Câu 45. Gọi
'd
là hình chiếu vuông góc của đường thẳng
5 2 4
:
11
2
x y z
d
lên mặt
phẳng
( ) : 2 0P x y z
. Tính góc giữa
d
và
'd
?
A.
6
B.
2
3
C.
4
3
D.
5
3
Câu 46:Trong không gian cho điểm A(1;1;1) v đường thẳng
14 4
:
52
xt
d y t
zt
.Xác định điểm
H l hình chiếu vuông gc của A lên d
A. H(2;3;-1) B H(2;-3;-1) C. H(2;-3;1) D. H(2;-3;-1)
Câu 47: Hình chiếu vuông góc của A(-2;4;3) trên mặt phẳng
2 3 6 19 0x y z
có tọa độ
là:
A. (1;-1;2) B.
20 37 3
( ; ; )
7 7 7
C.
2 37 31
( ; ; )
5 5 5
D. Kết quả khác
Câu 48: Xác định điểm đối xứng A' của điểm A(4;1;6) qua đường thẳng :
52
: 7 2
xt
d y t
zt
A. A’(27;26;14) B. A’(27;-26;14) C. A’(27;26;-14) D. A’(27;-26;-14)
Câu 49. Cho điểm A(1; 1; 1) v đường thẳng (d):
64
2
12
xt
yt
zt
. Tìm tọa độ hình chiếu vuông
góc của A lên đường thẳng (d).
Trang 9/10
A. (2; –3; –1) B. (2; 3; 1) C. (2; –3; 1) D. (–2; 3; 1)
Câu 50. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:
21
2 2 1
x y z
và
điểm A(–1; 0; 1). Tìm tọa độ điểm B đối xứng với A qua đường thẳng d.
A. (1; 2; 3) B. (1; 2; 1) C. (1; –2; 3) D. (0; 1; 1)
Câu 51.Cho A(–2; 2; 3) v đường thẳng (Δ):
1 2 3
2 2 1
x y z
. Tính khoảng cách từ A
đến(Δ).
A. 3
5
B. 5
3
C. 2
5
D. 5
2
Câu 52. Cho đường thẳng d:
2 3 1
2 3 3
x y z
và mặt phẳng (P): 3x + 5y – 2z – 4 = 0.
Tìm tọa độ giao điểm của d và (P).
A. (4; 0; 4) B. (0; 0; –2) C. (2; 0; 1) D. (–2; 2; 0)
Câu 53. Tìm tọa độ điểm A trên đường thẳng d:
1
2 1 1
x y z
sao cho khoảng cách từ A đến
mặt phẳng (P): x – 2y – 2z + 5 = 0 bằng 3. Biết rằng A c honh độ dương.
A. (2; –1; 0) B. (4; –2; 1) C. (–2; 1; –2) D. (6; –3; 2)
Câu 54. Tính khoảng cách giữa hai đường thẳng d
1
:
1 7 3
2 1 4
x y z
, d
2
:
1 2 2
1 2 1
x y z
.
A.
3
14
B.
2
14
C.
1
14
D.
5
14
Câu 55. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:
1 3 1
3 2 2
x y z
và
mặt phẳng (P): x – 3y + z – 4 = 0. Phương trình hình chiếu vuông góc của d trên mặt phẳng (P) là
A.
3 1 1
2 1 1
x y z
B.
2 1 1
2 1 1
x y z
C.
5 1 1
2 1 1
x y z
D.
11
2 1 1
x y z
Câu 56. Cho đường thẳng Δ:
12
2 1 1
x y z
và mặt phẳng (P): x − 2y + 2z – 3 = 0. Gọi C
l giao điểm của Δ với (P), M l điểm thuộc Δ. Tính khoảng cách từ M đến (P), biết MC =
6
.
Trang 10/10
A. 2 B. 3 C. 2/3 D. 4/3
Câu 57. Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): 2x + y – z – 3 = 0 và (Q):
x + y + z – 1 = 0. Phương trình đường giao tuyến của hai mặt phẳng (P) và (Q).
A. (d):
21
2 3 1
x y z
B. (d):
1 2 1
2 3 1
x y z
C. (d):
1 2 1
2 3 1
x y z
D. (d):
21
2 3 1
x y z
Câu 58. Cho mặt phẳng (P): 3x – 2y + z + 6 = 0 v điểm A(2; –1; 0). Tìm tọa độ hình chiếu của
A lên mặt phẳng (P).
A. (1; –1; 1) B. (–1; 1; –1) C. (3; –2; 1) D. (5; –3; 1)
Câu 59. Cho điểm A(1; 1; 1) v đường thẳng (d):
64
2
12
xt
yt
zt
. Tìm tọa độ hình chiếu vuông
góc của A lên đường thẳng (d).
A. (2; –3; –1) B. (2; 3; 1) C. (2; –3; 1) D. (–2; 3; 1)
Câu 60. Cho đường thẳng Δ:
1
2 1 2
x y z
. Xác định tọa độ điểm M trên trục hoành sao cho
khoảng cách từ M đến Δ bằng OM với O là gốc tọa độ.
A. (–1; 0; 0) hoặc (1; 0; 0) B. (2; 0; 0) hoặc (–2; 0; 0)
C. (1; 0; 0) hoặc (–2; 0; 0) D. (2; 0; 0) hoặc (–1; 0; 0)
| 1/10
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

BÀI TẬP PHƯƠNG TRÌNH ĐƯỜNG THẲNG
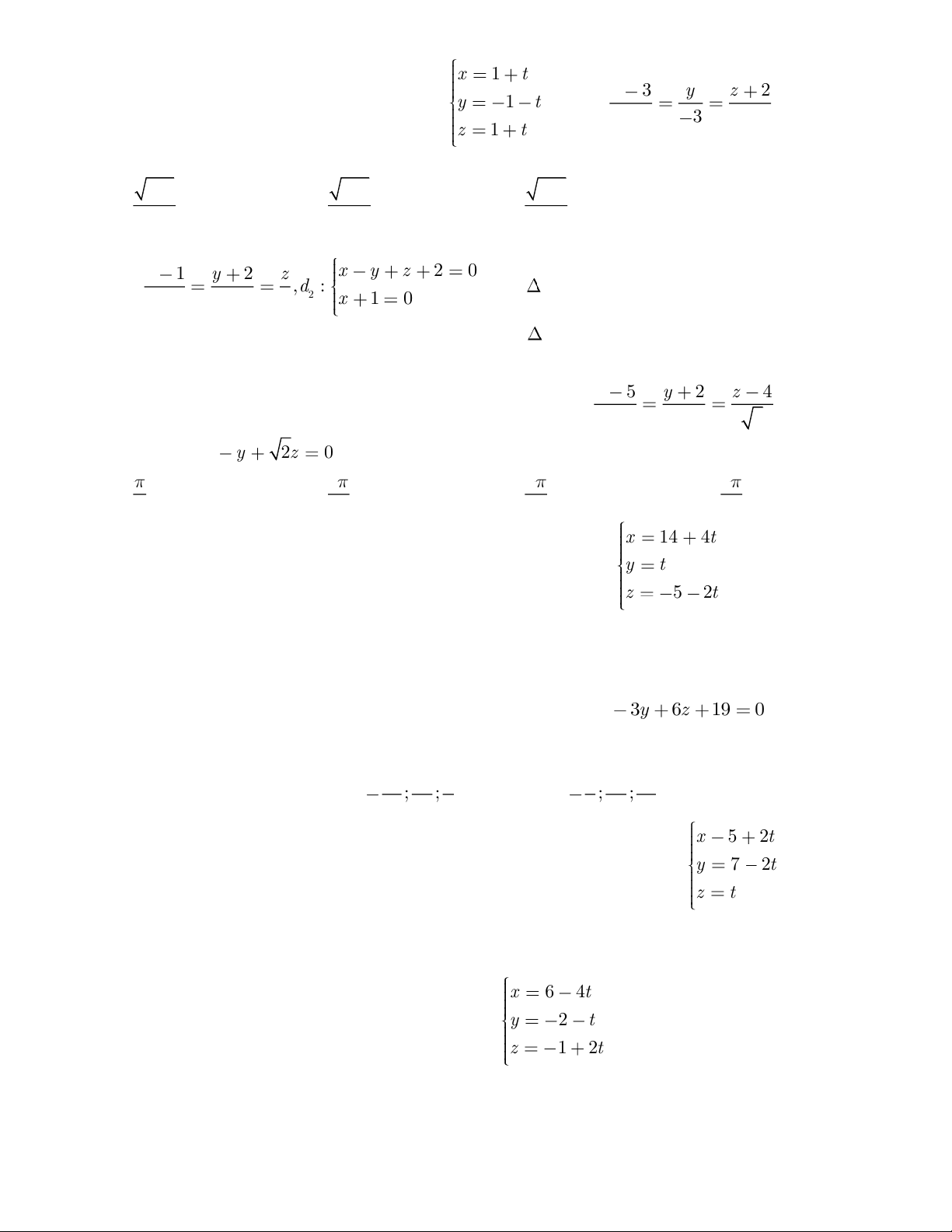
Câu 1 Viết phương trình đường thẳng d đi qua 2 điểm A(2; 1; 0), B(0; 1; 2) x t x 2 t x 2 t x t A. (d): y 0 B. (d): y 1 C. (d): y 1 D. (d): y 0 z t z t z t z 2 t
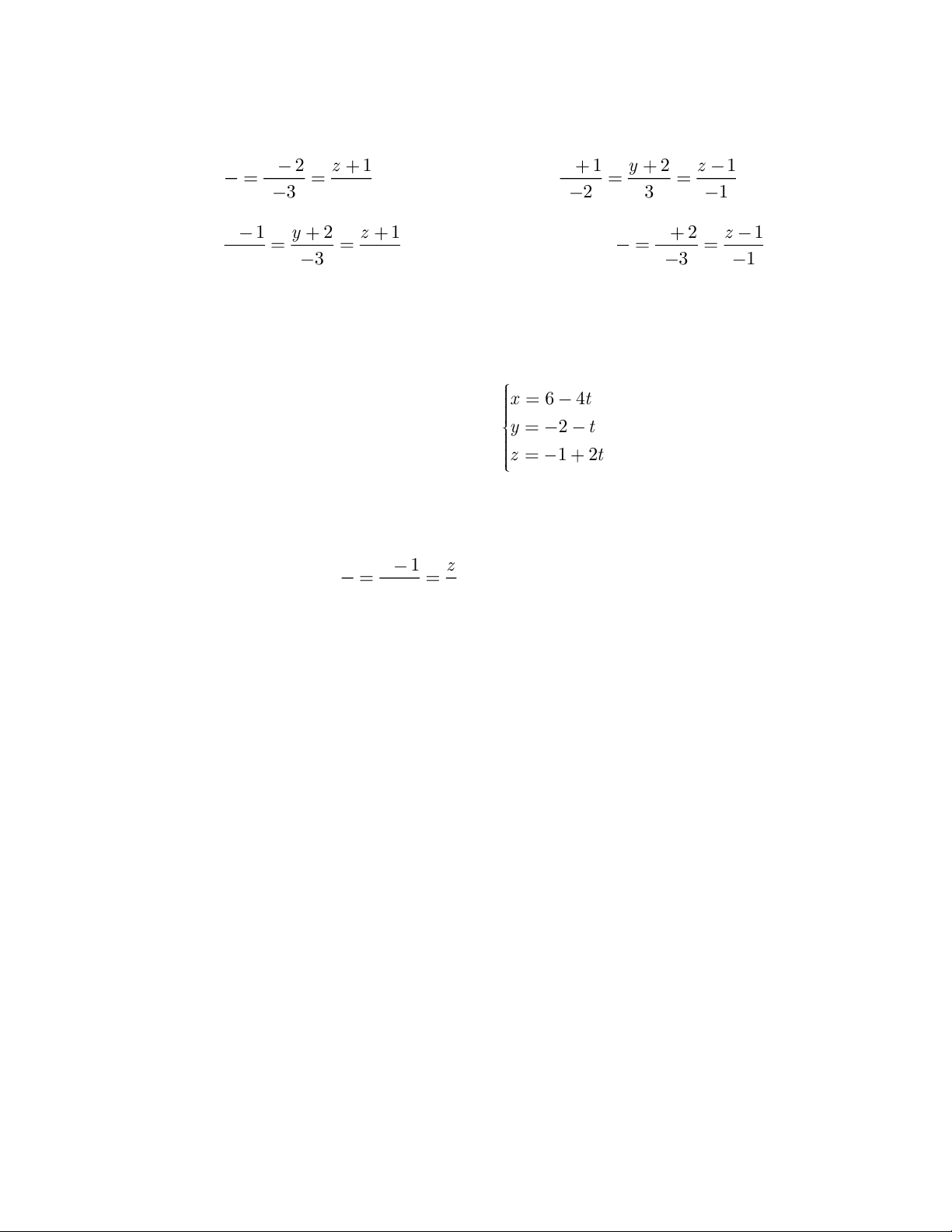
Câu 2. Viết phương trình đường thẳngd đi qua điểm A(4; –2; 2), song song với Δ: x 2 y 5 z 2 . 4 2 3 x 4 y 2 z 2 x 4 y 2 z 2 A. (d): B. (d): 4 2 3 4 2 3 x 4 y 2 z 2 x 4 y 2 z 2 C. (d): D. (d): 4 2 3 4 2 3
Câu 3. Viết phương trình đường thẳng(d) đi qua điểm A(–1; 0; 2), vuông góc với (P): 2x – 3y + 6z + 4 = 0. x 1 y z 2 x 1 y z 2 A. (d): B. (d): 2 3 6 2 3 6 x 1 y z 2 x 1 y z 2 C. (d): D. (d): 2 3 6 2 3 6
Câu 4. Viết phương trình giao tuyến của 2 mặt phẳng (P): 2x + y – z + 3 = 0; (Q): x + y + z – 1 = 0 x y 1 z 2 x y 1 z 2 A. (d): B. (d): 2 3 1 2 3 1 x y 2 z 1 x 1 y z 1 C. (d): D. (d): 2 3 1 2 3 1
Câu 5. Viết phương trình đường thẳng(d) đi qua điểm A(1; 0; 5), đồng thời vuông góc với hai x 1 y 3 z 1 x 1 y 2 z 3 đường thẳng (d1): và (d 2 2 1 2): 1 1 3 x 1 5t x 1 t x 1 t x 1 t A. (d): y 5t B. (d): y t C. (d): y t D. (d): y t z 5 4t z 5 z 5 z 5 Trang 1/10
Câu 6 Viết phương trình đường thẳng(d) đi qua điểm A(1; 2; –2), đồng thời vuông góc và cắt x y 1 z đường thẳng Δ: 1 1 2 x 1 y 2 z 2 x 1 y 2 z 2 A. B. 1 1 1 1 1 1 x 1 y 2 z 2 x 1 y 2 z 2 C. D. 1 1 1 1 1 1
Câu 7. Lập phương trình tổng quát của đường thẳng d đi qua điểm ( A 1;0;3) và ( B 4;2; 1)? 2x 3y 2 0 2x 3y 2 0 A. B. 4x 3z 13 0 4x 3z 13 0 2x 3y 2 0 2x 3y 2 0 C. D. 4x 3z 13 0 4x 3z 13 0
Câu 8. Phương trình chính tắc của đường thẳng d đi qua điểm M(1; 2;5) và vuông góc với mặt phẳng ( ) : 4x 3y 2z 5 0 là: x 1 y 2 z 5 x 1 y 2 z 5 A. B. 4 3 2 4 3 2 x 1 y 2 z 5 x 1 y 2 z 5 C. D. 4 3 2 4 3 2
Câu 9: Phương trình của mp(P) đi qua điểm A(1;-1;-1) và vuông góc với đường thẳng x 2 t d : y 1 t là: z 1 2t
A. x - y - 2z + 4=0 B. x - y + 2z - 4=0
C. x - y + 2z + 4=0 D.x – y – 2z – 4 = 0
Câu 10: Lập phương trình của mặt phẳng (P) đi qua điểm A(1;-1;-1) và vuông góc với đường thẳng x+3 1-y z+2 d : = = 2 3 4
A. 2x-3y +4z -1=0 B. 2x-3y +4z +1=0
C. 2x-3y -4z -1=0 D. 2x-3y -4z +1=0 Trang 2/10
Câu 11: Phương trình tham số của đường thẳng đi qua điểm A(1; 2;3) và có VTCP u ( 2; 0;1)là: x 1 2t x 1 2t x 1 t x 1 t A. d : y 2 B. d : y 2 C. d : y 2 D. d : y 2 z 3 t z 3 t z 3 t z 3 t
Câu 12: Lập phương trình tham số của đường thẳng d đi qua hai điểm A(1;2;3) và B(2;1;1) x 1 t x 1 t x 1 t x 1 t A. d : y 2
t B. d : y 2
t C. d : y 2
t D. d : y 2 t z 3 2t z 3 2t z 3 t z 3 t
Câu 13:Lập phương trình tham số của đường thẳng d đi qua điểm M(1;-2;3) và song song với x 1 2t đường thẳng Δ: y 2 t z 3 t x 1 2t x 1 2t x 1 2t A. d : y 2
t B. d : y 2
t C. d : y 2 t D. z 3 t z 3 t z 3 t x 1 2t d : y 2 t z 3 t x 2 2t
Câu 15: Cho đường thẳng d : y 3t
. Phương trình chính tắc của d là: z 3 5t x 2 y z 3 x 2 y z 3 A. B. 2 3 5 2 3 5
C. x -2 = y = z+3 D. x+2 = y = z - 3 x 2 2t
Câu 16: Cho đường thẳng d : y 3t
. Một véc tơ chỉ phương của d là : z 3 5t A. u (2; 0; 3) B. u (2; 3;5) u u C. (2; 3; 5) D. 2; 0;5 Trang 3/10 x 6 y 6 z 2 x 1 y 2 z 3
Câu 17. Cho hai đường thẳng d1: , d . Viết 2 2 1 2: 2 3 1
phương trình đường thẳng đồng thời cắt và vuông góc với cả hai đường thẳng d1, d2. x 3 t x 3 5t x 3 5t x 3 t A. d: y 8 B. d: y 8 t C. d: y 8 t D. d: y 8 z 1 2t z 1 10t z 1 10t z 1 2t
Câu18. Hãy tìm một vectơ chỉ phương của đường thẳng là giao tuyến của hai mặt phẳng 2x 3y 5z 8 0,x y 2z 1 0? A. u (11; 1; 5) B.u ( 11;1;5) C.u (11; 1;5) D.u (11;1;5) x 1 2t
Câu19. Tìm toạ độ giao điểm M của đường thẳng d : y 2 t và mặt phẳng z 1 t (P) : 4x y z 5 0 ?
A. M(1;1;2)
B. M(1; 1;2)
C. M(1;1; 2)
D. M( 1; 1;2)
Câu 20: Trong không gian Oxyz, cho mp(P) :x+ y +z -1 =0 và đường thẳng d có phương x 1 trình:d : y
t .Tìm giao điểm A của d và mp(P) z 1
A. A(1;1;-1) B. A(1;1;1) C. A(1;-1;-1) D. A(1;-1;1)
Câu 21: Cho điểm A(2;3;5) và mp (P): 2x +3y+z -17=0 , gọi d là đường thẳng đi qua A và vuông góc với mp(P) . Xác định giao điểm M của d và trục Oz.
A. M(0;0;2) B. M(0;0;3) C. M(0;0;4) D. M(0;0;-4) x=4+3t
Câu 22: Tìm giao điểm M của đường thẳng
: y=-6-3t và mặt phẳng (P) : 2x+ 4y - 3z - 1 =0 z=t
A. M(-1;1;-1) B. M(-1;-1;1) C. M(1;-1;-1) D.M(1;1;1) x 5 t
Câu 23. Góc giữa đường thẳng : y 2
t và mặt phẳng ( ) : x y 2z 7 0 z 4 2t bằng: A. B. C. D. 4 6 3 2 Trang 4/10 x 1 2t x 3 y 1 z 2
Câu 24. Tính góc giữa 2 đường thẳng d : y 2 2t và d : ? 1 2 2 1 2 z 3 A. B. C. D. 6 3 4 2 x 1 8t Câu 25. Toạ
độ giao điểm M của 2 đường thẳng d : y 1 3t và 1 z 2 5t x 7 y 3 z 5 d : là: 2 2 5 2
A. M(9;2;7)
B. M(9;2; 7)
C. M(9; 2; 7)
D. M(9; 2;7) x=3t
Câu 26: Tìm hình chiếu H của điểm A(2;-1;3) trên đường thẳng (D): y=-7 +5t z=2 +2t
A. H(3;-2;-4) B. H(3;2;4) C. H(-3;-2;4) D. Một điểm khác. x=3t
Câu 27: Tính khoảng cách d từ A (2;-1;3) đến đường thẳng (D): y=-7 +5t z=2 +2t A. d= 2 B. d= 3 C. d= 2 3 D. d= 3 2 x=3t
Câu 28: Xác định điểm A' đối xứng của điểm A(2;-1;3) qua đường thẳng d: y=-7 +5t z=2 +2t
A. A'(4;3;5) B. A'(4;3;-5) C. A'(4;-3;5) D. A'(4;-3;-5)
Câu 29: Cho mặt phẳng (P) 2x+y+3z+1=0 và đuờng thẳng d có phương trình tham số: x 3 t y 2
2t , trong các mệnh đề sau, mệnh đề nào đúng: z 1 A. d vuông góc với (P); B. d cắt (P); C. d song song với (P); D. d thuộc (P) Trang 5/10 x 1 2t x 2 y 2 z 3
Câu 30: Góc giữa 2 đuờng thẳng : va d : y 1 t là : 1 1 1 z 1 3t A. 00; B.300; C. 900; D.600 x 3 2t x 5 t '
Câu 31: Giao điểm của hai đường thẳng d : y 2
3t và d’ : y 1 4t ' là : z 6 4t z 20 t '
A. (-3;-2;6) B. (5;-1;20) C. (3;7;18) D.(3;-2;1) x 1 2t x 2 y 2 z 3
Câu 32:Khoảng cách giữa hai đường thẳng d: y 1 t và d’ : là 1 1 1 z 1 : 6 1 A. 6 B. C. D. 2 2 6 x 2 y z 1 x 7 y 2 z
Câu 33: Cho hai đường thẳng d1: và d2: . Vị trí 4 6 8 6 9 12
tương đối giữa d1 và d2 là: A. Trùng nhau B. Song song C. Cắt nhau D. Chéo nhau x 2 y z 1
Câu 34: Khoảng cách giữa hai đường thẳng d1: và d2: 4 6 8 x 7 y 2 z là: 6 9 12 35 35 854 854 A. B. C. D. 17 17 29 29 x y z x 1 y 5 z
Câu 35. Tìm m để 2 đường thẳng d : và d : cắt nhau? 1 2 3 m 2 3 2 1 A. m=1 B. m=2 C. m=3 D. m=4 Trang 6/10
Câu 36. Xác định toạ độ hình chiếu M ' của điểm M(1;2;6) lên đường thẳng x 2 y 1 z 3 d : ? 2 1 1
A. M '(0;2; 4)
B. M '(0; 2; 4)
C. M '(0; 2; 4)
D. M(0;2; 4) x 1 4t
Câu 37. Khoảng cách từ điểm (
A 2;3;1) đến đường thẳng d : y 2 2t bằng : z 1 4t A. 3 B. 5 C. 6 D. 7 x y 3 z 2
Câu 38. Khoảng cách giữa 2 đường thẳng song song d : và 1 1 2 1 x 3 y 1 z 2 d : bằng: 2 1 2 1 5 6 5 3 5 30 5 5 A. B. C. D. 6 6 6 6 Câu 39. Xét vị trí tương đối giữa 2 đường thẳng x 1 y 3 z 2 x 2 y 1 z 4 d : ,d :
ta được kết quả nào? 1 2 2 2 3 3 2 4 A. Cắt nhau B. Song song C. Chéo nhau D. Trùng nhau x 3 t
Câu 40. Cho mặt phẳng ( ) : 2x y 3z 1
0 và đường thẳng d : y 2 2t . Tìm mệnh z 1
đề đúng trong các mệnh đề sau? A. d ( ) B. d ( ) C. d ( )=M D. d ( ) x 2y z 2 0
Câu 41. Trong không gian với hệ trục toạ độ Oxyz cho đường thẳng d : . 2x z 5 0 Gọi M
d và u là vectơ chỉ phương của đường thẳng . Tìm nhận định đúng?
A. M(3; 1;1) và u(1; 1;2)
B. M(3;1; 1) và u(1;1; 2)
C. M(3;1; 1) và u(1;1;2)
D. Cả 3 đáp án trên đều sai x 1 t x 1 2u
Câu 42. Xét vị trí tương đối của 2 đường thẳng d : y 2
t và d ' : y 1 2u ? z 3 t z 2 2u
A. d và d ' chéo nhau
B. d d ' C. d d '=M D. d d ' Trang 7/10 x 1 t x 3 y z 2
Câu 43.Cho 2 đường thẳng chéo nhau d : y 1 t và d : . Độ dài 1 2 3 3 3 z 1 t
đường vuông góc chung của 2 đường thẳng trên bằng bao nhiêu? 112 104 114 A. B. C.
D. Đáp số A, B, C sai 3 3 3 Câu 44. Cho điểm M(0;1;1) và 2 đường thẳng x 1 y 2 z x y z 2 0 d : ,d : . Gọi
là đường thẳng đi qua điểm M vuông 1 2 3 1 1 x 1 0
góc với d , cắt d . Tính góc giữa 2 đường thẳng d và ? 1 2 2 A. 0 120 B. 0 30 C. 0 60 D. 0 45 x 5 y 2 z 4
Câu 45. Gọi d ' là hình chiếu vuông góc của đường thẳng d : lên mặt 1 1 2 phẳng (P) : x y 2z
0 . Tính góc giữa d và d ' ? 2 4 5 A. B. C. D. 6 3 3 3 x 14 4t
Câu 46:Trong không gian cho điểm A(1;1;1) và đường thẳng d : y t .Xác định điểm z 5 2t
H là hình chiếu vuông góc của A lên d
A. H(2;3;-1) B H(2;-3;-1) C. H(2;-3;1) D. H(2;-3;-1)
Câu 47: Hình chiếu vuông góc của A(-2;4;3) trên mặt phẳng 2x 3y 6z 19 0 có tọa độ là: 20 37 3 2 37 31 A. (1;-1;2) B. ( ; ; ) C. ( ; ; ) D. Kết quả khác 7 7 7 5 5 5 x 5 2t
Câu 48: Xác định điểm đối xứng A' của điểm A(4;1;6) qua đường thẳng :d : y 7 2t z t
A. A’(27;26;14) B. A’(27;-26;14) C. A’(27;26;-14) D. A’(27;-26;-14) x 6 4t
Câu 49. Cho điểm A(1; 1; 1) và đường thẳng (d): y 2
t . Tìm tọa độ hình chiếu vuông z 1 2t
góc của A lên đường thẳng (d). Trang 8/10 A. (2; –3; –1) B. (2; 3; 1) C. (2; –3; 1) D. (–2; 3; 1) x 2 y 1 z
Câu 50. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: và 2 2 1
điểm A(–1; 0; 1). Tìm tọa độ điểm B đối xứng với A qua đường thẳng d. A. (1; 2; 3) B. (1; 2; 1) C. (1; –2; 3) D. (0; 1; 1) x 1 y 2 z 3
Câu 51.Cho A(–2; 2; 3) và đường thẳng (Δ): . Tính khoảng cách từ A 2 2 1 đến(Δ). A. 3 5 B. 5 3 C. 2 5 D. 5 2 x 2 y 3 z 1
Câu 52. Cho đường thẳng d:
và mặt phẳng (P): 3x + 5y – 2z – 4 = 0. 2 3 3
Tìm tọa độ giao điểm của d và (P). A. (4; 0; 4) B. (0; 0; –2) C. (2; 0; 1) D. (–2; 2; 0) x y z 1
Câu 53. Tìm tọa độ điểm A trên đường thẳng d:
sao cho khoảng cách từ A đến 2 1 1
mặt phẳng (P): x – 2y – 2z + 5 = 0 bằng 3. Biết rằng A có hoành độ dương. A. (2; –1; 0) B. (4; –2; 1) C. (–2; 1; –2) D. (6; –3; 2) x 1 y 7 z 3
Câu 54. Tính khoảng cách giữa hai đường thẳng d1: , d 2 1 4 2: x 1 y 2 z 2 . 1 2 1 3 2 1 5 A. B. C. D. 14 14 14 14 x 1 y 3 z 1
Câu 55. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: và 3 2 2
mặt phẳng (P): x – 3y + z – 4 = 0. Phương trình hình chiếu vuông góc của d trên mặt phẳng (P) là x 3 y 1 z 1 x 2 y 1 z 1 A. B. 2 1 1 2 1 1 x 5 y 1 z 1 x y 1 z 1 D. C. 2 1 1 2 1 1 x 1 y z 2
Câu 56. Cho đường thẳng Δ:
và mặt phẳng (P): x − 2y + 2z – 3 = 0. Gọi C 2 1 1
là giao điểm của Δ với (P), M là điểm thuộc Δ. Tính khoảng cách từ M đến (P), biết MC = 6 . Trang 9/10 A. 2 B. 3 C. 2/3 D. 4/3
Câu 57. Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): 2x + y – z – 3 = 0 và (Q):
x + y + z – 1 = 0. Phương trình đường giao tuyến của hai mặt phẳng (P) và (Q). x y 2 z 1 x 1 y 2 z 1 A. (d): B. (d): 2 3 1 2 3 1 x 1 y 2 z 1 x y 2 z 1 C. (d): D. (d): 2 3 1 2 3 1
Câu 58. Cho mặt phẳng (P): 3x – 2y + z + 6 = 0 và điểm A(2; –1; 0). Tìm tọa độ hình chiếu của A lên mặt phẳng (P). A. (1; –1; 1) B. (–1; 1; –1) C. (3; –2; 1) D. (5; –3; 1) x 6 4t
Câu 59. Cho điểm A(1; 1; 1) và đường thẳng (d): y 2
t . Tìm tọa độ hình chiếu vuông z 1 2t
góc của A lên đường thẳng (d). A. (2; –3; –1) B. (2; 3; 1) C. (2; –3; 1) D. (–2; 3; 1) x y 1 z
Câu 60. Cho đường thẳng Δ:
. Xác định tọa độ điểm M trên trục hoành sao cho 2 1 2
khoảng cách từ M đến Δ bằng OM với O là gốc tọa độ.
A. (–1; 0; 0) hoặc (1; 0; 0)
B. (2; 0; 0) hoặc (–2; 0; 0)
C. (1; 0; 0) hoặc (–2; 0; 0)
D. (2; 0; 0) hoặc (–1; 0; 0) Trang 10/10