Chủ đề tương giao của đồ thị hàm số ôn thi tốt nghiệp THPT môn Toán

Tài liệu gồm 84 trang, được biên soạn bởi thầy giáo Phan Nhật Linh, tổng hợp lý thuyết trọng tâm, ví dụ minh họa và các dạng bài tập chủ đề tương giao của đồ thị hàm số ôn thi tốt nghiệp THPT môn Toán, có đáp án và lời giải chi tiết.

Môn:

Toán 12 3.9 K tài liệu

Thông tin:
84 trang 1 năm trước
Tác giả:
Student
Mai Nguyệt
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Chủ đề tương giao của đồ thị hàm số ôn thi tốt nghiệp THPT môn Toán

Tài liệu gồm 84 trang, được biên soạn bởi thầy giáo Phan Nhật Linh, tổng hợp lý thuyết trọng tâm, ví dụ minh họa và các dạng bài tập chủ đề tương giao của đồ thị hàm số ôn thi tốt nghiệp THPT môn Toán, có đáp án và lời giải chi tiết.

71 36 lượt tải Tải xuống

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số 375 tài liệu

Môn: Toán 12 3.9 K tài liệu

Thông tin:

84 trang 1 năm trước

Tác giả:

Profile Mai Nguyệt
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
1 | Facebook tác giả: Phan Nhật Linh
CHỦ ĐỀ 06 : TƯƠNG GIAO CỦA ĐỒ THỊ HÀM SỐ
❖ Tọa độ giao điểm của hai đồ thị hàm số:
• Phương pháp: Cho 2 hàm số
( ) ( )
==,y f x y g x
có đồ thị lần lượt là
( )
C
và
( )
C
.
▪ Lập phương trình hoành độ giao điểm của
( )
C
và
( )
C
:
( ) ( ) ( )
= *f x g x
▪ Giải phương trình tìm
x
từ đó suy ra
y
và tọa độ giao điểm.
▪ Số nghiệm của (*) là số giao điểm của
( )
C
và
( )
C
.
❖ Tương giao của đồ thị hàm bậc 3
• Phương pháp 1: Bảng biến thiên (phương pháp đồ thị)
▪ Lập phương trình hoành độ giao điểm dạng
( )
=,0F x m
(phương trình ẩn
x
tham số
)
▪ Cô lập
đưa phương trình về dạng
( )
=m f x
▪ Lập bảng biến thiên cho hàm số
( )
=y f x
.
▪ Dựa và giả thiết và bảng biến thiên từ đó suy ra
.
➢ Dấu hiệu: Sử dụng phương pháp bảng biến thiên khi
độc lập với
x
.
❖ Phương pháp 2: Nhẩm nghiệm – tam thức bậc 2.
▪ Lập phương trình hoành độ giao điểm
( )
=,0F x m
▪ Nhẩm nghiệm: (Khử tham số). Giả sử
=
0
xx
là 1 nghiệm của phương trình.
▪ Phân tích:
( ) ( ) ( )
( )
=
= − =
=
0
0
, 0 . 0
0
xx
F x m x x g x
gx
(là
( )
= 0gx
là phương trình bậc
hai ẩn
x
tham số
).
▪ Dựa vào yêu cầu bài toán đi xử lý phương trình bậc hai
( )
= 0gx
.
❖ Phương pháp 3: Cực trị
• Nhận dạng: Khi bài toán không cô lập được m và cũng không nhẩm được nghiệm.
• Quy tắc:
▪ Lập phương trình hoành độ giao điểm
( ) ( )
=, 0 1F x m
. Xét hàm số
( )
= ,y F x m
▪ Để
( )
1
có đúng 1 nghiệm thì đồ thị
( )
= ,y F x m
cắt trục hoành tại đúng
1
điểm.
▪ Hoặc hàm số luôn đơn điệu trên
hàm số không có cực trị
='0y
hoặc vô nghiệm
hoặc có nghiệm kép
'
0
y
▪ Hoặc hàm số có cực đại, cực tiểu và
.0
cd ct
yy
(tham khảo hình vẽ)
LÍ THUYẾT
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 2
▪ Để
( )
1
có đúng
3
nghiệm thì đồ thị
( )
= ,y F x m
cắt trục hoành tại
3
điểm phân biệt
Hàm số có cực đại, cực tiểu và
.0
cd ct
yy
(tham khảo hình vẽ).
▪ Để
( )
1
có đúng
2
nghiệm thì đồ thị
( )
= ,y F x m
cắt trục hoành tại
2
điểm phân biệt
Hàm số có cực đại, cực tiểu và
=.0
cd ct
yy
(tham khảo hình vẽ)
❖ Tương giao của hàm số phân thức
• Cho hàm số
( )
+
=
+
ax b
yC
cx d
và đường thẳng
=+:d y px q
. Phương trình hoành độ giao điểm
của
( )
C
và
( )
d
:
( )
+
= + =
+
,0
ax b
px q F x m
cx d
(phương trình bậc 2 ẩn
x
tham số
).
• Các câu hỏi thường gặp:
▪ Tìm
để
d
cắt
( )
C
tại
2
điểm phân biệt
( )
1
có 2 nghiệm phân biệt khác
−
d
c
.
▪ Tìm
để
d
cắt
( )
C
tại
2
điểm phân biệt cùng thuộc nhánh phải của (C)
( )
1
có 2
nghiệm phân biệt
12
,xx
và thỏa mãn
−
12
:
d
xx
c
.
▪ Tìm
để
d
cắt
( )
C
tại
2
điểm phân biệt cùng thuộc nhánh trái của
( )
C
( )
1
có 2
nghiệm phân biệt
12
,xx
và thỏa mãn
−
12
d
xx
c
.
▪ Tìm
để
d
cắt
( )
C
tại
2
điểm phân biệt thuộc hai nhánh của
( )
C
( )
1
có 2 nghiệm
phân biệt
12
,xx
và thỏa mãn
−
12
d
xx
c
.
▪ Tìm
để
d
cắt
( )
C
tại
2
điểm phân biệt
và
B
thỏa mãn điều kiện hình học cho trước:
✓ Đoạn thẳng
=AB kS
✓ Tam giác
ABC
vuông.
✓ Tam giác
ABC
có diện tích
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
3 | Facebook tác giả: Phan Nhật Linh
• Quy tắc:
▪ Tìm điều kiện tồn tại A, B
(1) có 2 nghiệm phân biệt.
▪ Xác định tọa độ của A và B (chú ý Vi ét)
▪ Dựa vào giả thiết xác lập phương trình ẩn m. Từ đó suy ra m.
• Chú ý: Công thức khoảng cách:
▪
( ) ( ) ( )
( )
= − + −
2
2
; , ; :
B
A A B B B A A
A x y B x y AB x x y y
▪
( )
( )
++
=
+ + =
+
00
00
22
00
;
,
:0
Ax By C
M x y
dM
Ax By C
AB
❖ Tương giao của hàm số bậc 4
• Nghiệm của phương trình bậc bốn trùng phương:
( )
+ + =
42
01ax bx c
• Nhẩm nghiệm:
▪ Nhẩm nghiệm: Giả sử
=
0
xx
là một nghiệm của phương trình.
▪ Khi đó ta phân tích:
( )
( )
( )
( )
=
= − =
=
0
22
0
,0
0
xx
f x m x x g x
gx
▪ Dựa vào giả thiết xử lý phương trình bậc hai
( )
= 0gx
• Ẩn phụ - tam thức bậc 2:
▪ Đặt
( )
=
2
,0t x t
. Phương trình:
+ + =
2
0at bt c
( )
2
.
▪ Để
( )
1
có đúng
1
nghiệm thì
( )
2
có nghiệm
12
,tt
thỏa mãn:
=
==
12
12
0
0
tt
tt
▪ Để
( )
1
có đúng
2
nghiệm thì
( )
2
có nghiệm
12
,tt
thỏa mãn:

=
12
12
0
0
tt
tt
▪ Để
( )
1
có đúng
3
nghiệm thì
( )
2
có nghiệm
12
,tt
thỏa mãn:
=
12
0 tt
▪
Để
( )
1
có đúng
4
nghiệm thì
( )
2
có nghiệm
12
,tt
thỏa mãn:

12
0 tt
• Bài toán: tìm
để
( ) ( )
= + +
42
:1C y ax bx c
cắt
Ox
tại bốn điểm có hoành độ lập thành một cấp
số cộng.
▪ Đặt
( )
=
2
,0t x t
. Phương trình:
+ + =
2
0at bt c
(2).
▪ Để
( )
1
cắt
Ox
tại 4 điểm phân biệt thì
( )
2
phải có 2 nghiệm dương
( )
1 2 1 2
,t t t t
thỏa mãn
=
21
9tt
.
▪ Kết hợp
=
21
9tt
vơi định lý vi – ét tìm được m.
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 4
Lời giải
Chọn D
Ta có
=+1ym
( )
d
và
= − −
42
32y x x
( )
C
.
Xét phương trình tương giao:
− − = +
42
3 2 1x x m
( )
− − + =
42
3 3 0x x m
.
( )
1
Đặt
=
2
0,tx
phương trình
( )
1
trở thành:
( )
− − + =
2
3 3 0t t m
.
( )
2
Phương trình
( )
2
có tích
= − − . 3 0a c m
khi
là số thực dương.
Suy ra phương trình
( )
2
luôn có hai nghiệm trái dấu

12
0.tt
Từ đó suy ra phương trình
( )
1
có hai nghiệm đối nhau
= − =
1 2 2 2
,x t x t
đồng thời
( )
d
và
( )
C
cắt nhau tại hai điểm phân biệt đối xứng nhau qua
Oy
là
( ) ( )
− + +
22
; 1 , , 1 .M t m N t m
Mặt khác tam giác
OMN
vuông tại
O
thì
=.0OM ON
( )
= +
2
2
1tm
.
Thay
( )
=+
2
2
1tm
vào phương trình
( )
2
ta được:
( ) ( ) ( )
+ − + − + =
42
1 3 1 3 0m m m
( ) ( ) ( )
+ − + − + − =
42
1 3 1 1 2 0m m m
.
Đặt
= + 11am
ta được phương trình
− − − =
42
3 2 0a a a
( )
( )
− + + + =
32
2 2 1 0a a a a
=2a
(do
1a
nên
+ + +
32
2 1 0a a a
).
Từ đó ta được
+=12m
=1m
(thỏa mãn
0m
). Vậy
= 1.m
Lời giải
Chọn D
VÍ DỤ 1: Gọi
là số thực dương sao cho đường thẳng
=+1ym
cắt đồ thị hàm số
= − −
42
32y x x
tại
hai điểm phân biệt
,MN
thỏa mãn tam giác
OMN
vuông tại
O
(
O
là gốc tọa độ). Kết luận nào sau
đây là đúng?
A.



11 15
;
44
m
. B.



13
;
24
m
. C.



79
;
44
m
. D.



35
;
44
m
.
VÍ DỤ 2: Cho hàm số
= ()y f x
xác định trên
\{1}
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như hình vẽ sau:
Tìm tập hợp tất cả các giá trị thực của tham số
sao cho phương trình
( )
+=1f x m
có đúng
ba nghiệm thực phân biệt.
A.
( )
−4; 2
. B.
(
−
;2
. C.
)
−
4; 2
. D.
( )
−3;3
.
VÍ DỤ MINH HỌA
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
5 | Facebook tác giả: Phan Nhật Linh
Phương trình
( ) ( )
+ = = −11f x m f x m
có đúng ba nghiệm phân biệt khi và chỉ khi đồ thị
hàm số
( )
=y f x
và đường thẳng
=−1ym
cắt nhau tại ba điểm phân biệt.
Căn cứ vào bảng biến thiên của hàm số
( )
=y f x
ta được
− − − 4 1 2 3 3.mm
Vậy
( )
−3;3 .m
Lời giải
Chọn C
Phương trình hoàn độ giao điểm của
= + + +
32
31y x x mx
và
= 1y
là:
( )
( )
=
+ + + = + + =
+ + =
3 2 2
2
0
3 1 1 6 0
6 0 *
x
x x mx x x x m
x x m
Để đồ thị hàm số
( )
=y f x
cắt đồ thị hàm số
= 1y
tại ba điểm phân biệt
( )
0;1 ,A
( )
11
;,B x y
( )
22
;C x y
thì phương trình
( )
*
có hai nghiệm phân biệt khác
0.



= −
0
0
9
9 4 0
4
m
m
m
m
. Theo hệ thức Viet ta có
+ = −
=
12
12
3
.
.
xx
x x m
Để tiếp tuyến của đồ thị hàm số
( )
=y f x
tại
,B
C
vuông góc với nhau thì
( ) ( )
( ) ( )

= − + + + + = −
22
1 2 1 1 2 2
. 1 3 6 . 3 6 1f x f x x x m x x m
( )
( )
( )
+ + + + + + + + + =
2 2 2 2 2
1 2 1 2 1 2 1 2 1 2 1 2
9 18 3 6 36 1 0x x x x x x m x x m x x x x m
+
=
+−
− + = = + =
−
=
2
9 65
9 65 9 65 9
8
4 9 1 0 .
8 8 4
9 65
8
m
m m S
m
Lời giải
VÍ DỤ 3: Cho hàm số
( )
= + + +
32
3 1.f x x x mx
Gọi
S
là tổng tất cả giá trị của tham số
để đồ thị
hàm số
( )
=y f x
cắt đường thẳng
= 1y
tại ba điểm phân biệt
( )
0;1 ,A
,B
C
sao cho các tiếp tuyến của
đồ thị hàm số
( )
=y f x
tại
,B
C
vuông góc với nhau. Gía trị của
S
bằng
A.
9
.
2
B.
9
.
5
C.
9
.
4
D.
11
.
5
VÍ DỤ 4: Cho hàm số
( )
=
−1
x
yC
x
và điểm
( )
−1;1 .A
Tìm
để đường thẳng
= − −:1d y mx m
cắt
( )
C
tại hai điểm phân biệt
,MN
sao cho
+
22
AM AN
đạt giá trị nhỏ nhất.
A.
=−1m
. B.
= 0m
. C.
=−2m
. D.
=−
2
3
m
.
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 6
Chọn A
Phương trình hoành độ giao điểm của
( )
C
và
d
là:
= − −
−
1
1
x
mx m
x
(đk:
1x
)
( )( )
= − − − = − − − + + − + + =
22
1 1 1 2 1 0 (*)x x mx m x mx m mx mx x mx mx m
Để
( )
C
và
d
cắt nhau tại hai điểm phân biệt
,MN
thì (*) phải có 2 nghiệm phân biệt khác
1
( )

= − + = −
− + +
2
0
' 1 0
2 1 0
m
m m m m
m m m
0m
Giả sử
( ) ( )
1 1 2 2
; , ;M x y N x y
. Theo hệ thức viét :
+
+ = =
1 2 1 2
1
2;
m
x x x x
m
( )
+ = + − − = − − = −
1 2 1 2
2 2 2 2 2 2y y m x x m m m
và
( )( ) ( )( ) ( )
= − − − − = − + + + +
2
2
1 2 1 2 1 2 1 2
. 1 1 1 1y y mx m mx m m x x m m x x m
( ) ( )
= + − + + + = +
2
( 1) 2 1 1 1m m m m m m
Ta có:
( ) ( ) ( ) ( )
+ = + + − + + + −
2 2 2 2
22
1 1 2 2
1 1 1 1AM AN x y x y
( ) ( )( ) ( ) ( )( )
= + + − + + + + − − − −
22
1 2 1 2 1 2 1 2
2 2 1 1 2 2 1 1x x x x y y y y
( ) ( ) ( ) ( )
( )
= + + − + + + + + − − − + +
22
1 2 1 2 1 2 1 2 1 2 1 2
2 2 1 2 2 1x x x x x x y y y y y y
( ) ( ) ( )
( )
+
= + − + + + − − − + − − +


22
1
2 2 2 2 1 2 2 2 1 2 1
m
m
m
+
= − − = − − − = + + − + =


−
1 1 1
18 2 2 18 2 2. 2 16 2. ( ) 16 2.2 20
m
m m m
m m m
(BĐT Cauchy)
Suy ra:
+
22
AM AN
đạt giá trị nhỏ nhất là
20
khi
=
= − =
=−
−
2
1
1
1
1
m
mm
m
m
Vậy
=−1m
(vì
0m
)
Lời giải
Chọn B
Vì đường thẳng
d
cắt đồ thị hàm số
()C
tại 3 điểm phân biệt nên đường thẳng
d
là đường thẳng
có hệ số góc dạng
=+y ax b
.
Phương trình hoành độ giao điểm của
d
và
()C
là:
− = +
42
2x x ax b
.
Mà phương trình là phương trình bậc 4 nên phương trình muốn có 3 nghiệm phân biệt thì trong
đó sẽ có 1 nghiệm kép gọi là
, hai nghiệm còn lại là
23
,xx
.
Suy ra đường thẳng
d
là tiếp tuyến của đồ thị
()C
, không mất tính tổng quát giả sử đường thẳng
d
tiếp xúc với đồ thị hàm số
()C
tại
.
VÍ DỤ 5: Cho hàm số
=−
42
2y x x
có đồ thị
()C
, có bao nhiêu đường thẳng
d
có đúng 3 điểm chung với
đồ thị
()C
và các điểm chung có hoành độ
1 2 3
,,x x x
thỏa mãn
+ + = −
3 3 3
1 2 3
1x x x
.
A.
0
. B.
1
. C.
2
. D.
3
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
7 | Facebook tác giả: Phan Nhật Linh
Gọi
d
là tiếp tuyến của
()C
tại điểm có hoành độ
,
d
cắt
()C
tại 2 điểm phân biệt có hoành độ
2 3 1
, ( )x x x
thỏa mãn
+ + = −
3 3 3
1 2 3
1x x x
. Ta có:
= − − + −
3 4 2
1 1 1 1 1
: (4 4 )( ) 2d y x x x x x x
.
Phương trình hoành độ giao điểm của
d
và
()C
là:
− = − − + −
4 2 3 4 2
1 1 1 1 1
2 (4 4 )( ) 2 (1)x x x x x x x x
Yêu cầu bài toán
(1)
có 3 nghiệm phân biệt thỏa mãn
+ + = −
3 3 3
1 2 3
1x x x
.
=
− + + − =
= + + − =
1
2 2 2
1 1 1
22
11
(1) ( ) ( 2 3 2) 0
( ) 2 3 2 0
xx
x x x x x x
f x x x x x
Để phương trình
(1)
có 3 nghiệm phân biệt thỏa mãn
+ + = −
3 3 3
1 2 3
1x x x
thì phương trình
=( ) 0fx
phải có 2 nghiệm phân biệt
23
,xx
khác
và thỏa mãn định lí Vi – ét:
+ = −
=−
2 3 1
2
2 3 1
2
. 3 2
x x x
x x x
Ta có:
= − +
+ + −
+ + − + = −
22
11
2 2 2
1 1 1
33
1 2 3 2 3 2 3
' 3 2 0
2 3 2 0
( ) 3 ( ) 1
xx
x x x
x x x x x x x
−
−
+ − − − − = −
1
2
1
3 3 2
1 1 1 1
11
3 1 0
( 2 ) 3(3 2).( 2 ) 1
x
x
x x x x
−+
=
1
11 165
22
x
. Vậy có đúng 1 đường thẳng thỏa mãn yêu cầu bài toán.
Lời giải
Chọn D
Ta có phương trình hoành độ giao điểm của đường thẳng và đồ thị hàm bậc ba đã cho là
( )
+ − − = − −
32
3 1 6 4x x x m x
( )
+ + − + =
32
3 3 0x x m x
( )
1
.
Giả sử
,
,
là ba nghiệm phân biệt của phương trình
( )
1
.
Theo hệ thức viet đối với phương trình bậc ba ta có :
+ + = −
+ + = −
=−
1 2 3
1 2 2 3 3 1
1 2 3
1
3
3
x x x
x x x x x x m
x x x
.
Nhận thấy tung độ của ba giao điểm thỏa mãn phương trình
( )
= − −64y m x
nên ta có được
( )
+ = −
11
46y m x
,
( )
+ = −
22
46y m x
và
( )
+ = −
33
46y m x
.
Khi đó
+ + =
+ + +
1 2 3
1 1 1 2
4 4 4 3y y y
( ) ( ) ( )
+ + =
− − −
1 2 3
1 1 1 2
3
6 6 6m x m x m x
++
=
−
1 2 2 3 3 1
1 2 3
12
.
63
x x x x x x
m x x x
−
=
−−
1 3 2
.
6 3 3
m
m
= 9m
.
VÍ DỤ 6: Có bao nhiêu số thực của tham số
để đường thẳng
( )
= − −64y m x
cắt đồ thị hàm số
= + − −
32
31y x x x
tại ba điểm phân biệt có tung độ
,
2
y
,
3
y
thỏa mãn
+ + =
+ + +
1 2 3
1 1 1 2
4 4 4 3y y y
.
A.
2
. B.
0
. C.
3
. D.
1
.
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 8
Thử lại với
= 9m
suy ra phương trình hoành độ giao điểm
+ − + =
32
6 3 0x x x
có ba nghiệm
phân biệt thỏa mãn giả thiết cho (Dùng casio để kiểm tra) . Vậy có một số thực
thỏa mãn .
Lời giải
Chọn D
Do đường thẳng cắt đồ thị hàm số
=−
42
2y x x
tại điểm có hoành độ là
0
nên phương trình
đường thẳng có dạng
=y ax
.
Phương trình hoành độ giao điểm của đường thẳng
=y ax
với đồ thị hàm số
=−
42
2y x x
là :
−=
42
2x x a x
− − =
42
20x x a x
( )
− − =
3
20x x x a
.
Do phương trình có bốn nghiệm là
0
,
1
,
,
n
nên ta có :
( )
( )( )( )
− − = − − −
3
21x x x a x x x m x n
( )
( )
− − = − − + −
32
2x x a x mx x m x n
− − = − − + − + + −
3 3 2 2 2
2x x a x nx mx mnx x nx mx mn
( ) ( )
− − = + − − − + + + −
3 3 2
21x x a x n m x m n mn x mn
( )
− − − =
+ = −
+ + = − = + = + − =

=−
− = −
2
22
10
1
2 2 3
1
mn
mn
m n mn S m n m n mn
mn
mn a
.
Lời giải
Chọn B
Ta có
( )
− + + − + =
2
22
3 8 2 0x x m x x m
( ) ( )

− + − + − + =


2
2 2 2
3 2 8 2 0x x m x x x m
( )( ) ( )
− + − + + − + =
2 2 2
4 2 2 4 0x x m x x m x x m
( )( )
− + − + + =
22
4 2 2 0x x m x x m
( )
( )
− + =
− + + =
2
2
4 0 1
2 2 0 2
x x m
x x m
.
Yêu cầu bài toán
mỗi phương trình
( )
1
và
( )
2
có
2
nghiệm phân biệt không trùng nhau.
Phương trình
( )
1
và
( )
2
có
2
nghiệm phân biệt
VÍ DỤ 7: Một đường thẳng cắt đồ thị hàm số
=−
42
2y x x
tại bốn điểm phân biệt có hoành độ là
0
,
1
,
và
n
. Tính
=+
22
S m n
.
A.
= 0S
. B.
= 1S
. C.
= 2S
. D.
= 3S
.
VÍ DỤ 7: Cho phương trình
( )
− + + − + =
2
22
3 8 2 0x x m x x m
. Có bao nhiêu giá trị nguyên của tham số
thuộc đoạn
−

20;20
để phương trình đã cho có
4
nghiệm phân biệt?
A.
19
. B.
18
. C.
17
. D.
20
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
9 | Facebook tác giả: Phan Nhật Linh
−
−

− − −

1
2
0
4 0 4
1
0
1 2 0 1
mm
m
mm
.
Giả sử phương trình
( )
1
và
( )
2
có nghiệm
trùng nhau
Hệ sau có nghiệm
( )
( )
− + =
− + + =
2
2
4 0 1
2 2 0 2
x x m
x x m
( )
− + − − + + =
22
0 0 0 0
4 2 2 0x x m x x m
= −
0
1x
.
Với
=−
0
1x
thay vào
( )
1
ta được
=−5m
.
Với
−5m
phương trình
( )
1
và
( )
2
không có nghiệm trùng nhau.
Kết hợp
là số nguyên thuộc đoạn
−

20;20
)
− − −
20; 1 \ 5m
.
Vậy có
18
số nguyên
thoả mãn yêu cầu bài toán.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
1 | Facebook tác giả: Phan Nhật Linh
Câu 1: Cho hàm số bậc ba
()y f x=
có đồ thị là đường cong trong hình vẽ bên. Số nghiệm thực phân
biệt của phương trình
(
)
22
1
41
2021
f x x− − − =
là
A.
24
. B.
14
. C.
12
. D.
10
.
Câu 2: Cho hai hàm số
( )
2
3
3
x
ux
x
+
=
+
và
( )
fx
, trong đó đồ thị hàm số
( )
y f x=
như hình vẽ bên.
Hỏi có bao nhiêu số nguyên
để phương trình
( )
( )
f u x m=
có đúng
3
nghiệm phân biệt?
A.
1
. B.
4
. C.
3
. D.
2
.
Câu 3: Cho hàm số
()y f x=
có đạo hàm cấp hai trên
R
và có đồ thị
'( )y f x=
là đường cong trong
hình vẽ bên.
Đặt
( ) ( '( ) 1)g x f f x=−
. Gọi
S
là tập nghiệm của phương trình
'( ) 0gx=
. Số phần tử của tập
S
là
A.
8
B.
6
C.
10
D.
9
Bài toán tương giao đồ thị hàm số 01
DẠNG 1
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 2
Câu 4: Cho hàm số
()fx
liên tục trên và có đồ thị như hình vẽ.
Có bao nhiêu giá trị nguyên của tham số
để phương trình
(
)
2
3sin cos 1
2 ( 2) 4
2cos sin 4
xx
f f m
xx
− −
+ = + +

−+

có nghiệm?
A.
3
. B.
5
. C.
4
. D.
2
.
Câu 5: Cho hàm số
( )
y f x=
liên tục trên có đồ thị như hình vẽ bên dưới.Gọi
( )
1
C
và
( )
2
C
lần
lượt là đồ thị của hai hàm số
( ) ( ) ( )
2
.y f x f x f x
=−


và
2021
x
y =
.Số giao điểm của
( )
1
C
và
( )
2
C
là
A.
1
B.
0
C.
2
D.
4
Câu 6: Biết hàm số
( )
32
f x ax bx cx d= + + +
đạt cực trị tại
1x =
và
2021x =
. Có bao nhiêu số nguyên
để phương trình
( ) ( )
f x f m=
có ba nghiệm phân biệt?
A.
4037
. B.
2019
. C.
4001
. D.
2021
.
Câu 7: Cho hàm số
( )
y f x=
liên tục trên có đồ thị hình vẽ.
Có bao nhiêu giá trị nguyên của tham số
để phương trình
( )
( )
4 2 cosf f x m+=
có nghiệm
0;
2
x



Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
3 | Facebook tác giả: Phan Nhật Linh
A.
4
. B.
5
. C.
3
. D.
2
.
Câu 8: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ sau:
Có bao nhiêu số nguyên
để phương trình
( )
3
1
2 6 2 5
2
f x x m− + = −
có 6 nghiệm phân biệt
thuộc đoạn
1;2−
?
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 9: Cho hàm số
y f x
liên tục trên và có bảng biến thiên như hình vẽ
Số nghiệm của phương trình
2f f x
là
A.
4
. B.
5
. C.
9
. D.
7
.
Câu 10: Cho hàm số
( )
2
y f x ax bx c= = + +
có đồ thị
( )
C
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
( )
( )
( )
2
2 3 0f x m f x m+ − + − =
có 6 nghiệm phân biệt?
A. 2. B. 3. C. 1. D. 4.
Câu 11: Biết đồ thị hàm số bậc bốn
( )
y f x=
được cho bởi hình vẽ bên dưới. Tìm số giao điểm của đồ
thị hàm số
( ) ( ) ( ) ( )
2
.y g x f x f x f x
= = −


và trục hoành:
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 4
A.
4
. B.
0
. C.
6
. D.
2
.
Câu 12: Cho hàm số
2
( ) 1f x x x= + +
. Số giá trị nguyên của tham số
để phương trình
( )
1 4 1
( ) 0
1 4 1
xm
xf x
f x m
+ + −
−=
− − + −
có hai nghiệm phân biệt là
A.
2
. B.
3
. C.
6
. D.
4
.
Câu 13: Cho hàm số
( )
( ) ( )
3 3 2 2 3
1 3 3 2 2 2f x m x mx m m x m m= − + + − + + +
với
là tham số. Có bao
nhiêu số nguyên
2020;2021m−
sao cho
( )
0fx
với mọi
2020;2021x
?
A.
2023
. B.
2022
. C.
2021
. D.
2020
.
Câu 14: Cho hàm số
( )
32
2 3 1y f x x x= = − +
. Tập hợp các giá trị
để phương trình
( )
2sin 1
2
x
f f f m
+

=




có nghiệm là đoạn
;ab
. Khi đó giá trị
2
48ab+
thuộc khoảng nào
sau đây?
A.
23
7;
2



. B.
( )
2;5−
. C.
43 39
;
32



. D.
37 65
;
34



.
Câu 15: Cho hàm số
( )
2
52
21
xx
fx
x
++
=
+
. Có tất cả bao nhiêu giá trị nguyên dương của tham số
để bất
phương trình
(
)
22
2021 3 18 28 3 18 28 4042f x x m x x m− + − − + +
nghiệm đúng với
mọi
x
thuộc đoạn
2;4
.
A.
673
. B.
808
. C.
135
. D.
898
.
Câu 16: Cho hàm số
()y f x=
liên tục trên và có bảng biến thiên như sau:
Số nghiệm của phương trình
( )
42
3 4 2
2 1 0
xx
f
−+
+=
là
A.
2
. B.
3
. C.
6
. D.
5
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
5 | Facebook tác giả: Phan Nhật Linh
Câu 17: Cho hàm số
( )
fx
có đồ thị như bên dưới
Số nghiệm phương trình
( )
2 1 6 3 1f x x+ − + =
là
A.
3
. B.
4
. C.
6
. D.
5
.
Câu 18: Cho hàm số
( )
3
1
8,
2
f x x mx m x= − + −
với
m
là một hằng số khác
0
. Biết rằng phương
trình
( )
0fx=
có đúng hai nghiệm phân biệt. Hỏi có bao nhiêu giá trị nguyên của
k
thỏa mãn
phương trình
( )
f x k=
có 3 nghiệm phân biệt ?
A.
3
. B.
34
. C.
6
. D.
34
.
Câu 19: Cho hàm đa thức
( )
y f x=
có đồ thị như hình vẽ.
Đặt
( )
( )
2
g x f x=
. Số nghiệm của phương trình
( ) ( )
. 2 1 0g x g x −=


là
A. 11. B. 10. C. 13. D. 12.
Câu 20: Hàm số
( )
y f x=
liên tục trên và có bảng biến thiên như hình vẽ
Phương trình
( )
2
2 3 2 5fx+ − =
có bao nhiêu nghiệm?
A.
3
. B.
5
. C.
6
. D.
4
.
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 6
Câu 21: Cho hai hàm
( )
y f x=
và
( )
y g x=
liên tục trên và có đồ thị như hình vẽ. Khi đó tổng số
nghiệm của phương trình
( )
( )
0f g x =
và
( )
( )
0g f x =
là
A.
25
. B.
22
. C.
21
. D.
26
.
Câu 22: Cho
( )
fx
là hàm số bậc ba. Hàm số
( )
fx
có đồ thị như sau:
Tìm tất cả các giá trị thực của tham số
để phương trình
( )
10+ − − =
x
f e x m
có hai nghiệm
thực phân biệt.
A.
( )
2mf
. B.
( )
21−mf
. C.
( )
1 ln 2−mf
. D.
( )
1 ln2+mf
.
Câu 23: Cho hàm số bậc ba
( )
y f x=
có đồ thị là đường cong trong hình bên dưới
Số nghiệm thực phân biệt của phương trình
( )
( )
3
10f x f x +=
là
A.
6
. B.
8
. C.
5
. D.
4
.
Câu 24: Cho hàm số
( )
4 3 2
y f x ax bx cx dx e= = + + + +
với
( , , , , )a b c d e
. Biết hàm số
( )
y f x
=
có
đồ thị như hình vẽ.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
7 | Facebook tác giả: Phan Nhật Linh
Có bao nhiêu giá trị nguyên của
trên
5;5−
để phương trình
( )
2
2f x x m e− + + =
có bốn
nghiệm phân biệt.
A.
0
. B.
2
. C.
5
. D.
7
.
Câu 25: Cho hàm số
( )
y f x=
liên tục trên có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của
tham số
để phương trình
( )
( )
4 2 cosf f x m+=
có nghiệm
0;
2
x


.
A.
4
. B.
3
. C.
2
. D.
5
.
Câu 26: Cho hàm số
( )
3
2
m
f x x x= + −
. Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
( )
( )
f f x x=
có nghiệm thuộc đoạn
1;2
.
A.
3.
B.
4.
C.
0.
D.
2.
Câu 27: Cho hàm số
dcxbxaxxfy +++==
23
)(
có đồ thị như hình dưới đây
Có tất cả bao nhiêu giá trị nguyên của tham số
( )
5;5−m
để phương trình
( )
2
( ) ( 4) ( ) 2 4 0 *f x m f x m− + + + =
có
6
nghiệm phân biệt
A.
2
. B.
4
. C.
3
. D.
5
.
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 8
Câu 28: Cho hàm số
( )
y f x=
có đồ thị là đường cong trong hình bên.
Số nghiệm thực phân biệt của phương trình
( )
( )
2
20f x f x +=
là
A.
8
. B.
12
. C.
6
. D.
9
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
9 | Facebook tác giả: Phan Nhật Linh
BẢNG ĐÁP ÁN
1.D
2.C
3.C
4.B
5.B
6.A
7.A
8.B
9.D
10.B
11.B
12.D
13.B
14.D
15.A
16.C
17.B
18.D
19.D
20.A
21.C
22.A
23.A
24.B
25.A
26.B
27.C
28.D
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Chọn D
(
)
22
( ) 4 1y g x f x x= = − − −
với
1
()
2021
gx=
Ta đặt:
2
4 , 2;2t x x= − −
thì suy ra
( )
2
( ) 3 , 0;2y g t f t t t= = − −
Suy ra:
2
2
2
3, 0; 3
( ) 3
3, 3;2
t t t
h t t t
t t t

+ −
= − − =

− + +

.
Từ đó ta có BBT của hàm số
()ht
như hình vẽ bên:
Đặt
2
3u t t= − −
thì ta cũng có BBT của
u
như sau:
Nhìn vào đồ thị
()y f x=
trên ta có được:
32
( ) , 0
2
0
3
(1) (2) 0, "(1) 0
f x ax bx cx a
a
f f f
= + +
=
= = =
Như vậy ta suy ra
( )( )
2
( ) 1 2
3
f x x x x= − −
. Mà hàm số đó có cực trị bằng
43
9
−
tại
0
xx=
nên
suy ra
( )
00
4 3 3 3
93
f x x
−+
= =
Như vậy:
( )
3 3 4 3
(3) 4, 3 0,2,
39
f f f

+−
= = − =



2
0
0
3
3
3
1
0
0
3
3
3
1
3
3
2
0
2
t
t
2
3
t
t
2
3
t
x
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 10
Từ đó, ta phác họa được đồ thị
( )
y f u=
với
2
3u t t= − −
như sau:
Dựa vào hình vẽ trên, ta kết luận phương trình
1
()
2021
gx=
có tất cả 10 nghiệm phân biệt.
Câu 2: Chọn C
Đặt
( )
2
3
3
x
t u x
x
+
==
+
;
( )
( )
( )
2
2
2
22
3
3
33
3
'
3
33
xx
x
x
x
ux
x
xx
+
+−
−
+
==
+
++
;
( )
' 0 1u x x= =
.
Dựa vào bảng biến thiên, ta có
( ) (
1;2ux−
.
Phương trình
( )
( )
f u x m=
trở thành
( )
f t m=
,
(
1;2t −
.
Dựa vào đồ thị đã cho ta có:
Khi
2m =
: phương trình
( )
0
2
2
t
ft
t
=
=
=
phương trình
( )
( )
f u x m=
có
2
nghiệm phân
biệt.
Khi
1m =
: phương trình
( )
1ft=
có
3
nghiệm
( ) ( ) ( )
1 2 3
1;0 , 0;1 , 1;2t t t −
phương
trình
( )
( )
f u x m=
có
4
nghiệm phân biệt.
Khi
0; 1; 2m − −
: phương trình
( )
f t m=
có
2
nghiệm
( ) ( )
12
0;1 , 1;2tt
phương trình
( )
( )
f u x m=
có
3
nghiệm phân biệt.
Khi
3m =−
: phương trình
( )
f t m=
có
1
nghiệm
1t =
phương trình
( )
( )
f u x m=
có
1
nghiệm.
Vậy
0; 1; 2m − −
.
Câu 3: Chọn C
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
11 | Facebook tác giả: Phan Nhật Linh
Ta có:
( ) ( '( ) 1) '( ) "( ). '( '( ) 1)g x f f x g x f x f f x= − = −
Phương trình
''( ) 0 ''( ) 0
'( ) 0
'( ) 0 '( ) 1 1 '( ) 0
'( '( ) 1) 0
'( ) 1 2 '( ) 3
f x f x
fx
g x f x f x
f f x
f x f x
==

=

= − = − =

−=

− = =

Ta có đồ thị
'( )y f x=
có cực trị tại
0
1
2
3
(1;2)
x
x
xx
=
−
=
=
0
"(1) 0
2
"0
3
''( ) 0
f
f
fx
=
−

=


=
''( ) 0fx=
có 3 nghiệm
0
1
;
2
3
x
xx
x
=
=
−
=
cùng với
1x =
là nghiệm bội chẵn
Tại phương trình
'( ) 0fx=
ta thấy có 2 nghiệm bội lẻ
1, 2xx= − =
và nghiệm bội chẵn
1x =
Tại phương trình
'( ) 3fx=
ta thấy có 2 nghiệm mà đường thẳng
3y =
cắt đồ thị
()y f x=
đó là
hai điểm
1
( ; 1)xx= − −
và
2
(2; )xx= +
Vậy từ đó ta thấy phương trình
'( ) 0gx=
tổng cộng có tất cả 10 nghiệm.
Câu 4: Chọn B
Ta có:
1 sin 1, 1 cos 1xx− −
nên suy ra
2cos sin 4 0,x x x− +
.
Đặt
3sin cos 1
(2cos sin 4) 3sin cos 1
2cos sin 4
xx
t t x x x x
xx
−−
= − + = − −
−+
(2 1)cos ( 3)sin (4 1)t x t x t + − + = − +
.
Phương trình trên có nghiệm khi
2 2 2
9
(2 1) ( 3) (4 1) 1 2 2 3
11
t t t t t
−
+ + + + +
.
Nhìn vào hình trên ta thấy hàm số
()fx
luôn đồng biến trên
2;3
nên phương trình
(
)
2
3sin cos 1
2 ( 2) 4
2cos sin 4
xx
f f m
xx
− −
+ = + +

−+

hay phương trình
( )
(
)
2
2 ( 2) 4f t f m+ = + +
có nghiệm khi và chỉ khi phương trình
2
2 ( 2) 4tm+ = + +
có nghiệm
t
thỏa mãn điều kiện
2 2 3t +
22
2 ( 2) 4 3 4 1 0 2 5 2 5m m m m + + + − − +
.
Mà
m
nên có tất cả 5 giá trị
m
thỏa mãn.
Câu 5: Chọn B
Số giao điểm
( )
1
C
và
( )
2
C
là nghiệm của phương trình
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 12
( ) ( ) ( ) ( )
2
. 2021 *
x
f x f x f x
−=


Từ đồ thị ta thấy
( )
fx
cắt trục
Ox
tại bốn điểm phân biệt có hoành độ lần lượt là
1 2 3 4
; ; ;x x x x
nên phương trình
( )
0fx=
có bốn nghiệm phân biệt
1 2 3 4
; ; ;x x x x
( ) ( )( )( )( )
1 2 3 4
f x a x x x x x x x x = − − − −
Nếu
( )
1
2
3
4
0
xx
xx
fx
xx
xx
=
=
=
=
=
thay vào
( )
*
ta thấy vế trái âm,vế phải dương nên phương trình
( )
*
vô nghiệm
Nếu
( )
0fx
nên ta có phương trình ta có phương trình
( )
*
tương đương với
2
2 2 2
( ) ( ) ( )
2021 ( ) 2021
[ ( )] [ ( )] ( ) [ ( )]
xx
f x f x f x
fx
f x f x f x f x


−


= =


Ta có:
( )( )( )( )
( )( )( )( )
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4 1 2 3 4
()
1 1 1 1
()
1 1 1 1 ( ) 1 1 1 1
( ) ( )
()
f x a x x x x x x x x
f x a x x x x x x x x
x x x x x x x x
fx
f x f x
x x x x x x x x f x x x x x x x x x
= − − − −

= − − − − + + +

− − − −


= + + + = + + +

− − − − − − − −

Khi đó:
1 2 3 4
( ) 1 1 1 1
()
fx
f x x x x x x x x x


= + + +


− − − −


( ) ( ) ( ) ( )
2 2 2 2
1 2 3 4
1 1 1 1
0
x x x x x x x x

= − + + +


− − − −

Mà
2
2021
0
[ ( )]
x
fx
nên phương trình
2
( ) 2020
( ) [ ( )]
x
fx
f x f x

=


vô nghiệm,do đó phương trình vô
nghiệm.
Câu 6: Chọn A
Ta có
( ) ( )
3 2 2
32f x ax bx cx d f x ax bx cx
= + + + = + +
Do hàm số có 2 điểm cực trị là:
1
1x =
và
2
2021x =
.
Nên:
12
12
2
2022
3033
3
3 6063
. 2021
3
b
xx
ba
a
ca
xx
a
+ = − =
=−

=
==
Xét phương trình:
( ) ( )
f x f m=
3 2 3 2
ax bx cx d am bm cm d+ + + = + + +
( ) ( )
( )
3 3 2 2
0a x m b x m c x m − + − + − =
( ) ( )
( )
3 3 2 2
3033 6063 0a x m a x m x m − − − + − =
( )
( )
22
3033 3033 6063 0x m x mx m x m − + + − − + =
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
13 | Facebook tác giả: Phan Nhật Linh
22
0
3033 3033 6063 0 (*)
xm
x mx m x m
−=
+ + − − + =
Để phương trình
( ) ( )
f x f m=
có 3 nghiệm phân biệt thì pt có 2 nghiệm phân biệt khác
m
.
( )
( )
( )
2
2
22
3033 4 3033 6063 0
3033 3033 6063 0
m m m
m m m m m
= − − − +
+ − + − +
( )
2 2 2
22
6063 3033 4 4.3033 4.6063 0
3033 3033 6063 0
m m m m
m m m m m
− + − + −
+ − + − +
1009 3031
2021; 1
m
mm
−

Vậy:
( )
1009;3031 \ 1;2021m−
có 4037 giá trị
m
nguyên.
Câu 7: Chọn A
Đặt
costx=
, với
0;
2
x



( )
0;1t
.
Từ đồ thị suy ra
( ) ( ) ( ) ( ) ( ) ( )
2;0 4 2 0;4 4 2 0;2f t f t u f t − + = +
.
Ta có
( )
f u m=
với
( )
0;2u
.
Phương trình đã cho có nghiệm
0;
2
x



khi và chỉ khi phương trình
( )
f u m=
có nghiệm
( )
0;2u
22m −
.
Do
m
nên
2; 1;0;1m − −
.
Vậy có 4 giá trị nguyên của tham số
m
thoả mãn yêu cầu bài toán.
Câu 8: Chọn B
Đặt:
( )
( )
3
2 6 2g x f x x= − +
;
( )
( ) ( )
23
6 6 . 2 6 2g x x f x x

= − − +
( )
0gx
=
⇔
( )
2
3
6 6 0 (1)
2 6 2 0 (2)
x
f x x
−=
− + =
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 14
Giải:
2
6 6 0x −=
⇔
1
1
x
x
=−
=
Giải:
( )
3
2 6 2 0f x x
− + =
⇔
3
3
3
3
2 6 2 2
2 6 2 0
2 6 2 3
2 6 2 6
xx
xx
xx
xx
− + = −
− + =
− + =
− + =
⇔
2 1;2
1 (nghi m k p)
1,87 1;2
0,34
1,53
1,64 1;2
0,16
1.81
1 (nghi m k p)
2
x
x
x
x
x
x
x
x
x
x
= − −
=
− −
− −
−
=−
=
ÖÐ
ÖÐ
Bảng biến thiên của
( )
gx
trên đoạn
1;2−
Số nghiệm của phương trình
( )
3
1
2 6 2 5
2
f x x m− + = −
bằng số giao điểm của đồ thị hàm số
( )
( )
3
2 6 2g x f x x= − +
và đường thẳng
1
5
2
ym=−
.
Kẻ đường thẳng
1
5
2
ym=−
trên cùng bảng biến thiên của
( )
gx
. Điều kiện để đường thẳng
1
5
2
ym=−
cắt đồ thị hàm số
( )
( )
3
2 6 2g x f x x= − +
tại 6 điểm phân biệt là:
1
0 5 2
2
m −
⇔
10 14m
. Vì
m
⇒
11;12;13m
Vậy có 3 số nguyên
thỏa mãn ycbt.
Câu 9: Chọn D
Ta có:
2
2
2
f f x
f f x
f f x
. Dựa vào bảng biến thiên ta thấy:
;4
2
3;
f x a a
f f x
f x b b
.
2f f x
4
1;3
3;
fx
f x d d
f x e e
.
x
1−
0.16−
0.34
1
1,53
1,81
2
( )
gx
0
+
0
−
0
+
0
−
0
+
0
−
0
( )
gx
13
4
−
7
2
0
2
0
7
2
13
4
−
1
5
2
ym=−
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
15 | Facebook tác giả: Phan Nhật Linh
;4f x a a
vô nghiệm;
3;f x b b
có
2
nghiệm.
4fx
có
1
nghiệm;
1;3f x d d
có
2
nghiệm.
3;f x e e
có 2 nghiệm
2f f x
có 7 nghiệm.
Câu 10: Chọn B
Xét phương trình
( )
( )
( )
2
2 3 0f x m f x m+ − + − =
.
Nhận thấy
( ) ( )
( )
( )
1
1 2 3 0
3
fx
mm
f x m
=−
− − + − =
=−
.
Từ đồ thị hàm số
( )
fx
, suy ra đồ thị hàm số
( )
fx
như sau:
Với
( )
1fx=−
, ta được 2 nghiệm
x
.
Để phương trình đã cho có 6 nghiệm phân biệt, tức là phương trình
( )
3f x m=−
có 4 nghiệm
phân biệt.
Hay
1 3 3 0 4 1;2;3
m
m m m
− − ⎯⎯⎯→
.
Như vậy có 3 giá trị nguyên của
m
thỏa mãn.
Câu 11: Chọn B
Ta có phương trình hoành độ giao điểm của hai đồ thị
( )
y g x=
và
Ox
là:
( ) ( ) ( ) ( ) ( ) ( )
( )
( )
22
. 0 . 0 0
fx
f x f x f x f x f x f x
fx

− = − = =


Ta thấy đồ thị hàm số
( )
y f x=
cắt trục
Ox
tại
4
điểm phân biệt có hoành độ
1 2 3 4
, , ,x x x x
.
Giả sử
( ) ( )( )( )( )
1 2 3 4 1 2 3 4
, 0,f x a x x x x x x x x a x x x x= − − − −
Ta có:
( ) ( )( )( ) ( )( )( )
2 3 4 1 3 4
f x a x x x x x x a x x x x x x
= − − − + − − −
( )( )( ) ( )( )( )
1 2 4 1 2 3
a x x x x x x a x x x x x x+ − − − + − − −
Ta có:
( )
( )
1 2 3 4
1 1 1 1
fx
f x x x x x x x x x
= + + +
− − − −
Ta có:
( )
( )
( ) ( ) ( ) ( )
2 2 2 2
1 2 3 4
1 1 1 1
00
fx
fx
x x x x x x x x

= − − − − =

− − − −

vô nghiệm.
Vậy số giao điểm của đồ thị hàm số
( )
y g x=
và trục hoành bằng
0
.
Câu 12: Chọn D
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 16
Ta có:
2
2
( ) 1 '( ) 1 0,
1
x
f x x x f x x
x
= + + = +
+
.
Suy ra hàm số
2
( ) 1f x x x= + +
luôn đồng biến trên .
Mặt khác, ta lại có:
2
2
11
( ) 1
()
1
f x x x
fx
xx
− = − + + = =
++
.
Nên phương trình tiếp theo tương đương với:
( )
1 4 1
( ) 0
1 4 1
xm
xf x
f x m
+ + −
−=
− − + −
.
( ) ( )
( ) 1 4 1 1 4 1 0xf x x m f x m − + + − + + − =
.
( ) ( )
( ) 1 4 1 1 4 1xf x x m f x m = + + − + + −
.
Đến đây ta xét hàm đặc trưng
(
)
2 2 2
( ) ( ) . 1 1y g t tf t t t t t t t= = = + + = + +
.
Có
2
2
2
'( ) 2 1 0,
1
t
g t t t t
t
= + + +
+
nên suy ra
()gt
luôn đồng biến trên .
( )
( ) 1 4 1 1 4 1 4 1 1g x g x m x x m x m x = + + − = + + − + − = −
.
Do
4 1 0xm+ −
nên suy ra
( )
2
2
10
1
62
4 1 1
x
x
m x x
x m x
−

= − +
+ − = −
.
Xét hàm
2
( ) 6 2, 1 ( ) 2 6 0 3y p x x x x p x x x
= = − + = − = =
.
Ta có bảng biến thiên của hàm
()px
như sau:
Dựa vào BBT trên để phương trình có hai nghiệm phân biệt thì
(
(
(3); (1) 7; 3m p p m − −
.
Như vậy, ta kết luận có tất cả 4 giá trị nguyên thỏa mãn yêu cầu đề bài.
Câu 13: Chọn B
( )
( ) ( )
( ) ( ) ( )
3 3 2 2 3
33
1 3 3 2 2 2 0 2020;2021
2 2 2020;2021 (1)
f x m x mx m m x m m x
x m x m mx mx x
= − + + − + + +
+ + + +
Xét hàm số
32
( ) 2 , '( ) 3 2 0f t t t f t t t= + = +
Vậy hàm số
()ft
đồng biến trên nên
( )
1
suy ra
2021
2020;2021 2020;2021 .
1 2020
x
x m mx x m x m
x
+
−
Vậy trên đoạn
2020;2021−
có
2022
giá trị nguyên của
thỏa mãn.
Câu 14: Chọn D
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
17 | Facebook tác giả: Phan Nhật Linh
Ta có:
2
66y x x
=−
;
0y
=
0
1
x
x
=
=
.
Bảng biến thiên:
Ta có:
2sin 1 1 1 3
sin ;
2 2 2 2
x
x
+

= + −


suy ra
2sin 1
0;1
2
x
f
+



nên
2sin 1
0;1
2
x
ff
+





.
Phương trình
( )
2sin 1
2
x
f f f m
+

=




có nghiệm
( )
01fm
32
32
2 3 1 0
2 3 0
mm
mm
− +
−
13
22
m −
.
Vậy
2
13
4 8 4. 8. 13
42
ab+ = + =
.
Câu 15: Chọn A
Đặt
( )( )
22
3 18 28 3( 3) 1 3 2 4 4u x x x x x= − + = − + = − − +
do đó ta có với
2;4x
thì
1;2u
.
Biến đổi BPT ta được
( )
2021 . 4042f u m u m− +
( ) ( )
2021 2 1f u m u − +

.
Ta có
( )
2
52
21
xx
fx
x
++
=
+
nên
( )
22
52
22
2 1 2 1
u u u u
fu
uu
+ + +
− = − =
++
do vậy bất phương trình được
biến đổi tiếp
( )
( )
2
2021
2021
1
2 1 2 1
uu
u
m u m
uu
+
+
++
.
Lúc này yêu cầu bài toán tương đương
2021
, 1;2
21
u
mu
u
+
1;2
min ( )
u
m g u

.
Xét hàm số
2021
( ) , 1;2
21
u
g u u
u
=
+
ta có
( )
2
2021
( ) 0, 1;2
21
g u u
u
=
+
do vậy hàm số
( )
gu
tăng trên đoạn
1;2
. Vì vậy
( )
1;2
2021 2021
min ( ) 1
2 1 3
u
u
g u g
u
= = =
+
.
Kết hợp với
là các số nguyên dương ta được
1;2;3;...;673m
.
Vậy tìm được
673
số nguyên dương thỏa mãn yêu cầu bài toán.
Câu 16: Chọn C
Câu 17: Chọn B
Đặt
1 6 3t x x= + − +
,
1
2
x −
.
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 18
Ta có
3
1 0 1
63
tx
x
= − = =
+
. Khi đó bảng biến thiên của hàm số là
Phương trình đã cho trở thành
( )
1
2
ft=
. Dựa và đồ thị ta thấy phương trình có 3 nghiệm là
( )
( )
( )
1;0
1;2
2;3
ta
tb
tc
= −
=
=
.
Dựa vào bảng biến thiên của hàm số
1 6 3t x x= + − +
ta có
Phương trình
1 6 3t a x x a= + − + =
có
2
nghiệm và phương trình
1 6 3t b x x b= + − + =
có
1
nghiệm và Phương trình
1 6 3t c x x c= + − + =
có
1
nghiệm.
Vậy phương trình
( )
2 1 6 3 1f x x+ − + =
có
4
nghiệm.
Câu 18: Chọn D
Ta có: hệ số
10a =
và
( )
0fx=
có đúng hai nghiệm phân biệt.
Đồ thị hàm số có 2 điểm cực trị và 1 điểm thuộc trục hoành.
( )
2
3
2
m
f x x
=−
.
( ) ( )
00
6
m
f x x m
= =
.
Trường hợp 1 :
3
1
80
6 2 6
mm
mm

− + − =



24m=
.
( )
3
24: 12 16m f x x x= = − +
.
( )
f x k=
có 3 nghiệm phân biệt
( )
0;32k
.
Có 31 giá trị nguyên của
k
thỏa mãn.
Trường hợp 1 :
3
1
80
6 2 6
mm
mm

− + + − =



6m=
.
( )
3
6: 3 2m f x x x= = − −
.
( )
f x k=
có 3 nghiệm phân biệt
( )
4;0k −
.
Có 3 giá trị nguyên của
k
thỏa mãn.
Vậy có 34 giá trị nguyên của
k
thỏa mãn.
Câu 19: Chọn D
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
19 | Facebook tác giả: Phan Nhật Linh
Ta có
( ) ( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
2
2
2
2
2
01
00
1
. 2 1 0 2
1
1
2
2
2
1
3
2
fx
g x f x
g x g x f x
gx
fx
fx
=
==
− = =


=
=
=−
.
Từ đồ thị hàm số
( )
y f x=
suy ra
+)
( ) ( )
2
2
2
1
1 0;1
1
xa
xb
xc
= −
=
=
. Suy ra phương trình có 4 nghiệm phân biệt.
+)
( )
( )
( ) ( )
( )
2
2
2
1,
2 0;1 ,
1,
x d d a
x e e b
x f f c
= −
=
=
. Suy ra phương trình có 4 nghiệm phân biệt khác 4 nghiệm
phân biệt của phương trình.
+)
( )
( )
( ) ( )
( )
2
2
2
1, ,
3 0;1 , ,
1, ,
x m m d a
x n n e b
x p p f c
= −
=
=
. Suy ra phương trình có 4 nghiệm phân biệt khác 4 nghiệm
phân biệt của phương trình và 4 nghiệm phân biệt của phương trình.
Vậy phương trình
( ) ( )
. 2 1 0g x g x −=


có tất cả 12 nghiệm
Câu 20: Chọn A
Gọi
( )
( )
2
2 3 2g x f x= + −
. Ta có:
( )
( )
2
' 4 . ' 2 3g x x f x=+
.
( )
2
2
0
' 0 2 3 1 0
2 3 3
x
g x x x
x
=
= + = − =
+=
.
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 20
Ta có bảng biến thiên:
Mà
( )
( )
( )
5
5
5
gx
gx
gx
=
=
=−
. Từ bảng biến thiên ta thấy phương trình có 3 nghiệm.
Câu 21: Chọn C
Ta có
( )
( )
( )
( ) ( )
( )
( )
2 (1)
0 , 0;1 (2)
3 (3)
fx
g f x f x
fx

=−
= =
=
.
Dựa vào đồ thị hàm số
( )
gx
suy ra phương trình
( )
1
có 4 nghiệm; phương trình
( )
2
có 5
nghiệm và phương trình
( )
3
có 1 nghiệm. Vậy phương trình
( )
( )
0g f x =
có 10 nghiệm.
Ta có
( )
( )
( )
( )
( )
( ) ( )
( )
( ) ( )
( )
3 (4)
1 (5)
0 1 (6)
, 1;2 (7)
, 4;5 (8)
gx
gx
f g x g x
g x a a
g x b b
=−
=−
= =
=
=
.
Dựa vào đồ thị hàm số
( )
gx
suy ra phương trình
( )
4
có 1 nghiệm; phương trình
( ) ( ) ( )
5 ; 6 ; 7
mỗi phương trình có 3 nghiệm và phương trình
( )
8
có 1 nghiệm. suy ra phương trình
( )
( )
0f g x =
có 11 nghiệm.
Vậy tổng số nghiệm của phương trình
( )
( )
0f g x =
và
( )
( )
0g f x =
là 21.
Câu 22: Chọn A
Ta có:
( ) ( )
( )
1 0 1 1+ − − = + − =
xx
f e x m f e x m
.
Đặt
1 0,
= + =
xx
t e t e x
. Ta có bảng biến thiên:
Với
( )
1 ln 1= + = −
x
t e x t
. Ta có:
( ) ( ) ( ) ( )
1 ln 1 2 − − =f t t m
.
Khi đó, phương trình đã cho có hai nghiệm thực phân biệt khi và chỉ khi phương trình
( )
2
có
hai nghiệm thực phân biệt lớn hơn 1.
Xét hàm số
( ) ( ) ( )
ln 1 , 1= − − g t f t t t
ta có:
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
21 | Facebook tác giả: Phan Nhật Linh
( ) ( ) ( ) ( )
11
,0
11
= − = =
−−
g t f t g t f t
tt
.
Dựa vào đồ thị các hàm số
( )
=y f x
và
1
1
=
−
y
x
ta có:
( )
1
2
1
= =
−
f t t
t
.
Ta có bảng biến thiên của hàm số
( )
gt
:
Số nghiệm của phương trình
( )
2
bằng số giao điểm của đồ thị hàm số
( )
gt
và đường thẳng
=ym
.
Dựa vào bảng biến thiên, phương trình
( )
2
có hai nghiệm thực phân biệt lớn hơn 1
( ) ( ) ( )
2 2 ln1 2 − m g m f m f
.
Câu 23: Phương trình
( )
( )
( )
( )
( ) ( ) ( )
( ) ( ) ( )
( ) ( )
3
3 3 3
3
3 1 1
1 0 1 5 3 2
03
x f x a a
f x f x f x f x x f x b b
x f x
= − −
+ = = − = − −
=
.
Xét phương trình
( ) ( )
3
3
k
x f x k f x
x
= =
.
Đặt
( )
3
k
gx
x
=
,
( )
4
3
0, 0
k
g x x
x
−
=
và
0k
.
( ) ( )
lim lim 0
xx
g x g x
→− →+
==
,
( )
0
lim
x
gx
−
→
= +
,
( )
0
lim
x
gx
+
→
= −
.
Ta có bảng biến thiên của hàm số
( )
gx
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 22
Dựa vào bảng biến thiên và đề bài, suy ra trong mỗi khoảng
( )
;0−
và
( )
0;+
phương trình
( ) ( )
f x g x=
có đúng một nghiệm.
Vì
,0ab
nên phương trình
( )
1
và
( )
2
mỗi phương trình có
2
nghiệm phân biệt khác nhau.
Xét phương trình
( ) ( )
( )
3
0
0
3 : 0
0
0
x
x
x f x
fx
xc
=
=
=
=
=
, với
c
khác các nghiệm của
( )
1
và
( )
2
.
Vậy phương trình
( )
( )
3
10f x f x +=
có đúng
6
nghiệm.
Câu 24: Chọn B
Dựa vào đồ thị hàm số
( )
'y f x=
, suy ra hàm số
( )
'y f x=
là hàm số bậc 3 qua 0 không đổi
dấu và đi qua 3 đổi dấu từ + sang -. Mặt khác
( )
lim '
x
fx
→+
= −
nên
0k
.
Do đó, hàm số
( )
'y f x=
có dạng
( ) ( )
2
' . . 3f x k x x=−
.
Vì
( )
' 2 1f =
nên
1
4
k =−
. Suy ra
( ) ( )
3 2 4 3
1 3 1 1
'
4 4 16 4
f x x x f x x x e= − + = − + +
Xét phương trình
( ) ( ) ( )
( ) ( )
( )
( )
43
2 2 2
2
3
22
2
11
2 2 2 0
16 4
2 0 1
2 2 4 0
2 4 0 2
f x x m e x x m x x m
x x m
x x m x x m
x x m
− + + = − − + + + − + + =
− + + =
− + + − + + − =
− + + − =
Phương trình
( )
2
2f x x m e− + + =
có bốn nghiệm phân biệt khi và chỉ khi phương trình
( )
1
,
( )
2
đều có hai nghiệm phân biệt
10
3
1 4 0
m
m
m
+
+ −
.
Mặt khác,
là số nguyên trên
5;5−
nên
4;5m
.
Vậy có 2 giá trị nguyên của
thoả yêu cầu bài toán.
Câu 25: Chọn A
Đặt
costx=
. Do
0;
2
x


nên
(
0;1t
( )
)
2;0ft −
( ) ( )
)
4 2 cos 4 2 0;2f x f t + = +
( )
( )
)
4 2 cos 2;2f f x + −
Vậy phương trình
( )
( )
4 2 cosf f x m+=
có nghiệm
0;
2
x


22m −
Do
nguyên nên
2; 1;0;1m − −
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
23 | Facebook tác giả: Phan Nhật Linh
Vậy có bốn giá trị của tham số
để phương trình
( )
( )
4 2 cosf f x m+=
có nghiệm
0;
2
x


.
Câu 26: Chọn B
Đặt:
( )
y f x=
ta có hệ:
( )
( )
( ) ( ) ( )
*
y f x
f y y f x x
f y x
=
+ = +
=
Xét hàm số:
( ) ( )
3
22
m
g t f t t t t= + = + −
( )
2
3 2 0g t t t
= +
( )
gt
luôn đồng biến trên
Từ phương trình
( )
*
ta có
( ) ( ) ( )
33
22
mm
g y g x y x f x x x x x x= = = + − = =
Để phương trình
( )
( )
f f x x=
có nghiệm thuộc đoạn
1;2
thì
33
1;2 1;2
2
m
xx
Min x Max x


1 2 8 0 3
m
m
,
là số nguyên nên
0;1;2;3m
Vậy Chọn B
Câu 27: Chọn C
Ta có
2
( ) ( 4) ( ) 2 4 0f x m f x m− + + + =
( )( )
( )
( )
( ) 2 1
( ) 2 ( ) 2 0
( ) 2 2
fx
f x f x m
f x m
=
− − − =
=+
Phương trình
( )
1
có 4 nghiệm phân biệt
Vậy để phương trình
( )
*
có 6 nghiệm phân biệt thì phương trình
( )
2
có 2 nghiệm phân biệt khác
nghiệm của phương trình
( )
1
.
Phương trình
( )
2
có hai nghiệm phân biệt khác nghiệm của phương
( )
1
khi và chi khi
2 0 2
2 4 2
mm
mm
+ = = −


+

. Vì
( )
; 5;5m Z m −
nên
2;3;4m =−
Vậy
m
có 3 giá trị.
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 24
Câu 28: Ta có:
( )
( )
( )
( )
22
2 0 2f x f x f x f x+ = = −
( )
( ) ( )
( ) ( )
( ) ( )
2
2
2
2
0
0;1
2;3
3;4
x f x
x f x
x f x
x f x
=
=
=
=
.
( )
2
0x f x =
( )
0
0
x
fx
=
=
. Phương trình
( )
0fx=
có 2 nghiệm phân biệt khác 0.
Xét phương trình
( )
2
x f x m=
với
0m
. Rõ ràng
0x =
không là nghiệm của phương trình.
Do đó ta có:
( )
2
x f x m=
( )
2
m
fx
x
=
.
Xét hàm số
( )
2
m
gx
x
=
có
( )
3
2m
gx
x
−
=
. Từ đó ta có BBT của
( )
gx
:
Suy ra đồ thị hàm số
( )
y g x=
luôn cắt đồ thị hàm số
( )
y f x=
tại 2 điểm phân biệt có hoành
độ khác 0 và khác hai nghiệm của phương trình
( )
0fx=
.
Vậy mỗi phương trình
( ) ( )
2
0;1x f x
=
,
( ) ( )
2
2;3x f x
=
,
( ) ( )
2
3;4x f x
=
có hai
nghiệm phân biệt. Các nghiệm của các phương trình này không trùng nhau, khác 0 và khác hai
nghiệm của phương trình
( )
0fx=
.
Do đó phương trình
( )
( )
2
20f x f x +=
có 9 nghiệm thực phân biệt.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
1 | Facebook tác giả: Phan Nhật Linh
Câu 1: Cho hai hàm số
1 1 2
1 2 3
x x x x
y
x x x x
− + +
= + + +
+ + +
và
2y x x m= + − −
(
m
là tham số thực) có đồ
thị lần lượt là
( ) ( )
12
,CC
. Tập hợp tất cả các giá trị của
m
để
( )
1
C
và
( )
2
C
cắt nhau tại đúng
bốn điểm phân biệt là
A.
( )
2;− +
. B.
(
;2− −
. C.
)
2;− +
. D.
( )
;2− −
.
Câu 2: Tìm tập hợp tất cả các giá trị của tham số
m
để đồ thị hai hàm số
( )
2
2 1 1y x x= + −
và
11 1
11
3 4 2
ym
xx
= − + +
−−
cắt nhau tại
2
điểm phân biệt?
A.
( )
;0−
. B.
( )
;1−
. C.
(
;1−
. D.
(
;2−
.
Câu 3: Có bao nhiêu cặp số thực
( ; )ab
để bất phương trình
( )( )
( )
2
1 2 2 0x x ax bx− + + +
nghiệm
đúng với mọi
x
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 4: Cho 2 hàm số
7 5 3
31y x x x m= + + + −
và
22y x x m= − − −
(
là tham số thực) có đồ thị lần
lượt là
( )
1
C
,
( )
2
C
. Tập hợp tất cả các giá trị của
để
( )
1
C
cắt
( )
2
C
là
A.
m
. B.
( )
2;m +
. C.
( )
;2m −
. D.
)
2;m +
.
Câu 5: Có bao nhiêu giá trị nguyên của tham số thực
m
thuộc đoạn
2019;2019−
để phương trình
( ) ( )
2
3 2 3 1 5 1 2 4 2 3x x m x x m x x+ + − + − − + = − − +
có nghiệm thực?
A.
2019
. B.
4032
. C.
4039
. D.
4033
.
Câu 6: Có bao nhiêu
m
nguyên dương để hai đường cong
( )
1
2
:2
10
Cy
x
=+
−
và
( )
2
:4C y x m=−
cắt nhau tại ba điểm phân biệt có hoành độ dương?
A. 35. B. 37. C. 36. D. 34.
Câu 7: Cho hàm số
( ) ( 1).( 2)...( 2020).f x x x x= − − −
Có bao nhiêu giá trị nguyên của
m
thuộc đoạn
2020;2020−
để phương trình
( ) . ( )f x m f x
=
có 2020 nghiệm phân biệt?
A. 2020. B. 4040. C. 4041. D. 2020.
Câu 8: Cho hai hàm số
2
ln
−
=
x
y
x
và
31
4 2020
2
= − + −
−
ym
xx
, Tổng tất các các giá trị nguyên của
tham số
m
để đồ thị hai hàm số cắt nhau tại một điểm duy nhất là
A.
506
. B.
1011
. C.
2020
. D.
1010
.
Bài toán tương giao đồ thị hàm số 02
DẠNG 2
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 2
Câu 9: Cho hai hàm số
( )( )( )
( )
1 2 1 3 1 2y x x x m x= + + + +
;
4 3 2
12 22 10 3y x x x x= − − − + +
có đồ thị
lần lượt là
( )
1
C
,
( )
2
C
. Có bao nhiêu giá trị nguyên của tham số
m
trên đoạn
2020;2020−
để
( )
1
C
cắt
( )
2
C
tại 3 điểm phân biệt?
A.
4040
. B.
2020
. C.
2021
. D.
4041
.
Câu 10: Cho hai hàm số
642
6 6 1y x x x= + + +
và
( )
3
15 3 15y x m x m x= − + −
có đồ thị lần lượt là
( )
1
C
và
( )
2
C
. Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
thuộc đoạn
2019;2019−
để
( )
1
C
và
( )
2
C
cắt nhau tại hai điểm phân biệt. Số phần tử của tập hợp
S
bằng
A.
2006
. B.
2005
. C.
2007
. D.
2008
.
Câu 11: Cho hàm số
( )
4 3 2
y f x =ax bx cx dx e= + + + +
có đồ thị như hình vẽ bên đây, trong đó
a,b,c,d,e
là các hệ số thực. Số nghiệm của phương trình
( )
( )
( ) ( )
2 1 0f f x f x f x+ + − =
là
A. 3. B. 4. C. 2. D. 0.
Câu 12: Cho hàm số
( )
=y f x
có bảng biến thiên như hình vẽ:
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
( )
2
64f x x m−=
có ít nhất ba
nghiệm thực phân biệt thuộc khoảng
( )
0;+
?
A. 25. B. 30. C. 29. D. 24.
Câu 13: Cho hàm số
( )
y f x=
liên tục trên đoạn
1;4−
và có đồ thị như hình vẽ.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
3 | Facebook tác giả: Phan Nhật Linh
Có bao nhiêu giá trị
nguyên của
m
thuộc đoạn
10;10−
để bất phương trình
( )
2f x m m+
đúng với mọi
x
thuộc đoạn
1;4−
.
A.
6
. B.
5
. C.
7
. D.
8
.
Câu 14: Cho hàm số
( )
y f x=
liên tục trên và có đồ thị như hình vẽ bên dưới. Gọi
S
là tập hợp tất
cả giá trị nguyên của tham số
m
để phương trình
( )
sin 2 2sinf x m x− + =
có nghiệm thuộc
khoảng
( )
0;
. Tổng các phần tử của
S
bằng
A.
4
. B.
1−
. C.
3
. D.
2
.
Câu 15: Cho hàm số
( )
3
2f x x x= + +
. Có tất cả bao nhiêu giá trị nguyên của tham số
m
để phương
trình
( ) ( )
(
)
33
3
2f f x f x m x x+ + = − − +
có nghiệm
1;2x−
?
A.
1750
. B.
1748
. C.
1747
. D.
1746
.
Câu 16: Cho hàm số
()fx
liên tục trên
2;4
và có bảng biến thiên như hình vẽ bên. Có bao nhiêu giá
trị nguyên của
để phương trình
2
2 2 . ( )x x x m f x+ − =
có nghiệm thuộc đoạn
2;4
?
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 4
A.
6
. B.
5
. C.
4
. D.
3
.
Câu 17: Cho hàm số
( )
=y f x
liên tục và có đạo hàm trên đoạn
2;4−
và có bảng biến thiên như sau
Có bao nhiêu giá trị nguyên của tham số
m
để hệ phương trình
( )
2
3
9
40
6 2 1 8 6 0
−
− + − + − =
x
f x x x m
có ba nghiệm phân biệt?
A.
9
. B.
11
. C.
10
. D.
8
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
5 | Facebook tác giả: Phan Nhật Linh
BẢNG ĐÁP ÁN
1.B
2.C
3.C
4.A
5.B
6.C
7.B
8.A
9.C
10.A
11.B
12.B
13.C
14.D
15.A
16.C
17.D
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Chọn B
Xét phương trình hoành độ giao điểm
( )
1 1 2 1 1 2
2 2 1
1 2 3 1 2 3
x x x x x x x x
x x m x x m
x x x x x x x x
− + + − + +
+ + + = + − − + + + − + + = −
+ + + + + +
Xét
( )
1 1 2
2 , \ 3; 2; 1;0
1 2 3
x x x x
f x x x x D
x x x x
− + +
= + + + − + + = − − −
+ + +
Ta có
( )
( )
( )
1
2
1 1 2
2, 2;
1 2 3
1 1 2
2 2, ; 2
1 2 3
x x x x
x D D
x x x x
fx
x x x x
x x D D
x x x x
− + +
+ + + − − + =
+ + +
=
− + +
+ + + + + − − =
+ + +
Có
( )
( ) ( ) ( )
( ) ( ) ( )
1
2 2 2
2
2
2 2 2
2
1 1 1 1
,
1 2 3
1 1 1 1
2,
1 2 3
xD
x
x x x
fx
xD
x
x x x
+ + +
+ + +
=
+ + + +
+ + +
Dễ thấy
( )
12
0,f x x D D
, ta có bảng biến thiên
Hai đồ thị cắt nhau tại đúng 4 điểm phân biện khi và chỉ khi phương trình
( )
1
có đúng 4 nghiệm
phân biệt, từ bảng biến thiên ta có:
22mm− −
.
Câu 2: Chọn C
Xét phương trình hoành độ giao điểm:
( )
( )
2
11 1
2 1 1 11 *
3 4 2
+ − = − + +
−−
x x m
xx
Điều kiện:
1 0 1
44
33
22
−








xx
xx
xx
Ta có:
( )
*
( )
2
11 1
2 1 1 11
3 4 2
x x m
xx
+ − − + − =
−−
-
2
-
-
-
+
+
+
+
-
+
+
+
+
f(x)
f'(x)
+
-
x
-3
-2
1
0
+
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 6
Xét hàm số
( )
2
11 1
( ) 2 1 1 11
3 4 2
f x x x
xx
= + − − + −
−−
trên
)
4
1; \ ;2
3

+


Nhận thấy, hàm số
( )
fx
liên tục trên các khoảng
( )
44
1; , ;2 , 2;
33
+
Ta có,
( )
2
11 1
( ) 2 1 1 11
3 4 2
f x x x
xx

= + − − + −

−−

( )
( ) ( )
2
22
1 33 1
4 1 2 1
21
3 4 2
x x x
x
xx
= − + + + +
−
−−
( ) ( )
2
22
10 8 1 33 1
0
21
3 4 2
xx
x
xx
−+
= + +
−
−−
với
)
4
1; \ ;2
3

+


x
Suy ra, hàm số
( )
fx
đồng biến trên
)
4
1; \ ;2
3

+


.
Bảng biến thiên
Từ bảng biến thiên ta suy ra đồ thị hai hàm số
( )
2
2 1 1y x x= + −
và
11 1
11
3 4 2
ym
xx
= − + +
−−
cắt nhau tại
2
điểm phân biệt khi
(
;1m −
.
Câu 3: Chọn C
Đặt
( ) ( )( )
( )
2
1 2 2f x x x ax bx= − + + +
Giả sử
1x =
không phải là nghiệm của phương trình
( ) ( )
( )
2
2 2 0g x x ax bx= + + + =
thì hàm
số
( ) ( )( )
( )
2
1 2 2f x x x ax bx= − + + +
sẽ đổi dấu khi qua điểm
1x =
, nghĩa là
( )( )
( )
2
1 2 2 0x x ax bx− + + +
không có nghiệm đúng với mọi
x
.
Do đó, để yêu cầu bài toán được thỏa mãn thì một điều kiện cần là
( ) ( )
( )
2
2 2 0g x x ax bx= + + + =
có nghiệm
1x =
suy ra
20ab+ + =
Lí luận tương tự có
( ) ( )
( )
2
1 2 0h x x ax bx= − + + =
cũng phải nhận
2x =−
là nghiệm, suy ra
4 2 2 0ab− + =
Từ và ta có hệ
2 0 1
4 2 2 0 1
a b a
a b b
+ + = = −


− + = = −

Điều kiện đủ:
Với
1
1
a
b
=−
=−
có
( ) ( )( )
( )
( ) ( )
22
2
1 2 2 1 2 0f x x x x x x x= − + − − + = − − +
,
x
.
Vậy không tồn tại cặp số thực
( ; )ab
nào thỏa mãn yêu cầu bài toán.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
7 | Facebook tác giả: Phan Nhật Linh
Câu 4: Chọn A
Xét phương trình hoành độ giao điểm:
7 5 3
3 1 2 2x x x m x x m+ + + − = − − −
7 5 3
2 5 1 (1)x x x x x m + + − − + = − +
.
Xét hàm số
7 5 3
( ) 2f x x x x x x= + + − − +
.
Ta có
)
( )
7 5 3
7 5 3
2 khi 2;
()
2 2 khi ;2
x x x x
fx
x x x x x
+ + + +
=
+ + + − −
.
( )
( )
6 4 2
6 4 2
7 5 3 0 khi 2;
()
7 5 3 2 0 khi ;2
x x x x
fx
x x x x
+ + +
=
+ + + −
.
( )
lim
x
fx
→−
= −
;
( )
lim
x
fx
→+
= +
.
Bảng biến thiên:
Từ bảng biến thiên ta thấy phương trình
( )
1
luôn có nghiệm với mọi
m
.Vậy để
( )
1
C
cắt
( )
2
C
thì
m
.
Câu 5: Chọn B
Đk:
3;1x−
.
Phương trình đã cho
( )( )
( )
11 3 4 3 1 2 1 3 0x x x m x x − − + − + − − + =
.
Đặt
( )
2 1 3t x x g x= − − + =
, với
( )( )
2
3;1 11 3 4 3 1 4x x x x t − − − + − = +
.
Có
( ) ( )
11
0, 3;1
1 2 3
g x x
xx
−
= − −
−+
. Suy ra
( )
gx
nghịch biến trên khoảng
( )
3;1−
.
( ) ( )
3;1
min 1 2g x g
−
= = −
:
( ) ( )
3;1
max 3 4 2;4g x g t
−
= − = −
.
Từ
2
40t mt + + =
.
Nếu
0 0 4 0t = + =
.
Nếu
2;4 \{0}t −
, ta có
( )
2
44t
m t f t
tt
−−
= = − − =
.
Có
( ) ( )
2
2
4
, 0 2
t
f t f t t
t
−

= = =
.
Bảng biến thiên
Từ bảng biến thiên, suy ra phương trình có nghiệm thực khi và chỉ khi
4
4
m
m
−
.
+
∞
∞
+
2
+
∞
∞
f '(x)
f(x)
x
+
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 8
Do đó
2019;2019
4
2019; 2018;....; 4;4;...;2018;2019
4
m
m
m
m
m
−
− − −
−
.
Vậy có
( )
2019 4 1 .2 4032− + =
giá trị nguyên của tham số thực
m
.
Câu 6: ChọnC
Điều kiện:
10
4
x
m
x
.
Xét trên
( )
0; \ 10+
, phương trình hoành độ giao điểm của
( )
1
C
và
( )
2
C
là
2
2 2 18
2 4 4
10 10
x
x m m x
xx
−

+ = − = −

−−

.
Đặt
( )
2
2 18
4
10
x
g x x
x
−

=−

−

với
( )
0; \ 10x +
.
Ta có:
( )
( )
3
2 18
41
10
x
gx
x

−
=+


−

;
( )
( )
4
4 34
10
x
gx
x
−+

=
−
.
( )
gx
có bảng biến thiên như sau
Suy ra phương trình
( )
0gx
=
có một nghiệm duy nhất
17
;10
2



. Lại có
( )
9,22 0g
nên
( )
9,22;10
. Ta có bảng biến thiên của
( )
gx
trên
( )
0; \ 10+
:
Từ đó suy ra phương trình
( )
m g x=
có 3 nghiệm dương phân biệt khi và chỉ khi
( )
81
25
mg
−

.
Trên khoảng
( )
9,22;10
thì
2
4 40
2 18
3
10
x
x
x
−


−

nên
( ) ( ) ( )
37 36;37g x g
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
9 | Facebook tác giả: Phan Nhật Linh
Vậy những giá trị
m
nguyên dương thỏa mãn yêu cẩu bài toán là 1; 2; 3; …; 36 hay có 36 giá
trị của
m
cần tìm.
Câu 7: Chọn B
Ta có nhận xét: khi
( ) 0fx=
thì phương trình
( ) . ( )f x m f x
=
vô nghiệm.
Do đó:
()
( ) . ( ) .
()
fx
f x m f x m
fx
= =
Xét hàm số
( ) 1 1 1 1
()
( ) 1 2 3 2020
fx
gx
f x x x x x
= = + + + +
− − − −
.
Ta có
( ) ( ) ( ) ( )
2 2 2 2
1 1 1 1
( ) 0, \ 1;2;3...;2020
1 2 3 2020
g x x
x x x x
− − − −
= + + + +
− − − −
Bảng biến thiên:
Dựa vào BBT, phương trình
( ) . ( )f x m f x
=
có 2020 nghiệm phân biệt khi và chỉ khi
0m
hoặc
0m
.
Kết hợp với điều kiện
m
là số nguyên thuộc
2020;2020−
nên
| 2020 2020, 0 .m n n n −
Vậy có tất cả 4040 giá trị
m
thỏa yêu cầu bài toán.
Câu 8: Chọn A
+ Phương trình hoành độ điểm chung của hai đồ thị hàm số là
2 3 1 2 3 1
ln 4 2020 ln 4 2020 (*)
22
−−
= − + − − + = −
−−
xx
mm
x x x x x x
Đồ thị của hai hàm số đã cho cắt nhau tại một điểm duy nhất khi và chỉ khi có duy nhất một
nghiệm.
+ Xét hàm số
1
2
3
31
( ) ln( 2) ln khi 2
2
2 3 1 3 1
ln ( ) ln(2 ) ln khi 0 2
22
31
( ) ln(2 ) ln( ) khi 0
2
= − − − +
−
−
= − + = = − − − +
−−
= − − − − +
−
g x x x x
xx
x
y g x x x x
x x x x x
g x x x x
xx
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 10
Ta có
2
/
1
2 2 2 2
2
/
2
2 2 2 2
2
/
3
2 2 2 2
1 1 3 1 4( 1)
( ) khi 2
2 ( 2) ( 2)
1 1 3 1 4( 1)
( ) khi 0 2
2 ( 2) ( 2)
1 1 3 1 4( 1)
( ) khi 0
2 ( 2) ( 2)
−
= − + − =
− − −
−−
= − + − =
− − −
−−
= − + − =
− − −
x
g x x
x x x x x x
x
g x x
x x x x x x
x
g x x
x x x x x x
, do vậy
1
0
1
=−
=
=
x
y
x
bảng biến thiên hàm số như sau
+ Qua bảng biến thiên này ta có có nghiệm duy nhất khi và chỉ khi
506
4 2020 4
2020 ln3
4 2020 ln3
4
=
−=
+
−=
=
m
m
m
m
+ Tư đây yêu cầu bài toán xãy ra khi và chỉ khi
506=m
.
Câu 9: Chọn C
Xét phương trình hoành độ giao điểm của hai đồ thị
( )
1
C
và
( )
2
C
:
( )( )( )
( )
4 3 2
1 2 1 3 1 2 12 22 10 3x x x m x x x x x+ + + + = − − − + +
Để đồ thị
( )
1
C
cắt
( )
2
C
tại 3 điểm phân biệt thì phương trình có 3 nghiệm phân biệt.
Với
11
1; ;
23
x

− − −


: Không là nghiệm của phương trình.
Với
11
1; ;
23
x

− − −


ta có:
( )
( )( )( )
4 3 2
12 22 10 3 1 1 1
1 2 2 2
1 2 1 3 1 1 2 1 3 1
x x x x
m x m x x
x x x x x x
− − − + +
= − = − − + + +
+ + + + + +
.
Xét hàm số
( )
1 1 1
22
1 2 1 3 1
f x x x
x x x
= − − + + +
+ + +
,
11
\ 1; ;
23
x

− − −

.
Suy ra:
( )
( ) ( ) ( )
2 2 2
2
2 1 2 3
2
1 2 1 3 1
x
fx
x x x
x
= − − − − −
+ + +
.
Ta có:
( )
( ) ( ) ( )
( )
( ) ( ) ( )
( )
2 2 2
2 2 2
1 2 3
4 khi 0;
1 2 1 3 1
1 2 3 1 1
khi ;0 \ 1; ;
23
1 2 1 3 1
x
x x x
fx
x
x x x
− − − − +
+ + +
=

− − − − − − −


+ + +
và
( )
fx
không
xác định tại
0x =
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
11 | Facebook tác giả: Phan Nhật Linh
Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy để phương trình có 3 nghiệm phân biệt thì
0m
. Do đó có 2021
giá trị nguyên của tham số
m
thỏa mãn yêu cầu bài toán.
Câu 10: Chọn A
Ta biết
( )
1
C
cắt
( )
2
C
tại hai điểm phân biệt khi và chỉ khi phương trình
( ) ( )
6 4 2 3
6 6 1 15 3 15 1x x x x m x m x+ + + = − + −
có hai nghiệm phân biệt.
Điều kiện:
( )
15 0 15 *m x m x−
.
Nếu
0x =
thì phương trình
( )
1
vô nghiệm. Suy ra
0x
.
Khi đó
( ) ( )
32
3
1
1 6 6 15 3 15x x x m x m x
x
+ + + = − + −
( )
3
3
11
3 15 3 15x x m x m x
xx
+ + + = − + −
.
Xét hàm số
( )
3
3f t t t=+
. Tập xác định
D =
.
( )
2
3 3 0,f t t t
= +
. Suy ra hàm số
( )
3
3f t t t=+
đồng biến trên .
Do đó
( ) ( )
1
1 15 2x m x
x
+ = −
.
Nếu
1
00xx
x
+
Phương trình
( )
2
vô nghiệm
0x
.
Khi đó
0
1
0
m
x
x
+
nên
( )
22
22
11
2 2 15 2 15x m x m x x
xx
+ + = − = + + +
.
Đặt
( )
2
2
1
2 15 , 0g x x x x
x
= + + +
.
( )
3
2
2 15g x x
x
= − +
.
Phương trình
( )
0gx
=
có một nghiệm
1
2
x =
trên khoảng
( )
0;+
.
Bảng biến thiên
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 12
Suy ra
( )
1
có hai nghiệm phân biệt khi và chỉ khi
55
4
m
.
Kết hợp với
m
nguyên và
2019;2019m−
ta có được
m
nguyên và
14;2019m
.
Khi đó
S
có
2019 14 1 2006− + =
phần tử.
Câu 11: Chọn B
Từ hình vẽ ta có dạng đồ thị của hàm trùng phương nên
( )
42
0b d f x ax cx e= = = + +
Ta có
( )
3
42f x ax cx.
=+
Từ đồ thị
( )
( )
( )
( )
42
10
4 2 0 1
0 0 0 0 2
12
11
f
a c a
f e e f x x x .
a c e c
f
=
+ = =


= = = = +
+ + = =
=

( )
2
2f x x x = +
và
( )
( )
( ) ( )
2
2f f x f x f x .=+
Như vậy phương trình
( )
( )
( ) ( )
2 1 0f f x f x f x .+ + − =
( ) ( ) ( ) ( )
2
2 2 1 0f x f x f x f x + + + − =
với
( )
0f x .
Đặt
( )( )
0t f x t=
ta được phương trình
( )
0gt=
với
( )
2
3 2 1g t t t t .= − − +
Nhận thấy: Hàm số
( )
gt
liên tục trên đoạn
01;
và
( ) ( )
0 1 0g .g
( )
0gt=
có ít nhất 1 nghiệm thuộc
( )
01;
.
Hàm số
( )
gt
liên tục trên đoạn
14;
và
( ) ( )
1 4 0g .g
( )
0gt=
có ít nhất 1 nghiệm thuộc
( )
14;
.
Mà
( )
0gt=
là phương trình bậc hai chỉ có tối hai nghiệm nên
( )
0gt=
có duy nhất một nghiệm
thuộc
( )
01;
. Suy ra
( )
( )
( ) ( )
2 1 0f f x f x f x+ + − =
có duy nhất một nghiệm
( ) ( )
01f x ; .
Suy ra phương trình
( )
f x a=
với
( )
01a;
luôn có 4 nghiệm x phân biệt.
Câu 12: Chọn B
Ta đặt:
( )
( )
2
4g x f x x=−
.
( ) ( )
( )
2
2 4 4g x x f x x

= − −
( )
( )( )( )
222
2 2 4 4 4 2 4x x x x x x x= − − + − + −
( )
( )
( )
3
2
2 2 4 2 4x x x x x= − − + −
.
Mặt khác:
( ) ( )
0 0 3gf= = −
;
( ) ( )
( )
2 2 2 2 2 2g g f− = + = − =
;
( ) ( )
2 4 2gf= − = −
;
( ) ( )
4 0 3gf= = −
. Ta có bảng biến thiên:
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
13 | Facebook tác giả: Phan Nhật Linh
Từ bảng biến thiên ta được: yêu cầu bài toán tương đương
32
6
m
−
18 12m −
. Vậy có tất cả 30 giá trị của tham số
m
thỏa mãn yêu cầu bài toán.
Câu 13: Chọn C
Để bất phương trình
( )
2f x m m+
có nghiệm ta suy ra điều kiện
0m
.
( ) ( )
2 2 2f x m m m f x m m+ − +
( )
( )
3f x m
f x m
−
.
Bất phương trình
( )
2f x m m+
đúng với mọi
x
thuộc đoạn
1;4−
( )
( )
3f x m
f x m
−
đúng
với mọi
x
thuộc đoạn
1;4−
( )
( )
1;4
1;4
3 min
max
m f x
m f x
−
−
−
.
Từ đồ thị hàm số
( )
y f x=
ta suy ra
( )
( )
1;4
1;4
min 2; max 3f x f x
−
−
= − =
.
( )
( )
1;4
1;4
2
3 min
32
3
3
3
max
3
m f x
m
m
m
m
m f x
m
−
−
−
− −


Vậy trên đoạn
10;10−
có
7
giá trị nguyên của
m
thỏa mãn điều kiện bài toán.
Câu 14: Chọn D
Đặt
sintx=
, với
( )
0;x
(
0;1t
.
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 14
Ta được phương trình:
( ) ( )
2 2 2 2f t t m f t t m− = − = + −
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số
( )
y f t=
và đường thẳng
( )
22y t m r= + −
.
Gọi
( )
: 2 1p y x=+
song song với đường thẳng
( )
:2yt=
và đi qua điểm
( )
0;1A
.
Gọi
: 2 3q y x=−
song song với đường thẳng
( )
:2yt=
và đi qua điểm
( )
1; 1B −
.
Để phương trình
( )
sin 2 2sinf x m x− + =
có nghiệm thuộc khoảng
( )
0;
thì phương trình
phải có nghiệm
(
0;1t
, suy ra đường thẳng
r
nằm trong miền nằm giữa hai đường thẳng
q
và
p
3 2 1 1 3 1;0;1;2 1;0;1;2m m m S − − − − = −
.
Do đó tổng các phần tử là:
1 0 1 2 2− + + + =
.
Câu 15: Chọn A
Xét hàm số
3
( ) 2f t t t= + +
, ta có
2
( ) 3 1 0,f t t t
= +
.
Do đó hàm số
f
đồng biến trên .
Ta có
(
)
3
3
( ) ( ) ( )f f x f x m f x+ + = −
3 3 3
3
( ) ( ) ( ) ( ) 0 (1)x f x f x m f x f x x m − = + + + + + =
Xét
33
( ) ( ) ( )h x f x f x x m= + + +
trên đoạn
[ 1;2]−
.
Ta có
2 2 2 2
( ) 3 ( ) ( ) ( ) 3 ( ) 3 ( ) 1 3 .h x f x f x f x x f x f x x

= + + = + +

Ta có
2
( ) 3 1 0, [ 1;2] ( ) 0, [ 1;2]f x x x h x x

= + − −
.
Hàm số
()hx
đồng biến trên
[ 1;2]−
nên
[ 1;2]
[ 1;2]
min ( ) ( 1) 1, max ( ) (2) 1748.h x h m h x h m
−
−
= − = − = = +
Phương trình
(1)
có nghiệm khi và chỉ khi
( ) ( ) ( ) ( )
( )( )
[ 1;2]
[ 1;2]
min max 0 1 2
1 1748 0
1748 1.
h x h x h h
mm
m
−
−
−
− +
−
Do
m
nguyên nên tập các giá trị
m
thỏa mãn là
{ 1748; 1747; ;0;1}S = − −
.
Vậy có tất cả 1750 giá trị nguyên của
m
thỏa mãn.
Câu 16: Chọn C
Dựa vào bảng biến thiên ta có
( )
2;4
(4) 2Min f x f==
và
( )
2;4
(2) 4Max f x f==
Hàm số
2
( ) 2 2g x x x x= + −
liên tục và đồng biến trên
2;4
Suy ra
( )
2;4
(2) 2Min g x g==
và
( )
2;4
(4) 4 4 2Max g x g= = +
Ta có
2
2
2 2 ( )
2 2 . ( )
( ) ( )
x x x g x
x x x m f x m m
f x f x
+−
+ − = = =
Xét hàm số
()
()
()
gx
hx
fx
=
liên tục trên
2;4
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
15 | Facebook tác giả: Phan Nhật Linh
Vì
( )
gx
nhỏ nhất và
( )
fx
lớn nhất đồng thời xảy ra tại
2x =
nên
( )
( )
( )
( )
2;4
2;4
2;4
2
1
( ) (2)
22
Min g x
g
Minh x h
Max f x f
= = = =
Vì
( )
gx
lớn nhất và
( )
fx
nhỏ nhất đồng thời xảy ra tại
4x =
nên
( )
( )
( )
( )
2;4
2;4
2;4
4
( ) (4) 2 2 2
4
Max g x
g
Maxh x h
Min f x f
= = = = +
Từ đó suy ra phương trình
()h x m=
có nghiệm khi và chỉ khi
1
2 2 2
2
m +
.
Vậy có 4 giá trị nguyên của m để phương trình có nghiệm.
Câu 17: Chọn D
Ta có:
2
2
22
33
9 4 0
9 9 4 3 3
4 0 0 ; \ 0
22
22
0
0
−
−
−

− −



x
x
x
x
xx
x
x
.
Xét phương trình
( ) ( )
33
6 2 1 8 6 0 6 2 1 8 6− + − + − = = − + − +f x x x m m f x x x
Xét hàm số
( ) ( )
3
6 2 1 8 6= − + − +g x f x x x
, với
33
; \ 0
22

−


x
.
Ta có
( ) ( ) ( )
22
12 2 1 24 6 6 2 2 1 4 1

= − − + − + = − − + + −

g x f x x f x x
Từ giả thiết ta suy ra
( )
2 1 2
11
2 1 0
2 1 0
22
− +
− + −
− +
x
f x x
x
;
( )
13
2 2 1 0
22
2 1 0
2 2 1 4 3 1
22

− − +
− +
− +
− −
x
x
fx
x
x
.
Bảng biến thiên của hàm số
( ) ( )
3
6 2 1 8 6= − + − +g x f x x x
trên
33
; \ 0
22

−


.
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 16
Từ bảng biến thiên ta suy ra hệ có đúng ba nghiệm
có đúng ba nghiệm
33
; \ 0
22

−


x
4 14
9

m
m
. Vì
5;6;7;8;10;11;12;13 =mm
. Vậy có
8
số nguyên
m
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
1 | Facebook tác giả: Phan Nhật Linh
Câu 1: Cho hàm số
32
21y x x= − −
có đồ thị
(C)
, đường thẳng
( )
:1d y mx=−
và điểm
( )
4;11K
.Biết
rằng
(C)
và
( )
d
cắt nhau tại ba điểm phân biệt
,,A B C
trong đó
( )
0; 1A −
còn trọng tâm tam
giác
KBC
nằm trên đường thẳng
21yx=+
. Mệnh đề nào sau đây đúng?
A.
4m =
. B.
2m =
. C.
3m =
. D. Không có
m
.
Câu 2: Gọi
S
là tập tất cả các giá trị của tham số
để đường thẳng
3y x m=+
tiếp xúc với đồ thị hàm
số
3
1yx=+
. Tổng các phần tử của
S
bằng
A.
0
. B.
3
. C.
2
. D.
1−
.
Câu 3: Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số
( )
3
22y x m x m= − + +
cắt
trục hoành tại 3 điểm phân biệt
A.
1
2
m
. B.
1
2
m
. C.
1
2
m −
. D.
1
; 4
2
mm −
.
Câu 4: Cho hàm số
( ) ( )
32
, , ,f x ax bx cx d a b c d= + + +
có đồ thị như hình vẽ sau.
Có tất cả bao nhiêu giá trị nguyên thuộc đoạn
2020;2020−
của tham số
m
để phương trình
( )
20f x m−=
có đúng
2
nghiệm thực phân biệt?
A.
2020
. B.
2022
. C.
2021
. D.
2019
.
Câu 5: Biết đường thẳng
( )
3 1 6 3y m x m= − + +
cắt đồ thị hàm số
32
31y x x= − +
tại ba điểm phân biệt
sao cho một giao điểm cách đều hai giao điểm còn lại. Khi đó
thuộc khoảng nào dưới đây?
A.
3
1;
2



. B.
( )
0;1
. C.
3
;2
2



. D.
( )
1;0−
.
Câu 6: Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
32
2 1 3 1 1y x m x m x m
cắt trục hoành tại 2 điểm phân biệt?
A.
4
. B.
2
. C.
3
. D.
1
.
Câu 7: Cho đồ thị
( ) ( )
32
: 2 1
m
C y x x m x m= − + − +
. Tìm tất cả các giá trị của tham số m để
( )
m
C
cắt
trục hoành tại ba điểm phân biệt có hoành độ
1 2 3
,,x x x
thỏa
222
1 2 3
4xxx+ + =
A.
0m
. B.
( )
0;2m
. C.
1m =
. D.
1
4
−m
và
0m
.
Tìm m liên quan đến tương giao hàm bậc 3
DẠNG 3
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 2
Câu 8: Gọi
S
là tập tất cả các giá trị thực của tham số
m
để đường thẳng
ym=
cắt đồ thị hàm số
32
3y x x=−
tại 3 điểm phân biệt
,,A B C
(
B
nằm giữa
,AC
) sao cho
2AB BC=
. Tính tổng
các phần tử thuộc
S
.
A.
4−
. B.
77
7
−
. C.
2−
. D.
0
.
Câu 9: Có bao nhiêu giá trị nguyên âm của
a
để đồ thị hàm số
( )
32
10 1y x a x x= + + − +
cắt trục
hoành tại đúng một điểm?
A.
10
. B.
8
. C.
. D.
9
.
Câu 10: Có bao nhiêu giá trị nguyên thuộc
2020;2021−
của hàm số
m
để đường thẳng
1y mx m= − −
cắt đồ thị của hàm số
32
3y x x x= − +
tại ba điểm phân biệt
,,A B C
sao cho
AB BC=
.
A.
2021
. B.
2023
. C.
2024
. D.
2022
.
Câu 11: Cho bao nhiêu giá trị
m
để đồ thị hàm số
32
2y x mx m= − + −
cắt trục
Ox
tại
3
điểm phân biệt
có hoành độ lập thành cấp số cộng.
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 12: Cho hàm số bậc ba
( )
y f x=
liên tục trên và có đồ thị như hình vẽ bên.
Tổng tất cả các giá trị nguyên của tham số
m
để phương trình
( )
( )
2 cosf f x m=
có nghiệm
;
2
x


A.
1−
. B.
0
. C.
1
. D.
2−
.
Câu 13: Gọi S là tập hợp các số nguyên m để phương trình
32
(2 1) 2(3 2) 8 0x m x m x− + + − − =
có ba
nghiệm lập thành một cấp số nhân. Tổng các phần tử của S bằng
A.
0
. B.
2−
. C.
3
. D.
1−
.
Câu 14: Cho hàm số
3
1
( ) 8 ,
2
f x x mx m x= − + −
với
là một hằng số khác
0
. Biết rằng phương
trình
( ) 0fx=
có đúng 2 nghiệm phân biệt thì có bao nhiêu giá trị nguyên dương
k
thỏa mãn
phương trình
()f x k=
có 3 nghiệm phân biệt?
A.
3
. B.
6
. C.
34
. D.
31
.
Câu 15: Cho hàm số
32
( 2) (2 13) 2y x m x m x m= − + − + − −
có đồ thị
( ),
m
C
đường thẳng
:8d y mx m= + +
và điểm
( )
1;4 .I
Tính tổng tất cả các giá trị của tham số
,m
biết rằng đường
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
3 | Facebook tác giả: Phan Nhật Linh
thẳng
d
cắt đồ thị
()
m
C
tại ba điểm phân biệt
,,A B C
với
A
có hoành độ bằng
2−
và tam giác
IBC
cân tại
.I
A.
12−
. B.
6−
. C.
4−
. D.
10−
.
Câu 16: Gọi
d
là đường thẳng đi qua
( )
2;0A
có hệ số góc
( )
0mm
cắt đồ thị
( )
32
: 6 9 2C y x x x= − + − +
tại ba điểm phân biệt
, , .A B C
Gọi
,BC

lần lượt là hình chiếu
vuông góc của
,BC
lên trục tung. Biết rằng hình thang
BB C C

có diện tích bằng
8,
giá trị của
m
thuộc khoảng nào sau đây?
A.
( )
5;8
. B.
( )
5;0−
. C.
( )
0;2
. D.
( )
1;5
.
Câu 17: Cho hàm số bậc ba
( )
y f x=
có đồ thị như hình vẽ
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
( ) ( )
( )
( )
3 2 2 2
2 3 9 3 9 0f x mf x m m f x m m− + − − + + =
có đúng
8
nghiệm phân biệt?
A.
3
. B.
4
. C.
5
. D.
6
.
Câu 18: Gọi
S
là tập hợp chứa tất cả các giá trị thực của tham số
m
để đồ thị hàm số
( ) ( ) ( )
32
6 1 3 2 1 2f x x m x m x= − + + + +
cắt trục
Ox
tại ba điểm phân biệt có hoành độ lớn hơn
1−
. Biết rằng
;
a
S
b
−

= +


; trong đó
,ab
là các số nguyên dương và phân số
a
b
là tối giản.
Giá trị biểu thức
T a b=+
tương ứng bằng
A.
4
. B.
8
. C.
5
. D.
7
.
Câu 19: Điều kiện cần và đủ của tham số thực
m
để đường thẳng
32y x m= + −
cắt đồ thị hàm số
( )
3
1yx=−
tại ba điểm phân biệt là
A.
31m−
. B.
31m−
. C.
13m−
. D.
13m−
.
Câu 20: Cho hàm số
32
3y x x m= + +
có đồ thị
( )
C
. Biết đồ thị
( )
C
cắt trục hoành tại 3 điểm phân biệt
,,A B C
sao cho
B
là trung điểm
AC
. Phát biểu nào sau đây đúng?
A.
( )
4;0m−
. B.
( )
0;m +
. C.
( )
;4m − −
. D.
( )
4; 2m − −
.
Câu 21: Cho hàm số
32
21y x x= − −
có đồ thị
( )
C
, đường thẳng
( )
d
:
1y mx=−
và điểm
(4;11)K
. Biết
rằng
( )
C
và
( )
d
cắt nhau tại ba điểm phân biệt
,,A B C
trong đó
(0; 1)A −
còn trọng tâm tam
giác
KBC
nằm trên đường thẳng
21yx=+
. Mệnh đề nào sau đây đúng?
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 4
A.
4m =
. B.
2m =
. C.
3m =
. D. Không tồn tại
m
Câu 22: Cho hàm số
( )
32
21y x x m x m= − + − +
có đồ thị
( )
C
. Tìm tất cả các giá trị thực của tham số
m
để
( )
C
cắt trục hoành tại 3 điểm phân biệt
1
x
,
2
x
,
3
x
sao cho
222
1 2 3
4xxx+ +
.
A.
1
1
4
0
m
m
−
. B.
1m
. C.
1
1
4
m−
. D.
1
1
4
m
.
Câu 23: Cho hàm số
( )
32
21y x x m x m= − + − +
có đồ thị
( )
C
. Tìm tất cả các giá trị thực của tham số
m
để
( )
C
cắt trục hoành tại
3
điểm phân biệt
1 2 3
,,x x x
sao cho
222
1 2 3
4xxx+ +
.
A.
1
1
4
0
m
m
−
. B.
1m
. C.
1
1
4
m−
. D.
1
1
4
m
.
Câu 24: Cho hàm số
( ) ( )
32
2 2 13 2y x m x m x m= − + − + − −
có đồ thị là
( )
m
C
, đường thẳng
:8d y mx m= + +
và điểm
( )
1;4I
. Tính tổng tất cả các giá trị của tham số
m
, biết rằng đường
thẳng
d
cắt đồ thị
( )
m
C
tại ba điểm phân biệt
,,A B C
với
A
có hoành độ bằng
2−
và tam giác
IBC
cân tại
I
.
A.
12−
. B.
6−
. C.
4−
. D.
10−
.
Câu 25: Cho hàm số
32
( ) 3 1f x x x= − +
. Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
( )
2021. ( )f f x m=
có 7 nghiệm phân biệt?
A. 8078. B. 0. C. 4041. D. 8076.
Câu 26: Cho hàm số
( )
( )
( )
3 3 2
1 3 4 2f x m x x m x= − + + − +
với
m
là tham số. Có bao nhiêu số tự nhiên
m
sao cho phương trình
( )
0fx=
có nghiệm trên đoạn
1
; 5
5



.
A.
4
. B.
7
. C.
6
. D.
5
.
Câu 27: Cho hàm số
( )
32
2 3 1y f x x x= = − +
. Tập hợp các giá trị
m
để phương trình
( )
2sin 1
2
x
f f f m
+

=




có nghiệm là đoạn
;ab
. Khi đó giá trị
2
48ab+
thuộc khoảng nào
sau đây?
A.
23
7;
2



. B.
( )
2;5−
. C.
43 39
;
32



. D.
37 65
;
34



.
Câu 28: Tìm tất cả các giá trị của tham số
m
để phương trình
3 2 1 2
2 3 2 2 0
m
xx
−
− + − =
có
3
nghiệm thực
phân biệt.
A.
1
1
2
m
. B.
10m−
. C.
1
0
2
m
. D.
1
1
2
m−
.
Câu 29: Cho hàm số có đồ thị là , với là tham
số. Tập S là tập hợp các giá trị nguyên của để cắt trục hoành tại
( ) ( )
32
2 1 5 1 2 2y x m x m x m= − + + + − −
()
m
C
m
m
( ( 2021;2021))m−
()
m
C
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
5 | Facebook tác giả: Phan Nhật Linh
ba điểm phân biệt sao cho trong hai điểm có một điểm nằm trong và một
điểm nằm ngoài đường tròn có phương trình . Tính số các phần tử của
S
?
A. B. C. D.
Câu 30: Cho hàm số
( ) ( )
32
21f x x mx m x= − + − +
với
m
là tham số. Có tất cả bao nhiêu giá trị nguyên
của
m
để phương trình sau có
3
nghiệm thực phân biệt
( )
( )
( )
( )
( ) ( )
..
f x f x
f x e f x f x f x

+ = +
A.
1
. B. vô số. C.
2
. D.
0
.
( )
2;0 , ,A B C
,BC
22
1+=xy
4041.
2020.
2021.
4038.
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 6
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
32
21y x x= − −
có đồ thị
(C)
, đường thẳng
( )
:1d y mx=−
và điểm
( )
4;11K
.Biết
rằng
(C)
và
( )
d
cắt nhau tại ba điểm phân biệt
,,A B C
trong đó
( )
0; 1A −
còn trọng tâm tam
giác
KBC
nằm trên đường thẳng
21yx=+
. Mệnh đề nào sau đây đúng?
A.
4m =
. B.
2m =
. C.
3m =
. D. Không có
m
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm của
(C)
và
( )
d
là:
( )
3 2 3 2 2
2
0
2 1 1 2 0 2 0
2 0(1)
x
x x mx x x mx x x x m
x x m
=
− − = − − − = − − =
− − =
Để
(C)
và
( )
d
cắt nhau tại ba điểm phân biệt thì (1) có hai nghiệm phân biệt khác 0. Ta có:
'
2
0 1 0 1
00
0 0 0
mm
mm
m
+ −



− −

Gọi
12
,xx
là nghiệm của (1), ta có
( ) ( )
1 1 2 2
B ; 1 ; ; 1x mx C x mx−−
. Trọng tâm G của tam giác
KBC
, ta có
12
12
4
2
3
11 2
29
33
G
G
xx
x
mx mx
m
y
++
==
+ + −
+
==
Theo giả thiết G thuộc đường thẳng
( )
: 2 1d y x=+
nên ta có:
( )
29
2.2 1 3
3
m
m tm
+
= + =
Câu 2: Gọi
S
là tập tất cả các giá trị của tham số
để đường thẳng
3y x m=+
tiếp xúc với đồ thị hàm
số
3
1yx=+
. Tổng các phần tử của
S
bằng
A.
0
. B.
3
. C.
2
. D.
1−
.
Lời giải
Chọn C
2
'3yx=
.
Giả sử đường thẳng
3y x m=+
tiếp xúc với đồ thị hàm số
3
1yx=+
tại điểm
0
x
thì
( )
00
3 1.y x x
= =
Đk đủ:
00
12xy= =
thì PTTT là
3 2 1y x m= − = −
.
00
10xy= − =
thì PTTT là
3 3 3y x m= + =
.
Tổng các phần tử của
S
bằng
2
.
Cách 2: Điều kiện tiếp xúc
3
3
2
13
13
1; 3.
1
33
x x m
x x m
mm
x
x
+ = +
+ − =

= − =

=
=
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
7 | Facebook tác giả: Phan Nhật Linh
Câu 3: Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số
( )
3
22y x m x m= − + +
cắt
trục hoành tại 3 điểm phân biệt
A.
1
2
m
. B.
1
2
m
. C.
1
2
m −
. D.
1
; 4
2
mm −
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm của đồ thị với trục Ox:
( )
3
2 2 0− + + =x m x m
3
2 2 0 − − + =x x mx m
( ) ( )
2
1 2 2 0 1

− + − =

x x x m
( )
2
1
2 2 0 2
=
+ − =
x
x x m
Để đồ thị hàm số cắt Ox tại 3 điểm phân biệt
( )
1
có 3 nghiệm phân biệt
( )
2
có 2 nghiệm phân biệt khác
1
.
( )
' 1 2 0
1 2 2 0
= +
= + −
m
gm
1
2
4
−
m
m
Câu 4: Cho hàm số
( ) ( )
32
, , ,f x ax bx cx d a b c d= + + +
có đồ thị như hình vẽ sau.
Có tất cả bao nhiêu giá trị nguyên thuộc đoạn
2020;2020−
của tham số
m
để phương trình
( )
20f x m−=
có đúng
2
nghiệm thực phân biệt?
A.
2020
. B.
2022
. C.
2021
. D.
2019
.
Lời giải
Chọn D
( )
20f x m−=
( )
( )
1
2
=
m
fx
Dựa vào đồ thị hàm
( )
=y f x
ta có: để phương trình
( )
1
có đúng 2 nghiệm thực phân biệt
3
6
2
2
1
2
=
=

−
−
m
m
mm
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 8
Vì
2020;2020−m
2020; 2019;...... 3;6 − − −m
. Vậy có 2019 số.
Câu 5: Biết đường thẳng
( )
3 1 6 3y m x m= − + +
cắt đồ thị hàm số
32
31y x x= − +
tại ba điểm phân biệt
sao cho một giao điểm cách đều hai giao điểm còn lại. Khi đó
thuộc khoảng nào dưới đây?
A.
3
1;
2



. B.
( )
0;1
. C.
3
;2
2



. D.
( )
1;0−
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm là
( )
32
3 1 6 3 3 1m x m x x− + + = − +
( ) ( )
32
3 3 1 6 2 0 1x x m x m − − − − − =
.
Xét hàm số
( ) ( ) ( )
32
3 3 1 6 2
m
g x x x m x m C= − − − − −
.
( ) ( )
2
3 6 3 1 6 6g x x x m g x x
= − − + = −
;
( )
01g x x

= =
.
Đồ thị
( )
m
C
có điểm uốn là
( )
1; 9 3Im−−
.
Để đường thẳng
( )
3 1 6 3y m x m= − + +
cắt đồ thị hàm số
32
31y x x= − +
tại ba điểm phân biệt
sao cho một giao điểm cách đều hai giao điểm còn lại
( ) ( )
( )
2
2
3 3. 3 1 0
1
3
1;0
1
3
3
m
m
m
I Ox
m
−
= − − − +

= − −

=−
.
Câu 6: Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
32
2 1 3 1 1y x m x m x m
cắt trục hoành tại 2 điểm phân biệt?
A.
4
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn D
Xét phương trình
3 2 2
2
2 1 3 1 1 0 1 2 1 0
1
2 1 0 *
x m x m x m x x mx m
x
x mx m
Theo yêu cầu bài toán phương trình
*
xảy ra 2 trường hợp
TH1: phương trình có nghiệm kép khác 1, tức là
2
10
1 2 1 0
mm
mm
loại, do nghiệm không
nguyên.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
9 | Facebook tác giả: Phan Nhật Linh
TH2: phương trình có 2 nghiệm phân biệt trong đó 1 là một nghiệm, tức là
2
10
2
1 2 1 0
mm
m
mm
.
Nhận xét: cụm từ “cắt trục hoành tại 2 điểm phân biệt” được người ra đề hiểu là “có đúng 2 điểm
chung với trục hoành”. Theo ý kiến chủ quan của người giải, ta nên phát biểu rõ ràng hơn.
Câu 7: Cho đồ thị
( ) ( )
32
: 2 1
m
C y x x m x m= − + − +
. Tìm tất cả các giá trị của tham số m để
( )
m
C
cắt
trục hoành tại ba điểm phân biệt có hoành độ
1 2 3
,,x x x
thỏa
222
1 2 3
4xxx+ + =
A.
0m
. B.
( )
0;2m
. C.
1m =
. D.
1
4
−m
và
0m
.
Lời giải
Chọn C
Để hàm số đã cho cắt trục hoành tại 3 điếm phàn biệt thì phưong trình hoành độ giao điểm
phải có 3 nghiệm phàn biệt:
32
2 (1 ) 0− + − + =x x m x m
( )
2
( 1) 0− − − =x x x m
Ta đặt
1
1=x
. Khi đó, đế phưong trình có 3 nghiệm phân biệt thì phương trình sau phải có 2
nghiệm phân biệt khác 1.
2
0− − =x x m
Do có nghiệm khác 1 nên
1 1 0− − m
hay
0.m
Ta có
14 = + m
Để có 2 nghiệm phàn biệt thì
0
hay
1
4
−m
.
Theo điều kiện của đề bài ta có
222
1 2 3
4+ + =xxx
( )
2
2 3 2 3
1 2 4 + + − =x x x x
( )
2
2 3 2 3
23 + − =x x x x
vói
23
,xx
là nghiệm của phương trình bậc 2 trên.
Áp dụng Viet ta có
2
1 2( ) 3− − =m
1=m
Kết hợp các điều kiện ta có
1=m
.
Câu 8: Gọi
S
là tập tất cả các giá trị thực của tham số
m
để đường thẳng
ym=
cắt đồ thị hàm số
32
3y x x=−
tại 3 điểm phân biệt
,,A B C
(
B
nằm giữa
,AC
) sao cho
2AB BC=
. Tính tổng
các phần tử thuộc
S
.
A.
4−
. B.
77
7
−
. C.
2−
. D.
0
.
Lời giải
Chọn A
Ta có BBT của hàm số
32
3y x x=−
như sau:
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 10
Suy ra đường thẳng
ym=
cắt đồ thị hàm số
32
3y x x=−
tại 3 điểm phân biệt
,,A B C
40m −
.
Khi đó
3, 0,
A B C A B B C C A A B C
x x x x x x x x x x x x m+ + = + + = =
.
Để
B
nằm giữa
,AC
và
2AB BC=
thì
( )
( )
2
2
A B C
B A C B
C B A
A B B C
xxx
x x x x
x x x
x x x x
− = −

− = −
3 2 4 3 6 5
B A C B C A B
x x x x x x x = + − = = −
.
Suy ra
( ) ( ) ( ) ( )
( ) ( )
6 5 . . 4 3 4 3 . 6 5 0 (*)
4 3 . . 6 5 (**)
B B B B B B
B B B
x x x x x x
x x x m
− + − + − − =
− − =
.
Từ (*) được
77
7
B
x
=
. Thay vào (**) được
98 20 7
49
m
+
=−
và
98 20 7
49
m
−+
=
.
Vậy
98 20 7 98 20 7
;
49 49
S

+ − +

=−



.
Câu 9: Có bao nhiêu giá trị nguyên âm của
a
để đồ thị hàm số
( )
32
10 1y x a x x= + + − +
cắt trục
hoành tại đúng một điểm?
A.
10
. B.
8
. C.
. D.
9
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm của đồ thị và trục hoành là:
( ) ( )
32
10 1 0 1x a x x+ + − + =
3 2 2
10 1x x x ax + − + = −
.
Ta thấy
0x =
không là nghiệm của phương trình nên
( )
1
32
2
10 1x x x
a
x
+ − +
− =
.
Xét hàm số
( )
32
2
10 1x x x
fx
x
+ − +
=−
với
\0x
Ta có
( )
( )
( )
2
3
33
1 . 2
2
x x x
xx
fx
xx
− + +
+−
= − = −
( )
01f x x
= =
.
Bảng biến thiên của hàm số
( )
fx
như sau:
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
11 | Facebook tác giả: Phan Nhật Linh
Từ bảng biến thiên ta thấy đồ thị hàm số đã cho cắt trục hoành tại đúng một điểm khi
( )
1
có
đúng 1 nghiệm
11a −
.
Do
a
nguyên âm nên
10, 9, 8,..., 1a − − − −
. Vậy có 10 giá trị của
a
thỏa mãn yêu cầu bài
toán
Câu 10: Có bao nhiêu giá trị nguyên thuộc
2020;2021−
của hàm số
m
để đường thẳng
1y mx m= − −
cắt đồ thị của hàm số
32
3y x x x= − +
tại ba điểm phân biệt
,,A B C
sao cho
AB BC=
.
A.
2021
. B.
2023
. C.
2024
. D.
2022
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm
( )
3 2 3 2
3 1 3 1 1 0x x x mx m x x m x m− + = − − − + − + + =
.
( )
( )
( )
2
2
1
1 2 1 0
2 1 0 1
x
x x x m
x x m
=
− − − − =
− − − =
Để để đường thẳng
1y mx m= − −
cắt đồ thị hàm số
32
3y x x x= − +
tại ba điểm phân biệt
A
,
B
,
C
thì phương trình
( )
1
có hai nghiệm phân biệt khác
1
20
2
20
m
m
m
+
−
− −
.
Khi đó phương trình
( )
1
có hai nghiệm
12
,xx
thỏa mãn
12
2xx+=
với mọi tham số
m
.
Trường hợp 1:
1
B
x =
.
Khi đó yêu cầu bài toán trở thành
( )
12
12
12
12
2
2
2
2 2 2
22
A C B
A C B
xx
x x x
xx
m x x m
y y y y y
+=
+=
+=

+ − + =
+ = + =
.
Điều này thỏa mãn với mọi
2m −
.
Trường hợp 2:
1
B
x
và giả sử
12
xx
.
Khi đó yêu cầu bài toán trở thành
( )( )
12
12
12
12
12
2
12
2 2 1 *
2 1 2
A C B
A C B
xx
x x x
xx
mx m mx m
y y y y y
+=
+=
+=

− + = − +
+ = + =
.
Ta có hệ
1 2 2
1 2 1
1 2 1
21
x x x
x x x
+ = =


+ = =

không thỏa mãn yêu cầu bài toán.
Vậy giá trị
m
cần tìm là
2m −
.
Vì
, 2020;2021 1;2021m m m − −
có
2023
giá trị của
m
.
Câu 11: Cho bao nhiêu giá trị
m
để đồ thị hàm số
32
2y x mx m= − + −
cắt trục
Ox
tại
3
điểm phân biệt
có hoành độ lập thành cấp số cộng.
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn B
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 12
Xét phương trình hoành độ giao điểm:
32
20x mx m− + − =
(*).
Giả sử phương trình (*) có
3
nghiệm phân biệt
1
x
,
2
x
,
3
x
theo thứ tự lập thành một cấp số
cộng, theo tính chất của cấp số cộng ta có:
1 3 2
2x x x+=
.
Áp dụng định lí Vi-et ta có:
1 2 3 2 2
3
3
m
x x x m x m x+ + = = =
.
Vì
2
3
m
x =
là một nghiệm của phương trình (*) nên ta có:
32
. 2 0
33
mm
mm
− + − =
3
0
2 54 0 3 3
33
m
m m m
m
=
− = =
=−
.
Thử lại:
+ Với
0m =
, phương trình trở thành:
3
00xx− = =
( loại).
+ Với
33m =
, phương trình trở thành:
1
32
2
3
33
3 3 6 3 0 3
33
x
x x x
x
= − +
− + − = =
=+
và
3
nghiệm
này lập thành 1 CSC.
+ Với
33m =−
, phương trình trở thành:
1
32
2
3
33
3 3 6 3 0 3
33
x
x x x
x
= − −
− − + = = −
=−
và
3
nghiệm
này lập thành 1 CSC.
Vậy có
2
giá trị của
m
thỏa yêu cầu bài toán là
33m =
và
33m =−
.
Câu 12: Cho hàm số bậc ba
( )
y f x=
liên tục trên và có đồ thị như hình vẽ bên.
Tổng tất cả các giá trị nguyên của tham số
m
để phương trình
( )
( )
2 cosf f x m=
có nghiệm
;
2
x


A.
1−
. B.
0
. C.
1
. D.
2−
.
Lời giải
Chọn D
Đặt
cos ,tx=
do
;
2
x


nên suy ra
(
1;0t −
.
Trên khoảng
( )
1;0−
hàm số nghịch biến nên suy ra
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
13 | Facebook tác giả: Phan Nhật Linh
Với
(
1;0t −
thì
( ) ( ) ( )
01f f t f −
hay
( )
02ft
.
Đặt
( )
2 cosu f x=
thì
( )
)
2 , 0;2u f t u=
. Khi đó bài toán trở thành:
Tìm
m
để phương trình
( )
f u m=
có nghiệm
)
0;2u
.
Quan sát đồ thị ta thấy rằng với
)
0;2u
thì
( )
)
2;2 2 2f u m − −
.
Vì
2; 1;0;1 2m m m − − = −
.
Câu 13: Gọi S là tập hợp các số nguyên m để phương trình
32
(2 1) 2(3 2) 8 0x m x m x− + + − − =
có ba
nghiệm lập thành một cấp số nhân. Tổng các phần tử của S bằng
A.
0
. B.
2−
. C.
3
. D.
1−
.
Lời giải
Chọn C
Giả sử
1 2 3
,,x x x
là ba nghiệm của phương trình
32
(2 1) 2(3 2) 8 0x m x m x− + + − − =
.
Khi đó ta có
( )( )( )
32
1 2 3
(2 1) 2(3 2) 8x m x m x x x x x x x− + + − − = − − −
Ta có
( )
1 2 3
1 2 3
1 2 2 3 3 1
21
8
2 3 2
x x x m
x x x
x x x x x x m
+ + = +
=
+ + = +
Do
1 2 3
,,x x x
lập thành một cấp số nhân nên ta có
1 2 3 2
82x x x x= =
.
Thay
2
2x =
vào phuognw trình
32
(2 1) 2(3 2) 8 0x m x m x− + + − − =
ta có
( ) ( )
8 2 1 .4 4 3 2 8 0 4 12 3m m m m− + + − − = = =
.
Thử lại với
3m =
ta thấy thỏa mãn. Vậy
3m =
. Dó đó tổng tất cả các giá trị của
bằng
3
Câu 14: Cho hàm số
3
1
( ) 8 ,
2
f x x mx m x= − + −
với
là một hằng số khác
0
. Biết rằng phương
trình
( ) 0fx=
có đúng 2 nghiệm phân biệt thì có bao nhiêu giá trị nguyên dương
k
thỏa mãn
phương trình
()f x k=
có 3 nghiệm phân biệt?
A.
3
. B.
6
. C.
34
. D.
31
.
Lời giải
Chọn D
( )
2
( ) 0 2 2 4 0
2
m
pt f x x x x

= − + + − =


có đúng 2 nghiệm phân biệt
( )
2
()
2
2 4 0 1
2
gx
x
m
xx
=
+ + − =
có đúng 2 nghiệm phân biệt
+
(2) 0 24gm= =
( nhận )
32
( ) 12 16 '( ) 3 12f x x x f x x= − + → = −
'( ) 0 2f x x= =
BBT
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 14
Phương trình
()f x k=
có 3 nghiệm phân biệt khi
0 32k
và
*
1;2;3;....;31kk → =
+
( )
1Pt
có nghiệm kép và khác
2
0
6
(2) 0
m
g
=
=
( nhận )
32
( ) 3 2 '( ) 3 3f x x x f x x= − − → = −
'( ) 0 1f x x= =
BBT
Phương trình
()f x k=
có 3 nghiệm phân biệt khi
40k−
và
*
kk →
Vậy có
31
giá trị
k
thỏa điều kiện bài toán.
Câu 15: Cho hàm số
32
( 2) (2 13) 2y x m x m x m= − + − + − −
có đồ thị
( ),
m
C
đường thẳng
:8d y mx m= + +
và điểm
( )
1;4 .I
Tính tổng tất cả các giá trị của tham số
,m
biết rằng đường
thẳng
d
cắt đồ thị
()
m
C
tại ba điểm phân biệt
,,A B C
với
A
có hoành độ bằng
2−
và tam giác
IBC
cân tại
.I
A.
12−
. B.
6−
. C.
4−
. D.
10−
.
Lời giải
Chọn B
+ Phương trình hoành độ giao điểm của
d
và
()
m
C
là:
3
2
( 2) (3 13) 2 10 0 1
5
x
x m x m x m x
xm
=−
− + − + − − = = −
=+
+ Để đường thẳng
d
cắt đồ thị
()
m
C
tại ba điểm phân biệt
,,A B C
thì
7
6
m
m
−
−
+ Giả sử
2
( 1;8), ( 5; 6 8)B C m m m− + + +
. Để tam giác
IBC
cân tại
I
thì
2 2 2 2 2
2
20 ( 4) ( 6 4) 6( )
23
m
IB IC m m m m l
m
=−
= = + + + + = −
= −
Vậy có ba giá trị của m thỏa mãn nên tổng các giá trị của m bằng
6−
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
15 | Facebook tác giả: Phan Nhật Linh
Câu 16: Gọi
d
là đường thẳng đi qua
( )
2;0A
có hệ số góc
( )
0mm
cắt đồ thị
( )
32
: 6 9 2C y x x x= − + − +
tại ba điểm phân biệt
, , .A B C
Gọi
,BC

lần lượt là hình chiếu
vuông góc của
,BC
lên trục tung. Biết rằng hình thang
BB C C

có diện tích bằng
8,
giá trị của
m
thuộc khoảng nào sau đây?
A.
( )
5;8
. B.
( )
5;0−
. C.
( )
0;2
. D.
( )
1;5
.
Lời giải
Chọn D
Phương trình đường thẳng
( )
: 2 .d y m x=−
Phương trình hoành độ giao điểm
( ) ( )
( )
( )
3 2 2
2
2 2;0
6 9 2 2 2 4 1 0 .
4 1 0
xA
x x x m x x x x m
x x m
=
− + − + = − − − + + =
− + + =
Để
( )
C
cắt
d
tại 3 điểm phân biệt thì
0 4 1 0 3.mm − −
Giả sử
( ) ( )
12
1 1 2 2
12
4
, 2 , , 2 .
1
xx
B x mx m C x mx m
x x m
+=
− −
=+
Ta có
( ) ( )
12
0, 2 , 0, 2 .B mx m C mx m

−−
( ) ( )
''
1
' 8 16.
2
BB C C
S B C BB CC B C BB CC
= + = + =
Mà
( )
1 2 1 2
, , .B C m x x BB x CC x
= − = =
Do
m
dương nên
12
10x x m= +
mà
1 2 1 2
4 0 0, 0.x x x x+ =
( )
1 2 1 2 1 2 1 2 1 2
' ' , ' , ' 16 4B C m x x BB x CC x m x x x x m x x = − = = − + = − =
( ) ( ) ( )
22
2 2 2
1 2 1 2 1 2
16 4 16 16 4 4 16m x x m x x x x m m

− = + − = − − =

( )
32
1
3 4 0
2
ml
mm
m
=−
− + =
=
Câu 17: Cho hàm số bậc ba
( )
y f x=
có đồ thị như hình vẽ
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
( ) ( )
( )
( )
3 2 2 2
2 3 9 3 9 0f x mf x m m f x m m− + − − + + =
có đúng
8
nghiệm phân biệt?
A.
3
. B.
4
. C.
5
. D.
6
.
Lời giải
Chọn B
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 16
( ) ( )
( )
( )
3 2 2 2
2 3 9 3 9 0f x mf x m m f x m m− + − − + + =
Đặt
( )
t f x=
, phương trình trở thành:
( )
3 2 2 2
2 3 9 3 9 0t mt m m t m m− + − − + + =
( ) ( )
22
3 2 3 3 0t t m t m m

+ − + + + =

( )( )( )
3 3 0t t m t m + − − − =
( ) ( )
( ) ( )
( ) ( )
31
3
2
3
33
fx
t
t m f x m
tm
f x m
=−
=−
= =
=+
=+
Nhận xét các phương trình
( )
2
và
( )
3
không có nghiệm chung.
Dựa vào đồ thị, ta thấy:
( )
1
xa
xb
=
=
YCBT
Các phương trình
( )
2
và
( )
3
đều có 3 nghiệm phân biệt khác
,ab
3 5 2
32
33
mm
m
mm
+

−

− −

Mà
m
là số nguyên nên
2; 1;0;1m − −
.
Câu 18: Gọi
S
là tập hợp chứa tất cả các giá trị thực của tham số
m
để đồ thị hàm số
( ) ( ) ( )
32
6 1 3 2 1 2f x x m x m x= − + + + +
cắt trục
Ox
tại ba điểm phân biệt có hoành độ lớn hơn
1−
.
Biết rằng
;
a
S
b
−

= +


; trong đó
,ab
là các số nguyên dương và phân số
a
b
là tối giản. Giá trị
biểu thức
T a b=+
tương ứng bằng
A.
4
. B.
8
. C.
5
. D.
7
.
Lời giải
Chọn C
Xét phương trình hoành độ giao điểm:
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
17 | Facebook tác giả: Phan Nhật Linh
( ) ( )
32
6 1 3 2 1 2 0x m x m x− + + + + =
( ) ( )
( )
2
1 6 5 2 0x x m x − − + − =
( ) ( )
2
1
6 5 2 0 *
x
x m x
=
− + − =
Yêu cầu bài toán tương đương với phương trình
( )
*
có hai nghiệm phân biệt
12
;xx
lớn hơn
1−
và khác
1
.Ta có:
( )( )
( )
2
12
12
2
0
36 60 33 0
2
6 5 2
2
1 1 0
3
6 4 0
1
1 6 5 2 0
mm
xx
m
m
xx
m
m
m

+ +
+ −
+ −
−


+ +
+


−
− + −
Do đó
2; 3 5a b T a b= = = + =
Câu 19: Điều kiện cần và đủ của tham số thực
m
để đường thẳng
32y x m= + −
cắt đồ thị hàm số
( )
3
1yx=−
tại ba điểm phân biệt là
A.
31m−
. B.
31m−
. C.
13m−
. D.
13m−
.
Lời giải
Chọn B
Xét phương trình:
( )
3
32
321 31x mx m x x= + − − +− =
(*).
Đường thẳng
32y x m= + −
cắt đồ thị
( )
3
1yx=−
tại ba điểm phân biệt khi và chỉ khi phương
trình (*) có ba nghiệm phân biệt.
Đặt
( ) ( )
3 2 2
0
3 1 ' 3 6 0
2
x
f x x x f x x x
x
=
= − + = − =
=
.
Ta có bảng biến thiên
Từ bảng biến thiên suy ra phương trình (*) có ba nghiệm phân biệt khi và chỉ khi đường thẳng
ym=
cắt đồ thị hàm số
( )
32
31f x x x= − +
tại ba điểm phân biệt. Vậy
31m−
.
Câu 20: Cho hàm số
32
3y x x m= + +
có đồ thị
( )
C
. Biết đồ thị
( )
C
cắt trục hoành tại 3 điểm phân biệt
,,A B C
sao cho
B
là trung điểm
AC
. Phát biểu nào sau đây đúng?
A.
( )
4;0m−
. B.
( )
0;m +
. C.
( )
;4m − −
. D.
( )
4; 2m − −
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm của
( )
C
và trục hoành là
( )
32
3 0 1x x m+ + =
.
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 18
Giả sử
( )
1
có 3 nghiệm phân biệt
( )
1 2 3 1 2 3
;;x x x x x x
thì
1 2 3
;;x x x
lần lượt là hoành độ của
,,A B C
và
( )( )( )
32
1 2 3
3x x m x x x x x x+ + = − − −
( ) ( )
3 2 3 2
1 2 3 1 2 2 3 3 1 1 2 3
3x x m x x x x x x x x x x x x x x x + + = − + + + + + −
Nên ta có
1 2 3
3x x x+ + = −
.
Để
B
là trung điểm
AC
thì
1 3 2
2x x x+=
nên
22
3 3 1xx= − = −
.
Tức là
( )
1
có 1 nghiệm là
1x =−
. Suy ra
1 3 0 2mm− + + = = −
.
Thử lại với
2m =−
thì
( )
1
trở thành
32
13
3 2 0 1
13
x
x x x
x
= − −
+ − = = −
= − +
(thỏa điều kiện bài toán).
Cách 2: Ta có
2
36y x x
=+
và
66yx

=+
nên
( )
C
có điểm uốn
( )
1; 2Im−+
.
Để
( )
C
cắt trục hoành tại 3 điểm phân biệt
,,A B C
sao cho
B
là trung điểm
AC
thì
I Ox
2 0 2mm + = = −
.
Câu 21: Cho hàm số
32
21y x x= − −
có đồ thị
( )
C
, đường thẳng
( )
d
:
1y mx=−
và điểm
(4;11)K
. Biết
rằng
( )
C
và
( )
d
cắt nhau tại ba điểm phân biệt
,,A B C
trong đó
(0; 1)A −
còn trọng tâm tam
giác
KBC
nằm trên đường thẳng
21yx=+
. Mệnh đề nào sau đây đúng?
A.
4m =
. B.
2m =
. C.
3m =
. D. Không tồn tại
m
Lời giải
Chọn C
Xét phương trình hoành độ:
3 2 3 2
2
0
2 1 1 2 0
2 0(1)
x
x x mx x x mx
x x m
=
− − = − − − =
− − =
Suy ra
(0; 1)A −
và hoành độ của điểm
B
và
C
là nghiệm của phương trình (1)
Để
( )
C
và
( )
d
cắt nhau tại ba điểm phân biệt
,,A B C
khi và chỉ khi phương trình (1) có hai nghiệm phân
biệt khác 0
Khi và chỉ khi:


+ −




(1)
'0
1 m 0 m 1
(*)
m 0 m 0
m0
Giả sử:
11
( ;m 1)B x x −
,
22
( ;m 1)C x x −
. Theo Vi–ét ta có
12
2xx+=
Gọi
G
là trọng tâm của tam giác
KBC
:
++
=
=

+



+

+ − + −
=


=
12
G
G
12
G
G
4 x x
x2
x
2m 9
3
G 2;
2m 9
11 mx 1 mx 1
3
y
y
3
3
Trọng tâm
G
nằm trên đường thẳng
21yx=+
suy ra
29
2.2 1 3
3
m
m
+
= + =
thỏa mãn
( )
*
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
19 | Facebook tác giả: Phan Nhật Linh
Câu 22: Cho hàm số
( )
32
21y x x m x m= − + − +
có đồ thị
( )
C
. Tìm tất cả các giá trị thực của tham số
m
để
( )
C
cắt trục hoành tại 3 điểm phân biệt
1
x
,
2
x
,
3
x
sao cho
222
1 2 3
4xxx+ +
.
A.
1
1
4
0
m
m
−
. B.
1m
. C.
1
1
4
m−
. D.
1
1
4
m
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm của
( )
C
và trục hoành là:
( ) ( )
( )
( )
3 2 2
2
1
2 1 0 1 0
0*
x
x x m x m x x x m
x x m
=
− + − + = − − − =
− − =
.
( )
C
cắt trục hoành tại 3 điểm phân biệt
( )
*
có hai nghiệm phân biệt khác 1
2
1
1 4 0
4
1 1 0
0
m
m
m
m
+
−


− −
.
Khi đó
1
1x =
,
2
x
và
3
x
là hai nghiệm của
( )
*
.
( )
2
222
1 2 3 2 3 2 3
4 2 3 1 2 3 1x x x x x x x m m+ + + − +
.
Vậy các giá trị cần tìm của
m
là
1
1
4
0
m
m
−
.
Câu 23: Cho hàm số
( )
32
21y x x m x m= − + − +
có đồ thị
( )
C
. Tìm tất cả các giá trị thực của tham số
m
để
( )
C
cắt trục hoành tại
3
điểm phân biệt
1 2 3
,,x x x
sao cho
222
1 2 3
4xxx+ +
.
A.
1
1
4
0
m
m
−
. B.
1m
. C.
1
1
4
m−
. D.
1
1
4
m
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm:
( ) ( )
( )
( )
3 2 2
2 1 0 1 0 1x x m x m x x x m− + − + = − − − =
( )
3
2
1
02
x
x x m
=
− − =
. Điều kiện để phương trình
( )
1
có 3 nghiệm phân biệt là phương trình
( )
2
có 2 nghiệm phân biệt khác
1
0
1
1
1 4 0
4
m
x
m
m


= +
−
.
Khi đó phương trình
( )
2
có 2 nghiệm phân biệt
12
,xx
.
Ta có
( )
2
2 2 2 2 2
1 2 3 1 2 1 2 1 2
4 3 2 3x x x x x x x x x+ + + + −
2
1 2 3 1mm +
.
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 20
Vậy
1
1
4
0
m
m
−
.
Câu 24: Cho hàm số
( ) ( )
32
2 2 13 2y x m x m x m= − + − + − −
có đồ thị là
( )
m
C
, đường thẳng
:8d y mx m= + +
và điểm
( )
1;4I
. Tính tổng tất cả các giá trị của tham số
m
, biết rằng đường
thẳng
d
cắt đồ thị
( )
m
C
tại ba điểm phân biệt
,,A B C
với
A
có hoành độ bằng
2−
và tam giác
IBC
cân tại
I
.
A.
12−
. B.
6−
. C.
4−
. D.
10−
.
Lời giải
Chọn C
Phương trình hoành độ giao điểm của
( )
m
C
với đường thẳng
:8d y mx m= + +
là
( ) ( )
32
2 2 13 2 8x m x m x m mx m− + − + − − = + +
( ) ( )
32
2 3 13 2 10 0x m x m x m − + − + − − =
( ) ( ) ( )
2
2 4 5 0x x m x m

+ − + − + =

( )
2
0
x
gx
=−
=
(với
( ) ( ) ( )
2
45g x x m x m= − + − +
)
Đồ thị
( )
m
C
cắt đường thẳng
d
tại
3
điểm phân biệt khi và chỉ khi
( )
0gx=
có hai nghiệm
12
,xx
phân biệt khác
2−
, nghĩa là
( )
20
0
g
g −

.
Ta có
( ) ( )
2
2
4 4 5 12 36 0, 6.
g
m m m m m = + + + = + + −
và
( )
27gm− = +
do vậy
( )
20
7 0 6
67
0
g
g
mm
mm
−
+ −


− −


(*).
Với điều kiện (*) ta có đồ thị
( )
m
C
cắt đường thẳng
d
tại
3
điểm phân biệt
( )
2;8Am−−
và hai
điểm
( ) ( )
1 1 2 2
; , ;B x y C x y
trong đó
12
,xx
là hai nghiệm của
( )
0gx=
và
12
4x x m+ = +
.
Gọi
K
là trung điểm của
BC
ta có
1 2 1 2
( ) 2 16
;
22
x x m x x m
K
+ + + +



hay
2
4 6 16
;
22
m m m
K

+ + +


.
Tam giác
IBC
cân tại
I
nên ta có
IK BC⊥
hay
IK
cùng phương với pháp tuyến của đường
thẳng
d
.
Ta có
2
2 6 8
;
22
m m m
IK
+ + +
=


và
( )
;1nm=−
là một pháp tuyến của đường thẳng
d
, do đó
ta cần có
2
32
2
2 6 8
6 9 2 0
1
23
m
m m m
m m m
m
m
=−
+ + +
= + + + =
−
= −
.
Kiểm tra lại thấy
2m =−
không thỏa do khi đó
Id
.
Vậy có 2 giá trị của tham số
m
để thỏa mãn bài toán và tổng tất cả các giá trị đó bằng
4−
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
21 | Facebook tác giả: Phan Nhật Linh
Câu 25: Cho hàm số
32
( ) 3 1f x x x= − +
. Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
( )
2021. ( )f f x m=
có 7 nghiệm phân biệt?
A. 8078. B. 0. C. 4041. D. 8076.
Lời giải
Chọn C
Ta có:
( ) ( )
2021. ( ) ( )
2021
m
f f x m f f x= =
.
Khảo sát hàm số
( )
()y f f x=
trên .
Đạo hàm:
( ) ( )
( )
( )
( )
( )
( )
(
)
( )
( )
1
2
2
2
0
2
. 3 6 3 6 0
0
2
xx
xx
y f x f f x x x f x f x
fx
fx
==
==
= = − − =
=
=
.
Chú ý rằng:
3
4
5
2,879
( ) 0 0,653
0,532
xx
f x x x
xx
=
= =
= −
và
6
( ) 2 3,104f x x x= =
.
Do 6 nghiệm trên đều là nghiệm đơn nên hàm số
( )
()y f f x=
có 6 cực trị là
i
x
,
1,2,...,6i =
.
Bảng biến thiên:
Phương trình
( )
( )
2021.f f x m=
có 7 nghiệm phân biệt
1 1 2021 2021
2021
m
m − −
Do
m
nguyên nên
2020, 2019,...,2019,2020m − −
, do đó có 4041 số thỏa yêu cầu bài toán.
Câu 26: Cho hàm số
( )
( )
( )
3 3 2
1 3 4 2f x m x x m x= − + + − +
với
m
là tham số. Có bao nhiêu số tự nhiên
m
sao cho phương trình
( )
0fx=
có nghiệm trên đoạn
1
; 5
5



.
A.
4
. B.
7
. C.
6
. D.
5
.
Lời giải
Chọn D
Ta có:
( ) ( ) ( )
33
0 1 1 (*)f x x x mx mx= + + + = +
.
Xét
( )
3
f t t t=+
với
t
.
( )
2
3 1 0 f t t t
= +
.
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 22
Suy ra hàm số
( )
ft
đồng biến trên .
Khi đó
( ) ( )
* 1 1 1x mx m x + = − =
.
Để phương trình có nghiệm trên đoạn
1
; 5
5



thì
1 0 1
1 1 6
56
5 1 5
mm
m
m
−




−

.
Vì
m
là số tự nhiên nên
2;3;4;5;6m
. Vậy có 5 giá trị
m
thỏa để.
Câu 27: Cho hàm số
( )
32
2 3 1y f x x x= = − +
. Tập hợp các giá trị
m
để phương trình
( )
2sin 1
2
x
f f f m
+

=




có nghiệm là đoạn
;ab
. Khi đó giá trị
2
48ab+
thuộc khoảng nào
sau đây?
A.
23
7;
2



. B.
( )
2;5−
. C.
43 39
;
32



. D.
37 65
;
34



.
Lời giải
Chọn D
Ta có:
2
66y x x
=−
.
0y
=
0
1
x
x
=
=
.
Bảng biến thiên:
Ta có:
2sin 1 1 1 3
sin ;
2 2 2 2
x
x
+

= + −


suy ra
2sin 1
0;1
2
x
f
+



nên
2sin 1
0;1
2
x
ff
+





.
Phương trình
( )
2sin 1
2
x
f f f m
+

=




có nghiệm
( )
01fm
32
32
2 3 1 0
2 3 0
mm
mm
− +
−
13
22
m −
.
Vậy
2
13
4 8 4. 8. 13
42
ab+ = + =
.
Câu 28: Tìm tất cả các giá trị của tham số
m
để phương trình
3 2 1 2
2 3 2 2 0
m
xx
−
− + − =
có
3
nghiệm thực
phân biệt.
A.
1
1
2
m
. B.
10m−
. C.
1
0
2
m
. D.
1
1
2
m−
.
Lời giải
Chọn C
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
23 | Facebook tác giả: Phan Nhật Linh
( )
3 2 1 2 3 2 1 2
2 3 2 2 0 2 3 2 2 1
mm
x x x x
−−
− + − = − + =
Xét hàm số
( )
32
2 3 2f x x x= − +
( )
2
66f x x x
=−
( )
2
0
0 6 6 0
1
x
f x x x
x
=
= − =
=
Bảng biến thiên
Phương trình
( )
1
có
3
nghiệm thực phân biệt
12
1
1 2 2 0 1 2 1 0
2
m
mm
−
−
Câu 29: Cho hàm số có đồ thị là , với là tham
số. Tập S là tập hợp các giá trị nguyên của để cắt trục hoành tại
ba điểm phân biệt sao cho trong hai điểm có một điểm nằm trong và một
điểm nằm ngoài đường tròn có phương trình . Tính số các phần tử của
S
?
A. B. C. D.
Lời giải
Chọn D
Xét phương trình
32
2( 1) (5 1) 2 2 0(1)− + + + − − =x m x m x m
2
(1) ( 2)( 2 1) 0x x mx m − − + + =
2
2
( ) 2 1 0 (2)
=
= − + + =
x
g x x mx m
m
C
) cắt trục Ox tại ba điểm phân biệt
(2)
có 2 nghiệm phân biệt
12
;xx
khác 2
2
'0
10
(2) 0
4 4 1 0
mm
g
mm

− −


− + +
1 5 1 5
;;
22
(*)
5
3
m
m
−+
− +
Khi đó:
12
(2;0), ( ;0), ( ;0)A B x C x
;
Hai điểm
,BC
thỏa mãn điều kiện đầu bài
( 1)( 1) 0OB OC − −
1 2 1 2 1 2
22
1 2 1 2 1 2
( 1)( 1) 0 1
( ) 1 ( ) 2
x x x x x x
x x x x x x
− − + +
+ + −
f(x)
+
2
∞
∞
+
+
1
f'(x)
x
0
0
0
1
∞
∞
+
( ) ( )
32
2 1 5 1 2 2y x m x m x m= − + + + − −
()
m
C
m
m
( ( 2021;2021))m−
()
m
C
( )
2;0 , ,A B C
,BC
22
1+=xy
4041.
2020.
2021.
4038.
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 24
2
3 4 4 0mm − −
2
( ; ) (2; )
3
m
−
− +
Kết hợp với đk ta có
2
( ; ) (2; )
3
m
−
− +
thỏa mãn ycbt.
Vậy số các phần tử của
S
là
4038
.
Câu 30: Cho hàm số
( ) ( )
32
21f x x mx m x= − + − +
với
m
là tham số. Có tất cả bao nhiêu giá trị nguyên
của
m
để phương trình sau có
3
nghiệm thực phân biệt
( )
( )
( )
( )
( ) ( )
..
f x f x
f x e f x f x f x

+ = +
A.
1
. B. vô số. C.
2
. D.
0
.
Lời giải
Chọn B
Xét
( )
( )
( )
( )
( ) ( ) ( )
. . *
f x f x
f x e f x f x f x

+ = +
.
Ta có
( ) ( ) ( ) ( ) ( ) ( )
3 2 2
2 1 1 1 1 1 .f x x mx m x x x m x x g x

= − + − + = − + − − = −

.
Với
( ) ( )
2
11g x x m x= + − −
và
( )
11gm=−
và
( )
11gm− = −
.
Lại có
( )
2
3 2 2f x x mx m
= − + −
với
( )
( )
11
10
fm
f
=−
=
.
Với
( )
1f
nếu
( )
1 0 1fm
thì
( )
0, 1f x x
suy ra
( )
( )
( )
( )
1
1
fx
fx
e f x
fx
+
+
.
Khi đó
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
* 1 ' 1 2 . 0 **f x f x f x f x f x f x f x f x
+ + + +
.
Trường hợp 1. Nếu
( )
0fx=
thì
( )
0fx
=
.
Trường hợp 2. Nếu
( )
0fx
thì
( )
( )
( )
** 0
fx
fx

.
Mặt khác
( )
( )
2
2
3 15
3 6 0, 0
24
fx
m m m m f x


= − + = − + =


luôn có hai nghiệm phân
biệt hay hàm số luôn có 2 điểm cực trị.
Giả sử rằng
( )
0fx=
có các nghiệm
( )
12
; ;...x x x=
, ta có
( )
( )
( )
1
1
0 1
n
i
i
fx
f x x x
=
=
−
.
Do
( )
0fx=
có ba nghiệm nên
( )
1
có
2
nghiệm (vô lí).
Như vậy
( )
( )
( ) ( )
( )
( )
( )
( )
2
2
22
1
0
1 1 0; 1 4 0
0
3 2 2 0; 3 6 0
gx
hx
x
fx
g x x m x m
fx
h x x mx m m m
=
=

= + − − = = − +

=
= − + − = = − +
.
Với
( )
1 0 1 0 1g m m= − = =
và
( )
1 0 1 0 1h m m= − + = =
.
Do đó với
1m
, phương trình
( )
( )
( )
( )
( ) ( )
..
f x f x
f x e f x f x f x

+ = +
luôn có
3
nghiệm thực
phân biệt.
Vậy có vô số giá trị của
m
thỏa đề.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
25 | Facebook tác giả: Phan Nhật Linh
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
1 | Facebook tác giả: Phan Nhật Linh
Câu 1: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
42
30x x m− + =
có
4
nghiệm
thực phân biệt?
A.
1
. B.
4
. C.
2
. D.
0
.
Câu 2: Biết đồ thị hàm số
( )( )
( )
2
1 1 7y x x x m= − + − −
cắt trục hoành tại 4 điểm phân biệt có hoành độ
là
1 2 3 4
, , , .x x x x
Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để
1 2 3 4
1 1 1 1
1.
1 1 1 1x x x x
+ + +
− − − −
A.
9
. B.
8
. C.
6
. D.
7
.
Câu 3: Đường thẳng
2
ym=
cắt đồ thị hàm số
42
10y x x− −=
tại hai điểm phân biệt
,AB
sao cho tam
giác
OAB
vuông (với
O
là gốc tọa độ). Mệnh đề nào sau đây đúng?
A.
( )
2
5;7m
. B.
( )
2
3;5m
. C.
( )
2
0;1m
. D.
( )
2
1;3m
.
Câu 4: Có tất cả bao nhiêu giá trị nguyên của tham số
m
để phương trình
42
2 3 2 0x x m− + − =
có
nghiệm thuộc
( )
2;2−
?
A.
4
. B.
3
. C.
5
. D.
6
.
Câu 5: Đường thẳng
2
ym=
cắt đồ thị hàm số
42
10y x x− −=
tại hai điểm phân biệt
,AB
sao cho
tam giác
OAB
vuông (với
O
là gốc tọa độ). Mệnh đề nào sau đây đúng?
A.
( )
2
5;7m
. B.
( )
2
3;5m
. C.
( )
2
0;1m
. D.
( )
2
1;3m
.
Câu 6: Đồ thị của hàm số
( )
42
2 1 2 1y x m x m= − + + +
cắt trục hoành tại bốn điểm phân biệt có hoành
độ lập thành một cấp số cộng. Mệnh đề nào dưới đây đúng?
A.
( )
6;9m
. B.
( )
6; 3m − −
. C.
( )
3;2m−
. D.
( )
2;6m
.
Câu 7: Cho hàm số
( )
42
3 2 3y x m x m= − + +
có đồ thị
( )
m
C
. Xác định tất cả các giá trị của tham số
thực
m
để
( )
m
C
cắt đường thẳng
1y =−
tại bốn điểm phân biệt
A.
0
1
3
m
m
−
. B.
0
1
3
m
m
−
. C.
1
3
m −
. D.
1
3
m −
.
Câu 8: Tập các giá trị của tham số
m
để phương trình
42
2 3 1 0x x m− − + =
có hai nghiệm phân biệt là
A.
( )
1; 0+
. B.
1
;0
3

+


. C.
( )
0;+
. D.
( )
1;+
.
Câu 9: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Tìm m liên quan đến tương giao hàm trùng phương
DẠNG 4
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 2
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
( )
2
64f x x m−=
có ít nhất
3
nghiệm thực phân biệt thuộc khoảng
( )
0;+
?
A.
25
. B.
30
. C.
29
. D.
24
.
Câu 10: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ
Xét hàm số
( ) ( )
3
2 2 4 3 6 5g x f x x x m= + − − −
với
m
là tham số thực. Điều kiện cần và đủ để
( )
0, 5; 5g x x

−

là:
A.
( )
2
0
3
mf
. B.
( )
2
5
3
mf−
. C.
( )
2
5
3
mf
. D.
( )
2
5
3
mf
.
Câu 11: Cho hàm số
( )
42
3 2 3y x m x m= − + +
có đồ thị
( )
m
C
. Xác định tất cả các giá trị của tham số
thực
m
để
( )
m
C
cắt đường thẳng
1y =−
tại bốn điểm phân biệt
A.
0
1
3
m
m
−
. B.
0
1
3
m
m
−
. C.
1
3
m −
. D.
1
3
m −
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
3 | Facebook tác giả: Phan Nhật Linh
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
42
30x x m− + =
có
4
nghiệm thực
phân biệt?
A.
1
. B.
4
. C.
2
. D.
0
.
Lời giải
Chọn C
Đặt
( )
2
0t x t=
. Ta được phương trình
( )
2
3 0, 1t t m− + =
.
Phương trình đã cho có
4
nghiệm thực phân biệt khi và chỉ khi phương trình có 2 nghiệm dương
phân biệt
0 9 4 0
9
0 3 0 0
4
00
m
Sm
Pm
−






.
Do
m
nguyên nên
1;2m
.
Vậy có 2 giá trị nguyên của tham số
m
thoả mãn yêu cầu bài toán.
Câu 2: Biết đồ thị hàm số
( )( )
( )
2
1 1 7y x x x m= − + − −
cắt trục hoành tại 4 điểm phân biệt có hoành độ
là
1 2 3 4
, , , .x x x x
Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để
1 2 3 4
1 1 1 1
1.
1 1 1 1x x x x
+ + +
− − − −
A.
9
. B.
8
. C.
6
. D.
7
.
Lời giải
Chọn C
Ta có
( )( )
( )
2 4 2
1 1 7 8 7y x x x m x x m= − + − − = − + −
.
Mặc khác ta có
3
0
' 4 16 0
2
x
y x x
x
=
= − =
=
. Ta có bảng biến thiên như sau:
Để phương trình có 4 nghiệm phân biệt thì
97m−
. Vì hàm số chẵn nên có 2 cặp nghiệm đối
xứng. Giả sử
12
0xx+=
và
34
0xx+=
.
Theo đề bài ta có:
( )
( )
22
31
22
2 2 2 2
1 1 3 3 1 3
3 1 3 1
42
1 1 1 1 2 2
1
1 1 1 1 1 1
1.
xx
x x x x x x
x x x x
−+
+ + + = + =
− + − + − −
− + +
( )
4 2.8
1 0 12.
1 8 7
m
m
−
− + −
Kết hợp điều kiện suy ra
0 7 1;2;3;4;5;6mm
.
Câu 3: Đường thẳng
2
ym=
cắt đồ thị hàm số
42
10y x x− −=
tại hai điểm phân biệt
,AB
sao cho tam
giác
OAB
vuông (với
O
là gốc tọa độ). Mệnh đề nào sau đây đúng?
A.
( )
2
5;7m
. B.
( )
2
3;5m
. C.
( )
2
0;1m
. D.
( )
2
1;3m
.
Lời giải
Chọn D
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 4
Xét:
42
10y x x− −=
3
0
2
' 4 2 0
2
2
2
x
y x x x
x
=
= − = =
=−
Vì
2
0m
với mọi
m
nên từ bảng biến thiên thấy đường thẳng
2
ym=
luôn cắt đồ thị hàm số
42
10y x x− −=
tại những cặp điểm đối xứng nhau qua
Oy
. Giả sử
( ) ( )
22
11
; ; ;A x m B x m−
.Tam giác
OAB
vuông (với
O
là gốc tọa độ)
2 4 2 4 2
1 1 1
. 0 0OAOB x m x m x m = − + = = =
( )
22
;A m m
vì
( )
22
;A m m
thuộc đồ thị hàm số nên
8 4 2 2
10 2m m m m− − = =
.
Câu 4: Có tất cả bao nhiêu giá trị nguyên của tham số
m
để phương trình
42
2 3 2 0x x m− + − =
có
nghiệm thuộc
( )
2;2−
?
A.
4
. B.
3
. C.
5
. D.
6
.
Lời giải
Chọn C
4 2 4 2
2 3 2 0 2 3 2x x m x x m− + − = − + =
Xét
( ) ( )
42
2 3, 2;2f x x x x= − + −
( )
3
1
4 4 3 0 0
1
x
f x x x x
x
=−
= − + = =
=
Bảng biến thiên
Theo yêu câu bài toán, có:
2 2 11 1 5,5mm
1,2,3,4,5mm
.
Câu 5: Đường thẳng
2
ym=
cắt đồ thị hàm số
42
10y x x− −=
tại hai điểm phân biệt
,AB
sao cho
tam giác
OAB
vuông (với
O
là gốc tọa độ). Mệnh đề nào sau đây đúng?
A.
( )
2
5;7m
. B.
( )
2
3;5m
. C.
( )
2
0;1m
. D.
( )
2
1;3m
.
Lời giải
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
5 | Facebook tác giả: Phan Nhật Linh
Chọn D
Xét:
42
10y x x− −=
3
0
2
' 4 2 0
2
2
2
x
y x x x
x
=
= − = =
=−
Vì
2
0m
với mọi
m
nên từ bảng biến thiên thấy đường thẳng
2
ym=
luôn cắt đồ thị hàm số
42
10y x x− −=
tại những cặp điểm đối xứng nhau qua
Oy
. Giả sử
( ) ( )
22
11
; ; ;A x m B x m−
.Tam giác
OAB
vuông (với
O
là gốc tọa độ)
2 4 2 4 2
1 1 1
. 0 0OAOB x m x m x m = − + = = =
( )
22
;A m m
vì
( )
22
;A m m
thuộc đồ thị hàm số nên
8 4 2 2
10 2m m m m− − = =
.
Câu 6: Đồ thị của hàm số
( )
42
2 1 2 1y x m x m= − + + +
cắt trục hoành tại bốn điểm phân biệt có hoành
độ lập thành một cấp số cộng. Mệnh đề nào dưới đây đúng?
A.
( )
6;9m
. B.
( )
6; 3m − −
. C.
( )
3;2m−
. D.
( )
2;6m
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm:
( )
42
2 1 2 1 0x m x m− + + + =
. (1)
Đặt
2
,0t x t=
. Phương trình trở thành
( )
2
2 1 2 1 0t m t m− + + + =
. (2)
Phương trình (1) có bốn nghiệm phân biệt khi và chỉ khi phương trình (2) có hai nghiệm dương
phân biệt, nghĩa là
( ) ( )
2
1 2 1 0
00
1
0 1 0 1
2
0
0 2 1 0 1
2
mm
m
m
S m m
m
Pm
m
+ − +
−
+ −
+
−
.
Cách 1. Gọi
( )
1 2 3 4 1 2 3 4
, , ,x x x x x x x x
là nghiệm của phương trình (1) và
( )
1 2 1 2
,t t t t
là
nghiệm của phương trình (2).
Theo giả thiết, ta có
4 3 3 2 2 1 4 3 3 2
2 1 1 1 2 1
90
x x x x x x x x x x
t t t t t t
− = − = − − = −
− = + =
Ta có hệ
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 6
( )
1
12
1 2 2
21
12
1
55
21
4
9 9 1 9 9
2 1 2 1
4
5 5 5 5 5 5
9
9
21
m
t
t t m
m
m m m
t t m t m
m
tt
t t m
=+
+ = +
=
= + = + + + = +

=−

=
=+
(nhận)
Cách 2. Với
0

, phương trình (1) có nghiệm
12
1, 2 1t t m= = +
. Biện luận như trên, ta có hai
trường hợp
21
12
4
9
4
9
9
m
tt
tt
m
=
=
=
=−
(nhận).
Câu 7: Cho hàm số
( )
42
3 2 3y x m x m= − + +
có đồ thị
( )
m
C
. Xác định tất cả các giá trị của tham số
thực
m
để
( )
m
C
cắt đường thẳng
1y =−
tại bốn điểm phân biệt
A.
0
1
3
m
m
−
. B.
0
1
3
m
m
−
. C.
1
3
m −
. D.
1
3
m −
.
Lời giải
Chọn B
Phương trình hoành độ giao điểm
( )
42
3 2 3 1x m x m− + + = −
( )
4 2 2
2 1 3 1 0x x m x − + − − =
( ) ( )
2
22
1 3 1 0x m x − − − =
( )( )
2
22
2
2
1, 1
10
1 3 1 0
31
3 1 0
xx
x
x x m
xm
xm
= = −
−=
− − − =
=+
− − =
Đồ thị
( )
m
C
cắt
1y =−
tại bốn điểm phân biệt khi và chỉ khi
2
31xm=+
có hai nghiệm phân
biệt khác
1
và
1−
.
Khi đó, ta có
1
3 1 0
3
3 1 1
0
m
m
m
m
+
−

+
.
Câu 8: Tập các giá trị của tham số
m
để phương trình
42
2 3 1 0x x m− − + =
có hai nghiệm phân biệt là
A.
( )
1; 0+
. B.
1
;0
3

+


. C.
( )
0;+
. D.
( )
1;+
.
Lời giải
Chọn B
Ta có:
42
2 3 1 0x x m− − + =
42
3 2 1m x x = − +
.
Xét hàm số
( )
42
21y f x x x= = − +
.
Tập xác định
D =
,
3
44y x x
=−
.
0
01
1
x
yx
x
=
= = −
=
.
Bảng biến thiên
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
7 | Facebook tác giả: Phan Nhật Linh
Yêu cầu bài toán tương đương đường thẳng
( )
:3d y m=
cắt đường cong
( ) ( )
:C y f x=
tại
hai điểm phân biệt.
Để phương trình có hai nghiệm phân biệt thì
30
31
m
m
=
0
1
3
m
m
=
.
Câu 9: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
( )
2
64f x x m−=
có ít nhất
3
nghiệm thực phân biệt thuộc khoảng
( )
0;+
?
A.
25
. B.
30
. C.
29
. D.
24
.
Lời giải
Chọn B
Đặt
( )
( )
( ) ( )
( )
22
4 2 4 . 4g x f x x g x x f x x

= − = − −
.
( ) ( )
( )
( )
2
2
2
2
2
2
2 4 0
22
2 4 0
44
0 2 4 . 4 0
22
40
42
0
40
4
x
x
x
x
xx
g x x f x x
x
f x x
xx
x
xx
x
=
−=
=+
−=
− = −

= − − =
=−
−=
− = −
=
−=
=
.
Ta có bảng biến thiên:
0
+
∞
0
1
0
1
+
∞
+
+
0
0
0
1
∞
+
∞
y
y'
x
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 8
Yêu cầu của bài toán
( )
6
m
gx=
có ít nhất
3
nghiệm thực phân biệt thuộc khoảng
( )
0;+
3 2 18 12
6
m
m − −
mà
m
nên
17; 16;...;11;12m − −
.
Vậy có
30
giá trị nguyên của
m
thỏa mãn yêu cầu bài toán.
Câu 10: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ
Xét hàm số
( ) ( )
3
2 2 4 3 6 5g x f x x x m= + − − −
với
m
là tham số thực. Điều kiện cần và đủ để
( )
0, 5; 5g x x

−

là:
A.
( )
2
0
3
mf
. B.
( )
2
5
3
mf−
. C.
( )
2
5
3
mf
. D.
( )
2
5
3
mf
.
Lời giải
Chọn D
Ta có:
( ) ( )
2
2 6 4g x f x x

= + −
,
( ) ( ) ( )
2
0 3 2 1g x f x x

= = − +
.
Vẽ parabol
2
32yx= − +
ta thấy phương trình
( )
1
có
3
nghiệm
5, 0, 5x x x= − = =
.
BBT
( )
0, 5; 5g x x

−

( )
2 5 3 0fm −
( )
2
5
3
mf
.
Phan Nhật Linh Fanpage: Luyện thi Đại học 2023
9 | Facebook tác giả: Phan Nhật Linh
Câu 11: Cho hàm số
( )
42
3 2 3y x m x m= − + +
có đồ thị
( )
m
C
. Xác định tất cả các giá trị của tham số
thực
m
để
( )
m
C
cắt đường thẳng
1y =−
tại bốn điểm phân biệt
A.
0
1
3
m
m
−
. B.
0
1
3
m
m
−
. C.
1
3
m −
. D.
1
3
m −
.
Lời giải
Chọn B
Phương trình hoành độ giao điểm
( )
42
3 2 3 1x m x m− + + = −
( )
4 2 2
2 1 3 1 0x x m x − + − − =
( ) ( )
2
22
1 3 1 0x m x − − − =
( )( )
2
22
2
2
1, 1
10
1 3 1 0
31
3 1 0
xx
x
x x m
xm
xm
= = −
−=
− − − =
=+
− − =
Đồ thị
( )
m
C
cắt
1y =−
tại bốn điểm phân biệt khi và chỉ khi
2
31xm=+
có hai nghiệm phân
biệt khác
1
và
1−
.
Khi đó, ta có
1
3 1 0
3
3 1 1
0
m
m
m
m
+
−

+
.
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 10
| 1/84

Tài liệu khác của Toán 12

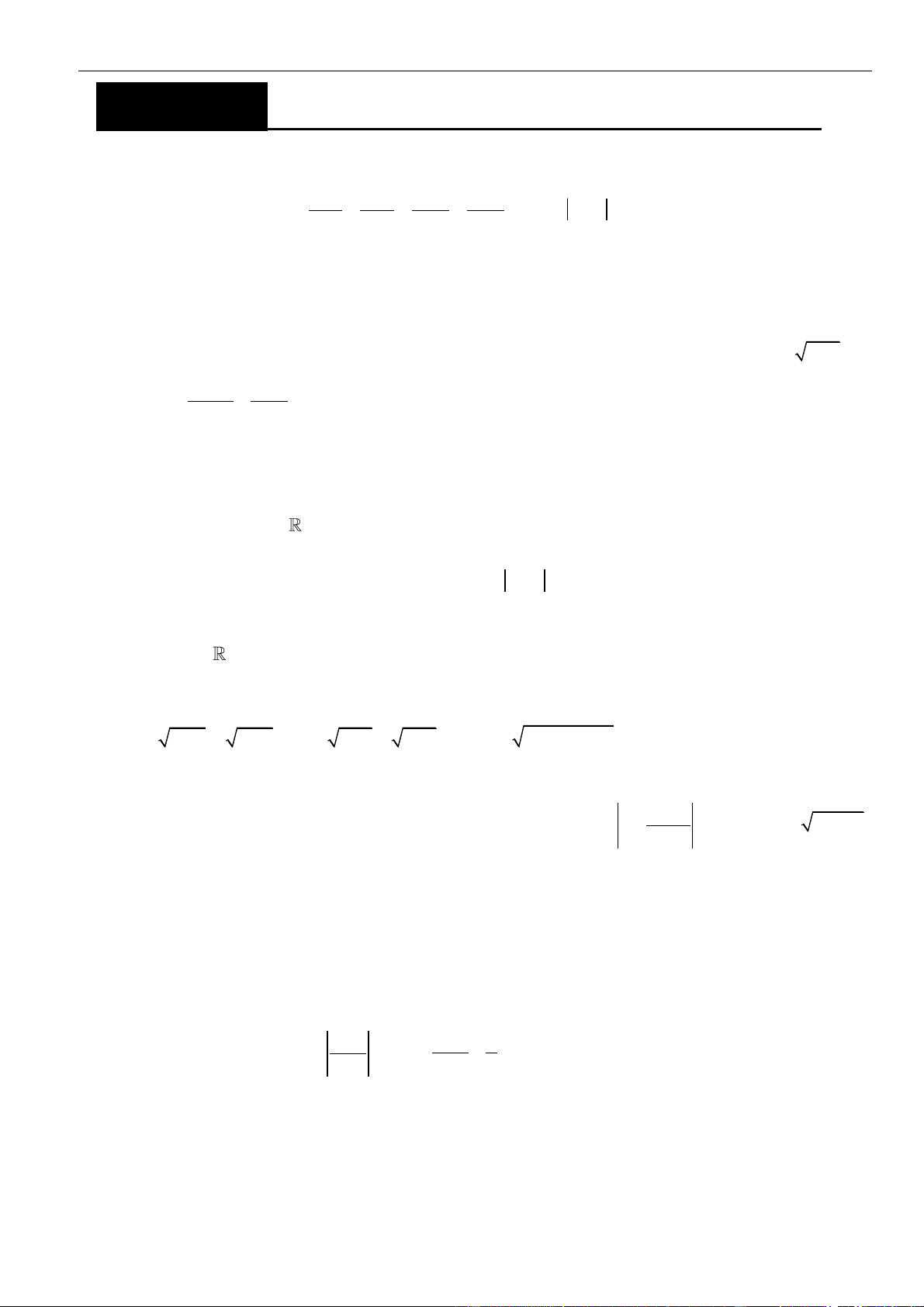
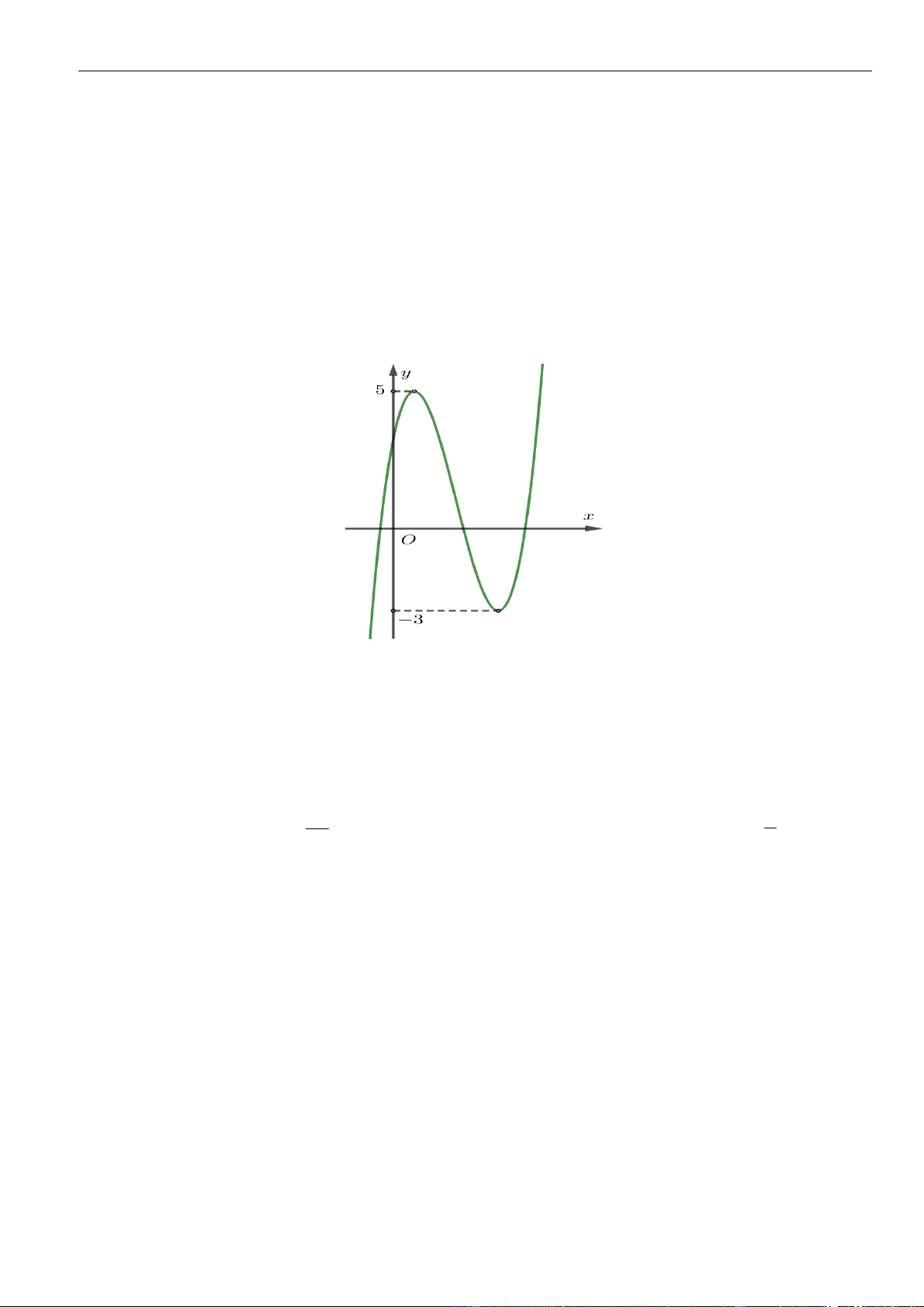
Preview text:

Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
CHỦ ĐỀ 06 : TƯƠNG GIAO CỦA ĐỒ THỊ HÀM SỐ LÍ THUYẾT
❖ Tọa độ giao điểm của hai đồ thị hàm số:
• Phương pháp: Cho 2 hàm số y = f (x),y = g(x) có đồ thị lần lượt là (C) và (C) .
▪ Lập phương trình hoành độ giao điểm của (C) và (C) : f (x) = g(x) (*)
▪ Giải phương trình tìm x từ đó suy ra y và tọa độ giao điểm.
▪ Số nghiệm của (*) là số giao điểm của (C) và (C) .
❖ Tương giao của đồ thị hàm bậc 3
• Phương pháp 1: Bảng biến thiên (phương pháp đồ thị)
▪ Lập phương trình hoành độ giao điểm dạng F (x,m) = 0 (phương trình ẩn x tham số m )
▪ Cô lập m đưa phương trình về dạng m = f (x)
▪ Lập bảng biến thiên cho hàm số y = f (x) .
▪ Dựa và giả thiết và bảng biến thiên từ đó suy ra m .
➢ Dấu hiệu: Sử dụng phương pháp bảng biến thiên khi m độc lập với x .
❖ Phương pháp 2: Nhẩm nghiệm – tam thức bậc 2.
▪ Lập phương trình hoành độ giao điểm F (x,m) = 0
▪ Nhẩm nghiệm: (Khử tham số). Giả sử x = x là 1 nghiệm của phương trình. 0 x = x
▪ Phân tích: F(x,m) = 0  (x − x ).g(x) = 0   0
(là g (x) = 0 là phương trình bậc 0 g(x) =  0
hai ẩn x tham số m ).
▪ Dựa vào yêu cầu bài toán đi xử lý phương trình bậc hai g(x) = 0 .
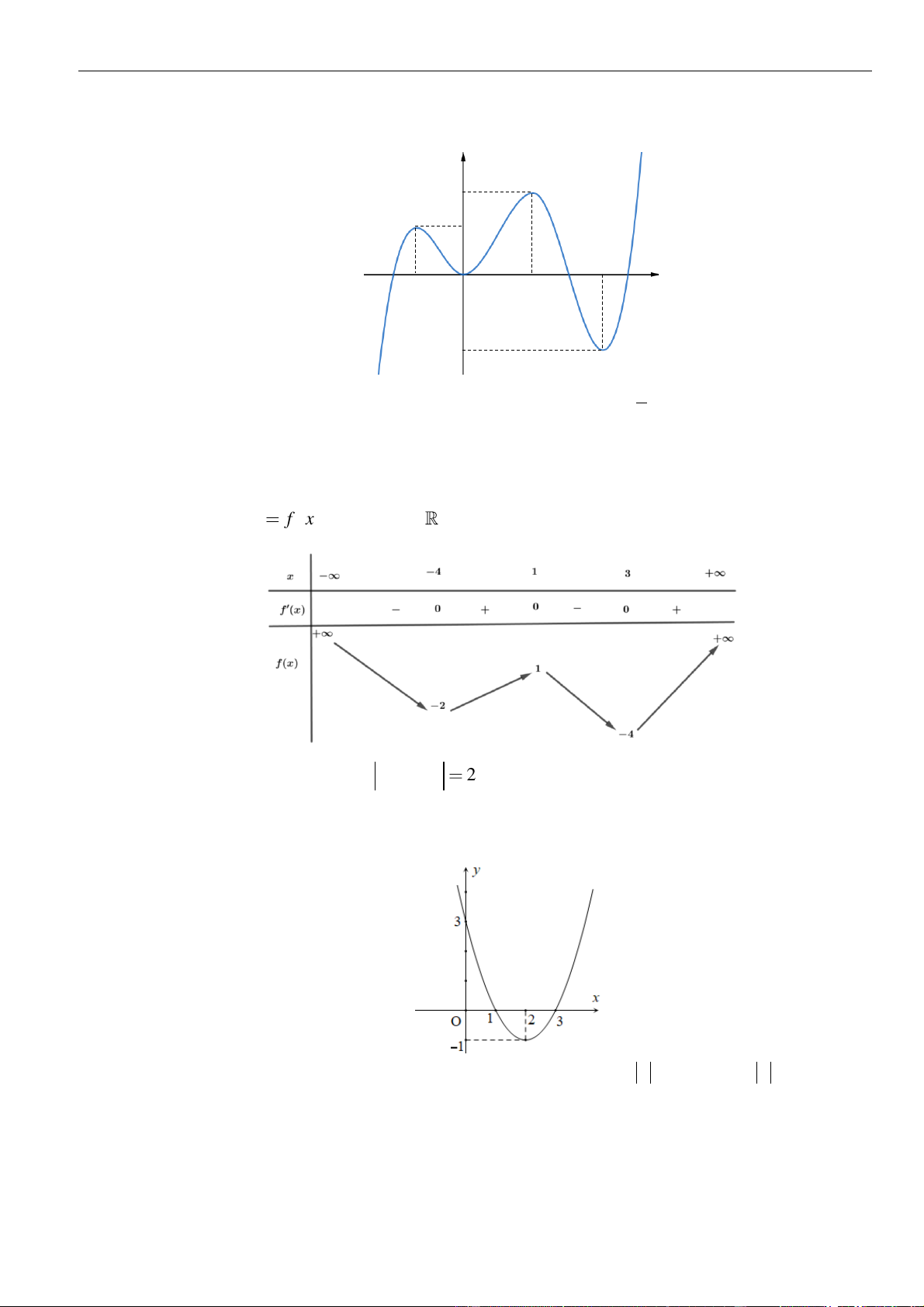
❖ Phương pháp 3: Cực trị
• Nhận dạng: Khi bài toán không cô lập được m và cũng không nhẩm được nghiệm. • Quy tắc:
▪ Lập phương trình hoành độ giao điểm F(x,m) = 0 (1) . Xét hàm số y = F(x,m) ▪ Để ( )
1 có đúng 1 nghiệm thì đồ thị y = F (x,m) cắt trục hoành tại đúng 1 điểm.
▪ Hoặc hàm số luôn đơn điệu trên  hàm số không có cực trị  y' = 0 hoặc vô nghiệm
hoặc có nghiệm kép    0 y'
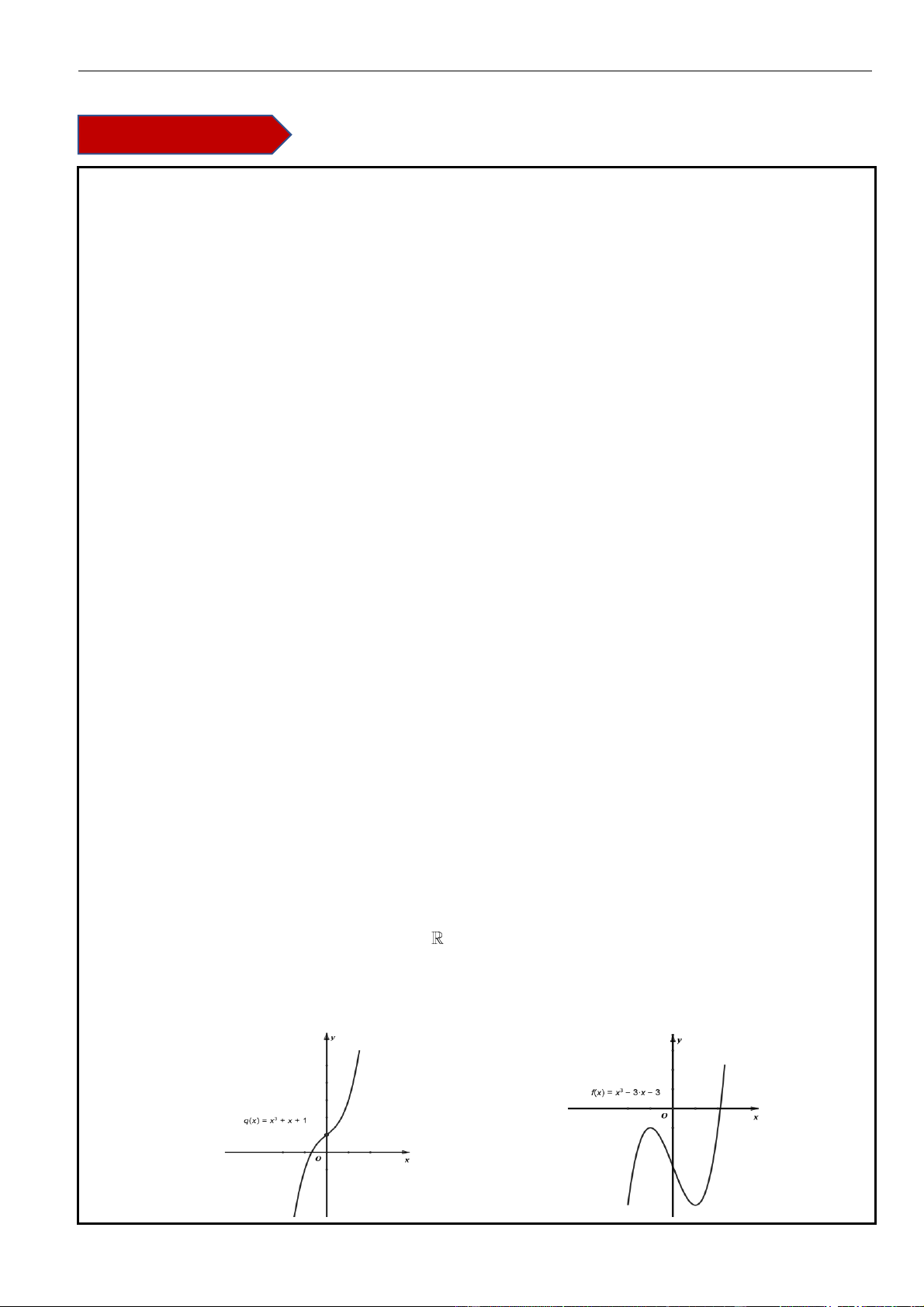
▪ Hoặc hàm số có cực đại, cực tiểu và y .y  0 (tham khảo hình vẽ) cd ct 1 | Facebook tá c giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số ▪ Để ( )
1 có đúng 3 nghiệm thì đồ thị y = F (x,m) cắt trục hoành tại 3 điểm phân biệt 
Hàm số có cực đại, cực tiểu và y .y  0 (tham khảo hình vẽ). cd ct ▪ Để ( )
1 có đúng 2 nghiệm thì đồ thị y = F (x,m) cắt trục hoành tại 2 điểm phân biệt 
Hàm số có cực đại, cực tiểu và y .y = 0 (tham khảo hình vẽ) cd ct
❖ Tương giao của hàm số phân thức • ax + b Cho hàm số y =
(C) và đường thẳng d : y = px +q . Phương trình hoành độ giao điểm cx + d ax + của ( b C) và (d) :
= px + q F(x,m) = 0 (phương trình bậc 2 ẩn x tham số m ). cx + d
• Các câu hỏi thường gặp:
▪ Tìm m để d cắt (C) tại 2 điểm phân biệt  (1) có 2 nghiệm phân biệt khác − d . c
▪ Tìm m để d cắt (C) tại 2 điểm phân biệt cùng thuộc nhánh phải của (C)  (1) có 2 nghiệm phân biệt d
x , x và thỏa mãn : −  x x . 1 2 1 2 c
▪ Tìm m để d cắt (C) tại 2 điểm phân biệt cùng thuộc nhánh trái của (C)  (1) có 2 nghiệm phân biệt d
x , x và thỏa mãn x x  − . 1 2 1 2 c
▪ Tìm m để d cắt (C) tại 2 điểm phân biệt thuộc hai nhánh của (C)  (1) có 2 nghiệm phân biệt d
x , x và thỏa mãn x  −  x . 1 2 1 2 c
▪ Tìm m để d cắt (C) tại 2 điểm phân biệt A và B thỏa mãn điều kiện hình học cho trước:
✓ Đoạn thẳng AB = kS
✓ Tam giác ABC vuông.
✓ Tam giác ABC có diện tích S 0
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 2 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 • Quy tắc:
▪ Tìm điều kiện tồn tại A, B  (1) có 2 nghiệm phân biệt.
▪ Xác định tọa độ của A và B (chú ý Vi ét)
▪ Dựa vào giả thiết xác lập phương trình ẩn m. Từ đó suy ra m.
• Chú ý: Công thức khoảng cách: 2 ▪ 2 A(x ; y B x y AB x x y y A A ) , ( ;B B): = ( − B A ) + ( − A B )
M(x ;y Ax By C 0 0 ) + + ▪   d(M,) = 0 0
 : Ax + By + C =  2 0 A + 2 0 0 B
❖ Tương giao của hàm số bậc 4
• Nghiệm của phương trình bậc bốn trùng phương: 4 ax + 2 bx + c = 0 (1) • Nhẩm nghiệm:
▪ Nhẩm nghiệm: Giả sử x = x là một nghiệm của phương trình. 0 x = x
▪ Khi đó ta phân tích: f (x,m) = ( 2 x − 2 x g x 0 0 ) ( ) =   0 g(x) =  0
▪ Dựa vào giả thiết xử lý phương trình bậc hai g(x) = 0
• Ẩn phụ - tam thức bậc 2: ▪ Đặt t = 2
x ,(t  0) . Phương trình: 2
at + bt + c = 0 (2) . t  0 = t ▪ Để ( )
1 có đúng 1 nghiệm thì (2) có nghiệm t ,t thỏa mãn:  1 2 1 2 t = t =  0 1 2 t  0  t ▪ Để ( )
1 có đúng 2 nghiệm thì (2) có nghiệm t ,t thỏa mãn:  1 2 1 2 0  t =  t 1 2 ▪ Để ( )
1 có đúng 3 nghiệm thì (2) có nghiệm t ,t thỏa mãn: 0 = t t 1 2 1 2 ▪ Để ( )
có nghiệm t ,t thỏa mãn: 0  t t
1 có đúng 4 nghiệm thì (2) 1 2 1 2
• Bài toán: tìm m để (C) y = 4 ax + 2 : bx + c ( )
1 cắt Ox tại bốn điểm có hoành độ lập thành một cấp số cộng. ▪ Đặt t = 2
x ,(t  0) . Phương trình: 2
at + bt + c = 0 (2). ▪ Để ( )
1 cắt Ox tại 4 điểm phân biệt thì (2) phải có 2 nghiệm dương t ,t (t t thỏa mãn 1 2 1 2 ) t = 9t . 2 1
▪ Kết hợp t = 9t vơi định lý vi – ét tìm được m. 2 1 3 | Faceboo
k tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số VÍ DỤ MINH HỌA Lời giải
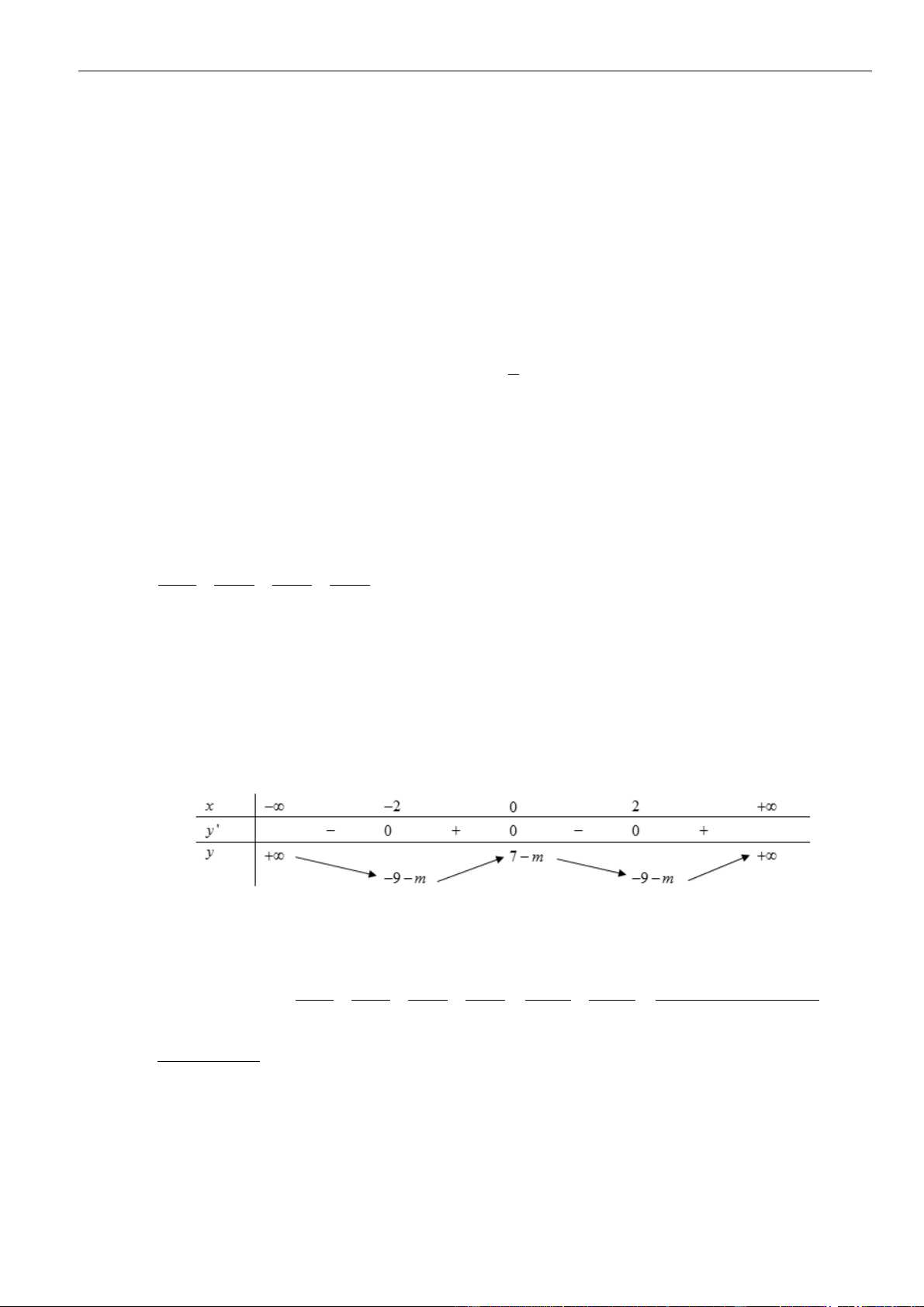
VÍ DỤ 1: Gọi m là số thực dương sao cho đường thẳng y = m + 1 cắt đồ thị hàm số y = 4 x − 2 3x − 2 tại
hai điểm phân biệt M,N thỏa mãn tam giác OMN vuông tại O (O là gốc tọa độ). Kết luận nào sau đây là đúng?  11 15   1 3   7 9   3 5  A. m  ;  .
B. m  ;  .
C. m  ;  .
D. m  ;  .  4 4   2 4   4 4   4 4  Chọn D
Ta có y = m + 1
(d) và y = 4x − 2 3x − 2 (C) .
Xét phương trình tương giao: 4 x − 2
3x − 2 = m + 1  4 x − 2
3x − (m + 3) = 0 . ( ) 1 Đặt t = 2
x  0, phương trình ( ) 1 trở thành: 2
t − 3t − (m + 3) = 0 . (2)
Phương trình (2) có tích .ac = −m − 3  0 khi m là số thực dương.
Suy ra phương trình (2) luôn có hai nghiệm trái dấu t  0  t . 1 2
Từ đó suy ra phương trình ( )
1 có hai nghiệm đối nhau x = − t ,x = t đồng thời (d) và (C) 1 2 2 2
cắt nhau tại hai điểm phân biệt đối xứng nhau qua Oy là M (− t ;m + )
1 , N ( t ,m +1 . 2 2 ) 2
Mặt khác tam giác OMN vuông tại O thì OM.ON = 0  t = m 1 . 2 ( + ) 2
Thay t = m 1 vào phương trình (2) ta được: 2 ( + ) ( 4 2
m + )4 − (m + )2 1 3
1 − (m + 3) = 0  (m + ) 1 − 3(m + ) 1 − (m + ) 1 − 2 = 0 .
Đặt a = m + 1  1 ta được phương trình 4 a − 2
3a − a − 2 = 0  (a − )( 3 a + 2 2
2a + a + 1) = 0  a = 2 (do a  1 nên 3 a + 2
2a + a + 1  0 ).
Từ đó ta được m + 1 = 2  m = 1 (thỏa mãn m  0 ). Vậy m = 1.
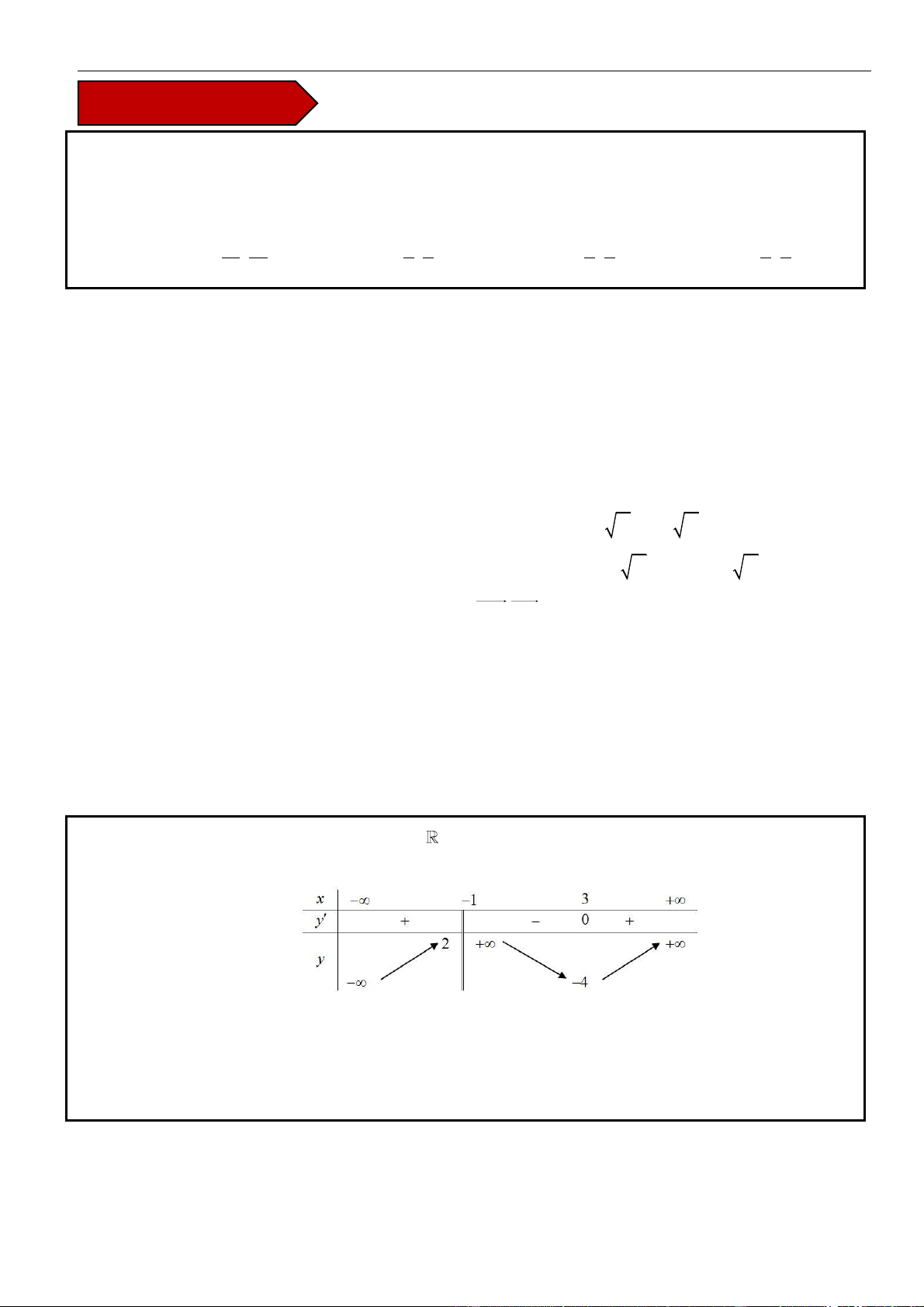
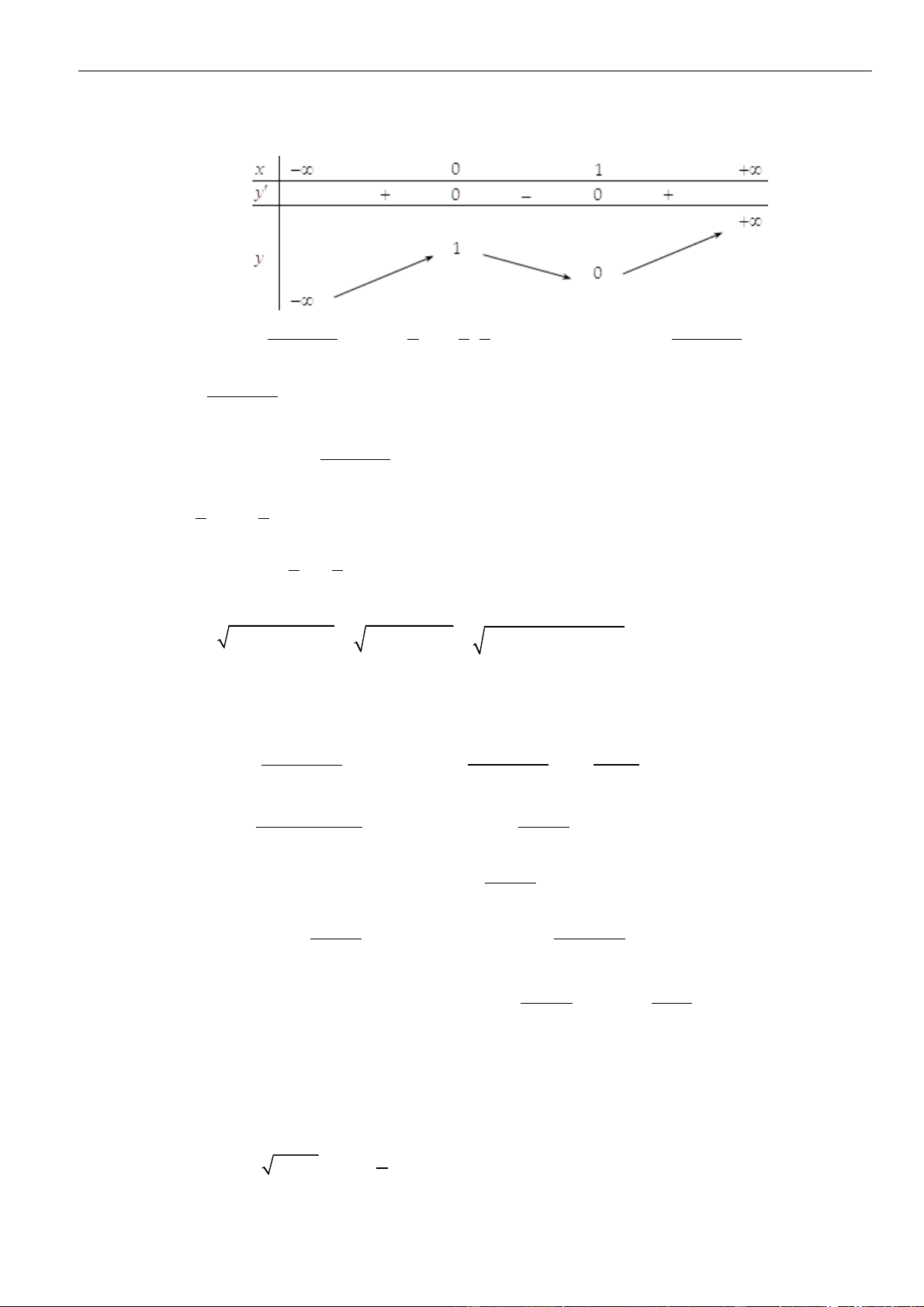
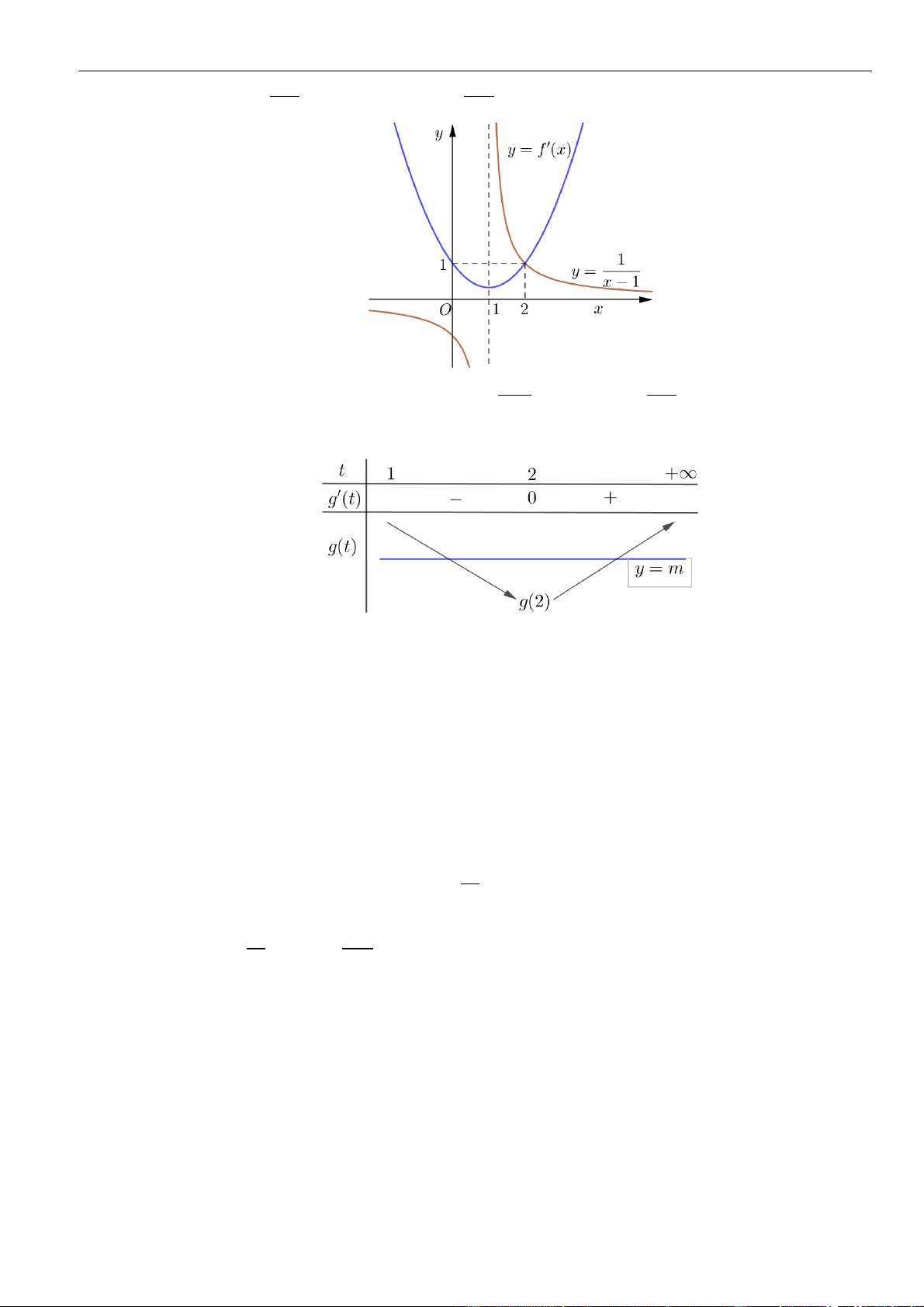
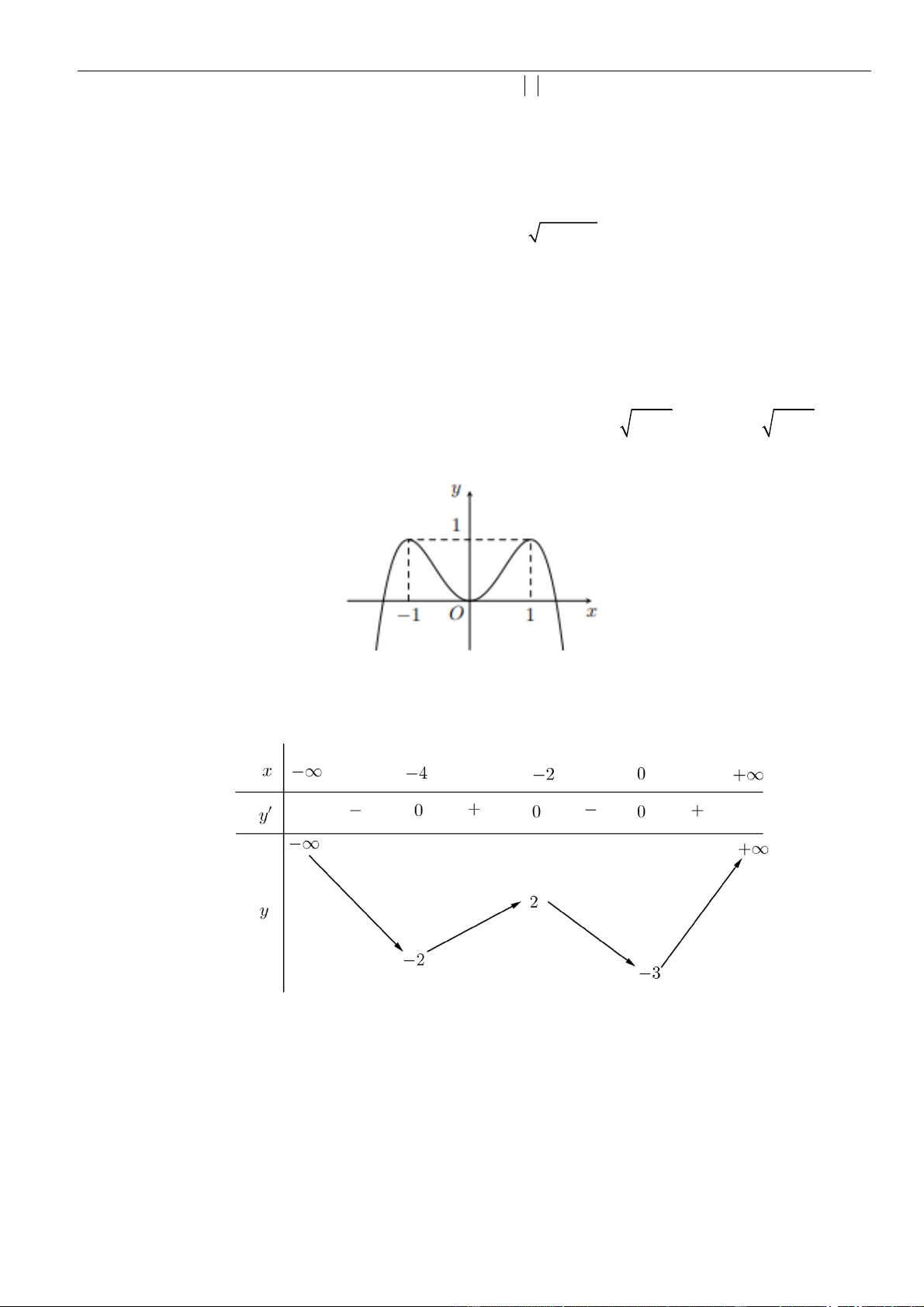
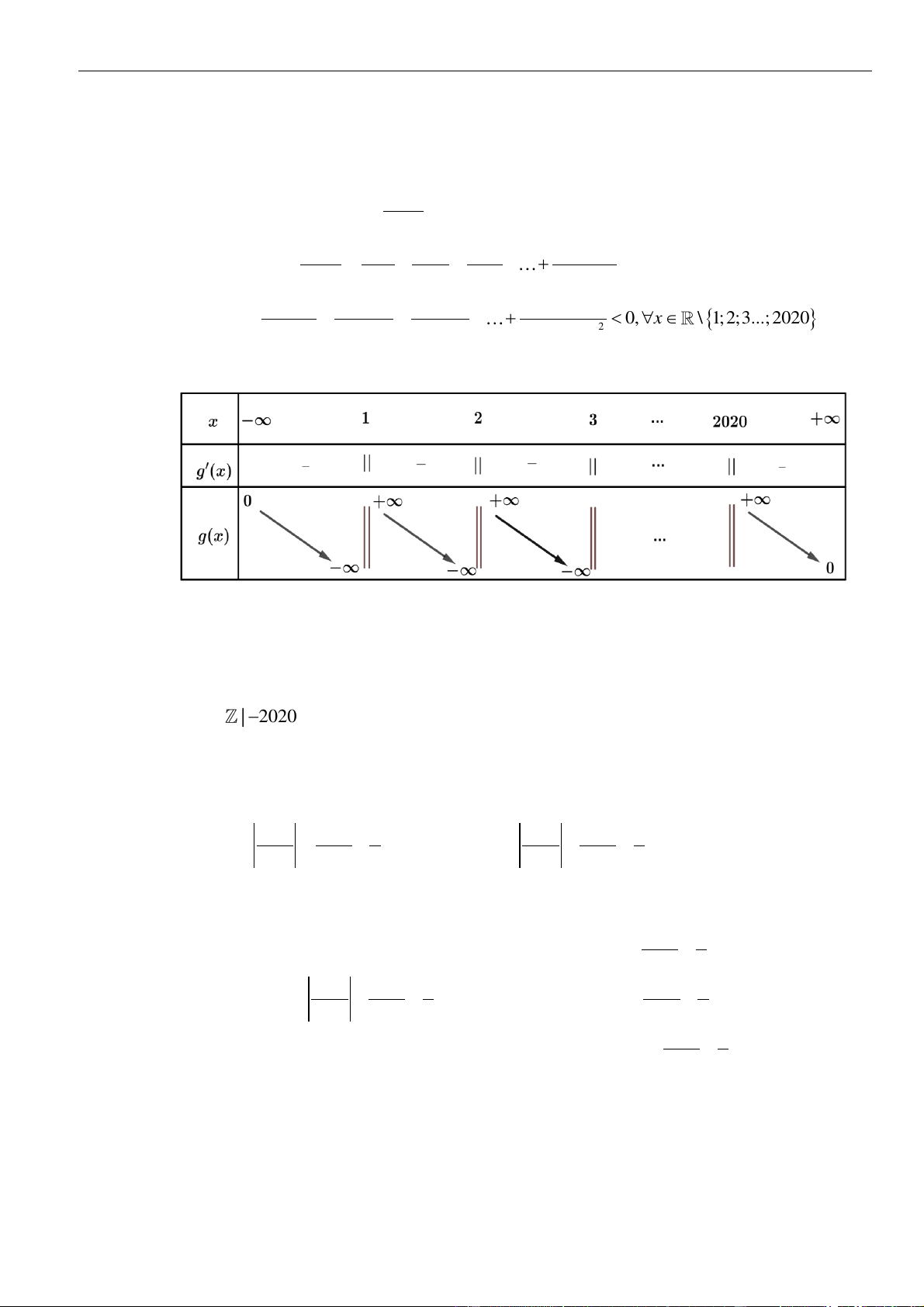
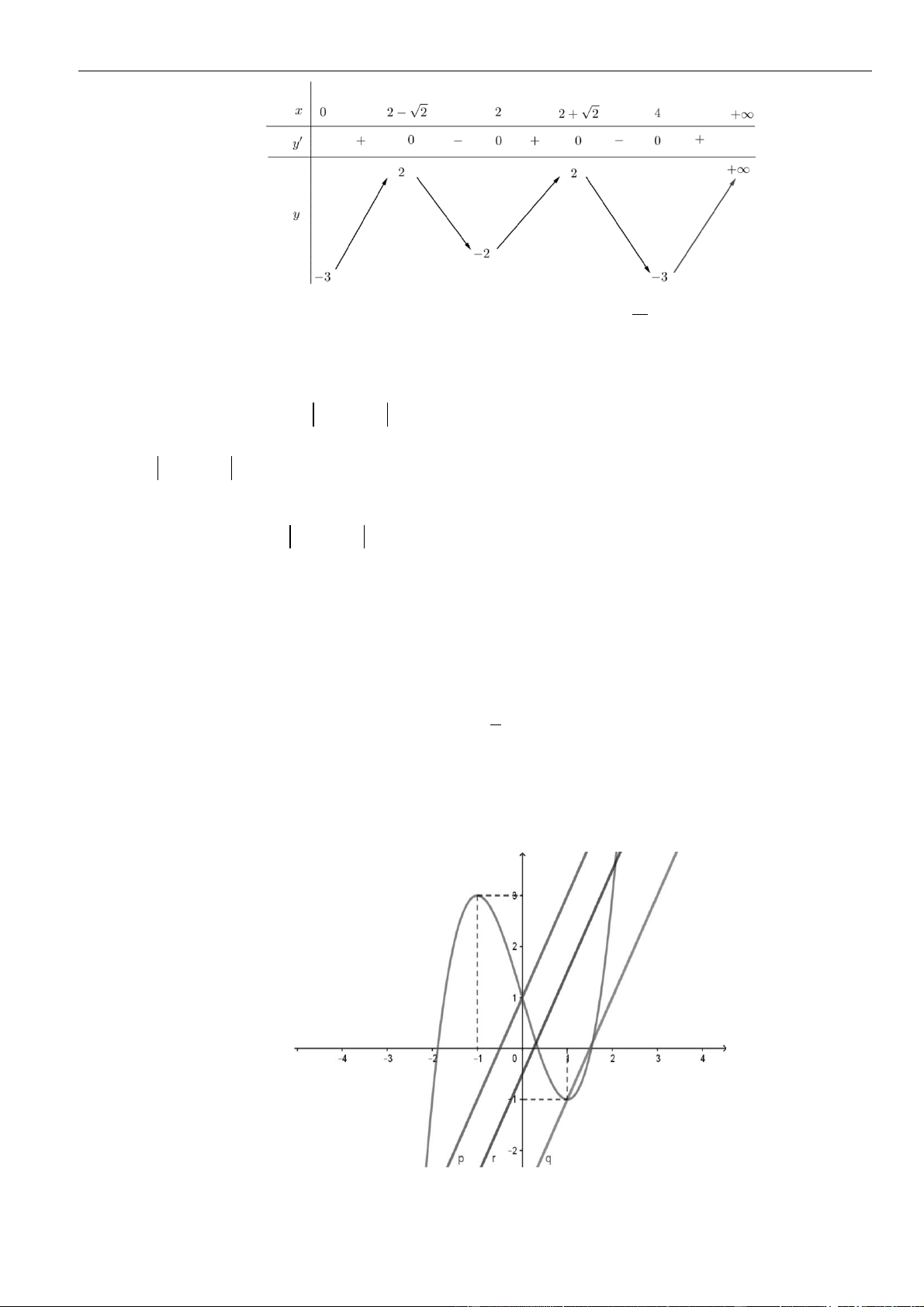
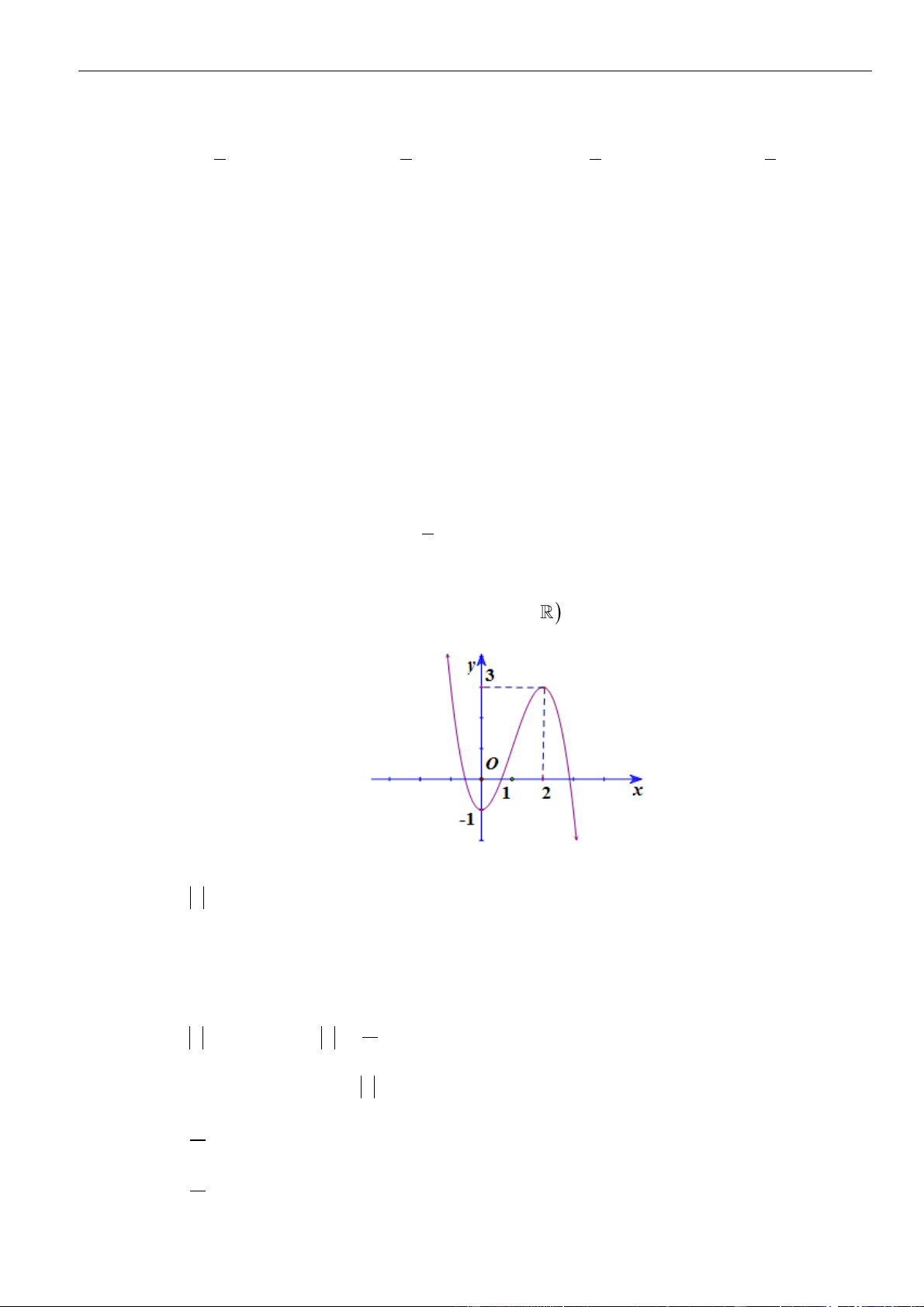
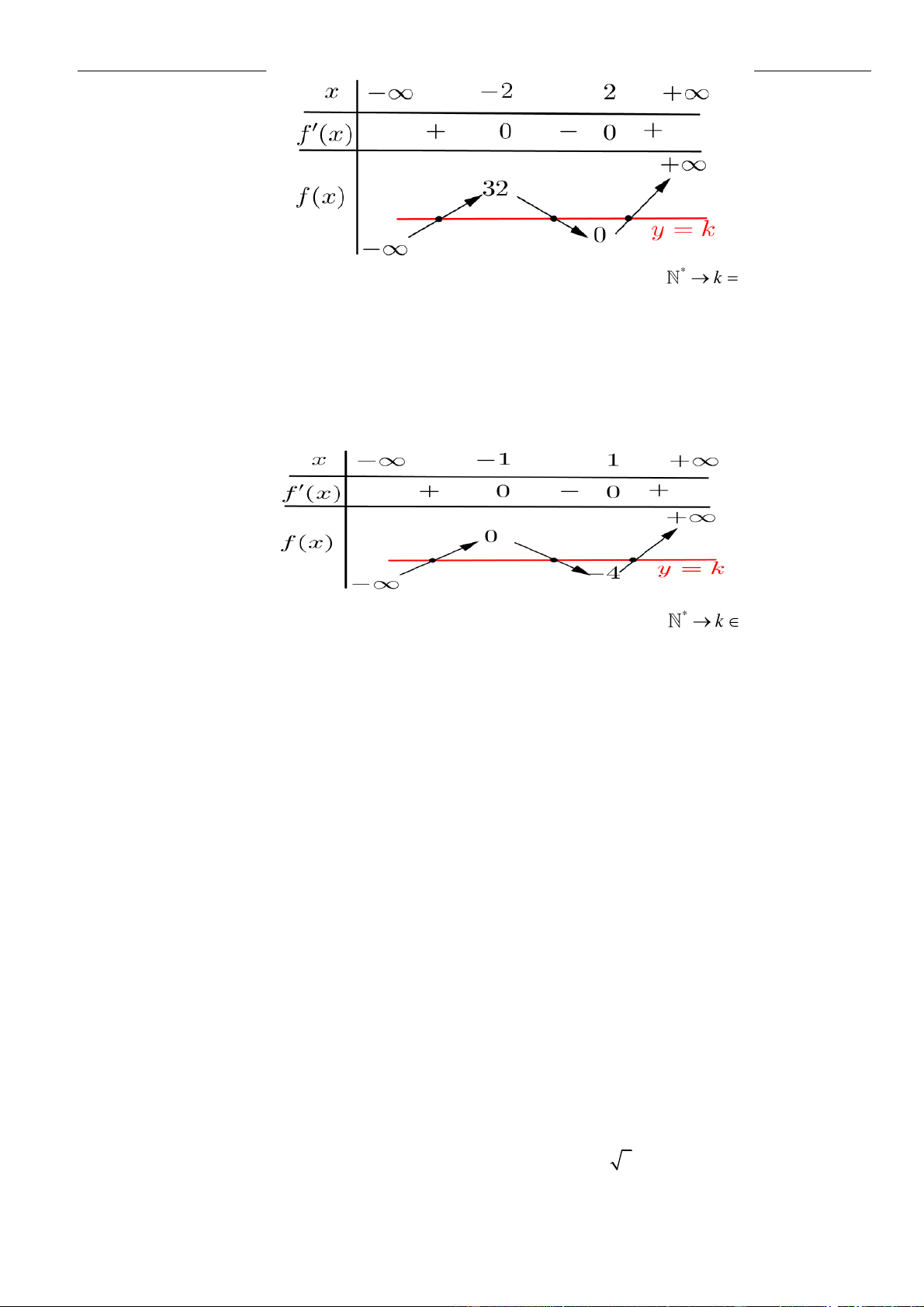
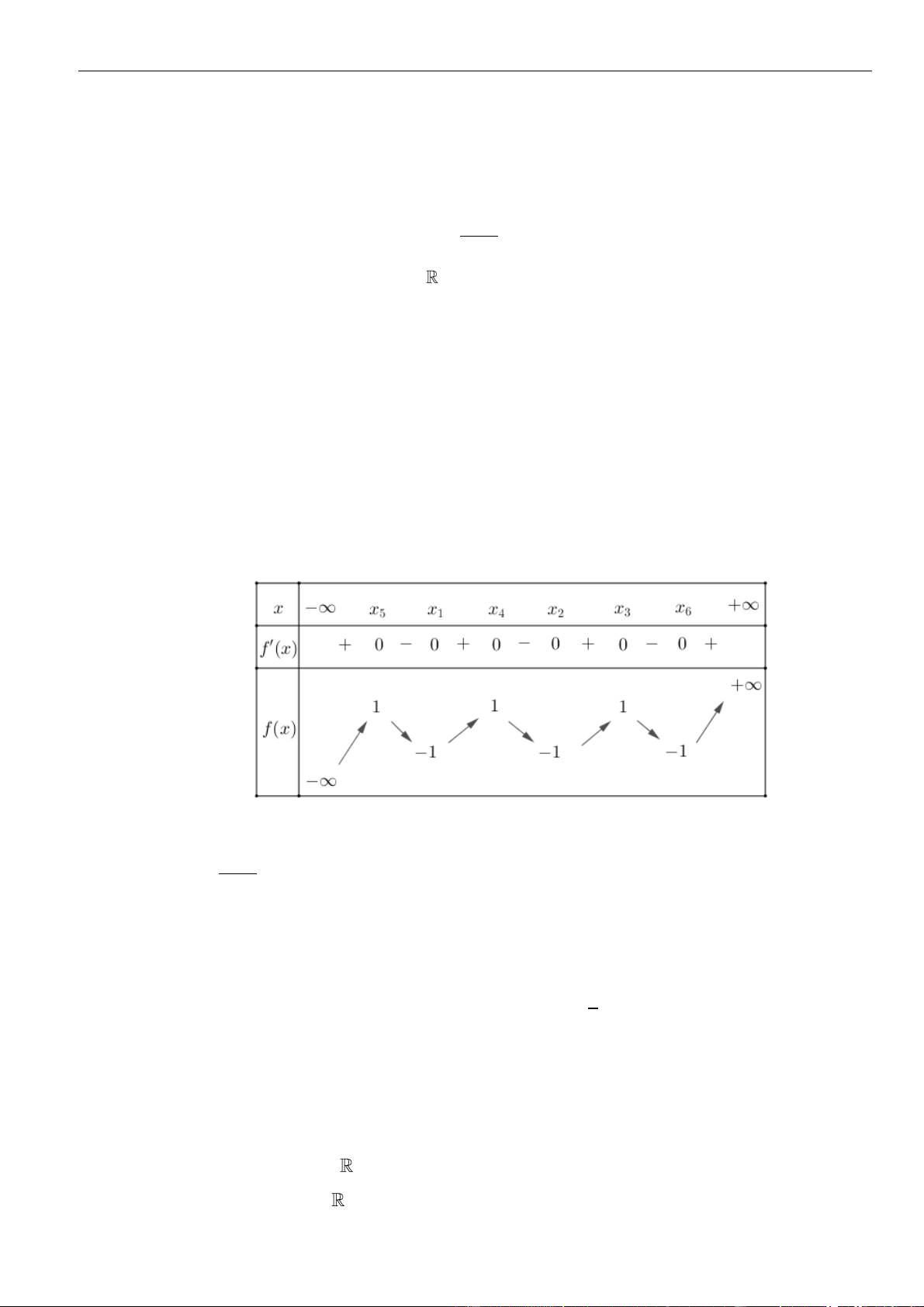
VÍ DỤ 2: Cho hàm số y = f (x) xác định trên \{1} , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau:
Tìm tập hợp tất cả các giá trị thực của tham số m sao cho phương trình f (x) + 1 = m có đúng
ba nghiệm thực phân biệt. A. (−4; 2) .
B. (−; 2 . C. −  4;2) . D. (−3; 3) . Lời giải Chọn D
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 4 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
Phương trình f (x) + 1 = m f (x) = m − 1 có đúng ba nghiệm phân biệt khi và chỉ khi đồ thị
hàm số y = f (x) và đường thẳng y = m − 1 cắt nhau tại ba điểm phân biệt.
Căn cứ vào bảng biến thiên của hàm số y = f (x) ta được −4  m − 1  2  −3  m  3. Vậy m  (−3;3).
VÍ DỤ 3: Cho hàm số f (x) = 3 x + 2
3x + mx + 1. Gọi S là tổng tất cả giá trị của tham số m để đồ thị
hàm số y = f (x) cắt đường thẳng y = 1 tại ba điểm phân biệt A(0;1) , B, C sao cho các tiếp tuyến của
đồ thị hàm số y = f (x) tại B, C vuông góc với nhau. Gía trị của S bằng 9 9 9 11 A. . B. . C. . D. . 2 5 4 5 Lời giải Chọn C
Phương trình hoàn độ giao điểm của y = 3 x + 2
3x + mx + 1 và y = 1 là: x 0 3 2 x 3x mx 1 1 x( 2 x 6x m)  = + + + =  + + = 0   2
x + 6x + m =  0 (*)
Để đồ thị hàm số y = f (x) cắt đồ thị hàm số y = 1 tại ba điểm phân biệt A(0;1), B(x ; y , 1 1 )
C (x ; y thì phương trình (*) có hai nghiệm phân biệt khác 0. 2 2 ) m  m  0  0 x + x = −  3   
. Theo hệ thức Viet ta có 1 2  =  . 9 − 4m  9  0 m   x .x = m   4 1 2
Để tiếp tuyến của đồ thị hàm số y = f (x) tại B, C vuông góc với nhau thì
f (x . f x 1 3x 6x m . 3x 6x m 1 1 ) ( 2 ) = −  ( 2 + + 1 1 ) ( 2 + + 2 2 ) = −  2 2 9x x + 18x x x x 3m x x 6m x x 36x x m 1 0 1 2 1 2 ( + 1 2 ) + ( 2 + 2 1 2 ) + ( + 1 2 ) + + 2 + = 1 2  9 + m = 65 8 9 + 65 9 −  2
4m − 9m + 1 = 0    S = + 65 = 9.  9 − 8 8 4 m = 65  8 x
VÍ DỤ 4: Cho hàm số y =
(C) và điểm A(−1;1). Tìm m để đường thẳng d : y = mx −m−1 cắt 1 − x
(C)tại hai điểm phân biệt M,N sao cho 2 + 2 AM
AN đạt giá trị nhỏ nhất.
A. m = −1 .
B. m = 0 .
C. m = −2 . D. m = − 2 . 3 Lời giải
5 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số Chọn A
Phương trình hoành độ giao điểm của ( x C) và d là:
= mx − m −1 (đk: x  1) 1 − x
x = ( − x)(mx − m − )  x = mx − m − − 2
mx + mx + x  2 1 1 1
mx − 2mx + m + 1 = 0 (*)
Để (C) và d cắt nhau tại hai điểm phân biệt M,N thì (*) phải có 2 nghiệm phân biệt khác 1 m  0   ' = 2
m − m(m + 1) = −m  0  m  0
m−2m+ m+1   0 m + Giả sử 1
M (x ; y ,N x ; y . Theo hệ thức viét : x + x = 2; x x = 1 1 ) ( 2 2) 1 2 1 2 m
y + y = m(x + x ) − 2m − 2 = 2m − 2m − 2 = −2 1 2 1 2 2
và y .y = mx m 1 mx m 1 m x x m m 1 x x m 1 1 2 ( − − 1 )( − − 2 ) = 2 − 1 2 ( + )( + 1 2 ) + ( + )
= m m + − m(m + ) + (m + )2 ( 1) 2 1 1 = m + 1 2 2 2 2 Ta có: 2 AM + 2 AN = (x + 1 y 1 x 1 y 1 1 ) +( − 1 ) +( + 2 ) +( − 2 ) = (x + x + 2 2 x 1 x 1 y y 2 2 y 1 y 1 1 2 )2 − ( + 1 )( + 2 )+( + − 1 2 )2 − ( − 1 )( − 2 ) = (x + x + 2 2 x x x x 1 y y 2 2 y y y y 1 1 2 )2 − ( + + + 1 2 1 2 )+( + − 1 2 )2 − ( − 1 2 ( + 1 2 ) + ) ( m 2 2)2  + 1  = + − 2
+ 2 + 1 + (−2 − 2)2 − 2(m+1−(−2) +   1)  m   m + 1 1  1  = 18 − 2
− 2m = 18 − 2 − 2. − 2m = 16 + 2. + (− ) m  16 + 2.2 =     20 (BĐT Cauchy)  m m −m  1 m = 1 Suy ra: 2 + 2 AM
AN đạt giá trị nhỏ nhất là 20 khi = −m  2 m = 1   −m m = −  1
Vậy m = −1 (vì m  0 )
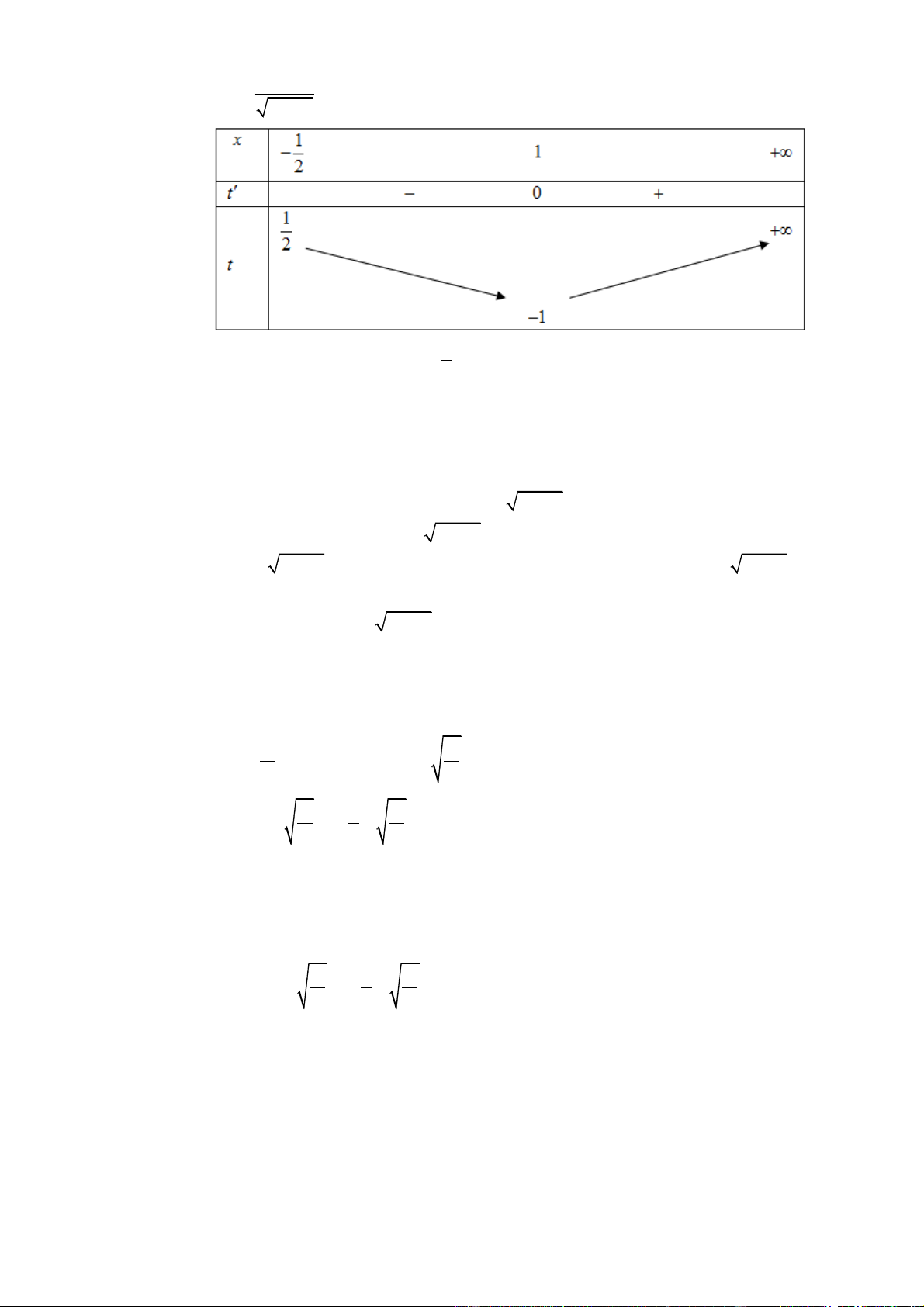
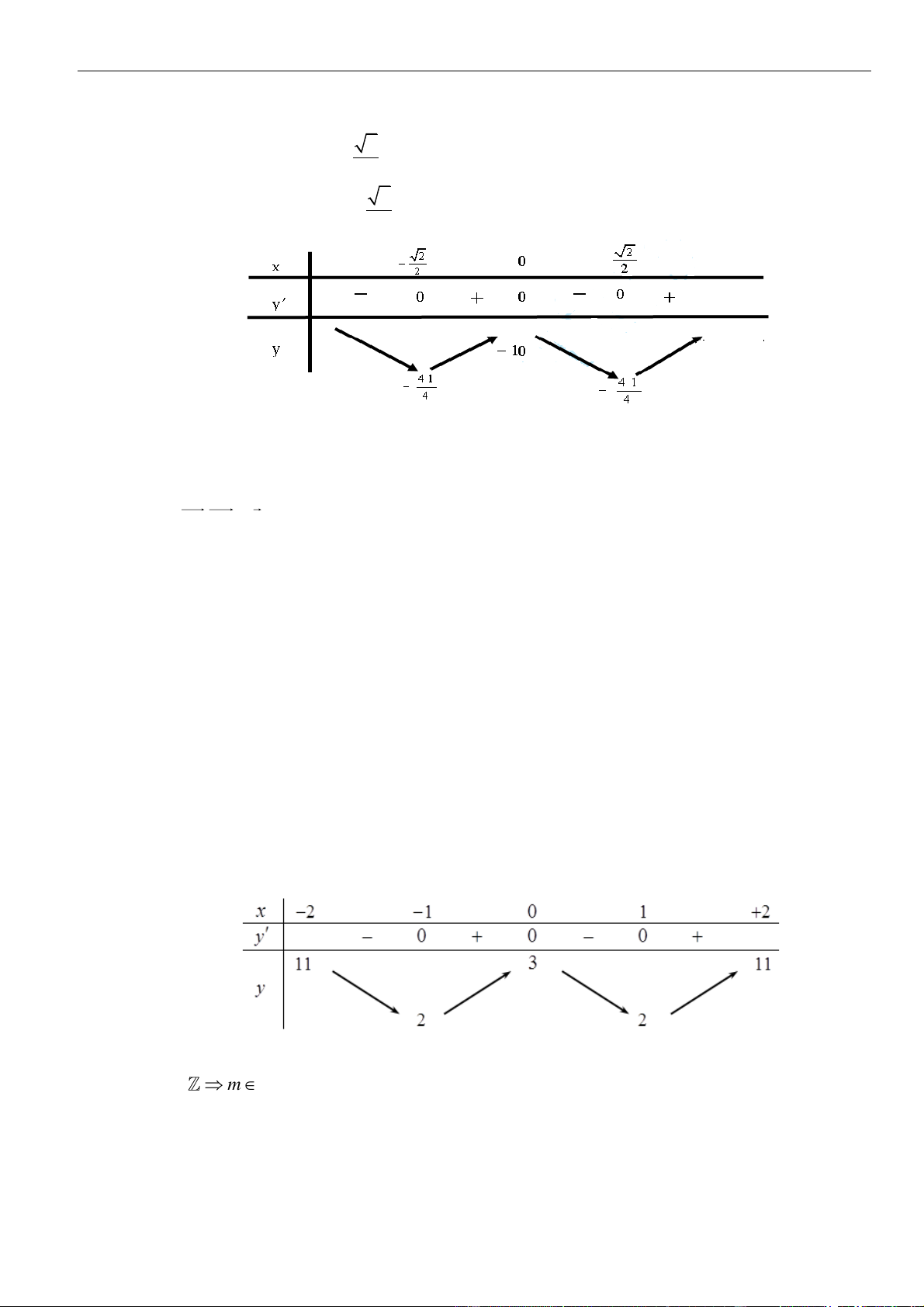
VÍ DỤ 5: Cho hàm số y = 4 x − 2
2x có đồ thị (C) , có bao nhiêu đường thẳng d có đúng 3 điểm chung với
đồ thị (C) và các điểm chung có hoành độ x ,x ,x thỏa mãn 3 x + 3 x + 3 x = −1 . 1 2 3 1 2 3 A. 0 . B. 1 . C. 2 . D. 3 . Lời giải Chọn B
Vì đường thẳng d cắt đồ thị hàm số (C) tại 3 điểm phân biệt nên đường thẳng d là đường thẳng
có hệ số góc dạng y = ax + b .
Phương trình hoành độ giao điểm của d và (C) là: 4 x − 2
2x = ax + b .
Mà phương trình là phương trình bậc 4 nên phương trình muốn có 3 nghiệm phân biệt thì trong
đó sẽ có 1 nghiệm kép gọi là x , hai nghiệm còn lại là x ,x . 1 2 3
Suy ra đường thẳng d là tiếp tuyến của đồ thị (C) , không mất tính tổng quát giả sử đường thẳng
d tiếp xúc với đồ thị hàm số (C) tại x . 1
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 6 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
Gọi d là tiếp tuyến của (C) tại điểm có hoành độ x , d cắt (C) tại 2 điểm phân biệt có hoành độ 1
x ,x ( x ) thỏa mãn 3 x + 3 x + 3
x = −1 . Ta có: d : y = 3
(4x − 4x )(x − x ) + 4 x − 2 2x . 2 3 1 1 2 3 1 1 1 1 1
Phương trình hoành độ giao điểm của d và (C) là: 4 x − 2 2x = 3
(4x − 4x )(x − x ) + 4 x − 2 2x (1) 1 1 1 1 1
Yêu cầu bài toán  (1) có 3 nghiệm phân biệt thỏa mãn 3 x + 3 x + 3 x = −1 . 1 2 3 x x 2 2 2  =
(1)  (x − x ) (x + 2x x + 3x − 2) = 0  1 1 1  1  f (x) = 2 x + 2x x + 2 3x − 2 =  0 1 1
Để phương trình (1) có 3 nghiệm phân biệt thỏa mãn 3 x + 3 x + 3
x = −1 thì phương trình 1 2 3
x + x = −2x
f (x) = 0 phải có 2 nghiệm phân biệt x , x khác x và thỏa mãn định lí Vi – ét:  2 3 1 2 3 1 x .x = 2 3x −  2 2 3 1 ' = 2 x − 2 3x + 2  0 −1  x  1  1 1  1 Ta có:  2 x + 2 2x + 2 3x − 2  0   2 3x − 1  0  1 1 1 1 3  x + (x + 3
x ) − 3x x (x + x ) = − 3 3 2  1
x + (−2x ) − 3(3x − 2).(−2x ) = −1 1 2 3 2 3 2 3  1 1 1 1 −11+  x =
165 . Vậy có đúng 1 đường thẳng thỏa mãn yêu cầu bài toán. 1 22
VÍ DỤ 6: Có bao nhiêu số thực của tham số m để đường thẳng y = (m − 6)x − 4 cắt đồ thị hàm số 1 1 1 2 y = 3 x + 2
x − 3x − 1 tại ba điểm phân biệt có tung độ y , y , y thỏa mãn + + = . 1 2 3 y + 4 y + 4 y + 4 3 1 2 3 A. 2 . B. 0 . C. 3 . D. 1 . Lời giải Chọn D
Ta có phương trình hoành độ giao điểm của đường thẳng và đồ thị hàm bậc ba đã cho là 3 x + 2
x − 3x − 1 = (m − 6)x − 4  3 x + 2
x + (3 − m)x + 3 = 0 ( ) 1 .
Giả sử x , x , x là ba nghiệm phân biệt của phương trình ( ) 1 . 1 2 3
x + x + x = −1  1 2 3
Theo hệ thức viet đối với phương trình bậc ba ta có : x x + x x + x x = 3 − m .  1 2 2 3 3 1 x x x = −  3 1 2 3
Nhận thấy tung độ của ba giao điểm thỏa mãn phương trình y = (m − 6)x − 4 nên ta có được
y + 4 = (m − 6 x , y + 4 = (m − 6 x và y + 4 = (m − 6 x . 3 ) 2 ) 1 ) 1 2 3 Khi đó 1 + 1 + 1 = 2 1 1 1 2  + + = y + 4 y + 4 y + 4 3
(m−6)x (m−6)x (m−6 x 3 1 2 ) 1 2 3 3 1 x x + x x + 1 3 −  x x 2 m 2 1 2 2 3 3 1 . =  . =  m = 9 . m − 6 x x x 3 m − 6 −3 3 1 2 3
7 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số
Thử lại với m = 9 suy ra phương trình hoành độ giao điểm 3 x + 2
x − 6x + 3 = 0 có ba nghiệm
phân biệt thỏa mãn giả thiết cho (Dùng casio để kiểm tra) . Vậy có một số thực m thỏa mãn .
VÍ DỤ 7: Một đường thẳng cắt đồ thị hàm số y = 4 x − 2
2x tại bốn điểm phân biệt có hoành độ là 0 , 1 ,
m và n . Tính = 2 + 2 S m n .
A. S = 0 .
B. S = 1 . C. S = 2 . D. S = 3 . Lời giải Chọn D
Do đường thẳng cắt đồ thị hàm số y = 4 x − 2
2x tại điểm có hoành độ là 0 nên phương trình
đường thẳng có dạng y = ax .
Phương trình hoành độ giao điểm của đường thẳng y = ax với đồ thị hàm số y = 4 x − 2 2x là : 4 x − 2 2x = a x  4 x − 2
2x − a x = 0  x( 3
x − 2x − a) = 0 .
Do phương trình có bốn nghiệm là 0 , 1, m , n nên ta có : x( 3
x − 2x − a) =x(x − )
1 (x − m)(x − n)  3
x − x − a = ( 2 2
x − mx − x + m)(x − n)  3
x − x − a = 3 x − 2 nx − 2 mx + mnx − 2 2
x + nx + mx − mn  3
x − x − a = 3
x + (−n − m − ) 2 2
1 x + (m + n + mn)x − mn
−m − n − 1 = 0  m + n = −  1
m + n + mn = −2 
S = m + n = (m + n)2 2 2 − 2mn = . mn = − 3   −mn = − 1  a 2
VÍ DỤ 7: Cho phương trình ( 2
x − x + m) + 2 3
x − 8x + 2m = 0 . Có bao nhiêu giá trị nguyên của tham số
m thuộc đoạn −20; 20 
 để phương trình đã cho có 4 nghiệm phân biệt? A. 19 . B. 18 . C. 17 . D. 20 . Lời giải Chọn B 2  2 2 2  Ta có ( 2
x − x + m) + 2 3
x − 8x + 2m = 0  (x − x + m) − x + ( 2 3
2x − 8x + 2m) =     0  ( 2
x − x + m)( 2
x − x + m) + ( 2 4 2
2 x − 4x + m) = 0  ( 2
x − x + m)( 2 4
x − 2x + m + 2) = 0  2
x − 4x + m = 0 (1)   .  2
x − 2x + m + 2 =  0 (2)
Yêu cầu bài toán  mỗi phương trình ( )
1 và (2) có 2 nghiệm phân biệt không trùng nhau. Phương trình ( )
1 và (2) có 2 nghiệm phân biệt
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 8 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023   0 4 − m  0 m   4  1      m  − .   0 1 − m − 2  0 m  − 1  1 2   Giả sử phương trình ( )
1 và (2) có nghiệm x trùng nhau 0  2
x − 4x + m =  0 (1)
 Hệ sau có nghiệm   2
x − 2x + m + 2 =  0 (2)  2
x − 4x + m− x 2x m 2 0  x = −1 . 0 0 ( 2 − + + 0 0 ) = 0
Với x = −1 thay vào ( )
1 ta được m = −5 . 0
 Với m  −5 phương trình ( )
1 và (2) không có nghiệm trùng nhau.
Kết hợp m là số nguyên thuộc đoạn −20; 20    m  − − ) −  20; 1 \  5 .
Vậy có 18 số nguyên m thoả mãn yêu cầu bài toán.
9 | Facebook tác giả: Phan Nhật Linh Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 D ẠNG 1
Bài toán tương giao đồ thị hàm số 01 Câu 1:
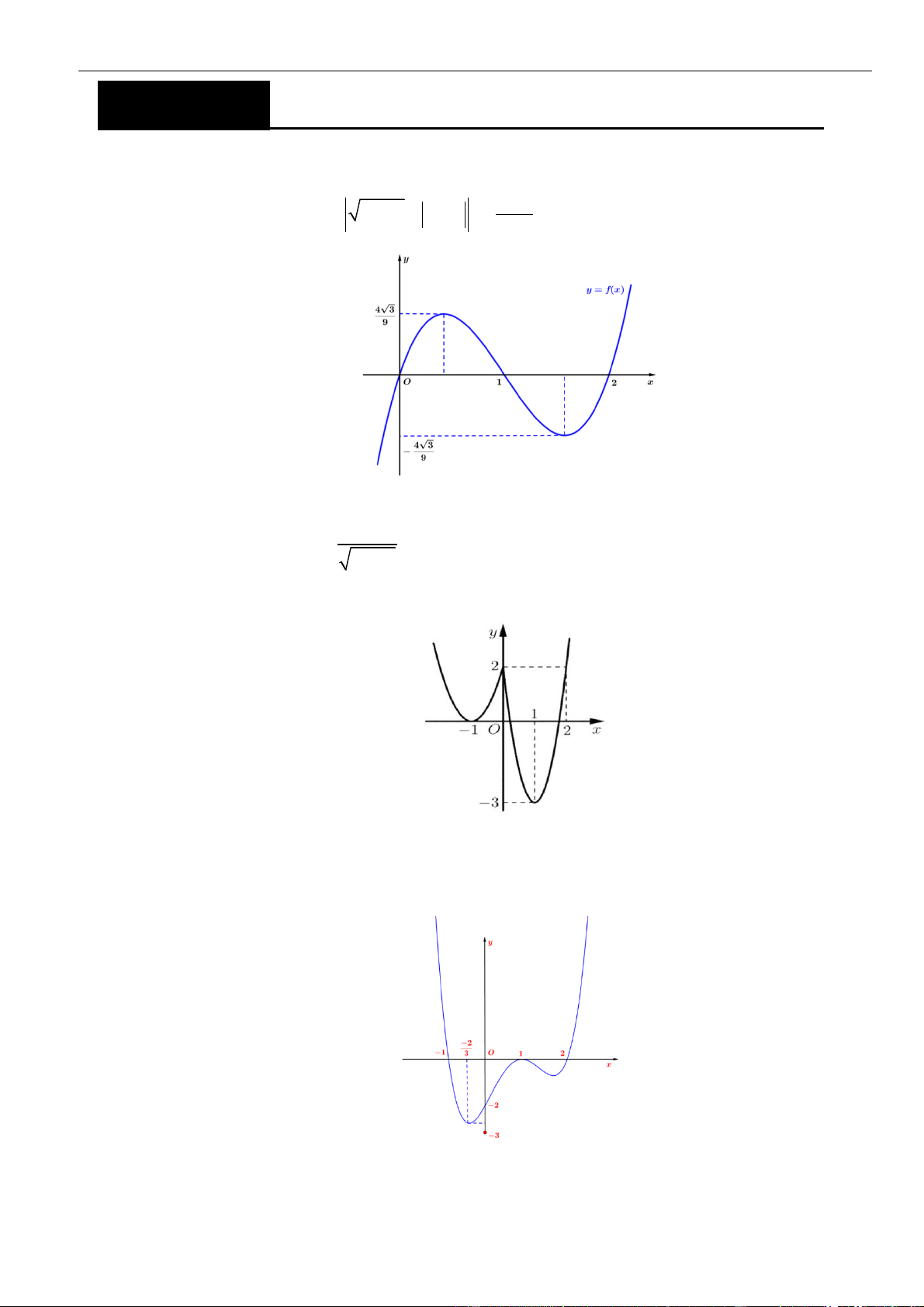
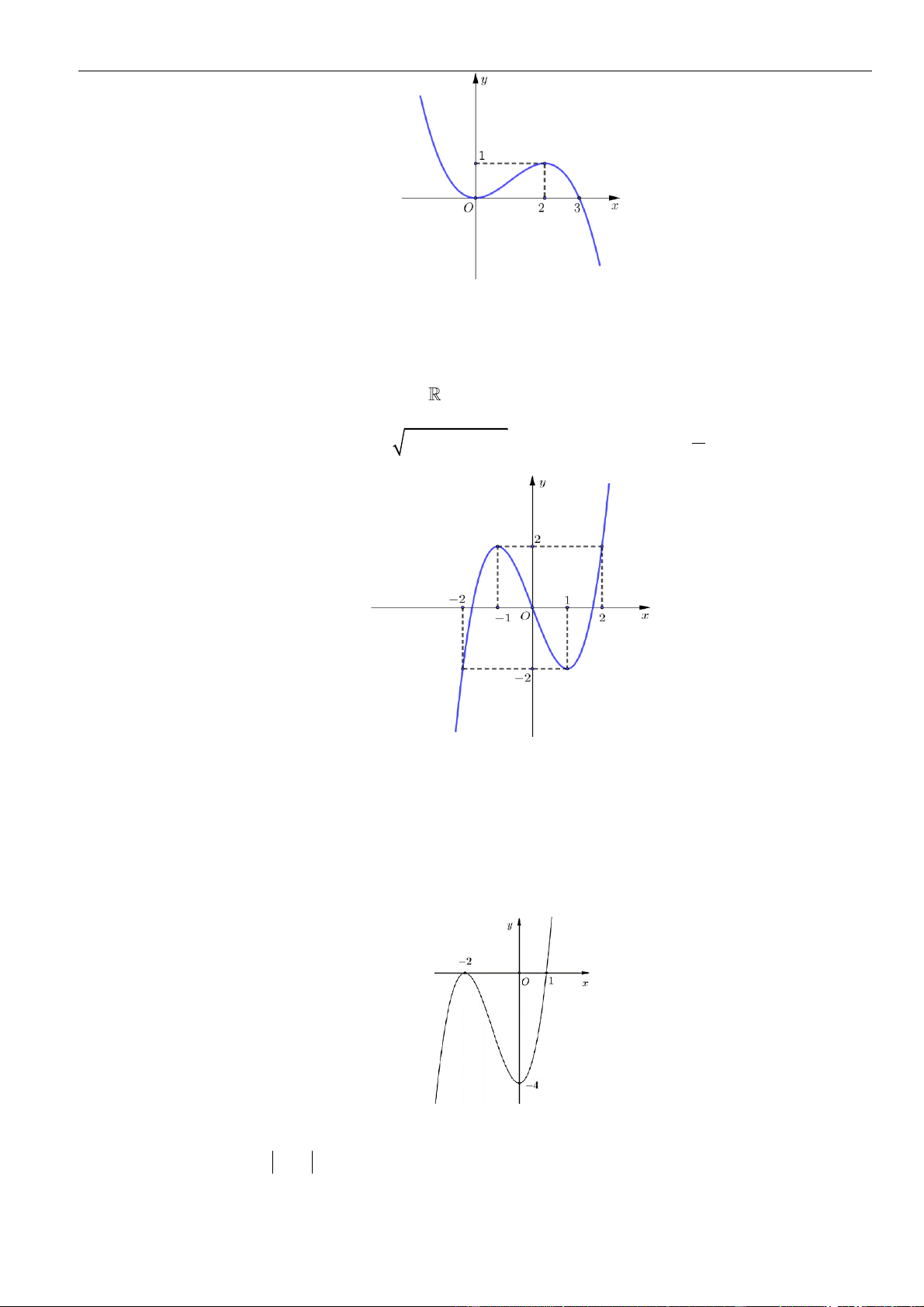
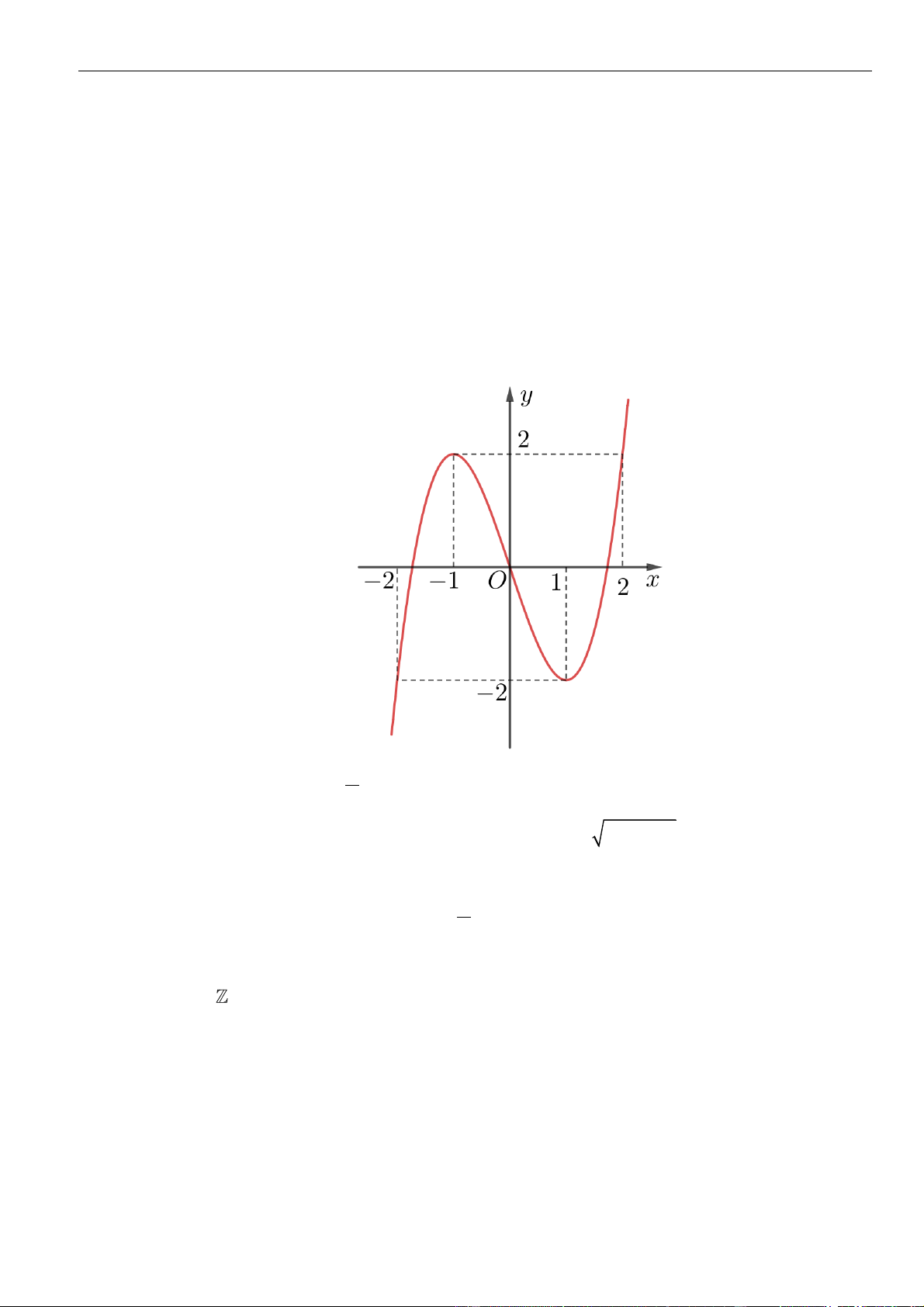
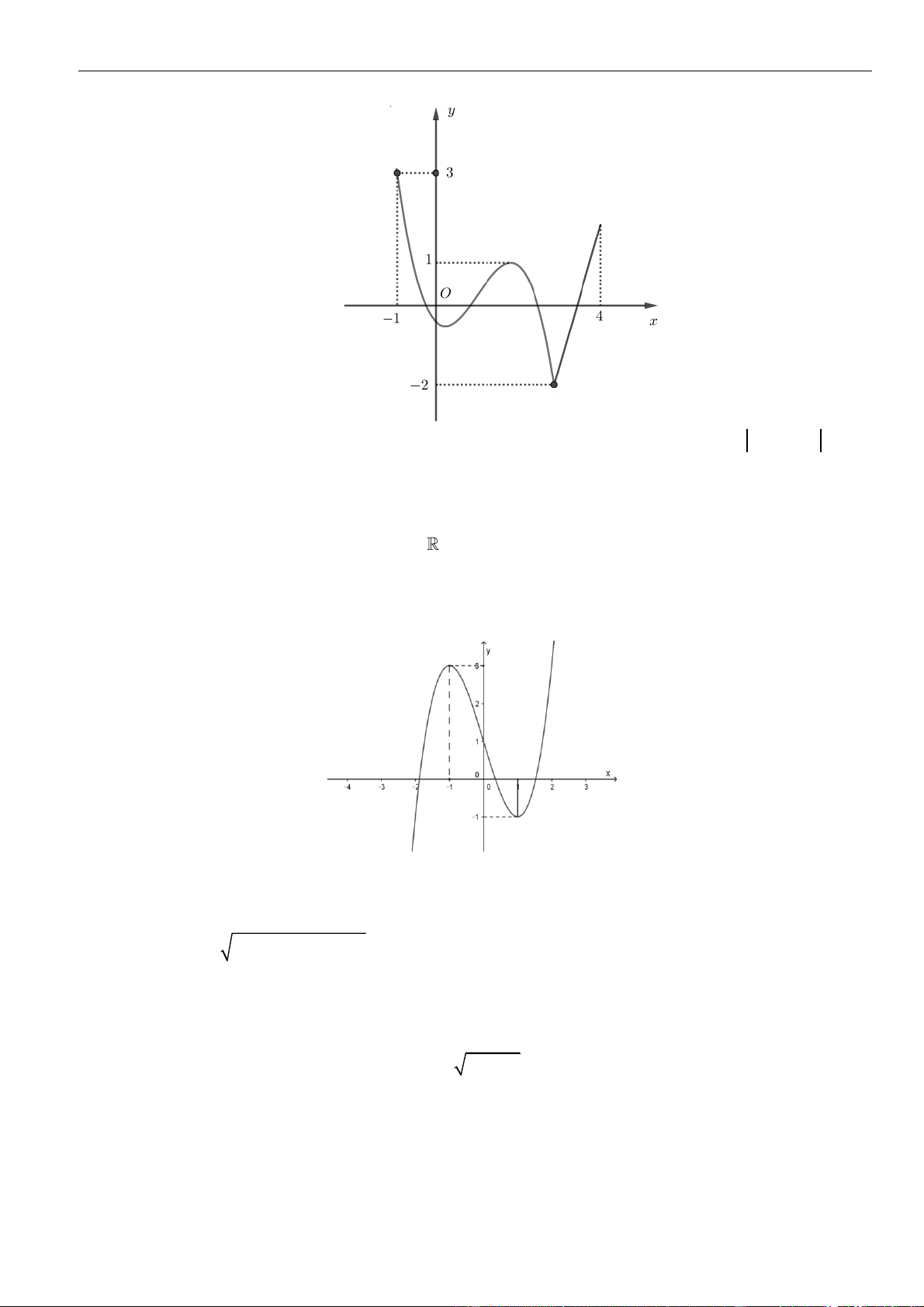
Cho hàm số bậc ba y = f (x) có đồ thị là đường cong trong hình vẽ bên. Số nghiệm thực phân
biệt của phương trình f ( 1 2 2
4 − x − x −1 ) = là 2021 A. 24 . B. 14 . C. 12 . D. 10 . x + 3 Câu 2:
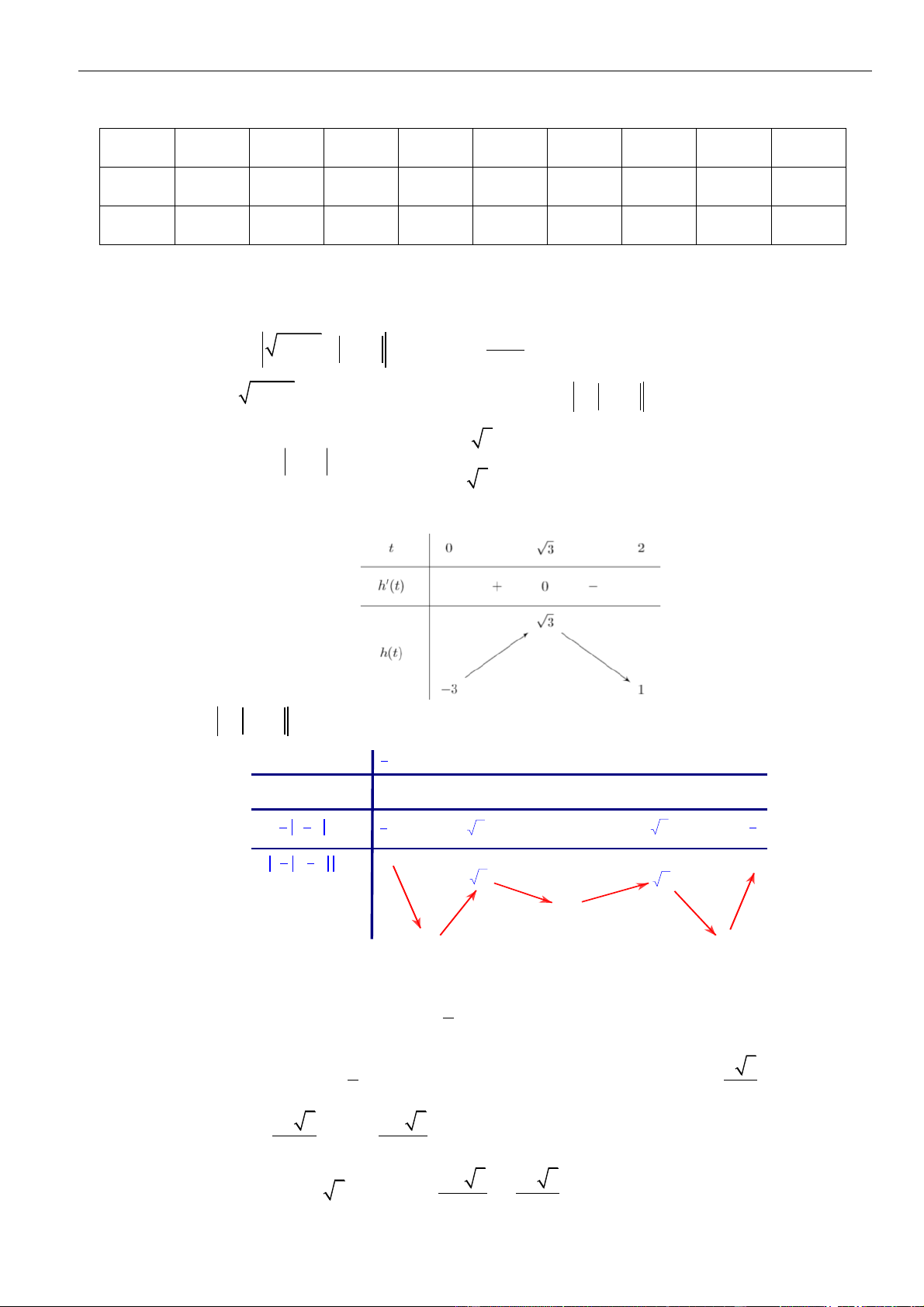
Cho hai hàm số u ( x) =
và f ( x) , trong đó đồ thị hàm số y = f ( x) như hình vẽ bên. 2 x + 3
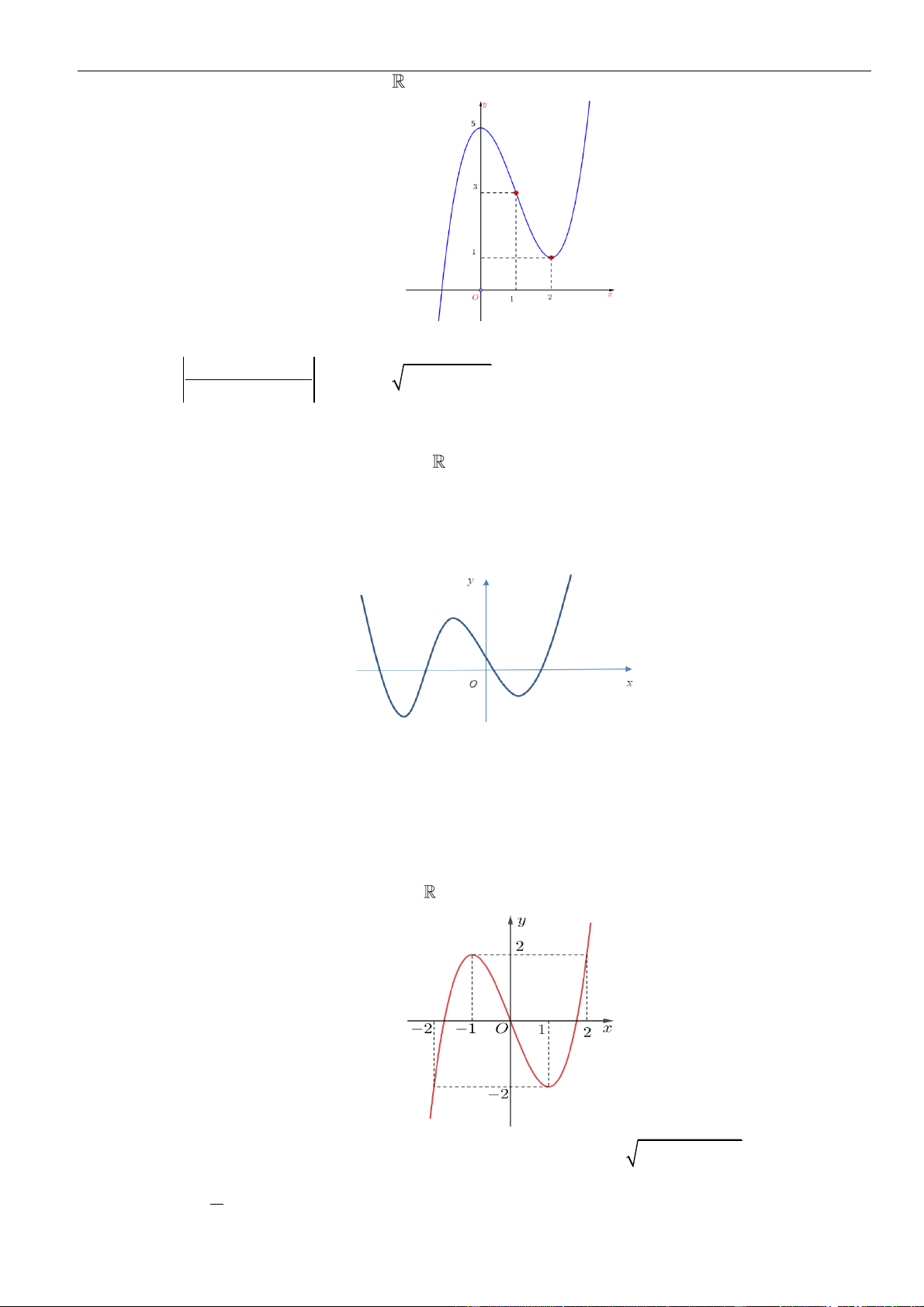
Hỏi có bao nhiêu số nguyên m để phương trình f (u ( x)) = m có đúng 3 nghiệm phân biệt? A. 1. B. 4 . C. 3 . D. 2 . Câu 3:
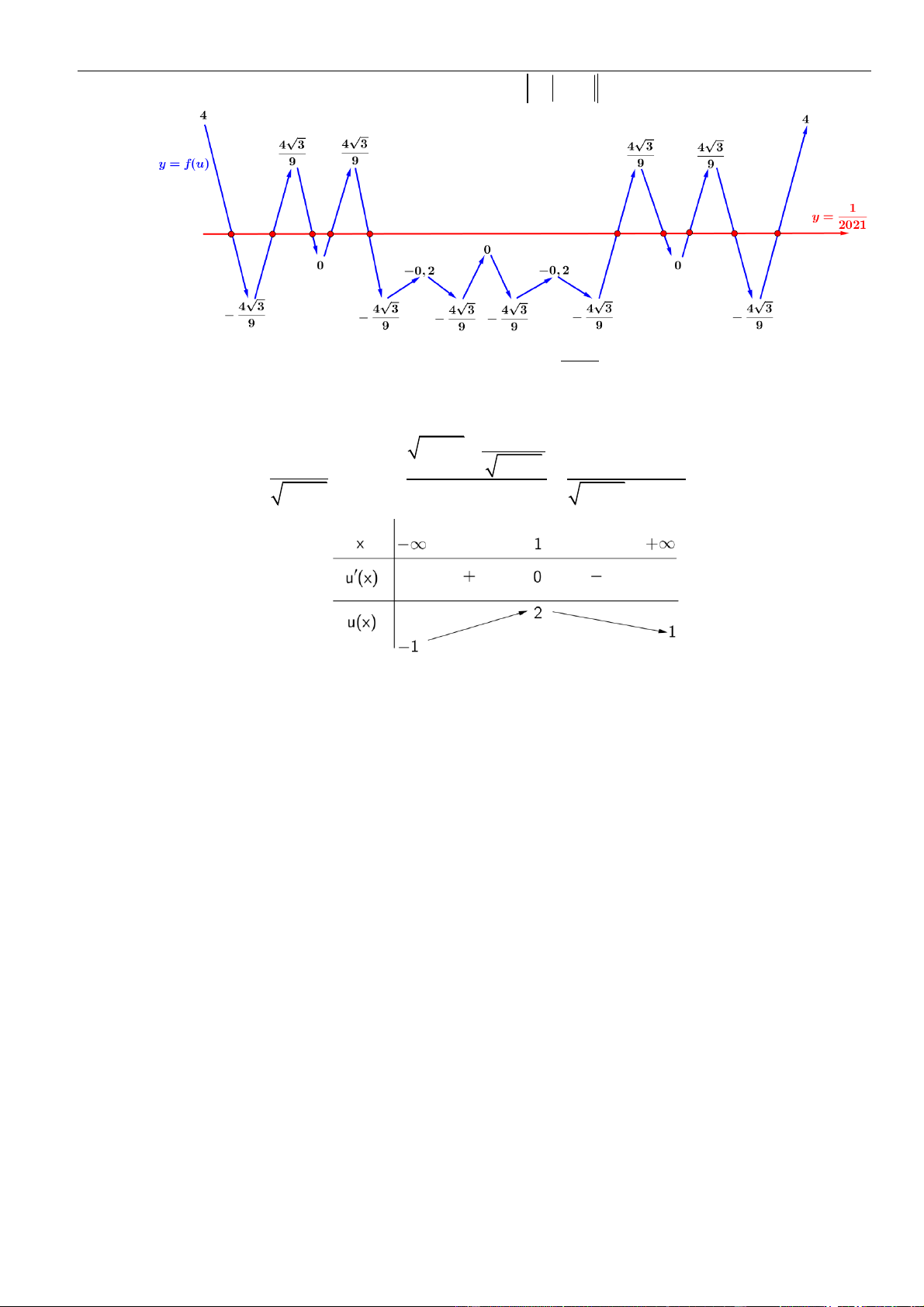
Cho hàm số y = f (x) có đạo hàm cấp hai trên R và có đồ thị y = f '(x) là đường cong trong hình vẽ bên.
Đặt g(x) = f ( f '(x) −1) . Gọi S là tập nghiệm của phương trình g '(x) = 0 . Số phần tử của tập S là A. 8 B. 6 C. 10 D. 9
1 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số Câu 4:
Cho hàm số f (x) liên tục trên
và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m để phương trình
 3sin x − cos x −1  f + 2 = f   ( 2
(m + 2) + 4 ) có nghiệm?
 2cos x − sin x + 4  A. 3 . B. 5 . C. 4 . D. 2 . Câu 5:
Cho hàm số y = f ( x) liên tục trên có đồ thị như hình vẽ bên dưới.Gọi (C và (C lần 2 ) 1 )
lượt là đồ thị của hai hàm số y = f  ( x) f ( x) −  f ( x) 2 .    và 2021x y =
.Số giao điểm của (C 1 ) và (C là 2 ) A. 1 B. 0 C. 2 D. 4 Câu 6: Biết hàm số ( ) 3 2
f x = ax + bx + cx + d đạt cực trị tại x = 1 và x = 2021. Có bao nhiêu số nguyên
m để phương trình f ( x) = f (m) có ba nghiệm phân biệt? A. 4037 . B. 2019 . C. 4001 . D. 2021 . Câu 7:
Cho hàm số y = f ( x) liên tục trên có đồ thị hình vẽ.
Có bao nhiêu giá trị nguyên của tham số m để phương trình f ( 4 + 2 f (cos x)) = m có nghiệm    x  0;    2 
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 2 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 A. 4 . B. 5 . C. 3 . D. 2 . Câu 8:
Cho hàm số y = f ( x) có đồ thị như hình vẽ sau: Có bao nhiêu số nguyên 1
m để phương trình f ( 3
2x − 6x + 2) = m − 5 có 6 nghiệm phân biệt 2 thuộc đoạn −1;2? A. 4 . B. 3 . C. 2 . D. 1. Câu 9: Cho hàm số y f x liên tục trên
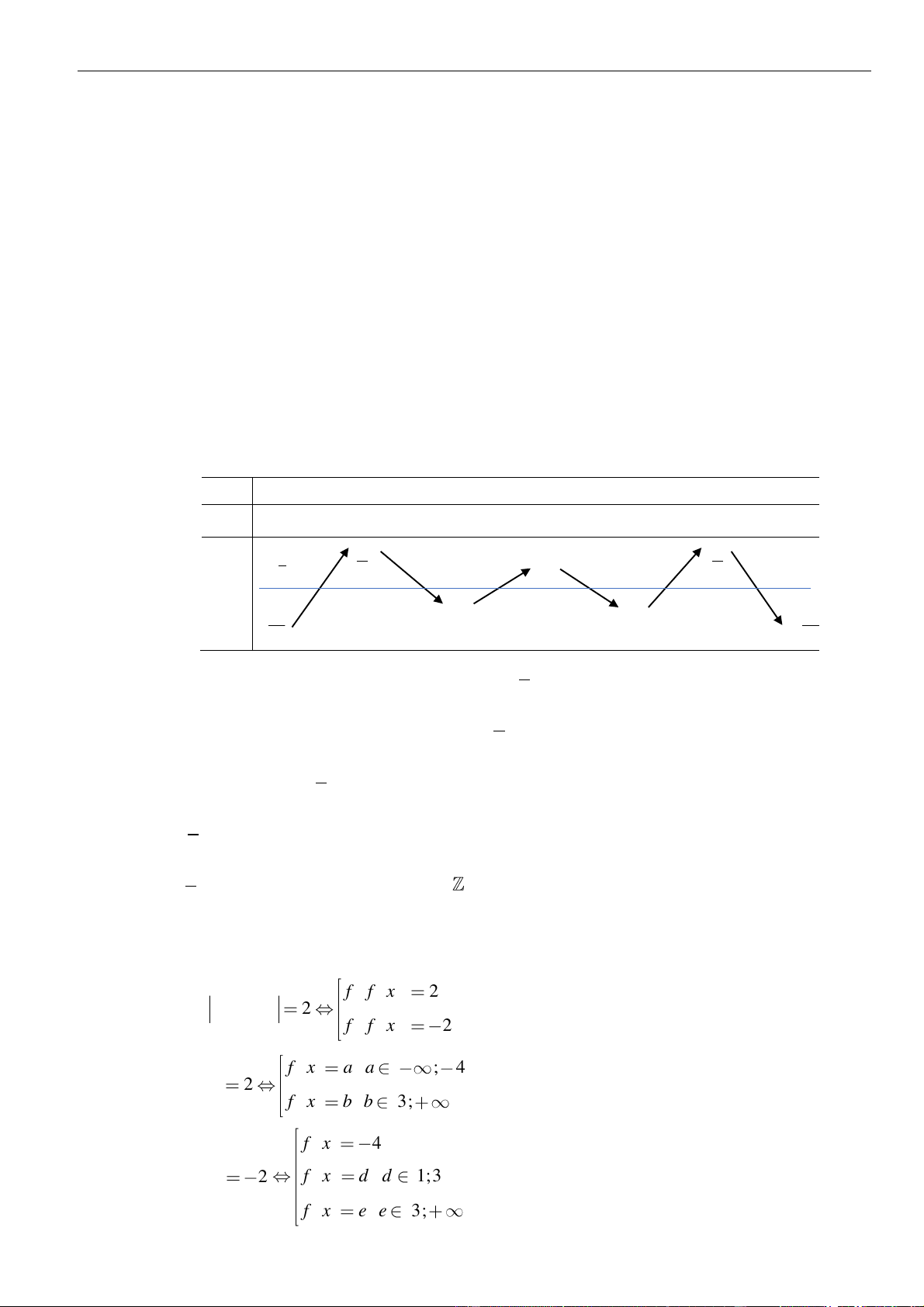
và có bảng biến thiên như hình vẽ
Số nghiệm của phương trình f f x 2 là A. 4 . B. 5 . C. 9 . D. 7 . Câu 10: Cho hàm số = ( ) 2 y
f x = ax + bx + c có đồ thị (C )
Có bao nhiêu giá trị nguyên của tham số m để phương trình 2
f ( x ) + (m − 2) f ( x ) + m − 3 = 0 có 6 nghiệm phân biệt? A. 2. B. 3. C. 1. D. 4.
Câu 11: Biết đồ thị hàm số bậc bốn y = f ( x) được cho bởi hình vẽ bên dưới. Tìm số giao điểm của đồ
thị hàm số y = g ( x) =  f   ( x) 2  − f
(x).f  (x) và trục hoành:
3 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số A. 4 . B. 0 . C. 6 . D. 2 . Câu 12: Cho hàm số 2
f (x) = x + 1+ x
. Số giá trị nguyên của tham số m để phương trình 1+ 4x + m −1 xf (x) −
= có hai nghiệm phân biệt là f (− − x + m − ) 0 1 4 1 A. 2 . B. 3 . C. 6 . D. 4 .
Câu 13: Cho hàm số f ( x) = ( 3 − m ) 3 2 x + mx + ( 2 m − m + ) 3 1 3 3 2
2 x + m + 2m với m là tham số. Có bao
nhiêu số nguyên m  20 − 20;20 
21 sao cho f ( x)  0 với mọi x 2020; 202  1 ? A. 2023 . B. 2022 . C. 2021 . D. 2020 .
Câu 14: Cho hàm số y = f ( x) 3 2
= 2x − 3x +1 . Tập hợp các giá trị m để phương trình   2sin x +1 f f = f   
(m) có nghiệm là đoạn a;b. Khi đó giá trị 2
4a + 8b thuộc khoảng nào   2  sau đây?  23   43 39   37 65  A. 7 ;   . B. (−2;5) . C. ;   . D. ;   .  2   3 2   3 4  x + x +
Câu 15: Cho hàm số f ( x) 2 5 2 =
. Có tất cả bao nhiêu giá trị nguyên dương của tham số m để bất 2x +1 phương trình f ( 2 x − x + ) 2 2021 3 18
28 − m 3x −18x + 28  m + 4042 nghiệm đúng với
mọi x thuộc đoạn 2;4. A. 673 . B. 808 . C. 135 . D. 898 .
Câu 16: Cho hàm số y = f (x) liên tục trên
và có bảng biến thiên như sau:
Số nghiệm của phương trình f ( 4 2 3x −4 x +2 2 )+1=0 là A. 2 . B. 3 . C. 6 . D. 5 .
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 4 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
Câu 17: Cho hàm số f ( x) có đồ thị như bên dưới
Số nghiệm phương trình 2 f (x +1− 6x +3) =1 là A. 3 . B. 4 . C. 6 . D. 5 . 1
Câu 18: Cho hàm số f ( x) 3
= x − mx + m −8, x  với m là một hằng số khác 0 . Biết rằng phương 2
trình f ( x) = 0 có đúng hai nghiệm phân biệt. Hỏi có bao nhiêu giá trị nguyên của k thỏa mãn
phương trình f ( x) = k có 3 nghiệm phân biệt ? A. 3 . B. 34 . C. 6 . D. 34 .
Câu 19: Cho hàm đa thức y = f ( x) có đồ thị như hình vẽ. Đặt ( ) = ( 2 g x
f x ) . Số nghiệm của phương trình g ( x).2g  (x)−1 = 0  là A. 11. B. 10. C. 13. D. 12.
Câu 20: Hàm số y = f ( x) liên tục trên
và có bảng biến thiên như hình vẽ Phương trình f ( 2
2x + 3) − 2 = 5 có bao nhiêu nghiệm? A. 3 . B. 5 . C. 6 . D. 4 .
5 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số
Câu 21: Cho hai hàm y = f ( x) và y = g ( x) liên tục trên
và có đồ thị như hình vẽ. Khi đó tổng số
nghiệm của phương trình f (g ( x)) = 0 và g ( f ( x)) = 0 là A. 25 . B. 22 . C. 21 . D. 26 .
Câu 22: Cho f ( x) là hàm số bậc ba. Hàm số f ( x) có đồ thị như sau:
Tìm tất cả các giá trị thực của tham số m để phương trình ( x f e + )
1 − x − m = 0 có hai nghiệm thực phân biệt.
A. m f (2) .
B. m f (2) −1.
C. m f ( ) 1 − ln 2 .
D. m f ( ) 1 + ln 2 .
Câu 23: Cho hàm số bậc ba y = f ( x) có đồ thị là đường cong trong hình bên dưới
Số nghiệm thực phân biệt của phương trình f ( 3
x f ( x)) +1 = 0 là A. 6 . B. 8 . C. 5 . D. 4 . Câu 24: Cho hàm số = ( ) 4 3 2 y
f x = ax + bx + cx + dx + e với (a, b, c, d , e  ) . Biết hàm số y = f ( x) có đồ thị như hình vẽ.
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 6 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
Có bao nhiêu giá trị nguyên của m trên −5;5 để phương trình f ( 2
−x + 2x + m) = e có bốn nghiệm phân biệt. A. 0 . B. 2 . C. 5 . D. 7 .
Câu 25: Cho hàm số y = f ( x) liên tục trên
có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của   
tham số m để phương trình f ( 4+ 2 f (cos x)) = m có nghiệm x 0;   .  2  A. 4 . B. 3 . C. 2 . D. 5 . Câu 26: Cho hàm số ( ) 3 = + − 2m f x x x
. Có bao nhiêu giá trị nguyên của tham số m để phương trình
f ( f ( x)) = x có nghiệm thuộc đoạn 1; 2 . A. 3. B. 4. C. 0. D. 2.
Câu 27: Cho hàm số y = f (x = ax3 )
+ bx2 + cx + d có đồ thị như hình dưới đây
Có tất cả bao nhiêu giá trị nguyên của tham số m  (− 5 ; 5 ) để phương trình 2
f (x) − (m + 4) f (x) + 2m + 4 = 0 (*) có 6 nghiệm phân biệt A. 2 . B. 4 . C. 3 . D. 5 .
7 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số
Câu 28: Cho hàm số y = f ( x) có đồ thị là đường cong trong hình bên.
Số nghiệm thực phân biệt của phương trình f ( 2
x f ( x)) + 2 = 0 là A. 8 . B. 12 . C. 6 . D. 9 .
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 8 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 BẢNG ĐÁP ÁN 1.D 2.C 3.C 4.B 5.B 6.A 7.A 8.B 9.D 10.B 11.B 12.D 13.B 14.D 15.A 16.C 17.B 18.D 19.D 20.A 21.C 22.A 23.A 24.B 25.A 26.B 27.C 28.D
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: Chọn D
y = g x = f ( 2 2 ( )
4 − x − x −1 ) với 1 g(x) = 2021 Ta đặt: 2
t = 4 − x , x   2
− ;2 thì suy ra y = g t = f ( 2 ( )
t − t − 3 ), t  0;2 2 t
 + t −3,t  0; 3    Suy ra: 2
h(t) = t − t − 3 =  . 2  t
− + t + 3,t   3;2   
Từ đó ta có BBT của hàm số h(t) như hình vẽ bên: Đặt 2
u = t − t − 3 thì ta cũng có BBT của u như sau: x 2 0 2 t 0 2 0 t t2 3 3 3 1 3 3 3 3 t t2 3 3 3 1 0 0
Nhìn vào đồ thị y = f (x) trên ta có được: 3 2
f (x) = ax + bx + cx,a  0 2    a =  0
f (1) = f (2) = 0, f "(1) = 0 3 Như vậy ta suy ra 2 f (x) = x ( x − )
1 ( x − 2) . Mà hàm số đó có cực trị bằng 4 3 −
tại x = x nên 0 3 9 4 − 3 3 + 3 suy ra f ( x =  x = 0 ) 0 9 3  +  − Như vậy: f = f ( ) 3 3 4 3 (3) 4, 3 = 0 − ,2, f   =   3 9  
9 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số
Từ đó, ta phác họa được đồ thị y = f (u) với 2
u = t − t − 3 như sau:
Dựa vào hình vẽ trên, ta kết luận phương trình 1 g(x) =
có tất cả 10 nghiệm phân biệt. 2021 Câu 2: Chọn C x x + 3 2 ( ) x + 3 − x + 3 2 x + 3 3 − 3x
Đặt t = u ( x) = ; u '( x) = =
; u '( x) = 0  x = 1 . 2 2 x + 3 2 x + 3 x + 3 ( 2 x + 3)
Dựa vào bảng biến thiên, ta có u ( x)( 1 − ;2 .
Phương trình f (u ( x)) = m trở thành f (t) = m , t ( 1 − ;2.
Dựa vào đồ thị đã cho ta có: t =
Khi m = 2 : phương trình f (t ) 0 = 2   
phương trình f (u ( x)) = m có 2 nghiệm phân t = 2 biệt.
Khi m = 1 : phương trình f (t ) = 1 có 3 nghiệm t  1
− ;0 ,t  0;1 ,t  1;2  phương 1 ( ) 2 ( ) 3 ( )
trình f (u ( x)) = m có 4 nghiệm phân biệt. Khi m 0; 1 − ;− 
2 : phương trình f (t ) = m có 2 nghiệm t  0;1 ,t  1; 2  phương trình 1 ( ) 2 ( )
f (u ( x)) = m có 3 nghiệm phân biệt.
Khi m = −3 : phương trình f (t ) = m có 1 nghiệm t = 1  phương trình f (u ( x)) = m có 1 nghiệm. Vậy m 0; 1 − ;−  2 . Câu 3: Chọn C
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 10 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
Ta có: g(x) = f ( f '(x) −1)  g '(x) = f "(x). f '( f '(x) −1)  f '(x) = 0  f '(x) = 0  = Phương f '(x) 0  
trình g '(x) = 0 
f '(x) −1 = 1
−  f '(x) = 0 
f '( f '(x) 1) 0   − =
f '(x) −1 = 2  f '(x) = 3   x = 1  −2
Ta có đồ thị y = f '(x) có cực trị tại x = 3 
x = x  (1;2)  0  f "(1) = 0  x = 1   2 −     f " = 0  
f '(x) = 0 có 3 nghiệm 
−2 ; x = x cùng với x = 1 là nghiệm bội chẵn 0   3  x =    3 f ' (x ) = 0  0
Tại phương trình f '(x) = 0 ta thấy có 2 nghiệm bội lẻ x = −1, x = 2 và nghiệm bội chẵn x = 1
Tại phương trình f '(x) = 3 ta thấy có 2 nghiệm mà đường thẳng y = 3 cắt đồ thị y = f (x) đó là
hai điểm x = x  (− ;  1
− ) và x = x  (2;+) 1 2
Vậy từ đó ta thấy phương trình g '(x) = 0 tổng cộng có tất cả 10 nghiệm. Câu 4: Chọn B Ta có: 1
−  sin x  1, −1  cos x  1 nên suy ra 2cos x − sin x + 4  0, x   . − − Đặt 3sin x cos x 1 t =
t(2cos x − sin x + 4) = 3sin x − cos x −1
2 cos x − sin x + 4
 (2t +1)cos x − (t + 3)sin x = −(4t +1) . −
Phương trình trên có nghiệm khi 9 2 2 2
(2t +1) + (t + 3)  (4t +1) 
t 1 2  t + 2  3 . 11
Nhìn vào hình trên ta thấy hàm số f (x) luôn đồng biến trên 2;  3 nên phương trình
 3sin x − cos x −1  f + 2 = f   ( 2
(m + 2) + 4 ) hay phương trình f ( t + ) = f ( 2 2 (m + 2) + 4 )
 2cos x − sin x + 4 
có nghiệm khi và chỉ khi phương trình 2
t + 2 = (m + 2) + 4 có nghiệm t thỏa mãn điều kiện 2  t + 2  3 2 2
 2  (m + 2) + 4  3  m + 4m −1 0  2 − 5  m  2 + 5 . Mà m
nên có tất cả 5 giá trị m thỏa mãn. Câu 5: Chọn B
Số giao điểm (C và (C là nghiệm của phương trình 2 ) 1 )
11 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số  ( ) ( ) −    ( ) 2 .  = 2021x f x f x f x  (*)
Từ đồ thị ta thấy f ( x) cắt trục Ox tại bốn điểm phân biệt có hoành độ lần lượt là x ; x ; x ; x 1 2 3 4
nên phương trình f ( x) = 0 có bốn nghiệm phân biệt x ; x ; x ; x 1 2 3 4
f (x) = a(x − x x − x x − x x − x 1 ) ( 2 ) ( 3 ) ( 4 ) x = x1 x = x Nếu  f ( x) 2 = 0  
thay vào (*) ta thấy vế trái âm,vế phải dương nên phương trình (*) x = x3 x = x  4 vô nghiệm
Nếu f ( x)  0 nên ta có phương trình ta có phương trình (*) tương đương với 2    ( )  ( ) − ( )   2021x     ( )  2021x f x f x f x f x =    = 2 2 2 [ f (x)] [ f (x)]  f (x)  [ f (x)] Ta có:
f (x) = a ( x − x x − x x − x x − x 1 ) ( 2 ) ( 3 ) ( 4 )  
f x = a ( 1 1 1 1 ( ) x − x x − x x − x x − x + + +   1 ) ( 2 ) ( 3 ) ( 4 ) x − x x − x x − x x − x  1 2 3 4   1 1 1 1  f   (x) 1 1 1 1
f (x) = f (x) + + +  = + + +   x − x x − x x − x x − x f (x) x − x x − x x − x x − x  1 2 3 4  1 2 3 4        Khi đó: f (x) 1 1 1 1   =  + + +   f (x)  x − x x − x x − x x − x  1 2 3 4   1 1 1 1  = − + + +    ( x x ) 0 2
(x x )2 (x x )2 (x x )2  − − − −  1 2 3 4    2021x  ( )  2020x f x Mà  0 nên phương trình   =
vô nghiệm,do đó phương trình vô 2 [ f (x)] 2  f (x)  [ f (x)] nghiệm. Câu 6: Chọn A Ta có f ( x) 3 2
= ax + bx + cx + d f (x) 2
= 3ax + 2bx + cx
Do hàm số có 2 điểm cực trị là: 1 x = 1 và 2 x = 2021.  2b + = − =  1 x 2 x 2022  b  = 3033 3 − a a Nên:    3  c = 6063a = = 1 x . 2 x 2021  3a
Xét phương trình: f ( x) = f (m) 3 2 3 2
ax + bx + cx + d = am + bm + cm + d a ( 3 3
x − m ) + b( 2 2
x − m ) + c(x − m) = 0  a( 3 3 x − m ) − a ( 2 2 3033
x − m ) + 6063(x − m) = 0  (x − m)( 2 2
x + mx + m − 3033x − 3033m + 6063) = 0
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 12 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 x − m = 0   2 2
x + mx + m − 3033x −3033m + 6063 = 0 (*)
Để phương trình f ( x) = f (m) có 3 nghiệm phân biệt thì pt có 2 nghiệm phân biệt khác m .  =  (m −3033)2 − 4( 2
m − 3033m + 6063)  0   2 m +  (m −3033) 2
m + m − 3033m + 6063  0 2 2 2
m −6063m +3033 − 4m + 4.3033m − 4.6063  0  1 − 009  m  3031     2 m +  (m −3033) 2
m + m − 3033m + 6063  0
m  2021; m  1 Vậy: m ( 1009 − ; ) 3031 \ 1; 
2021 có 4037 giá trị m nguyên. Câu 7: Chọn A   
Đặt t = cos x , với x  0;    t (0 ) ;1 .  2 
Từ đồ thị suy ra f (t)( 2
− ;0)  4 + 2 f (t)(0;4)  u = 4 + 2 f (t) (0;2) .
Ta có f (u) = m với u (0; 2) .   
Phương trình đã cho có nghiệm x  0; 
 khi và chỉ khi phương trình f (u) = m có nghiệm  2 
u  (0; 2)  −2  m  2 . Do m  nên m  2 − ; 1 − ;0  ;1 .
Vậy có 4 giá trị nguyên của tham số m thoả mãn yêu cầu bài toán. Câu 8: Chọn B
Đặt: g ( x) = f ( 3
2x − 6x + 2) ; g( x) = ( 2 x − ) f ( 3 6 6 . 2x − 6x + 2) 2 6x − 6 = 0 (1) 
g( x) = 0 ⇔  f   ( 3
2x − 6x + 2) = 0 (2)
13 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số x = 1 − Giải: 2 6x − 6 = 0 ⇔  x =1 x = 2 −  1 − ;2  x =1 (nghi m Ö k p) Ð x  1 − ,87   1 − ;2  3  
2x − 6x + 2 = −2 x  0, 34    3 
2x − 6x + 2 = 0  x 1,53 Giải:   f ( 3
2x − 6x + 2) = 0 ⇔  ⇔  3
2x − 6x + 2 = 3  x  1 − ,64 1 − ;2  3
2x −6x + 2 = 6 x  0 − ,16  x 1.81   x = 1 − (nghi m Ö k p) Ð  x = 2
Bảng biến thiên của g ( x) trên đoạn −1;2 x 1 − −0.16 0.34 1 1, 53 1,81 2 g( x) 0 + 0 − 0 + 0 − 0 + 0 − 0 g ( x) 7 7 1 y = m − 5 2 2 2 2 13 − 0 0 13 − 4 4
Số nghiệm của phương trình f ( 1 3
2x − 6x + 2) = m − 5 bằng số giao điểm của đồ thị hàm số 2
g ( x) = f ( 3
2x − 6x + 2) và đường thẳng 1 y = m − 5 . 2 Kẻ đường thẳng 1 y =
m − 5 trên cùng bảng biến thiên của g ( x) . Điều kiện để đường thẳng 2 1 y =
m − 5 cắt đồ thị hàm số g ( x) = f ( 3
2x − 6x + 2) tại 6 điểm phân biệt là: 2 1 0 
m − 5  2 ⇔ 10  m  14 . Vì m  ⇒ m 11;12;  13 2
Vậy có 3 số nguyên m thỏa mãn ycbt. Câu 9: Chọn D f f x 2 Ta có: f f x 2
. Dựa vào bảng biến thiên ta thấy: f f x 2 f x a a ; 4 f f x 2 . f x b b 3; f x 4 f f x 2 f x d d 1;3 . f x e e 3;
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 14 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 f x a a ; 4 vô nghiệm; f x b b 3; có 2 nghiệm. f x 4 có 1 nghiệm; f x d d 1;3 có 2 nghiệm. f x e e 3; có 2 nghiệm f f x 2 có 7 nghiệm. Câu 10: Chọn B Xét phương trình 2
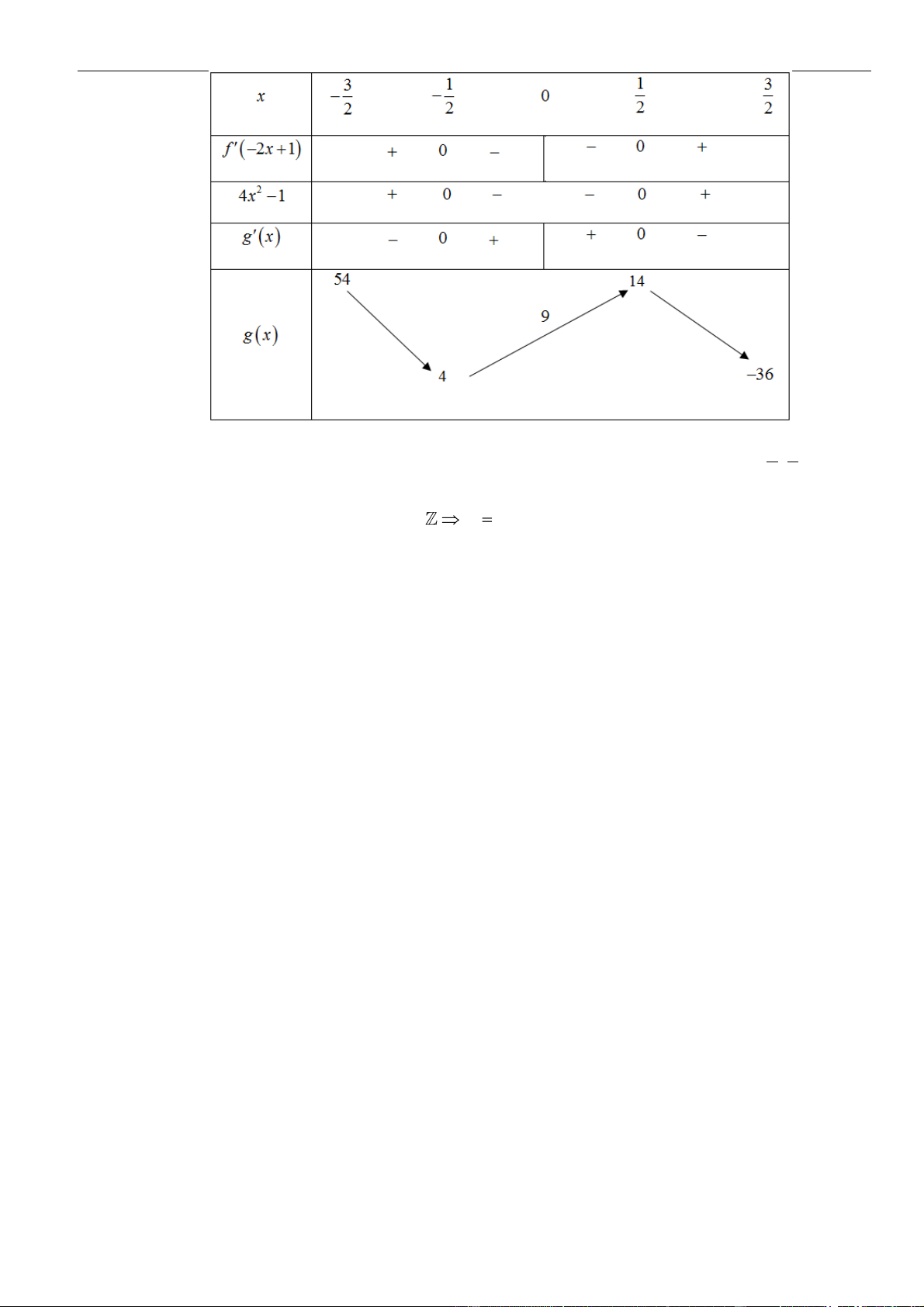
f ( x ) + (m − 2) f ( x ) + m − 3 = 0 .  f ( x ) = 1 −
Nhận thấy 1− (m − 2) + (m − 3) = 0   .  f
 ( x ) = 3 − m
Từ đồ thị hàm số f ( x) , suy ra đồ thị hàm số f ( x ) như sau:
Với f ( x ) = 1
− , ta được 2 nghiệm x .
Để phương trình đã cho có 6 nghiệm phân biệt, tức là phương trình f ( x ) = 3 − m có 4 nghiệm phân biệt.  Hay 1
−  3 −  3  0   4 m m m ⎯⎯⎯ →m1;2;  3 .
Như vậy có 3 giá trị nguyên của m thỏa mãn. Câu 11: Chọn B
Ta có phương trình hoành độ giao điểm của hai đồ thị y = g ( x) và Ox là:     ( )    2  −  ( ) f x f x
f x . f  ( x) = 0  f ( x). f  ( x) −  f   ( x) 2 ( )  = 0     = f  ( x) 0 
Ta thấy đồ thị hàm số y = f ( x) cắt trục Ox tại 4 điểm phân biệt có hoành độ x , x , x , x . 1 2 3 4
Giả sử f ( x) = a( x − x x − x x − x x − x
, a  0, x x x x 1 ) ( 2 ) ( 3 ) ( 4 ) 1 2 3 4
Ta có: f ( x) = a ( x − x x − x x − x + a x − x x − x x − x 2 ) ( 3 ) ( 4 ) ( 1 ) ( 3 ) ( 4 )
+a ( x − x x − x x − x + a x − x x − x x − x 1 ) ( 2 ) ( 4 ) ( 1 ) ( 2 ) ( 3 ) f ( x) 1 1 1 1 Ta có: = + + + f ( x) x − x x − x x − x x − x 1 2 3 4   f (x) 1 1 1 1 Ta có:   =  − − − − = vô nghiệm. f  ( x) 0  (x − x ) 0 2
(x − x )2 (x − x )2 (x − x )2 1 2 3 4
Vậy số giao điểm của đồ thị hàm số y = g ( x) và trục hoành bằng 0 . Câu 12: Chọn D
15 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số x Ta có: 2
f (x) = x + 1+ x f '(x) = 1+  0, x   . 2 1+ x Suy ra hàm số 2
f (x) = x + 1+ x luôn đồng biến trên . Mặt khác, ta lại có: 1 1 2
f (−x) = −x + 1+ x = = . 2 + + f (x) x 1 x + + −
Nên phương trình tiếp theo tương đương với: 1 4x m 1 xf (x) − = . f (− − x + m − ) 0 1 4 1
xf (x) − (1+ 4x + m−1) f (1+ 4x + m −1) = 0 .
xf (x) = (1+ 4x + m −1) f (1+ 4x + m −1) .
Đến đây ta xét hàm đặc trưng y = g t = tf t = t ( 2 t + t + ) 2 2 ( ) ( ) .
1 = t + t t +1 . 2 t Có 2
g '(t) = 2t + t +1 +  0, t  
nên suy ra g(t) luôn đồng biến trên . 2 t +1
g(x) = g (1+ 4x + m −1)  x =1+ 4x + m −1  4x + m −1 = x −1. x −1  0  x  1
Do 4x + m −1  0 nên suy ra    . 4x + m −1 =  (x − )2 2 1
m = x − 6x + 2 Xét hàm 2
y = p(x) = x − 6x + 2, x
  1 p (x) = 2x − 6 = 0  x = 3 .
Ta có bảng biến thiên của hàm p(x) như sau:
Dựa vào BBT trên để phương trình có hai nghiệm phân biệt thì m ( p(3); p(1)  m( 7 − ;−  3 .
Như vậy, ta kết luận có tất cả 4 giá trị nguyên thỏa mãn yêu cầu đề bài. Câu 13: Chọn B f ( x) = ( 3 1− m ) 3 2 x + 3mx + ( 2 3m − 2m + 2) 3
x + m + 2m  0 x  2020;  2021
 (x + m)3 + 2(x + m)  (mx)3 + 2mx x  2020;  2021 (1) Xét hàm số 3 2
f (t) = t + 2t, f '(t) = 3t + 2  0 t
Vậy hàm số f (t) đồng biến trên nên ( ) 1 suy ra +     x x m mx xm x    2021 2020; 2021 2020; 2021  m  . x −1 2020 Vậy trên đoạn  2020 − ; 
2021 có 2022 giá trị nguyên của m thỏa mãn. Câu 14: Chọn D
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 16 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 x = Ta có: 2
y = 6x − 6x ; y = 0 0   . x =1 Bảng biến thiên: 2sin x +1 1  1 3  2sin x +1 Ta có: = sin x +  − ;   suy ra f    0  ;1 nên 2 2  2 2  2    2sin x +1 f f     0  ;1 .   2    +  3 2
2m −3m +1 0 Phương trình 2sin x 1 f f = f   
(m) có nghiệm  0  f (m) 1     2  3 2
2m −3m  0 1 3  −  m  . 2 2 Vậy 1 3 2
4a + 8b = 4. + 8. =13. 4 2 Câu 15: Chọn A Đặt 2 2
u = 3x −18x + 28 = 3(x − 3) +1 = 3( x − 2)( x − 4) + 4 do đó ta có với x  2;4 thì u 1;2.
Biến đổi BPT ta được 2021 f (u) − .
m u m + 4042  2021 f (u) − 2  m(u +   ) 1 . x + x + u + u + u + u Ta có f ( x) 2 5 2 = f u − = − = 2x + nên ( ) 2 2 5 2 2 2 1 2u +1
2u + do vậy bất phương trình được 1 ( 2 2021 u + u) 2021u biến đổi tiếp  m(u + ) 1  m  2u +1 2u + . 1 2021u
Lúc này yêu cầu bài toán tương đương m  , u
 1;2  m  min g(u) . 2u +1 u   1;2 2021u 2021
Xét hàm số g(u) =
,u 1;2 ta có g (  u) =  0, u
  1;2 do vậy hàm số 2   2u +1 (2u + ) 1 2021u 2021
g (u) tăng trên đoạn 1;2 . Vì vậy min g(u) = = g ( ) 1 = . u   1;2 2u +1 3
Kết hợp với m là các số nguyên dương ta được m 1;2;3;...;  673 .
Vậy tìm được 673 số nguyên dương thỏa mãn yêu cầu bài toán. Câu 16: Chọn C Câu 17: Chọn B Đặt 1
t = x +1− 6x + 3 , x  − . 2
17 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số 3 Ta có t = 1−
= 0  x =1. Khi đó bảng biến thiên của hàm số là 6x + 3
Phương trình đã cho trở thành f (t) 1
= . Dựa và đồ thị ta thấy phương trình có 3 nghiệm là 2
t = a (−1;0) 
t = b (1;2) . t = c  (2;3)
Dựa vào bảng biến thiên của hàm số t = x +1− 6x + 3 ta có Phương trình
t = a x +1− 6x + 3 = a có 2 nghiệm và phương trình
t = b x +1− 6x + 3 = b có 1 nghiệm và Phương trình t = c x +1− 6x + 3 = c có 1 nghiệm.
Vậy phương trình 2 f (x +1− 6x +3) =1 có 4 nghiệm. Câu 18: Chọn D
Ta có: hệ số a = 1  0 và f ( x) = 0 có đúng hai nghiệm phân biệt.
Đồ thị hàm số có 2 điểm cực trị và 1 điểm thuộc trục hoành. m f ( x) m 2 = 3x −
. f ( x) = 0  x =  (m  0) . 2 6 3   Trường hợp m 1 m 1 :   − m + m − 8 = 0    m = 24 . 6 2 6   m = f ( x) 3 24 :
= x −12x +16 .
f ( x) = k có 3 nghiệm phân biệt  k (0;32) .
Có 31 giá trị nguyên của k thỏa mãn. 3   Trường hợp 1 m 1 m : −   + m + m − 8 = 0    m = 6 . 6 2 6   m = f ( x) 3 6 :
= x − 3x − 2 .
f ( x) = k có 3 nghiệm phân biệt  k ( 4 − ;0) .
Có 3 giá trị nguyên của k thỏa mãn.
Vậy có 34 giá trị nguyên của k thỏa mãn. Câu 19: Chọn D
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 18 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023   f ( 2 x ) = 0 ( ) 1 g (x) = 0  f ( 2x ) = 0    1
Ta có g ( x).2g  (x) −1 = 0     f    ( 2x) = (2 1 ) . g ( x) =    f ( 1 2 x ) 2 =  2  2   f ( 1 2 x ) = − (3)  2
Từ đồ thị hàm số y = f ( x) suy ra 2
x = a  −1  +) ( ) 2 1  x = b   (0; )
1 . Suy ra phương trình có 4 nghiệm phân biệt.  2 x = c  1  2
x = d  −1,(d a)  +) (2) 2
 x = e(0; )
1 , (e b) . Suy ra phương trình có 4 nghiệm phân biệt khác 4 nghiệm  2
x = f 1,( f c) 
phân biệt của phương trình. 2 x = m  1
− ,(m d,a)  +) (3) 2
 x = n(0 ) ;1 , (n  ,
e b) . Suy ra phương trình có 4 nghiệm phân biệt khác 4 nghiệm  2
x = p 1,( p f ,c) 
phân biệt của phương trình và 4 nghiệm phân biệt của phương trình.
Vậy phương trình g ( x).2g  (x)−1 = 0  có tất cả 12 nghiệm Câu 20: Chọn A
Gọi g ( x) = f ( 2
2x + 3) − 2 . Ta có: g ( x) = x f ( 2 ' 4 . ' 2x + 3) . x = 0  g '( x) 2 = 0  2x + 3 = 1 −  x = 0  . 2 2x + 3 = 3 
19 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số Ta có bảng biến thiên: g (x) = 5
Mà g ( x) = 5  
. Từ bảng biến thiên ta thấy phương trình có 3 nghiệm. g  ( x) = 5 − Câu 21: Chọn C f (x) = 2 − (1) 
Ta có g ( f ( x)) = 0   f ( x) = ,( (0 ) ;1 ) (2) .   f  ( x) = 3 (3)
Dựa vào đồ thị hàm số g ( x) suy ra phương trình ( )
1 có 4 nghiệm; phương trình (2) có 5
nghiệm và phương trình (3) có 1 nghiệm. Vậy phương trình g ( f ( x)) = 0 có 10 nghiệm. g (x) = 3 − (4)  g (x) = 1 − (5) 
Ta có f ( g ( x)) = 0  g ( x) = 1 (6) .
g(x) = a,(a  (1;2)) (7)
g(x) = b,  (b  (4;5)) (8)
Dựa vào đồ thị hàm số g ( x) suy ra phương trình (4) có 1 nghiệm; phương trình (5);(6);(7)
mỗi phương trình có 3 nghiệm và phương trình (8) có 1 nghiệm. suy ra phương trình
f ( g ( x)) = 0 có 11 nghiệm.
Vậy tổng số nghiệm của phương trình f (g ( x)) = 0 và g ( f ( x)) = 0 là 21. Câu 22: Chọn A Ta có:
( x + )1− − = 0  ( x f e x m f e + ) 1 − x = m ( ) 1 .
Đặt = x +1  = x t e t
e  0, x
. Ta có bảng biến thiên: Với = x t
e +1  x = ln (t − ) 1 . Ta có: ( )
1  f (t ) − ln (t − ) 1 = m (2) .
Khi đó, phương trình đã cho có hai nghiệm thực phân biệt khi và chỉ khi phương trình (2) có
hai nghiệm thực phân biệt lớn hơn 1.
Xét hàm số g (t) = f (t) − ln (t − ) 1 ,t  1 ta có:
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 20 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
g(t ) = f (t ) 1 −
g(t ) =  f (t ) 1 , 0 = . t −1 t −1
Dựa vào đồ thị các hàm số 1
y = f ( x) và y =
ta có: f (t ) 1 =  t = 2 . x −1 t −1
Ta có bảng biến thiên của hàm số g (t) :
Số nghiệm của phương trình (2) bằng số giao điểm của đồ thị hàm số g (t) và đường thẳng y = m .
Dựa vào bảng biến thiên, phương trình (2) có hai nghiệm thực phân biệt lớn hơn 1
m g (2)  m f (2) − ln1  m f (2) . 3
x f (x) = a ( 3 −  a  − ) 1 ( ) 1 
Câu 23: Phương trình f ( 3
x f ( x)) +1 = 0  f ( 3 x f ( x)) 3 = 1
−  x f (x) = b ( 5 −  b  3 − ) (2).  3 x f ( x) = 0 (3)  k Xét phương trình 3
x f ( x) = k f ( x) = . 3 x k 3 − k Đặt g ( x) = , g( x) =  0, x
  0 và k  0 . 3 x 4 x
lim g ( x) = lim g ( x) = 0 , lim g ( x) = + , lim g ( x) = − . − + x→− x→+ x→0 x→0
Ta có bảng biến thiên của hàm số g ( x)
21 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số
Dựa vào bảng biến thiên và đề bài, suy ra trong mỗi khoảng ( ;0
− ) và (0;+) phương trình
f ( x) = g ( x) có đúng một nghiệm.
Vì a, b  0 nên phương trình ( )
1 và (2) mỗi phương trình có 2 nghiệm phân biệt khác nhau. x = 0 x = 0 Xét phương trình (3) 3
: x f ( x) = 0    
, với c khác các nghiệm của ( ) 1 f  ( x) = 0 x = c  0 và (2) .
Vậy phương trình f ( 3
x f ( x)) +1 = 0 có đúng 6 nghiệm. Câu 24: Chọn B
Dựa vào đồ thị hàm số y = f '( x) , suy ra hàm số y = f '( x) là hàm số bậc 3 qua 0 không đổi
dấu và đi qua 3 đổi dấu từ + sang -. Mặt khác lim f '( x) = − nên k  0 . x→+
Do đó, hàm số y = f '( x) có dạng f ( x) 2 '
= k.x .(x −3). 1 1 3 1 1
Vì f '(2) = 1 nên k = − . Suy ra f '( x) 3 2
= − x + x f (x) 4 3 = − x + x + e 4 4 4 16 4 Xét phương trình
f (−x + x + m) 1 = e  −
(−x + x + m)4 1 2 2
+ (−x + 2x + m)3 2 2 2 = 0 16 4  (
−x + 2x + m = 0 1 2
−x + 2x + m) ( 2
−x + 2x + m − 4) 2 3 ( ) = 0   2
−x + 2x + m − 4 = 0  (2) Phương trình f ( 2
−x + 2x + m) = e có bốn nghiệm phân biệt khi và chỉ khi phương trình ( ) 1 , ( 1  + m  0
2) đều có hai nghiệm phân biệt    m  3. 1  + m − 4  0
Mặt khác, m là số nguyên trên −5;5 nên m4;  5 .
Vậy có 2 giá trị nguyên của m thoả yêu cầu bài toán. Câu 25: Chọn A   
Đặt t = cos x . Do x  0;   nên t (0; 
1  f (t )  2 − ;0)  2 
 4 + 2 f (cos x) = 4 + 2 f (t) 0;2)  f ( 4+ 2 f (cos x)) 2 − ;2)   
Vậy phương trình f ( 4+ 2 f (cos x)) = m có nghiệm x 0; 
  −2  m  2  2 
Do m nguyên nên m  2 − ; 1 − ;0  ;1
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 22 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
Vậy có bốn giá trị của tham số m để phương trình f ( 4+ 2 f (cos x)) = m có nghiệm    x  0;   .  2  Câu 26: Chọn B y = f  (x)
Đặt: y = f ( x) ta có hệ: 
f ( y) + y = f (x) + x (*)  f  ( y) = x Xét hàm số: ( ) = ( ) 3 + = + 2 − 2m g t f t t t tg(t) 2 = 3t + 2  0 t  
g (t) luôn đồng biến trên
Từ phương trình (*) ta có ( ) = ( )  =  ( ) 3 m 3 =  + − 2 =  = 2m g y g x y x f x x x x x x
Để phương trình f ( f (x)) = x có nghiệm thuộc đoạn 1;2 thì 3 3
Min x  2m Max x x   1;2 x   1;2
 1  2m  8  0  m  3, m là số nguyên nên m0;1;2;  3 Vậy Chọn B Câu 27: Chọn C Ta có 2
f (x) − (m + 4) f (x) + 2m + 4 = 0 (  =
f x − )( f x − − m) f (x) 2 ( ) 1 ( ) 2 ( ) 2 = 0  
f (x) = 2 + m  (2) Phương trình ( ) 1 có 4 nghiệm phân biệt
Vậy để phương trình (*) có 6 nghiệm phân biệt thì phương trình(2) có 2 nghiệm phân biệt khác
nghiệm của phương trình ( ) 1 .
Phương trình (2) có hai nghiệm phân biệt khác nghiệm của phương ( ) 1 khi và chi khi m + 2 = 0 m = 2 −   
. Vì m Z; m  ( 5 − ;5) nên m =  2 − ;3;  4 m + 2  4 m  2
Vậy m có 3 giá trị.
23 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số 2 x f (x) = 0  2
x f ( x) =  (0; ) 1
Câu 28: Ta có: f ( 2
x f ( x)) + =  f ( 2 2 0 x f ( x)) = 2 −   . 2
x f ( x) =    (2;3)  2
x f ( x) =    (3;4) x = 0 2
x f ( x) = 0  
. Phương trình f ( x) = 0 có 2 nghiệm phân biệt khác 0. f  ( x) = 0 Xét phương trình 2
x f ( x) = m với m  0 . Rõ ràng x = 0 không là nghiệm của phương trình. Do đó ta có: 2 m
x f ( x) = m f ( x) = . 2 x − Xét hàm số ( ) m 2m g x = có g( x) =
. Từ đó ta có BBT của g ( x) : 2 x 3 x
Suy ra đồ thị hàm số y = g ( x) luôn cắt đồ thị hàm số y = f ( x) tại 2 điểm phân biệt có hoành
độ khác 0 và khác hai nghiệm của phương trình f ( x) = 0 . Vậy mỗi phương trình 2
x f ( x) =  (0 ) ;1 , 2
x f ( x) =  (2;3) , 2
x f ( x) =  (3; 4) có hai
nghiệm phân biệt. Các nghiệm của các phương trình này không trùng nhau, khác 0 và khác hai
nghiệm của phương trình f ( x) = 0 .
Do đó phương trình f ( 2
x f ( x)) + 2 = 0 có 9 nghiệm thực phân biệt.
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 24 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 D ẠNG 2
Bài toán tương giao đồ thị hàm số 02 x − x x + x + Câu 1: Cho hai hàm số 1 1 2 y = + + +
và y = x + 2 − x − m ( m là tham số thực) có đồ x x +1 x + 2 x + 3
thị lần lượt là (C , C . Tập hợp tất cả các giá trị của m để (C và (C cắt nhau tại đúng 2 ) 1 ) 1 ) ( 2 )
bốn điểm phân biệt là A. ( 2; − + ) .
B. (−; − 2.
C. −2; + ) . D. (− ;  − 2) . Câu 2:
Tìm tập hợp tất cả các giá trị của tham số m để đồ thị hai hàm số y = ( 2 2x + ) 1 x −1 và 11 1 y = −
+11+ m cắt nhau tại 2 điểm phân biệt? 3x − 4 2 − x A. ( ; − 0). B. ( ) ;1 − . C. (  ;1 − . D. ( ; − 2 . Câu 3:
Có bao nhiêu cặp số thực (a;b) để bất phương trình ( x − )( x + )( 2 1 2
ax + bx + 2)  0 nghiệm
đúng với mọi x A. 3 . B. 2 . C. 0 . D. 1. Câu 4: Cho 2 hàm số 7 5 3
y = x + x + x + 3m −1 và y = x − 2 − x − 2m ( m là tham số thực) có đồ thị lần
lượt là (C , (C . Tập hợp tất cả các giá trị của m để (C cắt (C là 2 ) 1 ) 2 ) 1 ) A. m  .
B. m  (2; +) . C. m  (− ;  2) .
D. m 2; +) . Câu 5:
Có bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn  2019 −
; 2019 để phương trình + x (
+ x − m)+ − x ( − x + m) 2 3 2 3 1 5 1 2
= 4 −x − 2x + 3 có nghiệm thực? A. 2019 . B. 4032 . C. 4039 . D. 4033 . 2 Câu 6:
Có bao nhiêu m nguyên dương để hai đường cong (C : y = 2 +
và (C : y = 4x − m 2 ) 1 ) x −10
cắt nhau tại ba điểm phân biệt có hoành độ dương? A. 35. B. 37. C. 36. D. 34. Câu 7:
Cho hàm số f (x) = (x −1).(x − 2)...(x − 2020). Có bao nhiêu giá trị nguyên của m thuộc đoạn  2020 −
; 2020 để phương trình f (  x) = .
m f (x) có 2020 nghiệm phân biệt? A. 2020. B. 4040. C. 4041. D. 2020. − 3 1 Câu 8: Cho hai hàm số 2 = x y ln và y =
− + 4m − 2020 , Tổng tất các các giá trị nguyên của x x − 2 x
tham số m để đồ thị hai hàm số cắt nhau tại một điểm duy nhất là A. 506 . B. 1011. C. 2020 . D. 1010 .
1 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số Câu 9:
Cho hai hàm số y = (x + ) 1 (2x + ) 1 (3x + ) 1 (m + 2 x ) ; 4 3 2 y = 1
− 2x − 22x − x +10x + 3 có đồ thị
lần lượt là (C , (C . Có bao nhiêu giá trị nguyên của tham số m trên đoạn  2020 − ; 2020 để 2 ) 1 )
(C cắt (C tại 3 điểm phân biệt? 2 ) 1 ) A. 4040 . B. 2020 . C. 2021 . D. 4041 .
Câu 10: Cho hai hàm số 6 4 2
y = x + 6x + 6x +1 và 3 y = x
m −15x (m + 3 −15x) có đồ thị lần lượt là
(C và (C . Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc đoạn 2 ) 1 )  2019 −
; 2019 để (C và (C cắt nhau tại hai điểm phân biệt. Số phần tử của tập hợp S bằng 2 ) 1 ) A. 2006 . B. 2005 . C. 2007 . D. 2008 . Câu 11: Cho hàm số = ( ) 4 3 2 y
f x =ax + bx + cx + dx + e có đồ thị như hình vẽ bên đây, trong đó
a,b,c,d ,e là các hệ số thực. Số nghiệm của phương trình f ( f (x)) + f (x) + 2 f (x) −1= 0 là A. 3. B. 4. C. 2. D. 0.
Câu 12: Cho hàm số y = f ( x) có bảng biến thiên như hình vẽ:
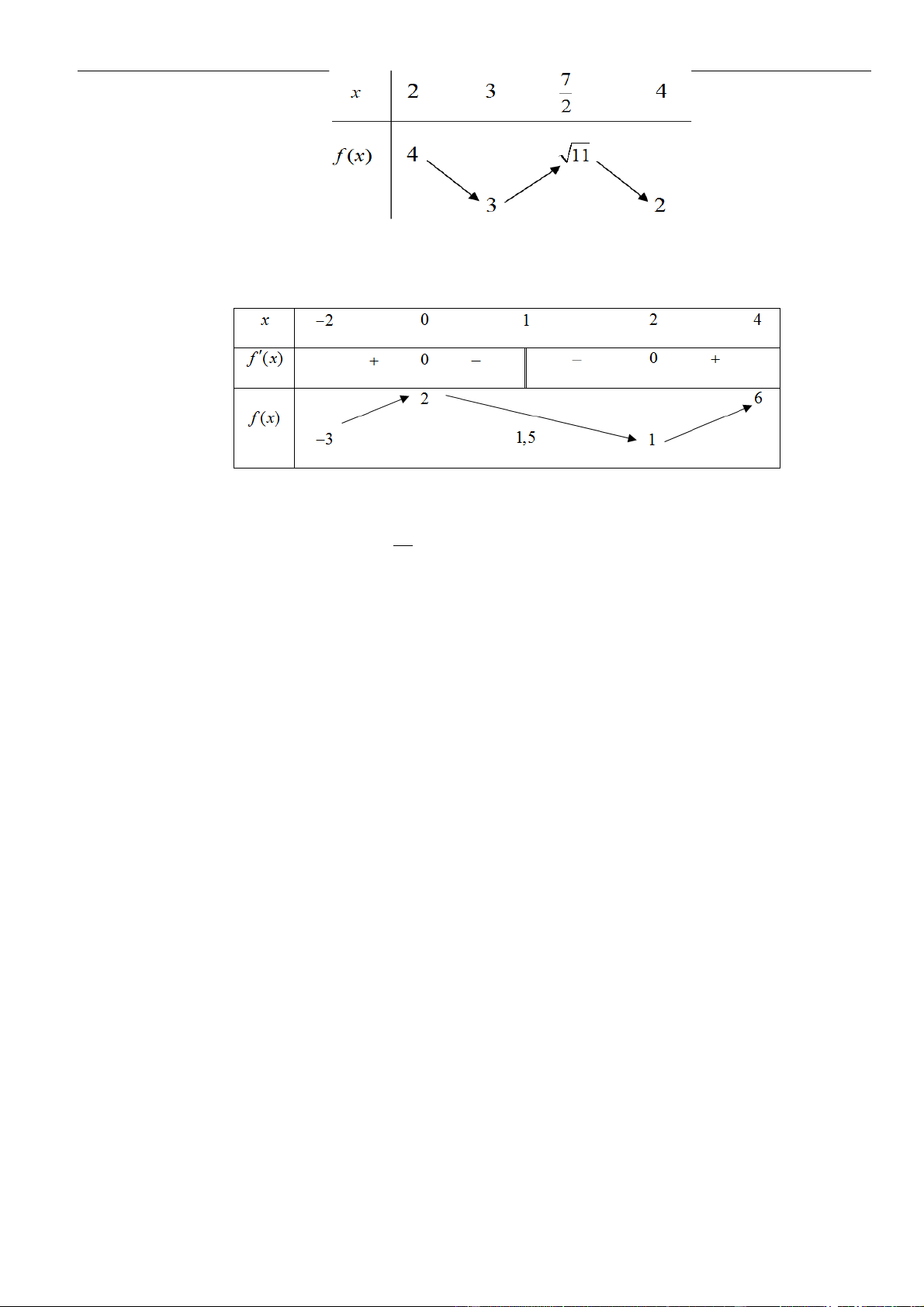
Có bao nhiêu giá trị nguyên của tham số m để phương trình f ( 2 6
x − 4x) = m có ít nhất ba
nghiệm thực phân biệt thuộc khoảng (0; + ) ? A. 25. B. 30. C. 29. D. 24.
Câu 13: Cho hàm số y = f ( x) −1;4 liên tục trên đoạn
và có đồ thị như hình vẽ.
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 2 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 Có bao nhiêu giá trị −10;10
nguyên của m thuộc đoạn
để bất phương trình f ( x) + m  2m đúng với mọi −1;4 x thuộc đoạn . A. 6 . B. 5 . C. 7 . D. 8 .
Câu 14: Cho hàm số y = f ( x) liên tục trên
và có đồ thị như hình vẽ bên dưới. Gọi S là tập hợp tất
cả giá trị nguyên của tham số m để phương trình f (sin x) − m + 2 = 2sin x có nghiệm thuộc
khoảng (0; ) . Tổng các phần tử của S bằng A. 4 . B. 1 − . C. 3 . D. 2 .
Câu 15: Cho hàm số f ( x) 3
= x + x + 2 . Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình f ( 3
f ( x) + f ( x) + m ) 3 3
= −x − x + 2 có nghiệm x  1 − ;2 ? A. 1750 . B. 1748 . C. 1747 . D. 1746 .
Câu 16: Cho hàm số f (x) liên tục trên 2; 4 và có bảng biến thiên như hình vẽ bên. Có bao nhiêu giá
trị nguyên của m để phương trình 2
x + 2 x − 2x = .
m f (x) có nghiệm thuộc đoạn 2; 4 ?
3 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số A. 6 . B. 5 . C. 4 . D. 3 .
Câu 17: Cho hàm số y = f ( x) liên tục và có đạo hàm trên đoạn −2; 4 và có bảng biến thiên như sau
Có bao nhiêu giá trị nguyên của tham số m để hệ phương trình  9  − 4  0 2  x 6  f ( 2 − x + ) 3
1 − 8x + 6x − m = 0 có ba nghiệm phân biệt? A. 9 . B. 11. C. 10 . D. 8 .
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 4 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 BẢNG ĐÁP ÁN 1.B 2.C 3.C 4.A 5.B 6.C 7.B 8.A 9.C 10.A 11.B 12.B 13.C 14.D 15.A 16.C 17.D
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: Chọn B
Xét phương trình hoành độ giao điểm x −1 x x +1 x + 2 x −1 x x +1 x + 2 + + +
= x + 2 − x − m  + + +
− x + 2 + x = −m ( ) 1 x x +1 x + 2 x + 3 x x +1 x + 2 x + 3 x −1 x x +1 x + 2 Xét f ( x) = + + +
− x + 2 + x, xD = \ 3 − ;− 2;−1;  0 x x +1 x + 2 x + 3  x −1 x x +1 x + 2 + + + − 2, x ( 2
− ;+ ) D = D  1  x x +1 x + 2 x + 3
Ta có f ( x) =  x −1 x x +1 x + 2  + + +
+ 2x + 2, x (− ;
 − 2) D = D2  x x +1 x + 2 x + 3  1 1 1 1 + + + , x   D  2 x  (x + )2 1 (x + 2)2 (x +3)2 1
Có f ( x) =  1 1 1 1  + + + + 2, x   D 2  x  (x + )2 1 (x + 2)2 (x +3)2 2
Dễ thấy f ( x)  0, x
  D D , ta có bảng biến thiên 1 2 x - -3 -2 1 0 + f'(x) + + + + + + + + + 2 f(x) - - - - -
Hai đồ thị cắt nhau tại đúng 4 điểm phân biện khi và chỉ khi phương trình ( ) 1 có đúng 4 nghiệm
phân biệt, từ bảng biến thiên ta có: −m  2  m  −2 . Câu 2: Chọn C 11 1
Xét phương trình hoành độ giao điểm: ( 2 2x + ) 1 x −1 = − +11+ m (*) 3x − 4 2 − xx −1  0 x  1     Điề 4 4 u kiện: x   x  3 3   x  2 x  2   Ta có: ( 11 1 *)  ( 2 2x + ) 1 x −1 − + −11 = m 3x − 4 2 − x
5 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số 11 1  
Xét hàm số f (x) = ( 2 2x + ) 1 x −1 − + −11 trên  + ) 4 1; \  ; 2 3x − 4 2 − x 3   4   4 
Nhận thấy, hàm số f ( x) liên tục trên các khoảng 1; , ; 2 , (2; +     )  3   3    11 1  Ta có, f (  x) = ( 2 2x + ) 1 x −1 − + −11  3x − 4 2 − x  2 − + = 10x 8x 1 33 1 4x x −1 + ( 1 33 1 2 2x + ) 1 + + = + +  0 2 2 2 x −1
(3x −4)2 (2− x)2 2 x −1
(3x −4) (2− x)  
với x  + ) 4 1; \  ; 2 3   
Suy ra, hàm số f ( x) đồng biến trên  + ) 4 1; \  ; 2. 3  Bảng biến thiên 11 1
Từ bảng biến thiên ta suy ra đồ thị hai hàm số y = ( 2 2x + ) 1 x −1 và y = − +11+ m 3x − 4 2 − x
cắt nhau tại 2 điểm phân biệt khi m  (−  ;1 . Câu 3: Chọn C
Đặt f ( x) = ( x − )( x + )( 2 1 2 ax + bx + 2)
Giả sử x = 1 không phải là nghiệm của phương trình g ( x) = ( x + )( 2 2
ax + bx + 2) = 0 thì hàm
số f ( x) = ( x − )( x + )( 2 1 2
ax + bx + 2) sẽ đổi dấu khi qua điểm x = 1 , nghĩa là
(x − )(x + )( 2 1 2
ax + bx + 2)  0 không có nghiệm đúng với mọi x  .
Do đó, để yêu cầu bài toán được thỏa mãn thì một điều kiện cần là
g ( x) = ( x + )( 2 2
ax + bx + 2) = 0 có nghiệm x = 1 suy ra a + b + 2 = 0
Lí luận tương tự có h( x) = ( x − )( 2
1 ax + bx + 2) = 0 cũng phải nhận x = −2 là nghiệm, suy ra
4a − 2b + 2 = 0 a + b + 2 = 0 a = 1 − Từ và ta có hệ   
4a − 2b + 2 = 0 b  = 1 − Điều kiện đủ: a = 1 − Với  2 2
có f ( x) = ( x − )( x + )( 2 1
2 −x − x + 2) = −( x − )
1 ( x + 2)  0 , x  . b  = 1 −
Vậy không tồn tại cặp số thực (a;b) nào thỏa mãn yêu cầu bài toán.
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 6 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 Câu 4: Chọn A
Xét phương trình hoành độ giao điểm: 7 5 3
x + x + x + 3m −1 = x − 2 − x − 2m 7 5 3
x + x + x − x − 2 + x = −5m +1 (1) . Xét hàm số 7 5 3
f (x) = x + x + x − x − 2 + x . 7 5 3
x + x + x + 2 khi x 2; +  )
Ta có f (x) =  . 7 5 3
x + x + x + 2x − 2 khi x   ( ; − 2) 6 4 2
7x + 5x + 3x  0 khi x  (2; +  ) f (  x) =  . 6 4 2
7x + 5x + 3x + 2  0 khi x   ( ; − 2)
lim f ( x) = − ; lim f ( x) = + . x→− x→+ Bảng biến thiên: x ∞ 2 +∞ + f '(x) + +∞ f(x) ∞
Từ bảng biến thiên ta thấy phương trình ( )
1 luôn có nghiệm với mọi m  .Vậy để (C cắt 1 ) (C thì m . 2 ) Câu 5: Chọn B Đk: x  3 −  ;1 .
Phương trình đã cho  11− 3x − 4 (3+ x)(1− x) + m(2 1− x − 3+ x ) = 0 .
Đặt t = 2 1− x − 3 + x = g ( x) , với x −
 − x − ( + x)( − x) 2 3;1 11 3 4 3 1 = t + 4 . 1 − 1 Có g( x) = −  0, x  ( 3 − )
;1 . Suy ra g ( x) nghịch biến trên khoảng (−3; ) 1 . 1− x 2 3 + x
 min g (x) = g ( ) 1 = 2
− : max g (x) = g ( 3
− ) = 4  t  2 − ;4 .  3 − ;  1  3 − ;  1 Từ 2
t + mt + 4 = 0 .
Nếu t = 0  0 + 4 = 0 . 2 t − − 4 4 Nếu t  2
− ;4 \{0}, ta có m = = t
− − = f (t) . t t 2 4 − t Có f (t ) =
, f t = 0  t = 2  . 2 ( ) t Bảng biến thiên m  4
Từ bảng biến thiên, suy ra phương trình có nghiệm thực khi và chỉ khi  . m  4 −
7 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số m  201 − 9; 2019  m  4 Do đó   m 
−2019;− 2018;....;− 4;4;...;2018;201  9 . m  4 − m  Vậy có (2019 − 4 + )
1 .2 = 4032 giá trị nguyên của tham số thực m . Câu 6: ChọnC x  10  Điều kiện:  m . x   4 Xét trên (0; +) \  
10 , phương trình hoành độ giao điểm của (C và (C là 2 ) 1 ) 2 2  2x −18  2 +
= 4x − m m = 4x −   . x −10  x −10  2  −  Đặt g (x) 2x 18 = 4x − 
 với x (0;+) \  10 .  x −10   2x 18  − 4 − x + 34
Ta có: g( x) = 41+    = ( ; g ( x) . x 10)3  −   (x −10)4
g( x) có bảng biến thiên như sau
Suy ra phương trình g( x) = 0 có một nghiệm duy nhất 17     ;10 
 . Lại có g(9, 22)  0 nên  2 
 (9,22;10). Ta có bảng biến thiên của g (x) trên (0;+) \  10 :
Từ đó suy ra phương trình m = g ( x) có 3 nghiệm dương phân biệt khi và chỉ khi 81
−  m g(). 25 4x  40  Trên khoảng (9,22;10) thì 2 
 2x −18  nên g ( x)  37  g ( )(36;37) . 3       x −10 
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 8 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
Vậy những giá trị m nguyên dương thỏa mãn yêu cẩu bài toán là 1; 2; 3; …; 36 hay có 36 giá
trị của m cần tìm. Câu 7: Chọn B
Ta có nhận xét: khi f (x) = 0 thì phương trình f (  x) = .
m f (x) vô nghiệm.  Do đó: f (x) f (  x) = .
m f (x)  m = . f (x)  Xét hàm số f (x) 1 1 1 1 g(x) = = + + + + . f (x) x −1 x − 2 x − 3 x − 2020 1 − 1 − 1 − 1 − Ta có g (  x) = + + + +  0, x   \ 1;2;3...;2020 2 2 2 2   (x − ) 1
(x − 2) (x −3) (x − 2020) Bảng biến thiên:
Dựa vào BBT, phương trình f (  x) = .
m f (x) có 2020 nghiệm phân biệt khi và chỉ khi m  0 hoặc m  0 . Kết hợp với điều kiện m là số nguyên thuộc  2020 − ; 2020 nên
m n  | 2
− 020  n  2020, n   0 .
Vậy có tất cả 4040 giá trị m thỏa yêu cầu bài toán. Câu 8: Chọn A
+ Phương trình hoành độ điểm chung của hai đồ thị hàm số là x − 2 3 1 x − 2 3 1 ln =
− + 4m − 2020  ln − + = 4m − 2020 (*) x x − 2 x x x − 2 x
Đồ thị của hai hàm số đã cho cắt nhau tại một điểm duy nhất khi và chỉ khi có duy nhất một nghiệm.  3 1
g (x) = ln(x − 2) − ln x − + khi x  2  1 x − 2  x x − 2 3 1  3 1 + Xét hàm số y = ln −
+ = g (x) = ln(2 − x) − ln x − + khi 0  x  2 2 x x − 2 x x − 2  x  3 1
g (x) = ln(2 − x) − ln(−x) − + khi x  0  3  x − 2 x
9 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số 2  1 1 3 1 4(x −1) / g (x) = − + − = khi x  2  1 2 2 2 2 x − 2 x (x − 2) x x (x − 2)  2  1 − 1 3 1 4(x −1) x = 1 − Ta có / g (x) = − + − =
khi 0  x  2 , do vậy y = 0   2 2 2 2 2 2 − x x (x − 2) x x (x − 2)  x =1  2 1 − 1 3 1 4(x −1) / g (x) = − + − = khi x  0 3 2 2 2 2  2 − x x (x − 2) x x (x − 2)
bảng biến thiên hàm số như sau
+ Qua bảng biến thiên này ta có có nghiệm duy nhất khi và chỉ khi m = 506 4m − 2020 = 4    2020 + ln 3 4m − 2020 = ln 3 m =   4
+ Tư đây yêu cầu bài toán xãy ra khi và chỉ khi m = 506 . Câu 9: Chọn C
Xét phương trình hoành độ giao điểm của hai đồ thị (C và (C : 2 ) 1 )
(x + )( x + )( x + )(m+ x ) 4 3 2 1 2 1 3 1 2 = 1
− 2x − 22x − x +10x + 3
Để đồ thị (C cắt (C tại 3 điểm phân biệt thì phương trình có 3 nghiệm phân biệt. 2 ) 1 )  1 1  Với x   1
− ;− ;− : Không là nghiệm của phương trình.  2 3  1 1  Với x   1 − ;− ;−  ta có:  2 3 ( ) 4 3 2 1
− 2x − 22x − x +10x + 3 1 1 1 1  m = ( )( −  = − − + + + . + x + )( x + ) 2 x m 2x 2 x x 1 2 1 3 1 x +1 2x +1 3x +1  1 1 
Xét hàm số f ( x) 1 1 1 = 2 − x − 2 x + + + , x   \  1 − ;− ;− . x +1 2x +1 3x +1  2 3 2x 1 2 3
Suy ra: f ( x) = 2 − − − − − . x (x + )2 1 (2x + )2 1 (3x + )2 2 1  1 2 3 4 − − − − khi x  0; +  2 2 2 ( ) (x + ) 1 (2x + ) 1 (3x +  ) 1
Ta có: f ( x) = 
và f ( x) không 1 2 3  1 1   − − − khi x − ;  0 \  1 − ;− ;−  2 2 2 ( )
 (x + )1 (2x + )1 (3x +  ) 1  2 3
xác định tại x = 0 .
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 10 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy để phương trình có 3 nghiệm phân biệt thì m  0 . Do đó có 2021
giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán. Câu 10: Chọn A Ta biết (C cắt (C
tại hai điểm phân biệt khi và chỉ khi phương trình 2 ) 1 ) 6 4 2 3
x + 6x + 6x +1 = x
m −15x (m + 3 −15x) ( )
1 có hai nghiệm phân biệt.
Điều kiện: m −15x  0  m  15x (*) .
Nếu x = 0 thì phương trình ( )
1 vô nghiệm. Suy ra x  0 . Khi đó ( ) 1 3 2
1  x + 6x + 6x +
= m −15x m + 3−15x 3 ( ) x 3      x + + x + =     ( m − x )3 1 1 3 15 + 3 m −15x .  x   x
Xét hàm số f (t) 3
= t + 3t . Tập xác định D = . f (t ) 2
= 3t + 3  0, t
  . Suy ra hàm số f (t) 3
= t + 3t đồng biến trên . Do đó ( ) 1 1  x + = m −15x (2). x Nếu 1 x  0  x +
 0  Phương trình (2) vô nghiệm x  0 . xm  0  Khi đó 1 1  1 nên (2) 2 2  x +
+ 2 = m −15x m = x + + 2 +15x . x +  0  2 2 x xx Đặt 2 g ( x) 1 2 = x +
+ 2 +15x, x  0 . g(x) = 2x − +15 . 2 x 3 x
Phương trình g( x) = 0 có một nghiệm 1 x = trên khoảng (0; +) . 2 Bảng biến thiên
11 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số Suy ra ( )
1 có hai nghiệm phân biệt khi và chỉ khi 55 m  . 4
Kết hợp với m nguyên và m  20
− 19;2019 ta có được m nguyên và m14;2019 .
Khi đó S có 2019 −14 +1 = 2006 phần tử. Câu 11: Chọn B
Từ hình vẽ ta có dạng đồ thị của hàm trùng phương nên b = d =  f ( x) 4 2 0
= ax + cx + e Ta có f ( x) 3 = 4ax + 2cx.f ( ) 1 = 0 4a + 2c = 0 a =1   
Từ đồ thị   f (0) = 0  e = 0
 e = 0  f (x) 4 2 = x + 2x .    f ( ) =
a + c + e = 1 c = 2 1 1     f ( x) 2
= x + 2x và f ( f (x)) 2
= f (x) + 2 f (x). Như vậy phương trình
f ( f (x)) + f (x) + 2 f (x) −1= 0. 2
f (x) + 2 f (x) + f (x) + 2 f (x) −1= 0 với f (x)  0.
Đặt t = f ( x)(t  0) ta được phương trình g (t) = 0 với g (t) 2
= t − 3t − 2 t +1.
Nhận thấy: Hàm số g (t) liên tục trên đoạn 0  1
; và g (0) .g ( ) 1  0
g (t) = 0 có ít nhất 1 nghiệm thuộc (0 ) 1 ; .
Hàm số g (t) liên tục trên đoạn 1;4 và g ( ) 1 .g (4)  0
g (t) = 0 có ít nhất 1 nghiệm thuộc (1;4) .
Mà g (t ) = 0 là phương trình bậc hai chỉ có tối hai nghiệm nên g (t ) = 0 có duy nhất một nghiệm thuộc (0 ) 1 ;
. Suy ra f ( f (x)) + f (x) + 2 f (x) −1= 0 có duy nhất một nghiệm
f ( x) (0; )
1 . Suy ra phương trình f ( x) = a với a  (0; )
1 luôn có 4 nghiệm x phân biệt. Câu 12: Chọn B
Ta đặt: g ( x) = f ( 2 x − 4x) .
g( x) = ( x − ) f ( 2 2 4
x − 4x) = ( x − )( 2 x − x + )( 2 x − x + )( 2 2 2 4 4 4 2 x − 4x) = (x − )3 ( 2 2 2
x − 4x + 2) x ( x − 4) .
Mặt khác: g (0) = f (0) = 3
− ; g (2− 2) = g (2+ 2) = f ( 2
− ) = 2 ; g (2) = f ( 4 − ) = 2 − ;
g (4) = f (0) = 3
− . Ta có bảng biến thiên:
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 12 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 m
Từ bảng biến thiên ta được: yêu cầu bài toán tương đương 3 −   2 6  18 −
m  12 . Vậy có tất cả 30 giá trị của tham số m thỏa mãn yêu cầu bài toán. Câu 13: Chọn C
Để bất phương trình f ( x) + m  2m có nghiệm ta suy ra điều kiện m  0 .  f
 ( x)  −3m
f ( x) + m  2m  2
− m f (x) + m  2m   .  f  ( x)  mf
 ( x)  −3m Bất phương trình −1;4
f ( x) + m  2m đúng với mọi x thuộc đoạn   đúng  f  ( x)  m
−3m  min f (x)  − với mọi −  1;4 1; 4 x thuộc đoạn   . m  max f  (x)   1 − ;4
Từ đồ thị hàm số y = f ( x) ta suy ra min f (x) = 2
− ; max f (x) = 3 .  1 − ;4  1 − ;4  3
− m  min f (x)  2   −  − 1 − ;4 3m 2 m         m m  max f  (x) 3 3 m  3     1 − ;4 m 3
Vậy trên đoạn −10;10 có 7 giá trị nguyên của m thỏa mãn điều kiện bài toán. Câu 14: Chọn D
Đặt t = sin x , với x  (0; )  t  (0  ;1 .
13 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số
Ta được phương trình: f (t) − 2t = m − 2  f (t) = 2t + m − 2
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số y = f (t) và đường thẳng
y = 2t + m − 2 (r ) .
Gọi ( p) : y = 2x +1 song song với đường thẳng () : y = 2t và đi qua điểm A(0; ) 1 .
Gọi q : y = 2x − 3 song song với đường thẳng () : y = 2t và đi qua điểm B (1;− ) 1 .
Để phương trình f (sin x) − m + 2 = 2sin x có nghiệm thuộc khoảng (0; ) thì phương trình
phải có nghiệm t  (0; 
1 , suy ra đường thẳng r nằm trong miền nằm giữa hai đường thẳng q và p  3
−  m − 2  1  1
−  m  3  m  1 − ;0;1;  2  S =  1 − ;0;1;  2 .
Do đó tổng các phần tử là: 1 − + 0 +1+ 2 = 2 . Câu 15: Chọn A Xét hàm số 3
f (t) = t + t + 2 , ta có 2 f (
t) = 3t +1  0, t   .
Do đó hàm số f đồng biến trên . Ta có f ( 3
3 f (x) + f (x) + m ) = f (−x) 3 3 3 3
 −x = f (x) + f (x) + m f (x) + f (x) + x + m = 0 (1) Xét 3 3
h(x) = f (x) + f (x) + x + m trên đoạn [−1; 2] . Ta có 2 2 2 2 h (
x) = 3 f (x) f (x) + f (x) + 3x = f (x) 3
f (x) +1 + 3x .   Ta có 2 f (
x) = 3x +1  0, x  [ 1
− ;2]  h (x)  0, x  [ 1 − ;2].
Hàm số h(x) đồng biến trên [−1; 2] nên min h(x) = h( 1
− ) = m −1, max h(x) = h(2) = m +1748. [ 1 − ;2] [ 1 − ;2]
Phương trình (1) có nghiệm khi và chỉ khi
min h ( x)  max h ( x)  0  h (− ) 1  h (2) [ 1 − ;2] [ 1 − ;2]  (m − ) 1 (1748 + m)  0  1 − 748  m 1.
Do m nguyên nên tập các giá trị m thỏa mãn là S = { 1748 − ; 1747 − ; ;  0;1} .
Vậy có tất cả 1750 giá trị nguyên của m thỏa mãn. Câu 16: Chọn C
Dựa vào bảng biến thiên ta có Min f ( x) = f (4) = 2 và Max f (x) = f (2) = 4 2;4 2;4 Hàm số 2
g(x) = x + 2 x − 2x liên tục và đồng biến trên 2; 4
Suy ra Min g ( x) = g(2) = 2 và Max g ( x) = g(4) = 4 + 4 2 2;4 2;4 2
x + 2 x − 2x g(x) Ta có 2
x + 2 x − 2x = . m f (x)  = m  = m f (x) f (x) g(x)
Xét hàm số h(x) = liên tục trên 2; 4 f (x)
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 14 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 Vì
g ( x) nhỏ nhất và
f ( x) lớn nhất đồng thời xảy ra tại x = 2 nên Min g ( x) 2;4 g (2) 1 Min h(x) = = = h(2) = 2;4 Max f ( x) f (2) 2 2;4 Vì
g ( x) lớn nhất và
f ( x) nhỏ nhất đồng thời xảy ra tại x = 4 nên Max g ( x) 2;4 g (4) Max h(x) = = = h(4) = 2 + 2 2 2;4 Min f ( x) f (4) 2;4 1
Từ đó suy ra phương trình h(x) = m có nghiệm khi và chỉ khi  m  2 + 2 2 . 2
Vậy có 4 giá trị nguyên của m để phương trình có nghiệm. Câu 17: Chọn D  3 3 2 2 9 9 − 4x 9  − 4x  0 −  x   3 3 Ta có: − 4  0   0     2 2  x  − ; \ 0 . 2 2     x xx  0   2 2 x  0
Xét phương trình f (− x + ) 3
− x + x − m =  m = f (− x + ) 3 6 2 1 8 6 0 6 2
1 − 8x + 6x   Xét hàm số 3 3
g ( x) = f (− x + ) 3 6 2
1 − 8x + 6x , với x  − ; \   0   .  2 2
Ta có g( x) = − f (− x + ) 2 − x +
= −  f (− x + ) 2 12 2 1 24 6 6 2 2 1 + 4x −1   − x + 
Từ giả thiết ta suy ra f (− x + ) 2 1 2 1 1 2 1  0  
 −  x  ;  2 − x +1  0 2 2 1 3  x  −  − x +   f (− x + ) 2 2 1 0 2 2 2 1  0     . 2  2 − x +1 4 3 1 −  x  −  2 2  
Bảng biến thiên của hàm số 3 3
g ( x) = f (− x + ) 3 6 2
1 − 8x + 6x trên − ; \   0   .  2 2
15 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số  
Từ bảng biến thiên ta suy 3 3
ra hệ có đúng ba nghiệm  có đúng ba nghiệm x  − ; \   0    2 2 4  m 14   . Vì m
m = 5;6;7;8;10;11;12;13 . Vậy có 8 số nguyên m . m  9
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 16 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 DẠNG 3
Tìm m liên quan đến tương giao hàm bậc 3 Câu 1: Cho hàm số 3 2
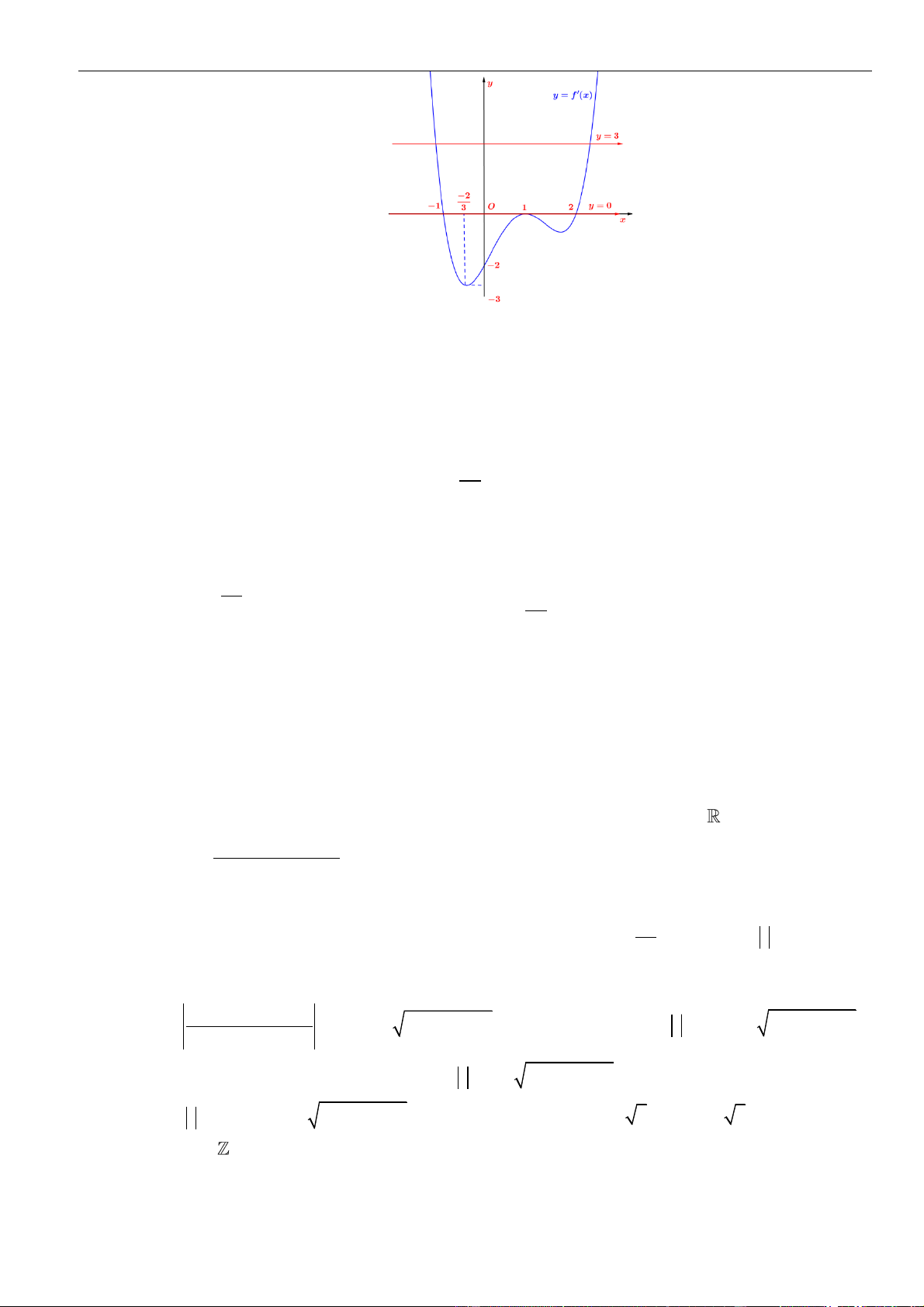
y = x − 2x −1 có đồ thị (C) , đường thẳng (d ) : y = mx −1 và điểm K (4;1 ) 1 .Biết
rằng (C) và (d ) cắt nhau tại ba điểm phân biệt ,
A B, C trong đó A(0; − ) 1 còn trọng tâm tam
giác KBC nằm trên đường thẳng y = 2x +1. Mệnh đề nào sau đây đúng?
A. m = 4 .
B. m = 2 .
C. m = 3 .
D. Không có m . Câu 2:
Gọi S là tập tất cả các giá trị của tham số m để đường thẳng y = 3x + m tiếp xúc với đồ thị hàm số 3
y = x +1 . Tổng các phần tử của S bằng A. 0 . B. 3 . C. 2 . D. 1 − . 3 Câu 3:
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y = 2x − (2 + m) x + m cắt
trục hoành tại 3 điểm phân biệt 1 1 1 1 A. m  . B. m  . C. m  − .
D. m  − ; m  4 . 2 2 2 2 Câu 4:
Cho hàm số f ( x) 3 2
= ax + bx + cx + d (a, b, c, d  ) có đồ thị như hình vẽ sau.
Có tất cả bao nhiêu giá trị nguyên thuộc đoạn  2020 −
; 2020 của tham số m để phương trình
2 f ( x ) − m = 0 có đúng 2 nghiệm thực phân biệt? A. 2020 . B. 2022 . C. 2021 . D. 2019 . Câu 5:
Biết đường thẳng y = (3m − )
1 x + 6m + 3 cắt đồ thị hàm số 3 2
y = x − 3x +1 tại ba điểm phân biệt
sao cho một giao điểm cách đều hai giao điểm còn lại. Khi đó m thuộc khoảng nào dưới đây?  3   3  A. 1;   . B. (0; ) 1 . C. ; 2   . D. (−1;0) .  2   2  Câu 6:
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 3 2 y x 2m 1 x 3m 1 x m
1 cắt trục hoành tại 2 điểm phân biệt? A. 4 . B. 2 . C. 3 . D. 1. Câu 7: Cho đồ thị (C ) 3 2
: y = x − 2x + (1− m x + m. Tìm tất cả các giá trị của tham số m để (C cắt m ) m )
trục hoành tại ba điểm phân biệt có hoành độ x , x , x thỏa 2 2 2
x + x + x = 4 1 2 3 1 2 3 1 A. m  0 .
B. m  (0; 2) . C. m = 1. D. m  − và m  0 . 4
1 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số Câu 8:
Gọi S là tập tất cả các giá trị thực của tham số m để đường thẳng y = m cắt đồ thị hàm số 3 2
y = x − 3x tại 3 điểm phân biệt ,
A B, C ( B nằm giữa ,
A C ) sao cho AB = 2BC . Tính tổng
các phần tử thuộc S . 7 − 7 A. 4 − . B. . C. 2 − . D. 0 . 7 3 2 Câu 9:
Có bao nhiêu giá trị nguyên âm của a để đồ thị hàm số y = x + (a +10) x − x +1 cắt trục
hoành tại đúng một điểm? A. 10 . B. 8 . C. 11. D. 9 .
Câu 10: Có bao nhiêu giá trị nguyên thuộc  2020 − ; 
2021 của hàm số m để đường thẳng y = mx − m −1
cắt đồ thị của hàm số 3 2
y = x − 3x + x tại ba điểm phân biệt ,
A B, C sao cho AB = BC . A. 2021 . B. 2023 . C. 2024 . D. 2022 .
Câu 11: Cho bao nhiêu giá trị m để đồ thị hàm số 3 2
y = −x + mx − 2m cắt trục Ox tại 3 điểm phân biệt
có hoành độ lập thành cấp số cộng. A. 1. B. 2 . C. 3 . D. 0 .
Câu 12: Cho hàm số bậc ba y = f ( x) liên tục trên
và có đồ thị như hình vẽ bên.
Tổng tất cả các giá trị nguyên của tham số m để phương trình f ( 2 f (cos x)) = m có nghiệm   x  ;    2  A. 1 − . B. 0 . C. 1. D. 2 − .
Câu 13: Gọi S là tập hợp các số nguyên m để phương trình 3 2
x − (2m +1)x + 2(3m − 2)x − 8 = 0 có ba
nghiệm lập thành một cấp số nhân. Tổng các phần tử của S bằng A. 0 . B. 2 − . C. 3 . D. 1 − . 1 Câu 14: Cho hàm số 3
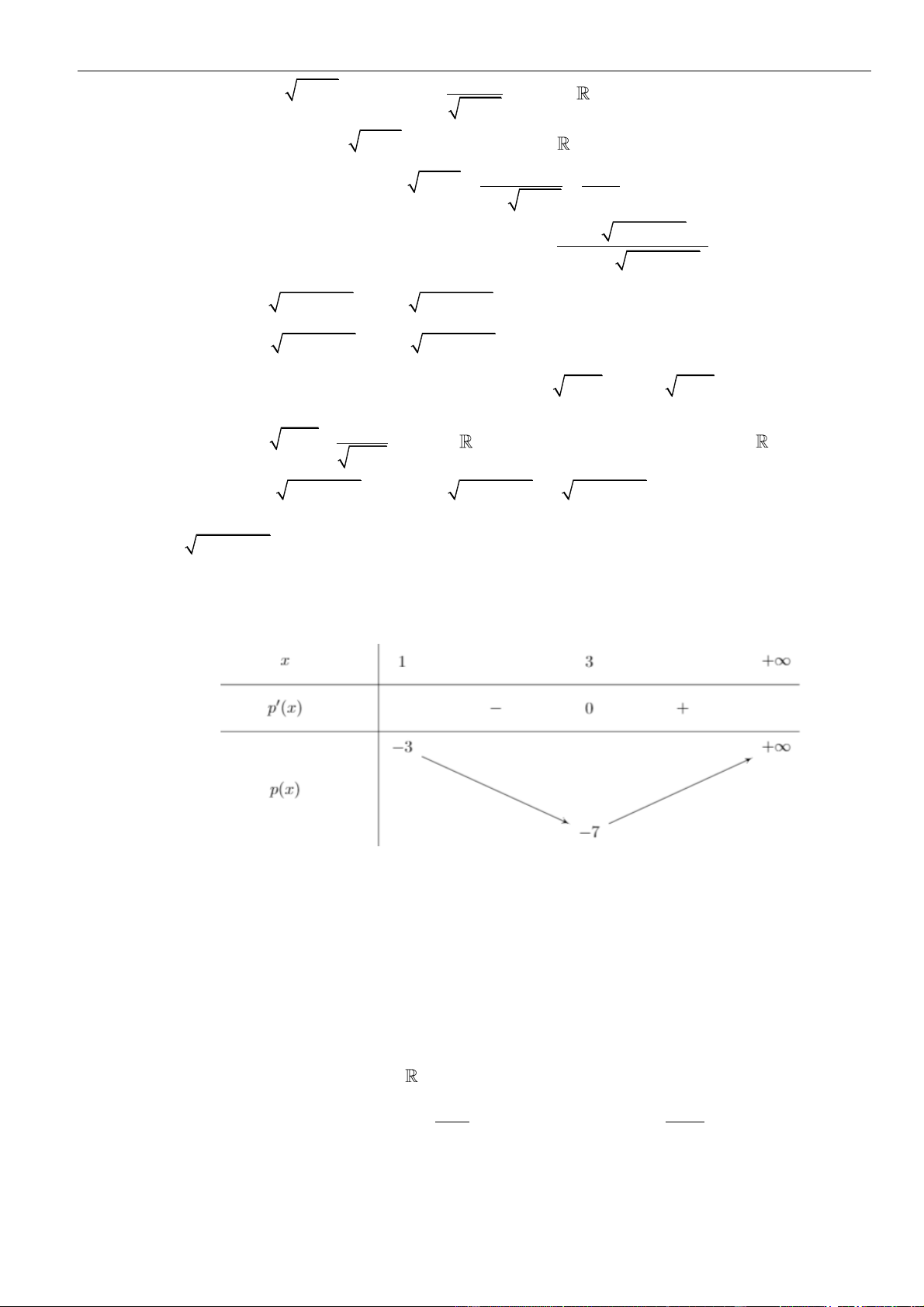
f (x) = x −
mx + m − 8 , x
với m là một hằng số khác 0 . Biết rằng phương 2
trình f (x) = 0 có đúng 2 nghiệm phân biệt thì có bao nhiêu giá trị nguyên dương k thỏa mãn
phương trình f (x) = k có 3 nghiệm phân biệt? A. 3 . B. 6 . C. 34 . D. 31. Câu 15: Cho hàm số 3 2
y = x − (m + 2)x − (2m +13)x − m − 2 có đồ thị (C ), đường thẳng m
d : y = mx + m + 8 và điểm I (1; 4). Tính tổng tất cả các giá trị của tham số ,
m biết rằng đường
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 2 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
thẳng d cắt đồ thị (C ) tại ba điểm phân biệt ,
A B, C với A có hoành độ bằng 2 − và tam giác m
IBC cân tại I . A. −12 . B. 6 − . C. 4 − . D. −10 .
Câu 16: Gọi d là đường thẳng đi qua A(2;0) có hệ số góc m (m  0) cắt đồ thị (C) 3 2
: y = −x + 6x − 9x + 2 tại ba điểm phân biệt ,
A B, C. Gọi B , C lần lượt là hình chiếu
vuông góc của B, C lên trục tung. Biết rằng hình thang BB CC
 có diện tích bằng 8, giá trị của
m thuộc khoảng nào sau đây? A. (5;8) . B. (−5;0) . C. (0; 2) . D. (1;5) .
Câu 17: Cho hàm số bậc ba y = f ( x) có đồ thị như hình vẽ
Có bao nhiêu giá trị nguyên của tham số m để phương trình 3 f ( x) 2 − mf (x) + ( 2
m − m − ) f ( x) 2 2 3 9
+ 3m + 9m = 0 có đúng 8 nghiệm phân biệt? A. 3 . B. 4 . C. 5 . D. 6 .
Câu 18: Gọi S là tập hợp chứa tất cả các giá trị thực của tham số m để đồ thị hàm số f ( x) 3 = x − (m + ) 2 6 1 x + 3(2m + )
1 x + 2 cắt trục Ox tại ba điểm phân biệt có hoành độ lớn hơn  −a  1 − . Biết rằng S = ; + 
 ; trong đó a,b là các số nguyên dương và phân số a là tối giản.  bb
Giá trị biểu thức T = a + b tương ứng bằng A. 4 . B. 8 . C. 5 . D. 7 .
Câu 19: Điều kiện cần và đủ của tham số thực m để đường thẳng y = 3x + m − 2 cắt đồ thị hàm số y = ( x − )3
1 tại ba điểm phân biệt là A. 3 −  m  1. B. 3 −  m  1.
C. −1  m  3 .
D. −1  m  3 . Câu 20: Cho hàm số 3 2
y = x + 3x + m có đồ thị (C) . Biết đồ thị (C) cắt trục hoành tại 3 điểm phân biệt ,
A B,C sao cho B là trung điểm AC . Phát biểu nào sau đây đúng? A. m ( 4 − ;0) .
B. m  (0;+) . C. m  ( ; − 4 − ) . D. m  ( 4 − ; 2 − ) . Câu 21: Cho hàm số 3 2
y = x − 2x −1 có đồ thị (C ) , đường thẳng (d ) : y = mx −1và điểm K (4;11) . Biết
rằng (C ) và (d ) cắt nhau tại ba điểm phân biệt ,
A B, C trong đó (
A 0; −1) còn trọng tâm tam
giác KBC nằm trên đường thẳng y = 2x +1. Mệnh đề nào sau đây đúng?
3 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số
A. m = 4 .
B. m = 2 .
C. m = 3 .
D. Không tồn tại m Câu 22: Cho hàm số 3 2
y = x − 2x + (1− m) x + m có đồ thị (C ) . Tìm tất cả các giá trị thực của tham số
m để (C ) cắt trục hoành tại 3 điểm phân biệt x , x , x sao cho 2 2 2
x + x + x  4 . 1 2 3 1 2 3  1 −  m  1 1 1 A.  4 .
B. m  1. C. −  m 1. D. m 1.  4 4 m  0 Câu 23: Cho hàm số 3 2
y = x − 2x + (1− m) x + m có đồ thị (C ) . Tìm tất cả các giá trị thực của tham số
m để (C ) cắt trục hoành tại 3 điểm phân biệt x , x , x sao cho 2 2 2
x + x + x  4 . 1 2 3 1 2 3  1 −  m  1 1 1 A.  4 .
B. m  1. C. −  m  1. D. m 1.  4 4 m  0 Câu 24: Cho hàm số 3
y = x − (m + ) 2
2 x − (2m +13) x − m − 2 có đồ thị là (C , đường thẳng m )
d : y = mx + m + 8 và điểm I (1; 4) . Tính tổng tất cả các giá trị của tham số m , biết rằng đường
thẳng d cắt đồ thị (C tại ba điểm phân biệt ,
A B, C với A có hoành độ bằng 2 − và tam giác m )
IBC cân tại I . A. −12 . B. 6 − . C. 4 − . D. −10 . Câu 25: Cho hàm số 3 2
f (x) = x − 3x +1. Có bao nhiêu giá trị nguyên của tham số m để phương trình
2021. f ( f (x)) = m có 7 nghiệm phân biệt? A. 8078. B. 0. C. 4041. D. 8076.
Câu 26: Cho hàm số f ( x) = ( 3 − m ) 3 2 1
x + 3x + (4 − m) x + 2 với m là tham số. Có bao nhiêu số tự nhiên  
m sao cho phương trình f ( x) = 0 có nghiệm trên đoạn 1 ; 5   . 5  A. 4 . B. 7 . C. 6 . D. 5 .
Câu 27: Cho hàm số y = f ( x) 3 2
= 2x − 3x +1 . Tập hợp các giá trị m để phương trình   2sin x +1 f f = f   
(m) có nghiệm là đoạn a;b. Khi đó giá trị 2
4a + 8b thuộc khoảng nào   2  sau đây?  23   43 39   37 65  A. 7 ;   . B. (−2;5) . C. ;   . D. ;   .  2   3 2   3 4 
Câu 28: Tìm tất cả các giá trị của tham số m để phương trình 3 2 1 2 2 3 2 2 m x x − − + − = 0 có 3 nghiệm thực phân biệt. 1 1 1 A. m 1.
B. −1  m  0 . C. 0  m  . D. 1 −  m  . 2 2 2 3 2
Câu 29: Cho hàm số y = x − 2(m + ) 1 x + (5m + )
1 x − 2m − 2 có đồ thị là (C ) , với m là tham m
số. Tập S là tập hợp các giá trị nguyên của m (m ( 2
− 021;2021)) để (C ) cắt trục hoành tại m
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 4 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
ba điểm phân biệt A(2;0), B,C sao cho trong hai điểm B,C có một điểm nằm trong và một
điểm nằm ngoài đường tròn có phương trình 2 2
x + y = 1. Tính số các phần tử của S ? A. 4041. B. 2020. C. 2021. D. 4038.
Câu 30: Cho hàm số f ( x) 3 2
= x − mx + (m − 2) x +1 với m là tham số. Có tất cả bao nhiêu giá trị nguyên của m để phương trình sau có 3 nghiệm thực phân biệt
f ( x) f (x) .e
+ f (x) f (x) .  
= f (x) + f (x) A. 1. B. vô số. C. 2 . D. 0 .
5 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: Cho hàm số 3 2
y = x − 2x −1 có đồ thị (C) , đường thẳng (d ) : y = mx −1 và điểm K (4;1 ) 1 .Biết
rằng (C) và (d ) cắt nhau tại ba điểm phân biệt ,
A B, C trong đó A(0; − ) 1 còn trọng tâm tam
giác KBC nằm trên đường thẳng y = 2x +1. Mệnh đề nào sau đây đúng?
A. m = 4 .
B. m = 2 .
C. m = 3 .
D. Không có m .
Lời giải Chọn A
Phương trình hoành độ giao điểm của (C) và (d ) là: x = 0 3 2 3 2
x − 2x −1 = mx −1  x − 2x − mx = 0  x ( 2
x − 2x − m) = 0   2
x − 2x − m = 0(1)
Để (C) và (d ) cắt nhau tại ba điểm phân biệt thì (1) có hai nghiệm phân biệt khác 0. Ta có: '   0 1  + m  0 m  1 −      2
0 − 0 − m  0 m  0 m  0
Gọi x , x là nghiệm của (1), ta có B( x ;mx −1 ;C x ;mx −1 . Trọng tâm G của tam giác 1 1 ) ( 2 2 ) 1 2 KBC , ta có  4 + x + x 1 2 x = = 2  G  3 
11+ mx + mx − 2 2m + 9  1 2 y = = G  3 3 +
Theo giả thiết G thuộc đường thẳng ( 2m 9
d ) : y = 2x +1 nên ta có:
= 2.2 +1 m = 3(tm) 3 Câu 2:
Gọi S là tập tất cả các giá trị của tham số m để đường thẳng y = 3x + m tiếp xúc với đồ thị hàm số 3
y = x +1 . Tổng các phần tử của S bằng A. 0 . B. 3 . C. 2 . D. 1 − .
Lời giải Chọn C 2 y ' = 3x .
Giả sử đường thẳng y = 3x + m tiếp xúc với đồ thị hàm số 3
y = x +1 tại điểm x0 thì y( =  =  0 x ) 3 0 x 1. Đk đủ: =  =
y = x −  m = − 0 x 1 0 y 2 thì PTTT là 3 2 1. = −  =
y = x +  m = 0 x 1 0 y 0 thì PTTT là 3 3 3 .
Tổng các phần tử của S bằng 2 . 3  3
x +1 = 3x + m
x +1− 3x = m
Cách 2: Điều kiện tiếp xúc   
m = −1;m = 3. 2 3  x = 3 x = 1
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 6 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 3 Câu 3:
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y = 2x − (2 + m) x + m cắt
trục hoành tại 3 điểm phân biệt 1 1 1 1 A. m  . B. m  . C. m  − .
D. m  − ; m  4 . 2 2 2 2
Lời giải Chọn D
Phương trình hoành độ giao điểm của đồ thị với trục Ox: 3
2x − (2 + m) x + m = 0 3
 2x − 2x − mx + m = 0  (x − ) 2
1 2x + 2x − m = 0 ( ) 1   x = 1   2
2x + 2x − m = 0  (2)
Để đồ thị hàm số cắt Ox tại 3 điểm phân biệt  ( ) 1 có 3 nghiệm phân biệt
 (2) có 2 nghiệm phân biệt khác 1.   1 ' = 1+ 2m  0  m  −     2 g ( ) 1 = 2 + 2 − m  0 m  4 Câu 4:
Cho hàm số f ( x) 3 2
= ax + bx + cx + d (a, b, c, d  ) có đồ thị như hình vẽ sau.
Có tất cả bao nhiêu giá trị nguyên thuộc đoạn  2020 −
; 2020 của tham số m để phương trình
2 f ( x ) − m = 0 có đúng 2 nghiệm thực phân biệt? A. 2020 . B. 2022 . C. 2021 . D. 2019 .
Lời giải Chọn D
2 f ( x ) − m = 0  ( ) = m f x ( ) 1 2
Dựa vào đồ thị hàm y = f ( x ) ta có: để phương trình ( )
1 có đúng 2 nghiệm thực phân biệt m = 3  m = 6 2     mm  2 −  1 −  2
7 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số Vì m  20
− 20;2020  m 20 − 20; 20 − 19;......− 3;  6 . Vậy có 2019 số. Câu 5:
Biết đường thẳng y = (3m − )
1 x + 6m + 3 cắt đồ thị hàm số 3 2
y = x − 3x +1 tại ba điểm phân biệt
sao cho một giao điểm cách đều hai giao điểm còn lại. Khi đó m thuộc khoảng nào dưới đây?  3   3  A. 1;   . B. (0; ) 1 . C. ; 2   . D. (−1;0) .  2   2 
Lời giải Chọn D
Phương trình hoành độ giao điểm là ( m − ) 3 2 3
1 x + 6m + 3 = x − 3x +1 3 2
x − 3x − (3m − )
1 x − 6m − 2 = 0 ( ) 1 .
Xét hàm số g ( x) 3 2
= x − 3x − (3m − )
1 x − 6m − 2 (C . m ) g( x) 2
= 3x − 6x − 3m +1 g (x) = 6x − 6; g(x) = 0  x =1.
Đồ thị (C có điểm uốn là I (1; 9 − m − 3) . m )
Để đường thẳng y = (3m − )
1 x + 6m + 3 cắt đồ thị hàm số 3 2
y = x − 3x +1 tại ba điểm phân biệt
sao cho một giao điểm cách đều hai giao điểm còn lại  2  = ( m  − 3 − )2 − 3.( 3 − m + ) 1  0  3 1      m = − ( 1 − ;0) .   1 I Ox 3 m = −  3 Câu 6:
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 3 2 y x 2m 1 x 3m 1 x m
1 cắt trục hoành tại 2 điểm phân biệt? A. 4 . B. 2 . C. 3 . D. 1.
Lời giải Chọn D  Xét phương trình 3 2 2 x 2m 1 x 3m 1 x m 1 0 x 1 x 2mx m 1 0 x 1 2 x 2mx m 1 0 *
 Theo yêu cầu bài toán phương trình * xảy ra 2 trường hợp 2 m m 1 0
TH1: phương trình có nghiệm kép khác 1, tức là loại, do nghiệm không 1 2m m 1 0 nguyên.
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 8 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
TH2: phương trình có 2 nghiệm phân biệt trong đó 1 là một nghiệm, tức là 2 m m 1 0 m 2 . 1 2m m 1 0
Nhận xét: cụm từ “cắt trục hoành tại 2 điểm phân biệt” được người ra đề hiểu là “có đúng 2 điểm
chung với trục hoành”. Theo ý kiến chủ quan của người giải, ta nên phát biểu rõ ràng hơn. Câu 7: Cho đồ thị (C ) 3 2
: y = x − 2x + (1− m x + m. Tìm tất cả các giá trị của tham số m để (C cắt m ) m )
trục hoành tại ba điểm phân biệt có hoành độ x , x , x thỏa 2 2 2
x + x + x = 4 1 2 3 1 2 3 1 A. m  0 .
B. m  (0; 2) . C. m = 1. D. m  − và m  0 . 4 Lời giải Chọn C
 Để hàm số đã cho cắt trục hoành tại 3 điếm phàn biệt thì phưong trình hoành độ giao điểm
phải có 3 nghiệm phàn biệt: 3 2
x − 2x + (1− m)x + m = 0 x − ( 2 (
1) x − x − m) = 0
 Ta đặt x = 1. Khi đó, đế phưong trình có 3 nghiệm phân biệt thì phương trình sau phải có 2 1
nghiệm phân biệt khác 1. 2
x − x − m = 0
 Do có nghiệm khác 1 nên 1−1− m  0 hay m  0. Ta có  = 1+ 4m  1
Để có 2 nghiệm phàn biệt thì   0 hay m  − . 4
 Theo điều kiện của đề bài ta có 2 2 2
x + x + x = 4 1 2 3
 1+ (x + x )2 − 2x x = 4 2 3 2 3
 (x + x )2 − 2x x = 3 2 3 2 3
vói x , x là nghiệm của phương trình bậc 2 trên. 2 3  Áp dụng Viet ta có 2
1 − 2(−m) = 3  m = 1
 Kết hợp các điều kiện ta có  m = 1. Câu 8:
Gọi S là tập tất cả các giá trị thực của tham số m để đường thẳng y = m cắt đồ thị hàm số 3 2
y = x − 3x tại 3 điểm phân biệt ,
A B, C ( B nằm giữa ,
A C ) sao cho AB = 2BC . Tính tổng
các phần tử thuộc S . 7 − 7 A. 4 − . B. . C. 2 − . D. 0 . 7
Lời giải Chọn A
 Ta có BBT của hàm số 3 2
y = x − 3x như sau:
9 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số
 Suy ra đường thẳng y = m cắt đồ thị hàm số 3 2
y = x − 3x tại 3 điểm phân biệt , A B, C  −4  m  0 .
 Khi đó x + x + x = 3, x x + x x + x x = 0, x x x = m . A B C A B B C C A A B C
x x xA B C 
x − x = 2 x − xB A ( C B )
 Để B nằm giữa ,
A C và AB = 2BC thì 
x x x  C B A
x − x = 2 x − xA B ( B C )
 3x = x + 2x  4x − 3 = x x = 6 − 5x . B A C B C A B (6−5x x + x x − + x − − x =  B ) . . B B ( 4 3 B ) (4 3 B ).(6 5 B ) 0 (*)  Suy ra ( .  4x − 3 x − x = mB ). .B(6 5 B ) (**)  + − +  98 20 7 Từ (*) được 7 7 x =
. Thay vào (**) được 98 20 7 m = − và m = . B 7 49 49  + − +   98 20 7 98 20 7 Vậy S = − ;  .  49 49   3 2 Câu 9:
Có bao nhiêu giá trị nguyên âm của a để đồ thị hàm số y = x + (a +10) x − x +1 cắt trục
hoành tại đúng một điểm? A. 10 . B. 8 . C. 11. D. 9 .
Lời giải Chọn A
 Phương trình hoành độ giao điểm của đồ thị và trục hoành là: 3 x + (a + ) 2
10 x − x +1 = 0( ) 1 3 2 2
x +10x − x +1 = −ax .
Ta thấy x = 0 không là nghiệm của phương trình nên ( ) 3 2
x +10x − x +1 1  − = a . 2 x
x +10x − x +1  = −
Xét hàm số f ( x) 3 2 với x  \   0 2 x + − ( − ) 1 .( 2 3 + + 2 2 x x x x x )
Ta có f ( x) = − = − 3 3 x x
f ( x) = 0  x = 1 .
Bảng biến thiên của hàm số f ( x) như sau:
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 10 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
 Từ bảng biến thiên ta thấy đồ thị hàm số đã cho cắt trục hoành tại đúng một điểm khi ( ) 1 có
đúng 1 nghiệm  a  −11. Do a − − − −
nguyên âm nên a  10, 9, 8,..., 
1 . Vậy có 10 giá trị của a thỏa mãn yêu cầu bài toán
Câu 10: Có bao nhiêu giá trị nguyên thuộc  2020 − ; 
2021 của hàm số m để đường thẳng y = mx − m −1
cắt đồ thị của hàm số 3 2
y = x − 3x + x tại ba điểm phân biệt ,
A B, C sao cho AB = BC . A. 2021 . B. 2023 . C. 2024 . D. 2022 .
Lời giải Chọn A
Phương trình hoành độ giao điểm 3 2 3 2
x − 3x + x = mx − m −1  x − 3x + (1− m) x + m +1 = 0 . ( − ) x = x 1 ( 1 2
x − 2x −1− m) = 0   2
x − 2x −1− m = 0  ( ) 1
Để để đường thẳng y = mx − m −1 cắt đồ thị hàm số 3 2
y = x − 3x + x tại ba điểm phân biệt A , 2 + m  0
B , C thì phương trình ( )
1 có hai nghiệm phân biệt khác 1    m  2 − .  2 − − m  0 Khi đó phương trình ( )
1 có hai nghiệm x , x thỏa mãn x + x = 2 với mọi tham số m . 1 2 1 2
Trường hợp 1: x = 1. B
x + x = 2xx + x = 2 x + x = 2 
Khi đó yêu cầu bài toán trở thành A C B 1 2 1 2      .
y + y = 2 y y + y = 2  
m x + x − 2m + 2 = 2 A C B 1 2  ( 1 2 )
Điều này thỏa mãn với mọi m  −2 .
Trường hợp 2: x  1 và giả sử x x . B 1 2
Khi đó yêu cầu bài toán trở thành
x + x = 2xx +1 = 2xx +1 = 2xA C B 1 2 1 2      .
y + y = 2 y y +1 = 2 y  
mx − m + 2 = 2 mx − m +1 * A C B 1 2  1 ( 2 )( ) x +1 = 2xx =1 Ta có hệ 1 2 2   
không thỏa mãn yêu cầu bài toán. x + x = 2 x = 1  1 2  1
Vậy giá trị m cần tìm là m  −2 .
Vì m  , m  2 − 020;202  1  m  1 − ;202 
1  có 2023 giá trị của m .
Câu 11: Cho bao nhiêu giá trị m để đồ thị hàm số 3 2
y = −x + mx − 2m cắt trục Ox tại 3 điểm phân biệt
có hoành độ lập thành cấp số cộng. A. 1. B. 2 . C. 3 . D. 0 .
Lời giải Chọn B
11 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số
 Xét phương trình hoành độ giao điểm: 3 2
−x + mx − 2m = 0 (*).
 Giả sử phương trình (*) có 3 nghiệm phân biệt x , x , x theo thứ tự lập thành một cấp số 1 2 3
cộng, theo tính chất của cấp số cộng ta có: x + x = 2x . 1 3 2  m
Áp dụng định lí Vi-et ta có: x + x + x = m  3x = m x = . 1 2 3 2 2 3  m Vì x =
là một nghiệm của phương trình (*) nên ta có: 2 3 m = 0 3 2  m   m   − + . m − 2m = 0     3
 2m − 54m = 0  m = 3 3  .  3   3  m = 3 − 3   Thử lại:
+ Với m = 0 , phương trình trở thành: 3
−x = 0  x = 0 ( loại). x = 3 − + 3 1 
+ Với m = 3 3 , phương trình trở thành: 3 2
−x + 3 3x − 6 3 = 0  x = 3 và 3 nghiệm 2  x = 3+ 3 3 
này lập thành 1 CSC.x = 3 − − 3 1  + Với m = 3
− 3 , phương trình trở thành: 3 2
−x − 3 3x + 6 3 = 0  x = − 3 và 3 nghiệm 2  x = 3− 3 3 
này lập thành 1 CSC.
 Vậy có 2 giá trị của m thỏa yêu cầu bài toán là m = 3 3 và m = 3 − 3 .
Câu 12: Cho hàm số bậc ba y = f ( x) liên tục trên
và có đồ thị như hình vẽ bên.
Tổng tất cả các giá trị nguyên của tham số m để phương trình f ( 2 f (cos x)) = m có nghiệm   x  ;    2  A. 1 − . B. 0 . C. 1. D. 2 − .
Lời giải Chọn D  
Đặt t = cos x, do x  ; 
 nên suy ra t  ( 1; − 0.  2 
Trên khoảng (−1;0) hàm số nghịch biến nên suy ra
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 12 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 Với t  ( 1;
− 0 thì f (0)  f (t)  f (− )
1 hay 0  f (t )  2 .
Đặt u = 2 f (cos x) thì u = 2 f (t),u 0;2). Khi đó bài toán trở thành:
Tìm m để phương trình f (u) = m có nghiệm u 0; 2) .
Quan sát đồ thị ta thấy rằng với u 0;2) thì f (u)  2 − ;2)  2 −  m  2 . Vì m   m  2 − ;−1;0  ;1  m = 2 − .
Câu 13: Gọi S là tập hợp các số nguyên m để phương trình 3 2
x − (2m +1)x + 2(3m − 2)x − 8 = 0 có ba
nghiệm lập thành một cấp số nhân. Tổng các phần tử của S bằng A. 0 . B. 2 − . C. 3 . D. 1 − .
Lời giải Chọn C
Giả sử x , x , x là ba nghiệm của phương trình 3 2
x − (2m +1)x + 2(3m − 2)x − 8 = 0 . 1 2 3 Khi đó ta có 3 2
x − (2m +1)x + 2(3m − 2)x − 8 = ( x − x x − x x − x 1 ) ( 2 ) ( 3 )
x + x + x = 2m +1 1 2 3  Ta có x x x = 8 1 2 3
x x + x x + x x = 2 3m+ 2  1 2 2 3 3 1 ( )
Do x , x , x lập thành một cấp số nhân nên ta có x x x = 8  x = 2 . 1 2 3 1 2 3 2
Thay x = 2 vào phuognw trình 3 2
x − (2m +1)x + 2(3m − 2)x − 8 = 0 ta có 2 8 − (2m + )
1 .4 + 4 (3m − 2) − 8 = 0  4m = 12  m = 3 .
Thử lại với m = 3 ta thấy thỏa mãn. Vậy m = 3 . Dó đó tổng tất cả các giá trị của m bằng 3 1 Câu 14: Cho hàm số 3
f (x) = x −
mx + m − 8 , x
với m là một hằng số khác 0 . Biết rằng phương 2
trình f (x) = 0 có đúng 2 nghiệm phân biệt thì có bao nhiêu giá trị nguyên dương k thỏa mãn
phương trình f (x) = k có 3 nghiệm phân biệt? A. 3 . B. 6 . C. 34 . D. 31.
Lời giải Chọn D   pt f x =  (x − ) m 2 ( ) 0 2 x + 2x + 4 − = 0  
có đúng 2 nghiệm phân biệt  2  x = 2  m 2
 x + 2x + 4 − = 0 ( )
1 có đúng 2 nghiệm phân biệt  2  g ( x)
+ g(2) = 0  m = 24 ( nhận ) 3 2
f (x) = x −12x +16 → f '(x) = 3x −12
f '(x) = 0  x = 2  BBT
13 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số
Phương trình f (x) = k có 3 nghiệm phân biệt khi 0  k  32 và * k
→ k = 1;2;3;....;  31  = 0 + Pt ( )
1 có nghiệm kép và khác 2  
m = 6 ( nhận )g(2)  0 3 2
f (x) = x − 3x − 2 → f '(x) = 3x − 3
f '(x) = 0  x = 1  BBT
Phương trình f (x) = k có 3 nghiệm phân biệt khi 4 −  k  0 và * k  → k 
Vậy có 31 giá trị k thỏa điều kiện bài toán. Câu 15: Cho hàm số 3 2
y = x − (m + 2)x − (2m +13)x − m − 2 có đồ thị (C ), đường thẳng m
d : y = mx + m + 8 và điểm I (1; 4). Tính tổng tất cả các giá trị của tham số ,
m biết rằng đường
thẳng d cắt đồ thị (C ) tại ba điểm phân biệt ,
A B, C với A có hoành độ bằng 2 − và tam giác m
IBC cân tại I . A. −12 . B. 6 − . C. 4 − . D. −10 .
Lời giải Chọn B + Phương trình hoành độ giao điểm của d và (C ) là: mx = 2 −  3
x − (m + 2)x − (3m +13)x − 2m −10 = 0  x = 1 −  x = m + 5  m  7 −
+ Để đường thẳng d cắt đồ thị (C ) tại ba điểm phân biệt , A B, C thì  mm  6 − + Giả sử 2 B( 1
− ;8),C(m + 5;m + 6m + 8) . Để tam giác IBC cân tại I m = 2 −  thì 2 2 2 2 2
IB = IC  20 = (m + 4) + (m + 6m + 4)  m = 6 − (l)   m = 2 −  3
Vậy có ba giá trị của m thỏa mãn nên tổng các giá trị của m bằng 6 − .
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 14 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
Câu 16: Gọi d là đường thẳng đi qua A(2;0) có hệ số góc m (m  0) cắt đồ thị (C) 3 2
: y = −x + 6x − 9x + 2 tại ba điểm phân biệt ,
A B, C. Gọi B , C lần lượt là hình chiếu
vuông góc của B, C lên trục tung. Biết rằng hình thang BB CC
 có diện tích bằng 8, giá trị của
m thuộc khoảng nào sau đây? A. (5;8) . B. (−5;0) . C. (0; 2) . D. (1;5) .
Lời giải Chọn D
Phương trình đường thẳng d : y = m( x − 2). Phương trình hoành độ giao điểm x =  A
−x + 6x − 9x + 2 = m(x − 2)  (x − 2)(x − 4x + m + ) 2 (2;0) 3 2 2 1 = 0   . 2
x − 4x + m +1= 0
Để (C) cắt d tại 3 điểm phân biệt thì   0  4 − m −1  0  m  3. x + x = 4
Giả sử B (x ,mx − 2m),C (x ,mx − 2m) 1 2   . 1 1 2 2 x x = m +1  1 2
Ta có B(0, mx − 2m , C 0, mx − 2m . 1 ) ( 2 ) 1 S = B C
  BB + CC ' = 8  B C
  BB + CC =16. BB 'C 'C ( ) ( ) 2 Mà B C
  = m(x − x , BB = x ,CC = x . 1 2 ) 1 2
Do m dương nên x x = m +1  0 mà x + x = 4  0  x  0, x  0. 1 2 1 2 1 2
B 'C ' = m x − x , BB ' = x ,CC ' = x m x − x x + x =16  m x − x = 4 1 2 1 2 1 2 ( 1 2 ) 1 2
m (x − x )2 =16  m (x + x )2 2 2 2
− 4x x  =16  m 16 − 4m − 4 =16 1 2 1 2 1 2 ( )   m = 1 − l 3 2 ( )
m − 3m + 4 = 0   m = 2
Câu 17: Cho hàm số bậc ba y = f ( x) có đồ thị như hình vẽ
Có bao nhiêu giá trị nguyên của tham số m để phương trình 3 f ( x) 2 − mf (x) + ( 2
m − m − ) f ( x) 2 2 3 9
+ 3m + 9m = 0 có đúng 8 nghiệm phân biệt? A. 3 . B. 4 . C. 5 . D. 6 . Lời giải Chọn B
15 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số 3 f ( x) 2 − mf (x) + ( 2
m − m − ) f ( x) 2 2 3 9 + 3m + 9m = 0
Đặt t = f ( x) , phương trình trở thành: 3 2 t − mt + ( 2 m − m − ) 2 2 3
9 t + 3m + 9m = 0  (t + ) 2 t − ( m + ) 2 3 2
3 t + m + 3m = 0  
 (t + 3)(t − m)(t − m −3) = 0  = −  f (x t ) = 3 − ( )1 3    t = m
  f (x) = m (2)   t = m + 3  f
 ( x) = m + 3 (3)
Nhận xét các phương trình (2) và (3) không có nghiệm chung.
Dựa vào đồ thị, ta thấy: ( ) x = a 1   x = b
YCBT  Các phương trình (2) và (3) đều có 3 nghiệm phân biệt khác a, b m + 3  5 m  2      3 −  m  2 m  3 − m  3 −
Mà m là số nguyên nên m  2 − ; 1 − ;0  ;1 .
Câu 18: Gọi S là tập hợp chứa tất cả các giá trị thực của tham số m để đồ thị hàm số f ( x) 3 = x − (m + ) 2 6 1 x + 3(2m + )
1 x + 2 cắt trục Ox tại ba điểm phân biệt có hoành độ lớn hơn 1 − .  −  Biết rằng a S = ; + 
 ; trong đó a,b là các số nguyên dương và phân số a là tối giản. Giá trị  bb
biểu thức T = a + b tương ứng bằng A. 4 . B. 8 . C. 5 . D. 7 .
Lời giải Chọn C
Xét phương trình hoành độ giao điểm:
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 16 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 3 x − (m + ) 2 6 1 x + 3(2m + ) 1 x + 2 = 0  (x − )( 2
1 x − (6m + 5) x − 2) = 0 x =1   2 x − 
(6m +5) x − 2 = 0(*)
Yêu cầu bài toán tương đương với phương trình (*) có hai nghiệm phân biệt x ; x lớn hơn 1 − 1 2 và khác 1.Ta có: 2   0 36
m + 60m + 33  0   x + x  2 −  1 2 6m + 5  2 − 2 − (     m x +1 x +1  0 +  1 )( 2 ) 6m 4 0 3   2 1  − 
(6m +5)− 2  0 m  1 −
Do đó a = 2;b = 3  T = a + b = 5
Câu 19: Điều kiện cần và đủ của tham số thực m để đường thẳng y = 3x + m − 2 cắt đồ thị hàm số y = ( x − )3
1 tại ba điểm phân biệt là A. 3 −  m  1. B. 3 −  m  1.
C. −1  m  3 .
D. −1  m  3 .
Lời giải Chọn B
Xét phương trình: ( x − )3 3 2 1
= 3x + m − 2  x − 3x +1 = m (*).
Đường thẳng y = 3x + m − 2 cắt đồ thị y = ( x − )3
1 tại ba điểm phân biệt khi và chỉ khi phương
trình (*) có ba nghiệm phân biệt. x = 0 Đặt f ( x) 3 2
= x − 3x +1 f '(x) 2
= 3x − 6x = 0   . x = 2 Ta có bảng biến thiên
Từ bảng biến thiên suy ra phương trình (*) có ba nghiệm phân biệt khi và chỉ khi đường thẳng
y = m cắt đồ thị hàm số f ( x) 3 2
= x − 3x +1 tại ba điểm phân biệt. Vậy 3 −  m  1. Câu 20: Cho hàm số 3 2
y = x + 3x + m có đồ thị (C) . Biết đồ thị (C) cắt trục hoành tại 3 điểm phân biệt ,
A B,C sao cho B là trung điểm AC . Phát biểu nào sau đây đúng? A. m ( 4 − ;0) .
B. m  (0;+) . C. m  ( ; − 4 − ) . D. m  ( 4 − ; 2 − ) .
Lời giải Chọn A
Phương trình hoành độ giao điểm của (C) và trục hoành là 3 2
x + 3x + m = 0( ) 1 .
17 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số Giả sử ( )
1 có 3 nghiệm phân biệt x ; x ; x
x x x
thì x ; x ; x lần lượt là hoành độ của 1 2 3 ( 1 2 3 ) 1 2 3 , A B,C và 3 2
x + 3x + m = ( x − x x − x x − x 1 ) ( 2 ) ( 3 ) 3 2 3
x + 3x + m = x − ( x + x + x ) 2
x + x x + x x + x x x − x x x 1 2 3 ( 1 2 2 3 3 1 ) 1 2 3
Nên ta có x + x + x = 3 − . 1 2 3
Để B là trung điểm AC thì x + x = 2x nên 3x = 3 −  x = 1 − . 1 3 2 2 2 Tức là ( )
1 có 1 nghiệm là x = −1 . Suy ra 1
− + 3 + m = 0  m = −2 . x = 1 − − 3 
Thử lại với m = −2 thì ( ) 1 trở thành 3 2
x + 3x − 2 = 0  x = 1 − 
(thỏa điều kiện bài toán). x = 1 − + 3  Cách 2: Ta có 2
y = 3x + 6x và y = 6x + 6 nên (C) có điểm uốn I ( 1 − ;m + 2) .
Để (C) cắt trục hoành tại 3 điểm phân biệt ,
A B,C sao cho B là trung điểm AC thì I Ox
m + 2 = 0  m = 2 − . Câu 21: Cho hàm số 3 2
y = x − 2x −1 có đồ thị (C ) , đường thẳng (d ) : y = mx −1và điểm K (4;11) . Biết
rằng (C ) và (d ) cắt nhau tại ba điểm phân biệt ,
A B, C trong đó (
A 0; −1) còn trọng tâm tam
giác KBC nằm trên đường thẳng y = 2x +1. Mệnh đề nào sau đây đúng?
A. m = 4 .
B. m = 2 .
C. m = 3 .
D. Không tồn tại m
Lời giải Chọn C
Xét phương trình hoành độ: x = 0 3 2 3 2
x − 2x −1 = mx −1  x − 2x − mx = 0   2
x − 2x − m = 0(1) Suy ra (
A 0; −1) và hoành độ của điểm B và C là nghiệm của phương trình (1)
Để (C ) và (d ) cắt nhau tại ba điểm phân biệt ,
A B, C khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác 0 '  0 1 m 0 m 1 (1)  +   Khi và chỉ khi:   −      (*) m   0 m   0 m   0
Giả sử: B(x ; m x −1) , C(x ; m x −1) . Theo Vi–ét ta có x + x = 2 1 1 2 2 1 2 Gọi G là trọng tâm của tam giác KBC :  4 + x + x x = 1 2 x =  2 G 3  G  2m + 9     +  G 2; 2m 9  11 + mx − 1 + mx − 1 y =  3 1 2  G   y = G   3 3 2m + 9
Trọng tâm G nằm trên đường thẳng y = 2x +1 suy ra
= 2.2 +1  m = 3 thỏa mãn (*) 3
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 18 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 Câu 22: Cho hàm số 3 2
y = x − 2x + (1− m) x + m có đồ thị (C ) . Tìm tất cả các giá trị thực của tham số
m để (C ) cắt trục hoành tại 3 điểm phân biệt x , x , x sao cho 2 2 2
x + x + x  4 . 1 2 3 1 2 3  1 −  m  1 1 1 A.  4 .
B. m  1. C. −  m 1. D. m 1.  4 4 m  0
Lời giải Chọn A
Phương trình hoành độ giao điểm của (C) và trục hoành là: x =1 3 2
x − 2x + (1− m) x + m = 0  ( x − ) 1 ( 2
x − x − m) = 0   . 2
x − x − m = 0  ( ) *
(C) cắt trục hoành tại 3 điểm phân biệt  (*) có hai nghiệm phân biệt khác 1  1 1  + 4m  0 m  −     4 . 2 1  −1− m  0 m  0
Khi đó x = 1, x và x là hai nghiệm của (*) . 1 2 3
x + x + x  4  ( x + x )2 2 2 2
− 2x x  3  1+ 2m  3  m  1. 1 2 3 2 3 2 3  1 −  
Vậy các giá trị cần tìm của m 1 m là  4 . m  0 Câu 23: Cho hàm số 3 2
y = x − 2x + (1− m) x + m có đồ thị (C ) . Tìm tất cả các giá trị thực của tham số
m để (C ) cắt trục hoành tại 3 điểm phân biệt x , x , x sao cho 2 2 2
x + x + x  4 . 1 2 3 1 2 3  1 −  m  1 1 1 A.  4 .
B. m  1. C. −  m  1. D. m 1.  4 4 m  0
Lời giải Chọn A
Phương trình hoành độ giao điểm: 3 2
x − x + ( − m) x + m =  ( x − )( 2 2 1 0
1 x − x − m) = 0 ( ) 1 x =1 3  
. Điều kiện để phương trình ( )
1 có 3 nghiệm phân biệt là phương trình 2
x − x − m = 0  (2) m  0 ( x  1 
2) có 2 nghiệm phân biệt khác 1     1 .  = 1+ 4m  0 m  −  4
Khi đó phương trình (2) có 2 nghiệm phân biệt x , x . 1 2
Ta có x + x + x  4  x + x  3  ( x + x )2 2 2 2 2 2 − 2x x  3 2
 1 + 2m  3  m  1. 1 2 3 1 2 1 2 1 2
19 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số  1 −  m  1 Vậy  4 . m  0 Câu 24: Cho hàm số 3
y = x − (m + ) 2
2 x − (2m +13) x − m − 2 có đồ thị là (C , đường thẳng m )
d : y = mx + m + 8 và điểm I (1; 4) . Tính tổng tất cả các giá trị của tham số m , biết rằng đường
thẳng d cắt đồ thị (C tại ba điểm phân biệt ,
A B, C với A có hoành độ bằng 2 − và tam giác m )
IBC cân tại I . A. −12 . B. 6 − . C. 4 − . D. −10 .
Lời giải Chọn C
Phương trình hoành độ giao điểm của (C với đường thẳng d : y = mx + m + 8 là m ) 3 x − (m + ) 2
2 x − (2m +13) x − m − 2 = mx + m + 8 3
x − (m + ) 2
2 x − (3m +13) x − 2m −10 = 0  (x + ) 2
2 x − (m + 4) x − (m + 5) = 0   x = 2 −   (với g ( x) 2
= x − (m + 4) x − (m + 5) ) g  ( x) = 0
Đồ thị (C cắt đường thẳng d tại 3 điểm phân biệt khi và chỉ khi g ( x) = 0 có hai nghiệm m ) g  ( 2 − )  0
x , x phân biệt khác 2 − , nghĩa là  . 1 2   0  g 2
Ta có  = (m + ) + (m + ) 2 4 4
5 = m +12m + 36  0, m   −6. và g ( 2 − ) = m + 7 do vậy gg  ( 2 − )  0 m + 7  0 m  6 −      (*).   0  m  6 − m  7 − g
Với điều kiện (*) ta có đồ thị (C cắt đường thẳng d tại 3 điểm phân biệt A( 2 − ;8 − m) và hai m )
điểm B ( x ; y ,C x ; y trong đó x , x là hai nghiệm của g ( x) = 0 và x + x = m + 4 . 1 1 ) ( 2 2 ) 1 2 1 2  + + + +  Gọi x x m(x x ) 2m 16 K là
trung điểm của BC ta có 1 2 1 2 K ;   hay  2 2  2
m + 4 m + 6m +16  K  ;  .  2 2 
Tam giác IBC cân tại I nên ta có IK ⊥ BC hay IK cùng phương với pháp tuyến của đường thẳng d . 2
m + 2 m + 6m + 8  Ta có IK =  ;  và n = ( ; m − )
1 là một pháp tuyến của đường thẳng d , do đó  2 2  2 + + + m = 2 − ta cần có m 2 m 6m 8 3 2 =
m + 6m + 9m + 2 = 0   . m 1 − m = 2 −  3
Kiểm tra lại thấy m = −2 không thỏa do khi đó I d .
Vậy có 2 giá trị của tham số m để thỏa mãn bài toán và tổng tất cả các giá trị đó bằng 4 − .
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 20 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 Câu 25: Cho hàm số 3 2
f (x) = x − 3x +1. Có bao nhiêu giá trị nguyên của tham số m để phương trình
2021. f ( f (x)) = m có 7 nghiệm phân biệt? A. 8078. B. 0. C. 4041. D. 8076.
Lời giải Chọn C m
Ta có: 2021. f ( f (x)) = m f ( f (x)) = . 2021
Khảo sát hàm số y = f ( f (x)) trên . x = 0 = x1 x = 2 = x Đạo hàm: 
y = f ( x). f ( f ( x)) = (3x − 6x)(3( f (x))2 − 6 f (x)) 2 2 = 0   . f ( x) = 0   f  ( x) = 2
x = x  2,879 3 Chú ý rằng: 
f (x) = 0  x = x  0, 653 và f (x) = 2  x = x  3,104 . 4  6 x = x  0 − ,532  5
Do 6 nghiệm trên đều là nghiệm đơn nên hàm số y = f ( f (x)) có 6 cực trị là x , i =1,2,...,6 . i Bảng biến thiên: Phương trình
2021. f ( f ( x)) = m có 7 nghiệm phân biệt m  1 −  1  2 − 021 m  2021 2021
Do m nguyên nên m  20 − 20, 20 − 19,..., 2019, 20 
20 , do đó có 4041 số thỏa yêu cầu bài toán.
Câu 26: Cho hàm số f ( x) = ( 3 − m ) 3 2 1
x + 3x + (4 − m) x + 2 với m là tham số. Có bao nhiêu số tự nhiên  
m sao cho phương trình f ( x) = 0 có nghiệm trên đoạn 1 ; 5   . 5  A. 4 . B. 7 . C. 6 . D. 5 .
Lời giải Chọn D 3 3
Ta có: f ( x) = 0  ( x + )
1 + x +1 = (mx) + mx (*) . Xét ( ) 3
f t = t + t với t  . f (t ) 2 = 3t +1  0 t   .
21 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số
Suy ra hàm số f (t) đồng biến trên .
Khi đó (*)  x +1 = mx  (m − ) 1 x = 1 . m −1  0 m  1    
Để phương trình có nghiệm trên đoạn 1 ; 5   thì    .  1 1 6 5    5  m  6   5 m −1 5
Vì m là số tự nhiên nên m 2;3; 4;5; 
6 . Vậy có 5 giá trị m thỏa để.
Câu 27: Cho hàm số y = f ( x) 3 2
= 2x − 3x +1 . Tập hợp các giá trị m để phương trình   2sin x +1 f f = f   
(m) có nghiệm là đoạn a;b. Khi đó giá trị 2
4a + 8b thuộc khoảng nào   2  sau đây?  23   43 39   37 65  A. 7 ;   . B. (−2;5) . C. ;   . D. ;   .  2   3 2   3 4 
Lời giải Chọn D Ta có: 2
y = 6x − 6x . x = y = 0 0   . x =1 Bảng biến thiên: 2sin x +1 1  1 3  2sin x +1 Ta có: = sin x +  − ;   suy ra f    0  ;1 nên 2 2  2 2  2    2sin x +1 f f     0  ;1 .   2    3 2 2sin x +1 
2m −3m +1 0 Phương trình f f = f   
(m) có nghiệm  0  f (m) 1     2  3 2
2m −3m  0 1 3  −  m  . 2 2 Vậy 1 3 2
4a + 8b = 4. + 8. =13. 4 2
Câu 28: Tìm tất cả các giá trị của tham số m để phương trình 3 2 1 2 2 3 2 2 m x x − − + − = 0 có 3 nghiệm thực phân biệt. 1 1 1 A. m 1.
B. −1  m  0 . C. 0  m  . D. 1 −  m  . 2 2 2
Lời giải Chọn C
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 22 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 3 2 1−2m 3 2 1−2 2 − 3 + 2 − 2
= 0  2 − 3 + 2 = 2 m x x x x ( ) 1
Xét hàm số f ( x) 3 2 = 2x − 3x + 2 f ( x) 2 = 6x − 6x  = f ( x) x 0 2
= 0  6x − 6x = 0   x =1 Bảng biến thiên x ∞ 0 1 + ∞ f'(x) + 0 0 + 2 + ∞ f(x) ∞ 1 Phương − m 1 trình ( )
1 có 3 nghiệm thực phân biệt 1 2  1 2
 2  0 1− 2m 1  0  m  2 3 2
Câu 29: Cho hàm số y = x − 2(m + ) 1 x + (5m + )
1 x − 2m − 2 có đồ thị là (C ) , với m là tham m
số. Tập S là tập hợp các giá trị nguyên của m (m ( 2
− 021;2021)) để (C ) cắt trục hoành tại m
ba điểm phân biệt A(2;0), B,C sao cho trong hai điểm B,C có một điểm nằm trong và một
điểm nằm ngoài đường tròn có phương trình 2 2
x + y = 1. Tính số các phần tử của S ? A. 4041. B. 2020. C. 2021. D. 4038.
Lời giải Chọn D Xét phương trình 3 2
x − 2(m + 1)x + (5m + 1)x − 2m − 2 = 0(1) x = 2 2
(1)  (x − 2)(x − 2mx + m + 1) = 0   2
g(x) = x − 2mx + m +1 = 0 (2)
C ) cắt trục Ox tại ba điểm phân biệt  (2) có 2 nghiệm phân biệt x ; x khác 2 m 1 2 2 '  0
m − m −1  0     g(2)  0
4 − 4m + m +1  0   1 − 5  1+ 5  m ; −    ;+   2 2       (*)  5 m   3 Khi đó: (
A 2;0), B(x ;0),C(x ;0) ; 1 2
Hai điểm B,C thỏa mãn điều kiện đầu bài  (OB −1)(OC −1)  0
 ( x −1)( x −1)  0  x x +1 x + x 1 2 1 2 1 2 2 2
 (x x ) +1 (x + x ) − 2x x 1 2 1 2 1 2
23 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số − 2
 3m − 4m − 4  2 0  m  (− ;  )  (2;+) 3 2 −
Kết hợp với đk ta có m  (− ; 
)  (2;+) thỏa mãn ycbt. 3
Vậy số các phần tử của S là 4038 .
Câu 30: Cho hàm số f ( x) 3 2
= x − mx + (m − 2) x +1 với m là tham số. Có tất cả bao nhiêu giá trị nguyên của m để phương trình sau có 3 nghiệm thực phân biệt
f ( x) f (x) .e
+ f (x) f (x) .  
= f (x) + f (x) A. 1. B. vô số. C. 2 . D. 0 .
Lời giải Chọn B
Xét f ( x) f (x) .e
+ f (x) f (x) .  
= f (x) + f (x) (*) . Ta có f ( x) 3 2
= x − mx + (m − ) x + = (x − ) 2 2 1
1 x + (1− m) x −1 = ( x − ) 1 .g ( x)   . Với g ( x) 2
= x + (1− m) x −1 và g ( )
1 = 1− m và g (m − ) 1 = −1 .  f   ( ) 1 = 1− m
Lại có f ( x) 2
= 3x − 2mx + m − 2 với  .  f  ( ) 1 = 0 f ( x) ef  (x)+1 Với f ( ) 1 nếu f ( )
1  0  m  1 thì f ( x)  0, x  1 suy ra  . f ( x)    f  (x)+1 Khi đó ( )
*  f ( x) + f ( x)  f ( x)  f
 (x) +1 + f  (x) f '
 (x) +1  2 f
(x).f (x)  0 (**) .
Trường hợp 1. Nếu f ( x) = 0 thì f ( x) = 0 . f x
Trường hợp 2. Nếu f ( x)  0 thì (* ) ( ) *   . f ( x) 0 2   Mặt khác 3 15 2 
= m − 3m + 6 = m − +  0, m
  f x =   luôn có hai nghiệm phân f x ( ) ( ) 0  2  4
biệt hay hàm số luôn có 2 điểm cực trị. f ( x) n Giả sử rằng 1
f ( x) = 0 có các nghiệm x = ( x ; x ;... , ta có =   0 1 . 1 2 ) f ( x) ( ) = x − x i 1 i
Do f ( x) = 0 có ba nghiệm nên ( )
1 có 2 nghiệm (vô lí). x =1  f  ( x) = 0  2  Như vậy   g (x) 2
= x + (1− m) x −1 = 0; = − m +  g x (1 ) 4 0  .  f   ( x) ( ) = 0 h(x) 2 2
= 3x − 2mx + m − 2 = 0; = m − m +   h  (x) 3 6 0 Với g ( )
1 = 0  1− m = 0  m = 1 và h ( )
1 = 0  −m +1 = 0  m = 1.
Do đó với m  1, phương trình f ( x) f (x) .e
+ f (x) f (x) .  
= f (x) + f (x) luôn có 3 nghiệm thực phân biệt.
Vậy có vô số giá trị của m thỏa đề.
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 24 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
25 | Facebook tác giả: Phan Nhật Linh Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 DẠNG 4
Tìm m liên quan đến tương giao hàm trùng phương Câu 1:
Có bao nhiêu giá trị nguyên của tham số m để phương trình 4 2
x − 3x + m = 0 có 4 nghiệm thực phân biệt? A. 1. B. 4 . C. 2 . D. 0 . Câu 2:
Biết đồ thị hàm số y = ( x − )( x + )( 2 1
1 x − 7) − m cắt trục hoành tại 4 điểm phân biệt có hoành độ
là x , x , x , x . Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để 1 2 3 4 1 1 1 1 + + + 1. 1− x 1− x 1− x 1− x 1 2 3 4 A. 9 . B. 8 . C. 6 . D. 7 . Câu 3: Đường thẳng 2
y = m cắt đồ thị hàm số 4 2
y = x − x − 10 tại hai điểm phân biệt , A B sao cho tam
giác OAB vuông (với O là gốc tọa độ). Mệnh đề nào sau đây đúng? A. 2 m  (5;7) . B. 2 m  (3;5) . C. 2 m  (0; ) 1 . D. 2 m  (1;3) . Câu 4:
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình 4 2
x − 2x + 3 − 2m = 0 có
nghiệm thuộc (−2; 2) ? A. 4 . B. 3 . C. 5 . D. 6 . Câu 5: Đường thẳng 2
y = m cắt đồ thị hàm số 4 2
y = x − x − 10 tại hai điểm phân biệt , A B sao cho
tam giác OAB vuông (với O là gốc tọa độ). Mệnh đề nào sau đây đúng? A. 2 m  (5;7) . B. 2 m  (3;5) . C. 2 m  (0; ) 1 . D. 2 m  (1;3) . Câu 6: Đồ thị của hàm số 4
y = x − (m + ) 2 2
1 x + 2m +1 cắt trục hoành tại bốn điểm phân biệt có hoành
độ lập thành một cấp số cộng. Mệnh đề nào dưới đây đúng?
A. m (6;9) . B. m ( 6 − ; 3 − ) . C. m ( 3 − ;2) . D. m (2;6) . Câu 7: Cho hàm số 4
y = x − ( m + ) 2 3
2 x + 3m có đồ thị (C
. Xác định tất cả các giá trị của tham số m )
thực m để (C
cắt đường thẳng y = −1 tại bốn điểm phân biệt m ) m  0    m 0  1 1 A.  1 . B.  1 .
C. m  − . D. m  − . m  −  m  −   3 3 3  3 Câu 8:
Tập các giá trị của tham số m để phương trình 4 2
x − 2x − 3m +1 = 0 có hai nghiệm phân biệt là  1 
A. (1; + )   0 . B. ; +       0 . C. (0; + ) . D. (1; + ) .  3  Câu 9:
Cho hàm số y = f ( x) có bảng biến thiên như sau
1 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số
Có bao nhiêu giá trị nguyên của tham số m để phương trình f ( 2 6
x − 4x) = m có ít nhất 3
nghiệm thực phân biệt thuộc khoảng (0;+)? A. 25 . B. 30 . C. 29 . D. 24 .
Câu 10: Cho hàm số y = f ( x) có đồ thị như hình vẽ
Xét hàm số g ( x) = f ( x) 3 2
+ 2x − 4x − 3m − 6 5 với m là tham số thực. Điều kiện cần và đủ để
g ( x)  0, x   − 5; 5   là: 2 2 2 2 A. m f (0) . B. m f (− 5). C. m f ( 5) . D. m f ( 5) . 3 3 3 3 Câu 11: Cho hàm số 4
y = x − ( m + ) 2 3
2 x + 3m có đồ thị (C
. Xác định tất cả các giá trị của tham số m )
thực m để (C
cắt đường thẳng y = −1 tại bốn điểm phân biệt m ) m  0    m 0  1 1 A.  1 . B.  1 . C. m  − . D. m  − . m  −  m  − 3 3   3  3
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 2 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1:
Có bao nhiêu giá trị nguyên của tham số m để phương trình 4 2
x − 3x + m = 0 có 4 nghiệm thực phân biệt? A. 1. B. 4 . C. 2 . D. 0 .
Lời giải Chọn C Đặt 2
t = x (t  0) . Ta được phương trình 2
t − 3t + m = 0, ( ) 1 .
Phương trình đã cho có 4 nghiệm thực phân biệt khi và chỉ khi phương trình có 2 nghiệm dương   0 9  − 4m  0   phân biệt 9  S  0  3   0  0  m  . 4   P  0 m  0  
Do m nguyên nên m 1;  2 .
Vậy có 2 giá trị nguyên của tham số m thoả mãn yêu cầu bài toán. Câu 2:
Biết đồ thị hàm số y = ( x − )( x + )( 2 1
1 x − 7) − m cắt trục hoành tại 4 điểm phân biệt có hoành độ
là x , x , x , x . Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để 1 2 3 4 1 1 1 1 + + + 1. 1− x 1− x 1− x 1− x 1 2 3 4 A. 9 . B. 8 . C. 6 . D. 7 .
Lời giải Chọn C
Ta có y = ( x − )( x + )( 2 x − ) 4 2 1 1
7 − m = x − 8x + 7 − m . x = 0 Mặc khác ta có 3
y ' = 4x −16x = 0  
. Ta có bảng biến thiên như sau: x = 2 
Để phương trình có 4 nghiệm phân biệt thì −9  m  7 . Vì hàm số chẵn nên có 2 cặp nghiệm đối
xứng. Giả sử x + x = 0 và x + x = 0 . 1 2 3 4 4 − 2 1 1 1 1 2 2 ( 2 2 x + x 3 1 ) Theo đề bài ta có: + + + = + =  1 2 2 1− x 1+ x 1− x 1+ x 1− x 1− x 1− ( 2 2 x + x ) 2 2 + x .x 1 1 3 3 1 3 3 1 3 1 4 − 2.8 (    
0  m  7  m  1; 2;3; 4;5;6 − + −
Kết hợp điều kiện suy ra  . m) 1 0 m 12. 1 8 7 Câu 3: Đường thẳng 2
y = m cắt đồ thị hàm số 4 2
y = x − x − 10 tại hai điểm phân biệt , A B sao cho tam
giác OAB vuông (với O là gốc tọa độ). Mệnh đề nào sau đây đúng? A. 2 m  (5;7) . B. 2 m  (3;5) . C. 2 m  (0; ) 1 . D. 2 m  (1;3) .
Lời giải Chọn D
3 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số Xét: 4 2
y = x − x −10 x = 0  2 3 
y ' = 4x − 2x = 0  x =  2  2 x = −  2 Vì 2
m  0 với mọi m nên từ bảng biến thiên thấy đường thẳng 2
y = m luôn cắt đồ thị hàm số 4 2
y = x − x − 10 tại những cặp điểm đối xứng nhau qua Oy . Giả sử A( 2
x ; m ); B ( 2
−x ;m .Tam giác OAB vuông (với O là gốc tọa độ) 1 1 ) 2 4 2 4 2  O .
A OB = 0  − x + m = 0  x = m x = m 1 1 1  A( 2 2
m ; m ) vì A( 2 2
m ; m ) thuộc đồ thị hàm số nên 8 4 2 2
m − m − 10 = m m = 2 . Câu 4:
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình 4 2
x − 2x + 3 − 2m = 0 có
nghiệm thuộc (−2; 2) ? A. 4 . B. 3 . C. 5 . D. 6 . Lời giải Chọn C 4 2 4 2
x − 2x + 3 − 2m = 0  x − 2x + 3 = 2m Xét f ( x) 4 2
= x − 2x + 3, x ( 2 − ;2) x = 1 −   f (x) 3
= 4x − 4x + 3 = 0  x = 0  x =1  Bảng biến thiên
Theo yêu câu bài toán, có: 2  2m  11  1  m  5, 5 m   m1,2,3,4,  5 . Câu 5: Đường thẳng 2
y = m cắt đồ thị hàm số 4 2
y = x − x − 10 tại hai điểm phân biệt , A B sao cho
tam giác OAB vuông (với O là gốc tọa độ). Mệnh đề nào sau đây đúng? A. 2 m  (5;7) . B. 2 m  (3;5) . C. 2 m  (0; ) 1 . D. 2 m  (1;3) .
Lời giải
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 4 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 Chọn D Xét: 4 2
y = x − x −10 x = 0  2 3 
y ' = 4x − 2x = 0  x =  2  2 x = −  2 Vì 2
m  0 với mọi m nên từ bảng biến thiên thấy đường thẳng 2
y = m luôn cắt đồ thị hàm số 4 2
y = x − x − 10 tại những cặp điểm đối xứng nhau qua Oy . Giả sử A( 2
x ; m ); B ( 2
−x ;m .Tam giác OAB vuông (với O là gốc tọa độ) 1 1 ) 2 4 2 4 2  O .
A OB = 0  − x + m = 0  x = m x = m 1 1 1  A( 2 2
m ; m ) vì A( 2 2
m ; m ) thuộc đồ thị hàm số nên 8 4 2 2
m − m − 10 = m m = 2 . Câu 6: Đồ thị của hàm số 4
y = x − (m + ) 2 2
1 x + 2m +1 cắt trục hoành tại bốn điểm phân biệt có hoành
độ lập thành một cấp số cộng. Mệnh đề nào dưới đây đúng?
A. m (6;9) . B. m ( 6 − ; 3 − ) . C. m ( 3 − ;2) . D. m (2;6) .
Lời giải Chọn D
Phương trình hoành độ giao điểm: 4 x − (m + ) 2 2
1 x + 2m +1 = 0 . (1) Đặt 2
t = x ,t  0 . Phương trình trở thành 2 t − 2(m + )
1 t + 2m +1 = 0 . (2)
Phương trình (1) có bốn nghiệm phân biệt khi và chỉ khi phương trình (2) có hai nghiệm dương     0 (m + )2 1 − (2m + ) 1  0 m  0  1     m  −
phân biệt, nghĩa là S  0  m +1  0  m  1 −   2 .     P  0 2m +1  0 1  m  0  m  −  2
Cách 1. Gọi x , x , x , x
x x x x là nghiệm của phương trình (1) và t ,t t t là 1 2 ( 1 2 ) 1 2 3 4 ( 1 2 3 4 )
nghiệm của phương trình (2). Theo giả thiết, ta có
x − x = x − x = x − x x − x = x − x 4 3 3 2 2 1 4 3 3 2
t − t = t + t t = 9t  0 2 1 1 1 2 1 Ta có hệ
5 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số  m 1 t = +  t  + t = (m + ) 1 5 5 2 1 1 2  m = 4   9m 9
m 1  9m 9   tt = 2m +1  t  = +  + + = 2m +1  (nhận) 1 2 2    4 5 5    5 5  5 5  m = − t = 9t  9 2 1  tt = 2m +1 1 2 
Cách 2. Với   0 , phương trình (1) có nghiệm t = 1,t = 2m +1. Biện luận như trên, ta có hai 1 2 m = 4 t = 9t trườ  ng hợp 2 1   4 (nhận). t = 9t   m = − 1 2  9 Câu 7: Cho hàm số 4
y = x − ( m + ) 2 3
2 x + 3m có đồ thị (C
. Xác định tất cả các giá trị của tham số m )
thực m để (C
cắt đường thẳng y = −1 tại bốn điểm phân biệt m ) m  0    m 0  1 1 A.  1 . B.  1 .
C. m  − . D. m  − . m  −  m  −   3 3 3  3
Lời giải Chọn B
Phương trình hoành độ giao điểm 4 x − ( m + ) 2 3 2 x + 3m = 1 − 4 2
x − x + − m( 2 2 1 3 x − ) 1 = 0  (x − )2 2 − m( 2 1 3 x − ) 1 = 0  (  − =  = = − x − ) x x x
1 ( x − 3m − ) 2 1 0 1, 1 2 2 1 = 0     2 2
x − 3m −1 = 0 x = 3m +1
Đồ thị (C cắt y = −1 tại bốn điểm phân biệt khi và chỉ khi 2
x = 3m +1 có hai nghiệm phân m ) biệt khác 1 và 1 − .  1 3  m +1  0   − Khi đó, ta có m    3 . 3  m +1  1 m  0 Câu 8:
Tập các giá trị của tham số m để phương trình 4 2
x − 2x − 3m +1 = 0 có hai nghiệm phân biệt là  1 
A. (1; + )   0 . B. ; +       0 . C. (0; + ) . D. (1; + ) .  3 
Lời giải Chọn B  Ta có: 4 2
x − 2x − 3m +1 = 0 4 2
 3m = x − 2x +1.
 Xét hàm số y = f ( x) 4 2 = x − 2x +1.
 Tập xác định D = , 3
y = 4x − 4x . x = 0  
y = 0  x = 1 −  . x =1   Bảng biến thiên
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 6 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 x ∞ 1 0 1 + ∞ y' 0 + 0 0 + + ∞ 1 + ∞ y 0 0
 Yêu cầu bài toán tương đương đường thẳng (d ) : y = 3m cắt đường cong (C) : y = f ( x) tại hai điểm phân biệt.  =  m 0 3m = 0
 Để phương trình có hai nghiệm phân biệt thì    1 . 3m  1 m   3 Câu 9:
Cho hàm số y = f ( x) có bảng biến thiên như sau
Có bao nhiêu giá trị nguyên của tham số m để phương trình f ( 2 6
x − 4x) = m có ít nhất 3
nghiệm thực phân biệt thuộc khoảng (0;+)? A. 25 . B. 30 . C. 29 . D. 24 .
Lời giải Chọn B
Đặt g ( x) = f ( 2
x − x)  g( x) = ( x − ) f ( 2 4 2 4 . x − 4x) .  x = 2  2x − 4 = 0 x = 2+ 2   2  − =  ( ) x x − x = −
g x = 0  (2x − 4). f ( 2 4 0 4 4 2
x − 4x) = 0       = − . f   ( 2 x − x) 2 x 2 2 4 = 0
x − 4x = −2    = 2 x 0  x − 4x = 0   x = 4 Ta có bảng biến thiên:
7 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số
Yêu cầu của bài toán  ( ) m g x =
có ít nhất 3 nghiệm thực phân biệt thuộc khoảng (0; +) 6 m  3 −   2  1
− 8  m  12 mà m  nên m 17 − ; 16 − ;...;11  ;12 . 6
Vậy có 30 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Câu 10: Cho hàm số y = f ( x) có đồ thị như hình vẽ
Xét hàm số g ( x) = f ( x) 3 2
+ 2x − 4x − 3m − 6 5 với m là tham số thực. Điều kiện cần và đủ để
g ( x)  0, x   − 5; 5   là: 2 2 2 2 A. m f (0) . B. m f (− 5). C. m f ( 5) . D. m f ( 5) . 3 3 3 3
Lời giải Chọn D
Ta có: g( x) = f ( x) 2 2
+ 6x − 4 , g(x) =  f (x) 2 0 = 3 − x + 2( ) 1 . Vẽ parabol 2 y = 3
− x + 2 ta thấy phương trình ( )
1 có 3 nghiệm x = − 5, x = 0, x = 5 . BBT 2
g ( x)  0, x
  − 5; 5  2 f ( 5)  m f ( 5)   − 3m  0 . 3
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 8 Phan Nhật Linh
Fanpage: Luyện thi Đại học 2023 Câu 11: Cho hàm số 4
y = x − ( m + ) 2 3
2 x + 3m có đồ thị (C
. Xác định tất cả các giá trị của tham số m )
thực m để (C
cắt đường thẳng y = −1 tại bốn điểm phân biệt m ) m  0    m 0  1 1 A.  1 . B.  1 . C. m  − . D. m  − . m  −  m  − 3 3   3  3
Lời giải Chọn B
Phương trình hoành độ giao điểm 4 x − ( m + ) 2 3 2 x + 3m = 1 − 4 2
x − x + − m( 2 2 1 3 x − ) 1 = 0  (x − )2 2 − m( 2 1 3 x − ) 1 = 0  (  − =  = = − x − ) x x x
1 ( x − 3m − ) 2 1 0 1, 1 2 2 1 = 0     2 2
x − 3m −1 = 0 x = 3m +1
Đồ thị (C cắt y = −1 tại bốn điểm phân biệt khi và chỉ khi 2
x = 3m +1 có hai nghiệm phân m ) biệt khác 1 và 1 − .  1 3  m +1  0   − Khi đó, ta có m    3 . 3  m +1  1 m  0
9 | Facebook tác giả: Phan Nhật Linh
Chủ đề 06: Tương giao của đồ thị hàm số
Tư duy toán học 4.0 – Luyện thi Đại học 2023 | 10
Document Outline

  • [06.D0] Lý thuyết và ví dụ minh họa về sự tương giao
  • [06.D1] BT tương giao 01
  • [06.D2] BT tương giao 02
  • [06.D3] Tìm điều kiện của m liên quan đến tương giao hàm bậc 3
  • [06.D4] Tìm điều kiện của m liên quan đến tương giao hàm trùng phương