













Preview text:
CHÙM BÀI TOÁN
TIẾP TUYẾN – CÁT TUYẾN ÔN THI VÀO 10 HƯỚNG DẪN GIẢI
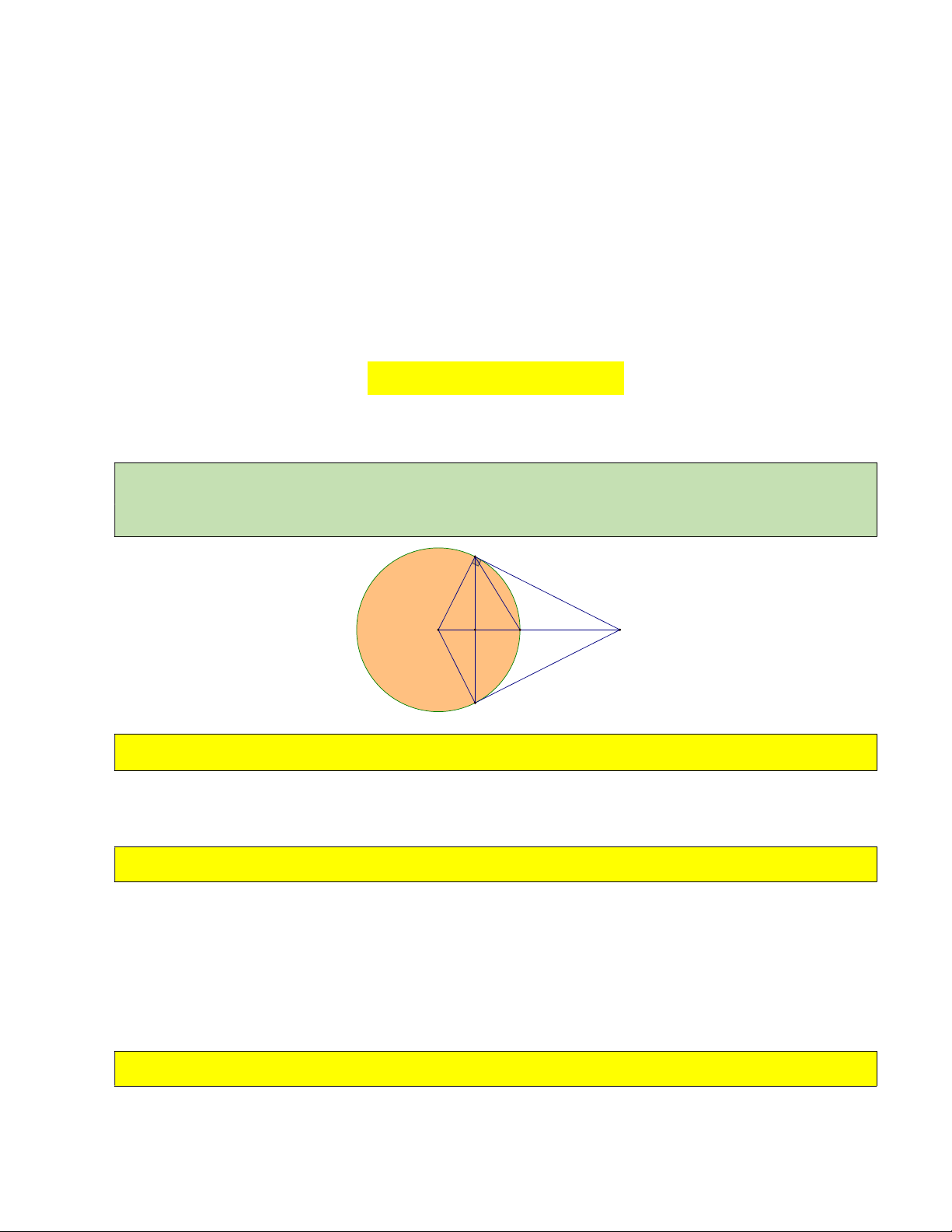
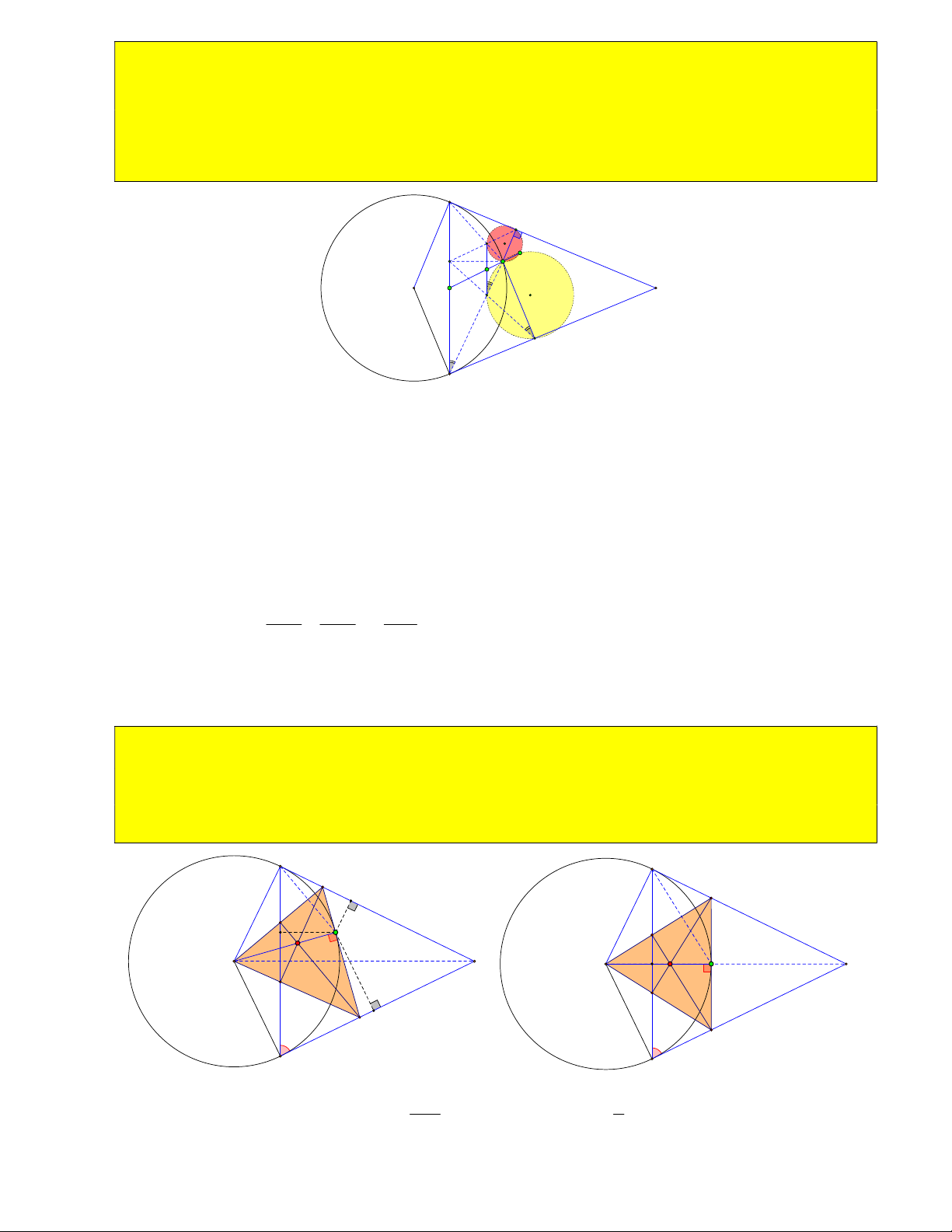
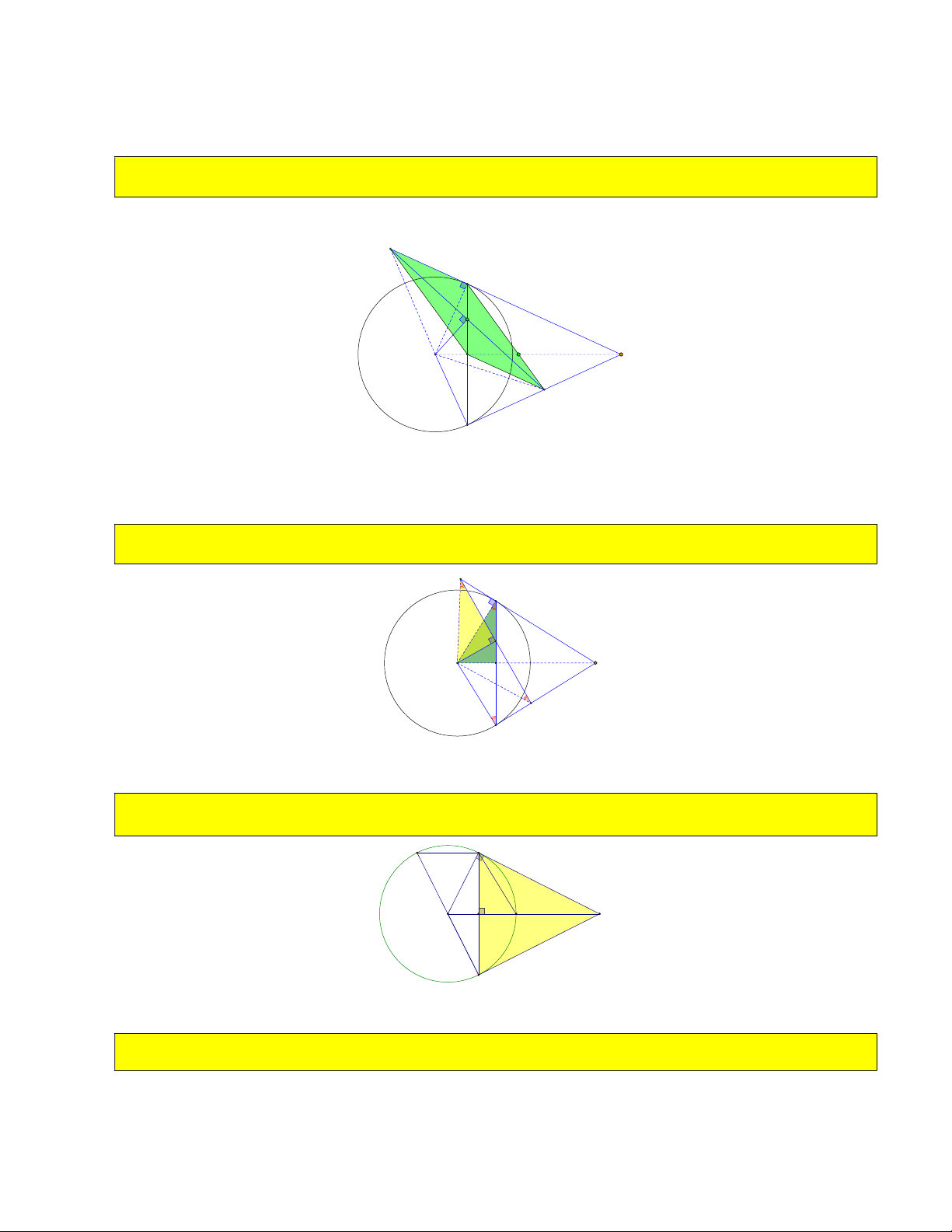
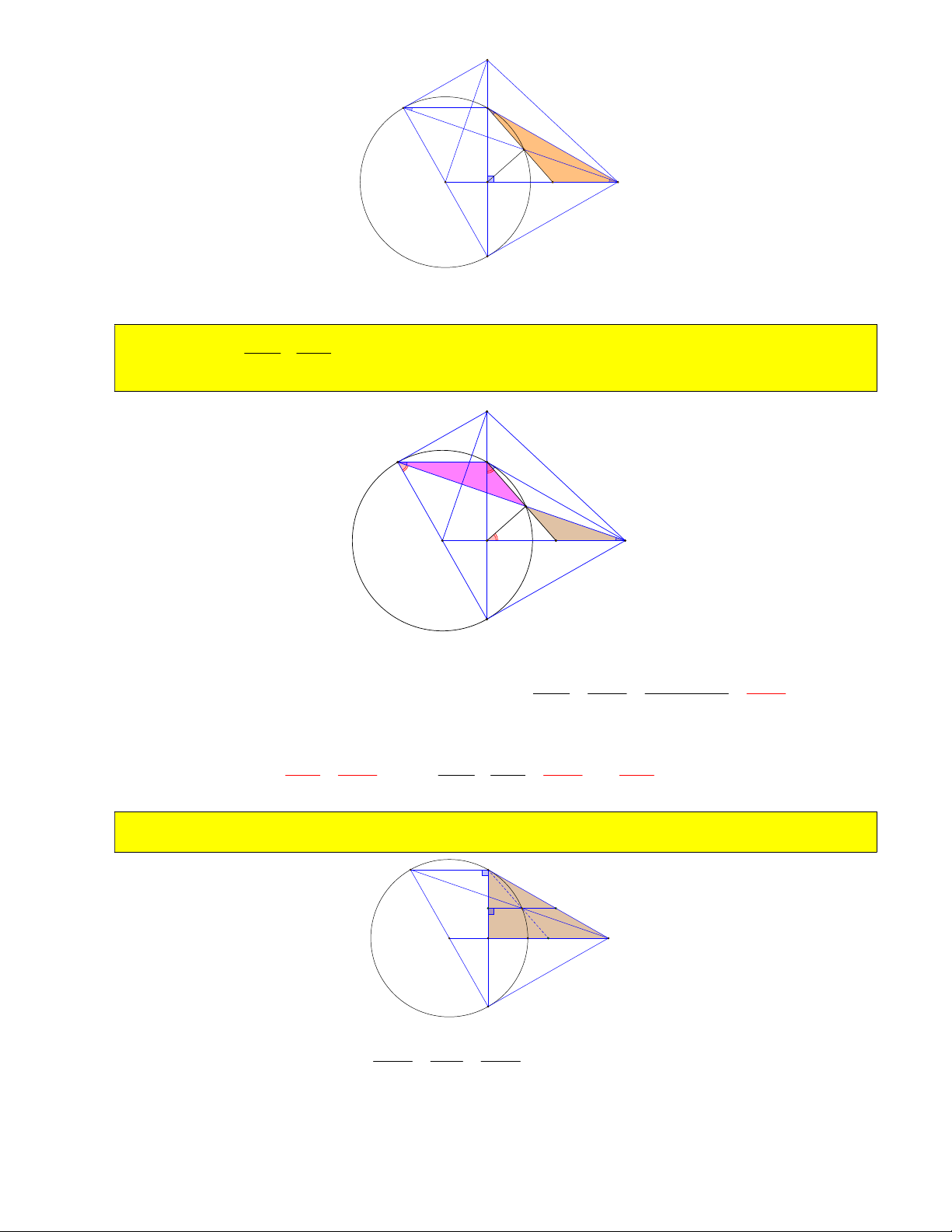
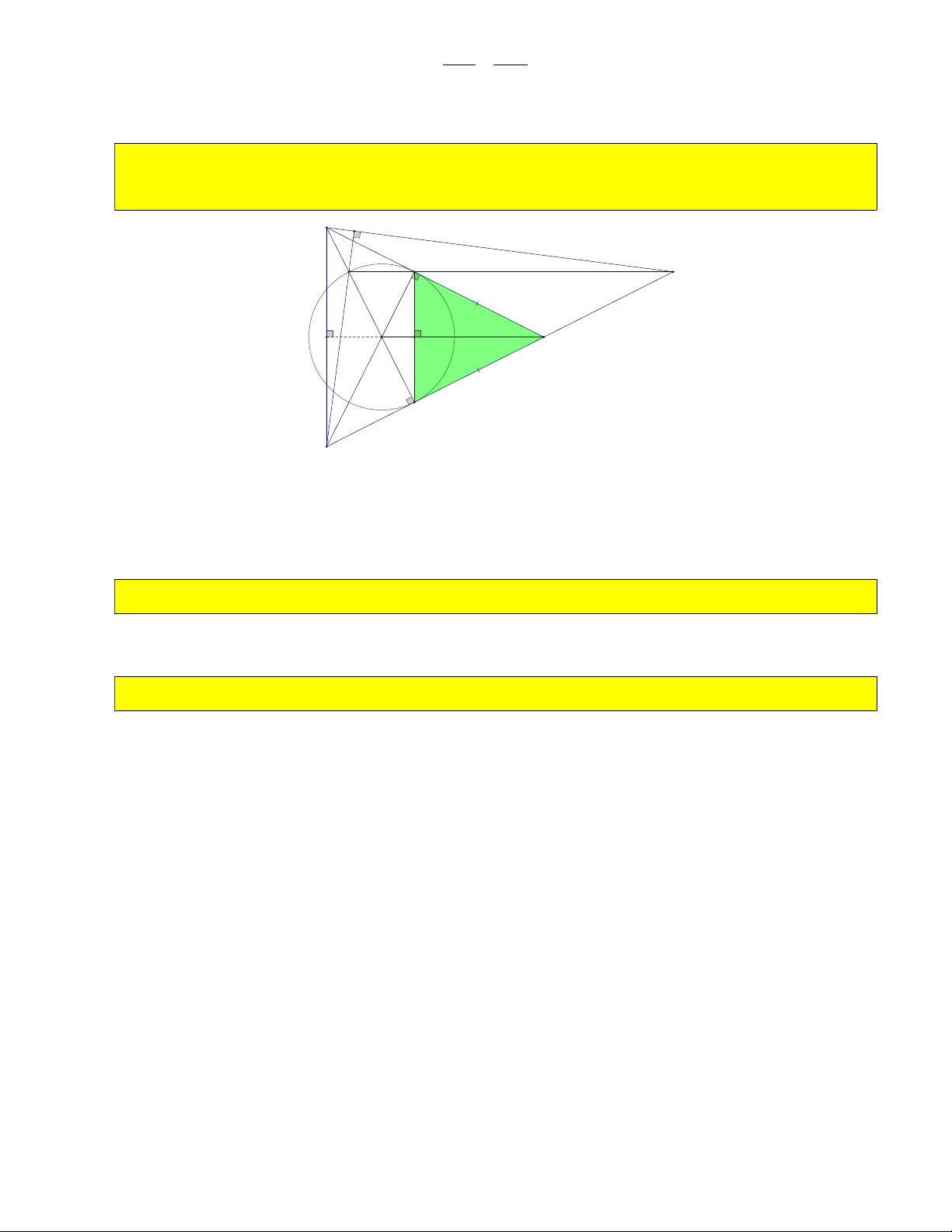
Bài 1: Cho O; R và điểm M nằm ngoài đường tròn. Kẻ tiếp tuyến MB với đường tròn, dây BC vuông góc OM tại H . B O M H I C 1) Chứng minh 2 OH.OM R .
Vì MB là tiếp tuyến O BM OB OBM vuông tại B, BH là đường cao .
Áp dụng hệ thức lượng cho tam giác vuông 2 2 OBM : OM .OH OB R
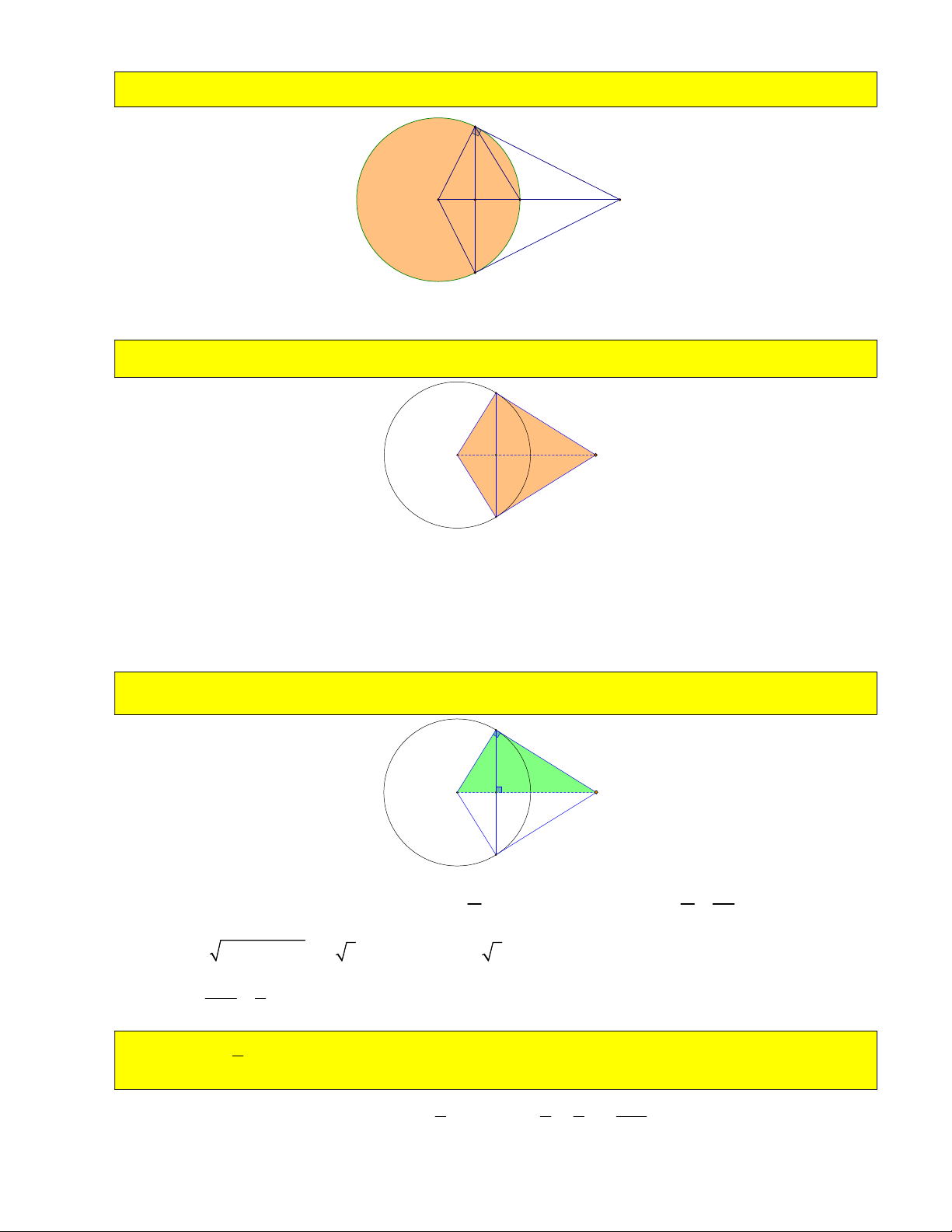
2) Chứng minh MB MC , HB HC .
Xét hai tam giác vuông OHB và OHC có OB OC R , OH chung. BOH COH
Từ đó chỉ ra OHB O HC 2cgv . HB HC Từ đó suy ra OMB O
MC c g c MB MC .
3) Chứng minh MC là tiếp tuyến đường tròn. Do OMB O MC OCM 0
OBM 90 CM là tiếp tuyến của O .
Giáo viên: Nguyễn Chí Thành
4) Chứng minh tứ giác MBOC nội tiếp đường tròn, tìm tâm đường tròn đó. B O M H I C Chỉ ra MBO 0
MCO 180 MBOC nội tiếp, tâm nằm ở trung điểm OM .
5) Bài có thể thay đổi lại đề bài, cho hai tiếp tuyến MB, MC . Chứng minh BC OM . B M O H C
+ Lập luận vì MB MC M nằm trên trung trực BC , OB OC O nằm trên trung trực BC .
Vậy OM là trung trực BC OM BC .
+ Hoặc chỉ ra MB MC và MO là phân giác góc
BMC ( tính chất tiếp tuyến) nên OM là đường cao M BC OM BC .
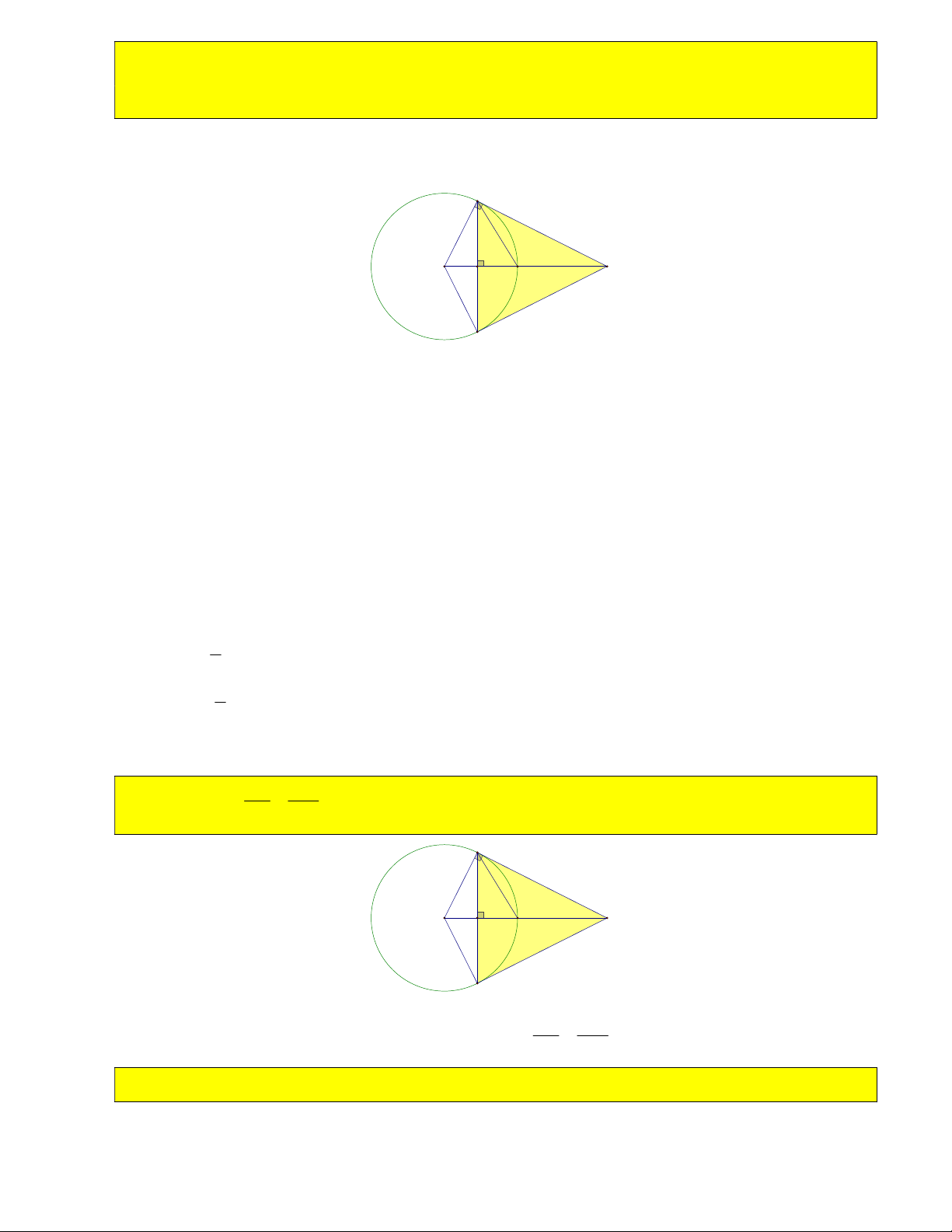
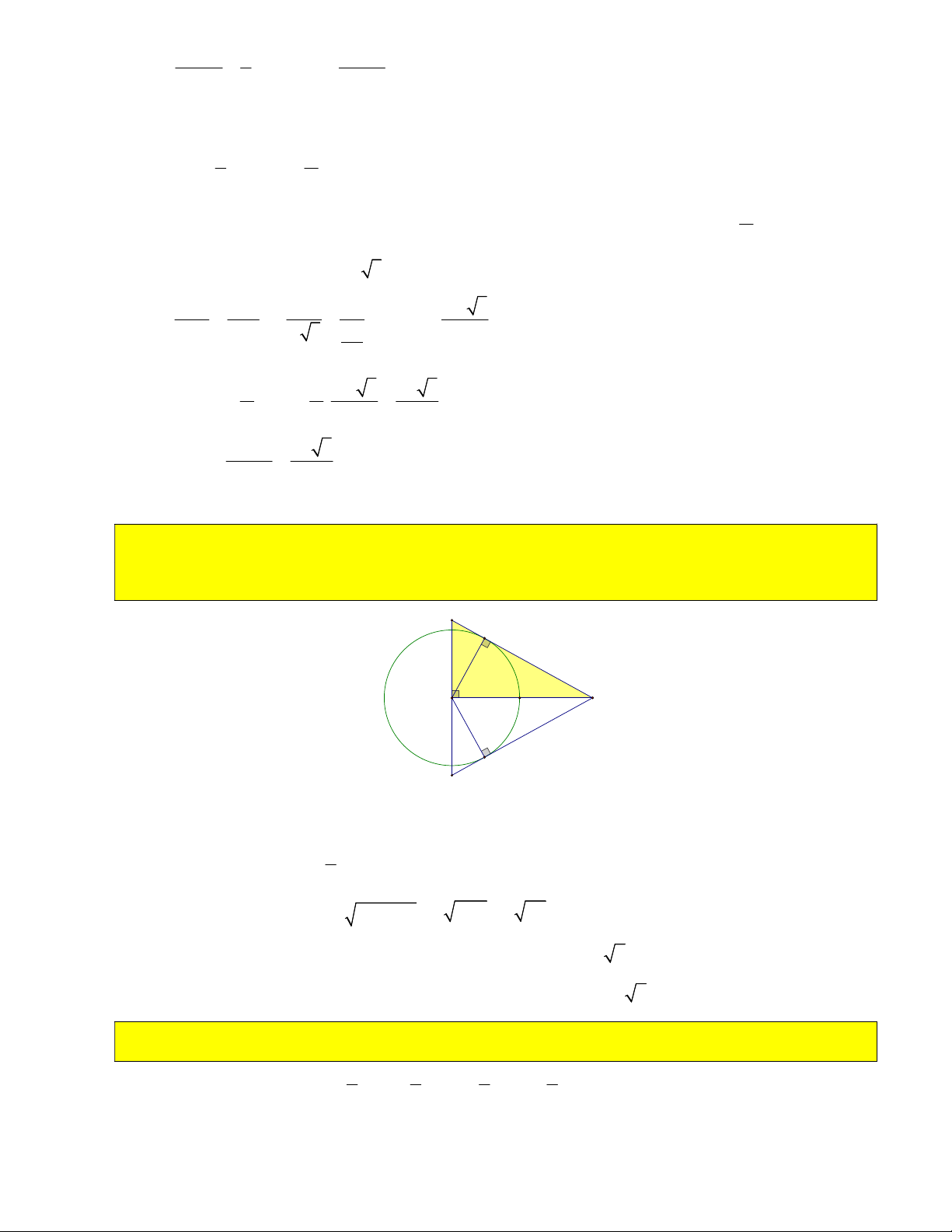
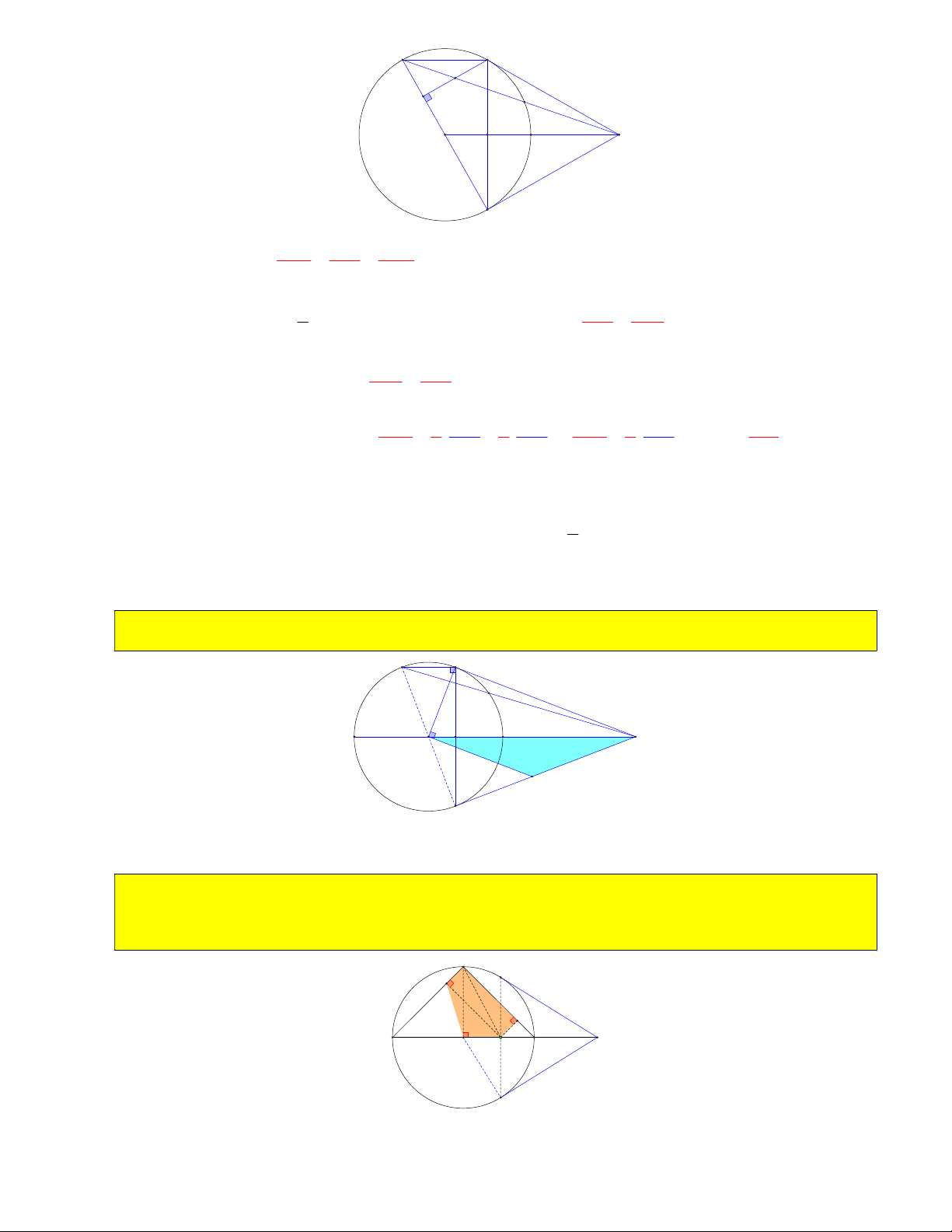
6) Tính OH , HM , MB, MC , góc BMC biết OM 2R . B M O H C R R 3R Chỉ ra 2 2
OB OH.OM R OH.2R OH
HM OM OH 2R . 2 2 2 Tính 2 2
BM OM OB R 3 MC MB R 3 . OB 1 sin BMO 0 BMO 30 BMC 2. 0 BMO 60 . OM 2 4
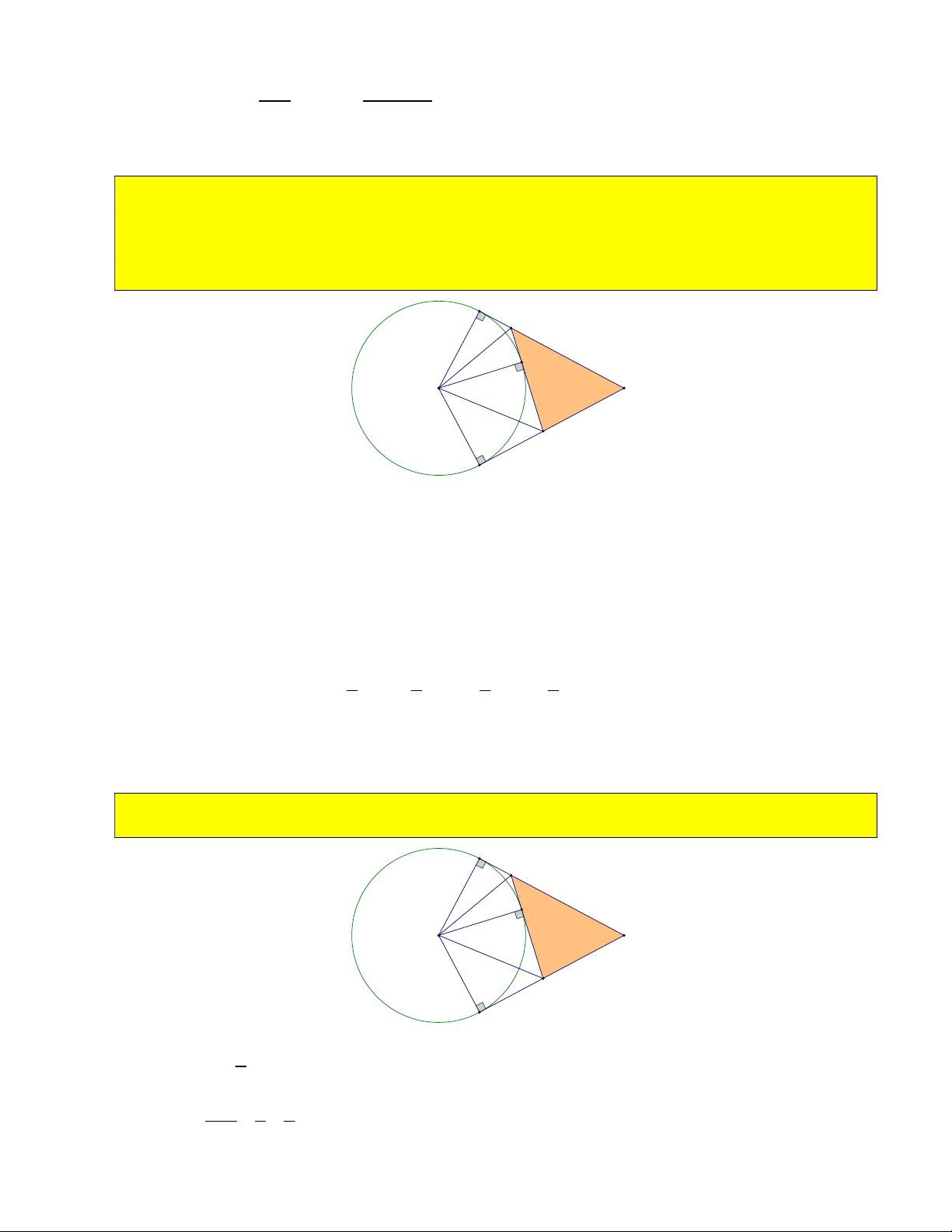
7) Cho CM R . Tính diện tích COBM . 3 2 1 1 4 4R Vì OBM OCM S 2S 2. .OC.CM 2. . . R R ( đơn vị diện tích) OBMC O CM 2 2 3 3
Giáo viên: Nguyễn Chí Thành
8) Gọi giao OM với O là I . Chứng minh BI là phân giác góc
MBC và I là tâm đường tròn nội tiếp M BC .
(Đề bài có thể đổi thành: Chứng minh khi M thay đổi, tâm đường tròn ngoại tiếp M BC luôn nằm trên
một đường tròn cố định – hoặc chứng minh I cách đều 3 cạnh BM ,CM , BC ) B O M H I C
Cách 1: Do MC, MB là hai tiếp tuyến cắt nhau tại M MO là phân giác góc BMC 1 . OBI 0 IBM 90 Ta có: HBI 0 HIB 90 HBI
IBM BI là phân giác góc CBM 2 . HIB OBI, OI OB R Từ
1 2 I là tâm đường tròn nội tiếp B CM .
Cách 2: Do MC, MB là hai tiếp tuyến cắt nhau tại M MO là phân giác góc BMC 1 . Ta có: BOM
COM ( tính chất hai tiếp tuyến cắt nhau) nên cung CI BI . 1 CBI sd CI Mà 2 CBI
IBM BI là phân giác góc CBM 2 . 1 IBM sd BI 2 Từ
1 2 I là tâm đường tròn nội tiếp B CM . IH HB 9) Chứng minh IM BM B O M H I C HI BH
Xét BHM có BI là phân giác trong của góc HBM
( tính chất phân giác) . IM BM
10) Tìm vị trí điểm M để BI MC ( hoặc CI MB ).
Vì BI là phân giác góc CBM , để BI CM C
BM cân tại B CB BM .
Giáo viên: Nguyễn Chí Thành Mà BM CM B
CM là tam giác đều nên 0 BMC 0 BOC 0 60 120 BOM 60 . OB OB Ta có: cos BOM OM 2R . OM cos BOM
Vậy để BI CM thì M ; O 2R .
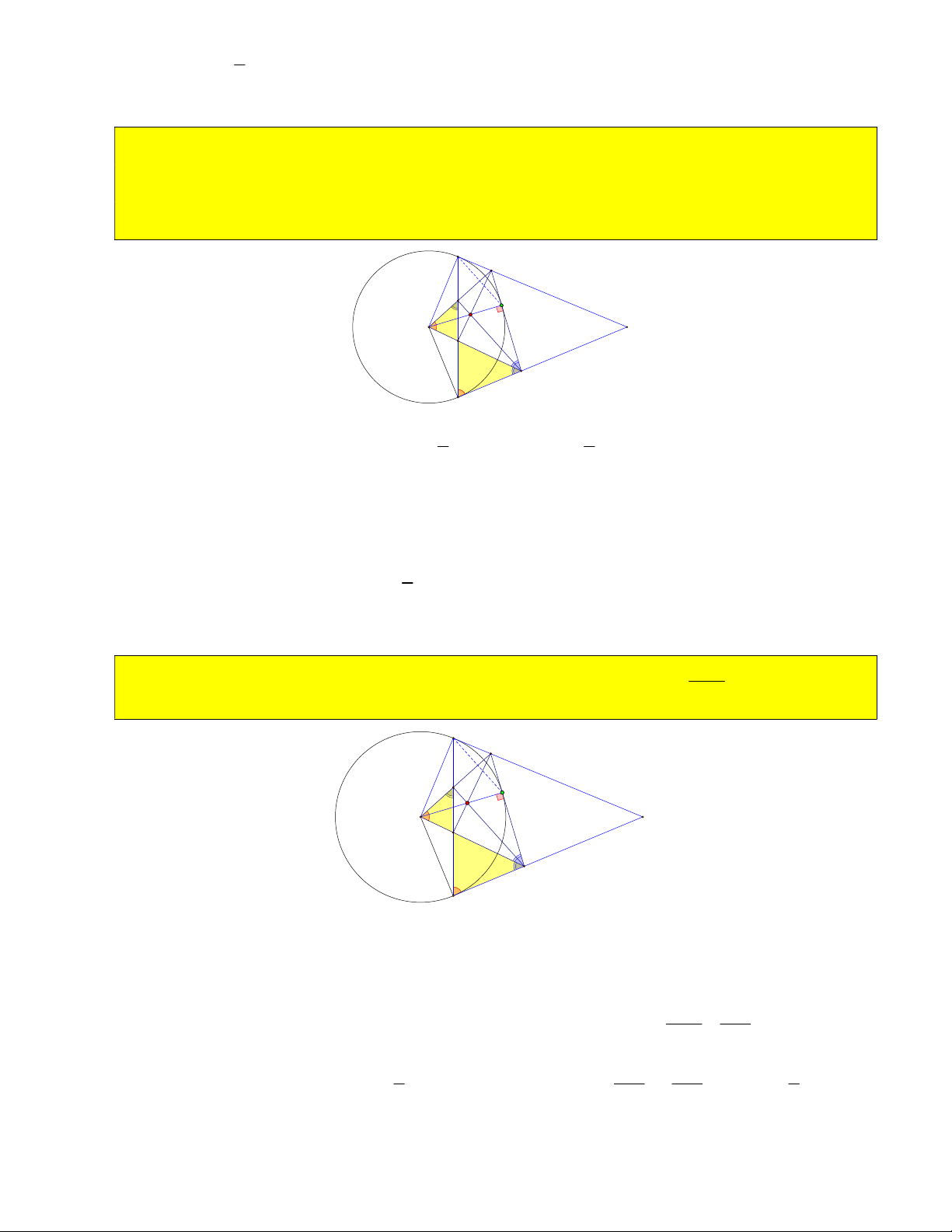
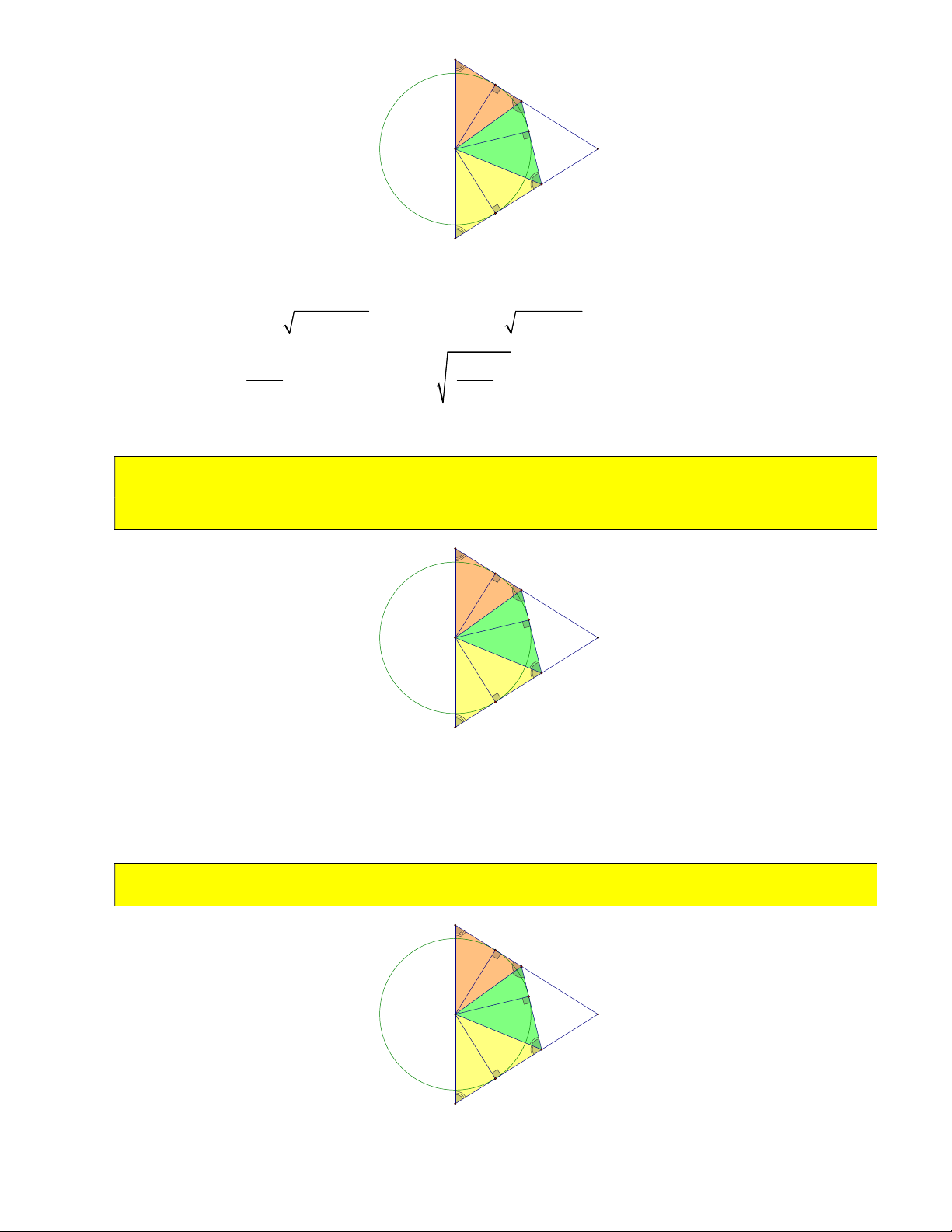
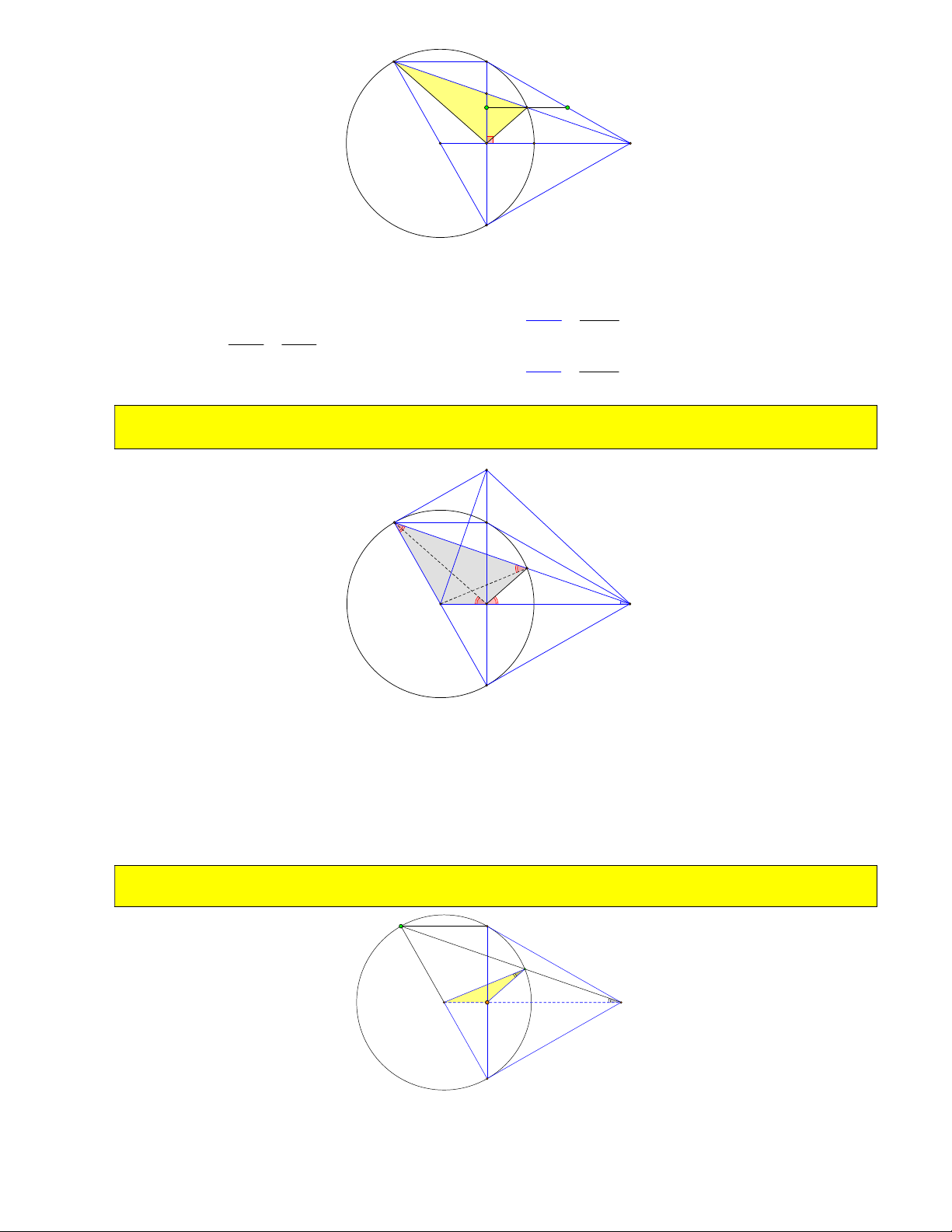
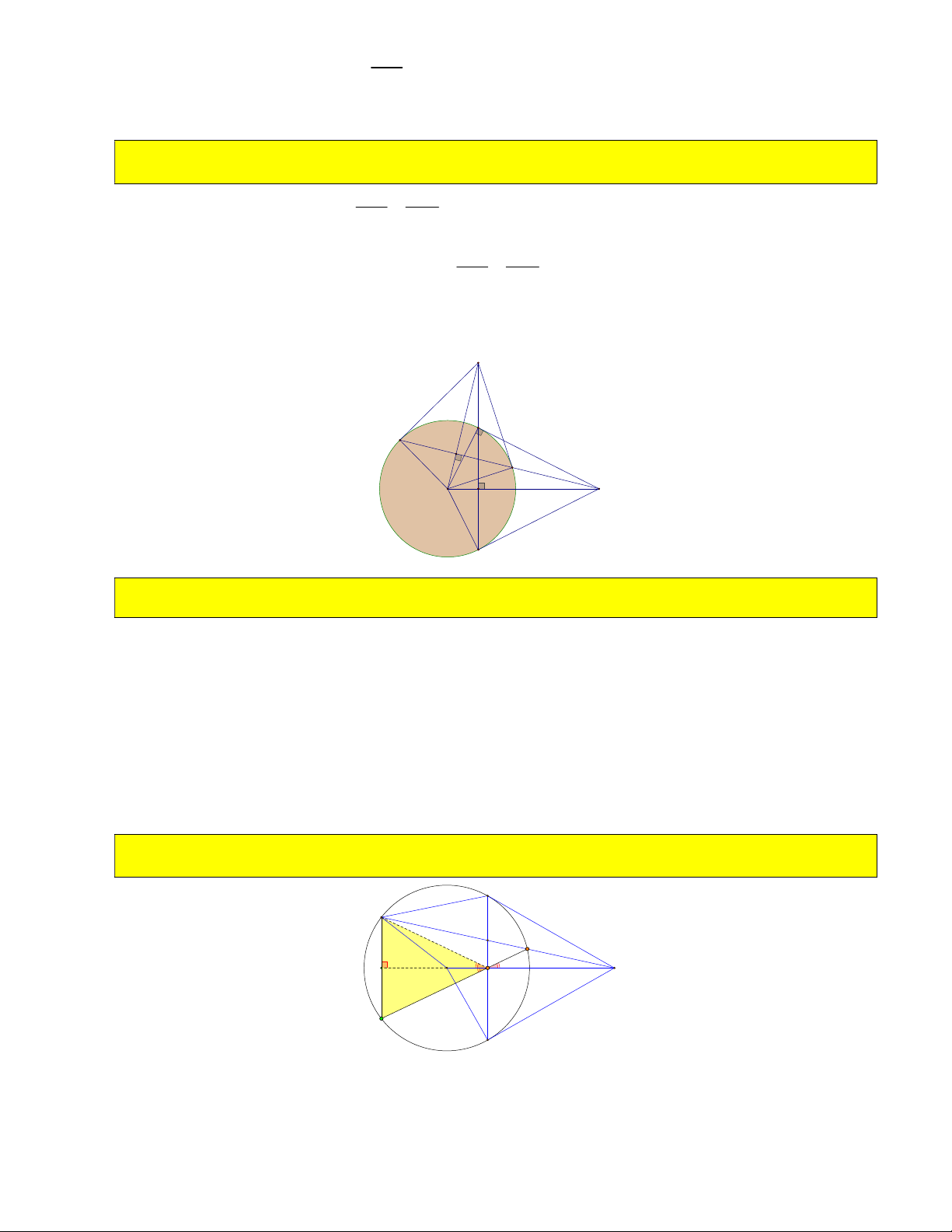
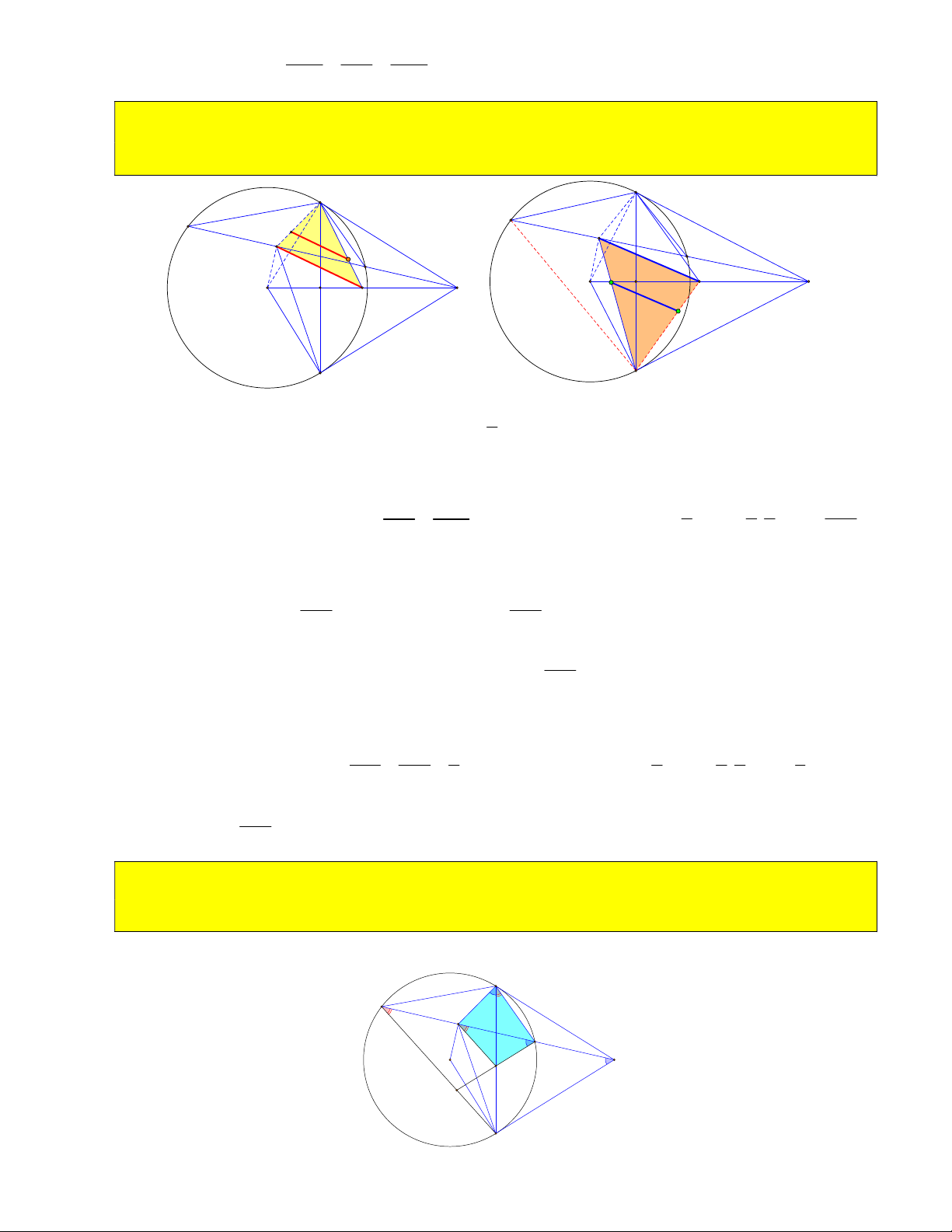
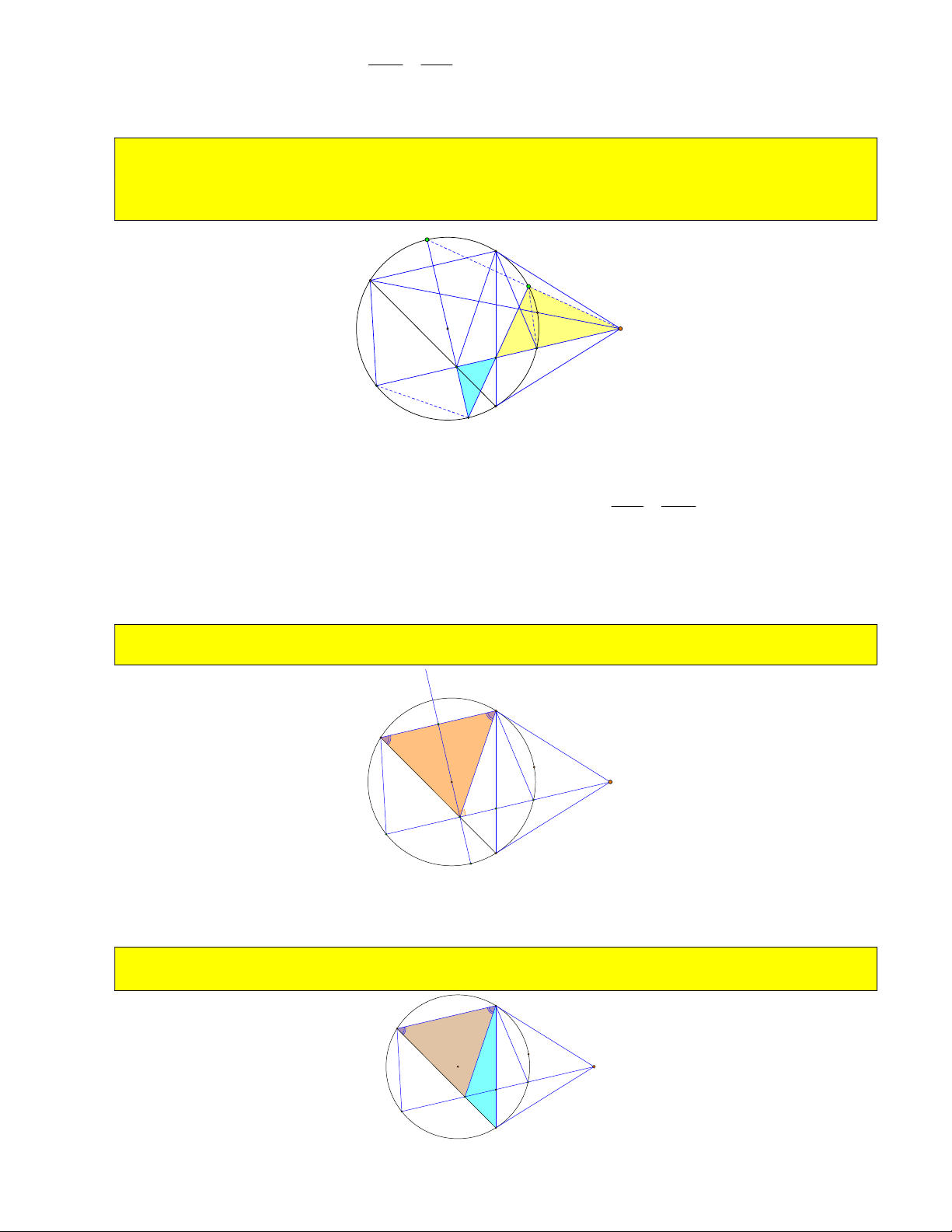
11) Từ điểm A trên cung nhỏ BC vẽ tiếp tuyến với đường tròn O . Tiếp tuyến này cắt MB, MC tại
A , A . Chứng minh chu vi MA A không đổi và độ lớn góc
A OA không phụ thuộc vào vị trí điểm 1 2 1 2 1 2
A khi A di chuyển trên cung nhỏ BC . B A1 A O M A2 C MB MC
Ta có: A B A A ( tính chất tiếp tuyến cắt nhau) . 1 1 A A A C 2 2
Chu vi MA A là: MA MA A A MA MA A A AA MA A A MA AA 1 2 1 2 1 2 1 2 1 1 2 2 1 2
MA A B MA CA MB MC 2MB không đổi khi A di chuyển trên cung nhỏ BC . 1 1 2 2 1 1 1 1 Ta có: A OA A OA AOA BAO AOC 0 BOC 180 BMC không đổi. 1 2 1 2 2 2 2 2
Vậy chu vi tam giác MA A và độ lớn góc
A OA không phụ thuộc vào vị trí điểm A . 1 2 1 2
12) Cho R 3cm, OM 6cm . Tính số đo góc A OA . 1 2 B A1 A O M A2 C 1 Ta có: 0 A OA 180
BMC . Trong tam giác vuông BMO ta có: 1 2 2 OB 3 1 sin BMO 0 BMO 30 0 BMC 60 . OM 6 2
Giáo viên: Nguyễn Chí Thành 1 Do đó 0 A OA 180 BMC 0 60 . 1 2 2
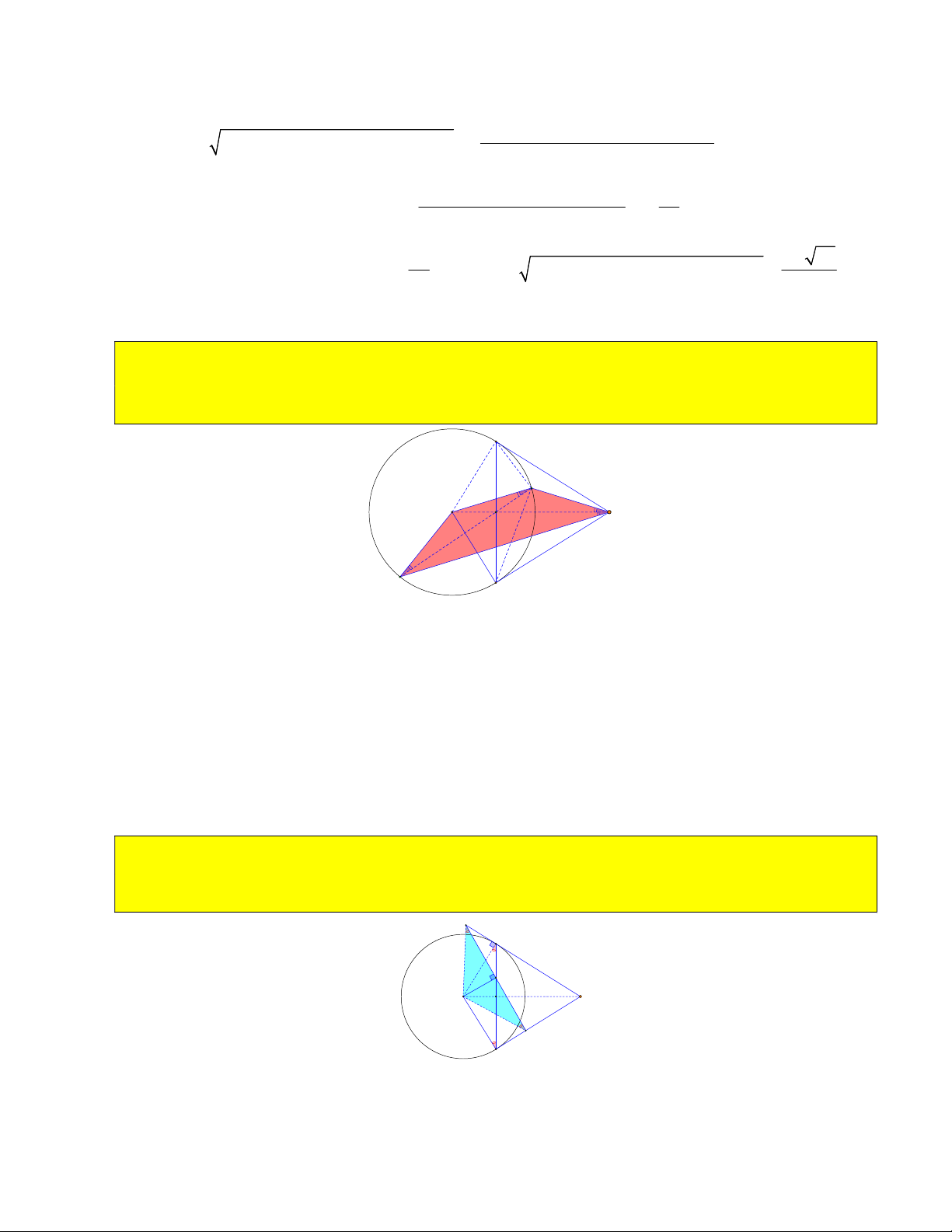
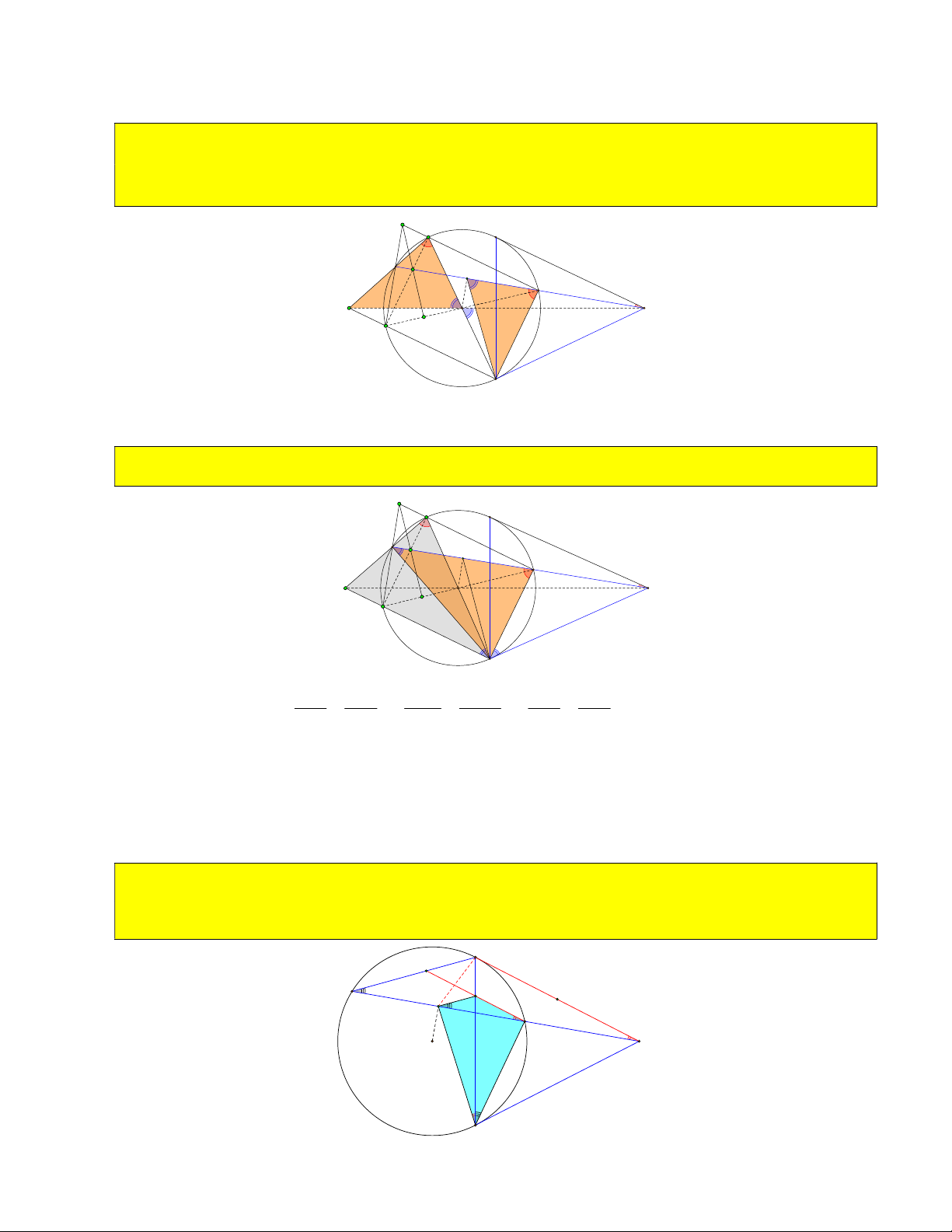
13) Gọi giao OA và OA với BC là A và A . Chứng minh A A OA và A A OA ( hoặc các câu 1 2 3 4 2 3 1 1 4 2
hỏi liên quan đến ba đường cao của O
A A hoặc chứng minh tứ giác OCA A và OBA A và 1 2 2 3 1 4
A A A A là tứ giác nội tiếp) 3 4 2 1 B A1 A3 A M O A4 A2 C 1 1
Ở trên các em đã chứng minh được A OA . BOC mà BCA .
BOC ( góc ở tâm và góc nt) 1 2 2 2 2 Suy ra A OA BCA . 1 2 2
Từ đó suy ra tứ giác OCA A là tứ giác nội tiếp nên OA A 0 OCA 90 . 2 3 3 2 2 1 Chứng minh tương tự: A OA CBA .
BOC tứ giác OBA A nội tiếp nên 1 2 1 2 1 4 OA A 0 OBA 90 A A OA . 4 1 1 1 4 2 A A 14) Cho góc 0
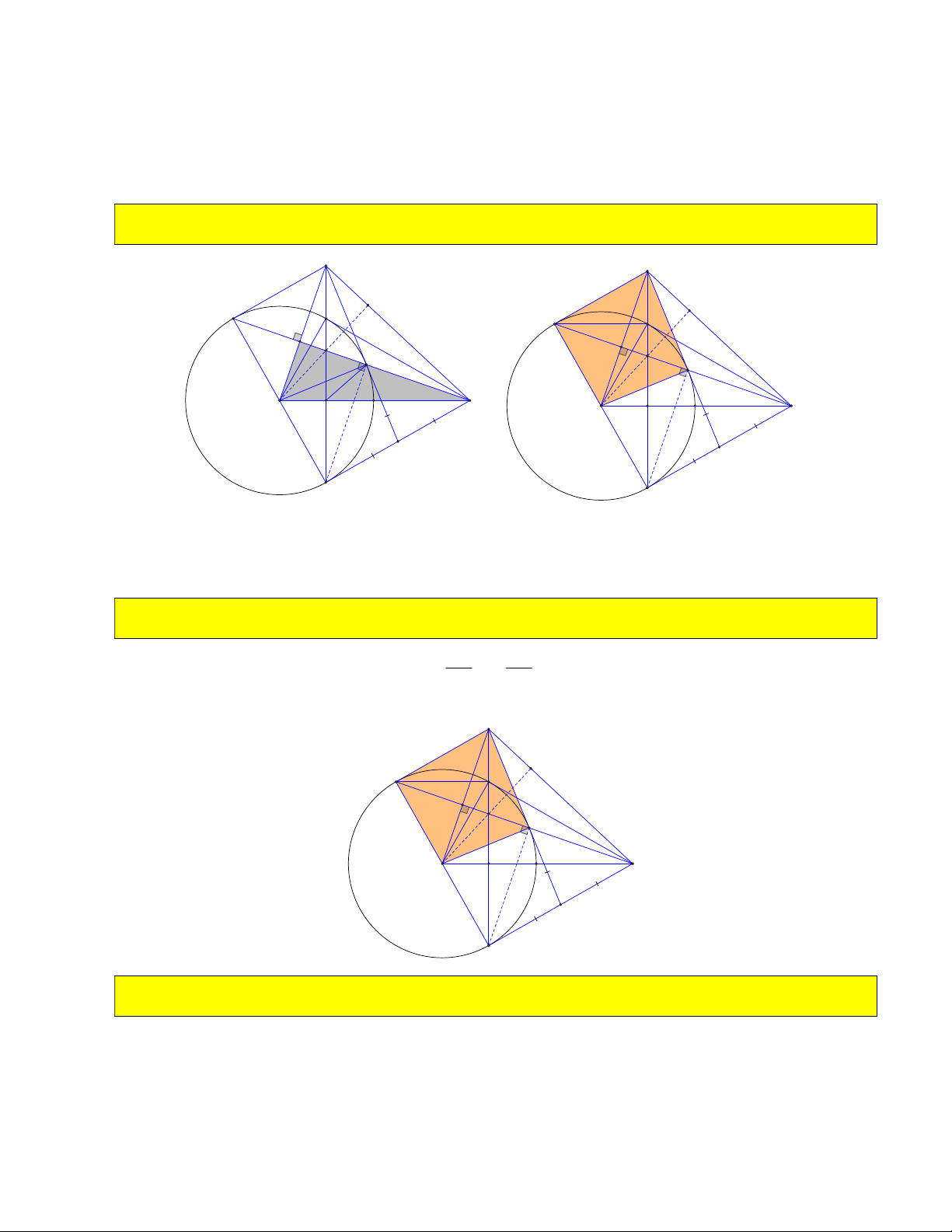
BMC 60 , gọi giao OA và OA với BC là A và A . Tính tỉ số 1 2 . 1 2 3 4 A A 3 4 B A1 A3 A M O A4 A2 C
Đầu tiên các em tính góc 0 BOC 120 .
Ở bài trên các em đã chứng minh được tứ giác OCA A nội tiếp nên OA C OA C OA A OA C 2 3 2 3 2 3 A A OA ( do OA C
OA A tính chất tt cắt nhau) . Từ đó suy ra 2 1 3 O A A ∽ O A A . 2 2 3 4 2 1 A A OA 3 4 2 1 OA OA 1 Do O A A vuông tại A và A OA . 0 BOC 60 nên cos 3 3 0 A OA cos60 . 3 2 3 3 2 2 3 4 OA OA 2 2 2
Giáo viên: Nguyễn Chí Thành A A OA 1 Vậy 2 1 3 A A OA 2 3 4 2 O A BC A 15) Cho góc 0 BMC 60 và 1 3
. Chứng minh AA . AA BA .CA . OA BC A 1 2 3 4 2 4 B A1 A3 A M O A4 A2 C Chỉ ra A BA A OA 0 A CA 60 . 1 3 1 2 2 4 A BA ∽ A OA g g 1 3 4 3 A B BA Chỉ ra 1 3 A BA ∽ A CA . A OA ∽ A CA g g A C CA 4 3 4 2 1 3 4 2 4 2 A B A A A A BA Mà 1 1 1 3 AA . AA BA .CA 1 2 3 4 CA AA A C AA 2 2 4 2
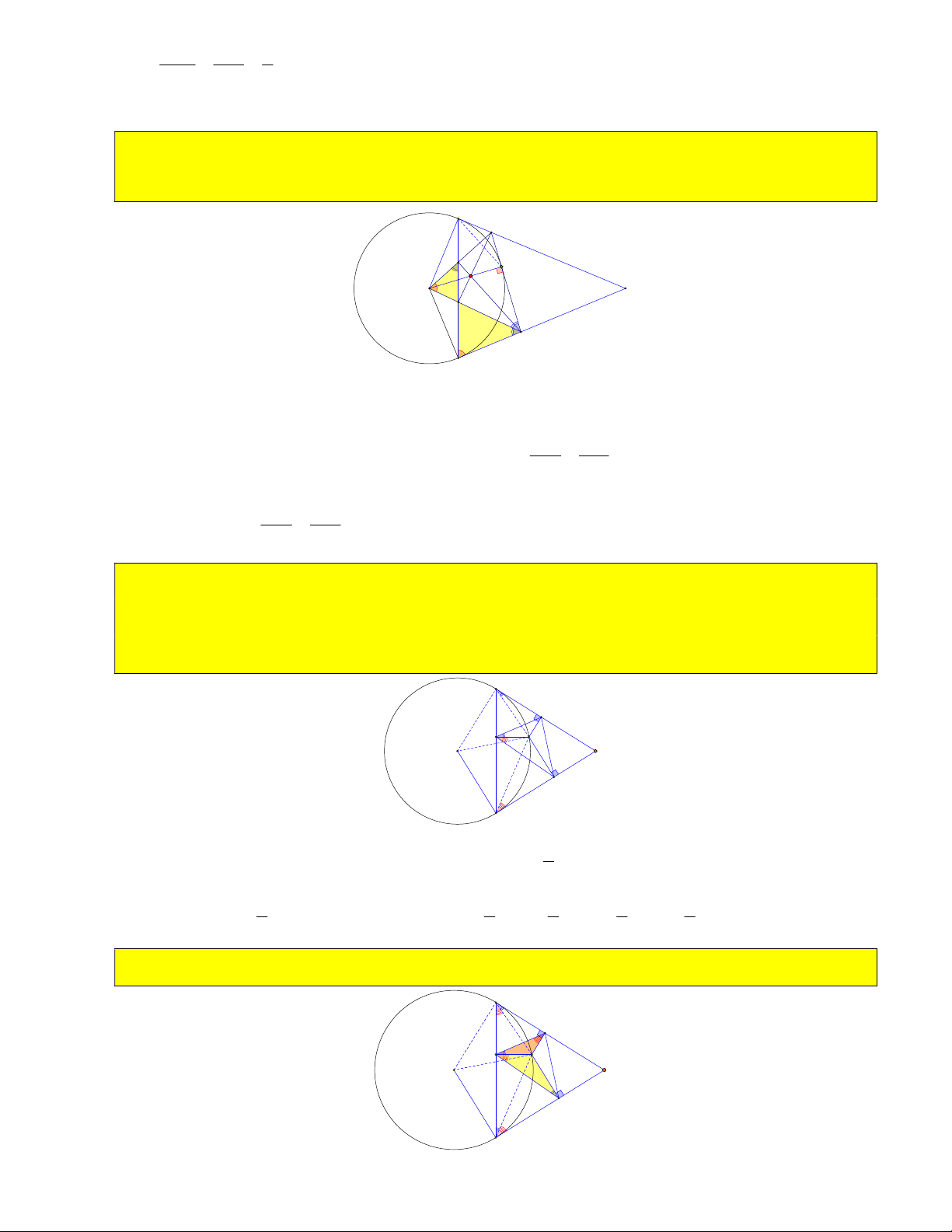
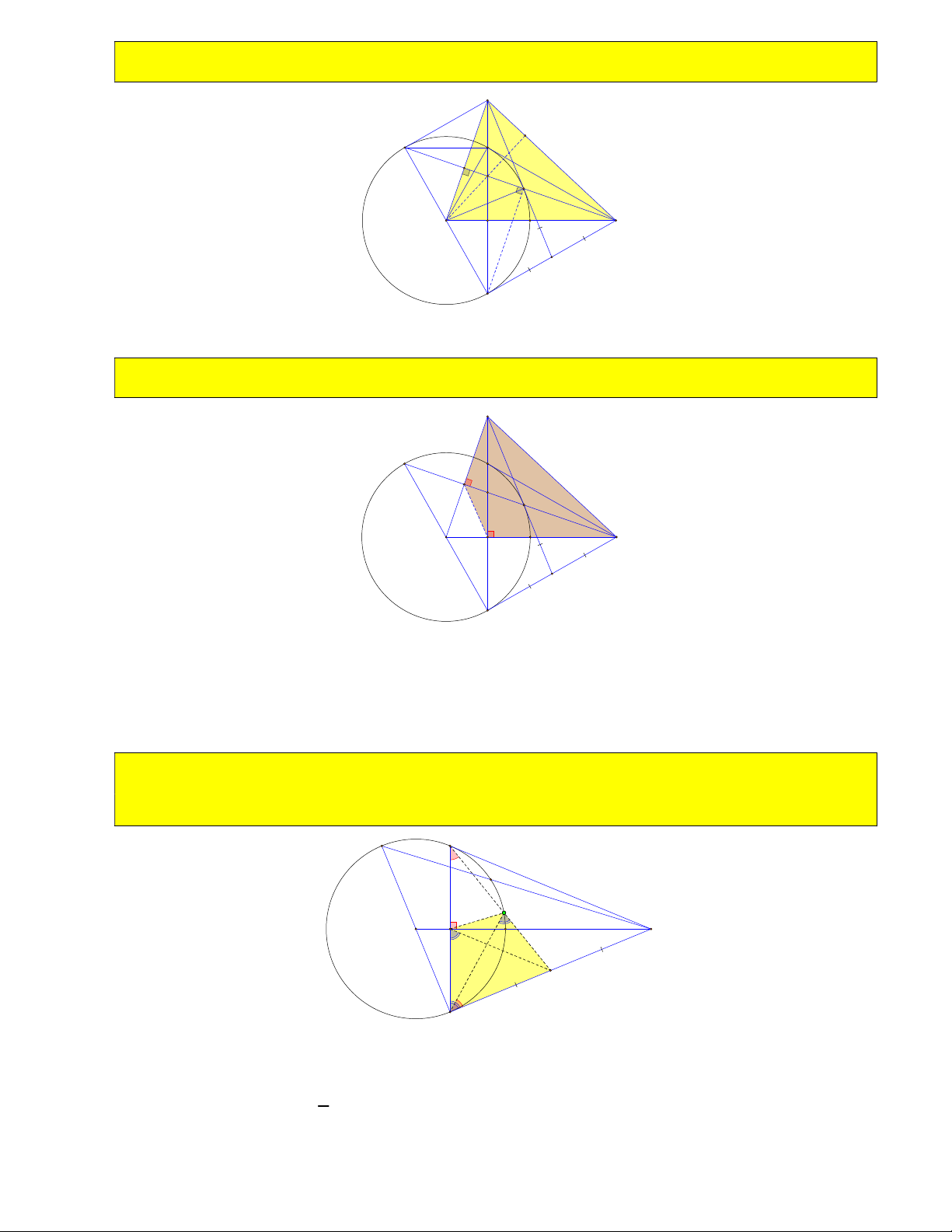
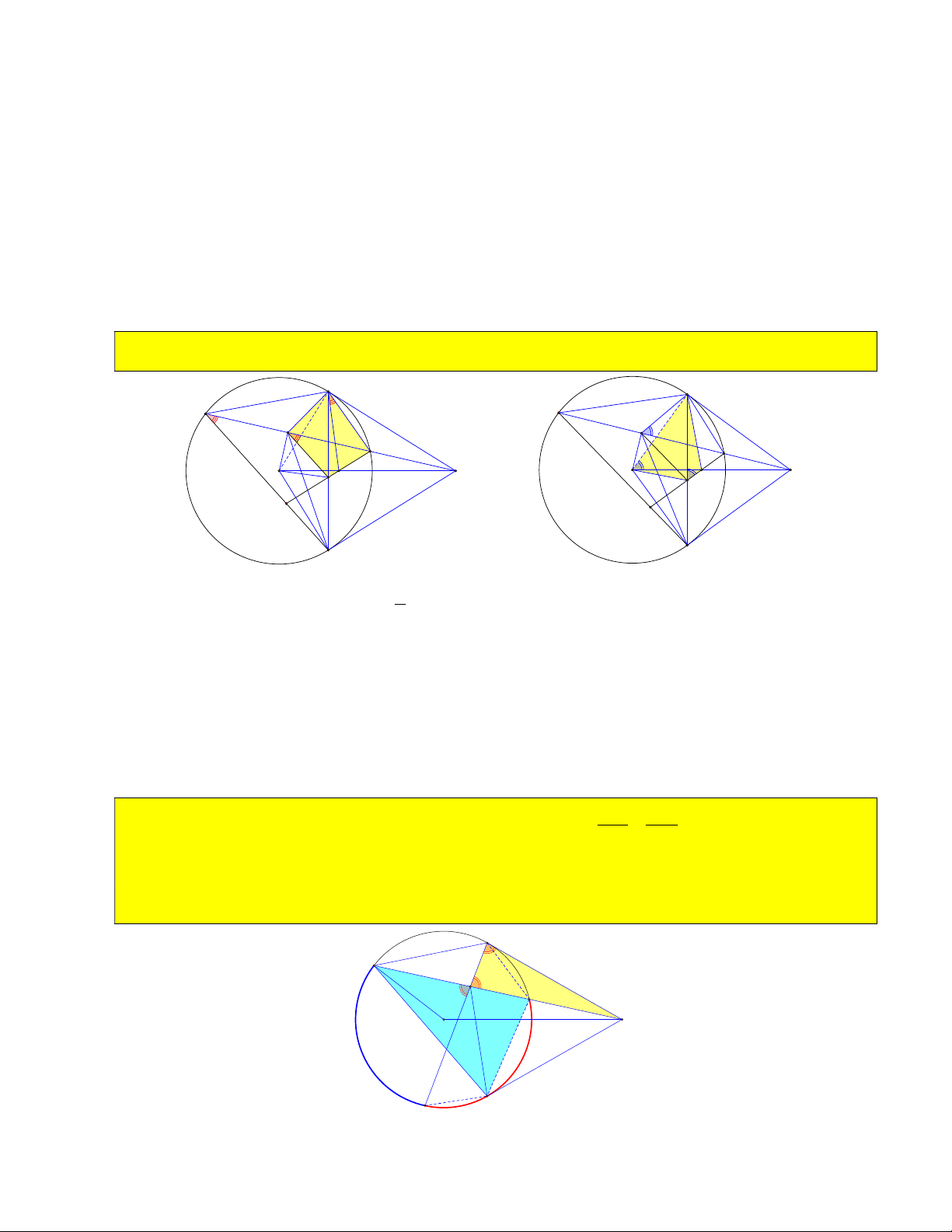
16) Từ điểm A trên cung nhỏ BC kẻ AR, AT , AY lần lượt vuông góc với CB, BM , CM tại R,T ,Y . Cho góc 0 BMC 60 . Tính góc
TRY ( hoặc chứng minh góc
TRY không đổi hoặc chứng minh TRY BMC ) B T R A M O Y C 1
Chỉ ra ATBR, AYCR là tứ giác nội tiếp nên ART ABT
BOA ( góc nt và góc ở tâm) 2 1 1 1 1 1 Và ARY ACY AOC TRY ART ARY BOA AOC 0 BOC 180 BMC 0 60 . 2 2 2 2 2 17) Chứng minh 2 AR AT.AY B T R A M O Y C
Giáo viên: Nguyễn Chí Thành AYR ACR ABT ART Chỉ ra góc
ARY ∽ATR g g ARY ACT ABC ATR AR AY Suy ra 2 AR AT.AY . AT AR
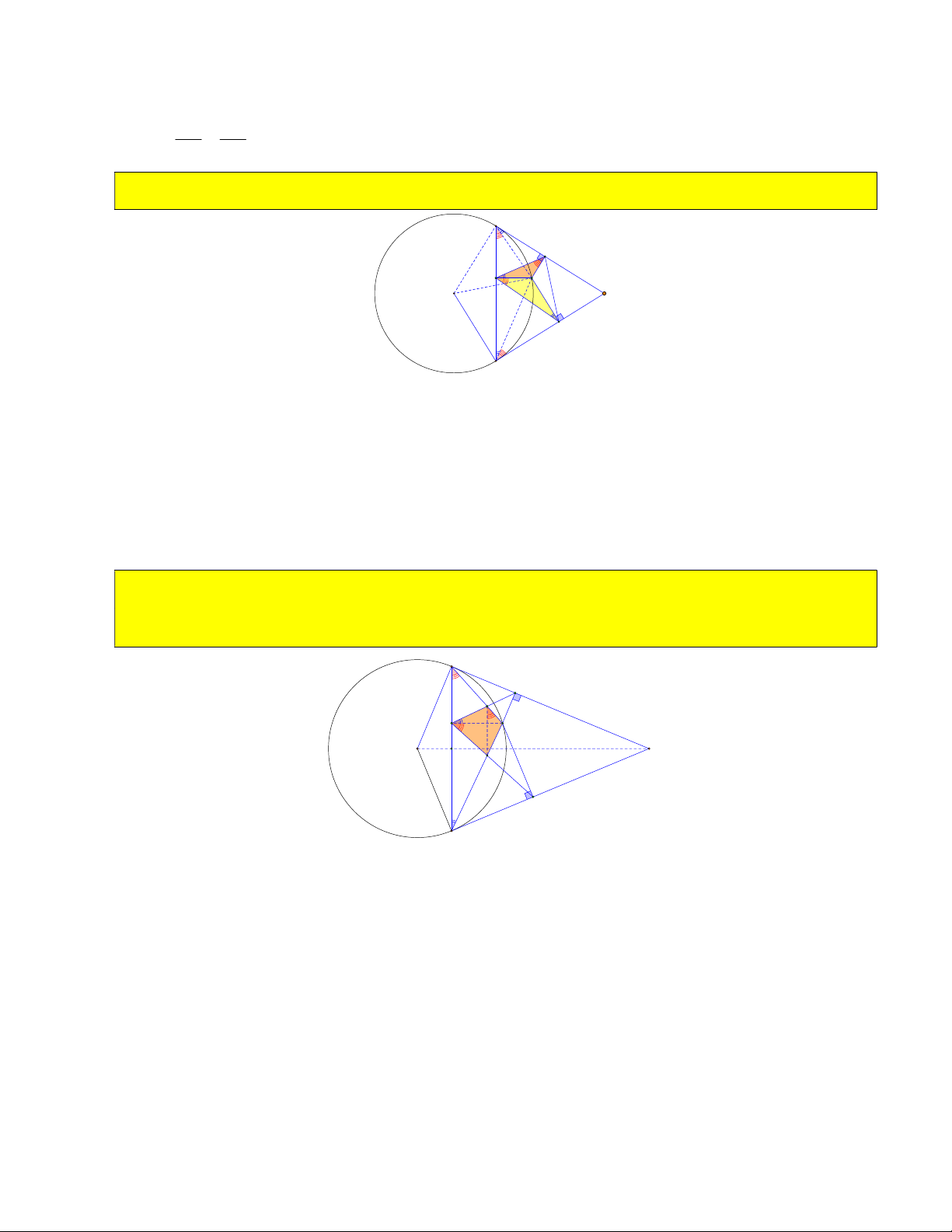
18) Tìm vị trí điểm A để AT. AR. AY đạt giá trị lớn nhất hoặc AT.AY đạt giá trị lớn nhất. B T R A M O Y C + Ta có: 2 AT.AY AR .
Do đó AT. AY đạt giá trị lớn nhất khi AR lớn nhất, suy ra AR AI A I . max + Ta có: 2 3
AT.AY AR AT.AY. AR AR
Do đó AT. AR. AY đạt giá trị lớn nhất khi AR lớn nhất, suy ra AR AI A I . max
( với I OM O ).
19) Gọi RT AB A , RY AC A . Chứng minh tứ giác AA RA nội tiếp và A A RA ( hoặc 5 6 5 6 5 6 A A / /BC ) 5 6 B T A5 R A O H M A6 Y C ARA ABT ACB Chỉ ra 5 . ARA ACY ABC 6 Suy ra A AA A RA A AA A RA ARA A AA ACB 0 ABC 180 . 5 6 5 6 5 6 5 6 5 6
Suy ra tứ giác AA RA nội tiếp. 5 6
Vì tứ giác AA RA nội tiếp nên A A A A RA ACY
CBA A A / /BC A A AR . 5 6 6 5 6 5 6 5 6
Giáo viên: Nguyễn Chí Thành 20) Cho ,
A B,Y thẳng hàng, kéo dài A A BM R . Chứng minh BR A R là hình bình hành ( hoặc khai 5 6 1 1 6
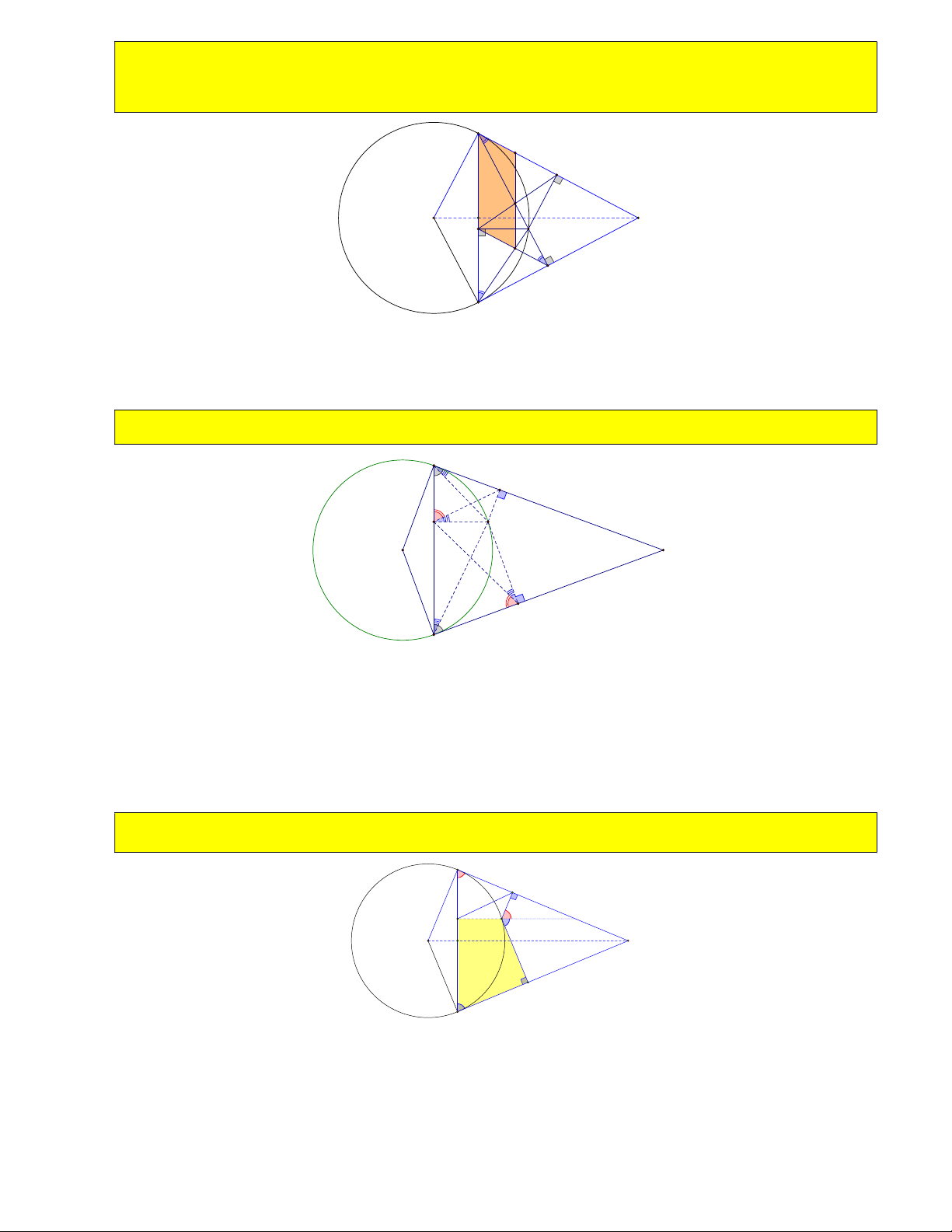
thác các yếu tố của hình bình hành này) B R1 T A5 H M O A R A6 Y C
Ở trên các em đã chỉ ra A A / /BC . 5 6 Mặt khác: ABT ACB
AYR RY / /BM . Từ đó suy ra BR A R là hình bình hành. 1 6
21) Chứng minh rằng nếu TR TB thì RY RC . B T R A O M Y C Chỉ ra AYR ACR ABT ART AYR ART . ART 0 TRB 90 Mà TRB . AYR RYC 0 RYC 90 Mặt khác TB TR TRB TBR RCY RCY RYC RY RC .
22) Chứng minh rằng tia đối của tia AR là phân giác của góc TAY . B T y R A O H M Y C
Gọi Ay là tia đối tia AR .
Chỉ ra tứ giác BTAR nội tiếp nên CBT TAy .
Chỉ ra tứ giác CYAR nội tiếp nên BCY YAy . Mà C T B BCY y
A là phân giác của góc TAY .
Giáo viên: Nguyễn Chí Thành AB RT A 23) Gọi 5
. Gọi O là đường tròn đi qua 3 điểm ATA , O là đường tròn đi qua 3 điểm 5 4 AC RY A 5 6
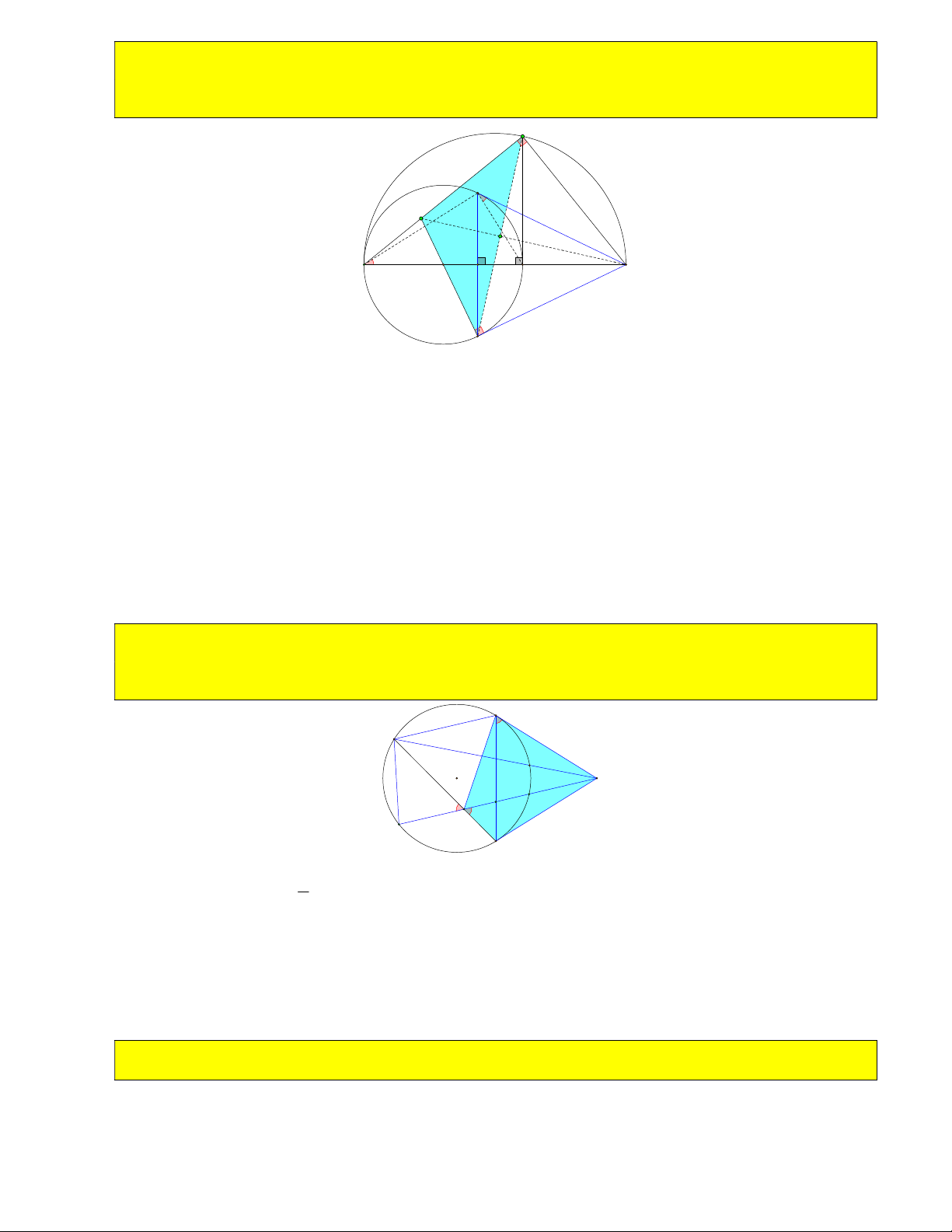
AYA và A là giao điểm thứ hai của O và O , H là trung điểm BC . Chứng minh A , , A H 5 4 6 7 7 thẳng hàng. B T O A 4 5 A7 R A A 8 O H M A6 O5 Y C
Gọi A là giao A A với A A và H là giao A A với BC . 8 7 5 6 7 Chỉ ra A A A BCA
A YA A A là tiếp tuyến của O . 5 5 6 6 5 6 Từ đó chỉ ra được 2 A A A A. A A . 8 6 8 8 7
Chứng minh tương tự : A A A BCT
A TA A A là tiếp tuyến của O 4 8 5 5 8 5 suy ra 2
A A A A. A A . Từ đó suy ra 2 2
A A A A A A A A A là trung điểm A A . 8 5 8 8 7 8 6 8 5 8 5 8 6 8 5 6 A A A A AA + Do 5 8 6 8 8 A A / /BC H B H C
H là trung điểm BC H H . 5 6 H B H C AH Vậy A , , A H thẳng hàng. 7 24) Cho góc 0
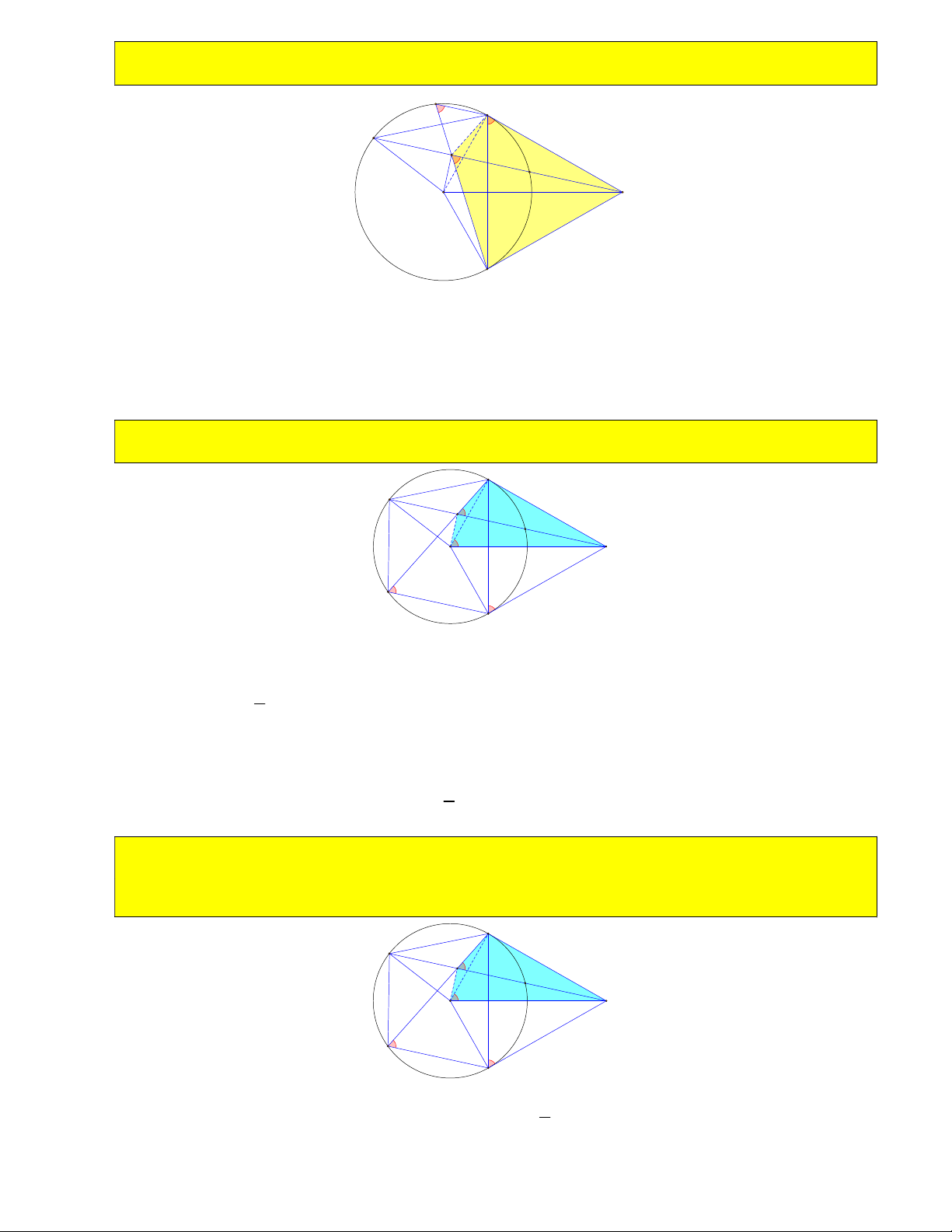
BOC 120 . Gọi giao OA và OA với BC là A và A . Tìm vị trí điểm A trên cung nhỏ 1 2 3 4
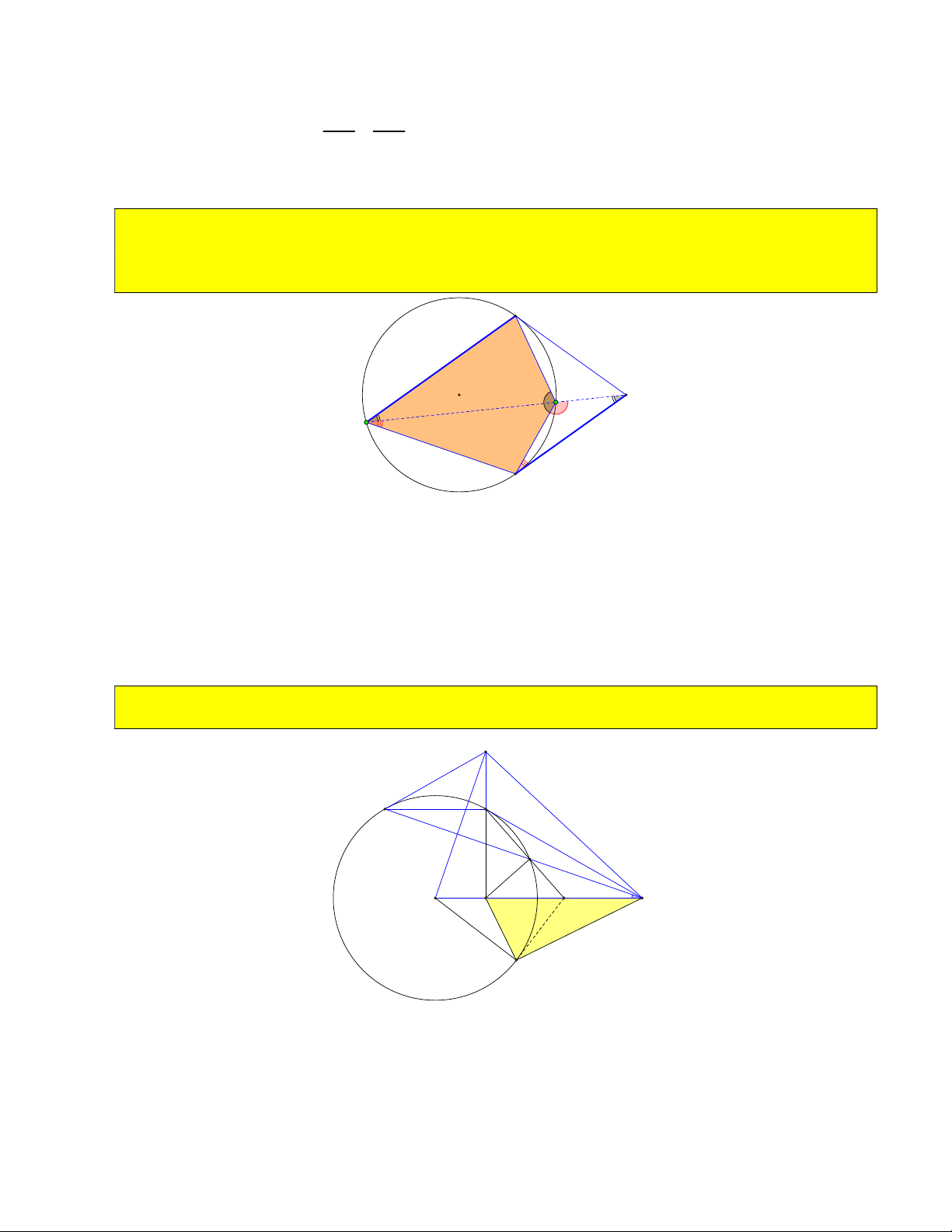
BC để diện tích tam giác OA A bé nhất và tìm giá trị bé nhất đó ( hoặc tìm vị trí điểm A để diện 3 4 tích O
A A bé nhất hoặc độ dài A A bé nhất) 1 2 1 2 B B A1 A T 1 A3 A A3 R M A M O O H A4 A4 Y A2 A2 C C OA 1 Ta có: OA A ∽ O A A theo tỉ số 3 K cos 0 A OA cos 60 . 3 4 2 1 3 2 OA 2 2
Giáo viên: Nguyễn Chí Thành S S O A A 1 Suy ra 3 4 O 2 A 1 A = S = . O 3 A 4 S 4 A 4 O 2 A 1 A Do đó S nhỏ nhất khi S nhỏ nhất. O 3 A 4 A O 2 A 1 A 1 R Mà S O . A A A
.A A nhỏ nhất khi A A nhỏ nhất. O 2 A 1 A 1 2 1 2 2 2 1 2 R
Mà A A nhỏ nhất khi A OM O . Khi đó OAB là tam giác đều nên OH HA và OM 2R . 1 2 2
Các em tính được BC 2BH R 3 và AM OM OA R . A A AM A A R 2 . R 3 Ta có: 1 2 1 2 A A 1 2 BC MH 3 R 3 R 3 2 2 R R 2 . R 3 R 3 Khi đó S .A A . . O 2 A 1 A 1 2 2 2 3 3 2 S OA A R 3 Nên 2 1 S = O 3 A 4 A 4 12
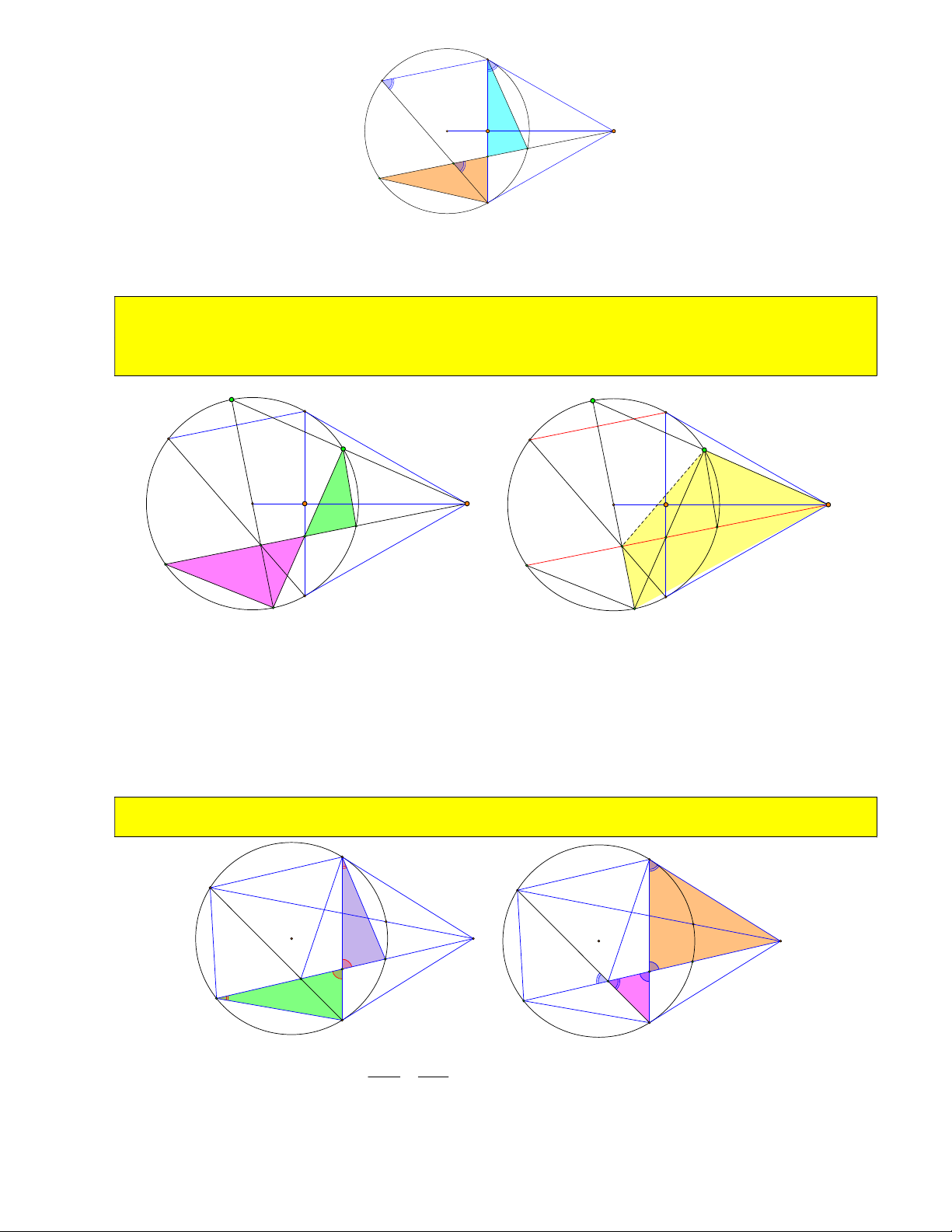
25) Qua O kẻ đường thẳng vuông góc với OM cắt MB, MC tại O và O . Tìm vị trí điểm M để diện 1 2
tích tam giác MO O bé nhất. 1 2 O1 B O M C O2
Xét MO O có: OM vừa là đường cao, vừa là đường phân giác nên MO O cân tại M . 1 2 1 2 1 Suy ra S 2S 2. O . B O M . R O M . M 1 O 2 O MO 1 O 1 1 2 Mặt khác 2 2 O M O B BM 2 O .
B BM 2 OB 2 R 2R . 1 1 1
Dấu bằng xảy ra khi O B BM O OM vuông cân nên OM R 2 . 1 1 Vậy 2 min S
2R khi điểm M nằm cách O một khoảng OM R 2 . M 1 O 2 O
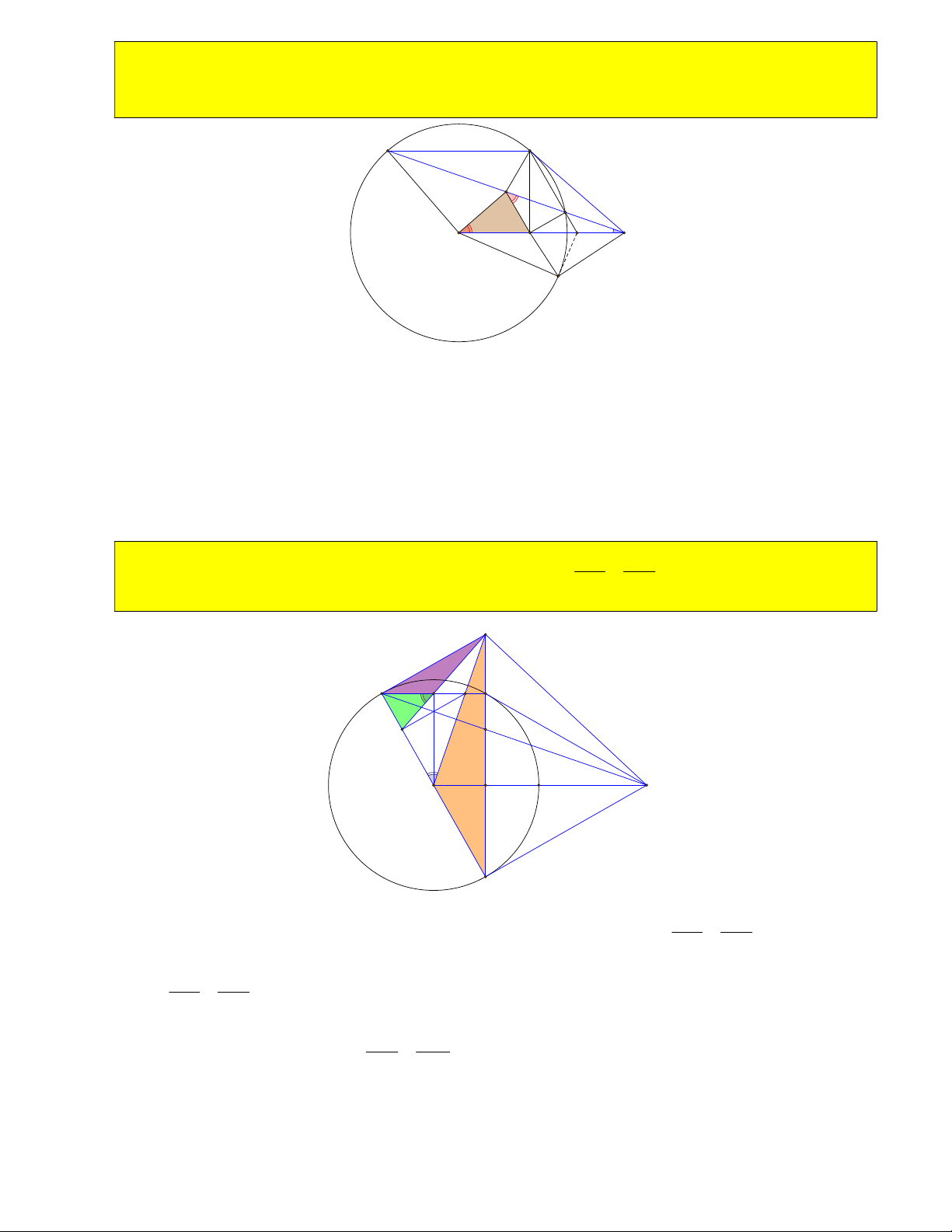
26) Chứng minh ba tam giác O
A O ∽ AOA ∽ O OA và O A .O A O O.O O . 1 1 1 2 2 2 1 1 2 2 2 1 1 1 1 1 Ta có: A OA A OA AOA POA AOC 0 BOC 180 M . 1 2 1 2 2 2 2 2
Giáo viên: Nguyễn Chí Thành
Do MO O cân tại M ( vì OM vừa là đường cao, vừa là phân giác) nên 1 2 0 180 M O O O O A OA . 1 2 1 2 1 2 2
Xét O A O và A OA có: 1 1 1 2 O A O
OA A ( Tính chất hai tiếp tuyến cắt nhau) 1 1 1 2 O A OA ( chứng minh trên) 1 1 2
Suy ra O A O ∽ AOA g g . 1 1 1 2
Chứng minh tương tự các em sẽ được AOA ∽ O OA . 1 2 2 2 Vậy O
A O ∽ AOA ∽ O OA . 1 1 1 2 2 2 O A O O Chỉ ra 1 1 1 O A O ∽ O OA
O A .O A O O.O O ( đpcm). 1 1 2 2 1 1 2 2 2 1 O O O A 2 2 2 O1 B A1 A O M A2 C O2
27) Chứng minh O A O A O O . 1 1 2 2 1 2 O1 B A1 A O M A2 C O2 Sử dụng BĐT Cosi:
Ta có: O A O A 2 O A .O A O A O A 2 O O.O O . 1 1 2 2 1 1 2 2 1 1 2 2 1 2 O O 2 O O Mà 1 2 O O O O nên 1 2 O A O A 2 O O . 1 2 2 1 1 2 2 1 2 2
28) Cho O; R và điểm M cố định. Tìm vị trí điểm A để O A O A nhỏ nhất. 1 1 2 2
Giáo viên: Nguyễn Chí Thành O1 B A1 A O M A2 C O2
Vì O; R và điểm M cố định nên O O không đổi. 1 2
Ta có: O A O A 2 O A .O A O A O A 2 O O.O O . 1 1 2 2 1 1 2 2 1 1 2 2 1 2 O O 2 O O Mà 1 2 O O O O nên 1 2 O A O A 2 O O . 1 2 2 1 1 2 2 1 2 2
Dấu bằng xảy ra khi O A O A A A / /O O A I ( với I OM O ) 1 1 2 2 1 2 1 2
29) Cho O và M cố định, điểm A di chuyển trên cung nhỏ BC . Chứng minh chu vi tam giác MA A 1 2
không phụ thuộc vào vị trí điểm A . O1 B A1 A O M A2 C O2 Chỉ ra chu vi M
A A là: MA A A AA A M MA A B CA A M MB C M 2 B M 1 1 2 2 1 1 2 2 1 2 không đổi.
Vậy chu vi tam giác MA A không phụ thuộc vào vị trí điểm A . 1 2
30) Cho O và M cố định . Tìm vị trí điểm A trên cung nhỏ BC để diện tích tam giác MA A lớn nhất. 1 2 O1 B A1 A O M A2 C O2
Giáo viên: Nguyễn Chí Thành
Như trên ta đã chứng minh: Chu vi M
A A không đổi và bằng 2MB . 1 2
Đặt MB a nửa chu vi M
A A là p a không đổi 1 2 4
p p MA p A A p MA và S p p MA p A A p MA M A A 1 1 2 2 1 1 2 2 1 2 4 3 3
p MA p A A p MA p
Ta có: p MA p A A p MA 1 1 2 2 1 1 2 2 3 27 4 p 2 p . 27 Nên p p MA p A A p MA S p p MA p A A p MA M A A 1 1 2 2 1 1 2 2 27 1 2 27
Dấu bằng xảy ra khi MA MA A là giao điểm của OM với O 1 2
31) Kéo dài AH O Z . Chứng minh tứ giác MAOZ là tứ giác nội tiếp và góc BMZ AMC ( hoặc chứng minh BMA
CMZ hoặc OM là phân giác góc AMZ ). B A O H M Z C 2 HM.HO HC Chỉ ra HM. O H H . A HZ . 2 H . A Z H H . B HC HC Từ đó suy ra HAM ∽ H
OZ c g c AZO
AMO tứ giác MAOZ là tứ giác nội tiếp. + Ta có: AMO
AZO (góc nt chắn cung OA ) mà OAZ AZO ( OAZ cân tại O) Và OAZ
OMZ (góc nt chắn cung OZ ) nên AMO OMZ mà BMO CMO nên BMA CMZ suy ra BMZ AMC .
32) Lấy điểm T bất kì trên BC , kẻ đường thẳng qua T và vuông góc OT , cắt MB, MC tại T ,T . Chứng 1 1 1 2 3 minh OT T cân. 2 3 T2 B T1 O H M T3 C
Giáo viên: Nguyễn Chí Thành O BT OT T
Chỉ ra tứ giác OT BT ; OT T C nội tiếp nên 1 2 1 mà 1 2 1 3 O T T OCT 3 1 1 OB OC OBT OCT OT T OT T O T T cân tại O . 1 2 2 1 3 1 2 3
33) Chứng minh rằng nếu T là trung điểm HB thì T là trung điểm CM , hoặc HT BT là hình bình hành 1 3 3 2
( hoặc cho T là trung điểm HB , chứng minh BT là trung tuyến BMC , hoặc MG 2GH ….) 1 3 T2 B T1 G O H M T3 C
Chỉ ra OT T cân nên T là trung điểm T T , mà T là trung điểm HB HT BT là hình bình hành, do 2 3 1 3 2 1 3 2
đó HT / /BT . Dựa vào MBC có HT / /BM mà H là trung điểm BC T là trung điểm CM . 3 2 3 3 34) Chứng minh OH.OT O . B OT 2 1 T2 B T1 O H M T3 C Chỉ ra OT T
OBT OT T ∽ OBH g g OH.OT O . B OT 2 1 1 2 1 2 1
35) Vẽ đường kính CK của đường tròn O . Chứng minh BK / /OM . K B O M H I C
Vì OB OC OK R C
KB vuông tại B BK BC mà OM BC BK / /OM .
36) Đường thẳng vuông góc KC tại O cắt BC tại E . Chứng minh 2 HE.HC H . O HM R .
Chỉ ra HOE ∽ HCO g g 2 HE.HC OH . Mà 2 2 2 2 2 H . O HM BH HE.HC H .
O HM OH HB OB R .
Giáo viên: Nguyễn Chí Thành
37) Cho R 3cm, OM 5cm . Tính độ dài các cạnh của tam giác MBC . Ta có: 2 2 2
BM OM OB 16 BM MC 4cm . OM .BM 3.4 12 BH.OM O . B BM BH cm BC 2BH 4,8cm . OM 5 5
38) Kẻ CP BM tại P , CP OM Q . Chứng minh Q là trực tâm M
BC và BQ MC . Tính BQ . K B B P P O M O H Q Q M H C C Xét M
BC có MH ,CP là đường cao nên Q là trực tâm M BC và BQ MC . O B / /CQ MB Chỉ ra O
C / /BQ MC OBQC là hình thoi nên BQ OB R . BC OQ
39) Giả sử O cố định và điểm M luôn chạy trên đường tròn ;
O 3R . Chứng minh khi đó Q chạy trên
một đường tròn cố định. R 2R 2R
Các em tính được độ dài OH OQ
Q luôn chạy trên đường tròn O; . 3 3 3
40) Chứng minh BC là phân giác của góc KCP . Chỉ ra BHQ C HQ 2cgv HBQ HCQ
Do QB / /KC ( cùng vuông góc CM ) nên HBQ KCB ( so le trong ) Suy ra KCB
BCQ BC là phân giác của góc KCP .
41) Tứ giác OBQC là hình gì ? Vì sao? OB / /CQ, MB
Chỉ ra OC / /BQ, CM OBQC là hình thoi. OQ BC
42) Gọi Q là trung điểm BK . Chứng minh OHBQ là hình chữ nhật. 1 1 K B Q1 M O H C
Giáo viên: Nguyễn Chí Thành Chỉ ra OQ B Q BH 0
BHO 90 OHBQ là hình chữ nhật. 1 1 1
43) Từ C kẻ đường thẳng song song MB và cắt O tại Y . Chứng minh 2 KY .OM 2R 2 2 K B M O H Y2 C
44) Từ C kẻ đường thẳng song song MB và cắt O tại Y . Tia MY cắt đường tròn tại M , gọi M là 2 2 3
điểm đối xứng với M qua OM . Chứng minh Y , H , M thẳng hàng. 2 3 B B M3 O H M M'3 O H M M' Y M' 2 Y2 C C Cách 1:
Gọi M là giao Y H với O . Chỉ ra tứ giác OHM Y nội tiếp. 3 2 2 Từ đó suy ra MHM OY M OM Y OHY M HM . 2 2 2 3
Từ đó suy ra M HM
MHM M và M đối xứng nhau qua OM M M . 3 3 3 3 Cách 2: 1
Do M đối xứng M qua MO nên M OM M O M . M OM M Y M . 3 3 3 3 2 2 Mặt khác tứ giác OHM Y nội tiếp nên M O M M Y H M Y H M Y M . 2 2 2 2 2
Vậy Y , H , M thẳng hàng. 2 3
45) Từ B kẻ BF KC tại F , BF KM F . Chứng minh F là trung điểm F B và BC là phân giác 2 2 2 3 3 2 góc MBF . 2
Giáo viên: Nguyễn Chí Thành K B F3 F K1 2 M O H C F F CM CM Chỉ ra 2 3 F F / /CM . 2 3 KF KC 2OC 2 1 F B HM Chỉ ra F KB HCM sd 2 BC F BK ∽ H MC g g . 2 2 2 KF HC 2 HM CM
Chỉ ra HOC ∽ HCM g g . HC OC F F 1 CM 1 F B F F 1 F B F B
Từ 3 đẳng thức trên các em suy ra : 2 3 2 2 3 2 2 . . . F F F là 2 3 3 KF 2 OC 2 KF KF 2 KF 2 2 2 2 2 trung điểm F B . 2 1 + Chỉ ra F BC CKB ( cùng phụ F BK ) mà CKB CBM sd BC . 2 2 2 Suy ra F BC
CBM BC là phân giác góc MBF . 2 2
46) Qua O kẻ đường thẳng vuông góc OB cắt MC tại Y . Chứng minh O Y M cân. 1 1 K B K1 H I I1 M O Y1 C
Chỉ ra OY / /MB OB Y OM OMB slt OMY O Y M cân tại Y . 1 1 1 1 1
47) Gọi B là điểm chính giữa cung I I . Từ H kẻ HH B I tại H , kẻ HH B I tại H . Chứng 3 1 3 3 1 3 4 3 4
minh 5 điểm O, H , H , B , H cùng thuộc một đường tròn. 4 3 3 B3 H B 3 H4 I1 O H I M C
Chỉ ra 5 điểm O, H , H , B , H cùng nằm trên đường tròn đường kính HB . 4 3 3 3
Giáo viên: Nguyễn Chí Thành
48) Gọi H là điểm đối xứng với H qua H H . Chứng minh H H B H là hình thang cân. 5 3 4 4 5 3 3 B3 B H3 H5 H4 I1 O H I M C H H H H Chỉ ra 4 4 5
( tính chất đối xứng trục) H H H H 3 3 5
nên H H H H HH g g g H H H 0
H HH 90 H H B H là tứ giác nội tiếp. 3 5 4 3 4 3 5 4 3 4 4 5 3 3 Vì H H HH B H B H H
H H H ( góc nt chắn hai cung bằng nhau) 4 5 4 3 3 3 5 3 4 3 5
Suy ra B H / /H H H H B H là hình thang. 3 5 3 4 4 5 3 3
Vì hình thang H H B H là tứ giác nội tiếp nên H H B H là hình thang cân. 4 5 3 3 4 5 3 3
49) Chứng minh rằng H O . 5 B3 B H3 H5 H4 I1 O H I M C O H H 0 OB H 45 Chỉ ra 5 3 3 3
, mà H H B H là tứ giác nội tiếp và H H B H nên góc 0 4 5 3 3 4 5 3 3 O B I 45 3 H B H B H H OB H
OH B OH B cân tại O OH OB R H O . 5 3 5 4 3 5 3 5 3 3 5 5 3 5 3
50) Tiếp tuyến tại H cắt OM tại H . Chứng minh H , H , H thẳng hàng. 5 6 3 4 6 B3 B H3 H5 H4 I1 O H I M H6 C
Giáo viên: Nguyễn Chí Thành 0
IHH OH H OB I 45 4 3 4 3
Tứ giác OHH H nội tiếp nên O H H 0 OB H 45 H HI 0 H H H 45 4 3 5 4 3 4 4 4 5 6 0 O H H 90 5 6 Mà H H H H HH HH H
H HH H H H H H nằm trên trung trực HH 4 5 4 5 5 6 5 6 6 5 6 6 5
Mà H H là trung trực HH nên H , H , H thẳng hàng. 3 4 5 3 4 6
51) Giả sử B cố định và M thay đổi sao cho MB là tiếp tuyến của O . Tìm quỹ tích điểm Q khi M thay đổi.
Do OBQC là hình thoi nên BQ OB R mà B cố định nên Q B; R . MK O K1
52) Gọi C là trung điểm CM , MK BC B . Chứng minh MK .MK MH.MO . 1 1 1 C K BC B 1 1 2 B2 B2 K B K B B K 1 1 B K 1 1 O H M O H M C1 C1 C C Chỉ ra C
KM vuông tại C và có CK là đường cao nên 2 MK .MK CM . 1 1 Chỉ ra O
CM vuông tại C có CH là đường cao nên 2 MH .MO CH .
Từ đó suy ra MK .MK MH.MO 1 MHK MKO 53) Chứng minh M K H ∽ MOK và góc 1
. Từ đó suy ra OKK H nội tiếp. 1 1 MK O MOK 1 B2 B2 K B K B B K 1 1 B K 1 1 M O H O H M C1 C1 C C
Giáo viên: Nguyễn Chí Thành MK MH Xét M K H và M OK có: góc KMO chung và 1 1 MO MK Từ đó suy ra M K H ∽ MOK . 1 MHK MKO Vì M K H ∽ MOK nên 1 . 1 MK O MOK 1 Xét tứ giác OKK H có OKK OHK K HM 0
OHK 180 , mà đây là hai góc đối nhau nên tứ giác 1 1 1 1 1
OKK H là tứ giác nội tiếp. 1
54) Chứng minh C K là tiếp tuyến của O . 1 1 B2 K B B K 1 1 M O H C1 C Chỉ ra C
MK vuông tại K K C C C C M C K C cân tại C . 1 1 1 1 1 1 1 1 1
Chỉ ra OC K OC C c c c OK C 0 OCC 90 . 1 1 1 1 1 1
Từ đó suy ra C K là tiếp tuyến của O . 1 1
55) Gọi K là trung điểm KK . Chứng minh B K là tiếp tuyến của O . 2 1 2 B' B2 K B K B K2 K2 B K 1 1 B K 1 1 M O H O H M C1 C1 C C O K KK Vì K là trung điểm 2 1 KK . 2 1 KOK K OK 2 1 2
giả sử OK BC B. Ta sẽ chứng minh B ' B , tức là chứng minh B ' K là tiếp tuyến O . 2 2 1
Giáo viên: Nguyễn Chí Thành Ta có: O
K M ∽ OHBg g 2 2 2
OK .OB OH.OM OB R OK 2 2 1 2
OK .OB OK OK K ∽ OK Bc g c OK B 0 OK K 90 B K là tiếp tuyến của 2 1 2 1 1 1 2 1 1 O , suy ra B B . 2
Từ OKB OK B c g c OKB 0
OK B 90 nên B K là tiếp tuyến của O . 2 1 2 2 1 2 2 56) Chứng minh M HB ∽ B HO . Từ đó suy ra 2 H . O HM HB . HB BH . 1 2 2 1 B' B2 K B K B K2 K2 B K 1 1 B K 1 1 M O H O H M C1 C1 C C Các em chỉ ra HMB HB O ( cùng phụ HPB ). 1 2 2 Từ đó suy ra M
HB ∽ B HO g g H . O HM HB .HB và 2 HO.HM BH . 1 2 2 1 57) Chứng minh 2 BC 4HB . HB . 1 2 2 BC BC Chỉ ra 2 BH HO.HM HB . HB mà 2 BH
HB .HB BC 4HB .HB . 2 1 2 1 1 2 2 2 B2 K B K2 B K 1 1 O H M C1 C 58) Chứng minh 2 2
OH .OM OK .OB R OB ( hoặc chứng minh OK .OB không đổi) 2 2 2 2 Chỉ ra K MO HB O ( cùng phụ HOB ) . 2 2 2 Từ đó suy ra K MO ∽ H
B O g g OH.OM OK .OB . 2 2 2 2 Mà 2 2 OH .OM OB R nên 2 2
OH .OM OK .OB R OB 2 2
Giáo viên: Nguyễn Chí Thành 59) Chứng minh OB B M 1 2 B2 K B K2 B K 1 1 O H M C1 C
Chỉ ra B là trực tâm OMB OB MB . 1 2 1 2
60) Chứng minh tứ giác MHK B nội tiếp từ đó suy ra OK .OB không đổi. 2 2 2 2 B2 K B K2 B K 1 1 O H M C1 C Xét tứ giác MHK B có: MHB 0
MK B 90 , mà đây là hai góc có đỉnh kề nhau cùng nhìn cạnh 2 2 2 2 2
MB , suy ra tứ giác MHK B là tứ giác nội tiếp. 2 2 2 Chỉ ra 2 2
OK .OB OH.OM OB R không đổi. 2 2
61) Gọi BC O J . Chứng minh C J C ∽ C CB , C MJ ∽ C
BM ; CH J C là tứ giác nội tiếp. 1 1 1 1 1 1 1 1 1 1
(hoặc bài có thể khai thác từ các yếu tố trên như chứng minh các góc, tỉ số đoạn thẳng…) K B K1 J1 M O H C1 C
Chỉ ra C H C C ( trung tuyến tam giác vuông) nên C CH C HC . 1 1 1 1 1 Mặt khác C CJ C BC sd CJ C J C ∽ C CB g g C J C C CB C HC . 1 1 1 1 1 1 1 1 1 1 1 2
Giáo viên: Nguyễn Chí Thành
Từ đó suy ra CH J C là tứ giác nội tiếp. 1 1 + Chỉ ra 2
C J C ∽ C CB CC C J .C B mà 1 1 1 1 1 1 1 2
C C C M C M C J .C B C
MJ ∽ C BM c g c 1 1 1 1 1 1 1 1 1
62) Kéo dài MJ cắt O tại J . Chứng minh J C là phân giác góc C J J 1 2 1 1 1 2 K B K1 J2 J1 M O H C1 C Do C MJ ∽ C BM C MJ C BM MJ B J B / /CM 1 1 1 1 1 1 2 2 J BC BCM CJ C 2 1 1 J J C J C là phân giác góc C J J . 1 1 1 2 J BC CJ C 2 1 1 1 J J C 2 2 1 2 K M K K .K B
63) Kéo dài BK OM K . Chứng minh 3 3 1 3
từ đó suy ra K là trung điểm HM và 1 3 2 K H K K .K B 3 3 3 1 3 HK BK . 1 1 B2 K B K1 M O H K3 C Chỉ ra K MK MKB ( sole trong) mà MKB
K BM ( tính chất góc nt và góc tạo bởi tt và dây cung) 3 3 Nên K MK
K BM . Từ đó suy ra K MK ∽ K
BM g g K M K K .K B . 3 1 3 2 3 3 3 3 1 3 + Do MK H ∽ M OK nên MHK MKO mà MKO HBK ( góc nt chắn cung CK ) 1 1 3 1
Từ đó suy ra K HK ∽ K BH g g 2 K H K K .K B . 3 1 3 3 3 1 3 2 K M K K .K B Vì 3 3 1 3
K M K H K là trung điểm MH . 3 3 3 2 K H K K .K B 3 3 1 3
Giáo viên: Nguyễn Chí Thành B2 K B K1 M O H K3 C + Ta có: K BH K HB K HK K HB 0
K HB 90 . Từ đó suy ra HK BK . 1 1 1 3 1 3 1 1 2 HC KK 64) Chứng minh 1 1. 2 HK MK 1 1 B2 K B K1 M O H K3 C 2 BH BK .BK 1 3 2 C H BK .BK 2 HC BK BK K K BK Chỉ ra 2 1 3 HK BK .K K . Suy ra 3 1 1 3 1 1. 1 1 1 3 2 HK BK .K K 2 HK K K K K K K 1 1 1 3 BH CH 1 1 3 1 3 1 3 KK BK 2 HC KK BK KK + Ta có: 1 1 BK / /OM suy ra 1 1 1 1 1. MK K K 2 HK K M K K MK 1 1 3 1 1 1 3 1
65) Từ K kẻ đường thẳng song song KB cắt BC, BM tại K , K . Chứng minh K là trung điểm K K . 1 5 6 1 5 6 K B K1 K6 K5 M O H K3 C KB / /OM K K BK K K Vì 1 5 1 1 6 K K / /HM
mà HK K M K K K K K là trung 5 6 K K / /KB HK BK K M 3 3 1 5 1 6 1 5 6 3 3 3 điểm K K . 5 6
Giáo viên: Nguyễn Chí Thành K B B1 K1 K6 K5 O H M C
Cách khác: Các em có thể thấy, HB là phân giác trong
KHK và HM HB HM là phân giác ngoài 1 1 K B K K 1 1 1 5 K B MK B K KB góc KHK 1 1 1
( tính chất phân giác) . Mà 1 K K K K . 1 B K MK 1 5 1 6 1 MK K K 1 1 6 MK KB
66) Chứng minh HB là phân giác góc KHK . 1 B2 K B K1 M O H C O KK K HM
Chỉ ra tứ giác OKK H là tứ giác nội tiếp nên 1 1 mà OKK OK K ( do OKK cân) 1 1 1 1 O K H OK K 1 BHK 0 OHK 90 Nên K HM OHK mà BHK
BHK HB là phân giác góc KHK . 1 1 B K H 1 0 K HM 90 1 1 67) Chứng minh 2
OK OH.OM từ đó chứng minh OK là tiếp tuyến của đường tròn ngoại tiếp H MK 1 1 1 K B K1 M O H C
Giáo viên: Nguyễn Chí Thành 2 O B OH.OM Chỉ ra 2 OK OH.OM . 1 OB OK 1 OK OM + Chỉ ra 2 1 OK OH.OM O HK ∽ O K M c g c . 1 1 1 OH OK1 Từ đó suy ra góc OK H
OMK OK là tiếp tuyến của đường tròn ngoại tiếp H MK . 1 1 1 1
68) Từ B kẻ đường thẳng song song MC cắt O tại B , nối MB O B . Chứng minh góc 4 4 5 BB C MB C 5 5 B B5 M O B4 C
Vì tứ giác BB CB nội tiếp nên BB C 0 BB C 180 . 4 5 4 5 BB B B MC slt 4 5 4 MB C B CM Chỉ ra 4 5 BB C CB M . BB B MB C 5 5 0 BB C 180 4 5 4 5 B MC B CM 0 CB M 180 4 5 5
69) Từ K kẻ tiếp tuyến K K với O , K là tiếp điểm . Chứng minh HK M vuông. 3 3 4 4 4 B2 K B K1 K3 O H M K4 Ta có: O K K vuông tại 2 2 2 2
K OK K K OK OH HK 4 4 3 4 3 3 4 3 2 2 2 2 2 2 2 2 2
OH HK 2.OH.HK OH HK OH.HM OH HK BH HK OB 3 3 3 3 3
Mà OK OB R K K HK K K HK K M H
K M vuông tại K ( tính chất trung 4 3 4 3 3 4 3 3 4 4
tuyến của tam giác vuông).
Giáo viên: Nguyễn Chí Thành
70) Giả sử KK 3K M và P là trung điểm KM . Chứng minh KM là tiếp tuyến của đường tròn ngoại 1 1 1 tiếp OHP . 1 K B P1 K1 M O H K3 K4 Ta có: 2 2
BM MK .MK MK .4MK 4MK BM 2MK mà MP 2MK PM MP . 1 1 1 1 1 1 1 1 Mặt khác: 2 2
BM MH.MO MP MH .MO . 1
Từ đó các em chứng minh MHP ∽ MPO c g c MP H MOP . 1 1 1 1
Suy ra MK là tiếp tuyến của đường tròn ngoại tiếp OHP . 1 B Q KO Q CB KB
71) Gọi trung điểm BK là Q , 2 1 2 . Chứng minh 2 2 và Q Q / /KB . 1 B OKB Q OC KQ 2 3 2 2 3 1 B2 K Q1 B Q3 B1 Q2 M O H C CB KB Chỉ ra 2 2 KB .KC K .
B CB KB .2OC 2KQ .CB KB .OC KQ .CB . 2 2 2 1 2 2 1 2 OC KQ1 CB KB + Từ 2 2
B Q K ∽ B OC c g c B Q K B OC Q Q K KOB . 2 1 2 2 1 2 2 1 2 OC KQ1 Q K Q K
Nên Q Q K ∽ Q OK g g 1 2 . 2 1 3 OK Q K 3
Giáo viên: Nguyễn Chí Thành Q K Q K Xét O Q K và Q Q K có OKB chung và 1 2 nên 1 3 2 OK Q K 3
OQ K ∽ Q Q K c g c Q Q K 0
OQ K 90 mà B K KC Q Q / /B K . 1 3 2 3 2 1 2 2 3 2 BM KC S 72) Cho
. Chứng minh M là trung điểm JC . C M KB J S K B J O H M C X MCB 0 MJB 90 Vì MB MC gt MBC MCB mà MJB cân tại M MBC MBJ MBJ 0 MBJ 90
MB MJ . Vì MB MC MJ M là trung điểm CJ .
73) OB CM X . Chứng minh SX / /BC .
Xét MSX có hai đường cao SC và XP nên O là trực tâm M SX MO SX . Vì MO BC SX / /BC . 74) Chứng minh XK SJ . Do BK / /MO BK SX . Xét S
JX có SC và KJ là đường cao nên K là trực tâm S JX XK SJ .
Giáo viên: Nguyễn Chí Thành 75)
Từ M kẻ cát tuyến MDD ( tia MD nằm giữa tia MB và MO ), gọi D là trung điểm DD, 1
OD BC D . Chứng minh các điểm O,C, M , B, D cùng nằm trên một đường tròn, các điểm 1 2 1
M , H , D , D cùng nằm trên một đường tròn. 1 2 D2 B D' D1 D O H M C
Chỉ ra các điểm O,C, M , B, D đều cách đều trung điểm của OM ( dựa vào tính chất trung tuyến tam giác 1
vuông) hoặc các đỉnh C, B, D đều nhìn MO dưới một góc vuông. 1
Chỉ ra các điểm M , H , D , D đều cách đều trung điểm của D M ( dựa vào tính chất trung tuyến tam giác 1 2 2 vuông) hoặc MHD 0 MD D 90 . 2 1 2 76)
Cho O và điểm M cố định. Khi cát tuyến MDD thay đổi, tìm quỹ tích điểm D . 1 D2 B D' D1 D O H M C Vì 0
OD M 90 nên điểm D nằm trên đường tròn đường kính OM . Do đó khi cát tuyến MDD thay 1 1
đổi, thì quỹ tích điểm D chạy trên đường tròn đường kính OM . 1 77) Chứng minh 2 2 2
OH.OM OD .OD OB R OD . 1 2 Chỉ ra OHD ∽ O
D M g g OH.OM OD .OD . 2 1 1 2 Chỉ ra 2 2
OH.OM OB R ( hệ thức lượng) Suy ra 2 2 2
OH.OM OD .OD OB OD R . 1 2
Giáo viên: Nguyễn Chí Thành D2 B D' D1 D O H M C 78) Chứng minh 2 CM M . D MD MH.MO . Cách 1: Ta có: M .
D MD MD D D MD D D MD D D MD D D 1 1
1 1 1 1 1 1 2 2 D M D D 2 2 OM D O 2 2 OD D O 2 2 2 2 2
OM OD OM OC CM ( đpcm) 1 1 1 1
+ Trong tam giác vuông OCM , đường cao 2 CH CM MH.MO . Cách 2: 1 Chỉ ra MBD MD B sd BD M BD ∽ M D B g g 2 2 BM M . D MD CM M . D MD 2 79) Chứng minh 2 OH.OM M . D MD MO . 2 O H.OM OB 2 2 2 OH.OM M .
D MD OB BM MO . 2 M . D MD MB 80)
Chứng minh MBD ∽ MD B và góc MBD MD B . Cách 1: Ta có: 2 2 CM M . D MD BM M . D MD .
Từ đó suy ra MBD ∽ MD B
c g c MBD MD B
( hai góc tương ứng) . 1 Cách 2: MBD MD B sd BD M BD ∽ M D B g g . 2 81) Chứng minh M DH ∽ M OD và góc MHD MD O . 2 MB M . D MD Do M . D MD MH.MO . 2 MB MH.MO
Từ đó suy ra MDH ∽ MODc g c MHD MD O
( hai góc tương ứng) . 82)
Giả sử độ dài dây cung DD không đổi. Chứng minh BC luôn đi qua điểm cố định khi M thay đổi.
Do DD nên khoảng cách từ O đến DD là OD không đổi. 1
Giáo viên: Nguyễn Chí Thành 2 R Mặt khác 2 OD .OD R OD
không đổi nên D cố định. 1 2 2 OD 2 1
Suy ra BC luôn đi qua điểm cố định là D . 2 83)
Chứng minh D D là tiếp tuyến của O ( hoặc chứng minh OD D D ) 2 2 OD OD Ta có: 2 2 1 OD .OD R OD . 1 2 OD OD2 OD OD Xét O D D và O D D có D O D chung và 1 nên OD D ∽ O D D c g c 1 2 1 2 1 OD OD2 Suy ra OD D 0
OD D 90 D D là tiếp tuyến của O . 2 1 2 D2 B D' D1 D O H M C 84)
Nếu đề bài đổi thành tiếp tuyến tại D và D cắt nhau tại D , chứng minh B,C, D thẳng hàng. 2 2 2 2 O H.OM OB R Chỉ ra
OH.OM OD .OD OHD ∽ O D M c g c 1 2 2 1 2 2 O D .OD D O R 1 2 OHD 0
OD M 90 HD OM mà BC OM B,C, D thẳng hàng. 2 1 2 2
Cách khác: Các em có thể chỉ ra hai tứ giác OD D D và OD D
H nội tiếp nên 5 điểm O, D, D, H , D 2 2
cùng thuộc một đường tròn, suy ra OHD 0
ODD 90 HD OH mà BC OH B,C, D thẳng 2 2 2 2 hàng. 85)
Từ D kẻ đường thẳng song song BC cắt O tại D . Chứng minh D , H, D thẳng hàng. 5 5 B D' D3 D M O H D5 C
Vì BH là phân giác góc D H
D ( đã chứng minh ở các câu khác) Mà OHB 0 MHB 90 OHD DHM .
Giáo viên: Nguyễn Chí Thành Vì D D
/ /BC OH là trung trực D D OHD OHD OHD DHM . 5 5 5 5 Ta có: OHD OHD DHM 0
OHD 180 D , H , D thẳng hàng. 5 5 86)
Gọi MO KD G , CG O G , D G DK G ,G K D D G . Chứng minh 1 1 2 2 3 2 4 CD D
KOG từ đó cứng minh OKG ∽ D
DC ( hoặc các tỉ số từ tam giác đồng dạng) 1 1 1 1 G3 K B D' D G 1 4 D G M 1 O G2 C Chỉ ra CD D MOC KOG và G KO D DC ( góc nt chắn cung D C ). 1 1 1 1 87)
Chứng minh G ,O, D thẳng hàng và G G G D . 2 3 4 2 G3 K B D' D G 1 4 D G M 1 O G2 C OK DD 2OK 2DD KC DD Vì 1 1 OKG ∽ D DC DCD∽ K G C c g c 1 1 1 KG DC KG DC KG DC 1 1 1 Suy ra KCG DD C DCM G CD G CO COD DCM 0
COD 90 G D là đường kính của 1 2 1 2
đường tròn O G , D,O thẳng hàng và G D D 0
G KD 90 G là trực tâm 2 2 2 4 G DG G G G D 2 3 3 4 2 88)
Từ D kẻ đường thẳng song song BM cắt BC, BD tại C , C . Chứng minh tứ giác CDC D nội 4 5 4 1
tiếp và C là trung điểm DC . 4 5 B C5 D' C4 D1 D M O C
Giáo viên: Nguyễn Chí Thành
Vì CD BM nội tiếp nên D CB D MB
D DC slt CDC D là tứ giác nội tiếp. 1 1 1 4 1 4 1
Vì CDC D nội tiếp nên DD C DCC mà DCC DD B DD B DD C D B / /D C . 4 1 1 4 4 4 1 4 1 4 Mà D là trung điểm D D
C là trung điểm DC . 1 4 5 89)
Gọi MD BC D . Chứng minh MD và D D là phân giác trong và ngoài của góc CD B và 3 1 1 2 1 BD .CD BD .CD . 2 3 3 2 D2 B D' D1 D3 D M O H C
+ Chỉ ra tứ giác OD BM là tứ giác nội tiếp nên MD B
MOB ( góc nt cùng chắn cung BM ) 1 1
+ Chỉ ra tứ giác OD MC nội tiếp nên MD C
MOC ( góc nt cùng chắn cung MC ). 1 1 Mà MOC MOB MD B
MD C MD là phân giác góc CD B . 1 1 1 1
Hoặc các em chỉ ra : 5 điểm M ,C,O, D , B cùng thuộc một đường tròn, 1 mà MB MC MD B
MD C ( góc nt chắn hai cung bằng nhau) 1 1
MD là phân giác góc CD B . 1 1
+ Vì D D D M D D là phân giác ngoài của góc CD B . 1 2 1 1 2 1 BD BD
Áp dụng tính chất phân giác ta có: 3 2 BD .CD BD .CD 2 3 3 2 CD CD 3 2 90) Chứng minh D D .D D D . B D C 3 3 3 3 B D' D D3 M O H C Chỉ ra D
BD∽ D DC g g D D .D D D . B D C . 3 3 3 3 3 3
Giáo viên: Nguyễn Chí Thành 91)
D C O C . Chứng minh C B / /D D . 1 2 2 C2 B D' D1 D M O C
Chỉ ra tứ giác BMCD nội tiếp, suy ra CD M
CBM ( góc nt cùng chắn cung CM ) 1 1 Mà CC B
CBM ( góc nt cùng chắn cung BC ) 2 Suy ra CD M
CC B , mà hai góc này ở vị trí đồng vị nên C B / /D D . 1 2 2 92)
Kéo dài BD O C . Chứng minh CC / /D D . 1 3 3 B D' D1 D M O C3 C
Chỉ ra tứ giác OD BM là tứ giác nội tiếp, suy ra MD B
MOB ( góc nt cùng chắn cung BM ) 1 1 1 Mặt khác CC B . COB
MOB ( tính chất góc nội tiếp và góc ở tâm) 2 2 Suy ra CC B
MD B , mà hai góc này ở vị trí đồng vị nên CC / /D D . 2 1 2 1
Các em cũng có thể chỉ ra CC B MCB sd BC
MD B ( góc nt chắn cung BM ) 2 1 2 93)
Đề bài có thể thay đổi, kẻ dây CC / /D D . Chứng minh góc C BO D M O hoặc chứng minh 3 3
C , D , B thẳng hàng, hoặc C B D D
D chứng minh D là trung điểm D D . 3 1 3 1 1 B D' D1 D M O C3 C 1
Gọi BC MD D . Vì CC / /D D C D D BC C sd BC 4 4 3 3 4 3 2
Giáo viên: Nguyễn Chí Thành 0 CD O 90 0 C D D 90 sd BC 4 3 4 1 1 Mà BMO 0 BMC 180 BOC 0 90 sd BC BMO CD O OMBD nội tiếp 4 4 2 2 nên OD M 0 OBM 90 OD D D D D . 4 4 4 1
Vì OMBD là tứ giác nội tiếp nên C BO D M O . 1 3 2 1 1 94)
Gọi MD BC D . Chứng minh M . D MD MD .MD và 3 3 1 MD MD MD 3 B D' D1 D3 D M O H C3 C 2 M . D MD BM Chỉ ra M . D MD MD .MD . 3 1 2 MD .MD MH.MO MB 3 1 + Ta có: MD .MD M .
D MD MD .MD MD .MD 2M . D MD 3 1 3 1 3 1
MD . MD DD MD . MD DD 2M . D MD 3 1 3 1
MD .MD MD .DD MD .MD MD .DD 2M . D MD 3 3 1 3 3 1
MD .MD MD .MD 2M . D MD 3 3 2 MD MD 2 1 1 MD MD MD 2M . D MD 3 MD M . D MD MD MD MD 3 3 95)
Kéo dài BD và BD cắt C C tại C , C . Chứng minh rằng C là trung điểm C C . 3 6 7 3 6 7 B D' C6 D1 D M O H C3 C C7 Chỉ ra D D
/ /C C ( đã chứng minh trên) 6 7
Giáo viên: Nguyễn Chí Thành D D BD DD Áp dụng định lí Talet: 1 1 1 , mà DD D D nên C C C C . C C BC C C 1 1 3 6 3 7 3 6 3 3 7 96)
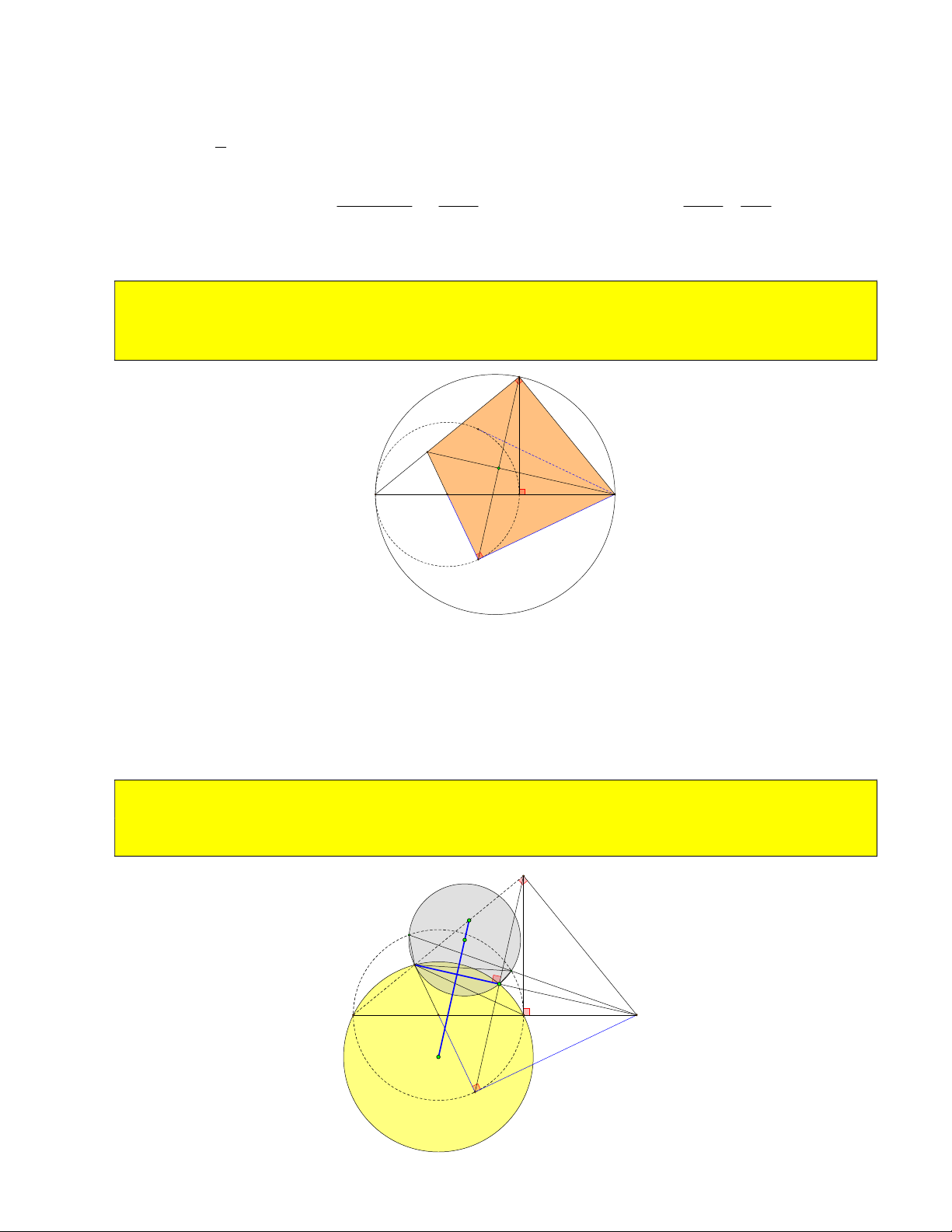
Cho O , M và B cố định. Chứng minh trọng tâm BD D và C D D luôn chạy trên một
đường tròn cố định ( hoặc chứng minh đường tròn ngoại tiếp BD D và C D D có cùng bán kính). B B D' D' G D1 D D1 D O2 O H M M G' O1 O H O1 O3 C C 1
Gọi O là trung điểm OM O cố định và O D OM không đổi. 1 1 1 1 2
+ Trên BO lấy điểm O sao cho BO 2O O O cố định ( do B,O cố định) 1 2 2 1 2 2 1 BG BO 2 2 1 OM
Gọi G là trọng tâm BD D . Ta có: 2
2 GO / /D O và GO D O . OM 2 1 1 GD O O 2 1 1 3 3 2 3 1 1 2 không đổi. OM OM Vì O cố định và GO không đổi nên G O ; . 2 2 3 2 3 OM Vậy trọng tâm BD D
luôn chạy trên một đường tròn O ; cố định. 2 3
+ Trên CO lấy điểm O sao cho CO 2O O O cố định ( do C,O cố định) 1 3 3 1 3 3 1 CG CO 2 2 2 1 1 Gọi G ' là trọng tâm 3 CD D G O / /D O và G O D O . OM OM . 3 1 1 CD CO 3 3 1 1 3 3 2 3 1 1 OM Do đó G O ; cố định. 3 3 97)
Từ D kẻ đường thẳng song song CM cắt BC, CD tại E, F . Chứng minh BDED là tứ giác nội 1
tiếp và E là trung điểm FD .
(Bài có thể thay đổi qua D kẻ đường thẳng song song CD cắt BC tại E ) 1 B D' D1 D O M E F C
Giáo viên: Nguyễn Chí Thành
Chỉ ra tứ giác D BMC nội tiếp nên góc D BC
D MC ( góc nt chắn cung D C ) 1 1 1 1 Mà D MC D DE ( đồng vị) nên D BC D DE D BE
D DE . Từ đó suy ra BDED là tứ giác nội 1 1 1 1 1 1 1 tiếp.
+ Vì BDED là tứ giác nội tiếp nên ED D
EBD ( góc nt chắn cung ED ) 1 1 Mà EBD CD D
( góc nt chắn cung DC ). Suy ra ED D CD D
, suy ra ED / /CD mà D là trung điểm D D
E là trung điểm DF ( tính chất 1 1 1 đường trung bình) . 98)
ED cắt OM tại F . Chứng minh ED BD và OEF B là tứ giác nội tiếp. 1 1 1 B B D' D' D1 D D1 D O F M O F M 1 E 1 E F F C C 1 + Chỉ ra ED D CD D slt CBD sd CD ED D EBD . 1 1 2
Từ đó suy ra ED BD là tứ giác nội tiếp. 1
+ Vì ED BD là tứ giác nội tiếp nên EDB
DD B (góc nt chắn cung BD ) 1 1
Mà tứ giác OMBD là tứ giác nội tiếp nên DD B
BOM ( góc nt chắn cung BM ) 1 1 Suy ra F EB
F OB OEF B là tứ giác nội tiếp. 1 1 1 BD CD 99) Phân giác góc
DBD cắt MD tại H . Chứng minh rằng : D B D C và CH là phân 1 1 BM MH CM 1 giác góc D C D . B D' H1 D O M C H2
Giáo viên: Nguyễn Chí Thành BD MB + Vì M DB ∽ MBD . D B D M DC MC BD CD + Tương tự: MDC ∽ M CD mà MC MB . D C D M D B D C BD H D BD CD CD H D + Ta có: 1
( tính chất phân giác) mà nên 1 D B H D D B D C D C H D 1 1
Suy ra CH là phân giác góc D C D . 1
+ Gọi BH O H . Vì H BD H BD D H DH . 1 2 2 2 2 2 1 1 1 Mà H BM sd BH sd BD sd DH sd BD sd D H BH M . 1 2 2 2 1 2 2 2 Do đó B
H M cân tại M MB MH mà MB MC nên BM MH CM 1 1 1
100) Chứng minh tứ giác D O HD nội tiếp. Vì M D O ∽ MHD MD O MHD OD D OHD DHM 0 OHD 180 . Xét tứ giác D O HD có DHM 0
OHD 180 mà đây là hai góc đối nhau nên D O
HD là tứ giác nội tiếp. B D' D M O H C
101) Đề bài có thể thay đổi thành: Chứng minh đường tròn ngoại tiếp HD D hoặc D O D luôn đi
qua một điểm cố định, hoặc tâm đường tròn ngoại tiếp HD D
luôn chạy trên một đường thẳng cố định…. B D' D M O H I C
+ Các em sẽ thấy, tứ giác OHDD là tứ giác nội tiếp nên đường tròn ngoại tiếp tam giác HD D luôn đi
qua điểm cố định O và đường tròn ngoại tiếp tam giác OD D
luôn đi qua điểm cố định H .
Giáo viên: Nguyễn Chí Thành
+ Vì OHDD là tứ giác nội tiếp nên tâm đường tròn ngoại tiếp HD D
luôn nằm trên đường trung trực đoạn OH .
102) Chứng minh DI là phân giác góc HDM ( với I MO O ) B D' D M O H I C MD MO MO Vì MD O ∽ M HD 1 . HD OD OB MI MB
Mà BI là phân giác góc HBM 2 IH BH MO MB MI Chỉ ra MHB ∽ M BO g g 3 . BO HB HI MD MI Từ 1 23
DI là phân giác góc HDM . HD HI 103) Chứng minh MOD 2 MDI B D' D M O H I C
Vì tứ giác HODD là tứ giác nội tiếp nên HOD HDM .
Mà DI là phân giác góc HDM HOD 2. MDI .
104) Kéo dài OM cắt O tại điểm thứ hai là I . Chứng minh M . D MD MI.MI 1 1 B D' D I1 O I M C
Vì IDD I là tứ giác nội tiếp nên D I I IDM . 1 1 Từ đó suy ra MID ∽ M D I g g M . D MD MI.MI . 1 1
Giáo viên: Nguyễn Chí Thành
105) Tiếp tuyến tại I cắt nửa đường tròn đường kính MI tại X , CO X I X . Chứng minh 1 1 1 1 2 MX CX 2 1 X1 B X2 O H I1 M I C Chỉ ra MBI ∽ M I B g g 2 BM MI.MI . 1 1 Mà 2
MX MI.MI ( hệ thức lượng) suy ra MX BM MC M X C cân. 1 1 1 1
Do đó M nằm trên đường trung trực CX . 1 MX C 0 CX X 90 M X C cân MX C MCX mà 1 1 2 CX X X CX X X C cân nên X 1 1 1 2 MCX 1 2 1 2 2 1 0 X CX 90 1 1 2
nằm trên đường trung trực CX . 1
Vậy MX là trung trực CX nên MX CX . 2 1 2 1
106) Từ M kẻ cát tuyến MPP song song BD , cát tuyến này cắt CB,CD tại P , P . Chứng minh tứ 1 4 2 3
giác MCP B là tứ giác nội tiếp và P là trung điểm P P ( hoặc OP P P ) 3 3 4 1 3 1 4 B D' D O M P1 P2 P3 P4 C 1 Chỉ ra MBC MD C sd BC MPC ( đồng vị) nên MBC MP C . 3 2 3
Từ đó suy ra MCP B là tứ giác nội tiếp. 3
+ Do M ,C,O, B cùng thuộc đường tròn đường kính OM 5 điểm M ,C,O, B, P cùng thuộc đường 3
tròn đường kính OM 0
OP M 90 OP PP P là trung điểm P P . 3 3 1 4 3 4 1
107) Chứng minh P P . P M P P. P P 2 3 2 2 1 2 4
Giáo viên: Nguyễn Chí Thành B D' M O H P1 P2 P3 P4 C P P .P M P C .P B Chỉ ra 2 3 2 2 1 2 P P .P M P P.P P 2 3 2 2 1 2 4 P P.P P P C .P B 2 1 2 4 2 1 2
108) Đường thẳng OP cắt O tại Y ,Y (Y nằm trên cung nhỏ D B
). Y P O Y . Chứng minh 2 2 3 2 3 3 4
Y ,Y , M thẳng hàng hoặc chứng minh tứ giác Y PY M nội tiếp. 3 4 2 3 4 Y3 Y3 B B D' D' Y4 Y4 M M O H O H P1 P1 P2 P2 P3 P3 P4 P4 C C Y2 Y2
Chỉ ra P P .P P PY .P Y mà P P . P M P P.P P nên P P . P M P Y .P Y 2 1 2 4 2 4 2 2 2 3 2 2 1 2 4 2 3 2 2 4 2 2
Từ đó chứng minh P PY ∽ P Y M c g c Y Y M 0
Y P M 90 Y Y Y M . 2 3 2 2 4 2 4 2 3 2 4 4
Vì Y Y là đường kính O Y Y Y Y . 2 3 2 4 3 4
Từ đó suy ra Y ,Y , M thẳng hàng. 3 4
109) Chứng minh P P . P M PP . P P 3 2 2 1 2 2 4 B B D' D' D D O M O M P1 P1 P2 P2 P3 P3 P4 P4 C C P P P C Chỉ ra P P C ∽ P BP g g 2 4 2 P P .P P P C .P B . 2 4 2 1 2 4 2 1 2 2 P B P P 2 2 1
Giáo viên: Nguyễn Chí Thành P C P P Chỉ ra P CP ∽ P MB g g P C .P B P P .P M . 2 3 2 2 2 3 2 2 2 3 2 P M P B 2 2
Từ đó suy ra P P . P M PP . P P . 3 2 2 1 2 2 4
110) Kéo dài OP cắt đường tròn O tại P , P ( P thuộc cung nhỏ BD ). Nối P P cắt đường tròn 3 5 6 5 6 2
O tại P . Chứng minh M, P , P thẳng hàng. 7 5 7 P5 B D' P7 D O M P1 P2 P3 P4 C P6
Vì P P là đường kính O P P P P 1 . 6 7 5 7 5 6 P P P P Ta có: 3 2 2 7
P P . P M PP . P P P P . P P P P . P M P P . P P . 3 2 2 1 2 2 4 2 7 2 6 3 2 2 2 7 2 6 P P P M 2 6 2
Từ đó suy ra P P M ∽ P P P c g c P P M 0
P P P 90 P P MP 2 . 2 7 2 3 6 2 7 2 3 6 2 7 7 Từ
1 2 M , P , P thẳng hàng. 5 7 111) Chứng minh D B P là tam giác cân. 3 B D' D M O P1 P2 P3 P4 C O P PP Vì 3 1 4
OP BD OP là trung trực BD nên BP P D B P D cân tại P . 3 3 PP / /BD 3 3 3 3 1 4
112) Cho B,C và O cố định. Tìm vị trí cát tuyến MDD để diện tích P BC lớn nhất. 3 B D' D M O P1 P2 P3 P4 C
Giáo viên: Nguyễn Chí Thành Ta có: BPC CD B P BD 2. CD B
( tính chất góc trong – góc ngoài tam giác) 3 3
Mà B,C,O cố định nên góc CD B không đổi, suy ra BPC 2. CD B không đổi. 3 1 Mà S .PC.P B.sin BPC S
lớn nhất khi PC. P B lớn nhất. 3 P BC 3 3 3 3 2 P BC 3 3 2 PC P D D C 2 2 D C 4R Ta có: 3 3 PC.P B PC.P D mà 2 CD 2R P C. P B R . 3 3 3 3 2 4 3 3 4 4
Dấu bằng xảy ra khi CD là đường kính của O .
113) Tiếp tuyến của đường tròn O tại I cắt đường tròn đường kính MI tại M , M I OC M . 1 1 1 1 2
Chứng minh tứ giác MCM M là tứ giác nội tiếp, MM MC ; CM MM . 2 1 1 1 2 M1 B M2 I1 O I M C
Vì MI là đường kính nên 0 M M M 90
M CM MCM M là tứ giác nội tiếp. 1 2 1 2 2 1 + Chỉ ra 2 2
MM MI.MI MC MM MC . 1 1 1
+ Vì tứ giác MCM M nội tiếp đường tròn đường kính MM mà MM MC MM là đường trung 2 1 2 1 2 trực CM CM MM . 1 1 2
114) Gọi E là tâm đường tròn ngoại tiếp IMI , E là tâm đường tròn ngoại tiếp M D D , E là 1 1 2 2 3
trung điểm của M M . Chứng minh E , E , E thẳng hàng. 1 2 1 2 3 M1 E3 D' E2 M2 D V I1 O I M E1 C
Giáo viên: Nguyễn Chí Thành
+ Gọi MM CM V . Ta có: 2 2
MV .MM MM MC MI.MI M . D MD . 2 1 2 1 1
Từ đẳng thức MV.MM M . D MD D D
VM nội tiếp nên V E . 2 2 2
Từ đẳng thức MV .MM MI.MI IVM I là tứ giác nội tiếp nên V E . 1 2 1 2 1
Suy ra E , E cắt nhau tại hai điểm M , V E E là trung trực VM . 1 2 2 1 2 2
Vì E E / /CM và E E đi qua trung điểm VM nên E E đi qua trung điểm M M . 1 2 1 1 2 2 1 2 1 2
Vậy E , E , E thẳng hàng. 1 2 3
Giáo viên: Nguyễn Chí Thành




