Chuỗi Maclaurin Taylor môn Toán ứng dụng | Trường Đại học Sư phạm Thành phố Hồ Chí Minh

lOMoAR cPSD| 22014077 5/23/2022 8.8
8.8.Chuỗi Taylor- Chuỗi Maclaurin 1)
Cho hàm số 𝑓(𝑥) có đạo hàm với mọi cấp tại 𝑥 = 𝑐.
Khi đó ta có khai triển hàm 𝑓(𝑥)thành chuỗi Taylor tại lân cận (quanh) điểm 𝑥 = 𝑐 là f c'( ) f ' ( )c f k ( )c f k ( )c k f x( ) f c( ) x c 2! x c 2 ... k! x c k ... k 0 k! x c 1! 2)
Chuỗi Maclaurin là trường hợp đặc biệt của công thức Taylor của
hàmsố 𝑓(𝑥) với 𝑐 = 0 lOMoAR cPSD| 22014077 5/23/2022
Khai triển hàm f (x) thành chuỗi Malaurin là f '(0) f ''(0) f k (0) f k (0) f x( ) f (0) x x2 ... xk ... xk 1! 2! k ! k 0 k ! CHUỖI TAYLOR CHUỖI MACLAURIN lOMoAR cPSD| 22014077 5/23/2022 Ví dụ 1
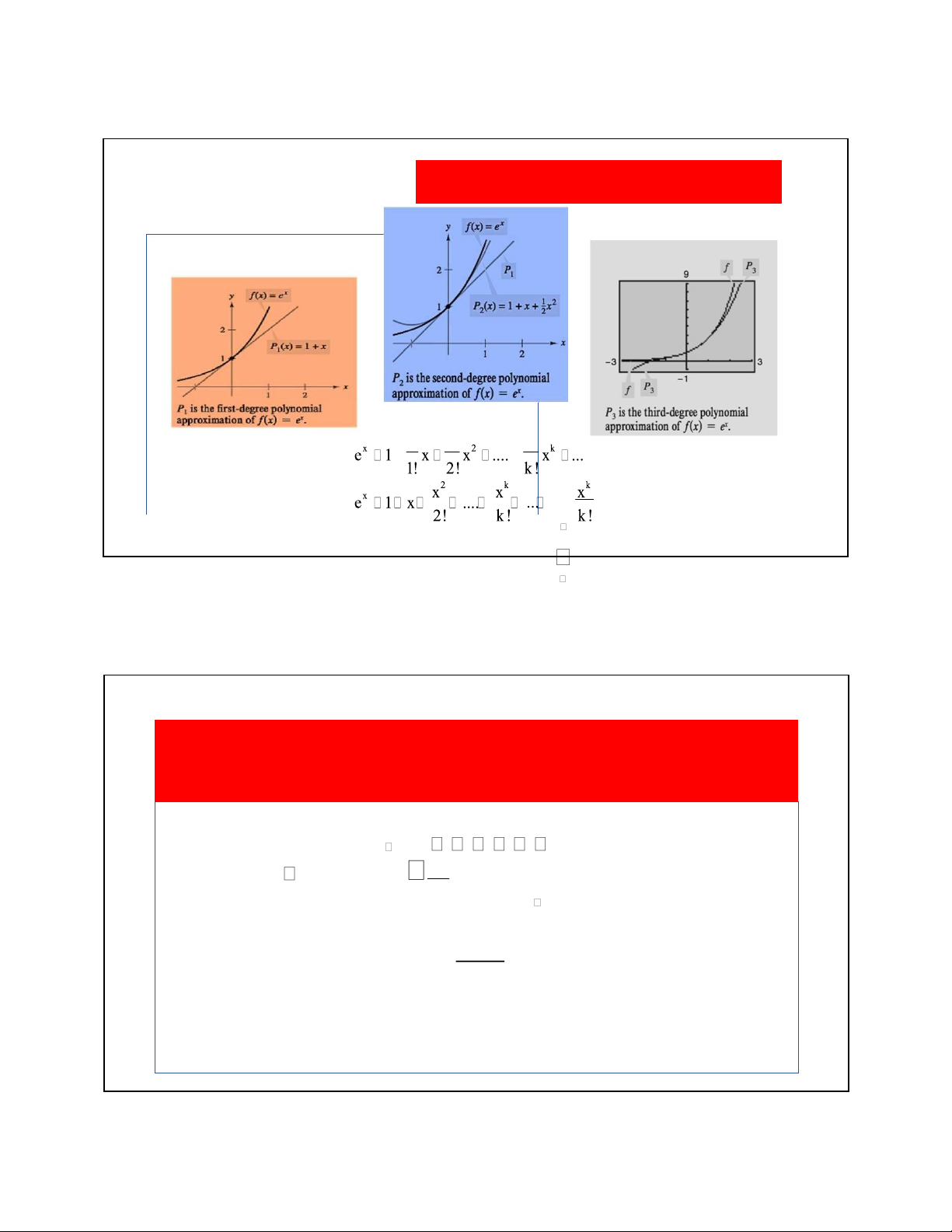
Dựa vào khai triển Maclaurin của hàm 𝑓 𝑥 = 𝑒 .
Tính tổng của các chuỗi số sau ∑. !
Giải. Ta có khai triển Maclaurin của hàm 𝑥 𝑒 = 𝑘! Tại x=1 ta có 𝑒 lOMoAR cPSD| 22014077 5/23/2022 ! Tại x=3 ta có ∑ 𝑒 Ví dụ 1
• Viết khai triển hàm số 𝑓 𝑥 = 𝑒 thành chuỗi Maclaurin
Giải.Ta có 𝑓 𝑥 = 𝑒
Đạo hàm cấp n của hàm f là 𝑓 𝑥 = 𝑒 với 𝑛 ≥ 1 Do vậy 𝑓
0 = 𝑒 = 1 , 𝑓 0 = 𝑒 =1
f '(0) f ''(0) f k (0) f k (0) Thay vào công
thức (2) f x( ) f (0) 1! x 2! x ta đượ 2 ... k! xk ... k 0 k ! xk c khai triển của
hàm 𝑓 𝑥 = 𝑒 thành chuỗi Maclaurin là 1 1 1 ex 1 x x2 .... xk ... 1! 2! k! 2 k k x x x ex 1 x 2! .... k! ... k 0 k! lOMoAR cPSD| 22014077 5/23/2022 Ví dụ 1 1 1 1 . .. k 1 Ví dụ 1 • Dựa vào khai triển x2 xk xk e 1 x .... ... 2! k! k 1 k!
• Tính gần đúng 𝑒 . ≅ 1 + 0.135 + . lOMoAR cPSD| 22014077 5/23/2022 Ví dụ 2
Tính tích phân ∫ 𝑑𝑥
Giải Ta có khai triển của hàm 𝑓 𝑥
= 𝑒 thành chuỗi Maclaurin là 𝑥 𝑥 𝑥𝑥 𝑒 = 1 + 𝑥 + 𝑘! Do vậy ∫ 𝑑𝑥 = ∫ + 1 + + ⋯ + + ⋯𝑑𝑥 ! ! 𝑥𝑥 = ln 𝑥 + 𝑥 +
Chúng ta có công thức sau trong bảng công thức tính tích phân lOMoAR cPSD| 22014077 5/23/2022 Ví dụ 4 lOMoAR cPSD| 22014077 5/23/2022
a) Viết khai triển hàm số 𝑓 𝑥 = 𝑥𝑒 thành chuỗi Maclaurin Giải 2 3 k k u u u u Ta có khai triển eu 1 u ... ... k! 2! 3! k! k 0
Thay 𝑢 = 3𝑥, ta được 2 3 k k 3x 3x 3x 3x 3x e 1 3x 2! 3! ... k! ... k 0 k! 3x 32 2x 33 3x 3k kx 3k kx e 1 3x ... ... k! 2! 3! k! k 0 Ví dụ 3: Viết khai triển hàm
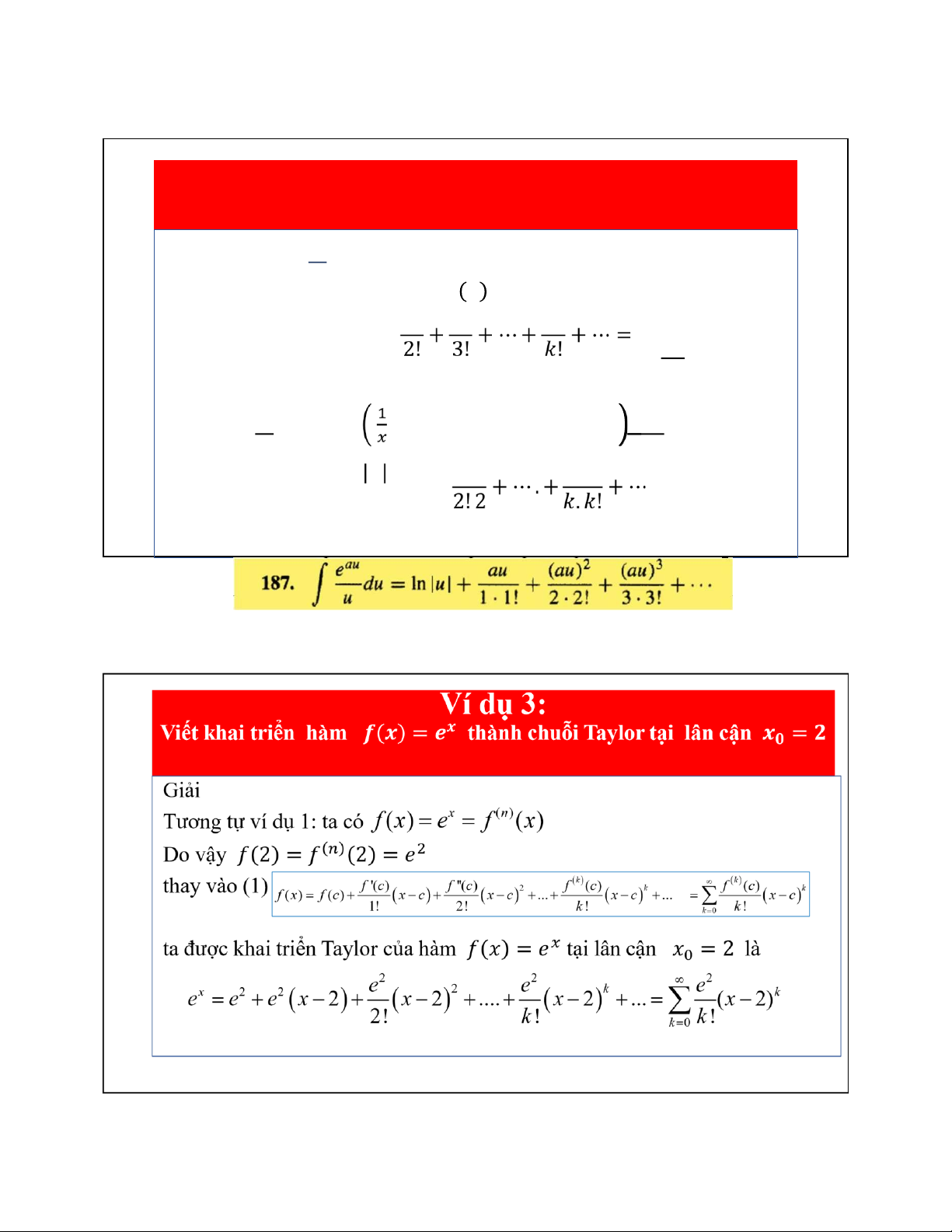
𝒇 𝒙 = 𝒆𝒙 thành chuỗi Taylor tại lân cận 𝒙𝟎 = 𝟐 lOMoAR cPSD| 22014077 5/23/2022 Cách 2 2 3 k k u u u u u Giải.Ta có khai triển e 1 u ... ... 2! 3! k! k 0 k! Mà 𝑓 𝑥 = 𝑒 = e = 𝑒 . 𝑒 2 3 k k (x 2)
(x 2) (x 2) (x 2) Thay 𝑢 = 𝑥 − 2, ta được ex 2 1 x 2 ... ... 2! 3! k! k 0 k!
Khai triển hàm số 𝑓 𝑥 = 𝑒
thành chuỗi chuỗi Taylor tại lân cận 𝒙𝟎 = 𝟐 2 x 2 2 (x 2)2 (x 2)3 (x 2)k 2 (x 2)k e2 k e e e 1 x 2 2! 3! ... k! ... e k 0 k! k 0 k!(x 2) lOMoAR cPSD| 22014077 5/23/2022 Ví dụ 4
a) Viết khai triển hàm số 𝑓 𝑥 = 𝑥𝑒 thành chuỗi Maclaurin Giải
Ta có khai triển hàm 𝑓 𝑥 = 𝑥𝑒 thành chuỗi Maclaurin là
32 2x 33 3x 3k kx 3k kx xe3x x 1 3x 2! 3! ... k! ... x k 0 k! k 32 3x 33 4x 3k kx ... k 1 3 x xe3x x 3x2 1 ... 2! 3! k! k! k 0 Ví dụ 4
Viết khai triển hàm số 𝑓 𝑥 = 𝑥𝑒
thành chuỗi Maclaurin. Dựa vào khai
triển thu được tính các đạo hàm 𝑓 0 , 𝑓
0 , 𝑓( )(0), 𝑓( )(0), 𝑓(0). Giải
Ta có khai triển hàm 𝑓 𝑥 = 𝑥𝑒 thành chuỗi Maclaurin là 3x 2 32 3x 33 4x 3k kx 1 3k kx 1 xe x 3x ... ... 2! 3! k! k 0 k! (a)
Đồng nhất hệ số với 𝑓 𝑥 𝑥(b) ! lOMoAR cPSD| 22014077 5/23/2022 Ví dụ 4 Nhắc lại
• 𝑓 𝑥 = 𝑎𝑥 + 𝑏𝑥 + 𝑐𝑥 + 𝑑 (1)
• 𝑓 𝑥 = 4𝑥 − 7𝑥 + 5 (2)
Đồng nhất hệ số giữa 1 và 2, ta được 𝑥a = 4 𝑥b = 0 𝑥c = - 7 𝑥d = 5 lOMoAR cPSD| 22014077 5/23/2022
Ví dụ 4: Viết khai triển hàm số 𝑓 𝑥 = 𝑥𝑒 thành chuỗi Maclaurin. Dựa vào khai triển thu được tính
các đạo hàm 𝑓 0 , 𝑓 0 , 𝑓( )(0), 𝑓( )(0), 𝑓 (0) lOMoAR cPSD| 22014077 5/23/2022 Ví dụ 5
• Khai triển hàm 𝑓 𝑥 = 𝑥𝑠𝑖𝑛 3𝑥
𝑡ℎà𝑛ℎ 𝑐ℎ𝑢ỗ𝑖
𝑀𝑎𝑐𝑙𝑎𝑢𝑟𝑖𝑛
• Ta có khai triển ( 1) ku2 1k sinu k 0 2k 1 !
• Thay u = 3𝑥 , ta có khai triển lOMoAR cPSD| 22014077 5/23/2022 Ví dụ 5 ( 1) 3 k 2 1 4 3k .x k
• Khai triển hàm 𝑓 𝑥 = 𝑥𝑠𝑖𝑛 3𝑥
𝑡ℎà𝑛ℎ 𝑐ℎ𝑢ỗ𝑖
𝑀𝑎𝑐𝑙𝑎𝑢𝑟𝑖𝑛 • Ta có khai triển sinu ( 1) 2kk u1 !2 1k k 0 !
• Thay u = 3𝑥 , ta có khai triển Maclaurin 2 1k k 2 k 2 1 4 2k k ( 1) 3x ( 1) 3 .x sin3x2 2k 1 ! k 0 2k 1 ! k 0 k 2 1 4 3k k ( 1) 3 .x xsin3x2 2k 1 ! k 0 lOMoAR cPSD| 22014077 5/23/2022 Ví dụ 6
• Viết khai triển hàm số 𝑓 𝑥 = ln (4 + 𝑥)
thành chuỗi Maclaurin Giải u2 u3 ( 1) k 1uk ( 1) k 1uk Ta có khai triển ln(1 u) u ... ... k 1 k 2 3 k Ta có ln 4 + 𝑥 =ln(1+3+x) Hoặc ln 4 + 𝑥 = ln 4 1 + = ln 4 + ln 1 + lOMoAR cPSD| 22014077 5/23/2022 Ví dụ 6
• Viết khai triển hàm số 𝑓 𝑥 = ln (4 + 𝑥)
thành chuỗi Maclaurin Giải u2 u3 ( 1) k 1uk ( 1) k 1uk Ta có khai triển ln(1 u) u 2 3 ... k ... k 1 k Ta có ln 4 + 𝑥 = ln 4 1 + = ln 4 + ln (1 + ) 3 Thay 𝑢 =, ta được ... ln(1 x) x 1 x 1 x ... ( 1) k 1 x k k 1 ( 1) kk 1 4x k lOMoAR cPSD| 22014077 5/23/2022 4 2 4 3 4 k 4 x 1 1 ( 1) k 1 ( 1) k 1 ln(1 ) 2 x2 3.43 x3 ... .4k xk ... k 1 k.4k xk 4 2.4 k
Sử dụng chuỗi lũy thừa của một số hàm cơ bản
• Chọn 𝑢 = 𝑎 𝑥 − 𝑐 ℎ𝑜ặ𝑐 𝑢 = • Chuỗi Maclaurin c = 0 lOMoAR cPSD| 22014077 5/23/2022 Ví dụ 6
• Viết khai triển hàm số 𝑓 𝑥 = ln (4 + 𝑥)
thành chuỗi Maclaurin. Dựa vào
khai triển thu được hãy tính tổng của các chuỗi số sau k 1 k ( 1) 1 3 S1 k , S2 k , S3 k , k.4 k.4 k.4 Giải k 1 k 1 k 1
Ta có khai triển hàm số 𝑓 𝑥 = ln (4 + 𝑥) thành chuỗi Maclaurin là k 1 ( 1) lOMoAR cPSD| 22014077 5/23/2022 ln(4 x) ln4 k xk k.4 k 1 k 1 k 1 ( 1) k ( 1) Với x=1 ta có ln(4 1)ln4 k.4k 1 S1 k 1 k.4k ln5 ln4 k 1 lOMoAR cPSD| 22014077 5/23/2022 Ví dụ 6
• Viết khai triển hàm số 𝑓 𝑥 = ln (4 + 𝑥)
thành chuỗi Maclaurin. Dựa vào khai
triển thu được hãy tính tổng của các chuỗi số sau k 1 k ( 1) 1 3 S1 k , S2 k , S3 k , k.4 k.4 k.4 Giải k 1 k 1 k 1
Ta có khai triển hàm số 𝑓 𝑥 = ln (4 + 𝑥) thành chuỗi Maclaurin là k 1 ( 1) k ln(4 x) ln4 k x k.4 k 1 k 1 ( 1) ( 1) Với x=-1 ta có ln(4 1)ln4 k.4k ( 1) k ln4 k 1 k.4k k 1 1 4 S2 k ln4 ln3 ln k 1 k.4 3