Chương 1. Bài 6: Hypebol | Bài giảng PowerPoint chuyên đề Toán 10 | Kết nối tri thức với cuộc sống

CHUYÊNC H ĐỀ Ư 2 Ơ . N P G HƯ I ƠNG PHÁP QUI
NẠP TOÁN HỌC. NHỊ THỨC NEWTON
Chứng minh rằng với mọi số tự nhiên
Chứng minh rằng với mọi số tự nhiên
n  1 Chứng minh rằng với mọi số tự nhiên , ta có n  1 , ta có n  1 , ta có CHUYÊN C Đ H Ề Ư 2. Ơ P N H G Ư Ơ I NG PHÁP QUI NẠP
TOÁN HỌC. NHỊ THỨC NEWTON TOÁN ĐẠI SỐ ➉ 1 1 2
BÀI TẬP CUỐI CHUYÊN ĐỀ 2 2 4 5
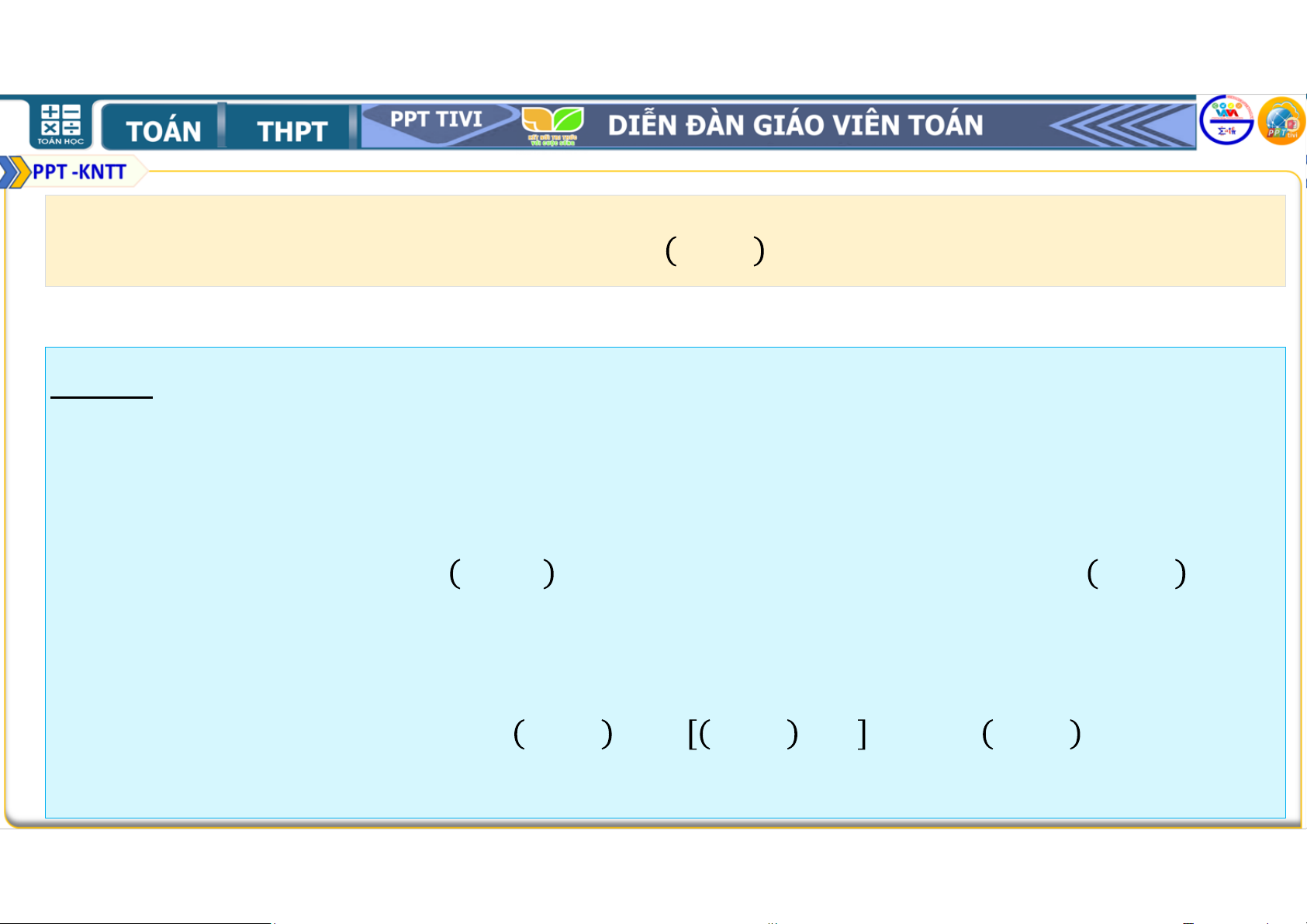
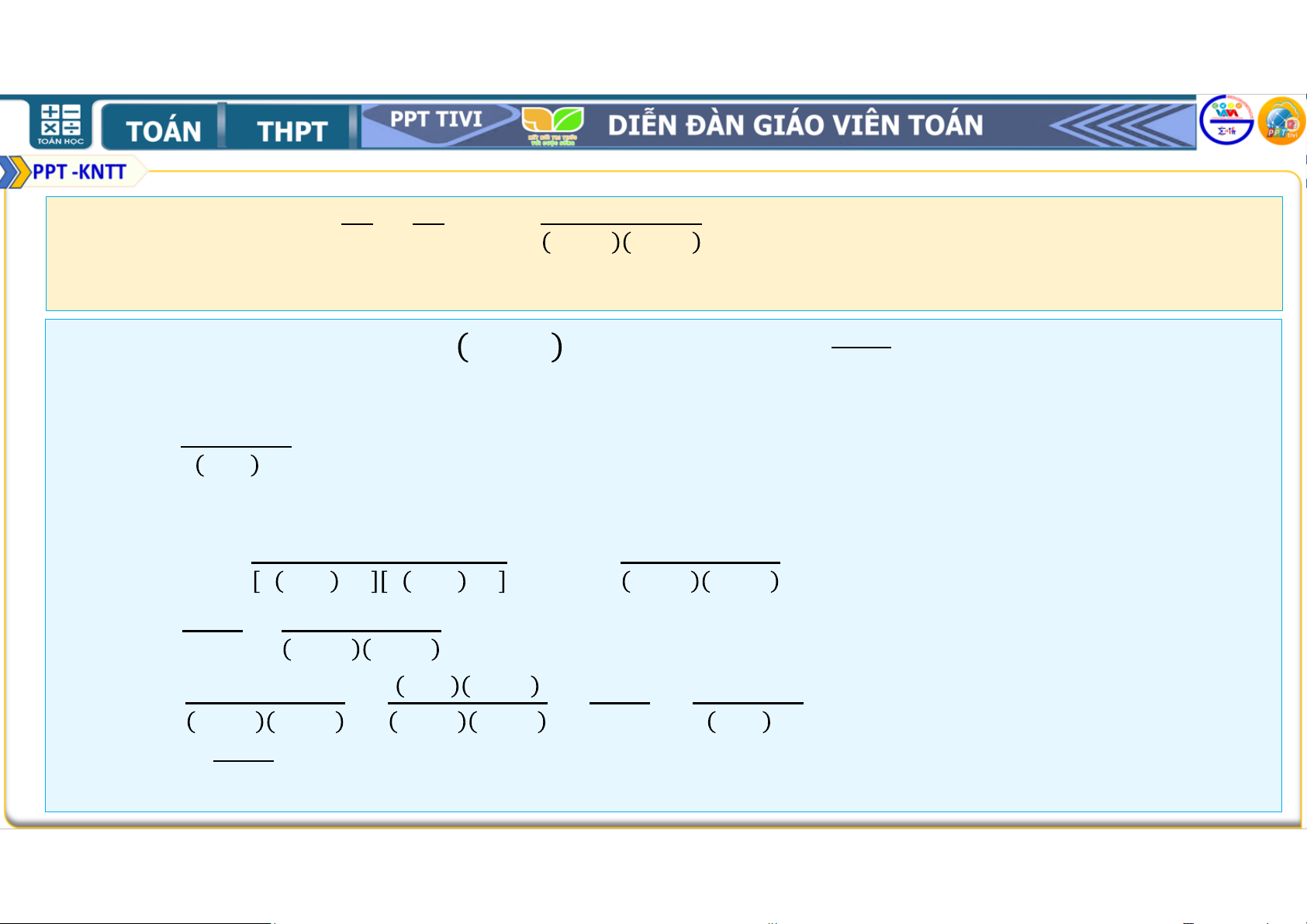
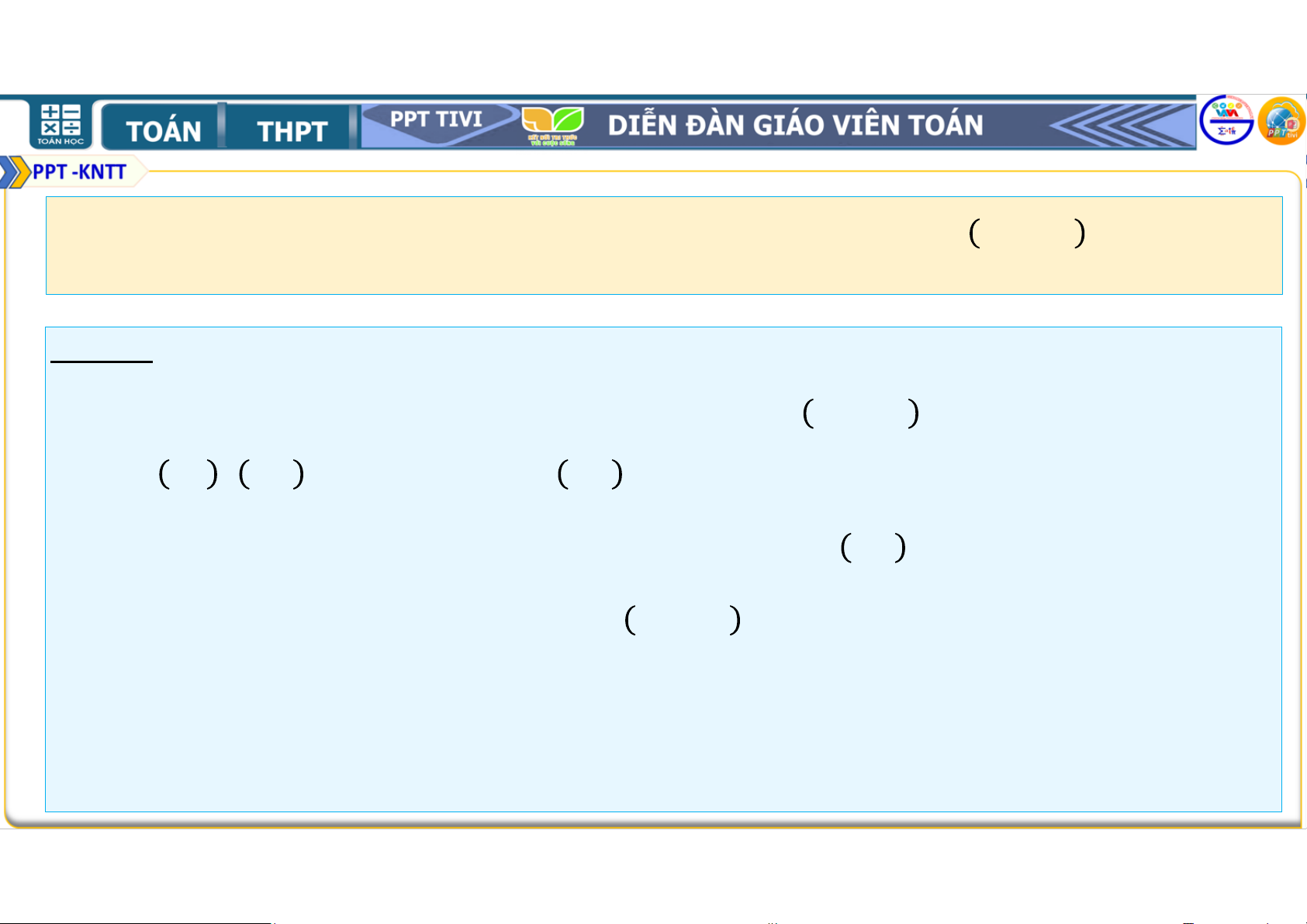
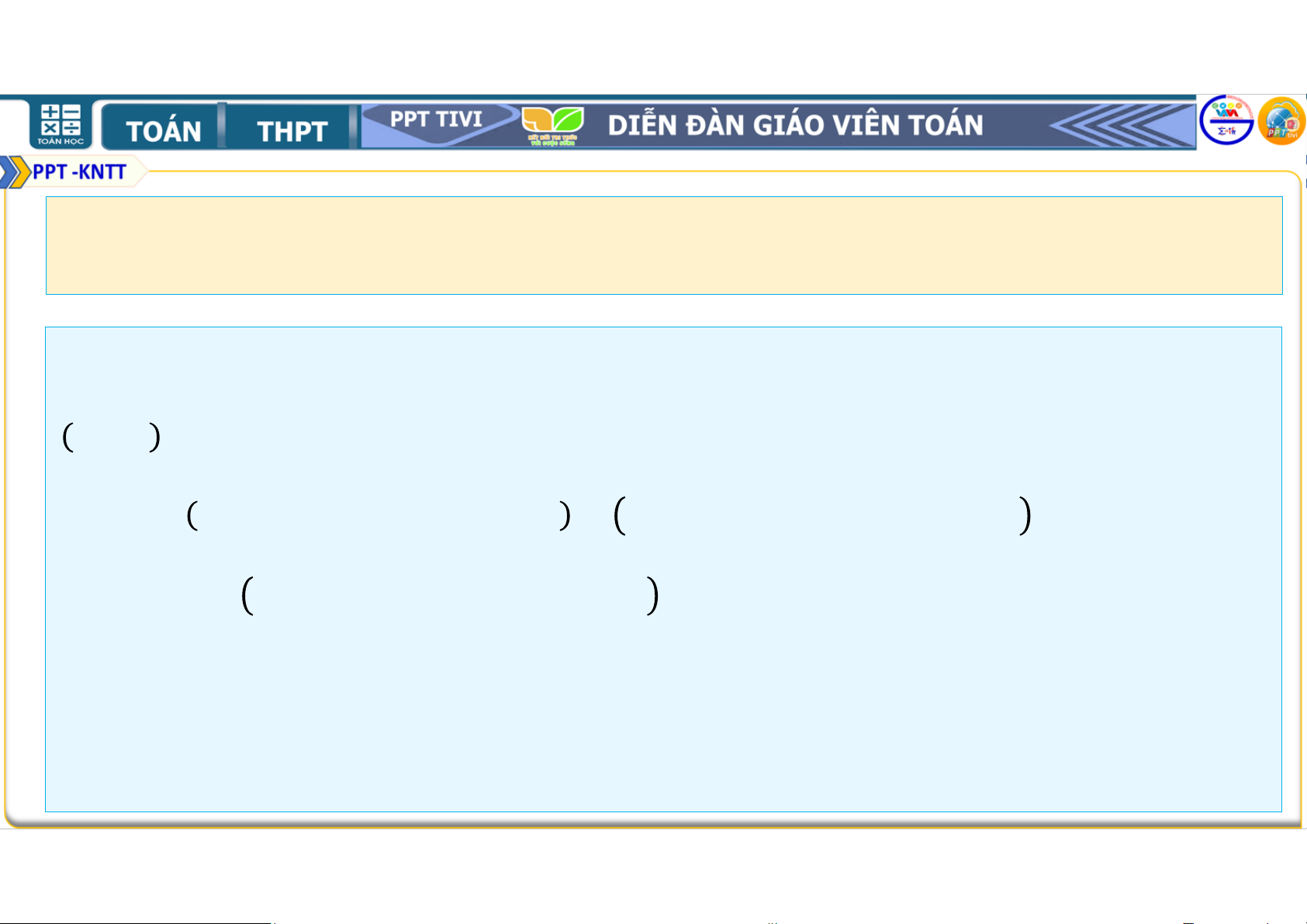
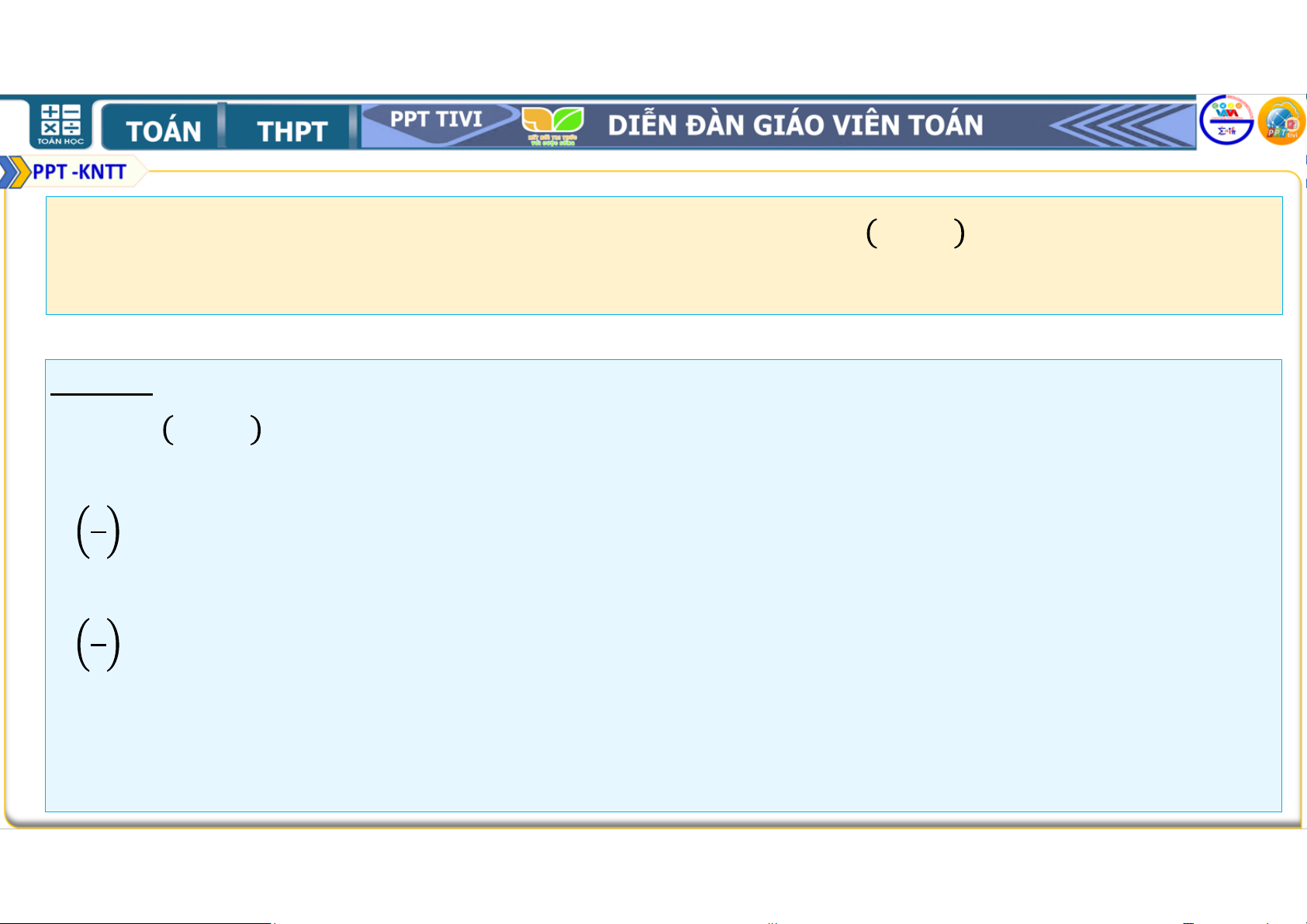
Bài 2.19. Chứng minh rằng với mọi số tự nhiên ≥ 1, ta có
2. 2 + 3. 2 + 4. 2 +. . . + + 1 . 2 = . 2 . (1) Lời giải:
• Ta chứng minh bằng quy nạp theo . • Với
= 1 ta có (1) 2. 2 = 4 = 1. 2
là mệnh đề đúng. Như vậy (1) đúng với = 1.
• Giả sử (1) đúng với =
≥ , tức là ta có 2.2 + 3.2 + 4.2 +. . . + + 1 .2 = .2 .
• Ta sẽ chứng minh rằng (1) cũng đúng với = + 1, nghĩa là ta sẽ chứng minh
2.2 + 3.2 + 4.2 +. . . + + 1 .2 + + 1 + 1 .2 = + 1 .2
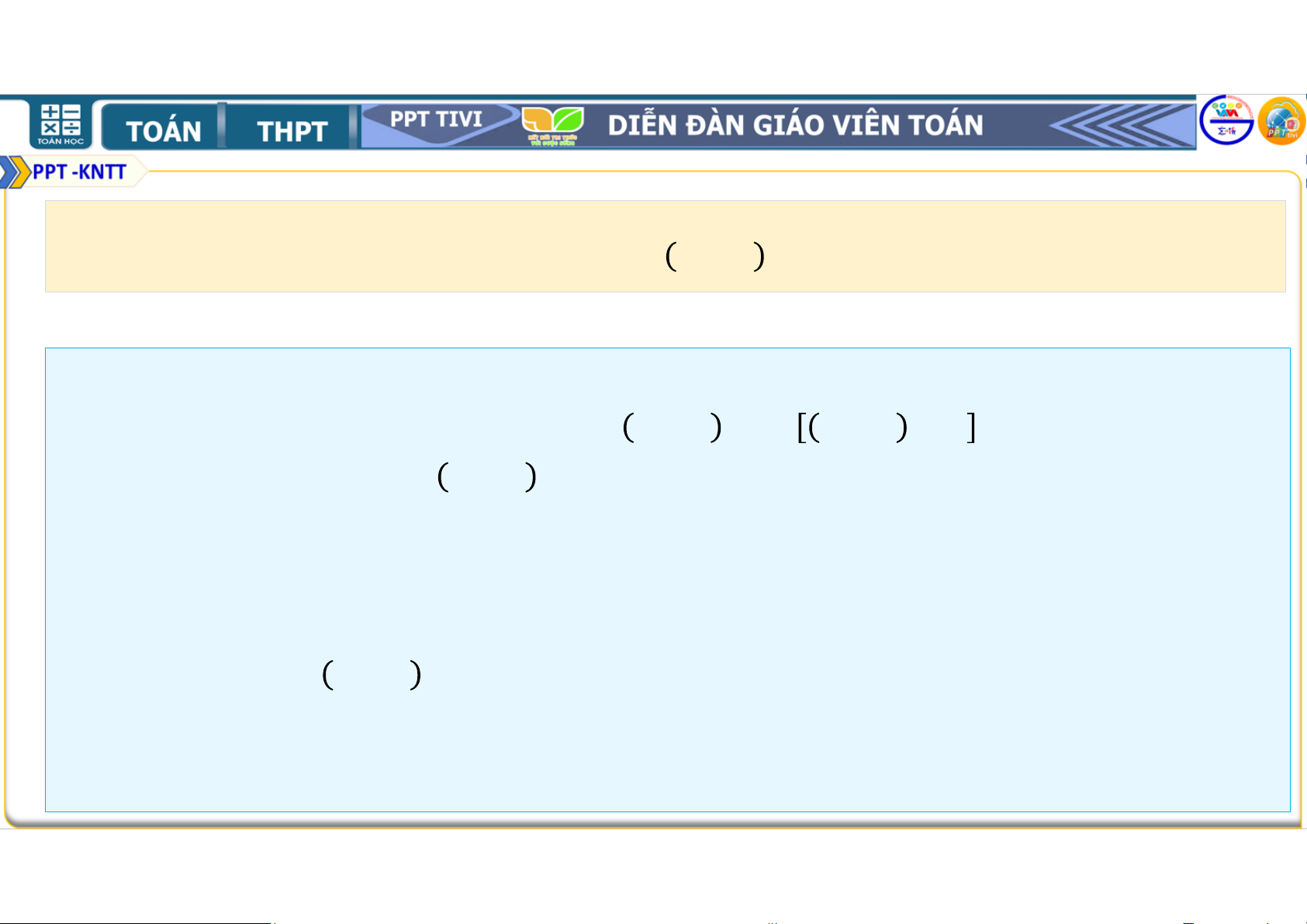
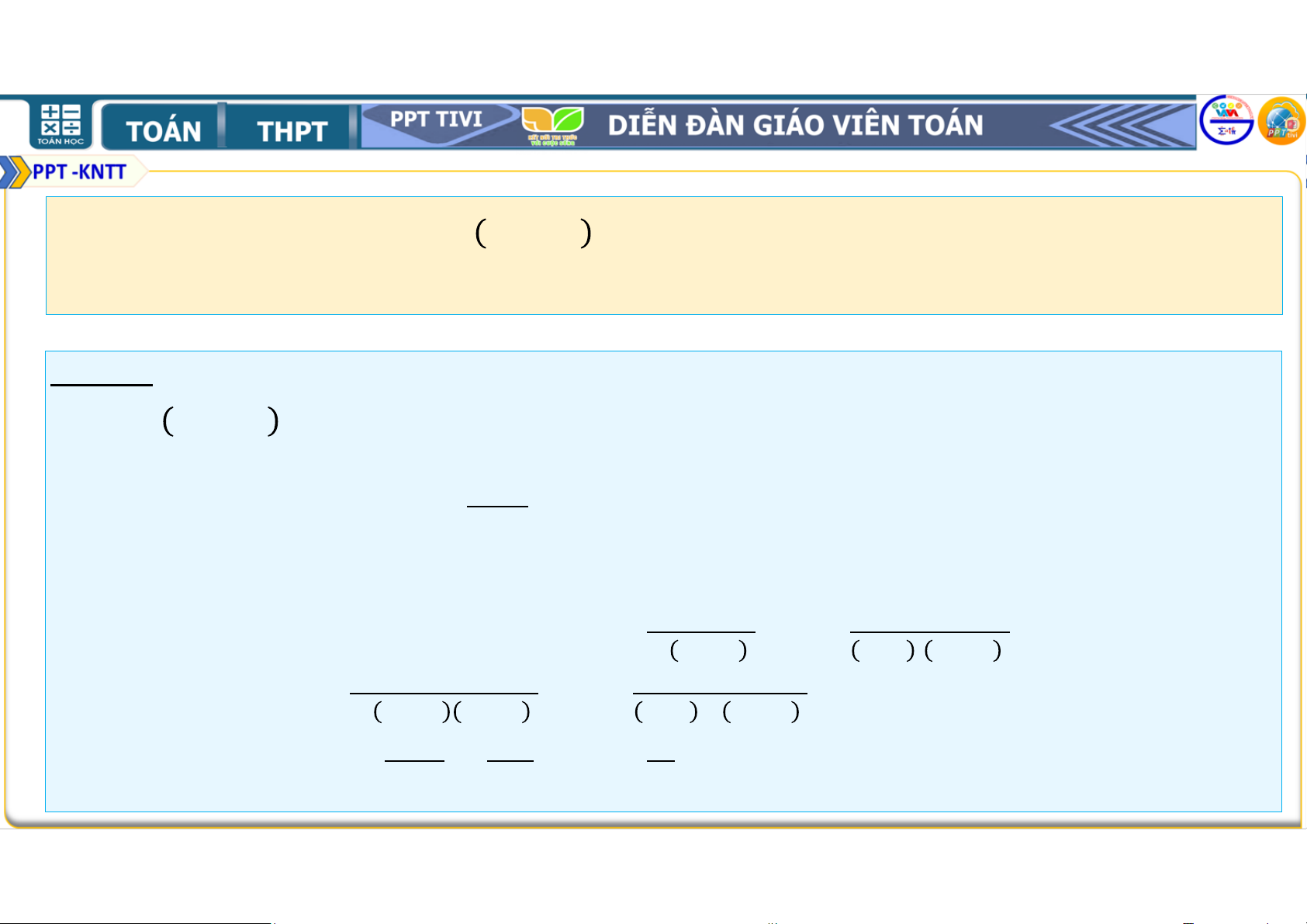
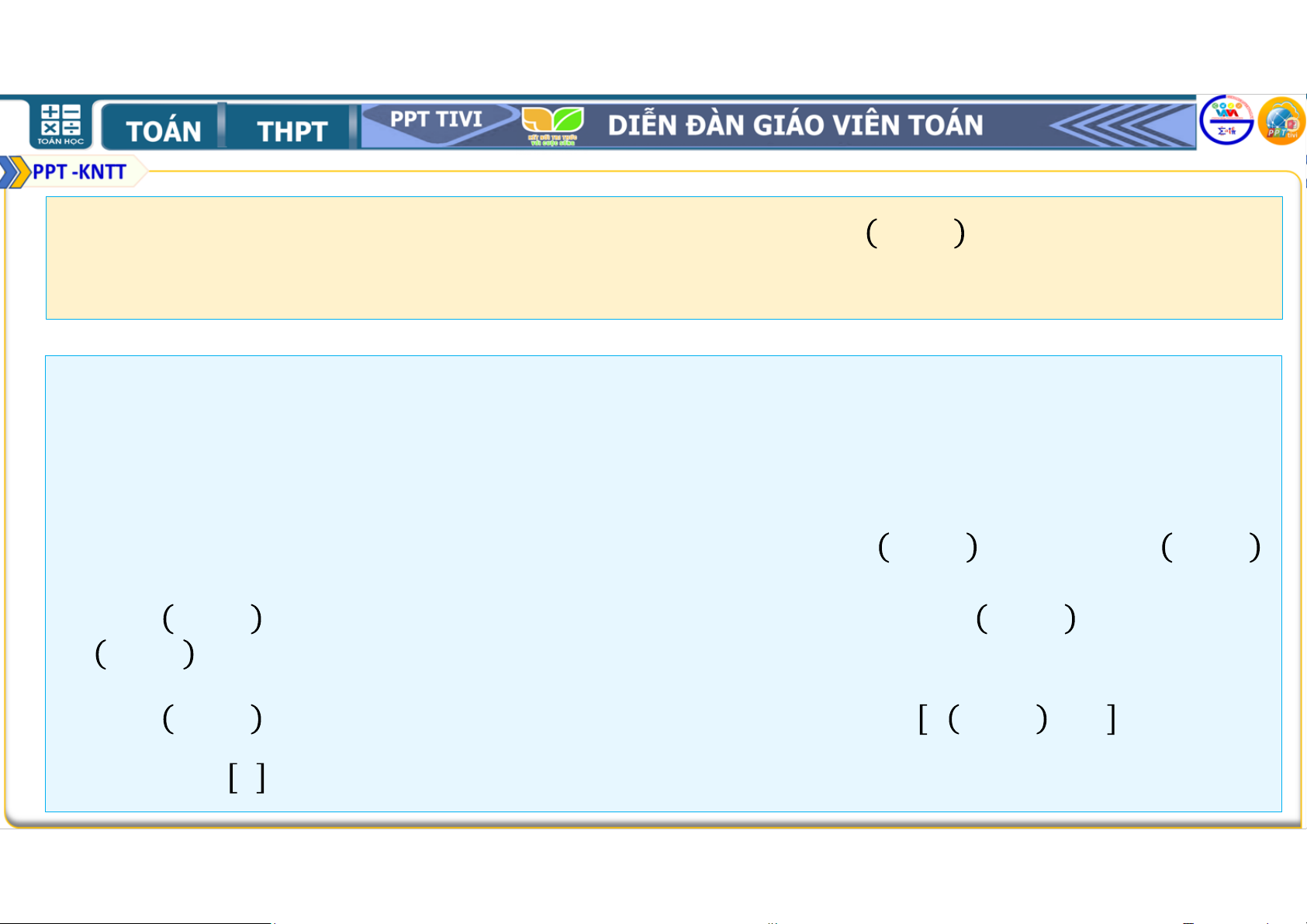
Bài 2.19. Chứng minh rằng với mọi số tự nhiên ≥ 1, ta có
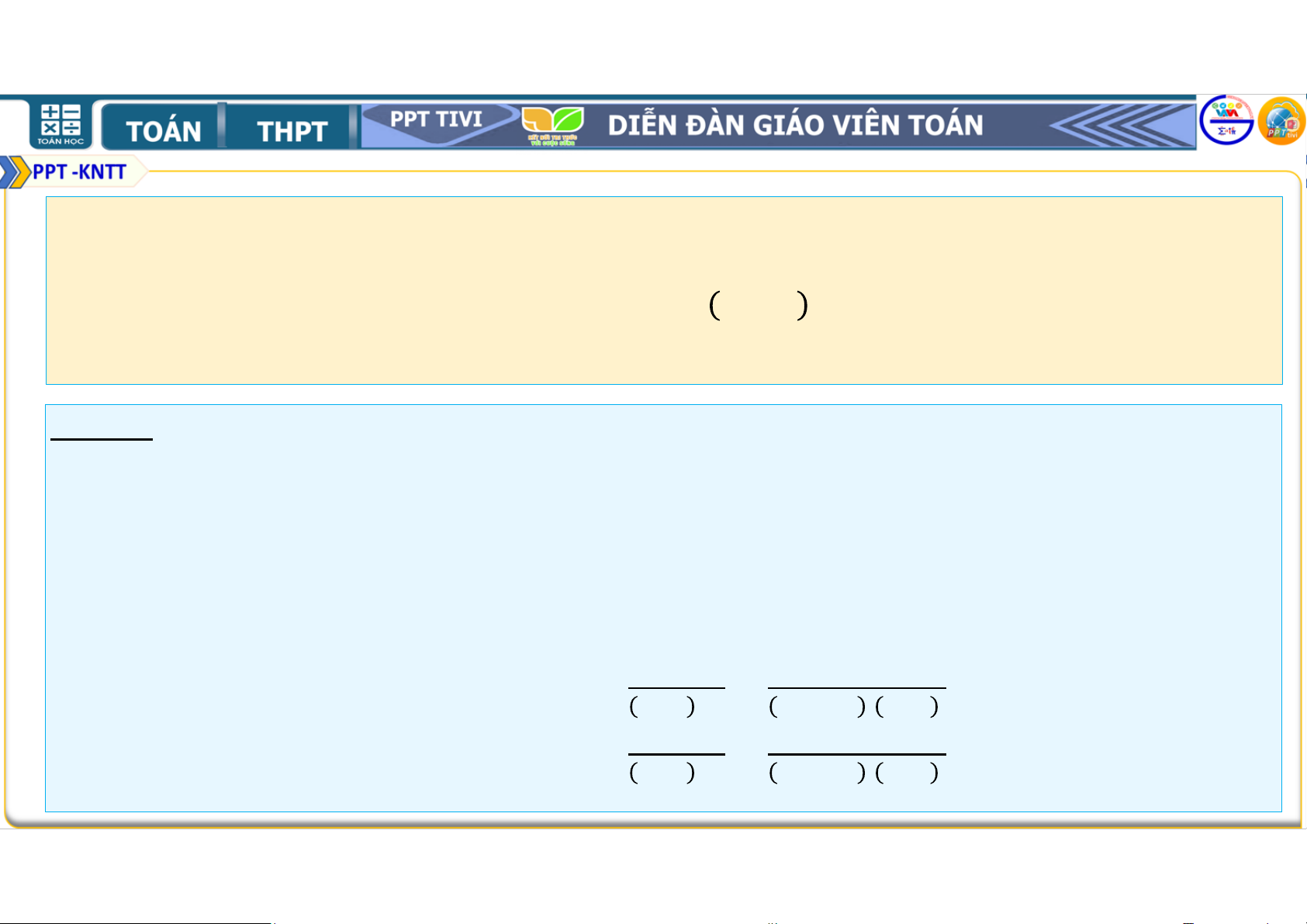
2. 2 + 3. 2 + 4. 2 +. . . + + 1 . 2 = . 2 . (1) • Thật vậy, ta có
2.2 + 3.2 + 4.2 +. . . + + 1 .2 + + 1 + 1 .2 = .2 + + 2 .2 = .2 + .2 +2.2 = 2 .2 +2.2 = .2 +2 = + 1 .2
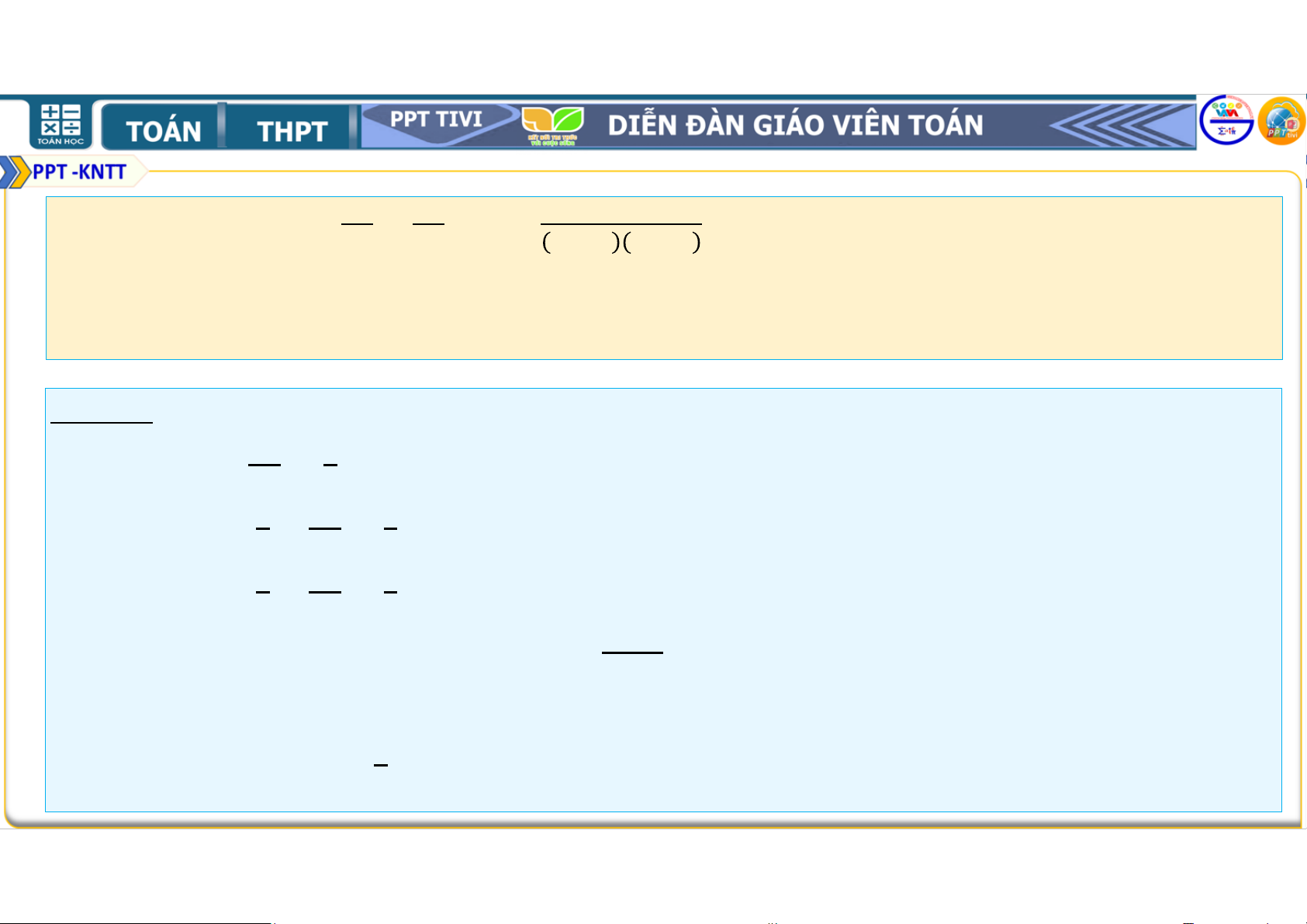
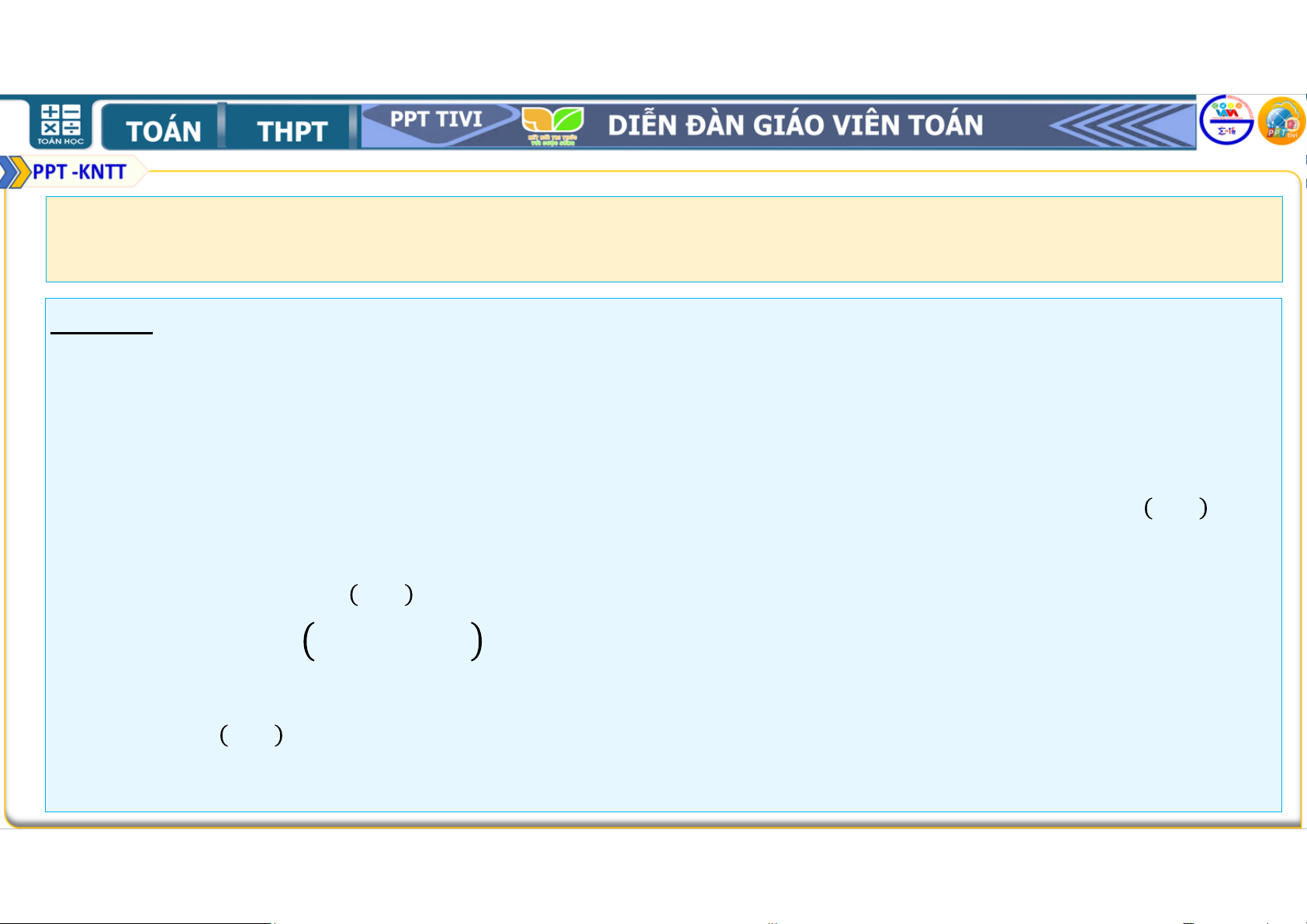
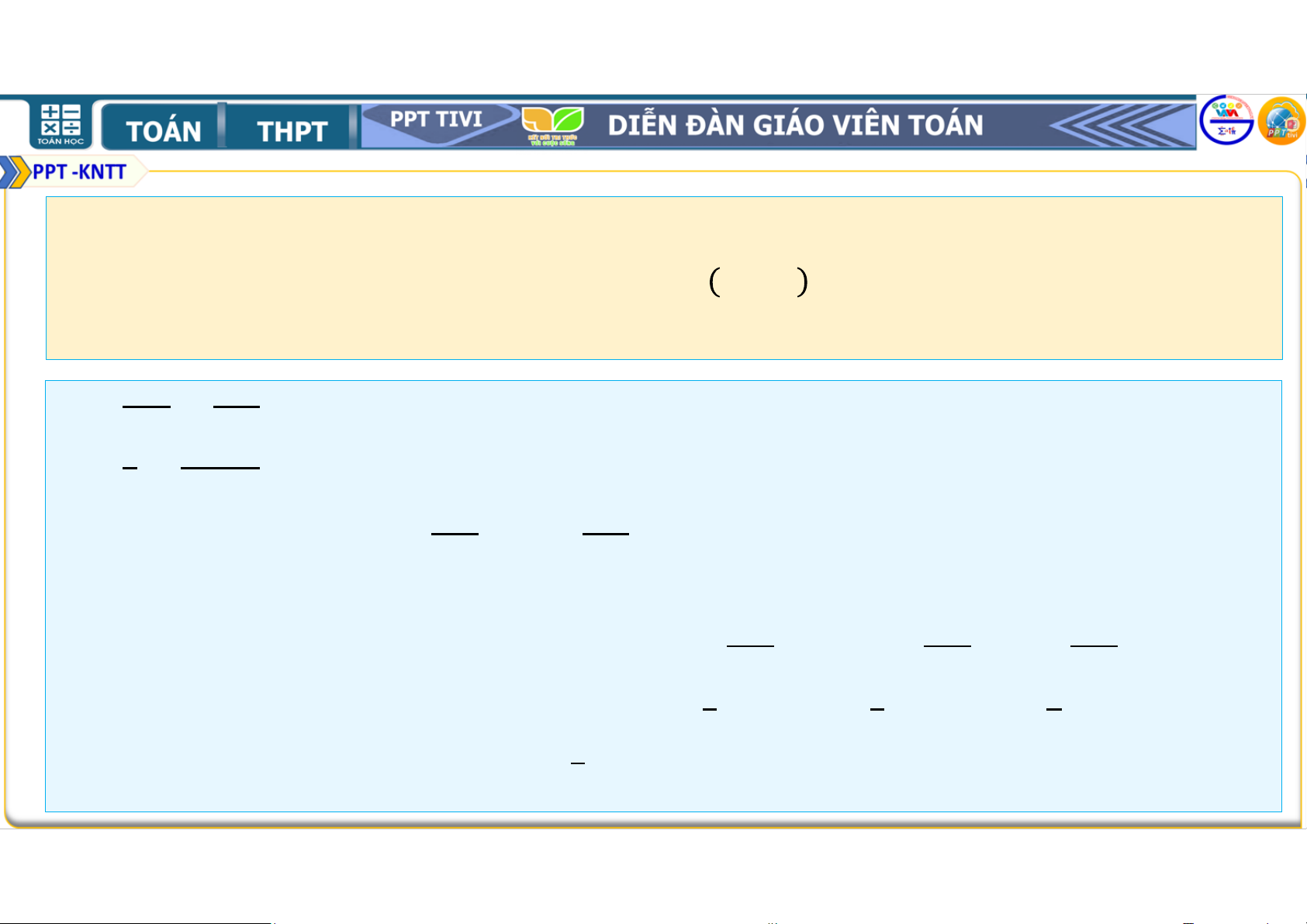
Vậy (1) đúng với mọi số tự nhiên ≥ 1. Bài 2.20. Đặt = + +. . . + . . . a) Tính , , .
b) Dự đoán công thức tính tổng
và chứng minh nó bằng quy nạp. Lời giải: a) Ta có = = . . = + = . . = + = . .
b) Từ kết quả câu a) ta dự đoán = (1)
• Ta chứng minh (1) bằng quy nạp theo , với ≥ . • Với = 1 ta có
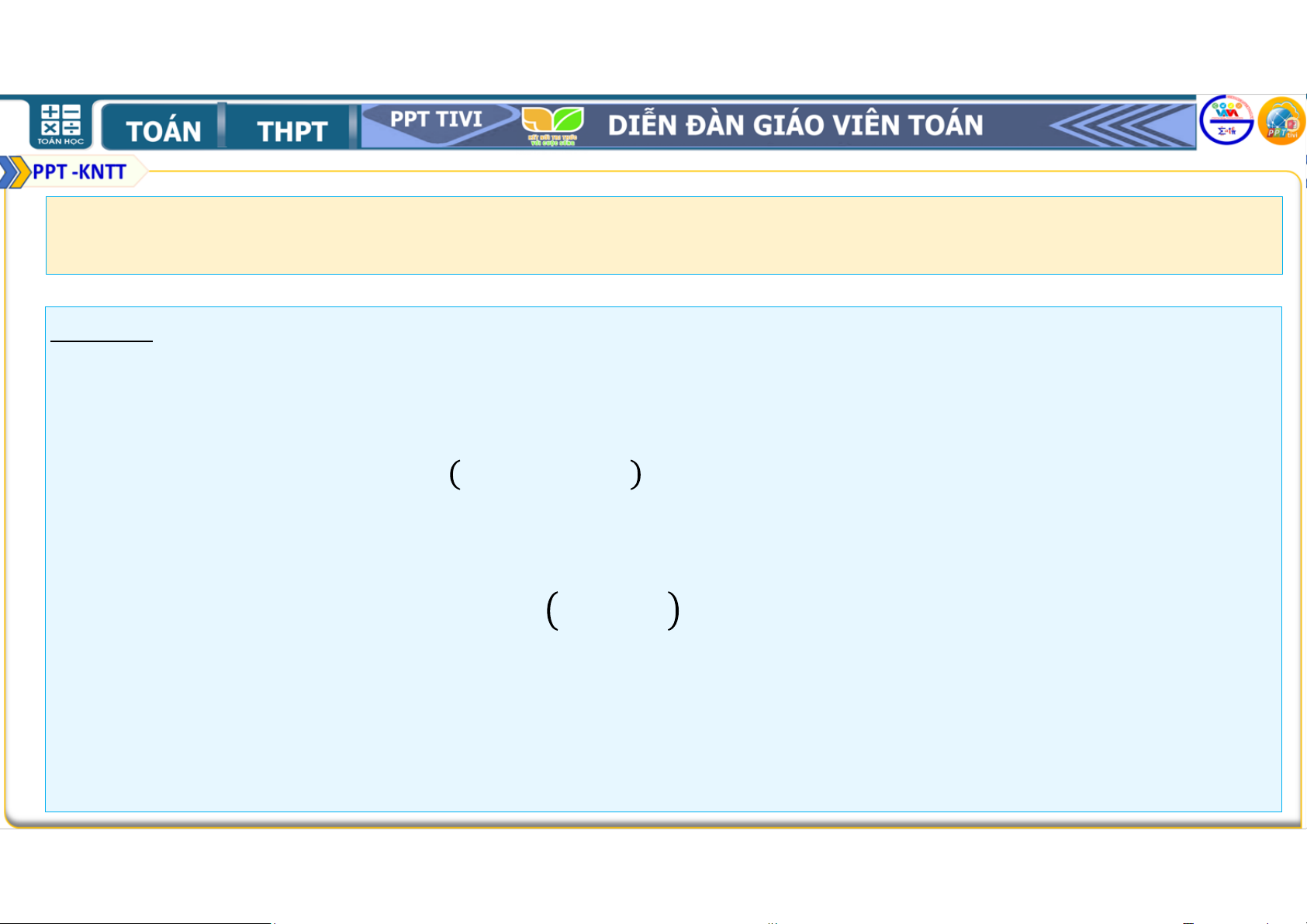
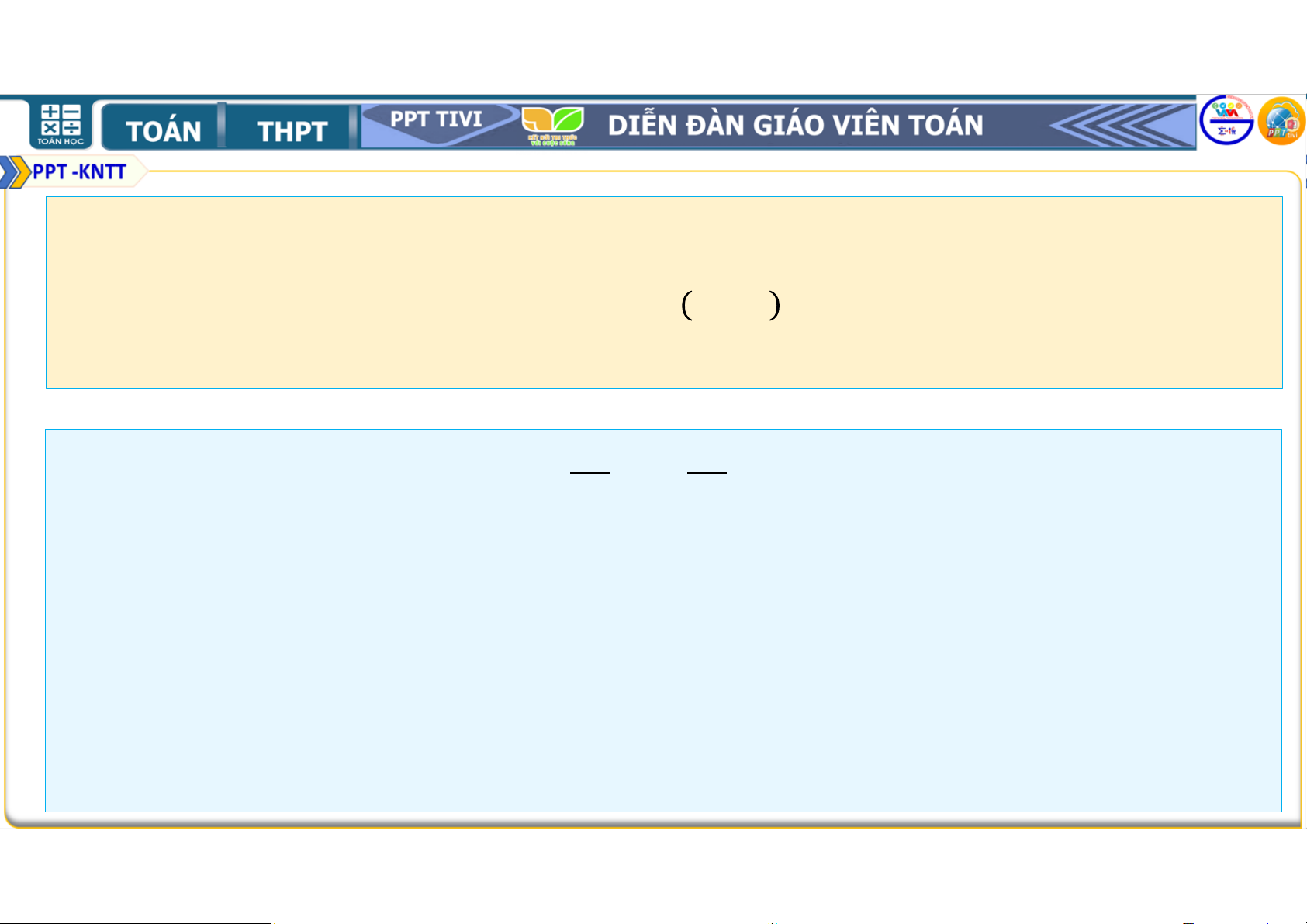
= . Như vậy (1) đúng với = 1. Bài 2.20. Đặt = + +. . . + . . .
b) Dự đoán công thức tính tổng
và chứng minh nó bằng quy nạp.
• Giả sử (1) đúng với n = k ≥ , tức là ta có = .
• Ta sẽ chứng minh rằng (1) cũng đúng với = + 1, nghĩa là ta sẽ chứng minh = . • Thật vậy, ta có • = + = + = + = = = = • Vậy = , với mọi ≥ 1.
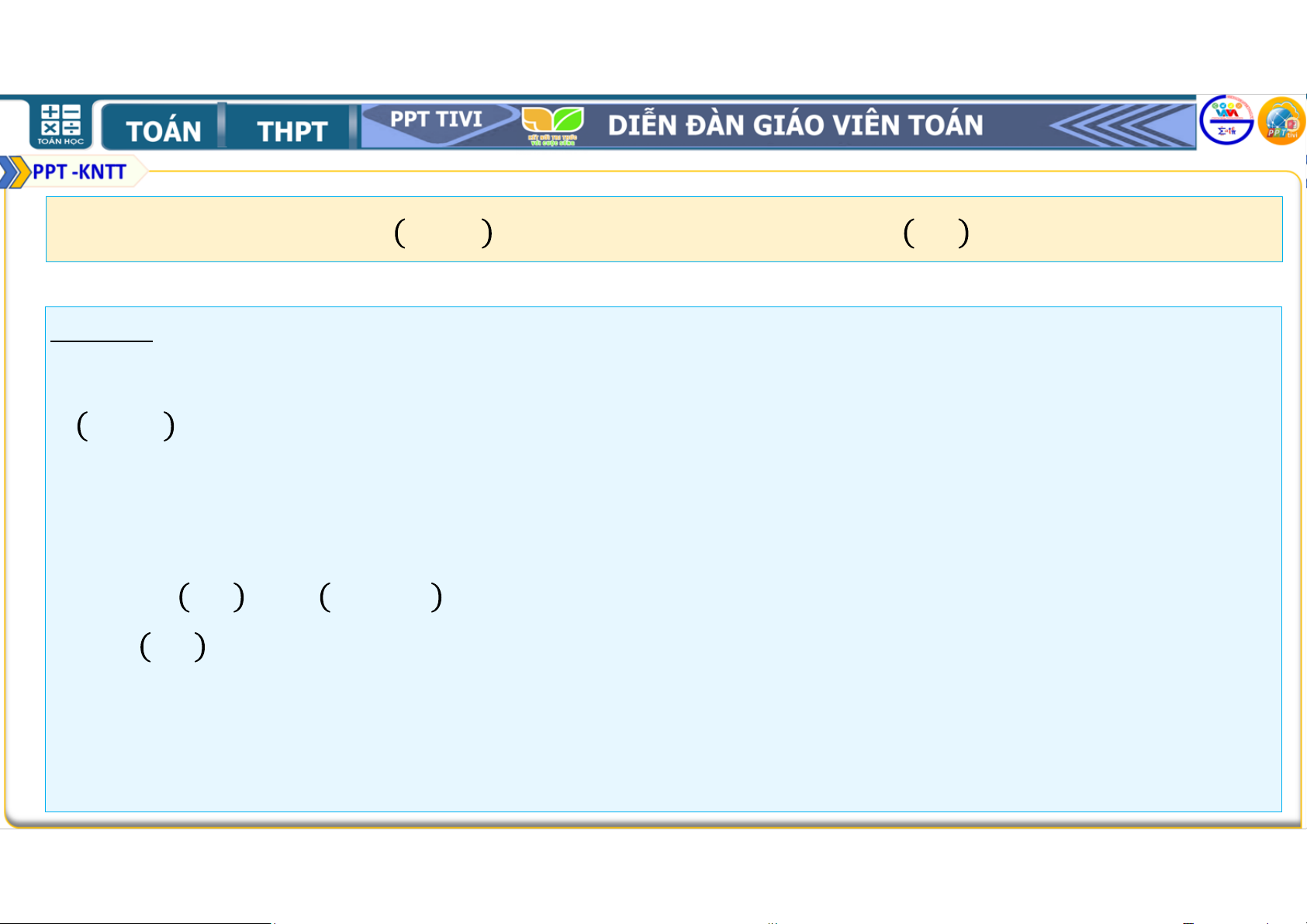
Bài 2.21. Chứng minh rằng với mọi số tự nhiên , ta có 10 + 1 chia hết cho 11. (1) Lời giải:
• Ta chứng minh (1) bằng quy nạp theo . • Với = 0 ta có 10 .
+ 1 = 11 chia hết cho 11. Vậy (1) đúng với = 0.
• Giả sử (1) đúng với = , (ĐK?) tức là 10 + 1 chia hết cho 11.
• Ta cần chứng minh (1) đúng với = + 1, nghĩa là ta sẽ chứng minh 10 + 1 chia hết cho 11. • Thật vậy, ta có 10 + 1 = 10 + 1 = 10 . 10 + 1 = 100.10 + 100 − 99 = 100 10 + 1 − 99
• Rõ ràng −99 chia hết cho 11 và 10
+ 1 chia hết cho 11 theo giả thiết quy nạp. • Vì thế 10 + 1 chia hết cho 11.
• Vậy (1) đúng với mọi số tự nhiên .
Bài 2.22. Chứng minh rằng với mọi số tự nhiên ≥ 2, ta có 5 ≥ 3 + 4 . (1) Lời giải:
• Ta chứng minh bất đẳng thức (1) bằng quy nạp theo , với ≥ 2.
• Với = 2 ta có 5 = 3 + 4 . Vậy (1) đúng với = 2.
• Giả sử (1) đúng với =
≥ 2, ∈ ℕ , tức là ta có 5 ≥ 3 + 4 .
• Ta cần chứng minh (1) đúng với = + 1, tức là chứng minh 5 ≥ 3 + 4 = 3. 3 + 4. 4 . • Thật vậy, ta có 5
= 5. 5 ≥ 5. 3 + 4 = 5. 3 + 5. 4 ≥ 3. 3 + 4. 4
• Vậy (1) đúng với mọi số tự nhiên ≥ 2.
Bài 2.23. a) Khai triển 1 + $ . b) So sánh 1,1 và 2. Lời giải:
a) Theo công thức nhị thức Newton, ta có • 1 + $
= % + % $ + % $ + % $ + %& $& + % $ + %' $' + % $ + %( $( + %) $) + % $
= 1 + 10$ + 45$ + 120$ + 210$& + 252$ + 210$' + 120$ + 45$( + 10$) + $ b) Ta có 1,1 = 1 + 0,1
= ∑ , % . 0, 1 > % + % . 0, 1 = 2 • Vậy 1,1 > 2.
Bài 2.24. Tìm hệ số của $) trong khai triển thành đa thức của 2$ − 3 .
Lời giải: bài này thầy/cô nên tìm số hạng TQ cho HS yếu dễ theo dõi
• Số hạng chứa $ (ĐK của k) trong khai triển của 2$ − 3 là % 2$ −3 hay % 2 −3 $
• Số hạng chứa $) ứng với = 9, tức là số hạng % 2) −3 $) hay 253440$).
• Vậy hệ số của $) trong khai triển của 2$ − 3 là 253440.
Bài 2.25. Khai triển đa thức 1 + 2$
thành dạng - + - $ + - $ +. . . +- $ . Tìm hệ số - lớn nhất. Lời giải: • Ta có 1 + 2$ = ∑ , % . 2 . $
• Do đó hệ số tổng quát trong khai triển là - = % 2
• Xét dãy số - = % 2 , = 1,12. • Ta có - = % 2 • Nếu - < - ⇔ % 2 < % 2 ⇔ ! . 2 < ! . 2 ! ! ! ! ⇔ ! . 2 < ! . 2. 2 ! ! ! ! ⇔ < ⇔ <
Bài 2.25. Khai triển đa thức 1 + 2$
thành dạng - + - $ + - $ +. . . +- $ . Tìm hệ số - lớn nhất.
• Suy ra - < - < - <. . . < -(.
• Ngược lại nếu - > -
⇔ > . Suy ra -( > -) > - > - > - .
• Vậy hệ số lớn nhất trong khai triển là -( = %( 2( = 126720
Bài 2.26. Chứng minh rằng % + % + %& +. . . +% = % + % + % +. . . +% . Lời giải: • Ta có 1 + $
= % + % $ + % $ + % $ + %& $&+. . . +% $ + % $ + % $ . (1)
• Thay $ = −1 vào (1) ta được 1 − 1 = % − % + % − % + %& −. . . +% − % + %
⇔ 0 = % − % + % − % + %& −. . . +% − % + %
⇔ % + % + %& +. . . +% = % + % + % +. . . +% (đpcm).
Bài 2.26. Chứng minh rằng % + % + %& +. . . +% = % + % + % +. . . +% .
• Thay $ = 1 vào (1) ta được 1 + 1
= % + % + % + % + %& +. . . +% + % + %
⇔ 2 = % + % + %& +. . . +% + % + % + % +. . . +%
• ⇔ 2 = 2. % + % + % +. . . +% • ⇒ % + % + % +. . . +% = 2
• Từ giả thiết suy ra 2 = 2048 ⇔ = 6
Bài 2.27. Tìm giá trị lớn nhất trong các giá trị % , % , . . . % .
Áp dụng: Tìm hệ số lớn nhất của khai triển - + 5 , biết rằng tổng các hệ số của khai triển bằng 4096. Lời giải:
• Ta có % = % = 1 không thể là giá trị lớn nhất.
• Xét % với 1 ≤ ≤ − 1
• Ta có % lớn nhất khi và chỉ khi 7% ≥ % % ≥ % ! ≥ ! • ⇔ 8 ! ! ! ! ! ≥ ! ! ! ! !
Bài 2.27. Tìm giá trị lớn nhất trong các giá trị % , % , . . . % .
Áp dụng: Tìm hệ số lớn nhất của khai triển - + 5 , biết rằng tổng các hệ số của khai triển bằng 4096. ≥ ⇔ 9 ⇔ : + 1 ≥ − ≥ − + 1 ≥ ⇔ − 1 ≤ 2 ≤ + 1 ⇔ ≤ ≤ .
Trường hợp 1: Nếu lẻ thì = 2; + 1 ⇒ ; ≤ ≤ ; + 1.
Suy ra tồn tại hai giá trị thỏa mãn là = ; = hoặc = + 1 = .
• Trường hợp 2: Nếu chẵn thì = 2; ⇒ ; − ≤ ≤ ; + ⇒ = ; = . <
• Vậy chẵn thì giá trị lớn nhất là % .
Bài 2.27. Tìm giá trị lớn nhất trong các giá trị % , % , . . . % .
Áp dụng: Tìm hệ số lớn nhất của khai triển - + 5 , biết rằng tổng các hệ số của khai triển bằng 4096. <=> <?> •
lẻ thì có hai giá trị lớn nhất là % và % . • Áp dụng
• Tổng các hệ số của khai triển bằng 4096 ⇒ 2 = 4096 ⇔ = 12
• Do chẵn, theo kết quả trên giá trị lớn nhất là %' = 924.
Bài 2.28. Tìm số hạng có giá trị lớn nhất của khai triển @ + A với @ > 0, A > 0, @ + A = 1. Lời giải: • Ta có @ + A = ∑ , % @ A
• Trường hợp 1: Số hạng đầu tiên lớn nhất khi và chỉ khi % @ ≥ % @ A ⇔ B ≥ % . C
• Trường hợp 2: Số hạng cuối cùng lớn nhất khi và chỉ khi % A ≥ % @ A ⇔ C ≥ % . B
Bài 2.28. Tìm số hạng có giá trị lớn nhất của khai triển @ + A với @ > 0, A > 0, @ + A = 1.
• Trường hợp 3: Hai số hạng đầu tiên và cuối cùng không phải là số lớn nhất Suy ra % @
A lớn nhất khi và chỉ khi 7% @ A ≥ % @ A ,với 1 ≤ ≤ − 1 % @ A ≥ % @ A ⇔ : ≥ A − @
≤ A + @ ⇔ A + 1 − 1 ≤ ≤ A + 1 .
• Nếu A + 1 − 1 nguyên thì tồn tại 2 giá trị thỏa mãn = A + 1 − 1 hoặc = A + 1 .
• Nếu A + 1 − 1 không nguyên thì là phần nguyên = A − 1 − 1 + 1, trong
đó kí hiệu $ là phần nguyên của $.