









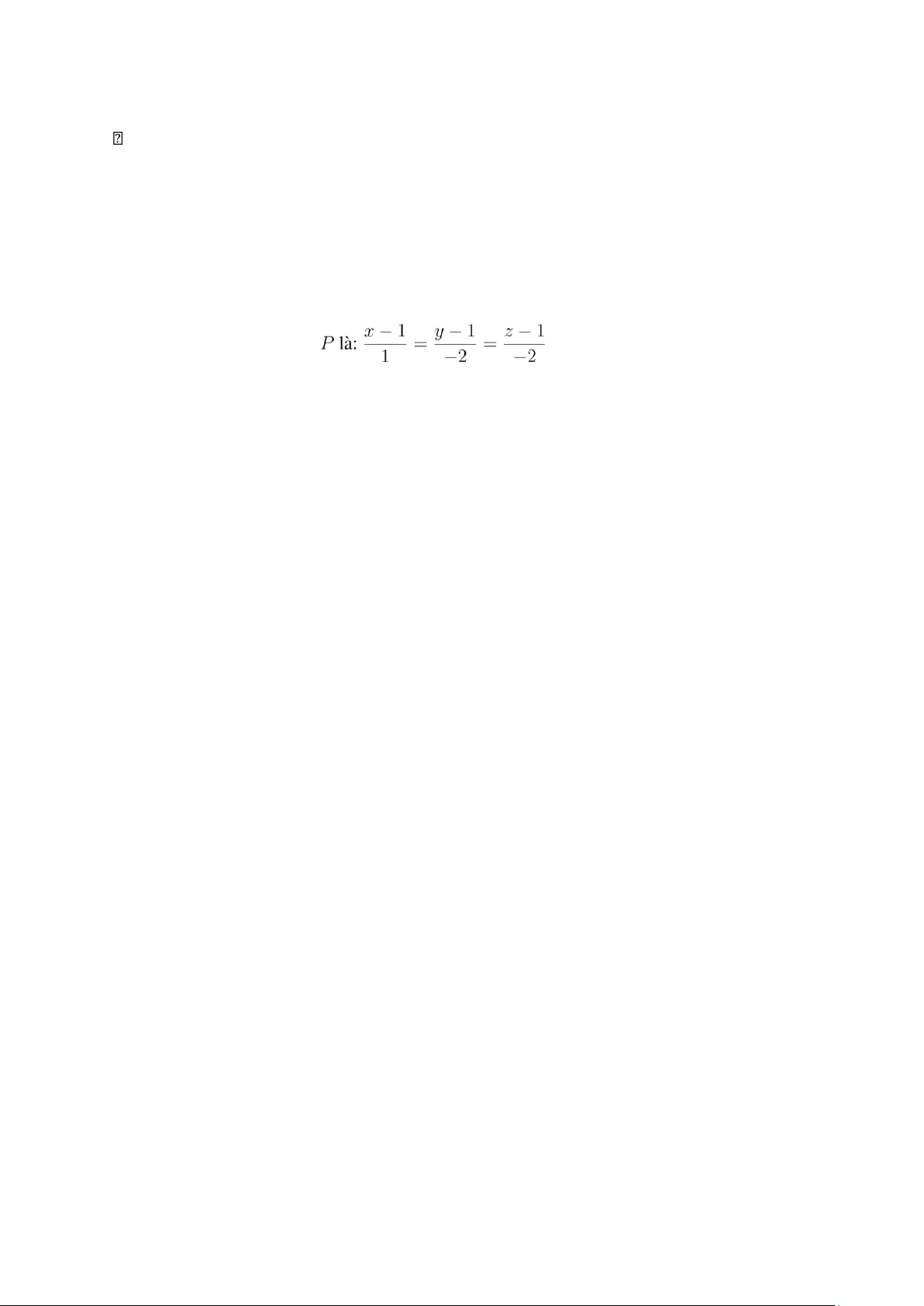


Preview text:
lOMoAR cPSD| 27879799
ỨNG DỤNG PHÉP TÍNH VI PHÂN TRONG HÌNH HỌC Mục lục
I Hàm véctơ ........................................................................................................................................................... 0
1 Định nghĩa, giới hạn, tính liên tục ................................................................................................................... 0
2 Các phép toán .................................................................................................................................................... 1
3 Đạo hàm, tính khả vi và tích phân ................................................................................................................... 2
4 Ví dụ..................................................................................................................................................................... 2
II Ứng dụng của phép tính vi phân trong hình học phẳng............................................................................. 4
1 Phương trình tiếp tuyến và pháp tuyến của đường cong ............................................................................ 4
1.1 Điểm chính quy ............................................................................................................................................... 4
1.2 Công thức phương trình tiếp tuyến, phương trình pháp tuyến của đường conghàm ẩn và đường
cong tham số ......................................................................................................................................................... 4
2 Hình bao của họ đường cong ........................................................................................................................... 5
2.1 Định nghĩa: ...................................................................................................................................................... 5
2.2 Quy tắc tìm hình bao của họ đường cong phụ thuộc một tham số: ....................................................... 5
2.3 Các lưu ý khi tìm hình bao: ........................................................................................................................... 5
3 Ví dụ..................................................................................................................................................................... 6
III Ứng dụng của phép tính vi phân trong hình học không gian ................................................................... 6
1 Đường cong trong không gian ......................................................................................................................... 6
2 Mặt cong trong không gian .............................................................................................................................. 7
3 Đường cong cho dưới dạng giao của 2 mặt cong ......................................................................................... 8
4 Ví dụ..................................................................................................................................................................... 8
IV Độ cong của đường cong ............................................................................................................................. 11
1 Định nghĩa và ý nghĩa ...................................................................................................................................... 11
2 Các công thức tính độ cong ............................................................................................................................ 11 3 Ví dụ
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 I Hàm véctơ
1 Định nghĩa, giới hạn, tính liên tục
Giả sử I là một khoảng trong R.
Định nghĩa 1. Ánh xạ I → Rn,t 7→ ⃗r(t) ∈ Rn được gọi là hàm véctơ của biến số t xác định trên R. lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Nếu n = 3, ta viết
⃗r(t) = x(t) ·⃗i + y(t) ·⃗j + z(t) ·⃗k.
Đặt M(x(t),y(t),z(t)), quỹ tích M khi t biến thiên trong I được gọi là tốc đồ của hàm véctơ ⃗r(t). ⃗ t → t 0 a →
lim | ⃗( t ) − ⃗| = 0 t → t 0 − r a
lim ⃗( t )= ⃗
t → t 0 r a ⃗( t )
I được gọi là liên tục tại t 0 ∈ I r
lim ⃗( t )= ⃗( t 0 t ) → t 0 r r
x ( t ) ,y ( t ) ,z ( t ) 2 Các phép toán
Định lý 2. Xét 2 véctơ ⃗a = (a1;a2;a3) và⃗b = (b1;b2;b3), k là số thực thì:
⃗a +⃗b = (a1 + b1;a2 + b2;a3 +
b3). ⃗a −⃗b = (a1 − b1;a2 − b2;a3 − b3).
k.⃗a = (ka1;ka2;ka3).
Định nghĩa 3. Tích vô hướng: Cho ⃗a(a1;a2;a3) và⃗b(b1;b2;b3) thì tích vô hướng:
⃗a ·⃗b = a1 · b1 + a2 · b2 + a3 · b3 Ta có: . Đặt
Định nghĩa 4. Tích có hướng: Với ⃗a = (a1,a2,a3);⃗b = (b1,b2,b3) ta có tích có hướng: ! 1 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập 3
Đạo hàm, tính khả vi và tích phân
⃗ = ( x ( t ) ,y ( t ) ,z ( t )) r b b b b ⃗( t ) dt =
⃗( t ) dt,
⃗( t ) dt,
⃗( t ) dt a r a x a y a z 4 Ví dụ d p⃗
( t)= e t · ⃗i + arctan t · ⃗j + arcsin t · ⃗ k ( (t
dt e t p⃗ )) t =0 Ta có
Ví dụ 2. Cho hàm vector p(t) = (sint,cost,t2). Tính q′(π) biết q(t) = (t2 + 1).p(t).
[Hướng dẫn giải]
Đặt r(t) = t2 + 1. 2 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Ta có q′(t) = r′(t).q(t) + r(t).q′(t) = 2t.(sint,cost,t2) + (t2 + 1).(cost,−sint,2t).
Thay t = π vào biểu thức trên ta có:
q′(π) = 2π.(sinπ,cosπ,π2) + (π2 + 1).(cosπ,−sinπ,2π) = (−π2 − 1,−2π,4π3 + 2π). 3 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập II
Ứng dụng của phép tính vi phân trong hình học phẳng
1 Phương trình tiếp tuyến và pháp tuyến của đường cong 1.1 Điểm chính quy
Định nghĩa 7. Trong hệ toạ độ Descarter, cho đường cong L có phương trình f(x,y) = 0. Điểm
M0(x0,y0) ∈ L gọi là điểm chính quy nếu fx′ (M0) và fy′(M0) không đồng thời bằng 0, gọi là điểm kỳ dị
trong trường hợp ngược lại.
1.2 Công thức phương trình tiếp tuyến, phương trình pháp tuyến của đường cong hàm ẩn và đường cong tham số
▶ Đường cong hàm ẩn:
Chúng ta biết rằng hệ số góc k của tiếp tuyến của đường cong C tại điểm M chính là . Do đó, nếu
đường cong cho bởi phương trình f(x,y) = 0 thì nó xác định một hàm ẩn y = y(x) và đạo hàm của nó tính theo công thức ( x = x(t) . M
( d ): f ′ x ( M ) · ( x − x 0 )+ f ′ y ( M ) · ( y − y 0 )=0 M x y ( − x 0 − y 0 d ′ ): = f ′ x ( M )
f ′ y ( M )
y = f ( x )
M ( x 0 ,y 0 ) chính quy là y − y 0 = f ′ ( x 0 )( x − x 0 )
Nếu đường cong (C) cho bởi phương trình tham sốthì: y = y(t) . 4 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
M ( x ( t 0 ) ,y ( t 0 )) x y ( − x ( t 0 ) − y ( t 0 ) d ): = x ′ ( t 0 ) y ′ ( t 0 )
Nói cách khác, véc tơ tiếp tuyến của đường cong C tại điểm M (x(t0),y (t0)) là ⃗n = (x′ (t0),y′ (t0)).
Công thức 4. Phương trình pháp tuyến tại M :
(d′) : x′ (t0) · (x − x(t0)) + y′ (t0) · (y − y (t0)) = 0
2 Hình bao của họ đường cong 2.1 Định nghĩa:
Định nghĩa 8. Cho họ đường cong (L) phụ thuộc vào một hay nhiều tham số. Nếu mỗi đường cong
trong họ (L) đều tiếp xúc với đường cong (E) tại một điểm nào đó trên E và ngược lại, tại mỗi điểm
thuộc (E) đều tồn tại một đường cong của họ (L) tiếp xúc với (E) tại điểm đó thì (E) được goi là
hình bao của họ đường cong (L). 2.2
Quy tắc tìm hình bao của họ đường cong phụ thuộc một tham số: F ( x,y,c )=0 c ( F ( x,y,c )=0
F ′ c ( x,y,c )=0
Dựa vào 2 phương trình trong hệ trên, ta khử c đi, rút ra được 1 phương trình mối liên hệ giữa x và y.
Đây chính là phương trình của hình bao (E). 2.3
Các lưu ý khi tìm hình bao: Lưu ý 3.
• Xét đến điểm kì dị: M(x0,y0) là điểm kì dị của đường cong và
• Nếu họ đường cong đã cho có điểm kì dị thì hệ phương trình trên bao gồm hình bao (E) và
quỹ tích các điểm kì dị thuộc họ các đường cong đã cho. 5 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập 3 Ví dụ 1+ x t = t 3 3 1 y = + 2 t 3 2 t A (2 , 2) Ta có : . Tại điểm
Phương trình tiếp tuyến của đường cong tại điểm A(2;2) là: − −
Phương trình pháp tuyến của đường cong tại điểm A(2;2) là:
(x′t(A))(x − x(A)) + (yt′(A))(y − y(A)) = 0 ⇔ −5(x − 2) − 5(y − 2) = 0 ⇔ x + y − 4 = 0. 1 y = cx + ( c L )
[Hướng dẫn giải] Đặt
. Điều kiện : c ̸= 0 Xét hệ:
FFyx′′((x,y,cx,y,c) = 1 = 0) = −c = 0 . ⇒ Họ đường cong không có điểm ki dị. Xét hệ :
Vậy hình bao của đường cong (L) đã cho là y2 = 4x, trừ điểm (0,0). III
Ứng dụng của phép tính vi phân trong hình học không gian
1 Đường cong trong không gian
Định nghĩa 9. Đường cong trong không gian R3 là 1 hàm vecto:
r : [a,b] → R3
⃗r(t) = x(t)⃗i + y(t)⃗j + z(t)⃗k 6 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
▶ Phương trình tiếp tuyến và pháp diện của đường cong cho bởi phương trình tham số.
x = x(t),
Đường cong L trong không gian cho bởi hàm vecto ⃗r(t), có phương trình tham số: y = y(t), . z = z(t)
Khi đó, véctơ tiếp tuyến của . r
M 0 ( x 0 ,y 0 ,z 0 ) x y z ( − x ( t 0 ) − y ( t 0 ) − z ( t 0 ) d ): = = x ′ ( t 0 ) y ′ ( t 0 ) z ′ ( t 0 )
( P ): x ′ ( t 0 )( x − x ( t 0 ))+ y ′ ( t 0 )( y − y ( t 0 ))+ z ′ ( t 0 )( z − z ( t 0 ))=0
2 Mặt cong trong không gian
Phương trình mặt cong trong không gian: ( S ): f ( x,y,z )=0
M ( x 0 ,y 0 ,z 0 )
[ f ′ x ( x 0 ,y 0 ,z 0 )] 2 +[ f ′ y ( x 0 ,y 0 ,z 0 )] 2 +[ f ′ z ( x 0 ,y 0 ,z 0 )] 2 > 0
▶ Phương trình pháp tuyến và phương trình tiếp diện của mặt cong.
Cho mặt cong S : f(x,y,z) = 0, có điểm chính quy M(x0,y0,z0). Vecto pháp tuyến của S tại điểm M là: . M x y z ( − x 0 − y 0 − z 0 d ): = = f ′ x ( M )
f ′ y ( M ) f ′ z ( M ) M
( P ): f ′ x ( M )( x − x 0 )+ f ′ y ( M )( y − y 0 )+ f ′ z ( M )( z − z 0 )=0 7 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
3 Đường cong cho dưới dạng giao của 2 mặt cong
f(x,y,z) = 0 ▶ Cho
đường cong xác định bởi giao của 2 mặt cong sau:. f x′ y′ z′ g(x,y,z) = 0
• Đặt n⃗ = (f (M),f (M),f (M)) là vecto pháp tuyến của mặt phẳng tiếp diện của mặt cong f(x,y,z) = 0 tại M.
• Đặt ⃗ng = (gx′ (M),gy′ (M),gz′ (M)) là vecto pháp tuyến của mặt phẳng tiếp diện của mặt cong g(x,y,z) = 0 tại M.
• Khi đó ⃗nf ∧ ⃗ng là vecto chỉ phương của tiếp tuyến đường cong đã cho tại M. 4 Ví dụ
Ví dụ 5. Viết phương trình tiếp diện và pháp tuyến của mặt cong x2 + y3 + z2 − 2xyz − 6 = 0 tại điểm P(1;2;3).
[Hướng dẫn giải] Đặt
F(x,y,z) = x2 + y3 + z2 − 2xyz − 6
Fxy′′(x,y,z) = 2x2− 2yz
Fzyx′′′(1,2,3) = −10 ⇒
Fz′(x,y,z) = 3y − 2xz ⇒
F (1,2,3) = 6
F (x,y,z) = 2z − 2xy
F (1,2,3) = 2 8 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
⇒ →−n = (−10,6,2) = −2(5,−3,−1) là vecto pháp tuyến của mặt cong tại P
⇒ Phương trình pháp tuyến tại
Phương trình tiếp diện tại P là: 5(x − 1) − 3(y − 2) − (z − 3) = 0 ⇒ 5x − 3y − z + 4 = 0
x 2 + y 2 + z 2 − 3 x 2 yz =0
Cho đường cong xác định bởi giao của 2 mặt cong sau x 3 + y + z 2 − 3 xy =0
A (1 , 1 , 1) Đặt
fzxy′′′ (x,y,z) = 2x − 6xyz22
fxzyxyz′′′′′′ (1,1,1) = −4
fg f (x,y,z) = 2y − 3x z
f (1,1,1) = −1 ⇒
fgzyx′′′ (x,y,zg
) = 3x2−−33xyy ⇒
fg (1(1,,11,,1) =1) = 0−1 ⇒
→−−nn→ = (0= (−,4−,2−,12),−1) f (x,y,z) = 2z 9 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
g (x,y,z) = 1 − 3x g (1,1,1) = −2 g (x,y,z) = 2z g (1,1,1) = 2
⇒ −n→ × →−n = (−4,8,8) = 4(1,−2,−2)
⇒ →−n = (1,−2,−2) là vecto chỉ phương của tiếp tuyến tại A
⇒ Phương trình pháp tuyến tại
Phương trình tiếp diện tại P là:(x − 1) − 2(y − 1) − 2(z − 1) = 0 ⇒ x − 2y − 2z + 3 = 0 10 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập IV
Độ cong của đường cong 1
Định nghĩa và ý nghĩa Cho đường cong ′( ( t )
t )= | ′( t ) | d
Độ cong của đường cong = ( t ) C = ds ( t )
s ( t ) là hàm độ dài.
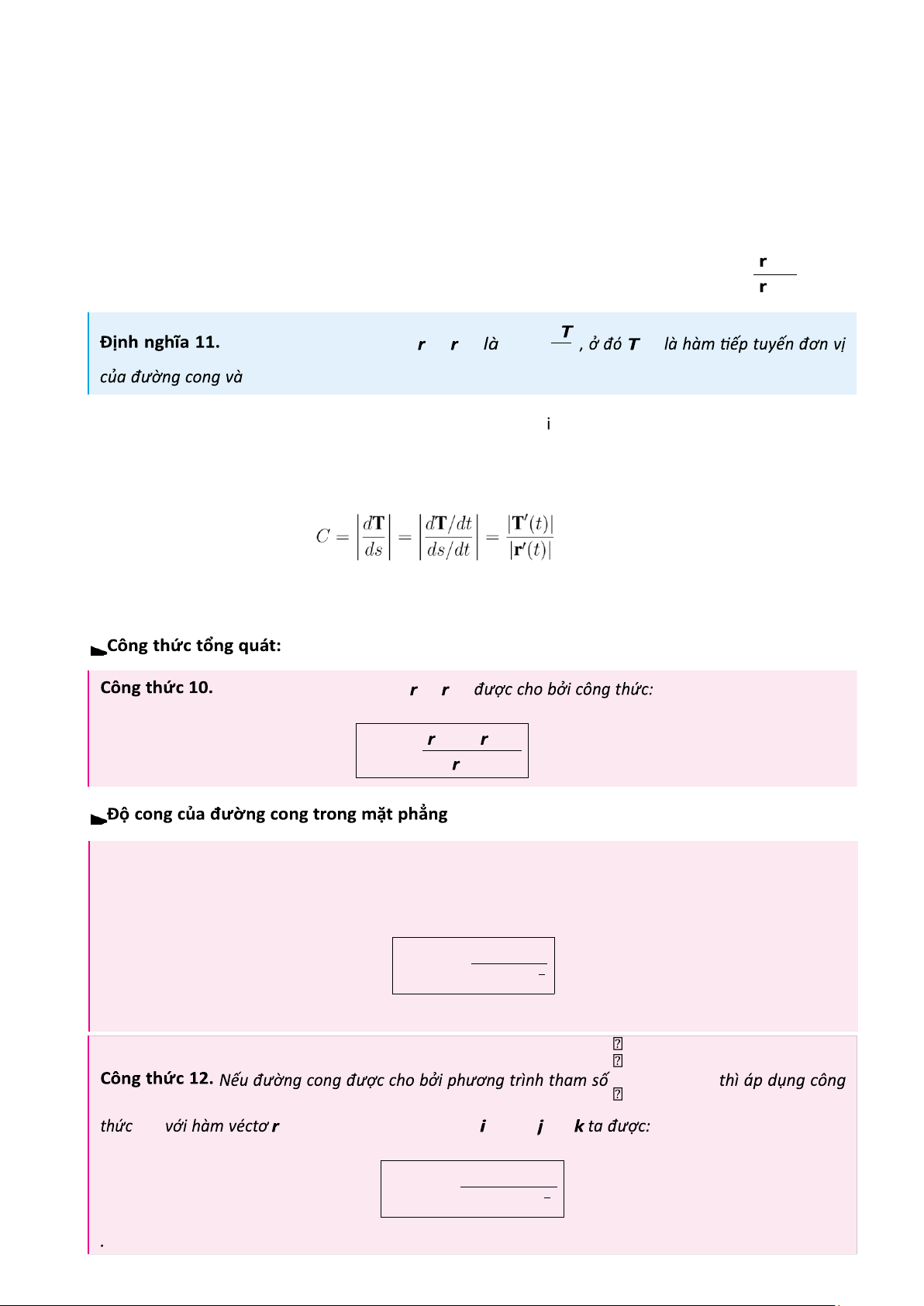
r = r(t). Khi đó véctơ tiếp tuyến đơn vị T(t) được xác định bởi: T
▶ Ý nghĩa: Độ cong của đường cong tại một điểm P là một đại lượng đo "tốc độ" thay đổi hướng của
đường cong tại điểm P đó. Một cách cụ thể, người ta định nghĩa độ cong của đường cong tại điểm P là
"tốc độ" thay đổi của véctơ tiếp tuyến đơn vị theo độ dài cung tại điểm P đó. Ta có:
2 Các công thức tính độ cong
Độ cong của đường cong = ( t ) | C
′ ( t ) ∧ ′′ ( t ) | ( t )= ( | ∗ ) ′( t ) | 3
Công thức 11. Nếu đường cong cho bởi phương trình y = f(x) thì ta áp dụng công thức (∗) với hàm
véctơ r = (x,f(x),0) = ti + f(t)j + 0k ta được: | C y ′′ | ( M )= (1+ 3 y ′ 2 ) 2 .
x = x ( t )
y = y ( t ) ( ∗ )
( t )=( x ( t ) ,y ( t ) , 0)= x ( t ) + y ( t ) +0 | C
x ′ y ′′ − x ′′ y ′ | ( M )= ( 3
x ′ 2 + y ′ 2 ) 2 11 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập | r
r 2 +2 r ′ 2 − rr ′′ | = r ( φ ) C ( M )= ( 3
r 2 + r ′ 2 ) 2
x = x ( t ) , y
= y ( t ) ,
z = z ( t ) v u u 2 2 2 t x ′ y ′ y ′ z ′ z ′ x ′ + +
x ′′ y ′′
y ′′ z ′′
z ′′ x ′′ C ( t )= ( 3
x ′ 2 + y ′ 2 + z ′ 2 ) 2
x = e t + sin t, t = 0
y = e t − cos t.
Ta có x′ = et + cost,x′′ = et − sint,y′ = et + sint,y′′ = et + cost.
Độ cong tại điểm M(1;0) ứng với t = 0 là
Ví dụ 8. Cho đường cong (L) trong không gian cho bởi hàm vecto r−−(→t), có phương trình tham
số x(t) = t2,y(t) = 3t2 + t,z(t) = t3.Tính độ cong của đường cong tại điểm M(1,4,1). [Hướng dẫn giải] Do
Tại M(1,4,1) ⇒ t = 1. Thay t = 1 vào ta tính được
Do độ cong của đường cong L cho bởi công thức: 12 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập 13




