Chương 2: Tích phân bội - Giải tích II (MI1120) | Trường Đại học Bách khoa Hà Nội

lOMoAR cPSD| 27879799 TÍCHPHÂNBỘI Mục lục I Tích phân kép 2 1
Định nghĩa, điều kiện khả tích và tính chất của tích phân kép . . . . . . . . . . . . . . . 2 2
Cách tính tích phân kép trong hệ tọa độ Descartes . . . . . . . . . . . . . . . . . . . . . 3 2.1
Tích phân có miền là hình chữ nhật hoặc hình thang cong . . . . . . . . . . . . . 3 2.2
Tích phân có chứa dấu giá trị tuyệt đối . . . . . . . . . . . . . . . . . . . . . . . 4 2.3
Tích phân có miền lấy tích phân là miền đối xứng . . . . . . . . . . . . . . . . . 4 3
Tính tích phân kép bằng cách đổi hệ tọa độ . . . . . . . . . . . . . . . . . . . . . . . . . 6 3.1
Công thức đổi biến trong tích phân kép
. . . . . . . . . . . . . . . . . . . . . . 6 3.2
Tính tích phân kép trong hệ tọa độ cực . . . . . . . . . . . . . . . . . . . . . . . 6 4
Ứng dụng của tích phân kép . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
II Tích phân bội ba 10 1
Định nghĩa, điều kiện khả tích và tính chất của tích phân bội ba . . . . . . . . . . . . . . 10 1.1 Định nghĩa
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 1.2
Định lý Fubini . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 1.3
Các tính chất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 2
Cách tính tích phân bội ba trong hệ tọa độ Descartes: . . . . . . . . . . . . . . . . . . . 12 3
Tính tích phân bội ba bằng cách đổi hệ tọa độ . . . . . . . . . . . . . . . . . . . . . . . 13 3.1
Công thứ đổi biến trong tích phân bội ba: . . . . . . . . . . . . . . . . . . . . . 13 3.2
Tính tích phân bội ba trong hệ tọa độ trụ: . . . . . . . . . . . . . . . . . . . . . 14 3.3
Tính tích phân bội ba trong hệ tọa độ cầu . . . . . . . . . . . . . . . . . . . . . 14 4
Ứng dụng của tích phân bội ba: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập I Tích phân kép 1
Định nghĩa, điều kiện khả tích và tính chất của tích phân kép
Định nghĩa 1. Cho z = f(x,y) là một hàm hai biến xác định trên miền đóng và bị chặn D.
• Phân hoạch miền D một cách tùy ý thành các miền con D1,D2,...,Dn sao cho các Dk không giao
nhau ngoại trừ biên của chúng.
• Gọi ∆Sk là diện tích của miền con Dk.
• Đặt d(Dk) là khoảng cách lớn nhất giữa hai điểm trong Dk và d = .
• Lấy Mk là điểm tùy ý trong Dk.
• Tổng tích phân của f(x,y) trên miền .
Nếu limIn tồn tại không phụ thuộc vào cách phân hoạch miền
và cách chọn các điểm Mk trong d→ , thì giới hạn này được gọi là tích phân
kép của hàm f trên miền D. Kí hiệu là mỗi miền
Lúc đó, ta nói hàm f(x,y) khả tích trên miền D.
Giả sử f(x,y) ) khả tích trên miền D. Khi đó, việc tính tích phân kép không phụ thuộc cách phân hoạch
miền D. Do đó, ta có thể phân hoạch miền D theo các đường song song với các trục tọa độ. Lúc đó, ∆Sk
= ∆x.∆y và ta có thể viết như sau:
¨ f(x,y)dS = ¨ f(x,y)dxdy D D
▶ Điều kiện khả tích:
Định lý 1. Nếu f(x,y) liên tục trên miền đóng, bị chặn D thì f khả tích.
▶ Các tính chất: Cho f(x,y), g(x,y) là các hàm khả tích trên miền D ∈ R2, và c,m,M là các số thực. Khi đó, •
diện tích miền D.
• ¨ [f(x,y) ± g(x,y)]dxdy = ¨ f(x,y)dxdy ± ¨ g(x,y)dxdy; D D D 1 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
• ¨ c.f(x,y)dxdy = c.¨ f(x,y)dxdy; D D
• Nếu D được chia thành 2 miền D1,D2 không giẫm lên nhau . • Nếu . • Nếu
, trong đó S là diện tích miền D. 2
Cách tính tích phân kép trong hệ tọa độ Descartes 2.1
Tích phân có miền là hình chữ nhật hoặc hình thang cong
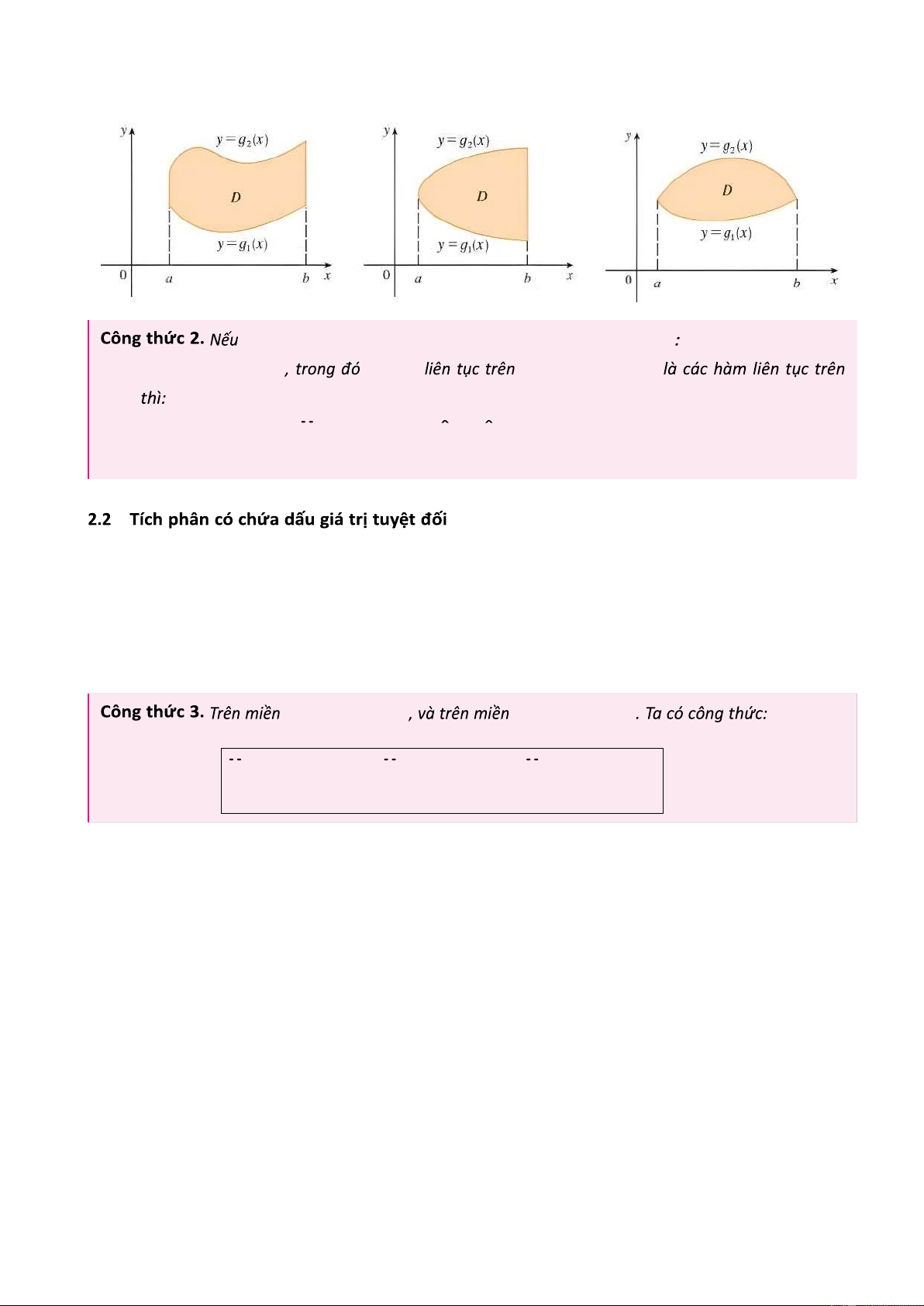
Định lý 2. Nếu D là miền hình chữ nhật: D = {(x,y)|a ≤ x ≤ b;c ≤ y ≤ d} và f(x,y) liên tục trên D, thì:
( Định lý Fubini ) .
Đặc biệt, nếu f(x,y) có thể phân tích thành tích của các hàm một biến, tức là f(x,y) = g(x).h(y), thì
tích phân kép trên miền D = [a,b] × [c,d] có thể viết thành tích của các tích phân xác định như sau: b d f ( x,y ) dxdy =
g ( x ) h ( y ) dxdy =
g ( x ) dx ·
h ( y ) dy a c D D D
Oy D = { ( x,y ) | a ≤ x ≤
b ; y ( x ) ≤ y ≤ y ( x ) } f ( x,y )
D và y ( x ) ,y ( x ) [ a ; b ] 1 2 1 2 b y 2 ( x ) ! f ( x,y ) dxdy =
f ( x,y ) dy dx a y 1 ( x ) D
Một số miền có dạng hình thang cong có cạnh đáy song song với Oy: 2 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
D là miền hình thang cong có các cạnh song song với Ox D = { ( x,y ) | c ≤ y ≤
d ; x ( y ) ≤ x ≤ x ( y ) } f ( x,y )
D và x ( y ) ,x ( y ) 1 2 1 2 [ c ; d ] d x 2 ( y ) ! f ( x,y ) dxdy =
f ( x,y ) dx dy c x 1 ( y ) D
▶ Giả sử cần tính ¨ |f(x,y)|dxdy. D
Mục đích của chúng ta là phá bỏ được dấu giá trị tuyệt đối. Vì vậy ta khảo sát dấu của hàm f(x,y). Do
tính liên tục của hàm f(x,y) nên đường cong f(x,y) = 0 sẽ chia miền D thành hai miền, D+ và D−.
D + ,f ( x,y ) ≥ 0
D − ,f ( x,y ) ≤ 0 |
f ( x,y ) | dxdy =
f ( x,y ) dxdy +
− f ( x,y ) dxdy ( ∗ ) D D + D −
▶ Các bước tính tích phân kép có chứa dấu giá trị tuyệt đối:
• Bước 1: Vẽ đường cong f(x,y) = 0 để tìm đường cong phân chia miền D.
• Bước 2: Giả sử đường cong tìm được chia miền D thành 2 miền. Để xác định miền nào là D+, miền
nào là D−, ta xét một điểm (x0,y0) bất kì, sau đó tính giá trị f(x0,y0). Nếu f(x0,y0) > 0 thì miền chứa
(x0,y0) là D+ và ngược lại.
• Bước 3: Sau khi xác định được các miền D+,D−, sử dụng công thức (∗) để tính tích phân. 3 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập 2.3
Tích phân có miền lấy tích phân là miền đối xứng D Ox Oy y x
f ( x,y ) dxdy =0 D
Công thức 5. Nếu miền D là miền đối xứng qua trục Ox (tương ứng với Oy) và hàm là hàm chẵn đối
với y (tương ứng đối với x) thì: f
( x,y ) dxdy =2
f ( x,y ) dxdy D D +
trong đó D+ là phần nằm bên trên trục Ox của D (tương ứng phía phải trục Oy của D). D f ( x,y )
f ( − x, − y ) = − f ( x,y )
f ( x,y ) dxdy =0 D 1 1
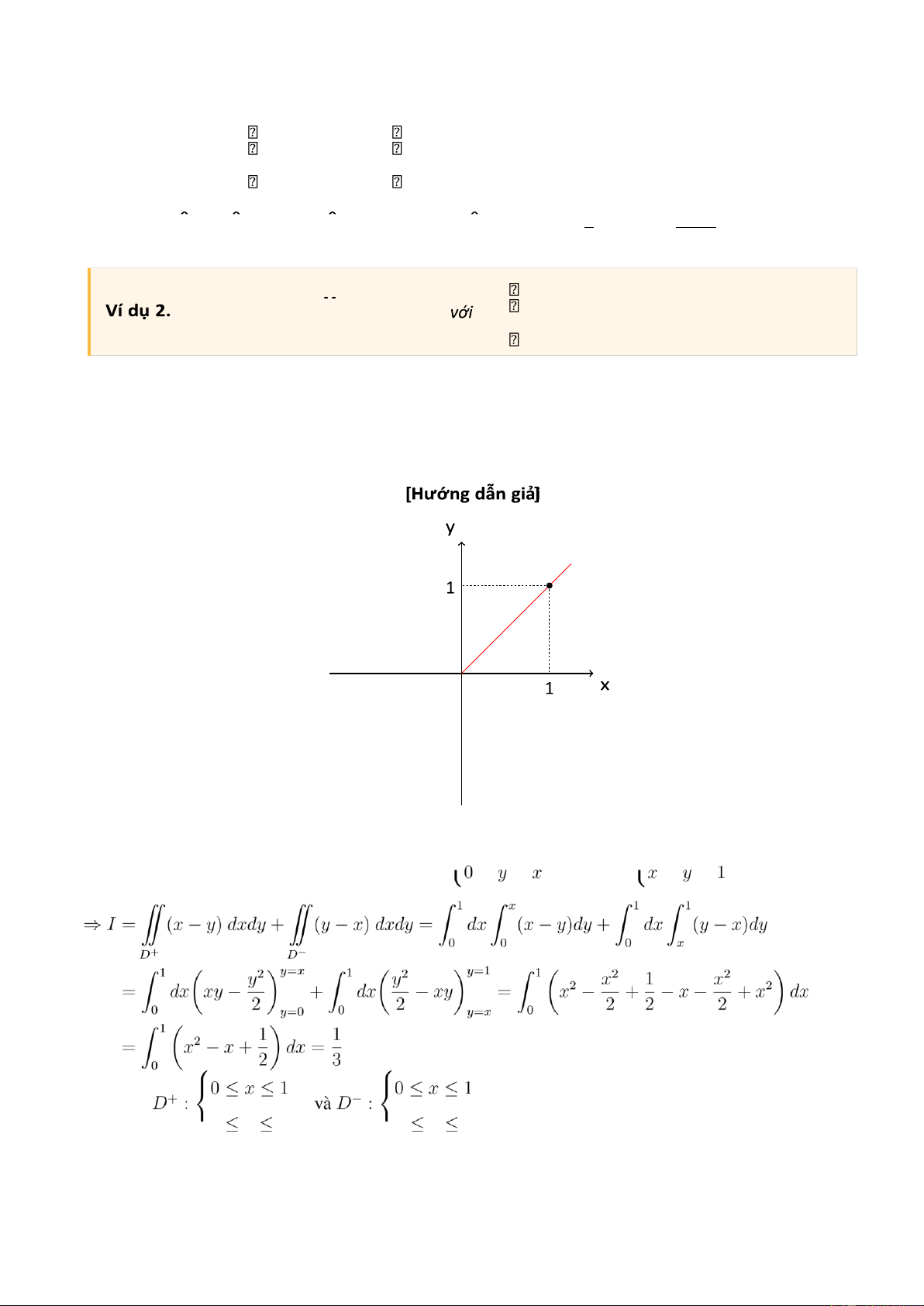
Ví dụ 1. Tính tích phân kép I =dy ˆ ex2dx. 0 y
[Hướng dẫn giải] Ta thấy tích phân
không tính được qua các hàm sơ cấp, vì vậy nếu tính trực tiếp tích phân trên
là vô cùng phức tạp. Lúc này nên nghĩ tới việc đổi thứ tự lấy tích phân qua 3 bước: + B1: Xác định miền D
+ B2: Biểu diễn miền D trên đồ thị
+ B3: Dựa vào hình vẽ thay đổi thứ tự lấy tích phân O 4 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập 0 ≤ y ≤ 1 0 ≤ x ≤ 1 D : ⇔ y ≤ x ≤ 1 0 ≤ y ≤ x 1 x 1 y = x 1 1 x =1 e I − 1 = dx
e x 2 dy =
dx.e x 2 y =
x.e x 2 dx = e x 2 = 0 0 0 y =0 0 2 x =0 2 0 ≤ x ≤ 1
Tính tích phân I =
| x − y | dxdy D : 0 D ≤ y ≤ 1 Từ hình vẽ ta có: Khi đó D − D + O Từ hình vẽ suy ra D = D+ ∪ D−, trong đó 5 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
3 Tính tích phân kép bằng cách đổi hệ tọa độ 3.1
Công thức đổi biến trong tích phân kép
Công thức 7. Giả sử ta cần tính tích phân I = ¨ f(x,y)dxdy. Thực hiện phép đổi biến x = D D(x,y) x′ x′
x(u,v),y = y(u,v) và tính định thức Jacobi: J = = yuu
yv′v, ∀(u,v) ∈ D′. Khi đó: D(u,v) ′
¨ f(x,y)dxdy = ¨ f(x(u,v),y(u,v)).|J|dudv D D′ −− → M ( r,ϕ )
ϕ = ( Ox, OM ) ,r = | OM | x = r. cos ϕ
0 ≤ ϕ ≤ 2 π M ( x,y ) Oxy ⇒
y = r. sin ϕ | J | = r f ( x,y ) dxdy =
f ( r. cos ϕ,r. sin ϕ ) rdrdϕ D D với miền
Ví dụ 3. Tính tích phân
[Hướng dẫn giải]
. Miền D trở thành Từ miền miền 6 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Đổi biến:
Ví dụ 4. Tính tích phân
[Hướng dẫn giải]
Lưu ý: Với bài này nhiều người sẽ đặt
, tuy nhiên ta nên ưu tiên biến đổi sao cho
biểu thức tích phân dễ tính thay vì biến đổi đưa về miền D dễ tính. Đặt
Từ x2 + y2 ≤ 2y ⇒ r2 ≤ 2r sinϕ ⇔ r ≤ 2sinϕ
Lại có r ≥ 0 ⇒ 2sinϕ
≥ 0 ⇒ 0 ≤ ϕ ≤ π. Miền D trở thành: 4 Ứng dụng của tích phân kép
▶ Tính thể tích một vật thể hình trụ:
Công thức 9. Vật hình trụ có đáy là miền D ⊂ mặt phẳng Oxy, mặt trên có phương trình z = f(x,y)
(f(x,y) ≥ 0, liên tục trên D). Thể tích của vật thể ấy là: V =
f ( x,y ) dxdy D 7 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập D S = dxdy D
▶ Tính diện tích mặt cong:
Công thức 11. Cho mặt cong S có phương trình z = f(x,y),f(x,y) liên tục, có các đạo hàm riêng cấp
một liên tục trên D. (D là hình chiếu của S trên mặt phẳng Oxy). Diện tích mặt phẳng S là S q = 1+ f ′ 2 x + f ′ 2 y dxdy D
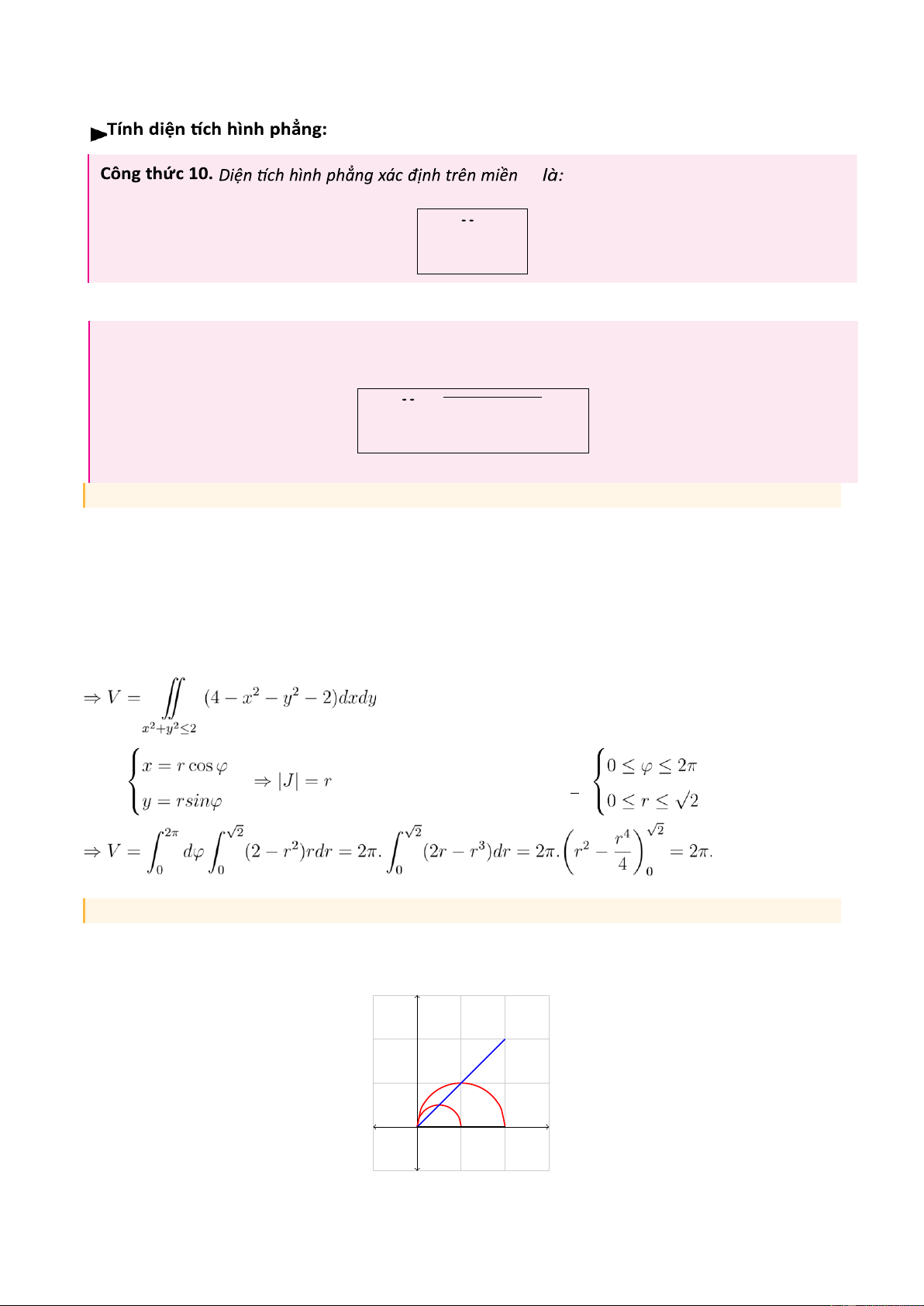
Ví dụ 5. Tính thể tích vật thể trong không gian Oxyz giới hạn bởi 2 mặt x2 + y2 + z = 4 và z = 2
[Hướng dẫn giải]
Nhận xét: Mặt phía trên là mặt paraboloid: z = 4 − x2 − y2 Mặt phía dưới
là mặt phẳng z = 2. ⇒ 2 ≤ 4 − x2 − y2 ⇔ x2 + y2 ≤ 2 Đặt , miền D trở thành:
Ví dụ 6. Tính diện tích miền D giới hạn bởi các đường: x2 + y2 = 2x,x2 + y2 = 4x,y = x,y = 0.
[Hướng dẫn giải] y y = x D x O 8 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Đặt
Từ 2x ≤ x2 + y2 ≤ 4x ⇒ 2r cosϕ ≤ r2 ≤ 4r cosϕ ⇔ 2cosϕ ≤ r ≤ 4cosϕ
Ta có 4cosϕ ≥ 2cosϕ ≥ 0 suy ra Lại có
. Miền D trở thành:
Ví dụ 7. Tính diện tích phần mặt nón z =
x2 + y2 nằm trong miền giới hạn D : x2 + y2 ≤ 2x. p
[Hướng dẫn giải] Ta có
(do miền D giới hạn bởi đường tròn có bán kính là 1) 9 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập II Tích phân bội ba 1
Định nghĩa, điều kiện khả tích và tính chất của tích phân bội ba 1.1 Định nghĩa
Định nghĩa 2. Cho hàm ba biến z = f(x,y,z) trên miền V đóng và bị chặn trong không gian Oxyz.
• Chia miền V một cách tùy ý thành n khối V1,...,Vn sao cho các Vk không giao nhau ngoại trừ biên.
• Gọi ∆Vk là thể tích của khối Vk.
• Đặt d(Vk) là khoảng cách lớn nhất giữa hai điểm trong khối Vk, và đặt .
• Lấy điểm Mk tùy ý trong mỗi khối Vk. n
• Tổng tích phân của f trên miền V là In = Xf(Mk).∆Vk k
Nếu limIn tồn tại không phụ thuộc vào cách phân hoạch miền và cách chọn các điểm Mk trong d→0 ,
thì giới hạn này được gọi là tích phân bội ba của hàm f trên miền V , kí hiệu là mỗi khối Vk
˚ f(x,y,z)dV. V
Lúc đó, ta nói hàm f(x,y,z) khả tích trên miền V .
Giả sử hàm f(x,y,z) khả tích trên miền V . Khi đó, việc tính tích phân bội ba không phụ thuộc cách phân
hoạch miền V . Do đó, ta có thể phân hoạch miền V theo họ các mặt phẳng song song với các mặt phẳng
tọa độ. Lúc đó, ∆Vk = ∆x · ∆y · ∆z và ta có thể viết như sau: f ( x,y,z ) dV =
f ( x,y,z ) dxdydz V V 1.2 Định lý Fubini
▶ Đổi thứ tự lấy tích phân - Định lý Fubini:
Định lý 3. Nếu f liên tục trên hình hộp B = [a,b] × [c,d] × [r,s], thì f khả tích trên B và
Lưu ý 2. Tích phân b d s
bội ba trên hình hộp f f
có thể được tính
( x,y,z ) dxdydz =
( x,y,z ) dxdydz theo sáu thứ tự khác a c r nhau. B 10 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
▶ Hệ quả của Định lý Fubini: Đặc biệt, nếu f(x,y,z) có thể phân tích thành tích của các hàm một biến,
tức là f(x,y,z) = g(x)h(y)k(z), thì tích phân bội ba trên miền B = [a,b] × [c,d] × [r,s] có thể viết thành
tích của các tích phân xác định như sau: b d s f
( x,y,z ) dxdydz =
g ( x ) h ( y ) k ( z ) dxdydz =
g ( x ) dx ·
h ( y ) dy ·
k ( z ) dz a c r B B 1.3 Các tính chất
Cho f(x,y,z), g(x,y,z) là các hàm khả tích trên miền D ∈ R2, và α,β,m,M là các số thực. Khi đó, •
• Nếu V được chia thành 2 miền con V1,V2 không giao nhau trừ trên biên, thì
• Nếu f(x,y,z) ≤ g(x,y,z) trong V thì
Đặc biệt, hàm |f(x,y,z)| cũng khả tích trong V , và • Nếu . Khi đó, m.
với Vol(V ) là thể tích của V .
• Nếu miền lấy tích phân V đối xứng qua mặt phẳng x = 0 (tương ứng y = 0,z = 0) và f(x,y,z) là hàm
lẻ theo biến x (tương ứng y,z), thì khi đó
f ( x,y,z ) dxdydz =0 V 11 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập 2
Cách tính tích phân bội ba trong hệ tọa độ Descartes: V =
{ ( x,y,z ) | ( x,y ) ∈ D,f ( x,y ) ≤ z ≤ f ( x,y ) } 1 2
f ( x,y ) ,f ( x,y ) D 1 2 f " 2 ( x,y ) # ρ
( x,y,z ) dxdydz =
ρ ( x,y,z ) dz dxdy f 1 ( x,y ) V D
V = { ( x,y,z ) | a ≤ x ≤ b,g 1 ( x ) ≤ y ≤ g 2 ( x ) ,f 1 ( x,y ) ≤ z ≤ f 2 ( x,y ) } b g f 2 ( x ) 2 ( x,y ) ρ
( x,y,z ) dxdydz =
ρ ( x,y,z ) dxdydz a g 1 ( x ) f 1 ( x,y ) V I 2 = xy dxdydz,
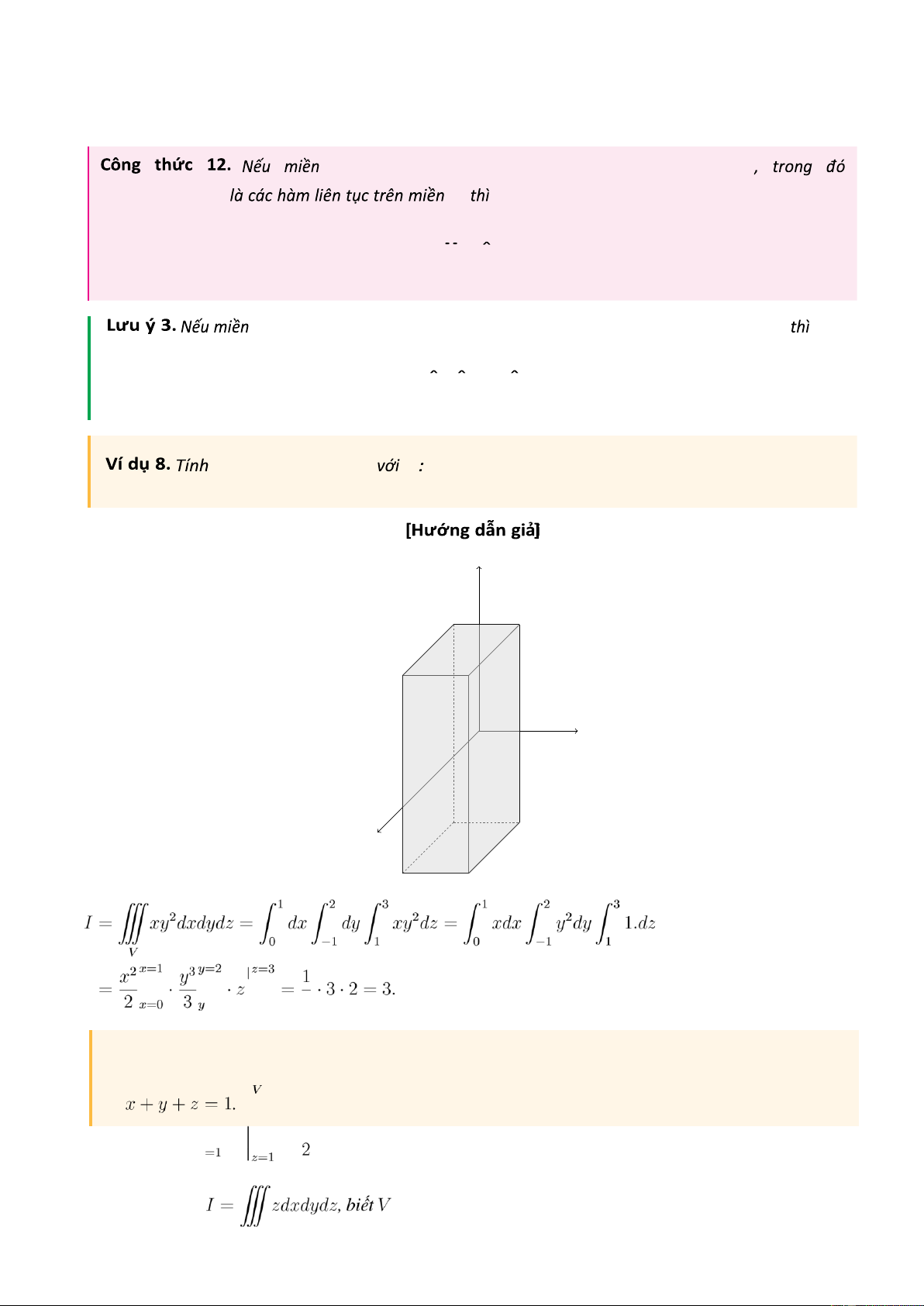
V 0 ≤ x ≤ 1 − 1 ≤ y ≤ 21 ≤ z ≤ 3 V y x z
Ví dụ 9. Tính
là khối tứ diện giới hạn bởi 4 mặt phẳng x = 0,y = 0,z = 0 và 12 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
[Hướng dẫn giải] y 1 x O 1 1 z Ta có 3
Tính tích phân bội ba bằng cách đổi hệ tọa độ
Giả sử ta cần tính tích phân I =
f ( x,y,z ) dxdydz V
x = x ( u,v,w ) ,y = y ( u,v,w ) ,z = z ( u,v,w ) x ′ D
u x ′ v x ′ w J ( x,y,z = = y D ′ ( u,v,w )
u y ′ v y ′ w z ′
u z ′ v z ′ w J =0 u ′ 1
x u ′ y u ′ z D = ( u,v,w ) = v J ′ D ( x,y,z
x v ′ y v ′ z w ′
x w ′ y w ′ z J =0 f
( x,y,z ) dxdydz =
f x ( u,v,w ) ,y ( u,v,w ) ,z ( u,v,w ) . | J | dudvdw V V ′ 3.2
Tính tích phân bội ba trong hệ tọa độ trụ: 13 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
▶ Xét tọa độ của một điểm P trong hệ tọa độ trụ là (r,ϕ,z) với (r,ϕ) là tọa độ cực của hình chiếu của
P lên mặt phẳng Oxy và z là cao độ của P. 3.3 Tính
x = r.cosϕ tích phân r.sinϕ bội ba trong hệ tọa độ
Giả sử P có tọa độ (x,y,z) trong Oxyz, ta có biến đổi y =
(x2 + y2 = r2) z = z r ≥ 0 ; 0
≤ ϕ ≤ 2 π | J | = r V Oxyz Orϕz
V = { ( r,ϕ,z ) | ϕ ≤ ϕ ≤ ϕ
( ϕ ) ≤ r ≤ ϕ
( r cos ϕ,r sin ϕ ) ≤ z ≤ f ( r cos ϕ,r sin ϕ ) } 1 2 ,r 1 2 ,f 1 2 ϕ r f 2 2 ( ϕ )
2 ( r cos ϕ,r sin ϕ ) f
( x,y,z ) dxdydz = dϕ dr
f ( r cos ϕ,r sin ϕ,z ) rdz ϕ 1 r 1 ( ϕ )
f 1 ( r cos ϕ,r sin ϕ ) V cầu
▶ Xét tọa độ của một điểm P trong hệ tọa độ cầu là (r,ϕ,θ), trong đó r = |OP|, ϕ là góc như trong tọa
độ trụ, và θ là góc tạo bởi tia Oz và tia OP. Khi đó ta có công thức chuyển đổi giữa tọa độ Descartes và
x = r.sinθ.cosϕ tọa độ cầu: y =
r.sinθ.sinϕ z = r.cosθ 2 2 2
Trong đó: r ≥ 0,
0 ≤ θ ≤ π,
0 ≤ ϕ ≤ 2π và
x + y + z = r2 14 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
J = − r 2 sin θ V
V = { ( r,θ,ϕ ) | a ≤ r ≤ b,θ ≤ θ ≤ θ 1
2 ,α ≤ ϕ ≤ β } β θ b 2 f 2
( x,y,z ) dxdydz = dϕ dθ
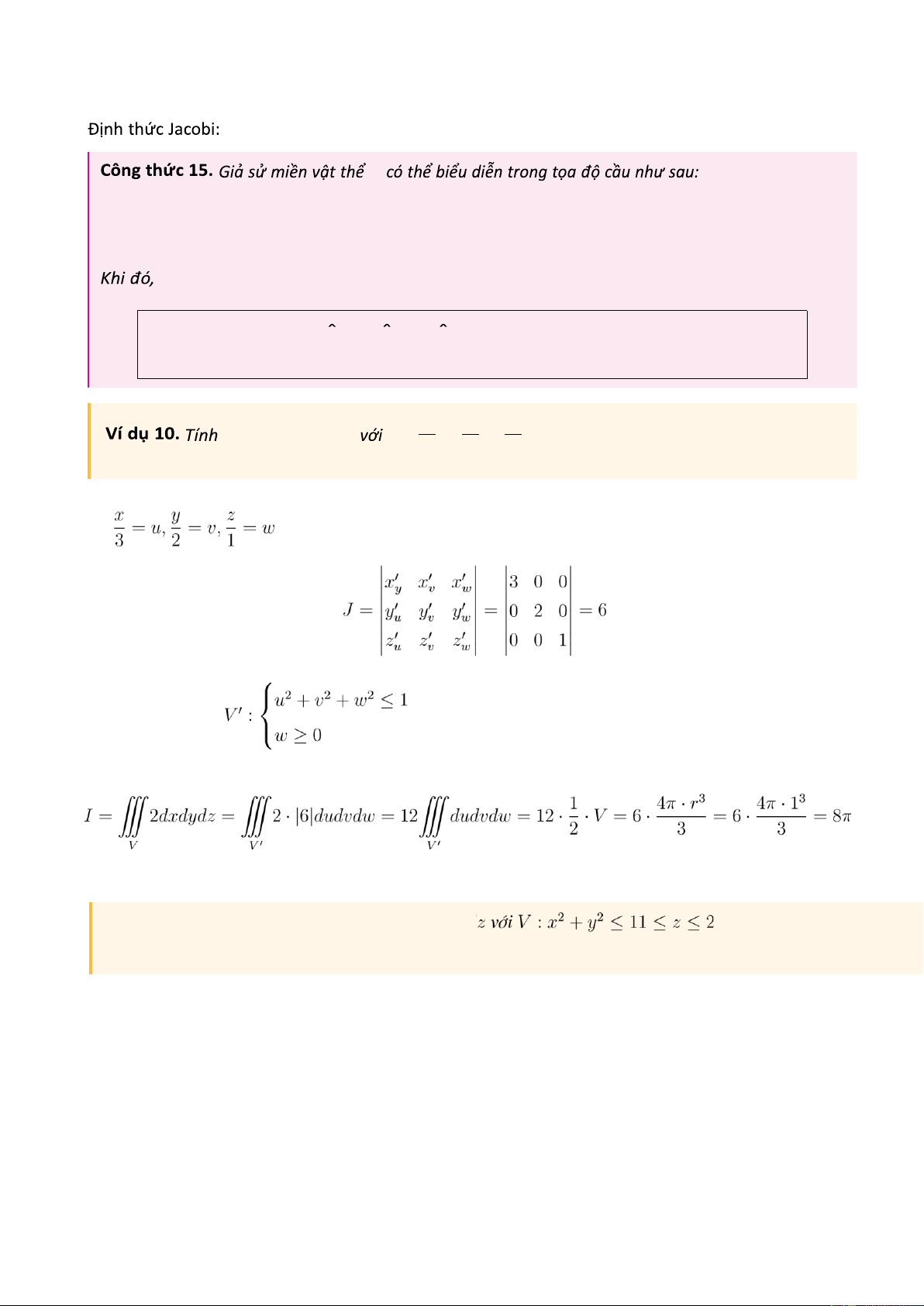
f ( r sin θ cos ϕ,r sin θ sin ϕ,r cos θ ) r sin θdr α θ 1 a V x y z 2 2 2 I = 2 dxdydz V : + + ≤ 9 1 ,z ≥ 0 4 1 V
[Hướng dẫn giải] Đặt
. Ta có x = 3u,y = 2v,z = w. Ta có Miền V trở thành Do đó, ta có :
( V ′ là mặt cầu bán kính bằng r = 1).
Ví dụ 11. Tính
[Hướng dẫn giải] 15 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập . Khi đó, ta có : Đặt
Ví dụ 12. Tính .
[Hướng dẫn giải]
Đặt x = ar sinθ cosϕy = br sinθ sinϕz = cr cosθ ⇒ |J| = abcr2 sinθ. Ta có . Đặt . Suy ra: 4
Ứng dụng của tích phân bội ba:
f ( x,y,z ) = 1
( x,y,z ) ∈ V . Khi đó, thể tích khối V V = dxdydz V 16 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
V trong không gian Oxyz ρ ( x,y,z ) m =
ρ ( x,y,z ) dxdydz V 17