Chương 2: Tín hiệu và Hệ thống liên tục trong miền thời gian CHƯƠNG 2
TÍN HIỆU VÀ HỆ THỐNG LIÊN TỤC
TRONG MIỀN THỜI GIAN (p2) 4.
PHAÂN TÍCH TÖÔNG QUAN TÍN HIEÄU 4.1. Heä soá töông quan
Tín hieäu coù theå ñöôïc bieåu dieãn nhö moät vectô trong moät khoâng gian metric thích hôïp
ñöôïc goïi laø khoâng gian tín hieäu. Ñeå so saùnh hai tín hieäu ngöôøi ta thöôøng xaùc ñònh
khoaûng caùch d( x , x ) giöõa chuùng, ñoù laø möùc ñoä khaùc nhahu giöõa hai tín hieäu, noù seõ 1 2
baèng khoâng neáu hai tín hieäu hoaøn toaøn gioáng nhau. Khoaûng caùch Ôcôlic cuûa hai tín
hieäu x ( )t vaø x (t) , xeùt trong khoaûng thôøi gian T ñöôïc xaùc ñònh theo coâng thöùc: 1 2 1 2 ö ö 2
d (x , x ) ý ÷ K x (t )  x (t )  dt 1 2 1 2 ÷ ÷÷ ø T ø
Coù theå thaáy raèng, naêng löôïng cuûa tín hieäu trong khoâng gian L2(0,T) coù khaùi nieäm töông
töï nhö bình phöông khoaûng caùch trong khoâng gian Rn. Do ñoù 2
d ( x , x ) ñöôïc hieåu laø 1 2
naêng löôïng cuûa tín hieäu, ñöôïc xaùc ñònh nhö sau: 
E ý d 2 (x , x ) ý
x t()  x t() *( ) *  ( )  y 1 2 1 2 x t x t 1 2 dt  2 2    ý x t ( ) dt  Re x t ( )x * t ( )dt  x t ( ) dt    1 1 2 2   
Naêng löôïng cuûa tín hieäu E phuï thuoäc vaøo tích voâ höôùng giöõa x (t) vaø x (t ), coù yù nghóa y 1 2
laø khoaûng caùch giöõa hai tín hieäu seõ cöïc ñaïi neáu tích voâ höôùng cuûa noù baèng khoâng
( x ( )t vaø x (t) tröïc giao), vaø cöïc tieåu (baèng khoâng) neáu x ( )t = x (t) . 1 2 1 2
Ngöôøi ta ñònh nghóa heä soá töông quan giöõa hai tín hieäu x , x laø tæ soá sau: 1 2  x t x t dt  1( ) 2( )  ( x x 1 , 2 )  ý ý (2.39) 12  2 ( x , x ) x (t) 1 1 dt  1 
Vaø heä soá töông quan giöõa hai tín hieäu x (t) vaø x ( )t : 2 1  *
x (t )x (t )dt  2 1 (x , x )  2 1  ý ý (2.40) 21  2 øx , x 2 2 ù x (t) dt  2 
Taát nhieân caùc tích voâ höôùng treân ñöôïc xaùc ñònh trong khoâng gian 2 L ( , 0 T ). www.hcmute.edu.vn 1
Chương 2: Tín hiệu và Hệ thống liên tục trong miền thời gian
Neáu  ý  ý 0 thì caùc tín hieäu x , x laø tröïc giao vaø ta coù naêng löôïng toång cuûa hai 12 21 1 2
tín hieäu baèng toång naêng löôïng cuûa töøng tín hieäu. Caùc heä soá  vaø  trong tröôøng hôïp 12 21
chung khoâng baèng nhau (   ). 12 21
Ngoaøi ra heä soá töông quan chuaån hoùa giöõa hai tín hieäu x , x coøn ñöôïc ñònh nghóa: 1 2 øx x x x 1, 2 ù ( 2, 1)  ý  . ý (2.41) 12 21
(x , x )(x , x ) 1 1 2 2
Coù theå thaáy raèng  laø moät soá thöïc coù giaù trò trong khoaûng 0 (    ) 1 . 4.2. Haøm töông quan
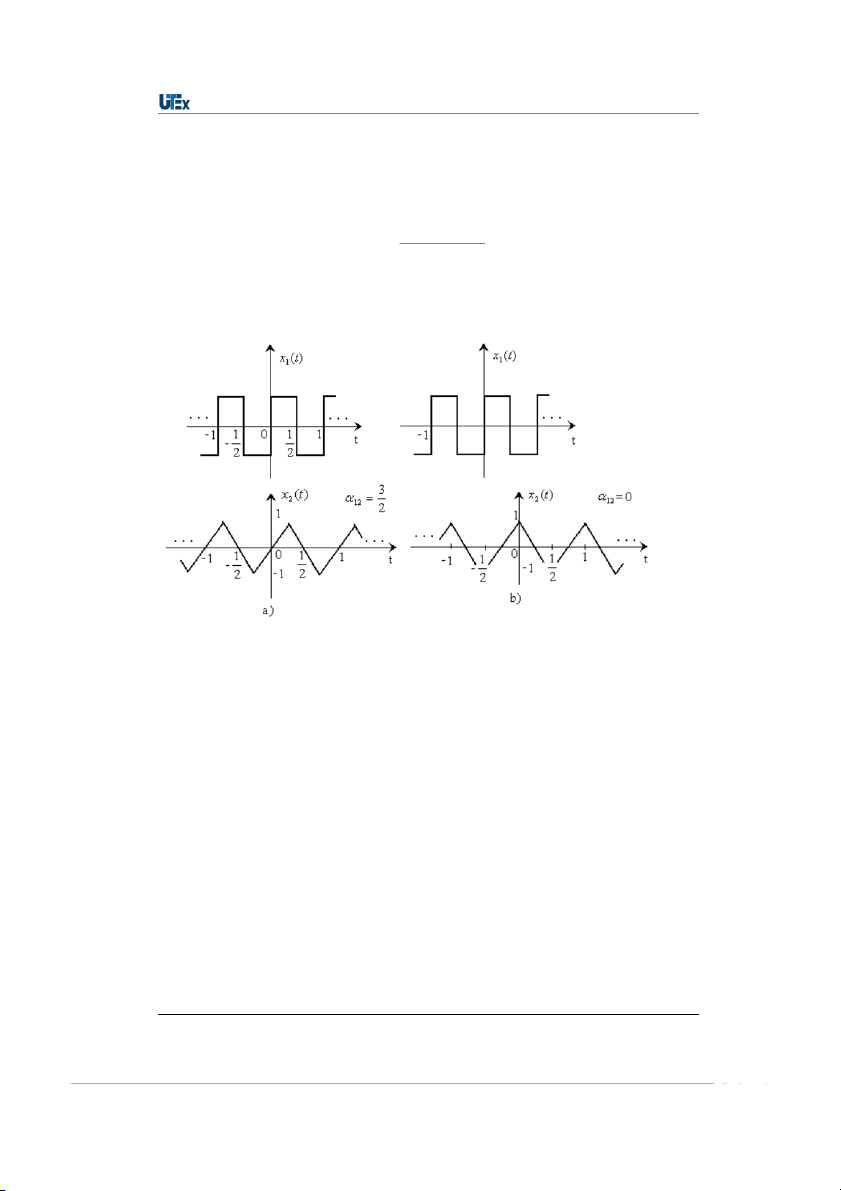
Hình 2.21: Söï phuï thuoäc cuûa heä soá töông quan  vaøo söï dòch chuyeån cuûa tín hieäu 12
Heä soá töông quan giöõa hai tín hieäu bieåi thò vò trí cuûa hai tín hieäu trong khoâng gian töông
öùng. Tuy nhieân, khi moät trong hai tín hieäu dòch chuyeån treân thang thôøi gian thì tích voâ
höôùng cuûa chuùng seõ thay ñoåi theo söï dòch chuyeån ñoù.
Neáu ta kí hieäu ñoä dòch chuyeån treân thang thôøi gian laø  , thì tích voâ höôùng giöõa hai tín
hieäu x , x seõ laø haøm cuûa  . Ñeå tieän lôïi cho vieäc so saùnh tín hieäu trong khoâng gian cuûa 1 2
noù ngöôøi ta ñöa ra khaùi nieäm veà haøm töông quan. 4.2.1.
Tín hieäu naêng löôïng höõu haïn
Haøm töông quan trong khoâng gian 2 L , 0
( T ) cuûa tín hieäu naêng löôïng ñöôïc kí hieäu laø  ,
noù ñöôïc xaùc ñònh bôûi tích voâ höôùng cuûa hai tín hieäu khi moät trong chuùng dòch chuyeån treân thang thôøi gian. 
 () ý x t()x* t(  d ) t (2.42) 12  1 2  
 ( ) ý x t()x* t(  dt (2.43) 21  ) 2 1  www.hcmute.edu.vn 2
Chương 2: Tín hiệu và Hệ thống liên tục trong miền thời gian
Caùc haøm  (), () coøn ñöôïc goïi laø haøm töông quan cheùo. Coù theå thaáy giaù trò cuûa 12 21
chuùng laø dieän tích giôùi haïn döôùi ñoà thò tích cuûa hai tín hieäu.
Ngoaøi ra, coøn coù khaùi nieäm veà haøm töï töông quan cuûa tín hieäu x(t) nhö sau: 
 () ý x(t) x* (t )dt  (2.44) xx 
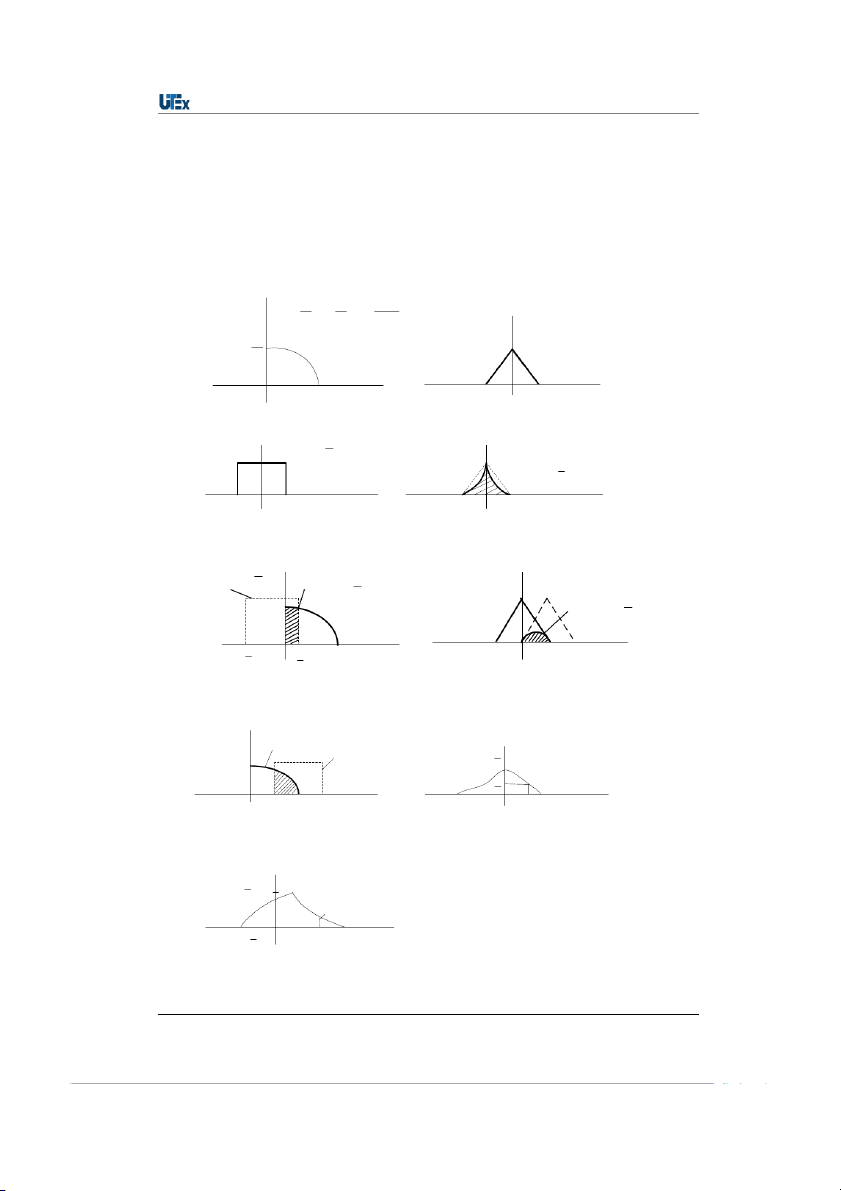
Caùch xaùc ñònh caùc haøm töông quan vaø haøm töï töông quan ñuôïc minh hoïa qua ví duï treân hình 2.22    ö t  ö x t t 1 ( ) ý cos  1 ÷ ÷ 4 4 ø 2 ø
 x(t) ý (t)  4 t   -1 1 2 4 -2 -1 0 1 2 3 ö t ö  x (t ) ý   ÷ ÷  ý 0 2 1 ø 2 ø 1 2 S ý  ) 0 ( ý 3 t t   -2 -1 0 1 2 3 4 -3 -2 -1 0 1 2 3 4 ö 1 ö x ÷ t  ÷  1  2 ö ö  ý 1 ø 2ø S ý  ÷  ÷ 12 ø 2 ø 1 x(t  ) 1 1 S ý  ) 1 ( ý 6  3  -2  -1 0 1 1 2 3 4 t -3 -2 -1 0 1 2 3 t 2 2  S ý  (2)  1 12 x (t  ) 2 2  ( ) 2 3  t 1  6  -2 -1 0 1 2 3 4 -3 -2 -1 0 1 2 3 5   (2) ö 1 ö 12  ÷ ÷ 12 1 ø 2 ø  () 12   -2 -1 1 0 2 3 4 1  2
Hình 2.22: Haøm töông quan vaø töï töông quan cuûa tín hieäu naêng löôïng www.hcmute.edu.vn 3
Chương 2: Tín hiệu và Hệ thống liên tục trong miền thời gian
Coù theå thaáy raèng, giaù trò cuûa haøm   seõ khoâng thay ñoåi khi x dòch sang phaûi moät 12 ( ) 2
ñoaïn  vaø ñöùng yeân, hoaëc khi x ñöùng yeân vaø x dòch sang traùi moät ñoaïn  . 2 1
Do ñoù haøm töông quan (2.42), (2.43) vaø haøm töï töông quan (2.44) coù theå vieát laïi döôùi daïng: 
 ( ) ý x t(  )x* t()dt  (2.45) 12 1 22  
 ( ) ý x t(  )x* t()dt  (2.46) 21 2 1    ( ) ý x t (  )x*  t ( )dt  (2.47) xx 
Caùc haøm töông quan cuõng coù theå kí hieäu laø  ( ), ( ), vaø haøm töï töông quan laø xy yx  ( ) . xx 
Caùc tính chaát quan troïng cuûa haøm töông quan vaø haøm töï töông quan:  Tính chaát 1: *   ý   ( ) ( ) xy yx (2.55)  Tính chaát 2:     ( )d ý x t ( ) y* t (  )dtd ý  xy       
ý [x(t) y* t
(   )d d ] t ý x t ( )dt y* t ( )dt     (2.56)    
Coù theå suy ra töø (2.56) laø dieän tích döôùi ñoà thò cuûa haøm töông quan baèng tích caùc dieän
tích döôùi ñoà thò cuûa moãi tín hieäu.  Tính chaát 3:  ( ) * ý  (   ) (2.57) xx xx
Haøm töông quan laø haøm Hermit. Vôùi tín hieäu thöïc, haøm töï töông quan laø haøm chaün.  Tính chaát 4: 2   ( ) 0 ý x t ( ) dt  (2.58)   Tính chaát 5: www.hcmute.edu.vn 4
Chương 2: Tín hiệu và Hệ thống liên tục trong miền thời gian      * 2 2
 ( )d ý x(t) x (t)dt ý [ Re x(t)dt]  [ I x(t)dt]      (2.59) xx m     
Vôùi tín hieäu thöïc dieän tích döôùi ñoà thò cuûa haøm töï töông quan baèng bình phöông dieän
tích döôùi ñoà thò cuûa tín hieäu.  Tính chaát 6:
Vôùi moïi giaù trò cuûa ta luoân coù:  ( )  0 ( ) (2.60) xx xx 4.2.2.
Tín hieäu coâng suaát trung bình höõu haïn a) Tín hieäu tuaàn hoaøn 2 L T
Haøm töông quan cuûa tín hieäu tuaàn hoaøn ta kí hieäu baèng chöõ () vaø ñöôïc ñònh nghóa nhö sau: T T 1 * 1  () ý
x(t) y (t   d ) t ý
x(t   ) y* (t) dt   (2.61a) xy T T 0 0 T T 1 * 1  ( )ý
y(t) x (t  d ) t ý
y(t  )x ( * t)dt   (2.61b) yx T T 0 0 T T 1 * 1  ( ) ý
x(t) x (t  d ) t ý x t (  x ) * t ( d ) t   (2.61c) xx T T 0 0 
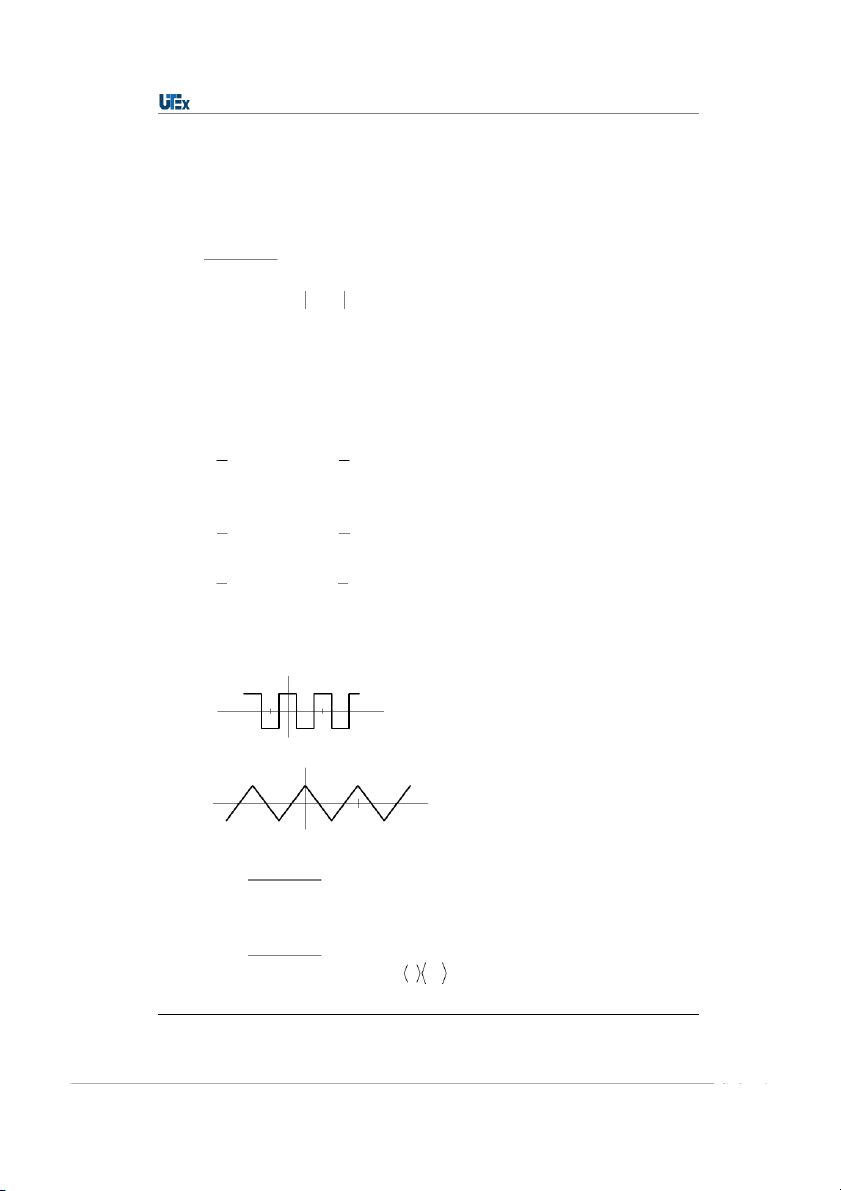
Caùc tính chaát cuûa haøm töông quan vaø töï töông quan cuûa tín hieäu tuaàn hoaøn.  x(t) 1 ... ... -T 0 T t   ( ) x 1 ... ... 0 T  Hình 2.23  Tính chaát 1:  ( ) * ý (   ) (2.62) xy yx  Tính chaát 2: * ü   (2.63) xy ( ) x y www.hcmute.edu.vn 5
Chương 2: Tín hiệu và Hệ thống liên tục trong miền thời gian  Tính chaát 3:  ( x  ) * ý (2.64) xx (   )  Tính chaát 4:  (0 ý 2 ) x ý P (2.65) xx x 
Tính chaát 5: Neáu tín hieäu x laø thöïc 2  ý x (2.66)  Tính chaát 6:  ( )  0 ( ) (2.67) xx xx b)
Tín hieäu khoâng tuaàn hoaøn
Trong khoâng gian cuûa tín hieäu coâng suaát trung bình höõu haïn khoâng coù khaùi nieäm veà tích
voâ höôùng. Tuy nhieân, ñoái vôùi moät soá tín hieäu cuûa khoâng gian naøy, vaãn toàn taïi caùc giôùi
haïn theo ñònh nghóa thoâng thöôøng. Vôùi nhöõng tín hieäu nhö vaäy, ngöôøi ta cuõng coù theå
ñònh nghóa caùc haøm töông quan nhö sau: T T  () ý 1 1 lim
x( t) y*( t  ) dt ý lim x t (   )y * t ( d ) t (2.68) xy T   T   T 2  T 2 T T T T  ( ) ý 1 1 lim
y( t) x*( t ) dt ý lim y t (   x ) * t ( d ) t (2.69) yx T   T   T 2  T 2 T T T T  ( ) ý 1 1 lim
x( t) x*( t  ) dt ý lim x t (  x ) * t ( d ) t (2.70) xx T   T   T 2  T 2 T T www.hcmute.edu.vn 6