Chương 3. Bài 5: Giá trị lớn nhất | Giáo án điện tử môn Toán 10 | Kết nối tri thức với cuộc sống
Giáo án PowerPoint Toán 10 Kết nối tri thức với cuộc sống là tài liệu cực kì hữu ích mà muốn giới thiệu đến quý thầy cô tham khảo. Bài giảng điện tử môn Toán 10 Kết nối tri thức bao gồm đầy đủ các bài giảng trong cả năm học được thiết kế dưới dạng file trình chiếu PowerPoint với nhiều hiệu ứng rất đẹp mắt. Với nội dung bài học trình bày chi tiết cho từng phần học và bám sát chương trình SGK Toán 10 Kết nối tri thức.
Chủ đề: Giáo án Toán 10
Môn: Toán 10
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Preview text:
CHƯƠNG III. HỆ T C H H Ứ Ư C Ơ L N Ư G Ợ N I G TRONG TAM GIÁC TOÁN HÌNH ➉ 5
GIÁ TRỊ LƯỢNG GIÁC CỦA
MỘT GÓC TỪ 00 ĐẾN 1800 1
GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC 2
MỐI QUAN HỆ GIỮA GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC BÙ NHAU 3 BÀI TẬP THUẬT NGỮ
KIẾN THỨC, KĨ NĂNG
• Giá trị lượng giác của một góc.
Nhận biết giác trị lượng giác của một góc từ ∘ đến ∘. • Hai góc bù nhau.
Giải thích hệ thức liên hệ giữa các giá trị lượng giác của
hai góc phụ nhau, bù nhau.
Sử dụng máy tính cầm tay để tính các giá trị lượng giác của một góc.
• Vận dụng giải một số bài toán có nội dung thực tiễn. = cos = Bạn đã biết tỉ số lượng giác của một góc nhọn. Đối với góc tù thì sao? = cot = B α
Nhắc lại định nghĩa a
tỉ số lượng giác c của góc nhọn? A C b Hình 3.1
1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC
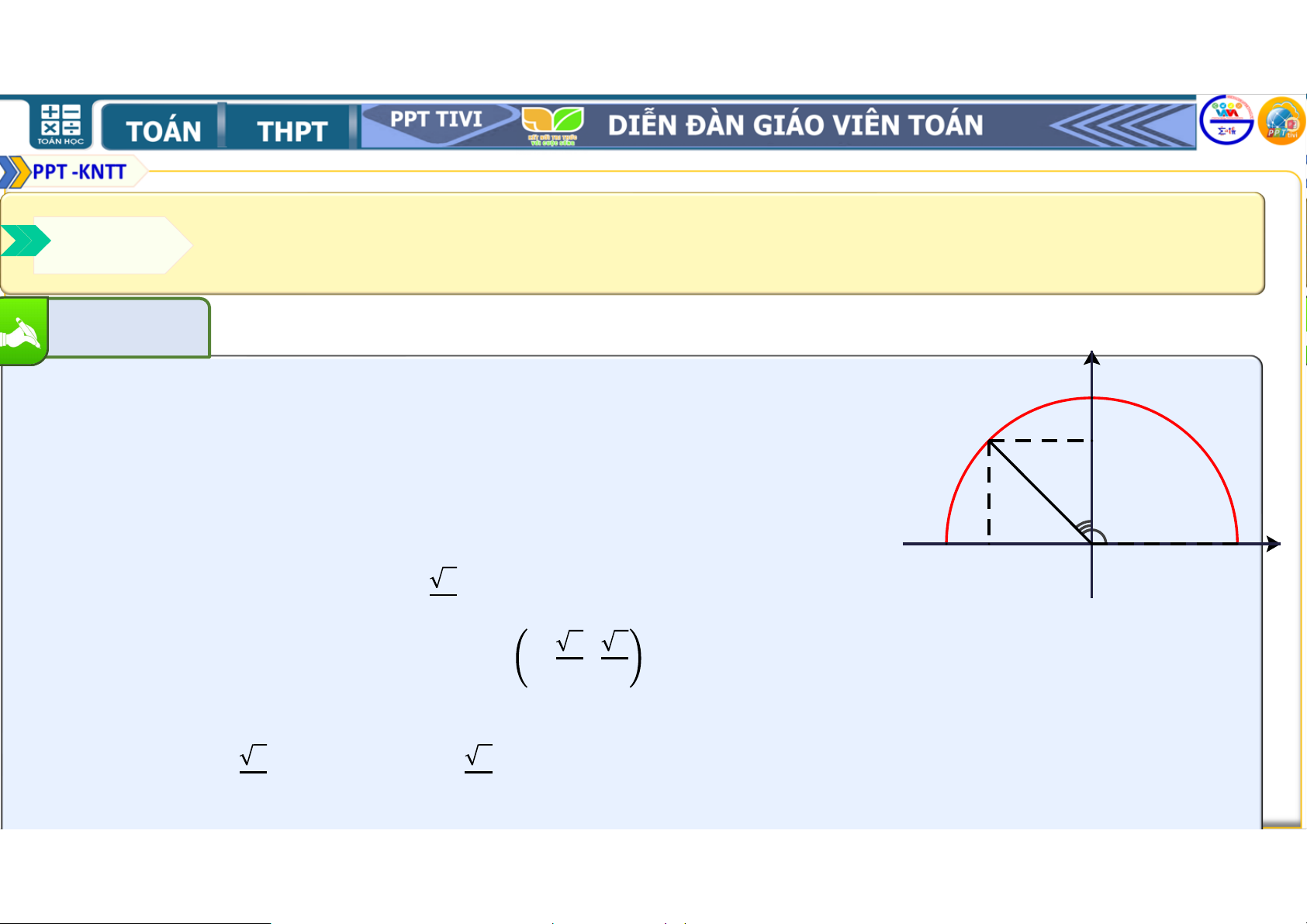
• Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O, bán kính = nằm
phía trên trục hoành (H.3.2) được gọi là nửa đường tròn đơn vị.
• Cho trước một góc , ∘ ≤ ≤
∘. Khi đó, có duy nhất điểm ( ; ) trên
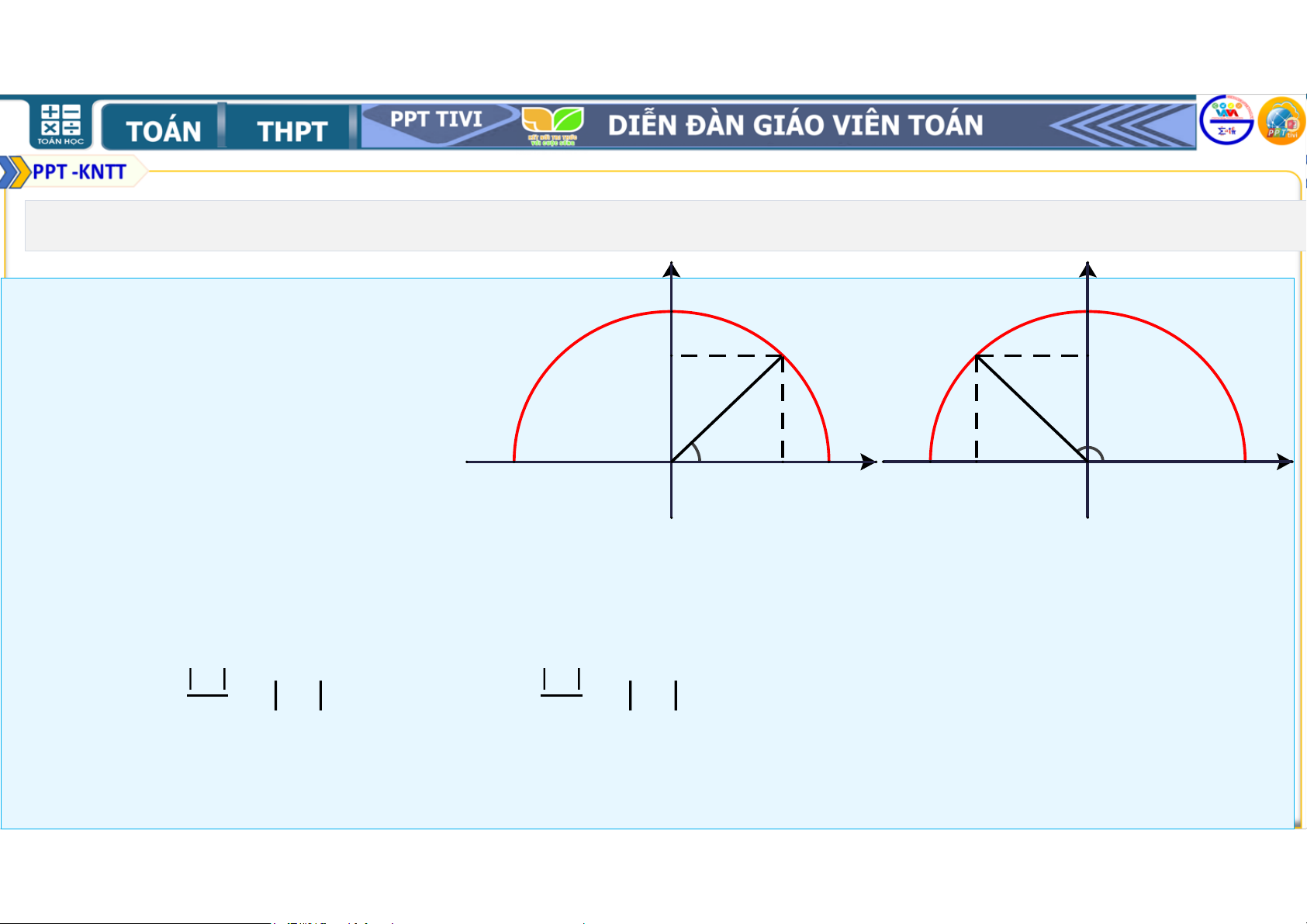
nửa đường tròn đơn vị nói trên để = . y y HĐ1: C 1 1 C M M y y 0 0
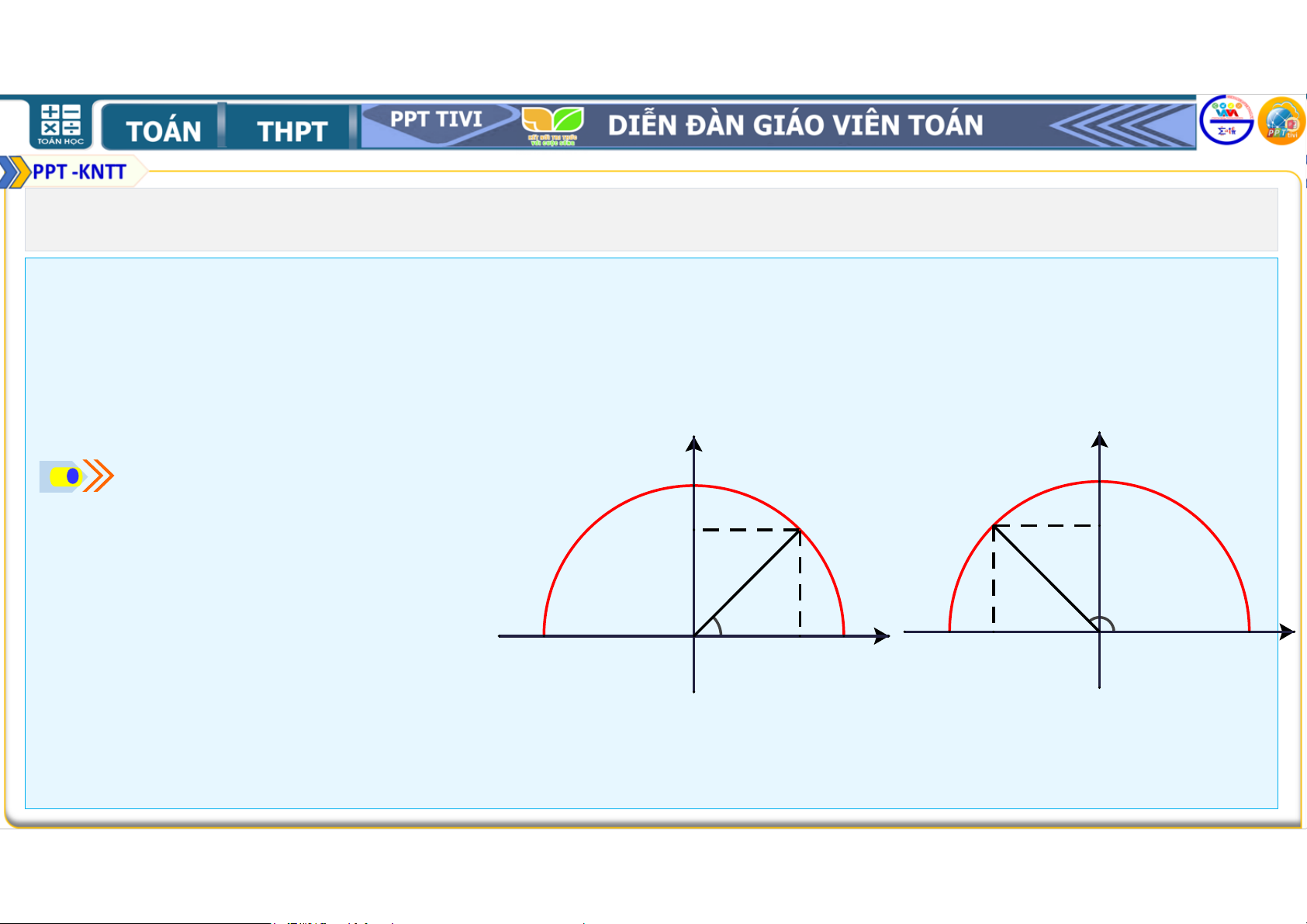
a) Nêu nhận xét về vị trí
của điểm M trên nửa đường
tròn đơn vị trong mỗi B B α α A A trường hợp sau: -1 O x x -1 O 1 x 0 1 x 0 = ∘; < ∘; > ∘. α < 90o α > 90o b) Khi ∘ < <
∘, nêu mối quan hệ giữa ,
với hoành độ và tung độ của điểm .
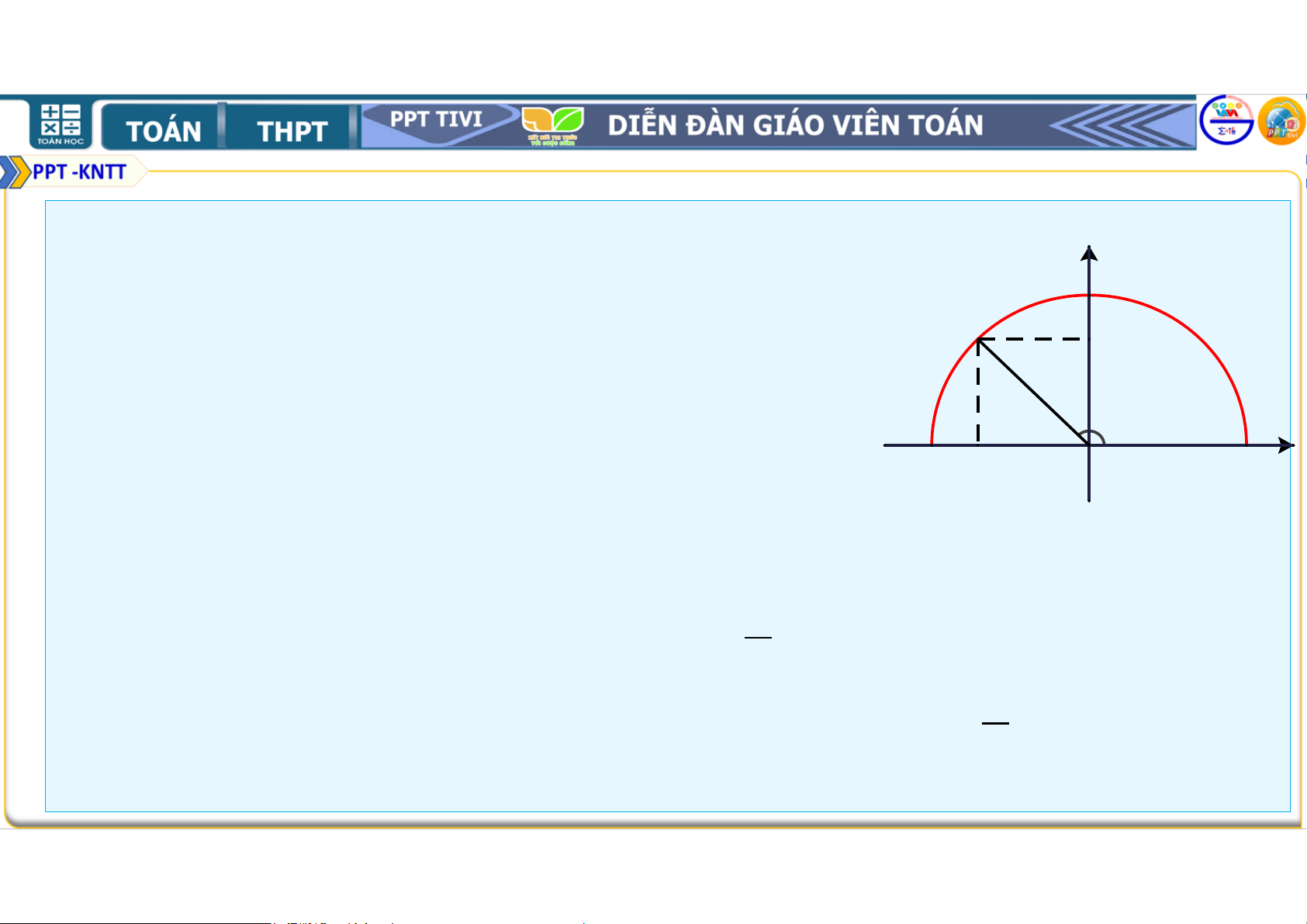
1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC y y C 1 1 C M M y0 y0 a) Khi = ∘, điểm trùng với điểm . (Vì = = ∘); B α A α B A -1 O x0 1 x x -1 0 O 1 x α < 90o α > 90o • Khi < ∘, điểm thuộc vào cung
(bên phải trục tung); • Khi > ∘, điểm
thuộc vào cung (bên trái trục tung). b) cos = = = ; = = = . Vì = = , thuộc tia nên > ; thuộc tia nên >
Vậy cos là hoành độ của của điểm , là tung độ của điểm .
• => Mở rộng khái niệm tỉ số lượng giác của một góc nhọn cho một góc bất
kì từ ∘ đến
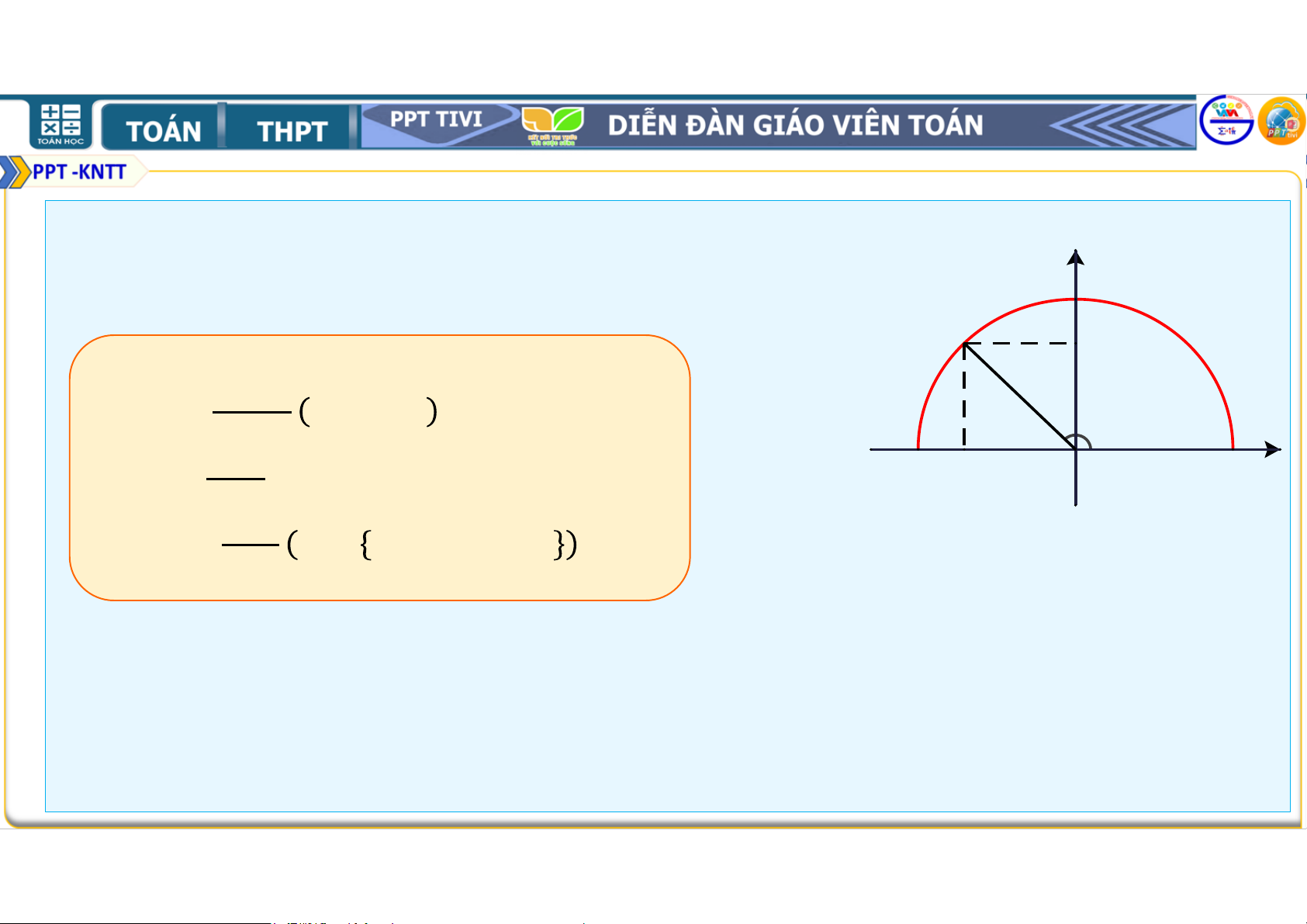
∘, ta có định nghĩa sau: y 1 C
Với mỗi góc ( ∘ ≤ ≤ ∘), gọi ( ; ) là M y0
điểm trên nửa đường tròn đơn vị sao cho = . Khi đó: α B A sin của góc là tung độ của điểm , x -1 0 O 1 x được kí hiệu là ; α > 90o Côsin của góc là hoành độ của điểm , được kí hiệu là ; Khi ≠ ∘ (hay là ≠ ), tang của
là , được kí hiệu là ; Khi ≠ ∘ và ≠ ∘ (hay là ≠ ), côtang của
là , được kí hiệu là . y
Từ định nghĩa trên, ta có: 1 C M y0 = ≠ ∘ ; α B A x -1 0 O 1 x = ( ≠ ∘và ≠ ∘); α > 90o = ∉ ∘; ∘; ∘
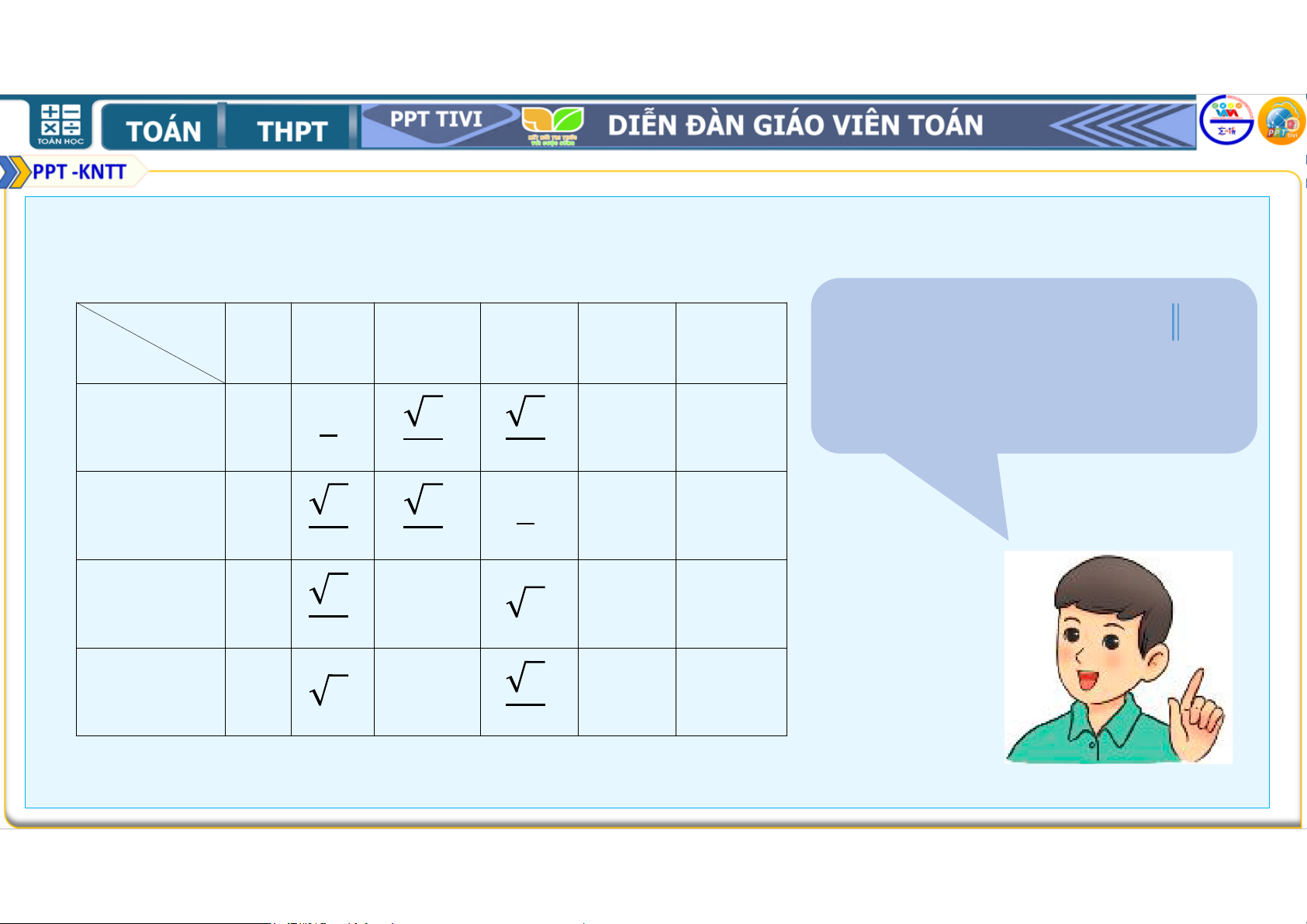
Sau đây là bảng giá trị lượng giác (GTLG) của một số góc
đặc biệt mà em nên nhớ. ,
Trong bảng, kí hiệu chỉ 180∘ 90∘ 60∘ 45∘ 30∘ 0∘ GTLG
giá trị lượng giác tương 1 2 3
ứng không xác định. ./0 , 0 1 0 2 2 2 3 2 1 cos, 1 0 −1 2 2 2 3 670 , 0 1 3 || 0 3 3 896 , || 3 1 0 || 3 Bảng 3.1 Ví dụ 1.
Tìm các giá trị lượng giác của góc :;∘. Bài giải y Gọi
là điểm trên nửa đường tròn đơn vị sao cho 1
= :;∘. Gọi <, > tương ứng là hình chiếu vuông M P góc của lên các trục , . 45o Vì = :;∘ nên < = ?;∘,
> = ?;∘. Vậy các tam 135o giác <,
> là vuông cân với cạnh huyền = . -1 N O 1 x Từ đó, ta có @ < = > = . Mặt khác, điểm nằm bên @ Hình 3.3
trái trục tung nên có tọa độ là @ @ − ; . @ @
Theo định nghĩa, ta có: @ @ :;∘ =
; cos135∘ = − ; :;∘ = − ; :;∘ = − . @ @ Luyện tập 1.
Tìm các giá trị lượng giác của góc @ ∘. Bài giải Gọi
là điểm trên nửa đường tròn đơn vị sao cho y 1
= @ ∘. Gọi <, > tương ứng là hình chiếu vuông góc của lên các trục M , . P Vì = @ ∘ nên < = A ∘, < = : ∘. Vậy < là 120o
đường cao của tam giác đều Q B có cạnh bằng 1. -1 N O 1 x Từ đó, ta có : < =
; < = . Mặt khác, điểm nằm bên @ @ Hình 3.4
trái trục tung nên có tọa độ là : − ; . @ @
Theo định nghĩa, ta có: : @ ∘ = ; cos120∘ = − ; @ ∘ = − :; @ ∘ = − . @ @ :
Ta có thể sử dụng máy tính cầm tay để tính (đúng hoặc
gần đúng) các giá trị lượng giác của một góc và tính góc
khi biết giá trị lượng giác của góc đó.
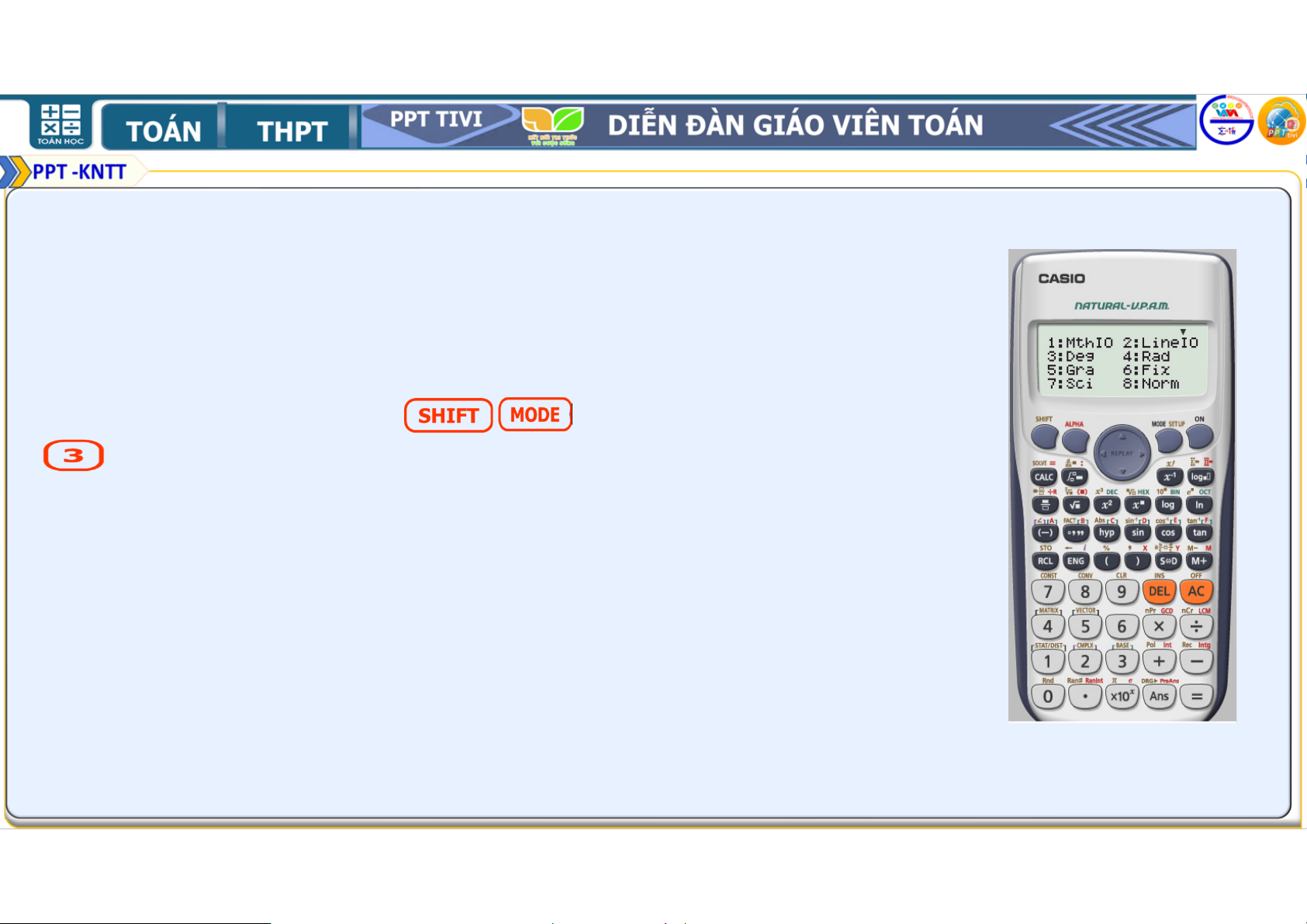
Chẳng hạn, với một loại máy tính cầm tay, sau khi mở máy ta cần bấm phím
(SETUP) rồi bấm phím
để chọn đơn vị đo góc là “độ”. Sau đó tính giá trị
lượng giác của góc hoặc tính góc khi biết giá trị lượng giác của góc đó.