CHƯƠNG III. C H H Ệ Ư TH Ơ Ứ N C G LƯ I ỢNG TRONG TAM GIÁC
§5. Giá trị lượng giác của một góc từ 00 đến 1800
§6. Hệ thức lượng trong tam giác
Bài tập cuối chương 3 CHƯƠNG III. HỆ T C H H Ứ Ư C Ơ L N Ư G Ợ N I G TRONG TAM GIÁC TOÁN ĐẠI SỐ 6
HỆ THỨC LƯỢNG TRONG TAM GIÁC ➉ 1 ĐỊNH LÍ CÔSIN 2 ĐỊNH LÍ SIN 3
GIẢI TAM GIÁC VÀ ỨNG DỤNG THỰC TẾ 4
CÔNG THỨC TÍNH DIỆN TÍCH TAM GIÁC 5 BÀI TẬP 6
BÀI TẬP TRẮC NGHIỆM 5 Ngắm Tháp Rùa từ bờ, chỉ với những dụng cụ đơn giản, dễ chuẩn bị, ta cũng có thể xác định được khoảng cách từ
vị trí ta đứng tới Tháp Rùa. Em có biết vì sao?
Tháp Rùa nằm trong lòng hồ Hoàn Kiếm ở Thủ đô Hà Nội 1. ĐỊNH LÍ CÔSIN HĐ1.
• c) Nếu sau khi đi được 2 giờ, tàu
chuyển sang hướng nam (thay vì
• Một tàu biển xuất phát từ cảng Vân
hướng đông nam) thì có thể dùng Định
Phong (Khánh Hòa) theo hướng đông với
lí Pythagore (Pi-ta-go) để tính chính
vận tốc 20 km/h. Sau khi đi được 1 giờ,
xác các số đo trong câu b hay không?
tàu chuyển sang hướng đông nam rồi giữ
nguyên vận tộc và đi tiếp.
• Đối với tam giác ta thường kí hiệu , ,
là các góc của tam giác tại đỉnh
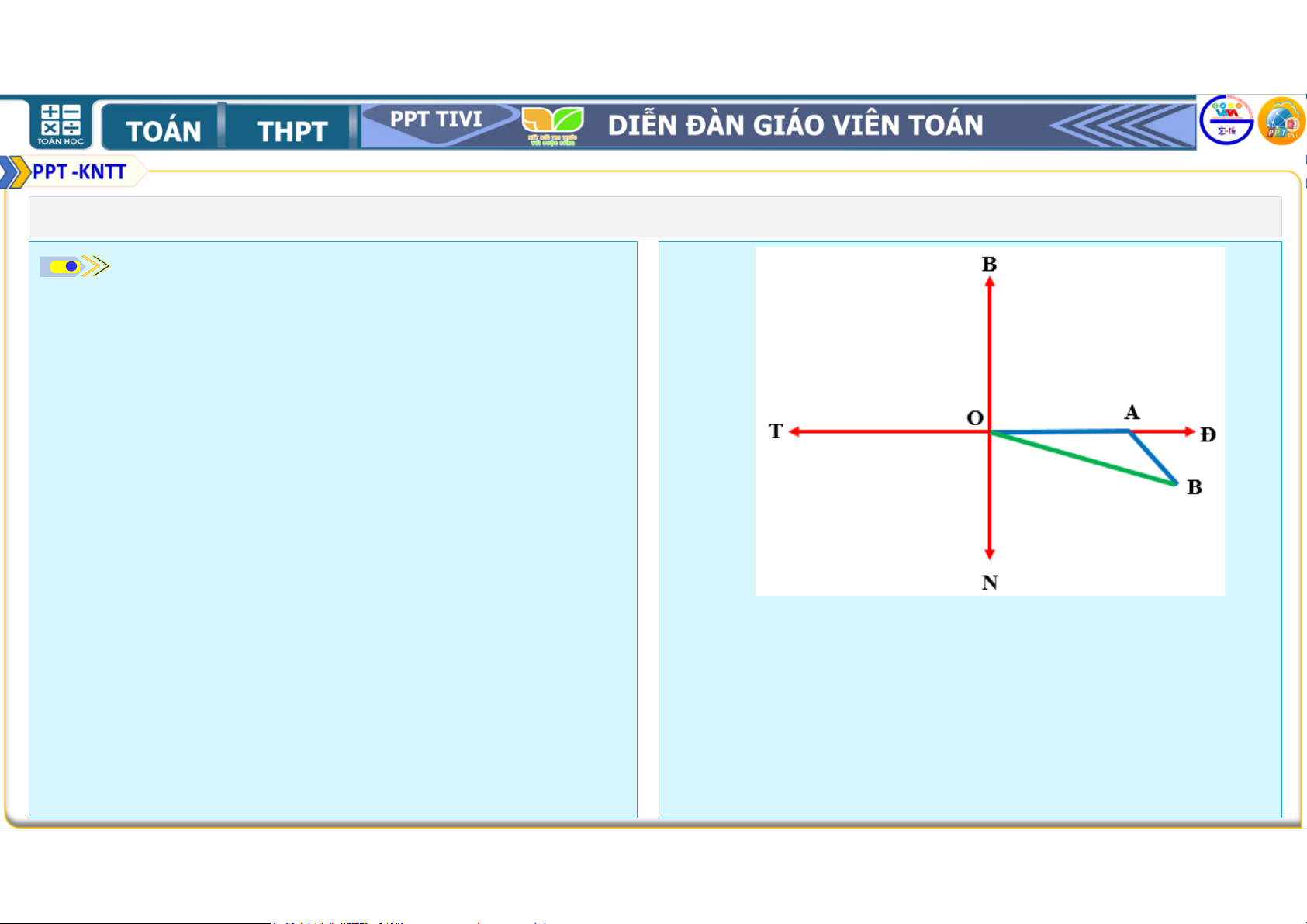
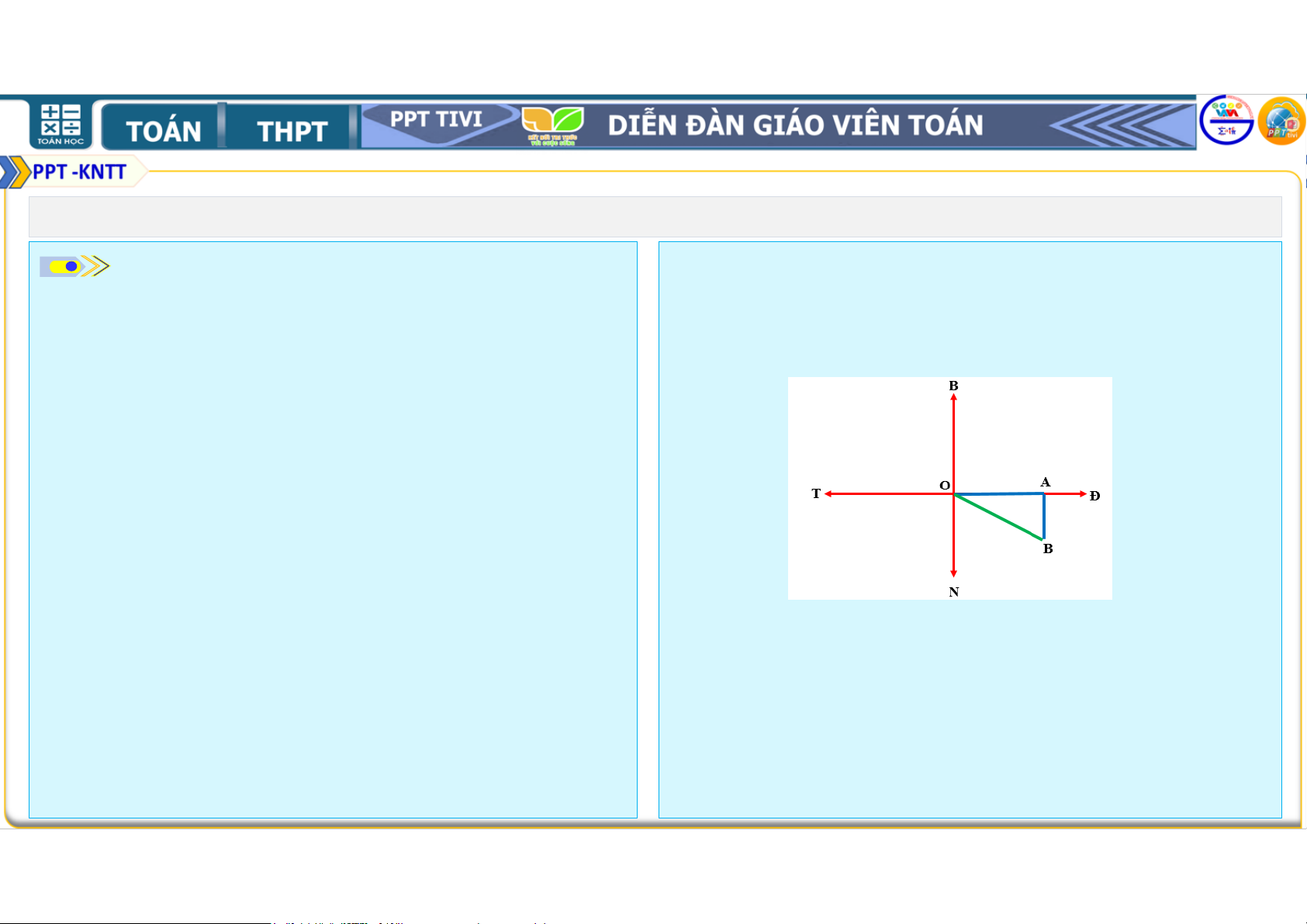
• a) Hãy vẽ sơ đồ đường đi của tàu trong
tương ứng; , , tương ứng là độ dài
1,5 giờ kể từ khi xuất phát (1 km trên
của các cạnh đối diện với đỉnh , , ;
thực tế ứng dụng với 1 cm trên bản vẽ).
là nữa chu vi; là diện tích; , tương
ứng là bán kính đường tròn ngoại tiếp,
• b) Hãy đo trực tiếp trên bản vẽ và cho biết nội tiếp tam giác.
sau 1,5 giờ kể từ khi xuất phát, tàu cách
cảng Vân Phong bao nhiêu kilômét (số đo gần đúng). 1. ĐỊNH LÍ CÔSIN HĐ1.
• Một tàu biển xuất phát từ cảng Vân
Phong (Khánh Hòa) theo hướng đông với
vận tốc 20 km/h. Sau khi đi được 1 giờ,
tàu chuyển sang hướng đông nam rồi giữ
nguyên vận tộc và đi tiếp.
• a) Hãy vẽ sơ đồ đường đi của tàu trong
1,5 giờ kể từ khi xuất phát (1 km trên
thực tế ứng dụng với 1 cm trên bản vẽ). • Lời giải
20.1 =20 (km) tương ứng với 20 cm trên sơ đồ.
a, Giả sử tàu biển xuất phát từ điểm O như
• Trong 0,5 giờ tiếp theo, tàu di chuyển từ A đến hình vẽ B với quãng
• Trong 1 giờ, tàu di chuyển từ O đến A với
• đường là: 20.0,5 = 10 (km) tương ứng với 10 quãng đường là: cm trên sơ đồ. 1. ĐỊNH LÍ CÔSIN HĐ1. Lời giải
• Một tàu biển xuất phát từ cảng Vân
Phong (Khánh Hòa) theo hướng đông với
vận tốc 20 km/h. Sau khi đi được 1 giờ,
tàu chuyển sang hướng đông nam rồi giữ
nguyên vận tộc và đi tiếp.
• a) Hãy vẽ sơ đồ đường đi của tàu trong
1,5 giờ kể từ khi xuất phát (1 km trên
thực tế ứng dụng với 1 cm trên bản vẽ).
• b) Hãy đo trực tiếp trên bản vẽ và cho biết
b) Trên sơ đồ, khoảng cách từ cảng
sau 1,5 giờ kể từ khi xuất phát, tàu cách
đến tàu là đoạn OB dài khoảng 28 cm.
cảng Vân Phong bao nhiêu kilômét (số đo gần đúng).
Do đó khoảng cách từ cảng đến tàu thực tế khoảng 28 km. 1. ĐỊNH LÍ CÔSIN HĐ1.
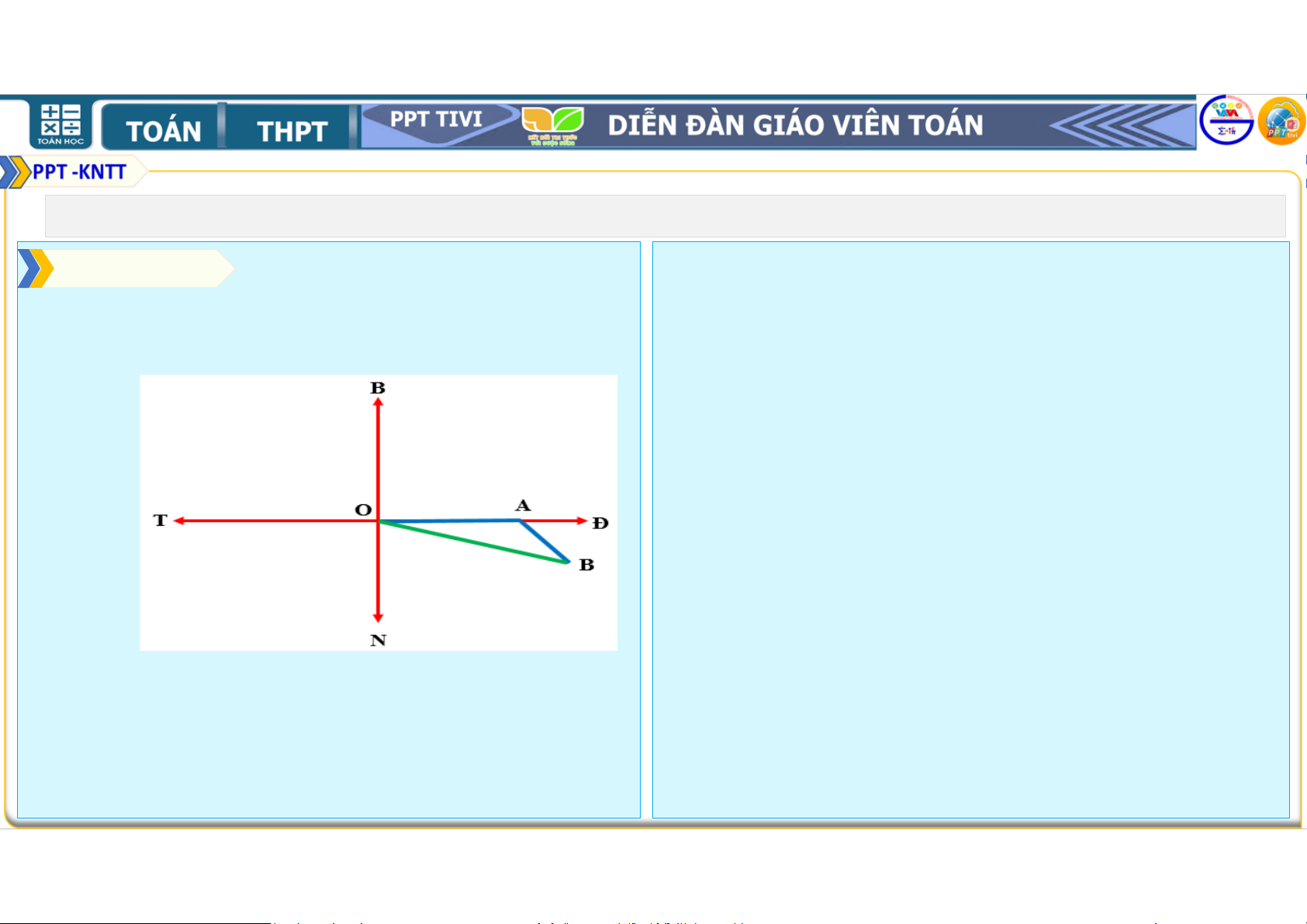
Sau 2 giờ đầu, tàu đi từ O đến A, với
• Một tàu biển xuất phát từ cảng Vân quãng đường là
Phong (Khánh Hòa) theo hướng đông với
20.2 = 40 (km) tương ứng 40 cm trên
vận tốc 20 km/h. Sau khi đi được 1 giờ, sơ đồ.
tàu chuyển sang hướng đông nam rồi giữ
Sau đó, tàu chuyển sang hướng nam, vị
nguyên vận tộc và đi tiếp.
trí của tàu là điểm B.
c) Nếu sau khi đi được 2 giờ, tàu chuyển
sang hướng nam (thay vì hướng đông
Khi đó ta có thể tính chính xác khoảng
nam) thì có thể dùng Định lí Pythagore
cách từ cảng đến
(Pi-ta-go) để tính chính xác các số đo
tàu, chính là đoạn OB (do tam giác
trong câu b hay không? OAB vuông tại A) Lời giải
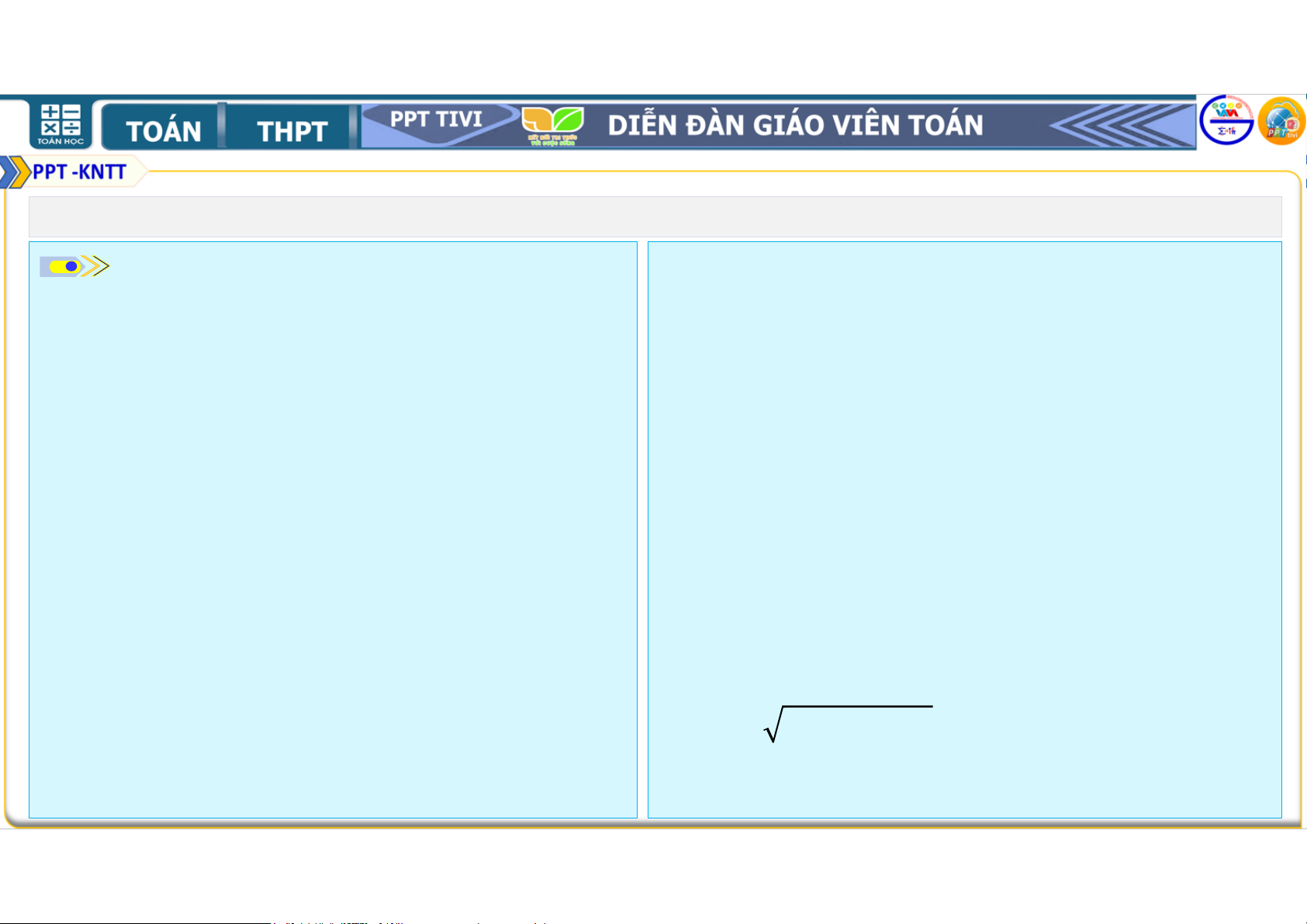
dựa vào định lí Pythagore:
c) Nếu sau khi đi được 2 giờ, tàu chuyển
sang hướng nam (thay vì hướng đông = + .
nam) thì sơ đồ đường đi của tàu như sau: 1. ĐỊNH LÍ CÔSIN HĐ2. Lời giải
• Trong hình 3.8, hãy thực hiện các a) Tam giác vuông :
bước sau để thiết lập công thức tính
theo , và giá trị lượng giác của góc = + . . b) = và a) Tính theo và . = + = + . . + b) Tính theo , và . ⇒ = + + c) Tính theo và . = + + . . d) Chứng minh = + . c) Tam giác vuông tại có : = ⇒ = .
d) Theo câu b) ta có : = + + . . = + + . . 1. ĐỊNH LÍ CÔSIN
d) Theo câu b) ta có : HĐ2.
• Trong hình 3.8, hãy thực hiện các = + + . . = + + . .
bước sau để thiết lập công thức
tính theo , và giá trị lượng giác • Chú ý. Người ta chứng minh được kết quả trong của góc .
HĐ2d đối với cả các trường hợp góc là góc vuông hoặc nhọn. a) Tính theo và .
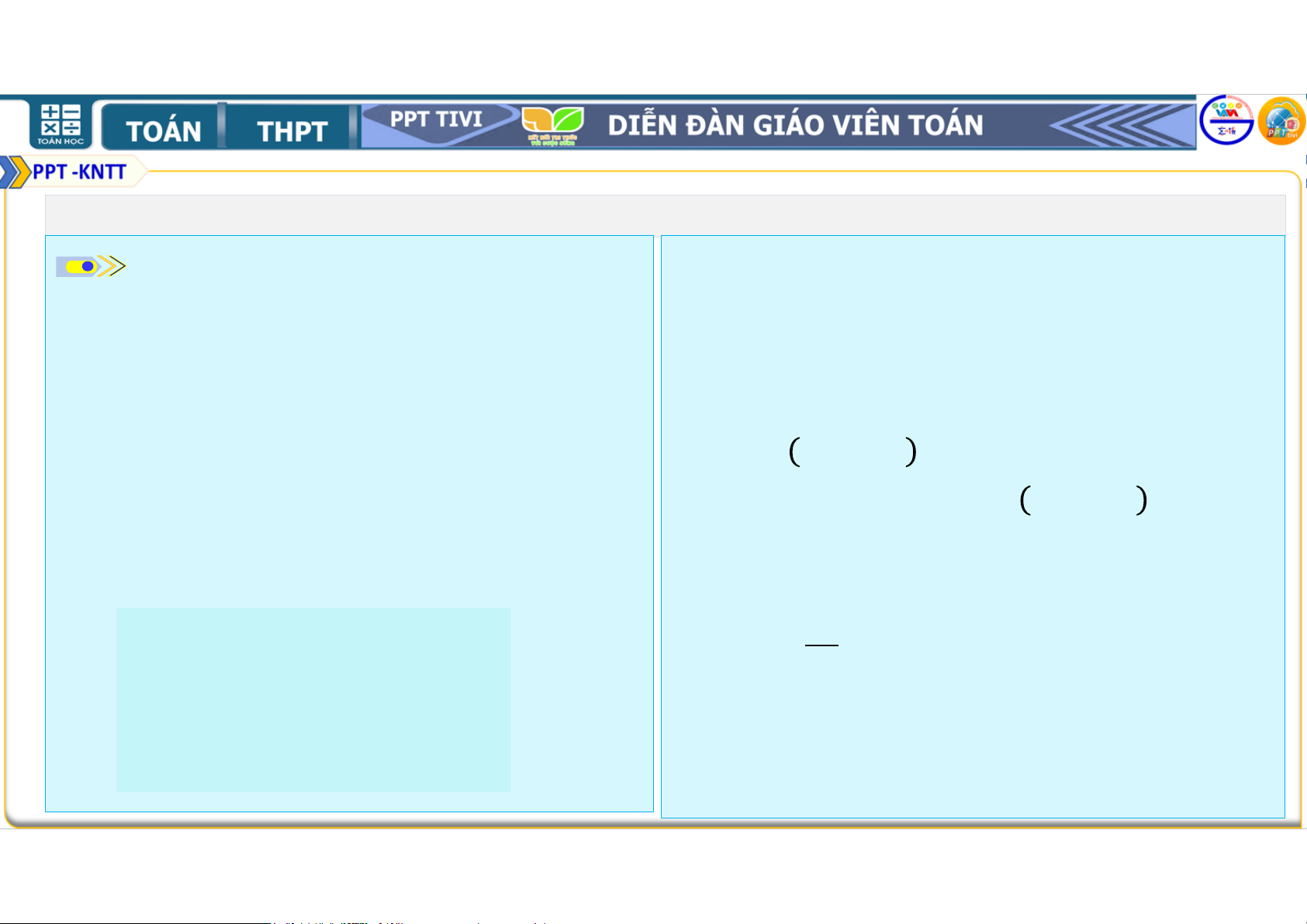
Định lí côsin. Trong tam giác : b) Tính theo , và . = + , c) Tính theo và . = + , d) CM: = + . = + . •
Định lí Pythagore có phải là một trường hợp đặc
biệt của Định lí côsin hay không? Lời giải
• Định lí Pythagore có phải là một trường hợp đặc
biệt của Định lí côsin bởi vì: • Khi = 90 ⇒ = 0: = ! + 1. ĐỊNH LÍ CÔSIN
• Chú ý. Người ta chứng minh được kết quả trong
HĐ2d đối với cả các trường hợp góc là góc vuông HĐ2.
hoặc nhọn. Định lí côsin. Trong tam giác :
• Trong hình 3.8, hãy thực hiện = + ,
các bước sau để thiết lập công = + ,
thức tính theo , và giá trị = + .
lượng giác của góc . •
Định lí Pythagore có phải là một trường hợp đặc biệt a) Tính theo và .
của Định lí côsin hay không? b) Tính theo , và . Lời giải c) Tính theo và .
• Định lí Pythagore có phải là một trường hợp đặc biệt
của Định lí côsin bởi vì: Khi " d) CM: = #$$ ⇒ = $: = + . = + ⇔ = + . • Khi " = #$$ ⇒ = $: = + ⇔ = + . • Khi " = #$$ ⇒ = $: = + ⇔ = + . 1. ĐỊNH LÍ CÔSIN
Từ Định lí côsin, hãy viết các Ví dụ 1. Khám phá. công thức tính Cho tam giác có " , , theo độ = ' $ và
dài các cạnh , , của tam giác . = (,
= ). Tính độ dài cạnh . Lời giải = + * + ⇔ = . = + • Giải (H.3.9) * + ⇔ = .
• Áp dụng Định lí côsin cho tam giác , ta có: • = + . . ' $ = + ' = ( + ) . (. ). = ' # + ⇔ = Vậy = ' #. 1. ĐỊNH LÍ CÔSIN Luyện tập 1. • " ≈ ')$$ ,($ #'$#. /, )0.. • Cho tam giác có = (, = ) và
≈ ,0$($′00, '2′′.
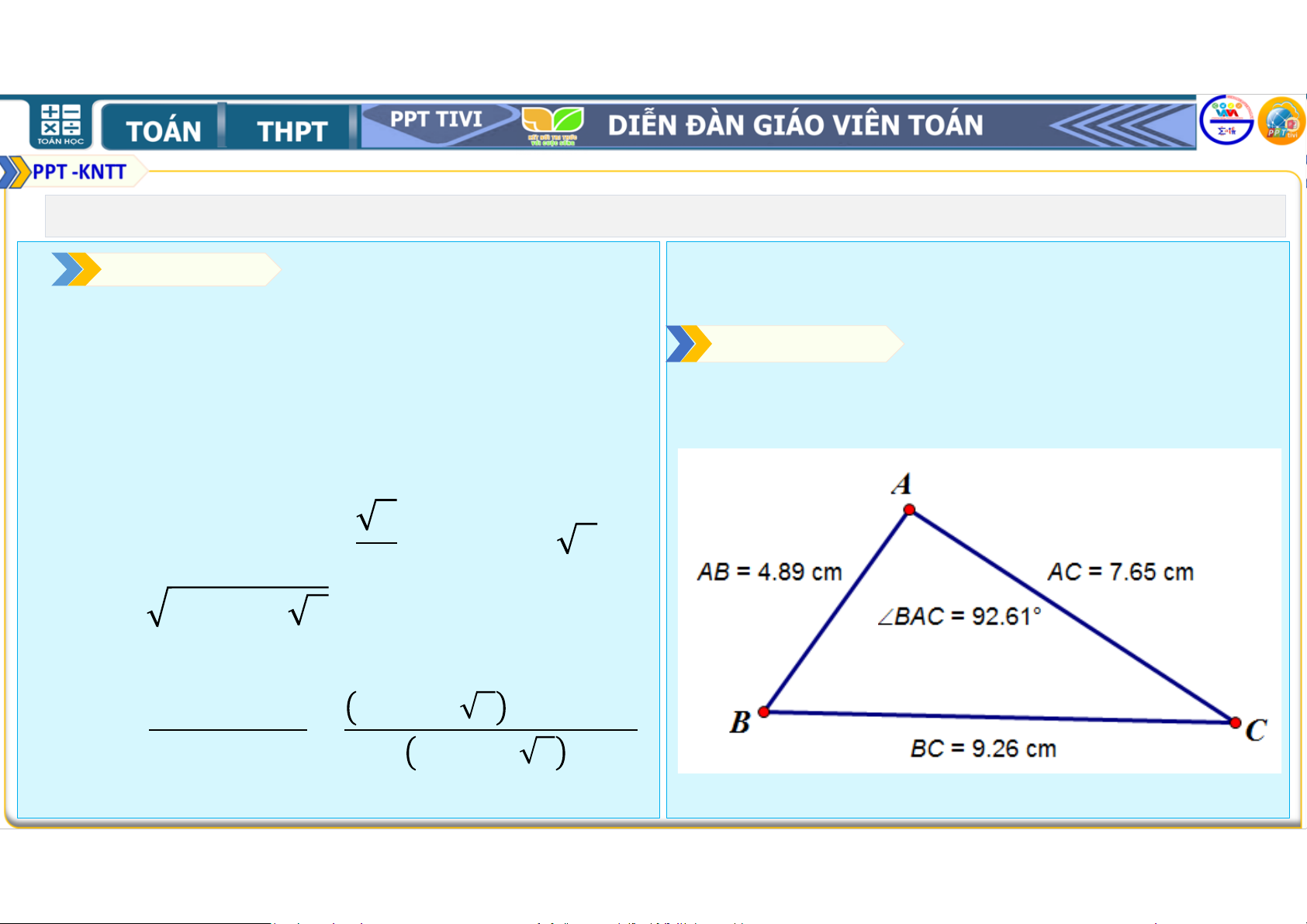
" = ,( . Tính độ dài các cạnh và độ lớn các • VẽTrm ảiộtn tgam hi ệ giá m. c
, sau đó đo độ dài các
góc còn lại của tam giác. cạnh, số đo góc
và kiểm tra tính đúng đắn của
Định lí côsin tại đỉnh
đối với tam giác đó.
• Giải: Áp dụng định lý cosin : • = + . . , ( = ( + ) . (. ). = )# ,$ ⇒ = )# ,$ .
• Áp dụng định lý cosin : + )# ,$ + ( ) = = )# ,$ . ( ≈ $, $ $ ⇒ " ≈ #'$#′ 1. ĐỊNH LÍ CÔSIN Trải nghiệm. Vẽ một tam giác
, sau đó đo độ dài các cạnh, số ⇔ ≈ )(, ), ⇔ ≈ #, / đo góc
và kiểm tra tính đúng đắn của Định lí côsin
Như vậy kết quả thu được từ định lí xấp xỉ tại đỉnh
đối với tam giác đó.
với kết quả đo được.
Lời giải Xét tam giác như hình vẽ sau:
Vậy định lí côsin tại đỉnh A là đúng.
Áp dụng Định lí côsin tại đỉnh A, ta có: = + . . ⇔ = 2, /( + ,, )# . 2, /(. ,, )#. # , /' 1. ĐỊNH LÍ CÔSIN Vận dụng 1.
Giả sử sau 1,5 giờ tàu ở vị trí điểm B.
Ta có quảng đường OA=20km, quảng đường
• Dùng Định lí côsin, tính khoảng cách được AB=10km.
đề cập trong HĐ1b.
Khoảng cách giữa tàu và cảng Vân Phong Lời giải chính là quảng đường OB.
Mặt khác, 3 = '0( (do tàu đi theo hướng đông nam).
Áp dụng Định lí côsin cho tam giác OAB tại đỉnh A, ta có: = + . . 3
Tàu xuất phát từ cảng Vân Phong, đi theo ⇔ = $ + '$ . $. '$. ' 0(
thướng Đông với vận tốc 20km/h. Sau khi ⇔ ≈ 2) , ),.
Vậy khoảng cách từ tài đến cảng Vân Phong
đi 1 giờ, tàu chuyển sang hướng đông xấp xỉ 27,98km.
nam rồi giữ nguyên vận tốc. Lời giải 2. ĐỊNH LÍ SIN HĐ3.
Xét tam giác MBC vuông tại C ta
• Trong mỗi hình dưới đây, hãy tính theo và có: 45 6 = = ⇒ = . 6 45 6 45 .
Từ Hình 3.10 a ta có: " = 6 " (cùng chắn cung nhỏ BC). ⇒ 45 = 45 6. Do đó = . 45
Hình 3.10 b ta có: " + 6 " = ')$
(tứ giác ABMC nội tiếp đường tròn tâm O, bán kính R). ⇒ 45 = 45 6. Do đó = . 45
Vậy ở hai hình ta đều có = . 45
Định lí sin. Trong tam giác : = = = . 45 45 45 2. ĐỊNH LÍ SIN Ví dụ 2. • Cho tam giác có " = '0( , ' " . 45 ' 0($ = ' ;
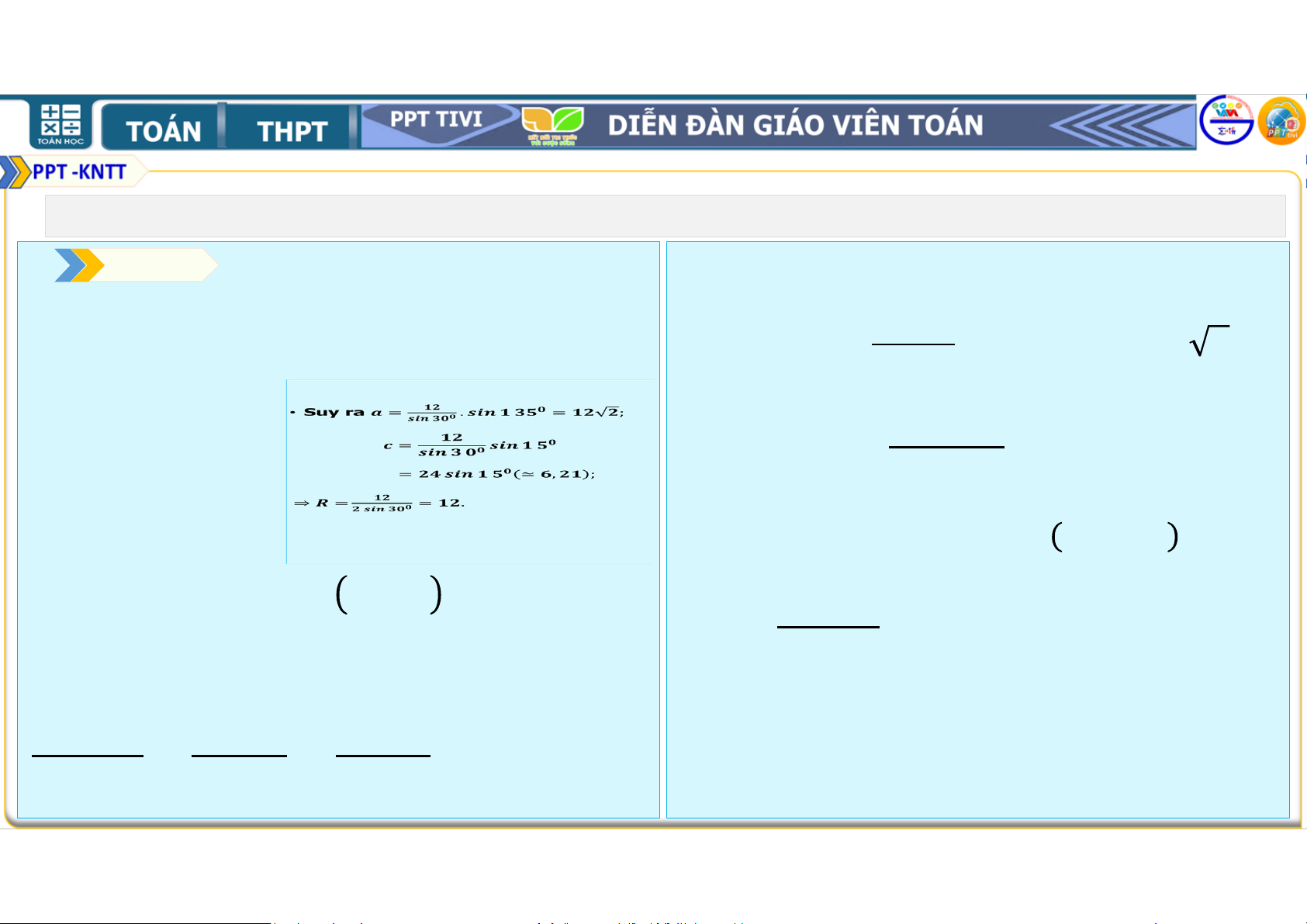
= '( và = ' . Tính , , và số đo • Suy ra = 45 0$$ góc . ' = 45 ' ($ 45 0 $$ • Giải ( H.3.11) = , 45 ' ($ ≃ /, ' ; • Ta có: " = ')$ " + " ' ⇒ = = ' . = ')$ 7'0( + '( 8 = 0$ . 45 0$$
• Áp dụng Định lí sin, ta có: ' = = = . 45 '0($ 45 0$$ 45 '($ 2. ĐỊNH LÍ SIN Luyện tập 2. • Cho tam giác có = ), = ( và " = . 45 (. 45 ) $$
)$ . Tính số đo các góc, bán kính đường 45 = = ≃ $, / )
tròn ngoại tiếp và độ dài cạnh còn lại của ⇒ ) tam giác. = = = ,, $/ 45 . 45 ) $$ Giải
• Áp dụng Định lí sin cho tam giác ta có: = = 45 45
3. GIẢI TAM GIÁC VÀ ỨNG DỤNG THỰC TẾ
Việc tính độ dài các cạnh và số đo các góc của một tam giác khi biết một số yếu
tố của tam giác đó gọi là giải tam giác. Ví dụ 3. Giải Giải tam giác
, biết = ', và • Ta có " = ')$ " + " " = /$ , " = ,$ . = ')$ 7/$ + ,$ 8 = )$ .
• Áp dụng Định lí sin ta có: ', = = . 45 /$$ 45 ,$$ 45 )$$ ',. 45 /$$ • Suy ra = ' , 0'; 45 )$$ ',. 45 ,$$ • = ≃ #, ',. 45 )$$
3. GIẢI TAM GIÁC VÀ ỨNG DỤNG THỰC TẾ Luyện tập 3. • Giải tam giác
, biết = ,(, = 0 và 0 . 45 )2$ " • Suy ra 45 = ≃ $, (# = )2 . (0,), ⇒ ≃ 0/$#′ . • Giải
• Áp dụng Định lí côsin cho tam giác , ta • Ta có " = ')$ " + " có: = ')$ 70/$#′ + )2 8 = (/ ('′. • = + .
• Chú ý. Áp dụng các Định lí côsin, sin và sử = 0 + ,( . 0 . ,(. ) 2$
dụng máy tính cầm tay, ta có thể tính (gần
đúng) các cạnh và các góc của một tam giác = )#), 2
trong các trường hợp sau: • Suy ra ≃ (0, ),.
• Biết hai cạnh và góc xen giữa;
• Áp dụng Định lí sin cho tam giác , ta có: (0,), 0 • Biết ba cạnh; = 45 )2$ 45
• Biết một cạnh và hai góc kề.