Chương 3. Bài 6: Hệ thức lượng trong tam giác | Giáo án điện tử môn Toán 10 | Kết nối tri thức với cuộc sống
Giáo án PowerPoint Toán 10 Kết nối tri thức với cuộc sống là tài liệu cực kì hữu ích mà muốn giới thiệu đến quý thầy cô tham khảo. Bài giảng điện tử môn Toán 10 Kết nối tri thức bao gồm đầy đủ các bài giảng trong cả năm học được thiết kế dưới dạng file trình chiếu PowerPoint với nhiều hiệu ứng rất đẹp mắt. Với nội dung bài học trình bày chi tiết cho từng phần học và bám sát chương trình SGK Toán 10 Kết nối tri thức.
Chủ đề: Bài giảng điện tử Toán 10
Môn: Toán 10
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Preview text:
CHƯƠNG I CHƯƠNG III
HỆ THỨC LƯỢNG TRONG TAM GIÁC
§5. Giá trị lượng giác của góc từ 00 đến 1800
§6. Hệ thức lượng trong tam giác
Bài tập cuối chương III CHƯƠNG ICIH I. Ư H Ơ Ệ N T G H
ỨIC LƯỢNG TRONG TAM GIÁC HÌNH HỌC ➉ 5
GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 00 ĐẾN 1800 1
GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC 2
MỐI QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC GÓC BÙ NHAU 3
BÀI TẬP TRẮC NGHIỆM
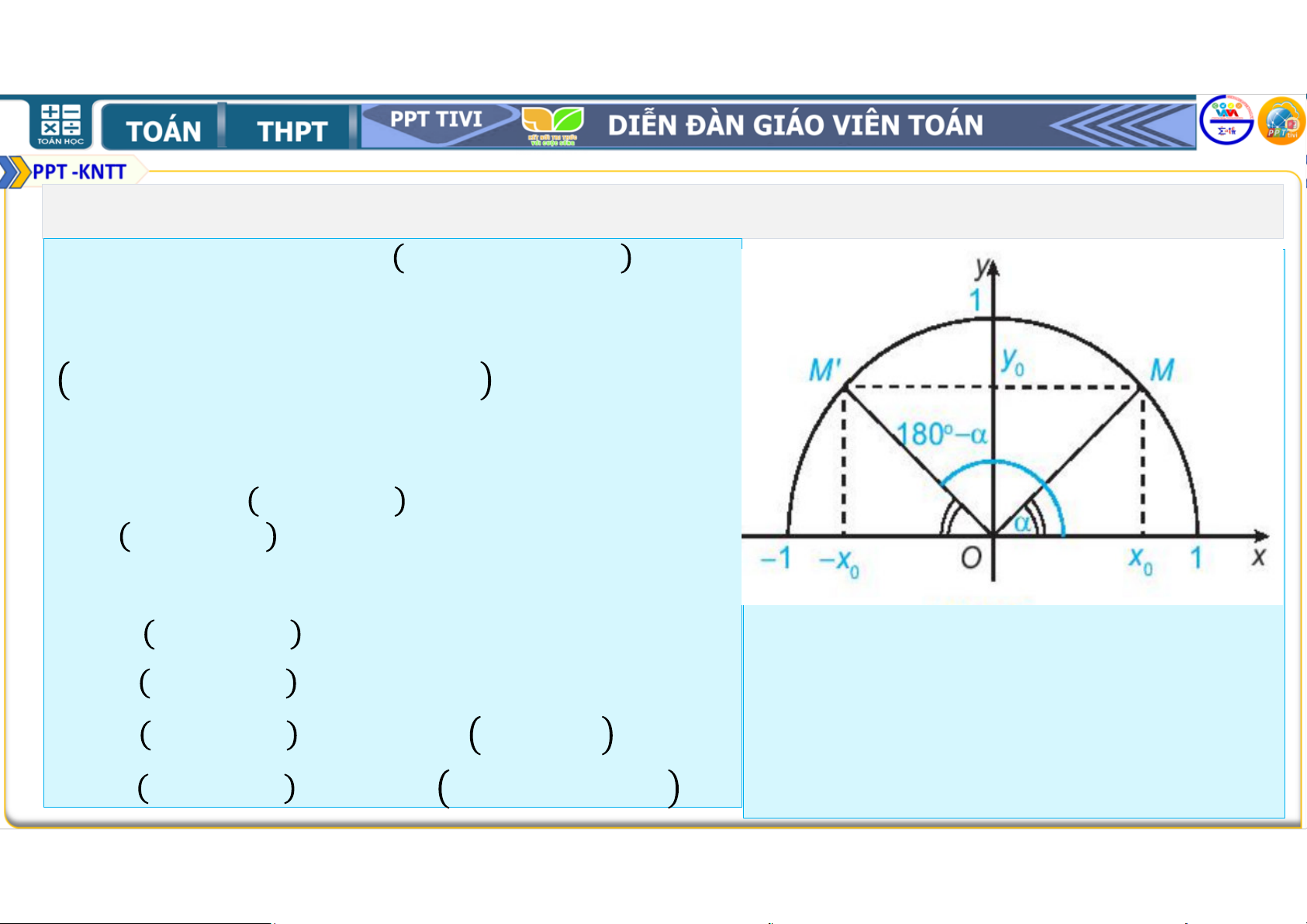
2. MỐI QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC BÙ NHAU
• Đối với một góc tùy ý ≤ ≤ , gọi ,
là hai điểm trên nửa đường tròn đơn vị
tương ứng với hai góc bù nhau và − = , = −
• Nêu nhận xét về vị trí của hai điểm , đối với trục
. Từ đó nêu các mối quan hệ giữa và − , giữa cos và cos − . • Hai điểm ,
đối xứng nhau trục . Do đó − = ,
Hai góc bằng nhau có sin bằng nhau; cos − = −cos .
côsin, tang, côtang đối nhau tan − = − ≠ ; cot − = −cot < < .
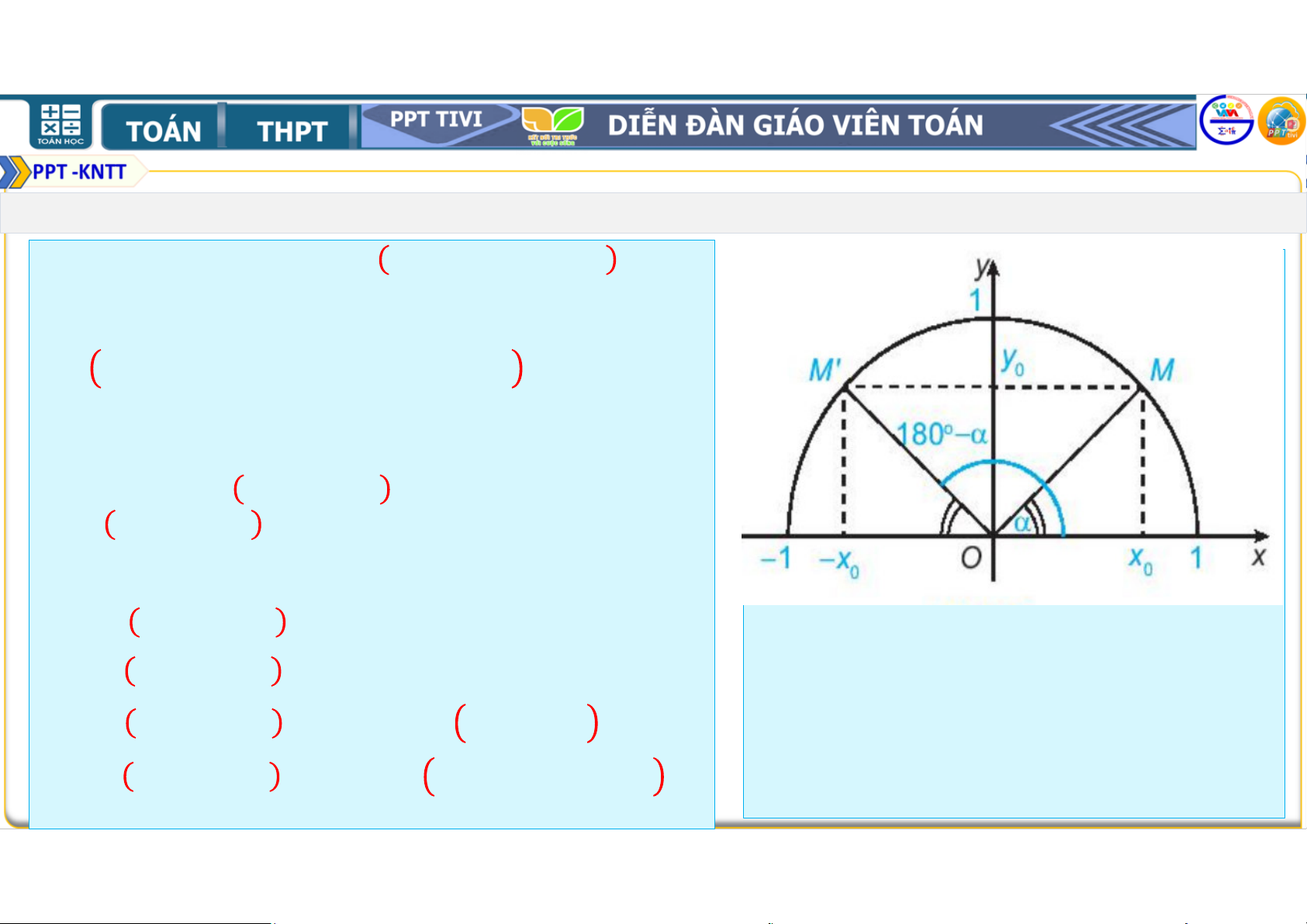
2. MỐI QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC BÙ NHAU
• Đối với một góc tùy ý ≤ ≤ , gọi ,
là hai điểm trên nửa đường tròn đơn vị
tương ứng với hai góc bù nhau và − = , = −
• Nêu nhận xét về vị trí của hai điểm , đối với trục
. Từ đó nêu các mối quan hệ giữa và − , giữa cos và cos − . • Hai điểm ,
đối xứng nhau trục . Do đó − = ,
Hai góc bằng nhau có sin bằng nhau; cos − = −cos .
côsin, tang, côtang đối nhau tan − = − ≠ ; cot − = −cot < < .
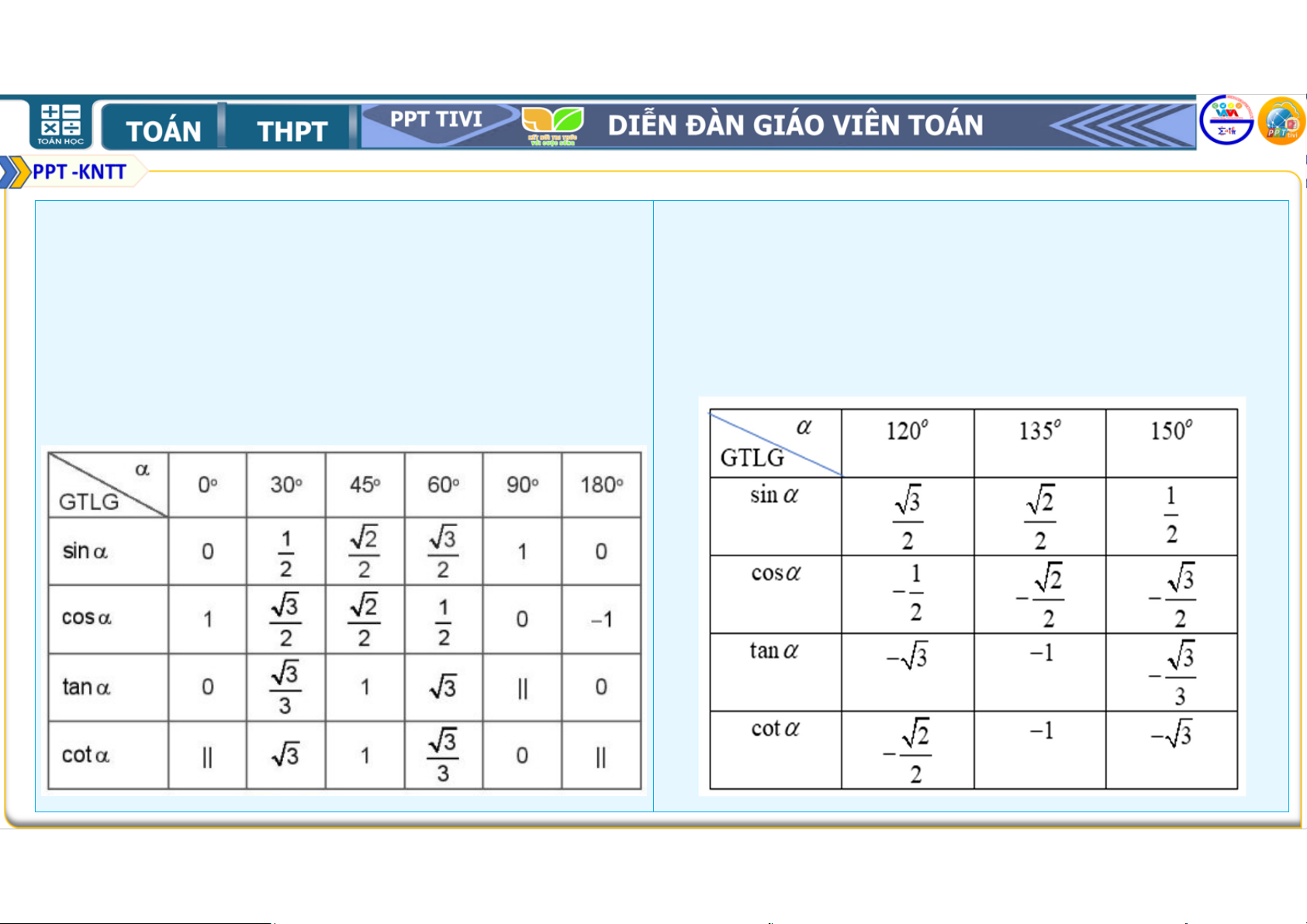
• Ví dụ 2: Tính các giá trị lượng giác của các LỜI GIẢI góc , , . Do các góc , , tương ứng
GỢI Ý TÌM LỜI GIẢI bù với các góc
, 4 , 3 nên từ bảng
3.1 ta cũng có bảng giá trị lượng giác sau: Các góc góc , , bù với các góc
nào trong bảng 3.1? Từ đó tính các giá trị
lượng giác của góc , , .
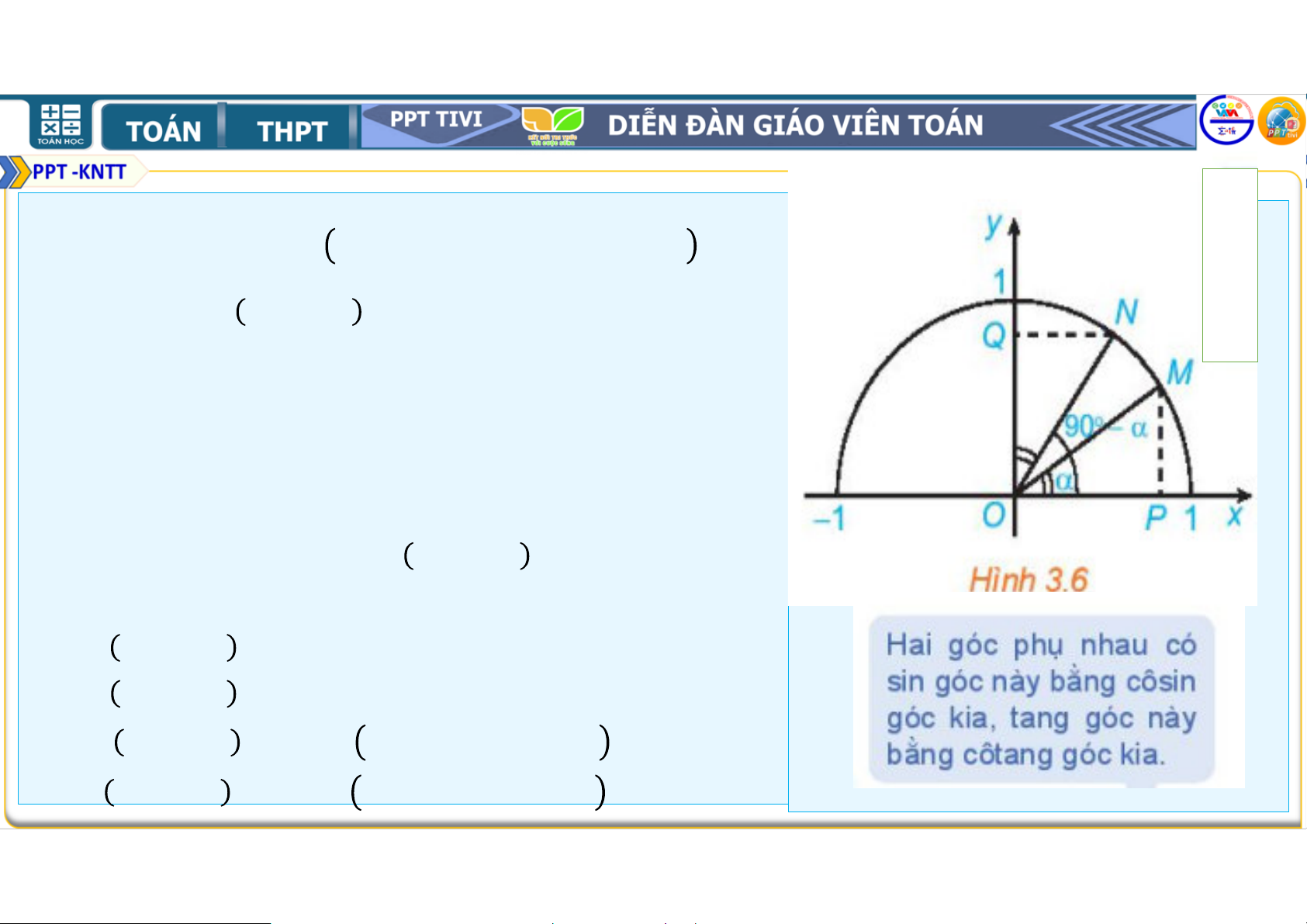
Luyện tập 2: Trong hình 3.6, hai điểm , ứng với hai góc phụ nhau và − = , = − . Chứng minh rằng =
. Từ đó nêu mối quan hệ giữa cos và − . LỜI GIẢI Ta có = − ⇒ = .
Xét hai tam giác vuông ; ta có = = = # ⇒ = . Ta có cos = = = − . Do đó − = $ , c − = . t − = $ ≠ , , ; cot − = ≠ , , . Vận dụng GỢI Ý GIẢI
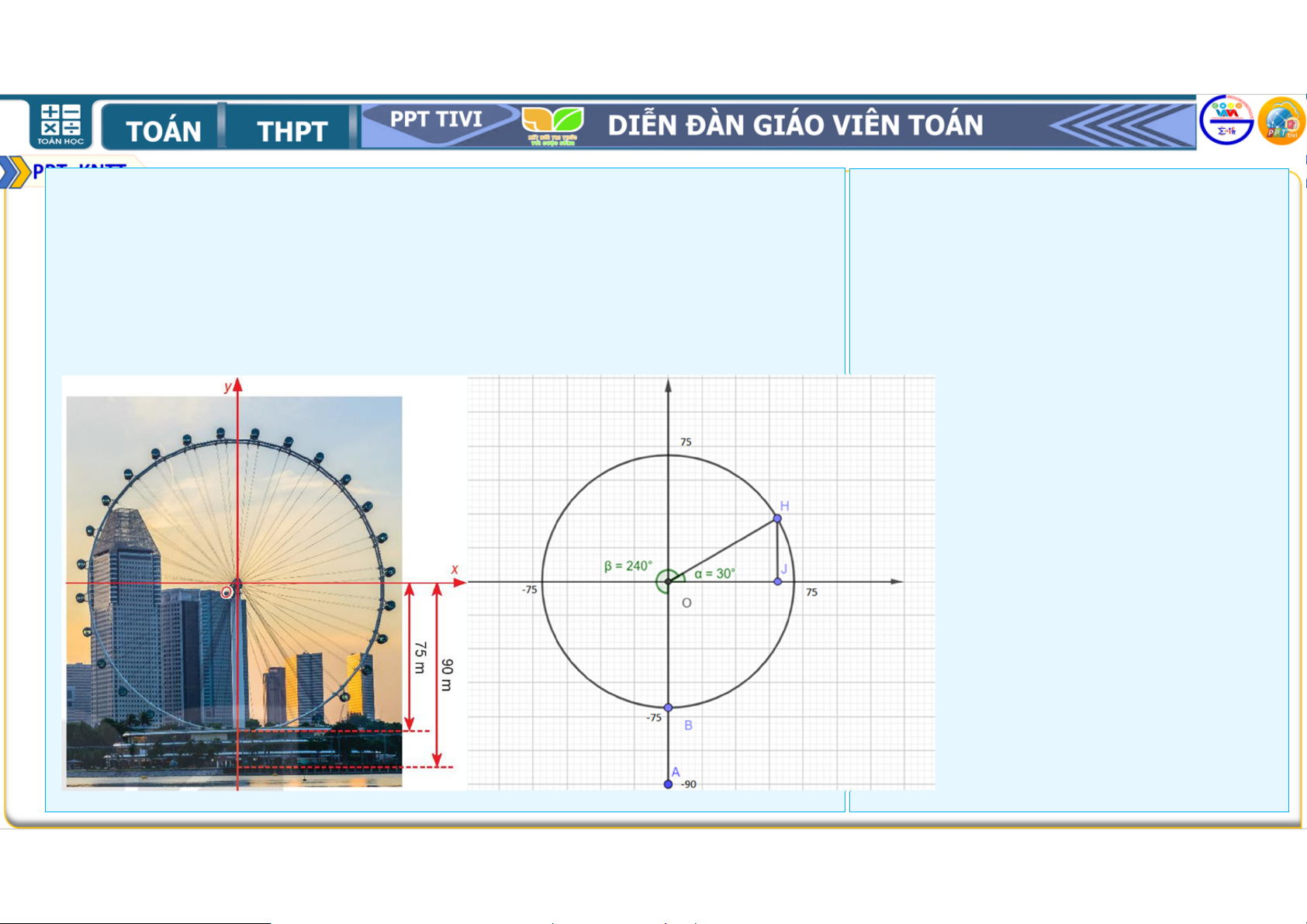
Một chiếc đu quay có bán kính % &, tâm của vòng quay ở độ
Gắn hệ trục vào đu quay ta được cao
& (H 3.7), thời gian thực hiện mỗi vòng quay của đu
một đường tròn lượng giác như quay là
phút. Nếu một người vào cabin tại vị trí thấp nhất hình vẽ
của vòng quay, thì sau
phút quay, người đó ở độ cao bao nhiêu mét? Đu quay sẽ quay theo
chiều dương hoặc theo chiều âm. Sửa thành: Đu quay sẽ quay cùng
chiều hoặc ngược chiều
quay của kim đồng hồ
Từ đó ta tính được độ
cao của người ngồi
trong cabin ở vị trí thấp nhất sau khi quay 20 phút. Vận dụng
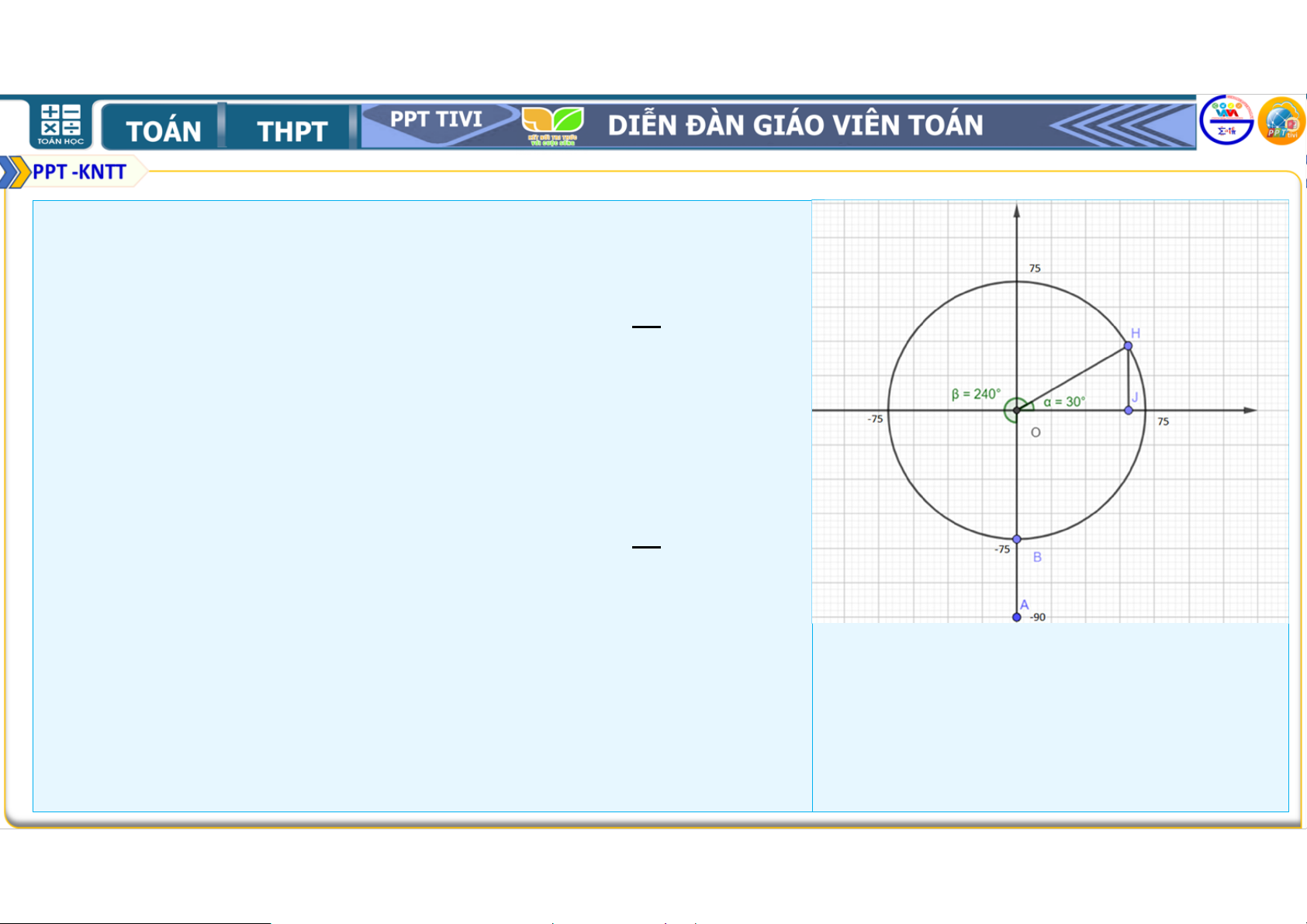
TH1: ĐU QUAY QUAY CÙNG CHIỀU KIM ĐỒNG HỒ
Sau 20 phút quay cabin đi được một góc là: . =
( tức là đến vị trí điểm ). Khi đó góc ) * = và )* =
. ) = %, +&,. Vậy sau phút quay,
người đó ở độ cao %, - = %, +&,.
TH2: ĐU QUAY QUAY NGƯỢC CHIỀU KIM ĐỒNG HỒ
Sau 20 phút quay cabin đi được một góc là: . =
( tức là đến vị trí điểm ., / đối xứng với 0 qua .
1 là hình chiếu của / trên trục 23. Khi đó góc . 4 = và /4 =
. . = %, +&,. Vậy sau phút quay,
người đó ở độ cao %, - = %, +&,. III
BÀI TẬP TRẮC NGHIỆM CỦNG CỐ CÂU 1 Giá trị 8 ( - ( bằng bao nhiêu? A . B 2. C 3. D . Bài giải
Bằng cách tra bảng giá trị lượng giác của các góc đặc biệt hay $ ( =
dùng MTCT ta được 7 ⇒ $ ( - ( = . ( =