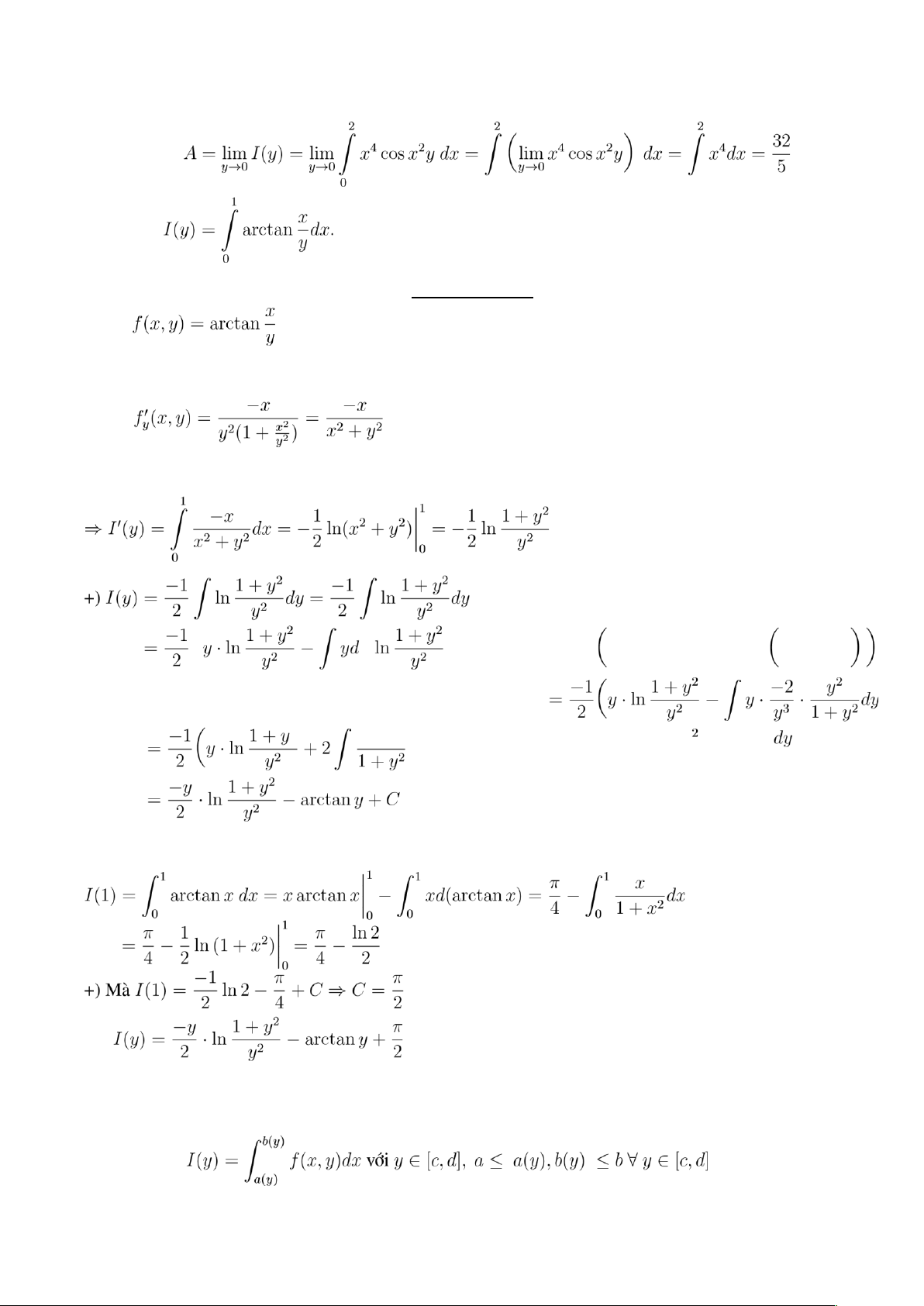





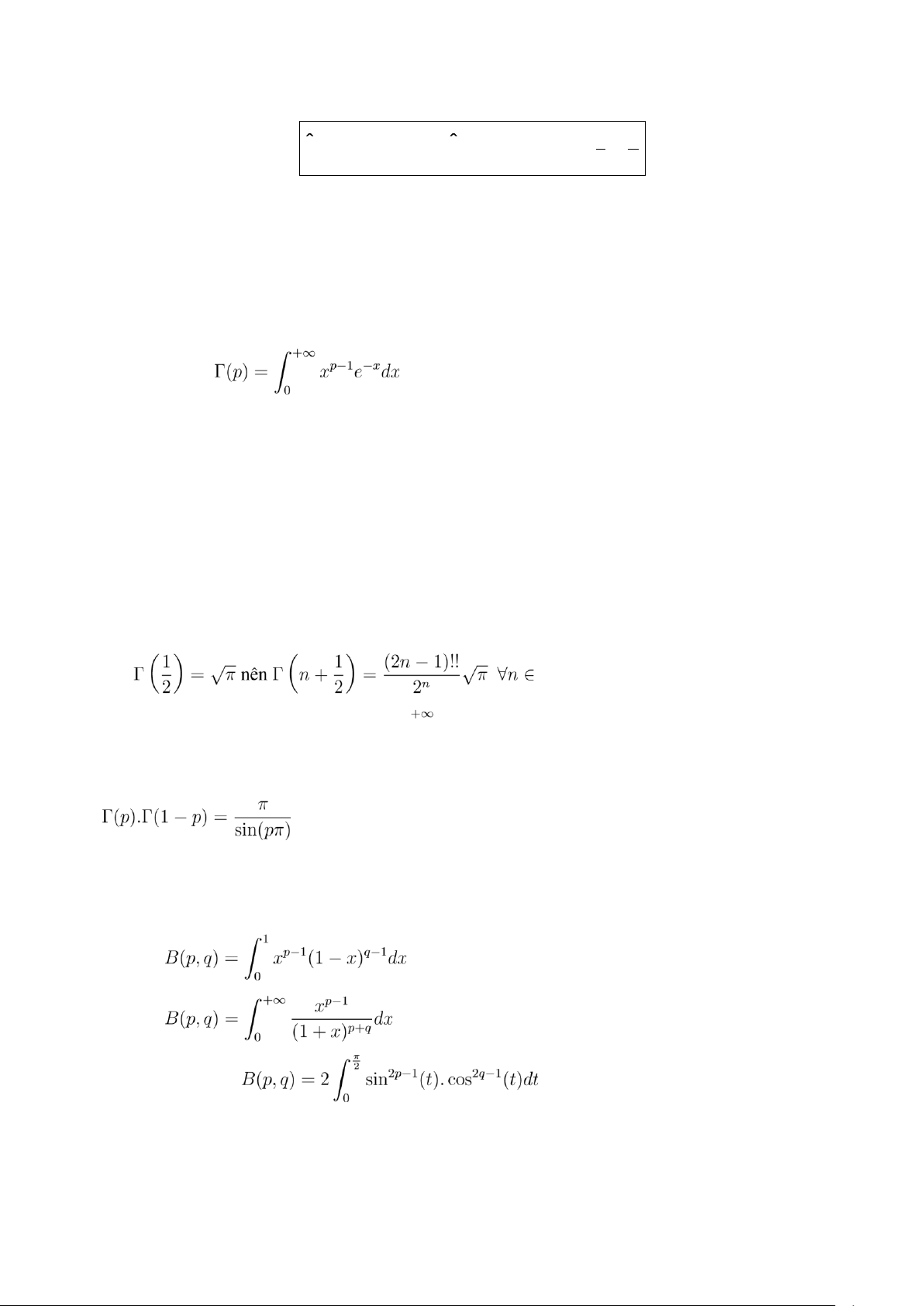


Preview text:
lOMoAR cPSD| 27879799
Chương 3: Tích Phân Phụ Thuộc Tham Số I
Tích phân xác định phụ thuộc tham số 1
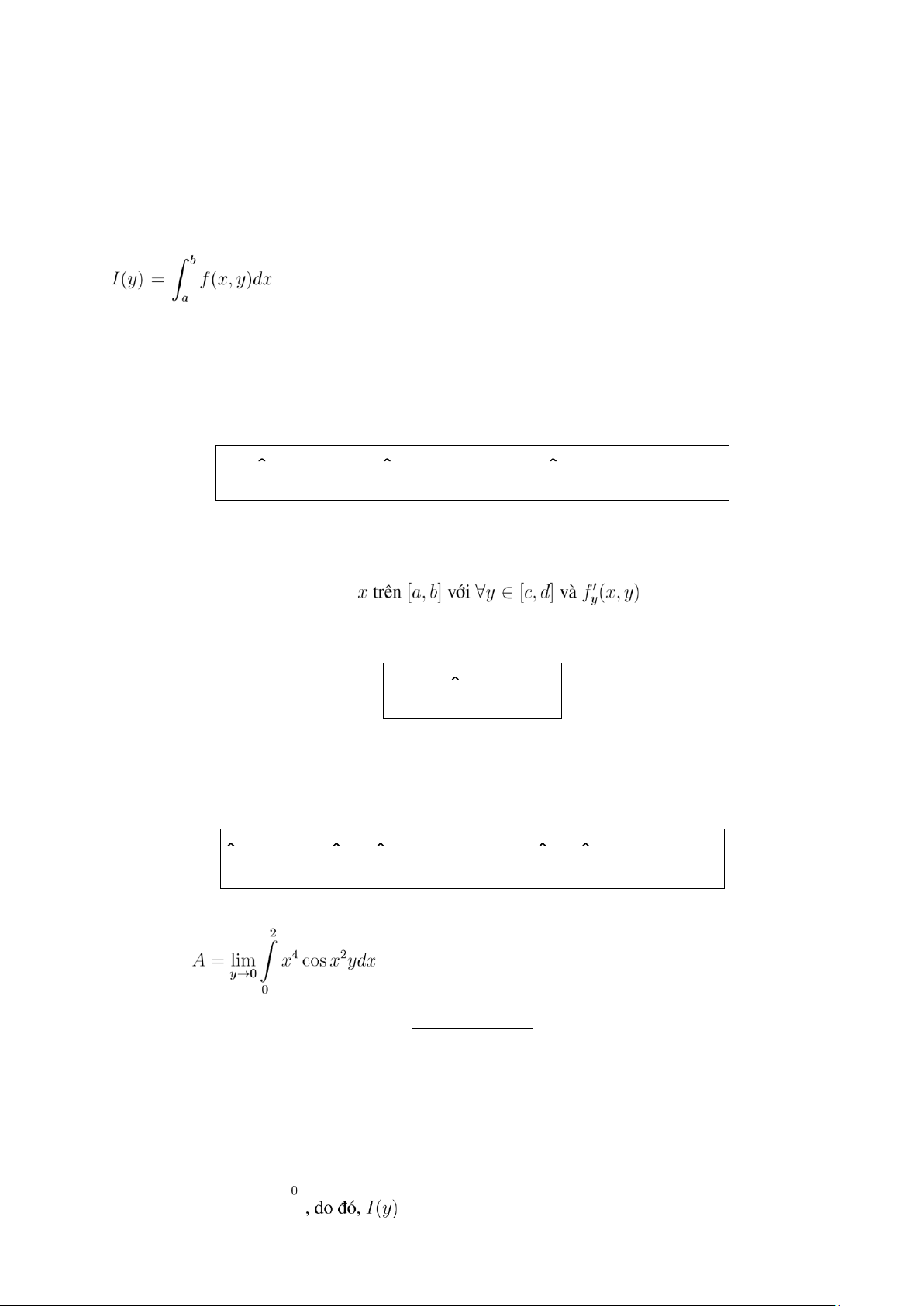
Tích phân xác định phụ thuộc tham số Xét
, trong đó f(x,y) khả tích theo x trên [a,b] với mỗi y ∈ [c,d]. Tích phân này
được gọi là tích phân phụ thuộc tham số y. 1.1 Tính liên tục
▶ Định lý 1: Nếu f(x,y) liên tục trên [a,b] × [c,d] thì I(y) liên tục trên [c,d] và: b b b lim
f ( x,y ) dx =
lim f ( x,y ) dx =
f ( x,y 0 ) dx = I ( y 0 )
y → y 0 a
a y → y 0 a 1.2 Tính khả vi
▶ Định lý 2: Nếu f(x,y) liên tục theo
liên tục trên [a,b] × [c,d] thì
I(y) là hàm số khả vi trên (c,d) và: b I ′ ( y )=
f ′ y ( x,y ) dx a 1.3 Tính khả tích
▶ Định lý 3: Nếu f(x,y) liên tục trên [a,b] × [c,d] thì I(y) là hàm số khả tích trên [c,d] và: d d b b d Ç å Ç å I ( y ) dy =
f ( x,y ) dx dy =
f ( x,y ) dy dx c c a a c Ví dụ 1: Tính:
Hướng dẫn giải
+) Xét hàm số f(x,y) = x4 cos2
x2y là hàm số liên tục trên [0,2] × [−1,1].
Do đó, hàm số I(y) = ylim ˆ x4 cosx2y dx liên tục trên [−1,1]. →0
Mà đoạn [−1,1] chứa điểm
0liên tục tại y = 0. +) Vậy ta có:. lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập 0 0 Ví dụ 2: Tính tích phân:
Hướng dẫn giải +) Đặt có:
• f(x,y) liên tục trên [0;1] × [c;d] với 0 ∈/ [c;d] •
liên tục trên [1;0] × [c;d] với 0 ∈/ [c;d]
⇒ I(y) khả vi ∀ y ̸= 0 å å
+) Thay y = 1 vào ta có: Vậy
2 Tích phân xác định với cận biến đổi Xét tích phân . 2.1 Tính liên tục 1 lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
▶ Định lý 1: Nếu f(x,y) liên tục trên [a,b] × [c,d], các hàm số a(y),b(y) liên tục trên [c,d] thỏa mãn
điều kiện a ≤ a(y),b(y) ≤ b ∀ y ∈ [c,d] thì I(y) là hàm số liên tục đối với y trên [c,d]. 2.2 Tính khả vi
▶ Định lý 2: Nếu hàm số
liên tục trên [a,b] × [c,d] và các hàm a(y),b(y) khả vi trên
[c,d] thỏa mãn điều kiện a ≤ a(y),b(y) ≤ b ∀ y ∈ [c,d] thì I(y) là hàm số khả vi đối với y trên [c,d] và: b (y ) I
′ ( y )= f ( b ( y ) ,y ) .b ′ y ( y ) − f ( a ( y ) ,y ) .a ′ y ( y )+
f ′ y ( x,y ) dx a ( y ) Ví dụ 3: Tính .
Nháp: Ta chọn x ∈ [0,2] chứa x = 1. Với x ∈ [0,2] ⇒ cos x ∈ [cos 2,1], (x + 1) ∈ [1,3] nên ta chọn
được cận y ∈ [cos 2,3].
Hướng dẫn giải +) Đặt .
+) Nhận thấy f(x,y) liên tục trên D = [0,2] × [cos 2,3].
+) Các hàm số: α(x) = cos x , β(x) = x + 1 liên tục ∀ x ∈ [0,2] và α(x),β(x) ∈ [cos 2,3] ∀x ∈ [0,2].
Do đó I(x) liên tục trên
liên tục tại x = 1. +) Vậy ta có: Ví dụ 4: Cho
. Tính I′(2).
Hướng dẫn giải +) Đặt 2 lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập +) Nhận thấy:
• f(x,y) liên tục trên [0,+∞) × [0,+∞) •
liên tục trên [0,+∞) × [0,+∞)
• B(y) = y và A(y) = 0 khả vi trên [0,+∞) nên ta có I(y) khả vi trên [0,+∞)
⇒ I(y) khả vi trên +) Vậy . II
Tích phân suy rộng phụ thuộc tham số Xét tích phân
, trong đó f(x,y) là hàm số xác định trên [a,+∞]×[c,d], với mỗi y ∈
[c,d] cố định, f(x,y) khả tích theo x trên [a,b], ∀b > a. 1
Khái niệm tích phân suy rộng phụ thuộc tham số
▶ Định nghĩa: Tích phân suy rộng phụ thuộc tham số là:
• Hội tụ tại điểm y0 ∈ [c,d] : ∀ϵ > 0,∃ b(ϵ,y0) > a ( phụ thuộc vào ϵ và y0) sao cho: b + ∞ I ( y 0 ) −
f ( x,y 0 ) dx =
f ( x,y 0 ) dx < ϵ, ∀ b>b ( ϵ,y 0 ) a b
• Hội tụ trên [c,d] nếu I(y) hội tụ tại mọi y ∈ [c,d].
• Hội tụ đều trên [c,d] : ∀ϵ > 0,∃ b(ϵ) > a ( chỉ phụ thuộc vào ϵ mà không phụ thuộc y ) sao cho: 3 lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập b + ∞ I ( y ) −
f ( x,y ) dx =
f ( x,y ) dx < ϵ, ∀ b>b ( ϵ ) , ∀ y ∈ [ c,d ] a b
| f ( x,y ) |≤ g ( x ) ∀ ( x,y ) ∈ [ a, + ∞ ] × [ c,d ] I ∞ ( y )=
f ( x,y ) dx y ∈ [ c,d ] a +
Ví dụ 5: Xét sự hội tụ đều của tích phân:
Hướng dẫn giải +) Ta có: +) Mà là tích phân xác định
Vậy tích phân đã cho hội tụ đều ∀y ∈ R. 2
Tính chất của tích phân suy rộng hội tụ đều 2.1 Tính liên tục
▶ Định lý 1: Nếu f(x,y) liên tục trên [a,+∞] × [c,d] và tích phân suy rộng hội tụ
đều đối với y ∈ [c,d] thì I(y) là hàm số liên tục trên [c,d], và: + ∞ + ∞ + ∞ lim I ( y )= lim
f ( x,y ) dx =
lim f ( x,y ) dx =
f ( x,y 0 ) dx = I ( y 0 ) y → y 0
y → y 0 a a y → y 0 a 2.2 Tính khả vi
▶ Định lý 2 : Giả sử hàm số f(x,y) xác định trên [a,+∞] × [c,d] sao cho với mỗi y ∈ [c,d], hàm số f(x,y) liên tục đối với+
liên tục trên [a,+∞] × [c,d]. Nếu tích phân suy rộng 4 lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập ∞
I(y) = ˆ f(x,y)dx hội tụ vàhội tụ
đều đối với y ∈ [c,d] thì I(y) là hàm số khả vi trên và: + ∞ ⇒ I ′ ( y )=
f ′ y ( x,y ) dx a 2.3 Tính khả tích
▶ Định lý 3: Nếu hàm số f(x,y) liên tục trên [a,+∞]×[c,d] và nếu tích phân suy rộng I(y) hội tụ đều đối
với y ∈ [c,d] thì I(y) là hàm số khả tích trên [c,d] và ta có thể đổi thứ tự lấy tích phân theo công thức: d d + + d Å ∞ å ∞ Ç å I ( y ) dy =
f ( x,y ) dx dy =
f ( x,y ) dy dx c c a a c ∞ Ví dụ 6: Tính
Hướng dẫn giải +) Xét hàm số
là hàm số liên tục trên ï o +) Ta có : . Lại có:
là tích phân xác định. hội tụ đều với
ï o theo tiêu chuẩn Weierstrass (2) +) Từ liên tục trên o 5 lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Ví dụ 7: Tính .
Hướng dẫn giải +) Ta thấy: +∞ β
Khi đó: I = ˆ Ñ ˆ e−yxdye dx. 0 α
+) Xét tích phân suy rộng phụ thuộc tham số
Ta có: f(x,y) = e−yx liên tục trên miền [0;+∞] × [α;β] (1) Và:
hội tụ với α > 0.
Do đó, theo tiêu chuẩn Weierstrass ta có:
hội tụ đều (2). +) Từ (1) và (2), ta có: .
3 Một số tích phân quan trọng 3.1 Tích phân Dirichlet + ∞ sin x π dx = 0 x 2 3.2 Tích phân Gauss + √ ∞ π e − x 2 dx = 0 2 3.3 Tích phân Fresnel 6 lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập + + ∞ ∞ 1… π sin( x 2 ) dx = cos( x 2 ) dx = 0 0 2 2 III Tích phân Euler 1 Hàm Gamma 1.1 Định nghĩa: ▶ Hàm Gamma:
, xác định trên (0,+∞) 1.2 Tính chất:
▶ Hạ bậc: Γ(p + 1) = pΓ(p), với p > 0. Ý nghĩa của tính chất này là ta chỉ cần nghiên cứu Γ(p) với 0 < p ≤ 1. ▶ Đặc biệt:
• Γ(1) = 1 nên Γ(n) = (n − 1)! ∀n ∈ N • N
▶ Đạo hàm của hàm Gamma: Γ(k)(p) = ˆ
xp−1.(lnk x).e−xdx 0 ▶
, với mọi 0 < p < 1 2 Hàm Beta 2.1 Định nghĩa: ▶ Dạng 1: ▶ Dạng 2:
▶ Dạng lượng giác: 2.2 Tính chất:
▶ Tính đối xứng: B(p,q) = B(q,p) 7 lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập ▶ Hạ bậc:
, nếu p > 1 nếu q > 1
Ý nghĩa của công thức trên ở chỗ muốn nghiên cứu hàm Beta ta chỉ cần xét trong khoảng (0,1] x (0,1] mà thôi.
▶ Đặc biệt, B(1,1) = 1 nên:
▶ Công thức liên hệ giữa hàm Beta và Gamma: ▶ Ví dụ 8: Tính
Hướng dẫn giải +) Đặt .
+) Tại x = 0 thì t = 0, khi x → +∞ thì t → +∞ +) Khi đó ta có: Ví dụ 9: Tính »
Hướng dẫn giải +) Đặt . x 0 3 Đổi cận: t 0 1 8 lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập 9




