TOÁN THPT
GIÁO ÁN ĐIỆN TỬ-DIỄN ĐÀN GIÁO VIÊN TOÁN CHƯƠNG IV.
HỆ THỨC LƯỢNG TRONG TAM GIÁC. VECTƠ
§5. Tích của một số với một vectơ Tiết 1 TOÁN THPT
GIÁO ÁN ĐIỆN TỬ-DIỄN ĐÀN GIÁO VIÊN TOÁN TOÁN HỌC
CHƯƠNG IV. HỆ THỨC LƯỢNG TRONG TAM GIÁC. VEC TƠ ➉ § 5
TÍCH CỦA MỘT SỐ VỚI MỘT VECTƠ I ĐỊNH NGHĨA II TÍNH CHẤT III MỘT SỐ ỨNG DỤNG TOÁN THPT
GIÁO ÁN ĐIỆN TỬ-DIỄN ĐÀN GIÁO VIÊN TOÁN KHỞI ĐỘNG Câu hỏi
1. Hãy nêu khái niệm tổng của hai vectơ? Trả lời * Định nghĩa:
Cho 2 vectơ 𝒂 và 𝒃 . Lấy 1 điểm 𝒂 𝒃
𝑨 tùy ý, rồi vẽ : 𝑨𝑩 = 𝒂, 𝑩𝑪 = 𝒃 . 𝑩
Vectơ 𝑨𝑪 được gọi là tổng
của hai vectơ 𝒂 và 𝒃. • Kí 𝑪
hiệu: 𝑨𝑪 = 𝒂 + 𝒃. 𝑨 𝒂 + 𝒃
Phép tìm tổng của hai vectơ còn
được gọi là phép cộng hai vectơ. TOÁN THPT
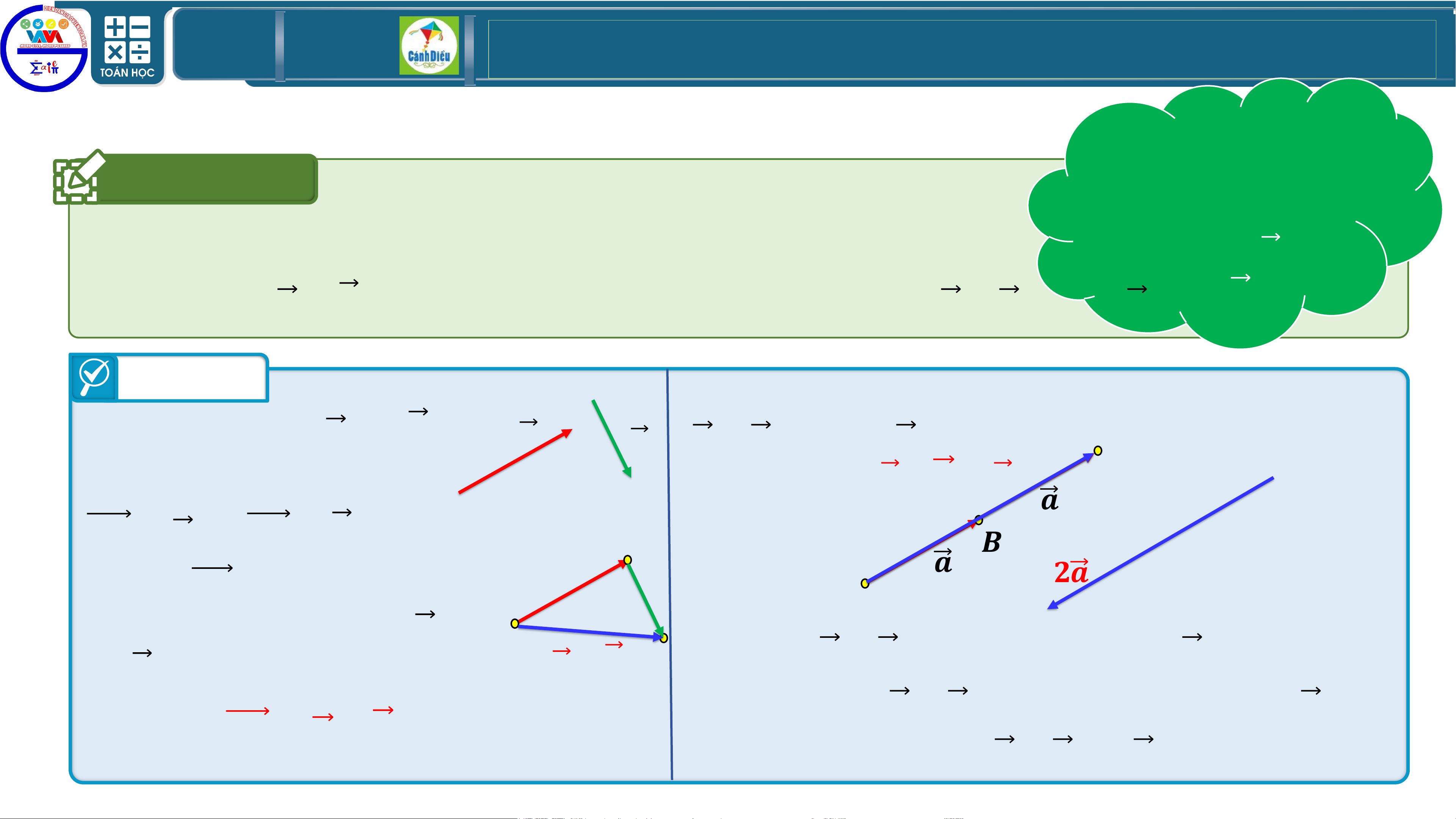
GIÁO ÁN ĐIỆN TỬ-DIỄN ĐÀN GIÁO VIÊN TOÁN KHỞI ĐỘNG Em hãy thử Câu hỏi dự đoán hướng và độ dài của
1. Hãy nêu khái niệm tổng của hai vectơ?
vectơ −𝟐𝒂 so 2. Cho với 𝒂 .
vectơ 𝒂 ≠ 𝟎, so sánh hướng và độ dài của vectơ 𝒂 + 𝒂 so với 𝒂. Trả lời
2. So sánh hướng và độ dài của vectơ
1. Cho 2 vectơ 𝒂 và 𝒃. 𝒂 𝒃
𝒂 + 𝒂 so với 𝒂. 𝒂 + 𝒂 =𝟐𝒂 𝑪
Lấy điểm 𝑨 tùy ý, vẽ: 𝒂
𝑨𝑩 = 𝒂 và 𝑩𝑪 = 𝒃. 𝑩 𝒂 𝑩 −𝟐𝒂
Vectơ 𝑨𝑪 được gọi là 𝑨 𝑨
tổng của hai vectơ 𝒂
𝒂 + 𝒃 𝑪 • Vectơ 𝒂 + 𝒂 cùng hướng với 𝒂 . và 𝒃.
• Độ dài của 𝒂 + 𝒂 gấp đôi độ dài của 𝒂 .
Kí hiệu: 𝑨𝑪 = 𝒂 + 𝒃.
• Người ta kí hiệu: 𝒂 + 𝒂 = 𝟐𝒂. TOÁN THPT
GIÁO ÁN ĐIỆN TỬ-DIỄN ĐÀN GIÁO VIÊN TOÁN I ĐỊNH NGHĨA Định nghĩa
Cho số 𝒌 ≠ 𝟎 và 𝒂 ≠ 𝟎. Tích của véctơ 𝒂 với số 𝒌 là một vectơ, kí hiệu 𝒌𝒂,
được xác định như sau:
+ Về hướng: 𝒌𝒂 cùng hướng với vectơ 𝒂 nếu 𝒌 > 𝟎
𝒌𝒂 ngược hướng với vectơ 𝒂 nếu 𝒌 < 𝟎
+ Về độ dài: 𝒌𝒂 = 𝒌 𝒂 .
* Qui ước: 𝟎. 𝒂 = 𝟎; 𝒌. 𝟎 = 𝟎.
Phép lấy tích của một số với một vectơ được gọi là phép nhân một số với một vectơ. TOÁN THPT
GIÁO ÁN ĐIỆN TỬ-DIỄN ĐÀN GIÁO VIÊN TOÁN Ví dụ 1
Cho 𝒂 và điểm 𝑶 như hình vẽ sau. Xác định hai điểm 𝑴 và 𝑵 sao cho: 𝑴 𝑶 𝑵
a) 𝑶𝑴 = 𝟑𝒂; 3𝒂 −𝟒𝒂
b) 𝑶𝑵 = −𝟒𝒂. 𝒂 Bài giải
- Vẽ d đi qua 𝑶 và song song với giá của 𝒂 .
- Do 𝑶𝑴 = 𝟑𝒂 suy ra 𝑴 ∈ 𝒅 sao cho 𝑶𝑴 = 𝟑 𝒂 và 𝑶𝑴 cùng hướng với 𝒂.
- Do 𝑶𝐍 = −𝟒𝒂 suy ra 𝑵 ∈ 𝒅 sao cho 𝑶𝐍 = 𝟒 𝒂 và 𝑶𝐍 ngược hướng với 𝒂. TOÁN THPT
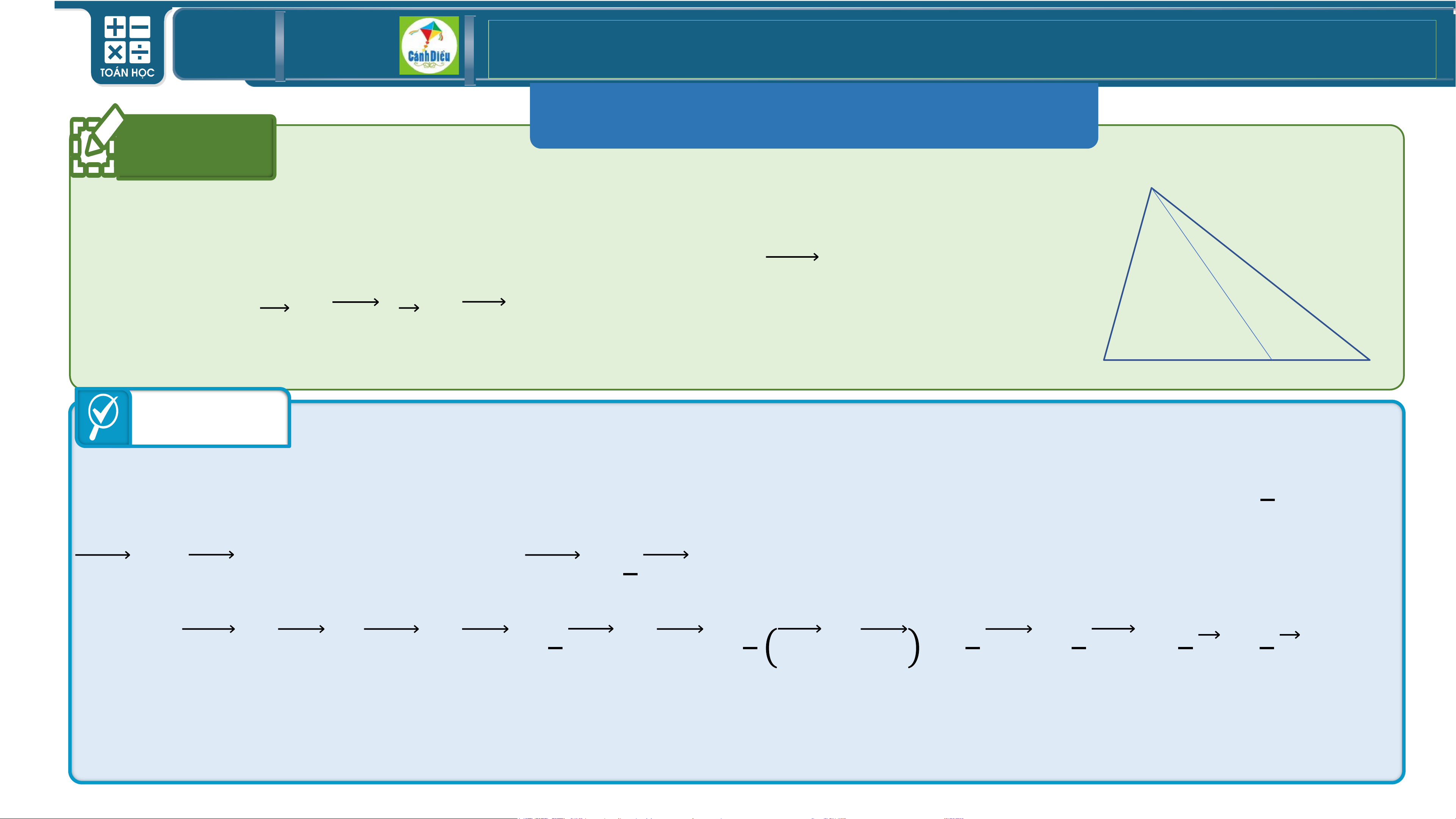
GIÁO ÁN ĐIỆN TỬ-DIỄN ĐÀN GIÁO VIÊN TOÁN Ví dụ 2
Cho tam giác 𝑨𝑩𝑪. Hai đường trung tuyến 𝑨𝑴 và 𝑩𝑵 cắt nhau tại 𝑮.
Tìm các số 𝒂, 𝒃 biết: 𝑨𝑮 = 𝒂𝑨𝑴; 𝑮𝑵 = 𝒃𝑮𝑩. Bài giải A
a) Ta có: 𝑨𝑮 và 𝑨𝑴 là 2 vectơ cùng hướng N
và 𝑨𝑮 = 𝟐 𝑨𝑴 𝟑 G 𝟐 𝟐
 𝑨𝑮 = 𝟑𝑨𝑴. Vậy 𝒂 = . B 𝟑 C M b) Ta có: 𝟏
𝑮𝑵 và 𝑮𝑩 là 2 vectơ ngược hướng và 𝑮𝑵 = 𝟐 𝑮𝑩 −𝟏 𝟏
 𝑮𝑵 = 𝟐 𝑮𝑩. Vậy 𝒃 = −𝟐. TOÁN THPT
GIÁO ÁN ĐIỆN TỬ-DIỄN ĐÀN GIÁO VIÊN TOÁN Ví dụ 3
Vật thứ nhất chuyển động thẳng đều từ
A đến B với tốc độ là 12 m/s và vật thứ 𝒗
hai chuyển động thẳng đều từ B đến A 𝟏
với tốc độ là 9m/s. Gọi 𝒗 𝒗
𝟏, 𝒗𝟐 lần lượt là 𝟐
các vectơ vận tốc của vật thứ nhất và
vật thứ hai. Có hay không một số thực
𝒌 thõa mãn 𝒗𝟏 = 𝒌𝒗𝟐 ? Bài giải
Do tỉ số tốc độ của vật thứ nhất và vật thứ hai là 𝟏𝟐 = 𝟒 𝟗 𝟑
đồng thời hai vật chuyển động ngược hướng nên hai vectơ vận tốc ngược hướng.
Suy ra 𝒗𝟏 = − 𝟒 𝒗 . 𝟑 𝟐.
Vậy 𝒌 = − 𝟒𝟑 TOÁN THPT GIÁO ÁN ĐIỆN TỬ II TÍNH CHẤT
Khởi động Em hãy nêu các tính chất phép nhân hai số thực?
Với 𝒂, 𝒃, 𝒄 là các số thực ta có:
• Tính chất giao hoán: 𝒂. 𝒃 = 𝒃. 𝒂
Tính chất tích của một số với một • Tính vectơ chất kết hợp:
có gì khác so với tính chất phép
𝒂. 𝒃 . 𝒄 = 𝒂. (𝒃. 𝒄) nhân các số thực?
• Tính chất phân phối:
𝒂. 𝒃 + 𝒄 = 𝒂. 𝒃 + 𝒂. 𝒄 TOÁN THPT GIÁO ÁN ĐIỆN TỬ II TÍNH CHẤT Ghi nhớ
Với hai véctơ bất kì 𝒂 và 𝒃, với hai số thực 𝒉 và 𝒌, ta có:
• 𝒌 𝒂 + 𝒃 = 𝒌𝒂 + 𝒌𝒃; 𝒌 𝒂 − 𝒃 = 𝒌𝒂 − 𝒌𝒃;
• (𝒉 + 𝒌)𝒂 = 𝒉𝒂 + 𝒌𝒂;
• 𝒉(𝒌𝒂) = (𝒉𝒌)𝒂;
• 𝟏𝒂 = 𝒂; (−𝟏)𝒂 = −𝒂.
* Nhận xét: 𝒌𝒂 = 𝟎 khi và chỉ khi 𝒌 = 𝟎 hoặc 𝒂 = 𝟎. TOÁN THPT GIÁO ÁN ĐIỆN TỬ II TÍNH CHẤT
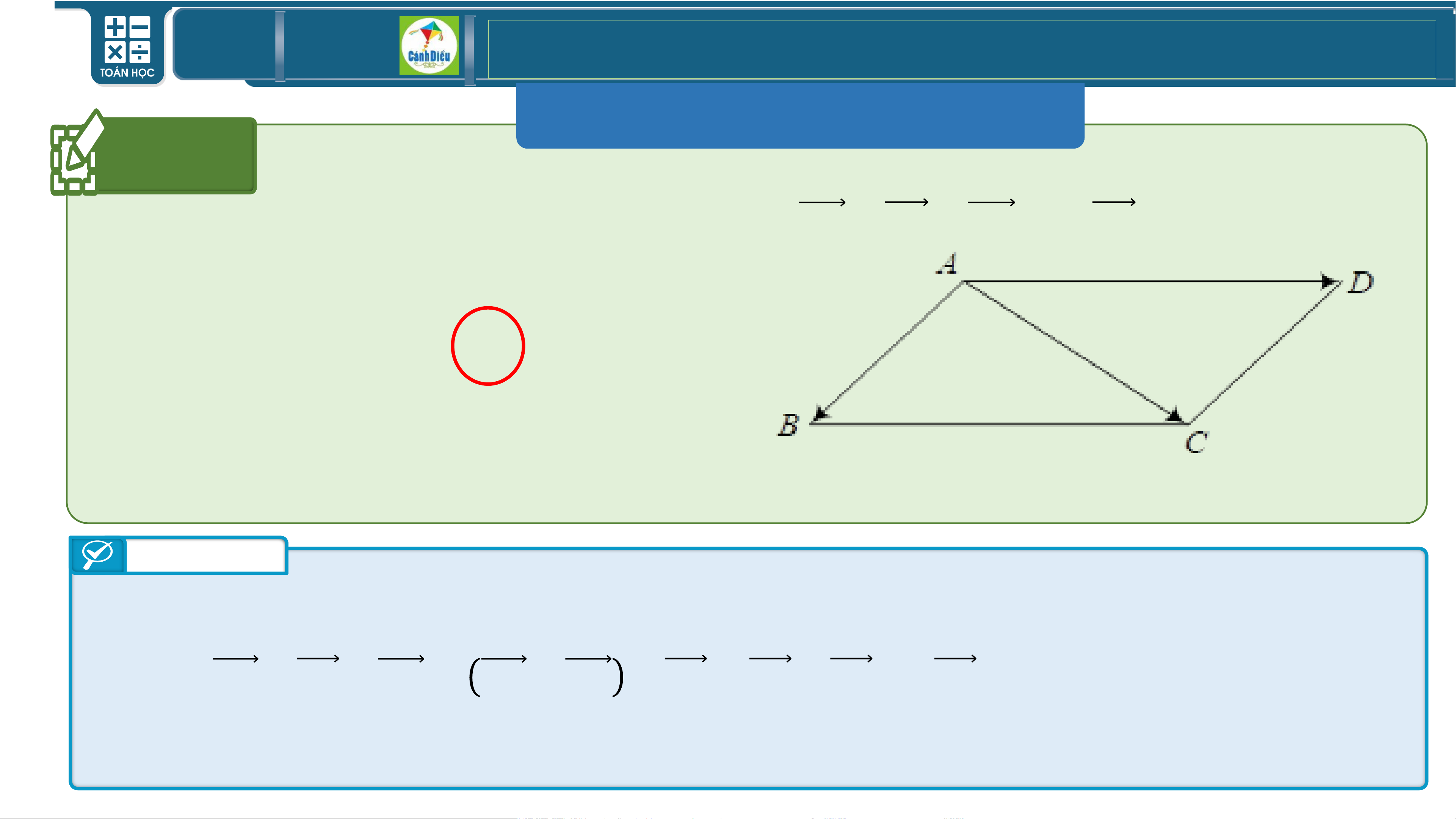
Ví dụ 1 Cho ba điểm A, B, C. Chứng minh:
𝐚) 𝟐𝑨𝑩 + 𝟐𝑩𝑪 = 𝟐𝑨𝑪;
𝐛) 𝟑 𝟓𝑨𝑪 + 𝑪𝑩 − 𝟏𝟒𝑨𝑪 = 𝑨𝑩. Bài giải a) Ta có:
𝟐𝑨𝑩 + 𝟐𝑩𝑪 = 𝟐 𝑨𝑩 + 𝑩𝑪 = 𝟐𝑨𝑪 b) Ta có:
𝟑 𝟓𝑨𝑪 + 𝑪𝑩 − 𝟏𝟒𝑨𝑪 = 𝟏𝟓𝑨𝑪 + 𝑪𝑩 − 𝟏𝟒𝑨𝑪 = 𝟏𝟓𝑨𝑪 − 𝟏𝟒𝑨𝑪 + 𝑪𝑩 = 𝑨𝑪 + 𝑪𝑩 = 𝑨𝑩 TOÁN THPT GIÁO ÁN ĐIỆN TỬ II TÍNH CHẤT Ví dụ 1
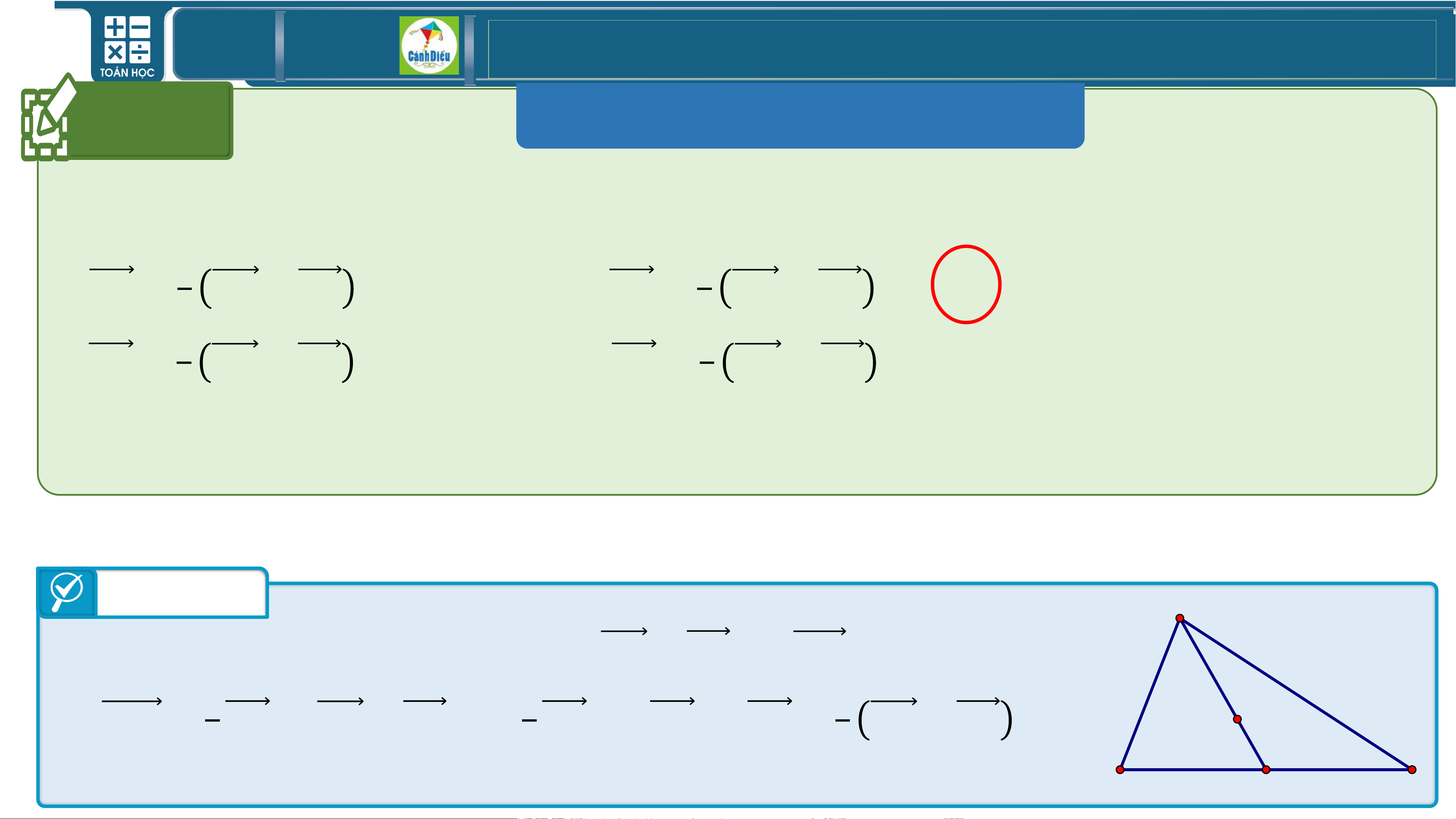
Cho ba điểm A, B, C. Chứng minh:
𝟑 𝑨𝑩 + 𝟐𝑩𝑪 − 𝟐 𝑨𝑩 + 𝟑𝑩𝑪 = 𝑨𝑩. Bài giải
𝟑 𝑨𝑩 + 𝟐𝑩𝑪 − 𝟐 𝑨𝑩 + 𝟑𝑩𝑪
= 𝟑𝑨𝑩 + 𝟔𝑩𝑪 − 𝟐𝑨𝑩 − 𝟔𝑩𝑪
= 𝟑𝑨𝑩 − 𝟐𝑨𝑩 + 𝟔𝑩𝑪 − 𝟔𝑩𝑪 = 𝑨𝑩. TOÁN THPT GIÁO ÁN ĐIỆN TỬ III MỘT SỐ ỨNG DỤNG
Nêu tính chất trung điểm của đoạn thẳng, trọng tâm của tam giác?
- Trung điểm của đoạn thẳng chia đoạn thẳng thành 2 đoạn thẳng bằng nhau.
- Trọng tâm tam giác cách đỉnh một khoảng bằng 𝟐 độ dài 𝟑
đường trung tuyến. TOÁN THPT GIÁO ÁN ĐIỆN TỬ III MỘT SỐ ỨNG DỤNG
Cho tam giác 𝑨𝑩𝑪, gọi 𝑰 là trung điểm của 𝑨𝑩, 𝑮 là
trọng tâm tam giác 𝑨𝑩𝑪, 𝑴 là điểm bất kì. Điền vào
dấu (...) 1 số hoặc 1 vectơ để được kết quả đúng.
a) 𝑰𝑨 =. . . 𝑰𝑩 ⇔ 𝑰𝑨 + 𝑰𝑩 =. . .;
b) 𝑴𝑨 + 𝑴𝑩 = 𝑴𝑰+. . . + 𝑴𝑰+. . . . = 𝟐𝑴𝑰 + . . . +. . . =. . .;
c) 𝑮𝑨 + 𝑮𝑩 + 𝑮𝑪 =. . .;
d)𝑴𝑨 + 𝑴𝑩 + 𝑴𝑪 = 𝑴𝑮+. . . + 𝑴𝑮+. . . + 𝑴𝑮+. . . = 𝟑𝑴𝑮 + . . . +. . . +. . . =. . . TOÁN THPT GIÁO ÁN ĐIỆN TỬ III MỘT SỐ ỨNG DỤNG
a) 𝑰𝑨 =. .-. 𝑰𝑩 ⇔ 𝑰𝑨 + 𝑰𝑩 =. . . 𝟎;
b) 𝑴𝑨 + 𝑴𝑩 = 𝑴𝑰+. . . 𝑰𝑨 + 𝑴𝑰+. . . .
𝑰𝑩 = 𝟐𝑴𝑰 + . . . 𝑰𝑨+. . . 𝑰𝑩 =. .𝟐. . ; 𝑴𝑰
c) 𝑮𝑨 + 𝑮𝑩 + 𝑮𝑪 =. . . 𝟎 ;
d) 𝑴𝑨 + 𝑴𝑩 + 𝑴𝑪 = 𝑴𝑮 + … . 𝑮𝑨 + 𝑴𝑮+ . . . 𝑮𝑩 + 𝑴𝑮+ . . . 𝑮𝑪 = 𝟑𝑴𝑮 + … . . 𝑮𝑨+ . . . 𝑮𝑩+ . . . 𝑮𝑪 = .𝟑. .𝑴𝑮 TOÁN THPT GIÁO ÁN ĐIỆN TỬ III MỘT SỐ ỨNG DỤNG Ghi nhớ
+ Nếu 𝑰 là trung điểm của đoạn 𝑨𝑩 thì với mọi điểm 𝑴 ta có:
𝑴𝑨 + 𝑴𝑩 = 𝟐𝑴𝑰;
+ Nếu 𝑮 là trọng tâm của tam giác 𝑨𝑩𝑪 thì với mọi điểm 𝑴 ta có:
𝑴𝑨 + 𝑴𝑩 + 𝑴𝑪 = 𝟑𝑴𝑮. TOÁN THPT GIÁO ÁN ĐIỆN TỬ III MỘT SỐ ỨNG DỤNG
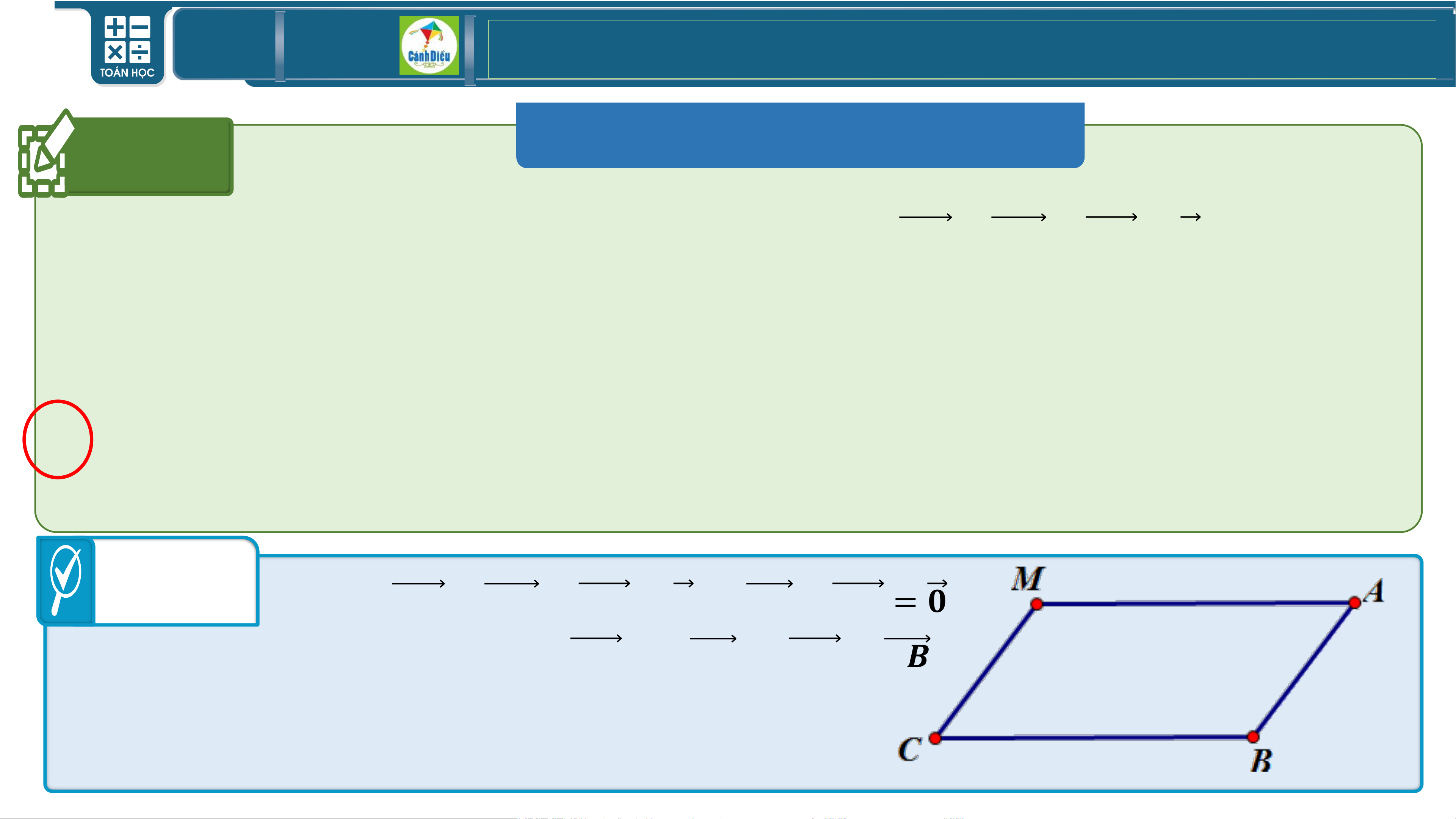
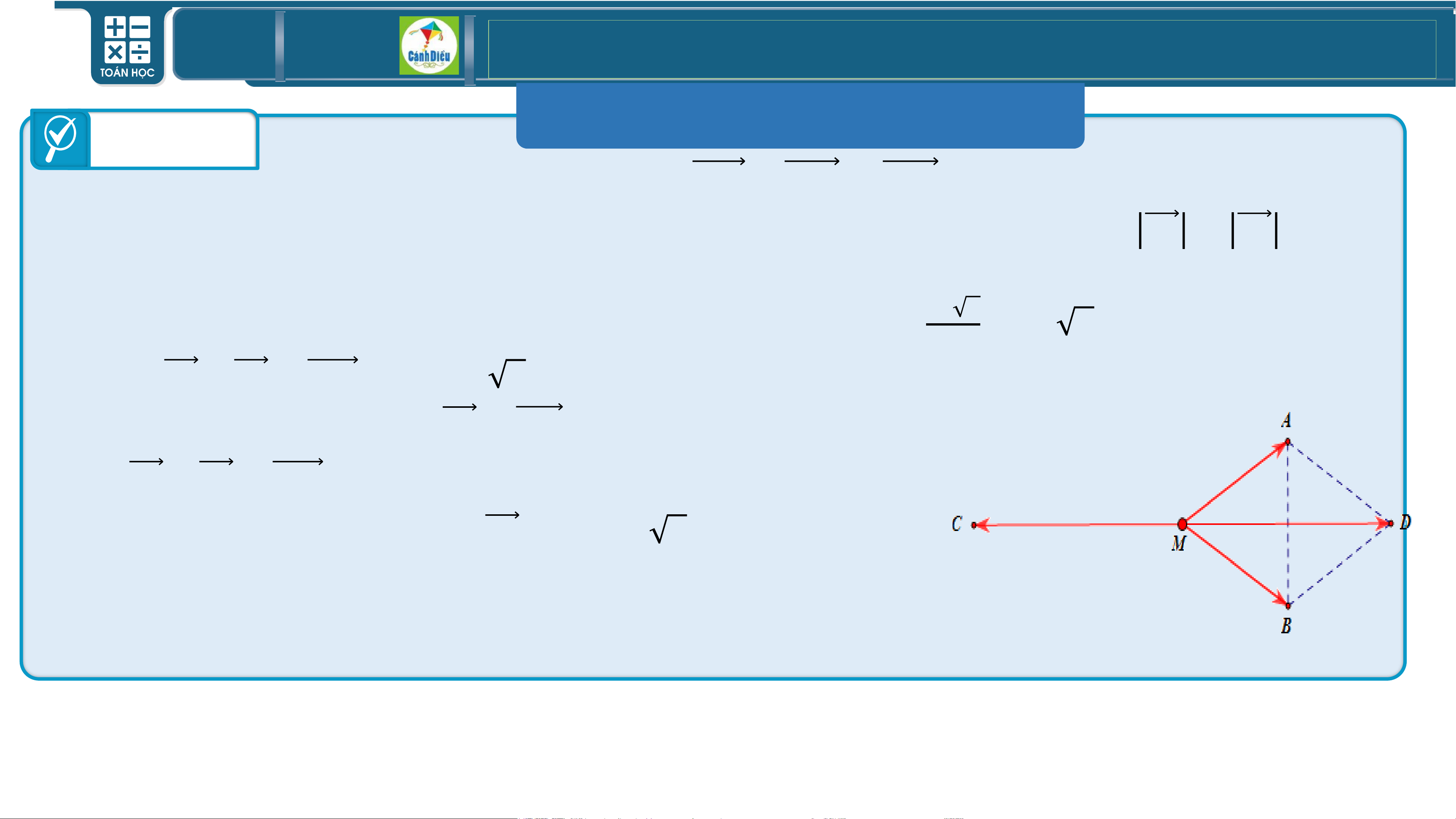
Ví dụ 3 Cho tứ giác ABCD có M, N lần lượt là trung điểm của hai cạnh AB
và CD. Gọi G là trung điểm của đoạn thẳng MN. Chứng minh:
𝑮𝑨 + 𝑮𝑩 + 𝑮𝑪 + 𝑮𝑫 = 𝟎. Bài giải
Vì M là trung điểm của AB nên 𝑮𝑨 + 𝑮𝑩 = 𝟐𝑮𝑴.
Vì N là trung điểm của CD nên 𝑮𝑪 + 𝑮𝑫 = 𝟐𝑮𝑵.
⇒ 𝑮𝑨 + 𝑮𝑩 + 𝑮𝑪 + 𝑮𝑫 = 𝟐𝑮𝑴 + 𝟐𝑮𝑵 = 𝟐 𝑮𝑴 + 𝑮𝑵 = 𝟎. TOÁN THPT GIÁO ÁN ĐIỆN TỬ III MỘT SỐ ỨNG DỤNG
Ví dụ 4 Cho tam giác ABC có G là trọng tâm. Chứng minh:
𝑨𝑩 + 𝑨𝑪 = 𝟑𝑨𝑮. Bài giải
Thay điểm M bằng điểm A trong hệ thức ở Ví dụ 4 ta được
𝑨𝑨 + 𝑨𝑩 + 𝑨𝑪 = 𝟑𝑨𝑮 hay 𝑨𝑩 + 𝑨𝑪 = 𝟑𝑨𝑮. TOÁN THPT GIÁO ÁN ĐIỆN TỬ
k > 0 cùng hướng 𝒂; k a
k < 0 ngược hướng 𝒂 Tổng kết
Độ dài bằng 𝒌 |𝒂| a
𝟎𝒂 = 𝟎, 𝒌𝟎 = 𝟎. Tích của một số Ứng dụng với một vectơ
• 𝒌 𝒂 + 𝒃 = 𝒌𝒂 + 𝒌𝒃;
𝑰 là trung điểm của đoạn 𝑨𝑩
• 𝒌 𝒂 − 𝒃 = 𝒌𝒂 − 𝒌𝒃;
𝑴𝑨 + 𝑴𝑩 = 𝟐𝑴𝑰, ∀ 𝑴.
• (𝒉 + 𝒌)𝒂 = 𝒉𝒂 + 𝒌𝒂;
• 𝒉(𝒌𝒂) = (𝒉𝒌)𝒂;
𝑮 là trọng tâm của tam giác 𝑨𝑩𝑪
• 𝟏𝒂 = 𝒂; (−𝟏)𝒂 = −𝒂.
𝑴𝑨 + 𝑴𝑩 + 𝑴𝑪 = 𝟑𝑴𝑮, ∀ 𝑴.
• 𝒌𝒂 = 𝟎 ⟺ 𝒌 = 𝟎 hoặc 𝒂 = 𝟎. TOÁN THPT
GIÁO ÁN ĐIỆN TỬ-DIỄN ĐÀN GIÁO VIÊN TOÁN CHƯƠNG IV.
HỆ THỨC LƯỢNG TRONG TAM GIÁC. VECTƠ
§5. Tích của một số với một vectơ Tiết 2 TOÁN THPT GIÁO ÁN ĐIỆN TỬ 3
Điều kiện để hai vectơ cùng phương. Điều kiện để ba điểm thẳng hàng Khởi động 𝒂
Cho vectơ 𝒂 (khác 𝟎) như hình vẽ.
a) Hãy vẽ các vectơ 𝒃 = 𝟑𝒂 và 𝒄 = −𝟐𝒂? 𝒃
b) Nhận xét gì về phương của
các vectơ 𝒂, 𝒃, 𝒄. 𝒄 TOÁN THPT GIÁO ÁN ĐIỆN TỬ 3
Điều kiện để hai vectơ cùng phương. Điều kiện để ba điểm thẳng hàng Ghi nhớ
❖ Điều kiện cần và đủ để hai vectơ 𝒂 và 𝒃 (𝒃 ≠ 𝟎) cùng phương là có một
số thực 𝒌 để 𝒂 = 𝒌𝒃. Câu hỏi Câu hỏi
Cho ba điểm phân biệt 𝑨, 𝑩, 𝑪.
a) Nếu ba điểm 𝑨, 𝑩, 𝑪 thẳng hàng thì hai vectơ 𝑨𝑩, 𝑨𝑪 có cùng phương hay không?
b) Ngược lại, nếu hai vectơ 𝑨𝑩, 𝑨𝑪 cùng phương thì ba điểm 𝑨, 𝑩, 𝑪 có
thẳng hàng hay không? TOÁN THPT GIÁO ÁN ĐIỆN TỬ 3
Điều kiện để hai vectơ cùng phương. Điều kiện để ba điểm thẳng hàng Câu hỏi Câu hỏi
Cho ba điểm phân biệt 𝑨, 𝑩, 𝑪. B A C
a) Nếu ba điểm 𝑨, 𝑩, 𝑪 thẳng hàng thì hai vectơ 𝑨𝑩, 𝑨𝑪 có cùng phương hay không?
b) Ngược lại, nếu hai vectơ 𝑨𝑩, 𝑨𝑪 cùng phương thì ba điểm 𝑨, 𝑩, 𝑪 có
thẳng hàng hay không? Trả lời
a) Hai vectơ 𝑨𝑩, 𝑨𝑪 cùng phương với nhau.
b) Nếu hai vectơ 𝑨𝑩, 𝑨𝑪 cùng phương với nhau thì hai đường thẳng 𝑨𝑩
và 𝑨𝑪 sẽ song song hoặc trùng nhau, mà chúng cùng đi qua điểm 𝑨 nên
trùng nhau, do đó ba điểm 𝑨, 𝑩, 𝑪 thẳng hàng. TOÁN THPT GIÁO ÁN ĐIỆN TỬ 3
Điều kiện để hai vectơ cùng phương. Điều kiện để ba điểm thẳng hàng Ghi nhớ
❖ Điều kiện cần và đủ để hai vectơ 𝒂 và 𝒃 (𝒃 ≠ 𝟎) cùng phương là có một
số thực 𝒌 để 𝒂 = 𝒌𝒃.
❖ Điều kiện cần và đủ để ba điểm phân biệt 𝑨, 𝑩, 𝑪 thẳng hàng là có số
thực 𝒌 để 𝑨𝑩 = 𝒌𝑨𝑪. TOÁN THPT GIÁO ÁN ĐIỆN TỬ 3
Điều kiện để hai vectơ cùng phương. Điều kiện để ba điểm thẳng hàng Ví dụ 1
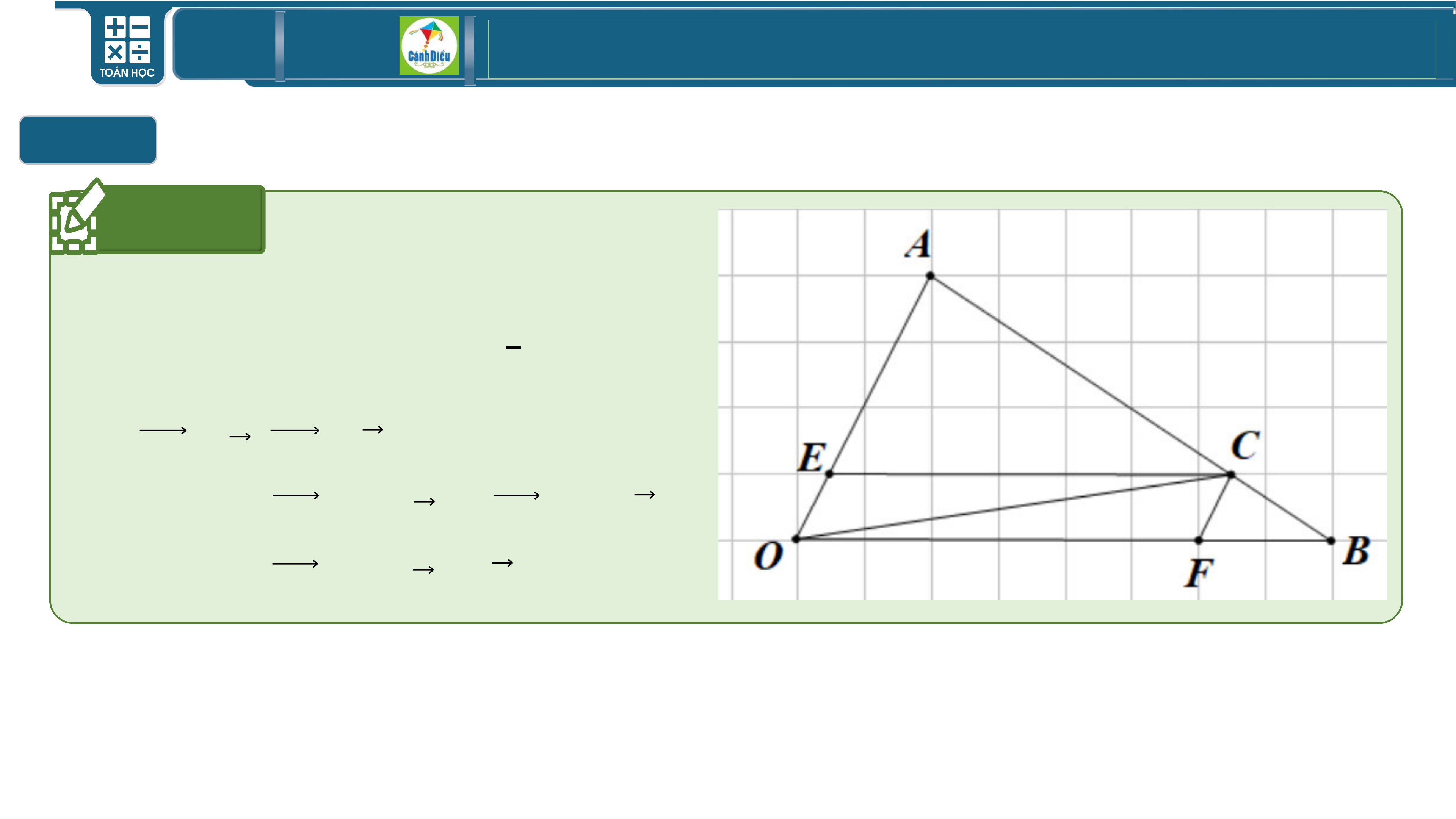
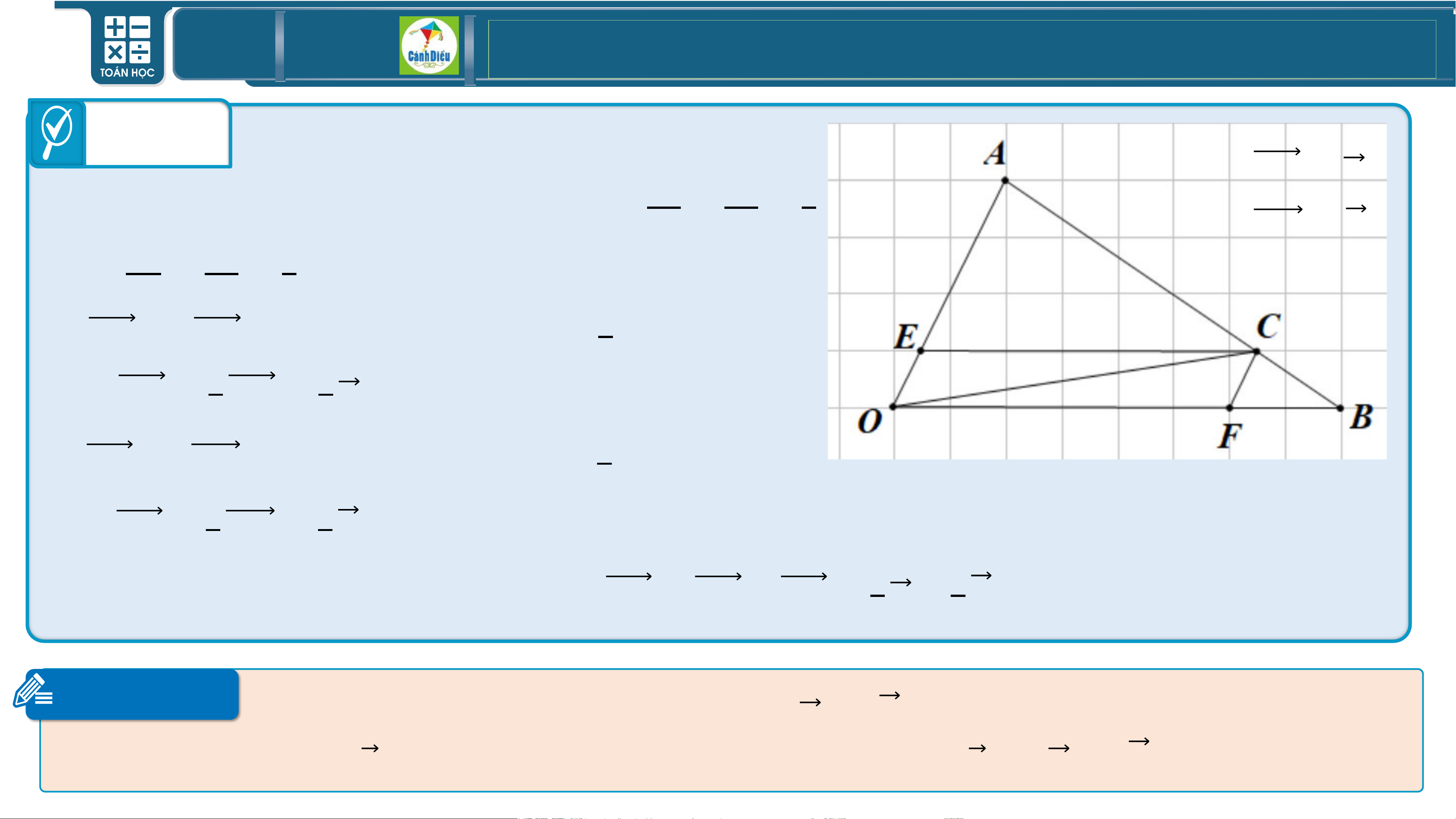
Cho tam giác 𝑶𝑨𝑩. Điểm 𝑪 thuộc
cạnh 𝑨𝑩 sao cho 𝑨𝑪 = 𝟑 𝑨𝑩. Dựng 𝟒
𝑪𝑬 // 𝑶𝑩, 𝑪𝑭 // 𝑶𝑨 (như hình). Giả
sử 𝑶𝑨 = 𝒂, 𝑶𝑩 = 𝒃.
a) Biểu thị 𝑶𝑬 theo 𝒂 và 𝑶𝑭 theo 𝒃.
b) Biểu thị 𝑶𝑪 theo 𝒂 và 𝒃. TOÁN THPT GIÁO ÁN ĐIỆN TỬ Trả lời 𝑶𝑨 = 𝒂 𝑶𝑬
a) Ta có 𝑪𝑬 // 𝑶𝑩, 𝑪𝑭 // 𝑶𝑨 suy ra = 𝑩𝑪 = 𝟏 𝑶𝑨 𝑩𝑨 𝟒 𝑶𝑩 = 𝒃
và 𝑶𝑭 = 𝑨𝑪 = 𝟑. 𝑶𝑩 𝑨𝑩 𝟒
Vì 𝑶𝑬 và 𝑶𝑨 cùng hướng và 𝑶𝑬 = 𝟏 𝑶𝑨 𝟒
nên 𝑶𝑬 = 𝟏 𝑶𝑨 = 𝟏 𝒂. 𝟒 𝟒
Vì 𝑶𝑭 và 𝑶𝑩 cùng hướng và 𝑶𝑭 = 𝟑 𝑶𝑩 𝟒
nên 𝑶𝑭 = 𝟑 𝑶𝑩 = 𝟑 𝒃. 𝟒 𝟒
b) Vì 𝑶𝑬𝑪𝑭 là hình bình hành nên 𝑶𝑪 = 𝑶𝑬 + 𝑶𝑭 = 𝟏 𝒂 + 𝟑 𝒃. 𝟒 𝟒
Nhận xét Trong mặt phẳng, cho hai vectơ 𝒂 và 𝒃 không cùng phương. Với mỗi
vectơ 𝒄 có duy nhất cặp số (𝒙; 𝒚) thỏa mãn 𝒄 = 𝒙𝒂 + 𝒚𝒃. TOÁN THPT GIÁO ÁN ĐIỆN TỬ CHƯƠNG IV.
HỆ THỨC LƯỢNG TRONG TAM GIÁC. VECTƠ
§5. Tích của một số với một vectơ Phần Luyện tập TOÁN THPT GIÁO ÁN ĐIỆN TỬ
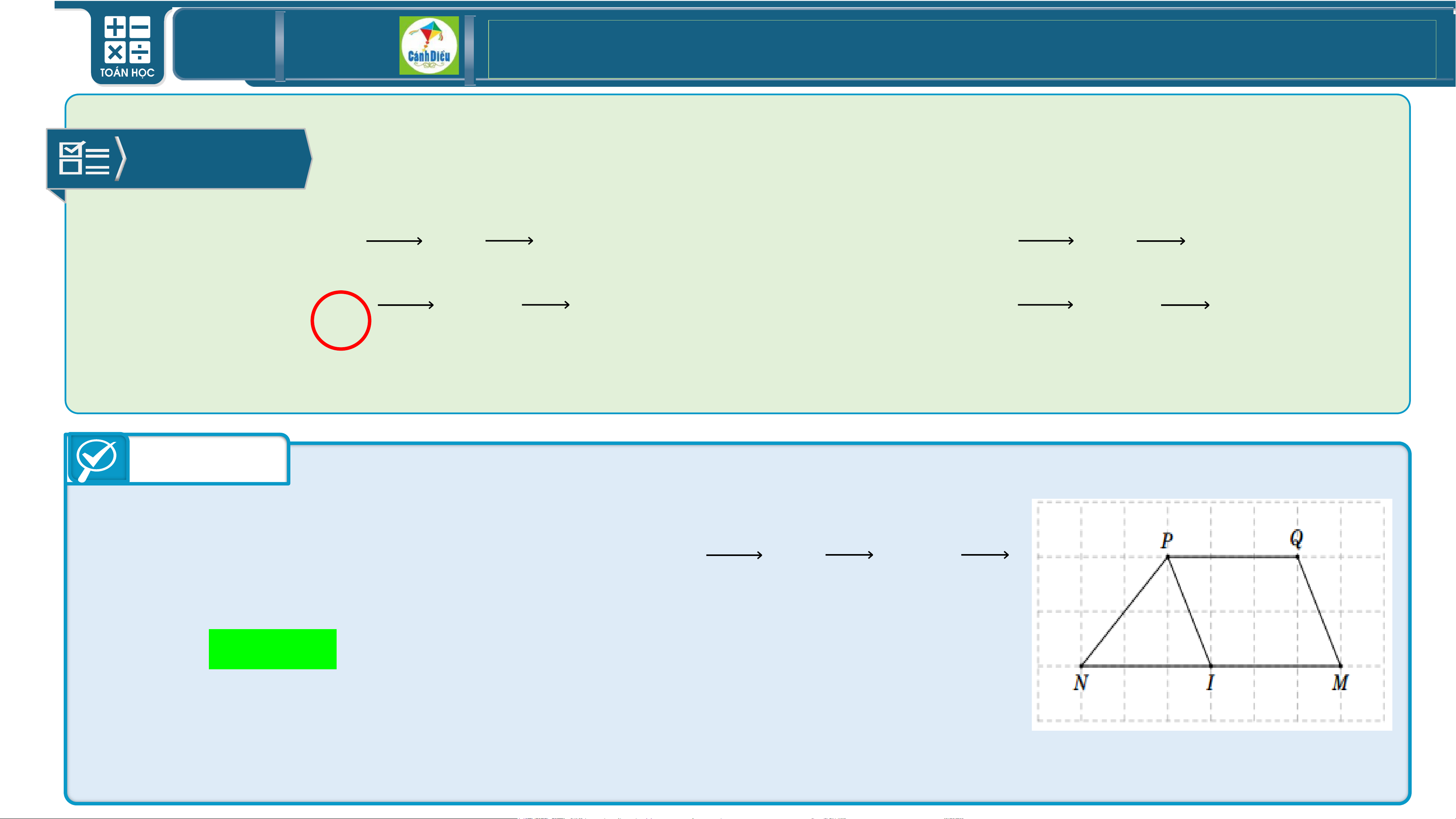
BÀI 1/Sgk Cho hình thang 𝑴𝑵𝑷𝑸, 𝑴𝑵 song song 𝑷𝑸, 𝑴𝑵 = 𝟐𝑷𝑸. Phát biểu nào sau đây đúng?
A. 𝑴𝑵 = 𝟐𝑷𝑸
B. 𝑴𝑸 = 𝟐𝑵𝑷
C. 𝑴𝑵 = −𝟐𝑷𝑸
D. 𝑴𝑸 = −𝟐𝑵𝑷 Trả lời
Gọi 𝑰 là trung điểm 𝑴𝑵. Ta có 𝑴𝑵 = 𝟐𝑸𝑷 = −𝟐𝑷𝑸 Chọn C. TOÁN THPT GIÁO ÁN ĐIỆN TỬ
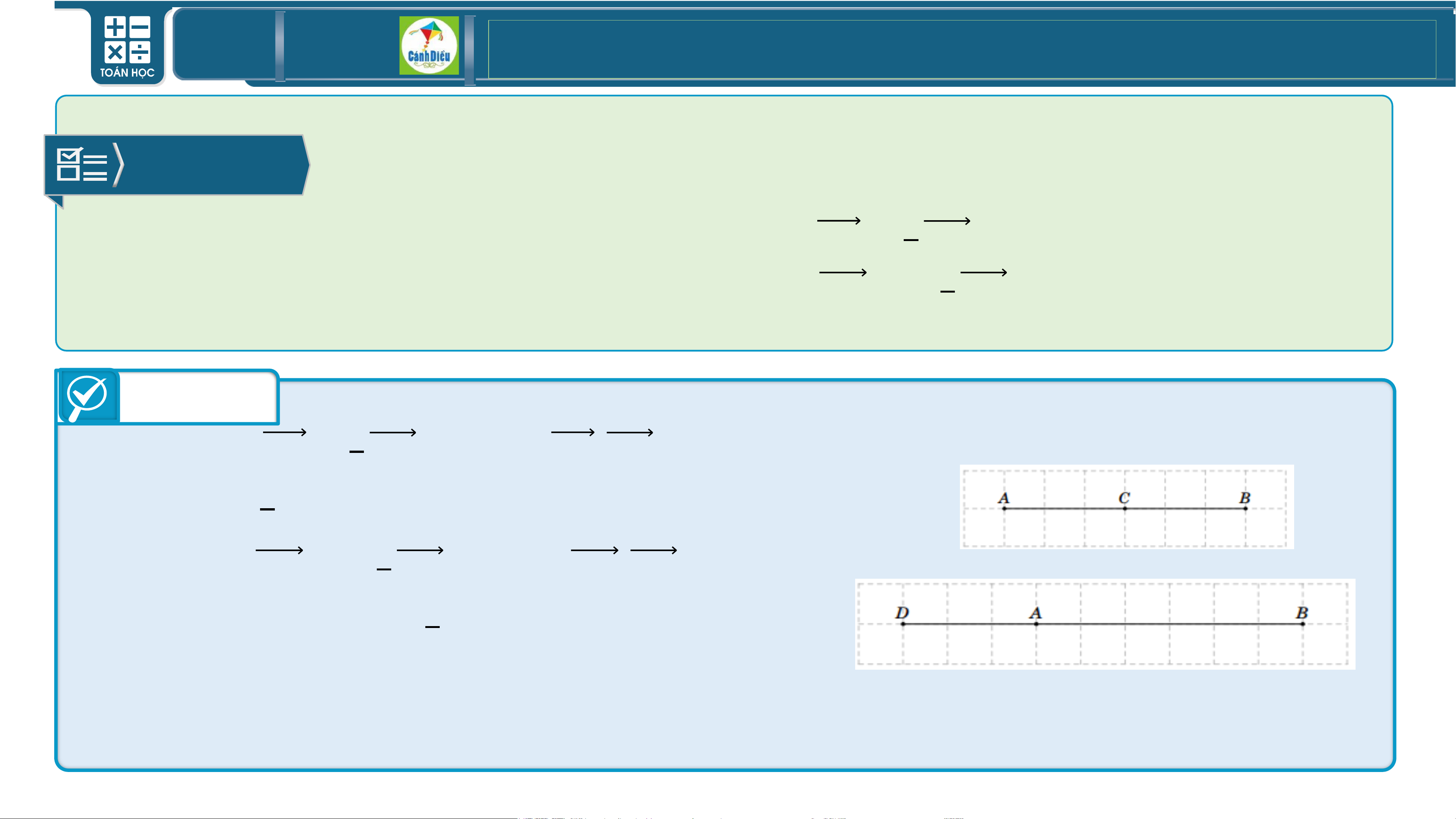
BÀI 2/Sgk Cho đoạn thẳng 𝑨𝑩 = 𝟔 𝒄𝒎
a) Xác định điểm 𝑪 thỏa mãn 𝑨𝑪 = 𝟏 𝑨𝑩 𝟐
b) Xác định điểm 𝑫 thỏa mãn 𝑨𝑫 = − 𝟏 𝑨𝑩. 𝟐 Trả lời
a) Vì 𝑨𝑪 = 𝟏 𝑨𝑩 , suy ra 𝑨𝑪, 𝑨𝑩 cùng hướng và 𝟐
𝑨𝑪 = 𝟏 𝑨𝑩. Do đó 𝑪 là trung điểm của đoạn 𝑨𝑩. 𝟐
b) Vì 𝑨𝑫 = − 𝟏 𝑨𝑩, suy ra 𝑨𝑫, 𝑨𝑩 ngược 𝟐
hướng và 𝑨𝑫 = 𝟏 𝑨𝑩. 𝟐
Do đó 𝑫 là điểm ngoài đoạn 𝑨𝑩 (nằm trên
đường thẳng 𝑨𝑩) sao cho 𝑫𝑨 + 𝑨𝑩 = 𝟗 𝒄𝒎. TOÁN THPT GIÁO ÁN ĐIỆN TỬ
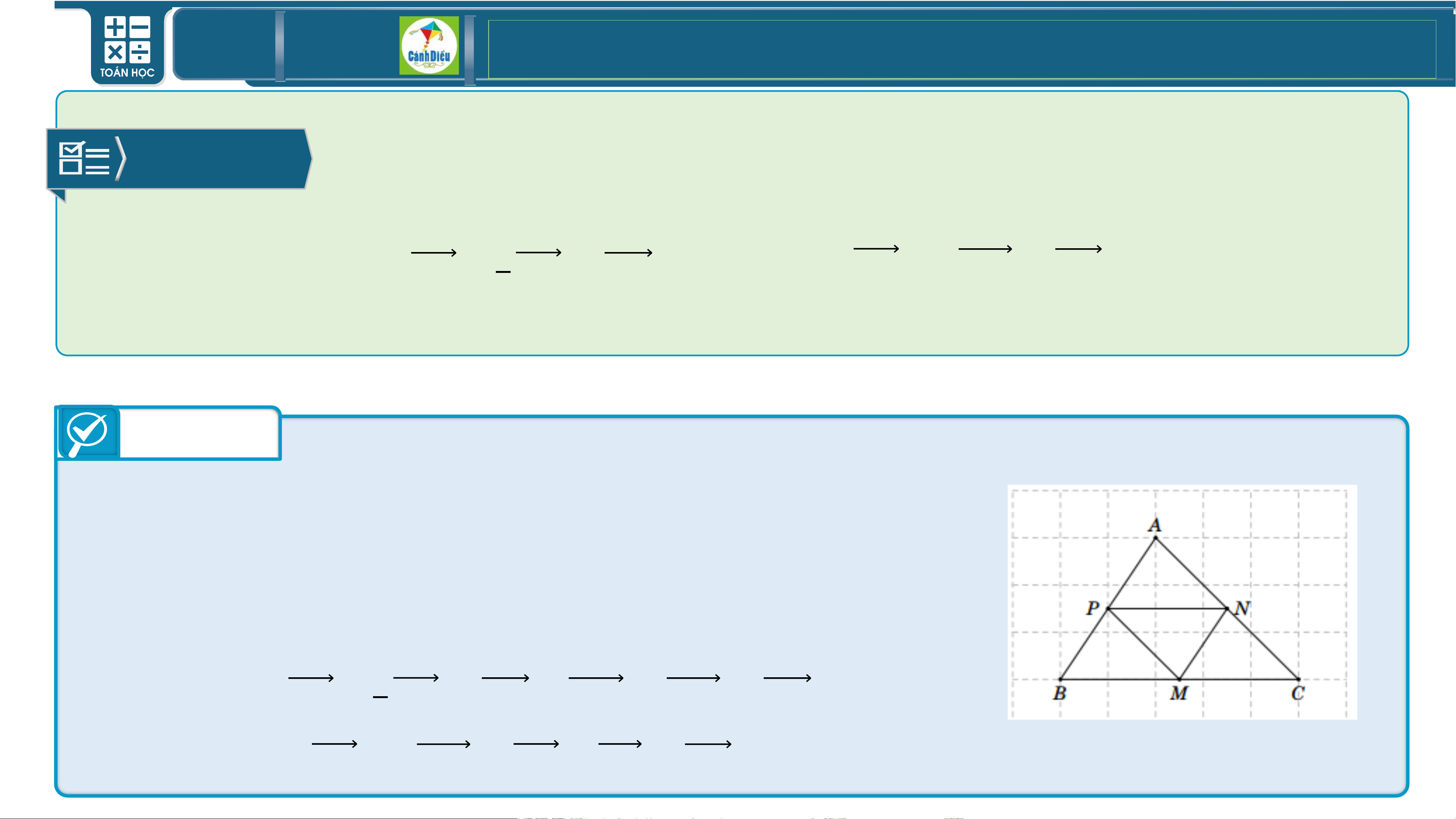
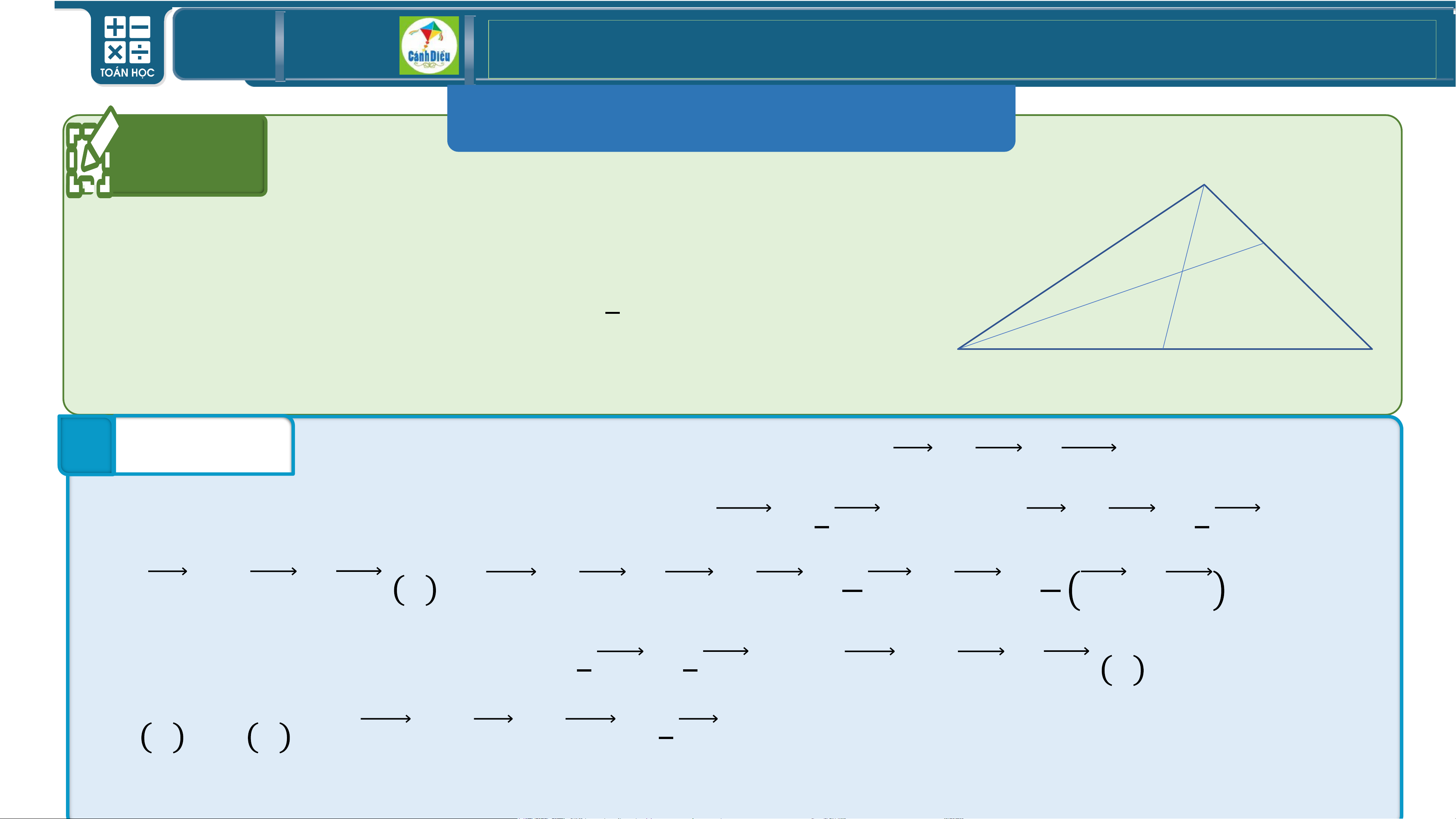
BÀI 3/Sgk Cho tam giác 𝑨𝑩𝑪 có 𝑴, 𝑵, 𝑷 lần lượt là trung điểm các cạnh
𝑩𝑪, 𝑪𝑨, 𝑨𝑩. Chứ ng minh rằng:
a) 𝑨𝑷 + 𝟏 𝑩𝑪 = 𝑨𝑵
b) 𝑩𝑪 + 𝟐𝑴𝑷 = 𝑩𝑨 𝟐 Trả lời
a) Theo tính chất đường trung bình của tam
giác, từ giả thiết ta có:
𝑷𝑴, 𝑵𝑴 lần lượt song song với 𝑨𝑪, 𝑨𝑩,
Suy ra tứ giác 𝑨𝑷𝑴𝑵 là hình bình hành.
Ta có 𝑨𝑷 + 𝟏 𝑩𝑪 = 𝑷𝑩 + 𝑩𝑴 = 𝑷𝑴 = 𝑨𝑵 (đpcm). 𝟐
b) Ta có 𝑩𝑪 + 𝟐𝑴𝑷 = 𝑩𝑪 + 𝑪𝑨 = 𝑩𝑨 (đpcm). TOÁN THPT GIÁO ÁN ĐIỆN TỬ
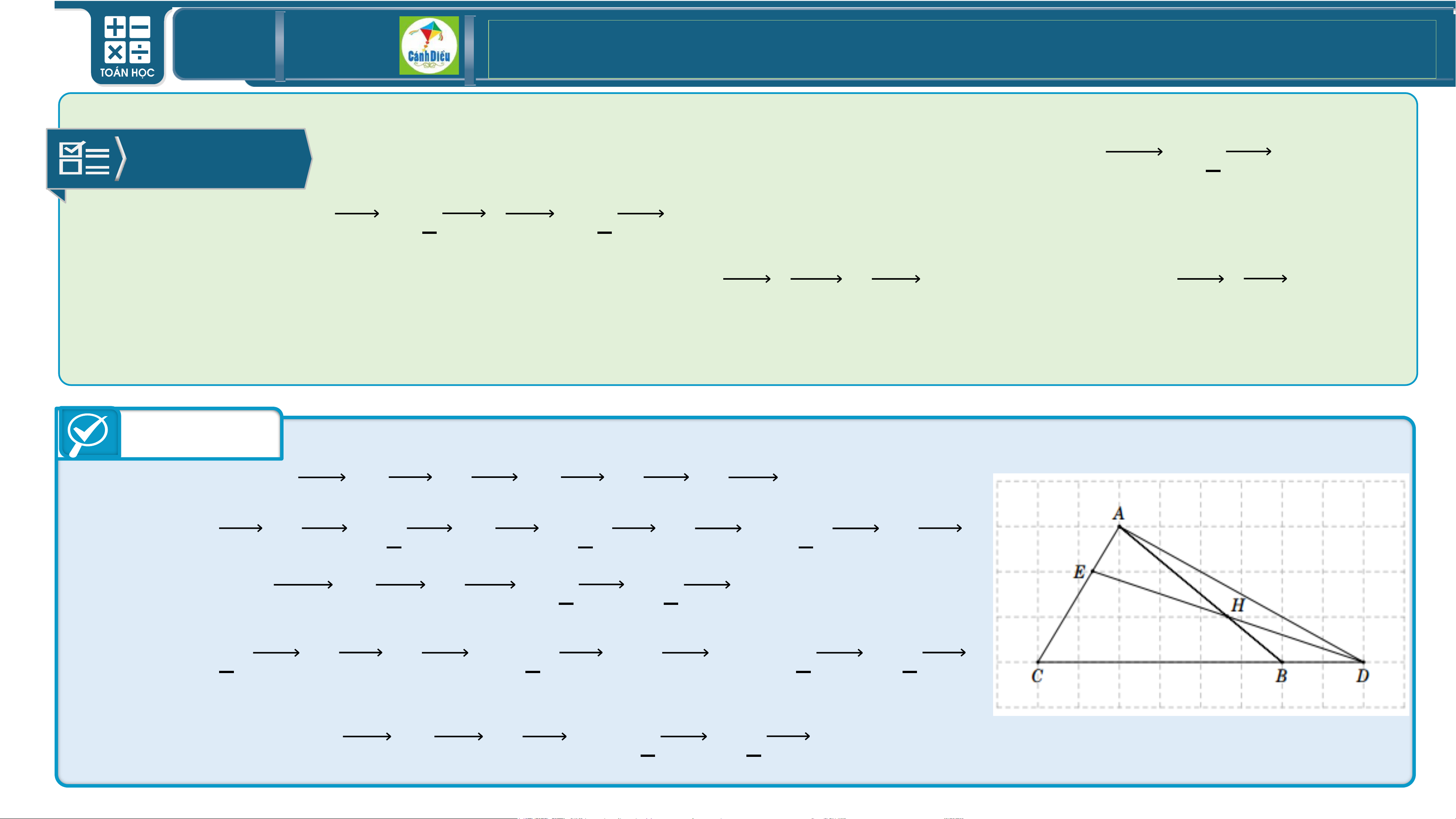
BÀI 7/Sgk Cho tam giác 𝑨𝑩𝑪 . Các điểm 𝑫,𝑬,𝑯 thỏa mãn 𝑫𝑩 = 𝟏𝑩𝑪, 𝟑
𝑨𝑬 = 𝟏 𝑨𝑪, 𝑨𝑯 = 𝟐 𝑨𝑩. 𝟑 𝟑
a) Biểu thị mỗi vectơ 𝑨𝑫, 𝑫𝑯 , 𝑯𝑬 theo hai vectơ 𝑨𝑩, 𝑨𝑪 .
b) Chứng minh 𝑫, 𝑬 , 𝑯 thẳng hàng. Trả lời
a) Ta có 𝑨𝑫 = 𝑨𝑪 + 𝑪𝑫 = 𝑨𝑪 + 𝑪𝑩 + 𝑩𝑫
= 𝑨𝑪 + 𝑪𝑩 + 𝟏 𝑪𝑩 = 𝑨𝑪 + 𝟒 (𝑪𝑨 + 𝑨𝑩) = 𝟒 (𝑨𝑩 − 𝑨𝑪). 𝟑 𝟑 𝟑
Ta có 𝑫𝑯 = 𝑫𝑩 + 𝑩𝑯 = 𝟏 𝑩𝑪 + 𝟏 𝑩𝑨 𝟑 𝟑
= 𝟏 (𝑩𝑨 + 𝑨𝑪 + 𝑩𝑨) = 𝟏 (𝑨𝑪 − 𝟐𝑨𝑩) = − 𝟐 𝑨𝑩 + 𝟏 𝑨𝑪. 𝟑 𝟑 𝟑 𝟑
Suy ra 𝑯𝑬 = 𝑯𝑨 + 𝑨𝑬 = − 𝟐 𝑨𝑩 + 𝟏 𝑨𝑪. 𝟑 𝟑 TOÁN THPT GIÁO ÁN ĐIỆN TỬ
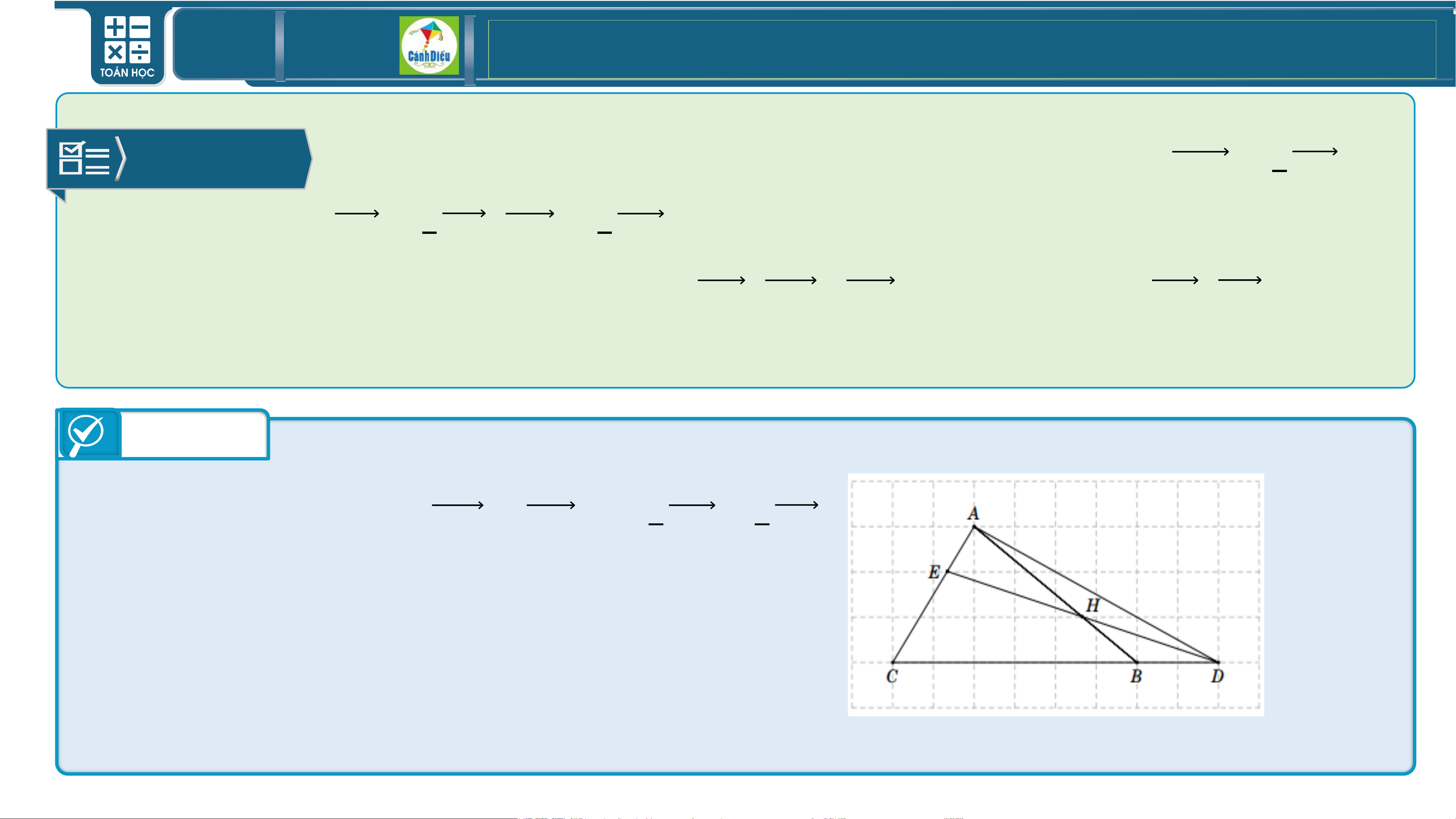
BÀI 7/Sgk Cho tam giác 𝑨𝑩𝑪 . Các điểm 𝑫,𝑬,𝑯 thoả mãn 𝑫𝑩 = 𝟏𝑩𝑪, 𝟑
𝑨𝑬 = 𝟏 𝑨𝑪, 𝑨𝑯 = 𝟐 𝑨𝑩. 𝟑 𝟑
a) Biểu thị mỗi vectơ 𝑨𝑫, 𝑫𝑯 , 𝑯𝑬 theo hai vectơ 𝑨𝑩, 𝑨𝑪 .
b) Chứng minh 𝑫, 𝑬 , 𝑯 thẳng hàng. Trả lời b) Ta thấy
𝑫𝑯 = 𝑯𝑬 = − 𝟐 𝑨𝑩 + 𝟏 𝑨𝑪. 𝟑 𝟑
Nên 3 điểm 𝑫, 𝑬 , 𝑯 thẳng hàng. TOÁN THPT GIÁO ÁN ĐIỆN TỬ BÀI 8
Cho tam giác 𝑨𝑩𝑪, xác định điểm 𝑴 để 𝑴𝑨 + 𝟑𝑴𝑩 + 𝟐𝑴𝑪 = 𝟎. Trả lời
Đẳng thức vectơ đã cho tương đương với
MA + 𝟑(MA + AB) + 𝟐(MA + AC) = 𝟎
⇔ 𝟔MA + 𝟑AB + 𝟐AC = 𝟎 𝟏 𝟏 ⇔ AM = 𝟐AB + 𝟑AC.
Lấy điểm 𝑬 là trung điểm của 𝑨𝑩 và điểm 𝑭
thuộc cạnh 𝑨𝑪 sao cho 𝑨𝑭 = 𝟏 𝑨𝑪. 𝟑
Khi đó 𝑨𝑬 = 𝟏 𝑨𝑩, 𝑨𝑭 = 𝟏 𝑨𝑪, vì vậy 𝑨𝑴 = 𝑨𝑬 + 𝑨𝑭. 𝟐 𝟑
Suy ra 𝑴 là đinh thứ tư của hình bình hành 𝑬𝑨𝑭𝑴. TOÁN THPT GIÁO ÁN ĐIỆN TỬ
Nhận xét Điểm khối tâm của hệ các chất điểm 𝑨𝟏,𝑨𝟐,…,𝑨𝒏 với các
khối lượng tương ứng 𝒎𝟏, 𝒎𝟐, … , 𝒎𝒏, được xác định bởi đẳng thức vectơ
𝒎𝟏𝑴𝑨𝟏 + 𝒎𝟐𝑴𝑨𝟐 + ⋯ + 𝒎𝒏𝑴𝑨𝒏 = 𝟎.
Vì vậy việc xác định điểm khối tâm được quy về việc
xác định điểm thỏa mãn đẳng thức vectơ tương ứng. TOÁN THPT GIÁO ÁN ĐIỆN TỬ
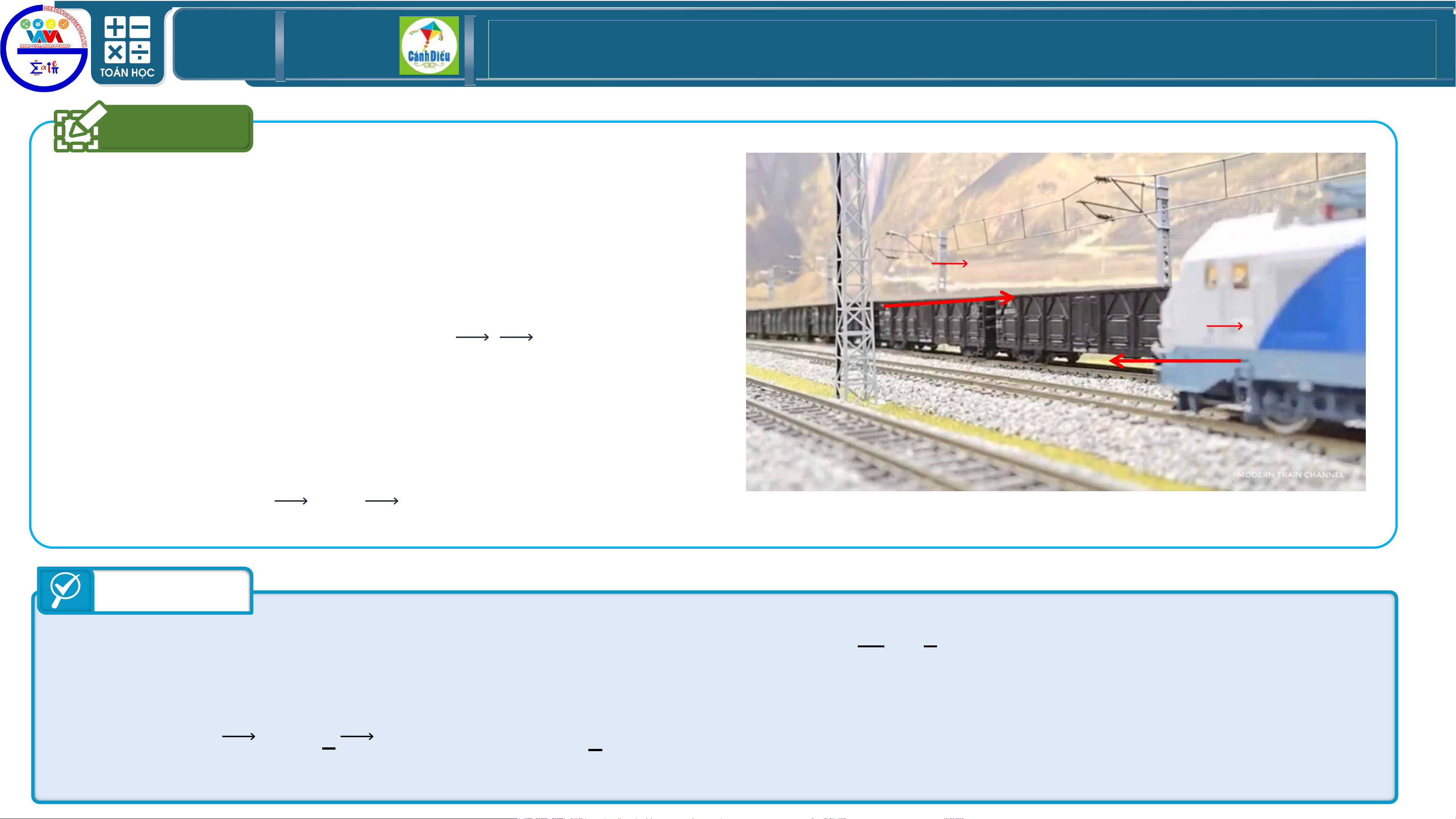
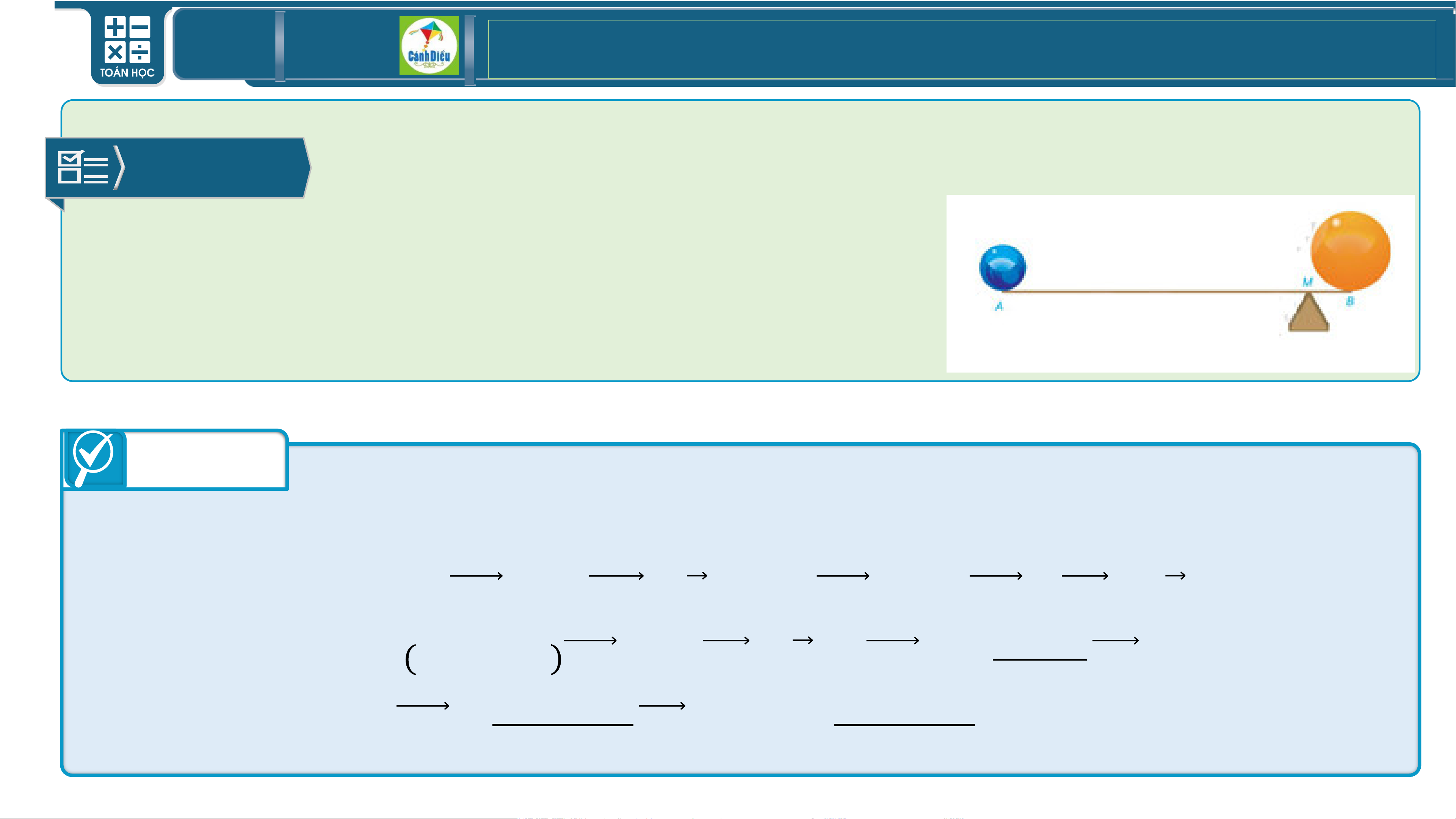
BÀI TOÁN Đặt 2 viên bi có khối lượng khác
nhau lên 2 đầu của một cánh tay đòn.
Xác định vị trí đặt trụ đỡ tam giác trên cánh tay
đòn sao cho cánh tay đòn ở trạng thái cân bằng. Trả lời
Khối lượng viên bi đặt ở đầu 𝑨 là 𝒎𝟏, đầu 𝑩 là 𝒎𝟐.
Chiều dài cánh tay đòn 𝑨𝑩. Do hệ vật cân bằng nên
𝒎𝟏𝑴𝑨 + 𝒎𝟐𝑴𝑩 = 𝟎 ⇔ 𝒎𝟏 𝑴𝑨 + 𝒎𝟐(𝑴𝑨 + 𝑨𝑩) = 𝟎
⇔ 𝒎𝟏 + 𝒎𝟐 𝑴𝑨 + 𝒎𝟐𝑨𝑩 = 𝟎 ⇔ 𝑴𝑨 = − 𝒎𝟐 𝑨𝑩 𝒎 𝒎 𝒎𝟏+𝒎𝟐 ⇔ 𝑨𝑴 = 𝟐 𝟐 𝒎 𝑨𝑩 ⇔ 𝑨𝑴 = 𝑨𝑩. 𝟏 + 𝒎𝟐 𝒎𝟏 + 𝒎𝟐 TOÁN THPT GIÁO ÁN ĐIỆN TỬ
Cho vectơ 𝒂 và số k  R. 𝒌𝒂 là một vectơ được xác định như sau: Định nghĩa
+ 𝒌𝒂 cùng hướng với 𝒂 nếu k > 0 và ngược hướng với 𝒂 nếu 𝒌 < 𝟎
+ 𝒌𝒂 = 𝒌 . 𝒂 . Tính chất
𝒌 𝒂 + 𝒃 = 𝒌𝒂 + 𝒌𝒃;
𝒉 + 𝒌 𝒂 = 𝒉𝒂 + 𝒌𝒂
𝒉 𝒌𝒂 = 𝒉𝒌 𝒂;
𝟏. 𝒂 = 𝒂, −𝟏 𝒂 = −𝒂 Trung điểm
I là trung điểm AB  𝑰𝑨 + 𝑰𝑩 = 𝟎  𝑴𝑨 + 𝑴𝑩 = 𝟐𝑴𝑰 (M tuỳ ý). Trọng tâm
G là trọng tâm ABC  𝑮𝑨 + 𝑮𝑩 + 𝑮𝑪 = 𝟎
 𝑴𝑨 + 𝑴𝑩 + 𝑴𝑪 = 𝟑𝑴𝑮 (M tuỳ ý). ĐK 2 vectơ
𝒂 và 𝒃 𝒗ớ𝒊 𝒃 ≠ 𝟎 cùng phương ⇔ ∃𝒌 ∈ ℝ: 𝒂 = 𝒌𝒃 cùng phương
Ba điểm phân biệt 𝑨, 𝑩, 𝑪 thẳng hàng ⇔ ∃𝒌 ∈ ℝ, 𝐤 ≠ 𝟎: 𝑨𝑩 = 𝒌𝑨𝑪. TOÁN THPT GIÁO ÁN ĐIỆN TỬ CHƯƠNG IV.
HỆ THỨC LƯỢNG TRONG TAM GIÁC. VECTƠ
§5. Tích của một số với một vectơ Bài tập làm thêm TOÁN THPT GIÁO ÁN ĐIỆN TỬ BÀI TẬP TỰ LUẬN Bài 1 A
Cho tam giác 𝑨𝑩𝑪. Điểm 𝑴 nằm trên cạnh 𝑩𝑪
sao cho 𝑴𝑩 = 𝟐𝑴𝑪. Hãy phân tích vectơ 𝑨𝑴 theo hai vectơ C
𝒖 = 𝑨𝑩, 𝒗 = 𝑨𝑪. B M Lời giải
Từ giả thiết điểm 𝑴 nằm trên cạnh 𝑩𝑪 sao cho 𝑴𝑩 = 𝟐𝑴𝑪 ta có 𝑩𝑴 = 𝟐 𝑩𝑪, 𝟑
𝑩𝑴 và 𝑩𝑪 cùng hướng nên 𝑩𝑴 = 𝟐 𝑩𝑪. 𝟑
Do đó 𝑨𝑴 = 𝑨𝑩 + 𝑩𝑴 = 𝑨𝑩 + 𝟐 𝑩𝑪 = 𝑨𝑩 + 𝟐 𝑨𝑪 − 𝑨𝑩 = 𝟏 𝑨𝑩 + 𝟐 𝑨𝑪 = 𝟏 𝒖 + 𝟐 𝒗. 𝟑 𝟑 𝟑 𝟑 𝟑 𝟑 TOÁN THPT GIÁO ÁN ĐIỆN TỬ BÀI TẬP TỰ LUẬN Bài 2 A
Cho tam giác 𝑨𝑩𝑪 có trung tuyến 𝑨𝑴. K Gọi 𝑰 là I
trung điểm 𝑨𝑴 và 𝑲 là điểm
thuộc cạnh 𝑨𝑪 sao cho 𝑨𝑲 = 𝟏 𝑨𝑪. Chứng 𝟑 B
minh ba điểm 𝑩, 𝑰, 𝑲 thẳng hàng. C M Lời giải
Ta có 𝑰 là trung điểm của 𝑨𝑴 ⇒ 𝟐𝑩𝑰 = 𝑩𝑨 + 𝑩𝑴.
Mặt khác 𝑴 là trung điểm của 𝑩𝑪 nên 𝑩𝑴 = 𝟏 𝑩𝑪. Do đó 𝟐𝑩𝑰 = 𝑩𝑨 + 𝟏 𝑩𝑪 𝟐 𝟐 𝟏 𝟏
⇔ 𝟒𝑩𝑰 = 𝟐𝑩𝑨 + 𝑩𝑪 𝟏 . 𝑩𝑲 = 𝑩𝑨 + 𝑨𝑲 = 𝑩𝑨 + 𝟑𝑨𝑪 = 𝑩𝑨 + 𝟑 𝑩𝑪 − 𝑩𝑨
= 𝟐 𝑩𝑨 + 𝟏 𝑩𝑪. ⇔ 𝟑𝑩𝑲 = 𝟐𝑩𝑨 + 𝑩𝑪 𝟐 𝟑 𝟑
Từ 𝟏 và 𝟐 ⇒ 𝟑𝑩𝑲 = 𝟒𝑩𝑰 ⇔ 𝑩𝑲 = 𝟒 𝑩𝑰. Suy ra 3 điểm 𝑩, 𝑰, 𝑲 thẳng hàng. 𝟑 TOÁN THPT GIÁO ÁN ĐIỆN TỬ BÀI TẬP TỰ LUẬN Bài 3
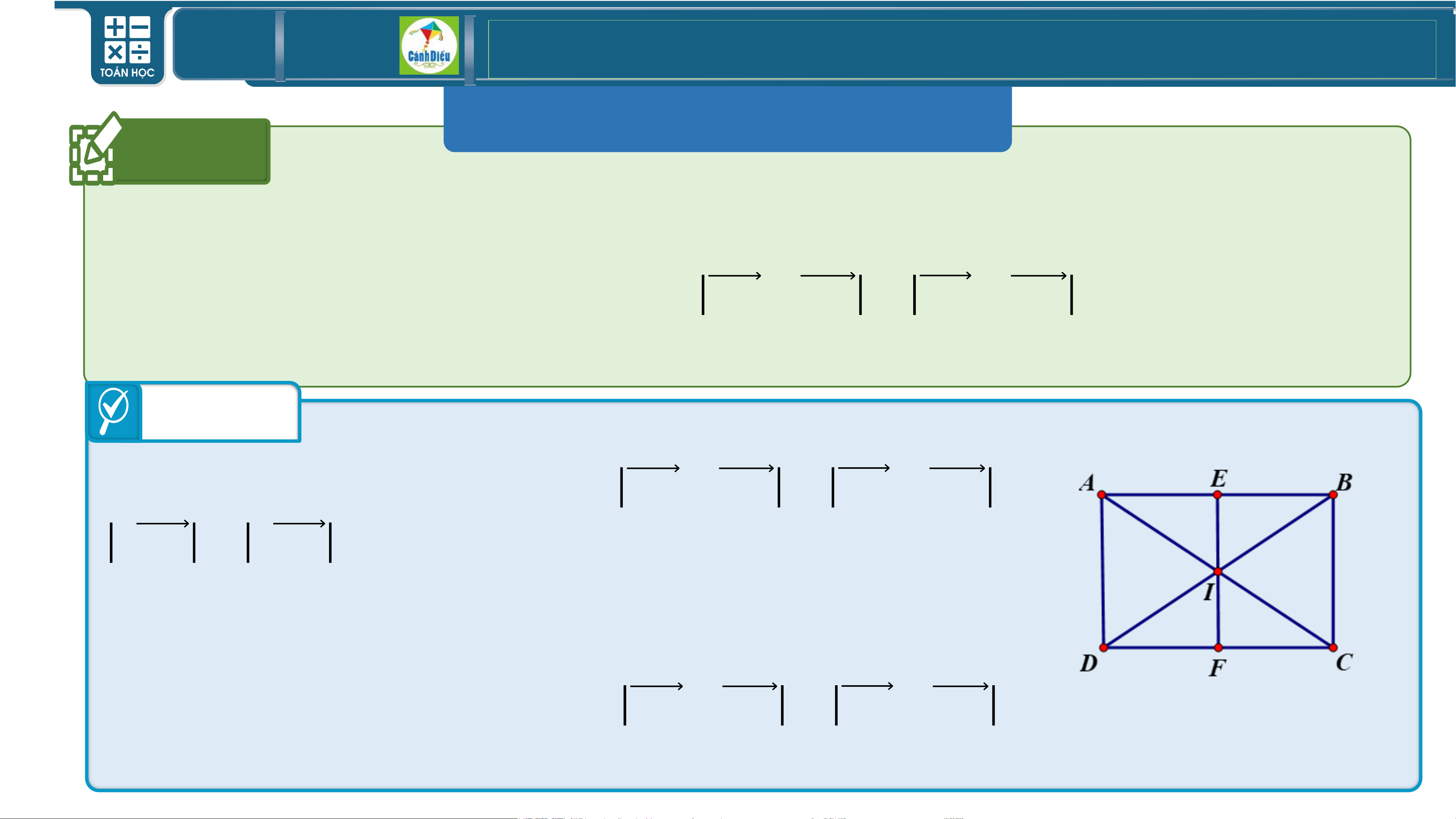
Cho hình chữ nhật 𝑨𝑩𝑪𝑫 và 𝑰 là giao điểm của hai đường chéo.
Tìm tập hợp các điểm 𝑴 thỏa mãn 𝑴𝑨 + 𝑴𝑩 = 𝑴𝑪 + 𝑴𝑫 .
Lời giải Gọi 𝑬 là trung điểm 𝑨𝑩, 𝑭 là trung điểm
𝑪𝑫. Giả sử điểm 𝑴 thoả mãn: 𝑴𝑨 + 𝑴𝑩 = 𝑴𝑪 + 𝑴𝑫 ⇔
𝟐𝑴𝑬 = 𝟐𝑴𝑭 ⇔ 𝑴𝑬 = 𝑴𝑭
⇔ 𝑴 nằm trên đường trung trực của đoạn thẳng 𝑬𝑭
⇔ 𝑴 nằm trên đường trung trực của đoạn thẳng 𝑨𝑫.
Vậy tập hợp điểm 𝑴 thỏa mãn 𝑴𝑨 + 𝑴𝑩 = 𝑴𝑪 + 𝑴𝑫 là
đường thẳng trung trực của đoạn thẳng 𝑨𝑫. TOÁN THPT GIÁO ÁN ĐIỆN TỬ
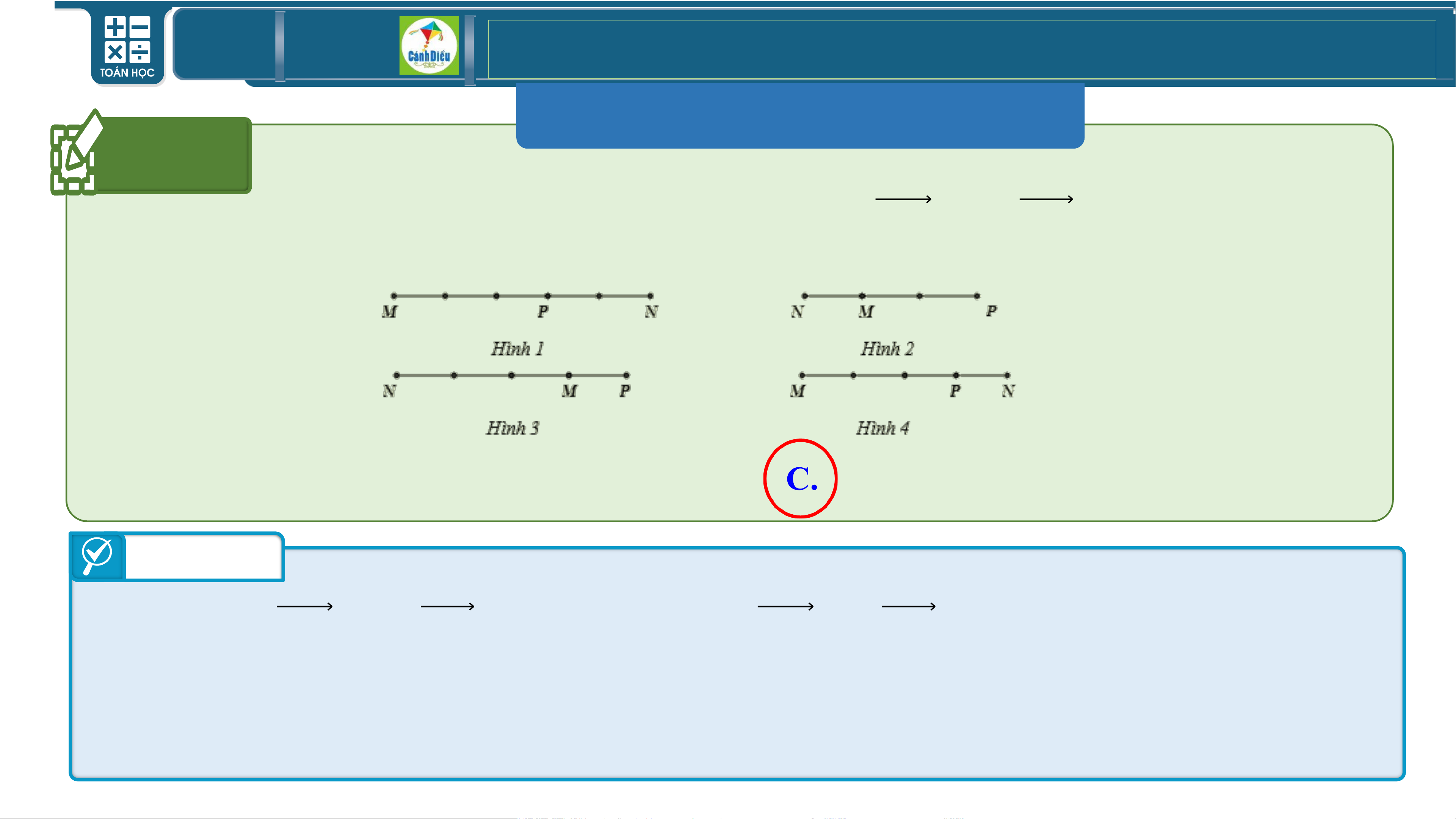
BÀI TẬP TRẮC NGHIỆM Câu 1
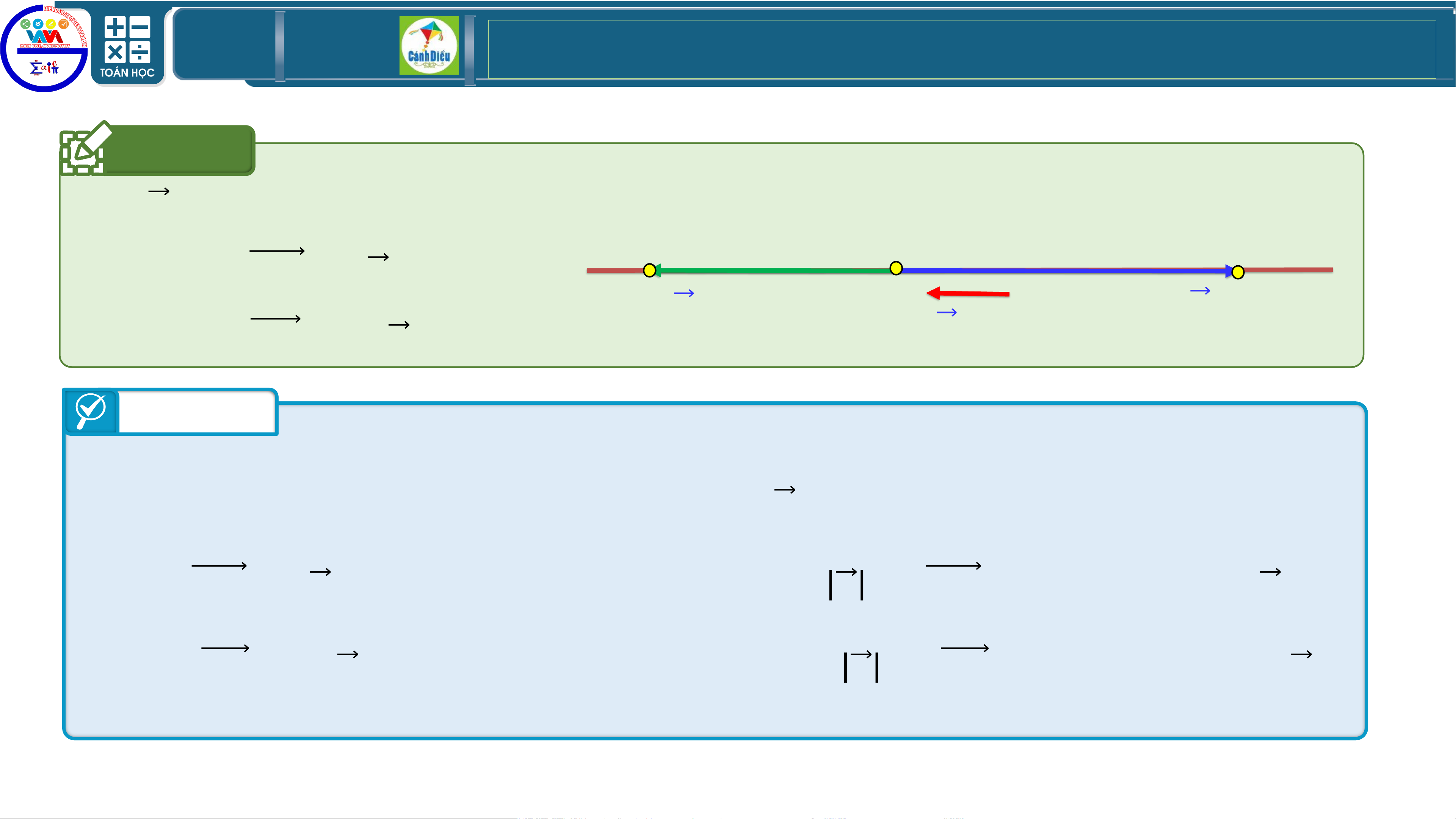
Trên đường thẳng 𝑴𝑵 lấy điểm 𝑷 sao cho 𝑴𝑵 = −𝟑𝑴𝑷. Điểm 𝑷 được
xác định đúng trong hình vẽ nào sau đây:
A. Hình 1.
B. Hình 2.
C. Hình 3. D. Hình 4. Trả lời
Ta có 𝑴𝑵 = −𝟑𝑴𝑷 nên 𝑴𝑵 = 𝟑𝑴𝑷; 𝑴𝑵 và 𝑴𝑷 ngược hướng. Chọn C. TOÁN THPT GIÁO ÁN ĐIỆN TỬ
BÀI TẬP TRẮC NGHIỆM Câu 2
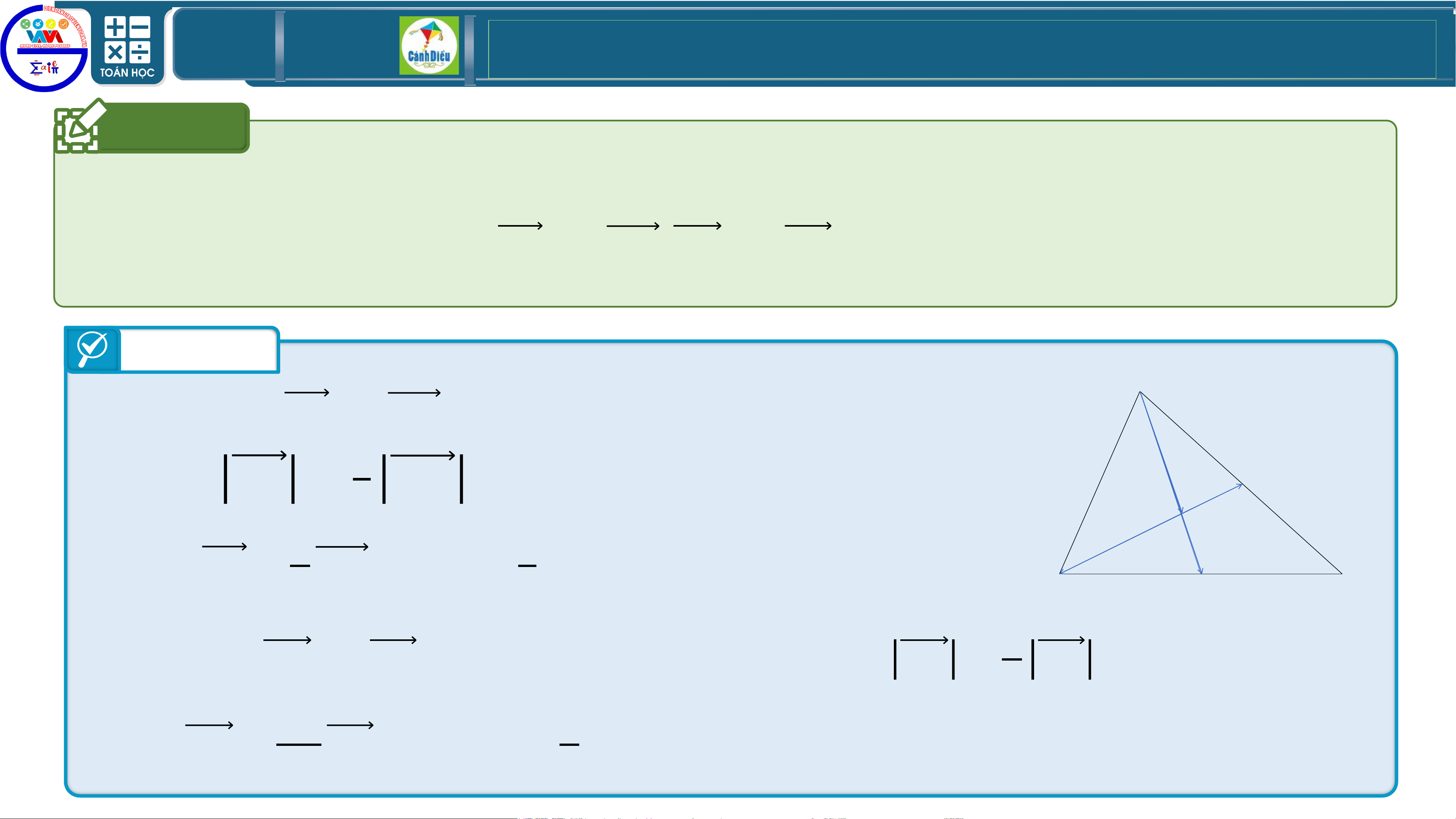
Cho hình bình hành 𝑨𝑩𝑪𝑫. Tìm 𝒏 ∈ ℝ, biết 𝑨𝑩 + 𝑨𝑪 + 𝑨𝑫 = 𝒏. 𝑨𝑪. A. 𝒏 = 𝟏. B. 𝒏 = 𝟒.
C. 𝒏 = 𝟑. D. 𝒏 = 𝟐. Trả lời
Ta có: 𝑨𝑩 + 𝑨𝑪 + 𝑨𝑫 = 𝑨𝑩 + 𝑨𝑫 + 𝑨𝑪 = 𝑨𝑪 + 𝑨𝑪 = 𝟐𝑨𝑪. Chọn D TOÁN THPT GIÁO ÁN ĐIỆN TỬ Câu 3
BÀI TẬP TRẮC NGHIỆM
Nếu 𝑮 là trọng tam giác 𝑨𝑩𝑪 thì đẳng thức nào sau đây đúng.
A. 𝑨𝑮 = 𝟏 𝑨𝑩 + 𝑨𝑪 .
B. 𝑨𝑮 = 𝟏 𝑨𝑩 + 𝑨𝑪 . 𝟐 𝟑
C. 𝑨𝑮 = 𝟑 𝑨𝑩 + 𝑨𝑪 .
D. 𝑨𝑮 = 𝟐 𝑨𝑩 + 𝑨𝑪 . 𝟐 𝟑 Trả lời A
Gọi 𝑴 là trung điểm của 𝑩𝑪 nên ta có 𝑨𝑩 + 𝑨𝑪 = 𝟐𝑨𝑴
Mà 𝑨𝑴 = 𝟑 𝑨𝑮 ⇒ 𝑨𝑩 + 𝑨𝑪 = 𝟐. 𝟑 𝑨𝑮 = 𝟑𝑨𝑮 ⇔ 𝑨𝑮 = 𝟏 𝑨𝑩 + 𝑨𝑪 . G 𝟐 𝟐 𝟑 Chọn B. B C M TOÁN THPT GIÁO ÁN ĐIỆN TỬ
BÀI TẬP TRẮC NGHIỆM Câu 4
Cho tam giác 𝑨𝑩𝑪. Để điểm 𝑴 thoả mãn điều kiện 𝑴𝑨 − 𝑴𝑩 + 𝑴𝑪 = 𝟎 thì 𝑴 phải
thỏa mãn mệnh đề nào?
A. 𝑴 là điểm sao cho tứ giác 𝑨𝑩𝑴𝑪 là hình bình hành.
B. 𝑴 là trọng tâm tam giác 𝑨𝑩𝑪.
C. 𝑴 là điểm sao cho tứ giác 𝑩𝑨𝑴𝑪 là hình bình hành.
D. 𝑴 thuộc trung trực của 𝑨𝑩. Trả lời
Ta có: 𝑴𝑨 − 𝑴𝑩 + 𝑴𝑪 = 𝟎 ⇔ 𝑩𝑨 + 𝑴𝑪 = 𝟎
⇔ 𝑴𝑪 = −𝑩𝑨 ⇔ 𝑴𝑪 = 𝑨𝑩
với 𝑨, 𝑩, 𝑪 không thẳng hàng nên tứ giác
𝑩𝑨𝑴𝑪 là hình bình hành. Chọn C TOÁN THPT GIÁO ÁN ĐIỆN TỬ
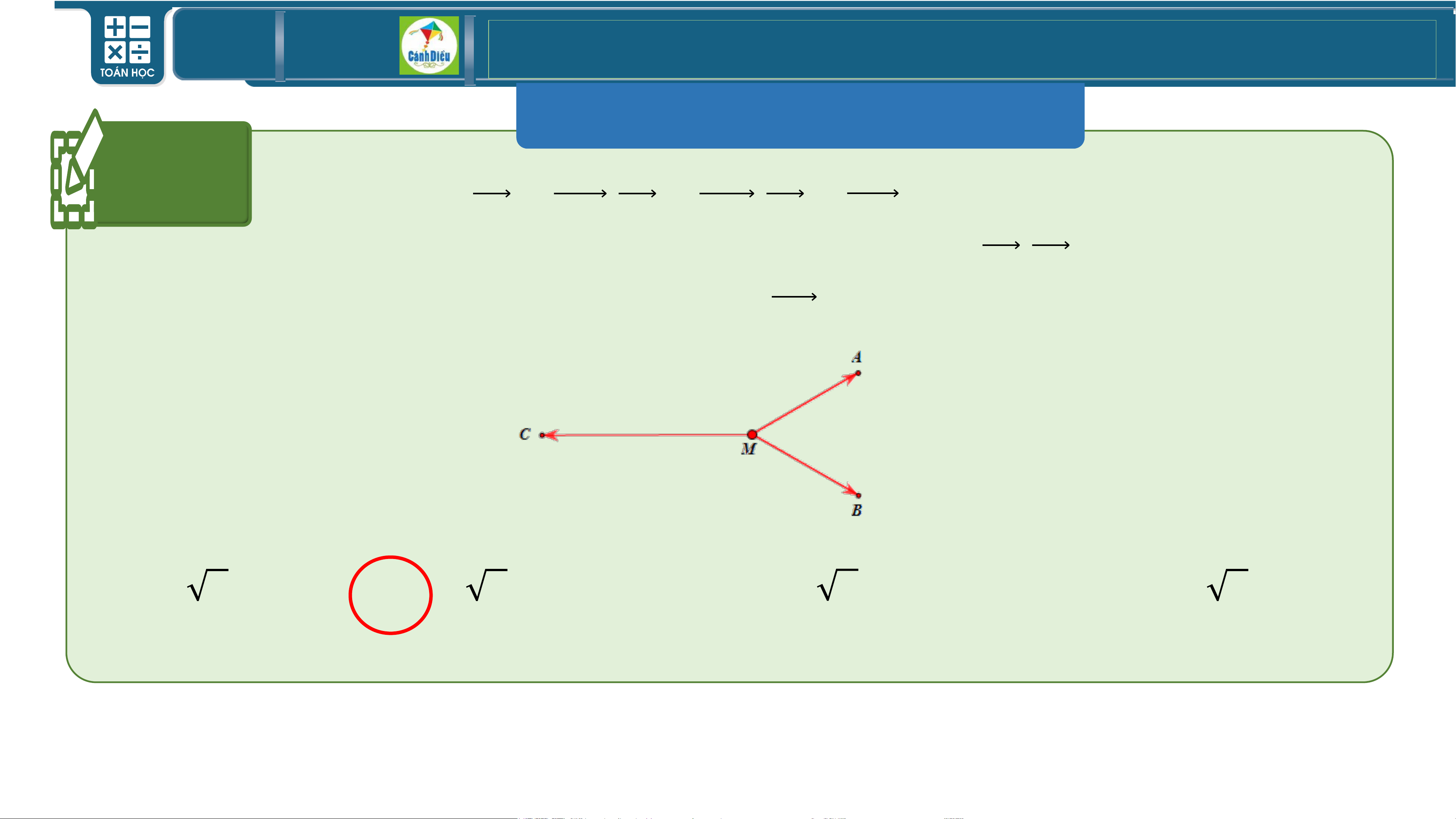
BÀI TẬP TRẮC NGHIỆM Câu 5
Cho ba lực 𝑭𝟏 = 𝑴𝑨, 𝑭𝟐 = 𝑴𝑩, 𝑭𝟑 = 𝑴𝑪 cùng tác động vào một vật
tại điểm 𝑴 và vật đứng yên. Cho biết cường độ của 𝑭𝟏, 𝑭𝟐 đều bằng 𝟓𝟎 𝑵 và góc ෣
𝑨𝑴𝑩 = 𝟔𝟎𝟎. Khi đó cường độ của lực 𝑭𝟑 là:
A. 𝟏𝟎𝟎 𝟑 𝑵.
B. 𝟓𝟎 𝟑 N.
C. 𝟓𝟎 𝟐 𝑵.
D. 𝟏𝟎 𝟑 N. TOÁN THPT GIÁO ÁN ĐIỆN TỬ Trả lời
BÀI TẬP TRẮC NGHIỆM
Gọi 𝑫 là điểm thỏa mãn 𝑴𝑨 + 𝑴𝑩 = 𝑴𝑫
thì ta có tứ giác 𝑴𝑨𝑫𝑩 là hình bình hành,
hơn nữa ta có 𝑴𝑨 = 𝑴𝑩 = 𝑭𝟏 = 𝑭𝟐
nên tứ giác 𝑴𝑨𝑫𝑩 là hình thoi.
Ta có tam giác 𝑨𝑴𝑩 đều cạnh 𝑴𝑨 = 𝟓𝟎 nên ta có 𝑴𝑫 = 𝟐. 𝟓𝟎 𝟑 = 𝟓𝟎 𝟑, hay cường độ của 𝟐
hợp lực 𝑭𝟏 + 𝑭𝟐 = 𝑴𝑫 bằng 𝟓𝟎 𝟑𝑵.
Vì vật đứng yên nên vectơ 𝑭𝟑 = 𝑴𝑪 là vectơ đối của
vectơ 𝑭𝟏 + 𝑭𝟐 = 𝑴𝑫 .
Từ đó ta có cường độ của lực 𝑭𝟑 bằng 𝟓𝟎 𝟑𝑵. Chọn B TOÁN THPT GIÁO ÁN ĐIỆN TỬ
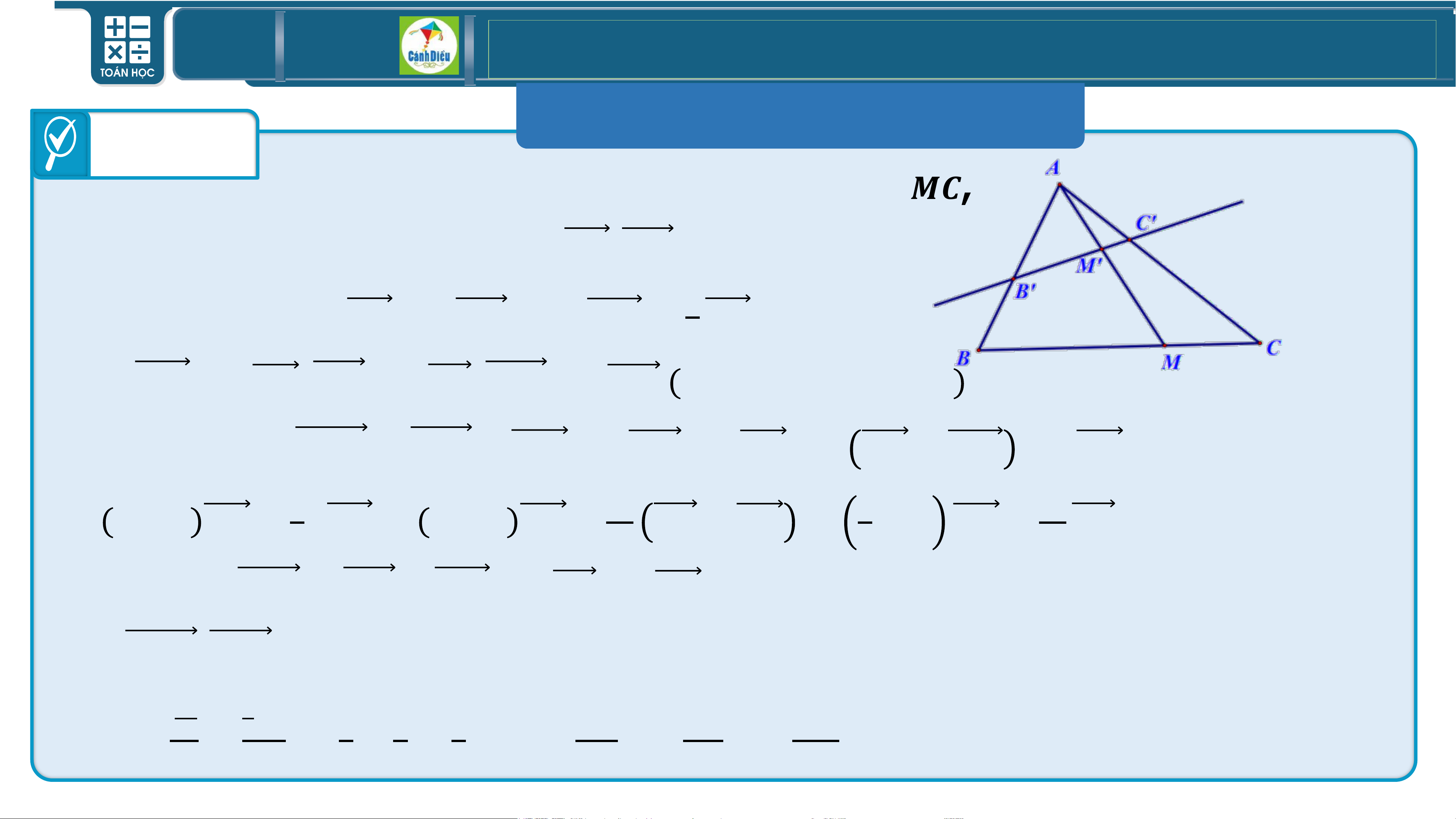
BÀI TẬP TRẮC NGHIỆM Câu 6
Cho tam giác 𝑨𝑩𝑪. 𝑴 là điểm nằm trên cạnh 𝑩𝑪 sao cho 𝑺𝑨𝑩𝑪 = 𝟑𝑺𝑨𝑴𝑪.
Một đường thẳng cắt các cạnh 𝑨𝑩, 𝑨𝑴, 𝑨𝑪 lần lượt tại 𝑩′, 𝑴′, 𝑪′ phân
biệt. Biết rằng 𝑨𝑩 + 𝟐 𝑨𝑪 = 𝒌 𝑨𝑴. Tìm số 𝒌. 𝑨𝑩′ 𝑨𝑪′ 𝑨𝑴′ A. 𝒌 = 𝟏.
B. 𝒌 = 𝟐. C. 𝒌 = 𝟑. D. 𝒌 = 𝟐 . 𝟑 TOÁN THPT GIÁO ÁN ĐIỆN TỬ Trả lời
BÀI TẬP TRẮC NGHIỆM
Theo giả thiết, 𝑺𝑨𝑩𝑪 = 𝟑𝑺𝑨𝑴𝑪 ⇔ 𝑩𝑪 = 𝟑𝑴𝑪,
với 𝑴 nằm trên cạnh 𝑩𝑪 ta có 𝑩𝑪, 𝑴𝑪 là hai vectơ
cùng hướng nên 𝑩𝑪 = 𝟑𝑴𝑪 hay 𝑩𝑴 = 𝟐 𝑩𝑪 . 𝟑
Đặt 𝑨𝑩′ = 𝒙𝑨𝑩; 𝑨𝑪′ = 𝒚𝑨𝑪; 𝑨𝑴′ = 𝒛𝑨𝑴 𝒙 > 𝟎, 𝒚 > 𝟎, 𝒛 > 𝟎 .
Khi đó, ta có :𝑩′𝑴′ = 𝑨𝑴′ − 𝑨𝑩′ = 𝒛𝑨𝑴 − 𝒙𝑨𝑩 = 𝒛 𝑨𝑩 + 𝑩𝑴 − 𝒙𝑨𝑩
= 𝒛 − 𝒙 𝑨𝑩 + 𝟐 𝒛𝑩𝑪 = 𝒛 − 𝒙 𝑨𝑩 + 𝟐𝒛 𝑨𝑪 − 𝑨𝑩 = 𝒛 − 𝒙 𝑨𝑩 + 𝟐𝒛 𝑨𝑪 (1). 𝟑 𝟑 𝟑 𝟑
Mặt khác 𝑩′𝑪′ = 𝑨𝑪′ − 𝑨𝑩′ = 𝒚𝑨𝑪 − 𝒙𝑨𝑩 (2).
Mà 𝑩′𝑴′, 𝑩′𝑪′ là hai vectơ cùng phương nên từ (1) và (2) ta có 𝟐𝒛 𝒛
𝟑 = 𝟑−𝒙 ⇔ 𝟏 + 𝟐 = 𝟑 𝑨𝑩 hay
+ 𝟐 𝑨𝑪 = 𝟑 𝑨𝑴 do đó 𝒌 = 𝟑. Chọn C 𝒚 −𝒙 𝒙 𝒚 𝒛 𝑨𝑩′ 𝑨𝑪′ 𝑨𝑴′
Document Outline