TOÁN THPT GIÁO ÁN ĐIỆN TỬ
CHƯƠNG IV. HỆ THỨC LƯỢNG TRONG TAM GIÁC. VECTƠ §6
BÀI TẬP CUỐI CHƯƠNG IV TOÁN THPT GIÁO ÁN ĐIỆN TỬ I TÓM TẮT LÝ THUYẾT Khởi động
Trong buổi trước thầy đã phân chia lớp thành 4 nhóm và
phân công nhiệm vụ cho 4 nhóm.
Nhóm 1, 2: Vẽ sơ đồ tư duy tóm tắt về các giá trị lượng giác của
góc bất kỳ từ 0 đến 180 , các hệ thức lượng trong tam giác
Nhóm 3, 4: Vẽ sơ đồ tư duy tóm tắt về vectơ và các phép toán vectơ.
Sau đây xin mời đại diện các nhóm treo sản phẩm của nhóm mình lên
bảng. Nhóm 1 và nhóm 3 cử đại diện lên thuyết trình kết quả của nhóm mình.
Cả lớp ở dưới theo dõi kết quả của các nhóm và cho nhận xét, góp ý bổ sung. TOÁN THPT GIÁO ÁN ĐIỆN TỬ
II BÀI TẬP VỀ HỆ THỨC LƯỢNG TRONG TAM GIÁC Bài Tập 1
Bài tập này thầy giao nhiệm vụ làm việc theo cặp đôi. Thầy sẽ
chọn ra 3 cặp đôi làm ra kết quả nhanh nhất để chấm điểm. Sau khi hoàn
thành các cặp đôi cử đại diện lên trình bày kết quả Cặp 1: Câu a Cặp 2: Câu b, c Cặp 3: câu d, e TOÁN THPT GIÁO ÁN ĐIỆN TỬ II BÀI TẬP Bài Tập 1
a) Áp dụng định lý cosin ta có: = + − 2 .
. cos = 3 + 4 − 2.3.4. cos120 = 37 ⇒ = 37 cos = = = ⇒ ≈ 34 . . . .
b) Bán kính đường tròn ngoại tiếp: " &&& ! = = = = #$% .#$%& ' c) Diện tích tam giác : & &
( = )*sin = . 3.4. sin120 = 3 3 d) . . / &&&?
Độ dài đường cao xuất phát từ : ℎ"= = = " TOÁN THPT GIÁO ÁN ĐIỆN TỬ II BÀITẬP Bài Tập 2
Bài tập này thầy xin mời 2 bạn lên trình bày nhanh kết quả
= (234 2 0 + sin70 5 + (*62 2 0 + *62 1 10 5
= 234 2 0 + 234 7 0 + 2. 234 2 0 . 234 7 0 + *62 2 0 + *62 1 10 + 2. *62 2 0 . *62 1 10 = 234 2 0 + *62 2 0
+ 2. 234 2 0 . *62 2 0 + *62 2 0 + 234 2 0 + 2. *62 2 0 . − 234 2 0 = 1 + 1 = 2
= tan20 + cot20 + tan110 + *69 110
= tan20 + cot20 + tan(90 + 20 5 + cot(90 + 20 5
= tan20 + cot20 + tan(90 + 20 5 + cot(90 + 20 5
= tan20 + cot20 − tan20 − cot 20 = 0 TOÁN THPT GIÁO ÁN ĐIỆN TỬ II BÀITẬP Bài Tập 3
Áp dụng định lý cosin ta có: < < ,& &/& *62 ; = = = − y .< .< . . > ⇒ ; ≈ 101 Vậy ?;@ A ≈ 101 B O A x TOÁN THPT GIÁO ÁN ĐIỆN TỬ II BÀITẬP Bài Tập 4 Xét tam giác ta có B = 180 − 60 + 45 = 75 .
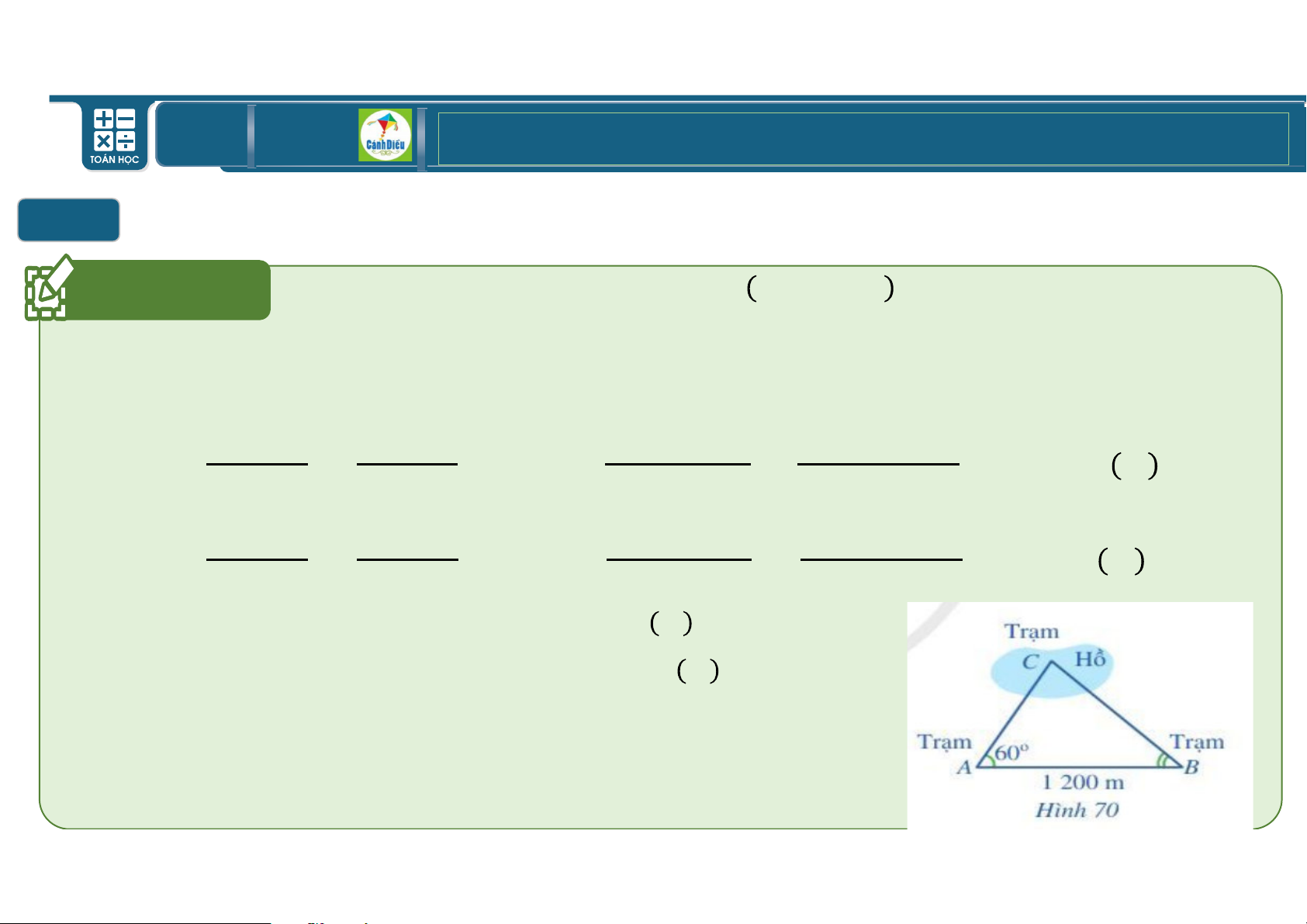
Khoảng cách từ trạm C đến trạm A và B lần lượt là độ dài các cạnh CA, CB
Theo định lý sin ta được: EFG H & .EFG / ' = ⇒ = = ≈ 1075,89 I EFG H EFG H EFG H EFG ' EFG H & .EFG ' = ⇒ = = ≈ 878,46 I EFG H EFG H EFG H EFG '
Vậy khoảng cách từ C đến trạm A là 878,46 I ;
kKhoảng cách từ C đến trạm B là 1075,89 I TOÁN THPT GIÁO ÁN ĐIỆN TỬ II BÀITẬP Bài Tập 5
Bài tập này thầy xin mời một bạn lên trình bày nhanh kết quả
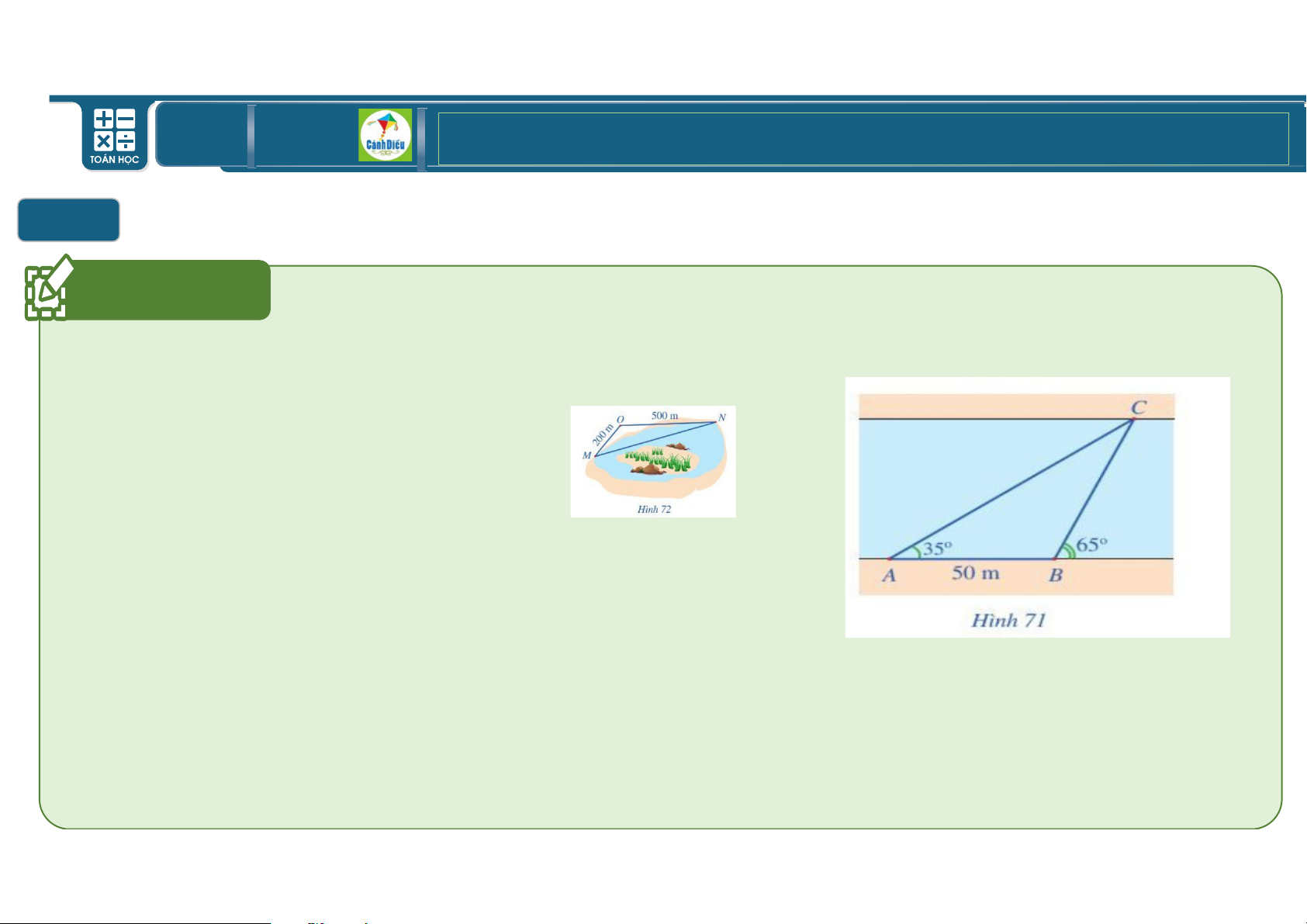
Chiều rộng của sông là 52 I. TOÁN THPT GIÁO ÁN ĐIỆN TỬ II BÀITẬP Bài Tập 6
Bài tập này thầy xin mời một bạn lên trình bày nhanh kết quả
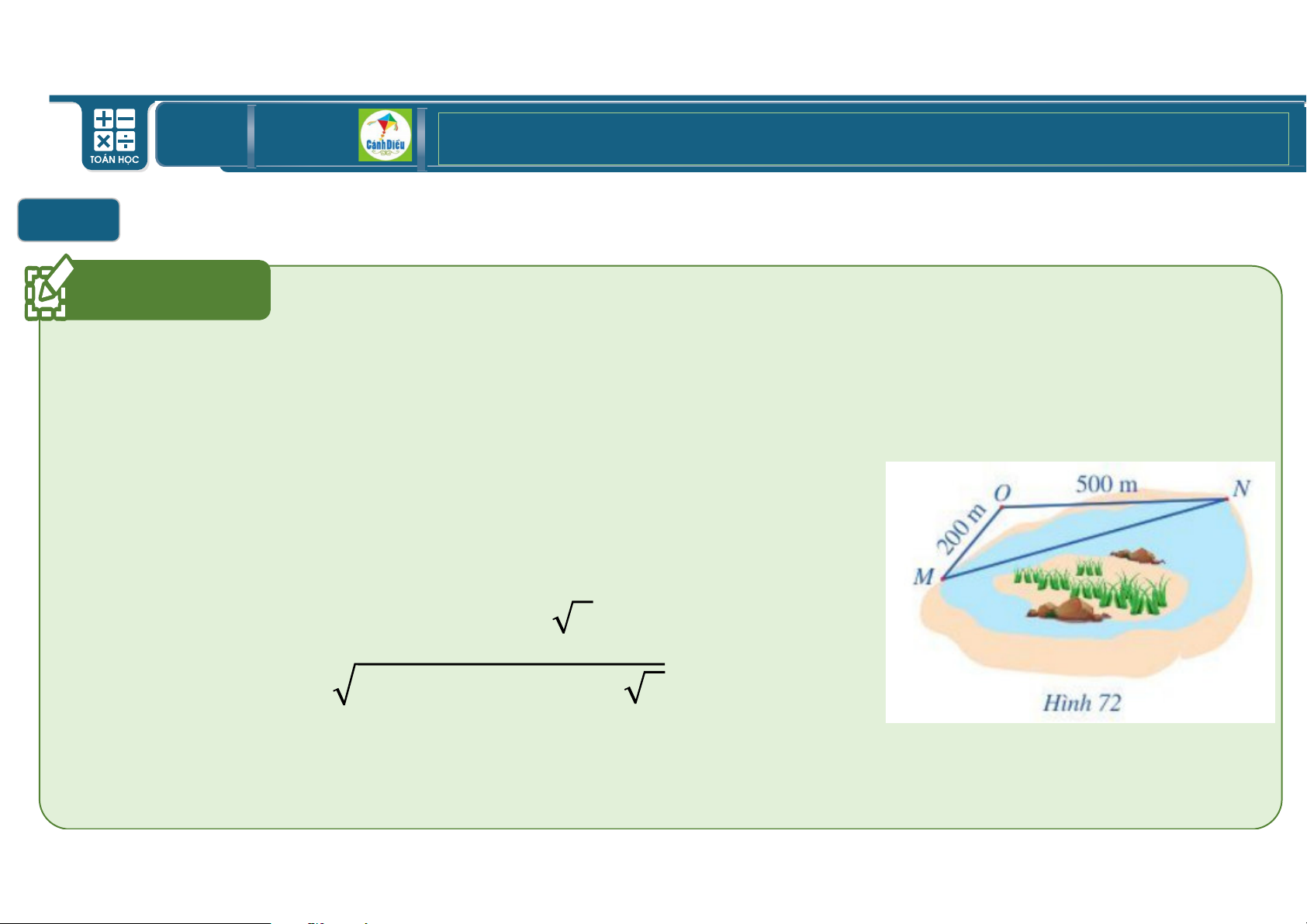
Khoảng cách giữa 2 vị trí K, L là độ dài đoạn KL.
Xét tam giác K;L, Theo định lý Cosin
KL = ;K + ;L − 2;K. ;L. *62 K;L H
= 200 + 500 − 2.200.500 *62 1 35 = 290000 + 100000 2 ⇒ KL = 290000 + 100000 2 ≈ 656,82I.
Kết luận: Khoảng cách giữa hai vị trí K, L là 657I. =VP2 TOÁN THPT GIÁO ÁN ĐIỆN TỬ Do I IiI BÀI TẬP VỀ VECTƠ Bài Tập 7 a) + M + N = N 1 Do
Mlà hình bình hanh nên ta có + M = ⇒ OP 1 = + M + N = + N = N = OQ 1 b) K + K + 2RL = 2KL 2 Ta có K + K = 2KR.
⇒ OP 2 = K + K + 2RL = 2KR + 2RL = 2 KR + RL = 2KL = OQ 2 TOÁN THPT GIÁO ÁN ĐIỆN TỬ I IiI BÀI TẬP VỀ VECTƠ Bài Tập 7
c) K + K + K − 3LU= 3LU
Do U là trọng tâm của tam giác nên ta có K + K + K = 3KU.
OP 3 = K + K + K − 3KL = 3KU − 3KL = 3 KU − KL = 3LU = OQ 3 =VP2 TOÁN THPT GIÁO ÁN ĐIỆN TỬ Do I IiI BÀI TẬP VỀ VECTƠ Bài Tập 8
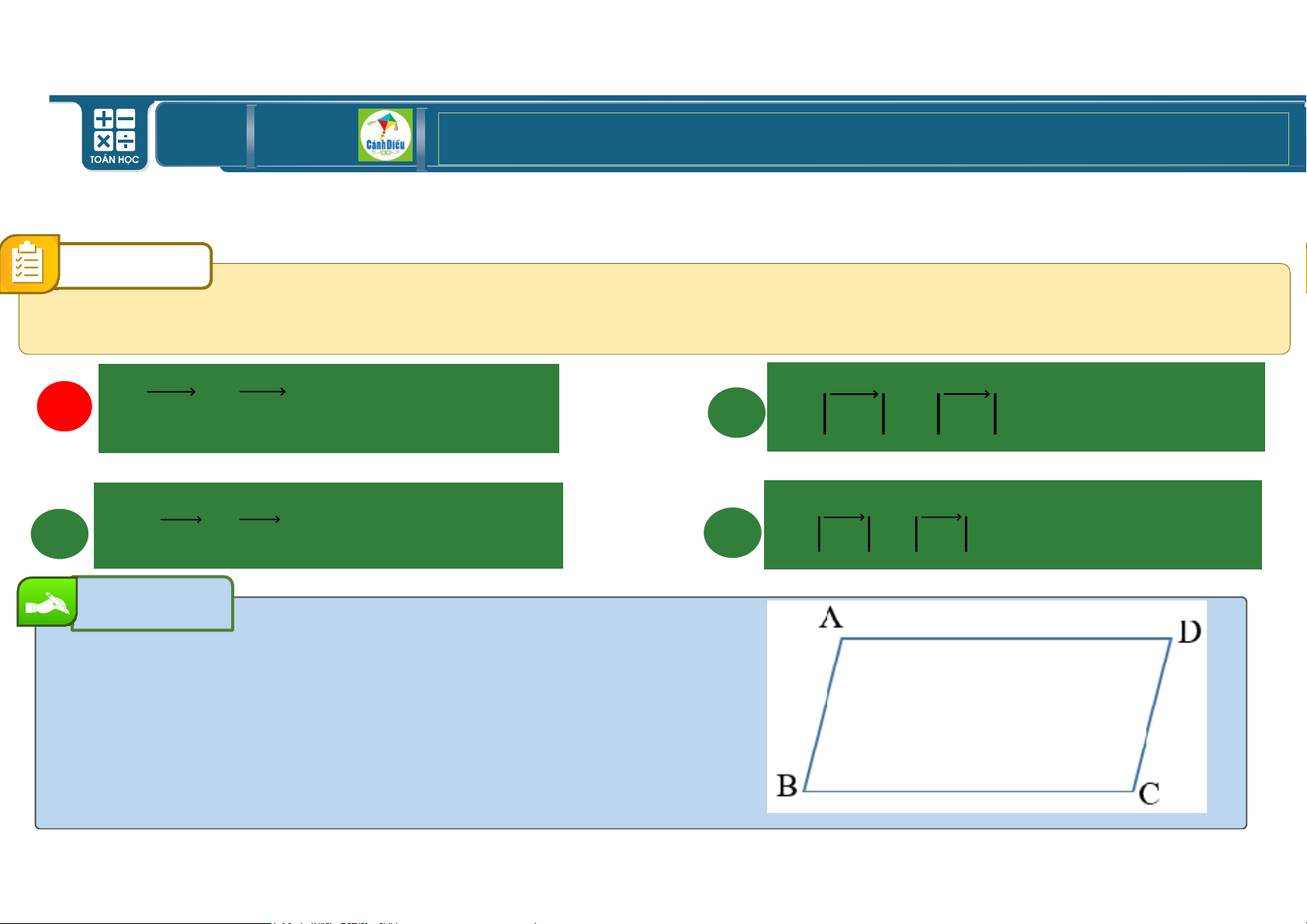
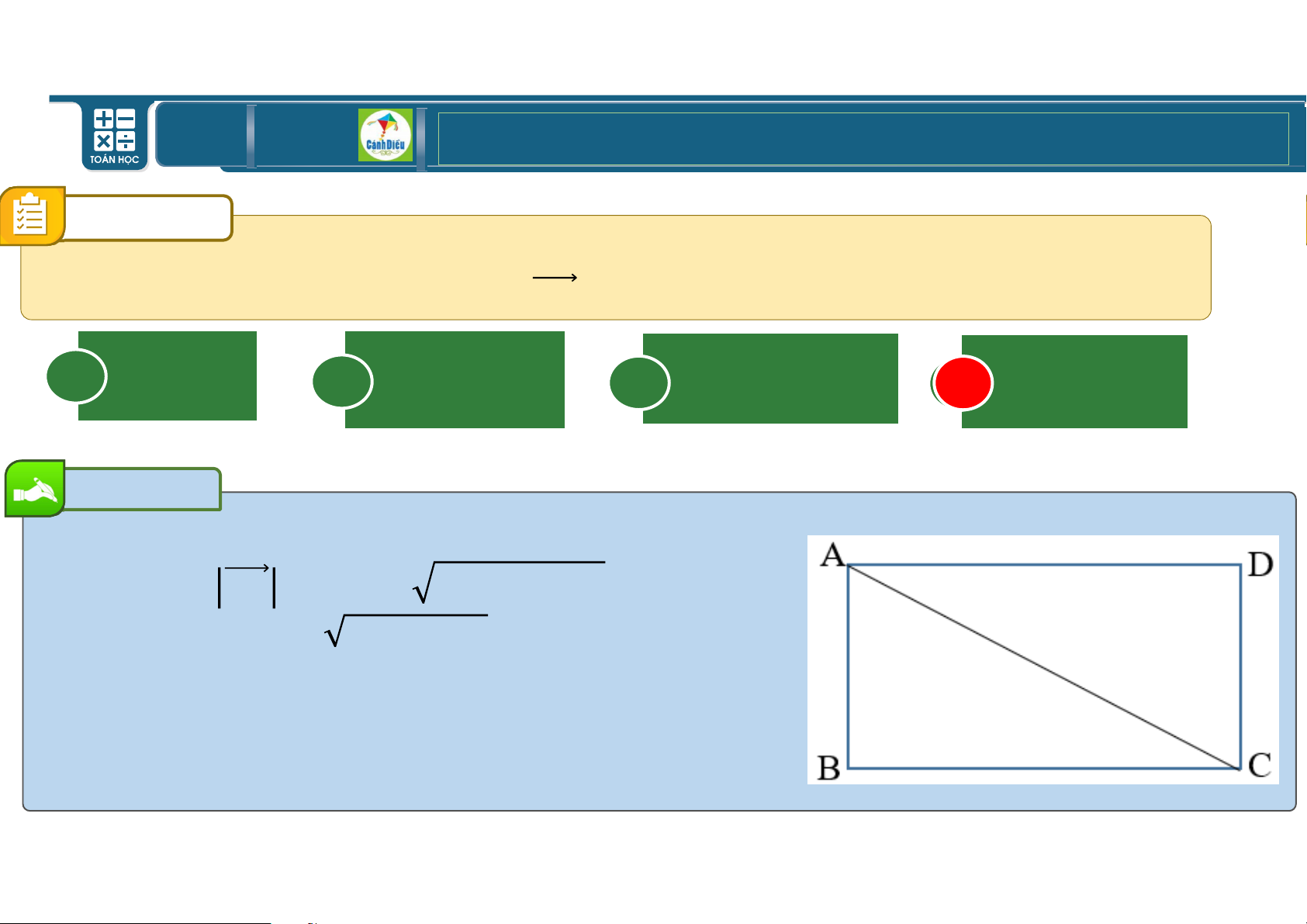
a) Theo quy tắc hình bình hành ta có: = + M
b) Tính các tích vô hướng +) & . M = . M. *62 M H = 4.6. *62 6 0 = 4.6. = 12 +5 . = . + M = + . M = 4 + 12 = 28 +5 M. = − + M + M = M − = 6 − 4 = 20 =VP2 TOÁN THPT GIÁO ÁN ĐIỆN TỬ Do I III BÀI TẬP VỀ VECTƠ Bài Tập 8
c) Tính độ dài đường chéo : M = ( + M5 = (− + M5 = − 2. . M + M = 16 − 12 + 36 = 4 ⇒ M = 40 ⇒ M = 40 = 2 10 = ( + M5 = + 2. . M + M = 16 + 12 + 36 = 64 ⇒ = 64 ⇒ = 8 TOÁN THPT GIÁO ÁN ĐIỆN TỬ
CÂU HỎI TRẮC NGHIỆM PHIẾU BÀI TẬP SỐ 1 CÂU 1 15 Cho tam giác 54
VWX bất kỳ có WX = Y, 9
VX = Z,VW = [. 6
Đẳng thức nào sai? A
Z\ = Y\ + [\ − \Y[ []^ W. B
Y\ = Z\ + [\ − \Z[ []^ V. C
[\ = Z\ + Y\ + \YZ []^ X. D
[\ = Z\ + Y\ − \YZ []^ X. Bài giải Mệnh đề Sai là C TOÁN THPT GIÁO ÁN ĐIỆN TỬ
CÂU HỎI TRẮC NGHIỆM CÂU 2 15 Trong tam giá 5 c 4
VWX bất kỳ cóWX = Y, 9
VX = Z,VW = [. Bán 6 kính đường
tròn ngoại tiếp tam giác VWX là Y A Y _ = . B Z _ = C _ = D Z ^`a V \ ^`a V R= \ ^`a V ^`a V Bài giải
Theo định lý sin, mệnh đề đúng là C TOÁN THPT GIÁO ÁN ĐIỆN TỬ
CÂU HỎI TRẮC NGHIỆM CÂU 3 15 Cho tam giác 5 V4
WX bất kỳ có WX = Y, 9
VX = Z,VW = [, b là 6 nửa chu
vi tam giác VWX. Diện tích tam giác VWX là A c = b b − Y b − Z b − [ B c = b − Y b − Z b − [ C c = b b − Y b − Z b − [ D c = b − Y b − Z b − [ Bài giải
Theo công thức Hê - rông, mệnh đề đúng là A TOÁN THPT GIÁO ÁN ĐIỆN TỬ
2. CÂU HỎI TRẮC NGHIỆM CÂU 4 15 Cho tam giác 5 V 4
WX có Y = d, Z = e và9
[ = d. Số đo của góc 6WVX nhận giá
trị nào trong các giá trị dưới đây? A idh B C ghh ehh D V f ghh Bài giải th1 Z\ + [\ − Y\ e\ + d\ − d\ e j []^ V = = = k = []^ g hh \Z[ \. e. d jh \ ⇒ V f ghh Chọn D Slide 17 th1 thuy ha, 03/01/2022 TOÁN THPT GIÁO ÁN ĐIỆN TỬ
CÂU HỎI TRẮC NGHIỆM CÂU 5 15 54 9 6
Cho tam giác VWX có VW = i, VX = g, V
l = ghh. Tính độ dài cạnh WX A n B \ n C e n D \m. Bài giải
Áp dụng định lý cosin tacó
WX\ = VW\ + VX\ − \VW. VX. []^ V
= i\ + g\ − \. i. g. cos6hh = \m ⇒ WX = \m = \ n. Chọn B. TOÁN THPT GIÁO ÁN ĐIỆN TỬ
CÂU HỎI TRẮC NGHIỆM CÂU 6 15 Cho tam giá 5 c 4
VWX có VW = i, VX = 9 g, V
l = ghh. Tính bán 6kính
đường tròn ngoại tiếp tam giác VWX A \ \j B \ n C \j D e n e e Bài giải Ta có j
c = VW. VX. ^`a V = j . i. g. ^`a g hh = g e. \ \ YZ[ YZ[ i.g.\ n \ \j c = ⇒ _ = = = . Chọn A i_ ic i.g e e TOÁN THPT GIÁO ÁN ĐIỆN TỬ
CÂU HỎI TRẮC NGHIỆM CÂU 7 15 Tam giác V 5 W 4
Xcó các cạnh thỏa mãn h 9
ệ thức Y + Z + [ Y 6 + Z − [ = eYZ.
Khi đó số đo của góc X là: A j\hh B ehh. C ohh D ghh Bài giải
Y + Z + [ Y + Z − [ = eYZ  Y\+Z\ − [\ = YZ Y\ Z\ [\ j  []^ X = = ⇒ X l = ghh. \YZ \ Chọn D. TOÁN THPT GIÁO ÁN ĐIỆN TỬ
CÂU HỎI TRẮC NGHIỆM CÂU 8 15 Cho tam giá5 c 4
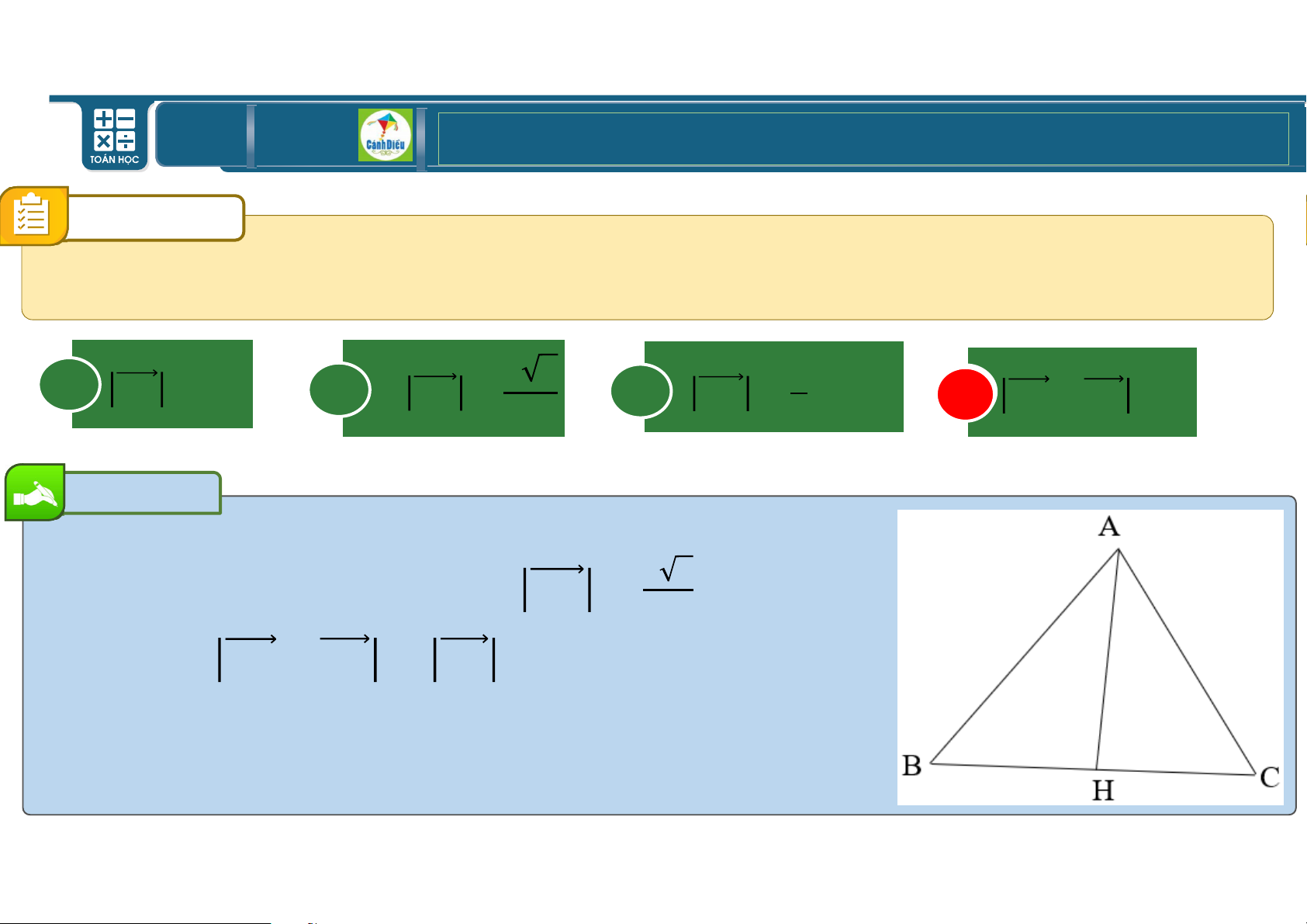
VWX vuông tại V có V9
W = [, AX = Z, AD l 6 à phân giác
trong của góc V. Độ dài của Vp bằng: A Z[ B Z[ \ C Z + [ Z + [ D . Z + [ Z + [ Z[ Z[ \ Bài giải Trong Wp Wp qVWp có Vp = = = \Wp ^`a W ^`a WVp H ^`a idh ⇒ Vp = \Wp ^`a W. Mà VX Z \ZWp \Z[ ^`a W = =  Vp = = . WX WX WX Z [ Chọn B. TOÁN THPT GIÁO ÁN ĐIỆN TỬ
CÂU HỎI TRẮC NGHIỆM CÂU 9 15 Cho tam giá 5
c 4VWX cân tại V nội tiếp 9đường tròn r; _ , A6B = x.
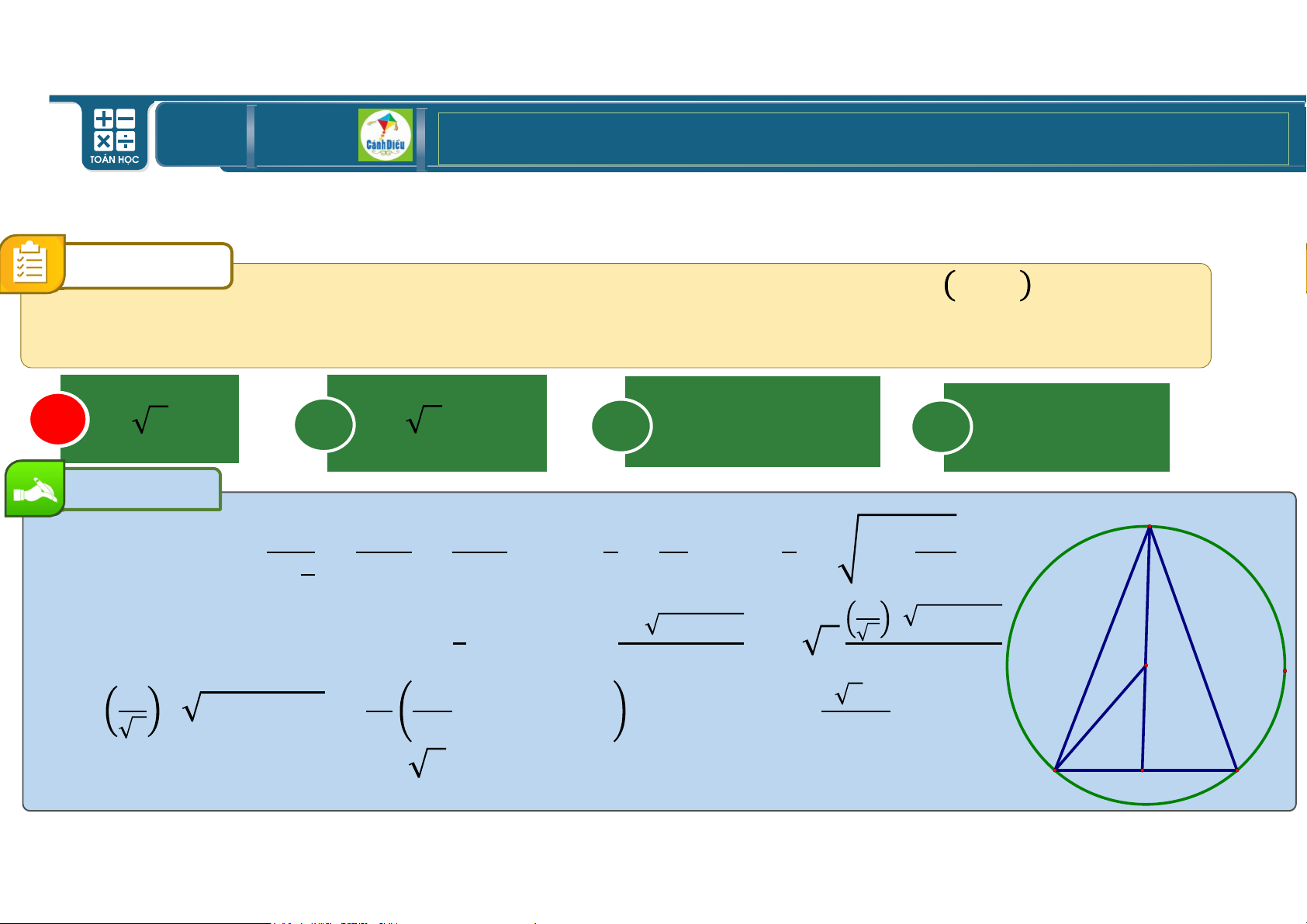
Tìm t để diện tích tam giác VWX lớn nhất. A _ e B _ \ C R D Đáp án khác Bài giải A Trong x x x x u ; có v = = ⇒ *62 =  234 = 1 − . w EFG EFG < EFG v v z y v x R Khi đó diện tích & xy v x u là: ( = ? 234 = = 3 3 y x v v O Do x & x v 4! − ? { + 4! − ? = !  ( { &/ R
Dấu bằng xảy ra khi ? = ! 3. Chọn A B C TOÁN THPT GIÁO ÁN ĐIỆN TỬ
CÂU HỎI TRẮC NGHIỆM CÂU 10 15 Cho góc tr 5 |
H 4= ehr. Gọi V và W là h9ai điểm di động lần l 6 ượt trên rt
và r| sao cho VW = j. Độ dài lớn nhất của đoạn rW bằng: A 1,5 B e C \ \ D \ Bài giải
Xét tam giác rVW có VW
= \ = \_ ⇒ _ = j. Với _ là bán kính ^`a tr| H
đường tròn ngoại tiếp tam giác rVW. Vậy rW lớn nhất khi rW là đường
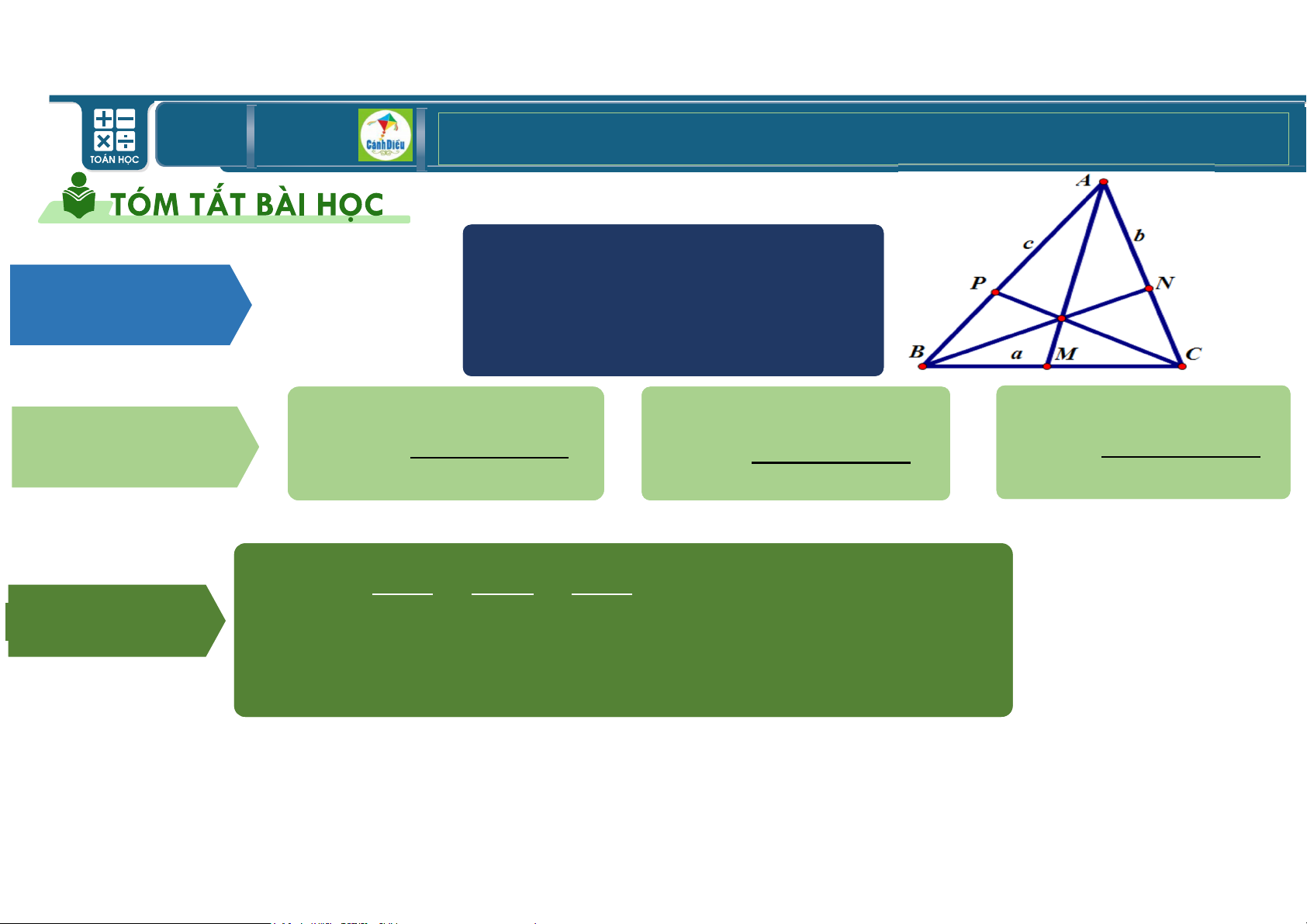
kính của đường tròn ngoại tiếp tam giác rVW. Khi đó rW = \. Chọn D TOÁN THPT GIÁO ÁN ĐIỆN TỬ • ~ = ) + * − 2). *. cos ĐỊNH LÍ CÔSIN • ) = ~ + * − 2~. *. cosB • * = ~ + ) − 2~. b. cosC b + * − ~ ~ + * − ) ~ + ) − * HỆ QUẢ *osA = *osB = *osC = 2)* 2~* 2~) ~ ) * = = = 2! ĐỊNH LÍ SIN sin sin sin
_: bán kính đường tròn ngoại tiếp TOÁN THPT GIÁO ÁN ĐIỆN TỬ 1 1 1 ( = ℎ ℎ ℎ 2 ". ~ = 2 „. ) = 2 …. * 1 1 ( = . ~. *. 234 = . ~. ) 234 2 2 ( = ƒ. †
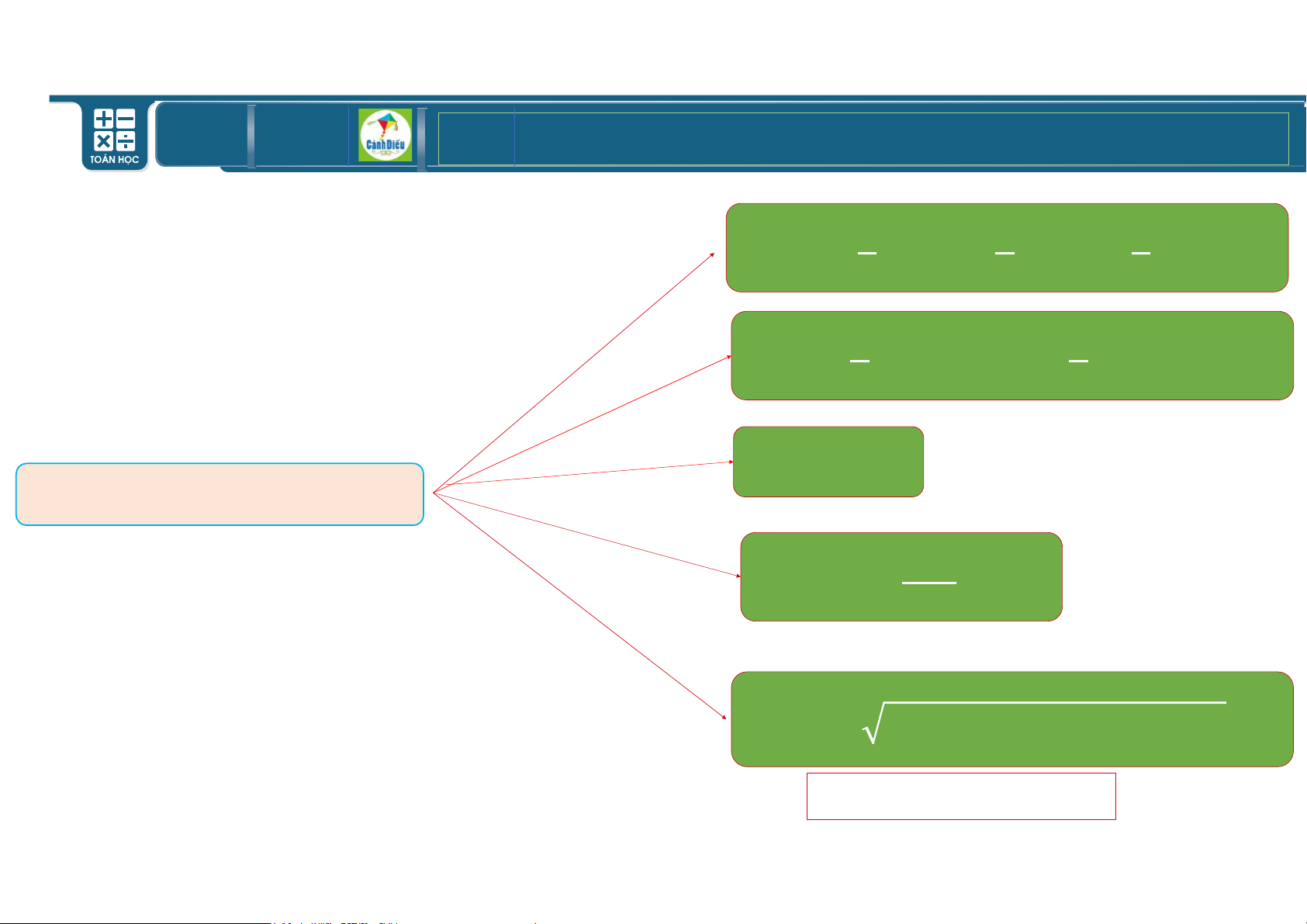
Diện tích tam giác S ~)* ( = 4! ( =
ƒ(ƒ − ~5(ƒ − )5(ƒ − *5 (Công thức Hê−rông) TOÁN THPT GIÁO ÁN ĐIỆN TỬ
CÂU HỎI TRẮC NGHIỆM PHIẾU BÀI TẬP SỐ 2 CÂU 1 15 54 9 6
Cho hình bình hành VWXp. Khẳng định nào dưới đây sai? A Vp = XW B Vp = XW C VW = pX D VW = Xp Bài giải Mệnh đề Sai là A TOÁN THPT GIÁO ÁN ĐIỆN TỬ CÂU 2
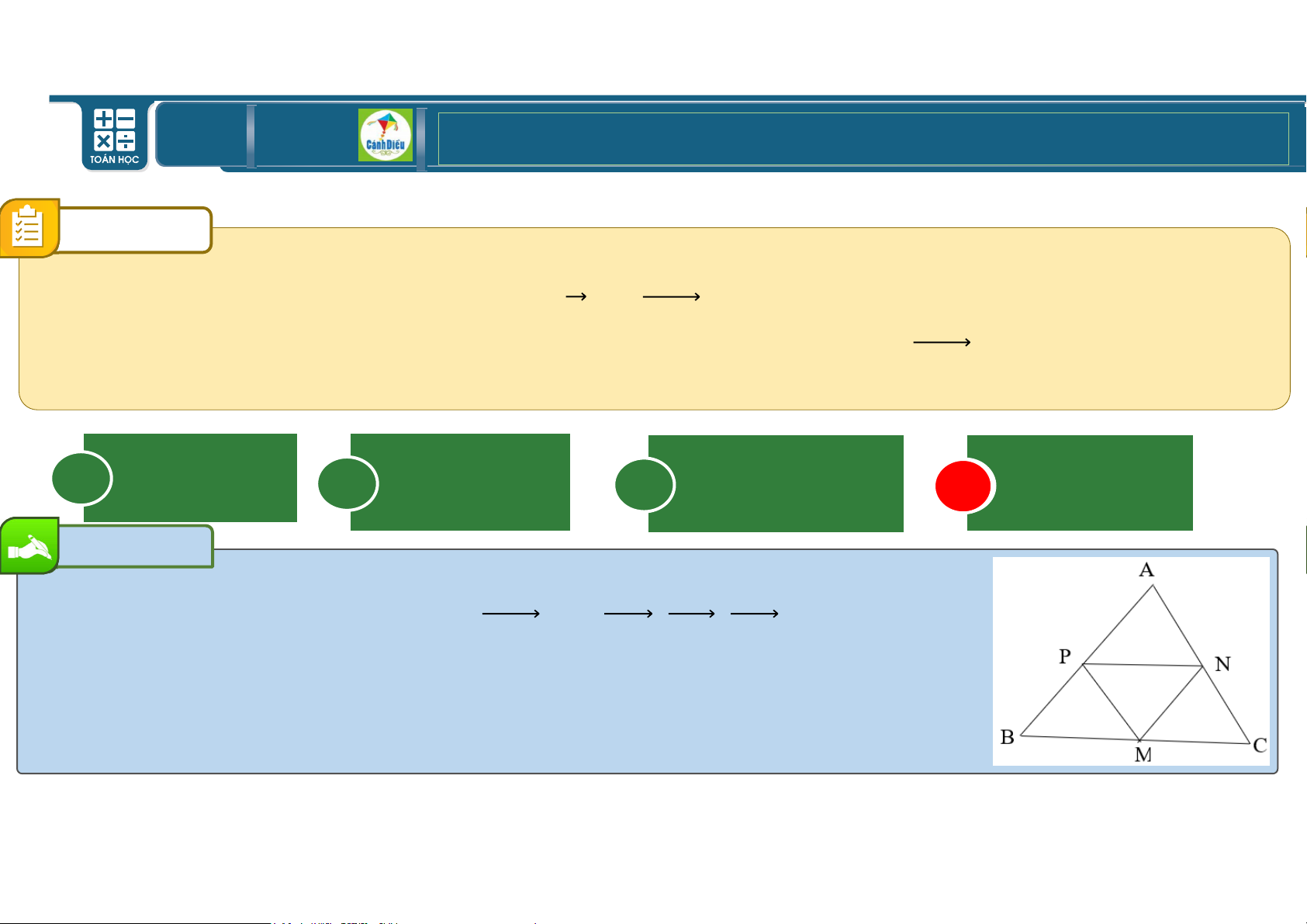
Cho tam giác VWX. Gọi ‡, ˆ, ‰ lần lượt là trung điểm của WX, XV, VW. 15 54 9 6
Có bao nhiêu vectơ khác vectơ h và ‡ˆ, có điểm đầu và điểm cuối là các
điểm V, W, X, ‡, ˆ, ‰ đồng thời cùng hướng với vectơ ‡ˆ? A i B d C \ D 3 Bài giải
Các vec tơ cùng hướng với ‡ˆ là: W‰, ‰V, WV Chọn D TOÁN THPT GIÁO ÁN ĐIỆN TỬ CÂU 3
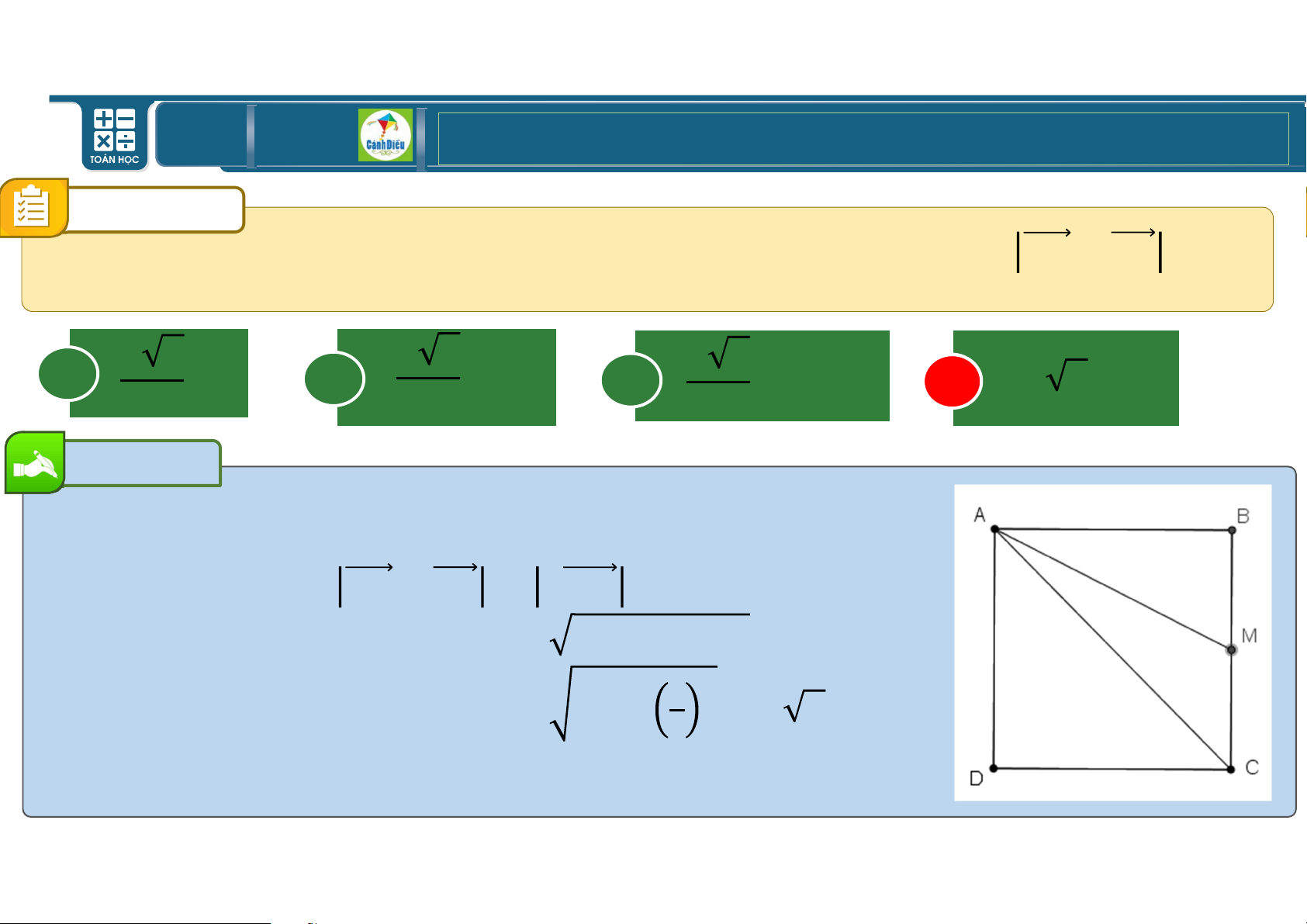
Cho tam giác VWX đều cạnh Y, Š là trung điểm của WX và gọi p là đ 1
iể5m thỏa mãn tứ giác V5X4Šp là hình bình hành. 9Độ dài của vectơ X 6 p bằng A Y B eY C \ eY D Y n \ \ e \ Bài giải D A
Vì p là điểm thỏa mãn tứ giác VXŠp là hình bình hành.
⇒ VŠWp là hình chữ nhật. th2 Ta có Xp = Xp.
Tam giác pWX vuông tại W nên eY\ Y n Xp = Wp\ + WX\ = VŠ\ + WX\ = + Y\ = . B H C i \ Chọn D Slide 28 th2 thuy ha, 03/01/2022 TOÁN THPT GIÁO ÁN ĐIỆN TỬ CÂU 4
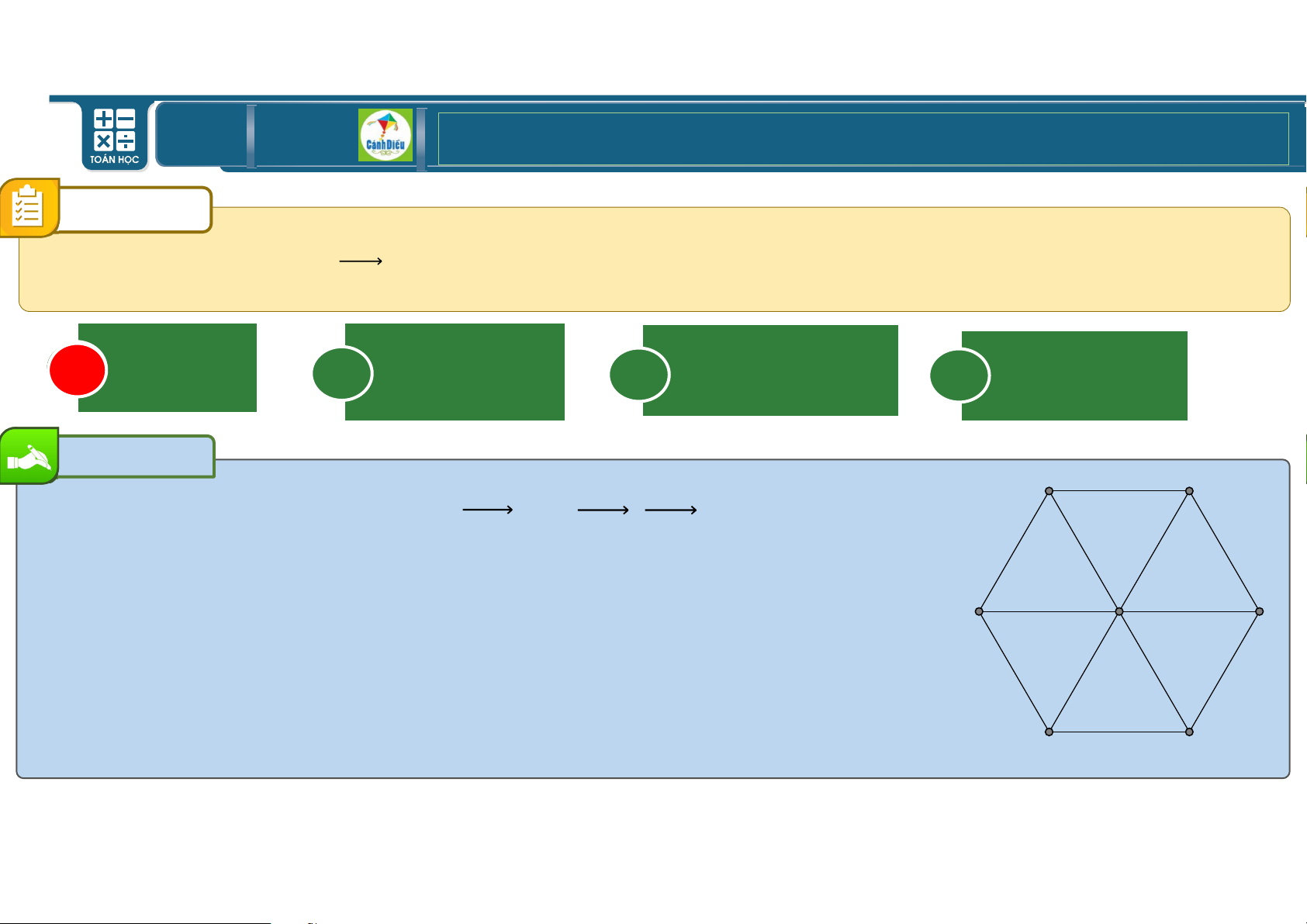
Cho lục giác đều VWXp‹Œ tâm r (tham khảo hình bên dưới). Có bao nhiêu
v1e5ctơ bằng vectơ rX c 5 ó 4
điểm đầu và điểm cuối9 là các đỉnh của lục 6 giác đã cho? A \ B e C i D g Bài giải C B
Các vec tơ bằng rX là: VW, ‹p Chọn A. D A O E F TOÁN THPT GIÁO ÁN ĐIỆN TỬ CÂU 5
Cho tứ giác VWXp. Gọi ‡, ˆ, ‰, • lần lượt là trung điểm của 15 VW, WX, Xp, 5 p 4
V. Khẳng định nào s 9 au đây là sai? 6 A ‡ˆ = •‰ B •‰ = ‡ˆ C ‡• = ˆ‰ D ‡ˆ = VX Bài giải Chọn D TOÁN THPT GIÁO ÁN ĐIỆN TỬ CÂU 6
Cho ba điểm V, W, X phân biệt. Khi đó vectơ VW + WX bằng 15 54 9 6 A VW B h C XW D VX Bài giải Chọn D TOÁN THPT GIÁO ÁN ĐIỆN TỬ CÂU 7
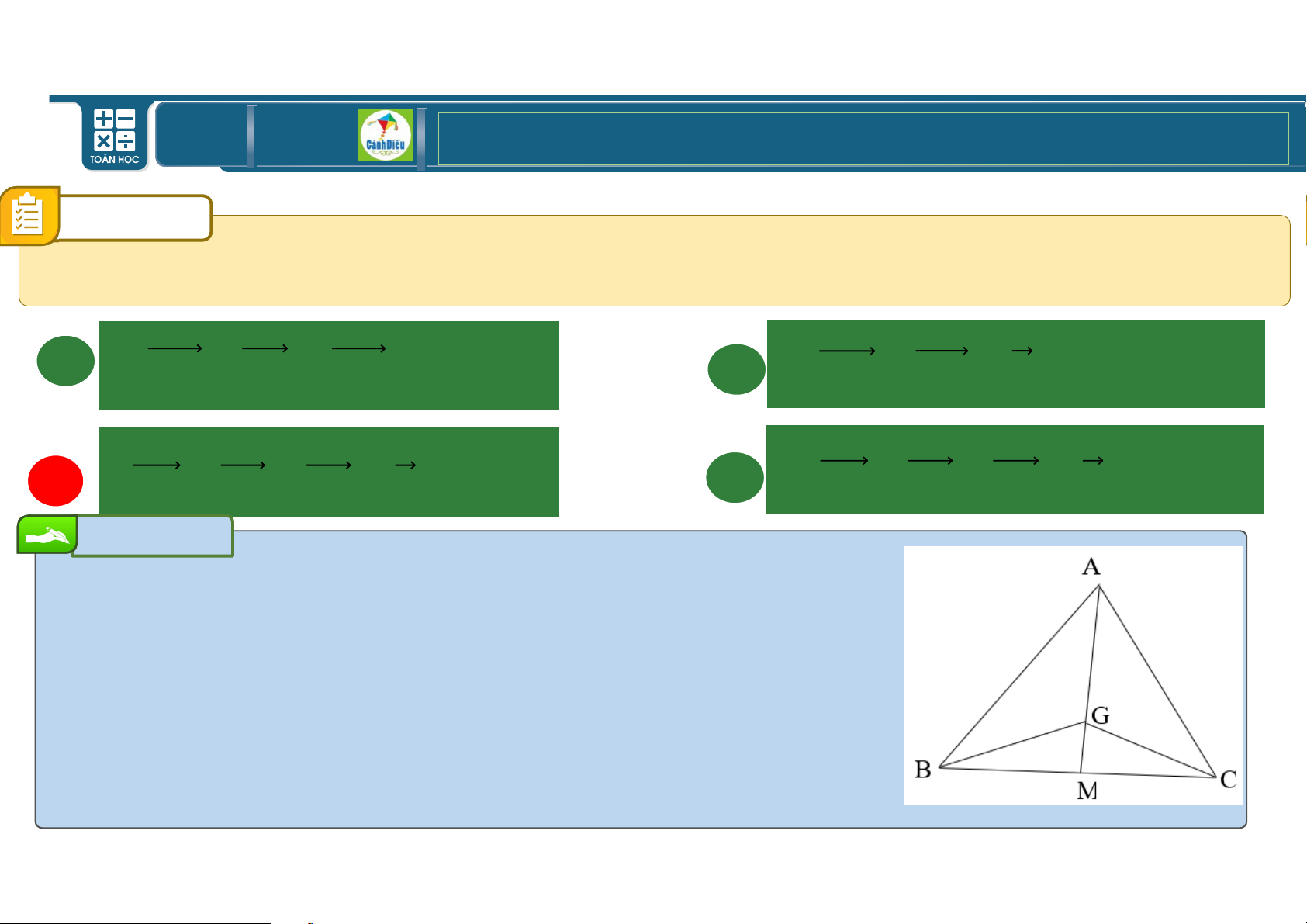
Cho tam giác VWX có ‡ là trung điểm của WX và Ž là trọng 15 tâm của tam5 4
giác VWX. Khẳng địn 9
h nào dưới đây sai?6 A Ž‡ + VŽ = V‡. B ‡W + ‡X = h C ŽW + ŽX − ŽV = h. D ŽW + ŽX + ŽV = h Bài giải Chọn C TOÁN THPT GIÁO ÁN ĐIỆN TỬ CÂU 8
Cho tam giác đều VWX cạnh bằng e và Š là trung điểm của WX. 15 Khẳng định 5 n 4 ào dưới đây sai? 9 6 A e VW = e B e e VŠ = C ŠW = D VW + WX = g \ \ Bài giải
Dùng Pytagore ta tính được e e VŠ = \ VW + WX = VX = e Chọn D TOÁN THPT GIÁO ÁN ĐIỆN TỬ CÂU 9
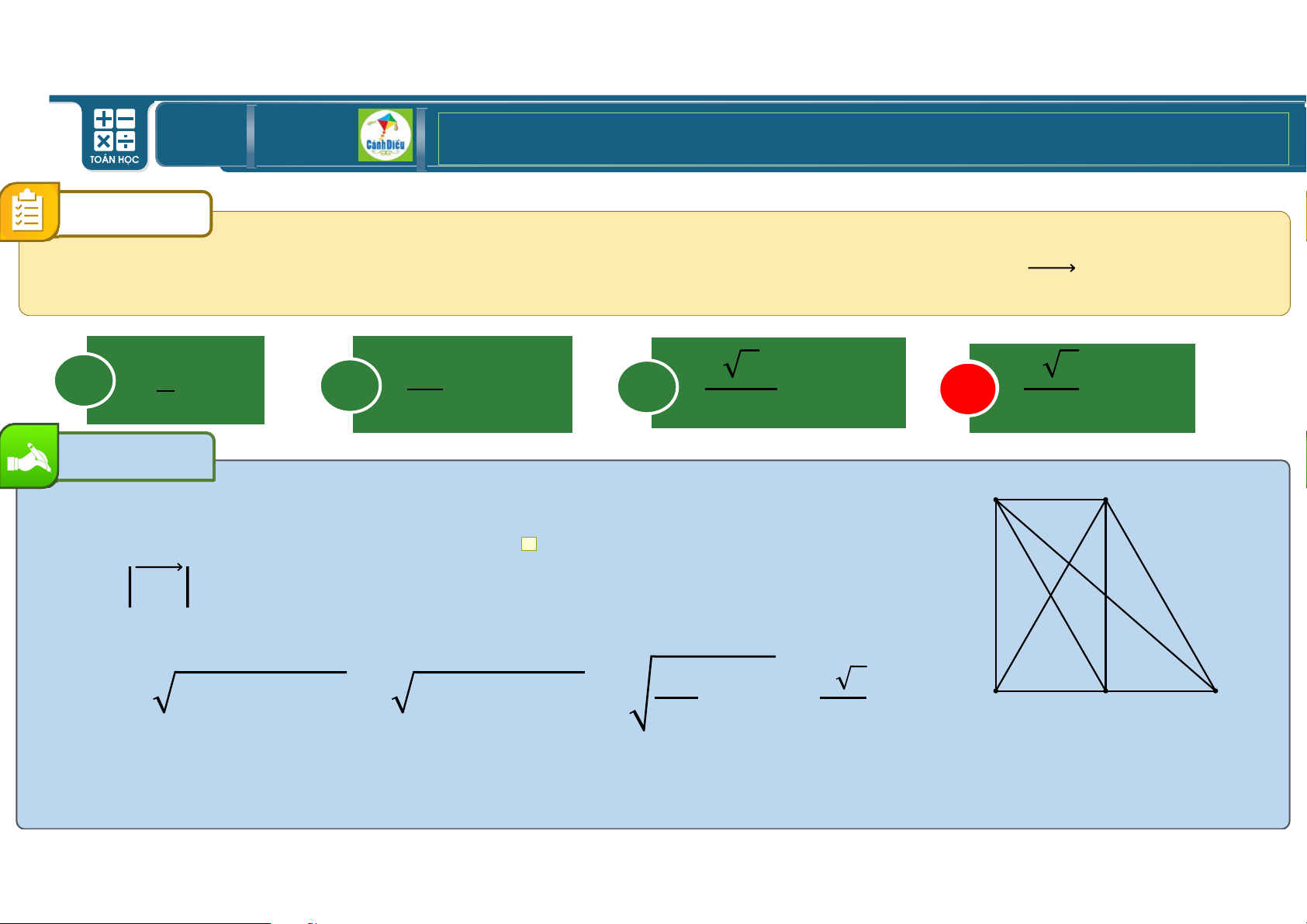
Cho hình chữ nhật VWXp có VW = dcm, WX = j\cm. 15 Độ dài của 5 4 vectơ VX bằng 9 6 A i[• B g[• C 8cm D 13cm Bài giải Ta có VX = VX = VW\ + Vp\ = \d + jii = jecm Chọn D TOÁN THPT GIÁO ÁN ĐIỆN TỬ CÂU 10
Cho hình vuông VWXp có cạnh bằng Y. Khi đó VW + VX bằng 15 54 9 6 A Y d Y e Y e B C D Y d \ \ e Bài giải
Gọi ‡ là trung điểm của WX.
Ta có: VW + VX = \V‡ = \V‡ = \ VW\ + W‡\ Y \ = \ Y\ + = Y d. \ Chọn D TOÁN THPT GIÁO ÁN ĐIỆN TỬ CÂU 11
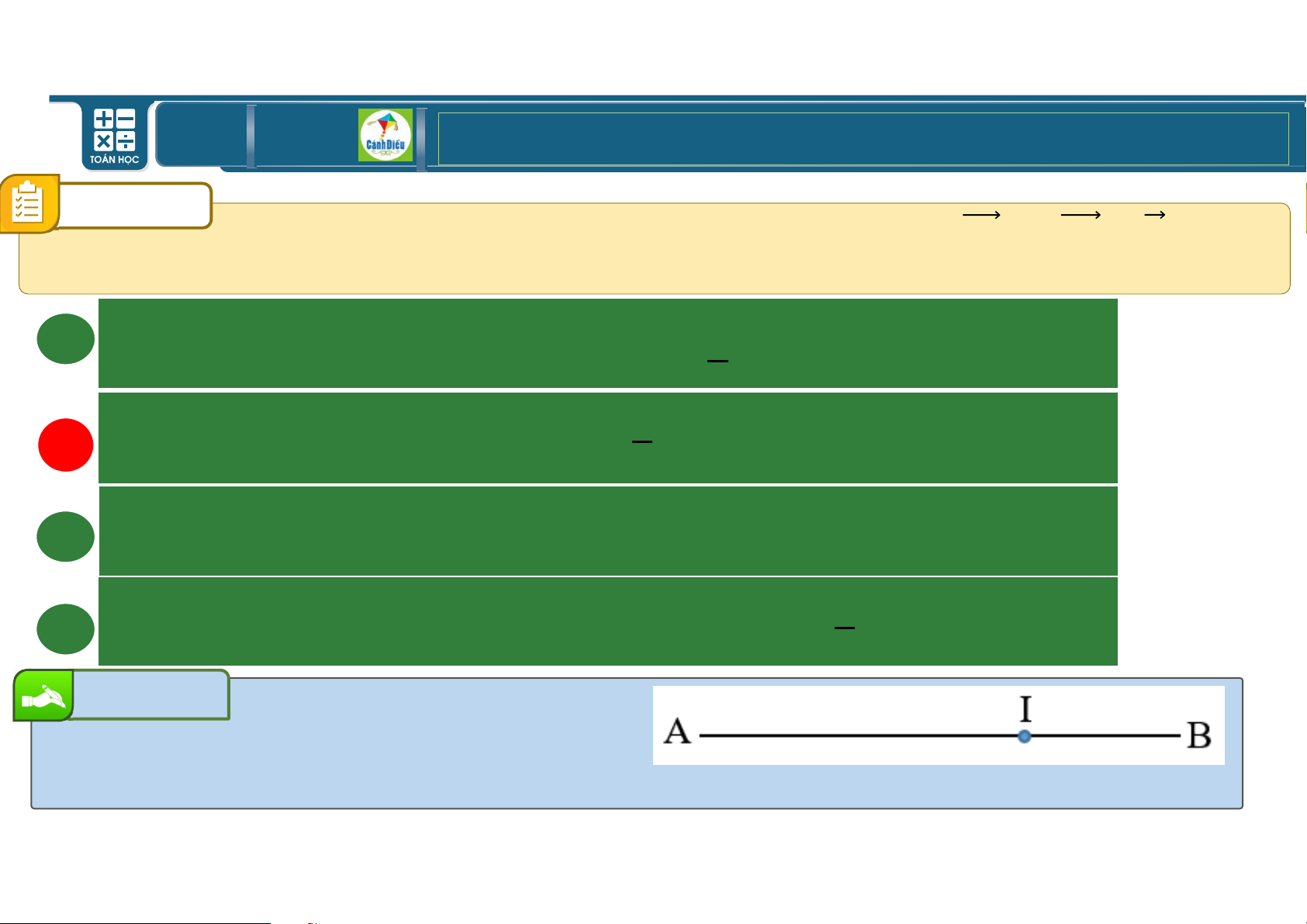
Cho hai điểm phân biệt V, W và điểm • thỏa mãn •V + \•W = h.
Khẳng định nào dưới đây đúng? 15 54 9 6 A j
Điểm • nằm ngoài đoạn VW và •W = VW e j B
Điểm • thuộc đoạnVW và •W = VW e C
Điểm • là trung điểm của đoạn VW j D
Điểm • nằm khác phía W đối với V và •W = VW e Bài giải Chọn B TOÁN THPT GIÁO ÁN ĐIỆN TỬ CÂU 12 Cho hai lực Œ
không cùng phương, cùng tác dụng vào một vật, j, Œ\ b1i5 ết Œ
c tổng hợp của hai lực đã cho
j = ehˆ và Œ\ 54
= mhˆ. Cường độ lự9 6
không thể nhận giá trị nào dưới đây? A 80N B jjhˆ C nhˆ D 60N Bài giải
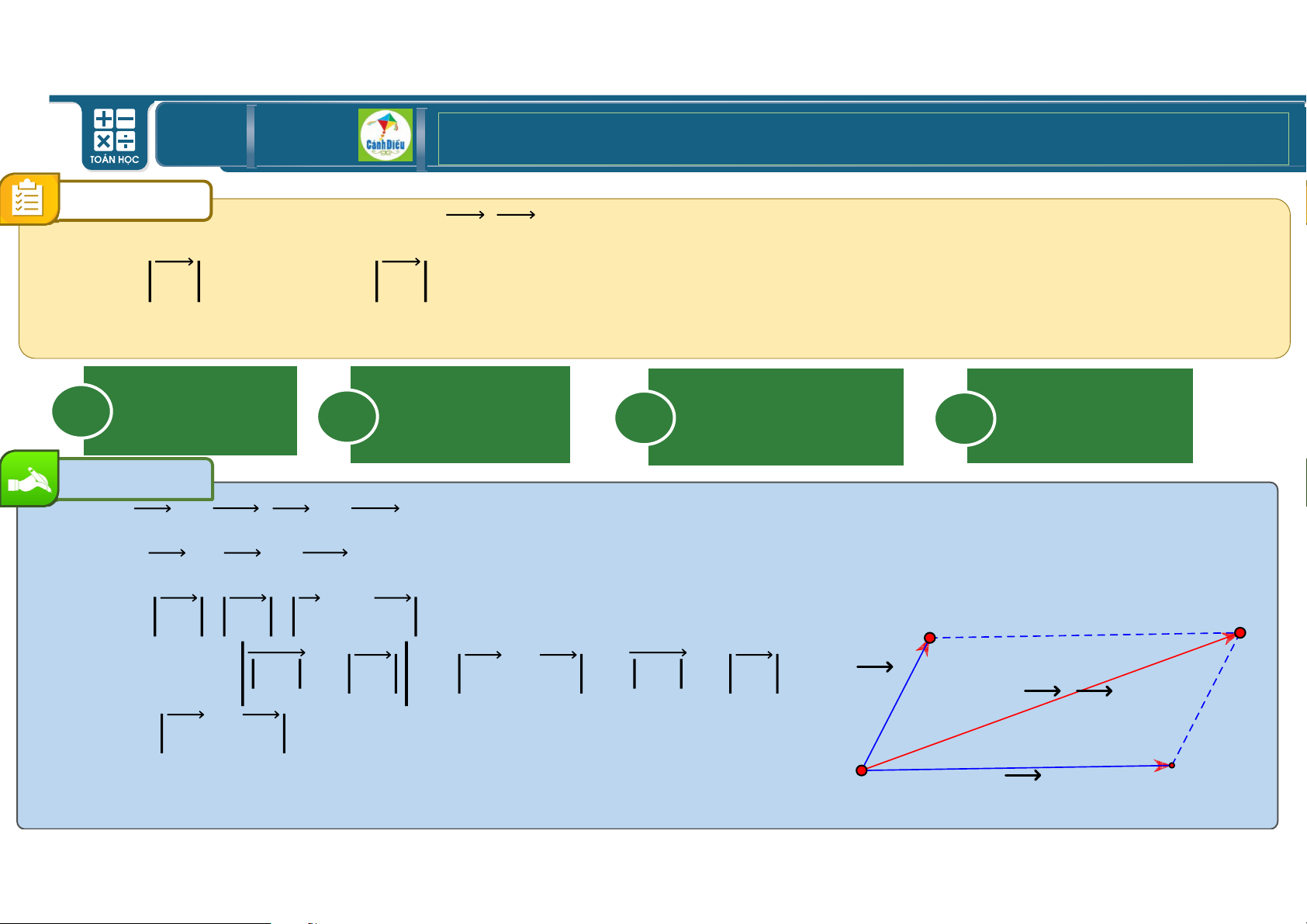
Dựng Œj = rV; Œ\ = rW.
Khi đó Œj + Œ\ = rX ( với X là đỉnh thứ tư của hình bình hành rVXW). Ta có: Œ
là ba cạnh của một j , Œ\ , Œj + Œ\ A C tam giác nên Œ . j − Œ\ { Œj + Œ\ { Œj + Œ\ F1
⇒ dh { Œj + Œ\ { jjh. F1+F2 O F2 B TOÁN THPT GIÁO ÁN ĐIỆN TỬ CÂU 12 Cho hai lực Œ
không cùng phương, cùng tác dụng vào một vật, j, Œ\ b1i5 ết Œ
c tổng hợp của hai lực đã cho
j = ehˆ và Œ\ 54
= mhˆ. Cường độ lự9 6
không thể nhận giá trị nào dưới đây? A 80N B jjhˆ C nhˆ D 60N Bài giải Œ cùng hướng,
j + Œ\ = jjh khi Œj, Œ\ Œ
ngược hướng ( không thỏa mãn do bài ra hai
j + Œ\ = dh khi Œj, Œ\ lực Œ không cùng phương) A C j, Œ\
⇒ dh k Œj + Œ\ k jjh F1
Vậy cường độ lực tổng hợp của hai lực F1+F2
không thể là jjhˆ. Chọn B O F2 B TOÁN THPT GIÁO ÁN ĐIỆN TỬ CÂU 13
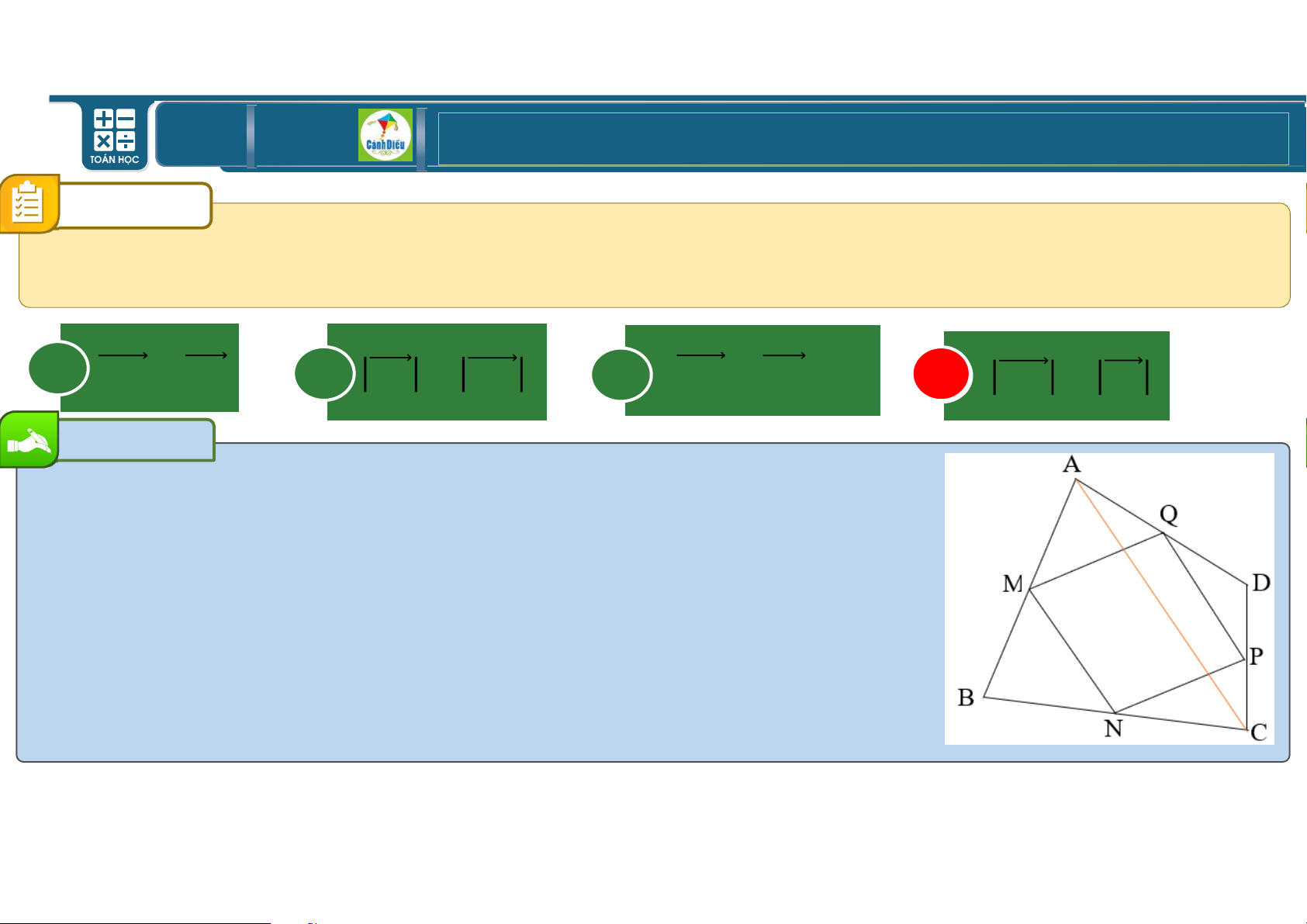
Cho tứ giác lồi VWXp. Gọi ‡, ˆ lần lượt là trọng tâm 15 tam giác V 5 W4
X và WXp. Khẳng định 9nào dưới đây đúng? 6 A MN//AB B MN//BC C MN//AD D MN//CD Bài giải Do K là trọng tâm u nên K + K + K = 0. C I Và L là trọng tâm u M nên L + L + LM = 0. B
Trừ các vế tương ứng của hai đẳng thức ta được: M N K − LM + K − L + K − L = 0 ⇔ K − LM + 2KL = 0. ⇔ KL + L − LM + 2KL = 0
⇔ M + 3KL = 0 ⇔ M = 3KL. A D
Vậy KL // M (do K ∉ M). Chọn C TOÁN THPT GIÁO ÁN ĐIỆN TỬ CÂU 14
Cho hình chữ nhật VWXp tâm r có VW = \WX = \Y. 15 Khi đó X 5 W 4 − \rX bằng 9 6 A \Y B \Y C D \ \Y Y Bài giải
Gọi ‡ là trung điểm VW. A M
Khi đó: XW − \rX = \r‡ − \rX B
= \ X‡ = \X‡ = \ \Y. ChọnC O D C TOÁN THPT GIÁO ÁN ĐIỆN TỬ CÂU 15
Cho tam giác VWX có WX = eY. Gọi ‡ là điểm thỏa mãn e 1 ‡ 5
V + \‡W − \‡X = 54
‡W − ‡X . Độ dài nh 9
ỏ nhất của vectơ W 6 ‡ − WV bằng A Y B eY C D eY \Y Bài giải
Gọi ; là điểm thỏa mãn: 3; + 2; − 2; = 0.
Khi đó: 3; + 2; − 2; = 0 ⇔ 3; + 2 = 0 A O M ⇔ ; =
Ta xác định được điểm ; cố định thỏa ; = Mặt khác: 3K + 2K − 2K = K − K 1 B C ⇔ 3K; + 3; + 2; − 2; = ⇔ K; = 3 Suy ra: K; = ~. TOÁN THPT GIÁO ÁN ĐIỆN TỬ CÂU 15
Cho tam giác VWX có WX = eY. Gọi ‡ là điểm thỏa mãn e 1 ‡ 5
V + \‡W − \‡X = 54
‡W − ‡X . Độ dài nh 9
ỏ nhất của vectơ W 6 ‡ − WV bằng A Y B eY C D eY \Y Bài giải
Do đó tập hợp các điểm ‡ thỏa đề bài là
đường tròn tâm r, bán kính bằng Y. A
Khi đó: W‡ − WV = V‡ = V‡ nhỏ nhất O M
khi r, ‡, V thẳng hàng và ‡ nằm giữa r, V.
Vậy V‡ = rV − ‡r = Y. Chọn A B C