CHƯƠNG I CHƯƠNG IV. VECTƠ
§7. Các khái niệm mở đầu
§8. Tổng và hiệu của hai vectơ
§9. Tích của một vectơ với một số
§10. Vectơ trong mặt phẳng tọa độ
§11. Tích vô hướng của hai vectơ
Bài tập cuối chương 4 CHƯƠNG I CHƯƠNG IV. VECTƠ TOÁN HÌNH HỌC ➉ ÔN CHƯƠNG IV 1 BÀI TẬP SKG 2 BÀI TẬP THÊM 3
BÀI TẬP TRẮC NGHIỆM 1. BÀI TẬP
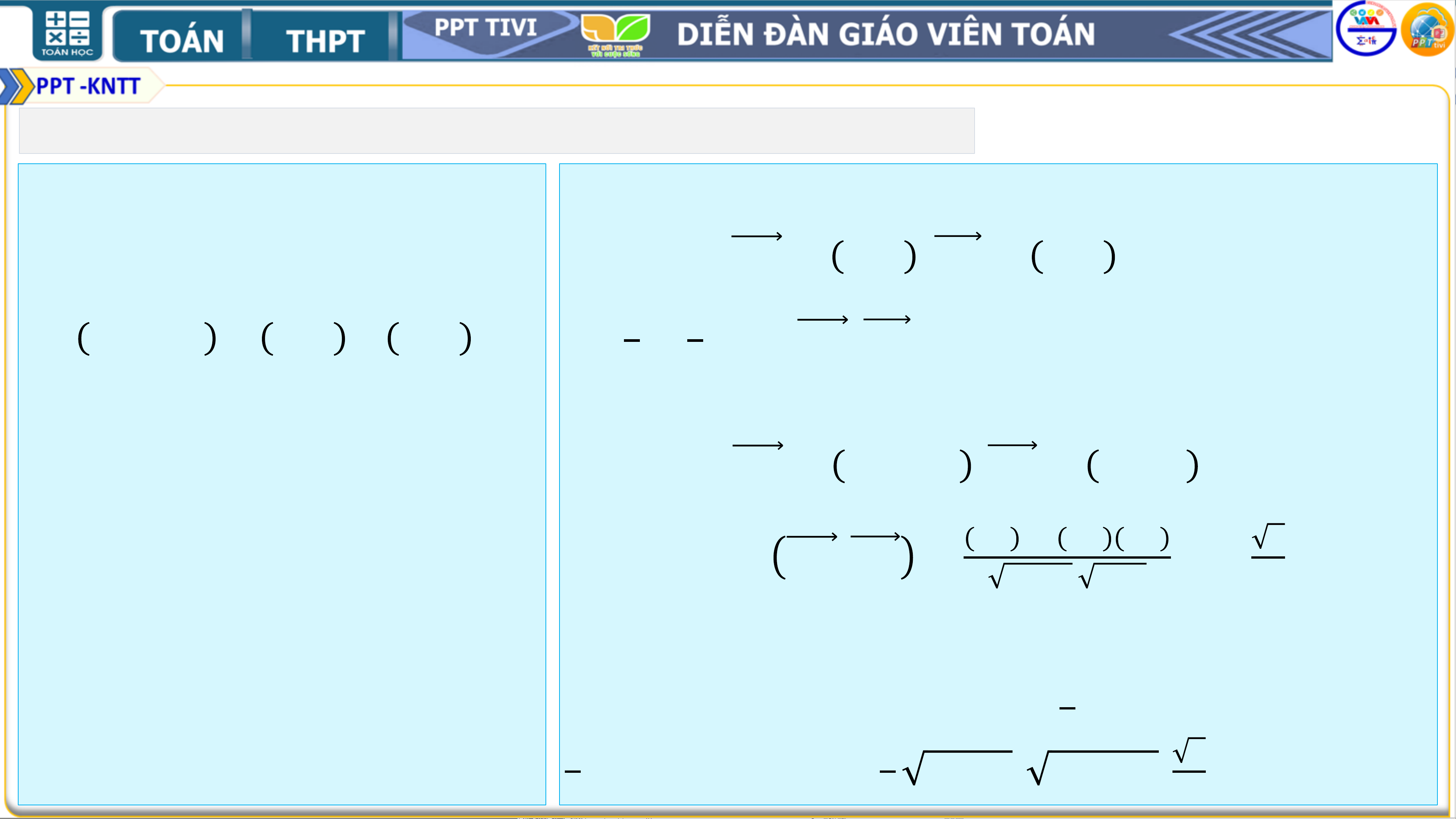
❖4.34. Cho hình bình hành 𝑨𝑩𝑪𝑫. ➢ Hướng dẫn:
Chứng minh rằng với mọi điểm 𝑴 Ta có:
ta có: 𝑴𝑨 + 𝑴𝑪 = 𝑴𝑩 + 𝑴𝑫.
𝑴𝑨 + 𝑴𝑪 = 𝑴𝑩 + 𝑩𝑨 + 𝑴𝑫 + 𝑫𝑪
= 𝑴𝑩 + 𝑴𝑫 + 𝑩𝑨 + 𝑫𝑪 = 𝑴𝑩 + 𝑴𝑫.
Vì 𝑨𝑩𝑪𝑫là hình bình hành nên
𝑨𝑩 = 𝑫𝑪 ⇒ 𝑩𝑨 + 𝑫𝑪 = 𝑩𝑨 + 𝑨𝑩 = 𝟎 1. BÀI TẬP
❖4.35. Trong mặt phẳng tọa độ ➢ Hướng dẫn:
𝑶𝒙𝒚 , cho 𝑨 𝟐; 𝟏 ; 𝑩 −𝟐; 𝟓 và a. 𝑩𝑨 = 𝟒; −𝟒 ; 𝑩𝑪 = −𝟑; −𝟑 . 𝑪 −𝟓; 𝟐
b. Ta thấy 𝟒 ≠ −𝟒 nên 2 vec-tơ 𝑩𝑨 và . −𝟑 −𝟑
a. Tìm tọa độ của các vectơ 𝑩𝑨 và 𝑩𝑪 không cùng phương suy ra 3 điểm 𝑨 𝑩𝑪.
, 𝑩 , 𝑪 không thẳng hàng do đó chúng
là 3 đỉnh của 1 tam giác.
b. Chứng minh rằng 𝑨, 𝑩, 𝑪 là ba
đỉnh của một tam giác vuông. Lại có: 𝑩𝑨. 𝑩𝑪 = 𝟒. −𝟑 + −𝟒 −𝟑 = 𝟎
Tính diện tích và chu vi của tam nên 𝑩𝑨 ⊥ 𝑩𝑪 suy ra 𝜟𝑨𝑩𝑪 vuông tại 𝑩. giác đó. 1. BÀI TẬP
❖4.35. Trong mặt phẳng tọa độ ➢ Hướng dẫn:
𝑶𝒙𝒚 , cho 𝑨 𝟐; 𝟏 ; 𝑩 −𝟐; 𝟓 và 𝑨𝑩 = 𝟒𝟐 + −𝟒 𝟐 = 𝟒 𝟐 ; 𝑪 −𝟓; 𝟐 𝑩𝑪 =
−𝟑 𝟐 + −𝟑 𝟐 = 𝟑 𝟐; .
a. Tìm tọa độ trọng tâm 𝑮 của 𝑨𝑪 =
−𝟕 𝟐 + 𝟏𝟐 = 𝟓 𝟐 ∆𝑨𝑩𝑪 . . 𝑺
𝑩𝑨. 𝑩𝑪 = 𝟏 . 𝟒 𝟐. 𝟑 𝟐 = 𝟏𝟐 (đvdt)
b. Tìm tọa độ của điểm 𝑫 sao cho 𝑨𝑩𝑪 = 𝟏𝟐 𝟐
tứ giác 𝑩𝑪𝑨𝑫 là một hình bình
Chu vi tam giác 𝑨𝑩𝑪 bằng hành.
𝑨𝑩 + 𝑩𝑪 + 𝑪𝑨 = 𝟒 𝟐 + 𝟑 𝟐 + 𝟓 𝟐 = 𝟏𝟐 𝟐 (đvcv). 1. BÀI TẬP
❖4.35. Trong mặt phẳng tọa độ ➢ Hướng dẫn: 𝑶𝒙𝒚
c. 𝑮 là trọng tâm của tam giác 𝑨𝑩𝑪 nên
, cho 𝑨 𝟐; 𝟏 ; 𝑩 −𝟐; 𝟓 và 𝑪 −𝟓; 𝟐 .
𝒙𝑮 = 𝒙𝑨+𝒙𝑩+𝒙𝑪 = 𝟐−𝟐−𝟓 = −𝟓 𝟑 𝟑 𝟑
c. Tìm tọa độ trọng tâm 𝑮 của ൞𝒚 = 𝟏+𝟓+𝟐 = 𝟖 ∆𝑨𝑩𝑪.
𝑮 = 𝒚𝑨+𝒚𝑩+𝒚𝑪 𝟑 𝟑 𝟑
d. Tìm tọa độ của điểm 𝑫 sao cho
Vậy 𝑮 − 𝟓 ; 𝟖 .
tứ giác 𝑩𝑪𝑨𝑫 là một hình bình 𝟑 𝟑 hành. 1. BÀI TẬP
❖4.35. Trong mặt phẳng tọa độ ➢ Hướng dẫn: 𝑶𝒙𝒚
d. Gọi 𝑫 𝒂, 𝒃 Do 𝑨𝑩𝑪 là một tam giác
, cho 𝑨 𝟐; 𝟏 ; 𝑩 −𝟐; 𝟓 và .
nên tứ giác 𝑩𝑪𝑨𝑫 là hình bình hành 𝑪 −𝟓; 𝟐 . 𝒙
c. Tìm tọa độ trọng tâm 𝑮
𝑪 − 𝒙𝑩 = 𝒙𝑨 − 𝒙𝑫 của
⇔ 𝑩𝑪 = 𝑫𝑨 ⇔ ቊ𝒚
𝑪 − 𝒚𝑩 = 𝒚𝑨 − 𝒚𝑫 ∆𝑨𝑩𝑪.
d. Tìm tọa độ của điểm 𝑫 sao cho ⇔ ቊ−𝟑 = 𝟐 − 𝒂
−𝟑 = 𝟏 − 𝒃 ⇔ ቊ𝒂 = 𝟓 𝒃 = 𝟒.
tứ giác 𝑩𝑪𝑨𝑫 là một hình bình hành.
Vậy 𝑫 𝟓; 𝟒 . 1. BÀI TẬP
❖4.36. Trong mặt phẳng tọa độ ➢ Hướng dẫn:
𝑶𝒙𝒚, cho 𝑨 𝟏; 𝟐 ; 𝑩 𝟑; 𝟒 ; 𝑪 −𝟏; −𝟐 a. 𝑨𝑩 = 𝟐; 𝟐 ; 𝑪𝑫 = 𝟕; 𝟕 . và 𝑫 𝟔; 𝟓
b. Ta thấy 𝟐 = 𝟐 nên 2 vec-tơ 𝑨𝑩 và 𝑪𝑫 . 𝟕 𝟕
a. Tìm tọa độ của vec cùng
-tơ 𝑨𝑩 và 𝑪𝑫. phương.
b. Hãy giải thích vì sao các vec-tơ
c. 𝑨𝑪 = −𝟐; −𝟒 ; 𝑩𝑬 = 𝒂 − 𝟑; −𝟑 .
𝑨𝑩 và 𝑪𝑫 cùng phương.
𝑨𝑪 và 𝑩𝑬 cùng phương
c. Giả sử 𝑬 là điểm có tọa độ 𝒂; 𝟏 . Tìm
⇔ −𝟐 −𝟑 = −𝟒 𝒂 − 𝟑 ⇔ 𝒂 = 𝟑 .
𝒂 để các vec-tơ 𝑨𝑪 và 𝑩𝑬 cùng 𝟐 phương. 1. BÀI TẬP
❖4.36. Trong mặt phẳng tọa độ ➢ Hướng dẫn:
𝑶𝒙𝒚, cho 𝑨 𝟏; 𝟐 ; 𝑩 𝟑; 𝟒 ; 𝑪 −𝟏; −𝟐 d. Khi 𝒂 = 𝟑 thì 𝑬 𝟑 ; 𝟏 . 𝟐 𝟐 và 𝑫 𝟔; 𝟓
Giả sử tồn tại bộ 𝒎, 𝒏 ∈ ℝ thỏa mãn .
c. Giả sử 𝑬 là điểm có tọa độ 𝒂; 𝟏 .
𝑨𝑬 = 𝒎𝑨𝑩 + 𝒏𝑨𝑪
Tìm 𝒂 để các vec-tơ 𝑨𝑪 và 𝑩𝑬 cùng 𝟏 phương. 𝒎 = 𝟏
⇔ ൝ = 𝟐𝒎 − 𝟐𝒏 𝟐 ⇔ ൝𝒏 = 𝟑 . d. Với 𝒂
−𝟏 = 𝟐𝒎 − 𝟒𝒏 𝟒
vừa tìm được, hãy biểu thị
vec-tơ 𝑨𝑬 theo các vectơ 𝑨𝑩 và 𝑨𝑪
Vậy 𝑨𝑬 = 𝑨𝑩 + 𝟑 𝑨𝑪. . 𝟒 1. BÀI TẬP ❖ ➢ Hướng dẫn:
4.37. Cho vectơ 𝒂 ≠ 𝟎 . Chứng
Ta có: 𝟏 𝒂 = 𝟏 𝒂 = 𝟏 và 𝟏 > 𝟎 nên
minh rằng 𝟏 𝒂 (hay còn được viết 𝒂 𝒂 𝒂 𝒂
𝟏 𝒂 là một vectơ đơn vị, cùng hướng 𝒂
là 𝒂 ) là một vectơ đơn vị, cùng với vectơ 𝒂. 𝒂
hướng với vectơ 𝒂. 1. BÀI TẬP
❖4.38. Cho ba vectơ 𝒂, 𝒃, 𝒖 với ➢ Hướng dẫn:
𝒂 = 𝒃 = 𝟏 và 𝒂 ⊥ 𝒃. Xét một hệ Giả sử: 𝒖 = 𝒙𝒂 + 𝒚𝒃, 𝒙, 𝒚 ∈ ℝ .
trục 𝑶𝒙𝒚 với các vectơ đơn vị Ԧ𝒊 = Ta có:
𝒂, Ԧ𝒋 = 𝒃. Chứng minh rằng:
𝒖 = 𝒖 . 𝒄𝒐𝒔 𝒖, 𝒂 𝒂 + 𝒖 . 𝒄𝒐𝒔 𝒖, 𝒃 𝒃
a) Vectơ 𝒖 có toạ độ là 𝒖 ⋅ 𝒂; 𝒖 ⋅ 𝒃 .
= 𝒖 . 𝒂 . 𝒄𝒐𝒔 𝒖, 𝒂 𝒂 + 𝒖 . 𝒃 . 𝒄𝒐𝒔 𝒖, 𝒃 𝒃
b) 𝒖 = 𝒖 ⋅ 𝒂 𝒂 + 𝒖 ⋅ 𝒃 𝒃.
= 𝒖 ⋅ 𝒂 𝒂 + 𝒖 ⋅ 𝒃 𝒃
Vậy vectơ 𝒖 có toạ độ là 𝒖 ⋅ 𝒂; 𝒖 ⋅ 𝒃 và
𝒖 = 𝒖 ⋅ 𝒂 𝒂 + 𝒖 ⋅ 𝒃 𝒃. 1. BÀI TẬP
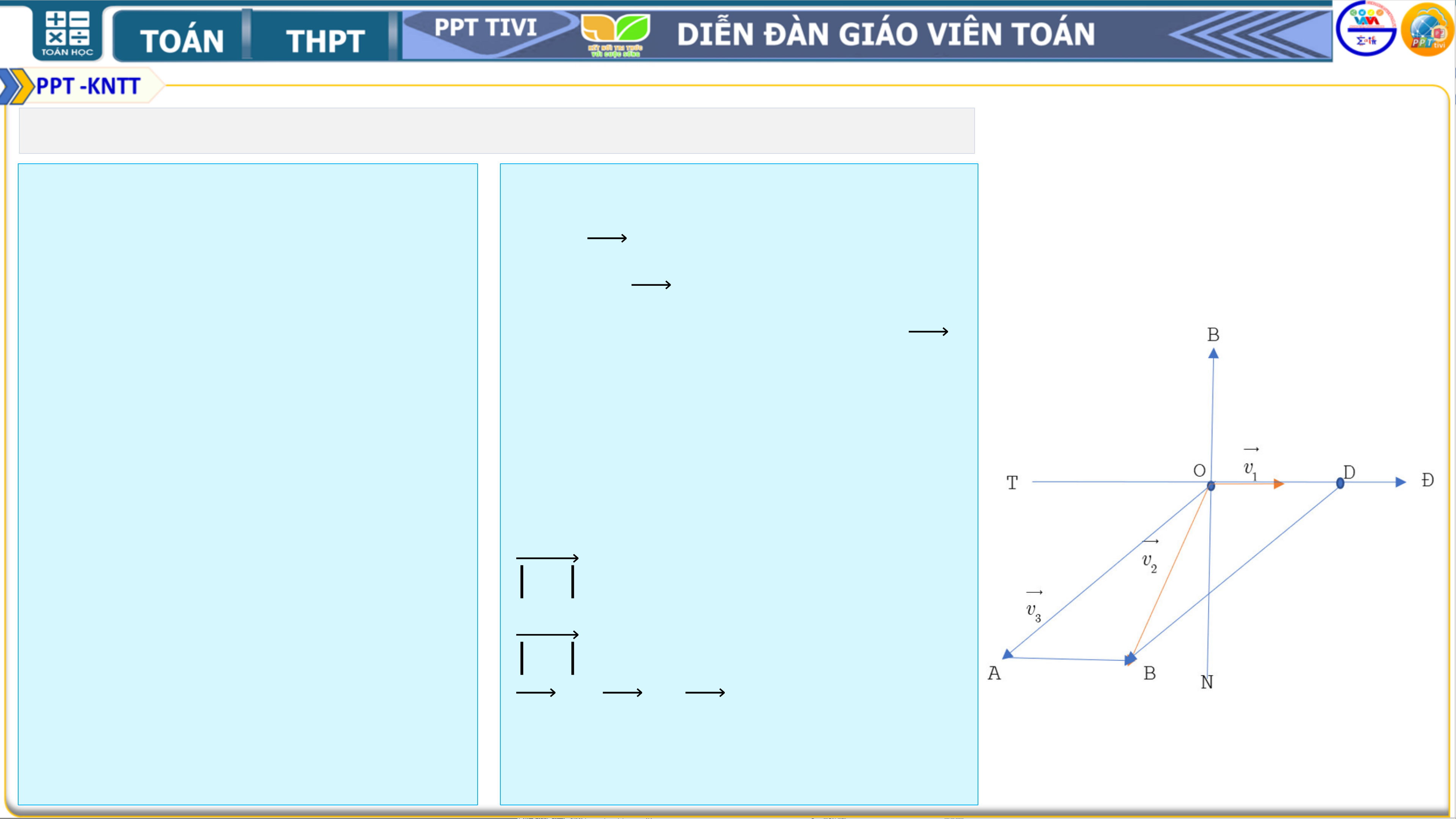
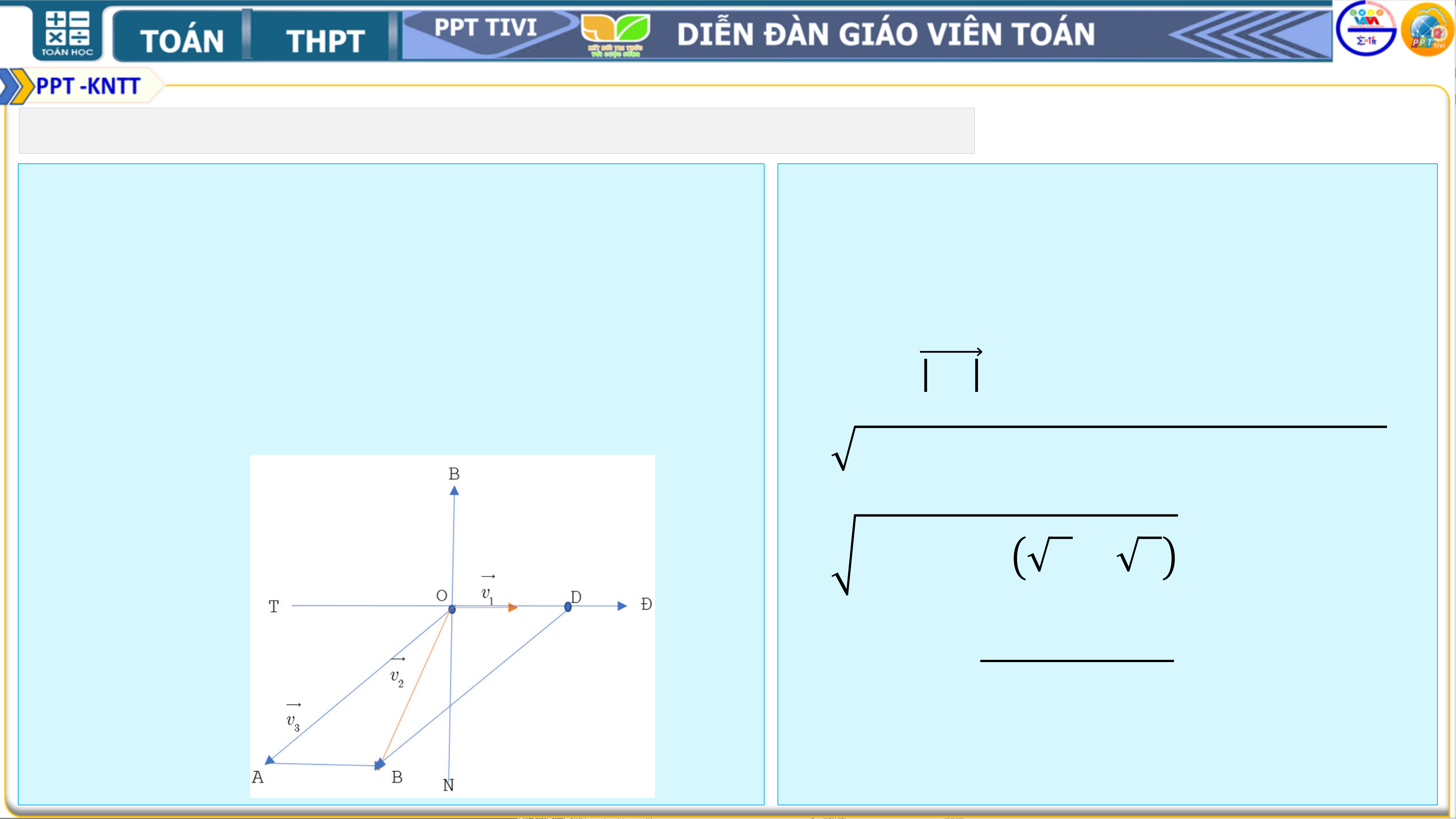
❖4.39. Trên sông, một ➢ Hướng dẫn:
ca nô chuyển động Gọi 𝒗 thẳng
𝟏 là vận tốc dòng
đều theo hướng nước; 𝒗 𝑺𝟏𝟓∘𝑬
𝟐 là vận tốc ca nô
với vận tốc có độ có sức cản của nước; 𝒗 lớn 𝟑
bằng 𝟐𝟎 km/𝒉 . là vận tốc riêng của ca
Tính vận tốc riêng của nô.
ca nô, biết rằng, nước
trên sông chảy về Từ đề bài ta có
hướng đông với vận 𝒗 tốc
𝟏 = 𝑶𝑫 = 𝟑𝒌𝒎/𝒉;
có độ lớn bằng 𝟑 km/𝒉.
𝒗𝟐 = 𝑶𝑩 = 𝟐𝟎𝒌𝒎/𝒉 và
𝒗𝟐 = 𝒗𝟏 + 𝒗𝟑. 1. BÀI TẬP
❖4.39. Trên sông, một ca nô chuyển ➢ Hướng dẫn:
động thẳng đều theo hướng 𝑺𝟏𝟓∘𝑬 với Ca nô chuyển động thẳng đều theo
vận tốc có độ lớn bằng 𝟐𝟎 km/𝒉. Tính hướng 𝑺𝟏𝟓°𝑬 thì ෣
𝑩𝑶𝑫 = 𝟏𝟎𝟓°.
vận tốc riêng của ca nô, biết rằng,
nước trên sông chảy về hướng đông Suy ra 𝒗𝟑 = 𝑶𝑨 = 𝑫𝑩
với vận tốc có độ lớn bằng 𝟑 km/𝒉.
= 𝑶𝑩𝟐 + 𝑶𝑫𝟐 − 𝟐𝑶𝑩. 𝑶𝑫. 𝒄𝒐𝒔 𝟏𝟎𝟓°
= 𝟒𝟎𝟗 + 𝟑𝟎 𝟔 − 𝟐 . 𝐜𝐨𝐬 ෣
𝑨𝑶𝑩 = 𝑶𝑨𝟐+𝑶𝑩𝟐−𝑨𝑩𝟐 ≈ 𝟎. 𝟗𝟗 𝟐.𝑶𝑨.𝑶𝑩 Suy ra ෣ 𝑨𝑶𝑩 ≈ 𝟖°. 1. BÀI TẬP
❖4.39. Trên sông, một ca nô chuyển ➢ Hướng dẫn:
động thẳng đều theo hướng 𝑺𝟏𝟓∘𝑬 với Suy ra ෣ 𝑨𝑶𝑩 ≈ 𝟖° vận .
tốc có độ lớn bằng 𝟐𝟎 km/𝒉. Tính
vận tốc riêng của ca nô, biết rằng, Vậy Cano đi một mình theo hướng
nước trên sông chảy về hướng đông 𝑺𝟐𝟑°𝑬 với vận tốc:
với vận tốc có độ lớn bằng 𝟑 km/𝒉.
𝟒𝟎𝟗 + 𝟑𝟎 𝟔 − 𝟐 𝒌𝒎/𝒉. 2. BÀI TẬP THÊM
❑Bài 1. Chứng minh rằng điểm 𝑰 là ➢ Hướng dẫn:
• Nếu 𝑰 là trung điểm của đoạn thẳng
trung điểm của đoạn thẳng 𝑨𝑩
𝑨𝑩 thì 𝑰𝑨 = 𝑰𝑩 và hai vec tơ 𝑰𝑨, 𝑰𝑩
khi và chỉ khi 𝑰𝑨 = −𝑰𝑩.
ngược hướng. Vậy 𝑰𝑨 = −𝑰𝑩.
• Ngược lại, nếu 𝑰𝑨 = −𝑰𝑩 thì 𝑰𝑨 = 𝑰𝑩 và
hai vec tơ 𝑰𝑨, 𝑰𝑩 ngược hướng. Do đó
𝑨, 𝑰, 𝑩 thẳng hàng.
Vậy 𝑰 là trung điểm của đoạn thẳng 𝑨𝑩. 2. BÀI TẬP THÊM ➢ Hướng dẫn:
❑Bài 2. Cho tam giác 𝑨𝑩𝑪 có
a) Vì 𝑰 là trung điểm của 𝑩𝑪 nên
trọng tâm 𝑮. Gọi 𝑰 là trung điểm
𝑩𝑰 = 𝑪𝑰 và 𝑩𝑰 cùng hướng với 𝑰𝑪 do đó
của 𝑩𝑪. Dựng điểm 𝑩′ sao cho hai vectơ 𝑩𝑰,𝑰𝑪 bằng nhau hay 𝑩𝑰 = 𝑰𝑪.
𝑩′𝑩 = 𝑨𝑮.
b) Ta có 𝑩′𝑩 = 𝑨𝑮 ⇒ 𝑩′𝑩 = 𝑨𝑮 và 𝑩𝑩′ ∥ 𝑨𝑮.
Do đó 𝑩𝑱, 𝑰𝑮 cùng hướng. (1)
a) Chứng minh rằng 𝑩𝑰 = 𝑰𝑪.
Vì 𝑮 là trọng tâm tam giác 𝑨𝑩𝑪 nên
b) Gọi 𝑱 là trung điểm của 𝑩𝑩′.
Chứng minh rằng 𝑩𝑱 = 𝑰𝑮.
𝑰𝑮 = 𝟏 𝑨𝑮, 𝑱 là trung điểm 𝑩𝑩′ suy ra A 𝟐 B'
𝑩𝑱 = 𝟏 𝑩𝑩′. Vì vậy 𝑩𝑱 = 𝑰𝑮. (2) 𝟐 G J
Từ (1) và (2) ta có 𝑩𝑱 = 𝑰𝑮. B C I 2. BÀI TẬP THÊM
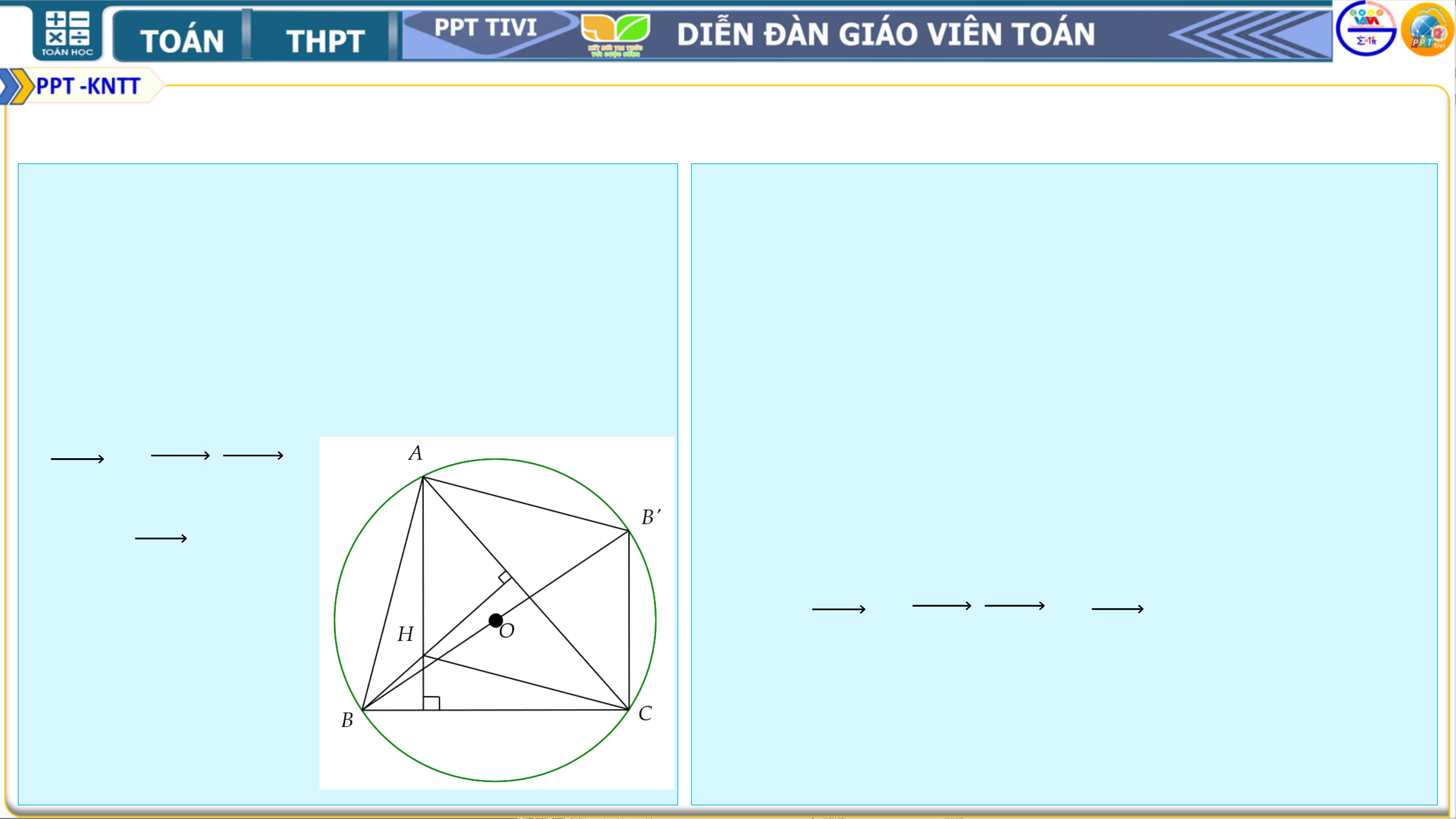
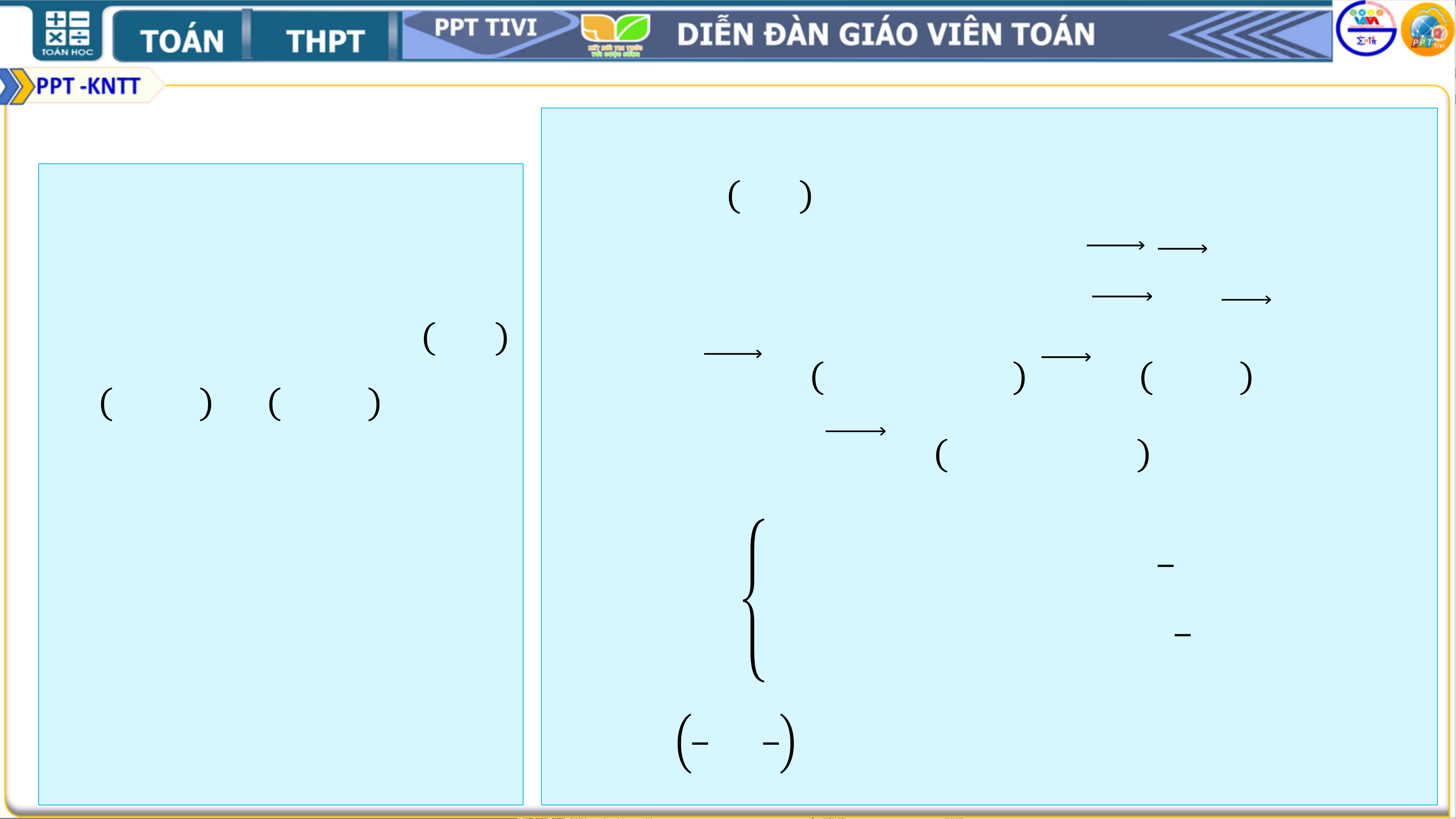
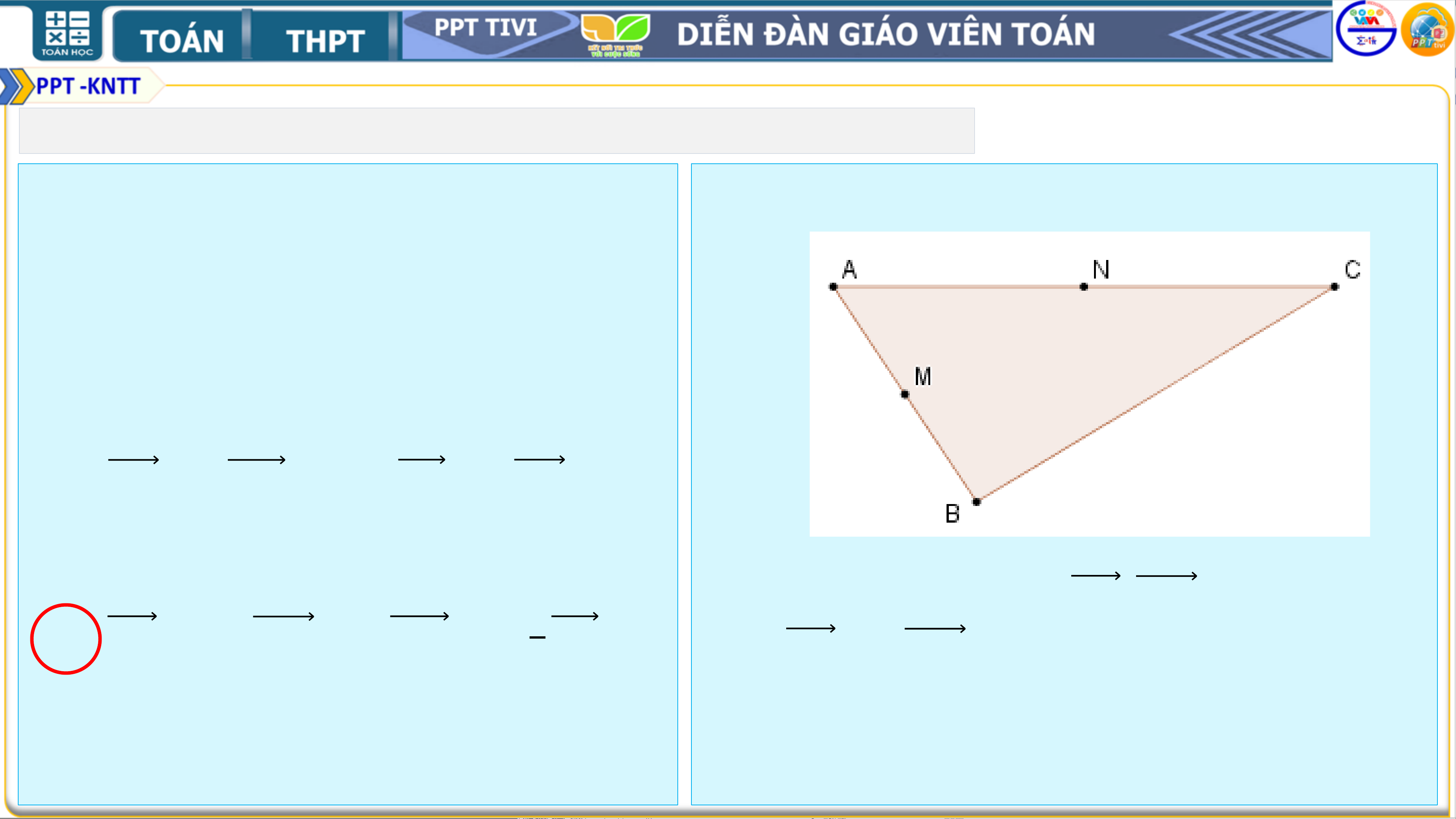
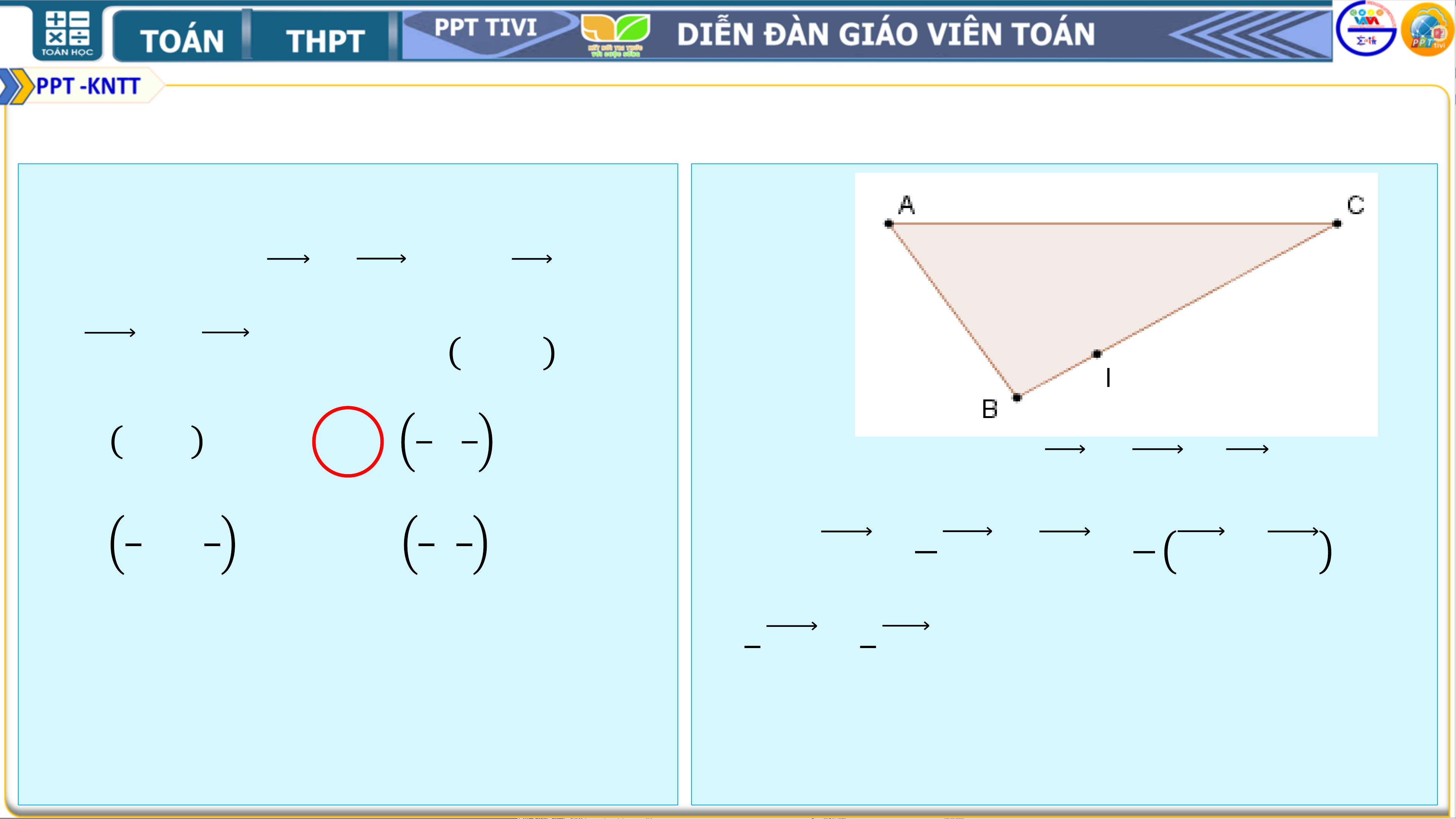
❑Bài 3. Cho tam giác 𝑨𝑩𝑪 có 𝑯 là ➢ Hướng dẫn: trực
• Vì 𝑩𝑩′ là đường kính của đường tròn
tâm và 𝑶 là tâm đường tròn
ngoại tiếp tam giác 𝑨𝑩𝑪 nên
ngoại tiếp. Gọi 𝑩′ là điểm đối ෣ 𝑩𝑨𝑩′ = ෣
𝑩𝑪𝑩′ = 𝟗𝟎°.
xứng của 𝑩 qua 𝑶. Chứng minh • Do đó 𝑪𝑯 ∥ 𝑩′𝑨 và 𝑨𝑯 ∥ 𝑩′𝑪
𝑨𝑯 = 𝑩′𝑪, 𝑨𝑩′
• Suy ra tứ giác 𝑨𝑩′𝑪𝑯 là hình bình = 𝑯𝑪. hành
• Vậy 𝑨𝑯 = 𝑩′𝑪, 𝑨𝑩′ = 𝑯𝑪. 2. BÀI TẬP THÊM
❑Bài 4. Cho năm điểm 𝑨, 𝑩, 𝑪, 𝑫, 𝑬. ➢ Hướng dẫn: Chứng
a) Biến đổi vế trái ta có minh rằng:
𝑽𝑻 = 𝑨𝑪 + 𝑪𝑩 + 𝑪𝑫 + 𝑬𝑫 + 𝑫𝑨
a) 𝑨𝑩 + 𝑪𝑫 + 𝑬𝑨 = 𝑪𝑩 + 𝑬𝑫.
= 𝑪𝑩 + 𝑬𝑫 + 𝑨𝑪 + 𝑪𝑫 + 𝑫𝑨
b) 𝑨𝑪 + 𝑪𝑫 − 𝑬𝑪 = 𝑨𝑬 − 𝑫𝑩 + 𝑪𝑩.
= 𝑪𝑩 + 𝑬𝑫 + 𝑨𝑫 + 𝑫𝑨 = 𝑪𝑩 + 𝑬𝑫 = 𝑽𝑷.
b) Đẳng thức tương đương với
𝑨𝑪 − 𝑨𝑬 + 𝑪𝑫 − 𝑪𝑩 − 𝑬𝑪 + 𝑫𝑩 = 𝟎
⇔ 𝑬𝑪 + 𝑩𝑫 − 𝑬𝑪 + 𝑫𝑩 = 𝟎
⇔ 𝑩𝑫 + 𝑫𝑩 = 𝟎
(đúng với mọi 𝑩, 𝑫) ⇒ (đpcm). 2. BÀI TẬP THÊM ➢ Hướng dẫn:
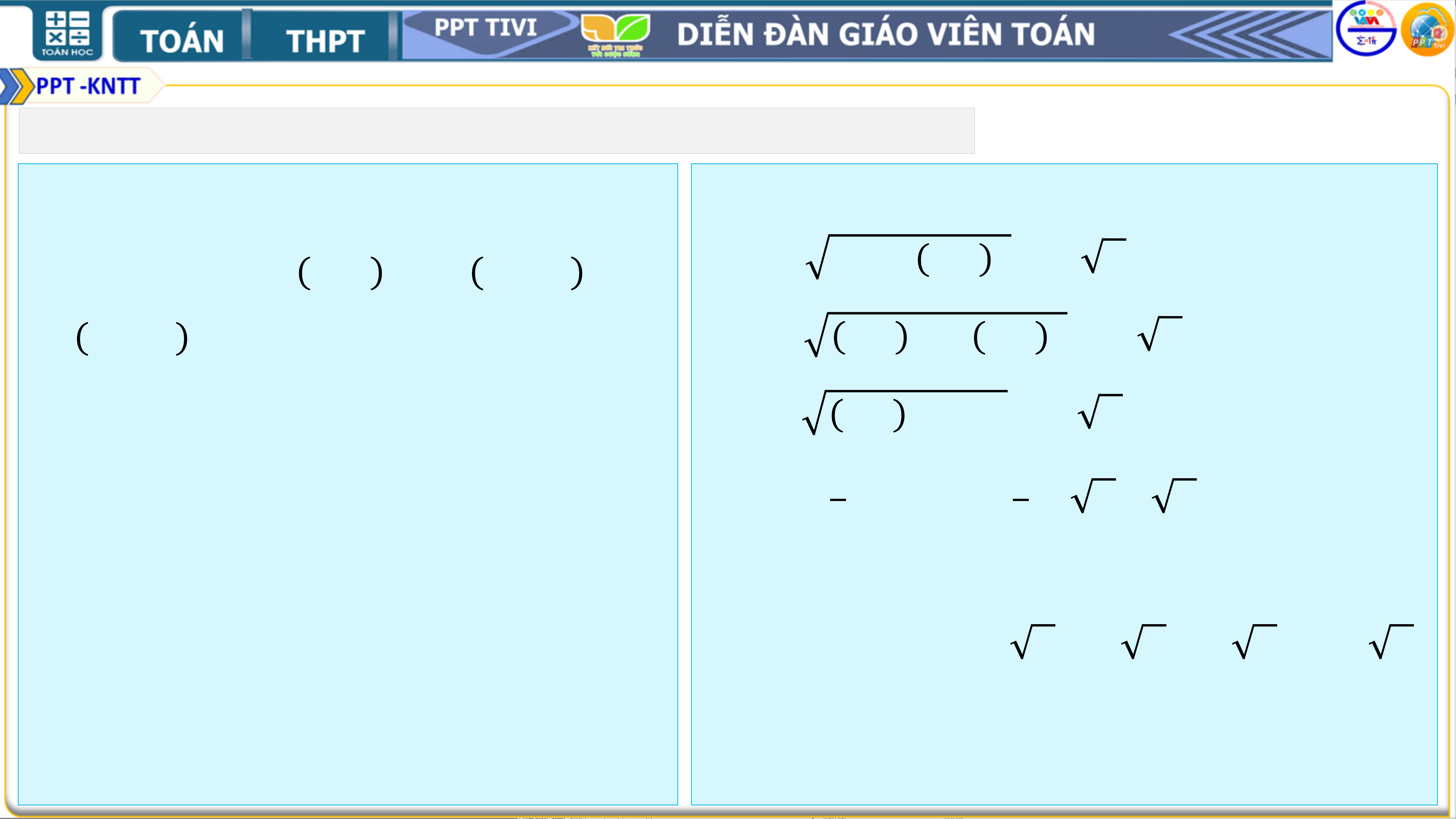
❑Bài 5. Cho 𝒖 = 𝟏 Ԧ𝒊 − 𝟓Ԧ𝒋 𝟐
Ta có 𝒖 = 𝟏 ; −𝟓 , 𝒗 = 𝒌; −𝟒 .
và 𝒗 = 𝒌Ԧ𝒊 − 𝟒Ԧ𝒋. Tìm 𝒌 để 𝟐
a) 𝒖 ⊥ 𝒗.
a) 𝒖 ⊥ 𝒗 ⇔ 𝟏 𝒌 + −𝟓 −𝟒 = 𝟎 ⇔ 𝒌 = −𝟒𝟎. 𝟐
b) 𝒖 = 𝒗 .
b) 𝒖 = 𝟏 + 𝟐𝟓 = 𝟏 𝟏𝟎𝟏 và 𝒗 = 𝒌𝟐 + 𝟏𝟔. 𝟒 𝟐
Do đó 𝒖 = 𝒗 ⇔ 𝒌𝟐 + 𝟏𝟔 = 𝟏 𝟏𝟎𝟏 𝟐
⇔ 𝒌𝟐 + 𝟏𝟔 = 𝟏𝟎𝟏 ⇔ 𝒌𝟐 = 𝟑𝟕 ⇔ 𝒌 = ± 𝟑𝟕. 𝟒 𝟒 𝟐 2. BÀI TẬP THÊM
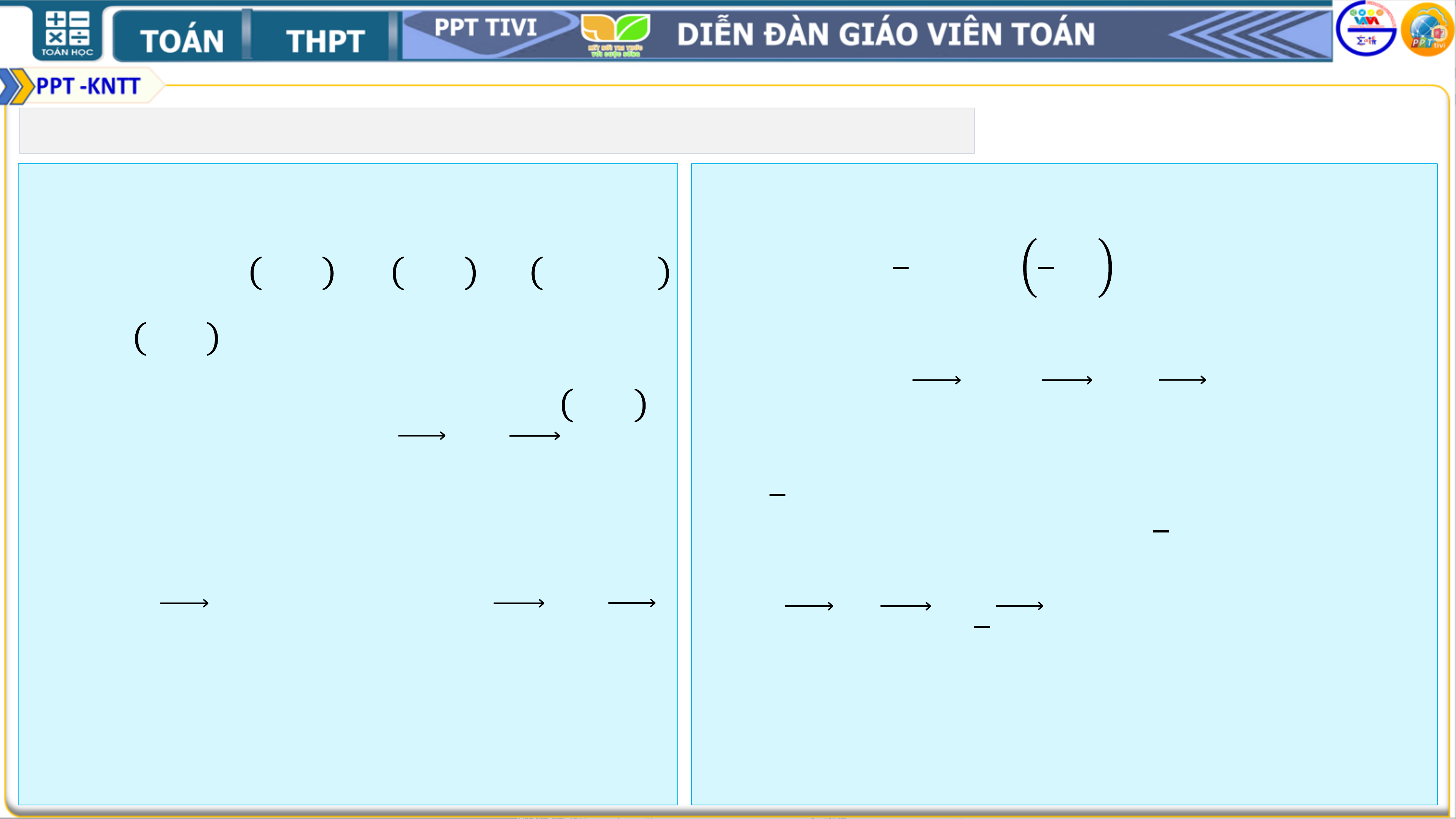
❑Bài 6. Trong mặt phẳng ➢ Hướng dẫn:
toạ độ 𝑶𝒙𝒚, cho các điểm a) Ta có 𝑨𝑩 = 𝟒; 𝟐 ; 𝑨𝑪 = 𝟕; 𝟏 .
𝑨 −𝟏; −𝟏 , 𝑩 𝟑; 𝟏 , 𝑪 𝟔; 𝟎 .
Vì 𝟒 ≠ 𝟐 nên 𝑨𝑩; 𝑨𝑪 không cùng phương, suy ra 𝟕 𝟏
a) Chứng minh ba điểm ba điểm 𝑨, 𝑩, 𝑪 không thẳng hàng.
𝑨, 𝑩, 𝑪 không thẳng hàng. b) Ta có 𝑩𝑨 = −𝟒; −𝟐 , 𝑩𝑪 = 𝟑; −𝟏 .
b) Tính góc 𝑩 và diện tích 𝒄𝒐𝒔 𝑩 = 𝒄𝒐𝒔 𝑩𝑨, 𝑩𝑪 = −𝟒 𝟑+ −𝟐 −𝟏 = − 𝟐. 𝟏𝟔+𝟒. 𝟗+𝟏 𝟐
của tam giác 𝑨𝑩𝑪.
Vậy ෡𝑩 = 𝟏𝟑𝟓°.
Hạ đường cao 𝑨𝑯 ta có 𝑺 = 𝟏 𝑩𝑪. 𝑨𝑯 = 𝟐
𝟏 𝑩𝑪.𝑨𝑩.𝒔𝒊𝒏𝟒𝟓° = 𝟏 𝟗 + 𝟏. 𝟏𝟔 + 𝟒. 𝟐 = 𝟓. 𝟐 𝟐 𝟐 2. BÀI TẬP THÊM
❑Bài 7. Trong mặt phẳng ➢ Hướng dẫn:
toạ độ 𝑶𝒙𝒚,
Gọi 𝑰 𝒙; 𝒚 là tâm đường tròn ngoại tiếp ∆𝑨𝑩𝑪, ta cho các có: điểm
𝑰𝑨 = 𝑰𝑩 = 𝑰𝑪 ⇔ 𝑰𝑨𝟐 = 𝑰𝑩𝟐 = 𝑰𝑪𝟐
𝑨 𝟒; 𝟔 , 𝑩 𝟓; 𝟏 , 𝑪 𝟏; 𝟑 . Tìm
⇔ ൝ 𝒙 − 𝟒 𝟐 + 𝒚 − 𝟔 𝟐 = 𝒙 − 𝟓 𝟐 + 𝒚 − 𝟏 𝟐
tọa độ tâm và bán
𝒙 − 𝟒 𝟐 + 𝒚 − 𝟔 𝟐 = 𝒙 − 𝟏 𝟐 + 𝒚 + 𝟑 𝟐
kính đường tròn ngoại tiếp
⇔ ቊ 𝟐𝒙 − 𝟏𝟎𝒚 = −𝟐𝟔
và 𝒚 = 𝟓.
tam giác 𝑨𝑩𝑪.
−𝟔𝒙 − 𝟏𝟖𝒚 = −𝟒𝟐 ⇔ 𝒙 = − 𝟏𝟐 𝟐
Vậy tâm 𝑰 − 𝟏 ; 𝟓 . 𝟐 𝟐 𝟐 𝟐 Bán kính 𝑰𝑨 =
− 𝟏 − 𝟒 + 𝟓 − 𝟔 = 𝟏𝟑𝟎. 𝟐 𝟐 𝟐 2. BÀI TẬP THÊM
❑Bài 8. Trong mặt phẳng toạ độ ➢ Hướng dẫn: 𝑶𝒙𝒚,
a) Tứ giác 𝑨𝑩𝑪𝑫 là hình bình hành khi
cho tam giác 𝑨𝑩𝑪 với
𝑨 𝟐; 𝟒 , 𝑩 −𝟑; 𝟏 , 𝑪 𝟑; −𝟏 .
𝑨𝑫 = 𝑩𝑪 ⇔ ൝ 𝒙𝑫 − 𝟐 = 𝟑 + 𝟑 𝒚
a) Tìm toạ độ điểm 𝑫 để tứ giác
𝑫 − 𝟒 = −𝟏 − 𝟏 ⇔ ቊ𝒙𝑫 = 𝟖 𝒚𝑫 = 𝟐.
𝑨𝑩𝑪𝑫 là hình bình hành.
Vậy 𝑫 𝟖; 𝟐 .
b) Tìm toạ độ chân đường cao vẽ
từ đỉnh 𝑨 của tam giác 𝑨𝑩𝑪. 2. BÀI TẬP THÊM ➢ Hướng dẫn:
❑Bài 8. Trong mặt phẳng b) Gọi 𝑨′ 𝒙; 𝒚 là chân đường cao 𝑨𝑨′ của tam
toạ độ 𝑶𝒙𝒚, cho tam giác 𝑨𝑩𝑪. Ta có ቊ𝑨𝑨′ ⊥ 𝑩𝑪 ⇔ ൝𝑨𝑨′.𝑩𝑪 = 𝟎 (*) giác 𝑨′ ∈ 𝑩𝑪 𝑩𝑨′ = 𝒌𝑩𝑪
𝑨𝑩𝑪 với 𝑨 𝟐; 𝟒 ,
𝑨𝑨′ = 𝒙 − 𝟐; 𝒚 − 𝟒 , 𝑩𝑪 = 𝟔; −𝟐 ;
𝑩 −𝟑; 𝟏 , 𝑪 𝟑; −𝟏 .
𝑩𝑨′ = 𝒙 + 𝟑; 𝒚 − 𝟏 .
a) Tìm toạ độ điểm 𝑫 để
tứ giác 𝑨𝑩𝑪𝑫 là hình bình 𝒙 = 𝟑 hành 𝟓 . Hệ (*) ⇔ 𝟔𝒙 − 𝟐𝒚 = 𝟒
−𝟐𝒙 − 𝟔𝒚 = 𝟎 ⇔ ൞ . 𝒚 = − 𝟏
b) Tìm toạ độ chân đường 𝟓
cao vẽ từ đỉnh 𝑨 của tam
giác 𝑨𝑩𝑪.
Vậy 𝑨′ 𝟑 ; − 𝟏 . 𝟓 𝟓
3. BÀI TẬP TRẮC NGHIỆM
➢Câu 1. Cho tam giác 𝑨𝑩𝑪. Gọi 𝑴, 𝑵 ➢ Hướng dẫn: lần Chọn A.
lượt là trung điểm của các
cạnh 𝑨𝑩, 𝑨𝑪. Hỏi cặp véctơ nào A
sau đây cùng hướng? M N
A. 𝑨𝑩 và 𝑴𝑩.
B. 𝑴𝑵 và 𝑪𝑩 . B C
C. 𝑴𝑨 và 𝑴𝑩 . D. 𝑨𝑵 và 𝑪𝑨 .
3. BÀI TẬP TRẮC NGHIỆM
➢Câu 2. Cho hình chữ nhật 𝑨𝑩𝑪𝑫 ➢ Hướng dẫn:
có 𝑨𝑩 = 𝟑cm, 𝑩𝑪 = 𝟓cm . Độ dài 𝑨𝑪 = 𝑨𝑪 = 𝑨𝑩𝟐 + 𝑨𝑫𝟐 = 𝟐𝟓 + 𝟏𝟒𝟒 = 𝟏𝟑.
của véctơ 𝑨𝑪 là Chọn D. A. 𝟒. B. 𝟔. C. 𝟖. D. 𝟏𝟑.
3. BÀI TẬP TRẮC NGHIỆM
➢Câu 3. Cho hình bình hành 𝑨𝑩𝑪𝑫 ➢ Hướng dẫn:
với 𝑰 là giao điểm của 2 đường A B
chéo. Khẳng định nào sau đây là I khẳng định sai? D C
A. 𝑰𝑨 + 𝑰𝑪 = 𝟎. B. 𝑨𝑩 = 𝑫𝑪.
𝑨𝑪 và 𝑩𝑫 không cùng phương nên 𝑨𝑪 = 𝑩𝑫 sai.
C. 𝑨𝑪 = 𝑩𝑫.
D. 𝑨𝑩 + 𝑨𝑫 = 𝑨𝑪. Chọn C.
3. BÀI TẬP TRẮC NGHIỆM
➢Câu 4. Cho tam giác 𝑨𝑩𝑪. Gọi 𝑴 ➢ Hướng dẫn:
và 𝑵 lần lượt là trung điểm của
𝑨𝑩 và 𝑨𝑪. Trong các mệnh đề sau tìm mệnh đề sai?
A. 𝑨𝑩 = 𝟐𝑨𝑴. B. 𝑨𝑪 = 𝟐𝑵𝑪.
Ta có: 𝑩𝑪 = 𝟐𝑴𝑵 và 𝑩𝑪; 𝑴𝑵 cùng hướng
C. 𝑩𝑪 = −𝟐𝑴𝑵. D. 𝑪𝑵 = − 𝟏 𝑨𝑪. 𝟐
nên 𝑩𝑪 = 𝟐𝑴𝑵. Chọn C.
3. BÀI TẬP TRẮC NGHIỆM
➢Câu 5. Cho tam giác 𝑨𝑩𝑪, điểm 𝑰
thoả mãn: 𝟒𝑩𝑰 = 𝑩𝑪. Nếu 𝑨𝑰 =
𝒎𝑨𝑩 + 𝒏𝑨𝑪 thì cặp số 𝒎; 𝒏 bằng 𝟑 A. 𝟑; 𝟒 . B. ; 𝟏 . 𝟒 𝟒
Ta phân tích được 𝑨𝑰 = 𝑨𝑩 + 𝑩𝑰 𝟏 𝟏 𝟏 𝟏 C. ; − 𝟏 . D. ; 𝟏 . 𝟑 𝟓 𝟒 𝟒
= 𝑨𝑩 + 𝟒𝑩𝑪 = 𝑨𝑩 + 𝟒 𝑨𝑪 − 𝑨𝑩 Hướng dẫn:
= 𝟑 𝑨𝑩 + 𝟏 𝑨𝑪. 𝟒 𝟒 Chọn B.
3. BÀI TẬP TRẮC NGHIỆM
➢Câu 6. Cho hai điểm 𝑴 𝟖; −𝟏 và ➢ Hướng dẫn:
𝑵 𝟑; 𝟐 . Nếu 𝑷là điểm đối xứng
• Giả sử 𝑷 𝒙𝑷; 𝒚𝑷 . với điểm 𝑴
• Vì 𝑷 là điểm đối xứng với điểm 𝑴 qua
qua điểm 𝑵 thì 𝑷 có 𝒙 tọa độ là
điểm 𝑵, ta có: ቊ 𝒑 = 𝟐𝒙𝑵 − 𝒙𝑴
𝒚𝑷 = 𝟐𝒚𝑵 − 𝒚𝑴
A. −𝟐; 𝟓 .
B. 𝟏𝟑; −𝟑 . 𝒙 ⇔ ቊ 𝒑 = −𝟐 𝟏𝟏 𝒚𝑷 = 𝟓
C. 𝟏𝟏; −𝟏 . D. ; 𝟏 . 𝟐 𝟐
• Vậy 𝑷 −𝟐; 𝟓 Chọn A.
3. BÀI TẬP TRẮC NGHIỆM
➢Câu 7. Véc-tơ đối của ➢ Hướng dẫn:
• Vec-tơ đối của vecto 𝒗 = −𝟒; −𝟏𝟏 là
𝒗 = −𝟒; −𝟏𝟏 là
−𝒗 = 𝟒; 𝟏𝟏 .
A. 𝒖 = −𝟏𝟏; −𝟒 . • Chọn A.
B. 𝒖 = 𝟒; −𝟏𝟏 .
C. 𝒖 = 𝟒; 𝟏𝟏 .
D. 𝒖 = −𝟒; 𝟏𝟏 .
3. BÀI TẬP TRẮC NGHIỆM
➢Câu 8. Trong mặt phẳng 𝑶𝒙𝒚, cho ➢ Hướng dẫn:
hai điểm 𝑨 −𝟑; 𝟐 , 𝑩 𝟏; 𝟒 . Tìm tọa • Gọi 𝑴 𝒙; 𝒚 . độ điểm 𝑴
• Ta có: 𝑨𝑴 = 𝒙 + 𝟑; 𝒚 − 𝟐 , 𝑨𝑩 = 𝟒; 𝟐
thỏa 𝑨𝑴 = −𝟐𝑨𝑩 là
• 𝑨𝑴 = −𝟐𝑨𝑩 ⇒ ቊ𝒙 + 𝟑 = −𝟖
𝒚 − 𝟐 = −𝟒 ⇒ ቊ𝒙 = −𝟏𝟏 𝒚 = −𝟐
A. 𝑴 𝟑; 𝟖 .
B. 𝑴 𝟖; −𝟒 . • Vậy 𝑴 −𝟏𝟏;−𝟐 . • Chọn D.
C. 𝑴 𝟔; −𝟐 .
D. 𝑴 −𝟏𝟏; −𝟐 .
3. BÀI TẬP TRẮC NGHIỆM
➢Câu 9. Trong mặt phẳng 𝑶𝒙𝒚, cho ➢ Hướng dẫn:
𝑨 𝒎 − 𝟏; 𝟏 , 𝑩 𝟐; 𝟔 − 𝟐𝒎 , 𝑪ሺ𝒎 +
Do 𝑨, 𝑩, 𝑪 thẳng hàng nên 𝑨𝑩 cùng phương với 𝑨𝑪 𝟏; )
𝟑 . Tìm giá trị của 𝒎 để 𝑨, 𝑩, 𝑪 thẳng hàng
𝑨𝑩 = 𝟑 − 𝒎; 𝟓 − 𝟐𝒎 , 𝑨𝑪 = 𝟐; 𝟐 . Khi đó :
A. 𝒎 = 𝟎 .
B. 𝒎 = 𝟐 .
𝟑 − 𝒎 𝟓 − 𝟐𝒎
C. 𝒎 = 𝟏 . D. 𝒎 = 𝟑 . 𝟐 = 𝟐 ⇔ 𝒎 = 𝟐 Chọn B.
3. BÀI TẬP TRẮC NGHIỆM
➢Câu 10. Cho tam giác 𝑨𝑩𝑪 ➢ Hướng dẫn:
có 𝑨 −𝟒; −𝟓
• TN: Biểu diễn toạ độ các điểm trên mặt
, 𝑩 𝟏; 𝟓 ,
phẳng toạ độ, bằng trực quan ta chọn được
𝑪 𝟒; −𝟏 . Toạ độ chân ngay đáp án B.
đường phân giác trong
• Tự luận: Gọi 𝑫 𝒂; 𝒃 là chân đường phân giác
của góc 𝑩 là
trong của góc 𝑩 thì 𝑫𝑨 = 𝑩𝑨 = 𝟓 𝟓 = 𝟓 𝑫𝑪 𝑩𝑪 𝟑 𝟓 𝟑
A. 𝟏; 𝟓 .
B. 𝟏; − 𝟓 . 𝟐 𝟐
• Do 𝑫 nằm trong đoạn 𝑨𝑪 nên 𝑫𝑨 = − 𝟓 𝑫𝑪 𝟑
−𝟒 − 𝒂 = − 𝟓 𝟒 − 𝒂 𝒂 = 𝟏
C. 𝟏; −𝟓 . D. 𝟓; 𝟏 . ⇔ ൞ 𝟑 ⇔ ൝ .
−𝟓 − 𝒂 = − 𝟓 −𝟏 − 𝒃 𝒃 = − 𝟓 𝟑 𝟐 • Chọn B.
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18
• Slide 19
• Slide 20
• Slide 21
• Slide 22
• Slide 23
• Slide 24
• Slide 25
• Slide 26
• Slide 27
• Slide 28
• Slide 29
• Slide 30
• Slide 31
• Slide 32
• Slide 33