Chương 4: Xác Định Chuyển Vị | Môn Cơ học kết cấu - Đại học Xây Dựng Hà Nội

lOMoAR cPSD| 58933639 lOMoAR cPSD| 58933639 à i l i u t h a k h ả Bài giảng môn học.
Lều Thọ Trình, Cơ học kết Lều Thọ Trình, Nguyễn
Mạnh Yên, Bài tập Cơ học
Lều Thọ Trình, Cơ học kết Lều Thọ Trình, Nguyễn
Mạnh Yên, Bài tập Cơ học lOMoAR cPSD| 58933639 Ơ 1 lOMoAR cPSD| 58933639 Công khả dĩ
Nguyên lý công khả dĩ cho hệ đàn hồi D U Ơ 1
Công thức chuyển vị trong hệ thanh đàn hồi tuyến tính Ví dụ áp dụng lOMoAR cPSD| 58933639 1. Công khả dĩ ảo của
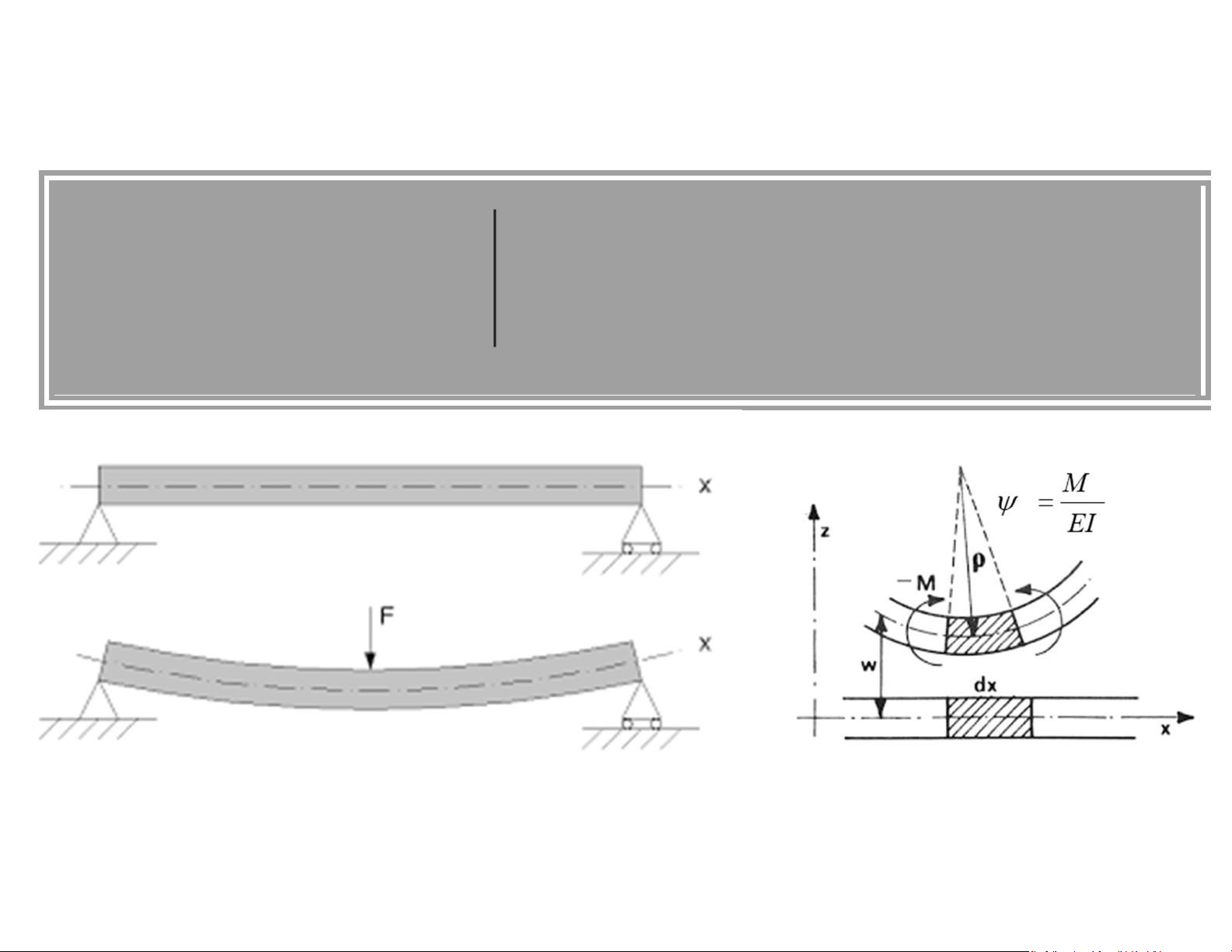
Định nghĩa: Công khả dĩ là công sinh ra bởi các nội lực và ngoại lực
nội lực và ngoại lực trên những biến dạng và
chuyển vị vô cùng bé do những nguyên nhân bất • kỳ nào đó sinh ra.
• Xét hệ đàn hồi ở hai trạng thái cân bằng khác nhau: lOMoAR cPSD| 58933639
Trạng thái “k”: Hệ chịu lực P
Trạng thái “m”: Hệ chịu nguyên nhân bất kỳ. lOMoAR cPSD| 58933639 n g k h ả d ĩ ả chuyển vị vô cùng bé bằng ủ a n g ạ i l ự lOMoAR cPSD| 58933639
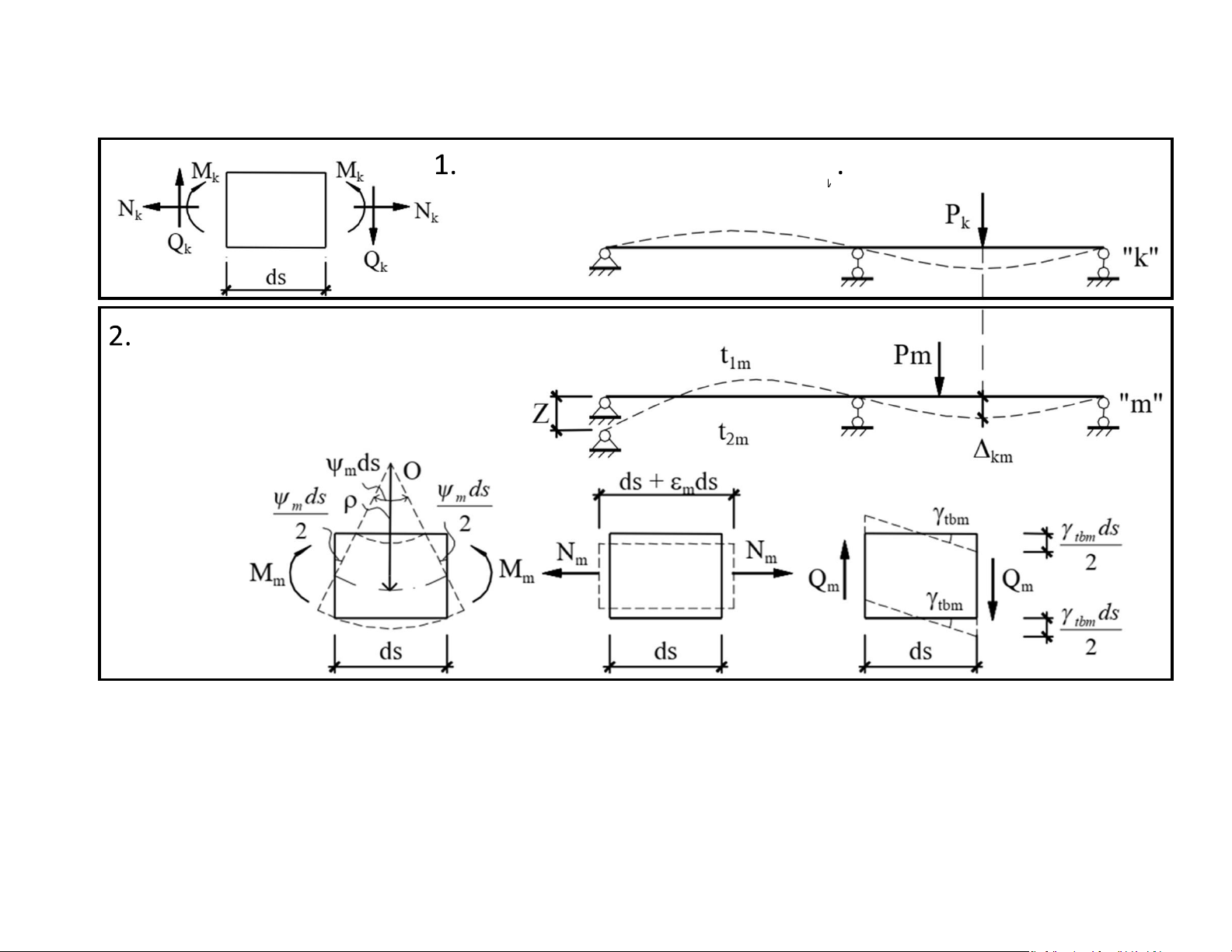
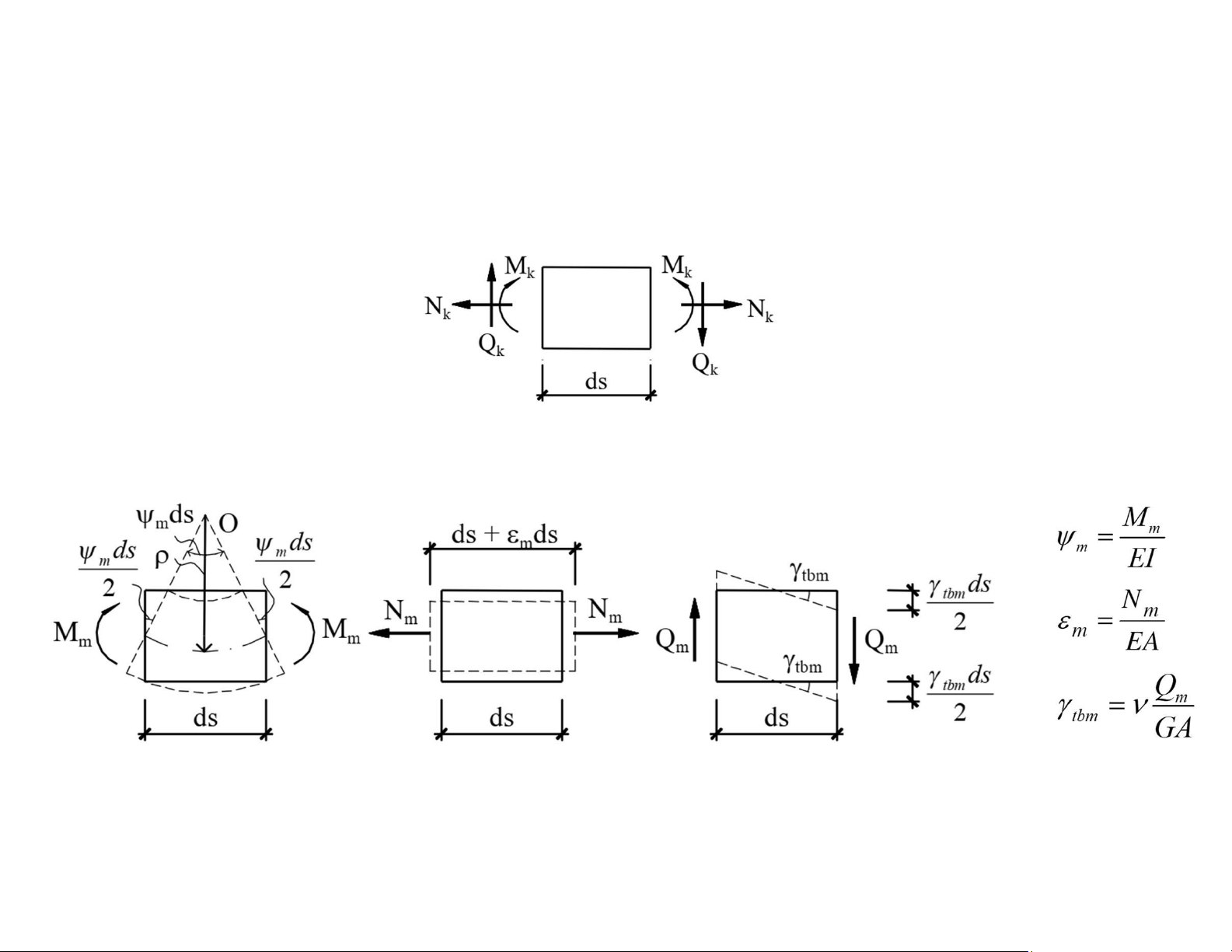
Công khả dĩ ảo của nội lực
• Ở trạng thái “k” tồn tại các thành phần phản lực phân tố Mk, Qk, Nk
• Ở trạng thái “m” tồn tại các thành phần biến dạng do Mm, Qm, Nm gây ra:
• Ở trạng thái “m” tồn tại các thành phần biến dạng do thay đổi nhiệt độ gây ra: lOMoAR cPSD| 58933639 Biến dạng dọc trục
Biến dạng góc xoay giữa hai tiết diện ở hai đầu phân tố • Vậy côn
g khả dĩ của phản lực phân tố ở trạng thái “k” trên các biến dạng khả dĩ ở trạng thái “m”: lOMoAR cPSD| 58933639
• Suy ra công khả dĩ của nội lực phân tố ở trạng thái “k” trên các biến dạng khả dĩ ở trạng thái “m”: lOMoAR cPSD| 58933639
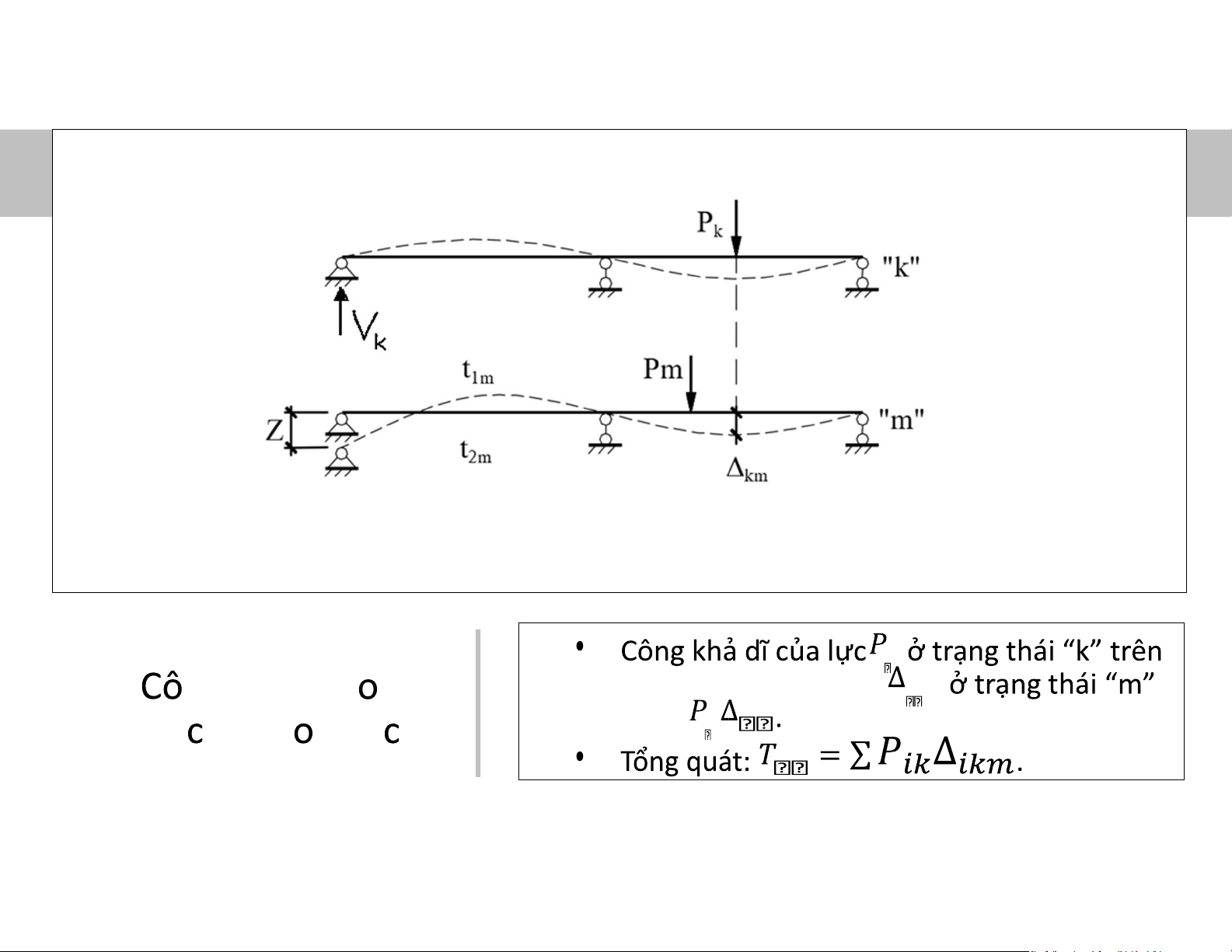
2. Nguyên lý công khả dĩ cho hệ đàn hồi
• Nếu một hệ biến dạng đàn hồi cô lập, cân bằng dưới tác dụng của các ngoại lực thì
tổng công khả dĩ Tkm của các ngoại lực trên những chuyển vị khả dĩ vô cùng bé lOMoAR cPSD| 58933639
tương ứng và công khả dĩ của các nội lực A*km trên những biến dạng đàn hồi khả
dĩ tương ứng phải bằng không. lOMoAR cPSD| 58933639
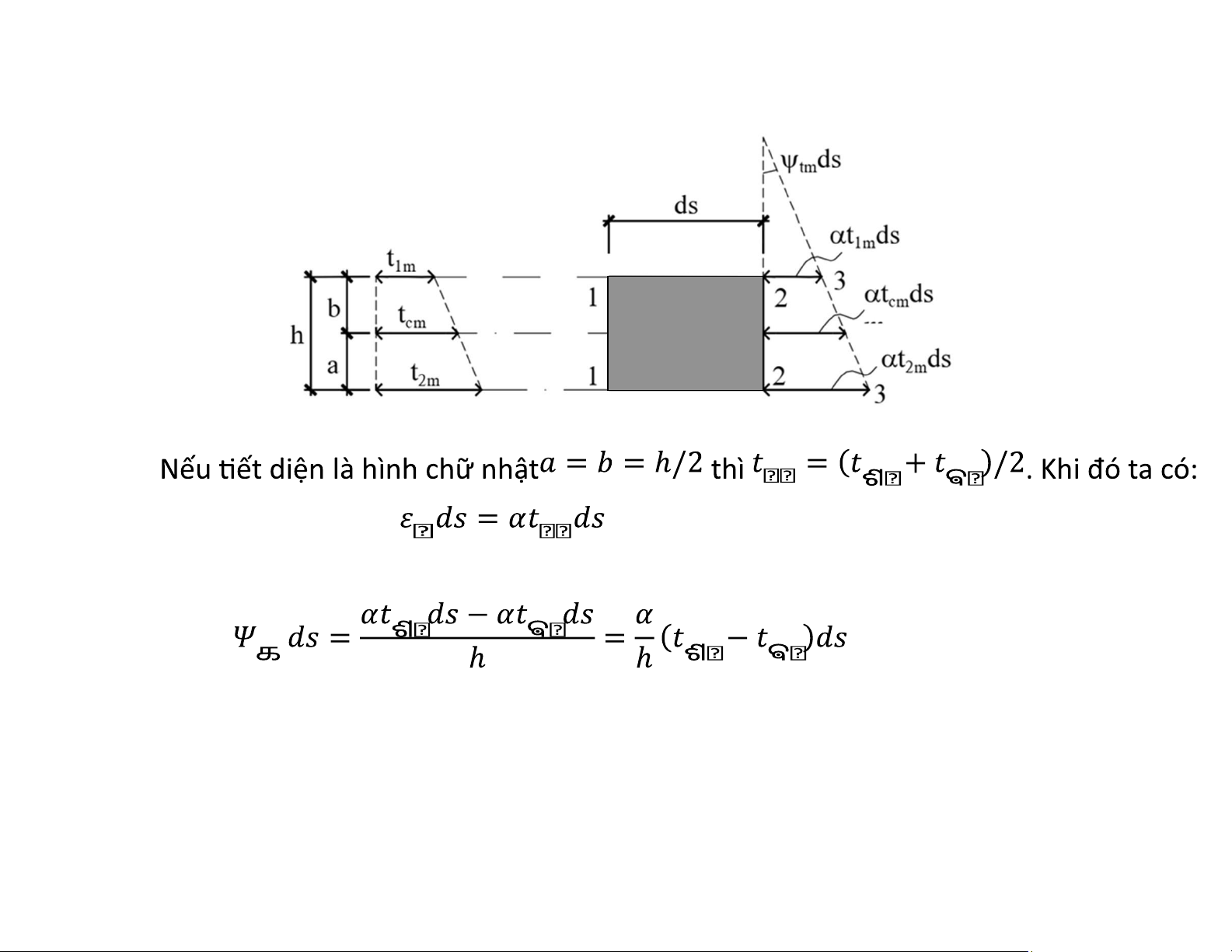
3. Công thức chuyển vị trong hệ thanh đàn hồi tuyến tính
• Xét hệ thanh đàn hồi tuyến tính chịu tác dụng của các nguyên nhân: tải trọng Pm,
chuyển vị cưỡng bức gối tựa Zm, sự biến thiên nhiệt độ t1m và t2m.
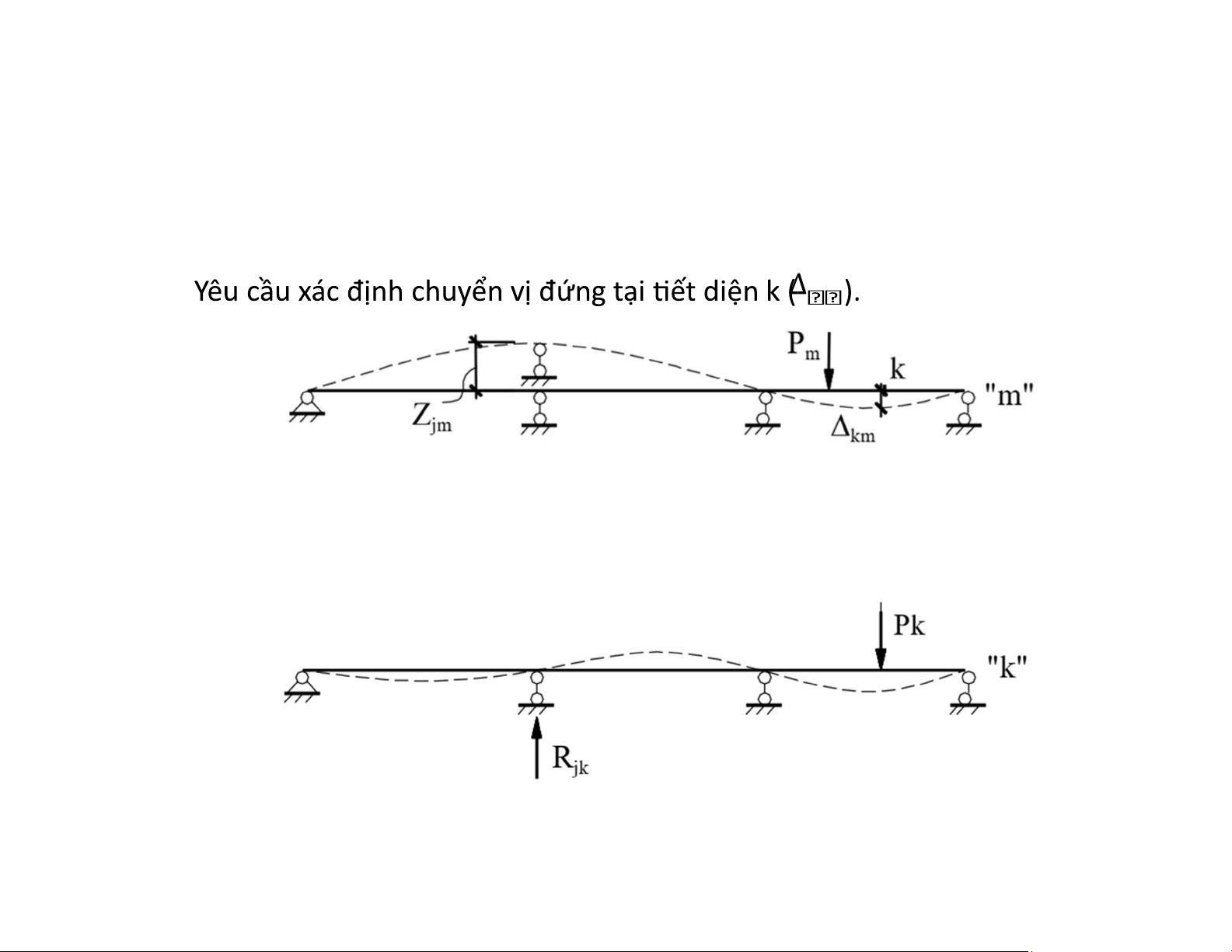
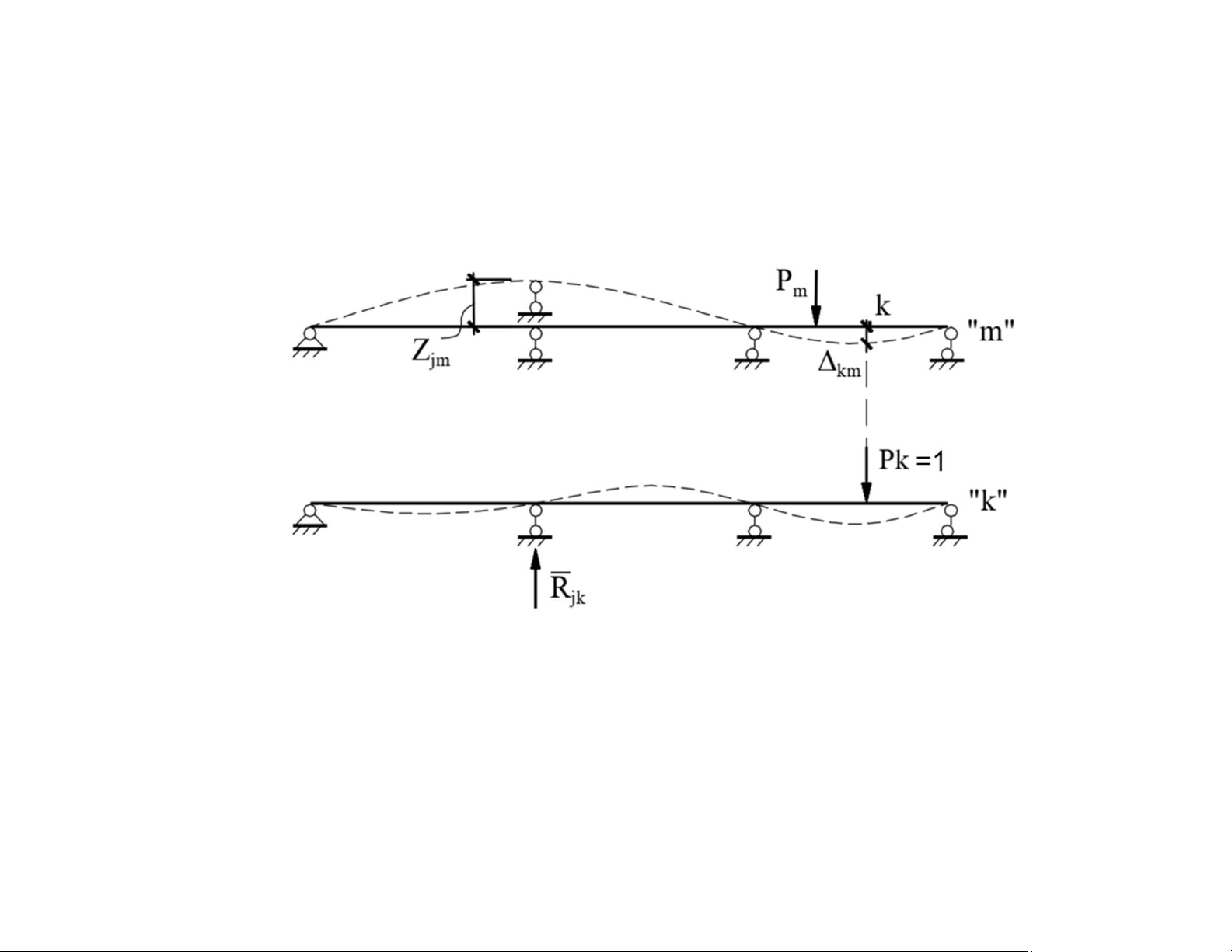
• Tạo một trạng thái khả dĩ “k”: bằng cách đặt lực lực Pk tương ứng với vị trí và
phương chuyển vị cần tìm (chiều tùy ý). lOMoAR cPSD| 58933639
• Áp dụng nguyên lý công khả dĩ (đã xây dựng bên trên) ta có:
• Chia hai vế cho Pk đồng thời ký hiệu
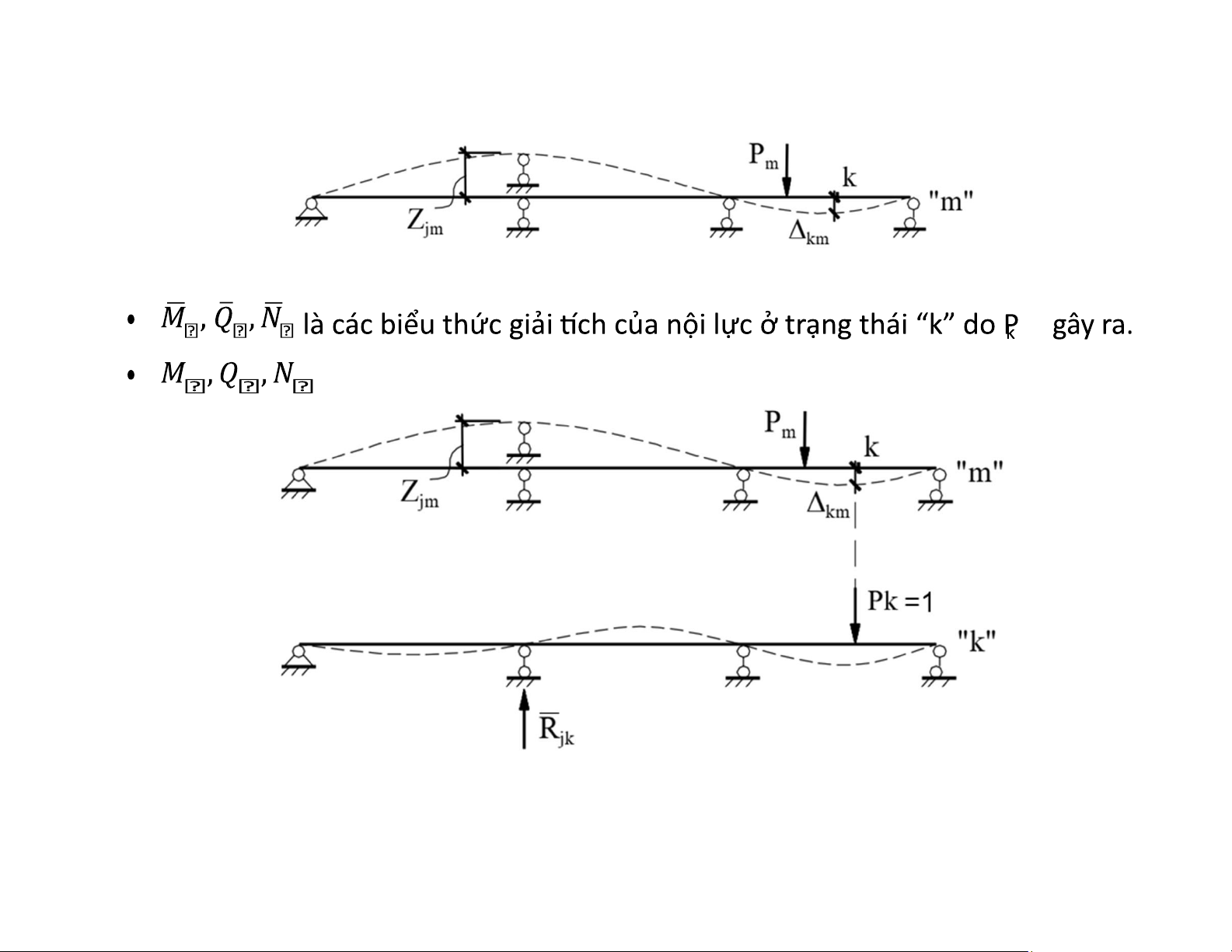
• Công thức xác định chuyển vị trong hệ thanh đàn hồi tuyến tính (Maxwell-Morh): Chú ý (tự đọc): lOMoAR cPSD| 58933639
• Trạng thái “k” chỉ đặt duy nhất 1 lực Pk=1 không thứ nguyên. Nếu cần tìm chuyển vị
thẳng thì Pk=1 là lực tập trung.
• Nếu cần tìm chuyển vị xoay thì Pk=1 là mô men tập trung. lOMoAR cPSD| 58933639 =1
• Công thức Maxwell-Morh phù hợp với các hệ thanh thẳng, không phân biệt hệ tĩnh định hay siêu tĩnh. lOMoAR cPSD| 58933639 =1
là các biểu thức giải tích của nội lực ở trạng thái “m”. lOMoAR cPSD| 58933639
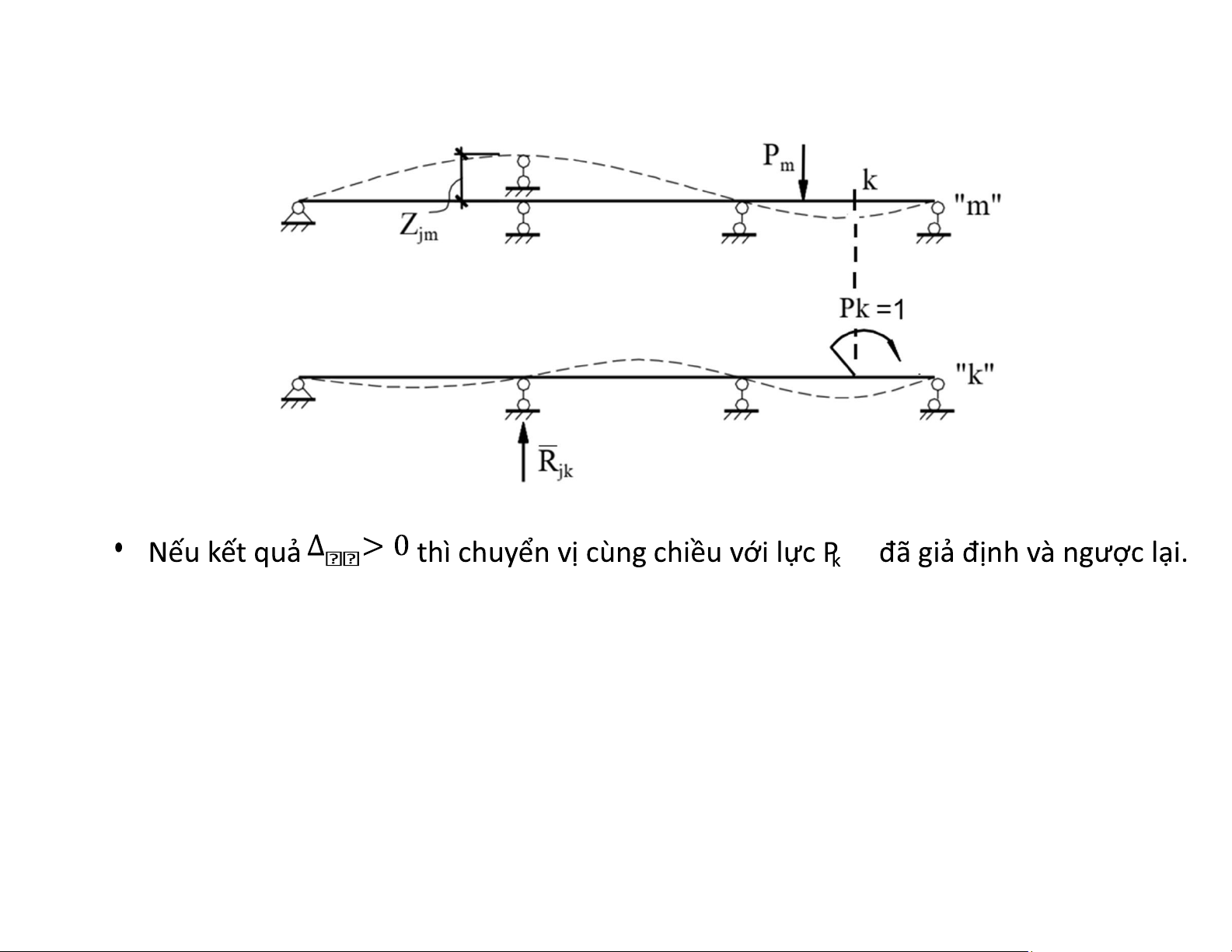
• Zjm là chuyển vị cưỡng bức tại gối tựa thứ j của hệ ở trạng thái “m”.
• ௝௝ là phản lực tại gối tựa thứ j (tương ứng với chuyển vị Zjm ) do lực Pk=1 gây ra ở trạng thái “k”.
• Tích số ௝௝ ௝௝ (công phản lực gối có lún) lấy dấu dương nếu cùng chiều và ngược lại. 4. Ví dụ áp dụng
a. Hệ dầm và khung chịu tải trọng:
• Trong hệ dầm khung ảnh hưởng của biến dạng đàn hồi dọc trục và trượt là rất nhỏ so với lOMoAR cPSD| 58933639
b. Hệ dàn chịu tải trọng:
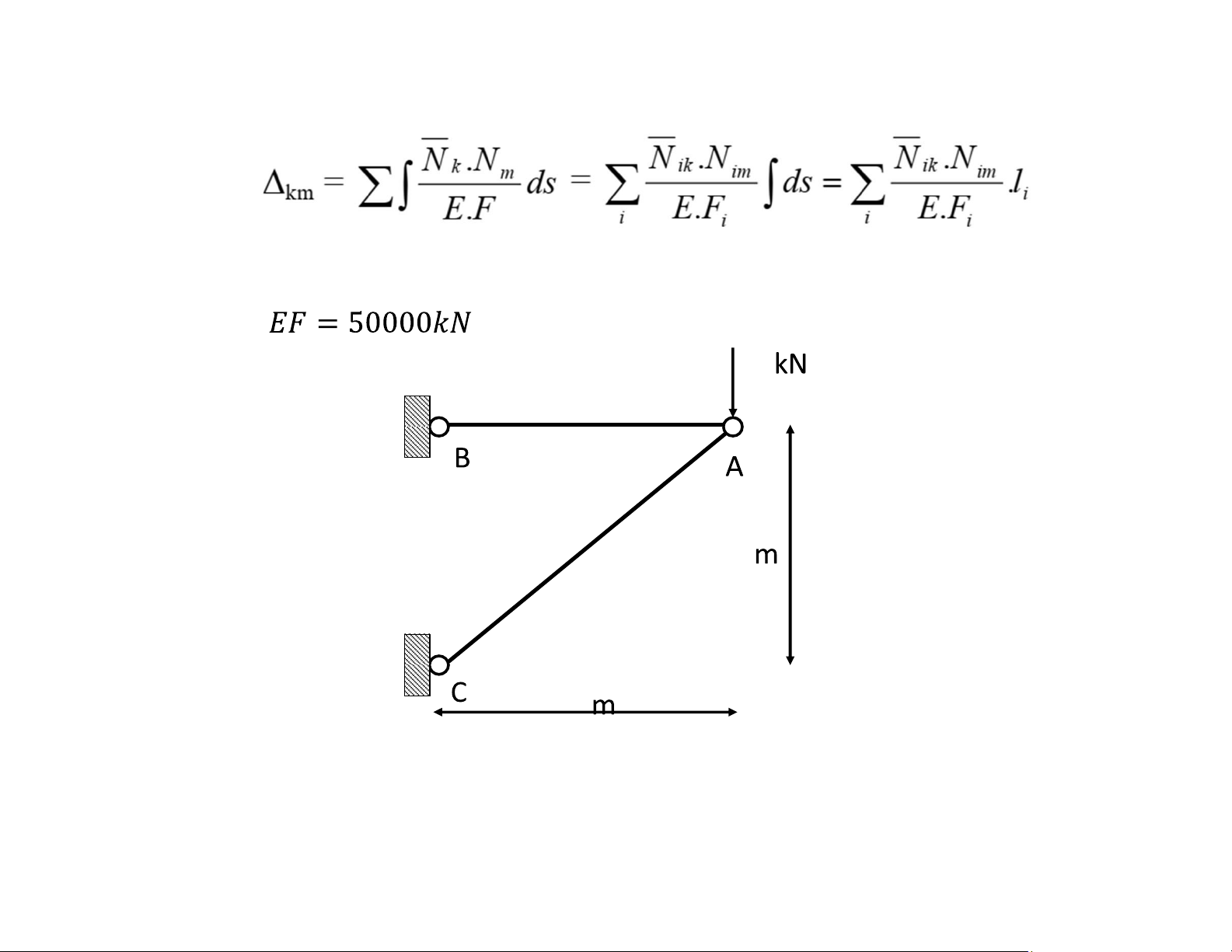
• Trong hệ dàn, các thanh chỉ tồn tại lực dọc và thường là hằng số trên từng thanh: lOMoAR cPSD| 58933639
Ví dụ: Xác định chuyển vị ngang tại mắt A của dàn bên dưới. Cho biết độ cứng dọc trục trong các thanh dàn là . 80 4 3