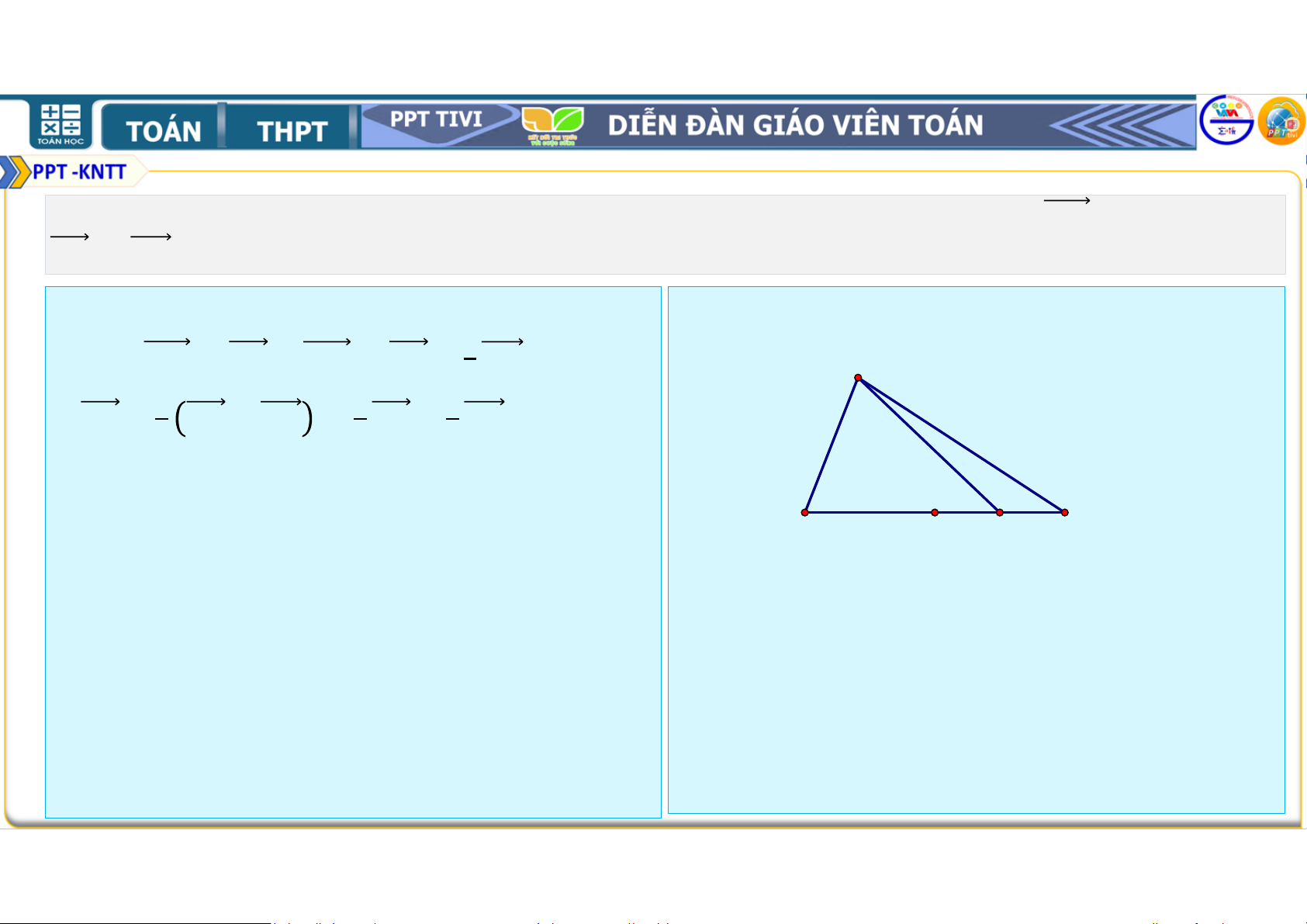
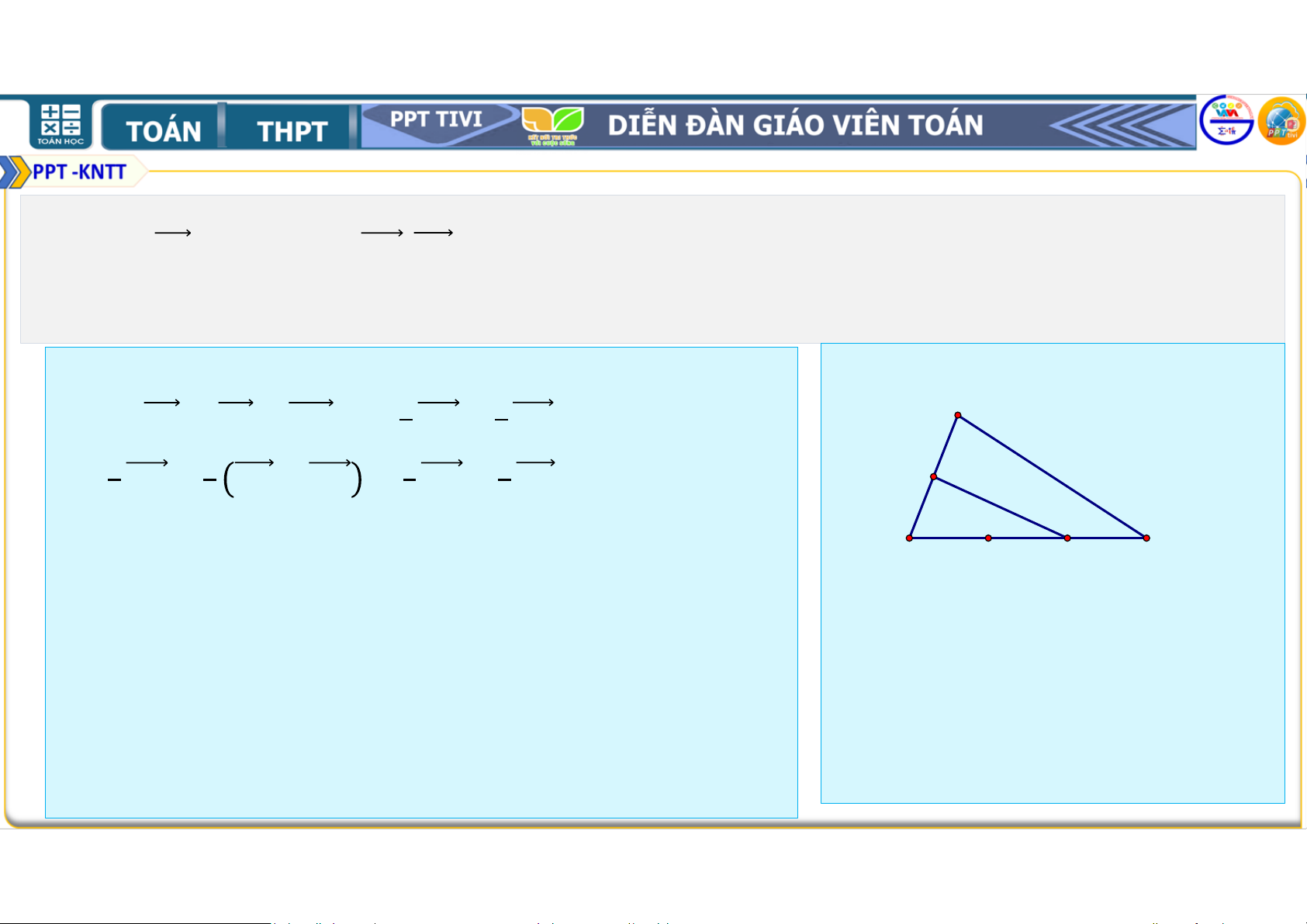
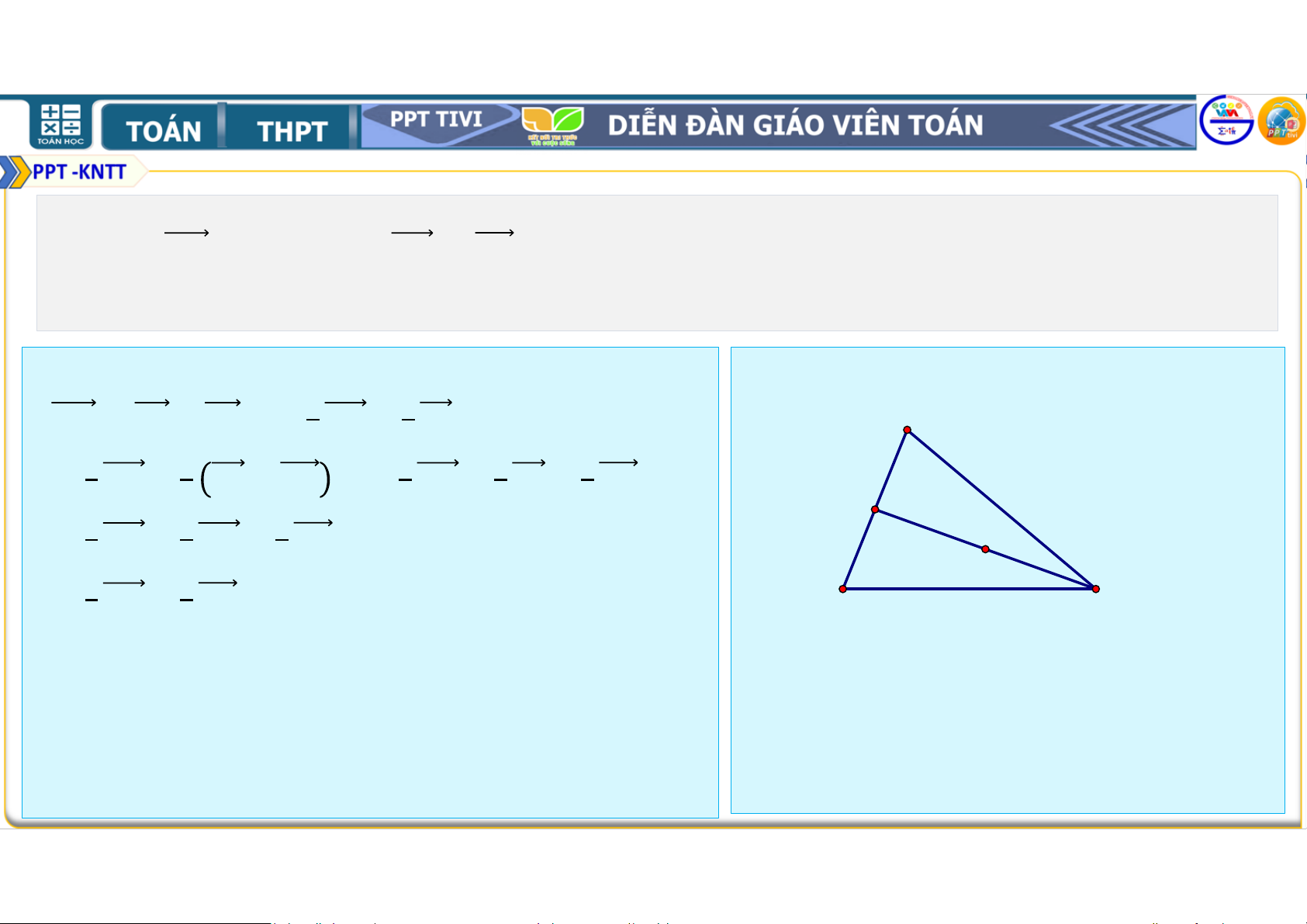
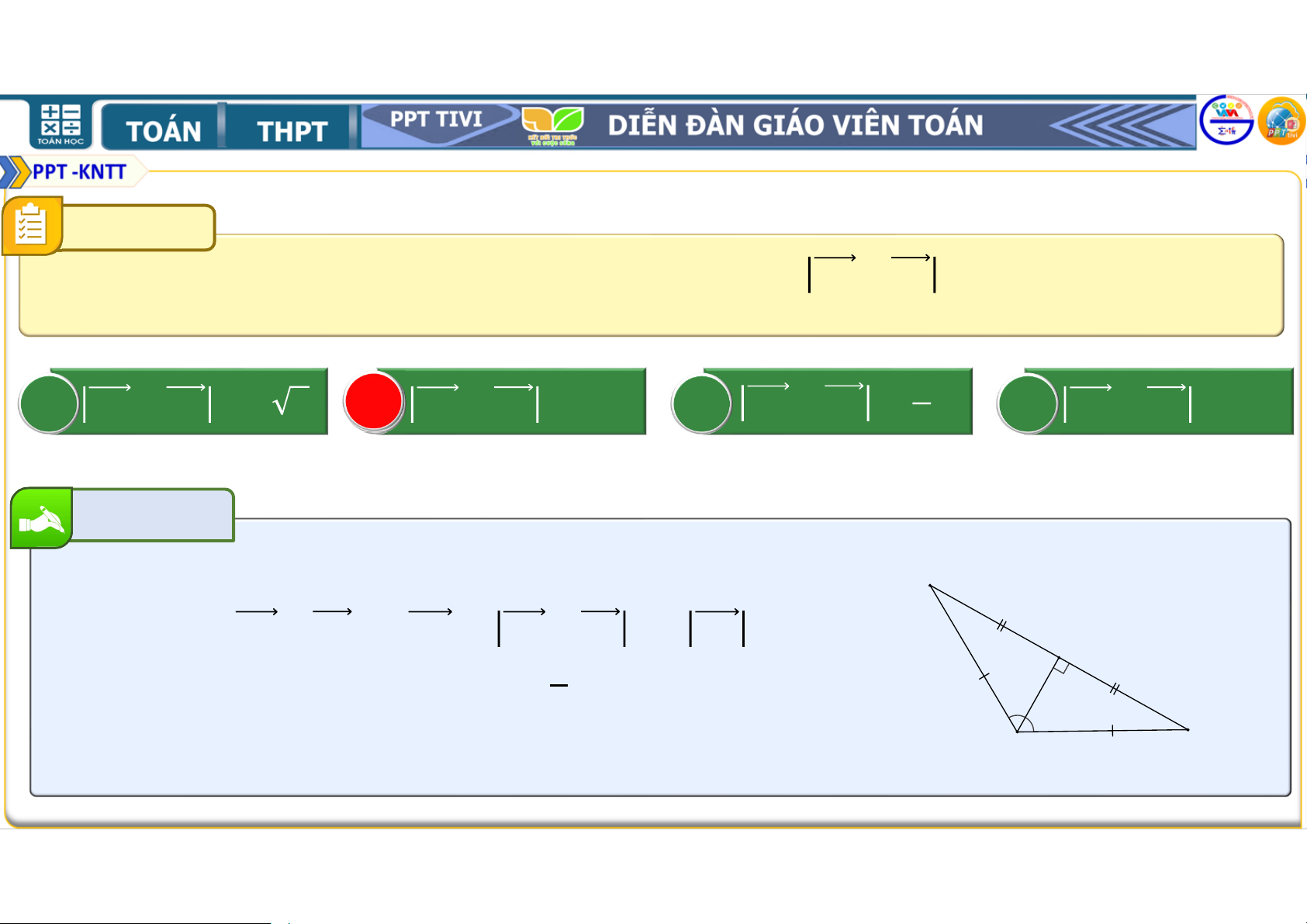
Ví dụ 3. Cho tam giác
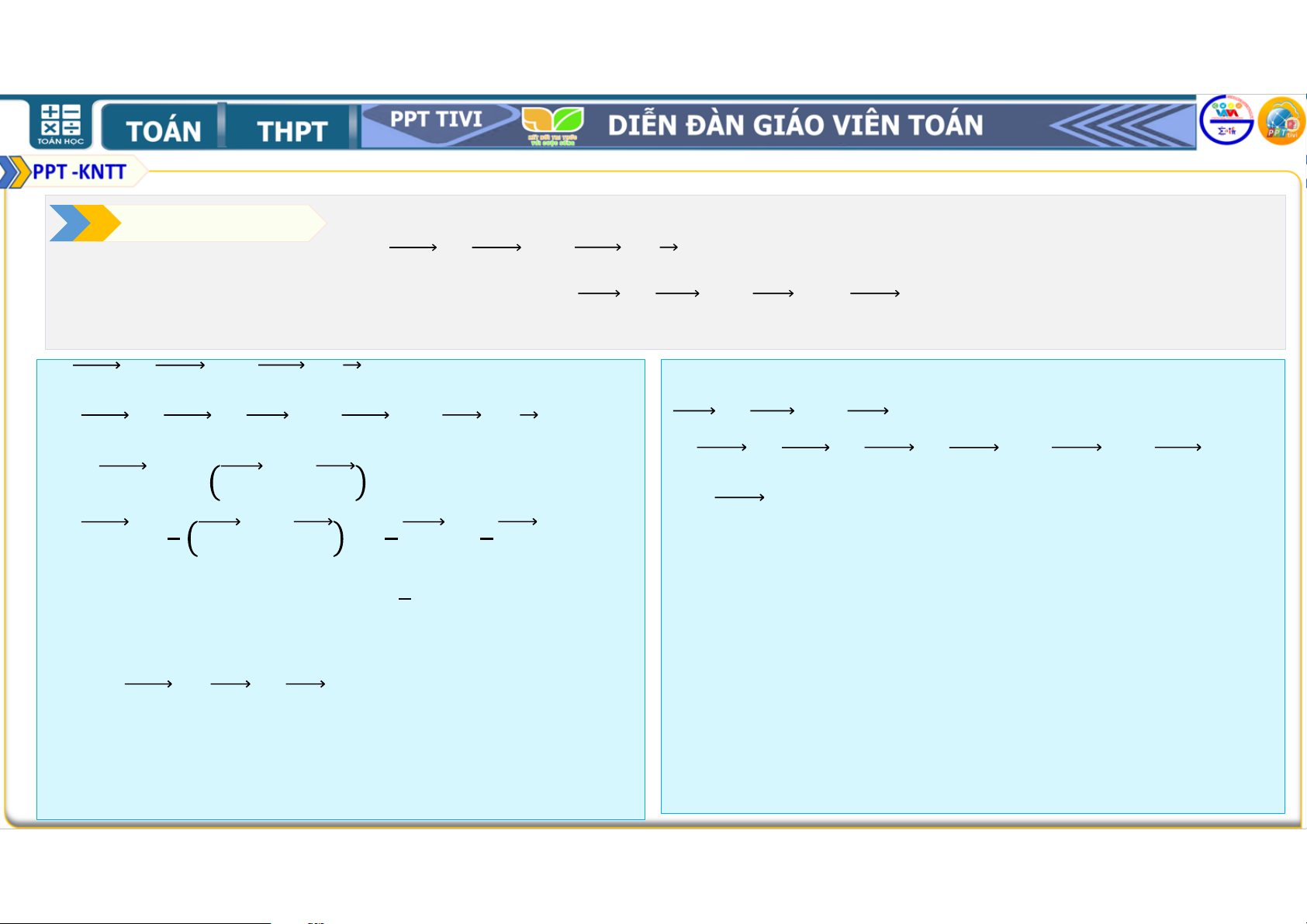
. Hãy xác định điểm để + + = . • Lời giải
• Đẳng thức vectơ đã cho tương đương với: • + + + + = ⇔ + + = ⇔ = + • Lấy điểm là trung điểm của và điểm thuộc cạnh sao cho = . • Khi đó = và = . Vì vậy = + . • Suy ra
là đỉnh thứ tư của hình bình hành .
Ta trở lại vấn đề đã được nêu trong phần đầu bài học. Điểm khối tâm của hệ các chất điểm , , . . . ,
với các khối lượng tương ứng , , . . . , được xác
định bởi đẳng thức vectơ + +. . . + = .
Vì vậy, việc xác định điểm khối tâm được quy về xác định điểm thỏa mãn đẳng
thức vec tơ tương ứng.
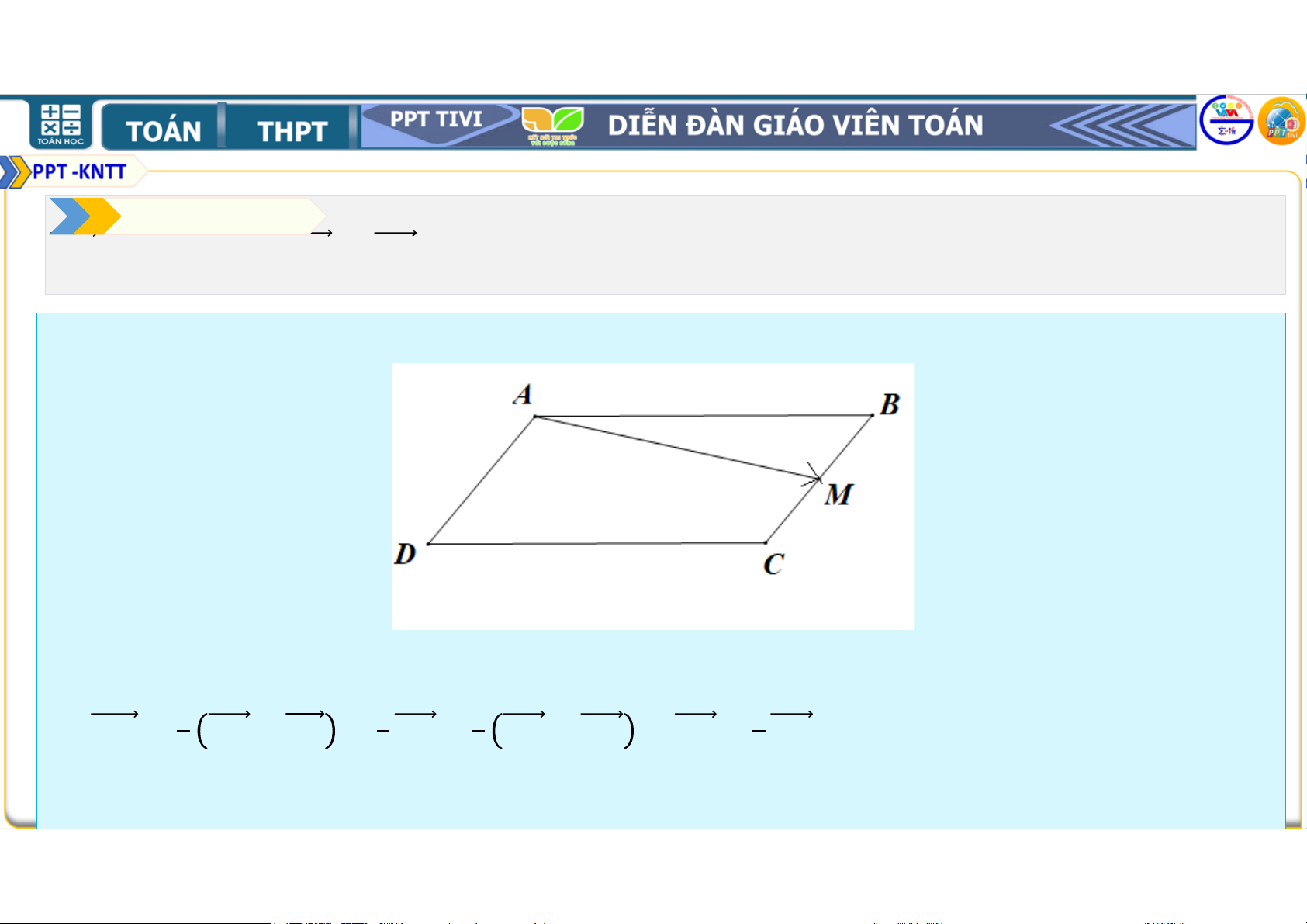
Bài tập 4.11. Cho hình bình hành . Gọi
là trung điểm của cạnh . Hãy biểu thị theo hai vectơ và . Lời giải • Ta có = + = + + = +
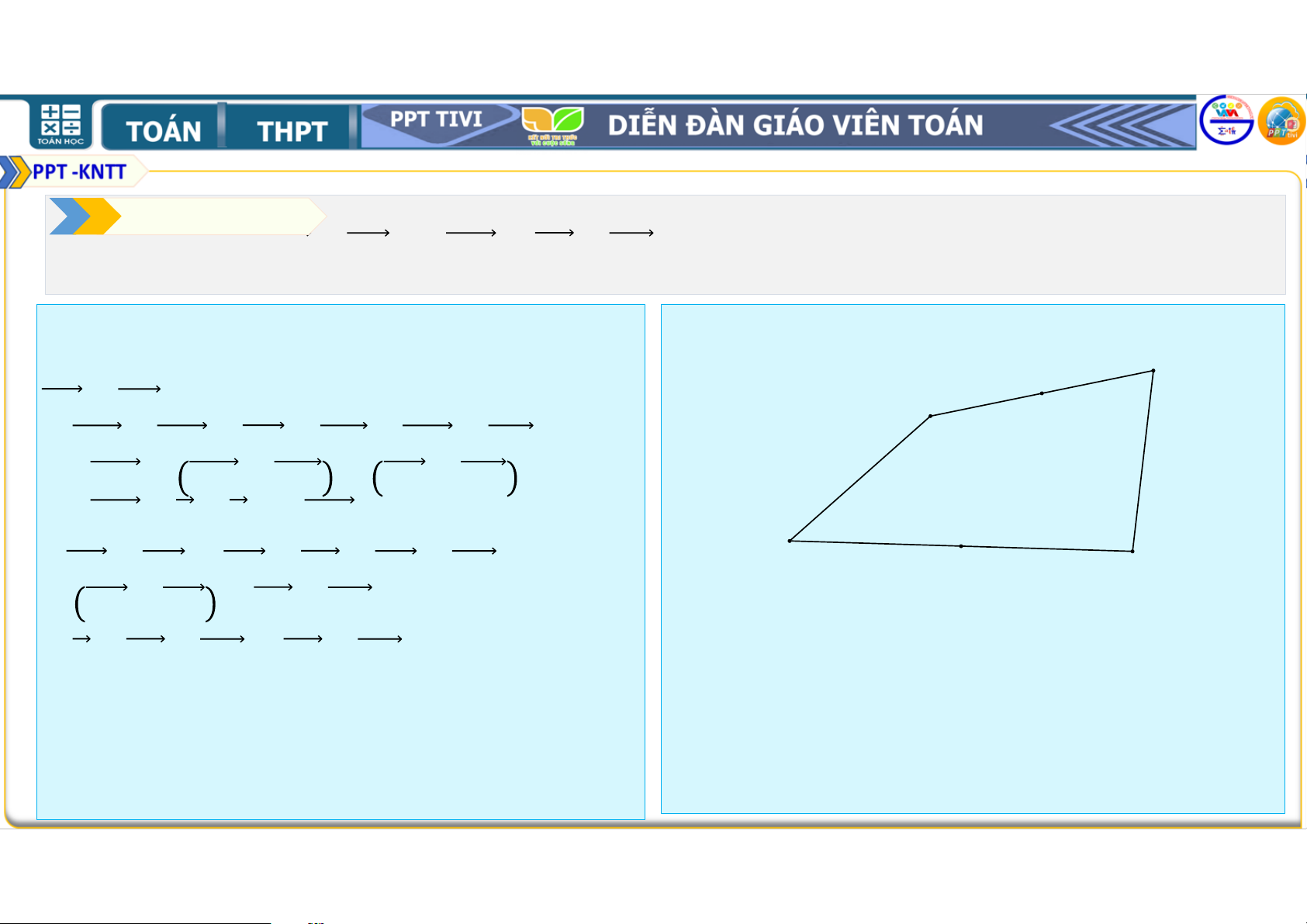
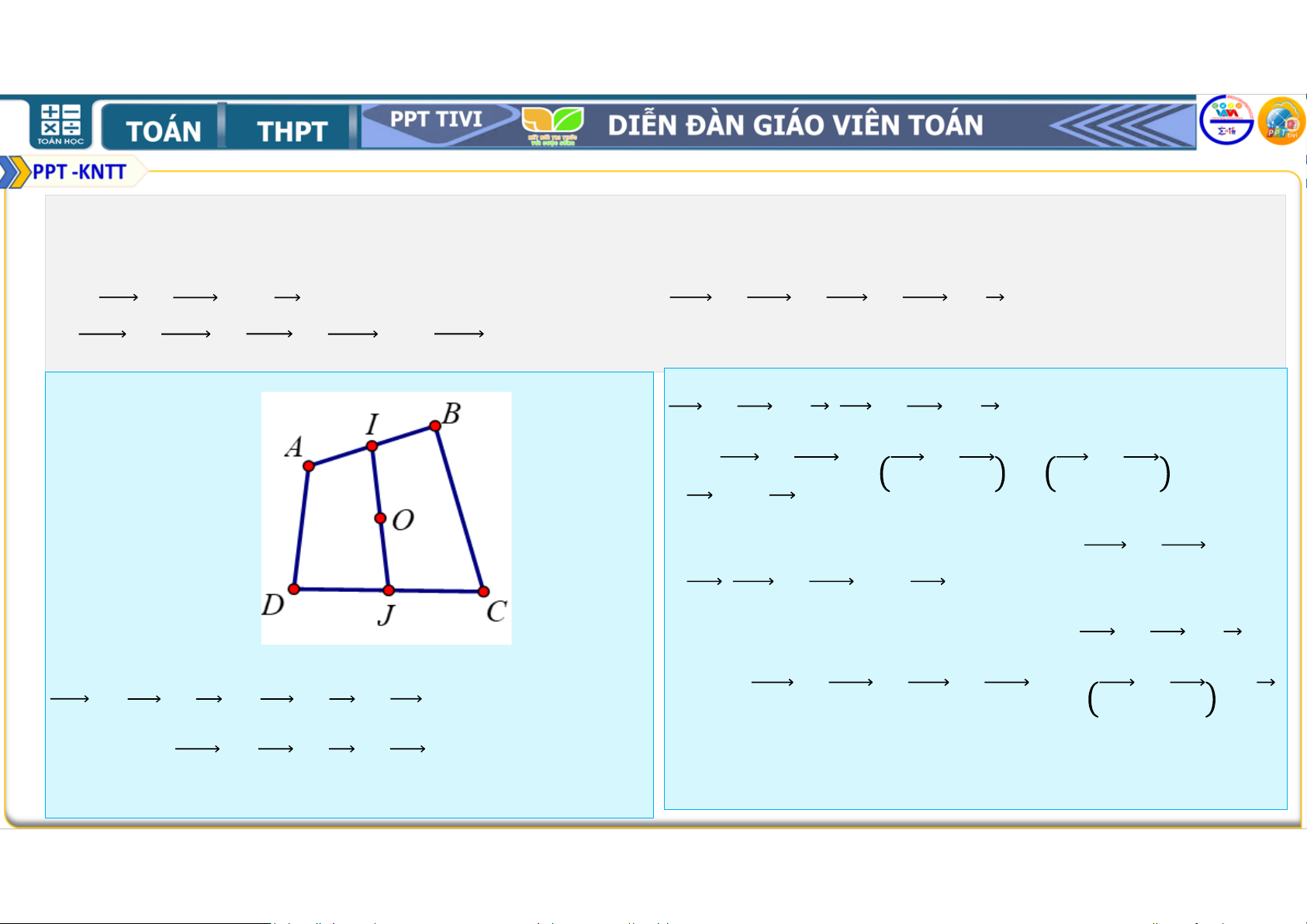
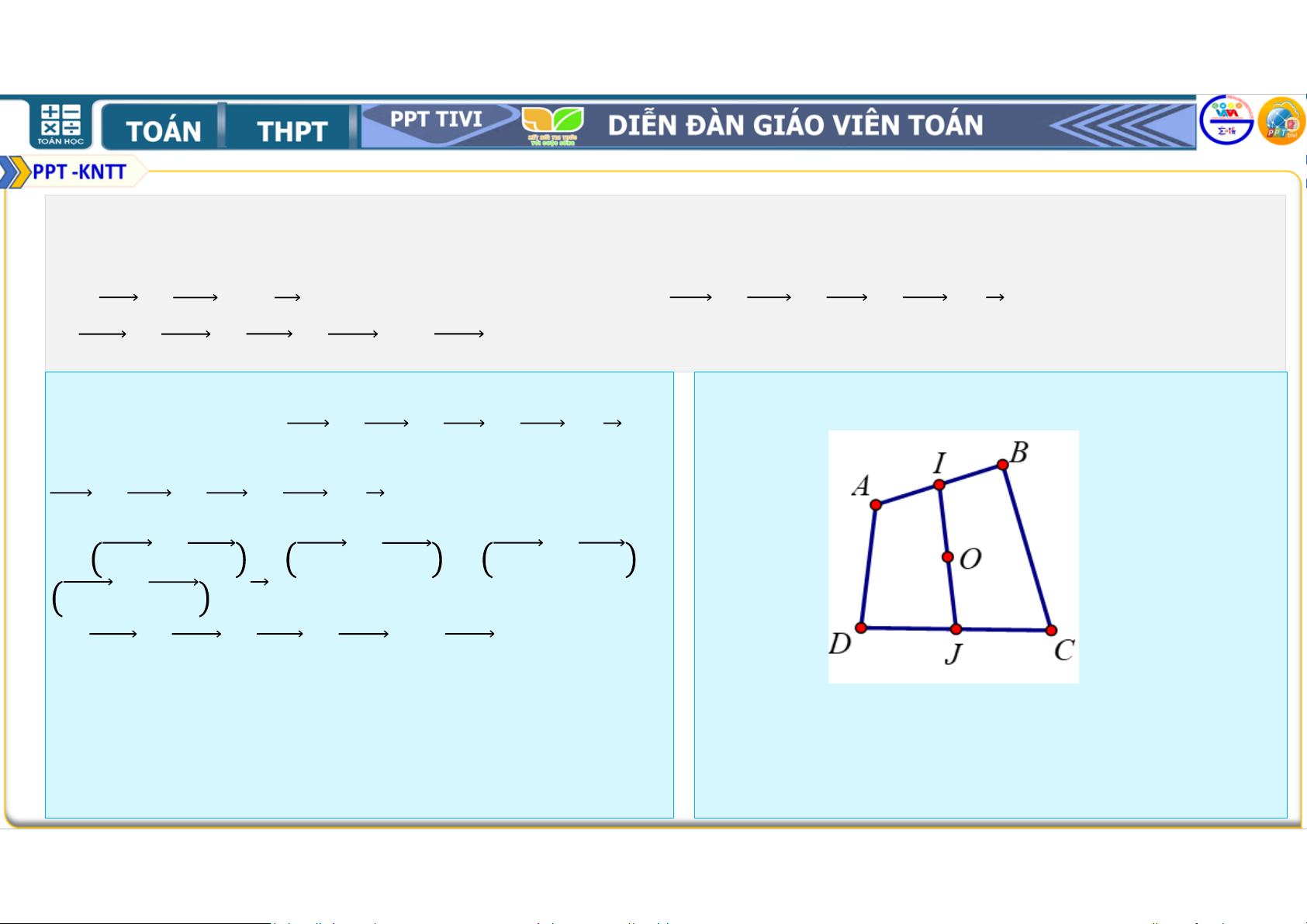
Bài tập 4.12. Cho tứ giác . Gọi
, tương ứng là trung điểm của các cạnh , . Chứng minh rằng + = = + . Lời giải B • Ta có M + A = + + + + + = + + + + = + + = D • + = + + + N C = + + + = + + = +
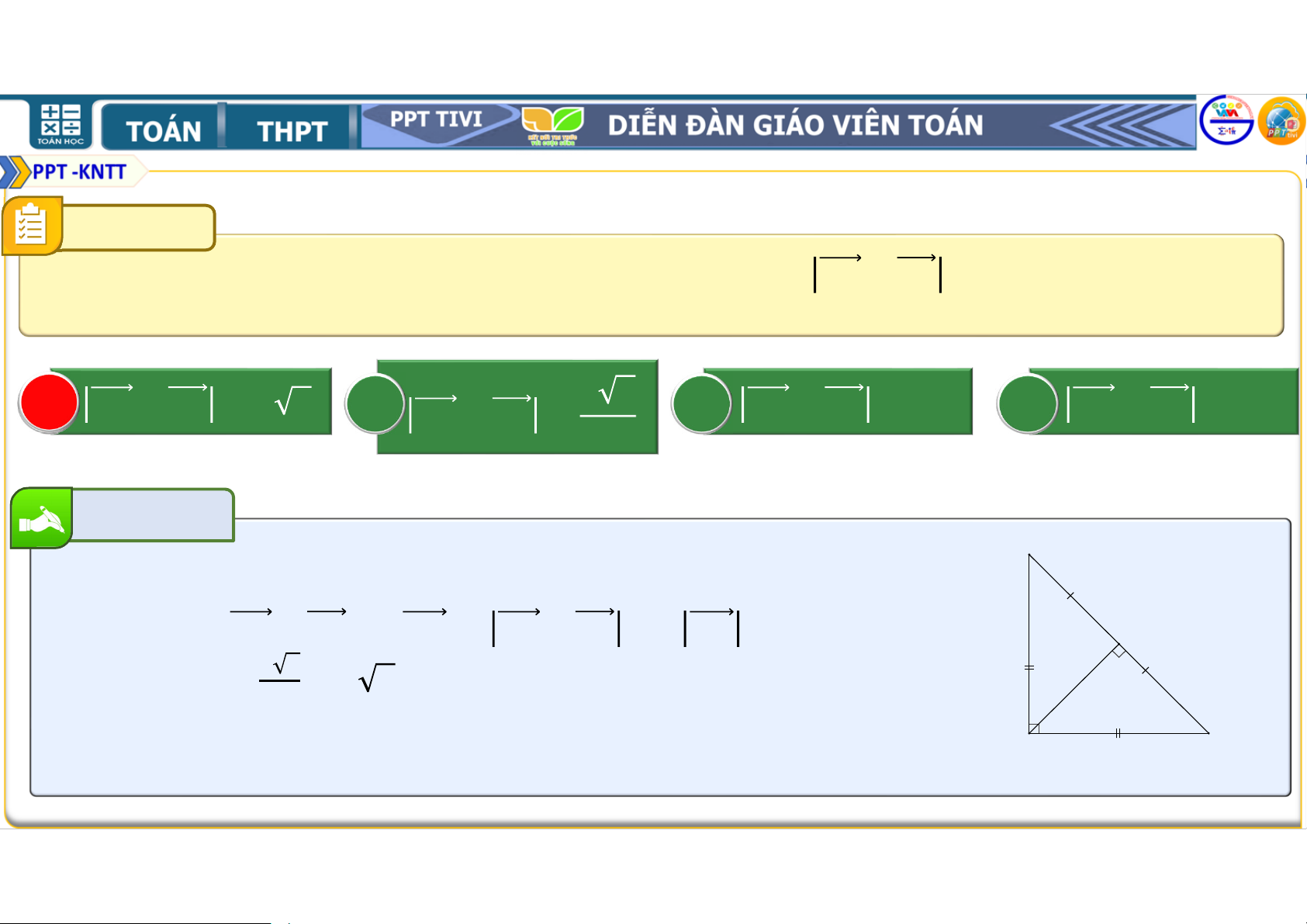
Bài tập 4.13. Cho hai điểm phân biệt và .
a) Hãy xác định điểm sao cho + = .
b) Chứng minh rằng với mọi điểm , ta có = + . a) + = ⇔ + + = b) Ta có: + = ⇔ = − ⇔ = − ⇔ = + = + + + Vậy ∈ sao cho = . = + + = + − + =
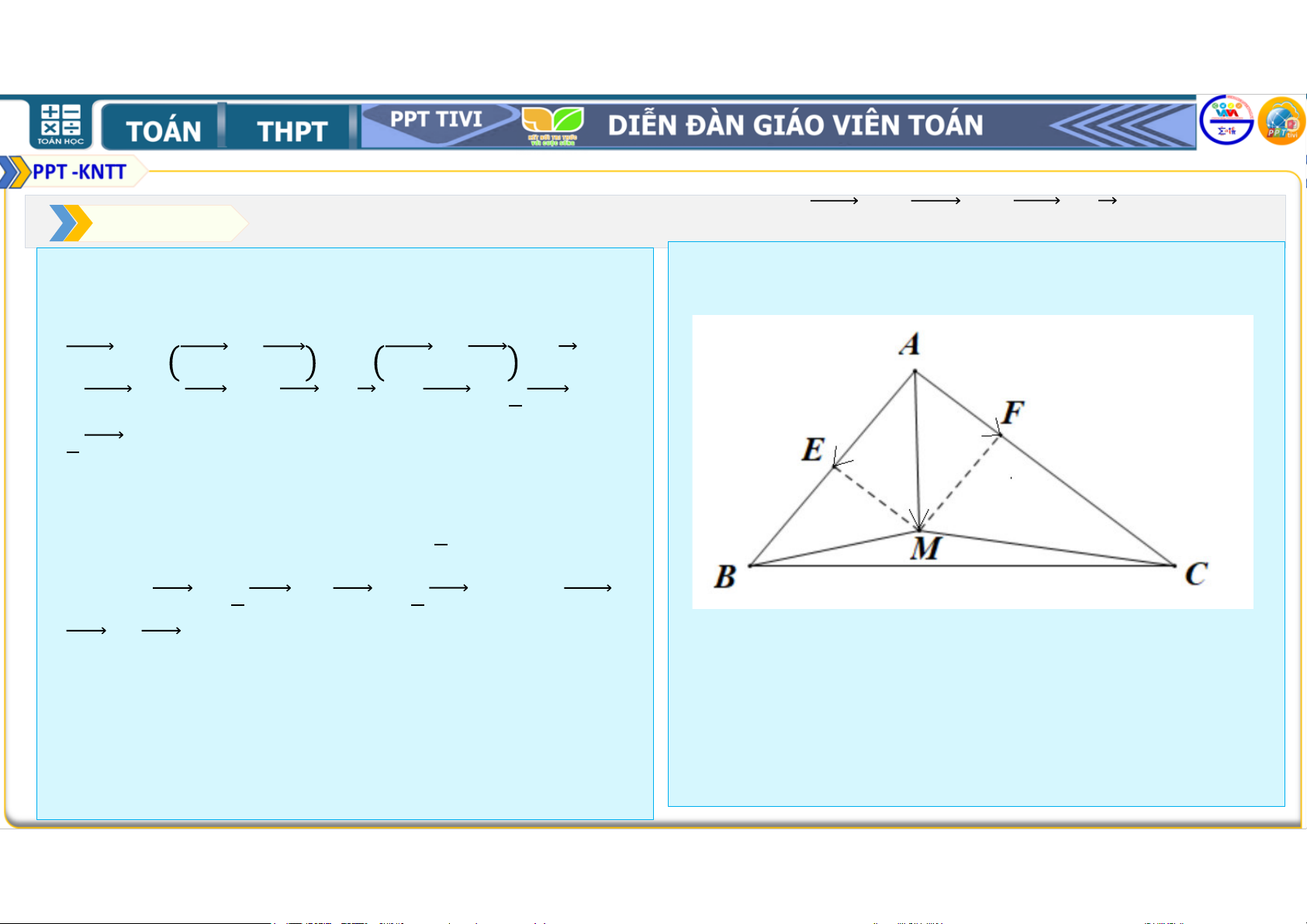
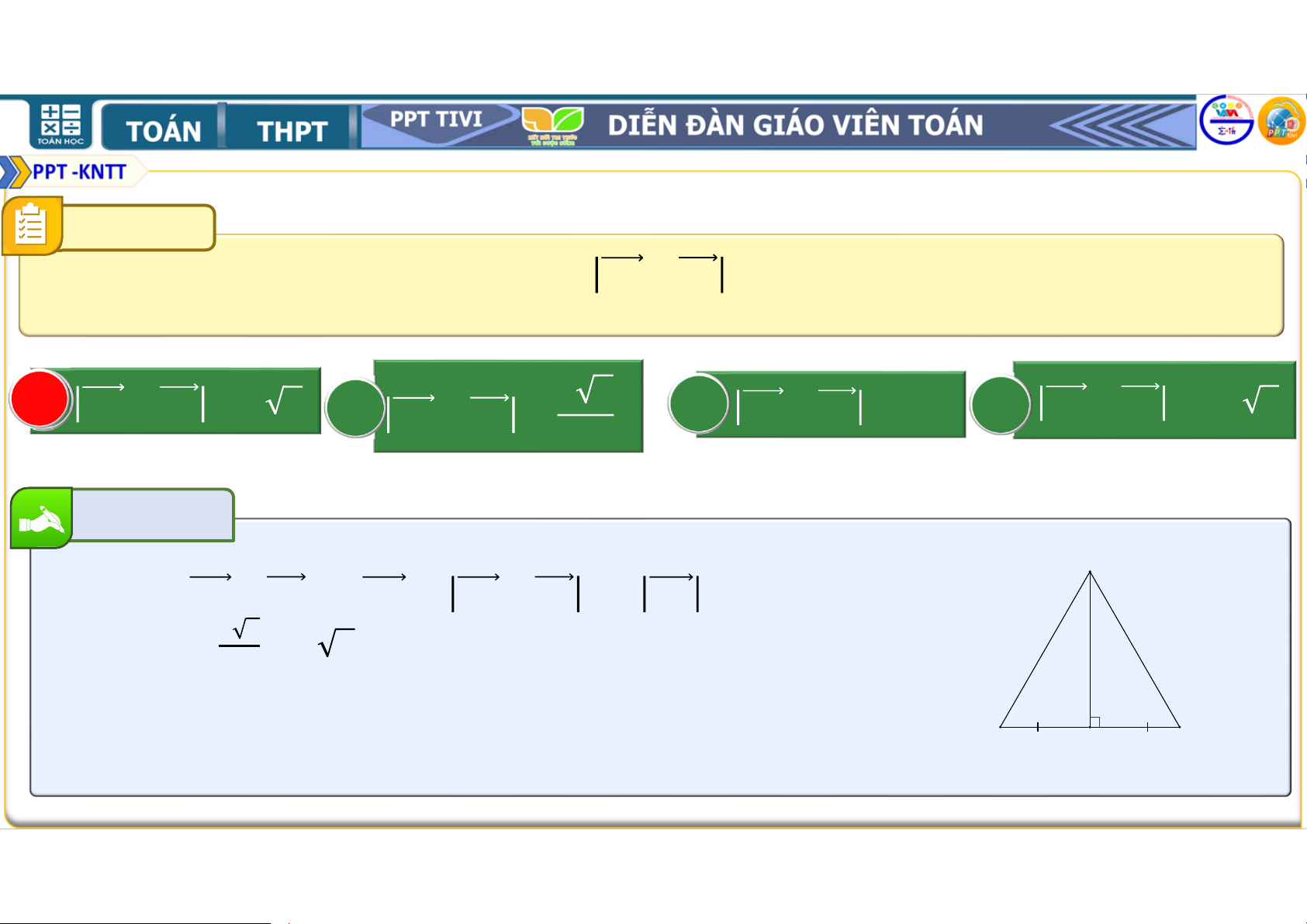
Bài tập 4.14. Cho tam giác .
a) Hãy xác định điểm để + + = .
b) Chứng minh rằng với mọi điểm , ta có + + = . a) + + = b) ⇔ + + + + = + + = + + + + + ⇔ = − + = ⇔ = + = + • Gọi ∈ sao cho = . • là trung điểm của Suy ra = + ⇒
là điểm thứ 4 của hình bình hành .
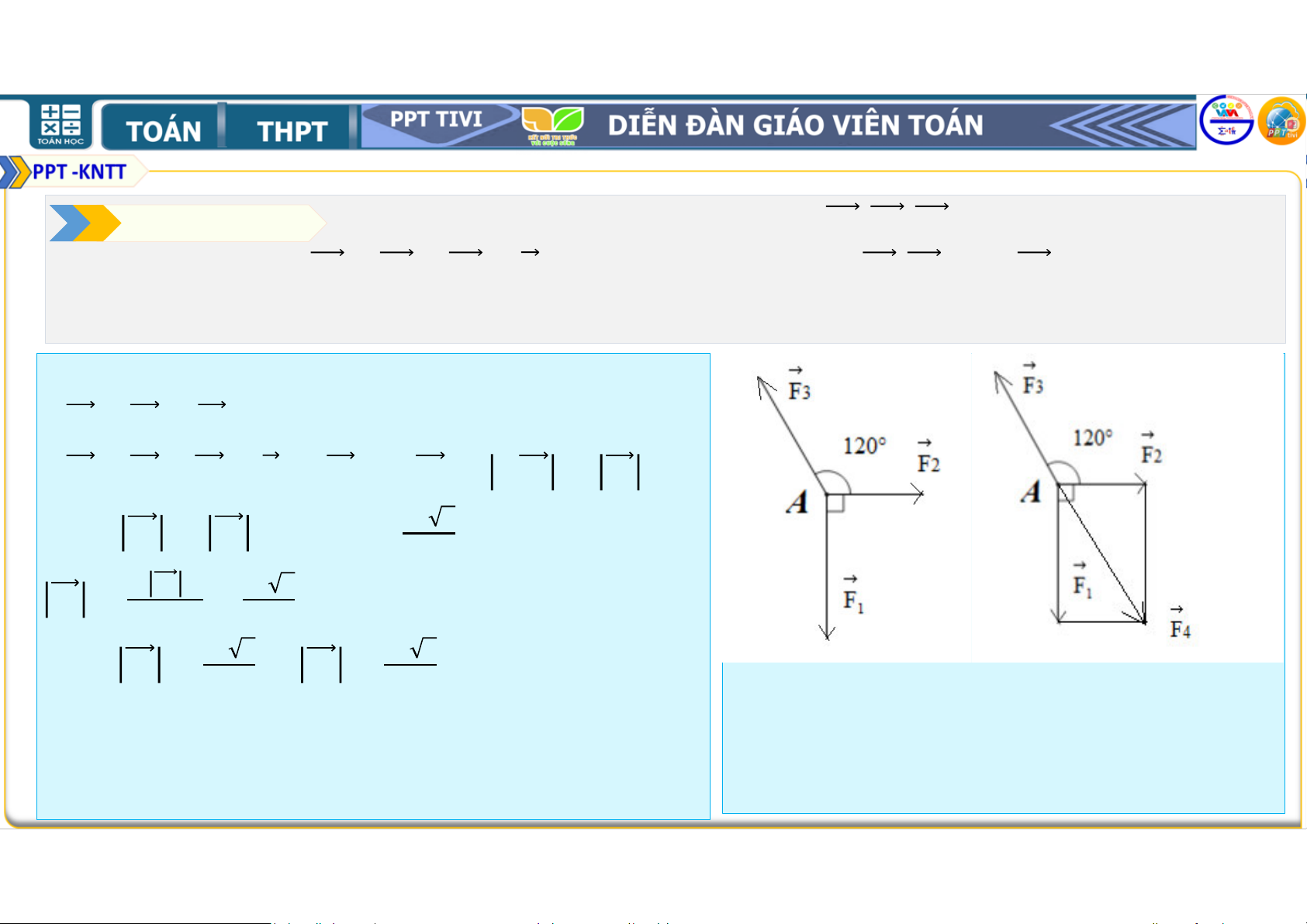
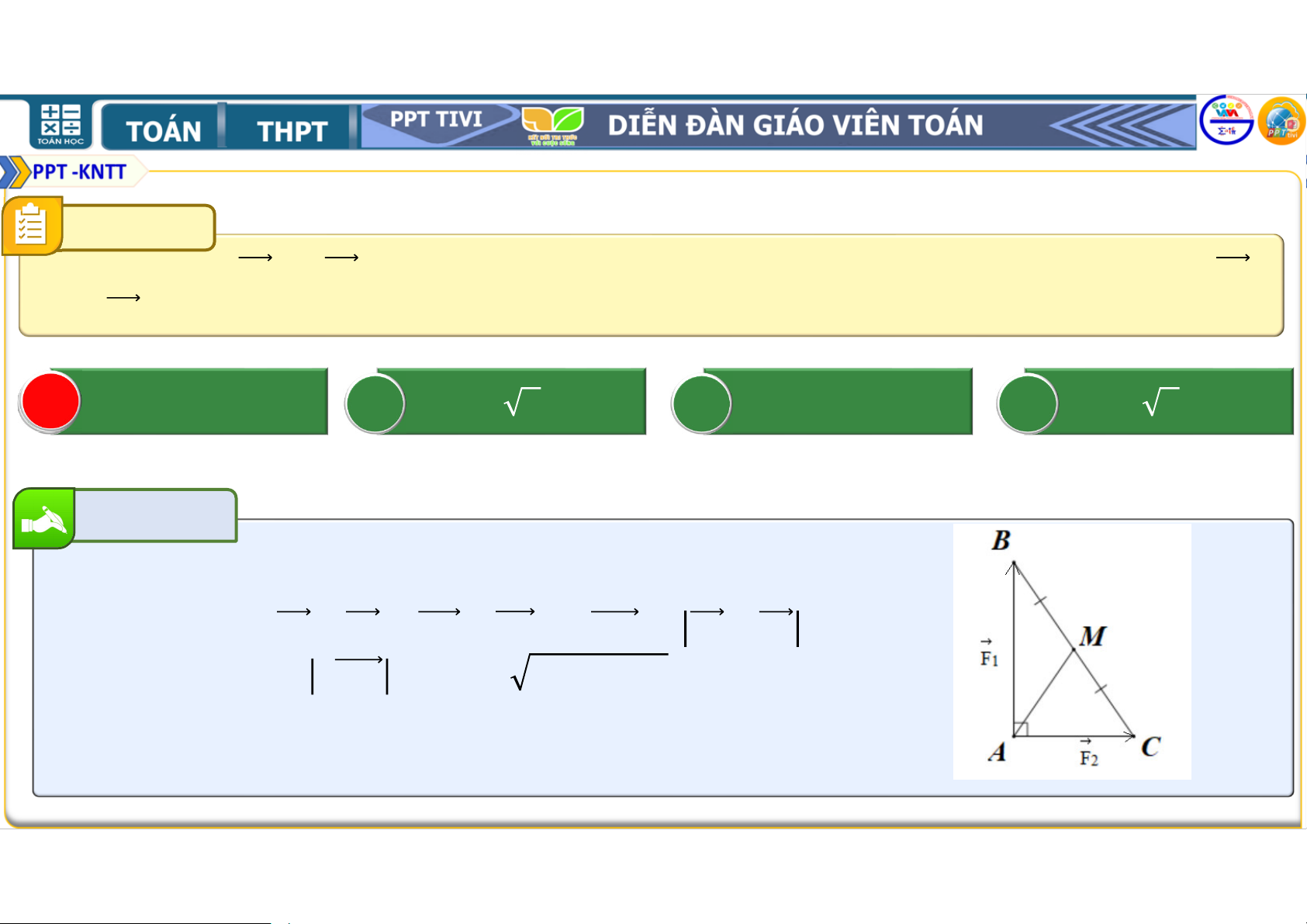
Bài tập 4.15. Chất điểm chịu tác động của ba lực , ,
như Hình 4.30 và ở trạng
thái cân bằng (tức là + +
= ). Tính độ lớn của các lực , , biết
có độ lớn là 20 N. Lời giải • + = • + + = 0 ⇔ = − ⇒ − = Ta có: = . !"# 3 0° = & ; = () = & ; cos3&° • Vậy = & N, = & N. Hình 4.30 • Em có biết ?
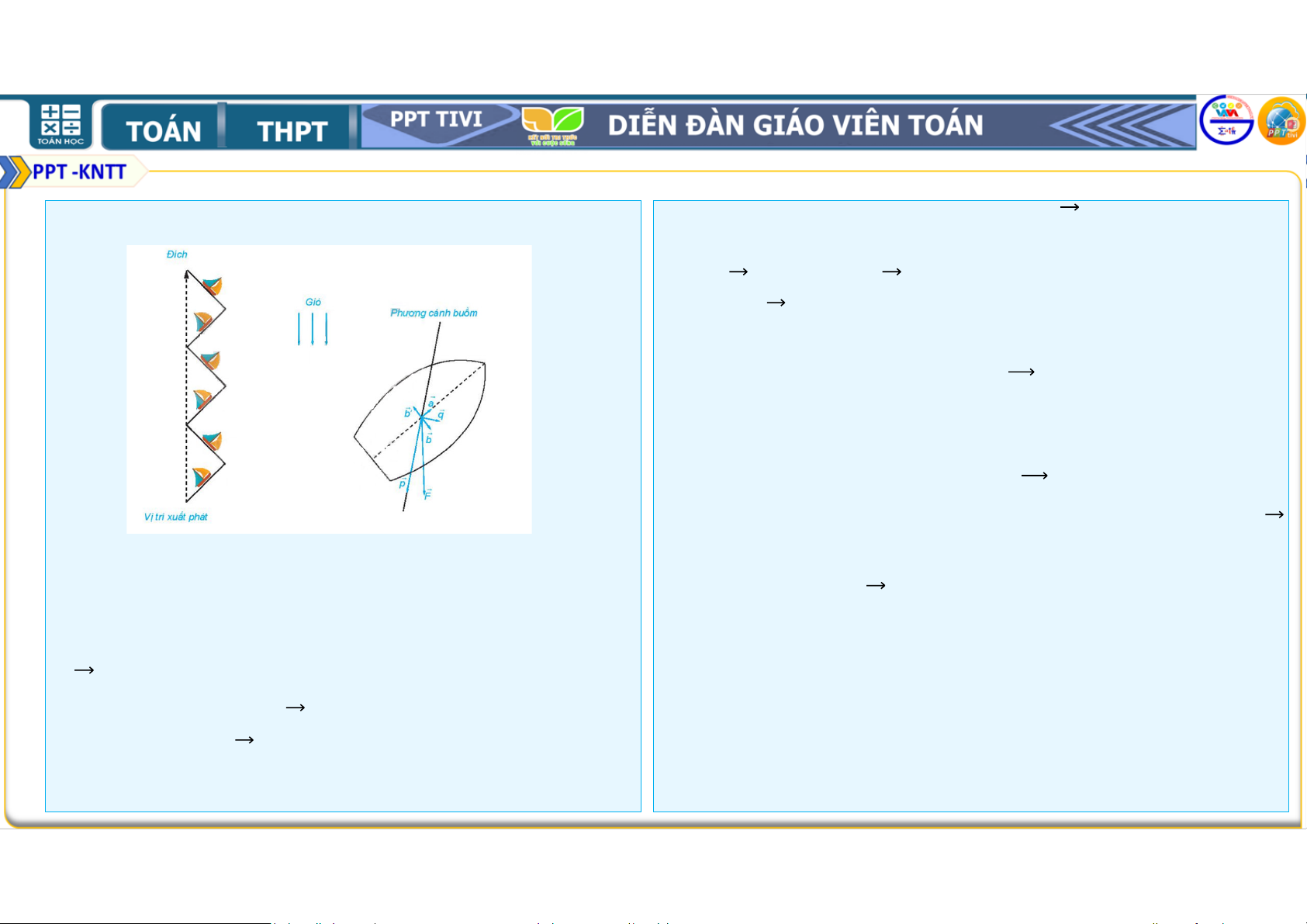
• Do cánh buồm mỏng nên lực * chỉ trượt đi mà
không tác động lên cánh buồm. Ta lại phân tích
lực + thành lực , cùng phương với sống thuyền
và lực - có phương vuông góc với sống thuyền.
Thuyền buồm có sống thuyền sâu (mũi nhọn)
nên nó chịu một lực cản -′ đáng kể của nước,
vuông góc với sống thuyền. Người ta điều chỉnh
hướng thuyền (hướng sống thuyền), phương
của cánh buồm để lực cản -′ của nước (lực này
không phụ thuộc vào sự điều chỉnh) thắng lực -
(có thể điều chỉnh độ lớn). Cuối cùng, dưới tác
• Ta hãy dùng kiến thức về vectơ để phân tích
động của lực , thuyền di chuyển và sau một
các lực chính tác động tới sự chuyển động
khoảng thời gian, nó lại được điều chỉnh
của thuyền buồm trong trường hợp này. Lực
hướng, để đi đến đích theo đường dích dắc.
do gió tác động vào cánh buồm được phân
tích thành lực * cùng phương với cánh
buồm và lực + vuông góc với cánh buồm. BÀI TẬP TƯƠNG TỰ 1. Cho tứ giác
. Gọi /, 0 lần lượt là trung điểm của và
, là trung điểm của /0 .Chứng minh rằng: a) + = /0 b) + + + = c) + + + =
với M là điểm bất kì Lời giải
Mà I, J lần lượt là trung điểm của AB và CD nên / + / = , 0 + 0 = Vậy + = / + / + 0 + 0 + /0 = /0 (đpcm)
b) Theo hệ thức trung điểm ta có + = /, + = 0
Mặt khác là trung điểm /0 nên / + 0 = .
a) Theo quy tắc ba điểm ta có = / + /0 = / + /0 + 0 Suy ra + + + = / + 0 = (đpcm) Tương tự = / + /0 + 0 BÀI TẬP TƯƠNG TỰ 1. Cho tứ giác
. Gọi /, 0 lần lượt là trung điểm của và
, là trung điểm của /0 .Chứng minh rằng: a) + = /0 b) + + + = c) + + + =
với M là điểm bất kì Lời giải c) Theo câu b ta có + + + = do
đó với mọi điểm thì + + + = ⇔ + + + + + + + = ⇔ + + + = (đpcm) 2. Cho hai tam giác và
có cùng trọng tâm G. Gọi 3 , 3 , 3 lần lượt là trọng tâm tam giác , , .
Chứng minh rằng 33 + 33 + 33 = . Lời giải
• Mặt khác hai tam giác và có
cùng trọng tâm G nên
• Vì 3 là trọng tâm tam giác nên 33 = 3 + 3 + 3 • 3 + 3 + 3 = và 3 + 3 + 3
• Tương tự 3 , 3 lần lượt là trọng tâm tam giác , suy ra
• Suy ra 33 + 33 + 33 = . • 33 = 3 + 3 + 3 và 33 = 3 + 3 + 3
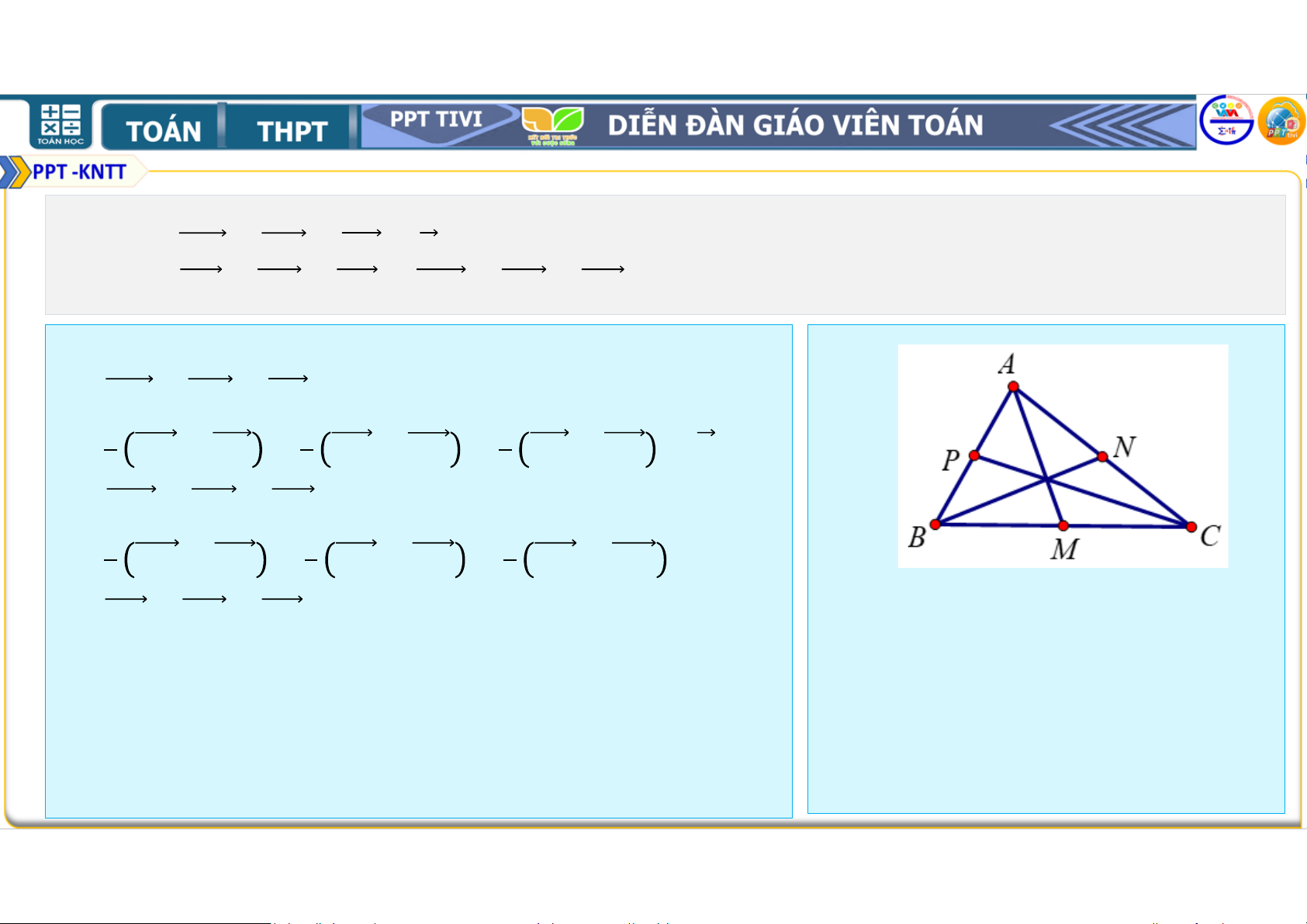
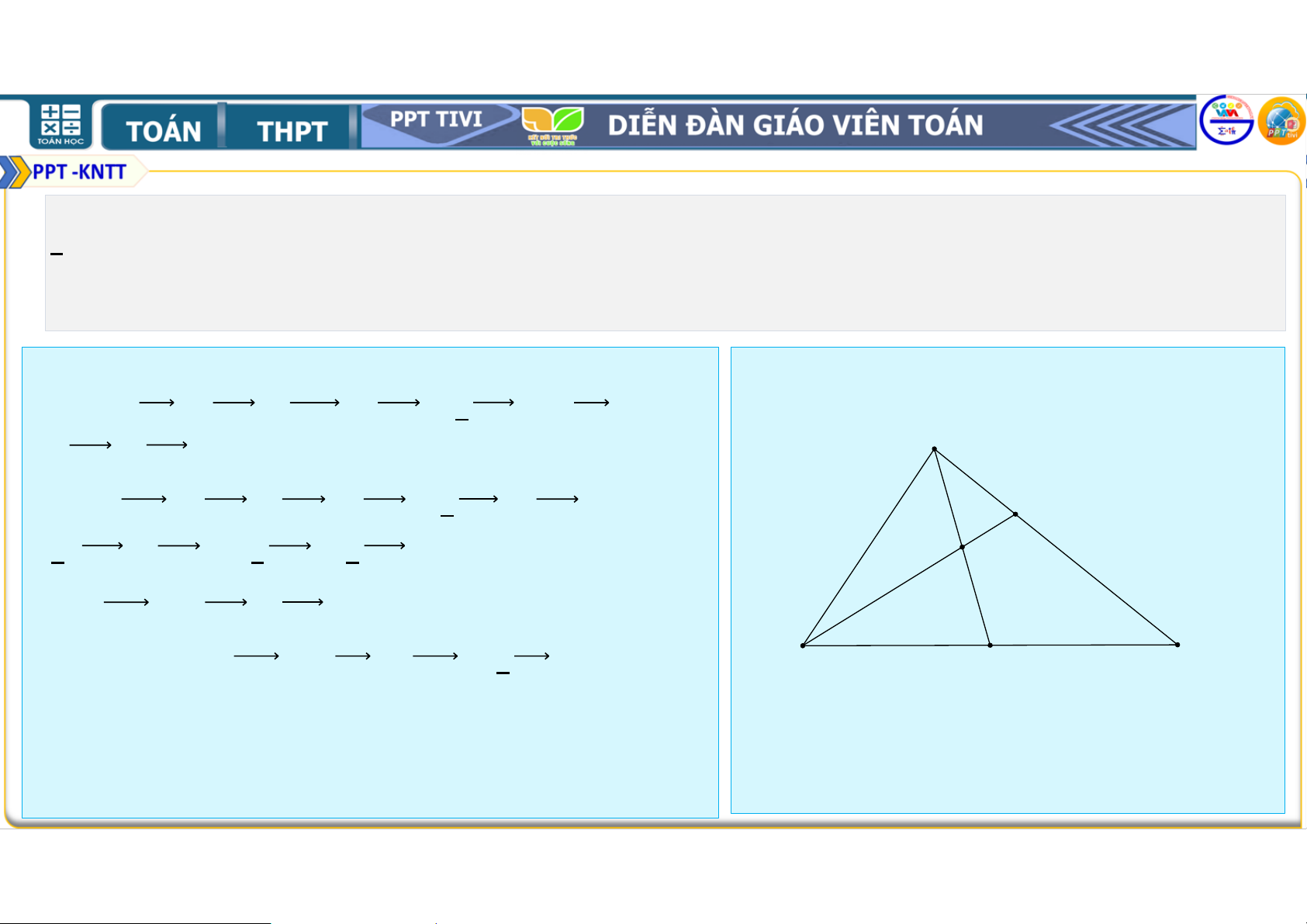
• Công theo vế với vế các đẳng thức trên ta có • 33 + 33 + 33 = 3 + 3 + 3 + 3 + 3 + 3 3. Cho tam giác
. Gọi , , 4 lần lượt là trung điểm của , , . Chứng minh rằng a) + + 4 = b) + + = +
+ 4 với O là điểm bất kỳ. • Lời giải • a) + + 4 • = + + + + + = • b) + + 4 • = + + + + + • = + + 4. Cho tam giác và một điểm
tùy ý. Chứng minh rằng + − = + . • Lời giải
• Ta có 56 = 289 + 8: − 38; = 2 8; + ;9 + 8; + ;: − 38; = 2;9 + ;: = 5<
5. Cho 4 điểm , , , . Gọi /, 0 lần lượt là trung điểm của , . Chứng minh = + / + 0 + > = . • Lời giải • 2 9: + 9? + @9 + A9 = 2 A: + 9? + @9 = 2 A: + @? = 2A: + 2@? = 3A:.
6. Xác định điểm biết + + = . • Lời giải
• Gọi /, 0 lần lượt là trung điểm và . Khi đó ta có + + = ⇔ + + + = ⇔ / + 0 = ⇔ / = − 0 Vậy điểm
cần tìm thuộc đoạn /0 sao cho / = 0. 7. Cho tam giác có thuộc cạnh sao cho = . Phân tích vectơ theo hai vectơ và . Lời giải • Ta có = + = + C = + + = + . A B M 8. Cho tam giác có thuộc cạnh sao cho =
và / là trung điểm của .
Phân tích / theo 2 vectơ , . • Lời giải A • Ta có / = / − = − − = − − − = − . I B C N 9. Cho tam giác
có /, lần lượt là trung điểm , /. Phân tích qua hai vectơ và . • Lời giải • = / + / = − + / A = − + / + = − + / + I = − − + D = − + . B C 10. Cho B có trung tuyến
. Gọi / là trung điểm và là điểm thuộc sao cho =
. Chứng minh ba điểm , /, thẳng hàng. • Lời giải • Ta có / = + = + ⇒ / = A + ( ) K • Ta có = + = + = + I ( − ) = + • ⇒ = + ( ) B C M
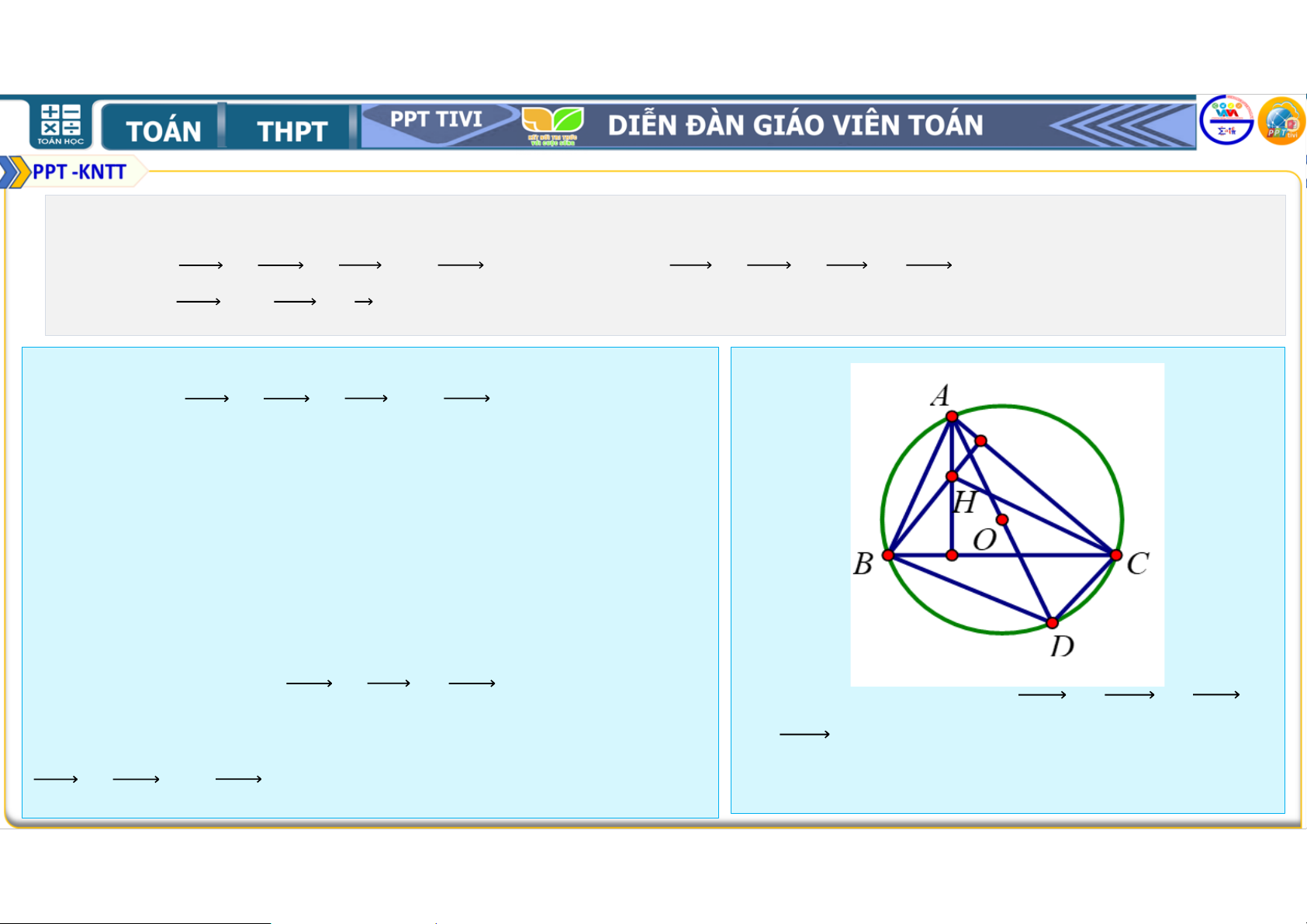
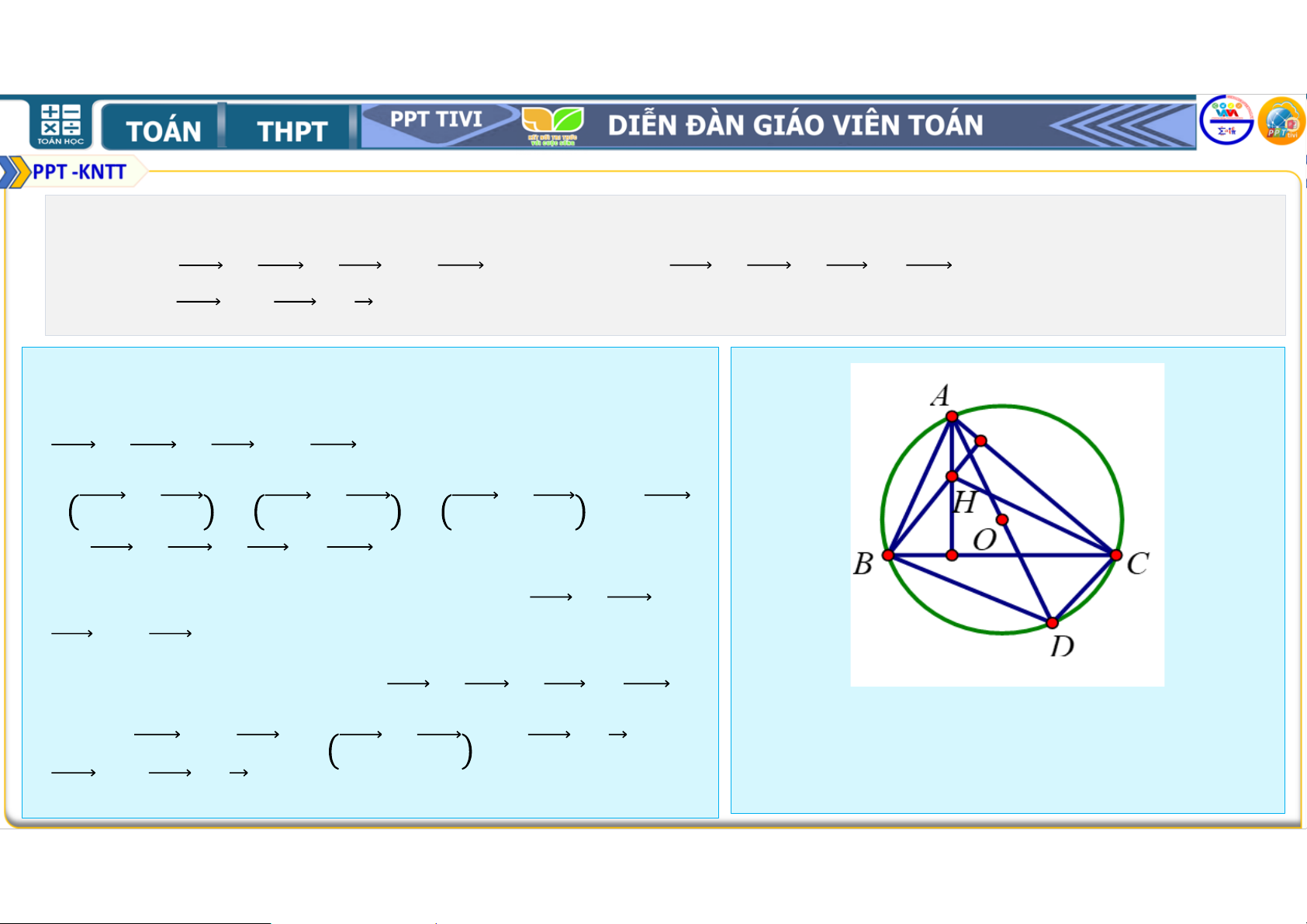
• Từ (1)&(2) = / ⇒ = /  B, I, K thẳng hàng. 11. Cho tam giác
có trực tâm D , trọng tâm 3 và tâm đường tròn ngoại tiếp . Chứng minh rằng a) D + D + D = D b) + + = D c) 3D + 3 = . • Lời giải
• a) Dễ thấy D + D + D = D nếu tam giác vuông. • Nếu tam giác
không vuông gọi D là điểm đối
xứng của A qua O khi đó • D//
(vì cùng vuông góc với AC) •
// D (vì cùng vuông góc với AB) • Suy ra
D là hình bình hành, do đó theo quy tắc
hình bình hành thì D + D = D (1)
• Từ (1) và (2) suy ra D + D + D =
• Mặt khác vì O là trung điểm của AD nên D D + D = D (2) 11. Cho tam giác
có trực tâm D , trọng tâm 3 và tâm đường tròn ngoại tiếp . Chứng minh rằng a) D + D + D = D b) + + = D c) 3D + 3 = . • Lời giải
• b) Theo câu a) ta có • D + D + D = D ⇔ D + + D + + D + = D • ⇔ + + = D đpcm
• c) Vì G là trọng tâm tam giác nên + + = 3
• Mặt khác theo câu b) ta có + + = D • Suy ra D = 3 ⇔ 3 + 3D − 3 = ⇔ 3D + 3 = .
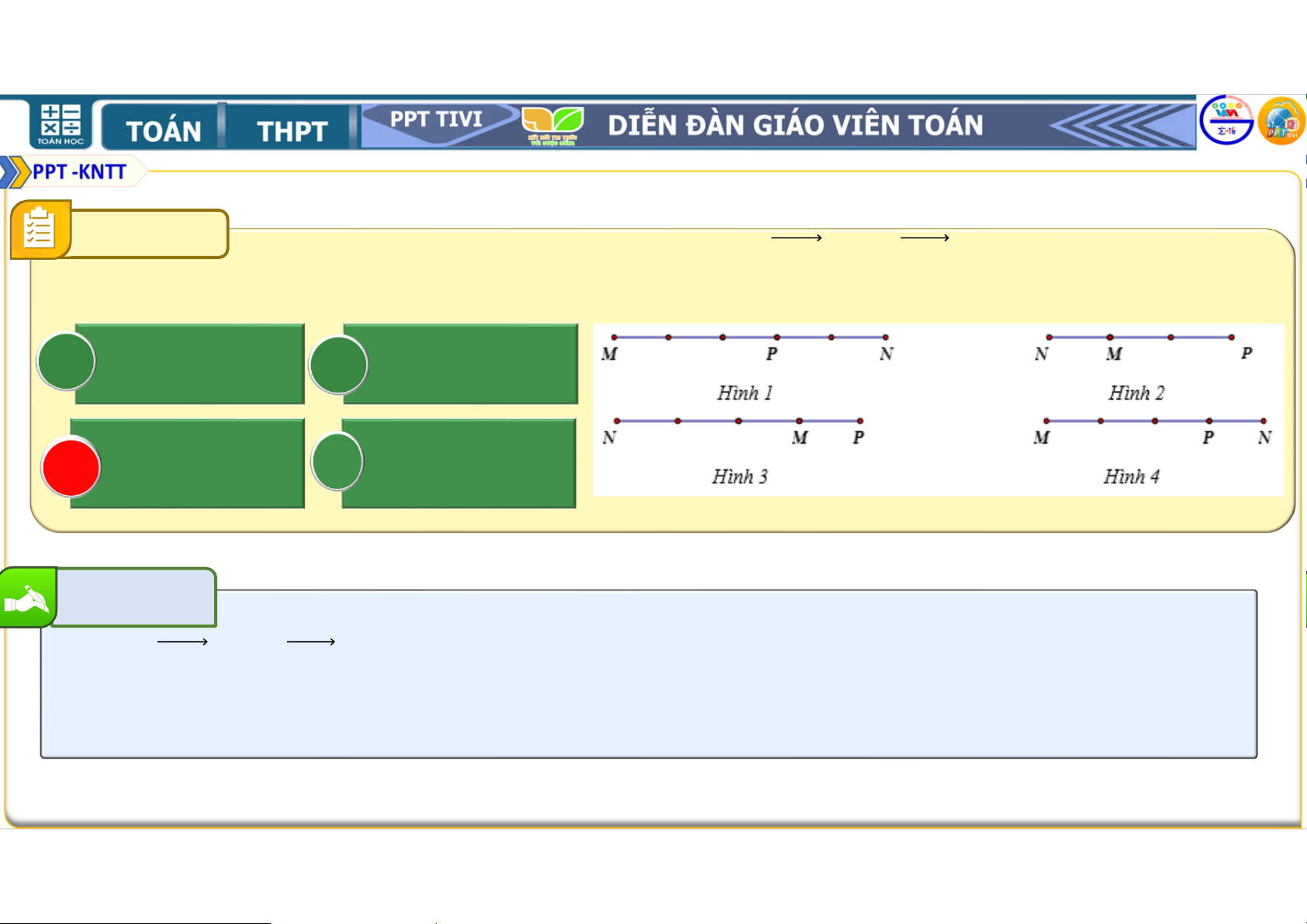
BÀI TẬP TRẮC NGHIỆM CỦNG CỐ CÂU 1 Trên đường thẳng
lấy điểm 4 sao cho = −
4. Điểm 4 được xác định
đúng trong hình vẽ nào sau đây? A Hình 1. B Hình 2. C Hình 3. C D Hình 4. Bài giải Vì = − 4 nên
nằm giữa , 4 và = 4. Chọn C CÂU 2
Đẳng thức nào sau đây mô tả đúng hình vẽ bên: I B A A 39? + 9: = 0 B 3?9 + ?: = 0. C :? + 3:9 = 0 D 9? + 39: = 0. Bài giải Vì
nằm giữa /, và = / nên / + = . Chọn A
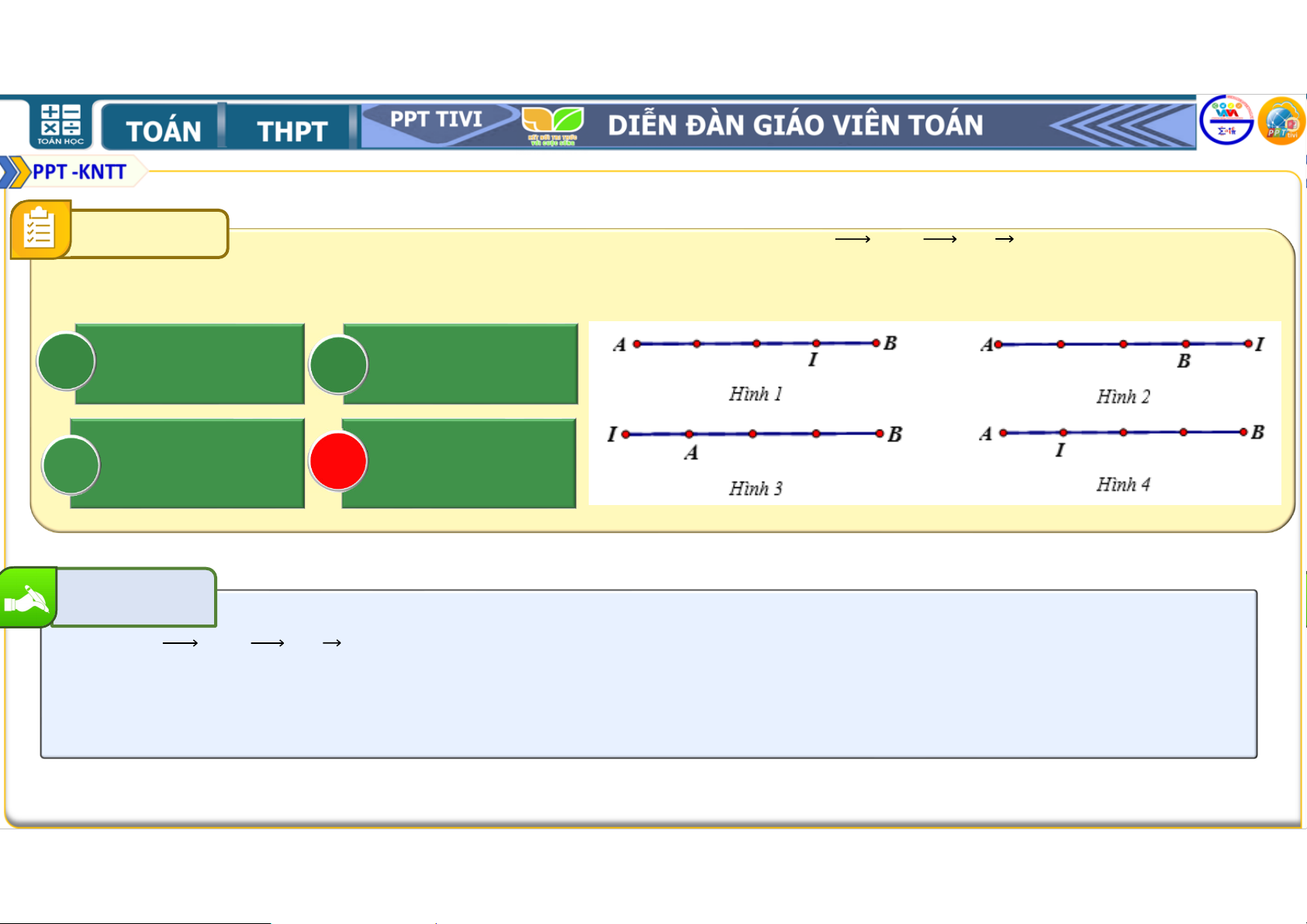
BÀI TẬP TRẮC NGHIỆM CỦNG CỐ CÂU 3 Cho đoạn thẳng
và điểm I thỏa mãn / + / = . Hình nào sau
đây mô tả đúng giả thiết này? A Hình 1. B Hình 2. C Hình 3. D Hình 4. Bài giải
Vì / + / = nên / nằm giữa , và / = / . Chọn D CÂU 4
Cho vectơ - J , , = − - , I = , + -. Khẳng định nào sau đây sai? A Hai vectơ B
- Hà I bằng nhau.
Hai vectơ - Hà I ngược hướng.
C Hai vectơ - Hà I cùng phương.
D Hai vectơ - Hà I đối nhau. Bài giải
Vì , = − -, I = , + - ⇒ I = − - + - = −-
Do đó: Hai vectơ - Hà I bằng nhau là khẳng định sai. Chọn C CÂU 5 Gọi
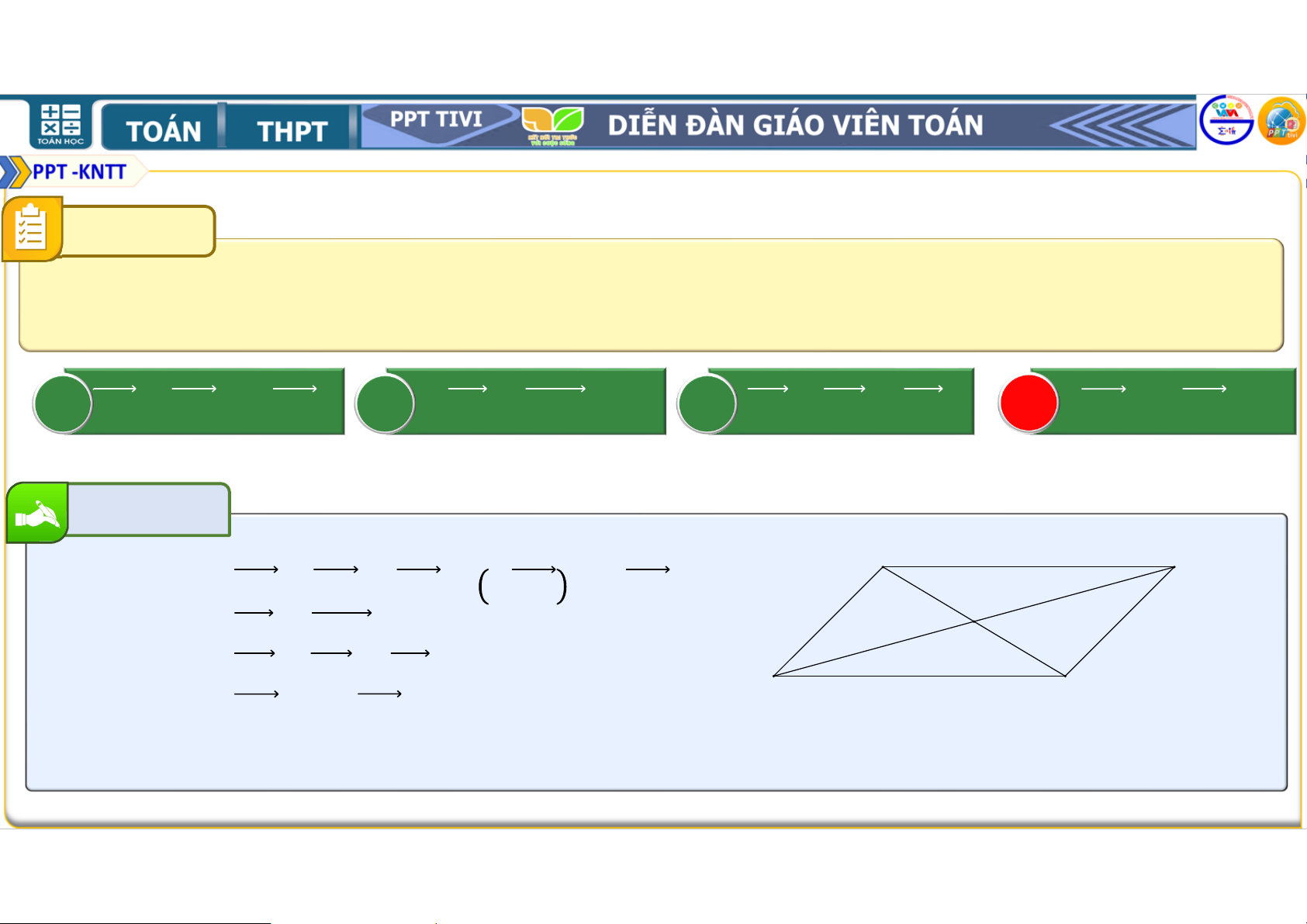
là giao điểm hai đường chéo và của hình bình hành . Đẳng thức
nào sau đây là đẳng thức sai? A − = . B = . C + = . D = . Bài giải A B − = − − = = O + = D C = − Chọn D CÂU 6 Cho hình vuông
cạnh , . Tính K = + ? A = ,. B = ,. C = , . D = , . Bài giải A B + = + = ⇒ + = = . = ,. O Chọn A D C CÂU 7 Cho hình bình hành , điểm thoả mãn: + = . Khi đó là trung điểm của: A . B . C . D . Bài giải + = A B ⇔ + + + = ⇔ + = O ⇔ = − ⇔ = D C Nên là trung điểm của . Chọn D CÂU 8 Cho tam giác
có 3 là trọng tâm và là trung điểm
. Khẳng định nào sau đây sai ? A 3 = − . B B + = 3. C 3 = 3 + 3. D 3 + 3 = 3 . Bài giải A + = = . 3 = 3 G B C M Chọn B CÂU 9 Cho tam giác vuông tại , là trung điểm của
. Khẳng định nào sau đây đúng ? A = = . B = . C = − . D = . Bài giải A = − . B C Chọn C M CÂU 10 Cho tam giác . Gọi và
lần lượt là trung điểm của và . Khẳng định nào sau đây sai ? A = . B = . C = − . D = − . Bài giải A Vì
là đường trung bình của tam giác nên // , = N M Suy ra = . Chọn C B C CÂU 11 Cho tam giác
đều cạnh ,. Tính + . A , + = , . B + = . C + = ,. D + = , . Bài giải A + = D ⇒ + = D = . , = , . B C Chọn A H CÂU 12 Cho tam giác vuông cân tại có = ,. Tính + . , A + = , . B + = . C + = ,. D + = ,. Bài giải C + = D ⇒ + = D = H . , = , . Chọn A A B CÂU 13 Tam giác có = = , và L = °. Tính + . , A + = , . B + = ,. C + = . D + = ,. Bài giải B + = D ⇒ + = D H = . . IMN ° = . ,. = ,. C Chọn B A CÂU 14 Cho tam giác
đều cạnh ,, D là trung điểm của . Tính − D . , , A , − D = . B − D = . C − D = . D − D = , O . Bài giải A
Gọi là trung điểm của D , , , , , O D = ; D = ⇒ = + = M , O , O − D = + D = ⇒ − D = = . = . B C Chọn D H CÂU 15 Cho hai lực và có điểm đặt
vuông góc với nhau. Cường độ của hai lực và lần lượt là Q ,
. Cường độ tổng hợp lực của hai lực đó là A B C P D P Bài giải + = + = ⇒ + = = = Q + = N Chọn A